Abstract
Many of the new -valued fuzzy structures, including intuitionistic, neutrosophic, or fuzzy soft sets, can be transformed into so-called almost -valued fuzzy sets, or, equivalently, fuzzy sets with values in dual pair of semirings (in symbols, -fuzzy sets). This transformation allows any construction of almost -valued fuzzy sets to be retransformed into an analogous construction for these new fuzzy structures. In that way, approximation theories for -fuzzy sets, rough -fuzzy sets theories, or F-transform theories for -fuzzy sets have already been created and then retransformed for these new fuzzy structures. In this paper, we continue this trend and define, on the one hand, the theory of extensional -fuzzy sets defined on sets with fuzzy similarity relations with values in dual pair of semirings and power sets functors related to this theory and, at the same time, the theory of cuts with relational morphisms of these structures. Illustratively, the reverse transformations of some of these concepts into new fuzzy structures are presented.
Keywords:
almost MV-valued fuzzy sets; dual pair of semirings; cut systems; extensional fuzzy sets; power set functors MSC:
03E72
1. Introduction
In the current development of fuzzy sets theory, and especially in the connection with the development of applicability in soft fields, there is a significant tendency to use completely new fuzzy structures and their mutual combinations in addition to the classic L-valued fuzzy sets. Let us mention, for example, intuitionistic fuzzy sets [1], fuzzy soft sets [2,3], or neutrosophic fuzzy sets [4] and their mutual combinations, such as intuitionistic fuzzy soft sets [5], etc.
Given that the individual fuzzy structures created in this way are defined relatively independently, the basic operations with these structures are also defined independently, with only a partial relationship to the operations of fuzzy structures of another type. Moreover, it very often happens that different variants of these operations are defined for one type of new fuzzy structure, which complicates the creation of one consistent and generally accepted theory of a new fuzzy structure. For example, fuzzy soft sets were introduced in [2] and modified in many other papers. The consequence of this is that there are a number of different definitions of basic operations with fuzzy soft sets, and some of these definitions do not correspond to the standards for these operations. For example, some of the operations introduced in that way do not meet DeMorgan’s laws. The consequence of this state, among other things, is that each of these new fuzzy structures creates its own independent theory, including the necessary theoretical results and their proofs.
Therefore, it is understandable that efforts are being made to unify at least part of these new fuzzy structures and to create a theory that would allow us to work with these fuzzy structures in a manner analogous to classic L-fuzzy sets. One of the possible approaches to this unification consists of the transformation of some of these L-valued fuzzy structures into a new structure called -valued fuzzy sets or, equivalently, -fuzzy sets, where is a dual pair of semirings (see, e.g., [6]). Although most of the new L-valued fuzzy structures in the set X do not represent mappings , after this transformation, individual fuzzy structures represent mappings , where only the dual pair of semirings with the underlying set R changes depending on the type of fuzzy structure. With the help of this transformation, not only can their basic operations and terms be consistently defined for these new fuzzy structures, but the reverse transformation to the original fuzzy structures can be applied to the entire theory of -fuzzy sets. This makes it possible to define -sets theory analogies for new fuzzy structures without the need for special definitions and new proofs.
Since the reverse transformation of the results related to the theory of -fuzzy sets to the results related to the new fuzzy structure is relatively simple, it is advisable to develop the theory of -fuzzy sets as much as possible so that it is possible to subsequently transform these results on analogical theory in new fuzzy structures. In previous papers, we dealt with, e.g., definitions and properties of the theory of approximations of -fuzzy sets, as well as definitions and properties of rough -fuzzy sets [7] or F-transform theory for -fuzzy sets [6]. All these notions can be relatively simply transformed (without any additional proofs) into analogical notions with analogical properties into new fuzzy structures that can be transformed into -fuzzy sets; moreover, due to the existence of two monads, the results are mostly defined in two adjoint variants.
In this paper, we want to continue the process of defining concepts and theories for -fuzzy sets, well known in the standard theories of classic L-valued fuzzy set theory. Naturally, the question may arise as to why the methods of classic L-fuzzy sets cannot be mechanically applied to define the theory of -fuzzy sets. The reason is in the formal tools that are used to work with -fuzzy sets. These tools are based on the use of two isomorphic monads in the category , which are created from a dual pair of semirings . The result of this approach is, among other things, that most of the constructions defined in this way are much clearer and simpler than if we tried to directly apply the classical tools of L-valued fuzzy theory sets to -sets.
In this paper, we focus on two concepts from the theory of classic L-fuzzy sets that are often used and the possibilities of their conversion into the concepts of -fuzzy sets.
The first concept concerns the so-called L-sets, whose origin is in the Wyler category [8] and was further developed in detail in the publications of Hohle [9] and other authors. This category represents a generalization of the classical category of sets, with the difference that the more general L-valued similarity relation is used instead of the classical identity. Among recent applications of L-sets theory is, for example, the theory of multilevel fuzzy sets, introduced by Šostak [10,11].
In the paper, for each dual pair of semirings , we introduce two terms of similarity R-relations and two related terms of -sets and -sets, as a pair , where X is a set and Q is an - or -similarity relation. For these objects, we define two isomorphic categories and , whose morphisms are again -relations, defined by the two monads already mentioned. Thus, these categories represent generalizations of the category . We introduce the concept of fuzzy sets defined over objects of these categories, which are, in fact, analogies of extensional fuzzy sets, and we show the construction of power sets of these extensional fuzzy sets. All these constructions can be applied to new fuzzy structures by using the transformation of new L-fuzzy structures into -fuzzy sets.
Another area of the theory of L-fuzzy sets, whose analogy we want to define in the paper on the theory of -fuzzy sets, concerns cut systems. It is well known that any L-fuzzy set can be equivalently defined as the cut system , satisfying some natural axioms. Between the cut systems in X and the fuzzy sets in X, there are some interesting relationships, and from some point of view, an investigation of the L-valued fuzzy sets can be substituted by the investigation of cut systems. Cut systems play a significant role in fuzzy topology [11], fuzzy algebra [12], fuzzy measure, fuzzy analysis [13] or [14], rule-based systems [15], and many other areas. For more information on the relationships between fuzzy sets and cut systems, see [16] or [17]. The cut systems are the natural bridge between the fuzzy sets and the classical sets.
In this paper, we define the theory of -cuts represented by two categories and , where the morphisms are again -relations defined using the mentioned monads. As the main result, we show that these categories are isomorphic to the categories and , respectively. Subsequently, this makes it possible to define the theory of cut systems in a universal and consistent way for any new fuzzy system that can be transformed into -fuzzy sets.
2. Preliminary Notions
The basic value structures that we use in the paper are dual pairs of semirings as the equivalent form of -algebras. All these notions have been introduced in a recent paper [7], and it is, therefore, appropriate to repeat the basic definitions and properties of these new structures. In this section, we present the basic definitions and properties of these structures.
Recall that a complete monoid is a monoid of type such that for an arbitrary set there exists a sum such that for an arbitrary partition of I, the equality holds.
We recall the definition of an idempotent semiring.
Definition 1
([18]). A complete commutative idempotent semiring (or a semiring, shortly) is an algebraic structure with the following properties:
- is a complete idempotent commutative monoid;
- is a commutative monoid;
- holds for all ;
- holds for all .
The definition of dual pairs of semirings was introduced in [7], which is presented below.
Definition 2.
Let and be complete idempotent commutative semirings with the same underlying set R. The pair is called the dual pair of semirings if there exists a semiring isomorphism and the following axioms hold:
- is the involutive isomorphism;
- ;
- , where is the complete operation in ;
Some properties of dual pairs of semirings are described in the following lemma:
Lemma 1
([7]). Let be a dual pair of semirings defined in Definition 3.
- Let the relations ≤ and be defined byThe following statements hold:
- (a)
- ≤ and are the order relations on R;
- (b)
- ;
- (c)
- ;
- (d)
- ;
- (e)
- and are lattice-ordered semirings, where, for arbitrary ,where is the sum of elements with respect to .
Using dual pairs of semirings , we can also introduce -fuzzy sets and operations with these fuzzy sets.
Definition 3
([7]). Let be a dual pair of semirings.
- A mapping is called a -fuzzy set in a set X.
- Operations with -fuzzy sets are defined by
- (a)
- The intersection is defined by , ;
- (b)
- The union is defined by , ;
- (c)
- Complement is defined by ;
- (d)
- The external multiplication ☆ by elements of R is defined by;
- (e)
- The order relation ≤ between is defined by where ≤ is the order relation defined in Lemma 1.
Another tool we use is the elementary theory of monads in categories, as introduced in [19]. This theory allows us to use a monad to define the concept of a monadic relation, which can be used to construct the general theory of upper and lower approximations and many other constructions. We use this theory in the context of dual pairs of semirings.
Definition 4
([19]). The structure is a monad in the category , where
- is the mapping of objects;
- η is a system of mappings ;
- For each pair of mappings , , there exists a composition (called a Kleisli composition) , which is associative;
- For every mapping , and hold;
- ◊ is compatible with the composition of mappings, i.e., for mappings , , we have .
In the following proposition, it is shown that any dual pair of semirings defines two monads in the category :
Proposition 1
([7]). Let be a complete commutative idempotent semiring and let the structure be defined by
- The mapping of objects is defined by ,
- For the mappings and their composition is defined by
- is the mapping defined by
Then, is a monad in the category .
Remark 1.
If is a dual pair of semirings, according to Proposition 1, there exists another monad , where for and ,
The last definition we need is the notion of a monadic relation. This notion was introduced by Manes [19]. For simplicity, we define this notion for monads and only.
Definition 5
([19]). Let be the monad in category from Proposition 1 and let be sets. A -relation Q from X to Y (denoted ) is a mapping . If and are -relations, their composition is the -relation . A -relation is called a -similarity relation if
- It is reflexive, that is, ;
- it is transitive, that is, ;
- it is symmetric, that is, , for arbitrary .
Remark 2.
- From Observation 1 it follows that for a dual pair of semirings we can introduce two types of monadic relations, namely -relation and -relation. From Definition 2, it follows that these monadic relations are identical objects. For this reason, we sometimes include these two objects under the common name -relations.
- If the composition of -relations is considered, we need to distinguish between -relations and -relations, depending on the compositions ◊ and , respectively.
- Since the notion of the -similarity relation is defined using terms from the monad , it is necessary to distinguish between the notions of the -similarity relation and the -similarity relation.
3. -Sets
In the classical theory of L-valued fuzzy sets, where L is a complete, distributive lattice with possible other operations, there are two basic categories of objects for which L-valued fuzzy sets are defined. The first of these categories is the classic category with sets as objects and mappings as morphisms. The second type of basic category is category , which represents a generalization of category . This category has its origin in Wyles’ category [8], developed in the work of Höhle [9] and other authors. Objects of the category are the so-called L-sets, that is, pairs , where X is a set, and delta is the equality valued L on X, that is, with natural axioms. Morphisms are structures that preserve mapping.
As we already mentioned in the introduction, many of the new fuzzy structures, traditionally called L-fuzzy structures, are, in fact, -fuzzy sets for suitably dual pairs of semirings . Just as L-sets are a generalization of classic sets, we can introduce the general concept of -sets, which will be a generalization of L-sets and it will be possible to apply them to all new fuzzy structures that can be transformed into -fuzzy sets.
Based on the current trend in fuzzy set theory categories, we introduce new categories and , respectively, which generalize the category of sets and the category of L-sets , respectively, with suitable types of relations such as morphisms instead of mappings. According to Remark 2, with any dual pair of semirings two types of relations are used, namely, and -relations and it follows that we obtain two types of these categories, namely and and and , respectively.
The analogies of the category but with -relations as morphisms are the following categories and .
Definition 6.
Let be a dual pair of semirings.
- The category of sets with -relations as morphisms is defined by
- (a)
- Objects are sets;
- (b)
- Morphisms from X to Y are -relations ;
- (c)
- The composition of morphisms is defined by ◊;
- (d)
- For arbitrary object X, .
- The category of sets with -relations as morphisms is defined by
- (a)
- Objects are sets;
- (b)
- Morphisms from X to Y are -relations ;
- (c)
- The composition of morphisms is defined by ;
- (d)
- For arbitrary object X, .
The analogies of the category are the categories and with sets as objects and with or -similarity relations, respectively.
Definition 7.
Let be a dual pair of semirings.
- The category of sets with -similarity relations is defined by
- (a)
- The objects are pairs , where X is a set and is a -similarity relation;
- (b)
- Morphisms are -relations such that , , where the order relation ≤ is defined point-wise;
- (c)
- The composition of the morphisms and is defined by ;
- (d)
- For arbitrary object , .
- The category of sets with -similarity relations is defined by
- (a)
- The objects are pairs , where X is a set and is a -similarity relation;
- (b)
- Morphisms are -relations such that , , where the order relation is defined point-wise;
- (c)
- The composition of the morphisms and is defined by ;
- (d)
- For the arbitrary object , .
Remark 3.
- It should be noted that objects of categories and are different. In fact, objects of are pairs , such that are -relations such that and , but objects of are pairs , such that Q are -relations such that and .
- According to the traditional designation of L-sets, the objects of the categories and , respectively, will be called -sets and -sets, respectively.
- It should be observed that conditions , and , , respectively, are equivalent to conditions and , respectively.
Proposition 2.
All categories , , , and are correctly defined.
The proof follows directly from the definitions of operations in and the corresponding monads, and will be omitted.
As we have already stated, both types of newly defined pairs of categories can be considered certain generalizations of the classical category . In the classical L-fuzzy set theory, the power set structure is the principal structure, which is the basis for many theoretical results. In the following part, we will, therefore, show how analogies of this power set structure can also be defined for new analogies of the category , mentioned in the previous definitions.
In what follows, we introduce new types of power set structures based on generalized categories of sets, which are defined as functors from these categories of sets to the classical category of sets. However, as mentioned above, we have two types of generalization of the category Set, ie, category and category . For this reason, for each set , we obtain two types generalizing the classical power set objects , namely, objects and objects . These two power set structures are represented by two pairs of functors
Theorem 1.
Let be a dual pair of semirings. There exist power set functors such that the following diagram commutes, where Δ and Ω are isomorphic functors.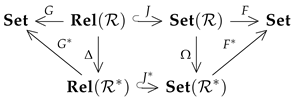

Proof.
(1) Let be a morphism in the category . The functor G is defined by
From Definition 6, it follows that and for another morphism we obtain , where is the composition of mappings. Therefore, G is the functor.
(2) Let be a morphism in the category . The functor is defined by
is the functor. In fact, we have . For arbitrary morphisms and , we have
(3) Let be a morphism in the category . The functor is defined by
It is straightforward to show that is the functor. We show that . In fact, . In addition, we have
and the diagram commutes.
(4) Let be a morphism in . The functor F is defined by
We show that this definition is correct. We have . In fact, for arbitrary ,
and . Furthermore, for and , we have
and it follows that . Therefore, . Finally, let and be morphisms in . Therefore, and and we obtain the following equation:
as follows from identities and composition rules for ◊. Therefore, F is the functor.
(5) Let be a morphism in . The functor is defined by
We show that this definition is correct. First, the following equalities hold for an arbitrary object :
In fact, for we have . On the other hand, and the first equality is proved. If , we obtain and it follows that .
We prove that preserves unity morphisms. According to (1), for arbitrary we have
and it follows that .
Let and be morphisms of . Using the identities and , we obtain the following:
Finally, we show that for arbitrary and arbitrary morphism , holds. In fact, we have
and, according to (1), we have .
(6) Let be a morphism in . The functor is defined by
Since is the -similarity relation, the definition is correct. We prove that the diagram commutes, that is, . In fact, according to (1), we have
Further, we have and obtain
(7) Let be a morphism in the category (or , equivalently). The embedding functors J and are defined by
It is easy to see that are functors and that . □
Remark 4.
As in the case of classic power set structures , the objects of and , respectively, will be called -extensional and -extensional -fuzzy sets, respectively, where and .
4. -Cut Systems
It is well known that the theory of classical L-valued fuzzy sets can be equivalently replaced by the theory of -cuts. In many theories, and especially in applications, this substitution is a more acceptable solution because it allows one to explicitly interpret the approximate solutions of a number of problems. A typical example can be problems related to fuzzy rough set theory, the goal of which is to approximate indeterminate (i.e., fuzzy) phenomena s with the help of the so-called upper and lower approximations and based on a suitable similarity Q. However, this approximation again represents L-valued fuzzy sets, and therefore, its visualization is somewhat problematic. Therefore, a suitable solution is to replace these approximations with their -cuts, which allows us to explicitly define sets of elements , representing the lower and upper estimate of the set of objects satisfying the given concept s with the degree at least .
Since in addition to classic L-fuzzy sets, other types of fuzzy structures are currently used in applications, it is appropriate to extend this more illustrative form of fuzzy sets and its theory to these new fuzzy structures as well. For this reason, in this section, we will focus on introducing the theory of cut systems for -sets and extensional -fuzzy sets. For individual types of fuzzy structures transformable to -fuzzy sets, their cut system theories are only special examples of the cut system theory for general -fuzzy sets. In this way, the theory of -cuts can be obtained, for example, for neutrosophic, intuitionistic, or L-fuzzy soft sets.
As we mentioned in the previous section, the basic categories for -fuzzy sets we use are the categories and . Our goal in this section is to show that these categories can be equivalently expressed by cut systems, which are introduced in the following definitions.
Definition 8.
Let be a dual pair of semirings and let , where for arbitrary , is a -relation.
- is called an -cut system in a set X, if for arbitrary ,
- (a)
- is a crisp -relation, that is, ;
- (b)
- ;
- (c)
- ;
- (d)
- ;
- (e)
- ;
- (f)
- For arbitrary , the set has the greatest element in .
- is called am -cut system in a set X, if for arbitrary ,
- (a)
- is a crisp -relation, that is, ;
- (b)
- ;
- (c)
- ;
- (d)
- ;
- (e)
- ;
- (f)
- For arbitrary , the set has the greatest element in .
Remark 5.
It should be noted that conditions (e) and (f) are equivalent to the following implications:
In fact, if is the greatest element of , for arbitrary we have and it follows that and we obtain . Therefore, .
In the following definition, we introduce two categories of cut systems:
Definition 9.
Let be a dual pair of semirings.
- The category of -cut systems is defined by
- (a)
- Objects are pairs , where is an -cut system in a set X;
- (b)
- Morphisms are -relations such that for all , , holds;
- (c)
- The composition of the morphisms and is defined by ;
- (d)
- For the arbitrary object , the unit morphism is defined by
- The category of -cut systems is defined by
- (a)
- Objects are pairs representing -cut systems in a set X;
- (b)
- Morphisms are -relations such that for all , , holds;
- (c)
- The composition of the morphisms and is defined by ;
- (d)
- For arbitrary object , the unit morphism is defined by
The main reason for introducing cut systems categories is to take advantage of the approximate representation of - and -sets, including methods for working with this approximate representation. Generally speaking, rather than working with the -set that is not very intuitive, we can use its approximation , where is a level of approximation, and is a classical crisp relation in a set X. The basis for defining this relation is the following theorem, which proves the existence of isomorphisms between the categories of -sets and -cut systems.
Theorem 2.
Let be a dual pair of semirings. There exist isomorphic functors and Φ such that the following diagram commutes, where Ω is from Theorem 1: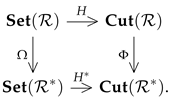

Proof.
For arbitrary we define the mappings by
(1) First, we show that the definition of the category is correct. We show that is a morphism. For , and , we have
as follows from the inequality . Therefore, is the morphism in . For an arbitrary morphism we have and . In fact, for we have
The other identity can be proven analogously and is defined correctly.
Let be a morphism in . The functor H is defined by
We prove that this definition is correct. It is clear that is a crisp -relation. Furthermore, using the equality , by a simple calculation we obtain
Analogously, we have . For , we have . For , and it follows that . Finally, the greatest element of the set equals . Hence, is the object in the category .
We prove that is a morphism in the category . In fact, we have
Therefore, H is defined correctly. To prove that H is a functor, we only need to show that . We have and for we have
(2) We define the inverse functor . Let be a morphism in . The functor is defined by
We show that this definition is correct. We have
Further, we have
Since , Q is the symmetric -relation and it follows that Q is the -similarity relation in X.
We show that is the morphism in . We have
Finally, we have
and is the functor. We show that are inverse functors. In fact, for and , we obtain the following.
as follows from a simple calculation and using Remark 5.
(3) We show that the definition of the category is correct. Most of the proof can be carried out similarly to the previous case. For illustration, we prove only the following identity:
We show that for an arbitrary object , is a morphism. For and we have
as follows from the inequality . Therefore, is the morphism in . The proof that is the unit morphism in is analogous to the proof that is the unit morphism in and will be omitted.
Let be a morphism in . The functor is defined by
We show that is the functor. We have . In fact,
Therefore, is the -cut system. Furthermore, is a morphism in , as can be verified by a simple calculation. Finally, we have , In fact, we have
(4) We define the inverse functor . For a morphism we set
The proofs that is the functor and are inverse functors are similar to these proofs for the functors and H of (2) and will be omitted.
(5) We define the isomorphic functor . Let be a morphism in the category and in the category . We set
We prove that and are defined correctly, that is, we show that and . We set and we have
and, finally, if , we have
Therefore, from Remark 5 it follows that . The proof for is similar and will be omitted.
We have and . The functors and are mutually inverse. For we have
(6) We prove that the diagram commutes, that is, . In fact, let be an object of . We have
and the diagram commutes. □
Just as we define the power set structure of all -extensional fuzzy sets, we can define the power set structure of -extensional cuts. To define the functor , we start with the definition of the object function of E.
Recall that for a -relation , the upper approximation mapping is defined by . For an arbitrary subset , we define the characteristic -fuzzy set of A by .
Definition 10.
Let be a dual pair of semirings.
- Let . A system is called an extensional -cut, if
- (a)
- ;
- (b)
- ;
- (c)
- .
- The object function is defined by
We first show that there is a strong relationship between -extensional cuts and -extensional fuzzy sets.
Proposition 3.
Let be an -set. There exist mutually inverse bijections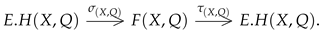
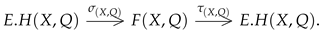
Proof.
According to the proof of Theorem 2, we have the following: , where . Let . The mapping is defined by
We show that this definition is correct, that is, is an -extensional fuzzy set. Using the identity from Theorem 2, we have
According to the definition of functor F, we have , and the definition of is correct. In contrast, let . The mapping is defined by
We show that is an extensional -cut. In fact, for arbitrary , we have
as follows from the inequality for arbitrary . Therefore, .
We show that and are mutually inverse mappings. For and , we have
as follows from the axioms of extensional -cut. □
The object function E can be extended to the powerset functor
Let be a morphism in , and let us consider the following diagram:
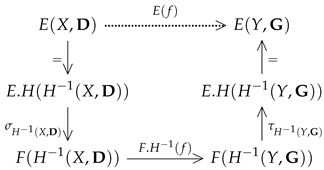 To make this diagram commutative, we can set
From the construction of , it follows that E respects the composition of morphisms and unit morphisms. Therefore, we obtain the theorem below, which expresses the equivalence between -extensional fuzzy sets and extensional cuts.
To make this diagram commutative, we can set
From the construction of , it follows that E respects the composition of morphisms and unit morphisms. Therefore, we obtain the theorem below, which expresses the equivalence between -extensional fuzzy sets and extensional cuts.
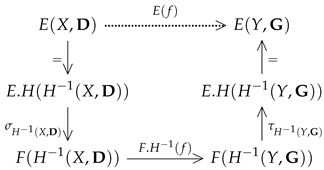 To make this diagram commutative, we can set
To make this diagram commutative, we can set
Theorem 3.
Let be a dual pair of semirings. The functors and F are naturally isomorphic, that is, and are natural inverse isomorphisms between these funtors,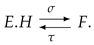
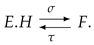
F.
Proof.
Let be a morphism in . We show that is the natural transformation, that is, the following diagram commutes:
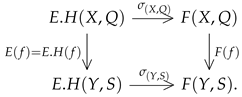 If we set , we obtain the following.
and the diagram commutes. Therefore, is the natural transformation and also the natural isomorphism. By analogy, it can be proved that is the natural isomorphism. □
If we set , we obtain the following.
and the diagram commutes. Therefore, is the natural transformation and also the natural isomorphism. By analogy, it can be proved that is the natural isomorphism. □
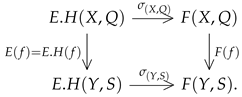 If we set , we obtain the following.
If we set , we obtain the following.
5. Examples
In this section, we show illustrative examples of how -cut systems can be used to approximate a standard construction used in the theory of fuzzy sets. As we have already stated in the previous sections, the advantage of the theory of -cut systems is the possibility to use this theory for arbitrary fuzzy systems that can be transformed into -fuzzy sets. Therefore, as an illustration of this procedure and its application in various fuzzy systems, in the following examples, we focus on classical -valued fuzzy sets, -valued intuitionistic fuzzy sets, and -valued fuzzy soft sets.
As an example of the method on which we will illustrate the possibility of using -cut systems, we chose the upper approximation defined by the -similarity relation. Recall that if is an -similarity relation on the set X, the upper approximation defined by Q is the mapping which is defined by the formula
It is obvious that if we fully know the -similarity relation Q, there is no need to perform any approximation of the output of the fuzzy structure s. However, a problem can arise if we only know approximately the -similarity relation. For example, instead of knowing the complete -similarity relation , we sometimes only know its approximations represented by several classical equivalence relations for some values . This classical equivalence relation then represents those pairs of points , for which we “estimate” . Therefore, it is natural to ask whether from these various local equivalence relations at least some approximation of the global upper approximation can be obtained for any . In this section, we will first show how this global approximation can be obtained for the case of general -fuzzy sets, and then we will illustrate the concrete procedure for the case of three fuzzy structures that can be transformed into -fuzzy sets, i.e., classical fuzzy sets, intuitionistic fuzzy sets, and fuzzy soft sets.
Example 1.
General approach: Approximation of for -sets.
Let be a dual pair of semirings and let X be a set. Suppose that instead of an -similarity relation we have at our disposal only a finite number of classical equivalence relations , where , , where represents our local opinions that the points x and are at least in a degree similar to Q (which we do not know as a global -similarity relation ).
Instead of the equivalence relations we can consider the -similarity relations , defined by . Let us further assume that our local equivalence relations are consistent, i.e., that it holds.
In that case, we obtain an approximation of an -cut in X, and using the functor of Theorem 2, we obtain the “approximation” of the unknown -set , where . Hence,
In general, does not need to be an -similarity relation, although and are symmetric. To obtain an “almost” -similarity relation, we can calculate for several copies of and this -relation can be considered a reasonable approximation of Q. Using this approximation , for arbitrary , we can calculate at least the lower estimate of the approximation , that is,
Analogously, as the -similarity relation Q, sometimes we are not able to fully describe -fuzzy set as the mapping . Instead of that, we know (or estimate) only a few cuts , . Using the inequality
for , the lower estimate of can be calculated by
In the following examples, we show how the calculation of the lower estimate of looks for concrete examples of -fuzzy sets, -intuitionistic fuzzy sets, and L-fuzzy soft sets. In these examples, we assume that is the complete ukasiewicz algebra , where
We use the notation of Example 1.
Example 2.
Lower approximation of for -fuzzy sets.
It is easy to see that -fuzzy sets can be transformed to -fuzzy sets, where is a dual pair of semirings, where
and is the involutive negation . In that case, the algebraic structure of -fuzzy sets is isomorphic to the algebraic structure of -fuzzy sets. Using the notation of Example 1 and the operations of , formula (2) is expressed by
Example 3.
Lower approximation of for -intuitionistic fuzzy sets.
In [6], we showed that -intuitionistic fuzzy sets can be transformed into fuzzy sets, where , and
- ;
- ;
- ;
- ;
- ;
- ;
- is defined by .
Then, is the dual pair of semirings and the algebraic structure of -intuitionistic fuzzy sets is isomorphic to the algebraic structure of -fuzzy sets. Using the notation of (2), for elements we can set
In that case, formula (2) can be transformed into the following formula for elements of R:
Example 4.
Lower approximation of for -fuzzy soft sets.
Recall [2] that an -fuzzy soft set in a set X is a pair , where and , such that for arbitrary , for all . Basic operations with L-fuzzy soft sets are defined by
The dual pair of semirings that transforms fuzzy soft sets into -fuzzy sets is defined by
where is defined by and .
- The semiring is defined by
- (a)
- , where is the supremum in ;
- (b)
- , where is defined by ;
- (c)
- , , where for arbitrarily , .
- The semiring is defined by
- (a)
- , where is the infimum in ;
- (b)
- , where ⊕ in is defined component-wise;
- (c)
- , , where for arbitrarily , .
- is defined by where is defined point-wise in .
Then, is the dual pair of semirings, and the algebraic structure of -fuzzy soft sets is isomorphic to the algebraic structure of the -fuzzy sets. Using the notation of (2), for elements we can set
where and , such that for . In that case, formula (2) can be transformed into the following formula for elements of R:
6. Discussion
A known disadvantage of the method that uses -fuzzy sets to unify new fuzzy structures is these new fuzzy structures need to be -valued. It is, therefore, appropriate to try to modify the concept of -fuzzy set in such a way as to enable the transformation of fuzzy structures based on complete residual lattices, for example. The second disadvantage is the fact that some of the new -valued fuzzy structures cannot be transformed into -fuzzy sets because the algebraic systems of the fuzzy sets of both structures are not isomorphic. An example can be hesitant fuzzy sets, where certain variants of the definitions of basic operations with hesitant fuzzy sets lead to the non-distributive nature of these operations, which is not possible for -fuzzy sets. The question, therefore, arises whether it would be appropriate to modify either some of these operations related to new fuzzy structures or, on the contrary, to define the operations with -fuzzy sets in a different way.
7. Conclusions
With the gradual development of fuzzy set applications, many new fuzzy structures were also developed, based on the theory of fuzzy sets, whose primary goal was to be a suitable tool, especially for certain types of applications. Over time, however, own theories began to be built even for these new fuzzy structures, which created a number of parallel theories, only loosely connected by some common methods from the general theory of fuzzy sets. Therefore, parallel to this development of theoretical tools for new fuzzy structures, there is naturally also an effort to unify these new fuzzy structures and their theories.
One of these unifications is the theory of fuzzy sets defined by a dual pair of semirings, briefly -fuzzy sets. For this reason, it was appropriate to create new theoretical foundations of the theory of -fuzzy sets, and, for example, the theory of approximations for -fuzzy sets, the theory of rough -fuzzy sets, or the F-transform theory for -fuzzy sets has already been created.
In this paper, we continued this development of the theory of -fuzzy sets and, as an analogy of the so-called L-sets, we defined the category - and -sets and a power set functor for these categories, formed by the so-called extensional -fuzzy sets. Due to the monadic structure used for the theory of -fuzzy sets, two isomorphic variants of this concept could be automatically created, i.e., upper and lower extensional -fuzzy sets. In parallel with these concepts, we defined cut systems of these structures, which can be used, among other things, as certain approximations of these structures. At the end of the paper, we presented several simple examples of how these notions of -fuzzy sets can be transformed into new original fuzzy structures.
Funding
This research received no external funding.
Data Availability Statement
No new data were created.
Conflicts of Interest
The author declares no conflict of interest.
References
- Atanassov, K.T. Intuitionistic fuzzy sets. Fuzzy Sets Syst. 1986, 20, 87–96. [Google Scholar] [CrossRef]
- Maji, P.K.; Roy, A.R.; Biswas, R. Fuzzy soft-sets. J. Fuzzy Math. 2001, 9, 589–602. [Google Scholar]
- Močkoř, J. Powerset Theory of Fuzzy Soft Sets. Int. J. Fuzzy Log. Intell. Syst. 2020, 20, 298–315. [Google Scholar] [CrossRef]
- James, J.; Mathew, S.C. Lattice valued neutrosophis sets. J. Math. Comput. Sci. 2021, 11, 4695–4710. [Google Scholar]
- Agarwal, M.; Biswas, K.K.; Hanmandlu, M. Generalized intuitionistic fuzzy soft sets with applications in decision-making. Appl. Soft Comput. 2013, 13, 3552–3566. [Google Scholar] [CrossRef]
- Močkoř, J. Semiring-valued Fuzzy Sets and F-transform. Mathematics 2021, 9, 3107. [Google Scholar] [CrossRef]
- Močkoř, J.; Hurtik, P.; Hýnar, D. Rough Semirings-valued Fuzzy Sets with Application. Mathematics 2022, 10, 2274. [Google Scholar] [CrossRef]
- Wyler, O. Fuzzy logic and categories of fuzzy sets. In Non-Clasical Logics and Their Applications to Fuzzy Subsets; Theory Decis. Libr., Ser. B. 32; Kluwer Acad. Publ.: Dordrecht, The Netherland, 1995; pp. 235–268. [Google Scholar]
- Höhle, U. M-valued Sets and Sheaves over Integral Commutative CL-Monoids. In Applications of Category Theory to Fuzzy Subsets; Rodabaugh, S., Klement, E., Höhle, U., Eds.; Kluwer Academic Publishers: Dordrecht, The Netherland, 1992. [Google Scholar]
- Šostak, A.; Elkins, A.; Uljane, I. Many-level fuzzy rough approximation spaces induced by many-level fuzzy preorders and the related ditopological structures. In Proceedings of the 11th Conference of the European Society for Fuzzy Logic and Technology; Atlantis Press: Dordrecht, The Netherland, 2019. [Google Scholar]
- Liu, Y.M.; Luo, M.K. Fuzzy Topology; World Scientific Publishing: Singapore, 1990. [Google Scholar]
- Mordeson, J.N.; Bhutani, K.R.; Rosenfeld, A. Fuzzy Group Theory; Springer: New York, NY, USA, 2005. [Google Scholar]
- Bertoluzza, C.; Solci, M.; Capodieci, M.L. Measure of a fuzzy set: The alpha-cut approach in the finite case. Fuzzy Sets Syst. 2001, 123, 93–102. [Google Scholar] [CrossRef]
- Garcia, J.N.; Kutalik, Z.; Cho, K.H.; Wolkenhauer, O. Level sets and minimum volume sets of probability density functions. Int. J. Appr. Reason. 2003, 34, 25–47. [Google Scholar] [CrossRef]
- Pourabdollah, A.; Mendel, J.M.; John, R.I. Alpha-cut representation used for defuzzification in rule-based systems. Fuzzy Sets Syst. 2020, 399, 110–132. [Google Scholar] [CrossRef]
- Jaballah, A.; Saidi, F.B. Uniqueness results in the representation of families of sets by fuzzy sets. Fuzzy Sets Syst. 2006, 157, 964–975. [Google Scholar] [CrossRef]
- Saidi, F.B.; Jaballah, A. Alternative characterizations for the representation of families of sets by fuzzy sets. Inform. Sci. 2008, 178, 2639–2647. [Google Scholar] [CrossRef]
- Gan, A.P.; Jiang, Y.L. On ordered ideals in ordered semirings. J. Math. Res. Expo. 2011, 31, 989–996. [Google Scholar]
- Manes, E.G. Algebraic Theories; Springer: Berlin, Germany, 1976. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).