Abstract
The problem of finding the optimal open-loop control for discrete-time stochastic dynamical systems is considered. It is assumed that the initial conditions and external influences are random. The average value of the Bolza functional defined on individual trajectories is minimized. It is proposed to solve the problem by means of classical and modified migrating optimization algorithms. The modification of the migrating algorithm consists of cloning the members of the initial population and choosing different strategies of migratory behavior for the main population and for populations formed by clones. At the final stage of the search for an extremum, an intensively clarifying migration cycle is implemented with the participation of three leaders of the populations participating in the search process. Problems of optimal control of bundles of trajectories of deterministic discrete dynamical systems, as well as individual trajectories, are considered as special cases. Seven model examples illustrating the performance of the proposed approach are solved.
Keywords:
discrete dynamical system; stochastic system; metaheuristic optimization method; optimal control; migrating algorithm MSC:
49M99
1. Introduction
Discrete system control problems have found wide application in solving engineering and economic problems [1,2,3,4]. For deterministic problems, as a rule, the discrete maximum principle or more general necessary conditions are used to search for optimal open-loop control [5] and the Bellman equation for the synthesis of systems with full feedback [1,6,7,8]. When solving problems with non-separable quality criteria, methodological problems arise in their use. As the dimension of the problem being solved increases, the computational difficulties can become insurmountable.
To solve stochastic problems in which the initial conditions and external influences are random, when searching for the optimal open-loop control, the stochastic discrete maximum principle [9,10,11] is used. To find the optimal control with full feedback on the state vector, the Bellman equation for discrete stochastic systems is usually applied [2,6,7]. Compared to deterministic problems, the complexity of the numerical solution increases significantly. Therefore, the direct search for optimal control for the described class of stochastic problems using various methods of global optimization, including metaheuristic algorithms, is relevant.
A special case of stochastic problems is the problem of optimal control of bundles of trajectories, in which it is assumed that there are no external influences on the system and the initial conditions belong to a given set of possible states. As a rule, the law of distribution of the initial states of the system is assumed to be uniform, which corresponds to the case of uncertainty in setting the initial conditions. Various necessary and sufficient conditions for the optimality of the control of bundles of trajectories of discrete systems, as well as computational procedures for their implementation, are considered in [12,13,14]. The problem of finding the optimal open-loop control of a separate trajectory of a discrete deterministic system starting from a given initial state can, in turn, be considered a special case of controlling bundles of trajectories.
Examples of solving discrete deterministic optimal control problems using various metaheuristic optimization algorithms, such as evolutionary methods, the Luus-Jaakola method, iterative dynamic programming, and methods that simulate the behavior of the tomtit flock and a flock of river perch, are described in [15,16,17,18]. Migrating optimization algorithms that use the processes of solution population evolution have been used in solving various applied problems [19,20]. The development of migrating algorithms was a modified migrating algorithm, which has proven itself to solve finite-dimensional technical problems [21].
The article proposes applying a modified migrating algorithm to solve the problem of finding the optimal open-loop control of nonlinear discrete stochastic systems. As special cases, we consider the solution of control problems for bundles of trajectories in the presence of uncertainty in setting the initial conditions and individual trajectories under a fixed initial condition.
The purpose of the article is to demonstrate the possibility of using migration metaheuristic optimization algorithms, including new ones, to solve a wide class of problems of finding optimal control of discrete dynamic systems. The solution procedure does not require the application of necessary optimality conditions and numerical methods for satisfying them. It is shown that the stated problems can be solved with relatively low computational costs. The completed research opens up the possibility of using a similar approach to solve more complex problems, namely the problems of finding control laws with complete and incomplete feedback.
The article has the following structure: In Section 2, the formulations of three optimal control problems for discrete dynamical systems are given. A description of the basic self-organizing migrating optimization algorithm and the modified one developed by the authors is presented. Section 3 contains solutions to seven model examples, two for each of the problem statements given in Section 2. Finally, conclusions are summarized in Section 4.
2. Materials and Methods
2.1. Statements of Optimal Control Problems
Problem 1
(average optimal open-loop control of a stochastic system). The behavior of a nonlinear discrete stochastic model of the control object is described using the following equation:
where is a discrete time, and the number is given; is a system state vector, ; is a control vector; is the set of admissible control values, which is a direct product of segments , is a continuous vector function; and is an -dimensional random vector with a known probability density .
A special case of model (1) is the equation
in which a random external influence on the control system enters additively; is a vector function of dimensions ; and is a matrix function of dimensions .
The initial conditions
are given by the initial probability density .
It is assumed that only discrete-time information is used in the control law. The set of admissible controls form sequences such that and the function is such that a solution to the system of Equation (1) with initial condition (2) exists and is unique.
Let us define the control quality functional for a separate trajectory in the Bolza form:
where are given continuous functions.
The quality of system control is proposed to be estimated by the value of the function
where denotes the operation of finding the mathematical expectation.
One needs to find a control such that
The desired control is called optimal on average since the average value of the functional (3) is minimized.
Problem 2
(average optimal control of a bundle of trajectories of a deterministic system). The behavior of the nonlinear deterministic discrete model of the control object is described by the difference equation as follows:
where is a discrete time, is a system state vector, ; is a system control vector, ; is the set of admissible control values, which is a direct product of segments , ; is a continuous vector function; and the number of discrete-time steps is given as .
The initial state is given by a compact set of positive measures:
The set of admissible controls form the sequences , where .
Let us define the control quality functional for a separate trajectory in the Bolza form:
or
where are given continuous functions, trajectory , and control Function (9) corresponds to the case of non-separable criteria.
To every admissible control and set , let us set in correspondence the bundle of trajectories of the system of Equation (6):
i.e., the union of solutions of Equation (6) over all possible initial states (7).
The quality of control of a bundle of trajectories is proposed to be estimated by the value of the functional
where is a set measure.
It is required to find a control such that
The desired control is called optimal on average, since the average value of the functional (8) or (9) is minimized on the given set of initial states.
It is further assumed that set of initial states is a parallelepiped defined by the direct product of the segments i.e., . All segments with a step are divided into segments, and parallelepiped is divided into elementary subsets . In each elementary subset the initial state (center of the parallelepiped) is set. These initial states and the applied control generate trajectories on which the value of the functional (8) or (9) is calculated. After averaging over all realizations, the value of functional (11) is found.
Problem 3
(optimal control of a separate trajectory of a dynamical deterministic system). The behavior of the nonlinear deterministic discrete model of the control object is described by the difference equation
where is a discrete time, is a system state vector, ; is a system control vector, ; is the set of admissible control values, which is a direct product of segments , ; is a continuous vector function; and a number of discrete-time steps is given as .
The initial state is given as follows:
The set of admissible processes is a set of pairs , including the trajectory and admissible control , where , satisfying the equation of state (13) and the initial condition (14).
On the set , let us define the control quality functional for a separate trajectory in the Bolza form as follows:
or
where , are given continuous functions.
We need to find a pair such that
Elements of a pair , i.e., desired trajectory and control are called the optimal trajectory and optimal control, respectively.
If any admissible control match single pair , then problem (17) can be rewritten in an equivalent form as the problem of finding the minimum of the functional on the set of admissible controls. Functional (16) is more general than the Bolza functional (15), and its application is typical for so-called non-separable problems.
2.2. Self-Organizing Migrating Optimization Algorithms
2.2.1. Optimization Problem Statement
Given an objective function defined on the set of admissible solutions It is required to find the constrained global minimum of the function on the set i.e., a point such that
where
2.2.2. Self-Organizing Migrating Algorithm (SOMA)
SOMA can be classified as the metaheuristic evolutionary optimization algorithm based on the self-organizing behavior of groups of individuals in a social environment. When solving the problem, finite sets of possible solutions, called populations, are used, where is an individual with number , is a population size.
The Self-Organizing Migrating Algorithm [19,20] simulates the evolution of the initial population and is an iterative process that explores the set D.
Initially, a population is created from individuals with randomly generated coordinates from the segment using the uniform distribution law.
Then, the migration cycles begin. Before each cycle, a leader is identified, i.e., an individual with the best value of the objective function . In these cycles, all individuals sequentially move towards the leader along the straight line connecting them, including moving behind him for some distance along the same straight line. In this case, the leader remains motionless. Then, the position of the individual is selected, which corresponds to the best value of the objective function obtained in the search process, and it is recorded in the next population.
The algorithm continues until the difference between the values of the objective function corresponding to the leader and the worst individual of the population becomes less than a predetermined value, or until the maximum number of migration cycles is reached.
Algorithm SOMA parameters that must be specified are as follows: control parameter NStep, determining the number of steps until the end of the movement; control parameter PRT, determining whether the individual will move along the chosen coordinate to the leader; control parameter NP, determining the size of the population of individuals; stop parameter Migration, determining the maximum number of iterations; and stop parameter MinDiv, showing the allowable difference in the value of the objective function between the leader and the worst individual.
2.2.3. Modified Self-Organizing Migrating Algorithm
When developing a modified self-organizing migrating optimization algorithm (MSOMA) [21], the basic version of the SOMA algorithm [19,20] was used.
Modifications consist of the selection of three leaders among the individuals that form the population. For each of the members of the population, two clones are generated with the same position. Thus, three populations are generated, each of which implements a migration cycle relative to its leader. For all members of the population, the best positions achieved during the cycle are found. During the search, the population is regularly updated with new individuals generated on the set of feasible solutions. They replace outgoing individuals with the worst objective function values. After the termination conditions are met, a refinement search (migration cycle) is performed, in which the three remaining leaders of the population participate. The best result is presented as a solution.
When solving the problem, finite sets of possible solutions, called populations, are used, where is an individual with number j, is a population size.
The Self-Organizing Migrating Algorithm simulates the evolution of the initial population and is an iterative process that explores the set D. The initial population is created from individuals with randomly generated coordinates from the segment . In this case, a uniform distribution law is used.
Further migration cycles are realized. Before each cycle, individuals are ordered, and three leaders are identified: individuals with the best values of the objective function . Each individual creates two individual clones with the same coordinates. Thus, three populations of total size are created. Each of the populations moves relative to one of the three leaders. In these cycles, all individuals sequentially, with a certain step, move in a straight line toward their leader and along the same straight line behind him for a certain distance. In this case, the leader remains motionless. Then, the position of the individual is selected, which corresponds to the best value of the objective function obtained in the search process. This position is written to the next population of size . After all individuals are recorded in the new population, individuals with worse objective function values are removed from it. Then, new individuals, according to the rules for the formation of the initial population, are generated to supplement the population to its original size NP in order to update the population and explore new areas in the set of feasible solutions.
The algorithm continues until the average deviation in the value of the function between the three leaders of the population becomes less than a predetermined value or until the maximum number of migration cycles is realized. Then, a clarifying migration cycle is implemented for the three leaders of the population relative to the absolute leader. As an approximate solution, the best position and the corresponding value of the objective function found during the search are presented.
- Algorithm MSOMA for solving the optimization problem
Step 1. Set the method parameters:
- Control parameter NStep, determining the number of steps until the end of the movement;
- Control parameter PRT, determining whether the individual will move along the chosen coordinate to the leader;
- Control parameter NP, determining the size of the population of individuals;
- Stop parameter Migration, determining the maximum number of iterations;
- Stop parameter MinDist, reflecting the value of the average deviation between the three leaders of the population in terms of the value of the function;
- Iteration counter MCount, necessary to stop the algorithm when it reaches the number Migration.
Set MCount = 1.
Step 2. Create an initial population.
Step 2.1. Create a population of individuals with randomly generated coordinates from a segment using the uniform distribution law:
Step 2.2. For each individual, calculate the objective function value and choose leaders (individuals with the best values). To do this, order the population in a non-decreasing order of the objective function. Then, select the first three individuals from it with the smallest values of the objective function.
Step 3. Realize a migration cycle regarding the three leaders.
Step 3.1. For all individuals, create two “clones”, i.e., the individuals with the same coordinates:
In this case, the parent individual moves toward the first leader, the first clone moves towards the second leader, and the second clone moves toward the third leader.
Step 3.2. Before starting the movement of an individual to one of the leaders, generate a random number on the segment for each coordinate of the individual and then compare it with PRT:
Vector thus formed defines the set of coordinate directions along which the search will be performed.
Step 3.3. Implement the movement of individuals to the appropriate leader. The movement takes place in steps until the end position is reached, according to the following formula:
- for the first leader:
- for the second leader:
- for the third leader:
Step 3.4. After all the steps performed for each individual, find the best position (at which the objective function value was the smallest), and the individual to take this position, and then move to the next population:
- for the first leader:
- for the second leader:
- for the third leader:
Step 3.5. Sort all individuals in non-decreasing order of the objective function value.
Step 4. Checking the conditions for completing the search.
If or if the migration limit (Migration) is reached, then go to step 6; otherwise, go to step 5.
Step 5. Update the current population.
Step 5.1. Sort all individuals in non-decreasing objective function value:
Step 5.2. Delete last individuals.
Step 5.3. Create new individuals:
Step 5.4. Increment iteration counter: and go to step 3.
Step 6. Realize the intensively clarifying migration cycle.
Step 6.1. Increase parameter NStep () and implement a migration cycle for the second and third leaders relative to the first leader. Before the individual moves towards the leader, generate a random number on the segment for each coordinate of the individual, and then compare with PRT:
Thus, to form , defining the set of coordinate directions along which the search will be performed.
The movement of the second and third leaders is implemented according to the formula as follows:
Step 6.2. Find a new leader position:
Step 6.3. Return the best solution found during the search:
The complete steps of the MSOMA algorithm are shown in the Algorithm 1.
| Algorithm 1 MSOMA Algorithm |
| 1: Initialize the algorithm parameters NStep, PRT, NP, Migration, MinDist, MCount 2: Set MCount = 1 3: Create an initial population: 4: for all do 5: 6: end for 7: for all calculate the objective function value 8: end for 9: Select the first three individuals with the smallest values of the objective function from the current population 10: Realize a migration cycles regarding the three leaders: 11: for all create two “clones” as 12: 13: end for 14: Implement the movement of individuals to the first leader: 15: for all do 16: for all do 17: generate a random number on the segment ; 18: 19: 20: 21: 22: end if 23: end for 24: for do 25: ; 26: end for 27: Calculate 28: end for 29: Implement the movement of individuals to the second leader: 30: for all do 31: for all , do 32: generate a random number on the segment ; 33: 34: 35: 36: 37: end if 38: end for 39: for do 40: ; 41: end for 42: Calculate 43: end for 44: Implement the movement of individuals to the third leader: 45: for all do 46: for all , do 47: generate a random number on the segment ; 48: 49: 50: 51: 52: end if 53: end for 54: for do 55: ; 56: end for 57: Calculate 58: end for 59: Sort all individuals in non-decreasing order of the objective function value 60: Check the conditions for completing the search 61: if ˅ Mcount = Migration, then 62: go to 75 63: else 64: go to 66 65: end if 66: Update the current population: 67: Sort all individuals in non-decreasing objective function value: 68: Delete last individuals and create new individuals: 69: for do 70: for do 71: 72: end for 73: end for 74: Set and go to 10 75: Realize the intensively clarifying migration cycle 76: Set 77: for do 78: for all , do 79: generate a random number on the segment ; 80: 81: 82: 83: 84: end if 85: end for 86: for do 87: ; 88: end for 89: Calculate 90: end for 91: Return the best solution |
3. Model Examples
The solutions of all model examples are implemented using the Jupyter Notebook software in the Phyton language. Macbook Pro 16 gb RAM, and M1 pro processor with a frequency of 3.2 GHz were used.
3.1. Optimal Open-Loop Control of a Stochastic Discrete Systems
Example 1.
The behavior of the control object model is described by the difference equation:
where , the control variable is constrained by and is the Gaussian random variable with zero mean and unit variance. We take the value of the parameter characterizing the intensity of external influences . The initial states are given by the uniform distribution law on the segment . Functional (3) has the form
It is required to find a control minimizing the value of the functional (4).
Set the number of discrete-time steps: , number of implementations . SOMA parameters are given in Table 1. Figure 1 shows the obtained optimal control and the family of trajectories. The resulting value of the quality functional for is ; numerical results were obtained in 3173.59 s.

Table 1.
SOMA parameters (Example 1).
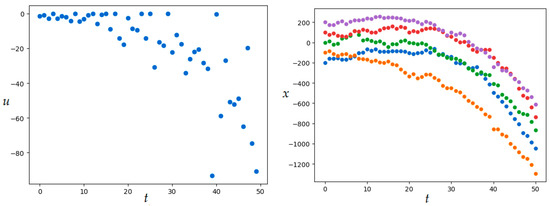
Figure 1.
Optimal control and trajectories in Example 1 (SOMA application).
MSOMA parameters are given in Table 2. The resulting value of the quality functional is ; numerical results were obtained in 1783.98 s. Figure 2 shows the obtained optimal control and the set of trajectories.

Table 2.
MSOMA parameters (Example 1).
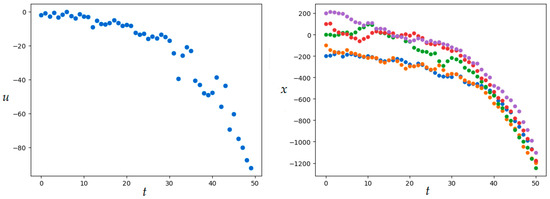
Figure 2.
Optimal control and trajectories in Example 1 (MSOMA application).
Example 2.
The behavior of the control object model is described by a system of difference equations:
where , are the independent Gaussian random variables with zero mean and unit variance. We take the values of the parameters characterizing the intensity of external influences . The initial states are described by the uniform distribution law on the set , the control variable is constrained by .
Functional (3) has the form
It is required to find the optimal open-loop control and the minimum value of the functional (4).
Let us set , number of implementations 25. SOMA parameters are given in Table 3. Figure 3 and Figure 4 show the resulting optimal control and trajectories. The resulting value of the quality functional is ; numerical results were obtained in 8504.02 s.

Table 3.
SOMA parameters (Example 2).
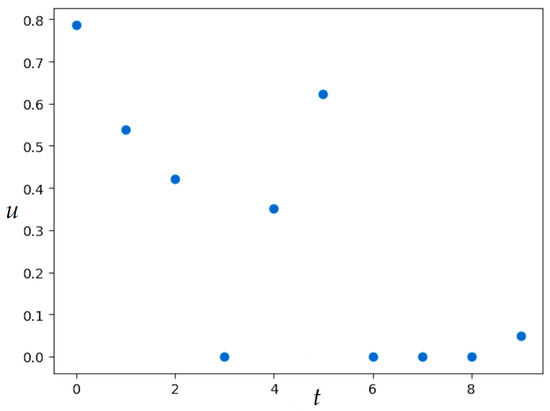
Figure 3.
Optimal control in Example 2 (SOMA application).
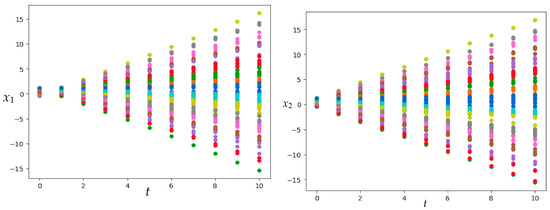
Figure 4.
Trajectories in Example 2 (SOMA application).
MSOMA parameters used are shown in Table 4. Figure 5 and Figure 6 show the obtained optimal control and trajectories of the discrete dynamical system. The resulting value of the quality functional is ; numerical results were obtained in 14,270.38 s.

Table 4.
MSOMA parameters (Example 2).
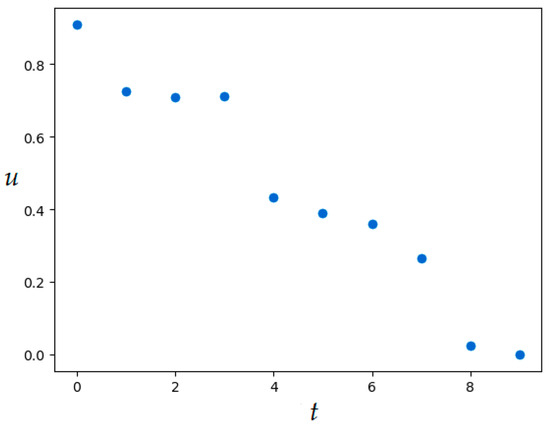
Figure 5.
Optimal control in Example 2 (MSOMA application).
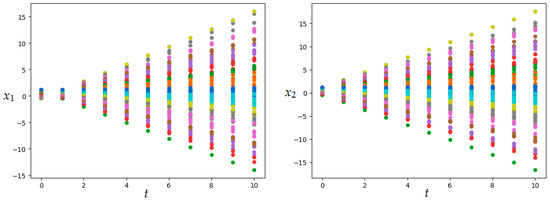
Figure 6.
Trajectories in Example 2 (MSOMA application).
3.2. Optimal Open-Loop Control of Bundles of Trajectories
Example 3.
The behavior of the control object model is described by the difference equation
where , The control variable is constrained by . The initial states are determined from the condition . Functional (8) has the form
It is required to find a control minimizing the value of the functional (11).
Set the number of discrete-time steps , number of implementations .
SOMA parameters are given in Table 5. Figure 7 shows the resulting optimal control and bundle of trajectories. The resulting value of the quality functional for is , numerical results were obtained in 520.52 s.

Table 5.
SOMA parameters in Example 3.
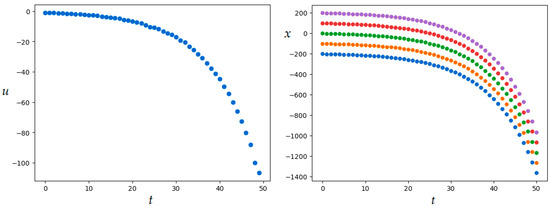
Figure 7.
Optimal control and bundle of trajectories in Example 3 (SOMA application).
MSOMA parameters are given in Table 6. Figure 8 shows the resulting optimal control and bundle of trajectories. The resulting value of the quality functional for is ; numerical results were obtained in 730.24 s.

Table 6.
MSOMA parameters in Example 3.
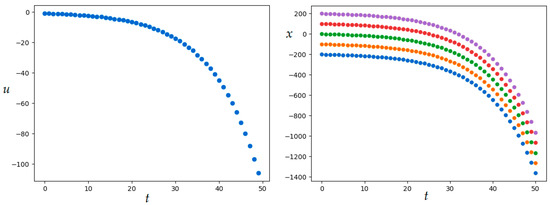
Figure 8.
Optimal control and bundle of trajectories in Example 3 (MSOMA application).
Example 4.
The behavior of the control object model is described by a system of difference equations:
where The initial states are determined from the condition . The control variable is constrained by . Functional (8) has the form
It is required to find the optimal program control and the minimum value of the functional (11).
Let us set , number of implementations 25. The results of the SOMA algorithm (the parameters are given in Table 5). Figure 9 and Figure 10 show the resulting optimal control and corresponding bundle of trajectories. The resulting value of the quality functional: ; numerical results were obtained in 225.58 s.
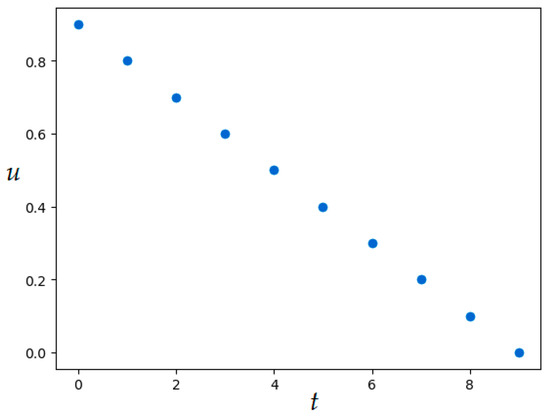
Figure 9.
Optimal control in Example 4 (SOMA application).
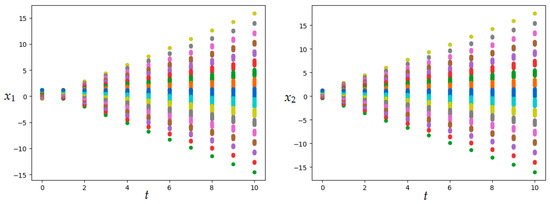
Figure 10.
Bundle of trajectories in Example 4 (SOMA application).
MSOMA parameters are given in Table 6. The resulting value of the quality functional is , numerical results were obtained in 868.34 s. Figure 11 and Figure 12 show the resulting optimal control and corresponding bundle of trajectories.
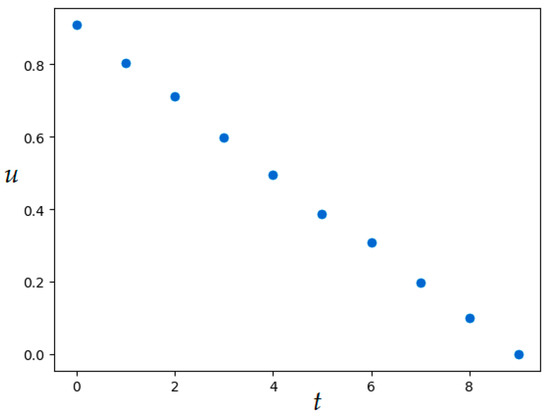
Figure 11.
Optimal control in Example 4 (MSOMA application).
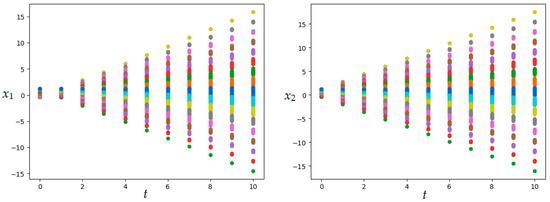
Figure 12.
Bundle of trajectories in Example 4 (MSOMA application).
3.3. Optimal Open-Loop Control of Individual Trajectories
Example 5.
The behavior of the control object model is described by the difference equation
where , The control variable is constrained by . The initial state is given by the condition .
On the set of admissible processes, the quality functional is defined as follows:
It is required to find the minimum value of the functional and the optimal process at which this value is reached.
The problem under consideration has an analytical solution presented as: ,
Set the number of discrete-time steps: . For the exact value of the quality functional is . SOMA parameters are given in Table 3. The resulting value of the quality functional is , numerical results were obtained in 2.2 min. Figure 13 shows the resulting optimal control and corresponding trajectory.
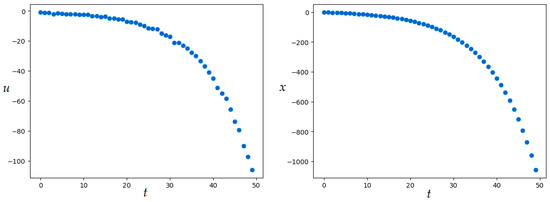
Figure 13.
Optimal control and trajectory in Example 5 (SOMA application).
MSOMA parameters are given in Table 4. The resulting value of the quality functional is ; numerical results were obtained in 10.7 min. Figure 14 shows the resulting optimal control and corresponding trajectory.
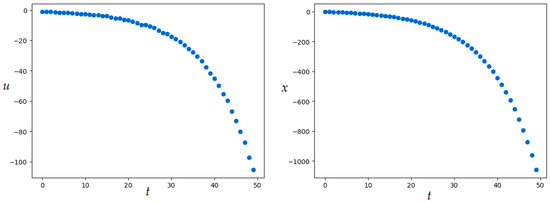
Figure 14.
Optimal control and trajectory in Example 5 (MSOMA application).
Example 6.
The behavior of the control object model is described by a system of difference equations:
where . The initial state is given by the condition . The control variable is constrained by .
On the set of admissible processes, a functional of the Bolza form
is defined. It is required to find the minimum value of the functional and the optimal process on which this value is reached.
The problem has an analytical solution: , . If one set , then .
SOMA parameters are given in Table 7. The resulting value of the quality functional is , numerical results were obtained in 26 s. Figure 15 and Figure 16 show the resulting optimal control and trajectory.

Table 7.
SOMA parameters in Example 6.
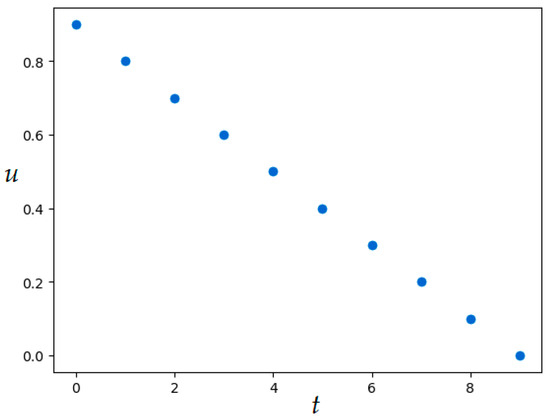
Figure 15.
Optimal control in Example 6 (SOMA application).
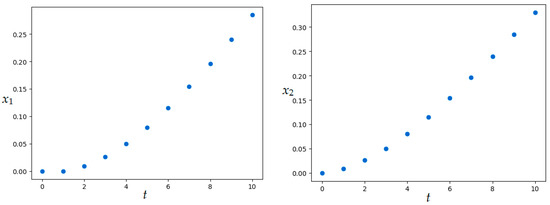
Figure 16.
Optimal trajectory in Example 6 (SOMA application).
MSOMA parameters are given in Table 8. The resulting value of the quality functional is ; numerical results were obtained in 12.7 s. Figure 17 and Figure 18 show the resulting optimal control and trajectory.

Table 8.
MSOMA parameters in Example 6.
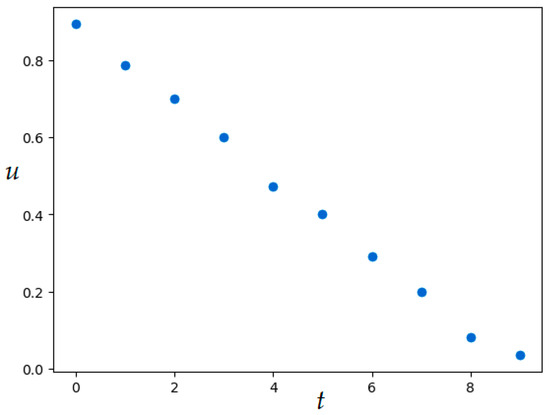
Figure 17.
Optimal control in Example 6 (MSOMA application).
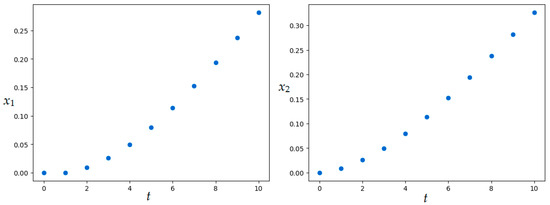
Figure 18.
Optimal trajectory in Example 6 (MSOMA application).
Example 7.
The behavior of the control object model is described by a difference equation:
where . The initial state is given by the condition , the control variable is constrained by .
On the set of admissible processes, a functional of the form
is defined. It is required to find the minimum value of the functional and the optimal process on which this value is reached.
The problem has an analytical solution. If one set then .
MSOMA parameters are given in Table 8. The resulting value of the quality functional:; numerical results were obtained in 5.7 s. The obtained control and state values are presented in Table 9. Figure 19 shows the resulting optimal control and trajectory.

Table 9.
Optimal control and state values in Example 7.
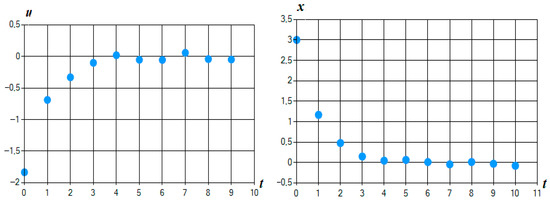
Figure 19.
Optimal control and trajectory in Example 7 (MSOMA application).
4. Discussion
Analysis of the results of solving Examples 5 and 6 indicates the ability of migrating optimization algorithms SOMA and MSOMA to find the optimal control and the corresponding trajectory for deterministic discrete dynamical systems with sufficiently high accuracy, which follows from a comparison with the exact solutions obtained by applying the discrete maximum principle. Example 7 shows that there are problems in which the control values tend to zero over time, and the coordinate values of the state vector tend to be stationary values.
The results of solving Examples 3 and 4 demonstrate the capabilities of metaheuristic migrating algorithms to solve optimal control problems under conditions of uncertainty in specifying initial conditions. In this case, the found control laws generate a fairly regular behavior of the trajectories forming the bundle. The disadvantages of using open loop control of trajectory bundles include the inability to concentrate trajectories in the desired neighborhood, which is demonstrated in Figure 10 and Figure 12 in Example 4. The optimal control and graphs in Figure 7 and Figure 8 obtained as a result of solving Example 3 demonstrate that the uncertainty generated by specifying a set of possible initial conditions when using open loop control at least does not decrease over time.
The results of solving Examples 1 and 2, presented in Figure 1, Figure 2, Figure 3, Figure 4, Figure 5 and Figure 6, demonstrate the influence of random external influences on the type of trajectories of a dynamical system. Comparing the graphs in Figure 1 and Figure 2 with Figure 7 and Figure 8 (Examples 1 and 3), as well as the graphs in Figure 3, Figure 4, Figure 5 and Figure 6 and Figure 9, Figure 10, Figure 11 and Figure 12 (Examples 2 and 4), one can conclude that the set of obtained trajectories of stochastic systems compared with a similar set of trajectories of deterministic systems are characterized by noticeable turbulence. At the same time, the patterns of behavior of controlled systems generally correspond to each other.
5. Conclusions and Future Work
The article demonstrates the application of metaheuristic migrating optimization algorithms to solving optimal control problems for discrete dynamical systems of different classes. Their use makes it possible to obtain a solution of acceptable quality at reasonable computational costs. It is noted that the proposed modified algorithm solves the problem of finding the optimal control of stochastic systems more successfully than the basic one. In problems of optimal control of bundles of trajectories and an individual trajectory, migrating algorithms are almost as accurate as each other.
Noting the shortcomings of the proposed approach, it should be emphasized that with a significant increase in the value of N, the complexity of the problems being solved also increases because of the number of variables on which the value of the functionals (4), (11), (15) and (16) depends increases. This fact leads to an increase in computational costs, which may be unjustified. One direction of development may be the search for the desired control law in parametric form with a relatively small number of characteristic parameters.
A further direction of research can be the search for an optimal control that depends on time and a set of coordinates of the state vector available for measurement, as well as solving problems of joint estimation and control. In this case, it is possible to use other metaheuristic optimization algorithms, namely methods of swarm intelligence, bio-inspired, multi-agent, and multi-start, as well as simulating physical and chemical processes.
Author Contributions
Conceptualization, A.P.; methodology, A.P. and V.R.; software, V.R. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Source code at https://github.com/Vradislav/MSOMA (accessed on 4 October 2023); numerical results at https://github.com/Vradislav/MSOMA/blob/main/MSOMA_application.ipynb (accessed on 4 October 2023).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Bertsekas, D.P. Dynamic Programming and Optimal Control; Athena Scientific: Belmont, MA, USA, 1995; Volume 1. [Google Scholar]
- Bertsekas, D.P.; Shreve, S.E. Stochastic Optimal Control: The Discrete Time Case; Academic: New York, NY, USA, 2004. [Google Scholar]
- Luus, R. Iterative Dynamic Programming, 1st ed.; Chapman & Hall/CRC: London, UK, 2000. [Google Scholar]
- Salinelli, E.; Tomarelli, F. Discrete Dynamical Models; Springer: Milan, Italy, 2014. [Google Scholar]
- Propoi, A.I. Problems of discrete control with phase constraints. USSR Comput. Math. Math. Phys. 1972, 12, 53–74. [Google Scholar] [CrossRef]
- Kwakernaak, H.; Sivan, R. Linear Optimal Control Systems; Wiley–Interscience: Hoboken, NJ, USA, 1972. [Google Scholar]
- Fleming, W.H.; Soner, H.M. Controlled Markov Processes and Viscosity Solutions; Springer: New York, NY, USA; Berlin/Heidelberg, Germany, 1993. [Google Scholar]
- Kushner, H.J. Approximation and Weak Convergence Methods for Random Processes with Applications to Stochastic Systems Theory; MIT Press: Cambridge, MA, USA, 1984. [Google Scholar]
- Kushner, H.J.; Schweppe, F.C. A maximum principle for stochastic control systems. J. Math. Anal. Appl. 1964, 8, 287–302. [Google Scholar] [CrossRef]
- Peng, S. A general stochastic maximum principle for optimal control problems. SIAM J. Control. Optim. 1990, 28, 966–979. [Google Scholar] [CrossRef]
- Lin, X.; Zhang, W. A maximum principle for optimal control of discrete-time stochastic systems with multiplicative noise. IEEE Trans. Autom. Control 2015, 60, 1121–1126. [Google Scholar] [CrossRef]
- Golovkina, A.; Ovsyannikov, D. Optimal control of trajectories ensemble for a class of discrete dynamic systems. IFAC-PapersOnLine 2020, 53, 6893–6898. [Google Scholar] [CrossRef]
- Kotina, E.D.; Ovsyannikov, D.A. Mathematical model of joint optimization of programmed and perturbed motions in discrete systems. In Prikladnaya Matematika, Informatika, Protsessy Upravleniya; Vestnik Sankt-Peterburgskogo Universiteta: St. Petersburg, FL, USA, 2021; Volume 17, pp. 213–224. [Google Scholar] [CrossRef]
- Kotina, E.D. Discrete optimization problem in beam dynamics. Nucl. Instrum. Methods Phys. Res. A 2006, 558, 292–294. [Google Scholar] [CrossRef]
- Floudas, C.; Pardalos, P. Encyclopedia of Optimization, 2nd ed.; Springer: New York, NY, USA, 2009. [Google Scholar]
- Gendreau, M. Handbook of Metaheuristics, 2nd ed.; Springer: New York, NY, USA, 2010. [Google Scholar]
- Panteleev, A.V.; Kolessa, A.A. Application of the tomtit flock metaheuristic optimization algorithm to the optimal discrete time deterministic dynamical control problem. Algorithms 2022, 15, 301. [Google Scholar] [CrossRef]
- Panteleev, A.V.; Kolessa, A.A. Optimal open-loop control of discrete deterministic systems by application of the perch school metaheuristic optimization algorithm. Algorithms 2022, 15, 157. [Google Scholar] [CrossRef]
- Davendra, D.; Zelinka, I. Self-Organizing Migrating Algorithm, 1st ed.; Methodology and Implementation; Studies in Computational Intelligence, 626; Springer: New York, NY, USA, 2016. [Google Scholar]
- Zelinka, I.; Lampinen, J. SOMA—Self-organizing migrating algorithm. In Proceedings of the International Conference on Soft Computing (Mendel 2000), Brno, Czech Republic, 10–12 July 2000; pp. 177–187. [Google Scholar]
- Panteleev, A.V.; Rakitianskii, V.M. Application of the modified self-organizing migration algorithm MSOMA in optimal open-loop control problems. J. Phys. Conf. Ser. 2021, 1925, 012017. [Google Scholar] [CrossRef]
- Horn, R.A.; Johnson, C.R. Matrix Analysis; Cambridge University Press: Cambridge, UK, 2012. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).