Congruence Representations via Soft Ideals in Soft Topological Spaces

Abstract

This article starts with a study of the congruence of soft sets modulo soft ideals. Different types of soft ideals in soft topological spaces are used to introduce new weak classes of soft open sets. Namely, soft open sets modulo soft nowhere dense sets and soft open sets modulo soft sets of the first category. The basic properties and representations of these classes are established. The class of soft open sets modulo the soft nowhere dense sets forms a soft algebra. Elements in this soft algebra are primarily the soft sets whose soft boundaries are soft nowhere dense sets. The class of soft open sets modulo soft sets of the first category, known as soft sets of the Baire property, is a soft $\sigma$-algebra. In this work, we mainly focus on the soft $\sigma$-algebra of soft sets with the Baire property. We show that soft sets with the Baire property can be represented in terms of various natural classes of soft sets in soft topological spaces. In addition, we see that the soft $\sigma$-algebra of soft sets with the Baire property includes the soft Borel $\sigma$-algebra. We further show that soft sets with the Baire property in a certain soft topology are equal to soft Borel sets in the cluster soft topology formed by the original one.

1. Introduction

Molodtsov [1] suggested the theory of soft sets through set-valued mappings as an important alternative to some preexisting mathematical techniques for dealing with uncertainty. Soft sets differ from probability theory, fuzzy set theory, and rough set theory in that accurate quantities such as membership grade and probability are not required. Due to the fact that in the majority of realistic scenarios, the underlying possibilities and grade of membership are not well understood enough to support the use of actual valuations, this feature makes certain applications possible. The idea of soft sets has received a lot of attention since it was first proposed, including several fruitful applications (see [2,3,4,5,6]).

A number of researchers have utilized soft set theory to numerous structures of mathematics, including soft ideal theory [7], soft group theory [8], soft ring theory [9], soft algebras, and soft $\sigma$-algebras [10,11], etc.

One of the structures is soft topology established in [12,13] as a mixture of the classical topology and soft set theory. The work of Çağman et al. [12] and Shabir and Naz [13] had a significant impact on the development of soft topology. Then, many traditional topological notions have been generalized and applied to soft set contexts, such as soft compact spaces [14], soft paracompact spaces [15], soft extremally disconnected spaces [16], soft separation axioms [13,17,18,19], soft separable spaces [17], and soft connected spaces [15].

It is known that soft open sets are the building blocks of soft topology, but other classes of soft sets can contribute to the growth of soft topology. Namely, soft $\omega$-open [20], soft dense [21], soft codense [22], soft nowhere dense [21], and soft meager (first category soft set) [21]. A question here would be: Can we construct a scheme for defining a category of soft sets that includes the earlier classes of soft sets? The main objective of this work is to introduce the concept of congruence modulo a soft ideal in soft topological spaces, which is the property that classifies soft open sets with respect to the given soft ideal. This technique is applied to define certain weak classes of soft open sets. The class of soft sets with the Baire property is one of the classes generated by soft open sets modulo soft sets of the first category. This class is vast and contains all the above-mentioned soft sets in soft topological spaces and even soft Borel sets.

This paper contributes to the advancement of the area of soft topology by introducing the class of soft sets with the Baire property. Soft sets with the Baire property can be represented in multiple different forms. Additionally, soft sets with the Baire property lead to the growth of soft measure and soft game theories, as they are approximately soft open sets and nicely related to soft Borel sets.

The paper’s primary portion is structured as follows: In Section 2, we provide a summary of the soft set theory and soft topology literature. Section 3 presents the concept of congruence of soft sets modulo a soft ideal. In Section 4, we introduce the class of soft open sets modulo a soft ideal. We establish a result representing this class of soft open sets modulo a soft ideal. In Section 5, we study the family of soft open sets modulo soft nowhere dense sets and find some of its characterizations. Section 6 defines soft sets with the Baire property in soft topological spaces, followed by some operations. Additionally, we demonstrate some properties and representations of such soft sets. Section 7 ends the work with a brief conclusion and possible lines of research.

2. Preliminaries

Let I be any index set, $\tilde{\beta }$ be a family that contains our parameters, and $2^X$ be the collection of the whole subsets of a universal set X.

Definition 1 

([1]). Let $\beta \subseteq \tilde{\beta }$. A soft set is defined to be the ordered pair $(E,\beta )=\left\{\right(\mu ,E\left(\mu \right)):\mu \in \beta \}$ such that $E:\beta \to 2^X$ is a mapping. In other word, a soft set $(E,\beta )$ over X can be expressed by

$$(E,\beta )=\left\{(\mu ,E\left(\mu \right)):\mu \in \beta ,E\left(\mu \right)\in 2^X\right\}.$$

Observe that one can directly extend a soft set $(E,\beta )$ to the soft set $(E,\tilde{\beta })$ by $E\left(\mu \right)=\varnothing$ for each $\mu \in \tilde{\beta }-\beta$.

The set of all soft subsets over X with respect to $\beta$ is symbolized by $SS\left(\widehat{X}\right)$.

Definition 2 

([4]). Let $(E,\beta )\in SS\left(\widehat{X}\right)$. A soft set ${(E,\beta )}^c=(E^c,\beta )$ is said to be the soft complement $(E,\beta )$ for which $E^c:\beta \to 2^X$ is a mapping that is defined by $E^c\left(\mu \right)=X-E\left(\mu \right)$ for each $\mu \in \beta$.

Notice that ${\left({(E,\beta )}^c\right)}^c=(E,\beta )$.

Definition 3 

([23]). Let $(E,\beta )\in SS\left(\widehat{X}\right)$. Then, $(E,\beta )$ is said to be null relates to β, denoted by Φ, if $E\left(\mu \right)=\varnothing$ for all $\mu \in \beta$. It is absolute relates to β, denoted by $\widehat{X}$, if $E\left(\mu \right)=X$ for all $\mu \in \beta$.

The null and absolute soft sets relate to $\tilde{\beta }$ are denoted by ${\Phi }_{\tilde{\beta }}$ and $(X,\tilde{\beta })$, respectively.

Evidently, ${\Phi }^c=\widehat{X}$ and ${\widehat{X}}^c=\Phi$.

Definition 4 

([24,25]). Let $(E,\beta )\in SS\left(\widehat{X}\right)$. Then, $(E,\beta )$ is called a soft element, denoted by $x_{\mu }$, if $E\left(\mu \right)=\left\{x\right\}$ and $F\left(\nu \right)=\varnothing$ for all $\nu \in \beta$ with $\mu \ne \nu$, where $\mu \in \beta$ and $x\in X$.

The soft element is called a soft point in [26]. We prefer to use the concept of soft point in the sequel.

By a statement $x_{\mu }\in (E,\beta )$ we mean $x\in E\left(\mu \right)$. By $SP\left(\widehat{X}\right)$, we denote the set of all soft points over X along with E.

Definition 5 

([27]). A soft set $(E,\beta )$ is said to be finite if $E\left(\mu \right)$ is finite for each $\mu \in \beta$. Otherwise, it is called infinite. The same can be said of a countable soft set.

Definition 6 

([4,28]). Let $\beta ,\lambda \subseteq \widehat{\beta }$. It is said that $(E,\beta )$ is a soft subset of $(F,\lambda )$, written by $(E,\beta )\tilde{\subseteq }(F,\lambda )$, if $\beta \subseteq \lambda$ and $E\left(\mu \right)\subseteq F\left(\mu \right)$ for all $\mu \in \beta$. And $(E,\beta )$ is soft equal to $(F,\beta )$, written by $(E,\beta )=(F,\lambda )$, if $(E,\beta )\tilde{\subseteq }(F,\lambda )$ and $(F,\lambda )\tilde{\subseteq }(E,\beta )$.

Definition 7 

([23,29]). Let $\{(E_i,\beta ):i\in I\}$ be a collection of soft sets over X. For all $i\in I$,

1.

The soft union of $(E_i,\beta )$ is a soft set $(E,\beta )={\tilde{\cup }}_{i\in I}(E_i,\beta )$ such that $E\left(\mu \right)={\cup }_{i\in I}{E}_i\left(\mu \right)$ for all $\mu \in \beta$.

2.

The soft intersection of $(E_i,\beta )$ is a soft set $(E,\beta )={\tilde{\cap }}_{i\in I}(E_i,\beta )$ such that $E\left(\mu \right)={\cap }_{i\in I}{E}_i\left(\mu \right)$ for each $\mu \in \beta$.

Definition 8 

([23,30]). Let $(E,\beta ),(G,\beta )\in SS\left(\widehat{X}\right)$.

1.

The soft set difference $(E,\beta )$ and $(G,\beta )$ is defined to be the soft set $(H,\beta )=(E,\beta )-(G,\beta )$, where $H\left(\mu \right)=E\left(\mu \right)-G\left(\mu \right)$ for all $\mu \in \beta$.

2.

The soft symmetric difference of $(E,\beta )$ and $(G,\beta )$ is defined by $(E,\beta )\tilde{\Delta }(G,\beta )=[(E,\beta )-(G,\beta )]\tilde{\cup }[(G,\beta )-(E,\beta )]$.

In what follow, by two distinct soft points $x_{\mu },y_{\nu }$, we mean either $x\ne y$ or $\mu \ne \nu$, and by two disjoint soft sets $(E,\beta ),(G,\beta )$ over X, we mean $(E,\beta )\tilde{\cap }(G,\beta )=\Phi$.

Definition 9 

([13]). A family $\tau \tilde{\subseteq }SS\left(\widehat{X}\right)$ is called a soft topology over X if

1.

$\Phi ,\widehat{X}\in \tau$,

2.

$(E,\beta ),(F,\beta )\in \tau$ implies $(E,\beta )\tilde{\cap }(F,\beta )\in \tau$, and

3.

$\{(E_i,\beta ):i\in I\}\tilde{\subseteq }\tau$ implies ${\tilde{\cup }}_{i\in I}(E_i,\beta )\in \tau$.

By $(X,\tau ,\beta )$, we mean a soft topological space. Soft open sets are elements of τ, and their complements are called soft closed sets. By ${\tau }^c$, we mean the collection of all soft closed sets. The lattice of soft topologies over X is denoted by $T\left(\widehat{X}\right)$ (see, [31]).

Definition 10 

([13]). Let $(Y,\beta )\ne \Phi$ be a soft subset of $(X,\tau ,\beta )$. Then, ${\tau }_{(Y,\beta )}=\{(G,\beta )\tilde{\cap }(Y,\beta ):(G,\beta )\in \tau \}$ is called a relative soft topology over Y and $(Y,{\tau }_{(Y,\beta )},\beta )$ is a soft subspace of $(Y,\tau ,\beta )$.

Lemma 1 

([13]). Let $(Y,{\tau }_{(Y,\beta )},\beta )$ be a soft subspace of $(Y,\tau ,\beta )$ and let $(E,\beta )\tilde{\subseteq }(Y,\beta )\in \tau$. Then, $(E,\beta )\in {\tau }_{(Y,\beta )}$ if $(E,\beta )\in \tau$.

Definition 11 

([25]). Let $(G,\beta )\in SS\left(\widehat{X}\right)$ and $\tau \in T\left(\widehat{X}\right)$. Then, $(G,\beta )$ is called a soft neighborhood of $x_{\mu }\in SP\left(\widehat{X}\right)$ if there exists $(U,\beta )\in \tau \left(x_{\mu }\right)$ such that $x_{\mu }\in (U,\beta )\tilde{\subseteq }(G,\beta )$, where $\tau \left(x_{\mu }\right)$ is the family of all elements of τ that contain $x_{\mu }$.

Definition 12 

([12]). A soft base for a soft topology τ is a subfamily $\mathcal{B}$ of τ that represents members of τ as unions of members of $\mathcal{B}$. And τ is said to have a countable soft base if $\mathcal{B}$ is countable.

Definition 13 

([31]). Let $\mathcal{C}\tilde{\subseteq }SS\left(\widehat{X}\right)$ and $\mathit{T}=\{{\tau }_i\in T\left(\widehat{X}\right):\mathcal{C}\tilde{\subseteq }{\tau }_i,i\in I\}$. The $\tilde{\cap }\mathit{T}={\tilde{\cap }}_{i\in I}{\tau }_i$ is called a soft topology generated by $\mathcal{C}$ and is denoted by $\tau ⟨\mathcal{C}⟩$.

Lemma 2 

([13]). Let $(X,\tau ,\beta )$ be a soft topological space. Then, for each $\mu \in \beta$, the collection $\tau \left(\mu \right)=\left\{E\right(\mu ):(E,\beta )\in \tau \}$ is a (crisp) topology on X.

Lemma 3 

([29]). Let $\beta =\left\{\mu \right\}$, $\tau =\left\{\right(\mu ,H\left(\mu \right)):H(\mu )\in Y\}$, $\tau \left(\mu \right)=\left\{H\right(\mu ):(\mu ,H\left(\mu \right))\in \tau \}$, where $Y\subseteq 2^X$. Then, τ is a soft topology if $\tau \left(\mu \right)$ is a (crisp) topology on X.

Definition 14 

([13]). Let $(H,\beta )\in SS\left(\widehat{X}\right)$ and $\tau \in T\left(\widehat{X}\right)$. Then, $cl(H,\beta )=\tilde{\cap }\{(E,\beta ):(H,\beta )\tilde{\subseteq }(E,\beta ),(E,\beta )\in {\tau }^c\}$ is the soft closure of $(H,\beta )$ and $int(H,\beta )=\tilde{\cup }\{(E,\beta ):(E,\beta )\tilde{\subseteq }$$(H,\beta ),(E,\beta )\in \tau \}$ is the soft interior of $(H,\beta )$.

Lemma 4 

([32]). Let $(E,\beta )\in SS\left(\widehat{X}\right)$ and $\tau \in T\left(\widehat{X}\right)$. Then,

$$int\left({(E,\beta )}^c\right)={\left(cl\left((E,\beta )\right)\right)}^c\mathrm{and}cl\left({(E,\beta )}^c\right)={\left(int\left((E,\beta )\right)\right)}^c.$$

Definition 15 

([32,33]). Let $(E,\beta )\in SS\left(\widehat{X}\right)$ and $\tau \in T\left(\widehat{X}\right)$. The soft boundary of $(E,\beta )$ is given by $b(E,\beta )=cl(E,\beta )-int(E,\beta )$.

Definition 16 

([7]). A non-null class $\tilde{I}\tilde{\subseteq }SS\left(\widehat{X}\right)$ is called a soft ideal over X if $\tilde{I}$ satisfies the following conditions:

1.

If $(E,\beta ),(G,\beta )\in \tilde{I}$, then $(E,\beta )\tilde{\cup }(G,\beta )\in \tilde{I}$, and

2.

If $(G,\beta )\in \tilde{I}$ and $(E,\beta )\tilde{\subseteq }(G,\beta )$, then $(E,\beta )\in \tilde{I}$.

$\tilde{I}$ is called a soft σ-ideal if (1) holds for countably many soft sets. We denote the family of soft ideals over X by $\mathcal{I}\left(\widehat{X}\right)$.

Definition 17 

([11,34]). A family $\mathcal{A}\tilde{\subseteq }SS\left(\widehat{X}\right)$ is said to be a soft algebra over X if $\mathcal{A}$ satisfies the following conditions:

1.

$\Phi \in \mathcal{A}$,

2.

If $(E,\beta )\in \mathcal{A}$, then ${(E,\beta )}^c\in \mathcal{A}$, and

3.

If $(E_m,\beta )\in \mathcal{A}$, for all $m=1,2,\cdots ,n$, then ${\tilde{\cup }}_{m=1}^n(E_m,\beta )\in \mathcal{A}$.

If (3) holds for countably infinite elements of $\mathcal{A}$, then $\mathcal{A}$ is said to be a soft $\sigma$-algebra over X (see, [10]).

Definition 18 

([34]). Let $\mathcal{C}\tilde{\subseteq }SS\left(\widehat{X}\right)$. The soft intersection of all soft σ-algebras over X containing $\mathcal{C}$ is a soft σ-algebra, and it is called the soft σ-algebra generated by $\mathcal{C}$ and is denoted by $\sigma \left(\mathcal{C}\right)$.

Definition 19. 

Let $(E,\beta ),(G,\beta )\in SS\left(\widehat{X}\right)$ and let $\tau \in T\left(\widehat{X}\right)$. Then, $(E,\beta )$ is called

1.

Soft clopen [35] if $(E,\beta )$ is both soft open and soft closed.

2.

Soft regular open [36] if $int\left(cl\right(E,\beta \left)\right)=(E,\beta )$.

3.

Soft dense in $(G,\beta )$[21,22] if $(G,\beta )\tilde{\subseteq }cl(E,\beta )$.

4.

Soft codense [22] if $int(E,\beta )=\Phi$.

5.

Soft $G_{\delta }$[22] if $(E,\beta )={\tilde{\cap }}_{n=1}^{\infty }(G_n,\beta )$, where $(G_n,\beta )\in \tau$.

6.

Soft $F_{\sigma }$[22] if $(E,\beta )={\tilde{\cup }}_{n=1}^{\infty }(E_n,\beta )$, where $(E_n,\beta )\in {\tau }^c$.

7.

Soft nowhere dense [21] if $int\left(cl\right(E,\beta \left)\right)=\Phi$.

8.

Soft meager [21,37] (or of the first category) if $(E,\beta )={\tilde{\cup }}_{n=1}^{\infty }(E_n,\beta )$, where each $(E_n,\beta )$ is soft nowhere dense, otherwise $(E,\beta )$ is of the second category.

The collection of all soft sets of the first category (resp. soft sets of the second category, soft nowhere dense sets) over X is denoted by $\mathcal{M}\left(\tau \right)$ (resp. $\mathcal{S}\left(\tau \right),\mathcal{N}\left(\tau \right)$).

Remark 1 

([37]). For any soft topological space $(X,\tau ,\beta )$, $\mathcal{M}\left(\tau \right)$ forms a soft σ-ideal and $\mathcal{N}\left(\tau \right)$ forms a soft ideal. By $\mathcal{C}\left(\tau \right)$ we mean a soft ideal of soft codense sets.

Definition 20 

([21,22]). Let $(X,\tau ,\beta )$ be a soft topological space. Then, $(X,\tau ,\beta )$ is said to be soft Baire whenever $\Phi \ne (G,\beta )\in \tau$ implies $(G,\beta )\notin \mathcal{M}\left(\tau \right)$.

Lemma 5 

([37]). Let $(N,\beta )\in SS\left(\widehat{X}\right)$ and let $\tau \in T\left(\widehat{X}\right)$. If $(N,\beta )\in \mathcal{N}\left(\tau \right)$, then $cl(N,\beta )\in \mathcal{N}\left(\tau \right)$.

Proposition 1 

([37]). Let $(M,\beta )\in SS\left(\widehat{X}\right)$ and let $\tau \in T\left(\widehat{X}\right)$. If $(M,\beta )\in \mathcal{M}\left(\tau \right)$, then $(M,\beta )\tilde{\subseteq }(E,\beta )$, where $(E,\beta )$ is a soft $F_{\sigma }$ set in $\mathcal{M}\left(\tau \right)$.

Definition 21 

([38]). Let $(E,\beta )\in SS\left(\widehat{X}\right)$, $\tau \in T\left(\widehat{X}\right)$, and $\tilde{I}\in \mathcal{I}\left(\widehat{X}\right)$. A soft point $x_{\mu }\in SP\left(\widehat{X}\right)$ is a cluster soft point of $(E,\beta )$ if $(E,\beta )\tilde{\cap }(U,\beta )\notin \tilde{I}$ for each $(U,\beta )\in \tau \left(x_{\mu }\right)$. The set of all the cluster soft points of $(E,\beta )$ is called the cluster soft set of $(E,\beta )$ and is denoted by ${\mathfrak{c}}_{(\tau ,\tilde{I})}(E,\beta )$ or shortly $\mathfrak{c}(E,\beta )$.

The family ${\tau }_{\mathfrak{c}}\left(\tilde{I}\right)=\{(E,\beta )\in SS\left(\widehat{X}\right):\mathfrak{c}\left({(E,\beta )}^c\right)\tilde{\subseteq }{(E,\beta )}^c\}$ is a soft topology over X and is called the cluster soft topology (or soft ideal topology). The Lemma 11 and Theorem 6 in [33] guarantee that the cluster soft topology is equivalent soft ${\tau }^{*}$-topology constructed differently in [7]. We may write simply ${\tau }_{\mathfrak{c}}$ instead of ${\tau }_{\mathfrak{c}}\left(\tilde{I}\right)$ if there is no confusion.

Lemma 6 

([38]). Let $\tau \in T\left(\widehat{X}\right)$, and $\tilde{I}\in \mathcal{I}\left(\widehat{X}\right)$. Then,

$${\mathcal{B}}_{\mathfrak{c}}\left(\tilde{I}\right)=\{(G,\beta )-(P,\beta ):(G,\beta )\in \tau ,(P,\beta )\in \tilde{I}\}$$

form a base for the cluster soft topology ${\tau }_{\mathfrak{c}}$.

Definition 22 

([38]). Given $\tau \in T\left(\widehat{X}\right)$ and $\tilde{I}\in \mathcal{I}\left(\widehat{X}\right)$. Then, $\tilde{I}$ is called a soft adherent ideal if $(R,\beta )-\mathfrak{c}(R,\beta )\in \tilde{I}$ for each $(R,\beta )\in SS\left(\widehat{X}\right)$.

Lemma 7 

([38]). If $\tau \in T\left(\widehat{X}\right)$ has a countable soft base, then each soft σ-ideal on X is soft adherent.

Lemma 8 

([38]). Let $\tau \in T\left(\widehat{X}\right)$ and $\tilde{I}\in \mathcal{I}\left(\widehat{X}\right)$. If τ has a countable soft base $\mathcal{B}$ and $\tilde{I}$ is a soft σ-ideal, then ${\tau }_{\mathfrak{c}}=\{(G,\beta )-(P,\beta ):(G,\beta )\in \tau ,(P,\beta )\in \tilde{I}\}$.

Lemma 9 

([38]). Let $\tau \in T\left(\widehat{X}\right)$, $\tilde{I}\in \mathcal{I}\left(\widehat{X}\right)$, and ${\tau }_{\mathfrak{c}}$ be the cluster soft topology generated by τ. Then, each element of $\tilde{I}$ is soft ${\tau }_{\mathfrak{c}}$-closed.

Definition 23 

([37]). Let $(E,\beta )\in SS\left(\widehat{X}\right)$ and $\tau \in T\left(\widehat{X}\right)$. It is said that $(E,\beta )$ is of the second category at a soft point $x_{\mu }\in SP\left(\widehat{X}\right)$ if $(E,\beta )\tilde{\cap }(U,\beta )\notin \mathcal{M}\left(\tau \right)$ for each $(U,\beta )\in \tau \left(x_{\mu }\right)$. Otherwise, $(E,\beta )$ is of the first category at $x_{\mu }$. The set of all soft points at which $(E,\beta )$ is of the first (resp. second) category is denoted by $C_1(E,\beta )$ (resp. $C_2(E,\beta )$).

Remark 2. 

Given $\tau \in T\left(\widehat{X}\right)$, evidently, $(E,\beta )\in SS\left(\widehat{X}\right)$ is of the first category at soft point $x_{\mu }\in SP\left(\widehat{X}\right)$ if there exists $(U,\beta )\in \tau \left(x_{\mu }\right)$ such that $(E,\beta )\tilde{\cap }(U,\beta )\in \mathcal{M}\left(\tau \right)$.

Lemma 10 

([37]). Let $\tau \in T\left(\widehat{X}\right)$ and $(E,\beta )\in SS\left(\widehat{X}\right)$. Then, $(E,\beta )\in \mathcal{M}\left(\tau \right)$ if $C_2(E,\beta )\tilde{\cap }(E,\beta )$$=\Phi$ if $C_2(E,\beta )=\Phi$.

Theorem 1 

([37]). Let $\tau \in T\left(\widehat{X}\right)$ and $(E,\beta )\in SS\left(\widehat{X}\right)$. If $(E,\beta )\in \mathcal{S}\left(\tau \right)$, then $(E,\beta )$ is of the second category at each soft point in some $\Phi \ne (G,\beta )\in \tau$. Equivalently, if $\{(E_i,\beta ):i\in I\}\tilde{\subseteq }SS\left(\widehat{X}\right)$ in which $(E_i,\beta )\in \mathcal{M}\left(\tau \right)$ and $(E_i,\beta )\in \tau$, then ${\tilde{\cup }}_{i\in I}(E_i,\beta )\in \mathcal{M}\left(\tau \right)$.

Lemma 11 

([37]). Let $(E,\beta ),(G,\beta )\in SS\left(\widehat{X}\right)$ and $\tau \in T\left(\widehat{X}\right)$. The following properties hold:

1.

If $(E,\beta )\tilde{\subseteq }(G,\beta )$, then $C_2(E,\beta )\tilde{\subseteq }{C}_2(G,\beta )$.

2.

$C_2\left((E,\beta )\tilde{\cap }(G,\beta )\right)\tilde{\subseteq }{C}_2(E,\beta )\tilde{\cap }{C}_2(G,\beta )$.

3.

$C_2\left((E,\beta )\tilde{\cup }(G,\beta )\right)=C_2(E,\beta )\tilde{\cup }{C}_2(G,\beta )$.

4.

$C_2(E,\beta )-C_2(G,\beta )\tilde{\subseteq }{C}_2\left((E,\beta )-(G,\beta )\right)$.

5.

$C_2(E,\beta )\tilde{\subseteq }cl(E,\beta )$.

6.

$C_2(E,\beta )\in {\tau }^c$.

7.

$C_2\left[C_2(E,\beta )\right]=C_2(E,\beta )$.

Lemma 12 

([37]). Let $\tau \in T\left(\widehat{X}\right)$ and $(E,\beta ),(G,\beta )\in SS\left(\widehat{X}\right)$. If $(G,\beta )\in \mathcal{M}\left(\tau \right)$, then $C_2[(E,\beta )\tilde{\cup }$$(G,\beta )]=C_2(E,\beta )=C_2[(E,\beta )-(G,\beta )]$.

Lemma 13 

([37]). Let $\tau \in T\left(\widehat{X}\right)$ and $(E,\beta )\in SS\left(\widehat{X}\right)$. Then,

1.

$C_2\left(C_1(E,\beta )\right)=\Phi$, i.e., $C_2((E,\beta )-C_2(E,\beta ))=\Phi$

2.

$C_2(E,\beta )=cl\left(int\left(C_2(E,\beta )\right)\right)$.

3. Congruence Modulo a Soft Ideal

Definition 24. 

Let $(E,\beta ),(G,\beta )\in SS\left(\widehat{X}\right)$ and let $\tilde{I}\in \mathcal{I}\left(\widehat{X}\right)$. It said that $(E,\beta )$ is congruent to $(G,\beta )$ modulo $\tilde{I}$, written as $(E,\beta )\approx (G,\beta ) \mathrm{mod} \tilde{I}$, if $(E,\beta )\tilde{\Delta }(G,\beta )\in \tilde{I}$.

If there is no confusion, we may simply write $(E,\beta )\approx (G,\beta )$ instead of $(E,\beta )\approx (G,\beta ) \mathrm{mod} \tilde{I}$.

Lemma 14. 

Let $(E,\beta ),(G,\beta ),(H,\beta )\in SS\left(\widehat{X}\right)$ and let $\tilde{I}\in \mathcal{I}\left(\widehat{X}\right)$. The relation “$\approx$” is equivalence.

Proof. 

Since $(G,\beta )\tilde{\Delta }(G,\beta )=\Phi \in \tilde{I}$, then $(G,\beta )\approx (G,\beta )$ and so “$\approx$” is reflexive. The symmetry follows easily since $(G,\beta )\tilde{\Delta }(E,\beta )=(E,\beta )\tilde{\Delta }(G,\beta )$. Suppose $(E,\beta )\approx (G,\beta )$ and $(G,\beta )\approx (H,\beta )$. Then, $(E,\beta )\tilde{\Delta }(G,\beta )=(P,\beta )$ and $(G,\beta )\tilde{\Delta }(H,\beta )=(Q,\beta )$ for some $(P,\beta ),(Q,\beta )\in \tilde{I}$. Now,

$$\begin{array}{cc}\hfill (E,\beta )\tilde{\Delta }(H,\beta )& =\left((E,\beta )\tilde{\Delta }(G,\beta )\tilde{\Delta }(G,\beta )\right)\tilde{\Delta }(H,\beta )\hfill \\ \hfill & =\left((E,\beta )\tilde{\Delta }(G,\beta )\right)\tilde{\Delta }\left((G,\beta )\tilde{\Delta }(H,\beta )\right)\hfill \\ \hfill & =(P,\beta )\tilde{\Delta }(Q,\beta )\hfill \\ \hfill & \tilde{\subseteq }(P,\beta )\tilde{\cup }(Q,\beta )\in \tilde{I}.\hfill \end{array}$$

Therefore, $(E,\beta )\approx (H,\beta )$. Hence, “$\approx$” is an equivalence relation. □

Lemma 15. 

Let $(D,\beta ),(E,\beta ),(G,\beta ),(H,\beta )\in SS\left(\widehat{X}\right)$ and let $\tilde{I}\in \mathcal{I}\left(\widehat{X}\right)$. If $(D,\beta )\approx (E,\beta )$ and $(G,\beta )\approx (H,\beta )$, then

1.

$(D,\beta )\tilde{\cup }(G,\beta )\approx (E,\beta )\tilde{\cup }(H,\beta )$.

2.

$(D,\beta )\tilde{\cap }(G,\beta )\approx (E,\beta )\tilde{\cap }(H,\beta )$.

3.

$(D,\beta )-(G,\beta )\approx (E,\beta )-(H,\beta )$.

Proof. 

Suppose $(D,\beta )\approx (E,\beta )$ and $(G,\beta )\approx (H,\beta )$. Then, $(D,\beta )\tilde{\Delta }(E,\beta )=(P,\beta )$ and $(G,\beta )\tilde{\Delta }(H,\beta )=(Q,\beta )$, where $(P,\beta ),(Q,\beta )\in \tilde{I}$. Therefore,

$$\begin{array}{cc}\hfill (D,\beta )\tilde{\cup }(G,\beta )\tilde{\Delta }(E,\beta )\tilde{\cup }(H,\beta )& =\left(\left[(D,\beta )\tilde{\cup }(G,\beta )\right]-\left[(E,\beta )\tilde{\cup }(H,\beta )\right]\right)\hfill \\ \hfill & \tilde{\cup }\left(\left[(E,\beta )\tilde{\cup }(H,\beta )\right]-\left[(D,\beta )\tilde{\cup }(G,\beta )\right]\right)\hfill \end{array}$$

After a long computation, we obtain

$$\begin{array}{cc}\hfill (D,\beta )\tilde{\cup }(G,\beta )\tilde{\Delta }(E,\beta )\tilde{\cup }(H,\beta )& \tilde{\subseteq }\left((D,\beta )\tilde{\Delta }(G,\beta )\right)\tilde{\cup }\left((E,\beta )\tilde{\Delta }(H,\beta )\right)\hfill \\ \hfill & =(P,\beta )\tilde{\cup }(Q,\beta )\in \tilde{I}.\hfill \end{array}$$

Thus, $(D,\beta )\tilde{\cup }(G,\beta )\approx (E,\beta )\tilde{\cup }(H,\beta )$.

The other cases can be proved similarly. □

Lemma 16. 

Let $(E_n,\beta ),(G_n,\beta )\in SS\left(\widehat{X}\right)$, for $n=1,2,3,\cdots$, and let $\tilde{I}\in \mathcal{I}\left(\widehat{X}\right)$ be a soft σ-ideal. If $(E_n,\beta )\approx (G_n,\beta )$ for each n, then ${\tilde{\cup }}_{n=1}^{\infty }(E_n,\beta )\approx {\tilde{\cup }}_{n=1}^{\infty }(G_n,\beta )$.

Proof. 

It follows from Lemma 15 (1). □

4. Soft Open Sets Modulo a Soft Ideal

Definition 25. 

Let $\tau \in T\left(\widehat{X}\right)$, $(E,\beta )\in SS\left(\widehat{X}\right)$, and $\tilde{I}\in \mathcal{I}\left(\widehat{X}\right)$. Then, $(E,\beta )$ is called soft open modulo $\tilde{I}$ if there exists $(G,\beta )\in \tau$ such that $(E,\beta )$ is congruent to $(G,\beta ) \mathrm{mod} \tilde{I}$, i.e., $(E,\beta )\approx (G,\beta )$. Clearly $(E,\beta )\approx (G,\beta )$ implies $(E,\beta )-(G,\beta )$ and $(G,\beta )-(E,\beta )$ belong to $\tilde{I}$. The set of all soft open sets modulo $\tilde{I}$ is denoted by ${\mathfrak{B}}_r(X,\tau ,\tilde{I},\beta )$ or simply ${\mathfrak{B}}_r(\tau ,\tilde{I})$.

Proposition 2. 

For any $\tau \in T\left(\widehat{X}\right)$ and $\tilde{I}\in \mathcal{I}\left(\widehat{X}\right)$, ${\mathfrak{B}}_r(\tau ,\tilde{I})$ is closed under finite soft intersections and finite soft unions. Furthermore, ${\mathfrak{B}}_r(\tau ,\tilde{I})$ is a soft algebra if ${\tau }^c\tilde{\subseteq }{\mathfrak{B}}_r(\tau ,\tilde{I})$.

Proof. 

Let $(D,\beta ),(E,\beta )\in {\mathfrak{B}}_r(\tau ,\tilde{I})$. Therefore, there exists $(G,\beta ),(H,\beta )\in \tau$ such that $(D,\beta )\approx (G,\beta )$ and $(E,\beta )\approx (H,\beta )$. By Lemma 15 (2), $(D,\beta )\tilde{\cap }(E,\beta )\approx (G,\beta )\tilde{\cap }(H,\beta )$. Since $(G,\beta )\tilde{\cap }(H,\beta )\in \tau$, so $(D,\beta )\tilde{\cap }(E,\beta )\in {\mathfrak{B}}_r(\tau ,\tilde{I})$. The case for finite soft unions is similar.

We now prove that ${\mathfrak{B}}_r(\tau ,\tilde{I})$ is closed under soft complements. Suppose $(E,\beta )\in {\mathfrak{B}}_r(\tau ,\tilde{I})$. Then, one can find $(G,\beta )\in \tau$ such that $(E,\beta )\approx (G,\beta )$. We need find $(H,\beta )\in \tau$ such that ${(E,\beta )}^c\approx (H,\beta )$. From $(E,\beta )\approx (G,\beta )$, we have ${(E,\beta )}^c\approx {(G,\beta )}^c$ and since ${(G,\beta )}^c\in {\tau }^c\tilde{\subseteq }{\mathfrak{B}}_r(\tau ,\tilde{I})$, then there exists $(H,\beta )\in \tau$ such that ${(G,\beta )}^c\approx (H,\beta )$. By transitivity, we obtain that ${(E,\beta )}^c\approx (H,\beta )$ and hence, ${(E,\beta )}^c\in {\mathfrak{B}}_r(\tau ,\tilde{I})$. And the other case is clear. □

Theorem 2. 

Let $\tau \in T\left(\widehat{X}\right)$ and $\tilde{I}\in \mathcal{I}\left(\widehat{X}\right)$.

1.

If $\mathcal{N}\left(\tau \right)\tilde{\subseteq }\tilde{I}$, then ${\mathfrak{B}}_r(\tau ,\tilde{I})$ is a soft algebra.

2.

If ${\mathfrak{B}}_r(\tau ,\mathcal{C}\left(\tau \right))$ is a soft algebra, then $\mathcal{N}\left(\tau \right)\tilde{\subseteq }\mathcal{C}\left(\tau \right)$.

Proof. 

(1) Suppose $\mathcal{N}\left(\tau \right)\tilde{\subseteq }\tilde{I}$. Let $(E,\beta )\in {\tau }^c$. Since $(E,\beta )-int(E,\beta )\in \mathcal{N}\left(\tau \right)$, so $(E,\beta )-int(E,\beta )\in \tilde{I}$ and therefore, $(E,\beta )\approx int(E,\beta )$. Since $int(E,\beta )\in \tau$, then $(E,\beta )\in {\mathfrak{B}}_r(\tau ,\tilde{I})$, by Proposition 2, ${\mathfrak{B}}_r(\tau ,\tilde{I})$ is a soft algebra.

(2) Suppose ${\mathfrak{B}}_r(\tau ,\mathcal{C}\left(\tau \right))$ is a soft algebra. Let $(E,\beta )\in \mathcal{N}\left(\tau \right)\tilde{\cap }{\tau }^c$. Since $(E,\beta )\in {\mathfrak{B}}_r(\tau ,\mathcal{C}\left(\tau \right))$, then $(E,\beta )\approx (G,\beta )$ for some $(G,\beta )\in \tau$ and therefore, $(E,\beta )\tilde{\Delta }(G,\beta )\in \mathcal{C}\left(\tau \right)$. This implies that $(G,\beta )-(E,\beta )\in \mathcal{C}\left(\tau \right)\tilde{\cap }\tau =\{\Phi \}$, which means that $(G,\beta )\tilde{\subseteq }int(E,\beta )=\Phi$. Thus, $(E,\beta )=(E,\beta )\tilde{\Delta }(G,\beta )\in \mathcal{C}\left(\tau \right)$. Hence, $\mathcal{N}\left(\tau \right)\tilde{\subseteq }\mathcal{C}\left(\tau \right)$. □

5. Soft Open Sets Modulo Soft Nowhere Dense Sets

Definition 26. 

Let $\tau \in T\left(\widehat{X}\right)$ and $(E,\beta )\in SS\left(\widehat{X}\right)$. Then, $(E,\beta )$ is called soft open modulo $\mathcal{N}\left(\tau \right)$ if there exists $(G,\beta )\in \tau$ such that $(E,\beta )$ is congruent to $(G,\beta )mod\mathcal{N}\left(\tau \right)$, i.e., $(E,\beta )\approx (G,\beta )$. Clearly $(E,\beta )\approx (G,\beta )$ implies $(E,\beta )-(G,\beta )$ and $(G,\beta )-(E,\beta )$ belong to $\mathcal{N}\left(\tau \right)$. The set of all soft open sets modulo $\mathcal{N}\left(\tau \right)$ shall be ${\mathfrak{B}}_r(\tau ,\mathcal{N}\left(\tau \right))$.

Lemma 17. 

Let $\tau \in T\left(\widehat{X}\right)$ and $(E,\beta )\in SS\left(\widehat{X}\right)$. If $(E,\beta )\in {\tau }^c\tilde{\cup }\tau$, then $(E,\beta )\in {\mathfrak{B}}_r(\tau ,\mathcal{N}\left(\tau \right))$.

Proof. 

If $(E,\beta )\in {\tau }^c$, then $(E,\beta )=cl(E,\beta )=int(E,\beta )\tilde{\cup }b(E,\beta )$. Clearly $b(E,\beta )=(E,\beta )-int(E,\beta )\in \mathcal{N}\left(\tau \right)$. Thus, $(E,\beta )\in {\mathfrak{B}}_r(\tau ,\mathcal{N}\left(\tau \right))$.

If $(E,\beta )\in \tau$, then, since $(E,\beta )=(E,\beta )\approx \Phi$, $(E,\beta )\in {\mathfrak{B}}_r(\tau ,\mathcal{N}\left(\tau \right))$. □

Proposition 3. 

Let $\tau \in T\left(\widehat{X}\right)$ and $(E,\beta )\in SS\left(\widehat{X}\right)$. Then, $(E,\beta )\in {\mathfrak{B}}_r(\tau ,\mathcal{N}\left(\tau \right))$ if there exists $(G,\beta )\in \tau$ such that $(G,\beta )\tilde{\subseteq }(E,\beta )$ and $(E,\beta )-(G,\beta )\in \mathcal{N}\left(\tau \right)$.

Proof. 

Suppose $(E,\beta )\in {\mathfrak{B}}_r(\tau ,\mathcal{N}\left(\tau \right))$. Then, there exists $(H,\beta )\in \tau$ such that $(E,\beta )\tilde{\Delta }(H,\beta )$$\in \mathcal{N}\left(\tau \right)$. That is, both $(E,\beta )-(H,\beta )$ and $(H,\beta )-(E,\beta )$ belong to $\mathcal{N}\left(\tau \right)$. Set $(G,\beta )=(H,\beta )\tilde{\cap }int(E,\beta )$. Therefore,

$$\begin{array}{cc}\hfill (E,\beta )-(G,\beta )& =((E,\beta )-(H,\beta ))\tilde{\cup }\left((E,\beta )\tilde{\cap }cl\left({(E,\beta )}^c\right)\right)\hfill \\ \hfill & =((E,\beta )-(H,\beta ))\tilde{\cup }\left((H,\beta )\tilde{\cap }(E,\beta )\tilde{\cap }cl\left({(E,\beta )}^c\right)\right)\hfill \\ \hfill & \tilde{\subseteq }((E,\beta )-(H,\beta ))\tilde{\cup }cl((H,\beta )-(E,\beta ))\mathrm{as}(H,\beta )\in \tau .\hfill \end{array}$$

By Lemma 5, $(E,\beta )-(G,\beta )\in \mathcal{N}\left(\tau \right)$ and obviously $(G,\beta )\tilde{\subseteq }(E,\beta )$.

Conversely, suppose there exists $(G,\beta )\in \tau$ such that $(G,\beta )\tilde{\subseteq }(E,\beta )$ and $(E,\beta )-(G,\beta )\in \mathcal{N}\left(\tau \right)$. Then, $(E,\beta )=(G,\beta )\tilde{\cup }[(E,\beta )-(G,\beta )]=(G,\beta )\tilde{\Delta }[(E,\beta )-(G,\beta )]$. Thus, $(E,\beta )\in {\mathfrak{B}}_r(\tau ,\mathcal{N}\left(\tau \right))$. □

Theorem 3. 

Let $\tau \in T\left(\widehat{X}\right)$ and $(E,\beta )\in SS\left(\widehat{X}\right)$. Then, $(E,\beta )\in {\mathfrak{B}}_r(\tau ,\mathcal{N}\left(\tau \right))$ if $b(E,\beta )\in \mathcal{N}\left(\tau \right)$.

Proof. 

Suppose $(E,\beta )\in {\mathfrak{B}}_r(\tau ,\mathcal{N}\left(\tau \right))$. Then, $(E,\beta )=(G,\beta )\tilde{\cup }(N,\beta )$ for some $(G,\beta )\in \tau$ and $(N,\beta )\in \mathcal{N}\left(\tau \right)$. From Lemma 4 (7) [33], we have $b(E,\beta )\tilde{\subseteq }b(G,\beta )\tilde{\cup }b(N,\beta )$. Since $b(G,\beta )\tilde{\cup }b(N,\beta )\in \mathcal{N}\left(\tau \right)$, then $b(E,\beta )\in \mathcal{N}\left(\tau \right)$.

Conversely, let $b(E,\beta )\in \mathcal{N}\left(\tau \right)$. Set $(G,\beta )=int(E,\beta )$ and $(N,\beta )=(E,\beta )-int(E,\beta )$. Therefore, $(N,\beta )\tilde{\subseteq }b(E,\beta )$. Thus, by assumption, $int\left(cl(N,\beta )\right)\tilde{\subseteq }int\left(b(E,\beta )\right)=\Phi$. Hence, $(N,\beta )\in \mathcal{N}\left(\tau \right)$. This implies that $(E,\beta )=(G,\beta )\tilde{\Delta }(N,\beta )\in {\mathfrak{B}}_r(\tau ,\mathcal{N}\left(\tau \right))$. □

6. Soft Sets with the Baire Property

Definition 27. 

Let $\tau \in T\left(\widehat{X}\right)$ and $(E,\beta )\in SS\left(\widehat{X}\right)$. Then, $(E,\beta )$ is called soft open modulo $\mathcal{M}\left(\tau \right)$ if there exists $(G,\beta )\in \tau$ such that $(E,\beta )$ is congruent to $(G,\beta )mod\mathcal{N}\left(\tau \right)$. That is, $(E,\beta )\approx (G,\beta )mod\mathcal{M}\left(\tau \right)$, which implies $(E,\beta )-(G,\beta )$ and $(G,\beta )-(E,\beta )$ belong to $\mathcal{M}\left(\tau \right)$. The set of all soft open sets modulo $\mathcal{M}\left(\tau \right)$ shall be ${\mathfrak{B}}_r(\tau ,\mathcal{M}\left(\tau \right))$. We call a soft open set modulo $\mathcal{M}\left(\tau \right)$ a soft set with the Baire property.

Remark 3. 

[30] Let $(E,\beta )\in SS\left(\widehat{X}\right)$ and let $\tau \in T\left(\widehat{X}\right)$. Then, $(E,\beta )$ has the Baire property if there exists $(G,\beta )\in \tau$ such that $(E,\beta )\tilde{\Delta }(G,\beta )\in \mathcal{M}\left(\tau \right)$, equivalently, if it is of the form $(E,\beta )=(G,\beta )\tilde{\Delta }(P,\beta )$, where $(G,\beta )\in \tau$ and $(P,\beta )\in \mathcal{M}\left(\tau \right)$. This follows from the fact that $(E,\beta )=(G,\beta )\tilde{\Delta }(P,\beta )$ if $(E,\beta )\tilde{\Delta }(G,\beta )=(P,\beta )$.

Proposition 4. 

Let $(E,\beta )\in SS\left(\widehat{X}\right)$ and let $\tau \in T\left(\widehat{X}\right)$. Then, $(E,\beta )\in {\mathfrak{B}}_r(\tau ,\mathcal{M}\left(\tau \right))$ if $(E,\beta )=(C,\beta )\tilde{\Delta }(Q,\beta )$, where $(C,\beta )\in {\tau }^c$ and $(Q,\beta )\in \mathcal{M}\left(\tau \right)$.

Proof. 

Let $(E,\beta )\in {\mathfrak{B}}_r(\tau ,\mathcal{M}\left(\tau \right))$. Then, $(E,\beta )=(G,\beta )\tilde{\Delta }(P,\beta )$ for some $(G,\beta )\in \tau$ and $(P,\beta )\in \mathcal{M}\left(\tau \right)$. If $(R,\beta )=cl(G,\beta )-(G,\beta )$, then $(R,\beta )\in \mathcal{N}\left(\tau \right)$. Therefore, $(Q,\beta )=(R,\beta )\tilde{\Delta }(P,\beta )\in \mathcal{M}\left(\tau \right)$. Set $(C,\beta )=cl(G,\beta )$. Then,

$$\begin{array}{cc}\hfill (E,\beta )& =(G,\beta )\tilde{\Delta }(P,\beta )\hfill \\ \hfill & =\left(cl(G,\beta )\tilde{\Delta }(R,\beta )\right)\tilde{\Delta }(P,\beta )\hfill \\ \hfill & =cl(G,\beta )\tilde{\Delta }\left((R,\beta )\tilde{\Delta }(P,\beta )\right)\hfill \\ \hfill & =(C,\beta )\tilde{\Delta }(Q,\beta ).\hfill \end{array}$$

Conversely, suppose $(E,\beta )=(C,\beta )\tilde{\Delta }(Q,\beta )$, where $(C,\beta )\in {\tau }^c$ and $(Q,\beta )\in \mathcal{M}\left(\tau \right)$. Set $(G,\beta )=int(C,\beta )$. Then, $(R,\beta )=(C,\beta )-(G,\beta )\in \mathcal{N}\left(\tau \right)$ and so $(P,\beta )=(Q,\beta )\tilde{\Delta }(R,\beta )$.

Therefore,

$$\begin{array}{cc}\hfill (E,\beta )& =(C,\beta )\tilde{\Delta }(Q,\beta )\hfill \\ \hfill & =\left((G,\beta )\tilde{\Delta }(R,\beta )\right)\tilde{\Delta }(Q,\beta )\hfill \\ \hfill & =(G,\beta )\tilde{\Delta }\left((R,\beta )\tilde{\Delta }(Q,\beta )\right)\hfill \\ \hfill & =(G,\beta )\tilde{\Delta }(P,\beta ).\hfill \end{array}$$

The proof is finished. □

Proposition 5. 

Let $(E,\beta )\in SS\left(\widehat{X}\right)$ and let $\tau \in T\left(\widehat{X}\right)$. If $(E,\beta )\in {\mathfrak{B}}_r(\tau ,\mathcal{M}\left(\tau \right))$, then ${(E,\beta )}^c\in {\mathfrak{B}}_r(\tau ,\mathcal{M}\left(\tau \right))$.

Proof. 

Suppose $(E,\beta )\in {\mathfrak{B}}_r(\tau ,\mathcal{M}\left(\tau \right))$. Then, $(E,\beta )=(G,\beta )\tilde{\Delta }(P,\beta )$ for some $(G,\beta )\in \tau$ and $(P,\beta )\in \mathcal{M}\left(\tau \right)$. Now,

$$\begin{array}{ccc}\hfill {(E,\beta )}^c={\left((G,\beta )\tilde{\Delta }(P,\beta )\right)}^c& =& {\left[((G,\beta )-(P,\beta ))\tilde{\cup }((P,\beta )-(G,\beta ))\right]}^c\hfill \\ & =& {[\left((G,\beta )\tilde{\cup }(P,\beta )\right)-\left((G,\beta )\tilde{\cap }(P,\beta )\right)]}^c\hfill \\ & =& {\left[\left((G,\beta )\tilde{\cup }(P,\beta )\right)\tilde{\cap }{\left((G,\beta )\tilde{\cap }(P,\beta )\right)}^c\right]}^c\hfill \\ & =& {\left((G,\beta )\tilde{\cup }(P,\beta )\right)}^c\tilde{\cup }\left((G,\beta )\tilde{\cap }(P,\beta )\right)\hfill \\ & =& \left({(G,\beta )}^c\tilde{\cap }{(P,\beta )}^c\right)\tilde{\cup }\left((G,\beta )\tilde{\cap }(P,\beta )\right)\hfill \\ & =& \left({(G,\beta )}^c\tilde{\cup }(P,\beta )\right)\tilde{\cap }\left((G,\beta )\tilde{\cup }{(P,\beta )}^c\right)\hfill \\ & =& \left({(G,\beta )}^c\tilde{\cup }(P,\beta )\right)\tilde{\cap }{\left({(G,\beta )}^c\tilde{\cap }(P,\beta )\right)}^c\hfill \\ & =& \left({(G,\beta )}^c\tilde{\cup }(P,\beta )\right)-\left({(G,\beta )}^c\tilde{\cap }(P,\beta )\right)\hfill \\ & =& {(G,\beta )}^c\tilde{\Delta }(P,\beta ).\hfill \end{array}$$

By Proposition 4, ${(E,\beta )}^c\in {\mathfrak{B}}_r(\tau ,\mathcal{M}\left(\tau \right))$. □

Proposition 6. 

Let $(E_n,\beta )\in SS\left(\widehat{X}\right)$, for $n=1,2,\cdots$, and let $\tau \in T\left(\widehat{X}\right)$. If $(E_n,\beta )\in {\mathfrak{B}}_r(\tau ,\mathcal{M}\left(\tau \right))$, then ${\tilde{\cup }}_{n=1}^{\infty }(E_n,\beta )\in {\mathfrak{B}}_r(\tau ,\mathcal{M}\left(\tau \right))$.

Proof. 

It follows from Lemmas 15 and 16. □

Theorem 4. 

For any $\tau \in T\left(\widehat{X}\right)$, ${\mathfrak{B}}_r(\tau ,\mathcal{M}\left(\tau \right))$ constitutes a soft σ-algebra over X. Furthermore, ${\mathfrak{B}}_r(\tau ,\mathcal{M}\left(\tau \right))$ is the soft σ-algebra generated by τ together with $\mathcal{M}\left(\tau \right)$.

Proof. 

Obviously, $\Phi \in {\mathfrak{B}}_r(\tau ,\mathcal{M}\left(\tau \right))$. Propositions 5 and 6 prove that ${\mathfrak{B}}_r(\tau ,\mathcal{M}\left(\tau \right))$ is a soft $\sigma$-algebra. On the other hand, suppose ${\mathfrak{B}}_r^{*}(X,\tau ,\tilde{I},\beta )$ is the soft $\sigma$-algebra generated by $\tau$ and $\tilde{I}=\mathcal{M}\left(\tau \right)$. Let $(E,\beta )\in {\mathfrak{B}}_r(\tau ,\mathcal{M}\left(\tau \right))$. Then, $(E,\beta )=(G,\beta )\tilde{\Delta }(P,\beta )$ for some $(G,\beta )\in \tau$ and $(P,\beta )\in \mathcal{M}\left(\tau \right)$. Hence, ${\mathfrak{B}}_r(\tau ,\mathcal{M}\left(\tau \right))\tilde{\subseteq }{\mathfrak{B}}_r^{*}(X,\tau ,\tilde{I},\beta )$. For the reverse of the inclusion, since $\Phi$ is both in $\tau$ and $\mathcal{M}\left(\tau \right)$, so each soft open or soft set of the first category $(E,\beta )$ can be written as $(E,\beta )=(E,\beta )\tilde{\Delta }\Phi$. Therefore, $(E,\beta )\in {\mathfrak{B}}_r(\tau ,\mathcal{M}\left(\tau \right))$ and thus ${\mathfrak{B}}_r^{*}(X,\tau ,\tilde{I},\beta )\tilde{\subseteq }{\mathfrak{B}}_r(\tau ,\mathcal{M}\left(\tau \right))$. Hence, ${\mathfrak{B}}_r^{*}(X,\tau ,\tilde{I},\beta )={\mathfrak{B}}_r(\tau ,\mathcal{M}\left(\tau \right))$. □

Proposition 7. 

Let $(E,\beta ),(Y,\beta )\in SS\left(\widehat{X}\right)$ and let $\tau \in T\left(\widehat{X}\right)$. If $(E,\beta )\in {\mathfrak{B}}_r(\tau ,\mathcal{M}\left(\tau \right))$, then $(E,\beta )\tilde{\cap }(Y,\beta )\in {\mathfrak{B}}_r({\tau }_{(Y,\beta )},{\mathcal{N}}_{(Y,\beta )})$.

Proof. 

Let $(E,\beta )\in {\mathfrak{B}}_r(\tau ,\mathcal{M}\left(\tau \right))$. Then, $(E,\beta )=[(G,\beta )-(P,\beta )]\tilde{\cup }(Q,\beta )$, where $(G,\beta )\in \tau$ and $(P,\beta ),(Q,\beta )\in \mathcal{M}\left(\tau \right)$. Therefore, $(E,\beta )\tilde{\cap }(Y,\beta )=[\left((G,\beta )\tilde{\cap }(Y,\beta )\right)-\left((P,\beta )\tilde{\cap }(Y,\beta )\right)]\tilde{\cup }$$\left((Q,\beta )\tilde{\cap }(Y,\beta )\right)$. Evidently, $(G,\beta )\tilde{\cap }(Y,\beta )\in {\tau }_{(Y,\beta )}$ and $(P,\beta )\tilde{\cap }(Y,\beta ),(P,\beta )\tilde{\cap }(Y,\beta )\in$$\mathcal{M}\left({\tau }_{(Y,\beta )}\right)$. Thus, $(E,\beta )\tilde{\cap }(Y,\beta )\in {\mathfrak{B}}_r({\tau }_{(Y,\beta )},{\mathcal{N}}_{(Y,\beta )})$. □

Proposition 8. 

Let $(E,\beta ),(Y,\beta )\in SS\left(\widehat{X}\right)$ and let $\tau \in T\left(\widehat{X}\right)$. If $(E,\beta )\in {\mathfrak{B}}_r({\tau }_{(Y,\beta )},$${\mathcal{N}}_{(Y,\beta )})$ and $(Y,\beta )\in {\mathfrak{B}}_r(\tau ,\mathcal{M}\left(\tau \right))$, then $(E,\beta )\in {\mathfrak{B}}_r(\tau ,\mathcal{M}\left(\tau \right))$.

Proof. 

Let $(E,\beta )\in {\mathfrak{B}}_r({\tau }_{(Y,\beta )},{\mathcal{N}}_{(Y,\beta )})$. Then, $(E,\beta )=(G,\beta )\tilde{\cup }(P,\beta )$, where $(G,\beta )$ is a soft $G_{\delta }$ set in $(Y,\beta )$ and $(P,\beta )\in \mathcal{M}\left({\tau }_{(Y,\beta )}\right)$. By definition, $(G,\beta )=(H,\beta )\tilde{\cap }(Y,\beta )$ for some soft $G_{\delta }$ set $(H,\beta )$ over X. By Theorem 4, $(E,\beta )\in {\mathfrak{B}}_r(\tau ,\mathcal{M}\left(\tau \right))$. Also, one can see that $(P,\beta )\in \mathcal{M}\left(\tau \right)$. Consequently, $(E,\beta )=(G,\beta )\tilde{\cup }(P,\beta )\in {\mathfrak{B}}_r(\tau ,\mathcal{M}\left(\tau \right))$. □

Proposition 9. 

Let $(E,\beta )\in SS\left(\widehat{X}\right)$ and let $\tau \in T\left(\widehat{X}\right)$. Then, $(E,\beta )\in {\mathfrak{B}}_r(\tau ,\mathcal{M}\left(\tau \right))$ if $(E,\beta )=[(G,\beta )-(P,\beta )]\tilde{\cup }(Q,\beta )$, where $(G,\beta )\in \tau$ and $(P,\beta ),(Q,\beta )\in \mathcal{M}\left(\tau \right)$.

Proof. 

Suppose $(E,\beta )\in {\mathfrak{B}}_r(\tau ,\mathcal{M}\left(\tau \right))$. Then, by Remark 3, there exists $(G,\beta )\in \tau$ such that $(E,\beta )-(G,\beta )$ and $(G,\beta )-(E,\beta )$ are in $\mathcal{M}\left(\tau \right)$. Set $(P,\beta )=(G,\beta )-(E,\beta )$ and $(Q,\beta )=(E,\beta )-(G,\beta )$, we have that $(E,\beta )=[(G,\beta )-(P,\beta )]\tilde{\cup }(Q,\beta )$.

Conversely, suppose $(E,\beta )=[(G,\beta )-(P,\beta )]\tilde{\cup }(Q,\beta )$ for some $(G,\beta )\in \tau$ and $(P,\beta ),(Q,\beta )$$\in \mathcal{M}\left(\tau \right)$. Therefore, $(E,\beta )-(G,\beta )\tilde{\subseteq }(Q,\beta )$ and $(G,\beta )-(E,\beta )\tilde{\subseteq }(P,\beta )$. By Remark 3, it follows that $(E,\beta )\in {\mathfrak{B}}_r(\tau ,\mathcal{M}\left(\tau \right))$. □

Proposition 10. 

Let $(E,\beta )\in SS\left(\widehat{X}\right)$ and let $\tau \in T\left(\widehat{X}\right)$. Then, $(E,\beta )\in {\mathfrak{B}}_r(\tau ,\mathcal{M}\left(\tau \right))$ if $(E,\beta )=[(D,\beta )-(R,\beta )]\tilde{\cup }(S,\beta )$, where $(D,\beta )\in {\tau }^c$ and $(R,\beta ),(S,\beta )\in \mathcal{M}\left(\tau \right)$.

Proof. 

It follows from Propositions 4 and 9. □

Proposition 11. 

Let $(E,\beta )\in SS\left(\widehat{X}\right)$ and let $\tau \in T\left(\widehat{X}\right)$. Then, $(E,\beta )\in {\mathfrak{B}}_r(\tau ,\mathcal{M}\left(\tau \right))$ if $(E,\beta )=(H,\beta )\tilde{\cup }(R,\beta )$, where $(H,\beta )$ is a soft $G_{\delta }$ set and $(R,\beta )\in \mathcal{M}\left(\tau \right)$.

Proof. 

Let $(E,\beta )\in {\mathfrak{B}}_r(\tau ,\mathcal{M}\left(\tau \right))$. By the definition, $(E,\beta )=(G,\beta )\tilde{\Delta }(P,\beta )$ for some $(G,\beta )\in \tau$ and $(P,\beta )\in \mathcal{M}\left(\tau \right)$. By Proposition 1, $(P,\beta )$ is a soft subset of some soft $F_{\sigma }$ set of the first category $(Q,\beta )$, say. Put $(H,\beta )=(G,\beta )-(Q,\beta )$. Clearly, $(H,\beta )$ is a soft $G_{\delta }$ set. Now, we have

$$\begin{array}{cc}\hfill (E,\beta )& =(G,\beta )\tilde{\Delta }(P,\beta )\hfill \\ \hfill & =\left([(G,\beta )-(Q,\beta )]\tilde{\Delta }\left[(G,\beta )\tilde{\cap }(Q,\beta )\right]\right)\tilde{\Delta }\left[(P,\beta )\tilde{\Delta }(Q,\beta )\right]\hfill \\ \hfill & =(H,\beta )\tilde{\Delta }\left(\left[(G,\beta )\tilde{\Delta }(P,\beta )\right]\tilde{\cap }(Q,\beta )\right).\hfill \end{array}$$

Set $(R,\beta )=(G,\beta )\tilde{\Delta }(P,\beta )]\tilde{\cap }(Q,\beta )$. Since $(Q,\beta )\in \mathcal{M}\left(\tau \right)$ and $(R,\beta )\tilde{\subseteq }(Q,\beta )$, so $(R,\beta )\in \mathcal{M}\left(\tau \right)$. Additionally, $(H,\beta )$ and $(R,\beta )$ are disjoint. Thus, $(E,\beta )=(H,\beta )\tilde{\cup }(R,\beta )$, where $(H,\beta )$ is a soft $G_{\delta }$ set and $(R,\beta )\in \mathcal{M}\left(\tau \right)$.

Conversely, if $(E,\beta )=(H,\beta )\tilde{\cup }(R,\beta )$, for some soft $G_{\delta }$ set $(H,\beta )$ and $(R,\beta )\in \mathcal{M}\left(\tau \right)$, by Theorem 4, $(E,\beta )\in {\mathfrak{B}}_r(\tau ,\mathcal{M}\left(\tau \right))$. □

Proposition 12. 

Let $(E,\beta )\in SS\left(\widehat{X}\right)$ and let $\tau \in T\left(\widehat{X}\right)$. Then, $(E,\beta )\in {\mathfrak{B}}_r(\tau ,\mathcal{M}\left(\tau \right))$ if $(E,\beta )=(D,\beta )-(Q,\beta )$, where $(D,\beta )$ is a soft $F_{\sigma }$ set and $(Q,\beta )\in \mathcal{M}\left(\tau \right)$.

Proof. 

Let $(E,\beta )\in {\mathfrak{B}}_r(\tau ,\mathcal{M}\left(\tau \right))$. By Proposition 5, ${(E,\beta )}^c\in {\mathfrak{B}}_r(\tau ,\mathcal{M}\left(\tau \right))$. Therefore, by Proposition 11, ${(E,\beta )}^c=(H,\beta )\tilde{\cup }(P,\beta )$, for some soft $G_{\delta }$ set $(H,\beta )$ and $(P,\beta )\in \mathcal{M}\left(\tau \right)$. Thus, $(E,\beta )={(H,\beta )}^c-(P,\beta )$. Set ${(H,\beta )}^c=(D,\beta )$ and $(P,\beta )=(Q,\beta )$.

Conversely, since ${\mathfrak{B}}_r(\tau ,\mathcal{M}\left(\tau \right))$ is a soft $\sigma$-algebra containing all soft $F_{\sigma }$ sets and all $(P,\beta )\in \mathcal{M}\left(\tau \right)$, hence, the conclusion follows. □

Lemma 18. 

Let $(G,\beta )\in SS\left(\widehat{X}\right)$ and let $\tau \in T\left(\widehat{X}\right)$. If $(G,\beta )\in \tau$, then it can be written as $(G,\beta )=(H,\beta )-cl(N,\beta )$, where $(H,\beta )$ is soft regular open and $(N,\beta )\in \mathcal{N}\left(\tau \right)$.

Proof. 

Let $(H,\beta )=int\left(cl\right(G,\beta \left)\right)$ and $(N,\beta )=(H,\beta )-(G,\beta )$. Then, $(H,\beta )$ is soft regular open and $(N,\beta )\in \mathcal{N}\left(\tau \right)$. If $(G,\beta )=(H,\beta )-(N,\beta )$, then $cl(N,\beta )\tilde{\subseteq }cl(H,\beta )-(G,\beta )$. Therefore, $(G,\beta )=(G,\beta )\tilde{\cap }(H,\beta )=(H,\beta )-[cl(H,\beta )-(G,\beta )]\tilde{\subseteq }(H,\beta )-cl(N,\beta )$. On the other hand, we always have $(H,\beta )-cl(N,\beta )\tilde{\subseteq }(H,\beta )-(N,\beta )=(G,\beta )$. Thus, $(G,\beta )=(H,\beta )-cl(N,\beta )$. □

Proposition 13. 

Let $(E,\beta )\in SS\left(\widehat{X}\right)$ and let $\tau \in T\left(\widehat{X}\right)$. If $(E,\beta )\in {\mathfrak{B}}_r(\tau ,\mathcal{M}\left(\tau \right))$, then it can be written as $(E,\beta )=(H,\beta )\tilde{\Delta }(Q,\beta )$, where $(H,\beta )$ is soft regular open and $(Q,\beta )\in \mathcal{M}\left(\tau \right)$. Moreover, if $(X,\tau ,\beta )$ is a soft Baire space, such a representation is unique.

Proof. 

Let $(E,\beta )\in {\mathfrak{B}}_r(\tau ,\mathcal{M}\left(\tau \right))$. Then, $(E,\beta )=(G,\beta )\tilde{\Delta }(P,\beta )$, where $(G,\beta )\in \tau$ and $(Q,\beta )\in \mathcal{M}\left(\tau \right)$. By Lemma 18, $(G,\beta )=(H,\beta )-cl(N,\beta )$, where $(H,\beta )$ is soft regular open and $(N,\beta )\in \mathcal{N}\left(\tau \right)$. Now,

$$\begin{array}{cc}\hfill (E,\beta )& =(G,\beta )\tilde{\Delta }(P,\beta )\hfill \\ \hfill & =[(H,\beta )-cl(N,\beta )]\tilde{\Delta }(P,\beta )\hfill \\ \hfill & =[(H,\beta )-cl(N,\beta )-(P,\beta )]\tilde{\cup }(P,\beta )-[(H,\beta )-cl(N,\beta )]\hfill \\ \hfill & =\left((H,\beta )-\left[(P,\beta )\tilde{\cup }cl(N,\beta )\right]\right)\tilde{\cup }\left(\left[\right(P,\beta )-cl(N,\beta \left)\right]-(H,\beta )\right)\hfill \end{array}$$

Set $(Q,\beta )=(P,\beta )-cl(N,\beta )$. Obviously, $(Q,\beta )\in \mathcal{M}\left(\tau \right)$. Therefore,

$$\begin{array}{cc}\hfill (E,\beta )& =[(H,\beta )-(Q,\beta )]\tilde{\cup }[(Q,\beta )-(H,\beta )]\hfill \\ \hfill & =(H,\beta )\tilde{\Delta }(Q,\beta ).\hfill \end{array}$$

We now prove that this representation is unique. Assume $(H,\beta )\tilde{\Delta }(Q,\beta )=(G,\beta )\tilde{\Delta }(P,\beta )$, where $(H,\beta )$ is soft regular open, $(G,\beta )\in \tau$, and $(Q,\beta ),(P,\beta )\in \mathcal{M}\left(\tau \right)$. Then, $(G,\beta )-cl(H,\beta )\tilde{\subseteq }(G,\beta )\tilde{\Delta }(H,\beta )=(P,\beta )\tilde{\Delta }(Q,\beta )$. This means that $(G,\beta )-cl(H,\beta )$ is a soft open set of the first category. Since $(X,\tau ,\beta )$ is soft Baire, so we must have $(G,\beta )-cl(H,\beta )=\Phi$. Therefore, $(G,\beta )\tilde{\subseteq }cl(H,\beta )$ and hence, $(G,\beta )\tilde{\subseteq }int\left(cl(H,\beta )\right)=(H,\beta )$. Thus, in this representation, soft regular open is larger than soft open, and each soft regular open is a soft open set. On the other hand, if both $(G,\beta )$, $(H,\beta )$ are soft regular open, then we have $(G,\beta )\tilde{\subseteq }(H,\beta )$ and $(H,\beta )\tilde{\subseteq }(G,\beta )$. Thus, $(G,\beta )=(H,\beta )$ and $(P,\beta )=(Q,\beta )$. □

Proposition 14. 

Let $(E,\beta )\in SS\left(\widehat{X}\right)$ and let $\tau \in T\left(\widehat{X}\right)$. Then, $(E,\beta )\in {\mathfrak{B}}_r(\tau ,\mathcal{M}\left(\tau \right))$ if there exists $(M,\beta )\in \mathcal{M}\left(\tau \right)$ such that $(E,\beta )-(M,\beta )$ is soft clopen in ${(M,\beta )}^c$.

Proof. 

Let $(E,\beta )\in {\mathfrak{B}}_r(\tau ,\mathcal{M}\left(\tau \right))$. By Propositions 9 and 10, $(E,\beta )=[(G,\beta )-(P,\beta )]\tilde{\cup }$$(Q,\beta )=[(D,\beta )-(R,\beta )]\tilde{\cup }(S,\beta )$, where $(G,\beta )\in \tau$, $(D,\beta )\in {\tau }^c$, and $(P,\beta ),(Q,\beta ),(R,\beta ),$$(S,\beta )\in \mathcal{M}\left(\tau \right)$. Set $(M,\beta )=(P,\beta )\tilde{\cup }(Q,\beta )\tilde{\cup }(R,\beta )\tilde{\cup }(S,\beta )$. Then, $(E,\beta )-(M,\beta )=(G,\beta )-(M,\beta )=(D,\beta )-(M,\beta )$. This proves that $(E,\beta )-(M,\beta )$ is a soft clopen set in ${(M,\beta )}^c$.

Conversely, suppose there exists $(M,\beta )\in \mathcal{M}\left(\tau \right)$ such that $(E,\beta )-(M,\beta )$ is soft clopen in ${(M,\beta )}^c$. Put $(E,\beta )-(M,\beta )=(G,\beta )\tilde{\cap }{(M,\beta )}^c$ for some soft clopen over X. Evidently, $(E,\beta )=(G,\beta )\tilde{\Delta }(M,\beta )$ and hence, $(E,\beta )\in {\mathfrak{B}}_r(\tau ,\mathcal{M}\left(\tau \right))$. □

Proposition 15. 

Let $(E,\beta )\in SS\left(\widehat{X}\right)$ and let $\tau \in T\left(\widehat{X}\right)$. Then, $(E,\beta )\in {\mathfrak{B}}_r(\tau ,\mathcal{M}\left(\tau \right))$ if $C_2(E,\beta )-(E,\beta )\in \mathcal{M}\left(\tau \right)$.

Proof. 

Assume $(E,\beta )\in {\mathfrak{B}}_r(\tau ,\mathcal{M}\left(\tau \right))$. If $(E,\beta )\in \mathcal{M}\left(\tau \right)$, by Lemma 10, $C_2(E,\beta )-(E,\beta )\in \mathcal{M}\left(\tau \right)$. On the other hand, assume $(E,\beta )\in \mathcal{S}\left(\tau \right)$. Suppose, otherwise that, $C_2(E,\beta )-(E,\beta )\in \mathcal{S}\left(\tau \right)$. By Theorem 1, $C_2(E,\beta )-(E,\beta )$ is of the second category in some nun-null soft open $(G,\beta )$. Since $C_2(E,\beta )\tilde{\cap }(G,\beta )\in \mathcal{S}\left(\tau \right)$, then there exists a soft point $x_{\mu }\in SP\left(\widehat{X}\right)$ such that $x_{\mu }\in C_2(E,\beta )\tilde{\cap }(G,\beta )$. Since $(G,\beta )\in \tau \left(x_{\mu }\right)$, so $(E,\beta )\tilde{\cap }(G,\beta )\in \mathcal{M}\left(\tau \right)$. Since $C_2(E,\beta )-(E,\beta )$ is of the second category in $(G,\beta )$ and $C_2(E,\beta )-(E,\beta )\tilde{\subseteq }{(E,\beta )}^c$ implies ${(E,\beta )}^c$ is of the second category in $(G,\beta )$. But $(G,\beta )-{(E,\beta )}^c=(G,\beta )\tilde{\cap }(E,\beta )\in \mathcal{M}\left(\tau \right)$, which is a contradiction. Hence, $C_2(E,\beta )-(E,\beta )\in \mathcal{M}\left(\tau \right)$.

Conversely, assume $C_2(E,\beta )-(E,\beta )\in \mathcal{M}\left(\tau \right)$. Consider

$$\begin{array}{c}\hfill (E,\beta )=[C_2(E,\beta )-(C_2(E,\beta )-(E,\beta ))]\tilde{\cup }[(E,\beta )-C_2(E,\beta )].\end{array}$$

Since $(P,\beta )=C_2(E,\beta )-(E,\beta )$, $(Q,\beta )=(E,\beta )-C_2(E,\beta )$ are in $\mathcal{M}\left(\tau \right)$ and $C_2(E,\beta )\in {\tau }^c$ (by Lemma 11), then $(E,\beta )\in {\mathfrak{B}}_r(\tau ,\mathcal{M}\left(\tau \right))$ from Proposition 10. □

Proposition 16. 

Let $(E,\beta )\in SS\left(\widehat{X}\right)$ and let $\tau \in T\left(\widehat{X}\right)$. Then, $(E,\beta )\in {\mathfrak{B}}_r(\tau ,\mathcal{M}\left(\tau \right))$ if $C_2(E,\beta )\tilde{\cap }{C}_2\left({(E,\beta )}^c\right)\in \mathcal{N}\left(\tau \right)$.

Proof. 

Suppose $(E,\beta )\in {\mathfrak{B}}_r(\tau ,\mathcal{M}\left(\tau \right))$. By Proposition 9, $(E,\beta )=((G,\beta )-(P,\beta ))\tilde{\cup }(Q,\beta )$, where $(G,\beta )\in \tau$ and $(P,\beta ),(Q,\beta )\in \mathcal{M}\left(\tau \right)$. By Proposition 5, ${(E,\beta )}^c={(G,\beta )}^c-(Q,\beta )\tilde{\cup }[(P,\beta )-(Q,\beta )]$ is also in $\mathcal{M}\left(\tau \right)$. By Lemma 12, $C_2(E,\beta )=C_2(G,\beta )$ and $C_2\left({(E,\beta )}^c\right)$$=C_2\left({(G,\beta )}^c\right)$. By Lemma 11, $C_2(G,\beta )\tilde{\subseteq }cl(G,\beta )$ and $C_2\left({(G,\beta )}^c\right)\tilde{\subseteq }cl\left({(G,\beta )}^c\right)$. Therefore, we obtain that

$$\begin{array}{c}\hfill C_2(E,\beta )\tilde{\cap }{C}_2\left({(E,\beta )}^c\right)\tilde{\subseteq }cl(G,\beta )\tilde{\cap }cl\left({(G,\beta )}^c\right)=cl(G,\beta )-(G,\beta ).\end{array}$$

Since $cl(G,\beta )-(G,\beta )\in \mathcal{N}\left(\tau \right)$, so $C_2(E,\beta )\tilde{\cap }{C}_2\left({(E,\beta )}^c\right)\in \mathcal{N}\left(\tau \right)$.

Conversely, assume $(E,\beta )\notin {\mathfrak{B}}_r(\tau ,\mathcal{M}\left(\tau \right))$. Let $(G,\beta )\in \tau$ such that for each $(H,\beta )\in \tau$ with $\Phi \ne (H,\beta )\tilde{\subseteq }(G,\beta )$, $(E,\beta )\tilde{\cap }(H,\beta )$ and ${(E,\beta )}^c\tilde{\cap }(H,\beta )$ are in $\mathcal{M}\left(\tau \right)$. From the following identity

$$(E,\beta )\tilde{\cap }(H,\beta )=\left[(E,\beta )\tilde{\cap }{C}_2(E,\beta )\tilde{\cap }(H,\beta )\right]\tilde{\cup }\left[((E,\beta )-C_2(E,\beta ))\tilde{\cap }(H,\beta )\right],$$

we obtain that $C_2(E,\beta )\tilde{\cap }(H,\beta )\in \mathcal{S}\left(\tau \right)$. Since $(H,\beta )$ we chosen arbitrarily, so $C_2(E,\beta )\in \mathcal{S}\left({\tau }_{(G,\beta )}\right)$. Therefore, $(G,\beta )-C_2(E,\beta )\in \mathcal{M}\left(\tau \right)$. By the same reason, $(G,\beta )-C_2\left({(E,\beta )}^c\right)$$\in \mathcal{M}\left(\tau \right)$. Now,

$$\begin{array}{cc}\hfill (G,\beta )& =\left[(G,\beta )\tilde{\cap }{C}_2(E,\beta )\tilde{\cap }{C}_2\left({(E,\beta )}^c\right)\right]\tilde{\cup }[(G,\beta )-C_2(E,\beta )]\hfill \\ \hfill & \tilde{\cup }\left[C_2(E,\beta )\tilde{\cap }((G,\beta )-C_2\left({(E,\beta )}^c\right))\right]\tilde{\cup }\left[((G,\beta )-C_2(E,\beta ))\tilde{\cap }((G,\beta )-C_2\left({(E,\beta )}^c\right))\right].\hfill \end{array}$$

From the above equation, one can see that $(G,\beta )\tilde{\cap }{C}_2(E,\beta )\tilde{\cap }{C}_2\left({(E,\beta )}^c\right)\in \mathcal{S}\left(\tau \right)$. Thus, $C_2(E,\beta )$$\tilde{\cap }{C}_2\left({(E,\beta )}^c\right)$ cannot be in $\mathcal{N}\left(\tau \right)$. □

Summing up all the above findings regarding soft sets with the Baire property yields the following conclusion:

Theorem 5. 

Let $(E,\beta )\in SS\left(\widehat{X}\right)$ and let $\tau \in T\left(\widehat{X}\right)$. The following properties are equivalent:

1.

$(E,\beta )\in {\mathfrak{B}}_r(\tau ,\mathcal{M}\left(\tau \right))$.

2.

If $(E,\beta )=(H,\beta )\tilde{\Delta }(P,\beta )$, where $(H,\beta )$ is soft regular open and $(P,\beta )\in \mathcal{M}\left(\tau \right)$.

3.

If $(E,\beta )=(C,\beta )\tilde{\Delta }(Q,\beta )$, where $(C,\beta )\in {\tau }^c$ and $(Q,\beta )\in \mathcal{M}\left(\tau \right)$.

4.

If $(E,\beta )=[(D,\beta )-(R,\beta )]\tilde{\cup }(S,\beta )$, where $(D,\beta )\in {\tau }^c$ and $(R,\beta ),(S,\beta )\in \mathcal{M}\left(\tau \right)$.

5.

If $(E,\beta )=[(G,\beta )-(M,\beta )]\tilde{\cup }(N,\beta )$, where $(G,\beta )\in \tau$ and $(M,\beta ),(N,\beta )\in \mathcal{M}\left(\tau \right)$.

6.

If $(E,\beta )=(U,\beta )\tilde{\cup }(L,\beta )$, where $(U,\beta )$ is a soft $G_{\delta }$ set and $(L,\beta )\in \mathcal{M}\left(\tau \right)$.

7.

If $(E,\beta )=(W,\beta )-(T,\beta )$, where $(W,\beta )$ is a soft $F_{\sigma }$ set and $(T,\beta )\in \mathcal{M}\left(\tau \right)$.

8.

If there exists $(V,\beta )\in \mathcal{M}\left(\tau \right)$ such that $(E,\beta )-(V,\beta )$ is soft clopen in ${(V,\beta )}^c$.

9.

$C_2(E,\beta )\tilde{\cap }{C}_2\left({(E,\beta )}^c\right)\in \mathcal{N}\left(\tau \right)$.

10.

$C_2(E,\beta )-(E,\beta )\in \mathcal{M}\left(\tau \right)$.

Proposition 17. 

Let $(E,\beta )\in SS\left(\widehat{X}\right)$ and let $\tau \in T\left(\widehat{X}\right)$. If $(E,\beta )\in {\mathfrak{B}}_r(\tau ,\mathcal{M}\left(\tau \right))$ such that no soft point $x_{\mu }\in SP\left(\widehat{X}\right)$ belongs to $C_1(E,\beta )$, Then, ${(E,\beta )}^c\in \mathcal{M}\left(\tau \right)$.

Proof. 

$(E,\beta )\in {\mathfrak{B}}_r(\tau ,\mathcal{M}\left(\tau \right))$ such that it not of the first category at any $x_{\mu }$. This means that $C_2(E,\beta )=\widehat{X}$. By Theorem 5 (9), $C_2\left({(E,\beta )}^c\right)\in \mathcal{N}\left(\tau \right)$, i.e., $int\left(cl\left(C_2\left({(E,\beta )}^c\right)\right)\right)=\Phi$. On the other hand, by Lemma 13 (2), $int\left(cl\left(C_2\left({(E,\beta )}^c\right)\right)\right)=C_2\left({(E,\beta )}^c\right)$. The latter statements imply that $C_2\left({(E,\beta )}^c\right)=\Phi$. By Lemma 10, ${(E,\beta )}^c\in \mathcal{M}\left(\tau \right)$. □

Proposition 18. 

Let $(E,\beta ),(G,\beta )\in SS\left(\widehat{X}\right)$ and let $\tau \in T\left(\widehat{X}\right)$. If $(E,\beta )\in {\mathfrak{B}}_r(\tau ,\mathcal{M}\left(\tau \right))$ and disjoint with $(G,\beta )$, then $int\left(C_2(E,\beta )\right)\tilde{\cap }int\left(C_2(G,\beta )\right)=\Phi$.

Proof. 

Suppose $(E,\beta )\in {\mathfrak{B}}_r(\tau ,\mathcal{M}\left(\tau \right))$. Since $(E,\beta )\tilde{\cap }(G,\beta )=\Phi$, so $(G,\beta )\tilde{\subseteq }{(E,\beta )}^c$. By Lemma 11, $C_2(G,\beta )\tilde{\subseteq }{C}_2\left({(E,\beta )}^c\right)$. Therefore, $C_2(G,\beta )\tilde{\cap }{C}_2(E,\beta )\tilde{\subseteq }{C}_2(E,\beta )\tilde{\cap }{C}_2\left({(E,\beta )}^c\right)$. By Proposition 16, $C_2(E,\beta )\tilde{\cap }{C}_2\left({(E,\beta )}^c\right)\in \mathcal{N}\left(\tau \right)$. Thus, $int\left(C_2(E,\beta )\right)\tilde{\cap }int\left(C_2(G,\beta )\right)=\Phi$. □

Definition 28. 

Let $\tau \in T\left(\widehat{X}\right)$. The soft σ-algebra generated by τ is called a soft Borel σ-algebra and is denoted by $\mathcal{B}\left(\tau \right)$. Members of $\mathcal{B}\left(\tau \right)$ are called soft Borel sets.

By Theorems 4 and 5, ${\mathfrak{B}}_r(\tau ,\mathcal{M}\left(\tau \right))$ includes $\tau$, ${\tau }^c$, all soft $G_{\delta }$ sets, all soft $F_{\sigma }$ sets, $\mathcal{N}\left(\tau \right)$, $\mathcal{C}\left(\tau \right)$, and $\mathcal{M}\left(\tau \right)$. Consequently, $\mathcal{B}\left(\tau \right)\tilde{\subseteq }{\mathfrak{B}}_r(\tau ,\mathcal{M}\left(\tau \right))$. That is, each soft Borel set is a soft set of the Baire property. The converse is not true in general. By Lemma 3, we can recall an example in classical topology. It is known that there are infinitely many subsets of the Cantor set that are not Borel. Any of such sets can be regarded as a soft set, which serves as a counterexample; for more details, see [39].

Theorem 6. 

Let $\tau \in T\left(\widehat{X}\right)$. If τ has a countable soft base, then ${\mathfrak{B}}_r(\tau ,\mathcal{M})=\mathcal{B}\left({\tau }_{\mathfrak{c}}\left(\mathcal{M}\right)\right)$, where $\mathcal{M}=\mathcal{M}\left(\tau \right)$.

Proof. 

Let $\tau \in T\left(\widehat{X}\right)$ have a countable soft base. Since $\mathcal{M}$ is a soft $\sigma$-ideal, by Lemma 7, soft open set with respect to ${\tau }_{\mathfrak{c}}\left(\mathcal{M}\right)$ are of the form $(G,\beta )-(P,\beta )$, where $(G,\beta )\in \tau$ and $(P,\beta )\in \mathcal{M}$ and soft closed set with respect to ${\tau }_{\mathfrak{c}}\left(\mathcal{M}\right)$ are of the form $(D,\beta )-(Q,\beta )$, where $(D,\beta )\in \tau$ and $(Q,\beta )\in \mathcal{M}$. Therefore, ${\tau }_{\mathfrak{c}}\left(\mathcal{M}\right)\tilde{\subseteq }{\mathfrak{B}}_r(\tau ,\mathcal{M})$. Since $\mathcal{B}\left({\tau }_{\mathfrak{c}}\left(\mathcal{M}\right)\right)$ is the smallest soft $\sigma$-algebra containing ${\tau }_{\mathfrak{c}}\left(\mathcal{M}\right)$, so $\mathcal{B}\left({\tau }_{\mathfrak{c}}\left(\mathcal{M}\right)\right)\tilde{\subseteq }{\mathfrak{B}}_r(\tau ,\mathcal{M})$.

Conversely, let $(E,\beta )\in {\mathfrak{B}}_r(\tau ,\mathcal{M})$. By Proposition 10, $(E,\beta )=[(D,\beta )-(P,\beta )]\tilde{\cup }$$(Q,\beta )$, where $(G,\beta )\in \tau$ and $(P,\beta ),(Q,\beta )\in \mathcal{M}$. Now, we have

$$\begin{array}{c}\hfill (E,\beta )=\left[(D,\beta )\tilde{\cup }(Q,\beta )\right]\tilde{\cap }\left[{(P,\beta )}^c\tilde{\cup }(Q,\beta )\right].\end{array}$$

Clearly, $(D,\beta )\tilde{\cup }(Q,\beta )$ is soft ${\tau }_{\mathfrak{c}}\left(\mathcal{M}\right)$-closed. On the other hand, ${(P,\beta )}^c\tilde{\cup }(Q,\beta )$ is soft ${\tau }_{\mathfrak{c}}\left(\mathcal{M}\right)$-open since ${\left[{(P,\beta )}^c\tilde{\cup }(Q,\beta )\right]}^c=(P,\beta )\tilde{\cap }{(Q,\beta )}^c\in \mathcal{M}$ and by Lemma 9, ${\left[{(P,\beta )}^c\tilde{\cup }(Q,\beta )\right]}^c$ is soft ${\tau }_{\mathfrak{c}}\left(\mathcal{M}\right)$-closed. Since $\mathcal{B}\left({\tau }_{\mathfrak{c}}\left(\mathcal{M}\right)\right)$ contains all soft ${\tau }_{\mathfrak{c}}\left(\mathcal{M}\right)$-open and soft ${\tau }_{\mathfrak{c}}\left(\mathcal{M}\right)$-closed set, and is closed under finite soft intersections, hence $(E,\beta )\in \mathcal{B}\left({\tau }_{\mathfrak{c}}\left(\mathcal{M}\right)\right)$. Thus, ${\mathfrak{B}}_r(\tau ,\mathcal{M})\tilde{\subseteq }$$\mathcal{B}\left({\tau }_{\mathfrak{c}}\left(\mathcal{M}\right)\right)$. Consequently, ${\mathfrak{B}}_r(\tau ,\mathcal{M})=\mathcal{B}\left({\tau }_{\mathfrak{c}}\left(\mathcal{M}\right)\right)$. □

This mission is completed by the diagram at the end of this work, which displays the relationships between the previously mentioned soft sets. We encourage that the reader compare Figure 1 here with Figure 1 in [40].

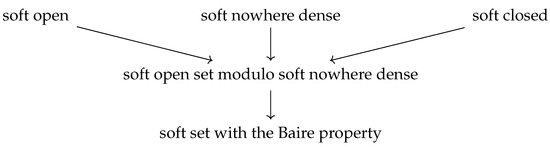
Figure 1. Generalized soft open sets.

Generally, none of the arrows in Figure 1 is reversible, it is shown in the following example:

Example 1. 

Let $\mathbb{R}$ be the set of real numbers and β be a set of parameters. Let τ be the soft topology on $\mathbb{R}$ generated by $\left\{\right(\mu ,E\left(\mu \right)):E(\mu )=(t,s);t,s\in \mathbb{R};t<s,\mu \in \beta \}$. The soft set $(H,\beta )=\left\{\right(\mu ,(-1,0)\cup (0,1)\cup \left\{2\right\}):\mu \in \beta \}$ is a soft open set modulo soft nowhere dense but neither soft open, soft closed, nor soft nowhere dense. While $(G,\beta )=\left\{\right(\mu ,\mathbb{R}-\mathbb{Q}):\mu \in \beta \}$ is a soft set with the Baire property but not soft open set modulo soft nowhere dense.

7. Conclusions and Future Work

The continuous launch of new classes of topological spaces, examples, properties, and relations has aided in the advancement of topology. As a result, it is necessary to similarly broaden the area of soft topology. By analyzing particular kinds of soft sets in soft topological spaces, we have made a novel contribution to the subject of soft topology. The research begins by recalling several essential conclusions and procedures for certain classes of soft sets in soft topological spaces. We have proposed the concept of congruence of soft sets modulo a soft ideal. By applying different types of soft ideals in soft topological spaces in this representation, we have defined classes of soft open sets modulo soft ideals. In particular, we have defined soft open sets modulo soft of soft nowhere dense sets and soft open sets modulo soft sets of the first category (known as soft sets with the Baire property). The first class forms a soft algebra, and the last one forms a soft $\sigma$-algebra. The soft $\sigma$-algebra of soft sets with the Baire property is identical to the soft $\sigma$-algebra generated by soft open sets and soft sets of the first category. The operations on elements of this soft $\sigma$-algebra are discussed, like restriction to a soft subspace or transferring from a soft subspace to a soft topological space. A characterization of soft sets with the Baire property is demonstrated, which asserts that a soft set with the Baire property can be represented via soft closed, soft clopen relative, soft $G_{\delta }$, soft $F_{\sigma }$, and soft regular open with the soft set(s) of the first category in various different ways. Then, we have proved that each soft Borel set is a soft set with the Baire property. On the other hand, there are soft sets with the Baire property that are not soft Borel. However, we have found two different soft topologies for which soft sets with the Baire property and soft Borel sets are identical. Namely, if $\tau$ is a soft topology over X with a countable soft base and ${\tau }_{\mathfrak{c}}\left(\mathcal{M}\right)$ is the cluster soft topology generated by $\tau$ and the soft $\sigma$-ideal $\mathcal{M}=\mathcal{M}\left(\tau \right)$, then the soft $\sigma$-algebra of soft sets with the Baire property in $\tau$ is similar to the soft Borel $\sigma$-algebra of ${\tau }_{\mathfrak{c}}\left(\mathcal{M}\right)$, i.e., ${\mathfrak{B}}_r(\tau ,\mathcal{M})=\mathcal{B}\left({\tau }_{\mathfrak{c}}\left(\mathcal{M}\right)\right)$.

The conclusions in this article are preliminary, and more study will be necessary. These findings can be seen as the foundation for researching new topics of soft topology (see [40]). Also, the obtained results are essential for the growth of soft measure theory. In particular, one can use soft sets of the first category to study the duality (similarity) between soft measure and soft category. Another aspect of this accomplishment is beneficial to the advancement of soft game theory. More precisely, on a specific soft topological space, the determinacy of the Banach-Mazur game can be studied.