On the Normalized Laplacian Spectrum of the Linear Pentagonal Derivation Chain and Its Application

Abstract

A novel distance function named resistance distance was introduced on the basis of electrical network theory. The resistance distance between any two vertices u and v in graph G is defined to be the effective resistance between them when unit resistors are placed on every edge of G. The degree-Kirchhoff index of G is the sum of the product of resistance distances and degrees between all pairs of vertices of G. In this article, according to the decomposition theorem for the normalized Laplacian polynomial of the linear pentagonal derivation chain $Q{P}_n$, the normalize Laplacian spectrum of $Q{P}_n$ is determined. Combining with the relationship between the roots and the coefficients of the characteristic polynomials, the explicit closed-form formulas for degree-Kirchhoff index and the number of spanning trees of $Q{P}_n$ can be obtained, respectively. Moreover, we also obtain the Gutman index of $Q{P}_n$ and we discovery that the degree-Kirchhoff index of $Q{P}_n$ is almost half of its Gutman index.

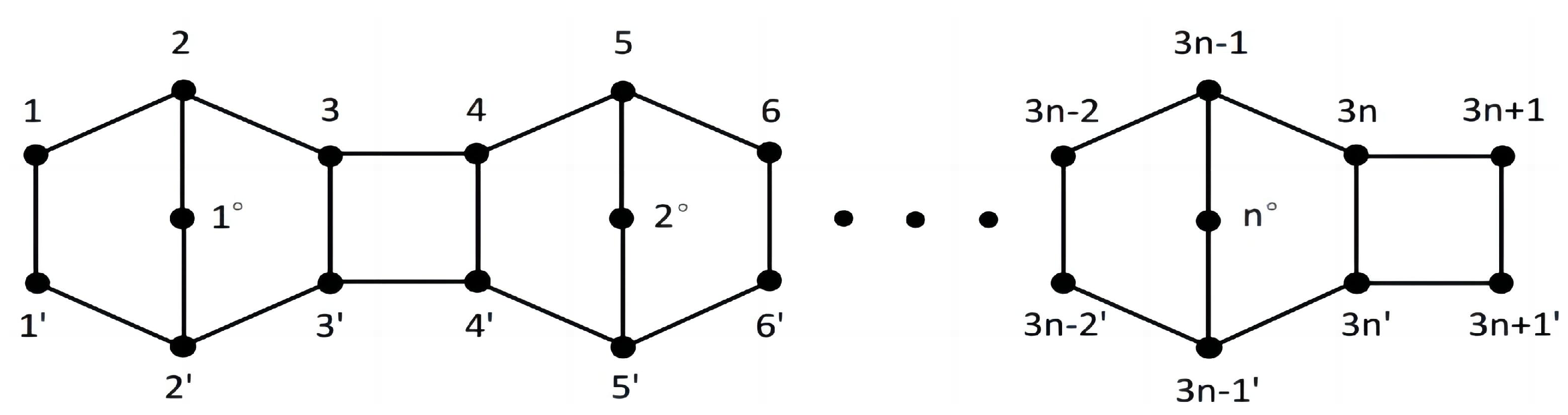
1. Introduction

Throughout this paper, we handle a simple, finite, and undirected graph. Let $G=\left(V\right(G),E(G\left)\right)$ be a graph with vertex set $V\left(G\right)=\{v_1,v_2,\dots ,v_n\}$ and edge set $E\left(G\right)$. For $v_i\in V\left(G\right)$, let $N_G\left(v_i\right)$ be the set of neighbors of $v_i$ in G. In particular, $d_i=\left|N_G\left(v_i\right)\right|$ is the degree of $v_i$ in G. The adjacency matrix of G, written as $A\left(G\right)$, is an $n\times n$ matrix whose $(i,j)$-entry is 1 if $v_i{v}_j\in E\left(G\right)$ or 0 otherwise. The Laplacian matrix $L\left(G\right)=D\left(G\right)-A\left(G\right)$, where $D\left(G\right)=diag(d_1,d_2,\dots ,d_n)$ is the diagonal matrix of G whose diagonal entry $d_i$ is the degree of $v_i$ for $1\le i\le n$.

The normalized Laplacian matrix [1] of a graph G, $\mathcal{L}\left(G\right)$, is defined to be

$$\mathcal{L}\left(G\right)=I-D^{\frac{1}{2}}\left(D^{-1}A\right)D^{-\frac{1}{2}}=D^{-\frac{1}{2}}L\left(G\right)D^{-\frac{1}{2}},$$

with the convention that $D{\left(G\right)}^{-1}(i,i)=0$ if $d_i=0$. Since the normalized Laplacian matrix is consistent with the eigenvalues in spectral geometry and random walks [1], it has attracted more and more researchers’ attention. From the definition of $\mathcal{L}\left(G\right)$, it is easy to obtain that:

$${\left(\mathcal{L}\left(G\right)\right)}_{ij}=\left\{\begin{array}{cccc}\hfill & 1,\hfill & \hfill & \mathrm{if}i=j;\hfill \\ \hfill & -\frac{1}{\sqrt{d_i{d}_j}},\hfill & \hfill & \mathrm{if}i\ne j\mathrm{and}{v}_i\mathrm{is} \mathrm{adjacent} \mathrm{to}{v}_j;\hfill \\ \hfill & 0,\hfill & \hfill & \mathrm{otherwise},\hfill \end{array}\right.$$

(1)

where ${\left(\mathcal{L}\left(G\right)\right)}_{ij}$ denotes the $(i,j)$-entry of $\mathcal{L}\left(G\right)$.

For an $n\times n$ matrix M, we denote the characteristic polynomial $det(x{I}_n-M)$ of M by ${\Phi }_M\left(x\right)$, where $I_n$ is the identity matrix of order n. In particular, for a graph G, ${\Phi }_{L\left(G\right)}\left(x\right)$ (respectively, ${\Phi }_{\mathcal{L}\left(G\right)}\left(x\right)$) is the Laplacian (respectively, normalized Laplacian) characteristic polynomial of G, and its roots are the Laplacian (respectively, normalized Laplacian) eigenvalues of G. The collection of eigenvalues of $L\left(G\right)$ (respectively, $\mathcal{L}\left(G\right)$) together with their multiplicities are called the L-spectrum (respectively, $\mathcal{L}$-spectrum) of G.

For a graph G, the distance between vertices $v_i$ and $v_j$ on G is defined as the length of the shortest path between the two vertices, denoted $d_{ij}$. One famous distance based parameter called the Wiener index [2], which is defined as the sum of the distances between all the vertices on the graph, was given by $W\left(G\right)={\sum }_{i<j}{d}_{ij}$. For more studies on the Wiener index, one may be referred to [3,4,5,6,7,8]. In 1994, Gutman presented an index based on degree and distance of vertex, Gutman index [9], which is $Gut\left(G\right)={\sum }_{i<j}{d}_i{d}_j{d}_{ij}.$ He also showed that when G is an n-order tree, the close relationship between the Wiener index and the Gutman index is $Gut\left(G\right)=4W\left(G\right)-(2n-1)(n-1)$.

Based on electrical network theory, Klein and Randić [10] proposed a novel distance function named resistance distance. Let G be a connected graph, and the resistance distance between vertices $v_i$ and $v_j$, denoted by $r_{ij}$, is defined as the effective resistance distance between vertices $v_i$ and $v_j$ in the electrical network obtained by replacing each edge in G with a unit resistance. The resistance distance is a better indicator of the connection between two vertices than the distance. In fact, the resistance distance parameter reflects the intrinsic properties of the graph and has many applications in chemistry [11,12].

One famous parameter called the Kirchhoff index [10], defined as the sum of resistance distances in a simple connected graph, was given by $Kf\left(G\right)={\sum }_{i<j}{r}_{ij}.$ In 1993, Klein and Randić [10] proved that $r_{ij}\le d_{ij}$ and $Kf\left(G\right)\le W\left(G\right)$ with equality if and only if G is a tree. The intrinsic correlation between the Kirchhoff index and the Laplacian eigenvalues of graph G is shown, independently, by Gutman and Mohar [13] and Zhu et al. [14] as

$$Kf\left(G\right)=\sum _{i<j}{r}_{ij}=n\sum _{i=2}^n\frac{1}{{\mu }_i},$$

where n is the number of vertices of the graph G and $0={\mu }_1<{\mu }_2\le \cdots \le {\mu }_n$ are the eigenvalues of $L\left(G\right)$.

As an analogue to the Gutman index, Chen and Zhang [15] presented another graph parameter, the degree-Kirchhoff index $K{f}^{*}\left(G\right)={\sum }_{i<j}{d}_i{d}_j{r}_{ij}$. Meanwhile, authors [15] proved that the degree-Kirchhoff index is closely related to the corresponding normalized Laplacian spectrum. Many researchers devote themselves to the study of normalized Laplacian spectrum and the degree-Kirchhoff index of some classes of graphs. One may be referred to those in [16,17,18,19,20,21,22].

As a structured descriptor of chemical molecular graphs, the topological index can reflect some structural characteristics of compounds. Like Kirchhoff index, degree-Kirchhoff index is also a topological index. Unfortunately, it is difficult to compute resistant distance and degree-Kirchhoff index in a graph from their computational complexity. Therefore, it is necessary to find a explicit closed-form formulas for the degree-Kirchhoff index. In fact, the degree-Kirchhoff index is difficult to calculate for general graphs, but it is computable for some graphs with good periodicity and good symmetry. Huang et al. studied the degree-Kirchhoff index of some graphs with a good structure, such as linear polyomino chain [23] and linear hexagonal chain [24]. In addition, there are also some studies on the normalized Laplacian spectrum and the degree-Kirchhoff index of phenylene chains [25,26].

The number of spanning trees of a graph (network) is an important quantity to evaluate the reliability of the graph [27]. Therefore, studying the number of spanning trees of graphs has a very important theoretical and practical significance.

Hexagonal systems are very important in theoretical chemistry because they are natural graphical representations of benzene molecular structures. In recent years, researchers have worked to study the topological index of hexagonal systems [4,28]. The linear pentagonal derivation chain studied in this paper is related to the hexagonal systems. A linear pentagonal chain of length n, denoted by $P_n$, is made up of $2n$ pentagons, where every two pentagons with two sides can be seen as a hexagon with one vertex and two sides. Then the linear pentagonal derivation chain, denoted by $Q{P}_n$, is the graph obtained by attaching four-membered rings to each hexagon composed of two pentagons of $P_n$, as showed in Figure 1. It is not difficult to verify that $\left|V\right(Q{P}_n\left)\right|=7n+2$, $\left|E\right(Q{P}_n\left)\right|=10n+1$.

Figure 1. The linear pentagonal derivation chain $Q{P}_n$.

The explicit closed-form formulas for Kirchhoff index and the number of spanning trees of the linear pentagonal derivation chain $Q{P}_n$ have been derived from the Laplacian spectrum [29]. Motivated by the above works, we consider the degree-Kirchhoff index and the number of spanning trees of linear pentagonal derivation chain in terms of the normalized Laplacian spectrum. Different from the method in [29], in this paper, we solve the number of spanning trees according to the normalized Laplacian spectrum, which gives a new way for calculating the number of spanning trees of $Q{P}_n$.

In this article, according to the decomposition theorem for the normalized Laplacian polynomial of the linear pentagonal derivation chain $Q{P}_n$, the normalized Laplacian spectrum of $Q{P}_n$ is determined. Combining with the relationship between the roots and the coefficients of the characteristic polynomials, the explicit closed-form formulas for degree-Kirchhoff index and the number of spanning trees of $Q{P}_n$ can be obtained, respectively. Meanwhile, we also get the Gutman index of $Q{P}_n$. For a general graph G, the ratio $\frac{Kf\left(G\right)}{W\left(G\right)}$ is not closely related to ${\displaystyle \frac{K{f}^{*}\left(G\right)}{Gut\left(G\right)}}$. However, we are surprised to discovery that for $Q{P}_n$ both ${\displaystyle \frac{Kf\left(Q{P}_n\right)}{W\left(Q{P}_n\right)}}\to {\displaystyle \frac{1}{2}}$ [29] and ${\displaystyle \frac{K{f}^{*}\left(Q{P}_n\right)}{Gut\left(Q{P}_n\right)}}\to {\displaystyle \frac{1}{2}}$ (based on our obtained results) as $n\to \infty$.

2. Preliminaries

In this section, we will give some notations and terminologies and some known results that will be used in our following section.

An automorphism of G is a permutation $\pi$ of $V\left(G\right)$, with the property that $v_i{v}_j$ is an edge of G if and only if $\pi \left(v_i\right)\pi \left(v_j\right)$ is an edge of G.

Suppose we mark the vertices of $Q{P}_n$ as shown in Figure 1 and denote $V_0=\{1^{\circ },2^{\circ },\dots ,n^{\circ }\},$$V_1=\{1,2,\dots ,3n+1\},V_2=\{1^{{}^{\prime }},2^{{}^{\prime }},\dots ,{(3n+1)}^{{}^{\prime }}\}.$ Then

$$\pi =\left(1^{\circ }\right)\left(2^{\circ }\right)\cdots \left(n^{\circ }\right)(1,1^{{}^{\prime }})(2,2^{{}^{\prime }})\cdots (3n+1,{(3n+1)}^{{}^{\prime }})$$

is an automorphism of $Q{P}_n$. For convenience, we abbreviate $\mathcal{L}\left(Q{P}_n\right)$ to $\mathcal{L}$. By a suitable arrangement of vertices in $Q{P}_n$, the normalized Laplacian matrix $\mathcal{L}$ can be written as the following block matrix

$$\mathcal{L}=\begin{array}{c}\left[\begin{array}{ccc}{\mathcal{L}}_{V_{00}}& {\mathcal{L}}_{V_{01}}& {\mathcal{L}}_{V_{02}}\\ {\mathcal{L}}_{V_{10}}& {\mathcal{L}}_{V_{11}}& {\mathcal{L}}_{V_{12}}\\ {\mathcal{L}}_{V_{20}}& {\mathcal{L}}_{V_{21}}& {\mathcal{L}}_{V_{22}}\end{array}\right]\end{array},$$

where ${\mathcal{L}}_{V_{ij}}$ is the submatrix composed by rows corresponding to vertices in $V_i$ and columns corresponding to vertices in $V_j$ for $i,j=0,1,2.$

Let

$$T=\begin{array}{c}\left[\begin{array}{ccc}{I}_n& \mathbf{0}& \mathbf{0}\\ \mathbf{0}& \frac{1}{\sqrt{2}}{I}_{3n+1}& \frac{1}{\sqrt{2}}{I}_{3n+1}\\ \mathbf{0}& \frac{1}{\sqrt{2}}{I}_{3n+1}& -\frac{1}{\sqrt{2}}{I}_{3n+1}\end{array}\right]\end{array}$$

be the block matrix so that the blocks have the same dimension as the corresponding blocks in $\mathcal{L}$. Note that ${\mathcal{L}}_{V_{01}}={\mathcal{L}}_{V_{02}}$, ${\mathcal{L}}_{V_{10}}={\mathcal{L}}_{V_{20}}$, ${\mathcal{L}}_{V_{11}}={\mathcal{L}}_{V_{22}}$ and ${\mathcal{L}}_{V_{12}}={\mathcal{L}}_{V_{21}}$. From the unitary transformation $T\mathcal{L}T$, we obtain

$$T\mathcal{L}T=\begin{array}{c}\left[\begin{array}{cc}{\mathcal{L}}_A& \mathbf{0}\\ \mathbf{0}& {\mathcal{L}}_S\end{array}\right]\end{array},$$

where

$$\begin{array}{c}\hfill \begin{array}{c}{\mathcal{L}}_A=\left[\begin{array}{cc}{\mathcal{L}}_{V_{00}}& \sqrt{2}{\mathcal{L}}_{V_{01}}\\ \sqrt{2}{\mathcal{L}}_{V_{10}}& {\mathcal{L}}_{V_{11}}+{\mathcal{L}}_{V_{12}}\end{array}\right],{\mathcal{L}}_S={\mathcal{L}}_{V_{22}}-{\mathcal{L}}_{V_{12}}\end{array}.\end{array}$$

(2)

According to the above analysis process, Huang et al. [24] derived the decomposition theorem of normalized Laplacian characteristic polynomial of G below.

Lemma 1

([24]). Suppose $\mathcal{L}$, ${\mathcal{L}}_A$ and ${\mathcal{L}}_S$ are defined as above. Then the normalized Laplacian characteristic polynomial of $Q{P}_n$ is as follows

$${\Phi }_{\mathcal{L}}\left(x\right)={\Phi }_{{\mathcal{L}}_A}\left(x\right){\Phi }_{{\mathcal{L}}_S}\left(x\right),$$

where ${\Phi }_{\mathcal{L}}\left(x\right),{\Phi }_{{\mathcal{L}}_A}\left(x\right)$ and ${\Phi }_{{\mathcal{L}}_S}\left(x\right)$ are characteristic polynomials of $\mathcal{L},{\mathcal{L}}_A$ and ${\mathcal{L}}_S$, respectively.

Lemma 2

([30]). Let $M_1$, $M_2$, $M_3$, $M_4$ be respectively $p\times p$, $p\times q$, $q\times p$, $q\times q$ matrices with $M_1$ and $M_4$ being invertible. Then

$$\begin{array}{cc}\hfill det\left(\begin{array}{cc}{M}_1& M_2\\ M_3& M_4\end{array}\right)& =det\left(M_1\right)·det(M_4-M_3{M}_1^{-1}{M}_2)\hfill \\ \hfill & =det\left(M_4\right)·det(M_1-M_2{M}_4^{-1}{M}_3),\hfill \end{array}$$

where $M_4-M_3{M}_1^{-1}{M}_2$ and $M_1-M_2{M}_4^{-1}{M}_3$ are called the Schur complements of $M_1$ and $M_4$, respectively.

Lemma 3.

Suppose G is a connected graph of order n with m edges, and $\{0={\lambda }_1<{\lambda }_2\le \cdots \le {\lambda }_n\}$ is the spectrum on the normalized Laplacian matrix $\mathcal{L}$ of G. Denote by $d_i$ is the degree of $v_i$ of G, $i=1,2,\dots ,n$. Then

(i)

[15] The degree-Kirchhoff index of G is $K{f}^{*}\left(G\right)=2m{\sum }_{i=2}^n\frac{1}{{\lambda }_i}$;

(ii)

[1] The number $\tau \left(G\right)$ of spanning trees of G is $\tau \left(G\right)=\frac{{\prod }_{i=1}^n{d}_i{\prod }_{k=2}^n{\lambda }_k}{2m}$.

3. The Normalized Laplacian Spectrum of ${\mathit{QP}}_{\mathit{n}}$

In this part, from Lemma 1, we first derive the normalized Laplacian eigenvalues of linear pentagonal derivation chain $Q{P}_n$. Then we present a complete description of the sum of the normalized Laplacian eigenvalues’ reciprocals and the product of the normalized Laplacian eigenvalues which will be used in getting the degree-Kirchhoff index and the number of spanning trees of $Q{P}_n$, respectively.

Given an $n\times n$ square matrix M, then we will use $M[i,j,\cdots ,k]$ to denote the sub-matrix obtained by deleting the i-th, j-th, $\cdots ,$ k-th rows and corresponding columns of M. In view of (1), ${\mathcal{L}}_{V_{00}}$, ${\mathcal{L}}_{V_{01}}$, ${\mathcal{L}}_{V_{12}}$ and ${\mathcal{L}}_{V_{11}}$ are given as follows:

$$\begin{array}{c}{\mathcal{L}}_{V_{00}}=I_n,{\mathcal{L}}_{V_{01}}={\left[\begin{array}{ccccccccc}0& -\frac{1}{\sqrt{6}}& 0& 0& 0& \cdots & 0& 0& 0\\ 0& 0& 0& 0& -\frac{1}{\sqrt{6}}& \cdots & 0& 0& 0\\ ⋮& ⋮& ⋮& ⋮& ⋮& \ddots & ⋮& ⋮& ⋮\\ 0& 0& 0& 0& 0& \cdots & -\frac{1}{\sqrt{6}}& 0& 0\end{array}\right]}_{n\times (3n+1)},\end{array}$$

$$\begin{array}{c}{\mathcal{L}}_{V_{11}}={\left[\begin{array}{ccccccc}1& -\frac{1}{\sqrt{6}}& 0& \cdots & 0& 0& 0\\ -\frac{1}{\sqrt{6}}& 1& -\frac{1}{3}& \cdots & 0& 0& 0\\ 0& -\frac{1}{3}& 1& \cdots & 0& 0& 0\\ ⋮& ⋮& ⋮& \ddots & ⋮& ⋮& ⋮\\ 0& 0& 0& \cdots & 1& -\frac{1}{3}& 0\\ 0& 0& 0& \cdots & -\frac{1}{3}& 1& -\frac{1}{\sqrt{6}}\\ 0& 0& 0& \cdots & 0& -\frac{1}{\sqrt{6}}& 1\end{array}\right]}_{(3n+1)\times (3n+1)},\end{array}$$

$$\begin{array}{c}{\mathcal{L}}_{V_{12}}={\left[\begin{array}{ccccccccc}-\frac{1}{2}& 0& 0& 0& \cdots & 0& 0& 0& 0\\ 0& 0& 0& 0& \cdots & 0& 0& 0& 0\\ 0& 0& -\frac{1}{3}& 0& \cdots & 0& 0& 0& 0\\ 0& 0& 0& -\frac{1}{3}& \cdots & 0& 0& 0& 0\\ ⋮& ⋮& ⋮& ⋮& \ddots & ⋮& ⋮& ⋮& ⋮\\ 0& 0& 0& 0& \cdots & -\frac{1}{3}& 0& 0& 0\\ 0& 0& 0& 0& \cdots & 0& 0& 0& 0\\ 0& 0& 0& 0& \cdots & 0& 0& -\frac{1}{3}& 0\\ 0& 0& 0& 0& \cdots & 0& 0& 0& -\frac{1}{2}\end{array}\right]}_{(3n+1)\times (3n+1)}.\end{array}$$

Since $\begin{array}{c}{\mathcal{L}}_{V_{10}}={\mathcal{L}}_{V_{01}}^T,{\mathcal{L}}_{V_{22}}={\mathcal{L}}_{V_{11}},\end{array}$ and $\begin{array}{c}{\mathcal{L}}_A=\left[\begin{array}{cc}{\mathcal{L}}_{V_{00}}& \sqrt{2}{\mathcal{L}}_{V_{01}}\\ \sqrt{2}{\mathcal{L}}_{V_{10}}& {\mathcal{L}}_{V_{11}}+L_{V_{12}}\end{array}\right],{\mathcal{L}}_S={\mathcal{L}}_{V_{22}}-{\mathcal{L}}_{V_{12}}\end{array}$ (see (2)),

we have

$${\mathcal{L}}_A={\left[\begin{array}{ccccccccccccc}1& 0& \cdots & 0& 0& -\frac{1}{\sqrt{3}}& 0& 0& 0& \cdots & 0& 0& 0\\ 0& 1& \cdots & 0& 0& 0& 0& 0& -\frac{1}{\sqrt{3}}& \cdots & 0& 0& 0\\ ⋮& ⋮& \ddots & ⋮& ⋮& ⋮& ⋮& ⋮& ⋮& \ddots & ⋮& ⋮& ⋮\\ 0& 0& \cdots & 1& 0& 0& 0& 0& 0& \cdots & -\frac{1}{\sqrt{3}}& 0& 0\\ 0& 0& \cdots & 0& \frac{1}{2}& -\frac{1}{\sqrt{6}}& 0& 0& 0& \cdots & 0& 0& 0\\ -\frac{1}{\sqrt{3}}& 0& \cdots & 0& -\frac{1}{\sqrt{6}}& 1& -\frac{1}{3}& 0& 0& \cdots & 0& 0& 0\\ 0& 0& \cdots & 0& 0& -\frac{1}{3}& \frac{2}{3}& -\frac{1}{3}& 0& \cdots & 0& 0& 0\\ 0& 0& \cdots & 0& 0& 0& -\frac{1}{3}& \frac{2}{3}& -\frac{1}{3}& \cdots & 0& 0& 0\\ 0& -\frac{1}{\sqrt{3}}& \cdots & 0& 0& 0& 0& -\frac{1}{3}& 1& \cdots & 0& 0& 0\\ ⋮& ⋮& \ddots & ⋮& ⋮& ⋮& ⋮& ⋮& ⋮& \ddots & ⋮& ⋮& ⋮\\ 0& 0& \cdots & -\frac{1}{\sqrt{3}}& 0& 0& 0& 0& 0& \cdots & 1& -\frac{1}{3}& 0\\ 0& 0& \cdots & 0& 0& 0& 0& 0& 0& \cdots & -\frac{1}{3}& \frac{2}{3}& -\frac{1}{\sqrt{6}}\\ 0& 0& \cdots & 0& 0& 0& 0& 0& 0& \cdots & 0& -\frac{1}{\sqrt{6}}& \frac{1}{2}\end{array}\right]}_{(4n+1)\times (4n+1)},$$

and

$${\mathcal{L}}_S={\left[\begin{array}{ccccccccccc}\frac{3}{2}& -\frac{1}{\sqrt{6}}& 0& 0& 0& 0& \cdots & 0& 0& 0& 0\\ -\frac{1}{\sqrt{6}}& 1& -\frac{1}{3}& 0& 0& 0& \cdots & 0& 0& 0& 0\\ 0& -\frac{1}{3}& \frac{4}{3}& -\frac{1}{3}& 0& 0& \cdots & 0& 0& 0& 0\\ 0& 0& -\frac{1}{3}& \frac{4}{3}& -\frac{1}{3}& 0& \cdots & 0& 0& 0& 0\\ 0& 0& 0& -\frac{1}{3}& 1& -\frac{1}{3}& \cdots & 0& 0& 0& 0\\ 0& 0& 0& 0& -\frac{1}{3}& \frac{4}{3}& \cdots & 0& 0& 0& 0\\ ⋮& ⋮& ⋮& ⋮& ⋮& ⋮& \ddots & ⋮& ⋮& ⋮& ⋮\\ 0& 0& 0& 0& 0& 0& \cdots & \frac{4}{3}& -\frac{1}{3}& 0& 0\\ 0& 0& 0& 0& 0& 0& \cdots & -\frac{1}{3}& 1& -\frac{1}{3}& 0\\ 0& 0& 0& 0& 0& 0& \cdots & 0& -\frac{1}{3}& \frac{4}{3}& -\frac{1}{\sqrt{6}}\\ 0& 0& 0& 0& 0& 0& \cdots & 0& 0& -\frac{1}{\sqrt{6}}& \frac{3}{2}\end{array}\right]}_{(3n+1)\times (3n+1)}.$$

It is easy to see that the normalized Laplacian spectrum of $Q{P}_n$ consists of eigenvalues of ${\mathcal{L}}_A$ and ${\mathcal{L}}_S$ from Lemma 1. Now, suppose that the eigenvalues of ${\mathcal{L}}_A$ and ${\mathcal{L}}_S$ are, respectively, denoted by ${\alpha }_0\le {\alpha }_1\le \cdots \le {\alpha }_{4n}$ and ${\beta }_1\le {\beta }_2\le \cdots \le {\beta }_{3n+1}$. Note that $\mathcal{L}\left(Q{P}_n\right)$ is positive semi-definite (see [1]). Hence, the eigenvalues of $\mathcal{L}\left(Q{P}_n\right)$ are non-negative. That is to say, ${\mathcal{L}}_A$ and ${\mathcal{L}}_S$ are positive semi-definite. And then, it is not difficult to verify that ${\alpha }_0=0$, ${\alpha }_i>0$$(i=1,2,\dots ,4n)$ and ${\beta }_j>0$$(j=1,2,\dots ,3n+1)$.

4. Degree-Kirchhoff Index and the Number of Spanning Trees of ${\mathit{QP}}_{\mathit{n}}$

In this section, we first introduce the following lemma which is a direct result of Lemma 3(i). Note that $\left|E\right(Q{P}_n\left)\right|=10n+1$.

Lemma 4.

Suppose $Q{P}_n$ is a linear pentagonal derivation chain with length n. Then we have

$$\begin{array}{cc}\hfill K{f}^{*}\left(Q{P}_n\right)& =2(10n+1)(\sum _{i=1}^{4n}\frac{1}{{\alpha }_i}+\sum _{j=1}^{3n+1}\frac{1}{{\beta }_j}),\hfill \end{array}$$

where $0={\alpha }_0<{\alpha }_1\le \cdots \le {\alpha }_{4n}$ and $0<{\beta }_1\le {\beta }_2\le \cdots \le {\beta }_{3n+1}$ are eigenvalues of ${\mathcal{L}}_A$ and ${\mathcal{L}}_S$, respectively.

Lemma 5.

Let $0={\alpha }_0<{\alpha }_1\le \cdots \le {\alpha }_{4n}$ be eigenvalues of ${\mathcal{L}}_A$. Then

$$\begin{array}{c}\hfill \sum _{i=1}^{4n}\frac{1}{{\alpha }_i}=\frac{50n^3+25n^2+n}{10n+1}.\end{array}$$

Proof.

According to the relationship between the roots and coefficients of ${\Phi }_{{\mathcal{L}}_A}\left(x\right)$, ${\sum }_{i=1}^{4n}\frac{1}{{\alpha }_i}$ are obtained respectively. Since ${\Phi }_{{\mathcal{L}}_A}\left(x\right)=x^{4n+1}+a_1{x}^{4n}+\cdots +a_{4n-1}{x}^2+a_{4n}x$ with $a_{4n}\ne 0$ and ${\alpha }_1,{\alpha }_2,\cdots ,{\alpha }_{4n}$ are the roots of ${\Phi }_{{\mathcal{L}}_A}\left(x\right)=0$. By Vieta’s Formula [31], we get

$$\begin{array}{c}\hfill \sum _{i=1}^{4n}\frac{1}{{\alpha }_i}=\frac{{\sum }_{i^{{}^{\prime }}=1}^{4n}{\prod }_{i=1,i\ne i^{{}^{\prime }}}^{4n}{\alpha }_i}{{\prod }_{i=1}^{4n}{\alpha }_i}=-\frac{a_{4n-1}}{a_{4n}}.\end{array}$$

(3)

In the subsequent of this part, it suffices to determine $a_{4n}$ and $-a_{4n-1}$ in Equation (3), respectively.

Claim 1.

$a_{4n}=\frac{10n+1}{12}{\left(\frac{1}{3}\right)}^{3n-2}.$

Proof.

One can see that the number $a_{4n}(={(-1)}^{4n}{a}_{4n})$ is the sum of the determinants obtained by deleting the i-th row and corresponding column of ${\mathcal{L}}_A$ for $i=1,2,\dots ,4n+1$ (see also in [32]), that is

$$\begin{array}{c}\hfill a_{4n}=\sum _{i=1}^{4n+1}det{\mathcal{L}}_A\left[i\right].\end{array}$$

(4)

Case 1. $1\le i\le n$. According to the structure of ${\mathcal{L}}_A$ (see details in (2)), deleting the i-th row and corresponding column of ${\mathcal{L}}_A$ is equivalent to deleting the i-th row and corresponding column of $I_n$, the i-th row of $\sqrt{2}{\mathcal{L}}_{V_{01}}$ and the i-th column of $\sqrt{2}{\mathcal{L}}_{V_{10}}$. We mark the resulting blocks of ${\mathcal{L}}_A\left[i\right]$, by $I_{n-1}$, $B_{(n-1)\times (3n+1)}$, $B_{(n-1)\times (3n+1)}^T$, $C_{(3n+1)\times (3n+1)}$, respectively. Then applying Lemma 2 to the resulting matrix, one has

$$\begin{array}{cc}\hfill det{\mathcal{L}}_A\left[i\right]=& \left|\begin{array}{cc}{I}_{n-1}& B_{(n-1)\times (3n+1)}\\ B_{(n-1)\times (3n+1)}^T& C_{(3n+1)\times (3n+1)}\end{array}\right|=\left|\begin{array}{cc}{I}_{n-1}& 0\\ 0& C_{(3n+1)\times (3n+1)}-B_{(n-1)\times (3n+1)}^T{B}_{(n-1)\times (3n+1)}\end{array}\right|\hfill \\ \hfill =& \left|\begin{array}{c}{C}_{(3n+1)\times (3n+1)}-B_{(n-1)\times (3n+1)}^T{B}_{(n-1)\times (3n+1)}\end{array}\right|,\hfill \end{array}$$

where

$$\begin{array}{c}C-B^{T}B={\left[\begin{array}{cccccccccc}\frac{1}{2}& -\frac{1}{\sqrt{6}}& 0& 0& \cdots & 0& \cdots & 0& 0& 0\\ -\frac{1}{\sqrt{6}}& \frac{2}{3}& -\frac{1}{3}& 0& \cdots & 0& \cdots & 0& 0& 0\\ 0& -\frac{1}{3}& \frac{2}{3}& -\frac{1}{3}& \cdots & 0& \cdots & 0& 0& 0\\ ⋮& ⋮& ⋮& ⋮& \ddots & ⋮& \ddots & ⋮& ⋮& ⋮\\ 0& 0& 0& 0& \cdots & 1& \cdots & 0& 0& 0\\ ⋮& ⋮& ⋮& ⋮& \ddots & ⋮& \ddots & ⋮& ⋮& ⋮\\ 0& 0& 0& 0& \cdots & 0& \cdots & \frac{2}{3}& -\frac{1}{3}& 0\\ 0& 0& 0& 0& \cdots & 0& \cdots & -\frac{1}{3}& \frac{2}{3}& -\frac{1}{\sqrt{6}}\\ 0& 0& 0& 0& \cdots & 0& \cdots & 0& -\frac{1}{\sqrt{6}}& \frac{1}{2}\end{array}\right]}_{(3n+1)\times (3n+1)},\end{array}$$

and there’s only one 1 on the diagonal in the $(3i-1)$-th row of $C-B^{T}B$ for $1\le i\le n$. By a direct calculation, we have $det(C-\frac{1}{2}{B}^{T}B)=\left(\frac{1}{4}\right){\left(\frac{1}{3}\right)}^{3n-1}.$ Therefore, for $1\le i\le n$, we obtain

$$\begin{array}{c}\hfill det{\mathcal{L}}_A\left[i\right]=\left(\frac{1}{4}\right){\left(\frac{1}{3}\right)}^{3n-1}.\end{array}$$

(5)

Case 2. $n+1\le i\le 4n+1.$ In this case, according to the structure of ${\mathcal{L}}_A$, deleting the i-th row and corresponding column of ${\mathcal{L}}_A$ is equal to deleting the $(i-n)$-th row and corresponding column of ${\mathcal{L}}_{V_{11}}+{\mathcal{L}}_{V_{12}}$, the $(i-n)$-th column of $\sqrt{2}{\mathcal{L}}_{V_{01}}$ and the $(i-n)$-th row of $\sqrt{2}{\mathcal{L}}_{V_{10}}$. Expressing the resulting blocks, respectively, as $I_n$, $B_{n\times 3n}$, $B_{n\times 3n}^T$, $C_{3n\times 3n}$. Then by Lemma 2, we obtain

$$\begin{array}{cc}\hfill det{\mathcal{L}}_A\left[i\right]=& \left|\begin{array}{cc}{I}_n& B_{n\times 3n}\\ B_{n\times 3n}^T& C_{3n\times 3n}\end{array}\right|=\left|\begin{array}{cc}{I}_n& 0\\ 0& C_{3n\times 3n}-B_{n\times 3n}^T{B}_{n\times 3n}\end{array}\right|\hfill \\ \hfill =& \left|\begin{array}{c}{C}_{3n\times 3n}-B_{n\times 3n}^T{B}_{n\times 3n}\end{array}\right|,\hfill \end{array}$$

where

$$\begin{array}{c}C-B^{T}B={\left[\begin{array}{cc}{E}_{(i-n-1)\times (i-n-1)}& 0\\ 0& F_{(4n+1-i)\times (4n+1-i)}\end{array}\right]}_{3n\times 3n},\end{array}$$

and the $E,F$ are as follows:

$$\begin{array}{c}E={\left[\begin{array}{ccccccc}\frac{1}{2}& \frac{-1}{\sqrt{6}}& 0& \cdots & 0& 0& 0\\ \frac{-1}{\sqrt{6}}& \frac{2}{3}& -\frac{1}{3}& \cdots & 0& 0& 0\\ 0& -\frac{1}{3}& \frac{2}{3}& \cdots & 0& 0& 0\\ ⋮& ⋮& ⋮& \ddots & ⋮& ⋮& ⋮\\ 0& 0& 0& \cdots & \frac{2}{3}& -\frac{1}{3}& 0\\ 0& 0& 0& \cdots & -\frac{1}{3}& \frac{2}{3}& -\frac{1}{3}\\ 0& 0& 0& \cdots & 0& -\frac{1}{3}& \frac{2}{3}\end{array}\right]}_{(i-n-1)\times (i-n-1)},\end{array}{\begin{array}{c}F=\left[\begin{array}{ccccccc}\frac{2}{3}& -\frac{1}{3}& 0& \cdots & 0& 0& 0\\ -\frac{1}{3}& \frac{2}{3}& -\frac{1}{3}& \cdots & 0& 0& 0\\ 0& -\frac{1}{3}& \frac{2}{3}& \cdots & 0& 0& 0\\ ⋮& ⋮& ⋮& \ddots & ⋮& ⋮& ⋮\\ 0& 0& 0& \cdots & \frac{2}{3}& -\frac{1}{3}& 0\\ 0& 0& 0& \cdots & -\frac{1}{3}& \frac{2}{3}& \frac{-1}{\sqrt{6}}\\ 0& 0& 0& \cdots & 0& \frac{-1}{\sqrt{6}}& \frac{1}{2}\end{array}\right]\end{array}}_{(4n+1-i)\times (4n+1-i)}.$$

By a direct calculation, we get

$$det{\mathcal{L}}_A\left[i\right]=det(C-B^{T}B)=\left\{\begin{array}{cc}\hfill \frac{1}{2}{\left(\frac{1}{3}\right)}^{3n-1},& i=n+1,i=4n+1;\hfill \\ \hfill \frac{1}{4}{\left(\frac{1}{3}\right)}^{3n-2},& n+2\le i\le 4n.\hfill \end{array}\right.$$

(6)

Together with (4)–(6) we have

$$\begin{array}{c}\hfill a_{4n}=\sum _{i=1}^{4n+1}det{\mathcal{L}}_A\left[i\right]=\sum _{i=1}^{n}det{\mathcal{L}}_A\left[i\right]+\sum _{i=n+1}^{4n+1}det{\mathcal{L}}_A\left[i\right]=\frac{10n+1}{12}{\left(\frac{1}{3}\right)}^{3n-2}.\end{array}$$

□

Claim 2.

$-a_{4n-1}=\frac{50n^3+25n^2+n}{36}{\left(\frac{1}{3}\right)}^{3n-3}.$

Proof.

One can see that $-a_{4n-1}(={(-1)}^{4n-1}{a}_{4n-1})$ is the sum of the determinants of the resulting matrix by deleting the i-th row, i-th column and the j-th row, j-th column for some $1\le i<j\le 4n+1$ in ${\mathcal{L}}_A$. That is

$$-a_{4n-1}=\sum _{1\le i<j\le 4n+1}det{\mathcal{L}}_A[i,j].$$

(7)

Case 1. $1\le i<j\le n$. In this case, deleting the i-th and j-th rows and corresponding columns of ${\mathcal{L}}_A$ is to deleting the i-th and j-th rows and corresponding columns of $I_n$, the i-th and j-th rows of $\sqrt{2}{\mathcal{L}}_{V_{01}}$ and the i-th and j-th columns of $\sqrt{2}{\mathcal{L}}_{V_{10}}$. Denote the resulting blocks, respectively, as $I_{n-2}$, $B_{(n-2)\times (3n+1)}$, $B_{(n-2)\times (3n+1)}^T$ and $C_{(3n+1)\times (3n+1)}$ and apply Lemma 2 to the resulting matrix. Then we have

$$\begin{array}{c}det{\mathcal{L}}_A[i,j]=\left|\begin{array}{cc}{I}_{n-2}& B_{(n-2)\times (3n+1)}\\ B_{(n-2)\times (3n+1)}^T& C_{(3n+1)\times (3n+1)}\end{array}\right|=|C-B^{T}B|,\end{array}$$

where

$$\begin{array}{c}C-B^{T}B={\left[\begin{array}{cccccccccc}\frac{1}{2}& -\frac{1}{\sqrt{6}}& 0& 0& 0& \cdots & 0& 0& 0& 0\\ -\frac{1}{\sqrt{6}}& \frac{2}{3}& -\frac{1}{3}& 0& 0& \cdots & 0& 0& 0& 0\\ 0& -\frac{1}{3}& \frac{2}{3}& -\frac{1}{3}& 0& \cdots & 0& 0& 0& 0\\ 0& 0& -\frac{1}{3}& \frac{2}{3}& -\frac{1}{3}& \cdots & 0& 0& 0& 0\\ 0& 0& 0& -\frac{1}{3}& 1& \cdots & 0& 0& 0& 0\\ ⋮& ⋮& ⋮& ⋮& ⋮& \ddots & ⋮& ⋮& ⋮& ⋮\\ 0& 0& 0& 0& 0& \cdots & 1& -\frac{1}{3}& 0& 0\\ 0& 0& 0& 0& 0& \cdots & -\frac{1}{3}& \frac{2}{3}& -\frac{1}{3}& 0\\ 0& 0& 0& 0& 0& \cdots & 0& -\frac{1}{3}& \frac{2}{3}& -\frac{1}{\sqrt{6}}\\ 0& 0& 0& 0& 0& \cdots & 0& 0& -\frac{1}{\sqrt{6}}& \frac{1}{2}\end{array}\right]}_{(3n+1)\times (3n+1)}\end{array},$$

and there exists one 1 on the diagonal in the $(3i-1)$-th and $(3j-1)$-th rows of $C-B^{T}B$ for $1\le i<j\le n$, respectively.

By a direct computing, we have

$$\begin{array}{c}\hfill det{\mathcal{L}}_A[i,j]=|C-B^{T}B|=\frac{1}{4}{\left(\frac{1}{3}\right)}^{3n-1}(3j-3i+2),1\le i<j\le n.\end{array}$$

(8)

Case 2. $n+1\le i<j\le 4n+1$. In this case, deleting the i-th and j-th rows and corresponding columns of ${\mathcal{L}}_A$ is to deleting the $(i-n)$-th and $(j-n)$-th rows and corresponding columns of ${\mathcal{L}}_{V_{11}}+{\mathcal{L}}_{V_{12}}$, the $(i-n)$-th and $(j-n)$-th columns of $\sqrt{2}{\mathcal{L}}_{V_{01}}$ and the $(i-n)$-th and $(j-n)$-th rows of $\sqrt{2}{\mathcal{L}}_{V_{10}}$. Similarly, denote the resulting blocks, respectively, as $C_{(3n-1)\times (3n-1)}$, $B_{n\times (3n-1)}$, $B_{n\times (3n-1)}^T$ and $I_n$. Then by Lemma 2 to the resulting matrix, we have

$$\begin{array}{c}det{\mathcal{L}}_A[i,j]=\left|\begin{array}{cc}{I}_n& B_{n\times (3n-1)}\\ B_{n\times (3n-1)}^T& C_{(3n-1)\times (3n-1)}\end{array}\right|=|C-B^{T}B|,\end{array}$$

where

$$\begin{array}{c}C-B^{T}B={\left[\begin{array}{ccc}{E}_{(i-n-1)\times (i-n-1)}& 0& 0\\ 0& F_{(j-i-1)\times (j-i-1)}& 0\\ 0& 0& G_{(4n+1-j)\times (4n+1-j)}\end{array}\right]}_{(3n-1)\times (3n-1)},\end{array}$$

and the $E,F,G$ are as follows:

$$\begin{array}{c}E={\left[\begin{array}{ccccccc}\frac{1}{2}& -\frac{1}{\sqrt{6}}& 0& \cdots & 0& 0& 0\\ -\frac{1}{\sqrt{6}}& \frac{2}{3}& -\frac{1}{3}& \cdots & 0& 0& 0\\ 0& -\frac{1}{3}& \frac{2}{3}& \cdots & 0& 0& 0\\ ⋮& ⋮& ⋮& \ddots & ⋮& ⋮& ⋮\\ 0& 0& 0& \cdots & \frac{2}{3}& -\frac{1}{3}& 0\\ 0& 0& 0& \cdots & -\frac{1}{3}& \frac{2}{3}& -\frac{1}{3}\\ 0& 0& 0& \cdots & 0& -\frac{1}{3}& \frac{2}{3}\end{array}\right]}_{(i-n-1)\times (i-n-1)},\end{array}{\begin{array}{c}F=\left[\begin{array}{ccccccc}\frac{2}{3}& -\frac{1}{3}& 0& \cdots & 0& 0& 0\\ -\frac{1}{3}& \frac{2}{3}& -\frac{1}{3}& \cdots & 0& 0& 0\\ 0& -\frac{1}{3}& \frac{2}{3}& \cdots & 0& 0& 0\\ ⋮& ⋮& ⋮& \ddots & ⋮& ⋮& ⋮\\ 0& 0& 0& \cdots & \frac{2}{3}& -\frac{1}{3}& 0\\ 0& 0& 0& \cdots & -\frac{1}{3}& \frac{2}{3}& -\frac{1}{3}\\ 0& 0& 0& \cdots & 0& -\frac{1}{3}& \frac{2}{3}\end{array}\right]\end{array}}_{(j-i-1)\times (j-i-1)},$$

$${\begin{array}{c}G=\left[\begin{array}{ccccccc}\frac{2}{3}& -\frac{1}{3}& 0& \cdots & 0& 0& 0\\ -\frac{1}{3}& \frac{2}{3}& -\frac{1}{3}& \cdots & 0& 0& 0\\ 0& -\frac{1}{3}& \frac{2}{3}& \cdots & 0& 0& 0\\ ⋮& ⋮& ⋮& \ddots & ⋮& ⋮& ⋮\\ 0& 0& 0& \cdots & \frac{2}{3}& -\frac{1}{3}& 0\\ 0& 0& 0& \cdots & -\frac{1}{3}& \frac{2}{3}& -\frac{1}{\sqrt{6}}\\ 0& 0& 0& \cdots & 0& -\frac{1}{\sqrt{6}}& \frac{1}{2}\end{array}\right]\end{array}}_{(4n+1-j)\times (4n+1-j)}.$$

By a direct calculation, we have

$$det{\mathcal{L}}_A[i,j]=det(C-B^{T}B)=\left\{\begin{array}{ccc}\hfill & \frac{1}{4}(j-i){\left(\frac{1}{3}\right)}^{3n-3},\hfill & \hfill n+2\le i<j\le 4n;\\ \hfill & \frac{1}{2}(j-n-1){\left(\frac{1}{3}\right)}^{3n-2},\hfill & \hfill i=n+1,n+2\le j\le 4n;\\ \hfill & \frac{1}{2}(4n-i+1){\left(\frac{1}{3}\right)}^{3n-2},\hfill & \hfill n+2\le i\le 4n,j=4n+1;\\ \hfill & 3n{\left(\frac{1}{3}\right)}^{3n-1},\hfill & \hfill i=n+1,j=4n+1.\end{array}\right.$$

(9)

Case 3. $1\le i\le n$, $n+1\le j\le 4n+1$. By using a similar method, deleting the i-th and j-th rows and corresponding columns of ${\mathcal{L}}_A$ is to deleting the i-th row and i-th column of $I_n$, the $(j-n)$-th row and $(j-n)$-th column of ${\mathcal{L}}_{V_{11}}+{\mathcal{L}}_{V_{12}}$, the i-th row and $(j-n)$-th column of $\sqrt{2}{\mathcal{L}}_{V_{01}}$ and the $(j-n)$-th row and i-th column of $\sqrt{2}{\mathcal{L}}_{V_{10}}$. We denote the resulting blocks, respectively, as $I_{(n-1)}$, $C_{3n\times 3n}$, $B_{(n-1)\times 3n}$ and $B_{(n-1)\times 3n}^T$ and apply Lemma 2 to the resulting matrix. Then we get

$$\begin{array}{c}det{\mathcal{L}}_A[i,j]=\left|\begin{array}{cc}{I}_{n-1}& B_{(n-1)\times 3n}\\ B_{(n-1)\times 3n}^T& C_{3n\times 3n}\end{array}\right|=|C-B^{T}B|.\end{array}$$

Subcase 3.1. If $1\le i\le n$, $j=n+1$, then the matrix $C-B^{T}B$ is

$$\begin{array}{c}{\left[\begin{array}{cccccccccc}\frac{2}{3}& -\frac{1}{3}& 0& 0& \cdots & 0& \cdots & 0& 0& 0\\ -\frac{1}{3}& \frac{2}{3}& -\frac{1}{3}& 0& \cdots & 0& \cdots & 0& 0& 0\\ 0& -\frac{1}{3}& \frac{2}{3}& -\frac{1}{3}& \cdots & 0& \cdots & 0& 0& 0\\ ⋮& ⋮& ⋮& ⋮& \ddots & ⋮& \ddots & ⋮& ⋮& ⋮\\ 0& 0& 0& 0& \cdots & 1& \cdots & 0& 0& 0\\ ⋮& ⋮& ⋮& ⋮& \ddots & ⋮& \ddots & ⋮& ⋮& ⋮\\ 0& 0& 0& 0& \cdots & 0& \cdots & \frac{2}{3}& -\frac{1}{3}& 0\\ 0& 0& 0& 0& \cdots & 0& \cdots & -\frac{1}{3}& \frac{2}{3}& -\frac{1}{\sqrt{6}}\\ 0& 0& 0& 0& \cdots & 0& \cdots & 0& -\frac{1}{\sqrt{6}}& \frac{1}{2}\end{array}\right]}_{3n\times 3n},\end{array}$$

and there is only one 1 on the diagonal in the $(3i-2)$-th row of $C-B^{T}B$ for $1\le i\le n$.

Subcase 3.2. If $1\le i\le n$, $j=4n+1$, then the matrix $C-B^{T}B$ is

$$\begin{array}{c}{\left[\begin{array}{cccccccccc}\frac{1}{2}& -\frac{1}{\sqrt{6}}& 0& 0& \cdots & 0& \cdots & 0& 0& 0\\ -\frac{1}{\sqrt{6}}& \frac{2}{3}& -\frac{1}{3}& 0& \cdots & 0& \cdots & 0& 0& 0\\ 0& -\frac{1}{3}& \frac{2}{3}& -\frac{1}{3}& \cdots & 0& \cdots & 0& 0& 0\\ ⋮& ⋮& ⋮& ⋮& \ddots & ⋮& \ddots & ⋮& ⋮& ⋮\\ 0& 0& 0& 0& \cdots & 1& \cdots & 0& 0& 0\\ ⋮& ⋮& ⋮& ⋮& \ddots & ⋮& \ddots & ⋮& ⋮& ⋮\\ 0& 0& 0& 0& \cdots & 0& \cdots & \frac{2}{3}& -\frac{1}{3}& 0\\ 0& 0& 0& 0& \cdots & 0& \cdots & -\frac{1}{3}& \frac{2}{3}& -\frac{1}{3}\\ 0& 0& 0& 0& \cdots & 0& \cdots & 0& -\frac{1}{3}& \frac{2}{3}\end{array}\right]}_{3n\times 3n},\end{array}$$

and there is only one 1 on the diagonal in the $(3i-1)$-th row of $C-B^{T}B$ for $1\le i\le n$.

Subcase 3.3. If $1\le i\le n$, $n+2\le j\le 4n$, then the matrix

$$\begin{array}{c}C-B^{T}B={\left[\begin{array}{cc}{E}_{(j-n-1)\times (j-n-1)}& 0\\ 0& F_{(4n+1-j)\times (4n+1-j)}\end{array}\right]}_{3n\times 3n},\end{array}$$

where

$$\begin{array}{c}E={\left[\begin{array}{ccccccccc}\frac{1}{2}& -\frac{1}{\sqrt{6}}& 0& \cdots & 0& \cdots & 0& 0& 0\\ -\frac{1}{\sqrt{6}}& \frac{2}{3}& -\frac{1}{3}& \cdots & 0& \cdots & 0& 0& 0\\ 0& -\frac{1}{3}& \frac{2}{3}& \cdots & 0& \cdots & 0& 0& 0\\ ⋮& ⋮& ⋮& \ddots & ⋮& \ddots & ⋮& ⋮& ⋮\\ 0& 0& 0& \cdots & 1& \cdots & 0& 0& 0\\ ⋮& ⋮& ⋮& \ddots & ⋮& \ddots & ⋮& ⋮& ⋮\\ 0& 0& 0& \cdots & 0& \cdots & \frac{2}{3}& -\frac{1}{3}& 0\\ 0& 0& 0& \cdots & 0& \cdots & -\frac{1}{3}& \frac{2}{3}& -\frac{1}{3}\\ 0& 0& 0& \cdots & 0& \cdots & 0& -\frac{1}{3}& \frac{2}{3}\end{array}\right]}_{(j-n-1)\times (j-n-1)},\end{array}$$

$$\begin{array}{c}F={\left[\begin{array}{ccccccc}\frac{2}{3}& -\frac{1}{3}& 0& \cdots & 0& 0& 0\\ -\frac{1}{3}& \frac{2}{3}& -\frac{1}{3}& \cdots & 0& 0& 0\\ 0& -\frac{1}{3}& \frac{2}{3}& \cdots & 0& 0& 0\\ ⋮& ⋮& ⋮& \ddots & ⋮& ⋮& ⋮\\ 0& 0& 0& \cdots & \frac{2}{3}& -\frac{1}{3}& 0\\ 0& 0& 0& \cdots & -\frac{1}{3}& \frac{2}{3}& -\frac{1}{\sqrt{6}}\\ 0& 0& 0& \cdots & 0& -\frac{1}{\sqrt{6}}& \frac{1}{2}\end{array}\right]}_{(4n+1-j)\times (4n+1-j)},\end{array}$$

and there is only one 1 in the $(3i-1)$-th row of E, or

$$\begin{array}{c}C-B^{T}B={\left[\begin{array}{cc}{E}_{(3i-2)\times (3i-2)}& 0\\ 0& F_{(3n-3i+2)\times (3n-3i+2)}\end{array}\right]}_{3n\times 3n},\end{array}$$

where

$$\begin{array}{c}E={\left[\begin{array}{ccccccc}\frac{1}{2}& -\frac{1}{\sqrt{6}}& 0& \cdots & 0& 0& 0\\ -\frac{1}{\sqrt{6}}& \frac{2}{3}& -\frac{1}{3}& \cdots & 0& 0& 0\\ 0& -\frac{1}{3}& \frac{2}{3}& \cdots & 0& 0& 0\\ ⋮& ⋮& ⋮& \ddots & ⋮& ⋮& ⋮\\ 0& 0& 0& \cdots & \frac{2}{3}& -\frac{1}{3}& 0\\ 0& 0& 0& \cdots & -\frac{1}{3}& \frac{2}{3}& -\frac{1}{3}\\ 0& 0& 0& \cdots & 0& -\frac{1}{3}& \frac{2}{3}\end{array}\right]}_{(3i-2)\times (3i-2)},\end{array}$$

$$\begin{array}{c}F={\left[\begin{array}{ccccccccc}\frac{2}{3}& -\frac{1}{3}& 0& \cdots & 0& \cdots & 0& 0& 0\\ -\frac{1}{3}& \frac{2}{3}& -\frac{1}{3}& \cdots & 0& \cdots & 0& 0& 0\\ 0& -\frac{1}{3}& \frac{2}{3}& \cdots & 0& \cdots & 0& 0& 0\\ ⋮& ⋮& ⋮& \ddots & ⋮& \ddots & ⋮& ⋮& ⋮\\ 0& 0& 0& \cdots & 1& \cdots & 0& 0& 0\\ ⋮& ⋮& ⋮& \ddots & ⋮& \ddots & ⋮& ⋮& ⋮\\ 0& 0& 0& \cdots & 0& \cdots & \frac{2}{3}& -\frac{1}{3}& 0\\ 0& 0& 0& \cdots & 0& \cdots & -\frac{1}{3}& \frac{2}{3}& -\frac{1}{\sqrt{6}}\\ 0& 0& 0& \cdots & 0& \cdots & 0& -\frac{1}{\sqrt{6}}& \frac{1}{2}\end{array}\right]}_{(3n-3i+2)\times (3n-3i+2)}.\end{array}$$

Hence, for $1\le i\le n$,

$$det{\mathcal{L}}_A[i,j]=det(C-B^{T}B)=\left\{\begin{array}{ccc}\hfill & \frac{1}{2}(3i-1){\left(\frac{1}{3}\right)}^{3n-1},\hfill & \hfill j=n+1;\\ \hfill & \frac{1}{2}(n-i+1){\left(\frac{1}{3}\right)}^{3n-2},\hfill & \hfill j=4n+1;\\ \hfill & \frac{1}{4}\left(\right|j-n-3i+1|+1){\left(\frac{1}{3}\right)}^{3n-2},\hfill & \hfill n+2\le j\le 4n.\end{array}\right.$$

(10)

Combining with (7)–(10), we obtain

$$\begin{array}{cc}\hfill -a_{4n-1}=& \sum _{1\le i<j\le 4n+1}det{\mathcal{L}}_A[i,j]\hfill \\ \hfill =& \sum _{1\le i<j\le n}det{\mathcal{L}}_A[i,j]+\sum _{n+1\le i<j\le 4n+1}det{\mathcal{L}}_A[i,j]+\sum _{1\le i\le n,n+1\le j\le 4n+1}det{\mathcal{L}}_A[i,j]\hfill \\ \hfill =& \frac{n^3+2n^2-3n}{8}{\left(\frac{1}{3}\right)}^{3n-1}+\frac{27n^3+9n^2+2n}{24}{\left(\frac{1}{3}\right)}^{3n-3}+\frac{18n^3+21n^2-n}{72}{\left(\frac{1}{3}\right)}^{3n-3}\hfill \\ \hfill =& \frac{50n^3+25n^2+n}{36}{\left(\frac{1}{3}\right)}^{3n-3}.\hfill \end{array}$$

□

Finally, substituting Claims 1 and 2 into (3), Lemma 5 holds directly. □

Lemma 6.

Let $0<{\beta }_1\le {\beta }_2\le \cdots \le {\beta }_{3n+1}$ be eigenvalues of ${\mathcal{L}}_S$. Then

$$\begin{array}{cc}\hfill \sum _{j=1}^{3n+1}\frac{1}{{\beta }_j}=& \frac{[(\mathrm{15,429}\sqrt{1365}+\mathrm{569,985})n+3356\sqrt{1365}+\mathrm{124,042}]{(37+\sqrt{1365})}^{n-1}}{[(5135\sqrt{1365}+\mathrm{189,735}){(37+\sqrt{1365})}^{n-1}+(5135\sqrt{1365}-\mathrm{189,735}){(37-\sqrt{1365})}^{n-1}]}\hfill \\ \hfill & +\frac{[(\mathrm{15,429}\sqrt{1365}-\mathrm{569,985})n+3356\sqrt{1365}-\mathrm{124,042}]{(37-\sqrt{1365})}^{n-1}}{[(5135\sqrt{1365}+\mathrm{189,735}){(37+\sqrt{1365})}^{n-1}+(5135\sqrt{1365}-\mathrm{189,735}){(37-\sqrt{1365})}^{n-1}]}.\hfill \end{array}$$

Proof.

Similarly, for ${\Phi }_{{\mathcal{L}}_S}\left(x\right)=x^{3n+1}+b_1{x}^{3n}+\cdots +b_{3n-1}{x}^2+b_{3n}x+b_{3n+1}$ with $b_{3n+1}\ne 0$, we know ${\beta }_1,{\beta }_2,\cdots ,{\beta }_{3n+1}$ are the roots of the ${\Phi }_{{\mathcal{L}}_S}\left(x\right)=0$. Applying Vieta’s Formulas [31], we get

$$\begin{array}{c}\hfill \sum _{j=1}^{3n+1}\frac{1}{{\beta }_j}=\frac{{\sum }_{j^{{}^{\prime }}=1}^{3n+1}{\prod }_{j=1,j\ne j^{{}^{\prime }}}^{3n+1}{\beta }_j}{{\prod }_{j=1}^{3n+1}{\beta }_j}=\frac{{(-1)}^{3n}{b}_{3n}}{det{\mathcal{L}}_S}.\end{array}$$

(11)

In order to determine ${(-1)}^{3n}{b}_{3n}$ and $det{\mathcal{L}}_S$ in (11), we consider the k order principal submatrix $W_k$ consisting of the first k rows and the first k columns of ${\mathcal{L}}_S$, $k=1,2,\dots ,3n+1$. Put $w_k:=det{W}_k$. Let’s prove the following fact first.

Fact 1. For $7\le k\le 3n$, $w_k$ satisfy the recurrence

$$w_k=\frac{37}{27}{w}_{k-3}-\frac{1}{729}{w}_{k-6},$$

with the initial conditions $w_1=\frac{3}{2},w_2=\frac{4}{3},w_3=\frac{29}{18},w_4=\frac{54}{27},w_5=\frac{295}{162},$ and $w_6=\frac{536}{243}.$

Proof.

By a direct calculation, we obtain that $w_1=\frac{3}{2},w_2=\frac{4}{3},w_3=\frac{29}{18},w_4=\frac{54}{27},w_5=\frac{295}{162},$ and $w_6=\frac{536}{243}$, expanding $det{W}_k$ with regard to its last row, we have

$$\left\{\begin{array}{ccc}\hfill w_{3i+2}& =w_{3i+1}-\frac{1}{9}{w}_{3i},\hfill & \hfill i=1,2,\dots ,n-1;\\ \hfill w_{3i}& =\frac{4}{3}{w}_{3i-1}-\frac{1}{9}{w}_{3i-2},\hfill & \hfill i=1,2,\dots ,n;\\ \hfill w_{3i+1}& =\frac{4}{3}{w}_{3i}-\frac{1}{9}{w}_{3i-1},\hfill & \hfill i=1,2,\dots ,n-1.\end{array}\right.$$

For $0\le i\le n-1$, let $e_i=w_{3i+2}$, for $1\le i\le n$, let $f_i=w_{3i}$ and for $0\le i\le n-1$, let $g_i=w_{3i+1}$. Then

$$\left\{\begin{array}{cc}\hfill e_i& =g_i-\frac{1}{9}{f}_i\hfill \\ \hfill f_i& =\frac{4}{3}{e}_{i-1}-\frac{1}{9}{g}_{i-1}\hfill \\ \hfill g_i& =\frac{4}{3}{f}_i-\frac{1}{9}{e}_{i-1}\hfill \end{array}\right..$$

Hence, $e_i=\frac{37}{27}{e}_{i-1}-\frac{1}{729}{e}_{i-2}$, $f_i=\frac{37}{27}{f}_{i-1}-\frac{1}{729}{f}_{i-2}$ and $g_i=\frac{37}{27}{g}_{i-1}-\frac{1}{729}{g}_{i-2}$. Therefore, for $7\le k\le 3n$, $w_k$ satisfies the recurrence

$$w_k=\frac{37}{27}{w}_{k-3}-\frac{1}{729}{w}_{k-6},$$

where $w_1=\frac{3}{2},w_2=\frac{4}{3},w_3=\frac{29}{18},w_4=\frac{54}{27},w_5=\frac{295}{162},$ and $w_6=\frac{536}{243}.$ □

Claim 3.

$det{\mathcal{L}}_S=\left(\frac{79}{72}+\frac{973}{24\sqrt{1365}}\right){\left(\frac{37+\sqrt{1365}}{54}\right)}^{n-1}+\left(\frac{79}{72}-\frac{973}{24\sqrt{1365}}\right){\left(\frac{37-\sqrt{1365}}{54}\right)}^{n-1}$.

Proof.

By Fact 1, the characteristic equations of $e_i$ is $x^2=\frac{37}{27}x-\frac{1}{729}$, whose roots are $x_1=\frac{37+\sqrt{1365}}{54}$, $x_2=\frac{37-\sqrt{1365}}{54}$. Suppose that $e_i=y_1{\left(\frac{37+\sqrt{1365}}{54}\right)}^i+y_2{\left(\frac{37-\sqrt{1365}}{54}\right)}^i$. Then according to the initial conditions $e_0=w_2=\frac{4}{3}$, $e_1=w_5=\frac{295}{162}$, we have the systems of equations

$$\left\{\begin{array}{cc}\hfill y_1+y_2& =\frac{4}{3}\hfill \\ \hfill y_1\frac{37+\sqrt{1365}}{54}+y_2\frac{37-\sqrt{1365}}{54}& =\frac{295}{162}\hfill \end{array}\right..$$

The only solution of this system of equations is $y_1=\frac{2}{3}+\frac{49}{2\sqrt{1365}},y_2=\frac{2}{3}-\frac{49}{2\sqrt{1365}}$, so

$$e_i=(\frac{2}{3}+\frac{49}{2\sqrt{1365}}){\left(\frac{37+\sqrt{1365}}{54}\right)}^i+(\frac{2}{3}-\frac{49}{2\sqrt{1365}}){\left(\frac{37-\sqrt{1365}}{54}\right)}^i.$$

By using a similar method, we can get $f_i$ and $g_i$ below

$$\left\{\begin{array}{cc}\hfill f_i& =\left(\frac{3}{4}+\frac{63}{4\sqrt{1365}}\right){\left(\frac{37+\sqrt{1365}}{54}\right)}^i+\left(\frac{3}{4}-\frac{63}{4\sqrt{1365}}\right){\left(\frac{37-\sqrt{1365}}{54}\right)}^i\hfill \\ \hfill g_i& =\left(\frac{3}{4}+\frac{105}{4\sqrt{1365}}\right){\left(\frac{37+\sqrt{1365}}{54}\right)}^i+\left(\frac{3}{4}-\frac{105}{4\sqrt{1365}}\right){\left(\frac{37-\sqrt{1365}}{54}\right)}^i\hfill \end{array}\right..$$

Since $w_{3i}=f_i,w_{3i+1}=g_i$ and $w_{3i+2}=e_i$, we get

$$w_i=\left\{\begin{array}{cc}\hfill & \left(\frac{3}{4}+\frac{63}{4\sqrt{1365}}\right){\left(\frac{37+\sqrt{1365}}{54}\right)}^{\frac{i}{3}}+\left(\frac{3}{4}-\frac{63}{4\sqrt{1365}}\right){\left(\frac{37-\sqrt{1365}}{54}\right)}^{\frac{i}{3}},ifi\equiv 0(mod3)\hfill \\ \hfill & \left(\frac{3}{4}+\frac{105}{4\sqrt{1365}}\right){\left(\frac{37+\sqrt{1365}}{54}\right)}^{\frac{i-1}{3}}+\left(\frac{3}{4}-\frac{105}{4\sqrt{1365}}\right){\left(\frac{37-\sqrt{1365}}{54}\right)}^{\frac{i-1}{3}},ifi\equiv 1(mod3)\hfill \\ \hfill & \left(\frac{2}{3}+\frac{49}{2\sqrt{1365}}\right){\left(\frac{37+\sqrt{1365}}{54}\right)}^{\frac{i-2}{3}}+\left(\frac{2}{3}-\frac{49}{2\sqrt{1365}}\right){\left(\frac{37-\sqrt{1365}}{54}\right)}^{\frac{i-2}{3}},ifi\equiv 2(mod3)\hfill \end{array}\right..$$

(12)

By expansion-formula, we can see $det{\mathcal{L}}_S$ with respect to its last row as

$$\begin{array}{cc}\hfill det{\mathcal{L}}_S=& \frac{3}{2}det{W}_{3n}-\frac{1}{6}det{W}_{3n-1}\hfill \\ \hfill =& \frac{3}{2}{w}_{3n}-\frac{1}{6}{w}_{3n-1}\hfill \\ \hfill =& \frac{3}{2}\left[\left(\frac{3}{4}+\frac{63}{4\sqrt{1365}}\right){\left(\frac{37+\sqrt{1365}}{54}\right)}^n+\left(\frac{3}{4}-\frac{63}{4\sqrt{1365}}\right){\left(\frac{37-\sqrt{1365}}{54}\right)}^n\right]\hfill \\ & -\frac{1}{6}\left[\left(\frac{2}{3}+\frac{49}{2\sqrt{1365}}\right){\left(\frac{37+\sqrt{1365}}{54}\right)}^{n-1}+\left(\frac{2}{3}-\frac{49}{2\sqrt{1365}}\right){\left(\frac{37-\sqrt{1365}}{54}\right)}^{n-1}\right]\hfill \\ \hfill =& \left(\frac{79}{72}+\frac{973}{24\sqrt{1365}}\right){\left(\frac{37+\sqrt{1365}}{54}\right)}^{n-1}+\left(\frac{79}{72}-\frac{973}{24\sqrt{1365}}\right){\left(\frac{37-\sqrt{1365}}{54}\right)}^{n-1}.\hfill \end{array}$$

It completes the proof of Claim 3. □

Claim 4.

$$\begin{array}{cc}\hfill {(-1)}^{3n}{b}_{3n}=& \left[\frac{\mathrm{15,429}n+3356}{4680}+\frac{\mathrm{569,985}n+\mathrm{124,042}}{4680\sqrt{1365}}\right]{\left(\frac{37+\sqrt{1365}}{54}\right)}^{n-1}\hfill \\ & +\left[\frac{\mathrm{15,429}n+3356}{4680}-\frac{\mathrm{569,985}n+\mathrm{124,042}}{4680\sqrt{1365}}\right]{\left(\frac{37-\sqrt{1365}}{54}\right)}^{n-1}.\hfill \end{array}$$

Proof.

Since ${(-1)}^{3n}{b}_{3n}$ is the sum of all those principal minors of ${\mathcal{L}}_S$ each of which is of size $3n\times 3n$, we have

$$\begin{array}{c}\hfill {(-1)}^{3n}{b}_{3n}=\sum _{i=1}^{3n+1}det{\mathcal{L}}_S\left[i\right]=\sum _{i=1}^{3n+1}\left|\begin{array}{cc}{W}_{i-1}& 0\\ 0& H\end{array}\right|=\sum _{i=1}^{3n+1}det{W}_{i-1}detH.\end{array}$$

(13)

Note that H is a $(3n+1-i)\times (3n+1-i)$ matrix obtain from $L_S$ deleting the first i rows and corresponding columns. Let $q_{3n+1-i}=detH$. Then we get $q_i=\frac{37}{27}{q}_{i-3}-\frac{1}{729}{q}_{i-6}$, where $q_1=\frac{3}{2},$$q_2=\frac{11}{6},$$q_3=\frac{5}{3},$$q_4=\frac{109}{54},$$q_5=\frac{203}{81},$$q_6=\frac{1109}{486}.$ Thus

$$q_l=\left\{\begin{array}{cc}\hfill & \left(\frac{3}{4}+\frac{69}{4\sqrt{1365}}\right){\left(\frac{37+\sqrt{1365}}{54}\right)}^{\frac{l}{3}}+\left(\frac{3}{4}-\frac{69}{4\sqrt{1365}}\right){\left(\frac{37-\sqrt{1365}}{54}\right)}^{\frac{l}{3}},ifl\equiv 0(mod3)\hfill \\ \hfill & \left(\frac{3}{4}+\frac{107}{4\sqrt{1365}}\right){\left(\frac{37+\sqrt{1365}}{54}\right)}^{\frac{l-1}{3}}+\left(\frac{3}{4}-\frac{107}{4\sqrt{1365}}\right){\left(\frac{37-\sqrt{1365}}{54}\right)}^{\frac{l-1}{3}},ifl\equiv 1(mod3)\hfill \\ \hfill & \left(\frac{11}{12}+\frac{135}{4\sqrt{1365}}\right){\left(\frac{37+\sqrt{1365}}{54}\right)}^{\frac{l-2}{3}}+\left(\frac{11}{12}-\frac{135}{4\sqrt{1365}}\right){\left(\frac{37-\sqrt{1365}}{54}\right)}^{\frac{l-2}{3}},ifl\equiv 2(mod3)\hfill \end{array}\right..$$

(14)

Therefore, by (13),

$$\begin{array}{cc}\hfill {(-1)}^{3n}{b}_{3n}& =\sum _{i=1}^{3n+1}{w}_{i-1}{q}_{3n+1-i}=\sum _{i=0}^{3n}{w}_i{q}_{3n-i}\hfill \\ \hfill & =\sum _{l=0}^n{w}_{3l}{q}_{3n-3l}+\sum _{l=0}^{n-1}{w}_{3l+1}{q}_{3n-(3l+1)}+\sum _{l=0}^{n-1}{w}_{3l+2}{q}_{3n-(3l+2)}.\hfill \end{array}$$

(15)

Combining (12) with (14), we know

$$\begin{array}{cc}\hfill \sum _{l=0}^n{w}_{3l}{q}_{3n-3l}=& \sum _{l=1}^{n-1}{w}_{3l}{q}_{3n-3l}+w_0{q}_{3n}+q_0{w}_{3n}\hfill \\ \hfill =& \sum _{l=1}^{n-1}\left[\left(\frac{3}{4}+\frac{63}{4\sqrt{1365}}\right){\left(\frac{37+\sqrt{1365}}{54}\right)}^l+\left(\frac{3}{4}-\frac{63}{4\sqrt{1365}}\right){\left(\frac{37-\sqrt{1365}}{54}\right)}^l\right]\hfill \\ \hfill & ·\left[\left(\frac{3}{4}+\frac{69}{4\sqrt{1365}}\right){\left(\frac{37+\sqrt{1365}}{54}\right)}^{n-l}+\left(\frac{3}{4}-\frac{69}{4\sqrt{1365}}\right){\left(\frac{37-\sqrt{1365}}{54}\right)}^{n-l}\right]\hfill \\ \hfill & +\left(\frac{3}{2}+\frac{132}{4\sqrt{1365}}\right){\left(\frac{37+\sqrt{1365}}{54}\right)}^n+\left(\frac{3}{2}-\frac{132}{4\sqrt{1365}}\right){\left(\frac{37-\sqrt{1365}}{54}\right)}^n\hfill \\ \hfill =& \left[\frac{369n+195}{520}+\frac{\mathrm{12,870}n+11283}{520\sqrt{1365}}\right]{\left(\frac{37+\sqrt{1365}}{54}\right)}^n\hfill \\ \hfill & +\left[\frac{369n+195}{520}-\frac{\mathrm{12,870}n+11283}{520\sqrt{1365}}\right]{\left(\frac{37-\sqrt{1365}}{54}\right)}^n,\hfill \end{array}$$

(16)

$$\begin{array}{cc}\hfill \sum _{l=0}^{n-1}{w}_{3l+1}{q}_{3n-(3l+1)}=& \sum _{l=0}^{n-1}\left[\left(\frac{3}{4}+\frac{105}{4\sqrt{1365}}\right){\left(\frac{37+\sqrt{1365}}{54}\right)}^l+\left(\frac{3}{4}-\frac{105}{4\sqrt{1365}}\right){\left(\frac{37-\sqrt{1365}}{54}\right)}^l\right]\hfill \\ \hfill & ·\left[\left(\frac{11}{12}+\frac{135}{4\sqrt{1365}}\right){\left(\frac{37+\sqrt{1365}}{54}\right)}^{n-l-1}+\left(\frac{11}{12}-\frac{135}{4\sqrt{1365}}\right){\left(\frac{37-\sqrt{1365}}{54}\right)}^{n-l-1}\right]\hfill \\ \hfill =& \left[\frac{139n+4}{104}+\frac{5135n+148}{104\sqrt{1365}}\right]{\left(\frac{37+\sqrt{1365}}{54}\right)}^{n-1}\hfill \\ \hfill & +\left[\frac{139n+4}{104}-\frac{5135n+148}{104\sqrt{1365}}\right]{\left(\frac{37-\sqrt{1365}}{54}\right)}^{n-1},\hfill \end{array}$$

(17)

and

$$\begin{array}{cc}\hfill \sum _{l=0}^{n-1}{w}_{3l+2}{q}_{3n-(3l+2)}=& \sum _{l=0}^{n-1}\left[\left(\frac{2}{3}+\frac{49}{2\sqrt{1365}}\right){\left(\frac{37+\sqrt{1365}}{54}\right)}^l+\left(\frac{2}{3}-\frac{49}{2\sqrt{1365}}\right){\left(\frac{37-\sqrt{1365}}{54}\right)}^l\right]\hfill \\ \hfill & ·\left[\left(\frac{3}{4}+\frac{107}{4\sqrt{1365}}\right){\left(\frac{37+\sqrt{1365}}{54}\right)}^{n-l-1}+\left(\frac{3}{4}-\frac{107}{4\sqrt{1365}}\right){\left(\frac{37-\sqrt{1365}}{54}\right)}^{n-l-1}\right]\hfill \\ \hfill =& \left[\frac{1529n+31}{1560}+\frac{56,485n+1147}{1560\sqrt{1365}}\right]{\left(\frac{37+\sqrt{1365}}{54}\right)}^{n-1}\hfill \\ \hfill & +\left[\frac{1529n+31}{1560}-\frac{\mathrm{56,485}n+1147}{1560\sqrt{1365}}\right]{\left(\frac{37-\sqrt{1365}}{54}\right)}^{n-1}.\hfill \end{array}$$

(18)

Hence, putting (16)–(18) into (15), Claim 4 follows immediately. □

In view of (11) and Claims 3 and 4, Lemma 6 holds directly. □

Note that $\left|E\right(Q{P}_n\left)\right|=10n+1$. Substituting Lemmas 5 and 6 into Lemma 4, we can easily obtain the following main result.

Theorem 1.

Suppose $Q{P}_n$ is a linear pentagonal derivation chain with length n. Then

$$\begin{array}{cc}\hfill K{f}^{*}\left(Q{P}_n\right)=& 2(10n+1)(-\frac{a_{4n-1}}{a_{4n}}+\frac{{(-1)}^{3n}{b}_{3n}}{det{\mathcal{L}}_S})\hfill \\ \hfill =& 100n^3+50n^2+2n\hfill \\ \hfill & +\frac{(20n+2)[(\mathrm{15,429}\sqrt{1365}+\mathrm{569,985})n+3356\sqrt{1365}+\mathrm{124,042}]{(37+\sqrt{1365})}^{n-1}}{[(5135\sqrt{1365}+\mathrm{189,735}){(37+\sqrt{1365})}^{n-1}+(5135\sqrt{1365}-\mathrm{189,735}){(37-\sqrt{1365})}^{n-1}]}\hfill \\ \hfill & +\frac{(20n+2)[(\mathrm{15,429}\sqrt{1365}-\mathrm{569,985})n+3356\sqrt{1365}-\mathrm{124,042}]{(37-\sqrt{1365})}^{n-1}}{[(5135\sqrt{1365}+\mathrm{189,735}){(37+\sqrt{1365})}^{n-1}+(5135\sqrt{1365}-\mathrm{189,735}){(37-\sqrt{1365})}^{n-1}]}.\hfill \end{array}$$

(19)

According to Theorem 1, we can have the degree-Kirchhoff indices of linear pentagonal derivation chains from $Q{P}_1$ to $Q{P}_{40}$, as shown in Table 1.

Table 1. The degree-Kirchhoff indices of linear pentagonal derivation chains from $Q{P}_1$ to $Q{P}_{40}$.

n	${\mathit{Kf}}^{*}\left({\mathit{QP}}_{\mathit{n}}\right)$	n	${\mathit{Kf}}^{*}\left({\mathit{QP}}_{\mathit{n}}\right)$	n	${\mathit{Kf}}^{*}\left({\mathit{QP}}_{\mathit{n}}\right)$	n	${\mathit{Kf}}^{*}\left({\mathit{QP}}_{\mathit{n}}\right)$
1	232.48	11	146,653.84	21	975,092.77	31	3,085,549.27
2	1283.82	12	188,906.94	22	1,118,547.63	32	3,390,205.89
3	3755.34	13	238,580.22	23	1,275,422.66	33	3,714,282.68
4	8247.04	14	296,273.67	24	1,446,317.87	34	4,058,379.65
5	15,358.91	15	362,587.30	25	1,631,833.26	35	4,423,096.79
6	25,690.96	16	438,121.11	26	1,832,568.82	36	4,809,034.11
7	39,843.19	17	523,475.09	27	2,049,124.56	37	5,216,791.60
8	58,415.59	18	619,249.25	28	2,282,100.48	38	5,646,969.27
9	82,008.16	19	726,043.58	29	2,532,096.56	39	610,0167.12
10	111,220.91	20	844,458.09	30	2,799,712.83	40	6,576,985.14

Now, we consider the explicit closed-form formula of the number of spanning trees of $Q{P}_n$. Note that

$$\begin{array}{c}\hfill \prod _{i=1}^{7n+2}{d}_i\left(Q{P}_n\right)=2^{n+4}·3^{6n-2},\left|E\left(Q{P}_n\right)\right|=10n+1.\end{array}$$

Based on Claims 1, 3 and Lemma 3, we can get the same results as the Theorem 3 [29], which further proves that the result of our calculation (Theorem 2) is correct.

Theorem 2.

Let $Q{P}_n$ denote a linear pentagonal derivation chain with length n. Then

$$\begin{array}{c}\hfill \tau \left(Q{P}_n\right)=2^{n-1}\left[\left(\frac{79}{2}+\frac{2919}{2\sqrt{1365}}\right){\left(\frac{37+\sqrt{1365}}{2}\right)}^{n-1}+\left(\frac{79}{2}-\frac{2919}{2\sqrt{1365}}\right){\left(\frac{37-\sqrt{1365}}{2}\right)}^{n-1}\right].\end{array}$$

5. A Relation between the Gutman Index and Degree-Kirchhoff of ${\mathit{QP}}_{\mathit{n}}$

At the end of this paper, we calculate the Gutman index and show that the degree-Kirchhoff index of $Q{P}_n$ is about half of its Gutman index.

Theorem 3.

Let $Q{P}_n$ denote a linear pentagonal derivation chain with length n. Then

$$\begin{array}{c}\hfill Gut\left(Q{P}_n\right)=200n^3+181n^2+31n+1.\end{array}$$

Proof.

Let the vertices of $Q{P}_n$ be labeled as in Figure 1. Recall that $Gut\left(G\right)={\sum }_{i<j}{d}_i{d}_j{d}_{ij}.$ Therefore, we evaluated $d_i{d}_j{d}_{ij}$ for all vertices, and then we summed them and divided by two. First, compute $d_i{d}_j{d}_{ij}$ for each type of vertices separately and the expression of each type of vertices are as follows:

▸ Fixed the vertices 1 or $1^{\prime }$ of $Q{P}_n$:

$$\begin{array}{cc}\hfill f_1(1,j)& =\sum _{j\ne 1}{d}_1{d}_j{d}_{1j}\hfill \\ \hfill & =2\times 2\times [3n+1+(3n+1)+\sum _{k=0}^{n-1}(3k+2)]+2\times 3\times (\sum _{k=1}^{3n-1}k+\sum _{k=2}^{3n}k)\hfill \\ \hfill & =60n^2+26n+2.\hfill \end{array}$$

▸ Fixed the vertices 2 or $2^{\prime }$ of $Q{P}_n$:

$$\begin{array}{cc}\hfill f_2(2,j)& =\sum _{j\ne 2}{d}_2{d}_j{d}_{2j}\hfill \\ \hfill & =2\times 3\times [1+(3n-1)+2+3n+\sum _{k=0}^{n-1}(3k+1)]+3\times 3\times (\sum _{k=1}^{3n-2}k+\sum _{k=2}^{3n-1}k+2)\hfill \\ \hfill & =90n^2-21n+30.\hfill \end{array}$$

▸ Fixed the vertices $3l$ or $3l^{\prime }$$(1\le l\le n)$ of $Q{P}_n$:

$$\begin{array}{cc}\hfill f_3(3l,j)=& \sum _{j\ne 3l}{d}_{3l}{d}_j{d}_{3lj}\hfill \\ \hfill =& 2\times 3\times [(3l-1)+(3n-3l+1)+(3n-3l+2)+3l+\sum _{k=0}^{l-1}(3k+2)+\sum _{k=1}^{n-l}3k]\hfill \\ \hfill & +3\times 3\times (\sum _{k=1}^{3l-2}k+\sum _{k=1}^{3n-3l}k+\sum _{k=1}^{3n-3l+1}k+\sum _{k=2}^{3l-1}k)\hfill \\ \hfill =& 90n^2+180l^2-180nl-114l+99n+21.\hfill \end{array}$$

▸ Fixed the vertices $3l+1$ or $3l+1^{\prime }$$(1\le l\le n-1)$ of $Q{P}_n$:

$$\begin{array}{cc}\hfill f_4(3l+1,j)=& \sum _{j\ne 3l+1}{d}_{3l+1}{d}_j{d}_{(3l+1)j}\hfill \\ \hfill =& 2\times 3\times [3l+(3n-3l)+(3l+1)+(3n-3l+1)+\sum _{k=1}^{l}3k+\sum _{k=0}^{n-l-1}(3k+2)]\hfill \\ \hfill & +3\times 3\times (\sum _{k=1}^{3l-1}k+\sum _{k=1}^{3n-3l-1}k+\sum _{k=1}^{3n-3l}k+\sum _{k=2}^{3l}k)\hfill \\ \hfill =& 90n^2+180l^2-180nl+6l+39n+3.\hfill \end{array}$$

▸ Fixed the vertices $3l+2$ or $3l+2^{\prime }$$(1\le l\le n-2)$ of $Q{P}_n$:

$$\begin{array}{cc}\hfill f_5(3l+2,j)=& \sum _{j\ne 3l+2}{d}_{3l+2}{d}_j{d}_{(3l+2)j}\hfill \\ \hfill =& 2\times 3\times [(3l+1)+(3n-3l-1)+(3l+2)+(3n-3l)+\sum _{k=1}^l(3k+1)+\sum _{k=0}^{n-l-1}(3k+1)]\hfill \\ \hfill & +3\times 3\times (\sum _{k=1}^{3l}k+\sum _{k=1}^{3n-3l-2}k+\sum _{k=2}^{3n-3l-1}k+\sum _{k=2}^{3l+1}k+2)\hfill \\ \hfill =& 90n^2+180l^2-180nl+126l-21n+30.\hfill \end{array}$$

▸ Fixed the vertices $3n-1$ or $3n-1^{\prime }$ of $Q{P}_n$:

$$\begin{array}{cc}\hfill f_6(3n-1,j)=& \sum _{j\ne 3n-1}{d}_{3n-1}{d}_j{d}_{(3n-1)j}\hfill \\ \hfill =& 2\times 3\times [(3n-2)+2+3+(3n-1)+\sum _{k=0}^{n-1}(3k+1)]\hfill \\ \hfill & +3\times 3\times (\sum _{k=1}^{3n-3}k+1+2+2+\sum _{k=2}^{3n-2}k)\hfill \\ \hfill =& 90n^2-75n+84.\hfill \end{array}$$

▸ Fixed the vertices $3n+1$ or $3n+1^{\prime }$ of $Q{P}_n$:

$$\begin{array}{cc}\hfill f_7(3n+1,j)=& \sum _{j\ne 3n+1}{d}_{3n+1}{d}_j{d}_{(3n+1)j}\hfill \\ \hfill & =2\times 2\times [3n+1+(3n+1)+\sum _{k=1}^{n}3k]+2\times 3\times (\sum _{k=1}^{3n-1}k+\sum _{k=2}^{3n}k)\hfill \\ \hfill & =60n^2+30n+2.\hfill \end{array}$$

▸ Fixed the vertex $1^{\circ }$ of $Q{P}_n$:

$$\begin{array}{cc}\hfill f_8(1^{\circ },j)=& \sum _{j\ne 1^{\circ }}{d}_{1^{\circ }}{d}_j{d}_{1^{\circ }j}\hfill \\ \hfill & =2\times 2\times [2\times 2+2\times 3n+\sum _{k=1}^{n-1}(3k+2)]+2\times 3\times (2\times \sum _{k=1}^{3n-1}k)\hfill \\ \hfill & =60n^2+8n+8.\hfill \end{array}$$

▸ Fixed the vertices $l^{\circ }$$(2\le l\le n-1)$ of $Q{P}_n$:

$$\begin{array}{cc}\hfill f_9(l^{\circ },j)=& \sum _{j\ne l^{\circ }}{d}_{l^{\circ }}{d}_j{d}_{l^{\circ }j}\hfill \\ \hfill =& 2\times 2\times [2\times (3l-1)+2\times (3n-3l+3)+\sum _{k=1}^{l-1}(3k+2)+\sum _{k=1}^{n-l}(3k+2)]\hfill \\ \hfill & +2\times 3\times (2\times \sum _{k=1}^{3l-2}k+2\times \sum _{k=2}^{3n-3l+2}k)\hfill \\ \hfill =& 60n^2+120l^2-120nl+128n-156l+44.\hfill \end{array}$$

▸ Fixed the vertex $n^{\circ }$ of $Q{P}_n$:

$$\begin{array}{cc}\hfill f_{10}(n^{\circ },j)=& \sum _{j\ne n^{\circ }}{d}_{n^{\circ }}{d}_j{d}_{n^{\circ }j}\hfill \\ \hfill & =2\times 2\times [2\times 3+2\times (3n-1)+\sum _{k=1}^{n-1}(3k+2)]+2\times 3\times (2\times 2+2\times \sum _{k=1}^{3n-2}k)\hfill \\ \hfill & =60n^2-28n+44.\hfill \end{array}$$

Hence,

$$\begin{array}{cc}\hfill Gut\left(Q{P}_n\right)& =\frac{1}{2}\times [2\times (f_1(1,j)+f_2(2,j)+\sum _{l=1}^n{f}_3(3l,j)+\sum _{l=1}^{n-1}{f}_4(3l+1,j)+\sum _{l=1}^{n-2}{f}_5(3l+2,j)\hfill \\ \hfill & +f_6(3n-1,j)+f_7(3n+1,j))+f_8(1^{\circ },j)+\sum _{l=2}^{n-1}{f}_9(l^{\circ },j)+f_{10}(n^{\circ },j)]\hfill \\ \hfill & =200n^3+181n^2+31n+1.\hfill \end{array}$$

□

Together with Theorems 1 and 3, Corollary 1 follows immediately.

Corollary 1.

Let $Q{P}_n$ denote a linear pentagonal derivation chain with length n. Then

$$\begin{array}{c}\hfill \underset{n\to \infty }{lim}\frac{K{f}^{*}\left(Q{P}_n\right)}{Gut\left(Q{P}_n\right)}=\frac{1}{2}.\end{array}$$

6. Conclusions

In this paper, the degree-Kirchhoff index, Gutman index and the number of spanning trees of linear pentagonal derivation chain are calculated. Moreover, we show that the degree-Kirchhoff index of the linear pentagonal derivation chain is approximately to one half of its Gutman index. For some linear chains, the method applied in this paper could be effective. But for some other family of graphs, it is difficult to obtain the closed formulas of the degree-Kirchhoff index. So we must look for new methods. This will be the direction we will study later.