Approximation Properties of the Blending-Type Bernstein–Durrmeyer Operators

Abstract

We construct the blending-type modified Bernstein–Durrmeyer operators and investigate their approximation properties. First, we derive the Voronovskaya-type asymptotic theorem for this type of operator. Then, the local and global approximation theorems are obtained by using the classical modulus of continuity and K-functional. Finally, we derive the rate of convergence for functions with a derivative of bounded variation. The results show that the new operators have good approximation properties.

1. Introduction

In [1], S. N. Bernstein constructed positive and linear operators (named after him) as Bernstein operators to prove the famous Weierstrass approximation theorem. The Bernstein operators attached to ℑ: $C_S$ (the space of continuous functions on S endowed with the max-norm $\parallel \Im \parallel =\underset{\chi \in S}{max}\left|\Im \left(\chi \right)\right|$) $\to C_S$ with $S:=[0,1]$ were defined by

$${\mathfrak{B}}_{\lambda }(\Im ;\chi )=\sum _{\nu =0}^{\lambda }{b}_{\lambda ,\nu }\left(\chi \right)\Im \left(\frac{\nu }{\lambda }\right),\chi \in S,\lambda \in {\mathbb{N}}_{+}:=\{1,2,\cdots \},$$

(1)

where $b_{\lambda ,\nu }\left(\chi \right)=\left(\genfrac{}{}{0pt}{}{\lambda }{\nu }\right){\chi }^{\nu }{(1-\chi )}^{\lambda -\nu }$, $\nu =0,1,\cdots ,\lambda$, $\Im \in C_S$. Later, many generalizations and modifications of these kinds of operators (1) have been constructed and considered, we refer the readers to these papers (see $\lambda$-Bernstein operators [2], generalized Bernstein operators [3,4], blending-type Bernstein operators [5,6,7], Durrmeyer-type Bernstein operators [8], genuine-type Bernstein operators [9,10], and so on).

In [11], F. Usta constructed a new modification of Bernstein operators attached to ℑ: $C_S\to C_S$ by means of the second-order central moments of the Bernstein operators (1) as:

$${\mathfrak{B}}_{\lambda }^{*}(\Im ;\chi )=\sum _{\nu =0}^{\lambda }{p}_{\lambda ,\nu }\left(\chi \right)\Im \left(\frac{\nu }{\lambda }\right),\chi \in S,\lambda \in {\mathbb{N}}_{+}$$

(2)

where

$$p_{\lambda ,\nu }\left(\chi \right)=\left\{\begin{array}{cc}\lambda \chi {(1-\chi )}^{\lambda -1},\hfill & \hfill \nu =0,\\ {(1-\lambda \chi )}^2{(1-\chi )}^{\lambda -2},\hfill & \hfill \nu =1,\\ \frac{1}{\lambda }{(\nu -\lambda \chi )}^2\left(\genfrac{}{}{0pt}{}{\lambda }{\nu }\right){\chi }^{\nu -1}{(1-\chi )}^{\lambda -\nu -1},\hfill & \hfill 1<\nu <\lambda -1,\\ {(\nu -\lambda \chi )}^2{\chi }^{\lambda -2},\hfill & \hfill \nu =\lambda -1,\\ \lambda (1-\chi ){\chi }^{\lambda -1},\hfill & \hfill \nu =\lambda .\end{array}\right.$$

In [12], Y. S. Wu et al. defined q-generalization of operators (2). In [13], Q. B. Cai et al. developed a Beta-type modification of operators (2). Recently, many generalizations and modifications of operators (2) were introduced and studied, we refer the readers to the articles [14,15]. Motivated by the above works, for $\Im \in C_S$, we present the blending-type modified Bernstein–Durrmeyer operators involving a strictly positive function $\theta \left(\chi \right)\in C_S$ and $\gamma >0$ as follows:

$${\mathcal{H}}_{\lambda ,\gamma }^{\theta }(\Im ;\chi )=\sum _{\nu =0}^{\lambda }{p}_{\lambda ,\nu }\left(\chi \right){\int }_0^1\frac{s^{\nu \gamma +\theta \left(\chi \right)-1}{(1-s)}^{(\lambda -\nu )\gamma +\theta \left(\chi \right)-1}}{\mathcal{B}(\nu \gamma +\theta (\chi ),(\lambda -\nu )\gamma +\theta (\chi \left)\right)}\Im \left(s\right)\mathrm{d}\mathrm{s},$$

(3)

where $\chi \in S$, $\lambda \in {\mathbb{N}}_{+}$ and Beta function $\mathcal{B}(u,v)={\int }_0^1{s}^{u-1}{(1-s)}^{v-1}\mathrm{d}\mathrm{s}$, $u,v>0$.

If we take $\gamma =\theta \left(\chi \right)=1$, then we obtain the operators defined in [13]. If we take $\theta \left(\chi \right)=1$, then we obtain the operators defined in [14].

In the rest part of the paper, we investigate the approximation properties of the operators $H_{\lambda ,\gamma }^{\theta }$. In Section 2, we yield the calculation formulas for the moment and central moment related to the operators $H_{\lambda ,\gamma }^{\theta }$. In Section 3, we yield an asymptotic formula for operators (3). In Section 4 and Section 5, we establish the local and global approximation theorems by using the classical modulus of continuity and K–functional. In Section 6, we derive the rate of convergence for functions with a derivative of bounded variation. In Section 7, we make the concluding remarks on our works. We show the advantage of the operators $H_{\lambda ,\gamma }^{\theta }$ by some numerical experiments.

2. Auxiliary Lemmas

In this section, we establish several lemmas to prove our main approximation properties for operators (3). Let $e_j\left(s\right)=s^j$, $j\in \mathbb{N}:=\{0,1,2,\cdots \}$ be the test functions, which play a key role in the study of the approximation properties of the positive linear operators.

Lemma 1. 

([12], Lemma 1 and Lemma 2, q = 1) Let $\theta \left(\chi \right)\in C_S$, $\lambda \in {\mathbb{N}}_{+}$, $\chi \in S$ and $j\in \mathbb{N}$. Then, the following relations hold:

$$\begin{array}{cc}\hfill & {\mathfrak{B}}_{\lambda }(e_0;\chi )=1,{\mathfrak{B}}_{\lambda }(e_1;\chi )=\chi ;\hfill \\ \hfill & {\mathfrak{B}}_{\lambda }(e_{j+1};\chi )=\frac{1}{\lambda }{\left({\mathfrak{B}}_{\lambda }(e_j;\chi )\right)}^{\prime }+\chi {\mathfrak{B}}_{\lambda }(e_j;\chi );\hfill \\ \hfill & {\mathfrak{B}}_{\lambda }^{*}(e_{j+1};\chi )=\frac{1}{\lambda }{\left({\left({\mathfrak{B}}_{\lambda }(e_j;\chi )\right)}^{\prime }\right)}^{\prime }+{\mathfrak{B}}_{\lambda }(e_j;\chi ).\hfill \end{array}$$

By using direct calculation, we obtain the following three lemmas.

Lemma 2. 

Let $\theta \left(\chi \right)\in C_S$, $\lambda \in {\mathbb{N}}_{+}$, $\chi \in S$ and $\gamma >0$, $e_j=s^j,j=\overline{0,4}$. We conclude

$$\begin{array}{cc}\hfill & {\mathcal{H}}_{\lambda ,\gamma }^{\theta }(e_0;\chi )=1;\hfill \\ \hfill & {\epsilon }_{\lambda ,\gamma }^{\theta }\left(\chi \right):={\mathcal{H}}_{\lambda ,\gamma }^{\theta }(e_1;\chi )=\frac{(\lambda -2)\gamma }{\lambda \gamma +2\theta \left(\chi \right)}\chi +\frac{\gamma +\theta \left(\chi \right)}{\lambda \gamma +2\theta \left(\chi \right)};\hfill \\ \hfill & {\mathcal{H}}_{\lambda ,\gamma }^{\theta }(e_2;\chi )=\frac{({\lambda }^2-7\lambda +6){\gamma }^2}{(\lambda \gamma +2\theta (\chi \left)\right)(\lambda \gamma +2\theta (\chi )+1)}{\chi }^2+\frac{(5\lambda -6){\gamma }^2+(\lambda -2)(2\theta \left(\chi \right)+1)\gamma }{(\lambda \gamma +2\theta (\chi \left)\right)(\lambda \gamma +2\theta (\chi )+1)}\chi \hfill \\ \hfill & +\frac{(\gamma +\theta (\chi \left)\right)(\gamma +\theta (\chi )+1)}{(\lambda \gamma +2\theta (\chi \left)\right)(\lambda \gamma +2\theta (\chi )+1)};\hfill \\ \hfill & {\mathcal{H}}_{\lambda ,\gamma }^{\theta }(e_3;\chi )=\frac{\lambda {\gamma }^3({\lambda }^2-15\lambda +38)}{(\lambda \gamma +2\theta (\chi \left)\right)(\lambda \gamma +2\theta (\chi )+1)(\lambda \gamma +2\theta (\chi )+2)}{\chi }^3\hfill \\ \hfill & +\frac{3\lambda {\gamma }^2(\lambda (4\gamma +\theta \left(\chi \right)+1)-(16\gamma +7\theta \left(\chi \right)+7))}{(\lambda \gamma +2\theta (t\left)\right)(\lambda \gamma +2\theta (t)+1)(\lambda \gamma +2\theta (\chi )+2)}{\chi }^2\hfill \\ \hfill & +\frac{\lambda \gamma (13{\gamma }^2+15\gamma \theta \left(\chi \right)+15\gamma +3{\theta }^2\left(\chi \right)+6\theta \left(\chi \right)+2)}{(\lambda \gamma +2\theta (\chi \left)\right)(\lambda \gamma +2\theta (\chi )+1)(\lambda \gamma +2\theta (\chi )+2)}\chi +o\left(\frac{1}{{\lambda }^2}\right);\hfill \\ \hfill & {\mathcal{H}}_{\lambda ,\gamma }^{\theta }(e_4;\chi )=\frac{{\lambda }^2{\gamma }^4({\lambda }^2-26\lambda +131)}{(\lambda \gamma +2\theta (\chi \left)\right)(\lambda \gamma +2\theta (\chi )+1)(\lambda \gamma +2\theta (\chi )+2)(\lambda \gamma +2\theta (\chi )+3)}{\chi }^4\hfill \\ \hfill & +\frac{{\lambda }^2{\gamma }^3(2\gamma (11\lambda -93)+2(\lambda -15)(2\theta \left(\chi \right)+3))}{(\lambda \gamma +2\theta (\chi \left)\right)(\lambda \gamma +2\theta (\chi )+1)(\lambda \gamma +2\theta (\chi )+2)(\lambda \gamma +2\theta (\chi )+3)}{\chi }^3\hfill \\ \hfill & +\frac{{\lambda }^2{\gamma }^2(61{\gamma }^2+24\gamma (2\theta \left(\chi \right)+3)+6{\theta }^2\left(\chi \right)+18\theta \left(\chi \right)+11)}{(\lambda \gamma +2\theta (\chi \left)\right)(\lambda \gamma +2\theta (\chi )+1)(\lambda \gamma +2\theta (\chi )+2)(\lambda \gamma +2\theta (\chi )+3)}{\chi }^2+o\left(\frac{1}{{\lambda }^2}\right).\hfill \end{array}$$

Lemma 3. 

Let $\theta \left(\chi \right)\in C_S$, $\lambda \in {\mathbb{N}}_{+}$, $\chi \in S$ and $\gamma >0$. We conclude

$$\begin{array}{cc}\hfill & A_{\lambda ,\gamma }^{\theta }\left(\chi \right):={\mathcal{H}}_{\lambda ,\gamma }^{\theta }(e_1-\chi ;\chi )=\frac{(\gamma +\theta (\chi \left)\right)(1-2\chi )}{\lambda \gamma +2\theta \left(\chi \right)};\hfill \\ \hfill & B_{\lambda ,\gamma }^{\theta }\left(\chi \right):={\mathcal{H}}_{\lambda ,\gamma }^{\theta }({(e_1-\chi )}^2;\chi )=\frac{\gamma (3\lambda \gamma +\lambda -6\gamma -4)-2\theta \left(\chi \right)(4\gamma +2\theta (\chi )+1)}{(\lambda \gamma +2\theta (\chi \left)\right)(\lambda \gamma +2\theta (\chi )+1)}\chi (1-\chi )\hfill \\ \hfill & +\frac{(\gamma +\theta (\chi \left)\right)(\gamma +\theta (\chi )+1)}{(\lambda \gamma +2\theta (\chi \left)\right)(\lambda \gamma +2\theta (\chi )+1)}.\hfill \end{array}$$

Lemma 4. 

For $\chi \in S$ and $\gamma >0$, we conclude

$$\begin{array}{cc}\hfill & \underset{\lambda \to \infty }{lim}\lambda {\mathcal{H}}_{\lambda ,\gamma }^{\theta }(e_1-\chi ;\chi )=\frac{(\gamma +\theta (\chi \left)\right)(1-2\chi )}{\gamma };\hfill \\ \hfill & \underset{\lambda \to \infty }{lim}\lambda {\mathcal{H}}_{\lambda ,\gamma }^{\theta }({(e_1-\chi )}^2;\chi )=\frac{3\gamma +1}{\gamma }\chi (1-\chi );\hfill \\ \hfill & \underset{\lambda \to \infty }{lim}{\lambda }^2{\mathcal{H}}_{\lambda ,\gamma }^{\theta }({(e_1-\chi )}^4;\chi )=\frac{3{\chi }^2{(1-\chi )}^2(5{\gamma }^2+6\gamma +1)}{{\gamma }^2}.\hfill \end{array}$$

Lemma 5. 

Let $\Im \in C_S$, $\theta \left(\chi \right)\in C_S$ and fix $\gamma >0$. Then, $\underset{\lambda \to \infty }{lim}{\mathcal{H}}_{\lambda ,\gamma }^{\theta }(\Im ;\chi )=\Im \left(\chi \right)$ holds uniformly on S.

Proof. 

Note that ${\mathcal{H}}_{\lambda ,\gamma }^{\theta }(e_0;\chi )=1$, ${\mathcal{H}}_{\lambda ,\gamma }^{\theta }(e_1;\chi )\to \chi$, ${\mathcal{H}}_{\lambda ,\gamma }^{\theta }(e_2;\chi )\to {\chi }^2$ as $\lambda \to \infty$ hold uniformly on S. Applying the classic Korovkin Theorem in [16], it follows that $\underset{\lambda \to \infty }{lim}{\mathcal{H}}_{\lambda ,\gamma }^{\theta }(\Im ;\chi )=\Im \left(\chi \right)$ holds uniformly on S.   □

Lemma 6. 

Let $\Im \in C_S$, $\theta \left(\chi \right)\in C_S$, $\lambda \in {\mathbb{N}}_{+}$ and fix $\gamma >0$. Then, we have $\parallel {\mathcal{H}}_{\lambda ,\gamma }^{\theta }(\Im )\parallel \le \parallel \Im \parallel$.

Proof. 

Using the definition of the operators ${\mathcal{H}}_{\lambda ,\gamma }^{\theta }$ and taking Lemma 2 into account, it follows

$$\left|{\mathcal{H}}_{\lambda ,\gamma }^{\theta }(\Im ;\chi )\right|\le \parallel \Im \parallel {\mathcal{H}}_{\lambda ,\gamma }^{\theta }(e_0;\chi )=\parallel \Im \parallel .$$

□

3. Voronovskaya-Type Asymptotic Theorem

In this section, we establish the following Voronovskaya-type asymptotic theorem for the operators ${\mathcal{H}}_{\lambda ,\gamma }^{\theta }$.

Theorem 1. 

Let $\Im \in C_S$, $\theta \left(\chi \right)\in C_S$ and $\gamma >0$. If ${\Im }^{″}$ exists at a point $\chi \in S$, then the following relation holds:

$$\underset{\lambda \to \infty }{lim}\lambda ({\mathcal{H}}_{\lambda ,\gamma }^{\theta }(\Im ;\chi )-\Im \left(\chi \right))=\frac{(\gamma +\theta (\chi \left)\right)(1-2\chi )}{\gamma }{\Im }^{\prime }\left(\chi \right)+\frac{3\gamma +1}{2\gamma }\chi (1-\chi ){\Im }^{″}\left(\chi \right).$$

Proof. 

By using Taylor’s expansion formula for the function ℑ, we get

$$\Im \left(s\right)=\Im \left(\chi \right)+{\Im }^{\prime }\left(\chi \right)(s-\chi )+\frac{1}{2}{\Im }^{″}\left(\chi \right){(s-\chi )}^2+\eta (s;\chi ){(s-\chi )}^2,$$

(4)

where

$$\eta (s;\chi )=\left\{\begin{array}{cc}\frac{\Im \left(s\right)-\Im \left(\chi \right)-{\Im }^{\prime }\left(\chi \right)(s-\chi )-\frac{1}{2}{\Im }^{″}\left(\chi \right){(s-\chi )}^2}{{(s-\chi )}^2},\hfill & \hfill s\ne \chi ;\\ 0,\hfill & \hfill s=\chi .\end{array}\right.$$

Using L’Hospital’s Rule, we have

$$\underset{s\to \chi }{lim}\eta (s;\chi )=\frac{1}{2}\underset{s\to \chi }{lim}\frac{{\Im }^{\prime }\left(s\right)-{\Im }^{\prime }\left(\chi \right)}{s-\chi }-\frac{1}{2}{\Im }^{″}\left(\chi \right)=0.$$

Thus, $\eta (s;\chi )\in C_S.$ Then, we obtain the following equality by applying the new operators ${\mathcal{H}}_{\lambda ,\gamma }^{\theta }$ to both sides of (4),

$${\mathcal{H}}_{\lambda ,\gamma }^{\theta }(\Im ;\chi )-\Im \left(\chi \right)={\Im }^{\prime }\left(\chi \right){\mathcal{H}}_{\lambda ,\gamma }^{\theta }(s-\chi ;\chi )+\frac{{\Im }^{″}\left(\chi \right)}{2}{\mathcal{H}}_{\lambda ,\gamma }^{\theta }({(s-\chi )}^2;\chi )+{\mathcal{H}}_{\lambda ,\gamma }^{\theta }(\eta (s;\chi ){(s-\chi )}^2;\chi ).$$

(5)

Multiplying (5) by $\lambda$ and taking the limit as $\lambda \to \infty$, we obtain

$$\begin{array}{cc}\hfill \underset{\lambda \to \infty }{lim}\lambda ({\mathcal{H}}_{\lambda ,\gamma }^{\theta }(\Im ;\chi )-\Im \left(\chi \right))& =\underset{\lambda \to \infty }{lim}\lambda {\Im }^{\prime }\left(\chi \right){\mathcal{H}}_{\lambda ,\gamma }^{\theta }(s-\chi ;\chi )+\underset{\lambda \to \infty }{lim}\lambda \frac{{\Im }^{″}\left(\chi \right)}{2}{\mathcal{H}}_{\lambda ,\gamma }^{\theta }({(s-\chi )}^2;\chi )\hfill \\ \hfill & +\underset{\lambda \to \infty }{lim}\lambda {\mathcal{H}}_{\lambda ,\gamma }^{\theta }(\eta (s;\chi ){(s-\chi )}^2;\chi ).\hfill \end{array}$$

By Lemma 4, we write

$$\begin{array}{c}\hfill \begin{array}{c}\hfill \underset{\lambda \to \infty }{lim}\lambda ({\mathcal{H}}_{\lambda ,\gamma }^{\theta }(\Im ;\chi )-\Im \left(\chi \right))=\frac{(\gamma +\theta (\chi \left)\right)(1-2\chi )}{\gamma }{\Im }^{\prime }\left(\chi \right)+\frac{3\gamma +1}{2\gamma }\chi (1-\chi ){\Im }^{″}\left(\chi \right)\\ \hfill +\underset{\lambda \to \infty }{lim}\lambda {\mathcal{H}}_{\lambda ,\gamma }^{\theta }(\eta (s;\chi ){(s-\chi )}^2;\chi ).\end{array}\end{array}$$

(6)

Applying the Cauchy–Buniakowsky–Schwarz inequality to the last term of (6), we have

$$\left|\lambda {\mathcal{H}}_{\lambda ,\gamma }^{\theta }(\eta (s;\chi ){(s-\chi )}^2;\chi )\right|\le \sqrt{{\mathcal{H}}_{\lambda ,\gamma }^{\theta }({\eta }^2(s;\chi );\chi )}\sqrt{{\lambda }^2{\mathcal{H}}_{\lambda ,\gamma }^{\theta }({(s-\chi )}^4;\chi )}.$$

(7)

Meanwhile, it is known from Lemma 4 that the term ${\lambda }^2{\mathcal{H}}_{\lambda ,\gamma }^{\theta }({(s-\chi )}^4;\chi )$ is bounded as $\lambda \to \infty$. On the other hand, ${\eta }^2(.;\chi )$ is continuous at $s\in S$ and $\underset{s\to \chi }{lim}{\eta }^2(s;\chi )=0$. Hence, by Lemma 5, we can deduce that

$$\underset{\lambda \to \infty }{lim}{\mathcal{H}}_{\lambda ,\gamma }^{\theta }({\eta }^2(s;\chi );\chi )={\eta }^2(\chi ;\chi )=0.$$

(8)

Therefore, from (7) and (8), we have

$$\underset{\lambda \to \infty }{lim}\lambda {\mathcal{H}}_{\lambda ,\gamma }^{\theta }(\eta (s;\chi ){(s-\chi )}^2;\chi )=0.$$

(9)

Combining (6) with (9), we get the desired result.   □

4. Local Approximation

In this section, we study the local approximation properties for the newly defined operators ${\mathcal{H}}_{\lambda ,\gamma }^{\theta }(\Im ;\chi )$ in terms of the modulus of continuity, Peetre’s K-functional, the Steklov mean function and the elements of Lipschitz function class. For $\Im \in C_S$, the classical modulus ${\omega }_1$ and the second-order modulus ${\omega }_2$ of ℑ are defined respectively by:

$$\begin{array}{c}\hfill {\omega }_1(\Im ;\sigma )=\underset{0<s\le \sigma }{sup}\underset{\chi ,\chi +s\in S}{sup}|\Im (\chi +s)-\Im \left(\chi \right)|,\\ \hfill {\omega }_2(\Im ;\sqrt{\sigma })=\underset{0<s\le \sqrt{\sigma }}{sup}\underset{\chi ,\chi +2s\in S}{sup}|\Im (\chi +2s)-2\Im (\chi +s)+\Im \left(\chi \right)|.\end{array}$$

The Peetre’s K-functional is given by

$$K_2(\Im ;\sigma )=\underset{\eta ,{\eta }^{″}\in C_S}{inf}\{\parallel \Im -\eta \parallel +\sigma \parallel {\eta }^{″}\parallel :\eta \in W^2\},\forall \Im \in C_S,\sigma >0.$$

It is known from [16] that

$$K_2(\Im ;\sigma )\le M{\omega }_2(\Im ;\sqrt{\sigma }),$$

(10)

where $M>0$ is a constant depending only on ℑ.

For $\Im \in C_S$ and $\sigma \in S$, the Steklov mean function is defined by

$${\Im }_{\sigma }\left(\chi \right)=\frac{4}{{\sigma }^2}{\int }_0^{\frac{\sigma }{2}}{\int }_0^{\frac{\sigma }{2}}(2\Im (\chi +x+y)-\Im (\chi +2(x+y)))\mathrm{d}x\mathrm{d}y.$$

From direct calculation, we have (i) $\parallel {\Im }_{\sigma }-\Im \parallel \le {\omega }_2(\Im ;\sigma )$.

(ii) ${\Im }_{\sigma }^{\prime },{\Im }_{\sigma }^{″}\in C_S$ and $\parallel {\Im }_{\sigma }^{\prime }\parallel \le \frac{5}{\sigma }\omega (\Im ;\sigma ),\parallel {\Im }_{\sigma }^{″}\parallel \le \frac{9}{{\sigma }^2}{\omega }_2(\Im ;\sigma )$.

In [17], Lenze introduced the following Lipschitz-type maximal function of order $\varrho$ for a function $\Im \in C_S$ as

$${\omega }_{\varrho }(\Im ;\chi )=\underset{s\ne \chi ,s\in S}{sup}\frac{|\Im (s)-\Im (\chi \left)\right|}{{|s-\chi |}^{\varrho }},\chi \in S\mathrm{and}\varrho \in (0,1].$$

(11)

In [18], M. A. Özarslan and H. Aktuğlu defined the following Lipschitz-type space involving two parameters ${\kappa }_1,{\kappa }_2\in [0,\infty )$ as

$${\mathrm{Lip}}_M^{{\kappa }_1,{\kappa }_2}\left(\varrho \right)=\left\{\Im \in C_B:|\Im \left(s\right)-\Im \left(\chi \right)|\le M_2\frac{{|s-\chi |}^{\varrho }}{(s+{\kappa }_1{\chi }^2+{\kappa }_2\chi )};s\in S,\chi \in (0,1]\right\},$$

where $\varrho \in (0,1]$ and $M_2$ is a positive constant depending at most on $\Im ,{\kappa }_1,{\kappa }_2$ and $\varrho$.

Now, we prove the following theorems on the local approximation properties of operators (3).

Theorem 2. 

Let $\Im \in C_S$, $\theta \left(\chi \right)\in C_S$, $\lambda \in {\mathbb{N}}_{+}$, $\gamma >0$ and $\chi \in S$. We have

$$|{\mathcal{H}}_{\lambda ,\gamma }^{\theta }(\Im ;\chi )-\Im \left(\chi \right)|\le 2{\omega }_1\left(\Im ;\sqrt{B_{\lambda ,\gamma }^{\theta }\left(\chi \right)}\right).$$

Proof. 

By using the property of ${\omega }_1$, we derive

$$|\Im \left(s\right)-\Im \left(\chi \right)|\le {\omega }_1(\Im ;\sigma )\left(\frac{{(s-\chi )}^2}{{\sigma }^2}+1\right).$$

Combining the linearity and the monotonicity of operators (3), we have

$$\begin{array}{cc}\hfill \left|{\mathcal{H}}_{\lambda ,\gamma }^{\theta }(\Im ;\chi )-\Im \left(\chi \right)\right|& \le {\mathcal{H}}_{\lambda ,\gamma }^{\theta }\left(|\Im (s)-\Im (\chi \left)\right|;\chi \right)\hfill \\ \hfill & \le {\omega }_1(\Im ;\sigma )\left(1+\frac{1}{{\sigma }^2}{\mathcal{H}}_{\lambda ,\gamma }^{\theta }\left({(s-\chi )}^2;\chi \right)\right).\hfill \end{array}$$

Choosing $\sigma =\sqrt{B_{\lambda ,\gamma }^{\theta }\left(\chi \right)}$, we get the desired result.   □

Theorem 3. 

Let ${\Im }^{\prime }\in C_S$, $\theta \left(\chi \right)\in C_S$, $\lambda \in {\mathbb{N}}_{+}$, $\gamma >0$ and $\chi \in S$. We have

$$|{\mathcal{H}}_{\lambda ,\gamma }^{\theta }(\Im ;\chi )-\Im \left(\chi \right)|\le |A_{\lambda ,\gamma }^{\theta }\left(\chi \right)\left|\right|{\Im }^{\prime }\left(\chi \right)|+2\sqrt{B_{\lambda ,\gamma }^{\theta }\left(\chi \right)}{\omega }_1({\Im }^{\prime };\sqrt{B_{\lambda ,\gamma }^{\theta }\left(\chi \right)}).$$

Proof. 

For any $s,\chi \in S$, we have

$$\Im \left(s\right)-\Im \left(\chi \right)={\Im }^{\prime }\left(\chi \right)(s-\chi )+{\int }_{\chi }^s({\Im }^{\prime }\left(x\right)-{\Im }^{\prime }\left(\chi \right))\mathrm{d}x.$$

Applying the operators ${\mathcal{H}}_{\lambda ,\gamma }^{\theta }(.;\chi )$ on both sides of the above equality, we can write

$${\mathcal{H}}_{\lambda ,\gamma }^{\theta }(\Im \left(s\right)-\Im \left(\chi \right);\chi )={\Im }^{\prime }\left(\chi \right){\mathcal{H}}_{\lambda ,\gamma }^{\theta }(s-\chi ;\chi )+{\mathcal{H}}_{\lambda ,\gamma }^{\theta }\left({\int }_{\chi }^s({\Im }^{\prime }\left(x\right)-{\Im }^{\prime }\left(\chi \right))\mathrm{d}x;\chi \right).$$

By using the property of ${\omega }_1$, we derive

$$|\Im \left(s\right)-\Im (\chi |\le {\omega }_1(\Im ;\sigma )\left(\frac{|s-\chi |}{\sigma }+1\right),\sigma >0.$$

Then, we have

$$\left|{\int }_{\chi }^s({\Im }^{\prime }\left(x\right)-{\Im }^{\prime }\left(\chi \right))\mathrm{d}x\right|\le {\omega }_1({\Im }^{\prime };\sigma )\left(\frac{{(s-\chi )}^2}{\sigma }+|s-\chi |\right).$$

It follows that

$$\begin{array}{cc}\hfill \left|{\mathcal{H}}_{\lambda ,\gamma }^{\theta }(\Im ;\chi )-\Im \left(\chi \right)\right|& \le |{\Im }^{\prime }\left(\chi \right)\left|\right|{\mathcal{H}}_{\lambda ,\gamma }^{\theta }(s-\chi ;\chi )|\hfill \\ \hfill & +{\omega }_1({\Im }^{\prime };\sigma )\left\{\frac{1}{\sigma }{\mathcal{H}}_{\lambda ,\gamma }^{\theta }({(s-\chi )}^2;\chi )+{\mathcal{H}}_{\lambda ,\gamma }^{\theta }\left(\right|s-\chi |;\chi )\right\}.\hfill \end{array}$$

Hence, by using the Cauchy–Buniakowsky–Schwarz inequality, we have

$$\begin{array}{cc}\hfill |{\mathcal{H}}_{\lambda ,\gamma }^{\theta }(\Im ;\chi )-\Im \left(\chi \right)|& \le |{\Im }^{\prime }\left(\chi \right)\left|\right|{\mathcal{H}}_{\lambda ,\gamma }^{\theta }(s-\chi ;\chi )|\hfill \\ \hfill & +{\omega }_1({\Im }^{\prime };\sigma )\left\{\frac{1}{\sigma }\sqrt{{\mathcal{H}}_{\lambda ,\gamma }^{\theta }({(s-\chi )}^2;\chi )}+1\right\}\sqrt{{\mathcal{H}}_{\lambda ,\gamma }^{\theta }({(s-\chi )}^2;\chi )}.\hfill \end{array}$$

Now, choosing $\sigma =\sqrt{B_{\lambda ,\gamma }^{\theta }\left(\chi \right)}$, we get the desired inequality.   □

Theorem 4. 

Let $\Im \in C_S$, $\theta \left(\chi \right)\in C_S$, $\lambda \in {\mathbb{N}}_{+}$, $\gamma >0$ and $\chi \in S$. Then, there exists a constant $M_1=4M$ such that for any $\chi \in S$

$$|{\mathcal{H}}_{\lambda ,\gamma }^{\theta }(\Im ;\chi )-\Im \left(\chi \right)|\le M_1{\omega }_2\left(\Im ;\frac{1}{2}{\delta }_{\lambda ,\gamma }^{\theta }\left(\chi \right)\right),+{\omega }_1\left(\Im ;|A_{\lambda ,\gamma }^{\theta }\left(\chi \right)|\right),$$

where ${\delta }_{\lambda ,\gamma }^{\theta }\left(\chi \right)=\sqrt{B_{\lambda ,\gamma }^{\theta }\left(\chi \right)+{\left(A_{\lambda ,\gamma }^{\theta }\left(\chi \right)\right)}^2}$.

Proof. 

For any $\lambda \in {\mathbb{N}}_{+},\gamma >0$ and $\chi \in S$, we construct the auxiliary operators as follows:

$${\Omega }_{\lambda ,\gamma }^{\theta }(\Im ;\chi )={\mathcal{H}}_{\lambda ,\gamma }^{\theta }(\Im ;\chi )+\Im \left(\chi \right)-\Im \left({\epsilon }_{\lambda ,\gamma }^{\theta }\left(\chi \right)\right).$$

(12)

Then, we can easily check that

$$\begin{array}{cc}\hfill {\Omega }_{\lambda ,\gamma }^{\theta }(e_0;\chi )& ={\mathcal{H}}_{\lambda ,\gamma }^{\theta }(e_0;\chi )=1,\hfill \\ \hfill {\Omega }_{\lambda ,\gamma }^{\theta }(e_1;\chi )& ={\mathcal{H}}_{\lambda ,\gamma }^{\theta }(e_1;\chi )+\chi -{\epsilon }_{\lambda ,\gamma }^{\theta }\left(\chi \right)=\chi .\hfill \end{array}$$

For any ${\pi }^{″}\in C_S$ and $s,\chi \in S$, by using Taylor’s expansion formula, we have

$$\pi \left(s\right)-\pi \left(\chi \right)={\pi }^{\prime }\left(\chi \right)(s-\chi )+{\int }_{\chi }^s(s-x){\pi }^{″}\left(x\right)\mathrm{d}x.$$

Applying the operators ${\Omega }_{\lambda ,\gamma }^{\theta }$ on both sides of the above equality, we can write

$${\Omega }_{\lambda ,\gamma }^{\theta }(\pi ;\chi )=\pi \left(\chi \right)+{\Omega }_{\lambda ,\gamma }^{\theta }\left({\int }_{\chi }^s(s-x){\pi }^{″}\left(x\right)\mathrm{d}x;\chi \right).$$

Therefore, we have

$${\Omega }_{\lambda ,\gamma }^{\theta }(\pi ;\chi )=\pi \left(\chi \right)+{\mathcal{H}}_{\lambda ,\gamma }^{\theta }\left({\int }_{\chi }^s(s-x){\pi }^{″}\left(x\right)\mathrm{d}x;\chi \right)-{\int }_{\chi }^{{\epsilon }_{\lambda ,\gamma }^{\theta }\left(\chi \right)}({\epsilon }_{\lambda ,\gamma }^{\theta }\left(\chi \right)-x){\pi }^{″}\left(x\right)\mathrm{d}x.$$

On the other hand,

$$|{\int }_{\chi }^s(s-x){\pi }^{″}{\left(x\right)\mathrm{d}x|\le (s-\chi )}^2\parallel {\pi }^{″}\parallel .$$

This means that

$$\begin{array}{cc}\hfill |{\Omega }_{\lambda ,\gamma }^{\theta }(\pi ;\chi )-\pi \left(\chi \right)|& \le \left|{\mathcal{H}}_{\lambda ,\gamma }^{\theta }({\int }_{\chi }^s(s-x){\pi }^{″}\left(x\right)\mathrm{d}x;\chi )\right|+|{\int }_{\chi }^{{\epsilon }_{\lambda ,\gamma }^{\theta }\left(\chi \right)}({\epsilon }_{\lambda ,\gamma }^{\theta }\left(\chi \right)-x){\pi }^{″}\left(x\right)\mathrm{d}x|\hfill \\ \hfill & \le {\mathcal{H}}_{\lambda ,\gamma }^{\theta }({(s-\chi )}^2;\chi )\parallel {\pi }^{″}\parallel +{({\epsilon }_{\lambda ,\gamma }^{\theta }\left(\chi \right)-\chi )}^2\parallel {\pi }^{″}\parallel \hfill \\ \hfill & \le (B_{\lambda ,\gamma }^{\theta }\left(\chi \right)+{\left(A_{\lambda ,\gamma }^{\theta }\left(\chi \right)\right)}^2)\parallel {\pi }^{″}\parallel .\hfill \end{array}$$

In view of (12) and Lemma 6, we obtain

$$|{\Omega }_{\lambda ,\gamma }^{\theta }(\Im ;\chi )|\le |{\mathcal{H}}_{\lambda ,\gamma }^{\theta }(\Im ;\chi )|+|\Im \left(\chi \right)|+|\Im \left({\epsilon }_{\lambda ,\gamma }^{\theta }\left(\chi \right)\right)|\le 3\parallel \Im \parallel .$$

(13)

Furthermore, using the definition (12) of the operators ${\Omega }_{\lambda ,\gamma }^{\theta }$ and (13), we obtain that

$$\begin{array}{cc}\hfill |{\mathcal{H}}_{\lambda ,\gamma }^{\theta }(\Im ;\chi )-\Im \left(\chi \right)|& =|{\Omega }_{\lambda ,\gamma }^{\theta }(\Im ;\chi )-\Im \left(\chi \right)+\Im \left({\epsilon }_{\lambda ,\gamma }^{\theta }\left(\chi \right)\right)-\Im \left(\chi \right)|\hfill \\ \hfill & \le |{\Omega }_{\lambda ,\gamma }^{\theta }(\Im -\pi ;\chi )|+|{\Omega }_{\lambda ,\gamma }^{\theta }(\pi ;\chi )-\pi \left(\chi \right)|\hfill \\ \hfill & +|\pi \left(\chi \right)-\Im \left(\chi \right)|+|\Im ({\epsilon }_{\lambda ,\gamma }^{\theta }\left(\chi \right))-\Im \left(\chi \right)|\hfill \\ \hfill & \le 4\parallel \Im -\pi \parallel +{\left({\epsilon }_{\lambda ,\gamma }^{\theta }\left(\chi \right)\right)}^2\parallel {\pi }^{″}\parallel +{\omega }_1(\Im ;|A_{\lambda ,\gamma }^{\theta }\left(\chi \right)\left|\right).\hfill \end{array}$$

Taking the infimum on the right-hand side over all ${\pi }^{″}\in C_S$ and combining inequality (10), we have

$$\begin{array}{cc}\hfill |{\mathcal{H}}_{\lambda ,\gamma }^{\theta }(\Im ;\chi )-\Im \left(\chi \right)|& \le 4K_2\left(\Im ;\frac{1}{4}{\left({\epsilon }_{\lambda ,\gamma }^{\theta }\left(\chi \right)\right)}^2\right)+{\omega }_1(\Im ;|A_{\lambda ,\gamma }^{\theta }\left(\chi \right)\left|\right)\hfill \\ \hfill & \le M_1{\omega }_2\left(\Im ;\frac{1}{2}{\epsilon }_{\lambda ,\gamma }^{\theta }\left(\chi \right)\right)+{\omega }_1(\Im ;|A_{\lambda ,\gamma }^{\theta }\left(\chi \right)\left|\right).\hfill \end{array}$$

Then, the proof of Theorem 4 is completed.   □

Theorem 5. 

Let $\Im \in C_S$, $\theta \left(\chi \right)\in C_S$, $\lambda \in {\mathbb{N}}_{+}$, $\gamma >0$ and $\chi \in S$. Then, we have

$$|{\mathcal{H}}_{\lambda ,\gamma }^{\theta }(\Im ;\chi )-\Im \left(\chi \right)|\le 5\sqrt{\lambda }\left|A_{\lambda ,\gamma }^{\theta }\left(t\right)\right|{\omega }_1\left(\Im ;\frac{1}{\sqrt{\lambda }}\right)+\left(\frac{9}{2}\lambda B_{\lambda ,\gamma }^{\theta }\left(\chi \right)+2\right){\omega }_2\left(\Im ;\frac{1}{\sqrt{\lambda }}\right).$$

Proof. 

For $\chi ,\sigma ,\chi +\sigma \in S$, using the definition of the Steklov mean, we obtain

$$|{\mathcal{H}}_{\lambda ,\gamma }^{\theta }(\Im ;\chi )-\Im \left(\chi \right)|\le {\mathcal{H}}_{\lambda ,\gamma }^{\theta }\left(\right|\Im -{\Im }_{\sigma }|;\chi )+|{\mathcal{H}}_{\lambda ,\gamma }^{\theta }({\Im }_{\sigma }-{\Im }_{\sigma }\left(\chi \right);\chi )|+|{\Im }_{\sigma }\left(\chi \right)-\Im \left(\chi \right)|.$$

Using property (i) of the Steklov mean and Lemma 6, we obtain

$$|{\mathcal{H}}_{\lambda ,\gamma }^{\theta }\left(\right|\Im -{\Im }_{\sigma }|;\chi )\le \parallel {\mathcal{H}}_{\lambda ,\gamma }^{\theta }\left(\right|\Im -{\Im }_{\sigma }\left|\right)\parallel |\le \parallel \Im -{\Im }_{\sigma }\parallel \le {\omega }_2(\Im ;\sigma ).$$

It follows from Taylor’s expansion formula that

$${\Im }_{\sigma }\left(s\right)={\Im }_{\sigma }\left(\chi \right)+{\Im }_{\sigma }^{\prime }\left(\chi \right)(s-\chi )+{\int }_{\chi }^s(s-x){\Im }_{\sigma }^{″}\left(x\right)\mathrm{d}x.$$

Again using property (i) of the Steklov mean and Lemma 6, we get

$$\begin{array}{cc}\hfill |{\mathcal{H}}_{\lambda ,\gamma }^{\theta }({\Im }_{\sigma };\chi )-{\Im }_{\sigma }\left(\chi \right)|& \le |{\mathcal{H}}_{\lambda ,\gamma }^{\theta }({\Im }_{\sigma }^{\prime }\left(\chi \right)(s-\chi );\chi )|+\left|{\mathcal{H}}_{\lambda ,\gamma }^{\theta }\left({\int }_{\chi }^s(s-x){\Im }_{\sigma }^{″}\left(x\right)\mathrm{d}x;\chi \right)\right|\hfill \\ \hfill & \le \parallel {\Im }_{\sigma }^{\prime }\parallel |{\mathcal{H}}_{\lambda ,\gamma }^{\theta }((s-\chi );\chi )|+\parallel {\Im }_{\sigma }^{″}\parallel \left|{\mathcal{H}}_{\lambda ,\gamma }^{\theta }\left({\int }_{\chi }^s(s-x)\mathrm{d}x;\chi \right)\right|\hfill \\ \hfill & \le \parallel {\Im }_{\sigma }^{\prime }\parallel |A_{\lambda ,\gamma }^{\theta }\left(\chi \right)|+\frac{1}{2}\parallel {\Im }_{\sigma }^{″}\parallel |B_{\lambda ,\gamma }^{\theta }\left(\chi \right)|\hfill \\ \hfill & \le \frac{5}{\sigma }\left|A_{\lambda ,\gamma }^{\theta }\left(\chi \right)\right|{\omega }_1(\Im ;\sigma )+\frac{9}{2{\sigma }^2}\left|B_{\lambda ,\gamma }^{\theta }\left(\chi \right)\right|{\omega }_2(\Im ;\sigma ).\hfill \end{array}$$

Hence, we have

$$|{\mathcal{H}}_{\lambda ,\gamma }^{\theta }({\Im }_{\sigma };\chi )-{\Im }_{\sigma }\left(\chi \right)|\le \frac{5}{\sigma }\left|A_{\lambda ,\gamma }^{\theta }\left(\chi \right)\right|{\omega }_1(\Im ;\sigma )+\left(\frac{9}{2{\sigma }^2}\left|B_{\lambda ,\gamma }^{\theta }\left(\chi \right)\right|+2\right){\omega }_2(\Im ;\sigma ).$$

(14)

Choosing $\sigma =\frac{1}{\sqrt{\lambda }}$, the proof of Theorem 5 is completed.   □

Theorem 6. 

Let $\varrho \in (0,1]$. If $\Im \in {\mathrm{Lip}}_M^{{\kappa }_1,{\kappa }_2}\left(\varrho \right)$, then we have

$$|{\mathcal{H}}_{\lambda ,\gamma }^{\theta }(\Im ;\chi )-\Im \left(\chi \right)|\le M_2{\left(\frac{B_{\lambda ,\gamma }^{\theta }\left(\chi \right)}{{\kappa }_1{\chi }^2+{\kappa }_2\chi }\right)}^{\frac{\varrho }{2}}.$$

Proof. 

We first deal with the case $\varrho =1$. We obtain

$$\begin{array}{cc}\hfill & |{\mathcal{H}}_{\lambda ,\gamma }^{\theta }(\Im ;\chi )-\Im \left(\chi \right)|\hfill \\ \hfill & \le \sum _{\nu =0}^{\lambda }{p}_{\lambda ,\nu }\left(\chi \right){\int }_0^1|\Im \left(s\right)-\Im \left(\chi \right)|\left(\frac{s^{\nu \gamma +\theta \left(\chi \right)-1}{(1-s)}^{(\lambda -\nu )\gamma +\theta \left(\chi \right)-1}}{\mathcal{B}(\nu \gamma +\theta ,(\lambda -\nu )\gamma +\theta (\chi \left)\right)}\right)\mathrm{d}s\hfill \\ \hfill & \le M_2\sum _{\nu =0}^{\lambda }{p}_{\lambda ,\nu }\left(\chi \right){\int }_0^1\frac{|s-\chi |}{\sqrt{s+{\kappa }_1{\chi }^2+{\kappa }_2\chi }}\left(\frac{s^{\nu \gamma +\theta \left(\chi \right)-1}{(1-s)}^{(\lambda -\nu )\gamma +\theta \left(\chi \right)-1}}{\mathcal{B}(\nu \gamma +\theta ,(\lambda -\nu )\gamma +\theta (\chi \left)\right)}\right)\mathrm{d}s.\hfill \end{array}$$

Using the fact that $\frac{1}{\sqrt{s+{\kappa }_1{\chi }^2+{\kappa }_2\chi }}<\frac{1}{\sqrt{{\kappa }_1{\chi }^2+{\kappa }_2\chi }}$ and the Cauchy–Buniakowsky–Schwarz inequality, we have

$$\begin{array}{cc}\hfill & |{\mathcal{H}}_{\lambda ,\gamma }^{\theta }(\Im ;\chi )-\Im \left(\chi \right)|\hfill \\ \hfill & \le \frac{M_2}{\sqrt{{\kappa }_1{\chi }^2+{\kappa }_2\chi }}\sum _{\nu =0}^{\lambda }{p}_{\lambda ,\nu }\left(\chi \right){\int }_0^1|s-\chi |\left(\frac{s^{\nu \gamma +\theta \left(\chi \right)-1}{(1-s)}^{(\lambda -\nu )\gamma +\theta \left(\chi \right)-1}}{\mathcal{B}(\nu \gamma +\theta ,(\lambda -\nu )\gamma +\theta (\chi \left)\right)}\right)\mathrm{d}s\hfill \\ \hfill & =\frac{M_2}{\sqrt{{\kappa }_1{\chi }^2+{\kappa }_2\chi }}{\mathcal{H}}_{\lambda ,\gamma }^{\theta }\left(\right|s-\chi |,\chi )\le M_2{\left(\frac{B_{\lambda ,\gamma }^{\theta }\left(\chi \right)}{{\kappa }_1{\chi }^2+{\kappa }_2\chi }\right)}^{\frac{1}{2}}.\hfill \end{array}$$

Thus, the inequality is obtained for $\varrho =1$. Next, we prove the inequality for the case $0<\varrho <1$. Applying the Hölder’s inequality with $p=\frac{2}{\varrho }$ and $q=\frac{2}{2-\varrho }$, we get

$$\begin{array}{cc}\hfill & |{\mathcal{H}}_{\lambda ,\gamma }^{\theta }(\Im ;\chi )-\Im \left(\chi \right)|\hfill \\ \hfill & \le \sum _{\nu =0}^{\lambda }{p}_{\lambda ,\nu }\left(\chi \right){\int }_0^1|\Im \left(s\right)-\Im \left(\chi \right)|\left(\frac{s^{\nu \gamma +\theta \left(\chi \right)-1}{(1-s)}^{(\lambda -\nu )\gamma +\theta \left(\chi \right)-1}}{\mathcal{B}(\nu \gamma +\theta ,(\lambda -\nu )\gamma +\theta (\chi \left)\right)}\right)\mathrm{d}s\hfill \\ \hfill & \le \sum _{\nu =0}^{\lambda }{p}_{\lambda ,\nu }\left(\chi \right){\left({{\int }_0^1|\Im \left(s\right)-\Im \left(\chi \right)|}^{\frac{2}{\varrho }}\left(\frac{s^{\nu \gamma +\theta \left(\chi \right)-1}{(1-s)}^{(\lambda -\nu )\gamma +\theta \left(\chi \right)-1}}{\mathcal{B}(\nu \gamma +\theta (\chi ),(\lambda -\nu )\gamma +\theta (\chi \left)\right)}\right)\mathrm{d}s\right)}^{\frac{\varrho }{2}}\hfill \\ \hfill & \le {\left\{\sum _{\nu =0}^{\lambda }{p}_{\lambda ,\nu }\left(\chi \right){{\int }_0^1|\Im \left(s\right)-\Im \left(\chi \right)|}^{\frac{2}{\varrho }}\left(\frac{s^{\nu \gamma +\theta \left(\chi \right)-1}{(1-s)}^{(\lambda -\nu )\gamma +\theta \left(\varrho \right)-1}}{\mathcal{B}(\nu \gamma +\theta ,(\lambda -\nu )\gamma +\theta (\varrho \left)\right)}\right)\mathrm{d}s\right\}}^{\frac{\varrho }{2}}\hfill \\ \hfill & \times {\left(\sum _{\nu =0}^{\lambda }{p}_{\lambda ,\nu }\left(\chi \right){\int }_0^1\left(\frac{s^{\nu \gamma +\theta \left(\chi \right)-1}{(1-s)}^{(\lambda -\nu )\gamma +\theta \left(\chi \right)-1}}{\mathcal{B}(\nu \gamma +\theta ,(\lambda -\nu )\gamma +\theta (\chi \left)\right)}\right)\mathrm{d}s\right)}^{\frac{2-\varrho }{2}}\hfill \\ \hfill & ={\left(\sum _{\nu =0}^{\lambda }{p}_{\lambda ,\nu }\left(\chi \right){\int }_0^1{|\Im \left(s\right)-\Im \left(\chi \right)|}^{\frac{2}{\varrho }}\left(\frac{s^{\nu \gamma +\theta \left(\chi \right)-1}{(1-s)}^{(\lambda -\nu )\gamma +\theta \left(\chi \right)-1}}{\mathcal{B}(\nu \gamma +\theta ,(\lambda -\nu )\gamma +\theta (\chi \left)\right)}\right)\mathrm{d}s\right)}^{\frac{\varrho }{2}}\hfill \\ \hfill & \le M_2{\left(\sum _{\nu =0}^{\lambda }{p}_{\lambda ,\nu }\left(\chi \right){\int }_0^1\frac{{(s-\chi )}^2}{(s+{\kappa }_1{\upsilon }^2+{\kappa }_2\chi )}\left(\frac{s^{\nu \gamma +\theta \left(\chi \right)-1}{(1-s)}^{(\lambda -\nu )\gamma +\theta \left(\chi \right)-1}}{\mathcal{B}(\nu \gamma +\theta ,(\lambda -\nu )\gamma +\theta (\chi \left)\right)}\right)\mathrm{d}s\right)}^{\frac{\varrho }{2}}\hfill \\ \hfill & \le \frac{M_2}{{({\kappa }_1{\chi }^2+{\kappa }_2\chi )}^{\frac{\chi }{2}}}{\left(\sum _{\nu =0}^{\lambda }{p}_{\lambda ,\nu }\left(\chi \right){\int }_0^1{(s-\chi )}^2\left(\frac{s^{\nu \gamma +\theta \left(\chi \right)-1}{(1-s)}^{(\lambda -\nu )\gamma +\theta \left(\chi \right)-1}}{\mathcal{B}(\nu \gamma +\theta ,(\lambda -\nu )\gamma +\theta (\chi \left)\right)}\right)\mathrm{d}s\right)}^{\frac{\varrho }{2}}\hfill \\ \hfill & =\frac{M_2}{{({\kappa }_1{\chi }^2+{\kappa }_2\chi )}^{\frac{\varrho }{2}}}{\left({\mathcal{H}}_{\lambda ,\gamma }^{\theta }({(s-\chi )}^2;\chi )\right)}^{\frac{\varrho }{2}}=M_2{\left(\frac{B_{\lambda ,\gamma }^{\theta }\left(\chi \right)}{({\kappa }_1{\chi }^2+{\kappa }_2\chi )}\right)}^{\frac{\varrho }{2}}.\hfill \end{array}$$

Hence, the desired result is obtained.   □

Theorem 7. 

Let $\Im \in C_S$ and $0<\varrho \le 1$. Then, for all $\chi \in S$, we have

$$|{\mathcal{H}}_{\lambda ,\gamma }^{\theta }(\Im ;\chi )-\Im \left(\chi \right)|\le {\omega }_{\varrho }(\Im ;\chi ){\left(B_{\lambda ,\gamma }^{\theta }\left(\chi \right)\right)}^{\frac{\varrho }{2}}.$$

Proof. 

By (11), we have

$$|{\mathcal{H}}_{\lambda ,\gamma }^{\theta }(\Im ;\chi )-\Im \left(\chi \right)|\le {\omega }_{\varrho }(\Im ;\chi ){\mathcal{H}}_{\lambda ,\gamma }^{\theta }{\left(\right|s-\chi |}^{\varrho };\chi ).$$

Applying the Hölder’s inequality with $p=\frac{2}{\varrho }$ and $q=\frac{2}{2-\varrho }$, we obtain

$$\begin{array}{cc}\hfill |{\mathcal{H}}_{\lambda ,\gamma }^{\theta }(\Im ;\chi )-\Im \left(\chi \right)|& \le {\omega }_{\varrho }(\Im ;\chi )({\mathcal{H}}_{\lambda ,\gamma }^{\theta }{\left(\right|s-\chi |}^2;\chi {\left)\right)}^{\frac{\rho }{2}}\hfill \\ \hfill & \le {\omega }_{\varrho }(\Im ;\chi ){\left(B_{\lambda ,\gamma }^{\theta }\left(\chi \right)\right)}^{\frac{\varrho }{2}}.\hfill \end{array}$$

□

5. Global Approximation

In this section, we yield a theorem on the global approximation properties of operators (3) by using the weighted first- and second-order modulus of smoothness. Let us define the space of functions $W^2\left(\psi \right)=\{\pi \in C_S:{\pi }^{\prime }\in {\mathrm{AC}}_{loc}[0,1],{\psi }^2{\pi }^{″}\in C_S\}$, where ${\pi }^{\prime }\in {\mathrm{AC}}_{loc}[0,1]$ means that $\pi$ is differentiable and ${\pi }^{\prime }$ is absolutely continuous on every closed interval $[c,d]\subset (0,1)$. Let $\Im \in C_S$ and $\sigma >0$. The weighted K-functional is defined by

$$K_2^{\psi }(\Im ;\sigma )=inf\{\parallel \Im -\pi \parallel +\sigma \parallel {\psi }^2{\pi }^{″}\parallel +{\sigma }^2\parallel {\pi }^{″}\parallel :\pi \in W^2\left(\psi \right)\}.$$

The weighted first- and second-order modulus of smoothness are defined by

$${\omega }_1^{\ell }(\Im ;\sigma )=\underset{0<s\le \sigma }{sup}\underset{\chi ,\chi +s\ell \left(\chi \right)\in S}{sup}|\Im (\chi +s\ell \left(\chi \right))-\Im \left(\chi \right)|,$$

and

$${\omega }_2^{\psi }(\Im ;\sqrt{\sigma })=\underset{0<s\le \sqrt{\sigma }}{sup}\underset{\chi ,\chi +s\psi \left(\chi \right)\in S}{sup}|\Im (\chi +s\psi \left(\chi \right))-2\Im \left(\chi \right)+\Im (\chi -s\psi \left(\chi \right))|,$$

where $\psi$ and ℓ above are admissible step-weight functions defined on S. By [19], there exists a constant $M>0$, such that

$$K_2^{\psi }(\Im ;\sigma )\le M{\omega }_2^{\psi }(\Im ;\sqrt{\sigma }).$$

(15)

Our next result is the following theorem.

Theorem 8. 

Let $\Im \in C_S$, $\theta \left(\chi \right)\in C_S$, $\lambda \in {\mathbb{N}}_{+}$, $\gamma >0$ and $\chi \in S$. Then

$$|{\mathcal{H}}_{\lambda ,\gamma }^{\theta }(\Im ;\chi )-\Im \left(\chi \right)|\le M_3{\omega }_2^{\psi }\left(\Im ;\frac{1}{\sqrt{\lambda \gamma }}\right)+{\omega }_1^{\ell }\left(\Im ;\frac{1}{\lambda \gamma }\right),$$

where $\psi \left(\chi \right)=\sqrt{\chi (1-\chi )}$, $\ell \left(\chi \right)=(\gamma +\theta (\chi \left)\right)|1-2\chi |$, $\chi \in S$ and $M_3>0$ is a constant.

Proof. 

Again, considering the auxiliary operators defined at (12) and for $\pi \in W^2\left(\psi \right)$, applying the operators ${\mathcal{H}}_{\lambda ,\gamma }^{\theta }$ on both sides of the inequality mentioned above, we have

$$|{\Omega }_{\lambda ,\gamma }^{\theta }(\pi ;\chi )-\pi \left(\chi \right)|\le {\mathcal{H}}_{\lambda ,\gamma }^{\theta }\left({\int }_{\chi }^s|s-\mu ||{\pi }^{″}\left(\mu \right)|\mathrm{d}\mu ;\chi \right)+{\int }_{\chi }^{{\epsilon }_{\lambda ,\gamma }^{\theta }\left(\chi \right)}|{\epsilon }_{\lambda ,\gamma }^{\theta }\left(\chi \right)-\mu \left|\right|{\pi }^{″}\left(\mu \right)|\mathrm{d}\mu .$$

(16)

Since ${\mathsf{\Lambda }}_{\lambda }\left(\chi \right)={\phi }^2\left(\chi \right)+\frac{1}{\lambda \gamma }$ is concave function on S, taking $\mu =\epsilon \chi +(1-\epsilon )s$, with $\epsilon \in [0,1]$ and $s<\mu <\chi$, we have

$$\frac{|s-\mu |}{{\mathsf{\Lambda }}_{\lambda }\left(\mu \right)}=\frac{\epsilon |s-\chi |}{{\mathsf{\Lambda }}_{\lambda }(\epsilon \chi +(1-\epsilon )s)}\le \frac{\epsilon |s-\chi |}{\epsilon {\mathsf{\Lambda }}_{\lambda }\left(\chi \right)+(1-\epsilon ){\mathsf{\Lambda }}_{\lambda }\left(s\right)}\le \frac{|s-\chi |}{{\mathsf{\Lambda }}_{\lambda }\left(\chi \right)}.$$

(17)

On the other hand, we observe that

$$|{\int }_{\chi }^s|s-\mu |{\pi }^{″}\left(\mu \right)\mathrm{d}\mu |=\left|{\int }_{\chi }^s\frac{|s-\mu |}{{\mathsf{\Lambda }}_{\lambda }\left(\mu \right)}{\pi }^{″}\left(\mu \right){\mathsf{\Lambda }}_{\lambda }\left(\mu \right)\mathrm{d}\mu \right|\le \frac{\parallel {\mathsf{\Lambda }}_{\lambda }{\pi }^{″}\parallel }{{\mathsf{\Lambda }}_{\lambda }\left(\chi \right)}{(s-\chi )}^2.$$

(18)

Combining (16)–(18), we have

$$\begin{array}{cc}\hfill |{\Omega }_{\lambda ,\gamma }^{\theta }(\pi ;\chi )-\pi \left(\chi \right)|& \le \frac{1}{{\mathsf{\Lambda }}_{\lambda }\left(\chi \right)}{\mathcal{H}}_{\lambda ,\gamma }^{\theta }({(x-\chi )}^2;\chi )\parallel {\mathsf{\Lambda }}_{\lambda }{\pi }^{″}\parallel \hfill \\ \hfill & +\frac{1}{{\mathsf{\Lambda }}_{\lambda }\left(\chi \right)}{\left(\frac{(\gamma +\theta (\chi \left)\right)(1-2\chi )}{\lambda \gamma +2\theta \left(\chi \right)}\right)}^2\parallel {\mathsf{\Lambda }}_{\lambda }{\pi }^{″}\parallel \hfill \\ \hfill & \le \frac{{(\gamma +\theta \left(\chi \right))}^2}{\lambda \gamma }\parallel {\mathsf{\Lambda }}_{\lambda }{\pi }^{″}\parallel .\hfill \end{array}$$

Applying the definition of $K_2^{\psi }(\Im ;\sigma )$ in this section, we find

$$|{\Omega }_{\lambda ,\gamma }^{\theta }(\Im ;\chi )-\Im \left(\chi \right)|\le \frac{{(\gamma +\theta \left(\chi \right))}^2}{\lambda \gamma }\left(\parallel {\psi }^2{\Im }^{″}\parallel +\frac{1}{\lambda \gamma }\parallel {\Im }^{″}\parallel \right).$$

Further, for $\Im \in C_S$, since the operators ${\Omega }_{\lambda ,\gamma }^{\theta }(\Im ;\chi )$ are uniformly bounded, using the above inequality, we have

$$\begin{array}{cc}\hfill |{\mathcal{H}}_{\lambda ,\gamma }^{\theta }(\Im ;\chi )-\Im \left(\chi \right)|& \le |{\Omega }_{\lambda ,\gamma }^{\theta }(\Im -\pi ;\chi )|+|{\Omega }_{\lambda ,\gamma }^{\theta }(\pi ;\chi )-\pi \left(\chi \right)|+|\Im \left(\chi \right)-\pi \left(\chi \right)|\hfill \\ \hfill & +|\Im \left(\frac{(\lambda -2)\gamma \chi +\gamma +\theta \left(\chi \right)}{\lambda \gamma +2\theta \left(\chi \right)}\right)-\Im \left(\chi \right)|\hfill \\ \hfill & \le 4{(\gamma +\theta \left(\chi \right))}^2\left(\parallel \Im -\pi \parallel +\left(\frac{1}{\lambda \gamma }\parallel {\psi }^2{\Im }^{″}\parallel +\frac{1}{{\lambda }^2{\gamma }^2}\parallel {\Im }^{″}\parallel \right)\right)\hfill \\ \hfill & +\left|\Im \left(\frac{(\lambda -2)\gamma \chi +\gamma +\theta \left(\chi \right)}{\lambda \gamma +2\theta \left(\chi \right)}\right)-\Im \left(\chi \right)\right|.\hfill \end{array}$$

Taking infimum over all $\pi \in W^2\left(\psi \right)$, we get

$$|{\mathcal{H}}_{\lambda ,\gamma }^{\theta }(\Im ;\chi )-\Im \left(\chi \right)|\le M_3{K}_2^{\psi }\left(\Im ;\frac{1}{\lambda \gamma }\right)+\left|\Im \left(\frac{(\lambda -2)\gamma \chi +\gamma +\theta \left(\chi \right)}{\lambda \gamma +2\theta \left(\chi \right)}\right)-\Im \left(\chi \right)\right|.$$

(19)

As for the last part above, we find

$$\begin{array}{cc}\hfill \left|\Im \left(\frac{(\lambda -2)\gamma \chi +\gamma +\theta \left(\chi \right)}{\lambda \gamma +2\theta \left(\chi \right)}\right)-\Im \left(\chi \right)\right|& =\left|\Im \left(\chi +\ell \left(\chi \right)\frac{(r+\theta (\chi \left)\right)(1-2\chi )}{\ell \left(\chi \right)(\lambda \gamma +2\theta (\chi \left)\right)}\right)-\Im \left(\chi \right)\right|\hfill \\ \hfill & \le \underset{x\in S}{sup}\left|\Im \left(x+\ell \left(x\right)\frac{(r+\theta (\chi \left)\right)(1-2\chi )}{\ell \left(\chi \right)(\lambda \gamma +2\theta (\chi \left)\right)}\right)-\Im \left(x\right)\right|\hfill \\ \hfill & \le {\omega }_1^{\ell }\left(\Im ;\frac{(r+\theta (\chi \left)\right)(1-2\chi )}{\ell \left(\chi \right)(\lambda \gamma +2\theta (\chi \left)\right)}\right)\hfill \\ \hfill & \le {\omega }_1^{\ell }\left(\Im ;\frac{1}{\lambda \gamma +2\theta \left(\chi \right)}\right)\le {\omega }_1^{\ell }\left(\Im ;\frac{1}{\lambda \gamma }\right).\hfill \end{array}$$

Combining (19) with the above results, we complete the proof of Theorem 8.   □

6. Rate of Convergence

The goal of this section is to study the convergence rate of ${\mathcal{H}}_{\lambda ,\gamma }^{\theta }(\Im ;\chi )$ for functions with a derivative of bounded variation on S. Let $DVB[0,1]$ denote the class of absolutely continuous functions defined on $[0,1]$, whose derivatives have bounded variation on $[0,1]$. It is well known that the functions $\Im \in DVB[0,1]$ possess a representation:

$$\Im \left(\chi \right)={\int }_0^{\chi }\pi \left(s\right)\mathrm{d}s+\Im \left(0\right),$$

where $\pi$ is a function with bounded variation on $[0,1]$. An integral representation of the operators ${\mathcal{H}}_{\lambda ,\gamma }^{\theta }$ can be given as follows:

$${\mathcal{H}}_{\lambda ,\gamma }^{\theta }(\Im ;\chi )={\int }_0^1{\mathbb{R}}_{\lambda ,\gamma }^{\theta }(\chi ;s)\Im \left(s\right)\mathrm{d}s,\chi \in S,$$

(20)

where the kernel ${\mathbb{R}}_{\lambda ,\gamma }^{\theta }(\chi ;s)={\displaystyle \sum _{\nu =0}^{\lambda }}{p}_{\lambda ,\nu }\left(\chi \right)\frac{s^{\nu \gamma +\theta \left(\chi \right)-1}{(1-s)}^{(\lambda -\nu )\gamma +\theta \left(\chi \right)-1}}{\beta (\nu \gamma +\theta (\chi ),(\lambda -\nu )\gamma +\theta (\chi \left)\right)}$.

Lemma 7. 

For a sufficiently large λ and a fixed $\chi \in (0,1)$, we have

(a) 

${\varpi }_{\lambda }(\chi ;y)={\int }_0^y{\mathbb{R}}_{\lambda ,\gamma }^{\theta }(\chi ;s)\mathrm{d}s\le \frac{B_{\lambda ,\gamma }^{\theta }\left(\chi \right)}{{(\chi -y)}^2},0\le y<\chi ,$

(b) 

$1-{\varpi }_{\lambda }(\chi ;z)={\int }_z^1{\mathbb{R}}_{\lambda ,\gamma }^{\theta }(\chi ;s)\mathrm{d}s\le \frac{B_{\lambda ,\gamma }^{\theta }\left(\chi \right)}{{(z-\chi )}^2},\chi <z<1$.

Proof. 

We prove (a) as follows.

By Lemma 3, we have

$$\begin{array}{cc}\hfill {\varpi }_{\lambda }(\chi ;y)& ={\int }_0^y{\mathbb{R}}_{\lambda ,\gamma }^{\theta }(\chi ;s)\mathrm{d}s\le {\int }_0^y{\left(\frac{\chi -s}{\chi -y}\right)}^2{\mathbb{R}}_{\lambda ,\gamma }^{\theta }(\chi ;s)\mathrm{d}s\hfill \\ \hfill & ={\mathcal{H}}_{\lambda ,\gamma }^{\theta }({(s-\chi )}^2;\chi ){(\chi -y)}^{-2}=\frac{B_{\lambda ,\gamma }^{\theta }\left(\chi \right)}{{(\chi -y)}^2}.\hfill \end{array}$$

The proof of (b) is similar to that of (a). We omit the details.   □

Theorem 9. 

Let $\Im \in DBV[0,1]$. Then, for every $\chi \in (0,1)$ and sufficiently large λ, the following inequality

$$\begin{array}{cc}\hfill |{\mathcal{H}}_{\lambda ,\gamma }^{\theta }(\Im ;\chi )-\Im \left(\chi \right)|& \le \frac{1}{2}|{\Im }^{\prime }(\chi +)+{\Im }^{\prime }(\chi -)||A_{\lambda ,\gamma }^{\theta }\left(\chi \right)|+\frac{1}{2}|{\Im }^{\prime }(\chi +)-{\Im }^{\prime }(\chi -)|\sqrt{B_{\lambda ,\gamma }^{\theta }\left(\chi \right)}\hfill \\ \hfill & +B_{\lambda ,\gamma }^{\theta }\left(\chi \right){\chi }^{-1}\sum _{j=1}^{\left[\sqrt{\lambda }\right]}\underset{\chi -\chi /j}{\overset{\chi }{\bigvee }}\left({\Im }_{\chi }^{\prime }\right)+\frac{\chi }{\sqrt{\lambda }}\underset{\chi -\chi /\sqrt{\lambda }}{\overset{\chi }{\bigvee }}\left({\Im }_{\chi }^{\prime }\right)\hfill \\ \hfill & +\frac{B_{\lambda ,\gamma }^{\theta }\left(\chi \right)}{1-\chi }\sum _{j=1}^{\left[\sqrt{\lambda }\right]}\underset{\chi }{\overset{\chi +(1-\chi )/j}{\bigvee }}\left({\Im }_{\chi }^{\prime }\right)+\frac{(1-\chi )}{\sqrt{\lambda }}\underset{\chi }{\overset{\chi +(1-\chi )/\sqrt{\lambda }}{\bigvee }}\left({\Im }_{\chi }^{\prime }\right)\hfill \end{array}$$

holds, where ${\bigvee }_a^b\left({\Im }_{\chi }^{\prime }\right)$ is the total variation of ${\Im }_{\chi }^{\prime }$ on $[a,b]$ and ${\Im }_{\chi }^{\prime }$ is defined by

$${\Im }_{\chi }^{\prime }\left(s\right)=\left\{\begin{array}{cc}{\Im }^{\prime }\left(s\right)-{\Im }^{\prime }(\chi -),\hfill & \hfill 0\le s<\chi ,\\ 0,\hfill & \hfill s=\chi ,\\ {\Im }^{\prime }\left(s\right)-{\Im }^{\prime }(\chi +),\hfill & \hfill \chi <s<1.\end{array}\right.$$

(21)

Proof. 

Since $H_{\lambda ,\gamma }^{\theta }(e_0;\chi )=1$, by (20), for each $\chi \in (0,1)$, we get

$$\begin{array}{cc}\hfill {\mathcal{H}}_{\lambda ,\gamma }^{\theta }(\Im ;\chi )-\Im \left(\chi \right)& ={\int }_0^1{\mathbb{R}}_{\lambda ,\gamma }^{\theta }(\chi ;s)(\Im \left(s\right)-\Im \left(\chi \right))\mathrm{d}s\hfill \\ \hfill & ={\int }_0^1{\mathbb{R}}_{\lambda ,\gamma }^{\theta }(\chi ;s){\int }_{\chi }^s{\Im }^{\prime }\left(u\right)\mathrm{d}u\mathrm{d}s.\hfill \end{array}$$

On the other hand, for any $\Im \in DBV[0,1]$, by (21), we decompose ${\Im }^{\prime }\left(u\right)$ as follows

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill {\Im }^{\prime }\left(u\right)& ={\Im }_{\chi }^{\prime }\left(u\right)+\frac{1}{2}({\Im }^{\prime }(\chi +)+{\Im }^{\prime }(\chi -))+\frac{1}{2}({\Im }^{\prime }(\chi +)-{\Im }^{\prime }(\chi -))\mathrm{sgn}(u-\chi )\hfill \\ \hfill & +{\delta }_{\chi }\left(u\right)\left({\Im }^{\prime }\left(u\right)-\frac{1}{2}({\Im }^{\prime }(\chi +)+{\Im }^{\prime }(\chi -))\right),\hfill \end{array}\end{array}$$

(22)

where

$${\delta }_{\chi }\left(u\right)=\left\{\begin{array}{cc}1,\hfill & \hfill u=\chi ,\\ 0,\hfill & \hfill u\ne \chi .\end{array}\right.$$

Therefore, we have

$${\int }_0^1\left({\int }_{\chi }^s\left({\Im }^{\prime }\left(u\right)-\frac{1}{2}({\Im }^{\prime }(\chi +)+{\Im }^{\prime }(\chi -))\right){\delta }_{\chi }\left(u\right)\mathrm{d}u\right){\mathbb{R}}_{\lambda ,\gamma }^{\theta }(\chi ;s)\mathrm{d}s=0.$$

(23)

From (20), we have

$$\begin{array}{c}\hfill \begin{array}{c}\hfill {\int }_0^1\left({\int }_{\chi }^s\frac{1}{2}\left({\Im }^{\prime }(\chi +)+{\Im }^{\prime }(\chi -)\right)\mathrm{d}u\right){\mathbb{R}}_{\lambda ,\gamma }^{\theta }(\chi ;s)\mathrm{d}s=\frac{1}{2}({\Im }^{\prime }(\chi +)+{\Im }^{\prime }(\chi -)){\mathcal{H}}_{\lambda ,\gamma }^{\theta }\left((s-\chi );s\right),\end{array}\end{array}$$

(24)

meanwhile, we have

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill & \left|{\int }_0^1{\mathbb{R}}_{\lambda ,\gamma }^{\theta }(\chi ;s)\left({\int }_{\chi }^s\frac{1}{2}({\Im }^{\prime }(\chi +)-{\Im }^{\prime }(\chi -))\mathrm{sgn}(u-\chi )\mathrm{d}u\right)\mathrm{d}s\right|\hfill \\ \hfill & \le \frac{1}{2}|{\Im }^{\prime }(\chi +)-{\Im }^{\prime }(\chi -)|{\int }_0^1|s-\chi |{\mathbb{R}}_{\lambda ,\gamma }^{\theta }(\chi ;s)\mathrm{d}s\hfill \\ \hfill & \le \frac{1}{2}|{\Im }^{\prime }(\chi +)-{\Im }^{\prime }(\chi -)|{\mathcal{H}}_{\lambda ,\gamma }^{\theta }\left(\right|s-\chi |;\chi )\hfill \\ \hfill & \le \frac{1}{2}|f^{\prime }(\chi +)-{\Im }^{\prime }(\chi -)|{\left({\mathcal{H}}_{\lambda ,\gamma }^{\theta }{(s-\chi )}^2;\chi \right)}^{\frac{1}{2}}.\hfill \end{array}\end{array}$$

(25)

Using Lemma 3 and considering (22)–(25), we obtain

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill |{\mathcal{H}}_{\lambda ,\gamma }^{\theta }(\Im ;\chi )-\Im \left(\chi \right)|& \le \frac{1}{2}|{\Im }^{\prime }(\chi +)+{\Im }^{\prime }(\chi -)||A_{\lambda ,\gamma }^{\theta }\left(\chi \right)|+\frac{1}{2}|{\Im }^{\prime }(\chi +)-{\Im }^{\prime }(\chi -)|\sqrt{B_{\lambda ,\gamma }^{\theta }\left(\chi \right)}\hfill \\ \hfill & +\left|{\int }_0^{\chi }\left({\int }_{\chi }^s{\Im }_{\chi }^{\prime }\left(u\right)\mathrm{d}u\right){\mathbb{R}}_{\lambda ,\gamma }^{\theta }(\chi ;s)\mathrm{d}s+{\int }_{\chi }^1\left({\int }_{\chi }^s{\Im }_{\chi }^{\prime }\left(u\right)\mathrm{d}u\right){\mathbb{R}}_{\lambda ,\gamma }^{\theta }(\chi ;s)\mathrm{d}s\right|.\hfill \end{array}\end{array}$$

(26)

Now, let

$${\mathfrak{E}}_{\lambda ,\gamma }^{\theta }({\Im }_{\chi }^{\prime };\chi )={\int }_0^{\chi }\left({\int }_{\chi }^s{\Im }_{\chi }^{\prime }\left(u\right)\mathrm{d}u\right){\mathbb{R}}_{\lambda ,\gamma }^{\theta }(\chi ;s)\mathrm{d}s,$$

$${\mathfrak{F}}_{\lambda ,\gamma }^{\theta }({\Im }_{\chi }^{\prime };\chi )={\int }_{\chi }^1\left({\int }_{\chi }^s{\Im }_{\chi }^{\prime }\left(u\right)\mathrm{d}u\right){\mathbb{R}}_{\lambda ,\gamma }^{\theta }(\chi ;s)\mathrm{d}s.$$

Thus, our task is to estimate the terms ${\mathfrak{E}}_{\lambda ,\gamma }^{\theta }({\Im }_{\chi }^{\prime };\chi )$ and ${\mathfrak{F}}_{\lambda ,\gamma }^{\theta }({\Im }_{\chi }^{\prime };\chi )$.

From the definition of ${\varpi }_{\lambda }(\chi ;s)$, we write

$$\left|{\mathfrak{E}}_{\lambda ,\gamma }^{\theta }({\Im }_{\chi }^{\prime };\chi )\right|=\left|{\int }_0^{\chi }\left({\int }_{\chi }^s{\Im }_{\chi }^{\prime }\left(u\right)\mathrm{d}u\right){\mathrm{d}}_s{\varpi }_{\lambda }(\chi ;s)\right|=\left|{\int }_0^{\chi }{\varpi }_{\lambda }(\chi ;s){\Im }_{\chi }^{\prime }\left(s\right)\mathrm{d}s\right|.$$

Since the inequality ${\int }_a^b{\mathrm{d}}_s{\varpi }_{\lambda }(\chi ;s)\le 1$ holds for any $[a,b]\subset [0,1]$, applying the integration by parts with putting $y=\chi -(\chi /\sqrt{\lambda })$, we obtain

$$\begin{array}{cc}\hfill |{\mathfrak{E}}_{\lambda ,\gamma }^{\theta }({\Im }_{\chi }^{\prime };\chi )|& \le ({\int }_0^y+{\int }_y^{\chi })\left|{\varpi }_{\lambda }(\chi ;s)\right||{\Im }_{\chi }^{\prime }\left(s\right)|\mathrm{d}s\hfill \\ \hfill & \le B_{\lambda ,\gamma }^{\theta }\left(\chi \right){\int }_0^y\underset{s}{\overset{\chi }{\bigvee }}\left({\Im }_{\chi }^{\prime }\right){(\chi -s)}^{-2}\mathrm{d}s+{\int }_y^{\chi }\underset{s}{\overset{\chi }{\bigvee }}\left({\Im }_{\chi }^{\prime }\right)\mathrm{d}s\hfill \\ \hfill & \le B_{\lambda ,\gamma }^{\theta }\left(\chi \right){\int }_0^{\chi -(\chi /\sqrt{\lambda })}\underset{s}{\overset{\chi }{\bigvee }}\left({\Im }_{\chi }^{\prime }\right){(\chi -s)}^{-2}\mathrm{d}s+\frac{\chi }{\sqrt{\lambda }}\underset{\chi -(\chi /\sqrt{\lambda })}{\overset{\chi }{\bigvee }}\left({\Im }_{\chi }^{\prime }\right).\hfill \end{array}$$

By considering $u=\chi /(\chi -s)$, we yield

$$\begin{array}{cc}\hfill B_{\lambda ,\gamma }^{\theta }\left(\chi \right){\int }_0^{\chi -(\chi -\sqrt{\lambda })}{(\chi -s)}^{-2}\underset{s}{\overset{\chi }{\bigvee }}\left({\Im }_{\chi }^{\prime }\right)\mathrm{d}s& =B_{\lambda ,\gamma }^{\theta }\left(\chi \right){\chi }^{-1}{\int }_1^{\sqrt{\lambda }}\underset{\chi -(\chi /u)}{\overset{\chi }{\bigvee }}\left({\Im }_{\chi }^{\prime }\right)\mathrm{d}u\hfill \\ \hfill & \le B_{\lambda ,\gamma }^{\theta }\left(\chi \right){\chi }^{-1}\sum _{j=1}^{\left[\sqrt{\lambda }\right]}{\int }_j^{j+1}\underset{\chi -(\chi /j)}{\overset{\chi }{\bigvee }}\left({\Im }_{\chi }^{\prime }\right)\mathrm{d}u\hfill \\ \hfill & \le B_{\lambda ,\gamma }^{\theta }\left(\chi \right){\chi }^{-1}\sum _{j=1}^{\left[\sqrt{\lambda }\right]}\underset{\chi -(\chi /j)}{\overset{\chi }{\bigvee }}\left({\Im }_{\chi }^{\prime }\right).\hfill \end{array}$$

Therefore,

$$\left|{\mathfrak{E}}_{\lambda ,\gamma }^{\theta }({\Im }_{\chi }^{\prime };\chi )\right|\le B_{\lambda ,\gamma }^{\theta }\left(\chi \right){\chi }^{-1}\sum _{j=1}^{\left[\sqrt{\lambda }\right]}\underset{\chi -(\chi /j)}{\overset{\chi }{\bigvee }}\left({\Im }_{\chi }^{\prime }\right)+\frac{\chi }{\sqrt{\lambda }}\underset{\chi -(\chi /\sqrt{\lambda })}{\overset{\chi }{\bigvee }}\left({\Im }_{\chi }^{\prime }\right).$$

(27)

Again, applying integration by parts to ${\mathfrak{F}}_{\lambda ,\gamma }^{\theta }({\Im }_{\chi }^{\prime };\chi )$, together with Lemma 7, we have

$$\begin{array}{cc}\hfill |{\mathfrak{F}}_{\lambda ,\gamma }^{\theta }({\Im }_{\chi }^{\prime };\chi )|& =\left|{\int }_{\chi }^1\left({\int }_{\chi }^s{\Im }_{\chi }^{\prime }\left(u\right)\mathrm{d}u\right){\mathbb{R}}_{\lambda ,\gamma }^{\theta }(\chi ;s)\mathrm{d}s\right|\hfill \\ \hfill & \le \left|{\int }_{\chi }^z\left({\int }_{\chi }^s{\Im }_{\chi }^{\prime }\left(u\right)\mathrm{d}u\right){\mathrm{d}}_s(1-{\varpi }_{\lambda }(\chi ;s))\right|+\left|{\int }_z^1\left({\int }_{\chi }^s{\Im }_{\chi }^{\prime }\left(u\right)\mathrm{d}u\right){\mathrm{d}}_s(1-{\varpi }_{\lambda }(\chi ;s))\right|\hfill \\ \hfill & =\left|{\left[{\int }_{\chi }^s{\Im }_{\chi }^{\prime }\left(u\right)(1-{\varpi }_{\lambda }(\chi ;s))\mathrm{d}u\right]}_{\chi }^z-{\int }_{\chi }^z{\Im }_{\chi }^{\prime }\left(s\right)(1-{\varpi }_{\lambda }(\chi ;s))\mathrm{d}s\right|\hfill \\ \hfill & +\left|{\int }_z^1\left({\int }_{\chi }^s{\Im }_{\chi }^{\prime }\left(u\right)\mathrm{d}u\right){\mathrm{d}}_s(1-{\varpi }_{\lambda }(\chi ;s))\right|\hfill \\ \hfill & =\left|{\int }_{\chi }^z{\Im }_{\chi }^{\prime }\left(u\right)\mathrm{d}u(1-{\varpi }_{\lambda }(\chi ;z))-{\int }_{\chi }^z{\Im }_{\chi }^{\prime }\left(s\right)(1-{\varpi }_{\lambda }(\chi ;s))\mathrm{d}s\right|\hfill \\ \hfill & +\left|{\left[{\int }_{\chi }^s{\Im }_{\chi }^{\prime }\left(u\right)\mathrm{d}u(1-{\varpi }_{\lambda }(\chi ;s))\right]}_z^1-{\int }_z^1{\Im }_{\chi }^{\prime }\left(s\right)(1-{\varpi }_{\lambda }(\chi ;s))\mathrm{d}s\right|\hfill \\ \hfill & =\left|{\int }_{\chi }^z{\Im }_{\chi }^{\prime }\left(s\right)(1-{\varpi }_{\lambda }(\chi ;s))\mathrm{d}s+{\int }_z^1{\Im }_{\chi }^{\prime }\left(s\right)(1-{\varpi }_{\lambda }(\chi ;s))\mathrm{d}s\right|\hfill \\ \hfill & \le B_{\lambda ,\gamma }^{\theta }\left(\chi \right){\int }_z^1\underset{\chi }{\overset{s}{\bigvee }}\left({\Im }_{\chi }^{\prime }\right){(s-\chi )}^{-2}\mathrm{d}s+{\int }_{\chi }^z\underset{\chi }{\overset{s}{\bigvee }}\left({\Im }_{\chi }^{\prime }\right)\mathrm{d}s\hfill \\ \hfill & =B_{\lambda ,\gamma }^{\theta }\left(\chi \right){\int }_{\chi +((1-\chi )/\sqrt{\lambda })}^1\underset{\chi }{\overset{s}{\bigvee }}\left({\Im }_{\chi }^{\prime }\right){(s-\chi )}^{-2}\mathrm{d}s+\frac{(1-\chi )}{\sqrt{\lambda }}\underset{\chi }{\overset{\chi +((1-\chi )/\sqrt{\lambda })}{\bigvee }}\left({\Im }_{\chi }^{\prime }\right).\hfill \end{array}$$

By the substitution of the values $u=(1-\chi )/(s-\chi )$, we get

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill |{\mathfrak{F}}_{\lambda ,\gamma }^{\theta }({\Im }_{\chi }^{\prime };\chi )|& \le B_{\lambda ,\gamma }^{\theta }\left(\chi \right){\int }_1^{\sqrt{\lambda }}\underset{\chi }{\overset{\chi +\left(\right(1-\chi )/u)}{\bigvee }}\left({\Im }_{\chi }^{\prime }\right){(1-\chi )}^{-1}\mathrm{d}u+\frac{(1-\chi )}{\sqrt{\lambda }}\underset{\chi }{\overset{\chi +((1-\chi )/\sqrt{\lambda })}{\bigvee }}\left({\Im }_{\chi }^{\prime }\right)\hfill \\ \hfill & \le \frac{B_{\lambda ,\gamma }^{\theta }\left(\chi \right)}{(1-\chi )}\sum _{j=1}^{\left[\sqrt{\lambda }\right]}{\int }_j^{j+1}\underset{\chi }{\overset{\chi +\left(\right(1-\chi )/u)}{\bigvee }}\left({\Im }_{\chi }^{\prime }\right)\mathrm{d}u+\frac{(1-\chi )}{\sqrt{\lambda }}\underset{\chi }{\overset{\chi +((1-\chi )/\sqrt{\lambda })}{\bigvee }}\left({\Im }_{\chi }^{\prime }\right)\hfill \\ \hfill & =\frac{B_{\lambda ,\gamma }^{\theta }\left(\chi \right)}{(1-\chi )}\sum _{j=1}^{\left[\sqrt{\lambda }\right]}\underset{\chi }{\overset{\chi +\left(\right(1-\chi )/j)}{\bigvee }}\left({\Im }_{\chi }^{\prime }\right)+\frac{(1-\chi )}{\sqrt{\lambda }}\underset{\chi }{\overset{\chi +((1-\chi )/\sqrt{\lambda })}{\bigvee }}\left({\Im }_{\chi }^{\prime }\right).\hfill \end{array}\end{array}$$

(28)

Collecting the estimates (26)–(28), we get the desired results. Hence, the proof of Theorem 9 is completed.   □

7. Conclusions

In our paper, we construct the blending-type modified Bernstein–Durrmeyer operators involving the strictly positive function $\theta \left(\chi \right)$ and the positive parameter $\gamma$. We derive many approximation properties of this type of operator. We first establish a Voronovskaya-type asymptotic theorem of them. Then, we establish the local and global approximation theorems by using the classical modulus of continuity and K-functional. Finally, we derive the convergence rate of the approximation for functions with a derivative of bounded variation.

We remark that our results are rather general. For instance, one can get the error estimates from our results for different existing Bernstein–Durrmeyer–type operators, such as operators given in [14,15], by selecting different parameters $\theta \left(\chi \right)$ and $\gamma$. Moreover, we can obtain the new operators, which provide better approximations for different target functions. In general, different target functions need different parameters. The choices of the parameters show the flexibility of the operators ${\mathcal{H}}_{\lambda ,\gamma }^{\theta }$. In fact, for a given target function ℑ, we can choose appropriate parameters to obtain a smaller error of the approximation by ${\mathcal{H}}_{\lambda ,\gamma }^{\theta }(\Im ;\chi )$. This feature will be of great interest to practical applications. We illustrate this feature by some numerical experiments.

Example 1. 

Let $\Im \left(\chi \right)={\chi }^2+\chi +1$, $\chi \in [0,1]$, $\gamma =5$, $\theta \left(\chi \right)={\chi }^{2}sin\left(\frac{\pi }{2}{\chi }^3\right)$ and $\lambda \in \{10,20,50,100\}$.

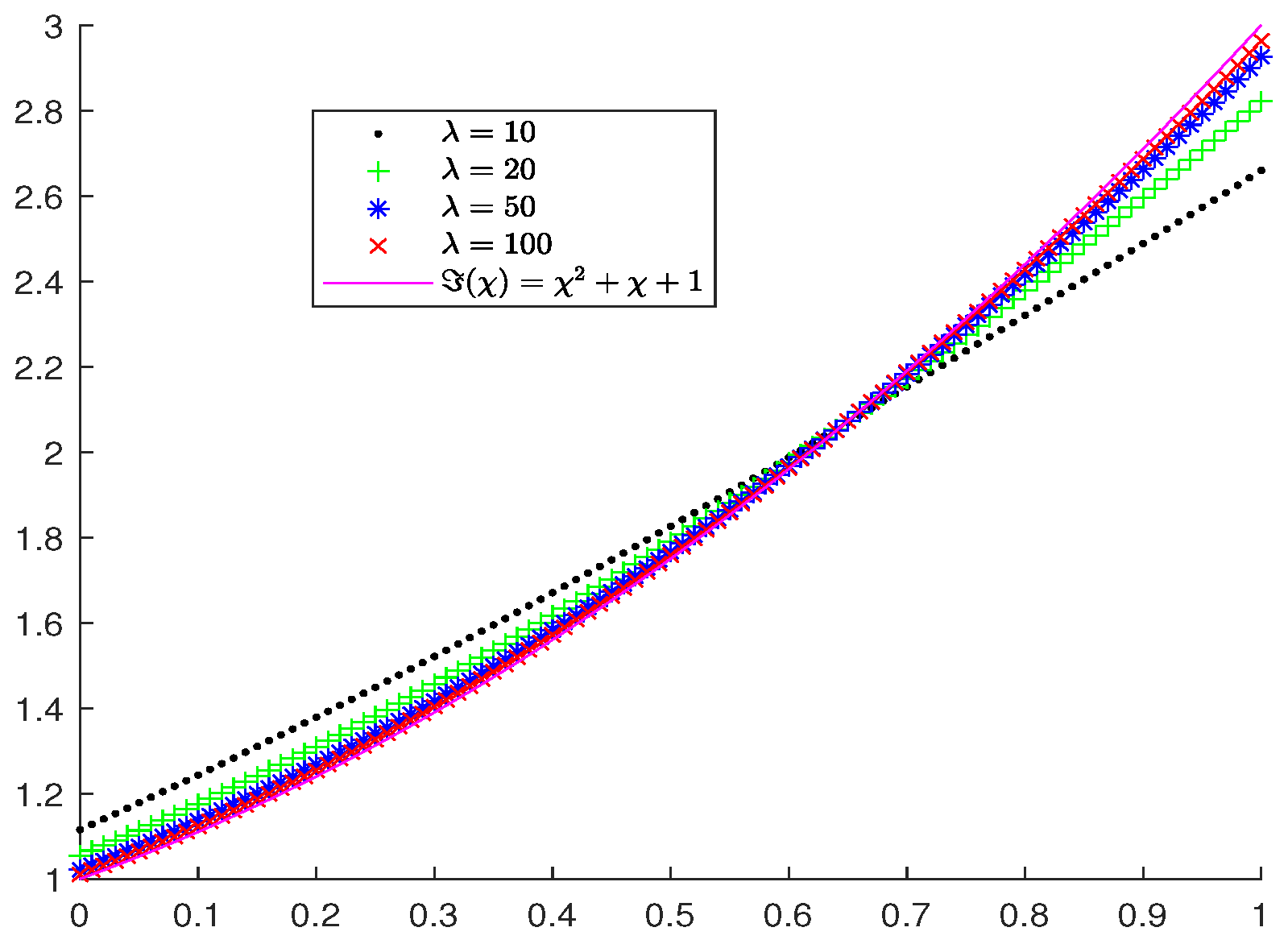
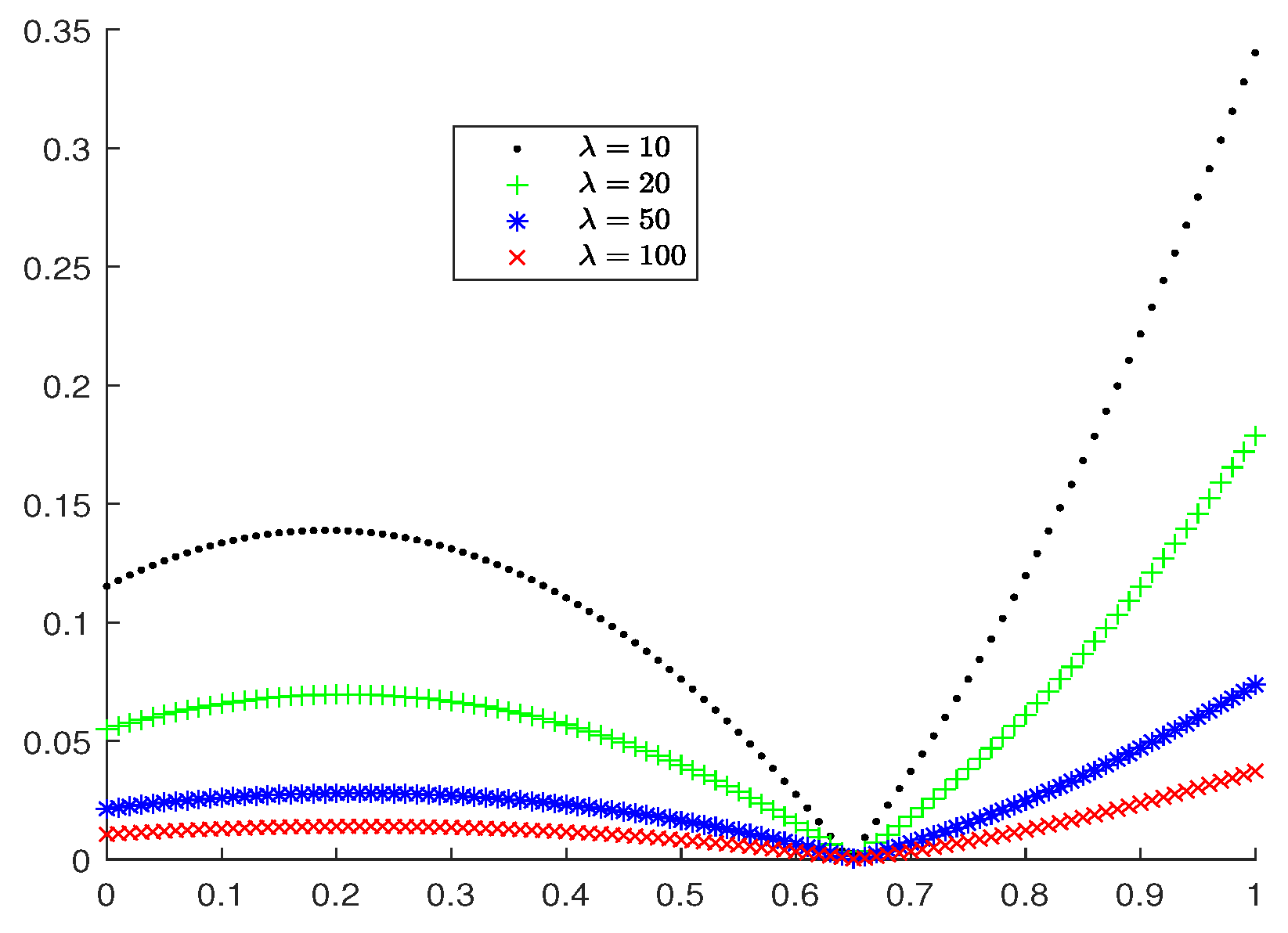
Figure 1 shows the convergence of the operators ${\mathcal{H}}_{\lambda ,\gamma }^{\theta }(\Im ;\chi )$ to the target function $\Im \left(\chi \right)$ while we choose different parameters $\lambda$. The larger the $\lambda$, the smaller of the error of the approximation by ${\mathcal{H}}_{\lambda ,\gamma }^{\theta }\left(\Im ;\chi \right)$. Combining with Figure 2, when $\chi \in [0,0.65]$, the error of the approximation $|{\mathcal{H}}_{\lambda ,\gamma }^{\theta }\left(\Im ;\chi \right)-\Im \left(\chi \right)|$ becomes smaller and smaller with the increase of variable $\chi$. When $\chi \in [0.65,1]$, contrary to what happens.

Figure 1. The operators ${\mathcal{H}}_{\lambda ,\gamma }^{\theta }(\Im ;\chi )$ and the target function $\Im \left(\chi \right)$.

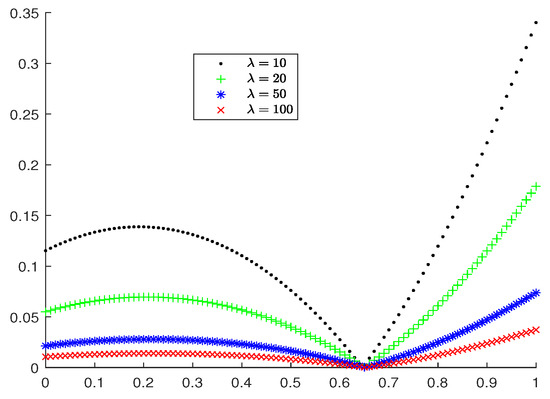
Figure 2. Error of approximation $|{\mathcal{H}}_{\lambda ,\gamma }^{\theta }\left(\Im ;\chi \right)-\Im \left(\chi \right)|$.

It is known that if we take $\theta \left(\chi \right)=1$ in operators (3), then we get the modified Bernstein–Durrmeyer-type operators ${\mathcal{H}}_{\lambda ,\gamma }^1(\Im ;\chi )$, which is defined in [14]. In the following example, we show that operators (3) with some different parameters provide better approximations than the operators ${\mathcal{H}}_{\lambda ,\gamma }^1(\Im ;\chi )$.

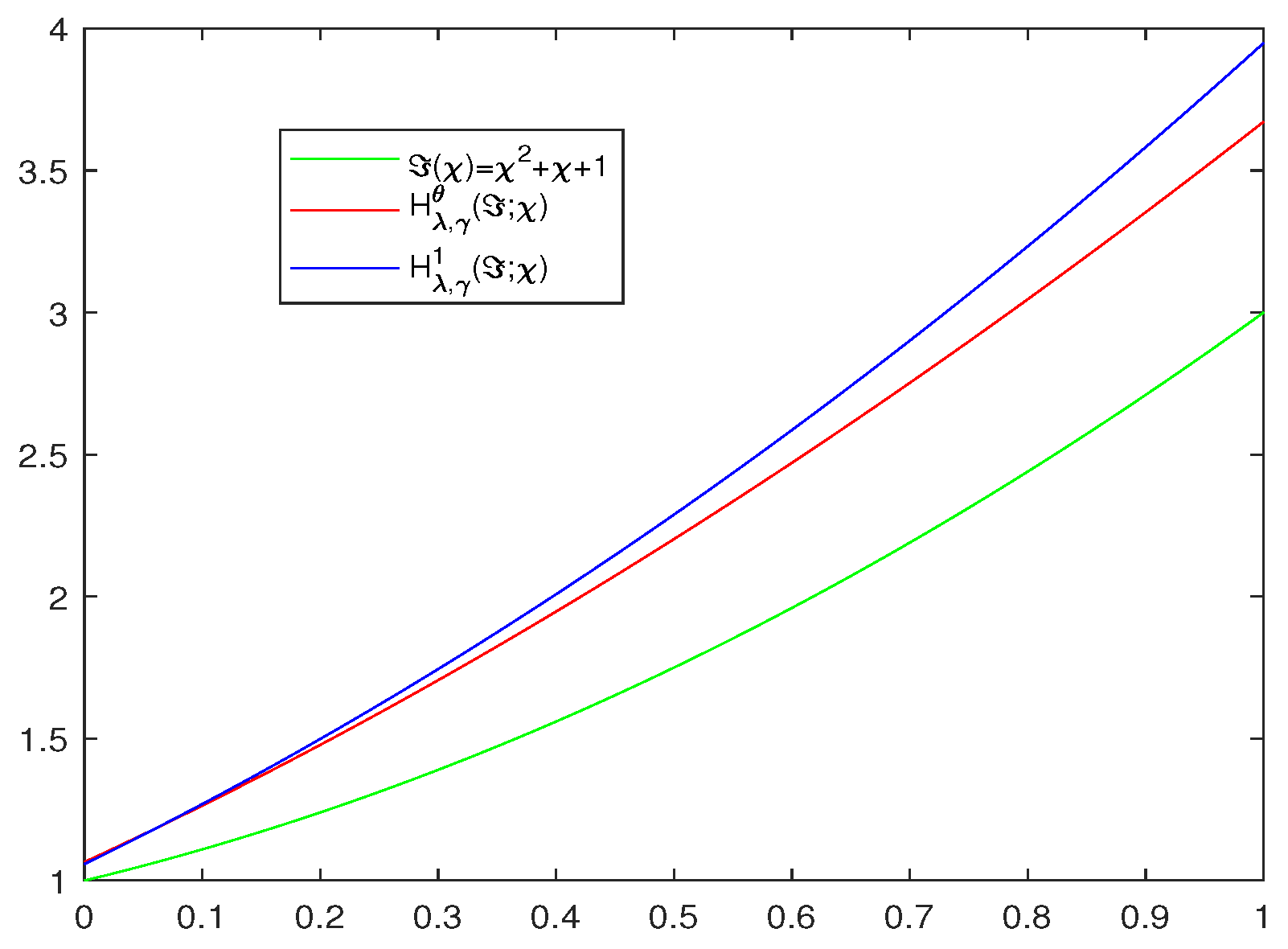
Example 2. 

Let $\Im \left(\chi \right)={\chi }^2+\chi +1$, $\chi \in [0,1]$, $\gamma =10$, $\theta \left(\chi \right)={(\chi +3)}^2$ and $\lambda =50$.

From Figure 3, we can see that, for the target function $\Im \left(\chi \right)$ (green), the operator ${\mathcal{H}}_{\lambda ,\gamma }^{\theta }(\Im ;\chi )$ (red) gives a better approximation to $\Im \left(\chi \right)$ than the modified Bernstein–Durrmeyer type operator ${\mathcal{H}}_{\lambda ,\gamma }^1(\Im ;\chi )$ (blue).

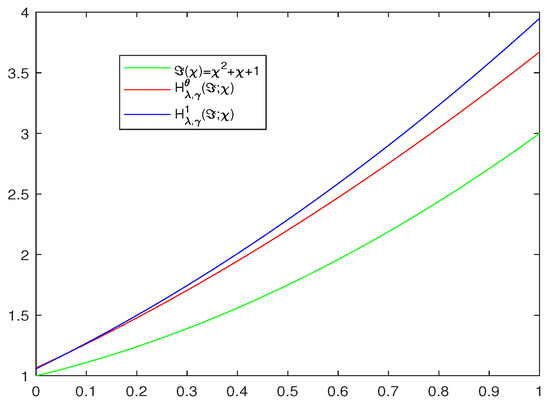
Figure 3. The target function $\Im \left(\chi \right)$ (green), the operator ${\mathcal{H}}_{\lambda ,\gamma }^{\theta }(\Im ;\chi )$ (red), the modified Bernstein–Durrmeyer type operator ${\mathcal{H}}_{\lambda ,\gamma }^1(\Im ;\chi )$ (blue).