An Approach for the Assessment of Multi-National Companies Using a Multi-Attribute Decision Making Process Based on Interval Valued Spherical Fuzzy Maclaurin Symmetric Mean Operators

Abstract

Many fuzzy concepts have been researched and described with uncertain information. Collecting data under uncertain information is a difficult task, especially when there is a difference between the opinions of experts. To deal with such situations, different types of operators have been introduced. This paper aims to develop the Maclaurin symmetric mean (MSM) operator for the information in the shape of the interval-valued spherical fuzzy set (IVSFS). In this article, a family of aggregation operators (AOs) is proposed which consists of interval valued spherical fuzzy Maclaurin symmetric mean operator (IVSFMSM), interval valued spherical fuzzy weighted Maclaurin symmetric mean (IVSFWMSM), interval valued spherical fuzzy dual Maclaurin symmetric mean (IVSFDMSM), and interval valued spherical fuzzy dual weighted Maclaurin symmetric mean (IVSFDWMSM) operators. In this paper, we studied an elucidative example to discuss the evaluation of multi-national companies for the application of the proposed operator. Then the obtained results from the proposed operators are compared. The results obtained are graphed and tabulated for a better understanding.

1. Introduction

A fuzzy set (FS) was introduced by Zadeh [1] in 1965 to deal with an uncertain situation. In FS, there is only one side we can read about how much a phenomenon relates to a set. To deal with the two-sided opinions of experts Atanassov [2] gave the idea of an intuitionistic fuzzy set (IFS), in which we use (MD) and (NMD), and an (RD) shows the accuracy of IFS. IFS also describes the disconnection of phenomena, and the sum is existing in $\left[0,1\right]$. Atanassov [3] extended IFS into the interval-valued intuitionistic fuzzy set (IVIFS). To increase the accuracy of IFS, Yager [4] proposed the idea of the Pythagorean fuzzy set (PyFS). In which, we take $0\le {\left(f\left(\nu \right)\right)}^2+{\left(w\left(\nu \right)\right)}^2\le 1$. Peng and Yager extended the concept of PyFS into an interval-valued Pythagorean fuzzy set (IVPyFS). Coung [5] introduced the concept of a picture fuzzy set (PFS), in which we use an abstain degree (AD). A picture-fuzzy set eliminates the loss of information due to four possibilities (MD, NMD, AD, and RD). Coung [6] also worked on the extended form of PFS and introduced the concept of an interval-valued picture fuzzy set (IVPFS). The concept of a spherical fuzzy set (SFS) was introduced by Ullah et al. [7]. The notion of q-Rung Orthopair Fuzzy Set (q-ROFS) was given by Yager [8], in which we use cubic power for the MD, NMD, AD, and RD. A (SFS) increases the range of accuracy by taking the square of all the degrees. FS theory plays an important role in different mathematical fields, such as work by Ghaznavi et al. [9] on the parametric fuzzy equation, and Jafri et al. [10] work on the fuzzy differential equation. Ullah et al. [11] also worked on the Interval Valued Spherical Fuzzy Set (IVSFS). Some more work on the SFS and TSFS can be found in [12,13,14].

Aggregation operators (AOs) [15] are important tools for gathering information under uncertain information. Over the last decade, a lot of AOs have been developed to aggregate the results of fuzzy concepts in undefined situations. AOs are very important due to the use of these operators in different fields of fuzzy theory. If we talk about AOs, the Bonferroni mean operator (BMO) was developed by Bonferroni [16], and Liang et al. extended it into the Weighted Pythagorean Fuzzy Geometric Bonferroni mean operator (WFGBM) [17]. Sykora had developed the Heronian Mean operator (HMO) [18], and Yu developed the concept of an intuitionistic fuzzy geometric weighted Heronian Mean operator (IFGHMO) [19]. The generalized Heronian mean operator based on q rung Orthopair (q-ROPFGHMO) [20] was developed by Wei et al. Over time, many mathematicians made extensions to (BMO), such as the partitioned Heronian mean (PHM) operator based on linguistic fuzzy numbers [21]. To solve (MADM) problems with more accuracy, Xing YP et al. [22] combined (HMO) with interactional operational law. Dombi t norm (t-conorm) is an elastic operator; the (DMO) based on (IFS) was developed by Liu et al. [23]. In fuzzy theory, Chen and Ye developed the concept of generalized Dombi operations (GDO) based on the neutrosophic cubic fuzzy set [24]. To solve (MADM) problem, Shi and Ye developed the idea of (WNSCFS) based on the t norm (t-conorm) [25]. Yang and Pang worked on more extensions to BMO and Dombi t norm (t-conorm) [26]. The related literature can be found in [13,27,28,29].

Maclaurin [30] gave the concept of the MSM operator, which is a high-significance form of AOs. MSM operators are very important due to their correlation with four (MD, NMD, AD, and RD) input arguments, like (BMO) and (HMO). As we know, all the existing operators correlate with two input arguments, but MSM eliminates the loss of information. Liu [31] proposed an extended form of the IFMSM operator, and Liu et al. [32] did extensive work on IVIFMSM. Wei and Lu [33] developed the PyFMSM operator, which was later expanded by Wei et al. [34]. The idea of PFMSM was given by Ullah et al. [35], and extended work on IVPMSM operators was done by Ashraf et al. [36]. The idea of q-ROPFMSM was developed by Liu [37], in which we take the cubic powers of MD, NMD, AD, and RD. MSM operators are unique due to their correlation with more than two input arguments. As we know, PFMSM [31] operators increased the range of accuracy, so if we take a square of the four possible degrees, the range of accuracy increases. More work on the MSM operator can be found in [38,39,40,41].

The IVSFS is the framework that covers information with the least amount of data loss from real-life scenarios. Furthermore, the MSM operator is an interesting AO that aggregates the information by preserving the relationship of the components of the information. The major contribution of this article is to develop a family of AOs for IVSFS based on the MSM operator. In Section 2, we define the background of FS theory and the importance of aggregation operators (AOs). We proposed IVSFMSM and IVSFWMSM in Section 3. In Section 4, we developed the concept of IVSFDMSM and IVSFDWMSM operators. We analyze some special cases of the developed AOs in Section 5. In Section 6, we applied the developed AOs to the MADM problem. In Section 7, we analyze the comparative study of developed AOs with traditional operators. Conclusive remarks are in Section 8.

2. Preliminaries

In this section, we define the SFS, IVSFS, MSM, and score function of the IVSFS. We also described the basic operations of the IVSFS and MSM operators.

Definition 1:

[11] For a universal set Z, a SFS is defined as $X=\left\{\left(v,\left(f\left(\nu \right),g\left(\nu \right),w\left(\nu \right)\right)\right):\nu \in Z\right\}$ where$f, g,$ and w are mapped from Z to$\left[0,1\right]$, with the condition that $0\le {\left(f\left(\nu \right)\right)}^2+{\left(g\left(\nu \right)\right)}^2+{\left(w\left(\nu \right)\right)}^2\le 1$. A refusal degree can be defined as $A\left(\nu \right)={\left(1-\left({\left(f\left(\nu \right)\right)}^2+{\left(g\left(\nu \right)\right)}^2+{\left(w\left(\nu \right)\right)}^2\right)\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}$ and a triplet $\left(f\left(\nu \right),g\left(\nu \right),w\left(\nu \right)\right)$ is known as SFV. Further, $f\left(\nu \right)$ shows MD $g\left(\nu \right)$ is AD, and $w\left(\nu \right)$ is ND.

Definition 2:

[11] In a universal set Z an IVSFS is defined as $X=\left\{\left(v,\left(f\left(\nu \right),g\left(\nu \right),w\left(\nu \right)\right)\right):\nu \in Z\right\}$ where $f, g$ and $w$ are mapped from Z to $\left[0,1\right]$ such that $f\left(\nu \right)=\left[f^{inf}\left(\nu \right),f^{sup}\left(\nu \right)\right]$,$g\left(\nu \right)=\left[g^{inf}\left(\nu \right),g^{sup}\left(\nu \right)\right]$ and $w\left(\nu \right)=\left[\left(w^{inf}\right)\left(\nu \right),w^{sup}\left(\nu \right)\right]$ with the condition that $0\le {\left(f{\left(\nu \right)}^{sup}\right)}^2+{\left(g{\left(\nu \right)}^{sup}\right)}^2+{\left(w{\left(\nu \right)}^{sup}\right)}^2\le 1$. A refusal degree can be derived as $A\left(\nu \right)=\left[A^{inf}\left(\nu \right),A^{sup}\left(\nu \right)\right]$

$$=\left[\begin{array}{c}{\left(1-\left({\left(f^{inf}\right)}^2\left(\nu \right)+{\left(g^{inf}\right)}^2\left(\nu \right)+{\left(w^{inf}\right)}^2\left(\nu \right)\right)\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.},\\ \left({\left(1-\left({\left(f^{sup}\right)}^2\left(\nu \right)+{\left(g^{sup}\right)}^2\left(\nu \right)+{\left(w^{sup}\right)}^2\left(\nu \right)\right)\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}\right)\end{array}\right]$$

and a triplet $\left(f\left(\nu \right),g\left(\nu \right),w\left(\nu \right)\right)=\left(\left[f^{inf}\left(\nu \right),f^{sup}\left(\nu \right)\right],\left[g^{inf}\left(\nu \right),g^{sup}\left(\nu \right)\right],\left[w^{inf}\left(\nu \right),w^{sup}\left(\nu \right)\right]\right)$ is known as IVSFV here $f\left(\nu \right)$ shows MD $g\left(\nu \right)$ are AD and $w\left(\nu \right)$ is ND.

The score function for IVSFVs is given below.

Definition 3:

Let $A_i=\left(\left[f^{inf}\left(\nu \right),f^{sup}\left(\nu \right)\right],\left[g^{inf}\left(\nu \right),g^{sup}\left(\nu \right)\right],\left[w^{inf}\left(\nu \right),w^{sup}\left(\nu \right)\right]\right)$be values of IVSFS, then score function is defined as

$$SC\left(\nu \right)=\frac{\begin{array}{c}{\left(f^{inf}\left(v\right)\right)}^2\left(1-{\left(g^{inf}\left(v\right)\right)}^2-{\left(w^{inf}\left(v\right)\right)}^2\right)+\\ {\left(f^{sup}\left(v\right)\right)}^2\left(1-{\left(g^{sup}\left(v\right)\right)}^2-{\left(w^{sup}\left(v\right)\right)}^2\right)\end{array}}{3}$$

(1)

the accuracy function is defined as

$$H\left(\nu \right)=\frac{\begin{array}{c}{\left(f^{inf}\left(v\right)\right)}^2\left(1+{\left(g^{inf}\left(v\right)\right)}^2+{\left(w^{inf}\left(v\right)\right)}^2\right)+\\ {\left(f^{sup}\left(v\right)\right)}^2\left(1+{\left(g^{sup}\left(v\right)\right)}^2+{\left(w^{sup}\left(v\right)\right)}^2\right)\end{array}}{3}$$

(2)

Definition 4:

[11] Let$L_1=\left(\left[f_1^{inf}\left(v\right),f_1^{sup}\left(v\right)\right],\left[g_1^{inf}\left(v\right),g_1^{sup}\left(v\right)\right],\left[w_1^{inf}\left(v\right),w_1^{sup}\left(v\right)\right]\right)$ and $L_2=\left(\left[f_2^{inf}\left(v\right),f_2^{sup}\left(v\right)\right],\left[g_2^{inf}\left(v\right),g_2^{sup}\left(v\right)\right],\left[w_2^{inf}\left(v\right),w_2^{sup}\left(v\right)\right]\right)$ be two IVSFVs, then we can define the following operations. Note that $\otimes$ and $\oplus$ denote the multiplication and addition of two IVSFVs.

$$L_1\otimes L_2=\left\{\left(\begin{array}{c}\left[f_1^{inf}\left(\nu \right)f_2^{inf}\left(\nu \right),f_1^{sup}\left(\nu \right)f_2^{sup}\left(\nu \right)\right]\\ \left[\begin{array}{c}1-\left(1-g_1^{inf}{\left(\nu \right)}^2\right){\left(1-g_2^{inf}{\left(\nu \right)}^2\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.},\\ {\left(1-\left(1-g_1^{sup}{\left(\nu \right)}^2\right)\left(1-g_2^{sup}{\left(\nu \right)}^2\right)\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}\end{array}\right]\\ \left[\begin{array}{c}{\left(1-\left(1-w_1^{inf}{\left(\nu \right)}^2\right)\left(1-w_2^{inf}{\left(\nu \right)}^2\right)\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.},\\ {\left(1-\left(1-w_1^{sup}{\left(\nu \right)}^2\right)\left(1-w_2^{sup}{\left(\nu \right)}^2\right)\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}\end{array}\right]\end{array},\right),\nu \in Z\right\}$$

$$L_1\oplus L_2=\left\{\left(\begin{array}{c}\left[\begin{array}{c}{\left(1-\left(1-f_1^{inf}{\left(\nu \right)}^2\right)\left(1-f_2^{sup}{\left(\nu \right)}^2\right)\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.},\\ {\left(1-\left(1-f_1^{sup}\left(\nu \right)\right)\left(1-f_2^{sup}\left(\nu \right)\right)\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}\end{array}\right]\\ \left[g_1^{inf}\left(\nu \right)g_2^{inf}\left(\nu \right),g_1^{sup}\left(\nu \right)g_2^{sup}\left(\nu \right)\right],\\ \left[w_1^{inf}\left(\nu \right)w_2^{inf}\left(\nu \right),w_1^{sup}\left(\nu \right)w_2^{sup}\left(\nu \right)\right]\end{array},\right),\nu \in Z\right\}$$

$$\xi L_1=\left\{\left(\begin{array}{c}\left[{\left(1-{\left(1-f_1^{inf}\left(\nu \right)\right)}^{\xi }\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.},{\left(1-{\left(1-f_1^{sup}\left(\nu \right)\right)}^{\xi }\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}\right],\\ \left[{\left(g_1^{inf}\left(\nu \right)\right)}^{\xi },{\left(g_1^{sup}\left(\nu \right)\right)}^{\xi }\right],\\ \left[{\left(w_1^{inf}\left(\nu \right)\right)}^{\xi },{\left(w_1^{sup}\left(\nu \right)\right)}^{\xi }\right]\end{array}\right), \nu \in Z\right\}$$

$$L_1{}^{\xi }=\left\{\left(\begin{array}{c}\left[{\left(f_1^{inf}\left(\nu \right)\right)}^{\xi },{\left(f_1^{sup}\left(\nu \right)\right)}^{\xi }\right],\\ \left[{\left(1-{\left(1-g_1^{inf}\left(\nu \right)\right)}^{\xi }\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.},{\left(1-{\left(1-g_1^{sup}\left(\nu \right)\right)}^{\xi }\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}\right],\\ \left[{\left(1-{\left(1-w_1^{inf}\left(\nu \right)\right)}^{\xi }\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.},{\left(1-{\left(1-w_1^{sup}\left(\nu \right)\right)}^{\xi }\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}\right]\end{array}\right), \nu \in Z\right\}$$

Definition 5:

[35] Let $A_i=\left(i=1,2,3,\dots ,r\right)$ be a collection of positive real numbers. Then

$$MS{M}^{\left(\nu \right)}\left(c_1,c_2,\dots ,c_r\right)={\left(\frac{{{\displaystyle \sum }}_{1\le i_1\le ,\dots ,i_{{\rm Y}}\le r}{{\displaystyle \prod }}_{\tau =1}^{{\rm Y}}{A}_{i_{\tau }}}{C_r^{{\rm Y}}}\right)}^{\frac{1}{{\rm Y}}}$$

is called MSM. Where $\left(c_1,c_2,\dots ,c_{{\rm Y}}\right)$ convert all the l-tuple combinations of $\left(1,2,\dots ,r\right)$ and $C_r^{{\rm Y}}$is the binomial coefficient.

Now we discuss the main work regarding this article.

3. Interval Valued Spherical Fuzzy Maclaurin Symmetric Mean (IVSFMSM) Operator

In this section, we developed the concept of the IVSFMSM and IVSFWMSM operators.

Definition 6:

Let $A_i=\left(\left[f_i^{inf}\left(v\right), f_i^{sup}\left(v\right)\right] \left[g_i^{inf}\left(v\right), g_i^{sup}\left(v\right)\right] \left[w_i^{inf}\left(v\right), w_i^{sup}\left(v\right)\right]\right)$and be two IVSFVs. Then, the IVSFMSM operator is given by

$$IVSFMSM\left(A_1,A_{2,\dots ,}{A}_r\right)={\left(\frac{\underset{1\le i_1\le ,\dots ,i_{{\rm Y}}\le r}{\oplus }\left(\stackrel{{\rm Y}}{\underset{\tau =1}{\otimes }}{A}_{i_{\tau }}\right)}{C_r^{{\rm Y}}}\right)}^{1/\dot{{\rm Y}}}.$$

(3)

Theorem 1:

Let $A_i=\left(\left[f_i^{inf}\left(v\right),f_i^{sup}\left(v\right)\right],\left[g_i^{inf}\left(v\right),g_i^{sup}\left(v\right)\right],\left[w_i^{inf}\left(v\right),w_i^{sup}\left(v\right)\right]\right)$be a collection of IVSFVs. Then, using IVSFMSM operator, we get

$$\begin{gathered} IVSFMSM\left(A_1,A_2,\cdots ,A_r\right) \\ =\left(\begin{array}{c}\begin{array}{c}\left[\begin{array}{c}{\left({\left(1-{\left({\displaystyle \prod _{1\le i_1\le ,\dots ,<i_{{\rm Y}}\le r}}\left(1-\left({\displaystyle \prod _{\tau =1}^{{\rm Y}}}{\left(f_{i_{\tau }}^{inf}\left(v\right)\right)}^2\right)\right)\right)}^{1/C_r^{{\rm Y}}}\right)}^{1/{\rm Y}}\right)}^{1/2}\\ {\left({\left(1-{\left({\displaystyle \prod _{1\le i_1\le ,\dots ,<i_{{\rm Y}}\le r}}\left(1-\left({\displaystyle \prod _{\tau =1}^{{\rm Y}}}{\left(f_{i_{\tau }}^{sup}\left(v\right)\right)}^2\right)\right)\right)}^{1/C_r^{{\rm Y}}}\right)}^{1/{\rm Y}}\right)}^{1/2}\end{array}\right],\\ \left[\begin{array}{c}1-{\left(1-{\left({\displaystyle \prod _{1\le i_1\le ,\dots ,<i_{{\rm Y}}\le r}}\left(1-\left({\displaystyle \prod _{\tau =1}^{{\rm Y}}}\left(1-{\left(g_{i_{\tau }}^{inf}\left(v\right)\right)}^2\right)\right)\right)\right)}^{1/C_r^{{\rm Y}}}\right)}^{1/\dot{{\rm Y}}},\\ 1-{\left(1-{\left({\displaystyle \prod _{1\le i_1\le ,\dots ,<i_{{\rm Y}}\le r}}\left(1-\left({\displaystyle \prod _{\tau =1}^{{\rm Y}}}\left(1-{\left(g_{i_{\tau }}^{sup}\left(v\right)\right)}^2\right)\right)\right)\right)}^{1/C_r^{{\rm Y}}}\right)}^{1/\dot{\dot{{\rm Y}}}}\end{array}\right],\\ \end{array}\\ \left[\begin{array}{c}{\left(1-{\left(1-{\left({\displaystyle \prod _{1\le i_1\le ,\dots ,<i_{{\rm Y}}\le r}}\left(1-\left({\displaystyle \prod _{\tau =1}^{\dot{{\rm Y}}}}\left(1-{\left(w_{i_{\tau }}^{inf}\left(v\right)\right)}^2\right)\right)\right)\right)}^{1/C_r^{{\rm Y}}}\right)}^{1/\dot{{\rm Y}}}\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.},\\ {\left(1-{\left(1-{\left({\displaystyle \prod _{1\le i_1\le ,\dots ,<i_{{\rm Y}}\le r}}\left(1-\left({\displaystyle \prod _{\tau =1}^{\dot{{\rm Y}}}}\left(1-{\left(w_{i_{\tau }}^{sup}\left(v\right)\right)}^2\right)\right)\right)\right)}^{1/C_r^{{\rm Y}}}\right)}^{1/\dot{{\rm Y}}}\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}\end{array}\right]\end{array}\right) \end{gathered}$$

Proof: 

By using Definition 6, we have

$$\stackrel{{\rm Y}}{\underset{\tau =1}{⨂}}{A}_{i_{\tau }}=\left(\begin{array}{c}\left[{\displaystyle \prod _{\tau =1}^{{\rm Y}}}{\left(f_{i_{\tau }}^{inf}\left(v\right)\right)}^2,{\displaystyle \prod _{\tau =1}^{{\rm Y}}}{\left(f_{i_{\tau }}^{sup}\left(v\right)\right)}^2\right],\\ \left[1-{\displaystyle \prod _{\tau =1}^{{\rm Y}}}\left(1-{\left(g_{i_{\tau }}^{inf}\left(v\right)\right)}^2\right),1-{\displaystyle \prod _{\tau =1}^{{\rm Y}}}\left(1-{\left(g_{i_{\tau }}^{sup}\left(v\right)\right)}^2\right)\right],\\ \left[1-{\displaystyle \prod _{\tau =1}^{{\rm Y}}}\left(1-{\left(w_{i_{\tau }}^{inf}\left(v\right)\right)}^2\right),1-{\displaystyle \prod _{\tau =1}^{{\rm Y}}}\left(1-{\left(w_{i_{\tau }}^{sup}\left(v\right)\right)}^2\right)\right]\end{array}\right),$$

$$\underset{1\le i_1\le ,\dots ,<i_{{\rm Y}}\le r}{⨁}\left(\stackrel{{\rm Y}}{\underset{\tau =1}{⨂}}{A}_{i_{\tau }}\right)=\left(\begin{array}{c}\left[\begin{array}{c}{\left(1-{\displaystyle \prod _{1\le i_1\le ,\dots ,<i_{{\rm Y}}\le r}}\left(1-{\displaystyle \prod _{\tau =1}^{{\rm Y}}}{\left(f_{i_{\tau }}^{inf}\left(v\right)\right)}^2\right)\right)}^{1/2},\\ {\left(1-{\displaystyle \prod _{1\le i_1\le ,\dots ,<i_{{\rm Y}}\le r}}\left(1-{\displaystyle \prod _{\tau =1}^{{\rm Y}}}{\left(f_{i_{\tau }}^{sup}\left(v\right)\right)}^2\right)\right)}^{1/2}\end{array}\right],\\ \left[\begin{array}{c}{\left(\left({\displaystyle \prod _{1\le i_1\le ,\dots ,<i_{{\rm Y}}\le r}}1-\left({\displaystyle \prod _{\tau =1}^{{\rm Y}}}\left(1-{\left(g_{i_{\tau }}^{inf}\left(v\right)\right)}^2\right)\right)\right)\right)}^{1/2}\\ ,{\left({\displaystyle \prod _{1\le i_1\le ,\dots ,<i_{{\rm Y}}\le r}}1-\left({\displaystyle \prod _{\tau =1}^{{\rm Y}}}\left(1-{\left(g_{i_{\tau }}^{sup}\left(v\right)\right)}^2\right)\right)\right)}^{1/2}\end{array}\right],\\ \left[\begin{array}{c}{\left({\displaystyle \prod _{1\le i_1\le ,\dots ,<i_{{\rm Y}}\le r}}1-\left({\displaystyle \prod _{\tau =1}^{{\rm Y}}}\left(1-{\left(w_{i_{\tau }}^{inf}\left(v\right)\right)}^2\right)\right)\right)}^{1/2},\\ {\left({\displaystyle \prod _{1\le {{\rm Y}}_1\le ,\dots ,<i_{{\rm Y}}\le r}^{{\rm Y}}}1-\left({\displaystyle \prod _{\tau =1}^{{\rm Y}}}\left(1-{\left(w_{i_{\tau }}^{sup}\left(v\right)\right)}^2\right)\right)\right)}^{1/2}\end{array}\right]\\ \end{array}\right)$$

$$\frac{1}{C_r^{{\rm Y}}}{\displaystyle \underset{1\le {{\rm Y}}_1\le ,\dots ,<{{\rm Y}}_{{\rm Y}}\le r}{⨂}}\left(\stackrel{{\rm Y}}{\underset{\tau =1}{⨂}}{A}_{i_{\tau }}\right)=\left(\begin{array}{c}\begin{array}{c}\left[\begin{array}{c}{\left(1-{\left({\displaystyle \prod _{1\le i_1\le ,\dots ,<i_{{\rm Y}}\le r}}\left(1-{{\displaystyle \prod _{\tau =1}^{{\rm Y}}}\left(f_{i_{\tau }}^{inf}\left(v\right)\right)}^2\right)\right)}^{1/C_r^{{\rm Y}}}\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.},\\ {\left(1-{\left({\displaystyle \prod _{1\le i_1\le ,\dots ,<i_{{\rm Y}}\le r}}\left(1-{\displaystyle \prod _{\tau =1}^{{\rm Y}}}{\left(f_{i_{\tau }}^{sup}\left(v\right)\right)}^2\right)\right)}^{1/C_r^{{\rm Y}}}\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}\end{array}\right],\\ \left[\begin{array}{c}{\left(1-{\left({\displaystyle \prod _{1\le {{\rm Y}}_1\le ,\dots ,<i_{{\rm Y}}\le r}}\left(1-{\displaystyle \prod _{\tau =1}^{{\rm Y}}}\left(1-{\left(g_{i_{\tau }}^{inf}\left(v\right)\right)}^2\right)\right)\right)}^{1/C_r^{{\rm Y}}}\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.},\\ {\left(1-{\left({\displaystyle \prod _{1\le i_1\le ,\dots ,<i_{{\rm Y}}\le r}}\left(1-{\displaystyle \prod _{\tau =1}^{{\rm Y}}}\left(1-{\left(g_{i_{\tau }}^{sup}\left(v\right)\right)}^2\right)\right)\right)}^{1/C_r^{{\rm Y}}}\right)}^{1/2}\end{array}\right]\end{array}\\ \left[\begin{array}{c}1-{\left({\displaystyle \prod _{1\le i_1\le ,\dots ,<i_{{\rm Y}}\le r}}\left(1-{\displaystyle \prod _{\tau =1}^{{\rm Y}}}\left(1-{\left(w_{i_{\tau }}^{inf}\left(v\right)\right)}^2\right)\right)\right)}^{1/C_r^{{\rm Y}}},\\ 1-{\left({\displaystyle \prod _{1\le {{\rm Y}}_1\le ,\dots ,<i_{{\rm Y}}\le r}}\left(1-{\displaystyle \prod _{\tau =1}^{{\rm Y}}}\left(1-{\left(w_{i_{\tau }}^{sup}\left(v\right)\right)}^2\right)\right)\right)}^{1/C_r^{{\rm Y}}}\end{array}\right]\end{array}\right)$$

therefore, we get

$$\begin{gathered} IVSFMSM\left(A_1,A_2,\dots ,A_r\right) \\ =\left(\begin{array}{c}\begin{array}{c}\\ \left[\begin{array}{c}{\left({\left(1-{\left({\displaystyle \prod _{1\le i_1\le ,\dots ,<i_{{\rm Y}}\le r}}\left(1-\left({\displaystyle \prod _{\tau =1}^{\dot{{\rm Y}}}}{\left(f_{i_{\tau }}^{inf}\left(v\right)\right)}^2\right)\right)\right)}^{1/C_r^{{\rm Y}}}\right)}^{1/\dot{{\rm Y}}}\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.},\\ {\left({\left(1-{\left({\displaystyle \prod _{1\le i_1\le ,\dots ,<i_{{\rm Y}}\le r}}\left(1-\left({\displaystyle \prod _{\tau =1}^{{\rm Y}}}{\left(f_{i_{\tau }}^{sup}\left(v\right)\right)}^2\right)\right)\right)}^{1/C_r^{{\rm Y}}}\right)}^{1/{\rm Y}}\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}\end{array}\right]\end{array},\\ \left[\begin{array}{c}{\left(1-{\left(1-{\left({\displaystyle \prod _{1\le i_1\le ,\dots ,<i_{{\rm Y}}\le r}}\left(1-\left({\displaystyle \prod _{\tau =1}^{{\rm Y}}}\left(1-{\left(g_{i_{\tau }}^{inf}\left(v\right)\right)}^2\right)\right)\right)\right)}^{1/C_r^{{\rm Y}}}\right)}^{1/\dot{{\rm Y}}}\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.},\\ {\left(1-{\left(1-{\left({\displaystyle \prod _{1\le i_1\le ,\dots ,<i_{{\rm Y}}\le r}}\left(1-\left({\displaystyle \prod _{\tau =1}^{{\rm Y}}}\left(1-{\left(g_{i_{\tau }}^{sup}\left(v\right)\right)}^2\right)\right)\right)\right)}^{1/C_r^{{\rm Y}}}\right)}^{1/\dot{\dot{{\rm Y}}}}\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}\end{array}\right],\\ \left[\begin{array}{c}{\left(1-{\left(1-{\left({\displaystyle \prod _{1\le i_1\le ,\dots ,<i_{{\rm Y}}\le r}}\left(1-\left({\displaystyle \prod _{\tau =1}^{\dot{{\rm Y}}}}\left(1-{\left(w_{i_{\tau }}^{inf}\left(v\right)\right)}^2\right)\right)\right)\right)}^{1/C_r^{{\rm Y}}}\right)}^{1/\dot{{\rm Y}}}\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.},\\ {\left(1-{\left(1-{\left({\displaystyle \prod _{1\le i_1\le ,\dots ,<i_{{\rm Y}}\le r}}\left(1-\left({\displaystyle \prod _{\tau =1}^{\dot{{\rm Y}}}}\left(1-{\left(w_{i_{\tau }}^{sup}\left(v\right)\right)}^2\right)\right)\right)\right)}^{1/C_r^{{\rm Y}}}\right)}^{1/\dot{{\rm Y}}}\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}\end{array}\right]\end{array}\right) \end{gathered}$$

as we know, an aggregation operator fulfills the criteria of three properties (boundedness, idempotency, and monotonicity). So, IVSFMSM operators satisfied these properties as given below

Property 1:

(Idempotency Property) Let ${\alpha }_i=\left(\left[f_i^{inf}\left(v\right) ,f_i^{sup}\left(v\right)\right],\left[g_i^{inf}\left(v\right) ,g_i^{sup}\left(v\right)\right],\left[w_i^{inf}\left(v\right), w_i^{sup}\left(v\right)\right]\right)$ and ${\alpha }_j=\left(\left[f_j^{inf}\left(v\right) ,f_j^{sup}\left(v\right)\right],\left[g_j^{inf}\left(v\right) ,g_j^{sup}\left(v\right)\right],\left[w_j^{inf}\left(v\right), w_j^{sup}\left(v\right)\right]\right)$ be two collections of IVSFVs. If $A_i=A$ then (all are identical)

$$IVSFMSM\left(A_1,A_2,A_3,\dots ,A_r\right)=A$$

Property 2:

(Monotonicity Property) Let $A_{i\tau }$ and${\check{A}}_{i\tau }$ be two IVSFVs. If$f_i^{inf}\left(v\right)\le {\check{f}}_i^{inf}\left(v\right)$,$f_i^{sup}\left(v\right)\le {\check{f}}_i^{sup}\left(v\right)$,$g_i^{inf}\left(v\right)\ge {\check{g}}_i^{inf}\left(v\right)$,$g_i^{sup}\left(v\right)\ge {\check{g}}_i^{sup}\left(v\right)$, and $w_i^{inf}\left(v\right)\ge {\check{w}}_i^{inf}\left(v\right)$, $w_i^{sup}\left(v\right)\ge {\check{w}}_i^{sup}\left(v\right)$ then

$$IVSFMSM\left(A_1,A_2,\dots ,A_r\right)\le IVSFMSM\left({\check{A}}_1,{\check{A}}_2,\dots ,{\check{A}}_r\right)$$

Property 3:

(Boundedness Property) Let $A_i=\left(\left[f_i^{inf}\left(v\right) ,f_i^{sup}\left(v\right)\right],\left[g_i^{inf}\left(v\right) ,g_i^{sup}\left(v\right)\right],\left[w_i^{inf}\left(v\right), w_i^{sup}\left(v\right)\right]\right)$ be a collection of IVSFVs and let$A^{inf}$and$A^{sup}$ denote the smallest and the greatest IVSFVs respectively. Then

$$A^{inf}\le IVSFMSM\left(A_1,A_2,\dots ,A_r\right)\le A^{sup}$$

Definition 7:

Let $A_i=\left(\left[f_i^{inf}\left(v\right) ,f_i^{sup}\left(v\right)\right],\left[g_i^{inf}\left(v\right) ,g_i^{sup}\left(v\right)\right],\left[w_i^{inf}\left(v\right), w_i^{sup}\left(v\right)\right]\right)$be a collection of IVSFVs and${\omega }_i$be the weight vector of$A_i$such that ${{\displaystyle \sum }}_{i=1}^n{\omega }_i=1$

. Then, the IVSFWMSM operator is defined by

$$IVSFWMSM\left(A_1,A_2,\dots ,A_r\right)=\left[{\left(\frac{\underset{1\le i_1\le ,\dots ,<i_{{\rm Y}}}{\otimes }{\left(\stackrel{{\rm Y}}{\underset{\tau =1}{\otimes \left(A_{i_{\tau }}\right)}}\right)}^{{\omega }_{i\tau }}}{C_r^{{\rm Y}}}\right)}^{1/\dot{{\rm Y}}}\right].$$

(4)

Theorem 2:

Let $A_i=\left(\left[f_i^{inf}\left(v\right) ,f_i^{sup}\left(v\right)\right],\left[g_i^{inf}\left(v\right) ,g_i^{sup}\left(v\right)\right],\left[w_i^{inf}\left(v\right), w_i^{sup}\left(v\right)\right]\right)$be a collection of IVSFVs. Then, using IVSFWMSM operator, we get

$$\begin{gathered} IVSFWMSM\left(A_1,A_2,\dots ..,A_r\right) \\ =\left(\begin{array}{c}\left[\begin{array}{c}{\left({\left(1-{\left({\displaystyle \prod _{1\le i_1\le ,\dots ,<i_{{\rm Y}}\le r}}\left(1-\left({\left({\left(f_{i_{\tau }}^{inf}\left(v\right)\right)}^2\right)}^{{\omega }_{i\tau }}\right)\right)\right)}^{1/C_r^{{\rm Y}}}\right)}^{1/\dot{\dot{{\rm Y}}}}\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.},\\ {\left({\left(1-{\left({\displaystyle \prod _{1\le i_1\le ,\dots ,<i_{{\rm Y}}\le r}}\left(1-\left({\left({\left(f_{i_{\tau }}^{sup}\left(v\right)\right)}^2\right)}^{{\omega }_{i\tau }}\right)\right)\right)}^{1/C_r^{{\rm Y}}}\right)}^{1/\dot{{\rm Y}}}\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}\end{array}\right],\\ \left[\begin{array}{c}{\left(1-{\left(1-{\left({\displaystyle \prod _{1\le {{\rm Y}}_1\le ,\dots ,<i_{{\rm Y}}\le r}}\left(1-\left({\displaystyle \prod _{\tau =1}^{{\rm Y}}}{\left(1-{\left(g_{i_{\tau }}^{inf}\left(v\right)\right)}^2\right)}^{{\omega }_{i\tau }}\right)\right)\right)}^{1/C_r^{{\rm Y}}}\right)}^{1/\dot{\dot{{\rm Y}}}}\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.},\\ {\left(1-{\left(1-{\left({\displaystyle \prod _{1\le {{\rm Y}}_1\le ,\dots ,<i_{{\rm Y}}\le r}}\left(1-\left({\displaystyle \prod _{\tau =1}^{{\rm Y}}}{\left(1-{\left(g_{i_{\tau }}^{sup}\left(v\right)\right)}^2\right)}^{{\omega }_{i\tau }}\right)\right)\right)}^{1/C_r^{{\rm Y}}}\right)}^{1/\dot{\dot{{\rm Y}}}}\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}\end{array}\right],\\ \left[\begin{array}{c}{\left(1-{\left(1-{\left({\displaystyle \prod _{1\le {{\rm Y}}_1\le ,\dots ,<i_{{\rm Y}}\le r}}\left(1-\left({\displaystyle \prod _{\tau =1}^{{\rm Y}}}{\left(1-{\left(w_{i_{\tau }}^{inf}\left(v\right)\right)}^2\right)}^{{\omega }_{i\tau }}\right)\right)\right)}^{1/C_r^{{\rm Y}}}\right)}^{1/\dot{\dot{{\rm Y}}}}\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.},\\ {\left(1-{\left(1-{\left({\displaystyle \prod _{1\le {{\rm Y}}_1\le ,\dots ,<i_{{\rm Y}}\le r}}\left(1-\left({\displaystyle \prod _{\tau =1}^{{\rm Y}}}{\left(1-{\left(w_{i_{\tau }}^{sup}\left(v\right)\right)}^2\right)}^{{\omega }_{i\tau }}\right)\right)\right)}^{1/C_r^{{\rm Y}}}\right)}^{1/\dot{\dot{{\rm Y}}}}\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}\end{array}\right]\end{array}\right). \end{gathered}$$

Proof: 

Proof is skipped.

4. Interval-Valued IVSFDMSM Operator

The main purpose of this part of the paper is to develop the ideas of IVSFDMSM and IVSFDWMSM by using MD, NMD, and AD.

Definition 8:

Let $A_i=\left(\left[f_i^{inf}\left(v\right) ,f_i^{sup}\left(v\right)\right],\left[g_i^{inf}\left(v\right) ,g_i^{sup}\left(v\right)\right],\left[w_i^{inf}\left(v\right), w_i^{sup}\left(v\right)\right]\right)$be a collection of IVSFVs. Then, IVSFDMSM is defined as

$$IVSFDMSM\left(A_1,A_2,\dots ,A_r\right)=\left[\frac{1}{{\rm Y}}\left(\underset{1\le i_1\le ,\dots ,<i_{{\rm Y}}\le r}{\oplus }{\left(\stackrel{{\rm Y}}{\underset{\tau =1}{\otimes }}{A}_{i_{\tau }}\right)}^{1/C_r^{{\rm Y}}}\right)\right]$$

Theorem 3:

Let $A_i=\left(\left[f_i^{inf}\left(v\right) ,f_i^{sup}\left(v\right)\right],\left[g_i^{inf}\left(v\right) ,g_i^{sup}\left(v\right)\right],\left[w_i^{inf}\left(v\right), w_i^{sup}\left(v\right)\right]\right)$denote the collection of IVSFVs. Then, by using IVSFDMSM operators, we have

$$\begin{gathered} IVSFDMSM\left(A_1,A_2,\dots ,A_r\right) \\ =\left(\begin{array}{c}\begin{array}{c}\left[\begin{array}{c}{\left(1-{\left(1-{\left({\displaystyle \prod _{1\le i_1\le ,\dots ,<i_{{\rm Y}}\le r}}\left(1-\left({\displaystyle \prod _{\tau =1}^{\dot{{\rm Y}}}}\left(1-{\left(f_{i_{\tau }}^{inf}\left(v\right)\right)}^2\right)\right)\right)\right)}^{1/C_r^{{\rm Y}}}\right)}^{1/\dot{{\rm Y}}}\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.},\\ {\left(1-{\left(1-{\left({\displaystyle \prod _{1\le i_1\le ,\dots ,<i_{{\rm Y}}\le r}}\left(1-\left({\displaystyle \prod _{\tau =1}^{\dot{{\rm Y}}}}\left(1-{\left(f_{i_{\tau }}^{sup}\left(v\right)\right)}^2\right)\right)\right)\right)}^{1/C_r^{{\rm Y}}}\right)}^{1/\dot{{\rm Y}}}\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}\end{array}\right],\\ \left[\begin{array}{c}{\left({\left(1-{\left({\displaystyle \prod _{1\le i_1\le ,\dots ,<i_{{\rm Y}}\le r}}\left(1-\left({\displaystyle \prod _{\tau =1}^{{\rm Y}}}{\left(g_{i_{\tau }}^{inf}\left(v\right)\right)}^2\right)\right)\right)}^{1/C_r^{{\rm Y}}}\right)}^{1/\dot{{\rm Y}}}\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.},\\ {\left({\left(1-{\left({\displaystyle \prod _{1\le i_1\le ,\dots ,<i_{{\rm Y}}\le r}}\left(1-\left({\displaystyle \prod _{\tau =1}^{{\rm Y}}}{\left(g_{i_{\tau }}^{sup}\left(v\right)\right)}^2\right)\right)\right)}^{1/C_r^{{\rm Y}}}\right)}^{1/\dot{{\rm Y}}}\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}\end{array}\right]\\ \end{array},\\ \left[\begin{array}{c}{\left({\left(1-{\left({\displaystyle \prod _{1\le i_1\le ,\dots ,<i_{{\rm Y}}\le r}}\left(1-\left({\displaystyle \prod _{\tau =1}^{{\rm Y}}}{\left(w_{i_{\tau }}^{inf}\left(v\right)\right)}^2\right)\right)\right)}^{1/C_r^{{\rm Y}}}\right)}^{1/\dot{{\rm Y}}}\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.},\\ {\left({\left(1-{\left({\displaystyle \prod _{1\le i_1\le ,\dots ,<i_{{\rm Y}}\le r}}\left(1-\left({\displaystyle \prod _{\tau =1}^{{\rm Y}}}{\left(w_{i_{\tau }}^{sup}\left(v\right)\right)}^2\right)\right)\right)}^{1/C_r^{{\rm Y}}}\right)}^{1/\dot{{\rm Y}}}\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}\end{array}\right]\end{array}\right). \end{gathered}$$

Proof: 

Using Definition 8, we have

$$\stackrel{{\rm Y}}{\underset{\tau =1}{⨂}}{A}_{i_{\tau }}=\left(\begin{array}{c}\left[{\left(1-{\displaystyle \prod _{\tau =1}^{\dot{{\rm Y}}}}\left(1-{\left(f_{i_{\tau }}^{inf}\left(v\right)\right)}^2\right)\right)}^{\frac{1}{2}},{\left(1-{\displaystyle \prod _{\tau =1}^{\dot{{\rm Y}}}}\left(1-{\left(f_{i_{\tau }}^{sup}\left(v\right)\right)}^2\right)\right)}^{\frac{1}{2}}\right],\\ \left[{\displaystyle \prod _{\tau =1}^{\dot{{\rm Y}}}}{g}_{i_{\tau }}^{inf}\left(v\right),{\displaystyle \prod _{\tau =1}^{\dot{{\rm Y}}}}{g}_{i_{\tau }}^{sup}\left(v\right)\right],\left[{\displaystyle \prod _{\tau =1}^{\dot{{\rm Y}}}}{w}_{i_{\tau }}^{inf}\left(v\right),{\displaystyle \prod _{\tau =1}^{\dot{{\rm Y}}}}{w}_{i_{\tau }}^{sup}\left(v\right)\right]\end{array}\right)$$

$${\left(\stackrel{{\rm Y}}{\underset{\tau =1}{⨂}}{A}_{i\tau }\right)}^{1/C_r^{{\rm Y}}}=\left(\begin{array}{c}\left[\begin{array}{c}{\left(1-{\displaystyle \prod _{\tau =1}^{{\rm Y}}}\left(1-{\left(f_{i_{\tau }}^{inf}\left(v\right)\right)}^2\right)\right)}^{1/C_r^{{\rm Y}}},\\ {\left(1-{\displaystyle \prod _{\tau =1}^{{\rm Y}}}\left(1-{\left(f_{i_{\tau }}^{sup}\left(v\right)\right)}^2\right)\right)}^{1/C_r^{{\rm Y}}}\end{array}\right],\\ \left[\begin{array}{c}1-{\left(1-\left({\displaystyle \prod _{\tau =1}^{{\rm Y}}}{\left(g_{i_{\tau }}^{inf}\left(v\right)\right)}^2\right)\right)}^{1/C_r^{{\rm Y}}},\\ 1-{\left(1-\left({\displaystyle \prod _{\tau =1}^{{\rm Y}}}{\left(g_{i_{\tau }}^{sup}\left(v\right)\right)}^2\right)\right)}^{1/C_r^{{\rm Y}}}\end{array}\right],\\ \left[\begin{array}{c}1-{\left(1-\left({\displaystyle \prod _{\tau =1}^{{\rm Y}}}{\left(w_{i_{\tau }}^{inf}\left(v\right)\right)}^2\right)\right)}^{1/C_r^{{\rm Y}}},\\ 1-{\left(1-\left({\displaystyle \prod _{\tau =1}^{{\rm Y}}}{\left(w_{i_{\tau }}^{sup}\left(v\right)\right)}^2\right)\right)}^{1/C_r^{{\rm Y}}}\end{array}\right]\end{array}\right)$$

$$\underset{1\le i_1\le ,\dots ,<i_{{\rm Y}}\le r}{\dot{⨂}}{\left(\stackrel{{\rm Y}}{\underset{\tau =1}{⨁}}{A}_{i_{\tau }}\right)}^{1/C_r^{{\rm Y}}}=\left(\begin{array}{c}\left[\begin{array}{c}{\left({\displaystyle \prod _{1\le i_1\le ,\dots ,<i_{{\rm Y}}\le r}}{\left(1-{\displaystyle \prod _{\tau =1}^{{\rm Y}}}\left(1-{\left(f_{i_{\tau }}^{inf}\left(v\right)\right)}^2\right)\right)}^{1/C_r^{{\rm Y}}}\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.},\\ {\left({\displaystyle \prod _{1\le i_1\le ,\dots ,<i_{{\rm Y}}\le r}}{\left(1-{\displaystyle \prod _{\tau =1}^{{\rm Y}}}\left(1-{\left(f_{i_{\tau }}^{sup}\left(v\right)\right)}^2\right)\right)}^{1/C_r^{{\rm Y}}}\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}\end{array}\right],\\ \left[\begin{array}{c}{\left(1-{\displaystyle \prod _{1\le i_1\le ,\dots ,<i_{{\rm Y}}\le r}}{\left(1-\left({\displaystyle \prod _{\tau =1}^{{\rm Y}}}{\left(g_{i_{\tau }}^{inf}\left(v\right)\right)}^2\right)\right)}^{1/C_r^{{\rm Y}}},\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}\\ {\left(1-{\displaystyle \prod _{1\le i_1\le ,\dots ,<i_{{\rm Y}}\le r}}{\left(1-\left({\displaystyle \prod _{\tau =1}^{{\rm Y}}}{\left(g_{i_{\tau }}^{sup}\left(v\right)\right)}^2\right)\right)}^{1/C_r^{{\rm Y}}}\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}\end{array}\right],\\ \left[\begin{array}{c}{\left(1-{\displaystyle \prod _{1\le i_1\le ,\dots ,<i_{{\rm Y}}\le r}}{\left(1-\left({\displaystyle \prod _{\tau =1}^{{\rm Y}}}{\left(w_{i_{\tau }}^{inf}\left(v\right)\right)}^2\right)\right)}^{1/C_r^{{\rm Y}}},\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}\\ {\left(1-{\displaystyle \prod _{1\le i_1\le ,\dots ,<i_{{\rm Y}}\le r}}{\left(1-\left({\displaystyle \prod _{\tau =1}^{{\rm Y}}}{\left(w_{i_{\tau }}^{sup}\left(v\right)\right)}^2\right)\right)}^{1/C_r^{{\rm Y}}}\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}\end{array}\right]\end{array}\right)$$

therefore, we get

$$\begin{gathered} IVSFDMSM\left(A_1,A_2,\dots ,A_r\right) \\ =\left(\begin{array}{c}\begin{array}{c}\left[\begin{array}{c}{\left(1-{\left(1-{\displaystyle \prod _{1\le i_1\le ,\dots ,<i_{{\rm Y}}\le r}}{\left(1-{\displaystyle \prod _{\tau =1}^{{\rm Y}}}\left(1-{\left(f_{i_{\tau }}^{inf}\left(v\right)\right)}^2\right)\right)}^{1/C_r^{{\rm Y}}}\right)}^{1/\dot{{\rm Y}}}\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.},\\ {\left(1-{\left(1-{\displaystyle \prod _{1\le i_1\le ,\dots ,<i_{{\rm Y}}\le r}}{\left(1-{\displaystyle \prod _{\tau =1}^{{\rm Y}}}\left(1-{\left(f_{i_{\tau }}^{sup}\left(v\right)\right)}^2\right)\right)}^{1/C_r^{{\rm Y}}}\right)}^{1/\dot{{\rm Y}}}\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}\end{array}\right],\\ \left[\begin{array}{c}{\left({\left(1-{\left({\displaystyle \prod _{1\le i_1\le ,\dots ,<i_{{\rm Y}}\le r}}\left(1-\left({{\displaystyle \prod _{\tau =1}^{{\rm Y}}}\left(g_{i_{\tau }}^{inf}\left(v\right)\right)}^2\right)\right)\right)}^{1/C_r^{{\rm Y}}}\right)}^{1/\dot{{\rm Y}}}\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.},\\ {\left({\left(1-{\left({\displaystyle \prod _{1\le i_1\le ,\dots ,<i_{{\rm Y}}\le r}}\left(1-\left({\displaystyle \prod _{\tau =1}^{{\rm Y}}}{\left(g_{i_{\tau }}^{sup}\left(v\right)\right)}^2\right)\right)\right)}^{1/C_r^{{\rm Y}}}\right)}^{1/\dot{{\rm Y}}}\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}\end{array}\right]\\ \end{array},\\ \left[\begin{array}{c}{\left({\left(1-{\left({\displaystyle \prod _{1\le i_1\le ,\dots ,<i_{{\rm Y}}\le r}}\left(1-\left({\displaystyle \prod _{\tau =1}^{{\rm Y}}}{\left(w_{i_{\tau }}^{inf}\left(v\right)\right)}^2\right)\right)\right)}^{1/C_r^{{\rm Y}}}\right)}^{1/\dot{{\rm Y}}}\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.},\\ {\left({\left(1-{\left({\displaystyle \prod _{1\le i_1\le ,\dots ,<i_{{\rm Y}}\le r}}\left(1-\left({\displaystyle \prod _{\tau =1}^{{\rm Y}}}{\left(w_{i_{\tau }}^{sup}\left(v\right)\right)}^2\right)\right)\right)}^{1/C_r^{{\rm Y}}}\right)}^{1/\dot{{\rm Y}}}\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}\end{array}\right]\end{array}\right) \end{gathered}$$

IVSFDMSM operators also satisfied the aggregation properties (Boundedness, Idempotency, and Monotonicity).

Property 4:

(Idempotency property) Let $A_i=\left(\left[f_i^{inf}\left(v\right), f_i^{sup}\left(v\right)\right] \left[g_i^{inf}\left(v\right), g_i^{sup}\left(v\right)\right] \left[w_i^{inf}\left(v\right), w_i^{sup}\left(v\right)\right]\right)$ and if $A_i=A$ then (all are identical)

$$IVSFDMSM\left(A_1,A_2,A_3,\dots ,A_r\right)=A.$$

Property 5:

(Boundedness Property) Let$A_i=\left(\left[f_i^{inf}\left(v\right),f_i^{sup}\left(v\right)\right],\left[g_i^{inf}\left(v\right),g_i^{sup}\left(v\right)\right],\left[w_i^{inf}\left(v\right),w_i^{sup}\left(v\right)\right]\right)$ be a collection of IVSFVs and let$A^{inf}$ and$A^{sup}$ denote the smallest and the greatest IVSFVs, respectively. Then

$$A^{inf}\le IVSFFDMSM\left(A_1,A_2,\dots ,A_r\right)\le A^{sup}.$$

Definition 9:

Let$A_i=\left(\left[f_i^{inf}\left(v\right),f_i^{sup}\left(v\right)\right],\left[g_i^{inf}\left(v\right),g_i^{sup}\left(v\right)\right],\left[w_i^{inf}\left(v\right),w_i^{sup}\left(v\right)\right]\right)$be a collection of IVSFVs. Then, the IVSFDWMSM operator is given as

$$\begin{gathered} IVSFDWMSM\left(A_1,A_2,\dots ,A_r\right) \\ =\left(\begin{array}{c}\begin{array}{c}\left[\begin{array}{c}{\left(1-{\left(1-{\displaystyle \prod _{1\le i_1\le ,\dots ,<i_{{\rm Y}}\le r}}{\left(1-{\displaystyle \prod _{\tau =1}^{{\rm Y}}}{\left(1-{\left(f_{i_{\tau }}^{inf}\left(v\right)\right)}^2\right)}^{{\omega }_{i\tau }}\right)}^{1/C_r^{{\rm Y}}}\right)}^{1/\dot{{\rm Y}}}\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.},\\ {\left(1-{\left(1-{\displaystyle \prod _{1\le i_1\le ,\dots ,<i_{{\rm Y}}\le r}}{\left(1-{\displaystyle \prod _{\tau =1}^{{\rm Y}}}{\left(1-{\left(f_{i_{\tau }}^{sup}\left(v\right)\right)}^2\right)}^{{\omega }_{i\tau }}\right)}^{1/C_r^{{\rm Y}}}\right)}^{1/\dot{{\rm Y}}}\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}\end{array}\right],\\ \left[\begin{array}{c}{\left({\left(1-{\left({\displaystyle \prod _{1\le i_1\le ,\dots ,<i_{{\rm Y}}\le r}}\left(1-\left({\displaystyle \prod _{\tau =1}^{{\rm Y}}}{\left({\left(g_{i_{\tau }}^{inf}\left(v\right)\right)}^2\right)}^{{\omega }_{i\tau }}\right)\right)\right)}^{1/C_r^{{\rm Y}}}\right)}^{1/\dot{{\rm Y}}}\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.},\\ {\left({\left(1-{\left({\displaystyle \prod _{1\le i_1\le ,\dots ,<i_{{\rm Y}}\le r}}\left(1-\left({\displaystyle \prod _{\tau =1}^{{\rm Y}}}{\left({\left(g_{i_{\tau }}^{sup}\left(v\right)\right)}^2\right)}^{{\omega }_{i\tau }}\right)\right)\right)}^{1/C_r^{{\rm Y}}}\right)}^{1/\dot{{\rm Y}}}\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}\end{array}\right]\\ \end{array},\\ \left[\begin{array}{c}{\left({\left(1-{\left({\displaystyle \prod _{1\le i_1\le ,\dots ,<i_{{\rm Y}}\le r}}\left(1-\left({\displaystyle \prod _{\tau =1}^{{\rm Y}}}{\left({\left(w_{i_{\tau }}^{inf}\left(v\right)\right)}^2\right)}^{{\omega }_{i\tau }}\right)\right)\right)}^{1/C_r^{{\rm Y}}}\right)}^{1/\dot{{\rm Y}}}\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.},\\ {\left({\left(1-{\left({\displaystyle \prod _{1\le i_1\le ,\dots ,<i_{{\rm Y}}\le r}}\left(1-\left({\displaystyle \prod _{\tau =1}^{{\rm Y}}}{\left({\left(w_{i_{\tau }}^{sup}\left(v\right)\right)}^2\right)}^{{\omega }_{i\tau }}\right)\right)\right)}^{1/C_r^{{\rm Y}}}\right)}^{1/\dot{{\rm Y}}}\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.},\end{array}\right]\end{array}\right). \end{gathered}$$

Theorem 4:

Let$A_i=\left(\left[f_i^{inf}\left(v\right),f_i^{sup}\left(v\right)\right],\left[g_i^{inf}\left(v\right),g_i^{sup}\left(v\right)\right],\left[w_i^{inf}\left(v\right),w_i^{sup}\left(v\right)\right]\right)$denote the collection of IVSPFNs. Then, by using IVSFDWMSM operators, we have

$$\begin{gathered} IVSFDWMSM\left(A_1,A_2,\dots ,A_r\right) \\ =\left(\begin{array}{c}\begin{array}{c}\left[\begin{array}{c}{\left(1-{\left(1-{\displaystyle \prod _{1\le i_1\le ,\dots ,<i_{{\rm Y}}\le r}}{\left(1-{\displaystyle \prod _{\tau =1}^{{\rm Y}}}{\left(1-{\left(f_{i_{\tau }}^{inf}\left(v\right)\right)}^2\right)}^{{\omega }_{i\tau }}\right)}^{1/C_r^{{\rm Y}}}\right)}^{1/\dot{{\rm Y}}}\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.},\\ {\left(1-{\left(1-{\displaystyle \prod _{1\le i_1\le ,\dots ,<i_{{\rm Y}}\le r}}{\left(1-{\displaystyle \prod _{\tau =1}^{{\rm Y}}}{\left(1-{\left(f_{i_{\tau }}^{sup}\left(v\right)\right)}^2\right)}^{{\omega }_{i\tau }}\right)}^{1/C_r^{{\rm Y}}}\right)}^{1/\dot{{\rm Y}}}\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}\end{array}\right],\\ \left[\begin{array}{c}{\left({\left(1-{\left({\displaystyle \prod _{1\le i_1\le ,\dots ,<i_{{\rm Y}}\le r}}\left(1-\left({\displaystyle \prod _{\tau =1}^{{\rm Y}}}{\left({\left(g_{i_{\tau }}^{inf}\left(v\right)\right)}^2\right)}^{{\omega }_{i\tau }}\right)\right)\right)}^{1/C_r^{{\rm Y}}}\right)}^{1/\dot{{\rm Y}}}\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.},\\ {\left({\left(1-{\left({\displaystyle \prod _{1\le i_1\le ,\dots ,<i_{{\rm Y}}\le r}}\left(1-\left({\displaystyle \prod _{\tau =1}^{{\rm Y}}}{\left({\left(g_{i_{\tau }}^{sup}\left(v\right)\right)}^2\right)}^{{\omega }_{i\tau }}\right)\right)\right)}^{1/C_r^{{\rm Y}}}\right)}^{1/\dot{{\rm Y}}}\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}\end{array}\right]\\ \end{array},\\ \left[\begin{array}{c}{\left({\left(1-{\left({\displaystyle \prod _{1\le i_1\le ,\dots ,<i_{{\rm Y}}\le r}}\left(1-\left({\displaystyle \prod _{\tau =1}^{{\rm Y}}}{\left({\left(w_{i_{\tau }}^{inf}\left(v\right)\right)}^2\right)}^{{\omega }_{i\tau }}\right)\right)\right)}^{1/C_r^{{\rm Y}}}\right)}^{1/\dot{{\rm Y}}}\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.},\\ {\left({\left(1-{\left({\displaystyle \prod _{1\le i_1\le ,\dots ,<i_{{\rm Y}}\le r}}\left(1-\left({\displaystyle \prod _{\tau =1}^{{\rm Y}}}{\left({\left(w_{i_{\tau }}^{sup}\left(v\right)\right)}^2\right)}^{{\omega }_{i\tau }}\right)\right)\right)}^{1/C_r^{{\rm Y}}}\right)}^{1/\dot{{\rm Y}}}\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.},\end{array}\right]\end{array}\right). \end{gathered}$$

Proof: 

The proof is the same as in Theorem 3 above.

We will discuss a numerical example to illustrate the calculation process.

We take the values $A_1=\left(\left[0.21,0.30\right],\left[0.18,0.25\right], \left[0.05,0.19\right]\right)$, $A_2=\left(\left[0.09,0.31\right],\left[0.15,0.20\right],\left[0.19,0.25\right]\right)$, $A_3=\left(\left[0.08,0.17\right],\left[0.14,0.20\right],\left[0.21,0.24\right]\right), A_4=\left(\left[0.17,0.31\right],\left[0.07,0.12\right],\left[0.20,0.25\right]\right)$ also $r=4$ and ${\rm Y}=1$. Now we take a weight vector such as ${\left(0.3, 0.2,0.1,0.4\right)}^T$.

For MD,

$$\begin{gathered} =\left(\left[\begin{array}{c}{\left(1-{\left(1-{\left(\begin{array}{c}1-{\left({\left({\left(1-0.21\right)}^2\right)}^{0.3}\times {\left(1-0.09\right)}^2\right)}^{0.2}\\ \times {\left({\left(1-0.08\right)}^2\right)}^{0.1}\times {\left({\left(1-0.17\right)}^2\right)}^{0.4}\end{array}\right)}^{\frac{1}{4}}\right)}^1\right)}^{\frac{1}{2}},\\ {\left(1-{\left(1-{\left(\begin{array}{c}1-{\left({\left({\left(1-0.30\right)}^2\right)}^{0.3}\times {\left(1-0.31\right)}^2\right)}^{0.2}\times \\ {\left({\left(1-0.17\right)}^2\right)}^{0.1}\times {\left({\left(1-0.31\right)}^2\right)}^{0.4}\end{array}\right)}^{1/4}\right)}^1\right)}^{1/2}\end{array}\right]\right), \\ =[0.11,0.12] \end{gathered}$$

for AD,

$$\begin{gathered} =\left[\begin{array}{c}{\left(1-{\left({\begin{array}{c}\left(1-{\left({\left(0.18\right)}^2\right)}^{0.3}\right)\times \left(1-{\left({\left(0.15\right)}^2\right)}^{0.2}\right)\times \\ \left(1-{\left({\left(0.14\right)}^2\right)}^{0.1}\right)\times \left(1-{\left({\left(0.07\right)}^2\right)}^{0.4}\right)\end{array}}^{\frac{1}{1}}\right)}^{\frac{1}{4}}\right)}^{\frac{1}{2}},\\ {\left(1-{\left({\begin{array}{c}\left(1-{\left({\left(0.25\right)}^2\right)}^{0.3}\right)\times \left(1-{\left({\left(0.20\right)}^2\right)}^{0.2}\right)\times \\ \left(1-{\left({\left(0.20\right)}^2\right)}^{0.1}\right)\times \left(1-{\left({\left(0.12\right)}^2\right)}^{0.4}\right)\end{array}}^{1/1}\right)}^{1/4}\right)}^{1/2}\end{array}\right], \\ =\left[0.01,0.04\right] \end{gathered}$$

for NMD,

$$\begin{gathered} =\left[\begin{array}{c}{\left(1-{\left({\begin{array}{c}\left(1-{\left({\left(0.05\right)}^2\right)}^{0.3}\right)\times \left(1-{\left({\left(0.19\right)}^2\right)}^{0.2}\right)\times \\ \left(1-{\left({\left(0.24\right)}^2\right)}^{0.1}\right)\times \left(1-{\left({\left(0.20\right)}^2\right)}^{0.4}\right)\end{array}}^{\frac{1}{1}}\right)}^{\frac{1}{4}}\right)}^{\frac{1}{2}},\\ {\left(1-{\left({\begin{array}{c}\left(1-{\left({\left(0.19\right)}^2\right)}^{0.3}\right)\times \left(1-{\left({\left(0.25\right)}^2\right)}^{0.2}\right)\times \\ \left(1-{\left({\left(0.21\right)}^2\right)}^{0.1}\right)\times \left(1-{\left({\left(0.25\right)}^2\right)}^{0.4}\right)\end{array}}^{1/1}\right)}^{1/4}\right)}^{1/2}\end{array}\right], \\ =\left[0.02,0.06\right] \end{gathered}$$

5. Special Cases Analysis

In this section, we observe the changes in the proposed operators in different frameworks. To begin, take the IVSFMSM abstinence values, which are zero, and convert them into IVPyFMSM operators such as $\left\{g_{i\tau }^{inf}=0, g_{i\tau }^{sup}=0\right\}$

$$\begin{gathered} IVSFMSM\left(A_1,A_2,\dots ..,A_r\right) \\ =\left(\begin{array}{c}\begin{array}{c}\\ \left[\begin{array}{c}{\left({\left(1-{\left({\displaystyle \prod _{1\le i_1\le ,\dots ,<i_{{\rm Y}}\le r}}\left(1-\left({\displaystyle \prod _{\tau =1}^{{\rm Y}}}{\left(f_{i_{\tau }}^{inf}\left(v\right)\right)}^2\right)\right)\right)}^{1/C_r^{{\rm Y}}}\right)}^{1/\dot{{\rm Y}}}\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.},\\ {\left({\left(1-{\left({\displaystyle \prod _{1\le i_1\le ,\dots ,<i_{{\rm Y}}\le r}}\left(1-\left({\displaystyle \prod _{\tau =1}^{{\rm Y}}}{\left(f_{i_{\tau }}^{inf}\left(v\right)\right)}^2\right)\right)\right)}^{1/C_r^{{\rm Y}}}\right)}^{1/\dot{{\rm Y}}}\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}\end{array}\right]\end{array},\\ \left[\begin{array}{c}{\left(1-{\left(1-{\left({\displaystyle \prod _{1\le i_1\le ,\dots ,<i_{{\rm Y}}\le r}}\left(1-\left({\displaystyle \prod _{\tau =1}^{{\rm Y}}}\left(1-{\left(g_{i_{\tau }}^{inf}\left(v\right)\right)}^2\right)\right)\right)\right)}^{1/C_r^{{\rm Y}}}\right)}^{1/\dot{{\rm Y}}}\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.},\\ {\left(1-{\left(1-{\left({\displaystyle \prod _{1\le i_1\le ,\dots ,<i_{{\rm Y}}\le r}}\left(1-\left({\displaystyle \prod _{\tau =1}^{{\rm Y}}}\left(1-{\left(g_{i_{\tau }}^{sup}\left(v\right)\right)}^2\right)\right)\right)\right)}^{1/C_r^{{\rm Y}}}\right)}^{1/\dot{{\rm Y}}}\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}\end{array}\right],\\ \left[\begin{array}{c},\\ {\begin{array}{c}\left(1-{\left(1-{\left({\displaystyle \prod _{1\le i_1\le ,\dots ,<i_{{\rm Y}}\le r}}\left(1-\left({\displaystyle \prod _{\tau =1}^{{\rm Y}}}\left(1-{\left(w_{i_{\tau }}^{inf}\left(v\right)\right)}^2\right)\right)\right)\right)}^{1/C_r^{{\rm Y}}}\right)}^{1/\dot{{\rm Y}}}\right)\\ {\left(1-{\left(1-{\left({\displaystyle \prod _{1\le i_1\le ,\dots ,<i_{{\rm Y}}\le r}}\left(1-\left({\displaystyle \prod _{\tau =1}^{{\rm Y}}}\left(1-{\left(w_{i_{\tau }}^{sup}\left(v\right)\right)}^2\right)\right)\right)\right)}^{1/C_r^{{\rm Y}}}\right)}^{1/\dot{{\rm Y}}}\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}\end{array}}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}\end{array}\right];\end{array}\right) \end{gathered}$$

$$\begin{gathered} IVSFDMSM\left(A_1,A_2,\dots ,A_r\right) \\ =\left(\begin{array}{c}\begin{array}{c}\left[\begin{array}{c},\\ {\left(1-{\left(1-{\displaystyle \prod _{1\le i_1\le ,\dots ,<i_{{\rm Y}}\le r}}{\left(1-{\displaystyle \prod _{\tau =1}^{{\rm Y}}}\left(1-{\left(f_{i_{\tau }}^{inf}\left(v\right)\right)}^2\right)\right)}^{1/C_r^{{\rm Y}}}\right)}^{1/\dot{{\rm Y}}}\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}\\ {\left(1-{\left(1-{\displaystyle \prod _{1\le i_1\le ,\dots ,<i_{{\rm Y}}\le r}}{\left(1-{\displaystyle \prod _{\tau =1}^{{\rm Y}}}\left(1-{\left(f_{i_{\tau }}^{sup}\left(v\right)\right)}^2\right)\right)}^{1/C_r^{{\rm Y}}}\right)}^{1/\dot{{\rm Y}}}\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}\end{array}\right],\\ \left[\begin{array}{c}{\left({\left(1-{\left({\displaystyle \prod _{1\le i_1\le ,\dots ,<i_{{\rm Y}}\le r}}\left(1-\left({\displaystyle \prod _{\tau =1}^{{\rm Y}}}{\left(g_{i_{\tau }}^{inf}\left(v\right)\right)}^2\right)\right)\right)}^{1/C_r^{{\rm Y}}}\right)}^{1/{\rm Y}}\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.},\\ {\left({\left(1-{\left({\displaystyle \prod _{1\le i_1\le ,\dots ,<i_{{\rm Y}}\le r}}\left(1-\left({\displaystyle \prod _{\tau =1}^{{\rm Y}}}{\left(g_{i_{\tau }}^{sup}\left(v\right)\right)}^2\right)\right)\right)}^{1/C_r^{{\rm Y}}}\right)}^{1/{\rm Y}}\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}\end{array}\right]\\ \end{array},\\ \left[\begin{array}{c}{\left({\left(1-{\left({\displaystyle \prod _{1\le i_1\le ,\dots ,<i_{{\rm Y}}\le r}}\left(1-\left({\displaystyle \prod _{\tau =1}^{{\rm Y}}}{\left(w_{i_{\tau }}^{inf}\left(v\right)\right)}^2\right)\right)\right)}^{1/C_r^{{\rm Y}}}\right)}^{1/\dot{{\rm Y}}}\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.},\\ {\left({\left(1-{\left({\displaystyle \prod _{1\le i_1\le ,\dots ,<i_{{\rm Y}}\le r}}\left(1-\left({\displaystyle \prod _{\tau =1}^{{\rm Y}}}{\left(w_{i_{\tau }}^{sup}\left(v\right)\right)}^2\right)\right)\right)}^{1/C_r^{{\rm Y}}}\right)}^{1/\dot{{\rm Y}}}\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}\end{array}\right]\end{array}\right) \end{gathered}$$

if we set $g_{i\tau }=0$ then IVSFMSM and IVSFDMSM change into IVPyFSMSM and IVPyDMSM operators.

$$\begin{gathered} IVPyFMSM\left(A_1,A_2,\dots ,A_r\right) \\ =\left(\begin{array}{c}\begin{array}{c}\begin{array}{c}\\ \left[\begin{array}{c}{\left(1-{\left({\displaystyle \prod _{1\le i_1\le ,\dots ,<i_{{\rm Y}}\le r}}\left(1-\left({\displaystyle \prod _{\tau =1}^{{\rm Y}}}{\left(f_{i_{\tau }}^{inf}\left(v\right)\right)}^2\right)\right)\right)}^{1/C_r^{{\rm Y}}}\right)}^{1/\dot{{\rm Y}}},\\ {\left(1-{\left({\displaystyle \prod _{1\le i_1\le ,\dots ,<i_{{\rm Y}}\le r}}\left(1-\left({\displaystyle \prod _{\tau =1}^{{\rm Y}}}{\left(f_{i_{\tau }}^{sup}\left(v\right)\right)}^2\right)\right)\right)}^{1/C_r^{{\rm Y}}}\right)}^{1/\dot{{\rm Y}}}\end{array}\right]\end{array},\\ \left[\begin{array}{c}1-{\left(1-{\left({\displaystyle \prod _{1\le i_1\le ,\dots ,<i_{{\rm Y}}\le r}}\left(1-\left({\displaystyle \prod _{\tau =1}^{{\rm Y}}}\left(1-{\left(w_{i_{\tau }}^{inf}\left(v\right)\right)}^2\right)\right)\right)\right)}^{1/C_r^{{\rm Y}}}\right)}^{1/\dot{\mathrm{{\rm Y}}}},\\ 1-{\left(1-{\left({\displaystyle \prod _{1\le i_1\le ,\dots ,<i_{{\rm Y}}\le r}}\left(1-\left({\displaystyle \prod _{\tau =1}^{{\rm Y}}}\left(1-{\left(w_{i_{\tau }}^{sup}\left(v\right)\right)}^2\right)\right)\right)\right)}^{1/C_r^{{\rm Y}}}\right)}^{1/\dot{{\rm Y}}}\end{array}\right]\end{array}\end{array}\right) \end{gathered}$$

now for, IVPyDFMSM,

$$\begin{gathered} IVPyFDMSM\left(A_1,A_2,\dots ,A_r\right) \\ =\left(\begin{array}{c}\begin{array}{c}{\left[\begin{array}{c}1-{\left(1-{\displaystyle \prod _{1\le i_1\le ,\dots ,<i_{{\rm Y}}\le r}}{\left(1-{\displaystyle \prod _{\tau =1}^{{\rm Y}}}\left(1-{\left(f_{i_{\tau }}^{inf}\left(v\right)\right)}^2\right)\right)}^{1/C_r^{{\rm Y}}}\right)}^{1/\dot{\dot{{\rm Y}}}},\\ 1-{\left(1-{\displaystyle \prod _{1\le i_1\le ,\dots ,<i_{{\rm Y}}\le r}}{\left(1-{\displaystyle \prod _{\tau =1}^{{\rm Y}}}\left(1-{\left(f_{i_{\tau }}^{sup}\left(v\right)\right)}^2\right)\right)}^{1/C_r^{{\rm Y}}}\right)}^{1/\dot{\dot{{\rm Y}}}}\end{array}\right]}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}\\ \end{array},\\ {\left[\begin{array}{c}{\left(1-{\left({\displaystyle \prod _{1\le i_1\le ,\dots ,<i_{{\rm Y}}\le r}}\left(1-\left({\displaystyle \prod _{\tau =1}^{{\rm Y}}}{\left(w_{i_{\tau }}^{inf}\left(v\right)\right)}^2\right)\right)\right)}^{1/C_r^{{\rm Y}}}\right)}^{1/\dot{{\rm Y}}},\\ {\left(1-{\left({\displaystyle \prod _{1\le i_1\le ,\dots ,<i_{{\rm Y}}\le r}}\left(1-\left({\displaystyle \prod _{\tau =1}^{{\rm Y}}}{\left(w_{i_{\tau }}^{sup}\left(v\right)\right)}^2\right)\right)\right)}^{1/C_r^{{\rm Y}}}\right)}^{1/\dot{{\rm Y}}}\end{array}\right]}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}\end{array}\right) \end{gathered}$$

when we take AD as zero, then the interval-valued spherical dual fuzzy MSM (IVSFDMSM) operator changes into the interval-valued Pythagorean fuzzy dual MSM (IVPyFDMSM) operator.

6. Application to MADM

In this section, we use the proposed operators in the MADM process. MADM is a process by which we can choose the better option in an uncertain situation [42,43,44]. In the MADM process, we take limited alternatives that depend on limited attributes [45,46,47]. In this way, the experts express their opinions in the form of interval-valued spherical fuzzy numbers (IVSFVs) and prefer different sources according to their thinking. The best option is chosen by basing the aggregation operators on expert recommendations. Suppose $\check{{\rm P}}=\left\{\check{{{\rm P}}_{1 }},\check{{{\rm P}}_2},\dots ,\check{{{\rm P}}_n}\right\}$ are the set of attributes that can choose the best option based on observations, and that the set of alternatives is $\check{k}=\left\{\check{k_1},\check{k_2},\dots ,\check{k_n}\right\}$. The data is given in the form of IVSFVs under uncertain information, where we have four facts from an expert’s opinion that can be aggregated for all the alternatives. In the proposed work, experts expressed their opinions in the form, “We use MSM operators to aggregate the result in the form of IVSFMSM and IVSFDMSM operators”. The details of this procedure are as follows:

Step 1. The experts use uncertain data in the form of MD, NMD, and AD restrictions for IVSFS. The results of alternatives $\check{{\rm P}}=\check{{{\rm P}}_i}$ concerning attributes $\check{k}=\check{k_i}$ are given in the form IVSFV.

$$\begin{gathered} A_{i_{\tau }}=\left(\left[f_{i_{\tau }}^{inf},f_{i_{\tau }}^{sup}\right],\left[g_{i_{\tau }}^{inf},g_{i_{\tau }}^{sup}\right],\left[w_{i_{\tau }}^{inf},w_{i_{\tau }}^{sup}\right]\right)\mathrm{such} \mathrm{that} \\ 0\le \left({\left(f_{i_{\tau }}^{sup}\right)}^2+{\left(g_{i_{\tau }}^{sup}\right)}^2+{\left(w_{i_{\tau }}^{sup}\right)}^2\right)\le 1 \end{gathered}$$

Step 2. In this step, we deal with two types of attributes (benefit and cost). To deal with the cost type of attributes, we use the process of normalization. In which we change all cost types of attributes into benefit types of attributes.

$$\begin{gathered} A_{i\tau }=\left(\left[f_{i_{\tau }}^{inf},f_{i_{\tau }}^{sup}\right],\left[g_{i_{\tau }}^{inf},g_{i_{\tau }}^{sup}\right],\left[w_{i_{\tau }}^{inf},w_{i_{\tau }}^{sup}\right]\right) \\ =\left\{\begin{array}{c}(\left[f_{i_{\tau }}^{inf},f_{i_{\tau }}^{sup}\right],\left[g_{i_{\tau }}^{inf},g_{i_{\tau }}^{sup}\right],\left[w_{i_{\tau }}^{inf},w_{i_{\tau }}^{sup}\right])\hspace{1em}\mathit{benefit\; type\; of\; attributes}\\ (\left[w_{i_{\tau }}^{inf},w_{i_{\tau }}^{sup}\right],\left[g_{i_{\tau }}^{inf},g_{i_{\tau }}^{sup}\right],\left[f_{i_{\tau }}^{inf},f_{i_{\tau }}^{sup}\right])\hspace{1em}\mathit{cost\; type\; of\; attributes}\end{array}\right\} \end{gathered}$$

Step 3. After using the process of normalization, we apply the two aggregation operators IVSFMSM and IVSFDMSM to the given uncertain data.

Step 4. After getting aggregated results by applying the proposed operators, we use Definition 3 to get the score function value of those results.

Step 5. By using score values, we get a ranking of the obtained results.

Example 1:

Consider the problem of evaluating of the progress of multinational companies. Suppose the multinational companies are evaluated based on some attributes as given below:

• $\check{k_1}$ for stock purchases;
• $\check{k_2}$ for stock award;
• $\check{k_3}$ for the charge of control;
• $\check{k_4}$ for the bonus of the company.

Consider four companies $\left\{\check{{{\rm P}}_1},\check{{{\rm P}}_2},\check{{{\rm P}}_3},\check{{{\rm P}}_4}\right\}$ be evaluated based on attributes $\left\{\check{k_1},\check{k_2},\check{k_3},\check{k_4}\right\}$. For this reason, the expert gave his opinion in the form of IVSFV, where $k_1$ represents stock purchases; $k_2$ shows stock awards; $k_3$ shows the charge of control, and $k_4$ shows the bonus of the company. In this scheme, each attribute is given the weight vector $w_{i\tau }={\left(0.2, 0.3, 0.1,0.4\right)}^T$ such that ${{\displaystyle \sum }}_{i=0}^n{w}_i=1$. The process of the multinational companies is given below. In this example, the values of $r$ are 4 and the parameter ${\rm Y}=3$.

In

Table 1. Values obtained from experts regarding companies in form of IVSFV.

	$\widetilde{{\mathit{P}}_1}$						$\widetilde{{\mathit{P}}_2}$
	$\widetilde{f\left(i\right)}$	$\widetilde{f\left(u\right)}$	$\widetilde{g\left(i\right)}$	$\widetilde{g\left(u\right)}$	$\widetilde{w\left(i\right)}$	$\widetilde{w\left(u\right)}$	$\widetilde{f\left(i\right)}$	$\widetilde{f\left(u\right)}$	$\widetilde{g\left(i\right)}$	$\widetilde{g\left(u\right)}$	$\widetilde{w\left(i\right)}$	$\widetilde{w\left(u\right)}$
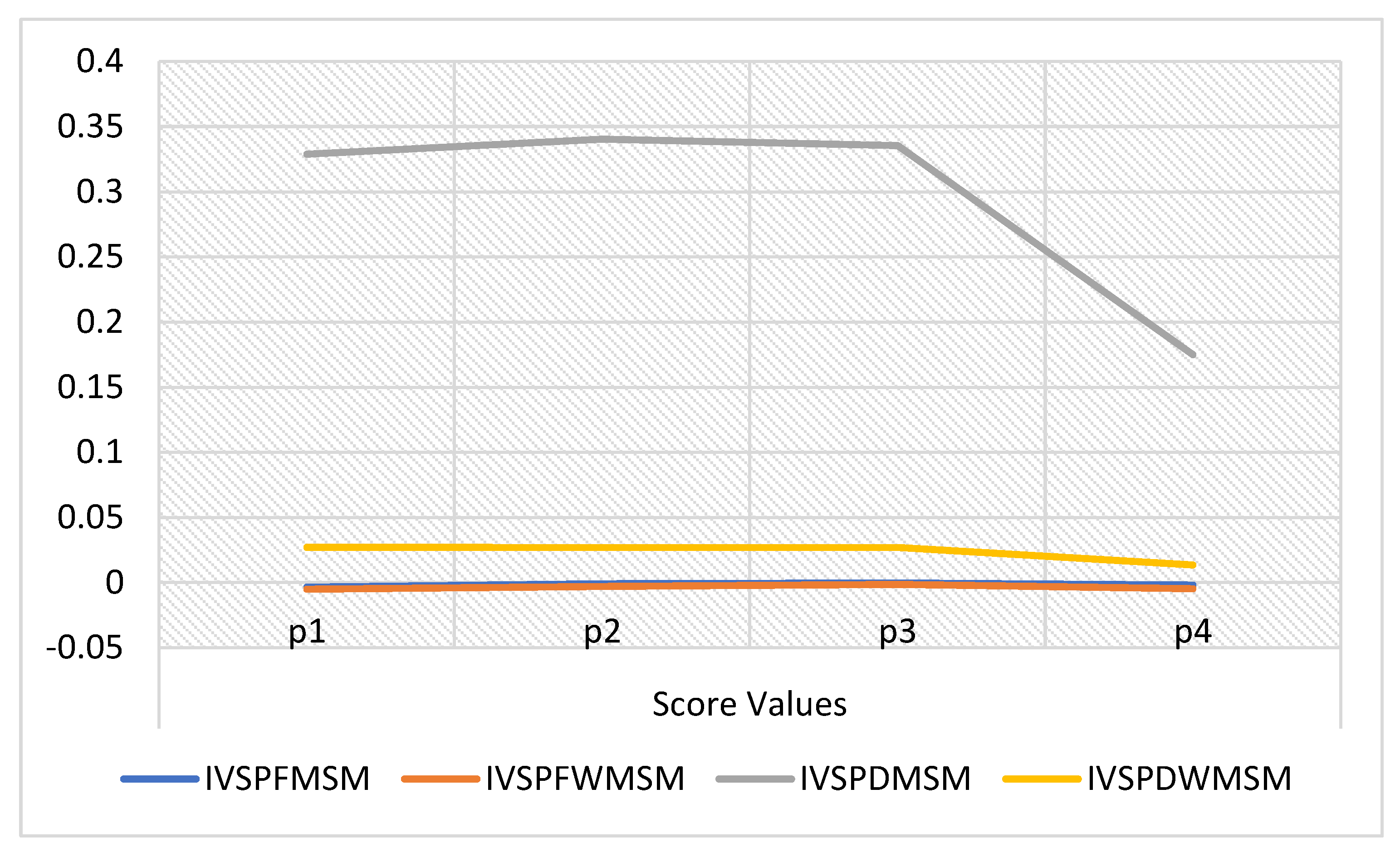
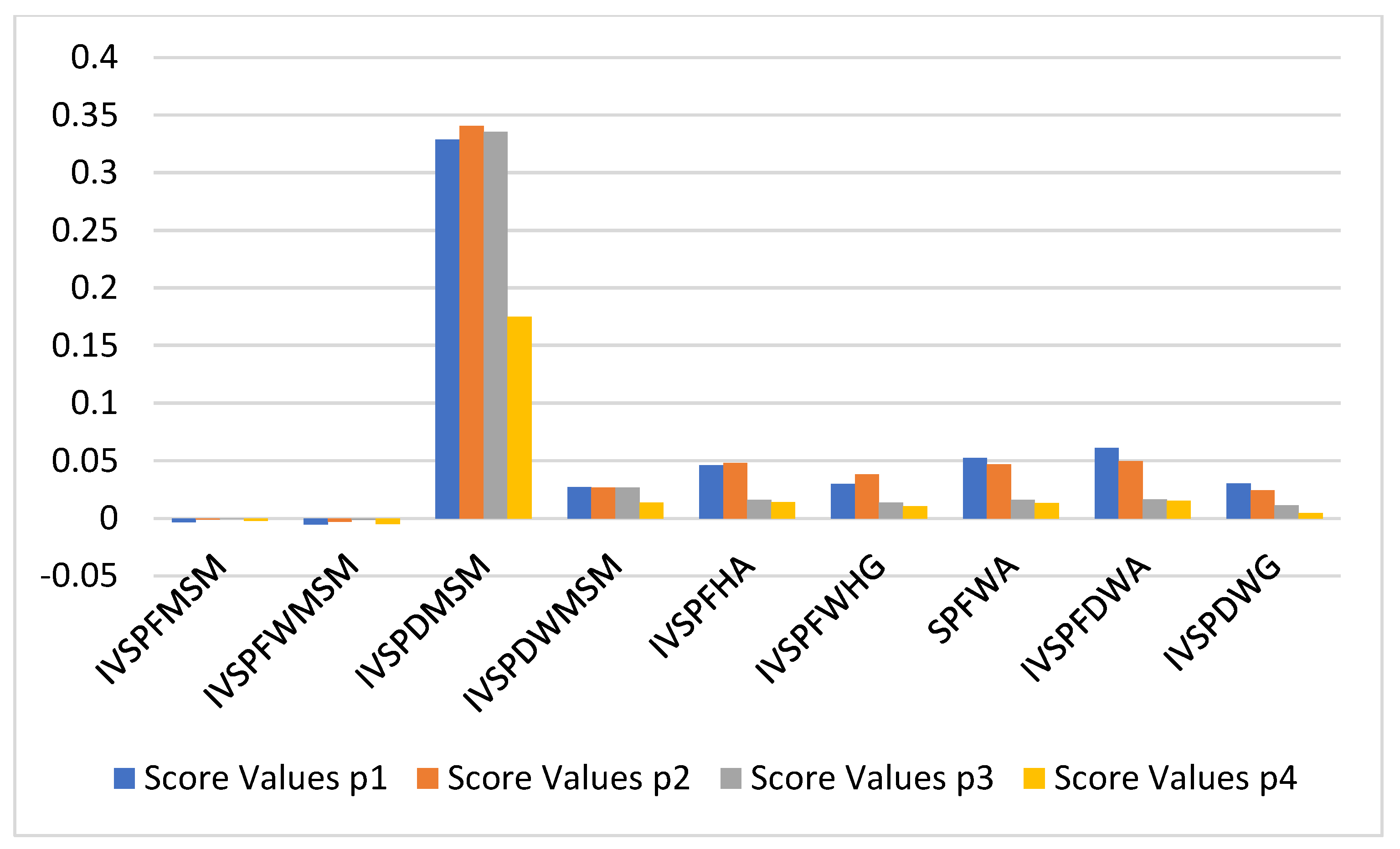
$\check{{\mathit{k}}_1}$	0.23	0.35	0.14	0.15	0.12	0.45	0.05	0.21	0.17	0.31	0.15	0.19
$\check{{\mathit{k}}_2}$	0.21	0.56	0.2	0.3	0.08	0.12	0.32	0.42	0.18	0.19	0.29	0.36
${\check{\mathit{k}}}_3$	0.15	0.21	0.09	0.18	0.29	0.41	0.19	0.34	0.25	0.28	0.17	0.22
${\check{\mathit{k}}}_4$	0.19	0.25	0.37	0.41	0.09	0.12	0.05	0.17	0.04	0.14	0.09	0.12
	$\tilde{{\mathit{{\rm P}}}_3}$						$\tilde{{\mathit{{\rm P}}}_4}$
	$\widetilde{f\left(i\right)}$	$\widetilde{f\left(u\right)}$	$\widetilde{g\left(i\right)}$	$\widetilde{g\left(u\right)}$	$\widetilde{w\left(i\right)}$	$\widetilde{w\left(u\right)}$	$\widetilde{f\left(i\right)}$	$\widetilde{f\left(u\right)}$	$\widetilde{g\left(i\right)}$	$\widetilde{g\left(u\right)}$	$\widetilde{w\left(i\right)}$	$\widetilde{w\left(u\right)}$
$\check{{\mathit{k}}_1}$	0.12	0.31	0.15	0.21	0.09	0.11	0.12	0.15	0.1	0.16	0.13	0.15
$\check{{\mathit{k}}_2}$	0.11	0.19	0.09	0.14	0.05	0.25	0.11	0.22	0.17	0.41	0.09	0.17
$\check{{\mathit{k}}_3}$	0.03	0.17	0.02	0.18	0.1	0.16	0.09	0.21	0.21	0.42	0.25	0.31
$\check{{\mathit{k}}_4}$	0.03	0.16	0.01	0.25	0.02	0.21	0.03	0.04	0.01	0.02	0.02	0.06

, we use undefined data in the form of IVSFVs as the opinions of experts of the company.

In

Table 2. The aggregated information with the IVSFMSM operator.

	$\widetilde{{\mathit{P}}_1}$						$\widetilde{{\mathit{P}}_2}$
	$\widetilde{f\left(i\right)}$	$\widetilde{f\left(u\right)}$	$\widetilde{g\left(i\right)}$	$\widetilde{g\left(u\right)}$	$\widetilde{w\left(i\right)}$	$\widetilde{w\left(u\right)}$	$\widetilde{f\left(i\right)}$	$\widetilde{f\left(u\right)}$	$\widetilde{g\left(i\right)}$	$\widetilde{g\left(u\right)}$	$\widetilde{w\left(i\right)}$	$\widetilde{w\left(u\right)}$
$\check{{\mathit{k}}_1}$	0.05	0.52	0.54	0.51	0.64	0.05	0.01	0.04	0.52	0.53	0.52	0.53
$\check{{\mathit{k}}_2}$	0.46	0.51	0.51	0.51	0.52	0.46	0.46	0.46	0.50	0.51	0.50	0.51
${\check{\mathit{k}}}_3$	0.57	0.02	0.03	0.01	0.12	0.57	0.52	0.55	0.01	0.03	0.01	0.02
${\check{\mathit{k}}}_4$	0.51	0.46	0.46	0.46	0.46	0.51	0.50	0.51	0.46	0.46	0.46	0.46
	$\tilde{{\mathit{{\rm P}}}_3}$						$\tilde{{\mathit{{\rm P}}}_4}$
	$\widetilde{f\left(i\right)}$	$\widetilde{f\left(u\right)}$	$\widetilde{g\left(i\right)}$	$\widetilde{g\left(u\right)}$	$\widetilde{w\left(i\right)}$	$\widetilde{w\left(u\right)}$	$\widetilde{f\left(i\right)}$	$\widetilde{f\left(u\right)}$	$\widetilde{g\left(i\right)}$	$\widetilde{g\left(u\right)}$	$\widetilde{w\left(i\right)}$	$\widetilde{w\left(u\right)}$
$\check{{\mathit{k}}_1}$	0.00	0.02	0.50	0.52	0.50	0.52	0.23	0.02	0.51	0.55	0.51	0.52
$\check{{\mathit{k}}_2}$	0.46	0.46	0.50	0.50	0.50	0.50	0.46	0.91	0.50	0.51	0.50	0.50
$\check{{\mathit{k}}_3}$	0.50	0.52	0.00	0.02	0.00	0.02	0.50	0.03	0.01	0.03	0.01	0.01
$\check{{\mathit{k}}_4}$	0.50	0.50	0.46	0.46	0.46	0.46	0.50	0.01	0.45	0.46	0.46	0.45

, the experts use proposed operators to aggregate the given undefined data, however, we provided the aggregated values obtained by the IVSFMSM operator. In the next step, we must find the score values of the alternatives.

In

Table 3. Score values of aggregated results by using the developed operator.

Score	$\tilde{{\mathit{{\rm P}}}_1}$	$\tilde{{\mathit{{\rm P}}}_2}$	$\tilde{{\mathit{{\rm P}}}_3}$	$\tilde{{\mathit{{\rm P}}}_4}$
IVSFMSM	−0.0035	−0.0008	−0.0003	−0.0021
IVSFWMSM	−0.0051	−0.0029	−0.0014	−0.0049
IVSFDMSM	0.3287	0.3403	0.3354	0.1749
IVSFDWMSM	0.0270	0.0269	0.0268	0.0135

, we use Definition 1 of the score function. The score values show that all the operators are much more fruitful, but IVSFDMSM is the most fruitful compared to other operators because it shows much more accuracy. IVSFDWMSM shows negative score values. The stepwise procedure of the evaluation of the multinational companies is given below:

The decision panel of the company gave opinions in the form of IVSFV;

Step 1. Then we aggregated the obtained information with proposed operators IVSFMSM, IVSFWMSM, IVSFDMSM, and IVSFDWMSM;

Step 2. In this step, we make a ranking of proposed operators by using score functions;

Step 3. This is the end of the procedure with the ranking of the companies.

From

Table 4. Ranking of the score values of the aggregated results from Table 2.

Operators	Ranking Values
IVSFMSM	$\widetilde{{{\rm P}}_4}<\widetilde{{{\rm P}}_3}<\widetilde{{{\rm P}}_2}<\widetilde{{{\rm P}}_1}$
IVSFWMSM	$\widetilde{{{\rm P}}_3}<\widetilde{{{\rm P}}_2}<\widetilde{{{\rm P}}_4}<\widetilde{{{\rm P}}_1}$
IVSFDMSM	$\widetilde{{{\rm P}}_3}<\widetilde{{{\rm P}}_2}<\widetilde{{{\rm P}}_4}<\widetilde{{{\rm P}}_1}$
IVSFDWMSM	$\widetilde{{{\rm P}}_4}<\widetilde{{{\rm P}}_3}<\widetilde{{{\rm P}}_2}<\widetilde{{{\rm P}}_1}$

, it is shown that the finest multinational company is $\widetilde{{{\rm P}}_4}$ using IVSFMSM and IVSFDWMSM. $\widetilde{{{\rm P}}_3}$ is the better option for the IVSFWMSM and IVSFDMSM operators.

Now we show the ranking values in Figure 1.

From Figure 1, we can see the behavior of the score values obtained as the result of all the developed AOs. In Figure 1, all the results are shown that are described in Table 1.

Now, we discuss sensitivity analysis, in which we compare the accuracy of the proposed operators by taking different values of parameter ${\rm Y}$, as in

Table 5. Sensitivity analysis of the proposed operators.

Operators	$\mathit{l}=1$	$\mathit{l}=2$	$\mathit{l}=3$	$\mathit{l}=4$
IVSFMSM	$\tilde{{\mathsf{{\rm P}}}_1}=\widetilde{{{\rm P}}_2}=\widetilde{{{\rm P}}_3}=\widetilde{{{\rm P}}_4}$	$\widetilde{{{\rm P}}_3}<\widetilde{{{\rm P}}_4}<\widetilde{{{\rm P}}_1}=\widetilde{{{\rm P}}_2}$	$\widetilde{{{\rm P}}_4}<\widetilde{p_3}<\widetilde{p_2}<\widetilde{{{\rm P}}_1}$	$\widetilde{{{\rm P}}_4}<\widetilde{{{\rm P}}_1}<\widetilde{{{\rm P}}_3}<\widetilde{{{\rm P}}_2}$
IVSFWMSM	$\widetilde{{{\rm P}}_3}<\widetilde{{{\rm P}}_1}<\widetilde{{{\rm P}}_4}<\widetilde{{{\rm P}}_2}$	$\widetilde{{{\rm P}}_3}<\widetilde{{{\rm P}}_1}<\widetilde{{{\rm P}}_2}<\widetilde{{{\rm P}}_4}$	$\widetilde{{{\rm P}}_3}<\widetilde{{{\rm P}}_3}<\widetilde{{{\rm P}}_4}<\widetilde{{{\rm P}}_1}$	$\widetilde{{{\rm P}}_4}<\widetilde{{{\rm P}}_1}<\widetilde{{{\rm P}}_3}<\widetilde{{{\rm P}}_2}$
IVSFDMSM	$\widetilde{{{\rm P}}_1}=\widetilde{{{\rm P}}_2}=\widetilde{{{\rm P}}_3}=\widetilde{{{\rm P}}_4}$	$\widetilde{{{\rm P}}_4}<\widetilde{{{\rm P}}_3}<\widetilde{{{\rm P}}_2}<\widetilde{{{\rm P}}_1}$	$\widetilde{{{\rm P}}_3}<\widetilde{{{\rm P}}_2}<\widetilde{{{\rm P}}_4}<\widetilde{{{\rm P}}_1}$	$\widetilde{{{\rm P}}_2}<\widetilde{{{\rm P}}_3}<\widetilde{{{\rm P}}_4}<\widetilde{{{\rm P}}_1}$
IVSFDWMSM	$\widetilde{{{\rm P}}_1}<\widetilde{{{\rm P}}_2}<\widetilde{{{\rm P}}_4}<\widetilde{{{\rm P}}_3}$	$\widetilde{{{\rm P}}_4}<\widetilde{{{\rm P}}_3}<\widetilde{{{\rm P}}_2}<\widetilde{{{\rm P}}_1}$	$\widetilde{{{\rm P}}_4}<\widetilde{{{\rm P}}_3}<\widetilde{{{\rm P}}_2}<\widetilde{{{\rm P}}_1}$	$\widetilde{{{\rm P}}_2}<\widetilde{{{\rm P}}_3}<\widetilde{{{\rm P}}_4}<\widetilde{{{\rm P}}_1}$

.

From Table 5 above, we show that the proposed operators (IVSFMSM, IVSFWMSM, IVSFDMSM, and IVSFDWMSM) show different accuracy by taking different values of parameter ${\rm Y}$. At ${\rm Y}=1,$ all the alternatives show the same result for IVSFMSM and IVSFDMSM. In IVSFWMSM $\widetilde{{{\rm P}}_3}$ is much more accurate and in IVSFDWMSM $\widetilde{{{\rm P}}_1}$ is much more effective. At ${\rm Y}=2$, $\widetilde{{{\rm P}}_3}$ is much more effective in IVSFMSM and IVSFWMSM. $\widetilde{{{\rm P}}_4}$ is much more accurate in IVSFDMSM and IVSFDWMSM. At ${\rm Y}=3$, $\widetilde{{{\rm P}}_3}$ is much more accurate in IVSFWMSM and IVSFDMSM operators. $\widetilde{{{\rm P}}_4}$ is effective in IVSFMSM and IVSFDWMSM operators. At ${\rm Y}=4$, $\widetilde{{{\rm P}}_4}$ is effective in IVSFMSM and IVSFWMSM also $\widetilde{{{\rm P}}_2}$ is much more accurate in IVSFDMSM and IVSFDWMSM operators.

7. Comparative Study

In this part of the article, we compare traditionally used aggregation operators with those proposed. As we know, SFS eradicates uncertainty due to its extended limits. In this section, we compare IVSFMSM operators with existing operators’ interval-valued spherical fuzzy weighted averaging (IVSFWA), interval-valued SF Hamacher weighted averaging (IVSFHWG), interval-valued SF weighted geometric (IVSFWG), interval-valued SF Dombi weighted averaging (IVSFDWA), and interval-valued SF Dombi weighted geometric (IVSFDWG) operators.

In

Table 6. A comparative analysis of different operators with newly developed IVSMSM, IVSWMSM, IVSDMSM, and IVSDWMSM.

Operators	Ranking
IVSFHWA [48]	$\check{{{\rm P}}_4}<\check{{{\rm P}}_3}<\check{{{\rm P}}_2}<\check{{{\rm P}}_1}$
IVSFHWG [48]	$\check{{{\rm P}}_1}<\check{{{\rm P}}_4}<\check{{{\rm P}}_3}<\check{{{\rm P}}_2}$
IVSFWA [49]	$\check{{{\rm P}}_4}<\check{{{\rm P}}_3}<\check{{{\rm P}}_2}<\check{{{\rm P}}_1}$
IVSFWG [50]	$\check{{{\rm P}}_4}<\check{{{\rm P}}_3}<\check{{{\rm P}}_2}<\check{{{\rm P}}_1}$
IVSFDWA [51]	$\check{{{\rm P}}_3}<\check{{{\rm P}}_2}<\check{{{\rm P}}_1}<\check{{{\rm P}}_4}$
IVSFMSM	$\widetilde{{{\rm P}}_4}<\widetilde{{{\rm P}}_3}<\widetilde{{{\rm P}}_2}<\widetilde{{{\rm P}}_1}$
IVSFWMSM	$\widetilde{{{\rm P}}_3}<\widetilde{{{\rm P}}_2}<\widetilde{{{\rm P}}_4}<\widetilde{{{\rm P}}_1}$
IVSFDMSM	$\widetilde{{{\rm P}}_3}<\widetilde{{{\rm P}}_2}<\widetilde{{{\rm P}}_4}<\widetilde{{{\rm P}}_1}$
IVSFDWMSM	$\widetilde{{{\rm P}}_4}<\widetilde{{{\rm P}}_3}<\widetilde{{{\rm P}}_2}<\widetilde{{{\rm P}}_1}$

, we show the ranking of various defined operators with proposed operators by using the score values of those operators. We show that $\widetilde{{{\rm P}}_1}$ is much more accurate in IVSFHWA, IVSFHWG, IVSFWA, IVFWG, IVSFDWA, IVSFMSM, and IVSFDMSM. $\widetilde{{{\rm P}}_2}$ is much more fruitful in IVSFWMSM and IVSFDWMSM.

From Figure 2. in a comparative analysis, it is clear that $\check{{{\rm P}}_4}$ is a much more effective proposed operator than other defined operators. The basic benefit of the MSM operator is to aggregate the interrelated data in fuzzy theory. Hamacher AOs and Dombi AOs are also very effective in fuzzy theory for aggregating undefined data. In Figure 2, we see that $\check{{{\rm P}}_4}$ is the most fruitful option.

8. Conclusions

In this paper, we proposed the MSM operator by using IVSF information. The main advantage of these proposed operators is that IVSFMSM gave more accuracy than other operators (IVFMSM). After proposing the operator, we investigated the properties (Boundedness, Monotonicity, and Idempotency) of each AO. The progress of the multinational companies is evaluated with the help of the MADM procedure. Then we compared the results obtained with Dombi weighted aggregation (DWAOs), Dombi weighted geometric mean operators (DWGOs), and Hamacher weighted aggregation operators (HWAMOs). We can see that the proposed operator is much more effective because IVSFMSM minimizes the loss of information under uncertain conditions. However, the IVSF information is also limited because sometimes the sum of the upper values of the intervals may exceed one. Hence, the developed AOs are also limited to only IVSF information and can be further extended to any other framework. In the future, we aim to extend the developed approach to the framework defined in [52].