On Fuzzy Implications Derived from General Overlap Functions and Their Relation to Other Classes

Abstract

There are distinct techniques to generate fuzzy implication functions. Despite most of them using the combination of associative aggregators and fuzzy negations, other connectives such as (general) overlap/grouping functions may be a better strategy. Since these possibly non-associative operators have been successfully used in many applications, such as decision making, classification and image processing, the idea of this work is to continue previous studies related to fuzzy implication functions derived from general overlap functions. In order to obtain a more general and flexible context, we extend the class of implications derived by fuzzy negations and t-norms, replacing the latter by general overlap functions, obtaining the so-called $(\mathcal{GO},N)$-implication functions. We also investigate their properties, the aggregation of $(\mathcal{GO},N)$-implication functions, their characterization and the intersections with other classes of fuzzy implication functions.

1. Introduction

In recent years, a plethora of fuzzy implication functions have been proposed in the literature [1,2,3,4]. These functions have been investigated from a more theoretical point of view [2,5,6] to the one involving practical applications [7,8,9]. They can be used in various fields such as approximate reasoning [10,11,12,13], decision making [14], image processing [15], and fuzzy mathematical morphology [16].

The first impact of fuzzy implications functions was the formalization of the “if… then…” rules in the fuzzy inference process used, for example, in fuzzy rule-based systems. Roughly speaking, it allows one to deduce a possible imprecise conclusion from a collection of imprecise premises. Therefore the implication operator is taken as a fuzzy relation, known as the generalized modus ponens/tollens [17,18,19]. For instance, in classification problems, the following schema may be applied in the fuzzy inference process, taking $A,B$ as being fuzzy concepts:

Premise: A belongs to class P;

Relation 1: A and B are close;

Relation 2: B is slightly smaller than A;

Conclusion: B belongs to class P.

There are many strategies to define fuzzy implication functions that either combine logical connectives (for instance, (S,N), R or QL-implications), or use univariate functions, such as Yager’s f and g-generated implications [13].

The class of implication functions constructed from a t-norm T and a fuzzy negation N was revisited by Pinheiro et al. [20] where the focus was on their properties and also the definition of fuzzy subsethood measures using the fuzzy implication functions called (T,N)-implications.

Most studies on fuzzy implication functions use t-norms and t-conorms [21,22]. However, different operators have been applied to construct implication-like functions, notably, uninorms or semi-uninorms [23,24,25], pseudo-t-norms [26,27], (dual) copulas, quasi- (semi-) copulas [28,29,30,31]. We also highlight the ones given from weaker operators such as overlap and grouping functions which are non-necessarily associative aggregation operators [32,33,34,35] and their interval-valued extensions. Notice that, in contrast with the work by Pinheiro et al. [20] mentioned above, Dimuro et al. [33] developed the more flexible concept of $QL$-operations and fuzzy implications functions derived from overlap and grouping functions, with the applications to the construction of fuzzy subsethood and entropy measures.

Note that, in classical logic, one can define the implication connective in distinct ways, meaning that if the truth tables are equal, then the operators are equivalent [36]. However, when one generalizes those equivalences to the unit interval $[0,1]$, different classes of fuzzy implication functions are obtained. For example, when we generalize the ∨ operator and replace it by the grouping function G, the ∧ operator by the overlap function O and ¬ by a fuzzy negation N, we can mention $(G,N)$-implication functions [34], which generalize the material implication used in Kleene algebra that can be defined according to the tautology: $p\to q\equiv \neg p\vee q$.

In [32], $R_O$-implication functions were proposed using overlap functions inspired on the generalization of Boolean implications resulted as the residuum of the conjunction of Heyting algebra considered in the intuitionistic logic and defined according to the identity: $A^{\prime }\cup B={(A-B)}^{\prime }=\bigcup \{C\in X:(A\cap C)\subseteq B\}$, where X is a universe set and $A,B\subseteq X$. Moreover, the implication functions defined in the quantum logic framework, were also generalized [33], using the following tautology: $p\to q\equiv \neg p\vee (p\wedge q)$, called QL-implication functions. Finally, we have D-implication functions [35] (also known as Dishkant implication), derived from the following generalization: $p\to q\equiv q\vee (\neg p\wedge \neg q)$.

Therefore, following the natural sequence of the investigation on fuzzy implication functions constructed from overlap and grouping functions, the tautology $p\to q\equiv \neg (p\wedge \neg q)$ still can be used to defined a new class. Despite being generalized by t-norms, and called $(T,N)$-implication functions, it seems that applying a more general and flexible context may be feasible when using general overlap functions instead of the standard overlap functions.

The aim of this paper is to provide a theoretical study on a new family of fuzzy implications entitled $(\mathcal{GO},N)$-implications, where $\mathcal{GO}$ is the set of general overlap functions and N is a fuzzy negation. The objectives are threefold: (i) the study of the main properties satisfied by this new class, (ii) $(\mathcal{GO},N)$-implication characterization, and (iii) analysis of the intersections between $(\mathcal{GO},N)$-implications and other families of implications defined via overlap and grouping functions.

The remaining sections of the paper is structured as follows. Section 2 recalls some definitions and important concepts used in our work. The major contributions related to the new class of $(\mathcal{GO},N)$-implication functions and the intersections between other classes are seen in Section 3 and Section 4. At last, we discuss the final remarks and future works in Section 5.

2. Preliminaries

2.1. Fuzzy Negations

Fuzzy negations have been deeply investigated [5,34,37]. Let us recall some important ideas.

Definition 1. 

A fuzzy negation is a function $N:[0,1]\to [0,1]$ satisfying:

 (N1)

N is decreasing, i.e., $N\left(x\right)\le N\left(y\right)$ if $y\le x$;

 (N2)

$N\left(0\right)=1$ and $N\left(1\right)=0$.

A fuzzy negation N is strict if (N3) N is continuous and (N4) $N\left(x\right)<N\left(y\right)$ whenever $y<x$.

A fuzzy negation N is strong if (N5) $N\left(N\right(x\left)\right)=x$, for each $x\in [0,1]$ and crisp if (N6) $N\left(x\right)\in \{0,1\}$, for all $x\in [0,1]$.

A fuzzy negation N is said to be frontier if it satisfies (N7) $N\left(x\right)\in \{0,1\}$ if and only if $x=0$ or $x=1$.

The standard (or Zadeh) negation is: $N_Z\left(x\right)=1-x$.

Remark 1. 

By [33], a fuzzy negation $N:[0,1]\to [0,1]$ is crisp if and only if there exists $\alpha \in \left[0,1\right)$ such that $N=N_{\alpha }$ or there exists $\alpha \in \left(0,1\right]$ such that $N=N^{\alpha }$, where

$$\begin{array}{c}\hfill N_{\alpha }\left(x\right)=\left\{\begin{array}{cc}0,\hfill & \mathit{if}x>\alpha \hfill \\ 1,\hfill & \mathit{if}x\le \alpha \hfill \end{array}\right.\mathit{and}{N}^{\alpha }\left(x\right)=\left\{\begin{array}{cc}0,\hfill & \mathit{if}x\ge \alpha \hfill \\ 1,\hfill & \mathit{if}x<\alpha .\hfill \end{array}\right.\end{array}$$

The smallest fuzzy negation $N_{\perp }$ and the greatest fuzzy negation $N_{\top }$ are examples of crisp fuzzy negations. They are defined by $N_{\perp }=N_{\alpha =0}$ and $N_{\top }=N^{\alpha =1}$, respectively.

In our next developments, the N-duality notion will play an important role.

Definition 2. 

Let N be a fuzzy negation and $f:{[0,1]}^n\to [0,1]$ be any function. The N-dual function of f, for all $x_1,\dots ,x_n\in [0,1]$, is given by:

$$\begin{array}{c}\hfill f_N(x_1,\dots ,x_n)=N\left(f(N\left(x_1\right),\dots ,N\left(x_n\right))\right).\end{array}$$

(1)

2.2. From Aggregation Functions to General Overlap Functions

Definition 3 

([38]). An n-ary aggregation function is a mapping $A:{[0,1]}^n\to [0,1]$ satisfying the following properties:

(A1)

$A(0,\dots ,0)=0$ and $A(1,\dots ,1)=1$;

(A2)

If $x_i\le y$, then $A(x_1,\dots ,x_n)\le A(x_1,\dots ,x_{i-1},y,x_{i+1},\dots ,x_n)$, for each $i\in \{1,\dots ,n\}$.

Proposition 1 

(Corollary 3.8 [12]). Let $A:{[0,1]}^n\to [0,1]$ be an aggregation function and N be a fuzzy negation. The N-dual function of A, denoted by $A_N:{[0,1]}^n\to [0,1]$, is also an aggregation function.

Definition 4 

(Definition 1.1 [39]). A bivariate aggregation function $T:{[0,1]}^2\to [0,1]$ is called a t-norm if it satisfies, for all $x,y,z\in [0,1]$,

(T1)

$T(x,y)=T(y,x)$;          (commutativity)

(T2)

$T(x,T(y,z\left)\right)=T\left(T\right(x,y),z)$;      (associativity)

(T3)

$T(x,y)\le T(x,z)$ whenever $y\le z$;     (monotonicity)

(T4)

$T(x,1)=x$.             (boundary condition)

Definition 5 

(Definition 15 [40]). A bivariate function $O:{[0,1]}^2\to [0,1]$ is an overlap function if it holds, for all $x,y,z\in [0,1]$:

(O1)

$O(x,y)=O(y,x)$;

(O2)

$O(x,y)=0$ if and only if $x=0$ or $y=0$;

(O3)

$O(x,y)=1$ if and only if $x=y=1$;

(O4)

O is increasing, i.e., if $x\le y$ then $O(x,z)\le O(y,z)$;

(O5)

O is continuous.

Remark 2. 

Note that whenever an overlap function has a neutral element, then, by (O3), it is necessarily 1.

Definition 6 

(Definition 3 [41]). A bivariate function $G:{[0,1]}^2\to [0,1]$ is a grouping function if it holds, for all $x,y,z\in [0,1]$,

(G1)

$G(x,y)=G(y,x)$;

(G2)

$G(x,y)=0$ if and only if $x=y=0$;

(G3)

$G(x,y)=1$ if and only if $x=1$ or $y=1$;

(G4)

G is increasing, i.e., if $x\le y$ then $G(x,z)\le G(y,z)$;

(G5)

G is continuous.

Remark 3. 

Note that whenever a grouping function has a neutral element, then, by (G2), this element is necessarily 0.

For further properties and related concepts on overlap/grouping functions, refer to [32,33,34,42,43,44,45].

Theorem 1 

(Theorem 2 [41]). Let O be an overlap function, and let N be a strict fuzzy negation. Then,

$$\begin{array}{c}\hfill G(x,y)=N\left(O\right(N\left(x\right),N\left(y\right)\left)\right)\end{array}$$

(2)

is a grouping function. Reciprocally, if G is a grouping function, then

$$\begin{array}{c}\hfill O(x,y)=N\left(G\right(N\left(x\right),N\left(y\right)\left)\right)\end{array}$$

(3)

is an overlap function.

In the following remark we show that if an overlap function O admits a neutral element, and if N is not a strong negation, then the dual grouping function G does not have a neutral element.

Remark 4. 

Let N be a strict and non-strong fuzzy negation and O be an overlap function. If O has a neutral element, then the grouping function G given by Equation (2) has no neutral element.

It is clear that since O has a neutral element, then $O(x,1)=x$, for all $x\in [0,1]$. However, as N is a non-strong fuzzy negation, there is $\tilde{x}\in [0,1]$ such that $N\left(N\left(\tilde{x}\right)\right)\ne \tilde{x}$, so: $G(\tilde{x},0)=N\left(O(N\left(\tilde{x}\right),1)\right)=N\left(N\left(\tilde{x}\right)\right)\ne \tilde{x}$. Therefore, G has no neutral element.

Next, we present the concept of general overlap function. Note that any t-norm is, in particular, a general overlap function in two variables.

Definition 7 

(Definition 8 [46]). A function $\mathcal{GO}:{[0,1]}^n$$\to [0,1]$ is a general overlap function (GOF, for short) if it satisfies the following properties, for all $\overrightarrow{x}=(x_1,\dots ,x_n)\in {[0,1]}^n$,

($\mathcal{GO}1$)

 $\mathcal{GO}(x_1,\dots ,x_n)=\mathcal{GO}(x_{j_1},\dots ,x_{j_n})$, where

$(x_{j_1},\dots ,x_{j_n})$ is any permutation of $(x_1,\dots ,x_n)$;

($\mathcal{GO}2$)

 If ${\prod }_{i=1}^n{x}_i=0$ then $\mathcal{GO}(\overrightarrow{x})=0$;

($\mathcal{GO}3$)

 If ${\prod }_{i=1}^n{x}_i=1$ then $\mathcal{GO}(\overrightarrow{x})=1$;

($\mathcal{GO}4$)

 $\mathcal{GO}$ is increasing;

($\mathcal{GO}5$)

 $\mathcal{GO}$ is continuous.

Some examples of overlap functions and GOF are given in Table 1, where ${\mathcal{GO}}_L$ is defined by ${\mathcal{GO}}_L(\overrightarrow{x})=max\{(({\displaystyle \sum _{i=1}^n}{x}_i)-(n-1),0)\}$ [46]. Notice that any overlap function is a bivariate general overlap function, but the converse does not necessarily hold.

Table 1. Examples of overlap functions O and general overlap functions $\mathcal{GO}$.

Overlap Functions	General Overlap Functions
$O_{mM}(x,y)=min\{x,y\}max\{x^2,y^2\}$	${\mathcal{GO}}_{max}(x,y)=max\{0,x^2+y^2-1\}$
$O_{DB}(x,y)=\left\{\begin{array}{cc}\frac{2xy}{x+y},\hfill & \mathrm{if}x+y\ne 0;\hfill \\ 0,\hfill & \mathrm{if}x+y=0.\hfill \end{array}\right.$	${\mathcal{GO}}_{T_L}(x,y)={(min\{x,y\})}^p·max\{0,x+y-1\},$ for $p>0$
$O_P(x,y)=x^p{y}^p,\mathrm{with}p>0.$	$$\begin{gathered} {\mathcal{GO}}_{PN}(\overrightarrow{x})= \\ {\displaystyle \prod _{i=1}^n}{x}_i·\left(\left\{\begin{array}{c}0,\mathrm{if}{\displaystyle \sum _{i=1}^n}{x}_i\le 1,\hfill \\ \bigwedge (\overrightarrow{x})=\bigwedge (x_1,\dots ,x_n),\hfill \\ \mathrm{otherwise}.\hfill \end{array}\right.\right) \end{gathered}$$
$O_V(x,y)=\left\{\begin{array}{c}\frac{1+{(2x-1)}^2{(2y-1)}^2}{2},\hfill \\ \mathrm{if}x,y\in [0.5,1],\hfill \\ min\{x,y\},\hfill \\ \mathrm{otherwise}.\hfill \end{array}\right.$	$$\begin{gathered} {\mathcal{GO}}_{GN}\left(\overrightarrow{x}\right)= \\ \sqrt[n]{{\displaystyle \prod _{i=1}^n}{x}_i}·\left(\left\{\begin{array}{c}0,\mathrm{if}{\displaystyle \sum _{i=1}^n}{x}_i\le 1,\hfill \\ \bigwedge (\overrightarrow{x})=\bigwedge (x_1,\dots ,x_n),\hfill \\ \mathrm{otherwise}.\hfill \end{array}\right.\right) \end{gathered}$$
$O_{min}(x,y)=min\{x,y\}$	${\mathcal{GO}}_G\left(\overrightarrow{x}\right)=\left\{\begin{array}{c}n{\mathcal{GO}}_L(\overrightarrow{x}),\mathrm{if}{\mathcal{GO}}_L(\overrightarrow{x})\le \frac{1}{n},\hfill \\ 1,\mathrm{otherwise}.\hfill \end{array}\right.$

2.3. Some New Results on General Overlap Functions

Proposition 2. 

Let O be an overlap function and take $a\in (0,1)$. Therefore, $O_a:{[0,1]}^2\to [0,1]$ defined, for all $x,y\in [0,1]$, by

$$\begin{array}{c}\hfill O_a(x,y)=\frac{max(0,O(x,y)-O(max(x,y),a\left)\right)}{1-O(max(x,y),a)}\end{array}$$

is a bivariate GOF which is not an overlap function.

Proof. 

By (O3), $O(max(x,y),a)\ne 1$ and, therefore, $O_a$ is well defined. Clearly, $O_a$ is commutative, increasing, satisfies ($\mathcal{GO}$2) and ($\mathcal{GO}$3) but does not satisfy (O2). In addition, let $x_i\in [0,1]$ be a sequence, such that ${lim}_{i\to \infty }{x}_i=a$. So, for each $y\in [0,1]$, we have two situations: (i) if $y\le a$, then ${lim}_{i\to \infty }{O}_a(x_i,y)=0=O_a(a,y)$ and (ii) if $y>a$ then, since O is continuous and commutative, ${lim}_{i\to \infty }{O}_a(x_i,y)={lim}_{i\to \infty }\frac{max(0,O(x_i,y)-O(y,a))}{1-O(y,a)}=0=O_a(a,y).$ Therefore, $O_a$ is continuous. □

Proposition 3. 

Consider a strict negation N and a bivariate general overlap function $\mathcal{GO}$. If $\mathcal{GO}$ satisfies the following conditions, for all $x,y\in [0,1]$,

($\mathcal{GO}2a$)

 If $\mathcal{GO}(x,y)=0$ then $xy=0$;

($\mathcal{GO}3a$)

 If $\mathcal{GO}(x,y)=1$ then $xy=1$,

then

$$\begin{array}{c}\hfill G(x,y)=N\left(\mathcal{GO}\right(N\left(x\right),N\left(y\right)\left)\right)\end{array}$$

(4)

is a grouping function. Reciprocally, if G is a grouping function, then

$$\begin{array}{c}\hfill \mathcal{GO}(x,y)=N\left(G\right(N\left(x\right),N\left(y\right)\left)\right)\end{array}$$

(5)

is a GOF satisfying ($\mathcal{GO}$2a) and ($\mathcal{GO}$3a).

Proof. 

Since such GOF is also an overlap function, then the result follows straight from Theorem 1. □

An element $a\in [0,1]$ is a neutral element of $\mathcal{GO}$ if for each $x\in [0,1]$, $\mathcal{GO}(x, \underset{(n-1)-times}{\underbrace{a,\dots ,a}})=x$.

Proposition 4. 

Let $\mathcal{GO}$ be a bivariate general overlap function. Then 1 is a neutral element of $\mathcal{GO}$ if and only if $\mathcal{GO}$ satisfies ($\mathcal{GO}$3a) and has a neutral element.

Proof. 

If $\mathcal{GO}(x,y)=1$ then, by ($\mathcal{GO}$4) and since 1 is a neutral element of $\mathcal{GO}$, one has that $x=\mathcal{GO}(x,1)=1$ and $y=\mathcal{GO}(1,y)=1$, i.e., $xy=1$. Conversely, if a bivariate general overlap function $\mathcal{GO}$ satisfies ($\mathcal{GO}$3a) and has a neutral element a then $a=1$. In fact, $\mathcal{GO}(a,1)=1$ and therefore, by ($\mathcal{GO}$3a), $a=1$. □

Remark 5. 

Observe that the result stated by Proposition 4 does not mean that when a bivariate GOF has a neutral element then it is equal to 1. In fact, for each $e\in (0,1]$, the function

$$\mathcal{GO}(x,y)=\left\{\begin{array}{cc}min(x,y),\hfill & ifmax(x,y)\le e\hfill \\ max(x,y),\hfill & ifmin(x,y)\ge e\hfill \\ \frac{xy}{e},\hfill & ifmin(x,y)<e<max(x,y)\hfill \end{array}\right.$$

is a GOF with e as the neutral element.

Since $\mathcal{GO}$ is an aggregation function, the following proposition is immediate.

Proposition 5. 

If 1 is the neutral element of a general overlap function $\mathcal{GO}$ and $\mathcal{GO}$ is idempotent, then $\mathcal{GO}$ is the minimum.

Lemma 1. 

Let $A:{[0,1]}^n\to [0,1]$ be an aggregation function and ${\mathcal{GO}}^{\ast }=\{{\mathcal{GO}}_i:{[0,1]}^k\to [0,1]\mid i\in \{1,2,\dots ,n\}\}$ be a family of general overlap functions. Then ${\mathcal{GO}}_A^{\ast }$ is a GOF whenever A is continuous.

Proof. 

We will verify that ${\mathcal{GO}}_A^{\ast }$ satisfies the conditions that define a GOF:

($\mathcal{GO}$1) Indeed, for all $x_1,\dots ,x_k\in [0,1]$, since ${\mathcal{GO}}_i$ is commutative for all $i\in \{1,\dots ,n\}$, we have for any $r,s\in \{1,\dots ,k\}$: ${\mathcal{GO}}_A^{\ast }(x_1,\dots ,x_r,\dots ,x_s,\dots ,x_k)=$

$$\begin{array}{ccc}& =& A({\mathcal{GO}}_1(x_1,\dots ,x_r,\dots ,x_s,\dots ,x_k),\dots ,{\mathcal{GO}}_n(x_1,\dots ,x_r,\dots ,x_s,\dots ,x_k))\hfill \\ & =& A({\mathcal{GO}}_1(x_1,\dots ,x_s,\dots ,x_r,\dots ,x_k),\dots ,{\mathcal{GO}}_n(x_1,\dots ,x_s,\dots ,x_r,\dots ,x_k))\hfill \\ & =& {\mathcal{GO}}_A^{\ast }(x_1,\dots ,x_s,\dots ,x_r,\dots ,x_k).\hfill \end{array}$$

($\mathcal{GO}$2) If ${\prod }_{i=1}^k{x}_i=0$, then, by ($\mathcal{GO}$2), ${\mathcal{GO}}_i(x_1,\dots ,x_k)=0$ for all $i\in \{1,\dots ,n\}$,

$$\begin{array}{ccc}\hfill {\mathcal{GO}}_A^{\ast }(x_1,\dots ,x_k)& =& A({\mathcal{GO}}_1(x_1,\dots ,x_k),\dots ,{\mathcal{GO}}_n(x_1,\dots ,x_k))\hfill \\ & =& A(0,\dots ,0)\stackrel{\left(A1\right)}{=}0.\hfill \end{array}$$

($\mathcal{GO}$3) If ${\prod }_{i=1}^k{x}_i=1$, then, by ($\mathcal{GO}$3), ${\mathcal{GO}}_i(x_1,\dots ,x_k)=1$ for all $i\in \{1,\dots ,n\}$,

$$\begin{array}{ccc}\hfill {\mathcal{GO}}_A^{\ast }(x_1,\dots ,x_k)& =& A({\mathcal{GO}}_1(x_1,\dots ,x_k),\dots ,{\mathcal{GO}}_n(x_1,\dots ,x_k))\hfill \\ & =& A(1,\dots ,1)\stackrel{\left(A1\right)}{=}1.\hfill \end{array}$$

($\mathcal{GO}$4) The result is immediate, since A and ${\mathcal{GO}}_i$ are increasing, $\forall i\in \{1,2,\dots ,n\}$.

($\mathcal{GO}$5) Since A and ${\mathcal{GO}}_i$ are continuous, $\forall i\in \{1,2,\dots ,n\}$, the result follows.

Therefore, ${\mathcal{GO}}_A^{\ast }$ is a general overlap function. □

2.4. Fuzzy Implications Derived from Overlap and Grouping Functions

The definition of fuzzy implication functions in [5,47,48], is given as follows:

Definition 8. 

A function $I:{[0,1]}^2\to [0,1]$ is a fuzzy implication function if, for all $x,y,z\in [0,1]$, the following properties are satisfied:

(I1)

If $x\le z$ then $I(x,y)\ge I(z,y)$;     (left antitonicity)

(I2)

If $y\le z$ then $I(x,y)\le I(x,z)$;     (right isotonicity)

(I3)

$I(0,y)=1$;          (left boundary condition)

(I4)

$I(x,1)=1$;         (right boundary condition)

(I5)

$I(1,0)=0$.

We denote by $\mathcal{FI}$ the set of all fuzzy implications.

Definition 9 

(Definition 11 [49]). A fuzzy implication function is said to be crisp if $I(x,y)\in \{0,1\}$, for each $x,y\in [0,1]$.

Proposition 6 

(Proposition 2 [49]). Let $I:{[0,1]}^2\to [0,1]$ be a fuzzy implication function. Then I is crisp if and only if one of the following conditions are satisfied, for all $x,y\in [0,1]$:

(C1) 

If there exists $\alpha \in (0,1]$ and $\beta \in [0,1)$ such that $I=I_{\underline{\alpha }}^{\overline{\beta }}$, where

$$I_{\underline{\alpha }}^{\overline{\beta }}(x,y)=\left\{\begin{array}{cc}0,\hfill & ifx\ge \alpha andy\le \beta \hfill \\ 1,\hfill & otherwise.\hfill \end{array}\right.$$

(C2) 

If there exists $\alpha \in [0,1)$ and $\beta \in (0,1]$ such that $I=I_{\alpha }^{\beta }$, where

$$I_{\alpha }^{\beta }(x,y)=\left\{\begin{array}{cc}0,\hfill & ifx>\alpha andy<\beta \hfill \\ 1,\hfill & otherwise.\hfill \end{array}\right.$$

(C3) 

If there exists $\alpha ,\beta \in (0,1]$ such that $I=I_{\underline{\alpha }}^{\beta }$, where

$$I_{\underline{\alpha }}^{\beta }(x,y)=\left\{\begin{array}{cc}0,\hfill & ifx\ge \alpha andy<\beta \hfill \\ 1,\hfill & otherwise.\hfill \end{array}\right.$$

(C4) 

If there exists $\alpha ,\beta \in [0,1)$ such that $I=I_{\alpha }^{\overline{\beta }}$, where

$$I_{\alpha }^{\overline{\beta }}(x,y)=\left\{\begin{array}{cc}0,\hfill & ifx>\alpha andy\le \beta \hfill \\ 1,\hfill & otherwise.\hfill \end{array}\right.$$

Definition 10 

(Definition 1.4.15 [5]). Let $I\in \mathcal{FI}$. The function $N_I:[0,1]\to [0,1]$ defined by

$$N_I\left(x\right)=I(x,0),x\in [0,1]$$

(6)

is called natural negation of I or negation induced by I.

It is clear $N_I$ is indeed a fuzzy negation. If I is crisp then $N_I$ is a crisp fuzzy negation. Other properties may be demanded for fuzzy implication functions. In the following, we highlight some of them:

Definition 11. 

A fuzzy implication function $I:{[0,1]}^2\to [0,1]$ satisfies, for all $x,y,z\in [0,1]$, the:

 (NP)

Left neutrality property if and only if $I(1,y)=y$;

 (IP)

Identity principle if and only if $I(x,x)=1$;

 (EP)

Exchange principle if and only if $I(x,I(y,z\left)\right)=I(y,I(x,z\left)\right)$;

 (EP1)

Exchange principle for 1 if and only if $I(x,I(y,z\left)\right)=1\Rightarrow I(y,I(x,z\left)\right)=1$;

 (IB)

Iterative Boolean law if and only if $I(x,I(x,y\left)\right)=I(x,y)$;

 (LOP)

 Left-ordering property, if $I(x,y)=1$ whenever $x\le y$;

 (ROP)

 Right-ordering property, if $I(x,y)\ne 1$ whenever $x>y$;

 (CP)

Law of contraposition (or the contrapositive symmetry) with respect to fuzzy negation N, if and only if $I(x,y)=I\left(N\right(y),N(x\left)\right)$;

 (L-CP)

 Law of left contraposition with respect to fuzzy negation N if and only if $I\left(N\right(x),y)=I\left(N\right(y),x)$;

 (R-CP)

 Law of right contraposition with respect to fuzzy negation N if and only if $I(x,N(y\left)\right)=I(y,N(x\left)\right)$.

If I satisfies the (left, right) contrapositive symmetry with respect to N, then we also will denote this by L-CP(N), R-CP(N), and CP(N), respectively.

A well-known result is that from bivariate operations on the unit interval $[0,1]$, it is possible to construct families (classes) of fuzzy implication functions [5]. Hence, one can also use overlap and grouping functions to obtain other classes of implication functions, such as $(G,N),QL,R_O$ and D-implication functions, defined as follows.

Definition 12. 

Let $O:{[0,1]}^2\to [0,1]$ be an overlap function, $G:{[0,1]}^2\to [0,1]$ be a grouping function and $N:[0,1]\to [0,1]$ be a fuzzy negation. Then, the functions $I_{G,N},I_{O,G,N_{\top }},I_O,I_G^D$$:{[0,1]}^2\to [0,1]$ are called:

 1.

$(G,N)$-implication function, given by [34], if

$$\begin{array}{c}\hfill I_{G,N}(x,y)=G(N\left(x\right),y).\end{array}$$

(7)

 2.

$QL$-implication function, given by [33] (where $N_{\top }$ is the crisp fuzzy negation defined according to Remark 1) if

$$\begin{array}{c}\hfill I_{O,G,N_{\top }}(x,y)=\left\{\begin{array}{cc}G(0,O(1,y\left)\right),\hfill & ifx=1;\hfill \\ 1,\hfill & ifx<1.\hfill \end{array}\right.\end{array}$$

 3.

A residual $R_O$-implication function, given by [32], if

$$\begin{array}{c}\hfill I_O(x,y)=max\{z\in [0,1]\mid O(x,z)\le y\}.\end{array}$$

 4.

D-implication function derived from G, given by [35], if

$$\begin{array}{c}\hfill I_G^D(x,y)=\left\{\begin{array}{cc}G(0,y),\hfill & ifx=1;\hfill \\ 1,\hfill & otherwise.\hfill \end{array}\right.\end{array}$$

3. $(\mathcal{GO},N)$-Implications

A class of fuzzy implication functions entitled $(T,N)$-implications was investigated in [20]. They were derived from the composition of a fuzzy negation and a t-norm, and many relevant properties were discussed. In the current study, a similar class of implication functions is investigated. However, we substitute the t-norm by a bivariate GOF. Thus, we provide a new class of implication function called $(\mathcal{GO},N)$-implications, defined as follows.

Definition 13. 

A function $I:{[0,1]}^2\to [0,1]$ is said to be a $(\mathcal{GO},N)$-implication if there exists a bivariate general overlap function $\mathcal{GO}:{[0,1]}^2\to [0,1]$ and a fuzzy negation $N:[0,1]\to [0,1]$ such that, for all $x,y\in [0,1]$

$$I(x,y)=N\left(\mathcal{GO}\right(x,N\left(y\right)\left)\right).$$

(8)

If N is strict, then I is called strict $(\mathcal{GO},N)$-implication. Analogously, if N is strong, I is called strong $(\mathcal{GO},N)$-implication.

Remark 6. 

The above definition agrees with the result given by Theorem 4.3 [50], which states that a function $I(x,y)=N\left(A\right(x,N\left(y\right)\left)\right)$ is an implication function if and only if A is a conjunctor. This result is dual to Theorem 33 [11].

From now on, whenever I is a $(\mathcal{GO},N)$-implication function generated from $\mathcal{GO}$ and N, it will be denoted by $I_{\mathcal{GO}}^N$.

Example 1. 

We can construct some examples of $I_{\mathcal{GO}}^N$.

 (i)

Consider the GOF: ${\mathcal{GO}}_{max}(x,y)=max\{0,x^2+y^2-1\}$ and the standard fuzzy negation $N_Z\left(x\right)=1-x$, then we have that:

$$\begin{array}{c}\hfill I_{{\mathcal{GO}}_{max}}^{N_Z}(x,y)=min\{1,1-x^2-y^2+2y\}.\end{array}$$

 (ii)

Take the GOF: ${\mathcal{GO}}_{T_L}(x,y)={(min\{x,y\})}^p·max\{0,x+y-1\}$, for $p=2$ and $N_Z\left(x\right)=1-x$, so:

$$\begin{array}{c}\hfill I_{{\mathcal{GO}}_{T_L}}^{N_Z}(x,y)=1-(min\{x^2,y^2-2y+1\}·max\{0,x-y\}).\end{array}$$

 (iii)

Consider the general overlap function ${\mathcal{GO}}_{max}$ and the crisp fuzzy negation $N_{\alpha }$, then we have that:

$$\begin{array}{c}\hfill I_{{\mathcal{GO}}_{max}}^{N_{\alpha }}(x,y)=\left\{\begin{array}{cc}0,\hfill & ify\le \alpha and x^2>\alpha .\hfill \\ 1,\hfill & ify>\alpha , or y\le \alpha and x^2\le \alpha .\hfill \end{array}\right.\end{array}$$

 (iv)

Take the GOF ${\mathcal{GO}}_{T_L}$, for $p=2$ and the crisp fuzzy negation $N^{\alpha }$, so:

$$\begin{array}{c}\hfill I_{{\mathcal{GO}}^{T_L}}^{N^{\alpha }}(x,y)=\left\{\begin{array}{cc}0,\hfill & if y<\alpha and x^3\ge \alpha .\hfill \\ 1,\hfill & if y\ge \alpha ,or y<\alpha and x^3<\alpha .\hfill \end{array}\right.\end{array}$$

Proposition 7. 

If I is a $(\mathcal{GO},N)$-implication function then $I\in \mathcal{FI}$.

Proof. 

Indeed, let I be a $(\mathcal{GO},N)$-implication function generated by a general overlap function $\mathcal{GO}$ and a fuzzy negation N, then

(I1) Given $x,y\in [0,1]$ such that $x\le y$, by ($\mathcal{GO}$4), for all $z\in [0,1]$, it holds that $\mathcal{GO}(x,N(z\left)\right)$$\le \mathcal{GO}(y,N(z\left)\right)$. So, $N\left(\mathcal{GO}\right(y,N\left(z\right)\left)\right)\le N\left(\mathcal{GO}\right(x,N\left(z\right)\left)\right)$, that is, $I_{\mathcal{GO}}^N(y,z)\le I_{\mathcal{GO}}^N(x,z)$.

(I2) Analogous to (I1).

(I3) For all $y\in [0,1]$, $I_{\mathcal{GO}}^N(0,y)=N\left(\mathcal{GO}(0,N\left(y\right))\right)\stackrel{\left(\mathcal{GO}2\right)}{=}N\left(0\right)=1$.

(I4) For all $x\in [0,1]$, $I_{\mathcal{GO}}^N(x,1)=N\left(\mathcal{GO}(x,N\left(1\right))\right)=N\left(\mathcal{GO}(x,0)\right)\stackrel{\left(\mathcal{GO}2\right)}{=}N\left(0\right)=1$.

(I5) $I_{\mathcal{GO}}^N(1,0)=N\left(\mathcal{GO}(1,N\left(0\right))\right)=N\left(\mathcal{GO}(1,1)\right)\stackrel{\left(\mathcal{GO}3\right)}{=}N\left(1\right)=0$.

Therefore, $I_{\mathcal{GO}}^N$ is a fuzzy implication function. □

The next result presents the conditions under which the class of (T,N)-implication functions is different from he class of $(\mathcal{GO},N)$-implication functions.

Proposition 8. 

Let N be a strict fuzzy negation and $\mathcal{GO}$ be a GOF. If $\mathcal{GO}$ has no neutral element, then $I_{\mathcal{GO}}^N\ne I_T^N$ for any t-norm T.

Proof. 

By hypothesis, $\mathcal{GO}$ has no neutral element, so there is $\tilde{y}\in (0,1)$ such that $\mathcal{GO}(1,\tilde{y})\ne \tilde{y}$. Since N is strict, given $\tilde{y}\in (0,1)$, there is $\tilde{x}\in (0,1)$ such that $N\left(\tilde{x}\right)=\tilde{y}$. So,

$$\begin{array}{ccc}\hfill \mathcal{GO}(1,N\left(\tilde{x}\right))\ne N\left(\tilde{x}\right)& \stackrel{N\mathrm{strict}}{\Rightarrow }& N\left(\mathcal{GO}(1,N\left(\tilde{x}\right))\right)\ne N\left(N\left(x\right)\right)\hfill \\ & \Rightarrow & I_{\mathcal{GO}}^N(1,\tilde{x})\ne N\left(N\left(\tilde{x}\right)\right).\hfill \end{array}$$

On the other hand, for any t-norm T, we have $I_T^N(1,\tilde{x})=N\left(T(1,N\left(\tilde{x}\right))\right)=N\left(N\left(\tilde{x}\right)\right)\ne I_{\mathcal{GO}}^N(1,\tilde{x})$. Therefore, $I_{\mathcal{GO}}^N\ne I_T^N$. □

Corollary 1. 

Let N be a strict fuzzy negation and ${\mathcal{GO}}_1$ and ${\mathcal{GO}}_2$ be general overlap functions. If ${\mathcal{GO}}_1$ has no neutral element, then $I_{{\mathcal{GO}}_1}^N\ne I_{{\mathcal{GO}}_2}^N$.

Example 2. 

Consider the GOF and the strict fuzzy negation respectively defined by ${\mathcal{GO}}_{max}(x,y)=max\{0,x^2+y^2-1\}$ and $N\left(x\right)=1-x^2$. So, one has that:

$$\begin{array}{ccc}\hfill I_{{\mathcal{GO}}_{max}}^N(x,y)& =& N\left({\mathcal{GO}}_{max}(x,N\left(y\right))\right)\hfill \\ & =& 1-{\left(max\{0,x^2+{(1-y^2)}^2-1\}\right)}^2.\hfill \end{array}$$

Observe that $I_{{\mathcal{GO}}_{max}}^N(1,y)=1-{\left(max\{0,1+{(1-y^2)}^2-1\}\right)}^2=1-{\left(1-y^2\right)}^4$ and for any t-norm T, we have that $I_T^N(1,y)=N\left(T(1,N\left(y\right))\right)=N\left(N\left(y\right)\right)=1-{(1-y^2)}^2$. Therefore, for all $y\in (0,1)$, $I_{{\mathcal{GO}}_{max}}^N(1,y)\ne I_T^N(1,y)$.

Observe that it is possible to recover the bivariate general overlap function from any $(\mathcal{GO},N)$-implication function which was constructed from such GOF and a strict fuzzy negation, as shown in the following proposition.

Proposition 9. 

Let $\mathcal{GO}:{[0,1]}^2\to [0,1]$ be a bivariate GOF and N be a fuzzy negation. If N is strict, then, for all $x,y\in [0,1]$,

$$\mathcal{GO}(x,y)=N^{-1}\left(I_{\mathcal{GO}}^N(x,N^{-1}\left(y\right))\right).$$

Proof. 

Straightforward. □

Corollary 2. 

Let $\mathcal{GO}$ be a bivariate GOF and N be a fuzzy negation. If N is strong, then $\mathcal{GO}(x,y)=N\left(I_{\mathcal{GO}}^N(x,N\left(y\right))\right)$, for all $x,y\in [0,1]$.

Proposition 10. 

Let $\mathcal{GO}$ and N be a GOF and a fuzzy negation, respectively. Then,

 (i)

If 1 is the neutral element of $\mathcal{GO}$, then $N_{I_{\mathcal{GO}}^N}=N$;

 (ii)

If N is strict and $N_{I_{\mathcal{GO}}^N}=N$, then 1 is the neutral element of $\mathcal{GO}$.

Proof. 

Indeed

 (i)

For all $x\in [0,1]$, one has that $N_{I_{\mathcal{GO}}^N}\left(x\right)=I_{\mathcal{GO}}^N(x,0)=N\left(\mathcal{GO}(x,N\left(0\right))\right)=N\left(\mathcal{GO}(x,1)\right)=N\left(x\right)$.

 (ii)

Since N is strict and $N_{I_{\mathcal{GO}}^N}=N$, for all $x\in [0,1]$, we have: $\mathcal{GO}(x,1)=N^{-1}\left(N\right(\mathcal{GO}$$(x,N(0\left)\right)\left)\right)=$$N^{-1}\left(I_{\mathcal{GO}}^N(x,0)\right)=N^{-1}\left(N\left(x\right)\right)=x$. □

Note that the converse of Proposition 10(i) is not always valid. There are non-strict negations N that satisfy $N_{I_{\mathcal{GO}}^N}=N$, but $\mathcal{GO}$ has no neutral element. See the following example:

Example 3. 

Take the fuzzy negation $N_{\top }$ given by

$$\begin{array}{c}\hfill N_{\top }\left(x\right)=\left\{\begin{array}{cc}0,\hfill & \mathit{if}x=1;\hfill \\ 1,\hfill & \mathit{if}x\ne 1,\hfill \end{array}\right.\end{array}$$

(9)

and consider a bivariate general overlap function $\mathcal{GO}$ that satisfies ($\mathcal{GO}$3a). Then, for all $x\in [0,1]$, one has that:

$$\begin{array}{ccc}\hfill N_{I_{\mathcal{GO}}^{N_{\top }}}\left(x\right)& =& I_{\mathcal{GO}}^{N_{\top }}(x,0)=N_{\top }\left(\mathcal{GO}(x,1)\right)\hfill \\ & =& \left\{\begin{array}{cc}0,\hfill & \mathit{if}\mathcal{GO}(x,1)=1\hfill \\ 1,\hfill & \mathit{if}\mathcal{GO}(x,1)\ne 1\hfill \end{array}\right.\hfill \\ & \stackrel{\left(\mathcal{GO}3\mathrm{a}\right)}{=}& \left\{\begin{array}{cc}0,\hfill & \mathit{if}x=1\hfill \\ 1,\hfill & \mathit{if}x\ne 1\hfill \end{array}\right.=N_{\top }\left(x\right).\hfill \end{array}$$

However, $\mathcal{GO}$ does not necessarily have a neutral element.

Proposition 11. 

Let $\mathcal{GO}$ be a bivariate GOF and N be a fuzzy negation such that $x\le N\left(N\right(x\left)\right)$, for all $x\in [0,1]$. Then:

 (i)

If $\mathcal{GO}(1,y)\le y$, then $y\le I_{\mathcal{GO}}^N(x,y)$;

 (ii)

If N is strict and $y\le I_{\mathcal{GO}}^N(x,y)$, then $\mathcal{GO}(1,y)\le y$.

Proof. 

Indeed,

(i)

By hypothesis, take $\mathcal{GO}(1,N(y\left)\right)\le N\left(y\right)$. Then, applying N on both sides, $N\left(N\right(y\left)\right)\le N\left(\mathcal{GO}\right(1,N\left(y\right)\left)\right)$. On the other hand,

$$\begin{array}{ccc}\hfill x\le 1& \stackrel{\left(\mathcal{GO}4\right)}{\Rightarrow }& \mathcal{GO}(x,N(y\left)\right)\le \mathcal{GO}(1,N(y\left)\right)\hfill \\ & \Rightarrow & N\left(\mathcal{GO}\right(1,N\left(y\right)\left)\right)\le N\left(\mathcal{GO}\right(x,N\left(y\right)\left)\right)\hfill \end{array}$$

for all $x,y\in [0,1]$. So, it follows that $y\le N\left(N\right(y\left)\right)\le N\left(\mathcal{GO}\right(1,N\left(y\right)\left)\right)\le N\left(\mathcal{GO}\right(x,$$N\left(y\right)\left)\right)$, and, therefore, $y\le I_{\mathcal{GO}}^N(x,y)$.

(ii)

Since $y\le I_{\mathcal{GO}}^N(x,y)$, for all $x,y\in [0,1]$, so, in particular, $y\le I_{\mathcal{GO}}^N(1,y)$, for all $y\in [0,1]$. Moreover, $y\le N\left(\mathcal{GO}(1,N\left(y\right))\right)\stackrel{\left(N1\right)}{\Rightarrow }N\left(N\left(\mathcal{GO}(1,N\left(y\right))\right)\right)\le N\left(y\right)$. Hence, by hypothesis,

$$\begin{array}{c}\hfill \mathcal{GO}(1,N(y\left)\right)\le N\left(N\right(\mathcal{GO}(1,N(y\left)\right)\left)\right)\le N\left(y\right),\end{array}$$

for all $y\in [0,1]$. So, $\mathcal{GO}(1,y)=\mathcal{GO}(1,N\left(N^{-1}\left(y\right)\right))\le N\left(N^{-1}\left(y\right)\right)=y$, since N is strict. Therefore, for all $y\in [0,1]$, $\mathcal{GO}(1,y)\le y$.

□

Proposition 12. 

Let $I_{\mathcal{GO}}^N$ be a $(\mathcal{GO},N)$-implication function. Then:

 (i)

$I_{\mathcal{GO}}^N$ satisfies L-CP(N);

 (ii)

If N is a strict negation, then $I_{\mathcal{GO}}^N$ satisfies R-CP(N⁻¹);

 (iii)

If $I_{\mathcal{GO}}^N$ satisfies R-CP(N) with a strict negation N and 1 is the neutral element of $\mathcal{GO}$, then N is a strong negation;

 (iv)

If N is a strong negation, then $I_{\mathcal{GO}}^N$ satisfies CP(N);

 (v)

If $I_{\mathcal{GO}}^N$ satisfies CP(N) with a strict negation N and 1 is the neutral element of $\mathcal{GO}$, then N is a strong negation.

Proof. 

(i) For all $x,y\in [0,1]$, it holds that: $I_{\mathcal{GO}}^N(N\left(x\right),y)=N\left(\mathcal{GO}(N\left(x\right),N\left(y\right))\right)\stackrel{\left(\mathcal{GO}1\right)}{=}N\left(\mathcal{GO}(N\left(y\right),N\left(x\right))\right)=I_{\mathcal{GO}}^N(N\left(y\right),x)$.

(ii) For all $x,y\in [0,1]$, one has that $I_{\mathcal{GO}}^N(x,N^{-1}\left(y\right))=N\left(\mathcal{GO}(x,N\left(N^{-1}\left(y\right)\right))\right)=N\left(\mathcal{GO}\right(x,$$y\left)\right)$$\stackrel{\left(\mathcal{GO}1\right)}{=}N\left(\mathcal{GO}(y,x)\right)=N\left(\mathcal{GO}(y,N\left(N^{-1}\left(x\right)\right))\right)=I_{\mathcal{GO}}^N(y,N^{-1}\left(x\right))$.

(iii) Since $I_{\mathcal{GO}}^N$ satisfies $R-CP\left(N\right)$, then $I_{\mathcal{GO}}^N(1,N\left(y\right))=I_{\mathcal{GO}}^N(y,N\left(1\right))$. Hence, since N is a strict negation, $\mathcal{GO}(1,N(N\left(y\right)\left)\right)=\mathcal{GO}(y,N(N\left(1\right)\left)\right)$ for all $y\in [0,1]$, i.e., $\mathcal{GO}(1,N(N\left(y\right)\left)\right)$$=\mathcal{GO}(y,1)$ for all $y\in [0,1]$. So, since 1 is the neutral element of $\mathcal{GO}$, $N\left(N\right(y\left)\right)=y$, for all $y\in [0,1]$.

(iv) For all $x,y\in [0,1]$, since N is strong: $I_{\mathcal{GO}}^N(N\left(y\right),N\left(x\right))=N\left(\mathcal{GO}\right(N\left(y\right),$ $N\left(N\left(x\right)\right)\left)\right)=N\left(\mathcal{GO}(N\left(y\right),x)\right)\stackrel{\left(\mathcal{GO}1\right)}{=}N\left(\mathcal{GO}(x,N\left(y\right))\right)=I_{\mathcal{GO}}^N(x,y)$.

(v) Since $I_{\mathcal{GO}}^N$ satisfies CP(N) and N is a strict negation, then $\mathcal{GO}(x,N(0\left)\right)=\mathcal{GO}\left(N\right(0),$$N\left(N\right(x\left)\right))$$\forall x\in [0,1]$, i.e., $\mathcal{GO}(x,1)=\mathcal{GO}(1,N(N\left(x\right)\left)\right)$$\forall x\in [0,1]$. So, since 1 is the neutral element of $\mathcal{GO}$, $N\left(N\right(x\left)\right)$$=x$, for all $x\in [0,1]$. □

Example 4. 

Consider a bivariate general overlap function $\mathcal{GO}$ with 1 being its neutral element, and the fuzzy negation $N_{\top }$ given by Equation (9). Then, for $x=1$ and for all $y\in [0,1]$, one has that:

$$\begin{array}{ccc}\hfill I_{\mathcal{GO}}^{N_{\top }}(N_{\top }\left(y\right),N_{\top }\left(1\right))& =& I_{\mathcal{GO}}^{N_{\top }}(N_{\top }\left(y\right),0)=N_{\top }\left(\mathcal{GO}(N_{\top }\left(y\right),1)\right)\hfill \\ & =& \left\{\begin{array}{cc}{N}_{\top }\left(\mathcal{GO}(0,1)\right),\hfill & \mathit{if}y=1\hfill \\ N_{\top }\left(\mathcal{GO}(1,1)\right),\hfill & \mathit{if}y\ne 1\hfill \end{array}\right.\hfill \\ & \stackrel{\left(\mathcal{GO}2\right)\left(\mathcal{GO}3\right)}{=}& \left\{\begin{array}{cc}1,\hfill & \mathit{if}y=1\hfill \\ 0,\hfill & \mathit{if}y\ne 1\hfill \end{array}\right..\hfill \end{array}$$

So,

$$\begin{array}{ccc}\hfill I_{\mathcal{GO}}^{N_{\top }}(1,y)& =& N_{\top }\left(\mathcal{GO}(1,N_{\top }\left(y\right))\right)=\left\{\begin{array}{cc}{N}_{\top }\left(\mathcal{GO}(1,0)\right),\hfill & \mathit{if}y=1\hfill \\ N_{\top }\left(\mathcal{GO}(1,1)\right),\hfill & \mathit{if}y\ne 1\hfill \end{array}\right.\hfill \\ & \stackrel{\left(\mathcal{GO}2\right)\left(\mathcal{GO}3\right)}{=}& \left\{\begin{array}{cc}1,\hfill & \mathit{if}y=1\hfill \\ 0,\hfill & \mathit{if}y\ne 1\hfill \end{array}\right.=I_{\mathcal{GO}}^{N_{\top }}(N_{\top }\left(y\right),N_{\top }\left(1\right)).\hfill \end{array}$$

Now, for $x\ne 1$ and for all $y\in [0,1]$:

$$\begin{array}{c}\hfill I_{\mathcal{GO}}^{N_{\top }}(N_{\top }\left(y\right),N_{\top }\left(x\right))=I_{\mathcal{GO}}^{N_{\top }}(N_{\top }\left(y\right),1)=N_{\top }\left(\mathcal{GO}(N_{\top }\left(y\right),0)\right)\stackrel{\left(\mathcal{GO}2\right)}{=}1.\end{array}$$

So,

$$\begin{array}{ccc}\hfill I_{\mathcal{GO}}^{N_{\top }}(x,y)& =& N_{\top }\left(\mathcal{GO}(x,N_{\top }\left(y\right))\right)=\left\{\begin{array}{cc}{N}_{\top }\left(\mathcal{GO}(x,0)\right),\hfill & \mathit{if}y=1\hfill \\ N_{\top }\left(\mathcal{GO}(x,1)\right),\hfill & \mathit{if}y\ne 1\hfill \end{array}\right.\hfill \\ & =& \left\{\begin{array}{cc}{N}_{\top }\left(0\right),\hfill & \mathit{if}y=1\hfill \\ N_{\top }\left(x\right),\hfill & \mathit{if}y\ne 1\hfill \end{array}\right.\stackrel{(1\mathit{neutral}\mathit{element})}{=}1=I_{\mathcal{GO}}^{N_{\top }}(N_{\top }\left(y\right),N_{\top }\left(x\right)).\hfill \end{array}$$

However, N does not need to necessarily be a strong fuzzy negation to $I_{\mathcal{GO}}^N$ satisfies the CP(N) property.

Proposition 13. 

Let $I_{\mathcal{GO}}^N$ be a $(\mathcal{GO},N)$-implication. If N is a strong negation, then

 (i)

$I_{\mathcal{GO}}^N$ satisfies (NP) if and only if 1 is the neutral element of $\mathcal{GO}$.

 (ii)

$I_{\mathcal{GO}}^N$ satisfies (EP) if and only if $\mathcal{GO}$ is associative.

Proof. 

Indeed,

(i) Consider $I_{\mathcal{GO}}^N(1,y)=y$, for all $y\in [0,1]$. Then, since N is strong, for all $y\in [0,1]$, $(\ast )\mathcal{GO}(1,N(y\left)\right)=N\left(y\right)$.

So, one has that $\mathcal{GO}(1,x)\stackrel{\left(N5\right)}{=}\mathcal{GO}(1,N\left(N\left(x\right)\right))\stackrel{(\ast )}{=}N\left(N\left(x\right)\right)\stackrel{\left(N5\right)}{=}x$, for all $x\in [0,1]$. Conversely, since 1 is neutral element of $\mathcal{GO}$, then for all $y\in [0,1]$, we have that $I_{\mathcal{GO}}^N(1,y)=N\left(\mathcal{GO}(1,N\left(y\right))\right)=N\left(N\left(y\right)\right)\stackrel{\left(N5\right)}{=}y$.

(ii) Consider that $I_{\mathcal{GO}}^N$ satisfies (EP). Then, for all $x,y,z\in [0,1]$, since N is a strong negation,

$$\begin{array}{ccc}\hfill N\left(\mathcal{GO}\right(x,\mathcal{GO}(y,z)\left)\right)& =& N\left(\mathcal{GO}\right(x,N\left(N\right(\mathcal{GO}(y,N(N\left(z\right)\left)\right)\left)\right)\left)\right)\hfill \\ & =& I_{\mathcal{GO}}^N(x,I_{\mathcal{GO}}^N(y,N\left(z\right)))=I_{\mathcal{GO}}^N(y,I_{\mathcal{GO}}^N(x,N\left(z\right)))\hfill \\ & =& N\left(\mathcal{GO}\right(y,\mathcal{GO}(x,z)\left)\right)\hfill \end{array}$$

and so, $\mathcal{GO}(x,\mathcal{GO}(y,z\left)\right)=\mathcal{GO}(y,\mathcal{GO}(x,z)$, for all $x,y,z\in [0,1]$. Therefore, $\mathcal{GO}$ is associative.

Conversely, $\forall x,y,z\in [0,1]$, since N is strong and $\mathcal{GO}$ is associative, then

$$\begin{array}{ccc}\hfill I_{\mathcal{GO}}^N(x,I_{\mathcal{GO}}^N(y,z))& =& N\left(\mathcal{GO}\right(x,\mathcal{GO}(y,N(z\left)\right)\left)\right)\hfill \\ & \stackrel{\mathcal{GO}\mathrm{Assoc}.}{=}& N\left(\mathcal{GO}\right(\mathcal{GO}(x,y),N\left(z\right)\left)\right)\hfill \\ & \stackrel{\left(\mathcal{GO}1\right)}{=}& N\left(\mathcal{GO}\right(\mathcal{GO}(y,x),N\left(z\right)\left)\right)\hfill \\ & \stackrel{\mathcal{GO}\mathrm{Assoc}.}{=}& N\left(\mathcal{GO}\right(y,\mathcal{GO}(x,N(z\left)\right)\left)\right)\hfill \\ & =& I_{\mathcal{GO}}^N(y,I_{\mathcal{GO}}^N(x,z)).\hfill \end{array}$$

Therefore, $I_{\mathcal{GO}}^N$ satisfies (EP). □

Proposition 14. 

Let $I_{\mathcal{GO}}^N$ be a $(\mathcal{GO},N)$-implication. If N is a strict negation, so $I_{\mathcal{GO}}^N(x,I_{\mathcal{GO}}^{N^{-1}}(y,z))$$=I_{\mathcal{GO}}^N(y,I_{\mathcal{GO}}^{N^{-1}}(x,z))$ if and only if $\mathcal{GO}$ is associative.

Proof. 

Indeed, consider that $I_{\mathcal{GO}}^N(x,I_{\mathcal{GO}}^{N^{-1}}(y,z))=I_{\mathcal{GO}}^N(y,I_{\mathcal{GO}}^{N^{-1}}(x,z))$. Then, for all $x,y,z\in [0,1]$,

$$\begin{array}{ccc}\hfill N\left(\mathcal{GO}\right(x,\mathcal{GO}(y,z)\left)\right)& =& N\left(\mathcal{GO}(x,N\left(N^{-1}\left(\mathcal{GO}(y,N^{-1}\left(N\left(z\right)\right))\right)\right))\right)\hfill \\ & =& I_{\mathcal{GO}}^N(x,I_{\mathcal{GO}}^{N^{-1}}(y,N\left(z\right)))=I_{\mathcal{GO}}^N(y,I_{\mathcal{GO}}^{N^{-1}}(x,N\left(z\right)))\hfill \\ & =& N\left(\mathcal{GO}\right(y,\mathcal{GO}(x,z)\left)\right).\hfill \end{array}$$

So, $\mathcal{GO}(x,\mathcal{GO}(y,z\left)\right)=\mathcal{GO}(y,\mathcal{GO}(x,z\left)\right)$, for all $x,y,z\in [0,1]$, since N is a strict negation. Therefore, $\mathcal{GO}$ is associative. Conversely, $\forall x,y,w\in [0,1]$, since $\mathcal{GO}$ is associative, then

$$\begin{array}{ccc}\hfill I_{\mathcal{GO}}^N(x,I_{\mathcal{GO}}^{N^{-1}}(y,N\left(w\right)))& =& N\left(\mathcal{GO}\right(x,\mathcal{GO}(y,w)\left)\right)\hfill \\ & \stackrel{\mathcal{GO}\mathrm{Assoc}.}{=}& N\left(\mathcal{GO}\right(y,\mathcal{GO}(x,w)\left)\right)\hfill \\ & =& I_{\mathcal{GO}}^N(y,I_{\mathcal{GO}}^{N^{-1}}(x,N\left(w\right))).\hfill \end{array}$$

So, for all $z\in [0,1]$, since N is continuous, there is $w\in [0,1]$ such that $N\left(w\right)=z$. Thus $I_{\mathcal{GO}}^N(x,I_{\mathcal{GO}}^{N^{-1}}(y,z))=I_{\mathcal{GO}}^N(y,I_{\mathcal{GO}}^{N^{-1}}(x,z))$, for all $x,y,z\in [0,1]$. □

Proposition 15. 

Let $\mathcal{GO}$ be a bivariate GOF satisfying ($\mathcal{GO}$2a), and $I_{\mathcal{GO}}^N$ be a $(\mathcal{GO},N)$-implication. If N is a frontier fuzzy negation, then $I_{\mathcal{GO}}^N$ satisfies (EP1).

Proof. 

Suppose that $I_{\mathcal{GO}}^N(x,I_{\mathcal{GO}}^N(y,z))=1$, for all $x,y,z\in [0,1]$. This means that $N\left(\mathcal{GO}\right(x$$,N\left(N\right(\mathcal{GO}(y,N(z\left)\right)\left)\right)\left)\right)=1$. In this case, since N is a frontier negation, then: $\mathcal{GO}(x,N(N($$\mathcal{GO}(y,N(z\left)\right)\left)\right))=0$.

By ($\mathcal{GO}$2a), either $x=0$ or $N\left(N\right(\mathcal{GO}(y,N(z\left)\right)\left)\right)$$=0$. Then, one has the following cases:

(1) For $x=0$, it follows: $I_{\mathcal{GO}}^N(y,I_{\mathcal{GO}}^N(0,z))=I_{\mathcal{GO}}^N(y,1)=N\left(\mathcal{GO}(y,0)\right)\stackrel{\left(\mathcal{GO}2\right)}{=}1$.

(2) For $N\left(N\right(\mathcal{GO}(y,N(z\left)\right)\left)\right)=0$, since N is a frontier negation, so $\mathcal{GO}(y,N(z\left)\right)$$=0$. So, by ($\mathcal{GO}$2a), $y=0$ or $z=1$. If $y=0$, then $I_{\mathcal{GO}}^N(0,I_{\mathcal{GO}}^N(x,z))=1$. On the other hand, if $z=1$, then $I_{\mathcal{GO}}^N(y,I_{\mathcal{GO}}^N(x,1))=I_{\mathcal{GO}}^N(y,1)=1$.

Thus, in any case, it holds that $I_{\mathcal{GO}}^N(y,I_{\mathcal{GO}}^N(x,z))=1$. □

Proposition 16. 

Let $I_{\mathcal{GO}}^N$ be a $(\mathcal{GO},N)$-implication with a strict fuzzy negation N.

 (i)

If $I_{\mathcal{GO}}^N$ satisfies (IB) and $\mathcal{GO}$ has 1 as neutral element, then N is strong and $\mathcal{GO}$ is idempotent.

 (ii)

If N is strong and $\mathcal{GO}$ is idempotent and associative, then $I_{\mathcal{GO}}^N$ satisfies (IB) and $\mathcal{GO}$ has 1 as neutral element.

Proof. 

Indeed,

(i) Since $I_{\mathcal{GO}}^N$ satisfies (IB), we have for $x=1$, $I_{\mathcal{GO}}^N(1,I_{\mathcal{GO}}^N(1,y))=I_{\mathcal{GO}}^N(1,y)$, $\forall y\in [0,1]$. So, $N\left(\mathcal{GO}\right(1,N\left(N\right(\mathcal{GO}(1,N(y\left)\right)\left)\right)\left)\right)=N\left(\mathcal{GO}\right(1,N\left(y\right)\left)\right)$. Therefore, $N\left(N\right(N\left(N\right(y\left)\right)\left)\right)=N\left(N\right(y\left)\right)$, for all $y\in [0,1]$, since 1 is neutral element of $\mathcal{GO}$. However, N being a strict negation, then $N\left(N\right(y\left)\right)=y$, for all $y\in [0,1]$ and, then, N is strong. Moreover, since $I_{\mathcal{GO}}^N(x,I_{\mathcal{GO}}^N(x,N\left(y\right)))=I_{\mathcal{GO}}^N(x,N\left(y\right))$, we have that $N\left(\mathcal{GO}\right(x,\mathcal{GO}(x,y)\left)\right)=N\left(\mathcal{GO}\right(x,y\left)\right)$, since N is strong. So, $\mathcal{GO}(x,\mathcal{GO}(x,y\left)\right)=\mathcal{GO}(x,y)$. In particular, for $y=1$, $\mathcal{GO}(x,x)=x$, for all $x\in [0,1]$, since 1 is the neutral element of $\mathcal{GO}$. Therefore, the general overlap function $\mathcal{GO}$ is idempotent.

(ii) For all $x,y\in [0,1]$,

$$\begin{array}{ccc}\hfill I_{\mathcal{GO}}^N(x,I_{\mathcal{GO}}^N(x,y))& =& N\left(\mathcal{GO}\right(x,\mathcal{GO}(x,N(y\left)\right)\left)\right)=N\left(\mathcal{GO}\right(x,\mathcal{GO}\left(N\right(y),x)\left)\right)\hfill \\ & \stackrel{\mathcal{GO}\mathrm{Assoc}.}{=}& N\left(\mathcal{GO}(N\left(y\right),\mathcal{GO}(x,x))\right)\stackrel{\mathcal{GO}\mathrm{Idem}.}{=}N\left(\mathcal{GO}(N\left(y\right),x)\right)\hfill \\ & =& N\left(\mathcal{GO}(x,N\left(y\right))\right)=I_{\mathcal{GO}}^N(x,y).\hfill \end{array}$$

So, $I_{\mathcal{GO}}^N$ satisfies (IB). In case $x=1$, since N is strong, $I_{\mathcal{GO}}^N(1,I_{\mathcal{GO}}^N(1,N^{-1}\left(y\right)))$$=I_{\mathcal{GO}}^N(1,N^{-1}$$\left(y\right))$. So, for all $y\in [0,1]$, $\mathcal{GO}(1,\mathcal{GO}(1,y\left)\right)=\mathcal{GO}(1,y)$. Since $\mathcal{GO}$ is continuous and increasing, for all $z\in [0,1]$, there is $y\in [0,1]$ such that $\mathcal{GO}(1,y)=z$. Thus, for all $z\in [0,1]$, $\mathcal{GO}(1,z)=\mathcal{GO}(1,\mathcal{GO}(1,y\left)\right)=\mathcal{GO}(1,y)=z$. Therefore, 1 is a neutral element of $\mathcal{GO}.$ □

Corollary 3. 

Let $I_{\mathcal{GO}}^N$ be a $(\mathcal{GO},N)$-implication with a strict fuzzy negation N. If $I_{\mathcal{GO}}^N$ satisfies (IB) and 1 is the neutral element of the bivariate general overlap function $\mathcal{GO}$, then $\mathcal{GO}$ is the minimum t-norm.

Proof. 

Straightforward from Propositions 16 and 5. □

Remark 7. 

Observe that, trivially, $I_{\mathcal{GO}}^N$ is crisp if and only if N is crisp. In fact, for each $\alpha \in (0,1)$, if 1 is a neutral element of $\mathcal{GO}$ then $I_{\mathcal{GO}}^{N^{\alpha }}=I_{\underline{\alpha }}^{\alpha }$ and $I_{\mathcal{GO}}^{N_{\alpha }}=I_{\alpha }^{\overline{\alpha }}$.

Proposition 17. 

Let $I_{\mathcal{GO}}^N$ be a crisp $(\mathcal{GO},N)$-implication, and let 1 be a neutral element of $\mathcal{GO}$, then:

 (i)

$I_{\mathcal{GO}}^N$ satisfies (EP) but it does not satisfy (NP);

 (ii)

$I_{\mathcal{GO}}^N$ satisfies (LOP) but it does not satisfy (ROP);

 (iii)

$I_{\mathcal{GO}}^N$ satisfies (IP);

 (iv)

$I_{\mathcal{GO}}^N$ satisfies (IB);

 (v)

$I_{\mathcal{GO}}^N$ satisfies (CP) with respect to N;

 (vi)

$I_{\mathcal{GO}}^N$ satisfies (R-CP) with respect to N.

Proof. 

Indeed,

(i)

Straightforward from Proposition 6 [49], considering Remark 7.

(ii)

Since N is crisp and 1 is a neutral element of $\mathcal{GO}$, it follows that:

(LOP)

For all $x,y\in [0,1]$ such that $x\le y$, two situations are possible:

(1) 

If there exists $\alpha \in \left(0,1\right)$ such that $N=N_{\alpha }$, so, by Remark 7 and (C4), we have that $I_{\mathcal{GO}}^N(x,y)=I_{\alpha }^{\overline{\alpha }}(x,y)$. Therefore,

$$\begin{array}{c}\hfill I_{\mathcal{GO}}^N(x,y)=\left\{\begin{array}{cc}0,\hfill & \mathrm{if}x>\alpha \mathrm{and}y\le \alpha .\hfill \\ 1,\hfill & \mathrm{if}y>\alpha \mathrm{or}x\le \alpha .\hfill \end{array}\right.\end{array}$$

(10)

For $y\le \alpha$, as $x\le y$, it holds that $x\le \alpha$. Hence one concludes that $I_{\mathcal{GO}}^N(x,y)=1$. For $y>\alpha$, it is immediate that $I_{\mathcal{GO}}^N(x,y)=1$.

(2) 

If there exists $\alpha \in \left(0,1\right)$ such that $N=N^{\alpha }$, so, by Remark 7 and (C3), we have $I_{\mathcal{GO}}^N(x,y)=I_{\underline{\alpha }}^{\alpha }(x,y)$. Thus,

$$\begin{array}{c}\hfill I_{\mathcal{GO}}^N(x,y)=\left\{\begin{array}{cc}0,\hfill & \mathrm{if}x\ge \alpha \mathrm{and}y<\alpha .\hfill \\ 1,\hfill & \mathrm{if}x<\alpha \mathrm{or}y\ge \alpha .\hfill \end{array}\right.\end{array}$$

(11)

For $y<\alpha$, as $x\le y$, it holds that $x<\alpha$. So one concludes that $I_{\mathcal{GO}}^N(x,y)=1$.

For $y\ge \alpha$, it is immediate that $I_{\mathcal{GO}}^N(x,y)=1$.

Therefore, it holds that $I_{\mathcal{GO}}^N$ satisfies $\left(LOP\right)$.

(ROP)

We also consider two situations:

(1) 

If $N=N_{\alpha }$, for some $\alpha \in \left(0,1\right)$, then take $x,y\in [0,1]$ such that $x>y>\alpha$. Consequently, by Equation (10), $I_{\mathcal{GO}}^N(x,y)=1$.

(2) 

If $N=N^{\alpha }$, for some $\alpha \in \left(0,1\right)$, then take $x,y\in [0,1]$ such that $y<x<\alpha$. Thus, by Equation (11), $I_{\mathcal{GO}}^N(x,y)=1$.

In both situations, there exists $x>y$, but $I_{\mathcal{GO}}^N(x,y)=1$. So $I_{\mathcal{GO}}^N$ does not satisfy $\left(ROP\right)$.

(iii)

Given $x\in [0,1]$, since N is crisp, either $N\left(x\right)=0$ or $N\left(x\right)=1$. If $N\left(x\right)=0$, then $I_{\mathcal{GO}}^N(x,x)=N\left(\mathcal{GO}(x,N\left(x\right))\right)=N\left(\mathcal{GO}(x,0)\right)\stackrel{\left(\mathcal{GO}2\right)}{=}1$. On the other hand, if $N\left(x\right)=1$, then $I_{\mathcal{GO}}^N(x,x)=N\left(\mathcal{GO}(x,N\left(x\right))\right)=N\left(\mathcal{GO}(x,1)\right)=N\left(x\right)=1$, since 1 is the neutral element of $\mathcal{GO}$.

(iv)

Given $y\in [0,1]$, as N is crisp, either $N\left(y\right)=0$ or $N\left(y\right)=1$.

(1) 

Take $N\left(y\right)=0$, and for all $x\in [0,1]$,

$$\begin{array}{ccc}\hfill I_{\mathcal{GO}}^N(x,I_{\mathcal{GO}}^N(x,y))& =& N\left(\mathcal{GO}\right(x,N\left(N\right(\mathcal{GO}(x,N(y\left)\right)\left)\right)\left)\right)\hfill \\ & =& N\left(\mathcal{GO}\right(x,N\left(N\right(\mathcal{GO}(x,0)\left)\right)\left)\right)\hfill \\ & \stackrel{\left(\mathcal{GO}2\right)}{=}& N\left(\mathcal{GO}(x,N\left(N\left(0\right)\right))\right)=N\left(\mathcal{GO}(x,0)\right)\stackrel{\left(\mathcal{GO}2\right)}{=}1\hfill \end{array}$$

and $I_{\mathcal{GO}}^N(x,y)=N\left(\mathcal{GO}(x,N\left(y\right))\right)=N\left(\mathcal{GO}(x,0)\right)\stackrel{\left(\mathcal{GO}2\right)}{=}1$.

(2) 

Now, $N\left(y\right)=1$, and $\forall x\in [0,1]$, since 1 is the neutral element of $\mathcal{GO}$,

$$\begin{array}{ccc}\hfill I_{\mathcal{GO}}^N(x,I_{\mathcal{GO}}^N(x,y))& =& N\left(\mathcal{GO}\right(x,N\left(N\right(\mathcal{GO}(x,N(y\left)\right)\left)\right)\left)\right)\hfill \\ & =& N\left(\mathcal{GO}\right(x,N\left(N\right(\mathcal{GO}(x,1)\left)\right)\left)\right)\hfill \\ & =& N\left(\mathcal{GO}\right(x,N\left(N\right(x\left)\right)\left)\right)\hfill \end{array}$$

and $I_{\mathcal{GO}}^N(x,y)=N\left(\mathcal{GO}(x,N\left(y\right))\right)=N\left(\mathcal{GO}(x,1)\right)=N\left(x\right)$. So, if $N\left(x\right)=0$, then $I_{\mathcal{GO}}^N(x,I_{\mathcal{GO}}^N(x,y))=N\left(\mathcal{GO}(x,1)\right)=N\left(x\right)=0$ and $I_{\mathcal{GO}}^N(x,y)=N\left(x\right)=0$. Now, if $N\left(x\right)=1$, then, by $\left(\mathcal{GO}2\right)$, $I_{\mathcal{GO}}^N(x,I_{\mathcal{GO}}^N(x,y))=N\left(\mathcal{GO}(x,0)\right)=1$ and $I_{\mathcal{GO}}^N(x,y)=N\left(x\right)=1$. Therefore, in any case, $I_{\mathcal{GO}}^N(x,I_{\mathcal{GO}}^N(x,y))=I_{\mathcal{GO}}^N(x,y)$.

(v)

Given $y\in [0,1]$, as N is crisp, either $N\left(y\right)=0$ or $N\left(y\right)=1$.

(1) 

For $N\left(y\right)=0$, then $I_{\mathcal{GO}}^N(x,y)=N\left(\mathcal{GO}(x,0)\right)\stackrel{\left(\mathcal{GO}2\right)}{=}1$, and therefore $I_{\mathcal{GO}}^N(N\left(y\right),$$N\left(x\right))=N\left(\mathcal{GO}(0,N\left(N\left(x\right)\right))\right)\stackrel{\left(\mathcal{GO}2\right)}{=}1$, for all $x\in [0,1]$.

(2) 

For $N\left(y\right)=1$, since 1 is the neutral element of $\mathcal{GO}$, $I_{\mathcal{GO}}^N(x,y)=N\left(\mathcal{GO}(x,N\left(y\right))\right)=N\left(\mathcal{GO}(x,1)\right)=N\left(x\right)$ and, we also have that

$$\begin{array}{ccc}\hfill I_{\mathcal{GO}}^N(N\left(y\right),N\left(x\right))& =& N\left(\mathcal{GO}\right(N\left(y\right),N\left(N\right(x\left)\right)\left)\right)\hfill \\ & =& N\left(\mathcal{GO}\right(1,N\left(N\right(x\left)\right)\left)\right)=N\left(N\right(N\left(x\right)\left)\right),\hfill \end{array}$$

for all $x\in [0,1]$. Since N is crisp, $N\left(N\right(N\left(x\right)\left)\right)=N\left(x\right)$ for all $x\in [0,1]$. Therefore, $I_{\mathcal{GO}}^N(N\left(y\right),N\left(x\right))=I_{\mathcal{GO}}^N(x,y)$.

(vi)

Given $y\in [0,1]$, as N is crisp, either $N\left(y\right)=0$ or $N\left(y\right)=1$.

(1) 

For $N\left(y\right)=0$, since 1 is the neutral element of $\mathcal{GO}$, for all $x\in [0,1]$,

$$\begin{array}{ccc}\hfill I_{\mathcal{GO}}^N(x,N\left(y\right))& =& N\left(\mathcal{GO}\right(x,N\left(0\right)\left)\right)=N\left(\mathcal{GO}\right(x,1\left)\right)=N\left(x\right)\hfill \end{array}$$

and $I_{\mathcal{GO}}^N(y,N\left(x\right))=N\left(\mathcal{GO}(y,N\left(N\left(x\right)\right))\right)$. If $N\left(x\right)$$=0$, consequently, $I_{\mathcal{GO}}^N(x,N\left(y\right))=0=N\left(y\right)=N\left(\mathcal{GO}(y,1)\right)=I_{\mathcal{GO}}^N(y,N\left(x\right))$. Moreover, if $N\left(x\right)=1$ then, $I_{\mathcal{GO}}^N(x,N\left(y\right))=1=N\left(0\right)=N\left(\mathcal{GO}(y,0)\right)=I_{\mathcal{GO}}^N(y,N\left(x\right))$.

(2) 

For $N\left(y\right)=1$, since 1 is the neutral element of $\mathcal{GO}$, $I_{\mathcal{GO}}^N(x,N\left(y\right))=N\left(\mathcal{GO}\right(x,$$N\left(1\right)\left)\right)=N\left(\mathcal{GO}(x,0)\right)\stackrel{\left(\mathcal{GO}2\right)}{=}1$. Moreover, $I_{\mathcal{GO}}^N(y,N\left(x\right))$$=N\left(\mathcal{GO}\right(y,N\left(N\right(x\left)\right)\left)\right)$, for all $x\in [0,1]$. So, if $N\left(x\right)=0$, then $I_{\mathcal{GO}}^N(y,$$N\left(x\right))=N(\mathcal{GO}(y,N(0\left)\right))=N(\mathcal{GO}(y,1))=N(y)=1$. However, if $N\left(x\right)=1$, then, by $\left(\mathcal{GO}2\right)$, we have that $I_{\mathcal{GO}}^N(y,N\left(x\right))=N\left(\mathcal{GO}(y,N\left(1\right))\right)=N\left(\mathcal{GO}(y,0)\right)=1$. So, in any case, $I_{\mathcal{GO}}^N(x,N\left(y\right))=I_{\mathcal{GO}}^N(y,N\left(x\right))$.□

Aggregating $(\mathcal{GO},N)$-Implications

In [12], the authors performed a study on ${\mathcal{I}}_A$ fuzzy implications obtained by the composition of an aggregation function A and a family $\mathcal{I}$ of fuzzy implication functions. Here we verify under which conditions an ${\mathcal{I}}_A$-operator is a $(\mathcal{GO},N)$-implication, whenever $\mathcal{I}$ is a family of $(\mathcal{GO},N)$-implication functions.

Definition 14 

(Definition 5.1 [12]). Let $A:{[0,1]}^n\to [0,1]$ be an aggregation function and take $\mathcal{F}=\{F_i:{[0,1]}^k\to [0,1]\mid i\in \{1,2,\dots ,n\}\}$ as a family of k-ary functions. An $(\mathbf{A},\mathcal{F})$-operator on $[0,1]$, denoted by ${\mathcal{F}}_A:{[0,1]}^k\to [0,1]$, is given by:

$$\begin{array}{c}\hfill {\mathcal{F}}_A(x_1,\dots ,x_k)=A(F_1(x_1,\dots ,x_k),F_2(x_1,\dots ,x_k),\dots ,F_n(x_1,\dots ,x_k)).\end{array}$$

(12)

In [12], it has been shown that ${\mathcal{F}}_A$ preserves some properties of $F_i$ for $i\in \{1,2,\dots ,n\}$. For example, if $F_i$ are fuzzy implication functions then ${\mathcal{F}}_A$ is also a fuzzy implication function.

Proposition 18. 

Let $A:{[0,1]}^n\to [0,1]$ be a continuous aggregation function and let $\mathcal{I}=\{I_{{\mathcal{GO}}_i}^{N_i}:{[0,1]}^2\to [0,1]\mid i\in \{1,\dots ,n\}\}$ be a family of $(\mathcal{GO},N)$-implication functions. Then, ${\mathcal{I}}_A$ is a $(\mathcal{GO},N)$-implication whenever $N_i=N$ for $i\in \{1,2,\dots ,n\}$ and N is a strong negation.

Proof. 

Consider the family of $(\mathcal{GO},N)$-implication functions represented by $\mathcal{I}=\{I_{{\mathcal{GO}}_i}^{N_i}$$:{[0,1]}^2\to [0,1]\mid i\in \{1,2,\dots ,n\}\}$. Then, since $N_i=N$ and N is a strong negation, for all $0\le i\le n$,

$$\begin{array}{ccc}\hfill {\mathcal{I}}_A(x,y)& \stackrel{\mathrm{Equation}\left(12\right)}{=}& A(I_{{\mathcal{GO}}_1}^{N_1}(x,y),\dots ,I_{{\mathcal{GO}}_n}^{N_n}(x,y))\hfill \\ & \stackrel{\mathrm{Equation}\left(8\right)}{=}& A(N_1\left({\mathcal{GO}}_1(x,N_1\left(y\right))\right),\dots ,N_n\left({\mathcal{GO}}_n(x,N_n\left(y\right))\right))\hfill \\ & =& A(N\left({\mathcal{GO}}_1(x,N\left(y\right))\right),\dots ,N\left({\mathcal{GO}}_n(x,N\left(y\right))\right))\hfill \\ & \stackrel{\mathrm{Equation}\left(1\right)/\left(N5\right)}{=}& N\left(A_N({\mathcal{GO}}_1(x,N\left(y\right)),\dots ,{\mathcal{GO}}_n(x,N\left(y\right)))\right)\hfill \\ & \stackrel{\mathrm{Equation}\left(12\right)}{=}& N\left({\mathcal{GO}}_{A_N}^{\ast }(x,N\left(y\right))\right)\hfill \\ & \stackrel{\mathrm{Equation}\left(8\right)}{=}& I_{{\mathcal{GO}}_{A_N}^{\ast }}^N(x,y).\hfill \end{array}$$

By Proposition 1, $A_N$ is an aggregation function. Furthermore, by the continuity of A and N, we have that $A_N$ is continuous. So, by Lemma 1, ${\mathcal{GO}}_{A_N}^{\ast }$ is a general overlap function. Therefore, since ${\mathcal{I}}_A=I_{{\mathcal{GO}}_{A_N}^{\ast }}^N$, then ${\mathcal{I}}_A$ is a $(\mathcal{GO},N)$-implication function. □

Corollary 4. 

Let $A:{[0,1]}^n\to [0,1]$ be a continuous aggregation function and let $\mathcal{I}=\{I_{{\mathcal{GO}}_i}^{N_i}$$:{[0,1]}^2\to [0,1]\mid i\in \{1,2,\dots ,n\}\}$, for $i\in \{1,2,\dots ,n\}$, be a family of $(\mathcal{GO},N)$-implication functions. If N is a strong negation, then for ${\mathcal{I}}_A$ with $N_i=N$ for $i\in \{1,2,\dots ,n\}$, it holds that:

 (i)

${\mathcal{I}}_A$ satisfies L-CP(N);

 (ii)

If N is also strict, then ${\mathcal{I}}_A$ satisfies R-CP(N⁻¹);

 (iii)

${\mathcal{I}}_A$ satisfies CP(N).

Proof. 

Straightforward from Propositions 12 and 18. □

4. Intersections between Families of Fuzzy Implications

In this section we present results regarding the intersections that exist among the families of fuzzy implications $(\mathcal{GO},N)$, $(G,N)$, $QL$, $R_O$ and D-implications derived from (general) overlap and grouping functions O and G, respectively, and fuzzy negations N. We will represent these families by ${\mathbb{I}}_{\mathcal{G}\mathbb{O}}^{\mathbb{N}},{\mathbb{I}}_{\mathbb{G},\mathbb{N}},{\mathbb{I}}_{\mathbb{O},\mathbb{G},\mathbb{N}}$, ${\mathbb{I}}_{\mathbb{O}}$ and ${\mathbb{I}}_{\mathbb{D}}$, respectively.

4.1. Intersections between $(\mathcal{GO},N)$ and $(G,N)$-Implications

Proposition 19. 

Let N and $N^{\prime }$ be fuzzy negations, $\mathcal{GO}$ be a bivariate general overlap function and G be a grouping function such that $I_{\mathcal{GO}}^N=I_{G,N^{\prime }}$.

 (i)

If N is strict and $N^{\prime }$ is frontier, then $\mathcal{GO}$ is an overlap function.

 (ii)

If 1 is the neutral element of $\mathcal{GO}$, then:

 (a)

If N is a strong negation, then $N=N^{\prime }$;

 (b)

If N is continuous and $N=N^{\prime }$, then N is strong;

 (c)

N is strong if and only if 0 is the neutral element of G.

 (iii)

If 0 is the neutral element of G, then:

 (a)

$N^{\prime }$ is strong if and only if $N^{\prime }=N$;

 (b)

$N^{\prime }$ is strong if and only if 1 is the neutral element of $\mathcal{GO}$.

Proof. 

(i)

Indeed, if $\mathcal{GO}(x,y)=0$, then

$$\begin{array}{ccc}\hfill N\left(\mathcal{GO}\right(x,y\left)\right)=1& \Rightarrow & I_{G,N}(x,N^{-1}\left(y\right))=I_{\mathcal{GO}}^N(x,N^{-1}\left(y\right))=1\hfill \\ & \Rightarrow & G(N\left(x\right),N^{-1}\left(y\right))=1\hfill \\ & \stackrel{\left(G3\right)}{\Rightarrow }& N\left(x\right)=1\mathrm{or}{N}^{-1}\left(y\right)=1\stackrel{\left(G3\right)}{\Rightarrow }x=0\mathrm{or}y=0.\hfill \end{array}$$

Moreover, if $\mathcal{GO}(x,y)=1$, then

$$\begin{array}{ccc}\hfill N\left(\mathcal{GO}\right(x,y\left)\right)=0& \Rightarrow & I_{G,N}(x,N^{-1}\left(y\right))=I_{\mathcal{GO}}^N(x,N^{-1}\left(y\right))=0\hfill \\ & \Rightarrow & G(N\left(x\right),N^{-1}\left(y\right))=0\hfill \\ & \stackrel{\left(G2\right)}{\Rightarrow }& N\left(x\right)=0\mathrm{and}{N}^{-1}\left(y\right)=0\stackrel{\left(G2\right)}{\Rightarrow }x=1\mathrm{and}y=1.\hfill \end{array}$$

Consequently, $\mathcal{GO}$ satisfies (O2) and (O3) and we conclude that $\mathcal{GO}$ is an overlap function.

(ii)

Indeed,

(a)

by Prop. 3.4(xxi) [34] we have that $I_{G,N^{\prime }}$ satisfies R-CP(N′), so

$$\begin{array}{ccc}\hfill N\left(y\right)& =& I_{\mathcal{GO}}^N(y,0)=I_{G,N^{\prime }}(y,0)\stackrel{\mathrm{R}-\mathrm{CP}\left({\mathrm{N}}^{\prime }\right)}{=}{I}_{G,N^{\prime }}(1,N^{\prime }\left(y\right))\hfill \\ & =& I_{\mathcal{GO}}^N(1,N^{\prime }\left(y\right))=N\left(\mathcal{GO}(1,N\left(N^{\prime }\left(y\right)\right))\right)\stackrel{\left(N5\right)}{=}{N}^{\prime }\left(y\right),\hfill \end{array}$$

for all $y\in [0,1]$. Therefore, $N=N^{\prime }$.

(b)

Since $I_{G,N^{\prime }}$ satisfies R-CP(N′) and $I_{\mathcal{GO}}^N=I_{G,N^{\prime }}$, $I_{\mathcal{GO}}^N(x,N^{\prime }\left(y\right))=I_{\mathcal{GO}}^N(y,N^{\prime }\left(x\right))$. So, for $x=1$, $I_{\mathcal{GO}}^N(1,N^{\prime }\left(y\right))=I_{\mathcal{GO}}^N(y,N^{\prime }\left(1\right))$, i.e.,

$$\begin{array}{c}\hfill N\left(\mathcal{GO}(1,N\left(N^{\prime }\left(y\right)\right))\right)=N\left(\mathcal{GO}(y,N\left(N^{\prime }\left(1\right)\right))\right).\end{array}$$

Since 1 is the neutral element of $\mathcal{GO}$ and $N=N^{\prime }$, for all $y\in [0,1]$, $N\left(N\right(N\left(y\right)\left)\right)=N\left(y\right)$. Now, since N is continuous, for every $x\in [0,1]$, there is $y\in [0,1]$ such that $x=N\left(y\right)$. So, $N\left(N\right(x\left)\right)=x$, for all $x\in [0,1]$.

(c)

For all $y\in [0,1]$, $N\left(N\left(y\right)\right)=N\left(\mathcal{GO}(1,N\left(y\right))\right)=I_{\mathcal{GO}}^N(1,y)=I_{G,N^{\prime }}(1,y)=G(N^{\prime }\left(1\right),y)$$=G(0,y)$. So the result holds.

(iii)

Indeed,

(a)

by Prop. 3.4(ii) [34] we have that $I_{G,N^{\prime }}$ satisfies (NP), so

$$\begin{array}{ccc}\hfill y& \stackrel{\left(\mathrm{NP}\right)}{=}& I_{G,N^{\prime }}(1,y)=I_{\mathcal{GO}}^N(N\left(0\right),y)\stackrel{\mathrm{Prop}.\left(\mathrm{i}\right)}{=}{I}_{\mathcal{GO}}^N(N\left(y\right),0)\hfill \\ & =& I_{G,N^{\prime }}(N\left(y\right),0)=N^{\prime }\left(N\left(y\right)\right),\hfill \end{array}$$

for all $y\in [0,1]$. Therefore, the result follows.

(b)

Consider $N^{\prime }$ as a strong negation, then by the previous item, $N^{\prime }=N$. So, $x=N^{\prime }\left(N^{\prime }\left(x\right)\right)=N^{\prime }\left(G(N^{\prime }\left(x\right),0)\right)=N^{\prime }\left(I_{G,N^{\prime }}(x,0)\right)=N^{\prime }\left(I_{\mathcal{GO}}^N(x,0)\right)=N^{\prime }\left(N\right(\mathcal{GO}(x,$$N\left(0\right)\left)\right))\stackrel{{\mathrm{N}}^{\prime }=\mathrm{N}}{=}\mathcal{GO}(x,1)$, for all $x\in [0,1]$. Therefore, 1 is the neutral element of $\mathcal{GO}$. Conversely, $N\left(x\right)=N\left(\mathcal{GO}(x,N\left(0\right))\right)=I_{\mathcal{GO}}^N(x,0)=I_{G,N^{\prime }}(x,0)=N^{\prime }\left(x\right)$, and therefore, by sub-item (a) of item (ii), $N^{\prime }$ is a strong negation. □

The next propositions show that strict $(\mathcal{GO},N)$-implication functions generated by general overlap functions satisfying ($\mathcal{GO}$2a) and ($\mathcal{GO}$3a) are strict $(G,N)$-implication functions and vice-versa.

Proposition 20. 

Let N be a strict fuzzy negation, $\mathcal{GO}$ be a GOF satisfying ($\mathcal{GO}$2a) and ($\mathcal{GO}$3a), and let G be the grouping function defined according to Equation (4). Then, one has that $I_{\mathcal{GO}}^N=I_{G,N^{-1}}$.

Proof. 

For all $x,y\in [0,1]$, since N is strict, it follows:

$$\begin{array}{ccc}\hfill I_{\mathcal{GO}}^N(x,y)& =& N\left(\mathcal{GO}(x,N\left(y\right))\right)=N\left(\mathcal{GO}(N\left(N^{-1}\left(x\right)\right),N\left(y\right))\right)\hfill \\ & \stackrel{\mathrm{Equation}\left(4\right)}{=}& G(N^{-1}\left(x\right),y)\stackrel{\mathrm{Equation}\left(7\right)}{=}{I}_{G,N^{-1}}(x,y).\hfill \end{array}$$

□

Proposition 21. 

Let N be a strict negation, G be a grouping function and $\mathcal{GO}$ be the general overlap function defined in Equation (3). Then, $I_{G,N}=I_{\mathcal{GO}}^{N^{-1}}$.

Proof. 

For all $x,y\in [0,1]$, since N is strict, it follows that:

$$\begin{array}{ccc}\hfill I_{G,N}(x,y)& \stackrel{\mathrm{Equation}\left(7\right)}{=}& N^{-1}\left(N\left(G(N\left(x\right),N\left(N^{-1}\left(y\right)\right))\right)\right)\hfill \\ & \stackrel{\mathrm{Equation}\left(3\right)}{=}& N^{-1}(\mathcal{GO}(x,N^{-1}\left(y\right))\stackrel{\mathrm{Equation}\left(8\right)}{=}{I}_{\mathcal{GO}}^{N^{-1}}(x,y).\hfill \end{array}$$

□

Corollary 5. 

Let I be a fuzzy implication function. Then, I is a strict $(\mathcal{GO},N)$-implication with $\mathcal{GO}$ satisfying conditions ($\mathcal{GO}$2a) and ($\mathcal{GO}$3a) if and only if I is a strict $(G,N)$-implication.

Proof. 

Straightforward from Propositions 20 and 21. □

By Corollary 5 we have that the intersection of $(\mathcal{GO},N)$ and $(G,N)$-implications is non-empty: ${\mathbb{I}}_{\mathcal{G}\mathbb{O}}^{\mathbb{N}}\cap {\mathbb{I}}_{\mathbb{G},\mathbb{N}}\ne \varnothing$. In addition, we also conclude that ${\mathbb{I}}_{\mathcal{G}\mathbb{O}}^{{\mathbb{N}}^{\ast }}={\mathbb{I}}_{\mathbb{G},{\mathbb{N}}^{\ast }}\subseteq {\mathbb{I}}_{\mathcal{G}\mathbb{O}}^{\mathbb{N}}\cap {\mathbb{I}}_{\mathbb{G},\mathbb{N}}$, where ${\mathbb{I}}_{\mathcal{G}\mathbb{O}}^{{\mathbb{N}}^{\ast }}$ is the family of all strict $(\mathcal{GO},N)$-implication functions and, analogously, ${\mathbb{I}}_{\mathbb{G},{\mathbb{N}}^{\ast }}$ is the family of all strict $(G,N)$-implication functions.

Next, we provide an example presenting an implication function belonging to both classes $(\mathcal{GO},N)$ and $(G,N)$-implications.

Example 5. 

Take the strict fuzzy negation N, defined by $N\left(x\right)=1-x^2$ and consider the grouping function G given by $G(x,y)=1-{(1-x)}^2{(1-y)}^2$. Then, for all $x,y\in [0,1]$, $I_{G,N}(x,y)=G(N\left(x\right),y)=1-{(1-N\left(x\right))}^2{(1-N\left(y\right))}^2=1-x^4{(1-y)}^2$. Now, consider the general overlap fuction $\mathcal{GO}(x,y)=N\left(G\right(N\left(x\right),N\left(y\right)\left)\right)$ (Equation (3)). Note that $\mathcal{GO}(x,y)=1-{(1-x^4{y}^4)}^2$ and $\mathcal{GO}$ satisfies ($\mathcal{GO}$2a) and ($\mathcal{GO}$3a). So since $N^{-1}\left(x\right)=\sqrt{1-x}$, we have that:

$$\begin{array}{ccc}\hfill I_{\mathcal{GO}}^{N^{-1}}(x,y)& =& N^{-1}\left(\mathcal{GO}(x,N^{-1}\left(y\right))\right)=\sqrt{1-\left(1-{\left(1-x^4{\left(\sqrt{1-y}\right)}^4\right)}^2\right)}\hfill \\ & =& 1-x^4{(1-y)}^2=I_{G,N}(x,y).\hfill \end{array}$$

Therefore, $I(x,y)=1-x^4{(1-y)}^2$ is a $(\mathcal{GO},N)$-implication and a $(G,N)$-implication.

Proposition 22. 

Let $I\in \mathcal{FI}$ such that $Ran\left(I\right)\ne [0,1]$. If I is a $(\mathcal{GO},N)$-implication function then I is not a $(G,N)$-implication function.

Proof. 

Suppose that I is a $(G,N)$-implication function. Then, there is a grouping G and a fuzzy negation N such that $I(x,y)=G\left(N\right(x),y)$ for each $x,y\in [0,1]$. However, since G is continuous and $G\left(N\right(0),0)=0$, $G\left(N\right(0),1)=1$, then for any $y\in [0,1]$ there exists $x\in [0,1]$ such that $I(0,x)=G(1,x)=y$. Therefore, $Ran\left(I\right)=[0,1]$. □

Corollary 6. 

Each crisp $(\mathcal{GO},N)$-implication function is not a $(G,N)$-implication function.

Let ${\mathbb{I}}_{\mathcal{G}\mathbb{O}}^{\mathbb{N}}=\{I\in {\mathbb{I}}_{\mathcal{G}\mathbb{O}}^{\mathbb{N}}|Ran\left(I\right)\ne [0,1]\}$. Proposition 22 proves that ${\mathbb{I}}_{\mathcal{G}\mathbb{O}}^{\mathbb{N}}\cap {\mathbb{I}}_{\mathbb{G},\mathbb{N}}=\varnothing$. Thus, there are $(\mathcal{GO},N)$-implication functions that are not $(G,N)$-implication functions and therefore, the class of $(\mathcal{GO},N)$-implication functions is not contained in the class of $(G,N)$-implication functions.

Note that the converse also holds as shown in the next proposition.

Proposition 23. 

There are $(G,N)$-implication functions that are not $(\mathcal{GO},N)$-implication functions.

Proof. 

Take the $(G,N)$-implication function $I_{G,N}$, where $G(x,y)=max(x,y)$ and $N=N_{\top }$. Thus,

$$\begin{array}{ccc}\hfill I_{G,N}(x,y)& =& max(N_{\top }\left(x\right),y)=\left\{\begin{array}{cc}max(0,y),\hfill & \mathrm{if}x=1\hfill \\ 1,\hfill & \mathrm{if}x<1\hfill \end{array}\right.=\left\{\begin{array}{cc}y,\hfill & \mathrm{if}x=1\hfill \\ 1,\hfill & \mathrm{if}x<1.\hfill \end{array}\right.\hfill \end{array}$$

Suppose there exists a GOF $\mathcal{GO}$ and a fuzzy negation N such that

$$I_{\mathcal{GO}}^N(x,y)=\left\{\begin{array}{cc}y,\hfill & \mathrm{if}x=1\hfill \\ 1,\hfill & \mathrm{if}x<1.\hfill \end{array}\right.$$

Thus, for $x=1$, $I_{\mathcal{GO}}^N(1,y)=y$, for all $y\in [0,1]$,

$$\begin{array}{c}\hfill N\left(\mathcal{GO}\right(1,N\left(y\right)\left)\right)=y.\end{array}$$

(13)

Furthermore, for $x<1$, $I_{\mathcal{GO}}^N(x,y)=1$, for all $y\in [0,1]$. So, in particular, for $y=0$, since $\mathcal{GO}$ is commutative,

$$\begin{array}{c}\hfill N\left(\mathcal{GO}\right(1,x\left)\right)=1\end{array}$$

(14)

for all $x<1$. Now, given $y\in (0,1)$, we have either $N\left(y\right)=1$ or $N\left(y\right)<1$. If $N\left(y\right)=1$ then, by Equation $\left(13\right)$ and $\left(\mathcal{GO}3\right)$, it follows $y=N\left(\mathcal{GO}\right(1,N\left(y\right)\left)\right)=N\left(\mathcal{GO}\right(1,1\left)\right)=N\left(1\right)=0$, which is a contradiction, since $y\in (0,1)$. Furthermore, if $N\left(y\right)<1$, then $y\stackrel{\mathrm{Equation}\left(13\right)}{=}N\left(\mathcal{GO}(1,N\left(y\right))\right)\stackrel{\mathrm{Equation}\left(14\right)}{=}1,$ which is a contradiction, since $y\in (0,1)$. In both cases we have a contradiction, so $I_{max,N_{\top }}$ is not a $(\mathcal{GO},N)$- implication function. □

The last two results ensure that ${\mathbb{I}}_{\mathcal{G}\mathbb{O}}^{\mathbb{N}}⊈{\mathbb{I}}_{\mathbb{G},\mathbb{N}}$ and ${\mathbb{I}}_{\mathbb{G},\mathbb{N}}⊈{\mathbb{I}}_{\mathcal{G}\mathbb{O}}^{\mathbb{N}}$.

4.2. Intersections between $(\mathcal{GO},N)$ and $QL$-Implication Functions

A tuple $(O,G,N)$, with O being an overlap function, G being a grouping function and N being a fuzzy negation, known as a $QL$-operator [33] is in fact an implication function if and only if $N=N_{\top }$. Then, we conclude that:

Proposition 24. 

There are no fuzzy implication functions that are simultaneously $QL$ implication functions and $(\mathcal{GO},N)$-implication functions.

Proof. 

Indeed, by Proposition 12(i), any $(\mathcal{GO},N)$-implication function $I_{\mathcal{GO}}^N$ satisfies L-CP(N). Moreover by Theorem 3.1(v) [33], any $QL$-implication $I_{O,G,N_{\top }}$ does not satisfy (L-CP) for any negation N. □

Corollary 7. 

There is no fuzzy implication function which is simultaneously a $QL$-implication function and a strict $(G,N)$-implication function.

Proof. 

Straightforward from Corollary 5 and Proposition 24. □

Therefore, one can conclude that the intersection of $QL$-implication functions and $(\mathcal{GO},N)$-implication functions is empty, i.e., ${\mathbb{I}}_{\mathcal{G}\mathbb{O}}^{\mathbb{N}}\cap {\mathbb{I}}_{\mathbb{O},\mathbb{G},\mathbb{N}}=\varnothing$. As a consequence, the intersection of $QL$-implication functions and $(G,N)$-implication functions with N being a strict negation, is also empty: ${\mathbb{I}}_{\mathbb{O},\mathbb{G},\mathbb{N}}\cap {\mathbb{I}}_{\mathbb{G},{\mathbb{N}}^{\ast }}=\varnothing$. In Theorem 5.1 [33], it is seen that $QL$-implication functions are included in the class of $(G,N)$-implications. Example 6 illustrates that.

Example 6. 

Consider the overlap function $O(x,y)=xy$, the grouping function $G(x,y)=1-{(1-x)}^2{(1-y)}^2$ and the fuzzy negation $N_{\top }$ given by Equation (9). Then, for all $x,y\in [0,1]$, one has that:

$$\begin{array}{ccc}\hfill I_{O,G,N_{\top }}(x,y)& =& G(N_{\top }\left(x\right),O(x,y)))=1-{\left(1-N_{\top }\left(x\right)\right)}^2{\left(1-O(x,y)\right)}^2\hfill \\ & =& \left\{\begin{array}{cc}1-{(1-y)}^2,\hfill & \mathit{if}x=1;\hfill \\ 1,\hfill & \mathit{if}x\ne 1\hfill \end{array}\right..\hfill \end{array}$$

On the other hand,

$$\begin{array}{ccc}\hfill I_{G,N_{\top }}(x,y)& =& G(N_{\top }\left(x\right),y)=1-{\left(1-N_{\top }\left(x\right)\right)}^2{\left(1-y\right)}^2\hfill \\ & =& \left\{\begin{array}{cc}1-{(1-y)}^2,\hfill & \mathit{if}x=1\hfill \\ 1,\hfill & \mathit{if}x\ne 1\hfill \end{array}\right..\hfill \end{array}$$

Therefore, $I(x,y)=\left\{\begin{array}{cc}1-{(1-y)}^2,\hfill & \mathit{if}x=1\hfill \\ 1,\hfill & \mathit{if}x\ne 1\hfill \end{array}\right.\in {\mathbb{I}}_{\mathbb{O},\mathbb{G},\mathbb{N}}\cap {\mathbb{I}}_{\mathbb{G},\mathbb{N}}$.

4.3. Intersections between $(\mathcal{GO},N)$ and $R_O$-implication Functions

Proposition 25. 

There are no fuzzy implication functions that are simultaneously $R_O$-implication functions and $(\mathcal{GO},N)$-implication functions.

Proof. 

Indeed, by Proposition 12(i), any $(\mathcal{GO},N)$-implication $I_{\mathcal{GO}}^N$ satisfies L-CP(N), however by Theorem 4.2 [32], it is guaranteed that every $R_O$-implication, $I_O$, does not satisfy (L-CP) for any negation N. □

Therefore, one can conclude that $(\mathcal{GO},N)$-implication functions and the family of $R_O$-implication functions do not intercept, i.e., ${\mathbb{I}}_{\mathcal{G}\mathbb{O}}^{\mathbb{N}}\cap {\mathbb{I}}_{\mathbb{O}}=\varnothing$.

4.4. Intersections between $(\mathcal{GO},N)$ and D-Implication Functions

From the results given in Theorem 4.1 [35] we know that every D-implication function is a $QL$-operation considering the greatest fuzzy negation. Still, from Theorem 4.2 [35] we know that every D-implication is a $(G,N)$-implication considering the greatest fuzzy negation. Therefore, it is straightforward that there are no intersections between $(\mathcal{GO},N)$ implication functions and D-implication or $(G,N)$-implication functions. Moreover, by Theorem 4.3 [35] one can say that there is no intersection between $(\mathcal{GO},N)$-implication functions and D-implication functions.

In Figure 1, we illustrate the main results presented in this section. Note that the intersections between the families of $(G,N)$, $QL$, $R_O$ and D-implication functions had already been presented in other works [32,33,34,35].

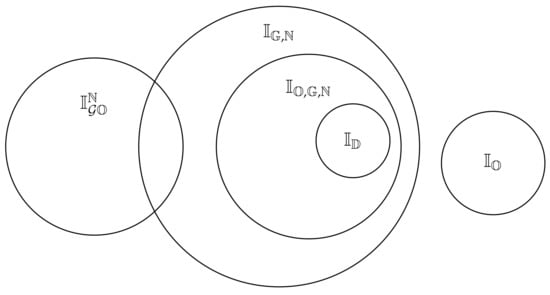
Figure 1. Intersections between families of fuzzy implication functions.

5. Final Remarks

In propositional logics, one may consider the negation (¬) and other logical connectives such as the implication (→), the disjunction (∨) or the conjunction (∧) as being primitive. Other connectives can be defined in a standard form using only two primitive connectives [36]. In particular, when the primitive connectives are the negation and the disjunction, the standard definition of the implication is given by (i) $p\to q\equiv \neg p\vee q$ and when the primitive connectives are the negation and the conjunction, the standard definition of the implication is given by (ii) $p\to q\equiv \neg (p\wedge \neg q)$. The first one, in fuzzy logics, had motived the introduction of several classes of fuzzy implication functions, such as the $(S,N)$, $(G,N)$ and $(A,N)$ implications, where the disjunction is given, respectively, by a t-conorm S, a grouping function G or a disjunctive aggregation function A (e.g., see [11,34,51]). The second one, using conjunctive operators, allowed the definition of implication functions based on t-norms [20]. In this work we introduced a class of implication function based on (ii), where the conjunction is given by generalized overlap functions.

The main contributions of this work are the investigation of properties satisfied by such implication functions, their characterization, and a study of the intersections between them and other classes of implication functions derived from (general) overlap/grouping functions. The summary of these intersections is illustrated in Figure 1. Actually, we complete this study by also considering the class of $(T,N)$-implication functions, denoted by ${\mathbb{I}}_{\mathbb{T}}^{\mathbb{N}}$, which is also based on the standard definition of the implication given by (ii), but using a t-norm instead of a general overlap function. Since each continuous t-norm is a general overlap function but the converse does not hold, then trivially we have that: ${\mathbb{I}}_{\mathcal{G}\mathbb{O}}^{\mathbb{N}}\cap {\mathbb{I}}_{\mathbb{T}}^{\mathbb{N}}\ne \varnothing$, ${\mathbb{I}}_{\mathcal{G}\mathbb{O}}^{\mathbb{N}}-{\mathbb{I}}_{\mathbb{T}}^{\mathbb{N}}\ne \varnothing$ and ${\mathbb{I}}_{\mathbb{T}}^{\mathbb{N}}-{\mathbb{I}}_{\mathcal{G}\mathbb{O}}^{\mathbb{N}}\ne \varnothing$. In addition, Table 2 shows some of the properties satisfied by the $(\mathcal{GO},N)$-implication functions and $(T,N)$-implication functions whenever we take into account: any fuzzy negation N, strong fuzzy negations (represented by ${\mathbb{N}}^{\ast }$), non-strong fuzzy negations (represented by ${\mathbb{N}}^{+}$) or crisp negations (represented by ${\mathbb{N}}_c$). For each property, yes/no means that the property is/is not held for each implication of that class. Additional restrictions may appear as follows: no^st means the property is not valid if N is strict, yes(no)${}^{ne}$ means the property is(not) valid when 1 is the neutral element of $\mathcal{GO}$, and yes${}^a$ means the property holds when $\mathcal{GO}$ is associative. Empty table cells mean that some implication functions of the class satisfy the property whereas others do not. We can notice that indeed $\mathcal{GO}$-implication functions are more general since more properties are verified.

Table 2. Some properties of fuzzy implication functions.

Property	${\mathbb{I}}_{\mathbb{T}}^{{\mathbb{N}}^{\ast }}={\mathbb{I}}_{\mathbb{S},{\mathbb{N}}^{\ast }}$	${\mathbb{I}}_{\mathbb{T}}^{{\mathbb{N}}^{+}}$	${\mathbb{I}}_{\mathbb{T}}^{{\mathbb{N}}_{\mathit{c}}}$	${\mathbb{I}}_{\mathcal{G}\mathbb{O}}^{{\mathbb{N}}^{\ast }}$	${\mathbb{I}}_{\mathcal{G}\mathbb{O}}^{{\mathbb{N}}_{\mathit{c}}}$
EP	yes	nost	yes	yes${}^a$	yes${}^{ne}$
NP	yes	no	no	yes${}^{ne}$	no${}^{ne}$
ROP			no		no${}^{ne}$
LOP			yes		yes${}^{ne}$
CP(N)	yes	nost	yes	yes	yes${}^{ne}$
L-CP(N)	yes	yes	yes	yes	yes
R-CP(N)	yes	nost	yes	yes	yes${}^{ne}$

Our future works include studying the use of $\mathcal{GO}$ operators on other classes of implication functions and the construction of other classes of fuzzy subsethood measures like it was made in [20,33], which can be used to generate fuzzy entropies, similarity measures and penalty functions, and applied in many ways.