Optimal Control for Parabolic Uncertain System Based on Wavelet Transformation

Abstract

In this paper, we study a new type of optimal control problem subject to a parabolic uncertain partial differential equation where the expected value criterion is adopted in the objective function. The basic idea of Haar wavelet transformation is to transform the proposed problem into an approximate uncertain optimal control problem with arbitrary accuracy because the dimension of Haar basis tends to infinity. The relative convergence theorem is proved. An application to an optimal control problem with an uncertain heat equation is dealt with to illustrate the efficiency of the proposed method.

1. Introduction

Differential equations are essential mathematical tools for describing control systems. Modern optimal control theory can be divided into three main parts by the control systems. The first part is the lumped parameter system (LPS). It mainly discusses the optimal control problem of an ordinary differential equation (ODE). The second part is the optimal control of a distributed parameter system (DPS). A distributed parameter optimal control problem consists of an objective function and a partial differential equation (PDE) system. The third part is the optimal control problem with disturbances in a system of equations. That is, the system is characterized by stochastic differential equations (SDE) or uncertain differential equations (UDE).

In the late sixties, Lions systematically studied a situation in which the performance index is quadratic and studied the optimal control problem (OCP) of DPS utilizing a variational inequality and convex analysis. It is worth mentioning that Lions [1] described the optimal control theory of PDEs in a more complete and detailed manner. He carried out in-depth research on the solution of the OCP for parabolic, hyperbolic and elliptic PDEs. Ahmed and Teo [2] discussed a DPS in Banach space using tools such as operator semigroups, adjoint systems and variational inequalities. Paymond and Zidani [3], Fernández [4], Case and Kunisch [5], Bokalo and Tsebenko [6] and Abdulla et al. [7,8,9] further worked on OCPs governed by PDEs. In 2007, based on normality, self-duality, subadditivity and product axioms, Liu [10] proposed the uncertain measure and developed uncertainty theory. Liu [11] defined the UDE with uncertain process of describing dynamic changes of uncertain factors. Chen and Liu [12] proved that, when the coefficients meet linear growth and Lipschitz conditions, the solution of an UDE exists and is unique. For cases where the analytical solution of the UDE does not exist, Gu and Zhu [13] proposed an Adams prediction correction method to obtain the numerical solution of the UDE. Based on UDEs, in 2010, Zhu [14] proposed an uncertain optimal control problem (UOCP) under the expected value criterion. The principle of optimality and equation of optimality of UOCP were obtained by Bellman dynamic programming method. Furthermore, Ge and Zhu [15] considered UOCP from the perspective of the variational method. They showed a necessary condition of optimality of UOCP under the expected value criterion. Since then, various types of UOCPs have been discussed, such as UOCP with jumps [16], continuous-time uncertain bang–bang control problems [17], UOCP under Hurwicz criterion and optimistic value criterion [18], OCP for switched systems [19], uncertain linear–quadratic optimal parameter control problems [20], UOCP for singular systems [21] and optimal control for time-delay uncertain systems [22]. As we know, in practice, mathematical physical equations presented by PDEs have many applications. However, the distributed parameter UOCP—the system of which is described as an uncertain partial differential equation (UPDE)—has not been studied. In 2017, Yang and Yao [23] introduced the parabolic uncertain partial differential equation (pUPDE). This gives research on the optimal control problem based on pUPDEs a foundation, while in most cases it is challenging to obtain solutions to PDEs. Solutions of PDEs with uncertain processes are more tricky to obtain. Furthermore, the OCPs with UPDE system are much harder to solve. However, many problems in practice are suited to being described by OCPs with UPDE systems, such as the metal-temperature-control problem in an environment with uncertain heat sources. Hence, the OCP with a UPDE system is worth discussing.

Wavelet transform allows a function over an interval to be represented on an orthogonal basis. Haar wavelet basis—as an orthogonal function system—has excellent integral operation properties [24]. Many primary functions could also convert integral operations into algebraic operations, such as Legendre polynomials, Chebyshev polynomials and Genocchi polynomials [25]. The simplest complete orthogonal basis is Haar wavelet basis. By the orthogonal function approximation method, PDEs can be transformed into ordinary differential equations. Our problem is one of whether the pUPDE can be transformed into an ordinary UDE. We ask the following question: what is the optimal solution for a UOCP based on the pUPDE system? As far as we know, the above issues have not yet been answered. This paper focuses on such problems to fill the gap. Based on Zhu’s work [14] on UOCP, we consider a more complex case where the control system is a pUPDE. The main work of wavelet transformation is to transform the pUDE into an ordinary UDE. The optimal control obtained by the approximate problem is an approximation of the optimal control of the parabolic UOCP. As the dimension tends to infinity, these two optimal controls can be arbitrarily close.

In the next section, some concepts are reviewed, including uncertain process and UPDE. In Section 3, a parabolic UOCP is discussed. Section 4 shows an approximate form of parabolic UOCP by Haar wavelet transformation. In Section 5, the inverse uncertainty distribution solution of the system equation after Haar wavelet transformation is discussed. After that, the convergence is obtained in Section 6. In the final section, the validity of the proposed method is confirmed by an control problem of metal temperature with uncertain energy source.

2. Preliminaries

In this section, the concepts of the uncertain measure, uncertain variable, independence and uncertain process are shown as follows. As a particular case of PDE with uncertain process, uncertain parabolic PDE is shown.

Definition 1

([10]). The set function $\mathcal{M}$ on $\mathcal{L}$ is called an uncertain measure if it satisfies the normality, $\mathcal{M}\{\Gamma \}=1$, for the universal set, Γ; the duality, $\mathcal{M}\{\Lambda \}+\left\{{\Lambda }^C\right\}=1$, for any event, Λ, in $\mathcal{L}$, which is a σ-algebra over Γ; and the subadditivity axioms, $\mathcal{M}\left\{{\bigcup }_{i=1}^{\infty }{\Lambda }_i\right\}\le {\sum }_{i=1}^{\infty }\mathcal{M}\left\{{\Lambda }_i\right\}.$

Definition 2

([10]). An uncertain variable is a function, ξ, from an uncertain space, $(\Gamma ,\mathcal{L},\mathcal{M})$, to the set of real numbers, such that $\{\xi \in B\}$ is an event for any Borel set, B.

Definition 3

([26]). The uncertain variables ${\xi }_1$, ${\xi }_2$, … and ${\xi }_n$ are said to be independent if

$$\mathcal{M}\left\{{\bigcap }_{i=1}^n({\xi }_i\in B_i)\right\}={\bigwedge }_{i=1}^n\mathcal{M}\{{\xi }_i\in B_i\}$$

for any Borel sets—$B_1$, $B_2$, … and $B_n$.

Definition 4

([10]). The uncertain sequence $\left\{{\xi }_n\right\}$ is said to be convergent in measure to ξ if

$${lim}_{n\to \infty }\mathcal{M}\left\{\right|{\xi }_n-\xi |\ge \epsilon \}=0$$

for every $\epsilon >0$.

Definition 5

([26]). An uncertain process, $C_t$, is said to be Liu process if

(i) 

$C_0=0$ and almost all sample paths are Lipschitz continuous;

(ii) 

$C_t$ has stationary and independent increments;

(iii) 

every increment $C_{s+t}-C_s$ is a normal uncertain variable with expected value 0 and variance $t^2$, whose uncertainty distribution is

$${\mathsf{\Phi }}_t\left(x\right)={\left(1+exp\left({\displaystyle \frac{-\pi x}{\sqrt{3}t}}\right)\right)}^{-1},x\in \mathcal{R}$$

and inverse uncertainty distribution is

$${\mathsf{\Phi }}_t^{-1}\left(\alpha \right)={\displaystyle \frac{t\sqrt{3}}{\pi }}ln{\displaystyle \frac{\alpha }{1-\alpha }}$$

that are homogeneous linear functions of time, t, for any given $\alpha \in (0,1)$.

Yang [23] defined an uncertain partial differential equation (UPDE). Next, for a parabolic uncertain partial differential equation (pUPDE), we give its $\alpha$-path.

Definition 6

([27]). Let α be a number with $0<\alpha <1$. An uncertain differential equation

$$\mathrm{d}{X}_t=f(t,X_t)\mathrm{d}t+g(t,X_t)\mathrm{d}{C}_t$$

is said to have an α-path $X_t^{\alpha }$ if it solves the corresponding ordinary differential equation:

$$\mathrm{d}{X}_t^{\alpha }=f(t,X_t^{\alpha })\mathrm{d}t+\left|g(t,X_t^{\alpha })\right|{\mathsf{\Phi }}^{-1}\left(\alpha \right)\mathrm{d}t,$$

where ${\mathsf{\Phi }}^{-1}\left(\alpha \right)$ is the inverse standard normal uncertainty distribution.

Theorem 1

([27]). Let $X_t$ and $X_t^{\alpha }$ be the solution and α-path of the uncertain differential equation

$$\mathrm{d}{X}_t=f(t,X_t)\mathrm{d}t+g(t,X_t)\mathrm{d}{C}_t,$$

respectively. Then, the solution $X_t$ has an inverse uncertainty distribution

$${\mathsf{\Psi }}_t^{-1}\left(\alpha \right)=X_t^{\alpha }.$$

Definition 7.

Let α be a number with $0<\alpha <1$. An UPDE

$${\displaystyle \frac{\partial Y_{t,x}}{\partial t}}-\sum _{i,j=1}^n{a}_{ij}{\displaystyle \frac{{\partial }^2{Y}_{t,x}}{\partial x_i\partial x_j}}+\sum _{i=1}^n{b}_i{\displaystyle \frac{\partial Y_{t,x}}{\partial x_i}}+c{Y}_{t,x}=q_t{\dot{C}}_t$$

(1)

is said to have an α-path $Y_{t,x}^{\alpha }$ if it solves the corresponding PDE

$${\displaystyle \frac{\partial Y_{t,x}^{\alpha }}{\partial t}}-\sum _{i,j=1}^n{a}_{ij}{\displaystyle \frac{{\partial }^2{Y}_{t,x}^{\alpha }}{\partial x_i\partial x_j}}+\sum _{i=1}^n{b}_i{\displaystyle \frac{\partial Y_{t,x}^{\alpha }}{\partial x_i}}+c{Y}_{t,x}^{\alpha }=\left|q_t\right|{\mathsf{\Phi }}^{-1}\left(\alpha \right),$$

(2)

where ${\mathsf{\Phi }}^{-1}\left(\alpha \right)$ is the inverse standard normal uncertainty distribution.

Theorem 2

([11]). Let ${\xi }_1,{\xi }_2,\dots ,{\xi }_n$ be independent uncertain variables with regular uncertainty distribution ${\mathsf{\Phi }}_1,{\mathsf{\Phi }}_2,\dots ,{\mathsf{\Phi }}_n$, respectively. If f is a strictly increasing function, then the uncertain variable

$$\xi =f({\xi }_1,{\xi }_2,\dots ,{\xi }_n)$$

has an inverse uncertainty distribution

$${\mathsf{\Psi }}^{-1}\left(\alpha \right)=f({\mathsf{\Phi }}_1^{-1}\left(\alpha \right),{\mathsf{\Phi }}_2^{-1}\left(\alpha \right),\dots ,{\mathsf{\Phi }}_n^{-1}\left(\alpha \right)).$$

From Theorem 1, we can see that the solution $X_t$ of UDE has an inverse uncertainty distribution $X_t^{\alpha }$. The inverse uncertainty distribution $X_t^{\alpha }$ is the $\alpha$-path. Similarly, the solution $Y_{t,x}$ of UPDE has an inverse uncertainty distribution $Y_{t,x}^{\alpha }$. Combining with Theorem 2, for any increasing function $f\left(Y_{t,x}\right)$, the inverse uncertainty distribution of $f\left(Y_{t,x}\right)$ is $f\left(Y_{t,x}^{\alpha }\right)$.

Based on the existing work above, we consider the optimal control for parabolic uncertain system.

3. Problem Formulations

In daily life, many phenomena need to be described by PDEs. This part we consider a system described by parabolic PDEs. Moreover, because of the environment’s complexity, it is necessary to consider uncertain processes. The cost function in the optimal control problem is considered as an expected value function. Consider the following expected-value-based parabolic uncertain optimal control problem:

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{\displaystyle J(0,y_{0,x})\equiv \underset{u\in \mathcal{U}}{min}E\left[{\int }_0^1{\int }_0^{T}f(Y_{t,x},u_{t,x})\mathrm{d}t\mathrm{d}x+G\left(Y_{T,1}\right)\right]}\hfill \\ \mathrm{subject}\mathrm{to}\hfill \\ {\displaystyle {\displaystyle \frac{\partial Y_{t,x}}{\partial t}}-a{\displaystyle \frac{{\partial }^2{Y}_{t,x}}{\partial x^2}}+b{\displaystyle \frac{\partial Y_{t,x}}{\partial x}}+c{Y}_{t,x}+h{u}_{t,x}=q_t{\dot{C}}_t,t\in [0,T],x\in [0,1],}\hfill \\ {\displaystyle Y_{0,x}=y_{0,x},x\in [0,1],}\hfill \\ {\displaystyle Y_{t,0}=g_{1t},t\in [0,T],}\hfill \\ {\displaystyle {\displaystyle \frac{\partial Y_{t,x}}{\partial x}}\left|{}_{x=0}=g_{2t}\right.,t\in [0,T].}\hfill \end{array}\right.\end{array}$$

(3)

It can be seen that the DPS is an uncertain, linear, time-invariant parabolic control system:

$${\displaystyle \frac{\partial Y_{t,x}}{\partial t}}-a{\displaystyle \frac{{\partial }^2{Y}_{t,x}}{\partial x^2}}+b{\displaystyle \frac{\partial Y_{t,x}}{\partial x}}+c{Y}_{t,x}+h{u}_{t,x}=q_t{\dot{C}}_t,(t,x)\in [0,T]\times [0,1],$$

(4)

where $Y_{t,x}$ is the state variable. Let $\mathcal{U}$ be a given nonempty subset of $\mathcal{R}$. The function $u_{t,x}:[0,T]\times [0,1]\to \mathcal{U}$ called the control variable is piecewise continuous. The coefficients $a,b,c,h\in \mathcal{R}$ are crisp numbers; $q_t:[0,T]\to \mathcal{R}$ is a continuous function.

The initial condition is

$$Y_{0,x}=y_{0,x},x\in [0,1],$$

(5)

where $y_{0,x}\in C\left([0,1]\right).$

The boundary condition is described as

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{Y}_{t,0}=g_{1t},\hfill \\ {\displaystyle \frac{\partial Y_{t,x}}{\partial x}}\left|{}_{x=0}=g_{2t},\right.\hfill \end{array}\right.\end{array}$$

(6)

where $g_{1t},g_{2t}:[0,T]\to \mathcal{R}$.

The objective function is an expected value based index function

$$J(0,y_{0,x})\equiv \underset{u\in \mathcal{U}}{min}E\left[{\int }_0^1{\int }_0^{T}f(Y_{t,x},u_{t,x})\mathrm{d}t\mathrm{d}x+G\left(Y_{T,1}\right)\right],$$

(7)

where $f(Y_{t,x},u_{t,x})$ is a strictly monotonic continuous function in $Y_{t,x}$. $G\left(Y_{T,1}\right)$ is a function of terminal reward at $t=T$ and $x=1$. We denote $J(s,y_{s,x})$ as the optimal value obtained in $s\in [t,T]$.

4. Wavelet Transformation

The parabolic uncertain optimal control problem is challenging because of the uncertain process and partial differential equation in the system. The difficulty of the problem can be reduced by transforming the parabolic uncertain optimal control problem into a known uncertain optimal control problem. Wavelet transformation is an excellent tool to transform a DPS into an LPS. Some more sophisticated methods to uncertain optimal control problems with UDEs can be applied to optimal control problems for parabolic UPDEs. The Haar wavelet with orthogonality is one of the commonly used wavelets. $F\left(t\right)$—which belongs to $C[0,1]$ or $L^p(0,1)(1\le p<\infty )$—may be approximated by a finite term summation based on the Haar basis.

A set of orthogonal wavelet basis can be described as $\{{\psi }_{m,k}\left(t\right),m,k\in \mathbb{N}\}$, where

$${\psi }_{m,k}\left(t\right)=2^{\frac{m}{2}}\psi (2^{m}t-k)$$

and $\mathbb{N}$ is the set of natural numbers. For Haar wavelet, the mother wavelet $\psi \left(t\right)$ is expressed as

$$\begin{array}{c}\hfill \psi \left(t\right)=\left\{\begin{array}{cc}& 1,t\in [0,{\displaystyle \frac{1}{2}})\hfill \\ & -1,t\in [{\displaystyle \frac{1}{2}},1)\hfill \\ & 0,otherwise,\hfill \end{array}\right.\end{array}$$

(8)

and the corresponding scaling function $\varphi \left(t\right)$ is expressed as

$$\varphi \left(t\right)=\left\{\begin{array}{cc}& 1,t\in [0,1)\hfill \\ & 0,otherwise.\hfill \end{array}\right.$$

The wavelet series expansion of the function $F\left(t\right)$ is

$$F\left(t\right)\sim c_0\varphi \left(t\right)+{\sum }_{m,k}{c}_{m.k}{\psi }_{m,k}\left(t\right),F\left(t\right)\in C[0,1],$$

where the coefficient $c_{m,k}$ is the inner product ${\int }_0^1{\psi }_{m,k}\left(t\right)F\left(t\right)\mathrm{d}t$. What is more, use the n-term wavelet series summation to approximate the function $F\left(t\right)$. Then, $F\left(t\right)$ can be approximated as

$$F\left(t\right)\simeq c_0\varphi \left(t\right)+\sum _{m=0}^n\sum _{k=0}^{2^m-1}{c}_{m.k}{\psi }_{m,k}\left(t\right),F\left(t\right)\in C[0,1].$$

(9)

Wavelet function can transform integral operation into an algebraic operation, as follows:

$${\int }_0^t{\mathsf{\Psi }}_{sN}\mathrm{d}s=P_N{\mathsf{\Psi }}_{tN},$$

(10)

where ${\mathsf{\Psi }}_{tN}$ is the vector consisting of reordering of ${\psi }_{m,k}\left(t\right)$, $m=0,1,2,\dots ,n$, $k=0$, 1, 2, …, $2^m-1$, and $P_N$ is an N-dimensional constant square matrix. If $N=4$, then ${\mathsf{\Psi }}_{t4}={({\psi }_{t1},{\psi }_{t2},{\psi }_{t3},{\psi }_{t4})}^{\tau }$, where $\tau$ stands for transposition, and

$$\begin{array}{cc}& {\psi }_{t1}=\varphi \left(t\right)=1,\hfill \\ & {\psi }_{t2}={\psi }_{0,0}\left(t\right)=\psi \left(t\right),\hfill \\ & {\psi }_{t3}={\psi }_{1,0}\left(t\right)=\sqrt{2}\psi \left(2t\right),\hfill \\ & {\psi }_{t4}={\psi }_{1,1}\left(t\right)=\sqrt{2}\psi (2t-1).\hfill \end{array}$$

Another characteristic of Haar wavelet function is

$$I_N={\int }_0^1{\mathsf{\Psi }}_{tN}{\left({\mathsf{\Psi }}_{tN}\right)}^{\tau }\mathrm{d}t,$$

(11)

where $I_N$ is the identity matrix of order N.

Furthermore, the Haar wavelet series can approximate the function $F\left(t\right)\in C[0,1]$ with arbitrary accuracy. Suppose the partial summation $S_N\left(F\right)$ of wavelet series expansion with respect to $F\left(t\right)$ is $S_N\left(F\right)={\displaystyle \sum _{n=1}^N}{c}_n\left(F\right){\psi }_{tn}$. With Haar wavelet series expansion, the parabolic distributed parameter uncertain optimal problem (3) may be approximated by a series of lumped parameter uncertain optimal problems.

For DPS (4) of problem (3),

$${\displaystyle \frac{\partial Y_{t,x}}{\partial t}}-a{\displaystyle \frac{{\partial }^2{Y}_{t,x}}{\partial x^2}}+b{\displaystyle \frac{\partial Y_{t,x}}{\partial x}}+c{Y}_{t,x}+h{u}_{t,x}=q_t{\dot{C}}_t,$$

integrating both sides of the above equation simultaneously, we have

$$\begin{array}{ccc}\hfill & & {\int }_0^x{\int }_0^x{\displaystyle \frac{\partial Y_{t,x}}{\partial t}}\mathrm{d}x\mathrm{d}x-{\int }_0^x{\int }_0^{x}a{\displaystyle \frac{{\partial }^2{Y}_{t,x}}{\partial x^2}}\mathrm{d}x\mathrm{d}x+{\int }_0^x{\int }_0^{x}b{\displaystyle \frac{\partial Y_{t,x}}{\partial x}}\mathrm{d}x\mathrm{d}x\hfill \\ & +& {\int }_0^x{\int }_0^x\left(c{Y}_{t,x}+hu(t,x)\right)\mathrm{d}x\mathrm{d}x\hfill \\ & =& {\int }_0^x{\int }_0^x{q}_t{\dot{C}}_t\mathrm{d}x\mathrm{d}x.\hfill \end{array}$$

(12)

For the integral ${\int }_0^x{\int }_0^{x}b{\displaystyle \frac{\partial Y_{t,x}}{\partial x}}\mathrm{d}x\mathrm{d}x$ in Equation (12), it holds that

$${\int }_0^x{\int }_0^{x}b{\displaystyle \frac{\partial Y_{t,x}}{\partial x}}\mathrm{d}x\mathrm{d}x=b\left({\int }_0^x{Y}_{t,x}\mathrm{d}x-{\int }_0^x{Y}_{t,0}\mathrm{d}x\right).$$

(13)

About ${\int }_0^x{\int }_0^{x}a{\displaystyle \frac{{\partial }^2{Y}_{t,x}}{\partial x^2}}\mathrm{d}x\mathrm{d}x$ in Equation (12), by the first boundary condition Equation (6), we have

$$\begin{array}{ccc}\hfill {\int }_0^x{\int }_0^{x}a{\displaystyle \frac{{\partial }^2{Y}_{t,x}}{\partial x^2}}\mathrm{d}x\mathrm{d}x& =& a\left({\int }_0^x{\displaystyle \frac{\partial Y_{t,x}}{\partial x}}\mathrm{d}x-{\int }_0^x{\displaystyle \frac{\partial Y_{t,x}}{\partial x}}{|}_{x=0}\mathrm{d}x\right)\hfill \\ & =& a\left(Y_{t,x}-g_{1t}-{\int }_0^x{g}_{2t}\mathrm{d}x\right).\hfill \end{array}$$

(14)

Substituting Equations (13) and (14) into Equation (12), there is

$$\begin{array}{ccc}\hfill & & {\int }_0^x{\int }_0^x{\displaystyle \frac{\partial Y_{t,x}}{\partial t}}\mathrm{d}x\mathrm{d}x-a\left(Y_{t,x}-g_{1t}-{\int }_0^x{g}_{2t}\mathrm{d}x\right)+b\left({\int }_0^x\left(Y_{t,x}-g_{1t}\right)\mathrm{d}x\right)\hfill \\ & +& {\int }_0^x{\int }_0^{x}c{Y}_{t,x}\mathrm{d}x\mathrm{d}x+{\int }_0^x{\int }_0^{x}hu(t,x)\mathrm{d}x\mathrm{d}x\hfill \\ & =& {\int }_0^x{\int }_0^x{q}_t{\dot{C}}_t\mathrm{d}x\mathrm{d}x.\hfill \end{array}$$

(15)

Next, to transform the parabolic distributed parameter uncertain optimal control to lumped parameter uncertain optimal control, a kind of Haar wavelet transformation is used to the functions in the parabolic equation. Compared with the deterministic optimal control problem, the question of how to deal with the uncertain process, $C_t$, is important.

Expanding function $q_t{\dot{C}}_t$, state function $Y_{t,x}$, control function $u_{t,x}$, initial condition (I.C.) and the boundary condition (B.C.) on Haar basis, the following is obtained:

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}& Y_{t,x}\simeq {\left({\overline{Y_t}}_N\right)}^{\tau }{\mathsf{\Psi }}_{xN}\hfill \\ & u_{t,x}\simeq {\left({\overline{u_t}}_N\right)}^{\tau }{\mathsf{\Psi }}_{xN}\hfill \\ & q_t{\dot{C}}_t=q_t{\dot{C}}_t{\left(e_N\right)}^{\tau }{\mathsf{\Psi }}_{xN}\hfill \\ I.C.\hfill & Y_{0,x}=y_{0,x}\simeq {\left({\overline{y}}_{0N}\right)}^{\tau }{\mathsf{\Psi }}_{xN}\hfill \\ B.C.\hfill & \left\{\begin{array}{c}{Y}_{t,0}=g_{1t}=g_{1t}{\left(e_N\right)}^{\tau }{\mathsf{\Psi }}_{xN}\\ {\displaystyle \frac{\partial Y_{t,x}}{\partial x}}{|}_{x=0}=g_{2t}=g_{2t}{\left(e_N\right)}^{\tau }{\mathsf{\Psi }}_{xN}\end{array}\right.\hfill \end{array}\right.\end{array}$$

(16)

where the coefficients ${\overline{Y_t}}_N,{\overline{u_t}}_N$ on Haar basis are vectors in ${\mathcal{R}}^n$. Since $u\in \mathcal{U}$, we have ${\overline{u}}_N\in \overline{\mathcal{U}}$. The unit vector $e_N={(1,0,\dots ,0)}^{\tau }\in R^n$. Then, Equation (15) after Haar wavelet transformation may be written as

$$\begin{array}{ccc}\hfill & & {\int }_0^x{\int }_0^x{\displaystyle \frac{\mathrm{d}{\left({\overline{Y_t}}_N\right)}^{\tau }}{\mathrm{d}t}}{\mathsf{\Psi }}_{xN}\mathrm{d}x\mathrm{d}x-a\left({\left({\overline{Y_t}}_N\right)}^{\tau }{\mathsf{\Psi }}_{xN}-g_{1t}{\left(e_N\right)}^{\tau }{\mathsf{\Psi }}_{xN}-{\int }_0^x{g}_{2t}{\left(e_N\right)}^{\tau }{\mathsf{\Psi }}_{xN}\mathrm{d}x\right)\hfill \\ & +& b\left({\int }_0^x{\left({\overline{Y_t}}_N\right)}^{\tau }{\mathsf{\Psi }}_{xN}\mathrm{d}x-{\int }_0^x{g}_{1t}{\left(e_N\right)}^{\tau }{\mathsf{\Psi }}_{xN}\mathrm{d}x\right)+{\int }_0^x{\int }_0^{x}c{\left({\overline{Y_t}}_N\right)}^{\tau }{\mathsf{\Psi }}_{xN}\mathrm{d}x\mathrm{d}x\hfill \\ & +& {\int }_0^x{\int }_0^{x}h{\left({\overline{u_t}}_N\right)}^{\tau }{\mathsf{\Psi }}_{xN}\mathrm{d}x\mathrm{d}x={\int }_0^x{\int }_0^x{q}_t{\dot{C}}_t{\left(e_N\right)}^{\tau }{\mathsf{\Psi }}_N\left(x\right)\mathrm{d}x\mathrm{d}x.\hfill \end{array}$$

(17)

With the help of the integral operation matrix of Haar wavelet (10), we obtain

$$\begin{array}{ccc}\hfill & & {\displaystyle \frac{\mathrm{d}{\left({\overline{Y_t}}_N\right)}^{\tau }}{\mathrm{d}t}}{P}_N^2{\mathsf{\Psi }}_{xN}-a\left({\left({\overline{Y_t}}_N\right)}^{\tau }{\mathsf{\Psi }}_{xN}-g_{1t}{\left(e_N\right)}^{\tau }{\mathsf{\Psi }}_{xN}-g_{2t}{\left(e_N\right)}^{\tau }{P}_N{\mathsf{\Psi }}_{xN}\right)\hfill \\ & +& b\left({\left({\overline{Y_t}}_N\right)}^{\tau }{P}_N{\mathsf{\Psi }}_{xN}-g_{1t}{\left(e_N\right)}^{\tau }{P}_N{\mathsf{\Psi }}_{xN}\right)+c{\left({\overline{Y_t}}_N\right)}^{\tau }{P}_N^2{\mathsf{\Psi }}_{xN}+h{\left({\overline{u_t}}_N\right)}^{\tau }{P}_N^2{\mathsf{\Psi }}_{xN}\hfill \\ & =& q_t{\dot{C}}_t{\left(e_N\right)}^{\tau }{P}_N^2{\mathsf{\Psi }}_{xN}.\hfill \end{array}$$

(18)

Note that the wavelet series expansion of a function is unique. The following can be obtained:

$$\begin{array}{cc}& {\displaystyle \frac{\mathrm{d}{\left({\overline{Y_t}}_N\right)}^{\tau }}{\mathrm{d}t}}{P}_N^2-a\left({\left({\overline{Y_t}}_N\right)}^{\tau }-g_{1t}{\left(e_N\right)}^{\tau }-g_{2t}{\left(e_N\right)}^{\tau }{P}_N\right)+b\left({\left({\overline{Y_t}}_N\right)}^{\tau }{P}_N-g_{1t}{\left(e_N\right)}^{\tau }{P}_N\right)\hfill \\ & +c{\left({\overline{Y_t}}_N\right)}^{\tau }{P}_N^2+h{\left({\overline{u_t}}_N\right)}^{\tau }{P}_N^2=q_t{\dot{C}}_t{\left(e_N\right)}^{\tau }{P}_N^2.\hfill \end{array}$$

Transposing both sides of the above equation at the same time, it follows that

$$\begin{array}{cc}& {\left(P_N^2\right)}^{\tau }{\displaystyle \frac{\mathrm{d}{\overline{Y_t}}_N}{\mathrm{d}t}}-a\left({\overline{Y_t}}_N-g_{1t}{e}_N-{\left(P_N\right)}^{\tau }{g}_{2t}{e}_N\right)+b\left({\left(P_N\right)}^{\tau }{\overline{Y_t}}_N-{\left(P_N\right)}^{\tau }{g}_{1t}{e}_N\right)\hfill \\ & +c{\left(P_N^2\right)}^{\tau }{\overline{Y_t}}_N+h{\left(P_N^2\right)}^{\tau }{\overline{u_t}}_N={\left(P_N^2\right)}^{\tau }{q}_t{\dot{C}}_t{e}_N.\hfill \end{array}$$

Multiply the both sides of the above equation by ${\left(P_N^{-2}\right)}^{\tau }$, and it reduces to

$$\begin{array}{cc}& {\displaystyle \frac{\mathrm{d}{\overline{Y_t}}_N}{\mathrm{d}t}}-a{\left(P_N^{-2}\right)}^{\tau }\left({\overline{Y_t}}_N-g_{1t}{e}_N\right)-a{\left(P_N^{-1}\right)}^{\tau }{g}_{2t}{e}_N+b{\left(P_N^{-1}\right)}^{\tau }\left({\overline{Y_t}}_N-g_{1t}{e}_N\right)\hfill \\ & +c{\overline{Y_t}}_N+h{\overline{u_t}}_N=q_t{\dot{C}}_t{e}_N.\hfill \end{array}$$

We get

$$\begin{array}{ccc}\hfill {\displaystyle \frac{\mathrm{d}{\overline{Y_t}}_N}{\mathrm{d}t}}& =& \left[a{\left(P_N^{-2}\right)}^{\tau }-b{\left(P_N^{-1}\right)}^{\tau }-c{I}_N\right]{\overline{Y_t}}_N-h{\overline{u_t}}_N+\left[-a{\left(P_N^{-2}\right)}^{\tau }{g}_{1t}+a{\left(P_N^{-1}\right)}^{\tau }{g}_{2t}\right.\hfill \\ & & +\left.b{\left(P_N^{-1}\right)}^{\tau }{g}_{1t}\right]e_N+q_t{\dot{C}}_t{e}_N.\hfill \end{array}$$

(19)

Set

$$\begin{array}{c}\hfill \left\{\begin{array}{ccc}{A}_N\hfill & =\hfill & a{\left(P_N^{-2}\right)}^{\tau }-b{\left(P_N^{-1}\right)}^{\tau }-c{I}_N,\hfill \\ B_{tN}\hfill & =\hfill & \left[-a{\left(P_N^{-2}\right)}^{\tau }{g}_{1t}+a{\left(P_N^{-1}\right)}^{\tau }{g}_{2t}+b{\left(P_N^{-1}\right)}^{\tau }{g}_{1t}\right]e_N,\hfill \\ H_N\hfill & =\hfill & -h{I}_N,\hfill \\ Q_{tN}\hfill & =\hfill & q_t{e}_N.\hfill \end{array}\right.\end{array}$$

(20)

Then, Equation (19) can be written as

$$\mathrm{d}{\overline{Y_t}}_N=\left[A_N{\overline{Y_t}}_N+B_{tN}+H_N{\overline{u_t}}_N\right]\mathrm{d}t+Q_{tN}\mathrm{d}{C}_t.$$

(21)

Note that Equation (21) is a lumped parameter UDE. In other words, parabolic uncertain distributed parameter system (4) in problem (3) has been transformed into an uncertain LPS.

We now prepare to consider the index function. It follows from the transformation Equation (16) that the objective function Equation (7) is transformed to

$${\overline{J}}_N(0,{\overline{y}}_{0N})\equiv \underset{{\overline{u}}_N\in \overline{\mathcal{U}}}{min}E\left[{\int }_0^{T}f({\left({\overline{Y_t}}_N\right)}^{\tau }{\mathsf{\Psi }}_{xN},{\left({\overline{u_t}}_N\right)}^{\tau }{\mathsf{\Psi }}_{xN})\mathrm{d}t+G\left({\overline{Y}}_{T,1}\right)\right].$$

(22)

By virtue of property (9), functions in problem (3) can be approximated by the sum of finite terms of wavelet series. Combining (21) with (22), we obtain the lumped parameter UOCP after approximation with the N-dimensional wavelet series

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{\displaystyle {\overline{J}}_N(0,{\overline{y}}_{0N})\equiv \underset{{\overline{u}}_N\in \overline{\mathcal{U}}}{min}E\left[f({\left({\overline{Y_t}}_N\right)}^{\tau }{\mathsf{\Psi }}_{xN},{\left({\overline{u_t}}_N\right)}^{\tau }{\mathsf{\Psi }}_{xN})\mathrm{d}t+G\left({\overline{Y}}_{T,1}\right)\right]}\hfill \\ \mathrm{subject}\mathrm{to}\hfill \\ {\displaystyle \mathrm{d}{\overline{Y_t}}_N=\left[A_N{\overline{Y_t}}_N+B_{tN}+H_N{\overline{u_t}}_N\right]\mathrm{d}t+Q_{tN}\mathrm{d}{C}_t,}\hfill \\ {\displaystyle {\overline{Y_0}}_N={\overline{y}}_{0N},}\hfill \end{array}\right.\end{array}$$

(23)

where ${\overline{Y_0}}_N$ represents the initial state of ${\overline{Y_t}}_N$ at time 0 with N-dimensional Haar basis, the coefficients matrix defined as Equation (20).

5. Inverse Uncertainty Distribution of Solution

In this section, we will discuss the solution of the system equation in problem (23). When the uncertain differential equation is one-dimensional, Theorem 3 shows the analytical solution. The following lemma shows the analytical solution when the equation is N-dimensional. After that, we obtain the inverse distribution of the solution of the system Equation (21).

Theorem 3

([12]). Let $u_{1t},$$u_{2t},$$v_{1t},$$v_{2t}$ be integrable uncertain processes. Then, the linear UDE

$$\mathrm{d}{X}_t=({\mu }_{1t}{X}_t+u_{2t})\mathrm{d}t+({\nu }_{1t}{X}_t+{\nu }_{2t})\mathrm{d}{C}_t$$

has a solution

$$X_t=U_t\left(X_0+{\int }_0^t{\mu }_{2s}{U}_s^{-1}\mathrm{d}s+{\int }_0^t{\nu }_{2s}{U}_s^{-1}\mathrm{d}{C}_s\right),$$

where

$$U_t=exp\left({\int }_0^t{\mu }_{1s}\mathrm{d}s+{\int }_0^t{\nu }_{1s}\mathrm{d}{C}_s\right).$$

Lemma 1.

Let $C_t$ be a Liu process. Suppose that $A_N$ is a matrix in ${\mathcal{R}}^{N\times N}$, $B_{tN},Q_{tN}$ are N-dimensional vector valued functions, and each component is continuous with respect to t. Then, the N-dimensional linear uncertain differential equation

$$\mathrm{d}{\overline{Y_t}}_N=\left[A_N{\overline{Y_t}}_N+B_{tN}\right]\mathrm{d}t+Q_{tN}\mathrm{d}{C}_t$$

(24)

has a solution

$${\overline{Y_t}}_N=exp\left(A_{N}t\right)\left({\overline{Y}}_{0N}+{\int }_0^{t}exp(-A_{N}s)B_{sN}\mathrm{d}s+{\int }_0^{t}exp(-A_{N}s)Q_{sN}\mathrm{d}{C}_s\right).$$

Proof. 

Note

$$\begin{array}{c}\mathrm{d}{U}_{tN}=A_N{U}_{tN}\mathrm{d}t,\hfill \\ \mathrm{d}{V}_{tN}=U_{tN}^{-1}{B}_{tN}\mathrm{d}t+U_{tN}^{-1}{Q}_{tN}\mathrm{d}{C}_t,\hfill \end{array}$$

where $U_{tN}$ is an N-dimensional invertible matrix function. Each component of $U_{tN}$ is a continuous function respect to t. Furthermore, for $t\in [0,1]$. $V_{tN}$ is an N-dimensional uncertain process.

Then, we have ${\overline{Y}}_t=U_{tN}{V}_{tN}$ because

$$\begin{array}{cc}\mathrm{d}{\overline{Y}}_{tN}\hfill & =\mathrm{d}{U}_{tN}{V}_{tN}+U_{tN}\mathrm{d}{V}_t\hfill \\ & =A_N{U}_{tN}{V}_{tN}\mathrm{d}t+B_{tN}\mathrm{d}t+Q_{tN}\mathrm{d}{C}_t\hfill \\ & =A_N{\overline{Y}}_{tN}\mathrm{d}t+B_{tN}\mathrm{d}t+Q_{tN}\mathrm{d}{C}_t.\hfill \end{array}$$

It is been remarkable watching $U_{tN}=exp\left(A_{N}t\right)$, and $V_t={\overline{Y}}_{0N}+{\int }_0^{t}exp(-A_{N}s)B_{sN}\mathrm{d}s$ $+exp(-A_{N}s)$$Q_{sN}$$\mathrm{d}{C}_s$. We obtain the solution of (24) as

$${\overline{Y}}_{tN}=exp\left(A_{N}t\right)\left({\overline{Y}}_{0N}+{\int }_0^{t}exp(-A_{N}s)B_{sN}\mathrm{d}s+{\int }_0^{t}exp(-A_{N}s)Q_{sN}\mathrm{d}{C}_s\right).$$

The proof is completed. □

Lemma 2.

Let α be a number with $0<\alpha <1$. The coefficient matrices $A_N$, $B_{tN}$ and $Q_{tN}$ are defined as Equation (20). The inverse uncertainty distribution of solution $Y_{tN}^{\alpha }$ of the system equation in problem (23) is

$$\begin{array}{cc}{\overline{Y}}_{tN}^{\alpha }\hfill & =exp\left(A_{N}t\right)\left({\overline{Y}}_{0N}+{\int }_0^{t}exp(-A_{N}s)(B_{sN}+H_N{\overline{u}}_s)\mathrm{d}s\right.\hfill \\ & +\left.{\int }_0^{t}exp(-A_{N}s)\left|q_t\right|e_N{\mathsf{\Phi }}^{-1}\left(\alpha \right)\mathrm{d}s\right),\hfill \end{array}$$

where ${\mathsf{\Phi }}^{-1}\left(\alpha \right)=\frac{\sqrt{3}}{\pi }ln\frac{\alpha }{1-\alpha }$, $e_N={(1,0,\dots ,0)}^{\tau }\in {\mathcal{R}}^N$, ${\overline{Y}}_{tN}^{\alpha }\in {\mathcal{R}}^N$.

Proof. 

Set solution ${\overline{Y}}_{tN}={({\overline{Y}}_{tN,1},{\overline{Y}}_{tN,2},\dots ,{\overline{Y}}_{tN,N})}^{\tau }$, where N is the dimension of the vector. Note $A_N={(A_{N,1},A_{N,2},\dots ,A_{N,i},\dots ,A_{N,N})}^{\tau }$, and $A_{N,i}=(A_{N,i1},A_{N,i2},\dots ,$$A_{N,ij}$, …, $A_{N,iN})$, $i=1,2,\dots ,N$, $j=1,2,\dots ,N$, $B_{tN}={(B_{tN,1},B_{tN,2},\dots ,B_{tN,N})}^{\tau }$, $H_N={(H_{N,1},H_{N,2},\dots ,H_{N,N})}^{\tau }$. Then, the multi-dimensional uncertain differential equation may be written as

$$\begin{array}{cc}& \mathrm{d}{\overline{Y}}_{tN,1}=\left[A_{N,11}{\overline{Y}}_{tN,1}+\left({\displaystyle \sum _{j=2}^N}{A}_{N,1j}{\overline{Y}}_{tN,j}+B_{tN,1}+H_{N,1}{\overline{u}}_t\right)\right]\mathrm{d}t+q_t\mathrm{d}{C}_t,\hfill \\ & \mathrm{d}{\overline{Y}}_{tN,i}=\left[A_{N,i1}{\overline{Y}}_{tN,i}+\left({\displaystyle \sum _{j=1,j\ne i}^N}{A}_{N,ij}{\overline{Y}}_{tN,j}+B_{tN,i}+H_{N,i}{\overline{u}}_t\right)\right]\mathrm{d}t,i=2,3,\dots ,N.\hfill \end{array}$$

For the first dimension, ${\overline{Y}}_{tN,1}$ solves a one-dimensional UODE. By virtue of Theorem 2, the first dimension inverse uncertainty distribution of solution ${\overline{Y}}_{tN,1}^{\alpha }$ satisfies

$$\mathrm{d}{\overline{Y}}_{tN,1}^{\alpha }=\left[A_{N,11}{\overline{Y}}_{tN,1}^{\alpha }+\sum _{j=2}^N{A}_{N,1j}{\overline{Y}}_{tN,j}+B_{tN,1}+H_{N,1}{\overline{u}}_t+\left|q_t\right|{\mathsf{\Phi }}^{-1}\left(\alpha \right)\right]\mathrm{d}t.$$

When $i=2,3,\dots ,N$, ${\overline{Y}}_{tN,i}$ is the solution of the determined differential equation corresponding to ${\overline{Y}}_{tN,1}^{\alpha }$. Hence, the inverse uncertainty distribution of solution ${\overline{Y}}_t^{\alpha }$ satisfies

$$\begin{array}{cc}& \mathrm{d}{\overline{Y}}_{tN,1}^{\alpha }=\left[A_{N,11}{\overline{Y}}_{tN,1}^{\alpha }+{\displaystyle \sum _{j=2}^N}{A}_{N,1j}{\overline{Y}}_{tN,j}+B_{tN,1}+H_{N,1}{\overline{u}}_t+\left|q_t\right|{\mathsf{\Phi }}^{-1}\left(\alpha \right)\right]\mathrm{d}t,\hfill \\ & \mathrm{d}{\overline{Y}}_{tN,i}=\left[A_{N,i1}{\overline{Y}}_{tN,i}+\left({\displaystyle \sum _{j=1,j\ne i}^N}{A}_{N,ij}{\overline{Y}}_{tN,j}+B_{tN,i}+H_{N,i}{\overline{u}}_t\right)\right]\mathrm{d}t,i=2,3,\dots ,N.\hfill \end{array}$$

We find that ${\overline{Y}}_{tN}^{\alpha }$ satisfies

$$\begin{array}{c}\hfill \mathrm{d}{\overline{Y}}_{tN}^{\alpha }=\left[A_N{\overline{Y}}_{sN}^{\alpha }+B_{sN}\mathrm{d}t+H_N{\overline{u}}_t+\left|q_t\right|{\mathsf{\Phi }}^{-1}\left(\alpha \right)e_N\right]\mathrm{d}t.\end{array}$$

(25)

Hence, we have

$$\begin{array}{cc}{\overline{Y}}_{tN}^{\alpha }\hfill & =exp\left(A_{N}t\right)\left({\overline{Y}}_{0N}+{\int }_0^{t}exp(-A_{N}s)\left(B_{sN}+H_N{\overline{u}}_s+\left|q_s\right|e_N{\mathsf{\Phi }}^{-1}\left(\alpha \right)\right)\mathrm{d}s\right.\hfill \\ & +\left.{\int }_0^{t}exp(-A_{N}s)\mathrm{d}s\right).\hfill \end{array}$$

□

6. Convergence Analysis

The conversion between problems (3) and (23) is based on the wavelet series expansions of $Y_{t,x}$ and $u_{t,x}$. We demonstrate that, as N tends to infinity, ${\overline{J}}_N(0,{\overline{y}}_{0N})$ converges to $J(0,y_{0,x})$.

Lemma 3

([28]). The Haar series expansion $S_N\left(F\right)$ of $F\left(t\right)\in C[0,1]$ is convergent to $F\left(t\right)$ on $[0,1]$, and

$$\parallel F-S_N{\left(F\right)\parallel }_C\le 3{sup}_{\begin{array}{c}0\le t<t+h\le 1\\ 0<h\le {\displaystyle \frac{1}{N}}\end{array}}\left|F(t+h)-F\left(t\right)\right|,$$

where ${\parallel ·\parallel }_C$ represents the maximum norm of continuous function space $C[0,1]$.

Theorem 4.

Suppose that uncertain sequence ${\left({\overline{Y_t}}_N\right)}^{\tau }{\mathsf{\Psi }}_{xN}$ is an Haar wavelet approximation sequence of the uncertain variable $y_{t,x}$. Then, ${\left({\overline{Y_t}}_N\right)}^{\tau }{\mathsf{\Psi }}_{xN}$ is convergent in measure to the $Y_{t,x}$ as N tends to infinity.

Proof. 

According to Lemma 3, for any $\gamma \in \Gamma$,

$$|Y_{t,x}\left(\gamma \right)-{\left({\overline{Y_t}}_N\right)}^{\tau }{\mathsf{\Psi }}_{xN}\left(\gamma \right)|\le 3{sup}_{\begin{array}{c}0\le x<x+h\le 1\\ 0<h\le {\displaystyle \frac{1}{N}}\end{array}}|Y_{t,x+h}\left(\gamma \right)-Y_{t,x}\left(\gamma \right)|.$$

Hence, for $\epsilon >0$, we have

$$\mathcal{M}\left\{\right|Y_{t,x}-{\left({\overline{Y_t}}_N\right)}^{\tau }{\mathsf{\Psi }}_{xN}|<\epsilon ,fort\in (0,T]\}\ge \mathcal{M}\{\left|Y_{t,x+h}\left(\gamma \right)-Y_{t,x}\left(\gamma \right)\right|<\frac{\epsilon }{3},fort\in (0,T]\}.$$

(26)

Note that $Y_{t,x}\left(\gamma \right)$ is continuous with respect to $x\in [0,1]$ and $t\in [0,T]$. Furthermore, on $[0,1]\times [0,T]$, $Y_{t,x}\left(\gamma \right)$ is uniformly continuous concerning x and t. Hence

$$\mathcal{M}\{\left|Y_{t,x+h}\left(\gamma \right)-Y_{t,x}\left(\gamma \right)\right|<\frac{\epsilon }{3},fort\in (0,T]\}⟶1(ash⟶0).$$

We find that

$${lim}_{N\to \infty }\mathcal{M}\{\left|Y_{t,x+h}-{\left({\overline{Y_t}}_N\right)}^{\tau }{\mathsf{\Psi }}_{xN}\right|<\epsilon ,fort\in (0,T]\}=1.$$

□

Theorem 5.

The optimal value ${\overline{J}}_N(0,{\overline{y}}_{0N})$ of the approximate problem (23) converges to the optimal value $J(0,y_{0,x})$ of the problem (3) as N tends to infinity.

Proof. 

Suppose $u_{t,x}^{*}$ is the optimal control of problem (3), and ${\overline{u}}_{tN}^{*}$ is the optimal control of the approximate problem (23) by Haar wavelet transformation.

The corresponding optimal state of problem (3) and (23) are $Y_{t,x}^{*}$ and ${\overline{Y_{tN}}}^{*}$, respectively. That is

$$\begin{array}{cc}& J(0,y_{0,x})=E\left[{\int }_0^1{\int }_0^{T}f(Y_{t,x}^{*},u_{t,x}^{*})\mathrm{d}t\mathrm{d}x+G(Y_{T,1}^{*})\right],\hfill \\ & {\overline{J}}_N(0,{\overline{y}}_{0N})=E\left[{\int }_0^1{\int }_0^{T}f({({\overline{Y}}_{tN}^{*})}^{\tau }{\mathsf{\Psi }}_{xN},{\left({\overline{u}}_{tN}^{*}\right)}^{\tau }{\mathsf{\Psi }}_{xN})\mathrm{d}t\mathrm{d}x+G({\overline{Y}}_{T,1}^{*})\right].\hfill \end{array}$$

Since $f(Y_{t,x},u_{t,x})$ is a strictly monotonic continuous function with respect to $Y_{t,x}$, by Theorem 2, we have

$$\begin{array}{c}\hfill J(0,y_{0,x})={\int }_0^1\left[\left[{\int }_0^1{\int }_0^{T}f(Y_{t,x}^{*\alpha },u_{t,x}^{*\alpha })\mathrm{d}t\mathrm{d}x\right]+G(Y_{T,1}^{*\alpha })\right]\mathrm{d}\alpha ,\end{array}$$

(27)

and

$$\begin{array}{c}\hfill {\overline{J}}_N(0,{\overline{y}}_{0N})={\int }_0^1\left[\left[{\int }_0^1{\int }_0^{T}f({({\overline{Y}}_{tN}^{*\alpha })}^{\tau }{\mathsf{\Psi }}_{xN},{({\overline{u}}_{tN}^{*\alpha })}^{\tau }{\mathsf{\Psi }}_{xN})\mathrm{d}t\mathrm{d}x\right]+G({\overline{Y}}_{T,1}^{*\alpha })\right]\mathrm{d}\alpha .\end{array}$$

(28)

We have known that ${({\overline{Y_T}}_N^{*\alpha })}^{\tau }{e}_N=Y_T^{*\alpha }$, ${\left({\overline{Y}}_{tN}^{\alpha }\right)}^{\tau }{\mathsf{\Psi }}_{xN}$ and ${\left({\overline{u}}_{tN}^{*\alpha }\right)}^{\tau }{\mathsf{\Psi }}_{xN}$ are the wavelet approximation of $Y_{t,x}^{\alpha }$ and $u_{t,x}^{*\alpha }$, respectively. According to Lemma 3, we have ${\left({\overline{Y}}_{tN}^{\alpha }\right)}^{\tau }{\mathsf{\Psi }}_{xN}\to Y_{t,x}^{\alpha }$ and ${\left({\overline{u}}_{tN}^{*\alpha }\right)}^{\tau }{\mathsf{\Psi }}_{xN}\to u_{t,x}^{*\alpha }$ as $N\to \infty$. Then

$$\underset{N\to \infty }{lim}f({({\overline{Y}}_{tN}^{*\alpha })}^{\tau }{\mathsf{\Psi }}_{xN},{({\overline{u}}_{tN}^{*\alpha })}^{\tau }{\mathsf{\Psi }}_{xN})=f(Y_{t,x}^{*\alpha },u_{t,x}^{*\alpha }).$$

By virtue of the Lebesgue-dominated convergence theorem,

$$\begin{array}{cc}& \underset{N\to \infty }{lim}{\int }_0^1\left[\left[{\int }_0^1{\int }_0^{T}f({({\overline{Y}}_{tN}^{*\alpha })}^{\tau }{\mathsf{\Psi }}_{xN},{({\overline{u}}_{tN}^{*\alpha })}^{\tau }{\mathsf{\Psi }}_{xN})\mathrm{d}t\mathrm{d}x\right]+G\left({\overline{Y}}_{T,1}^{*\alpha }\right)\right]\mathrm{d}\alpha \hfill \\ =\hfill & {\int }_0^1\left[\left[{\int }_0^1{\int }_0^{T}f(Y_{t,x}^{*\alpha },u_{t,x}^{*\alpha })\mathrm{d}t\mathrm{d}x\right]+G\left(Y_{T,1}^{*\alpha }\right)\right]\mathrm{d}\alpha .\hfill \end{array}$$

We find that

$$\underset{N\to \infty }{lim}{\overline{J}}_N(0,{\overline{y}}_{0N})=J(0,y_{0,x}).$$

The proof is completed.

Theorem 5 shows that the solution of problem (23) may be approximated to the solution of problem (3). □

7. Application to Metal-Temperature-Control Problem

When there is an unknown heat source around an object, the process of metal temperature transformation may be described with a stochastic heat equation which is driven by the Wiener process. However, Yang and Yao [23] pointed out that a stochastic heat equation describes a process with infinite heat-conduction velocity or unbounded second-order partial derivatives to space. In real life, all objects have bounded heat-conduction velocities and bounded second-order partial derivatives. It is unreasonable to describe a heat-conduction process by a stochastic heat equation.

Therefore, based on the characteristics of the uncertain process, it is more reasonable to use an uncertain heat equation to describe the temperature change process of an object when there is an unknown heat source around.

Suppose there is a metal of length L, and the temperature of the metal is $Y_{t,x}$ as a function of position, x, and time, t. An uncertain heat source, ${\overline{q}}_t{\dot{C}}_t$, affects the metal’s temperature. We add an induction heater, $u_{t,x}$, to keep the metal temperature in equilibrium. We know that the heat passing through metal per unit of time is proportional to the rate of change of temperature to time and inversely proportional to the direction of temperature increase. Then, the heat passing through a metal per unit of time can be expressed as

$$-K\frac{\partial Y_{t,x}}{\partial x},$$

where K is the thermal conductivity. Then, the heat change of region $[x-\Delta x,x+\Delta x]$ during $[t-\Delta t,t+\Delta t]$ can be described as

$$K{\int }_{t-\Delta t}^{t+\Delta t}{\int }_{x-\Delta x}^{x+\Delta x}\frac{{\partial }^2{Y}_{s,z}}{\partial z^2}\mathrm{d}z\mathrm{d}s.$$

The energy from the induction heater and an external uncertain heat source passing through the region $[x-\Delta x,x+\Delta x]$ in time $[t-\Delta t,t+\Delta t]$ is

$${\int }_{t-\Delta t}^{t+\Delta t}{\int }_{x-\Delta x}^{x+\Delta x}(u_{s,z}+{\overline{q}}_s{\dot{C}}_s)\mathrm{d}z\mathrm{d}s.$$

Denote energy as $\tilde{Q}$. At this time, the change of energy, ${\displaystyle \frac{\mathrm{d}\tilde{Q}}{\mathrm{d}t}}$, is proportional to the change in temperature, ${\displaystyle \frac{\mathrm{d}{Y}_{t,x}}{\mathrm{d}t}}$, with respect to time, t, which can be expressed as

$$\frac{\mathrm{d}\tilde{Q}}{\mathrm{d}t}=c_{\rho }\rho \frac{\mathrm{d}{Y}_{t,x}}{\mathrm{d}t},$$

where $c_{\rho }$ is the specific heat capacity, and $\rho$ is the mass density. Then, the exchange of heat in region $[x-\Delta x,x+\Delta x]$ at $[t-\Delta t,t+\Delta t]$ is

$$c_{\rho }\rho {\int }_{x-\Delta x}^{x+\Delta x}\left(Y_{t+\Delta t,z}-Y_{t-\Delta t,z}\right)\mathrm{d}z=c_{\rho }\rho {\int }_{t-\Delta t}^{t+\Delta t}{\int }_{x-\Delta x}^{x+\Delta x}\frac{\partial Y_{s,z}}{\partial s}\mathrm{d}z\mathrm{d}s.$$

According to the law of conservation of energy, we obtain

$$\begin{array}{cc}& K{\int }_{t-\Delta t}^{t+\Delta t}{\int }_{x-\Delta x}^{x+\Delta x}\frac{{\partial }^2{Y}_{s,z}}{\partial z^2}\mathrm{d}z\mathrm{d}s+{\int }_{t-\Delta t}^{t+\Delta t}{\int }_{x-\Delta x}^{x+\Delta x}(u_{s,z}+{\overline{q}}_s{\dot{C}}_s)\mathrm{d}z\mathrm{d}s\hfill \\ =\hfill & c_{\rho }\rho {\int }_{t-\Delta t}^{t+\Delta t}{\int }_{x-\Delta x}^{x+\Delta x}\frac{\partial Y_{s,z}}{\partial s}\mathrm{d}s\mathrm{d}z.\hfill \end{array}$$

Then, the uncertain heat-conduction equation can be expressed as

$$\frac{\partial Y_{t,x}}{\partial t}-\frac{K}{c_{\rho }\rho }\frac{{\partial }^2{Y}_{s,x}}{\partial x^2}=\frac{1}{c_{\rho }\rho }(u_{t,x}+{\overline{q}}_t{\dot{C}}_t).$$

Set $a^2=\frac{K}{c_{\rho }\rho }$, $h=-\frac{1}{c_{\rho }\rho }$, $q_t=\frac{1}{c_{\rho }\rho }{\overline{q}}_t$. The system equation is

$$\frac{\partial Y_{t,x}}{\partial t}-a^2\frac{{\partial }^2{Y}_{s,x}}{\partial x^2}=-h{u}_{t,x}+q_t{\dot{C}}_t.$$

Consider an optimal control problem where the system is an uncertain heat equation. Let the initial temperature be $Y_{0,x}=y_{0,x}$. As we know, absolute zero is −273.15 °C. The measurement method for temperature $Y_{t,x}$ in the system is the Celsius scale plus 273.15 °C. Therefore, temperature $Y_{t,x}$ is greater than 0 °C. The boundary conditions are $Y_{t,0}=g_{1t}$ and ${\displaystyle \frac{\partial Y_{t,x}}{\partial x}}{|}_{x=0}=g_{2t}$. Set $g_{1t}=0$, $g_{2t}=0$, and the control $u_{t,x}\subset R$; the length of metal is $L=1$, $T=1$. In order to minimize the change of the temperature from metal and induction heater, we use

$$J(0,y_{0,x})\equiv \underset{u_{t,x}\in U}{min}E\left[{\int }_0^1{\int }_0^1{Y}_{t,x}^2+u_{t,x}^2\mathrm{d}t\mathrm{d}x\right]$$

as the objective function to minimize the change of temperature in metal and induction heater. Since temperature is greater than 0 °C, the objective function monotonically increases concerning temperature.

The control problem of metal temperature may be described as

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{\displaystyle J(0,y_{0,x})\equiv \underset{u_{t,x}\in U}{min}E\left[{\int }_0^1{\int }_0^1\left(Y_{t,x}^2+u_{t,x}^2\right)\mathrm{d}t\mathrm{d}x\right]}\hfill \\ \mathrm{subject}\mathrm{to}\hfill \\ {\displaystyle {\displaystyle \frac{\partial Y_{t,x}}{\partial t}}-a^2{\displaystyle \frac{{\partial }^2{Y}_{t,x}}{\partial x^2}}+h{u}_{t,x}=q_t{\dot{C}}_t,}\hfill \\ {\displaystyle Y_{0,x}=y_{0,x},}\hfill \\ {\displaystyle Y_{t,0}=g_{1t},}\hfill \\ {\displaystyle {\displaystyle \frac{\partial Y_{t,x}}{\partial x}}\left|{}_{x=0}=g_{2t}.\right.}\hfill \end{array}\right.\end{array}$$

(29)

Although problem (29) describes the process of temperature transformation and the conditions that need to be optimized well, the existing methods cannot directly obtain their optimal solution. It can be known from Theorem 5 that the optimal solution of problem (29) may be approximated by the optimal solution of the following problem

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{\displaystyle {\overline{J}}_N(0,{\overline{y}}_{0N})\equiv \underset{{\overline{u_t}}_N\in U^N}{min}E\left[{\int }_0^1\left({\left({\overline{Y_t}}_N\right)}^{\tau }{\overline{Y_t}}_N+{\left({\overline{u_t}}_N\right)}^{\tau }{\overline{u_t}}_N\right)\mathrm{d}t\right]}\hfill \\ \mathrm{subject}\mathrm{to}\hfill \\ {\displaystyle \mathrm{d}{\overline{Y_t}}_N=\left[A_N{\overline{Y_t}}_N+H_N{\overline{u_t}}_N\right]\mathrm{d}t+Q_{tN}\mathrm{d}{C}_t,}\hfill \\ {\displaystyle {\overline{Y_0}}_N={\overline{y}}_{0N},}\hfill \end{array}\right.\end{array}$$

(30)

where $A_N=a^2{\left(P_N^{-2}\right)}^{\tau }$, $H=-h{I}_N$, $Q_N=q_t{e}_N$, and the initial condition $Y_{0,x}={({\overline{Y}}_{0N})}^{\tau }$${\mathsf{\Psi }}_{xN}$=${\left({\overline{y}}_{0N}\right)}^{\tau }{\mathsf{\Psi }}_{xN}$.

By the method of solving quadratic uncertain optimal control in [22], the equation of optimality for (30) is

$$-{\displaystyle \frac{\mathrm{d}{\overline{J}}_N(t,{\overline{Y}}_{tN})}{\mathrm{d}t}}=\underset{{\overline{u_t}}_N\in {\mathcal{R}}^N}{min}\left\{\left({\left({\overline{Y}}_{tN}\right)}^{\tau }{\overline{Y}}_{tN}+{\left({u_t}_N\right)}^{\tau }{u_t}_N\right)+{\left[A{\overline{Y}}_{tN}+{\overline{u_t}}_N\right]}^{\tau }{\nabla }_{{\overline{Y}}_{tN}}{\overline{J}}_N(t,{\overline{Y}}_{tN})\right\}.$$

The optimal control ${\overline{u}}_{tN}^{*}$ of (30) is

$$\begin{array}{c}\hfill {\overline{u}}_{tN}^{*}=-\frac{1}{2}{\overline{P}}_{tN}{\overline{Y}}_{tN},\end{array}$$

(31)

where ${\overline{P}}_{tN}$ satisfies the following Riccati equation

$$\left\{\begin{array}{c}\hfill {\displaystyle \frac{\mathrm{d}{\left({\overline{P}}_{tN}\right)}^{\tau }}{\mathrm{d}t}=-2I_N-a^2{P}_N^{-2}{\overline{P}}_{tN}-a^2{\left({\overline{P}}_{tN}\right)}^{\tau }{\left(P_N^{-2}\right)}^{\tau }+\frac{1}{2}{\left({\overline{P}}_{tN}\right)}^{\tau }{\left({\overline{P}}_{tN}\right)}^{\tau }}\\ {\displaystyle {\overline{P}}_{tN}=\mathbf{0},}\end{array}\right.$$

(32)

and the optimal value ${\overline{J}}_N^{*}(0,{\overline{y}}_{0N})$ of (30) is

$$\begin{array}{c}\hfill {\overline{J}}_N^{*}(0,{\overline{y}}_{0N})=\frac{1}{2}{\left({\overline{y}}_{0N}\right)}^{\tau }{\overline{P}}_{0N}{\overline{y}}_{0N}.\end{array}$$

(33)

Substituting Equation (31) to the system equation in problem (30), we have

$$\mathrm{d}{\overline{Y_t}}_N=\left(a^2{\left(P_N^{-2}\right)}^{\tau }+\frac{h}{2}{\overline{P}}_{tN}\right){\overline{Y_t}}_N\mathrm{d}t+q_t{e}_N\mathrm{d}{C}_t.$$

By Lemma 1, the solution ${\overline{Y_t}}_N$ of the above equation is

$${\overline{Y_t}}_N=exp\left(a^{2}t{\left(P_N^{-2}\right)}^{\tau }+\frac{ht}{2}{\overline{P}}_{tN}\right)\left({\overline{y}}_{0N}+{\int }_0^{t}exp\left(-a^{2}s{\left(P_N^{-2}\right)}^{\tau }-\frac{hs}{2}{\overline{P}}_{tN}\right)q_s{e}_N\mathrm{d}{C}_s\right).$$

Substituting the above equation to Equation (31), we have

$$\begin{array}{ccc}\hfill & & {\overline{u}}_{tN}^{*}=-\frac{1}{2}{\overline{P}}_{tN}exp\left(a^{2}t{\left(P_N^{-2}\right)}^{\tau }+\frac{ht}{2}{\overline{P}}_{tN}\right){\overline{y}}_{0N}-\frac{1}{2}{\overline{P}}_{tN}exp\left(a^{2}t{\left(P_N^{-2}\right)}^{\tau }+\frac{ht}{2}{\overline{P}}_{tN}\right)\hfill \\ & & \cdot {\int }_0^{t}exp\left(-a^{2}s{\left(P_N^{-2}\right)}^{\tau }-\frac{hs}{2}{\overline{P}}_{tN}\right)q_s{e}_N\mathrm{d}{C}_s.\hfill \end{array}$$

(34)

By the inverse wavelet transformation of ${\overline{u_t}}_N^{*}$, the approximated optimal control of problem (30) is

$$\begin{array}{ccc}\hfill u_{t,x}^{*}& =& -\frac{1}{2}{\left({\overline{P}}_{tN}\right)}^{\tau }exp\left(a^{2}t{P}_N^{-2}+\frac{ht}{2}{\left({\overline{P}}_{tN}\right)}^{\tau }\right)\left({\left({\overline{y}}_{0N}\right)}^{\tau }\right.\hfill \\ & & +\left.{\int }_0^{t}exp\left(-a^{2}s{P}_N^{-2}-\frac{hs}{2}{\left({\overline{P}}_{tN}\right)}^{\tau }\right){\left(q_s\left(e_N\right)\right)}^{\tau }\mathrm{d}{C}_s\right){\mathsf{\Psi }}_{xN}.\hfill \end{array}$$

(35)

Based on Lemma 2, the inverse distribution ${\overline{Y_t}}_N^{\alpha }$ of solution ${\overline{Y_t}}_N$ is

$$\begin{array}{cc}{\overline{Y}}_{tN}^{\alpha }=\hfill & exp\left(a^{2}t{\left(P_N^{-2}\right)}^{\tau }+\frac{ht}{2}{\overline{P}}_{tN}\right)\left({\overline{y}}_{0N}\right.\hfill \\ & +\left.{\int }_0^{t}exp\left(-a^{2}s{\left(P_N^{-2}\right)}^{\tau }-\frac{hs}{2}{\overline{P}}_{tN}\right)\frac{\sqrt{3}\left|q_s\right|}{\pi }ln\frac{\alpha }{1-\alpha }{e}_N\mathrm{d}s\right).\hfill \end{array}$$

Hence, the inverse distribution of ${\overline{u_t}}_N^{*}$ is

$$\begin{array}{ccc}\hfill {\overline{u_t}}_N^{\alpha *}& =& -\frac{1}{2}{\overline{P}}_{tN}exp\left(a^{2}t{\left(P_N^{-2}\right)}^{\tau }+\frac{ht}{2}{\overline{P}}_{tN}\right){\overline{y}}_{0N}\hfill \\ & & -\frac{1}{2}{\overline{P}}_{tN}exp\left(a^{2}t{\left(P_N^{-2}\right)}^{\tau }+\frac{ht}{2}{\overline{P}}_{tN}\right){\int }_0^{t}exp\left(-a^{2}s{\left(P_N^{-2}\right)}^{\tau }-\frac{hs}{2}{\overline{P}}_{tN}\right)\hfill \\ & & \cdot \frac{\sqrt{3}\left|q_s\right|}{\pi }ln\frac{\alpha }{1-\alpha }{e}_N\mathrm{d}s\hfill \end{array}$$

(36)

and the inverse distribution of $u_{t,x}^{*}$ is

$$\begin{array}{ccc}\hfill u_{t,x}^{\alpha *}& =& -\frac{1}{2}{\left({\overline{P}}_{tN}\right)}^{\tau }exp\left(a^{2}t\left(P_N^{-2}\right)+\frac{ht}{2}{\left({\overline{P}}_{tN}\right)}^{\tau }\right){\left({\overline{y}}_{0N}\right)}^{\tau }{\mathsf{\Psi }}_{xN}\hfill \\ & & -\frac{1}{2}{\left({\overline{P}}_{tN}\right)}^{\tau }exp\left(a^{2}t\left(P_N^{-2}\right)+\frac{ht}{2}{\left({\overline{P}}_{tN}\right)}^{\tau }\right){\int }_0^{t}exp\left(-a^{2}s\left(P_N^{-2}\right)-\frac{hs}{2}{\left({\overline{P}}_{tN}\right)}^{\tau }\right)\hfill \\ & & \cdot \frac{\sqrt{3}\left|q_s\right|}{\pi }ln\frac{\alpha }{1-\alpha }{\left(e_N\right)}^{\tau }\mathrm{d}s{\mathsf{\Psi }}_{xN}.\hfill \end{array}$$

(37)

Set the coefficients $a=\frac{1}{100}$, $h=-1$, $q_t=t$, the initial condition $y_{0,x}=\frac{3}{2}{x}^2$.

For $N=8$, ${\mathsf{\Psi }}_{x8}=\left(1,\psi \left(x\right),\sqrt{2}\psi \left(2x\right),\sqrt{2}\psi (2x-1)\right.$, $2\psi \left(4x\right)$, $2\psi (4x-1)$, $2\psi (4x-2)$, ${\left.2\psi (4x-3)\right)}^{\tau }.$ Furthermore, the initial value

$$\begin{array}{ccc}{\overline{y}}_{08}\hfill & =\hfill & \left({\int }_0^1{y}_{0,x}\mathrm{d}x,{\int }_0^1\psi \left(x\right)y_{0,x}\mathrm{d}x,{\int }_0^1\sqrt{2}\psi \left(2x\right)y_{0,x}\mathrm{d}x,{\int }_0^1\sqrt{2}\psi (2x-1)y_{0,x}\mathrm{d}x,\right.\hfill \\ & & {\left.{\int }_0^{1}2\psi \left(4x\right)y_{0,x}\mathrm{d}x,{\int }_0^{1}2\psi (4x-1)y_{0,x}\mathrm{d}x,{\int }_0^{1}2\psi (4x-2)y_{0,x}\mathrm{d}x,{\int }_0^{1}2\psi (4x-3)y_{0,x}\mathrm{d}x\right)}^{\tau }\hfill \\ & =\hfill & {\left(\frac{1}{2},-\frac{3}{8},-\frac{3\sqrt{2}}{64},-\frac{9\sqrt{2}}{64},-\frac{3}{256},-\frac{9}{256},-\frac{15}{256},-\frac{21}{256}\right)}^{\tau }.\hfill \end{array}$$

According to the 4th order explicit Runge–Kutta method, we obtain ${\overline{P}}_{t8}$ by solving the Riccati Equation (32). The plots of elements in ${\overline{P}}_{t8}$ with respect to t are shown in Figure 1.

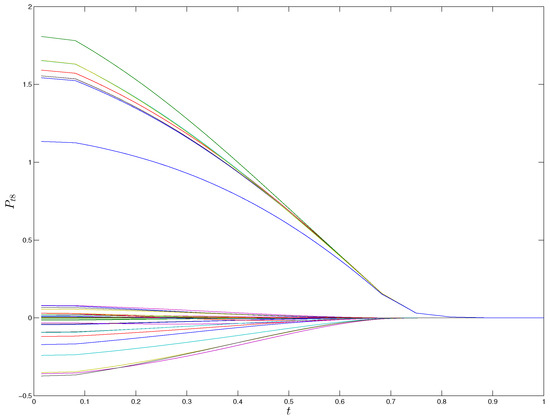
Figure 1. Elements in ${\overline{P}}_{t8}$ with respect to t.

Substituting ${\overline{P}}_{t8}$ into Equation (34), we have the optimal control of problem (30) by

$$\begin{array}{ccc}{\overline{u_t}}_8^{*}\hfill & =\hfill & -\frac{1}{2}{\overline{P}}_{t8}exp\left({10}^{-4}t{\left(P_8^{-2}\right)}^{\tau }+\frac{t}{2}{\overline{P}}_{t8}\right)\left({\overline{y_0}}_8+{\int }_0^{t}exp\left(-{10}^{-4}s{\left(P_8^{-2}\right)}^{\tau }\right.\right.\hfill \\ & & -\left.\left.\frac{s}{2}{\overline{P}}_{t8}\right)\mathrm{d}{C}_s\right).\hfill \end{array}$$

By Equation (35), the approximated optimal control of problem (29) is

$$\begin{array}{ccc}{u}_{t,x}^{*}\hfill & =\hfill & -\frac{1}{2}{\left({\overline{P}}_{t8}\right)}^{\tau }exp\left({10}^{-4}t{P}_8^{-2}-\frac{t}{2}{\left({\overline{P}}_{t8}\right)}^{\tau }\right)\left({\left({\overline{y_0}}_8\right)}^{\tau }+{\int }_0^{t}exp\left(-{10}^{-4}s{P}_8^{-2}\right.\right.\hfill \\ & & +\left.\left.\frac{s}{2}{\left({\overline{P}}_{t8}\right)}^{\tau }\right){\left(s\left(e_8\right)\right)}^{\tau }\mathrm{d}{C}_s\right){\mathsf{\Psi }}_{x8}.\hfill \end{array}$$

By Equation (36), the inverse distribution ${\overline{u_t}}_8^{\alpha *}$ of ${\overline{u_t}}_8^{*}$ is

$$\begin{array}{ccc}{\overline{u_t}}_8^{\alpha *}\hfill & =\hfill & -\frac{1}{2}{\overline{P}}_{t8}exp\left({10}^{-4}t{\left(P_8^{-2}\right)}^{\tau }-\frac{t}{2}{\overline{P}}_{t8}\right){\overline{y_0}}_8-\frac{1}{2}{\overline{P}}_{t8}exp\left({10}^{-4}t{\left(P_8^{-2}\right)}^{\tau }-\frac{t}{2}{\overline{P}}_{t8}\right)\hfill \\ & & \cdot {\int }_0^{t}exp\left(-{10}^{-4}s{\left(P_8^{-2}\right)}^{\tau }+\frac{s}{2}{\overline{P}}_{t8}\right)\frac{\sqrt{3}s}{\pi }ln\frac{\alpha }{1-\alpha }{e}_8\mathrm{d}s.\hfill \end{array}$$

According to Equation (37), the inverse distribution $u_{t,x}^{\alpha *}$ of $u_{t,x}^{*}$ is

$$\begin{array}{ccc}{u}_{t,x}^{\alpha *}\hfill & =\hfill & -\frac{1}{2}{\left({\overline{P}}_{t8}\right)}^{\tau }exp\left({10}^{-4}t\left(P_8^{-2}\right)-\frac{t}{2}{\left({\overline{P}}_{t8}\right)}^{\tau }\right){\left({\overline{y_0}}_8\right)}^{\tau }{\mathsf{\Psi }}_{x8}-\frac{1}{2}{\left({\overline{P}}_{t8}\right)}^{\tau }exp\left({10}^{-4}t\left(P_8^{-2}\right)\right.\hfill \\ & & \left.-\frac{t}{2}{\left({\overline{P}}_{t8}\right)}^{\tau }\right){\int }_0^{t}exp\left(-{10}^{-4}s\left(P_8^{-2}\right)+\frac{s}{2}{\left({\overline{P}}_{t8}\right)}^{\tau }\right)\frac{\sqrt{3}s}{\pi }ln\frac{\alpha }{1-\alpha }{\left(e_8\right)}^{\tau }\mathrm{d}s{\mathsf{\Psi }}_{x8}.\hfill \end{array}$$

When $\alpha =0.5$, elements of ${\overline{u}}_{t8}^{\alpha *}\left(i\right),i=1,2,\dots ,8$ with respect to t are shown in Figure 2 and Figure 3. It can be seen from the figures that ${\overline{u}}_{t8}^{\alpha *}\left(4\right)$ and ${\overline{u}}_{t8}^{\alpha *}\left(8\right)$ have the most significant influence on ${\overline{u}}_{t8}^{\alpha *}$. Furthermore, the control directions of these two dimensions are opposite. Figure 4 shows $u_{t,x}^{\alpha *}$ with respect of t and x. For different positions, x, $u_{t,x}^{\alpha *}$ exhibits a positive and negative staggered form. The wavelet transform influences this form. As the wavelet basis dimension increases, the surface becomes smoother.

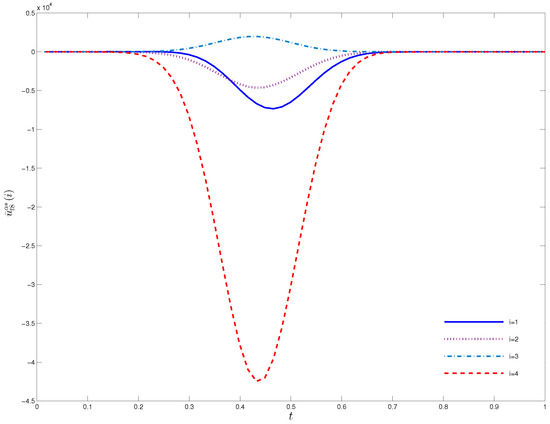
Figure 2. ${\overline{u}}_{t8}^{\alpha *}\left(i\right)$ with respect to t for $\alpha =0.5$, i = 1, 2, 3, 4.

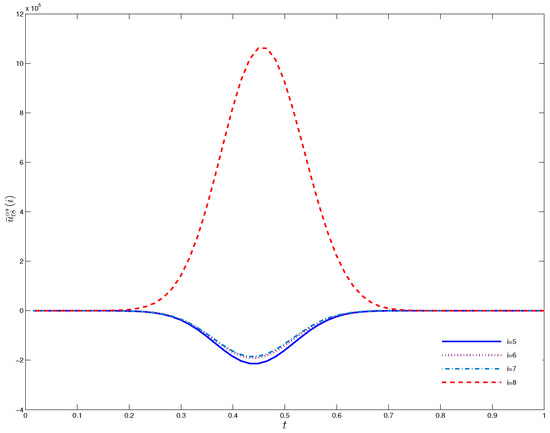
Figure 3. ${\overline{u}}_{t8}^{\alpha *}\left(i\right)$ with respect to t for $\alpha =0.5$, i = 5, 6, 7, 8.

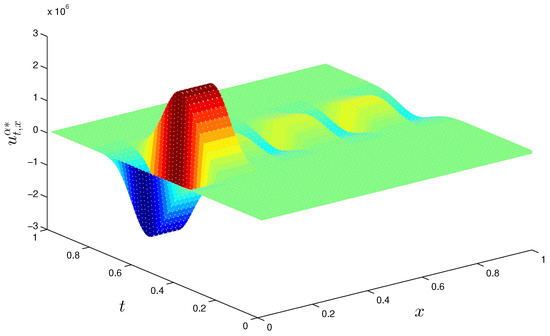
Figure 4. $u_{t,x}^{\alpha *}$ with respect to t and x for $\alpha =0.5$.

Substituting ${\overline{P}}_{08}$ to Equation (33), we obtain the optimal value of problem (30) is ${\overline{J}}_8^{*}=0.3336$. This suggests that the approximated optimal value of problem (29) for $N=8$ after wavelet transformation is $J=0.3336$. In an environment with uncertain heat source, when we use an induction heater to keep the metal temperature stable, the approximated sum of the square of the temperature change of the metal itself and the temperature raised by the induction heater over time [0, 1] is at least $0.3336$.

8. Conclusions

In this paper, a class of optimal control problem with parabolic uncertain system was proposed and investigated. With the help of Haar wavelet transformation, the proposed problem was approximated by an uncertain optimal control problem. Thus, the optimal control of the uncertain optimal control problem is regarded as an approximated solution of the proposed problem. However, the method cannot guarantee convergence when the approximated function in the model is discontinuous. The Haar wavelet basis is composed of piecewise, constantly valued functions, it is also well-defined at the junction of each dimension basis of the approximation function. In the following work, we will try smooth orthogonal basis with the property of algebraic integral transformation to obtain more refined results on the solution of the problem on the one hand; on the other hand, we will consider the case where the constant coefficients in the system are continuous functions so that the model can be applied more widely.