Abstract
The purpose of this study is to provide a mathematical construction based on the novel singular perturbed model of the second kind (NSPM-SK) using the standard form of the Lane–Emden. The singular Lane–Emden types of the models have abundant applications in astrophysics. The inclusive features of this model are provided using the perturbed, pantograph, singular point together and the shape factor based on the NSPM-SK. These models become more complicated by using these factors through the artificial neural networks (ANNs) together with the optimization procedures of the swarming particle swarm optimization (PSO) paradigms and the local sequential quadratic programming (SQP). An objective function is provided based on the differential form of the NSPM-SK and then optimization is performed through the hybridization of the PSOSQP. The exactness of the model is attained to solve three different variations of the mathematical NSPM-SK by using the overlapping of the obtained and true results. The stability, robustness, and convergence of the designed numerical approach are perceived by using different statistical performances of the ANNs together with the optimization of the PSOSQP for 30 independent executions.
Keywords:
singular; perturbed; pantograph; artificial neural networks; swarming approach; sequential quadratic programming MSC:
92F05; 85A04
1. Introduction
The use of perturbation factors makes differential models complex and challenging due to the boundary layer behavior. The variations of these systems are assumed to be rapid inside the thin layers or within the range of the system. Few of the schemes that have been used in this study are finite difference, which works to the performance of the exponential factor in the perturbed form of the differential system [1,2,3], the numeric special mesh scheme that is used to model the reaction–diffusion systems [4,5], the perturbed form of the convection–diffusion system of second order [6], and the diffusion reaction semi-linear model [7]. Therefore, it is necessary to design few appropriate techniques to provide the solutions of these singular perturbed systems [8,9,10,11,12,13,14]. These conventional methods have been used to show singular perturbation model solutions that cannot produce satisfying results when small values of the perturbed components are used. The differential pantograph models are very important for researchers due to the diversity of applications in the field of medicine, shipping controls, biology, population dynamics, chemistry, economics, engineering, physics, electrodynamics, infectious diseases, pharmaceutical kinetics, quantum mechanics, electronics, and physiology [15,16]. Ockendon et al. proposed the “pantograph” in the 7th decade of the 19th century by working on different experiments [17]. Based on the consequence of the pantograph types of models, some analytical and numerical approaches have been provided, such as multi-dimensional homotopy optimal method [18], Least-Squares-Epsilon-Ritz [19], Chebyshev spectral [20], Taylor operation [21], spectral tau [22], Genocchi operational matrix [23], and many more [24,25].
The singular based mathematical systems have huge significance and are considered tough to present the solutions by applying the analytical and numerical methods. The singular models occur in the modeling of the gas cloud, quantum mechanics, and astrophysics. Some of the deterministic approaches that have been applied to assess the singular systems are described in these investigations [26,27]. In astrophysics, there are various types of singular models that have been used such as ABC singular Lane–Emden model [28], shifted ultraspherical operational matrices of derivatives [29], fractional differential and integral operators with non-singular and non-local kernel schemes [30], Bernoulli polynomials with their differentiation matrix [31], a novel Chebyshev neural network approach [32], combining a pair of one-step hybrid block Nyström methods [33], a new Bernoulli wavelet operational matrix of derivative method [34], Haar wavelet approximate scheme [35], analytic solution of system of singular nonlinear differential equations with Neumann–Robin boundary conditions [36], Adomian decomposition method [37], and Hermite wavelets technique coupled with a numerical iteration technique such as the Newton Raphson approach [38]. The general form of the singular model based on Lane–Emden is provided as [39]:
where is the shape vector and the singular point arises at . The motive of these investigations is to construct a novel singular perturbed model of the second kind (NSPM-SK) using the traditional form of the Lane–Emden. The singular models become more complicated by using these factors through the artificial neural networks (ANNs) together with the optimization procedures of the swarming particle swarm optimization (PSO) paradigms and the local sequential quadratic programming (SQP). The solution of the singular types of the Lane–Emden models is not easy to present due to the singularity. These models become complex, stiffer, and more difficult with the pantograph and perturbed terms. Hence, a numerical stochastic ANNs-PSOSQP procedure is presented to solve such complicated natured novel linear/nonlinear models. The worthy stochastic measures are not only familiar to solve the integer order models, but also have been executed for the fractional kinds of systems. Some prominent recent applications of these solvers are nervous stomach [40], medical smoking [41], food chain supply [42,43], and thermal explosion model [44,45]. The novel features of the ANNs-PSOSQP for solving the differential NSPM-SK are presented as:
- The construction of a mathematical NSPM-SK is presented through the perturbed, pantograph, and singular terms.
- Soft computing schemes using the ANNs along with the hybridization of PSOSQP solver have been applied to present the numerical performances of the nonlinear NSPM-SK.
- The competence of the designed NSPM-SK as well as stochastic computing ANNs along with the hybridization of PSOSQP solver is perceived by using the comparison of the obtained and true solutions.
- Three different cases based on small values of the perturbation terms have been provided to check the capability of the proposed scheme.
- The performances of the scheme to solve the designed NSPM-SK are also observed by using the absolute error (AE) values, which have been proven in good measures.
- The convergence, stability, and reliability of the ANNs-PSOSQP for solving the differential NSPM-SK is observed via statistical procedures based semi-interquartile range (SIR), variance mean square error (MSE), and variance account for (VAF).
- Beside the precise performances of the designed NSPM-SK, smooth processes, ease of understanding, comprehensive applicability, and robustness are other esteemed benefits of the ANNs-PSOSQP solver.
The remaining sections of this paper are presented as follows. Section 2 provides the mathematical design of the NSPM-SK. Section 3 designates the stochastic procedure. Section 4 presents the implementations procedures of the scheme for solving the model. The concluding reports are provided in the final section.
2. Construction of the NSPM-SK
The current section performs the construction of NSPM-SK by using the perturbation term, delay differential form along with the traditional type of the Lane–Emden. Recently, some novel singular models that have been designed are pantograph/delay singular models, functional form of the differential model of the fourth kind, prediction singular models, fifth and sixth kind of singular models, fractional kind of differential delay, and pantograph differential singular models [46]. Keeping in view these applications, the current investigations based on the mathematical form of the NSPM-SK are presented. The mathematical form of the NSPM-SK is given as:
where shows a positive value of a constant. To solve the mathematical form of the NSPM-SK, and q are given as:
The efficient form of above Equation is given as:
The updated values are given as:
The achieved mathematical NSPM-SK form is shown as:
The above model represents the NSPM-SK form, shows the pantograph, is the perturbed term and defines the singularity. In Equation (6), the single singularity arises, is the shape factor, while the pantograph and perturbed terms appear two times. Figure 1 illustrates the flow-chart descriptions to achieve the mathematical form of the NSPM-SK.
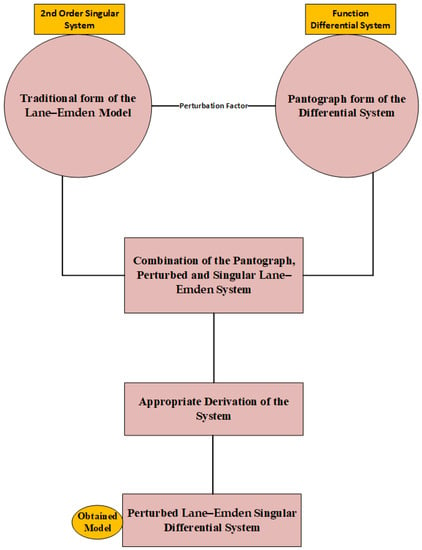
Figure 1.
Flow-chart descriptions to achieve the mathematical form of the NSPM-SK.
3. ANNs Procedure along with the Optimization of PSOSQP
In this section, the proposed ANNs together with the optimization procedures of the swarming schemes and SQP for solving the mathematical NSPM-SK. An objective function is provided using the differential NSPM-SK and then optimized through the hybridization of the PSOSQP. The proposed ANNs-PSOSQP structure to solve the mathematical NSPM-SK is provided in Figure 2.
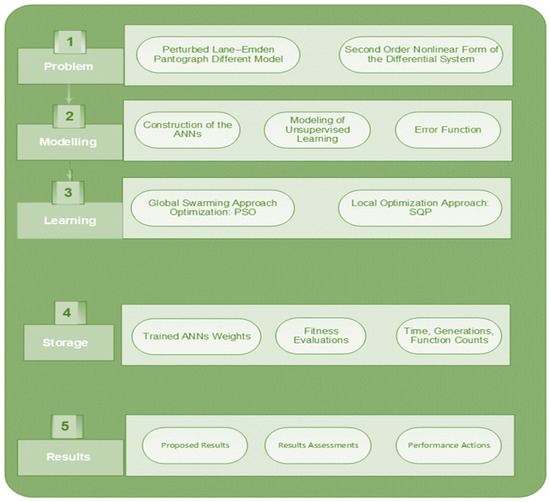
Figure 2.
Proposed ANNs-PSOSQP structure for the mathematical form of the NSPM-SK.
3.1. ANN Modeling
To present the numerical solutions of the mathematical NSPM-SK, the proposed solutions are designated as , while is the n kind of derivative. The mathematical details of these outcomes are presented as:
where represents the neurons, is the merit function (), and presents the vth component of . The using the log-sigmoid function is written as:
A merit function () is given as:
Here, and signifies the associated to singular perturbed form of the differential system provided in Equation (6). The performances of the are written as:
where and .
3.2. Performance Operators
This section indicates the performance indices of the VAF, MSE, and SIR for the mathematical NSPM-SK by using the ANNs together with the optimization procedures of the swarming schemes and SQP. The descriptions of the VAF, SIR, and MSE are provided as:
where and are the true and proposed results.
3.3. Networks Optimization
The parameter optimization scheme for the mathematical NSPM-SK by using the ANNs structure along with the PSOSQP are presented in this section.
The global search computational optimization algorithm PSO is a Neuro swarming technique, which is applied to the replacement of genetic algorithm. Kennedy and Eberhart introduced the PSO scheme in the last century [47]. PSO shows the results of the numerous complex and complicated systems to regulate the precise population by using the method of optimal training. The accomplishment of PSO is simple due to the short requirements of memory [48]. Recently, PSO has been used in numerous applications, e.g., multimodal multi-objective schemes [49], engineering systems [50], solar energy systems [51], plant diseases investigations [52], classifying the photovoltaic parameters of the single, double, and triple diode [53], constructions for image organization [54], green coal manufacture systems [55], and reduction of particle filter noise using the diagnosis of the mechanical responsibility [56]. These extraordinary submissions inspired the authors to apply the swarming schemes to solve the NSPM-SK.
PSO is a sluggish approach and the hybridization process by using the local search is applied for quick convergence. Therefore, SQP is a local search approach that is applied to obtain the rapid convergence. The optimal performances of the PSO are used as a primary input in the SQP process. SQP is an eminent form that is used in the modeling of the constrained and unconstrained problems. Some significant SQP applications are the approximation of nonlinear least squares and its submission [57], chilled water plant [58], engineering system optimization [59], constrained optimization of the nonconvex, non-smooth models [60], dynamic dispatch of the economic networks [61], optimal organization of directional relays by incorporating the dispersed generation [62], analysis of stiffened plates [63], optimal sizing and location the DGs in DC grids [64], and modeling of the hydro unit commitment [65].
4. Implementations
In this section, the implementations procedures based on the numerical solutions of the mathematical NSPM-SK using the proposed ANNs-PSOSQP structure is provided as:
- The ANNs have been applied for the proposed solutions .
- The Log-sigmoid function is used in the hidden layer and the nth order derivatives have been used provided.
- A merit function is designed based on the differential 2nd order perturbed pantograph Lane–Emden model and its boundary or initial conditions.
- The optimization of the merit function is performed by using the hybrid computing procedure based on the global swarming and local sequential quadratic programming schemes.
- The solutions are performed in terms of unidentified weight vectors.
5. Simulations and Results
The current section of this study provides the numerical representations for the mathematical nonlinear form of the NSPM-SK using the ANNs together with the optimization procedures of the swarming schemes and SQP. Thirty numbers of accomplishments have been used to validate the consistency of the scheme for the nonlinear mathematical NSPM-SK. The important graphical and representations to authenticate the convergence of the stochastic scheme are also provided.
Case 1:
Suppose a mathematical nonlinear form of the NSPM-SK is obtained by using the values of , , , and in Equation (6) as:
where
The true result of above Equation is The becomes:
Case 2:
Suppose a mathematical nonlinear form of the NSPM-SK is obtained by using the values of , , , and in Equation (6) as:
where
The true form of Equation (16) is The becomes:
Case 3:
Suppose a mathematical nonlinear form of the NSPM-SK is obtained by using the values of , , , and in Equation (6) as:
where
The exact value of Equation (16) is The function becomes:
The performances of each case of the mathematical nonlinear form of the NSPM-SK are accomplished using the stochastic ANNs procedures. Thirty numbers of independent trials have been achieved to designate the dependability of the ANNs together with the optimization procedures of the swarming schemes and SQP. The obtained results through these stochastic solvers based on the mathematical performances to find the unknown weights are shown as:
The achieved numerical results using the ANNs together with the optimization procedures of the swarming schemes and SQP are provided in Equations (20)–(22). Figure 3 presents the graphic illustrations to solve the mathematical nonlinear form of the NSPM-SK. The mean, worst, and best results are also provided in the 2nd part of Figure 3 for the NSPM-SK that shows the overlapping of the solutions. These obtained precise performances represent the brilliance of the proposed stochastic procedure for solving the NSPM-SK. The performances of the AE are illustrated in Figure 3g, which are measured as 10−4–10−6, 10−5–10−6, and 10−5–10−7 for case 1 to 3. The MSE, Fitness, and EVAF operator measures are given in Figure 3h for solving the NSPM-SK. It is observed that the best form of the Fitness measures was found as 10−9–10−10 for the 1st and 3rd case, however for the 2nd case these measures lie as 10−8–10−9. The EVAF performances of the operator that found as 10−8–10−9 for case 1, 2, and 3 for the NSPM-SK. Similarly, the MSE measures lie as 10−9–10−10 for case 1, 2, and 3 for the NSPM-SK. These best optimal values designate the correctness and precision of the stochastic approach for the mathematical NSPM-SK.
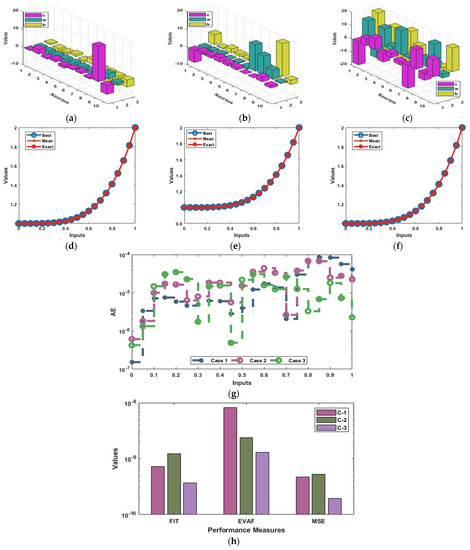
Figure 3.
Graphic illustrations based on the best weight vectors, AE, and convergence performances to solve the NSPM-SK. (a) Weights for C-1. (b) Weights for C-2. (c) Weights for C-3. (d) C-1: Results. (e) C-2: Results. (f) C-3: Results. (g) Performances of the AE for the NSPM-SK. (h) Performance indices for the NSPM-SK.
The convergence measures are drawn in Figure 4, Figure 5 and Figure 6, using the Fitness, EVAF, and MSE with the histograms (HGs) and boxplots (BPs) to solve the nonlinear NSPM-SK. The Fitness values have been illustrated in Figure 4, which shows that most of the values are calculated as 10−6 to 10−9 for case 1, 2, and 3 for the NSPM-SK. Likewise, Figure 5 shows that most of the EVAF performances lie as 10−6 to 10−10 for case 1, 2, and 3 for the NSPM-SK. Figure 6 indicates that most of the EVAF measures are calculated as 10−5 to 10−9 for each case of the NSPM-SK. These optimal best achieved values based on these statistical operators validate the correctness of the ANNs together with the optimization procedures of the swarming schemes and SQP.
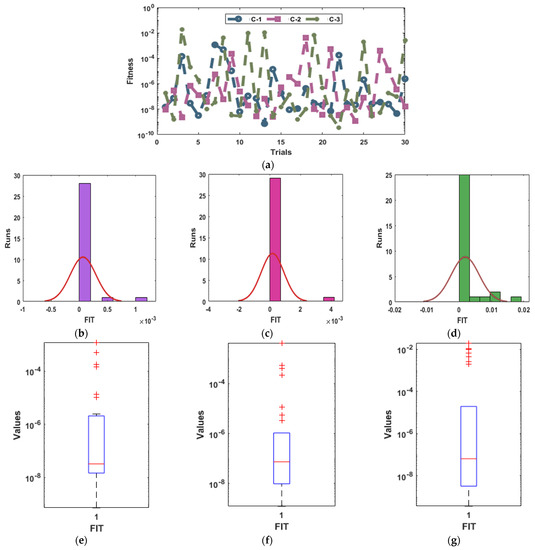
Figure 4.
Performances through the statistical measures for the Fitness values based on the NSPM-SK. (a) Performances of the Fitness for case 1 to 3. (b) Hist of C-1. (c) Hist of C-2. (d) Hist of C-3. (e) BPs of C-1. (f) BPs of C-2. (g) BPs of C-3.
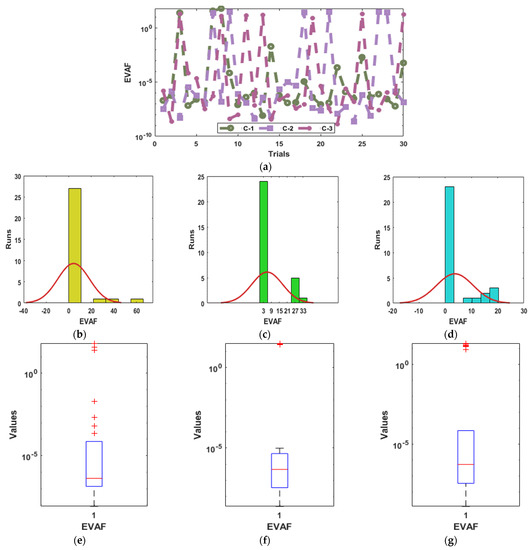
Figure 5.
Performances through the statistical measures for the EVAF values based on the NSPM-SK. (a) Performances of the EVAF for case 1 to 3. (b) Hist of C-1. (c) Hist of C-2. (d) Hist of C-3. (e) BPs of C-1. (f) BPs of C-2. (g) BPs of C-3.
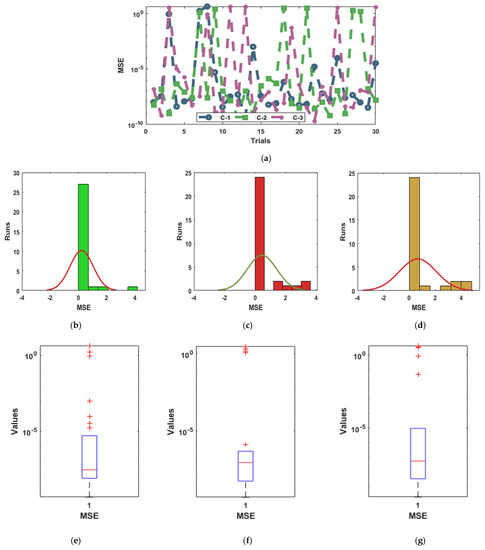
Figure 6.
Performances through the statistical measures for the MSE values based on the NSPM-SK. (a) Performances of the MSE for case 1 to 3. (b) Hist of C-1. (c) Hist of C-2. (d) Hist of C-3. (e) BPs of C-1. (f) BPs of C-2. (g) BPs of C-3.
To observe the precision and accurateness of the proposed ANNs together with the optimization procedures of the swarming schemes and SQP, the statistical performances were provided by applying the minimum, SIR, mean, standard deviation (STD), and median for 30 runs in Table 1, Table 2 and Table 3. The best performances were provided based on the Minimum operator, while the mathematical form of the MSE and SIR are shown in the statistical measures section. One can perform the performance and constancy of the proposed ANNs together with the optimization procedures of the swarming schemes and SQP for each case of the NSPM-SK.

Table 1.
Statistical measures for the stochastic operators based on case 1 for the NSPM-SK.

Table 2.
Statistical measures for the stochastic operators based on case 2 for the NSPM-SK.

Table 3.
Statistical measures for the stochastic operators based on case 3 for the NSPM-SK.
The convergence plots through the ANNs together with the optimization procedures of the swarming schemes and SQP for each case of the NSPM-SK-based global MSE, Fitness, and EVAF for 30 implementations are provided in Table 4. For each variation of the NSPM-SK, the performances of the Minimum operators-based global Fitness, EVAF, and MSE were calculated as 10−4–10−6, 10−1–10−2, and 10−4–10−5. The SIR measures for these measures were found as 10−7–10−8, 10−3–10−4, and 10−7–10−8. These global measures through the optimal performances present the accuracy of the ANNs together with the optimization procedures of the swarming schemes and SQP for each case of the NSPM-SK.

Table 4.
Global performances of the mathematical form of the NSPM-SK.
6. Conclusions
The aim of this study is to present the mathematical construction based on the novel singular perturbed model of the second kind using the standard form of the Lane–Emden. The singular form of the models has abundant applications in astrophysics. The inclusive features of this model have been provided using the perturbed, pantograph, and singular point together with the shape factor based on the NSPM-SK. The singular kinds of the models become more complicated by using these factors through the artificial neural networks together with the optimization swarming procedures and the local sequential quadratic programming. An objective function has been designed using the differential form of the NSPM-SK and then optimization is performed through the hybridization of the PSOSQP. The exactness of the model is attained to solve three different variations of the mathematical NSPM-SK by using the overlapping of the obtained and true results. The AE is noticed in good measures for solving the perturbed singular model, which are found as 10−6 to 10−8 for each case. The stability, robustness, and convergence of the designed numerical approach are perceived by using the different statistical performances of the ANNs together with the optimization of the PSOSQP for 30 independent executions. The statistical measures through the Minimum, Fitness, EVAF, mean, MSE, STD, and SIR are accomplished through 30 implementations to validate the steadiness and reliability of the stochastic scheme. Furthermore, it is authenticated that the mathematical NSPM-SK becomes complicated by using the singular, perturbed, and pantograph factors. Therefore, these kinds of the system are not easy to solve by using the traditional approaches. Hence, ANNs together with the optimization procedures based on the swarming schemes and SQP are a good choice for solving the NSPM-SK.
In upcoming works, the mathematical form of the higher order NSPM can be designed and provided by using the ANNs together with the optimization procedures of the swarming schemes and SQP. Moreover, the proposed scheme can be implemented to solve the various fractional and nonlinear differential systems [66,67,68,69,70,71,72,73,74,75].
Author Contributions
Conceptualization, M.A.N. and Z.S.; methodology, Z.S. and M.A.N.; software, Z.S. and M.A.N.; validation, M.A.N. and Z.S.; formal analysis, Z.S.; investigation, Z.S. and M.A.N.; resources, M.A.N. and Z.S.; data curation, M.A.N. and Z.S.; writing—original draft preparation, Z.S.; writing—review and editing, M.A.N.; visualization, M.A.N. and Z.S.; supervision, M.A.N. and Z.S.; project administration, Z.S. and M.A.N.; funding acquisition, M.A.N. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the Deanship of Scientific Research, Vice Presidency for Graduate Studies and Scientific Research, King Faisal University, Saudi Arabia (Project No. GRANT691).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data that support the findings of this study are available from the corresponding author upon reasonable request. The data are not publicly available due to [insert reason here].
Acknowledgments
The authors acknowledge the Deanship of Scientific Research at King Faisal University, Saudi Arabia for their financial support [Project No. GRANT691].
Conflicts of Interest
The authors declare no conflict of interest.
References
- Holevoet, D.; Daele, M.V.; Berghe, G.V. The Optimal Exponentially-Fitted Numerov Method for Solving Two-Point Boundary Value Problems. J. Comp. Appl. Math. 2010, 230, 260–269. [Google Scholar] [CrossRef]
- Phaneendra, K.; Pramod Chakravarthy, P.; Reddy, Y.N. A Fitted Numerov Method for Singular Perturbation Problems Exhibiting Twin Layers. Appl. Math. Inf. Sci. 2010, 4, 341–352. [Google Scholar]
- Patidar, K.C. High order fitted operator numerical method for self-adjoint singular perturbation problems. Appl. Math. Comp. 2005, 171, 547–566. [Google Scholar] [CrossRef]
- Kondo, S.; Miura, T. Reaction-diffusion model as a framework for understanding biological pattern formation. Science 2010, 329, 1616–1620. [Google Scholar] [CrossRef]
- Bawa, R.K. A Paralel aproach for self-adjoint singular perturbation problems using Numerov’s scheme. Int. J. Comput. Math. 2007, 84, 317–323. [Google Scholar] [CrossRef]
- Amiraliyeva, I.G.; Erdogan, F.; Amiraliyev, G.M. A uniform numerical method for dealing with a singularly perturbed delay inital value problem. Appl. Math. Lett. 2010, 23, 1221–1225. [Google Scholar] [CrossRef]
- Kopteva, N.; Stynes, M. Numerical analysis of a singularly perturbed nonlinear reaction–diffusion problem with multiple solutions. Appl. Numer. Math. 2002, 51, 273–288. [Google Scholar] [CrossRef]
- Doolan, E.R.; Miller, J.J.H.; Schilders, W.H.A. Uniform Numerical Methods for Problems with Initial and Boundary Layers; Boole Press: Dublin, Ireland, 1980. [Google Scholar]
- Roos, H.G.; Stynes, M.; Tobiska, L. Numerical Methods for Singularly Perturbed Differential Equations: Convection-Diffusion and Flow Problems; Springer: Berlin/Heidelberg, Germany, 1996. [Google Scholar]
- Farrell, P.A.; Hegarty, A.F.; Miller, J.J.H.; O’Riordan, E.; Shishkin, G.I. Robust Computational Techniques for Boundary Layers; Chapman-Hall: New York, NY, USA; CRC Press: New York, NY, USA, 2000. [Google Scholar]
- Miller, J.J.H.; O’Riordan, E.; Shishkin, G.I. Fitted Numerical Methods for Singular Perturbation Problems: Error Estimates in the Maximum Norm for Linear Problems in One and Two Dimensions; World Scientific: Singapore, 2012. [Google Scholar]
- Linss, T. Layer-adapted meshes for convection–diffusion problems. Comput. Methods Appl. Mech. Eng. 2003, 192, 1061–1105. [Google Scholar] [CrossRef]
- Erdogan, F.; Sakar, M.G.; Saldır, O. A finite difference method on layer-adapted mesh for singularly perturbed delay differential equations. Appl. Math. Nonlinear Sci. 2020, 5, 425–436. [Google Scholar] [CrossRef]
- Linss, T.; Stynes, M. A hybrid difference scheme on a Shishkin mesh for linear convection-diffusion problems. Appl. Numer. Math. 1999, 31, 255–270. [Google Scholar] [CrossRef]
- Bogachev, L.; Derfel, G.; Molchanov, S.; Ochendon, J. On bounded solutions of the balanced generalized pantograph equation. In Topics in Stochastic Analysis and Nonparametric Estimation; The IMA Volumes in Mathematics and Its Applications; Chow, P.L., George, Y., Mordukhovich, B., Eds.; Springer: New York, NY, USA, 2008; Volume 145, pp. 29–49. [Google Scholar]
- Vanani, S.K.; Hafshejani, J.S.; Soleymani, F.; Khan, M. On the numerical solution of generalized pantograph equation. World Appl. Sci. J. 2011, 13, 2531–2535. [Google Scholar]
- Ockendon, J.R.; Tayler, A.B. The dynamics of a current collection system for an electric locomotive. Proc. R. Soc. Lond. A Math. Phys. Eng. Sci. 1971, 322, 447–468. [Google Scholar]
- Anakira, N.R.; Jameel, A.; Alomari, A.K.; Saaban, A.; Almahameed, M.; Hashim, I. Approximate solutions of multi-pantograph type delay differential equations using multistage optimal homotopy asymptotic method. J. Math. Fundam. Sci. 2018, 50, 221–232. [Google Scholar] [CrossRef]
- Yousefi, S.A.; Noei-Khorshidi, M.; Lotfi, A. Convergence analysis of least squares-Epsilon-Ritz algorithm for solving a general class of pantograph equations. Kragujev. J. Math. 2018, 42, 431–439. [Google Scholar] [CrossRef]
- Ezz-Eldien, S.S.; Wang, Y.; Abdelkawy, M.A.; Zaky, M.A.; Aldraiweesh, A.A.; Machado, J.T. Chebyshev spectral methods for multi-order fractional neutral pantograph equations. Nonlinear Dyn. 2020, 100, 3785–3797. [Google Scholar] [CrossRef]
- Yüzbaşi, S.; Ismailov, N. A Taylor operation method for solutions of generalized pantograph type delay differential equations. Turk. J. Math. 2018, 42, 395–406. [Google Scholar] [CrossRef]
- Ezz-Eldien, S.S. On solving systems of multi-pantograph equations via spectral tau method. Appl. Math. Comput. 2018, 321, 63–73. [Google Scholar] [CrossRef]
- Isah, A.; Phang, C. A collocation method based on Genocchi operational matrix for solving Emden-Fowler equations. J. Phys. Conf. Ser. 2020, 1489, 012022. [Google Scholar] [CrossRef]
- Gul, H.; Alrabaiah, H.; Ali, S.; Shah, K.; Muhammad, S. Computation of solution to fractional order partial reaction diffusion equations. J. Adv. Res. 2020, 25, 31–38. [Google Scholar] [CrossRef]
- Amin, R.; Shah, K.; Asif, M.; Khan, I.; Ullah, F. An efficient algorithm for numerical solution of fractional integro-differential equations via Haar wavelet. J. Comput. Appl. Math. 2021, 381, 113028. [Google Scholar] [CrossRef]
- Sabir, Z.; Sakar, M.G.; Yeskindirova, M.; Saldir, O. Numerical investigations to design a novel model based on the fifth order system of Emden–Fowler equations. Theor. Appl. Mech. Lett. 2020, 10, 333–342. [Google Scholar] [CrossRef]
- Abdelkawy, M.A.; Sabir, Z.; Guirao, J.L.G.; Saeed, T. Numerical investigations of a new singular second-order nonlinear coupled functional Lane–Emden model. Open Phys. 2020, 18, 770–778. [Google Scholar] [CrossRef]
- Arqub, O.A.; Osman, M.S.; Abdel-Aty, A.H.; Mohamed, A.B.A.; Momani, S. A numerical algorithm for the solutions of ABC singular Lane–Emden type models arising in astrophysics using reproducing kernel discretization method. Mathematics 2020, 8, 923. [Google Scholar] [CrossRef]
- Abd-Elhameed, W.M.; Youssri, Y.; Doha, E.H. New solutions for singular Lane-Emden equations arising in astrophysics based on shifted ultraspherical operational matrices of derivatives. Comput. Methods Differ. Equ. 2014, 2, 171–185. [Google Scholar]
- Atangana, A.; Aguilar, J.F.G.; Kolade, M.O.; Hristov, J.Y. Fractional differential and integral operators with non-singular and non-local kernel with application to nonlinear dynamical systems. Chaos Solitons Fractals 2020, 132, 109493. [Google Scholar] [CrossRef]
- Adel, W. A Numerical Technique for Solving a Class of Fourth-Order Singular Singularly Perturbed and Emden–Fowler Problems Arising in Astrophysics. Int. J. Appl. Comput. Math. 2022, 8, 220. [Google Scholar] [CrossRef]
- Mall, S.; Chakraverty, S. A novel Chebyshev neural network approach for solving singular arbitrary order Lane-Emden equation arising in astrophysics. Netw. Comput. Neural Syst. 2020, 31, 142–165. [Google Scholar] [CrossRef] [PubMed]
- Rufai, M.A.; Ramos, H. Numerical solution of second-order singular problems arising in astrophysics by combining a pair of one-step hybrid block Nyström methods. Astrophys. Space Sci. 2020, 365, 96. [Google Scholar] [CrossRef]
- Balaji, S. A new Bernoulli wavelet operational matrix of derivative method for the solution of nonlinear singular Lane–Emden type equations arising in astrophysics. J. Comput. Nonlinear Dyn. 2016, 11, 051013. [Google Scholar] [CrossRef]
- Kaur, H.; Mittal, R.C.; Mishra, V. Haar wavelet approximate solutions for the generalized Lane–Emden equations arising in astrophysics. Comput. Phys. Commun. 2013, 184, 2169–2177. [Google Scholar] [CrossRef]
- Singh, R. Analytic solution of system of singular nonlinear differential equations with Neumann-Robin boundary conditions arising in astrophysics. arXiv 2020, arXiv:2007.01653. [Google Scholar]
- Wazwaz, A.M. Analytical solution for the time-dependent Emden–Fowler type of equations by Adomian decomposition method. Appl. Math. Comput. 2005, 166, 638–651. [Google Scholar] [CrossRef]
- Ali, M.R.; Hadhoud, A.R.; Ma, W.X. Evolutionary numerical approach for solving nonlinear singular periodic boundary value problems. J. Intell. Fuzzy Syst. 2020, 39, 7723–7731. [Google Scholar] [CrossRef]
- Adel, W.; Sabir, Z. Solving a new design of nonlinear second-order Lane–Emden pantograph delay differential model via Bernoulli collocation method. Eur. Phys. J. Plus 2020, 135, 427. [Google Scholar] [CrossRef]
- Guerrero Sánchez, Y.; Sabir, Z.; Günerhan, H.; Baskonus, H.M. Analytical and approximate solutions of a novel nervous stomach mathematical model. Discret. Dyn. Nat. Soc. 2020, 2020, 5063271. [Google Scholar] [CrossRef]
- Sabir, Z.; Saed, T.; Alhodaly, M.S.; Alsulami, H.H.; Sánchez, Y.G. An advanced heuristic approach for a nonlinear mathematical based medical smoking model. Results Phys. 2021, 32, 105137. [Google Scholar]
- Sabir, Z.; Ali, M.R.; Sadat, R. Gudermannian neural networks using the optimization procedures of genetic algorithm and active set approach for the three-species food chain nonlinear model. J. Ambient Intell. Humaniz. Comput. 2022, 2022, 1–10. [Google Scholar] [CrossRef]
- Sabir, Z. Stochastic numerical investigations for nonlinear three-species food chain system. Int. J. Biomath. 2021, 15, 2250005. [Google Scholar] [CrossRef]
- Sabir, Z. Neuron analysis through the swarming procedures for the singular two-point boundary value problems arising in the theory of thermal explosion. Eur. Phys. J. Plus 2022, 137, 638. [Google Scholar] [CrossRef]
- Sabir, Z.; Wahab, H.A.; Ali, M.R.; Sadat, R. Neuron analysis of the two-point singular boundary value problems arising in the thermal explosion’s theory. Neural Process. Lett. 2022, 1–28. [Google Scholar] [CrossRef]
- Sabir, Z.; Raja, M.A.Z.; Nguyen, T.G.; Fathurrochman, I.; Sadat, R.; Ali, M.R. Applications of neural networks for the novel designed of nonlinear fractional seventh order singular system. Eur. Phys. J. Spec. Top. 2022, 231, 1831–1845. [Google Scholar] [CrossRef]
- Shi, Y.; Eberhart, R.C. Empirical study of particle swarm optimization. In Proceedings of the 1999 Congress on Evolutionary Computation-CEC99, Washington, DC, USA, 6–9 July 1999; Volume 3, pp. 1945–1950. [Google Scholar]
- Engelbrecht, A.P. Computational Intelligence: An Introduction, 2nd ed.; John Wiley & Sons Ltd.: Chichester, UK, 2007. [Google Scholar]
- Zhang, X.; Liu, H.; Tu, L. A modified particle swarm optimization for multimodal multi-objective optimization. Eng. Appl. Artif. Intell. 2020, 95, 103905. [Google Scholar] [CrossRef]
- De Almeida, B.S.G.; Leite, V.C. Particle swarm optimization: A powerful technique for solving engineering problems. In Swarm Intelligence-Recent Advances, New Perspectives and Applications; Books on Demand: McFarland, WI, USA, 2019; pp. 31–51. [Google Scholar]
- Elsheikh, A.H.; Abd Elaziz, M. Review on applications of particle swarm optimization in solar energy systems. Int. J. Environ. Sci. Technol. 2019, 16, 1159–1170. [Google Scholar] [CrossRef]
- Darwish, A.; Ezzat, D.; Hassanien, A.E. An optimized model based on convolutional neural networks and orthogonal learning particle swarm optimization algorithm for plant diseases diagnosis. Swarm Evol. Comput. 2020, 52, 100616. [Google Scholar] [CrossRef]
- Yousri, D.; Thanikanti, S.B.; Allam, D.; Ramachandaramurthy, V.K.; Eteiba, M.B. Fractional chaotic ensemble particle swarm optimizer for identifying the single, double, and three diode photovoltaic models’ parameters. Energy 2020, 195, 116979. [Google Scholar] [CrossRef]
- Junior, F.E.F.; Yen, G.G. Particle swarm optimization of deep neural networks architectures for image classification. Swarm Evol. Comput. 2019, 49, 62–74. [Google Scholar] [CrossRef]
- Cui, Z.; Zhang, J.; Wu, D.; Cai, X.; Wang, H.; Zhang, W.; Chen, J. Hybrid many-objective particle swarm optimization algorithm for green coal production problem. Inf. Sci. 2020, 518, 256–271. [Google Scholar] [CrossRef]
- Chen, H.; Fan, D.L.; Fang, L.; Huang, W.; Huang, J.; Cao, C.; Yang, L.; He, Y.; Zeng, L. Particle swarm optimization algorithm with mutation operator for particle filter noise reduction in mechanical fault diagnosis. Int. J. Pattern Recognit. Artif. Intell. 2020, 34, 2058012. [Google Scholar] [CrossRef]
- Fu, Z.; Liu, G.; Guo, L. Sequential quadratic programming method for nonlinear least squares estimation and its application. Math. Probl. Eng. 2019, 2019, 3087949. [Google Scholar]
- Olson, R.T.; Liebman, J.S. Optimization of a chilled water plant using sequential quadratic programming. Eng. Optim. 1990, 15, 171–191. [Google Scholar] [CrossRef]
- Fesanghary, M.; Mahdavi, M.; Minary-Jolandan, M.; Alizadeh, Y. Hybridizing harmony search algorithm with sequential quadratic programming for engineering optimization problems. Comput. Methods Appl. Mech. Eng. 2008, 197, 3080–3091. [Google Scholar] [CrossRef]
- Curtis, F.E.; Overton, M.L. A sequential quadratic programming algorithm for nonconvex, nonsmooth constrained optimization. SIAM J. Optim. 2012, 22, 474–500. [Google Scholar] [CrossRef]
- Basu, M. Hybridization of bee colony optimization and sequential quadratic programming for dynamic economic dispatch. Int. J. Electr. Power Energy Syst. 2013, 44, 591–596. [Google Scholar] [CrossRef]
- ElSayed, S.K.; Elattar, E.E. Hybrid Harris hawks optimization with sequential quadratic programming for optimal coordination of directional overcurrent relays incorporating distributed generation. Alex. Eng. J. 2021, 60, 2421–2433. [Google Scholar] [CrossRef]
- Bedair, O.K. Analysis of stiffened plates under lateral loading using sequential quadratic programming (SQP). Comput. Struct. 1997, 62, 63–80. [Google Scholar] [CrossRef]
- Montoya, O.D.; Gil-González, W.; Grisales-Noreña, L.F. Relaxed convex model for optimal location and sizing of DGs in DC grids using sequential quadratic programming and random hyperplane approaches. Int. J. Electr. Power Energy Syst. 2020, 115, 105442. [Google Scholar] [CrossRef]
- Finardi, E.C.; da Silva, E.L. Solving the hydro unit commitment problem via dual decomposition and sequential quadratic programming. IEEE Trans. Power Syst. 2006, 21, 835–844. [Google Scholar] [CrossRef]
- Aghilí, A. Complete solution for the time fractional diffusion problem with mixed boundary conditions by operational method. Appl. Math. Nonlinear Sci. 2021, 6, 9–20. [Google Scholar] [CrossRef]
- Sulaiman, T.A.; Bulut, H.; Baskonus, H.M. On the exact solutions to some system of complex nonlinear models. Appl. Math. Nonlinear Sci. 2021, 6, 29–42. [Google Scholar] [CrossRef]
- Gençoglu, M.T.; Agarwal, P. Use of quantum differential equations in sonic processes. Appl. Math. Nonlinear Sci. 2021, 6, 21–28. [Google Scholar] [CrossRef]
- Baskonus, H.M.; Bulut, H.; Sulaiman, T.A. New complex hyperbolic structures to the lonngren-wave equation by using sine-gordon expansion method. Appl. Math. Nonlinear Sci. 2019, 4, 141–150. [Google Scholar] [CrossRef]
- Che, Y.; Keir, M.Y.A. Study on the training model of football movement trajectory drop point based on fractional differential equation. Appl. Math. Nonlinear Sci. 2021, 7, 425–430. [Google Scholar] [CrossRef]
- Touchent, K.A.; Hammouch, Z.; Mekkaoui, T. A modified invariant subspace method for solving partial differential equations with non-singular kernel fractional derivatives. Appl. Math. Nonlinear Sci. 2020, 5, 35–48. [Google Scholar] [CrossRef]
- İlhan, E.; Kıymaz, İ.O. A generalization of truncated M-fractional derivative and applications to fractional differential equations. Appl. Math. Nonlinear Sci. 2020, 5, 171–188. [Google Scholar] [CrossRef]
- Sajjan, K.; Shah, N.A.; Ahammad, N.A.; Raju, C.S.K.; Kumar, M.D.; Weera, W. Nonlinear Boussinesq and Rosseland approximations on 3D flow in an interruption of Ternary nanoparticles with various shapes of densities and conductivity properties. AIMS Math. 2022, 7, 18416–18449. [Google Scholar] [CrossRef]
- Priyadharshini, P.; Archana, M.V.; Ahmmad, N.A.; Raju, C.S.K.; Yook, S.-J.; Shah, N.A. Gradient descent machine learning regression for MHD flow: Metallurgy process. Int. Commun. Heat Mass Transf. 2022, 138, 106307. [Google Scholar] [CrossRef]
- Durur, H.; Tasbozan, O.; Kurt, A. New analytical solutions of conformable time fractional bad and good modified Boussinesq equations. Appl. Math. Nonlinear Sci. 2020, 5, 447–454. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).