Approximate Methods for Calculating Singular and Hypersingular Integrals with Rapidly Oscillating Kernels

Abstract

The article is devoted to the issue of construction of an optimal with respect to order passive algorithms for evaluating Cauchy and Hilbert singular and hypersingular integrals with oscillating kernels. We propose a method for estimating lower bound errors of quadrature formulas for singular and hypersingular integral evaluation. Quadrature formulas were constructed for implementation of the obtained estimates. We constructed quadrature formulas and estimated the errors for hypersingular integrals with oscillating kernels. This method is based on using similar results obtained for singular integrals.

1. Introduction

Recent years have shown the importance of evaluating singular and hypersingular integrals with rapidly oscillating kernels in mathematical modeling of wave processes in many areas of physics and technology: electrodynamics (waveguides, gyrotrons), aerodynamics, geophysics (transformation of gravity and magnetic fields), etc.

Today, there are very few manuscripts devoted to approximate methods for evaluating singular integrals with rapidly oscillating kernels. We are unaware of papers dealing with approximate methods for evaluating hypersingular integrals with rapidly oscillating kernels.

In this paper, we construct an optimal with respect to order quadrature formulas for evaluating singular and hypersingular integrals on Hölder functions and differentiable function classes.

The paper is organized as follows:

Section 1 contains the review of publications evaluating singular integrals with rapidly oscillating functions. In this section, we give the definitions of singular and hypersingular integrals and optimal algorithms for their evaluation.

In Section 2, Levin’s method is extended to singular and hypersingular integrals.

In Section 3, we introduce an optimal with respect to order quadrature formulas for calculating singular integrals with oscillating functions.

In Section 4, we present methods for evaluating the hypersingular integrals with rapidly oscillating functions.

In Section 5, we give the conclusions of our study.

1.1. Literature Review

An extensive literature exists regarding approximate methods for singular and hypersingular integral evaluation. Detailed reviews are given in [1,2,3,4,5,6,7,8]. Very few publications concentrate on approximate methods for evaluating singular integrals with oscillating kernels [9,10,11,12,13,14,15,16,17].

Here, we give a brief overview of the manuscripts considering singular integrals with oscillating kernels.

The chapter “Oscillatory Singular Integrals” in [18] is devoted to the study of oscillatory singular integrals. The authors consider singular integrals of the form

$$Tf(x)=p.v.{\int }_{R^n}{e}^{ip(x,y)}K(x-y)f(y)dy,$$

(1)

where

(i)

K is a $C^1$ function away from the origin;

(ii)

K is homogeneous of degree -n;

(iii)

the mean value of K on the unit sphere vanishes;

(iiii)

$p(x,y)$ is a real-value polynomial on $R^n\times R^n$.

The boundedness of the operator T is investigated in a number of function spaces. Integrals of the form (1) are widely used in the Radon transform.

The paper [11] deals with approximate methods for evaluating the integral

$$I(f,w)={\int }_{-1}^1\frac{f(x)}{x}coswxdx,$$

(2)

where $f(x)$ is an analytic function in $[-1;1]$, $w\in R \backslash \left\{0\right\}$. The integral (2) is converted to the form

$$I(f,w)={\int }_{-1}^1\frac{coswx-1}{x}f(x)dx+{\int }_{-1}^1\frac{f(x)}{x}dx=I_0(f)+I(f).$$

(3)

Philon’s method is used for the integral $I_0(f)$.

The second method proposed in [11] consists in approximating the function $f(x)$ in $I_0(f)$ by segment of the Taylor series. The well-known methods are used to approximate the integral $I(f)$ [19].

In [20], Levin’s method [21,22] for evaluating integrals with oscillating kernels was extended to weakly singular integrals with logarithmic singularities.

Approximate methods for evaluating singular integrals with oscillating kernels of the form

$$K(f,w)(t)={\int }_{-1}^1{e}^{iwx}\frac{f(x)}{x-t}dx$$

(4)

have been studied in [9].

In [16], quadrature formulas are constructed for evaluating singular integrals of the form

$$I(w,a)={\int }_{-1}^1\frac{e^{iwx}}{\sqrt{1-x^2}}\frac{f(x)}{x-a}dx,$$

(5)

where w is a large positive number, $-1<a<1$.

To construct a quadrature formula, the function f (x) is approximated by interpolation polynomial $P_n(f,x)$ on nodes $x_1,x_2,\dots ,x_n,a$, and a does not match $x_1,x_2,\dots ,x_n$. As a result, the integral (5) is approximated by the quadrature formula

$$I(w,a)={\int }_{-1}^1\frac{e^{iwx}{P}_n(f,x)}{\sqrt{1-x^2}(x-a)}dx+R_n(f,a).$$

The estimate for $R_n(f,a)$ is given in [16].

1.2. Definitions of Singular and Hypersingular Integrals

Recall the definitions of function classes.

Let $\gamma$ be the unit circle centered at the origin in the plane of the complex variable. Let $A=[-1,1]$ or $A=\gamma$.

Definition 1.

Hölder function class $H_{\alpha }(M;A)(0<\alpha \le 1)$ consists of functions $f(x)$ defined on A satisfying the inequality $|f(x^{\prime })-f(x^{″})|\le M|x^{\prime }-x^{″}{|}^{\alpha }$.

Definition 2.

The class $W^r(M;A),$ $r=1,2,\dots ,$ consists of functions $f\in C[a,b]$ which have absolutely continuous derivatives of orders $j=0,1,\dots ,r-1$ and a piecewise continuous derivative $f^{(r)}$ satisfying $\parallel f^{(r)}(x)\parallel \le M.$

Definition 3.

The class $W^r{H}_{\alpha }(M;A)$ consists of functions $f(x)$ belonging to the class $W^r(M;A)$ and satisfying the additional condition $f^{(r)}(x)\in H_{\alpha }(M,A)$.

Consider the integral

$$\underset{a}{\overset{b}{\int }}\frac{f(\tau )}{\tau -t}d\tau ,a<t<b.$$

(6)

Definition 4.

The Cauchy principal value of the singular integral (6) is called the limit

$$\underset{\eta \to 0}{lim}\left[\underset{a}{\overset{c-\eta }{\int }}\frac{f(\tau )}{\tau -c}d\tau +\underset{c+\eta }{\overset{b}{\int }}\frac{f(\tau )}{\tau -c}d\tau \right].$$

Recall the definitions of hypersingular integrals. Hadamard [23] introduced a new type of integral, hypersingular integrals:

Definition 5.

The integral of the type

$$\underset{a}{\overset{b}{\int }}\frac{A(x)dx}{{(b-x)}^{p+\alpha }}$$

(7)

for an integer p and $0<\alpha <1$ defines a value of the above integral (“finite part”) as the limit of the sum

$$\underset{a}{\overset{x}{\int }}\frac{A(t)dt}{{(b-t)}^{p+\alpha }}+\frac{B(x)}{{(b-x)}^{p+\alpha -1}},$$

as $x\to b$ if one assumes that $A(x)$ has p derivatives in the neighborhood of point b. Here, $B(x)$ is any function that satisfies the following two conditions:

(i)

The above limit exists;

(ii)

$B(x)$ has at least p derivatives in the neighborhood of a point $x=b$.

An arbitrary choice of $B(x)$ does not depend on the value of the limit in (i). Condition (ii) defines the values of first $(p-1)$ derivatives of $B(x)$ at point b. An arbitrary additional term in the numerator is infinitesimal, of order ${(b-x)}^p$.

Notation 1.

Hadamard [24] gave a fascinating report of various aspects of the creative process in solving mathematical problems and, in particular, on his discovery of hypersingular integrals.

Chikin [25] introduced the definition of the Cauchy–Hadamard type integral that generalized a singular integral in the Cauchy principal and Hadamard sense.

Definition 6.

The Cauchy–Hadamard principal sense of the following integral

$$\underset{a}{\overset{b}{\int }}\frac{\phi (\tau )d\tau }{{(\tau -c)}^p},a<c<b$$

is defined as the limit of the expression

$$\underset{a}{\overset{b}{\int }}\frac{\phi (\tau )d\tau }{{(\tau -c)}^p}=\underset{v\to 0}{lim}\left[\underset{a}{\overset{c-v}{\int }}\frac{\phi (\tau )d\tau }{{(\tau -c)}^p}+\underset{c+v}{\overset{b}{\int }}\frac{\phi (\tau )d\tau }{{(\tau -c)}^p}+\frac{\xi (v)}{v^{p-1}}\right],$$

where $\xi (v)$ is a function chosen so as to provide the existence of the limit above.

In some cases, it is more convenient to use the following definition of hypersingular integrals, which is equivalent to Definition 6.

Definition 7.

Let $f(t)\in W^r{H}_{\alpha }(M;[-1,1]),r=1,2,\dots ,0<\alpha \le 1.$ A hypersingular integral with order of $p+1$ singularity, $p\le r,$ is defined by

$$\underset{-1}{\overset{1}{\int }}\frac{f(\tau )}{{(\tau -t)}^{p+1}}d\tau =\frac{1}{p!}\frac{{\partial }^p}{\partial t^p}\underset{-1}{\overset{1}{\int }}\frac{f(\tau )}{\tau -t}d\tau .$$

1.3. Optimal Quadrature Formulas for Calculating Singular and Hypersingular Integrals

Formulation of the problem of constructing the best quadrature formula belongs to Kolmogorov. Bakhvalov introduced [26] the concepts of asymptotically optimal and optimal with respect to order passive algorithms for solving problems in numerical analysis. Other approaches to determine optimal passive algorithms are given in [27,28,29].

We give now the definition of optimal quadrature formulas for singular integrals.

Consider the quadrature rule

$$C\phi \equiv \underset{-1}{\overset{1}{\int }}\frac{\phi (\tau )}{\tau -t}d\tau =\sum _{k=1}^N\sum _{l=0}^{\rho }{p}_{kl}(s){\phi }^{(l)}(t_k)+R_N(\phi ,t,p_{kl},t_k).$$

(8)

The error (8) is

$$R_N(\phi ,p_{kl},t_k)=\underset{-1<t<1}{sup}|R_N(\phi ,t,p_{kl},t_k)|.$$

The error of (8) on $\mathsf{\Psi }$ class is

$$R_N(\mathsf{\Psi },p_{kl},t_k)=\underset{\phi \in \mathsf{\Psi }}{sup}{R}_N(\phi ,p_{kl},t_k)|.$$

We introduce the functional

$${\zeta }_N\left[\mathsf{\Psi }\right]=\underset{p_{kl},t_k}{inf}{R}_N(\mathsf{\Psi },p_{kl},t_k),$$

where the lower bound takes over all the nodes $t_k,$ $-1<t_k<1,$ and the coefficients $p_{kl},$ $k=1,2,\dots ,N,$ $l=0,1,\dots ,\rho .$

The quadrature Formula (8) is defined by a set of nodes $t_k^{*},$ $k=1,2,\dots ,N,$ and coefficients $p_{kl}^{*},$ $k=1,2,\dots ,N,$ $l=0,1,\dots ,\rho ,$ called optimal, asymptotically optimal and optimal with respect to order if ${\zeta }_N\left[\mathsf{\Psi }\right]/R_N(p_{kl}^{*},t_k^{*},\mathsf{\Psi })=1,\sim 1,\asymp 1,$ respectively.

In a similar way, the concept of optimal, asymptotically optimal and optimal with respect to order quadrature formulas for evaluating hypersingular integrals is introduced.

Remark 1.

Let $\mathsf{\Psi }=W^r([-1,1],1).$ Let the integral $C\phi$ be evaluated with quadrature formula

$$C\phi =\sum _{k=1}^N\sum _{l=0}^{\rho }{p}_{kl}(t){\phi }^{(l)}(t_k)+R_N(\phi ,t,p_{kl},t_k)$$

with fixed nodes $t_k,$ $k=1,2,\dots ,N,$ and fixed coefficients $p_{kl}(t),$ $k=1,2,\dots ,N,$ $l=0,1,\dots ,\rho .$ In this case, the functional $R_N(\mathsf{\Psi },p_{kl},t_k)$ is equivalent to the Peano constant. Theory of the Peano constants is a very important part of classical numerical theory (see [30]). Comparing the definitions of the Peano constant and optimal quadrature formulas, one can observe that the Peano constant theory is a special case of optimal algorithms theory.

2. Levin’s Method for Evaluating Singular and Hypersingular Integrals with Rapidly Oscillating Kernels

We present an application of Levin’s method for evaluating hypersingular integrals with rapidly oscillating kernels.

Consider the integral

$$\underset{-1}{\overset{1}{\int }}\frac{f(\tau )e^{i\omega g(\tau )}}{{(\tau -t)}^p}d\tau ,-1<t<1,p=1,2,\dots$$

(9)

The integral (9) is associated with the differential equation

$$\frac{d}{d\tau }\left[x(\tau )e^{i\omega g(\tau )}\right]=\frac{f(\tau )e^{i\omega g(\tau )}}{{(\tau -t)}^p},$$

where t is a parameter.

Differentiating the left-hand side, we have

$$x^{\prime }(\tau )e^{i\omega g(\tau )}+i\omega g^{\prime }(\tau )x(\tau )e^{i\omega g(\tau )}=\frac{f(\tau )e^{i\omega g(\tau )}}{{(\tau -t)}^p},$$

moreover, it is enough to consider the equation

$$x^{\prime }(\tau )+i\omega g^{\prime }(\tau )x(\tau )=\frac{f(\tau )}{{(\tau -t)}^p}.$$

(10)

If it is possible to find an analytical solution of Equation (10), then

$$\begin{array}{c}\underset{-1}{\overset{1}{\int }}\frac{f(\tau )e^{i\omega g(\tau )}}{{(\tau -t)}^p}d\tau =\underset{-1}{\overset{1}{\int }}d\left[x(\tau )e^{i\omega g(\tau )}\right]=\hfill \\ =x(1)e^{i\omega g(1)}-x(-1)e^{i\omega g(-1)}.\hfill \end{array}$$

(11)

Note that when solving the differential Equation (11), the singularity can be avoided for $\tau =t.$

Indeed, by the definition of the hypersingular integral, we have

$$\begin{array}{c}\underset{-1}{\overset{1}{\int }}\frac{f(\tau )e^{i\omega g(\tau )}d\tau }{{(\tau -t)}^p}=\underset{\eta \to 0}{lim}\left[\underset{-1}{\overset{t-\eta }{\int }}\frac{f(\tau )e^{i\omega g(\tau )}}{{(\tau -t)}^p}d\tau +\right.\hfill \\ +\left.\underset{t+\eta }{\overset{1}{\int }}\frac{f(\tau )e^{i\omega g(\tau )}}{{(\tau -t)}^p}d\tau +\frac{\phi (\tau )}{{\eta }^{p-1}}\right].\hfill \end{array}$$

(12)

The function $\phi (\tau )$ has continuous derivatives up to $p-1$ order in a neighborhood of zero and is chosen such that the limit exists.

Taking the integrals separately on the right-hand side of (12) and applying the formula (11) to each of them, we have

$$\begin{array}{c}\underset{-1}{\overset{1}{\int }}\frac{f(\tau )e^{i\omega g(\tau )}d\tau }{{(\tau -t)}^p}=\underset{\eta \to 0}{lim}\left[x(1)e^{i\omega g(1)}+x(t-\eta )e^{i\omega g(t-\eta )}-\right.\hfill \\ \left.-x(t+\eta )e^{i\omega g(t+\eta )}-x(-1)e^{i\omega g(-1)}+\frac{\phi (\eta )}{{\eta }^{p-1}}\right].\hfill \end{array}$$

The functions $x(t\pm \eta )e^{i\omega g(t\pm \eta )}$ can be represented as a sum:

$$x(t\pm \eta )e^{i\omega g(t\pm \eta )}=x_1(t\pm \eta )e^{i\omega g(t\pm \eta )}+x_2(t\pm \eta )e^{i\omega g(t\pm \eta )},$$

where the first term tends to infinity as $\eta \to 0$, and the second term tends to the finite limit.

Obviously,

$$\begin{array}{c}\underset{-1}{\overset{1}{\int }}\frac{f(\tau )e^{i\omega g(\tau )}d\tau }{{(\tau -t)}^p}=\underset{\eta \to 0}{lim}\left[x(1)e^{i\omega g(1)}+x_2(t-\eta )e^{i\omega g(t-\eta )}-\right.\hfill \\ \left.-x_2(t+\eta )e^{i\omega g(t+\eta )}-x(-1)e^{i\omega g(-1)}\right].\hfill \end{array}$$

(13)

Assuming that $f(t),g(t)\in W^p([-1,1],M),$ the function $\psi (t)=\underset{-1}{\overset{1}{\int }}\frac{f(\tau )e^{i\omega g(\tau )}d\tau }{{(\tau -t)}^p}$ is continuous at $t\in (-1,1)$ [4]. Then, ${lim}_{\eta \to 0}(x_2(t-\eta )e^{i\omega g(t-\eta )}-x_2(t+\eta )e^{i\omega g(t+\eta )})=0$ and from (13) the final formula follows:

$$\underset{-1}{\overset{1}{\int }}\frac{f(\tau )e^{i\omega g(\tau )}d\tau }{{(\tau -t)}^p}=x(1)e^{i\omega g(1)}-x(-1)e^{i\omega g(-1)}.$$

Thus, the analogue of the Newton–Leibniz formula for hypersingular integrals has been obtained. The application of the Newton–Leibniz formula for hypersingular integrals for certain function classes has been shown in [31].

It follows from the above that for evaluating hypersingular integrals with rapidly oscillating kernels, one can use numerical methods for solving ordinary differential equations.

3. Quadrature Formulas for Evaluating Singular Integrals with Rapidly Oscillating Functions

In this section, we study methods for evaluating the following types of singular integrals with rapidly oscillating functions

$$(C\phi )(t)\equiv \frac{1}{\pi i}\underset{\gamma }{\int }\frac{\phi (\tau ){\tau }^{m}d\tau }{\tau -t},t\in \gamma ,$$

(14)

$$(H\phi )(s)\equiv \underset{0}{\overset{2\pi }{\int }}\phi (\sigma )\{\begin{array}{c}sinm\sigma \hfill \\ cosm\sigma \hfill \end{array}\}ctg\frac{\sigma -s}{2}d\sigma ,s\in [0,2\pi ),$$

(15)

where m is a natural number.

Note that integral (14) is reduced by the Hilbert transformation to integral (15). Therefore, in this section we can restrict ourselves to considering the integral (15).

3.1. Lower Bound Estimates for Quadrature Formula Errors

First, we find a lower bound estimate for the quadrature formula errors using N values of integrands.

The integral (15) will be evaluated using the quadrature formula

$$(H\phi )(s)=\sum _{j=1}^N{p}_j(s)\phi (w_j)+R_N(s,p_j(s),w_j,\phi ).$$

(16)

We find a lower bound estimate of the error for (16) provided that $\phi \in H_1([0,2\pi ],1).$

In doing so, we generalize the method for constructing optimal quadrature formulas for evaluating singular integrals proposed in [1,3].

There are two cases: (1) $N\le 2m;$ (2) $N\ge 2m.$

First, assume $N\le 2m.$

Introduce the nodes $t_k=2k\pi /N,$ $k=0,1,\dots ,N,$ $s_l=l\pi /m,$ $l=0,1,\dots ,2m.$ Note $t_0=t_N,s_0=s_{2m}$.

Let $v_j$ form a union of nodes $t_k,$ $k=0,1,\dots ,N,$ $w_i,$ $i=1,2,\dots ,N,$ and $s_l,$ $l=0,1,\dots ,2m.$ Without loss of generality, assume the sets of nodes $t_k,$ $k=0,1,\dots ,N,$ $w_i,$ $i=1,2,\dots ,N,$ and $s_l=0,1,\dots ,2m,$ do not intersect.

It follows from below that when some nodes coincide, the lower bound error of the quadrature formula does not decrease. Thus, we assume that the number of nodes $v_j$, $j=0,1,\dots ,n-1,$ is equal to $n=2m+2N$.

Let ${\Delta }_k$ be segments ${\Delta }_k=[v_k,v_{k+1}],$ $k=0,1,\dots ,n-1,$ $v_n=v_0.$

To each node $t_k,$ $k=0,1,\dots ,N-1,$ we assign the following function

$${\phi }_k(s)=\left\{\begin{array}{c}(\mathrm{sgn}(sinms))min(|s-v_i|,|v_{i+1}-s|),s\in [v_i,v_{i+1}],[v_i,v_{i+1}]\subset [t_j,t_{j+1}],\\ j=k,k+1,\dots ,k+[N/2]-1;\\ -(\mathrm{sgn}(sinms))min(|s-v_i|,|v_{i+1}-s|),s\in [v_i,v_{i+1}],[v_i,v_{i+1}]\subset [t_j,t_{j+1}],\\ j=k+[N/2]+1,k+[N/2]+2,\dots ,k+N-1;\\ 0,s\in [k+t_{[N/2]-1},k+t_{[N/2]+1}].\end{array}\right.$$

(17)

Then,

$$\begin{array}{c}(H{\phi }_k)(t_k)={\displaystyle \underset{0}{\overset{2\pi }{\int }}}{\phi }_k(\sigma )sinm\sigma ctg\frac{\sigma -t_k}{2}d\sigma \ge \hfill \\ \ge {\displaystyle \sum _{l=1}^{[N/2]-2}}\underset{t_{l+k}}{\overset{t_{l+k+1}}{\int }}{\phi }_k(\sigma )sinm\sigma ctg\frac{\sigma -t_k}{2}d\sigma +\hfill \\ +{\displaystyle \sum _{l=[N/2]+1}^{N-1}}\underset{t_{l+k}}{\overset{t_{l+k+1}}{\int }}{\phi }_k(\sigma )sinm\sigma ctg\frac{\sigma -t_k}{2}\ge \hfill \\ \ge {\displaystyle \sum _{l=1}^{[N/2]-2}}ctg\frac{\pi (l+1)}{N}\underset{t_{l+k}}{\overset{t_{l+k+1}}{\int }}|{\phi }_k(\sigma )||sinm\sigma |d\sigma +\hfill \\ +{\displaystyle \sum _{l=[N/2]+1}^{N-1}}ctg\frac{\pi l}{N}\underset{t_{l+k}}{\overset{t_{l+k+1}}{\int }}|{\phi }_k(\sigma )||sinm\sigma |d\sigma .\hfill \end{array}$$

Let us average the previous inequality over $k,$ $k=0,1,\dots ,N-1.$ We have

$$\begin{array}{c}\underset{0\le l\le N-1}{max}(H{\phi }_l)(t_l)\ge \frac{1}{N}{\displaystyle \sum _{k=0}^{N-1}}(H{\phi }_k)(t_k)\ge \hfill \\ \ge \frac{1}{N}{\displaystyle \sum _{k=0}^{N-1}}{\displaystyle \sum _{l=1}^{[N/2]-2}}ctg\frac{\pi (l+1)}{N}\underset{t_{l+k}}{\overset{t_{l+k+1}}{\int }}|{\phi }_k(\sigma )||sinm\sigma |d\sigma +\hfill \\ +\frac{1}{N}{\displaystyle \sum _{k=0}^{N-1}}{\displaystyle \sum _{[N/2]+1}^{N-1}}ctg\frac{\pi l}{N}\underset{t_{l+k}}{\overset{t_{l+k+1}}{\int }}|{\phi }_k(\sigma )||sinm\sigma |d\sigma =\hfill \\ =\frac{1}{N}{\displaystyle \sum _{l=1}^{[N/2]-2}}ctg\frac{\pi (l+1)}{N}\underset{0}{\overset{2\pi }{\int }}{\phi }^{*}(\sigma )|sinm\sigma |d\sigma +\hfill \\ +\frac{1}{N}{\displaystyle \sum _{l=[N/2]+1}^{N-1}}ctg\frac{\pi l}{N}\underset{0}{\overset{2\pi }{\int }}{\phi }^{*}(\sigma )|sinm\sigma |d\sigma =\hfill \\ =(1+o(1))\frac{2}{N}\underset{0}{\overset{2\pi }{\int }}{\phi }^{*}(\sigma )|sinm\sigma |d\sigma {\displaystyle \sum _{l=1}^{[N/2]-2}}ctg\frac{\pi (l+1)}{N}.\hfill \end{array}$$

(18)

Here, ${\phi }^{*}(\sigma )=min(|\sigma -v_i|,|v_{i+1}-\sigma |),$ $\sigma \in [v_i,v_{i+1}],$ $i=0,1,\dots ,n.$

Estimate from below the integral $\underset{0}{\overset{2\pi }{\int }}{\phi }^{*}(\sigma )|sinm\sigma |d\sigma$ under the following conditions: (1) the function ${\phi }^{*}(\sigma )\in H_1([0,2\pi ],1);$ (2) the function ${\phi }^{*}(\sigma )$ is non-negative; (3) the function ${\phi }^{*}(\sigma )$ vanishes at points $v_k,$ $k=0,1,\dots ,n-1.$

The set of nodes $\left\{v_k\right\}$ is a union of three sets $\left\{t_i\right\},$ $i=0,1,\dots ,N-1,$ $\left\{w_i\right\},$ $i=1,2,\dots ,N,$ $\left\{s_j\right\},$ $j=0,1,\dots ,2m-1.$

Let $N\le m/2.$

Then, there are at least $2m-2N$ segments $[s_l,s_{l+1}],$ in which there are no nodes from the sets $\left\{w_j\right\},j=1,2,\dots ,N$, and $\left\{t_i\right\},$ $i=0,1,\dots ,N-1.$ We call such segments marked.

It is easy to see that in the marked segments

$$\underset{s_l}{\overset{s_{l+1}}{\int }}{\phi }^{*}(\sigma )|sinm\sigma |d\sigma =\underset{0}{\overset{\pi /2m}{\int }}\sigma sinm\sigma d\sigma +\underset{\pi /2m}{\overset{\pi /m}{\int }}(\frac{\pi }{m}-\sigma )sinm\sigma d\sigma =\frac{2}{m^2}.$$

(19)

Thus, for $N\le m/2$, we have the estimate

$$\underset{0}{\overset{2\pi }{\int }}{\phi }^{*}(\sigma )|sinm\sigma |d\sigma \ge (2m-2N)\frac{C}{m^2}=\frac{C}{m}.$$

From this estimate and the inequality (18), we have

$$R_N(H_1([-1,1],1))\ge \frac{C}{mN}\sum _{k=1}^{N-2}ctg\frac{k+1}{N}=\frac{C}{m}lnN.$$

(20)

Here, and below C, are the constants independent of N and $m.$

For $\frac{m}{2}\le N\le 2m$, we must change the proof. Let $\left\{v_i\right\},i=0,1,\dots ,n$ be a union of node sets $\left\{w_k\right\},k=1,2,\dots ,N$ and $\left\{s_l\right\},i=0,1,\dots ,2m$.

Let

$${\phi }^{*}(s)=min(|s-v_i|,|v_{i+1}-s|),s\in [v_i,v_{i+1}],i=0,1,\dots ,n-1.$$

Each node $s_l$ is associated with the function

$${\phi }_l(s)=\left\{\begin{array}{c}(sgn(sinms))min(|s-v_i|,|v_{i+1}-s|),s\in [v_i,v_{i+1}],\hfill \\ [v_i,v_{i+1}]\subset [s_j,s_{j+1}],j=l,l+1,\dots ,m-1;\hfill \\ -(sgn(sinms))min(|s-v_i|,|v_{i+1}-s|),s\in [v_i,v_{i+1}],\hfill \\ [v_i,v_{i+1}]\subset [s_j,s_{j+1}],j=m+1,\dots ,2m-1.\hfill \end{array}\right.$$

Then,

$$\begin{array}{c}(H{\phi }_l)(s_l)\ge \sum _{k=1}^{m-2}ctg\frac{\pi (k+1)}{m}{\int }_{s_{l+k}}^{s_{l+k+1}}|{\phi }_l(\sigma )||sinm\sigma |d\sigma +\hfill \\ +\sum _{k=m+1}^{2m-1}ctg\frac{k\pi l}{m}{\int }_{t_{l+k}}^{t_{l+k+1}}|{\phi }_l(\sigma )||sinm\sigma |d\sigma .\hfill \end{array}$$

Averaging the previous inequality over $l,l=0,1,\dots ,2m-1,$ we have

$$\begin{array}{c}\underset{0\le l\le 2m-1}{max}(H{\phi }_l)(s_l)\ge \frac{1}{2m}\sum _{k=1}^{m-2}ctg\frac{\pi (k+1)}{m}{\int }_0^{2\pi }{\phi }^{*}(\sigma )|sinm\sigma |d\sigma +\hfill \\ \frac{1}{2m}\sum _{k=m+1}^{2m-1}ctg\frac{k\pi }{m}{\int }_0^{2\pi }{\phi }^{*}(\sigma )|sinm\sigma |d\sigma =\hfill \\ =(1+o(1))\frac{1}{m}{\int }_0^{2\pi }{\phi }^{*}(\sigma )|sinm\sigma |d\sigma \sum _{k=1}^{m-2}ctg\frac{\pi (k+1)}{m}.\hfill \end{array}$$

(21)

Estimate from below the integral

$${\int }_0^{2\pi }{\phi }^{*}(\sigma )|sinm\sigma |d\sigma .$$

The integral takes the smallest value if in each interval $(s_i,s_{i+1})$ there is at most one node $w_j,j=1,2,\dots ,N$.

It was shown above (19) that if there are no nodes $w_j,j=1,2,\dots ,N$ in $(s_i,s_{i+1})$, then

$${\int }_{s_i}^{s_{i+1}}{\phi }^{*}(\sigma )|sinm\sigma |d\sigma =\frac{2}{m^2}.$$

(22)

Next, consider the case when the interval $(s_i,s_{i+1})$ contains more than one node from $\left\{w_j\right\},j=1,2,\dots ,N$. Without loss of generality, we assume $N=2m$.

First, let the interval $(s_i,s_{i+1})$ contain one node from the set $\left\{w_j\right\},j=1,2,\dots ,N$. Obviously,

$$\begin{array}{c}{\int }_{s_i}^{s_{i+1}}{\phi }^{*}(\sigma )|sinm\sigma |d\sigma \ge 2{\int }_{s_i}^{s_i+\frac{\pi }{4m}}(\sigma -s_i)|sinm\sigma |d\sigma +\hfill \\ +2{\int }_{s_i+\frac{\pi }{4m}}^{s_i+\frac{\pi }{2m}}(s_i+\frac{\pi }{2m}-\sigma )|sinm\sigma |d\sigma =\hfill \\ =\frac{2}{m^2}\left|2sinm\frac{2s_i+\frac{\pi }{2m}}{2}-sinm{s}_i-sinm\left(s_i+\frac{\pi }{2m}\right)\right|=\hfill \\ =\frac{2}{m^2}\left|2sinm\left(s_i+\frac{\pi }{4m}\right)-sinm{s}_i-sinm\left(s_i+\frac{\pi }{2m}\right)\right|=\hfill \\ =\frac{2}{m^2}\left|2cosi\pi sin\frac{\pi }{4}-(cosi\pi )sin\frac{\pi }{2}\right|=\hfill \\ =\frac{2}{m^2}{|(-1)}^i\sqrt{2}-{(-1)}^i|=\frac{2}{m^2}|\sqrt{2}-1|\approx \frac{2}{m^2}0.41.\hfill \end{array}$$

(23)

Assume now that the interval $(s_i,s_{i+1})$ contains two nodes from $\left\{w_j\right\},j=1,2,\dots ,N$. This means there is an interval $(s_l,s_{l+1}),$ which does not contain nodes from $\left\{w_j\right\},j=1,2,\dots ,N$.

From (22) and (23), we have

$$\begin{array}{c}{\int }_{s_i}^{s_{i+1}}{\phi }^{*}(\sigma )|sinm\sigma |d\sigma +{\int }_{s_l}^{s_{l+1}}{\phi }^{*}(\sigma )|sinm\sigma |d\sigma =\hfill \\ =\frac{2}{m^2}+{\int }_{s_l}^{s_{l+1}}{\phi }^{*}(\sigma )|sinm\sigma |d\sigma \ge \frac{2}{m^2}0.82.\hfill \end{array}$$

Thus, the minimum of the integral ${\int }_0^{2\pi }{\phi }^{*}(\sigma )|sinm\sigma |d\sigma$ is achieved under the assumption that each interval has at most one node $\left\{w_j\right\},j=1,2,\dots ,N$.

Other cases for the distribution of nodes $w_j,j=1,2,\dots ,N$ over intervals $(s_i,s_{i+1}),i=0,1,\dots ,2m-1$ are studied similarly.

Thus, from (21)–(23), we have for $\frac{m}{2}\le N\le 2m$

$$R_N(H_1([-1,1],1))\ge \frac{C}{m^2}\sum _{k=1}^{m-2}ctg\frac{(k+1)\pi }{m}=\frac{C}{m}lnm=\frac{C}{N}lnN.$$

From this estimate and the inequality (20), we have for $N\le 2m$

$$R_N(H_1([-1,1],1))\ge \frac{C}{m^2}\sum _{k=1}^{m-2}ctg\frac{(k+1)\pi }{m}=\frac{C}{m}lnN.$$

(24)

For the second case, consider $N\ge 2m.$ It is enough to introduce additional nodes $t_k=2k\pi /q,k=0,1,\dots ,q,q=3N.$ Let the set $v_k,$ $v_k=0,1,\dots ,n,$ $n=N+2m+q=4N+2m,$ be the union of nodes $w_i,i=1,2,\dots ,N,$ $s_j,j=0,1,\dots ,2m,$ $t_l,l=0,1,\dots ,q.$ Each node $t_k,k=0,1,\dots ,q-1,$ is associated with the function ${\psi }_k(s),$ constructed by analogy with the function ${\phi }_k(s)$ (see (17)). It is easy to see that there are at least N intervals $(t_l,t_{l+1}),$ in which there are no nodes from the sets $s_l,$ $i=0,1,\dots ,2m,$ and $w_j,j=1,2,\dots ,N.$

Repeating the above arguments yields

$$R_N\left[H_1(1)\right]\ge \frac{C}{N^2}\sum _{k=1}^{q-1}ctg\frac{\pi (k+1)}{2q}=\frac{C}{N}lnN.$$

(25)

From the inequalities (24) and (25), the next statement follows.

Theorem 1.

Let $\phi (t)\in H_1(1).$ For all possible quadrature formulas of the form (16) using N nodes, the following estimate holds

$$R_N(H_1([0,2\pi ],1))\ge \{\begin{array}{c}{C}_1\frac{lnN}{m},N\le 2m;\hfill \\ C_2\frac{lnN}{N},N\ge 2m,\hfill \end{array}$$

(26)

where $C_1,C_2$ are constants independent of N.

Making the proof more difficult yields the following statement.

Theorem 2.

Let be $\phi (t)\in H_{\alpha }(1),0<\alpha \le 1.$ For all possible quadrature formulas of the form (16) using N nodes, the following estimate holds:

$$R_N(H_{\alpha }([0,2\pi ],1))\ge \{\begin{array}{c}{C}_1\frac{lnN}{m^{\alpha }},N\le 2m;\hfill \\ C_2\frac{lnN}{N^{\alpha }},N\ge 2m.\hfill \end{array}$$

(27)

Estimate from below the error of quadrature formulas of (16) on the $W^r([0,2\pi ],1),$ $r=1,2,\dots$ class.

In order to simplify the presentation, we give the proof for $N/2\le m$ only.

We introduce the nodes $\left\{t_k\right\},$ $t_k=2k\pi /N,k=0,1,\dots ,N-1;$ $w_j,j=1,2,\dots ,N;$ $\left\{s_k\right\},$ $k=0,1,\dots ,2m-1;$ $\left\{v_j\right\},$ $j=1,2,\dots ,n,$ $n=2N+2m.$

To each node $t_k,$ $k=0,1,\dots ,N-1$ we assign the function

$${\phi }_k(s)=\left\{\begin{array}{c}A\frac{{(s-v_l)}^r{(v_{l+1}-s)}^r}{h_l^r}\mathrm{sgn}sin\mathrm{ms},\mathrm{s}\in [{\mathrm{v}}_{\mathrm{l}},{\mathrm{v}}_{\mathrm{l}+1}],[{\mathrm{v}}_{\mathrm{l}},{\mathrm{v}}_{\mathrm{l}+1}]\in [{\mathrm{t}}_{\mathrm{j}},{\mathrm{t}}_{\mathrm{j}+1}]\\ j=k,k+1,\dots ,k+[N/2]-1;\\ -A\frac{{(s-v_l)}^r{(v_{l+1}-s)}^r}{h_l^r}\mathrm{sgn}sin\mathrm{ms},\mathrm{s}\in [{\mathrm{v}}_{\mathrm{l}},{\mathrm{v}}_{\mathrm{l}+1}],[{\mathrm{v}}_{\mathrm{l}},{\mathrm{v}}_{\mathrm{l}+1}]\in [{\mathrm{t}}_{\mathrm{j}},{\mathrm{t}}_{\mathrm{j}+1}]\\ j=k+[n/2]+1,k+[N/2]+2,\dots ,k+N-1;\\ 0,s\in [v_{k+[N/2]-1]},[v_{k+[N/2]+1]},\end{array}\right.$$

$h_l=|v_{l+1}-v_l|,l=0,1,\dots ,n-1.$

Estimating the integral

$$\underset{0}{\overset{2\pi }{\int }}{\phi }_k(\sigma )sinm\sigma ctg\frac{\sigma -t_k}{2}d\sigma$$

and then averaging the result over $k,$ $k=0,1,\dots ,N-1,$ we obtain the required estimate for $N/2\le m$.

Theorem 3.

Let $\phi \in W^r([0,2\pi ],1).$ For all possible quadrature formulas of the form (16) using N nodes, the following estimate holds:

$$R_N(W^r([0,2\pi ],1))\ge \{\begin{array}{c}{C}_1\frac{lnN}{m^r},N\le 2m;\hfill \\ C_2\frac{lnN}{N^r},N\ge 2m.\hfill \end{array}$$

(28)

3.2. Quadrature Formulas

Let us construct quadrature formulas for evaluating integrals of (15).

We start by considering singular integrals with the Hilbert kernel:

$$\frac{1}{2\pi }{\int }_0^{2\pi }f(\sigma )\left\{\begin{array}{c}cosm\sigma \\ sinm\sigma \end{array}\right\}ctg\frac{\sigma -s}{2}d\sigma ,$$

where $f\in W^r([0,2\pi ],M),M$ is an integer.

First, we consider the integral

$$Hf=\frac{1}{2\pi }{\int }_0^{2\pi }f(\sigma )sinm\sigma ctg\frac{\sigma -s}{2}d\sigma .$$

The function $f(s)$ is approximated by the interpolation polynomial

$$f_n(s)=\sum _{k=0}^{2n}f(s_k){\psi }_k(s),$$

where ${\psi }_k(s)=\frac{1}{2n+1}\frac{sin\frac{2n+1}{2}(s-s_k)}{sin\frac{s-s_k}{2}}=\frac{1}{2n+1}(1+2cos(s-s_k)+\dots +2cosn(s-s_k)).$

We have for $m>n$

$$\begin{array}{c}Hf=\frac{1}{2n+1}\sum _{k=0}^{2n}f(s_k)\frac{1}{2\pi }{\int }_0^{2\pi }sinm\sigma ctg\frac{\sigma -s}{2}d\sigma +\hfill \\ +\frac{1}{2n+1}\sum _{k=0}^{2n}f(s_k)\frac{1}{\pi }{\int }_0^{2\pi }\sum _{l=1}^{n}cosl(\sigma -s_k)sinm\sigma ctg\frac{\sigma -s}{2}d\sigma +R_n(f)=\hfill \\ =\frac{1}{2n+1}\sum _{k=0}^{2n}f(s_k)cosms+\frac{1}{2n+1}\sum _{k=0}^{2n}f(s_k)\frac{1}{2\pi }{\int }_0^{2\pi }\sum _{l=1}^n[(sin(m+l)\sigma )(cosl{s}_k)-\hfill \\ -(cos(m+l)\sigma )(sinl{s}_k)+\hfill \\ +(sin(m-l)\sigma )(cosl{s}_k)-(cos(m-l)\sigma )(sinl{s}_k)]ctg\frac{\sigma -s}{2}d\sigma +R_n(f)=\hfill \\ =\frac{1}{2n+1}\sum _{k=0}^{2n}f(s_k)cosms+\frac{1}{2n+1}\sum _{k=0}^{2n}f(s_k)\sum _{l=1}^n[(cos(m+l)s)(cosl{s}_k)+\hfill \\ +(sin(m+l)s)(sinl{s}_k)+(cos(m-l)s)(cosl{s}_k)+sin(m-l)s)(sinl{s}_k)]+R_n(f)=\hfill \\ =\frac{1}{2n+1}\sum _{k=0}^{2n}f(s_k)\left[cosms+\right.\hfill \\ +\left.2\sum _{l=1}^n[(cosms)(cosls)(cosl{s}_k)+(cosms)(sinls)(sinl{s}_k)]\right]=\hfill \\ =\frac{1}{2n+1}\left[cosms\sum _{k=0}^{2n}f(s_k)\left[1+2\sum _{l=1}^{n}cosl(s-s_k)\right]\right]=\hfill \\ =cosms\sum _{k=0}^{2n}f(s_k){\psi }_k(s)=(cosms)f_n(s).\hfill \end{array}$$

(29)

Above, we used ([32], p.36)

$$\frac{1}{2\pi }{\int }_{-\pi }^{\pi }{e}^{im\sigma }ctg\frac{\sigma -s}{2}d\sigma =\left\{\begin{array}{c}0,m=0\\ i{e}^{ims},m>0\\ -i{e}^{ims},m<0\end{array}\right.$$

for m integer.

Next, consider the integral

$$Kf=\frac{1}{2\pi }{\int }_0^{2\pi }f(\sigma )cosm\sigma ctg\frac{\sigma -s}{2}d\sigma .$$

As above, the function $f(s)$ is approximated by the interpolation polynomial $f_n(s)$.

Obviously, for $m>n$,

$$\begin{array}{c}Kf=\frac{1}{2n+1}\sum _{k=0}^{2n}f(s_k)\frac{1}{2\pi }{\int }_0^{2\pi }cosm\sigma ctg\frac{\sigma -s}{2}d\sigma +\hfill \\ +\frac{1}{2n+1}\sum _{k=0}^{2n}f(s_k)\left[\sum _{l=1}^n\frac{1}{\pi }{\int }_0^{2\pi }cosl(\sigma -s_k)cosm\sigma ctg\frac{\sigma -s}{2}d\sigma \right]+R_n(f)=\hfill \\ =-\frac{1}{2n+1}\sum _{k=0}^{2n}f(s_k)\left[sinms-cosmscosec\frac{s-s_k}{2}\left[cos\frac{s-s_k}{4}+cos\frac{2n+1}{2}\frac{(s-s_k)}{2}\right]\right]+R_n(f).\hfill \end{array}$$

(30)

Now, we study error estimates for constructed quadrature formulas. It is enough to consider the quadrature Formula (29). It is easy to see that the error of (29) is estimated by the inequality

$$\begin{array}{c}|R_n(f)|=\left|\frac{1}{2\pi }{\int }_0^{2\pi }{\psi }_n(\sigma )sinm\sigma ctg\frac{\sigma -s}{2}d\sigma \right|\le \hfill \\ \le \left|\frac{1}{2\pi }{\int }_0^{2\pi }({\psi }_n(\sigma )-{\psi }_n(s))sinm\sigma ctg\frac{\sigma -s}{2}d\sigma \right|+\left|\frac{1}{2\pi }{\psi }_n(s){\int }_0^{2\pi }sinm\sigma ctg\frac{\sigma -s}{2}d\sigma \right|=\hfill \\ =I_1(s)+I_2(s).\hfill \end{array}$$

Here, ${\psi }_n(s)=f(s)-f_n(s)$.

Evaluate each term separately,

$$I_2(s)=|{\psi }_n(s)cosms|\le C{E}_n(f)lnn,$$

where $E_n(f)$ is the best approximation in the uniform metric for the function f by nth-order trigonometric polynomials

$$\begin{array}{c}{I}_1(s)\le \left|\frac{1}{2\pi }{\int }_0^{2\pi }|{\psi }_n(\sigma )-{\psi }_n{(s)|}^{1-\beta }|{\psi }_n(\sigma )-{\psi }_n{(s)|}^{\beta }|sinm\sigma ||ctg\frac{\sigma -s}{2}|d\sigma \right|\le \hfill \\ \le \left|\frac{1}{2\pi }{\int }_0^{2\pi }|{\psi }_n(\sigma )-{\psi }_n{(s)|}^{1-\beta }|{\psi }_n^{{}^{\prime }}{(s+\theta (\sigma -s)(\sigma -s))|}^{\beta }|ctg\frac{\sigma -s}{2}|d\sigma \right|\le \hfill \\ \le C(\underset{0\le s\le 2\pi }{max}|{\psi }_n{(s)|)}^{1-\beta }(\underset{0\le s\le 2\pi }{max}|{\psi }_n^{{}^{\prime }}(s){|)}^{\beta }{\int }_0^{2\pi }\frac{d\sigma }{{(\sigma -s)}^{1-\beta }}d\sigma \le \hfill \\ \le \frac{C}{\beta }(\underset{0\le s\le 2\pi }{max}|{\psi }_n{(s)|)}^{1-\beta }(\underset{0\le s\le 2\pi }{max}|{\psi }_n^{{}^{\prime }}(s){|)}^{\beta }.\hfill \end{array}$$

The following statement is well known.

Theorem 4

([33]). Let $f(t)\in \tilde{C}[0,2\pi ],P_n(t)$ be an n-order trigonometric polynomial satisfying the inequality $|f(t)-P_n(t)|\le {\eta }_n.$

Then, $|f^{\prime }(t)-P_n^{\prime }(t)|\le Cn{\eta }_n,$ where C is a constant independent of n.

Thus

$$(\underset{0\le s\le 2\pi }{max}|{\psi }_n^{{}^{\prime }}(s){|)}^{\beta }\le C{(E_n(f)lnn)}^{\beta }.$$

Setting $\beta =\frac{1}{lnn}$, we have

$$I_2\le C{E}_n(f){ln}^{2}n.$$

From the estimates $I_1$ and $I_2$, we have

$$|R_n(f)\le C{E}_n(f){ln}^{2}n,$$

and, therefore, on the function class $W^r{H}_{\alpha }([0,2\pi ],M).$

$$R_n(W^r{H}_{\alpha })\le C\frac{{ln}^{2}n}{n^{r+\alpha }}.$$

(31)

The final estimate is valid for any $m\ge 1$.

Now, we consider the following quadrature formula for $Hf$ evaluation.

We approximate the function $f(s)$ by the polygon $f_N(s)$, constructed on the nodes $t_k=2k\pi /N,k=0,1,\dots ,N.$

The integral $Hf$ will be evaluated using the quadrature formula

$$(Hf)(s)\equiv \underset{0}{\overset{2\pi }{\int }}{f}_N(\sigma )sinm\sigma ctg\frac{\sigma -s}{2}d\sigma +R_N(s,p_k(s),t_k,f).$$

(32)

The error of (32) is estimated by

$$|R_N(s,s_k,f)|\le |\sum _{l=0}^{N-1}\underset{t_l}{\overset{t_{l+1}}{\int }}(f(\sigma )-f_N(\sigma ))sinm\sigma ctg\frac{\sigma -s}{2}d\sigma |.$$

(33)

Consider two cases: (1) $2m\le N,$ (2) $N<2m$.

Start with the first one.

Let be $s\in {\Delta }_j,{\Delta }_k=[t_k,t_{k+1}],k=0,1,\dots ,N-1.$

Estimate the integral

$$J_1=|\underset{t_l}{\overset{t_{l+1}}{\int }}{\psi }_N(\sigma )sinm\sigma ctg\frac{\sigma -s}{2}d\sigma |$$

(34)

for $j\ne l-1,l,l+1$.

Set ${\psi }_N(s)=f(s)-f_N(s).$ Obviously, ${\psi }_N(t_l)={\psi }_N(t_{l+1})=0$.

Obviously,

$$\begin{array}{c}|\underset{t_l}{\overset{t_{l+1}}{\int }}{\psi }_N(\sigma )sinm\sigma ctg\frac{\sigma -s}{2}d\sigma |\le \hfill \\ \le \underset{t_l}{\overset{t_{l+1}}{\int }}|{\psi }_N(\sigma )||ctg\frac{\sigma -s}{2}|d\sigma \le \frac{2\pi }{N^2}max(|ctg\frac{(l-j-1)\pi }{N}|,|ctg\frac{(j-l-1)\pi }{N}|).\hfill \end{array}$$

(35)

Let $s\in {\Delta }_j,j=l.$ Estimate the integral

$$J_2=\underset{t_{l-1}}{\overset{t_{l+2}}{\int }}{\psi }_N(\sigma ))sinm\sigma ctg\frac{\sigma -s}{2}d\sigma .$$

Let $d=min(|t_{l+2}-s|,|s-t_{l-1}|)$. Set $d=|s-t_{l-1}|$.

Represent the previous integral as

$$\begin{array}{c}{J}_2=\underset{t_{l-1}}{\overset{t_{l+2}}{\int }}{\psi }_N(\sigma ))sinm\sigma ctg\frac{\sigma -s}{2}d\sigma =\hfill \\ =\underset{t_{l-1}}{\overset{s+d}{\int }}{\psi }_N(\sigma ))sinm\sigma ctg\frac{\sigma -s}{2}d\sigma +\hfill \\ +\underset{s+d}{\overset{t_{l+2}}{\int }}{\psi }_N(\sigma ))sinm\sigma ctg\frac{\sigma -s}{2}d\sigma =J_{21}+J_{22}.\hfill \end{array}$$

(36)

Estimate each of the integrals $J_{21},J_{22}$ separately.

Obviously,

$$|J_{22}|\le \underset{s+d}{\overset{t_{l+2}}{\int }}|{\psi }_N(\sigma )||ctg\frac{\sigma -s}{2}|d\sigma \le \frac{4{\pi }^2}{N^2}ctg\frac{\pi }{N}.$$

(37)

Estimate the integral $J_{21}$. We have

$$\begin{array}{c}|J_{21}|=|\underset{s_{l-1}}{\overset{s+d}{\int }}{\psi }_N(\sigma )sinm\sigma ctg\frac{\sigma -s}{2}d\sigma |\le \hfill \\ \le |\underset{t_{l-1}}{\overset{s+d}{\int }}({\psi }_N(\sigma )-{\psi }_N(s))sinm\sigma ctg\frac{\sigma -s}{2}d\sigma |+\hfill \\ +|\underset{s_{l-1}}{\overset{s+d}{\int }}{\psi }_N(s)(sinm\sigma -sinms)ctg\frac{\sigma -s}{2}d\sigma |=J_{211}+J_{212}.\hfill \end{array}$$

(38)

Estimate $J_{211},j_{212}$.

Obviously,

$$J_{211}\le \underset{t_{l-1}}{\overset{s+d}{\int }}|{\psi }_N(\sigma )-{\psi }_N(s)||ctg\frac{\sigma -s}{2}|d\sigma \le \frac{6{\pi }^2}{N},$$

(39)

$$J_{212}\le \underset{s_{l-1}}{\overset{s+d}{\int }}|{\psi }_N(s)||sinm\sigma -sinms||ctg\frac{\sigma -s}{2}|d\sigma \le \frac{6{\pi }^{2}m}{N^2}.$$

(40)

From inequalities (36)–(40), it follows

$$|J_2|\le \frac{C}{N}.$$

(41)

From inequalities (33)–(41), it follows that for $2m<N$ the inequality holds

$$R_N(H_1(1))\le \frac{ClnN}{N}.$$

(42)

The inequality

$$R_N(H_{\alpha }(1))\le \frac{ClnN}{N^{\alpha }}$$

(43)

is proved in a similar way.

Consider the second case, $N<2m$. Let $s\in {\Delta }_j,{\Delta }_k=[t_k,t_{k+1}],k=0,1,\dots ,N-1.$

Estimating (34), we again consider two cases, $j\ne l-1,l,l+1$ and $j=l$.

For the first one, after making some calculations, it can be shown that the largest error is yielded for functions of the form ${\psi }_N(s)=(min(s-s_i,s_{i+1}-s)\mathrm{sgn}sin\mathrm{ms},$ $s\in [s_i,s_{i+1}],s_i=\pi i/m,i=0,1,\dots ,2m$.

Then,

$$J_1=|\underset{t_l}{\overset{t_{l+1}}{\int }}{\psi }_N(\sigma )sinm\sigma ctg\frac{\sigma -s}{2}d\sigma |\le \frac{2{\pi }^2}{m^2}max(|ctg\frac{(l-j+1)\pi }{N}|,|ctg\frac{(j-l-1)\pi }{N}|).$$

(44)

Now, let $j=l,s\in [t_j,t_{j+1}]$ and $s\in [s_v,s_{v+1}].$

We represent the integral $J_1$ as

$$\begin{array}{c}{J}_1\le |\underset{t_{j-1}}{\overset{s_{v-1}}{\int }}{\psi }_N(\sigma )sinm\sigma ctg\frac{\sigma -s}{2}d\sigma |+\hfill \\ +|\underset{s_{v-1}}{\overset{s_{v+2}}{\int }}{\psi }_N(\sigma )sinm\sigma ctg\frac{\sigma -s}{2}d\sigma |+|\underset{s_{v+2}}{\overset{t_{j+1}}{\int }}{\psi }_N(\sigma )sinm\sigma ctg\frac{\sigma -s}{2}d\sigma |=\hfill \\ =J_{11}+J_{12}+J_{13}.\hfill \end{array}$$

Obviously,

$$\begin{array}{c}{J}_{11}\le C\frac{1}{m^2}{\displaystyle \sum _{l=1}^{L-1}}ctg\frac{l\pi }{2m}\le \frac{C}{m}lnm;\hfill \\ J_{13}\le C\frac{1}{m^2}{\displaystyle \sum _{l=1}^{L-1}}ctg\frac{l\pi }{2m}\le \frac{C}{m}lnm;\hfill \\ J_{12}=|\underset{s_{v-1}}{\overset{s_{v+2}}{\int }}({\psi }_N(\sigma )sinm\sigma -{\psi }_N(s)sinms)ctg\frac{\sigma -s}{2}d\sigma |\le \frac{C}{m},\hfill \end{array}$$

where $L=\lceil 2m/N\rceil$.

Making calculations similar to those above, we obtain the estimate

$$J_1\le \{\begin{array}{c}{C}_1\frac{1}{N}lnN,2m\le N;\hfill \\ C_2\frac{1}{m}lnm,N\le 2m,\hfill \end{array}$$

(45)

where constants $C_1,C_2$ are independent of N.

Theorem 1 and inequalities (33)–(45) yield the following statement.

Theorem 5.

Among all quadrature formulas of the form (16) using N nodes, the optimal with respect to order on the function class $H_1(1)$ turns out to be Formula (32). The estimate is valid:

$$R_N(H_1(1))\le \{\begin{array}{c}{C}_1\frac{1}{N}lnN,2m\le N;\hfill \\ C_2\frac{1}{m}lnm,N\le 2m,\hfill \end{array}$$

where constants $C_1,C_2$ are independent of N.

Similarly, we can prove the following.

Theorem 6.

Among all quadrature formulas of the form (16) using N nodes, the optimal with respect to order on the function class $H_{\alpha }(1)$ turns out to be Formula (32). The estimate holds:

$$R_N(H_{\alpha }(1))\le \{\begin{array}{c}{C}_1\frac{1}{N^{\alpha }}lnN,2m\le N;\hfill \\ C_2\frac{1}{m^{\alpha }}lnm,N\le 2m,\hfill \end{array}$$

where constants $C_1,C_2$ are independent of N.

Using the Hilbert transformation, we obtain

$$\begin{array}{c}Cf=\frac{1}{\pi i}{\int }_{\gamma }\frac{f(\tau ){\tau }^m}{\tau -t}d\tau =\hfill \\ =\frac{1}{2\pi i}{\int }_0^{2\pi }f(e^{i\sigma })cosm\sigma ctg\frac{\sigma -s}{2}d\sigma +\frac{1}{2\pi }{\int }_0^{2\pi }f(e^{i\sigma })sinm\sigma ctg\frac{\sigma -s}{2}d\sigma +\hfill \\ +\frac{1}{2\pi }{\int }_0^{2\pi }f(e^{i\sigma })cosm\sigma d\sigma +\frac{i}{2\pi }{\int }_0^{2\pi }f(e^{i\sigma })sinm\sigma d\sigma .\hfill \end{array}$$

To evaluate the integral $Cf$, we use the quadrature formula

$$\begin{array}{c}Cf=\frac{1}{2\pi i}{\int }_0^{2\pi }{P}_n\left[f(e^{i\sigma })\right]cosm\sigma ctg\frac{\sigma -s}{2}d\sigma +\hfill \\ +\frac{1}{2\pi }{\int }_0^{2\pi }{P}_n\left[f(e^{i\sigma })\right]sinm\sigma ctg\frac{\sigma -s}{2}d\sigma +\hfill \\ +\frac{1}{2\pi }{\int }_0^{2\pi }{P}_n\left[f(e^{i\sigma })\right]cosm\sigma d\sigma +\frac{i}{2\pi }{\int }_0^{2\pi }{P}_n\left[f(e^{i\sigma })\right]sinm\sigma d\sigma +R_n\left[f\right],\hfill \end{array}$$

(46)

where $P_n$ is a projection operator onto a set of interpolating trigonometric polynomials on nodes $s_k=2\pi k/(2n+1),k=0,1,\dots ,2n$.

The error of (46) is estimated by

$$\begin{array}{c}|R_n(f)|\le \left|\frac{1}{2\pi }{\int }_0^{2\pi }{\psi }_n(\sigma )cosm\sigma ctg\frac{\sigma -s}{2}d\sigma \right|+\hfill \\ +\left|\frac{1}{2\pi }{\int }_0^{2\pi }{\psi }_n(\sigma )sinm\sigma ctg\frac{\sigma -s}{2}d\sigma \right|+\hfill \\ +\left|\frac{1}{2\pi }{\int }_0^{2\pi }{\psi }_n(\sigma )cosm\sigma d\sigma \right|+\left|\frac{1}{2\pi }{\int }_0^{2\pi }{\psi }_n(\sigma )sinm\sigma d\sigma \right|=\hfill \\ =I_1+I_2+I_3+I_4,\hfill \end{array}$$

(47)

where ${\psi }_n(t)=f(t)-P_n\left[f\right](t).$

The estimates $I_1$ and $I_2$ have been obtained above (see (31)).

The estimates hold:

$$I_3\le C{E}_n(f)lnn,$$

(48)

$$I_4\le C{E}_n(f)lnn.$$

(49)

The inequalities (31), (48) and (49) yield the estimate

$$|R_n(f)\le C{E}_n(f){ln}^{2}n.$$

(50)

Transform the integrals

$$\frac{1}{2\pi i}{\int }_0^{2\pi }{P}_n\left[f(e^{i\sigma })\right]cosm\sigma ctg\frac{\sigma -s}{2}d\sigma$$

and

$$\frac{1}{2\pi i}{\int }_0^{2\pi }{P}_n\left[f(e^{i\sigma })\right]sinm\sigma ctg\frac{\sigma -s}{2}d\sigma .$$

It was shown above that

$$\begin{array}{c}\frac{1}{2\pi i}{\int }_0^{2\pi }{P}_n\left[f(e^{i\sigma })\right]sinm\sigma d\sigma =P_n\left[f(e^{is})\right]cosms=\hfill \\ =(cosms)\frac{1}{2n+1}\sum _{k=0}^{2n}f(e^{i{s}_k})\left[1+2\sum _{l=1}^{m}cosl(s-s_k)\right]=\hfill \\ \frac{1}{2}\left(e^{ims}+e^{-ims}\right)\frac{1}{2n+1}\sum _{k=0}^{2n}f(e^{i{s}_k})\left[1+\sum _{l=1}^m\left(e^{il(s-s_k)}+e^{-il(s-s_k)}\right)\right]=\hfill \\ =\frac{1}{2}\left(t^m+t^{-m}\right)\frac{1}{2n+1}\sum _{k=0}^{2n}f(t_k)\left[1+\sum _{l=1}^m\left(\frac{t^l}{t_k^l}+\frac{t_k^l}{t^l}\right)\right];\hfill \end{array}$$

(51)

$$\begin{array}{c}\frac{1}{2\pi i}{\int }_0^{2\pi }{P}_n\left[f(e^{i\sigma })\right]cosm\sigma d\sigma =\hfill \\ =-\frac{1}{2n+1}\sum _{k=0}^{2n}f(e^{i{s}_k})\left[sinms+2cosms\sum _{l=1}^{m}sinl(s-s_k)\right]=\hfill \\ =-\frac{1}{2}\sum _{k=0}^{2n}f(t_k)\left[\frac{1}{2i}\left(e^{ims}+e^{-ims}\right)+\left(e^{ims}+e^{-ims}\right)\times \right.\hfill \\ \left.\times \sum _{l=1}^n\frac{1}{2i}\left(e^{il(s-s_k)}+e^{-il(s-s_k)}\right)\right]=\hfill \\ =-\frac{1}{2n+1}\sum _{k=0}^{2n}f(t_k)\left[\frac{1}{2i}\left(t^m-t^{-m}\right)+\left(t^m-t^{-m}\right)\sum _{l=1}^n\frac{1}{2i}\left(\frac{t^l}{t_k^l}-\frac{t_k^l}{t^l}\right)\right].\hfill \end{array}$$

(52)

Thus, the following quadrature formula is valid:

$$\begin{array}{c}C\phi =\frac{1}{2}\left(t^m-t^{-m}\right)\frac{1}{2n+1}\sum _{k=0}^{2n}f(t_k)\left[1+\sum _{l=1}^m\left(\frac{t^l}{t_k^l}-\frac{t_k^l}{t^l}\right)\right]-\hfill \\ -\frac{1}{i}\frac{1}{2n+1}\sum _{l=1}^{2n}f(t_k)\left[\frac{1}{2i}\left(t^m-t^{-m}\right)+\left(t^m-t^{-m}\right)\sum _{l=1}^n\frac{1}{2i}\left(\frac{t^l}{t_k^l}-\frac{t_k^l}{t^l}\right)\right]+\hfill \\ +\frac{1}{2\pi }{\int }_0^{2\pi }{P}_n\left[f(e^{i\sigma })\right]cosm\sigma d\sigma +\frac{1}{2\pi }{\int }_0^{2\pi }{P}_n\left[f(e^{i\sigma })\right]sinm\sigma d\sigma +R_n(f).\hfill \end{array}$$

(53)

Estimates (48)–(50) hold:

$$|R_n(f)|\le C{E}_n(f){ln}^{2}n,$$

where $E_n(f)$ is the best uniform approximation of the function f by trigonometric polynomials of order n.

Let us take a look at an illustration of the quadrature formulas we have discussed. Consider an integral

$$J_m(s)=\frac{1}{2\pi }{\int }_{-\pi }^{\pi }\frac{\sigma (\sigma -2\pi )(\sigma -\pi )}{12}sinm\sigma ctg\frac{\sigma -s}{2}d\sigma =cosms\sum _{k=1}^{\infty }\frac{sinks}{k^3}$$

(54)

where m is integer. Let us apply the quadrature Formula (29) for evaluation of the integral:

$$J_m(s)=\frac{1}{2n+1}cosms\sum _{k=0}^{2n}f(s_k)\left[1+2\sum _{l=0}^{n}cosl(s-s_k)\right],$$

(55)

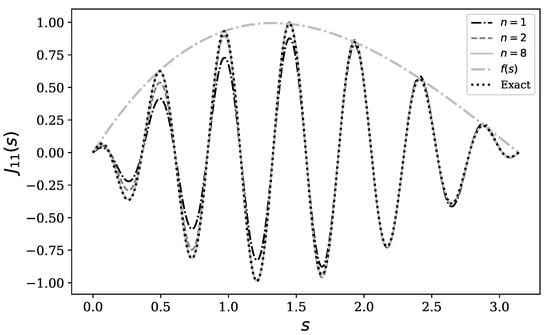
where $f(s)=\frac{s(s-2\pi )(s-\pi )}{12}$ and $s_k=\frac{2k\pi }{2n+1}$ for $k=0,1,\dots ,2n$. We present the results of evaluation of the integral by series summation and by quadrature formula in Figure 1. We observe rapid convergence of the quadrature formula to the exact value of the integral. We also show that the amplitude of the oscillations is determined by the function $f(s)$, as is suggested by Equation (29).

4. Approximate Evaluation of Hypersingular Integrals with Rapidly Oscillating Functions

In this section, we study approximate methods for evaluating hypersingular integrals of the form

$$(Hf)(t)=\frac{1}{\pi i}{\int }_{\gamma }\frac{f(\tau e^{im\tau })d\tau }{{(\tau -t)}^p},t\in \gamma ,p=2,3,\dots .$$

(56)

Here, $\gamma =\{z:|z|=1\}-$ is a unit circle centered at the origin in the complex plane, m is a natural number. To obtain a lower bound estimate for the error of the quadrature formula, we use the Hilbert transformation from the integral (56) to the hypersingular integral with a Hilbert kernel. We change the variables in (56): $\tau =e^{i\sigma },$ $t=e^{is},$ $\sigma \in [0,2\pi ].$

Now, we have

$$\frac{1}{\pi i}{\int }_{\gamma }\frac{f(\tau )e^{im\tau }d\tau }{{(\tau -t)}^p}=\frac{1}{\pi }{\int }_0^{2\pi }\frac{f(e^{i\sigma })(cosm\sigma +isinm\sigma )e^{i\sigma }d\sigma }{{(e^{i\sigma }-e^{is})}^p}.$$

Converting the fraction yields

$$\begin{array}{c}\frac{1}{{(e^{i\sigma }-e^{is})}^p)}=\frac{e^{-i\frac{\sigma -s}{2}p}}{{(e^{i\sigma }-e^{is})}^p{e}^{-i\frac{\sigma -s}{2}p}}=\hfill \\ ={\left(\frac{e^{-\frac{\sigma -s}{2}}}{(e^{i\sigma }-e^{is})e^{-i\frac{\sigma +s}{2}}}\right)}^p=\hfill \\ ={\left(\frac{cos\frac{\sigma -s}{2}-isin\frac{\sigma -s}{2}}{e^{i\frac{\sigma -s}{2}}-e^{-i\frac{\sigma -s}{2}}}\right)}^p={\left(\frac{cos\frac{\sigma -s}{2}+isin\frac{\sigma -s}{2}}{2isin\frac{\sigma -s}{2}}\right)}^p=\hfill \\ =\frac{{(-1)}^p}{2^p}{\left(ictg\frac{\sigma -s}{2}+1\right)}^p.\hfill \end{array}$$

Thus, to estimate from below the error for evaluation integrals of the form (56) by quadrature formulas constructed on N nodes, it is enough to study the integrals of the form

$$\frac{1}{2\pi }{\int }_0^{2\pi }\phi (\sigma )\left\{\begin{array}{c}sinm\sigma \hfill \\ cosm\sigma \hfill \end{array}\right\}ct{g}^p\frac{\sigma -s}{2}d\sigma .$$

Evaluate the hypersingular integral

$$F\phi =\underset{0}{\overset{2\pi }{\int }}\phi (\sigma )sinm\sigma ct{g}^p\frac{\sigma -s}{2}d\sigma$$

by the quadrature formula

$$F\phi =\sum _{k=1}^N{p}_k(s)\phi (w_k)+R_N(s,p_k(s),w_k,\phi )$$

(57)

on the function class $W^r([0,2\pi ],1),r\ge p.$

When estimating the error of the quadrature formula from below, two cases should be considered:

(1)

p is an even natural number;

(2)

p is an odd natural number.

Let us first study an integral with a singularity of the even order.

Let $t_k=2k\pi /N,$ $k=0,1,\dots ,N-1.$

The set of nodes $\left\{v_j\right\},$ $j=0,1,\dots ,n-1,$ $n=2N+2m$ is obtained by merging $\left\{t_k\right\},$ $k=0,1,\dots ,N-1,$ $\left\{w_k\right\},$ $k=1,\dots ,N,$ and $s_j=\pi j/m,$ $j=0,1,\dots ,2m-1.$

We introduce the function

$${\phi }^{*}(s)=\underset{0\le i\le 2N+2m}{min}A\frac{{(s-v_i)}^r{(v_{i+1}-s)}^r}{h_i^r},$$

$s\in [v_i,v_{i+1}],h_i=|v_{i+1}-v_i|,i=0,1,\dots ,n-1.$

The constant A is chosen such that ${\phi }^{*}\in W^r([0,2\pi ],1).$

To each node $t_k,$ $k=0,1,\dots ,N-1,$ we assign the function

$${\phi }_k(s)={\phi }^{*}(s)\mathrm{sgn}sin\mathrm{ms}.$$

Then,

$$\begin{array}{c}(F{\phi }_k)(s_k)=\underset{0}{\overset{2\pi }{\int }}{\phi }_k(\sigma )sinm\sigma ct{g}^p\frac{\sigma -s_k}{2}d\sigma =\hfill \\ ={\displaystyle \sum _{l=0}^{N-1}}\underset{t_l}{\overset{t_{l+1}}{\int }}{\phi }_k(\sigma )sinm\sigma ct{g}^p\frac{\sigma -s_k}{2}d\sigma \ge \hfill \\ \ge {\displaystyle \sum _{l=0}^{[N/2]-1}}\underset{t_{k+l}}{\overset{t_{k+l+1}}{\int }}{\phi }_k(\sigma )sinm\sigma ct{g}^p\frac{\sigma -s_k}{2}d\sigma +\hfill \\ +{\displaystyle \sum _{l=[N/2]+1}^{N-2}}\underset{t_{k+l}}{\overset{t_{k+l+1}}{\int }}{\phi }_k(\sigma )sinm\sigma ct{g}^p\frac{\sigma -s_k}{2}d\sigma \ge \hfill \\ \ge {\displaystyle \sum _{l=0}^{[N/2]-1}}ct{g}^p\frac{(l+1)\pi }{m}\underset{t_{k+l}}{\overset{t_{k+l+1}}{\int }}{\phi }^{*}(\sigma )|sinm\sigma |d\sigma +\hfill \\ +{\displaystyle \sum _{l=[N/2]+1}^{N-2}}ct{g}^p\frac{l\pi }{m}\underset{t_{k+l}}{\overset{t_{k+l+1}}{\int }}{\phi }^{*}(\sigma )|sinm\sigma |d\sigma .\hfill \end{array}$$

Averaging the previous inequality over $k,$ $k=0,1,\dots ,N-1$, we have

$$\begin{array}{c}\underset{0\le j\le N-1}{max}(F{\phi }_j)(s_j)\ge \frac{1}{N}{\displaystyle \sum _{k=0}^{N-1}}(F{\phi }_k)(s_k)\ge \hfill \\ \ge \frac{1}{N}{\displaystyle \sum _{k=0}^{N-1}}{\displaystyle \sum _{l=0}^{[N/2]-1}}ct{g}^p\frac{(l+1)\pi }{N}\underset{t_{k+l}}{\overset{t_{k+l+1}}{\int }}{\phi }^{*}(\sigma )|sinm\sigma |d\sigma +\hfill \\ +\frac{1}{N}{\displaystyle \sum _{k=0}^{N-1}}{\displaystyle \sum _{l=[N/2]+1}^{N-2}}ct{g}^p\frac{l\pi }{N}\underset{t_{k+l}}{\overset{t_{k+l+1}}{\int }}{\phi }^{*}(\sigma )|sinm\sigma |d\sigma =\hfill \\ =\frac{2(1+o(1))}{N}{\displaystyle \sum _{l=0}^{[N/2]-1}}ct{g}^p\frac{(l+1)\pi }{N}\underset{0}{\overset{2\pi }{\int }}{\phi }^{*}(\sigma )|sinm\sigma |d\sigma .\hfill \end{array}$$

Now, we obtain the estimate of the integral $\underset{0}{\overset{2\pi }{\int }}{\phi }^{*}(\sigma )|sinm\sigma |d\sigma$ under the following assumptions:

(1)

${\phi }^{*}(\sigma )\in W^r(1);$

(2)

${({\phi }^{*})}^{(i)}(v_k)=0,i=0,1,\dots ,r-1,$$k=0,1,\dots ,n;$

(3)

${\phi }^{*}(s)\ge 0,s\in [0,2\pi ].$

First, let $N\le 2m.$ Repeating the arguments above when studying singular integrals, we have

$$\underset{0}{\overset{2\pi }{\int }}{\phi }^{*}(\sigma )|sinm\sigma |d\sigma \ge \frac{C}{m^r}.$$

For $2m<N$, we have

$$\underset{0}{\overset{2\pi }{\int }}{\phi }^{*}(\sigma )|sinm\sigma |d\sigma \ge \frac{C}{N^r}.$$

Thus, for even p, we obtain the estimate

$$R_N(W^r(1))\ge \{\begin{array}{c}{C}_1\frac{1}{m^r}\frac{1}{N}{\displaystyle \sum _{k=0}^{[N/2]-1}}ct{g}^p\frac{k\pi }{N}=\frac{1}{m^r{N}^{1-p}},N\le 2m;\hfill \\ C_2\frac{1}{N^r}\frac{1}{N}{\displaystyle \sum _{k=0}^{[N/2]-1}}ct{g}^p\frac{k\pi }{N}=\frac{1}{N^{r+1-p}},2m\le N.\hfill \end{array}$$

For odd p, the construction is more complicated. Nevertheless, we are sure that the following estimate is valid:

$$R_N(W^r(1))\ge \{\begin{array}{c}{C}_1\frac{1}{m^r}\frac{1}{N}{\displaystyle \sum _{k=0}^{[N/2]-1}}ct{g}^p\frac{k\pi }{N}=\frac{1}{m^r{N}^{1-p}},N\le 2m;\hfill \\ C_2\frac{1}{N^r}\frac{1}{N}{\displaystyle \sum _{k=0}^{[N/2]-1}}ct{g}^p\frac{k\pi }{N}=\frac{1}{N^{r+1-p}},2m\le N.\hfill \end{array}$$

Finally, the theorem is proved.

Theorem 7.

Let $\phi \in W^r(1).$ Then, for all possible quadrature formulas of the form (57), the estimate

$$R_N(W^r(1))\ge \{\begin{array}{c}{C}_1\frac{1}{m^r}\frac{1}{N}{\displaystyle \sum _{k=0}^{[N/2]-1}}ct{g}^p\frac{k\pi }{N}=\frac{1}{m^r{N}^{1-p}},N\le 2m;\hfill \\ C_2\frac{1}{N^r}\frac{1}{N}{\displaystyle \sum _{k=0}^{[N/2]-1}}ct{g}^p\frac{k\pi }{N}=\frac{1}{N^{r+1-p}},2m\le N.\hfill \end{array}$$

is valid.

When constructing quadrature formulas for hypersingular integral evaluation, we will use Definition 7, which allows us to construct methods for hypersingular integral evaluation based on well-known methods for evaluating singular integrals.

From Definition 7, it follows that

$$\begin{array}{c}\frac{1}{\pi i}{\int }_{\gamma }\frac{f(\tau ){\tau }^m}{{(\tau -t)}^p}d\tau =\frac{1}{(p-1)!}\frac{d^{p-1}}{d{t}^{p-1}}\frac{1}{\pi i}{\int }_{\gamma }\frac{f(\tau ){\tau }^m}{\tau -t}d\tau =\hfill \\ =\frac{1}{(p-1)!}\frac{d^{p-1}}{d{t}^{p-1}}\left[\frac{1}{2}\left(t^m-t^{-m}\right)+\frac{1}{2n+1}\sum _{k=0}^{2n}f(t_k)\left[1+\sum _{l=1}^m\left(\frac{t^l}{t_k^l}-\frac{t_k^l}{t^l}\right)\right]\right.-\hfill \\ \left.-\frac{1}{i}\frac{1}{2n+1}\sum _{k=0}^{2n}f(t_k)\left[\frac{1}{2i}\left(t^m-t^{-m}\right)+\left(t^m-t^{-m}\right)\sum _{l=1}^n\frac{1}{2i}\left(\frac{t^l}{t_k^l}-\frac{t_k^l}{t^l}\right)\right]\right]+R_n(f).\hfill \end{array}$$

(58)

To estimate $|R_n(f)|$, note that the integrals

$$\frac{1}{2\pi }{\int }_0^{2\pi }{P}_n\left[f(e^{i\sigma })\right]sinm\sigma ctg\frac{\sigma -s}{2}d\sigma$$

and

$$\frac{1}{2\pi }{\int }_0^{2\pi }{P}_n\left[f(e^{i\sigma })\right]cosm\sigma ctg\frac{\sigma -s}{2}d\sigma .$$

are trigonometric polynomials of the $(n+m)$th order.

As shown above,

$$\begin{array}{c}\left|\frac{1}{2\pi }{\int }_0^{2\pi }f(e^{m\sigma })\left\{\begin{array}{c}cosm\sigma \\ sinm\sigma \end{array}\right\}ctg\frac{\sigma -s}{2}d\sigma -\frac{1}{2\pi }{\int }_0^{2\pi }{P}_n\left[f(e^{m\sigma })\right]\left\{\begin{array}{c}cosm\sigma \\ sinm\sigma \end{array}\right\}ctg\frac{\sigma -s}{2}d\sigma \right|\le \hfill \\ \le C{E}_n(f){ln}^{2}n.\hfill \end{array}$$

(59)

Using Theorem 5, we obtain the estimate

$$|R_n{(f)|\le C(n+m)}^{p-1}{E}_n(f){ln}^{2}n.$$

Setting $f\in W^r{H}_{\alpha }(\gamma ,1)$, we finally have

$$R_n[W^r{H}_{\alpha }([0,2\pi ]),1]\le C\frac{{(n+m)}^{p-1}}{n^{r+\alpha }}{ln}^{2}n.$$

5. Conclusions

We studied approximate methods for evaluating Cauchy and Hilbert singular and hypersingular integrals with rapidly oscillating kernels. In the case of periodic integrable functions, lower and upper bound quadrature formula estimates have been obtained. Optimals with respect to order quadrature formulas for certain classes of functions have been constructed. We developed a method for constructing and estimating quadrature formulas for hypersingular integrals, based on similar results for singular integrals.

Finally, we point out a few key points of our study presented in this paper:

(1) We introduced a method to estimate below quadrature formulas for evaluating singular and hypersingular integrals with rapidly oscillating kernels (in this paper, a method to obtain lower bound estimates by functional ${\zeta }_N\left[\mathsf{\Psi }\right]$ in the class of functions $\mathsf{\Psi }$). Moreover, these estimates can be obtained from any set of N nodes located in the range of integration and N values of integrand function.

The method can be extended to singular and hypersingular integrals defined on other varieties, to polysingular and polyhypersingular integrals and to many dimensional singular and hypersingular integrals. The existence of lower bound estimates of functional ${\zeta }_N\left[\mathsf{\Psi }\right]$ allows us to construct an optimal with respect to order (to accuracy) passive algorithms for evaluating corresponding integrals in the classes of functions $\mathsf{\Psi }$.

(2) We proposed a method to construct quadrature formulas for evaluating hypersingular integrals and their error estimates based on quadrature formulas for evaluating singular integrals.

(3) We proposed optimals with respect to order quadrature formulas, which are apparently the most effective among known methods for evaluating singular and hypersingular integrals with rapidly oscillating kernels. We made a comparison of the efficiency of quadrature Formulas (29), (30) and (58) with well-known rules.

Using Levin’s method, one must analytically solve the equation

$$x^{\prime }(\tau )+iw{g}^{\prime }(\tau )x(\tau )=\frac{f(\tau )}{{(\tau -t)}^p},$$

where g and f are known functions.

Applying numerical methods to solve this equation might cause some difficulties due to singularity at point t on the right-hand side of the equation.

Thus, Levin’s method has some application limitations.

In [16], an interpolation quadrature formula was constructed to evaluate integrals of the type

$${\int }_{-1}^1\frac{f(x)dx}{\sqrt{1-x^2}(x-a)}$$

with fixed singularity a.

When constructing a quadrature formula, function $f(x)$ is approximated by an interpolation polynomial with $n+1$ nodes. A set of nodes contains a particular point a.

Thus, in [16], it was necessary to construct the quadrature formula for each value of $-1<t<1$.

Implementation of other methods, constructed in the cited literature here, causes greater smoothness of integrand functions than in our computations.