Oscillatory Behavior of Third-Order Quasi-Linear Neutral Differential Equations

Abstract

In this paper, we consider a class of quasilinear third-order differential equations with a delay argument. We establish some conditions of such certain third-order quasi-linear neutral differential equation as oscillatory or almost oscillatory. Those criteria improve, complement and simplify a number of existing results in the literature. Some examples are given to illustrate the importance of our results.

1. Introduction

Consider the third-order neutral delay differential equation of the form

$${\left(r\left(t\right){\left(y^{″}\left(t\right)\right)}^{\alpha }\right)}^{\prime }+q\left(t\right)f\left(x\left(\sigma \left(t\right)\right)\right)=0,$$

(1)

where $y\left(t\right)=x\left(t\right)+p\left(t\right)x\left(\tau \left(t\right)\right)$ and we assume that the following hypotheses are satisfied:

(I₁)

$r\in C\left(\left[t_0,\infty \right),\mathbb{R}\right)$ is positive and $\pi \left(t\right)<\infty ,$ where

$$\pi \left(t\right)={\int }_t^{\infty }{r}^{-1/\alpha }\left(s\right)\mathrm{d}s;$$

(I₂)

$p,q\in C\left(\left[t_0,\infty \right),\mathbb{R}\right),$$p\le p_0<\infty ,$q is non-negative and does not eventually vanish (i.e., $q\left(t\right)$ is not eventually zero on any half line $[t_{\ast },\infty )$ for $t_{\ast }\ge$ $t_0$);

(I₃)

$\sigma ,\tau \in C^1\left(\left[t_0,\infty \right),\mathbb{R}\right),$$\sigma \left(t\right)<t,$$\tau \left(t\right)<t,$${\tau }^{\prime }\left(t\right)\ge {\tau }_0>0,$$\sigma \circ \tau =\tau \circ \sigma$ and ${\lim }_{t\to \infty }\sigma \left(t\right)={\lim }_{t\to \infty }\tau \left(t\right)=\infty ;$

(I₄)

$f\in C\left(\mathbb{R},\mathbb{R}\right)$ and satisfies

$$f\left(x\right)>k{x}^{\alpha } \mathrm{for} \mathrm{all} k>0.$$

where $\alpha$ is the quotient of odd positive integers.

By a solution of (1), we mean a nontrivial function $x\in C\left([T_x,\infty ),\mathbb{R}\right)$ with $T_x\ge t_0$, which satisfies the property $r{\left(y^{″}\right)}^{\alpha }\in C^1\left([T_x,\infty ),\mathbb{R}\right)$, moreover, satisfies (1) on $[T_x,\infty ).$ We only consider those solutions of (1) satisfying, on some half-line, $[T_x,\infty )$ and satisfying the condition $\sup \{\left|x\left(t\right)\right|:T\le t<\infty \}>0$ for any $T\ge T_x$. A solution of (1) is oscillatory if it has arbitrarily large zeros on $[T_x,\infty )$; otherwise, it is said to be nonoscillatory. The equation itself is termed oscillatory if all its solutions oscillate, and is said to be almost oscillatory if all its solutions are oscillatory or asymptotically convergent to zero.

The neutral differential equations have numerous applications in electrical engineering, chemical reactions analysis, and economics.

Such equations are essential tools to model and study the dynamics and stability properties of electrical power systems, as in the works of Milano et al. [1,2]. The asymptotic behavior of solutions of associated delay differential equations have been used to describe the behavior of solutions to third-order partial differential equations. Additionally, they are employed for the study of distributed networks containing lossless transmission lines; see [3,4] for more details.

Recently, there has been much research activity concerning the oscillation of second-order differential equations with delay. See, for example, [5,6] and the references cited therein. Compared to the development of the oscillation for the second-order equations, the oscillation for third-order equations has received considerably less attention from researchers; see [7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24].

Baculikova and Dzurina [25,26] and Grace et al. [27] considered the third-order nonlinear delay differential equation

$${\left(r\left(t\right){\left(x^{″}\left(t\right)\right)}^{\alpha }\right)}^{\prime }+q\left(t\right)f\left(x\left(\sigma \left(t\right)\right)\right)=0,$$

in the case where $\pi \left(t\right)=\infty$ or $\pi \left(t\right)<\infty .$

Saker and Dzurina [28] studied the third-order nonlinear delay differential equation

$${\left(r\left(t\right){\left(x^{″}\left(t\right)\right)}^{\alpha }\right)}^{\prime }+q\left(t\right)x^{\beta }\left(\sigma \left(t\right)\right)=0,$$

(2)

and obtained several oscillation criteria, which guarantee that all non-oscillatory solutions of such Equation (2) tend towards zero.

Ravi et al. [29] investigated a third-order delay differential equation

$${\left(r_2\left(t\right){\left(r_1\left(t\right)\left(x^{\prime }\left(t\right)\right)\right)}^{\prime }\right)}^{\prime }+q\left(t\right)x^{\beta }\left(\sigma \left(t\right)\right)=0,$$

and established some oscillation results that supplemented and improved the results in [27]. Sidorov and Trufanov [30] considered nonlinear operator equations with a functional perturbation of the argument of neutral type and reduced the problem to quasilinear operator equations with a functional perturbation of the argument.

Moaaz, in [11], studied a third-order nonlinear delay differential (2) under the condition $\pi \left(t\right)=\infty$; he developed some results of previous references and established several sufficient conditions, which ensure that all solutions of (2) are oscillatory.

In previous papers, the authors used an integral averaging technique and a Riccati transformation to establish some sufficient conditions which ensure that any solution of (1) oscillates or converges to zero. The purpose of this paper is to improve and generalize these results and present some new sufficient conditions, which ensure that any solution of (1) oscillates or, for all its nonoscillatory solutions, tend towards zero as $t\to \infty .$

2. Auxiliary Results

In this section, we state and prove the following lemmas, which will be useful in the proofs of the main results.

Lemma 1

([29]). Assume $x\left(t\right)$ is nonoscillatory solution of (1). Then, $y\left(t\right)>0$ and there are three possible cases of $y\left(t\right)$:

$$\begin{array}{cc}{\mathbf{N}}_1\hfill & y^{\prime }\left(t\right)>0, y^{″}\left(t\right)>0,\hfill \\ {\mathbf{N}}_2& y^{\prime }\left(t\right)>0, y^{″}\left(t\right)<0,\hfill \\ {\mathbf{N}}_3& y^{\prime }\left(t\right)<0, y^{″}\left(t\right)>0.\hfill \end{array}$$

Lemma 2

([31]). Let $h\left(u\right)=Au-B{\left(u-C\right)}^{\left(\alpha +1\right)/\alpha },$ where $B>0$, A and C are constants, α bea ratio of two odd positive numbers. Then, h attains its maximum value on $\mathbb{R}$ at $u^{\ast }=C+{\left(\frac{\alpha A}{\left(\alpha +1\right)B}\right)}^{\alpha }$ such that

$$\underset{u\in \mathbb{R}}{\max }h\left(u\right)=h\left(u^{\ast }\right)=AC+\frac{{\alpha }^{\alpha }}{{\left(\alpha +1\right)}^{\alpha +1}}\frac{A^{\alpha +1}}{B^{\alpha }}.$$

Lemma 3

([32]). Assume that $c_1,c_2\in [0,\infty )$ and $\gamma >0$. Then

$${\left(c_1+c_1\right)}^{\gamma }\le \mu \left(c_1^{\gamma }+c_2^{\gamma }\right),$$

where

$$\mu :=\left\{\begin{array}{cc}1\hfill & if \gamma \le 1\\ \hfill 2^{\gamma -1}& if \gamma >1\end{array}\right.$$

Lemma 4.

Let x be a positive solution of (1), $y^{\prime }\left(t\right)>0$ and $p\left(t\right)\in \left(0,1\right).$ Then,

$${\left(r\left(t\right){\left(y^{″}\left(t\right)\right)}^{\alpha }\right)}^{\prime }+kQ\left(t\right)y^{\alpha }\left(\sigma \left(t\right)\right)\le 0,$$

(3)

where

$$Q\left(t\right)=q\left(t\right){\left(1-p\left(\sigma \left(t\right)\right)\right)}^{\alpha }.$$

Proof. 

Assume that x is a positive solution of (1). From hypothesis (I${}_4$), (1) becomes

$${\left(r\left(t\right){\left(y^{″}\left(t\right)\right)}^{\alpha }\right)}^{\prime }+kq\left(t\right)x^{\alpha }\left(\sigma \left(t\right)\right)\le 0.$$

(4)

Since $y^{\prime }\left(t\right)>0$, we find

$$\begin{array}{ccc}\hfill x\left(t\right)& =& y\left(t\right)-p\left(t\right)x\left(\tau \left(t\right)\right)\ge y\left(t\right)-p\left(t\right)y\left(\tau \left(t\right)\right)\hfill \\ & \ge & y\left(t\right)-p\left(t\right)y\left(t\right)=y\left(t\right)\left(1-p\left(t\right)\right).\hfill \end{array}$$

That is

$$x^{\alpha }\left(\sigma \left(t\right)\right)\ge y^{\alpha }\left(\sigma \left(t\right)\right){\left(1-p\left(\sigma \left(t\right)\right)\right)}^{\alpha }.$$

(5)

Combining (4) and (5), we have

$${\left(r\left(t\right){\left(y^{″}\left(t\right)\right)}^{\alpha }\right)}^{\prime }+kQ\left(t\right)y^{\alpha }\left(\sigma \left(t\right)\right)\le 0.$$

This completes the proof. □

Lemma 5.

Assume that $x\left(t\right)$ is a positive solution of (1). Then,

$${\left(r\left(t\right){\left(y^{″}\left(t\right)\right)}^{\alpha }+\frac{p_0^{\alpha }}{{\tau }_0}r\left(\tau \left(t\right)\right){\left(y^{″}\left(\tau \left(t\right)\right)\right)}^{\alpha }\right)}^{\prime }\le -\frac{k}{\mu }\widehat{O}\left(t\right)y^{\alpha }\left(\sigma \left(t\right)\right),$$

(6)

where $\widehat{O}\left(t\right):=\min \left\{q\left(t\right),q\left(\tau \left(t\right)\right)\right\}.$

Proof. 

Let $x\left(t\right)$ be a positive solution of (1). Then, there exists $t_1\ge t_0$ such that $x\left(\sigma \left(t\right)\right)>0$ and $x\left(\tau \left(t\right)\right)>0$ for all $t\ge t_1$. From Lemma 3 and $\sigma \circ \tau =\tau \circ \sigma$, we obtain

$$y^{\alpha }\left(\sigma \left(t\right)\right)=\mu \left(x^{\alpha }\left(\sigma \left(t\right)\right)+p_0^{\alpha }{x}^{\alpha }\left(\sigma \left(\tau \left(t\right)\right)\right)\right).$$

(7)

In view of (I${}_3$), (4) implies

$$\begin{array}{ccc}\hfill 0& \ge & \frac{p_0^{\alpha }}{{\tau }^{\prime }\left(t\right)}{\left(r\left(\tau \left(t\right)\right){\left(y^{″}\left(\tau \left(t\right)\right)\right)}^{\alpha }\right)}^{\prime }+p_0^{\alpha }kq\left(\tau \left(t\right)\right)x^{\alpha }\left(\sigma \left(\tau \left(t\right)\right)\right)\hfill \\ & \ge & \frac{p_0^{\alpha }}{{\tau }_0}{\left(r\left(\tau \left(t\right)\right){\left(y^{″}\left(\tau \left(t\right)\right)\right)}^{\alpha }\right)}^{\prime }+p_0^{\alpha }kq\left(\tau \left(t\right)\right)x^{\alpha }\left(\tau \left(\sigma \left(t\right)\right)\right).\hfill \end{array}$$

Using (4) with the above inequality, and taking into account (7), we have

$$\begin{array}{ccc}\hfill {\left(r\left(t\right){\left(y^{″}\left(t\right)\right)}^{\alpha }\right)}^{\prime }+\frac{p_0^{\alpha }}{{\tau }_0}{\left(r\left(\tau \left(t\right)\right){\left(y^{″}\left(\tau \left(t\right)\right)\right)}^{\alpha }\right)}^{\prime }+k\widehat{O}\left(t\right)\left(x^{\alpha }\left(\sigma \left(t\right)\right)+p_0^{\alpha }{x}^{\alpha }\left(\tau \left(\sigma \left(t\right)\right)\right)\right)& \le & 0\hfill \\ \hfill {\left(r\left(t\right){\left(y^{″}\left(t\right)\right)}^{\alpha }\right)}^{\prime }+\frac{p_0^{\alpha }}{{\tau }_0}{\left(r\left(\tau \left(t\right)\right){\left(y^{″}\left(\tau \left(t\right)\right)\right)}^{\alpha }\right)}^{\prime }+\frac{k}{\mu }\widehat{O}\left(t\right)y^{\alpha }\left(\sigma \left(t\right)\right)& \le & 0.\hfill \end{array}$$

Thus,

$${\left(r\left(t\right){\left(y^{″}\left(t\right)\right)}^{\alpha }+\frac{p_0^{\alpha }}{{\tau }_0}r\left(\tau \left(t\right)\right){\left(y^{″}\left(\tau \left(t\right)\right)\right)}^{\alpha }\right)}^{\prime }+\frac{k}{\mu }\widehat{O}\left(t\right)y^{\alpha }\left(\sigma \left(t\right)\right)\le 0.$$

This completes the proof. □

Lemma 6.

Assume that $x\left(t\right)$ is a positive solution of (1) and $y^{\prime }\left(t\right)>0$. Then

$$y\left(\sigma \left(t\right)\right)\ge ć\sigma \left(t\right), where ć:=c\varsigma .$$

(8)

Proof. 

Since $y^{\prime }$ is nondecreasing, this implies that

$$y^{\prime }\left(t\right)\ge y^{\prime }\left(t_1\right)=:c \mathrm{on} [t_1,\infty ).$$

Integrating from $\sigma \left(t\right)$ to $t_1$, we get

$$y\left(\sigma \left(t\right)\right)\ge c\left(\sigma \left(t\right)-t_1\right).$$

Hence, for any $\varsigma \in (0,1)$ and $t\ge t_2,$ we see that

$$y\left(\sigma \left(t\right)\right)\ge ć\sigma \left(t\right).$$

The proof is complete. □

Lemma 7.

Let $x\left(t\right)$ be a positive solution of (1). If

$${\int }_{t_0}^{\infty }\widehat{O}\left(t\right){\sigma }^{\alpha }\left(t\right)\mathrm{d}t=\infty ,$$

(9)

then case ${\mathbf{N}}_1$ is impossible.

Proof. 

Assume that $x\left(t\right)$ is a positive solution of (1) on $[t_0,\infty )$. Then, there exists $t_1\ge t_0$ such that $x\left(\tau \left(t\right)\right)>0$ and $x\left(\sigma \left(t\right)\right)>0$ for all $t\ge t_1$. On the contrary, assume that $y\left(t\right)$ satisfies case ${\mathbf{N}}_1$. Integrating (6) from $t_2$ to t and using (8), we get

$$\begin{array}{ccc}& & r\left(t\right){\left(y^{″}\left(t\right)\right)}^{\alpha }+\frac{p_0^{\alpha }}{{\tau }_0}r\left(\tau \left(t\right)\right){\left(y^{″}\left(\tau \left(t\right)\right)\right)}^{\alpha }\hfill \\ & \le & r\left(t_2\right){\left(y^{″}\left(t_2\right)\right)}^{\alpha }+\frac{p_0^{\alpha }}{{\tau }_0}r\left(\tau \left(t_2\right)\right){\left(y^{″}\left(\tau \left(t_2\right)\right)\right)}^{\alpha }-{\left(ć\right)}^{\alpha }\frac{k}{\mu }{\int }_{t_2}^t\widehat{O}\left(t\right){\sigma }^{\alpha }\left(t\right)\mathrm{d}t,\hfill \end{array}$$

(10)

which is a contradiction. □

Lemma 8.

Let $y\left(t\right)$ be a positive increasing solution of (1). If

$${\int }_{t_0}^{\infty }\frac{1}{r^{1/\alpha }\left(t\right)}{\left({\int }_{t_0}^t\widehat{O}\left(t\right){\sigma }^{\alpha }\left(s\right)\mathrm{d}s\right)}^{1/\alpha }\mathrm{d}t=\infty ,$$

(11)

then y satisfies case ${\mathbf{N}}_2$ for $t\ge t_1$ and

(a)

$y\left(t\right)\ge t{y}^{\prime }\left(t\right)$ and $y\left(t\right)/t$ is decreasing, and ${\lim }_{t\to \infty }y\left(t\right)/t=y^{\prime }=0$,

(b)

$y^{\prime }\left(t\right)\ge -\pi \left(t\right)r^{\frac{1}{\alpha }}\left(t\right)y^{″}\left(t\right)$ and $y^{\prime }\left(t\right)/\pi \left(t\right)$ is increasing.

Proof. 

Assume that $x\left(t\right)$ is a positive solution of (1) on $[t_0,\infty )$. Then, there exists $t_1\ge t_0$ such that $x\left(\tau \left(t\right)\right)>0$ and $x\left(\sigma \left(t\right)\right)>0$ for all $t\ge t_1$. Since y is increasing, y satisfies either case ${\mathbf{N}}_1$ or ${\mathbf{N}}_2$. In view of $\pi \left(t\right)<\infty$ and (11), we see that (9) hold. By Lemma 7, $y\left(t\right)$ satisfies case ${\mathbf{N}}_2$.

On the other hand, it follows from $y^{\prime }\left(t\right)$ is decreasing, such that there exists a constant $\lambda \ge 0$ such that ${\lim }_{t⟶\infty }{y}^{\prime }\left(t\right)=\lambda \ge 0$. We claim that $\lambda =0.$ As the proof of Lemma 7 we have (10). Take into account ${\left(r\left(t\right){\left(y^{″}\left(t\right)\right)}^{\alpha }\right)}^{\prime }\le 0$ and $y^{″}\left(t\right)<0$, we have

$$r\left(t\right){\left(y^{″}\left(t\right)\right)}^{\alpha }\left(1+\frac{p_0^{\alpha }}{{\tau }_0}\right)\le -{\left(ć\right)}^{\alpha }\frac{k}{\mu }{\int }_{t_1}^t\widehat{O}\left(s\right){\sigma }^{\alpha }\left(s\right)\mathrm{d}s.$$

It follows that

$$y^{″}\left(t\right)\le -ć{\left(\frac{1}{r\left(t\right)}\left(\frac{k{\tau }_0}{\mu \left({\tau }_0+p_0^{\alpha }\right)}\right)\right)}^{1/\alpha }{\left({\int }_{t_1}^t\widehat{O}\left(s\right){\sigma }^{\alpha }\left(s\right)\mathrm{d}s\right)}^{1/\alpha }.$$

Integrating from $t_2$ to t, we obtain

$$y^{\prime }\left(t\right)\le y^{\prime }\left(t_2\right)-ć{\left(\frac{k{\tau }_0}{\mu \left({\tau }_0+p_0^{\alpha }\right)}\right)}^{\frac{1}{\alpha }}{\int }_{t_2}^t\frac{{\left({\int }_{t_2}^u\widehat{O}\left(s\right){\sigma }^{\alpha }\left(s\right)\mathrm{d}s\right)}^{\frac{1}{\alpha }}}{r^{\frac{1}{\alpha }}\left(u\right)}\mathrm{d}u.$$

In view of (11), this contradicts the positivity of $y^{\prime }\left(t\right)$. Thus $\lambda =0$. By “Hospital’s rule”, we see that

$$\underset{t\to \infty }{\lim }\frac{y\left(t\right)}{t}=0 \mathrm{and} \underset{t\to \infty }{\lim }{y}^{\prime }\left(t\right)=0.$$

Thus,

$$y\left(t_1\right)-y^{\prime }\left(t\right)t_1>0.$$

(12)

Therefore,

$$y\left(t\right)>y^{\prime }\left(t\right)t_1,$$

for $t\ge t_2.$ Hence, by the monotonicity of $y^{\prime }\left(t\right),$ one can obtain that

$$y\left(t\right)=y\left(t_1\right)+{\int }_{t_1}^t{y}^{\prime }\left(s\right)\mathrm{d}s\ge y\left(t_1\right)+y^{\prime }\left(t\right)\left(t-t_1\right).$$

By (12), we have

$${\left(\frac{y\left(t\right)}{t}\right)}^{\prime }=\frac{t{y}^{\prime }-y}{t^2}<0.$$

Now, it is easy to see that

$$y^{\prime }\left(t\right)\ge -{\int }_t^{\infty }\frac{1}{r^{1/\alpha }\left(s\right)}{r}^{1/\alpha }\left(s\right)y^{″}\left(s\right)\mathrm{d}s\ge -r^{1/\alpha }\left(t\right)y^{″}\left(t\right)\pi \left(t\right).$$

Thus,

$${\left(\frac{y^{\prime }\left(t\right)}{\pi \left(t\right)}\right)}^{\prime }=\frac{r^{1/\alpha }\left(t\right)y^{″}\left(t\right)\pi \left(t\right)+y^{\prime }\left(t\right)}{r^{1/\alpha }\left(t\right){\pi }^2\left(t\right)}\ge 0.$$

The proof is complete. □

3. Main Results

Theorem 1.

If

$${\int }_{t_0}^{\infty }\frac{1}{r^{1/\alpha }\left(t\right)}{\left({\int }_{t_0}^t\widehat{O}\left(s\right)\mathrm{d}s\right)}^{1/\alpha }\mathrm{d}t=\infty ,$$

(13)

then possible positive solution of (1) satisfies case ${\mathbf{N}}_3$.

Proof. 

Assume that $x\left(t\right)$ is a positive solution of (1) on $[t_0,\infty )$. Then, there exists $t_1\ge t_0$ such that $x\left(\tau \left(t\right)\right)>0$ and $x\left(\sigma \left(t\right)\right)>0$ for all $t\ge t_1$. Suppose that $y\left(t\right)$ satisfies case ${\mathbf{N}}_1$ or ${\mathbf{N}}_2.$ Since y is increasing, then it follows that

$$y\left(t\right)\ge y\left(t_1\right)=\varrho \mathrm{for} t\ge t_2.$$

(14)

Set

$$\varpi \left(t\right)=r\left(t\right){\left(y^{″}\left(t\right)\right)}^{\alpha }+\frac{p_0^{\alpha }}{{\tau }_0}r\left(\tau \left(t\right)\right){\left(y^{″}\left(\tau \left(t\right)\right)\right)}^{\alpha }.$$

(15)

In (6), we obtain

$${\varpi }^{\prime }\left(t\right)\le -\frac{k}{\mu }\widehat{O}\left(t\right)y^{\alpha }\left(\sigma \left(t\right)\right).$$

(16)

Since ${\varpi }^{\prime }\left(t\right)\le 0,$ by (15), we have

$$\varpi \left(t\right)\ge r\left(t\right){\left(y^{″}\left(t\right)\right)}^{\alpha }\left(1+\frac{p_0^{\alpha }}{{\tau }_0}\right).$$

(17)

Integrating (16) from $t_2$ to t and using (14), we obtain

$$\varpi \left(t\right)\le \varpi \left(t_1\right)-\frac{{\varrho }^{\alpha }k}{\mu }{\int }_{t_2}^t\widehat{O}\left(s\right)\mathrm{d}s.$$

(18)

First, let $y\left(t\right)$ satisfies case ${\mathbf{N}}_1$. We note that $\varpi \left(t\right)>0$. Using the fact $\pi \left(t\right)<\infty$ together with (13) yields that ${\int }_{t_0}^t\widehat{O}\left(s\right)\mathrm{d}s$ contradicts the positivity of $\varpi \left(t\right)$.

If $y\left(t\right)$ satisfies case ${\mathbf{N}}_2$, using (17) in (18) becomes

$$r\left(t\right){\left(y^{″}\left(t\right)\right)}^{\alpha }\left(1+\frac{p_0^{\alpha }}{{\tau }_0}\right)\le -\frac{{\varrho }^{\alpha }k}{\mu }{\int }_{t_2}^t\widehat{O}\left(s\right)\mathrm{d}s,$$

that is

$$y^{″}\left(t\right)\le -\varrho {\left(\frac{k{\tau }_0}{\mu \left({\tau }_0+p_0^{\alpha }\right)}\right)}^{\frac{1}{\alpha }}{\left(\frac{1}{r\left(t\right)}{\int }_{t_2}^t\widehat{O}\left(s\right)\mathrm{d}s\right)}^{\frac{1}{\alpha }}.$$

Integrating from $t_2$ to t, we have

$$y^{\prime }\left(t\right)\le y^{\prime }\left(t_2\right)-\varrho {\left(\frac{k{\tau }_0}{\mu \left({\tau }_0+p_0^{\alpha }\right)}\right)}^{\frac{1}{\alpha }}{\int }_{t_2}^t{\left(\frac{1}{r\left(u\right)}{\int }_{t_2}^u\widehat{O}\left(s\right)\mathrm{d}s\right)}^{\frac{1}{\alpha }}\mathrm{d}u.$$

we obtain a cotradiction with the positivity of $y^{\prime }\left(t\right)$. The proof of the theorem is complete. □

Theorem 2.

If

$$\underset{t\to \infty }{\lim \inf }{\int }_{\sigma \left(t\right)}^t{\left(\frac{1}{r\left(u\right)}{\int }_{t_2}^u\widehat{O}\left(s\right){\sigma }^{\alpha }\left(s\right)\mathrm{d}s\right)}^{\frac{1}{\alpha }}\mathrm{d}u>{\left(\frac{\mu \left({\tau }_0+p_0^{\alpha }\right)}{k{\tau }_0{e}^{\alpha }}\right)}^{\frac{1}{\alpha }},$$

(19)

then, a possible positive solution to (1) satisfies case ${\mathbf{N}}_3$.

Proof. 

Assume that $x\left(t\right)$ is a positive solution of (1) on $[t_0,\infty )$. Then, there exists $t_1\ge t_0$ such that $x\left(\tau \left(t\right)\right)>0$ and $x\left(\sigma \left(t\right)\right)>0$ for all $t\ge t_1$. Suppose that y satisfies case ${\mathbf{N}}_1$ or ${\mathbf{N}}_2$. In view of (19), (11) holds. Hence, by Lemma 8, $y\left(t\right)$ satisfies case ${\mathbf{N}}_2$ and properties (a) and (b) in Lemma 8. This implies that

$$y\left(\sigma \left(t\right)\right)\ge \sigma \left(t\right)y^{\prime }\left(\sigma \left(t\right)\right).$$

Combining the above inequality along with (6), we get

$${\left(r{\left(y^{″}\left(t\right)\right)}^{\alpha }+\frac{p_0^{\alpha }}{{\tau }_0}r{\left(y^{″}\left(\tau \left(t\right)\right)\right)}^{\alpha }\right)}^{\prime }\le -\frac{k}{\mu }\widehat{O}\left(t\right){\sigma }^{\alpha }\left(t\right){\left(y^{\prime }\left(\sigma \left(t\right)\right)\right)}^{{}^{\alpha }}.$$

Integrating from $t_2$ to t and using (17), we have

$$-r\left(t\right){\left(y^{″}\left(t\right)\right)}^{\alpha }\left(1+\frac{p_0^{\alpha }}{{\tau }_0}\right)\ge \frac{k}{\mu }{\int }_{t_2}^t\widehat{O}\left(s\right){\sigma }^{\alpha }\left(s\right){\left(y^{\prime }\left(\sigma \left(t\right)\right)\right)}^{{}^{\alpha }}\mathrm{d}s.$$

(20)

Using the fact that $y^{″}\left(t\right)<0,$ we see that

$$-y^{″}\left(t\right)\ge {\left(\frac{k{\tau }_0}{\mu \left({\tau }_0+p_0^{\alpha }\right)}\right)}^{\frac{1}{\alpha }}{y}^{\prime }\left(\sigma \left(t\right)\right){\left(\frac{1}{r\left(t\right)}{\int }_{t_2}^t\widehat{O}\left(s\right){\sigma }^{\alpha }\left(s\right)\mathrm{d}s\right)}^{\frac{1}{\alpha }}.$$

Now, set $\chi \left(t\right)=y^{\prime }\left(t\right);$ we obtain

$${\chi }^{\prime }\left(t\right)+{\left(\frac{k{\tau }_0}{\mu \left({\tau }_0+p_0^{\alpha }\right)}\right)}^{\frac{1}{\alpha }}{\left(\frac{1}{r\left(t\right)}{\int }_{t_2}^t\widehat{O}\left(s\right){\sigma }^{\alpha }\left(s\right)\mathrm{d}s\right)}^{\frac{1}{\alpha }}\chi \left(\sigma \left(t\right)\right) \le 0.$$

(21)

In view of ([13], Theorem 1), however, the associated delay Equation (21) has a positive solution, which is a contradiction. The proof is complete. □

Remark 1.

Theorem 2 does not require the existence of auxiliary functions such as ([27], Theorem 3), which uses the same principles (compared with first-order delay equations).

Theorem 3.

Assume that (11) hold. If

$$\underset{t\to \infty }{\lim \sup } {\pi }^{{}^{\alpha }}\left(t\right){\int }_{t_0}^t\widehat{O}\left(s\right){\sigma }^{\alpha }\left(s\right)\mathrm{d}s>\frac{\mu \left({\tau }_0+p_0^{\alpha }\right)}{k{\tau }_0},$$

(22)

then, the possible positive solution to (1) satisfies case ${\mathbf{N}}_3$.

Proof. 

Suppose that y satisfies case ${\mathbf{N}}_1$ or ${\mathbf{N}}_2$. We see that (9) holds due to $\pi \left(t\right)<\infty$ (this mean that ${\lim }_{t\to \infty }\pi \left(t\right)=0$) and condition (22). Hence, by Lemma 8, $y\left(t\right)$ satisfies case ${\mathbf{N}}_2$ in addition to properties (a) and (b) in Lemma 8. As in the proof of Theorem 2 with the fact $r\left(t\right){\left(y^{″}\left(t\right)\right)}^{\alpha }$ is nonincreasing, and from (20), we obtain

$$-r\left(t\right){\left(y^{″}\left(t\right)\right)}^{\alpha }\left(1+\frac{p_0^{\alpha }}{{\tau }_0}\right)\ge -\frac{k}{\mu }{\pi }^{{}^{\alpha }}\left(t\right)r\left(t\right){\left(y^{″}\left(t\right)\right)}^{{}^{\alpha }}{\int }_{t_2}^t\widehat{O}\left(s\right){\sigma }^{\alpha }\left(s\right)\mathrm{d}s.$$

That is,

$$\frac{k{\tau }_0}{\mu \left({\tau }_0+p_0^{\alpha }\right)}{\pi }^{{}^{\alpha }}\left(t\right){\int }_{t_2}^t\widehat{O}\left(s\right){\sigma }^{\alpha }\left(s\right)\mathrm{d}s\le 1.$$

This contradicts (22). The proof is complete. □

Theorem 4.

Assume that (11) holds. If ${\sigma }^{\prime }\left(t\right)>0$ and there exists a nondecreasing function $\rho \in C^1\left(\left[t_0,\infty \right),\left(0,\infty \right)\right)$, such that

$$\underset{t\to \infty }{\lim \sup }{\int }_T^t\left({\left(\frac{k{\tau }_0}{\mu \left({\tau }_0+p_0^{\alpha }\right)}\right)}^{\frac{1}{\alpha }}\frac{\rho \left(u\right)}{\sigma \left(u\right)r^{\frac{1}{\alpha }}\left(u\right)}{\int }_{t_0}^t\widehat{O}\left(s\right){\sigma }^{\alpha }\left(s\right)\mathrm{d}s-\frac{{\rho }^{\prime 2}\left(u\right)}{4\rho \left(u\right){\sigma }^{\prime }\left(u\right)}\right)\mathrm{d}u=\infty ,$$

(23)

for any $T\in \left[t_0,\infty \right)$, then a possible positive solution to (1) satisfies case ${\mathbf{N}}_3$.

Proof. 

Assume that $x\left(t\right)$ is a positive solution of (1) on $[t_0,\infty )$. Then, there exists $t_1\ge t_0$ such that $x\left(\tau \left(t\right)\right)>0$ and $x\left(\sigma \left(t\right)\right)>0$ for all $t\ge t_1$. Suppose that y satisfies case ${\mathbf{N}}_1$ or ${\mathbf{N}}_2$. By Lemma 8, $y\left(t\right)$ satisfies case ${\mathbf{N}}_2$ and the properties (a) and (b). Define the function $w\left(t\right)$ by

$$w\left(t\right):=\rho \left(t\right)\frac{y^{\prime }\left(t\right)}{y\left(\sigma \left(t\right)\right)} .$$

(24)

Then $w\left(t\right)>0$, and

$$w^{\prime }\left(t\right)=\frac{{\rho }^{\prime }\left(t\right)}{\rho \left(t\right)}w\left(t\right)+\frac{\rho \left(t\right)y^{″}\left(t\right)}{y\left(\sigma \left(t\right)\right)}-\frac{\rho \left(t\right)y^{\prime }\left(t\right)y^{\prime }\left(\sigma \left(t\right)\right){\sigma }^{\prime }\left(t\right)}{y^2\left(\sigma \left(t\right)\right)}.$$

Using the fact that $y^{\prime }\left(t\right)$ is decreasing, we have

$$\begin{array}{ccc}\hfill w^{\prime }\left(t\right)& \le & \frac{{\rho }^{\prime }\left(t\right)w\left(t\right)}{\rho \left(t\right)}+\rho \left(t\right)\frac{y^{″}\left(t\right)}{y\left(\sigma \left(t\right)\right)}-\rho \left(t\right)\frac{{\left(y^{\prime }\left(t\right)\right)}^2{\sigma }^{\prime }\left(t\right)}{y^2\left(\sigma \left(t\right)\right)}\hfill \\ & =& \frac{{\rho }^{\prime }\left(t\right)w\left(t\right)}{\rho \left(t\right)}+\rho \left(t\right)\frac{y^{″}\left(t\right)}{y\left(\sigma \left(t\right)\right)}-\frac{{\sigma }^{\prime }\left(t\right)}{\rho \left(t\right)}{\left(\rho \left(t\right)\frac{y^{\prime }\left(t\right)}{y\left(\sigma \left(t\right)\right)}\right)}^2.\hfill \end{array}$$

By (24), we obtain

$$w^{\prime }\left(t\right)\le \frac{{\rho }^{\prime }\left(t\right)w\left(t\right)}{\rho \left(t\right)}+\rho \left(t\right)\frac{y^{″}\left(t\right)}{y\left(\sigma \left(t\right)\right)}-\frac{{\sigma }^{\prime }\left(t\right)}{\rho \left(t\right)}{w}^2\left(t\right).$$

(25)

Integrating (6) from $t_2$ to t and ${\left(y\left(\sigma \left(t\right)\right)/\sigma \left(t\right)\right)}^{\prime }<0,$ we have

$$\begin{array}{ccc}\hfill -\left(r\left(t\right){\left(y^{″}\left(t\right)\right)}^{\alpha }+\frac{p_0^{\alpha }}{{\tau }_0}r\left(\tau \left(t\right)\right){\left(y^{″}\left(\tau \left(t\right)\right)\right)}^{\alpha }\right)& \ge & -\left(r\left(t_2\right){\left(y^{″}\left(t_2\right)\right)}^{\alpha }+\frac{p_0^{\alpha }}{{\tau }_0}r\left(t_2\right){\left(y^{″}\left(\tau \left(t_2\right)\right)\right)}^{\alpha }\right)\hfill \\ & & +\frac{k}{\mu }{\int }_{t_2}^t\widehat{O}\left(s\right)y^{\alpha }\left(\sigma \left(s\right)\right)\mathrm{d}s\hfill \\ & \ge & -\left(r\left(t_2\right){\left(y^{″}\left(t_2\right)\right)}^{\alpha }+\frac{p_0^{\alpha }}{{\tau }_0}r\left(t_2\right){\left(y^{″}\left(\tau \left(t_2\right)\right)\right)}^{\alpha }\right)\hfill \\ & & +\frac{k}{\mu }{\left(\frac{y\left(\sigma \left(t\right)\right)}{\sigma \left(t\right)}\right)}^{\alpha }{\int }_{t_2}^t\widehat{O}\left(s\right){\sigma }^{\alpha }\left(s\right)\mathrm{d}s.\hfill \end{array}$$

(26)

Since ${\lim }_{t\to \infty }y\left(t\right)/t=0,$ there exists $t_3>t_2$ such that

$$-\left(r\left(t_2\right){\left(y^{″}\left(t_2\right)\right)}^{\alpha }+\frac{p_0^{\alpha }}{{\tau }_0}r\left(t_2\right){\left(y^{″}\left(\tau \left(t_2\right)\right)\right)}^{\alpha }\right)-\frac{k}{\mu }{\left(\frac{y\left(\sigma \left(t\right)\right)}{\sigma \left(t\right)}\right)}^{\alpha }{\int }_{t_0}^{t_2}\widehat{O}\left(s\right){\sigma }^{\alpha }\left(s\right)\mathrm{d}s>0.$$

Combining the above inequality in (27) implies

$$\begin{array}{ccc}\hfill -\left(r\left(t\right){\left(y^{″}\left(t\right)\right)}^{\alpha }+\frac{p_0^{\alpha }}{{\tau }_0}r\left(\tau \left(t\right)\right){\left(y^{″}\left(\tau \left(t\right)\right)\right)}^{\alpha }\right)& \ge & -{\left(r{\left(y^{″}\left(t_2\right)\right)}^{\alpha }+\frac{p_0^{\alpha }}{{\tau }_0}r\left(y^{\prime \prime }\left(\tau \left(t_2\right)\right)\right)\right)}^{\alpha }\hfill \\ & & +\frac{k}{\mu }{\left(\frac{y\left(\sigma \left(t\right)\right)}{\sigma \left(t\right)}\right)}^{\alpha }{\int }_{t_0}^t\widehat{O}\left(s\right){\sigma }^{\alpha }\left(s\right)\mathrm{d}s\hfill \\ & & -\frac{k}{\mu }{\left(\frac{y\left(\sigma \left(t\right)\right)}{\sigma \left(t\right)}\right)}^{\alpha }{\int }_{t_0}^{t_2}\widehat{O}\left(s\right){\sigma }^{\alpha }\left(s\right)\mathrm{d}s\hfill \\ & \ge & \frac{k}{\mu }{\left(\frac{y\left(\sigma \left(t\right)\right)}{\sigma \left(t\right)}\right)}^{\alpha }{\int }_{t_0}^t\widehat{O}\left(s\right){\sigma }^{\alpha }\left(s\right)\mathrm{d}s.\hfill \end{array}$$

Using (17), we have

$$-r\left(t\right){\left(y^{″}\left(t\right)\right)}^{\alpha }\left(1+\frac{p_0^{\alpha }}{{\tau }_0}\right)\ge \frac{k}{\mu }{\left(\frac{y\left(\sigma \left(t\right)\right)}{\sigma \left(t\right)}\right)}^{\alpha }{\int }_{t_0}^t\widehat{O}\left(s\right){\sigma }^{\alpha }\left(s\right)\mathrm{d}s,$$

that is,

$$\frac{y^{″}\left(t\right)}{y\left(\sigma \left(t\right)\right)}\le -{\left(\frac{k{\tau }_0}{\mu \left({\tau }_0+p_0^{\alpha }\right)}\right)}^{\frac{1}{\alpha }}\frac{1}{\sigma \left(t\right)r^{\frac{1}{\alpha }}\left(t\right)}{\int }_{t_0}^t\widehat{O}\left(s\right){\sigma }^{\alpha }\left(s\right)\mathrm{d}s.$$

(27)

Substituting (27) in (25), yields

$$\begin{array}{ccc}\hfill w^{\prime }\left(t\right)& \le & \frac{{\rho }^{\prime }\left(t\right)}{\rho \left(t\right)}w\left(t\right)-\frac{\rho \left(t\right)}{\sigma \left(s\right)}{\left(\frac{k{\tau }_0}{\mu \left({\tau }_0+p_0^{\alpha }\right)}\right)}^{\frac{1}{\alpha }}\frac{1}{r^{\frac{1}{\alpha }}\left(t\right)}{\int }_{t_0}^t\widehat{O}\left(s\right){\sigma }^{\alpha }\left(s\right)\mathrm{d}s-\frac{{\sigma }^{\prime }\left(t\right)}{\rho \left(t\right)}{w}^2\left(t\right)\hfill \\ & =& -\frac{{\sigma }^{\prime }\left(t\right)}{\rho \left(t\right)}{\left(w\left(t\right)-\frac{{\rho }^{\prime }\left(t\right)}{2{\sigma }^{\prime }\left(t\right)}\right)}^2+\frac{{\rho }^{\prime 2}\left(t\right)}{4p\left(t\right){\sigma }^{\prime }\left(t\right)}\hfill \\ & & -\frac{\rho \left(t\right)}{\sigma \left(s\right)}{\left(\frac{k{\tau }_0}{\mu \left({\tau }_0+p_0^{\alpha }\right)}\right)}^{\frac{1}{\alpha }}\frac{1}{r^{\frac{1}{\alpha }}\left(t\right)}{\int }_{t_0}^t\widehat{O}\left(s\right){\sigma }^{\alpha }\left(s\right)\mathrm{d}s.\hfill \end{array}$$

Hence,

$$w^{\prime }\left(t\right)\le -\frac{\rho \left(t\right)}{\sigma \left(s\right)}{\left(\frac{k{\tau }_0}{\mu \left({\tau }_0+p_0^{\alpha }\right)}\right)}^{\frac{1}{\alpha }}\frac{1}{r^{\frac{1}{\alpha }}\left(t\right)}{\int }_{t_0}^t\widehat{O}\left(s\right){\sigma }^{\alpha }\left(s\right)\mathrm{d}s+\frac{{\rho }^{\prime 2}\left(t\right)}{4p\left(t\right){\sigma }^{\prime }\left(t\right)}.$$

Integrating from $t_3$ to t, we have

$$w\left(t\right)\le w\left(t_3\right)-{\int }_{t_3}^t\left({\left(\frac{k{\tau }_0}{\mu \left({\tau }_0+p_0^{\alpha }\right)}\right)}^{\frac{1}{\alpha }}\frac{\rho \left(u\right)}{\sigma \left(u\right)r^{\frac{1}{\alpha }}\left(u\right)}{\int }_{t_0}^t\widehat{O}\left(s\right){\sigma }^{\alpha }\left(s\right)\mathrm{d}s-\frac{{\rho }^{\prime 2}\left(u\right)}{4p\left(u\right){\sigma }^{\prime }\left(u\right)}\right)\mathrm{d}u,$$

which is a contradiction. The proof is complete. □

By choosing $\rho \left(t\right)=\frac{1}{\pi }$, we conclude the following corollary.

Corollary 1.

Assume that (11) holds. If there is a nondecreasing function $\rho \in C^1\left(\left[t_0,\infty \right),\left(0,\infty \right)\right)$ and ${\sigma }^{\prime }\left(t\right)>0$, such that

$$\underset{t\to \infty }{\lim \sup }{\int }_T^t\left(\frac{{\left(\frac{k{\tau }_0}{\mu \left({\tau }_0+p_0^{\alpha }\right)}\right)}^{\frac{1}{\alpha }}}{\pi \left(u\right)\sigma \left(u\right)r^{\frac{1}{\alpha }}\left(u\right)}{\int }_{t_0}^t\widehat{O}\left(s\right){\sigma }^{\alpha }\left(s\right)\mathrm{d}s-\frac{r^{-2/\alpha }\left(u\right)}{4{\sigma }^{\prime }\left(u\right){\pi }^3\left(u\right)}\right)\mathrm{d}u=\infty ,$$

(28)

for any $T\in \left[t_0,\infty \right)$, then possible positive solution of (1) satisfies case ${\mathbf{N}}_3$.

Theorem 5.

Assume that (11) holds. If there is a nondecreasing function $\delta \in C^1\left(\left[t_0,\infty \right),\left(0,\infty \right)\right)$, such that

$$\underset{t\to \infty }{\lim \sup }{\int }_{t_2}^t\left(\delta \left(s\right)k\frac{\widehat{O}\left(s\right)}{\mu }-\frac{{\left({\delta }^{\prime }\left(s\right)\right)}^{\alpha +1}}{{\left(\alpha +1\right)}^{\alpha +1}{\left({\sigma }^{{}^{\prime }}\left(s\right)\right)}^{\alpha }{\pi }^{\alpha }\left(s\right){\delta }^{\alpha }\left(s\right)}\right)\mathrm{d}s>\frac{\delta \left(t\right)}{{\pi }^{\alpha }\left(t\right){\sigma }^{\alpha }\left(t\right)},$$

(29)

then, the possible positive solution to (1) satisfies case ${\mathbf{N}}_3$.

Proof. 

Assume that $x\left(t\right)$ is a positive solution of (1) on $[t_0,\infty )$; then, there exists $t_1\ge t_0$ such that $x\left(\tau \left(t\right)\right)>0$ and $x\left(\sigma \left(t\right)\right)>0$ for all $t\ge t_1$. Suppose that y satisfies case ${\mathbf{N}}_1$ or ${\mathbf{N}}_2$. By Lemma 8, $y\left(t\right)$ satisfies case ${\mathbf{N}}_2$ and the properties (a) and (b).

Define the function $w\left(t\right)$ by

$$w\left(t\right):=\delta \left(t\right)\left(\frac{r{\left(y^{″}\left(t\right)\right)}^{\alpha }}{y^{\alpha }\left(\sigma \left(t\right)\right)}+\frac{1}{{\pi }^{\alpha }{\sigma }^{\alpha }\left(t\right)}\right).$$

(30)

From Lemma 8, it is easy to see that

$$y\left(\sigma \left(t\right)\right)\ge \sigma \left(t\right)y^{\prime }\left(\sigma \left(t\right)\right)\ge \sigma \left(t\right)y^{\prime }\left(t\right)\ge -\sigma \left(t\right)\pi \left(t\right)r^{\frac{1}{\alpha }}\left(t\right)y^{″}\left(t\right).$$

(31)

That is, $w\left(t\right)>0$ and

$$-\frac{\delta \left(t\right)r{\left(y^{″}\left(t\right)\right)}^{\alpha }}{y^{\alpha }\left(\sigma \left(t\right)\right)}\le \frac{\delta \left(t\right)}{{\pi }^{\alpha }{\sigma }^{\alpha }\left(t\right)}.$$

(32)

Using (16) and the fact $y^{\prime }\left(t\right)$ is decreasing, we have.

$$\begin{array}{ccc}\hfill w^{\prime }\left(t\right)& =& \frac{{\delta }^{\prime }\left(t\right)}{\delta \left(t\right)}w\left(t\right)+\frac{\delta \left(t\right){\left(r\left(t\right){\left(y^{″}\left(t\right)\right)}^{\alpha }\right)}^{\prime }}{y^{\alpha }\left(\sigma \left(t\right)\right)}-\frac{\alpha \delta \left(t\right)r\left(t\right){\left(y^{″}\left(t\right)\right)}^{\alpha }{y}^{\prime }\left(\sigma \left(t\right)\right){\sigma }^{\prime }\left(t\right)}{y^{\alpha +1}\left(\sigma \left(t\right)\right)}\hfill \\ & & +\frac{\alpha \delta \left(t\right)}{{\left(\pi \left(t\right)\sigma \left(t\right)\right)}^{\alpha +1}}\left(\frac{\sigma \left(t\right)}{r^{\frac{1}{\alpha }}\left(t\right)}-{\sigma }^{\prime }\left(t\right)\pi \left(t\right)\right)\hfill \\ & \le & \frac{{\delta }^{\prime }\left(t\right)}{\delta \left(t\right)}w\left(t\right)-\delta \left(t\right)\frac{k}{\mu }\widehat{O}\left(t\right)\hfill \\ & & -\frac{\alpha {\sigma }^{{}^{\prime }}\left(t\right)y^{\prime }\left(t\right)}{{\delta }^{\frac{1}{\alpha }}\left(t\right)r^{\frac{1}{\alpha }}\left(t\right)y^{″}\left(t\right)}{\left(w\left(t\right)-\frac{\delta \left(t\right)}{\pi \left(t\right)\sigma \left(t\right)}\right)}^{\frac{1}{\alpha }+1}+\frac{\alpha \delta \left(t\right)}{{\left(\pi \left(t\right)\sigma \left(t\right)\right)}^{\alpha +1}}\left(\frac{\sigma \left(t\right)}{r^{\frac{1}{\alpha }}\left(t\right)}-{\sigma }^{\prime }\left(t\right)\pi \left(t\right)\right).\hfill \end{array}$$

In view of (b) in Lemma 8, we find

$$\begin{array}{ccc}\hfill w^{\prime }\left(t\right)& \le & \frac{{\delta }^{\prime }\left(t\right)}{\delta \left(t\right)}w\left(t\right)-\delta \left(t\right)k\frac{\widehat{O}\left(t\right)}{\mu }\hfill \\ & & -\frac{\alpha {\sigma }^{{}^{\prime }}\left(t\right)\pi \left(t\right)}{{\delta }^{\frac{1}{\alpha }}\left(t\right)}{\left(w\left(t\right)-\frac{\delta \left(t\right)}{{\pi }^{\alpha }\left(t\right){\sigma }^{\alpha }\left(t\right)}\right)}^{\frac{1}{\alpha }+1}+\frac{\alpha \delta \left(t\right)}{{\left(\pi \left(t\right)\sigma \left(t\right)\right)}^{\alpha +1}}\left(\frac{\sigma \left(t\right)}{r^{\frac{1}{\alpha }}\left(t\right)}-{\sigma }^{\prime }\left(t\right)\pi \left(t\right)\right).\hfill \end{array}$$

Set

$$A:=\frac{{\delta }^{\prime }\left(t\right)}{\delta \left(t\right)}, B:=\frac{\alpha {\sigma }^{{}^{\prime }}\left(t\right)\pi \left(t\right)}{{\delta }^{\frac{1}{\alpha }}\left(t\right)}, C:=\frac{\delta \left(t\right)}{{\pi }^{\alpha }\left(t\right){\sigma }^{\alpha }\left(t\right)}.$$

Using Lemma 2, we obtain

$$\begin{array}{ccc}\hfill w^{\prime }\left(t\right)& =& -\delta \left(t\right)k\frac{\widehat{O}\left(t\right)}{\mu }+\frac{{\delta }^{\prime }\left(t\right)}{{\pi }^{\alpha }\left(t\right){\sigma }^{\alpha }\left(t\right)}+\frac{1}{{\left(\alpha +1\right)}^{\alpha +1}}\frac{{\left({\delta }^{\prime }\left(t\right)\right)}^{\alpha +1}}{{\left({\sigma }^{{}^{\prime }}\left(t\right)\right)}^{\alpha }{\pi }^{\alpha }\left(t\right){\delta }^{\alpha }\left(t\right)}\hfill \\ & & +\frac{\alpha \delta \left(t\right)}{{\left(\pi \left(t\right)\sigma \left(t\right)\right)}^{\alpha +1}}\left(\frac{\sigma \left(t\right)}{r^{\frac{1}{\alpha }}\left(t\right)}-{\sigma }^{\prime }\left(t\right)\pi \left(t\right)\right).\hfill \end{array}$$

(33)

It is clear that

$${\left(\frac{\delta \left(t\right)}{{\pi }^{\alpha }\left(t\right){\sigma }^{\alpha }\left(t\right)}\right)}^{\prime }=\frac{{\delta }^{\prime }\left(t\right)}{{\pi }^{\alpha }\left(t\right){\sigma }^{\alpha }\left(t\right)}+\frac{\alpha \delta \left(t\right)}{{\left(\pi \left(t\right)\sigma \left(t\right)\right)}^{\alpha +1}}\left(\frac{\sigma \left(t\right)}{r^{\frac{1}{\alpha }}\left(t\right)}-{\sigma }^{\prime }\left(t\right)\pi \left(t\right)\right).$$

In (33), we obtain

$$w^{\prime }\left(t\right)=-\delta \left(t\right)k\frac{\widehat{O}\left(t\right)}{\mu }+{\left(\frac{\delta \left(t\right)}{{\pi }^{\alpha }\left(t\right){\sigma }^{\alpha }\left(t\right)}\right)}^{\prime }+\frac{1}{{\left(\alpha +1\right)}^{\alpha +1}}\frac{{\left({\delta }^{\prime }\left(t\right)\right)}^{\alpha +1}}{{\left({\sigma }^{{}^{\prime }}\left(t\right)\right)}^{\alpha }{\pi }^{\alpha }\left(t\right){\delta }^{\alpha }\left(t\right)}.$$

Integrating the above inequality from $t_2$ to t yields

$$\begin{array}{ccc}& & {\int }_{t_2}^t\left(\delta \left(s\right)k\frac{\widehat{O}\left(s\right)}{\mu }-\frac{{\left({\delta }^{\prime }\left(s\right)\right)}^{\alpha +1}}{{\left(\alpha +1\right)}^{\alpha +1}{\left({\sigma }^{{}^{\prime }}\left(s\right)\right)}^{\alpha }{\pi }^{\alpha }\left(s\right){\delta }^{\alpha }\left(s\right)}\right)\mathrm{d}s+\frac{\delta \left(t\right)}{{\pi }^{\alpha }\left(t\right){\sigma }^{\alpha }\left(t\right)}-\frac{\delta \left(t_2\right)}{{\pi }^{\alpha }\left(t_2\right){\sigma }^{\alpha }\left(t_2\right)}\hfill \\ & \le & w\left(t_2\right)-w\left(t\right).\hfill \end{array}$$

From (30), we are led to

$$\begin{array}{ccc}& & {\int }_{t_2}^t\left(\delta \left(s\right)k\frac{\widehat{O}\left(s\right)}{\mu }-\frac{{\left({\delta }^{\prime }\left(s\right)\right)}^{\alpha +1}}{{\left(\alpha +1\right)}^{\alpha +1}{\left({\sigma }^{{}^{\prime }}\left(s\right)\right)}^{\alpha }{\pi }^{\alpha }\left(s\right){\delta }^{\alpha }\left(s\right)}\right)\mathrm{d}s+\frac{\delta \left(t\right)}{{\pi }^{\alpha }\left(t\right){\sigma }^{\alpha }\left(t\right)}\hfill \\ & & -\frac{\delta \left(t_2\right)}{{\pi }^{\alpha }\left(t_2\right){\sigma }^{\alpha }\left(t_2\right)}\hfill \\ & \le & \delta \left(t_2\right)\left(\frac{r{\left(y^{″}\left(t_2\right)\right)}^{\alpha }}{y^{\alpha }\left(\sigma \left(t_2\right)\right)}\right)-\delta \left(t\right)\left(\frac{r{\left(y^{″}\left(t\right)\right)}^{\alpha }}{y^{\alpha }\left(\sigma \left(t\right)\right)}\right).\hfill \end{array}$$

(34)

By (32), (35) becomes

$${\int }_{t_2}^t\left(\delta \left(s\right)k\frac{\widehat{O}\left(s\right)}{\mu }-\frac{{\left({\delta }^{\prime }\left(s\right)\right)}^{\alpha +1}}{{\left(\alpha +1\right)}^{\alpha +1}{\left({\sigma }^{{}^{\prime }}\left(s\right)\right)}^{\alpha }{\pi }^{\alpha }\left(s\right){\delta }^{\alpha }\left(s\right)}\right)\mathrm{d}s\le \frac{\delta \left(t\right)}{{\pi }^{\alpha }{\sigma }^{\alpha }\left(t\right)}.$$

The proof is complete. □

Lemma 9.

Let $x\left(t\right)$ be a positive solution to (1) and $y\left(t\right),$ satisfying case ${\mathbf{N}}_3.$ If

$${\int }_{t_0}^{\infty }\widehat{O}\left(s\right)\mathrm{d}s=\infty$$

(35)

or

$${\int }_{t_0}^{\infty }\frac{1}{r\left(s\right)}{\left({\int }_t^{\infty }\widehat{O}\left(u\right)\mathrm{d}u\right)}^{\frac{1}{\alpha }}\mathrm{d}s=\infty ,$$

(36)

then ${\lim }_{t\to \infty }y\left(t\right)=0$.

Proof. 

Assume that $x\left(t\right)$ is a positive solution of (1) on $[t_0,\infty )$, there exists $t_1\ge t_0$ such that $x\left(\tau \left(t\right)\right)>0$ and $x\left(\sigma \left(t\right)\right)>0$ for all $t\ge t_1$. Since $y\left(t\right)>0$ and $y^{\prime }\left(t\right)<0,$ there is $\lambda \ge 0$, such that ${\lim }_{t\to \infty }y\left(t\right)=\lambda .$ Assume that $\lambda >0.$ Integrating (6) from $t_2$ to t, we have

$$\begin{array}{ccc}\hfill r\left(t\right){\left(y^{″}\left(t\right)\right)}^{\alpha }+\frac{p_0^{\alpha }}{{\tau }_0}r{\left(y^{″}\left(\tau \left(t\right)\right)\right)}^{\alpha }& \le & r\left(t_1\right){\left(y^{″}\left(t_1\right)\right)}^{\alpha }+\frac{p_0^{\alpha }}{{\tau }_0}r\left(\tau \left(t_1\right)\right){\left(y^{\prime \prime }\left(\tau \left(t_1\right)\right)\right)}^{\alpha }\hfill \\ & & -\frac{k}{\mu }{\int }_{t_2}^t\widehat{O}\left(s\right)y^{\alpha }\left(\sigma \left(s\right)\right)\mathrm{d}s\hfill \\ & \le & r\left(t_1\right){\left(y^{″}\left(t_1\right)\right)}^{\alpha }+\frac{p_0^{\alpha }}{{\tau }_0}r\left(\tau \left(t_1\right)\right){\left(y^{″}\left(\tau \left(t_1\right)\right)\right)}^{\alpha }\hfill \\ & & -\frac{k}{\mu }{\lambda }^{\alpha }{\int }_{t_2}^t\widehat{O}\left(s\right)\mathrm{d}s.\hfill \end{array}$$

This contradicts (35). Hence $\lambda =0.$ The proof is complete. □

Theorem 6.

Let $x\left(t\right)$ be a positive solution of (1). If

$$\underset{t\to \infty }{\lim \sup }{\int }_{\sigma \left(t\right)}^t\widehat{O}\left(s\right)R\left(\sigma \left(t\right),\sigma \left(s\right)\right)\mathrm{d}s>\frac{{\tau }_0}{{\tau }_0+p_0^{\alpha }},$$

(37)

then case ${\mathbf{N}}_3$ is impossible, where $R(v,u)={\int }_u^v{\int }_{\zeta }^v\frac{1}{r^{\frac{1}{\alpha }}\left(\zeta \right)}\mathrm{d}\zeta .$

Proof. 

Since $r{\left(y^{″}\left(t\right)\right)}^{\alpha }$ is nonincreasing, pick $t_1\in [t_0,\infty )$ for $t\ge t_1$, we see that

$$-y^{\prime }\left(u\right)\ge {\int }_u^v\frac{1}{r^{\frac{1}{\alpha }}\left(s\right)}{r}^{\frac{1}{\alpha }}\left(s\right)y^{″}\left(s\right)\mathrm{d}s\ge r^{\frac{1}{\alpha }}\left(v\right)y^{″}\left(v\right){\int }_u^v\frac{1}{r^{\frac{1}{\alpha }}\left(s\right)}\mathrm{d}s,$$

for $v\ge u$. Integrating above inequality from u to v, we have

$$y\left(u\right)\ge r^{\frac{1}{\alpha }}\left(v\right)y^{″}\left(v\right){\int }_u^v{\int }_{\zeta }^v\frac{1}{r^{\frac{1}{\alpha }}\left(\zeta \right)}\mathrm{d}\zeta =r^{\frac{1}{\alpha }}\left(v\right)y^{″}\left(v\right)R(v,u).$$

(38)

Integrating (6) from $\sigma \left(t\right)$ to t and using (38), we get (17)

$$\begin{array}{ccc}\hfill \left(r\left(\sigma \left(t\right)\right){\left(y^{″}\left(\sigma \left(t\right)\right)\right)}^{\alpha }+\frac{p_0^{\alpha }}{{\tau }_0}r\left(\tau \left(\sigma \left(t\right)\right)\right)\left(y^{″}{\left(\tau \left(\sigma \left(t\right)\right)\right)}^{\alpha }\right)\right)& \ge & \frac{k}{\mu }{\int }_{\sigma \left(t\right)}^t\widehat{O}\left(s\right)y^{\alpha }\left(\sigma \left(s\right)\right)\mathrm{d}s\hfill \\ & \ge & \frac{k}{\mu }r\left(\sigma \left(t\right)\right){\left(y^{″}\left(\sigma \left(t\right)\right)\right)}^{\alpha }{\int }_{\sigma \left(t\right)}^t\widehat{O}\left(s\right)R^{\alpha }(\sigma \left(t\right),\sigma \left(s\right))\mathrm{d}s.\hfill \end{array}$$

Using the fact that ${\left(r\left(t\right){\left(y^{″}\left(t\right)\right)}^{\alpha }\right)}^{\prime }<0$ and (17), we obtain

$$r\left(\sigma \left(t\right)\right){\left(y^{″}\left(\sigma \left(t\right)\right)\right)}^{\alpha }<r\left(\tau \left(\sigma \left(t\right)\right)\right){\left(y^{″}\left(\tau \left(\sigma \left(t\right)\right)\right)\right)}^{\alpha },$$

and

$$\begin{array}{ccc}\hfill r\left(\tau \left(\sigma \left(t\right)\right)\right)\left(y^{″}{\left(\tau \left(\sigma \left(t\right)\right)\right)}^{\alpha }\right)\left(1+\frac{p_0^{\alpha }}{{\tau }_0}\right)& \ge & -\frac{k}{\mu }r\left(\sigma \left(t\right)\right){\left(y^{″}\left(\sigma \left(t\right)\right)\right)}^{\alpha }{\int }_{\sigma \left(t\right)}^t\widehat{O}\left(s\right)R^{\alpha }(\sigma \left(t\right),\sigma \left(s\right))\mathrm{d}s\hfill \\ & \ge & -\frac{k}{\mu }r\left(\tau \left(\sigma \left(t\right)\right)\right){\left(y^{″}\left(\tau \left(\sigma \left(t\right)\right)\right)\right)}^{\alpha }{\int }_{\sigma \left(t\right)}^t\widehat{O}\left(s\right)R^{\alpha }(\sigma \left(t\right),\sigma \left(s\right))\mathrm{d}s.\hfill \end{array}$$

Hence,

$$\left(1+\frac{p_0^{\alpha }}{{\tau }_0}\right)\ge -\frac{k}{\mu }{\int }_{\sigma \left(t\right)}^t\widehat{O}\left(s\right)R^{\alpha }(\sigma \left(t\right),\sigma \left(s\right))\mathrm{d}s.$$

This led to a contradiction. The proof is complete. □

4. Applications

4.1. Asymptotic Properties

By combining Theorems 2–5 with Lemma 9, one can easily provide new criteria for the asymptotic properties of (1) as follows

Theorem 7.

Assume that (13) holds. Then, (1) is almost oscillatory.

Theorem 8.

Assume that (19) and (35) or (36) hold. Then (1) is almost oscillatory.

Theorem 9.

Assume that (11), (22) and either (35) or (36) hold. Then, (1) is almost oscillatory.

Theorem 10.

Assume that (11) holds and, if there is a nondecreasing function $\rho \in C^1\left(\left[t_0,\infty \right),\left(0,\infty \right)\right)$ and ${\sigma }^{\prime }\left(t\right)>0$, such that (28) and either (35) or (36) hold, then (1) is almost oscillatory.

Theorem 11.

Assume that (11) holds and if there is a nondecreasing function $\delta \in C^1\left(\left[t_0,\infty \right),\left(0,\infty \right)\right)$, such that (29) and either (35) or (36) hold, then (1) is almost oscillatory.

4.2. Oscillation

In the following Theorem, we combine Theorems 2–5 with Theorem (37) to obtain new criteria for oscillation of (1)

Theorem 12.

If all assumptions of Theorem 1 or 2 or 3 or 4 or 5 and (37) hold, then (1) is oscillatory.

Remark 2.

Compared to the existing results of [25,26], oscillation of (1) is attained by easier conditions.

Example 1.

Consider the third-order neutral delay differential equation

$${\left(t^2{\left(x\left(t\right)+p_{0}x\left(ϵt\right)\right)}^{″}\right)}^{\prime }+\frac{q_0}{t}y\left(0.5t\right)=0, t\ge 1,$$

(39)

where $ϵ\in \left(0,1\right)$ and $q_0>0.$ We note that $r=t^2,\sigma \left(t\right)=0.5t$, $\tau \left(t\right)=ϵt$, $p\left(t\right)=p_0$. It can easily be verified that $\widehat{O}\left(t\right)=\frac{q_0}{t}.$ By choosing $\delta \left(t\right)=\pi \left(t\right)\tau \left(t\right)=ϵ,$ Condition (19), (29), (28) and (37) become

$$\begin{array}{ccc}\hfill q_0& >& \frac{2\left({\tau }_0+p_0\right)}{\ln \left(2\right){\tau }_{0}e},\hfill \end{array}$$

(40)

$$\begin{array}{ccc}\hfill q_0& >& \frac{2}{\left(1-p_0\right)},\hfill \end{array}$$

(41)

$$\begin{array}{ccc}\hfill q_0& >& \frac{\left({\tau }_0+p_0\right)}{2{\tau }_0}\hfill \end{array}$$

(42)

and

$$q_0>\frac{{\tau }_0}{\left({\tau }_0+p_0\right)\left(0.5+\ln 0.5+\frac{1}{2}{\ln }^{2}0.5\right),}$$

respectively. Using Theorems 8, 10 and 11, Equation (39) is almost oscillatory if (40) or (41) or (42) holds. Moreover, by Theorem 12, we see that (39) is oscillatory if

$$q_0>\max \left\{\frac{{\tau }_0}{\left({\tau }_0+p_0\right)\left(0.5+\ln 0.5+\frac{1}{2}{\ln }^{2}0.5\right)},\frac{2\left({\tau }_0+p_0\right)}{\ln \left(2\right){\tau }_{0}e}\right\}.$$

Remark 3.

It is easy to verify that condition (13) fails; therefore, Theorem 1 does not apply.

Remark 4.

If $p_0=1$ then our results are reduced to the results of Chatzarakis in [14].

Example 2.

Consider the third-order neutral delay differential equation

$${\left(t^2{\left({\left(x\left(t\right)+p_{0}x\left(ϵt\right)\right)}^{″}\right)}^{\alpha }\right)}^{\prime }+\frac{q_0}{t}{y}^{\alpha }\left(\lambda t\right)=0, t\ge 1,$$

(43)

where $q_0>0$ and $\lambda ,ϵ\in \left(0,1\right).$ Condition (19), (28) and (37) reduse to

$$\begin{array}{ccc}\hfill C1:q_0& >& \frac{ϵ+p_0}{\lambda ϵe\ln \left(\frac{1}{\lambda }\right)},\hfill \\ \hfill C2:q_0& >& \frac{\mu {\left(ϵ+p_0^{\alpha }\right)}^{1/\alpha }}{4\lambda {ϵ}^{1/\alpha }}\hfill \end{array}$$

and

$$C3:q_0>\frac{ϵ}{\left(ϵ+p_0^{\alpha }\right)\left(1-\lambda +\ln \lambda +\frac{1}{2}{\ln }^2\lambda \right),}$$

respectively. Therefore, by Theorem 12, we see that (43) is oscillatory if

$$q_0>\max \left\{\frac{ϵ+p_0}{\lambda ϵe\ln \left(\frac{1}{\lambda }\right)},\frac{ϵ}{\left(ϵ+p_0^{\alpha }\right)\left(1-\lambda +\ln \lambda +\frac{1}{2}{\ln }^2\lambda \right)}\right\}$$

(44)

or

$$q_0>\max \left\{\frac{\mu {\left(ϵ+p_0^{\alpha }\right)}^{1/\alpha }}{4\lambda {ϵ}^{1/\alpha }},\frac{ϵ}{\left(ϵ+p_0^{\alpha }\right)\left(1-\lambda +\ln \lambda +\frac{1}{2}{\ln }^2\lambda \right)}\right\}.$$

(45)

Remark 5.

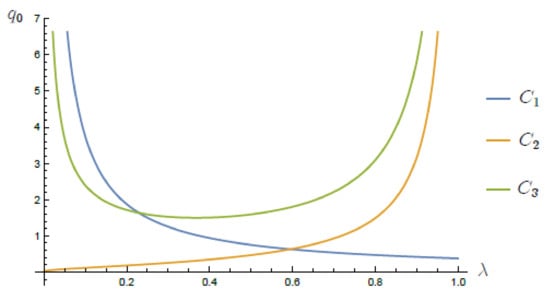
Consider a particular case of (43), namely,

$${\left(t^2\left({\left(x\left(t\right)+\frac{1}{4}x\left(\frac{t}{2}\right)\right)}^{″}\right)\right)}^{\prime }+\frac{q_0}{t}y\left(\lambda t\right)=0,$$

(46)

Conditions (44) and (45) reduce to

$$q_0>\max \left\{\frac{\frac{3}{4}}{\frac{1}{4}\lambda e\ln \left(\frac{1}{\lambda }\right)},\frac{\frac{1}{2}}{\left(\frac{3}{4}\right)\left(1-\lambda +\ln \lambda +\frac{1}{2}{\ln }^2\lambda \right)}\right\}$$

(47)

and

$$q_0>\max \left\{\frac{3}{8\lambda },\frac{2}{3\left(1-\lambda +\ln \lambda +\frac{1}{2}{\ln }^2\lambda \right)}\right\},$$

(48)

respectively; see Figure 1. Thus, by Theorem 12, Equation (46) is oscillatory if (47) or (48) satisfies. So, For a given $\lambda \in \left(0,0.21\right),$ Condition (47) is sharp for oscillation, but in $\lambda \in \left(0.21,1\right)$ Condition (48) is sharp for oscillation.

Figure 1. Test of the strength of criteria for (46).

On the other hand, consider a particular case of (43), namely,

$${\left(t^2{\left({\left(x\left(t\right)+\frac{1}{4}x\left(\frac{t}{2}\right)\right)}^{″}\right)}^{\alpha }\right)}^{\prime }+\frac{q_0}{t}y\left(\frac{t}{4}\right)=0,$$

(49)

where $\alpha >1$. Conditions (44) and (45) reduce to

$$q_0>\max \left\{\frac{3}{e\ln 2},\frac{1}{2}\frac{2^{2\alpha +1}}{\left(2^{2\alpha }+2\right)\left(2{\ln }^{2}2-2\ln 2+\frac{3}{4}\right)}\right\}$$

or

$$q_0>\max \left\{\frac{2}{17}{2}^{\alpha }{\left(\frac{1}{2^{2\alpha }}\left(2^{2\alpha }+2\right)\right)}^{\frac{1}{\alpha }},\frac{1}{2}\frac{2^{2\alpha +1}}{\left(2^{2\alpha }+2\right)\left(2{\ln }^{2}2-2\ln 2+\frac{3}{4}\right)}\right\}.$$

Remark 6.

It is easy to notice that the effect of the delay argument on the oscillation parameters varies from one example to another, and no consistent pattern can be found to determine this effect. Additionally, the oscillation test depends on two different conditions, so we notice the change in the effect of the delay argument on oscillation (from inverse to direct relationship). This also applies to the effect of α.

5. Conclusions

In this paper, we introduced a simplified theorem for near oscillation; furthermore, we established oscillation criteria for (1). Using comparison theorems and the Riccati technique, we established criteria to check the oscillation under fewer restrictions, and compared this with some results published in the literature. Our results are an extension of and complement to existing results in some previous studies, such as [15,27,29].

The establishment of criteria for the oscillation of Equation (1) without the need for a condition $\sigma \circ \tau =\tau \circ \sigma$ and ${\tau }^{\prime }\left(t\right)\ge {\tau }_0$ remains an open problem.