1. Introduction
Multiple criteria decision-making (MCDM) is still a very actual area of operational research. For solving many decision-making problems, numerous MCDM methods have been proposed so far. On the other hand, a number of their extensions have also been proposed, such as grey, fuzzy, or neutrosophic extensions, in order to enable their usage for solving a number of complex decision problems.
The following can be mentioned as some of the prominent, or newly proposed, MCDM methods, also used in presented research: Technique for Order of Preference by Similarity to Ideal Solution (the TOPSIS method) [
1], Multi-criteria Optimization and Compromise Solution (the VIKOR method) [
2] and Multi-Objective Optimization by Ratio Analysis plus the full multiplicative form (the MULTIMOORA method) [
3], the Additive Ratio Assessment (the ARAS method) method [
4], the Weighted Aggregated Sum Product Assessment (the WASPAS method) [
5], and the Combined Compromise Solution (the CoCoSo method) [
6].
Stanujkic et al. [
7] proposed a new MCDM approach based on the integration of the WS and WP methods, which also integrates some approaches implemented in the ARAS, WASPAS, CoCoSo and MULTIMOORA methods, the Simple Weighted Sum Product (WISP) method.
In order to enable wider application of the Simple WISP method, a combative study between the results obtained by using the Simple WISP method and several selected MCDM methods is presented in this article. Analyses and computational procedures were performed by using the Python programming language and its NumPy library.
Accordingly, the article is structured as follows: In
Section 2, the Simple WISP method and cosine similarity measure are presented in detail, whereas in
Section 3, several analyses of the results obtained using Simple WISP and several selected MCDM methods were performed, with analyses performed using Python and its NymPy library. In
Section 4, the effectiveness of the Simple WISP method was demonstrated in the case of solving a real MCDM problem, where the obtained results were also compared with the results obtained using some selected MCDM methods. In
Section 5, a brief discussion is given. Finally, the conclusions are presented at the end.
3. Comparison of the WISP Method and Some Efficient MCDM Methods
This part presents a comparative study of the ranking results obtained by using the WISP method and some noticeable MCDM methods, namely TOPSIS, SAW, ARAS, WASPAS, and CoCoSo methods. The analysis was performed on an MCDM example containing five alternatives and four criteria, with the first two criteria being beneficial and the remaining two non-beneficial. In the conducted analysis, all criteria have the same weight, which is why the weight vector looks as follows: wj = {0.25, 0.25, 0.25, 0.25}.
In the conducted analyses, the ratings of alternative A1 were generated using Python for in-range loops, while ratings of alternatives A2 to A5 were generated using the numpy.random.randint (1, 6) function and numpy.random.seed (0).
The utility of the considered alternatives obtained using the mentioned MCDM methods, for different variations of the ratings of criteria
C1–
C4 of the alternative
A1, is shown graphically in
Figure 2 and
Figure 3.
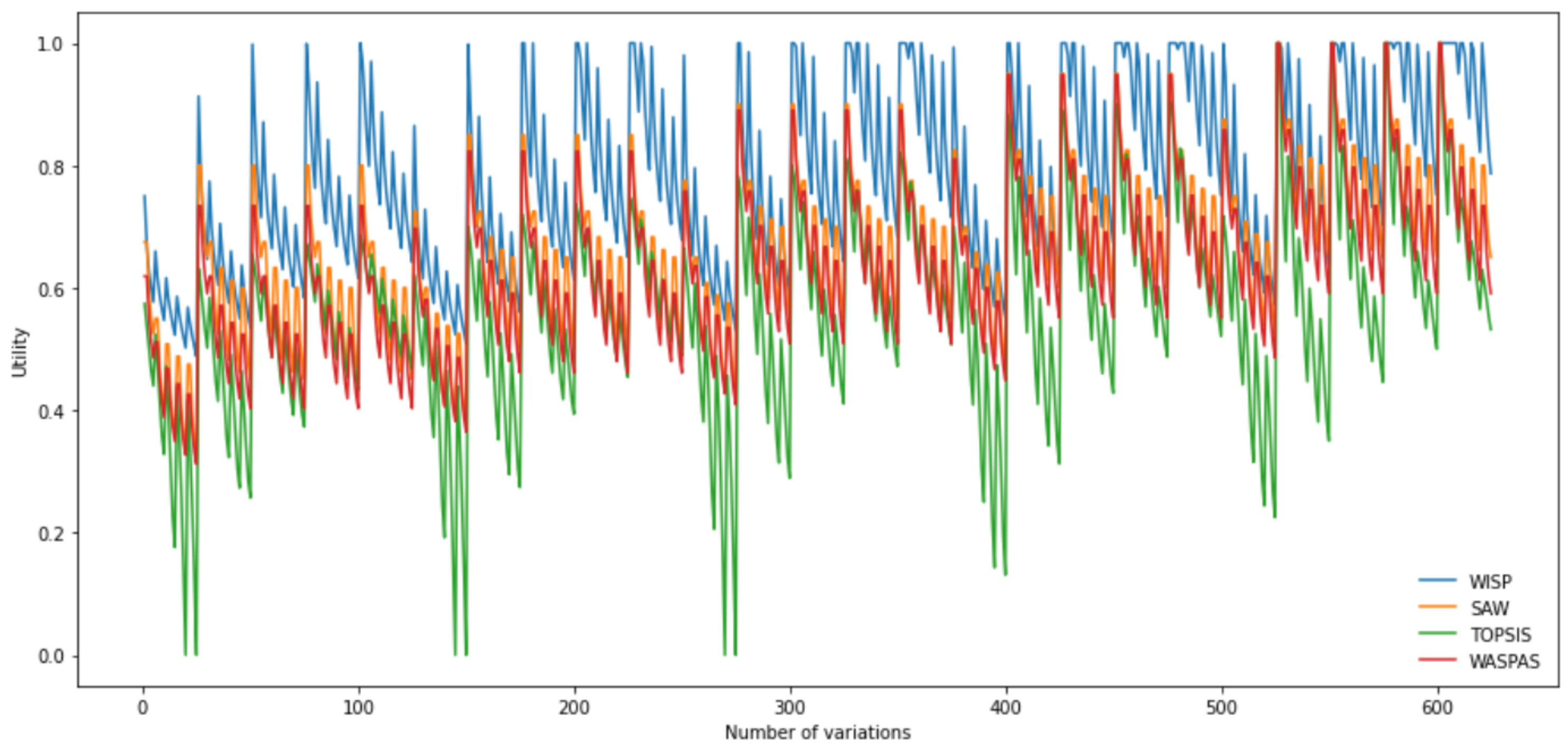
Figure 2 shows the utility of considered alternatives based on 625 variations of the ratings of criteria
C1–
C4 of the alternative
A1,
, which were formed using the Python for in range (1, 6) loops.
A similar, somewhat clearer,
Figure 2 was formed based on 225 variations of the ratings of criteria
C1–
C4,
, and
where the ratings of criteria
C2 and
C4 were formed using the Python for in range (1, 6, 2) loops.
From
Figure 2 and
Figure 3, a significant correlation in the trend of increasing and decreasing utility of alternatives obtained by applying the considered MCDM methods can be noticed.
To determine to what extent the results obtained by applying the WISP method are consistent with the results obtained by applying the above-mentioned MCDM methods, several analyses were performed, which are described below.
The first analysis. In the first of the five conducted analyses, the correlation between ranking orders of alternatives was obtained by using the WISP method and ranking orders of alternatives obtained by applying TOPSIS, SAW, ARAS, WASPAS, and CoCoSo methods. The correlation was examined based on four “randomly selected” initial decision-making matrices.
The four initial decision-making matrices were selected from a set of 81 decision-making matrices formed by using the Python for in range (1, 6, 2) loops. Further evaluation is selected every twentieth initial decision-making matrix, i.e., the matrix for which the following condition is met number_of_variation % 20 == 0.
The first of four selected initial decision-making matrices is shown in
Table 1, while the ranking results and ranking orders of alternatives are shown in
Table 2 and
Table 3.
From
Table 3, it can be noticed that there is some difference in the ranking orders of alternatives obtained by applying the WISP method and some of the considered MCDM methods. However, the cosine similarity measure calculated between the ranking results obtained using WISP and the considered MCDM methods, also shown in
Table 3, indicates a significant similarity between the obtained ranking orders of alternatives.
Table 7,
Table 8 and
Table 9 show a significantly higher agreement between the ranking corresponding to the WISP method and the ranking results obtained using the ARAS, SAW, WASPAS, and TOPSIS methods, which is also confirmed by the high values of cosine similarity measures between ranking orders of alternatives achieved using the WISP method and ranking orders of alternatives achieved using mentioned MCDM methods.
Contrary to the above, the achieved results indicate a slightly lower agreement between the results achieved using WISP and CoCoSo methods.
The second analysis. In the second of the five conducted analyses, the correlation of the ranks of alternative A1 concerning the ranks of the same alternative obtained by applying the selected MCDM methods was examined.
Determining the correlation of the ranks of alternative A1 was performed for five cases, with a different number of variations of the values of criteria C1–C4, where different number of variations was realized by using different combinations of range (1,6) and range (1,6,2) function in the Python for in loop. In each of the five cases, for each MCDM method used, a vector containing the rank of alternative A1 was formed.
The achieved values of the cosine similarity measure between the vectors of the WISP method and the vectors of other MCDM methods are shown in
Table 10.
From
Table 10, it can be seen that there is a high correlation in the rank of alternative
A1 between WISP–WASPAS, WISP–SAW, and WISP–ARAS methods. There is a high correlation that also exists between WISP–TOPSIS and WISP–CoCoSo methods, but it is lower compared to the above-mentioned.
The third analysis. In the third analysis, the correlation between the best-ranked alternatives obtained by applying several MCDM methods was examined. As in the previous analysis, the correlation was performed for five cases with a different numbers of variations.
The achieved values of the cosine similarity measure between the vectors of the WISP method and the vectors of other MCDM methods are shown in
Table 11.
From
Table 11, a high correlation of the best-placed alternative can be observed between WISP–WASPAS, WISP–SAW, and WISP–ARAS methods. A slightly lower correlation can also be observed between WISP–TOPSIS and WISP–CoCoSo methods.
The fourth analysis. The fourth analysis was conducted to determine the similarity between the ranking orders of alternatives obtained by applying WISP and mentioned MCDM methods. As in previous cases, the analysis was performed on five cases with different numbers of variations. The obtained results of this analysis are shown in
Table 12.
As in the previous analysis, a high correlation of the ranking orders of alternatives can be observed between WISP–WASPAS, WISP–SAW, WISP–ARAS and WISP–TOPSIS methods.
The fifth analysis. Unlike previous analyses, in this analysis, the values of alternative
A2 are also varied, as in the case of alternative
A1. In this analysis, the similarity of the first-ranked method obtained using WISP and the above-mentioned MCDM methods was checked. The results of the calculation, i.e., the similarity of the obtained ranks calculated using the cosine similarity measure are shown in
Table 13.
As in the previous analysis, a high correlation of the best-placed alternative can be observed between WISP–WASPAS, WISP–ARAS, WISP–SAW and WISP–TOPSIS methods.
Based on the above analysis, it may be realized that the WISP method produces comparable ranking results as the WASPAS, ARAS, SAW, and TOPSIS methods.
4. A Numerical Illustration
In order to demonstrate the application of the WISP method, an example of a flotation machine selection was borrowed from Stirbanovic et al. [
14]. In this example, the evaluation of the flotation machine was performed on the basis of 10 criteria, which were classified into three groups:
- ―
Constructional parameters;
- ―
Economical parameters;
- ―
Technical parameters.
The evaluation criteria, their optimization direction (Opt.), and their weights are shown in
Table 14.
The ratings of the five alternatives in relation to the selected set of criteria is shown in
Table 15.
The mentioned example of selection is interesting because the applied MCDM methods, TOPSIS and VIKOR, gave different ranking orders of alternatives, as shown in
Table 16.
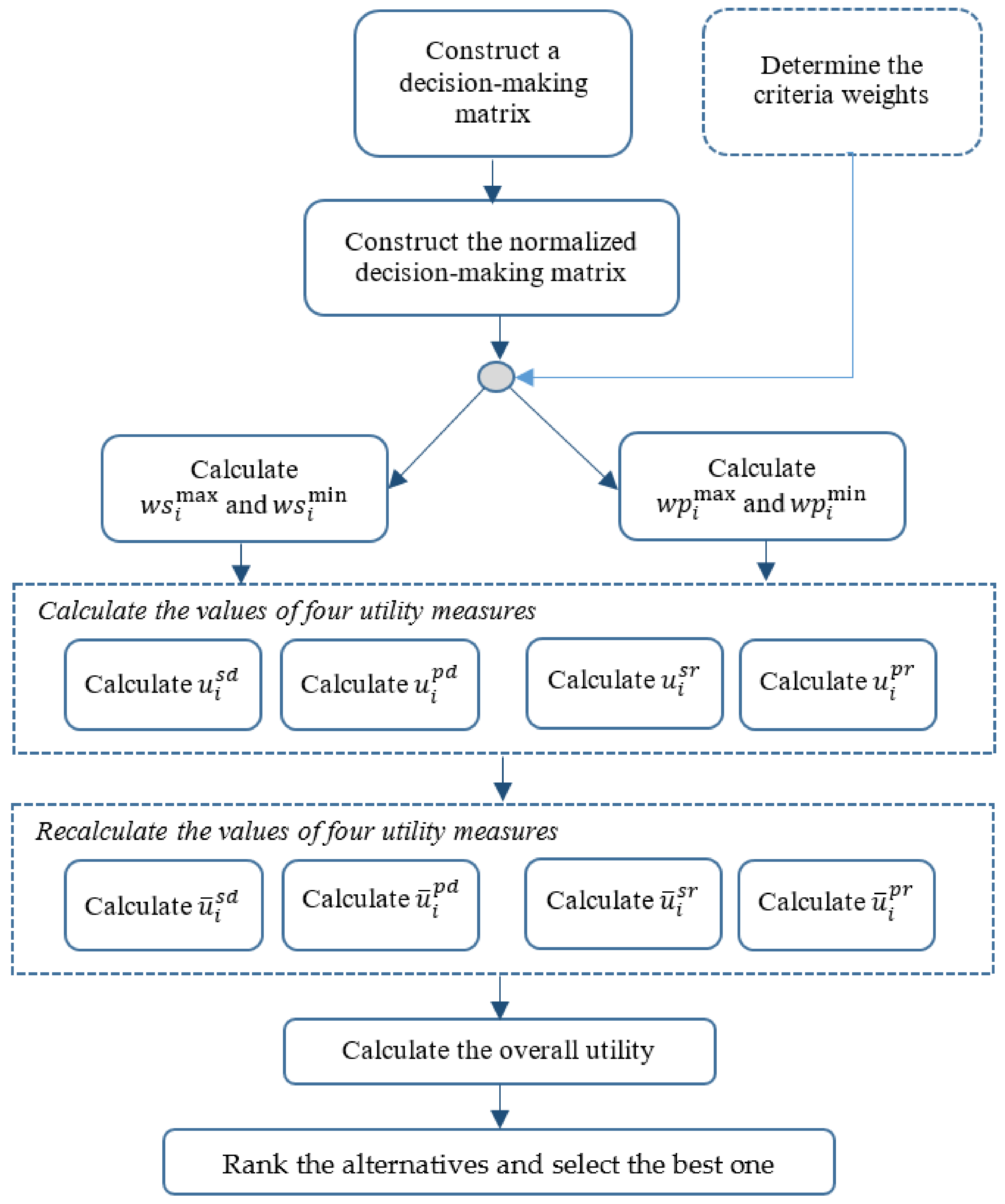
Normalized decision table, constructed using Equation (1), is shown in
Table 17.
The values of four utility measures
,
,
, and
, calculated using Equations (2)–(5), are shown in
Table 18.
The normalized values of four utility measures
,
and
, calculated using Equations (6)–(9), are shown in
Table 19.
The overall utility of each of the five alternatives, calculated using Equation (14), is shown in
Table 20. The ranking order of alternatives obtained using the WISP method is also shown in
Table 20.
From the above table, it can be noticed that the ranking order of alternatives obtained using the WISP method is identical to the order of ranked alternatives obtained by means of the TOPSIS method, and that alternative A4 is the most acceptable in the case of applying both methods.
In order to determine which alternative is indeed the most acceptable, an evaluation was performed using several MCDM methods, and the results are summarized in
Table 21 and
Table 22.
As can be seen from
Table 22, the ranking orders of alternatives are quite similar, but there are some deviations regarding the first-ranked alternative in the case of using VIKOR and CoCoSo methods.
The problem of the emergence of different ranking orders of alternatives obtained using different MCDM methods is discussed in Stanujkic et al. [
15], and it arises as a consequence of the using different normalization procedures, different aggregation procedures, and certain relationships between criteria weights. For example, in this case, by decreasing the weight of criterion
C7 from 0.12 to 0.054, with a corresponding increase of weights of other criteria in order to meet the following constraint, or more precisely by applying the weighting vector
wj = {0.075, 0.075, 0.075, 0.150, 0.215, 0.086, 0.054, 0.134, 0.054, 0.081}, all alternatives gave the same ranking order of alternatives, as it is shown in
Table 23.
As can be seen from
Table 23, the decrease of the weight of criterion
C7 caused that all MCDM methods gave the same ranking order of alternatives, i.e., that the alternative
A3 is the most acceptable by applying all considered MCDM methods. In this case, criterion
C7 was chosen because of its significant weight. Similar analyses can be performed with increasing or decreasing weights of other criteria with higher weights, or with groups of criteria with lower weights.
Similarly, reducing the weight of criterion
C8 from 0.125 to 0.022, i.e., by applying the weighting vector
wj = {0.078, 0.078, 0.078, 0.157, 0.224, 0.089, 0.134, 0.022, 0.056, 0.084}, the alternative
A4 will become most appropriate, except by applying the CoCoSo method, as shown in
Table 24.
Based on the above-conducted analysis, it is obvious that the WISP method produces similar ranking results as other prominent MCDM methods in solving real DM problems.