Abstract
Meta-analyses combine the estimators of individual means to estimate the common mean of a population. However, the common mean could be undefined or uninformative in some scenarios where individual means are “ordered” or “sparse”. Hence, assessments of individual means become relevant, rather than the common mean. In this article, we propose simultaneous estimation of individual means using the James–Stein shrinkage estimators, which improve upon individual studies’ estimators. We also propose isotonic regression estimators for ordered means, and pretest estimators for sparse means. We provide theoretical explanations and simulation results demonstrating the superiority of the proposed estimators over the individual studies’ estimators. The proposed methods are illustrated by two datasets: one comes from gastric cancer patients and the other from COVID-19 patients.
1. Introduction
Meta-analysis is a statistical method used to summarize results from published studies [1]. While it has been applied to all areas of science, meta-analysis has been a particularly important tool in educational studies [2,3] and medical studies [4,5]. Especially, meta-analysis has played an important role in studies on the impact of COVID-19 [6,7,8].
The most basic method in meta-analyses uses a fixed-effect model, where all of the studies have a common mean [5,9]. This model has long been recognized in mathematical statistics and stratified sampling designs, where the common mean estimator has rigorously been investigated (pp. 55–103 of [10]; [11,12,13]).
Another basic model is the random-effects model [14], where the studies have different means. This model imposes normally distributed random-effects to account for between-study deviations from the common mean [15]. In either model, the goal of meta-analyses is to estimate the common mean by combining the estimators of individual means.
However, in some scenarios, the common mean is undefined or uninformative. In these scenarios, the focus of meta-analyses can be on individual studies’ means. While individual means are estimated by published studies, they could be improved by statistical techniques. For instance, Raudenbush and Bryk [16] pointed out the possibility for improving individual studies’ estimators in meta-analyses by using empirical Bayes estimators under the normal random-effects. Schmid [17] also considered similar Bayes estimators that improve upon individual studies’ estimators. Röver and Friede [18,19] tried to improve an individual estimator by another individual estimator. All these Bayes estimators are defined by posterior means under the normal priors (random-effects). Evidently, the posterior means are related to but different from the individual studies’ estimates. However, there are some cases where the normal priors (random-effects) do not apply (Section 2.2). This motivates us to develop non-Bayesian estimation.
In this article, we consider some improved estimation methods of individual means without normal random-effects. First, we will explain how to employ shrinkage estimators to obtain improved estimators of individual means. Unlike the existing Bayes estimators, our frequentist shrinkage estimators do not involve any prior distribution. Next, we will provide theoretical and numerical results to show the superiority of the proposed estimators over the individual studies’ estimators. Finally, we will analyze two datasets to illustrate the proposed methods.
This article is organized as follows. Section 2 provides a background including a review of meta-analyses. Section 3 proposes the estimators of individual means and studies their theoretical properties. Section 4 conducts simulation studies, and Section 5 analyzes real datasets. Section 6 concludes the article.
2. Background
2.1. Meta-Analysis
This subsection reviews the basic models for meta-analysis under the normal distribution, including the fixed-effect model and random-effects model [1,5].
First, we introduce some mathematical notations and basic assumptions for meta-analyses. Let be the number of studies ( stands for Groups) in a meta-analysis. For , the i-th study provides an estimate for an unknown mean with a known variance . This implies that each study provides as the standard error (SE) of the estimate . Hence, in meta-analyses, the variance is known. We note that there could be a different setting, where the variance is unknown [20,21].
Next, we further assume the normal model . This model’s special case, the fixed-effect model, imposes the common mean assumption. That is, . The random-effects model imposes normally distributed means given by for . In either case, the main goal of meta-analyses is to estimate by optimally combining s [1,5,9].
In a meta-analysis, observed data consist of . An example is the two-sample t-test for a continuous outcome, where is the (standardized) mean difference estimator from the i-th study, and is the pooled variance estimator [5]. Another example is the table analysis for association between an event and a risk factor, where is the logarithm of the risk ratio (or odds ratio), and is estimated variance [5]. Another example is a survival analysis for censored data, where can be the logarithm of an estimate of relative risks from the Cox model. Without loss of generality, we assume that corresponds to the null value.
Finally, we describe the main idea of meta-analyses. The idea is to optimally combine the results from the studies, based on either the fixed-effect model or random-effects model. The first model leads to the fixed-effect meta-analysis under the assumption . The second model leads to the random-effects meta-analysis under the assumption . In either case, the target is to estimate the common (overall) mean by
where the value of is an estimator from the data [5,14].
2.2. Does the Estimation of the Common Mean Make Sense?
Given the data of , one usually conducts the fixed-effect meta-analysis and/or random-effects meta-analysis. The Q test for homogeneity can help select between the fixed-effect and random-effects model [1,5]. If the fixed-effect model is rejected (i.e., the random-effects model is selected), one might explore a systematic source of heterogeneity by meta-regression. One might also test the goodness-of-fit of the normal random-effects model [22]. In any case, statistical inference for the common mean depends on some statistical models.
However, the above statistical models do not always fit the data at hand. If the studies have a monotonic-effect, e.g., , the model is neither fixed nor random. Thus, there is no general way to estimate the common parameter unless some specific models are imposed. If a covariate is available to explain some structure among s, a meta-regression may be used (Chapter 20 of [1]). However, we do not wish to assume the presence of covariates to conduct meta-regression in this article.
While the common mean estimate can be an informative summary of individual estimates, this single value rarely describes the whole results. Thus, meta-analysis typically displays individual estimates , providing an opportunity for learning the data. For instance, forest plots show the individual estimates along with their 95% confidence intervals (CIs): . Funnel plots show against; see [1,5,23,24] for these plots. In some cases, one is interested in the that has the largest size [16]. Therefore, reporting individual estimates is an important part of meta-analysis.
2.3. Individual Estimates Could Be Improved
Despite the potential advantages of improving the individual estimators by the shrinkage methods [11,12,25,26], the development of such estimators has rarely been discussed in the literature of meta-analyses. In other words, the goal of meta-analyses has been the estimation of the common mean by disregarding the individual means. This causes a gap between meta-analyses and shrinkage estimation methods. Therefore, there is room for improving the standard individual estimators for in some scenarios.
We raise scenarios where the common mean is undefined or uninformative.
The first example is the case of the monotonic-effect, , where the common mean seems to be not well-defined. In this case, an alternative is to perform meta-regression with the aid of observable covariates. We however do not assume the availability of covariates in this article.
The second example is the case of sparse normal means [27,28], where most of s are equal to zero, e.g., . This is relevant to meta-analyses that fail to reject many null hypotheses. In this case, the interest may be in the estimation of the nonzero means rather than the common mean.
3. Proposed Estimators
We propose a variety of shrinkage estimators for simultaneously estimating individual means, and discuss their properties. In particular, we theoretically prove that the proposed estimators have better precision than the individual studies’ estimates in terms of a mean squared error criterion under some conditions.
The problem setting is as follows: Let be an estimator for an unknown mean under a known variance for . As mentioned in Section 2, the variance is known from the -th study. Observed data consist of . We regard as a simultaneous estimator of . That is, we regard as an observable random vector to estimate the unknown vector .
Let be a simultaneous estimator for . We state that improves upon if
We then call an improved estimator of .
We call the standard unbiased estimator because of the unbiasedness . It is a benchmark estimator for comparing different estimators. Recall that is simply the collection of the individual studies’ estimates. If “” in the criterion (2) holds only for a restricted parameter space, is only locally improved.
The criteria (1) and (2) employ the weighted mean squared errors (WMSEs). The inverse variance weights guarantee the equal contributions of all studies to the estimation error. The weighs also make it convenient to apply the classical decision theory. The special case of gives the total MSE (TMSE), defined as [11,25,29]. We use the WMSEs for theoretical convenience while the TMSE criterion is also a relevant criterion. We will use both the WMSE and TMSE in our numerical assessments.
Indeed, there are infinitely many estimators that improve upon , including very complex and unrealistic ones [25]. In addition, it is quite easy to find an estimator that locally improves upon , such as . While the problem of deriving/assessing estimators has been intensively discussed in the statistical decision theory, it has rarely been appreciated in meta-analytical settings. The goal of this article is to facilitate the applications of shrinkage estimators in the context of meta-analyses.
In the subsequent sections, we will introduce three estimators that help reduce the WMSE and TMSE by shrinking toward a restricted space of . Section 3.1 will discuss the shrinkage towards the zero vector , the most traditional shrinkage scheme. Section 3.2 will consider the shrinkage toward under constraints . Section 3.3 will explore the shrinkage towards the sparse space .
3.1. Shrinkage Estimation for Means
To estimate , we propose the James–Stein (JS) estimator of the form
This estimator is a modification of the original JS estimator [29] that was derived under the unit variances ( for ). See Appendix A.1 for the details. The JS estimator reduces variance by shrinking the vector toward while it produces bias. The degree of shrinkage is determined by the factor that usually ranges from 0 (0% shrinkage) to 1 (100% shrinkage), and occasionally becomes greater than 1 (overshrinkage).
It can be shown in Appendix A.1 that has the following WMSE
where is a random variable having a noncentral -distribution with the noncentral parameter and the degrees of freedom . Thus, has a smaller WMSE than when . Indeed, the WMSE is minimized at at which the WMSE is by the inverse moment of the central -distribution with. Thus, the JS estimator gains the greatest advantage if all the individual means are zero. This gain is appealing for meta-analyses for small individual effects (true means close to zero). Even if , the JS estimator has a smaller WMSE than . The reduction of the WMSE diminishes as departs from zero.
One might ask where the special formula of the JS estimator comes from. The JS estimator can be derived as an empirical Bayes estimator under the prior :
where the shrinkage factor is the estimator of . See Appendix A.2 for the detailed derivations. Thus, if , the JS estimator minimizes the Bayes risk, and hence, is the optimal estimator under the prior.
A minor modification to the JS estimator can reduce the WMSE further. The modification is made in order to avoid the effect of an overshrinkage, , by which all the signs of are reverted. The overshrinkage phenomenon occurs with a small probability, and therefore, the modification is minor in the majority of cases. A modified estimator is the positive-part JS estimator
where . Consequently, has a smaller WMSE than (p. 356, Theorem 5.4 of [25].
In summary, this subsection proposes two estimators ( and ) that improve upon the standard unbiased estimator .
3.2. Estimation under Ordered Means
Our next proposal is a shrinkage estimator under ordered means. We consider the case where the ordering constraints are known by the study design. Thus, the parameter is known to be restricted on the space . For instance, suppose that represents the time index ( for the oldest study, and for the newest study) at which a treatment effect is estimated. Then, one may assume a trend due to the improvements of treatments over time.
For instance, the true means may be . This trend could be modeled by a meta-regression with , where values and are unknown. In practice, one does not know any structure of the means (e.g., linear regression) except for . If some knowledge, such as a linear model on covariates, is true, one could use meta-regression. However, we do not adopt any model, permitting various non-linear settings such as and .
The use of the standard unbiased estimator is not desirable under the ordering constraints. Due to random variations, the estimator can be outside the parameter space, namely, . Under this setting, an estimator accounting for the parameter restriction improves upon the unrestricted estimator , even though the former is a biased estimator [30].
The restricted maximum likelihood (RML) estimator satisfying is calculated by the pool-adjacent-violators algorithm (PAVA)
This gives the RML estimator , which has a smaller WMSE than . For an example of , one has the data of , and the PAVA results in
Hence, is equal to itself or an average including . Of course, if . For theories and applications of the PAVA, we refer to [31,32,33]. The max min formula written above can be found in Chapter 8 of [30] or [34].
It is clear that is different from order statistics that are a permutation of and also improve the WMSE in some cases [34]. However, the permuted estimator loses the information of individual studies’ identifications, and therefore, is not considered in this article.
Below, we further improve with the aid of the JS estimator. Let be the indicator function; or if is true or false, respectively. We adjust the estimator of Chang [35] who proposed the JS-type estimator under the order restriction as follows:
where “RJS” stands for “Restricted JS”. Note that has a smaller WMSE than , and hence, the former improves upon the latter [35].
We further improve the RJS estimator by the positive-part RJS estimator given by
Consequently, has a smaller WMSE than (Theorem 5.4 of Lehmann and Casella [25]). Note that, if is not satisfied, then .
In summary, this subsection proposes three estimators (, , and ) that improve upon the standard unbiased estimator under .
3.3. Estimation under Sparse Means
Our third proposal is a shrinkage estimator under sparse normal means where most of the s are zero [27,28]. The vector is called sparse if the number is much smaller than , e.g., . In practice, one does not know which components are zeros, and how many components are zero. Nonetheless, one could assume that many of are zero. However, the elements of are almost always nonzero, which disagree with the true values .
Under the sparse means, it is quite reasonable to estimate as exactly zero if is close to zero. Accordingly, one can use a thresholding estimator for a critical value . The idea was proposed by Bancroft [36] who formulated pretest estimators that incorporate a preliminary hypothesis test into estimation. Judge and Bock [37] extensively studied pretest estimators with applications to econometrics; see also more recent works [38,39,40,41,42,43]. Among all, we particularly note that Shih et al. [41] proposed the general pretest (GPT) estimator that includes empirical Bayes and Types I-II shrinkage pretest estimators for the univariate normal mean.
We modify the GPT estimator to be adopted to meta-analyses as follows:
for , , and is the upper p-th quantile of for . To implement the GPT estimator, the values of and , and the probability function must be chosen. They cannot be chosen to minimize the WMSE and TMSE criteria since pretest estimators do not permit tractable forms of MSEs [38,41]. Fortunately, for any value of and , and a function , one can show that has smaller WMSE and TMSE values than provided ; see Appendix A.3 for the proof.
For the above reasons, we apply statistically interpretable choices of , , and . The special case of leads to the usual pretest estimator
for which is arbitrary. Thus, we retain if is rejected in favor of at the 5% level. Otherwise, we discard , and conclude .
For the GPT estimator, we set (50% shrinkage) as suggested by Shih et al. [41]. To facilitate the interpretability of pretests, we chose (5% level) and (10% level). Thus, we propose the estimator
Thus, if is rejected at the 5% level, we set . If is accepted at the 5% level, but rejected at the 10% level, we set . If is accepted at the 10% level, we set . Thus, gives a weaker shrinkage than does. Obviously, we obtain a relationship .
The GPT estimator introduced above is not an empirical Bayesian estimator. If , , and were chosen, the resultant GPT estimator would be an empirical Bayes estimator [41]. However, we do not consider this estimator in our analysis.
In summary, this subsection proposes two estimators ( and ) that improve upon the standard unbiased estimator provided .
4. Simulation
We conducted Monte Carlo simulations to examine the performance of the proposed estimators. The purpose of the simulations is to clarify how the proposed estimators improve upon the standard unbiased estimator in terms of the WMSE and TMSE, defined as
We also examined the bias defined as,
4.1. Simulation Design
We generated normally distributed data , , under the following scenarios:
Scenario (a):
Common means: ,
Scenario (b):
Zero means: ,
Scenario (c):
Ordered means: ,
Scenario (d):
Sparse means: .
For the known variances, we generated , restricted in the interval , as previously considered [15,44], leading to . Figure 1 depicts simulated data and under Scenarios (a) and (c). Using the data, we computed the proposed estimators , , , , , , and for estimating . Our interest is to see how and when these estimators improve upon the standard unbiased estimator . The WMSE, TMSE and Bias of all the estimators were computed by the Monte Carlo average of 10,000 replications of such data.
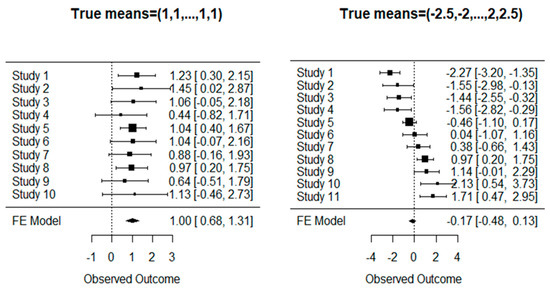
Figure 1.
Simulated values and the 95%CI , where , and being restricted in the interval , for. The “FE Model” is the common mean estimator and its 95%CI under the fixed-effect (FE) model.
4.2. Simulation Results
Table 1, Table 2, Table 3 and Table 4 summarize the simulation results for comparing eight estimators: , , ,, , , , and .

Table 1.
Simulation results under Scenario (a): .

Table 2.
Simulation results under Scenario (b): ).

Table 3.
Simulation results under Scenario (c): .

Table 4.
Simulation results under Scenario (d): .
The JS estimators ( and ) improved upon in all the scenarios (see the WMSE and TMSE in Table 1, Table 2, Table 3 and Table 4). Scenario (b) produced the greatest reduction in the values of the WMSE and TMSE, where all the true means are equal to zero (Table 2). This is exactly what the theoretical results imply (Section 3.1). The two estimators and showed similar performance except for Scenario (b), where exhibited smaller values for the WMSE and TMSE than (Table 2). In summary, we observed a clear advantage of the two JS estimators ( and ) over the standard estimator () in all the scenarios examined.
The order-restricted estimators (, and ) were even more advantageous than and according to the smallest values of the WMSE and TMSE in Table 1 and Table 3. The substantially reduced values of the WMSE and TMSE were brought by the strict constraints by isotonic regression. We found that had the smallest value of the WMSE and TMSE under Scenarios (a) and (c) (Table 1 and Table 3). However, we observed large and systematic biases of the order-restricted estimators, which are caused by isotonic regression.
The pretest estimator showed the best performance under Scenario (d) (Table 4), followed by the general pretest estimator . However, the comparison between and depends on the scenarios: was better in Scenarios (b) and (d) while was better in Scenarios (a) and (c). Both and did not perform well in Scenarios (a) and (c), where the sparsity hypothesis fails. Naturally, the sparsity of individual means is essential for the pretest estimators to perform well.
In summary, our simulations have shown that the proposed estimators have their own advantageous scenarios: for Scenario (b); for Scenarios (a) and (c); or for Scenario (d). These proposed estimators substantially reduced the values of the WMSE and TMSE over the standard estimator . Furthermore, the proposed estimators , ,, , and improved upon across all the scenarios. We therefore conclude that there are good reasons to apply the proposed estimators to estimate in order to improve the accuracy of estimation.
5. Data Analyses
We analyze two datasets to illustrate the proposed method. One dataset comes from gastric cancer patients and the other from COVID-19 pneumonia patients.
5.1. Gastric Cancer Data
We illustrate the proposed methods using a dataset from the Global Advanced/Adjuvant Stomach Tumor Research International Collaboration (GASTRIC) [45]. The data provide survival times for gastric cancer patients from 14 studies. One of the goals of this collaboration is to estimate the effects of chemotherapy on disease-free survival (DFS) for gastric cancer patients [46]. We used the data available in the R package surrosurv [47].
Let be the estimator for a Cox regression coefficient for a treatment indicator (1=treatment vs. 0=control) and let be the SE for . Table 5 summarizes , , and sample sizes for the 14 studies. It is reasonable to assume the asymptotic normal approximation since the sample size of each study is large enough. Table 5 also shows the p-values for testing through Z-values .

Table 5.
The 14 studies on gastric cancer patients for estimating the effects of chemotherapy on DFS.
Table 5 shows that only two studies reached 5% significance. Thus, it is reasonable to assume , and therefore, the JS estimators are suitable. It is also reasonable to assume for most of s, and therefore, the PT and GPT estimators are suitable. We therefore calculated , , , and to estimate as shown in Table 6.

Table 6.
Estimates of the treatment effects on DFS from the 14 studies on gastric cancer patients.
Table 6 shows that and shrink the values of by 45%, namely, . We also observe that and cause 0%, 50% or 100% shrinkage of . The values of suggested the null effects () for 12 studies while the values of suggested the null effects for 10 studies. By shrinkage, the estimators , , , and more accurately estimate than do. The reason is that the data structure resembles Scenario (b), where and performed the best (Table 2) or Scenario (d), where and performed the best (Table 4).
5.2. COVID-19 Data
We illustrate the proposed methods using data from Pranata et al., [7] who examined the effect of hypertension on mortality for patients with COVID-19 pneumonia. One of their conclusions was that hypertension increases mortality. We obtained mortality data from Pranata et al. [7], consisting of 11 published studies (Table 7).

Table 7.
Summary of the 11 studies (shown by the author and publication year) on COVID-19 patients for examining the effects of hypertension on mortality.
Let , , be the log of the risk ratio (RR) calculated from two-by-two contingency tables examining the association (mortality vs. hypertension). Let be the SE for . Table 7 summarizes the 11 studies. Table 7 also shows the p-values for testing the no association () by Z-values assuming .
Before applying the proposed methods, we changed the order of the 11 studies by the percentages of male patients (Table 8). The largest percentage (82%) gave the smallest RR () while the smallest percentage (45%) gave the largest RR (). However, the values of s are not monotonically increasing (in Table 8). While Pranata et al. [7] regressed s on the percentages by meta-regression, we prefer not to assume a linear model. Alternatively, we considered the order-restricted estimators (, , and ) by merely assuming that the true means are ordered by the percentages of male patients.

Table 8.
Estimated effects of hypertension on mortality from the 11 studies on COVID-19 patients.
Table 8 shows the proposed estimators , , , , and . The JS shrinkage estimators were . They reduced only 5% of , and hence gave very weak shrinkage toward zero. This is because s are unlikely to be zero. The order-restricted estimator successfully enforced order restrictions, , which was not achieved by . Since the order restrictions were not met for , we had by definition. Thus, the last three estimators can clearly incorporate the knowledge that hypertension-related mortality is monotonically influenced by gender without imposing a linear model.
In summary, it would be advantageous and informative to add the order restriction to individual studies’ estimators on the association (mortality vs. hypertension). The resultant order-restricted estimators are expected to provide more accurate estimates than individual studies’ estimators. The reason is that the data structure resembles Scenario (c), where , , and performed the best (Table 3).
6. Conclusions and Future Extensions
We have shown that the proposed shrinkage estimators can be more precise than the standard unbiased estimators for estimating individual means in meta-analyses. Theoretical evidence (Section 3) and simulation studies (Section 4) identified the remarkable advantages of the proposed estimators under certain scenarios of the true individual means. However, no single estimator is the best for all the scenarios. Hence, it is important to choose a suitable estimator for each scenario. We have provided two data examples to demonstrate the scenarios under which the proposed estimators are beneficial (Section 5). However, the choice of estimators depends on the goal of research, and hence, it is difficult to set a purely statistical strategy to choose the estimator. What we have concluded in this article is that there is good potential for the proposed estimators by their careful applications to real meta-analyses.
Recall that the shrinkage effects on the general pretest estimators, , are component-wise, and hence, do not involves the JS-type shrinkage as in Section 3.1 and Section 3.2. In the presence of pretests, it is unclear how the JS-type shrinkage can be introduced. This issue is an interesting topic, yet it is beyond the scope of the article.
This article focused on the shrinkage toward zero because a meta-analysis is typically a collection of individual studies of weak effects. However, other shrinkage schemes can also be considered, such as the shrinkage toward an arbitrary mean vector, a truncated space, a polyhedral convex, or a positive halfplane [12,25,48,49,50,51,52,53,54]. Different shrinkage schemes could be considered depending on the goals of meta-analyses. Therefore, there is good potential for shrinkage estimation methods to work with meta-analyses.
This article focuses on univariate response. One may consider extensions of this article to multiple (e.g., bivariate) responses. For instance, educational research may involve meta-analyses of bivariate test scores on verbal and mathematics tests [55], and mathematics and statistics tests [44]. In our data example of gastric cancer patients (Section 5.1), bivariate correlated endpoints are of great interest [55]. Correlations between responses should be employed to improve the efficiency and reduce the bias of univariate analyses [56,57,58,59,60,61,62,63,64,65] and to predict a primary outcome by the secondary outcome [66,67,68,69]. Multivariate shrinkage estimators of multivariate normal means, such as [70,71], can be considered for this extension.
One may also consider extensions of this article to non-normal (e.g., gamma distributed) responses. For non-normal distributions, shrinkage estimators exist, such as [72] for gamma distribution. Thus, introduction of shrinkage estimators to multivariate and/or non-normal models, and even their regression models, is a promising future direction.
Finally, we note that all meta-analyses are valid under the questionable assumption of no publication bias. Frequentist and Bayesian models for checking the publication biases are often considered [73,74]. It would be interesting to see if the proposed shrinkage methods can mitigate the effect of publication biases.
Author Contributions
Conceptualization, N.T. and T.E.; methodology, N.T. and T.E.; data curation, N.T. and T.E.; writing, N.T., T.E., Y.K. and Y.-T.C.; supervision, T.E., Y.K., and Y.-T.C.; funding acquisition, Y.-T.C. All authors have read and agreed to the published version of the manuscript.
Funding
Chang YT is financially supported by JSPS KAKENHI Grant Number JP26330047 and JP18K11196.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
The authors thank referees for their valuable suggestions that improved the article. The authors kindly thank Leila Zhang from MDPI for her invitation to submit our work to Axioms free of article processing charge.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
Appendix A.1. Derivations of the JS Estimator
Define and . Then, we obtain , where is the identity matrix of dimension G. The random vector having the unit variance is the traditional setup of the simultaneous inference (pp. 346–355 of [25]). Now, is a maximum likelihood estimator of . Consider an arbitrary estimator of under the square error loss . Let the JS estimator be
It can be shown that
where is the noncentral -distribution with the noncentral parameter ; see p. 355 of [25] for the proofs. From this equation,
for . Thus, improves upon for . Rewriting the above results, we arrive at
Appendix A.2. Derivations of the Empirical Bayes Estimator
Under the prior , the Bayes estimator is derived as
It can be shown that the marginal distribution of is . Thus, , a central -distribution with degrees of freedom. Taking the inverse,
Taking the expectation for left and right sides,
Thus, by the method of moment estimation,
This estimator is unbiased since
Appendix A.3. Proof for the Pretest Estimators
The proofs for the WMSE and TMSE are similar. Thus, we focus on the latter. Then, it suffices to show
It follows that
There exists a small value such that for
Thus, for ,
References
- Borenstein, M.; Hedges, L.V.; Higgins, J.P.; Rothstein, H.R. Introduction to Meta-Analysis; John Wiley & Sons: Hoboken, NJ, USA, 2011. [Google Scholar]
- Kaiser, T.; Menkhoff, L. Financial education in schools: A meta-analysis of experimental studies. Econ. Educ. Rev. 2020, 78, 101930. [Google Scholar] [CrossRef]
- Leung, Y.; Oates, J.; Chan, S.P. Voice, articulation, and prosody contribute to listener perceptions of speaker gender: A systematic review and meta-analysis. J. Speech Lang. Hear. Res. 2018, 61, 266–297. [Google Scholar] [CrossRef]
- DerSimonian, R.; Laird, N. Meta-analysis in clinical trials revisited. Contemp. Clin. Trials 2015, 45, 139–145. [Google Scholar] [CrossRef] [PubMed]
- Fleiss, J.L. Review papers: The statistical basis of meta-analysis. Stat. Methods Med. Res. 1993, 2, 121–145. [Google Scholar] [CrossRef]
- Batra, K.; Singh, T.P.; Sharma, M.; Batra, R.; Schvaneveldt, N. Investigating the psychological impact of COVID-19 among healthcare workers: A meta-analysis. Int. J. Environ. Res. Public Health 2020, 17, 9096. [Google Scholar] [CrossRef] [PubMed]
- Pranata, R.; Lim, M.A.; Huang, I.; Raharjo, S.B.; Lukito, A.A. Hypertension is associated with increased mortality and severity of disease in COVID-19 pneumonia: A systematic review, meta-analysis and meta-regression. J. Renin-Angiotensin-Aldosterone Syst. 2020, 21, 1470320320926899. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Kala, M.P.; Jafar, T.H. Factors associated with psychological distress during the coronavirus disease 2019 (COVID-19) pandemic on the predominantly general population: A systematic review and meta-analysis. PLoS ONE 2020, 15, e0244630. [Google Scholar] [CrossRef] [PubMed]
- Rice, K.; Higgins, J.P.; Lumley, T. A re-evaluation of fixed effect (s) meta-analysis. J. R. Stat. Soc. Ser. A 2018, 181, 205–227. [Google Scholar] [CrossRef]
- Lehmann, E.L. Elements of Large-Sample Theory; Springer Science & Business Media: Berlin, Germany, 2010. [Google Scholar]
- Shinozaki, N.; Chang, Y.T. Minimaxity of empirical Bayes estimators of the means of independent normal variables with unequal variances. Commun. Stat.-Theor. Methods 1993, 8, 2147–2169. [Google Scholar] [CrossRef]
- Shinozaki, N.; Chang, Y.T. Minimaxity of empirical Bayes estimators shrinking toward the grand mean when variances are unequal. Commun. Stat.-Theor. Methods 1996, 25, 183–199. [Google Scholar] [CrossRef]
- Singh, H.P.; Vishwakarma, G.K. A family of estimators of population mean using auxiliary information in stratified sampling. Commun. Stat. -Theor. Methods 2008, 37, 1038–1050. [Google Scholar] [CrossRef]
- DerSimonian, R.; Laird, N. Meta-analysis in clinical trials. Control Clin. Trials 1986, 7, 177–188. [Google Scholar] [CrossRef]
- Kontopantelis, E.; Reeves, D. Performance of statistical methods for meta-analysis when true study effects are non-normally distributed: A simulation study. Stat. Methods Med. Res. 2012, 21, 409–426. [Google Scholar] [CrossRef] [PubMed]
- Raudenbush, S.W.; Bryk, A.S. Empirical bayes meta-analysis. J. Educ. Stat. 1985, 10, 75–98. [Google Scholar] [CrossRef]
- Schmid, C. Using bayesian inference to perform meta-analysis. Eval. Health Prof. 2001, 24, 165–189. [Google Scholar] [CrossRef] [PubMed]
- Röver, C.; Friede, T. Dynamically borrowing strength from another study through shrinkage estimation. Stat. Methods Med. Res. 2020, 29, 293–308. [Google Scholar] [CrossRef]
- Röver, C.; Friede, T. Bounds for the weight of external data in shrinkage estimation. Biom. J. 2021, 63, 1131–1143. [Google Scholar] [CrossRef]
- Malekzadeh, A.; Kharrati-Kopaei, M. Inferences on the common mean of several normal populations under hetero-scedasticity. Comput. Stat. 2018, 33, 1367–1384. [Google Scholar] [CrossRef]
- Shinozaki, N. A note on estimating the common mean of k normal distributions and the stein problem. Commun. Stat. -Theory Methods 1978, 7, 1421–1432. [Google Scholar] [CrossRef]
- Chen, Z.; Zhang, G.; Li, J. Goodness-of-fit test for meta-analysis. Sci. Rep. 2015, 5, 16983. [Google Scholar] [CrossRef]
- Everitt, B. Modern Medical Statistics: A Practical Guide; Wiley: Hoboken, NJ, USA, 2003. [Google Scholar]
- Lin, L. Hybrid test for publication bias in meta-analysis. Stat. Methods Med. Res. 2020, 29, 2881–2899. [Google Scholar] [CrossRef] [PubMed]
- Lehmann, E.L.; Casella, G. Theory of Point Estimation, 2nd ed.; Springer: New York, NY, USA, 1998. [Google Scholar]
- Shao, J. Mathematical Statistics; Springer: New York, NY, USA, 2003. [Google Scholar]
- Johnstone, I.M. On minimax estimation of a sparse normal mean vector. Ann. Stat. 1994, 22, 271–289. [Google Scholar] [CrossRef]
- van der Pas, S.; Salomond, J.-B.; Schmidt-Hieber, J. Conditions for posterior contraction in the sparse normal means problem. Electron. J. Stat. 2016, 10, 976–1000. [Google Scholar] [CrossRef]
- James, W.; Stein, C. Estimation with quadratic loss. In Breakthroughs in Statistics; Springer: New York, NY, USA, 1992; Volume 1, pp. 443–460. [Google Scholar]
- van Eeden, C. Restricted Parameter Space Estimation Problems; Springer: New York, NY, USA, 2006. [Google Scholar]
- Li, W.; Li, R.; Feng, Z.; Ning, J. Semiparametric isotonic regression analysis for risk assessment under nested case-control and case-cohort designs. Stat. Methods Med. Res. 2020, 29, 2328–2343. [Google Scholar] [CrossRef] [PubMed]
- Robertson, T.; Wright, F.T.; Dykstra, R. Order Restricted Statistical Inference; Wiley: Chichester, UK, 1988. [Google Scholar]
- Silvapulle, M.J.; Sen, P.K. Constrained Statistical Inference: Inequality, Order, and Shape Restrictions; Wiley: Hoboken, NJ, USA, 2005. [Google Scholar]
- Tsukuma, H. Simultaneous estimation of restricted location parameters based on permutation and sign-change. Stat. Pap. 2012, 53, 915–934. [Google Scholar] [CrossRef]
- Chang, Y.T. Stein-type estimators for parameters restricted by linear inequalities. Keio Sci. Technol. Rep. 1981, 34, 83–95. [Google Scholar]
- Bancroft, T.A. On biases in estimation due to the use of preliminary tests of significance. Ann. Math. Stat. 1944, 15, 190–204. [Google Scholar] [CrossRef]
- Judge, G.G.; Bock, M.E. The Statistical Implications of Pre-Test and Stein-Rule Estimators in Econometrics; Elsevier: Amsterdam, The Netherland, 1978. [Google Scholar]
- Khan, S.; Saleh, A.K.M.E. On the comparison of the pre-test and shrinkage estimators for the univariate normal mean. Stat. Pap. 2001, 42, 451–473. [Google Scholar] [CrossRef]
- Magnus, J.R. The traditional pretest estimator. Theory Probab. Its Appl. 2000, 44, 293–308. [Google Scholar] [CrossRef]
- Magnus, J.R.; Wan, A.T.; Zhang, X. Weighted average least squares estimation with nonspherical disturbances and an application to the Hong Kong housing market. Comput. Stat. Data Anal. 2011, 55, 1331–1341. [Google Scholar] [CrossRef]
- Shih, J.-H.; Konno, Y.; Chang, Y.-T.; Emura, T. A class of general pretest estimators for the univariate normal mean. Commun. Stat. -Theory Methods 2021. [Google Scholar] [CrossRef]
- Shih, J.-H.; Lin, T.-Y.; Jimichi, M.; Emura, T. Robust ridge M-estimators with pretest and Stein-rule shrinkage for an intercept term. Jpn. J. Stat. Data Sci. 2021, 4, 107–150. [Google Scholar] [CrossRef]
- Kibria, B.G.; Saleh, A.M.E. Optimum critical value for pre-test estimator. Commun. Stat. -Simul. Comput. 2006, 35, 309–319. [Google Scholar] [CrossRef]
- Shih, J.-H.; Konno, Y.; Chang, Y.-T.; Emura, T. Estimation of a common mean vector in bivariate meta-analysis under the FGM copula. Statistics 2019, 53, 673–695. [Google Scholar] [CrossRef]
- GASTRIC (Global Advanced/Adjuvant Stomach Tumor Research International Collaboration) Group. Role of chemotherapy for advanced/recurrent gastric cancer: An individual-patient-data meta-analysis. Eur. J. Cancer 2013, 49, 1565–1577. [Google Scholar] [CrossRef]
- Oba, K.; Paoletti, X.; Alberts, S.; Bang, Y.J.; Benedetti, J.; Bleiberg, H.; Catalano, P.; Lordick, F.; Michiels, S.; Morita, S.; et al. Disease-free survival as a surrogate for overall survival in adjuvant trials of gastric cancer: A meta-analysis. J. Natl. Cancer Inst. 2013, 105, 1600–1607. [Google Scholar] [CrossRef]
- Rotolo, F.; Paoletti, X.; Michiels, S. Surrosurv: An R package for the evaluation of failure time surrogate endpoints in individual patient data meta-analyses of randomized clinical trials. Comput. Methods Programs Biomed. 2018, 155, 189–198. [Google Scholar] [CrossRef]
- Kubokawa, T. Shrinkage and modification techniques in estimation of variance and the related problems: A review. Commun. Stat. -Theory Methods 1999, 28, 613–650. [Google Scholar] [CrossRef]
- Fourdrinier, D.; Strawderman, W.E.; Wells, M.T. Shrinkage Estimation; Springer: New York, NY, USA, 2018. [Google Scholar]
- Fourdrinier, D.; Ouassou, I.; Strawderman, W.E. Estimation of a parameter vector when some components are re-stricted. J. Multivar. Anal. 2003, 86, 14–27. [Google Scholar] [CrossRef]
- Kuriki, S.; Takemura, A. Shrinkage estimation towards a closed convex set with a smooth boundary. J. Multivar. Anal. 2000, 75, 79–111. [Google Scholar] [CrossRef][Green Version]
- Tripathi, Y.M.; Kumar, S. Estimating a positive normal mean. Stat. Pap. 2007, 48, 609–629. [Google Scholar] [CrossRef]
- Tsukuma, H. Shrinkage estimation in elliptically contoured distribution with restricted parameter space. Stat. Decis. 2009, 27, 25–35. [Google Scholar] [CrossRef]
- Tsukuma, H.; Kubokawa, T. Stein’s phenomenon in estimation of means restricted to a polyhedral convex cone. J. Multivar. Anal. 2008, 99, 141–164. [Google Scholar] [CrossRef]
- Gleser, L.J.; Olkin, L. Stochastically dependent effect sizes. In the Handbook of Research Synthesis; Russel Sage Foundation: New York, NY, USA, 1994. [Google Scholar]
- Emura, T.; Matsui, S.; Rondeau, V. Survival Analysis with Correlated Endpoints: Joint Frailty-Copula Models; Springer: Singapore, 2019. [Google Scholar]
- Emura, T.; Nakatochi, M.; Murotani, K.; Rondeau, V. A joint frailty-copula model between tumour progression and death for meta-analysis. Stat. Methods Med. Res. 2017, 26, 2649–2666. [Google Scholar] [CrossRef] [PubMed]
- Emura, T.; Sofeu, C.L.; Rondeau, V. Conditional copula models for correlated survival endpoints: Individual patient data meta-analysis of randomized controlled trials. Stat. Methods Med. Res. 2021. [Google Scholar] [CrossRef]
- Mavridis, D.; Salanti, G. A practical introduction to multivariate meta-analysis. Stat. Methods Med. Res. 2013, 22, 133–158. [Google Scholar] [CrossRef]
- Peng, M.; Xiang, L. Correlation-based joint feature screening for semi-competing risks outcomes with application to breast cancer data. Stat. Methods Med. Res. 2021, 09622802211037071. [Google Scholar]
- Riley, R.D. Multivariate meta-analysis: The effect of ignoring within-study correlation. J. R. Stat. Soc. Ser. A 2009, 172, 789–811. [Google Scholar] [CrossRef]
- Copas, J.B.; Jackson, D.; White, I.R.; Riley, R.D. The role of secondary outcomes in multivariate meta-analysis. J. R. Stat. Soc. Ser. C 2018, 67, 1177–1205. [Google Scholar] [CrossRef]
- Sofeu, C.L.; Emura, T.; Rondeau, V. A joint frailty-copula model for meta-analytic validation of failure time surrogate endpoints in clinical trials. Biom. J. 2021, 63, 423–446. [Google Scholar] [CrossRef]
- Wu, B.H.; Michimae, H.; Emura, T. Meta-analysis of individual patient data with semi-competing risks under the Weibull joint frailty–copula model. Comput. Stat. 2020, 35, 1525–1552. [Google Scholar] [CrossRef]
- Yamaguchi, Y.; Maruo, K. Bivariate beta-binomial model using Gaussian copula for bivariate meta-analysis of two binary outcomes with low incidence. Jpn. J. Stat. Data Sci. 2019, 2, 347–373. [Google Scholar] [CrossRef]
- Emura, T.; Nakatochi, M.; Matsui, S.; Michimae, H.; Rondeau, V. Personalized dynamic prediction of death according to tumour progression and high-dimensional genetic factors: Meta-analysis with a joint model. Stat. Methods Med. Res. 2018, 27, 2842–2858. [Google Scholar] [CrossRef] [PubMed]
- Kawakami, R.; Michimae, H.; Lin, Y.-H. Assessing the numerical integration of dynamic prediction formulas using the exact expressions under the joint frailty-copula model. Jpn. J. Stat. Data Sci. 2021, 1–29. [Google Scholar] [CrossRef]
- Noughabi, M.S.; Kayid, M. Bivariate quantile residual life: A characterization theorem and statistical properties. Stat. Pap. 2019, 60, 2001–2012. [Google Scholar] [CrossRef]
- Shinohara, S.; Lin, Y.-H.; Michimae, H.; Emura, T. Dynamic lifetime prediction using a Weibull-based bivariate failure time model: A meta-analysis of individual-patient data. Commun. Stat. -Simul. Comput. 2020, 1–20. [Google Scholar] [CrossRef]
- Bilodeau, M.; Kariya, T. Minimax estimators in the normal MANOVA model. J. Multivar. Anal. 1989, 28, 260–270. [Google Scholar] [CrossRef]
- Konno, Y. On estimation of a matrix of normal means with unknown covariance matrix. J. Multivar. Anal. 1991, 36, 44–55. [Google Scholar] [CrossRef]
- Vishwakarma, G.K.; Gupta, S. Shrinkage estimator for scale parameter of gamma distribution. Commun. Stat. -Simul. Comput. 2020, 1–8. [Google Scholar] [CrossRef]
- Copas, J.B.; Shi, J.Q. A sensitivity analysis for publication bias in systematic reviews. Stat. Methods Med Res. 2001, 10, 251–265. [Google Scholar] [CrossRef]
- Larose, D.T.; Dey, D.K. Modeling publication bias using weighted distributions in a Bayesian framework. Comput. Stat. Data Anal. 1998, 26, 279–302. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).