Abstract
As semi-airborne mineral exploration has a limited budget, it is critical to design experimental procedures that generate data to maximize desired information. We investigated the effects of transmitter–receiver geometries for a variety of anomalies and semi-airborne layouts. Our simulations indicated that flight line spacing of 200 m and a point distance of 100 m provides the optimal trade-off between coverage and survey progress for various targets. Based on the target size and distance between the transmitter and the target, the transmitter length should be at least equal to the length of the target. However, where the distance between the transmitter and the target is more than 1 km, the transmitter length should be at least two or three times the target size. Of similar importance are the location and direction of the transmitter cables, which can have a significant impact on the result of inversion and should be parallel to the target strike. By using more than one transmitter, better results can be obtained. If the strike of the target is known, transmitters should be parallel to each other, and if not, it is better to use perpendicular transmitters. The results of this study showed that the optimal distance between transmitters is 3 km. Our simulations showed that it is even possible to recover targets just below the transmitter in corresponding areas of masked data.
1. Introduction
Considering the role of minerals in providing the basic needs of various industries, it seems necessary to search for them with efficient methods. Nowadays, it is not possible to search for mineral resources by using surface geological information alone. Electromagnetic geophysical methods are highly effective at searching for the mentioned sources. These methods are used in almost all stages of exploration operations, and they are cheap, reliable, and in many cases reduce large investment risks. By using geophysics, it is possible to identify parts of the earth that have different physical characteristics from the surrounding environment, such as mineralized zones. The ultimate goal of all applied geophysical explorations is to achieve an accurate picture of the properties of materials below the surface of the earth. The actual structures below the Earth’s surface are often very complex. Therefore, an attempt can be made to provide a simpler model of the earth that is controlled by a finite number of parameters. Resistivity is among the most important geophysical parameters, and is used to identify and explore areas prone to mineralization. The required steps are preliminary geological investigations, data collection, and finally, interpretation. Most geophysical studies deal with mathematics, governing problems with data processing, modelling and inversion [1,2,3].
An important link that has barely been addressed is the data collection itself and the related design of surveys that ultimately dictate the quality of subsurface information provided from the practical implementation of geophysical methods. One of the most expensive stages of exploration is collecting geophysical data. In the DESMEX project, Becken et al. [1] developed a new semi-airborne electromagnetic (SAEM) system, with data analysis in the frequency domain. This method uses ground-based transmitters and airborne magnetic field receivers, as illustrated in Figure 1. This method allows the use of powerful transmitters on the ground, whereas the advantages of survey efficiency and spatial coverage of AEM can be partially maintained when a passive sensor system is carried by an aircraft in the vicinity of the transmitter cable [2]. This is an expensive method. The costs include the cost of each minute of helicopter flight, running the generator and transmitter, and people on the ground. Naturally, the more points that are collected, the higher the cost, but this does not necessarily achieve a better result. Considering all of these factors, a trade-off should be achieved, which can be used to reach an acceptable result, while minimizing costs. Very few studies and research have been carried out on the design of electromagnetic data survey design, especially in the field of semi-airborne design, which is one of the methods used in the Leibniz Institute of Applied Geophysics (LIAG). This was one of our main motivations for conducting this study, which can ultimately help to reduce project costs. King and Constable [4] investigated resolution and depth sensitivity in different CSEM (controlled-source electro-magnetic) systems. They found the trade-offs between different systems, such as nodal and towed CSEM, and reached a greater depth with better resolution. Maurer et al. [5] used examples from direct-current electrical and frequency-domain EM applications, with approaches to quantitative experimental design. Henning et al. [6] introduced a procedure to reduce the number of geoelectrical multielectrode measurements of a survey. Coscia et al. [7] designed optimized electrode configurations to employ cross-hole electrical resistivity tomography for monitoring fast hydrological processes. Loke and Wilkinson [8] also worked on optimizing arrays for electrical imaging surveys. They worked on optimizing non-traditional arrays. Nowruzi [9] and Ahmadi [10] investigated the theoretical and practical concepts of geometric probabilities and presented the relations of geometric probabilities to determine the probability of the intersection of various geometric shapes with different types of grids (Buffon’s needle problem). Agocs [11] was one of the first to study the effect of changing the distance of flight lines and the location of these lines in airborne surveys by using the relationships related to the probability of discovery, obtained based on geometric probability theories and Buffon’s needle problem. McCammon [12] and Chung [13] also used this theory to study the effect of the distance of the parallel survey lines on the possibility of deposit exploration. There are other studies that have been carried out using other methods, for example, seismic tomography [14,15] and reflection surveys [16,17,18].
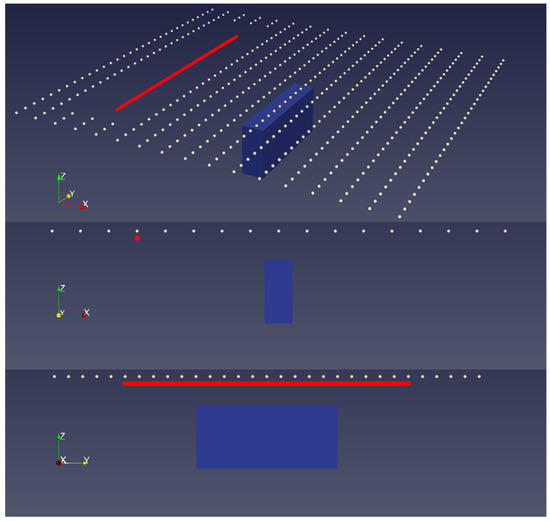
Figure 1.
Sketch of the 3D SAEM model. White points are receivers (50 m in the air); red line is the ground transmitter. Data points are removed within a distance of 400 m from the transmitter. The resistivities of the block and background were 1 and 300 m.
There have only been very few studies on the survey design of AEM, especially semi-airborne EM. Smirnova et al. [19] studied the source parameters such as current, cable length, and frequency on simple 1D models and showed how fields behave on different backgrounds for a 2-km source. They demonstrated how the field decays and goes into the noise level based on current and cable length for two different frequencies. They used 3D synthetic models to show the dependence of the response on frequency, depth and thickness of the conductor, and transmitter–receiver distance on real data. Chen and Sun [20] used layered synthetic models to investigate the characteristics of semi-airborne transient EM (SATEM) with different parameters such as flight altitude, offsets, and geometric positions, and defined an ellipse equation to separate suitable and unsuitable areas for survey with SATEM system. This ellipse equation fitted better to short-line sources, not long sources. Ke et al. [21] worked on the multi-component 3D inversion of SATEM systems in the presence of topography. They used synthetic modelling to demonstrate the importance of multi-component inversion. They first used single-component 3D inversion to detect a plate in vertical and horizontal situations. Their study showed that using single-component inversion does not give good results. For example, using just the z-component, they could only detect the top of the vertical plate. Then, they presented different complex models using multi-component inversion. In the following sections, we will first discuss the inversion method, followed by the survey parameters involved in data collection, cost, and time.
2. Methodology
2.1. Scheme
Airborne electromagnetic (AEM) methods measure the magnetic field to calculate the resistivity distribution of the earth’s subsurface and are widely used for mineral exploration and groundwater studies [22,23]. AEM surveys can cover large areas in a short time and are much more efficient than ground geophysics. Most importantly, they can handle rough or even inaccessible terrain and topography. As the power of a pure airborne transmitter is practically limited, the penetration depth of pure airborne EM is limited to a few hundred meters. However, modern exploration targets are at increasingly greater depths of up to 1 km, requiring greater transmitter moments (the strength of a dipole source) for sufficient signal-to-noise ratios. However, SAEM combines strong transmitter currents with fast data coverage, achieving both advantages at the same time. In this study, for modelling and inversion, we used frequencies from 16 to 1024 Hz in octave steps that were similar to mid-range frequencies of the “SQUID bird” that was developed jointly by the Leibniz Institute of Photonic Technology and Supracon AG, Jena, Germany [24,25].
2.2. Forward Problem and Inversion
We solve the total-field formulation of the Maxwell equations (Equation (1)) based on accurate second-order finite element forward operator, using the open-source toolbox custEM [26]
where ω is the angular frequency, σ is the electric conductivity, and je is the source-current density. The custEM implements a finite-element discretization on unstructured meshes and Nédélec basis functions in collaboration with the direct solver MUMPS. The time-harmonic curl-curl equation was used for the electric field with the common quasi-static approximation for the frequency range of CSEM methods reads. Finally, we solved a linear system of equations AE = b for each frequency and calculated the magnetic field using Equation (2) [26,27].
Most recently, Rochlitz [28] presented a new inversion workflow based on the pyGIMLi [29] framework, which solves Equation (3) with a least squares conjugate gradient solver [30], avoiding any matrix–matrix multiplication.
where J is the Jacobian matrix containing sensitivities of N data observations d to M model parameters m (the logarithmized conductivities), f(m) is the forward response of the model m, Wd is the error-weighting matrix with inverse errors, and Wm is the smoothness operator. The inverse solver also involves the model and data transformations, whose inner derivatives are used to scale the model, data, and the Jacobian matrix. We use a two-sided logarithmic transformation [31] to constrain the resistivity between and Ωm (Equation (4)).
In addition to performance and convenience improvements, custEM includes sub-modules for explicit Jacobian calculations and a communication interface with pyGIMLi’s inverse solver. All vectors are only assembled locally on cells, avoiding equivalent vector derivative expressions for system matrix derivatives. Various shapes of receiver patches with individual field components and transmitter relationships allow grouping electric- and magnetic field data sets without memory or computation overhead. Additionally, we eliminated unnecessary back-substitutions for masked data, i.e., below the noise level [28].
2.3. Synthetic Experiments
For the experimental design, we conducted synthetic experiments using a relatively simple model of a conducting block in a resistive background. The resistivities of the block and background were 1 and 300 Ωm. Gaussian noise was added to the data and the regularization parameter was selected such that the data would fit within the noise level and have a smoother result. As the error model (standard deviation of the noise and inverse weighting), we used a relative error of 5% and an optimistic absolute error level of 1 pT/A. The flight altitude was 50 m above the ground. The receivers covered an area of approximately 10 km2 (3 km × 3.2 km).
Since the field was very strong at the location of the transmitter and decayed rapidly near the transmitter, in many cases, the data surveyed on or near the transmitter could not be used for inversion because they could cause artificial effects and mask the anomalies [26,32]. In these cases, we did not consider the data up to a certain distance from the transmitter (in our case, 400 m) and removed data around the transmitter.
3. Single- and Multi-Component Inversion
In the single-component method, only one of the field components was used for inversion, while in the multi-component method, all three magnetic field components were used simultaneously [28]. The synthetic model consisted of a block with the dimensions of 200 m × 1000 m × 500 m, buried at a depth of 150 m from the ground level. Figure 1 displays a sketch of this model. In this model, the transmitter was a 2-km-long cable, placed parallel to the block strike. All computations were run on a Dell® PowerEdge R940 server with four Intel® Xeon® 2 Gold 6154 processors and 48 LRDIMM 64 GB, DDR4-2666 Quad Ranks with shared random access memory (RAM). Figure 2 shows the inversion results; Figure 2a–d represent the case of a single component inversion, and Figure 2a,b represent the x-component results, better describing the edges of the body in the x direction. The anomaly of the body was less inclined towards the transmitter, but on the other hand, the effect of the body reached the surface. In the same way, in Figure 2c,d (z-component result), the resistivity was more limited to the edges in the z direction but tended more towards the transmitter. We could recover the body properly with a lower resistivity resolution. Figure 2e,f show that, using multi-component inversion, the block edges were better recovered in all directions; moreover, the maximum resistivity values were higher. Another way to confirm our conclusion here was that all subfigures showed the minimum (min) and mean of the resistivity of cells located inside of the target. For example, by using only a single component, the X minimum of the resistivity was 76 Ωm and the mean of resistivity of the cells inside the body was 108 Ωm; in the case of multi-component inversion, these numbers dropped down to 27 and 66 Ωm and became closer to the synthetic model. Our results were in agreement with those of Ke et al. [21], who were studying multi-component inversion. As a result, all of the other modellings you will see hereafter are multi-component inversion results.
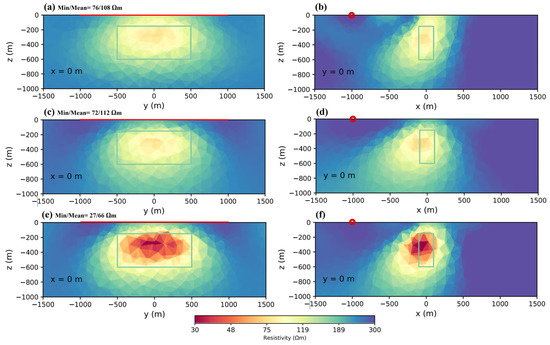
Figure 2.
Cross-sections (y–z and x–z planes) of inversion results for different components: (a,b) x-component; (c,d) z-component; and (e,f) xyz (multi)-component. In all figures in this paper, when the transmitter was perpendicular to the plane, it is shown as a red circle, whereas it is shown as a red straight line when it was parallel to the plane. In the title, the minimum and mean resistivity values inside of the target dimensions (blue rectangles) are provided as a quantitative measure of resolution.
4. Survey Parameters
4.1. Surveying Data Density
With a point and line spacing parameter, we examined the effect of data point density on the result of inversion, number of flight lines, or cost. Table 1 shows the variables of this modeling.

Table 1.
Summary of the data point spacing, number of data points, and runtime.
Figure 3 shows the results. Figure 3a,b are the results for a 100 m × 100 m survey grid, and we can better see the result that is closer to the body properties or higher resolution, as the figures show that the minimum of the cells was 15 Ωm and the mean was 44, taking 19 h to run. Figure 3c,d are the results for the 200 m × 100 m grid size that gave a reasonable result with a minimum of 27 and mean of 66 Ωm with respect to the run time and resolution. Most importantly, in this case, the flight lines were half of the 100 m × 100 m grid, resulting in a lower cost. Figure 3e,f show the 200 m × 200 m result that was lower in resolution. Based on the results of the inversions with different grid sizes. The more the flight lines spacing increased and therefore the number of data points decreased, the lower the resolution became. However, a denser flight line spacing increased the number of flight lines and more data points increased the inversion time by a factor of 2 or 3, as shown in Table 1. Therefore, we used the 200 m × 100 m data spacing for modelling in this study because it was faster to run and needed less flight lines in the survey.
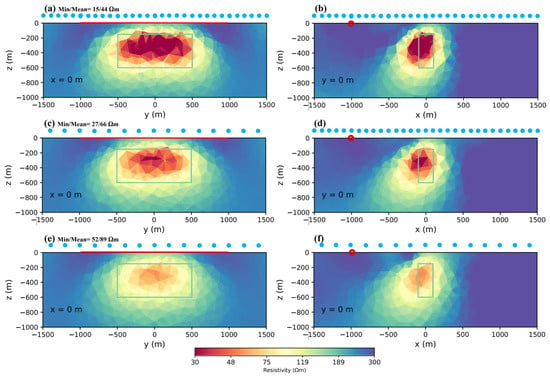
Figure 3.
Inversion results for different measuring grid sizes: (a,b) 100 m × 100 m; (c,d) 200 m × 100 m; (e,f) 200 m × 200 m. Blue dots are receiver positions.
4.2. Transmitter Length
In this step, we examined the effect of the transmitter length. We considered the same model, but this time, the block was located at a depth of 50 m. It is worth mentioning that we could have used a long transmitter (10 km or more), but we considered the practical limitations of the transmitter layout for real surveys. Therefore, the objective was to achieve a good trade-off between resolution and installation effort. Starting with the block being 1 km from the transmitter, the transmitter length increased from 1 km to 3 km. In this case, the block was close to the transmitter and as a result, the signal was strong at the block. Figure 4a indicates that using a transmitter length of at least equal to the length of the target provided a good target recovery. To obtain a good result with a higher resolution, it was better to use a transmitter with twice the length of the target (Figure 4c). In terms of numbers, using a 1-km transmitter produced good results, min/mean of 11/40, and using the 2-km-length transmitter helped to improve the numbers slightly to 10/35. However, thereafter, numerical changes were not very significant and were not worth the practical work.
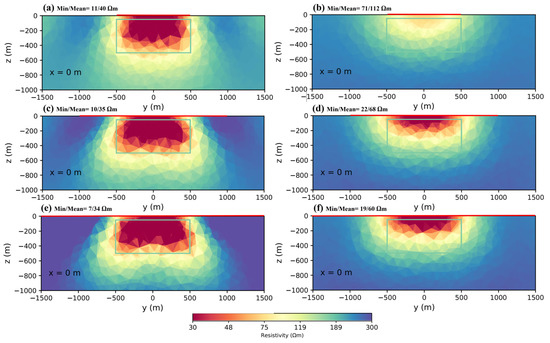
Figure 4.
Inversion results for different transmitter lengths: (a,b) 1 km; (c,d) 2 km; (e,f) 3 km. The conductive body is located: (a,c,e) 1 km from the transmitter; (b,d,f) 2 km from the transmitter.
Next, we placed the block 2 km away from the transmitter, and at this distance, the signal was weaker in comparison to the previous model (Figure A1). Again, the transmitter length changed from 1 km to 3 km. We can see from Figure 4b that the 1-km transmitter did not produce a strong enough primary field at the block. We reached a min/mean of 71/112 that was far from the synthetic model, and the result resolution was low. A transmitter with twice the length of the target block gave a fair result (Figure 4d), and using a transmitter three times the length of the target (Figure 4f) gave a better result at this distance. Figure 4f shows the min/mean of 19/60 that was much closer to the model. In this situation, it was better to use a transmitter with three times the length of the target.
In the last model, the block was 3 km from the transmitter. In this situation, the signal at the block location was weak (Figure 5). Figure 5a shows that with the 1-km transmitter, we could not see the block at all because of the weak signal at that distance. As the figure shows, the inversion reached the minimum resistivity of 192 Ωm and the mean of the cells was 245 Ωm. These numbers were closer to the background than the target. Using the 2- and 3-km length transmitter did not provide reasonable results. We could see the numbers changing significantly, but even with the 3-km transmitter, the min/mean was 68/111; these were not good results (Figure 5b,c). We even used a 4-km transmitter, but the results were just slightly better in resolution, and the numbers for the minimum and mean of the cells resistivity were 50 and 99 Ωm. (Figure 5d). Another important point here is that, even with a long transmitter such as one with a 4-km range, the maximum distance that we could rely upon the data for was 3 km from the transmitter. We therefore recommend that, for long distances, it is better to use transmitters with at least four times the length of the target.
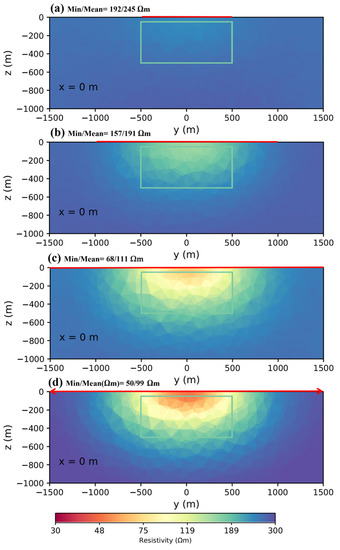
Figure 5.
Inversion results for different transmitter lengths ((a) 1 km, (b) 2 km, (c) 3 km, (d) 4 km), in this case, the conductive body was located 3 km away from the transmitter.
4.3. Transmitter Orientation with Respect to the Block
In many cases of mineral exploration, there is at least some geological and geometric information on the target, based on preliminary studies. In this situation, we have some general knowledge of the target, and it is the best-case scenario because we know we should lay down the transmitter cable parallel to the main strike of the target to have the best coupling of the transmitter and target. To demonstrate this, we assumed the same model as in the previous section. Figure 4c shows that the best results were obtained when the target was closer to the transmitter (1 km) and the transmitter length was twice the length of the target. This time, we laid down the cable perpendicular to the body. Figure 6a,b shows that, in this model, the block was perpendicular to the transmitter. In this situation, even when the right side of the block was located only 500 m from the transmitter, the results were not good. We could not recover the body boundaries, except when the block was just in front of the body. This result can be seen based on the obtained numbers. The minimum resistivity was 47 Ωm; this was not too bad, compared with the situation when the transmitter was parallel to the block and the minimum was between 10 and 25 Ωm. However, the mean of the cells inside of the target (218 Ωm) showed the result was not good and this number was closer to the background. This means we could not detect the whole body. In Figure 6c,d, the conductive body was 2 km away from the transmitter and we could not even see the front of the body in good resolution. The min/mean was 186/260 Ωm, and it was hard to distinguish the body from the background. This examination shows the importance of carrying out geological studies to obtain information on the target geometry before designing the survey.
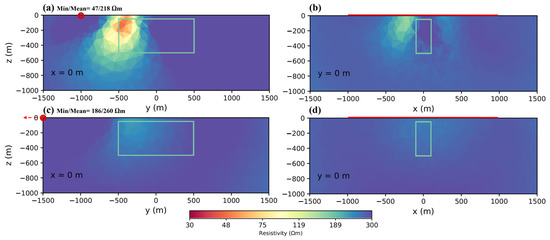
Figure 6.
Inversion results of transmitter at different distances of (a,b) 1 km away from the center of the conductive body; and (c,d) 2 km away from the center of the conductive body. Transmitter was perpendicular to the general strike of the body.
4.4. Using More Than One Transmitter
In the previous modellings, we used only one transmitter. By looking closely at the results (Figure 3b,d,f), the anomaly tended toward the transmitter and this could mislead the interpretation. For example, we could lose the symmetry of the target. Another consequence of using only one transmitter was that if a conductive body was located behind the front body, it could mask the front body (Figure 7a). A significant decay occurred in the field after the front body, and this caused a loss of accuracy in the interpretation behind the block. Figure 7a shows that, for the front body, the min/mean was 29/59 Ωm, but the results for the second body were a min/mean of 144/183. This means we could not see the body and it was covered by the effect of the front body. To overcome these problems, it was better to use more than one transmitter on both sides. Figure 7b shows that, using two transmitters, both blocks were recovered in a good resolution, and the min/mean for second body improved to 26/57 Ωm; consequently, both targets had almost the same resolutions and we could distinguish them. Later on in this paper, we have provided the results from greater depths of 300 m. Using multiple transmitters helped to improve the resolution at greater depths. Therefore, it is important to use more than one transmitter. In the following section, we have explained how to use these transmitters in terms of their orientation and distance.
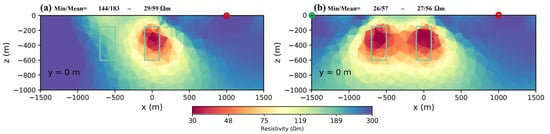
Figure 7.
Inversion result for using single and double transmitters, the first transmitter (Tx1) is displayed in red and the second transmitter (Tx2) is displayed in green. Inversion results of (a) two conductive bodies and one transmitter; and (b) two conductive bodies and two transmitters on both sides.
4.5. Transmitter Orientation with Respect to Each Other
In previous models, we assumed that we knew the general strike of the target and we laid down the Tx cable parallel and also perpendicular to it. The results showed that the parallel configuration was much better. If we did not know the target geometry, one reasonable idea would be to use more than one transmitter in a way that the transmitters are perpendicular to each other. A sketch of such a model is presented in Figure A2 as an Appendix A. Figure 8 shows the results using the perpendicular layout. The body was recovered with a higher resolution and the resistivity distribution was more limited to the body. To prove this design method, we considered a more complex model that included a dipping plate with dimensions of 100 m × 500 m × 100 m, a dip angle of 45 degrees, and an azimuth of 45 degrees. The center of the plate was located at a depth of 300 m from the surface of the earth. Figure 9a shows the front view and Figure 9b shows the side view of the plate inversion. The plate was recovered with a good resolution so that the resistivity distribution followed the plate geometry. The min/mean was 15/52 Ωm, representing good results compared with the block numbers of min/mean = 9/40 Ωm. In addition, the block was bigger and easier to detect. In the absence of information concerning the target, it is better to use at least two perpendicular transmitters. From a logistical point of view (i.e., the installation of grounding points), it is better if one end of the transmitter is close to the other; alternatively, the same grounding station can be used at the same end (Figure A2 and Figure A3 in the Appendix A).
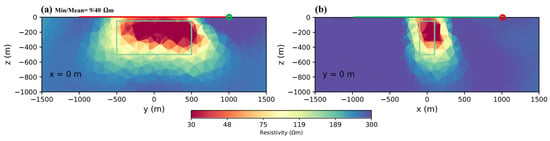
Figure 8.
Inversion results of using two transmitters perpendicular to each other. Cross-sections (a) y–z plane and (b) x–z plane of inversion results.
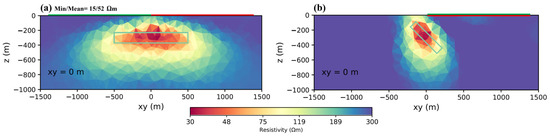
Figure 9.
Inversion results of using two transmitters perpendicular to each other; in this case, the conductive body is a dipping plate. Cross-sections (a) front view and (b) side view of inversion results. For a better understanding of the plane views, please refer to the Appendix A, Figure A3.
4.6. The Distance of the Transmitters from Each Other
In case we have general information on the target, we can use parallel transmitters on both sides of the target. Next, we investigated the optimal distance between these two transmitters and how this distance affected the depth of investigation. We considered a model that included a block at different depths of 150, 300, and 500 m from the surface of the earth. Two transmitters were considered parallel to this block. The geometry of this model is presented in the Appendix A, Figure A4, located at a distance of 2, 3, and 4 km from each other.
First, we investigated the case when the transmitter distance was 2 km. Figure 10a shows the result for a body located at a depth of 150 m. The body was recovered with a high resolution so that the resistivity distribution was more limited to the edges. We could see the geometry or edges of the target more effectively. In the same way, Figure 10d,g shows the results for the body located at depths of 300 and 500 m. As the body moved towards the depth, the resolution decreased; however, we still could not detect it. Figure 10a,d,g shows the mean resistivity of the cells inside the target changed from 40 to 149 Ωm. This shows the high importance of the depth of the target and having prior geological information about the target, which can be very useful when deciding the distance of the transmitters and achieving the result of the inversion. This meant that by using a 2-km distance between transmitters, we could detect target at a depth of up to 1 km.
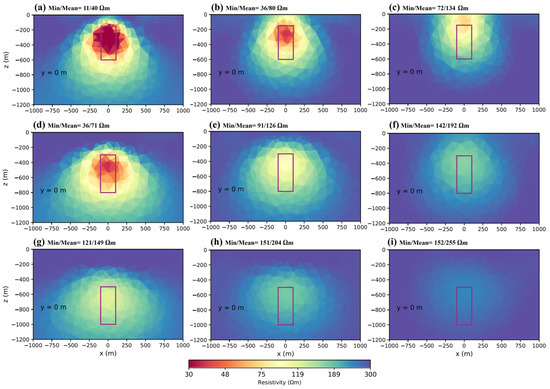
Figure 10.
Inversion results for a body located at different depths: (a–c) 150 m; (d–f) 300 m; and (g–i) 500 m from the surface, and for different transmitter distances: (a,d,g) 2 km; (b,e,h) 3 km; and (c,f,i) 4 km.
For further investigation and to achieve the optimal distance, the distance between transmitters changed to 3 and 4 km. Figure 10b shows that, for the block near the surface (150 m) and in the case where the distance between the transmitters was approximately 3 km, it was still possible to determine the location of the block. In this case, the min/mean was 36/80 Ωm; compared to transmitters that were 2 km away from each other, this result was considered to be good. However, Figure 10c shows that, with a 4-km distance between the transmitters, the resistivity distribution moved toward the surface; the min/mean increased to 72/134 Ωm, but we could still see the body with a lower resolution. When the same block went to a depth of 300 m, we could detect it with acceptable resolution using a 3-km distance between the transmitters (Figure 10e). Figure 10f shows that using a 4-km distance between the transmitters meant that the body was recovered with a low resolution (min/mean of 142/192 Ωm).
Figure 10g–i shows the results for the body located at a depth of 500 m. Based on Figure 10h, when the distance between the transmitters was 3 km, we could recover the body with a low resolution. However, Figure 10i shows that, for a distance of 4 km, it was practically impossible to detect the boundaries or location of the block.
The results showed that the closer the transmitters, the better the results (Figure 10a,d,g); however, this proximity caused a smaller area to be covered per helicopter flight, resulting in more flights and thus increased costs. As a result, the optimal distance between two transmitters in this case, for exploration up to a maximum depth of 1 km, is 3 km (Figure 10b,e,h). It is important to note that the length of the transmitter was 2 km, which was close to the average length of the surveys carried out by the LIAG [19,28]. Of course, you can use a transmitter of any length, but the limitations in the field do not allow it in most cases.
4.7. Anomalies under the Transmitter
As mentioned previously, we did not consider the data points up to a certain distance from the transmitter, typically 400 m [28,32]. By considering a respective model, as before, we removed the data around the transmitter up to a distance of 400 m from each side. The results showed that, in this case, when the block was located at a depth of 150 m below the transmitter, it was recovered well (Figure 11a,b). In the second case, when the block was placed at a depth of 300 m, it was relatively well recovered (Figure 11c,d); however, when it went to a depth of 500 m, it became difficult to identify its location and the numbers increased drastically (Figure 11e,f). As explained in the previous section, it is better to use two transmitters. Using this method, we could use one of the transmitters to cover the data near the other one, which helped to estimate the depth of the investigation and provide better resolution of the results. Figure 12 shows that covering the masked data point with another transmitter helped to image the block at a depth of 500 m with a higher resolution, compared to using one transmitter. Figure 11e,f and Figure 12e,f show that, for the target at 500 m, in the case of just one transmitter, we could reach a min/mean of 188/213 Ωm. By using two transmitters, the resolution increased and we reached a min/mean of 140/161 Ωm. We thus conclude that we can still recover an anomaly underneath the transmitter without data points being located exactly on top of the body.
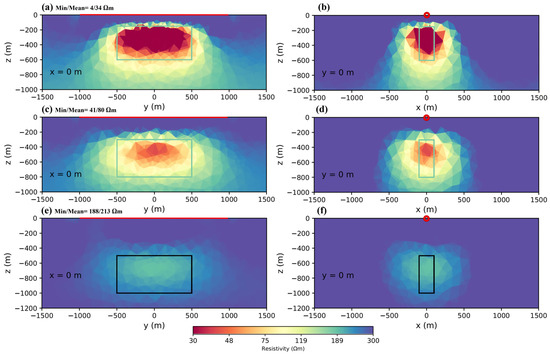
Figure 11.
Inversion results using a body located under the transmitter and different depths below the surface: (a,b) 150 m; (c,d) 300 m; and (e,f) 500 m.
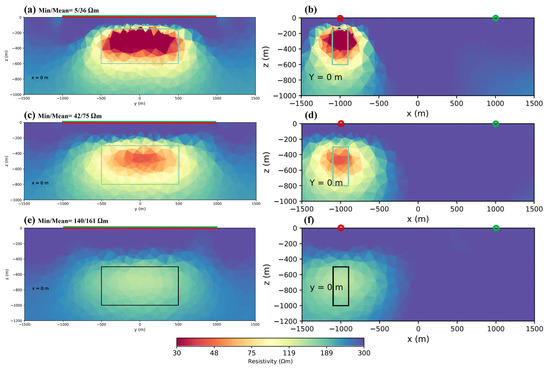
Figure 12.
Inversion results using a body located under two transmitter and different depths of (a,b) 150 m; (c,d) 300 m; and (e,f). 500 m. In this case, the body was located exactly under the transmitter, Tx1, and 2 km away from transmitter, Tx2.
5. Discussion
We used synthetic modelling and inversion to examine how different field survey parameters affected the inversion results and aimed to optimize them. At first, we demonstrated the importance of multicomponent inversion. Using all three components increases the accuracy of recovering the resistivity of the body and its boundaries. Table 2 shows the numerical analyses of results for different parameters. The electrical resistivity numbers showed that the use of multicomponent inversion greatly increased the resolution, and the numbers were close to the synthetic model. Our results were in agreement with those of Ke et al. [21]. The number of flight lines is one of the most important factors affecting the cost of such surveys. In general, denser lines lead to better data coverage, which suggests a steadily increasing resolution of inversion. Table 2 also shows the increase in the resolution; by increasing the data points, the numbers improve and become closer to the synthetic model. However, depending on the target size and geometry, there is a reasonable limit of data density to recover conductive bodies well. Collecting more data hardly increases the resolution and only produces additional survey costs, as well as processing and inversion runtimes. By examining different models, we concluded that a line spacing of 200 m with 100 m in-line spacing provides the optimal trade-off between cost and resolution.

Table 2.
Numerical analyses of results for different parameters: the minimum (min) and mean resistivity value inside of the target dimensions is provided as a quantitative measure of resolution. Recommended values of parameters are highlighted.
The longer the transmitter is, the stronger the signal will be. However, the installation of the transmitter, including finding suitable grounding locations and laying out cables, is strongly controlled by the field conditions. The models showed that, in general, if the distance between the transmitter and the target was 1 km, the minimum length of the transmitter should be at least equal to the largest target dimension. For better results, it should be twice the target dimension. The minimum and mean numbers confirmed this conclusion. By changing the transmitter length from 1 to 2 km, the numbers decrease, but with a longer transmitter, the change is small; therefore, it is not worth the effort of laying down more cable. If the target is located within 2 km of the transmitter, the minimum length of the transmitter should be three times the length of the target, and if the target is within 3 km, a transmitter with a length of at least four times is needed. Figure A1 shows that the signal became extremely weak and unreliable after 3 km and went below the typical noise level.
An important issue to be considered before installing a transmitter is its orientation relative to the target geometry. In this case, it is necessary to use geological studies before geophysical surveying to determine the general strike of the target and install the cable parallel to it, in order to obtain the highest coupling. The results showed that the transmitter orientation had a great impact on the inversion result. If the cable was roughly perpendicular to the target, it was difficult to image the whole target (Figure 6). We also showed that if one body was placed behind another, it was difficult to distinguish both or even to detect the further body, as it is masked by the first (Figure 7). As a result, we suggest using more than one transmitter. When information regarding the strike direction is available, two transmitters should be installed parallel on both sides of the target, with an optimal distance of 3 km, assuming transmitter lengths of 2 km (Figure 7 and Figure 10). If the available information regarding the strike direction is limited, the best method is to use transmitters with different orientations depending on local conditions (Figure 8 and Figure 9). Finally, our studies showed that even if data are removed in a certain distance from the transmitter, the body under the transmitter can still be recovered. In the case of larger target depths, it is suggested to use multiple transmitters for improving the resolution at depth. For example, Table 2 shows that, for anomalies under the transmitter when the target was placed at a depth of 500 m and just one transmitter was used, the min/mean was 188/213 Ωm; however, using two transmitters changed the results, with a min/mean = 140/160 Ωm.
We used simple synthetic models for our study. To obtain a better result, it is necessary to use more complex models. This complexity includes various things, for example, models with different thicknesses and different geometric shapes, and the simultaneous use of several targets placed in different positions. With this, it is possible to give a more detailed opinion regarding the parameters of the investigation and their optimized value. It should also be kept in mind that the real environment of the earth is very complex. As a result, targets with different contrasts with the background should be used. One way to draw a conclusion is based on observing the output of inversion or visualization, which can be concluded according to the obtained resolution. This type of conclusion can be biased and cause mistakes in determining the optimal values. However, the proper and more accurate way is to use numerical values and compare them with real values (synthetic models). By changing each parameter, the change in the inversion result and the decrease or increase in the distance between the result and the actual values should be checked, and thus, a definite result will be reached. In the table of numerical results (Table 2), we have provided some of the investigated parameters.
The main reason for using a semi-airborne EM system is to cover wide areas in a short timeframe with superior signal-to-noise ratios, compared to pure airborne EM systems. Furthermore, airborne methods, in general, facilitate work being undertaken when there is arbitrary topography, e.g., impassable or rough terrain. Our study tried to find general rules to optimize the trade-off between resolution and costs. Summarizing the individual survey parameters and arguments discussed previously, we suggest a survey layout scheme using eight main transmitters with lengths of 2 to 3 km (Figure 13). For this design with overlapping injection points, we only needed nine grounding positions (using main transmitters only) instead of the 16 that were needed with eight separated transmitters, which means less logistic effort was required. Here, six of the transmitters were parallel to each other and two others were perpendicular. With this layout, we minimized the number of perpendicular transmitters to just two. As was demonstrated previously, this approach helped to image the subsurface with a much higher resolution. This layout can cover an area of 36 km2 with high resolution (inside of the 2 × 2 transmitter square) and a total area of 84 km2 (outside). The optional transmitters (green lines) will further improve the resolution, particularly in cases of unknown strike direction, and increase this area to 144 km2. It is worth noting that this scheme can be arbitrarily extended to larger survey areas by moving the transmitter combinations by increments of 3 km in all directions.
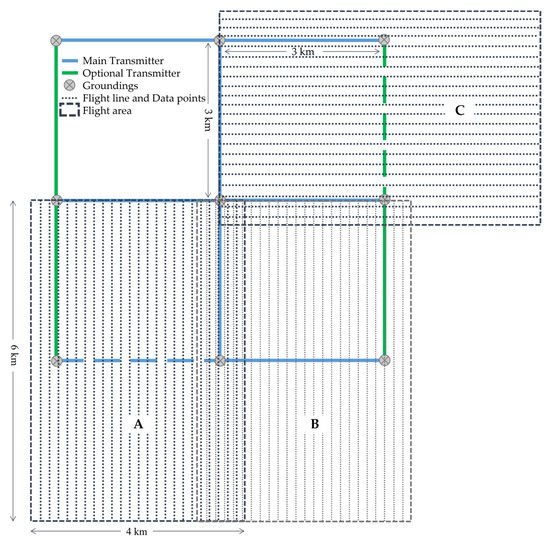
Figure 13.
Recommended optimized survey layout (to be adapted to field conditions). The length of all transmitters and spacing between parallel transmitters was 3 km, using common groundings that reduced logistic effort. Three of the overlapping flight patches are given as examples (each covering an area of 24 km2): (A) over the lower-left Tx (dashed blue), (B) over the lower-right Tx (solid blue), and (C) over the optional Tx (dashed green).
We used comparatively simple models in terms of conductivity and geometry. For future studies, we suggest moving toward more realistic geological settings for addressing goals in real mineral exploration scenarios. One of the most important features of the real world is topography. In the presence of topography, sometimes helicopters need to fly at higher altitudes, which means larger offsets. Motional noise can affect the data processing and extraction of x, y, and z components. One interesting future study could involve using the total magnetic field vector in terms of amplitude and phase for the inversion. Using different error models should also be studied. In this study, we used 7 frequencies from 16 to 1024. This was a limited range of frequencies for our modelling and we suggest using lower and higher frequencies to examine the outcome in the future.
6. Conclusions
Our experiments showed that multi-component EM surveying and inversion provides significantly improved chances for recovering deep conductive targets. Since many mineral deposits are embedded in more complex geological structures compared with our idealistic model setup, the advantages become even more important in practice. Corresponding multi-component surveying capabilities have become increasingly available in recent years, though SAEM exploration costs can be considered more expensive compared to established AEM and surface EM methods. As an efficient compromise between costs and data coverage, our modellings suggest 200-m flight line spacing. Data gaps in the vicinity of the transmitters do not significantly limit the resolution capabilities just below the transmitters. In reality, the length of the transmitter is often controlled by the field conditions. Our results strongly suggest using multiple transmitters instead of only one, with lengths of at least 2 km for recovering conductive targets up to a distance of 3 km from the transmitter and down to a depth of several hundred meters. However, even the most promising setups have underestimated the true target conductivity by approximately one order of magnitude. By using appropriate geological studies before designing survey plans, the mineralization type and strike can be determined to some extent. A parallel transmitter layout according to this information maximizes the target resolution capabilities. In cases where mineralization is very complex, several perpendicular transmitters should be used. Finally, we presented a general scheme that is very suitable for covering large areas effectively with helicopter-towed receivers. We suggested quantitative measures such as the mean and minimum recovered resistivities inside the target volume and a percentual metric of recovery on a logarithmic scale to generalize our synthetic inversion results. We are confident that these and other measures can support comparing our results with related EM modeling studies in the future.
Author Contributions
Conceptualization and methodology, T.G. and S.N.; software, R.R. and T.G.; formal analysis, S.N.; writing—original draft preparation, S.N.; writing—review and editing, R.R. and T.G.; visualization, S.N. and T.G.; project administration and funding acquisition, T.G. All authors have read and agreed to the published version of the manuscript.
Funding
The paper was financially supported by the Federal Ministry of Education and Research (BMBF) of Germany as part of the DESMEX-II and DESMEX-real projects under grant numbers 033R385D and 033R130DN.
Data Availability Statement
All data and files for running the simulations are available on request. In addition, a representative selection of data and scripts to reproduce our examples are available on https://gitlab.com/Rochlitz.R/custem-examples. The open-source software custEM and pyGIMLi are available at https://gitlab.com/Rochlitz.R/custEM and https://www.pygimli.org.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
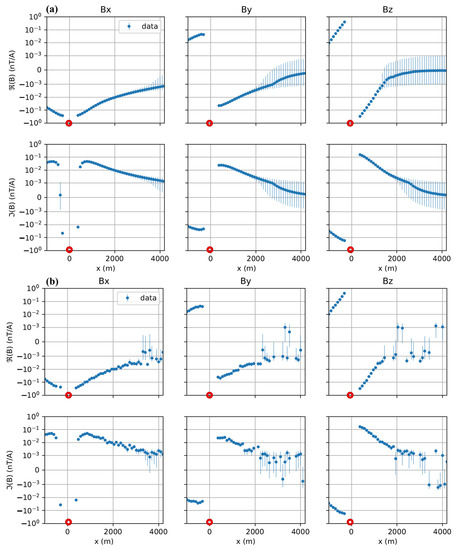
Figure A1.
Synthetic data of one flight line over a homogeneous half space at 300 Ωm. Frequency was 512 Hz. (a) Data without noise; (b) noisy data.
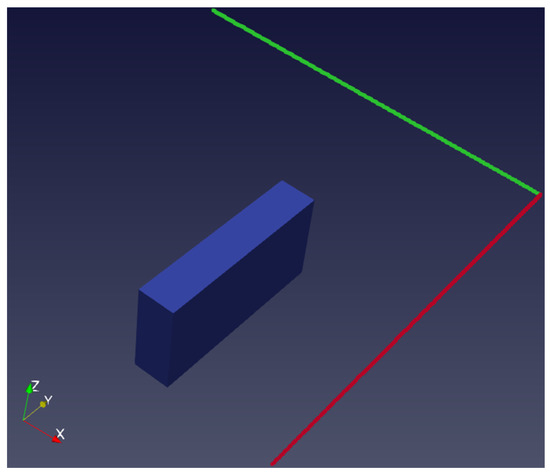
Figure A2.
Sketch of the model using two transmitters perpendicular to each other. Red line is the Transmitter 1 and green line is Transmitter 2.
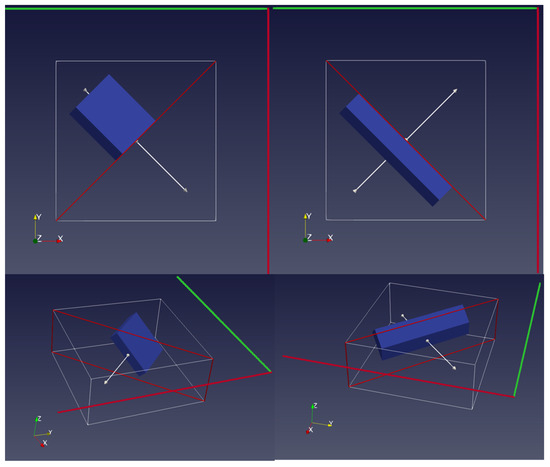
Figure A3.
Sketch of the dipping plate using two transmitters perpendicular to each other. Plane views are 45 degrees in x–y plane. Red line is Transmitter 1 and green line is Transmitter 2.
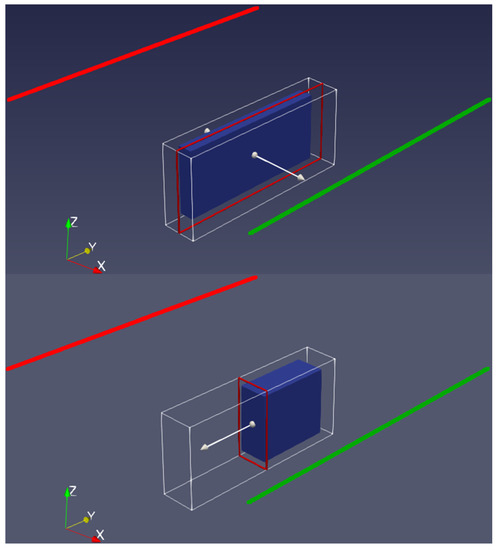
Figure A4.
Sketch of the model using two transmitter parallel to each other. Red line is Transmitter 1 and green line is Transmitter 2.
References
- Becken, M.; Nittinger, C.G.; Smirnova, M.; Steuer, A.; Martin, T.; Petersen, H. DESMEX Working Group. DESMEX: A novel system development for semi-airborne electromagnetic exploration. Geophysics 2008, 85, E253–E267. [Google Scholar] [CrossRef]
- Kearey, P.; Brooks, M.; Hill, I. An Introduction to Geophysical Exploration; John Wiley & Sons: Hoboken, NJ, USA, 2002. [Google Scholar]
- Dentith, M.; Mudge, S.T. Geophysics for the Mineral Exploration Geoscientist; Cambridge University Press: Cambridge, UK, 2014. [Google Scholar]
- King, R.B.; Constable, S. How low can you go: An investigation of depth sensitivity and resolution using towed marine CSEM systems. Geophys. Prospect. 2023, 71, 722–733. [Google Scholar] [CrossRef]
- Maurer, H.; Boerner, D.E.; Curtis, A. Design strategies for electromagnetic geophysical surveys. Inverse Probl. 2000, 16, 1097. [Google Scholar] [CrossRef]
- Hennig, T.; Weller, A.; Möller, M. Object orientated focussing of geoelectrical multielectrode measurements. J. Appl. Geophys. 2008, 65, 57–64. [Google Scholar] [CrossRef]
- Coscia, I.; Marescot, L.; Maurer, H.; Greenhalgh, S.; Linde, N. Experimental design for crosshole electrical resistivity tomography data sets. In Near Surface 2008—14th EAGE European Meeting of Environmental and Engineering Geophysics; cp-64-00054; EAGE Publications B.V.: Houten, The Netherlands, 2008. [Google Scholar] [CrossRef]
- Loke, M.H.; Wilkinson, P. Rapid parallel computation of optimized arrays for electrical imaging surveys. In Near Surface 2009—15th EAGE European Meeting of Environmental and Engineering Geophysics; cp-134-00049; EAGE Publications B.V.: Houten, The Netherlands, 2009. [Google Scholar] [CrossRef]
- Nowruzi, G.H. Optimum Design of Survey Grid in Magnetic Studies; University College of Engineering: Tehran, Iran, 1997; Volume 30. [Google Scholar]
- Ahmadi, R. Application of geometric probability to design exploration grid of mineral deposits, case study: Porphyry copper index located in the south-west of Kerman. J. Anal. Numer. Methods Min. Eng. 2018, 8, 39–54. [Google Scholar] [CrossRef]
- Agocs, W.B. Line spacing effect and determination of optimum spacing illustrated by Marmora, Ontario magnetic anomaly. Geophysics 1955, 20, 871–885. [Google Scholar] [CrossRef]
- McCammon, R.B. Target intersection probabilities for parallel line and continuous grid types of search. J. Math. Geol. 1977, 9, 369–382. [Google Scholar] [CrossRef]
- Chung, C.F. Application of the Buffon needle problem and its extensions to parallel-line search sampling scheme. J. Int. Assoc. Math. Geol. 1981, 13, 371–390. [Google Scholar] [CrossRef]
- Ajo-Franklin, J.B. Optimal experiment design for time-lapse traveltime tomography. Geophysics 2009, 74, Q27–Q40. [Google Scholar] [CrossRef]
- Brenders, A.J.; Pratt, R.G. Waveform tomography of marine seismic data: What can limited offset offer. In 2007 SEG Annual Meeting; OnePetro: Richardson, TX, USA, 2007. [Google Scholar]
- Curtis, A.; Snieder, R. Reconditioning inverse problems using the genetic algorithm and revised parameterization. Geophysics 1997, 62, 1524–1532. [Google Scholar] [CrossRef]
- Liner, C.L.; Underwood, W.D.; Gobeli, R. 3-D seismic survey design as an optimization problem. Lead. Edge 1999, 18, 1054–1060. [Google Scholar] [CrossRef]
- Sirgue, L.; Pratt, R.G. Efficient waveform inversion and imaging: A strategy for selecting temporal frequencies. Geophysics 2004, 69, 231–248. [Google Scholar] [CrossRef]
- Smirnova, M.V.; Becken, M.; Nittinger, C.; Yogeshwar, P.; Mörbe, W.; Rochlitz, R.; Steuer, A.; Costabel, S.; Smirnov, M. DESMEX Working Group. A novel semiairborne frequency-domain controlled-source electromagnetic system: Three-dimensional inversion of semiairborne data from the flight experiment over an ancient mining area near Schleiz, Germany. Geophysics 2019, 84, E281–E292. [Google Scholar] [CrossRef]
- Chen, C.; Sun, H. Characteristic analysis and optimal survey area definition for semi-airborne transient electromagnetics. J. Appl. Geophys. 2020, 180, 104134. [Google Scholar] [CrossRef]
- Ke, Z.; Liu, Y.; Su, Y.; Wang, L.; Zhang, B.; Ren, X.; Ma, X. Three-Dimensional Inversion of Multi-Component Semi-Airborne Electromagnetic Data in an Undulating Terrain for Mineral Exploration. Minerals 2023, 13, 230. [Google Scholar] [CrossRef]
- Siemon, B.; Christiansen, A.V.; Auken, E. A review of helicopter-borne electromagnetic methods for groundwater exploration. Near Surf. Geophys. 2009, 7, 629–646. [Google Scholar] [CrossRef]
- Smith, R. Electromagnetic induction methods in mining geophysics from 2008 to 2012. Surv. Geophys. 2014, 35, 123–156. [Google Scholar] [CrossRef]
- Stolz, R.; Zakosarenko, V.; Schulz, M.; Chwala, A.; Fritzsch, L.; Meyer, H.G.; Köstlin, E.O. Magnetic full-tensor SQUID gradiometer system for geophysical applications. Lead. Edge 2006, 25, 178–180. [Google Scholar] [CrossRef]
- Rudd, J.; Chubak, G.; Larnier, H.; Stolz, R.; Schiffler, M.; Zakosarenko, V.; Meyer, M. Commercial operation of a SQUID-based airborne magnetic gradiometer. Lead. Edge 2022, 41, 486–492. [Google Scholar] [CrossRef]
- Rochlitz, R.; Skibbe, N.; Günther, T. custEM: Customizable finite-element simulation of complex controlled-source electromagnetic data. Geophysics 2019, 84, F17–F33. [Google Scholar] [CrossRef]
- Rochlitz, R. Analysis and Open-Source Implementation of Finite Element Modeling Techniques for Controlled-Source Electromagnetics. Ph.D. Thesis, Westfälische Wilhelms-Universität Münster, Münster, Germany, 2020. [Google Scholar]
- Rochlitz, R.; Becken, M.; Günther, T. Three-dimensional inversion of semi-airborne electromagnetic data with a second-order finite-element forward solver. Geophys. J. Int. 2023, 234, 528–545. [Google Scholar] [CrossRef]
- Rücker, C.; Günther, T.; Wagner, F.M. pyGIMLi: An open-source library for modelling and inversion in geophysics. Comput. Geosci. 2017, 109, 106–123. [Google Scholar] [CrossRef]
- Günther, T.; Rücker, C.; Spitzer, K. Three-dimensional modelling and inversion of DC resistivity data incorporating topography—II. Inversion. Geophys. J. Int. 2006, 166, 506–517. [Google Scholar] [CrossRef]
- Kim, H.J.; Kim, Y. A unified transformation function for lower and upper bounding constraints on model parameter in electrical and electromagnetic inversion. J. Geophys. Eng. 2011, 8, 21–26. [Google Scholar] [CrossRef]
- Steuer, A.; Smirnova, M.; Becken, M.; Schiffler, M.; Günther, T.; Rochlitz, R.; Müller, F. Comparison of novel semi-airborne electromagnetic data with multi-scale geophysical, petrophysical and geological data from Schleiz, Germany. J. Appl. Geophys. 2020, 182, 104172. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).