Predictive Mapping of Prospectivity for Gold in the Central Portion of the Tapajós Mineral Province, Brazil
Abstract
:1. Introduction
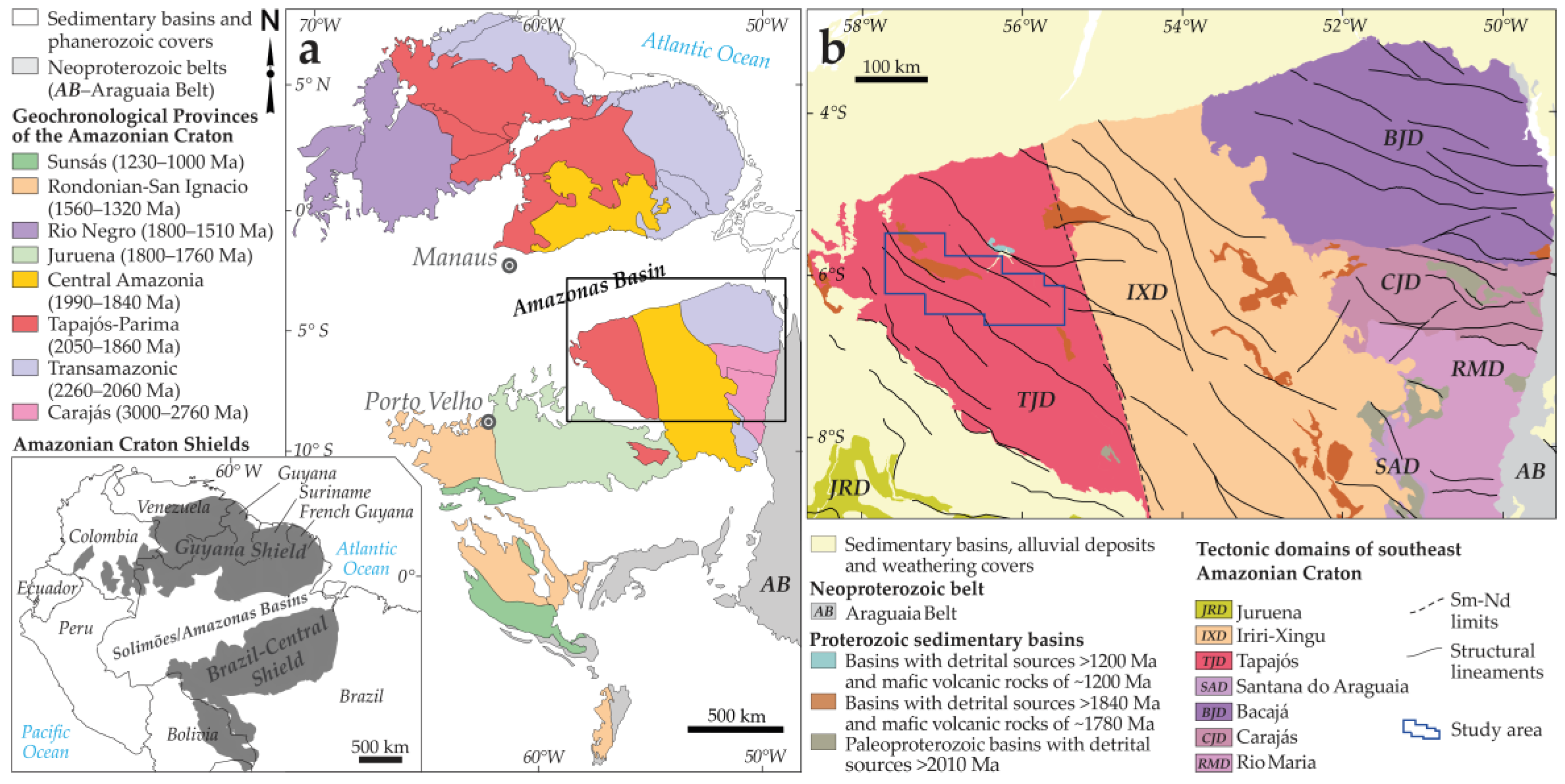
2. Geological Setting
Structures, Metallogeny, and Gold Mineralization
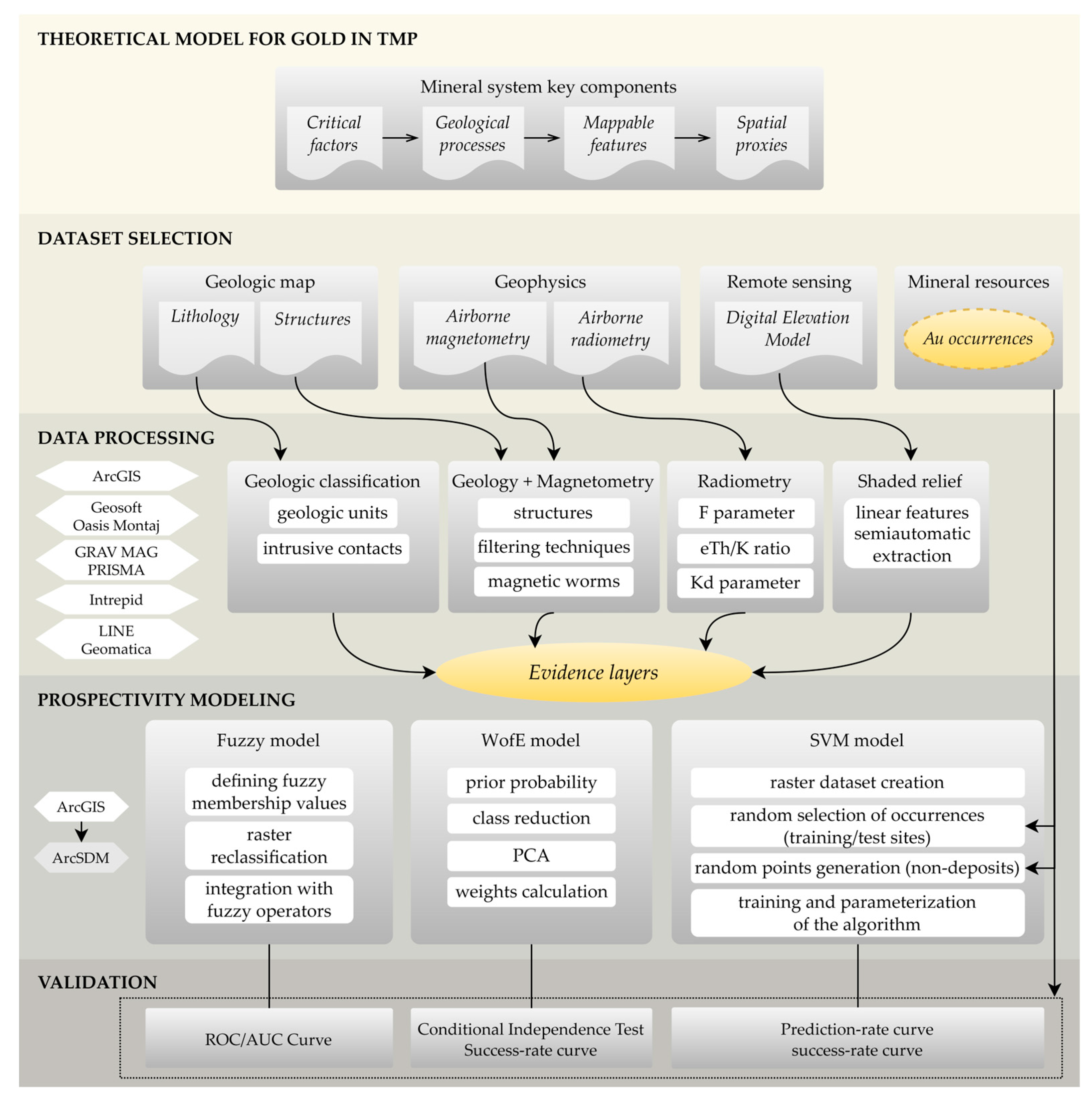
3. Materials and Methods
3.1. Dataset
3.2. Data Processing
3.3. Mineral Prospectivity Modelling
4. Results
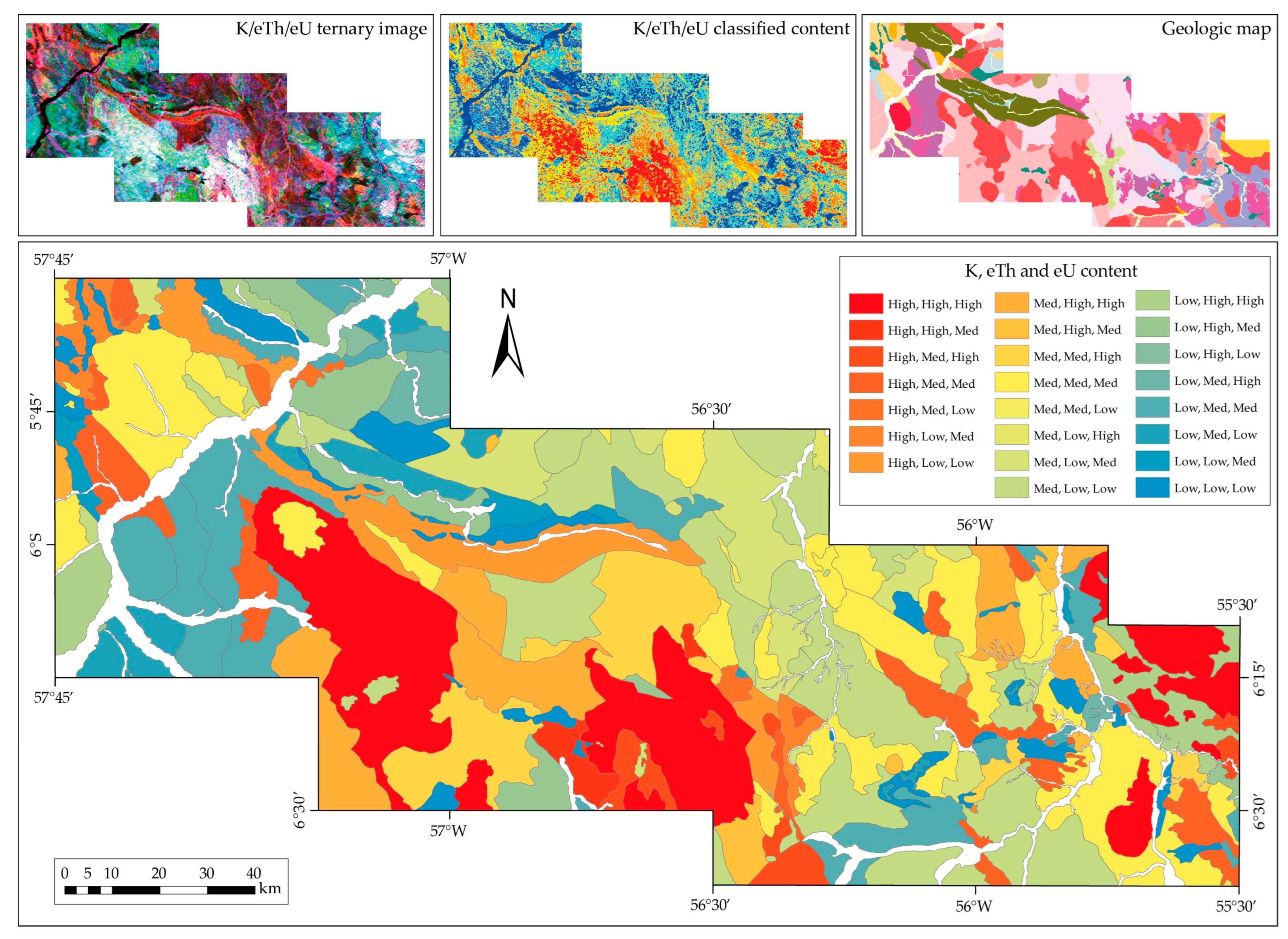
4.1. Hydrothermal Alteration Mapping with Gamma-ray Spectrometry
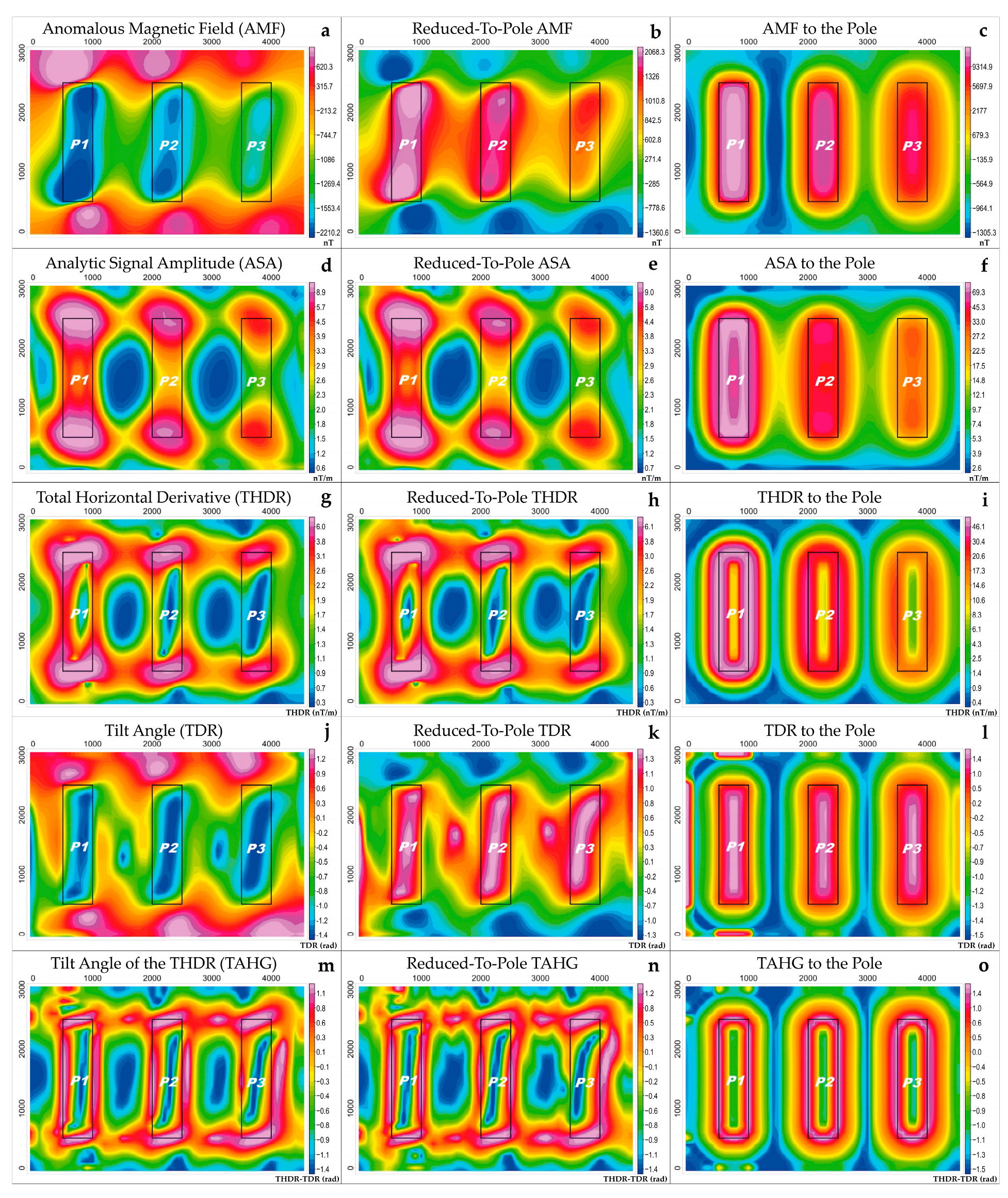
4.2. Interpretation of Magnetic Lineaments
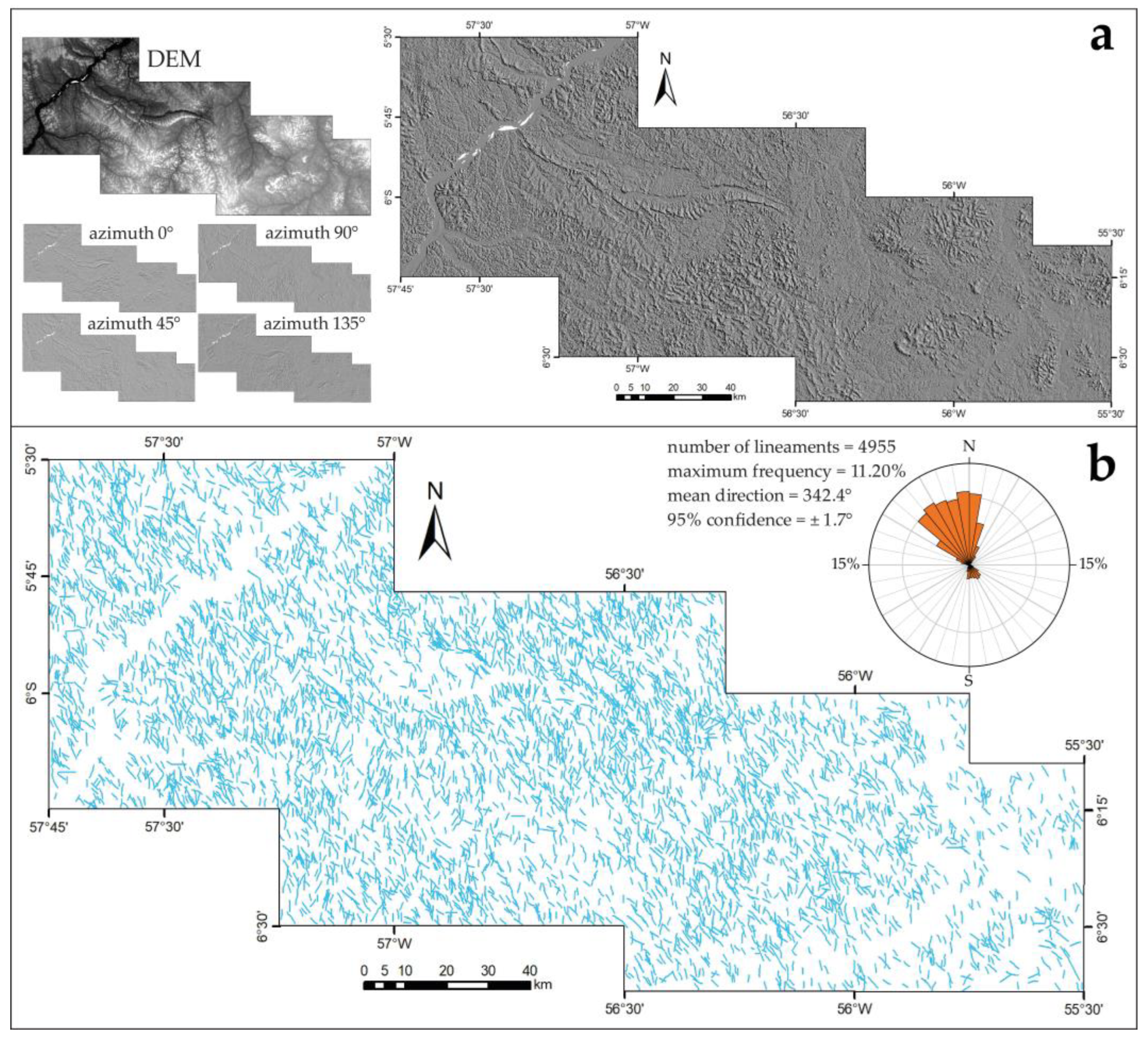
4.3. Semi-Automatic Surface Linear Features
4.4. Data Integration
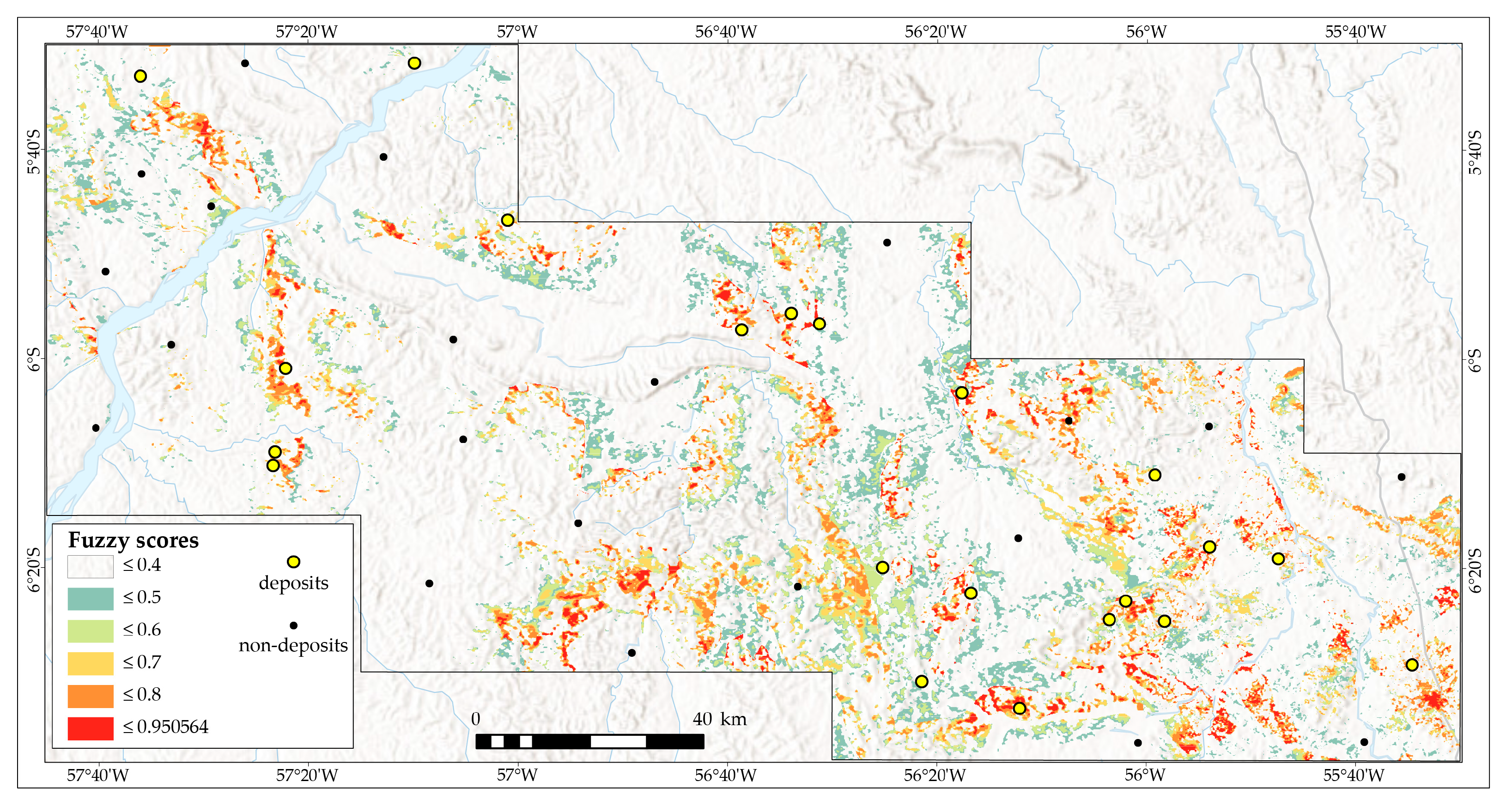
4.4.1. Fuzzy Model
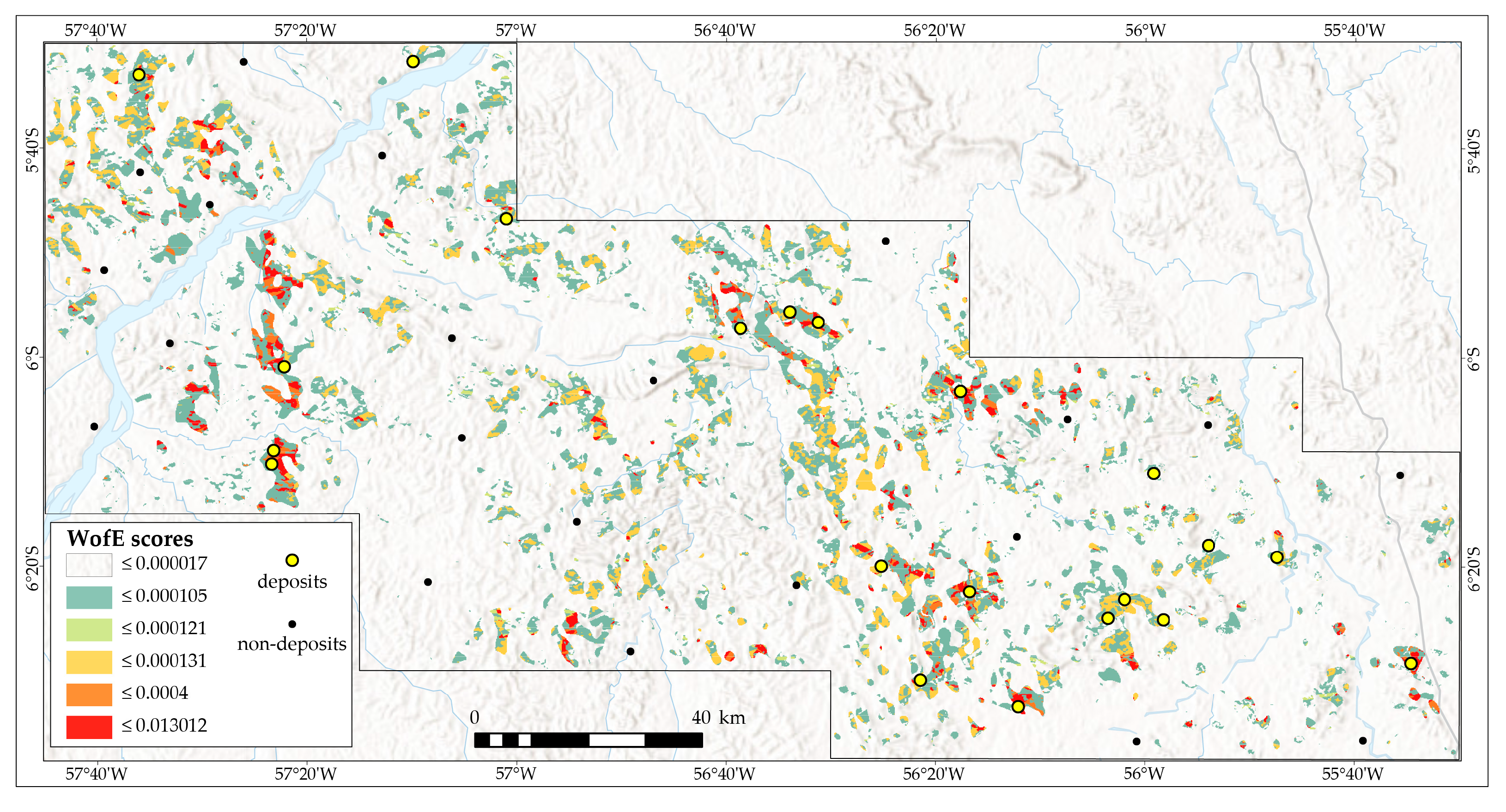
4.4.2. WofE Model
4.4.3. Support Vector Machine (SVM) Model
4.5. Validation
5. Discussions
6. Conclusions
- Radiometric data enhancement is effective for mapping K-enrichment and identifying gold-related hydrothermal alteration zones based on higher intensities of the parameters examined.
- Magnetic data processing with enhancement filters produced satisfactory results for interpreting the structural framework, despite challenges in calculating RTP at low magnetic latitudes.
- Semi-automated extraction of linear features from DEM provided valuable information on morphostructural lineaments in the study area, which is difficult to access in a tropical zone with high vegetation and cloud cover. The distribution of features is consistent with the regional tectonic framework of the area, and the density reflects the higher incidence of structuring at intermediate to shallow crustal levels.
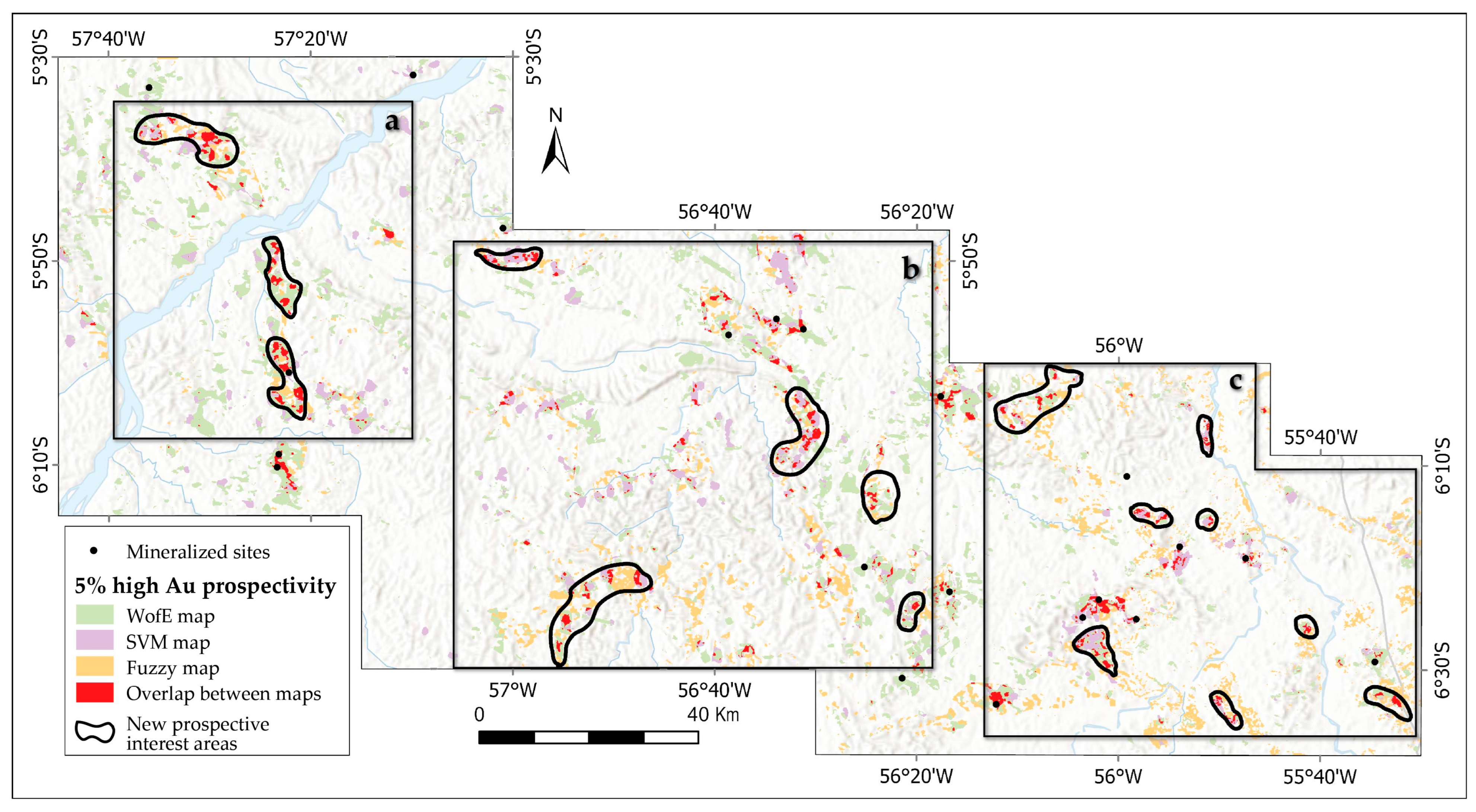
- Three different methods for data integration were used for prospectivity modeling in the central portion of the TMP, resulting in prospectivity sites indicative of the main deposits in the region.
- The fuzzy model (i) effectively identified potential targets, especially in the eastern portion, reflecting the data availability panorama; and (ii) mapped known mineralization sites reasonably, although some deposits had low or zero prospectivity scores. The model validation with an ROC/AUC curve of 0.980 demonstrates high confidence in the degree of randomness explored to map the mineralizing event.
- The WofE method (i) indicated elongated potential zones aligned with prospective structural trends; and (ii) mapped most of the known deposits in areas of higher probability and performed well with points not used in the modeling, attested by an AUC of 0.948 and an ROC curve demonstrating excellent model efficiency in mapping known deposits and predicting new potential targets.
- The ML algorithm (SVM) (i) presented better-defined prospectivity sites and (ii) mapped nearly all known deposits in areas of higher scores and performed even better with omitted points, achieving an AUC of 0.969—the closest to the best classification value. Although the training data set is limited and not ideal, satisfactory results using a limited training data set (<20) can be achieved (e.g., [8,53,123]). The advancement in the use of more sophisticated machine learning techniques, as well as the use of classical methods guided by knowledge or data, can substantially contribute to the risk reduction in mineral exploration and enable decision making through indirect spatial information complementary to field data.
- An agreement map combining the top 5% scores from each model pinpointed the best prospective interest areas, offering valuable insights for future exploration.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Carranza, E.J.M. Geochemical Anomaly and Mineral Prospectivity Mapping in GIS, 11th ed.; Elsevier: Amsterdam, The Netherlands, 2009. [Google Scholar]
- Bonham-Carter, G.F. Geographic Information Systems for Geoscientists: Modeling with GIS; Pergamon: Oxford, UK, 1994; ISBN 978-0-08-041867-4. [Google Scholar]
- Magalhães, L.A.; Souza Filho, C.R.d. Targeting of Gold Deposits in Amazonian Exploration Frontiers Using Knowledge- and Data-Driven Spatial Modeling of Geophysical, Geochemical, and Geological Data. Surv. Geophys. 2012, 33, 211–241. [Google Scholar] [CrossRef]
- Elliott, B.A.; Verma, R.; Kyle, J.R. Prospectivity Modeling for Cambrian–Ordovician Hydraulic Fracturing Sand Resources Around The Llano Uplift, Central Texas. Nat. Resour. Res. 2016, 25, 389–415. [Google Scholar] [CrossRef]
- Brown, W.M.; Gedeon, T.D.; Groves, D.I.; Barnes, R.G. Artificial Neural Networks: A New Method for Mineral Prospectivity Mapping. Aust. J. Earth Sci. 2000, 47, 757–770. [Google Scholar] [CrossRef]
- Rodriguez-Galiano, V.; Sanchez-Castillo, M.; Chica-Olmo, M.; Chica-Rivas, M. Machine Learning Predictive Models for Mineral Prospectivity: An Evaluation of Neural Networks, Random Forest, Regression Trees and Support Vector Machines. Ore Geol. Rev. 2015, 71, 804–818. [Google Scholar] [CrossRef]
- Geranian, H.; Tabatabaei, S.H.; Asadi, H.H.; Carranza, E.J.M. Application of Discriminant Analysis and Support Vector Machine in Mapping Gold Potential Areas for Further Drilling in the Sari-Gunay Gold Deposit, NW Iran. Nat. Resour. Res. 2016, 25, 145–159. [Google Scholar] [CrossRef]
- McKay, G.; Harris, J.R. Comparison of the Data-Driven Random Forests Model and a Knowledge-Driven Method for Mineral Prospectivity Mapping: A Case Study for Gold Deposits Around the Huritz Group and Nueltin Suite, Nunavut, Canada. Nat. Resour. Res. 2016, 25, 125–143. [Google Scholar] [CrossRef]
- Zhang, N.; Zhou, K.; Li, D. Back-Propagation Neural Network and Support Vector Machines for Gold Mineral Prospectivity Mapping in the Hatu Region, Xinjiang, China. Earth Sci. Inform. 2018, 11, 553–566. [Google Scholar] [CrossRef]
- Ghezelbash, R.; Maghsoudi, A.; Carranza, E.J.M. Performance Evaluation of RBF- and SVM-Based Machine Learning Algorithms for Predictive Mineral Prospectivity Modeling: Integration of S-A Multifractal Model and Mineralization Controls. Earth Sci. Inform. 2019, 12, 277–293. [Google Scholar] [CrossRef]
- Chudasama, B.; Torppa, J.; Nykänen, V.; Kinnunen, J.; Lerssi, J.; Salmirinne, H. Target-Scale Prospectivity Modeling for Gold Mineralization within the Rajapalot Au-Co Project Area in Northern Fennoscandian Shield, Finland. Part 1: Application of Knowledge-Driven- and Machine Learning-Based-Hybrid- Expert Systems for Exploration Targeting and Addressing Model-Based Uncertainties. Ore Geol. Rev. 2022, 147, 104937. [Google Scholar] [CrossRef]
- Wyborn, L.A.I.; Heinrich, C.A.; Jaques, A.L. Australian Proterozoic Mineral Systems: Essential Ingredients and Mappable Criteria. In Proceedings of the Australian Institute of Mining and Metallurgy Annual Conference, Melbourne, Australia, 5–9 August 1994; pp. 109–115. [Google Scholar]
- Hagemann, S.G.; Lisitsin, V.A.; Huston, D.L. Mineral System Analysis: Quo Vadis. Ore Geol. Rev. 2016, 76, 504–522. [Google Scholar] [CrossRef]
- Klein, E.L.; Almeida, M.E.; Vasquez, M.L.; Bahia, R.B.C.; Quadros, M.L.d.E.S.; Ferreira, A.L. Geologia e Recursos Minerais Da Província Mineral Do Tapajós. Folhas SB.21-V-D, SB.21-Y-B, SB.21-X-C e SB.21-Z-C. Estados Do Pará e Amazonas; CPRM: Brasília, Brazil, 2001. [Google Scholar]
- Jacques, P.D.; Lee, S.; Coutinho, M.G.d.N.; Lee, H.-J.; Oh, H.J. Mapa Previsional Para Ouro Em Sistema de Informação Geográfica (SIG). In Província Mineral do Tapajós: Geologia, Metalogenia e Mapa Provisional Para Ouro em SIG; Coutinho, M.G.d.N., Ed.; Serviço Geológico do Brasil-CPRM: Rio de Janeiro, Brazil, 2008; pp. 329–352. [Google Scholar]
- Souza Gaia, S.M.d.; Vasquez, M.L.; Chaves, C.L. Mapa de Favorabilidade Para Ouro: Lineamento Tocantinzinho—Setor Leste; SGB/CPRM: Belém, Brazil, 2021. [Google Scholar]
- Souza Gaia, S.M.d.; Vasquez, M.L. Mapa de Favorabilidade Para Ouro: Lineamento Tocantinzinho—Setor Oeste; SGB/CPRM: Belém, Brazil, 2022. [Google Scholar]
- Santos, J.O.S.; Groves, D.I.; Hartmann, L.A.; Moura, M.A.; McNaughton, N.J. Gold Deposits of the Tapajós and Alta Floresta Domains, Tapajós-Parima Orogenic Belt, Amazon Craton, Brazil. Miner. Depos. 2001, 36, 278–299. [Google Scholar] [CrossRef]
- Vasquez, M.L.; Rosa-Costa, L.T.d.; Silva, C.M.G.d.; Klein, E.L. Compartimentação Tectônica. In Geologia e Recursos Minerais do Estado do Pará: Sistema de Informações Geográficas—SIG: Texto Explicativo dos Mapas Geológico e Tectônico e de Recursos Minerais do Estado do Pará; Vasquez, M.L., da Rosa-Costa, L.T., Eds.; CPRM: Belém, Brazil, 2008; pp. 39–112. [Google Scholar]
- Santos, J.O.S.; Hartmann, L.A.; Gaudette, H.E.; Groves, D.I.; McNaughton, N.J.; Fletcher, I.R. A New Understanding of Provinces of the Amazon Craton Based on Integration of Filed Mapping and U-Pb Geochronology. Gondwana Res. 2000, 3, 453–488. [Google Scholar] [CrossRef]
- Tassinari, C.C.G.; Macambira, M.J.B. Geochronological Provinces of the Amazonian Craton. Episodes 1999, 22, 174–182. [Google Scholar] [CrossRef] [PubMed]
- Cordani, U.G.; Brito Neves, B.B.d. The Geologic Evolution of South America during the Archean and Early Proterozoic. Rev. Bras. Geociências 1982, 12, 78–88. [Google Scholar]
- Tassinari, C.C.G.; Macambira, M.J.B. A Evolução Tectônica Do Cráton Amazônico. In Geologia do Continente Sul-Americano: Evolução da Obra de Fernando Flávio Marques de Almeida; Mantesso-Neto, V., Bartorelli, A., Carneiro, C.D.R., de Brito Neves, B.B., Eds.; Beca: São Paulo, Brazil, 2004; pp. 471–485. ISBN 85-87256-45-9. [Google Scholar]
- Delgado, I.d.M. Metalogenia Previsional Da Província Aurífera Do Tapajós. (Relatório de Viagem); CPRM—DEGEO/DIGEOB: Salvador, Brazil, 1999. [Google Scholar]
- Almeida, M.E.; Ferreira, A.L.; Brito, M.d.F.L.d.; Monteiro, M.A.S. Evolução Tectono-Estrutural Da Província Tapajós Com Base Na Geologia Das Folhas Vila Mamãe Anã e Jacareacanga (1:250.000), Região Limite Dos Estados Do Amazonas e Pará. In Contribuições à Geologia da Amazônia; CPRM: Manaus, Brazil, 2001; pp. 57–112. [Google Scholar]
- Santos, R.A.d.; Coutinho, M.G.d.N. Geologia Estrutural. In Província Mineral do Tapajós: Geologia, Metalogenia e mapa Previsional para ouro em SIG; CPRM: Belém, Brazil, 2008; pp. 95–134. [Google Scholar]
- Santos, J.O.S. Geotectônica Dos Escudos Da Guiana e Brasil Central. In Geologia, Tectônica e Recursos Minerais do Brasil. Texto, mapas e SIG; Bizzi, L.A., Schobbenhaus, C., Vidotti, R.M., Gonçalves, J.H., Eds.; Serviço Geológico do Brasil-CPRM: Brasília, Brazil, 2003; pp. 169–226. [Google Scholar]
- Vasquez, M.L.; Souza Gaia, S.M.d.; Chaves, C.L.; Silva, C.M.G.d. Áreas de Relevante Interesse Mineral—Evolução Crustal e Metalogenia Da Província Mineral Do Tapajós—ARIM Tapajós; SGB/CPRM: Belém, Brazil, 2023. [Google Scholar]
- Cordani, U.G.; Ramos, V.A.; Fraga, L.M.; Cegarra, M.; Delgado, I.d.M.; Souza, K.G.; Gomes, F.E.M.; Schobbenhaus, C. Tectonic Map of South America, Scale 1:5.000.000; CGMW-CPRM-SEGEMAR: Brasília, Brazil, 2016; ISBN 978-2-917310-26-7. [Google Scholar]
- Santos, J.O.S.; Van Breemen, O.B.; Groves, D.I.; Hartmann, L.A.; Almeida, M.E.; McNaughton, N.J.; Fletcher, I.R. Timing and Evolution of Multiple Paleoproterozoic Magmatic Arcs in the Tapajós Domain, Amazon Craton: Constraints from SHRIMP and TIMS Zircon, Baddeleyite and Titanite U-Pb Geochronology. Precambrian Res. 2004, 131, 73–109. [Google Scholar] [CrossRef]
- Vasquez, M.L.; Rosa-Costa, L.T.d. Unidades Litoestratigráficas. In Geologia e Recursos Minerais do Estado do Pará: Sistema de Informações Geográficas—SIG: Texto Explicativo dos Mapas Geológico e Tectônico e de Recursos Minerais do Estado do Pará; Vasquez, M.L., Rosa-Costa, L.T.d., Eds.; CPRM: Belém, Brazil, 2008; pp. 113–215. [Google Scholar]
- Almeida, M.E.; Brito, M.d.F.L.d.; Ferreira, A.L.; Monteiro, M.A.S. Geologia e Recursos Minerais Da Folha Vila Mamãe Anã (SB.21-V-D), Estados Do Amazonas e Pará. Escala 1:250.000; CPRM: Belém, Brazil, 2000. [Google Scholar]
- Vasquez, M.L.; Ricci, P.S.F.; Klein, E.L.; Santos, A.; Martins, R.C. Descrição Das Unidades Litoestratigráficas e Litodêmicas. In Geologia e Recursos Minerais da Folha Vila Riozinho–SB; CPRM: Belém, Brazil, 2000. [Google Scholar]
- Ferreira, A.L.; Almeida, M.E.; Brito, M.d.F.L.d.; Monteiro, M.A.S. Geologia e Recursos Minerais Da Folha Jacareacanga: Folha SB.21-Y-B; CPRM: Belém, Brazil, 2000. [Google Scholar]
- Vasquez, M.L.; Ricci, P.d.S.F.; Klein, E.L. Granitóides Pós-Colisionais Da Porção Leste Da Província Tapajós. Contrib. à Geol. Amaz. 2002, 3, 67–84. [Google Scholar] [CrossRef]
- Vasquez, M.L.; Chaves, C.L.; Moura, E.M.; Oliveira, J.M.d.; Lafon, J.-M. Eventos Magmáticos de 2020-1980 Ma Nas Folhas São Domingos e Jardim Do Ouro, Porção Leste Do Domínio Tapajós. In Proceedings of the Anais do 13o Simpósio de Geologia da Amazônia, Belém, Brazil, 22–26 September 2013; pp. 209–212. [Google Scholar]
- Vasquez, M.L.; Chaves, C.L.; Moura, E.M.; de Oliveira, J.K.M. Geologia e Recursos Minerais Das Folhas São Domingos, SB. 21-ZA-II e Jardim Do Ouro, SB. 21-ZA-III: Estado Do Pará; CPRM: Belém, Brazil, 2017; ISBN 8574993255. [Google Scholar]
- Queiroz, J.D.D.S.; Klein, E.L.; Rodrigues, J.B. Rochas Intrusivas Na Formação Castelo Dos Sonhos, Cráton Amazônico: Petrografia, Geocronologia, Geoquímica e Implicações Para as Idades de Sedimentação e Da Mineralização No Depósito Aurífero Castelo de Sonhos. Bol. Mus. Para. Emílio Goeldi-Ciências Nat. 2015, 10, 341–380. [Google Scholar] [CrossRef]
- Klein, E.L.; Rodrigues, J.B.; Queiroz, J.D.d.S.; Oliveira, R.G.; Guimarães, S.B.; Chaves, C.L. Deposition and Tectonic Setting of the Palaeoproterozoic Castelo Dos Sonhos Metasedimentary Formation, Tapajós Gold Province, Amazonian Craton, Brazil: Age and Isotopic Constraints. Int. Geol. Rev. 2017, 59, 864–883. [Google Scholar] [CrossRef]
- Lamarão, C.N.; Dall’Agnol, R.; Lafon, J.-M.; Lima, E.F. Geology, Geochemistry, and Pb/Pb Zircon Geochronology of the Paleoproterozoic Magmatism of Vila Riozinho, Tapajós Gold Province, Amazonian Craton, Brazil. Precambrian Res. 2002, 119, 189–223. [Google Scholar] [CrossRef]
- Vasquez, M.L.; Klein, E.L.; Macambira, M.J.B.; Santos, A.; Bahia, R.B.C.; Ricci, P.d.S.F.; Quadros, M.L.d.E.S. Geochronology of Granitoids, Mafic Intrusions and Mineralizations of the Tapajós Gold Province, Amazonian Craton, Brazil. In Proceedings of the 31 International Geological Congress, Rio de Janeiro, Brazil, 6–17 August 2000. [Google Scholar]
- Vasquez, M.L.; Chaves, C.L.; Pinheiro, F.G.R.; Castro, J.M.R.; Costa Neto, M.C.; Cruz, V.L.; Chiba, B.F.F.; Amaral, J.A.F. Projeto Evolução Crustal e Metalogenia Da Província Mineral Do Tapajós—ARIM Tapajós: Ação Avaliação Dos Recursos Minerais Do Brasil; Relatório Técnico Anual; CPRM: Belém, Brazil, 2016. [Google Scholar]
- Lamarão, C.N. Geologia, Geoquímica e Geocronologia Do Magmatismo Paleoproterozoico Da Região de Vila Riozinho, Província Aurífera Do Tapajós, Cráton Amazônico. Ph.D. Thesis, Universidade Federal do Pará, Belém, Brazil, 2001. [Google Scholar]
- Klein, E.L.; Almeida, M.E.; Rosa-Costa, L.T.d. The 1.89-1.87 Ga Uatumã Silicic Large Igneous Province, Northern South America. Available online: http://www.largeigneousprovinces.org/12nov (accessed on 25 June 2019).
- Quadros, M.L.d.E.S.; Bahia, R.B.C.; Almeida, M.E. Geologia, Petrografia e Geoquímica Preliminar Da Suíte Intrusiva Cachoeira Seca, Província Mineral Do Tapajós, Sudoeste Do Pará. In Proceedings of the Congresso Brasileiro de Geologia, Anais, Belo Horizonte, Brazil, 11–16 November 1998; SGB: Belo Horizonte, Brazil, 1998; p. 468. [Google Scholar]
- Bahia, R.B.C.; Quadros, M.L.d.E.S. Geologia e Recursos Minerais Da Folha Caracol (SB-21-X-C), Estado Do Pará, Escala 1:250.000. Projeto Especial Província Mineral Do Tapajós (PROMIN Tapajós); CPRM: Brasília, Brazil, 2000. [Google Scholar]
- Klein, E.L.; Vasquez, M.L.; Rosa-Costa, L.T.d.; Carvalho, J.M.d.A. Geology of Paleoproterozoic Gneiss-and Granitoid-Hosted Gold Mineralization in Southern Tapajós Gold Province, Amazonian Craton, Brazil. Int. Geol. Rev. 2002, 44, 544–558. [Google Scholar] [CrossRef]
- Santos, R.A.d. Controle Estrutural Das Mineralizações de Ouro Da Província Mineral Do Tapajós—Síntese de Análise Estrutural Dos Prospectos; CPRM: Salvador, Brazil, 1999. [Google Scholar]
- Knox-Robinson, C.M.; Wyborn, L.A.I. Towards a Holistic Exploration Strategy: Using Geographic Information Systems as a Tool to Enhance Exploration. Aust. J. Earth Sci. 1997, 44, 453–463. [Google Scholar] [CrossRef]
- Hronsky, J.M.A.; Groves, D.I. Science of Targeting: Definition, Strategies, Targeting and Performance Measurement. Aust. J. Earth Sci. 2008, 55, 3–12. [Google Scholar] [CrossRef]
- Czarnota, K.; Blewett, R.S.; Goscombe, B. Predictive Mineral Discovery in the Eastern Yilgarn Craton, Western Australia: An Example of District Scale Targeting of an Orogenic Gold Mineral System. Precambrian Res. 2010, 183, 356–377. [Google Scholar] [CrossRef]
- Mccuaig, T.C.; Hronsky, J.M.A. The Mineral System Concept: The Key to Exploration Targeting. Spec. Publ. 2014, 18, 153–175. [Google Scholar] [CrossRef]
- Carranza, E.J.M.; Laborte, A.G. Random Forest Predictive Modeling of Mineral Prospectivity with Small Number of Prospects and Data with Missing Values in Abra (Philippines). Comput. Geosci. 2015, 74, 60–70. [Google Scholar] [CrossRef]
- Agterberg, F.P.; Cheng, Q. Conditional Independence Test for Weights-of-Evidence Modeling. Nat. Resour. Res. 2002, 11, 249–255. [Google Scholar] [CrossRef]
- Leite, E.P.; de Souza Filho, C.R. Artificial Neural Networks Applied to Mineral Potential Mapping for Copper-Gold Mineralizations in the Carajás Mineral Province, Brazil. Geophys. Prospect. 2009, 57, 1049–1065. [Google Scholar] [CrossRef]
- Leite, E.P.; Souza Filho, C.R.d. Probabilistic Neural Networks Applied to Mineral Potential Mapping for Platinum Group Elements in the Serra Leste Region, Carajás Mineral Province, Brazil. Comput. Geosci. 2009, 35, 675–687. [Google Scholar] [CrossRef]
- Carranza, E.J.M. Data-Driven Evidential Belief Modeling of Mineral Potential Using Few Prospects and Evidence with Missing Values. Nat. Resour. Res. 2015, 24, 291–304. [Google Scholar] [CrossRef]
- Klein, E.L.; Vasquez, M.L. Geologia e Recursos Minerais Da Folha Vila Riozinho SB.21-Z-A, Estado Do Pará. Escala 1:250.000; CPRM: Brasília, Brazil, 2000. [Google Scholar]
- Souza, S.R.C.d. Petrografia, Litogeoquímica, Geocronologia e Geoquímica Isotópica Da Mineralização Aurífera e Rochas Hospedeiras Do Prospecto Água Branca, Província Tapajós. Master’s Thesis, Universidade de Brasília, Brasília, Brazil, 2009. [Google Scholar]
- Corrêa-Silva, R.H.; Juliani, C.; Nunes, C.M.D.; Bettencourt, J.S. Petrographic Characterization of the Hydrothermal Alteration Zones Associated with Gold Mineralization in Granitic Rocks of the Batalha Gold Field, Tapajós (Pará)—Brazil. Rev. Bras. Geociências 2000, 30, 242–245. [Google Scholar] [CrossRef]
- Juliani, C.; Corrêa-Silva, R.H.; Monteiro, L.V.S.; Bettencourt, J.S.; Nunes, C.M.D. The Batalha Au-Granite System—Tapajós Gold Province, Amazonian Craton, Brazil: Hydrothermal Alteration and Regional Implications. Precambrian Res. 2002, 119, 225–256. [Google Scholar] [CrossRef]
- Santos, R.A.d. Contribuição à Análise Estrutural de Jazimentos Auríferos Do Rio Tapajós, SW Do Pará e SE Do Amazonas. In Garimpos Abacaxis, Espírito Santo, Bom Jesus, Goiano, Fazenda Pison, Ouro Mil, Santa Isabel, Majestade e Carneirinho; CPRM: Brasília, Brazil, 1997. [Google Scholar]
- Araújo, A.C.S. Estudos Isotópicos e de Inclusões Fluidas No Depósito Central Do Campo Mineralizado Do Cuiú-Cuiú, Província Aurífera Do Tapajós, Estado Do Pará. Master’s Thesis, Universidade Federal do Pará, Belém, Brazil, 2014. [Google Scholar]
- McMahon, A.M. Resource Estimate and Technical Report for the Cuiú-Cuiú Project Tapajós Region, North-Central Brazil; Micon International Limited: Belo Horizonte, Brazil, 2011. [Google Scholar]
- Assunção, R.F.S.; Klein, E.L. The Moreira Gomes Deposit of the Cuiú-Cuiú Goldfield: Fluid Inclusions and Stable Isotope Constraints and Implications for the Genesis of Granite-Hosted Gold Mineralization in the Tapajós Gold Province, Brazil. J. S. Am. Earth Sci. 2014, 49, 85–105. [Google Scholar] [CrossRef]
- Veloso, Â.S.R.; Santos, M.D. Geologia, Petrografia e Geocronologia Das Rochas Do Depósito Aurífero Ouro Roxo, Província Tapajós, Jacareacanga (PA), Brasil. Braz. J. Geol. 2013, 43, 22–36. [Google Scholar] [CrossRef]
- Montgomery, M.; Harvey, L. Fofoca Prospect São Domingos Project, Para, Brazili; Resource Report; Aurora Gold: Zug, Switzerland, 2010. [Google Scholar]
- Aurora Gold. São Domingo Project Summary; Aurora Gold Corporation: Zug, Switzerland, 2012. [Google Scholar]
- Borges, A.W.G. Geologia e Metalogênese Do Depósito Aurífero São Jorge, Província Aurífera Do Tapajós, Novo Progresso—PA. Master’s Thesis, Universidade Federal do Pará, Belém, Brazil, 2010. [Google Scholar]
- Villas, R.N.N.; Santiago, É.S.B.; Castilho, M.P. Contexto Geológico, Estudos Isotópicos (C, O e Pb) e Associação Metálica Do Depósito Aurífero Tocantinzinho, Domínio Tapajós, Província Tapajós-Parima. Geol. USP. Série Científica 2013, 13, 119–138. [Google Scholar] [CrossRef]
- Briggs, I.C. Machine Contouring Using Minimum Curvature. Geophysics 1974, 39, 39–48. [Google Scholar] [CrossRef]
- Gnojek, I.; Přichystal, A. A New Zinc Mineralization Detected by Airborne Gamma-Ray Spectrometry in Northern Moraiva (Czechoslovakia). Geoexploration 1985, 23, 491–502. [Google Scholar] [CrossRef]
- Pascholati, E.M. Caracterização Geofísica Da Suíte Intrusiva de Itu. Master’s Thesis, Universidade de São Paulo, São Paulo, Brazil, 1990. [Google Scholar]
- Ferreira, F.J.F. Aerogamaespectrometria e Aeromagnetometria de Um Trato Ocidental Do Pré-Cambriano Paulista. Ph.D. Thesis, Universidade de São Paulo, São Paulo, Brazil, 1991. [Google Scholar]
- Abd El Nabi, S.H. Role of γ-Ray Spectrometry in Detecting Potassic Alteration Associated with Um Ba’anib Granitic Gneiss and Metasediments, G. Meatiq Area, Central Eastern Desert, Egypt. Arab. J. Geosci. 2013, 6, 1249–1261. [Google Scholar] [CrossRef]
- Akingboye, A.S.; Ogunyele, A.C.; Jimoh, A.T.; Adaramoye, O.B.; Adeola, A.O.; Ajayi, T. Radioactivity, Radiogenic Heat Production and Environmental Radiation Risk of the Basement Complex Rocks of Akungba-Akoko, Southwestern Nigeria: Insights from in Situ Gamma-Ray Spectrometry. Environ. Earth Sci. 2021, 80, 228. [Google Scholar] [CrossRef]
- Saunders, D.F.; Terry, S.A.; Thompson, C.K. Test of National Uranium Resource Evaluation Gamma-ray Spectral Data in Petroleum Reconnaissance. Geophysics 1987, 52, 1547–1556. [Google Scholar] [CrossRef]
- Pires, A.C.B. Identificação Geofísica de Áreas de Alteração Hidrotermal, Crixás-Guarinos, Goiás. Rev. Bras. Geociências 1995, 25, 61–68. [Google Scholar] [CrossRef]
- Barbuena, D.; de Souza Filho, C.R.; Leite, E.P.; Miguel Junior, E.; de Assis, R.R.; Xavier, R.P.; Ferreira, F.J.F.; Paes de Barros, A.J. Airborne Geophysical Data Analysis Applied to Geological Interpretation in the Alta Floresta Gold Province, MT. Rev. Bras. Geofísica 2013, 31, 169–186. [Google Scholar] [CrossRef]
- Campos, L.D.; Souza, S.M.d.; de Sordi, D.A.; Tavares, F.M.; Klein, E.L.; Lopes, E.C.d.S. Predictive Mapping of Prospectivity in the Gurupi Orogenic Gold Belt, North–Northeast Brazil: An Example of District-Scale Mineral System Approach to Exploration Targeting. Nat. Resour. Res. 2017, 26, 509–534. [Google Scholar] [CrossRef]
- Galbraith, J.H.; Saunders, D.F. Rock Classification by Characteristics of Aerial Gamma-Ray Measurements. J. Geochem. Explor. 1983, 18, 49–73. [Google Scholar] [CrossRef]
- Dickson, B.L.; Scott, K.M. Interpretation of Aerial Gamma-Ray Surveys—Adding the Geochemical Factors. AGSO J. Aust. Geol. Geophys. 1997, 17, 187–200. [Google Scholar]
- Baranov, V. A New Method for Interpretation of Aeromagnetic Maps: Pseudo-gravimetric Anomalies. Geophysics 1957, 22, 359–382. [Google Scholar] [CrossRef]
- Li, X. Magnetic Reduction-to-the-Pole at Low Latitudes: Observations and Considerations. Lead. Edge 2008, 27, 990–1002. [Google Scholar] [CrossRef]
- Bongiolo, A.d.B.e.S. Contribuição Ao Estudo Da Bacia Do Amazonas E Seu Embasamento Através Da Magnetometria E Gravimetria. Ph.D. Thesis, Universidade Federal do Paraná, Belém, Brazil, 2011. [Google Scholar]
- Bongiolo, A.d.B.e.S.; Souza, J.d.; Ferreira, F.J.F.; Castro, L.G.d. GRAV_MAG_PRISM: A MATLAB®/Octave Program to Generate Gravity and Magnetic Anomalies Due to Rectangular Prismatic Bodies. Rev. Bras. Geofísica 2013, 31, 347–363. [Google Scholar] [CrossRef]
- Nettleton, L.L.; Cannon, J.R. Investigation of Upward Continuation System. Geophysics 1962, 27, 796–806. [Google Scholar] [CrossRef]
- Gunn, P.J. Linear Transformations of Gravity and Magnetics Fields. Geophys. Prospect. 1975, 23, 300–312. [Google Scholar] [CrossRef]
- Evjen, H.M. The Place of the Vertical Gradient in Gravitational Interpretations. Geophysics 1936, 1, 127–136. [Google Scholar] [CrossRef]
- Blakely, R.J. Potential Theory in Gravity and Magnetic Applications; Cambridge University Press: Cambridge, UK, 1995; ISBN 9780511549816. [Google Scholar]
- Nabighian, M.N. The Analytic Signal of Two-Dimensional Magnetic Bodies with Polygonal Cross-Section: Its Properties and Use for Automated Anomaly Interpretation. Geophysics 1972, 37, 507–517. [Google Scholar] [CrossRef]
- Nabighian, M.N. Additional Comments on the Analytic Signal of Two-Dimensional Magnetic Bodies with Polygonal Cross-Section. Geophysics 1974, 39, 85–92. [Google Scholar] [CrossRef]
- Roest, W.R.; Verhoef, J.; Pilkington, M. Magnetic Interpretation Using the 3-D Analytic Signal. Geophysics 1992, 57, 116–125. [Google Scholar] [CrossRef]
- Debeglia, N.; Corpel, J. Automatic 3-D Interpretation of Potential Field Data Using Analytic Signal Derivatives. Geophysics 1997, 62, 87–96. [Google Scholar] [CrossRef]
- Cordell, L.; Grauch, V.J.S. Mapping Basement Magnetization Zones from Aeromagnetic Data in the San Juan Basin, New Mexico. In The Utility of Regional Gravity and Magnetic Anomaly Maps; Society of Exploration Geophysicists: Tulsa, OK, USA, 1985; pp. 181–197. [Google Scholar]
- Milligan, P.R.; Gunn, P.J. Enhancement and Presentation of Airborne Geophysical Data. AGSO J. Aust. Geol. Geophys. 1997, 17, 63–75. [Google Scholar]
- Miller, H.G.; Singh, V. Potential Field Tilt a New Concept for Location of Potential Field Sources. J. Appl. Geophys. 1994, 32, 213–217. [Google Scholar] [CrossRef]
- Ferreira, F.J.F.; Souza, J.d.; Bongiolo, A.d.B.e.S.; Castro, L.G.d. Enhancement of the Total Horizontal Gradient of Magnetic Anomalies Using the Tilt Angle. Geophysics 2013, 78, J33–J41. [Google Scholar] [CrossRef]
- Archibald, N.; Gow, P.; Boschetti, F. Multiscale Edge Analysis of Potential Field Data. Explor. Geophys. 1999, 30, 38–44. [Google Scholar] [CrossRef]
- Salui, C.L. Methodological Validation for Automated Lineament Extraction by LINE Method in PCI Geomatica and MATLAB Based Hough Transformation. J. Geol. Soc. India 2018, 92, 321–328. [Google Scholar] [CrossRef]
- Souza Filho, C.R.d.; Nunes, A.R.; Leite, E.P.; Monteiro, L.V.S.; Xavier, R.P. Spatial Analysis of Airborne Geophysical Data Applied to Geological Mapping and Mineral Prospecting in the Serra Leste Region, Carajás Mineral Province, Brazil. Surv. Geophys. 2007, 28, 377–405. [Google Scholar] [CrossRef]
- Zadeh, L.A. Fuzzy Sets. Inf. Control 1965, 8, 338–353. [Google Scholar] [CrossRef]
- An, P.; Moon, W.M.; Rencz, A. Application of Fuzzy Set Theory to Integrated Mineral Exploration. Can. J. Explor. 1991, 27, 1–11. [Google Scholar]
- Brown, W.M.; Groves, D.I.; Gedeon, T.D. Use of Fuzzy Membership Input Layers to Combine Subjective Geological Knowledge and Empirical Data in a Neural Network Method for Mineral-Potential Mapping. Nat. Resour. Res. 2003, 12, 183–200. [Google Scholar] [CrossRef]
- Tsoukalas, L.H.; Uhrig, R.E. Fuzzy and Neural Approaches in Engineering; John Wiley and Sons, Inc.: New York, NY, USA, 1997. [Google Scholar]
- Raines, G.L.; Sawatzky, D.L.; Bonham-Carter, G.F. Incorporating Expert Knowledge: New Fuzzy Logic Tools in ArcGIS 10. ArcUser 2010, 49, 8–13. [Google Scholar]
- Zuo, R.; Carranza, E.J.M. Support Vector Machine: A Tool for Mapping Mineral Prospectivity. Comput. Geosci. 2011, 37, 1967–1975. [Google Scholar] [CrossRef]
- Vapnik, V.N. The Nature of Statistical Learning Theory; Springer New York: New York, NY, USA, 2000; ISBN 978-1-4419-3160-3. [Google Scholar]
- Burges, C.J.C. A Tutorial on Support Vector Machines for Pattern Recognition. Data Min. Knowl. Discov. 1998, 2, 121–167. [Google Scholar] [CrossRef]
- Ben-Hur, A.; Weston, J. A User’s Guide to Support Vector Machines. In Data Mining Techniques for the Life Sciences; Carugo, O., Eisenhaber, F., Eds.; Humana Press: Totowa, NJ, USA, 2010; pp. 223–239. [Google Scholar]
- Huang, C.; Davis, L.S.; Townshend, J.R.G. An Assessment of Support Vector Machines for Land Cover Classification. Int. J. Remote Sens. 2002, 23, 725–749. [Google Scholar] [CrossRef]
- Kavzoglu, T.; Colkesen, I. A Kernel Functions Analysis for Support Vector Machines for Land Cover Classification. Int. J. Appl. Earth Obs. Geoinf. 2009, 11, 352–359. [Google Scholar] [CrossRef]
- Van Rijsbergen, C.J. Information Retrieval, 2nd ed.; Butterworth-Heinemann: Woburn, MA, USA, 1979; ISBN 978-0-408-70929-3. [Google Scholar]
- Fawcett, T. An Introduction to ROC Analysis. Pattern Recognit. Lett. 2006, 27, 861–874. [Google Scholar] [CrossRef]
- Chen, Y.; Wu, W. A Prospecting Cost-Benefit Strategy for Mineral Potential Mapping Based on ROC Curve Analysis. Ore Geol. Rev. 2016, 74, 26–38. [Google Scholar] [CrossRef]
- Johnson, A.; Cheeseman, S.; Ferris, J. Improved Compilation of Antarctic Peninsula Magnetic Data by New Interactive Grid Suturing and Blending Methods. Ann. Geofis. 1999, 42, 249–259. [Google Scholar] [CrossRef]
- Lafon, J.-M.; Coutinho, M.G.d.N. Isótopos Radiogênicos de Chumbo. In Província Mineral do Tapajós: Geologia, Metalogenia e Mapa Provisional Para Ouro em SIG; Coutinho, M.G.d.N., Ed.; CPRM: Belém, Brazil, 2008; pp. 251–262. [Google Scholar]
- Franca-Rocha, W.; Bonham-Carter, G.F.; Misi, A. GIS Modeling for Mineral Potential Mapping of Carbonate-Hosted Pb-Zn Deposits. Rev. Bras. Geociências 2003, 33, 191–196. [Google Scholar] [CrossRef]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-Learn: Machine Learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar] [CrossRef]
- Plutowski, M.; Sakata, S.; White, H. Cross-Validation Estimates IMSE. Adv. Neural Inf. Process. Syst. 1993, 6, 391–398. [Google Scholar]
- Agterberg, F.P.; Bonham-Carter, G.F. Measuring the Performance of Mineral-Potential Maps. Nat. Resour. Res. 2005, 14, 1–17. [Google Scholar] [CrossRef]
- Ostrovskiy, E.Y. Antagonism of Radioactive Elements in Wallrock Alterations Fields and Its Use in Aerogamma Spectrometric Prospecting. Int. Geol. Rev. 1975, 17, 461–468. [Google Scholar] [CrossRef]
- Oshiro, T.M.; Perez, P.S.; Baranauskas, J.A. How Many Trees in a Random Forest? In Machine Learning and Data Mining in Pattern Recognition, Proceedings of the 8th International Conference, MLDM 2012, Berlin, Germany, 13–20 July 2012; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2012; Volume 7376, pp. 154–168. [Google Scholar]






| Occurrence | Mineralization Style | Alteration | Structural Control | References |
|---|---|---|---|---|
| Abacate | qz veins | sil, tur | N80E/70SE | [32] |
| Água Branca | qz veins | sil, carb, sulf, ser, cl | 88/125, 35/290, 65/315 | [58,59] |
| Asa Branca | qz veins | sulf, epid | 88/175, 88/125 | [14,58] |
| Batalha | stockwork, qz veins | ser, potas, alb, epid, sil, cl | 70/315, 90/300 | [32,60,61] |
| Boa Esperança | qz veins | arg, ser, cl, sulf | 220/75SW, 80/80SE | [14] |
| Cantagalo | qz veins, stockwork, disseminations | sulf, lim, sil, kaol, arg, ser | 85/060, 90/055, 80/350 | [32,34,62] |
| Cuiú–Cuiú/Central | qz veins, hydrothermal breccia | ser, cl, carb | 75/075 | [58,63] |
| Cuiú–Cuiú/Moreira Gomes | stockwork, veins | ser, sulf, carb, cl, sil, epid | 31/305, 10/341 | [64,65] |
| Carneirinho | stockwork | sulf, sil, ser, epid, potas | N80W/85NE, N15/85SE | [14,62] |
| Davi | qz veins | ser, carb, sulf, epid, cl, potas | 90/135, 90/305 | [32,62] |
| Mamoal | mafic dykes disseminations | sulf, potas | 88/020 | [58,62] |
| Ouro Roxo | disseminations, py and qz-py veins | ser, cl, carb | 65/090, 35/095 | [32,34,66] |
| Palito | veins | ser, sulf, epid, cl, carb, potas | 88/045 | [58] |
| Pimenteiras | veins | sulf | 90/095 | [34] |
| São Chico | veins | ser, cl, sulf, epid, musc, kaol, sil | 50/170, 88/170 | [58] |
| São Domingos/Fofoca | qz-sulphide veins, stockwork | ser, sil, sulf, epid | 88/165, 72/320 | [58,67] |
| São Domingos/Tucano | stockwork, qz-sulphide veins | ser, sil, sulf, epid | 60/75NW | [58,68] |
| São João | qz veins | epid, arg, sulf | N45–65E, N30E/75SE | [37] |
| São Jorge | qz veins, stockwork disseminations | sulf, musc, cl, carb | 80/160 | [58,69] |
| Sucuba | qz veins | sil, cl | EW | [37] |
| Tocantinzinho | qz veins, stockwork | mic, cl, ser, sil, carb | 80/125, 80/345 | [58,70] |
| Parameters | K (%) | eTh (ppm) | eU (ppm) | |
|---|---|---|---|---|
| Mean (M) | 0.324491 | 19.620647 | 2.358534 | |
| Standard Deviation (σ) | 0.166002 | 10.636025 | 0.932671 | |
| Class | Interval | |||
| Low | <M − ½σ | <0.24 | <14.30 | <1.89 |
| Intermediate | >M − ½σ and <M + ½σ | 0.24–0.41 | 14.30–24.94 | 1.89–2.83 |
| High | >M + ½σ | >0.41 | >24.94 | >2.83 |
| Data Source | Evidence Map | Classifying Process | Prospective Thresholds | Fuzzy Operators | Integrative Operator |
|---|---|---|---|---|---|
| Geologic map, scale 1:100,000 | Favorable host rocks | Data classified according to the frequency of occurrences and geochemical signature. | - | - | GAMMA, index 0.75 |
| Geologic map, scale 1:100,000 | Intrusive contacts | Proximity analysis of deposits with the contacts of intrusive bodies. | 5000 m | - | |
| Airborne magnetometry | Magnetic lineaments | Proximity to lineaments interpreted from magnetometry, which represent the magnetic signature of mineralized shear zones, secondary deposit controls, and mineralized late veins. Euclidean distance. | 2000 m (NW) 1000 m (NE and EW) 2500 m (NS) | OR | |
| Radar image | Density of surface traces | Density of lineaments extracted from DEM. | Densities > 1 | ||
| Airborne radiometry | F parameter | Statistical classification of the values of parameters F, Kd, and Ud and the eTh/K ratio, which represent the signature of The hydrothermal alteration with positive a correlation with mineralization. | Values > M + 1σ | GAMMA, index 0.75 | |
| Kd parameter | Values > M + 1σ | ||||
| Ud parameter | Values < M − ½σ | ||||
| eTh/K ratio | Values < 0.7 |
| PC1 | PC2 | PC3 | PC4 | |
|---|---|---|---|---|
| F | 0.34639 | −0.89043 | 0.29401 | 0.02670 |
| Kd | 0.20787 | −0.17201 | −0.70639 | −0.65438 |
| Ud | 0.17715 | −0.11325 | −0.62031 | 0.75565 |
| eTh/K | 0.89745 | 0.40587 | 0.17258 | −0.00790 |
| Fuzzy | WofE | SVM | |
|---|---|---|---|
| Advantages | (1) Easy implementation and operator knowledge-based control. | (1) Allows analysis of the weight of each evidence map and selection of the best ones for integration. | (1) Greater robustness, and handles both linear and non-linear data; (2) generalization ability, even with few training and testing points; (3) effective separation of data with a maximum margin; (4) increases decision-making resolution. |
| Disadvantages | (1) Less precise propositions and data inputs being more susceptible to bias; (2) Many steps and parameters to define (e.g., membership functions, data classification rules, integration operators). | (1) Need to reduce the number of classes (reclassification of evidential maps); (2) the assumption of conditional independence burdened and invalidated the modeling numerous times, a problem which can be minimized with the use of PCA. | (1) Requires extensive knowledge of ML architectures and programming languages. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Souza Gaia, S.M.d.; Souza Filho, C.R.d. Predictive Mapping of Prospectivity for Gold in the Central Portion of the Tapajós Mineral Province, Brazil. Minerals 2023, 13, 1432. https://doi.org/10.3390/min13111432
Souza Gaia SMd, Souza Filho CRd. Predictive Mapping of Prospectivity for Gold in the Central Portion of the Tapajós Mineral Province, Brazil. Minerals. 2023; 13(11):1432. https://doi.org/10.3390/min13111432
Chicago/Turabian StyleSouza Gaia, Sulsiene Machado de, and Carlos Roberto de Souza Filho. 2023. "Predictive Mapping of Prospectivity for Gold in the Central Portion of the Tapajós Mineral Province, Brazil" Minerals 13, no. 11: 1432. https://doi.org/10.3390/min13111432
APA StyleSouza Gaia, S. M. d., & Souza Filho, C. R. d. (2023). Predictive Mapping of Prospectivity for Gold in the Central Portion of the Tapajós Mineral Province, Brazil. Minerals, 13(11), 1432. https://doi.org/10.3390/min13111432






