Abstract
The goal of this paper is to compare and analyze the forecasting performance of two artificial neural network models (i.e., MLP (multi-layer perceptron) and DNN (deep neural network)), and to conduct an experimental investigation by data flow, not economic flow. In this paper, we investigate beyond the scope of simple predictions, and conduct research based on the merits and data of each model, so that we can predict and forecast the most efficient outcomes based on analytical methodology with fewer errors. In particular, we focus on identifying two models of neural networks (NN), a multi-layer perceptron (i.e., MLP) model and an excellent model between the neural network (i.e., DNN) model. At this time, predictability and accuracy were found to be superior in the DNN model, and in the MLP model, it was found to be highly correlated and accessible. The major purpose of this study is to analyze the performance of MLP and DNN through a practical approach based on an artificial neural network stock forecasting method. Although we do not limit S&P (i.e., Standard&Poor’s 500 index) to escape other regional exits in order to see the proper flow of capital, we first measured S&P data for 100 months (i.e., 407 weeks) and found out the following facts: First, the traditional artificial neural network (ANN) model, according to the specificity of each model and depending on the depth of the layer, shows the model of the prediction well and is sensitive to the index data; Second, comparing the two models, the DNN model showed better accuracy in terms of data accessibility and prediction accuracy than MLP, and the error rate was also shown in the weekly and monthly data; Third, the difference in the prediction accuracy of each model is not statistically significant. However, these results are correlated with each other, and are considered robust because there are few error rates, thanks to the accessibility to various other prediction accuracy measurement methodologies.
1. Introduction
The stock market index, which is shaking many capital markets around the world, can be used as an inflection point in the economy for a measure of important changes [1,2,3,4]. There are many ways of predicting objects as data. However, as a part of traditional supervised learning, we used an artificial neural network (i.e., ANN) model that uses labels as data. There are many examples [5,6,7], based on forecasting purpose data research, which are sometimes correct. However, this approach is worth investigating even the results are not correct. Numerous model design and performance analysis studies for stock forecasting have been carried out with various economic and statistical approaches [8,9,10,11,12]. From the viewpoint of prediction and forecasting, it is most important to establish each model by identifying the neural networks (NN) model and data learning method.
Therefore, due to the uniqueness and volatility of the stock market, many researchers and scientists seek prediction using models similar to neural network (NN) models. Since neural networks models have a long history of development regarding the number of layers (in this case, x), that is, deep-learning can occur, we aim to determine how accurately predictions and forecasting can be made possible through simple model comparisons [13,14,15].
Although the neural network-based method for stock forecasting has already been studied [13,16,17], it is necessary to conduct a scientific analysis of the stock forecasting method by comparing neural network models of single-layer and multi-layer networks. A comparison of the two above models, multi-layer perceptron (MLP) and deep neural network (DNN), reveals that it is meaningful to compare the data at the stage of establishing the two models. In addition, the stock market of a country can be seen as a flow of data rather than as a relation of capital flow. The greatest difference between MLP and DNN is to avoid overfitting, which includes random error or noise. For example, when MLP is applied, overfitting occurs and it is difficult to compare performance with DNN. In order to avoid this statistical error phenomenon, [18,19,20] studies use dropout, early stopping, and weights regulation for MLP. In this study, one statistical solution, dropout, is applied as a method to avoid overfitting. In addition, the MLP assumes that there is one hidden layer (i.e., 1-HL), and that the DNN has two or more hidden layers (i.e., 3-HL).
To compare the two artificial neural network models for stock forecasting, S&P 500 (i.e., Standard&Poor’s 500 index) was selected because it could see data flow for the week, month, and year according to accessibility and change. We also want to analyze in more detail the success of forecasting and forecasting in the areas of statistics and econometrics to create basic data for actual data usage analysis.
2. Data Acquisition
It is difficult to prove the excellence of objective data in the absence of local specificity. However, in order to collect the most efficient and objective data, S&P 500 data are accessed in this text. However, these statistical results are based on real measurements and show in the public domain a good prediction for an individual as well as for a large economic impact on society. In fact, the dataset spans from 31 May 2009 to 12 March 2017, totaling 100 months (i.e., 407 weeks) of observations. Statistical analysis for these eight years is a condition that should not be excluded or influenced by other data.
Actual data can be subdivided for viewing and forecasting, and thus divided into several ranges. As a result of efforts to determine the potential impact and efficiency of a given index data for the ultimate goal of prediction accuracy, the following results were obtained: 20% of the total number of observations were in the long-term range, 13–8% were in the intermediate range, and 6% were in the short-term range. The actual data tends to be grouped by scope, and if they are outside of this range, they cannot prove to be effective. Of the first long-range predictions, 330 weeks of data were used for model identification and estimation, and the remaining 77 weeks of data (about 20% of 407 weeks) were used to evaluate the performance of the MLP and DNN models. The intermediate range and short range were also defined in a similar way. After obtaining the middle range (31–50 weeks ahead) and the short range (23 weeks ahead) forecast horizon, it becomes necessary to check once again the soundness and efficiency of the data.
Once again, we present three predicted horizons (20%: long-term range, 13%: intermediate range, 8%: short-term range) and acknowledge that all the data used are obtained for the purpose of prediction and forecasting. At the same time, all results can be viewed in real time in order to see the flow of data.
3. Forecasting Methodology
3.1. MLP and DNN Model Methodology
In this section, we discuss the accuracy prediction methodology along with the basics of the neural network theory that can be found by increasing the number of layers (x) by elements of the traditional NN model. We also present the prediction efficiency of each model when the NN models are developed as back-propagation neural networks. The main reason for adopting MLP is because it is a partial differential of the network error function. Thus, it is an efficient way to develop a network model that minimizes discrepancies between the actual data and the output from the network model. In this case, the number of outputs per layer is increased and the output has an important scientific meaning in terms of efficiency, and it is a factor used to measure the quality of learning. In fact, MLP and DNN can have more than two hidden layers. However, in this study, we designed a stock forecasting model based on DNN with one hidden layer, as well as a model with two or more hidden layers. In the case of MLP, a method of avoiding overfitting is applied.
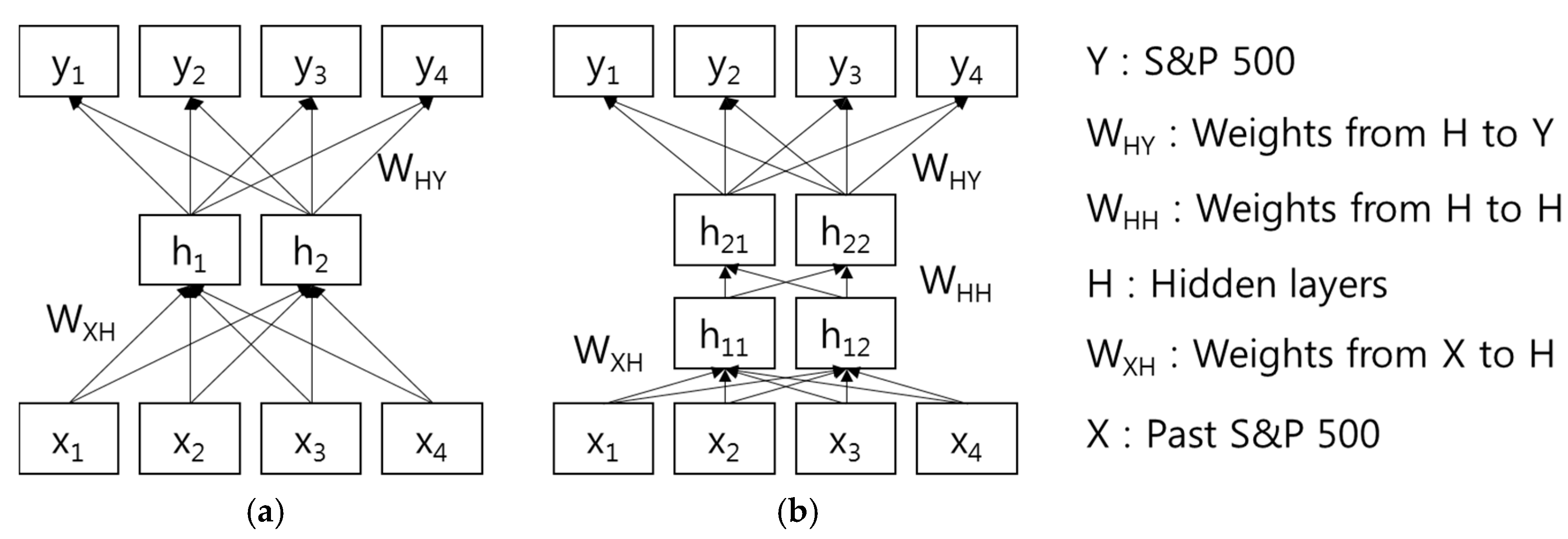
Figure 1 shows an illustration of the artificial neural network model methodology, in particular a Back-Propagation Neural Network (MLP and DNN). We designed an artificial neural network based on MLP and DNN models that predicts the future by using past S&P 500 data as input data. In addition, input and output data are normalized based on the highest index of S&P 500.
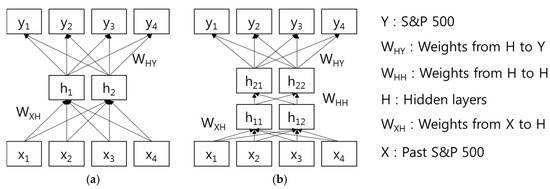
Figure 1.
Illustration of the MLP and DNN model methodology. (a) MLP with 1-HL; (b) DNN with 2-HL.
In particular, MLP and DNN can be trained using the historical data of a time series in order to capture the non-linear characteristics of the specific time series. Each model parameter will be adjusted iteratively by a process of minimizing the forecasting errors. For time series forecasting, the relationship between the output (Y) and the inputs (X) can be described by the following mathematical formula:
where aj (j = 0, 1, 2, …, n) is a bias on the jth unit; wij (i = 0, 1, 2, …, m; j = 0, 1, 2, …, n) is the connection weights between layers of the model; h(·) is the transfer function of the hidden layer; m is the number of input nodes; and n is the number of hidden nodes. The MLP model performs a nonlinear functional mapping from past observations (yk−1, yk−2, …, yk−p), to future values (yk), i.e.,
where w is a vector of all parameters and is a function determined by the network structure and connection weights.
In addition, it is necessary to explain the expanded method of neural network theory in order to increase the number of layers (x) of existing ANN models, and increase the forecast and prediction by the time series methodology. Therefore, we investigated the DNN model in the same context but with a different approach. In order to obtain the corresponding estimates of S&P 500, we used the multi-layer neural network [20] model to find the best fit of a time series model by using past values, and this method generated the optimal weights in hidden layers.
As these forecasting methodologies are important, there is a need to check for inadequate outlooks and susceptibility to errors. Therefore, the forecast error (er (k)) of each model is another important factor. It is mainly expressed as the method of subtracting the forecasted value from the actual value (price or profit) of our S&P 500 data and subtracting the difference from the absolute value of the actual data as follows:
where ABS(k) = actual value of S&P 500 in period (k) function, and FORECASTING (k) = forecasted value of S&P 500 in period (k) function.
3.2. Implementation and Avioding the Overfitting Problem
In this paper, DNN is implemented as shown in Algorithm 1 using Python. Algorithm 1 shows the implementation method when there are three hidden layers. In Step 1, the values of the input node and output node are stored in x, y. In addition, layer-1 to layer-n are initialized for n hidden layers. To calculate the hidden layer, we define two variables: layer and synapse. The layer stores the objective value of the hidden layer, and the synapse stores the value of the weights. Note that, since layer-0 is defined as the input layer, the value of x is substituted. It also generates and initializes variables from synapse_0 to synapse_n. In Step 2, the non-linear sigmoid is used to update the result between layers. In Step 3, we apply the dropout operation to avoid the overfitting problem. Step 4 calculates the error rate of the input and output between layers. In Step 5, we update each synapse with an error using the correction value. The same operation is repeated through 500 iterations from Step 2 to Step 5 to optimize the synapse values.
In the ANN proposed in this work, the dropout, early stopping, and weight regularization techniques are applied to avoid the overfitting phenomenon and to ensure good performance and the best generalization of the implemented model. Since it is already verified that dropout can solve the problem of overfitting that frequently occurs in the neural network model, we apply the dropout method between the hidden layer and the final classification layer of MLP and DNN models to apply the effect of regularization. Also, for every learning process, the epoch for each data is fixed as 500.
Note that we developed the MLP and DNN by using Python programming [21,22,23], which is used to train data for model developments and test data for the forecasting accuracy of the models developed. Here, the stop criteria for the supervised training of the networks are specified as follows. The maximum epochs specify how many iterations (over the training set) will be done if no other criterion kicks in. The training terminates when one of the following four conditions is met: (i) when the mean square error of the validation set begins to rise, indicating that overfitting might be happening; (ii) when the threshold is less than 0.01, i.e., we are on effectively flat ground; (iii) when the training time has reached 500 epochs; or (iv) when the goal (the difference between output and target is less than 0.01) has been met. After the training was completed, its epochs and the simulation procedure were completed successfully, which indicates that the network was trained and was predicting the output as desired. This is similar to the predictions we are currently pursuing in the Convolution Neural Network (CNN) of Artificial Intelligence (AI).
| Algorithm 1. MLP and DNN by using Python Language | |
| Step 1: | x <- Input nodes y <- Output nodes INIT(layer1, layer2, layer3) # <- random values with normalized 0 to 1 dropout_percent, do_dropout = (0.2, True) layer_0 <- x INIT(synapse_0, synapse_1, synapse_2, synapse_3) # <- random values with normalized 0 to 1 alpha <- 0.1 |
| Step 2: | for j in range(500): for i in range (len(x)): layer_0 = x[i] layer_1 = sigmoid(np.dot(layer_0,synapse_0)) layer_2 = sigmoid(np.dot(layer_1,synapse_1)) layer_3 = sigmoid(np.dot(layer_2,synapse_2)) |
| Step 3: | if(do_dropout): layer_1*=np.random.binomial([np.ones((len(X),hidden_dim))], 1-dropout_percent)[0] * (1.0/(1-dropout_percent) layer_2*=np.random.binomial([np.ones((len(H),hidden_dim))], 1-dropout_percent)[0] * (1.0/(1-dropout_percent)) |
| Step 4: | layer_3_error = layer_3 – y[i] #layer_3_error = y [i]- layer_3 layer_3_delta = layer_3_error * sigmoid_output_to_derivative(layer_3) layer_2_error = layer_3_delta.dot(synapse_2.T) layer_2_delta = layer_2_error * sigmoid_output_to_derivative(layer_2) layer_1_error = layer_2_delta.dot(synapse_1.T) layer_1_delta = layer_1_error * sigmoid_output_to_derivative(layer_1) |
| Step 5: | #layer_3_error = layer_3 − y synapse_2 −= alpha * np.reshape(layer_2,( −1,1))*layer_3_delta synapse_1 −= alpha * np.reshape(layer_1,( −1,1))*layer_2_delta synapse_0 −= alpha * np.reshape(layer_0,( −1,1))*layer_1_delta #layer_3_error = y - layer_3 synapse_2 += alpha * np.reshape(layer_2,(−1,1))*layer_3_delta synapse_1 += alpha * np.reshape(layer_1,( −1,1))*layer_2_delta synapse_0 += alpha * np.reshape(layer_0,( −1,1))*layer_1_delta |
In particular, it is necessary to apply the principle of Ockham’s razor [24], which is one of the many tools used in the development of philosophical and theoretical models of scientists. It is very important to identify the fundamental principles at this time. Aristotle's scientific curiosity was conveyed by Stephen Hawking [25] in a modernized sense as a measure of the path and process theories determined by the amount of neural weight delivered, which states that neural network theory is intelligent. The simplest network topology is used to produce the correct result of the prediction. As you increase the number of layers, it should be noted that you have to create the layers of the network in the order of input 2, layer 1, and output 1. In other words, this means that two input layers, one hidden layer, and one output layer are related to the accuracy of the prediction regardless of the order of propagation. At the same time, the hidden layer value in the middle, x, can be changed and can be set to various variables such as 2, 3, 4, and 5. Of course, 1 means simply that the value of the hidden layer is 1, but sometimes there is a best result when there is a hidden layer. The topology of the propagated network becomes an important factor.
4. Analysis and Results
4.1. Optimal Paramters
We first experimentally determined the number of hidden nodes to compare the performance of MLP and DNN by using weekly and monthly data. The number of hidden nodes in MLP is selected as 150%, 100%, 50%, and 25% of the number of input nodes. In addition, the number of hidden nodes in DNN is three times the number of hidden nodes in MLP. Finally, overfitting was avoided using dropout, and the epoch was fixed at 500.
Table 1 shows the results using MLP-based weekly and monthly data. The number of hidden nodes in the input nodes 77, 50, 31, 23, 17, 11, and 7 is 35, 25, 15, 23, 17, and 11, respectively. In addition, the results using DNN-based weekly and monthly data are shown in Table 2. In the input nodes 77, 50, 31, 23, 17, 11, and 7, the number of hidden nodes is 105, 36, 21, 33, 24, and 15, respectively.

Table 1.
MLP (1-HL) by using weekly and monthly data.

Table 2.
DNN (3-HL) by using weekly and monthly data.
4.2. Analysis and Results
In this section, descriptive statistics of forecast errors (er) from the MLP model and DNN model using S&P data are presented in Table 1. Those statistics of forecast errors (FE) for four different forecasting horizons such as 77 weeks ahead (long range), 50 weeks ahead (upper mid range), 31 weeks ahead (lower mid range), and 23 weeks ahead (short range) are presented in Table 1. As shown, statistical results such as average Mean, MAE (mean absolute error), MSE were applied with the measuring horizons of 77, 50, 31 and 23, respectively. What is unusual is that the DNN model provides a smaller MAE and MSE than the MLP model does for all forecast horizons, with the exception of the short forecast horizon (23 weeks ahead). These results were statistically significant at all predicted horizon measurement points by nonparametric Wilcoxon test [15]. The point that can be deduced, as mentioned by Wang et al. [16], is that the DNN model provides a more accurate prediction than the MLP model.
In particular, in Table 3 and Table 4, the hidden nodes of MLP and DNN are set to about half the number of inputs and outputs. In the case of DNN, the hidden layers are all set to six. Therefore, the number of hidden nodes is six times larger than that of MLP.

Table 3.
Statistical analysis and forecasting accuracy of each model by actual weekly data.

Table 4.
Statistical analysis and forecasting accuracy of each model by actual monthly data.
In terms of the prediction horizon, the NN model, which is a time series rather than the MLP model, has a small MAE and MSE. However, the difference was statistically significant for 11 months compared to the values initially predicted. Because α < 0.01, the statistical observations were reasonably judged. In conclusion, the results of the weekly data and monthly data are consistent.
Table 5 and Table 6 show the results of MLP and DNN with the number of hidden nodes increased. Although increasing the number of hidden nodes increases the learning time, it can confirm the relative increase in the accuracy. The execution time required for the learning time can be reduced through parallel processing or cloud computing [24,25,26]. The results of Table 5 and Table 6 show that the hidden nodes are twice as many as the input and output numbers, compared to Table 3 and Table 4, in which the hidden nodes are about half of the input and output counts. As a result, a slight improvement in the accuracy performance was confirmed as the result of increased hidden nodes in the weekly and monthly data-based MLP and DNN.

Table 5.
Statistical analysis and forecasting accuracy of each model by actual weekly data.

Table 6.
Statistical analysis and forecasting accuracy of each model by actual monthly data.
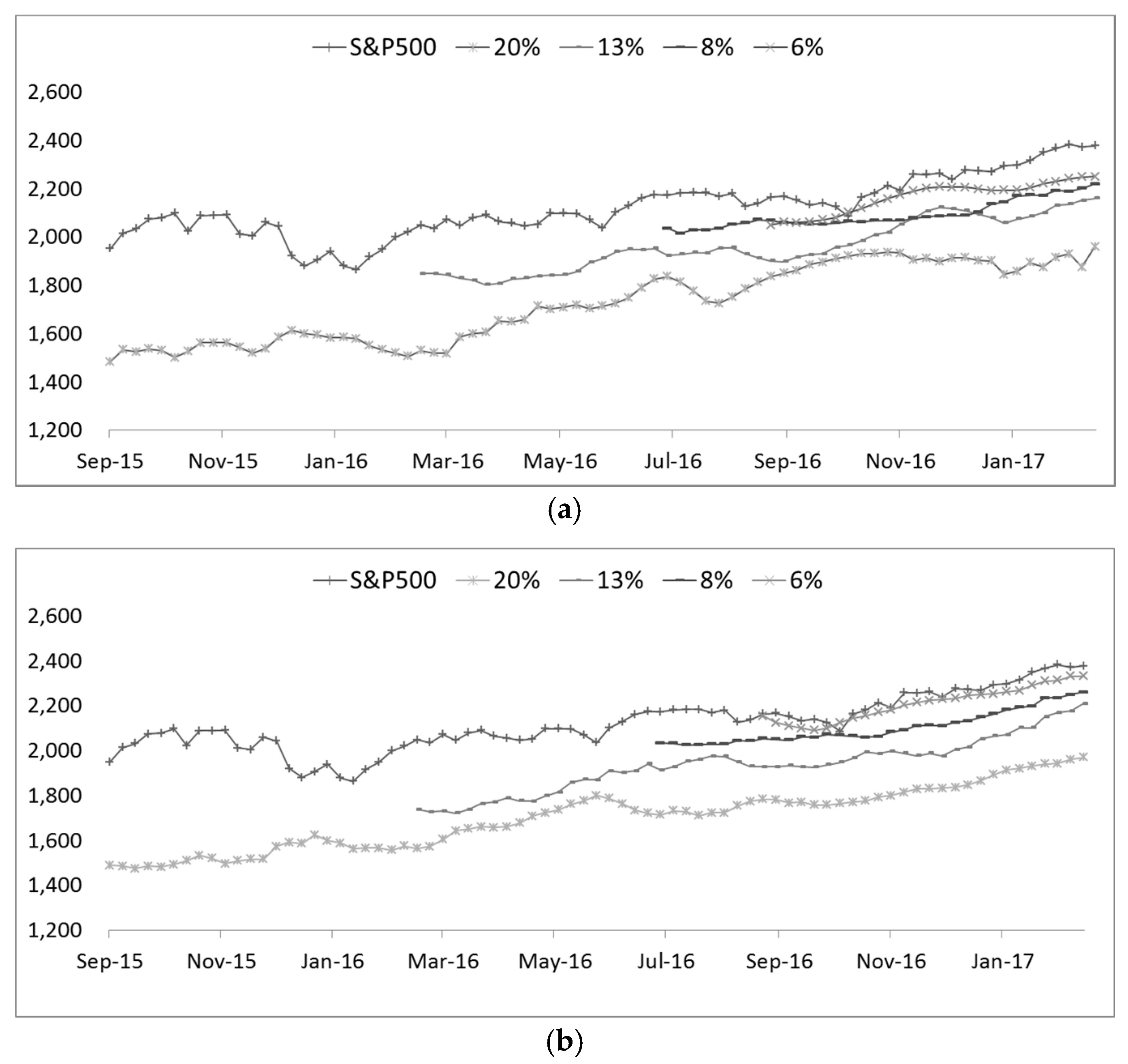
As described above, annual data can be inferred from the data of the week and month taken from the time series data. As the forecasting horizon changes, it is meaningless in the Neural Network Perspective. Below, we can see the recent yearly data from 2015 to 2017 for comparison. Figure 2 shows that a comparison of the recent yearly data by layer x = 0, which includes real data, 20%, 13%, 8%, and 6 %, respectively. Each colored line shows five layer-by-layer predictions, and the legend on the left shows the stock price index of the S&P 500 [27,28] in Figure 3. It can be seen that the main inflection point and the amount of network applied are very similar to the real data, that is, the actual measured data.
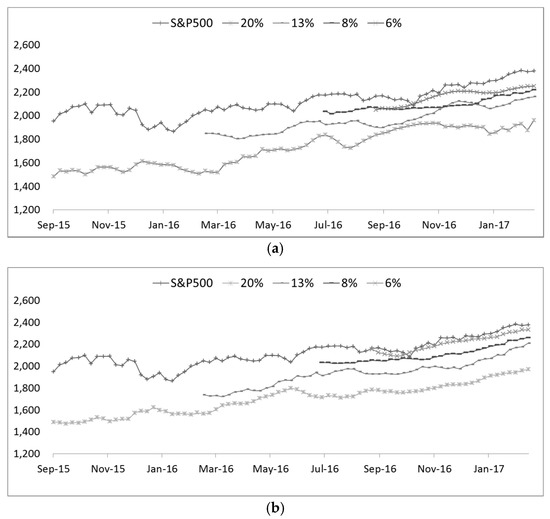
Figure 2.
Comparison of recent yearly data by x = 0 values from 20%, 10%, 8%, 6%, respectively. (a) MLP(1-HL); (b) DNN (3-HL).
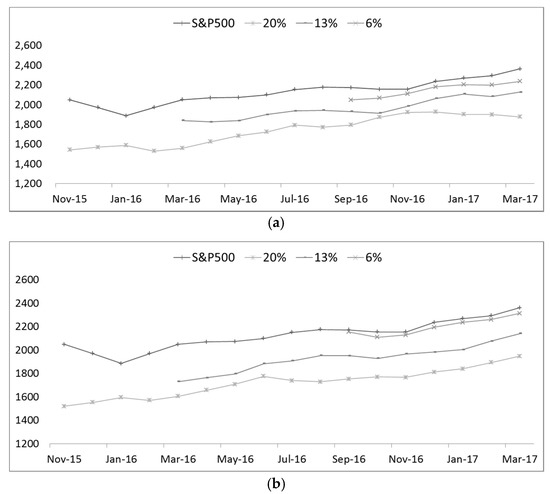
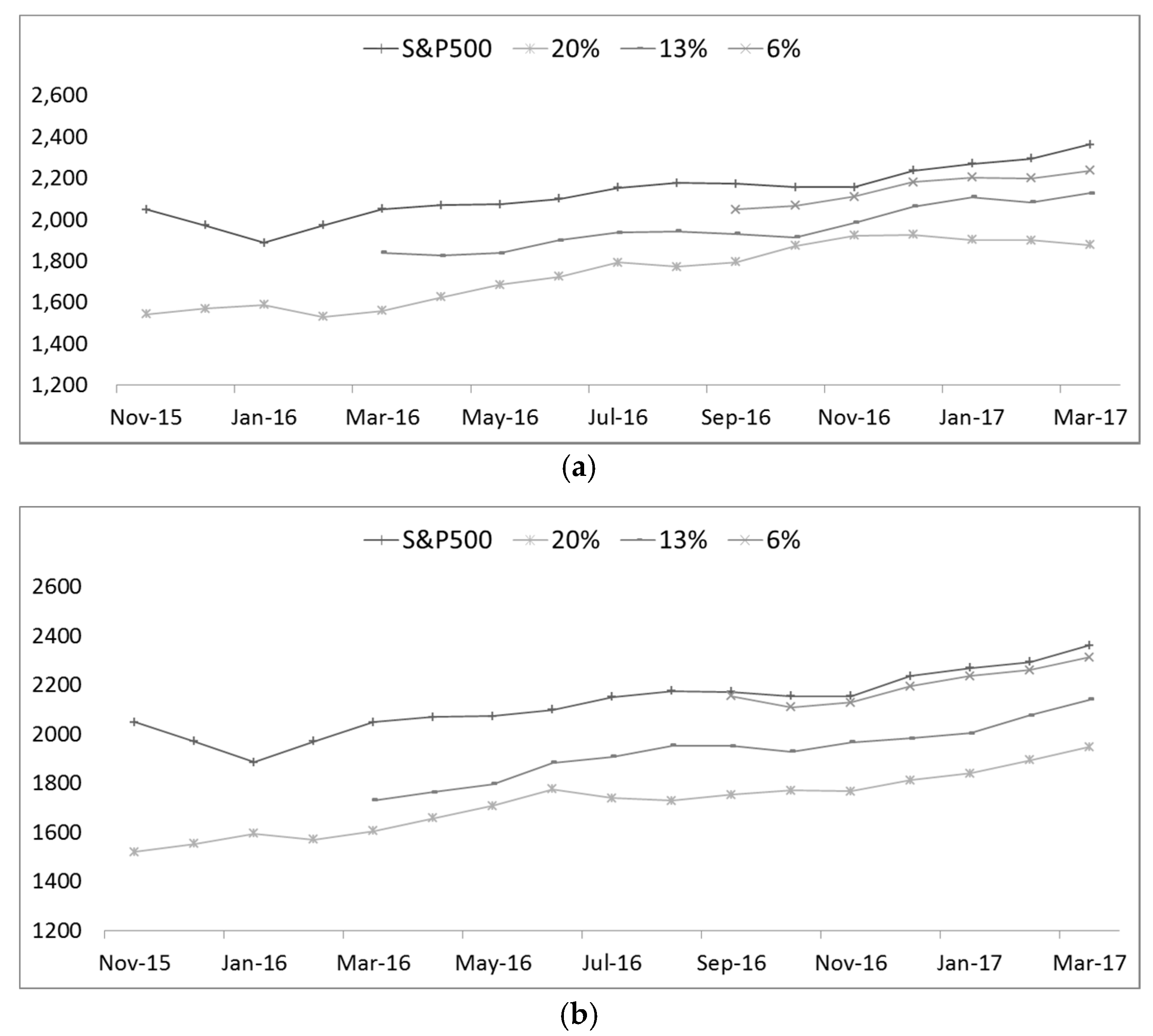
Figure 3.
Comparison of recent yearly data by x = 0 values from 20%, 13%, 6%, respectively. (a) MLP (1-HL); (b) DNN (3-HL).
Furthermore, in the case of the real data, that is, the actually measured data, the layer is 6%, and the reason for this is as follows. First, the error rate tends to be lower than other data. On the other hand, the higher the percentage of the layer, the more likely it is that the initial value will be the same as the real data.
5. Conclusions
The ultimate goal of this paper was to compare and analyze the forecasting performance of two artificial neural network (ANN) models, and to conduct scientific analysis by data flow, not economic flow. In particular, we investigated which is the better model between the multi-layer perceptron (MLP) model and the deep neural network (DNN) model by forecasting the Stock Price Index (S&P 500) during a certain time frame. Particularly, forecasting performance was measured by the forecast accuracy metrics, such as the absolute forecasting errors and square forecasting errors of each model.
As a result, DNN was found to perform better than MLP. In addition, although the method of input data is limited to the past stock index data in this study, monthly data learning results provided better prediction performance than weekly data learning results. It should be noted that the use of an artificial neural network, which is a scientific approach, can grasp the flow of stock trends, though it is difficult to predict detailed stock changes.
There is a first task of comparing and analyzing the models by limiting the object of S&P 500, as well as showing the flow of data and the viewpoint of analysis. S&P 500 data and its return data over a period of 100 months (i.e., 407 weeks), extending from 2009 to 2017, were analyzed. We found the followings: first, the DNN model generally provided more accurate forecasts for the S&P 500 than the MLP model. Although the ANN models have evolved continuously, it may be good for a deep running perspective, but since the approach between the models is different and the utility is different, it was not statistically reliable to predict on S&P 500 returns. It was observed that these results are applicable to both weekly, monthly, and annual data shown in DNN and are useful for accurate prediction without error rate. Since the accuracy of forecasting values is dependent on the developing process of forecasting models, the results of this study may also be sensitive to the developing process of the MLP model and DNN model.
Acknowledgments
This work has been supported by the Basic Science Research through NRF (Korea) grant 2015R1C1A1A02037688, 2017R1A1A2059115. This work was supported by Institute for IITP (Korea) grant funded by the Korea government, MSIP, 2017-0-00403.
Author Contributions
Sungju Lee developed stimuli, and interpreted the results; Taikyeong Jeong supervised the project, conducted model’s data analysis and wrote the paper. Authorship must be limited to those who have contributed substantially to the research reported.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Coch, D.; Ansari, D. Thinking about mechanisms is crucial to connecting neuroscience and education. Cortex 2009, 45, 546–547. [Google Scholar] [CrossRef] [PubMed]
- Hamid, S.A.; Iqbal, Z. Using neural networks for forecasting volatility of S&P 500 Index futures prices. J. Bus. Res. 2004, 57, 1116–1125. [Google Scholar]
- Huang, G.B.; Saratchandran, P.; Sundararajan, N. A generalized growing and pruning RBF (GGAP-RBF) neural network for function approximation. IEEE Trans. Neural Netw. 2005, 16, 57–67. [Google Scholar] [CrossRef] [PubMed]
- Jain, A.; Kumar, A.M. Hybrid neural network models for hydrologic time series forecasting. Appl. Soft Comput. 2007, 7, 585–592. [Google Scholar] [CrossRef]
- Singh, K.P.; Basant, A.; Malik, A.; Jain, G. Artificial neural network modeling of the river water quality—A case study. Ecol. Model. 2009, 220, 888–895. [Google Scholar] [CrossRef]
- Eakins, S.G.; Stansell, S.R. Can value-based stock selection criteria yield superior risk-adjusted returns: An application of neural networks. Int. Rev. Financ. Anal. 2003, 12, 83–97. [Google Scholar] [CrossRef]
- Trinkle, B.S.; Baldwin, A.A. Interpretable credit model development via artificial neural networks. Intell. Syst. Account. Financ. Manag. 2007, 15, 123–147. [Google Scholar] [CrossRef]
- Leung, M.T.; Daouk, H.; Chen, A.-S. Forecasting stock indices: A comparison of classification and level estimation models. Int. J. Forecast. 2000, 16, 173–190. [Google Scholar] [CrossRef]
- Enke, D.; Thawornwong, S. The use of data mining and neural networks for forecasting stock market returns. Expert Syst. Appl. 2005, 29, 927–940. [Google Scholar] [CrossRef]
- Atsalakis, G.S.; Valavanis, K.P. Surveying stock market forecasting techniques—Part II: Soft computing methods. Expert Syst. Appl. 2009, 36, 5932–5941. [Google Scholar] [CrossRef]
- Avellaneda, M.; Lee, J.-H. Statistical arbitrage in the US equities market. Quant. Financ. 2010, 10, 761–782. [Google Scholar] [CrossRef]
- Fama, E.F.; French, K.R. A five-factor asset pricing model. J. Financ. Econ. 2015, 116, 1–22. [Google Scholar] [CrossRef]
- Dixon, M.; Klabjan, D.; Bang, J.H. Implementing deep neural networks for financial market prediction on the Intel Xeon Phi. In Proceedings of the 8th Workshop on High Performance Computational Finance, New York, NY, USA, 15 November 2015; pp. 1–6. [Google Scholar]
- Hagan, M.T.; Menhaj, M.B. Training feedforward networks with the Marquardt algorithm. IEEE Trans. Neural Netw. 1994, 5, 989–993. [Google Scholar] [CrossRef] [PubMed]
- Lozano, A.M.; Lang, A.E.; Galvez-Jimenez, N.; Miyasaki, J.; Duff, J.; Hutchinson, W.D.; Dostrovsky, J.O. Effect of GPi pallidotomy on motor function in Parkinson’s disease. Lancet 1995, 346, 1383–1387. [Google Scholar] [CrossRef]
- Donaldson, R.G.; Kamstra, M. Forecast combining with neural networks. J. Forecast. 1996, 15, 49–61. [Google Scholar] [CrossRef]
- Zhang, Y.; Wu, L. Stock market prediction of S&P 500 via combination of improved BCO approach and BP neural network. Expert Syst. Appl. 2009, 36, 8849–8854. [Google Scholar]
- Mario, C.; Giovanni, P. An innovative approach for forecasting of energy requirements to improve a smart home management system based on BLE. IEEE Trans. Green Commun. Netw. 2017, 1, 112–120. [Google Scholar]
- Manabe, Y.; Chakraborty, B. Estimating embedding parameters using structural learning of neural network. In Proceedings of the IEEE 2005 International Workshop on Nonlinear Signal and Image Processing (NSIP 2005), Sapporo, Japan, 18–20 May 2005. [Google Scholar]
- Wu, S.L.; Li, K.L.; Huang, T.Z. Exponential stability of static neural networks with time delay and impulses. J. IET Control Theory Appl. 2011, 5, 943–951. [Google Scholar] [CrossRef]
- Hornik, K.; Stinchcombe, M.; White, H. Multi-layered feedforward networks are universal approximators. Neural Netw. 1989, 2, 359–366. [Google Scholar] [CrossRef]
- Huang, W.; Nakamori, Y.; Wang, S. Forecasting stock market movement direction with support vector machine. Comput. Oper. Res. 2005, 32, 2513. [Google Scholar] [CrossRef]
- Nils, O.; Alessandra, N.; Pierre, C. MLP Tools: A PyMOL plugin for using the molecular lipophilicity potential in computer-aided drug design. J. Comput. Aided Mol. Des. 2014, 28, 587–596. [Google Scholar]
- Jefferys, W.H.; Berger, J.O. Ockham’s razor and Bayesian analysis. Am. Sci. 1992, 80, 64–72. [Google Scholar]
- Gardner, H. Frames of Mind: The Theory of Multiple Intelligences; Basic books: New York, NY, USA, 2011. [Google Scholar]
- Lee, S.; Kim, H.; Park, D.; Chung, Y.; Jeong, T. CPU-GPU hybrid computing for feature extraction from video stream. IEICE Electron. Express 2014, 11. [Google Scholar] [CrossRef]
- Lee, S.; Kim, H.; Sa, J.; Park, B.; Chung, Y. Real-time processing for intelligent-surveillance applications. IEICE Electron. Express 2017, 14. [Google Scholar] [CrossRef]
- Lee, S.; Jeong, T. Cloud-based parameter-driven statistical services and resource allocation in a heterogeneous platform on enterprise environment. Symmetry 2016, 8, 103. [Google Scholar] [CrossRef]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).