Abstract
In the latest studies concerning the sentiment polarity of words, the authors mostly consider the positive and negative constructions, without paying too much attention to the neutral words, which can have, in fact, significant sentiment degrees. More precisely, not all the neutral words have zero positivity or negativity scores, some of them having quite important nonzero scores for these polarities. At this moment, in the literature, a word is considered neutral if its positive and negative scores are equal, which implies two possibilities: (1) zero positive and negative scores; (2) nonzero, but equal positive and negative scores. It is obvious that these cases represent two different categories of neutral words that must be treated separately by a sentiment analysis task. In this paper, we present a comprehensive study about the neutral words applied to English as is developed with the aid of SentiWordNet 3.0: the publicly available lexical resource for opinion mining. We designed our study in order to provide an accurate classification of the so-called “neutral words” described in terms of sentiment scores and using measures from neutrosophy theory. The intended scope is to fill the gap concerning the neutrality aspect by giving precise measurements for the words’ objectivity.
1. Introduction
Emotion is the root of any social dialogue. From the natural language processing (NLP) point of view, words are the root for emotion detection by some special constructions used in each language in order to describe feelings. This polarity is usually considered as having three possible values: positive, negative or neutral. Representation of the polarity in a natural language utterance, more precisely of its positivity, neutrality and negativity scores, has been a long-standing problem in NLP [1], the solving of which was attempted by various knowledge representation techniques including frames [2], conceptual dependency or semantic nets [3]. An extension of semantic nets was proposed under the name of fuzzy semantic nets [4,5,6] in order to include inexactitude and imprecision.
Most of the existing opinion mining algorithms attempt to identify the polarity of sentiment expressed in natural language texts. However, in most of the cases, the texts are not exclusively positive or exclusively negative, and the neutrality of some opinions could not be so neutral, as was, perhaps, the author’s intention. The reason is that, for all the sentiment polarities, there are many degrees that make the difference between an accurate opinion mining analysis and a common one, as the texts usually contain a mix of positive and negative sentiments. Therefore, for some applications, it is necessary to detect simultaneously these polarities and also to detect the strength of the expressed sentiments.
For instance, programs that monitor the sentiments expressed in online media communication (chats, blogs, social forums and networks) have to be designed in order to identify all these polarity degrees and strengths [7] that are intervening if inappropriate emotions or inappropriate (at-risk) users (inappropriate users or at-risk users are considered those persons that use both positive and negative expressions at a very high level of strength [8]) are detected. In addition, basic research to understand the role of emotion in online communication [9,10] would also benefit from fine-grained sentiment detection, as would the growing body of psychology and other social science research into the role of sentiment in various types of discussion or general discourse [11].
The study presented in this paper was constructed based on SentiWordNet 3.0: a publicly available lexical resource for opinion mining [12] constructed upon the synsets of Princeton WordNet 3.0. WordNet contains English nouns, verbs, adjectives and adverbs organized in the so-called “synsets”, which can be seen as logical groups of cognitive synonyms, in fact logical groups of word forms. Each word form can be a single word or a collocation (a sequence of two or more words connected by underscores). The synsets are linked through semantic pointers that describe the relationship between the connected elements, such as [13]:
- Nouns are connected through “hyperonymy” and “hyponymy” (inverse of “hyperonymy”) relations or “meronymy” and “holonymy” (inverse of “meronymy”) relations. The links defined between noun synsets form a hierarchy, which is rooted in the “entity” synset.
- Verbs are organized by means of the “troponym”, “hypernym” and “entailment” relations.
- Adjectives are linked to their antonyms, and relational adjectives point to their related nouns.
- Adverbs form the smallest group of synsets. They are mostly derived from adjectives and are linked to them via the “pertainym” relation.
SentiWordNet extends the WordNet lexicon by adding sentiment scores to the synsets. More precisely, in SentiWordNet, all the synsets are annotated according to their degree of neutrality, positiveness and negativity. A sentiment score is a value that represents the synset’s negative, positive or objective (neutral) connotation. Always, the sum of these three values is 1.0.
Each synset s is associated with three sentiment scores: , and , indicating how neutral (the value of ) or how affective (the values of and ) the terms contained in the synset are. Each of these three scores ranges between 0.0 and 1.0 values, and the sum of them is always 1.0 for each synset. For this reason, only the positivity and negativity scores are given in SentiWordNet, as the objectivity of a word is being measured by the difference: .
A synset (and all its including words) that has value 1.0 for the objectivity scores indicates that the term is objective, while 0.0 means that the term conveys some strong sentimental (positive or negative) meaning [14]. A subjective term is considered a term with important positive or negative polarity (-polarity), while an objective term can be defined as a term that does not have either positive or negative characteristics [12] or, in the presence of nonzero positive and negative scores, the objective score is the highest. Nevertheless, none these works make a distinction between different senses of a word, so that the term, and not its senses, are classified, although there are some works [15,16] that distinguish between different parts-of-speech data of a word [12].
The task of determining whether a term is a marker of opinionated content (i.e., subjective) has received much attention [12,17,18,19], with less attention concerning the analysis of the words’ objectivity degree, even if its results could help a fine-grained sentiment detection. A hard classification method will probably label as objective any term that has no strong -polarity, like “short” or “alone” [12]. In this assumption, if a sentence contains many such terms, an opinion mining analysis based on a hard classification will probably miss its subtly subjective character, while a fine-graded sentiment classification may provide enough information to capture such nuances.
This paper addresses the problem of objectivity degrees of neutral words by applying the neutrosophic theory on the words’ sentiment scores. In this approach, a word w is considered as a single-valued neutrosophic set [20] being represented by its three sentiment scores , where , and denote the positivity, objectivity and, respectively, negativity scores of the word w. These scores are determined by implementing a weighted average upon all the sentiment scores of the SentiWordNet synsets in which the word w appears. The data upon which the study was conducted are represented by the SentiWordNet lexical resource. From this resource, a special lexicon of neutral words was manually created in order to evaluate the proposed method. The main aim of this work is to enhance the performance of the sentiment analysis tasks by resolving the incorrect sentiment classification problem due to an improper interpretation of the words’ sentiment scores.
The purpose of this paper is to show that there is no basis for considering that neutrality means equal positive and negative scores. Therefore, we propose a precise mechanism that measures the objectivity degrees of the words by considering all the involved aspects concerning the sentiment polarity of the words. The mechanism is formalized with the help of neutrosophic functions, which are used for measuring the objectivity degrees of the words based on their sentiment scores. This is a word-level study in which words are considered as single entities. This means that no contextual information is taking into account, as we are not dealing with sequences of words in which the polarity of a word can be affected by the polarity of the surrounding words, as in “non-negative”. We recognize the problem of detecting the polarity for pieces of texts (sequences of more than one word), and we intend to address it in our future works; however, for this present study, we analyze the words by considering them in a neutral environment, in which their polarities are not affected by external circumstances.
The paper is organized as follows: in the following section, we review the literature in the domain of the neutrality theory. Section 3 presents the neutrosophic theory we have used in order to model the words’ sentiment polarities. Section 4 is dedicated to the neutrosophic approach we have developed for neutral words classes, while Section 5 presents the neutrosophic concepts used for modeling the words’ objectivity degrees. The last section summarizes the conclusions of the proposed mechanism and our future studies’ goals.
2. Related Works
In the literature, the typical studies concerning opinion mining concentrate on the (very) positive and (very) negative emotion words detected in texts [21], the so-called “positive versus negative” problem. This kind of approach has several weakness concerning not only these two contrasting types of data, but also by neglecting the so-called “neutral words”. Thus, despite the fact that neutral words could improve, under specific conditions, the opinion mining task’s accuracy, they are ignored by most researchers. In the few studies that mainly address neutrality, several technique are being used: the lexicon-based techniques take into account the neutrality score of the words in order to detect neutral opinions [22] or in order to filter them out for enabling algorithms to focus only on the words with positive and negative sentiment [23]; also, the statistical techniques filter all the information considered as neutral to focus only on the affective utterances in order to improve the binary classification of the texts into positive and negative ones [24,25].
It is also our belief that “so far, to our knowledge, there is yet no theory of emotion really elaborating on the structures and/or processes underlying stimulus neutrality” [26]. Moreover, some authors suggested [27] that as in every polarity detection problem, all three categories must be identified (namely, positive, negative and neutral), and therefore, the detection of the neutral category along with the other two can even improve the overall precision. Additionally, when the objectivity of the so-called “neutral words” is not so objective (as we will prove in the next sections), the precise recognition of the objectivity degrees of the words is even more necessary.
As is stated in the literature, neutrality can arise from two possible situations: (1) the neutrality can be caused by a state of no or insignificant affective involvement or (2) the neutrality can signify a balanced state of positive and negative affect. In our study, we have considered all these cases, and we have seen important differences from the sentiment polarity point of view between these two neutrality situations (see Section 4).
3. Neutrosophic Representation of Word Sentiment Scores
The approach deployed in this paper for the degrees of neutrality is formalized using neutrosophy theory concepts. The name “neutrosophy” is derived from the Latin word “neuter”, which means neutral, and the Greek word “Sophia”, which stands for skill or wisdom. Neutrosophy is a branch of philosophy that studies the origin, nature and scope of neutralities [28]. Florentin Smarandache had generalized the fuzzy logic by introducing two new concepts [29]: “neutrosophy”, the study of neutralities as an extension of dialectics and its derivative “neutrosophic”, such as “neutrosophic logic”, “neutrosophic set”, “neutrosophic probability” and “neutrosophic statistics”. Neutrosophy is the basis of neutrosophic logic, neutrosophic probability, neutrosophic sets and neutrosophic statistics.
A neutrosophic set () is a general framework that generalizes the concept of the classic set and fuzzy set and for which the indeterminacy is quantified explicitly and truth-membership (truth-degree), indeterminacy-membership (indeterminacy-degree) and false-membership (falsity-degree) are independent [30,31].
Let X be a universe of discourse, with a generic element in X denoted by x, then a neutrosophic set [32] A is an object having the form where the functions define respectively the degree of membership (or truth), the degree of indeterminacy and the degree of non-membership (or falsehood) of the element to the set A fulfilling the condition . As stated in [1], the three notions of truth, indeterminacy and falsehood can be substituted by the notions of positivity, neutrality and negativity, respectively.
Definition 1.
[33] Let X be a universe of discourse. The set is called a single-valued neutrosophic set (), if each element has, with respect to A, a degree of membership (), a degree of indeterminate-membership () and a degree of non-membership (), where and . We write .
A single-valued neutrosophic number [34] is a special single-valued neutrosophic set on the set of real numbers . Let be a single-valued neutrosophic number, where . The component t (truth) is considered as a positive quality, while i (indeterminacy) and f (falsehood) are considered negative qualities.
In this paper, we make use of special representations in which a word w is considered as a single-valued neutrosophic set of the form:
where , and denote the positivity, objectivity and, respectively, negativity scores of the word w. In this manner, all the properties involving the concept of the single-valued neutrosophic set and its refinement, the single-valued neutrosophic number, can be used and exploited.
In order to exemplify this representation, let us consider a word labeled as “neutral” because of its sentiment scores where the notation specifies the parts-of-speech of the word, in this case an adjective, and the triple specifies the positive, negative and, respectively, objective scores of the synset that contains the adjective “hydrostatic”.
The representation of the word “hydrostatic” considered as a single-value neutrosophic number becomes where the triplet specifies the word positivity, objectivity and neutrality scores. Obviously: the conditions imposed on these three values are preserved:
- , , and
- .
If a word has more than one sense, it will appear in more than one synset, one for each sense. Because the neutrosophic representation of the words is determined based on the scores triplet specified for the SentiWordNet synsets, in the case of multi-sense words, a weighted average must be implemented in order to obtain a single sentiment score triplet (the presented formulas approximate the sentiment value of a word by weighing the synset scores according to their rank (after [35])) :
where by , , , we denote the first, the second, respectively, the n-th sense of the considered word w. We used this weighted average formula as it pays attention to the frequency of a word’s senses such that the first sense, which is the most used one, is preserved as it is, while the second, which is less used, is divided by two, etc.
Definition 2.
[36] The average positive quality neutrosophic function (also known as the neutrosophic score function) of a neutrosophic number is defined as:
Definition 3.
[36] The average negative quality neutrosophic function of a neutrosophic number is defined as:
Definition 4.
[36] The neutrosophic accuracy function is defined by:
Definition 5.
[36] The neutrosophic certainty function is:
Theorem 1.
[36] The average positive quality neutrosophic function and the average negative quality neutrosophic function are complementary to each other, or .
All the above functions can be used in order to define a ranking (comparison) between two neutrosophic numbers in multi-criteria decision making. More precisely, using the functions presented above: neutrosophic score function, neutrosophic accuracy function and neutrosophic certainty function, one can define a total order on the set of neutrosophic numbers [36], noted here with . Indeed, if we consider two single-valued neutrosophic numbers and , where , then:
- if , then ;
- if = and > , then ;
- if and = and , then ;
- if and = and , then = .
In the study presented in this paper, we make use of these functions in order to distinguish between the word scores, in an attempt to investigate how objective the neutral words are. As will be shown, there are precise values of these function based on which we can accurately identify the objectivity degrees of the neutral words.
At this moment, in the literature, a word is considered neutral if its positive and negative scores are equal, as it is usually interpreted as “a combination of positive and negative valence for the same stimulus” [26]. At the sentence level, this situation can be exemplified by the construction “I have some good news and some bad news.” [26]. At the word level, we can have two possibilities: (1) words with zero positive and negative scores; (2) words with nonzero, but equal positive and negative scores. It is obvious that these cases represent two different categories of neutral words that must be treated separately by a sentiment analysis task.
In this paper, we propose a new mechanism for measuring the objectivity degrees of the words that pays attention to all characteristics that can alter the objectivity of the words. Our study was developed with the aid of the SentiWordNet 3.0, the publicly available lexical resource for opinion mining. The results of our study can be used in order to construct a formalism based on which the sentiment strength of the words can be determined in a very precise manner. The paper exemplifies all the involved computations for the words considered neutral with respect to their sentiment scores. Surprisingly enough, the reader will discover that the objectivity degree of the so-called “neutral words” is not as great as it should be.
4. Objectivity Classes for Neutral Words
The programs that make use of SentiWordNet data [12] consider the same set of rules in order to label the words of this lexical resource with sentiment category. At this moment, seven sentiment categories are proposed and used in the literature: neutral, positive, negative, weak positive, weak negative, strong positive and strong negative.
In Algorithm 1, we give the code proposed by Alvin Alexander [37] for these seven sentiment labels (From the very beginning, we have to point out that on the SentiWordNet site (http://sentiwordnet.isti.cnr.it/), the program code for processing the SentiWordNet database does not include any function for labeling the words with sentiment categories. We consider that the reason for this derives from the fact that sentiment labeling is, at the present moment, an open problem, for which we intend to find an accurate solution.), where score is considered as a pondered difference between the positivity and negativity scores of a word (a word with multiple senses has multiple sentiment score pairs, one for each sense). More precisely, if a word appears in n synsets, then for each i-th synset in which the word appears, its score, noted here with , is taken as:
| Algorithm 1: Sentiment word labels based on SentiWordNet scores. |
| function classForScore(score) |
| sent <- ‘‘neutral’’ |
| if(score >= 0.75) sent <- ‘‘strong_positive’’ |
| else if(score > 0.25 && score <= 0.5) sent <- ‘‘positive’’ |
| else if(score > 0 && score<=0.25) sent <- ‘‘weak_positive’’ |
| else if(score < 0 && score>=-0.25) sent <- ‘‘weak_negative’’ |
| else if(score < -0.25 && score >= -0.5) sent <- ‘‘negative’’ |
| else if(score <= -0.75) sent <- ‘‘strong_negative’’ |
| return sent |
| endfunction |
The score over all n synsets in which the word appears is calculated using the weighted average formula (after [35]):
In what follows, we will name “neutral words” all the words that are labeled with “neutral” by the rules of Algorithm 1. This means that all the words that have zero scores (calculated as in Equation (4)) are labeled as “neutral words”. Two questions arise:
- Question: What does score = 0 mean?Answer: This means zero positive and negative scores or equal positive and negative scores for non-zero for positivity and negativity values.
- Question: What does equal positive and negative scores mean?Answer: Considering that all the words of SentiWordNet have the sum of the positive, negative and objective scores equal to one, this means that the positive and negative scores can have values between zero (the minimum value) and 0.5 (the maximum value)
Surprisingly enough, by extracting all the words that are labeled as “neutral words” by the set of rules indicated above, we identified three classes of these words (see Figure 1), each group acting differently from the sentiment score point of view, and moreover, having different values for the average quality neutrosophic functions.
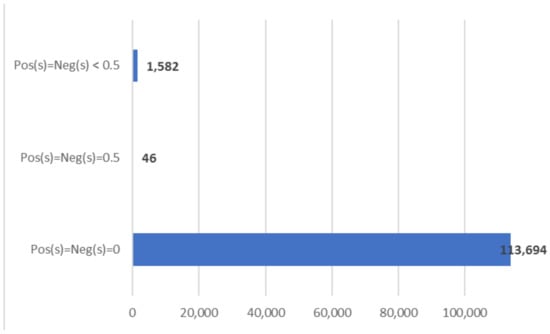
Figure 1.
The “neutral words” grouped by the positivity and negativity scores.
More precisely, from a total of 115,322 “neutral words”, almost all of them (113,694) have zero positive and negative scores and the maximum value (one) for objectivity, that is their sentiment score tuple is . We will consider these words as pure objective words.
A very small number of “neutral words”, only 46 words, have positive and negative scores values equal to 0.5, that is their sentiment score tuple is . As a direct consequence of these values for the positive and negative scores, the objectivity score of these words is zero, despite their “neutral” label. We will name these words as half positive-half negative words.
The last discussed category, quite small considering the total number of neutral words, includes only 1582 words. However, this is very interesting, from the point of view of our study, because the phenomena identified for these words was also seen at some sentiment words, such as “weak positive” and “weak negative” words (we take here the same set of rules of Algorithm 1 for labeling the words with “weak positive” or “weak negative”). As opposed to the first two categories presented above: the pure objective words (with the objective score equal to one) and the half positive-half negative words (with the objective score equal to zero), for this last category of “neutral words”, the values of the objective score vary from 0.166 to 0.98, that is the values of this score include almost all possible values this score can have.
More precisely, because this last category consists of instances with equal positive and negative scores having values greater than zero and smaller than 0.5, the objectivity scores vary between 0.166667 (when the positive and negative scores reach their maximum value for this category, that is 0.416667) and 0.9878 (when the positive and negative scores reach their minimum, 0.006). We will call the words in this last category as positive and negative balanced words, as they represent in fact “a balanced state of positive and negative affect” [26].
For this last category of positive and negative balanced words, we identified two groups:
- one group has instances with (0.125, 0.125, 0.75) sentiment scores (see Figure 2);
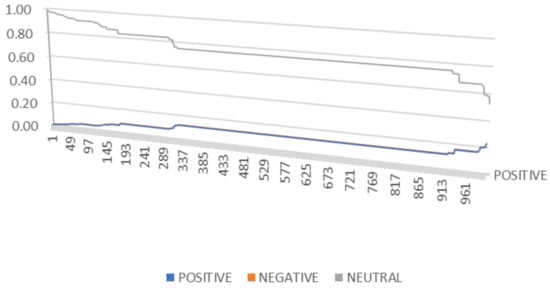 Figure 2. The (0.125, 0.125, 0.75) set of words from the positive and negative balanced words class.
Figure 2. The (0.125, 0.125, 0.75) set of words from the positive and negative balanced words class. - the second group corresponds to instances with (0.25, 0.25, 0.5) sentiment scores (see Figure 3).
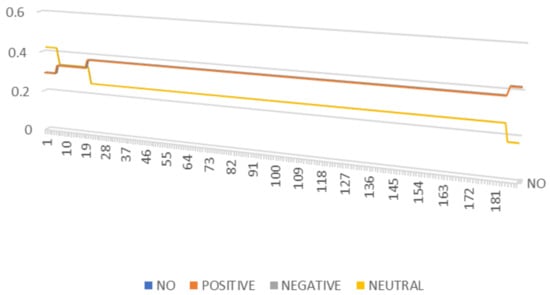 Figure 3. The (0.375, 0.375, 0.25) set of words from the positive and negative balanced words class.
Figure 3. The (0.375, 0.375, 0.25) set of words from the positive and negative balanced words class.
This particular category of “neutral words” has, as we already pointed out, both affective polarity (when the positive and negative scores are greater than the objective ones; few cases); but also objective polarity (when the reverse situation occurs; the majority of cases). For this reason, we consider that the results obtained for the positive and negative balanced words can be applied also to the affective words (especially for the (weak) positive words and (weak) negative words). This represent the direction for our future studies.
5. Neutrosophic Measures for the Objectivity Degrees of Neutral Words
As was presented in the previous section, using the rules of Algorithm 1, the resulting “neutral word” labels correspond to instances with different affective polarities. There is thus a need for a more accurate mapping based on which the sentiment polarity of the words would be more precisely evidenced.
In this section, we present a precise mechanism for measuring the words’ objectivity degrees, which maps any neutral word in one of the three objectivity classes proposed in the previous section.
The measuring mechanism described in Algorithm 2 is bidirectional, which means that one can measure the words’ objectivity degrees (by applying the average negative quality neutrosophic function and the relation) as well as the words’ affective degrees (by applying the average positive quality neutrosophic function and the relation).
| Algorithm 2: Objectivity class labeling (the three input scores are determined according to Equations (1) to (3).) |
| Input: (Pos(w), Obj(w), Neg(w)) such that Pos(w)=Neg(w) |
| Output: Objectivity Class Label |
| function objectivityLabel(Pos(w), Obj(w), Neg(w)) |
| t <- Pos(w) |
| f <- Neg(w) |
| i <- Obj(w) |
| if (s+(t,i,f) = 0.33 || s-(t,i,f) = 0.67) |
| output ‘‘Pure Neutral Word’’ |
| else if (s+(t,i,f) = 0.67 || s-(t,i,f) = 0.33) |
| output ‘‘Half Positive-Half Negative Word’’ |
| else if (0.33 < s+(t,i,f) < 0.67 || 0.33 < s-(t,i,f) < 0.67) |
| output ‘‘Positive and Negative Balanced Word’’ |
| endif |
| endif |
| endif |
| output ‘‘affectivity degree:’’, s+ |
| output ‘‘objectivity degree:’’, s- |
| endfunction |
We choose to use these neutrosophic functions on the words’ SentiWordNet scores as these functions impose on the considered words an order that suits our proposed objectivity classes for neutral words perfectly: pure neutral words (), positive and negative balanced words (), half positive-half negative words (50%-50%). As can be seen in Figure 4, both functions have two extremity points, 0.33 and 0.67, points that are shared by the pure neutral words and half positive-half negative words classes and a continuous set of values between these two points, which corresponds to the elements of positive and negative balanced words class.
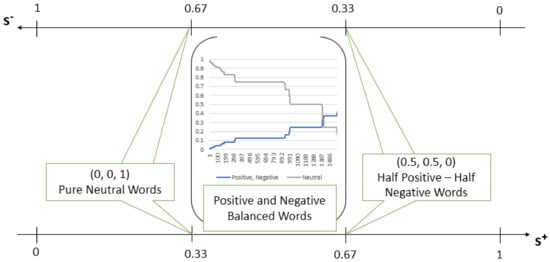
Figure 4.
The neutrosophic functions and values corresponding to the proposed “neutral words” classes.
It is evident that Algorithm 2 is sound and complete: it provides a solution for any word that respects the input conditions: equal positivity and negative scores and the provided solution is correct by the fact that the values of the functions used ( or ) match perfectly with the three objectivity classes.
Based on the values of the function, an ascending order of the words’ sentiment degree (noted here with ) can be established between the proposed objectivity classes:
Indeed, the pure neutral words have zero sentiment degree (zero positivity and negativity scores), while the half positive-half negative words have the strongest -polarity among the studied words (see Table 1).

Table 1.
The proposed classes for “neutral words” together with their values for the sentiment scores and , functions values.
Correspondingly, based on the function values, we obtain an ascending order of the words’ objectivity degrees (noted here with ). Indeed, the half positive-half negative words have the minimum objectivity degree (zero objectivity score), while the pure neutral words reach the maximum with respect to the objectivity degree (see also Table 1):
In Figure 5, we graphically represent the positive and negative balanced words and half positive-half negative words grouped by their values for the function. As can be seen, we obtain an important number of words for which the function is equal to 0.42 (611 occurrences), followed by the group of words having the function equal to 0.5 (395 occurrences).
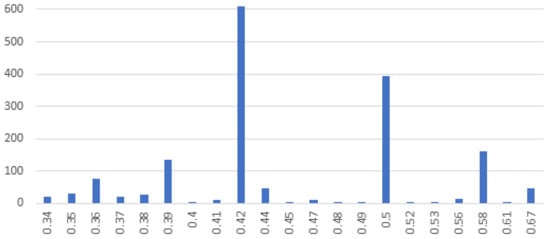
Figure 5.
Positive and negative balanced words and half positive-half negative words grouped by the function values.
All the words of the positive and negative balanced words and half positive-half negative words classes were manually annotated for their -polarity. Surprisingly enough, from a total of 1628 words, 567 words were marked by a linguist expert as having -polarity. By determining, for each possible value of the function, the average number of words that were manually labeled with -polarity, another interesting result was obtained, which confirms the proposed neutrosophic-based measuring approach for words’ objectivity degrees: we get a strong correlation between the average number of the words marked with -polarity and the three interval values of the function, as is shown in the Pareto chart of Figure 6. A Pareto chart is a type of chart that contains both bars and a line graph, where individual values are represented in descending order by bars, and the cumulative total is represented by the line [38].
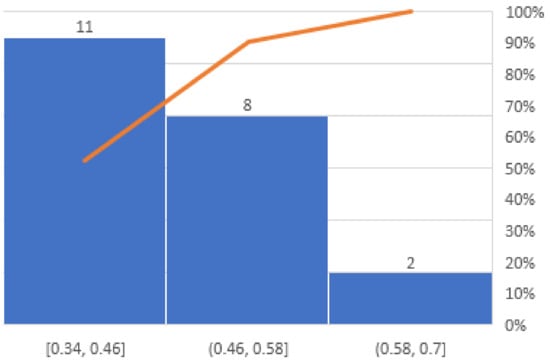
Figure 6.
The Pareto chart corresponding to the function interval values and their corresponding average number of words with -polarity.
As is shown in the chart of Figure 6, if we consider the values of the function partitioned in three intervals: , and , then the average number of the words marked with -polarity is strongly correlated with the values of the function, that is the highest values of this function; the values of the interval correspond to the group of words that were mostly labeled as having -polarity. In this way, another validation for the correctness of the and definitions given in Equations (5) and (6) was obtained.
Evidently, our study will be completed only when all the words, not only the “neutral words”, are analyzed with respect to their function values (or, correspondingly, function values). However, from this very first study developed on words having equal positive and negative scores, we discover that the values of average quality neutrosophic functions range from to , and moreover, we obtained a strong correlation between the proposed three classes and the corresponding values of these two functions. More precisely, the pure neutral words (maximum objectivity degree/minimum -degree) correspond to the lowest value of the function, while the half positive-half negative words (minimum objectivity degree/maximum -degree) correspond to the highest value of function. The words of the positive and negative balanced words class have values between these two extremities.
In our future studies, we propose to investigate the rest of the SentiWordNet words, that is the words with non-equal positive and negative scores, being marked with (weak/strong) positive or negative labels by the rules of Algorithm 1. The intended scope of all these studies is to establish a correlation between the values of average quality neutrosophic functions and all these words’ sentiment polarities.
6. Conclusions and Future Works
This paper addresses the problem of objectivity degrees of neutral words by applying the neutrosophic theory on the words’ sentiment scores. As was presented, there are precise values of average quality neutrosophic functions based on which we can accurately identify the objectivity degrees of the neutral words.
In Figure 7, we resume the workflow of the mechanism proposed in this paper: starting from the sentiment scores extracted from SentiWordNet, we determine the sentiment classes for the words under analysis by means of their corresponding values for average quality neutrosophic functions. Three main conclusions resulted from applying the neutrosophic theory on the words considered as neutral. We summarized these conclusions in terms of the function values, as the function values correspond to the reverse cases:
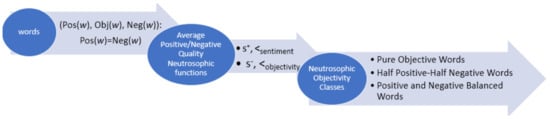
Figure 7.
The workflow of the proposed labeling mechanism for objectivity sentiment classes.
- the lowest value of the function, that is 0.33, was obtained for the words that have the highest objectivity degree (or, corresponding, the smallest -polarity): the pure neutral words class
- the highest value of the function, that is 0.67, was obtained for the words that have the smallest objectivity degree (or, equivalently, the highest -polarity): the half positive-half negative words class
- the values between these extremities, that is the values from the interval (0.33, 0.67), correspond to the words of the positive and negative balanced words class, where we can find a group of words with a mixture of sentiment polarities; nevertheless, the words with the objectivity scores bigger than the -scores have smaller values than the words for which the -scores overcome the objectivity scores.
For our future studies, we propose to apply the same formalism on the other words of the SentiWordNet: the sentiment-carrying words of this lexical resource, and then, to correlate the results obtained for the words considered as neutral with the future obtained results. The scope of our investigations is to determine a precise measurement for the words’ sentiment polarities formalized by means of neutrosophic theory.
Author Contributions
The three co-authors drew together the plan and the ideational reinforcement of the work. Mihaela Colhon made the part of calculations, did the integration of the contributions and provided the theoretical neutrosophic foundation. Ştefan Vlăduţescu and Xenia Negrea provided the corpus of examples, finalized the bibliography and performed the checks. All three authors accepted the final form of the work.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Lakra, S.; Prasad, T.V.; Ramakrishna, G. Representation of a Sentence using a Polar Fuzzy Neutrosophic Semantic Net. Int. J. Adv. Comput. Sci. Appl. Spec. Issue Nat. Lang. Process. 2014, 4, 1–8. [Google Scholar] [CrossRef]
- Minsky, M. A Framework for Representing Knowledge. In The Psychology of Computer Vision; Winston, P., Ed.; McGraw Hill: New York, NY, USA, 1975; pp. 211–277. [Google Scholar]
- Peirce, C.S. Existential Graphs. Collected Papers of Charles Sanders Peirce. 1994. Available online: https://colorysemiotica.files.wordpress.com/2014/08/peirce-collectedpapers.pdf (accessed on 8 October 2017).
- Guo, J.F.; Shao, X.D. A fine fuzzy spatial partitioning model for line objects based on computing with words and application in natural language spatial query. J. Intell. Fuzzy Syst. 2017, 32, 2017–2032. [Google Scholar] [CrossRef]
- Hightower, R.R. Fuzzy Semantic Networks. Master’s Thesis, Kansas State University, Manhattan, KS, USA, 1986. [Google Scholar]
- O’Neill, E.T.; Kammerer, K.A.; Bennett, R. The Aboutness of Words. J. Assoc. Inf. Sci. Technol. 2017, 68, 2471–2483. [Google Scholar] [CrossRef]
- Jiang, D.D.; Luo, X.F.; Xuan, J.Y.; Xu, Z. Sentiment Computing for the News Event Based on the Social Media Big Data. IEEE Access 2017, 5, 2373–2382. [Google Scholar] [CrossRef]
- Huang, Y.; Goh, T.; Liew, C. Hunting suicide notes in Web 2.0—Preliminary findings. In Proceedings of the Ninth IEEE International Symposium on Multimedia Workshops, Beijing, China, 10–12 December 2017; IEEE Computer Society: Los Alamitos, CA, USA, 2007; pp. 517–521. [Google Scholar]
- Derks, D.; Bos, A.E.R.; von Grumbkow, J. Emoticons and online message interpretation. Soc. Sci. Comput. Rev. 2008, 26, 379–388. [Google Scholar] [CrossRef]
- Nardi, B.A. Beyond bandwidth: Dimensions of connection in interpersonal communication. Comput. Support. Coop. Work 2005, 14, 91–130. [Google Scholar] [CrossRef]
- Thelwall, M.; Buckley, K.; Paltoglou, G.; Cai, D.; Kappas, A. Sentiment strength detection in short informal text. J. Am. Soc. Inf. Sci. Technol. 2010, 61, 2544–2558. [Google Scholar] [CrossRef]
- Esuli, A.; Sebastiani, F. SENTIWORDNET: A Publicly Available Lexical Resource for Opinion Mining. In Proceedings of the 5th Conference on Language Resources and Evaluation (LREC’06), Genoa, Italy, 24–26 May 2006; pp. 417–422. [Google Scholar]
- Kreutzer, J.; White, N. Opinion Mining Using SentiWordNet; Uppsala University: Uppsala, Sweden, 2013. [Google Scholar]
- Baldoni, M.; Baroglio, C.; Patti, V.; Rena, P. From tags to emotions: Ontology-driven sentiment analysis in the social semantic web. Intell. Artif. 2012, 6, 41–54. [Google Scholar]
- Hatzivassiloglou, V.; Wiebe, J.M. Effects of adjective orientation and gradability on sentence subjectivity. In Proceedings of the 18th International Conference on Computational Linguistics (COLING-00), Saarbrücken, Germany, 31 July–4 August 2000; pp. 174–181. [Google Scholar]
- Kamps, J.; Marx, M.; Mokken, R.J.; De Rijke, M. Using WordNet to measure semantic orientation of adjectives. In Proceedings of the 4th International Conference on Language Resources and Evaluation (LREC-04), Lisbon, Portugal, 26–28 May 2004; Volume IV, pp. 1115–1118. [Google Scholar]
- Ren, F.J.; Wang, L. Sentiment analysis of text based on three-way decisions. J. Intell. Fuzzy Syst. 2017, 33, 245–254. [Google Scholar] [CrossRef]
- Riloff, E.; Wiebe, J.; Wilson, T. Learning subjective nouns using extraction pattern bootstrapping. In Proceedings of the 7th Conference on Natural Language Learning (CONLL-03), Edmonton, CA, USA, 31 May–1 June 2013; pp. 25–32. [Google Scholar]
- Vegnaduzzo, S. Acquisition of subjective adjectives with limited resources. In Proceedings of the AAAI Spring Symposium on Exploring Attitude and Affect in Text: Theories and Applications, Palo Alto, CA, USA, 22–24 March 2004. [Google Scholar]
- Smarandache, F. Symbolic Neutrosophic Theory; Europa Nova: Brussels, Belgium, 2015. [Google Scholar]
- Kissler, J.; Herbert, C. Emotion, Etmnooi, or Emitoon?—Faster lexical access to emotional than to neutral words during reading. Biol. Psychol. 2013, 92, 464–479. [Google Scholar] [CrossRef] [PubMed]
- Ding, X.; Liu, B.; Yu, P.S. A holistic lexicon-based approach to opinion mining. In Proceedings of the 2008 International Conference on Web Search and Data Mining (WSDM ’08), Palo Alto, CA, USA, 11–12 February 2008; pp. 231–240. [Google Scholar]
- Taboada, M.; Brooke, J.; Tofiloski, M.; Voll, K.; Stede, M. Lexicon-Based Methods for Sentiment Analysis. Comput. Linguist. 2010, 37, 267–307. [Google Scholar] [CrossRef]
- Pang, B.; Lee, L. A sentimental education: Sentiment analysis using subjectivity summarization based on minimum cuts. In Proceedings of the 42nd Annual Meeting on Association for Computational Linguistics (ACL ’04), Barcelona, Spain, 21–26 July 2004. Article 271. [Google Scholar]
- Wilson, T.; Wiebe, J.; Hoffmann, P. Recognizing contextual polarity in phrase-level sentiment analysis. In Proceedings of the Conference on Human Language Technology and Empirical Methods in Natural Language Processing (HLT ’05), Vancouver, BC, Canada, 6–8 October 2005; pp. 347–354. [Google Scholar]
- Kuhlmann, M.; Hofmann, M.J.; Jacobs, A.M. If You Don’t Have Valence, Ask Your Neighbor: Evaluation of Neutral Words as a Function of Affective Semantic Associates. Front. Psychol. 2017, 8, 343. [Google Scholar] [CrossRef] [PubMed]
- Koppel, M.; Schler, J. The importance of neutral examples for learning sentiment. Comput. Intell. 2006, 22, 100–109. [Google Scholar] [CrossRef]
- Smarandache, F. Neutrosophy, a New Branch of Philosophy. Mult. Valued Log. Int. J. 2002, 8, 297–384. [Google Scholar]
- Smarandache, F. A Unifying Field in Logics: Neutrosophic Logic, Neutrosophy, Neutrosophic Set, Neutrosophic Probability; American Research Press: Rehoboth, MA, USA, 2000. [Google Scholar]
- Ye, J. Similarity measures between interval neutrosophic sets and their applications in multicriteria decision-making. J. Intell. Fuzzy Syst. 2014, 26, 165–172. [Google Scholar]
- Ye, J. Vector similarity measures of simplified neutrosophic sets and their application in multi-criteria decision-making. Int. J. Fuzzy Syst. 2014, 16, 204–215. [Google Scholar]
- Smarandache, F. Neutrosophy/Neutrosophic Probability, Set, and Logic; American Research Press: Rehoboth, MA, USA, 1998. [Google Scholar]
- Wang, H.; Smarandache, F.; Zhang, Y.; Sunderraman, R. Single Valued Neutrosophic Sets. Tech. Sci. Appl. Math. 2010, 4, 410–413. [Google Scholar]
- Liang, W.; Zhao, G.; Wu, H. Evaluating Investment Risks of Metallic Mines Using an Extended TOPSIS Method with Linguistic Neutrosophic Numbers. Symmetry 2017, 9, 149. [Google Scholar]
- Tönberg, P. The Demo Java Class for the SentiWordNet Website. Available online: http://sentiwordnet.isti.cnr.it/code/SentiWordNetDemoCode.java (accessed on 8 October 2017).
- Smarandache, F. Neutrosophic Perspectives: Triplets, Duplets, Multisets, Hybrid Operators, Modal Logic, Hedge Algebras and Applications; Pons Publishing House: Brussels, Belgium, 2017. [Google Scholar]
- Alexander, A. Free Java Source Code, Examples, Software, Applets (Java Source Code Warehouse). The SWN3.java Java Example Source Code. Available online: https://alvinalexander.com/java/jwarehouse/deeplearning4j/deeplearning4j-scaleout/deeplearning4j-nlp/src/main/java/org/deeplearning4j/text/corpora/sentiwordnet/SWN3.java.shtml (accessed on 8 October 2017).
- Gould, R.; Ryan, C.N. Essential Statistics: Exploring the World through Data; Pearson: Boston, MA, USA, 2014. [Google Scholar]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).