A Data Mining Approach for Cardiovascular Disease Diagnosis Using Heart Rate Variability and Images of Carotid Arteries

Abstract

In this paper, we proposed not only an extraction methodology of multiple feature vectors from ultrasound images for carotid arteries (CAs) and heart rate variability (HRV) of electrocardiogram signal, but also a suitable and reliable prediction model useful in the diagnosis of cardiovascular disease (CVD). For inventing the multiple feature vectors, we extract a candidate feature vector through image processing and measurement of the thickness of carotid intima-media (IMT). As a complementary way, the linear and/or nonlinear feature vectors are also extracted from HRV, a main index for cardiac disorder. The significance of the multiple feature vectors is tested with several machine learning methods, namely Neural Networks, Support Vector Machine (SVM), Classification based on Multiple Association Rule (CMAR), Decision tree induction and Bayesian classifier. As a result, multiple feature vectors extracted from both CAs and HRV (CA+HRV) showed higher accuracy than the separative feature vectors of CAs and HRV. Furthermore, the SVM and CMAR showed about 89.51% and 89.46%, respectively, in terms of diagnosing accuracy rate after evaluating the diagnosis or prediction methods using the finally chosen multiple feature vectors. Therefore, the multiple feature vectors devised in this paper can be effective diagnostic indicators of CVD. In addition, the feature vector analysis and prediction techniques are expected to be helpful tools in the decisions of cardiologists.

1. Introduction

According to the recent World Health Organization (WHO)’s report about the main causes of death, the top two causes are still cardiovascular diseases (CVD) [1]. In South Korea, CVD is ranked second in causes of death which turns the country into a demographical structure of high incidence of the disease [2]. Consequently, early diagnosis and the reliability of the diagnosis has been recognized as a very important social issue. The current method of diagnosis for CVD at a hospital includes echocardiography cardiac ultrasound, electrocardiogram (ECG) inspection, the magneto cardiogram (MEG) and the coronary angiography inspection. However, the majority of inspections are invasive and unreliable [3,4].

Nowadays, early diagnosis of CVD has been realized after the introduction of a method measuring carotid arterial intima-media thickness by ultrasound that can prescreen the CVD. The thickness of the common carotid artery (CCA) has been identified to be related with CVD in various studies and has become one of the typical cardiovascular risk factors together with hypertension of blood, hyperlipidemia, smoking and diabetes mellitus. It is also known as an independent predictor of CVD [5,6,7].

The correlation between the autonomic nervous system and mortality of CVD including sudden cardiac death has been proved as a significant factor during the past 30 years. The development of indicators that can evaluate quantitatively the activity of the autonomic nervous system is urgently required, and heart rate variability (HRV) has been one of the most promising indicators. The wide variety of linear and nonlinear characteristics of HRV have been studied as indicators to improve the diagnostic accuracy. Dynamic stability of the cardiovascular system is achieved by the heart rate’s quick reactions and automatically adjusting to internal or external stimuli [8,9,10].

Heart rate changes are complexly reacted to these stimuli and are stimulated intensively by the two systems: the sympathetic nervous system and the parasympathetic nervous system. The activation of the sympathetic nervous system slows the heart rate and the activation of the parasympathetic nervous system increases the speed of the heart beat with the growth of contractility. By this difference, the two systems of the autonomic nervous systems operate on different frequencies, and it allows us to know whether the variability of heart rate changes is dominantly related to the sympathetic nervous system or the parasympathetic one [11]. The level of sympathetic and parasympathetic nerve activity can be evaluated quantitatively through linear and/or nonlinear feature analysis. For instance, if we analyze the variability of the heart rates of patients with coronary artery disease (CAD), the regulatory role of the autonomic nervous system is reduced, and the risk of death in the case of acute myocardial infarction is reduced when the autonomic nervous system is actively interact. However, there is a problem with not directly introducing the developed algorithms and feature vectors standardized for western patients because it is reportedly known that feature vectors may cause different diagnosis results due to racial pathological and physiological deviations.

Therefore, the carotid artery (CA) and HRV diagnostic feature vectors need to be analyzed to ensure the reliability and early diagnosis for CVD of South Koreans. In order to analyze diagnostic feature vectors for South Korean CVD patients, we proposed an extraction methodology of multiple feature vectors from CA and HRV. The details of the proposed methods and how to perform the steps for the diagnosis of CVD are as follows:

(1)

Extracting diagnostic feature vectors: the feature vectors significant to disease diagnosis are extracted by applying image processing to the CA images taken by ultrasound;

(2)

Evaluation on feature vector and classification method for diagnosis of CVD: some diagnostic feature vectors that are significant by types of CVD through statistical analysis of the data should be selected as a preprocessing step. Classification or prediction algorithm is applied to the selected diagnostic feature vectors for CVD, and the vectors were evaluated.

For effective understanding of the paper, the paper is organized as follows. CA imaging and HRV analysis through complex diagnostic feature vector extraction process will be explained in Section 2 and Section 3, respectively. In Section 4, a feature vector selection process as pre-processing steps and experimental evaluations results using classification of forecasting techniques for disease diagnosis will be described. Finally, concluding remarks will be shown in Section 5.

2. Carotid Artery Scanning and Image Processing

The CA consists of common carotid artery (CCA), carotid bifurcation (BIF), internal carotid artery (ICA), and external carotid artery (ECA). The intima-media thickness (IMT) of the carotid can be measured at the far wall CCA region 10 mm proximal to bifurcation of carotid rather than the ICA or CA or BIF itself (see Figure 1). Intima is the high-density band-shaped and the media looks like a band with a low brightness between intima and adventitia. Adventitia generally has the brightest pixel value and it corresponds to the thick part below the intima-media having the high brightness. In addition, since the intima is thinnest among the three floors and its brightness is so similar to that of media, the endometrial thickness is difficult to detect. Thus, In general, It is sufficient to measure IMT including the intima and media.

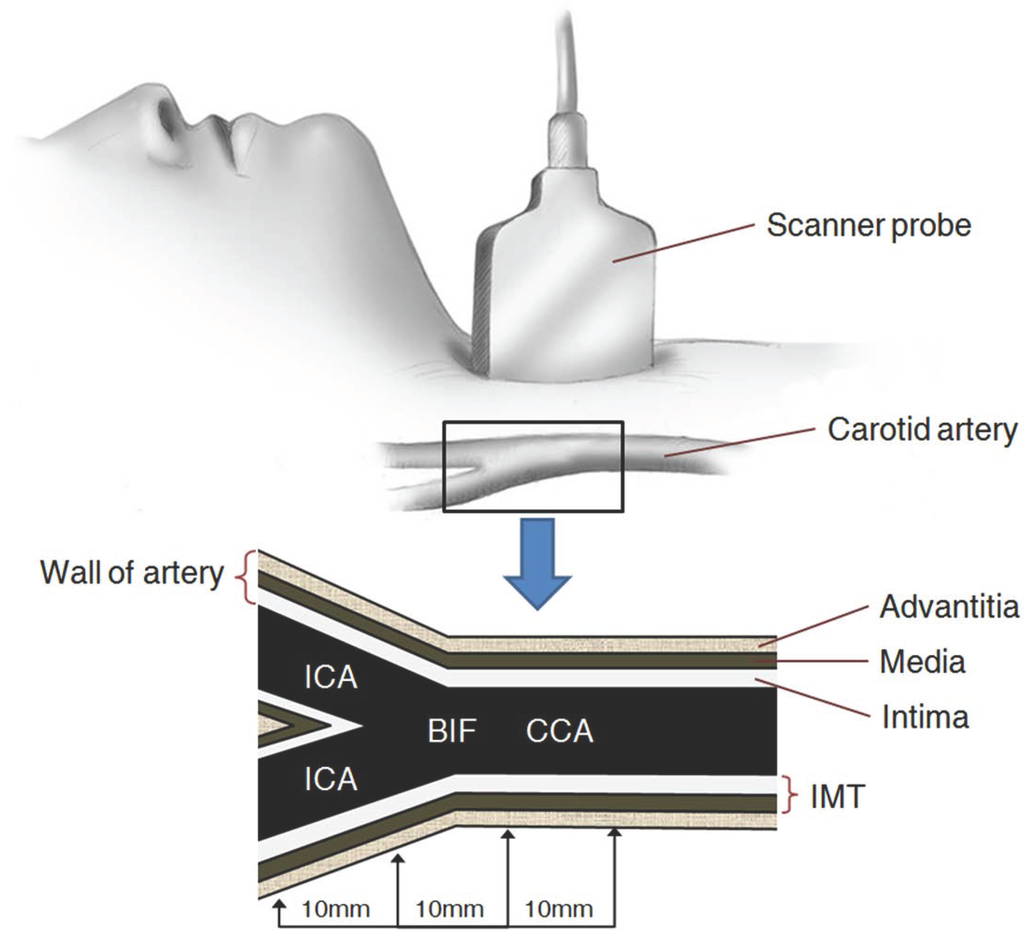
Figure 1. The measurement of intima-media thickness in the carotid artery using ultrasonograph. IMT: intima-media thickness, CCA: common carotid artery, BIF: bifurcation, ICA: internal carotid artery.

The Common Carotid Arterial scanning using a high-resolution ultrasound system can acquire the image by scanning the right side ICA longitudinally at R-peak of the electrocardiogram. At first, we load the ultrasound image of target common carotid arterial scanning from computer hard-disc memory in order to measure the carotid artery intima-media. Next, the calibration factor of pixel length is determined using electronic range caliper in a B-mode ultrasound system. After we select at least the 10 mm–long image of the Region of Interest (ROI) picture at 10 mm proximal around the area of BIF transition to CCA, we can evaluate the quality of the selected ROI image and remove speckle noise. After obtaining the edge image by applying the edge detection algorithm, IMT is measured [12].

After the acquisition of carotid image and IMT measurement, all of the diagnostic feature vectors for CVDs are extracted. The feature vector extraction will be performed in the following eight steps [13]:

(1)

The ROI image with $64\times 100$ pixels is acquired by defining the area of two ’+’ markers (from $\overline{)\mathrm{a}}$ to $\overline{)\mathrm{b}}$) on the image of the carotid IMT in Figure 2a;

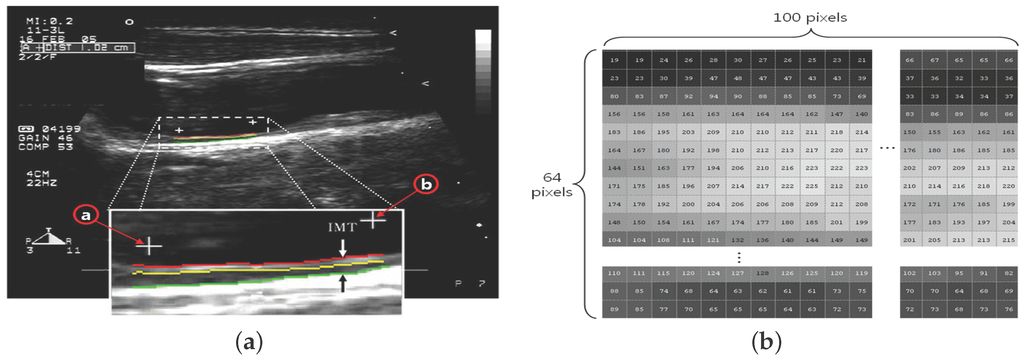
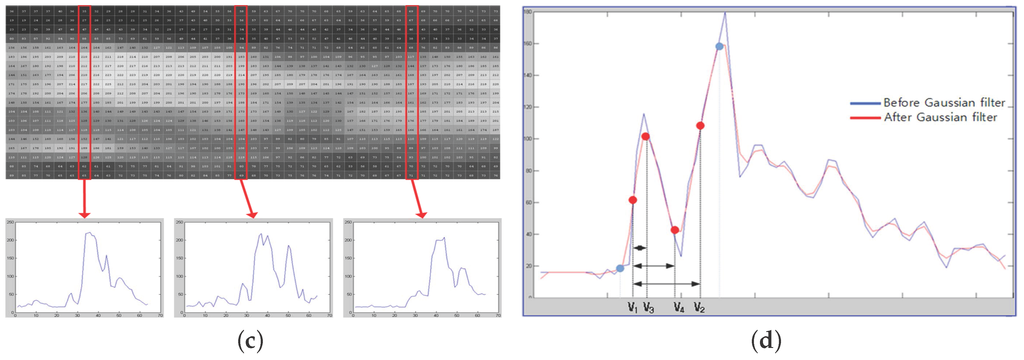Figure 2. Carotid artery image processing and feature vector extraction step. (a) acquisition of carotid image and IMT measurement; (b) the acquired Region of Interest (ROI) image ($64\times 100$ pixels); (c) graph for the trend of variation of each vertical line; and (d) computation of four basic feature vectors (points).

(2)

Each pixel is expressed by a number in the range of 0–$255\left(2^8\right)$ for the brightness (Figure 2b);

(3)

The trend of variation is shown in a graph in a vertical line (Figure 2c);

(4)

Thirty vertical lines are randomly selected as samples among a total of 100 vertical lines (Figure 2d);

(5)

The difference between $V_1$ and $V_2$ is calculated using the 30 random samples of vertical lines;

(6)

Only IMT $(V_1-V_2)$ values within one sigma in Gaussian distribution are extracted;

(7)

Four basic feature vectors are extracted and an average value is calculated;

(8)

The other 18 additional feature vectors are extracted through a calculation using the four basic feature vectors in Figure 2d, and the mean value is obtained.

All the feature vectors extracted from carotid image and IMT measurement are described in Table 1.

Table 1. All the extracted vectors of carotid arteries.

Feature vector	Index	Description
Carotid basic feature	$V_1$	Starting point of intima
	$V_2$	Starting point of adventitia
	$V_3$	Max. point between $V_1$ and $V_2$
	$V_4$	Min. point between $V_1$ and $V_2$
Carotid calculated feature	$V_5$	Distance between $V_1$ and $V_2$
	$V_6$	Area of the vector $V_5$
	$V_7$	Value of the point $V_3$
	$V_8$	Distance between $V_1$ and $V_3$
	$V_9$	Area of the vector $V_8$
	$V_{10}$	Value of the point $V_4$
	$V_{11}$	Distance between $V_1$ and $V_4$
	$V_{12}$	Area of the vector $V_{11}$
	$V_{13}$	Slope between $V_1$ and $V_3$
	$V_{14}$	Slope between $V_3$ and $V_4$
	$V_{15}$	Slope between $V_1$ and $V_2$
	$V_{16}$	$V_3$ - $V_1$
	$V_{17}$	$V_3$ - $V_4$
	$V_{18}$	Standard deviation between $V_1$ and $V_4$
	$V_{19}$	Variance between $V_1$ and $V_4$
	$V_{20}$	Skewness between $V_1$ and $V_4$
	$V_{21}$	Kurtosis between $V_1$ and $V_4$
	$V_{22}$	Moment between $V_1$ and $V_4$
IMT	$V_{23}$	Intima-media thickness

3. Linear and Non-Linear Feature Vectors of HRV

Extracting the linear and non-linear indicators of HRV, the main diagnostic indices for CVDs such as angina pectoris or acute coronary syndrome, starts from ECG. The ECG signal is measured during five minutes using a Lead II channel. The sampling frequency obtained from ECG signals with such measurements show 500 Hz, and ectopic beats and artifacts are removed. HRV is the physiological phenomenon of variation in the time interval between heartbeats. It is measured by the variation in the beat-to-beat interval. Other terms used are RR variability. where R is a point corresponding to the peak of the QRS complex which is the name for the combination of three of the graphical deflections seen on a typical ECG. RR is the interval between successive Rs. To analyze HRV, all RR intervals of the ECG signal are calculated by Thomkin’s algorithm [14], and time-series data is generated as shown in Figure 3. RR interval times-series data are re-sampled at a rate of 4 Hz in order to extract the indicators in the frequency domain, which is one of the linear analysis methods. We extract linear feature vectors in the time and frequency domain and extract non-linear feature vectors of HRV. The literature on HRV feature vector extraction was described in detail in [15].

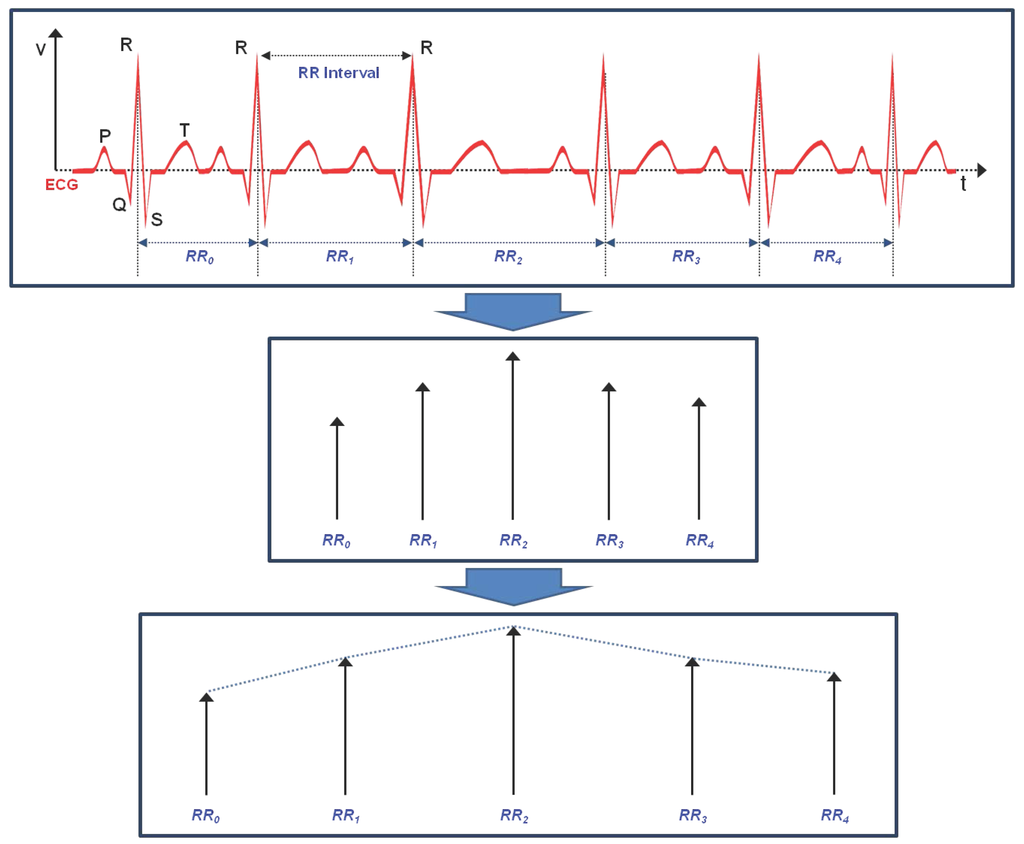
Figure 3. RR interval extraction process in electrocardiogram (ECG) signals.

3.1. Linear Feature Vectors in Time Domain

Time domain statistics are generally calculated on RR intervals without re-sampling. In a continuous ECG record, each QRS complex was detected and the RR intervals or the instantaneous heart rates were determined. RR intervals is denoted by $R{R}_n$, with $n=0,...,N$. For practical purposes, the following basic properties are true: $E\left[R{R}_n\right]=E\left[R{R}_{n+m}\right]$ and $E\left[R{R}_n^2\right]=E\left[R{R}_{n+m}^2\right]$. The standard time domain measures of HRV are as follows [16].

The standard deviation of the RR intervals (SDRR) is often employed as a measure of overall HRV. It is defined as the square root of the variance of the RR intervals as follows:

$$SDRR=\sqrt{E\left[R{R}_n^2\right]-{\overline{RR}}^2},$$

(1)

where the mean of RR interval is denoted by $\overline{RR}=E\left[R{R}_n\right]$. The standard deviation of the successive differences of the RR intervals (SDSD) is an important measure of short-term HRV. It is defined as the square root of the variance of the sequence $\Delta R{R}_n=R{R}_n-R{R}_{n+1}$ (the delta-RR intervals):

$$SDSD=\sqrt{E[\Delta R{R}_n^2]-{\overline{\Delta R{R}_n}}^2}.$$

(2)

Where, $\overline{\Delta R{R}_n}=E\left[R{R}_n\right]-E\left[R{R}_{n+1}\right]=0$ for stationary intervals. This means that the root mean square (rms) of the successive differences is statistically equivalent to the standard deviation of the successive differences as follows:

$$SDSD=rmsSD=\sqrt{E\left[{(R{R}_n-R{R}_{n+1})}^2\right]}.$$

(3)

Linear feature vectors in time domains include the mean of RR intervals ($\overline{RR}$), the standard deviation of the RR Intervals (SDRR), and the standard deviation of successive differences of the RR intervals (SDSD).

3.2. Linear Feature Vectors in Frequency Domain

The feature vectors in frequency mode use power spectral density (PSD) analysis and extract seven types of feature vectors as follows [13,15]:

(1)

Total power ($TP$), from 0 Hz to 0.4 Hz;

(2)

Very Low Frequency ($VLF$) power, from 0 Hz to 0.04 Hz;

(3)

Low Frequency ($LF$) power, from 0.04 Hz to 0.15 Hz;

(4)

High Frequency ($HF$) power, from 0.15 Hz to 0.4 Hz;

(5)

Normalized value of $LF$ ($nLF={\displaystyle \frac{(TP-VLF)}{LF}}\times 100$);

(6)

Normalized value of $HF$ ($nHF={\displaystyle \frac{(TP-VLF)}{HF}}\times 100$);

(7)

The ratio of $LF$ and $HF$ ($LF/HF$).

Diagnostic feature vector employs only three vectors; $nLF$ to reflect sympathetic activity, $nHF$ to show parasympathetic activity and $LF/HF$ ratio to mirror the sympathovagal balance (see Table 2).

Table 2. Diagnostic indicators from heart rate variability (HRV) analysis.

Feature Vector			Description
$\begin{array}{c}\mathrm{Linear}\\ \mathrm{features}\end{array}$	$\begin{array}{c}\mathrm{Frequency}\\ \mathrm{domain}\end{array}$	$nLF$	Normalized low frequency power ($nLF={\displaystyle \frac{(TP-VLF)}{LF}}\times 100$).
		$nHF$	Normalized high frequency power ($nHF={\displaystyle \frac{(TP-VLF)}{HF}}\times 100$).
		$LF/HF$	The ratio of low- and high-frequency power.
	$\begin{array}{c}\mathrm{Time}\\ \mathrm{domain}\end{array}$	$\overline{RR}$	The mean of RR intervals.
		SDRR	Standard deviation of the RR intervals.
		SDSD	Standard deviation of the successive differences RR intervals.
$\begin{array}{c}\mathrm{Nonlinear}\\ \mathrm{features}\end{array}$		$SD1$	Standard deviation of the distance of $RR\left(i\right)$ from the line $y=x$ in the Poincare
		$SD2$	Standard deviation of the distance of $RR\left(i\right)$ from the line $y=-x+2\overline{RR}$ in the Poincare
		$SD2/SD1$	The ratio $SD2$ to $SD1$
		$SD1·SD2$	$SD1\times SD2$
		$ApEn$	Approximate Entropy
		H	Hurst Exponent
		$f_{\alpha }$	1/f scaling of Fourier spectra

3.3. Poincare Plot of Nonlinear Feature Vectors

The Poincare plot may be analyzed quantitatively by fitting an ellipse to the plotted shape. The center of the ellipse is determined by the average RR intervals. $SD1$ refers to the standard deviation of the distances of points from the $y=x$ axis, $SD2$ stands for the standard deviation of the distances of points from $y=-x+2\overline{RR}$ axis, where $\overline{RR}$ is the mean of RR intervals as shown in Figure 4. We also compute the features, $SD2/SD1$, and $SD1·SD2$, describing the relationship between $SD1$ and $SD2$ in our study.

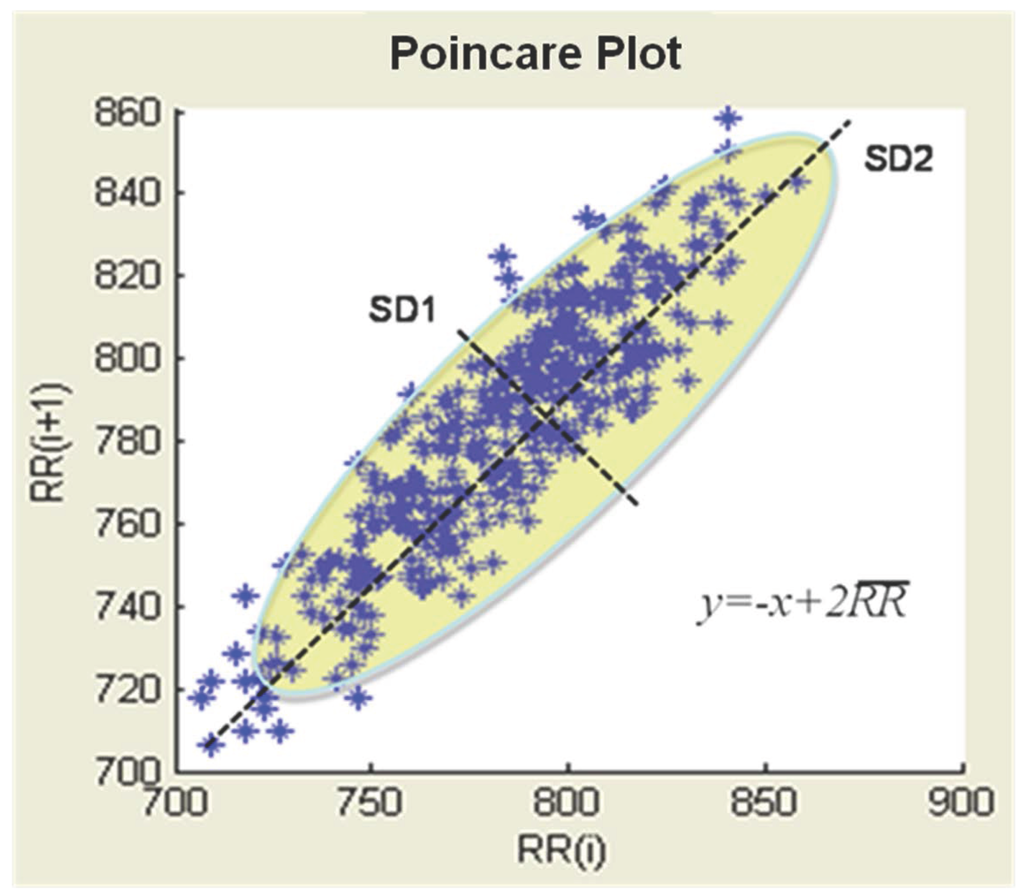
Figure 4. Diagnostic indicators in a Poincare plot.

3.4. A Non-Linear Vector: Approximate Entropy (ApEn)

Defined as the rate of information production, entropy quantifies the chaos of motion. $ApEn$ quantifies the regularity of time series, and is also called a "regularity statistic". It is represented as a simple index for the overall complexity and predictability of each time series. In this study, $ApEn$ quantifies the regularity of the RR intervals. The more regular and predictable the RRI series, the lower will be the value of $ApEn$. First of all, we reconstructed the RRI time series in the n-dimensional phase space using Takens’ theorem [17]. Takens suggested the following time delay method for the reconstruction of the state space as follows:

$$D_t=[RR\left(t\right),RR(t+\tau ),...,RR(t+(n-1)\tau )],$$

(4)

where n is the embedding dimension and τ is the time delay. In this study, the optimal value of τ was 10. The mean of the fraction of patterns with length m that resembles the pattern with the same length beginnings at interval i is defined by

$${\Phi }^m\left(r\right)=\frac{1}{N-m+1}\sum _{i=1}^{N-m+1}ln\left[\frac{\text{number}\text{of}\left|D_m\left(j\right)-D_m\left(i\right)\right|<r}{N-m-1}\right].$$

(5)

In the equation above, $D_m\left(i\right)$ and $D_m\left(j\right)$ are state vectors in the embedding dimension m. Given N data points, we can define $ApEn$ as $ApEn(m,r,N)={\varphi }^m\left(r\right)-{\Phi }^{m+1}\left(r\right)$, where $ApEn$ estimates the logarithmic likelihood that the next intervals after each of the patterns will differ. In general, the embedding dimension m, and the tolerance, r are fixed at $m=2$ and $r=0.2\times SD$ in physiological time series data.

3.5. Hurst Exponent (H) Non-Linear Vector)

The Hurst Exponent H is the measure of the smoothness of a fractal time series based on the asymptotic behavior of the rescaled range of the process. H is defined as, $\frac{log(R/S)}{log\left(T\right)}$, where T is the duration of the sample of data and $R/S$ is the corresponding value of the rescaled range. If $H=0.5$, the behavior of the time series is similar to a random walk. If $H<0.5$, the time series covers less distance than a random walk. If $H>0.5$, the time series covers more distance than a random walk.

3.6. Exponent α of the $1/f$ Spectrum ($f_{\alpha }$) Non-Linear Vector

Self-similarity is the most distinctive property of fractal signals. Fractal signals usually have a power spectrum of the inverse power law form, $1/f^{\alpha }$, where f is frequency, and the amplitude of the fluctuations is small at high frequencies and large at low frequencies. The exponent α is calculated by a first least-squares fit in a $log-log$ spectrum, after finding the power spectrum from RR intervals. The exponent is clinically significant because it has different values for healthy and heart rate failure patients.

All feature vectors extracted from linear and non-linear analysis of HRV are described in Table 2.

4. Evaluation of Diagnostic Feature Vectors

All the data used in our experiment were provided as a sample by the Bio-signal Research Center of the Korea Research Institute of Standards and Science. In this experiment, after coronary arteriography was performed for each of the 214 cardiovascular patients, patients showing more than 50% of stenosis are categorized as Coronary Artery Disease (CAD), whereas other patients having less than 50% stenosis are designated as the control group. Furthermore, CAD patients are also re-sorted by cardiologists into two groups, Angina Pectoris (AP) and Acute Coronary Syndrome (ACS). Clinical characteristics of the studied patients are shown in Table 3.

Table 3. Clinical characteristics of the study subjects.

Group	N	Sex (Male/Female)	Age (Years)
AP	102	50/52	59.98±8.41
Control	72	40/46	56.70±9.23
ACS	40	18/22	58.94±8.68

* AP: Angina Pectoris; ACS: Acute Coronary Syndrome.

4.1. Data Preprocessing

The extracted vectors from carotid imaging and HRV are evaluated in order to determine whether those vectors can be representative indicators of cardiovascular diseases or not by applying typical classification or prediction models of machine learning.

As a pre-processing step, feature selection method is used for eliminating the improper information to disease diagnosis. The performing steps are composed of feature ranking and feature selection steps. Selection algorithms evaluate the redundancy in feature vectors and prediction capability of each vector. Feature ranking considers one feature at a time to see how well each feature alone predicts the target class. The features are ranked according to a user-defined criterion. Available criteria depend on the measurement levels of the target class and feature. In the feature vector selection problem, a ranking criterion is used to find feature vectors that discriminate between healthy and diseased patients. The ranking value of each feature is calculated as ($1-p$), where p is the p-value of appropriate statistical tests of association between the candidate features and the target class. All diagnostic feature vectors are continuous-valued, and we use p-values based on F-statistics. This method is to perform a one-way ANOVA F-test [18] for each continuous feature.

Let C denote a target class with J categories, N be a total number of cases and X is the feature under consideration with I categories. The p-value based on F-statistics is calculated by;

$$\begin{array}{c}\hfill \begin{array}{ccc}\hfill Pr\left(F\right(J-1,N-J)>F),& & \hfill F=\frac{\frac{{\displaystyle \sum _{j=1}^J}{N}_j(\overline{x_j}-\tilde{x}{)}^2}{(J-1)}}{\frac{{\displaystyle \sum _{j=1}^J}(N_j-1)s_j^2}{(N-1)}},\end{array}\end{array}$$

(6)

where $N_j$ is the number of cases with $C=j$, $\overline{x_j}$ is the mean of feature X for target class $C=j$, $s_j^2$ is the sample variance of feature X for class $C=j$, $\tilde{x}$ is the grand mean of feature X and $F(J-1,N-J)$ is a random variable follows a F-distribution with degrees of freedom $J-1$ and $N-J$. If the denominator for a feature is zero, set the p-value = 0 for the feature. Features are ranked by p-value in ascending order. In this study, any p-value less than 0.1 significant test threshold was accepted as significant. A feature relevance score ($1-p$) is calculated. The features having values less than 0.1 indicate that they have low score and therefore they are removed. Afterwards, this subset of features is presented as input to the classification methods. We perform feature selection only once for each dataset and then different classification methods are evaluated. The results of feature selection and evaluation for each dataset (CA, HRV and CA+HRV) are described in Table 4.

Table 4. Selected feature vectors of carotid artery (CA), HRV and CA+HRV.

Rank	CA		HRV		CA+HRV
	Feature	RS($\mathbf{1}\mathbf{-}\mathit{p}$)	Feature	RS($\mathbf{1}\mathbf{-}\mathit{p}$)	Feature	RS($\mathbf{1}\mathbf{-}\mathit{p}$)
1	$V_3$	1.000	$SD2$	0.999	$V_3$	1.000
2	$V_{10}$	1.000	$SDRR$	0.998	$V_{10}$	1.000
3	$V_{18}$	0.998	$f_{\alpha }$	0.993	$SD2$	0.998
4	$V_2$	0.997	$SD2/SD1$	0.991	$SDRR$	0.997
5	$V_8$	0.997	$SD1$	0.986	$f_{\alpha }$	0.986
6	$V_{21}$	0.995	H	0.984	$SD2/SD1$	0.985
7	$V_{23}$	0.989	$SD1\times SD2$	0.975	$SD1$	0.979
8	$V_{20}$	0.989	$nLF$	0.968	$V_2$	0.979
9	$V_4$	0.975	$nHF$	0.967	$V_{18}$	0.965
10	$V_{11}$	0.968	$ApEn$	0.961	$SD1\times SD2$	0.965
11	$V_6$	0.968	$\overline{RR}$	0.958	H	0.965
12	$V_{16}$	0.967	$LF/HF$	0.955	$V_8$	0.963
13	$V_{13}$	0.966			$V_{21}$	0.962
14	$V_{19}$	0.962			$V_{23}$	0.962
15	$V_5$	0.961			$nLF$	0.960
16	$V_{17}$	0.953			$nHF$	0.958
17					$ApEn$	0.955
18					$V_{20}$	0.954
19					$V_{11}$	0.952
20					$V_{16}$	0.951

* CA: Carotid Artery, HRV: Heart Rate Variability, RS: Relevance score.

4.2. Verification of Feature Vectors Using Classification Methods

In order to determine whether the combined 20 feature vectors extracted from both CA and HRV (indicated as CA+HRV) can be effective diagnostic indicators of CVDs than feature vectors of CA and HRV separately, the famous classification or prediction method of machine learning is used as the way of evaluation. The classification method generates and compares several models including Neural Networks (NNs), Bayesian classifiers, decision tree induction model, Support Vector Machine (SVM) and Classification Based on Multiple Association Rules (CMAR).

4.2.1. Neural Networks

The NNs method uses back propagation to classify instances [19]. NNs are composed of nodes (neurons) and their interconnections. In general, input values are converted into values ranging from zero to one. Each input node is connected to an output node through the link with weight value. We use the back-propagation multi-layer perceptron (MLP) consisting of three layers: input, hidden, and output layers. An NNs learns through changes in the weight of each node, and its goal is to determine the weight w that minimizes the sum of the squared error between target class y and predicted class $\widehat{y}$, which is calculated using in the following equation below:

$$\begin{array}{c}\hfill \begin{array}{c}\hfill E\left(w\right)=\frac{1}{2}\sum _{i=1}^N{(y_i-\widehat{y})}^2.\end{array}\end{array}$$

(7)

4.2.2. Bayesian Network

The Bayesian Network chooses the highest posterior probability class using the prior probability computed from the training data set. The Naïve Bayes classifier assumes that the effect of an attribute on a given class is independent of the values of the other attributes. This assumption is called class conditional independence. However, attribute values of CA and HRV data may not be entirely independent from each other. In order to address this problem, we considered a set of extended Bayesian classifiers known to work well with correlated data, including Tree Augmented Naïve Bayes (TAN) [20].

4.2.3. Decision Tree Induction (C4.5)

C4.5 [21] is one of the most popular decision trees. A decision tree can be viewed as a partitioning of the instance space. Each partition, called a leaf, represents a number of similar instances that belong to the same class. C4.5 is also a decision tree generating algorithm based on the ID3 algorithm. It contains several improvements especially needed for software implementation. These improvements contain: (1) choosing an appropriate attribute selection measure; (2) handling training data with missing attribute values; (3) handling attributes with differing costs; and (4) handling continuous attributes. In order to perform experiments, we used the j48.part method that implemented the C4.5 algorithm [19].

4.2.4. Support Vector Machine (SVM)

The SVM is basically a two-class classifier and can be extended for multi-class classification. The main reason for interest in support vector and kernel methods is their flexibility and remarkable resistance to overfitting, and their simplicity and theoretical elegance, all appealing to practitioners as well as theoreticians. In our model, each object is mapped to a point in a high dimensional space, each dimension corresponding to features. The coordinates of the point are the frequencies of the features in the corresponding dimensions. The SVM learns, in the training step, the maximum-margin hyper-planes separating each class. In the testing step, it classifies a new object by mapping it to a point in the same high-dimensional space divided by the hyper-plane learned in the training step. For our experiments, we applied the sequential minimal optimization (SMO) algorithm by using the radial basis function (RBF) kernel for training a support vector classifier [19].

4.2.5. Classification Based on Multiple Association Rules (CMAR)

CMAR classifiers [22] extend CBA by using more than one rule to classify a new case. It is a two-step process: (1) rule generation and (2) classification. In rule generation, CMAR uses an approache based on the FP-growth method [23] to find the complete set of rules satisfying the minimum confidence and minimum support thresholds. FP-growth uses a tree structure called FP-tree, which retains the item set association information contained in the given data set D. CMAR uses an enhanced FP-tree that maintains the distribution of various class labels among tuples satisfying frequent item sets. From the FP-tree, created rules can be generated immediately. Thus, CMAR allows rule generation and frequent item set mining in a single step. Once a rule is generated, it is stored in a CR-tree. The CR-tree is a prefix tree data structure. Its function is to store and retrieve rules efficiently and prune rules based on confidence, correlation and database coverage. Whenever a rule is inserted into the CR2-tree, it starts a pruning rule. Highly specialized rules with low confidence can be pruned if more generalized rules with higher confidence exist. CMAR also prunes rules based on ${\chi }^2$ and database coverage [22,24].

In our experiment, four classifiers, except for the CMAR classifier, utilize the following source code provided by the Java WEKA project (University of Waikato, Hamiton, New Zealand) [19]. The CMAR classifier utilizes CMAR software provided by the LUCS-KDD group (University of Liverpool, Liverpool, England) [25].

• weka.classifiers.bayes.BayesNet (TAN)
• weka.classifiers.tree.j48.J48 (C4.5)
• weka.classifiers.funtions.SMO (SVM)
• weka.classifiers.functions.MultilayerPerceptron (MLP)

Through the statistical analysis of all the diagnostic feature vectors listed in Table 1 and Table 2, we apply each classification model to the data set that passed the feature selection step. We build the above classifiers from the preprocessed training data. Accuracy was obtained by using the methodology of stratified 10-fold cross-validation (CV-10) for three classes. To evaluate classification performance with respect to the number of instances and class labels, we used a confusion matrix. We also used $Precision$, $Recall$, F-$measure$ and $Accuracy$ to evaluate the classifiers’ performance for analyzing our training sets with imbalanced class distribution. Formal definitions of these measures are given in the equations below [15,26,27]:

$$\begin{array}{c}\hfill \begin{array}{cc}& Precision=\frac{TP}{TP+FP}\hfill \\ & Recall=\frac{TP}{TP+FN}\hfill \\ & F-measure=\frac{2\times Precision\times Recall}{Precision+Recall}\hfill \\ & Accuracy=\frac{TP+TN}{TP+FP+TN+FN},\hfill \end{array}\end{array}$$

(8)

where, $TP$ is True Positive, $TN$ is True Negative, $FP$ is False Positive, and $FN$ is False Negative in the confusion matrix. In the performance evaluation with $Precision$, $Recall$ and $F-measure$, Table 5 shows the features used for each data set which are CA, HRV and CA+HRV (combining CA and HRV).

Table 5. A description of summary results (all features).

Classifier	CA			HRV			CA+HRV			Class
	(Using 16 Features)			(Using 12 Features)			(Using 20 Features)
	Precision	Recall	${\mathit{F}}_{\mathbf{1}}$	Precision	Recall	${\mathit{F}}_{\mathbf{1}}$	Precision	Recall	${\mathit{F}}_{\mathbf{1}}$
$\begin{array}{c}\mathrm{NNs}\\ \left(\mathrm{MLP}\right)\end{array}$	0.701	0.754	0.727	0.681	0.749	0.713	0.763	0.913	0.831	AP
	0.707	0.714	0.711	0.696	0.713	0.704	0.835	0.749	0.790	Control
	0.519	0.409	0.457	0.480	0.336	0.395	0.833	0.568	0.675	ACS
$\begin{array}{c}\mathrm{BayesNet}\\ \left(\mathrm{TAN}\right)\end{array}$	0.627	0.782	0.696	0.589	0.749	0.659	0.660	0.871	0.751	AP
	0.669	0.541	0.598	0.632	0.532	0.578	0.768	0.553	0.643	Control
	0.595	0.425	0.496	0.501	0.297	0.373	0.725	0.499	0.591	ACS
C4.5	0.656	0.716	0.685	0.669	0.727	0.697	0.734	0.870	0.796	AP
	0.722	0.706	0.714	0.727	0.711	0.719	0.846	0.742	0.790	Control
	0.488	0.394	0.436	0.463	0.378	0.416	0.645	0.482	0.552	ACS
SVM	0.756	0.810	0.782	0.685	0.804	0.740	0.872	0.854	0.863	AP
	0.795	0.735	0.764	0.803	0.745	0.773	0.864	0.926	0.894	Control
	0.621	0.592	0.606	0.376	0.258	0.305	0.718	0.664	0.690	ACS
CMAR	0.719	0.814	0.764	0.617	0.818	0.703	0.839	0.945	0.889	AP
	0.669	0.769	0.716	0.702	0.774	0.736	0.836	0.845	0.840	Control
	0.694	0.462	0.554	0.542	0.235	0.328	0.855	0.692	0.765	ACS

* $F_1$: F-$measure$; NNs: Neural networks; MLP: Multi-layer perceptron; BayesNet: Bayesian network; TAN: Tree augmented naïve bayes; C4.5: Decision tree induction; SVM: Support vector machine; CMAR: Classification based on multiple association rules.

The parameters of the five classification methods were set as follows. For the CMAR algorithm, the minimum support was set to 0.4%, the minimum confidence to 70%, and the database coverage was set to 3.75 (critical threshold for a 5% “significance” level, assuming degree of freedom is equivalent to one). For the SVM, the soft margin allowed errors during training. We set 0.1 for the two-norm soft margin value. The Neural Networks (MLP), Bayesian classifier (TAN) and C4.5 parameters were default values.

In addition, summarizing classifiers’ performance with a single number would make it more convenient to compare the performance of diffenent classifiers. This can be done using a performance metric such as accuracy and Root Mean Squared Error (RMSE). The results of RMSE and the accuracy for each classifier are shown in Table 6 and Figure 5, respectively.

Table 6. A comparison of the classifiers’ root mean squared error (RMSE).

Classifier	CA (Using 16 Features)	HRV (Using 12 Features)	CA+HRV (Using 20 Features)
NNs (MLP)	0.405	0.442	0.293
BayesNet (TAN)	0.443	0.509	0.395
C4.5	0.422	0.426	0.342
SVM	0.301	0.437	0.216
CMAR	0.355	0.472	0.201

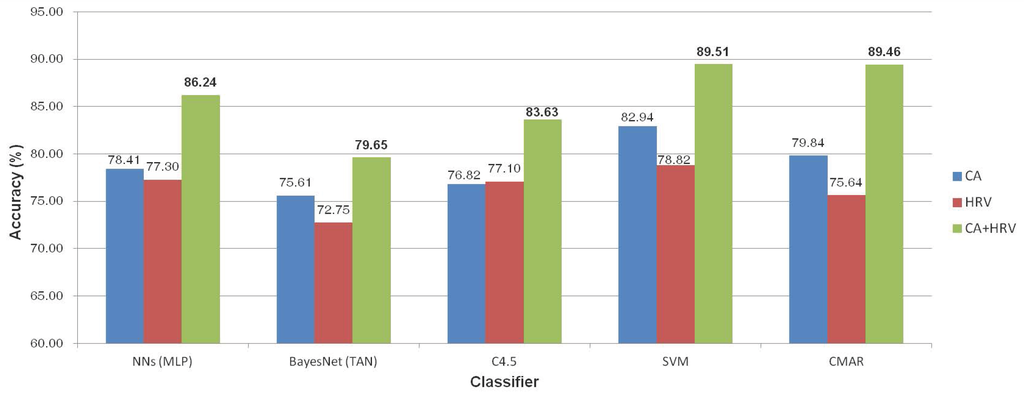
Figure 5. Accuracy comparison.

According to the result, shown in Figure 5, the highest accuracy for CA (16 features) and HRV (12 features) is 82.94% and 78.82%, respectively. However, both accuracies are lower than the highest accuracy rate, 89.51%, obtained from various features of CA+HRV (20 features), considering CA and HRV separately. Therefore, we anticipated that the use of the multi-features for CA+HRV will produce more effective diagnostic indicators than using features of CA and HRV. In order to address this expectation, we used the confusion matrix of classification results for each feature in Table 7. As SVM and CMAR give higher accuracy in comparison to other methods, we apply these two best classifiers in the following experiment. Table 7 records the hit rates (correctly classified instance rate) of SVM and CMAR in a confusion matrix, and the results are reasonably good. The hit rates of SVM for AP, Control and ACS classes are 85.42%, 92.55% and 66.39%. The hit rates of CMAR are also 94.51%, 84.51% and 69.23%, respectively. In particular, ACS class can not be correctly separated from AP class when we used features for each CA and HRV (see Table 7). These results indicate that using the multiple features of CA+HRV gives more effective results in discriminating between the groups.

Table 7. Confusion matrix for SVM and CMAR (use of each feature for CA, HRV and CA+HRV).

Features	Classifier	Actual Class	Predicted Class
			AP (%)	Control (%)	ACS (%)
$\begin{array}{c}\mathbf{CA}\\ \left(16\mathrm{features}\right)\end{array}$	SVM	AP	81.01	6.29	12.7
		Control	24.4	73.51	2.09
		ACS	22.66	18.12	59.22
	CMAR	AP	81.37	7.84	10.79
		Control	18.04	76.89	5.07
		ACS	26.92	26.92	46.16
$\begin{array}{c}\mathbf{HRV}\\ \left(12\mathrm{features}\right)\end{array}$	SVM	AP	80.4	6.05	13.55
		Control	20.85	74.52	4.63
		ACS	56.66	17.5	25.84
	CMAR	AP	81.82	7.28	10.9
		Control	18.13	77.43	4.44
		ACS	53.94	22.57	23.49
$\begin{array}{c}\mathbf{CA}+\mathbf{HRV}\\ \left(20\mathrm{features}\right)\end{array}$	SVM	AP	85.42	4.6	9.98
		Control	7.1	92.55	0.35
		ACS	19.06	14.55	66.39
	CMAR	AP	94.51	1.57	3.92
		Control	9.27	84.51	6.22
		ACS	16.39	14.38	69.23

5. Conclusions

This paper suggests multiple diagnostic feature vectors with the CA and HRV analyses for the purpose of more accurate prediction and early diagnosis of CVD, recently growing at a rapid speed. Moreover, we performed experiments and evaluations to verify the reliability of the prediction system and test the significance of diagnostic feature vectors. According to the results of experiments, 20 types of feature vectors are determined as the essential elements for disease diagnosis and SVM and CMAR show an excellent result in terms of the appropriate classification or prediction algorithm. These kind of complex diagnostic indicators would be useful for the automatic diagnosis of CVDs in Korea. The limitation of this paper is in the fact that the sample data provided by a certain organization without collecting sufficient data from the domestic hospitals. Data accumulation of various ages and genders is required to secure high reliability of the developed systems and play a reference database role in this disease area.