Neutrino Signals in Electron-Capture Storage-Ring Experiments
Abstract
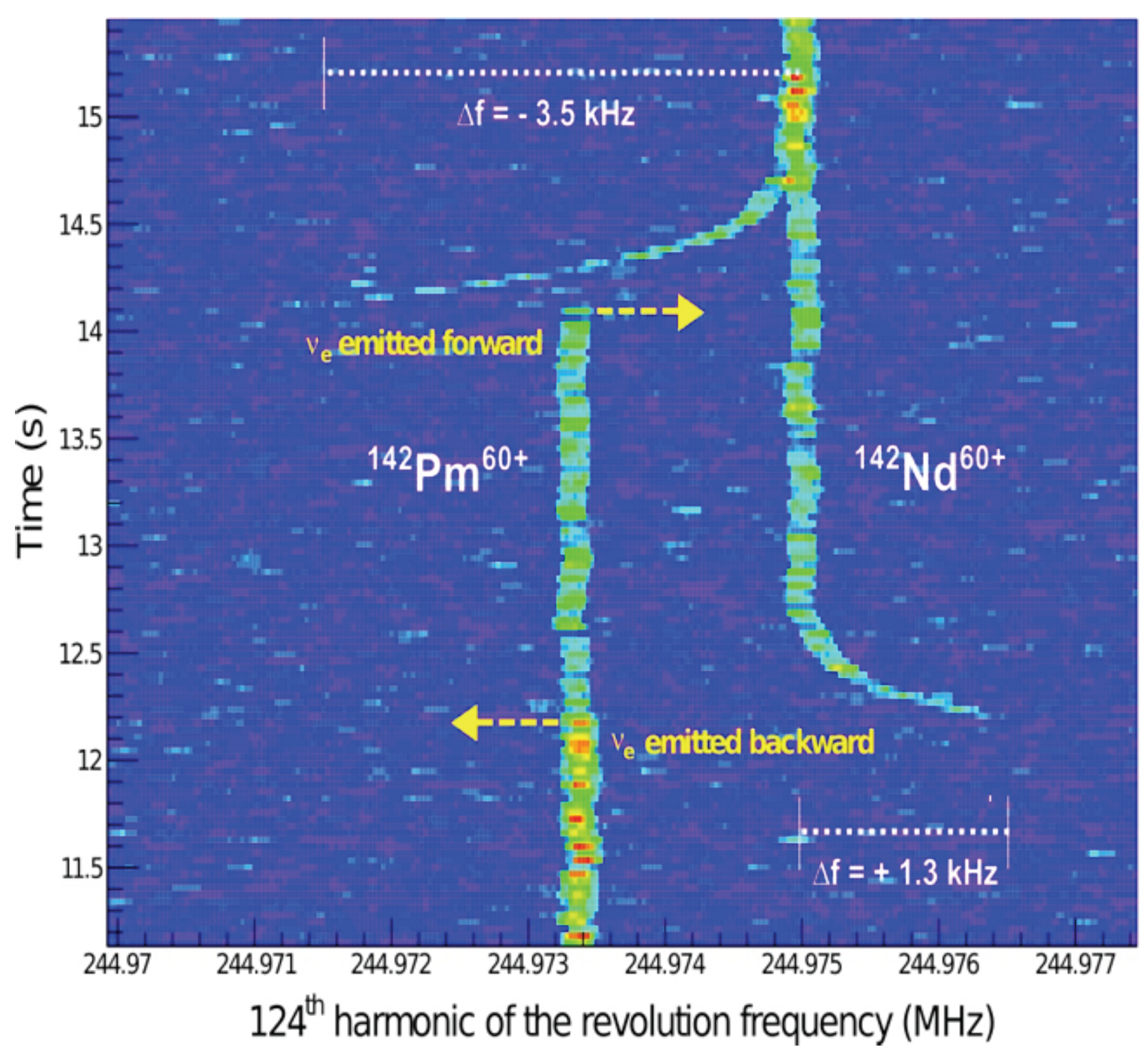
:1. Introduction
2. Daughter-Ion Oscillations in Two-Body EC
2.1. Daughter-Ion Oscillations in Two-Body EC: Non Storage-Ring Motion
2.2. Daughter-Ion Oscillations in Two-Body EC: Storage-Ring Motion I
2.3. Daughter-Ion Oscillations in Two-Body EC: Storage-Ring Motion II
3. Results
3.1. Center-of-Mass Oscillation Expressions
3.2. Laboratory Frame Oscillation Expressions
4. Conclusions
Acknowledgments
Conflicts of Interest
References and Notes
- Litvinov, Yu.A.; Bosch, F.; Winckler, N.; Boutin, D.; Essel, H.G.; Faestemann, T.; Geissel, H.; Hess, S.; Kienle, P.; Knöbel, R.; et al. Observation of non-exponential orbital electron capture decays of hydrogen-like 140Pr and 142Pm ions. Phys. Lett. B 2008, 664, 162–168. [Google Scholar] [CrossRef]
- Kienle, P.; Bosch, F.; Bühler, P.; Faestemann, T.; Litvinov, Yu.A.; Sanjari, M.S.; Shubina, B.B.; Winckler, N.; Atanasov, D.; Geissel, H.; et al. (Two-Body-Weak-Decays Collaboration). High-resolution measurement of the time-modulated orbital electron capture and of the β+ decay of hydrogen-like 142Pm ions. Phys. Lett. B 2013, 726, 638–645. [Google Scholar]
- Vetter, P.A.; Clark, R.M.; Dvorak, J.; Freedman, S.J.; Gregorich, K.E.; Jeppesen, H.B.; Mittelberger, D.; Wiedeking, M. Search for oscillation of the electron-capture decay probability of 142Pm. Phys. Lett. B 2008, 670, 196–199. [Google Scholar] [CrossRef]
- Faestermann, T.; Bosch, F.; Hertenberger, R.; Maier, L.; Krücken, R.; Rugel, G. Could the GSI decay rate oscillations be observed in a standard electron capture decay experiment? Phys. Lett. B 2009, 672, 227–229. [Google Scholar] [CrossRef]
- Piotrovski, J.; Chen, X.; Litvinov, Yu.A.; Sanjari, M.S.; Two-Body-Weak-Decays collaboration. Performance of the ESR kicker magnet during E082. GSI Scientific Report 2014 unpublished work. 2015. [Google Scholar] [CrossRef]
- Abe, K.; Hayato, Y.; Iida, T.; Ikeda, M.; Ishihara, G.; Iyogi, K.; Kameda, J.; Kobayashi, K.; Koshio, Y.; Kozuma, Y.; et al. (Super-Kamiokande Collaboration). Solar neutrino results in Super-Kamiokande-III. Phys. Rev. D 2011, 83, 052010. [Google Scholar] [CrossRef]
- Ivanov, A.N.; Kienle, P. Time Modulation of the K-Shell Electron Capture Decay Rates of H-like Heavy Ions at GSI Experiments. Phys. Rev. Lett. 2009, 103, 062502. [Google Scholar] [CrossRef] [PubMed]
- Giunti, C. Rates of processes with coherent production of different particles and the GSI time anomaly. Phys. Lett. B 2008, 665, 92–94. [Google Scholar] [CrossRef]
- Kienert, H.; Kopp, J.; Lindner, M.; Merle, A. The GSI anomaly. J. Phys. Conf. Ser. 2008, 136, 022049. [Google Scholar] [CrossRef]
- Cohen, A.G.; Glashow, S.L.; Ligeti, Z. Disentangling neutrino oscillations. Phys. Lett. B 2009, 678, 191–196. [Google Scholar] [CrossRef]
- Merle, A. Why a splitting in the final state cannot explain the GSI-Oscillations. Phys. Rev. C 2009, 80, 054616. [Google Scholar] [CrossRef]
- Flambaum, V.V. Comment on “Time Modulation of the K-Shell Electron Capture Decay Rates of H-like Heavy Ions at GSI Experiments”. Phys. Rev. Lett. 2010, 104, 159201. [Google Scholar] [CrossRef] [PubMed]
- Wu, J.; Hutasoit, J.A.; Boyanovsky, D.; Holman, R. Dynamics of disentanglement, density matrix, and coherence in neutrino oscillations. Phys. Rev. D 2010, 82, 013006. [Google Scholar] [CrossRef]
- Gal, A. Neutrino magnetic moment effects in electron-capture measurements at GSI. Nucl. Phys. A 2010, 842, 102–112. [Google Scholar] [CrossRef]
- Peshkin, M. Oscillating decay rate in electron capture and the neutrino mass difference. Phys. Rev. C 2015, 91, 042501. [Google Scholar] [CrossRef]
- Steck, M.; Beller, P.; Beckert, K.; Franzke, B.; Nolden, F. Electron cooling experiments at the ESR. Nucl. Instrum. Methods A 2004, 532, 357–365. [Google Scholar] [CrossRef]
- Kayser, B. Neutrino Oscillation Physics. In Proceedings of the International School of Physics “Enrico Fermi”; Bellini, G., Ludhova, L., Eds.; IOS Press: Amsterdam, The Netherlands, 2012; pp. 1–14. [Google Scholar]
- For a recent discussion of decay-rate frame dependence, see Alavi, S.A.; Giunti, C. Which is the quantum decay law of relativistic particles? Europhys. Lett. 2015, 109, 60001. [Google Scholar]

© 2016 by the author; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gal, A. Neutrino Signals in Electron-Capture Storage-Ring Experiments. Symmetry 2016, 8, 49. https://doi.org/10.3390/sym8060049
Gal A. Neutrino Signals in Electron-Capture Storage-Ring Experiments. Symmetry. 2016; 8(6):49. https://doi.org/10.3390/sym8060049
Chicago/Turabian StyleGal, Avraham. 2016. "Neutrino Signals in Electron-Capture Storage-Ring Experiments" Symmetry 8, no. 6: 49. https://doi.org/10.3390/sym8060049
APA StyleGal, A. (2016). Neutrino Signals in Electron-Capture Storage-Ring Experiments. Symmetry, 8(6), 49. https://doi.org/10.3390/sym8060049




