Abstract
We analyze the effect of the tensor force and other components of the nucleon-nucleon interaction on the nuclear symmetry energy and its density dependence by using the Hellmann–Feynman theorem. The analysis is performed within the microscopic Brueckner–Hartree–Fock approach using the Argonne V18 potential plus a Urbana IX three-nucleon force. Our results show that the potential part of the nuclear Hamiltonian, and in particular its tensor component, gives the largest contribution to the symmetry energy. The decomposition of the symmetry energy into a kinetic part and a potential energy part provides physical insight on the correlated nature of the system, indicating that pure neutron matter is less correlated than symmetric nuclear matter.1. Introduction
The density dependence of the nuclear symmetry energy, Esym(ρ), is a crucial ingredient of the nuclear equation of state (EoS) needed to understand many important properties of isospin-rich nuclear systems such as exotic nuclei, supernovae and neutron stars [1–4]. Experimental information on Esym(ρ) below, close to, and above nuclear saturation density, ρ0, can be obtained from a number of nuclear structure and heavy ion collision observables such as giant and pigmy resonances in heavy nuclei, n/p and t/3 He ratios in nuclear reactions, isospin diffusion and isospin scaling in nuclear multi-fragmentation, neutron-proton correlation functions at low relative momenta, isospin diffusion/transport in heavy-ion collisions, neutron-proton differential flow, isobaric analog states, or π−/π+ and K−/K+ ratios in heavy ion collisions. Accurate measurements of the neutron skin thickness δR in heavy nuclei, via parity violating experiments or by means of antiprotonic atom data, can also help to constrain Esym(ρ), since its derivative is strongly correlated with δR. Additional information on Esym(ρ) can be extracted from the astrophysical observation of compact objects, which opens a window into both the bulk and the microscopic properties of nuclear matter at extreme isospin asymmetries. In particular, the characterization of the core-crust transition in neutron stars or the analysis of power-law correlations, such as the relation between the radius of a neutron star and the equation of state, can put stringent constraints on Esym(ρ).
Theoretically, Esym(ρ) has been determined using both phenomenological and microscopic many-body approaches. Phenomenological approaches, either relativistic or non-relativistic, are based on effective interactions that are frequently built to reproduce the properties of nuclei. Since many of such interactions are built to describe systems close to the symmetric case, predictions at high asymmetries should be, however, taken with care. Microscopic approaches start from realistic nucleon-nucleon (NN) interactions that reproduce the scattering and bound state properties of the free two-nucleon system and naturally include the isospin dependence. In-medium correlations are then built using many-body techniques that microscopically account for isospin asymmetry effects such as the difference in the Pauli blocking factors and self-energies of neutrons and protons in asymmetric matter.
Nevertheless, in spite of the experimental and theoretical efforts (see [1] and references therein) carried out in the last years and the significant recent progress in studying the properties of isospin-asymmetric nuclear systems, Esym(ρ) is still uncertain. Its value at saturation, S0, is more or less well-established (~30 MeV), and its behavior below saturation is now much better known [5]. However, for densities above saturation, Esym(ρ) is not yet well constrained, and the predictions from different models strongly diverge. Why Esym(ρ) is so uncertain is still an open question whose answer is related to our limited knowledge of the nuclear force, and in particular to its spin and isospin dependence.
In this work we analyze the effect of the tensor force and other components of the NN interaction on Esym(ρ), and discuss how the isospin dependence of the NN correlations affects it. This analysis is carried out with the help of the Hellmann–Feynman theorem [6,7] within the framework of the microscopic Brueckner–Hartree–Fock (BHF) approach [8,9]. This theorem allows the decomposition of the total energy per particle of both pure neutron matter (PNM) and symmetric nuclear matter (SNM), and therefore of the nuclear symmetry energy, in the kinetic and potential energy contributions. We explore the different effects of NN correlations on SNM and PNM and discuss how the isospin dependence of these correlations affects the density dependence of the nuclear symmetry energy. To such end we compare the kinetic and potential energy contributions with those of the free Fermi gas and the so-called correlation energy. We note that a similar analysis was already performed in [10,11]. Consequently, the present work can be considered a short review of these previous publications with a focus in some different aspects that provide new physical insights into the problem. We would like to point out that a more exhaustive and complete study requires the use of other nuclear Hamiltonians and many-body techniques. Particularly promising would be the use of chiral effective field theory interactions and Renormalization Group methods (see, e.g., [12–15] for recent developments). However, this is out of the scope of the present work. Such more exhaustive and complete study will eventually be considered in the future.
This paper is organized in the following way. In Section 2 we briefly review the BHF approach of asymmetric nuclear matter. Our results are presented in Section 3. Finally, a summary and our main conclusions are given in Section 4.
2. The BHF Approach of Asymmetric Nuclear Matter
Assuming charge symmetry for nuclear forces, the energy per particle of asymmetric nuclear matter can be well approximated as
It is common to characterize the density dependence of the energy per particle of SNM around the saturation density ρ0 in terms of a few bulk parameters by expanding it in a Taylor series around ρ0,
The coefficients denote, respectively, the energy per particle, the incompressibility coefficient and the third derivative of the energy of SNM at saturation,
Similarly, the behavior of the symmetry energy around saturation can also be characterized in terms of a few bulk parameters,
The BHF approach is the lowest order of the Brueckner–Bethe–Goldstone many-body theory [8,9]. In this theory, the ground-state energy of nuclear matter is evaluated in terms of the so-called hole-line expansion, where the perturbative diagrams are grouped according to the number of independent hole lines. The expansion is derived by means of the in-medium two-body scattering G matrix, which describes the effective interaction between two nucleons in the presence of a surrounding medium. It is obtained by solving the well-known Bethe–Goldstone equation, schematically written as
3. Results
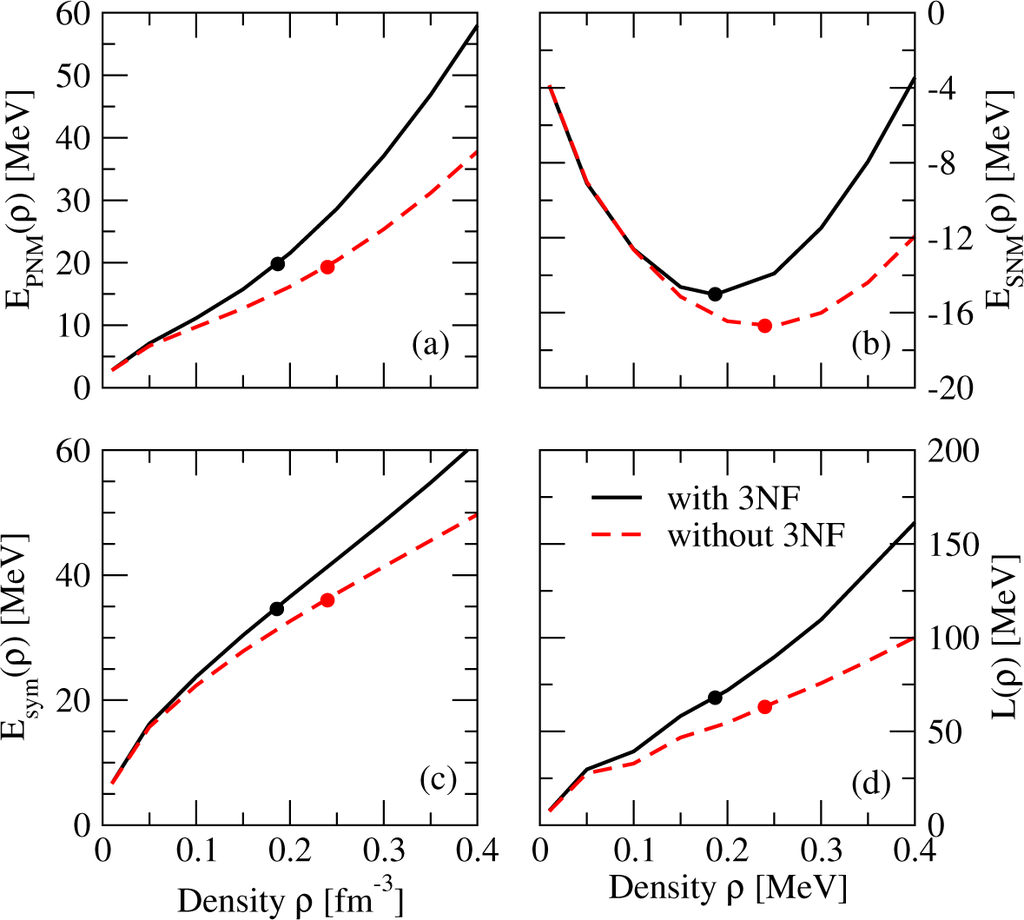
The discussion of our results starts by showing in Table 1 the bulk parameters characterizing the density dependence of the energy of SNM and the symmetry energy around saturation density. Results are shown for calculations with and without 3NF. Note that, in general, the effect of the 3NF seems to be more important on the isoscalar properties than on the isovector ones. In fact, by looking at the table it seems that the parameters L, Ksym and Qsym describing the density dependence of the symmetry energy around saturation are little affected by the effect of 3NF. However, we should notice that the value of the saturation density is different when 3NFs are considered (ρ0 = 0.187 fm−3) or not (ρ0 = 0.240 fm−3) in the calculation. Therefore, one has to be careful when comparing the value of these parameters in the two cases. To clarify the role of 3NF in the isovector properties of the nuclear equation of state, we show in Figure 1 the energy per particle of PNM (panel a) and SNM (panel b), as well as the symmetry energy (panel c) and its slope parameter (panel d), defined as L(ρ) = 3ρ∂Esym(ρ)/∂ρ, as a function of the density. The circles show the results at saturation density. As expected in the low density regime the role of 3NFs is basically negligible. Overall, for densities in 0.1–0.3 fm−3, there is a moderate dependence of Esym(ρ) and L(ρ) on the 3NF, even though its effect on PNM and SNM is not small. This dependence becomes stronger and stronger when increasing the density. The importance of 3NFs has been recently revised in the context of chiral effective field theory [29–34]. New fitting protocols of two-nucleon forces seem to indicate that the effect of 3NF could actually be rather small in PNM. Nevertheless, the relative importance of the two- and three-body contributions changes with the resolution scale. It is not clear whether such observations, valid for somewhat soft chiral interactions, still apply when considering a harder interaction like Av18.

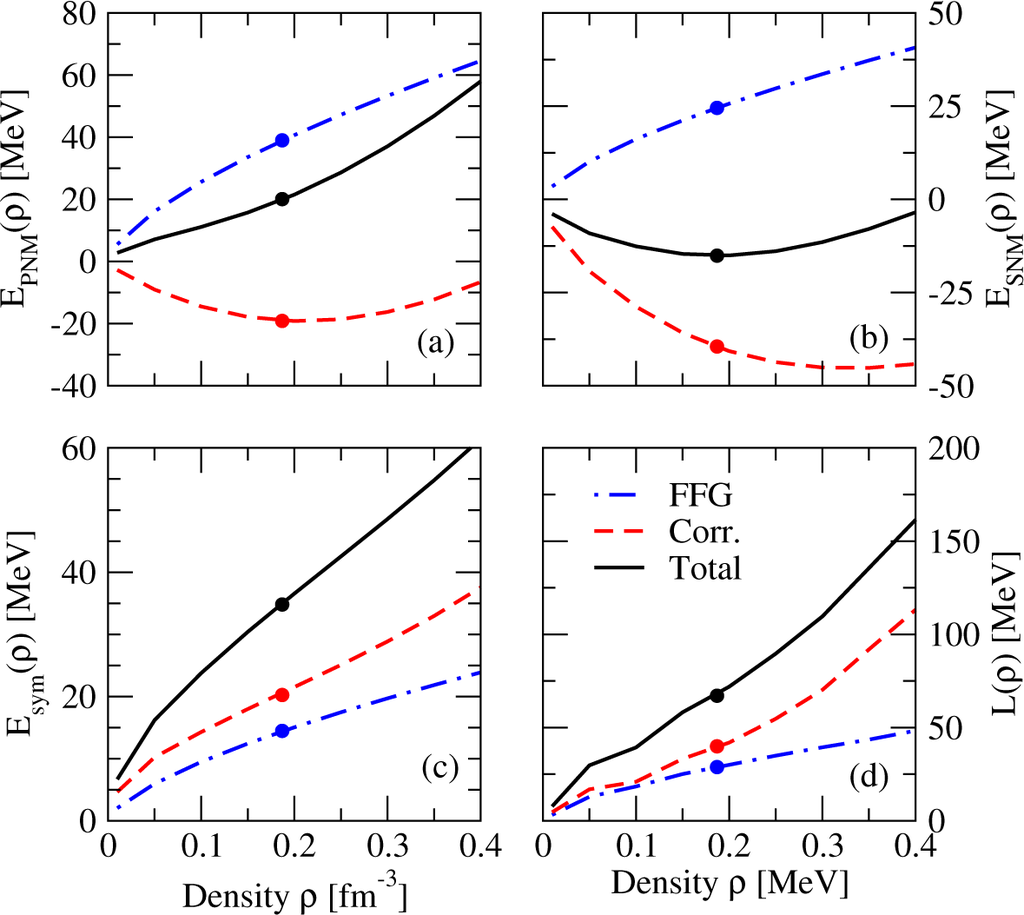
In Figure 2 we show the free Fermi gas and correlation energy contributions to the energy per particle of both PNM (panel a) and SNM (panel b) as well as to the symmetry energy (panel c) and its slope parameter (panel d) as a function of the density obtained in our BHF calculation with Av18 + 3NF. The particular values of these contributions at the saturation density of our calculation ρ0 = 0.187 fm−3 are denoted by circles and are reported in Table 2. The symmetry energy is calculated, as mentioned before, as the difference of the total energy per particle of PNM and SNM. As it is seen in the figure (see also Figure 4) the FFG energy of PNM is always larger than the corresponding one of SNM and, therefore, its contribution to the symmetry energy is positive throughout the explored density range and, in particular, amounts to ~14.38 MeV at ρ0. The correlation energy, Ecorr, contributes also positively (~19.92 MeV at ρ0) to the symmetry energy for all the densities, since it gives smaller attraction in PNM than in SNM. This contribution is larger than that of the FFG. The addition of both contributions, which are of the same order at ρ0, provides a symmetry energy of ~34.3 MeV at this density. The contributions to L can be decomposed similarly. In this case the contribution of the correlation energy is much larger than that of the FFG, except at very low densities where both contributions are similar.

To get a further physical insight on the role of the correlation energy, it is useful to look at its spin–isospin (S, T) decomposition, shown in Table 3. As expected, the main contribution is that of the (1, 0) channel, which is acting only in SNM and has a large attractive contribution. It is precisely in this channel where the tensor component of the nuclear force is active. Notice that the T = 1 channels give similar contributions in PNM and SNM and, therefore, the contribution to the symmetry energy is small. The channel (0, 0) gives a repulsive contribution to the total energy in SNM and since it does not play any role in PNM, its contribution to the total symmetry energy is negative. Note again that the tensor force is not acting in this channel.

Let us further continue this analysis by looking at the contributions of the different partial waves to Ecorr. Contributions up to J = 8 have been considered. These contributions are shown in Table 4. Notice that the 1S0 contribution, which is dominated by the central component of the NN potential, has a similar large contribution to both PNM and SNM and, therefore, its effect on the symmetry energy is almost negligible. The largest contribution is provided by the 3S1–3D1 channel, which corresponds to T = 0, active only in SNM. For larger values of the total angular momentum J, the contributions become smaller and many cancellations take place. In general, one observes that the final energy in SNM is the result of a large cancellation between EFFG and Ecorr, and that the absolute value of Ecorr for PNM is significantly smaller than for SNM. These observations point to the well-accepted fact that neutron matter is less correlated than symmetric matter.

By using different phase shift equivalent NN potentials, it has been shown that the total binding energy of the deuteron is the result of a strong cancellation between the kinetic and the potential energy [35,36]. However, this observation should be taken with care when using softer modern low-momentum or chiral NN interactions, since in this case this cancellation may be not so strong. The large kinetic energy, in the deuteron case, is a consequence of the NN correlations existing in the 3S1–3D1 channel. In that sense we would like to study the decomposition of the total energy of the infinite system in the kinetic and potential energy. Due to NN correlations, the kinetic energy will be larger than the FFG energy. Therefore, the difference between the kinetic energy of a correlated nuclear system and that of a FFG can be used to quantify the effect of NN correlations.
Unfortunately, the BHF approach does not give direct access to the separate contributions of the kinetic and potentials energies because it does not provide the correlated many-body wave function, |Ψ⟩. However, it has been shown [37–40] that the Hellmann–Feynman theorem [6,7] can be used to estimate the ground-state expectation values of both contributions from the derivative of the total energy with respect to a properly introduced parameter. Writing the nuclear matter Hamiltonian as H = T + V, and defining a λ-dependent Hamiltonian H(λ) = T + λV, the expectation value of the potential energy is given as
Then, the kinetic energy contribution ⟨T⟩ can be simply obtained by subtracting ⟨V⟩ from the total energy E.
In Figure 3 we show the kinetic and potential energy contributions to the energy per particle of both PNM (panel a) and SNM (panel b) as well as to the symmetry energy (panel c) and its slope parameter (panel d) as a function of the density obtained by applying the Hellmann–Feynman theorem, as explained above, to our BHF calculation with Av18 + 3NF. The values of all these contributions at saturation density are denoted by circles and reported in Table 5.
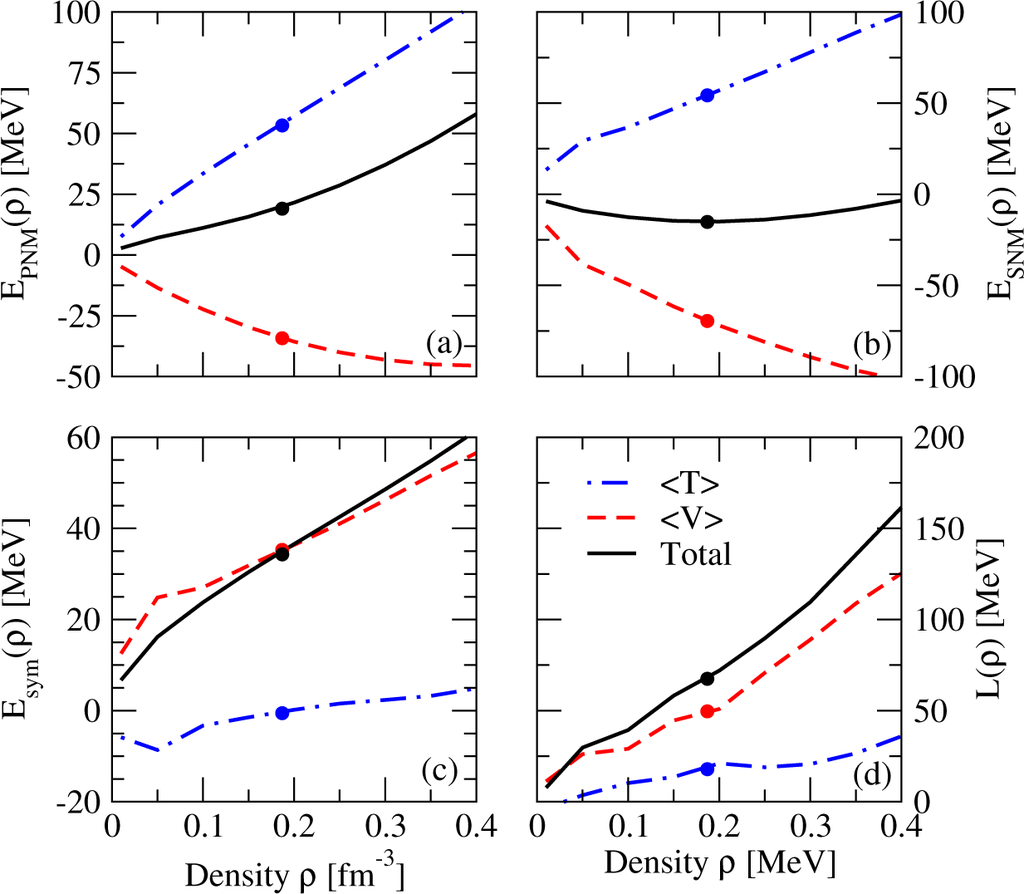

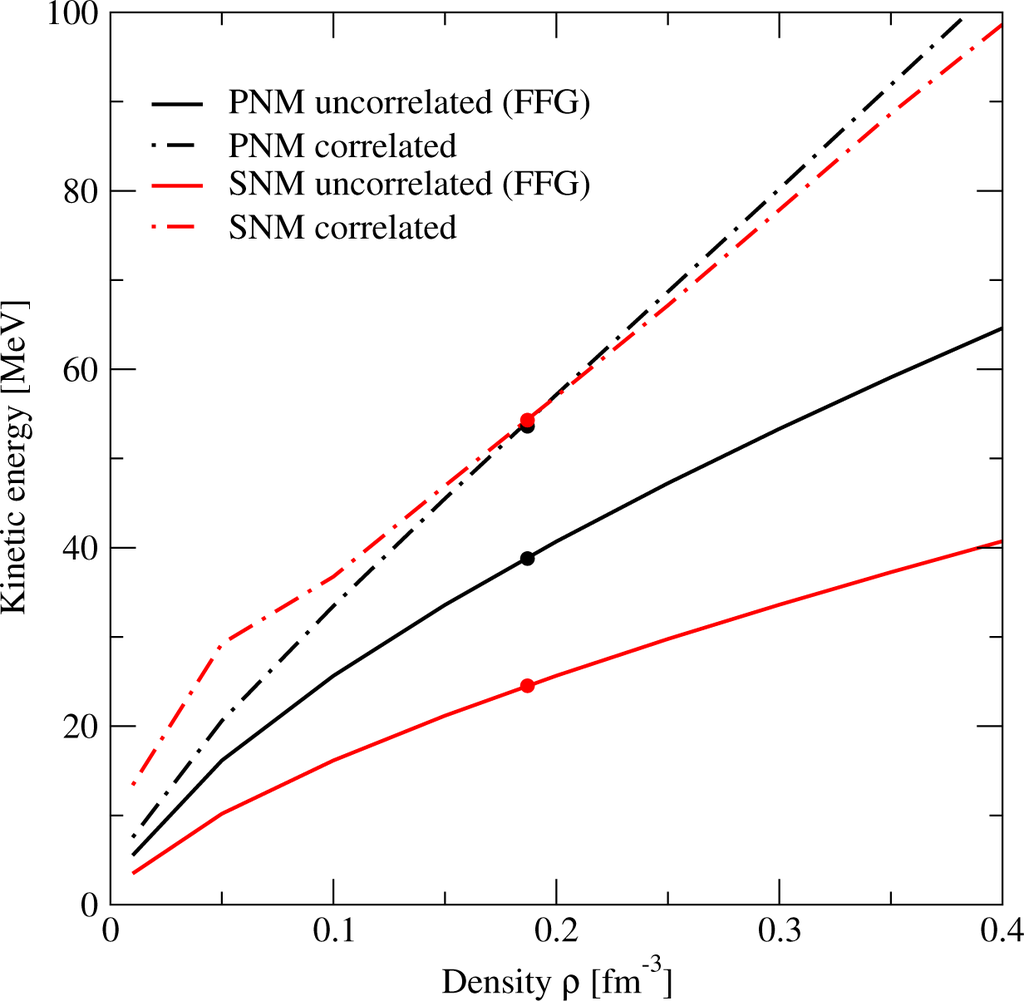
As in the case of the deuteron, both the total energy of PNM and that of SNM are the result of a strong cancellation between the kinetic and potential energies. It is worth noticing that the kinetic energy contribution to Esym is very small in the whole density range, being slightly negative for ρ ≤ 0.2 fm−3. This is in contrast to the results for the FFG (see Figure 2 and Table 2). The increase of the kinetic energy with respect to the FFG energy is probably due to the strong isospin dependence of the short-range NN correlations (SRC) induced by the tensor force. This observation has been also recently pointed out by Xu and Li [41] and Hen et al. [42] using a phenomenological model for the nucleon momentum distribution n(k), and by Carbone et al. [43] using the self-consistent Green’s function approach with the Av18 and the CDBONN [44] potentials. To illustrate this point, we show in Figure 4 the kinetic energy of uncorrelated (i.e., FFG energy) and correlated PNM and SNM as a function of density. Results at saturation density are also shown in this case by the circles. It can be seen that the increase of the kinetic energy of SNM due to SRC is always much larger than that of PNM. This is an indication that, at the same fixed density, SNM is always more correlated than PNM. Note also that the kinetic energy of both correlated systems is of similar order and that their strong cancellation gives the almost negligible contribution to the kinetic part of Esym noticed before. It is also worth mentioning that the kinetic contribution to L is smaller than the corresponding one of the FFG in the full density range. Clearly, the major contribution to both the symmetry energy and its slope parameter is due to the potential energy part. Note that at saturation density (see Table 5) this contribution is practically equal to the total value of the symmetry energy at saturation, and it represents ~78% of L.
The spin–isospin (S, T) channel decomposition of the potential energy of PNM and SNM at saturation, as well as of its contribution to Esym and L, is also illustrative. This is reported in Table 6. As in the case of the correlation energy, the largest contribution to the potential part of both Esym and L is provided by the (S = 1, T = 0) channel, for which the tensor is active. Interestingly, the S = 0 channels have a smaller and similar negative contribution to Esym and also a moderate negative contribution to L. However, the origin of these contributions is qualitatively different. While the channel (S = 0, T = 0) does not contribute to PNM and gives a small repulsive contribution to SNM, the contribution of the channel (S = 0, T = 1) to Esym is the result of a strong cancellation of large attractive contributions of this channel in both PNM and SNM. Analogous conclusions can be obtained from Table 7, where the partial wave decomposition of the potential energy is reported. Note that similar arguments have been already pointed out by other authors [41–43,45–57].


Finally, we analyze the role played by the different terms of the nuclear force, particularly the one of the tensor force, in the determination of Esym and L. To such end, we apply the Hellmann–Feynman theorem to the separate components of the Av18 and the Urbana IX 3NF. The Av18 potential has 18 components of the form with
As we said above, the Urbana IX three-body force is reduced to an effective density-dependent two-body force when used in the BHF approach. For simplicity, in the following we refer to it as the reduced Urbana force. This force is made of three components of the type where
The separate contributions of the various components of the Av18 potential and the reduced Urbana force to the energy per particle of PNM and SNM, and to the symmetry energy and its slope parameter at the saturation density, are given in Table 8. The contribution from the tensor component to Esym and L (contributions ⟨VSij⟩ and from the Av18 potential, and from the reduced Urbana force) is 36.056 MeV and 69.968 MeV, respectively. These results clearly confirm that the tensor force gives the largest contribution to both Esym and L. The contributions from the other components either are negligible, as for instance the contribution from the charge symmetry breaking terms , or almost cancel out.

4. Summary and Conclusions
In this work we have analyzed the effect of the tensor force and other components of the nucleon-nucleon (NN) interaction on the nuclear symmetry energy and its slope parameter for a wide range of densities. We have also discussed the role of the isospin dependence of the NN correlations on both quantities. This analysis has been carried out with the help of the Hellmann–Feynman theorem within the framework of the microscopic Brueckner–Hartree–Fock (BHF) approach using the Av18 potential plus an effective density-dependent two-body force deduced from the Urbana IX three-body force. The theorem allowed the decomposition of the total energy per particle of PNM and SNM into their kinetic and potential energy contributions. Our results showed that the potential part of the nuclear Hamiltonian gives the main contribution to both Esym and L. The kinetic contribution to Esym is very small throughout the explored density range, being even slightly negative for ρ ≤ 0.2 fm−3. We have explored the different effects of NN correlations on SNM and PNM and discussed how the isospin dependence of these correlations affects the density dependence of the nuclear symmetry energy. To such end, we have compared the kinetic and potential energy contributions to the energy per particle of PNM and SNM and to Esym(ρ) and L(ρ) with those of the free Fermi gas and the correlation energy. We found that PNM is less correlated than SNM, in agreement with recent results [41–43]. Finally, we have performed a partial wave and a spin–isospin channel decomposition of the potential part of Esym and L, showing that the major contribution to them is given by the spin-triplet (S = 1) and isospin-singlet (T = 0) channel. As we have explicitly shown, this is due to the dominant effect of the tensor force, which gives the largest contribution to both Esym and L. In conclusion, our results confirm the critical role of the tensor force in the determination of the symmetry energy and its density dependence. We would like to finish by noticing that at present there are no experimental or theoretical constraints to control the role of the tensor forces beyond the saturation density, although there are indications, based on large Nc QCD arguments (see, e.g., [58–60]), that tensor forces could undergo non-trivial modifications at densities not too far above saturation density, due to either the topology changes in the nucleon structure or the emergence of strongly interacting quark degrees of freedom. Consequently, the reader should take our results above saturation density with care.
Acknowledgments
This work has been partially supported by the project PEst-OE/FIS/UI0405/2014 developed under the initiative QREN financed by the UE/FEDER through the program COMPETE-“Programa Operacional Factores de Competitividade”, by the grant No. FIS2011-24154 from MICINNC (Spain) and grant No. 2014SGR401 from Generalitat de Catalunya (Spain), by the Consolider Ingenio 2010 Programme CPAN CSD2007-0042; STFC, through grants ST/1005528/1 and ST/J000051/1, and “NewCompstar”, COST Action MP1304.
Author Contributions
Isaac Vidaña was responsible for the calculations and the writting of the manuscript; Artur Polls and Constança Providência contributed to the writting of the manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Li, B.A.; Ramos, A.; Verde, G.; Vidaña, I. Topical issue on nuclear symmetry energy. Eur. Phys. J. A 2014, 50. [Google Scholar] [CrossRef]
- Baran, V.; Colonna, M.; Greco, V.; di Toro, M. Reaction dynamics with exotic nuclei. Phys. Rep 2005, 410, 335–466. [Google Scholar]
- Li, B.A.; Chen, W.; Ko, C.M. Recent progress and new challenges in isospin physics with heavy-ion reactions. Phys. Rep 2008, 464, 113–281. [Google Scholar]
- Steiner, A.W.; Prakash, M.; Lattimer, J.; Ellis, P.J. Isospin asymmetry in nuclei and neutron stars. Phys. Rep 2005, 411, 325–375. [Google Scholar]
- Tsang, M.B.; Stone, J.R.; Camera, F.; Danielewicz, P.; Gandolfi, S.; Hebeler, K.; Horowitz, C.J.; Lee, J.; Lynch, W.G.; Kohley, Z.; et al. Constraints on the symmetry energy and neutron skins from experiments and theory. Phys. Rev. C 2012, 86. [Google Scholar] [CrossRef]
- Hellmann, H. Einfüring in Die Quantenchemie; Franz Deuticke: Leipzig, Germany, 1937; p. 285. [Google Scholar]
- Feynman, R.P. Forces in molecules. Phys. Rev 1936, 56, 340–343. [Google Scholar]
- Day, B.D. Elements of Brueckner–Goldstone theory of nuclear matter. Rev. Mod. Phys 1967, 39, 719–744. [Google Scholar]
- Baldo, M. Nuclear Methods and the Nuclear Equation of State; World Scientific: Singapore, 1999. [Google Scholar]
- Vidaña, I.; Polls, A.; Providência, C. Nuclear symmetry energy and the role of the tensor force. Phys. Rev. C 2011, 84. [Google Scholar] [CrossRef]
- Carbone, A.; Polls, A.; Providência, C.; Rios, A.; Vidaña, I. Tensor force effects and high-momentum components in the nuclear symmetry energy. Eur. Phys. J. A 2014, 50. [Google Scholar] [CrossRef]
- Hagen, G.; Papenbrock, T.; Ekström, A.; Wendt, K.A.; Baardsen, G.; Gandolfi, S.; Hjorth-Jensen, M.; Horowitz, C.J. Coupled-cluster calculations of nucleonic matter. Phys. Rev. C 2014, 89. [Google Scholar] [CrossRef]
- Holt, J.W.; Kaiser, N.; Weise, W. Nuclear chiral dynamics and thermodynamics. Prog. Part. Nucl. Phys 2013, 73, 35–83. [Google Scholar]
- Furnstahl, R.J.; Hebeler, K. New applications of renormalization group methods in nuclear physics. Rept. Prog. Phys 2013, 76. [Google Scholar] [CrossRef]
- Hebeler, K.; Bogner, S.K.; Furnstahl, R.J.; Nogga, A.; Schwenk, A. Improved nuclear matter calculations from chiral low-momentum interactions. Phys. Rev. C 2011, 83. [Google Scholar] [CrossRef]
- Song, H.Q.; Baldo, M.; Giansiracusa, G.; Lombardo, U. Bethe–Brueckner–Goldstone expansion in nuclear matter. Phys. Rev. Lett 1998, 81, 1584–1587. [Google Scholar]
- Song, H.Q.; Baldo, M.; Giansiracusa, G.; Lombardo, U. Three-hole line contribution in nuclear matter revisited. Phys. Lett. B 1999, 411, 237–243. [Google Scholar]
- Jekeune, J.P.; Lejeune, A.; Mahaux, C. Many-body theory of nuclear matter. Phys. Rep 1976, 25, 83–174. [Google Scholar]
- Wiringa, R.B.; Stoks, V.G.J.; Schiavilla, R. Accurate nucleon-nucleon potential with charge-independence breaking. Phys. Rev. C 1995, 51, 38–51. [Google Scholar]
- Pudliner, B.S.; Pandharipande, V.R.; Carlson, J.; Wiringa, R.B. Quantum Monte Carlo calculations of A ≤ 6 nuclei. Phys. Rev. Lett 1995, 74, 4396–4399. [Google Scholar]
- Pudliner, B.S.; Pandharipande, V.R.; Carlson, J.; Pieper, S.C.; Wiringa, R.B. Quantum Monte Carlo calculations of nuclei with A ≤ 7. Phys. Rev. C 1997, 56, 1720–1750. [Google Scholar]
- Loiseau, B.A.; Nogami, Y.; Ross, C.K. Nucleon-nucleon correlation and two-pion exchange three-body force in nuclear matter. Nucl. Phys. A 1971, 165, 601–624. [Google Scholar]
- Grangé, P.; Martzolff, M.; Nogami, Y.; Sprung, D.W.L.; Ross, C.K. Three-body force in nuclear matter. Phys. Lett. B 1976, 60, 237–240. [Google Scholar]
- Baldo, M.; Ferreira, L. Nuclear liquid-gas phase transition. Phys. Rev. C 1999, 59, 682–703. [Google Scholar]
- Vidaña, I.; Providência, C.; Polls, A.; Rios, A. Density dependence of the nuclear symmetry energy: A microscopic perspective. Phys. Rev. C 2009, 80. [Google Scholar] [CrossRef]
- Zhou, X.R.; Burgio, G.F.; Lombardo, U.; Schulze, H.-J.; Zuo, W. Three-body forces and neutron star structure. Phys. Rev. C 2004, 69. [Google Scholar] [CrossRef]
- Li, Z.H.; Lombardo, U.; Schulze, H.-J.; Zuo, W. Consistent nucleon-nucleon potentials and three-body forces. Phys. Rev. C 2008, 77. [Google Scholar] [CrossRef]
- Li, Z.H.; Schulze, H.-J. Neutron star structure with modern nucleonic three-body forces. Phys. Rev. C 2008, 78. [Google Scholar] [CrossRef]
- Epelbaum, E.; Hammer, H.-W.; Meißner, U.-G. Modern theory of nuclear forces. Rev. Mod. Phys 2009, 81, 1773–1825. [Google Scholar]
- Machleidt, R.; Entem, D.R. Chiral effective field theory and nuclear forces. Phys. Rep 2011, 503, 1–75. [Google Scholar]
- Hammer, H.-W.; Nogga, A.; Schwenk, A. Three-body forces: From cold atoms to nuclei. Rev. Mod. Phys 2013, 85. [Google Scholar] [CrossRef]
- Carbone, A.; Polls, A.; Rios, A. Symmetric nuclear matter with chiral three-nucleon forces in the self-consistent Green’s functions approach. Phys. Rev. C 2013, 88. [Google Scholar] [CrossRef]
- Carbone, A.; Cipollone, A.; Barbieri, C.; Rios, A.; Polls, A. Self-consistent Green’s function formalism with three-body interactions. Phys. Rev. C 2013, 88. [Google Scholar] [CrossRef]
- Ekström, A.; Baardsen, G.; ForssÃl’n, C.; Hagen, G.; Hjorth-Jensen, M.; Jansen, G.R.; Machleidt, R.; Nazarewicz, W.; Papenbrock, T.; Sarich, J.; et al. Optimized chiral nucleon-nucleon interaction at next-to-next-to-leading order. Phys. Rev. Lett 2013, 110. [Google Scholar] [CrossRef]
- Polls, A.; Müther, H.; Machleidt, R.; Hjorth-Jensen, M. Phaseshift equivalent NN potentials and the deuteron. Phys. Lett. B 1998, 432, 1–7. [Google Scholar]
- Baldo, M.; Polls, A.; Rios, A.; Schulze, H.-J.; Vidaña, I. Comparative study of neutron and nuclear matterwith simplified Argonne nucleon-nucleon potentials. Phys. Rev. C 2012, 86. [Google Scholar] [CrossRef]
- Müther, H.; Polls, A. Correlations derived from modern nucleon-nucleon potentials. Phys. Rev. C 1999, 61. [Google Scholar] [CrossRef]
- Sartor, R. Diagrammatic analysis of the Hellmann–Feynman theorem. Phys. Rev. C 2000, 62. [Google Scholar] [CrossRef]
- Sartor, R. Diagrammatic analysis of the Hellmann–Feynman theorem: Numerical applications. Phys. Rev. C 2001, 64. [Google Scholar] [CrossRef]
- Bombaci, I.; Fabrocini, A.; Polls, A.; Vidaña, I. Spin-orbit and tensor interactons in homogeneous matter of nucleons: Accuracy of many-body theories. Phys. Lett. B 2005, 609, 232–240. [Google Scholar]
- Xu, C.; Li, B.A. Tensor force induced isospin-dependence of short-range nucleon-nucleon correlation and high density behavious of nuclear symmetry energy, 2011. Available online: http://arxiv.org/abs/1104.2075 accessed on 8 December 2014.
- Hen, O.; Li, B.A.; Guo, W.-J.; Weinstein, L.B.; Piasetzky, E. Kinetic symmetry energy of nucleonic matter with tensor correlations, 2014. Available online: http://arxiv.org/abs/1408.0772 accessed on 8 December 2014.
- Carbone, A.; Polls, A.; Rios, A. High momentum components in the nuclear symmetry energy. EuroPhys. Lett 2012, 97. [Google Scholar] [CrossRef]
- Machleidt, R.; Sammarruca, F.; Song, Y. Nonlocal nature of the nuclear force and its impact on nuclear structure. Phys. Rev. C 1996, 53, R1483–R1487. [Google Scholar]
- Bombaci, I.; Lombardo, U. Asymmetric nuclear matter equation of state. Phys. Rev. C 1991, 44, 1892–1900. [Google Scholar]
- Engvik, L.; Hjorth-Jensen, M.; Machleidt, R.; Müther, H.; Polls, A. Modern nucleon-nucleon potentials and symmetry energy in infinite matter. Nucl. Phys. A 1997, 627, 85–100. [Google Scholar]
- Pandharipande, V.R.; Garde, V.K. Effect of tensor forces on composition of dense matter. Phys. Lett. B 1972, 39, 608–610. [Google Scholar]
- Wiringa, R.B.; Fiks, V.; Fabrocini, A. Equation of state for dense nucleon matter. Phys. Rev. C 1988, 38, 1010–1037. [Google Scholar]
- Brown, G.E.; Rho, M. In-medium stiffening of the nucleon-nucleon spin-isospin interaction. Phys. Lett. B 1990, 237, 3–7. [Google Scholar]
- Müther, H.; Prakash, M.; Ainsworth, T.L. The nuclear symmetry energy in relativistic Brueckner–Hartree–Fock calculations. Phys. Lett. B 1987, 199, 469–574. [Google Scholar]
- Zuo, W.; Bombaci, I.; Lombardo, U. Asymmetric nuclear matter from an extended Brueckner–Hartree–Fock appriach. Phys. Rev. C 1999, 60. [Google Scholar] [CrossRef]
- Zuo, W.; Lejeune, A.; Lombardo, U.; Mathiot, J.F. Microscopic three-body force for asymmetric nuclear matter. Eur. Phys. J. A 2002, 14, 469–475. [Google Scholar]
- Dieperink, A.E.L.; Dewulf, Y.; van Neck, D.; Waroquier, M.; Rodin, V. Nuclear symmetry energy and the neutron skin in neutron-rich nuclei. Phys. Rev. C 2003, 68. [Google Scholar] [CrossRef]
- Li, Z.H.; Lombardo, U.; Schulze, H.-J.; Zuo, W.; Chen, L.W.; Ma, H.R. Nuclear matter saturation point and symmetry enegy with modern nucleon-nucleon potentials. Phys. Rev. C 2006, 74. [Google Scholar] [CrossRef]
- Xu, C.; Li, B.A. Understanding the major uncertainties in the nuclear symmetry energy at suprasaturation densities. Phys. Rev. C 2010, 81. [Google Scholar] [CrossRef]
- Li, A.; Li, B.A. Short-range tensor interaction and high-density nuclear symmetry energy, 2011. Available online: http://arxiv.org/abs/1107.0496 accessed on 8 December 2014.
- Sammarruca, F. Contribution of isovector mesons to the symmetry energy in a microscopic model. Phys. Rev. C 2011, 84. [Google Scholar] [CrossRef]
- Kyu, H.; Rho, M. Topology change and tensor forces for the EoS of dense baryonic matter. Eur. Phys. J. A 2014, 50. [Google Scholar] [CrossRef]
- Seo, Y.; Sin, S.-J. Symmetry energy from holographic QCD. Eur. Phys. J. A 2014, 50. [Google Scholar] [CrossRef]
- Sang, K.; Lee, S.H. Symmetry energy from QCD sum rules. Eur. Phys. J. A 2014, 50. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).