Abstract
Recent vigorous investigations of topological order have not only discovered new topological states of matter, but also shed new light on “already known” topological states. One established example with topological order is the valence bond solid (VBS) states in quantum antiferromagnets. The VBS states are disordered spin liquids with no spontaneous symmetry breaking, but most typically manifest a topological order known as a hidden string order on the 1D chain. Interestingly, the VBS models are based on mathematics analogous to fuzzy geometry. We review applications of the mathematics of fuzzy supergeometry in the construction of supersymmetric versions of VBS (SVBS) states and give a pedagogical introduction of SVBS models and their properties. As concrete examples, we present detailed analysis of supersymmetric versions of and VBS states, i.e., and SVBS states, whose mathematics are closely related to fuzzy two- and four-superspheres. The SVBS states are physically interpreted as hole-doped VBS states with a superconducting property that interpolates various VBS states, depending on the value of a hole-doping parameter. The parent Hamiltonians for SVBS states are explicitly constructed, and their gapped excitations are derived within the single-mode approximation on 1D SVBS chains. Prominent features of the SVBS chains are discussed in detail, such as a generalized string order parameter and entanglement spectra. It is realized that the entanglement spectra are at least doubly degenerate, regardless of the parity of bulk (super)spins. The stability of the topological phase with supersymmetry is discussed, with emphasis on its relation to particular edge (super)spin states.
1. Introduction
Strongly correlated systems, such as cuprate superconductors, quantum Hall systems, and quantum anti-ferromagnets (QAFM), have been offering arenas for unexpected emergent phenomena brought about by strong many-body correlation. In particular, the study of QAFM bears the longest history since Heisenberg introduced the celebrated quantum-spin model [1,2] and Bethe [3] found the first non-trivial exact solution to the quantum many-body problem, and it is still providing us with attractive topics in modern physics. Generally, in the presence of a many-body interaction, it is very hard to obtain exact many-body ground-state wave functions, and even if possible, it is rare that we are able to write them down in compact and physically meaningful forms. Fortunately, in the above mentioned three cases (superconductivity (SC), quantum Hall effects (QHE), and QAFM), the paradigmatic ground-state wave functions have been known and greatly contributed to our understanding of the exotic physics of these systems: the Bardeen-Cooper-Schrieffer (BCS) state [4] for SC, the Laughlin wave function [5] for QHE and for QAFM, the valence bond solid (VBS) states [6,7], which are the exact ground states of a certain class of quantum-spin models called the VBS models. In the present paper, we give a pedagogical review of the VBS models and their supersymmetric (SUSY) extension, i.e., the supersymmetric valence bond solid (SVBS) models [8,9,10], with particular emphasis on their relation to fuzzy geometry. The VBS models had been originally introduced by Affleck, Kennedy, Lieb and Tasaki (AKLT) [6,7] as a class of “exactly solvable” models that exhibit the properties conjectured by Haldane [11,12], namely the qualitative difference in excitation gaps and spin correlations in one-dimensional (1D) QAFM between half-odd-integer-spin and integer-spin cases.
As with other quantum-disordered paramagnets, the VBS states have a finite excitation gap and exponentially decaying spin correlations. However, the VBS states are not “mere” disordered non-magnetic spin states; the spin-S VBS states necessarily have gapless modes at their edges or, more specifically, emergent spin- edge spins [13,14]. This might remind the readers of the (chiral) gapless modes at the edge of the QHE systems, where excitations are gapful in the bulk (see Figure 1). Similar features are found in topological insulators, as well, [15,16,17] and considered as a hallmark of the topological state of matter. Furthermore, in 1D, the VBS states are known to exhibit a non-local order, called the hidden string order [18,19]. What is prominent in the VBS states is that they most typically exhibit a certain kind of topological order even in 1D, while QHE needs at least 2 D to work. This is a great advantage for the investigation of the VBS states, since in 1D, most calculations of physical quantities can be carried out exactly by using the matrix product state (MPS) representation [20,21,22,23,24,25] combined with the transfer-matrix method.
Since the topological character of a system is believed to be encoded in the many-body ground-state wave functions rather than in its Hamiltonian one, the relatively simple structure of the VBS wave function is suitable to investigate its topological properties by using such modern means as entanglement entropy [26,27] or the entanglement spectrum [28]. For the above reasons, the VBS states or, more generally, the MPS as a class of model states that satisfy the so-called area-law constraint [29] have attracted renewed attention as a “theoretical laboratory” in the recent study of topological states of matter. In fact, the MPS representation is now regarded as a natural and efficient way to describe quantum entangled many-body states and for a given (1D) Hamiltonian, the density matrix renormalization group (DMRG) [30] provides a powerful tool to find the optimized variational wave function in the form of MPS (see [31,32,33] for more details about the MPS method and DMRG). The key idea here is that for generic short-range interacting systems, only a small part of the entire Hilbert space is important, and depending on the problems in question, there are variety of ways to parametrize this physically relevant subspace. Although the Wigner’s -symbol may give a convenient description of -invariant MPS states [34,35,36], we adopt in the present paper the Schwinger-particle formalism (see, for instance, chapters 7 and 19 of [37]) to emphasize the analogies to the lowest Landau level physics. The list of possible applications includes a convenient description of gapped quantum ground states [29,38,39], as well as its application to efficient simulations of dynamics [40,41,42,43,44,45] and variational calculations [46,47,48,49]. Due to their simple structure, the entanglement entropy of the VBS states comes only from the bond(s) cut by the entanglement bipartition [50,51,52,53].
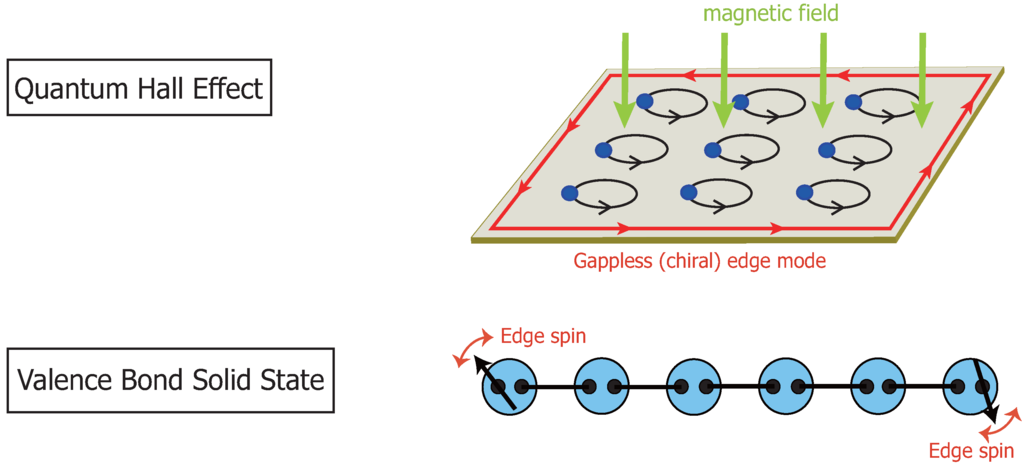
Figure 1.
(Color online) Physical analogies between quantum Hall effects (QHE) and valence bond solid (VBS) state. The bulk excitation on QHE is gapful, while the edge mode is a gapless (chiral) mode. Meanwhile, the bulk excitation on the VBS state is gapful while the motion of edge spins is a freely rotating gapless mode.
In some “anisotropic” MPSs, it is known that generalized quantum phase transitions (QPT) occur as the parameters contained in the MPSs are varied [54,55,56,57]. However, a remark is in order about the interpretation of this kind of “quantum phase transitions” in MPS. Normally, these QPTs in MPS are characterized by the divergence of spatial correlation lengths [57]. In generic lattice models, on the other hand, the diverging spatial correlation does not necessarily mean the vanishing of the excitation gap, while in the Lorentz-invariant systems, these two occur hand-in-hand. In fact, by the structure of MPS, the block (with size L) entanglement entropy never exceeds the L-independent value, [58] (with D being the dimension of the MPS matrix), while in quantum critical ground systems, whose low-energy physics is well described by conformal field theories, the block entanglement entropy is proportional to [58,59,60]. Therefore, one should take the QPTs in MPS mentioned above in a wider sense. This kind of phase transition in the VBS-type of states in 2D have been discussed in [54,55].
Finally, we would like to mention the recent application of MPS to the classification of the gapped topological phases in 1D. As is well-known, there is no true topological phase characterized by long-range entanglement [61,62]. However, if certain symmetries (e.g., time reversal) are imposed, topological phases characterized by short-range entanglement are possible. Since this kind of topological phase is stable only in the presence of certain protecting symmetries, they are called symmetry-protected topological (SPT) [63]. As has been mentioned above, an appropriate choice of MPS faithfully represents any given gapped (short-range entangled) ground state. Therefore, the problem of classifying all possible gapped topological phases reduces to classifying all possible MPSs by using group cohomology [61,62,64]. This program has been carried out for such elementary symmetries as time-reversal and link-parity in [65,66] (for the fermionic systems, see [67,68]) and for the Lie-group symmetries in [69,70]. Topological quantum phase transitions among these SPT phases have been discussed in, e.g., References [63,71,72].
In a sense, the second important keyword of this paper, fuzzy (super)geometry obtained by replacing the ordinary (commuting) coordinates with non-commutative ones, is again closely related to Heisenberg, who made a pioneering contribution in physics when he had built quantum mechanics on the basis of non-commuting phase-space variables. Snyder first substantiated Heisenberg’s idea of non-commutative coordinates in his paper “quantized space-time” [73] (see [74] for Heisenberg’s contribution to the original idea of non-commutative geometry and related historical backgrounds.) In fact, the VBS models have many interesting connections to QHE and fuzzy geometry. To explain the interesting relationship among them, let us begin with an analogy between the VBS states and the Laughlin wave functions of fractional quantum Hall effects (FQHE). Soon after the proposal of AKLT [6,7], Arovas, Auerbach and Haldane [75] realized that the Laughlin wave function and the VBS states (generalized to higher-spin cases) have analogous mathematical structures upon identifying the odd integer, m, which characterizes the filling fraction, , and the spin quantum number, S. Specifically, the VBS state is transformed to the Laughlin wave function of the electron system on a two-sphere, i.e., the Laughlin-Haldane wave function [76], by using the coherent-state representation of the VBS states and assigning appropriate correspondences between their physical quantities. In such a translation, the symmetry (or -rotation of the spatial coordinates) of the Laughlin-Haldane wave function for QHE on a two-sphere is translated into the symmetry (or spin- symmetry) of the VBS states for the integer-spin chains. This analogy can be generalized, and one can readily see that the Laughlin-Haldane wave functions with some external symmetry are generally transformed to give the VBS states with the identical symmetry.
In the past decade, there have been remarkable developments in higher-dimensional generalization of QHE (see [77,78] for reviews). So far, the set-up [5,76] of 2D QHE has been generalized to higher-dimensional manifolds, such as 4D [79], 8D [80], [81] and [82,83]. There also exist q-deformed QHE [84] and QHE on non-compact manifolds [85,86,87,88]. As is well-known, QHE is a physical realization of the non-commutative geometry [89], and non-commutative geometry brings exotic properties to QHE [90,91,92,93]. Therefore, for each higher-dimensional QHE, one can think of the underlying higher-dimensional fuzzy geometry, such as fuzzy two-sphere [94,95,96], four-sphere [97], sphere [98,99,100,101,102,103], [104,105,106], q-deformed sphere [107] and fuzzy hyperboloids [108,109,110,111].
On the other hand, we have already seen that the Bloch spin-coherent state enables us to relate the Laughlin-Haldane wave functions to the VBS states. In correspondence with such QHE, a variety of VBS models have been constructed with the symmetries, such as , [112,113,114], [115,116,117,118], [119,120] and q-deformed [22,23,121,122,123] [see Figure 2]. The VBS states demonstrate manifest relevance to fuzzy geometry also, by adopting the Schwinger operator formalism (see Section 2.1).
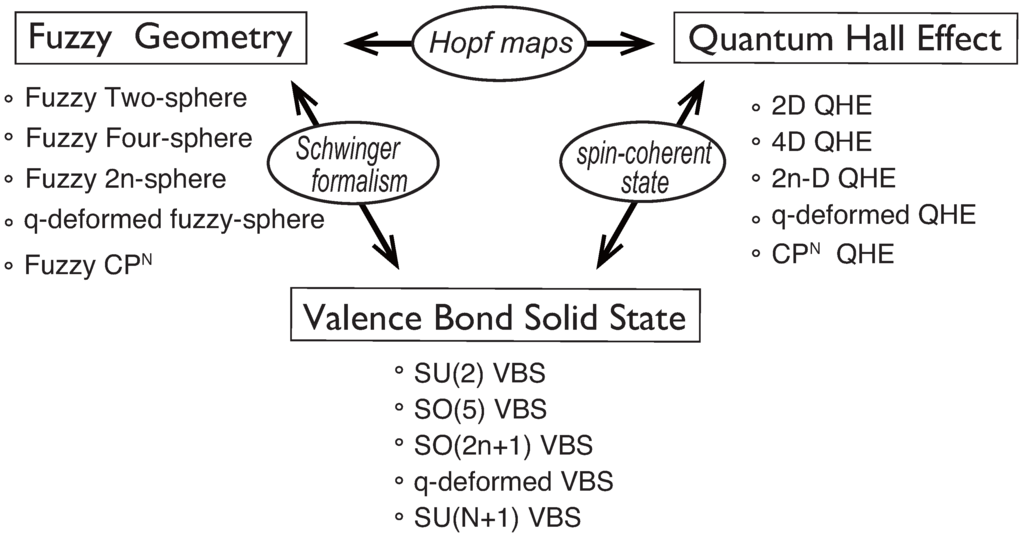
Figure 2.
Close relations among fuzzy geometry, QHE and VBS. They are “transformed” to each other with appropriate translations.
One of the main goals of this review is to illustrate their relations, which have been less emphasized in previous literature. As an explicit demonstration of the correspondence, we discuss a supersymmetric (SUSY) generalization of the VBS models. Since fuzzy super-spheres have already been explored in [124,125,126,127,128] and the SUSY QHE in [129,130,131,132] (a variety of super Landau models with super-unitary symmetries have been constructed in [133,134,135,136,137,138,139] and fuzzy supergeometries have also been investigated in [110,140,141,142]), we can develop a SUSY version of the VBS models (SVBS models) based on the mutual relations [8,9,10]. For the inclusion of fermionic degrees of freedom, the SVBS states exhibit particular features not observed in the VBS states with higher dimensional groups. For instance, while the VBS states only exhibit a property of quantum magnets, the SVBS states accommodate two distinct sectors, spin sector and charge sector, due to the inclusion of fermionic degrees of freedom. Physically, the SVBS states can be interpreted as hole-doped VBS states with superconducting property. Mathematically, the SVBS states are regarded as a type of “superfield” in terminology of SUSY field theory. As the superfield unifies various fields as its components, the SVBS states realize a variety of ordinary VBS states as the coefficients of the expansion with respect to Grassmann quantities.
By investigating topological features of the SVBS states, we address how SUSY affects the stability of topological phase or entanglement spectrum. As concrete examples, we discuss topological feature of the SVBS states with and symmetries, which we call type-I and type-II SVBS states, respectively. To perform detailed analyses of the SVBS states on a 1D chain, we develop a SUSY version of the MPS formalism (SMPS) [21,24,25]. MPS formalism is now regarded as an appropriate formalism to treat gapped 1D quantum systems [29,38]. Since the MPS formalism naturally incorporates edge states, MPS provides a powerful formalism to discuss relations between topological order and edge state. Taking this advantage, we can obtain general lessons for SUSY effects in topological phases. Specifically, the robustness of the topological phase in the presence of SUSY is discussed in light of the modern symmetry-protected topological order argument, with emphasis on the edge superspin picture. We also generalize the lower SUSY analyses to the case of higher SUSY: fuzzy four-superspheres and SVBS states.
The following is the organization of the present paper. In Section 2, we give a brief introduction to the original VBS states and explain its relations to fuzzy two-sphere and the 2D QHE through the Schwinger-operator representation and the Hopf map. In Section 3, the SUSY extensions of fuzzy two-sphere are presented in detail. The corresponding SVBS states and their basic properties are reviewed in Section 4. In Section 5, the SMPS formalism is introduced for the analysis of SVBS states. Gapped excitations of SVBS states are derived with use of SMPS formalism within single mode approximation. We investigate topological properties of the SVBS states in Section 6, where the entanglement spectrum and entanglement entropy are derived (unpublished results for SVBS chain are also included here). The stability of topological phases in the presence of SUSY is discussed, too. In Section 7, we extend the discussions to the case of fuzzy four-superspheres and the SVBS states. Section 8 is devoted to summary and discussions. In Appendix A, we provide mathematical supplements for the super-Lie group, . Fuzzy four-superspheres with an arbitrary number of SUSY are described in Appendix B.
2. Fuzzy Geometry and Valence Bond Solid States
In this section, we give a quick introduction to fuzzy two-spheres and the (bosonic) VBS states. Their mutual relations will be discussed, too.
The original idea of quantization of two-sphere was first introduced by Berezin in the 70s [94]. In the beginning of the 80s, Hoppe [95] explored the algebraic structure and field theories on a quantized sphere, and subsequently in the early 90s, Madore [96] further examined their structures, coining the name “fuzzy sphere”. Unlike the ordinary sphere, the fuzzy sphere has a minimum scale of area, while respecting the (rotational) symmetry as the ordinary two-sphere. This is a remarkable property of the fuzzy sphere, when we consider the field theories on it. In fact, in the other regularized field theories, such as lattice field theories, the extrinsic cut-off cures the UV divergence at the cost of continuous symmetries, and the resulting theories only respect the space-group symmetry of the lattice on which they are defined. On the other hand, field theories defined on the fuzzy manifolds contain an intrinsic “cut-off” coming from the minimum area of the fuzzy sphere, and the non-commutative field theories constructed on it were expected to have the innate property that might soften the UV divergence to be appropriately renormalized in conventional field theories.
In the middle of 90s, Grosse et al. [97] generalized the notion of the fuzzy two-sphere to construct four-dimensional fuzzy spheres and supersymmetric fuzzy spheres, i.e., fuzzy superspheres [124,125]. In the late 90s, fuzzy geometry was rediscovered in the context of the “second revolution of string theory” and attracted a lot of attention. Researchers began to recognize that the fuzzy geometry is closely related to the geometry that the string theory attempts to describe: the geometry of multiple D-branes is naturally described by fuzzy geometry (see [143,144,145] as reviews), and fuzzy manifolds are also known to arise as classical solutions of Matrix theory (see, e.g., References [98,146]). Similarly, field theories on fuzzy superspheres provide a set-up for SUSY field theories with UV regularization [124,147,148], and the fuzzy superspheres were also found to arise as classical solutions of supermatrix models [149,150]. For details and applications of the fuzzy sphere, interested readers may consult References [151,152,153,154]. Non-commutative geometry and fuzzy physics also found their applications in gravity [155,156,157] and in condensed matter physics [90,91,92,93].
2.1. Fuzzy Two-Spheres and the Lowest Landau Level Physics
The fuzzy two-sphere [94,95,96] is one of the simplest curved fuzzy manifolds (The fuzzy spheres also play a crucial role in studies of string theory; see [158,159,160] for reviews). The coordinates of the fuzzy two-sphere, , are regarded as the operators that are constituted of the generators
Here, R denotes the radius of the sphere, and d is the dimension of the irreducible representation:
with the Casimir index j , and are the matrices of the corresponding representation that satisfy:
and
where denotes unit matrix. The “coordinates”, , defined in Equation (1), satisfy:
Since takes the eigenvalues, , the eigenvalues of are given by:
Each “latitude” of corresponds to a patch of width, , i.e., the minimum state, on the fuzzy sphere ( here, two different viewpoints are possible; one assumes, as is done here, R to be fixed and, in the large-d (or large-j) limit, the width of the patch, , becomes zero to recover the continuous space). The other fixes the width, , and the radius of the fuzzy two-sphere, , diverges in the large-d limit. The former is reminiscent of the scaling limit of lattice field theories upon identifying R with the physical mass. If the limit of large representation, (with fixed radius R), is taken, the patches become invisible, and the discrete nature of the fuzzy sphere is smeared off. In fact, one readily sees and , and the discrete spectrum (6) of becomes continuum raging between and R. In this sense, the fuzzy sphere reduces to the ordinary (commutative) sphere with radius, R, in the limit, .
As a realization of the fuzzy two-sphere, a convenient way is to utilize the Schwinger operator formalism [153,161] and introduce the following operator:
whose components satisfy the following ordinary bosonic commutation relations:
By sandwiching the Pauli matrices with the Schwinger operators, Φ, one may simply represent the coordinates of the fuzzy two-sphere as:
where are the Pauli matrices:
This is the well-known construction of the angular momentum operators introduced by Schwinger [162]. In fact, one can easily check that satisfies the standard commutation relations (3) and that the Schwinger-operator representation (9) coincides with the original definition (1). The square of the radius is given by:
where n denotes the eigenvalues of the number operator for the Schwinger bosons, . Comparing this with Equation (5), one sees and:
Since we utilize the Schwinger operator, the irreducible representation is given by the fully symmetric representation of :
where and are non-negative integers that satisfy . Physically, stand for a finite number of basis states constituting fuzzy two-spheres, which are the eigenstates of with the eigenvalues:
where . The dimension of the space spanned by the basis states (13) is given by . From the expression, (14), it is not obvious that the definition (9) respects the rotational symmetry of the fuzzy two-sphere. However, this is an artifact of the particular choice of the -diagonal basis states (13). Any other complete sets of the basis states of the fuzzy two-sphere can be obtained by applying transformations to the basis set (13). In this sense, the whole Hilbert space of fuzzy two-sphere is “symmetric” with respect to the transformation, and hence, the fuzzy two-sphere is (rotationally) symmetric, like the ordinary (continuum) sphere.
Another description of fuzzy two-sphere is to utilize the coherent state (the coherent state here is usually referred to as the Bloch spin coherent state in the literature.) formalism, which will be useful in understanding the connection with the VBS states. The coherent state, , or, more precisely, the Hopf spinor, that is labeled by a point on the two-sphere, , is defined as a two-component complex vector satisfying (the usual coherent “state” (for ), defined as , satisfies
Expressing the above in the basis and , we obtain Equation (15)).
In general, the (normalized) coherent state is represented in terms of the Euler angles as:
where (, , ) and denotes an arbitrary phase factor. The relation between the point, , on a two-sphere and the two-component Hopf spinor is given by the so-called first Hopf map (for construction of higher dimensional Hopf maps, see Reference [77], for instance):
which maps the three-sphere, , onto the two-sphere, :
In fact, a space of normalized two-component complex spinors, , subject to is isomorphic to , and Equation (17) gives the mapping onto :
The Hopf spinor, , is regarded as the classical counterpart of the Schwinger operator, Φ [Equation (7)] that satisfies:
If we note that , in the limit, , the resemblance between (15) and (20) is clear. Multiplying from the right to both sides of Equation (20) and using , we reproduce Equation (11). By replacing the Schwinger operator with the Hopf spinor, one sees that the Schwinger operator construction (9) of fuzzy coordinates is an operator-generalization (, ) of the Hopf map (17) [163].
The fully symmetric, , representation in terms of the Hopf spinor is obtained if the Schwinger operator in (13) is replaced with the Hopf spinor :
with , .
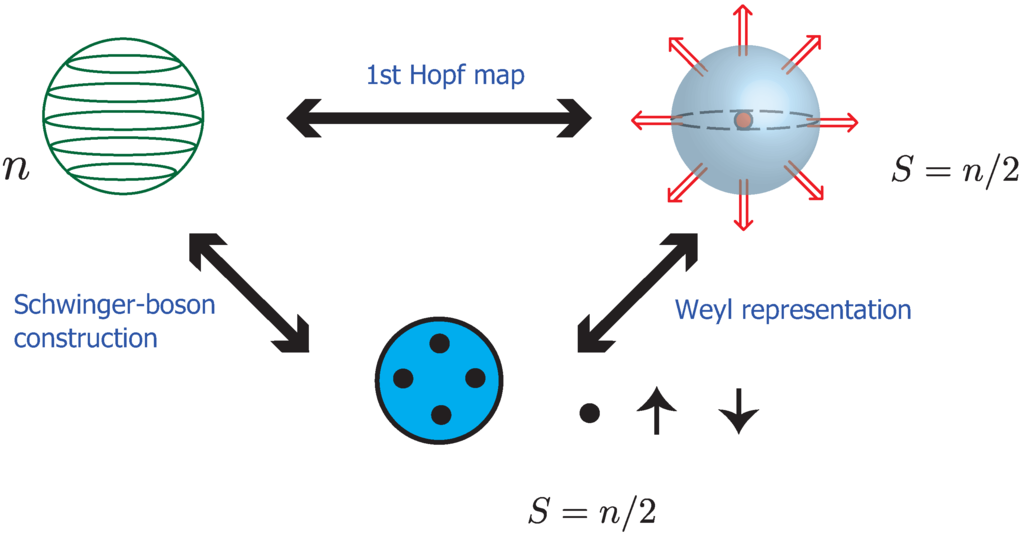
Figure 3.
(Color online) One-body-level relationship among fuzzy two-sphere (upper left), Haldane sphere (upper right) and local spin states of the VBS state (lower middle). The fuzzy two-sphere consists of a finite number of patches, i.e., the basis states, with width, . The Haldane sphere is a two-sphere with a Dirac monopole at its center. The is the monopole charge quantized as a half-integer or an integer by the Dirac quantization condition. In the local spin state of the VBS state (lower center), each blob denotes spin- degrees of freedom, and n blobs amount to local spin by a large Hund coupling on each site.
So far, are just the two auxiliary variables needed to realize the fuzzy two-sphere. However, if we regard them as the physical coordinates of the usual two-dimensional sphere [via the Hopf map (18)], we may think that represents the wave functions of a certain kind of quantum-mechanical systems in two dimensions. In fact, the wave functions, (21), coincide with those of the lowest eigenstates of the Landau Hamiltonian on a two-sphere (with radius R) in the Dirac monopole background, (i.e., the so-called Haldane’s sphere [76]):
where are the covariant angular momenta:
in the presence of the gauge field, , generated by the Dirac monopole at the origin:
In the fuzzy geometry side, the monopole charge, , corresponds to the quantized radius of the fuzzy two-sphere (11) (see also Figure 3). Thus, the lowest Landau level eigenfunctions (on a two-sphere) can be “derived” from the fuzzy two-sphere by switching from the Schwinger operator formalism to the coherent state formalism (or the Weyl representation). This is the key observation of correspondence between fuzzy geometry and the lowest Landau level physics [77].
2.2. Valence Bond Solid States
In order to translate the above features to those of QAFM, we first express the spin, , state in terms of the Schwinger bosons:
The fully symmetric representation (13) constructed out of n Schwinger operators automatically realizes the local spin defined on each site with the spin magnitude:
Physically, this bosonic construction realizes the ferromagnetic (Hund) coupling among n spin-1/2s to yield the maximal spin, , at each site. We have already seen that the spin wave function, written in terms of the Hopf spinor , coincides with those of the non-interacting electrons moving on a two-sphere in the presence of the monopole magnetic field.
Now, we demonstrate that a similar analogy exists even when we switch on strong interactions. Specifically, the exact ground-state wave functions of a class of interacting spin models, called the valence-bond solid (VBS) model [6,7,75], closely resemble the Laughlin wave functions on a two-sphere. The ground states of the VBS models (dubbed the VBS states) on a lattice with coordination number, z (see Figure 4), are constructed as follows. As the first step of the construction, we prepare n () local spins (auxiliary spins) on each vertex (site) of the lattice. Next, we connect every pair of two spin-1/2s on the nearest neighbor sites by spin-singlet bonds (since the spin-singlet state of the two spin-1/2s maximizes the entanglement entropy, the pair is sometimes called maximally entangled in modern literature.) called the valence bonds (VB) (see Figure 4). Last, we project the entire -dimensional Hilbert space of n spin-1/2s onto the subspace with the desired value of the (physical) spin S () on each site to obtain the spin-S many-body singlet state. Depending on which irreducible representation we use to realize the physical spin, we obtain different states even for the same lattice structure (some examples may be found in, e.g., Reference [114]). This kind of construction (valene-bond construction) applies to any lattice in any dimensions (see Figure 4 for typical examples in 1D and 2D), and the state obtained thereby is called the VBS state or, in modern terminology, the projected entangled-pair state (PEPS) [164,165].
It is also possible to construct the VBS states for other symmetry groups (e.g., [115,116] and [112,113]), with due extension of the notion of the singlet valence bond. In these examples, the VBS states thus constructed are constrained by specific symmetry groups, and normally, they do not have any tunable parameter (however, the parent Hamiltonians (i.e., the VBS models) may have tunable parameters. For instance, the parent Hamiltonian of the spin-2 VBS state (in 1D) allows one free parameter to tune even after we fix the overall energy scale.) However, if we use the matrix-product representation [21] in 1D or, in general, tensor-product representation (or, equivalently, the vertex-state representation [54,55]) in higher dimensions to express the VBS states and consider their “anisotropic” extensions of the tensors, it is possible to obtain parameter-dependent states. These generalized VBS states are known to have interesting properties; see, for instance, References [21,23,56] for 1D and References [54,55] for 2D honeycomb and square lattices.
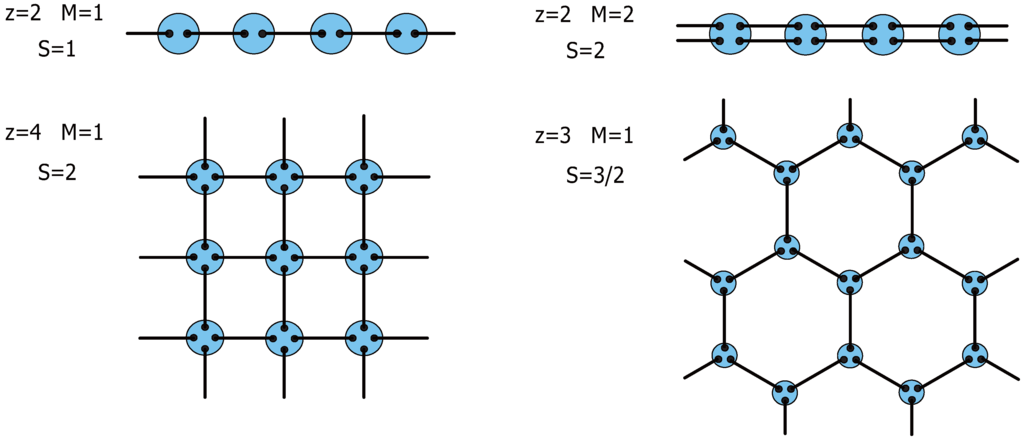
Figure 4.
(Color online) VBS states on 1D and 2D lattices. Filled circles denote auxiliary spin-1/2 objects, which are finally symmetrized to form physical spins at each site. Solid lines stand for singlet valence bonds between the spin-1/2s.
Now, let us come back to the SU(2) VBS states. If we represent the up and down degrees of freedom of auxiliary spin-1/2 by the Schwinger bosons, and (see Equation (25)), the singlet valence bond on the bond reads:
Physically, the spin singlet bond denotes the state with no specific spin polarization made of two spin 1/2 states, and hence, the valence bond represents a non-magnetic spin pairing between the two neighboring sites.
Of course, we can promote the power of the singlet bond from one to an arbitrary integer, M:
to represent M valence bonds between the sites, i and j. Thus, one sees that the original valence-bond construction [6,7] of the VBS states is equivalent to the following representation in terms of the Schwinger bosons [75]:
where implies that the product is taken over all nearest-neighbor bonds, , and denotes the vacuum of the Schwinger bosons. From (), it is obvious that the state Equation (29) is spin-singlet. As z bonds emanate from each site of the lattice (for instance, is for 1D chain and for D-dimensional hypercubic lattice), we have Schwinger bosons per site in the VBS state (29):
and, hence, the local spin quantum number, , is given by:
In particular, for the 1D (i.e., ) VBS state, we have:
and the local Hilbert space is spanned by the following three basis states:
We were a bit sloppy in writing down Equation (29). When considering a finite open chain (with length L), we should be careful in dealing with the edges of the system, while, for the VBS states on a circle, the expression (29) is correct without any modification. In fact, in (29), the number of the Schwinger bosons at sites 1 and L is M (half of that of the other sites), and we have to add the extra edge degrees of freedom represented by the M-th order homogeneous polynomials in and to recover the correct spin-Ms at the edges. The edge polynomials for are given by:
This representation naturally incorporates the physical emergent edge spins [13,14] localized around the two edges. For general M, the precise form of the VBS states on an open chain reads as
Since the VBS Hamiltonian is defined as the projection operator for the Hilbert space of a pair of neighboring spins (see Section 4.3 for detail), the state of the form (29) is the ground state regardless of the edge polynomials. Therefore, there appear degenerate ground states for the spin-S() VBS state on a finite open chain (see Figure 5) [7]. From similar considerations, it is obvious that the higher-dimensional VBS ground states (e.g., those in Figure 4) have degeneracy exponentially large in the size of the boundary. In the following, unless otherwise stated, we implicitly assume that the VBS state is defined in 1D and will focus on the spin-1 case.
Let us look at some key features of the VBS states in more detail. Classically, AFM on a bipartite lattice assumes the Néel-ordered state, where any pair of neighboring spins point the opposite directions. To be specific, in the Néel state of (classical) spin-1 AFM, the z-component of local spins at the site, i, takes either or , depending on to which sublattice the site belongs. (without loss of generality, we may assume that ordered spins are parallel to the z-axis). The spin configuration described by the VBS state is totally different from that of the classical Néel state described above. First of all, we note that the VBS state is -invariant (being a product of singlet bonds between pairs of adjacent sites; see Equation (29) and Figure 4) and is non-degenerate (this is true for a periodic chain and the bulk in a infinite chain; on a finite open chain, the ground state may not be spin-singlet and, hence, may show degeneracy corresponding to the edge states), while the classical ground state, i.e., the Néel state, is infinitely degenerate with respect to the rotational symmetry. This implies that though the magnitude of the local spin is , its expectation value is zero, , in the bulk (on a finite open chain, may take a non-zero finite value near the two boundaries and decays exponentially to zero toward the center of the system; in this sense, magnetism revives near the boundaries, and this is the manifestation of the emergent edge states), and the system is non-magnetic. In this sense, the VBS state is purely quantum-mechanical and does not have any classical counterpart.

Figure 5.
(Color online) For the VBS state on a finite open chain, there exist spin-1/2 degrees of freedom at each edge. By construction, the VBS state is the ground state of the VBS Hamiltonian, regardless of the spin states at the edges.
For better understanding of the VBS state, let us expand the spin-1 VBS state in the -basis:
where the coefficient in front of each term on the right-hand side is omitted for simplicity. What is remarkable with the above VBS state is that all the states appearing on the right-hand side have a very special feature; the states, and , appear in an alternating manner with intervening states. Namely, the ground state exhibits an analogue of the classical Néel order, called the string order [18,19], albeit “diluted” by randomly inserted zeros (see Section 6.1 for further detail). Unlike in the case of the classical Néel order, by the SU(2) symmetry of the state, the existence of the string order does not rely on the particular choice of the quantization axis (z-axis, here).
For the sake of later discussions, we introduce here a concise representation of the VBS state and point out remarkable similarity [75] to the Laughlin-Haldane wave function [76] for FQHE on a two-sphere. First, we note that by using the invariant matrix given by the 2 × 2 antisymmetric matrix (see Appendix A):
the VBS states (29) on generic lattices can be rewritten compactly as:
where denotes the Schwinger operator on the site i:
Then, we rewrite the VBS state (38) into the form of the wave function on a two-sphere. Specifically, by replacing the Schwinger operator with the Hopf spinor:
we obtain the coherent-state (or Weyl) representation of the VBS state (precisely, if we use the coherent-state basis
for the local spin- states and expand the VBS state in these basis, we obtain the “wave function” ):
Now, the formal similarity to the Laughlin-Haldane wave function of QHE:
on a two-sphere [75] is clear. By the stereographic projection from a two-sphere to a complex plane:
(42) is, in the thermodynamic limit, reduced to the celebrated Laughlin wave function:
Though the physical interpretation of the quantities appearing in these wave functions are different (Table 1), mathematical similarities between the VBS model and QHE may be manifest from the above constructions. Similarities between topological properties of VBS and QHE have also been discussed in References [166,167].

Table 1.
Correspondences between physical quantities of many-body wavefunctions of QHE and quantum anti-ferromagnets (QAFM).
| QHE | QAFM | |
|---|---|---|
| Many-body state | Laughlin-Haldane wave function | VBS state |
| Power | m: inverse of filling factor | M: number of VBs between neighboring sites |
| Charge | : monopole charge | : local spin magnitude |
3. Fuzzy Two-Supersphere
Next, we proceed to the SUSY version of fuzzy two-sphere (fuzzy superspheres are also realized as a classical solution of supermatrix models [149,150].) and generalized VBS states. We mostly focus on the cases of the SUSY numbers, and 2.
3.1.
First, we introduce SUSY algebra, [168,169,170], which contains the algebra as its maximal bosonic subalgebra. The algebra consists of the five generators, three of which are (bosonic) generators, , and the remaining two are fermionic spinors, , which amount to satisfy:
The Casimir is constructed as:
and its eigenvalues are given by : j is referred to as the superspin taking the non-negative integer or half-integer values, . The irreducible representation with the superspin index, j, consists of the j and spin representations, and hence, the dimension of the representation of superspin j is given by:
The fundamental representation matrices of the generators are expressed by the following 3 × 3 matrices:
where () are:
Equation (48) may be regarded as a SUSY extension of the Pauli matrices. They are “Hermitian” in the sense:
where ‡ signifies the super-adjoint defined by:
Similar to the case of fuzzy sphere (9), the coordinates of fuzzy two-superspheres [124,125] are constructed by the graded version of the Schwinger operator formalism [127,128,129]. The graded Schwinger operator consists of two bosonic components, a and b, and one fermion component, f:
with satisfying:
With the use of Ψ, the coordinates of a fuzzy two-supersphere, (two on the left to | denotes the bosonic degrees of freedom, while two on the right to | denotes the fermionic degrees of freedom), are constructed as:
which satisfy:
where with The square of the radius of fuzzy supersphere is given by the Casimir:
Notice that the zero-point energy in (56) reflects the difference between the bosonic and fermionic degrees of freedom. The basis states on fuzzy supersphere consist of the graded fully symmetric representation specified by the superspin, :
where and are non-negative integers that satisfy . is the fermionic counterpart of , and thus, and exhibit SUSY. The bosonic and fermionic basis states are the eigenstates of the fermion parity, , with the eigenvalues, and , respectively. Their degrees of freedom are also respectively given by:
and the total degrees of freedom is:
The eigenvalues of for (57) read as:
where . Even k () correspond to the bosonic states (57a), while odd k () to the the fermionic states (57b). Compare the eigenvalues of fuzzy supersphere (60) with those of the fuzzy (bosonic) sphere (14): the degrees of freedom of fuzzy supersphere for even k are accounted for by those of a fuzzy sphere with radius, n, while those for odd k are by a fuzzy sphere with radius . In this sense, the fuzzy two-supersphere, , of radius, n, can be regarded as a “compound” of two fuzzy spheres with different radii, and [Figure 6]:
The first accounts for the bosonic degrees of freedom (57a), while the second does so for the fermionic degrees of freedom (57b).
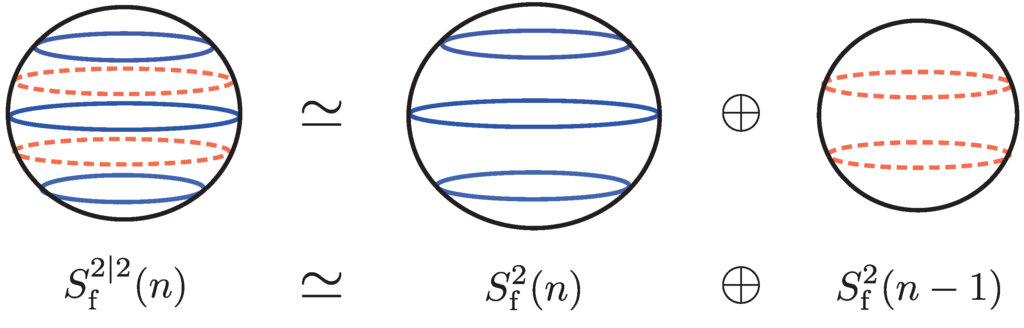
Figure 6.
(Color online) fuzzy supersphere is a “compound” of two fuzzy two-spheres with radii, and . This figure corresponds to .
Similar to the first Hopf map, we can construct a graded version of the first Hopf map [171,172]:
where and are the matrices of fundamental representation (48) and ψ denotes a normalized superspinor:
with:
Here, the super-adjoint of the superspinor is defined by [see, also, Equation (51)], and * represents the pseudo-conjugation (the pseudo-conjugation is defined as and for Grassmann odd quantities; see Refernence [173], for instance). The first two components of ψ are Grassmann-even. and the third component is Grassmann-odd. The ψ subject to the normalization (64) can be regarded as a coordinate of the manifold . From (62), we find that and satisfy the condition of :
Consequently, the map (62) represents:
The bosonic part of (66) exactly corresponds to the first Hopf map. Note that ψ satisfies the super-coherent state equation:
and ψ is referred to as the super-coherent state or spin-hole coherent state [37] in the literature. are Grassmann even, but not usual c-numbers, since the square of is not a c-number, , as seen from (65). Instead of , one can introduce c-number quantities, , as:
which denoting coordinates on , the “body” of , as confirmed from . With the use of the coordinates on , ψ can be expressed as [129]:
where stands for the arbitrary phase factor. The last expression on the right-hand side manifests the graded Hopf fibration, (here, ∼ denotes local equivalence): the -fiber, , is canceled in the graded Hopf map (62), and the other quantities, and in (69), correspond to the coordinates on .
3.2.
As the geometric structure of is determined by the algebra, the fuzzy supersphere, , is formulated by the algebra. The algebra contains the bosonic subalgebra, , and is isomorphic to . The dimension is given by:
Denoting the four bosonic generators as and Γ and the four fermionic generators as and , we can express the algebra as:
where . and form the subalgebra. There are two sets of fermionic generators, and , which bring SUSY. The algebra has two Casimirs, quadratic:
and cubic ones [169].
To specify a fuzzy manifold, an appropriate choice of irreducible representation is crucial as well. The irreducible representation of is classified into two categories: typical representation and atypical representation [169,170]. Since the quadratic Casimir (72) is identically zero for atypical representation, we adopt typical representation for the construction of [128]. The matrices for typical representation for minimal dimension are represented by the following matrices:
Applying the Schwinger construction, we introduce the coordinates of as:
where Ψ signifies the four-component, , Schwinger operator:
and with . Here, a and b are bosonic operators, while f and g are fermionic operators that satisfy:
It is straightforward to evaluate the square of the radius of :
With a given n, the basis states of are constituted of the graded fully symmetric representation of the :
where , , , , , , and denote non-negative integers that satisfy . The dimension of bosonic basis states, and , and that of fermionic basis states, and , are found to be equal:
and the total degrees of freedom amount to:
The square of the radius of (77) does not have the zero-point, “energy”, since the bosonic and fermionic degrees of freedom are canceled exactly (in the cases of fuzzy superspheres based on the algebra for , the dimension of fermionic basis states is larger than that of the bosonic basis states, and the zero-point “energy” becomes minus; in other words, the radius of fuzzy supersphere would become minus for the representations with sufficiently small dimensions; thus, we only deal with the fuzzy superspheres for ). The four sets of the basis states (78) forms the SUSY multiplet and suggests the following geometrical structure of :
The latitudes for the the basis states (78) are given by:
with . The even ks (, ) correspond to the bosonic basis states, (78a) and (78b), while odd ks (, ) to the fermionic basis states, (78c) and (78d) (Figure 7). Except for non-degenerate states at the north and south poles , all the other eigenvalues of (82) are doubly-degenerate.

Figure 7.
(Color online) is a “compound” made of four fuzzy two-spheres that are considered as superpartners. The above picture corresponds to .
4. Supersymmetric Valence Bond Solid States
In this section, we review the basic properties of the SVBS states [8,9] and discuss its intriguing connection to the SUSY QH wave function and BCS function.
4.1. Construction of SVBS States
4.1.1.
Here, we consider the SVBS states with SUSY (), which we shall call the type-I SVBS states. We apply the mathematical procedure of the constructions of the VBS states described in Section 2.2. The first we prepare is the invariant matrix (see Appendix A):
with the parameter dependent Schwinger operator:
the type-I SVBS state is constructed as:
The operators ,, and , are components of the graded Schwinger operator defined on each site, i, and satisfy the commutation relations, and . Physically, the three fundamental states, , and , are interpreted as spin ↑, ↓ and spinless hole states (see Table 2) (in Refernece [174], such a triplet is dubbed the superqubit). Since the fermions always appear in pairs of the form (i, j are adjacent), the SVBS states can be regarded as hole-pair doped VBS states, and r stands for a hole doping parameter.
Here, some comments are added. The -specific feature does not enter the local Hilbert space on each site. For instance, (57) can also be regarded as an irreducible representation of . Meanwhile, in the construction of the type-I SVBS states (85), the invariant matrix was utilized, and then the structure explicitly enters in the many-body states. This implies that (super)spin interaction between adjacent sites reduces the symmetry on each site to the lower symmetry in many-body physics.

Table 2.
The physical interpretation of the local states made by the Schwinger operators. denotes the hole degrees of freedom.
| Schwinger operator | quantum number | Spin state |
|---|---|---|
| 1/2 | ||
| 0 |
In the type-I SVB states (85), the total particle number of the Schwinger particles at each site is given by:
Since the fermion number takes either 0 or 1, the following two eigenvalues are possible for the local spin quantum number :
In particular, for , each site can take two spin values:
and the local Hilbert space is spanned by the five (, in general) basis states:
These constitute a SUSY multiplet with the superspin . Similarly, the edge states consist of SUSY multiplet with the superspin :
As we will see in Section 5, the ground state of a finite open chain is nine-fold degenerate (corresponding to matrix-components of the type-I SVBS states).
Intriguingly, the type-I SVBS chain interpolates two VBS states in the two extreme limits of the hole doping: in the limit , reproduces the original spin-1 VBS state :
while in the limit, , reduces to the Majumdar-Ghosh (MG) dimer state [175,176] ,
where is either of the two dimerized states of the MG model (the open boundary condition has been implicitly assumed here; if the periodic boundary condition had been used, the two states would have been summed up with a minus sign, due to the anti-commutating property of the holes) [Figure 8]:
For larger M, should be replaced with the inhomogeneous VBS states [75], where the number of valence bonds alternates from bond to bond.
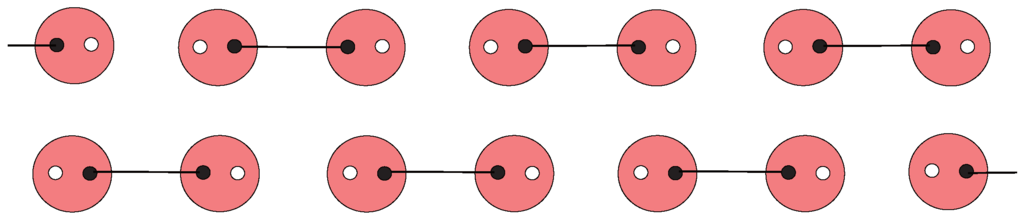
Figure 8.
(Color online) Two MG dimer states related by translation.
In the super-coherent state (63) representation (in the following discussion, the explicit form of the superspinor is not important; only the Grassmann property of the components matters), the SVBS state is expressed as [8]:
From the Grassmann (odd) property of η, (94) can be rewritten as:
where is the coherent state representation of the original VBS state (41). We can deduce a nice physical interpretation of the SVBS states from this expression. Since the SVBS states are written as a “product” of the exponential and the original VBS wave function , all physics inherent in the SVBS must be included in this exponential factor:
Since every time when the factor:
acts to the VBS wave function, the VB between the adjacent sites, i and j, is replaced with a hole-pair (see Figure 9):
one sees that the SVBS wave function (95) may be expanded as:
Thus, the SVBS chain is expressed as the superposition of many-body states on the right-hand side (r.h.s.) of (99). The first term on the r.h.s. is the original VBS chain (which is consistent with (91)). The second term is the VBS chain with one hole-pair doped, and the third term is the VBS chain with two hole-pairs doped. In general, the nth term represents the VBS chain with hole pairs doped. As the last term, partially dimerized chains, i.e., the VB chains whose half sites are occupied with hole-pairs, are realized (see Figure 10) (for general M and the arbitrary lattice coordination number, z, the last term of the expansion realizes a resonating valence bond (RVB) state [177]; for instance, on a 2D square lattice, the SVBS state with SUSY gives the Rokhsar-Kivelson RVB state [178] as the last term). For , the last term gives rise to the Majumdar-Ghosh dimer states:
where and are the coherent state representation of and (93). Now, the physical meaning of the SVBS states is transparent: the SVBS states signify a superposed state by all possible hole-pair doped VBS states, which can be viewed as a generalization of the resonating valence bond state [177] (see Section 4.2 for more details).

Figure 9.
(Color online) When the exponential factor (97) acts on the VBS state, the factor breaks the VB between i and sites and creates a hole-pair instead. The figure and caption are taken from [8].
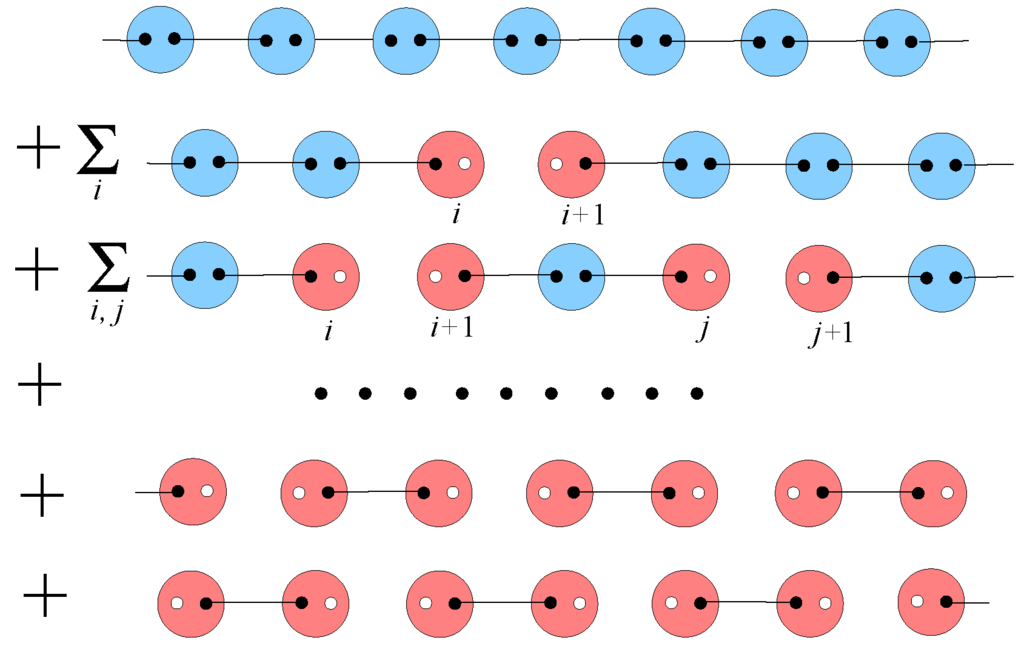
Figure 10.
(Color online) The type-I SVBS is a superposed state of hole-pair-doped VBS states. With the finite hole-doping parameter, r, all of the hole-pair-doped VBS states are superposed to form the SVBS state, and the SVBS state exhibits the SC property. At , the SVBS state is reduced to the original VBS state (depicted as the first chain), while for , the SVBS state is reduced to the MG dimer state (depicted as the last two chains). The figure and caption are taken from [9].
As in the original correspondence between VBS and QHE, the super-coherent state representation of SVBS (94) shows striking analogies to the SUSY Laughlin-Haldane wave function [130]:
Furthermore, for one-particle mechanics, there exists apparent relations between the SVBS and the SUSY Landau problem. Indeed, the super-coherent state representation of the basis states (57):
gives the lowest Landau level eigenstates of a SUSY Landau Hamiltonian [129]. Here, , , and are non-negative integers that satisfy . By the stereographic projection, and , the SUSY Laughlin-Haldane wave function, (101), is transformed to the SUSY Laughlin wave function defined by:
By expanding the polynomial part in the Grassmann odd quantities, we have:
where N is the total number of particles (which we assumed to be an even integer) and coincides with the Laughlin wave function on a 2D plane (up to the Grassmann factor ):
Interestingly, the Pfaffian wave function, , for the ground state of the non-Abelian QHE [179] appears in the last term of the expansion (104) at .
4.1.2.
The SVBS states, which we call the type-II SVBS states, are constructed as invariant VBS states. With the invariant matrix:
and Schwinger operator:
we introduce the type-II SVBS states:
The inclusion of two species of holes, f and g, allows us to write down a wave function more symmetric with respect to the bosonic and fermionic degrees of freedom. The new fermionic degrees of freedom, , are interpreted as another species of a (spinless) hole, and satisfy the standard anti-commutation relations, , , etc. In the type-II VBS states, there appear local sites, such as , with spin-0, which are not realized in the type-I SVBS states.
We have two species of fermions, and the total particle number of the Schwinger particles at each site i reads as:
Since the eigenvalues of and can take either 0 or 1, in the type-II SVBS chain , the following four eigenvalues are allowed for the local spin quantum number, :
In particular, for the SVBS chain, the local spin values are given by:
and the local Hilbert space is spanned by the following nine basis states:
The edge states are now given by
and correspondingly, there appear degenerate ground states for the type-II SVBS chain.
The type-II SVBS chain has the following properties. As in the type-I SVBS state, the type-II SVBS state reproduces the original VBS state for :
On the other hand, when , it reduces to the totally uncorrelated fermionic (F) state filled with holes:
Here, we have assumed the open boundary condition (if the periodic boundary condition is used, we have a zero state for odd-length chains; the sign factor depends on both the parity of the system size and the edge states). Note that, unlike type-I, type-II SVBS states have no spin degrees of freedom for . The super-coherent state representation of is given by:
By expanding the exponentials in terms of r, the type-II SVBS states can be expressed as a superposition of the hole-pair doped VBS states, as shown in Figure 11.
4.2. Superconducting Properties
In both and , the fermions always appear in pairs, and the wave functions can be expressed by a superposition of fermion pairs. We can point out interesting similarities between the SVBS states and BCS state of SC [180]:
with electron operator, , and coherence factor, . can be expressed as:
This expansion may remind us of the hole-pair expansion of the SVBS state (99). Furthermore, in the limit, , the BCS state reduces to the electron vacuum (no fermions), and for , it coincides with the filled Fermi sphere :
These also show apparent similarities with the asymptotic behaviors of the type-II SVBS chain, (114) and (115), under the correspondence:
From the analogies to the BCS state, the SVBS states are expected to exhibit a SC property in the charge sector by the immersion of hole-pairs to (insulating) VBS states (see Figure 12). This is quite similar to the mechanism of the Anderson’s RVB picture of high Tc SC [177]: a finite amount of hole-doping transforms the insulator of resonating valence bond state to a high Tc SC state. In the following, we explore qualitative arguments for the SC aspect of the SVBS states.
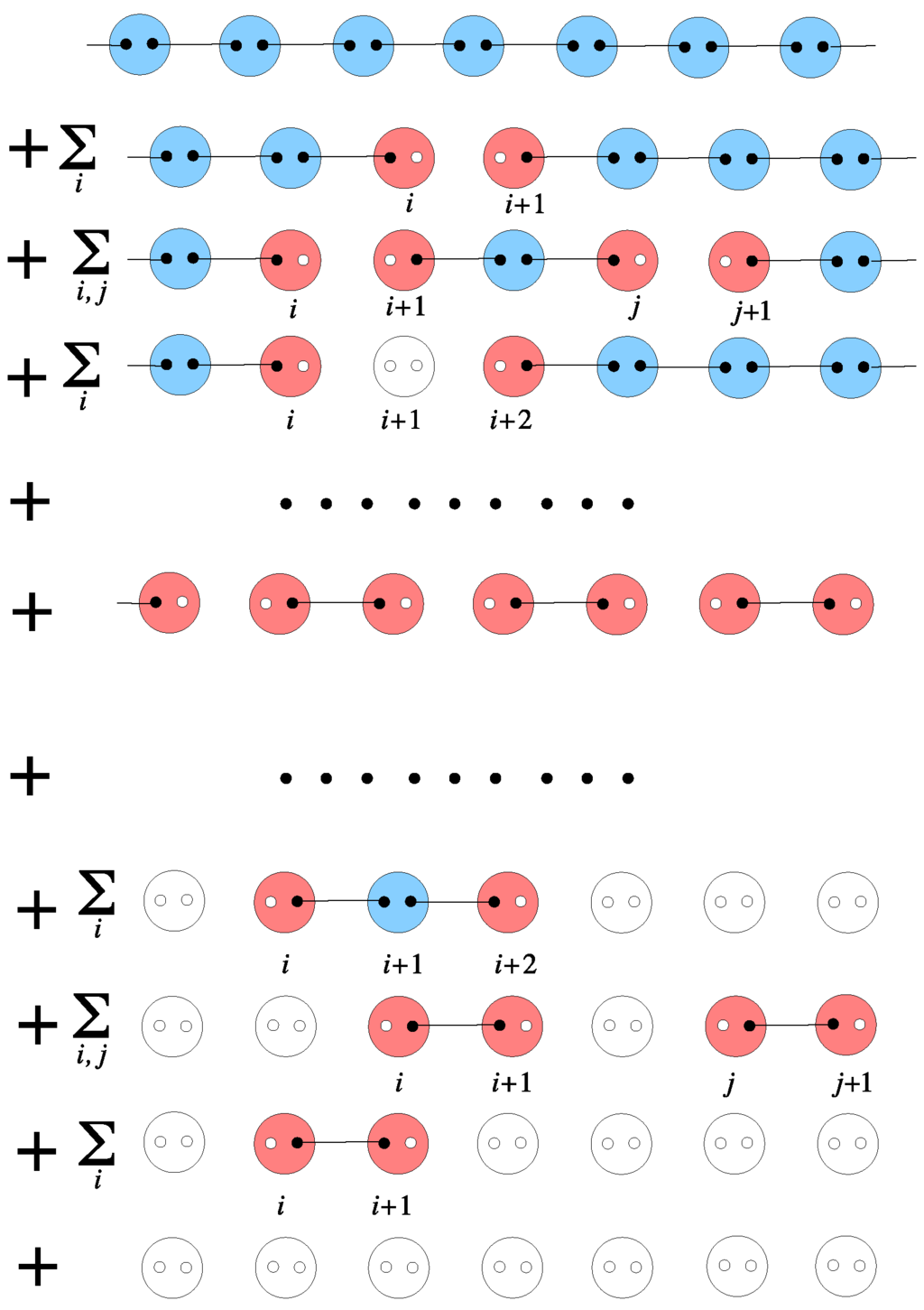
Figure 11.
(Color online) Like the type-I SVBS chain, the type-II SVBS chain is also expressed as a superposition of the hole-pair doped VBS chains. What is different to the type-I SVBS chain is the appearance of the spinless sites, depicted by the large white circles with double holes. The MG states are realized in the “middle” of the sequence. The original VBS state and the hole-VBS state are respectively realized in the first and last lines. The figure and caption are taken from [9].

Figure 12.
The SVBS states exhibit a superconducting property in the charge sector with finite r in addition to a quantum AFM property in the spin sector.
4.2.1.
Since the naive SC order parameter, such as , vanishes due to the violation of particle number conservation at each site, as the SC order parameter of the type-I VBS state, we adopt the following quantity:
which is calculated as:
It takes the maximum value:
at:
In particular, for , . The expectation values for the boson and fermion numbers, and , are respectively calculated as:
As expected, with an increase of the hole doping, , monotonically decreases, while monotonically increases. The fluctuations for the boson and fermion numbers, and , are given by:
and their maximum is met at
The behaviors of such quantities are depicted in Figure 13.
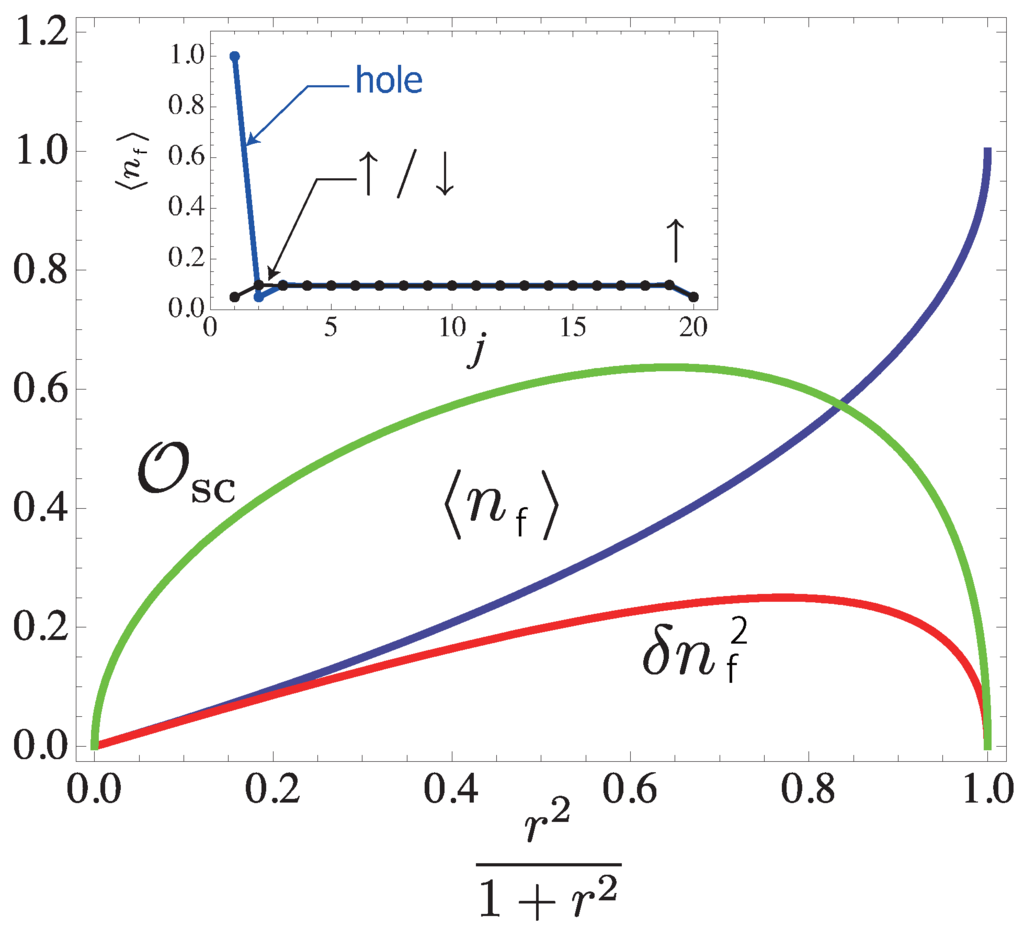
Figure 13.
(Color online) Plot of , the hole density, , and the hole-number fluctuation, , as a function of r. Here,the bulk values are plotted. Inset: pProfile of the hole density () for a finite system () with different left edge states (↑, ↓ and “hole”). Only the left edge state is changed with the right one fixed to . The hole density approaches exponentially to the bulk value as we move away from the edge. The figure and caption are taken from [9].
While the BCS state (117) has the particle-hole symmetry (for (117), the order parameter, , the electron number, , and its fluctuation, , are calculated as:
and are symmetric under , due to the particle-hole symmetry. The SVBS state does not show an exact particle-hole symmetry, (see the SC order parameter (122), for instance). This is because of the unequal properties between boson and fermion operators, .
4.2.2.
We define the order parameter for the type-II SVBS state (108) as follows:
In Figure 14, we plotted its expectation value:
the hole-number , and hole fluctuation, :
The SC order parameter, takes its maximal value at for . Comparing Figure 13 and Figure 14, one may find that the behavior of the order parameter of the type-II SVBS chain is more symmetric with respect to than that of the type-I SVBS chain. This is because of the almost compensation of the contributions from the equal number of the boson and fermion species in the type-II SVBS states.
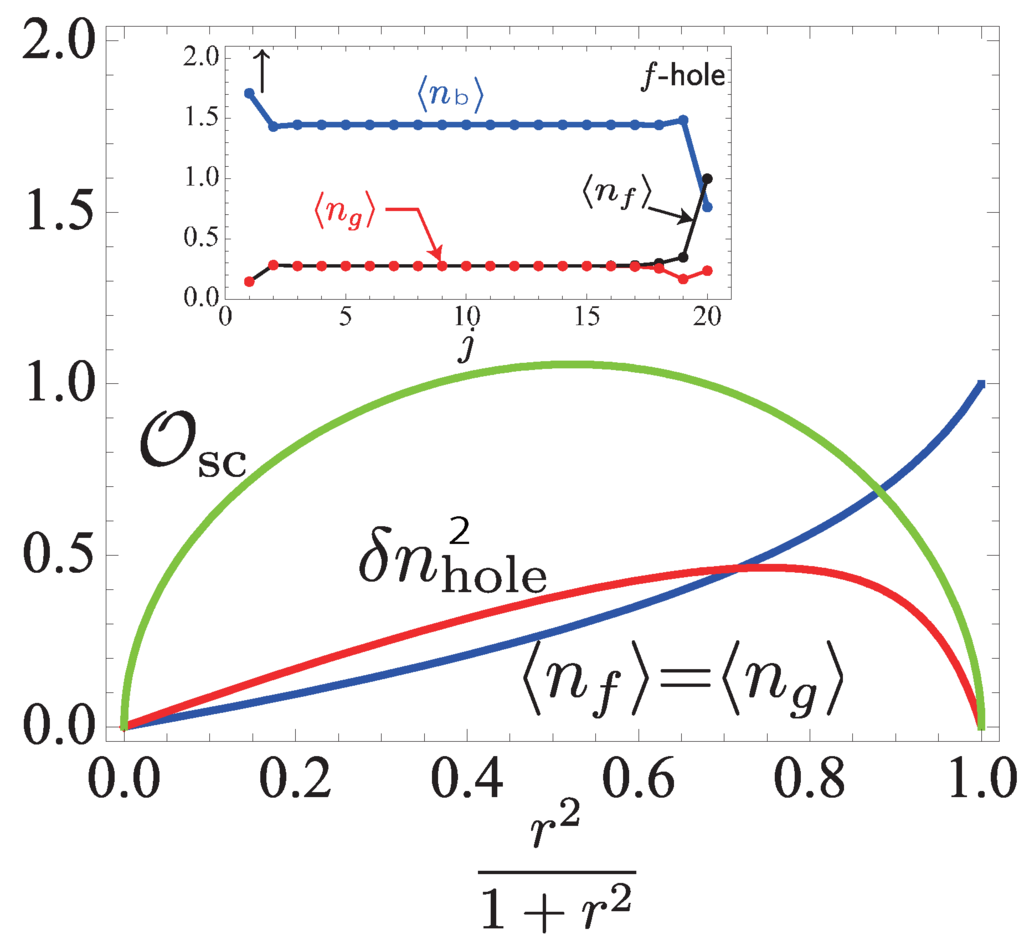
Figure 14.
(Color online) Plot of , the hole density, , and the hole-number fluctuation, , as a function of r. Inset: profile of the hole density () for a finite system (). Only the left edge state is changed with the right one fixed to . The figure and caption are taken from [9].
4.3. Parent Hamiltonians
The VBS state is the exact and unique ground state of a many-body Hamiltonian, which we call the parent Hamiltonian [6,7]. The relation between the VBS state and its parent Hamiltonian is quite unique. Usually in quantum mechanics, Hamiltonian is firstly given, and then we solve the eigenvalue problem of the given Hamiltonian. In most cases, particularly in the presence of many-body interaction, it is formidable to exactly solve the eigenvalue problem, and so, we need to rely on some appropriate approximation method. Interestingly, in VBS models, the procedure is completely : the many-body state (VBS state) is firstly given, and next the parent Hamiltonian is constructed, such that its ground state is exactly given by the VBS state.
We briefly review the procedure for the construction of the parent Hamiltonian. Consider the VBS chain with bulk spin 1. The decomposition rule of two spin 1 gives the total spin :
However, the values for the bond spin of the VBS chain does not take , since in that case, all four 1/2 spins are aligned to a same direction and do not form the spin-singlet bond between neighboring sites (see Figure 15).

Figure 15.
(Color online) The bond spin, , cannot be realized in the VBS chain.
Hence, the VBS state satisfies the condition:
where denotes a projection operator to the bond spin, . Since the eigenvalue of the projection operator is either 0 or 1 for arbitrary adjacent sites, the minimum eigenvalue of the “many-body operator”, , is zero. This simple fact is the key observation for the construction of the parent Hamiltonian. We then construct the parent Hamiltonian for the VBS chain as:
where denotes a positive coefficient ( can depend on the lattice site, i, but here, we postulate lattice translation symmetry and drop the lattice index, i). It is obvious that the eigenvalues of the parent Hamiltonian (134) are semi-positive definite, and its ground-state energy is zero. Furthermore, remember that the VBS state vanishes by the projection operators in the parent Hamiltonian, and hence:
Therefore, the VBS chain is a zero-energy ground state of the parent Hamiltonian (134). There is uniqueness to the ground state (on a finite-size chain, the ground state is, by construction, either unique (for a periodic chain) or degenerate with respect to the edge states (for an open chain)). In order to prove the uniqueness in the infinite-size system, one has to define the infinite-size ground state carefully [7].) for the parent Hamiltonian (up to the degeneracy coming from the edge degrees of freedom), which can also be proven [7]. The projection operator is explicitly derived as:
In the present case, , is given by:
After all, for the VBS chain, the parent Hamiltonian takes the following form:
where the overall proportional factor, , has been absorbed in the coefficient, V. The parameter, V, simply determines the energy scale of the system and is not important in the dynamical behaviors of the system. The construction of the parent Hamiltonian is rather technical, but the resulting parent Hamiltonian (138) appears to be “physical”: the spin-spin interaction represents the Heisenberg AFM, though it contains the quadratic term whose coefficient is one-third of the first Heisenberg AFM term. It may be obvious from the above discussion that the VBS state is the exact ground state of the parent Hamiltonian, but if the Hamiltonian (138) was firstly given, one might think that it is almost impossible to derive its exact energy spectra and corresponding many-body states. However, at least for the ground-state, we know the exact form of the wave function and its energy. Taking this advantage, we can develop precise discussions about physical quantities relevant to the ground-state, such as entanglement spectrum. For excitations, we need to rely on some approximation technique to extract useful information from the parent Hamiltonian (see Section 5.3.2). It should also be emphasized that the present construction can be generalized to higher spin VBS states on an arbitrary lattice in any dimensions. Generally, the parent Hamiltonian is given by:
where denotes a positive coefficient and is given by:
In QHE, the parent Hamiltonian for the Laughlin-Haldane wave function is called the Haldane’s pseudo-potential Hamiltonian [76]. As discussed in Section 2.2, the mathematical structure of the VBS state and the QHE is similar to each other, and the pseudo-potential Hamiltonian for QHE can also be obtained by applying the translations between QHE and VBS (Table 1). Indeed, the resultant pseudo-potential Hamiltonian for the Laughlin-Haldane wave function takes the form similar to (139):
where denotes the projection operator to two-body angular momentum, J.
4.3.1.
By replacing the operators with ones, we readily construct the parent Hamiltonian for the type-I SVBS states, which are invariant under transformations generated by the bosonic generators, :
and the parameter-dependent fermionic operators, :
where is defined by (84). Notice that and satisfy the algebra (45). With use of the generators, it is straightforward to construct the parent Hamiltonian for the SVBS states with the value of the parameter, r. First, we need to derive the projection operators to the subspaces of bond-superspin, J. The decomposition rule for the two superspins is given by:
Note that the decomposition rule is similar to that of the , except for the bond-superspin decreasing by . The SVBS state does not contain any bond superspins larger than and is the exact zero-energy ground state of the parent Hamiltonian:
where are positive coefficients and are the projection operator onto the superspin-J representation of , written in terms of the Casimir operator as:
which projects to the two-site subspace of the bond superspin, J. Here, and . Since the projection operators (146) are invariant, the parent Hamiltonian is (145), as well. Following similar discussions about the uniqueness of the VBS state in Reference [7], we can prove that the SVBS state is the unique zero-energy ground-state of the parent Hamiltonian (145).
For concreteness, we demonstrate the derivation of the parent Hamiltonian for the SVBS chain (, and then ). From (144), we obtain the parent Hamiltonian (145) for the type-I SVBS chain as:
Here, we add several comments. Since the Casimir operator, , contains pair-creation terms of fermions, such as , the Hamiltonian (147) does not preserve the total fermion number, (though the total particle number, i.e., the sum of boson number and fermion number, is conserved). This fermion number non-conserving term is a particular structure of the BCS Hamiltonian, and this is in agreement with the SC property of the SVBS model (see Section 4.2).
The fermionic generators, , are non-Hermitian, and then the type-I parent Hamiltonian (145) is non-Hermitian, as well. As a reasonable Hermitian extension of the type-I Hamiltonian, one may adopt:
The definition (148) is a natural generalization of the original type-I parent Hamiltonian, since, if the projection operators were Hermitian, from the property , Equation (148) would be reduced to the original one (145).
4.3.2.
The irreducible representation of the group is specified by , which signify the indices of the largest bosonic subalgebra, (we denote the eigenvalues of the Casimir operator, , as (.) and arbitrary complex number eigenvalues of the operator, B, as b.) The irreducible representation is classified into two categories: the typical representation and atypical representation. For , the irreducible representation is called the typical representation with dimension, , while for , the irreducible representation becomes the atypical representation with dimension . The eigenvalues of the quadratic Casimir operator (72) for representation are generally given by:
Then, for the atypical representation, , the Casimir eigenvalues identically vanish. Since the Casimir corresponds to the square of the radius of fuzzy manifold, it may not be probable to explore fuzzy geometry based on the atypical representation. Meanwhile, the typical representation consists of four representations, , , , , each of which carries the spin index S as:
For instance, an eight-dimensional typical representation, , is constructed with the use of the components of the Schwinger operator (107):
They give rise to a SUSY multiplet. The superspin operators can also be given by:
with , , and γ (73). Obviously, and are the generators of the subalgebra . The basis states (151) carry the indices as:
For a two-site system, the bond superspin operators are constructed as , , , , and the quadratic Casimir operator is expressed as:
where (the graded fully symmetric representation made of the Schwinger operator carries the indices, ), and is defined as:
The tensor product of two identical typical representations is decomposed as:
For instance, (on the right-hand sides of (157) and (156)) is replaced by a not-completely reducible atypical representation consisting of a semi-direct sum of atypical representations, , , , (for details, see Section 2.5.3 in [173]).
Similar to the decomposition (144), the bond superspins decrease by 1/2 [see the right-hand side of (157)]. As also observed in (157), B is specified by J: for integer, J, , while for half-integer, J, or . Hence, the square of B is uniquely determined as a function of J:
Invoking the usual arguments of constructing the parent Hamiltonian, we derive the type-II parent Hamiltonian as:
where stand for the projection operators of the bond superspin J:
Here, and are given by (158). For a type-II SVBS chain, the parent Hamiltonian is given by:
where the projection operators are:
With the use of , the type-II parent Hamiltonian (161) can be rewritten as:
It is noticed that, unlike the type-I parent Hamiltonians (145), the type-II parent Hamiltonians (159) themselves are Hermitian, since the Casimir itself (154) is given by a Hermitian operator.
5. Supersymmetric Matrix Product State Formalism
This section reviews the MPS formalism and its supersymmetric version, SMPS. In the formalism, the edge degrees of freedom are naturally incorporated. Practically, the MPS formalism provides a powerful method to calculate physical quantities, such as excitation gap, string order and entanglement spectrum.
5.1. Bosonic Matrix Product State Formalism
As we have discussed above, the VBS state is expressed as a product of valence bonds defined on two adjacent sites. In 1D, the VBS state (29) can be rewritten as a product of matrices defined on local site [21,24]:
where the “state-valued” matrix is given by:
It is clear, by the Schwinger-boson construction, that the row and the column of the matrix, , correspond, respectively, to the valence bonds going from the site, i, to its adjacent left and right sites. Sometimes, it is convenient to write (165) in a slightly different way:
or
In the first representation, the c-number matrices, , are given by:
while, in the second, is given by the Pauli matrices (). Using these representation, we can recast (164) into the form where the c-number coefficients and the basis part are separated explicitly:
The state (164) or (168) represents a collection of the states (with D being the matrix size) specified by the matrix indices, . In the above case, have a clear physical meaning that they specify the states of the two emergent edge spins.
It is convenient to represent [and ] by the following simple tripod diagrams:
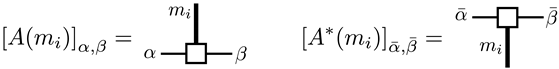 where the thick and the thin lines, respectively, denote the d-dimensional physical Hilbert space (here, spin-1 states labeled by or ) and the D-dimensional auxiliary space (-dimensional space spanned by the spinors and ); the matrix multiplication amounts to connecting open thin lines on the adjacent sites. Then, the Bra and the ket vectors may be depicted by strings of these tripods (Figure 16). Quantum states, which can be written in the form of (164) or (168), are in general called matrix-product states (MPS). As has been mentioned in Section 1, any gapped short-range states fall into this category. We refer the readers to recent readable reviews [32,33] for more details and the applications.
where the thick and the thin lines, respectively, denote the d-dimensional physical Hilbert space (here, spin-1 states labeled by or ) and the D-dimensional auxiliary space (-dimensional space spanned by the spinors and ); the matrix multiplication amounts to connecting open thin lines on the adjacent sites. Then, the Bra and the ket vectors may be depicted by strings of these tripods (Figure 16). Quantum states, which can be written in the form of (164) or (168), are in general called matrix-product states (MPS). As has been mentioned in Section 1, any gapped short-range states fall into this category. We refer the readers to recent readable reviews [32,33] for more details and the applications.
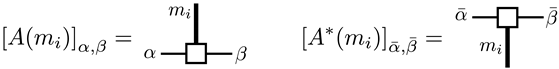
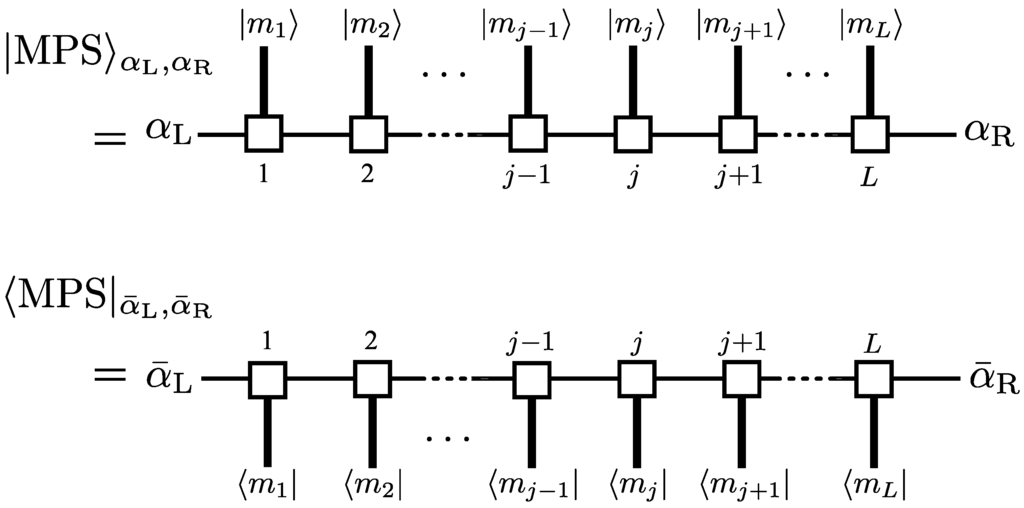
Figure 16.
Diagrammatic representation of MPS and its dual.
We would like to comment on an interesting property of MPS (168). When rotation acts on the state in (166b) as , the local MPS matrix, , transforms, like:
where R is a three-dimensional rotation matrix and U is the corresponding spinor representation. Namely, the original symmetry for the local spin-1 objects “fractionalizes” into that for the two spin-1/2 objects (spinors). From this, it is evident that the spin-1 VBS state on a finite open chain [represented by the MPS (164)] transforms, under rotation, as if there were two spin-1/2 objects (“quark” and “anti-quark”) at the ends of the chain. The above is the simplest example of more general symmetry fractionalization property of MPS, which will be extensively used in Section 6.4.
We can generalize the strategy to construct the parent Hamiltonian for the VBS state in Section 4.3 to any MPS. The idea is to prepare a cluster Hamiltonian and tune the parameters, so that the Hamiltonian annihilates all the states (i.e., matrix elements) of the MPS on that cluster. In fact, it can be shown that for any given MPS, there exists the parent Hamiltonian for which the MPS (164) or (168) gives the (degenerate) ground states [25]. By construction, the degree of degeneracy is equal to the number of matrix elements (). For example, the ground state of the parent Hamiltonian of the spin-S VBS state (the VBS model) is shown to have -fold degeneracy, when the model is defined on a finite open chain [6,7]. This exact degeneracy on a finite chain is peculiar to the VBS model and, if we slightly deviate from the solvable VBS point, the emergent edge spins () start interacting with each other with a coupling constant exponentially small in system size to (partially) resolve the degeneracy. For a periodic chain, on the other hand, we have to take the trace over the matrix indices:
and hence the ground state is not degenerate.
5.2. Supermatrix-Product State (SMPS) Formalism and Edge States
The Schwinger boson construction described in the previous section can be generalized to SUSY cases by using the Schwinger operator, which contains both bosons and fermion(s).
5.2.1.
Now let us consider the MPS representation for the type-I VBS chain [9]. The SVBS chain (85) is written as a string of 3×3 matrices :
where:
From the expression (172), it is clear that the nine-fold degenerate ground states correspond to different possible choices of the edge states:
The row index specifies the left edge states and the column one the right. On the left (right) edge, the matrix indices correspond respectively to ().
By looking at the form of (173), one sees that the matrix has a block structure:
where and respectively denote “bosonic” and “fermionic” (i.e., anti-commuting) matrices of the dimension, . Therefore, it is convenient to regard as a supermatrix. Thus, the SVBS chain can be expressed in the form of a supermatrix-product state (SMPS), and the matrix size of the SMPS is directly related to the number of edge degrees of freedom. The (S)VBS states with different edge states have finite overlaps with each other, which exponentially decrease by the system size, L. That is, two (S)VBS states with different edge states are orthogonal to each other only in the infinite-size limit.
In constructing the SVBS state on a periodic chain, one has to treat the fermion sign carefully, and one sees that the trace operation used in the standard MPS representation (171) should be replaced with the supertrace:
where the supertrace is defined as:
From these -matrices, we obtain the following 9×9 T-matrices (transfer matrix):
Here, is obtained from by and complex conjugation.
Using the matrices, , and the diagrammatic representation introduced in Section 5.1, the transfer matrix may be expressed as:
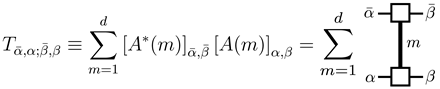 The transfer matrix naturally appears in the calculations of the MPS formalism. For instance, by using the diagrammatic representation in Figure 16 and the orthogonality of the local basis states, , one can show that the overlap of the two (S)MPSs with edge states and can be written as (for the bosonic MPS, this is straightforward; for the SMPS, one has to treat the fermion sign carefully, but at the end of the day, we can check that the final result is the same) (see Figure 17a):
where the matrix multiplication is taken over the tensor index .
The transfer matrix naturally appears in the calculations of the MPS formalism. For instance, by using the diagrammatic representation in Figure 16 and the orthogonality of the local basis states, , one can show that the overlap of the two (S)MPSs with edge states and can be written as (for the bosonic MPS, this is straightforward; for the SMPS, one has to treat the fermion sign carefully, but at the end of the day, we can check that the final result is the same) (see Figure 17a):
where the matrix multiplication is taken over the tensor index .
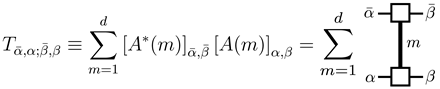
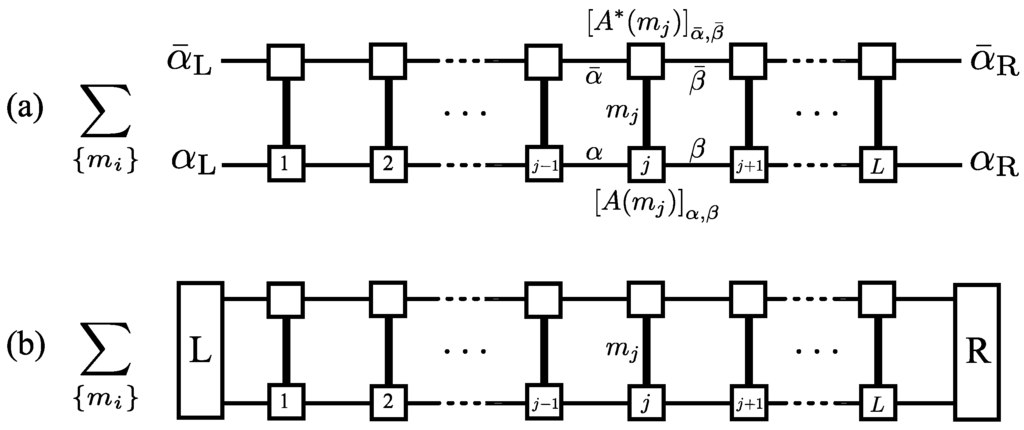
Figure 17.
(a) Diagrammatic representation of overlap of two supermatrix-product states (SMPSs); (b) more general boundary conditions, which are linear combinations of different s may be used. In those cases, edge states are expressed by -dimensional vectors, “L” and “R” (for instance, in the simplest case (a), the edge-state vector has the components, ).
In the periodic case, the above expression is modified:
where:
Notice that the transfer matrix directly appears in the right-hand side of (180), and hence, the calculation is boiled down to that of the power of the transfer matrix. The eigenvalues of the transfer matrix (177) are computed as:
and plotted in Figure 18. The largest eigenvalue of the transfer matrix, , will be relevant in the thermodynamic limit.
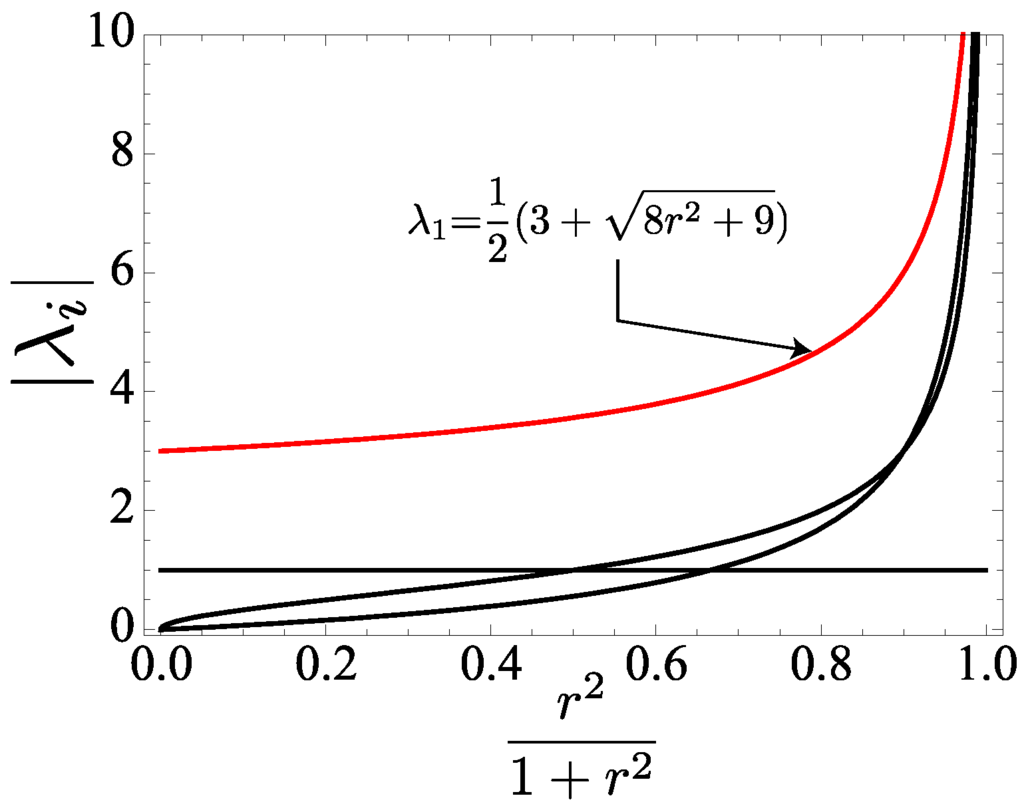
Figure 18.
(Color online) Plot of absolute values of the five different eigenvalues of T. The largest eigenvalue is always unique and non-degenerate (except for ). The figure and caption are taken from [9].
5.2.2.
Similar to the type-I SVBS chain, we can express the type-II SVBS chain in the form of SMPS:
where:
As in the type-I SVBS state, the supertrace is necessary for the periodic system:
where . The corresponding transfer matrix is a 16 × 16 matrix and has seven different eigenvalues:
where . Regardless of the value of r, the largest eigenvalue is:
5.3. Excitations
In this section, we delve into dynamical properties, i.e., low-lying excitations on the SVBS chain. In Section 4.3, we have already obtained the parent Hamiltonian from the VBS state. Given the form of the Hamiltonian, we can, in principle, investigate dynamical properties of the system. Unfortunately, however, even though we have the exact ground state in hand, only limited (exact or rigorous) information about the excitations is available [181,182]. Nevertheless, when the explicit form of the (whether exact or approximate) ground-state wave function is known, the single-mode approximation (SMA) gives reasonably good results [75,91,92]:
The SMA not only provides us with a simple transparent way of calculating (approximate) excitation spectrum, but also sets a rigorous upper bound for the true spectrum.
5.3.1. Fixing Parent Hamiltonian
Since the type-I Hamiltonian (147) contains one extra parameter up to the overall factor, i.e., the ratio of to , we begin with fixing the form of the parent Hamiltonian. One way to fix the remaining coupling is to require that the SUSY parent Hamiltonian (147) should reduce to the original VBS Hamiltonian (138) in the limit . This naturally fixes the two coupling constants in the type-I parent Hamiltonian (147) as:
and we have:
Some of the matrix elements in the fermionic sector have a factor, , and in the limit, , they are divergent. However, they are harmless in the limit, since the ground states contain no fermion in the limit. Consequently, the type-I parent Hamiltonian projected onto the bosonic sector coincides with the spin-1 VBS Hamiltonian (138).
5.3.2. Crackion Excitation
Now, we are ready to derive the excitation spectra by using SMA. The paradigmatic picture of the low-lying excitations in the half-odd-integer-spin chains is provided by the so-called Lieb–Schultz–Mattis construction [183], where we apply a slow twist along one of the symmetry axis (say, the z-axis) of the spin Hamiltonian. Physically, this boosts the quasi-particles in the system and thereby creates low-lying excitations [with energies of the order of ] at a special momentum determined solely by the total magnetization. Unfortunately, this construction does not work in the usual VBS state [24]. Instead, as we will see, an excited triplet bond (crackion [184], i.e., a “crack” created in a “solid” of valence bonds; see Figure 19) in the VBS gives, to good approximation, a physical low-lying excitation. Due to the simple structure of the VBS states, the excitations considered in the SMA essentially coincide with the crackions [24,184]. In the Schwinger-boson construction of the VBS states (29), the crackion excitation is obtained by replacing one of the singlet valence bonds, , by a triplet one (either or or ). Since a single Schwinger boson or describes a spin-1/2 spinon, we may thought of the triplet crackion as the confined triplet pair of two spinons. The notion of crackion excitations can be generalized in other VBS-type models (states) with higher symmetries (e.g., ), where an intriguing picture on the relation between spinon confinement and the existence of “Haldane gaps” has been proposed [116,118].
Now, let us consider the crackions in the SVBS chains [9]. Since we are dealing with a SUSY system, we consider two different types of excitations (see Figure 19) that may be regarded as super-partners of each other:
- Spin excitation:Spin triplet excitation () created by bosonic operators
- Spinon-hole excitation:Spin doublet excitation () paired with a hole created by fermionic operators
They are schematically represented in Figure 19.
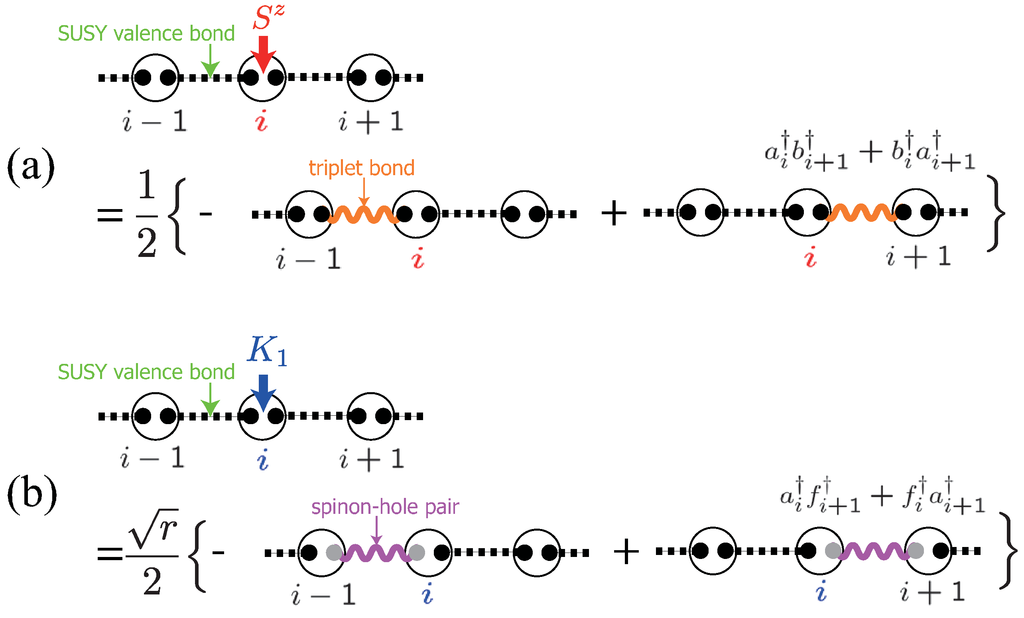
Figure 19.
(Color online) Action of bosonic (spin) operator, (a), and fermionic generator, (b), onto the SVBS state. The local operators, () and , respectively, create a triplet bond and a spinon-hole pair on either of the two adjacent bonds, and . The figure and caption are taken from [9].
In the SMA, the (unnormalized) excited-state wave function is assumed to be given (for the spin excitation) by:
where denotes the Fourier transform of the local spin operator . Then, the excitation spectrum (or the Bijl–Feynman frequency [185,186]) is obtained by calculating the following quantity:
where is given by (189) and is the ground-state energy. We can consider other types of excitations by changing to other operators.
5.3.3. Spin Excitation
Let us start by investigating the action of local spin operators:
on the SVBS state. A little algebra shows that these spin operators create triplet bonds around the site i (see Figure 19):
where and are obtained by replacing the SUSY valence bond, , by triplet bonds, and , respectively. By taking the Fourier transform of Equations (193a) and (193b), one immediately sees that the triplon-crackion equivalence (except for the momentum-dependent form factor) found in the ordinary VBS states [24,184] holds in the SVBS case, as well. By simple algebra, it is easy to show the following bound for the true spin-excitation spectrum :
The last inequality is proven by noting that the left-hand side can be rewritten as the following average:
and using the spectral decomposition of the dynamical structure factor, . The spin-excitation spectrum obtained [9] in this way is shown in Figure 20. At , the dispersion reduces to the well-known result of the original VBS chain [75]:
In the limit, , on the other hand, the spin excitation loses its dispersion. This is easily understood by noticing that the ground-state reduces to the Majumdar-Ghosh dimer states on which excitations cannot move.
5.3.4. Spinon-Hole Excitations
The dynamics of doped holes in the spin-gapped background is in its own right interesting [187]. In the context of the VBS models, some (both exact and approximate) results have been obtained. For instance, in [188], the motion of spin-0 holes in the spin-1 VBS background is considered and the exact one-hole spectrum is obtained. Motivated by the experiments carried out for hole-doped spin-1 compound, Penc and Shiba [189] introduced a realistic model and investigated the motion of a single spin-1/2 hole immersed in the gapped spin-1 VBS background.
Figure 20.
(Color online) The spin excitation (triplon) spectrum obtained by SMA. At , it reduces to the well-known dispersion of the spin-1 VBS model. When (Majumdar-Ghosh limit), dispersion becomes flat. The figure and caption are taken from [9].
A similar strategy can be used to obtain the spectrum of the charged (hole, ) excitation, which is always paired with the spinon ( or ). These excitations are created by applying the two fermionic generators of :
to the VBS ground state. By using the explicit form of the ground-state wave function, it is easy to show:
where the crackion state, , is obtained by replacing the SUSY valence bond, , with a spinon-hole pair, (see Figure 19b). The excited state, , is defined similarly with in the above expression replaced with . For , the spectrum is given by:
The behavior of the spectrum as a function of r [9] is plotted in Figure 21.
We add some comments about distinctions between and . Since SUSY relates the bosonic generators, S, and the two fermionic generators, , one might naively expect the same spectra for their corresponding excitations. However, this expectation relies on the existence of a “unitary” transformation, which linearly transforms the set of the SUSY generators onto themselves. Since no such transformation exists in the present SUSY, the spectra for the spin and charge sectors indeed exhibit different behaviors.
Figure 21.
(Color online) The excitation spectrum, , of a spinon-hole pair obtained by SMA. This spinon-hole pair state is created by fermionic generator, , except at , where the transition matrix elements of from the ground state vanish. The figure and caption are taken from [9].
6. Topological Order
As has been discussed in Section 1, no true topological order is possible in 1D systems [61,62]. However, if we impose a certain kind of symmetries, there can be topologically non-trivial phases protected by the symmetries dubbed symmetry-protected topological phases. One of the typical examples would be a non-trivial topological phase with the Majorana edge mode in 1D interacting fermions [190]. We already know that there exists an analogous “topological” phase with (almost) free edge spins () at the edges in 1D spin systems, as well. In this section, we give detailed discussions about the topological properties of the SVBS states [9,10]. In particular, we investigate the string order and the entanglement spectrum of type-I and type-II VBS states. Then, we generalize the MPS argument of the symmetry-protected topological order [65,66] to SUSY cases to understand the degeneracy structure in the entanglement spectrum.
6.1. Hidden Antiferromagnetic Order and String Order Parameter
Before proceeding to the SUSY cases, we briefly recapitulate the hidden non-local order in 1D spin systems. The concept of hidden order is an isotropic generalization of the Néel order. As we have seen in Section 2.2, the Néel order for antiferromagnetic spin chains looks like (if we assume that the ordering occurs in the z-axis):
Here, + stands for and − for . Clearly, the spin-spin correlation:
depends on the parity of the number, n, of sites between i and j. A simple way of turning this position-dependent (or alternating) correlation into the smooth ferromagnetic one would be to insert a phase factor, , between the two spins:
in order to cancel the sign factor coming from the alternating and between the sites, j and . Namely, the Néel antiferromagnetic correlation translates to the ferromagnetic correlation in .
On the other hand, as is seen in the expansion of the VBS state [see (36)], a typical sequence appearing in the state reads as:
As has been pointed out already in Section 2.2, by removing zeros in the sequence, we can reproduce the usual Néel order. In this sense, there still exists a certain kind of Néel order, though “disordered” by randomly inserted zeros, called the hidden string order (however, there is a striking difference from the usual Néel order. As has been mentioned in Section 2.2, the string order exists regardless of the choice of the quantization axis, while the Néel AF order is observed only in a particular direction) [18,19]. However, the trick used above does not work, since, due to the intervening zeros, the positions of and are random (though they still appear in an alternating way) and the phase cannot cancel the sign factor. Nevertheless, a little thought tells that the following choice will do the job:
where:
stands for the partial sum of between an arbitrary pair of sites, i and j. Therefore, it is suggested that we should use instead of Equation (202), the following pair of non-local order parameters:
known as the string order parameters [18,19], in order to characterize the non-trivial spin order in the () VBS state. In the first line, is defined similarly to [see Equation (205)].
The above expressions have been guided by a simple physical intuition. However, as has been pointed out in [191,192], the string order parameters have in fact a deeper meaning than we expect from the above simple argument. To see this, first we note that the string correlation functions can be recasted in a suggestive way:
where and are defined as:
The physical meaning of these operators may be best understood by considering the “height plot” of the VBS spin configurations [18,24], where the value is represented by the “height” between the sites, j and (hence, itself is a “step” at the site j). Figure 23a is a plot of a typical -configuration of the spin-1 VBS state when the left edge state is ↑. One can clearly see that the meandering steps are always confined between the heights 0 and . A similar analysis in the case with the left edge state ↓ shows that the heights are either 0 or . From these observations, it is concluded that the string attached to the left of the operator, , somehow suppresses the strong fluctuations in and that takes either 0 or (0 or ) when the left edge state is ↑ (↓). Similarly, one can show that becomes weakly ferromagnetic depending on the right edge states. In short, non-zero string order parameters translate to the existence of a certain kind of weakly ferromagnetic order in the x and the z directions (i.e., for ).
Remarkably, the following unitary transformation [193]:
relating the two operators, and , as:
transforms the original [SU(2)-invariant] Hamiltonian into the one, , which is invariant only under the dihedral group, (or ), consisting of two π rotations with respect to the x and the z axes [191,192]. Therefore, we can interpret the existence of the string order (both in x and z) in the original system as a consequence of the spontaneous breakdown of the -symmetry in the transformed system, and the resulting (weak) ferromagnetic order in .
The idea of non-local hidden order and edge states has been to some extent generalized [24,167,193,194,195] to other values of integer-spin-S, although the hidden -symmetry is never broken [193] in the case of even-S (see Figure 22) (this does not mean that -symmetry never breaks down in any even-S chains. In fact, even when even, one can construct the model ground states that have non-vanishing string order parameters.) In the course of these studies, it has been recognized that there are some differences [24,193] in the ground-state properties according to the parity of S. Nevertheless, by analogy with the quantum-Hall systems [166], the ground state of generic integer-spin antiferromagnetic chains, including the original VBS state and its higher-spin generalizations [75], characterized by certain kinds of non-local correlations and emergent edge states, have been called “topological” in a rough sense.
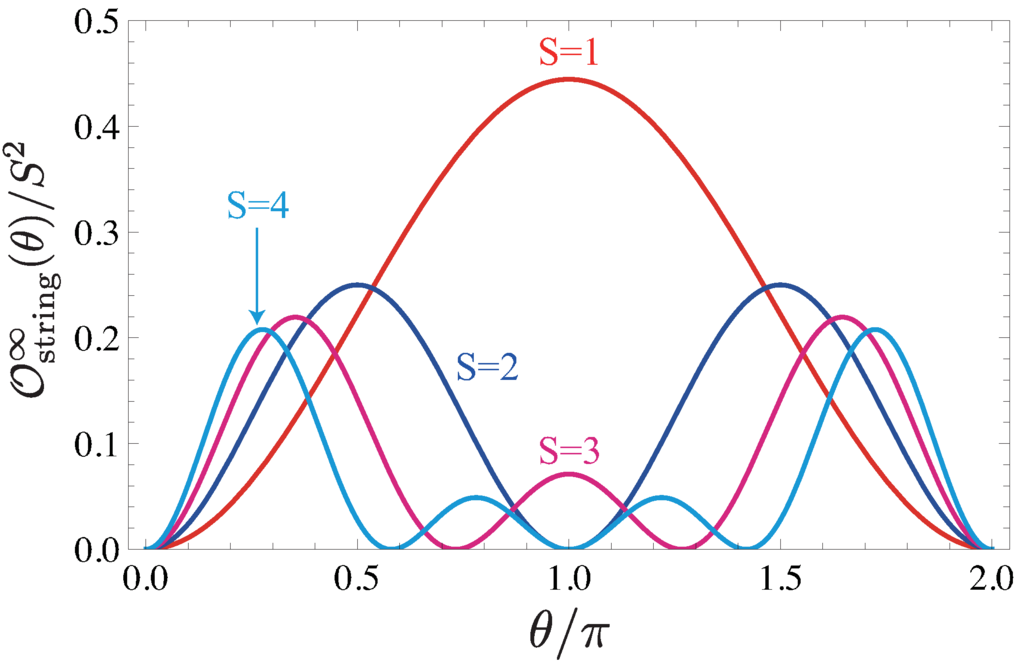
Figure 22.
(Color online) The behaviors of string order parameters in correspondence with magnitude of bulk spins. In particular, at , the string order parameters of even spin VBS vanish, while those of odd spin VBS, , have finite values.
To illustrate distinct behaviors depending on the parity of spin, S, we may introduce the following generalized (angle-dependent) string order parameter [193]:
where the parameter, θ, has been introduced for convenience (the introduction of the θ parameter is mainly motivated by the idea that the intermediate string might somehow cancel the fluctuations between the two spins, and ; for , this works perfectly in the VBS state; except for (ordinary spin-spin correlation) and (string correlation), no symmetry-related reason has been found so far). When , it reduces to the usual spin-spin correlation, and when , it coincides with the string order parameter discussed above. The behaviors of the generalized string order parameter (211) are shown for several values of bulk spin, S, in Figure 22 [24]. The string order parameters are symmetric with respect to and generally have S peaks for the spin-S VBS state. As is expected from the ground state being magnetically disordered, the infinite-distance limit of the usual spin-spin correlation function () vanishes regardless of the value of S. On the other hand, Figure 22 demonstrates that takes finite values for the odd-S VBS states, while it vanishes for even-S. Therefore, in the sense of the -symmetry argument [191,192] mentioned above, this hidden symmetry is never broken [193] in the even-S VBS models.
6.2. Generalized Hidden String Order in SVBS Chain
6.2.1.
Unlike the original VBS chains, and generally appear in the sequence of the SVBS chain, and a typical sequence of the SVBS chains is given by (it may be worthwhile to give some comments on the relation to the ferrimagnetic spin chains that also consist of alternating spin 1 and spin 1/2 [47]) Though both the ferrimagnetic chains and the present SVBS chains contain spin-1 and spin-1/2 degrees of freedom, in the SVBS chains, the spin 1 and spin 1/2 are not necessarily alternating (see (212) and Figure 10). More importantly, while the ferrimagnetic spin chain can exhibit a long-range magnetic order as the order parameter commutes with the Hamiltonian, the ground state of the SVBS chain itself is spin-singlet and the -symmetry is never broken (spontaneously).
From the sequence, one can “derive” the ordinary hidden order. First, we search the spin-half sites from the left, and whenever we encounter a pair of spin-half sites, we sum the two values to have the effective (e.g., ):
Next, we remove the zeros in the sequence to recover the standard Néel pattern:
This observation leads to the existence of a (generalized) hidden order of the SVBS chain. Figure 23 shows a typical height configuration corresponding to the usual VBS chain and its SUSY counterpart. Reflecting the existence of hidden order, the height configuration is always meandering between the height 0 and the height 1 (the same reasoning applies to the general spin-S VBS cases, and the height configurations are confined within a region of width S [24]). It should also be noted that the height-configuration (205) is directly reflected in the components of the SMPS (174):
To substantiate the existence of the hidden order, we explicitly calculate the string parameter for the SVBS chains. The behaviors of the string order are depicted in Figure 24 with respect to the hole doping parameter.
From Figure 24, one can find distinct behaviors of the string parameter in terms of the parity of bulk superspin. The string parameters of odd superspin SVBS chains generally decrease with increase of the hole doping, while those of the even superspin SVBS chains increase. Since the hole-doping simply reduces the spin degrees of freedom on the spin chain, the decrease of the string order of the odd superspin SVBS chains may be naturally understood. On the other hand, the string order behavior of the even superspin SVBS chains is quite interesting, since the string order revives with the hole doping. An intuitive explanation may go as follows. For instance, consider SVBS chain. At , the SVBS chain is exactly identical to the VBS chain, which is essentially constituted of two VBS chains, upper and lower chains. By doping the holes to the VBS chain, the spin degrees of freedom, say, on the upper VBS chain, decrease to have deficits in the chain. Below the deficits on the upper chain, the spin degrees of freedom on the lower VBS chain emerge and come into effect. In this way, the spin degrees of freedom of the lower VBS chain contribute to generate the finite string order with the increase of hole doping to the VBS chain. This intuitive explanation can be applicable to the revival of the string orders of general, even superspin, SVBS chains. Consequently, the SVBS states bear a finite string order with a finite amount of hole-doping of the parity of the bulk superspin. This is the salient SUSY effect to the topological stability of quantum spin chains. We revisit this effect in the context of the symmetry protected topological order in Section 6.3 and Section 6.4.
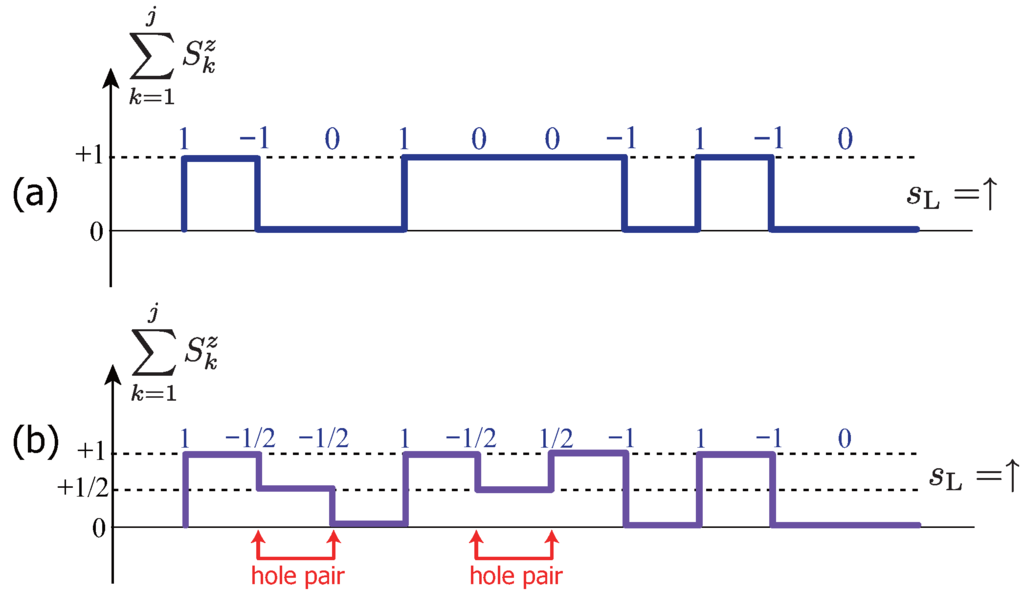
Figure 23.
(Color online) Height plot of typical spin configurations in VBS chain (a) and SVBS chain (b). Note that heights are confined within a region of width 1. Although a simple “diluted” Néel picture does not hold, because of the presence of hole pairs, still, we can find a string order when hole pairs are grouped together in (b). The figure and caption are taken from [9].
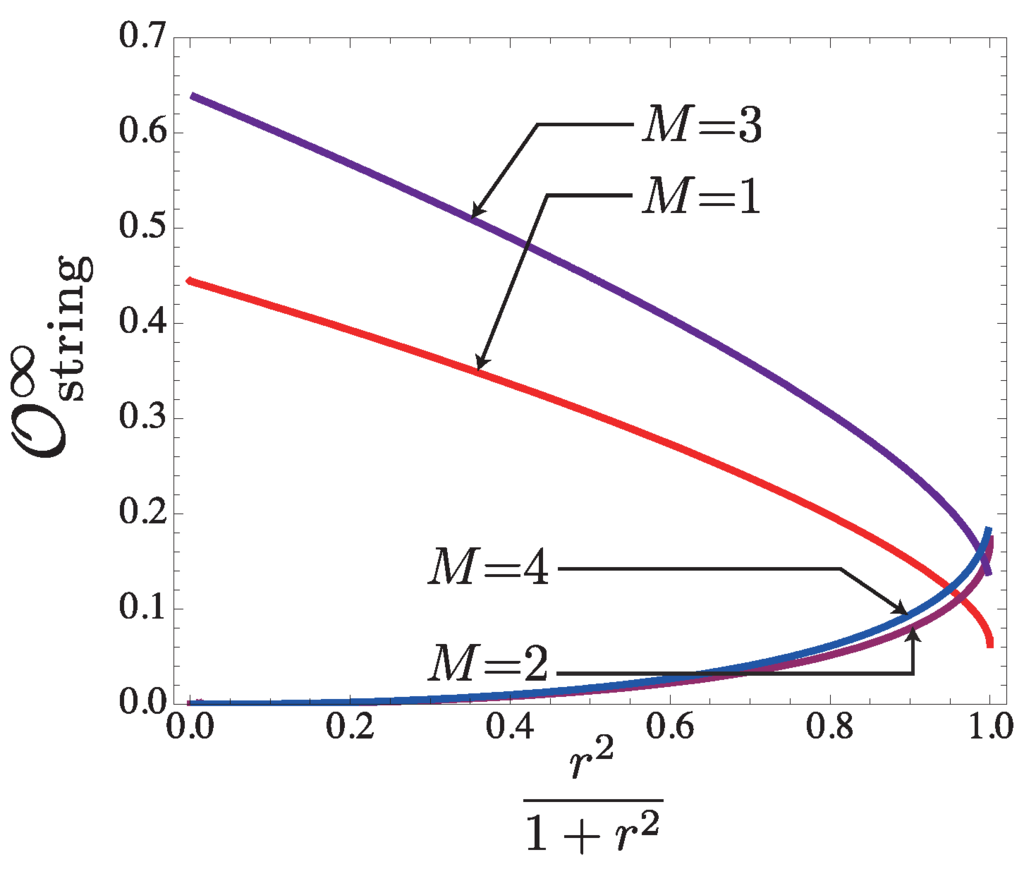
Figure 24.
(Color online) The string correlation function (206) of the SVBS infinite-chain for several values of the superspin, , is plotted as a function of r. Notice that, in the limit , the string order parameter, , for the SVBS chain reproduces that of the VBS chain. The figure and caption are taken from [9].
6.2.2.
For the type-II SVBS infinite chain, the string correlation is computed as:
which is plotted in Figure 25. The string order (216) takes the value of the VBS chain, , at , like the type-I chain, while approaches to zero in the limit, unlike the type-I chain. Since spin degrees of freedom completely disappear from the type-II chain in the limit (Figure 11), the string order of the type-I and II chains shows qualitatively different behaviors.
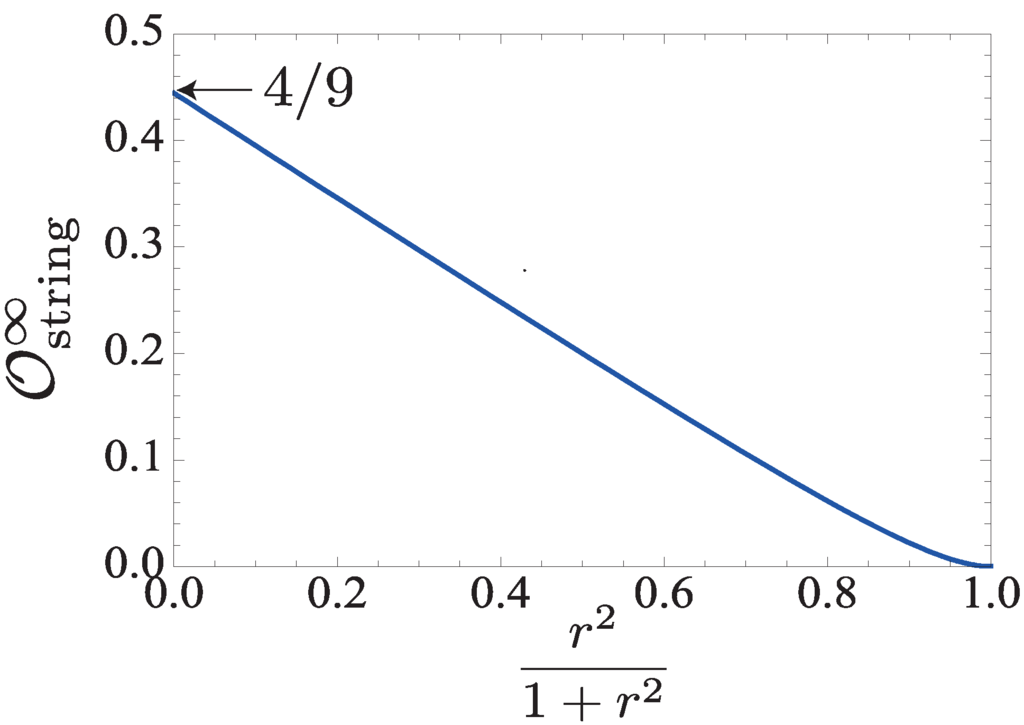
Figure 25.
The infinite-distance limit of the string correlation function (206) as a function of r. The value of string correlation smoothly decreases from the original VBS value, , to 0 (no spins left). The figure and caption are taken from [9].
6.3. Entanglement Spectrum and Edge States
As discussed above, the string order of type-I SVBS chains with even bulk-superspin revives upon hole doping. This suggests that, in contrast to their bosonic counterpart, even the SVBS states with even superspin can host the stable topological phase. Though the string order parameter is appealing in its similarity to the order parameter in FQHE [166] and its relation to the hidden -symmetry, its fragility under perturbations has also been discussed recently [63,196], and the alternative “order parameter” has been sought.
Recent development in quantum-information-theoretic approaches to quantum many-body problems enables us to extract information on the bulk topological order from the entanglement properties of the ground-state wave function [28,197,198]. The topological states in one-dimensional (1D) spin systems have been reconsidered [63,65,66] from the modern point of view, and the precise meaning of the topological Haldane phase has been clarified. In these studies, the string order parameters and the edge states, which in general are not robust against small perturbations, are replaced by more robust objects (i.e., the structure of the entanglement spectrum or the structure of tensor-network). In particular, it has been shown in [65,66] that the existence of (at least one of) the discrete symmetries (time-reversal, link-inversion and symmetry) divides all states of matter in 1D into two categories: topologically-non-trivial ones and the rest. Generic odd-integer-S spin chains belong to the former, while even-S chains to the latter. The hallmark of the topological phase protected by the above discrete symmetries is that all entanglement levels are even-fold degenerate. In this formulation, the difference between the odd-S VBS states and the even-S ones are naturally understood in terms of the entanglement structure, the degenerate structure exists only for odd-S cases (this does not mean that all the odd-S spin chains have the degenerate entanglement spectrum. We can construct an odd-S spin state without the even-fold degeneracy.) It should also be mentioned that the topological phases of one-dimensional gapped spin systems have been classified by group cohomology [61,62,64] and the detailed analyses based on the Lie group symmetries are reported in [69,70].
Following the proposal of Li and Haldane (Li and Haldane proposed to take the degeneracy of entanglement spectrum as the hallmark of topological phases, which can be applicable to general topological phases beyond QAFM) [28], we use the structure of the entanglement spectrum (e.g., degeneracy of the entanglement levels) as the fingerprint of topological phases. Then, the problem of the topological stability of the SVBS chains translates to the stability of the degenerate structure of the entanglement spectrum. Before proceeding to the details, we briefly introduce characteristic features of the entanglement entropy of the original -invariant VBS states. It has been reported that the entanglement entropy of the spin-S VBS state on an infinite chain is given by a constant (on the other hand, for gapless spin chains, the entanglement entropy diverges as with L the length of a subsystem for which entanglement entropy is defined [58]) determined essentially by the degrees of freedom of the edge spins [51,52]:
Corresponding to the parity of the bulk spin of the VBS chains, there appear either integer or half-integer spin at the edge. Meanwhile, in the presence of SUSY, there necessarily appears both integer and half-integer spins at the edge, since SUSY relates integer and half-integer spin degrees of freedom (Figure 26). Such a particular feature of the edge spins is crucial in understanding the salient structures of the entanglement spectrum of the SVBS chains.
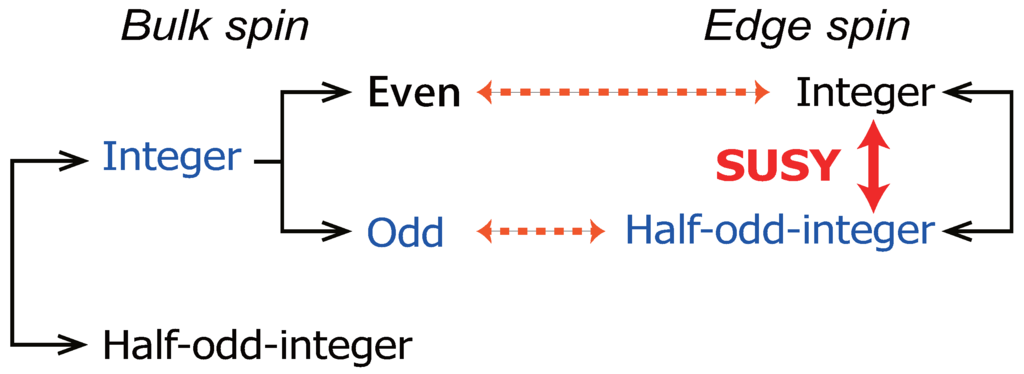
Figure 26.
(Color online) SUSY relates the edge spins with different parity.
6.3.1. Schmidt Decomposition and Canonical Form of MPS
Before going into the detailed discussion, it would also be worthwhile here to give the derivation of the entanglement spectrum using MPS. Suppose we divide a system into the two parts, A and B (see Figure 27). Then, we can express any wave function (state) as [26]:
with non-zero coefficients . Here, (; : Hilbert space of A) and () are orthonormal basis states in the subspaces, A and B, respectively:
The expansion (218), called the Schmidt decomposition, defines the Schmidt coefficients and describes the entanglement between the two subsystems. The Schmidt number χ is the number of non-zero Schmidt coefficients and never exceeds the minimum of the dimensions of the Hilbert subspaces. From the normalization of ; the Schmidt coefficients satisfy . The “spectrum” of the entanglement energy defined by:
is called the entanglement spectrum [28]. In terms of the Schmidt coefficients, the (von Neumann) entanglement entropy is given by [26]:
It is interesting to observe that may be viewed as the ordinary thermodynamic entropy if we introduce a fictitious “temperature”, T, and “partition function” as:
and define:
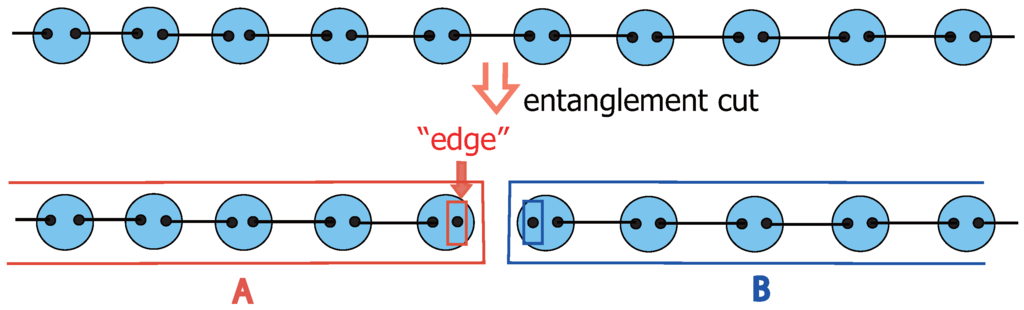
Figure 27.
The VBS state is divided into two parts and the edge degrees of freedom emerge at the cut.
In the MPS formulation, the derivation of the Schmidt coefficients are rather straightforward. Since the MPS is represented as the product of matrices, , defined on each site, one can easily write down an analogue of the Schmidt decomposition (218) (see Section 5.2 for the physical meaning of the matrix indices):
where D is the size of the matrix, , and each state-valued matrix, , is expanded explicitly in terms of the c-numbered matrices, , and the orthogonal local basis states, as:
(d: dimension of local physical Hilbert space). For simplicity of argument, we assume that the system is uniform [] and defined on an open chain.
One may think that (224) already completes the Schmidt decomposition (218) with the identification:
However, the orthonormality condition (219) are not always satisfied for the above choice. Normally, we use “gauge ambiguity” [25,32] to find an appropriate set of edge states in such a way that the following overlap matrices may equal to identity:
This procedure can be carried out both for finite systems and for infinite-sized systems by using the singular-value decomposition (SVD) [40,41,45]. As a result, we obtain, instead of a single matrix, , two different MPS matrices, for the left subsystem A and for the right subsystem B. The (diagonal) matrix elements of the diagonal matrix Λ coincide with the Schmidt coefficients:
The MPS characterized by the set of matrices () is called canonical [25] and automatically completes the Schmidt decomposition (218) as [40,41,45]:
(For a rather comprehensive account of the use of SVD in MPS, see, for instance, [33].)
Figure 28.
(Color online) Norm of MPS on a semi-infinite system. If the MPS is pure, the norm is essentially determined only by the dominant eigenvector, (except for the boundary factor, which depends on the boundary condition imposed on the edge states). Similar relation holds for the right semi-infinite system.
In infinite-size systems, the overlap calculation, (227), simplifies a lot, since () reduces essentially to the left (right) eigenvector, (), with the largest eigenvalue (dominant eigenvector; see Figure 28 for a diagrammatic representation; when the MPS is not of the canonical form, we can take and (and hence, ).) of the transfer matrix, (), defined by:
Specifically, except for the unimportant factors determined solely by the edge states, the overlap matrices (227) coincide with the (-dimensional) eigenvectors, and of and , respectively (see Figure 28):
If our infinite-size MPS (iMPS) assumes the canonical form, and , by definition (with being the D-dimensional identity matrix), and therefore the two transfer matrices satisfy (by the assumption of pure MPS, the largest eigenvalue is unique [21,199]; MPS is called a pure MPS when transfer matrix has non-degenerate maximal eigenvalue; in the infinite-size limit, the pure MPS is reduced to a pure state, and hence, the name, pure MPS). When the value of the largest eigenvalue is not 1, we can rescale the matrices, , so that it may be 1) [21,199] (see Figure 29).
and:
Notice that these equations can also be regarded as the eigenvalue equations for the transfer matrices: is the left (right) eigenstate of the transfer matrix, (), with the eigenvalue, 1. Equation (232) may be thought of as the conditions in order that the iMPS is of the canonical form.
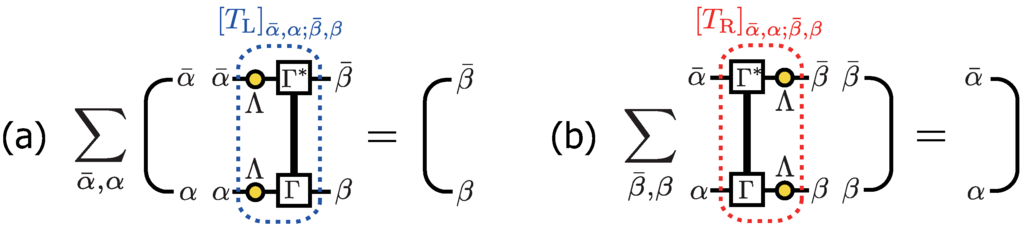
On the other hand, when the MPS in question satisfies (this is the case for all the (S)MPSs treated in this paper):
in the infinite-size limit, the Schmidt decomposition for the infinite chain is obtained very easily, just by rescaling the MPSs for the subsystems. The normalized state, , is constructed as:
where is the magnitude of :
With these normalization constants, the normalized MPS is written as:
Comparing this expansion with (218), one may read off the Schmidt coefficients as:
In the infinite limit, is not relevant to the polarization of the edge spins, and . Therefore, for the infinite (S)VBS chain, we only need to evaluate the magnitude of the matrix product to obtain the Schmidt coefficients, and thus, the derivation of Schmidt coefficients is boiled down to the computation of the normalization constants, (235).
6.3.2.
To substantiate the topological stability of the SVBS chain, we investigate two type-I chains with distinct bulk superspins, and .
(i) Superspin
From the formula (237), the entanglement spectrum of the type-I state (on an infinite chain) is derived as:
They are shown in Figure 30a with the entanglement entropy (right-figure). At , the SVBS state reduces to the VBS state and reproduces both the entanglement spectra and entanglement entropy of the VBS chain, i.e., and , which should be compared with (217) for . Similarly, in the limit, , the SVBS chain reduces to the MG chains, and the entanglement entropy of SVBS chain also reproduces the finite entanglement entropy of the MG chain (Figure 30b).
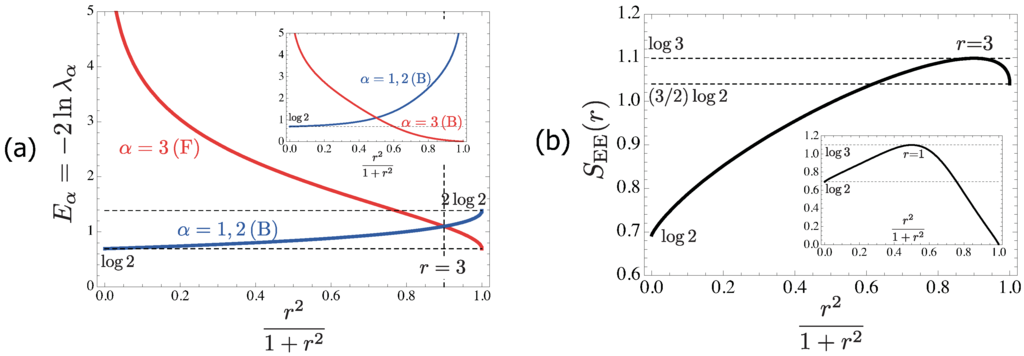
Figure 30.
The change of the entanglement spectra as a function of r (a) and entanglement entropy (b) of the type-I chain. The insets are the results for the bosonic-pair VBS chain. The figure and caption are taken from [10].
As in the entanglement spectra of the left of Figure 30, we have two distinct entanglement spectra, one of which is doubly degenerate spectrum (blue curve) for the “bosonic” Schmidt coefficients corresponding to those of the original VBS chain (238a), and the other is the non-degenerate spectrum (red curve) for the “fermionic” Schmidt coefficient (238b).
The existence of such two types of entanglement spectra is a salient feature of the SUSY state and can be readily understood based on the following edge state picture. For SVBS chain, its edge superspin states are given by the multiplet with superspin that consists of the ordinary states with spin, (Figure 31):
or:
The edge spin states generate the double degeneracy in the entanglement spectra, while the edge spin state gives the non-degenerate one. Due to the existence of spin edge degrees of freedom, the double degeneracy is guaranteed (we will give a detailed discussion in Section 6.4), and hence, we find that the type-I SVBS chain is in the topological phase.
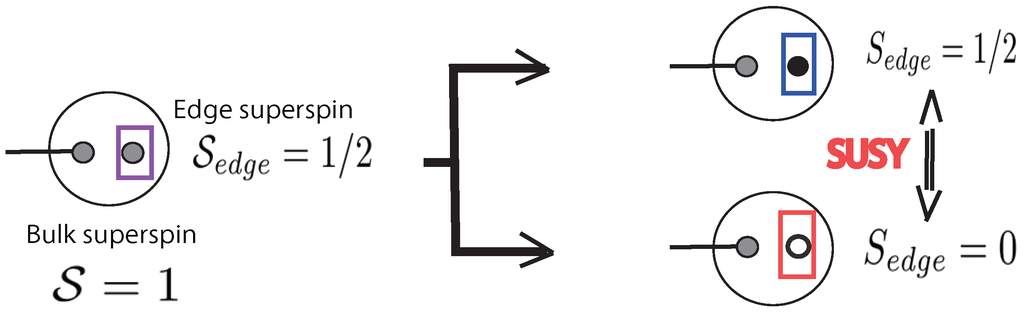
Figure 31.
(Color online) There always exist half-integer and integer edge spin states as the super-partner of the SUSY. The half-integer edge spin states play a crucial role in the stability of topological phases.
To highlight the effect of SUSY, we consider the non-SUSY (i.e., purely bosonic) cases and replace the fermion operator, , with the boson operator, (), to define the following boson-pair VBS chain:
As the insets of Figure 30, we depicted the entanglement spectra and entanglement entropy. The crucial difference to the SUSY case will be apparent in the limit, ; is reduced to a simple product state:
and the entanglement entropy vanishes (the inset of the right figure of Figure 30).
(ii) Superspin
Next, we examine the entanglement spectrum of the type-I SVBS chain. Though the topological phase of its bosonic counterpart, VBS chain, is fragile under perturbation [196], the type-I SVBS chain itself is topologically stable with a finite amount of hole doping. As we shall see below, SUSY plays a crucial role for the stability of the topological phase. At , the SVBS chain is reduced to the VBS chain, while in the limit, , the SVBS chain is reduced to the partially dimerized chain. We have the following five Schmidt coefficients for the SVBS chain:
Thus, the five Schmidt coefficients are split into the triply degenerate (243a) and doubly degenerate (243b) spectra showing distinct behaviors in Figure 32. Again, such splitting of the Schmidt coefficients are readily understood by the edge state picture for the SUSY chain. For the type-I SVBS chain, the edge superspin is given by that consists of the edge spin and (Figure 33):
or:
The degrees of freedom generate the triple degeneracy in the entanglement spectra, while the degrees of freedom give the double degeneracy. Due to the existence of SUSY, the SVBS chain necessarily contains the edge spin degrees of freedom that do not originally exist in the VBS chain (Figure 33), and they guarantee the double degeneracy in the entanglement spectra, i.e., the stability of the topological phase [65,66].
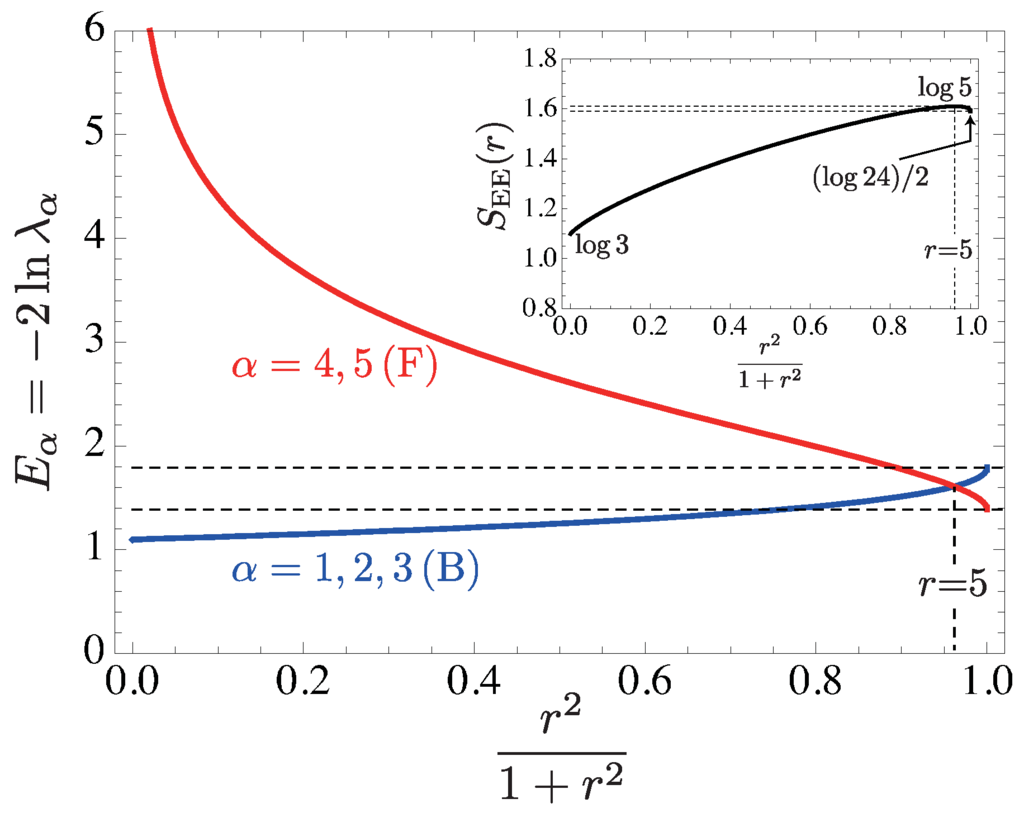
Figure 32.
The behaviors of the Schmidt coefficients (243) and the entanglement entropy (inset) of the type-I SVBS chain. The figure and caption are taken from [10].
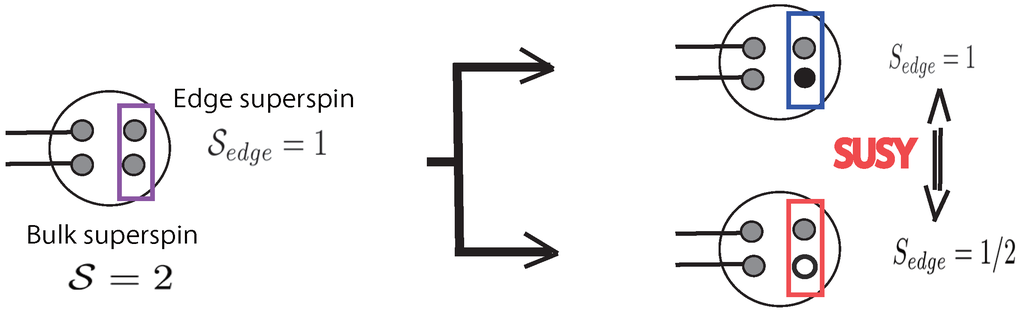
Figure 33.
(Color online) generates the stability of topological phase of the type II SVBS chain.
From the above demonstrations for and type I SVBS chains, one may see that regardless of the parity of bulk superspin, the SUSY introduces the half-integer edge-spin states that necessitate at least double degeneracy in the entanglement spectrum.
6.3.3.
It is also straightforward to calculate the Schmidt coefficients for the type-II SVBS chain:
The four Schmidt coefficients are split into two groups showing distinct behaviors (Figure 34) according to the decomposition of the edge superspin state:
or:
The first 2 on the right-hand side of (248) corresponds to the doubly degenerate blue curve in Figure 34, while the remaining represents the doubly degenerate red curve.
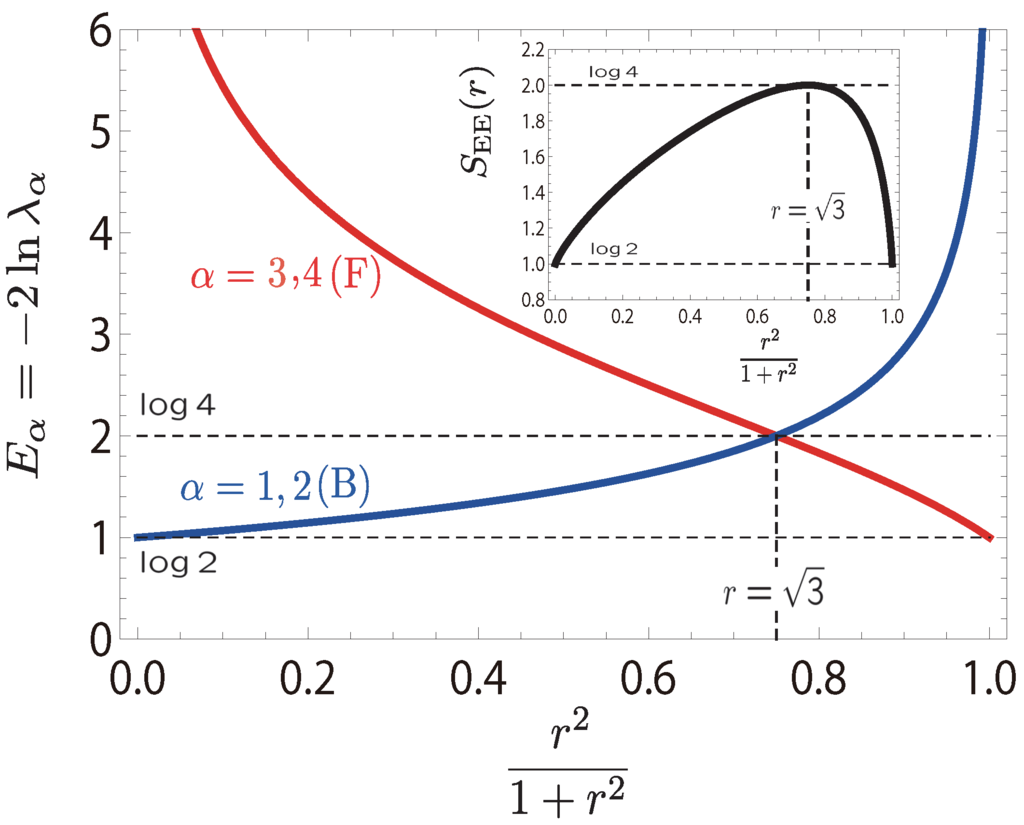
Figure 34.
The behaviors of the Schmidt coefficients and the entanglement entropy (inset) of the type-II SVBS chain.
6.4. Supersymmetry-Protected Topological Order
In this section, we clarify the relation between the structure of the entanglement spectra discussed in the previous sections and the symmetry-protected topological order [63]. To this end, we use the MPS representation established in Section 5. Because of its simplicity in the entanglement structure and the wide applicability to gapped states in 1D, the MPS approach provides us with a powerful tool in investigating the topological phases in 1D [61,62,64,65,66,67,68].
6.4.1. Symmetry Operation and MPS
For later convenience, we give a quick summary of some tools used in the MPS approach. As has been discussed in Section 5 and Section 6.3.1, any MPS on an open chain may be written as:
or in terms of the c-number matrices, (, d being the dimension of the local physical Hilbert space), as:
As has been mentioned in Section 6.3.1, we can “gauge-transform” this into the canonical form, which conforms with the Schmidt decomposition; on the left of the entanglement cut, we use the MPS matrix, , and on the right, . In the following sections, our arguments will be based on the canonical form characterized by the MPS data ().
Now, let us consider unitary operations on MPS. A given MPS () is said to be invariant under a unitary operation if the product of local unitary operators leaves the MPS invariant (up to an overall phase) [199,200]:
The local unitary operation, , acts on in a site-wise manner:
where we have used the completeness relation on each site, . If the symmetry operation is anti-unitary (like time-reversal), the complex-conjugation, , should be taken in Equation (252).
Then, it can be shown that the above unitary invariance is equivalent to the existence of the following unitary operator, U, acting on [199]:
where denotes a -dependent phase. Once the unitary is given, U is uniquely determined [199] up to an overall phase. To be more precise, if we define a generalized transfer matrix
the D-dimensional unitary matrix, U, is given essentially by its left eigenvector with the largest eigenvalue (we have assumed that is rescaled in such a way that the largest (or dominant) right-eigenvalue of is unity), (see Equation (270) and the explanations around it). Since U leaves the MPS invariant, it is natural to assume that U does not change the physical entanglement spectrum, Λ, i.e.,
Physically, the above relation (253) implies that the original symmetry operation (acting on the physical Hilbert space at each site) “fractionalizes” into the ones (U and ), which act on the edge states on both ends of the system. The equation (253) plays a crucial role in the following discussions.
6.4.2. Case of SMPS
Now we extend the arguments developed by Pollmann et al. [65,66] for the bosonic MPS to the SUSY case. First remember that degeneracy in energy spectra of quantum mechanical Hamiltonian can be attributed to some symmetry of the Hamiltonian. Meanwhile, since the entanglement spectrum is solely determined by a ground-state wave function, the degeneracy of entanglement spectrum is expected to stem from some symmetry of the ground-state wave function. Indeed, several discrete symmetries are identified to guarantee degeneracy in the entanglement spectrum. Since the degeneracy of the entanglement spectrum is the hallmark of the topological order, it is said that the topological order is protected by the symmetry of the ground-state wave function and, hence, the name symmetry protected topological order. In the following, we will show that the SUSY guarantees the existence of at least two-fold degeneracy of entanglement spectrum, , the parity of superspin, provided that at least one of the three symmetries, inversion, time-reversal and is present. We will also find that the (S)MPS formalism plays a crucial role in the discussions.
As has been discussed in Section 5.2, the SMPS is generally represented as [9]:
where are supermatrices defined on the sites, i. Then, we follow the same steps as in Section 6.4.1 to transform the SMPS into the canonical form. When a given unitary operation leaves the MPS invariant [in the sense of Equation (251)], the unitary operation, , fractionalizes into U and , and acts like:
In fact, the local symmetry operation need not be unitary (as will be in the following sections). In this case, the left-hand side may be replaced with the general form, . Therefore, the most general form reads as:
where the phase, , depends on the symmetry operation considered. In the above equations, m labels both bosonic and fermionic states, i.e., , and are given, for , by:
where and are c-number matrices.
Here, a remark is in order about the form of U. The (c-number) unitary matrix, U, in (257) may be postulated as:
where and are unitary matrices that act on the two bosonic subspaces having different fermion numbers. The reason for choosing the above form may be seen as follows. First, we note that Equation (257) implies that the MPS on a periodic chain transforms like:
where the supertrace STr is defined for general supermatrices as [see also Equation (176b)]:
We expect that for a periodic chain, which does not have edges, is fully invariant under the unitary operation, i.e., the expression (261) coincides with the original MPS (up to an overall phase). While in the case of bosonic MPS, this, combined with , immediately implies ; the relation holds only when A and B are super-matrices (that contain the Grassmann-odd blocks in their off-diagonal parts):
In fact, if an arbitrary pair of two super matrices, A and B, were merely c-number matrices, A and B, in general, would not commute inside : . In order to satisfy only with c-number matrices, either A or B is forbidden to have c-number components in the off-diagonal blocks.
For later convenience, we derive a useful property of pure canonical MPSs [25,45]. In the following sections, we assume that the MPS in question is defined on an infinite-size system. The Equation (258) is the most general statement about how a given symmetry of MPS is realized by a projective representation. However, sometimes it happens that for a certain symmetry operation, and in these cases, we can draw an interesting conclusion about the properties of U [10,65,66]. Suppose that we have a pure MPS whose canonical form is characterized by the MPS data [10,25], , and that it satisfies the following relation for some unitary matrix U:
Since the MPS is canonical, the following holds [see Equation (232a)]:
Physically, it states that the -dimensional vector, :
is the dominant left-eigenvector of the left transfer matrix (see Figure 29):
Plugging into (265), we obtain:
or equivalently:
This implies that the unitary matrix:
when viewed as a -dimensional vector, is the left-eigenvector of with the eigenvalue, :
Since, by assumption of canonical MPS, is the only left-eigenvector having the eigenvalue , we conclude:
Since, in deriving the above, we have only assumed that the (infinite-system) MPS in question is pure and takes the canonical form, (271) holds for any MPS (including SMPS) satisfying the assumption.
6.4.3. Inversion Symmetry
Now, let us look at what inversion symmetry, , with respect to a given link, implies the structure of the entanglement spectrum. It is convenient to consider an inversion transformation on a circle:
The inversion on a given link transforms the SMPS chain as:
By the relation, , (273) can be rewritten as:
where “st” stands for supertransposition, defined by:
It is easy to verify that applying the supertrace twice does not return a supermatrix to the original one:
where the matrix:
has been defined in such a way that its adjoint action, , multiples the fermionic blocks by a factor, ( and correspond to the unit matrices of two bosonic subspaces and should not be confused with the unit matrix ).
Therefore, at the level of the local MPS matrix, the inversion, , is realized as:
Finally, from Equation (258), one sees that when Ψ has the inversion symmetry, the -matrix should satisfy the relation: [45]
Note that at this stage, we can not apply the argument in Section 6.4.2, since Equation (279) does not assume exactly the same form as Equation (264) (the LHS is not ).
In order to obtain the relation of the form (264), we combine Equation (279) with the fact that the link-inversion squared to unity, . Applying supertransposition, , to (279), once again and using (Equation (276)), we obtain (in the bosonic case, the matrix, P, is not necessary [65,66]):
This is of the form of Equation (264) and then (271) immediately implies that:
After multiplying from the right and making transposition, we deduce:
(note: by Equations (260) and (277)). Therefore, we obtain [10]:
Equation (283) states that when is symmetric (anti-symmetric), is anti-symmetric (symmetric). It should be noted that unlike in the bosonic case [65,66], the symmetry constraint is imposed on each of the spin-S “bosonic” sector, , and , the “fermionic” sector, , in the case of SUSY.
When is anti-symmetric, for instance, the sector with must have a special structure in its entanglement spectrum. In fact, by computing the determinant of :
one can immediately see that should be even (the same argument applies to as well). From this, one can conclude that either the fermionic (when the sign + occurs) or bosonic (−) sector has even-fold degeneracy in each entanglement level, which we can be used as the fingerprint [63,65,66] of the SUSY-protected topological order [10].
6.4.4. Time-Reversal Symmetry
We can draw a similar conclusion for the time-reversal symmetry . Let us recall the time-reversal operation for the superspin, and :
with complex conjugation operator, K. The set of equations (285) implies that, for integer superspins, , satisfies (recall that, in the case, for integer S). When superspin, , is a half-odd-integer, the time reversal-operator satisfies, (this is indeed a generalization of for the half-integer spin case):
where the d-dimensional matrix, , which acts on the physical Hilbert space and multiples a minus sign when the state is fermionic (i.e., when the fermion number ), is analogous to the D-dimensional matrix, P (see Equation (277)) acting on the auxiliary space.
From (285), one sees that, in terms of the canonical matrix, the time reversal transformation is represented as:
where and . For instance, is given, for superspin , by:
Again, by Equation (258), the time-reversal invariance implies that there exists a unitary matrix that satisfies:
Applying this twice and using , we obtain
Using the relation, , we may rewrite (290) into the following form:
to which we can apply the argument presented in Section 6.4.2 (see Equation (264)). Thus, we obtain:
(the value of cannot be determined by this method). This is of exactly the same form as (281), and we deduce the same conclusion:
Therefore, as in the previous case (see Equation (283)), we see that time-reversal symmetry guarantees the existence of at least double degeneracy in the entanglement spectrum of (either of the bosonic or the fermionic sector).
6.4.5. Symmetry
Lastly, we consider the two independent π rotations around the x [] and the z axes [] (note that is redundant, since ). As will be seen below, or alone does not lead to any significant conclusion. However, the combination of the two [65,66] leads to a similar conclusion about the entanglement spectrum. Under the π rotation around the x (z) axis, (), SMPS transforms as:
When the SMPS respects such a symmetry, we have:
where for integer superspin, . Again, we follow the same steps as before to show:
Note that the phase factor, , can be absorbed in the definition of , and hereafter, we assume (). Unlike in the previous cases, this relation alone does not give any useful information about .
On the other hand, the combination of the “commutation relation”, , and Equation (295), implies, in terms of :
and hence gives
In obtaining Equation (297), the phase factor appears. However, it cancels out in the final expression (297).
Since the phases of and have been already fixed, the phase of cannot be arbitrary and has a definite physical meaning. By multiplying and from the left and the right of (298), respectively, and using repeatedly, one can show:
which is combined with (298) to give . To summarize, the two unitary matrices and obey the following commutation relation:
n terms of the block components, and , Equation (300) reads as:
As in the previous cases, (301) immediately implies at least double degeneracy of each entanglement levels in the sector (1 or 2), taking the minus sign in the above equation.
6.4.6. String Order Parameters and Entanglement Spectrum
In the previous sections, we have shown that, as in the purely bosonic cases [63,65,66], such elementary symmetries, as inversion and time-reversal, protect the Haldane phase from collapsing into trivial gapped phases on the basis of the assumption that the even-fold degeneracy in the entanglement spectrum either in the fermionic or in the bosonic sector is the entanglement fingerprint of the topological “Haldane phase” in SUSY systems. On the other hand, the string order parameters (see Section 6.1) have been used traditionally to characterize the Haldane phase [18,19]. Then, a natural question arises: is there any connection between the description by the string order parameters and the modern characterization in terms of the entanglement spectrum? In this section, we give the answer to this question.
Let us first consider the structure of the string order parameters, and (Equation (206)), from the MPS viewpoint [24,199]. When we evaluate them using MPSs, we encounter the following matrices [24]:
as well as the usual transfer matrix, T. By using these matrices, the MPS expression of the string order parameter is given as:
where we have omitted the denominator necessary to normalize the MPS. The parts, and , are easy; for the canonical MPS, they reduce, in the infinite-size limit, to (see Section 6.3.1):
The boundary dependent factors, and , are canceled by those coming from the denominator. Therefore, the quantity which we have to compute is:
Since we are interested in the long-distance limit, , we need know the asymptotic behavior of the string, . First we note that may be thought of as the overlap:
with () (see Equation (251)). Then, it can be shown [199] that in order for the string, , not to vanish in the long-distance limit, the MPS should be invariant under both of the π-rotations and .
Then, from the discussion in Section 6.4.5 (we just replace to obtain the results for the purely bosonic case), we see that there exists a pair of unitary matrices satisfying (295) and:
(see Equation (300)). Unfortunately, we cannot tell whether the even-fold degeneracy in the entanglement spectrum, which is the fingerprint of the topological Haldane phase, happens or not, since we do not know which of the ± signs is chosen.
Now, we show that when the string order parameters are non-vanishing , the minus sign in fact realizes (i.e., and anti-commute) in Equation (307), and the entanglement spectrum exhibits the degenerate structure. To this end, we investigate Equation (305). Since the largest (right) eigenvalue of is (see Section 6.4.1), reduces essentially to a phase, . The price to pay is the following boundary factors appearing at the two end points of the string correlators (see Figure 35):
where () denotes the left (right) dominant eigenvector of and the tensor notations are defined as:
In fact, the eigenvalues of precisely coincides with those of T for all the spin-S VBS states, and the different behaviors in the string order for the odd-S and the even-S chains comes only from these boundary factors.
To see whether the boundary factors are non-vanishing or not, we consider the right-boundary factor, , of . First, we rewrite it by using (see the second figure of Figure 36):
The unitary operators, and , appearing on both sides of , can be absorbed into the MPS matrices by using Equation (295) (the third figure of Figure 36). By re-arranging the unitary matrices, , with the help of Equation (307) (the fourth figure of Figure 36), we arrive at the expression:
Therefore, we see that the boundary factor, , vanishes (and so does the string order parameter, ) when and are commuting (i.e., when the minus sign in the last expression is chosen). By the explicit construction of and , we can easily see that for the even-S VBS state, holds. Therefore, it immediately results that the string order parameters identically vanish for the even-S VBS state solely for a symmetry reason.
Figure 35.
(Color online) Diagrammatic representation of the main part of string correlation function, . denotes the dominant eigenvector of . The figure has been adapted from [10].
In short, the existence of non-vanishing string order parameters, and , implies that the existence of the two anti-commuting unitary matrices, and , and, thereby, guarantees the even-fold degeneracy in the entanglement spectrum. To put it another way, the string order parameters work as the sufficient condition for the topological Haldane phase. It is crucial that both of the string order parameters are finite. For instance, if we “deform” the original -invariant VBS state by using the quantum group, , we obtain a VBS state with uniaxial anisotropy [23], where one of the string order parameters () vanishes, while the other is still finite [121]. In this case, the unitary does not exist, and the existence of the degenerate structure in the entanglement spectrum is no longer guaranteed. In fact, explicit calculation shows that the two-fold degenerate entanglement levels in the VBS state split into two non-degenerate levels in the deformed state.
Figure 36.
(Color online) Rewriting the boundary factor, (for ), using (see Equation (311)). When and are anti-commuting, the minus sign coming from is canceled and an overall plus sign is recovered. The figure has been adapted from [10].
It is straightforward to generalize [10] this to SUSY cases by taking into account the appearance of the P-matrix. Again, by using and , the second factor of the right-hand side of Equation (308) can be recasted as:
Since this implies:
 we see that one of the two components (bosonic or fermionic) vanishes just by symmetry:
we see that one of the two components (bosonic or fermionic) vanishes just by symmetry:


In conclusion, we have established the connection between the string order parameters, which have been commonly used [167,201,202,203,204] to characterize the Haldane phase and the entanglement spectrum [28], which is a modern tool to look at the topological properties in the bulk. As has been shown in Section 6.4.3, Section 6.4.4 and Section 6.4.5, SUSY guarantees, regardless of the parity of the bulk superspin , the existence of the even-fold degeneracy in the entanglement spectrum of either of the bosonic or the fermionic sector, provided at least one of the three symmetries (inversion, time-reversal and ) is present. Therefore, in contrast to the usual bosonic (i.e., ) VBS states, in which the Haldane phase is stable only for odd-integer spins, in the SVBS states, SUSY plays the crucial role in protecting the topological Haldane phase. The “revival” of the string order parameters upon doping the system (discussed in Section 6.2) may be naturally understood by the above argument.
As has been seen above, that both of the two string order parameters are non-vanishing is the sufficient condition for the symmetry-protected Haldane phase. However, one may seek more faithful order parameters and, in fact, some results have been obtained in this direction. See, for instance, References [205] and [206] for recent attempts at finding better order parameters.
7. Higher Symmetric Generalizations
In this section, we extend the previous SUSY formulation to the higher symmetric case. We begin with the construction of fuzzy four-supersphere based on the algebra [128]. As the coordinates of fuzzy four-sphere correspond to the gamma matrices [97], the coordinates of the fuzzy four-supersphere are constructed from “super gamma matrices” of the algebra. Next, based on the structure, we derive the SVBS state [10], whose bosonic counterpart is the VBS state [112,113,114] (there still exists the correspondences among fuzzy geometry, QHE and VBS in the higher dimension case; the VBS corresponds to the Laughlin-Haldane wave function in 4D QHE [79,207], and 4D QHE realizes the fuzzy geometry of fuzzy four-sphere). We also develop the SMPS formalism for the SVBS state and investigate the topological properties.
7.1. Fuzzy Four-Supersphere
Here, we utilize algebra to construct fuzzy four-supersphere with SUSY. It may be worthwhile to first point out a nice correspondence between algebras and fuzzy spheres. For fuzzy two-sphere, we have:
and for fuzzy four-sphere:
The algebra is constituted of fourteen generators:
ten of which are the bosonic generators, (the generators), and the remaining four are the fermionic ones, (the spinor). They amount to satisfy the following algebra:
where C is the charge conjugation matrix:
and are the matrices. In the following discussion, we take the matrices as:
The quadratic Casimir is given by:
The fundamental five-dimensional representation matrices of are constructed as follows. From the (bosonic) “gamma matrices” of algebra:
with:
we can derive the generators:
The fermionic “gamma matrices” are also constructed as:
where:
They satisfy the “hermiticity” condition:
where the super-adjoint ‡ is defined in (50). It is straightforward to check that (324) and (325) satisfy the algebra (318). In the similar manner to the case of (74), we introduce the coordinates of , and , as:
where Ψ is the Schwinger operator:
Here, and f, respectively, denote four bosonic and one fermionic operators that satisfy:
The square of the radius of fuzzy four-supersphere is also readily derived as:
In the Schwinger formalism, the Casimir (321) is represented as:
where:
Notice that in the Schwinger operator formalism the Casimir (332) is equivalent to (331) up to coefficient on the r.h.s. The basis states on fuzzy four-supersphere are given by the graded fully symmetric representation:
where are all non-negative integers satisfying the constraint, . Therefore, the dimensions of bosonic states (334a) and fermionic states (334b) are, respectively, given by:
and the total dimension is:
The bosonic and fermionic degrees of freedom (335) are respectively accounted for by the symmetric basis states with the Casimir indices, n and , and hence, the fuzzy four-supersphere can be regarded as a “compound” of two fuzzy four-spheres with different radii n and :
The eigenvalues of take the following values:
with . These eigenvalues are equal to those of of fuzzy two-supersphere (60), except for the degeneracy of the basis states at each latitude. The degeneracies at the latitude (338) for even and for odd are respectively given by:
which reproduce the total dimensions of bosonic and fermionic basis states (335) as:
From (331), one may find that the condition for fuzzy four-supersphere is invariant under the rotation of the Schwinger operator Ψ, which is larger than the original symmetry. It may be pedagogical to demonstrate how such “hidden” structure is embedded in the algebra of fuzzy four-supersphere. First, notice that the fuzzy four-supersphere coordinates, and , do not satisfy a closed algebra by themselves:
On the right-hand sides of (341), there appear “new” operators:
where and are, respectively, given by (324) and:
and , respectively, act as antisymmetric two-rank tensor and spinor. Commutation relations for these new operators can be derived as:
where the last equation further yields another new operator:
with:
Commutation relations with Z are obtained as:
Consequently, for the closure of the algebra of the fuzzy coordinates, and , we have introduced the fifteen new “coordinates”, , and Z. In total, with the original coordinates, they amount to twenty four operators that satisfy the algebra. The basic concept of the non-commutative geometry is the algebraic construction of geometry, and the structure, the symmetry of the basis states on fuzzy four-supersphere, has indeed appeared as the fundamental algebra of the fuzzy four-supersphere.
7.2. SVBS States
Similar to the SVBS case, the SVBS states (to be precise, there exist two types of VBS states, one of which is the tensor type (348) and the other is the vector type [10]; here, we focus on the tensor type.) can be constructed as:
where denotes the parameter-dependent Schwinger operator:
and signifies the invariant matrix:
The spin magnitude on site i reads as:
In the following, we focus on the SVBS chain and its corresponding SMPS representation:
where is a supermatrix given by:
with the matrix elements:
The basis states and are 10-dimensional adjoint representations, while are 4-dimensional spinors. In total, the components of consist of 14-dimensional representation of the graded fully symmetric representation (334) for .
7.3. Entanglement Spectrum and Symmetry
For the SVBS infinite chain, the Schmidt coefficients are computed as:
The bosonic Schmidt coefficients are quadratically degenerate, while the fermionic one is non-degenerate. The behaviors of the Schmidt coefficients and the entanglement entropy, , are plotted in Figure 37. The qualitative behaviors of the entanglement spectra of the VBS chain are quite similar to those of the type-I SVBS chain (see Figure 30), except for the quadratical degeneracy in the blue curve.
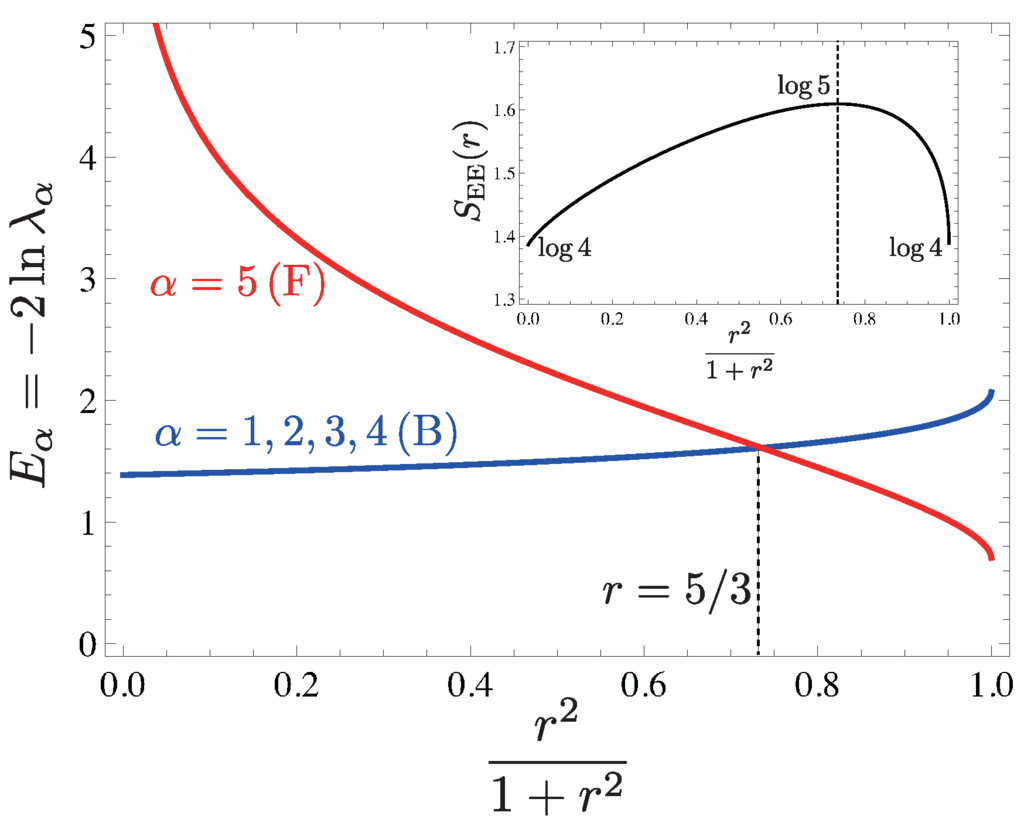
Figure 37.
The behaviors of the Schmidt coefficients and entanglement entropy (inset) of the VBS chain. The figure and caption are taken from [10].
The degeneracy of the entanglement spectra of the SVBS chain can be understood based on the arguments of the symmetry protected topological order. Before proceeding to the case of , we introduce the original arguments for its bosonic counterpart, the VBS state [112,113,114]. Each of inversion symmetry and time reversal symmetry guarantees at least double degeneracy of the entanglement spectra of the VBS states, as proven by a similar manner to the VBS states. This is simply because each of the inversion symmetry, and time reversal symmetry is a realization of symmetry. The crucial difference to the case is the existence of symmetry of the VBS states originating from the spin degrees of freedom at the edge [208]. The rotation represents a rotation in five-dimensional space, and we “divide” the five-dimensional coordinates (1, 2, 3, 4, 5) to two three-dimensional subsectors, (1, 2, 5) and (3, 4, 5). The π-rotational symmetry around x and z axes in each sector generates the symmetry, and in total, two independent sets of such discrete rotations give rise to symmetry in the five-dimensional space. The group elements of consist of 16 bases:
where are the group elements of π rotation generated by the generator :
As the symmetry generates at least doubly degeneracy in the entanglement spectra, the symmetry guarantees the four-fold degeneracy of the entanglement spectra of the VBS chain. For the SUSY case, just as we have discussed in the SVBS case, symmetry transformations are attributed to those of the bosonic and fermionic sectors:
Similar to the discussions about double degeneracy in the case, either of the bosonic and fermionic sectors brings the quadruple degeneracy to the entanglement spectra of the SVBS state in the presence of symmetry.
8. Summary and Discussions
We reviewed the constructions and basic properties of the fuzzy superspheres and SVBS models. Particularly, fuzzy superspheres and SVBS models with , and symmetries were discussed in detail. We clarified the mutual relations among the fuzzy spheres; QHE and VBS states were also emphasized based on the Schwinger operator formalism. It was illustrated that, though the SVBS states incorporate fermionic degrees of freedom, they “inherit” all the nice properties of the VBS:
- Solvable parent Hamiltonian
- Gapped bulk and gapless edge excitations
- Generalized hidden order.
We explicitly derived the spectra for gapped excitations (magnon and hole excitations) on 1D SVBS chain within SMA. Physical properties of the SVBS models are qualitatively different from those of the other generalized VBS models based on bosonic Lie groups, in the sense that the SVBS states accommodate the charge sector in addition to the spin sector. In each sector, the SVBS states exhibit the following properties:
- In the charge sector, the SVBS states have the superconducting property (SSB).
- In spin sector, the SVBS states show a non-trivial topological order of QAFM (no SSB).
We also established the SMPS formalism for the SVBS states, which naturally incorporates the edge degrees of freedom to provide a powerful tool in investigating topological property. For practical use, the (S)MPS formalism greatly simplifies the calculations of physical quantities, such as the string order and entanglement spectrum. The SVBS states bear a finite string order, regardless of the parity of the bulk superspin, unlike the original VBS states. From the explicit calculations of the entanglement spectra of the SVBS chains, we demonstrated that there exists a hallmark of topological phase, the double degeneracy in SUSY entanglement spectrum. The degeneracy is naturally understood by invoking particular edge states in the SUSY chain: since SUSY relates the integer and half-integer edge-spin states, the SVBS chains always accommodate half-integer edge spin (as well as integer edge spin), which guarantees at least double degeneracy of the entanglement spectra. Consequently, the topological order is stabilized regardless of the parity of bulk-spin in the presence of SUSY.
Though we focused on the SVBS states, the arguments of the present SUSY protected topological order are applicable to general boson-fermion systems. By reformulating the boson-fermion system, such as the boson-fermion mixture cold atom system [209] with SUSY, we may apply the present results to discuss the stability for their topological phases. The idea of the topological insulator has begun to be applied to the particle theory model [210]. It may also be interesting to apply the present arguments to other SUSY models that are not directly related to condensed matter physics.
Acknowledgment
K.H. would like to thank Daniel P. Arovas, Xiaoliang Qi and Shoucheng Zhang for bringing him the idea of SVBS states and the collaboration from which the sequent works were initiated. The authors also thank H. Katsura and F. Pollmann for very useful discussions. This work was supported in part by Grants-in-Aid for Scientific Research (B) 23740212 (K.H.), (C) 20540375, (C) 24540402 (K.T.) and by the global COE (GCOE) program, “The next generation of physics, spun from university and emergent” of Kyoto University.
Appendix
A.
Here, we summarize the basic properties of algebra. We denote the generators of the orthosymplectic group, as , which satisfy the following relation (the minus sign in front of in (358) is not important for the definition of , but added to be consistent with the notation of the present paper.):
where the supertranspose, , is defined in (275), denotes the unit matrix and represents the invariant matrix:
can be expressed by a linear combination of the following matrices:
where α and β are the indices of and l and m are those of (). stand for arbitrary matrices, while and , respectively, signify and matrices that satisfy:
The algebra contains the maximal bosonic subalgebra, , whose generators are and . The off-diagonal block matrices, , are fermionic generators that transform as the fundamental representation under each of the transformations of and . The matrices are antisymmetric matrices (361a), and then, we can take the indices of to be antisymmetric, . In the following, we consider the real antisymmetric matrices, the generators of , with real degrees of freedom. Meanwhile, from the relation (361b), the generators of take the form of:
where k stands for an arbitrary complex matrix and, similarly, s and are symmetric complex matrices. If the Hermiticity condition is imposed, are reduced to the generators of that take the form of:
where h represents an arbitrary Hermitian matrix and s also signifies an arbitrary symmetric complex matrix. Consequently, generators consist of (360), whose blocks satisfy (361) and (363). The real independent degrees of freedom of are . Then, for matrices , we can take the indices to be symmetric, Meanwhile, the real degrees of freedom of the fermionic generators, , are . Then in total, the real degrees of freedom of are given by:
In the present paper, instead of (359), we adopt the following matrix (which is unitarily equivalent to ):
and the following invariant matrix:
For instance, for the , and , are, respectively, given by:
B. Fuzzy Four-Supersphere with Higher Supersymmetries
By generalizing the construction of fuzzy four-supersphere based on (Section 7.1), we can construct -SUSY fuzzy four-sphere with use of the algebra [128]. The dimension of the algebra is given by:
We denote the bosonic generators of as , and fermionic generators as . In total, they satisfy:
where C is the charge conjugation matrix (319) and are generators given by:
We introduce the coordinates of as (; , do not satisfy a closed algebra by themselves, and the minimally extended closed algebra including these operators is [128]):
where denotes the Schwinger operator whose first four components, , are the bosonic operators, while the remaining components, , are the fermionic operators. The sandwiched matrices in (371):
are the fundamental representation matrices of . Here, denotes zero-matrix, and are given by (326). The square of the radius of the -SUSY fuzzy four-supersphere is readily derived as:
with . Notice that the square of the radius of -SUSY fuzzy supersphere is proportional to and takes negative values for sufficiently small n that satisfy . For the positive definiteness of the radius, the SUSY number should be restricted to . The basis states on -SUSY fuzzy supersphere are given by the graded fully symmetric representation:
where . Therefore, with (335a), the dimension of (374) is given by:
for . The degrees of freedom of the basis states (374) imply that can be interpreted as a “compound” of lower SUSY fuzzy four-spheres with different radii:
More explicitly:
For , this reproduces the relation for (61).
References and Notes
- Heisenberg, W. Mehrkörperproblem und resonanz in der quantenmechanik. Z. Phys. 1926, 38, 411–426. [Google Scholar] [CrossRef]
- Heisenberg, W. Zur theorie des ferromagnetismus. Z. Phys. 1928, 49, 619–636. [Google Scholar] [CrossRef]
- Bethe, H.A. Zur theorie der metalle i. eigenwerte und eigenfunktionen der linearen atomkette. Z. Phys. 1931, 71, 205–226. [Google Scholar] [CrossRef]
- Bardeen, J.; Cooper, L.N.; Schrieffer, J.R. Microscopic theory of superconductivity. Phys. Rev. 1957, 106, 162–164. [Google Scholar] [CrossRef]
- Laughlin, R.B. Anomalous quantum Hall effect: An incompressible quantum fluid with fractionally charged excitations. Phys. Rev. Lett. 1983, 50, 1395–1398. [Google Scholar] [CrossRef]
- Affleck, I.; Kennedy, T.; Lieb, E.; Tasaki, H. Rigorous results on valence-bond ground states in antiferromagnets. Phys. Rev. Lett. 1987, 59, 799–802. [Google Scholar] [CrossRef] [PubMed]
- Affleck, I.; Kennedy, T.; Lieb, E.; Tasaki, H. Valence bond ground states in isotropic quantum antiferromagnets. Commun. Math. Phys. 1988, 115, 477–528. [Google Scholar] [CrossRef]
- Arovas, D.P.; Hasebe, K.; Qi, X.-L.; Zhang, S.-C. Supersymmetric Valence Bond Solid States. Phys. Rev. 2009, B79, 224404:1–224404:20. [Google Scholar] [CrossRef]
- Hasebe, K.; Totsuka, K. Hidden order and dynamics in supersymmetric valence bond solid states–super-matrix product state formalism. Phys. Rev. 2011, B84, 104426:1–104426:19. [Google Scholar] [CrossRef]
- Hasebe, K.; Totsuka, K. Quantum entanglement and topological order in hole-doped valence bond solid states. Phys. Rev. B 2013, 87, 045115:1–045115:21. [Google Scholar] [CrossRef]
- Haldane, F.D.M. Continuum dynamics of the 1-D Heisenberg antiferromagnet: Identification with the O(3) nonlinear sigma model. Phys. Lett. A 1983, 93, 464–468. [Google Scholar] [CrossRef]
- Haldane, F.D.M. Nonlinear field theory of large-spin Heisenberg antiferromagnets: Semiclassically quantized solitons of the one-dimensional easy-axis Néel state. Phys. Rev. Lett. 1983, 50, 1153–1156. [Google Scholar] [CrossRef]
- Hagiwara, M.; Katsumata, K.; Affleck, I.; Halperin, B.I.; Renard, J.P. Observation of S = 1/2 degrees of freedom in an S = 1 linear-chain Heisenberg antiferromagnet. Phys. Rev. Lett. 1990, 65, 3181–3184. [Google Scholar] [CrossRef] [PubMed]
- Kennedy, T. Exact diagonalisations of open spin-1 chains. J. Phys. Condens. Matter 1990, 2, 5737–5745. [Google Scholar] [CrossRef]
- Qi, X.-L.; Zhang, S.-C. The quantum spin Hall effect and topological insulators. Phys. Today 2010, 63, 33–38. [Google Scholar] [CrossRef]
- Hasan, M.Z.; Kane, C.L. Topological insulators. Rev. Mod. Phys. 2010, 82, 3045–3067. [Google Scholar] [CrossRef]
- Qi, X.-L.; Zhang, S.-C. Topological insulators and superconductors. Rev. Mod. Phys. 2011, 83, 1057–1110. [Google Scholar] [CrossRef]
- den Nijs, M.; Rommelse, K. Preroughening transitions in crystal surfaces and valence-bond phases in quantum spin chains. Phys. Rev. B 1989, 40, 4709–4734. [Google Scholar] [CrossRef]
- Tasaki, H. Quantum liquid in antiferromagnetic chains: A stochastic geometric approach to the Haldane gap. Phys. Rev. Lett. 1991, 66, 798–801. [Google Scholar] [CrossRef] [PubMed]
- Fannes, M.; Nachtergaele, B.; Werner, R.F. Exact antiferromagnetic ground states of quantum spin chains. Europhys. Lett. 1989, 10, 633–637. [Google Scholar] [CrossRef]
- Fannes, M.; Nachtergaele, B.; Werner, R.F. Finitely correlated states on quantum spin chains. Commun. Math. Phys. 1992, 144, 443–490. [Google Scholar] [CrossRef]
- Klu¨mper, A.; Schadschneider, A.; Zittartz, J. Equivalence and solution of anisotropic spin-1 models and generalized t-J fermion models in one dimension. J. Phys. A Math. Gen. 1991, 24, L955–L959. [Google Scholar] [CrossRef]
- Klu¨mper, A.; Schadschneider, A.; Zittartz, J. Ground-state properties of a generalized VBS-model. Z. Phys. B Conds. Matter 1992, 87, 281–287. [Google Scholar] [CrossRef]
- Totsuka, K.; Suzuki, M. Matrix formalism for the VBS-type models and hidden order. J. Phys. Condens. Matter 1995, 7, 1639–1662. [Google Scholar] [CrossRef]
- Pérez-García, D.; Verstraete, F.; Wolf, M.M.; Cirac, J.I. Matrix product state representations. Quantum Inf. Comput. 2007, 7, 401–430. [Google Scholar]
- Nielsen, M.A.; Chuang, I.L. Quantum Computation and Quantum Information; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Amico, L.; Fazio, R.; Osterloh, A.; Vedral, V. Entanglement in many-body systems. Rev. Mod. Phys. 2008, 80, 517–576. [Google Scholar] [CrossRef]
- Li, H.; Haldane, F.D.M. Entanglement spectrum as a generalization of entanglement entropy: Identification of topological order in non-abelian fractional quantum Hall effect states. Phys. Rev. Lett. 2008, 101, 010504:1–010504:4. [Google Scholar] [CrossRef]
- Hastings, M.B. An area law for one-dimensional quantum systems. J. Stat. Mech. Theory Exp. 2007, P08024:1–P08024:14. [Google Scholar] [CrossRef]
- White, S.R. Density matrix formulation for quantum renormalization groups. Phys. Rev. Lett. 1992, 69, 2863–2866. [Google Scholar] [CrossRef] [PubMed]
- Östlund, S.; Rommer, S. Thermodynamic limit of the density matrix renormalization for the spin-1 Heisenberg chain. Phys. Rev. Lett. 1995, 75, 3537–3540. [Google Scholar] [CrossRef] [PubMed]
- Verstraete, F.; Murg, V.; Cirac, J.I. Matrix product states, projected entangled pair states, and variational renormalization group methods for quantum spin systems. Adv. Phys. 2008, 57, 143–224. [Google Scholar] [CrossRef]
- Schollwöck, U. The density-matrix renormalization group in the age of matrix product states. Ann. Phys. 2011, 326, 96–192. [Google Scholar] [CrossRef]
- Dukelsky, J.; Martin-Delgado, M.A.; Nishino, T.; Sierra, G. Equivalence of the variational matrix product method and the density matrix renormalization group applied to spin chains. Europhys. Lett. 1998, 43, 457–462. [Google Scholar] [CrossRef]
- Roman, J.M.; Sierra, G.; Dukelsky, J.; Martin-Delgado, M.A. The matrix product approach to quantum spin ladders. J. Phys. A Math. Gen. 1998, 31, 9729–9759. [Google Scholar] [CrossRef]
- Fledderjohann, A.; Klu¨mper, A.; Mu¨tter, K.-H. Diagrammatics for SU(2) invariant matrix product states. J. Phys. A Math. Gen. 2011, 44, 475302:1–475302:18. [Google Scholar] [CrossRef]
- Auerbach, A. Interacting Electrons and Quantum Magnetism; Springer: Heidelberg, Germany, 1994. [Google Scholar]
- Verstraete, F.; Cirac, J.I. Matrix product states represent ground states faithfully. Phys. Rev. B 2006, 73, 094423:1–094423:8. [Google Scholar] [CrossRef]
- Hastings, M.B. Solving gapped Hamiltonians locally. Phys. Rev. B 2006, 73, 085115:1–085115:13. [Google Scholar] [CrossRef]
- Vidal, G. Efficient classical simulation of slightly entangled quantum computations. Phys. Rev. Lett. 2003, 91, 147902:1–147902:4. [Google Scholar] [CrossRef]
- Vidal, G. Efficient simulation of one-dimensional quantum many-body systems. Phys. Rev. Lett. 2004, 93, 040502:1–040502:4. [Google Scholar] [CrossRef]
- White, S.R.; Feiguin, A.E. Real-time evolution using the density matrix renormalization group. Phys. Rev. Lett. 2004, 93, 076401:1–076401:4. [Google Scholar] [CrossRef]
- Daley, A.J.; Kollath, C.; Schollwoöck, U.; Vidal, G. Time-dependent density-matrix renormalization-group using adaptive effective Hilbert spaces. J. Stat. Mech. Theory Exp. 2004, P04005:1–P04005:28. [Google Scholar] [CrossRef]
- Vidal, G. Classical simulation of infinite-size quantum lattice systems in one spatial dimension. Phys. Rev. Lett. 2007, 98, 070201:1–070201:4. [Google Scholar] [CrossRef]
- Orús, R.; Vidal, G. Infinite time-evolving block decimation algorithm beyond unitary evolution. Phys. Rev. B 2008, 78, 155117:1–155117:11. [Google Scholar] [CrossRef]
- Schadschneider, A.; Zittartz, J. Variational study of isotropic spin-1 chains. Ann. Phys. 1995, 4, 157–163. [Google Scholar] [CrossRef]
- Kolezhuk, A.; Mikeska, H.-J.; Yamamoto, S. Matrix-product-states approach to Heisenberg ferrimagnetic spin chains. Phys. Rev. B 1997, 55, R3336–R3339. [Google Scholar] [CrossRef]
- Weichselbaum, A.; Verstraete, F.; Schollwöck, U.; Cirac, J.I.; von Delft, J. Variational matrix-product-state approach to quantum impurity models. Phys. Rev. B 2009, 80, 165117:1–165117:7. [Google Scholar] [CrossRef]
- Porras, D.; Verstraete, F.; Cirac, J.I. Renormalization algorithm for the calculation of spectra of interacting quantum systems. Phys. Rev. B 2006, 73, 014410:1–014410:7. [Google Scholar] [CrossRef]
- Fan, H.; Korepin, V.; Roychowdhury, V. Entanglement in a valence-bond solid state. Phys. Rev. Lett. 2004, 93, 227203:1–227203:4. [Google Scholar] [CrossRef]
- Katsura, H.; Hirano, T.; Hatsugai, Y. Exact analysis of entanglement in gapped quantum spin chains. Phys. Rev. B 2007, 76, 012401:1–012401:4. [Google Scholar] [CrossRef]
- Katsura, H.; Hirano, T.; Korepin, V.E. Entanglement in an SU(n) valence-bond-solid state. J. Phys. A Math Theor. 2008, 41, 135304:1–135304:13. [Google Scholar] [CrossRef]
- Xu, Y.; Katsura, H.; Hirano, T.; Korepin, V.E. Entanglement and density matrix of a block of spins in AKLT model. J. Stat. Phys. 2008, 133, 347–377. [Google Scholar] [CrossRef]
- Niggemann, H.; Klu¨mper, A.; Zittartz, J. Quantum phase transition in spin-3/2 systems on the hexagonal lattice - optimum ground state approach. Z. Phys. B 1997, 104, 103–110. [Google Scholar] [CrossRef]
- Niggemann, H.; Klu¨mper, A.; Zittartz, J. Ground state phase diagram of a spin-2 antiferromagnet on the square lattice. Eur. Phys. J. B 2000, 13, 15–19. [Google Scholar] [CrossRef]
- Klümper, A.; Schadschneider, A.; Zittartz, J. Matrix product ground states for one-dimensional spin-1 quantum antiferromagnets. Eur. Phys. Lett. 1993, 24, 293–297. [Google Scholar] [CrossRef]
- Wolf, M.M.; Ortiz, G.; Verstraete, F.; Cirac, J.I. Quantum phase transitions in matrix product systems. Phys. Rev. Lett. 2006, 97, 110403:1–110403:4. [Google Scholar] [CrossRef]
- Vidal, G.; Latorre, J.I.; Rico, E.; Kitaev, A. Entanglement in quantum critical phenomena. Phys. Rev. Lett. 2003, 90, 227902:1–227902:4. [Google Scholar] [CrossRef]
- Calabrese, P.; Cardy, J. Entanglement entropy and quantum field theory. J. Stat. Mech. 2004, P06002:1–P06002:27. [Google Scholar] [CrossRef]
- Calabrese, P.; Cardy, J. Entanglement entropy and conformal field theory. J. Phys. A Math. Theor. 2009, 42, 504005:1–504005:36. [Google Scholar] [CrossRef]
- Chen, X.; Gu, Z.-C.; Wen, X.-G. Classification of gapped symmetric phases in one-dimensional spin systems. Phys. Rev. B 2011, 83, 035107:1–035107:19. [Google Scholar] [CrossRef]
- Chen, X.; Gu, Z.-C.; Wen, X.-G. Complete classification of one-dimensional gapped quantum phases in interacting spin systems. 2011; 84, 235128:1–235128:14. [Google Scholar]
- Gu, Z.-C.; Wen, X.-G. Tensor-entanglement-filtering renormalization approach and symmetry-protected topological order. Phys. Rev. B 2009, 80, 155131:1–155131:26. [Google Scholar] [CrossRef]
- Schuch, N.; Pérez-García, D.; Cirac, I. Classifying quantum phases using matrix product states and projected entangled pair states. Phys. Rev. B 2011, 84, 165139:1–165139:21. [Google Scholar] [CrossRef]
- Pollmann, F.; Turner, A.M.; Berg, E.; Oshikawa, M. Entanglement spectrum of a topological phase in one dimension. Phys. Rev. B 2010, 81, 064439:1–064439:10. [Google Scholar] [CrossRef]
- Pollmann, F.; Berg, E.; Turner, A.M.; Oshikawa, M. Symmetry protection of topological order in one-dimensional quantum spin systems. Phys. Rev. B 2012, 85, 075125:1–075125:9. [Google Scholar] [CrossRef]
- Turner, A.; Pollmann, F.; Berg, E. Topological phases of one-dimensional fermions: An entanglement point of view. Phys. Rev. B 2011, 83, 075102:1–075102:11. [Google Scholar] [CrossRef]
- Fidkowski, L.; Kitaev, A. Topological phases of fermions in one dimension. Phys. Rev. B 2011, 83, 075103:1–075103:13. [Google Scholar] [CrossRef]
- Duivenvoorden, K.; Quella, T. On topological phases of spin chains. Phys. Rev. B 2013, 87, 125145:1–125145:16. [Google Scholar] [CrossRef]
- Duivenvoorden, K.; Quella, T. A discriminating string order parameter for topological phases of gapped SU(N) spin chains. Phys. Rev. B 2012, 86, 235142:1–235142:13. [Google Scholar] [CrossRef]
- Zang, J.; Jiang, H.-C.; Weng, Z.-Y.; Zhang, S.-C. Topological quantum phase transition in an S = 2 spin chain. Phys. Rev. B 2010, 81, 224430:1–224430:6. [Google Scholar] [CrossRef]
- Zheng, D.; Zhang, G.-M.; Xiang, T.; Lee, D.-H. Continuous quantum phase transition between two topologically distinct valence bond solid states associated with the same spin value. Phys. Rev. B 2011, 83, 014409:1–014409:7. [Google Scholar] [CrossRef]
- Snyder, H.S. Quantized space-time. Phys. Rev. 1947, 71, 38–41. [Google Scholar] [CrossRef]
- Balachandran, A.P.; Qureshi, B.A. Noncommutative geometry: Fuzzy spaces, the groenewold-moyal plane. SIGMA 2006, 2, 094:1–094:9. [Google Scholar] [CrossRef]
- Arovas, D.P.; Auerbach, A.; Haldane, F.D.M. Extended Heisenberg models of antiferromagnetism: Analogies to the fractional quantum Hall effect. Phys. Rev. Lett. 1988, 60, 531–534. [Google Scholar] [CrossRef] [PubMed]
- Haldane, F.D.M. Fractional quantization of the Hall effect: A hierarchy of incompressible quantum fluid states. Phys. Rev. Lett. 1983, 51, 605–608. [Google Scholar] [CrossRef]
- For a review, see Hasebe, K. Hopf maps, lowest landau level, and fuzzy spheres. SIGMA 2010, 6, 071:1–071:42. [Google Scholar]
- Karabali, D.; Nair, V.P. Quantum Hall effect in higher dimensions, matrix models and fuzzy geometry. J. Phys. A 2006, 39, 12735–12764. [Google Scholar] [CrossRef]
- Zhang, S.-C.; Hu, J.-P. A four-dimensional generalization of the quantum Hall effect. Science 2001, 294, 823–828. [Google Scholar] [CrossRef] [PubMed]
- Bernevig, B.A.; Hu, J.-P.; Toumbas, N.; Zhang, S.-C. The eight dimensional quantum Hall effect and the octonions. Phys. Rev. Lett. 2003, 91, 236803:1–236803:4. [Google Scholar] [CrossRef]
- Hasebe, K.; Kimura, Y. Dimensional hierarchy in quantum Hall effects on fuzzy spheres. Phys. Lett. 2004, B602, 255–260. [Google Scholar] [CrossRef]
- Karabali, D.; Nair, V.P. Quantum Hall effect in higher dimensions. Nucl. Phys. 2002, B641, 533–546. [Google Scholar] [CrossRef]
- Bellucci, S.; Casteill, P.-Y.; Nersessian, A. Four-dimensional Hall mechanics as a particle on CP3. Phys. Lett. B 2003, 574, 121–128. [Google Scholar] [CrossRef]
- Geloun, J.B.; Govaerts, J.; Hounkonnou, M.N. A (p,q)-deformed Landau problem in a spherical harmonic well: Spectrum and noncommuting coordinates. Europhys. Lett. 2007, 80, 30001:1–37005:6. [Google Scholar] [CrossRef]
- Jellal, A. Quantum Hall effect on higher dimensional spaces. Nucl. Phys. B 2005, 725, 554–576. [Google Scholar] [CrossRef]
- Daoud, M.; Jellal, A. Quantum Hall effect on the flag manifold F2. Int. J. Mod. Phys. A 2008, 23, 3129–3154. [Google Scholar] [CrossRef]
- Hasebe, K. Hyperbolic supersymmetric quantum Hall effect. Phys. Rev. D 2008, 78, 125024:1–125024:13. [Google Scholar] [CrossRef]
- Hasebe, K. Split-quaternionic Hopf map, quantum Hall effect and twistor theory. Phys. Rev. D 2010, 81, 041702(R):1–041702(R):5. [Google Scholar] [CrossRef]
- Bellissard, J.; van Elst, A.; Schulz Baldes, H. The noncommutative geometry of the quantum Hall effect. J. Math. Phys. 1994, 35, 5373–5451. [Google Scholar] [CrossRef]
- Girvin, S.M.; Jach, T. Formalism for the quantum Hall effect: Hilbert space of analytic functions. Phys. Rev. B 1984, 29, 5617–5625. [Google Scholar] [CrossRef]
- Girvin, S.M.; MacDonald, A.H.; Platzman, P.M. Collective-excitation gap in the fractional quantum Hall effect. Phys. Rev. Lett. 1985, 54, 581–583. [Google Scholar] [CrossRef] [PubMed]
- Girvin, S.M.; MacDonald, A.H.; Platzman, P.M. Magneto-roton theory of collective excitations in the fractional quantum Hall effect. Phys. Rev. B 1986, 33, 2481–2494. [Google Scholar] [CrossRef]
- Ezawa, Z.F.; Tsitsishvili, G.; Hasebe, K. Noncommutative geometry, extended W(infty) algebra and grassmannian solitons in multicomponent quantum Hall systems. Phys. Rev. B 2003, 67, 125314:1–125314:16. [Google Scholar] [CrossRef]
- Berezin, F.A. General concept of quantization. Commun. Math. Phys. 1975, 40, 153–174. [Google Scholar] [CrossRef]
- Hoppe, J. Quantum Theory of a Massless Relativistic Surface and a Two-Dimensional Bound State Problem. Ph.D. Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 1982. [Google Scholar]
- Madore, J. The fuzzy sphere. Class. Quant. Grav. 1992, 9, 69–87. [Google Scholar] [CrossRef]
- Grosse, H.; Klimcik, C.; Presnajder, P. On finite 4D quantum field theory in non-commutative geometry. Commun. Math. Phys. 1996, 180, 429–438. [Google Scholar] [CrossRef]
- Kabat, D.; Taylor, W. Spherical membranes in Matrix theory. Adv. Theor. Math. Phys. 1998, 2, 181–206. [Google Scholar]
- Ramgoolam, S. On spherical harmonics for fuzzy spheres in diverse dimensions. Nucl. Phys. B 2001, 610, 461–488. [Google Scholar] [CrossRef]
- Ho, P.-M.; Ramgoolam, S. Higher dimensional geometries from matrix brane constructions. Nucl. Phys. B 2002, 627, 266–288. [Google Scholar] [CrossRef]
- Kimura, Y. Noncommutative gauge theory on fuzzy four-sphere and matrix model. Nucl. Phys. B 2002, 637, 177–198. [Google Scholar] [CrossRef]
- Kimura, Y. On higher dimensional fuzzy spherical branes. Nucl. Phys. B 2003, 664, 512–530. [Google Scholar] [CrossRef]
- Azuma, T.; Bagnoud, M. Curved-space classical solutions of a massive supermatrix model. Nucl. Phys. B 2003, 651, 71–86. [Google Scholar] [CrossRef]
- Alexanian, G.; Balachandran, A.P.; Immirzi, G.; Ydri, B. Fuzzy CP2. J. Geom. Phys. 2002, 42, 28–53. [Google Scholar] [CrossRef]
- Balachandran, A.P.; Dolan, B.P.; Lee, J.; Martin, X.; O’Connor, D. Fuzzy complex projective spaces and their star-products. J. Geom. Phys. 2002, 43, 184–204. [Google Scholar] [CrossRef]
- Carow-Watamura, U.; Steinacker, H.; Watamura, S. Monopole bundles over fuzzy complex projective spaces. J. Geom. Phys. 2005, 54, 373–399. [Google Scholar] [CrossRef]
- Podles, P. Quantum spheres. Lett. Math. Phys. 1987, 14, 193–202. [Google Scholar] [CrossRef]
- Ho, P.-M.; Li, M. Large N expansion from fuzzy AdS2. Nucl. Phys. 2000, B590, 198–212. [Google Scholar] [CrossRef]
- Fakhri, H.; Imaanpur, A. Dirac operator on fuzzy AdS2. J. High Energy Phys. 2003, 0303, 003:1–003:16. [Google Scholar] [CrossRef]
- DeBellis, J.; Sa¨mann, Ch.; Szabo, R.J. Quantized nambu-poisson manifolds and n-lie algebras. J. Math. Phys. 2010, 51, 122303:1–122303:34. [Google Scholar] [CrossRef]
- Hasebe, K. Non-compact Hopf maps and fuzzy ultra-hyperboloids. Nucl. Phys. B 2012, 865, 148–199. [Google Scholar] [CrossRef]
- Tu, H.; Zhang, G.; Xiang, T. String order and hidden topological symmetry in the SO(2n + 1) symmetric matrix product states. J. Phys. A 2008, 41, 415201:1–415201:7. [Google Scholar] [CrossRef]
- Tu, H.; Zhang, G.; Xiang, T. Class of exactly solvable SO(n) symmetric spin chains with matrix product ground states. Phys. Rev. B 2008, 78, 094404:1–094404:10. [Google Scholar] [CrossRef]
- Tu, H.-H.; Zhang, G.-M.; Xiang, T.; Liu, Z.-X.; Ng, T.-K. Topologically distinct classes of valence bond solid states with their parent Hamiltonians. Phys. Rev. B 2009, 80, 014401:1–014401:11. [Google Scholar] [CrossRef]
- Greiter, M.; Rachel, S.; Schuricht, D. Exact results for SU(3) spin chains: Trimer states, valence bond solids, and their parent Hamiltonians. Phys. Rev. B 2007, 75, 060401(R):1–060401(R):4. [Google Scholar] [CrossRef]
- Greiter, M.; Rachel, S. Valence bond solids for SU(n) spin chains: Exact models, spinon confinement, and the Haldane gap. Phys. Rev. B 2007, 75, 184441:1–184441:25. [Google Scholar] [CrossRef]
- Arovas, D. Simplex solid states of SU(N) quantum antiferromagnets. Phys. Rev. B 2008, 77, 104404:1–104404:14. [Google Scholar]
- Rachel, S.; Thomale, R.; Führinger, M.; Schmitteckert, P.; Greiter, M. Spinon confinement and the Haldane gap in SU(n) spin chains. Phys. Rev. B 2009, 80, 180420(R):1–180420(R):4. [Google Scholar] [CrossRef]
- Schuricht, D.; Rachel, S. Valence bond solid states with symplectic symmetry. Phys. Rev. B 2008, 78, 014430:1–014430:9. [Google Scholar] [CrossRef]
- Rachel, S. Spin 3/2 dimer model. Europhys. Lett. 2009, 86, 37005:1–37005:6. [Google Scholar] [CrossRef]
- Totsuka, K.; Suzuki, M. Hidden symmetry breaking in a generalized valence-bond solid model. J. Phys. A Math. Gen. 1994, 27, 6443–6456. [Google Scholar] [CrossRef]
- Arita, C.; Motegi, K. Spin-spin correlation functions of the q-valence-bond-solid state of an integer spin model. J. Math. Phys. 2011, 52, 063303:1–063303:15. [Google Scholar] [CrossRef]
- Santos, R.A.; Paraan, F.N.C.; Korepin, V.E.; Klu¨mper, A. Entanglement spectra of q-deformed higher spin VBS states. J. Phys. A Math. Theor. 2012, 45, 175303:1–175303:14. [Google Scholar] [CrossRef]
- Grosse, H.; Klimcik, C.; Presnajder, P. Field theory on a supersymmetric lattice. Commun. Math. Phys. 1997, 185, 155–175. [Google Scholar] [CrossRef]
- Grosse, H.; Reiter, G. The fuzzy supersphere. J. Geom. Phys. 1998, 28, 349–383. [Google Scholar] [CrossRef]
- Landi, G. Projective modules of finite type over the supersphere S2,2. J. Geom. Phys. 2001, 37, 47–62. [Google Scholar] [CrossRef]
- Balachandran, A.P.; Kurkcuoglu, S.; Rojas, E. The star product on the fuzzy supersphere. J. High Energy Phys. 2002, 0207, 056:1–056:23. [Google Scholar] [CrossRef]
- Hasebe, K. Graded Hopf maps and fuzzy superspheres. Nucl. Phys. B 2011, 853, 777–827. [Google Scholar] [CrossRef]
- Hasebe, K.; Kimura, Y. Fuzzy supersphere and supermonopole. Nucl. Phys. 2005, 94, 94–114. [Google Scholar] [CrossRef]
- Hasebe, K. Supersymmetric quantum-Hall effect on a fuzzy supersphere. Phys. Rev. Lett. 2005, 94, 206802:1–206802:4. [Google Scholar] [CrossRef]
- Hasebe, K. Quantum Hall liquid on a noncommutative superplane. Phys. Rev. D 2005, 72, 105017:1–105017:9. [Google Scholar] [CrossRef]
- Hasebe, K. Supersymmetric Chern-Simons theory and supersymmetric quantum Hall liquid. Phys. Rev. D 2006, 74, 045026:1–045026:12. [Google Scholar] [CrossRef]
- Ivanov, E.; Mezincescu, L.; Townsend, P.K. A super-flag landau model. 2004. arXiv:hep-th/0404108. Avaliable online: http://arxiv.org/abs/hep-th/0404108 (accessed on 16 April 2004).
- Ivanov, E.; Mezincescu, L.; Townsend, P.K. Planar super-landau models. J. High Energy Phys. 2006. [Google Scholar] [CrossRef]
- Curtright, Th.; Ivanov, E.; Mezincescu, L.; Townsend, P.K. Planar super-landau models revisited. J. High Energy Phys. 2007, 0704, 020:1–020:24. [Google Scholar] [CrossRef]
- Beylin, A.; Curtright, Th.L.; Ivanov, E.; Mezincescu, L.; Townsend, P.K. Unitary spherical super-landau models. J. High Energy Phys. 2008, 0810, 069:1–069:47. [Google Scholar] [CrossRef]
- Beylin, A.; Curtright, Th.; Ivanov, E.; Mezincescu, L. Generalized N = 2 super landau models. J. High Energy Phys. 2010. arXiv:1003.0218. Avaliable online: http://arxiv.org/abs/1003.0218 (accessed on 28 February 2010). [Google Scholar]
- Bychkov, V.; Ivanov, E. N = 4 Supersymmetric landau models. Nucl. Phys. B 2012, 863, 33–64. [Google Scholar] [CrossRef]
- Goykhman, M.; Ivanov, E.; Sidorov, S. Super landau models on odd cosets. Phys. Rev. D 2013, 87, 025026:1–025026:18. [Google Scholar] [CrossRef]
- Ivanov, E.; Mezincescu, L.; Townsend, P.K. Fuzzy CP(n|m) as a quantum superspace. 2003. arXiv:hep-th/0311159. Avaliable online: http://arxiv.org/abs/hep-th/0311159 (accessed on 18 November 2003).
- Murray, S.; Saemann, C. Quantization of flag manifolds and their supersymmetric extensions. Adv. Theor. Math. Phys. 2008, 12, 641–710. [Google Scholar] [CrossRef]
- Lazaroiu, C.I.; McNamee, D.; Saemann, C. Generalized Berezin-Toeplitz quantization of Kaehler supermanifolds. J. High Energy Phys. 2009, 0905, 055:1–055:44. [Google Scholar]
- Johnson, C.V. D-brane primer. 2000. arXiv:hep-th/0007170. Avaliable online: http://arxiv.org/abs/hep-th/0007170 (accessed on 21 July 2000).
- Taylor, W. M(atrix) theory: Matrix quantum mechanics as a fundamental theory. Rev. Mod. Phys. 2001, 73, 419–462. [Google Scholar] [CrossRef]
- Szabo, R.J. D-branes in noncommutative field theory. 2005. arXiv:hep-th/0512054. Avaliable online: http://arxiv.org/abs/hep-th/0512054 (accessed on 5 December 2005).
- Myers, R.C. Dielectric-branes. J. High Energy Phys. 1999. [Google Scholar] [CrossRef]
- Klimcik, C. A nonperturbative regularization of the supersymmetric Schwinger model. Commun. Math. Phys. 1999, 206, 567–586. [Google Scholar]
- Klimcik, C. An extended fuzzy supersphere and twisted chiral superfields. Commun. Math. Phys. 1999, 206, 587–601. [Google Scholar]
- Iso, S.; Umetsu, H. Gauge theory on noncommutative supersphere from supermatrix model. Phys. Rev. D 2004, 69, 1050033:1–1050033:7. [Google Scholar] [CrossRef]
- Iso, S.; Umetsu, H. Note on gauge theory on fuzzy supersphere. Phys. Rev. D 2004, 69, 105014:1–105014:7. [Google Scholar] [CrossRef]
- Douglas, M.R.; Nekrasov, N.A. Noncommutative field theory. Rev. Mod. Phys. 2001, 73, 977–1029. [Google Scholar] [CrossRef]
- Azuma, T. Matrix models and the gravitational interaction. 2004. arXiv:hep-th/0401120. Avaliable online: http://arxiv.org/abs/hep-th/0401120 (accessed on 18 January 2004).
- Balachandran, A.P.; Kurkcuoglu, S.; Vaidya, S. Lectures on Fuzzy and Fuzzy SUSY Physics; World Scientific Publishers Co. Inc.: Hackensack, NJ, USA, 2007. [Google Scholar]
- Abe, Y.C. Construction of Fuzzy Spaces and Their Applications to Matrix Models. Ph.D. Thesis, City College of the CUNY, New York, NY, USA, December 2005. [Google Scholar]
- Aschieri, P.; Blohmann, C.; Dimitrijevic, M.; Meyer, F.; Schupp, P.; Wess, J. A gravity theory on noncommutative spaces. Class. Quant. Grav. 2005, 22, 3511–3532. [Google Scholar] [CrossRef]
- Calmet, X.; Kobakhidze, A. Noncommutative general relativity. Phys. Rev. D 2005, 72, 045010:1–045010:5. [Google Scholar] [CrossRef]
- Kurkcuoglu, S.; Saemann, C. Drinfeld twist and general relativity with fuzzy spaces. Class. Quant. Grav. 2007, 24, 291–312. [Google Scholar] [CrossRef]
- Taylor, W. Lectures on D-Branes, Gauge Theory and M(atrices); The ICTP Series in Theoretical Physics; Volume 14, Gava, E., Masiero, A., Narain, K.S., Randjbar-Daemi, S., Senjanovic, G., Smirnov, A., Shafi, Q., Eds.; World Scientific Publishers Co. Inc.: Hackensack, NJ, USA, 1998; p. 192. [Google Scholar]
- Azuma, T. Matrix models and the gravitational interaction. Ph.D. Thesis, Kyoto University, Kyoto, Japan, January 2004. [Google Scholar]
- Abe, Y. Construction of fuzzy spaces and their applications to matrix models. 2010. arXiv:1002.4937. Avaliable online: http://arxiv.org/abs/1002.4937 (accessed on 26 February 2010).
- Carow-Watamura, U.; Watamura, S. Chirality and dirac operator on noncommutative sphere. Commun. Math. Phys. 1997, 183, 365–382. [Google Scholar] [CrossRef]
- Schwinger, J. On Angular Momentum. In Quantum Theory of Angular Momentum; Biedenharn, L.C., van Dam, H., Eds.; Academic Press: New York, NY, USA, 1965; pp. 229–279. [Google Scholar]
- Grosse, H.; Klimcik, C.; Presnajder, P. Topologically nontrivial field configurations in noncommutative geometry. Commun. Math. Phys. 1996, 178, 507–526. [Google Scholar] [CrossRef]
- Verstraete, F.; Wolf, M.M.; Pérez-García, D.; Cirac, J.I. Criticality, the area law, and the computational power of projected entangled pair states. Phys. Rev. Lett. 2006, 96, 220601:1–220601:4. [Google Scholar] [CrossRef]
- Pérez-García, D.; Verstraete, F.; Ignacio Cirac, J.; Wolf, M.M. PEPS as unique ground states of local Hamiltonians. Quantum Inf. Comput. 2008, 8, 0650–0663. [Google Scholar]
- Girvin, S.; Arovas, D. Hidden topological order in integer quantum spin chains. Phys. Scr. T 1989, 27, 156–159. [Google Scholar] [CrossRef]
- Hatsugai, Y. String correlation of quantum antiferromagnetic spin chains with S = 1 and 2. J. Phys. Soc. Jpn. 1992, 61, 3856–3860. [Google Scholar] [CrossRef]
- Pais, A.; Rittenberg, V. Semisimple graded Lie algebras. J. Math. Phys. 1975, 16, 2062:1–2062:12. [Google Scholar] [CrossRef]
- Scheunert, M.; Nahm, W.; Rittenberg, V. Irreducible representations of the osp(2,1) and spl(2,1) graded Lie algebra. J. Math.Phys. 1977, 18, 155:1–155:8. [Google Scholar] [CrossRef]
- Marcu, M. The representations of spl(2,1)-an example of representations of basic superalgebras. J. Math. Phys. 1980, 21, 1277:1–1277:7. [Google Scholar] [CrossRef]
- Landi, G.; Marmo, G. Extensions of lie superalgebras and supersymmetric abelian gauge fields. Phys. Lett. B 1987, 193, 61–66. [Google Scholar] [CrossRef]
- Bartocci, C.; Bruzzo, U.; Landi, G. Chern-Simons forms on principal superfiber bundles. J. Math. Phys. 1990, 31, 45:1–45:10. [Google Scholar] [CrossRef]
- Frappat, L.; Sciarrino, A.; Sorba, P. Dictionary on Lie Algebras and Superalgebras; Academic Press: Waltham, MA, USA, 2000. [Google Scholar]
- Borsten, L.; Dahanayake, D.; Duff, M.J.; Rubens, W. Superqubits. Phys. Rev. D 2010, 81, 105023:1–105023:16. [Google Scholar] [CrossRef]
- Majumdar, C.; Ghosh, D. On next-nearest-neighbor interaction in linear chain. II. J. Math. Phys. 1969, 10, 1388–1399. [Google Scholar] [CrossRef]
- Majumdar, C. Antiferromagnetic model with known ground state. J. Phys. C 1970, 3, 911–916. [Google Scholar] [CrossRef]
- Anderson, P. The resonating valence bond state in La2CuO4 and superconductivity. Science 1987, 235, 1196–1198. [Google Scholar] [CrossRef] [PubMed]
- Rokhsar, D.S.; Kivelson, S.A. Superconductivity and the quantum hard-core dimer gas. Phys. Rev. Lett. 1988, 61, 2376–2379. [Google Scholar] [CrossRef] [PubMed]
- Moore, G.; Read, N. Nonabelions in the fractional quantum Hall effect. Nucl. Phys. B 1991, 360, 362–396. [Google Scholar] [CrossRef]
- Schrieffer, J.R. Theory of Superconductivity; Advanced Book Classics; Westview Press: New York, NY, USA, 1999. [Google Scholar]
- Knabe, S. Energy gaps and elementary excitations for certain VBS-quantum antiferromagnets. J. Stat. Phys. 1988, 52, 627–638. [Google Scholar] [CrossRef]
- Arovas, D.P. Two exact excited states for the S = 1 AKLT chain. Phys. Lett. A 1989, 137, 431–433. [Google Scholar] [CrossRef]
- Lieb, E.; Schultz, T.; Mattis, D. Two soluble models of an antiferromagnetic chain. Ann. Phys. (N.Y.) 1961, 16, 407–466. [Google Scholar] [CrossRef]
- Fáth, G.; Sólyom, J. Solitonic excitations in the Haldane phase of a S = 1 chain. J. Phys. Condens. Matter 1993, 5, 8983–8998. [Google Scholar] [CrossRef]
- Bijl, A. The lowest wave function of the symmetrical many particles system. Physica 1940, 7, 869–886. [Google Scholar] [CrossRef]
- Feynman, R.P. Atomic theory of the two-fluid model of liquid helium. Phys. Rev. 1954, 94, 262–277. [Google Scholar] [CrossRef]
- Xu, G.; Aeppli, G.; Bisher, M.E.; Broholm, C.; DiTusa, J.F.; Frost, C.D.; Ito, T.; Oka, K.; Paul, R.L.; Takagi, H.; Treacy, M.M.J. Holes in a quantum spin liquid. Science 2000, 289, 419–422. [Google Scholar] [CrossRef] [PubMed]
- Zhang, S.-C.; Arovas, D.P. Hole motion in an S = 1 chain. Phys. Rev. B 1989, 40, 2708–2711. [Google Scholar] [CrossRef]
- Penc, K.; Shiba, H. Propagating S = 1/2 particles in S = 1 Haldane-gap systems. Phys. Rev. B 1995, 52, R715–R718. [Google Scholar] [CrossRef]
- Kitaev, A.Y. Unpaired Majorana fermions in quantum wires. Phys.-Usp. 2001, 44, 131–136. [Google Scholar] [CrossRef]
- Kennedy, T.; Tasaki, H. Hidden Z2×Z2 symmetry breaking and the Haldane phase in the S = 1/2 quantum spin chain with bond alternation. Phys. Rev. B 1992, 45, 304–307. [Google Scholar] [CrossRef]
- Kennedy, T.; Tasaki, H. Hidden symmetry breaking and the Haldane phase S = 1 quantum spin chains. Commun. Math. Phys. 1992, 147, 431–484. [Google Scholar] [CrossRef]
- Oshikawa, M. Hidden Z2×Z2 symmetry in quantum spin chains with arbitrary integer spin. J. Phys. Condens. Matter 1992, 4, 7469–7488. [Google Scholar] [CrossRef]
- Schollwöck, U.; Jolicœur, T. Haldane gap and hidden order in the S = 2 antiferromagnetic quantum spin chain. Europhys. Lett. 1995, 30, 493–498. [Google Scholar] [CrossRef]
- Schollwöck, U.; Golinelli, O.; Jolicœur, T. S = 2 antiferromagnetic quantum spin chain. Phys. Rev. B 1996, 54, 4038–4051. [Google Scholar] [CrossRef]
- Anfuso, F.; Rosch, A. Fragility of string orders. Phys. Rev. B 2007, 76, 085124:1–085124:6. [Google Scholar] [CrossRef]
- Levin, M.; Wen, X.-G. Detecting topological order in a ground state wave function. Phys. Rev. Lett. 2006, 96, 110405:1–110405:4. [Google Scholar] [CrossRef]
- Kitaev, A.; Preskill, J. Topological entanglement entropy. Phys. Rev. Lett. 2006, 96, 110404:1–110404:4. [Google Scholar] [CrossRef]
- Pérez-García, D.; Wolf, M.M.; Sanz, M.; Verstraete, F.; Cirac, J.I. String order and symmetries in quantum spin lattices. Phys. Rev. Lett. 2008, 100, 167202:1–167202:4. [Google Scholar] [CrossRef]
- Sanz, M.; Wolf, M.M.; Pérez-García, D.; Cirac, J.I. Matrix product states: Symmetries and two-body Hamiltonians. Phys. Rev. A 2009, 79, 042308:1–042308:10. [Google Scholar] [CrossRef]
- Hatsugai, Y.; Kohmoto, M. Numerical study of the hidden antiferromagnetic order in the Haldane phase. Phys. Rev. B 1991, 44, 11789–11794. [Google Scholar] [CrossRef]
- Alcaraz, F.C.; Hatsugai, Y. String correlation functions in the anisotropic spin-1 Heisenberg chain. Phys. Rev. B 1992, 46, 13914–13918. [Google Scholar] [CrossRef]
- Yamamoto, S.; Miyashita, S. Thermodynamic properties of S = 1 antiferromagnetic Heisenberg chains as Haldane systems. Phys. Rev. B 1993, 48, 9528–9538. [Google Scholar] [CrossRef]
- Nishiyama, Y.; Totsuka, K.; Hatano, N.; Suzuki, M. Real-space renormalization-group analysisof the S = 2 antiferromagnetic Heisenberg chain. J. Phys. Soc. Jpn. 1995, 64, 414–422. [Google Scholar] [CrossRef]
- Haegeman, J.; Pérez-García, D.; Cirac, I.; Schuch, N. Order parameter for symmetry-protected phases in one dimension. Phys. Rev. Lett. 2012, 109, 050402:1–050402:5. [Google Scholar] [CrossRef]
- Pollmann, F.; Turner, A.M. Detection of symmetry-protected topological phases in one dimension. Phys. Rev. B 2012, 86, 125441:1–125441:13. [Google Scholar] [CrossRef]
- Zhang, S.-C. Exact microscopic wave function for a topological quantum membrane. Phys. Rev. Lett. 2003, 90, 196801:1–196801:4. [Google Scholar] [CrossRef]
- Tu, H.-H.; Orus, R. Intermediate Haldane phase in spin-2 quantum chains with uniaxial anisotropy. Phys. Rev. B 2011, 84, 140407(R):1–140407(R):4. [Google Scholar] [CrossRef]
- Yu, Y.; Yang, K. Supersymmetry and goldstino-like mode in bose-fermi mixtures. Phys. Rev. Lett. 2008, 100, 090404:1–090404:4. [Google Scholar] [CrossRef]
- Kaplan, D.B.; Sun, S. Spacetime as a topological insulator: Mechanism for the origin of the fermion generations. Phys. Rev. Lett. 2012, 108, 181807:1–181807:4. [Google Scholar] [CrossRef]
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).