Abstract
We describe computer algorithms that produce the complete set of isohedral tilings by n-omino or n-iamond tiles in which the tiles are fundamental domains and the tilings have 3-, 4-, or 6-fold rotational symmetry. The symmetry groups of such tilings are of types p3, p31m, p4, p4g, and p6. There are no isohedral tilings with p3m1, p4m, or p6m symmetry groups that have polyominoes or polyiamonds as fundamental domains. We display the algorithms’ output and give enumeration tables for small values of n. This expands earlier works [1,2] and is a companion to [3].
1. Introduction
Polyominoes and polyiamonds and their tiling properties have been the subject of computational geometry research that investigated which polyominoes can tile the plane isohedrally and which can tile by translations alone [4,5]. In earlier papers [1,2], we gave algorithms to create polyominoes and polyiamonds that were fundamental domains for isohedral tilings having p3, p4, or p6 symmetry groups. In this article, we consider the expanded task of producing polyomino and polyiamond tiles that generate isohedral tilings of types p3, p3m1, p31m, p4, p4m, p4g, p6 or p6m and for which the tiles are fundamental domains of the tiling. Recently an extension of this study was published as a separate paper [3] in which we carried out these investigations for symmetry groups of types pmm, pmg, pgg, and cmm.
The following definitions are noted in [3], and are included here for completeness. A polyomino (or n-omino) is a tile homeomorphic to a disk, made up of n unit squares that are connected at their edges; that is, the intersection of two unit squares in the polyomino is either empty or an edge of both squares. Similarly a polyiamond (or n-iamond) is a tile homeomorphic to a disk, made up of n unit equilateral triangles that are connected at their edges; the intersection of two unit triangles in the polyiamond is either empty or an edge of both triangles.
An isohedral tiling of the plane is a tiling by congruent tiles in which the symmetry group of the tiling acts transitively on the tiles. A fundamental domain (sometimes called a generating region) for an isohedral tiling is a region of least area that generates the whole tiling when acted on by the symmetry group of the tiling. Thus a fundamental domain for an isohedral tiling must not contain two points that are identical under the action of the symmetry group of the tiling. This implies the following fact that is important for our algorithm.
Lemma 1.
In an isohedral tiling in which each tile is a fundamental domain, no tile can contain a rotation center or axis of reflection for the whole tiling except on its boundary.
We note that while an isohedral tiling may have fundamental domains of many different shapes, all have the same area. The simplest fundamental domains have triangle or quadrilateral shapes [6]. Lemma 1 and the definitions of polyomino and polyiamond immediately exclude several symmetry groups from our consideration.
Theorem 1.
There are no p3, p31m, p3m1, p6, or p6m isohedral tilings by polyominoes. There are no p4, p4g, or p4m isohedral tilings by polyiamonds.
Proof.
Isohedral tilings of types p3, p31m, p3m1, p6, or p6m all have 3-fold centers, and by Lemma 1, if the tiles are fundamental domains, these centers must lie on the boundaries of the tiles. But if the tiles are polyominoes, a 120 rotation about such a center cannot map a tile fully onto another tile (since unit squares will not be mapped to unit squares). Thus such a tiling is impossible. Similarly, a 4-fold center is impossible in an isohedral tiling by polyiamonds (since a 90 rotation cannot map unit triangles to unit triangles), so there can be no such tilings of types p4, p4g, or p4m.
In each of the sections that follow, we begin with a fixed lattice of symmetry elements for a symmetry group G (that is, a fixed array of rotation centers, reflection axes and glide-reflection axes for elements of G) and give a backtracking procedure to produce a complete set of polyominoes (or polyiamonds) that are fundamental domains for G. A polyomino or polyiamond tile T is a fundamental domain for a symmetry group G if the action of G on T produces an isohedral tiling and T is a region of minimal area for which G can generate that tiling. G will be contained in (or equal to) the full symmetry group of the tiling.
As we consider symmetries of our isohedral tilings, the following theorem will be useful [3].
Theorem 2.
Let G be one of the 17 two-dimensional symmetry groups and an isohedral tiling generated by G acting on a tile T that is a fundamental domain for G. Let be the full symmetry group of . If G is a proper subgroup of , there is an element of (other than the identity) that leaves T invariant. In this case, a fundamental domain for has area smaller than T.
2. p4
2.1. Creating Polyominoes as Fundamental Domains for p4 Symmetry Groups
We begin with a lattice of unit squares as shown in Figure 1. Our n-omino tiles that are fundamental domains for a p4 group G will be built from these unit squares. By Lemma 1, the 4-fold rotation centers for G must be located on the boundary of the polyomino tiles that are fundamental domains for G. A 4-fold center can only occur at a lattice point that is a “corner” of the polyomino tile, that is, only one unit square of the polyomino contains that point.
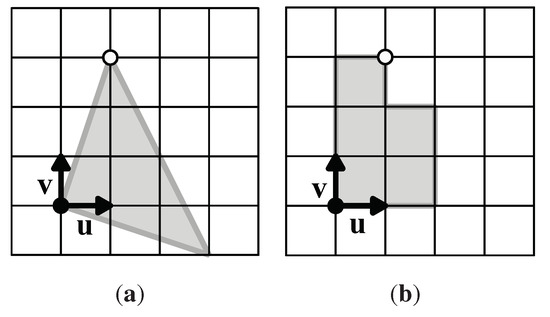
Figure 1.
A lattice of unit squares with black and white 4-fold rotation centers that generate a p4 group G. At left, a simple triangular fundamental domain (shaded) for G; at right, a polyomino fundamental domain (shaded) for G. Here , ; the area of each fundamental domain is 5 square units.
So, first we place a 4-fold rotation center, (a black circle) at a lattice point and call this the origin. We then place orthogonal unit vectors and at the origin (see Figure 1). Next we place a second 4-fold rotation center, the white circle in Figure 1, at , where x and y are nonnegative integers, not both 0. These two choices of 4-fold rotation centers determine a whole p4 lattice of rotation centers; rotations about the two placed black and white centers generate a p4 group G.
The area S of a fundamental domain for this p4 group G is given by [1,2]
taking the area of a unit square as 1. Since we want our n-omino to be a fundamental domain, and S must be an integer. Therefore, x and y must have the same parity, and
where two pairs , namely, and correspond to . All unit squares in the lattice are classified into n equivalence classes by the action of the p4 group G. We denote the equivalence class of a unit square e as .
We construct a set of n-ominoes that are fundamental domains for the p4 group G and a given n by following Procedure 1 below, using these definitions:
- T is a set of unit squares; is a set of unit squares that are edge-adjacent to the squares in T; is a set of n-ominoes.
- When T is the empty set, we define as the set of four squares around the origin (the four unit squares at the lower left in Figure 1.)
- We define , the Boolean function of T, which is true if and a white circle is on the boundary of T. Otherwise is false.
- . This is the set of all unit squares that are edge-adjacent to those in T, but not equivalent to any unit squares in T.
Procedure 1 creates a sequence of pairs of sets , in which is the set of unit squares that can be added to T to create the next set T in the sequence. The sets T are built up, one element at a time, until a set T is achieved for which is true, at which time T is added to the collection . When this takes place, the procedure backtracks to the most recent previous pair for which , and repeats the process.
Procedure 1.
- Fix n (from the list in (2) above). Begin with empty.
- Make T empty. Make . Make . Make .
- For in , if , choose an element e (a unit square) of . Remove e from and save the pair in .
- Increase k by 1. Add e (from step 3) to T to create a new -omino T, and let for the new T. Add the new pair to .
- If and , quit the procedure.
- If is true, an n-omino tile is completed and add T to provided there is no equivalent tile in . We regard two n-ominoes equivalent if conditions (a) and (b) below are satisfied.
- (a)
- The tiles are congruent (including mirror reflection).
- (b)
- When the tiles are superimposed, the positions of m-fold rotational centers on the boundaries of the tiles are the same. If there are several m-fold rotation centers for the same m, they can be permuted appropriately before comparison.
- If , decrease k by 1.
- Go back to step 3.
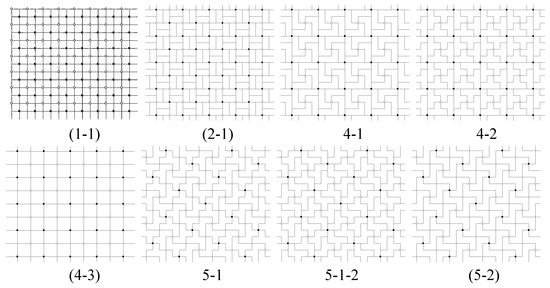
Figure 2 shows the set of inequivalent n-ominoes in for . From each of these n-ominoes we can obtain the associated p4 tiling by using the black and white circles as 4-fold rotation centers. Figure 3 shows the corresponding isohedral tilings produced by n-ominoes in Figure 2 for .
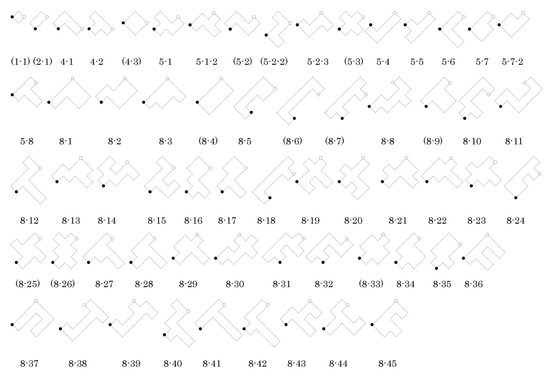
Figure 2.
List of n-ominoes produced by the procedure in Section 2.1 for [2]. The tiles are fundamental domains for the p4 group used to construct them. The labels indicate n followed by the tile number for that n. Parentheses indicate that the tiles produce tilings having more symmetries than the p4 group that generates the tilings.
2.2. Symmetries of Tiles
The list of isohedral tilings corresponding to tiles in Figure 2 includes some tilings having symmetry group larger than the p4 group G generated by 4-fold rotations about the black and white rotation centers. By Theorem 2, in every case where this occurs, the n-omino that generates the tiling must have reflection and/or rotation symmetry.
We outline below how to identify polyominoes whose corresponding isohedral tilings have symmetry groups larger than the group G that generated the tiling. Such tiles in Figure 2 and their tilings in Figure 3 are identified by parentheses around their labels.
- Select a polyomino that has rotation and/or reflection symmetry, and examine its tiling generated by G.
- Look at all vertices and centers of unit squares in a polyomino in except for the original 4-fold centers we have chosen (black and white centers), and determine whether or not is invariant under a 4-fold rotation about such a point. If so, then it is a new 4-fold center for , and this symmetry is not in G. For example, in Figure 3, tilings (5-2) and (5-2-2), while generated differently, are the same tiling and have 4-fold centers at every vertex where 4 tiles meet. Tiling (5-3) has 4-fold rotation centers at the centers of the “cross” tiles and at every vertex where 4 tiles meet. These tilings have full symmetry groups of type p4, with G as a proper subgroup.
- Other new symmetry elements of can be sought by using Chart 2 in [6]. If the line joining the black and white 4-fold centers we placed is an axis of mirror reflection for , then is type p4m. For example, in Figure 3, tilings (1-1) and (4-3) are type p4m. If this line is not a mirror reflection axis, but the line connecting two adjacent (nearest) 2-fold centers for is a mirror reflection axis for , then is type p4g. For example, in Figure 3, tiling (2-1) is type p4g.
3. p4g
3.1. Creating Polyominoes as Fundamental Domains for p4g Symmetry Groups
A p4g symmetry group contains 4-fold rotations, reflections, and glide-reflections; the subgroup generated by its 4-fold rotations is type p4. Thus we begin as in Section 2 with a lattice of unit squares and place a 4-fold rotation center (a black circle) at a lattice point and call this the origin. Orthogonal unit vectors and are then placed at the origin (see Figure 4(a)). Next, we place a reflection axis nearest to the origin; this must lie along the edges of unit squares according to Lemma 1, so we place it at or , where x is a positive integer. The placement of the origin and choice of x determine the whole p4g lattice of rotation centers, reflection axes and glide-reflection axes since the p4g group G is generated by 4-fold rotations about the origin and reflections in the placed axis (see Figure 4(b)).
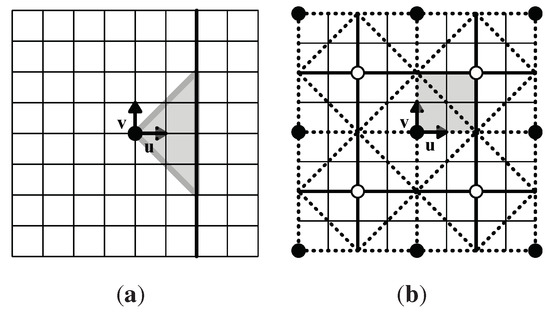
Figure 4.
(a) A lattice of unit squares with a 4-fold rotation center (black circle, the origin) and reflection axis (thick line) at that generate a p4g symmetry group G. The shaded triangle is a fundamental domain for G; (b) The lattice of all symmetry elements for G: 4-fold centers are black circles, 2-fold centers are white circles, reflection axes are thick solid lines, glide-reflection axes are dotted lines. The shaded square region is a polyomino fundamental domain for G. Here ; the area of each fundamental domain for G is 4.
The area S of a fundamental domain for the group G is given by
where the area of a unit square is 1. Since we want our n-omino to be a fundamental domain, . Therefore,
Action by the group G partitions the unit squares into n equivalence classes; as before, we denote the equivalence class of a unit square e as . We construct the set of n-ominoes that are fundamental domains for G using Procedure 1 in Section 2, with n chosen from the list in (4) and the additional constraint that unit squares in the set T must be in the region bounded by the mirror reflection axes nearest to the origin.
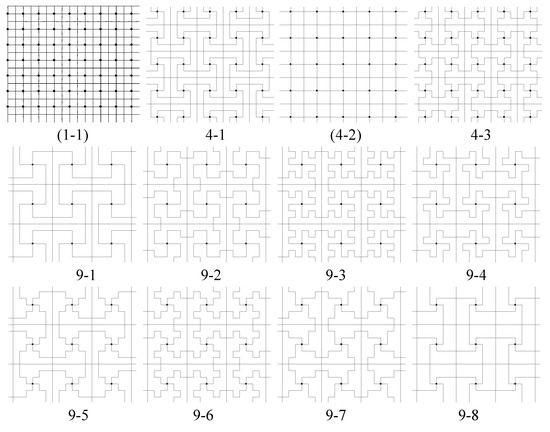
Figure 5 shows the set of inequivalent tiles in for . We can obtain the associated p4g tilings by using the origin as a 4-fold rotation center to fill out the square bounded by the reflection axes nearest the origin, then reflecting this square in its edges. Figure 6 shows the corresponding isohedral tilings produced by polyominoes in Figure 5.
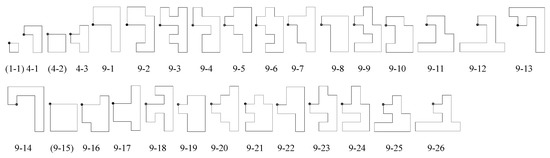
Figure 5.
List of n-ominoes produced as described in Section 3.1 for ; these are fundamental domains for the p4g group used to construct them. The labels indicate n followed by the tile number for that n. Parentheses indicate that the tiles produce tilings having more symmetries than the p4g group that generates the tilings.
3.2. Symmetries of Tiles
The only tilings in Figure 6 having symmetry group larger than the p4g group G that generated them are tilings with square polyomino tiles. In fact, this is always true.
Theorem 3.
Every tiling by a polyomino T produced by our algorithm in Section 3.1 has as its full symmetry group the p4g group that generated it and T is a fundamental domain for the tiling, except in the case when the shape of T is square. In that case, the tiling has symmetry group p4m and T is not a fundamental domain.
Proof.
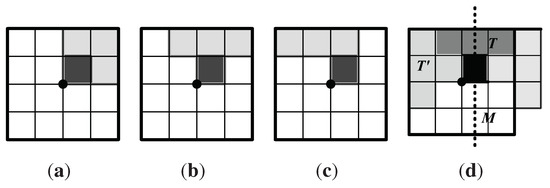
Let be the full symmetry group of a tiling produced by a p4g group G acting on a polyomino T that is a fundamental domain for G, constructed as described in Section 3.1. If G is a proper subgroup of , then by Theorem 2, there is a 2-fold or 4-fold rotation or reflection symmetry g in that is also a symmetry of T. By its construction, one corner of T is a 4-fold center for G at the origin; without loss of generality, we may assume that T contains the unit square shown in black in Figure 7.

Figure 7.
(a)–(c) The derivation of polyomino fundamental domains T for a p4g group G by removing unit squares from and adding equivalent unit squares to the original square polyomino fundamental domain in (a). Here ; (d) The polyomino T in (b) has reflection symmetry with mirror axis M, but this is not a symmetry of the tiling having T as fundamental domain, since , the image of T by a rotation about the origin, is mapped by a reflection in M to a tile that crosses a reflection axis for G.
T can also be obtained by beginning with an square polyomino fundamental domain for G as in Figure 7(a), then removing unit squares (except for the black unit square) and adding other unit squares equivalent (by a rotation of or about the origin) to these, always keeping the new tile homeomorphic to a disc. Figure 7(b,c) illustrates this for . Unit squares of T that abut one reflection axis for G are equivalent to unit squares along an adjacent reflection axis, and so T has on its boundary at least x unit squares in a straight row. Since g maps T onto itself, g maps the longest straight edge on the boundary of T to a congruent edge on the boundary of T.
If g is a rotation, the image of the longest edge of T is distinct from that edge. Since T cannot have two different straight edges on its boundary formed by more than x unit squares, the only possibility is that T is an square polyomino.
If g is a reflection, and T is not an square polyomino, then g must map the longest straight edge on the boundary of T onto itself. The reflection axis M for g is the perpendicular bisector of the edge of T that it leaves fixed. Since the length of this edge is greater than x and less than , M cannot have distance from the origin, and M cannot go through the origin. Let and be the images of T under and rotations about the origin. Then the reflections of and in M are not tiles in —these images partially overlap and and one of these images crosses a reflection axis of G. A simple example is illustrated in Figure 7(d). Thus the only possibility for g to be a reflection symmetry for T is that T be an square polyomino.
4. p4m
The rotation and reflection symmetry elements of a p4m group are shown in Figure 8. Black circles are 4-fold centers, white circles are 2-fold centers, and solid lines are mirror reflection axes. The shaded region is a fundamental domain for the p4m group. A polyomino that is a fundamental domain for the tiling must have its edges on the reflection axes, by Lemma 1. But this is clearly impossible.
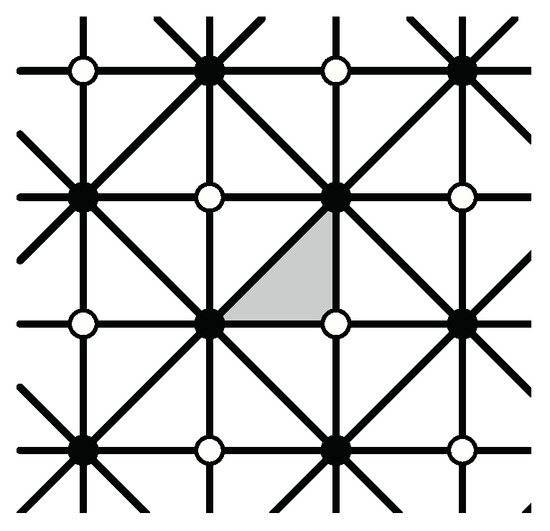
Figure 8.
The rotation and reflection symmetry elements of a p4m group G. Black circles are 4-fold centers, white circles are 2-fold centers, and lines are reflection axes. (Glide-reflection axes are not shown.) The shaded area is a fundamental domain for G.
Theorem 4.
There are no p4m isohedral tilings having polyominoes as fundamental domains.
5. p3
5.1. Creating Polyiamonds as Fundamental Domains for p3 Symmetry Groups
To build our n-iamond tiles that will be fundamental domains for a p3 isohedral tiling, we begin with a lattice of unit equilateral triangles. By Lemma 1, the 3-fold rotation centers for a p3 symmetry group must be located on the boundary of the tile, and in addition, these centers must be located at a lattice point that is a “corner” of the tile at which no more than two unit triangles meet. So first we place a 3-fold rotation center, a black circle, at a lattice point and call this the origin, then place vectors and at the origin along edges of a unit triangle. Next we place a second 3-fold rotation center, a white circle, at , where x and y are nonnegative integers, not both zero. See Figure 9(a). These two choices of 3-fold rotation centers determine the whole p3 lattice of rotation centers; 3-fold rotations about the black and white centers generate the whole p3 symmetry group.
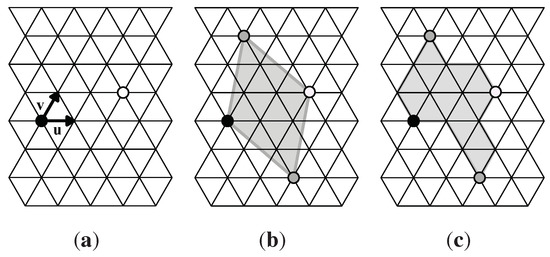
Figure 9.
(a) A lattice of unit triangles with two 3-fold rotation centers that generate a p3 group G; (b) A simple rhombic fundamental domain (shaded) for G; (c) A polyiamond fundamental domain (shaded) for G. Here , ; the area of each fundamental domain is 14 triangular units.
Figure 9(b,c) shows two fundamental domains for the p3 group G generated by the black and white 3-fold centers: a simple rhombic shape, and a polyiamond tile. Note that both fundamental domains contain the black and white 3-fold centers. The other two circles (shown in gray) that are on the boundaries of these fundamental domains are also 3-fold centers for G.
The area S of a fundamental domain for G is given by [2]
taking the area of a unit triangle as 1. Since we want our n-iamond to be a fundamental domain, . Therefore,
where two pairs , namely, and correspond to .
All unit triangles are classified into n equivalence classes by the action of G, and we denote the equivalence class of a unit triangle e as .
We construct a set of n-iamonds that are fundamental domains for G by modifying Procedure 1 in Section 2, choosing n from the list in (6), and replacing definitions in Section 2 with these:
- T is a set of unit triangles; is a set of unit triangles that are edge-adjacent to the triangles in T; is a set of n-iamonds.
- When T is the empty set, we define as the set of six triangles around the origin in Figure 9(a).
- We define , the Boolean function of T, which is true if and a white circle is on the boundary of T . Otherwise is false.
- . This is the set of all unit triangles that are edge-adjacent to those in T, but not equivalent to any unit triangles in T.
The procedure creates a sequence of pairs of sets , in which is the set of unit triangles that can be added to T to create the next set T in the sequence.
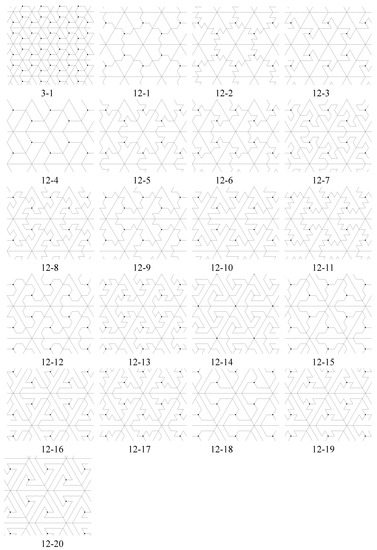
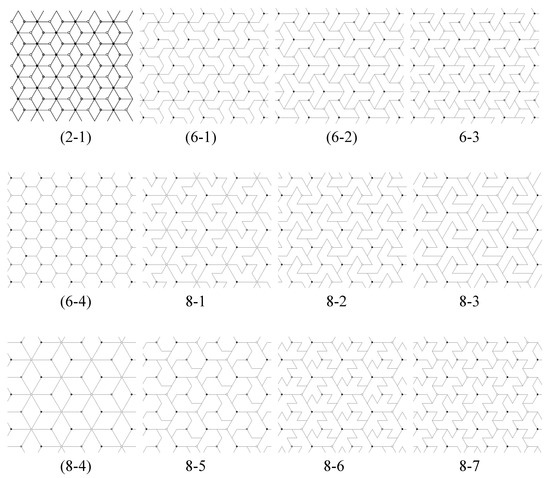
Figure 10 shows the set of inequivalent n-iamonds in for . From each of these we can obtain the associated p3 tiling by using the black and white circles as 3-fold rotation centers. Figure 11 shows the corresponding isohedral tilings produced by n-iamonds in Figure 10.
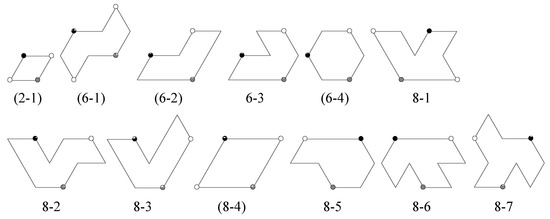
Figure 10.
List of n-iamonds produced as described in Section 5.1 for [2]. The tiles are fundamental domains for the p3 group used to construct them. The labels indicate n followed by the tile number for that n. Parentheses indicate that the tiles produce tilings having more symmetries than the p3 group that generates the tilings.
We note that the discussion in this section amplifies that in Section 3 in [2], and obtains the same list of polyomino fundamental domains for isohedral tilings with p3 symmetry. However, here we analyze the symmetries of those tilings, and lay the groundwork for our investigation in Section 5.1 of tilings by polyiamonds that are fundamental domains for symmetry groups of types p31m and p3m1. In our older article [1], we constructed p3 isohedral tilings by polyiamonds that were built up from units that were rhombuses, and so the list in [1] of such p3 tilings is a proper subset of our present results.
5.2. Symmetries of Tiles
The list of isohedral tilings in Figure 11 includes some tilings having symmetry group larger than the p3 group G generated by 3-fold rotations about the black and white rotation centers. By Theorem 2, when this occurs, the n-iamond that generates the tiling must have reflection and/or 3-fold rotation symmetry. The full symmetry group of the tiling could be of any of these types: p3, p3m1, p31m, p6, or p6m. The tilings in Figure 11 that have additional symmetries, and the n-iamonds in Figure 10 that generate them are indicated by parentheses in their labels. We outline below how to identify these polyiamonds.
- Select a polyiamond T that has rotation and/or reflection symmetry, and examine its tiling generated by G.
- Look at all vertices and centers of unit triangles in T except for those centers of rotation in G (black, white and gray centers), and determine whether or not any can be new 3-fold centers for . If a new 3-fold center is found, then the full symmetry group of contains G as a proper subgroup and T is not a fundamental domain for . If a new 3-fold center is a 6-fold center, is type p6m if there is a reflection axis joining it to any nearest 3-fold center; otherwise, is type p6. Tiling (6-4) in Figure 11 is type p6m, and has a 6-fold center at the center of the hexagonal 6-iamond. If there are new 3-fold centers but none are 6-fold centers, then is type p3.
- If the tiling contains only 3-fold centers for G, we seek new symmetry elements by using Chart 2 in [6].
- If some 3-fold center for G is a 6-fold center, the tiling will have p6m symmetry if the line joining a 6-fold center to a nearest 3-fold center is a reflection axis for , otherwise it will have p6 symmetry. In Figure 11, tilings (2-1) and (8-4) have p6m symmetry, and tiling (6-1) has p6 symmetry.
6. p31m
6.1. Creating Polyiamonds as Fundamental Domains for p31m Symmetry Groups
We begin with a lattice of unit triangles as in Section 5.1, since a p31m symmetry group contains 3-fold rotations, reflections, and glide-reflections; the subgroup generated by its 3-fold rotations is type p3. To build an n-iamond tile that is a fundamental domain for a p31m isohedral tiling, we first place a 3-fold rotation center, a black circle, at a lattice point and call this the origin. Then we place vectors and at the origin along edges of a unit triangle (see Figure 12(a)).
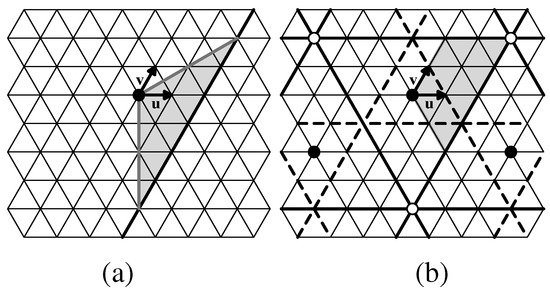
Figure 12.
(a) A lattice of unit triangles with a 3-fold rotation center at the origin (black circle) and reflection axis (solid line); together these generate a p31m group G; (b) Repeated 3-fold rotations about the origin and reflections about the axis in (a) generate the whole lattice of symmetry elements for G, which includes reflection axes (solid heavy lines), 3-fold rotation centers (black and white circles), and glide-reflection axes (dashed lines). A shaded triangular fundamental domain for G is shown in (a), and a shaded trapezoidal polyiamond fundamental domain for G is shown in (b). Here ; the area of each fundamental domain is 12 triangular units.
Next, we place a reflection axis that is nearest the origin; this must lie along the edges of unit triangles according to Lemma 1 (Figure 12(a)). Applying rotations to this reflection axis produces three reflection axes that intersect at the points , , and , where x is a positive integer; their intersections are equivalent 3-fold rotation centers (shown as a white circles in Figure 12(b)). The placement of the origin and choice of x determine the whole p31m lattice of rotation centers, reflection axes and glide-reflection axes since the p31m group G is generated by 3-fold rotations about the origin and reflections in one of the three reflection axes.
The area S of a fundamental domain for the tiling is one-third the area enclosed by the three reflection axes closest to the origin, which is
where the area of a unit triangle is 1. Since we want our n-iamond to be a fundamental domain, . Therefore,
The action of G classifies all unit triangles into n equivalence classes and we denote the equivalence class of a unit triangle e as . We construct a set of n-iamonds that are fundamental domains for G as described in Section 5.1, choosing n from the list in (8) and having the additional constraint that the unit triangles in the set T must be in the region bounded by the mirror reflection axes in Figure 12(b).
Figure 13 shows the set of inequivalent n-iamonds in for . Figure 14 shows the corresponding p31m tilings obtained by performing a 3-fold rotation about the origin (black circle) to fill out the triangle bounded by reflection axes (Figure 12(b)), then reflecting this triangle in its edges.
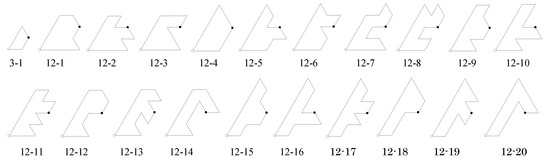
Figure 13.
List of n-iamonds produced as described in Section 6.1 for . The tiles are fundamental domains for the p31m group used to construct them. The labels indicate n followed by the tile number for that n.
6.2. Symmetries of Tiles
Theorem 5.
Every isohedral tiling by a polyiamond T produced by our algorithm in Section 6.1 has as its symmetry group the p31m group that generated it and T is a fundamental domain for the tiling.
Proof.
Our proof is analogous to that for Theorem 3. Let be the full symmetry group of a tiling produced by a p31m group G acting on a polyiamond T that is a fundamental domain for G, as described in Section 6.1. If G is a proper subgroup of , then by Theorem 2, there is a reflection symmetry or 3-fold rotation symmetry in that is also a symmetry of T. T can be obtained from the shaded fundamental domain shown in Figure 12(b) by removing unit triangles and adding unit triangles equivalent to these (by a rotation about the origin), always keeping the new tile homeomorphic to a disc and bounded by reflection axes as in Figure 12(b). This process shows that one edge of T that lies on a reflection axis will have length at least , and at most one other edge of T (lying on an adjacent reflection axis of G) will have this same length (see Figure 13). From this, it follows that T cannot have 3-fold rotation symmetry.
Suppose that T has reflection symmetry. If the two straight edges of T that lie on reflection axes for G have the same length, then the reflection that leaves T fixed must map these edges to each other. But this reflection cannot leave T invariant, since the other edges of T are related by a 3-fold rotation about the origin (see, for example, tiles 12-1, 12-2, 12-3 in Figure 13). If the two straight edges of T that lie on reflection axes for G have different lengths, then a reflection that fixes T must leave the longer edge fixed, and so is perpendicular to that edge. This can only happen if T is the rhombic fundamental domain in Figure 12(b), and in this case, the reflection symmetry for T is not a symmetry for the tiling (see tiling 12-4 in Figure 14).
7. p3m1
The lattice of reflection axes and 3-fold rotation centers of a p3m1 symmetry group is shown in Figure 15; black, white, and grey circles denote three inequivalent 3-fold rotation centers. Here, unlike the p31m case, all 3-fold centers lie on reflection axes. The shaded region bounded by reflection axes is a fundamental domain for the p3m1 group that generates the tiling by reflections in those axes. By Lemma 1, this is the only polyiamond tile possible having the area of a fundamental domain. But the full symmetry group of this tiling is type p6m, which has a fundamental domain with area 1/6 that of the shaded tile. Thus,
Theorem 6.
There are no p3m1 isohedral tilings having polyiamonds as fundamental domains.
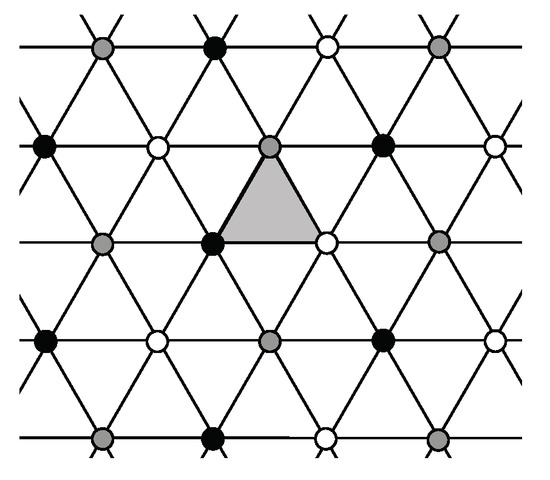
Figure 15.
The lattice of reflection axes and 3-fold rotation centers of a p3m1 group (glide-reflection axes are not shown). Three inequivalent 3-fold centers are black, grey, and white circles. Lines are reflection axes. The shaded region is a fundamental domain for the p3m1 group generated by reflections in the axes surrounding the region.
We note that if the shaded region in Figure 15 is decorated with an asymmetric motif then there are n-iamonds (where , k a positive integer) having the shape of an equilateral triangle, for which the decorated triangle is a fundamental domain for a p3m1 isohedral tiling.
8. p6
8.1. Creating Polyiamonds as Fundamental Domains for p6 Symmetry Groups
A p6 symmetry group G contains 6-fold, 3-fold, and 2-fold rotations; the subgroup generated by its 3-fold rotations is type p3. Thus we begin as in Section 5.1, with a lattice of equilateral triangles, to build n-iamond tiles that are fundamental domains for G. By Lemma 1, 6-fold and 3-fold centers for G are located on the boundaries of tiles, and we have seen that 3-fold centers can only occur at lattice points that are “corners” of the tiles where at most two unit triangles meet. Clearly 6-fold centers can only occur at lattice points that are “corners” where just one unit triangle in the tile meets that point.
So first we place a 6-fold rotation center, a black circle, at a lattice point and call this the origin, then place vectors and at the origin, along edges of a unit triangle. Next we place a 3-fold rotation center, a white circle, at , where x and y are nonnegative integers, not both 0. See Figure 16(a). These choices of 6-fold and 3-fold rotation centers determine the whole p6 lattice of rotation centers; rotations about the two chosen black and white centers generate G.
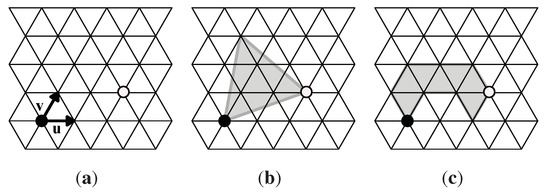
Figure 16.
(a) A lattice of unit triangles with a black 6-fold rotation center and white 3-fold rotation center that generate a p6 group G; (b) A triangular fundamental domain (shaded) for G; (c) A polyiamond fundamental domain (shaded) for G. Here , ; the area of each fundamental domain is 7 triangular units.
Figure 16(b) shows a simple triangular fundamental domain (shaded) for G, and Figure 16(c) shows a polyiamond fundamental domain (shaded) for G. The area of a fundamental domain for this p6 group is given by [2]
taking the area of a unit triangle as 1. Since we want our n-iamond to be a fundamental domain, . Therefore,
where two pairs of , namely, and correspond to .
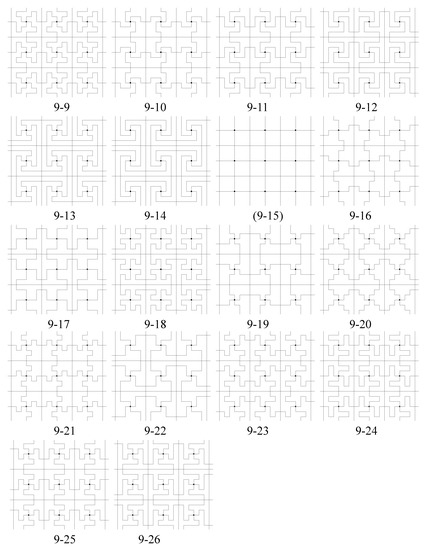
The action of the p6 group classifies all unit triangles into n equivalence classes and we denote the equivalence class of a unit triangle e as . We construct a set of n-iamonds that are fundamental domains for the given p6 group as in Section 5.1, with n chosen from the list in (10). Figure 17 shows the set of inequivalent n-iamonds in for . From each of these n-iamonds we obtain the associated p6 tiling by using the black circles as 6-fold rotation centers and white circles as 3-fold rotation centers. Figure 18 shows the corresponding isohedral tilings produced by n-iamonds in Figure 17.
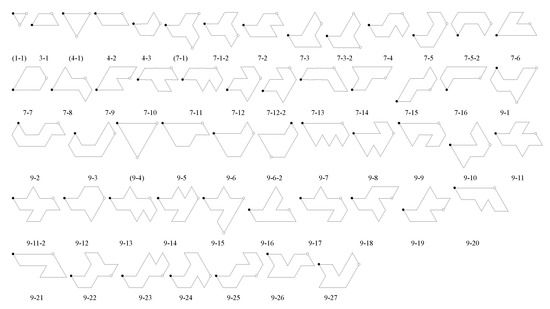
Figure 17.
List of n-iamonds produced as described in Section 8.1 for [2]. The tiles are fundamental domains for the p6 group used to construct them. The labels indicate n followed by the tile number for that n. Parentheses indicate that the tiles produce tilings having more symmetries than the p6 group that generates the tilings.
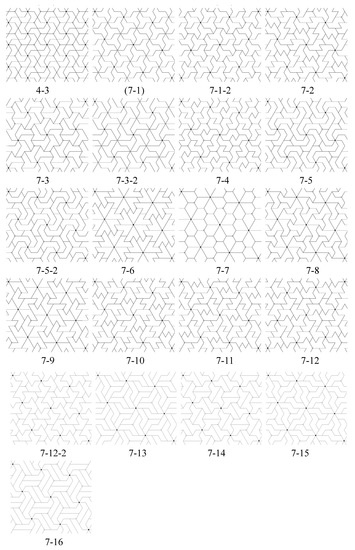
We note that the discussion in this section amplifies that in Section 3 in [2], and obtains the same list of polyomino fundamental domains for isohedral tilings with p6 symmetry. However, in our next Section 8.2 we analyze the symmetries of those tilings. In our older article [1], we presented a list of polyiamond tiles for p6 isohedral tilings constructed from rhombic units. Every tile in that list can be obtained by performing a half-turn about the 2-fold center on the boundary of a tile in our list here in Figure 17.
8.2. Symmetries of Tiles
Some tilings in Figure 18 have symmetries in addition to those in the p6 group G that generated them. These tilings and their polyiamond tiles in Figure 17 are indicated by parentheses in their labels. We can identify these polyiamonds as follows.
- Select a polyiamond that has rotation and/or reflection symmetry, and examine its tiling generated by G.
- If the line connecting adjacent 6-fold and 3-fold centers (black to white) is a reflection axis for , the tiling has p6m symmetry. Tilings (1-1) and (4-1) in Figure 18 have p6m symmetry. These tilings also have 3-fold centers for the tiling at the centers of the polyiamond tiles.
- Otherwise, look at all vertices and centers of unit triangles in a polyiamond in except for those black and white rotation centers in the p6 group we have generated and determine whether or not they can be new 3-fold centers for . If new 3-fold centers are found, the full symmetry group of the tiling contains G as a proper subgroup. Tiling (7-1) in Figure 18 has a larger p6 symmetry group than G since there are 3-fold rotation centers for at the centers of the rotor-like polyiamond tiles. Note that the same tiles appear in tiling 7-1-2, but in this tiling, the centers of the tiles are not 3-fold centers of rotation for .
9. p6m
Figure 19 shows the rotation and reflection symmetry elements of a p6m group. Black, white, and gray circles are the 6-, 3-, and 2-fold centers, respectively. Solid lines are reflection axes. The shaded - - -triangle is a fundamental domain. A polyiamond that is a fundamental domain for the tiling must have its edges on the reflection axes, by Lemma 1. But this is clearly impossible. Thus,
Theorem 7.
There are no p6m isohedral tilings having polyiamonds as fundamental domains.
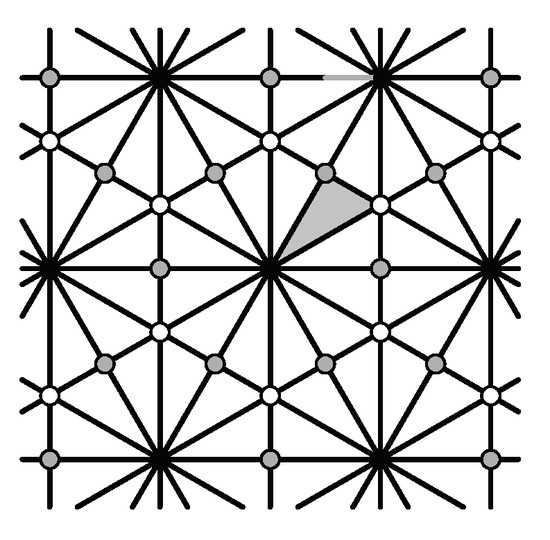
Figure 19.
The lattice of rotation and reflection symmetry elements for a p6m group G. Solid lines are reflection axes, black, white, and gray circles are 6-, 3-, and 2-fold centers respectively. (Glide-reflection axes are not shown.) The shaded region is a fundamental domain for G.
10. Enumeration Tables
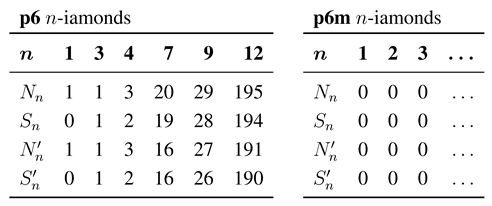
Table 1, Table 2 and Table 3 give the number of tiles and isohedral tilings that we have generated in Section 2 through Section 9. is the number of inequivalent tiles T in for a given symmetry group G of type p3, p31m, p3m1, p4, p4m, p4g, p6, or p6m that generate an isohedral tiling having the n-omino or n-iamond tiles as fundamental domain. Tiles are equivalent only if they generate the same tiling by the action of the group G when each tile is marked with an asymmetric motif. For example, the tiles 5-2 and 5-2-2 in Figure 3 are congruent and their corresponding tilings are the same, but the placement of their 4-fold centers is different, and so if the tiles are marked with an asymmetric motif, they generate different isohedral tilings.

Table 1.
The number of isohedral tilings of types p3, p31m and p3m1 having n-ominoes or n-iamonds as fundamental domains.

Table 2.
The number of isohedral tilings of types p4, p4g and p4m having n-ominoes or n-iamonds as fundamental domains.

Table 3.
The number of isohedral tilings of types p6 and p6m having n-ominoes or n-iamonds as fundamental domains.
Marking each tile with an asymmetric motif also guarantees that the group that generates the tiling is the full symmetry group of the tiling. So is also the number of isohedral tilings having G as full symmetry group and having n-omino or n-iamond tiles as fundamental domain, when each tile is marked with an asymmetric motif.
is the corresponding number of the tilings when the asymmetric motif of each tile is removed. That is, is the number of isohedral tilings having full symmetry group G and having (unmarked) n-ominoes or n-iamonds as fundamental domains. In our figures that depict the isohedral tilings for small values of n, these tilings do not have parentheses around their labels. These are the most important “counting” results in this article. is the number of non-congruent tiles in the tilings, counted by ignoring rotation centers attached to tiles; similarly, is the number of non-congruent tiles in the tilings.
For example, for symmetry group p6 and , there are 20 tiles in Figure 17, with corresponding isohedral tilings in Figure 18, so . Since tiling 7-1 of Figure 18 has parentheses around its label, . From Figure 17, we can see that four pairs of tiles are congruent: 7-1 and 7-1-2; 7-3 and 7-3-2; 7-5 and 7-5-2; 7-12 and 7-12-2. Thus . Among the 19 tiles counted for , there are also 16 non-congruent tiles, so .
11. Summary
We have described computer algorithms that can enumerate and display isohedral tilings by n-omino or n-iamond tiles for given n in which the tiles are fundamental domains and the tilings have 3-, 4-, or 6-fold rotational symmetry. Their symmetry groups are of types p3, p31m, p4, p4g, and p6. We have shown that there are no isohedral tilings with symmetry groups of types p3m1, p4m, or p6m that have polyominoes or polyiamonds as fundamental domains. For symmetry groups of types p3, p31m, p4, p4g, and p6 we used the backtracking Procedure 1 to obtain a set of n-omino or n-iamond tiles where each tile produced one isohedral tiling, generated by a given symmetry group G of one of these five types. We can denote as the set for that symmetry group G and the corresponding set of isohedral tilings.
We investigated the symmetries of tilings in the set and noted those tilings that satisfy the following two conditions: (1) the full symmetry group of the tiling is G; and (2) the tiles are fundamental domains for G. We denote the subset of that satisfies (1) and (2) as and the corresponding set of tiles as . (For small values of n, these tiles and their tilings were displayed with labels without parentheses.) The enumeration of is the main counting result of this article. Although the n-omino or n-iamond tiles produced by our algorithm are not always fundamental domains for the isohedral tilings they generate, if we mark these tiles with an asymmetric motif, then the set is the set of all isohedral tilings with symmetry group G in which the corresponding tiles in are fundamental domains. The set can then also include a marked fundamental domain for a p3m1 symmetry group. In Table 1, Table 2 and Table 3 of Section 10, we used the notation and .
Acknowledgement
The authors thank the referees for their helpful comments on an earlier draft of this article. This research has been supported by Grand-in-Aid for Scientific Research 20540127 JSPS.
References
- Fukuda, H.; Mutoh, N.; Nakamura, G.; Schattschneider, D. A method to generate polyominoes and polyiamonds for tilings with rotational symmetry. Graphs Comb. 2007, 23, 259–267. [Google Scholar] [CrossRef]
- Fukuda, H.; Mutoh, N.; Nakamura, G.; Schattschneider, D. Enumeration of Polyominoes, Polyiamonds and Polyhexes for Isohedral Tilings with Rotational Symmetry. In Computational Geometry and Graph Theory; Springer: Berlin/Heidelberg, Germany, 2008; Volume 4535, pp. 68–78. [Google Scholar]
- Fukuda, H.; Kanomata, C.; Mutoh, N.; Nakamura, G.; Schattschneider, D. Polyominoes and polyiamonds as fundamental domains for isohedral tilings of crystal class D2. Symmetry 2011, 3, 325–364. [Google Scholar] [CrossRef]
- Rhoads, G.C. Tilings by polyomoinoes, polyhexes, and polyiamonds. J. Comput. Appl. Math. 2005, 174, 329–353. [Google Scholar] [CrossRef]
- Keating, K.; Vince, A. Isohedral polyomino tiling of the plane. Discret. Comput. Geom. 1999, 21, 615–630. [Google Scholar] [CrossRef]
- Schattschneider, D. The plane symmetry groups: Their recognition and notation. Am. Math. Mon. 1978, 85, 439–450. [Google Scholar] [CrossRef]
© 2011 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/.)