An Application of the Extended Global SO(3) × SO(3) × U(1) Symmetry of the Hubbard Model on a Square Lattice: The Spinon, η-Spinon, and c Fermion Description

Abstract

In this paper we review recent results on the preliminary applications of the new-found extended global $SO(3)\times SO(3)\times U(1)$ symmetry of the Hubbard model on a bipartite lattice. Our results refer to the particular case of the bipartite square lattice. Specifically, we review a general description for such a model with nearest-neighbor transfer integral t and on-site repulsion U on a square lattice with $N_a^2\gg 1$ sites consistent with its extended global symmetry. It refers to three types of elementary objects whose occupancy configurations generate the state representations of the model extended global symmetry. Such objects emerge from a suitable electron-rotated-electron unitary transformation. An application to the spin spectrum of the parent compound La${}_2$CuO${}_4$ is shortly reviewed.

1. Introduction

The Hubbard model on a bipartite lattice is the simplest realistic toy model for description of the electronic correlation effects in general many-electron problems with short-range interaction on such a lattice. The model involves two effective parameters: the in-plane nearest-neighbor transfer integral t and the effective on-site repulsion U. Despite that it is among the mostly studied models in condensed matter and ultra-cold atom physics, except for the one-dimensional (1D) bipartite lattice [1,2,3] there is no exact solution and few controlled approximations exist for finite $U/4t$ values.

An exact result for the Hubbard model on any bipartite lattice is that in addition to the spin $SU(2)$ symmetry it has a second global $SU(2)$ symmetry [4], called by some authors and in this paper $\eta$-spin symmetry [5]. A trivial result is that at vanishing onsite interaction $U=0$ the global symmetry of the Hubbard model on a bipartite lattice at vanishing chemical potential and magnetic field is $O(4)=SO(4)\times Z_2$. Here the factor $Z_2$ refers to the particle-hole transformation on a single spin under which the model Hamiltonian is not invariant for $U\ne 0$ and $SO(4)=[SU(2)\times SU(2)]/Z_2$ contains the two $SU(2)$ symmetries. Yang and Zhang considered the most natural possibility that the $SO(4)$ symmetry inherited from the $U=0$ Hamiltonian $O(4)=SO(4)\times Z_2$ symmetry was the model global symmetry for $U\ne 0$ [5].

However, a recent study of the problem by the authors and collaborator reported in Reference [6] reveals an exact extra hidden global $U(1)$ symmetry emerging for $U\ne 0$ in addition to $SO(4)$. It is related to the $U\ne 0$ local $SU(2)\times SU(2)\times U(1)$ gauge symmetry of the Hubbard model on a bipartite lattice with vanishing transfer integral [7]. Such a local $SU(2)\times SU(2)\times U(1)$ gauge symmetry becomes for finite U and t a group of permissible unitary transformations. It is such that the corresponding local $U(1)$ canonical transformation is not the ordinary $U(1)$ gauge subgroup of electromagnetism. Instead it is a “nonlinear" transformation [7].

Consistently, for $U\ne 0$ the related new found global symmetry of the model on any bipartite lattice is larger than $SO(4)$ and given by $[SU(2)\times SU(2)\times U(1)]/Z_2^2=[SO(4)\times U(1)]/Z_2=SO(3)\times SO(3)\times U(1)$. The factor $1/Z_2$ (and $1/Z_2^2$) in $SO(4)=[SU(2)\times SU(2)]/Z_2$ (and in $[SU(2)\times SU(2)\times U(1)]/Z_2^2$) imposes that $[S_{\eta }+S_s]$ is an integer number (and both $[S_s+S_c]$ and $[S_{\eta }+S_c]$ are integer numbers). Here $S_{\eta }$, $S_s$, and $S_c$ are the $\eta$-spin, the spin, and one-half the eigenvalue $2S_c$ of the generator of the new global $U(1)$ symmetry, respectively. The latter is found in Reference [6] to be the number of rotated-electron singly occupied sites. This refers to any of the infinite electron-rotated-electron unitary transformations of Reference [8], such that rotated-electron single and double occupancy are good quantum numbers for $U/4t\ne 0$. $2S_c$ is then the number of rotated-electron singly occupied sites. Within the present notation, $S_{\eta }^{x_3}=-[N_a^D-N]/2$ and $S_s^{x_3}=-[N_{\uparrow }-N_{\downarrow }]/2$ are the $\eta$-spin projection and spin projection, respectively, and $N_a^D\gg 1$ denotes the number of lattice sites. For the bipartite 1D and square lattices considered in this paper the labeling index D in $N_a^D\equiv {[N_a]}^D$ reads $D=1$ and $D=2$, accounting for the $N_a\gg 1$ and $N_a^2=N_a\times N_a\gg 1$ lattice sites, respectively. The square and 1D lattices have spacing a and length edge and chain length $L=N_{a}a$, respectively.

An important point is that although addition of chemical-potential and magnetic-field operator terms to the Hubbard model on a bipartite lattice Hamiltonian lowers its symmetry, such terms commute with it. Therefore, the global symmetry being $SO(3)\times SO(3)\times U(1)$ implies that the set of independent rotated-electron occupancy configurations that generate the model energy and momentum eigenstates generate state representations of that global symmetry for all values of the electronic density n and spin density m. It then follows that the total number of such independent representations must equal the Hilbert-space dimension, $4^{N_a^D}$. The results of Reference [6] confirm that for the model on a bipartite lattice in its full Hilbert space the number of independent representations of the group $SO(3)\times SO(3)\times U(1)$ is indeed $4^{N_a^D}$. In contrast, the number of independent representations of the group $SO(4)$ is found to be smaller than the Hilbert-space dimension $4^{N_a^D}$.

In this paper we review an application of the extended global $SO(3)\times SO(3)\times U(1)$ symmetry of the Hubbard model on a square lattice. It refers to a rotated-electron related operator description in terms of spin-$1/2$ spinons, $\eta$-spin-$1/2$ $\eta$-spinons, and spin-less and $\eta$-spin-less c fermions [9,10]. Such an operator description involves an electron-rotated-electron unitary transformation of the type considered in Reference [8]. A property specific to the specific transformation associated with the operator description reviewed in this paper is that the $U>0$ energy eigenstates can be generated from suitable chosen $U/4t\to \infty$ energy eigenstates upon application onto the latter states of the corresponding electron-rotated-electron unitary operator. The related set of state representations of the group $SO(3)\times SO(3)\times U(1)$ that emerge from our description are energy eigenstates yet are generated by exactly the same electron-rotated-electron unitary transformation from corresponding $U/4t\to \infty$ states.

Their rotated electron occupancy configurations are simpler to describe in terms of the above-mentioned three types of elementary objects directly related to the rotated electrons whose numbers and designations are: $M_s=2S_c$ spin-$1/2$ spinons, $M_{\eta }=[N_a^D-2S_c]$ $\eta$-spin-$1/2$ $\eta$-spinons, and $N_c=2S_c$ spin-less and $\eta$-spin-less charge c fermions. The latter live on a lattice with $N_a^D=[N_c+N_c^h]$ sites identical to the original lattice. Here $N_c^h=[N_a^D-2S_c]$ gives the number of c fermion holes. The relation of such objects to the rotated electrons is as follows. The $M_s=2S_c$ spin-$1/2$ spinons describe the spin degrees of freedom of the $2S_c$ rotated electrons that singly occupy sites. The charge degrees of freedom of such rotated electrons are described by the $N_c=2S_c$c fermions. The $M_{\eta }=[N_a^D-2S_c]$ $\eta$-spin-$1/2$ $\eta$-spinons describe the $\eta$-spin degrees of freedom of the $[N_a^D-2S_c]$ sites doubly occupied and unoccupied by rotated electrons. Specifically, the $\eta$-spinons of $\eta$-spin projection $-1/2$ and $+1/2$ refer to the sites doubly occupied and unoccupied, respectively, by rotated electrons. The remaining degrees of freedom of such rotated-electron occupancy configurations are described by the $N_c^h=[N_a^D-2S_c]$ c fermion holes. The expression of the rotated-electron operators in terms of these three elementary objects is for $U>0$ identical to that of the electron operators for large U values in terms of the three objects obtained from the exact transformation for separation of spin-$1/2$ fermions without constraints considered in Reference [11].

Interestingly, $\eta$-spinon (and spinons) that are not invariant under the electron-rotated-electron unitary transformation considered in this paper have $\eta$-spin $1/2$ (and spin $1/2$) but are anti-bound within $\eta$-spin-neutral (and bound within spin-neutral) $2\nu$-$\eta$-spinon (and $2\nu$-spinon) composite $\eta \nu$ fermions (and $s\nu$ fermions). Here $\nu =1$, 2, … is the number of anti-bound $\eta$-spinon (and bound spinon) pairs. In this paper we follow the notation of Reference [9] and call such spinons and $\eta$-spinons, confined spinons and confined $\eta$-spinons, respectively. We emphasize though that by “confinement” is meant here that the spinons and $\eta$-spinons are bound and anti-bound within such composite $s\nu$ and $\eta \nu$ fermions, respectively, alike for instance protons and neutrons are bound within the nucleus. Whether the potential associated with such a behavior is in some limit confining remains an interesting open question. The reason for the notation of Reference [9] is that the term confined can be used both for spinons and $\eta$-spinons. A possible alternative notation would be bound spinons and anti-bound $\eta$-spinons, which would be different for spinons and $\eta$-spinons. We thus stress that within our notation the term confined is not equivalent to the high-energy physics concept of confinement.

Moreover, again we follow the notation of Reference [9] and call deconfined spinons and deconfined $\eta$-spinons those that are invariant under the electron-rotated-electron unitary transformation. Here deconfined means just that such objects are not bounded and anti-bounded within $s\nu$ fermions and $\eta \nu$ fermions, respectively. In case that future research reveals that the potential behind the energetic relations of $s\nu$ fermions and $\eta \nu$ fermions discussed below in Section 4.3 is at least in some limit confining, any possible relation to the concept of deconfined quantum criticality of Reference [12] should be clarified.

The paper is organized as follows. A uniquely defined rotated-electron description for the Hubbrad model on the square lattice and its relation to the global $SO(3)\times SO(3)\times U(1)$ symmetry are the subjects of Section II. In Section III the c fermion, $\eta$-spin-$1/2$ $\eta$-spinon, and spin-$1/2$ spinon and corresponding c, $\eta$-spin, and spin effective lattices are reviewed. The vacua of the theory, the transformation laws under the electron-rotated-electron unitary transformation of such objects, and the subspaces they refer to are issues also addressed in that section. The composite $\alpha \nu$ bond particles and $\alpha \nu$ fermions, corresponding $\alpha \nu$ effective lattices, ground-state occupancy configurations, and a complete set of momentum eigenstates are the problems studied in Section IV. 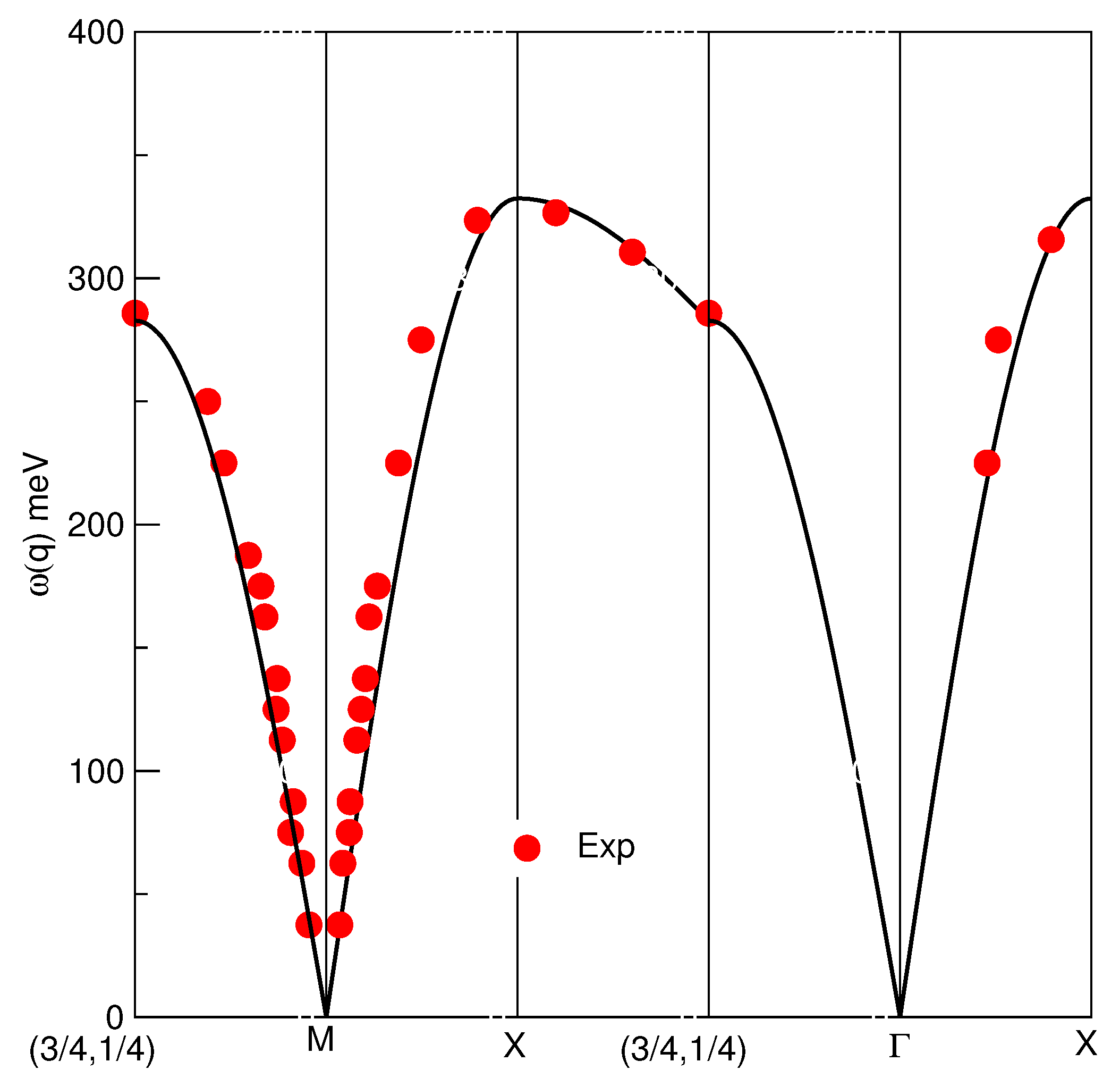The c and $s1$ fermion square-lattice quantum liquid and corresponding one- and two-electron subspace are the subjects discussed in Section V. Moreover, in that section a preliminary application of the present operator description to the inelastic neutron scattering of the Mott–Hubbard insulator parent compound La${}_2$CuO${}_4$ (LCO) [13] is presented. Our description leads to simple expressions that agree both with the LCO inelastic neutron scattering and the results of Reference [14], which involved the summation of an infinite number of diagrams. Finally, the concluding remarks are presented in Section VI.

2. The Model, a Suitable Rotated-Electron Description, and Relation to the Global $SO(3)\times SO(3)\times U(1)$ Symmetry

The Hubbard model on a square (or 1D) lattice with a very large number $N_a^D\gg 1$ of sites reads,

$$\begin{array}{cc}\hfill \widehat{H}& =t\widehat{T}+U[N_a^D-\widehat{Q}]/2\hfill \\ \hfill \widehat{T}& =-{\displaystyle \sum _{\langle {\overrightarrow{r}}_j{\overrightarrow{r}}_{j^{\prime }}\rangle }}{\displaystyle \sum _{\sigma }}[c_{{\overrightarrow{r}}_j,\sigma }^{†}{c}_{{\overrightarrow{r}}_{j^{\prime }},\sigma }+h.c.]\hfill \\ \hfill \widehat{Q}& =\sum _{j=1}^{N_a^D}{\displaystyle \sum _{\sigma =\uparrow ,\downarrow }}{\widehat{n}}_{{\overrightarrow{r}}_j,\sigma }(1-{\widehat{n}}_{{\overrightarrow{r}}_j,-\sigma })\hfill \end{array}$$

(1)

Periodic boundary conditions and torus periodic boundary conditions are considered for the 1D lattice for which $D=1$ and the square lattice for which $D=2$, respectively. Moreover, in Equation (1) t is the nearest-neighbor transfer integral, $\widehat{T}$ is the kinetic-energy operator in units of t, and $\widehat{Q}$ is the operator that counts the number of electron singly occupied sites. Hence the operator $\widehat{D}=[\widehat{N}-\widehat{Q}]/2$ counts the number of electron doubly occupied sites. Moreover, ${\widehat{n}}_{{\overrightarrow{r}}_j,\sigma }=c_{{\overrightarrow{r}}_j,\sigma }^{†}{c}_{{\overrightarrow{r}}_j,\sigma }$ where $-\sigma =\uparrow$ (and $-\sigma =\downarrow$) for $\sigma =\downarrow$ (and $\sigma =\uparrow$), $\widehat{N}={\sum }_{\sigma }{\widehat{N}}_{\sigma }$, and ${\widehat{N}}_{\sigma }={\sum }_{j=1}^{N_a^D}{\widehat{n}}_{{\overrightarrow{r}}_j,\sigma }$. We focus our attention onto ground states with hole concentration $x=[N_a^D-N]/N_a^D\ge 0$ and spin density $m=[N_{\uparrow }-N_{\downarrow }]/N_a^D=0$ and their excited states. Such an hole-concentration range corresponds to electronic densities $n=N/N_a^D\in (0,1)$. We are particularly interested in the LWS subspace spanned by the lowest-weight states (LWSs) of both the $\eta$-spin and spin algebras. Such energy eigenstates refer to values of $S_{\alpha }$ and $S_{\alpha }^{x_3}$ such that $S_{\alpha }=-S_{\alpha }^{x_3}$ for $\alpha =\eta ,s$.

The kinetic-energy operator $\widehat{T}$ can be expressed in terms of the operators,

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill {\widehat{T}}_0& =-{\displaystyle \sum _{\langle {\overrightarrow{r}}_j{\overrightarrow{r}}_{j^{\prime }}\rangle }}{\displaystyle \sum _{\sigma }}[{\widehat{n}}_{{\overrightarrow{r}}_j,-\sigma }{c}_{{\overrightarrow{r}}_j,\sigma }^{†}{c}_{{\overrightarrow{r}}_{j^{\prime }},\sigma }{\widehat{n}}_{{\overrightarrow{r}}_{j^{\prime }},-\sigma }+(1-{\widehat{n}}_{{\overrightarrow{r}}_j,-\sigma })c_{{\overrightarrow{r}}_j,\sigma }^{†}{c}_{{\overrightarrow{r}}_{j^{\prime }},\sigma }(1-{\widehat{n}}_{{\overrightarrow{r}}_{j^{\prime }},-\sigma })+h.c.]\hfill \\ \hfill {\widehat{T}}_{+1}& =-{\displaystyle \sum _{\langle {\overrightarrow{r}}_j{\overrightarrow{r}}_{j^{\prime }}\rangle }}{\displaystyle \sum _{\sigma }}{\widehat{n}}_{{\overrightarrow{r}}_j,-\sigma }{c}_{{\overrightarrow{r}}_j,\sigma }^{†}{c}_{{\overrightarrow{r}}_{j^{\prime }},\sigma }(1-{\widehat{n}}_{{\overrightarrow{r}}_{j^{\prime }},-\sigma })\hfill \\ \hfill {\widehat{T}}_{-1}& =-{\displaystyle \sum _{\langle {\overrightarrow{r}}_j{\overrightarrow{r}}_{j^{\prime }}\rangle }}{\displaystyle \sum _{\sigma }}(1-{\widehat{n}}_{{\overrightarrow{r}}_j,-\sigma })c_{{\overrightarrow{r}}_j,\sigma }^{†}{c}_{{\overrightarrow{r}}_{j^{\prime }},\sigma }{\widehat{n}}_{{\overrightarrow{r}}_{j^{\prime }},-\sigma }\hfill \end{array}\end{array}$$

(2)

as $\widehat{T}={\widehat{T}}_0+{\widehat{T}}_{+1}+{\widehat{T}}_{-1}$. These three kinetic operators play an important role in the physics. The operator ${\widehat{T}}_0$ does not change electron double occupancy whereas the operators ${\widehat{T}}_{+1}$ and ${\widehat{T}}_{-1}$ change it by $+1$ and $-1$, respectively.

The studies of Reference [6] consider unitary operators $\widehat{V}=\widehat{V}(U/4t)$ and corresponding rotated-electron operators,

$${\tilde{c}}_{{\overrightarrow{r}}_j,\sigma }^{†}={\widehat{V}}^{†}{c}_{{\overrightarrow{r}}_j,\sigma }^{†}\widehat{V};{\tilde{c}}_{{\overrightarrow{r}}_j,\sigma }={\widehat{V}}^{†}{c}_{{\overrightarrow{r}}_j,\sigma }\widehat{V};{\tilde{n}}_{{\overrightarrow{r}}_j,\sigma }={\tilde{c}}_{{\overrightarrow{r}}_j,\sigma }^{†}{\tilde{c}}_{{\overrightarrow{r}}_j,\sigma }$$

(3)

Those are such that rotated-electron single and double occupancy are good quantum numbers for $U/4t>0$. The global $U(1)$ symmetry generator $2{\tilde{S}}_c$ of eigenvalue $2S_c$ reads [6],

$$2{\tilde{S}}_c=\sum _{j=1}^{N_a^D}{\tilde{s}}_{{\overrightarrow{r}}_j,c};{\tilde{s}}_{{\overrightarrow{r}}_j,c}={\displaystyle \sum _{\sigma =\uparrow ,\downarrow }}{\tilde{n}}_{{\overrightarrow{r}}_j,\sigma }(1-{\tilde{n}}_{{\overrightarrow{r}}_j,-\sigma })$$

(4)

It follows that $2{\tilde{S}}_c={\widehat{V}}^{†}2{\widehat{S}}_c\widehat{V}$ where $2{\widehat{S}}_c=\widehat{Q}$ and the operator $\widehat{Q}$ is given in Equation (1). As mentioned in the previous section, $2S_c$ is the number of rotated-electron singly occupied sites. Most choices of the unitary operators $\widehat{V}$ correspond to choices of $U/4t\to \infty$ sets $\{|{\Psi }_{\infty }\rangle \}$ of $4^{N_a^D}$ energy eigenstates such that the states $|{\Psi }_{U/4t}\rangle ={\widehat{V}}^{†}|{\Psi }_{\infty }\rangle$ are not energy and momentum eigenstates for finite $U/4t$ values yet belong to a subspace with fixed and well-defined values of $S_c$, $S_{\eta }$, and $S_s$.

Let $\{|{\Psi }_{U/4t}\rangle \}$ be a complete set of $4^{N_a^D}$ energy, momentum, $\eta$-spin, $\eta$-spin projection, spin, and spin-projection eigenstates for $U/4t>0$. In the limit $U/4t\to \infty$ such states correspond to one of the many choices of sets $\{|{\Psi }_{\infty }\rangle \}$ of $4^{N_a^D}$ $U/4t$-infinite energy eigenstates. Both the sets of states $\{|{\Psi }_{U/4t}\rangle \}$ and $\{|{\Psi }_{\infty }\rangle \}$, respectively, are complete and the model Hilbert space is the same for all $U/4t>0$ values considered here. Hence it follows from basic quantum mechanics Hilbert-space and operator properties that for this choice there exists exactly one unitary operator $\widehat{V}=\widehat{V}(U/4t)$ such that $|{\Psi }_{U/4t}\rangle ={\widehat{V}}^{†}|{\Psi }_{\infty }\rangle$. Here we consider such a unitary operator and corresponding generator ${\tilde{S}}_c={\widehat{V}}^{†}{\widehat{S}}_c\widehat{V}$ given in Equation (4) and rotated-electron operators provided in Equation (3). The states $|{\Psi }_{U/4t}\rangle ={\widehat{V}}^{†}|{\Psi }_{\infty }\rangle$ (one for each value of $U/4t>0$) that are generated from the same initial state $|{\Psi }_{\infty }\rangle$ belong to the same V tower.

A complete set $\{|{\mathsf{\Phi }}_{U/4t}\rangle \}$ of related momentum eigenstates $|{\mathsf{\Phi }}_{U/4t}\rangle ={\widehat{V}}^{†}|{\mathsf{\Phi }}_{\infty }\rangle$ is introduced in Reference [9]. Such states are generated by occupancy configurations of the quantum objects of the general description considered in this paper. The unitary operator ${\widehat{V}}^{†}$ appearing in the general expression of such states is what also appears in the general expression $|{\Psi }_{U/4t}\rangle ={\widehat{V}}^{†}|{\Psi }_{\infty }\rangle$ of the above energy and momentum eigenstates. However the states $|{\mathsf{\Phi }}_{U/4t}\rangle$ are not in general energy eigenstates of the Hubbard model on the square lattice. The interest of the states $|{\mathsf{\Phi }}_{U/4t}\rangle ={\widehat{V}}^{†}|{\mathsf{\Phi }}_{\infty }\rangle$ is that those contained in the one- and two-electron subspace defined below are both momentum and energy eigenstates of that model. Fortunately, the present general description is physically most useful and important for the Hubbard model on the square lattice in that subspace, which refers to the square-lattice quantum liquid further investigated in Reference [10].

Alike in Reference [6], we associate with any operator $\widehat{O}$ an operator $\tilde{O}={\widehat{V}}^{†}\widehat{O}\widehat{V}$ that has the same expression in terms of rotated-electron creation and annihilation operators as $\widehat{O}$ in terms of electron creation and annihilation operators, respectively. Our convention is that marks placed over letters being a caret or a tilde denote operators. (An exception are the electron operators of Equation (3), which we denote by $c_{{\overrightarrow{r}}_j,\sigma }^{†}$ and $c_{{\overrightarrow{r}}_j,\sigma }$ rather than by ${\widehat{c}}_{{\overrightarrow{r}}_j,\sigma }^{†}$ and ${\widehat{c}}_{{\overrightarrow{r}}_j,\sigma }$, respectively.) Any operator $\widehat{O}$ can then be written in terms of rotated-electron creation and annihilation operators as,

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill \widehat{O}& =\widehat{V}\tilde{O}{\widehat{V}}^{†}=\tilde{O}+[\tilde{O},\widehat{S}]+\frac{1}{2}[[\tilde{O},\widehat{S}],\widehat{S}]+\dots =\tilde{O}+[\tilde{O},\tilde{S}]+\frac{1}{2}[[\tilde{O},\tilde{S}],\tilde{S}]+\dots \hfill \\ \hfill \widehat{S}& =-\frac{t}{U}\left[{\widehat{T}}_{+1}-{\widehat{T}}_{-1}\right]+\mathcal{O}(t^2/U^2);\tilde{S}=-\frac{t}{U}\left[{\tilde{T}}_{+1}-{\tilde{T}}_{-1}\right]+\mathcal{O}(t^2/U^2)\hfill \end{array}\end{array}$$

(5)

The operator $\widehat{S}$ appearing in this equation is related to the unitary operator as ${\widehat{V}}^{†}=e^{\widehat{S}}$ and $\widehat{V}=e^{-\widehat{S}}$. Although the general expression of $\widehat{S}$ remains unknown, an exact result is that it involves only the kinetic operators ${\widehat{T}}_0$, ${\widehat{T}}_{+1}$, and ${\widehat{T}}_{-1}$ of Equation (2) and numerical $U/4t$ dependent coefficients [8,9]. For $U/4t>0$ that expression can be expanded in a series of $t/U$. The corresponding first-order term has the universal form given in Equation (5). To arrive to the expression of $\widehat{O}$ in terms of the operator $\tilde{S}$ also given in Equation (5), the property that the operator $\widehat{V}$ commutes with itself is used. It implies that $\widehat{V}=e^{-\widehat{S}}=\tilde{V}=e^{-\tilde{S}}$ and $\widehat{S}=\tilde{S}$. Hence both the operators $\widehat{V}$ and $\widehat{S}$ have the same expression in terms of electron and rotated-electron creation and annihilation operators. This justifies why the expansion $\tilde{S}=-(t/U)[{\tilde{T}}_{+1}-{\tilde{T}}_{-1}]+\mathcal{O}(t^2/U^2)$ given in that equation for the operator $\tilde{S}$ has the same form as that of $\widehat{S}$.

The higher-order terms of the operator $\tilde{S}$ expression can be written as a product of operator factors. Their expressions involve the rotated kinetic operators ${\tilde{T}}_0$, ${\tilde{T}}_{+1}$, and ${\tilde{T}}_{-1}$. The full expression of the operator $\widehat{S}=\tilde{S}$ can for $U/4t>0$ be written as $\widehat{S}=-\widehat{S}(\infty )-\delta \widehat{S}=-\tilde{S}(\infty )-\delta \tilde{S}$. Here $\widehat{S}(\infty )=\tilde{S}(\infty )$ corresponds to the operator $S(l)$ at $l=\infty$ defined in Equation (61) of Reference [8]. Moreover, $\delta \widehat{S}=\delta \tilde{S}$ has the general form provided in Equation (64) of that paper. The unitary operator $\widehat{V}=e^{-\widehat{S}}=e^{-\tilde{S}}$ considered here corresponds to exactly one choice of the coefficients $D^{(k)}(\mathbf{m})$ of that equation. Here the index $k=1$, 2, … refers to the number of rotated-electron doubly occupied sites. The problem of finding the explicit form of the operators $\widehat{V}=\tilde{V}$ and $\widehat{S}=\tilde{S}$ is equivalent to finding all coefficients $D^{(k)}(\mathbf{m})$ associated with the electron-rotated-electron unitary transformation as defined above.

For finite $U/4t$ values the Hamiltonian $\widehat{H}$ of Equation (1) does not commute with the unitary operator $\widehat{V}=e^{-\widehat{S}}$. Hence when expressed in terms of the rotated-electron creation and annihilation operators of Equation (3) it has an infinite number of terms. According to Equation (5) it reads,

$$\widehat{H}=\widehat{V}\tilde{H}{\widehat{V}}^{†}=\tilde{H}+[\tilde{H},\tilde{S}]+\frac{1}{2}[[\tilde{H},\tilde{S}],\tilde{S}]+\dots$$

(6)

The commutator $[\tilde{H},\tilde{S}]$ does not vanish except for $U/4t\to \infty$ so that $\widehat{H}\ne \tilde{H}$ for finite values of $U/4t$. Fortunately, there is strong evidence that for approximately $U/4t>1$, out of the infinite terms on the right-hand-side of Equation (6) only the first few Hamiltonian terms play an active role in the physics of the Hubbard model on the square lattice in the one- and two-electron subspace [10]. This follows in part from in that subspace the rotated-electron configurations expressed in Reference [9] in terms of related c and $s1$ fermion operators referring to energy eigenstates. For instance, the spin spectrum used below in Section 5.4 was derived in Reference [10] under the assumption that for approximately $U/4t>1$ only the first few Hamiltonian terms on the right-hand side of Equation (6) play an active role in the model physics. For $U/4t=1.525$ the validity of that assumption is consistent with the very good agreement with both results obtained by the standard formalism of many-body physics for the model spin spectrum [14] and the inelastic neutron scattering of LCO reported in that Section. Note, however, that this property is expected to hold provided that the unitary transformation used to generate the rotated electrons from the electrons is that considered above.

Alike the operator $\tilde{S}$, the Hamiltonian expression in terms of rotated-electron operators Equation (6) can be expanded in a series of $t/U$. Its terms generated up to fourth order in $t/U$ are within a unitary transformation the equivalent to the $t-J$ model with ring exchange and various correlated hoppings [15]. Furthermore, at half filling the terms of the Hamiltonian Equation (6) expansion in $t/U$ with odd powers in t vanish due to the particle-hole symmetry and the resulting invariance of the spectrum under $t\to -t$. In turn, for finite hole concentration $x>0$ the expansion in powers of $t/U$ of the Hamiltonian Equation (6) involves terms with odd powers in t, absent at $x=0$. This is consistent with the effects of increasing $U/4t$ being often different at $x=0$ and for $x>0$ [16].

It is shown in Reference [8] that all infinite electron-rotated-electron unitary transformations are well defined except at $U=0$. This applies to the specific choice of electron-rotated-electron unitary transformation associated with the operational description reviewed in this paper. Given the unitarity character of that transformation, it may be used in two different physical problems, which however are mathematically and technically fully equivalent. These two physical problems are considered in Reference [8] and References [9,10], respectively. Specifically, in Reference [8] it is considered that the rotated creation and annihilation operators of Equation (3) refer to electrons. Within that choice, except for $U/4t\to \infty$ the Hamiltonian on the right-hand side of Equation (6) is not the Hubbard Hamiltonian. Instead it is an Hamiltonian for which electron double occupancy and single occupancy are good quantum numbers. In turn, within the alternative physical problem studied here and in References [9,10], the rotated creation and annihilation operators of Equation (3) refer to rotated electrons, which except for $U/4t\to \infty$ are objects different from electrons. In this case, provided that both the on-site interaction $U\ne 0$ is finite and one accounts for all higher-order terms on the right-hand-side of Equation (6), the corresponding expression refers to the Hubbard model in terms of rotated-electron creation and annihilation operators. Hence within the operational description reviewed in this paper the general expression given in Equation (6) is not a mapping of the Hubbard model onto some generalized $t-J$ model. Indeed the electron-rotated-electron unitary transformation considered here has been constructed to inherently rotated-electron double occupancy and singly occupancy being good quantum numbers for the Hubbard model with $U\ne 0$. Hence unlike in the derivation of $t-J$ models of References [17,18], the range of applicability of the Hubbard model expression given in Equation (6) refers to all finite $U\ne 0$ values.

In Reference [6] it is found that, in contrast to the Hamiltonian, the three components of the momentum operator $\widehat{\overrightarrow{P}}$, three generators of the spin $SU(2)$ symmetry, and three generators of the $\eta$-spin $SU(2)$ symmetry commute with the electron-rotated-electron unitary operator $\widehat{V}=\tilde{V}$. This also holds for the specific choice of that operator associated with the rotated-electron description considered in this paper. Hence the above operators have the same expression in terms of electron and rotated-electron creation and annihilation operators, so that the momentum operator reads,

$$\widehat{\overrightarrow{P}}={\displaystyle \sum _{\sigma =\uparrow ,\downarrow }}{\displaystyle \sum _{\overrightarrow{k}}}\overrightarrow{k}{c}_{\overrightarrow{k},\sigma }^{†}{c}_{\overrightarrow{k},\sigma }={\displaystyle \sum _{\sigma =\uparrow ,\downarrow }}{\displaystyle \sum _{\overrightarrow{k}}}\overrightarrow{k}{\tilde{c}}_{\overrightarrow{k},\sigma }^{†}{\tilde{c}}_{\overrightarrow{k},\sigma }$$

(7)

Furthermore, the above-mentioned six generators are given by,

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill {\widehat{S}}_{\eta }^{x_3}& =\sum _{j=1}^{N_a^D}{\widehat{s}}_{{\overrightarrow{r}}_j,\eta }^{x_3}=\sum _{j=1}^{N_a^D}{\tilde{s}}_{{\overrightarrow{r}}_j,\eta }^{x_3};{\widehat{S}}_{\eta }^{†}=\sum _{j=1}^{N_a^D}{\widehat{s}}_{{\overrightarrow{r}}_j,\eta }^{+}=\sum _{j=1}^{N_a^D}{\tilde{s}}_{{\overrightarrow{r}}_j,\eta }^{+};{\widehat{S}}_{\eta }=\sum _{j=1}^{N_a^D}{\widehat{s}}_{{\overrightarrow{r}}_j,\eta }^{-}=\sum _{j=1}^{N_a^D}{\tilde{s}}_{{\overrightarrow{r}}_j,\eta }^{-}\hfill \\ \hfill {\widehat{S}}_s^{x_3}& =\sum _{j=1}^{N_a^D}{\widehat{s}}_{{\overrightarrow{r}}_j,s}^{x_3}=\sum _{j=1}^{N_a^D}{\tilde{s}}_{{\overrightarrow{r}}_j,s}^{x_3};{\widehat{S}}_s^{†}=\sum _{j=1}^{N_a^D}{\widehat{s}}_{{\overrightarrow{r}}_j,s}^{+}=\sum _{j=1}^{N_a^D}{\tilde{s}}_{{\overrightarrow{r}}_j,s}^{+};{\widehat{S}}_s=\sum _{j=1}^{N_a^D}{\widehat{s}}_{{\overrightarrow{r}}_j,s}^{-}=\sum _{j=1}^{N_a^D}{\tilde{s}}_{{\overrightarrow{r}}_j,s}^{-}\hfill \end{array}\end{array}$$

(8)

However, except for $U/4t\to \infty$ the local rotated-electron operators,

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill {\tilde{s}}_{{\overrightarrow{r}}_j,\eta }^{x_3}& =-\frac{1}{2}[1-{\tilde{n}}_{{\overrightarrow{r}}_j,\uparrow }-{\tilde{n}}_{{\overrightarrow{r}}_j,\downarrow }];{\tilde{s}}_{{\overrightarrow{r}}_j,\eta }^{+}=e^{i\overrightarrow{\pi }·{\overrightarrow{r}}_j}{\tilde{c}}_{{\overrightarrow{r}}_j,\downarrow }^{†}{\tilde{c}}_{{\overrightarrow{r}}_j,\uparrow }^{†};{\tilde{s}}_{{\overrightarrow{r}}_j,\eta }^{-}=e^{-i\overrightarrow{\pi }·{\overrightarrow{r}}_j}{\tilde{c}}_{{\overrightarrow{r}}_j,\uparrow }{\tilde{c}}_{{\overrightarrow{r}}_j,\downarrow }\hfill \\ \hfill {\tilde{s}}_{{\overrightarrow{r}}_j,s}^{x_3}& =-\frac{1}{2}[{\tilde{n}}_{{\overrightarrow{r}}_j,\uparrow }-{\tilde{n}}_{{\overrightarrow{r}}_j,\downarrow }];{\tilde{s}}_{{\overrightarrow{r}}_j,s}^{+}={\tilde{c}}_{{\overrightarrow{r}}_j,\downarrow }^{†}{\tilde{c}}_{{\overrightarrow{r}}_j,\uparrow };{\tilde{s}}_{{\overrightarrow{r}}_j,s}^{-}={\tilde{c}}_{{\overrightarrow{r}}_j,\uparrow }^{†}{\tilde{c}}_{{\overrightarrow{r}}_j,\downarrow },j=1,2,\dots ,N_a^D\hfill \end{array}\end{array}$$

(9)

and corresponding local electron operators,

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill {\widehat{s}}_{{\overrightarrow{r}}_j,\eta }^{x_3}& =-\frac{1}{2}[1-{\widehat{n}}_{{\overrightarrow{r}}_j,\uparrow }-{\widehat{n}}_{{\overrightarrow{r}}_j,\downarrow }];{\widehat{s}}_{{\overrightarrow{r}}_j,\eta }^{+}=e^{i\overrightarrow{\pi }·{\overrightarrow{r}}_j}{\widehat{c}}_{{\overrightarrow{r}}_j,\downarrow }^{†}{\widehat{c}}_{{\overrightarrow{r}}_j,\uparrow }^{†};{\widehat{s}}_{{\overrightarrow{r}}_j,\eta }^{-}=e^{-i\overrightarrow{\pi }·{\overrightarrow{r}}_j}{\widehat{c}}_{{\overrightarrow{r}}_j,\uparrow }{\widehat{c}}_{{\overrightarrow{r}}_j,\downarrow }\hfill \\ \hfill {\widehat{s}}_{{\overrightarrow{r}}_j,s}^{x_3}& =-\frac{1}{2}[{\widehat{n}}_{{\overrightarrow{r}}_j,\uparrow }-{\widehat{n}}_{{\overrightarrow{r}}_j,\downarrow }];{\widehat{s}}_{{\overrightarrow{r}}_j,s}^{+}={\widehat{c}}_{{\overrightarrow{r}}_j,\downarrow }^{†}{\widehat{c}}_{{\overrightarrow{r}}_j,\uparrow };{\widehat{s}}_{{\overrightarrow{r}}_j,s}^{-}={\widehat{c}}_{{\overrightarrow{r}}_j,\uparrow }^{†}{\widehat{c}}_{{\overrightarrow{r}}_j,\downarrow },j=1,2,\dots ,N_a^D\hfill \end{array}\end{array}$$

(10)

appearing in the expressions given in Equation (8) of such six generators are different operators. We emphasize though that in the $U/4t\to \infty$ limit such two sets of six local operators become the same operators and in addition are the six out of seven generators of the local $SU(2)\times SU(2)\times U(1)$ gauge symmetry reported in Reference [7]. The vector $\overrightarrow{\pi }$ appearing in Equations (9) and (10) has Cartesian components $\overrightarrow{\pi }=[\pi ,\pi ]$ (and component $\pi$) for the model on the square (and 1D) lattice.

In contrast, the generator $2{\tilde{S}}_c$ of the charge independent $U(1)$ symmetry given in Equation (4) does not commute with the unitary operator $\widehat{V}$. This is behind the hidden character of such a symmetry. On the contrary of the Hamiltonian, that generator has a complicated expression in terms of electron creation and annihilation operators and a simple expression given in that equation in terms of rotated-electron creation and annihilation operators. The operator of Equation (4) plus the six operators provided in Equation (8) are the seven generators of the group $[SO(4)\times U(1)]/Z_2=SO(3)\times SO(3)\times U(1)$ associated with the global symmetry of the Hamiltonian Equation (1).

3. Three Elementary Quantum Objects and Corresponding c, $\eta$-Spin, and Spin Effective Lattices

Within the operational description reviewed this paper, three rotated-electron related elementary objects naturally emerge from the local operators that in the $U/4t\to \infty$ limit generate the local $SU(2)\times SU(2)\times U(1)$ gauge symmetry of Reference [7]. Summation over the $N_a$ sites of such operators gives for $U/4t>0$ the generators of the corresponding model extended global $[SU(2)\times SU(2)\times U(1)]/Z_2^2=SO(3)\times SO(3)\times U(1)$ symmetry. Such elementary objects are mapped from the rotated electrons by an exact local transformation that does not introduce constraints. Given their direct relation to the generators of the model extended symmetry, their occupancy configurations naturally generate representations of the global symmetry algebra.

In the $U/4t\to \infty$ limit and except for unimportant phase factors, the c fermion creation operators and the spinon and $\eta$-spinon operators introduced below become the quasicharge annihilation operators and the local spin and pseudospin operators, respectively, of Reference [11]. The representation associated with the latter operators refers to all dimensions and lattices. For instance, in Reference [11] it is used in the study of the Hubbard model on the square lattice. The unitarity and remaining properties of the electron-rotated-electron transformation considered in this paper assures that the corresponding c fermion, spinon, and $\eta$-spinon operator representation introduced in the following for $U/4t>0$ applies as well to the Hubbard model on the square lattice.

3.1. Elementary Quantum Objects and Their Operators

The local c fermion annihilation operator $f_{{\overrightarrow{r}}_j,c}$ and corresponding creation operator $f_{{\overrightarrow{r}}_j,c}^{†}={(f_{{\overrightarrow{r}}_j,c})}^{†}$ are constructed in terms of the rotated-electron operators of Equation (3). Within the LWS representation the latter operator reads,

$$f_{{\overrightarrow{r}}_j,c}^{†}={(f_{{\overrightarrow{r}}_j,c})}^{†}={\tilde{c}}_{{\overrightarrow{r}}_j,\uparrow }^{†}(1-{\tilde{n}}_{{\overrightarrow{r}}_j,\downarrow })-e^{-i\overrightarrow{\pi }·{\overrightarrow{r}}_j}{\tilde{c}}_{{\overrightarrow{r}}_j,\uparrow }{\tilde{n}}_{{\overrightarrow{r}}_j,\downarrow };f_{{\overrightarrow{q}}_j,c}^{†}=\frac{1}{\sqrt{N_a^D}}\sum _{j^{\prime }=1}^{N_a^D}{e}^{+i{\overrightarrow{q}}_j·{\overrightarrow{r}}_{j^{\prime }}}{f}_{{\overrightarrow{r}}_{j^{\prime }},c}^{†}$$

(11)

In Equation (11) we have introduced as well the corresponding c fermion momentum-dependent operators and $e^{i\overrightarrow{\pi }·{\overrightarrow{r}}_j}$ is $\pm 1$ depending on which sub-lattice site ${\overrightarrow{r}}_j$ is on. (For the 1D lattice that phase factor can be written as ${(-1)}^j$.) The c momentum band is studied in Reference [10] and has the same shape and momentum area as the electronic first-Brillouin zone.

The three spin local rotated operators ${\tilde{s}}_{{\overrightarrow{r}}_j,s}^l$ and the three $\eta$-spin local rotated operators ${\tilde{s}}_{{\overrightarrow{r}}_j,\eta }^l$ such that $l=\pm ,x_3$, given in Equation (9) are associated with the spinons and $\eta$-spinons, respectively, as defined in this paper. Consistently with the $f_{{\overrightarrow{r}}_j,c}^{†}$ expression given in Equation (11), the local rotated operator ${\tilde{s}}_{{\overrightarrow{r}}_j,c}$ and such spin and $\eta$-spin local rotated operators may be rewritten as,

$${\tilde{s}}_{{\overrightarrow{r}}_j,c}=n_{{\overrightarrow{r}}_j,c}=f_{{\overrightarrow{r}}_j,c}^{†}{f}_{{\overrightarrow{r}}_j,c};{\tilde{s}}_{{\overrightarrow{r}}_j,s}^l=n_{{\overrightarrow{r}}_j,c}{\tilde{q}}_{{\overrightarrow{r}}_j}^l;{\tilde{s}}_{{\overrightarrow{r}}_j,\eta }^l=(1-n_{{\overrightarrow{r}}_j,c}){\tilde{q}}_{{\overrightarrow{r}}_j}^l,l=\pm ,x_3$$

(12)

Here ${\tilde{q}}_{{\overrightarrow{r}}_j}^{\pm }={\tilde{q}}_{{\overrightarrow{r}}_j}^{x_1}\pm i{\tilde{q}}_{{\overrightarrow{r}}_j}^{x_2}$ where $x_1,x_2,x_3$ denotes the Cartesian coordinates of the rotated quasi-spin operators ${\tilde{q}}_{{\overrightarrow{r}}_j}^{x_i}$ with $i=1,2,3$. The former rotated quasi-spin operators ${\tilde{q}}_{{\overrightarrow{r}}_j}^l={\tilde{s}}_{{\overrightarrow{r}}_j,s}^l+{\tilde{s}}_{{\overrightarrow{r}}_j,\eta }^l$ such that $l=\pm ,x_3$ have for $U/4t>0$ the following expression in terms of rotated-electron operators,

$${\tilde{q}}_{{\overrightarrow{r}}_j}^{-}=({\tilde{c}}_{{\overrightarrow{r}}_j,\uparrow }^{†}+e^{-i\overrightarrow{\pi }·{\overrightarrow{r}}_j}{\tilde{c}}_{{\overrightarrow{r}}_j,\uparrow }){\tilde{c}}_{{\overrightarrow{r}}_j,\downarrow };{\tilde{q}}_{{\overrightarrow{r}}_j}^{+}={(q_{{\overrightarrow{r}}_j}^{-})}^{†};{\tilde{q}}_{{\overrightarrow{r}}_j}^{x_3}={\tilde{n}}_{{\overrightarrow{r}}_j,\downarrow }-\frac{1}{2}$$

(13)

Since the electron-rotated-electron transformation generated by the operator $\widehat{V}$ is unitary, the operators ${\tilde{c}}_{{\overrightarrow{r}}_j,\sigma }^{†}$ and ${\tilde{c}}_{{\overrightarrow{r}}_j,\sigma }$ of Equation (3) have the same anticommutation relations as $c_{{\overrightarrow{r}}_j,\sigma }^{†}$ and $c_{{\overrightarrow{r}}_j,\sigma }$, respectively. Straightforward manipulations based on Equations (11)–(13) then lead to the following algebra for the c fermion operators,

$$\{f_{{\overrightarrow{r}}_j,c}^{†},f_{{\overrightarrow{r}}_{j^{\prime }},c}\}={\delta }_{j,j^{\prime }};\{f_{{\overrightarrow{r}}_j,c}^{†},f_{{\overrightarrow{r}}_{j^{\prime }},c}^{†}\}=\{f_{{\overrightarrow{r}}_j,c},f_{{\overrightarrow{r}}_{j^{\prime }},c}\}=0$$

(14)

and c fermion operators and rotated quasi-spin operators,

$$[f_{{\overrightarrow{r}}_j,c}^{†},q_{{\overrightarrow{r}}_{j^{\prime }}}^l]=[f_{{\overrightarrow{r}}_j,c},q_{{\overrightarrow{r}}_{j^{\prime }}}^l]=0$$

(15)

In turn, the rotated quasi-spin operators $q_{{\overrightarrow{r}}_j}^{x_1}$, $q_{{\overrightarrow{r}}_j}^{x_2}$, and $q_{{\overrightarrow{r}}_j}^{x_3}$ and the related operators $q_{{\overrightarrow{r}}_j}^{\pm }=q_{{\overrightarrow{r}}_j}^{x_1}\pm i{q}_{{\overrightarrow{r}}_j}^{x_2}$ obey the following algebra,

$$\begin{array}{}\mathrm{(16)}& \hfill [q_{{\overrightarrow{r}}_j}^{x_p},q_{{\overrightarrow{r}}_{j^{\prime }}}^{x_{p^{\prime }}}]& =i{\delta }_{j,j^{\prime }}{\displaystyle \sum _{p^{″}}}{ϵ}_{p{p}^{\prime }{p}^{″}}{q}_{{\overrightarrow{r}}_j}^{x_{p^{″}}};\hfill & p,p^{\prime },p^{″}\hfill & =1,2,3\hfill \mathrm{(17)}& \hfill \{q_{{\overrightarrow{r}}_j}^{+},q_{{\overrightarrow{r}}_j}^{-}\}& =1,\hfill & \hfill \{q_{{\overrightarrow{r}}_j}^{\pm },q_{{\overrightarrow{r}}_j}^{\pm }\}& =0;\hfill \mathrm{(18)}& \hfill [q_{{\overrightarrow{r}}_j}^{+},q_{{\overrightarrow{r}}_{j^{\prime }}}^{-}]& ={\delta }_{j,j^{\prime }}{q}_{{\overrightarrow{r}}_j}^{x_3};\hfill & \hfill [q_{{\overrightarrow{r}}_j}^{\pm },q_{{\overrightarrow{r}}_{j^{\prime }}}^{\pm }]& =0\hfill \end{array}$$

Hence the operators $q_{{\overrightarrow{r}}_j}^{\pm }$ anticommute on the same site and commute on different sites. The same applies to three spinon operators $s_{{\overrightarrow{r}}_j}^l$ and three $\eta$-spinon operators $p_{{\overrightarrow{r}}_j}^l$, respectively, whose expressions are given in Equation (12).

The relations provided in Equations (14)–(18) confirm that the c fermions associated with the hidden global $U(1)$ symmetry are $\eta$-spinless and spinless fermionic objects. They are consistent as well with the spinons and $\eta$-spinons being spin-$1/2$ and $\eta$-spin-$1/2$ objects, respectively, whose local operators obey the usual corresponding $SU(2)$ algebras.

On inverting the relations given in Equations (11) and (13), the rotated-electron creation and/or annihilation operators of Equation (3) are written in terms of the operators of the c fermions and rotated quasi-spin operators. For the LWS subspace considered here this leads to,

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill {\tilde{c}}_{{\overrightarrow{r}}_j,\uparrow }^{†}& =\left(\frac{1}{2}-{\tilde{q}}_{{\overrightarrow{r}}_j}^{x_3}\right)f_{{\overrightarrow{r}}_j,c}^{†}-e^{-i\overrightarrow{\pi }·{\overrightarrow{r}}_j}\left(\frac{1}{2}+{\tilde{q}}_{{\overrightarrow{r}}_j}^{x_3}\right)f_{{\overrightarrow{r}}_j,c}\hfill \\ \hfill {\tilde{c}}_{{\overrightarrow{r}}_j,\downarrow }^{†}& ={\tilde{q}}_{{\overrightarrow{r}}_j}^{+}{f}_{{\overrightarrow{r}}_j,c}^{†}+e^{-i\overrightarrow{\pi }·{\overrightarrow{r}}_j}{\tilde{q}}_{{\overrightarrow{r}}_j}^{+}{f}_{{\overrightarrow{r}}_j,c}\hfill \\ \hfill {\tilde{c}}_{{\overrightarrow{r}}_j,\uparrow }& =\left(\frac{1}{2}-{\tilde{q}}_{{\overrightarrow{r}}_j}^{x_3}\right)f_{{\overrightarrow{r}}_j,c}-e^{i\overrightarrow{\pi }·{\overrightarrow{r}}_j}\left(\frac{1}{2}+{\tilde{q}}_{{\overrightarrow{r}}_j}^{x_3}\right)f_{{\overrightarrow{r}}_j,c}^{†}\hfill \\ \hfill {\tilde{c}}_{{\overrightarrow{r}}_j,\downarrow }& ={\tilde{q}}_{{\overrightarrow{r}}_j}^{-}{f}_{{\overrightarrow{r}}_j,c}+e^{i\overrightarrow{\pi }·{\overrightarrow{r}}_j}{\tilde{q}}_{{\overrightarrow{r}}_j}^{-}{f}_{{\overrightarrow{r}}_j,c}^{†}\hfill \end{array}\end{array}$$

(19)

The relations given in Equations (11)–(13) and (19) between the c fermion, spinon, and $\eta$-spinon operators and the rotated-electron operators differ from those of References [9,10] by unimportant phase factors. For $U/4t\to \infty$ the rotated electrons become electrons. In that limit and as mentioned above, except for unimportant phase factors the c fermion creation operators become the quasicharge annihilation operators of Reference [11] and the spinon and $\eta$-spinon operators become the local spin and pseudospin operators, respectively, of that reference. Consistently, in that limit and again unimportant phase factors Equations (11)–(19) are equivalent to Equations (1)–(3) of Reference [11] with the rotated-electron operators replaced by the corresponding electron operators and the c fermion creation operator $f_{{\overrightarrow{r}}_j,c}^{†}$ replaced by the quasicharge annihilation operator ${\widehat{c}}_r$.

Alike the transformation considered in Reference [11], that considered here does not introduce Hilbert-space constraints. Hence suitable occupancy configurations of c fermions, spinons, and $\eta$-spinons generate a complete set of finite-$U/4t$ states of the form $|{\mathsf{\Phi }}_{U/4t}\rangle ={\widehat{V}}^{†}|{\mathsf{\Phi }}_{\infty }\rangle$. Those are both state representations of the model global $SO(3)\times SO(3)\times U(1)$ symmetry and momentum eigenstates. In general the energy and momentum eigenstates $|{\Psi }_{U/4t}\rangle ={\widehat{V}}^{†}|{\Psi }_{\infty }\rangle$ of the Hubbard model on the square lattice are a superposition of a sub-set of states $|{\mathsf{\Phi }}_{U/4t}\rangle$ with the same momentum eigenvalue.

3.2. Interplay of the Global Symmetry with the Transformation Laws Under the Operator $\widehat{V}$: Three Basic Effective Lattices and the Theory Vacua

It follows from the results of Reference [6] that the $\eta$-spin $SU(2)$ and spin $SU(2)$ state representations correspond to the $\eta$-spin and spin degrees of freedom of independent rotated-electron occupancy configurations of $[N_a^D-2S_c]$ sites and $2S_c$ sites, respectively, of the original lattice. This applies to any choice of electron-rotated-electron unitary transformation and thus applies as well to that associated with the present description. In turn, the state representations associated with the new-found hidden $U(1)$ symmetry of the global $SO(3)\times SO(3)\times U(1)=[SU(2)\times SU(2)\times U(1)]/Z_2^2$ symmetry refer to the relative positions in the original lattice of the sites involved in each of these two types of configurations. In the present $N_a^D\gg 1$ limit it is useful to consider the following numbers,

$$N_{a_{\eta }}^D=N_a^D-2S_c;N_{a_s}^D=2S_c$$

(20)

such that $N_a^D=N_{a_{\eta }}^D+N_{a_s}^D$. Here the integer numbers $N_{a_{\eta }}^D$ and $N_{a_s}^D$ are the number of sites of the original lattice singly occupied by rotated electrons and unoccupied plus doubly occupied by rotated electrons, respectively. Below such numbers are found to play the role of number of sites of a $\eta$-spin and spin effective lattice, respectively. For the $D=2$ square lattice the number $N_a^2=N_a\times N_a$ is chosen so that the number $N_a$ of sites in a row or column is an integer. However, the designations $N_{a_{\eta }}^D$ and $N_{a_s}^D$ do not imply that the corresponding numbers $N_{a_{\eta }}$ and $N_{a_s}$ are integers. In general they are not integers. For finite values of x and $(1-x)$ and $N_a^D\to \infty$ we use for the numbers $N_{a_{\eta }}$ and $N_{a_s}$ of sites in a row and column of the $\eta$-spin and spin effective square lattices, respectively, the corresponding closest integer numbers.

Importantly, the numbers given in Equation (20) are fully controlled by the eigenvalue $2S_c$ of the generator Equation (4) of the hidden global $U(1)$ symmetry. This confirms the important role played by such a symmetry in the present general description. The degrees of freedom of the rotated-electron occupancy configurations of each of the sets of $N_{a_{\eta }}^D=[N_a^D-2S_c]$ and $N_{a_s}^D=2S_c$ sites of the original lattice that generate the $S_{\eta }$, $S_{\eta }^{x_3}$, $S_s$, $S_s^{x_3}$, $S_c$, and momentum eigenstates studied in Reference [9], which refer to state representations of the model global $SO(3)\times SO(3)\times U(1)$ symmetry, naturally separate as follows:

(i)

The occupancy configurations of the c fermions associated with the operators $f_{{\overrightarrow{r}}_j,c}^{†}={(f_{{\overrightarrow{r}}_j,c})}^{†}$ of Equation (11) where $j=1,\dots ,N_a^D$ correspond to the state representations of the hidden global $U(1)$ symmetry found in Reference [6]. Such c fermions live on the c effective lattice. It is identical to the original lattice. Its occupancies are related to those of the rotated electrons: The number of c fermion occupied and unoccupied sites is given by $N_c=N_{a_s}^D=2S_c$ and $N_c^h=N_{a_{\eta }}^D=[N_a^D-2S_c]$, respectively. Indeed, the c fermions occupy the sites singly occupied by the rotated electrons. In turn, the rotated-electron doubly-occupied and unoccupied sites are those unoccupied by the c fermions. Hence the c fermion occupancy configurations describe the relative positions in the original lattice of the $N_{a_{\eta }}^D=[N_a^D-2S_c]$ sites of the η-spin effective lattice and $N_{a_s}^D=2S_c$ sites of the spin effective lattice.

(ii)

The remaining degrees of freedom of rotated-electron occupancies of the sets of $N_{a_{\eta }}^D=[N_a^D-2S_c]$ and $N_{a_s}^D=2S_c$ original-lattice sites correspond to the occupancy configurations associated with the $\eta$-spin $SU(2)$ symmetry and spin $SU(2)$ symmetry state representations, respectively. The occupancy configurations of the set of $N_{a_{\eta }}^D=[N_a^D-2S_c]$ sites of the $\eta$-spin effective lattice and set of $N_{a_s}^D=2S_c$ sites of the spin effective lattice are independent. The former configurations refer to the operators $p_{{\overrightarrow{r}}_j}^l$ of Equation (12), which act only onto the $N_{a_{\eta }}^D=[N_a^D-2S_c]$ sites of the $\eta$-spin effective lattice. The latter configurations correspond to the operators $s_{{\overrightarrow{r}}_j}^l$ given in the same equation, which act onto the $N_{a_s}^D=2S_c$ sites of the spin effective lattice. This is assured by the operators $(1-n_{{\overrightarrow{r}}_j,c})$ and $n_{{\overrightarrow{r}}_j,c}$ in their expressions provided in that equation, which play the role of projectors onto the $\eta$-spin and spin effective lattice, respectively.

For $U/4t>0$ the degrees of freedom of each rotated-electron singly occupied site then separate into a spin-less c fermion carrying the electronic charge and a spin-down or spin-up spinon. Furthermore, the degrees of freedom of each rotated-electron doubly-occupied or unoccupied site separate into a $\eta$-spin-less c fermion hole and a $\eta$-spin-down or $\eta$-spin-up $\eta$-spinon, respectively. The $\eta$-spin-down or $\eta$-spin-up $\eta$-spinon refers to the $\eta$-spin degrees of freedom of a rotated-electron doubly-occupied or unoccupied site, respectively, of the original lattice.

Hence a key feature of the operational description reviewed in this paper is that for $U/4t>0$ its quantum objects correspond to rotated-electron configurations whose numbers of spin-down and spin-up single occupied sites, double occupied sites, and unoccupied sites are good quantum numbers. This is in contrast to descriptions in terms of electron configurations, whose numbers of spin-down and spin-up single occupied sites, double occupied sites, and unoccupied sites are good quantum numbers only for $U/4t\gg 1$ [19].

The transformation laws under the electron-rotated-electron unitary transformation of the $\eta$-spinons (and spinons) play a major role in the description of the $\eta$-spin (and spin) $SU(2)$ state representations in terms of the occupancy configurations of the $N_{a_{\eta }}^D=[N_a^D-2S_c]$ sites of the $\eta$-spin effective lattice (and set of $N_{a_s}^D=2S_c$ sites of the spin effective lattice). Indeed, a well-defined number of $\eta$-spinons (and spinons) remain invariant under that unitary transformation. Those are called deconfined $\pm 1/2$ $\eta$-spinons (and deconfined $\pm 1/2$ spinons). As further discussed below, they play the role of unoccupied sites of the $\eta$-spin (and spin) effective lattice. The values of the numbers $M_{\eta ,\pm 1/2}^{de}$ of deconfined $\pm 1/2$ $\eta$-spinons and $M_{s,\pm 1/2}^{de}$ of deconfined $\pm 1/2$ spinons are fully controlled by the $\eta$-spin $S_{\eta }$ and $\eta$-spin projection $S_{\eta }^{x_3}=-\frac{x}{2}{N}_a^D$ and spin $S_s$ and spin projection $S_s^{x_3}=-\frac{m}{2}{N}_a^D$, respectively, of the state under consideration as follows,

$$M_{\alpha }^{de}=[M_{\alpha ,-1/2}^{de}+M_{\alpha ,+1/2}^{de}]=2S_{\alpha };M_{\alpha ,\pm 1/2}^{de}=[S_{\alpha }\mp S_{\alpha }^{x_3}];\alpha =\eta ,s$$

(21)

The invariance of such deconfined $\eta$-spinons (and deconfined spinons) stems from the off diagonal generators of the $\eta$-spin (and spin) algebra, which flip their $\eta$-spin (and spin), commuting with the unitary operator $\widehat{V}$. This justifies why such generators have for $U/4t>0$ the same expressions in terms of electron and rotated-electron operators, as given in Equation (8).

It follows that the number of sites of the $\eta$-spin ($\alpha =\eta$) and spin ($\alpha =s$) effective lattice can be written as,

$$N_{a_{\alpha }}^D=[2S_{\alpha }+M_{\alpha }^{co}]=[M_{\alpha }^{de}+M_{\alpha }^{co}]=M_{\alpha };\alpha =\eta ,s$$

(22)

As justified below, here $M_{\alpha }^{co}$ is the confined $\eta$-spinon ($\alpha =\eta$) or confined spinon ($\alpha =s$) even number. The $\eta$-spin or spin degrees of freedom of the occupancy configurations in a set of $2S_{\alpha }=M_{\alpha }^{de}$ sites out of the whole set of $N_{a_{\alpha }}^D$ sites have for $U/4t>0$ the same form in terms of electrons and rotated electrons. In turn, for finite values of $U/4t$ and spin density $-(1-x)<m<(1-x)$ the corresponding c fermion occupancy configurations that store the information on the relative positions in the original lattice of the $N_{a_s}^D$ sites of the spin effective lattice and $N_{a_{\eta }}^D=[N_a^D-N_{a_s}^D]$ sites of the $\eta$-spin effective lattice are not invariant under the electron-rotated-electron unitary transformation.

Such an invariance of the $\eta$-spin degrees of freedom of the above occupancy configurations implies that in each state representation there are exactly $2S_{\eta }=[M_{\eta ,-1/2}^{de}+M_{\eta ,+1/2}^{de}]=M_{\eta }^{de}$ sites such that $M_{\eta ,-1/2}^{de}$ sites are doubly occupied and $M_{\eta ,+1/2}^{de}$ sites are unoccupied both by electrons and rotated electrons. Furthermore, the invariance of the spin degrees of freedom of the sites singly occupied by rotated electrons implies that there are exactly $2S_s=[M_{s,-1/2}^{de}+M_{s,+1/2}^{de}]=M_s^{de}$ sites of the original lattice such that $M_{s,-1/2}^{de}$ sites are singly occupied both for spin-down electrons and spin-down rotated electrons and $M_{s,+1/2}^{de}$ sites are singly occupied both for spin-up electrons and spin-up rotated electrons. The state representation is in general a superposition of such occupancy configurations whose positions of the $[2S_{\eta }+2S_s]=[M_{\eta }^{de}+M_s^{de}]$ sites are different.

In turn, out of the set of $[M_{\eta }^{co}+M_s^{co}]$ sites of the original lattice left over, a set of $M_{\eta }^{co}/2$ sites are unoccupied by rotated electrons, a set of $M_{\eta }^{co}/2$ sites are doubly occupied by rotated electrons, a set of $M_s^{co}/2$ sites are singly occupied by spin-up rotated electrons, and a set of $M_s^{co}/2$ sites are singly occupied by spin-down rotated electrons. However, in terms of electrons that set of $[M_{\eta }^{co}+M_s^{co}]$ sites of the original lattice has for finite $U/4t$ values very involved occupancies. Indeed for electrons and except for $U/4t\to \infty$ singly and doubly occupancy are not good quantum numbers and thus are not conserved. The important point brought about by the present description is that due to the transformation laws under the electron-rotated-electron unitary transformation this refers only to a sub-set of $[M_{\eta }^{co}+M_s^{co}]$ sites out of the $N_a^D$ sites of the original lattice. Indeed for the remaining $[2S_{\eta }+2S_s]=[M_{\eta }^{de}+M_s^{de}]$ sites singly and doubly occupancy are good quantum numbers both for electrons and rotated electrons.

The site numbers $M_{\eta }^{co}\ge 0$ and $M_s^{co}\ge 0$ are good quantum numbers given by,

$$M_{\eta }^{co}=[N_{a_{\eta }}^D-2S_{\eta }]=[N_a^D-2S_c-2S_{\eta }];M_s^{co}=[N_{a_s}^D-2S_s]=[2S_c-2S_s]$$

(23)

Hence their values are fully determined by those of the eigenvalue $2S_c$ of the hidden global $U(1)$ symmetry generator and $\eta$-spin $S_{\eta }$ or spin $S_s$, respectively. This reveals that $M_{\eta }^{co}$ and $M_s^{co}$ are not independent quantum numbers.

The physics behind the hidden $U(1)$ symmetry found in Reference [6] includes that brought about by the rotated-electron occupancy configurations of the set of $[M_{\eta }^{co}+M_s^{co}]$ sites of Equation (23). The use of the corresponding model global $SO(3)\times SO(3)\times U(1)$ symmetry reveals that the numbers $M_{\alpha }^{co}=0$, 2, 4, … are always even integers. Moreover, the application onto $S_{\alpha }=0$ states of the off-diagonal generators of the $\eta$-spin $(\alpha =\eta )$ or spin $(\alpha =s)$ algebra provided in Equation (8) gives zero. For such states $N_{a_{\alpha }}^D=M_{\alpha }^{co}$. In turn, application of these generators onto $S_{\alpha }>0$ states flips the $\eta$-spin ($\alpha =\eta$) or spin ($\alpha =s$) of a deconfined $\eta$-spinon ($\alpha =\eta$) or deconfined spinon ($\alpha =s$) but leaves invariant the rotated-electron occupancy configurations of the above considered set of $M_{\alpha }^{co}$ sites. It follows that such set of $M_{\eta }^{co}$ (and $M_s^{co}$) sites refers to $\eta$-spin-singlet (and spin-singlet) configurations involving $M_{\eta }^{co}/2$ (and $M_s^{co}/2$) $-1/2$ $\eta$-spinons (and $-1/2$ spinons) and an equal number of $+1/2$ $\eta$-spinons (and $+1/2$ spinons).

It follows from the above discussions that the total numbers of $\eta$-spinons ($\alpha =\eta$) and spinons ($\alpha =s$) read,

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill M_{\alpha }& =N_{a_{\alpha }}^D=[M_{\alpha }^{de}+M_{\alpha }^{co}]=[M_{\alpha ,-1/2}^{de}+M_{\alpha ,+1/2}^{de}+M_{\alpha }^{co}]\hfill \\ \hfill M_{\alpha ,\pm 1/2}& =[M_{\alpha ,\pm 1/2}^{de}+M_{\alpha }^{co}/2];\alpha =\eta ,s\hfill \\ \hfill M_{\eta }& =N_{a_{\eta }}^D=[N_a^D-2S_c];M_s=N_{a_s}^D=2S_c\hfill \end{array}\end{array}$$

(24)

The $\eta$-spinon and spinon operator algebra refers to well-defined subspaces spanned by states whose number of each of these basic objects is conserved and given in Equations (21), (23), and (24). Hence in such subspaces the number $2S_c$ of rotated-electron singly occupied sites and the numbers $N_{a_{\eta }}^D$ and $N_{a_s}^D$ of sites of the $\eta$-spin and spin effective lattices, respectively, are fixed. For hole concentrations $0\le x<1$ and maximum spin density $m=(1-x)$ (or $m=-(1-x)$) reached at some critical magnetic field $H_c$ aligned parallel to the square-lattice plane for $D=2$ and pointing along the chain for $D=1$ the c fermion operators are invariant under the electron-rotated-electron unitary transformation. There is a corresponding fully polarized vacuum $|0_{\eta s}\rangle$ that remains invariant under such a transformation. It reads,

$$|0_{\eta s}\rangle =|0_{\eta };N_{a_{\eta }}^D\rangle \times |0_s;N_{a_s}^D\rangle \times |G{S}_c;2S_c\rangle$$

(25)

Here the $\eta$-spin $SU(2)$ vacuum $|0_{\eta };N_{a_{\eta }}^D\rangle$ associated with $N_{a_{\eta }}^D$ deconfined $+1/2$ $\eta$-spinons, the spin $SU(2)$ vacuum $|0_s;N_{a_s}^D\rangle$ with $N_{a_s}^D$ deconfined $+1/2$ spinons, and the c$U(1)$ vacuum $|G{S}_c;2S_c\rangle$ with $N_c=2S_c$c fermions remain invariant under the electron-rotated-electron unitary transformation. The latter vacuum may be expressed as ${\prod }_{\overrightarrow{q}}{f}_{\overrightarrow{q},c}^{†}|G{S}_c;0\rangle$. Here the vacuum $|G{S}_c;0\rangle$ corresponds to the electron and rotated-electron vacuum. Its form is that given in Equation (25) with $N_{a_{\eta }}^D=N_a^D$ and $N_{a_s}^D=2S_c=0$.

For $U/4t>0$ only for a $m=(1-x)$ fully polarized state are the occupancy configurations of the state $|G{S}_c;2S_c\rangle$ and the corresponding $N_c=2S_c$ c fermions invariant under the electron-rotated-electron unitary transformation. For the corresponding vacuum $|0_{\eta };N_{a_{\eta }}^D\rangle$ (and $|0_s;N_{a_s}^D\rangle$), the $M_{\eta }=M_{\eta ,+1/2}^{de}$ deconfined $+1/2$ $\eta$-spinons refer to $N_{a_{\eta }}^D=M_{\eta ,+1/2}^{de}$ sites of the original lattice unoccupied by rotated electrons (and the $M_s=M_{s,+1/2}^{de}$ deconfined $+1/2$ spinons to the spins of $N_{a_s}^D=M_{s,+1/2}^{de}$ spin-up rotated electrons that singly occupy sites of such a lattice). At maximum spin density $m=(1-x)$ the c fermions are the non-interacting spinless fermions that describe the charge degrees of freedom of the electrons of the fully polarized ground state. At that spin density there are no electron doubly occupied sites and the quantum problem is non-interacting for $U/4t>0$.

Below we confirm that within the present description, out of the $N_{a_{\alpha }}^D=M_{\alpha }=[M_{\alpha }^{de}+M_{\alpha }^{co}]=[2S_{\alpha }+M_{\alpha }^{co}]$ sites of the $\eta$-spin ($\alpha =\eta$) and spin ($\alpha =s$) effective lattice, the $2S_{\alpha }=M_{\alpha }^{de}$ sites whose occupancies $\eta$-spin ($\alpha =\eta$) and spin ($\alpha =s$) degrees of freedom are invariant under electron-rotated-electron unitary transformation play the role of unoccupied sites. In turn, the remaining $M_{\alpha }^{co}$ sites play the role of occupied sites. This is a natural consequence of the $\eta$-spin $SU(2)$ vacuum $|0_{\eta };N_{a_{\eta }}^D\rangle$ (and spin $SU(2)$ vacuum $|0_s;N_{a_s}^D\rangle$) being for all $U/4t$ and m values invariant under the electron-rotated-electron unitary transformation. Indeed that vacuum is such that $N_{a_{\eta }}^D=2S_{\eta }=M_{\eta }^{de}$ (and $N_{a_s}^D=2S_s=M_s^{de}$), so that $M_{\eta }^{co}=0$ (and $M_s^{co}=0$.)

3.3. Important Energy Scales

For processes associated with one- and two-electron excitations the large-$U/4t$ energy scale U is for finite $U/4t$ values and $x\ne 0$ replaced by twice the absolute value of chemical potential, $2|\mu |$. This is because for $x\in (0,1)$ (and $x\in (-1,0)$) and finite $U/4t$ values the minimum energy for creation onto the ground state of a rotated-electron doubly occupied site (and unoccupied site) is given by $2|\mu |$. In turn, at $x=0$ the chemical potential $\mu$ belongs to the range $\mu \in (-{\mu }^0,{\mu }^0)$ whose energy width $2{\mu }^0\equiv {lim}_{x\to 0}2\mu$ equals the Mott–Hubbard gap. We use the convention that for $x\ne 0$ the chemical potential $\mu$ sign is that of the hole concentration $x\in (-1,1)$. For spin densities $m\ne 0$ we consider that the corresponding magnetic field points in directions such that $H>0$ for spin density $m>0$ and $H<0$ for $m<0$. The minimum magnitude of the energy ${\mathsf{\Delta }}_{D_{rot}}$ for creation of a number $D_{rot}=M_{\eta ,-1/2}=M_{\eta ,-1/2}^{de}+M_{\eta }^{co}/2$ of rotated-electron doubly occupied sites onto a $m=0$ and $x=0$ ground state and a $m=0$ and $x>0$ ground state is,

$$\begin{array}{c}\hfill \begin{array}{cccc}\hfill \min {\mathsf{\Delta }}_{D_{rot}}& =\left[({\mu }^0+\mu )M_{\eta ,-1/2}^{de}+{\mu }^0{M}_{\eta }^{co}\right],\hfill & \hfill \mathrm{at}& x=0\mathrm{and}\mu \in (-{\mu }^0,{\mu }^0)\hfill \\ & =2\mu [M_{\eta ,-1/2}^{de}+M_{\eta }^{co}/2],\hfill & \hfill \mathrm{for}& x>0\hfill \end{array}\end{array}$$

(26)

respectively. Similar expressions apply to the minimum magnitude of the energy ${\mathsf{\Delta }}_{D_{rot}^h}$ for creation of a number $D_{rot}^h=M_{\eta ,+1/2}=M_{\eta ,+1/2}^{de}+M_{\eta }^{co}/2$ of rotated-electron unoccupied sites onto a $m=0$ and $x=0$ ground state and a $m=0$ and $x<0$ ground state, respectively, provided that $\mu$ is replaced by $-\mu$ and $M_{\eta ,-1/2}^{de}$ by $M_{\eta ,+1/2}^{de}$. Hence for $\mu \in (-{\mu }^0,{\mu }^0)$ the minimum energy for creation onto the $m=0$ and $x=0$ ground state of one rotated-electron doubly occupied site and rotated-electron unoccupied site is $({\mu }^0+\mu )$ and $({\mu }^0-\mu )$, respectively. For the chemical potential in the middle of the Mott–Hubbard gap so that $\mu =0$ at $x=0$ the minimum energy of either process is given by ${\mu }^0$.

For the model on the 1D (and square) lattice at $m=0$ the important $x=0$ energy scale $2{\mu }^0$ appearing in Equation (26), which is the Mott–Hubbard gap, has the following exact (and approximate) limiting behaviors,

$$2{\mu }^0\approx \frac{U}{{\pi }^2}{\left(\frac{{[8\pi ]}^{2}t}{U}\right)}^{D/2}{e}^{-2\pi {\left(\frac{t}{U}\right)}^{1/D}},U/4t\ll 1;2{\mu }^0\approx [U-4Dt],U/4t\gg 1,D=1,2$$

(27)

These half-filling results are consistent with the properties of the $x=0$ and $m=0$ absolute ground state [10]. In turn, for $0<x<1$ and $m=0$ the chemical potential reads $\mu \approx U/2$ for $U/4t\to \infty$ and for finite $U/4t$ values is an increasing function of the hole concentration x such that,

$${\mu }^0\le \mu (x)\le {\mu }^1;0<x<1,m=0$$

(28)

Here ${\mu }^1\equiv {lim}_{x\to 1}\mu$. The related energy scale $2{\mu }^1$ reads,

$$2{\mu }^1=U+4Dt;D=1,2$$

(29)

The expression given in Equation (29) is exact both for the Hubbard model on a 1D and square lattice. It can be explicitly derived for both lattices. It refers to the non-interacting limit of vanishing electronic density. For the model on the square lattice the limiting behaviors reported in Equation (27) read $2{\mu }^0\approx 64t{e}^{-2\pi \sqrt{t/U}}$ and $2{\mu }^0\approx U$ for $U/4t\ll 1$ and $U/4t\gg 1$, respectively. They are those of the related zero-temperature gap of Equation (13) of Reference [20], which although showing up in the spin degrees of freedom equals half the charge Mott–Hubbard gap [10].

3.4. Spacing and Occupied and Unoccupied Sites of the $\eta$-Spin and Spin Effective Lattices

One may consider a configuration in which a original-lattice compact square domain of $N_{a_s}^D=2S_c=[2S_s+M_s^{co}]=N_c$ sites whose edge contains $N_{a_s}$ sites is singly occupied by rotated electrons, and the complementary two-dimensional (2D) compact domain of $N_{a_{\eta }}^2=[N_a^2-2S_c]=[2S_{\eta }+M_{\eta }^{co}]=N_c^h$ sites refers to rotated-electron unoccupied or doubly occupied sites. Obviously, in 2D there are many other shapes for compact domains of $N_{a_{\eta }}^2=[N_a^2-2S_c]=[2S_{\eta }+M_{\eta }^{co}]=N_c^h$ sites. The square shape will be justified below. In this configuration and considering processes of energy lower than $2|\mu |$, either the Pauli principle or the onsite repulsion prevents the rotated electrons to move (except for those on the lines referring to the square edges separating the two 2D domains). Although in this configuration there is no direct interaction between the rotated electrons, through an intermediate state with energy $2|\mu |$ neighboring rotated electrons can see each other’s spins, and rotated electrons with different spins can change position. Alike for 1D, the situation with the rotated-electron unoccupied and doubly occupied sites is similar for a original-lattice compact square domain of $N_{a_{\eta }}^2=[N_a^2-2S_c]=[2S_{\eta }+M_{\eta }^{co}]=N_c^h$ sites. Unfortunately and unlike for 1D, for a finite system the corresponding spinon and $\eta$-spinon distributions may change if the square-shape compact domain of rotated-electron singly occupied sites is “diluted” by rotated-electron unoccupied and doubly occupied sites. Indeed, for a 2D system there is no order equivalent to the 1D uniquely defined chain order.

However, within the $N_a^2\to \infty$ limit that the present description refers to the dominant c fermion occupancy configurations refer to an average uniform distribution of the c effective lattice occupied sites. In contrast to a finite system, configurations where for instance the c fermion occupied and unoccupied sites refer to two compact domains have vanishing weight as $N_a^2\to \infty$. Specifically, the c fermion positions of such a uniform configuration correspond to the average positions of the c fermions in an energy eigenstate. Indeed, the c fermion momentum occupancy configurations of such a state are a superposition of all compatible real-space c effective lattice occupancy configurations. Fortunately, for the average configuration in which the rotated-electron singly occupied sites are uniformly “diluted” by rotated-electron unoccupied and doubly occupied sites the spinon and $\eta$-spinon distributions of the above original-lattice square-shape compact domain of $N_{a_s}^2=2S_c=[2S_s+M_s^{co}]=N_c$ sites do not change. They may be described by corresponding occupancy configurations of an effective square lattice with $N_{a_s}^2=2S_c=[2S_s+M_s^{co}]=N_c$ sites and edge length L whose average spacing is for $x\ne 0$ larger than that of the original lattice. The same arguments apply to the $\eta$-spinon distributions. This reveals that for the Hubbard model on the square lattice with $N_a^2\to \infty$ sites the concepts of a spin effective square lattice and $\eta$-spin square effective lattice apply provided that $n=(1-x)$ and x are finite, respectively.

That the above considered initial reference original-lattice compact domain of $N_{a_s}^2=2S_c=[2S_s+M_s^{co}]=N_c$ (and $N_{a_{\eta }}^2=[N_a^2-2S_c]=[2S_{\eta }+M_{\eta }^{co}]=N_c^h$) sites has a square shape follows from only that compact domain shape transforming into a corresponding uniform “diluted” domain fully contained in the original square lattice. Any other initial reference compact-domain shape would transform into a uniform “diluted” domain that is not fully contained in the original square lattice and thus is neither physically nor mathematically acceptable. Here we are considering that the 2D crystal has a square shape whose edge is $L=a{N}_a$. If the square-lattice crystal has any other shape the compact domain should have a similar shape with an area reduced by a factor of $2S_c/N_a^2$ for the spin effective lattice (and of $[N_a^2-2S_c]/N_a^2$ for the $\eta$-spin effective lattice). Only then it transforms into a corresponding uniform “diluted” domain fully contained in the crystal. The final result is though the same, the obtained effective lattice being a square lattice whose spacing is given by,

$$a_{\alpha }=\frac{L}{N_{a_{\alpha }}}=\frac{N_a}{N_{a_{\alpha }}}a;\alpha =\eta ,s$$

(30)

where $N_{a_{\alpha }}={(N_{a_{\alpha }}^D)}^{1/D}$.

This spinon and $\eta$-spinon distributions “average invariance” under “site dilution” emerging for the square lattice in the $N_a^D\to \infty$ limit is behind the description of such distributions in terms of the occupancy configurations of independent $\eta$-spin and spin effective square lattices, respectively, and the direct propagation of c fermions in terms of occupancy configurations in an independent c effective lattice. While for $0<x<1$ and $0<m<n$ the former two lattices have both for 1D and 2D a number of sites smaller than $N_a^D$, the c effective lattice is identical to the original lattice.

Within the $N_a^D\gg 1$ limit of the present description the concept of a spin (and $\eta$-spin) effective lattice is well defined for finite values of the electronic density $n=(1-x)$ (and hole concentration x). The reasoning for the validity of the use of the corresponding effective lattices occupancy configurations may be summarized by the two following statements:

(1)

The representation associated with the present description contains full information about the relative positions of the sites of the $\eta$-spin and spin effective lattices in the original lattice. For each energy-eigenstate rotated-electron real-space occupancy configuration, that information is stored in the corresponding occupancy configurations of the c fermions in their c effective lattice. The latter lattice is identical to the original lattice. Such configurations correspond to the state representations of the $U(1)$ symmetry in the subspaces spanned by states with fixed values of $S_c$, $S_{\eta }$, and $S_s$. Indeed, the sites of the $\eta$-spin (and spin) effective lattice have in the original lattice the same real-space coordinates as the sites of the c effective lattice unoccupied (and occupied) by c fermions.

(2)

Within the $N_a^D\gg 1$ limit that the rotated-electron related operational description refers to, provided that the electronic density $n=(1-x)$ (and hole concentration x) is finite, the dominant c effective lattice occupancy configurations of an energy eigenstate of the Hubbard model on the square lattice refer to a nearly uniform distribution of the c fermions occupied sites (and unoccupied sites). Hence due to the spinon and $\eta$ spinon distribution “average order” emerging for the model on the square lattice in the $N_a^D\to \infty$ limit, the spin and $\eta$-spin effective lattices may be represented by square lattices. Moreover, the chain order invariance occurring for the 1D model both for the finite system and in that limit justifies why such effective lattices are 1D lattices. For both models the corresponding spin effective lattice spacing $a_s$ and $\eta$-spin effective lattice spacing $a_{\eta }$ refers to the average spacing between the c effective lattice occupied sites and between such a lattice unoccupied sites, respectively, given in Equation (30). Such spin and $\eta$-spin effective lattices obey the physical requirement condition that in the $x\to 0$ and $x\to \pm 1$ limit, respectively, equal the original lattice. Note that in the $x\to 0$ (and $x\to \pm 1$) limit one has that $N_{a_s}^D=N_a^D$ and the $\eta$-spin effective lattice does not exist (and $N_{a_{\eta }}^D=N_a^D$ and the spin effective lattice does not exist.)

The validity for $N_a^D\gg 1$ of the concept of a spin effective square lattice as constructed in this paper is confirmed by the behavior of the expectation value $\delta d=\langle \Psi |\delta \widehat{d}|\Psi \rangle$ of any energy eigenstate $|\Psi \rangle$. Here $\delta \widehat{d}$ is the operator associated with the distance in real space of any of the $N_{a_s}^D$ sites of the spin effective lattice from the rotated-electron singly occupied site of the original lattice closest to it. The state $|\Psi \rangle$ belongs to a subspace with fixed number of rotated-electron singly occupied sites. The point is that $\delta d=\langle \Psi |\delta \widehat{d}|\Psi \rangle$ vanishes in the $N_a^D\to \infty$ limit. We recall that the $N_{a_s}^D=2S_c$ sites of the spin effective lattice occupancies describe the spin degrees of freedom of the $N_c=2S_c$ rotated-electron singly occupied sites of the original lattice. The same applies to the $\eta$-spin effective lattice.

Consistently with the expression $a_{\alpha }=L/N_{a_{\alpha }}=[N_a/N_{a_{\alpha }}]a$ of Equation (30) where $\alpha =\eta ,s$, the $\eta$-spin (and spin) effective lattice has both for 1D and 2D the same length and edge length L, respectively, as the original lattice. Furthermore, the requirement that for the 2D case when going through the whole crystal of square shape along the $o{x}_1$ or $o{x}_2$ directions a $\eta$-spinon (and spinon) passes an overall distance L is met by an effective $\eta$-spin (and spin) square lattice. Since the number of sites sum-rule $[N_{a_{\eta }}^D+N_{a_s}^D]=N_a^D$ holds, the $\eta$-spin and spin effective lattices have in general a number of sites $N_{a_{\eta }}^D$ and $N_{a_s}^D$, respectively, smaller than that of the original lattice, $N_a^D$. It follows that their lattice spacings Equation (30) are larger than that of the original lattice.

4. The Composite $\alpha \nu$ Fermions

The global $SO(3)\times SO(3)\times U(1)$ symmetry of the model on any bipartite lattice implies that some features of the corresponding state representations are common to all such lattices. Our extension of the 1D model $M_s^{co}=[2S_c-2S_s]$-site spin-neutral and $M_{\eta }^{co}=[N_a^D-2S_c-2S_{\eta }]$-site $\eta$-spin-neutral rotated-electron occupancy configurations in terms of those of composite $s\nu$ fermions and $\eta \nu$ fermions, respectively, to the model on the square lattice accounts for the basic differences between the physics of the two models.

4.1. The $M_{\eta }^{co}$-$\eta$-Spinon and $M_s^{co}$-Spinon Configuration Partitions

Within the rotated-electron occupancy configurations that generate the exact energy eigenstates $|{\Psi }_{U/4t}\rangle ={\widehat{V}}^{†}|{\Psi }_{\infty }\rangle$ considered above, there are $[M_{\eta }^{co}+M_s^{co}]$ sites out of the $N_a^D$ sites of the original lattice whose rotated-electron occupancy configurations are not invariant under the electron-rotated-electron unitary transformation. The $\eta$-spin (and spin) degrees of freedom of $M_{\eta }^{co}$ (and $M_s^{co}$) of such sites refer to $\eta$-spin-neutral (and spin-neutral) configurations involving $M_{\eta }^{co}/2$ $+1/2$ $\eta$-spinons (and $M_s^{co}/2+1/2$ spinons) and an equal number $M_{\eta }^{co}/2$ of $-1/2$ $\eta$-spinons (and $M_s^{co}/2$ of $-1/2$ spinons).

This holds as well for the related momentum eigenstates $|{\mathsf{\Phi }}_{U/4t}\rangle ={\widehat{V}}^{†}|{\mathsf{\Phi }}_{\infty }\rangle$ considered in Reference [9]. For the model on the square lattice, the latter states refer in general to a partition different from that of the energy eigenstates $|{\Psi }_{U/4t}\rangle ={\widehat{V}}^{†}|{\Psi }_{\infty }\rangle$ of the $\eta$-spin-neutral (and spin-neutral) configurations of such $M_{\eta }^{co}$ (and $M_s^{co}$) $\eta$-spinons (and spinons), in terms of smaller configurations. Specifically, for a given momentum eigenstate there is for each branch involving $\nu =1,2,\dots$ pairs of $\eta$-spinons (and spinons) a well-defined number $N_{\eta \nu }$ of $\eta$-spin-neutral $2\nu$-$\eta$-spinon composite $\eta \nu$ fermions (and $N_{s\nu }$ of spin-neutral $2\nu$-spinon composite $s\nu$ fermions). The set of such composite objects describes the $\eta$-spinon (and spinon) occupancy configurations of exactly $M_{\eta }^{co}$ (and $M_s^{co}$) sites of the original lattice. Hence the following two sum rules hold for all momentum eigenstates,

$$\begin{array}{c}\hfill M_{\alpha }^{co}=[M_{\alpha }-2S_{\alpha }]=2\sum _{\nu =1}^{\infty }\nu N_{\alpha \nu };\alpha =\eta ,s\end{array}$$

(31)

Such sum rules refer to subspaces spanned by states with fixed values of $S_c$, $S_{\eta }$, and $S_s$.

One $\eta$-spin neutral $2\nu$-$\eta$-spinon composite $\eta \nu$ fermion describes the $\eta$-spin degrees of freedom of a $\eta$-spin-singlet occupancy configuration involving $\nu \le M_{\eta }^{co}/2$ sites of the original lattice unoccupied by rotated electrons and an equal number of sites doubly occupied by rotated electrons. The remaining degrees of freedom of such a rotated-electron occupancy configuration are described by $2\nu$ unoccupied sites of the c effective lattice whose spatial coordinates are those of the corresponding $2\nu$ sites of the original lattice.

Similarly, one spin neutral $2\nu$-spinon composite $s\nu$ fermion describes the spin degrees of freedom of a spin-singlet occupancy configuration involving $\nu \le M_s^{co}/2$ sites of the original lattice singly occupied by spin-up rotated electrons and an equal number of sites singly occupied by spin-down rotated electrons. The remaining degrees of freedom of that rotated-electron occupancy configuration are described by $2\nu$ occupied sites of the c effective lattice whose spatial coordinates are those of the corresponding $2\nu$ sites of the original lattice.

For each $\eta \nu$ fermion branch (and $s\nu$ fermion branch), one may consider a $\eta \nu$ effective lattice (and $s\nu$ effective lattice). It refers to occupancy configurations of $\eta$-spin-neutral (and spin-neutral) bonds of $2\nu$ confined $\eta$-spinons (and spinons). Hence each “occupied site” of such an effective lattice corresponds to $2\nu$ sites of the $\eta$-spin (and spin) effective lattice. In turn, the $M_{\eta }^{de}=2S_{\eta }$ (and $M_s^{de}=2S_s$) $\eta$-spin (and spin) effective lattice sites referring to the deconfined $\eta$-spinons (and deconfined spinons) and some of such a lattice sites referring to $2{\nu }^{\prime }$-$\eta$-spinon composite $\eta {\nu }^{\prime }$ fermions (and $2{\nu }^{\prime }$-spinon composite $s{\nu }^{\prime }$ fermions) of ${\nu }^{\prime }>\nu$ branches are found below to play the role of “unoccupied sites” of such a $\eta \nu$ effective lattice (and $s\nu$ effective lattice). The conjugate of the $\alpha \nu$ effective lattice site space variables are the $\alpha \nu$ band discrete momentum values. Their number equals that of the $\alpha \nu$ effective lattice sites. (For 1D, such a momentum values are good quantum numbers.)

Within chromodynamics the quarks have color but all quark-composite physical particles are color-neutral [21]. Here the $\eta$-spinon (and spinons) that are not invariant under the electron-rotated-electron unitary transformation have $\eta$-spin $1/2$ (and spin $1/2$) but are confined within $\eta$-spin-neutral (and spin-neutral) $2\nu$-$\eta$-spinon (and $2\nu$-spinon) composite $\eta \nu$ fermions (and $s\nu$ fermions). The exact and detailed internal $2\nu$-spinon configuration and $2\nu$-$\eta$-spinon configuration of a composite $s\nu$ fermion and $\eta \nu$ fermion, respectively, is in general an involved unsolved problem. (In 1D the exact BA solution takes implicitly into account such internal configurations.) Fortunately, however, the problem simplifies for the model in the one- and two-electron subspace reviewed below for which the only composite object that plays an active role is the two-spinon $s1$ fermion. Its internal structure is an issue studied in Reference [9]. Such a two-spinon object is related to the resonating-valence-bond pictures for spin-singlet occupancy configurations of ground states [22,23].

In the following we consider all multi-$\eta$-spinon and multi-spinon composite objects. Full information on the $2\nu$-$\eta$-spinon $(\alpha =\eta )$ or $2\nu$-spinon $(\alpha =s)$ configurations associated with the internal degrees of freedom of the composite $\alpha \nu$ fermions is not needed for the goals of this paper. Indeed, within the present $N_a^D\gg 1$ limit the problem of the internal degrees of freedom of the composite $\alpha \nu$ fermions and $\alpha \nu$ bond particles separates from that of their positions in the corresponding effective lattices. The partial information on the internal degrees of freedom of the composite $\alpha \nu$ fermions needed for the studies reported in this paper is accessed in the following by suitable use of their transformation laws under the electron-rotated-electron unitary transformation. In turn, the deconfined $\eta$-spinons and deconfined spinons are invariant under that transformation. Thus they are non-interacting deconfined objects that are not part of composite $\eta \nu$ fermions and composite $s\nu$ fermions, respectively.

4.2. The $\alpha \nu$ Fermion Operators

For the $\alpha \nu$ effective lattice, one local $\alpha \nu$ fermion “occupied site” refers to $2\nu$ sites of the $\eta$-spin ($\alpha =\eta$) or spin ($\alpha =s$) effective lattice. Alike for the corresponding latter lattice, the $2S_{\alpha }$ sites occupied by deconfined $\eta$-spinons ($\alpha =\eta$) or deconfined spinons ($\alpha =s$) are among those playing the role of the $\alpha \nu$ effective lattice “unoccupied sites”. Unlike for the former lattice, it is found below that a number $2({\nu }^{\prime }-\nu )$ of sites of each $\alpha {\nu }^{\prime }$ fermion with a number ${\nu }^{\prime }>\nu$ of confined $\eta$-spinons ($\alpha =\eta$) or confined spinons ($\alpha =s$) play as well the role of $\alpha \nu$ effective lattice “unoccupied sites”.

The conjugate variables of the $\alpha \nu$ effective lattice real-space coordinates are the discrete momentum values of the $\alpha \nu$ band. As shown in Reference [9], for the 1D model such discrete momentum values are the quantum numbers of the exact BA solution. For the Hubbard model on the square lattice the $s1$ band momentum discrete values of state representations belonging to the one- and two-electron subspace reviewed below are good quantum numbers as well.

As reported in Reference [10] for the $s1$ fermion operators, the $\alpha \nu$ fermion operators can be generated from the operators of corresponding hard-core $\alpha \nu$ bond-particle operators as follows,

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill f_{{\overrightarrow{r}}_j,\alpha \nu }^{†}& =e^{i{\varphi }_{j,\alpha \nu }}{g}_{{\overrightarrow{r}}_j,\alpha \nu }^{†};{\varphi }_{j,\alpha \nu }={\displaystyle \sum _{j^{\prime }\ne j}}{f}_{{\overrightarrow{r}}_{j^{\prime }},\alpha \nu }^{†}{f}_{{\overrightarrow{r}}_{j^{\prime }},\alpha \nu }{\varphi }_{j^{\prime },j,\alpha \nu };{\varphi }_{j^{\prime },j,\alpha \nu }=arctan\left(\frac{{x_{j^{\prime }}}_2-{x_j}_2}{{x_{j^{\prime }}}_1-{x_j}_1}\right)\hfill \\ \hfill f_{{\overrightarrow{q}}_j,\alpha \nu }^{†}& =\frac{1}{\sqrt{N_{a_{\alpha \nu }}^D}}\sum _{j^{\prime }=1}^{N_{a_{\alpha \nu }}^D}{e}^{+i{\overrightarrow{q}}_j·{\overrightarrow{r}}_{j^{\prime }}}{f}_{{\overrightarrow{r}}_{j^{\prime }},\alpha \nu }^{†}\hfill \end{array}\end{array}$$

(32)

Such expressions are valid provided that $(1-x)>0$ for the $\alpha \nu =s1$ branch and $S_{\alpha }/N_a^D>0$ for the remaining $\alpha \nu \ne s1$ branches. Explicit expressions for the operators $f_{{\overrightarrow{r}}_j,s1}^{†}$ and $g_{{\overrightarrow{r}}_j,s1}^{†}$ are given in Reference [9]. The quantity ${\varphi }_{j,\alpha \nu }$ appearing in Equation (32) is the Jordan–Wigner phase [10,24] operator, the indices $j^{\prime }$ and j refer to sites of the $\alpha \nu$ effective lattice, and $f_{{\overrightarrow{q}}_j,\alpha \nu }^{†}$ are the corresponding momentum-dependent $\alpha \nu$ fermion operators. The number $N_{a_{\alpha \nu }}^D$ of discrete momentum values of the $\alpha \nu$ momentum band equals that of sites of the $\alpha \nu$ effective lattice. Its expression is derived below.

The $\eta$-spin-neutral $2\nu$-$\eta$-spinon composite $\eta \nu$ bond-particle operators and spin-neutral $2\nu$-spinon composite $s\nu$ bond-particle operators denoted in Equation (32) by $g_{{\overrightarrow{r}}_j,\alpha \nu }^{†}$ where $\alpha =\eta ,s$ are constructed to inherently upon acting onto their $\alpha \nu$ effective lattice anticommuting on the same site and commuting on different sites. Hence they are hard-core like and can be transformed into fermionic operators, as given in that equation. For $\nu >1$ the algebra behind their construction in terms of the elementary $\eta$-spinon or spinon operators of Equations (12) and (13) is much more cumbersome than that of the two-spinon $s1$ bond particles studied in Reference [9]. Fortunately, the only property needed for the goals of this paper is that upon acting onto their $\alpha \nu$ effective lattice they are hard-core like.

The expressions given in Equation (32) apply to $\alpha \nu \ne s1$ branches provided that $S_{\alpha }/N_a^D>0$. One can also handle the problem when $S_{\alpha }=0$ and $N_{\alpha \nu }/N_a^D\ll 1$ for a given $\alpha \nu \ne s1$ branch. Then provided that $N_{\alpha {\nu }^{\prime }}=0$ for all remaining $\alpha {\nu }^{\prime }$ branches with a number of $\eta$-spinon or spinon pairs ${\nu }^{\prime }>\nu$ one finds below that $N_{a_{\alpha \nu }}^D=N_{\alpha \nu }$. The momentum of the operators $f_{{\overrightarrow{q}}_j,\alpha \nu }^{†}$ is in that limiting case given by ${\overrightarrow{q}}_j\approx 0$. For the states that span the corresponding $S_{\alpha }=0$ and $N_{\alpha \nu }/N_a^D\ll 1$ subspace all sites of the $\alpha \nu$ effective lattice are occupied and the $\alpha \nu$ momentum band is full. If $N_{\alpha \nu }$ is finite one has $N_{a_{\alpha \nu }}^D=N_{\alpha \nu }$ discrete momentum values ${\overrightarrow{q}}_j\approx 0$ compactly distributed around zero momentum. Their Cartesian components momentum spacing is $2\pi /L$. A case of interest is when $S_{\alpha }=0$ and $N_{\alpha \nu }=1$. Then the $\alpha \nu$ effective lattice has a single site and the corresponding $\alpha \nu$ band a single discrete momentum value, $\overrightarrow{q}=0$. In that case ${\varphi }_{\alpha \nu }={\varphi }_{j,\alpha \nu }=0$. Hence $f_{\overrightarrow{r},\alpha \nu }^{†}=g_{\overrightarrow{r},\alpha \nu }^{†}$ and $f_{\overrightarrow{q},\alpha \nu }^{†}=f_{\overrightarrow{r},\alpha \nu }^{†}$ where $\overrightarrow{q}=0$.

The operators $f_{{\overrightarrow{q}}_j,\alpha \nu }^{†}$ act onto subspaces with fixed values for the set of numbers $S_{\alpha }$, $N_{\alpha \nu }$, and $\{N_{\alpha {\nu }^{\prime }}\}$ for ${\nu }^{\prime }>\nu$ branches. (Below it is shown that this is equivalent to fixed values for the set of numbers $S_c$ and $\{N_{\alpha {\nu }^{\prime }}\}$ for all ${\nu }^{\prime }=1$, 2, … including $\nu$.) Such subspaces are spanned by mutually neutral states. Those are states with fixed values for the numbers of $\alpha \nu$ fermions and $\alpha \nu$ fermion holes. Hence such states can be transformed into each other by $\alpha \nu$ band particle-hole processes. Creation of one $\alpha \nu$ fermion is a process that involves the transition between two states belonging to different such subspaces. It is a well-defined process whose generator is the product of two operators. The first operator may add sites to or remove sites from the $\alpha \nu$ effective lattice. Alternatively, it may introduce corresponding changes in the $\alpha \nu$ momentum band. The second operator is the creation operator $f_{\overrightarrow{r},\alpha \nu }^{†}$ or $f_{\overrightarrow{q},\alpha \nu }^{†}$ appropriate to the excited-state subspace.

Provided that $(1-x)$ is finite for $s1$ fermions [10] and $S_{\alpha }/N_a^D>0$ as $N_a^D\to \infty$ for $\alpha \nu \ne s1$ fermions, the phases ${\varphi }_{j,\alpha \nu }$ given in Equation (32) are associated with an effective vector potential [24,25],

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill {\overrightarrow{A}}_{\alpha \nu }({\overrightarrow{r}}_j)& ={\mathsf{\Phi }}_0{\displaystyle \sum _{j^{\prime }\ne j}}{n}_{{\overrightarrow{r}}_{j^{\prime }},\alpha \nu }\frac{{\overrightarrow{e}}_{x_3}\times ({\overrightarrow{r}}_{j^{\prime }}-{\overrightarrow{r}}_j)}{{({\overrightarrow{r}}_{j^{\prime }}-{\overrightarrow{r}}_j)}^2};n_{{\overrightarrow{r}}_j,\alpha \nu }=f_{{\overrightarrow{r}}_j,\alpha \nu }^{†}{f}_{{\overrightarrow{r}}_j,\alpha \nu }\hfill \\ \hfill {\overrightarrow{B}}_{\alpha \nu }({\overrightarrow{r}}_j)& ={\overrightarrow{\nabla }}_{{\overrightarrow{r}}_j}\times {\overrightarrow{A}}_{\alpha \nu }({\overrightarrow{r}}_j)={\mathsf{\Phi }}_0{\displaystyle \sum _{j^{\prime }\ne j}}{n}_{{\overrightarrow{r}}_{j^{\prime }},\alpha \nu }\delta ({\overrightarrow{r}}_{j^{\prime }}-{\overrightarrow{r}}_j){\overrightarrow{e}}_{x_3}\hfill \end{array}\end{array}$$

(33)

For the model on the square lattice the vector ${\overrightarrow{e}}_{x_3}$ appearing here is the unit vector perpendicular to the plane. (Often we use units such that the fictitious magnetic flux quantum is given by ${\mathsf{\Phi }}_0=1$.)

The components of the microscopic momenta of the $\alpha \nu$ fermions are eigenvalues of the two (and one for 1D) $\alpha \nu$ translation generators ${\widehat{q}}_{\alpha \nu x_1}$ and ${\widehat{q}}_{\alpha \nu x_2}$ in the presence of the fictitious magnetic field ${\overrightarrow{B}}_{\alpha \nu }({\overrightarrow{r}}_j)$. That seems to imply that for the model on the square lattice the components $q_{x1}$ and $q_{x2}$ of the microscopic momenta $\overrightarrow{q}=[q_{x1},q_{x2}]$ refer to operators that do not commute. However, in the subspaces where the operators $f_{{\overrightarrow{q}}_j,\alpha \nu }^{†}$ act onto such are commuting operators. Indeed, those subspaces are spanned by neutral states [25]. Since $[{\widehat{q}}_{\alpha \nu x_1},{\widehat{q}}_{\alpha \nu x_2}]=0$ in such subspaces, for the model on the square lattice the $\alpha \nu$ fermions carry a microscopic momentum $\overrightarrow{q}=[q_{x1},q_{x2}]$ where the components $q_{x1}$ and $q_{x2}$ are well-defined simultaneously.

4.3. Ranges of the c and $\alpha \nu$ Fermion Energies, Their Transformation Laws, and the Ground-State Occupancies

Since the microscopic momenta of the c fermions are good quantum numbers both for the Hubbard model on the square and 1D lattices, one may define an energy dispersion ${ϵ}_c(\overrightarrow{q})$ [10]. For the 1D model also the $\alpha \nu$ energy dispersions ${ϵ}_{\alpha \nu }(q)$ are well defined. In turn, for the model on the square lattice an energy dispersion ${ϵ}_{\alpha \nu }(\overrightarrow{q})$ is for $\alpha \nu \ne s1$ branches well defined for the momentum values for which such objects are invariant under the electron-rotated-electron unitary transformation. For general $\alpha \nu$ fermion momentum values there is not in general a dispersion ${ϵ}_{\alpha \nu }={ϵ}_{\alpha \nu }(\overrightarrow{q})$ defining a one-to-one correspondence between the energy ${ϵ}_{\alpha \nu }$ and momentum $\overrightarrow{q}$. However, the range of the $\alpha \nu$ fermion energy ${ϵ}_{\alpha \nu }$ remains well defined. A $s1$ fermion energy dispersion ${ϵ}_{s1}={ϵ}_{s1}(\overrightarrow{q})$ is well defined for the square-lattice quantum liquid [10]. Indeed for the Hubbard model in the one- and two-electron subspace the $s1$ band momentum values become good quantum numbers [9].

The quantum-object occupancy configurations of the ground state are found below. They are consistent with the energies for creation onto such states of our description quantum objects. For instance, the elementary energies ${ϵ}_{s,-1/2}=2{\mu }_{B}H$ and ${ϵ}_{\eta ,-1/2}=2\mu$ correspond to creation onto a $m\ge 0$ and $x>0$ ground state of a deconfined $-1/2$ spinon and a deconfined $-1/2$ $\eta$-spinon, respectively. Here ${\mu }_B$ is the Bohr magneton and as above H and $\mu$ are the magnetic field and the chemical potential, respectively. The energy ${ϵ}_{s,-1/2}=2{\mu }_{B}H$ (and ${ϵ}_{\eta ,-1/2}=2\mu$) refers to an elementary spin-flip (and $\eta$-spin-flip) process. It transforms a deconfined $+1/2$ spinon (and deconfined $+1/2$ $\eta$-spinon) into a deconfined $-1/2$ spinon (and deconfined $-1/2$ $\eta$-spinon). Such elementary energies control the range of several physically important energy scales. Within the LWS representation, a deconfined $+1/2$ spinon (and deconfined $+1/2$ $\eta$-spinon) has vanishing energy so that ${ϵ}_{s,+1/2}=0$ (and ${ϵ}_{\eta ,+1/2}=0$). It follows that the energy of a pair of deconfined spinons (and deconfined $\eta$-spinons) with opposite projections is $2{\mu }_{B}H$ (and $2\mu$). Indeed due to the invariance of such objects under the electron-rotated-electron unitary transformation, they are not energy entangled and the total energy is the sum of their individual energies.

In the following we confirm that ground states have no $\eta \nu$ fermions and no $s\nu$ fermions with $\nu >1$ spinon pairs. The corresponding energies ${ϵ}_{\eta \nu }$ and ${ϵ}_{s\nu }$, respectively, considered below refer to creation onto the ground state of one of such objects. We start by providing a set of useful properties. We emphasize that some of these properties are not valid for descriptions generated by rotated-electron operators associated with the general unitary operators $\widehat{V}$ considered in Reference [6]. The following properties rather refer to the specific operator description associated with the rotated-electron operators ${\tilde{c}}_{{\overrightarrow{r}}_j,\sigma }^{†}={\widehat{V}}^{†}{c}_{{\overrightarrow{r}}_j,\sigma }^{†}\widehat{V}$ of Equation (3) as defined above.

Some of the following results are obtained from extension to the model on the square lattice of exact results extracted from the 1D model BA solution. However such an extension accounts for the different physics of such models. Both for the model on the square and 1D lattice, the range of the energy ${ϵ}_{\alpha \nu }$ for addition onto the ground state of one $\alpha \nu$ fermion derived below is that consistent with the interplay of the transformation laws of the $\alpha \nu$ fermions under the electron-rotated-electron unitary transformation with the model global $SO(3)\times SO(3)\times U(1)$ symmetry.

The $\eta \nu$ Fermion Energy Range

Alike for 1D, for the model on the square lattice one $\eta \nu$ fermion is a $\eta$-spin-neutral anti-bounding configuration of a number $\nu =1,2,\dots$ of confined $-1/2$ $\eta$-spinons and an equal number of confined $+1/2$ $\eta$-spinons. Symmetry implies that for $U/4t>0$ there is no energy overlap between the ${ϵ}_{\eta \nu }$ ranges corresponding to different $\nu =1,2,\dots$ branches. Fermions belonging to neighboring $\eta \nu$ and $\eta \nu +1$ branches differ in the number of $\eta$-spinon pairs by one. The requirement for the above lack of energy overlap is then that the energy bandwidth of the ${ϵ}_{\eta \nu }$ range is smaller than or equal to $2|\mu |$. For all x values, the energy scale $2|\mu |=[{ϵ}_{\eta ,-1/2}+{ϵ}_{\eta ,+1/2}]$ where $\mu ={\mu }^0$ at $x=0$ refers to the energy of a pair of deconfined $\eta$-spinons of opposite $\eta$-spin projection. Such properties imply the following range for the energy ${ϵ}_{\eta \nu }$,

$$2\nu |\mu |\le {ϵ}_{\eta \nu }<2(\nu +i_{\eta \nu })|\mu |;0\le i_{\eta \nu }\le 1$$

(34)

where $\mu ={\mu }^0$ at $x=0$. Deconfined $\eta$-spinons are invariant under the electron-rotated-electron unitary transformation. Consistently and as justified below, they are non-interacting and their energies are additive. For all x values $2\nu |\mu |$ is the energy of $\nu$ deconfined $-1/2$ $\eta$-spinons and $\nu$ deconfined $+1/2$ $\eta$-spinons. For instance, for $x>0$ the energy $2\nu \mu$ is as well that for creation of a number $\nu =1$, 2, … of deconfined $-1/2$ $\eta$-spinons onto a $S_{\eta }=\nu$ ground state with $2\nu$ deconfined $+1/2$ $\eta$-spinons. Such a creation refers to $\nu$ $\eta$-spin-flip processes (transformation of $\nu$ rotated-electron unoccupied sites into $\nu$ rotated-electron doubly occupied sites.) For $m=0$ and $x>0$ the number $i_{\eta \nu }$ decreases continuously for increasing values of $U/4t$. It has the limiting behaviors $i_{\eta \nu }\to 1$ for $U/4t\to 0$ and $i_{\eta \nu }\to 0$ for $U/4t\to \infty$. Hence the ${ϵ}_{\eta \nu }$ range vanishes for $U/4t\to \infty$. The latter behavior is associated with the full degeneracy of the $\eta$-spin configurations reached as $U/4t\to \infty$. In turn, at $m=0$ and $x=0$ the number $i_{\eta \nu }$ vanishes and ${ϵ}_{\eta \nu }=2\nu {\mu }^0$ for the whole finite interaction range $U/4t>0$. As discussed below, this behavior follows from the invariance under the electron-rotated-electron unitary transformation of a $\eta \nu$ fermion created onto a $x=0$ and $m=0$ ground state.

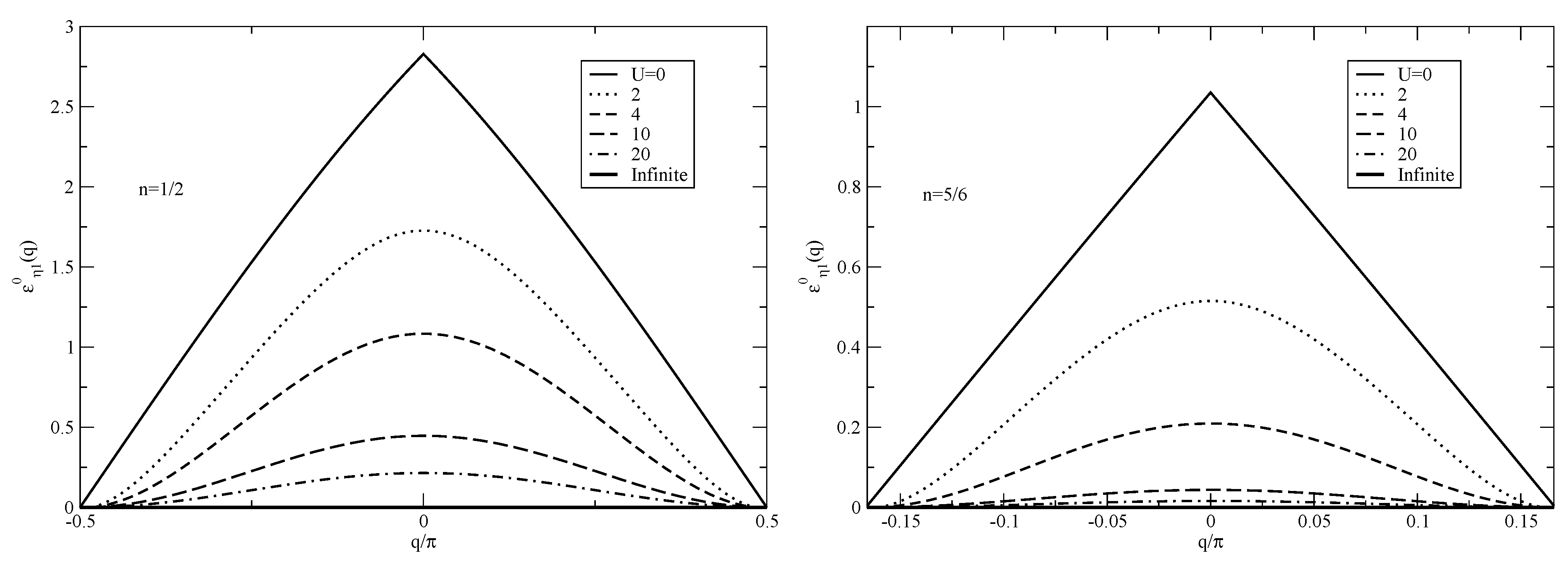
For the 1D Hubbard model one can define momentum dependent $\eta \nu$ fermion energy bands [26]. The $\eta 1$ and $\eta 2$ fermion bands are plotted in Figure 1 and Figure 2, respectively, in units of t for electronic densities $n=(1-x)=1/2,5/6$, spin density $m=0$, and different $U/t$ values. In the figures the lower energy level of the bands was shifted to zero. According to the above analysis, for $U/t\to 0$ and $U/t\to \infty$ the energy bandwidth of all $\eta \nu$ bands should read $2|\mu |$ and 0, respectively. For electronic densities $1/2$ and $5/6$ and $U/t\to 0$ one has that twice the chemical-potential absolute value reads $2|\mu |=2\sqrt{2}t\approx 2.828t$ and $2|\mu |=4tcos(5\pi /12)\approx 1.035t$, respectively. Consistently, notice that in the $U/t\to 0$ limit the energy bandwidths of the $\eta 1$ and $\eta 2$ fermion bands plotted in the figures are $2\sqrt{2}t\approx 2.828t$ and $4tcos(5\pi /12)\approx 1.035t$ for electronic densities $1/2$ and $5/6$, respectively, Furthermore, in the limit $U/t\to \infty$ the energy bandwidths of the $\eta 1$ and $\eta 2$ fermion bands indeed vanish. The parameter $i_{\eta \nu }$ appearing in Equation (34), which controls such energy bandwidths, has the same limiting behaviors $i_{\eta \nu }\to 1$ for $U/t\to 0$ and $i_{\eta \nu }\to 0$ for $U/t\to \infty$ for all remaining $\eta \nu$ bands corresponding to a number $\nu =1$, 2, 3, … of confined $\eta$-spinon pairs.

The $s\nu$ Fermion Energy Range

A $s\nu$ fermion is a spin-neutral bounding configuration of a number $\nu =1$, 2, … of confined $-1/2$ spinons and an equal number of confined $+1/2$ spinons. Again, symmetry implies that for $U/4t>0$ there is no energy overlap between the ${ϵ}_{s\nu }$ ranges of different $\nu =1$, 2, … branches. For $s\nu$ branches with a number of spinon pairs $\nu >1$ such an energy range bandwidth is for the present bounding configurations and for the same reasoning as for the $\eta \nu$ fermion smaller than or equal to $2{\mu }_B|H|$. For all m values, $2{\mu }_B|H|=[{ϵ}_{s,-1/2}+{ϵ}_{s,+1/2}]$ equals the energy of a pair of deconfined spinons of opposite spin projection. Hence the range of the energy ${ϵ}_{s\nu }$ for addition onto the ground state of one $s\nu$ fermion with $\nu >1$ spinon pairs is,

$$2(\nu -i_{s\nu }){\mu }_B|H|\le {ϵ}_{s\nu }\le 2\nu {\mu }_B|H|;\nu >1,0\le i_{s\nu }\le 1$$

(35)

Deconfined spinons are invariant under the electron-rotated-electron unitary transformation. Thus their energies are additive. It follows that for all m values $2\nu {\mu }_B|H|$ is the energy of $\nu$ deconfined $-1/2$ spinons and $\nu$ deconfined $+1/2$ spinons. For example, for $m>0$ the energy $2\nu {\mu }_{B}H$ is that for creation of a number $\nu =1$, 2, … of deconfined $-1/2$ spinons onto a $S_s=\nu$ ground state with $2\nu$ deconfined $+1/2$ spinons. Such a creation refers to $\nu$ spin-flip processes. The number $i_{s\nu }$ decreases continuously for increasing values of $U/4t$. For any fixed m value it has the limiting behaviors $i_{s\nu }\to 1$ for $U/4t\to 0$ and $i_{s\nu }\to i_{s\nu }^{\infty }$ for $U/4t\to \infty$ where $0\le i_{s\nu }^{\infty }<1$. Since for a non fully polarized state $2\nu {\mu }_{B}H\to 0$ as $U/4t\to \infty$, the energy bandwidth of the ${ϵ}_{s\nu }$ range vanishes for $U/4t\to \infty$. Such a behavior is associated with the full degeneracy of the spin configurations reached for $U/4t\to \infty$. Figures similar to those of Figure 1 and Figure 2 for the $\eta 1$ and $\eta 2$ fermion bands, respectively, confirm such a $i_{s\nu }$ behavior for the $s\nu$ bands associated with $\nu >1$ confined spinon pairs, but with the $U/4t\to 0$ energy bandwidth $2|\mu |$ replaced by $2{\mu }_B|H|$ and the electronic densities $n=(1-x)<1$ replaced by spin densities $m>0$. Note that at $m=0$ and thus $H=0$ one has that ${ϵ}_{s\nu }=0$ for the whole finite interaction range $U/4t>0$. This behavior follows from the invariance under the electron-rotated-electron unitary transformation of a $s\nu$ fermion with $\nu >1$ spinon pairs created onto a $m=0$ ground state.

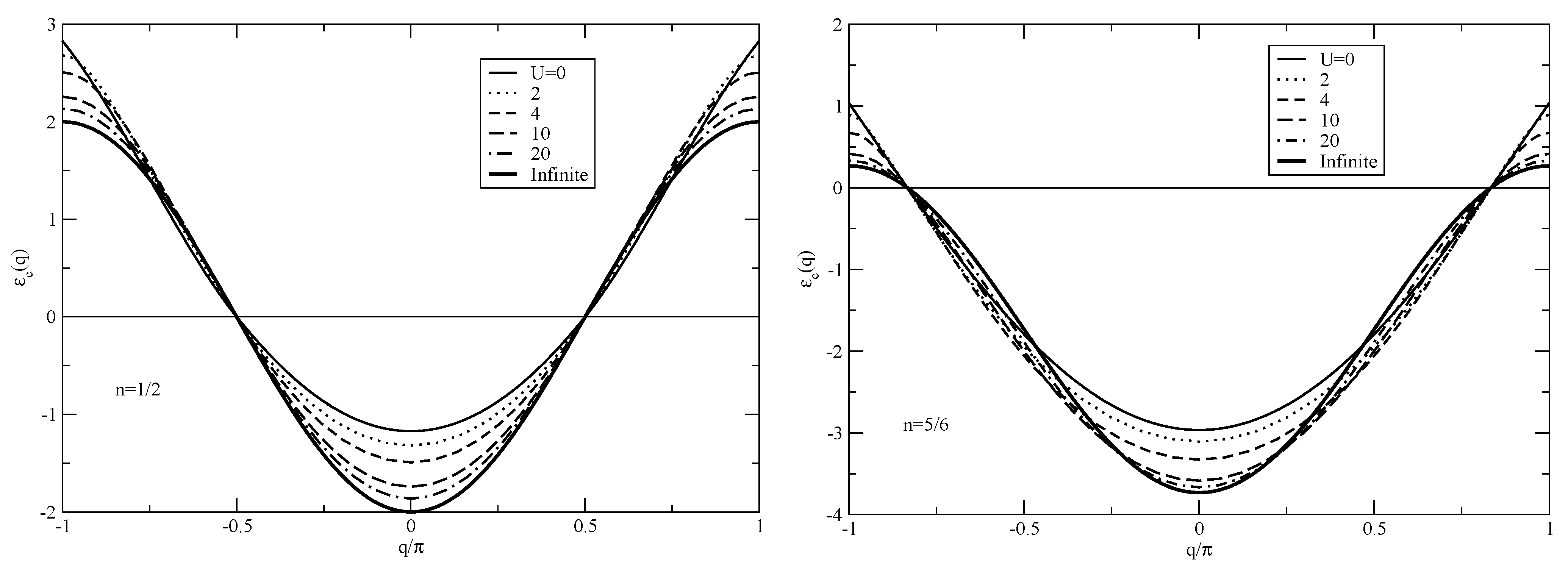
In turn, it is found below that for a $m=0$ and $x\ge 0$ ground state all sites of the $s1$ effective lattice are occupied. Hence the corresponding $s1$ momentum band is full. The range of the energy $-{ϵ}_{s1}$ for removal from that state of one $s1$ fermion then is,

$$0\le -{ϵ}_{s1}\le \max \{W_{s1},|\mathsf{\Delta }|\}$$

(36)

Here $|\mathsf{\Delta }|$ vanishes for 1D. The $s1$ fermion energy band is plotted in units of t in Figure 3 for the 1D Hubbard model at electronic densities $n=(1-x)=1/2$ and $n=5/6$, spin density $m=0$, and a set of $U/t$ values. For the Hubbard model on the square lattice, $|\mathsf{\Delta }|$ denotes the $s1$ fermion pairing energy per spinon considered in Reference [10]. There is strong evidence of the occurrence in the half-filling Hubbard model on the square lattice of strong short-range antiferromagnetic correlations for $T>0$ and below a crossover temperature called $T_x$ in Reference [20]. This is consistent with then the system being driven into a phase with short-range spin order. Within the representation of Reference [9], the occurrence of long-range antiferromagnetic order requires that $T=0$, $N_{a_{\eta }}^2=0$, and $N_{a_s}^2=N_a^2$. This is then consistent with the short-range spin order occurring for $m=0$, $0<x\ll 1$, and $0\le T<T_x$ being similar to that occurring for $m=0$, $x=0$, and $0<T<T_x$. The latter order was studied previously in Reference [20] for $0<T\ll T_x$. For small finite hole concentrations $0<x\ll 1$ the $s1$ fermion pairing energy $2|\mathsf{\Delta }|$ is identified with $2{\mathsf{\Delta }}_0\approx 2k_B{T}_x$. In turn, for $U/4t>0$ and $x=0$ its magnitude $2|\mathsf{\Delta }|={\mu }^0$ is larger than for $x\to 0$ and the $s1$ fermion spinon pairing refers to an antiferromagnetic long-range order [10].

The temperature $T_x$ of Reference [20] is plotted in Figure 3 of that reference. Its $U/4t$ dependence is qualitatively correct. $T_x$ vanishes both in the limits $U/4t\to 0$ and $U/4t\to \infty$. It goes through a maximum magnitude at an intermediate value $5/4<U/4t<3/2$. Nevertheless, the interpolation function used to produce it, provided in Ref. 74 of such a paper, is poor for intermediate values of $U/4t$. That used in the studies of Reference [10] is such that $2{\mathsf{\Delta }}_0\approx 2k_B{T}_x$ vanishes both in the $U/4t\to 0$ and $U/4t\to \infty$ limits and goes through a maximum value $\max \{2{\mathsf{\Delta }}_0\}\approx 2t/\pi$ at $U/4t\approx 1.3$. At fixed $U/4t$ values, $2|\mathsf{\Delta }|$ decreases for increasing x as $2|\mathsf{\Delta }|\approx 2{\mathsf{\Delta }}_0(1-x/x_{*})$ and vanishes for $x>x_{*}$. Here $x_{*}\in (0.23,0.28)$ for $U/4t\in (1.3,1.6)$ is a critical hole concentration below which the $s1$ fermion pairing refers to a spin short-range order [10].

On the other hand, at $m=0$ the energy scale $W_{s1}$ is the $s1$ fermion energy nodal bandwidth defined in Reference [10]. Its maximum magnitude is reached at $U/4t=0$. For $U/4t>0$ it decreases monotonously for increasing values of $U/4t$, vanishing for $U/4t\to \infty$. That $W_{s1}\to 0$ for $U/4t\to \infty$ is associated with the full degeneracy of the spin configurations reached in that limit. In it the spectrum of the two-spinon composite $s1$ fermions becomes dispersionless for the square-lattice quantum liquid of Reference [10].

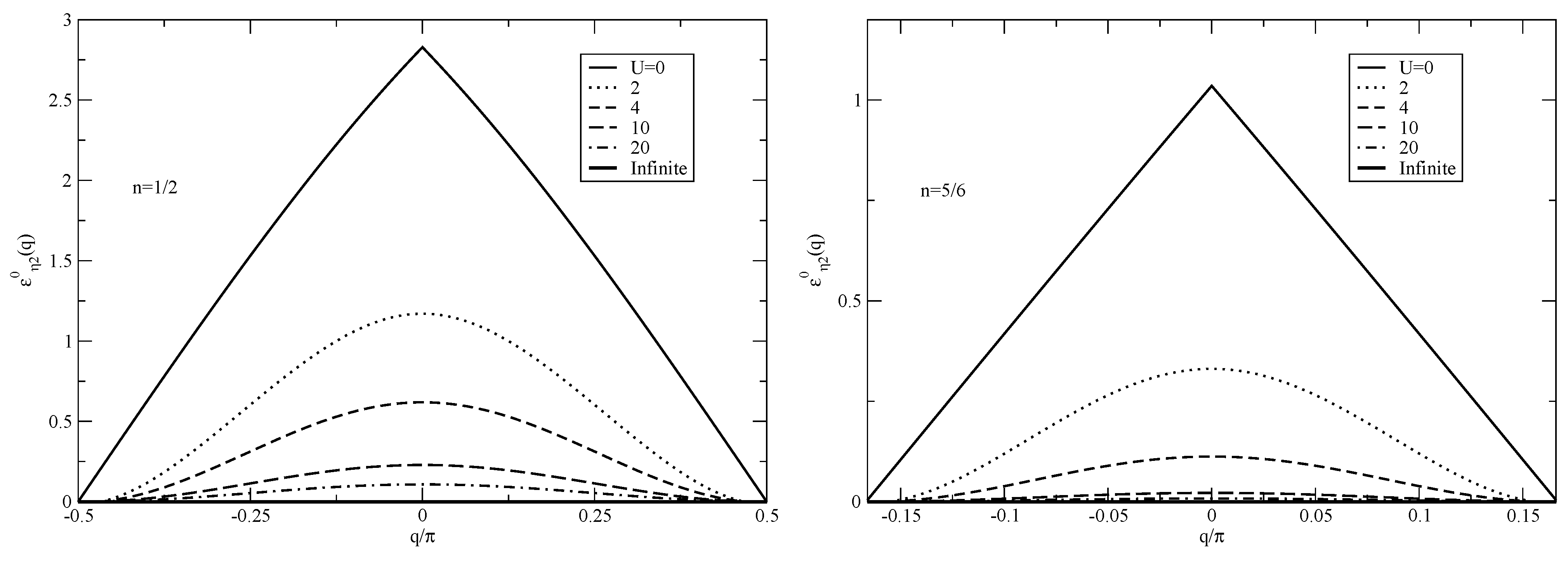
The c Fermion Energy Range

The energy ${ϵ}_c$ for addition onto the ground state of one c fermion of a given momentum and the energy $-{ϵ}_c$ for removal from that state of such a c fermion have the following ranges,

$$0\le {ϵ}_c\le W_c^h=[4Dt-W_c^p];0\le -{ϵ}_c\le W_c^p,D=1,2$$

(37)

respectively. Here $W_c^h=[4Dt-W_c^p]\in (0,4Dt)$ increases monotonously for increasing values of hole concentration $x\in (0,1)$. The energy bandwidth $W_c^p$ depends little on $U/4t$. For $U/4t>0$ it has the following limiting behaviors,

$$\begin{array}{c}\hfill \begin{array}{cccc}\hfill W_c^p& =4Dt,\hfill & \hfill x& =0\hfill \\ \hfill W_c^p& =0;\hfill & \hfill x& =1\hfill \end{array}\end{array}$$

(38)

The behaviors reported here for ${ϵ}_c$ are justified in Reference [10]. The c fermion energy band is plotted in units of t in Figure 4 for the 1D Hubbard model at electronic densities $n=(1-x)=1/2,5/6$, spin density $m=0$, and a set of $U/t$ values. Note that for 1D (and the square lattice) its energy bandwidth is $4t$ (and $8t$) for all density values and the whole $U/4t$ range.

Transformation Laws of $\alpha \nu$ Fermions and c Fermions under the Electron-Rotated-Electron Unitary Transformation

The minimum magnitude of the energy ${\mathsf{\Delta }}_{D_{rot}}$ for creation of a number $D_{rot}=M_{\eta ,-1/2}$ of rotated-electron doubly occupied sites onto a $m=0$ and $x\ge 0$ ground state given in Equation (26) may be expressed in terms of both the numbers of deconfined $\eta$-spinons and $\eta \nu$ fermions as follows,

$$\begin{array}{c}\hfill \begin{array}{cccc}\hfill \min {\mathsf{\Delta }}_{D_{rot}}& =({\mu }^0+\mu )M_{\eta ,-1/2}^{de}+\sum _{\nu =1}^{\infty }2\nu {\mu }^0{N}_{\eta \nu }\hfill & \hfill \mathrm{at}& x=0\mathrm{and}\mu \in (-{\mu }^0,{\mu }^0)\hfill \\ & =2\mu M_{\eta ,-1/2}^{de}+\sum _{\nu =1}^{\infty }2\nu \mu N_{\eta \nu }\hfill & \hfill \mathrm{for}& x>0\hfill \end{array}\end{array}$$

(39)

Here ${\mu }^0\equiv {lim}_{x\to 0}\mu$ is the energy scale whose limiting behaviors are given in Equation (27). Consistently, the following $\eta$-spinon and $\eta \nu$ fermion energy magnitudes hold,

$$\begin{array}{c}\hfill \begin{array}{ccccccc}\hfill {ϵ}_{\eta ,\pm 1/2}& =({\mu }^0\mp \mu );\hfill & \hfill {ϵ}_{\eta \nu }& =2\nu {\mu }^0\hfill & \mathrm{at}\hfill & \hfill x& =0\mathrm{and}\mu \in (-{\mu }^0,{\mu }^0)\hfill \\ \hfill {ϵ}_{\eta ,-1/2}& =2\mu ;\hfill & \hfill {ϵ}_{\eta ,+1/2}& =0;\hfill & \min \hfill & \hfill {ϵ}_{\eta \nu }& =2\nu \mu \mathrm{for}x>0\hfill \\ \hfill {ϵ}_{\eta ,-1/2}& =0;\hfill & \hfill {ϵ}_{\eta ,+1/2}& =2|\mu |;\hfill & \min \hfill & \hfill {ϵ}_{\eta \nu }& =2\nu |\mu |\mathrm{for}x<0\hfill \end{array}\end{array}$$

(40)

The corresponding energy magnitudes concerning creation of deconfined spinons and $s\nu$ fermions with $\nu >1$ spinon pairs onto $x\ge 0$ ground states with arbitrary values of m read,

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill {ϵ}_{s,\pm 1/2}& ={ϵ}_{s\nu }=0\mathrm{at}m=0\mathrm{and}{\mu }_{B}H=0,\hfill \\ \hfill {ϵ}_{s,-1/2}& =2{\mu }_{B}H;{ϵ}_{s,+1/2}=0;\max {ϵ}_{s\nu }=2\nu {\mu }_{B}H\mathrm{for}\nu >1\mathrm{and}m>0\hfill \\ \hfill {ϵ}_{s,-1/2}& =0;{ϵ}_{s,+1/2}=2{\mu }_B|H|;\max {ϵ}_{s\nu }=2\nu {\mu }_B|H|\mathrm{for}\nu >1\mathrm{and}m<0\hfill \end{array}\end{array}$$

(41)

Hence for all hole concentrations x and all spin densities m the inequalities ${ϵ}_{\eta \nu }\ge \nu [{ϵ}_{\eta ,-1/2}+{ϵ}_{\eta ,+1/2}]=2\nu |\mu |$ where $\mu ={\mu }^0$ at $x=0$ and ${ϵ}_{s\nu }\le \nu [{ϵ}_{s,-1/2}+{ϵ}_{s,+1/2}]=2\nu {\mu }_B|H|$, respectively, hold. Furthermore, $[{ϵ}_{\eta ,-1/2}+{ϵ}_{\eta ,+1/2}]=2|\mu |$ where again $\mu ={\mu }^0$ at $x=0$ and $[{ϵ}_{s,-1/2}+{ϵ}_{s,+1/2}]=2{\mu }_B|H|$.

The deconfined $\eta$-spinon and deconfined spinon energies provided in Equations (40) and (41), respectively, refer to a choice of the zero-energy level such that the ground-state energy vanishes. In the absence of the corresponding chemical-potential and magnetic-field terms, the deconfined $\eta$-spinon and deconfined spinon energies vanish. For that choice of zero-energy level, the absolute energies of the c fermions and $\alpha \nu$ fermions are consistently shifted. Such a deconfined $\eta$-spinon and deconfined spinon vanishing energy refers to all energy eigenstates. Also the vanishing momenta of the $\pm 1/2$ spinons and $+1/2$ $\eta$-spinons and the momentum $\overrightarrow{\pi }$ of the $-1/2$ $\eta$-spinons remain unchanged for all energy eigenstates. As a result, such objects do not undergo inelastic scattering processes, since they do not interchange energy and momentum. In addition, they do not undergo zero-momentum forward scattering. In 1D this leads to a corresponding lack of phase shifts [9,26]. This invariance of their energy and momentum values is behind their non-interacting character.

A related important property is that $\eta \nu$ fermions of any $\nu =1$, 2, … branch and $s\nu$ fermions with $\nu >1$ spinon pairs whose energy obeys the following relations,

$$\begin{array}{c}\hfill \begin{array}{ccc}\hfill {ϵ}_{\eta \nu }& =\nu [{ϵ}_{\eta ,-1/2}+{ϵ}_{\eta ,+1/2}]=2\nu |\mu |,\hfill & \nu =1,2,\dots \mathrm{for}x\ne 0\hfill \\ & =\nu [{ϵ}_{\eta ,-1/2}+{ϵ}_{\eta ,+1/2}]=2\nu {\mu }^0,\hfill & \nu =1,2,\dots \mathrm{at}x=0\hfill \\ \hfill {ϵ}_{s\nu }& =\nu [{ϵ}_{s,-1/2}+{ϵ}_{s,+1/2}]=2\nu {\mu }_B|H|,\hfill & \nu =2,3,\dots \hfill \end{array}\end{array}$$

(42)

remain invariant under the electron-rotated-electron unitary transformation. Those are non-interacting objects such that their energy is additive in the individual energies of the corresponding $2\nu$ $\eta$-spinons and $2\nu$ spinons, respectively. Therefore, for $U/4t>0$ they refer to the same occupancy configurations in terms of both rotated electrons and electrons. This refers to the $\eta$-spin and spin degrees of freedom, respectively, of such rotated-electron occupancy configurations. The corresponding rotated-electron degrees of freedom associated with the c fermion $U(1)$ symmetry are not in general invariant under that transformation.

Another important property is that a $s\nu$ fermion with $\nu >1$ spinon pairs (and a $\eta \nu$ fermion) created onto an initial $S_s=0$ and $H=0$ (and $S_{\eta }=0$) ground state remains invariant under the electron-rotated-electron unitary transformation. Indeed and as reported above, such an object has a uniquely defined energy ${ϵ}_{s\nu }=0$ (and ${ϵ}_{\eta \nu }=2\nu {\mu }^0$). Furthermore, its momentum is $\overrightarrow{q}={\overrightarrow{q}}_s=0$ (and $\overrightarrow{q}={\overrightarrow{q}}_{\eta }=0$). Hence it obeys indeed to the condition given in Equation (42). In turn, $s\nu$ fermions with $\nu >1$ spinon pairs (and $\eta \nu$ fermions) created onto initial $S_s>0$ (and $S_{\eta }>0$) ground states may have energy ${ϵ}_{s\nu }$ smaller than $2\nu {\mu }_B|H|$ (and energy ${ϵ}_{\eta \nu }$ larger than $2\nu |\mu |$), so that they are not necessarily invariant under the electron-rotated-electron unitary transformation.

To understand this property, we consider a set of $2\nu$ deconfined $\eta$-spinons (and $2\nu$ deconfined spinons) involving $\nu$ deconfined $+1/2$ $\eta$-spinons (and $\nu$ deconfined $+1/2$ spinons) and $\nu$ deconfined $-1/2$ $\eta$-spinons (and $\nu$ deconfined $-1/2$ spinons). Such a set of $2\nu$ deconfined $\eta$-spinons (and $2\nu$ deconfined spinons) refers to a $S_{\eta }=\nu$ and $S_{\eta }^{x_3}=0$ $\eta$-spin multiplet configuration of energy $2\nu |\mu |$ where $\mu ={\mu }^0$ at $x=0$ (and a $S_s=\nu$ and $S_s^{x_3}=0$ spin multiplet configuration of energy $2\nu {\mu }_B|H|$). In turn, the $2\nu$ $\eta$-spinons (and spinons) of a $\eta \nu$ fermion (and $s\nu$ fermion) correspond to a $S_{\eta }=S_{\eta }^{x_3}=0$ $\eta$-spin singlet configuration of energy ${ϵ}_{\eta \nu }\ge 2\nu |\mu |$ (and a $S_s=S_s^{x_3}=0$ spin singlet configuration of energy ${ϵ}_{s\nu }\le 2\nu {\mu }_B|H|$). The point is that only when the energy ${ϵ}_{\eta \nu }$ (and ${ϵ}_{s\nu }$) of a $\eta \nu$ fermion (and $s\nu$ fermion) $2\nu$-$\eta$-spinon $\eta$-spin singlet configuration (and $2\nu$-spinon spin singlet configuration) reads ${ϵ}_{\eta \nu }=2\nu |\mu |$ (and ${ϵ}_{s\nu }=2\nu {\mu }_B|H|$), as given in Equation (42), is it degenerated with that of the above $2\nu$-deconfined $\eta$-spinon $\eta$-spin multiplet configuration (and $2\nu$-deconfined spinon spin multiplet configuration). Only when that occurs is such a $\eta \nu$ fermion (and $s\nu$ fermion) invariant under the electron-rotated-electron unitary transformation.

On the other hand, $\eta \nu$ fermions of any $\nu =1$, 2, … branch and $s\nu$ fermions with $\nu >1$ spinon pairs whose energies obey the inequalities ${ϵ}_{\eta \nu }>2\nu |\mu |$ and ${ϵ}_{s\nu }<2\nu {\mu }_B|H|$, respectively, are not invariant under the electron-rotated-electron transformation. Furthermore, for finite $U/4t$ values c fermions and $s1$ fermions are not in general invariant under that transformation.

For the 1D model the $\alpha \nu$ fermion energy ${ϵ}_{\alpha \nu }(q)$ depends on the $\alpha \nu$ fermion momentum q, which is a good quantum number. For $U/4t>0$ and the $s\nu$ branches with $\nu >1$ spinon pairs and all $\eta \nu$ branches such momenta belong to the range $q\in (-m\pi ,+m\pi )$ and $q\in (-x\pi ,+x\pi )$, respectively. Only at the limiting momenta $q=q_{\eta }=\pm x\pi$ (and $q=q_s=\pm m\pi$) is the invariance condition given in Equation (42) met by the $\eta \nu$ fermion energy ${ϵ}_{\eta \nu }(q)$ (and $s\nu$ fermion energy ${ϵ}_{s\nu }(q)$ for $\nu >1$ branches). The $\eta \nu$ fermion energy dispersions ${ϵ}_{\eta \nu }(q)$ are plotted for the $\eta 1$ (and $\eta 2$) branches in Figures 8(a) and 9(a) (and Figures 8(b) and 9(b)) of Reference [26] as a function of q for several $U/4t$ values and electronic density $n=1/2$ and $n=5/6$, respectively. (In that reference the $\eta \nu$ fermions are called $c,\nu$ pseudoparticles.) The zero-energy level of Figures 8(a) and 9(a) (and Figures 8(b) and 9(b)) refers to the energy $2|\mu |$ (and $4|\mu |$) of the invariance condition given in Equation (42) for $\nu =1$ (and $\nu =2$).

For the Hubbard model on the square lattice the $\alpha \nu$ fermions whose energy obeys the invariance condition given in that equation have a well-defined momentum ${\overrightarrow{q}}_{\alpha }$, which can point in different directions. At $x=0$ (and $m=0$) the momentum ${\overrightarrow{q}}_{\eta }$ (and ${\overrightarrow{q}}_s$) vanishes. This is alike for the above corresponding momentum $q_{\eta }=\pm x\pi$ (and $q_s=\pm m\pi$) of the 1D model, which vanishes at $x=0$ (and $m=0$). While at 1D the momentum $q_{\eta }=\pm x\pi$ (and $q_s=\pm m\pi$) can for $x>0$ (and $m>0$) have two values, for the square-lattice model the momentum ${\overrightarrow{q}}_{\eta }$ (and ${\overrightarrow{q}}_s$) can for $x>0$ (and $m>0$) point to several directions. For instance, for $x<x_{*}$ and $m=0$ where $x_{*}$ is the hole concentration considered in Reference [10] below which the ground-state $s1$ fermion spinon pairing is associated with a short-range spin order, a good approximation for the momentum ${\overrightarrow{q}}_{\eta }$ centered at $-\overrightarrow{\pi }=[-\pi ,-\pi ]$ is,

$${\overrightarrow{q}}_{\eta }={\overrightarrow{q}}_{Fc}^h=q_{Fc}^h{\overrightarrow{e}}_{{\varphi }_c};q_{Fc}^h\approx 2\sqrt{x\pi };{\varphi }_c\in (0,2\pi )$$

(43)

Here ${\overrightarrow{q}}_{Fc}^h$ is the c fermion hole Fermi momentum considered in Reference [10] and ${\overrightarrow{e}}_{{\varphi }_c}$ is a unit vector centered at $-\overrightarrow{\pi }$ of Cartesian components $[cos{\varphi }_c,sin{\varphi }_c]$. As required, ${\overrightarrow{q}}_{\eta }\to 0$ as $x\to 0$.

Ground State Occupancies

Consistent with the energy values given in Equations (40) and (41), one finds that both for the model on the 1D and square lattice in the subspace spanned by the $x>0$ and $m>0$ LWS ground states and their excited energy eigenstates of energy $\omega <\min \{2\mu ,2{\mu }_{B}H\}$ the $\eta$-spinon and spinon numbers are given by $M_{\eta ,-1/2}=M_{\eta }^{co}/2=M_{\eta ,-1/2}^{de}=0$, $M_{\eta ,+1/2}=M_{\eta ,+1/2}^{de}=2S_{\eta }=x{N}_a^D$ and $M_{s,-1/2}=M_s^{co}/2=N_{\downarrow }$, $M_{s,+1/2}=M_s^{co}/2+M_{s,+1/2}^{de}=N_{\uparrow }$, respectively, so that $M_{s,+1/2}^{de}=2S_s=m{N}_a^D$. Hence for such energy eigenstates the numbers of $\eta \nu$ fermions and $s{\nu }^{\prime }$ fermions with ${\nu }^{\prime }>1$ spinon pairs vanish and the number of c fermions is $N_c=2S_c=N$ and that of $s1$ fermions is conserved and reads $N_{s1}=N_{\downarrow }$.

Except that the $-1/2$ $\eta$-spinons and $-1/2$ spinons play the role of the $+1/2$ $\eta$-spinons and $+1/2$ spinons, respectively, and vice versa, similar results are reached for highest-weight states (HWSs) of the $\eta$-spin and spin algebras. Comparison of the occupancies of the spin LWS ground states ($m>0$) and spin HWS ground states ($m<0$) provides useful information. From it and again consistently with the energy values of Equations (40) and (41), one finds that a $m=0$ ground state for which N is even and $x\ge 0$ has $M_{\eta ,\pm 1/2}$ and $N_c$ values as given above whereas $M_{s,\pm 1/2}=M_s^{co}/2=N/2$ so that $M_{s,\pm 1/2}^{de}=0$ and $N_{s1}=N/2$.

4.4. The Site Numbers and Spacing of the $\alpha \nu$ Effective Lattices

The number of sites of the $\alpha \nu$ effective lattice, which equals that of $\alpha \nu$ band discrete momentum values, has the general form,

$$N_{a_{\alpha \nu }}^D=[N_{\alpha \nu }+N_{\alpha \nu }^h]$$

(44)

where $N_{\alpha \nu }^h$ is the number of unoccupied sites whose expression is derived in Reference [9] on use of symmetry representation counting and reads,

$$\begin{array}{cc}\hfill N_{\alpha \nu }^h& =[M_{\alpha }^{de}+2\sum _{{\nu }^{\prime }=\nu +1}^{\infty }({\nu }^{\prime }-\nu )N_{\alpha {\nu }^{\prime }}]\hfill \\ & =[N_{a_{\alpha }}^D-\sum _{{\nu }^{\prime }=1}^{\infty }(\nu +{\nu }^{\prime }-|\nu -{\nu }^{\prime }|)N_{\alpha {\nu }^{\prime }}];\alpha =\eta ,s;\nu =1,2,\dots ,\infty \hfill \end{array}$$

(45)

where $M_{\alpha }^{de}=2S_{\alpha }$. Importantly, this expression is also that obtained from the BA exact solution for the 1D Hubbard model. However, it is fully determined by state-representation dimension requirements of the global $SO(3)\times SO(3)\times U(1)$ symmetry that apply to the Hubbard model on the square lattice as well. (Note that the equivalence of the two expressions given in Equation (45) confirms that the $N_c=2S_c$ and $\{N_{\alpha {\nu }^{\prime }}\}$ values with ${\nu }^{\prime }=1$, 2, … remaining fixed is equivalent to the $\eta$-spin $S_{\eta }$ ($\alpha =\eta$) or spin $S_s$ ($\alpha =s$) and values of the set of numbers $\{N_{\alpha {\nu }^{\prime }}\}$ with ${\nu }^{\prime }=\nu$, $\nu +1$, … remaining fixed as well. In both cases that implies that the $N_{a_{\alpha \nu }}^D$ value remains fixed.)

Provided that $N_{a_{\alpha \nu }}^D/N_a^D$ remains finite as $N_a^D\to \infty$, the related $\alpha \nu$ effective lattices can for the 1D and square-lattice models be represented by 1D and square lattices, respectively, of spacing,

$$a_{\alpha \nu }=\frac{L}{N_{a_{\alpha \nu }}}=\frac{N_a}{N_{a_{\alpha \nu }}}a=\frac{N_{a_{\alpha }}}{N_{a_{\alpha \nu }}}{a}_{\alpha };N_{a_{\alpha \nu }}\ge 1$$

(46)

Here $\nu =1$, 2, … and $\alpha =\eta ,s$. The arguments behind the lattice geometry and the average distance $a_{\alpha \nu }$ between the sites of the $\alpha \nu$ effective lattice playing the role of lattice spacing are similar to those used for the lattice geometry and spacing of the $\eta$-spin and spin effective lattices. In turn, the corresponding $\alpha \nu$ bands whose number of discrete momentum values is also given by $N_{a_{\alpha \nu }}^D$ are well defined even when $N_{a_{\alpha \nu }}^D$ is given by a finite small number, $N_{a_{\alpha \nu }}^D=1$, 2, …

5. The Square-Lattice Quantum Liquid: A Two-Component Fluid of Charge c Fermions and Spin-Neutral Two-Spinon $s1$ Fermions

In this section we review a suitable one- and two-electron subspace. (For hole concentrations $x>0$ our studies refer to excitation energies below $2\mu$ for which $M_{\eta ,-1/2}=0$ for that subspace.) For $x\ge 0$ the picture that emerges is that of a two-component quantum liquid of charge c fermions and spin neutral two-spinon $s1$ fermions. It refers to the square-lattice quantum liquid further investigated in Reference [10]. Moreover, a preliminary application of the description reviewed here is presented.

5.1. The One- and Two-Electron Subspace

General $\mathcal{N}$-Electron Subspaces

We consider a $x\ge 0$ and $m=0$ ground state $|{\Psi }_{GS}\rangle$. Application onto it of a $\mathcal{N}$-electron operator ${\widehat{O}}_{\mathcal{N}}$ generates a state,

$${\widehat{O}}_{\mathcal{N}}|{\Psi }_{GS}\rangle ={\displaystyle \sum _j}{C}_j|{\Psi }_{U/4t}(j)\rangle ;C_j=\langle {\Psi }_{U/4t}(j)|{\widehat{O}}_{\mathcal{N}}|{\Psi }_{GS}\rangle$$

(47)

contained in a $\mathcal{N}$-electron subspace. This is a subspace spanned by the set of energy eigenstates $\{|{\Psi }_{U/4t}(j)\rangle \}$ such that ${\sum }_j{|C_j|}^2\approx 1$. It is thus associated with a given $\mathcal{N}$-electron operator ${\widehat{O}}_{\mathcal{N}}$. Generally, such operators can be written as a product of

$$\mathcal{N}={\displaystyle \sum _{l_{\eta },l_s=\pm 1}}{\mathcal{N}}_{l_{\eta },l_s};l=\pm 1$$

(48)

one-electron creation and annihilation operators. Here ${\mathcal{N}}_{l_{\eta },l_s}$ is the number of electron creation and annihilation operators in the operator ${\widehat{O}}_{\mathcal{N}}$ expression for $l_{\eta }=-1$ and $l_{\eta }=+1$, respectively, and with spin down and spin up for $l_s=-1$ and $l_s=+1$, respectively.

A general local $\mathcal{N}$-electron operator ${\widehat{O}}_{\mathcal{N},j}$ refers to a product of $\mathcal{N}$ local electron creation and annihilation operators. For $\mathcal{N}>1$ such an operator has a well defined local structure. It involves ${\mathcal{N}}_{-1,l_s}$ electron creation operators of spin projection $l_s/2$ and ${\mathcal{N}}_{+1,l_s}^l$ electron annihilation operators of spin projection $l_s/2$ whose real-space coordinates refer in general to a compact domain of neighboring lattice sites. Such a local $\mathcal{N}$-electron operator ${\widehat{O}}_{\mathcal{N},j}$ may be labelled by the real-space coordinate ${\overrightarrow{r}}_j$ of a corresponding central site. A second type of $\mathcal{N}$-electron operator is denoted by ${\widehat{O}}_{\mathcal{N}}(\overrightarrow{k})$ and carries momentum $\overrightarrow{k}$. It is related to a local operator ${\widehat{O}}_{\mathcal{N},j}$ by a Fourier transform.

The general $\mathcal{N}$-electron operators ${\widehat{O}}_{\mathcal{N}}$ considered here belong to one of these two types and are such that the ratio $\mathcal{N}/N_a^D$ vanishes in the thermodynamic limit. The operators ${\widehat{O}}_{\mathcal{N}}(\overrightarrow{k})$ of physical interest correspond in general to operators ${\widehat{O}}_{\mathcal{N},j}$ whose $\mathcal{N}$ elementary electronic operators create or annihilate electrons in a compact domain of lattice sites. The more usual cases for the description of experimental studies correspond to the $\mathcal{N}=1$ one-electron and $\mathcal{N}=2$ two-electron operators. Therefore, in this section we are mostly interested in the corresponding one- and two-electron subspace.

Application onto a $x\ge 0$ and $m\ge 0$ ground state of a general $\mathcal{N}$-electron operator ${\widehat{O}}_{\mathcal{N}}$ leads to electron number deviations $\delta N=\delta N_{\uparrow }+\delta N_{\downarrow }$ and $\delta N_{\uparrow }-\delta N_{\downarrow }$. As a result of the expressions and relations given above in this paper, such deviations may be expressed in terms of corresponding deviations in the number of c fermions, $\alpha \nu$ fermions, deconfined $\eta$-spinons, and deconfined spinons as follows,

$$\delta N=\delta N_c+2M_{\eta ,-1/2}^{de}+M_{\eta }^{co}=\delta N_c+2M_{\eta ,-1/2}^{de}+2\sum _{\nu =1}^{\infty }\nu N_{\eta \nu }$$

(49)

and

$$\delta (N_{\downarrow }-N_{\uparrow })=2\delta N_{s1}-\delta N_c+2M_{s,-1/2}^{de}+2\sum _{\nu =2}^{\infty }\nu N_{s\nu }$$

(50)

respectively. (Note that $M_{\eta ,-1/2}^{de}=M_{\eta }^{co}=N_{\eta \nu }=M_{s,-1/2}^{de}=N_{s\nu }{|}_{\nu >1}=0$ for the initial ground state so that $\delta M_{\eta ,-1/2}^{de}=M_{\eta ,-1/2}^{de}$, $\delta M_{\eta }^{co}=M_{\eta }^{co}$, $\delta N_{\eta \nu }=N_{\eta \nu }$, $\delta M_{s,-1/2}^{de}=M_{s,-1/2}^{de}$, and $\delta N_{s\nu }{{|}_{\nu >1}=N_{s\nu }|}_{\nu >1}$.) Hence only transitions to excited states associated with deviations obeying the sum rules Equations (49) and (50) are permitted. The electron number deviations Equations (49) and (50) are associated with sum rules obeyed by the numbers ${\mathcal{N}}_{l_{\eta },l_s}$ of Equation (48) specific to the $\mathcal{N}$-electron operator ${\widehat{O}}_{\mathcal{N}}$ under consideration, which read,

$$\delta N={\displaystyle \sum _{l_{\eta },l_s=\pm 1}}(-l_{\eta }){\mathcal{N}}_{l_{\eta },l_s};\delta (N_{\downarrow }-N_{\uparrow })={\displaystyle \sum _{l_{\eta },l_s=\pm 1}}(l_{\eta }{l}_s){\mathcal{N}}_{l_{\eta },l_s}$$

(51)

Furthermore, it is straightforward to show that useful exact selection rules hold for excitations of well-defined initial ground states. For instance, the values of the numbers $M_{\eta }^{de}=[M_{\eta ,-1/2}^{de}+M_{\eta ,+1/2}^{de}]=2S_{\eta }$ of deconfined $\eta$-spinons and $M_{\eta ,\pm 1/2}^{de}$ of $\pm 1/2$ deconfined $\eta$-spinons generated by application onto a $S_{\eta }=S_s=0$ ground state of a $\mathcal{N}$-electron operator ${\widehat{O}}_{\mathcal{N}}$ are restricted to the following ranges,

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill M_{\eta }^{de}& =2S_{\eta }=0,1,\dots ,\mathcal{N}\hfill \\ \hfill M_{\eta ,\pm 1/2}^{de}& =0,1,\dots ,{\displaystyle \sum _{l_s=\pm 1}}{\mathcal{N}}_{\pm 1,l_s}\hfill \end{array}\end{array}$$

(52)

respectively. Here $S_{\eta }$ denotes the excited-state $\eta$-spin and the numbers ${\mathcal{N}}_{l_{\eta },l_s}$ are those of Equation (48) specific to the $\mathcal{N}$-electron operator.

In the case of an initial $S_s=0$ ground state with hole concentration $x>\mathcal{N}/N_a^D$ or $x=0$ one finds that the numbers $M_s^{de}=[M_{s,-1/2}^{de}+M_{s,+1/2}^{de}]=2S_s$ and $M_{s,\pm 1/2}^{de}$ of deconfined spinons generated by application onto that state of a $\mathcal{N}$-electron operator are restricted to the ranges,

$$\begin{array}{c}\hfill \begin{array}{ccc}\hfill M_s^{de}& =0,1,\dots ,\mathcal{N}\hfill & \mathrm{for}x>\mathcal{N}/N_a^D\hfill \\ \hfill M_{s,\pm 1/2}^{de}& =0,1,\dots ,{\displaystyle \sum _{l_{\eta },l_s=\pm 1}}{\delta }_{l_{\eta },\mp l_s}{\mathcal{N}}_{l_{\eta },l_s}\hfill & \mathrm{for}x>\mathcal{N}/N_a^D\hfill \\ \hfill M_s^{de}& =0,1,\dots ,{\displaystyle \sum _{l_s=\pm 1}}{\mathcal{N}}_{+1,l_s}\hfill & \mathrm{at}x=0\hfill \\ \hfill M_{s,\pm 1/2}^{de}& =0,1,\dots ,{\mathcal{N}}_{+1,\mp 1}\hfill & \mathrm{at}x=0\hfill \end{array}\end{array}$$

(53)

The range restrictions of Equations (52) and (53) are exact for both the model on the square and 1D lattice, as well as for any other bipartite lattice.

For $x>0$ we limit our considerations to the vanishing rotated-electron double occupancy subspace. Consistently with the ${\mathsf{\Delta }}_{D_{rot}}$ energy spectrum of Equations (26) and (39), this is accomplished merely by limiting the excitation energy to values below $2\mu$, so that the $M_{\eta ,-1/2}=0$ constraint is automatically fulfilled: It follows from the form of such a spectrum that excited states with ${\mathsf{\Delta }}_{D_{rot}}<2\mu$ have vanishing rotated-electron double occupancy. Indeed creation of one rotated-electron doubly occupied site onto an initial $x>0$ and $m=0$ ground state is a process of minimum energy $2\mu$. In turn, at $x=0$ we consider both states with vanishing and finite rotated-electron double occupancy.

Creation onto the $S_{\eta }=0$, $\mu =0$, and $S_s=0$ ground state of one $\eta \nu$ fermion is a vanishing momentum process whose finite energy is exactly given by ${ϵ}_{\eta \nu }=2\nu {\mu }^0$. That object then obeys the criterion of Equation (42) for invariance under the electron-rotated-electron unitary transformation. It follows that the $\eta$-spin degrees of freedom of such a $\eta \nu$ fermion exactly involve $\nu$ electron doubly occupied sites. Furthermore, creation onto an initial $x\ge 0$ and $S_s=0$ ground state of one $s\nu$ fermion with a number $\nu >1$ of spinon pairs is a vanishing energy and momentum process. Since vanishing spin $S_s=0$ refers to vanishing magnetic field $H=0$, such an object obeys the criterion ${ϵ}_{s\nu }=2\nu {\mu }_B|H|=0$ of Equation (42). Thus it is invariant under the electron-rotated-electron unitary transformation. It follows that for $U/4t>0$ creation of such an object involves occupancy configurations whose spin degrees of freedom are similar in terms of both rotated-electron and electron occupancy configurations. That reveals that such a $s\nu$ fermion describes the spin degrees of freedom of a number $2\nu$ of electrons.

It then follows from the invariance under the electron-rotated-electron unitary transformation of the $\eta$-spin and spin degrees of freedom of the above $\eta \nu$ fermion and $s\nu$ fermion, respectively, that for $x>\mathcal{N}/N_a^D$ where $\mathcal{N}/N_a^D\to 0$ as $N_a^D\to \infty$ and excitation energy $\omega <2\mu$ and any excitation energy at $x=0$ nearly the whole spectral weight generated by application onto the above ground states of $\mathcal{N}$-electron operators refers to a subspace spanned by excited states with numbers in the following range,

$$\begin{array}{c}\hfill \begin{array}{ccc}\hfill M_{\eta }^{de}& =2S_{\eta }=M_{\eta ,+1/2}^{de}=x{N}_a^D\hfill & \mathrm{for}x>\mathcal{N}/N_a^D\mathrm{and}\omega <2\mu \hfill \\ \hfill M_{\eta ,-1/2}^{de}& =M_{\eta }^{co}=0\hfill & \mathrm{for}x>\mathcal{N}/N_a^D\mathrm{and}\omega <2\mu \hfill \\ \hfill M_{\eta }& =M_{\eta }^{de}+M_{\eta }^{co}=0,1,\dots ,\mathcal{N}\hfill & \mathrm{at}x=0\hfill \\ \hfill M_{\eta ,\pm 1/2}& =M_{\eta ,\pm 1/2}^{de}+M_{\eta }^{co}/2=0,1,\dots ,{\displaystyle \sum _{l_s=\pm 1}}{\mathcal{N}}_{\pm 1,l_s}\hfill & \mathrm{at}x=0\hfill \\ \hfill M_s-2B_s& =M_s^{de}+M_s^{co}-2B_s=0,1,\dots ,\mathcal{N}\hfill & \mathrm{for}x>\mathcal{N}/N_a^D\hfill \\ & =0,1,\dots ,{\displaystyle \sum _{l_s=\pm 1}}{\mathcal{N}}_{+1,l_s}\hfill & \mathrm{at}x=0\hfill \\ \hfill M_{s,\pm 1/2}-B_s& =M_{s,\pm 1/2}^{de}+M_s^{co}/2\hfill \\ & =0,1,\dots ,{\displaystyle \sum _{l_{\eta },l_s=\pm 1}}{\delta }_{l_{\eta },\mp l_s}{\mathcal{N}}_{l_{\eta },l_s}\hfill & \mathrm{for}x>\mathcal{N}/N_a^D\hfill \\ & =0,1,\dots ,{\mathcal{N}}_{+1,\mp 1}\hfill & \mathrm{at}x=0\hfill \end{array}\end{array}$$

(54)

Here $M_{\alpha }^{co}=2{\sum }_{\nu =1}^{\infty }\nu N_{\alpha \nu }$ where $\alpha =\eta ,s$ and $B_s={\sum }_{\nu =1}^{\infty }{N}_{s\nu }$. The quantities $M_{\eta }^{de}$, $M_{\eta ,\pm 1/2}^{de}$, $M_{\eta }^{co}$, $M_s^{de}$, $M_{s,\pm 1/2}^{de}$, and $M_s^{co}$ appearing in Equation (54) are good quantum numbers. Moreover, provided that $\mathcal{N}/N_a^D\to 0$ and $[B_s-S_c+S_s]/N_a^D\to 0$ as $N_a^D\to \infty$, the number $B_s={\sum }_{\nu }{N}_{s\nu }$ is a good quantum number for the model on the square lattice, alike for 1D.

The selection rules given in Equations (52) and (53) are exact. In turn, for $x>0$ and $m=0$ initial ground states and excitation energy $\omega <2\mu$ (and an initial $x=0$ and $m=0$ ground state and any excitation energy) nearly the whole $\mathcal{N}$-electron spectral weight is generated by excited states whose numbers obey the approximate selection rules given in Equation (54). Indeed excited states with numbers $[M^{co}-2B_s]>\mathcal{N}$ for $x>0$ (and $M_{\eta }>\mathcal{N}$ and $[M_s-2B_s>{\sum }_{l_s=\pm 1}{\mathcal{N}}_{+1,l_s}]$ at $x=0$) generate a very small amount yet non-vanishing $\mathcal{N}$-electron spectral weight.

Why, in spite of the invariance under the electron-rotated-electron unitary transformation of the $s\nu$ fermions with a number $\nu >1$ of spinon pairs created onto an initial $x\ge 0$ and $m=0$ ground state (and that of the $\eta \nu$ fermions created onto an initial $x=0$ and $m=0$ ground state), are the selection rules provided in Equation (54) not exact? The reason is that while the spin degrees of freedom of the $2\nu$-electron occupancy configurations involved in a $s\nu$ fermion are exactly described by that object, their hidden $U(1)$ symmetry degrees of freedom are not invariant under the electron-rotated-electron unitary transformation. The same applies to the $\eta$-spin degrees of freedom of the $2\nu$-electron occupancy configurations exactly described by a $\eta \nu$ fermion created onto a $x=0$ ground state. Their corresponding hidden $U(1)$ symmetry degrees of freedom are not in general invariant under that transformation. The spin degrees of freedom of the $2\nu$-electron occupancy configurations involved in a $s\nu$ fermion are for $U/4t>0$ exactly the same as those of the corresponding $2\nu$-rotated-electron occupancy configurations. In turn, the occupancy configurations of the $2\nu$c fermions that describe the hidden $U(1)$ symmetry degrees of freedom of the $2\nu$ rotated electrons under consideration are slightly different from those of the corresponding $2\nu$ electrons. The same applies to the $\eta$-spin degrees of freedom and hidden $U(1)$ symmetry degrees of freedom of the $2\nu$ electrons and corresponding $2\nu$ rotated electrons involved in a $\eta \nu$ fermion created onto a $x=0$ ground state. The former and the latter are and are not invariant under that transformation. Hence that the selection rules of Equation (54) are not exact but a very good approximation stems from the lack of invariance under the electron-rotated-electron unitary transformation of the degrees of freedom associated with the hidden $U(1)$ symmetry of the Hubbard model. This applies both to the model on the 1D and square lattice.

The $\mathcal{N}$-electron spectral weight generated by excited states of initial $x>0$ and $m=0$ ground states of excitation energy $\omega <2\mu$ and numbers $[M_s-2B_s]>\mathcal{N}$ is extremely small. The same applies to excited states of initial $x=0$ and $m=0$ ground states of numbers $M_{\eta }>\mathcal{N}$ and $[M_s-2B_s]>{\sum }_{l_s=\pm 1}{\mathcal{N}}_{+1,l_s}$. Therefore, in this paper we define the $\mathcal{N}$-electron subspace as that spanned by an initial $x\ge 0$ and $m=0$ ground state plus the set of excited states whose numbers obey the approximate selection rules given in Equation (54). Note that the latter set of excited states depends on the specific $\mathcal{N}$-electron operator under consideration. (For hole concentrations $x>0$ this definition refers to excitation energy $\omega <2\mu$.)

The One- and Two-Electron Subspace

The concept of a $\mathcal{N}$-electron subspace as defined above refers to a specific operator. In contrast, rather than referring to a specific $\mathcal{N}$-electron operator, the one- and two subspace is the set of $\mathcal{N}=1$ and $\mathcal{N}=2$ subspaces associated with the one-electron operator and all simple two-electron operators, respectively. Besides the $\mathcal{N}=1$ one-electron operator ${\widehat{O}}_1(\overrightarrow{k})=c_{\overrightarrow{k},\sigma }$ (measured in the angle-resolved photoelectron spectroscopy), this includes a set of $\mathcal{N}=2$ operators ${\widehat{O}}_{\mathcal{N}}(\overrightarrow{k})$ such as the spin-projection $\sigma$ density operator ${\widehat{O}}_2^{\sigma sd}(\overrightarrow{k})=[1/\sqrt{N_a^D}]{\sum }_{{\overrightarrow{k}}^{\prime }}{c}_{\overrightarrow{k}+{\overrightarrow{k}}^{\prime },\sigma }^{†}{c}_{{\overrightarrow{k}}^{\prime },\sigma }$, the transverse spin-density operator ${\widehat{O}}_2^{sdw}(\overrightarrow{k})=[1/\sqrt{N_a^D}]{\sum }_{{\overrightarrow{k}}^{\prime }}{c}_{\overrightarrow{k}+{\overrightarrow{k}}^{\prime },\uparrow }^{†}{c}_{{\overrightarrow{k}}^{\prime },\downarrow }$, and the charge density operator (measured in density-density electron energy loss spectroscopy and inelastic X-ray scattering). The latter operator is written in terms of the above spin-up and spin-down density operators. Moreover, the set of $\mathcal{N}=2$ operators includes several superconductivity operators whose pairing symmetries are in general different at 1D and for the square lattice. The local operators ${\widehat{O}}_{\mathcal{N},j}$ corresponding to the operators ${\widehat{O}}_{\mathcal{N}}(\overrightarrow{k})$ whose explicit expression is provided above read ${\widehat{O}}_{1,j}=c_{{\overrightarrow{r}}_j,\sigma }$, ${\widehat{O}}_{2,j}^{\sigma sd}=c_{{\overrightarrow{r}}_j,\sigma }^{†}{c}_{{\overrightarrow{r}}_j,\sigma }$, and ${\widehat{O}}_{2,j}^{sdw}=c_{{\overrightarrow{r}}_j,\uparrow }^{†}{c}_{{\overrightarrow{r}}_j,\downarrow }$, respectively.

In the case of excitations of $x>0$ and $m=0$ ground states, in the remaining of this paper we are mostly interested in the subspace obtained from the overlap of the one- and two-electron subspace with the vanishing rotated-electron double occupancy subspace. Such a subspace is the one- and two-electron subspace for excitation energy $\omega <2\mu$. For finite hole concentrations this is the subspace of interest for the one- and two-electron physics. In turn, concerning the excitations of a $x=0$ and $m=0$ ground state we consider the whole one- and two-electron subspace, which refers both to the spin lower-Hubbard band physics and one-electron and charge upper-Hubbard band physics.

As discussed above concerning the general $\mathcal{N}$-electron spectral weight, for the model on the 1D and square lattices there is for $x>0$ an extremely small amount of one- and two-electron spectral weight that for excitation energy $\omega <2\mu$ is generated by states that do not obey the approximate selection rules of Equation (54) for $\mathcal{N}=1$, 2. Nearly all such very small amount of spectral weight refers to $N_{s3}=1$ excited states. (States with $N_{s4}=1$ or $N_{s2}=2$ generate nearly no spectral weight.) That very small weight is neglected within the present definition of the one- and two-electron subspace, which refers to excitation energies below $2\mu$. In turn, concerning the one- and two-electron excitations of a $x=0$ and $m=0$ ground state the very small amount of spectral weight generated by states that do not obey the approximate selection rules of Equation (54) refers to $N_{s3}=1$ and/or $N_{\eta 2}=1$ or $N_{\eta 1}=2$ excited states. That very small weight is also neglected within the definition of the one- and two-electron subspace. (Both the $N_{\eta 2}=1$ and $N_{\eta 1}=2$ excited states have energy much larger than the upper-Hubbard band $M_{\eta ,-1/2}^{de}=1$, 2 or $N_{\eta 1}=1$ excited states that obey the selection rules of Equation (54) for $\mathcal{N}=1$, 2.)

Initial $x>0$ and $m=0$ ground states and their excited states of energy $\omega <2\mu$ that span the one- and two-electron subspace considered in this paper have no $-1/2$ $\eta$-spinons, no $\eta \nu$ fermions, and no $s{\nu }^{\prime }$ fermions with ${\nu }^{\prime }>2$ spinon pairs, so that $N_{\eta \nu }=0$ and $N_{s{\nu }^{\prime }}=0$ for ${\nu }^{\prime }>2$. In turn, initial $x=0$ and $m=0$ ground states and their excited states that span the one- and two-electron subspace have no $\eta \nu$ fermions with $\nu >1$ $\eta$-spinon pairs and no $s{\nu }^{\prime }$ fermions with ${\nu }^{\prime }>2$ spinon pairs, so that $N_{\eta \nu }=0$ for $\nu >1$ and $N_{s{\nu }^{\prime }}=0$ for ${\nu }^{\prime }>2$. Thus, consistent with the approximate selection rules of Equation (54), the values of the object numbers of such ground states and their excited states that span the subspace considered here are restricted to the following ranges,

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill M_{\eta }^{de}& =2S_{\eta }=M_{\eta ,+1/2}^{de}=x{N}_a^D\mathrm{for}x>0\mathrm{and}\omega <2\mu \hfill \\ \hfill M_{\eta ,-1/2}^{de}& =M_{\eta }^{co}=0\mathrm{for}x>0\mathrm{and}\omega <2\mu \hfill \\ \hfill M_{\eta }& =0,\dots ,\mathcal{N}\mathrm{for}\mathcal{N}=1,2\mathrm{at}x=0\hfill \\ \hfill M_{\eta ,\pm 1/2}& =0,\dots ,{\displaystyle \sum _{l_s=\pm 1}}{\mathcal{N}}_{\pm 1,l_s}\mathrm{for}{\displaystyle \sum _{l_s=\pm 1}}{\mathcal{N}}_{\pm 1,l_s}=0,1,2\mathrm{at}x=0\hfill \\ \hfill M_s-2B_s& =0,\dots ,\mathcal{N}\mathrm{for}\mathcal{N}=1,2\mathrm{and}x>0\hfill \\ & =0,\dots ,{\displaystyle \sum _{l_s=\pm 1}}{\mathcal{N}}_{+1,l_s}\mathrm{for}{\displaystyle \sum _{l_s=\pm 1}}{\mathcal{N}}_{+1,l_s}=0,1,2\mathrm{at}x=0\hfill \\ \hfill M_{s,\pm 1/2}-B_s& =0,\dots ,{\displaystyle \sum _{l_{\eta },l_s=\pm 1}}{\delta }_{l_{\eta },\mp l_s}{\mathcal{N}}_{l_{\eta },l_s}\mathrm{for}{\displaystyle \sum _{l_{\eta },l_s=\pm 1}}{\delta }_{l_{\eta },\mp l_s}{\mathcal{N}}_{l_{\eta },l_s}=0,1,2\mathrm{for}x>0\hfill \\ & =0,\dots ,{\mathcal{N}}_{+1,\mp 1}\mathrm{for}{\mathcal{N}}_{+1,\mp 1}=0,1,2\mathrm{at}x=0\hfill \end{array}\end{array}$$

(55)

We emphasize that the maximum values of the numbers $[{\sum }_{l_s}{\mathcal{N}}_{\pm 1,l_s}]$, $[{\sum }_{l_s}{\mathcal{N}}_{+1,l_s}]$, $[{\sum }_{l_{\eta },l_s}{\delta }_{l_{\eta },\mp l_s}{\mathcal{N}}_{l_{\eta },l_s}]$, and ${\mathcal{N}}_{+1,\mp 1}$ appearing in this equation must be consistent with the inequality requirement $\mathcal{N}={\sum }_{l_{\eta },l_s}{\mathcal{N}}_{l_{\eta },l_s}\le 2$. Furthermore, the hole concentrations in the inequality $x>0$ and equality $x=0$ also appearing here refer to the initial ground states and in the inequality $x>0$ we have neglected $1/N_a^D$ and $2/N_a^D$ corrections. We recall that the numbers $\mathcal{N}=1$, 2 and ${\mathcal{N}}_{l_{\eta },l_s}$ correspond to a specific $\mathcal{N}$-electron operator ${\widehat{O}}_{\mathcal{N}}$ whose application onto a ground state $|{\Psi }_{GS}\rangle$ generates $\mathcal{N}$-electron excited states, as given in Equation (47). The subspace considered here refers though to the whole set of such subspaces associated with the one-electron operator and the set of simple two-electron operators mentioned above.

Fortunately, the subspace spanned by states whose numbers have values in the ranges given in Equation (55) is a $[M_s^{co}/2-B_s]=N_{s2}=0$, 1 and $[M_{\eta }^{co}/2-B_{\eta }]=0$ a subspace (A) as defined in Reference [9]. For initial $x>0$ and $m=0$ (and $x=0$ and $m=0$) ground states it is such that $M_s^{co}=[2N_{s1}+4N_{s2}]$, $B_s=[N_{s1}+N_{s2}]$, and $M_{\eta }^{co}=B_{\eta }=0$ (and $M_s^{co}=[2N_{s1}+4N_{s2}]$, $B_s=[N_{s1}+N_{s2}]$, and $M_{\eta }^{co}/2=B_{\eta }=N_{\eta 1}=0$, 1.) Hence the following c and $s1$ fermion numbers are conserved both for the subspaces with initial $x=0$ and $x>0$ ground states,

$$N_{a_c}^D=[N_c+N_c^h]=N_a^D;N_c=2S_c;N_c^h=N_a^D-2S_c$$

(56)

and

$$N_{a_{s1}}^D=[N_{s1}+N_{s1}^h]=[S_c+S_s];N_{s1}=[S_c-S_s-2N_{s2}];N_{s1}^h=[2S_s+2N_{s2}]=0,1,2$$

(57)

respectively. The hidden $U(1)$ symmetry generator eigenvalue $2S_c$ appearing here and the $\eta$-spin $S_{\eta }$ and spin $S_s$ have in the present subspace the following values,

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill 2S_c& =(1-x)N_a^D=N\mathrm{for}x>0\mathrm{and}\omega <2\mu \hfill \\ & =N-2M_{\eta ,-1/2}^{de}-2N_{\eta 1}\mathrm{for}\mathrm{the}\mathrm{initial}x=0\mathrm{GS}\mathrm{excitations}\hfill \\ \hfill S_{\eta }& =\frac{1}{2}x{N}_a^D\mathrm{for}x>0\mathrm{and}\omega <2\mu \hfill \\ & =\frac{1}{2}x{N}_a^D+M_{\eta ,-1/2}^{de}=0,\frac{1}{2},1\mathrm{for}\mathrm{the}\mathrm{initial}x=0\mathrm{GS}\mathrm{excitations}\hfill \\ \hfill S_s& =S_c-N_{s1}-2N_{s2}=0,\frac{1}{2},1\mathrm{for}x\ge 0\hfill \end{array}\end{array}$$

(58)

Furthermore, for the subspace considered here the following number associated with the $\alpha \nu =s1$ branch is conserved,

$$P_{s1}^h\equiv e^{i\pi N_{s1}^h}=e^{i2\pi S_s}=e^{i2\pi S_c}=e^{i\pi N}=\pm 1$$

(59)

Combination of this exact relation between $N_{s1}^h$ and the number of electrons N with the expressions and values of Equations (55) and (57) reveals that the one- and two-electron subspace considered here is spanned by states whose deviation $\delta N_c^h$ in the number of c band holes and number $N_{s1}^h$ of $s1$ band holes may only have the following values,

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill \delta N_c^h& =-2\delta S_c=-\delta N=0,\mp 1,\mp 2\hfill \\ \hfill N_{s1}^h& =2S_s+2N_{s2}=0,1,2\hfill \end{array}\end{array}$$

(60)

(The initial $x\ge 0$ and $m=0$ ground states have zero holes in the $s1$ band so that $\delta N_{s1}^h=N_{s1}^h$ for their excited states.) For $N_{s1}^h=0$ ground states and their charge excited states all $M_s=2S_c$ spinons are confined within the two-spinon bonds of the $N_{s1}=M_s/2$ $s1$ fermions.

The number $P_{s1}^h=\pm 1$ of Equation (59) is associated with an important exact selection rule. One of its consequences is that one- and two-electron excitations of $x\ge 0$ and $m=0$ ground states contain no states with an even and odd number $N_{s1}^h$ of $s1$ fermion holes in the $s1$ momentum band, respectively. For such initial ground states we consider that N is an even integer number. Since, as given in Equation (59), $e^{i\pi {\prod }_l{N}_{s1}^h(l)}=e^{i\pi N}$, for one-electron excited states for which the deviation in the value of N reads $\delta N=\pm 1$ the number of $s1$ fermion holes $N_{s1}^h$ must be always an odd integer. On the other hand, for both $\delta N=0$ and $\delta N=\pm 2$ two-electron excited states $N_{s1}^h$ must always be an even integer. Such exact selection rules play an important role in the one- and two-electron spectra of the square-lattice quantum liquid further studied in Reference [10]. That quantum liquid refers to the Hamiltonian Equation (1) in the one- and two-electron subspace for initial $x\ge 0$ and $m=0$ ground states.

5.2. The Spin and $s1$ Effective Lattices for the One- and Two-Electron Subspace

According to the restrictions and numbers values of Equations (55) and (60), the states that span the one- and two-electron subspace may involve none or one $s2$ fermion. As confirmed in the studies of Reference [10], it is convenient to express the one- and two-electron excitation spectrum relative to initial $x\ge 0$ and $m=0$ ground states in terms of the deviations in the numbers of c effective lattice unoccupied sites and $s1$ effective lattice unoccupied sites. Those are given explicitly in Equation (60) and equal the corresponding deviations in the numbers of c band fermion holes and $s1$ band fermion holes, respectively. Note that for $x>0$ and $\omega <2\mu$ states the $s1$ fermion related numbers provided in Equation (57) can be written as $N_{a_{s1}}^D=[N/2+S_s]$, $N_{s1}=[N/2-S_s-2N_{s2}]$, and $N_{s1}^h=[2S_s+2N_{s2}]=0$, 1, 2 where $S_s=0$ for $N_{s2}=1$ and $S_s=0,1/2,1$ for $N_{s2}=0$. In turn, for excited states of the $x=0$ and $m=0$ ground state they read $N_{a_{s1}}^D=[N/2-M_{\eta ,-1/2}^{de}-N_{\eta 1}+S_s]$, $N_{s1}=[N/2-M_{\eta ,-1/2}^{de}-N_{\eta 1}-S_s-2N_{s2}]$, and $N_{s1}^h=[2S_s+2N_{s2}]=0$, 1, 2 where $S_s$ and $N_{s2}$ may have the same values as above and $M_{\eta ,-1/2}^{de}=0$ for $N_{\eta 1}=1$ and $M_{\eta ,-1/2}^{de}=0$, 1, 2 for $N_{\eta 1}=0$. Provided that $n=(1-x)$ is finite, the corrections to $N_{a_{s1}}^D\approx N/2$ and $N_{s1}\approx N/2$ are in both cases of the order of $1/N_a^D$, whereas $N_{s1}^h=[2S_s+2N_{s2}]=0$, 1, 2 has the same expression and allowed values.

As discussed above, for $N_{s2}=1$ spin-singlet excited energy eigenstates the single $s2$ fermion has vanishing energy and momentum. Consistent with Equation (42), for vanishing magnetic field $H=0$ it is invariant under the electron-rotated-electron unitary transformation. The same applies to the single $\eta 1$ fermion of $N_{\eta 1}=1$ $\eta$-spin-singlet excited states of the $x=0$, $\mu =0$, and $m=0$ ground state. Therefore, the only effect of creation and annihilation of such two objects is in the numbers of sites and occupied sites of the $s1$ effective lattice. Their creation can then be merely accounted for by small changes in the occupancies of the discrete momentum values of the $s1$ band. Hence the only composite object whose internal occupancy configurations are important for the physics of the Hamiltonian Equation (1) in the one- and two-electron subspace is the spin-neutral two-spinon $s1$ fermion and related spin-singlet two-spinon $s1$ bond particle [10].

It turns out that for the Hubbard model in the one- and two-electron subspace and alike for the $s2$ fermion and/or the $\eta 1$ fermion, the presence of deconfined spinons is felt through the numbers of occupied and unoccupied sites of the $s1$ effective lattice. For excited states of $x\ge 0$ and $m=0$ ground states the number of deconfined $\eta$-spinons equals that of the unoccupied sites of the c effective lattice. For excited states of the $x=0$, $\mu =0$, and $m=0$ ground state the presence of deconfined $\eta$-spinons is felt in addition through the above numbers of sites and occupied sites of the $s1$ effective lattice. Those may be rewritten as $N_{a_{s1}}^D=[N_a^D/2-M_{\eta }^{de}/2-N_{\eta 1}+S_s]$ and $N_{s1}=[N_a^D/2-M_{\eta }^{de}/2-N_{\eta 1}-S_s-2N_{s2}]$, respectively, where $M_{\eta }^{de}=2S_{\eta }=0$, 1, 2. Therefore, when acting onto the one- and two-electron subspace, the Hubbard model refers to a two-component quantum liquid that can be described only in terms of c fermions and $s1$ fermions. For excited states of $x>0$ and $m=0$ ground states this analysis applies to excitation energies $\omega <2\mu$. For those of the $x=0$, $\mu =0$, and $m=0$ ground state the $\eta$-spin degrees of freedom are in addition behind the finite energy ${\mathsf{\Delta }}_{D_{rot}}$ given in Equation (39) and the related energy ${\mathsf{\Delta }}_{D_{rot}}^h$. Those are associated with rotated-electron doubly occupied sites and rotated-electron unoccupied sites, respectively, of excited states with finite occupancy $M_{\eta }^{de}=1$, 2 of deconfined $\eta$-spinons or $N_{\eta 1}=1$ of a single $\eta 1$ fermion. However, the magnitude of that energy is fixed for each branch of excitations of that ground state. Hence for it and its excited states the square-lattice quantum liquid may again be described solely in terms of c fermions and $s1$ fermions.

For excited states of $x>0$ and $m=0$ ground states belonging to the one- and two-electron subspace the spin effective lattice has a number of sites given by $N_{a_s}^D=(1-x)N_a^D$. For those of the $x=0$, $\mu =0$, and $m=0$ ground state it reads $N_{a_s}^D=[N_a^D-M_{\eta }^{de}-2N_{\eta 1}]$ so that $N_{a_s}^D$ may have the values $N_a^D$, $[N_a^D-1]$, and $[N_a^D-2]$. For $x>0$ its value is smaller than that of the original lattice. Within the $N_a^D\gg 1$ limit one may neglect corrections of the order $1/N_a^D$ so that for both types of excited states the lattice spacing $a_s$ is that provided in Equation (30) for $\alpha =s$. For the model on the square lattice it reads $a_s\approx a/\sqrt{1-x}$. Both it and its general expression given in Equation (30) are such that the area $L^2={[a_s\times N_{a_s}]}^2={[a\times N_a]}^2$ of the system is preserved. The concept of a spin effective lattice is valid only within the $N_a^D\gg 1$ limit that the description reviewed in this paper refers to. For the model on the square lattice, the corresponding $s1$ fermion spinon occupancy configurations are expected to be a good approximation provided that the ratio $N_{a_s}^2/N_a^2$ and thus the electronic density $n=(1-x)$ remain finite as $N_a^2\to \infty$. This is met for the hole concentration range $x\in (0,x_{*})$ considered in the studies of Reference [10].

Within the present $N_a^2\gg 1$ limit there is for the one- and two-electron subspace of the model on the square lattice commensurability between the real-space distributions of the $N_{a_{s1}}^2\approx N_{s1}$ sites of the $s1$ effective lattice and the $N_{a_s}^2\approx 2N_{s1}$ sites of the spin effective lattice. For $(1-x)\ge 1/N_a^2$ and $N_a^2\gg 1$ the spin effective lattice has $N_{a_s}^2\approx (1-x)N_a^2$ sites and from the use of the expression given in Equation (57) for the number of $s1$ effective lattice sites $N_{a_{s1}}^2$ and Equation (46) for the corresponding spacing $a_{s1}$ we find,

$$a_{s1}=a_s\sqrt{\frac{2}{1+\frac{2S_s}{(1-x)N_a^2}}}\approx \sqrt{2}{a}_s\left(1-\frac{2S_s}{2(1-x)}\frac{1}{N_a^2}\right)\approx \sqrt{2}{a}_s,S_s=0,\frac{1}{2},1$$

(61)

Our general description refers to a very large number of sites $N_a^2\gg 1$. Although very large, we assume that $N_a^D$ is finite and only in the end of any calculation take the $N_a^D\to \infty$ limit. For $N_a^D\gg 1$ very large but finite the $m=0$ ground state spin effective lattice is full and both at $x=0$ and for $x>0$ such a state is a spin-singlet state. (For $m=0$ and $x=0$ this agrees with the exact theorem of Reference [4].) For $N_{s1}^h=0$ states such as $x\ge 0$ and $m=0$ ground states and their charge excited states the spin effective square lattice has two well-defined sub-lattices, which we call sub-lattice 1 and 2, respectively. (For the $N_{s1}^h=1$, 2 states of the present subspace the spin effective lattice has two bipartite lattices as well, with the one or two extra sites accounted for by suitable boundary conditions.) The two spin effective sub-lattices have spacing $a_{s1}\approx \sqrt{2}{a}_s$. The fundamental translation vectors of the sub-lattices 1 and 2 read,

$${\overrightarrow{a}}_{s1}=\frac{a_{s1}}{\sqrt{2}}({\overrightarrow{e}}_{x_1}+{\overrightarrow{e}}_{x_2}),{\overrightarrow{b}}_{s1}=-\frac{a_{s1}}{\sqrt{2}}({\overrightarrow{e}}_{x_1}-{\overrightarrow{e}}_{x_2})$$

(62)

respectively. Here ${\overrightarrow{e}}_{x_1}$ and ${\overrightarrow{e}}_{x_2}$ are unit vectors pointing in the direction associated with the Cartesian coordinates $x_1$ and $x_2$, respectively. The vectors given in this equation are the fundamental translation vectors of the $s1$ effective square lattice.

In the case of $x\ge 0$, $m=0$, and $N_{s1}^h=0$ ground states whose $s1$ momentum band is full and all $N_{a_{s1}}^2=N_{a_{s1}}\times N_{a_{s1}}$ sites of the $s1$ effective square lattice are occupied, we consider that the square root $N_{a_s}$ of the number $N_{a_s}^2=N_{a_s}\times N_{a_s}$ of sites of the corresponding spin effective square lattice is an integer. Although the square root $N_{a_{s1}}$ of the number $N_{a_{s1}}^2=N_{a_{s1}}\times N_{a_{s1}}$ of sites of the $s1$ effective lattice is not in general an integer number, within the present $N_a^2\gg 1$ limit we consider that it is the closest integer to it.

5.3. The Square-Lattice Quantum Liquid of c and $s1$ Fermions

It follows from the above results that when acting onto the one- and two-electron subspace, the Hubbard model on a 1D or square lattice refers to a two-component quantum liquid described in terms of two types of objects on the corresponding effective lattices and momentum bands: The charge c fermions and spin-neutral two-spinon $s1$ fermions. The one- and two-electron subspace can be divided into smaller subspaces that conserve $S_c$ and $S_s$. When expressed in terms of c and $s1$ fermion operators, the Hubbard model on a square lattice in the one- and two-electron subspace is the square-lattice quantum liquid further studied in Reference [10].

The quantum-liquid c fermions are $\eta$-spinless and spinless objects without internal degrees of freedom and structure whose effective lattice is identical to the original lattice. For the complete set of $U/4t>0$ energy eigenstates that span the full Hilbert space, the occupied sites (and unoccupied sites) of the c effective lattice correspond to those singly occupied (and doubly occupied plus unoccupied) by the rotated electrons. The corresponding c band has the same shape and momentum area as the first Brillouin zone [10].

In contrast, the quantum-liquid composite spin-neutral two-spinon $s1$ fermions have internal structure. Thus the spinon occupancy configurations that describe such objects are a more complex problem for the one- and two-electron subspace. It is simplified by the property that the number of unoccupied sites of the $s1$ effective lattice is in that subspace limited to the values $N_{s1}^h=0$, 1, 2.

That the square-lattice quantum liquid is constructed to inherently the c and $s1$ fermion discrete momentum values being good quantum numbers is behind the suitability of the present description in terms of occupancy configurations of the c and $s1$ effective lattices and corresponding c and $s1$ band discrete momentum values. The latter c and $s1$ values are the conjugate of the real-space coordinates of the c and $s1$ effective lattice, respectively. Are the approximations used in the construction of the $s1$ effective lattice inconsistent with the $s1$ band discrete momentum values being good quantum numbers? The answer is no. Indeed, such approximations concern the relative positions of the $j=1$, …, $N_{a_{s1}}^2$ sites of the $s1$ effective lattice [10]. Those control the shape of the $s1$ momentum band boundary. They do not affect the $s1$ band discrete momentum values being good quantum numbers. At $x=0$ the spin effective lattice is identical to the original square lattice and the $s1$ effective lattice is one of its two sub-lattices. Consistently, at $x=0$ and $m=0$ the boundary of the $s1$ momentum band is accurately known. Then the $s1$ band coincides with an antiferromagnetic reduced Brillouin zone of momentum area $2{\pi }^2$ such that $|q_{x_1}|+|q_{x_2}|\le \pi$ [10]. In turn, it is known that for $x>0$ and $m=0$ the $s1$ band boundary encloses a smaller momentum area $(1-x)2{\pi }^2$ yet its precise shape remains an open issue.

The general problem of expressing the 1D Hubbard model in terms of c and $\alpha \nu$ fermion operators is beyond the goals of this paper. Fortunately, the problem of physical interest is simpler. It refers to the expression of the Hamiltonian $\widehat{H}$ of Equation (6) in the one- and two-electron subspace alone. This leads to an expression in terms of only c fermion and $s1$ fermion operators. However, this remains a problem of some complexity. It is discussed in Section 4.1 of Reference [10]. The corresponding general energy spectrum involves c and $s1$ momentum bands and corresponding energy dispersions. Such dispersions and associated velocities are studied in that reference.

5.4. A Preliminary Application: The Inelastic Neutron Scattering of LCO

It is desirable that the results of the square-lattice quantum liquid studied in this paper are compared with those of the standard formalism of many-body physics. Unfortunately, such a quantum liquid is non-perturbative in terms of electron operators so that, in contrast to a 3D isotropic Fermi liquid [27], rewriting the theory in terms of it is an extremely complex problem.

In spite of the lack of an exact solution for the model on a square lattice and the non-perturbative character of the quantum problem in terms of electrons, in this subsection results achieved by the square-lattice quantum liquid description are compared with those obtained by methods relying on the standard formalism of many-body physics. Unfortunately, there are not many controlled results for the Hubbard model on the square lattice from approximations relying on that formalism. Here we consider the interesting problem of the spin-excitation spectrum of the half-filling Hubbard model on the square lattice.

Within the present description and as discussed below, since the c and $s1$ fermion momentum values are for the model in the one- and two-electron subspace good quantum numbers, that problem refers to an effectively non-interacting limit whereas in terms of electrons it is an involved many-body problem. Fortunately, there are reliable results on that particular problem obtained by controlled approximations of the standard formalism of many-electron physics: within such approximations its solution requires summing up an infinite set of ladder diagrams, to find the spin-wave dispersion of the half-filled Hubbard model on the square lattice in a spin-density-wave-broken symmetry ground state [14]. In turn, within the present description the spin spectrum involves the creation of two holes in the $s1$ band. Agreement between the two methods is both a further checking of the validity of the description and a confirmation that the c and $s1$ fermion interactions are indeed residual and their momentum values good quantum numbers for the model on the square lattice in the one- and two-electron subspace.

The spin-triplet excitations relative to the $x=0$ and $m=0$ absolute ground state involve creation of two holes in the $s1$ band along with a shift $\overrightarrow{\pi }/N_a^2$ of all discrete momentum values of the full c band so that the their spectrum reads,

$$\omega (\overrightarrow{k})=[-{ϵ}_{s1}(\overrightarrow{q})-{ϵ}_{s1}(\overrightarrow{q}{}^{\prime })];\overrightarrow{k}=[\overrightarrow{\pi }-\overrightarrow{q}-\overrightarrow{q}{}^{\prime }]$$

(63)

where $\overrightarrow{\pi }=\pm [\pi ,\pm \pi ]$ and for approximately $U/4t\ge 1.3$, excitation energy $\omega$ below ${\mu }^0$, and temperatures T below $\omega /k_B$, the $s1$ fermion energy dispersion ${ϵ}_{s1}(\overrightarrow{q})$ reads [10],

$$\begin{array}{c}\hfill \begin{array}{cccc}\hfill {ϵ}_{s1}(\overrightarrow{q})& =-\sqrt{|{ϵ}_{s1}^0(\overrightarrow{q}){|}^2+{|{\mathsf{\Delta }}_{s1}(\overrightarrow{q})|}^2};\hfill & \hfill {ϵ}_{s1}^0(\overrightarrow{q})& =-\frac{W_{s1}^0}{2}[cos{q}_{x_1}+cos{q}_{x_2}]\hfill \\ \hfill |{\mathsf{\Delta }}_{s1}(\overrightarrow{q})|& =\frac{{\mu }^0}{2}{F}_{s1}(\overrightarrow{q});\hfill & \hfill F_{s1}(\overrightarrow{q})& =\frac{|cos{q}_{x_1}-cos{q}_{x_2}|}{2}\hfill \end{array}\end{array}$$

(64)

Here the maximum gap magnitude ${\mu }^0/2$ of the $s1$ fermion energy dispersion equals the maximum $s1$ fermion pairing energy per spinon for $x=0$ and $m=0$. It corresponds to the $s1$ band momentum values belonging to the $s1$ boundary line and pointing in the anti-nodal directions.

The $x=0$ and $m=0$ $s1$ energy dispersion Equation (64) is derived in Reference [10]. The main point is that in the absence of any spin order, the $s1$ fermion spinon-pairing energy would vanish and the energy dispersion ${ϵ}_{s1}(\overrightarrow{q})$ of the $s1$ fermions would be given by the auxiliary energy dispersion ${ϵ}_{s1}^0(\overrightarrow{q})$, also provided in that equation. An important issue for the Reference [10] derivation of the $s1$ fermion energy dispersion ${ϵ}_{s1}(\overrightarrow{q})$ in the presence of such an order as $N_a^2\to \infty$, is that for excitation energy below the energy scale ${\mu }^0$ one can ignore the amplitude fluctuations of the order parameter and the problem can be handled by a suitable mean-field theory where the occurrence of that order is described for the $x=0$ and $m=0$ problem by a $s1$ energy dispersion of the general form $-\sqrt{|{ϵ}_{s1}^0(\overrightarrow{q}){|}^2+{|{\mathsf{\Delta }}_{s1}(\overrightarrow{q})|}^2}$, where $|{\mathsf{\Delta }}_{s1}(\overrightarrow{q})|$ is the $s1$ fermion pairing energy per spinon given in Equation (64).

We emphasize that for small $U/4t$ values the energy scale ${\mu }^0/2$ becomes small and given by ${\mu }^0/2\approx 16t{e}^{-\pi \sqrt{4t/U}}$, so that the amplitude fluctuations of the order parameter cannot be ignored and thus the energy dispersion provided in Equation (64) is not expected to be a good approximation. Indeed and as discussed in Reference [10], within the c and $s1$ fermion description the small-$U/4t$ physics corresponds to a non-trivial problem. This applies to the derivation of the $s1$ fermion dispersion ${ϵ}_{s1}(\overrightarrow{q})$ for small values of $U/4t$, which remains an unsolved issue. Fortunately, the energy dispersion Equation (64) is expected to be a good approximation for $U/4t\ge 1.3$. Furthermore, as confirmed in the following the relation of the present quantum problem to the unusual physics of the Mott–Hubbard insulator parent compounds such as LCO refers to a value $U/4t\approx 1.525>1.3$, so that the description introduced in References [9,10] is of interest for the study of such materials.

For $x=0$ and $m=0$ both the c and $s1$ bands are full for the initial ground state and since the c band remains full for the excited states one can ignore the $s1$-$s1$ and $s1$-c fermion interactions. Indeed, then the residual fermion interactions have little effect on the occupancy configurations of the two holes created in the $s1$ band upon the two-electron spin-triplet excitations. This is consistent with the lack of a c Fermi line for the initial ground state and the lack of $s1$ band holes other than the two holes created upon the spin-triplet excitation so that in spite of the $s1$-$s1$ fermion long-range interactions associated with the effective vector potential of Equation (33) the exclusion principle, phase-space restrictions, and momentum and energy conservation drastically limit the number of available momentum occupancy configurations of the final excited states.

The excitation spectrum Equation (63) refers both to coherent and incoherent spin spectral weight. In contrast to the 1D case where a suitable c and $s1$ fermion dynamical theory is available [28,29], for the square-lattice quantum liquid there are within the present status of the theory no suitable tools to calculate matrix elements between the ground state and one- and two-electron excited states. Hence, one cannot calculate explicitly spin-spin correlation functions. Within the 1D c and $s1$ fermion dynamical theory, the sharp features of the spin two-electron spectral weight distributions result from processes where one of the two $s1$ fermion holes is created at the $s1$ boundary line.

The coherent spin spectral weight is here associated with a Goldstone-mode-like gapless spin-wave spectrum. It consists of sharp $\delta$-peaks having as background the incoherent spectral-weight distribution. From comparison with the results of Reference [14], we have confirmed that such spectral weight is generated by processes corresponding to well-defined values of the momenta $\overrightarrow{q}$ and $\overrightarrow{q}{}^{\prime }$ of the general spectrum Equation (63) such that one hole is created at a momentum pointing in the nodal directions of the $s1$ band and the other hole at a momentum belonging the $s1$ band boundary line, as expected from analogy with the 1D spectral-weight distributions. The incoherent part corresponds to the remaining values of $\overrightarrow{q}$ and $\overrightarrow{q}{}^{\prime }$ of the excitation spectrum Equation (63). The occurrence of the Goldstone-mode-like gapless spin-wave spectrum follows from the long-range antiferromagnetic order of the initial $x=0$ and $m=0$ ground state. In turn, for the $x>0$ short-range spin ordered phase the spin weight distribution has no coherent part. In 1D it has not coherent part both for $x=0$ and $x>0$, due to the lack of a ground-state long-range antiferromagnetic order.

As mentioned above, for the original electrons the problem is highly correlated and involves an infinite set of ladder diagrams and no simple analytical expression was found for the spin-wave energy spectrum [14]. In contrast, for the $s1$ fermion description it is effectively non-interacting and described by simple analytical expressions. Let us profit from symmetry and limit the present analysis to the sector $k_x\in (0,\pi )$ and $k_y\in (0,k_x)$ of the $(\overrightarrow{k},\omega )$ space. Within the description of the quantum problem used here, for $1/k_{B}T\to \infty$ the coherent spin-spectral-weight distribution derived in Reference [14] corresponds to a surface of energy and momentum given by,

$$\omega (\overrightarrow{k})=\frac{{\mu }^0}{2}\left|sin\left(\frac{k_x+k_y}{2}\right)\right|+W_{s1}^0\left|sin\left(\frac{k_x-k_y}{2}\right)\right|;\overrightarrow{k}=\overrightarrow{\pi }-\overrightarrow{q}-\overrightarrow{q}{}^{\prime }$$

(65)

This is a particular case of the general spin spectrum given in Equation (63), which corresponds to the above-mentioned specific processes associated with the following choices for $\overrightarrow{\pi }$, $\overrightarrow{q}$, and $\overrightarrow{q}{}^{\prime }$,

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill \overrightarrow{\pi }& =[\pi ,-\pi ]\hfill \\ \hfill \overrightarrow{q}& =\left[\frac{\pi }{2}-\frac{(k_x+k_y)}{2},-\frac{\pi }{2}-\frac{(k_x+k_y)}{2}\right]\hfill \\ \hfill \overrightarrow{q}{}^{\prime }& =\left[\frac{\pi }{2}-\frac{(k_x-k_y)}{2},-\frac{\pi }{2}+\frac{(k_x-k_y)}{2}\right]\hfill \end{array}\end{array}$$

(66)

for the sub-sector such that $k_x\in (0,\pi )$, $k_y\in (0,k_x)$ for $k_x\le \pi /2$, and $k_y\in (0,\pi -k_x)$ for $k_x\ge \pi /2$ and,

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill \overrightarrow{\pi }& =[\pi ,\pi ]\hfill \\ \hfill \overrightarrow{q}& =\left[\frac{\pi }{2}-\frac{(k_x+k_y)}{2},\frac{3\pi }{2}-\frac{(k_x+k_y)}{2}\right]\hfill \\ \hfill \overrightarrow{q}{}^{\prime }& =\left[\frac{\pi }{2}-\frac{(k_x-k_y)}{2},-\frac{\pi }{2}+\frac{(k_x-k_y)}{2}\right]\hfill \end{array}\end{array}$$

(67)

for the sub-sector such that $k_y\in (0,\pi )$, $k_x\in (\pi -k_y,\pi )$ for $k_y\le \pi /2$, and $k_x\in (k_y,\pi )$ for $k_y\ge \pi /2$, respectively. Note that as mentioned above, the components of the $s1$ band momenta $\overrightarrow{q}$ appearing in Equations (66) and (67) are such that $q_{x_1}-q_{x_2}=-\pi$ and thus belong to the half-filling $s1$ boundary line, whereas those of the momenta $\overrightarrow{q}{}^{\prime }$ in the same equations obey the relation ${q^{\prime }}_{x_1}=-{q^{\prime }}_{x_2}$ so that point in the nodal directions.

The curves plotted in Figure 5 of Reference [14] refer to the high symmetry directions in the Brillouin zone. The use of the above general expression given in Equation (65) leads for $U/4t=1.525$ to an excellent agreement with such curves. These directions correspond also to those measured by high-resolution inelastic neutron scattering in LCO, as plotted in Figure 3(A) of Reference [13]. We denote such symmetry directions by $MO$, $\Gamma O$, $XM$, $\Gamma X$, and $XO$. They connect the momentum-space points $M=[\pi ,\pi ]$, $O=[\pi /2,\pi /2]$, $\Gamma =[0,0]$, and $X=[\pi ,0]$ of the general spin-wave spectrum provided in Equation (65).

Such a spin-wave excitation spectrum is plotted for the above symmetry directions in Figure 1 (solid line) for ${\mu }^0=565.6$ meV and $W_{s1}^0=49.6$ meV together with the experimental results (circles) for $T=10$ K. This gives a Mott–Hubbard gap $2{\mu }^0=1131.2$ meV. The spin-spectrum expression given in Equation (65) refers to the first Brillouin zone. In Figure 1 we plot it in the second Brillouin zone, alike in Figure 3(A) of Reference [13] and Figure 5 of Reference [14]. An excellent quantitative agreement is reached for these magnitudes of the involved energy scales, which according to the complementary results of Reference [14] correspond to $U/4t\approx 1.525$ and $t\approx 295$ meV.

The above results confirm that the predictions of the square-lattice quantum liquid theory concerning the spin spectrum at half filling agree both with experiments on the parent compound LCO and results obtained by the standard formalism of many-body physics.

6. Concluding Remarks

In this paper a general operator description valid for both the Hubbard model on the 1D and square lattice in terms of three types of elementary quantum objects introduced in References [9,10] was reviewed. Such a rotated-electron related operational description is an application of the Hubbard model on a bipartite lattice extended global $SO(3)\times SO(3)\times U(1)$ symmetry recently found in Reference [6]. The occupancy configurations of such objects correspond to state representations of such an extended global symmetry. The physical interest of the present rotated-electron related operational description refers mostly to the model in the one- and two-electron subspace. However, the definition of that subspace requires the use of general properties of the full-Hilbert-space description summarized in this paper.

Although the operator description reviewed in this paper is compatible with and in part inspired in the exact solution of the 1D model, it accounts for the basic differences between the physics of the Hubbard model on the 1D and square lattice, respectively. For instance, in 1D the occurrence of an infinite set of conservation laws associated with the model integrability implies that the c-$s1$ fermion residual interactions refer only to zero-momentum forward-scattering. They merely give rise to phase shifts whose expressions may be extracted from the BA solution. This allows the introduction of a pseudofermion dynamical theory, which provides finite-energy spectral and correlation function expressions involving phase shifts [28,29]. Hence in 1D such interactions do not involve interchange of energy and momentum. In contrast, they do for the Hubbard model on the square lattice, yet they are much simpler than the corresponding electronic correlations. Indeed the quantum problem is non-perturbative in terms of electron operators. It follows that in contrast to a 3D isotropic Fermi liquid [27], rewriting the square-lattice quantum-liquid theory in terms of the standard formalism of many-electron physics is in general an extremely complex problem. Fortunately, such a quantum liquid dramatically simplifies when expressed in terms of the c fermion and $s1$ fermion operators [10].

The problem is simplest at $x=0$ for spin excitations for which the c band remains full and the effects of the c-$s1$ fermion interactions are frozen. The preliminary investigations reported in this paper on the physical consequences of the model on the square lattice new found global symmetry in actual materials in terms of the c and $s1$ fermion description refer to $x=0$. Such results confirm that the present description is useful for the further understanding of the role played by the electronic correlations in the spin spectrum of the parent compound LCO [13]. Indeed, it is quantitatively described by the corresponding spin spectrum of the square-lattice quantum liquid at $U/4t\approx 1.525$ and $t\approx 295$ meV.

A similar good quantitative agreement with the LCO spin-wave spectrum is reached by use of the Hubbard model on the square lattice for $U/4t$ values in the range $U/4t\in (1.5,2.0)$ and suitable different magnitudes of t. For instance, the studies of References [10,14] find $U/4t=1.525$ alike here whereas those of References [30] and [31] use $U/4t=1.625$ and $U/4t=2.000$, respectively. Consistent with the results of References [17,18], the Hubbard model in the subspace of vanishing rotated-electron double occupancy is related to the t-J model only for larger $U/4t$ values. Importantly, for arbitrary $U/4t>0$ values the usual large-U energy scale $4t^2/U$ is replaced by the $s1$ fermion energy nodal bandwidth $W_{s1}$ of Equation (36). Its maximum magnitude $W_{s1}=4t$ is reached for $U/4t\to 0$. For $U/4t>0$ it decreases monotonously for increasing values of $U/4t$, vanishing for $U/4t\to \infty$ as $W_{s1}\propto 4t^2/U$ [10]. Hence the $4t^2/U$ magnitude found here and in References [10,14,30,31] for the description of the LCO spin-wave spectrum within the Hubbard model should not be compared with that used by t-J model descriptions of the same spectrum. Indeed for the above intermediate $U/4t$ values there is no direct relation between the two models.

Further investigations on more complex $x>0$ and $m=0$ 2D problems for which the effects of doping are accounted for in terms of c-$s1$ fermion residual inelastic interactions will be also fulfilled elsewhere.