Abstract
We numerically study a quasi-one-dimensional classical Poisson–Nernst–Planck system with two oppositely charged ion species under different setups. Of particular interest is the following: (i) to numerically identify ten critical potentials, which play critical roles in characterizing the qualitative properties of individual fluxes; (ii) to numerically verify some interesting scaling laws related to boundary concentrations of the system; and (iii) to investigate the effects on the individual fluxes from finite ion sizes. Some numerical results support the analytical ones obtained in previous work and provide more intuitive illustrations of the abstract results, while some others provide important insights for future studies; particularly, the scaling law observed with both small permanent charges and finite ion sizes is quite different from previous results.
MSC:
34A26; 34B16; 34D15; 37D10; 92C35
1. Introduction
Ion channels, large protein complexes embedded within cell membranes, play a critical role in mediating the exchange of ion species between cells and their external environment. These channels are indispensable for a wide range of cellular processes. For example, sodium and potassium channels, which are widely distributed in neurons and cardiac tissues, are integral to the rapid transitions between action and resting potentials, enabling the propagation of stimuli across these cells. Similarly, in muscle cells, the coordinated activity of multiple ion channels facilitates muscle contraction [].
The study of ion channels encompasses two major, interlinked areas: structural characterization and ionic flow analysis. The physical arrangement of ion channels is determined by their structure (geometry) and the distribution of both fixed and dynamic charges within that structure, including polarization charges. Breakthroughs in structural analysis, such as those enabled by cryo-electron microscopy−recognized by the 2017 Nobel Prize−have laid the groundwork for deeper exploration. However, despite these advancements, current experimental methods for studying ion channels primarily rely on external input–output measurements, which limits our ability to understand the detailed internal ionic dynamics within the channels []. This gap presents a significant challenge to fully understand the properties of ion channels.
Mathematical analysis, informed by physically realistic models such as the Poisson–Nernst–Planck (PNP) system, is crucial for studying ion channel behavior [,,,,,,,,,]. The PNP system, a reduced model derived under specific conditions from molecular dynamics [], Boltzmann equations [], and variational principles [,,], is well suited for analyzing and simulating ionic flows within biological systems due to its key features, which has been extensively studied both analytically [,,,,,,,,,], particularly those under geometric singular perturbation theory [,,,,,,,,,,,] for the PNP model without finite ion sizes and [,,,,,,,] for the PNP model with steric effects) and numerically [,,,,,,,]. In particular, we refer the reader to [,] for numerical and scientific computing studies with a formal analysis of the computational complexity [] and also in the case of simulations with thousands of cells [].
Recently, in [], the authors systematically investigated the effects on ionic flows from small permanent charges via a quasi-one-dimensional classical PNP system under electroneutrality boundary conditions. More precisely, the authors in [] viewed small compared to boundary concentrations, employed regular perturbation analysis, and obtained the individual fluxes of the following form for
where is the leading term that contains the effect from small permanent charges. Based on the analysis of the leading terms, some non-intuitive and interesting results are obtained. Particularly, it was shown that, to maximize the impact of a small permanent charge in an ion channel, the narrowest section of the channel where the charge is localized should be “short” and “narrow”. This structure aligns with the typical architecture of ion channels, which have constricted regions designed to guide ionic flows. Interesting scaling laws are observed. More precisely, for any ,
Also, some critical potentials are identified, which play important roles in characterizing the permanent charge effects on ionic flows. Particularly, the critical potentials and (see []) that balance the small permanent charge effects on the individual fluxes and are defined by
Most importantly, the critical potentials and can be experimentally estimated. Taking the critical potential , for example, one can take an experimental individual flux as and numerically (or analytically) compute for an ideal case that allows one to obtain an estimate of by identifying the zero of the quantity
The studies in [,] have indicated the importance of the effects on the internal dynamics of ionic flows through membrane channels from nonzero permanent charges. Motivated by those interesting results and for a better understanding, in the current work, we will develop a numerical approach to the PNP system with steric effects, a more realistic setup, and, as a result, obtain numerical individual flux curves from which we investigate the permanent charge effects on ionic flows. This, on one hand, will provide more intuitive illustrations of the theoretical results obtained in [,] and will allow one to better understand the mechanism of the ionic flows through membrane channels. On the other hand, this will provide insights into future mathematical analysis of the interplays between nonzero permanent charges and finite ion sizes.
1.1. A Quasi-One-Dimensional Poisson–Nernst–Planck Model with Local Hard-Sphere Electrochemical Potentials
In this work, we adopt the following quasi-one-dimensional PNP model for a mixture of n ion species through a single channel (first proposed in [])
where is the coordinate along the axis of the channel that is normalized to , and is the area of cross-section of the channel over the location x.
For the system (4), we impose the following boundary conditions (see [] for a reasoning), for ,
where e is the elementary charge, is the Boltzmann constant, T is the absolute temperature, is the electric potential, is the permanent charge density of the channel, is the local dielectric coefficient, is the relative dielectric coefficient, represents the area of the cross-section over the point x, and n is the number of distinct types of ion species; for the jth ion species, is the number density, is the valence, is the electrochemical potential, is the number flux density, and is the diffusion coefficient.
1.2. Permanent Charges
The distribution of permanent charge is the primary factor differentiating various channel types []. Permanent charges, present in both ion channels and semiconductors, significantly influence their complex behavior. In ion channels, these charges, reflecting the channel protein’s structure, are particularly critical. The permanent charge is generally modeled through a piecewise constant function. To be specific, we assume, for a partition of into m subintervals, for where s are constants with . For a more detailed discussion of the permanent charge, one may refer to [].
In this work, we adopt the following relatively simple profile for the permanent charge
where is a constant.
1.3. Electrochemical Potentials
The electrochemical potential consists of two components: the ideal component given by
with some characteristic number density and the excess component . The ideal component contains contributions of ion particles as point charges and ignores the ion-to-ion interaction, while the excess component accounts for ion sizes, which is a crucial component for many important properties of ion channels such as selectivity (see [,] for a more detailed discussion). In this work, in addition to the ideal component, we will also include a local hard-sphere model for to account for finite ion size effects given by (see [] for a detailed derivation)
where is the diameter of the jth ion species.
1.4. Further Assumptions
For the BVP (4)–(5), we will take the same setting as that in [], except that the finite ion size effects are included; that is,
- (A1).
- We consider two ion species () with .
- (A2).
- For in (6), we assume is small relative to s and s.
- (A3).
- (A4).
- We assume that and are constants.
Furthermore, with the re-scaling
the BVP (4)–(5) reads, for , as follows:
where and for are defined as follows:
The boundary conditions are now given by
Recall that and are the diameters of the two ion species. While and are small, their ratio is of order . We thus set, for some ,
Correspondingly, one can rewrite and above for as
To end this section, we point out that there is a symmetry for the current problem. More precisely, if we flip the ion channel, then the parameter converts to and converts to . From the consideration of biology, one would have the fluxes s become s.
2. Numerical Methods and Setups
2.1. “bvp4c” Solver
We employ “bvp4c” in Matlab [] as the solver for (9)–(10). It solves systems of first order ordinary differential equations with two-point boundary conditions of the following form:
Given a mesh partition , the numerical solution of (12) is approximated by a piecewise cubic polynomial function . The approximated solution satisfies the boundary conditions, and it is a cubic Hermite interpolation polynomial for each subinterval .
For , let and let . The s are evaluated by solving the algebraic equations
Here,
where
The algebraic system (13) is solved by simplified Newton’s method with a weak line search. The global Jacobian that uses finite difference approximation by default is required, and the structure of the Jacobian is crucial for the linear solver in each Newton’s iteration. The residual of is then calculated by , and the residual in the boundary conditions is . The adaptive mesh strategy has been used to control the residual in “bvp4c” (see [] for details). We comment that taking the advantage of the detailed analysis from [,], we are able to choose the best initial guess for our numerical study. This makes the computational cost cheap.
2.2. Problem Setups
To get started, we rewrite the system (9)–(10) as a system of first-order ordinary differential equations. Upon introducing , one has
with boundary conditions
We comment that the choice of is based on the fact that the ion channel is cylindrical-like, and the variable cross-section area is chosen to reflect the fact that the channel is not uniform and much narrower in the neck than other regions []. We further take , and the function is then continuous at the jumping points and . Different models for may be chosen, and similar numerical results should be obtained.
2.3. Main Interest
The studies in [,] have indicated the important role played by the nonzero permanent charges, while those in [,] emphasize the importance of the effects from the finite ion sizes. The characterization of the nonlinear interplays between different system parameters involved in the model in both directions provides the most efficient way to adjust/control boundary conditions to observe distinct dynamics of ionic flows through membrane channels. This is not only important for future mathematical studies of ion channel problems but also critical for biological experiments. For further understandings of those properties of ionic flows, in the current work, we focus on the following:
- (i)
- Numerically identifying some critical potentials, particularly those that balance the small permanent charge effects on individual fluxes (see (3) for definitions), from which the effects from small permanent charges are examined;
- (ii)
- Numerically verifying the scaling law stated in (2) under different setups;
- (iii)
- Numerically examining the effects from finite ion sizes.
3. Results
Based on the description in Section 2.3, we perform numerical simulations to the system (14)–(15) under two different setups:
- (a)
- The PNP system with small permanent charges, which provides more intuitive illustrations of the analytical results obtained in [];
- (b)
- The PNP system with both small permanent charges and steric effects, which provides important insights for our future mathematical analysis.
We have the following observations:
- (i)
- We numerically identified ten critical potentials under the two different setups stated above. Figure 1 and Figure 2 are under setup (a), while Figure 3 is under setup (b). We demonstrate that the numerical results under setup (a) are consistent with those obtained in []. Those critical potentials play critical roles in characterizing the effects on ionic flows from small permanent charges and finite ion sizes. For example, for , one has
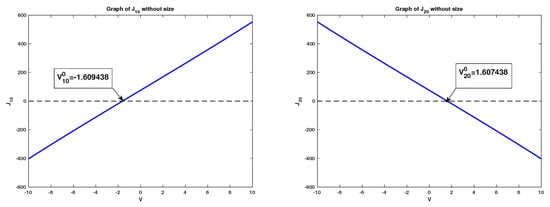 Figure 1. Identification of critical potentials and and graphs of and for without finite ion size effects.
Figure 1. Identification of critical potentials and and graphs of and for without finite ion size effects.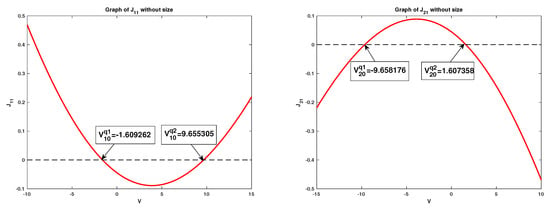 Figure 2. Identification of critical potentials and and approximations of , and without finite ion size effects for .
Figure 2. Identification of critical potentials and and approximations of , and without finite ion size effects for .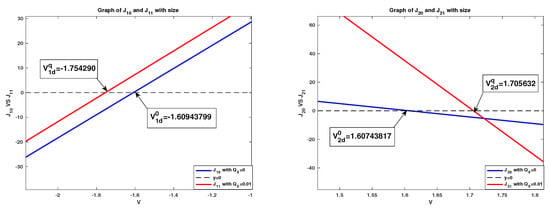 Figure 3. Identification of critical potentials , and , graphs of and , and approximations of and with finite ion size effects for .
Figure 3. Identification of critical potentials , and , graphs of and , and approximations of and with finite ion size effects for .- –
- , which indicates that the small permanent charge enhances the individual flux ;
- –
- , which implies that the small permanent charge reduces the magnitude of .
Similar discussions can be applied to other potential intervals split by the critical potentials, such as and identified in Figure 2. The numerical results obtained under setup (b), particularly, for , are quite different. More precisely, under setup (a), has two zeroes, while under setup (b), it has a unique zero. The numerical investigation indicates the finite ion size has important effects on ionic flows. Particularly, the interactions between small permanent charges and the finite ion size are critical to understand the internal dynamics of ionic flows through membrane channels, and this needs detailed mathematical analysis and will be studied in our near future project. - (ii)
- We numerically investigate the rescaling laws for the individual fluxes under the two setups (a) and (b). Our numerical simulation shows that
- –
- For the zeroth order individual fluxes and in small permanent charges, the finite ion size does not affect the scaling law observed in []. To be specific, approximately, one hasas shown in Figure 4.
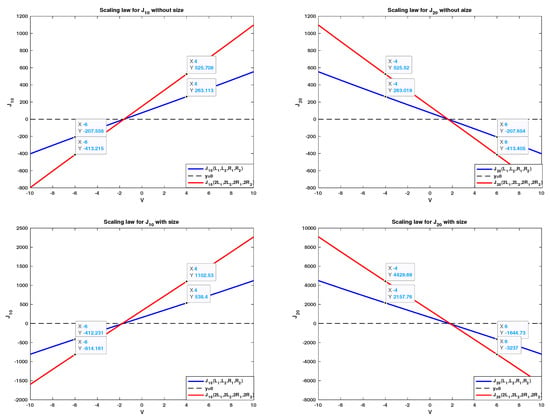 Figure 4. Scaling law verification for and for . The graphs in the first row are obtained without considering finite ion sizes, while the ones in the second row are obtained with finite ion size effects.
Figure 4. Scaling law verification for and for . The graphs in the first row are obtained without considering finite ion sizes, while the ones in the second row are obtained with finite ion size effects. - –
- However, the finite ion size does have great effects on the scaling law. More precisely, as observed in [], without considering the finite ion size, one hasas illustrated in the first row of Figure 5. However, with the finite ion size, approximately, one haswhich is quite different from those without finite ion sizes. The numerical observation provides important information for future mathematical analysis of the interplay between the small permanent charge and the finite ion size.
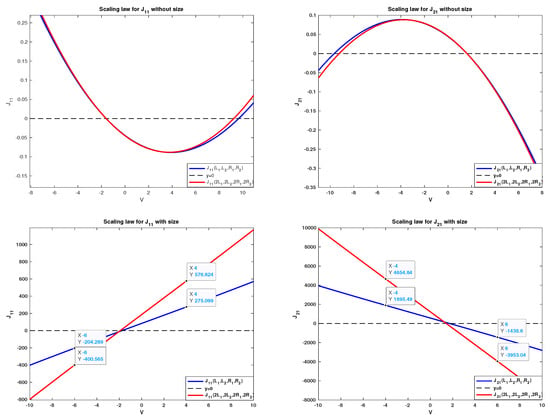 Figure 5. Scaling law verification for and for . The graphs in the first row are obtained without considering finite ion sizes, while the ones in the second row are obtained with finite ion size effects.
Figure 5. Scaling law verification for and for . The graphs in the first row are obtained without considering finite ion sizes, while the ones in the second row are obtained with finite ion size effects.
- (iii)
- We consider the effects on the individual fluxes from finite ion sizes by directly considering the difference for fixed boundary concentrations (see Figure 6)
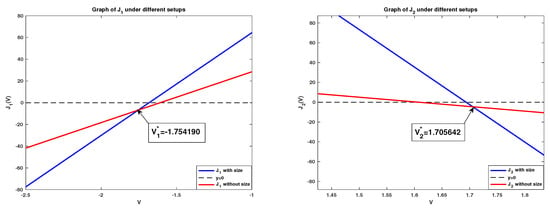 Figure 6. Finite ion size effect investigation for .Critical potentials and are numerically identified, which satisfy
Figure 6. Finite ion size effect investigation for .Critical potentials and are numerically identified, which satisfy- –
- For the individual flux , one has for while for ;
- –
- For the individual flux , one has for while for
4. Discussion
The numerical results presented here provide a multifaceted understanding of ionic transport in a charged, confined system beyond what classical PNP theory offers. By incorporating finite ion size and nonzero permanent charges into a quasi-one-dimensional PNP model, we uncovered several critical phenomena that enrich both the mathematical description and physical interpretation of ion-channel behavior. Notably, a series of critical potentials were identified, delineating distinct regimes in the individual ionic fluxes. These critical voltages—ten in total across the conditions studied—serve as threshold points at which qualitative changes occur in how each ion species’ flux responds to an applied bias. For example, in the absence of steric effects, two important critical potentials and mark the voltages at which the influence of a small permanent charge is exactly balanced for species 1 (the cation) and species 2 (the anion), respectively. At , the contribution of the fixed charge causes the net flux of species 1 to vanish (), analogous to a reversal potential where that ion’s current switches direction. The ability to determine such points is not just a theoretical exercise—it has practical implications since these critical potentials can be experimentally estimated by comparing flux–voltage curves with and without the permanent charge present. Identifying a voltage at which the difference between the real (charged) channel current and an ideal (uncharged) reference is zero provides a direct way to infer the magnitude of fixed charges inside channels. Thus, our numerical finding of multiple critical potentials offers both a confirmation of earlier analytical predictions and a tangible metric for experimental validation of channel properties. Beyond pinpointing critical bias values, our study rigorously examined how scaling laws of ionic flux with respect to concentration are altered by steric interactions. In line with previous theory, we verified that for a channel without finite-size effects, the baseline fluxes scale linearly with all boundary concentrations (i.e., doubling all concentrations doubles the zero-charge flux), while the first-order correction due to a small permanent charge remains invariant under such concentration scaling. This elegant scaling symmetry was analytically predicted in earlier perturbation analyses, and our numerics confirm its validity in the idealized (point-ion) scenario. However, once finite ion size is introduced, the classical scaling law no longer holds exactly, reflecting the onset of crowding-induced saturation. Our simulations under steric conditions demonstrate that although the zeroth-order flux still grows with concentration in a roughly proportional manner, the presence of finite ion volume imposes an upper limit on how effectively flux can increase. Physically, this manifests as a sub-linear increase in current at high concentrations—a hallmark of steric hindrance, where ions cannot pack arbitrarily densely, and thus additional concentration yields diminishing returns in flux. More strikingly, the influence of the permanent charge (quantified by the perturbation term) was found to deviate from the concentration-invariant law observed without steric effects. In the sterically inclusive model, the enhancement or suppression of flux due to a fixed charge became dependent on the absolute concentration level, implying that at higher salt conditions, the fixed charge’s relative effect is attenuated by ionic crowding. In essence, when the channel environment is crowded, a given small permanent charge produces a smaller perturbation in flux than it would in a dilute scenario—a qualitative departure from the predictions of the ideal PNP model. This breakdown of the neat scaling law underlines the importance of including finite ion sizes in models intended to operate beyond the dilute limit or at strong driving forces. The interaction between permanent charges and steric effects emerges as a crucial factor influencing ionic flux characteristics. Our comparative analysis of the two simulation setups—(a) with a small permanent charge alone and (b) with both that charge and finite-size effects—highlights how steric repulsion can fundamentally alter charge-induced transport phenomena. For instance, under the ideal model (a), the first-order flux correction for the cation species was observed to cross zero at two distinct voltages. This implies that the fixed charge’s effect on cation flux can switch signs twice, enhancing the flux in one voltage range but reducing it in another. Such behavior, predicted by earlier analytic work, points to a nuanced competition between electrostatic attraction/repulsion and the driving force. Yet, when finite ion size is accounted for (setup b), our results show that has only a single zero-crossing—the permanent charge’s effect changes sign only once across the full-voltage spectrum. The steric hindrance effectively damps out one of the regimes where the fixed charge would have inverted its impact on flux. In other words, crowding smooths the flux response, removing the secondary reversal of the fixed-charge effect. This simplification suggests that volume exclusion can suppress certain subtle nonlinear effects of fixed charges, likely by preventing excessive local accumulation of ions that would otherwise occur in an ideal model and give rise to complex multi-regime behavior. Moreover, we identified new critical potentials and that specifically characterize how finite size influences flux: these are the voltages at which the difference between flux with steric effects and flux without steric effects vanishes for each ion species. Notably, for species 1 (e.g., cations), when , the inclusion of finite ion size actually increases the flux relative to the no-size case, whereas for , steric effects reduce its flux. The anion (species 2) shows the opposite trend, with steric inclusion benefiting its flux at lower voltages but impeding it beyond a threshold . This finding is counter-intuitive at first glance—one might expect steric constraints to always hinder transport—but it underscores that steric effects modulate the multi-ion competition in a charged channel in nontrivial ways. At certain voltages, volume exclusion of one species can free up phase space or alter electrostatic screening in a manner that favorably influences the other species’ throughput. Such interplay between fixed-charge attraction and steric exclusion results in a delicate balance that can either boost or curb a particular ionic current depending on the operating conditions. From a broader perspective, these insights bear direct biological relevance and deepen our understanding of ion channel function. Real cellular channels are narrow, highly charged pores—conditions under which finite ion size (crowding) and fixed charges are known to dictate conductance properties. Our result that a small permanent charge can dramatically alter ionic flux in a short, narrow region is consonant with the architecture of selectivity filters in channels: nature often concentrates charged amino acids in tight vestibules to maximize their influence on permeating ions. The quantitative demonstration that a localized charge’s impact is maximized in a constricted geometry lends theoretical support to this design principle. Likewise, the concept of critical potentials for zero net flux parallels the physiological notion of reversal potential for ions; the shifts in those critical voltages caused by steric effects could translate to altered apparent reversal potentials in crowded pores. This implies that experiments measuring I–V curves of ion channels or synthetic nanopores might detect different reversal voltages or conductance regimes depending on ionic strength—an observation our model can rationalize. Furthermore, the saturation of current at high concentrations emerging from our steric PNP model mirrors the experimentally observed saturation of channel conductance (often described by Michaelis–Menten kinetics or Langmuir isotherms in ion transport) once the pore becomes crowded with ions. Standard PNP theory without finite-size effects would overestimate the conductance in such regimes as it ignores the volume exclusion that in reality limits how many ions can reside in the pore. By correcting this, our model aligns more closely with experimental reality, emphasizing that any quantitative modeling of channels under physiological conditions must include steric terms to avoid unrealistic predictions of unbounded ion uptake and flow. Mathematically, the findings obtained here open the door for new theoretical investigations. The numerically identified critical potentials provide concrete targets for asymptotic analysis and perturbation theory: for example, one could attempt to derive the existence of a unique when steric effects are included, contrasting with the double roots found in the absence of steric terms. The fact that volume exclusion collapses a pair of critical points into one suggests an underlying change in the structure of the governing equations (such as a different effective order of the polynomial governing ’s sign, or a merger of two solution branches into one). Developing an analytical understanding of how steric nonlinearities modify the bifurcation structure of steady-state solutions would be a valuable future contribution. Additionally, the observed breakdown of scaling invariance when permanent charge and finite size are both present calls for a refined mathematical framework. While prior work successfully applied regular perturbation expansions in the limit of small , those analyses assumed an ideal solution behavior. Extending those methods or devising new multi-scale perturbation approaches to accommodate finite-size corrections (perhaps treating steric effects as a separate asymptotic regime or using a singular perturbation if the steric parameter is small) could yield analytical expressions to complement our numerics. Such analysis would not only corroborate our computational findings but also generalize them, possibly revealing whether the altered scaling law we observed is universal or depends on specific model parameters (e.g., the ion size or channel geometry). Finally, this study suggests several avenues for future research. From a modeling perspective, it would be intriguing to explore channels with larger or spatially variable permanent charges, moving beyond the small regime to see if new types of critical behavior emerge when the fixed charge is strong enough to significantly perturb ionic distributions on its own. Similarly, investigating different shapes of confinement (wider channels or asymmetric tapers) under the influence of steric repulsion could clarify how general our conclusions are for other geometries. On the computational side, one could extend our numerical scheme to fully dynamic simulations or to higher-dimensional domains, thereby relaxing the quasi-1D assumption and bringing the model closer to realistic biological channels or synthetic nanopores. It would also be valuable to include additional ionic species or explicitly model ion–ion correlations beyond steric hindrance (such as electrostatic correlation effects that are missing in meanfield PNP) to assess how these factors might further modify flux properties. On the experimental front, our predictions invite validation: for instance, one could measure ionic currents through a nanopore with a known fixed charge at various salt concentrations to test the predicted deviation from classical scaling or vary the pore diameter to observe the influence of crowding on the critical reversal potentials. Overall, the discussion above illustrates that by marrying mathematical analysis with numerical simulation, we gain a deeper, integrated understanding of how permanent charges and steric effects jointly govern ionic flux. These insights not only bridge gaps between theory and experiment but also chart a clear course for subsequent investigations to build upon the complex, fascinating interplay unveiled by our results.
5. Conclusions
In this work, we numerically study the PNP system under different setups focusing on the qualitative properties of the individual fluxes. Critical potentials are numerically identified, which play key roles in studying the qualitative properties of the individual fluxes. Interesting scaling laws in boundary concentrations are further investigated, and some new observations provide further understanding of the sensitive nonlinear interplays between different system parameters. Most importantly, the scaling law provides an efficient way to control the boundary conditions to either reduce or enhance the effects from small permanent charges and finite ion sizes. Finite ion size effects on the individual fluxes with small permanent charges are also numerically studied, which is a starting point of future mathematical analysis. Meanwhile, we point out that our study in the current work is based on a dimensionless PNP model and might not be able to capture some biological concerns.
To end this section, we further emphasize that the potentials identified in [] and numerically identified in the current work are significant. They play unique and critical roles in describing the qualitative properties of ionic flows through membrane channels. More importantly, some of these potential values can be experimentally estimated. Take the potentials identified in Figure 2 for example, one can take an experimental individual flux as and numerically (or analytically) compute for an ideal case that allows one to obtain an estimate of
Author Contributions
Conceptualization, H.L., Z.L., J.Y., and M.Z.; methodology, X.D., H.L., Z.L., and J.Y.; formal analysis, X.D., H.L., Z.L., and M.Z.; writing—original X.D., H.L., and J.Y.; writing—review and editing, M.Z.; funding acquisition, M.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Simons Foundation USA (No. 628308).
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| PNP | Poisson–Nernst–Planck |
| BVP | Boundary value problem |
References
- Moody, W.; Bosma, M. Ion Channel Development, Spontaneous Activity, and Activity-Dependent Development in Nerve and Muscle Cells. Physiol. Rev. 2005, 85, 883–941. [Google Scholar] [CrossRef]
- Eisenberg, B. Crowded charges in ion channels. In Advances in Chemical Physics; Rice, S.A., Ed.; John Wiley & Sons: Hoboken, NJ, USA, 2011; pp. 77–223. [Google Scholar]
- Eisenberg, R.S. From Structure to Function in Open Ionic Channels. J. Memb. Biol. 1999, 171, 1–24. [Google Scholar] [CrossRef]
- Eisenberg, B. Proteins, channels, and crowded ions. Biophys. Chem. 2003, 100, 507–517. [Google Scholar] [CrossRef]
- Gillespie, D.; Eisenberg, R.S. Physical descriptions of experimental selectivity measurements in ion channels. Eur. Biophys. J. 2002, 31, 454–466. [Google Scholar] [CrossRef]
- Gillespie, D.; Nonner, W.; Eisenberg, R.S. Coupling Poisson-Nernst-Planck and density functional theory to calculate ion flux. J. Phys. Condens. Matter 2002, 14, 12129–12145. [Google Scholar] [CrossRef]
- Henderson, L.J. The Fitness of the Environment: An Inquiry Into the Biological Significance of the Properties of Matter; Macmillan: New York, NY, USA, 1927. [Google Scholar]
- Im, W.; Roux, B. Ion permeation and selectivity of OmpF porin: A theoretical study based on molecular dynamics, Brownian dynamics, and continuum electrodiffusion theory. J. Mol. Biol. 2002, 322, 851–869. [Google Scholar] [CrossRef]
- Noskov, S.Y.; Berneche, S.; Roux, B. Control of ion selectivity in potassium channels by electrostatic and dynamic properties of carbonyl ligands. Nature 2004, 431, 830–834. [Google Scholar] [CrossRef] [PubMed]
- Noskov, S.Y.; Roux, B. Ion selectivity in potassium channels. Biophys. Chem. 2006, 124, 279–291. [Google Scholar] [CrossRef] [PubMed]
- Roux, B.; Allen, T.W.; Berneche, S.; Im, W. Theoretical and computational models of biological ion channels. Quat. Rev. Biophys. 2004, 37, 15–103. [Google Scholar] [CrossRef]
- Roux, B.; Crouzy, S. Theoretical studies of activated processes in biological ion channels. In Classical and Quantum Dynamics in Condensed Phase Simulations; Berne, B.J., Ciccotti, G., Coker, D.F., Eds.; World Scientific Ltd.: Singapore, 1998; pp. 445–462. [Google Scholar]
- Schuss, Z.; Nadler, B.; Eisenberg, R.S. Derivation of Poisson and Nernst-Planck equations in a bath and channel from a molecular model. Phys. Rev. E 2001, 64, 036116. [Google Scholar] [CrossRef]
- Barcilon, V. Ion flow through narrow membrane channels: Part I. SIAM J. Appl. Math. 1992, 52, 1391–1404. [Google Scholar] [CrossRef]
- Hyon, Y.; Fonseca, J.; Eisenberg, B.; Liu, C. Energy variational approach to study charge inversion (layering) near charged walls. Discrete Contin. Dyn. Syst. Ser. B 2012, 17, 2725–2743. [Google Scholar] [CrossRef]
- Hyon, Y.; Liu, C.; Eisenberg, B. PNP equations with steric effects: A model of ion flow through channels. J. Phys. Chem. B 2012, 116, 11422–11441. [Google Scholar] [CrossRef] [PubMed]
- Hyon, Y.; Eisenberg, B.; Liu, C. A mathematical model for the hard sphere repulsion in ionic solutions. Commun. Math. Sci. 2010, 9, 459–475. [Google Scholar]
- Barcilon, V.; Chen, D.-P.; Eisenberg, R.S. Ion flow through narrow membrane channels: Part II. SIAM J. Appl. Math. 1992, 52, 1405–1425. [Google Scholar] [CrossRef]
- Barcilon, V.; Chen, D.-P.; Eisenberg, R.S.; Jerome, J.W. Qualitative properties of steady-state Poisson-Nernst-Planck systems: Perturbation and simulation study. SIAM J. Appl. Math. 1997, 57, 631–648. [Google Scholar]
- Boda, D.; Busath, D.; Eisenberg, B.; Henderson, D.; Nonner, W. Monte Carlo simulations of ion selectivity in a biological Na+ channel: Charge-space competition. Phys. Chem. Chem. Phys. 2002, 4, 51545160. [Google Scholar] [CrossRef]
- Kilic, M.S.; Bazant, M.Z.; Ajdari, A. Steric effects in the dynamics of electrolytes at large applied voltages. II. Modified Poisson-Nernst-Planck equations. Phys. Rev. E 2007, 75, 021503. [Google Scholar] [CrossRef]
- Liu, J.L.; Eisenberg, B. Poisson-Nernst-Planck-Fermi theory for modeling biological ion channels. J. Chem. Phys. 2014, 141, 12B640. [Google Scholar] [CrossRef]
- Liu, C.; Wang, C.; Wise, S.; Yue, X.; Zhou, S. A positivity-preserving, energy stable and convergent numerical scheme for the Poisson-Nernst-Planck system. Math. Comput. 2021, 90, 2071–2106. [Google Scholar] [CrossRef]
- Park, J.-K.; Jerome, J.W. Qualitative properties of steady-state Poisson-Nernst-Planck systems: Mathematical study. SIAM J. Appl. Math. 1997, 57, 609–630. [Google Scholar] [CrossRef]
- Singer, A.; Gillespie, D.; Norbury, J.; Eisenberg, R.S. Singular perturbation analysis of the steady-state Poisson-Nernst-Planck system: Applications to ion channels. European J. Appl. Math. 2008, 19, 541–560. [Google Scholar] [CrossRef]
- Singer, A.; Norbury, J. A Poisson-Nernst-Planck model for biological ion channels–An asymptotic analysis in a three-dimensional narrow funnel. SIAM J. Appl. Math. 2009, 70, 949–968. [Google Scholar] [CrossRef]
- Wang, X.-S.; He, D.; Wylie, J.; Huang, H. Singular perturbation solutions of steady-state Poisson-Nernst-Planck systems. Phys. Rev. E 2014, 89, 022722. [Google Scholar] [CrossRef]
- Abaid, N.; Eisenberg, R.S.; Liu, W. Asymptotic expansions of I-V relations via a Poisson-Nernst-Planck system. SIAM J. Appl. Dyn. Syst. 2008, 7, 1507–1526. [Google Scholar] [CrossRef][Green Version]
- Bates, P.W.; Jia, Y.; Lin, G.; Lu, H.; Zhang, M. Individual flux study via steady-state Poisson-Nernst-Planck systems: Effects from boundary conditions. SIAM J. Appl. Dyn. Syst. 2017, 16, 410–430. [Google Scholar] [CrossRef]
- Chen, J.; Wang, Y.; Zhang, L.; Zhang, M. Mathematical analysis of Poisson-Nernst-Planck models with permanent charges and boundary layers: Studies on individual fluxes. Nonlinearity 2021, 34, 3879–3906. [Google Scholar] [CrossRef]
- Eisenberg, B.; Liu, W.; Xu, H. Reversal permanent charge and reversal potential: Case studies via classical Poisson-Nernst-Planck models. Nonlinearity 2015, 28, 103–128. [Google Scholar] [CrossRef]
- Liu, W.; Sun, N. Flux rations for effects of permanent charges on ionic flows with three ion species: New phenomena from a case study. J. Dyn. Diff. Equat. 2024, 36, 27–62. [Google Scholar]
- Liu, W.; Wang, B. Poisson-Nernst-Planck systems for narrow tubular-like membrane channels. J. Dynam. Diff. Equat. 2010, 22, 413–437. [Google Scholar] [CrossRef]
- Liu, W.; Xu, H. A complete analysis of a classical Poisson-Nernst-Planck model for ionic flow. J. Differ. Equations 2015, 258, 1192–1228. [Google Scholar] [CrossRef]
- Mofidi, H. Reversal permanent charge and concentrations in ionic flows via Poisson-Nernst-Planck models. Quart. Appl. Math. 2021, 79, 581–600. [Google Scholar] [CrossRef]
- Mofidi, H. New insights into the effects of small permanent charge on ionic flows: A higher order analysis. Math. Biosci. Eng. 2024, 21, 6042–6076. [Google Scholar] [CrossRef]
- Mofidi, H.; Eisenberg, B.; Liu, W. Effects of diffusion coefficients and permanent charge on reversal potentials in ionic channels. Entropy 2022, 22, 325. [Google Scholar] [CrossRef]
- Mofidi, H.; Liu, W. Reversal potential and reversal permanent charge with unequal diffusion coefficients via classical Poisson-Nernst-Planck models. SIAM J. Appl. Math. 2020, 80, 1908–1935. [Google Scholar] [CrossRef]
- Li, H.; Li, Z.; Pan, C.; Song, J.; Zhang, M. Cubic-like features of I-V relations via classical Poisson-Nernst-Planck systems under relaxed electroneutrality boundary conditions. Axioms 2024, 13, 790. [Google Scholar] [CrossRef]
- Wen, Z.; Bates, P.W.; Zhang, M. Effects on I-V relations from small permanent charge and channel geometry via classical Poisson-Nernst-Planck equations with multiple cations. Nonlinearity 2021, 34, 4464–4502. [Google Scholar] [CrossRef]
- Wen, Z.; Zhang, L.; Zhang, M. Dynamics of classical Poisson-Nernst-Planck systems with multiple cations and boundary layers. J. Dynam. Diff. Equat. 2021, 33, 211–234. [Google Scholar] [CrossRef]
- Yan, L.; Xu, H.; Liu, W. Poisson-Nernst-Planck models for three ion species: Monotonic profiles vs. oscillatory profiles. J. Appl. Anal. Comput. 2022, 12, 1211–1233. [Google Scholar] [CrossRef]
- Aitbayev, R.; Bates, W.P.; Lu, H.; Zhang, L.; Zhang, M. Mathematical studies of Poisson-Nernst-Planck systems: Dynamics of ionic flows without electroneutrality conditions. J. Comput. Appl. Math. 2019, 362, 510–527. [Google Scholar] [CrossRef]
- Ji, S.; Liu, W. Poisson-Nernst-Planck systems for ion flow with density functional theory for hard-sphere potential: I-V relations and critical potentials. Part I: Analysis. J. Dyn. Diff. Equat. 2012, 24, 955–983. [Google Scholar] [CrossRef]
- Lin, G.; Liu, W.; Yi, Y.; Zhang, M. Poisson-Nernst-Planck systems for ion flow with density functional theory for local hard-sphere potential. SIAM J. Appl. Dyn. Syst. 2013, 12, 1613–1648. [Google Scholar] [CrossRef]
- Liu, X.; Song, J.; Zhang, L.; Zhang, M. Roles played by critical potentials in the study of Poisson-Nernst-Planck models with steric effects under relaxed neutral boundary conditions. Axioms 2025, 14, 69. [Google Scholar] [CrossRef]
- Sun, L.; Liu, W. Non-localness of Excess Potentials and Boundary Value Problems of Poisson-Nernst-Planck Systems for Ionic Flow: A Case Study. J. Dyn. Diff. Equat. 2018, 30, 779–797. [Google Scholar] [CrossRef]
- Ding, J.; Wang, C.; Zhou, S. Convergence analysis of structure-preserving numerical methods based on Slotboom transformation for the Poisson-Nernst-Planck equations. Commun. Math. Sci. 2023, 21, 459–484. [Google Scholar] [CrossRef]
- Burger, M.; Eisenberg, R.S.; Engl, H.W. Inverse problems related to ion channel selectivity. SIAM J. Appl. Math. 2007, 67, 960–989. [Google Scholar] [CrossRef][Green Version]
- Cardenas, A.E.; Coalson, R.D.; Kurnikova, M.G. Three-Dimensional Poisson-Nernst-Planck Theory Studies: Influence of Membrane Electrostatics on Gramicidin A Channel Conductance. Biophys. J. 2000, 79, 80–93. [Google Scholar] [CrossRef] [PubMed]
- Chen, D.P.; Eisenberg, R.S. Charges, currents and potentials in ionic channels of one conformation. Biophys. J. 1993, 64, 1405–1421. [Google Scholar] [CrossRef] [PubMed]
- Coalson, R.; Kurnikova, M. Poisson-Nernst-Planck theory approach to the calculation of current through biological ion channels. IEEE Trans. Nanobioscience 2005, 4, 81–93. [Google Scholar] [CrossRef] [PubMed]
- Qian, Y.; Wang, C.; Zhou, S. A positive and energy stable numerical scheme for the Pois- son–Nernst–Planck–Cahn–Hilliard equations with steric interactions. J. Comput. Phys. 2021, 426, 109908. [Google Scholar] [CrossRef]
- Ding, J.; Zhou, S. Second-order, Positive, and Unconditional Energy Dissipative Scheme for Modified Poisson-Nernst-Planck Equations. J. Comput. Phys. 2024, 510, 113094. [Google Scholar] [CrossRef]
- Bortoli, A.L.D.; Negro, E.; Noto, V.D. Generalized modified Poisson-Nernst-Planck model for electrical double layer with steric, correlation and thermal effects applied to fuel cells. Electrochim. Acta 2025, 525, 146070. [Google Scholar] [CrossRef]
- Benedusi, P.; Ferrari, P.; Rognes, M.E.; Serra-Capizzano, S. Modeling excitable cells with the EMI equations: Spectral analysis and iterative solution strategy. J. Sci. Comput. 2024, 98, 58. [Google Scholar] [CrossRef]
- Ellingsrud, A.J.; Benedusi, P.; Kuchta, M. A splitting, discontinuous Galerkin solver for the cell-by-cell electroneutral Nernst-Planck framework. SIAM J. Sci. Comput. 2025, 47, B477–B504. [Google Scholar] [CrossRef]
- Ji, S.; Liu, W.; Zhang, M. Effects of (small) permanent charge and channel geometry on ionic flows via classical Poisson-Nernst-Planck models. SIAM J. Appl. Math. 2015, 75, 114–135. [Google Scholar] [CrossRef]
- Bates, P.W.; Wen, W.; Zhang, M. Small permanent charge effects on individual fluxes via Poisson-Nernst-Planck models with multiple cations. J. Nonlinear Sci. 2021, 31, 55. [Google Scholar] [CrossRef]
- Nonner, W.; Eisenberg, R.S. Ion permeation and glutamate residues linked by Poisson-Nernst-Planck theory in L-type Calcium channels. Biophys. J. 1998, 75, 1287–1305. [Google Scholar] [CrossRef] [PubMed]
- Eisenberg, B.; Liu, W. Poisson-Nernst-Planck systems for ion channels with permanent charges. SIAM J. Math. Anal. 2007, 38, 1932–1966. [Google Scholar] [CrossRef]
- Gillespie, D. A Singular Perturbation Analysis of the Poisson-Nernst-Planck System: Applications to Ionic Channels. Ph.D. Thesis, Rush University at Chicago, Chicago, IL, USA, 1999. [Google Scholar]
- Kierzenka, J.; Shampine, L. A BVP Solver Based on Residual Control and the Matlab PSE. ACM Trans. Math. Softw. 2001, 27, 299–316. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).