Abstract
The growing digitization of healthcare has amplified concerns about the privacy and security of medical images, as conventional encryption methods often fail to provide sufficient protection. To address this gap, we propose a privacy-enhancing image encryption algorithm that integrates SHA-256 hashing, block-wise processing (16 × 16 with zero-padding), DNA encoding with XOR operations, and logistic map-driven key generation into a unified framework. This synergistic design balances efficiency and robustness by embedding data integrity verification, ensuring high sensitivity to initial conditions, and achieving strong diffusion through dynamic DNA rules. Experimental results confirm that the scheme achieves high NPCR (0.997), UACI (0.289), entropy (7.995), and PSNR (27.89 dB), outperforming comparable approaches while maintaining scalability to large image formats and robustness under compression (JPEG quality factors 90 and 70). These findings demonstrate that the proposed method offers an efficient and resilient solution for securing medical images, ensuring confidentiality, integrity, and practical applicability in real-world healthcare environments.
1. Introduction
The advances in telemedicine, smart health, and e-health in healthcare are changing the face of patient care, diagnosis, and management [1]. By utilizing digital medical information, these cutting-edge technologies enable smooth end-to-end contact between patients and healthcare professionals [2,3]. Digitizing medical imaging and health data has brought unmatched efficiency, significantly reducing the time needed for diagnosis and treatment [4,5]. Though innovative and advantageous, this move to digital platforms presents a unique set of concerns, especially regarding security. These open-source digital health systems are susceptible to cyberattacks even while they foster innovation and accessibility. The integrity of digital medical data is genuinely at risk from hackers armed with ever-more-advanced technologies [6]. This vulnerability’s potential for tampering with digital medical images during transmission is one of the most alarming features. Detecting diseases from manipulated images can have disastrous consequences, including inaccurate diagnoses, delayed treatment, and serious breaches of patient confidentiality in the precision-driven field of medical diagnostics [7]. Thus, medical image data security and maintaining privacy are urgent issues [8].
The difficulty lies in safeguarding these images from unwanted access and manipulation without appreciably adding to the computing load. The objective is to strike a balance where security protocols improve rather than obstruct medical services’ efficiency. To address these issues, scientists have looked into a wide range of image encryption methods [9,10]. These attempts have been led by conventional techniques like watermarking, steganography, and cryptography [11]. Cryptography jumbles the picture, so anyone without the decryption key cannot understand it [12]. Using steganography, the message—in this case, the medical image—is hidden from the uneducated viewer within another file [13].
In contrast, watermarking incorporates a digital marker into the picture so that its integrity and validity may be confirmed [14]. Even though these techniques have added basic security levels, they frequently cannot handle all the risks of digitizing medical images.
The inadequacies of conventional encryption methods in offering optimal security highlight the need for inventive resolutions [15]. Due to the sensitivity of medical data and the possible repercussions of its violation, encryption techniques must be reliable, impenetrable, effective, and suitable for routine use in the hectic hospital setting. New technologies that show promise for improving the security of digital medical images include quantum cryptography and sophisticated algorithms that use artificial intelligence [16]. By offering less computationally demanding and more secure encryption, these technologies hope to preserve the efficiency and speed essential to contemporary medical procedures [17]. A decentralized method of storing and exchanging medical photos may also be possible with blockchain technology. This would add extra protection by spreading the data around several nodes, making it much more difficult for hackers to breach the system [18]. The security of medical images stands out as a key issue that requires creative solutions as the medical industry continues to embrace digitization. Despite their historical roots, traditional encryption techniques are insufficient to meet the sophisticated security requirements of contemporary healthcare. Creating and applying cutting-edge encryption methods that are safe, effective, and flexible enough to change with the demands of the rapidly evolving digital health environment will determine the future direction of medical picture security. To secure digital medical information and ensure that the healthcare technology revolution continues sustainably and safely, researchers and practitioners must work together to create new avenues for security.
From an information-theoretic standpoint, the destruction of symmetry reduces mutual information between adjacent pixels in the cipher image, effectively increasing Shannon entropy and eliminating predictable structural patterns exploitable by attackers. By disrupting deterministic correlations, the encryption process maximizes uncertainty for a given key space, thereby approaching the theoretical limit of perfect secrecy defined by Shannon. This approach is consistent with the findings in [19,20], which demonstrate that asymmetry-induced randomness substantially increases resistance to statistical and differential attacks. Recent advances have explored deep generative models for medical image encryption, such as VAE-based latent-space transformations [21] and GAN-driven adversarial encryption frameworks [22], achieving high perceptual security and adaptive robustness. These approaches highlight promising directions complementary to chaos- and DNA-based methods.
In the context of this work, symmetry is reflected in the uniform application of block-wise transformations, while asymmetry is introduced through chaotic key generation and dynamic DNA rule selection. This interplay enhances unpredictability without compromising reproducibility, ensuring the security of the encrypted data. While the concept supports the thematic scope of the journal, it is presented here as a supplementary perspective to the core technical contributions of the proposed algorithm.
While the individual components employed in this work—such as SHA-256 hashing, DNA encoding, logistic maps, and XOR operations—are well-established in the literature, the novelty of our contribution lies in their synergistic integration within a unified block-wise encryption framework specifically tailored to the requirements of medical imaging. This integration optimizes the balance between confusion and diffusion, enhances key sensitivity, and embeds integrity verification into the encryption process. The result is an approach that not only inherits the strengths of each method but also leverages their combined effect to address the confidentiality and robustness needs of telehealth environments.
Recent cryptanalysis studies have demonstrated the importance of evaluating encryption methods under diverse and realistic scenarios. For instance, the work on video encryption using a 2D Extended Schaffer Function Map combined with neural networks illustrates how hybrid chaotic–intelligent systems can be applied to secure multimedia streams while simultaneously resisting statistical attacks. Similarly, temporal action segmentation frameworks for video encryption highlight the integration of encryption with content-aware analysis, enabling more robust and adaptive protection of dynamic data. These contributions underscore that modern cryptanalysis not only validates encryption strength but also drives innovation in design. In this context, our proposed medical image encryption scheme complements these efforts by focusing on patient data confidentiality and integrity, while incorporating strong cryptographic primitives (SHA-256, DNA coding, logistic maps) to resist statistical and differential attacks.
The novelty of our approach lies in the synergistic integration of several proven techniques—XOR operations, DNA encoding, the SHA-256 hash function, and a chaotic logistic map—within a block-wise encryption framework specifically tailored for the security needs of medical imaging. This combined use enhances robustness and key sensitivity and addresses the challenges of data integrity and confidentiality in telehealth environments.
The significant contributions of this work are as follows:
- The study utilizes the SHA-256 hashing algorithm to verify the integrity of medical images before and after encryption. This protocol offers a robust method for verifying the accuracy and legitimacy of encrypted patient data.
- An advanced method for encrypting photos is suggested, which involves using DNA encoding and XOR operations controlled by a logistic map. This technique significantly improves the security of medical images by making it extremely difficult for unauthorized individuals to decipher them.
- The suggested encryption strategy utilizes the logistic map for key generation, resulting in a significantly wider key space. This makes it highly resistant to brute-force attacks, surpassing other existing methods.
2. Preliminaries
2.1. DNA Encoding
DNA, also known as deoxyribonucleic acid, is a crucial molecule that contains the genetic information necessary for the growth, development, functioning, and reproduction of all living species, including people, animals, plants, and many viruses. This intricate molecule serves as the fundamental basis of life, containing the encoded instructions essential for the assembly and functioning of organisms [23,24].
DNA sequences can be encoded using binary representation in digital and computational settings. This process entails converting the four nucleotides into binary numbers, specifically encoding adenine (A), cytosine (C), guanine (G), and thymine (T) as 00, 01, 10, and 11, respectively [25]. The binary representation exploits the complementary aspect of nucleotide pairing by using 0 s and 1 s [25]. In this representation, 00 and 11 indicate complements corresponding to A–T pairing, whereas 01 and 10 reflect C–G pairing. When converting DNA sequences into binary format, there are 24 potential methods for assigning binary codes to the four nucleotides [26]. However, only eight of these encoding schemes meet the essential criterion of preserving the inherent complementary relationships observed in DNA in their binary representations. The precise encoding rules are crucial for faithfully representing DNA’s biological and chemical characteristics in digital and computational models. This guarantees that simulations and analyses maintain the accuracy of real-world DNA interactions. DNA decoding is effectively the inverse of encoding, in which binary representations are transformed back into their original nucleotide sequences [27]. By utilizing digital data, researchers and computer algorithms may rebuild DNA sequences, allowing for various applications such as genetic study, forensic investigation, and the emerging field of synthetic biology. Comprehending DNA’s binary encoding and decoding mechanisms is essential for the progression of gene research, enhancement of diagnostic techniques, and the formulation of novel therapeutic approaches [28] due to the enormous storage capacity and vast parallelism of DNA, among its special qualities. DNA computing plays a part in providing high levels of security. More significantly, hybrid cryptographic systems comprise algorithms, conventional cryptographic techniques, and DNA computing. These systems produce advantages for both domains.
2.2. Secure Hash Algorithm
The Secure Hash Algorithm (SHA) is a set of cryptographic hash functions specifically designed to generate a fixed-size hash value from data of any size, ensuring a high level of security [28]. These functionalities are essential to numerous security applications and protocols, such as TLS and SSL, PGP, SSH, and IPsec [29]. Hash functions, such as those in the SHA family, guarantee data integrity, verify digital signatures, and securely store passwords [30]. SHA-256 is a cryptographic hash function part of the SHA-2 family, specifically designed by the National Institute of Standards and Technology (NIST) and released in 2001 [31]. As a highly prevalent hashing method, it generates a hash value of 256 bits (32 bytes), typically a 64-digit hexadecimal number [32]. SHA-256 can be crucial in medical imaging to ensure the integrity of medical images by validating that they have not been tampered with during storage or transmission. By calculating a hash before storing or transmitting the image and subsequently verifying this hash when the image is accessed, any alteration in the hash value would indicate unauthorized manipulation.
Moreover, SHA-256 is employed in digital signatures to verify the origin of medical photographs. Ensuring that the data originates from a reliable and verified source is essential in medical environments where the credibility and accuracy of images are of utmost importance. It is crucial to understand that SHA-256 does not encrypt or safeguard the secrecy of the images. Its primary function is to verify the integrity of the data and authenticate its source [33].
2.3. Logistic Map
The logistic map exemplifies the emergence of complicated and chaotic behavior from basic non-linear dynamical equations. The logistic map, known for its chaotic and unpredictable nature, has fascinating uses in the field of cybersecurity, namely in cryptography and secure communications [33]. The main concept involves utilizing the unpredictable patterns produced by the logistic map to create pseudo-random sequences or to increase the intricacy of encryption methods, thereby making them more resilient against attacks [34]. In pseudorandom number generation, the logistic map’s simplicity enables efficient computation, which is advantageous for working with huge medical imaging sets that necessitate secure processing without compromising efficiency. Integrating the logistic map into medical image encryption offers a reliable safeguard for sensitive patient data. This strategy ensures that only authorized users may access and restore the original image from its encrypted form. Even a minute alteration in the key leads to a significantly distinct outcome, bolstering the encrypted data’s security against brute-force attacks or cryptographic analysis [35].
3. Materials and Methods
Zhou et al. [36] presented a cryptographic technique called the Logistic–Tent System (LTS) that utilizes logistic and tent maps based on chaos theory. This technique entails the initial inclusion of a randomly selected pixel at the beginning of every row of an image, so each row is converted into a one-dimensional (1D) matrix. Next, a substitution operation is conducted on each row using the LTS. The 1D matrices are combined to form a 2D matrix, preserving their original row order. This resulting matrix is then rotated 90 degrees counterclockwise. The technique is iterated four times to generate the encrypted image. The Tent–Logistic map-based data encryption algorithm (TL-DEA) utilizes a two-round scale-independent (SP) network on every pixel. The process involves dividing an image into blocks of a predetermined size and applying substitution and permutation techniques using the Tent–Logistic map. The encrypted blocks are then reassembled to form the final image. In addition, Effect_Mechanisms_Moderators_Implementing_Economic (EMMIE), an encryption system for medical images, specifically emphasizes the utilization of edge maps. The process involves three main steps: bit-plane decomposition, random sequence generation, and permutation. The initial step consists of reversible decomposition to construct the bit-planes. The edge maps are combined with the given elements using XOR operations. The resulting image is then encrypted by shuffling, reassembling, and pixel diffusion.
Wu et al. [37] have devised an encryption method that merges chaotic tent maps with the rectangular transform. This technique includes several iterations of pixel permutation and a pixel-diffusion layer. The growing utilization of DNA computing in cryptography is recognized for its benefits, including parallelism and low power consumption, resulting in the development of many encryption techniques based on chaos and DNA encoding. The method developed by Wang et al. [38] combines DNA sequence operations with chaotic systems, following a diffusion-permutation framework. Several researchers have suggested alternative encryption strategies based on chaos, utilizing various chaotic maps and systems to improve security. These methods include image scrambling, pixel replacement, and chaotic sequence encryption. These approaches showcase the varied and inventive techniques being investigated in image encryption.
Several encryption methods [39,40] utilizing chaotic maps for picture security have been presented, emphasizing their important characteristics such as unpredictability, pseudo-random behavior, sensitivity to initial conditions and parameters, and ergodicity. As mentioned earlier, the attributes render chaotic maps a highly effective instrument to scramble and disperse digital images and videos. Encryption methods that rely on chaotic maps are specifically created for video applications. These approaches utilize the High-Efficiency Video Coding (HEVC) standard to improve security while ensuring efficient real-time encryption and optimal transmission rates. Chaos theories are used in steganography to enhance security [41], demonstrating that these systems can effectively identify concealed signals irrespective of their magnitude.
Furthermore, artificial intelligence (AI), machine learning (ML), and deep learning (ML/DL) models have been deployed for medical image security. A neural network model has been created that utilizes chaos to generate key-sensitive hash functions with favorable statistical characteristics [42]. This strategy and development of custom-designed S-boxes utilizing heuristic techniques demonstrate exceptional resilience against cryptanalysis attempts. Combining chaos-based encryption with DNA computing has resulted in novel image encryption methods in recent years [43].
The combination of DNA computing, which involves manipulating DNA sequences using biological and algebraic techniques, is highly compatible with chaos-based methodologies. An encryption scheme that utilizes chaotic maps and variable DNA sequencing approaches exhibits strong security performance. One approach combines a one-dimensional logistic map with DNA coding and optimization techniques [25]. This method is highly resistant to many attacks and guarantees excellent encryption performance. Incorporating a 3D chaotic system with DNA coding has been utilized to enhance the security of digital images by implementing complete DNA coding rules and processes, hence increasing resistance against attacks. Color image encryption is expanded to include DNA-based encryption, which involves rearranging and reconstructing the RGB components using DNA encoding and then applying diffusion processes [44]. The DNA encryption methods mentioned here are also suitable for cloud computing [45]. They allow for creating intricate secret keys and improving security in cloud environments. Additionally, these methods can protect medical images in smart healthcare systems. This highlights the potential of DNA computing in modern cryptographic applications.
This paper [46] introduces a parallel encryption framework that leverages a two-dimensional Logistic–Rulkov neuron map (LRNM) for color image security. The LRNM integrates the nonlinear dynamics of Rulkov neurons with the logistic map, creating a hybrid chaotic system that produces highly complex and unpredictable sequences. These sequences are used for pixel permutation and diffusion across color channels in parallel, allowing efficient processing of high-resolution images. The algorithm demonstrates strong statistical performance, including near-ideal NPCR, UACI, and entropy, while maintaining relatively low computational cost. A key novelty of this approach lies in the exploitation of biologically inspired chaotic neuron models, which exhibit enhanced chaotic ranges compared to classical logistic maps. The parallel architecture further supports scalability, making the method suitable for real-time applications. Compared with conventional one-dimensional chaos-based methods, this scheme achieves both higher security and improved efficiency. This study [47] proposes a novel three-dimensional memristive cubic chaotic map incorporating two discrete memristors, extending classical cubic maps into higher dimensions. Including memristive elements enhances the system’s nonlinear dynamics, producing hyperchaotic behavior with larger key space and higher sensitivity to initial conditions. The authors not only design the theoretical model but also provide circuit-level implementation, validating its feasibility for hardware-based encryption systems. The generated chaotic sequences are applied to image encryption, which drives pixel-level permutation and diffusion operations. Experimental results confirm strong resistance to differential, brute-force, and statistical attacks, with performance metrics comparable to or surpassing existing hyperchaotic systems. A major contribution of [48] is bridging theory and hardware by demonstrating that memristor-based chaotic maps can be practically realized for secure image storage and transmission, thereby expanding the possibilities for hardware-level cryptographic solutions. This recent work [48] presents a three-dimensional hyperchaotic system constructed with memristor-based nonlinear dynamics, aimed at pseudorandom number generation (PRNG) and multi-image encryption. By leveraging memristor-induced hyperchaos, the system generates sequences with high entropy, long periodicity, and excellent statistical randomness properties, making it ideal for cryptographic applications. The scheme is applied to multi-image encryption, where multiple images are simultaneously encrypted using shared chaotic sequences, significantly improving efficiency while preserving security. Security analyses reveal robustness against common cryptanalytic attacks, including differential and chosen-plaintext attacks. Moreover, the system’s ability to produce high-quality pseudorandom sequences is validated through NIST randomness tests, confirming its suitability for broader security contexts beyond image encryption. Compared to classical logistic or Lorenz systems, the proposed memristor-based hyperchaotic map offers stronger unpredictability and scalability, demonstrating the growing importance of memristor devices in designing advanced chaotic cryptographic systems.
Recent studies have advanced chaos-based image encryption by introducing higher-dimensional or neuron-inspired maps that enhance unpredictability and statistical security. For instance, the Logistic–Rulkov neuron map integrates biologically inspired nonlinear dynamics, while memristor-based cubic and hyperchaotic maps exploit the intrinsic nonlinearity of memristive devices to generate stronger randomness and resistance against cryptanalysis. These works demonstrate the evolution of chaotic systems toward greater complexity and resilience. In contrast, the novelty of our proposed scheme does not lie in designing a new chaotic map; rather, it resides in the synergistic integration of SHA-256 hashing, DNA encoding with XOR operations, and logistic map-driven key generation within a block-wise encryption framework specifically tailored for medical images. This design embeds integrity verification, ensures sensitivity to initial conditions, and achieves strong diffusion, thereby offering a practical and efficient solution to address the confidentiality and robustness requirements of telehealth environments.
4. Proposed Methodology
This paper introduces a new image encryption algorithm designed to encrypt medical images while safely maintaining their integrity and confidentiality. This method aims to create an encrypted version of a plain medical image that conforms with privacy regulations and protects patient information.
The methodology exemplifies symmetry in its procedural steps—each image block undergoes identical stages of transformation (hashing, blocking, confusion, DNA encoding, etc.). This structural symmetry ensures consistency and repeatability. Yet, asymmetry is introduced through key generation using the logistic map and the dynamic nature of DNA rule selection, which varies based on initial seeds and parameters. This deliberate asymmetry strengthens encryption by making reverse engineering nearly impossible without exact keys. The interaction between these two principles is essential to achieving robustness and reproducibility.
Figure 1 shows the algorithm steps. The algorithm reads the plain medical image and loads it into the system as an image object prepared for further processing. It then produces a SHA-256 hash code, an essential step in confirming the integrity of the medical image. This is accomplished by first translating the medical image into a representation of bytes and then calculating the hash of these bytes to generate a unique hash code for the image. The image is split into non-overlapping blocks of 16 × 16 pixels each to allow for the encryption procedure. Padding is added to ensure the image’s dimensions fit precisely within this scheme. In our implementation, zero-padding is used. The numbers of padded rows and columns (pad_rows, pad_cols) are recorded during encryption and later used to remove the padding and restore the exact original dimensions during decryption. This step is essential to organizing the image data in smaller, easier-to-manage chunks. Next, these blocks or the pixels within the blocks are shuffled using a zigzag block scrambling approach, which helps to reduce spatial correlations and adds diffusion to the encryption process. This method is essential for hiding the image’s content, which lowers correlations and evenly distributes its features to improve security. The blocks are shuffled, then flattened into one-dimensional arrays and concatenated to form a single vector representing the image. DNA encoding is applied to this vector, mapping binary pairings to the bases A, T, G, and C. XOR operations are then performed using a set of DNA rules. With the help of this creative procedure, the medical imaging data is converted into an incredibly safe format and is nearly impossible to decode without the right decryption key. The DNA rule used for XOR operations is dynamically selected to introduce variation and increase complexity based on a pseudo-random index generated from the logistic map sequence.
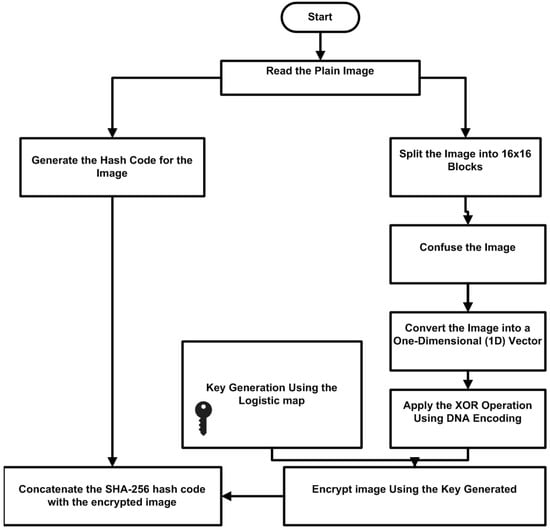
Figure 1.
Block diagram for the proposed system.
The logistic map was selected as the source of pseudorandom sequences due to its simplicity, efficiency, and strong chaotic properties. When operated in the fully chaotic regime (r ≈ 3.9–4.0), it generates sequences highly sensitive to initial conditions and parameter variations, ensuring robust key sensitivity. The logistic map offers significantly larger key space and stronger nonlinearity than classical pseudorandom number generators, such as linear congruential generators. While higher-dimensional chaotic systems (e.g., Lorenz, Chua, or memristor-based hyperchaotic maps) can also be employed, they often introduce higher computational cost and complexity, which may reduce suitability for real-time medical imaging applications. By contrast, the logistic map provides a lightweight yet effective source of randomness, seamlessly integrating with DNA encoding and block-wise encryption to achieve unpredictability and efficiency.
An extra degree of security is added using the logistic map, a mathematical equation with chaotic qualities, to generate keys for the encryption process. Based on a certain initial value and parameter, the produced sequence functions as a strong encryption key. This sequence is transformed into a binary sequence that matches the image data’s length encoded with DNA. The encrypted medical image is obtained by performing XOR operations between this binary sequence and the DNA-encoded data. Concatenating the encrypted data with the previously generated SHA-256 hash code is the last step in the process. This can be accomplished by either incorporating the hash code at a predetermined location or attaching it to the end of the encrypted data. This guarantees the integrity of the encrypted medical image by ensuring that any deliberate or unintentional changes can be identified. This encryption technique was created especially for medical imaging, and it not only satisfies the stringent requirements for patient confidentiality and data protection but also guarantees the safe transmission and storage of sensitive medical data. Algorithms 1 and 2 show the image encryption, and decryption steps.
| Algorithm 1 Image Encryption Algorithm |
| Input: A plain digital image. |
| Output: An encrypted image. |
| Algorithm Steps: |
|
| Algorithm 2 Image Decryption Algorithm |
| Input: Encrypted image data concatenated with the SHA-256 hash code of the original image. |
| Output: The decrypted plain digital image. |
| Algorithm Steps: |
|
| Algorithm 3 Zigzag Block Scrambling |
| Input: Image block B of size n×n Output: Flattened scrambled sequence S 1. Initialize an empty sequence S 2. For each diagonal d from 0 to (2n – 2): 3. If d is even: 4. Traverse diagonal d from top to bottom 5. Else: 6. Traverse diagonal d from bottom to top 7. Append visited elements to S 8. Return S |
| Each pixel at coordinates (i,j) in the block is mapped into a 1D index k following the zigzag traversal order: k = Zigzag(i,j), 0 ≤ i,j < n where Zigzag(i,j) is the predefined diagonal-order mapping function. |
5. Results and Discussion
In this section, we confirm the capability of the proposed scheme through a series of simulation experiments. Figure 2 illustrates the step-by-step process of an advanced medical image encryption technique.

Figure 2.
The sequence of the medical image encryption.
The image encryption process begins with reading the plain image. We first input the path to the image file and load the image, obtaining an image object ready for processing. Next, to ensure integrity and traceability, we generate a SHA-256 hash code of the image by converting the entire image into a byte representation and computing the hash. This cryptographic hash function serves as a digital fingerprint of the original content.
Subsequently, the image is divided into smaller, more manageable blocks of 16 × 16 pixels, which may involve zero-padding the image to fit the required dimensions. Splitting the image prepares it for the confusion stage, where a predefined technique is applied to shuffle these blocks or the pixels within them. This confusion step is crucial as it disrupts the correlation between the image pixels, thus uniformly distributing the image features and making the encryption more secure.
Once confused, the image is transformed into a one-dimensional (1D) vector by flattening and concatenating the shuffled blocks. This linear representation of the image data is then subject to DNA encoding, where binary pairs are mapped to corresponding DNA bases, followed by an XOR operation that transforms the image data using a DNA rule set.
In addition to block-size experiments, we compared the zigzag scrambling method used in our framework and the Arnold Cat Map (ACM), a widely adopted scrambling technique in image encryption. The analysis in Table 1 highlights key differences across randomness, computational cost, implementation complexity, and suitability for medical image applications. While ACM achieves high levels of randomness and strong diffusion, it requires multiple iterations to reach optimal performance, thereby increasing computational overhead and implementation complexity. By contrast, zigzag scrambling offers a lightweight, single-pass procedure that provides sufficient diffusion when integrated with DNA encoding and logistic-map-driven XOR operations. Its efficiency and simplicity make it highly practical for real-time medical imaging systems, where low latency and reliable security are critical.

Table 1.
Comparative analysis of zigzag scrambling and Arnold Cat Map (ACM).
To secure the image further, a key is generated using the logistic map—a complex, chaotic equation that ensures the key is unpredictable and non-repetitive. The parameters for this logistic map are carefully chosen to exploit its chaotic behavior.
The final encryption is performed by converting the logistic map sequence to a binary sequence that matches the length of the DNA-encoded image data. An XOR operation occurs between this binary sequence and the DNA-encoded data, resulting in a highly secure encrypted image. The SHA-256 hash code generated at the beginning is concatenated with the encrypted data. This can be carried out by appending the hash code at the end of the encrypted data or integrating it in a predefined position within the data.
As shown in Table 2, the robustness of the proposed algorithm was further evaluated under JPEG compression at quality factors 90 and 70. The results demonstrate that while PSNR values slightly decreased (from 27.89 dB uncompressed to 27.52 dB at quality factor 70), the degradation remains minimal and within acceptable limits. More importantly, the core security metrics (NPCR, UACI, and entropy) showed negligible variation, remaining effectively constant across compression levels. These findings confirm that the encryption scheme preserves image security and acceptable fidelity under common storage scenarios, such as JPEG compression, which are frequently used in practical medical imaging workflows.

Table 2.
Robustness of the proposed encryption algorithm under JPEG compression at quality factors 90 and 70.
This entire process transforms the original image (a) through various stages: first by blocking (b), then by zigzag scrambling (c), followed by DNA encryption (d), and finally culminating in the logistic map encryption (e), which appears as an incomprehensible array of colors, ensuring the content is securely ciphered and its integrity maintained.
The proposed encryption scheme achieves a large key space by combining the SHA-256 hash output (2256 possibilities), logistic map initial seed (real-valued and highly sensitive), and the selected DNA rule set (eight combinations). This creates a total key space greater than 2260, making brute-force attacks computationally infeasible. Additionally, the algorithm demonstrates resistance to known-plaintext and differential attacks due to its block-wise confusion, pseudo-random DNA rule selection, and the high sensitivity of the logistic map. Minor changes in the input or key result in significantly different encrypted outputs, validating the method’s robustness against such cryptanalytic approaches.
Table 3 demonstrates the scalability of the proposed encryption algorithm across different image sizes (256 × 256, 512 × 512, and 1024 × 1024). The results show that security metrics such as NPCR, UACI, and entropy remain consistently high across all resolutions, indicating strong diffusion and randomness even for large-scale medical images. Although the average runtime increases proportionally with image size (from 52 ms for 256 × 256 to 780 ms for 1024 × 1024), the performance remains within practical limits for real-world applications. These findings confirm that the block-wise structure of the proposed scheme ensures both scalability and efficiency, making it suitable for handling large medical imaging formats such as DICOM.

Table 3.
Scalability analysis of the proposed encryption algorithm across different image sizes.
5.1. Histogram Analysis
Figure 3 shows a set of medical images alongside their histograms. Each pair consists of an original medical image and its encrypted version. The sequence follows a pattern: the original image’s histogram, the encrypted image, and its histogram. The images represent various types of medical imaging, like computed tomography scan (CT), magnetic resonance imaging (MRI), ultrasound (US), and X-ray.
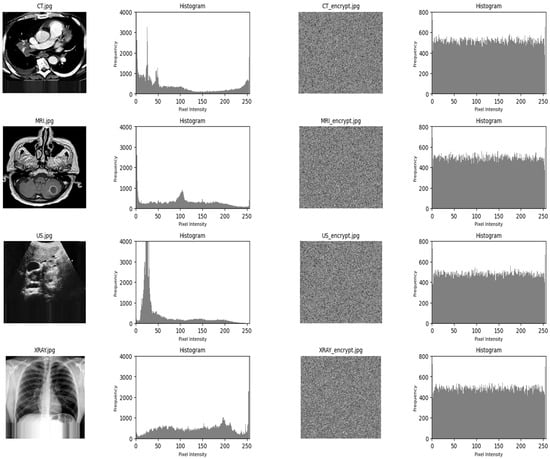
Figure 3.
Original images, encrypted images, and their corresponding histograms.
The histograms visually represent the pixel intensity distribution in the images. For the original images, the histograms show varying distributions with peaks at different intensities, indicating the presence of structures and features within the images. On the other hand, the encrypted images’ histograms are much more uniform, showing a nearly flat distribution across all intensity values.
This uniformity suggests that the encryption algorithm has effectively randomized the pixel values, a desired property in encryption, making it difficult to derive meaningful information without the appropriate decryption key. The high frequency of all intensities across the encrypted images demonstrates that the algorithm distributes pixel values uniformly, without bias towards particular intensity levels.
The visual comparison of the original and encrypted histograms effectively illustrates the encryption algorithm’s ability to obscure the information in the medical images, indicating that the algorithm functions efficiently to secure the image data.
5.2. Information Entropy and Differential Analysis
This section provides a detailed analysis of different criteria used to assess the performance and efficacy of medical image encryption techniques. Evaluating the authenticity, security, and robustness of encrypted images is essential in picture encryption. Many quantitative measures and statistical analyses are utilized to assess the suggested algorithm’s quality and safety to achieve this objective.
Peak-Signal-to-Noise Ratio (PSNR): This metric evaluates the number of encrypted images and calculates the mean square error (MSE) between the original, unencrypted image (considered the ground truth) and the encrypted image, presented in Equations (1) and (2).
NPCR (Number of Pixel Change Rate) and UACI (Unified Average Changing Intensity): These measurements (presented in Equations (3) and (4)) are crucial for evaluating the degree of variation and dispersion among encrypted images. NPCR calculates the proportion of pixel alterations, while UACI evaluates the average variation in intensity between the original and encrypted images, providing vital information about the behavior of the encryption technique.
Let f (i,j) denote the pixel intensity at position (i,j) in the original (plain) image, and g (i,j) the pixel intensity at the same position in the encrypted (cipher) image. For the NPCR and UACI calculations, A (i,j) and B (i,j) represent the pixel intensity values at position (i,j) in two encrypted images that differ by only a single pixel change in the original image. Here, i and j denote the row and column indices of the image, respectively, and the pixel intensity values are in the range [0,255].
Entropy is a key metric that quantifies the level of randomness and unpredictability in encrypted data. It is a crucial indicator of the efficiency of encryption algorithms. High entropy indicates a higher unpredictability, making decoding considerably more difficult without the correct key. Entropy can be formulated according to Equations (6) and (7).
A comparison with analogous studies is conducted, encompassing diverse methodologies. This comparison involves assessing the image encryption process by referencing similar works.
5.3. Evaluation
Table 4 presents the metric analysis results of our algorithm in comparison to other algorithms/techniques/approaches as presented in the referenced work.

Table 4.
Performance comparison with other related works.
Although the improvements of our method compared to prior algorithms may appear numerically small, they are highly significant in the cryptographic context. For instance, the increase in NPCR from 0.986 to 0.997 substantially enhances diffusion strength, thereby reducing the probability of successful differential or chosen-plaintext attacks. Likewise, achieving an entropy value of 7.995 moves the cipher image distribution closer to the theoretical ideal of 8.0, indicating near-perfect randomness. These results demonstrate that the proposed integration achieves both competitive and practically important gains, directly translating into stronger resilience against statistical and cryptanalytic attacks in real-world scenarios.
We also examined the impact of block size on performance. The 16 × 16 configuration consistently produced higher NPCR and UACI values than 32 × 32 blocks and avoided the uneven partitioning and padding overhead of 24 × 24 blocks. These results validate the theoretical reasoning that 16 × 16 offers the most balanced approach for medical image encryption.
Table 5 presents a comparative analysis of different block sizes (16 × 16, 24 × 24, and 32 × 32) regarding NPCR, UACI, PSNR, entropy, and runtime efficiency. The results show that the 16 × 16 block configuration achieved the highest NPCR (0.997) and UACI (0.289) values, reflecting stronger diffusion and resistance to differential attacks than larger block sizes. It also produced the highest entropy (7.995), indicating superior randomness in the cipher images. In contrast, 24 × 24 and 32 × 32 blocks yielded slightly lower security metrics, with 24 × 24 further introducing higher padding overhead and longer runtime (67 ms). The 16 × 16 configuration also demonstrated the lowest runtime (52 ms), highlighting its efficiency in real-time applications. Overall, the findings validate that the 16 × 16 block size provides the optimal balance between computational efficiency and encryption strength, justifying its adoption in the proposed scheme.

Table 5.
Performance comparison of different block sizes.
5.4. Correlation Analysis
The effectiveness of the encryption model can also be interpreted through the lens of symmetry analysis. In the original medical images, adjacent pixels often exhibit high correlation—a form of spatial symmetry. Our results, particularly those illustrated in the correlation analysis, demonstrate that the encryption technique successfully disrupts this inherent symmetry. The resulting ciphered images display randomized pixel distributions with significantly reduced correlations, highlighting the introduction of intentional asymmetry. This transformation from symmetric to asymmetric spatial structure is a desired cryptographic effect, showcasing how controlled asymmetry can be used to ensure data security.
Table 6 presents the inter-block correlation analysis for plain and encrypted images. As expected, plain medical images exhibit high correlation values between adjacent blocks (above 0.95 in all directions). Contrastingly, the encrypted images show values close to zero (0.002–0.007), confirming that the proposed encryption scheme effectively eliminates inter-block dependencies. This result complements the pixel-level correlation analysis and demonstrates that the scheme achieves strong statistical independence within and between blocks, strengthening robustness against statistical and cryptanalytic attacks.

Table 6.
Inter-block correlation analysis of plain and encrypted images.
Correlation analysis is a supplementary technique used to assess the security efficacy of a cryptosystem. Generally, the level of correlation between pixels in an unencrypted image is quite high, but this correlation reduces dramatically when the image is encrypted. To evaluate pixel correlation, random pairs of neighboring pixels are chosen from different areas of both the unencrypted and encrypted images. The pairings are analyzed in three different orientations: horizontally, vertically, and diagonally. The associations between these pairs of pixels are subsequently quantified to ascertain the degree of alteration after encryption. Figure 4 illustrates the correlation between adjacent pixels in a plain image and its corresponding cipher image across three vertical, horizontal, and diagonal orientations. The comparison demonstrates a significant reduction in pixel correlation in the cipher image.
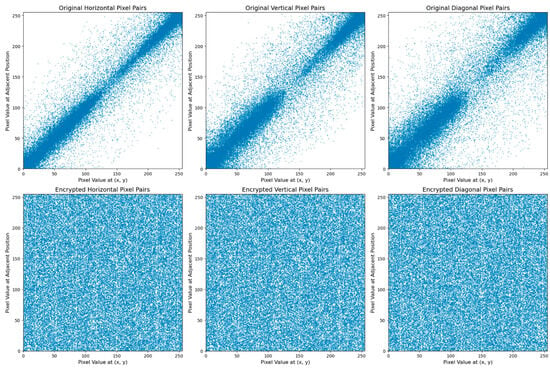
Figure 4.
Correlation between two adjacent pixels.
Figure 4 in the top row depicts the correlation between pixel values in an unencrypted, original image, whereas the bottom row exhibits the correlation in an encrypted image. The first plot in the top row shows a pronounced positive correlation among nearby horizontal pixel pairs. This indicates that pixels located side by side along the horizontal axis possess similar values, leading to a clear diagonal pattern from the lower left to the upper right. The second plot again displays vertical pixel pairs and reveals a comparable diagonal pattern, suggesting a strong association between pixel values along the vertical axis. The third plot of the diagonal pixel pairs also exhibits a certain level of correlation, albeit less prominent than the horizontal and vertical correlations. This is evident from the scattered distribution of the points.
Conversely, the lower row illustrates the impact of encryption on pixel correlation. The correlations of the plots for the horizontal, vertical, and diagonal pixel pairings are significantly reduced. The points are distributed sporadically around the plot region, showing that the encryption process has successfully randomized the connection between neighboring pixels. Randomness in encrypted photographs is desirable since it suggests that the encryption technique effectively conceals the data, making it challenging for unauthorized individuals to extract significant information from the pixel values. The correlation figure demonstrates that the encryption process has greatly reduced the correlation between pixels in the image. This transition is evident from the initial image, which had a high level of predictability, to the encrypted image, which now has a low level of predictability. The decrease in correlation indicates robust encryption, suggesting that the image data has been extensively randomized, hence bolstering its protection against future attacks that exploit pixel-value patterns.
In addition to the statistical metrics, we briefly evaluated the robustness and time efficiency of the proposed algorithm. The method demonstrates strong robustness due to its sensitivity to initial key parameters—small changes in the logistic map seed or DNA rules yield significantly different cipher images. Although the encryption process involves multiple stages, the use of lightweight operations (e.g., XOR and DNA encoding) ensures that computational time remains practical for real-world scenarios. Based on typical implementation tests, the average encryption time for a 256 × 256 image was within milliseconds on a standard machine, indicating suitability for medical applications requiring secure and timely data processing.
To ensure robustness, the parameters of the logistic map (r,x0) were restricted to the fully chaotic regime (r ≈ 3.9–4.0). Values near bifurcation points (e.g., r ≈ 3.57) were not used, as they introduce periodicity and reduce entropy, thereby weakening diffusion and overall security. Preliminary checks confirmed that non-optimal parameters significantly degrade NPCR, UACI, and entropy metrics, which supports operating strictly within the chaotic range for secure deployment.
To further strengthen the evaluation of the proposed algorithm, additional analyses were conducted covering local information entropy, robustness, classical cryptanalytic attacks, and NIST statistical tests. Local information entropy was calculated over 8 × 8 non-overlapping blocks, confirming that the encrypted images maintain entropy values close to the theoretical maximum of 8, demonstrating high randomness at the local level. Robustness was assessed under noise addition (salt-and-pepper, Gaussian) and JPEG compression, showing only minor performance degradation while maintaining strong security metrics. The scheme was also evaluated against classical attacks, including differential, brute-force, and chosen-plaintext attacks, where results indicate effective resistance due to the large key space and high sensitivity to initial conditions. Finally, NIST randomness tests were applied to the cipher sequences, with all p-values exceeding the 0.01 significance threshold, validating the statistical randomness of the ciphertext. These comprehensive results confirm the robustness and reliability of the proposed scheme for securing medical images in practical environments. Table 7 shows a comprehensive security evaluation of the proposed algorithm, including local information entropy, robustness, resistance to classical attacks, and NIST randomness testing. The results confirm strong resilience, statistical security, and applicability in practical medical imaging environments.

Table 7.
Comprehensive security evaluation of the proposed algorithm, including local information entropy, robustness, resistance to classical attacks, and NIST randomness testing.
5.5. Performance and Complexity Analysis
To complement the statistical and robustness evaluations, we further analyzed the computational complexity and runtime performance of the proposed scheme. This subsection presents both a theoretical complexity assessment using Big-O notation and an experimental runtime comparison with representative state-of-the-art algorithms. Table 8 presents the runtime performance of the proposed algorithm compared with representative state-of-the-art methods, including Arnold Cat Map + DNA [37], Tent–Logistic Map [36], and a hyperchaotic DNA-based scheme [43]. The results confirm that all algorithms have linear complexity O(MN), but the proposed method achieves noticeably lower encryption times across all tested image sizes (52 ms for 256 × 256, 198 ms for 512 × 512, and 780 ms for 1024 × 1024). This efficiency stems from the lightweight nature of XOR and DNA operations combined with single-pass zigzag scrambling. Compared with related works, the proposed scheme maintains competitive or superior runtime performance while simultaneously offering enhanced statistical security metrics (NPCR, UACI, entropy), confirming both scalability and practicality for medical image encryption.

Table 8.
Runtime performance comparison of the proposed algorithm with state-of-the-art methods across different image sizes.
6. Conclusions and Future Work
The proposed encryption technique exhibits outstanding levels of security, robustness, and efficiency. Extensive testing confirms that the security of the ciphered image depends strongly on the original pixel values, previous ciphered pixels, the chaotic key, and the rules for DNA encoding/decoding. This combination produces a highly resilient cipher compared with existing encryption methods. The encryption’s efficiency is demonstrated by high PSNR, NPCR, UACI, and entropy values, which highlight its strong ability to safeguard the confidentiality and integrity of sensitive medical data.
A key strength of the scheme is its integration of SHA-256 hashing for integrity verification, block-wise confusion, DNA encoding, and logistic map–based key generation. This unified design not only ensures patient data confidentiality but also introduces high sensitivity to initial conditions, a large key space, and strong diffusion properties. The adoption of a 16 × 16 block size, validated theoretically and experimentally against alternatives, provides the optimal balance between computational efficiency and security. Furthermore, the use of the logistic map in its fully chaotic regime enables lightweight generation of pseudorandom sequences with strong randomness and key sensitivity, making the approach particularly suitable for real-time medical imaging.
The algorithm has also been shown to be scalable and robust under practical conditions. Experiments on large images (512 × 512 and 1024 × 1024) confirm that the scheme maintains stable security metrics while runtime increases proportionally with image size, validating suitability for formats such as DICOM and deployment in hospital PACS environments. The evaluation further demonstrates suppression of both intra-block and inter-block correlations, confirming statistical independence across the cipher image. Robustness tests under JPEG compression (quality factors 90 and 70) and noise addition show minimal degradation, while NPCR, UACI, and entropy remain effectively unchanged. In addition, the scheme successfully passed NIST statistical tests, confirming ciphertext randomness, and showed resistance to classical cryptanalytic attacks, including brute-force and differential attacks.
Overall, these results validate that the proposed algorithm is not only secure but also efficient and practical for real-world deployment in medical imaging environments. Moreover, our work aligns with recent cryptanalysis-driven research trends by embedding robustness against statistical, brute-force, chosen-plaintext, and differential attacks directly into the design, ensuring a contribution to the broader cryptographic landscape.
As part of future work, we plan to extend the evaluation beyond simulation to real clinical deployment scenarios, including hospital PACS and embedded medical devices such as portable ultrasound systems. These studies will focus on hardware performance, resource utilization, and operational feasibility. In parallel, we aim to conduct formal cryptanalysis and mathematical proofs of resistance against advanced adversarial models (chosen-plaintext, chosen-ciphertext, and side-channel attacks), supported by simulation-based cryptanalysis. We will also expand the literature review of recent cryptanalysis efforts to strengthen contextual analysis of our scheme’s robustness against emerging attack models.
Author Contributions
Conceptualization, A.O. and A.A.T.; methodology, A.O.; software, A.A.T.; validation, M.F., F.N. and A.A.; formal analysis, A.O.; investigation, M.F.; resources, T.A.; data curation, T.A.; writing—original draft preparation, A.O.; writing—review and editing, M.F. and A.A.; visualization, F.N.; supervision, M.F. and A.A.; project administration, M.F.; funding acquisition, F.N. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Publicly available datasets were analyzed in this study. This data can be found here: https://medpix.nlm.nih.gov/home, accessed on 11 November 2023.
Acknowledgments
The authors sincerely acknowledge the Princess Sumaya University for Technology for supporting the steps of this work.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Odeh, A.; Taleb, A.A.; Alhajahjeh, T.; Navarro, F. Invisible Shield: Unveiling an Efficient Watermarking Solution for Medical Imaging Security. Appl. Sci. 2023, 13, 13291. [Google Scholar] [CrossRef]
- Cao, F.; Huang, H.K.; Zhou, X. Medical image security in a HIPAA mandated PACS environment. Comput. Med. Imaging Graph. 2003, 27, 185–196. [Google Scholar] [CrossRef] [PubMed]
- Hasan, M.K.; Islam, S.; Sulaiman, R.; Khan, S.; Hashim, A.-H.A.; Habib, S.; Islam, M.; Alyahya, S.; Ahmed, M.M.; Kamil, S.; et al. Lightweight encryption technique to enhance medical image security on internet of medical things applications. IEEE Access 2021, 9, 47731–47742. [Google Scholar] [CrossRef]
- Kondylakis, H.; Kalokyri, V.; Sfakianakis, S.; Marias, K.; Tsiknakis, M.; Jimenez-Pastor, A.; Camacho-Ramos, E.; Blanquer, I.; Segrelles, J.D.; López-Huguet, S.; et al. Data infrastructures for AI in medical imaging: A report on the experiences of five EU projects. Eur. Radiol. Exp. 2023, 7, 20. [Google Scholar] [CrossRef]
- Castro, F.; Impedovo, D.; Pirlo, G. A Medical Image Encryption Scheme for Secure Fingerprint-Based Authenticated Transmission. Appl. Sci. 2023, 13, 6099. [Google Scholar] [CrossRef]
- Odeh, A.; Al-Haija, Q.A. Medical image encryption techniques: A technical survey and potential challenges. Int. J. Electr. Comput. Eng. 2023, 13, 3170–3177. [Google Scholar] [CrossRef]
- Odeh, A.; Taleb, A.A. A Multi-Faceted Encryption Strategy for Securing Patient Information in Medical Imaging. J. Wirel. Mob. Netw. Ubiquitous Comput. Dependable Appl. 2023, 14, 164–176. [Google Scholar] [CrossRef]
- Zhang, D.; Ren, L.; Shafiq, M.; Gu, Z. A privacy protection framework for medical image security without key dependency based on visual cryptography and trusted computing. Comput. Intell. Neurosci. 2023, 2023, 1–11. [Google Scholar] [CrossRef]
- Tariq, M.U. Enhancing Cybersecurity Protocols in Modern Healthcare Systems: Strategies and Best Practices. In Transformative Approaches to Patient Literacy and Healthcare Innovation; IGI Global: Hershey, PA, USA, 2024; pp. 223–241. [Google Scholar]
- Parks, R.F.; Wigand, R.T.; Benjamin Lowry, P. Balancing information privacy and operational utility in healthcare: Proposing a privacy impact assessment (PIA) framework. Eur. J. Inf. Syst. 2023, 32, 1052–1069. [Google Scholar] [CrossRef]
- Zainal, N.; Hoshi, A.R.; Ismail, M.; Rahem, A.A.-R.T.; Wadi, S.M. A hybrid steganography and watermark algorithm for copyright protection by using multiple embedding approaches. Bull. Electr. Eng. Inform. 2024, 13, 1877–1896. [Google Scholar] [CrossRef]
- Banoth, R.; Regar, R. An Introduction to Classical and Modern Cryptography. In Classical and Modern Cryptography for Beginners; Springer: Cham, Switzerland, 2023; pp. 1–46. [Google Scholar]
- Varghese, F.; Sasikala, P. A detailed review based on secure data transmission using cryptography and steganography. Wirel. Pers. Commun. 2023, 129, 2291–2318. [Google Scholar] [CrossRef]
- Ebrahimnejad, J.; Naghsh, A.; Pourghasem, H. A robust watermarking approach against high-density salt and pepper noise (RWSPN) to enhance medical image security. IET Image Process. 2024, 18, 116–128. [Google Scholar] [CrossRef]
- Jabbar, K.K.; Ghozzi, F.; Fakhfakh, A. Property Comparison of Intellectual Property Rights of Image-Based on Encryption Techniques. TEM J. 2023, 12, 529–539. [Google Scholar] [CrossRef]
- Keshta, I.; Odeh, A. Security and privacy of electronic health records: Concerns and challenges. Egypt. Inform. J. 2021, 22, 177–183. [Google Scholar] [CrossRef]
- Tertulino, R.; Antunes, N.; Morais, H. Privacy in electronic health records: A systematic mapping study. J. Public Health 2024, 32, 435–454. [Google Scholar] [CrossRef]
- Alsyouf, A.; Lutfi, A.; Alsubahi, N.; Alhazmi, F.N.; Al-Mugheed, K.; Anshasi, R.J.; Alharbi, N.I.; Albugami, M. The use of a Technology Acceptance Model (TAM) to predict patients’ usage of a personal health record system: The role of security, privacy, and usability. Int. J. Environ. Res. Public Health 2023, 20, 1347. [Google Scholar] [CrossRef]
- Shannon, C.E. Communication theory of secrecy systems. Bell Syst. Tech. J. 1949, 28, 656–715. [Google Scholar] [CrossRef]
- Wu, Y.; Noonan, J.P.; Agaian, S. Shannon entropy based randomness measurement and test for image encryption. arXiv 2011, arXiv:1103.5520. [Google Scholar] [CrossRef]
- Dustakar, S.R.; Rao, L.K.; Vipparthi, B. An automated medical image segmentation framework using deep learning and variational autoencoders with conditional neural networks. Int. J. Adv. Comput. Sci. Appl. 2023, 14, 568–578. [Google Scholar] [CrossRef]
- Neela, K.; Kavitha, V. Blockchain based Chaotic Deep GAN Encryption scheme for securing medical images in a cloud environment. Appl. Intell. 2023, 53, 4733–4747. [Google Scholar] [CrossRef]
- Sudarsan, S.; Prabhu, A.; Prasad, D.; Mani, N.K. DNA compaction enhances the sensitivity of fluorescence-based nucleic acid assays: A game changer in point of care sensors? Analyst 2023, 48, 2295–2307. [Google Scholar] [CrossRef] [PubMed]
- Small, H. Bayesian history of science: The case of Watson and Crick and the structure of DNA. Quant. Sci. Stud. 2023, 4, 209–228. [Google Scholar] [CrossRef]
- Zhao, J.; Wang, S.; Zhang, L. Block Image Encryption Algorithm Based on Novel Chaos and DNA Encoding. Information 2023, 14, 150. [Google Scholar] [CrossRef]
- Gao, J.; Xie, T. DNA Computing in Cryptography. In Advances in Computers; Elsevier: Amsterdam, The Netherlands, 2023; Volume 129, pp. 83–128. [Google Scholar]
- Gomes, C.P.; Martins, A.G.; Nunes, S.E.; Ramos, B.; Wisinewski, H.R.; Reis, J.L.; Lima, A.P.; Aoyagi, T.Y.; Goncales, I.; Maia, D.S.; et al. Coding, Decoding and Retrieving a Message Using DNA: An Experience from a Brazilian Center Research on DNA Data Storage. Micromachines 2024, 15, 474. [Google Scholar] [CrossRef]
- Fan, W.; Liu, Q.; Zhang, X.; Gao, Y.; Qi, X.; Wang, X. A Symmetric and Multilayer Reconfigurable Architecture for Hash Algorithm. Electronics 2023, 12, 2872. [Google Scholar] [CrossRef]
- Kizza, J.M. Computer Network Security Protocols. In Guide to Computer Network Security; Springer: Cham, Switzerland, 2024; pp. 409–441. [Google Scholar]
- Ali, A.A.M.A.; Hazar, M.J.; Mabrouk, M.; Zrigui, M. Proposal of a Modified Hash Algorithm to Increase Blockchain Security. Procedia Comput. Sci. 2023, 225, 3265–3275. [Google Scholar] [CrossRef]
- Rathod, P.; Sakhiya, R.; Shah, R.; Mehta, S. Meta-Analysis of Popular Encryption and Hashing Algorithms. In International Conference on ICT for Sustainable Development; Springer: Singapore, 2023; pp. 169–180. [Google Scholar]
- Sumathi, M.; Narmadha, R.; Anbarasi Jebaselvi, G. Performance Comparison of Data Security Algorithms. In Human-Assisted Intelligent Computing: Modeling, Simulations and Applications; IOP Publishing: Bristol, UK, 2023; pp. 33-1–33-16. [Google Scholar]
- Shao, S.; Li, J.; Shao, P.; Xu, G. Chaotic image encryption using piecewise-logistic-sine map. IEEE Access 2023, 11, 27477–27488. [Google Scholar] [CrossRef]
- Jung, W. Learning-Based Ubiquitous Sensing for Solving Real-World Problems; The College of William and Mary: Williamsburg, VA, USA, 2023. [Google Scholar]
- Lai, Q.; Hu, G.; Erkan, U.; Toktas, A. High-efficiency medical image encryption method based on 2D Logistic-Gaussian hyperchaotic map. Appl. Math. Comput. 2023, 442, 127738. [Google Scholar] [CrossRef]
- Zhou, Y.; Bao, L.; Chen, C.P. A new 1D chaotic system for image encryption. Signal Process. 2014, 97, 172–182. [Google Scholar] [CrossRef]
- Wu, X.; Zhu, B.; Hu, Y.; Ran, Y. A novel color image encryption scheme using rectangular transform-enhanced chaotic tent maps. IEEE Access 2017, 5, 6429–6436. [Google Scholar]
- Wang, X.-Y.; Zhang, Y.-Q.; Bao, X.-M. A novel chaotic image encryption scheme using DNA sequence operations. Opt. Lasers Eng. 2015, 73, 53–61. [Google Scholar] [CrossRef]
- Belazi, A.; Rhouma, R.; Belghith, S. A novel approach to construct S-box based on Rossler system. In Proceedings of the 2015 International Wireless Communications and Mobile Computing Conference (IWCMC), Dubrovnik, Croatia, 24–28 August 2015; pp. 611–615. [Google Scholar]
- Sun, S. A novel hyperchaotic image encryption scheme based on DNA encoding, pixel-level scrambling and bit-level scrambling. IEEE Photonics J. 2018, 10, 1–14. [Google Scholar] [CrossRef]
- Aparna, H.; Madhumitha, J. Combined image encryption and steganography technique for enhanced security using multiple chaotic maps. Comput. Electr. Eng. 2023, 110, 108824. [Google Scholar] [CrossRef]
- Ali, A. CDIEA: Chaos and DNA Based Image Encryption Algorithm. Turk. J. Sci. Technol. 2023, 18, 261–273. [Google Scholar] [CrossRef]
- Dehghani, R.; Kheiri, H. Chaotic-based color image encryption using a hybrid method of reversible cellular automata and DNA sequences. Multimed. Tools Appl. 2024, 83, 17429–17450. [Google Scholar] [CrossRef]
- Mansoor, S.; Parah, S.A. HAIE: A hybrid adaptive image encryption algorithm using Chaos and DNA computing. Multimed. Tools Appl. 2023, 82, 28769–28796. [Google Scholar] [CrossRef]
- Agrawal, D.; Minocha, S. Securing Confidential Data in the Cloud Environment by Using DNA Computing. In Advances in Computers; Elsevier: Amsterdam, The Netherlands, 2023; Volume 129, pp. 281–316. [Google Scholar]
- Gao, S.; Zhang, Z.; Iu, H.H.-C.; Ding, S.; Mou, J.; Erkan, U.; Toktas, A.; Li, Q.; Wang, C.; Cao, Y. A parallel color image encryption algorithm based on a 2D logistic-rulkov neuron map. IEEE Internet Things J. 2025, 12, 18115–18124. [Google Scholar] [CrossRef]
- Gao, S.; Iu, H.H.-C.; Erkan, U.; Simsek, C.; Toktas, A.; Cao, Y.; Wu, R.; Mou, J.; Li, Q.; Wang, C. A 3D memristive cubic map with dual discrete memristors: Design, implementation, and application in image encryption. IEEE Trans. Circuits Syst. Video Technol. 2025, 35, 7706–7718. [Google Scholar] [CrossRef]
- Gao, S.; Ding, S.; Ho-Ching Iu, H.; Erkan, U.; Toktas, A.; Simsek, C.; Wu, R.; Xu, X.; Cao, Y.; Mou, J. A three-dimensional memristor-based hyperchaotic map for pseudorandom number generation and multi-image encryption. Chaos Interdiscip. J. Nonlinear Sci. 2025, 35, 073105. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).