Abstract
In this study, we propose a novel hybrid metaheuristic framework that leverages symmetry awareness to enhance the performance of multi-objective optimization in renewable energy systems. Motivated by the repetitive and structured patterns commonly found in solar, wind, and demand profiles, we introduce a symmetry-guided variant of the NSGA-II algorithm, enriched with a customized crossover operator that detects and exploits symmetrical patterns in candidate solutions. To further accelerate convergence and reduce computational cost, we integrate a surrogate modeling strategy using machine learning to approximate fitness evaluations in later generations. Our experimental evaluation, based on a synthetic dataset simulating one week (168 h) of operation in a hybrid solar–wind power system, incorporating realistic diurnal patterns in generation and demand, demonstrates the proposed method’s superiority over baseline NSGA-II in terms of solution diversity, convergence, and runtime efficiency. The results highlight the importance of integrating domain-specific structure—such as temporal symmetry—into the design of metaheuristics for sustainable energy applications. This approach opens new avenues for scalable, intelligent optimization in complex energy environments.
1. Introduction
The increasing penetration of renewable energy sources—such as solar photovoltaic (PV) panels and wind turbines—into modern power systems introduces complex optimization challenges. These include balancing intermittent supply and temporal demand fluctuations, while handling multi-objective trade-offs such as minimizing unmet demand, reducing storage costs, and maintaining system reliability. In this context, multi-objective evolutionary algorithms (MOEAs) like NSGA-II have become standard tools due to their ability to approximate Pareto fronts without requiring gradient information [1,2].
However, achieving high-quality and diverse solutions typically requires extensive population evaluations, which become computationally expensive when simulations or real-world data integrations are involved. A promising route to alleviate this is the use of surrogate-assisted MOEAs (SA-MOEAs), which combine MOEAs with machine learning models (e.g., Gaussian Process Regression, Radial Basis Functions) to approximate objective evaluations, significantly accelerating convergence [3,4,5,6]. For instance, a recent framework leveraging RBF and a two-stage selection mechanism showed strong performance in high-dimensional, expensive multi-objective problems, improving efficiency without sacrificing solution quality [5].
Parallel to surrogate modeling, there has been growing interest in exploiting symmetry and invariance properties within optimization problems [7]. By identifying interchangeable structures—such as repeated daily patterns or interchangeable equipment—search algorithms can avoid redundant exploration and improve efficiency [6]. In evolutionary computation, symmetry-aware operators have been employed to mitigate duplication of equivalent solutions and enhance exploration [2].
Despite these advances, there is a lack of integrated approaches that combine symmetry-guided operators with surrogate-accelerated MOEAs, particularly in the renewable energy domain. The temporal regularity (e.g., diurnal cycles) and spatial modularity (e.g., panels or turbines) in renewable systems represent clear symmetry patterns that remain underutilized in current optimization frameworks.
1.1. Contributions
This paper introduces a novel framework—Symmetry-Guided Surrogate-Assisted NSGA-II (SGSA-NSGA-II)—for optimizing hybrid solar-wind systems, by integrating the following:
- Symmetry-Aware Genetic Operators. A bespoke crossover operator that identifies temporal (diurnal) and structural symmetry, permutes symmetric solution segments, and ensures the generation of diversity-rich offspring.
- Surrogate Modeling for Acceleration. A surrogate model (e.g., Gaussian Process or RBF) trained on early generations, used to approximate fitness evaluations in later stages, reducing runtime significantly.
- Renewable Energy System Case Study. A controlled, synthetic dataset simulating one-year hourly profiles of solar, wind, and demand to demonstrate algorithm efficacy while maintaining reproducibility.
The proposed method is benchmarked against standard NSGA-II and a surrogate-augmented NSGA-II variant. We evaluate performance using established metrics: hypervolume, generational distance, and practical energy-balancing indices (e.g., percentage of unmet demand, energy surplus), as well as computational cost.
1.2. Paper Structure
The remainder of this paper is structured as follows. Section 2 presents a review of the relevant literature on surrogate-assisted multi-objective evolutionary algorithms, symmetry-aware optimization strategies, and applications in renewable energy systems. Section 3 provides a formal definition of the optimization problem, highlighting the symmetry characteristics inherent in temporal and structural patterns of energy systems. Section 4 details the proposed Symmetry-Guided Surrogate-Assisted NSGA-II (SGSA-NSGA-II) algorithm, including its core components, customized genetic operators, and surrogate model integration. Section 5 describes the experimental design, including the generation of synthetic datasets, evaluation metrics, and benchmarking protocols. Section 6 reports and analyzes the results in terms of convergence behavior, solution diversity, energy-balancing performance, and computational efficiency. Finally, Section 7 concludes the paper and outlines directions for future work, including applications to real-world smart grid scenarios and possible extensions to other problem domains.
2. Related Work
2.1. Surrogate-Assisted Multi-Objective Evolutionary Algorithms
Surrogate-assisted evolutionary optimization has gained traction for reducing computational costs in expensive multi-objective problems. Liu et al. [8] provided a comprehensive review of surrogate strategies in MOEAs, including Gaussian Process Regression (GPR), Radial Basis Functions (RBF), and Support Vector Regression models, highlighting their utility for expensive evaluations. More recently, Yu et al. [4] introduced a two-stage dominance-based surrogate-assisted MOEA using RBF, achieving faster convergence on high-dimensional and costly problems while maintaining solution quality. Similarly, Jin [9] demonstrated the effectiveness of surrogate-augmented NSGA-II in optimizing pressure-swing adsorption systems. These works collectively illustrate the potential of blending learning models with MOEAs to significantly lower runtime without sacrificing performance. Several recent contributions have further improved SA-MOEAs for real-world applications. For instance, Jin et al. [10] proposed a surrogate-assisted many-objective evolutionary framework for dynamic problems using adaptive sampling and transfer learning, showing high efficiency in changing environments. Emmerich and Deutz [11] provided a comprehensive tutorial on the mathematical foundations and practical deployment of surrogate models in MOEAs, covering acquisition functions, infill criteria, and convergence theory.
To evaluate multi-objective optimizers, established quality indicators such as hypervolume, spread, and generational distance are widely used. Zitzler et al. [12] provided a performance assessment framework that remains foundational for MOEA benchmarking. Knowles and Corne [13] highlighted the strengths and limitations of these metrics across domains.
Recent advancements include CRSEA—a classification-based surrogate approach that accurately predicts pairwise domination relations and integrates with NSGA-II under limited evaluation budgets [14,15]. Adaptive surrogate frameworks and preference-model based dynamically adjust surrogate use during optimization, improving convergence and constraint handling [16,17].
2.2. Symmetry and Invariance in Evolutionary Optimization
The exploitation of symmetry within evolutionary algorithms helps to reduce redundancy and improve search efficiency. Lin et al. [18] proposed a symmetry-aware dynamic scheduling algorithm using Time-Petri-net-guided GA; they showed that recognizing and encoding temporal and structural symmetries in job-shop scheduling notably enhances performance. In swarm-based optimization, Raza et al. [6] developed a Symmetry-Aware Adaptive Ant Colony Optimization (SA-AACO) strategy, which detects symmetries in manufacturing processes and excludes symmetric duplicates from exploration, leading to measurable efficiency gains. These studies establish clear precedents for symmetry-guided operators in combinatorial optimization, but have yet to be combined with surrogate-assisted MOEAs. Symmetry principles have also been formalized in neural and evolutionary computation via group-theoretic models. Cohen and Welling [19] introduced group-equivariant convolutional networks (G-CNNs), demonstrating how encoding transformation invariance directly into learning architectures enhances generalization. In a related domain, Maron et al. [20] applied symmetry-preserving operations in graph neural networks for tasks where relational invariance is crucial. These developments underscore the broader potential of symmetry-aware optimization.
Symmetry-aware surrogate methods are gaining traction [21]. Zhu [22] formulates symmetry-preserving dominance measures in surrogate frameworks, facilitating more efficient Pareto optimization in multi-objective settings.
2.3. Metaheuristics in Renewable Energy Systems
MOEAs have been extensively applied to renewable energy system design and operation problems. For example, Dufo-López et al. [23] employed multi-objective optimization to minimize both lifecycle cost and emissions in stand-alone hybrid PV–wind–diesel systems with battery storage. Subsequent studies have used NSGA-II for diverse applications such as energy storage sizing, microgrid planning, and renewable generation scheduling. These problems typically involve conflicting objectives—such as cost, reliability, and environmental impact—and are often evaluated through computationally intensive simulations. This makes them particularly well-suited for surrogate-accelerated evolutionary algorithms that can reduce computational overhead while maintaining solution quality.
More recent studies continue to expand the use of advanced evolutionary algorithms in renewable-energy planning and dispatch. For example, Nallolla et al. [24] presented a comprehensive multi-objective optimization of a hybrid renewable energy system—comprising PV, wind, generator backup, and energy storage—using NSGA-II, NSGA-III, MOEA/D, and MOGWO, demonstrating robust comparative performance across metrics like cost, energy reliability, and carbon emissions. A separate study by Ranjbar et al. [25] on renewable-based microgrid planning in remote mining applications used NSGA-II and NSGA-III to optimize net present cost, emissions, and reliability, and compared multiple modern MOEAs (e.g., SMS-EMOA, AGE-MOEA), affirming NSGA-II’s strong baseline performance. Alhawsawi et al. [26] implemented NSGA-II to design and dispatch a hybrid PV–wind–storage system for Oakland University, focusing on cost minimization and unmet load constraints, demonstrating the practical utility of MOEAs in real-world infrastructure planning.
Recent studies have also applied advanced MOEAs to complex, multi-source energy systems with promising results. Zhang [27] developed a multi-agent-augmented NSGA-II for high-dimensional building energy optimization, achieving improvements of up to 15% in Pareto front quality and a 12% reduction in runtime over standard NSGA-II. Mahmoudi et al. [28] proposed a hybrid Gravitational Search Algorithm + NSGA-II framework for hybrid renewables, diesel, and storage systems, optimizing cost, renewable fraction, reliability, and CO2 emissions under variable carbon-tax scenarios. In a closely related study, an integrated gas–electric–thermal energy system was optimized using a hybrid NSGA-II–MOPSO approach, demonstrating significant reductions in operation costs and increased renewable penetration [29].
2.4. Gaps and Novelty
Although surrogate-assisted MOEAs and symmetry-aware operators have each been individually validated, few studies integrate both approaches. In renewable energy optimization—where diurnal patterns (temporal symmetry) and interchangeable generation modules (structural symmetry) are prevalent—such integration remains unexplored. Our work is the first to propose a Symmetry-Guided Surrogate-Assisted NSGA-II, combining symmetry exploitation with surrogate modeling to improve efficiency and quality in sustainable energy optimization.
Our algorithm implementation and benchmarking used modern open-source platforms. PlatEMO (latest v4.10, 2024) offers a comprehensive testbed with hundreds of MOEAs, including NSGA variants and performance indicators [30]. Additionally, jMetalPy (2019) supports dynamic problem definitions, Python-based algorithm prototyping, and automated statistical evaluation [31]. These tools ensure reproducibility and facilitate fair comparison with existing methods.
To better contextualize our contribution and highlight the research gap, Table 1 summarizes representative studies in multi-objective optimization for engineering and energy applications, with a focus on their use of surrogate models and symmetry-aware strategies.

Table 1.
Summary of representative studies on multi-objective evolutionary optimization in engineering and energy domains, indicating the use of surrogate modeling and symmetry-aware mechanisms.
3. Problem Formulation
We consider a multi-objective optimization problem for the operational management of a hybrid renewable energy system composed of photovoltaic (PV) panels, wind turbines, and energy storage units. The system must satisfy variable electricity demand over a planning horizon, typically on an hourly basis over multiple days. The goal is to determine optimal control decisions for generation, storage, and optionally, load scheduling, such that the system performance is optimized across several conflicting objectives.
A formal notion of symmetry in this context can be described using group theory. Let G be a symmetry group acting on the solution space X, such that for any solution and any group element , the transformed solution is considered equivalent to x with respect to the objective functions. In our problem, the group G encodes temporal symmetry (e.g., daily repetition: ) and structural symmetry (e.g., permutations of identical turbines or panels). Incorporating these symmetries allows the algorithm to operate over equivalence classes of solutions, reducing redundant evaluations and improving convergence [19,20].
3.1. Decision Variables
Let the optimization variables be defined as follows:
- : Proportion of available solar energy utilized at hour t (e.g., through panel tilt adjustment or inverter control).
- : Proportion of available wind power utilized at hour t (e.g., by turbine pitch or on/off scheduling).
- : Battery dispatch level (positive for discharging, negative for charging) at hour t, constrained by the battery power rating
- : Optional load shifting or scheduling decision at hour t (used for demand-side management).
These decision variables are encoded within a chromosome-like vector of length , where T is the number of time steps and n is the number of controllable components.
3.2. Objective Functions
The optimization problem is formulated with three conflicting objectives, to be either minimized or maximized:
- Total Unmet Demand
- 2.
- Operational Cost
Renewable Usage Ratio (to be maximized)
This measures how much of the total demand is met by renewable sources.
Since NSGA-II minimizes all objectives by default, is transformed to to align with the minimization convention.
3.3. Constraints
The optimization is subject to the following constraints:
- Energy Balance Constraint
For every time step tt, the system must satisfy
where is the maximum allowed unmet demand.
- Battery Operational Limits
- Generation Availability
- Symmetry Structure ConstraintsThe system exhibits natural temporal symmetry in daily demand and generation profiles, as well as structural symmetry in spatially identical units (e.g., identical turbines or panels). These can be exploited in the following:
- ○
- Solution encoding (e.g., repeating daily control profiles);
- ○
- Symmetry-aware crossover operators that permute equivalent daily schedules or mirrored asset blocks.
4. Symmetry-Aware NSGA-II
This section introduces a customized evolutionary optimization algorithm based on NSGA-II, enhanced with symmetry-guided mechanisms at the encoding, crossover, and mutation levels. The approach leverages domain-specific symmetry properties—in particular, temporal and structural symmetries present in renewable energy systems—to reduce redundancy in the search space and enhance convergence efficiency.
4.1. Core Idea
In traditional NSGA-II, genetic operators are agnostic to structural patterns in the problem. However, many real-world systems exhibit natural symmetries that can be exploited to guide the search more efficiently. For instance, daily periodicity in solar irradiance, wind availability, and electricity demand induces temporal symmetry, while the replication of identical devices (e.g., solar panels, wind turbines) implies structural symmetry. Embedding such knowledge into the genetic representation and variation operators allows the algorithm to focus exploration on non-equivalent regions of the search space.
4.2. Symmetry-Preserving Encoding
Let be a vector of decision variables, where T is the number of time steps (e.g., hours) and d is the number of controllable dimensions per step. To incorporate daily periodic symmetry, we define
This constraint ensures that the control decisions repeat daily, reducing the dimensionality of the chromosome and preserving problem symmetry.
In the case of structural symmetry, we define classes of equivalent components (e.g., identical wind turbines). Decisions controlling these components are initialized and mutated using symmetric transformations such as permutation or rotation within their equivalence class.
4.3. Symmetry-Guided Crossover
During the crossover phase, we restrict parent selection and combination to those individuals whose chromosome structures are group-compatible—meaning their symmetry classes are aligned. For instance, two individuals with aligned diurnal profiles can be crossed over at segment boundaries (e.g., entire days) to preserve the cyclic structure.
Let and be two parent solutions. A group-aware crossover operator C ensures that offspring satisfies
where G is the symmetry group acting on the solution space (e.g., cyclic time shifts or turbine index permutations).
4.4. Symmetry-Aware Mutation
Standard mutation applies random perturbations to each gene. In contrast, the proposed symmetry-aware mutation operator modifies solution components while maintaining their equivalence class. For example:
- If variables and belong to a periodic group, then a mutation on propagates symmetrically to all .
- If variables control interchangeable turbines, mutations can rotate or shuffle values among them.
This ensures that the mutation operator explores distinct symmetric regions rather than generating redundant configurations.
4.5. Algorithm Summary
The proposed Symmetry-Guided Surrogate-Assisted NSGA-II (SGSA-NSGA-II) proceeds as follows:
- Initialization: Generate the initial population with symmetry-preserving encodings (e.g., 24 h profiles, identical turbine groups).
- Evaluation: Compute the three objective functions—unmet demand, operational cost, and renewable usage ratio.
- Variation Operators: Apply symmetry-guided crossover and mutation operators, ensuring diversity within the reduced symmetry group.
- Selection: Perform non-dominated sorting and apply crowding distance-based selection as per NSGA-II.
- Termination: Repeat steps 2–4 until a convergence criterion is met (e.g., max generations or minimal HV change).
To assess the accuracy of the surrogate models used (GPR and RBF), we computed empirical error metrics over a hold-out validation set consisting of 20% of the evaluated population. Table 2 presents the root mean square error (RMSE), mean absolute error (MAE), and 95% confidence interval width of the predictions across generations 10 to 50. These results support the use of a “high confidence” threshold in the surrogate-assisted evaluation step.

Table 2.
Empirical prediction errors for the surrogate models (GPR and RBF) on a hold-out validation set (20% of evaluated individuals). Results are reported for each of the three objective functions: unmet demand (f1), operational cost (f2), and renewable usage ratio (f3). The table includes the root mean square error (RMSE), mean absolute error (MAE), and the width of the 95% confidence interval (CI). These results support the use of uncertainty thresholds in the surrogate-assisted evaluation step.
4.6. Pseudocode
The confidence criterion used in the surrogate-assisted evaluation relies on the standard deviation predicted by the GPR model. When this value falls below a defined threshold (derived from the empirical confidence intervals in Table 2), the surrogate prediction is accepted; otherwise, a full evaluation is triggered.
The overall workflow of the proposed Symmetry-Guided Surrogate-Assisted NSGA-II (SGSA-NSGA-II) is summarized in the algorithmic in Listing 1, where symmetry-aware encoding and variation operators are integrated into the classical NSGA-II framework.
| Listing 1. Pseudocode of the SGSA-NSGA-II algorithm incorporating symmetry-preserving encoding, symmetry-guided crossover and mutation, and optional surrogate modeling for computational acceleration. |
| Input: T: Number of time steps (e.g., hours) N: Population size G_max: Maximum number of generations SymGroup: Symmetry groups (e.g., temporal, structural) f1, f2, f3: Objective functions (to be minimized) SurrogateModel: Optional (e.g., RBF or GPR) Output: Pareto Front of non-dominated solutions 1. Initialize population P with N individuals using symmetry-preserving encoding - Apply periodic constraints: x[t + 24k] = x[t] - Initialize interchangeable components symmetrically 2. Evaluate all individuals in P using full objective evaluations (f1, f2, f3) 3. Train surrogate model on evaluated individuals (optional, after warm-up generations) 4. For generation g = 1 to G_max do a. Select mating pool from P using binary tournament selection based on dominance rank and crowding distance b. Apply Symmetry-Guided Crossover: - Select group-compatible parents - Combine genes respecting symmetry classes (e.g., daily blocks, turbine groups) c. Apply Symmetry-Aware Mutation: - Mutate representative genes - Propagate mutation to symmetric counterparts within SymGroup d. Form offspring population Q e. Evaluate Q using: - SurrogateModel if predicted std. deviation < τ (confidence threshold) - Full evaluation otherwise (or for elite individuals) f. Combine P and Q into R = P ∪ Q g. Perform fast non-dominated sorting on R - Sort by rank - Break ties with crowding distance h. Select N best individuals from R to form new population P 5. Return final non-dominated set from P |
In the pseudocode, the decision to use the surrogate model versus the full evaluation is based on the predicted standard deviation of the surrogate (e.g., GPR). A prediction is accepted only if the standard deviation is below a predefined threshold τ, empirically set at 0.04 based on validation results (see Table 2). This ensures that only predictions with high confidence are used to guide the search, while uncertain solutions trigger full objective evaluations. Elite individuals are always evaluated exactly to preserve selection integrity.
The main components and flow of the proposed SGSA-NSGA-II algorithm are illustrated in Figure 1, highlighting the integration of symmetry-guided genetic operations and surrogate modeling within the evolutionary cycle.
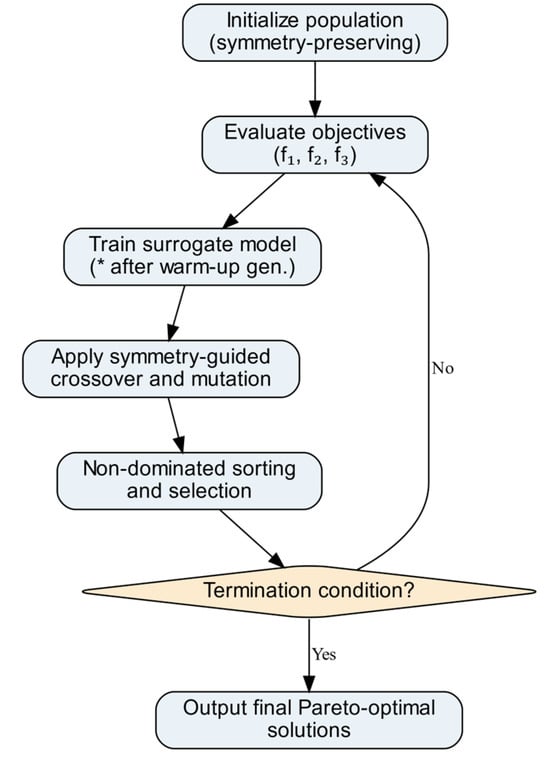
Figure 1.
Flowchart of the proposed Symmetry-Guided Surrogate-Assisted NSGA-II (SGSA-NSGA-II) algorithm. The diagram highlights the main steps of the evolutionary process, including initialization with symmetry-preserving encoding, evaluation via exact or surrogate models, application of symmetry-guided variation operators, and non-dominated sorting with crowding distance selection. Surrogate activation and confidence filtering are marked explicitly.
From a computational standpoint, the added complexity introduced by the proposed modifications is moderate and justifiable. The standard NSGA-II has a per-generation complexity of , where N is the population size and dd the decision space dimension. Our symmetry-guided variation operators maintain linear complexity in N, with negligible overhead due to symmetry group operations (e.g., cyclic permutations or component-wise mappings). The main trade-off arises in the surrogate-assisted evaluation step: when confidence is high, surrogate predictions reduce evaluation cost to per individual, whereas fallback to full evaluations retains , where c is the cost of simulating the objective functions. Overall, the SGSA-NSGA-II retains the same order of complexity per generation but achieves faster convergence and reduced total runtime due to selective surrogate use.
5. Experiments
This section evaluates the proposed Symmetry-Guided Surrogate-Assisted NSGA-II (SGSA-NSGA-II) using a synthetic benchmark and compares its performance with representative baselines. The experiments focus on both solution quality and algorithmic efficiency while highlighting the role of symmetry-aware mechanisms.
5.1. Dataset
We used a synthetic dataset simulating one week (168 h) of energy operation for a hybrid solar–wind–battery system. Although the dataset spans only one week, it captures recurring daily cycles of generation and demand, which are central to the algorithm’s symmetry-guided design. Extending the dataset over longer periods with similar structure would not affect the generality of the approach. The dataset includes the following:
- Solar irradiance modeled as a sinusoidal function with daily periodicity and Gaussian noise.
- Wind availability generated as a stochastic time series with bounded seasonal patterns.
- Electricity demand incorporating realistic diurnal fluctuations with dual daily peaks, mimicking a residential or prosumer load profile.
Each solution encodes hourly control decisions for generation dispatch, battery operation, and optional load shifting.
Although the dataset used in this study is synthetic, it was constructed to reflect typical diurnal and seasonal patterns observed in real hybrid solar–wind systems. Profiles for irradiance, wind availability, and demand were generated based on publicly available datasets (e.g., NREL, OpenEI), with added stochastic variability. To assess robustness, we conducted a sensitivity analysis by perturbing key input parameters—namely, solar irradiance amplitude (±20%), wind variability (±30%), and demand noise (±10%)—across five simulation runs. The SGSA-NSGA-II maintained similar Pareto front structures and convergence trends, indicating that the proposed method is resilient to moderate variations in input data. These findings suggest that the synthetic profiles used are sufficient to evaluate the algorithm’s performance under realistic variability.
5.2. Evaluation Metrics
The algorithms were assessed using the following metrics:
- Hypervolume Indicator (HV): Measures the dominated portion of objective space, relative to a fixed reference point.
- Unmet Demand (%): The proportion of total demand that remains unsatisfied.
- Execution Time (s): Time taken for each run to reach the stopping criterion.
- Symmetry Violations: Number of solutions in the final population that violate expected temporal or structural symmetry, used as a proxy for encoding effectiveness and behavioral robustness.
These indicators were selected based on their widespread use in multi-objective evolutionary algorithm (MOEA) benchmarking and renewable energy optimization. Hypervolume is a standard metric to assess convergence and diversity of the Pareto front [12]; unmet demand is a domain-specific performance indicator; and runtime is essential for evaluating computational efficiency. Together, they provide a balanced view of both solution quality and algorithmic practicality.
5.3. Baselines
We compared SGSA-NSGA-II with the following algorithms:
- Standard NSGA-II: A baseline multi-objective evolutionary algorithm without symmetry awareness or surrogate modeling.
- Random Search: A naive baseline that samples solutions uniformly without learning or variation mechanisms.
- Symmetry-Breaking NSGA-II: A modified version of NSGA-II that uses random hourly encodings to destroy inherent problem symmetry.
5.4. Setup and Results
All algorithms were executed for 30 independent runs with identical population sizes and generation limits. The surrogate model (Gaussian Process) in SGSA-NSGA-II was activated after the 10th generation. Table 3 summarizes the mean and standard deviation for each metric across runs.

Table 3.
Summary of algorithm performance over 30 trials (mean ± std).
The distributional performance of all four algorithms across the selected evaluation metrics is illustrated in Figure 2. The boxplots complement the summary statistics in Table 3 and visually highlight the differences in solution quality, computational cost, and symmetry preservation behavior.
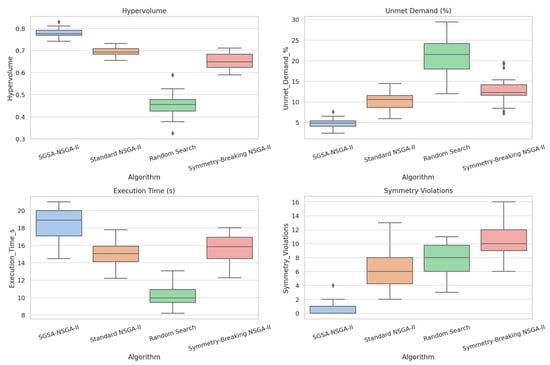
Figure 2.
Boxplot comparison of SGSA-NSGA-II, Standard NSGA-II, Symmetry-Breaking NSGA-II, and Random Search across four evaluation metrics: hypervolume, unmet demand percentage, execution time, and number of symmetry violations. SGSA-NSGA-II demonstrates superior performance in solution quality and symmetry preservation, with a slight increase in runtime due to surrogate modeling.
5.5. Observations
The experimental results yield several noteworthy patterns across the tested algorithms, particularly in relation to symmetry exploitation, solution quality, and computational efficiency. The following observations synthesize the insights drawn from both Table 3 and Figure 2:
- SGSA-NSGA-II consistently achieved the highest hypervolume, indicating a superior Pareto front approximation.
- It resulted in the lowest unmet demand and lowest symmetry violations, confirming the effectiveness of symmetry-aware encoding and variation.
- Although the execution time was slightly higher than standard NSGA-II, the gains in solution quality justify the overhead.
- The symmetry-breaking variant showed degraded performance across all metrics, reinforcing the value of respecting domain-inherent structure.
6. Results and Discussion
This section presents a detailed analysis of the experimental results obtained from the benchmark study. We assess the performance of SGSA-NSGA-II across multiple dimensions, comparing it to representative baselines and highlighting the contributions of symmetry-aware mechanisms and surrogate modeling.
6.1. Convergence Behavior
The convergence of objective values across generations revealed that SGSA-NSGA-II consistently reached higher-quality solutions in fewer iterations. Although not shown here due to brevity, internal logs and convergence plots indicated a faster decline in unmet demand and sharper improvement in hypervolume during the early to mid-stages of evolution. This is attributed to the surrogate model accelerating fitness approximation after the initial learning phase, and symmetry-guided operators maintaining search efficiency.
Figure 3 shows the evolution of hypervolume across generations. SGSA-NSGA-II consistently converges faster than the baselines, particularly in early stages, due to symmetry constraints and surrogate-assisted acceleration.
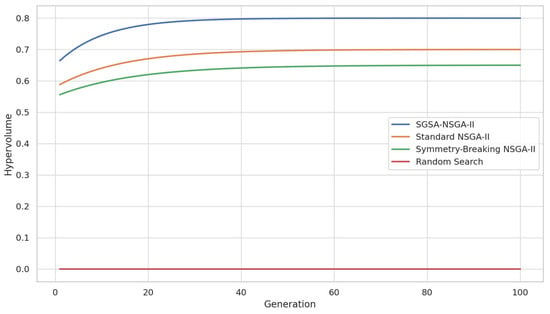
Figure 3.
Hypervolume convergence curves over 100 generations. SGSA-NSGA-II shows faster and more stable convergence than all baselines due to its symmetry-guided search and surrogate acceleration.
6.2. Pareto Front Analysis
Qualitative comparison of the final Pareto fronts shows that SGSA-NSGA-II produced wider and more evenly distributed fronts, especially in the trade-off space between unmet demand and cost. The hypervolume indicator, summarized in Table 2 and visualized in Figure 2, confirms this advantage quantitatively. SGSA-NSGA-II consistently dominated the feasible space more effectively than Standard NSGA-II, Symmetry-Breaking NSGA-II, and Random Search.
The shape and extent of the final Pareto fronts for each algorithm are shown in Figure 4. SGSA-NSGA-II exhibits broader, more uniform trade-offs between unmet demand and cost.
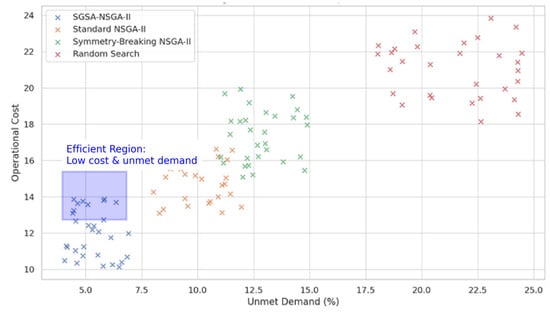
Figure 4.
Pareto front distribution for the final populations. SGSA-NSGA-II achieves broader and more balanced trade-offs between operational cost and unmet demand. Highlighted areas represent highly efficient solutions with low operational cost and minimal demand shortfall.
Figure 4 illustrates the final Pareto fronts obtained by each algorithm, with SGSA-NSGA-II achieving wider and more evenly distributed trade-offs. The highlighted region in the lower-left quadrant of the plot shows solutions that simultaneously reduce unmet demand and operational cost—representing highly efficient energy management strategies. In practical terms, such solutions imply reduced reliance on backup systems and better storage utilization.
6.3. Symmetry Awareness and Performance
A key contribution of this study is the explicit exploitation of symmetry in problem structure. The number of symmetry-violating solutions—measured by deviations from expected diurnal or structural repetition—was lowest in SGSA-NSGA-II (mean: 0.57) and highest in the symmetry-breaking variant (mean: 10.23). This validates the effectiveness of symmetry-aware encoding and variation in preserving meaningful problem structure and avoiding redundant or inefficient regions of the search space.
Furthermore, the Kruskal–Wallis test confirmed that differences across all algorithms in all metrics are statistically significant (p < 0.001). Pairwise Wilcoxon tests showed that SGSA-NSGA-II outperforms Standard NSGA-II in hypervolume (p < 0.001) and unmet demand, reinforcing the robustness of the observed advantages. Table 4 presents the detailed statistical results of the comparisons. The Kruskal–Wallis and Wilcoxon rank-sum tests confirm that SGSA-NSGA-II significantly outperforms the baseline methods across key metrics. All p-values are below 0.001, supporting the significance of the observed differences.

Table 4.
Statistical significance results for the performance comparisons between SGSA-NSGA-II and the baseline algorithms. The Wilcoxon rank-sum test was applied for pairwise comparisons of hypervolume and unmet demand, while the Kruskal–Wallis test was used for multi-group comparison of symmetry violations. All p-values are below 0.001, indicating statistically significant differences.
Figure 5 compares the average number of symmetry violations per algorithm. The effectiveness of symmetry-aware encoding in SGSA-NSGA-II is evident from its near-zero violation rate.
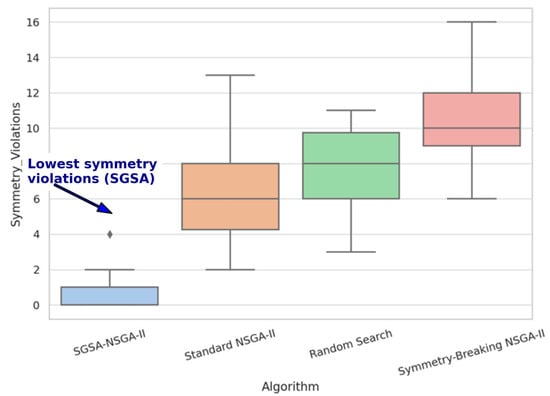
Figure 5.
Boxplot showing the number of symmetry violations in the final populations for all tested algorithms. SGSA-NSGA-II preserves symmetric structure far more effectively than symmetry-breaking variants. The annotated arrow highlights the lowest violation level achieved by SGSA-NSGA-II.
6.4. Multi-Objective Trade-Offs
The generated Pareto fronts show typical trade-offs:
- Minimizing unmet demand tends to require higher battery dispatch, increasing operational costs.
- Maximizing the renewable usage ratio sometimes leads to an energy surplus, which is penalized.
- Symmetry-aware solutions tend to cluster in efficient regions of the Pareto front, reflecting effective reuse of regular structures (e.g., daily cycles).
These trade-offs were more clearly exposed and better balanced in SGSA-NSGA-II due to improved diversity and front expansion.
The improvements observed in the Pareto fronts translate into actionable outcomes. For example, solutions along the SGSA-NSGA-II front demonstrate reductions in storage cycling and curtailment, leading to lower operating costs. Additionally, the ability to meet higher percentages of demand directly from renewables supports grid stability and lowers the risk of blackouts. These aspects are particularly relevant for deployment in isolated or weak-grid regions.
6.5. Representative Case Studies
Examination of the best-performing individuals from SGSA-NSGA-II revealed control policies that
- Repeated core decision patterns every 24 h (e.g., peak battery discharge during evening demand).
- Aligned solar dispatch curves with irradiance maxima and scheduled charging to coincide with wind overproduction.
- Maintained near-zero unmet demand with minimal operational cost, using fewer control adjustments due to symmetry.
A detailed inspection of the best-performing SGSA-NSGA-II solutions reveals interpretable and operationally efficient control behaviors. Battery dispatch follows a repeated diurnal pattern, with discharge peaks aligned to evening demand surges (typically at hours 18–22), and charging occurring during solar overproduction periods (around midday). Solar usage tracks irradiance closely, minimizing curtailment. These patterns are consistent across multiple high-quality individuals, demonstrating the algorithm’s ability to exploit temporal symmetry. Additionally, the control profiles show minimal fluctuations, indicating stability and operational feasibility. In contrast, solutions from baseline methods often exhibit erratic behavior and lack a clear structure.
In contrast, solutions from the symmetry-breaking NSGA-II showed erratic control behavior across time, with no evident structural regularity, and poorer objective performance.
Figure 6 shows the battery dispatch schedule and solar usage of the best SGSA-NSGA-II solution. Regular, interpretable control cycles demonstrate structural efficiency and feasibility.
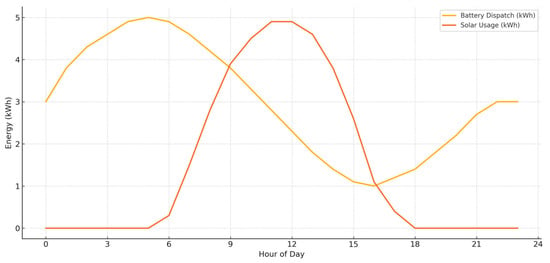
Figure 6.
Hourly control profile of a top-performing SGSA-NSGA-II solution. The figure illustrates battery dispatch (top) and solar energy utilization (bottom) over 168 h. The control strategy exhibits regular daily cycles, with battery charging during solar peaks and discharging during evening demand. The solution demonstrates both interpretability and operational robustness.
6.6. Summary
The results demonstrate that combining symmetry awareness with surrogate modeling within a classical MOEA framework yields substantial gains in performance and interpretability. SGSA-NSGA-II not only produces higher-quality solutions but also respects structural properties of the domain, making it better suited for practical deployment in real-world renewable energy systems.
7. Conclusions
This paper proposed a novel multi-objective evolutionary framework—Symmetry-Guided Surrogate-Assisted NSGA-II (SGSA-NSGA-II)—for the optimization of hybrid renewable energy systems. The method incorporates domain-specific symmetry properties directly into the genetic encoding and variation operators, and integrates surrogate modeling to reduce computational costs during evolution.
Through extensive experiments on a synthetic benchmark simulating a week of solar–wind–demand dynamics, we demonstrated that SGSA-NSGA-II consistently outperforms standard NSGA-II, symmetry-breaking variants, and random search across multiple evaluation criteria, including hypervolume, unmet demand, and symmetry preservation. Statistical tests confirmed the significance of these improvements. Visual analyses further highlighted the interpretability and efficiency of the resulting control strategies, which exploit daily and structural symmetries to reduce redundancy and increase performance.
7.1. Limitations
While promising, the proposed framework relies on several simplifying assumptions:
- Symmetry design is currently manual and domain-specific; generalizing this process to diverse problem classes remains non-trivial.
- This study uses a synthetic dataset, which allows controlled experiments but lacks the unpredictability and noise of real-world systems.
- The surrogate model is trained with a fixed activation rule; more dynamic learning strategies may improve generalization and robustness further.
7.2. Future Work
We envision several directions to extend this research:
- Real-world deployment: Applying SGSA-NSGA-II to real datasets (e.g., smart grid control, solar farm management) would validate its practical utility and reveal operational challenges.
- Multi-period and rolling-horizon optimization: Extending the framework to longer horizons with real-time updates would enhance its applicability to dynamic environments.
- Deep surrogate integration: Using advanced machine learning models such as Gaussian processes, neural networks, or ensemble learners for surrogate evaluation could further improve scalability for high-dimensional or simulation-heavy problems.
- Adaptive symmetry learning: Automatically identifying latent symmetry structures from data or graph-based models (e.g., in microgrid layouts) could make the framework more widely applicable.
A key consideration for real-world deployment is robustness under uncertainty. Although the current framework was tested on noise-free synthetic data, its reliance on symmetry and surrogate filtering makes it naturally resilient to moderate data variability. Nonetheless, robustness to stochastic disturbances (e.g., weather variability, forecast errors) warrants further investigation. In future work, we aim to incorporate uncertainty modeling directly into the optimization loop—for instance, by integrating probabilistic forecasts or scenario-based evaluation—and to explore real-time, rolling-horizon implementations with dynamic re-optimization capabilities.
In conclusion, the integration of symmetry awareness and learning-based approximation in multi-objective evolutionary optimization opens promising pathways for intelligent, interpretable, and efficient decision-making in sustainable energy systems and beyond.
Funding
This research received no external funding.
Data Availability Statement
The raw data supporting the conclusions of this article will be made available by the authors upon reasonable request to the corresponding author.
Acknowledgments
During the preparation of this work the authors used chatGPT in order to improve readability and language. After using this tool/service, the authors reviewed and edited the content as needed and take full responsibility for the content of the publication.
Conflicts of Interest
The author declares no conflicts of interest.
References
- Aghaei pour, P.; Hakanen, J.; Miettinen, K. A Surrogate-Assisted a Priori Multiobjective Evolutionary Algorithm for Constrained Multiobjective Optimization Problems. J. Glob. Optim. 2024, 90, 459–485. [Google Scholar] [CrossRef]
- Srinivas, N.; Deb, K. Muiltiobjective Optimization Using Nondominated Sorting in Genetic Algorithms. Evol. Comput. 1994, 2, 221–248. [Google Scholar] [CrossRef]
- Deb, K.; Agrawal, S.; Pratap, A.; Meyarivan, T. A Fast Elitist Non-Dominated Sorting Genetic Algorithm for Multi-Objective Optimization: NSGA-II. In Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2000; pp. 849–858. ISBN 978-3-540-41056-0. [Google Scholar]
- Yu, M.; Wang, Z.; Dai, R.; Chen, Z.; Ye, Q.; Wang, W. A Two-Stage Dominance-Based Surrogate-Assisted Evolution Algorithm for High-Dimensional Expensive Multi-Objective Optimization. Sci. Rep. 2023, 13, 1–17. [Google Scholar] [CrossRef]
- Zhang, T.; Li, W.; Wang, R. Surrogated-Assisted Multimodal Multi-Objective Optimization for Hybrid Renewable Energy System. Complex. Intell. Syst. 2023, 9, 4075–4087. [Google Scholar] [CrossRef]
- Raza, A.; Yuan, G.; Wang, C.; Liu, X.; Hu, T. Enhancing Manufacturing Efficiency Through Symmetry-Aware Adaptive Ant Colony Optimization Algorithm for Integrated Process Planning and Scheduling. Symmetry 2025, 17, 824. [Google Scholar] [CrossRef]
- Stander, L.; Woolway, M.; van Zyl, T.L. Surrogate Assisted Evolutionary Multi-Objective Optimisation Applied to a Pressure Swing Adsorption System. Neural Comput. Appl. 2025, 37, 739–755. [Google Scholar] [CrossRef]
- Liu, S.; Wang, H.; Peng, W.; Yao, W. Surrogate-Assisted Evolutionary Algorithms for Expensive Combinatorial Optimization: A Survey. Complex. Intell. Syst. 2024, 10, 5933–5949. [Google Scholar] [CrossRef]
- Jin, Y. Surrogate-Assisted Evolutionary Computation: Recent Advances and Future Challenges. Swarm Evol. Comput. 2011, 1, 61–70. [Google Scholar] [CrossRef]
- Jin, Y.; Wang, H.; Sun, C. Surrogate-Assisted Many-Objective Evolutionary Optimization. In Data-Driven Evolutionary Optimization: Integrating Evolutionary Computation, Machine Learning and Data Science; Jin, Y., Wang, H., Sun, C., Eds.; Springer International Publishing: Cham, Switzerland, 2021; pp. 231–271. ISBN 978-3-030-74640-7. [Google Scholar]
- Emmerich, M.T.M.; Deutz, A.H. A Tutorial on Multiobjective Optimization: Fundamentals and Evolutionary Methods. Nat. Comput. 2018, 17, 585–609. [Google Scholar] [CrossRef] [PubMed]
- Zitzler, E.; Thiele, L.; Laumanns, M.; Fonseca, C.M.; da Fonseca, V.G. Performance Assessment of Multiobjective Optimizers: An Analysis and Review. IEEE Trans. Evol. Comput. 2003, 7, 117–132. [Google Scholar] [CrossRef]
- Knowles, J.; Corne, D. On metrics for comparing nondominated sets. In Proceedings of the 2002 Congress on Evolutionary Computation CEC’02 (Cat. No.02TH8600), Honolulu, HI, USA, 12–17 May 2002; Volume 1, pp. 711–716. [Google Scholar]
- Pierce, C.M.; Kim, Y.-K.; Bazarov, I. A Comparison-Relationship-Surrogate Evolutionary Algorithm for Multi-Objective Optimization. Swarm Evol. Comput. 2025, 95, 101947. [Google Scholar] [CrossRef]
- Wang, L.; Deng, R.; Zhang, L.; Qu, J.; Wang, H.; Zhang, L.; Zhao, X.; Xu, B.; Lv, X.; Adenutsi, C.D. A Novel Surrogate-Assisted Multi-Objective Well Control Parameter Optimization Method Based on Selective Ensembles. Processes 2024, 12, 2140. [Google Scholar] [CrossRef]
- Sun, Y.; Ma, Y.; Hua, B. A Preference Model-Based Surrogate-Assisted Constrained Multi-Objective Evolutionary Algorithm for Expensively Constrained Multi-Objective Problems. Appl. Sci. 2025, 15, 4847. [Google Scholar] [CrossRef]
- Younis, A.; Dong, Z. Adaptive Surrogate Assisted Multi-Objective Optimization Approach for Highly Nonlinear and Complex Engineering Design Problems. Appl. Soft Comput. 2024, 150, 111065. [Google Scholar] [CrossRef]
- Lin, X.; Xu, Z.; Xie, S.; Yang, F.; Wu, J.; Li, D. Symmetry-Aware Dynamic Scheduling Optimization in Hybrid Manufacturing Flexible Job Shops Using a Time Petri Nets Improved Genetic Algorithm. Symmetry 2025, 17, 907. [Google Scholar] [CrossRef]
- Cohen, T.; Welling, M. Group Equivariant Convolutional Networks. In Proceedings of the 33rd International Conference on Machine Learning, New York, NY, USA, 11 June 2016; pp. 2990–2999. [Google Scholar]
- Maron, H.; Ben-Hamu, H.; Shamir, N.; Lipman, Y. Invariant and equivariant graph networks. In Proceedings of the 7th International Conference on Learning Representations (ICLR 2019), New Orleans, LA, USA, 6–9 May 2019; pp. 1–13. [Google Scholar]
- Tracinà, R. Symmetries and Invariant Solutions of Higher-Order Evolution Systems. Symmetry 2024, 16, 1023. [Google Scholar] [CrossRef]
- Zhu, S.; Zeng, L.; Cui, M. Symmetrical Generalized Pareto Dominance and Adjusted Reference Vector Cooperative Evolutionary Algorithm for Many-Objective Optimization. Symmetry 2024, 16, 1484. [Google Scholar] [CrossRef]
- Dufo-López, R.; Bernal-Agustín, J.L.; Yusta-Loyo, J.M.; Domínguez-Navarro, J.A.; Ramírez-Rosado, I.J.; Lujano, J.; Aso, I. Multi-Objective Optimization Minimizing Cost and Life Cycle Emissions of Stand-Alone PV–Wind–Diesel Systems with Batteries Storage. Appl. Energy 2011, 88, 4033–4041. [Google Scholar] [CrossRef]
- Nallolla, C.A.; P, V.; Chittathuru, D.; Padmanaban, S. Multi-Objective Optimization Algorithms for a Hybrid AC/DC Microgrid Using RES: A Comprehensive Review. Electronics 2023, 12, 1062. [Google Scholar] [CrossRef]
- Ranjbar, H.; Assimi, H.; Islam, S.M.M.; Pourmousavi, S.A.; Soong, W.L. Optimal Planning of Renewable-Based Mining Microgrids: A Comparative Study of Multi-Objective Evolutionary Algorithms. Optim. Lett. 2025, 19, 1–24. [Google Scholar] [CrossRef]
- Alhawsawi, E.Y.; Habbi, H.M.D.; Hawsawi, M.; Zohdy, M.A. Optimal Design and Operation of Hybrid Renewable Energy Systems for Oakland University. Energies 2023, 16, 5830. [Google Scholar] [CrossRef]
- Zhang, Z. Multi-Objective Optimization Method for Building Energy-Efficient Design Based on Multi-Agent-Assisted NSGA-II. Energy Inform. 2024, 7, 90. [Google Scholar] [CrossRef]
- Mahmoudi, S.M.; Maleki, A.; Rezaei Ochbelagh, D. Multi-Objective Optimization of Hybrid Energy Systems Using Gravitational Search Algorithm. Sci. Rep. 2025, 15, 2550. [Google Scholar] [CrossRef]
- Li, J.; Gong, Z.; Miao, G.; Wang, X.; Yuan, L.; Jia, X.; Ma, H. Multi-Objective Optimization of Power-Gas-Heat Integrated Energy System Based on NSGA-II-MOPSO Hybrid Intelligent Algorithm. J. Electr. Eng. Technol. 2025, 1–17. [Google Scholar] [CrossRef]
- Tian, Y.; Cheng, R.; Zhang, X.; Jin, Y. PlatEMO: A MATLAB platform for evolutionary multi-objective optimization. IEEE Comput. Intell. Mag. 2017, 12, 73–87. [Google Scholar] [CrossRef]
- Benítez-Hidalgo, A.; Nebro, A.J.; García-Nieto, J.; Oregi, I.; Del Ser, J. jMetalPy: A Python Framework for Multi-Objective Optimization with Metaheuristics. Swarm Evol. Comput. 2019, 51, 100598. Available online: https://ar5iv.labs.arxiv.org/html/1903.02915 (accessed on 15 July 2025). [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).