An Efficient Spectral Method for a Class of Asymmetric Functional-Order Diffusion–Wave Equations Using Generalized Chelyshkov Wavelets

Abstract

Asymmetric functional-order (variable-order) fractional diffusion–wave equations (FO-FDWEs) introduce considerable computational challenges, as the fractional order of the derivatives can vary spatially or temporally. To overcome these challenges, a novel spectral method employing generalized fractional-order Chelyshkov wavelets (FO-CWs) is developed to efficiently solve such equations. In this approach, the Riemann–Liouville fractional integral operator of variable order is evaluated in closed form via a regularized incomplete Beta function, enabling the transformation of the governing equation into a system of algebraic equations. This wavelet-based spectral scheme attains extremely high accuracy, yielding significantly lower errors than existing numerical techniques. In particular, numerical results show that the proposed method achieves notably improved accuracy compared to existing methods under the same number of basis functions. Its strong convergence properties allow high precision to be achieved with relatively few wavelet basis functions, leading to efficient computations. The method’s accuracy and efficiency are demonstrated on several practical diffusion–wave examples, indicating its suitability for real-world applications. Furthermore, it readily applies to a wide class of fractional partial differential equations (FPDEs) with spatially or temporally varying order, demonstrating versatility for diverse applications.

1. Introduction

Unlike the classical derivative, the use of fractional derivatives in many real-world phenomena can help to capture information of the current state from all its previous states. With this non-local property, fractional differential equations (FDEs) are used in many practical problems, such as modeling heat transfer [1], earthquakes [2], physics and mechanics [3,4,5], chemistry and dynamics in biological tissues [6], engineering [7], control theory [8,9,10], and option pricing [11].

In recent decades, FDEs have been extended to variable-order FDEs (VFDEs). In this equation, the orders of the derivatives can be non-constant functions [12,13,14,15,16,17]. This generalization enhances the fractional derivative’s ability to capture non-local effects, thus popularizing the applications of VFDEs (see [18] and references therein). The advantages of VFDEs in comparison with FDEs have been discussed in [19], while some results on the consistency of this kind of equation and the uniqueness of the analytical solutions of VFDEs have been given in [20,21,22]. The VFDEs occurring in the applications usually do not have a solution which can be expressed via elementary functions. Therefore, it is crucial to design efficient methods for approximating solutions of VFDEs. The available methods can be seen in [23,24,25,26,27,28,29,30]. Recently, wavelets have become an important tool for solving fractional calculus problems. For example, Legendre wavelets have been used efficiently in various methods [31]. Chebyshev wavelets demonstrated high accuracy in many methods [32,33]. Some other useful wavelets are the Bernoulli and Taylor wavelets [34,35].

In [36] and [37], fractional-order Laguerre and Legendre functions are introduced to improve the accuracy of solutions for FDEs that contain power terms of fractional-order. In addition, generalized Legendre and Bernoulli wavelets were given in [38] and [39]. In these methods, finding the Riemann–Liouville integral operator with functional-order(RLI-FO) of the bases was an important step. The RLI-FO of hybrid Bernoulli polynomials was derived in [40,41] by using Laplace transforms. The same argument was used for Taylor wavelets in [35,42]. However, the Laplace transform cannot be used to find the closed-form formula for the RLI-FO of any generalized form in both cases of polynomials and wavelets.

In this work, we consider an asymmetric functional-order fractional diffusion–wave equation of the following form [43]:

$$\begin{array}{cc}\hfill & D_{\mathbf{t}}^{\omega (\mathbf{x},\mathbf{t})}p(\mathbf{x},\mathbf{t})+\sum _{i=1}^m{a}_i{D}_{\mathbf{t}}^{{\omega }_i(\mathbf{x},\mathbf{t})}p(\mathbf{x},\mathbf{t})+a{\displaystyle \frac{\partial }{\partial \mathbf{x}}}p(\mathbf{x},\mathbf{t})+b{p}^n(\mathbf{x},\mathbf{t})=c{\displaystyle \frac{{\partial }^2}{\partial {\mathbf{x}}^2}}p(\mathbf{x},\mathbf{t})+q(\mathbf{x},\mathbf{t}),\hfill \end{array}$$

(1)

$$\begin{array}{cc}\hfill & p(\mathbf{x},0)=r_0\left(\mathbf{x}\right),p_{\mathbf{t}}(\mathbf{x},0)=r_1\left(\mathbf{x}\right),\hfill \end{array}$$

(2)

$$\begin{array}{cc}\hfill & p(0,\mathbf{t})=s_0\left(\mathbf{t}\right),p(1,\mathbf{t})=s_1\left(\mathbf{t}\right),\hfill \end{array}$$

(3)

where $(\mathbf{x},\mathbf{t})\in {[0,1]}^2$; $a,b,c,a_i$ are constants; $1<{\omega }_m(\mathbf{x},\mathbf{t})<\dots <{\omega }_1(\mathbf{x},\mathbf{t})<\omega (\mathbf{x},\mathbf{t})\le 2$; $r_0\left(\mathbf{x}\right),r_1\left(\mathbf{x}\right),s_0\left(\mathbf{t}\right)$ and $s_1\left(\mathbf{t}\right)$ are known functions. Here, $D_{\mathbf{t}}^{\omega (\mathbf{x},\mathbf{t})}$ and $D_{\mathbf{t}}^{{\omega }_i(\mathbf{x},\mathbf{t})}$ denote the Caputo functional-order derivative (CFD) defined by

$$\begin{array}{cc}\hfill & D_{\mathbf{t}}^{\omega (\mathbf{x},\mathbf{t})}p(\mathbf{x},\mathbf{t})=\left\{\begin{array}{cc}{\displaystyle \frac{1}{\mathrm{\Gamma }(2-\omega (\mathbf{x},\mathbf{t}\left)\right)}}{\int }_0^{\mathbf{t}}{(\mathbf{t}-s)}^{1-\omega (\mathbf{x},\mathbf{t})}{\displaystyle \frac{{\partial }^{2}p(\mathbf{x},s)}{\partial s^2}}ds,\hfill & 1<\omega (\mathbf{x},\mathbf{t})<2,\hfill \\ p_{\mathbf{tt}}(\mathbf{x},\mathbf{t}),\hfill & \omega (\mathbf{x},\mathbf{t})=2.\hfill \end{array}\right.\hfill \\ \hfill & D_{\mathbf{t}}^{{\omega }_i(\mathbf{x},\mathbf{t})}p(\mathbf{x},\mathbf{t})={\displaystyle \frac{1}{\mathrm{\Gamma }(2-{\omega }_i(\mathbf{x},\mathbf{t}))}}{\int }_0^{\mathbf{t}}{(\mathbf{t}-s)}^{1-{\omega }_i(\mathbf{x},\mathbf{t})}{\displaystyle \frac{{\partial }^{2}p(\mathbf{x},s)}{\partial s^2}}ds,i=1,\dots ,m.\hfill \end{array}$$

In the current paper, we numerically solve the FO-FDWE given in Equations (1)–(3) by using FO-CWs. The FO-CW technique provides several benefits, including orthogonality and spectral accuracy properties [44,45]. The regularized incomplete Beta functions are used to derive an exact value for the RLI-FO of order $\omega \left(x\right)$ for the FO-CWs. This exact value can be used to simplify Equations (1)–(3) into a system of algebraic equations. In general, this system can be computationally complex and require a large storage space for large systems. However, by using FO-CWs, the computational complexity can be reduced [46]. The structure of this article is arranged as follows. The RLI-FO, the CFD, and the regularized incomplete Beta functions are recalled in Section 2. In Section 3, we construct the FO-CWs and find the exact value of their RLI-FO by using the regularized incomplete Beta functions. In Section 4 and Section 5, we present the idea of the method and its error estimation. In Section 6, several examples are included. In addition, in Example 1, we will get the exact solution which was not obtained in [43]. In Example 2–4, we will point out that we will obtain better solutions than other methods in the literature.

2. Preliminaries

This section provides the foundational background necessary for the development of our numerical method. We begin by revisiting key notions from fractional calculus, including the definitions of the Riemann–Liouville integral of variable order (RLI-FO) and the Caputo fractional derivative (CFD), which together form the analytical basis of our approach. We also present relevant properties of the regularized incomplete Beta function, a classical special function that plays a crucial role in our derivations. Leveraging this function, we obtain an explicit formula for the variable-order fractional integral of the truncated power-type function $x^{\gamma }{\mu }_c\left(x\right)$. This result is instrumental for computing the fractional integrals of the wavelet basis functions used in our proposed spectral method.

Definition 1.

The RLI-FO of order $\omega \left(x\right)$ of a function $p\left(\mathit{x}\right)$ is defined as [47]

$$\begin{array}{ccc}\hfill I^{\omega \left(\mathit{x}\right)}p\left(\mathit{x}\right)& =& {\displaystyle \frac{1}{\mathrm{\Gamma }\left(\omega \right(\mathit{x}\left)\right)}}{\int }_0^{\mathit{x}}p\left(\mathit{t}\right){(\mathit{x}-\mathit{t})}^{\omega \left(\mathit{x}\right)-1}d\mathit{t},\mathit{x}\ge 0.\hfill \end{array}$$

(4)

The CFD of order $\omega \left(x\right)$ of a function $p\left(\mathit{x}\right)$ is defined as [47]

$$\begin{array}{c}\hfill D^{\omega \left(\mathit{x}\right)}p\left(\mathit{x}\right)={\displaystyle \frac{1}{\mathrm{\Gamma }(\nu -\omega (\mathit{x}\left)\right)}}{\int }_0^{\mathit{x}}{p}^{\left(\nu \right)}\left(\mathit{t}\right){(\mathit{x}-\mathit{t})}^{\nu -\omega \left(\mathit{x}\right)-1}d\mathit{t},\nu -1<\omega \left(\mathit{x}\right)\le \nu ,\nu \in \mathbb{N}.\end{array}$$

(5)

The CFD and the RLI-FO are linear operators. Moreover, we have

(i)

For $\gamma >-1$, we have

$$\begin{array}{c}\hfill I^{\omega \left(\mathbf{x}\right)}{\mathbf{x}}^{\gamma }={\displaystyle \frac{\mathrm{\Gamma }(1+\gamma )}{\mathrm{\Gamma }(1+\gamma +\omega (\mathbf{x}\left)\right)}}{x}^{\gamma +\omega \left(\mathbf{x}\right)},\end{array}$$

(ii)

For $\gamma >\nu -1$,

$$\begin{array}{c}\hfill D^{\omega \left(\mathbf{x}\right)}{\mathbf{x}}^{\gamma }={\displaystyle \frac{\mathrm{\Gamma }(1+\gamma )}{\mathrm{\Gamma }(1+\gamma -\omega (\mathbf{x}\left)\right)}}{\mathbf{x}}^{\gamma -\omega \left(\mathbf{x}\right)}.\end{array}$$

The Regularized Beta functions, denoted by $\mathbb{I}(\mathbf{x};c_1,c_2)$, are defined as [48]

$$\mathbb{I}(\mathbf{x};c_1,c_2)={\displaystyle \frac{\mathrm{\Gamma }(c_1+c_2)}{\mathrm{\Gamma }\left(c_1\right)\mathrm{\Gamma }\left(c_2\right)}}{\int }_0^{\mathbf{x}}{\mathbf{t}}^{c_1-1}{\left(1-\mathbf{t}\right)}^{c_2-1}d\mathbf{t},c_1>0,c_2>0,0\le \mathbf{x}\le 1,$$

where

$$\mathrm{\Gamma }\left(u\right)={\int }_0^{\infty }{e}^{-\mathbf{t}}{\mathbf{t}}^{u-1}d\mathbf{t},u>0$$

is the Gamma function.

By using the regularized incomplete Beta functions, we get the following lemma:

Lemma 1.

Let $c\ge 0$, $\gamma \ge -1$, then

$$I^{\omega \left(\mathit{x}\right)}\left({\mathit{x}}^{\gamma }{\mu }_c\left(\mathit{x}\right)\right)={\displaystyle \frac{\mathrm{\Gamma }(1+\gamma ){\mathit{x}}^{\gamma +\omega \left(\mathit{x}\right)}}{\mathrm{\Gamma }(1+\gamma +\omega (\mathit{x}\left)\right)}}\left[1-\mathbb{I}\left({\displaystyle \frac{c}{\mathit{x}}};1+\gamma ,\omega \left(\mathit{x}\right)\right)\right]{\mu }_c\left(\mathit{x}\right)$$

where

$${\mu }_c\left(\mathit{x}\right)=\left\{\begin{array}{cc}0,\hfill & \mathit{if}\mathit{x}<c,\hfill \\ 1,\hfill & \mathit{if}\mathit{x}\ge c.\hfill \end{array}\right.$$

Proof. 

For $\mathbf{x}\ge c$, applying Equation (4), we obtain the following:

$$\begin{array}{ccc}\hfill I^{\omega \left(\mathbf{x}\right)}\left({\mathbf{x}}^{\gamma }{\mu }_c\left(\mathbf{x}\right)\right)& =& {\displaystyle \frac{1}{\mathrm{\Gamma }\left(\omega \right(\mathbf{x}\left)\right)}}{\int }_0^{\mathbf{x}}{s}^{\gamma }{\mu }_c\left(s\right){(\mathbf{x}-s)}^{\omega \left(\mathbf{x}\right)-1}ds\hfill \\ & =& {\displaystyle \frac{1}{\mathrm{\Gamma }\left(\omega \right(\mathbf{x}\left)\right)}}{\int }_0^{\mathbf{x}}{s}^{\gamma }{(\mathbf{x}-s)}^{\omega \left(\mathbf{x}\right)-1}ds-{\displaystyle \frac{1}{\mathrm{\Gamma }\left(\omega \right(\mathbf{x}\left)\right)}}{\int }_0^c{s}^{\gamma }{(\mathbf{x}-s)}^{\omega \left(\mathbf{x}\right)-1}ds\hfill \end{array}$$

Thus,

$$\begin{array}{ccc}\hfill I^{\omega \left(\mathbf{x}\right)}\left({\mathbf{x}}^{\gamma }{\mu }_c\left(\mathbf{x}\right)\right)& =& I^{\omega \left(\mathbf{x}\right)}\left({\mathbf{x}}^{\gamma }\right)-{\displaystyle \frac{1}{\mathrm{\Gamma }\left(\omega \right(\mathbf{x}\left)\right)}}{\int }_0^c{\left({\displaystyle \frac{s}{\mathbf{x}}}\right)}^{\gamma }{\mathbf{x}}^{\gamma }{\left(1-{\displaystyle \frac{s}{\mathbf{x}}}\right)}^{\omega \left(\mathbf{x}\right)-1}{\mathbf{x}}^{\omega \left(\mathbf{x}\right)-1}\mathbf{x}d\left({\displaystyle \frac{s}{\mathbf{x}}}\right)\hfill \\ & =& I^{\omega \left(\mathbf{x}\right)}\left({\mathbf{x}}^{\gamma }\right)-{\displaystyle \frac{{\mathbf{x}}^{\gamma +\omega \left(\mathbf{x}\right)}}{\mathrm{\Gamma }\left(\omega \right(\mathbf{x}\left)\right)}}{\int }_0^{{\displaystyle \frac{c}{\mathbf{x}}}}{\mathbf{t}}^{\gamma }{\left(1-\mathbf{t}\right)}^{\omega \left(\mathbf{x}\right)-1}d\mathbf{t}\hfill \\ & =& I^{\omega \left(\mathbf{x}\right)}\left({\mathbf{x}}^{\gamma }\right)-{\displaystyle \frac{{\mathbf{x}}^{\gamma +\omega \left(\mathbf{x}\right)}}{\mathrm{\Gamma }\left(\omega \right(\mathbf{x}\left)\right)}}\mathbb{I}\left({\displaystyle \frac{c}{\mathbf{x}}};1+\gamma ,\omega \left(\mathbf{x}\right)\right){\displaystyle \frac{\mathrm{\Gamma }(1+\gamma )\mathrm{\Gamma }\left(\omega \right(\mathbf{x}\left)\right)}{\mathrm{\Gamma }(1+\gamma +\omega (\mathbf{x}\left)\right)}}\hfill \\ & =& {\displaystyle \frac{\mathrm{\Gamma }(1+\gamma )}{\mathrm{\Gamma }(1+\gamma +\omega (\mathbf{x}\left)\right)}}{\mathbf{x}}^{\gamma +\omega \left(\mathbf{x}\right)}\left(1-\mathbb{I}\left({\displaystyle \frac{c}{\mathbf{x}}};1+\gamma ,\omega \left(\mathbf{x}\right)\right)\right).\hfill \end{array}$$

This completes the proof. □

3. Fractional-Order Chelyshkov Wavelets and Function Approximations in Two-Dimensional Space

The Chelyshkov polynomials are defined as

$$\begin{array}{c}\hfill {\rho }_{m,}\left(\mathbf{x}\right)=\sum _{l=0}^{\mathbb{M}-m}{a}_{l,m}.{\mathbf{x}}^{m+l},m=0,1,\dots ,\mathbb{M},\end{array}$$

where

$$\begin{array}{c}\hfill a_{l,m}={(-1)}^l\left(\begin{array}{c}\mathbb{M}-m\\ l\end{array}\right)\left(\begin{array}{c}\mathbb{M}+m+l+1\\ \mathbb{M}-m\end{array}\right).\end{array}$$

Let $\mathbb{k},\mathbb{M}$ be non-negative integers. The Chelyshkov wavelets ${\psi }_{n,m}\left(\mathbf{x}\right)$ for $n=0,1,\dots ,2^{\mathbb{k}}-1$ and $m=0,1,\dots ,\mathbb{M}$ are defined on $[0,1)$ as

$$\begin{array}{c}\hfill {\psi }_{n,m}\left(\mathbf{x}\right)=\left\{\begin{array}{cc}\sqrt{2^{\mathbb{k}}(2m+1)}{\rho }_{m,\mathbb{M}}(2^{\mathbb{k}}\mathbf{x}-n),\hfill & \mathrm{if}\mathbf{x}\in \left[{\displaystyle \frac{n}{2^{\mathbb{k}}}},{\displaystyle \frac{n+1}{2^{\mathbb{k}}}}\right),\hfill \\ 0,\hfill & \mathrm{otherwise}.\hfill \end{array}\right.\end{array}$$

The FO-CWs are obtained by using the transformation $\mathbf{x}={\mathbf{t}}^{\alpha }$ for some $\alpha >0$, as

$$\begin{array}{c}\hfill {\psi }_{n,m}^{\alpha }\left(\mathbf{t}\right)=\left\{\begin{array}{cc}\sqrt{2^{\mathbb{k}}(2m+1)}{\rho }_{m,\mathbb{M}}(2^{\mathbb{k}}{\mathbf{t}}^{\alpha }-n),\hfill & \mathrm{if}t\in \left[{\left({\displaystyle \frac{n}{2^{\mathbb{k}}}}\right)}^{{\displaystyle \frac{1}{\alpha }}},{\left({\displaystyle \frac{n+1}{2^{\mathbb{k}}}}\right)}^{{\displaystyle \frac{1}{\alpha }}}\right),\hfill \\ 0,\hfill & \mathrm{otherwise}.\hfill \end{array}\right.\end{array}$$

The FO-CWs form an orthonormal basis for $L_{w^{\alpha }}^2[0,1]$, i.e.,

$$\begin{array}{c}⟨{\psi }_{n_1,m_1}^{\alpha }\left(t\right),{\psi }_{n_2,m_2}^{\alpha }\left(\mathbf{t}\right)⟩={\int }_0^1{\psi }_{n_1,m_1}^{\alpha }\left(t\right){\psi }_{n_2,m_2}^{\alpha }\left(\mathbf{t}\right)w^{\alpha }\left(\mathbf{t}\right)dt={\delta }_{n_1,n_2}·{\delta }_{m_1,m_2},\end{array}$$

where $w^{\alpha }\left(\mathbf{t}\right)=\alpha {\mathbf{t}}^{\alpha -1}$ is the weight function. Therefore, a function $p\left(\mathbf{t}\right)\in L_{w^{\alpha }}^2\left([0,1]\right)$ can be expressed as

$$p\left(\mathbf{t}\right)\approx \sum _{n=0}^{\mathbb{M}}\sum _{n=0}^{2^{\mathbb{k}}-1}{u}_{n,m}{\psi }_{n,m}^{\alpha }\left(\mathbf{t}\right)=C^T{\mathrm{\Psi }}_{\mathbb{k},\mathbb{M}}^{\alpha }\left(t\right),$$

where

$$\begin{array}{c}{C}^T=\left[u_{0,0},\dots ,u_{0,\mathbb{M}},u_{1,0},\dots ,u_{1,\mathbb{M}},\dots ,u_{2^{\mathbb{k}}-1,0},\dots ,u_{2^{\mathbb{k}}-1,\mathbb{M}}\right],\end{array}$$

and

$$\begin{array}{c}{\mathrm{\Psi }}_{\mathbb{k},\mathbb{M}}^{\alpha }\left(\mathbf{t}\right)={\left[{\psi }_{0,0}^{\alpha }\left(\mathbf{t}\right),\dots ,{\psi }_{0,\mathbb{M}}^{\alpha }\left(\mathbf{t}\right),{\psi }_{1,0}^{\alpha }\left(\mathbf{t}\right),\dots ,{\psi }_{1,\mathbb{M}}^{\alpha }\left(\mathbf{t}\right)\dots ,{\psi }_{2^{\mathbb{k}}-1,0}^{\alpha }\left(\mathbf{t}\right),\dots ,{\psi }_{2^{\mathbb{k}}-1,\mathbb{M}}^{\alpha }\left(\mathbf{t}\right)\right]}^T.\end{array}$$

The theorem below establishes a closed-form expression for the variable-order Riemann–Liouville integral of fractional-order Chelyshkov wavelets. This result serves as the foundation for constructing a novel numerical scheme for solving variable-order fractional diffusion–wave equations in the subsequent section.

Theorem 1—Closed-form of the RLI-FO of the FO-CWs.

Theorem 1.

Let $\alpha >0$, we have

$$I^{\omega \left(\mathit{t}\right)}{\psi }_{n,m}^{\alpha }\left(\mathit{t}\right)=\left\{\begin{array}{cc}0,\hfill & \mathit{if}\mathit{t}\le c_1,\hfill \\ A\left(\mathit{t}\right),\hfill & \mathit{if}{c}_1\le \mathit{t}<c_2,\hfill \\ B\left(\mathit{t}\right),\hfill & \mathit{t}\ge c_2,\hfill \end{array}\right.$$

where

$$\begin{array}{cc}\hfill A\left(\mathit{t}\right)& =\sqrt{2^{\mathbb{k}}(2m+1)}\sum _{l=0}^{\mathbb{M}-m}\sum _{k=0}^{m+l}{a}_{l,m}\left({\displaystyle \genfrac{}{}{0pt}{}{m+l}{k}}\right)2^{\mathbb{k}l}{(-n)}^{m+l-k}\hfill \\ \hfill & \times {\displaystyle \frac{\mathrm{\Gamma }(1+\alpha k)}{\mathrm{\Gamma }(1+\alpha k+\omega (\mathit{t}\left)\right)}}·{\mathit{t}}^{\alpha k+\omega \left(\mathit{t}\right)}\left[1-\mathbb{I}\left({\displaystyle \frac{c_1}{\mathit{t}}};1+\alpha k,\omega \left(\mathit{t}\right)\right)\right],\hfill \end{array}$$

$$\begin{array}{cc}\hfill B\left(\mathit{t}\right)& =\sqrt{2^{\mathbb{k}}(2m+1)}\sum _{l=0}^{\mathbb{M}-m}\sum _{k=0}^{k+l}{a}_{l,m}\left({\displaystyle \genfrac{}{}{0pt}{}{m+l}{k}}\right)2^{\mathbb{k}k}{(-n)}^{n+l-k}\hfill \\ \hfill & \times {\displaystyle \frac{\mathrm{\Gamma }(1+\alpha k)}{\mathrm{\Gamma }(1+\alpha k+\omega (\mathit{t}\left)\right)}}·{\mathit{t}}^{\alpha k+\omega \left(\mathit{t}\right)}·\mathbb{I}\left({\displaystyle \frac{c_2}{\mathit{t}}},{\displaystyle \frac{c_1}{\mathit{t}}};1+\alpha k,\omega \left(\mathit{t}\right)\right),\hfill \end{array}$$

and

$$c_1={\left({\displaystyle \frac{n}{2^{\mathbb{k}}}}\right)}^{{\displaystyle \frac{1}{\alpha }}},c_2={\left({\displaystyle \frac{n+1}{2^{\mathbb{k}}}}\right)}^{{\displaystyle \frac{1}{\alpha }}}.$$

Proof. 

First, we reformulate the FO-CWs in the following form:

$$\begin{array}{ccc}\hfill {\psi }_{m,n}^{\alpha }\left(\mathbf{t}\right)& =& \sqrt{2^{\mathbb{k}}(2m+1)}{\rho }_{m,\mathbb{M}}\left(2^{\mathbb{k}}{\mathbf{t}}^{\alpha }-n\right)\left({\mu }_{c_1}\left(\mathbf{t}\right)-{\mu }_{c_2}\left(\mathbf{t}\right)\right)\hfill \\ & =& \sqrt{2^{\mathbb{k}}(2m+1)}\left(\sum _{l=0}^{\mathbb{M}-m}{a}_{l,m}{\left(2^{\mathbb{k}}{\mathbf{t}}^{\alpha }-n\right)}^{m+l}\left[{\mu }_{c_1}\left(\mathbf{t}\right)-{\mu }_{c_2}\left(\mathbf{t}\right)\right]\right)\hfill \\ & =& \sqrt{2^{\mathbb{k}}(2m+1)}\sum _{l=0}^{\mathbb{M}-m}\sum _{k=0}^{m+l}{a}_{l,m}\left(\begin{array}{c}m+l\\ k\end{array}\right)2^{\mathbb{k}k}{(-n)}^{m+l-k}\hfill \\ & & \times \left[{\mathbf{t}}^{\alpha k}{\mu }_{c_1}\left(\mathbf{t}\right)-{\mathbf{t}}^{\alpha k}{\mu }_{c_2}\left(\mathbf{t}\right)\right],\hfill \end{array}$$

Then,

$$\begin{array}{ccc}\hfill I^{\omega \left(\mathbf{t}\right)}\left({\psi }_{n,m}^{\alpha }\left(\mathbf{t}\right)\right)& =& \sqrt{2^{\mathbb{k}}(2m+1)}\sum _{l=0}^{\mathbb{M}-m}\sum _{k=0}^{m+l}{a}_{l,m}\left(\begin{array}{c}m+l\\ k\end{array}\right)2^{\mathbb{k}k}{(-n)}^{m+l-k}\hfill \\ & \times & \left[I^{\omega \left(\mathbf{t}\right)}{(}^{\alpha k}{\mu }_{c_1}\left(\mathbf{t}\right))-I^{\omega \left(\mathbf{t}\right)}\left({\mathbf{t}}^{\alpha k}{\mu }_{c_2}\left(\mathbf{t}\right)\right)\right].\hfill \end{array}$$

After that, we apply Lemma 1 to obtain

$$\begin{array}{ccc}\hfill I^{\omega \left(\mathbf{t}\right)}\left({\psi }_{n,m}^{\alpha }\left(\mathbf{t}\right)\right)& =& \sqrt{2^{\mathbb{k}}(2m+1)}\sum _{l=0}^{\mathbb{M}-m}\sum _{k=0}^{m+l}{a}_{l,m}\left(\begin{array}{c}m+l\\ k\end{array}\right)2^{\mathbb{k}k}{(-n)}^{m+l-k}\hfill \\ & & \times \left[{\displaystyle \frac{\mathrm{\Gamma }(1+\alpha k)}{\mathrm{\Gamma }(1+\alpha k+\omega (\mathbf{t}\left)\right)}}{\mathbf{t}}^{\alpha k+\omega \left(\mathbf{t}\right)}\left(1-\mathbb{I}\left({\displaystyle \frac{c_1}{\mathbf{t}}};1+\alpha k,\omega \left(\mathbf{t}\right)\right)\right){\mu }_{c_1}\left(\mathbf{t}\right)\right.\hfill \\ & & \left.-{\displaystyle \frac{\mathrm{\Gamma }(1+\alpha k)}{\mathrm{\Gamma }(1+\alpha k+\omega (\mathbf{t}\left)\right)}}{\mathbf{t}}^{\alpha k+\omega \left(\mathbf{t}\right)}\left(1-\mathbb{I}\left({\displaystyle \frac{c_2}{\mathbf{t}}};1+\alpha k,\omega \left(\mathbf{t}\right)\right)\right){\mu }_{c_2}\left(\mathbf{t}\right)\right].\hfill \end{array}$$

If $\mathbf{t}<c_1$ then $I^{\omega \left(\mathbf{t}\right)}\left[{\psi }_{n,m}^{\alpha }\left(\mathbf{t}\right)\right]=0$. In case $c_1\le \mathbf{t}<c_2$, then

$$\begin{array}{ccc}\hfill I^{\omega \left(\mathbf{t}\right)}\left({\psi }_{n,m}^{\alpha }\left(\mathbf{t}\right)\right)& =& \sqrt{2^{\mathbb{k}}(2m+1)}\sum _{l=0}^{\mathbb{M}-m}\sum _{k=0}^{m+l}{a}_{l,m}\left(\begin{array}{c}m+l\\ k\end{array}\right)2^{\mathbb{k}k}{(-n)}^{m+l-k}\hfill \\ & & \times \left[{\displaystyle \frac{\mathrm{\Gamma }(1+\alpha k)}{\mathrm{\Gamma }(1+\alpha k+\omega (\mathbf{t}\left)\right)}}{\mathbf{t}}^{\alpha k+\omega \left(\mathbf{t}\right)}\left(1-\mathbb{I}\left({\displaystyle \frac{c_1}{\mathbf{t}}};1+\alpha k,\omega \left(\mathbf{t}\right)\right)\right)\right].\hfill \end{array}$$

For $\mathbf{t}\ge c_2$, we have

$$\begin{array}{c}\hfill I^{\omega \left(\mathbf{t}\right)}\left({\psi }_{n,m}^{\alpha }\left(\mathbf{t}\right)\right)=\sqrt{2^{\mathbb{k}}(2m+1)}\sum _{l=0}^{\mathbb{M}-m}\sum _{k=0}^{m+l}{a}_{l,m}\left(\begin{array}{c}m+l\\ k\end{array}\right)2^{\mathbb{k}k}{(-n)}^{m+l-k}\\ \hfill \times {\displaystyle \frac{\mathrm{\Gamma }(1+\alpha k)}{\mathrm{\Gamma }(1+\alpha k+\omega (\mathbf{t}\left)\right)}}{\mathbf{t}}^{\alpha k+\omega \left(\mathbf{t}\right)}\left[\mathbb{I}\left({\displaystyle \frac{c_2}{\mathbf{t}}};1+\alpha k,\omega \left(\mathbf{t}\right)\right)-\mathbb{I}\left({\displaystyle \frac{c_1}{\mathbf{t}}};1+\alpha k,\omega \left(\mathbf{t}\right)\right)\right]\\ \hfill =\sqrt{2^{\mathbb{k}}(2m+1)}\sum _{l=0}^{\mathbb{M}-m}\sum _{k=0}^{m+l}{a}_{l,m}\left(\begin{array}{c}m+l\\ k\end{array}\right)2^{\mathbb{k}k}{(-n)}^{m+l-k}\\ \hfill \times {\displaystyle \frac{\mathrm{\Gamma }(1+\alpha k)}{\mathrm{\Gamma }(1+\alpha k+\omega (\mathbf{t}\left)\right)}}{\mathbf{t}}^{\alpha k+\omega \left(\mathbf{t}\right)}\left[\mathbb{I}\left({\displaystyle \frac{c_2}{\mathbf{t}}},{\displaystyle \frac{c_1}{\mathbf{t}}};1+\alpha k,\omega \left(\mathbf{t}\right)\right)\right].\end{array}$$

The theorem is then proved. □

In the two-dimensional case, for $\alpha ,{\alpha }^{\prime }>0$, and non-negative integers $\mathbb{k},{\mathbb{k}}^{\prime },\mathbb{M},{\mathbb{M}}^{\prime }$ the set

$$\begin{array}{c}\mathcal{O}:=\left\{({\psi }_{m,n}^{\alpha }·{\psi }_{m^{\prime },n^{\prime }}^{{\alpha }^{\prime }})\right|0\le m\le 2^{\mathbb{k}}-1,0\le n\le \mathbb{M};0\le m^{\prime }\le 2^{{\mathbb{k}}^{\prime }}-1,0\le n^{\prime }\le {\mathbb{M}}^{\prime }\}\end{array}$$

forms an orthonormal set in $L_{w^{*}}^2([0,1]\times [0,1])$. Here, the norm ${\parallel .\parallel }_{w^{*}}$ is defined by

$${\parallel p(\mathbf{x},\mathbf{t})\parallel }_{w^{*}}^2={\int }_0^1{\int }_0^1{\left[p(\mathbf{x},\mathbf{t})\right]}^2{w}^{\alpha }\left(\mathbf{x}\right)w^{{\alpha }^{\prime }}\left(\mathbf{t}\right)d\mathbf{x}d\mathbf{t},$$

where $w^{\alpha }\left(\mathbf{x}\right)=\alpha {\mathbf{x}}^{\alpha -1}$ and $w^{{\alpha }^{\prime }}\left(\mathbf{x}\right)={\alpha }^{\prime }{\mathbf{x}}^{{\alpha }^{\prime -1}}$. To create a new arrangement, let ${\psi }_i^{\alpha }\left(\mathbf{x}\right)={\psi }_{m,n}^{\alpha }\left(\mathbf{x}\right),$ and ${\psi }_j^{{\alpha }^{\prime }}\left(\mathbf{t}\right)={\psi }_{m,n}^{{\alpha }^{\prime }}\left(\mathbf{t}\right)$, where $i=n(\mathbb{M}+1)+m+1,\mathrm{and}j=n^{\prime }({\mathbb{M}}^{\prime }+1)+m^{\prime }+1$, then the orthonormal set $\mathcal{O}$ becomes

$$\{{\psi }_i^{\alpha }\left(\mathbf{x}\right)·{\psi }_j^{{\alpha }^{\prime }}\left(\mathbf{t}\right)|i=1,\dots \widehat{\mathbb{M}},j=1,\dots ,{\widehat{\mathbb{M}}}^{\prime }\},$$

where $\widehat{\mathbb{M}}=2^{\mathbb{k}}(\mathbb{M}+1)\mathrm{and}{\widehat{\mathbb{M}}}^{\prime }=2^{{\mathbb{k}}^{\prime }}({\mathbb{M}}^{\prime }+1)$. Any function $p(\mathbf{x},\mathbf{t})\in L_{w^{*}}^2\left({[0,1]}^2\right)$ can be represented by

$$\begin{array}{c}p(\mathbf{x},\mathbf{t})\approx \overline{p}(\mathbf{x},\mathbf{t})=\sum _{i=1}^{\widehat{\mathbb{M}}}\sum _{j=1}^{{\widehat{\mathbb{M}}}^{\prime }}{c}_{i,j}{\psi }_i^{\alpha }\left(\mathbf{x}\right){\psi }_j^{{\alpha }^{\prime }}\left(\mathbf{t}\right)={\mathrm{\Psi }}_{\mathbb{k},\mathbb{M}}^{\alpha }{\left(\mathbf{x}\right)}^T·\mathrm{\Delta }·{\mathrm{\Psi }}_{{\mathbb{k}}^{\prime },{\mathbb{M}}^{\prime }}^{{\alpha }^{\prime }}\left(\mathbf{t}\right),\end{array}$$

where ${\mathrm{\Psi }}_{\mathbb{k},\mathbb{M}}^{\alpha }\left(\mathbf{x}\right)$ and ${\mathrm{\Psi }}_{{\mathbb{k}}^{\prime },{\mathbb{M}}^{\prime }}^{{\alpha }^{\prime }}\left(\mathbf{t}\right)$ are given as

$$\begin{array}{c}{\mathrm{\Psi }}_{\mathbb{k},\mathbb{M}}^{\alpha }\left(\mathbf{x}\right)={\left[{\psi }_1^{\alpha }\left(\mathbf{x}\right),{\psi }_2^{\alpha }\left(\mathbf{x}\right),\dots ,{\psi }_{\widehat{\mathbb{M}}}^{\alpha }\left(\mathbf{x}\right)\right]}^T,\end{array}$$

(6)

$$\begin{array}{c}{\mathrm{\Psi }}_{{\mathbb{k}}^{\prime },{\mathbb{M}}^{\prime }}^{{\alpha }^{\prime }}\left(\mathbf{t}\right)={\left[{\psi }_1^{{\alpha }^{\prime }}\left(\mathbf{t}\right),{\psi }_2^{{\alpha }^{\prime }}\left(\mathbf{t}\right),\dots ,{\psi }_{{\widehat{\mathbb{M}}}^{\prime }}^{{\alpha }^{\prime }}\left(\mathbf{t}\right)\right]}^T,\end{array}$$

(7)

and $\mathrm{\Delta }=\left[u_{i,j}\right]$ is an $\widehat{\mathbb{M}}\times {\widehat{\mathbb{M}}}^{\prime }$ matrix with

$$\begin{array}{ccc}\hfill u_{i,j}& =& {⟨{\psi }_i^{\alpha }\left(\mathbf{x}\right),{⟨p(\mathbf{x},\mathbf{t}),{\psi }_j^{{\alpha }^{\prime }}\left(\mathbf{t}\right)⟩}_{w^{{\alpha }^{\prime }}\left(\mathbf{t}\right)}⟩}_{w^{\alpha }\left(\mathbf{x}\right)}\hfill \\ & =& {\int }_0^1{\int }_0^1{\psi }_i^{\alpha }\left(\mathbf{x}\right){\psi }_j^{{\alpha }^{\prime }}\left(\mathbf{t}\right)p(\mathbf{x},\mathbf{t}){\omega }^{\alpha }\left(\mathbf{x}\right){\omega }^{{\alpha }^{\prime }}\left(\mathbf{t}\right)d\mathbf{x}d\mathbf{t}.\hfill \end{array}$$

Remark 1.

The fractional-order Chelyshkov wavelets employed in this work generate an orthogonal basis that offers both theoretical simplicity and practical advantages for numerical computation. Their algebraic structure allows for straightforward manipulation and efficient integration into the spectral discretization framework. A central feature of our approach is that the variable-order Riemann–Liouville integral of each basis function can be computed in closed form, which significantly simplifies the development of the numerical algorithm.

Regarding the tuning parameters, k and M determine the resolution level and polynomial degree, respectively, thus influencing the number of basis elements and the expressive power of the approximation space. Although increasing k and M typically enhances accuracy, it also raises computational demands. To provide additional flexibility, we introduce a scaling parameter α, which adjusts the distribution and behavior of the basis functions. This parameter enables improved accuracy under fixed computational cost and contributes to the robustness of the proposed spectral method.

4. Error Bound

In this section, we derive rigorous estimates for the approximation error associated with the proposed numerical scheme. The resulting upper bounds not only guarantee the convergence of the method but also offer valuable insights into how the accuracy depends on the variation of the basis function parameters. These results are formalized in the theorem below.

Theorem 2.

Let $\mathrm{\Omega }=[0,1]\times [0,1]$ and let $p:\mathrm{\Omega }\to \mathbb{R}$ be a smooth function. Suppose that $\overline{p}$ is the best approximation of p out of

$$Span\{{\psi }_i^{\alpha }\left(\mathit{x}\right){\psi }_j^{{\alpha }^{\prime }}\left(\mathbf{t}\right),1\le i\le \widehat{\mathbb{M}},1\le j\le {\widehat{\mathbb{M}}}^{\prime }\}.$$

with respect to the norm in $L_{w^{*}}^2\left(\mathrm{\Omega }\right)$. Then,

$$\begin{array}{ccc}\hfill \parallel p(\mathit{x},\mathbf{t})-\overline{p}{(\mathit{x},\mathbf{t})\parallel }_{w^{*}}^2& \le & {\displaystyle \frac{2^{1-(\mathbb{k}+2)(\mathbb{M}+1)}}{{\alpha }^{\mathbb{M}+1}·(\mathbb{M}+1)!}}·L_1+{\displaystyle \frac{2^{1-({\mathbb{k}}^{\prime }+2)({\mathbb{M}}^{\prime }+1)}}{{{\alpha }^{\prime }}^{{\mathbb{M}}^{\prime }+1}·({\mathbb{M}}^{\prime }+1)!}}·L_2\hfill \\ & +& {\displaystyle \frac{2^{2-(\mathbb{k}+2)(\mathbb{M}+1)-({\mathbb{k}}^{\prime }+2)({\mathbb{M}}^{\prime }+1)}}{{\alpha }^{\mathbb{M}+1}·{{\alpha }^{\prime }}^{{\mathbb{M}}^{\prime }+1}·(\mathbb{M}+1)!({\mathbb{M}}^{\prime }+1)!}}·L_3,\hfill \end{array}$$

where $L_1,L_2,\mathrm{and}{L}_2$ are constants satisfying

$$\underset{(\mathit{x},\mathit{t})\in \mathrm{\Omega }}{max}\left|{\displaystyle \frac{{\partial }^{\mathbb{M}+1}p(\mathit{x},\mathit{t})}{\partial {\mathit{x}}^{\mathbb{M}+1}}}\right|\le L_1,\underset{(\mathit{x},\mathit{t})\in \mathrm{\Omega }}{max}\left|{\displaystyle \frac{{\partial }^{{\mathbb{M}}^{\prime }+1}p(\mathit{x},\mathit{t})}{\partial {\mathit{t}}^{{\mathbb{M}}^{\prime }+1}}}\right|\le L_2,\underset{(\mathit{x},\mathit{t})\in \mathrm{\Omega }}{max}\left|{\displaystyle \frac{{\partial }^{\mathbb{M}+{\mathbb{M}}^{\prime }+2}p(\mathit{x},\mathit{t})}{\partial {\mathit{x}}^{\mathbb{M}+1}\partial {\mathit{t}}^{{\mathbb{M}}^{\prime }+1}}}\right|\le L_3.$$

Proof. 

We denote $I_{n,\mathbb{k}}^{\alpha }=\left[{\left({\displaystyle \frac{n}{2^{\mathbb{k}}}}\right)}^{{\displaystyle \frac{1}{\alpha }}},{\left({\displaystyle \frac{n+1}{2^{\mathbb{k}}}}\right)}^{{\displaystyle \frac{1}{\alpha }}}\right)$ and $I_{n^{\prime },{\mathbb{k}}^{\prime }}^{{\alpha }^{\prime }}=\left[{\left({\displaystyle \frac{n^{\prime }}{2^{{\mathbb{k}}^{\prime }}}}\right)}^{{\displaystyle \frac{1}{{\alpha }^{\prime }}}},{\left({\displaystyle \frac{n^{\prime }+1}{2^{{\mathbb{k}}^{\prime }}}}\right)}^{{\displaystyle \frac{1}{{\alpha }^{\prime }}}}\right)$. Suppose that the polynomial $v(\mathbf{x},\mathbf{t})$ interpolates the function $p(\mathbf{x},\mathbf{t})$ at the points $(x_i,t_j)$, where $x_i$s and $t_{j}s$ are the roots of the Chebyshev polynomial of $(\mathbb{M}+1)$-degree in $I_{n,\mathbb{k}}^{\alpha }$ and $({\mathbb{M}}^{\prime }+1)$-degree in $I_{n^{\prime },{\mathbb{k}}^{\prime }}^{{\alpha }^{\prime }}$ correspondingly.

Thus,

$$\begin{array}{c}\hfill \parallel p(\mathbf{x},\mathbf{t})-\overline{p}{(\mathbf{x},\mathbf{t})\parallel }_{\infty }\le {\parallel p(\mathbf{x},\mathbf{t})-v(\mathbf{x},\mathbf{t})\parallel }_{\infty }.\end{array}$$

(8)

Similar to the methods in References [43,49,50,51], we have

$$\begin{array}{ccc}\hfill p(\mathbf{x},\mathbf{t})-v(\mathbf{x},\mathbf{t})& =& {\displaystyle \frac{1}{(\mathbb{M}+1)!}}·{\displaystyle \frac{{\partial }^{\mathbb{M}+1}u(\eta ,\mathbf{t})}{\partial {\mathbf{x}}^{\mathbb{M}+1}}}·\prod _{i=0}^{\mathbb{M}}(\mathbf{x}-x_i)\hfill \\ \hfill & +& {\displaystyle \frac{1}{({\mathbb{M}}^{\prime }+1)!}}·{\displaystyle \frac{{\partial }^{{\mathbb{M}}^{\prime }+1}u(\mathbf{x},\xi )}{\partial {\mathbf{t}}^{{\mathbb{M}}^{\prime }+1}}}·\prod _{j=0}^{{\mathbb{M}}^{\prime }}(\mathbf{t}-t_j)\hfill \\ \hfill & -& {\displaystyle \frac{1}{(\mathbb{M}+1)!({\mathbb{M}}^{\prime }+1)!}}·{\displaystyle \frac{{\partial }^{\mathbb{M}+{\mathbb{M}}^{\prime }+2}u(\overline{\eta },\overline{\xi })}{\partial {\mathbf{x}}^{\mathbb{M}+1}\partial {\mathbf{t}}^{{\mathbb{M}}^{\prime }+1}}}·\prod _{i=0}^{\mathbb{M}}(\mathbf{x}-x_i)·\prod _{j=0}^{{\mathbb{M}}^{\prime }}(\mathbf{t}-t_j),\hfill \\ \hfill \end{array}$$

where $(\eta ,\xi ),(\overline{\eta },\overline{\xi })\in [0,1]\times [0,1]$. So we obtain

$$\begin{array}{ccc}\hfill {\parallel p(\mathbf{x},\mathbf{t})-v(\mathbf{x},\mathbf{t})\parallel }_{\infty }& \le & {\displaystyle \frac{1}{(\mathbb{M}+1)!}}·\underset{(\mathbf{x},\mathbf{t})\in \mathrm{\Omega }}{max}\left|{\displaystyle \frac{{\partial }^{\mathbb{M}+1}u(\eta ,\mathbf{t})}{\partial {\mathbf{x}}^{\mathbb{M}+1}}}\right|·\parallel \prod _{i=0}^{\mathbb{M}}(\mathbf{x}-x_i){\parallel }_{\infty }\hfill \\ \hfill & +& {\displaystyle \frac{1}{({\mathbb{M}}^{\prime }+1)!}}·\underset{(\mathbf{x},\mathbf{t})\in \mathrm{\Omega }}{max}\left|{\displaystyle \frac{{\partial }^{{\mathbb{M}}^{\prime }+1}u(\mathbf{x},\xi )}{\partial {\mathbf{t}}^{{\mathbb{M}}^{\prime }+1}}}\right|·\parallel \prod _{j=0}^{{\mathbb{M}}^{\prime }}(\mathbf{t}-t_j){\parallel }_{\infty }\hfill \\ \hfill & +& {\displaystyle \frac{1}{(\mathbb{M}+1)!({\mathbb{M}}^{\prime }+1)!}}·\underset{(\mathbf{x},\mathbf{t})\in \mathrm{\Omega }}{max}\left|{\displaystyle \frac{{\partial }^{\mathbb{M}+{\mathbb{M}}^{\prime }+2}u(\overline{\eta },\overline{\xi })}{\partial {\mathbf{x}}^{\mathbb{M}+1}\partial {\mathbf{t}}^{{\mathbb{M}}^{\prime }+1}}}\right|\hfill \\ \hfill & ·& \parallel \prod _{i=0}^{\mathbb{M}}(\mathbf{x}-x_i){\parallel }_{\infty }·\parallel \prod _{j=0}^{{\mathbb{M}}^{\prime }}(\mathbf{t}-t_j){\parallel }_{\infty }.\hfill \\ \hfill \end{array}$$

(9)

Since $p(\mathbf{x},\mathbf{t})$ is a smooth function on the compact domain $\mathrm{\Omega }$, then there exist $L_1,L_2,\mathrm{and}{L}_3$ satisfying

$$\underset{(\mathbf{x},\mathbf{t})\in \mathrm{\Omega }}{max}\left|{\displaystyle \frac{{\partial }^{\mathbb{M}+1}p(\mathbf{x},\mathbf{t})}{\partial {\mathbf{x}}^{\mathbb{M}+1}}}\right|\le L_1,\underset{(\mathbf{x},\mathbf{t})\in \mathrm{\Omega }}{max}\left|{\displaystyle \frac{{\partial }^{{\mathbb{M}}^{\prime }+1}p(\mathbf{x},\mathbf{t})}{\partial {\mathbf{t}}^{{\mathbb{M}}^{\prime }+1}}}\right|\le L_2,\underset{(\mathbf{x},\mathbf{t})\in \mathrm{\Omega }}{max}\left|{\displaystyle \frac{{\partial }^{\mathbb{M}+{\mathbb{M}}^{\prime }+2}p(\mathbf{x},\mathbf{t})}{\partial {\mathbf{x}}^{\mathbb{M}+1}\partial {\mathbf{t}}^{{\mathbb{M}}^{\prime }+1}}}\right|\le L_3.$$

(10)

To evaluate $\parallel {\prod }_{i=0}^{\mathbb{M}}(\mathbf{x}-x_i){\parallel }_{\infty }$, we consider the mapping

$$\mathbf{x}={\displaystyle \frac{a}{2^{\frac{\mathbb{k}}{\alpha }+1}}}·\mathbf{z}+{\displaystyle \frac{b}{2^{\frac{\mathbb{k}}{\alpha }+1}}},$$

where $a={(n+1)}^{{\displaystyle \frac{1}{\alpha }}}-n^{{\displaystyle \frac{1}{\alpha }}}$, and $b={(n+1)}^{{\displaystyle \frac{1}{\alpha }}}+n^{{\displaystyle \frac{1}{\alpha }}}$ between the intervals $[-1,1]$ and $\left[{\left({\displaystyle \frac{n}{2^{\mathbb{k}}}}\right)}^{{\displaystyle \frac{1}{\alpha }}},{\left({\displaystyle \frac{n+1}{2^{\mathbb{k}}}}\right)}^{{\displaystyle \frac{1}{\alpha }}}\right)$, we get

$$\begin{array}{ccc}\hfill \underset{x_i\in [0,1]}{min}\underset{\mathbf{x}\in [0,1]}{max}\left|\prod _{i=0}^{\mathbb{M}}(\mathbf{x}-x_i)\right|& =& {\displaystyle \frac{a^{\mathbb{M}+1}}{2^{(\mathbb{M}+1)(\frac{\mathbb{k}}{\alpha }+1)}}}·\underset{z_i\in [-1,1]}{min}\underset{z\in [-1,1]}{max}\left|\prod _{i=0}^{\mathbb{M}}(\mathbf{z}-z_i)\right|\hfill \\ \hfill & \le & {\displaystyle \frac{a^{\mathbb{M}+1}}{2^{(\mathbb{M}+1)(\frac{\mathbb{k}}{\alpha }+2)-1}}},\hfill \end{array}$$

where $z_0,z_1,\dots ,z_{\mathbb{M}}$ are the solutions of the Chebyshev polynomial of degree $\mathbb{M}+1$. Furthermore, by applying the mean value theorem,

$$\begin{array}{c}\hfill a={(n+1)}^{{\displaystyle \frac{1}{\alpha }}}-n^{{\displaystyle \frac{1}{\alpha }}}={\displaystyle \frac{1}{\alpha }}·{\zeta }^{{\displaystyle \frac{1}{\alpha }}-1},\zeta \in (n,n+1).\end{array}$$

We get

$$\begin{array}{c}\hfill a^{\mathbb{M}+1}={\displaystyle \frac{1}{{\alpha }^{\mathbb{M}+1}}}·{\zeta }^{(\mathbb{M}+1)({\displaystyle \frac{1}{\alpha }}-1)}\le {\displaystyle \frac{1}{{\alpha }^{\mathbb{M}+1}}}·2^{\mathbb{k}(\mathbb{M}+1)({\displaystyle \frac{1}{\alpha }}-1)}.\end{array}$$

So we obtain

$$\begin{array}{c}\hfill \underset{x_i\in [0,1]}{min}\underset{\mathbf{x}\in [0,1]}{max}\left|\prod _{i=0}^{\mathbb{M}}(\mathbf{x}-x_i)\right|\le {\displaystyle \frac{2^{1-(\mathbb{k}+2)(\mathbb{M}+1)}}{{\alpha }^{\mathbb{M}+1}}}.\end{array}$$

(11)

Similarly, we receive

$$\underset{t_j\in [0,1]}{min}\underset{\mathbf{t}\in [0,1]}{max}\left|\prod _{j=0}^{{\mathbb{M}}^{\prime }}(\mathbf{t}-t_j)\right|\le {\displaystyle \frac{2^{1-({\mathbb{k}}^{\prime }+2)({\mathbb{M}}^{\prime }+1)}}{{{\alpha }^{\prime }}^{{\mathbb{M}}^{\prime }+1}}}.$$

(12)

From Equations (9)–(12) we obtain

$$\begin{array}{c}\hfill {\parallel p(\mathbf{x},\mathbf{t})-v(\mathbf{x},\mathbf{t})\parallel }_{\infty }\le \mathbf{L},\end{array}$$

(13)

where

$$\begin{array}{ccc}\hfill \mathbf{L}& =& {\displaystyle \frac{2^{1-(\mathbb{k}+2)(\mathbb{M}+1)}}{{\alpha }^{\mathbb{M}+1}·(\mathbb{M}+1)!}}·L_1+{\displaystyle \frac{2^{1-({\mathbb{k}}^{\prime }+2)({\mathbb{M}}^{\prime }+1)}}{{{\alpha }^{\prime }}^{{\mathbb{M}}^{\prime }+1}·({\mathbb{M}}^{\prime }+1)!}}·L_2\hfill \\ & +& {\displaystyle \frac{2^{2-(\mathbb{k}+2)(\mathbb{M}+1)-({\mathbb{k}}^{\prime }+2)({\mathbb{M}}^{\prime }+1)}}{{\alpha }^{\mathbb{M}+1}·{{\alpha }^{\prime }}^{{\mathbb{M}}^{\prime }+1}·(\mathbb{M}+1)!({\mathbb{M}}^{\prime }+1)!}}·L_3.\hfill \end{array}$$

Note that $\mathrm{\Omega }$ is divided to $2^{\mathbb{k}+{\mathbb{k}}^{\prime }}$ subdomains ${\mathrm{\Omega }}^{\prime }=I_{n,\mathbb{k}}^{\alpha }\times I_{n^{\prime },{\mathbb{k}}^{\prime }}^{{\alpha }^{\prime }}$, we have

$$\begin{array}{ccc}\hfill \parallel p(\mathbf{x},\mathbf{t})-\overline{p}{(\mathbf{x},\mathbf{t})\parallel }_{w^{*}}^2& =& \sum _{n=0}^{2^{\mathbb{k}}-1}\sum _{n^{\prime }=0}^{2^{{\mathbb{k}}^{\prime }}-1}{\int }_{{\left({\displaystyle \frac{n}{2^{\mathbb{k}}}}\right)}^{{\displaystyle \frac{1}{\alpha }}}}^{{\left({\displaystyle \frac{n+1}{2^{\mathbb{k}}}}\right)}^{{\displaystyle \frac{1}{\alpha }}}}{\int }_{{\left({\displaystyle \frac{n^{\prime }}{2^{{\mathbb{k}}^{\prime }}}}\right)}^{{\displaystyle \frac{1}{{\alpha }^{\prime }}}}}^{{\left({\displaystyle \frac{n^{\prime }+1}{2^{{\mathbb{k}}^{\prime }}}}\right)}^{{\displaystyle \frac{1}{{\alpha }^{\prime }}}}}{w}^{\alpha }\left(\mathbf{x}\right)w^{{\alpha }^{\prime }}\left(\mathbf{t}\right){(p(\mathbf{x},\mathbf{t})-\overline{p}(\mathbf{x},\mathbf{t}))}^{2}d\mathbf{x}d\mathbf{t}.\hfill \end{array}$$

From Equations (8) and (13), we get

$$\begin{array}{ccc}\hfill \parallel p(\mathbf{x},\mathbf{t})-\overline{p}{(\mathbf{x},\mathbf{t})\parallel }_{w^{*}}^2& \le & \mathbf{L}·\sum _{n=0}^{2^{\mathbb{k}}-1}\sum _{n^{\prime }=0}^{2^{{\mathbb{k}}^{\prime }}-1}{\int }_{{\left({\displaystyle \frac{n}{2^{\mathbb{k}}}}\right)}^{{\displaystyle \frac{1}{\alpha }}}}^{{\left({\displaystyle \frac{n+1}{2^{\mathbb{k}}}}\right)}^{{\displaystyle \frac{1}{\alpha }}}}{\int }_{{\left({\displaystyle \frac{n^{\prime }}{2^{{\mathbb{k}}^{\prime }}}}\right)}^{{\displaystyle \frac{1}{{\alpha }^{\prime }}}}}^{{\left({\displaystyle \frac{n^{\prime }+1}{2^{{\mathbb{k}}^{\prime }}}}\right)}^{{\displaystyle \frac{1}{{\alpha }^{\prime }}}}}{w}^{\alpha }\left(\mathbf{x}\right)w^{{\alpha }^{\prime }}\left(\mathbf{t}\right)d\mathbf{x}d\mathbf{t}\hfill \\ \hfill & \le & \mathbf{L}·\sum _{n=0}^{2^{\mathbb{k}}-1}\sum _{n^{\prime }=0}^{2^{{\mathbb{k}}^{\prime }}-1}{\int }_{{\left({\displaystyle \frac{n}{2^{\mathbb{k}}}}\right)}^{{\displaystyle \frac{1}{\alpha }}}}^{{\left({\displaystyle \frac{b+1}{2^{\mathbb{k}}}}\right)}^{{\displaystyle \frac{1}{\alpha }}}}{\int }_{{\left({\displaystyle \frac{n^{\prime }}{2^{{\mathbb{k}}^{\prime }}}}\right)}^{{\displaystyle \frac{1}{{\alpha }^{\prime }}}}}^{{\left({\displaystyle \frac{b^{\prime }+1}{2^{{\mathbb{k}}^{\prime }}}}\right)}^{{\displaystyle \frac{1}{{\alpha }^{\prime }}}}}\alpha {\mathbf{x}}^{\alpha -1}·{\alpha }^{\prime }{\mathbf{t}}^{{\alpha }^{\prime }-1}d\mathbf{x}d\mathbf{t}\hfill \\ \hfill & =& \mathbf{L}.\hfill \end{array}$$

The theorem is proved. □

5. Numerical Method

We use FO-CWs to establish a numerical method for solving the Equation (1) associated with Conditions (2) and (3). First, we approximate

$$\begin{array}{c}{\displaystyle \frac{{\partial }^4}{\partial {\mathbf{x}}^2\partial {\mathbf{t}}^2}}p(\mathbf{x},\mathbf{t})\approx {\mathrm{\Psi }}_{\mathbb{k},\mathbb{M}}^{\alpha }{\left(\mathbf{x}\right)}^T·\mathrm{\Delta }·{\mathrm{\Psi }}_{{\mathbb{k}}^{\prime },{\mathbb{M}}^{\prime }}^{{\alpha }^{\prime }}\left(\mathbf{t}\right),\end{array}$$

where ${\mathrm{\Psi }}_{\mathbb{k},\mathbb{M}}^{\alpha }\left(\mathbf{x}\right),{\mathrm{\Psi }}_{{\mathbb{k}}^{\prime },{\mathbb{M}}^{\prime }}^{{\alpha }^{\prime }}\left(\mathbf{t}\right)$ are given in Equations (6) and (7). By integrating both sides of the above equation with respect to t twice and applying the Equation (2)

$$\begin{array}{c}{\displaystyle \frac{{\partial }^2}{\partial {\mathbf{x}}^2}}p(\mathbf{x},\mathbf{t})\approx {\mathrm{\Psi }}_{\mathbb{k},\mathbb{M}}^{\alpha }{\left(\mathbf{x}\right)}^T·\mathrm{\Delta }·I_{\mathbf{t}}^2{\mathrm{\Psi }}_{{\mathbb{k}}^{\prime },{\mathbb{M}}^{\prime }}^{{\alpha }^{\prime }}\left(\mathbf{t}\right)+{\displaystyle \frac{d^2}{d{\mathbf{x}}^2}}{r}_0\left(\mathbf{x}\right)+{\displaystyle \frac{d^2}{d{\mathbf{x}}^2}}{r}_1\left(\mathbf{x}\right)\mathbf{t}.\end{array}$$

(14)

Integrating both sides of Equation (14) with respect to $\mathbf{x}$ twice and using the conditions (3) we get

$$\begin{array}{ccc}\hfill p(\mathbf{x},\mathbf{t})& \approx & I_{\mathbf{x}}^2{\mathrm{\Psi }}_{\mathbb{k},\mathbb{M}}^{\alpha }{\left(\mathbf{x}\right)}^T·\mathrm{\Delta }·I_{\mathbf{t}}^2{\mathrm{\Psi }}_{{\mathbb{k}}^{\prime },{\mathbb{M}}^{\prime }}^{{\alpha }^{\prime }}\left(\mathbf{t}\right)-\mathbf{x}{I}_{\mathbf{x}}^2{\mathrm{\Psi }}_{\mathbb{k},\mathbb{M}}^{\alpha }{\left(1\right)}^T·\mathrm{\Delta }·I_{\mathbf{t}}^2{\mathrm{\Psi }}_{{\mathbb{k}}^{\prime },{\mathbb{M}}^{\prime }}^{{\alpha }^{\prime }}\left(\mathbf{t}\right)\hfill \\ & +& (1-\mathbf{x})\left[s_0\left(\mathbf{t}\right)+(r_0\left(\mathbf{x}\right)-r_0\left(0\right))+(r_1\left(\mathbf{x}\right)-r_1\left(0\right))\mathbf{t}\right]+\mathbf{x}{s}_1\left(\mathbf{t}\right),\hfill \end{array}$$

(15)

where

$$\begin{array}{c}{I}_{\mathbf{x}}^2{\mathrm{\Psi }}_{\mathbb{k},\mathbb{M}}^{\alpha }\left(\mathbf{x}\right)={\left[I_{\mathbf{x}}^2{\psi }_1^{\alpha }\left(\mathbf{x}\right),I_{\mathbf{x}}^2{\psi }_2^{\alpha }\left(\mathbf{x}\right),\dots ,I_{\mathbf{x}}^2{\psi }_{\mathbf{M}}^{\alpha }\left(\mathbf{x}\right)\right]}^T,\end{array}$$

and

$$\begin{array}{c}{I}_{\mathbf{t}}^2{\mathrm{\Psi }}_{{\mathbb{k}}^{\prime },{\mathbb{M}}^{\prime }}^{{\alpha }^{\prime }}\left(\mathbf{t}\right)={\left[I_{\mathbf{t}}^2{\psi }_1^{{\alpha }^{\prime }}\left(\mathbf{t}\right),I_{\mathbf{t}}^2{\psi }_2^{{\alpha }^{\prime }}\left(\mathbf{t}\right),\dots ,I_{\mathbf{t}}^2{\psi }_{{\mathbf{M}}^{\prime }}^{{\alpha }^{\prime }}\left(\mathbf{t}\right)\right]}^T.\end{array}$$

Therefore

$$\begin{array}{ccc}\hfill D_{\mathbf{t}}^{\omega (\mathbf{x},\mathbf{t})}p(\mathbf{x},\mathbf{t})& \approx & I_{\mathbf{x}}^2{\mathrm{\Psi }}_{\mathbb{k},\mathbb{M}}^{\alpha }{\left(\mathbf{x}\right)}^T·\mathrm{\Delta }·I_{\mathbf{t}}^{2-\omega (\mathbf{x},\mathbf{t})}{\mathrm{\Psi }}_{{\mathbb{k}}^{\prime },{\mathbb{M}}^{\prime }}^{{\alpha }^{\prime }}\left(\mathbf{t}\right)-\mathbf{x}·I_{\mathbf{x}}^2{\mathrm{\Psi }}_{\mathbb{k},\mathbb{M}}^{\alpha }{\left(1\right)}^T·\mathrm{\Delta }·I_{\mathbf{t}}^{2-\omega (\mathbf{x},\mathbf{t})}{\mathrm{\Psi }}_{{\mathbb{k}}^{\prime },{\mathbb{M}}^{\prime }}^{{\alpha }^{\prime }}\left(\mathbf{t}\right)\hfill \\ & +& (1-\mathbf{x})\left[D_{\mathbf{t}}^{\omega (\mathbf{x},\mathbf{t})}{s}_0\left(\mathbf{t}\right)+{\displaystyle \frac{r_1\left(\mathbf{t}\right)-r_1\left(0\right)}{\mathrm{\Gamma }(2-\omega (\mathbf{x},\mathbf{t})}}{\mathbf{t}}^{1-\omega (\mathbf{x},\mathbf{t})}\right]+\mathbf{x}{D}_{\mathbf{t}}^{\omega (\mathbf{x},\mathbf{t})}{s}_1\left(\mathbf{t}\right),\hfill \end{array}$$

(16)

and

$$\begin{array}{ccc}\hfill D_{\mathbf{t}}^{{\omega }_i(\mathbf{x},\mathbf{t})}p(\mathbf{x},\mathbf{t})& \approx & I_{\mathbf{x}}^2{\mathrm{\Psi }}_{\mathbb{k},\mathbb{M}}^{\alpha }{\left(\mathbf{x}\right)}^T·\mathrm{\Delta }·I_{\mathbf{t}}^{2-{\omega }_i(\mathbf{x},\mathbf{t})}{\mathrm{\Psi }}_{{\mathbb{k}}^{\prime },{\mathbb{M}}^{\prime }}^{{\alpha }^{\prime }}\left(\mathbf{t}\right)\hfill \\ & -& \mathbf{x}·I_{\mathbf{x}}^2{\mathrm{\Psi }}_{\mathbb{k},\mathbb{M}}^{\alpha }{\left(1\right)}^T·\mathrm{\Delta }·I_t^{2-{\omega }_i(\mathbf{x},\mathbf{t})}{\mathrm{\Psi }}_{{\mathbb{k}}^{\prime },{\mathbb{M}}^{\prime }}^{{\alpha }^{\prime }}\left(\mathbf{t}\right)\hfill \\ & +& (1-\mathbf{x})\left[D_{\mathbf{t}}^{{\omega }_i(\mathbf{x},\mathbf{t})}{s}_0\left(\mathbf{t}\right)+{\displaystyle \frac{r_1\left(\mathbf{x}\right)-r_1\left(0\right)}{\mathrm{\Gamma }(2-{\omega }_i(\mathbf{x},\mathbf{t})}}{\mathbf{t}}^{1-{\omega }_i(\mathbf{x},\mathbf{t})}\right]+\mathbf{x}{D}_{\mathbf{t}}^{{\omega }_i(\mathbf{x},\mathbf{t})}{s}_1\left(\mathbf{t}\right),\hfill \end{array}$$

(17)

where

$$\begin{array}{c}{I}_{\mathbf{t}}^{2-\omega (\mathbf{x},\mathbf{t})}{\mathrm{\Psi }}_{{\mathbb{k}}^{\prime },{\mathbb{M}}^{\prime }}^{{\alpha }^{\prime }}\left(\mathbf{t}\right)={\left[I_{\mathbf{t}}^{2-\omega (\mathbf{x},\mathbf{t})}{\psi }_1^{{\alpha }^{\prime }}\left(\mathbf{t}\right),I_{\mathbf{t}}^{2-\omega (\mathbf{x},\mathbf{t})}{\psi }_2^{{\alpha }^{\prime }}\left(\mathbf{t}\right),\dots ,I_{\mathbf{t}}^{2-\omega (\mathbf{x},\mathbf{t})}{\psi }_{{\mathbf{M}}^{\prime }}^{{\alpha }^{\prime }}\left(\mathbf{t}\right)\right]}^T,\end{array}$$

$$\begin{array}{c}{I}_{\mathbf{t}}^{2-{\omega }_i(\mathbf{x},\mathbf{t})}{\mathrm{\Psi }}_{{\mathbb{k}}^{\prime },{\mathbb{M}}^{\prime }}^{{\alpha }^{\prime }}\left(\mathbf{t}\right)={\left[I_{\mathbf{t}}^{2-{\omega }_i(\mathbf{x},\mathbf{t})}{\psi }_1^{{\alpha }^{\prime }}\left(\mathbf{t}\right),I_{\mathbf{t}}^{2-{\omega }_i(\mathbf{x},\mathbf{t})}{\psi }_2^{{\alpha }^{\prime }}\left(\mathbf{t}\right),\dots ,I_{\mathbf{t}}^{2-{\omega }_i(\mathbf{x},\mathbf{t})}{\psi }_{{\mathbf{M}}^{\prime }}^{{\alpha }^{\prime }}\left(\mathbf{t}\right)\right]}^T,\end{array}$$

and $D_{\mathbf{t}}^{\omega (\mathbf{x},\mathbf{t})}{s}_i\left(\mathbf{t}\right),D_{\mathbf{t}}^{{\omega }_i(\mathbf{x},\mathbf{t})}{s}_i\left(\mathbf{t}\right);i=0,1,$ are given in Equation (5). From Equation (15) we obtain

$$\begin{array}{ccc}\hfill {\displaystyle \frac{\partial p(\mathbf{x},\mathbf{t})}{\partial \mathbf{t}}}& =& I_{\mathbf{x}}^2{\mathrm{\Psi }}_{\mathbb{k},\mathbb{M}}^{\alpha }{\left(\mathbf{x}\right)}^T·\mathrm{\Delta }·I_{\mathbf{t}}^1{\mathrm{\Psi }}_{{\mathbb{k}}^{\prime },{\mathbb{M}}^{\prime }}^{{\alpha }^{\prime }}\left(\mathbf{t}\right)-\mathbf{x}{I}_{\mathbf{x}}^2{\mathrm{\Psi }}_{\mathbb{k},\mathbb{M}}^{\alpha }{\left(1\right)}^T·\mathrm{\Delta }·I_{\mathbf{t}}^1{\mathrm{\Psi }}_{{\mathbb{k}}^{\prime },{\mathbb{M}}^{\prime }}^{{\alpha }^{\prime }}\left(\mathbf{t}\right)\hfill \\ & +& (1-\mathbf{x})[s_0^{\prime }\left(\mathbf{t}\right)+r_1\left(\mathbf{x}\right)-r_1\left(0\right)]+\mathbf{x}{s}_1^{\prime }\left(\mathbf{t}\right).\hfill \end{array}$$

(18)

By substituting Equations (14)–(18) in Equation (1), we get an algebraic equation. By collocating at $\widehat{\mathbb{M}}·{\widehat{\mathbb{M}}}^{\prime }$ nodes given by

$$(x_i,t_j)=\left({\left({\displaystyle \frac{2i-1}{2\widehat{\mathbb{M}}}}\right)}^{{\displaystyle \frac{1}{\alpha }}},{\left({\displaystyle \frac{2j-1}{2{\widehat{\mathbb{M}}}^{\prime }}}\right)}^{{\displaystyle \frac{1}{{\alpha }^{\prime }}}}\right),i=1,\dots ,\widehat{\mathbb{M}};j=1,\dots ,{\widehat{\mathbb{M}}}^{\prime },$$

we can find the $\widehat{\mathbb{M}}·{\widehat{\mathbb{M}}}^{\prime }$ unknowns $u_{i,j}$.

The following schematic outlines the key steps of the proposed numerical procedure:

FO-FDWE formulation⟶Wavelet-based function approximation⟶Fractional integration via Beta functions⟶Discrete collocation⟶Algebraic system of equations

6. Illustrative Examples

We compare the experimental results obtained by using our method and with known methods, such as shifted Chebyshev cardinal functions [49], Chebyshev wavelets [43], and generalized polynomials [52], in the following examples:

Example 1

(See ([43], Example 1)). Consider the following FO-FDWE:

$$D_t^{\omega (\mathit{x},\mathit{t})}p(\mathit{x},\mathit{t})+D_t^{{\omega }_1(\mathit{x},\mathit{t})}p(\mathit{x},\mathit{t})+p_{\mathit{t}}(\mathit{x},\mathit{t})=p_{\mathbf{xx}}(\mathit{x},\mathit{t})+q(\mathit{x},\mathit{t}),$$

(19)

where $\omega (\mathit{x},\mathit{t})=2-0.3e^{-\mathbf{xt}},{\omega }_1(\mathit{x},\mathit{t})=2-0.6e^{-\mathbf{xt}}$,

$$\begin{array}{ccc}\hfill q(\mathit{x},\mathit{t})& =& 100{\mathit{x}}^{3-a}{\mathit{t}}^3(1-\mathit{x})\left({\displaystyle \frac{6}{\mathrm{\Gamma }(4-\omega (\mathit{x},\mathit{t}\left)\right)}}{\mathit{t}}^{-\omega (\mathit{x},\mathit{t})}-{\displaystyle \frac{24}{\mathrm{\Gamma }(5-\omega (\mathit{x},\mathit{t}\left)\right)}}{\mathit{t}}^{1-\omega (\mathit{x},\mathit{t})}\right)\hfill \\ & +& 100{\mathit{x}}^{3-a}{\mathit{t}}^3(1-\mathit{x})\left({\displaystyle \frac{6}{\mathrm{\Gamma }(4-{\omega }_1(\mathit{x},\mathit{t}))}}{\mathit{t}}^{-{\omega }_1(\mathit{x},\mathit{t})}-{\displaystyle \frac{24}{\mathrm{\Gamma }(5-{\omega }_1(\mathit{x},\mathit{t}))}}{\mathit{t}}^{1-{\omega }_1(\mathit{x},\mathit{t})}\right)\hfill \\ & +& 100{\mathit{x}}^{3-a}(1-\mathit{x})(3{\mathit{t}}^2-4{\mathit{t}}^3)-100{\mathit{t}}^3(1-\mathit{t})((3-a)(2-1){\mathit{x}}^{1-a}-(4-a)(3-a){\mathit{x}}^{2-a}),\hfill \end{array}$$

and the conditions in Equations (2) and (3) are given so that

$$p(\mathit{x},\mathit{t})=100{\mathit{x}}^{3-a}{\mathit{t}}^3(1-\mathit{x})(1-\mathit{t}).$$

This example was considered in [43] with $a=0$. Here, we applied our method with $\mathbb{k}={\mathbb{k}}^{\prime }=1,\mathbb{M}={\mathbb{M}}^{\prime }=2,\mathrm{and}\alpha ={\alpha }^{\prime }=1$. First, we evaluate

$$\begin{array}{c}{\displaystyle \frac{{\partial }^4}{\partial {\mathbf{x}}^2\partial {\mathbf{t}}^2}}p(\mathbf{x},\mathbf{t})\approx {\mathrm{\Psi }}_{\mathbb{k},\mathbb{M}}^{\alpha }{\left(\mathbf{x}\right)}^T·\mathrm{\Delta }·{\mathrm{\Psi }}_{{\mathbb{k}}^{\prime },{\mathbb{M}}^{\prime }}^{{\alpha }^{\prime }}\left(\mathbf{t}\right)\end{array}$$

where

$$\begin{array}{c}{\mathrm{\Psi }}_{\mathbb{k},\mathbb{M}}^{\alpha }\left(\mathbf{x}\right)={\left[{\psi }_1^1\left(\mathbf{x}\right),{\psi }_2^1\left(\mathbf{x}\right),{\psi }_3^1\left(\mathbf{x}\right),{\psi }_4^1\left(\mathbf{x}\right),{\psi }_5^1\left(\mathbf{x}\right),{\psi }_6^1\left(\mathbf{x}\right)\right]}^T,\end{array}$$

$$\begin{array}{c}{\mathrm{\Psi }}_{{\mathbb{k}}^{\prime },{\mathbb{M}}^{\prime }}^{{\alpha }^{\prime }}\left(\mathbf{t}\right)={\left[{\psi }_1^1\left(\mathbf{t}\right),{\psi }_2^1\left(\mathbf{t}\right),{\psi }_3^1\left(\mathbf{t}\right),{\psi }_4^1\left(\mathbf{t}\right),{\psi }_5^1\left(\mathbf{t}\right),{\psi }_6^1\left(\mathbf{t}\right)\right]}^T,\end{array}$$

and

$$\mathrm{\Delta }={\left(u_{i,j}\right)}_{i,j=1,\dots ,6}$$

From Equations (14) and (15) we obtain the following.

$${\displaystyle \frac{{\partial }^2}{\partial {\mathbf{x}}^2}}p(\mathbf{x},\mathbf{t})\approx {\mathrm{\Psi }}_{\mathbb{k},\mathbb{M}}^{\alpha }{\left(\mathbf{x}\right)}^T·\mathrm{\Delta }·I_{\mathbf{t}}^2{\mathrm{\Psi }}_{{\mathbb{k}}^{\prime },{\mathbb{M}}^{\prime }}^{{\alpha }^{\prime }}\left(\mathbf{t}\right),$$

(20)

$$p(\mathbf{x},\mathbf{t})=I_{\mathbf{x}}^2{\mathrm{\Psi }}_{\mathbb{k},\mathbb{M}}^{\alpha }{\left(\mathbf{x}\right)}^T·\mathrm{\Delta }·I_{\mathbf{t}}^2{\mathrm{\Psi }}_{{\mathbb{k}}^{\prime },{\mathbb{M}}^{\prime }}^{{\alpha }^{\prime }}\left(\mathbf{t}\right)-\mathbf{x}{I}_{\mathbf{x}}^2{\mathrm{\Psi }}_{\mathbb{k},\mathbb{M}}^{\alpha }{\left(1\right)}^T·\mathrm{\Delta }·I_{\mathbf{t}}^2{\mathrm{\Psi }}_{{\mathbb{k}}^{\prime },{\mathbb{M}}^{\prime }}^{{\alpha }^{\prime }}\left(\mathbf{t}\right),$$

(21)

where

$$\begin{array}{c}{I}_{\mathbf{x}}^2{\mathrm{\Psi }}_{\mathbb{k},\mathbb{M}}^{\alpha }\left(\mathbf{x}\right)={\left[I_{\mathbf{x}}^2{\psi }_1^1\left(\mathbf{x}\right),I_{\mathbf{x}}^2{\psi }_2^1\left(\mathbf{x}\right),I_{\mathbf{x}}^2{\psi }_3^1\left(\mathbf{x}\right),I_{\mathbf{x}}^2{\psi }_4^1\left(\mathbf{x}\right),I_{\mathbf{x}}^2{\psi }_5^1\left(\mathbf{x}\right),I_{\mathbf{x}}^2{\psi }_6^1\left(\mathbf{x}\right)\right]}^T,\end{array}$$

$$\begin{array}{c}{I}_{\mathbf{t}}^2{\mathrm{\Psi }}_{{\mathbb{k}}^{\prime },{\mathbb{M}}^{\prime }}^{{\alpha }^{\prime }}\left(\mathbf{t}\right)={\left[I_{\mathbf{t}}^2{\psi }_1^1\left(\mathbf{t}\right),I_{\mathbf{t}}^2{\psi }_2^1\left(\mathbf{t}\right),I_{\mathbf{t}}^2{\psi }_3^1\left(\mathbf{t}\right),I_{\mathbf{t}}^2{\psi }_4^1\left(\mathbf{t}\right),I_{\mathbf{t}}^2{\psi }_5^1\left(\mathbf{t}\right),I_{\mathbf{t}}^2{\psi }_6^1\left(\mathbf{t}\right)\right]}^T,\end{array}$$

$$\begin{array}{c}{I}_{\mathbf{x}}^2{\mathrm{\Psi }}_{\mathbb{k},\mathbb{M}}^{\alpha }\left(1\right)={\left[I_{\mathbf{x}}^2{\psi }_1^1\left(1\right),I_{\mathbf{x}}^2{\psi }_2^1\left(1\right),I_{\mathbf{x}}^2{\psi }_3^1\left(1\right),I_{\mathbf{x}}^2{\psi }_4^1\left(1\right),I_{\mathbf{x}}^2{\psi }_5^1\left(1\right),I_{\mathbf{x}}^2{\psi }_6^1\left(1\right)\right]}^T.\end{array}$$

By using Equations (16) and (17) we get

$$\begin{array}{c}{D}_{\mathbf{t}}^{\omega (\mathbf{x},\mathbf{t})}p(\mathbf{x},\mathbf{t})\approx I_{\mathbf{x}}^2{\mathrm{\Psi }}_{\mathbb{k},\mathbb{M}}^{\alpha }{\left(\mathbf{x}\right)}^T·\mathrm{\Delta }·I_{\mathbf{t}}^{2-\omega (\mathbf{x},\mathbf{t})}{\mathrm{\Psi }}_{{\mathbb{k}}^{\prime },{\mathbb{M}}^{\prime }}^{{\alpha }^{\prime }}\left(\mathbf{t}\right)-\mathbf{x}{I}_{\mathbf{x}}^2{\mathrm{\Psi }}_{\mathbb{k},\mathbb{M}}^{\alpha }{\left(1\right)}^T·\mathrm{\Delta }·I_{\mathbf{t}}^{2-\omega (\mathbf{x},\mathbf{t})}{\mathrm{\Psi }}_{{\mathbb{k}}^{\prime },{\mathbb{M}}^{\prime }}^{{\alpha }^{\prime }}\left(\mathbf{t}\right),\end{array}$$

(22)

and

$$\begin{array}{c}{D}_{\mathbf{t}}^{{\omega }_1(\mathbf{x},\mathbf{t})}p(\mathbf{x},\mathbf{t})\approx I_{\mathbf{x}}^2{\mathrm{\Psi }}_{\mathbb{k},\mathbb{M}}^{\alpha }{\left(\mathbf{x}\right)}^T·\mathrm{\Delta }·I_{\mathbf{t}}^{2-{\omega }_1(\mathbf{x},\mathbf{t})}{\mathrm{\Psi }}_{{\mathbb{k}}^{\prime },{\mathbb{M}}^{\prime }}^{{\alpha }^{\prime }}\left(\mathbf{t}\right)-\mathbf{x}{I}_{\mathbf{x}}^2{\mathrm{\Psi }}_{\mathbb{k},\mathbb{M}}^{\alpha }{\left(1\right)}^T·\mathrm{\Delta }·I_{\mathbf{t}}^{2-{\omega }_1(\mathbf{x},\mathbf{t})}{\mathrm{\Psi }}_{{\mathbb{k}}^{\prime },{\mathbb{M}}^{\prime }}^{{\alpha }^{\prime }}\left(\mathbf{t}\right),\end{array}$$

(23)

where

$$\begin{array}{ccc}\hfill I_{\mathbf{t}}^{2-\omega (\mathbf{x},\mathbf{t})}{\mathrm{\Psi }}_{{\mathbb{k}}^{\prime },{\mathbb{M}}^{\prime }}^{{\alpha }^{\prime }}\left(\mathbf{t}\right)& =& {\left[I_{\mathbf{t}}^{2-\omega (\mathbf{x},\mathbf{t})}{\psi }_0^1\left(\mathbf{t}\right),I_{\mathbf{t}}^{2-\omega (\mathbf{x},\mathbf{t})}{\psi }_1^1\left(\mathbf{t}\right),\dots ,I{\mathbf{t}}^{2-\omega (\mathbf{x},\mathbf{t})}{\psi }_6^1\left(\mathbf{t}\right)\right]}^T,\hfill \end{array}$$

and

$$\begin{array}{ccc}\hfill I_{\mathbf{t}}^{2-{\omega }_i(\mathbf{x},\mathbf{t})}{\mathrm{\Psi }}_{{\mathbb{k}}^{\prime },{\mathbb{M}}^{\prime }}^{{\alpha }^{\prime }}\left(\mathbf{t}\right)& =& {\left[I_{\mathbf{t}}^{2-{\omega }_i(\mathbf{x},\mathbf{t})}{\psi }_0^1\left(\mathbf{t}\right),I_{\mathbf{t}}^{2-{\omega }_i(\mathbf{x},\mathbf{t})}{\psi }_1^1\left(\mathbf{t}\right)\dots ,I_{\mathbf{t}}^{2-{\omega }_i(\mathbf{x},\mathbf{t})}{\psi }_6^1\left(\mathbf{t}\right)\right]}^T.\hfill \end{array}$$

From Equation (18) we get

$$p_{\mathbf{t}}(\mathbf{x},\mathbf{t})\approx I_{\mathbf{x}}^2{\mathrm{\Psi }}_{\mathbb{k},\mathbb{M}}^{\alpha }{\left(\mathbf{x}\right)}^T·\mathrm{\Delta }·I_{\mathbf{t}}^1{\mathrm{\Psi }}_{{\mathbb{k}}^{\prime },{\mathbb{M}}^{\prime }}^{{\alpha }^{\prime }}\left(\mathbf{t}\right)-\mathbf{x}{I}_{\mathbf{x}}^2{\mathrm{\Psi }}_{\mathbb{k},\mathbb{M}}^{\alpha }{\left(1\right)}^T·\mathrm{\Delta }·I_{\mathbf{t}}^1{\mathrm{\Psi }}_{{\mathbb{k}}^{\prime },{\mathbb{M}}^{\prime }}^{{\alpha }^{\prime }}\left(\mathbf{t}\right),$$

(24)

where

$$\begin{array}{ccc}\hfill I_{\mathbf{t}}^1{\mathrm{\Psi }}_{{\mathbb{k}}^{\prime },{\mathbb{M}}^{\prime }}^{{\alpha }^{\prime }}\left(\mathbf{t}\right)& =& {\left[I_{\mathbf{t}}^1{\psi }_1^1\left(\mathbf{t}\right),I_{\mathbf{t}}^1{\psi }_2^1\left(\mathbf{t}\right),I_{\mathbf{t}}^1{\psi }_3^1\left(\mathbf{t}\right),I_{\mathbf{t}}^1{\psi }_4^1\left(\mathbf{t}\right),I_{\mathbf{t}}^1{\psi }_5^1\left(\mathbf{t}\right),I_{\mathbf{t}}^1{\psi }_6^1\left(\mathbf{t}\right)\right]}^T.\hfill \end{array}$$

By substituting Equations (20) and (22)–(24) in Equation (19) and collocating the resulted equation at the nodes

$$\begin{array}{c}\left(x_i,y_j\right)=\left({\displaystyle \frac{2i-1}{12}},{\displaystyle \frac{2j-1}{12}}\right),i,j=\overline{1,6},\end{array}$$

a system of 36 algebraic equations in 36 unknowns $u_{i,j}$ is obtained. The solution of the system is presented in the symmetric matrix below:

$$\begin{array}{c}\mathrm{\Delta }={\displaystyle \frac{1}{8}}\left(\begin{array}{cccccc}0& 0& 0& 0& 0& 0\\ 0& 75& 15\sqrt{15}& 0& -75& -135\sqrt{15}\\ 0& 15\sqrt{15}& 45& 0& 15\sqrt{15}& -405\\ 0& 0& 0& 0& 0& 0\\ 0& -75& 15\sqrt{15}& 0& 75& -135\sqrt{15}\\ 0& -135\sqrt{15}& -405& 0& -135\sqrt{15}& 3645\end{array}\right).\end{array}$$

By substituting this solution into Equation (21), we get the exact solution $p(\mathbf{x},\mathbf{t})=100{\mathbf{x}}^3{\mathbf{t}}^3(1-\mathbf{x})(1-\mathbf{t})$. This solution was not obtained in [43].

Example 2

(See ([43], Example 2)). Consider the FO-FDWE

$$D_{\mathit{t}}^{\omega (\mathit{x},\mathit{t})}p(\mathit{x},\mathit{t})+a_1{D}_{\mathit{t}}^{{\omega }_1(\mathit{x},\mathit{t})}p(\mathit{x},\mathit{t})+a_2{D}_{\mathit{t}}^{{\omega }_2(\mathit{x},\mathit{t})}p(\mathit{x},\mathit{t})+p_{\mathit{t}}(\mathit{x},\mathit{t})=b{p}_{\mathbf{xx}}(\mathit{x},\mathit{t})+q(\mathit{x},\mathit{t}),(\mathit{x},\mathit{t})\in {[0,1]}^2,$$

where

$$q(\mathit{x},\mathit{t})=\left[{\displaystyle \frac{6{\mathit{t}}^{-\omega (\mathit{x},\mathit{t})}}{\mathrm{\Gamma }\left[4-\omega (\mathit{x},\mathit{t})\right]}}+{\displaystyle \frac{6a_1{\mathit{t}}^{-{\omega }_1(\mathit{x},\mathit{t})}}{\mathrm{\Gamma }\left[4-{\omega }_1(\mathit{x},\mathit{t})\right]}}+{\displaystyle \frac{6a_2{\mathit{t}}^{-{\omega }_2(\mathit{x},\mathit{t})}}{\mathrm{\Gamma }\left[4-{\omega }_2(\mathit{x},\mathit{t})\right]}}\right]{\mathit{t}}^3{e}^{\mathit{x}}+\left(3-b\mathit{t}\right){\mathit{t}}^2{e}^{\mathit{x}},$$

$\omega (\mathit{x},\mathit{t})=0.3sin\left(\mathbf{xt}\right)+1.7$, ${\omega }_1(\mathit{x},\mathit{t})=0.3sin\left(\mathbf{xt}\right)+1.5$, ${\omega }_2(\mathit{x},\mathit{t})=0.3sin\left(\mathbf{xt}\right)+1.3$, $a_1={\displaystyle \frac{1}{2}},a_2={\displaystyle \frac{1}{3}}$ and $b={\displaystyle \frac{1}{2}}$. The conditions in Equations (2) and (3) are given such that $p(\mathit{x},\mathit{t})={\mathit{t}}^3{e}^{\mathit{x}}$.

First, we solve this problem with $\mathbb{k}={\mathbb{k}}^{\prime }=1,\mathbb{M}={\mathbb{M}}^{\prime }=3$. Table 1 presents the maximum of the relative errors (REs) in various pairs of fractional orders $(\alpha ,{\alpha }^{\prime })$, and the minimal of these errors is reached at $(\alpha ,{\alpha }^{\prime })=(1,{\displaystyle \frac{1}{2}})$. In Table 2, we compare the REs for this method with those in [43]. The comparison is based on the same number of elements in the bases of the function approximation. The table suggests that the present method provides approximate solutions with lower error. In Table 2, M is the degree of Chebyshev polynomials. Figure 1 illustrates the graphs of the approximated solution and the absolute error function (AEF) for $\mathbb{k}={\mathbb{k}}^{\prime }=1,\mathbb{M}={\mathbb{M}}^{\prime }=9,\mathrm{and}\alpha =1,{\alpha }^{\prime }={\displaystyle \frac{1}{2}}$. Here, the relative errors (REs) and absolute error function (AEF) are defined by

$$\begin{array}{cc}\hfill \mathrm{REs}& =\left|{\displaystyle \frac{\mathrm{Numerical}\mathrm{solution}-\mathrm{Exact}\mathrm{solution}}{\mathrm{Exact}\mathrm{solution}}}\right|,\mathrm{and}\hfill \\ \hfill \mathrm{AEF}& =\left|\mathrm{Numerical}\mathrm{solution}-\mathrm{Exact}\mathrm{solution}\right|.\hfill \end{array}$$

Table 1. The relative errors for Example 2 with $\mathbb{k}={\mathbb{k}}^{\prime }=1,\mathbb{M}={\mathbb{M}}^{\prime }=3$ and various values of $\alpha ,{\alpha }^{\prime }$.

	${\mathit{\alpha }}^{\prime }$	$1/5$	$1/4$	$1/3$	$1/2$	1
${\mathit{\alpha }}^{\prime }$
$1/5$		$1.68841·{10}^{-4}$	$1.68718·{10}^{-4}$	$1.68488·{10}^{-4}$	$1.6842·{10}^{-4}$	$1.68621·{10}^{-4}$
$1/4$		$6.77442·{10}^{-5}$	$6.76307·{10}^{-5}$	$6.75261·{10}^{-5}$	$6.7548·{10}^{-5}$	$6.7544·{10}^{-5}$
$1/3$		$1.5636·{10}^{-4}$	$3.34059·{10}^{-4}$	$1.77233·{10}^{-5}$	$1.77229·{10}^{-5}$	$1.77255·{10}^{-5}$
$1/2$		$1.48302·{10}^{-4}$	$2.73862·{10}^{-5}$	$5.98422·{10}^{-6}$	$5.96328·{10}^{-6}$	$5.99829·{10}^{-6}$
$\mathbf{1}$		$2.84523·{10}^{-5}$	$9.24415·{10}^{-4}$	$1.59389·{10}^{-7}$	$\mathbf{1.59301}·{\mathbf{10}}^{-\mathbf{7}}$	$1.78903·{10}^{-7}$

Table 2. The relative errors for Example 2 with $\alpha =1,{\alpha }^{\prime }={\displaystyle \frac{1}{2}},\mathbb{k}={\mathbb{k}}^{\prime }=1$ and various values of $\mathbb{M}={\mathbb{M}}^{\prime }$ in comparison with the method in [43].

$(\mathit{x},\mathit{t})$	Method in [43]			Present Method with $\mathbb{M}={\mathbb{M}}^{\prime }$
	$\mathbf{M}=\mathbf{4}$	$\mathbf{M}=\mathbf{5}$	$\mathbf{M}=\mathbf{6}$	$\mathbb{M}=\mathbf{3}$	$\mathbb{M}=\mathbf{4}$	$\mathbb{M}=\mathbf{5}$
$(0.1,0.1)$	$4.23·{10}^{-4}$	$1.83·{10}^{-5}$	$2.17·{10}^{-7}$	$1.60·{10}^{-8}$	$2.96·{10}^{-10}$	$4.11·{10}^{-12}$
$(0.2,0.2)$	$4.21·{10}^{-5}$	$1.55·{10}^{-6}$	$5.86·{10}^{-9}$	$2.10·{10}^{-9}$	$1.15·{10}^{-10}$	$5.44·{10}^{-13}$
$(0.3,0.3)$	$1.17·{10}^{-5}$	$6.19·{10}^{-7}$	$1.26·{10}^{-9}$	$1.32·{10}^{-9}$	$7.82·{10}^{-11}$	$1.01·{10}^{-12}$
$(0.4,0.4)$	$6.28·{10}^{-6}$	$1.60·{10}^{-7}$	$8.87·{10}^{-9}$	$1.26·{10}^{-8}$	$4.09·{10}^{-10}$	$1.30·{10}^{-11}$
$(0.5,0.5)$	$2.96·{10}^{-5}$	$1.56·{10}^{-7}$	$9.92·{10}^{-10}$	$1.09·{10}^{-7}$	$6.54·{10}^{-10}$	$8.09·{10}^{-11}$
$(0.6,0.6)$	$1.90·{10}^{-5}$	$1.64·{10}^{-7}$	$1.19·{10}^{-8}$	$2.24·{10}^{-8}$	$1.36·{10}^{-10}$	$2.28·{10}^{-11}$
$(0.7,0.7)$	$1.77·{10}^{-5}$	$3.54·{10}^{-7}$	$1.51·{10}^{-9}$	$1.02·{10}^{-8}$	$1.42·{10}^{-10}$	$9.83·{10}^{-12}$
$(0.8,0.8)$	$1.87·{10}^{-5}$	$3.70·{10}^{-7}$	$2.99·{10}^{-9}$	$2.29·{10}^{-10}$	$1.05·{10}^{-11}$	$2.93·{10}^{-12}$
$(0.9,0.9)$	$1.68·{10}^{-5}$	$2.68·{10}^{-7}$	$1.61·{10}^{-8}$	$1.23·{10}^{-8}$	$3.12·{10}^{-10}$	$3.69·{10}^{-12}$

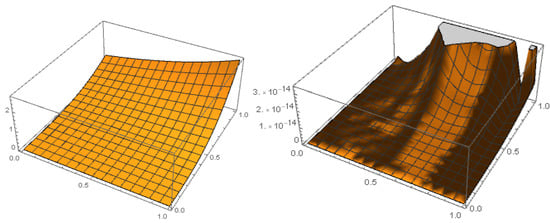
Figure 1. The graphs of the approximated solution (left) and the AEF (right) in Example 2 with $\mathbb{k}={\mathbb{k}}^{\prime }=1,\mathbb{M}={\mathbb{M}}^{\prime }=8,\alpha =1,{\alpha }^{\prime }={\displaystyle \frac{1}{2}}$.

Example 3

(See ([43], Example 4)). Consider the nonlinear FO-FDWE

$$D_{\mathit{t}}^{\omega (\mathit{x},\mathit{t})}p(\mathit{x},\mathit{t})+\sum _{i=1}^4{a}_i{D}_{\mathit{t}}^{{\omega }_i(\mathit{x},\mathit{t})}p(\mathit{x},\mathit{t})+u_{\mathit{t}}(\mathit{x},\mathit{t})=b{p}_{\mathbf{xx}}(\mathit{x},\mathit{t})+q(\mathit{x},\mathit{t}),(\mathit{x},\mathit{t})\in {[0,1]}^2,$$

where

$$\begin{array}{c}q(\mathit{x},\mathit{t})=\left({\displaystyle \frac{6{\mathit{t}}^{-\omega (\mathit{x},\mathit{t})}}{\mathrm{\Gamma }(4-\omega (\mathit{x},\mathit{t}\left)\right)}}+\sum _{i=1}^4{a}_i{\displaystyle \frac{6{\mathit{t}}^{-{\omega }_i(\mathit{x},\mathit{t})}}{\mathrm{\Gamma }(4-{\omega }_i(\mathit{x},\mathit{t}))}}\right){\mathit{t}}^{3}sin\left(\pi \mathit{x}\right)+(3+a{\pi }^2\mathit{t}){\mathit{t}}^{2}sin\left(\pi \mathit{x}\right),\end{array}$$

$\omega (\mathit{x},\mathit{t})=2-0.3e^{-\mathit{xt}};{\omega }_i(\mathit{x},\mathit{t})=2-{\displaystyle \frac{i+3}{10}}{e}^{-\mathit{xt}},a_i={\displaystyle \frac{1}{i+1}},i=1,\dots ,4;$ and $b={\displaystyle \frac{1}{3}}$. The conditions in Equations (2) and (3) are given such that $p(\mathit{x},\mathit{t})={\mathit{t}}^{3}sin\left(\pi \mathit{x}\right)$.

Table 3 provides the maximal AEs of the approximated solutions using our method in the case $\mathbb{k}={\mathbb{k}}^{\prime }=1,\mathbb{M}={\mathbb{M}}^{\prime }=3$ and various pairs of fractional orders $(\alpha ,{\alpha }^{\prime })$. The table shows that the minimum occurred at $(\alpha ,{\alpha }^{\prime })=(1.25,0.5)$. Figure 2 shows the graph of the solution and AEF in cases $\mathbb{k}={\mathbb{k}}^{\prime }=1,\mathbb{M}={\mathbb{M}}^{\prime }=8$ and $\alpha =1.25,{\alpha }^{\prime }=0.5$. Table 4 and Table 5 compare the REs of numerical solutions using our method with the method in [43] with different values of $\mathbb{M}={\mathbb{M}}^{\prime }$. These tables indicate that the present method yields more accurate solutions with fewer errors.

Table 3. The AEF of the numerical solution for Example 3 with $\mathbb{k}={\mathbb{k}}^{\prime }=1$, $\mathbb{M}={\mathbb{M}}^{\prime }=3$ and various values of $\alpha ,{\alpha }^{\prime }$.

	${\mathit{\alpha }}^{\prime }$	$0.25$	$0.5$	$0.75$	1	$1.25$	$1.5$
${\mathit{\alpha }}^{\prime }$
$0.25$		$2.43·{10}^{-3}$	$2.39·{10}^{-3}$	$2.45·{10}^{-3}$	$2.39·{10}^{-3}$	$1.79·{10}^{-3}$	$2.32·{10}^{-3}$
$0.5$		$4.23·{10}^{-4}$	$4.18·{10}^{-4}$	$4.29·{10}^{-4}$	$4.18·{10}^{-4}$	$6.44·{10}^{-4}$	$1.89·{10}^{-3}$
$0.75$		$6.83·{10}^{-5}$	$7.12·{10}^{-5}$	$2.32·{10}^{-4}$	$7.12·{10}^{-5}$	$4.62·{10}^{-4}$	$1.91·{10}^{-3}$
1		$2.27·{10}^{-5}$	$9.91·{10}^{-5}$	$1.64·{10}^{-4}$	$9.91·{10}^{-5}$	$9.91·{10}^{-5}$	$4.08·{10}^{-4}$
$1.25$		$4.29·{10}^{-5}$	$1.28·{10}^{-5}$	$6.62·{10}^{-5}$	$1.28·{10}^{-5}$	$4.52·{10}^{-4}$	$1.90·{10}^{-3}$
$1.5$		$1.14·{10}^{-4}$	$1.22·{10}^{-4}$	$6.68·{10}^{-5}$	$1.22·{10}^{-4}$	$5.41·{10}^{-4}$	$1.92·{10}^{-3}$
2		$2.11·{10}^{-4}$	$2.37·{10}^{-4}$	$9.48·{10}^{-3}$	$2.37·{10}^{-4}$	$9.64·{10}^{-3}$	$1.01·{10}^{-2}$

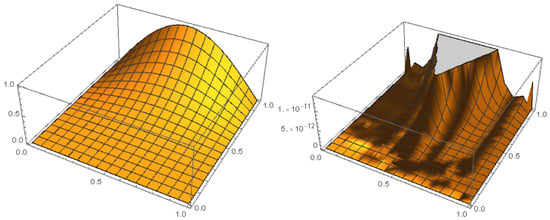
Figure 2. The graph of the numerical solution (left) and the AEF (right) in Example 3 with $\mathbb{k}={\mathbb{k}}^{\prime }=1,\mathbb{M}={\mathbb{M}}^{\prime }=8,\mathrm{and}\alpha =1.25,{\alpha }^{\prime }=0.5$.

Table 4. The REs of the approximated solution for Example 3 with $\mathbb{k}={\mathbb{k}}^{\prime }=1$, $\alpha =1.25$, ${\alpha }^{\prime }=0.5$ and different values of $\mathbb{M}={\mathbb{M}}^{\prime }$ in comparison with the method in [43].

$(\mathit{x},\mathit{t})$	Method in [43]			Present Method
	$\mathbf{M}=\mathbf{4}$	$\mathbf{M}=\mathbf{5}$	$\mathbf{M}=\mathbf{6}$	$\mathbb{M}=\mathbf{3}$	$\mathbb{M}=\mathbf{4}$	$\mathbb{M}=\mathbf{5}$
$(0.1,0.1)$	$1.04·{10}^2$	$5.47·{10}^0$	$2.78·{10}^{-1}$	$8.48·{10}^{-5}$	$8.36·{10}^{-6}$	$2.06·{10}^{-5}$
$(0.2,0.2)$	$6.67·{10}^0$	$6.47·{10}^{-1}$	$1.21·{10}^{-2}$	$6.46·{10}^{-5}$	$1.68·{10}^{-5}$	$1.64·{10}^{-6}$
$(0.3,0.3)$	$2.46·{10}^{-1}$	$3.77·{10}^{-2}$	$7.82·{10}^{-3}$	$7.22·{10}^{-6}$	$3.72·{10}^{-6}$	$2.26·{10}^{-7}$
$(0.4,0.4)$	$5.08·{10}^{-1}$	$3.78·{10}^{-2}$	$7.55·{10}^{-4}$	$7.77·{10}^{-7}$	$8.31·{10}^{-7}$	$5.27·{10}^{-7}$
$(0.5,0.5)$	$2.15·{10}^{-1}$	$2.54·{10}^{-2}$	$1.16·{10}^{-3}$	$4.03·{10}^{-7}$	$4.09·{10}^{-6}$	$6.84·{10}^{-7}$
$(0.6,0.6)$	$7.66·{10}^{-2}$	$9.81·{10}^{-3}$	$6.70·{10}^{-4}$	$7.92·{10}^{-6}$	$1.18·{10}^{-5}$	$2.27·{10}^{-6}$
$(0.7,0.7)$	$1.80·{10}^{-2}$	$2.63·{10}^{-3}$	$2.30·{10}^{-5}$	$3.29·{10}^{-6}$	$3.82·{10}^{-6}$	$2.11·{10}^{-6}$
$(0.8,0.8)$	$2.77·{10}^{-2}$	$3.97·{10}^{-3}$	$1.28·{10}^{-4}$	$3.48·{10}^{-6}$	$1.49·{10}^{-6}$	$7.80·{10}^{-7}$
$(0.9,0.9)$	$2.30·{10}^{-3}$	$1.96·{10}^{-3}$	$8.83·{10}^{-6}$	$2.67·{10}^{-7}$	$1.25·{10}^{-6}$	$3.81·{10}^{-7}$

Table 5. The REs of the numerical solution for Example 3 with $\mathbb{k}={\mathbb{k}}^{\prime }=1$, $\alpha =1.25$, ${\alpha }^{\prime }=0.5$ and several values of $\mathbb{M}={\mathbb{M}}^{\prime }$ in comparison with the result in [43].

$(\mathit{x},\mathit{t})$	Method in [43]			Present Method
	$\mathbf{M}=\mathbf{7}$	$\mathbf{M}=\mathbf{8}$	$\mathbf{M}=\mathbf{9}$	$\mathbb{M}=\mathbf{6}$	$\mathbb{M}=\mathbf{7}$	$\mathbb{M}=\mathbf{8}$
$(0.1,0.1)$	$4.31·{10}^{-1}$	$1.06·{10}^{-2}$	$1.01·{10}^{-3}$	$1.52·{10}^{-5}$	$9.19·{10}^{-6}$	$5.12·{10}^{-6}$
$(0.2,0.2)$	$4.05·{10}^{-2}$	$6.75·{10}^{-4}$	$1.63·{10}^{-4}$	$4.47·{10}^{-7}$	$2.83·{10}^{-7}$	$6.33·{10}^{-8}$
$(0.3,0.3)$	$2.49·{10}^{-3}$	$6.85·{10}^{-5}$	$1.22·{10}^{-6}$	$2.33·{10}^{-7}$	$7.04·{10}^{-9}$	$1.79·{10}^{-8}$
$(0.4,0.4)$	$5.56·{10}^{-5}$	$5.13·{10}^{-6}$	$2.60·{10}^{-7}$	$3.00·{10}^{-8}$	$1.45·{10}^{-8}$	$9.05·{10}^{-9}$
$(0.5,0.5)$	$3.01·{10}^{-5}$	$1.46·{10}^{-5}$	$3.03·{10}^{-6}$	$6.49·{10}^{-7}$	$5.48·{10}^{-7}$	$4.32·{10}^{-7}$
$(0.6,0.6)$	$2.32·{10}^{-6}$	$3.41·{10}^{-7}$	$4.76·{10}^{-7}$	$3.67·{10}^{-6}$	$4.47·{10}^{-7}$	$1.55·{10}^{-7}$
$(0.7,0.7)$	$1.97·{10}^{-4}$	$9.78·{10}^{-7}$	$2.20·{10}^{-7}$	$1.23·{10}^{-6}$	$7.69·{10}^{-7}$	$5.13·{10}^{-7}$
$(0.8,0.8)$	$8.60·{10}^{-5}$	$3.36·{10}^{-7}$	$2.82·{10}^{-7}$	$4.57·{10}^{-7}$	$2.84·{10}^{-7}$	$1.89·{10}^{-7}$
$(0.9,0.9)$	$4.18·{10}^{-6}$	$3.26·{10}^{-7}$	$6.94·{10}^{-7}$	$2.13·{10}^{-7}$	$1.31·{10}^{-7}$	$8.63·{10}^{-8}$

Example 4.

In particle physics, anomalous diffusion processes were formulated in terms of diffusion equations by using fractional derivatives and distributed-order derivatives in [53]. As a generalization, we consider the following diffusion equation with variable-order derivative:

$$\begin{array}{c}{D}_{\mathit{t}}^{\omega (\mathit{x},\mathit{t})}Q(\mathit{x},\mathit{t})=\nu {\displaystyle \frac{{\partial }^{2}Q(\mathit{x},\mathit{t})}{\partial {\mathit{x}}^2}}\end{array}$$

(25)

where $(\mathit{x},\mathit{t})\in (-\infty ,+\infty )\times (0,+\infty )$, $Q(\mathit{x},\mathit{t})$ is the pdf (probability density function) of the diffusion process, and ν is the diffusion coefficient of physical dimension (cm²/sec). Following [53], we consider the following diffusion equation:

$$\begin{array}{cc}\hfill & Q(\mathit{x},0)=\underset{\mathit{t}\to 0}{lim}Q(\mathit{x},\mathit{t})=1,\hfill \end{array}$$

(26)

$$\begin{array}{cc}\hfill & Q(\pm \infty ,\mathit{t})=0.\hfill \end{array}$$

(27)

We scale the problem to finite intervals by setting

$$\begin{array}{c}\mathit{x}=ln\left({\displaystyle \frac{\mathit{z}}{1-\mathit{z}}}\right),\mathit{or}\mathit{equivalently}\mathit{z}={\displaystyle \frac{1}{1+e^{-\mathit{x}}}}.\end{array}$$

(28)

Then $\mathit{z}\in (0,1)$ and Equations (25)–(27) become

$$\begin{array}{cc}\hfill & D_{\mathit{t}}^{\omega (\mathit{x},\mathit{t})}Q(\mathit{z},\mathit{t})=\nu {\displaystyle \frac{\partial Q(\mathit{z},\mathit{t})}{\partial \mathit{x}}}\mathit{z}(1-\mathit{z})(1-2\mathit{z})+\nu {\displaystyle \frac{{\partial }^{2}Q(\mathit{z},\mathit{t})}{\partial {\mathit{x}}^2}}{\mathit{z}}^2{(1-\mathit{z})}^2\hfill \\ \hfill & Q(1,\mathit{t})=0,Q(0,\mathit{t})=0,Q(\mathit{z},0)=\underset{\mathit{t}\to 0}{lim}Q(\mathit{z},\mathit{t})=1,\hfill \end{array}$$

(29)

where

$$\begin{array}{c}p(\mathit{z},\mathit{t})=Q(\mathit{z},\mathit{t})=Q\left(ln(\mathit{z}/(1-\mathit{z})),\mathit{t}\right).\end{array}$$

(30)

Following [53], we consider this equation with $\nu ={\displaystyle \frac{1}{2}}$. In addition, we use $k_1=k_2=1$, $({\alpha }_1,{\alpha }_2)=(1,0.5)$ and different values of $\mathbb{M}={\mathbb{M}}^{\prime }$. The numerical solution is illustrated in Figure 3. Table 6 reports the maximum residual errors along with the convergence order (CO). Here, for each numerical solution $\tilde{u}$, the maximal residual error is

$$\mathrm{MaxRE}=\underset{(\mathbf{z},\mathbf{t})\in {[0,1]}^2}{max}\left|D_{\mathbf{t}}^{\omega (\mathbf{x},\mathbf{t})}\tilde{p}(\mathbf{z},\mathbf{t})-\nu {\displaystyle \frac{\partial \tilde{p}(\mathbf{z},\mathbf{t})}{\partial \mathbf{x}}}\mathbf{z}(1-\mathbf{z})(1-2\mathbf{z})-\nu {\displaystyle \frac{{\partial }^2\tilde{p}(\mathbf{z},\mathbf{t})}{\partial {\mathbf{z}}^2}}{\mathbf{z}}^2{(1-\mathbf{z})}^2\right|.$$

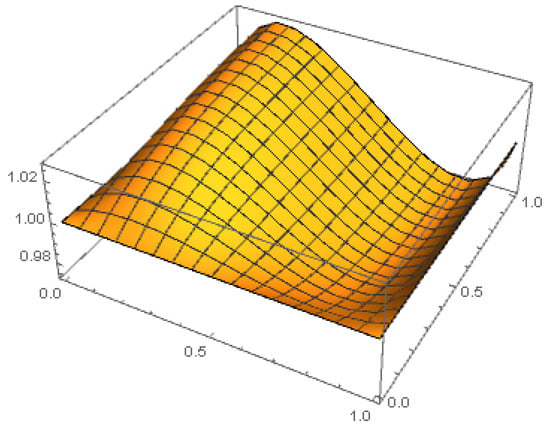
Figure 3. The numerical solution of Example 4 with $\nu ={\displaystyle \frac{1}{2}},k_1=k_2=1$, $({\alpha }_1,{\alpha }_2)=(1,0.5)$ and $\mathbb{M}={\mathbb{M}}^{\prime }$.

Table 6. The maximal residual errors for Example 4 with $k_1=k_2=1$, $\mathbb{M}={\mathbb{M}}^{\prime }$, and $({\alpha }_1,{\alpha }_2)=(1,0.5)$.

$\mathbb{M}={\mathbb{M}}^{\prime }$	MaxRE	CO
1	$1.47·{10}^{-3}$	−
2	$3.14·{10}^{-3}$	$1.119$
3	$2.04·{10}^{-3}$	$1.202$
4	$5.33·{10}^{-3}$	$1.004$
5	$7.27·{10}^{-3}$	$1.257$

7. Conclusions

This research presented a spectral method based on generalized Chelyshkov wavelets of fractional order for addressing functional-order fractional diffusion–wave equations. The technique demonstrates clear strengths in terms of computational efficiency and numerical accuracy, particularly when applied to two-dimensional partial differential equations involving variable-order or fractional derivatives. A key advantage lies in the derivation of exact analytical formulas for the functional-order Riemann–Liouville integrals corresponding to the chosen basis functions, which significantly improves both precision and stability. Moreover, the incorporation of a tunable parameter $\alpha$ into the wavelet construction enables flexible and effective control of approximation errors. Nevertheless, the method shares a common constraint found in many spectral techniques—namely, the increased computational demand as the number of basis elements grows, especially in problems with higher dimensionality.

Future investigations will aim to generalize this framework to broader categories of fractional partial differential equations with variable orders, including multidimensional domains and nonlinear systems. Emphasis will be placed on practical applications in physics and engineering where anomalous diffusion and memory-dependent dynamics are essential. To enhance scalability and performance, future efforts will explore adaptive refinement procedures and efficient solvers that preserve accuracy while reducing computational overhead.