Abstract
We numerically construct compact stars in the scalar–tensor theory of gravity with non-minimal derivative coupling of a scalar field to the curvature and nonzero cosmological constant. There are two free parameters in this model of gravity: the non-minimal derivative coupling parameter ℓ and the cosmological constant parameter . We study the relationship between the model parameters and characteristic of the neutron star, which allowed us to limit the permissible range of and ℓ. In particular, in the case , the external geometry of the neutron star coincides with the Schwarzschild–anti-de Sitter geometry, while the internal geometry of the star differs from the case of the standard gravity theory. Many realistic equations of the state of neutron star matter were considered. In general, the neutron star model in the theory of gravity with a non-minimal derivative coupling does not contradict astronomical data and is viable.
1. Introduction
1.1. Mass and Radius of a Neutron Star
The concept of neutron stars was suggested by Baade and Zwicky in 1932 [1] and was discovered many years later in 1967 as rapidly rotating stars with strong magnetic fields, now known as pulsars [2]. Since the discovery of neutron stars, methods for observing them have been improved, and knowledge about their nature has changed. Detailed reviews of the neutron stars can be found in [3,4,5,6,7,8,9].
Neutron stars belong to the class of compact stars, as the white Little Persons and quark stars [10], which are so far undetected. It is generally accepted that a canonical neutron star has a mass and radius km. The density at the center of a neutron star can exceed the nuclear saturation density by 5–10 times. The nature of such matter is still not clear, and there are various models to describe it. The structure of a neutron star is described by the Tolman–Oppenheimer–Volkoff equations [11,12]. The Tolman–Oppenheimer–Volkoff equations connect such macroscopic parameters of a star as mass and radius with microphysics, which is described by the equation of the state of super-dense matter.
Twenty years ago, estimates of the mass of radio pulsars showed a narrow distribution interval of about [13]. Thanks to more recent studies [14,15,16], we know now that neutron star masses span a wide range, between 1.2 and at least 2 . Evidence for neutron stars with more than two and almost three solar masses was found. The most massive neutron stars presently known in light of recent findings can be found in [17]. It is generally accepted that the radius of a neutron star takes values in the range 10–14 km [14]. For example, in the work [18], one finds that the radius of a neutron star is km (90% credible interval).
1.2. Neutron Stars in Modified Theory of Gravity
Today, modified theories of gravity have attracted significant attention. Modifications are often introduced to build cosmological models and explain phenomena in the universe on large scales, including dark matter or the accelerated expansion of the universe. Reviews on modified theories of gravity, including the motivations to consider extensions of general relativity, can be found in [19,20,21,22,23,24].
In context of the modification of general relativity, one needs to consider not only cosmological problems but stellar structures too. Due to the fact that neutron stars have a very strong gravitational field and are composed of super-dense matter, they provide information about both the theory of gravity and nuclear interactions that we cannot obtain from laboratory tests. Observations of neutron stars offer opportunities for measuring the effects of general relativity, as well as testing its modifications. Neutron star solutions have been constructed in various alternative theories of gravity [25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41]. For a recent review of compact star models in modified theories of gravity, see [42,43,44,45] and the references therein.
1.3. Neutron Stars in the Theory of Gravity with Non-Minimal Derivative Coupling
Horndeski’s theory [46,47,48] is the most general scalar–tensor theory of gravity having second-order field equations in four dimensions. There are four arbitrary functions in the theory. By taking these functions appropriately, one can reproduce any second-order scalar–tensor theory as a specific case, including quintessence and k-essence, gravity, Brans–Dicke theory, Einstein–dilaton–Gauss–Bonnet gravity, etc. Both cosmological and astrophysical aspects (including neutron stars) of Horndeski’s theory have been widely studied (for a review, see [49] and the references therein).
The interesting subclass of Horndeski’s gravity is the theory of gravity with non-minimal derivative coupling of a scalar field with the Einstein tensor with the action
where is the action for ordinary matter fields, which is supposed to be minimally coupled to gravity in the usual way. The real parameter corresponds to the usual kinetic term of the scalar field , while determines the modified part of the kinetic term. The theory (1) has very interesting cosmological properties [50,51,52,53,54], admitting black hole [55,56,57,58,59,60,61] and wormhole [62,63] solutions.
Black hole solutions in Horndeski’s theory were intensively considered in the literature. In 2013, Hui and Nicolis [55] have proved a no-hair theorem (with the no-hair meaning a trivial scalar field solution in this case) for shift-symmetric Horndeski gravity, i.e., the subclass of the Horndeski action which remains invariant under a transformation of the scalar field. The theorem is applicable to vacuum, static, spherically symmetric and asymptotically flat black holes. In this case, it is proved that the scalar field of the black hole solution must be constant, and by exploiting the shift symmetry, we can set its value to zero. Consequently, black holes cannot sustain non-trivial scalar field profiles in this case. However, hairy solutions can be obtained by violating some of the assumptions that enter the proof of the no-hair theorem. In particular, for the non-minimal derivative coupling theory, we found hairy solutions with [59]. Among the solutions constructed in this way, the non-minimally coupled theory with admits a “stealth” solution, where a Schwarzschild black hole metric supports a non-trivial, regular scalar field configuration which does not backreact in spacetime. Non-trivial scalar fields are also possible in the case of non-asymptotically flat black hole solutions [56,57,58]. In paper [56], a solution was found that describes black holes in the special case . This solution was later generalized to the arbitrary case . Black hole solutions with AdS asymptotics were also obtained [59], where the effective cosmological constant is given by geometric coupling constants in the action.
Neutron stars in the theory of gravity with non-minimal derivative coupling have also been widely explored [64,65,66,67,68]. An overview of solutions describing neutron stars can be found in the literature [67,69]. In work [69], a no-hair theorem was presented for the spherically symmetric and static star configurations in shift-symmetric Horndeski theories with minimal matter coupling. It was noted [69] that the regular spherically symmetric and static solution with an asymptotically flat spacetime in the shift-symmetric Horndeski theory with a minimally coupled matter sector with the action that is analytic around a trivial scalar field configuration has a constant scalar field and, in particular, star solutions are identical to their general relativity counterpart. However, there is possibilities to escape the assumption of the no-hair theorem and consider neutron stars in the asymptotically de Sitter universe, with a time-dependent scalar field, etc. [64,65,66].
Spherically symmetric neutron star solutions in the theory (1) with with a scalar field are linear in times . Moreover, a usual equation for the matter fluid with a polytrope equation of state was constructed in [64]; in this case, the external geometry is identical to the Schwarzschild metric, but the interior structure is considerably different from standard general relativity. Subsequently, this solution was generalized. Slowly rotating stars were considered in the theory with using several realistic equations of state [65,66].
Previously, we construct neutron star configurations with AdS asymptotics within the framework of the full theory (1) without imposing any restrictions on the parameters and [70]. However, the previous work considered the simplest polytrope equation of state. Now, our goal is to explore neutron star configurations in the full theory (1) and the realistic equation of the state of neutron star matter. This paper is organized as follows. In Section 2, we derive general equations describing an internal configuration of a neutron star in the theory of gravity with non-minimal derivative coupling. The external vacuum solution is presented in Section 3. Section 4 describes the numerical integration scheme and presents the main results describing the parameters of neutron stars for a set of realistic equations of state.
2. Basic Equations
2.1. Action and Field Equations
In this section, we will present the basic equations. We will use the notation of our previous work [70]. A detailed calculation can be found in the mentioned article. Here, we will briefly present the equations in a form convenient for numerical integration. A gravitational theory (1) can be represented as
where ℓ is a characteristic length characterizing the non-minimal derivative coupling between the scalar field and curvature, and . We will consider matter in the form of a perfect fluid with the stress–energy tensor
where is a unit time-like 4-vector, , is energy density, and p is isotropic pressure. The spacetime of a neutron star we will describe by the static spherically symmetric metric is as follows:
Assuming also that , , and , we can write down nonzero independent components of the gravitational field equations and scalar field equations in the following form [70]:
where ,
and dimensionless values
Equations (5) and (8) of the system contain the denominator . In the case where , this value can decrease to zero. Therefore, the solution of (5)–(8) will be divergent. Subsequently, in order to provide a regularity of solutions, we will consider a choice . The choice means that and have different signs, and the usual kinetic term and the modified term enter into the Lagrangian (1) with different signs. Despite this, the sign in (8) is still undefined. can be obtained from the requirement of the positivity of , from which it follows that condition must be satisfied.
2.2. Equation of State
To make the system of four field Equations (5)–(8) complete, one needs to add an equation of state relating the pressure and the energy density. In this work, we will use polytropic and 31 realistic equations of state.
2.2.1. Polytropic Equation of State
In the previous work [70], we considered the polytropic equation of state to construct neutron stars in the model (2)
where is baryonic mass density, is the adiabatic index, and K is the polytropic constant. In particular, we used and cgs. This equation of state is widely used to model neutron star configurations, it is used in general relativity [5,71] and it is used in various modified theories of gravity [29,36,37,38,39,40,41], including Horndeski’s theory [64,66,67,68]. However, Equation (10) is the simplest model equation of state which is not able to describe the whole complexity of the neutron star structure. For this reason, in the present work, we will consider a set of more realistic (though still model) equations of state.
2.2.2. Realistic Equation of State
It is generally accepted that the equation of state has a one-parameter character. Many equations of state have been proposed by considering different kinds of interactions into account. Equations of state are usually given in the form of tables. However, using the table is not always convenient, especially for considering the modified theory of gravity. In some cases, it is convenient to use a piecewise polytropic approach [72,73] or an analytical representations of equation of state [74,75,76,77]. Here, we use the analytical representations of 31 unified equations of state, presented in the works [74,75,76,77]. A standard abbreviation is used for equations of state; detailed references can be found, for example, in review [78].
The equation of state can be represented as a function of density from pressure, i.e., . Analytical representations of FPS (Friedman–Pandharipande–Skyrme) and SLy (Skyrme–Lyon) equations of state [79,80] are derived in the work [74]. The parametrization reads
where
and -given constants [74]. Here, represents full energy density, including the rest energies of the matter constituents divided by , i.e., . Function fits the original tables [79,80] in density from to within a typical error of 1–2%. In the dimensionless form, we have
We also use unified Brussels–Montreal–Skyrme equations of state in our work, labeled BSk19, BSk20, and BSk21 [81,82] and BSk22, BSk24, BSk25, and BSk26 [76]. At the much higher densities, they differ greatly in their stiffness. It was argued that the real equation of state can probably not be much stiffer than BSk26, and certainly not much softer than BSk22, BSk24 or BSk25. Analytic parametrization of reads [76,77]
which fits the numerical tables [81,82] for with a typical error of 1%. Equations (11) and (14) differ in the numbering of parameters and numerical value of .
In the work [75], an analytical unified representation for 22 equations of state of dense matter in neutron stars was presented: AP1–4, engvik, gm1nph, gm2nph, gm3nph, mpa1, ms00, ms2, ms1506, pal2, pclnphq, wff1, wff2, wff3, wff4, schaf1, schaf2, prakdat, ps. The function is
where
describe the low- and high-density regimes, respectively; the values of the fit parameters and for are given in the tables [75].
Some equations of state becomes superluminal above critical density , i.e., the speed of sound v
which is larger than the speed of light c, with representing causality limits. For example, in the case of BSk24, the equation of state . Apparently, in the case , the equation of state does not give a complete description and causality breaks down, as was discussed in [77].
2.3. Boundary Conditions
Equations (5)–(7) form a closed system of ordinary differential equations for functions , and , where the pressure and the energy are related by the equation of state . The scalar field can be found using Equation (8). Boundary conditions are usually determined at the center of a star
where is the central pressure, and the value of will be fixed after matching internal and external solutions at the star boundary. Therefore, the only free parameter is the value of the pressure in the center of the star, .
3. External Vacuum Solution
At the boundary of the star, the internal solution is continuously matched to the external vacuum solution. In this section, we briefly discuss the vacuum solution. Vacuum solution ( and ) of the system (5)–(7) has the form
where
and and are constants of integration. The asymptotical behavior of and at has the following form:
and corresponds to anti-de Sitter–Schwarzschild spacetime geometry outside the star. In the case where t is the time of a distant observer, the constant before the bracket in Equation (24) must be equal to , which allows us to determine the value of . The metric functions and must have the same sign. Therefore, constant is positive, or
Substituting the constants of integration and using the dimensional radial coordinate , we obtain the following asymptotic behavior:
where
and
Here, we would like to emphasize that the condition (26) provides the negativity of given by (29). Therefore, is an effective negative cosmological constant, and the vacuum solution (27) corresponds asymptotically to the anti-de Sitter–Schwarzschild spacetime. (Static spherically symmetric vacuum solutions were obtained and are considered in detail in refs. [56,57,58,59,60,61,70].) Equation (28) gives the so-called asymptotic mass of the neutron star. Constant is found from the condition of continuity on
where and are the values of the interior and exterior functions at the boundary of the neutron star . Substituting the value of the constant into Formula (28), we find the asymptotic mass M.
In the case where , the solution exactly represents the anti-de Sitter–Schwarzschild black hole as follows:
where and the integration constants are fixed as and .
In the classical theory of gravity, the nucleon and asymptotic mass coincide due to Einstein’s equations. However, in this case, the nucleon mass will differ from the asymptotic one and is calculated using following formula:
The sign can be determined from the requirement of the positivity of (22). Generally, when , we obtain
4. Internal Solution
4.1. Scheme of Numerical Integration
We were numerically solving the system of Equations (5)–(8) using various values of the model parameters and ℓ. Pressure and energy are related by one of the equations of state (11)–(15). The scheme of numerical integration we used was the following: First, we obtained numerical solutions and from Equations (5) and (6) using the following boundary conditions: , . In the case of the polytropic equation of state, ; in the case of realistic equations, , where . The radius of the star is defined as . From the continuity condition , where is the internal numerical solution and is the external vacuum solution (20), we determine the value of the constant . By substituting into Equations (28) and (29), we find the asymptotic mass M and the effective cosmological constant . By substituting numerical solutions and into Equations (7) and (8), we find and . The boundary condition for Equation (7) is the continuity condition , where is the vacuum solution given by Equation (21).
4.2. Results of Numerical Integration
4.2.1. The Special Case
In the special case where , i.e., , the vacuum solution (30) takes a particularly simple form that corresponds to a Schwarzschild–anti-de Sitter black hole. Also note that due to Equation (8); hence, due to the relation . In Figure 1, Figure 2, Figure 3, Figure 4 and Figure 5, we represent the results of numerical integration.
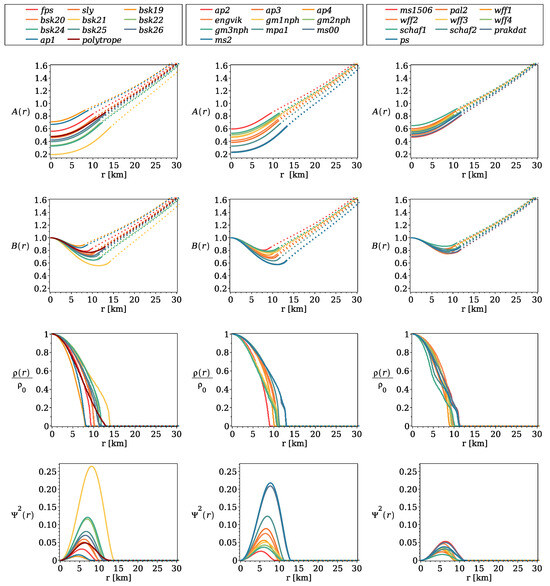
Figure 1.
Plots of , , and are shown for different equations of state in the case , km and the central mass density . The dotted line marks the vacuum solution.
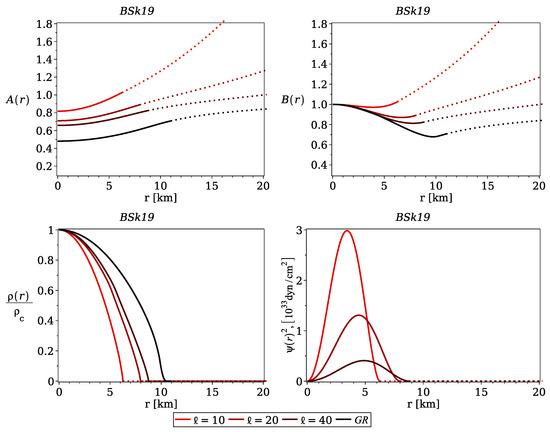
Figure 2.
Plots of , , and for the BSk19 equation of state in the case , where the central baryonic mass density , are shown for three different values, , 20 and 40 km. The dotted line marks the vacuum solution.
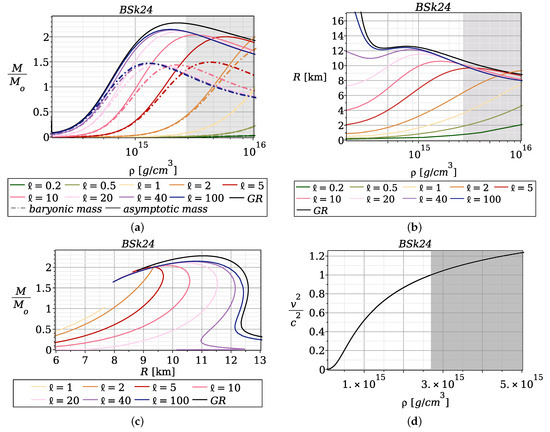
Figure 3.
Parameters of the stars in the case , 0.2, 0.5, 1, 2, 5, 10, 20, and 100 km for the BSk24 equation of state: (a) Mass M dependence from the central density ; the solid line corresponds to the asymptotic mass and the dashed dotted line to the baryonic mass. (b) The dependence of the star radius R from the central density . (c) The mass/radius diagram in the range . (d) The sound speed dependence from the density . The correspondence between style of lines and values ℓ is given in the legends; the black curve corresponds to Einstein’s theory of gravity (GR). The gray area in the figures corresponds to the density at which the equation of state becomes superluminal.
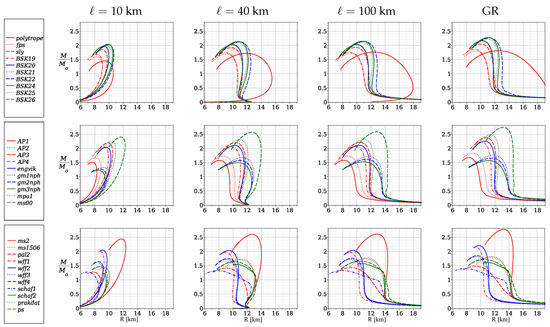
Figure 4.
The mass/radius diagram for different equations of state in the case and , 40 and 100 km. The left column with pictures corresponds to km, the next column corresponds to km and the third column corresponds to km; the right column corresponds to the unmodified theory of gravity (GR). The top row of these figures corresponds to the polytrope, FPS, SLY, BSk19–22, and BSk24–26 equations of state; the middle row corresponds to AP1–4, engvik, gm1nph, gm2nph, gm3nph, mpa1, and ms00; and the bottom row corresponds to ms2, ms1506, pal2, wff1, wff2, wff3, wff4, schaf1, schaf2, prakdat, and ps. The correspondence between the equation of state and the curve style is indicated on the left.
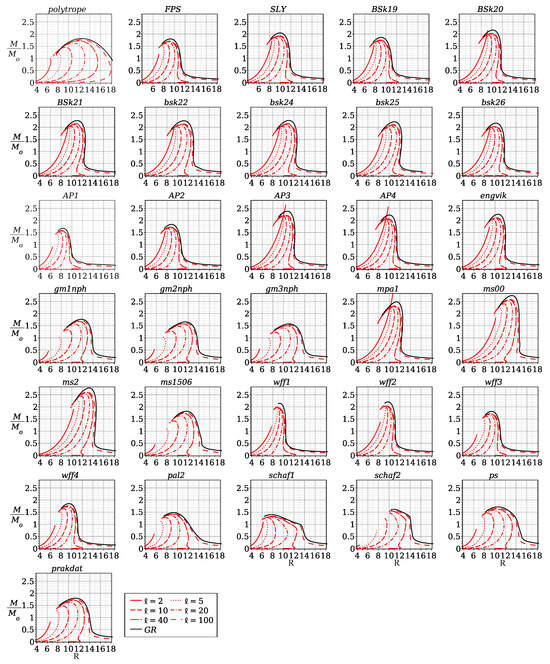
Figure 5.
The mass/radius diagram in the case and , 5, 10, 20, 40, and 100 km for different equations of state. The black curves correspond to the unmodified theory of gravity (GR). The red curves of different styles correspond to different values of ℓ.
The typical behavior of functions , , and inside and outside the star is shown in Figure 1 and Figure 2. Figure 1 shows the r dependence of this functions in the case km and the central baryonic mass density for different equations of state. For convenience, 31 equations of state were divided into three groups. Each column of the figures shows functions for this set of equations of state. The correspondence between the curve color and the equation of state is clarified in the legends at the top of the figure. The solid line corresponds to the internal solution, the dotted line corresponds to the external vacuum solution. The internal and vacuum solutions are continuously glued at the boundary of the star . The matter density monotonically decreases and equals zero at the boundary of the star. The solution of equals zero outside the star as well. As already mentioned, in the case where , the vacuum solutions of and coincide, but the internal solutions differ.
Despite the diversity of equations of state, many conclusions will be common for each of them. Therefore, we will consider one illustrative example to demonstrate these common properties. Next, we chose BSk equations only for the sake of demonstrativeness. Figure 2 shows the r dependence of the functions , , and in the case of the BSk19 equation of state, and , 20 and 40 km. The correspondence between the curve style and ℓ is given in the legend; the black curve corresponds to the unmodified theory of gravity (GR). As the parameter ℓ increases, the curves shift towards to the unmodified solution (GR), the scalar field tends to zero, and the radius of the star increases. Other equations of state have a similar appearance.
More detailed information about neutron star configurations can be extracted from a mass/radius diagram. As an example, we will choose the BSk24 equation of state. For this purpose, different values ℓ for the BSk24 equation of state are presented in Figure 3: (a) the dependence of the neutron star mass M on central density , (b) the dependence of the neutron star radius R on central density , and (c) the mass/radius diagram. The correspondence between the curve style and the ℓ value is given in the legend; the black curve corresponds to the unmodified theory of gravity (GR). Also, Figure 3d shows the dependence of the sound speed v on the density for the BSk24 equation of state. Densities at which the sound speed exceeds the speed of light are marked in gray in Figure 3a,b,d.
Here, we would like to remind the reader that the hydrostatic stability of a star needs to fulfill the condition . Therefore, in Figure 3a, unstable configurations correspond to the parts of curves to the right of their maxima, and in Figure 3c to the left of their maxima. The same feature is also shown in Figure 4, Figure 5, Figure 6 and Figure 7 for all diagrams. For this reason, we could only draw the curves on the mass/radius diagram up to their maxima. However, we used the other strategy. Namely, we fixed the parameters and ℓ, and we also chose the specific equation of state. Then, we constructed a mass/radius diagram using the same range of values of the central density for all sets of the parameters and equations of state. In practice, we considered the range . This strategy allowed us to isolate and remove obviously non-physical configurations.
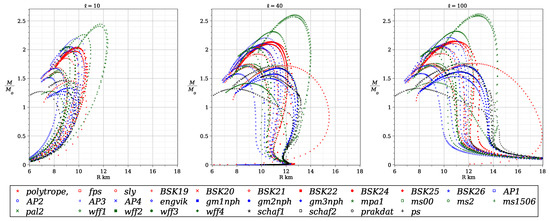
Figure 6.
The mass/radius diagram in the case and , 20 and 100 km for different equations of state.
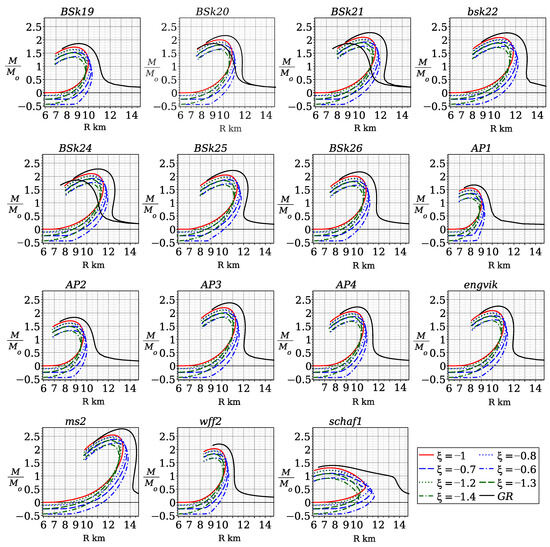
Figure 7.
The mass/radius diagram in the case km and , , , , , , and for different equations of state. The black curves correspond to the unmodified theory of gravity (GR); the red curves correspond to the case ; the green curves correspond to the case ; and the blue curves correspond to the case .
One more restriction for possible models of neutron stars comes from the model equations of state that are used for describing the inner structures of stars. The point is that the speed of sound, , could become larger than the speed of light for some values of density . This provides restrictions for possible values of , since it is obvious that the models with contradict the principle of causality. In Figure 3d, we show the dependence of on for the BSk24 equation of state. One can see that there is a domain such that (highlighted in gray). (Note that the causality limits for the BSk22-26 equations of states were discussed in [77].) The same domain in gray is shown in Figure 3a,b, and one can see that the configurations with small values of the non-minimal coupling parameter are non-physical. For example, let us discuss the graph with in Figure 3a. Its part corresponding to is located at densities significantly exceeding the permissible range of central densities. On the other hand, the permissible range of central densities corresponds to masses significantly smaller than . Thus, the case encompassing small values of the non-minimal coupling parameter ℓ takes us away from the applicability area of the equation of state or observable range of neutron star masses. For this reason, we will consider only the relatively large values of the non-minimal coupling parameter .
In Figure 4 and Figure 5, we present the mass/radius diagrams obtained for different values of the non-minimal derivative coupling parameter ℓ in the case for 31 equations of state.
For indicativeness, the diagrams are presented in two versions: In Figure 4, the diagrams are grouped by the values of parameter ℓ. In Figure 5, the diagrams are grouped by the equation of state. Each curve corresponds to the following range of central densities: .
In Figure 4, 31 equations of state were divided into three subgroups for convenience. The top row of the pictures corresponds to the polytrope, FPS, SLY, BSk19–21, BSk22, and BSk24–26 equations of state; the central row corresponds to AP1-4 engvik, gm1nph, gm2nph, gm3nph, mpa1, and ms00; and the bottom row corresponds to ms2, ms1506, pal2, wff1, wff2, wff3, wff4, schaf1, schaf2, prakdat, and ps. The left column of pictures in Figure 4 corresponds to km, the middle column corresponds to km, and the right column corresponds to km. The correspondence between the equation of state and the curve style is indicated on the left.
In Figure 5, the mass/radius diagrams are presented in the case and ℓ = 2, 5, 10, 20, 40, and 100 km for different equations of state. The black curves correspond to the unmodified theory of gravity (GR). The red curves of different styles correspond to different values of ℓ. Finally, the diagrams for all equations of state are given in Figure 6.
It is worth noting that mass/radius diagrams obtained in our work essentially differ from those obtained in GR. Neutron stars in the modified theory of gravity have smaller masses and radii compared to stars in the unmodified theory. As the parameter ℓ increases, the diagrams shift towards larger masses and larger radii, and in the limit of large values of ℓ, the relation of mass and radius tends to that in GR. There is a qualitative difference between the diagrams for large values ( km) and small values ( km). In the case of a small km, the mass of the star increases with an increasing radius. Such behavior corresponds to the so-called bare strange stars or quark stars (see [83] and the references therein). The essential feature of strange stars is that, for stars with small enough masses, their radii decrease monotonically with decreasing M, so that . This feature finds its explanation in the Bag Model for describing quark matter [83]. However, as we discussed in our previous work [70], the specific ‘strange’ relation between the mass and radius in our case forms due to the negative cosmological constant given by Equation (29). In the case of a large km, the form of the diagrams changes, and a vertical section appears in the diagrams, where the mass of the star increases practically without an increase in the radius. The values of the masses and radii significantly differ not only from the case of the unmodified gravity theory but also strongly depend on the choice of the equation of state. In general, realistic equations of state give larger masses compared to the polytropic equation that we considered earlier in [70]. The largest masses are given by ms00 and ms2 ( ), as well as by BSk22, BSk24 and AP3 ( ). The smallest masses are given by schaf1 ( ).
Here, we would like to stress that all theoretical results obtained by us above must, of course, be compared with known observable data. More recent analysis tells us that the reliably measured maximum mass of a neutron star is 2 (see ref. [16]). The constraints for the measured radii of neutron stars are not so strict. There is currently a consensus that their radii are within 10–14 km (see [16] and also [14]). Therefore, we should critically analyze the set of mass/radius diagrams obtained for different model parameters and equations of state, and exclude some of them from consideration due to being non-physical. For example, models that do not allow diagrams with masses greater than 2 contradict observations and should be rejected. In particular, based on Figure 5, we can conclude that the models with equations of state SLy, BSk20–22, BSk24–26, AP3, AP4, engvik, mpa1, ms00, ms2, wff1, and wff2 are surviving. Moreover, we have already noticed that the models with small values of the non-minimal coupling parameter correspond to the radii R of neutron stars of less than 10 km and hence also contradict observations.
4.2.2. The Case
In this section, we will shortly discuss the case . Generally, takes a value within the interval . We show mass/radius diagrams for various values of in Figure 7. It is seen that the mass/radius diagrams are shifted down and left in the case , and they are shifted down and right in the case in comparison to the case . Furthermore, we would like to note that the mass/radius diagrams in the case shift into the region of negative asymptotic masses. Despite this, the baryonic mass (31) of the star remains positive. Obviously, the negativity of asymptotic mass is not permissible from a physical point of view. Therefore, probably, all models with are non-physical. At the moment, we have no answer as to why the case is so degenerate. The study of this problem is beyond the scope of this paper. However, we intend to consider it in the future.
5. Summary
In this paper, we considered the subclass of Horndeski’s gravity represented by models with non-minimal derivative coupling of a scalar field with the Einstein tensor and the cosmological constant . We numerically constructed neutron star configurations. The matter had a form of a perfect fluid and obeyed the equation of the state of neutron matter. In [70], the matter obeyed the polytropic equation of state with the adiabatic index . The polytropic equation of state does not describe the complexity of matter in neutron stars. In the present work, besides the polytropic equation, many realistic equations of the state of neutron star matter were considered. We used the analytical representations of following unified equations of state: polytrope equation, FPS, SLY, BSk19–22, BSk24–26, AP1–4, engvik, gm1nph, gm2nph, gm3nph, mpa1, ms00, ms2, ms1506, pal2, wff1, wff2, wff3, wff4, schaf1, schaf2, prakdat, and ps. The model contained three parameters: ℓ, and . Parameter ℓ is a characteristic length that characterizes the non-minimal derivative coupling between the scalar field and curvature. is a dimensionless cosmological constant and takes the values , which provides the required metric signature. Note that is a `bare’ (i.e., unobserved) cosmological constant, and an observed effective negative cosmological constant appears as a certain combination of and the parameter of non-minimal derivative coupling ℓ. In order to provide the regularity of solutions, must be equal to . This means that the usual kinetic term of a scalar field and the modified term with an Einstein tensor enter into the Lagrangian with different signs. The results of numerical integration demonstrate the behavior of the metric functions, scalar field, baryonic density and the mass/radius diagram for different equations of state and different values of the model parameters, ℓ and .
The case was analyzed in more detail because, in this case, the vacuum solution takes a particularly simple form of the Schwarzschild–anti-de Sitter black hole. In the case of a small km, the mass/radius diagram displays an essential difference compared with that in general relativity: specifically, the radius decreases monotonically with decreasing mass. As such, the mass/radius relation corresponds to the so-called bare strange stars or quark stars in general relativity. The specific ‘strange’ relation between the mass and radius in our case forms due to the effective negative cosmological constant . In the case of a large km, the form of the diagrams changes, and a vertical section appears in the diagram, where the mass of the star increases practically without increasing the radius. As the parameter ℓ increases, the diagrams shift towards larger masses and larger radii. In the general case, the relation of the mass and radius tends to that obtained for the case of the unmodified theory in the limit of large values of ℓ.
The case of small values of the non-minimal coupling parameter km takes us away from the applicability area of the realistic equation of state or the observable range of stellar masses. In this case, stars with masses more than the mass of the Sun correspond to densities significantly exceeding the permissible range of central densities for selected equations of state. Oppositely, the permissible range of central densities corresponds to masses significantly smaller than .
Applying observable restrictions for the mass and radius of a neutron star, we obtain the restrictions on the parameter ℓ, namely . In particular, in the case , the mass/radius diagram approaches the results [64,71] without a kinetic term of a scalar field in the Lagrangian. In this case, the contribution of the kinetic term is much lower than the one of the modified term with an Einstein tensor in the Lagrangian, while the effective negative cosmological constant is small.
In the general case , the mass/radius diagrams are shifted down and left in the case , and they are shifted down and right in the case . It is also necessary to note that mass/radius diagrams are shifted in the region of negative asymptotic masses. Of course, the baryonic mass of the star remains positive.
Author Contributions
Conceptualization, S.V.S.; Methodology, P.E.K. and S.V.S.; Software, A.A.L.; Validation, P.E.K. and A.A.L.; Formal analysis, P.E.K. and S.V.S.; Investigation, P.E.K. and A.A.L.; Data curation, A.A.L.; Writing—original draft, P.E.K. and S.V.S. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the Russian Science Foundation, grant No. 25-22-00163.
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Baade, W.; Zwicky, F. Supernovae and cosmic rays. Phys. Rev. 1934, 45, 138. [Google Scholar]
- Hewish, A.; Bell, S.J.; Pilkington, J.D.H.; Scott, P.F.; Collins, R.A. Observation of a rapidly pulsating radio source. Nature 1968, 217, 709. [Google Scholar] [CrossRef]
- Rezzolla, L.; Pizzochero, P.; Jones, D.I.; Rea, N.; Vidaña, I. (Eds.) The Physics and Astrophysics of Neutron Stars; Springer: Cham, Switzerland, 2018; Volume 457. [Google Scholar]
- Chandrasekhar, S. Introduction to the Study of Stellar Structure; The University of Chicago Press: Chicago, IL, USA, 1939. [Google Scholar]
- Shapiro, S.L.; Teukolsky, S.A. Black Holes, White Dwarfs and Neutron Stars: The Physics of Compact Objects; Wiley: New York, NY, USA, 1983. [Google Scholar]
- Haensel, P.; Potekhin, A.Y.; Yakovlev, D.G. (Eds.) Neutron Stars: Equation of State and Structure; Springer: New York, NY, USA, 2007. [Google Scholar]
- Potekhin, A.Y. The physics of neutron stars. Physics-Uspekhi 2010, 53, 1235–1256. [Google Scholar] [CrossRef]
- Lattimer, J.M.; Prakash, M. The Physics of Neutron Stars. Science 2004, 304, 536–542. [Google Scholar] [CrossRef]
- Lattimer, J.M. Introduction to neutron stars. AIP Conf. Proc. 2015, 1645, 61–78. [Google Scholar]
- Weber, F. Strange Quark Matter and Compact Stars. Prog. Part. Nucl. Phys. 2005, 54, 193–288. [Google Scholar] [CrossRef]
- Tolman, R.C. Static Solutions of Einstein’s Field Equations for Spheres of Fluid. Phys. Rev. 1939, 55, 364–373. [Google Scholar] [CrossRef]
- Oppenheimer, J.R.; Volkoff, G.M. On Massive Neutron Cores. Phys. Rev. 1939, 55, 374. [Google Scholar] [CrossRef]
- Thorsett, S.E.; Chakrabarty, D. Neutron Star Mass Measurements. I. Radio Pulsars. Astrophys. J. 1999, 512, 288. [Google Scholar] [CrossRef]
- Ozel, F.; Freire, P. Masses, Radii, and the Equation of State of Neutron Stars. Annu. Rev. Astron. Astrophys. 2016, 54, 401. [Google Scholar] [CrossRef]
- Nättilä, J.; Miller, M.C.; Steiner, A.W.; Kajava, J.J.E.; Suleimanov, V.F.; Poutanen, J. Neutron star mass and radius measurements from atmospheric model fits to X-ray burst cooling tail spectra. Astron. Astrophys. 2017, 608, A31. [Google Scholar] [CrossRef]
- Fonseca, E.; Cromartie, H.T.; Pennucci, T.T.; Ray, P.S.; Kirichenko, A.Y.; Ransom, S.M.; Demorest, P.B.; Stairs, I.H.; Arzoumanian, Z.; Guillemot, L.; et al. Refined Mass and Geometric Measurements of the High-mass PSR J0740+6620. Astrophys. J. Lett. 2021, 915, L12, 15. [Google Scholar] [CrossRef]
- Linares, M. Super-Massive Neutron Stars and Compact Binary Millisecond Pulsars. arXiv 2019, arXiv:1910.09572. [Google Scholar]
- Capano, C.D.; Tews, I.; Brown, S.M.; Margalit, B.; De, S.; Kumar, S.; Brown, D.A.; Krishnan, B.; Reddy, S. Stringent constraints on neutron-star radii from multimessenger observations and nuclear theory. Nat. Astron. 2020, 4, 625–632. [Google Scholar] [CrossRef]
- Clifton, T.; Ferreira, P.G.; Padilla, A.; Skordis, C. Modified Gravity and Cosmology. Phys. Rep. 2012, 513, 1–189. [Google Scholar]
- Myrzakulov, R.; Sebastiani, L.; Zerbini, S. Some aspects of generalized modified gravity models. Int. J. Mod. Phys. D 2013, 22, 1330017. [Google Scholar] [CrossRef]
- Langlois, D. Dark energy and modified gravity in degenerate higher-order scalar–tensor (DHOST) theories: A review. Int. J. Mod. Phys. D 2019, 28, 1942006. [Google Scholar] [CrossRef]
- Capozziello, S.; De Laurentis, M. Extended Theories of Gravity. Phys. Rep. 2011, 509, 167–321. [Google Scholar] [CrossRef]
- Nojiri, S.; Odintsov, S.D.; Oikonomou, V.K. Modified gravity theories on a nutshell: Inflation, bounce and late-time evolution. Phys. Rep. 2017, 692, 1–104. [Google Scholar] [CrossRef]
- Berti, E.; Barausse, E.; Cardoso, V.; Gualtieri, L.; Pani, P.; Sperhake, U.; Stein, L.C.; Wex, N.; Yagi, K.; Baker, T.; et al. Testing General Relativity with Present and Future Astrophysical Observations. Class. Quant. Grav. 2015, 32, 243001. [Google Scholar] [CrossRef]
- Astashenok, A.V.; Capozziello, S.; Odintsov, S.D. Extreme neutron stars from Extended Theories of Gravity. J. Cosmol. Astropart. Phys. 2015, 2015, 001. [Google Scholar] [CrossRef]
- Astashenok, A.V.; Odintsov, S.D. Neutron Stars in f(R)-Gravity and Its Extension with a Scalar Axion Field. Particles 2020, 3, 532–542. [Google Scholar] [CrossRef]
- Astashenok, A.V.; Capozziello, S.; Odintsov, S.D.; Oikonomou, V.K. Extended Gravity Description for the GW190814 Supermassive Neutron Star. Phys. Lett. B 2020, 811, 135910. [Google Scholar] [CrossRef]
- Doneva, D.D.; Yazadjiev, S.S. Neutron star solutions with curvature induced scalarization in the extended Gauss-Bonnet scalar-tensor theories. J. Cosmol. Astropart. Phys. 2018, 1804, 011. [Google Scholar] [CrossRef]
- Horbatsch, M.W.; Burgess, C.P. Semi-Analytic Stellar Structure in Scalar-Tensor Gravity. J. Cosmol. Astropart. Phys. 2011, 1108, 027. [Google Scholar] [CrossRef][Green Version]
- Doneva, D.D.; Yazadjiev, S.S. Non-topological spontaneously scalarized neutron stars in tensor-multi-scalar theories of gravity. Phys. Rev. D 2020, 101, 104010. [Google Scholar] [CrossRef]
- Mendes, R.F.P.; Ortiz, N.; Stergioulas, N. Nonlinear dynamics of oscillating neutron stars in scalar-tensor gravity. Phys. Rev. D 2021, 104, 104036. [Google Scholar] [CrossRef]
- Odintsov, S.D.; Oikonomou, V.K. Neutron stars in scalar–tensor gravity with quartic order scalar potential. Ann. Phys. 2022, 440, 168839. [Google Scholar] [CrossRef]
- Rosca-Mead, R.; Moore, C.J.; Sperhake, U.; Agathos, M.; Gerosa, D. Structure of Neutron Stars in Massive Scalar-Tensor Gravity. Symmetry 2020, 12, 1384. [Google Scholar] [CrossRef]
- Oliveira, A.M.; Velten, H.E.S.; Fabris, J.C.; Casarini, L. Neutron Stars in Rastall Gravity. Phys. Rev. D 2015, 92, 044020. [Google Scholar] [CrossRef]
- Harko, T.; Lobo, F.S.N.; Mak, M.K.; Sushkov, S.V. Structure of neutron, quark, and exotic stars in Eddington-inspired Born-Infeld gravity. Phys. Rev. D 2013, 88, 044032. [Google Scholar] [CrossRef]
- Babichev, E.; Langlois, D. Relativistic stars in f(R) gravity. Phys. Rev. D 2009, 80, 121501. [Google Scholar] [CrossRef]
- Babichev, E.; Langlois, D. Relativistic stars in f(R) and scalar-tensor theories. Phys. Rev. D 2010, 81, 124051. [Google Scholar] [CrossRef]
- Cooney, A.; DeDeo, S.; Psaltis, D. Neutron stars in f(R) gravity with perturbative constraints. Phys. Rev. D 2010, 82, 064033. [Google Scholar] [CrossRef]
- Pace, M.; Said, J.L. A Perturbative Approach to Neutron Stars in f(R,T)-Gravity. Eur. Phys. J. C 2017, 77, 283. [Google Scholar] [CrossRef]
- Ilijic, S.; Sossich, M. Compact stars in f(T) extended theory of gravity. Phys. Rev. D 2018, 98, 064047. [Google Scholar] [CrossRef]
- Pani, P.; Berti, E.; Cardoso, V.; Read, J. Compact stars in alternative theories of gravity. Einstein-Dilaton-Gauss-Bonnet gravity. Phys. Rev. D 2011, 84, 104035. [Google Scholar] [CrossRef]
- Olmo, G.J.; Rubiera-Garcia, D.; Wojnar, A. Stellar structure models in modified theories of gravity: Lessons and challenges. Phys. Rep. 2020, 876, 1–75. [Google Scholar] [CrossRef]
- Lehebel, A. Compact astrophysical objects in modified gravity. arXiv 2018, arXiv:1810.04434. [Google Scholar]
- Doneva, D.D.; Pappas, G. Universal Relations and Alternative Gravity Theories. Astrophys. Space Sci. Libr. 2018, 457, 737–806. [Google Scholar]
- Blazquez-Salcedo, J.L.; Kleihaus, B.; Kunz, J. Compact Objects in Alternative Gravities. Universe 2022, 8, 153. [Google Scholar] [CrossRef]
- Horndeski, G.W. Second-order scalar-tensor field equations in a four-dimensional space. Int. J. Theor. Phys. 1974, 10, 363–384. [Google Scholar] [CrossRef]
- Charmousis, C.; Copeland, E.J.; Padilla, A.; Saffin, P.M. General second order scalar-tensor theory, self tuning, and the Fab Four. Phys. Rev. Lett. 2012, 108, 051101. [Google Scholar] [CrossRef] [PubMed]
- Deffayet, C.; Gao, X.; Steer, D.A.; Zahariade, G. From k-essence to generalised Galileons. Phys. Rev. D 2011, 84, 064039. [Google Scholar] [CrossRef]
- Kobayashi, T. Horndeski theory and beyond: A review. Rep. Prog. Phys. 2019, 82, 086901. [Google Scholar] [CrossRef]
- Sushkov, S.V. Exact cosmological solutions with nonminimal derivative coupling. Phys. Rev. D 2009, 80, 103505. [Google Scholar] [CrossRef]
- Saridakis, E.N.; Sushkov, S.V. Quintessence and phantom cosmology with non-minimal derivative coupling. Phys. Rev. D 2010, 81, 083510. [Google Scholar] [CrossRef]
- Sushkov, S. Realistic cosmological scenario with non-minimal kinetic coupling. Phys. Rev. D 2012, 85, 123520. [Google Scholar] [CrossRef]
- Starobinsky, A.A.; Sushkov, S.V.; Volkov, M.S. The screening Horndeski cosmologies. J. Cosmol. Astropart. Phys. 2016, 2016, 007. [Google Scholar] [CrossRef]
- Starobinsky, A.A.; Sushkov, S.V.; Volkov, M.S. Anisotropy screening in Horndeski cosmologies. Phys. Rev. D 2020, 101, 064039. [Google Scholar] [CrossRef]
- Hui, L.; Nicolis, A. A no-hair theorem for the galileon. Phys. Rev. Lett. 2013, 110, 241104. [Google Scholar] [CrossRef] [PubMed]
- Rinaldi, M. Black holes with non-minimal derivative coupling. Phys. Rev. D 2012, 86, 084048. [Google Scholar] [CrossRef]
- Minamitsuji, M. Solutions in the scalar-tensor theory with nonminimal derivative coupling. Phys. Rev. D 2014, 89, 064017. [Google Scholar] [CrossRef]
- Anabalon, A.; Cisterna, A.; Oliva, J. Asymptotically locally AdS and flat black holes in Horndeski theory. Phys. Rev. D 2014, 89, 084050. [Google Scholar] [CrossRef]
- Babichev, E.; Charmousis, C. Dressing a black hole with a time-dependent Galileon. J. High Energy Phys. 2014, 1408, 106. [Google Scholar] [CrossRef]
- Kobayashi, T.; Tanahashi, N. Exact black hole solutions in shift symmetric scalar–tensor theories. Prog. Theor. Exp. Phys. 2014, 2014, 073E02. [Google Scholar] [CrossRef]
- Babichev, E.; Charmousis, C.; Hassaine, M. Charged Galileon black holes. J. Cosmol. Astropart. Phys. 2015, 2015, 031. [Google Scholar] [CrossRef]
- Sushkov, S.V.; Korolev, R. Scalar wormholes with nonminimal derivative coupling. Class. Quant. Grav. 2012, 29, 085008. [Google Scholar] [CrossRef]
- Korolev, R.V.; Sushkov, S.V. Exact wormhole solutions with nonminimal kinetic coupling. Phys. Rev. D 2014, 90, 124025. [Google Scholar] [CrossRef]
- Cisterna, A.; Delsate, T.; Rinaldi, M. Neutron stars in general second order scalar-tensor theory: The case of nonminimal derivative coupling. Phys. Rev. D 2015, 92, 044050. [Google Scholar] [CrossRef]
- Cisterna, A.; Delsate, T.; Ducobu, L.; Rinaldi, M. Slowly rotating neutron stars in the nonminimal derivative coupling sector of Horndeski gravity. Phys. Rev. D 2016, 93, 084046. [Google Scholar] [CrossRef]
- Maselli, A.; Silva, H.O.; Minamitsuji, M.; Berti, E. Neutron stars in Horndeski gravity. Phys. Rev. D 2016, 93, 124056. [Google Scholar] [CrossRef]
- Silva, H.O.; Maselli, A.; Minamitsuji, M.; Berti, E. Compact objects in Horndeski gravity. Int. J. Mod. Phys. D 2016, 25, 1641006. [Google Scholar] [CrossRef]
- Blazquez-Salcedo, J.L.; Eickhoff, K. Axial quasinormal modes of static neutron stars in the nonminimal derivative coupling sector of Horndeski gravity: Spectrum and universal relations for realistic equations of state. Phys. Rev. D 2018, 97, 104002. [Google Scholar] [CrossRef]
- Lehebel, A.; Babichev, E.; Charmousis, C. A no-hair theorem for stars in Horndeski theories. J. Cosmol. Astropart. Phys. 2017, 2017, 037. [Google Scholar] [CrossRef]
- Kashargin, P.E.; Sushkov, S.V. Anti-de Sitter neutron stars in the theory of gravity with nonminimal derivative coupling. J. Cosmol. Astropart. Phys. 2023, 2023, 005. [Google Scholar] [CrossRef]
- Tooper, R.F. Adiabatic Fluid Spheres in General Relativity. Astrophys. J. 1965, 142, 1541–1562. [Google Scholar] [CrossRef]
- Read, J.S.; Lackey, B.D.; Owen, B.J.; Friedman, J.L. Constraints on a phenomenologically parametrized neutron-star equation of state. Phys. Rev. D 2009, 79, 124032. [Google Scholar] [CrossRef]
- Read, J.S.; Markakis, C.; Shibata, M.; Uryu, K.; Creighton, J.D.E.; Friedman, J.L. Measuring the neutron star equation of state with gravitational wave observations. Phys. Rev. D 2009, 79, 124033. [Google Scholar] [CrossRef]
- Haensel, P.; Potekhin, A.Y. Analytical representations of unified equations of state of neutron-star matter. Astron. Astrophys. 2004, 428, 191–197. [Google Scholar] [CrossRef]
- Can Gungor, K.; Eksi, Y. Analytical Representation for Equations of State of Dense Matter. arXiv 2011, arXiv:1108.2166. [Google Scholar]
- Potekhin, A.Y.; Fantina, A.F.; Chamel, N.; Pearson, J.M.; Goriely, S. Analytical representations of unified equations of state for neutron-star matter. Astron. Astrophys. 2013, 560, A48. [Google Scholar] [CrossRef]
- Pearson, J.M.; Chamel, N.; Potekhin, A.Y.; Fantina, A.F.; Ducoin, C.; Dutta, A.K.; Goriely, S. Unified equations of state for cold non—Accreting neutron stars with Brussels—Montreal functionals. I. Role of symmetry energy. Mon. Not. R. Astron. Soc. 2018, 481, 2994–3026. [Google Scholar] [CrossRef]
- Lattimer, J.M.; Prakash, M. Neutron Star Structure and the Equation of State. Astrophys. J. 2001, 550, 426E442. [Google Scholar] [CrossRef]
- Douchin, F.; Haensel, P. A unified equation of state of dense matter and neutron star structure. Astron. Astrophys. 2001, 380, 151. [Google Scholar] [CrossRef]
- Pandharipande, V.R.; Ravenhall, D.G. Hot Nuclear Matter. In Nuclear Matter and Heavy Ion Collisions; NATO ADS Series; Soyeur, M., Flocard, H., Tamain, B., Porneuf, M., Eds.; Reidel: Dordrecht, The Netherlands, 1989; Volume B205, p. 103. [Google Scholar]
- Goriely, S.; Chamel, N.; Pearson, J.M. Further explorations of Skyrme-Hartree-Fock-Bogoliubov mass formulas. XII: Stiffness and stability of neutron-star matter. Phys. Rev. C 2010, 82, 035804. [Google Scholar] [CrossRef]
- Pearson, J.M.; Goriely, S.; Chamel, N. Properties of the outer crust of neutron stars from Hartree-Fock-Bogoliubov mass models. Phys. Rev. C 2011, 83, 065810. [Google Scholar] [CrossRef]
- Haensel, P.; Potekhin, A.Y.; Yakovlev, D.G. Neutron Stars 1: Equation of State and Structure, Astrophysics and Space Science Library; Springer: New York, NY, USA, 2007. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).