Abstract
In recent years, hashing-based algorithms have garnered significant attention as vital technologies for cross-modal retrieval tasks. They leverage the inherent symmetry between different data modalities (e.g., text, images, or audio) to bridge their semantic gaps by embedding them into a unified representation space. This symmetry-preserving approach would greatly enhance retrieval performance. However, challenges persist in mining and enriching multi-modal semantic feature information. Most current methods use pre-trained models for feature extraction, which limits information representation during hash code learning. Additionally, these methods map multi-modal data into a unified space, but this mapping is sensitive to feature distribution variations, potentially degrading cross-modal retrieval performance. To tackle these challenges, this paper introduces a novel method called Attention-based Multi-scale Graph Fusion Hashing (AMGFH). This approach first enhances the semantic representation of image features through multi-scale learning via an image feature enhancement network. Additionally, graph convolutional networks (GCNs) are employed to fuse multi-modal features, where the self-attention mechanism is incorporated to enhance feature representation by dynamically adjusting the weights of less relevant features. By optimizing a combination of loss functions and addressing the diverse requirements of image and text features, the proposed model demonstrates superior performance across various dimensions. Extensive experiments conducted on public datasets further confirm its outstanding performance. For instance, AMGFH exceeds the most competitive baseline by 3% and 4.7% in terms of mean average precision (MAP) when performing image-to-text and text-to-image retrieval tasks at 32 bits on the MS COCO dataset.
1. Introduction
As technology rapidly advances, we are witnessing a surge in multimedia data across the Internet, including text, audio, images, and videos. This variety enhances user engagement and experience. To address the demand for effective retrieval techniques in this diverse landscape, cross-modal retrieval has emerged as a promising solution, allowing equivalent semantic content to be extracted from one data modality using information from another [,,]. It relies on the concept of symmetry to establish meaningful connections between diverse data types, such as text, images, and audio. By embedding these modalities into a unified representation space, symmetrical learning methods—like contrastive or metric learning—enable seamless bidirectional retrieval (e.g., finding images from text queries or vice versa). This symmetry-driven alignment ensures balanced and consistent mappings across modalities, mirroring how geometric symmetry governs structural harmony in natural and engineered systems [,,].
Cross-modal retrieval offers significant advantages over traditional single-modal methods by accurately representing features across different modalities and understanding their semantic connections [,,,]. A key challenge is effectively managing the retrieval of images and text, which both contain intricate features and semantic information, while addressing discrepancies and heterogeneous characteristics between the modalities.
As cross-modal retrieval algorithms continue to progress, finding methods that achieve efficient and precise retrieval remains a significant challenge. In recent years, hashing-based retrieval algorithms have gained considerable interest in the academic community due to their low storage costs and high computational efficiency []. These algorithms use hash functions to convert complex, high-dimensional features into a compact binary representation. This dimensionality reduction streamlines data management while preserving essential semantic information, making hash retrieval algorithms particularly effective for cross-modal retrieval of images and text [,,,,]. However, challenges persist in practical applications; these algorithms often face difficulties related to inadequate feature mining and the representation of multi-modal data. A lack of both intra-modal and inter-modal representation can result in skewed and biased retrieval outcomes, emphasizing the need for continuous improvement in this area.
To address these challenges, this paper presents a novel deep learning framework called Attention-based Multi-scale Graph Fusion Hashing (AMGFH). First, the framework performs multi-scale learning of image features through an image feature enhancement network, which refines semantic information and improves the representation of image features. Additionally, the fusion of multi-modal features is achieved using specialized graph convolutional networks (GCNs) in the graph feature fusion module. This module incorporates a self-attention mechanism to enhance feature representation by dynamically adjusting the weights of the features that are not actively used. Taking into account the diverse characteristics of image and text features, the model demonstrates optimal performance across various aspects and ultimately generates differentiated hash codes by optimizing a series of loss functions. This leads to improved performance in the cross-modal retrieval systems. In summary, the main contributions of this paper are as follows:
- In this paper, we propose a novel deep cross-modal hashing model called AMGFH, designed to achieve efficient cross-modal retrieval. The model enhances image feature representation by incorporating an image feature enhancement network, the self-attention mechanism, GCNs, and hybrid loss functions. This architecture guides the generation of hash codes that carry rich semantic information, enabling efficient and accurate cross-modal retrieval.
- The proposed image enhancement learning network facilitates the analysis of image information across multiple scales, allowing for a comprehensive extraction of diverse feature details. By leveraging this multi-scale approach, the network enhances our ability to uncover intricate details and subtle nuances within the image. Consequently, the semantic representation of image features is greatly enriched, resulting in a more sophisticated understanding of the visual content and its various elements.
- The combination of multi-modal features is achieved through GCNs in the graph feature fusion module. A self-attention mechanism dynamically adjusts feature weights to optimize the loss function, resulting in the generation of a binary hash code for efficient retrieval. Experiments on public datasets show that this method outperforms other baseline approaches across various metrics.
This paper is organized as follows: Section 2 discusses related technical studies. In Section 3, we present the overall framework of the proposed method, including the image enhancement network, feature fusion, and hash function learning. Section 4 details the specific experimental aspects of the proposed method. Finally, Section 5 summarizes and concludes the work.
2. Related Works
In cross-modal hash learning, researchers aim to improve similarity measures and retrieval efficiency across different data types. By using both supervised and unsupervised learning techniques, they are reinforcing the theory behind cross-modal hash learning while also enhancing practical applications in multimedia data retrieval.
2.1. Supervised Hashing
Supervised learning plays a crucial role in cross-modal hashing by utilizing annotated data to guide model learning, which in turn improves retrieval accuracy and similarity metrics. Shen et al. [] proposed the Subspace Relational Learning Cross-Modal Hashing approach, which optimizes the representation of various modalities in a low-dimensional Hamming subspace. This method leverages the relational information of labels in the semantic space to bring similar data closer together in the subspace, enhancing retrieval performance. Ma et al. [] introduced Multi-Level Correlation Adjacency Hashing (MLCAH). This algorithm efficiently encodes multi-level correlation information, including global, local, and tag information, through global and local semantic alignment mechanisms. Additionally, it incorporates a label-consistent attention mechanism with adversarial training to explore local cross-modal similarities in multi-modal data, further improving retrieval performance.
Furthermore, Liu et al. [] developed a network that employs a triple fusion network and a zero-padding operation to bridge the semantic gap between balanced and unbalanced data. Their approach includes an adversarial training mechanism tailored for unbalanced cross-modal data, providing an effective solution for handling such datasets. Wang et al. [] proposed a supervised adversarial hashing method based on a two-path attention mechanism. This method is applicable to unbalanced cross-modal data by deeply mining the fine-grained semantic correlations between different modalities and integrating adversarial learning to enhance the model’s ability to learn cross-modal semantic correlations.
2.2. Unsupervised Hashing
Unsupervised learning methods develop effective hash representations by utilizing the structure and relationships inherent in the data itself, without relying on labeled data. Wu et al. [] proposed a multi-modal semantics constrained hashing approach that uses neighborhood matrices to guide the generation of hash codes. This method applies the neighborhood structure to feature representations from different modalities, reconstructing cross-modal features that contain structural information, which significantly enhances the quality of hash code generation. Xie et al. [] introduced a multiplexed consistency-preserving adversarial hashing method that features a consistency refinement module (CR) designed to separate the representations of different modalities. Additionally, they proposed a multi-task adversarial learning module (MA) to align the public representations of different modalities in terms of feature distribution and semantic consistency. This approach improves the effectiveness of cross-modal retrieval in an unsupervised manner. Zhu et al. [] developed an unsupervised deep cross-modal hash learning framework that simultaneously models and encodes heterogeneous semantic associations and identity semantics of multi-modal data. This method constructs a multi-modal cooperation graph to illustrate the associations between different multi-modalities and designs an identity semantics reconstruction process that enhances the descriptive identity semantics of the hash codes.
Moreover, Song et al. [] proposed an unsupervised cross-modal hash retrieval method based on concordant semantic distribution. This method leverages not only paired data but also pairs with unpaired unimodal data. The consideration of semantic similarity is achieved by constructing a concordant semantic similarity matrix along with fusion feature generation, offering a new perspective on unsupervised cross-modal hash learning. Wu et al. [] suggested aligning global and local features from different modalities through hierarchical alignment while generating multi-length hash codes simultaneously, which improves retrieval performance. Cao et al. [] developed an efficient zero-sample cross-modal hashing method utilizing the pre-trained CLIP model. They designed suitable cues for multilabel images, guiding the model to recognize the multilabel characteristics of these images, and introduced a multilevel hashing loss function to generate hash codes with stronger discriminative properties. Huang et al. [] introduced a multilevel cross-modal similarity method with a unified perspective, establishing a one-to-many correspondence relationship for cross-modal data through the integration of local similarities and the design of similarity metrics. This method effectively addresses fine-grained cross-modal information processing. Huo et al. [] proposed a framework for learning distinguishable embedding spaces by incorporating learnable shared class agents and uniform distribution constraints, ensuring that the original neighborhood relationships are maintained. This approach enhances the robustness and retrieval accuracy of the hash codes. Song et al. [] also suggested maximizing the Normalized Discounted Cumulative Gain (NDCG) quota via a new ranking loss to learn the ranking distribution in cross-modal retrieval. This method improves the hash code’s discriminative ability on out-of-distribution (OOD) data by constructing auxiliary pseudo-OOD data.
Lastly, Sun et al. [] introduced a method for learning discriminative hash codes, offering greater flexibility through double-layer hash functions for image retrieval tasks. Their approach employs an energy preservation strategy to minimize energy loss during hash projection and incorporates a semantic reconstruction mechanism to ensure that semantic information is effectively retained in the hash codes. Additionally, Dong et al. [] proposed a hierarchical feature aggregation algorithm based on GCNs to promote the semantic integrity of objects. This method hierarchically synthesizes content about the objects and their relationships in both image and text modalities. They also presented a transformer-based cross-modal feature fusion method to mitigate differences between modalities, facilitating cross-modal feature fusion by synthesizing object features and global features from another modality.
3. Proposed Method
3.1. Overall Framework
As illustrated in Figure 1, which presents the foundational learning framework of our proposed method, our objective is to direct the generation of hash functions using the learned hash codes of cross-modal features. This approach enables the conversion of image features and text features into binary hash codes, thereby achieving efficient and accurate cross-modal retrieval.
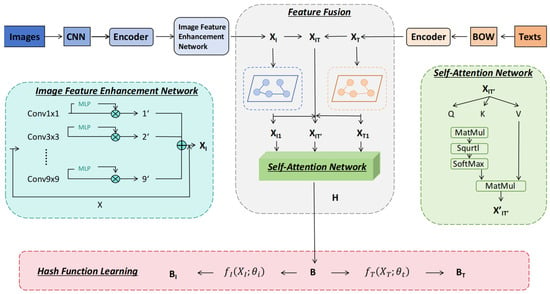
Figure 1.
The overall framework of the proposed AMGFH. Three main parts are included: the image feature enhancement network, graph feature fusion module, and hash function learning. AlexNet and BoW models are utilized to extract image and text features, respectively. The image features are then fed into the image feature enhancement network to obtain enhanced image features. Subsequently, the enhanced features and text features are spliced, and then feature fusion is performed by graph feature fusion module, which ultimately generates a unique binary hash code and combines it with the loss function in order to guide the learning of the hash function.
Our framework for learning cross-modal hash codes comprises three main components: an image feature enhancement network, a self-attention-based graph feature fusion module, and the hash function learning. We utilize AlexNet and BoW networks to extract image and text features, respectively. First, we feed the image features into the image feature enhancement network to improve their quality, resulting in enhanced image features . Next, we combine these enhanced image features with the text features to create a fused feature representation . We also construct an adjacency matrix for the enhanced image features and the text features to enable subsequent GCN-based feature fusion. Following this, we apply GCN to perform feature fusion on the enhanced image features, text features, and the fused features. The GCN processed enhanced image features , text features , and fused features then undergo a self-attention operation to produce enhanced representations for each. After completing the self-attention process, we splice the three enhanced features together to create new fused feature representations . Finally, a unique binary hash code is generated for these new features, which is used alongside a loss function to guide the learning of the hash function.
The image feature enhancement network enhances the representation of image features by performing multi-scale learning on features extracted from the images. In the graph feature fusion module, we achieve cross-modal feature fusion by applying graph convolutional networks across different modalities, which enhances the interaction between inter-modal features. Additionally, we introduce a self-attention mechanism to dynamically adjust the weights of image features, text features, and complementary features. This adjustment improves the representation of important information, leading to a more refined feature representation.
Secondly, in the hash function learning part, we generate a unique binary hash code by utilizing the new features obtained from this self-attention-based feature fusion. This result is further processed using a hash function to create a distinctive binary hash code. This process guides the development of both the image hash function and the text hash function . Ultimately, the input features are efficiently mapped into a compact and semantically consistent hash space, allowing us to obtain both the image hash code and the text hash code, thereby enabling effective cross-modal retrieval.
3.2. Image Feature Enhancement Network
In academic research, multi-scale feature learning has garnered significant attention and has been applied across various fields []. This approach enhances the semantic information of images by extracting local features at different scales, allowing for more effective representation of images in complex scenes. However, existing studies might not fully capture the comprehensive and rich semantic information needed for more intricate image scenarios. Therefore, this section will focus on strategies to better express this rich semantic information at the initial stage, to aid in subsequent experiments.
Firstly, the image feature enhancement network is mainly designed to dynamically fuse multi-scale local and global features through multi-scale feature learning, so as to obtain the enhanced expression of image features. Specifically, it is to extract multi-scale image feature representation (i.e., ) by different sizes of convolution kernels (1 × 1, 3 × 3, 5 × 5, 7 × 7, 9 × 9) from after completing the image feature extraction and weighted fusion by the dynamic feature and ultimately to obtain the enhanced representation of the image feature , where denotes the intermediate feature output of multi-scale feature learning. Thus, we can derive the calculation below:
where denotes these different kernel sizes. The weights for each scale are dynamically learned by applying the constructed MLP network to , thus resulting in the following:
The final convolution is performed through a 1 × 1 kernel (i.e., ), which is convolved and linked to to obtain an enhanced version of the image feature representation , and then the dimensions are unified as . The computational formula is expressed as follows:
3.3. Graph Feature Fusion Module
Recently, GCN has garnered significant attention, which excels at capturing complex relationships and features among nodes in images and has experienced rapid advancements in both image processing and natural language processing [,]. In this work, we will utilize GCN to fuse cross-modal features and apply varying weights to enhance the important information within these features through a self-attention mechanism. This approach aims to improve the expressive capabilities of the features and enrich the semantic representation among cross-modal features. In this process, symmetry is represented by the use of symmetrical image–text pairs during training. We utilize similarity matrices to establish and preserve this symmetrical relationship when applying GCN for feature learning. This approach helps to more accurately capture the correlation between multi-modal features and enhances the effectiveness of feature learning. In this context, the nodes of a graph network represent feature points extracted from images or text. The edges connecting these nodes are represented by an adjacency matrix, which indicates the similarity between the image or text data points. Initially, the features from the images and text are processed by their respective GCN encoders. These features are then combined to create fused features. The processing can be mathematically detailed using feature fusion as an example, as outlined below.
First, we constructed the adjacency matrix for the enhanced image features and text features , and is calculated by the following formula:
where denotes the similarity matrix of the image modality, denotes the similarity matrix of the text modality, and is the balance parameter. The computation rules of and are the same, and the formula for each element of is as follows:
where denotes the cosine similarity between the two vectors, and and denote the instance features of the th and -th images, respectively.
In the feature fusion stage, first we spliced the already obtained image feature representation and text feature representation to obtain the new feature representation (features fused from and ) and used GCN to obtain the new feature after the fusion of and image–text features. The new feature representation is given by the following formula:
where denotes the adjacency matrix, is the degree matrix of , and is the tier learnable weight matrix.
In order to further enhance the representation of the features, we subsequently continued the self-attention operation for , , and , respectively, in which the weights of the features are dynamically adjusted by calculating the interrelationships among the features, thus enhancing the representation of the features , , and . Taking as an example, the input feature is with dimension , where is the number of samples and is the feature dimension. We define three linear transformations: , , and , where ,, and are learnable weight matrices that are used to compute the query, key, and value, respectively. Subsequently, the dot product of the query and key is computed and normalized by the function to obtain the attention weights with dimension . Attention weights are calculated by the following formula:
where is the dimension of the key, which is used to scale the dot product result to prevent the gradient from disappearing. The values are then weighted and summed using the attention weights to obtain enhanced feature representation. The formula for weighted summation is the following:
Among them, and have the same dimension , so the output dimension of is . Finally, the representations , , and of the enhanced features obtained by the self-attention operation are subjected to feature fusion to obtain the new representation . In the self-attention calculations, we enhanced the representation of important features by incorporating an attention mechanism into image features, text features, and fused features. This is achieved by calculating and dynamically adjusting the self-attention weights through a fully connected layer.
3.4. Hash Function Learning
This research aims to develop an effective cross-modal hash retrieval algorithm using hash functions. After completing the image–text feature fusion process, the newly generated features will undergo further processing with hash functions to create unique binary hash codes. These codes will guide the development of both image and text hash functions, which will be optimized by minimizing target functions. This approach will enable the efficient mapping of input features into a compact and semantically consistent hash space. By leveraging hash functions, we aim to preserve the semantic information of multi-modal data, thereby improving both the efficiency and accuracy of cross-modal retrieval.
Specifically, the hash learning is performed on the new feature matrix after performing feature fusion, where is the number of samples and is the feature dimension, which is mapped to a lower dimension by a hash function , denoted by Equation (7):
The fused features after hash coding can be expressed as . The fusion of features of the hash code guides the learning of the image hash function and text hash function . Optimization of image hash function and text hash function is adjusted through the target function, and the formula is as follows:
where is the image features, is the text features, is the parameters of the image hash function, and is the parameters of the text hash function. The final image hash code is denoted as , and the text hash code is denoted as . Overall, we first learn the uniform hash code representation through the feature learning process in the above sections. The hash function learning process is implemented by using this hash code as supervision. Furthermore, we introduce a series of loss terms in the next subsection to ensure that the proximity of the data points is preserved during the learning process.
3.5. Loss Functions
The overall loss function of AMGFH consists of several components. First, the discretization loss (i.e., DIS) ensures that the generated hash code closely resembles binarization, thereby enhancing the retrieval efficiency of the hash code. The specific formula is as follows:
where denotes the generated hash code. By minimizing this loss function, the model can learn how to generate hash codes that are close to binarization, thus improving retrieval efficiency.
Subsequently, the regularization loss (i.e., REG) is used to prevent model overfitting by constraining the model parameters through regularization. The specific formula is as follows:
where is the regularization parameter, and is the model parameter. By minimizing this loss function, the model is able to avoid overfitting, thus improving the generalization ability of the model.
Then, the adversarial loss (i.e., ADV) is used to enhance the generation of hash codes, which is prompted by the idea of generative adversarial network (GAN) training to make the generated hash codes more effective. The specific formula for this term is as follows:
where is the discriminator, is the generator, is the true data distribution, and is the generated data distribution. By minimizing this loss function, the model is able to learn how to generate more realistic hash codes, thus improving retrieval performance. By combining Equations (8)–(11), the overall loss function is optimized in an iterative training process, where the network converges in the end to perform the subsequent cross-modal retrieval.
4. Experiment and Discussions
4.1. Dataset Details
The dataset used in this research is a total of three datasets typical in the field of image–text cross-modal retrieval, i.e., MIRFLICKR-25K, NUS-WIDE, and MS COCO for experimental comparisons.
- The MIRFLICKR-25K [] dataset contains 25,000 image–text pairs collected from the Flickr website, organized into 24 different image categories. To ensure fair comparisons, pairs with fewer than 20 tags were removed, resulting in a total of 20,015 valid pairs. In this study, 5000 pairs were selected for the training set and 2000 pairs for the test set.
- The NUS-WIDE [] dataset includes 269,648 image–text pairs collected from real-world scenes, categorized into 81 labels. To maintain consistency with previous studies, 186,577 pairs corresponding to the 10 most common concepts were selected. From these, 5000 pairs were randomly chosen for the training set and 2000 pairs for the test set.
- The MS COCO [] dataset consists of 123,287 image–text pairs. Similarly to the previous datasets, 5000 pairs were randomly selected for the training set and 2000 pairs for the test set. All instances, except those in the test sets, are used as the retrieval set across all datasets.
4.2. Experimental Settings
In this experiment, we compare the performance of the proposed method against several state-of-the-art baselines, including CMFH [], JDSH [], DJSRH [], MESDCH [], DCHMT [], and DSPH []. The results from these baselines are tuned and reported as per their respective studies. For the comparison, we obtained retrieval results at three different bit levels: 16, 32, and 64. We implemented the proposed AMGFH using the PyTorch 1.12.0 framework, and the experimental platform is equipped with an NVIDIA RTX 3080 graphics card. The code will be made available at https://github.com/tempdirec/multiscale-graph-hashing, accessed on 28 May 2025. In the training process, the learning rate was set to 0.001 on the MIRFLICKR-25K dataset. On the NUS-WIDE dataset, the learning rate was 0.0001, while it was 0.001 on the MS COCO dataset. For the loss function, the weights were set as follows, with a discretization loss of 1, a regularization loss of 0.001, and an adversarial loss of 0.01.
Following previous research, AMGFH first extracts features from the original image using AlexNet and from text using the BoW model. The feature dimensions extracted by AlexNet are 4096. For the BoW model, the dimensions are 1386 for MIRFLICKR-25K, 1000 for NUS-WIDE, and 2000 for MS COCO [,,,]. The extracted image features are then processed through an image feature enhancement network. After this, the processed image features and text features are combined, and feature fusion is performed using a GCN to learn the relationships between these features. Finally, the representation capability of the features is enhanced using a self-attention mechanism to generate the final hash code. In this, the image feature enhancement network uses different convolutional layers to extract different scale features and process them with batch normalization and ReLU activation function. Both the image and text encoders are three-layered and are first dimensionally transformed by fully connected layers, which are subsequently normalized and nonlinearly transformed.
4.3. Evaluation Metrics
Three widely used evaluation metrics in the field of graphical retrieval are mean average precision (MAP), Precision–Recall curve (PR), and Precision@Top-N. Here, the mean average precision (MAP) is mainly used to evaluate the proposed method in comparison with other baselines.
4.4. Comparison with State-of-the-Art Baselines
In this section, the MAP values for different methods in cross-modal retrieval tasks, specifically image-to-text (I-T) and text-to-image (T-I), are presented in Table 1 and Table 2 for three datasets. The results indicate that the proposed AMGFH method outperforms all other baseline methods at each bit size. For instance, on the MIRFLICKR-25K dataset, the MAP values for I-T retrieval using 16, 32, and 64 bits are 0.887, 0.913, and 0.923, respectively, which are at least 7.7% higher than those of the DJSRH method. Similarly, on the NUS-WIDE dataset, the MAP values for 16, 32, and 64 bits of I-T are 0.799, 0.822, and 0.848, respectively, exceeding DJSRH by at least 7.5%. On the MS COCO dataset, the MAP values for T-I retrieval for 16, 32, and 64 bits are 0.752, 0.781, and 0.775, respectively, showing an improvement of at least 10.2% over DJSRH.

Table 1.
Performance variations in terms of MAP at different bit sizes (i.e., 16, 32, and 64) on three datasets (Image->Text). The bold values indicate the best results.

Table 2.
Performance variations in terms of MAP at different bit sizes (i.e., 16, 32, and 64) on three datasets (Text->Image). The bold values indicate the best results.
To summarize, the retrieval performance of the proposed AMGFH shows a consistent advantage across all three datasets and their respective bit sizes. Additionally, we plotted the Precision–Recall (PR) and Precision@Top-N curves for the proposed method in Figure 2, where the overall trends align with the results presented in the tables.
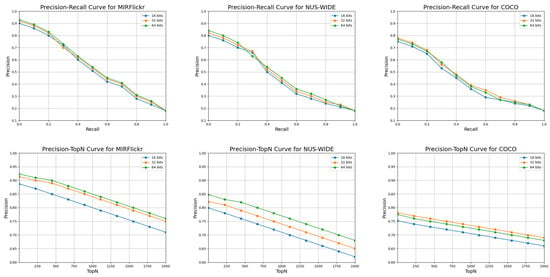
Figure 2.
Curves of PR (top) and Precision@Top-N (bottom) at 16, 32, and 64 bits (from left to right) on MIRFLICKR-25K, NUS-WIDE, and MS COCO datasets. Blue, orange, and green lines represent the curves at 16, 32, and 64 bits, respectively.
4.5. Ablation Study
In this section, we perform ablation experiments to analyze the contributions of different components such as image feature enhancement networks and loss functions.
4.5.1. Performance Analysis of Diverse Components
The MAP performance for 16, 32, 64, and 128 bits when changing the image feature enhancement network (i.e., IFN) and self-attention (i.e., SA) mechanism components on the MIRFLICKR-25K dataset is summarized in Table 3. When de-pointing the image feature enhancement network, the model performance decreases, from 0.887 to 0.882 at 16 bits. This means that the image feature enhancement network can improve model performance by enhancing the feature representation. After removing the GCN, it goes from 0.887 to 0.875 at 16 bits. This means that GCN can capture more complex relationships between image and text features. In addition to this, after de-pointing the self-attention mechanism, the model performance decreases, from 0.913 to 0.903 over 32 bits. This means that the self-attention network can enhance semantic information expression by dynamically adjusting the different weights to improve the model performance.

Table 3.
Performance variations in terms of MAP on diverse network components. Note that AMGFH-IFN refers to the removal of IFN from the original AMGFH. The same meanings apply to AMGFH-SA and AMGFH-GCN. The bold values indicate the best results.
4.5.2. Loss Function Analysis
The MAP performance for 16, 32, and 64 bits when changing various loss functions on the MIRFLICKR-25K dataset is summarized in Table 4. We can see that the MAP values of Text->Image for all these loss functions decreased at 16 bits, which proves that the combination of multiple loss functions can have some effect on the model. However, some of the data remain consistent, indicating that this combination of loss functions can continue to be optimized to improve the performance of the model even more.

Table 4.
Performance variations in terms of MAP on loss functions. Note that AMGFH-DIS refers to the removal of DIS from the original AMGFH. The same meanings apply to AMGFH-REG and AMGFH-ADV. The bold values indicate the best results.
4.5.3. Performance Analysis of Different Feature Concatenation Strategies
In the proposed AMGFH, GCN is employed to facilitate the additive fusion of graph features with image and text features. To assess the impact of various concatenation methods within this module, we performed several ablation experiments. One of the methods we tested involved feature concatenation, referred to as AMGFH-concat. The experimental results presented in Table 5 demonstrate that the fusion strategy in the proposed original AMGFH outperforms the AMGFH-concat approach.

Table 5.
Performance variations in terms of MAP of different feature concatenation strategies. Note that AMGFH-concat refers to the usage of the concatenation feature. The bold values indicate the best results.
4.5.4. Performance Evaluations of Different Weights in the Loss Function
To evaluate the effect of different weight parameters on loss terms such as DIS, REG, and ADV, we conducted ablation experiments using various weights at 128 bits on the MIRFLICKR-25K dataset. The results are presented in Table 6. From these results, it is evident that the weighting parameters in the proposed model yield the best performance. For instance, regarding DIS, we explored the impact of different weight parameters across five groups (0.1, 0.5, 1, 2, and 4). The data in the table demonstrate that the weight parameter we selected performed better than the others when the REG and ADV weight parameters remained unchanged. Additionally, the performance of the original parameter choices for the other two terms aligns with these findings.

Table 6.
Performance variations in terms of MAP of different weights of loss terms on MIRFLICKR-25K at 128 bits. For instance, regarding the loss term of DIS, the performance from five different weight parameters (i.e., 0.1, 0.5, 1, 2, and 4) is investigated.
4.6. Training Efficiency Analysis
Specifically, in the computational efficiency evaluation, Table 7 presents various metrics, including training time, FLOPs, and GPU usage for the proposed AMGFH method alongside other baseline methods. The performance results in the table indicate that the efficiency of the AMGFH method is significantly higher than that of the other methods, particularly for the lesser training time required at the 128-bit code length of the MIRFLICKR-25K dataset.

Table 7.
Training efficiency analysis on MIRFLICKR-25K at the code length of 128 bits. The bold values indicate the best results.
4.7. Discussions
This section examines the limitations of existing approaches from two key perspectives. First, while AMGFH is specifically designed for image–text cross-modal retrieval, multi-modal data encompass diverse forms such as speech and video. Future research should extend cross-modal retrieval techniques to accommodate these additional data modalities, thereby addressing a broader spectrum of retrieval requirements. Additionally, certain components of the current framework, including the image feature enhancement network and the self-attention mechanism, could be further optimized through more advanced architectural refinements to improve overall performance. For example, in this study, we used only the AlexNet and BoW models for image and text feature extraction for fair comparison. In future research, we will explore the use of more advanced models and methods, such as transformer-based models, BERT, CLIP, and others, to improve feature representation capability. The top five retrieval results from the text-to-image task on the MIRFLICKR-25K dataset are shown as an example in Figure 3. It is evident that semantic ambiguity is present in the retrieved results. Based on the label of the query text, we can infer that the images may represent a “close-up of red flowers”, a “close-up of flowers and insects”, and similar interpretations. However, it is worth noting that the image of a “Nikon” camera appears directly in the figure instead of the expected close-up of flowers. This semantic ambiguity may arise because the method relies on the simple BoW model to extract text features. A promising solution is to utilize more advanced text feature modeling techniques to process semantic information in future work.

Figure 3.
A top-5 text-to-image retrieval example on the MIRFLICKR-25K dataset. Red markers indicate the irrelevant samples returned to the query.
Moreover, the proposed method incorporates several key modules, such as the image feature enhancement network, GCN-based feature fusion, self-attention mechanism, and loss function, which possess potential applicability beyond the current scope. These components can enhance semantic representation learning by capturing richer intra- and inter-modal relationships, thereby improving cross-modal alignment. Future work will explore the generalization of these techniques across different domains to further validate their effectiveness. Furthermore, we only employed an attention-based approach for the feature fusion process. It is also possible to integrate different architecture or strategies for feature fusion. In the future, we plan to explore other approaches, such as transformer-based and co-attention networks [,,], for feature fusion to further enhance the model’s performance.
Despite some limitations, the proposed cross-modal retrieval algorithm has significant practical value in large-scale multimedia searching, recommendation systems, and multi-modal artificial intelligence platforms. For instance, in a recommendation system, it enables users to utilize flexible retrieval methods and receive cross-modal recommendations. Firstly, users can input their query requirements through various modalities, and the system will return matching results across different formats. For example, if a user uploads a photo of their home, the system can recommend furniture that matches the style of that image. Secondly, in a music application, when a user listens to a song, the system can suggest the corresponding lyrics or related music videos. These practical applications will further enhance the optimization and innovation of this type of cross-modal retrieval algorithm.
5. Conclusions
In this paper, we introduce the AMGFH to enhance the performance of cross-modal retrieval between images and texts. Specifically, AMGFH utilizes an image feature enhancement network to perform multi-scale learning of image features. This approach refines the semantic information embedded in the image features and improves their overall representation. Additionally, we employ GCNs to facilitate the fusion of cross-modal features, where the symmetry-driven alignment ensures balanced and consistent mappings across modalities. We also incorporate a self-attention mechanism to dynamically adjust the weights of unused features, thereby enhancing feature representation. Through these operations, the semantic expression of the features can be further strengthened during the hash function learning process, which helps establish the relationship between image and text features. This ultimately enables the generation of differentiated high-quality hash codes. By optimizing the combinations of loss functions, we address the multifaceted requirements of image–text features, enabling the model to achieve optimal performance across various aspects, thereby improving overall retrieval efficiency. Experimental results on three public datasets demonstrate that AMGFH surpasses other baseline methods. In future work, we plan to continue refining the model’s performance by exploring additional methods for cross-modal retrieval tasks to further enhance its retrieval capabilities.
Author Contributions
Conceptualization, J.L. and G.W.; methodology, J.L. and G.W.; software, J.L.; validation, J.L. and G.W.; formal analysis, J.L. and G.W.; investigation, J.L. and G.W.; resources, J.L. and G.W.; data curation, J.L. and G.W.; writing—original draft preparation, J.L.; writing—review and editing, J.L. and G.W.; visualization, J.L.; supervision, G.W.; project administration, G.W.; funding acquisition, G.W. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Science and Technology Development Fund, Macao SAR. Grant number: 0004/2023/ITP1.
Data Availability Statement
Data will be made available on request.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Song, X.; Chen, J.; Wu, Z.; Jiang, Y.-G. Spatial-Temporal Graphs for Cross-Modal Text2Video Retrieval. IEEE Trans. Multimed. 2022, 24, 2914–2923. [Google Scholar] [CrossRef]
- Zhou, K.; Hassan, F.H.; Hoon, G.K. The state of the art for cross-modal retrieval: A survey. IEEE Access 2023, 11, 138568–138589. [Google Scholar] [CrossRef]
- Han, Z.; Bin Azman, A.; Mustaffa, M.R.B.; Khalid, F.B. Cross-modal retrieval: A review of methodologies, datasets, and future perspectives. IEEE Access 2024, 12, 115716–115741. [Google Scholar] [CrossRef]
- Xia, B.; Yang, R.; Ge, Y.; Yin, J. A Review of Cross-Modal Retrieval for Image-Text. In Proceedings of the Fifteenth International Conference on Graphics and Image Processing (ICGIP 2023), Suzhou, China, 10–12 November 2023; Volume 13089, pp. 389–400. [Google Scholar]
- Zhen, L.; Hu, P.; Wang, X.; Peng, D. Deep Supervised Cross-Modal Retrieval. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 10394–10403. [Google Scholar]
- Qin, Q.; Wu, L.; Zhang, W.; Huang, L.; Nie, J. Deep Semantic-consistent Penalizing Hashing for Cross-modal Retrieval. IEEE Trans. Multimed. 2025, 1, 1–14. [Google Scholar] [CrossRef]
- Zhu, L.; Zheng, C.; Guan, W.; Li, J.; Yang, Y.; Shen, H.T. Multi-Modal Hashing for Efficient Multimedia Retrieval: A Survey. IEEE Trans. Knowl. Data Eng. 2024, 36, 239–260. [Google Scholar] [CrossRef]
- Ou, W.; Deng, J.; Zhang, L.; Gou, J.; Zhou, Q. Cross-Modal Generation and Pair Correlation Alignment Hashing. IEEE Trans. Intell. Transp. Syst. 2023, 24, 3018–3026. [Google Scholar] [CrossRef]
- Zheng, C.; Zhu, L.; Zhang, S.; Zhang, H. Efficient Parameter-Free Adaptive Multi-Modal Hashing. IEEE Signal Process. Lett. 2020, 27, 1270–1274. [Google Scholar] [CrossRef]
- Wu, G.; Lin, Z.; Han, J.; Liu, L.; Ding, G.; Zhang, B.; Shen, J. Unsupervised Deep Hashing via Binary Latent Factor Models for Large-Scale Cross-Modal Retrieval. In Proceedings of the Twenty-Seventh International Joint Conference on Artificial Intelligence IJCAI, Stockholm, Sweden, 13–19 July 2018; Volume 1, p. 5. [Google Scholar]
- Wu, G.; Han, J.; Lin, Z.; Ding, G.; Zhang, B.; Ni, Q. Joint image-text hashing for fast large-scale cross-media retrieval using self-supervised deep learning. IEEE Trans. Ind. Electron. 2018, 66, 9868–9877. [Google Scholar] [CrossRef]
- Zhou, X.; Wu, G.; Sun, X.; Hu, P.; Liu, Y. Attention-Based Multi-Kernelized and Boundary-Aware Network for image semantic segmentation. Neurocomputing 2024, 597, 127988. [Google Scholar] [CrossRef]
- Hu, P.; Zhen, L.; Peng, D.; Liu, P. Scalable deep multimodal learning for cross-modal retrieval. In Proceedings of the 42nd International ACM SIGIR Conference on Research and Development in Information Retrieval, Paris, France, 21–25 July 2019; pp. 635–644. [Google Scholar]
- Shen, H.T.; Liu, L.; Yang, Y.; Xu, X.; Huang, Z.; Shen, F.; Hong, R. Exploiting subspace relation in semantic labels for cross-modal hashing. IEEE Trans. Knowl. Data Eng. 2021, 33, 3351–3365. [Google Scholar] [CrossRef]
- Ma, X.; Zhang, T.; Xu, C. Multi-Level Correlation Adversarial Hashing for Cross-Modal Retrieval. IEEE Trans. Multimed. 2020, 22, 3101–3114. [Google Scholar] [CrossRef]
- Liu, X.; Cheung, Y.-M.; Hu, Z.; He, Y.; Zhong, B. Adversarial tri-fusion hashing network for imbalanced cross-modal retrieval. IEEE Trans. Emerg. Topics Comput. Intell. 2021, 5, 607–619. [Google Scholar] [CrossRef]
- Wang, X.; Liang, M.; Cao, X.; Du, J. Dual-Pathway Attention Based Supervised Adversarial Hashing for Cross-Modal Retrieval. In Proceedings of the 2021 IEEE International Conference on Big Data and Smart Computing (BigComp), Jeju Island, Republic of Korea, 17–20 January 2021; pp. 168–171. [Google Scholar] [CrossRef]
- Wu, Z.; Yu, Y. MLSCH: Multi-Layer Semantic Constraints Hashing for Unsupervised Cross-Modal Retrieval. In Proceedings of the 2023 IEEE International Conference on Control, Electronics and Computer Technology (ICCECT), Jilin, China, 28–30 April 2023; pp. 1479–1484. [Google Scholar] [CrossRef]
- Xie, D.; Deng, C.; Li, C.; Liu, X.; Tao, D. Multi-task consistency-preserving adversarial hashing for cross-modal retrieval. IEEE Trans. Image Process. 2020, 29, 3626–3637. [Google Scholar] [CrossRef]
- Zhu, L.; Wu, X.; Li, J.; Zhang, Z.; Guan, W.; Shen, H.T. Work Together: Correlation-Identity Reconstruction Hashing for Unsupervised Cross-Modal Retrieval. IEEE Trans. Knowl. Data Eng. 2023, 35, 8838–8851. [Google Scholar] [CrossRef]
- Song, R.; Liang, Y.; Wang, M.; Yan, F. Paired and Unpaired: Unsupervised Cross-Modal Hash Retrieval Based on Collaborative Semantic Distribution. In Proceedings of the 2022 4th International Conference on Frontiers Technology of Information and Computer (ICFTIC), Qingdao, China, 2–4 December 2022; pp. 180–184. [Google Scholar] [CrossRef]
- Wu, Q.; Zhang, Z.; Liu, Y.; Zhang, J.; Nie, L. Contrastive Multi-bit Collaborative Learning for Deep Cross-modal Hashing. IEEE Trans. Knowl. Data Eng. 2024, 36, 5835–5848. [Google Scholar] [CrossRef]
- Cao, L.; Xiao, H.; Song, W.; Li, H. A Highly Efficient Zero-Shot Cross-Modal Hashing Method Based on CLIP. In Proceedings of the 2024 5th International Seminar on Artificial Intelligence, Networking and Information Technology (AINIT), Nanjing, China, 22–24 March 2024; pp. 868–873. [Google Scholar] [CrossRef]
- Huang, Y.; Wang, Q.; Zhang, Y.; Hu, B. A Unified Perspective of Multi-level Cross-Modal Similarity for Cross-Modal Retrieval. In Proceedings of the 2022 5th International Conference on Information Communication and Signal Processing (ICICSP), Shenzhen, China, 14–16 March 2022; pp. 466–471. [Google Scholar] [CrossRef]
- Huo, Y.; Qibing, Q.; Dai, J.; Zhang, W.; Huang, L.; Wang, C. Deep Neighborhood-aware Proxy Hashing with Uniform Distribution Constraint for Cross-modal Retrieval. ACM Trans. Multimed. Comput. Commun. Appl. 2024, 20, 169. [Google Scholar] [CrossRef]
- Song, G.; Huang, K.; Su, H.; Song, F.; Yang, M. Deep Ranking Distribution Preserving Hashing for Robust Multi-Label Cross-Modal Retrieval. IEEE Trans. Multimed. 2024, 26, 7027–7042. [Google Scholar] [CrossRef]
- Sun, Y.; Dai, J.; Ren, Z.; Li, Q.; Peng, D. Relaxed Energy Preserving Hashing for Image Retrieval. IEEE Trans. Intell. Transp. Syst. 2024, 25, 7388–7400. [Google Scholar] [CrossRef]
- Dong, X.; Zhang, H.; Zhu, L.; Nie, L.; Liu, L. Hierarchical Feature Aggregation Based on Transformer for Image-Text Matching. IEEE Trans. Circuits Syst. Video Technol. 2022, 32, 6437–6447. [Google Scholar] [CrossRef]
- Wei, S.; Tan, A.; Wang, Y. A Multiscale Hybrid Model for Natural and Remote Sensing Image-Text Retrieval. In Proceedings of the 2024 6th International Conference on Machine Learning, Big Data and Business Intelligence (MLBDBI), Hangzhou, China, 1–3 November 2024; pp. 41–45. [Google Scholar] [CrossRef]
- Wu, Z.; Pan, S.; Chen, F.; Long, G.; Zhang, C.; Yu, P.S. A Comprehensive Survey on Graph Neural Networks. IEEE Trans. Neural Netw. Learn. Syst. 2021, 32, 4–24. [Google Scholar] [CrossRef]
- Sapijaszko, G.; Mikhael, W.B. An Overview of Recent Convolutional Neural Network Algorithms for Image Recognition. In Proceedings of the 2018 IEEE 61st International Midwest Symposium on Circuits and Systems (MWSCAS), Windsor, ON, Canada, 5–8 August 2018; pp. 743–746. [Google Scholar] [CrossRef]
- Huiskes, M.J.; Lew, M.S. The MIR Flickr Retrieval Evaluation. In Proceedings of the 1st ACM International Conference on Multimedia Information Retrieval (MIR ‘08), New York, NY, USA, 30–31 October 2008; pp. 39–43. [Google Scholar]
- Chua, T.-S.; Tang, J.; Hong, R.; Li, H.; Luo, Z.; Zheng, Y. NUS-WIDE: A Real-World Web Image Database from National University of Singapore. In Proceedings of the ACM International Conference on Image and Video Retrieval (CIVR ‘09), New York, NY, USA, 6 January 2009; pp. 1–9, Article 48. [Google Scholar]
- Lin, T.-Y.; Maire, M.; Belongie, S.; Hays, J.; Perona, P.; Ramanan, D.; Zitnick, C.L. Microsoft Coco: Common Objects in Context. In Proceedings of the European Conference on Computer Vision, Zurich, Switzerland, 6–12 September 2014; pp. 740–755. [Google Scholar]
- Ding, G.; Guo, Y.; Zhou, J. Collective Matrix Factorization Hashing for Multimodal Data. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition Workshops, Columbus, OH, USA, 25 September 2014; pp. 2075–2082. [Google Scholar]
- Liu, S.; Qian, S.; Guan, Y.; Zhan, J.; Ying, L. Joint-Modal Distribution-Based Similarity Hashing for Large-Scale Unsupervised Deep Cross-Modal Retrieval. In Proceedings of the 43rd International ACM SIGIR Conference on Research and Development in Information Retrieval, Xi’an, China, 25–30 July 2020; pp. 1379–1388. [Google Scholar]
- Su, S.; Zhong, Z.; Zhang, C. Deep Joint-Semantics Reconstructing Hashing for Large-Scale Unsupervised Cross-Modal Retrieval. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Seoul, Republic of Korea, 27 October–2 November 2019; pp. 3027–3035. [Google Scholar]
- Zou, X.; Wu, S.; Bakker, E.M.; Wang, X. Multi-label enhancement based self-supervised deep cross-modal hashing. Neurocomputing 2022, 467, 138–162. [Google Scholar] [CrossRef]
- Tu, J.; Liu, X.; Lin, Z.; Hong, R.; Wang, M. Differentiable Cross-Modal Hashing via Multimodal Transformers. In Proceedings of the 30th ACM International Conference on Multimedia, Lisbon, Portugal, 10–14 October 2022; pp. 453–461. [Google Scholar]
- Huo, Y.; Qin, Q.; Dai, J.; Wang, L.; Zhang, W.; Huang, L.; Wang, C. Deep semantic-aware proxy hashing for multi-label cross-modal retrieval. IEEE Trans. Circuits Syst. Video Technol. 2023, 34, 576–589. [Google Scholar] [CrossRef]
- Taheri, R.; Ahmadzadeh, M.; Kharazmi, M.R. A new approach for feature selection in intrusion detection system. Fen Bilim. Dergisi. CFD 2015, 36, 1344–1357. [Google Scholar]
- Parsaei, M.R.; Taheri, R.; Javidan, R. Perusing the effect of discretization of data on accuracy of predicting naive bayes algorithm. J. Curr. Res. Sci. 2016, 1, 457–462. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).