Abstract
The thick-walled thickness effect in layered-symmetrical structure is very important for considering the external thermal heating on the surface of functionally graded material (FGM) plates. Dynamic thermal vibration with advanced shear correction on the FGM plates are presented. The third-order shear deformation theory (TSDT) is included to calculate the values of advanced shear correction for the thick plates based on the displacement assumed in the middle symmetry plane. The values of advanced shear correction coefficient are in nonlinear variation with respect to the power-law index value for FGM. The dynamic stresses are calculated when the displacements and shear rotations are obtained for the given natural frequency of displacements, frequency of applied heat flux and time. The natural frequencies of sinusoidal displacements and shear rotations are obtained by using the determinant of the coefficient matrix in the fully homogeneous equation. Only the numerical dynamic results of displacements and stresses subjected to sinusoidal applied heat loads are investigated. The heating study in symmetry structure of FGMs to induce thermal vibration is interesting in the field of engineering and materials. The center displacements can withstand a higher temperature of 1000 K and a power-law index of 5, for which the length-to-thickness ratio 5 is better than that for 10.
1. Introduction
It is very important to study how the thick-walled thickness effect mainly contributes to shear stresses and displacements of functionally graded material (FGM) plates. A thick-walled structure can be defined as one for which the ratio of length to thickness is not less than a value of ten. The study of layered-symmetrical structure is also important to consider the external thermal heating on the surface, then induce the stresses and displacements of FGM plates. The dynamic states are also important to study for the time responses and transient responses of stresses and displacements for the FGM plates. The nonlinear type verse with thickness-axis direction of shear deformation theory for displacement should be considered in the layered-symmetrical structure. The advanced nonlinear shear correction coefficient used in the stiffness calculation is also very important to compute the stress values in a varied and accurate form. The values of advanced shear correction coefficient are in nonlinear variation with respect to the power-law index value for FGM symmetrical structures.
Studies of dynamic vibration have been investigated in the FGM symmetrical and asymmetrical structures. Kumar and Jana (2024) [1] applied the dynamic stiffness method (DSM) and first-order shear deformation theory (FSDT) to study the free vibration natural frequencies for the power-law FGM. Omar et al. (2024) [2] studied the natural frequencies and free vibration of displacements for FGM plates on elastic foundations. Narayanan and Banerjee (2024) [3] used the finite element method (FEM) and FSDT to present the free vibration and forced vibration for cutouts of FGM plates. Ledda et al. (2024) [4] applied the DSM, Euler–Bernoulli (EB) and Timoshenko beam models to study the natural frequencies of FGM beams. Do and Tran (2024) [5] used the FEM and refined FSDT to study the random vibration of moving load on FGM plates. Wang et al. (2023) [6] used the semi-analytical Chebyshev–Ritz method to investigate the stability behavior for asymmetric de-laminated FGM plates. Shariati et al. (2020) [7] studied the natural frequencies and stability of asymmetrical visco-elastic FGM beams by using Rayleigh and EB beam models. Duc et al. (2018) [8] applied the Runge–Kutta method and FSDT to study the dynamic response of porous FGM plates on elastic foundations. Singh and Harsha (2019) [9] applied the stress-function Galerkin method to investigate the nonlinear dynamic responses of sandwich FGM plates with inverse hyperbolic shear theory. Javani et al. (2019) [10] applied the generalized differential quadrature (GDQ) method to investigate the thermal vibrations of annular FGM plates with FSDT. Duc et al. (2016) [11] presented the nonlinear dynamic responses of piezoelectric layer in FGM plates with FSDT. Ta and Noh (2015) [12] applied the trigonometric refined plate theory to investigate the dynamic responses of FGM plates resting on elastic foundation. Dogan (2013) [13] presented the nonlinear dynamic vibration of FGM plates under thermal load and random excitation pressure loads. Sun and Luo (2011) [14] presented the dynamic response of FGM plates under impulse loads with FSDT. In the above literatures are investigated by linear FSDT study for displacement model and thin-walled structures. For thick-walled structures, it is needed to apply the nonlinear study for displacement model to understand thickness effect on displacement and stress. Do et al. (2020) [15] applied the finite element method to investigate the dynamic transient behaviors of nano-tube FGM plates with higher-order shear theory. Xia and Shen (2009) [16] presented the nonlinear dynamic response of piezoelectric FGM plates with third-order shear deformation theory (TSDT). Huang and Shen (2004) [17] applied the improved perturbation technique to investigate the nonlinear dynamic response of FGM plates with TSDT.
Symmetrical presentations for thick FGM structures have been applied by using the advanced varied shear correction coefficient. Hong (2024) [18] presented the frequency study of cylindrical shells with TSDT and advanced shear correction. The advanced shear correction was calculated directly with TSDT, and the fully homogeneous equation was used to obtain the frequency values. Presentations of GDQ also have been applied previously by using the shear factor 5/6 or simply modified shear correction factor. Hong (2023) [19] presented the thermal dynamic vibration with the simply modified shear correction factor. The effects of TSDT and the simply homogeneous equation on symmetrical plates were also considered. In the present manuscript, advanced shear correction and fully homogeneous equation studies are the only two items that are different from previous work [19], which was with the simply modified shear correction factor and simply homogeneous equation. Further, it is a novel study in the vibrations of nonlinear TSDT, fully homogeneous equation and advanced shear correction due to sinusoidal applied heat loads only in symmetry plane of FGMs. The purpose of this work is to use the computing GDQ method with advanced shear correction to study many effects on the stress and displacement for the FGM plates. The effects of length-to-thickness ratio, heat flux frequency, environment temperature and power law index on the vibrations of thick FGM plates are also studied. The heating studies in symmetry structure of FGMs to induce thermal vibrations are very important in the field of engineering and materials.
The text that follows describes the originality and relevance of the formulation of the proposed mechanical model to the thick symmetry plate problem addressed in materials, methods, research background, future research directions, and possible applications of the research. FGM materials are usually used in extremely high temperature—for example, a 1000 K environment—to reduce the displacement and stress of materials actuated by outer load, e.g., time sinusoidal applied heat load. For the studied thermal vibration problem, thick plates with TSDT are more complex and difficult than thin plates with FSDT and classical laminated plate theory (CLPT). The thick plates usually use a ratio value of length to thickness, which is less than 10 in the studied problem. Various property types of layered FGM materials are used distribution in functions of thickness coordinate, e.g., power law, exponential law, trigonometric law, etc. In general, the increasing of temperature on conventional materials would give the extension of plates, also in extremely high temperature, very great tension stress. To endure heat in extremely high temperature with materials of FGM would be available. The applied heat loads usually use the heat conduction equation with the assumptions of no heat source generation, linear, uncoupled and functions of temperature difference to obtain the frequency of applied heat flux. The nonlinear versus thickness coordinate in the displacement models could be TSDT or high-order shear deformation theory (HSDT) to derive the dynamic equation of motions. The value effects of various shear correction factor on the displacements and stresses could be in constant 5/6, simply modified and advanced types.
The numerical method used in the experimental simulation could be the finite difference method (FDM), FEM, boundary element method (BEM), GDQ method, etc. The implemented program used in the calculation could be commercial software, e.g., Abaqus, Ansys, Catia, and high-level language, e.g., Python, Matlab, Mathematica, Maple, C++, Lahey–Fujitsu Fortran, etc. For experimental details, the hardware would be waited in the future research directions, if possible. For possible applications, the research would be applied to the engine field of aircrafts and missiles. The main aim of this work is to use the GDQ method to study the effects of advanced shear correction, length-to-thickness ratio, heat flux frequency, environmental temperature and power law index on the stress and displacement of FGM symmetry plates. The principal time response results for the dynamic stress and displacement are obtained. The general key benefit of using GDQ over other numerical methods like FEM or FDM for this type of analysis is that it uses less computational time and grid points. In this study, the author would like to explicitly point out the combined study regarding thick-walled effects, layered-symmetrical structures, thermal heating in the symmetry plane and the specific advanced shear correction and fully homogeneous equation used on the FGM material. The main objective of the paper is to obtain the thermal vibration results for thick FGM plates with advanced nonlinear shear and a fully homogeneous equation. To provide the highlighting in focus and innovation of main researches, Section 2 introduces the work about power law FGM materials in functions of index and temperature and the TSDT displacement model in functions of nonlinear terms of z3, in which z is the thickness direction in a coordinate system and time, applied thermal loading in sinusoidal type, shear correction factor in advanced type, and the GDQ method is used to solve the dynamic differential equation. Section 3 introduces the work about numerical results for the fundamental frequency of the fully homogeneous equation, heat flux frequency of applied thermal loading, convergence study of center displacement and parameter effect on displacement and stress, including length-to-thickness ratio, power law index, temperature, TSDT and FSDT.
2. Materials and Methods
The presented formulation used in the study is described as follows. The power-law function property type of layered FGM materials is used. The TSDT displacement model is used and studied in the thermal vibration problem of thick plates in layered-symmetrical structures. Sinusoidal applied heat loads are used to study the thermal vibration of FGM plates. The advanced type of shear correction factor is included to study the thermal stress and displacement in nonlinear TSDT dynamic equations of motion. The GDQ numerical method is used in the simulation, and the Lahey–Fujitsu Fortran 7.8 Microsoft Visual Studio 2015 high-level language is implemented in the software program. The novelty of the research presented is in the well-known FG materials Si3N4 and SUS304, with well-known formulations in advanced type of shear correction factor and fully homogeneous equation being employed. It is very important to investigate the data for the fully homogeneous equation used in this study.
2.1. Power-Law FGM
The FGM plate under applied heat loads with temperature difference is presented in Figure 1 with respect to , and directions of the Cartesian coordinate system. Symbolic parameters and denote lengths, denotes thickness of constituent material 1, and denotes thickness of constituent material 2. Thus, denotes total thickness. For the two-material FGM plate, the material property Young’s modulus of the FGM plate is the dominated one in the expression , in which and are the Young’s modulus of constituent material 1 and material 2, and and are the volume fractions of constituent material 1 and material 2, meet in the expression and use the power-law function where is the power-law index [19]. Thus,
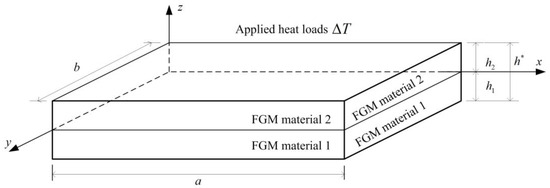
Figure 1.
Two constituent materials of FGM plates in layered-symmetrical structures under sinusoidal heat.
The other material properties, e.g., Poisson’s ratio and density , of the FGM plate are all assumed in average form as follows:
in which and are the Poisson’s ratio of constituent material 1 and material 2, and and are the density of constituent material 1 and material 2, respectively.
denotes the material properties of individual constituents; e.g., , , , , and etc. are applied in functions of temperature as follows [19]:
in which and denote temperature coefficients. Material properties, constants of two constituent materials of FGM used for Si3N4 and SUS304, are presented in Table 1 and are referred to in 2005 by Pradhan [20], in 1998 by Reddy and Chin [21], in 2008 by Shariyat [22] as follows.

Table 1.
Material properties, constants of two constituent materials of FGM.
2.2. TSDT Displacement Model
The TSDT model used for , components of displacements in , directions of thick plates are obtained in functions of time t and in nonlinear terms of z3 and shear rotations with . And the TSDT does not fit for the in transverse component of displacements; only use it varied on the mid-surface of the x-y plane and in function of t and listed in matrix form of TSDT model as follows [23]:
in which , is displacement in the middle symmetry plane of plates, is shear rotation, and . If = 0, then (5) becomes the FSDT model. If = 0, and = 0, then (5) becomes the CLPT model. The FSDT and CLPT models are inadequate for thick FGMs since they are more adequate for thin FGMs. The TSDT is one of the HSDT models and adequate for the thick FGMs approach.
2.3. Sinusoidal Applied Heat Loads
In preliminary study, this sinusoidal specific type of thermal loading is chosen to make a general understanding of thermal vibration. The stresses , in normal directions and stresses , , in shear directions in the layer of composited FGM plates due to of applied heat loads are formulated in reduced stiffness, strains and thermal coefficients in directions of expansion and shear, listed in matrix form as follows [24]:
in which is stress, is strain, is the coefficient of thermal expansion in x, y directions and thermal shear,
and with subscripts i, j = 1,2,4,5 and 6 is the stiffness of FGM. The sinusoidal equation of applied heat load with is formulated in the linear function of z and temperature amplitude , in sinusoidal functions of x, y, t and heat flux frequency listed as follows, for = 0 is assumed in the middle symmetry plane z = 0 of plates:
in which is assumed to satisfy initially no heat generation, linear and uncouple case of thermo-mechanics properties for the heat conduction expression , thus the parameter meets expression , in which , is thermal conductivity in average expression , and is specific heat in average expression . For FGM symmetry plates [19], property values for Si3N4 and SUS304 are presented in Table 1. These property values are used to obtain the FGM structure under temperature value.
2.4. Advanced SHEAR Correction Factor
The nonlinear dynamic equations of motion for a TSDT composited plate are formulated. Also, the dynamic nonlinear equilibrium differential equations for a TSDT composited plate under applied thermal loads and inertia terms are formulated in the matrix expressions listed as follows [19]:
in which denotes a 5 by 5 matrix, denotes a 5 by 12 matrix, denotes a 5 by 8 matrix, denotes a 5 by 9 matrix, denotes a 5 by 6 matrix, denotes a 5 by 10 matrix, and denotes a 5 by 5 matrix, e.g.,
= … = = … = = … = = … = , , , , and .
And , , , , denote the external loads, in which and denote the in-plane distributed forces, denotes the external pressure load, and denote the applied thermal loads as follows:
with the stiffness and advanced in the direction of axis integrated in the stiffness coefficients as follows:
in which , , and denotes the shear correction coefficient. When the advanced type of is used and called the advanced shear correction coefficient, the equation is formulated directly in expression as follows [18]:
where parameter FGMZSV is in function of ()6, and parameter FGMZIV is in function of ()5; thus, would be in non-dimensional value. The stress distribution can be identified from (6) and in functions of stiffness , strain and . Also, stiffness coefficients can be calculated from (13) contained , and displacements and shear rotation are contained in the strain. Thus, can affect stress distribution under strain and for the FGM plates. The nonlinear nature values of advanced are usually functions of , and . The application with advanced shear correction factor is particularly necessary when used in the thick-walled material of the proposed model. The stiffness coefficients contain different power law indices in matrices HM, EM, FM, AM, BM, KE and FQ, under applied thermal load, and different temperatures lead to sensitivities of the displacement results.
2.5. GDQ Numerical Method
The GDQ method is applied in the calculation for a with subscripts i = 1,2,…,N and j = 1,2,…,M, in which and denote the grid numbers. The time displacement and shear rotations of thermal vibrations are formulated in sinusoidal forms with the frequency in subscript integer mode number and for the fully homogeneous equation of thick FGM plates. And the GDQ discrete dynamic equation can be obtained in the following expression [19]:
in which denotes an × matrix with and contains stiffness coefficients, inertia terms and weighting parameters of GDQ. denotes an × 1 unknown matrix for displacements and shear rotations. denotes an × 1 external loads matrix.
More details on the implementation of the GDQ method in the software are discussed as follows. Boundary conditions incorporated into the numerical model at the boundary grid point usually contain the corresponding summation terms in the interior grid point. The different kinds of boundary conditions receive different kinds of interior grid point for displacement and shear rotation expressions. For four sides of the simply supported boundary, at left and right grid points and , in which j = 2, 3,…, M1, the displacement and shear rotation equations can be expressed in the following [25]:
where , , and .
At down and top grid points and , in which i = 2, 3,…, N1, the displacement and shear rotation equations also can be expressed in the following:
where , , and .
Thus, , derivative terms in discrete summation expressions, can be expressed in interior grid points, e.g., , , in which and are weighting parameters of GDQ for superscript m th-order derivative of displacement, shear rotation and thermal load functions in x and directions, respectively. And non-dimensional parameters , , , in which are applied for the grid points. The application with the GDQ method is usually applied for dynamic differential equation and boundary condition to become a GDQ discrete equation and internal grids.
3. Results
The nonlinear dynamic thermal stresses in the layer are found while solving the displacements and shear rotations for a given vibration frequency , advanced value and time t by implementing with the Fortran program. The fundamental of the fully homogeneous equation for boundary condition in four sides simply supported is applied; e.g., for a/h* = 10, the = 0.003201/s used in = 0.5; for a/h* = 5, the = 0.001928/s used in = 0.5. The material 1 is SUS304, and the material 2 is Si3N4, which is subjected to sinusoidal heat loads , and only; i.e., = = = 0 and = 0 is assumed in the middle symmetry plane z = 0 of the plates. The nonlinear dynamic convergence of center displacements (a/2,b/2) (mm) is obtained with basic parameter values of a/b = 1, = = 0.6 mm in layered-symmetrical structures, = 1.2 mm, = 0.925925/mm2, = 100 K, and = 100 K. The (a/2,b/2) values for a/h* = 10 with = 0.2618004/s and a/h* = 5 with = 0.2618019/s at t = 6 s, respectively, are presented in Table 2. There are some factors that contribute to the
center displacement convergence, e.g., material, boundary condition, external load, homogeneous equation type, kα value, a/h* value, value and grid size. Usually, the odd numbers of grid size, for example, N = M = 7, 9, 11, 13, and advanced value are calculated to study the convergence of center displacement. The percentage difference is 0.000681% for the (a/2,b/2) of = 2 and a/h* = 10 between grid size = 11 × 11 and 13 × 13; thus, = 11 × 11 or 13 × 13 are already in the convergence state used for center displacement numerical results.

Table 2.
Dynamic convergence of (a/2,b/2) with advanced nonlinear .
The advanced value also affects the center displacement when compared to the published article with simply modified shear correction factor in 2023 by Hong [19], which used more grid numbers, from 13 × 13 to 23 × 23. Of course, it is not necessary to use more grid numbers if the advanced value is used and considered in the convergence study. The 13 × 13 grid is considered to be in very good convergence condition at t = 6 s. And it can be considered in a steady state, nearly t = 6 s. For a/b = 1, values from 0.12 mm to 12 mm, the calculated values of advanced nonlinear under T = 600 K are presented in Table 3. They are used in the calculations for the displacements and stresses. When the values of presently advanced are compared with the published article in 2023 by Hong [19], which used the value of simply modified shear correction factor, they are totally in different values under T = 600 K; e.g., in Table 3, when used in TSDT model, advanced values are not functions of , and in almost constant values for each value, they can be in negative value = −1.096615 for = 0.5 or in positive value = 1.560072 for = 2. When , it is simply used for the FSDT displacement model. In article [19], presented with simply modified shear correction factor values, which are all in not negative values and in functions of , e.g., in = 1.2 mm, positive value = 0.089181 for = 0.5 and positive value = 0.191371 for = 2.

Table 3.
Advanced nonlinear vs. c1, and = 600 K.
The values of (a/2,b/2) (mm) are calculated with and varied , e.g., = 15.707964/s used at t = 0.1 s and = 0.523601/s used at t = 3.0 s. Figure 2 presents the response values of (a/2,b/2) (mm) vs. t for a/h* = 5 and 10, respectively, by using advanced values, = 600 K, = 100 K and t = 0.1 s–3.0 s. The (a/2,b/2) values of response converge with time. The maximum (a/2,b/2) is −2.656838 mm, obtained at t = 0.1 s for a/h* = 5 and = −3.535402, then the magnitude decreases and converges to 0.011554 mm at t = 3 s. And it can be considered in a steady state, nearly t = 3 s. The maximum (a/2,b/2) is −0.122967 mm, obtained at t = 0.1 s for a/h* = 10 and = −3.535402, then the magnitude decreases and converges to −0.025922 mm at t = 3 s. The (a/2,b/2) magnitudes in a/h* = 5 are greater than those in a/h* = 10. Figure 3 presents the time responses of (GPa) on x = a2, y = b/2, z = −0.5 h* for = 1, a/h* = 5 and 10, respectively. The maximum stress is −8.684167 × 10−4 GPa, obtained at t = 0.1 s for a/h* = 5, then the magnitude decreases to −8.181136 × 10−4 GPa at t = 3 s. The minimum stress is −7.837108 × 10−4 GPa, obtained at t = 0.1 s for a/h* = 10, then the magnitude increases to −7.937552 × 10−4 GPa at t = 3 s. The magnitudes in a/h* = 5 are greater than those in a/h* = 10.
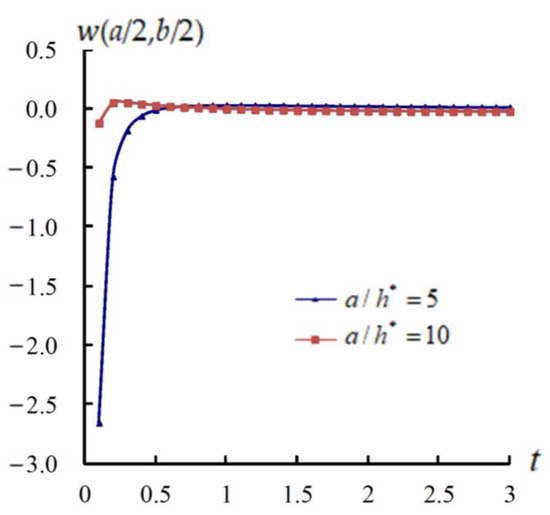
Figure 2.
(a/2,b/2) (mm) vs. t (s).
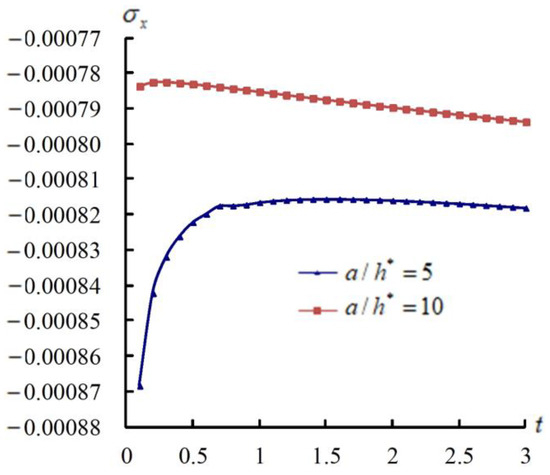
Figure 3.
(GPa) vs. t (s).
In Figure 4, the (a/2,b/2) (mm) vs. (K) of values vary from 0.1 to 10 at = 0.1 s with advanced values, = 100 K, a/h* = 5 and 10, respectively. The (a/2,b/2) (mm) vs.(K) for a/h* = 5; the maximum (a/2,b/2) is 16.269870 mm obtained on = 1000 K and = 10. The (a/2,b/2) values are increasing vs. varied from 600 K to 1000 K for = 0.2 and 10, they cannot withstand a higher T = 1000 K. The (a/2,b/2) values keep constant vs. for = 0.1, 0.5, 1 and 2. The (a/2,b/2) values decrease vs. varied from 600 K to 1000 K for = 5; they can withstand a higher = 1000 K. The (a/2,b/2) (mm) vs. (K) for a/h* = 10; the maximum (a/2,b/2) is −514.445740 mm obtained at = 1000 K and = 1. The (a/2,b/2) values increase vs. varied from 600 K to 1000 K for = 0.5, 1 and 2; they cannot withstand a higher = 1000 K. The (a/2,b/2) values are constant vs. for = 0.1, 0.2, 5 and 10. This is a typical property for FGM in proper power-law index design to decrease displacement at higher temperatures. Thus, the (a/2,b/2) can withstand a higher temperature of 1000 K and = 5, for which a/h* = 5 is better than that for a/h* = 10. The (a/2,b/2) results for TSDT vs. FSDT are compared and provided in Figure 4c for a/h* = 5, = 5 and in 4d for a/h* = 10, = 5. For TSDT of a/h* = 5 results, it is 4.036842 mm at T = 100 K, it is 14.289893 mm at T = 600 K, and it is −2.966549 mm at T = 1000 K. For the FSDT of a/h* = 5 results, it is −0.018941 mm at T = 100 K, it is −0.022558 mm at T = 600 K, and it is −0.016263 mm at T = 1000 K. Thus, the FSDT (a/2,b/2) result in linear line is underestimated vs. TSDT in improved nonlinear curve for the thick-walled a/h* = 5. Also, for TSDT of a/h* = 10 results, it is 63.253192 mm at T = 100 K, it is 2.341578 mm at T = 600 K, and it is −0.220947 mm at T = 1000 K. For the FSDT of a/h* = 10 results, it is 0.006162 mm at T = 100 K, it is 0.001586 mm at T = 600 K, and it is 0.000323 mm at T = 1000 K. Thus, the FSDT (a/2,b/2) result in linear line is underestimated vs. TSDT in improved nonlinear curve for the moderate thick-walled a/h* = 10. These are the practical implications for the ranges of identified optimal power law indices from 0.1 to 10 and thick-walled thickness ratios 5 and 10 used in the design of FGM structures for high-temperature environments from 100 K to 1000 K.
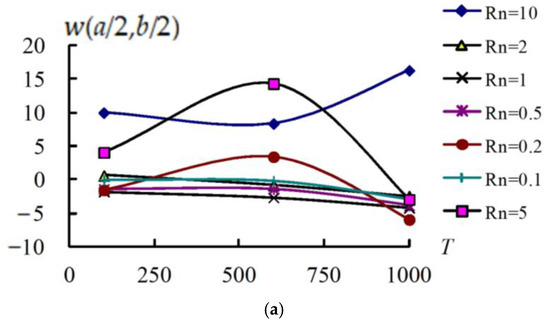
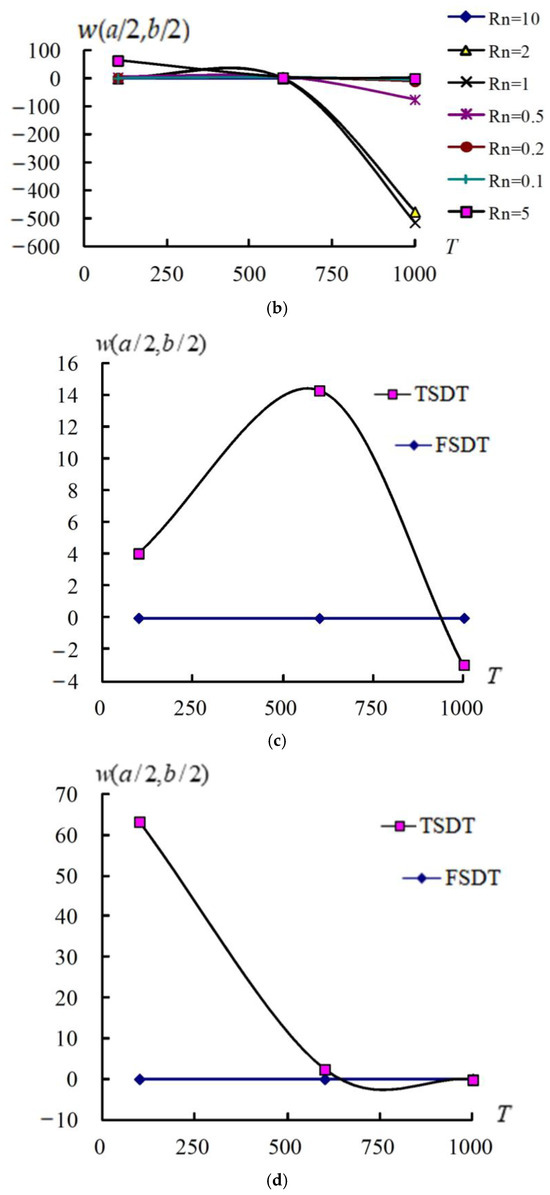
Figure 4.
(a/2,b/2) (mm) vs. (K) and varied from 0.1 to 10: (a) for a/h* = 5; (b) for a/h* = 10; (c) compared TSDT and FSDT for a/h* = 5, = 5; (d) compared TSDT and FSDT for a/h* = 10, = 5.
In Figure 5, the (GPa) on x = a/2, y = b/2, z = −0.5 h* vs. of values vary from 0.1 to 10, and a/h* = 5. The values vs. decrease from 100 K to 600 K and increase from 600 K to 1000 K for = 0.2, 5 and 10, they cannot withstand higher T = 1000 K. The values of are constant vs. for the others’ . The maximum is 1.020618 × 10−2 GPa, obtained on = 100 K and = 5. Thus cannot withstand a higher temperature of 1000 K and = 5, for a/h* = 5. The compare results for TSDT vs. FSDT are provided in Figure 5b for a/h* = 5, = 5. For TSDT of a/h* = 5 results, it is 1.020618 × 10−2 GPa at T = 100 K, it is 9.565207 × 10−4 GPa at T = 600 K, and it is −1.141790 × 10−3 GPa at T = 1000 K. For FSDT of a/h* = 5 results, it is 4.199531 × 10−4 GPa at T = 100 K, it is 5.283282 × 10−4 GPa at T = 600 K, and it is 4.527381 × 10−4 GPa at T = 1000 K. Thus, the FSDT result in linear line is underestimated vs. TSDT in improved nonlinear curve for the thick-walled a/h* = 5.
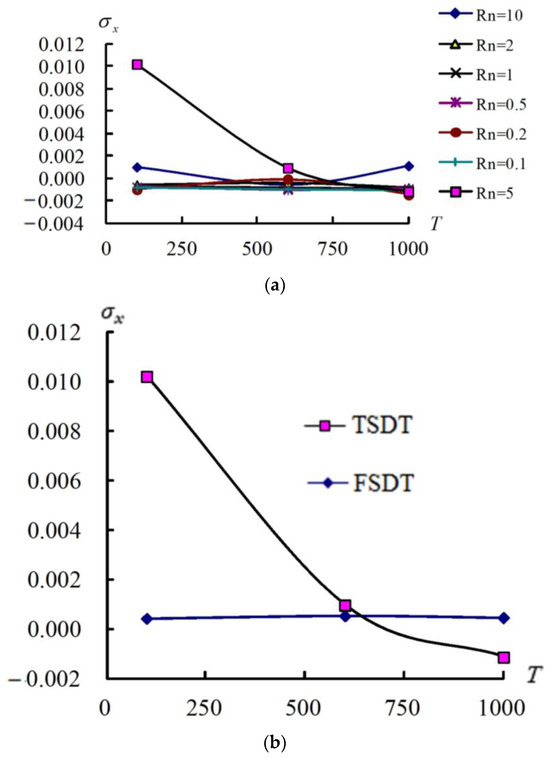
Figure 5.
(GPa) vs. (K) and for a/h* = 5 (a) varied from 0.1 to 10; (b) compared TSDT and FSDT for = 5.
The transient responses of (a/2,b/2) (mm) are obtained. Figure 6a presents the compared transient response of (a/2,b/2) vs. with = 0.001989/s, , advanced = −3.535402, = 600 K, and = 100 K. Two values for = 284314.1/s and = 785.3982/s are presented during t = 0.001 s–0.025 s. The greater (a/2,b/2) values are obtained in greater values. The maximum (a/2,b/2) is −273.793610 mm, obtained at t = 0.001 s for = 284314.1/s. The transient responses of (a/2,b/2) are in converging tendency. Thus, the corruption of (a/2,b/2) could happen in the higher value of heat flux frequency varied greater than 785.3982/s during t = 0.001 s–0.005 s. The compare results of transient responses by Lee et al. (2004) for a/h* = 5, CFRP [23] in Figure 6b are provided in a similarly convergent tendency.
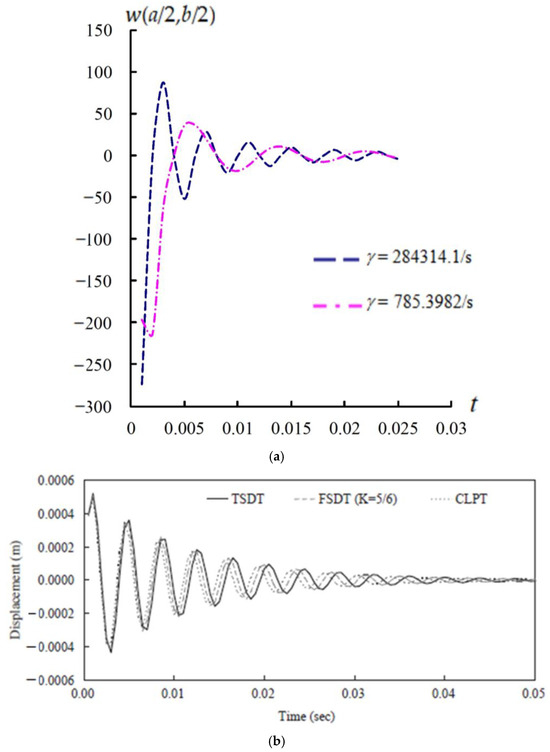
Figure 6.
Transient (a/2,b/2) (mm) vs. t (s) (a) for a/h* = 10; (b) compare results by Lee et al. (2004) for a/h* = 5, CFRP [23].
4. Discussion
The details of GDQ method, including a flowchart, are provided in Figure 7. The GDQ numerical results are successfully computed for many effects of length-to-thickness ratio, heat flux frequency, environmental temperature and power-law index on the symmetrical FGM plates under external thermal heating. The time responses and transient responses of stresses and displacements are obtained, respectively, by considering the nonlinear advanced values of the shear correction coefficient. The presented thermal vibrations are engaged from the first mode vibration frequency and applied heat flux frequency. Thus, it could become further research for the second mode vibration frequency and some applied heat flux frequencies by using the nonlinear TDST and advanced shear correction coefficient, if possible, in the future. The main differences between the present study and ref. [19] are listed in Table 4. The current methods with advanced nonlinear type shear correction and fully homogeneous equation are more significant and advantageous than previous methods with simply linear type shear correction and simply homogeneous equation. A summary, Table 5, of all test parameters used for the simulations is provided to clarify the numerical setting and improve reproducibility. Figure 8 represents transverse shear stress (GPa) vs. z/h* and (GPa) vs. z/h* of the FGM plate at t = 0.1 s, x = a/2, y = b/2, a/h* = 5, = 1, a/b = 1 under T = 600 K and = 100 K. The values of are linear, increasing across the thickness of the FGM plate. The absolute values of are nonlinear, first increasing and then decreasing across the thickness of the FGM plate.
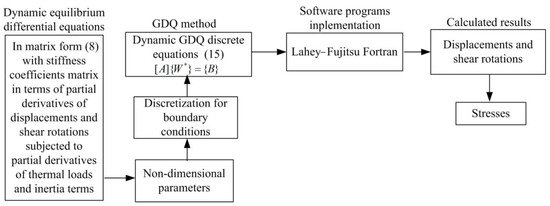
Figure 7.
GDQ method flowchart.

Table 4.
Main differences between the present study and ref. [19].

Table 5.
Test parameters used for the simulations.
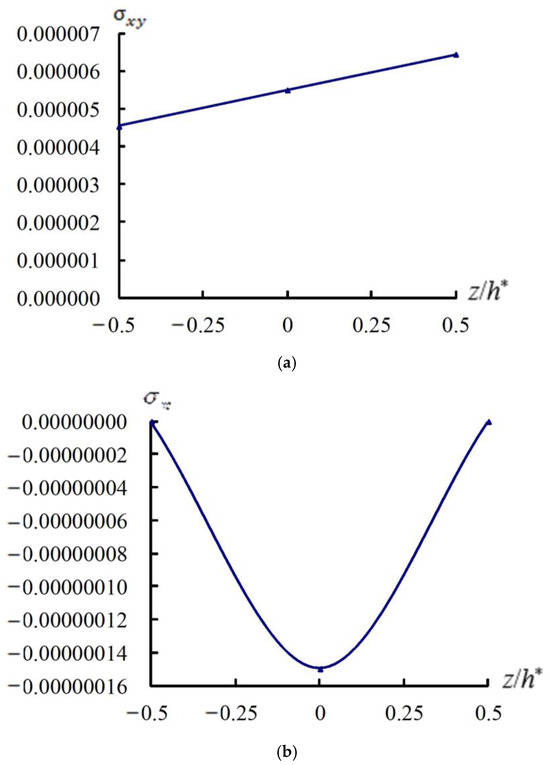
Figure 8.
Transverse shear stress (a) (GPa) vs. z/h*; (b) (GPa) vs. z/h*.
The dynamic response for boundary condition in four sides simply supported due to symmetry type is obtained. Other boundary conditions in the analysis, e.g., clamp or free, would cause some different results in the vibration, which is also very interesting and would warrrant further research, if possible, in the future. The practical relevance of functionally graded material could be in the fields of semiconductors, hip implants, thermal and sound insulated structural walls, interference colors of car-body coating and sports, as discussed in 2013 by Miyamoto et al. [26]. FGM could also be applied to the aerospace, nuclear energy, biological, electromagnetic, optical, and energy emitter fields, as discussed in 2018 by Li and Han [27]. The practical application might be applied to the semiconductor field for the symmetrical FGM plates study under external thermal heating, if possible, in the future. There would be an experimental study for the proposed nonlinear shear correction model in future, if possible. Temperature dependency formulation is explained in more detail in a 2025 article by Ghandehari et al. [28]. A literature review of recent articles with the same methodology and formulations can be found in a 2024 study by Ghandehari et al. [29]. Some new references about the research subject can be developed by using the numerical methods, such as the differential quadrature method (DQM), discussed in 2019 by Pankaj Sharma [30], meshless methods (MMs) in 2014 by Stach [31], the discrete singular convolution (DSC) method in 2013 by Pindza and Maré [32] or FEM in 2023 by El-Amin [33]. The superiority of the present GDQ method for computational issues is that less grid and CPU time used. Similar research into FGM subjects, e.g., in 2018 by Yang et al. [34], in 2024 by Rahmani et al. [35], in 2022 by Sobhani [36], also can be pointed out to make a bridge for studies and investigations.
5. Conclusions
The nonlinear dynamic responses of displacements and stresses for nonlinear TSDT thick FGM plates subjected to sinusoidal heat are presented. The layered-symmetrical FGM structures in the thermal vibration with the effects of advanced shear correction, temperature and power-law index are investigated. The GDQ method is used to calculate the thermal vibration numerical results. The advanced shear correction coefficient values are in variations with TSDT coefficient , power-law index and temperature. The maximum amplitude value of center displacement is −2.656838 mm, obtained at time t = 0.1 s for length
to thickness ratio a/h* = 5, environment temperature T = 600 K, applied heat temperature amplitude = 100 K, advanced shear correction coefficient = −3.535402 and applied heat flux frequency = 15.707964/s. The greater transient values of displacements (a/2,b/2) are obtained, corresponding to greater values. Also, the transient responses of (a/2,b/2) are in converging tendency. The (a/2,b/2) can withstand a higher environment temperature of 1000 K and a power-law index of = 5, in the a/h* = 5 case, is better than that in the a/h* = 10 case. But the normal stress cannot withstand a higher environment temperature of 1000 K and = 5 in the a/h* = 5 case. The (a/2,b/2) and results in FSDT linear line are underestimated vs. TSDT results in improved nonlinear curve for the thick-walled a/h* = 5 and = 5.
Funding
The funding of this paper is NSTC 112-2221-E-164-001 from National Science and Technology Council (NSTC), Taiwan.
Data Availability Statement
In the manuscript, the data used to generate the figures and tables are completely presented. All the data are generated by the author and are openly available.
Acknowledgments
The author expresses his thanks to the people helping and the valuable suggestions from the reviewers.
Conflicts of Interest
The author declares no conflict of interest.
References
- Kumar, R.; Jana, P. Free vibration analysis of uniform thickness and stepped P-FGM plates: A FSDT-based dynamic stiffness approach. Mech. Based Des. Struct. Mach. Int. J. 2024, 52, 447–476. [Google Scholar] [CrossRef]
- Omar, M.; Khaled, B.; Mohammed, S.; Otbi, B. Analytical modeling contribution of the vibration dynamics of FGM plates placed on elastic foundations. Stud. Eng. Exact Sci. 2024, 5, e12589. [Google Scholar] [CrossRef]
- Narayanan, N.I.; Banerjee, S. Free and forced vibration analysis of FGM plates with and without cutouts using heterosis finite element method. J. Vib. Eng. Technol. 2024, 12, 2129–2145. [Google Scholar] [CrossRef]
- Ledda, L.; Greco, A.; Fiore, I.; Caliò, I. Closed-form exact solution for free vibration analysis of symmetric functionally graded beams. Symmetry 2024, 16, 1206. [Google Scholar] [CrossRef]
- Do, N.T.; Tran, T.T. Random vibration analysis of FGM plates subjected to moving load using a refined stochastic finite element method. Def. Technol. 2024, 34, 42–56. [Google Scholar] [CrossRef]
- Wang, J.F.; Cao, G.; Song, Z.W.; Lai, S.K. Dynamic analysis of FGM plates with variable delamination parameters by the Chebyshev–Ritz method. Int. J. Struct. Stab. Dyn. 2023, 23, 2340013. [Google Scholar] [CrossRef]
- Shariati, A.; Jung, D.W.; Mohammad-Sedighi, H.; Zur, K.K.; Habibi, M.; Safa, M. Stability and dynamics of viscoelastic moving rayleigh beams with an asymmetrical distribution of material parameters. Symmetry 2020, 12, 586. [Google Scholar] [CrossRef]
- Duc, N.D.; Quang, V.D.; Nguyen, P.D.; Chien, T.M. Nonlinear dynamic response of functionally graded porous plates on elastic foundation subjected to thermal and mechanical loads. J. Appl. Comput. Mech. 2018, 4, 245–259. [Google Scholar]
- Singh, S.J.; Harsha, S.P. Nonlinear dynamic analysis of sandwich S-FGM plate resting on Pasternak foundation under thermal environment. Euro. J. Mech. A/Solids 2019, 76, 155–179. [Google Scholar] [CrossRef]
- Javani, M.; Kiani, Y.; Eslami, M.R. Large amplitude thermally induced vibrations of temperature dependent annular FGM plates. Compos. Part B 2019, 163, 371–383. [Google Scholar] [CrossRef]
- Duc, N.D.; Cong, P.H.; Quang, V.D. Nonlinear dynamic and vibration analysis of piezoelectric eccentrically stiffened FGM plates in thermal environment. Int. J. Mech. Sci. 2016, 115–116, 711–722. [Google Scholar] [CrossRef]
- Ta, H.D.; Noh, H.C. Analytical solution for the dynamic response of functionally graded rectangular plates resting on elastic foundation using a refined plate theory. Appl. Math. Model. 2015, 39, 6243–6257. [Google Scholar] [CrossRef]
- Dogan, V. Nonlinear vibration of FGM plates under random excitation. Compos. Struct. 2013, 95, 366–374. [Google Scholar] [CrossRef]
- Sun, D.; Luo, S.N. The wave propagation and dynamic response of rectangular functionally graded material plates with completed clamped supports under impulse load. Euro. J. Mech. A/Solids 2011, 30, 396–408. [Google Scholar] [CrossRef]
- Do, V.N.V.; Jeon, J.T.; Lee, C.H. Dynamic analysis of carbon nanotube reinforced composite plates by using Bézier extraction based isogeometric finite element combined with higher order shear deformation theory. Mech. Mater. 2020, 142, 103307. [Google Scholar]
- Xia, X.K.; Sheen, H.S. Nonlinear vibration and dynamic response of FGM plates with piezoelectric fiber reinforced composite actuators. Compos. Struct. 2009, 90, 254–262. [Google Scholar] [CrossRef]
- Huang, X.L.; Sheen, H.S. Nonlinear vibration and dynamic response of functionally graded plates in thermal environments. Int. J. Solids Struct. 2004, 41, 2403–2427. [Google Scholar] [CrossRef]
- Hong, C.C. Advanced frequency of thick FGM cylindrical shells with fully homogeneous equation. J. Struct. Eng. Appl. Mech. 2024, 7, 69–83. [Google Scholar] [CrossRef]
- Hong, C.C. GDQ computation for thermal vibration of thick FGM plates by using third-order shear deformation theory. Mater. Sci. Eng. B 2023, 294, 116208. [Google Scholar] [CrossRef]
- Pradhan, S.C. Vibration suppression of FGM shells using embedded magnetostrictive layers. Int. J. Solids Struct. 2005, 42, 2465–2488. [Google Scholar] [CrossRef]
- Reddy, J.N.; Chin, C.D. Thermoelastical analysis of functionally graded cylinders and plate. J. Therm. Stress. 1998, 21, 593–626. [Google Scholar] [CrossRef]
- Shariyat, M. Dynamic buckling of suddenly loaded imperfect hybrid FGM cylindrical shells with temperature dependent material properties under thermo-electromechanical loads. Int. J. Mech. Sci. 2008, 50, 1561–1571. [Google Scholar] [CrossRef]
- Lee, S.J.; Reddy, J.N.; Rostam-Abadi, F. Transient analysis of laminated composite plates with embedded smart-material layers. Finite Elem. Anal. Des. 2004, 40, 463–483. [Google Scholar] [CrossRef]
- Whitney, J.M. Structural Analysis of Laminated Anisotropic Plates; Technomic Publishing Company, Inc.: Lancaster, PA, USA, 1987. [Google Scholar]
- Shu, C.; Du, H. Implementation of clamped and simply supported boundary conditions in the GDQ free vibration analyses of beams and plates. Int. J. Solids Struct. 1997, 34, 819–835. [Google Scholar] [CrossRef]
- Miyamoto, Y.; Kaysser, W.A.; Rabin, B.H.; Kawasaki, A.; Ford, R.G. Functionally Graded Materials: Design, Processing and Applications; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Li, W.; Han, B. Research and application of functionally gradient materials. IOP Conf. Ser. Mater. Sci. Eng. 2018, 394, 022065. [Google Scholar] [CrossRef]
- Ghandehari, M.A.; Masoodi, A.R.; Hosseininia, E.S. Temperature-dependency and boundary condition impacts on the multiscale vibrational behavior of laminated nested dual conical shell structure semi-AUV applications. Appl. Ocean. Res. 2025, 154, 104425. [Google Scholar] [CrossRef]
- Ghandehari, M.A.; Masoodi, A.R.; Panda, S.K. Thermal frequency analysis of double CNT-reinforced polymeric straight beam. J. Vib. Eng. Technol. 2024, 12, 649–665. [Google Scholar] [CrossRef]
- Sharma, P. Vibration Analysis of Functionally Graded Piezoelectric Actuators; Springer Nature Link eBook: Berlin/Heidelberg, Germany, 2019; pp. 19–26. Available online: https://link.springer.com/book/10.1007/978-981-13-3717-8 (accessed on 9 January 2019).
- Stach, S. ch.11 Modelling fracture processes in orthopaedic implants. In Computational Modelling of Biomechanics and Biotribology in the Musculoskeletal System; Elsevier Ltd. eBook: Amsterdam, The Netherlands, 2014; pp. 331–368. Available online: https://www.sciencedirect.com/science/article/abs/pii/B9780857096616500115 (accessed on 16 May 2014).
- Pindza, E.; Maré, E. Discrete singular convolution method for numerical solutions of fifth order Korteweg-De Vries equations. J. Appl. Math. Phys. 2013, 1, 40717. [Google Scholar] [CrossRef]
- El-Amin, M.F. ch.4 Temporal numerical discretization schemes. In Numerical Modeling of Nanoparticle Transport in Porous Media, Matlab/Python Approach, Micro and Nano Technologies; Elsevier Inc. eBook: Amsterdam, The Netherlands, 2023; pp. 105–123. [Google Scholar]
- Yang, J.; Chen, D.; Kitipornchai, S. Buckling and free vibration analyses of functionally graded graphene reinforced porous nanocomposite plates based on Chebyshev-Ritz method. Compos. Struct. 2018, 193, 281–294. [Google Scholar] [CrossRef]
- Rahmani, F.; Kamgar, R.; Rahgozar, R.; Dimitri, R.; Tornabene, F. Nurl-Based isogeometric analysis for free vibration of functionally graded sandwich plates using higher order formulations. Int. J. Struct. Stab. Dyn. 2024. [Google Scholar] [CrossRef]
- Sobhani, E.; Masoodi, A.R.; Civalek, O.; Ahmadi-Pari, A.R. Agglomerated impact of CNT vs. GNP nanofillers on hybridization of polymer matrix for vibration of coupled hemispherical-conical-conical shells. Aerosp. Sci. Technol. 2022, 120, 107257. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).