Statistical Inference of Inverse Weibull Distribution Under Joint Progressive Censoring Scheme

Abstract

In recent years, there has been an increasing interest in the application of progressive censoring as a means to reduce both cost and experiment duration. In the absence of explanatory variables, the present study employs a statistical inference approach for the inverse Weibull distribution, using a progressive type II censoring strategy with two independent samples. The article expounds on the maximum likelihood estimation method, utilizing the Fisher information matrix to derive approximate confidence intervals. Moreover, interval estimations are computed by the bootstrap method. We explore the application of Bayesian methods for estimating model parameters under both the squared error and LINEX loss functions. The Bayesian estimates and corresponding credible intervals are calculated via Markov chain Monte Carlo (MCMC). Finally, comprehensive simulation studies and real data analysis are carried out to validate the precision of the proposed estimation methods.

1. Introduction

The modeling and analysis of lifetimes play a crucial role in many scientific and technological fields. In practice, studying a complete sample is often impractical because increasing product reliability results in longer lifetime data (see [1]). To save time and reduce costs, various censoring schemes have been proposed in reliability and survival analysis. Among them, the type II censoring scheme is one of the most commonly applied methods. Nevertheless, within industrial contexts, the manufacture of products occurs on multiple production lines, thus necessitating comparative lifecycle analyses. In the evaluation of the reliability of two populations produced by different lines, joint censoring schemes are a more appropriate methodology. In their seminal work, Balakrishnan et al. [2] pioneered the introduction of a novel joint type II censoring scheme, providing a framework for statistical inferences concerning two exponential distributions.

Unlike conventional type II censoring, which involves unit withdrawal only at the experiment’s termination, progressive type II censoring, as pioneered by [3] removes units at each failure occurrence. This strategy saves time by discarding observations with excessively long lifetimes, thereby allowing parameter estimation even without continuous data collection throughout the experiment. Compared to standard censoring techniques, progressive type II censoring provides notable benefits. For a detailed review of work on progressive censoring, please refer to [4].

Relying solely on censoring methods for a single population poses several limitations. While progressive type II censoring removes some data, obtaining sufficient observations remains costly. Moreover, experiments based on one population cannot capture the interaction between different groups. To overcome these drawbacks, Rasouli and Balakrishnan [5] proposed the joint progressive type II censoring (JPC) scheme. This method records failures from two distinct populations, reducing the time needed to collect comparable data and enabling direct comparison of failure times under identical conditions.

Within this framework, two independent samples of sizes m and n are selected from each production line. Both samples are drawn from each production line. Both samples undergo simultaneous life-testing experiments. This method is particularly efficient for ending life tests once a specified number of failures is observed.

Several studies have investigated JPC and its related inference methods. Balakrishnan et al. [6] proposed likelihood-based inference for k exponential distributions under JPC, while Doostparast et al. [7] examined Bayesian estimation using a linear exponential loss function with JPC data. Mondal and Kundu [8] focused on point and interval estimation for Weibull parameters under JPC. Goel and Krishna [9] studied likelihood and Bayesian inference for k Lindley populations under joint type II censoring, with Krishna and Goel [10] extending this framework to JPC. Hassan et al. [11] addressed inference for the Burr type III distribution under JPC, while Kumar and Kumari [12] explored likelihood and Bayesian estimation for two inverse Pareto populations. More recently, Hasaballah et al. [13] analyzed reliability for two Nadarajah–Haghighi populations, and Abo-Kasem et al. [14] investigated inference for two Gompertz populations under similar censoring schemes.

The two-parameter inverse Weibull distribution (IWD) was first proposed by Kaller and Kamath [15] to model the degradation of diesel engine components. Since its introduction, the IWD has gained widespread recognition as a suitable model for lifetime data analysis. Langlands et al. [16] demonstrated its effectiveness in modeling breast cancer mortality data. Abhijit and Anindya [17] demonstrated that the IWD outperforms the normal distribution in analyzing ultrasonic pulse velocity data on concrete structures. Elio et al. [18] introduced a mixed IWD model to address extreme wind speed scenarios.

The IWD finds extensive applications in reliability research. Azm et al. [19] explored the estimation of unknown IWD parameters under competing risks using an adaptive type I progressive hybrid censoring scheme. They employed both maximum likelihood and Bayesian estimation methods, deriving asymptotic, bootstrap, and highest posterior density confidence intervals, and validated their approach with two real datasets. Bi and Gui [20] investigated stress–strength reliability estimation based on the IWD. They proposed an approximate maximum likelihood approach for point estimation and confidence interval construction, alongside Bayesian estimation and highest posterior density intervals derived via Gibbs sampling.

In another study, Alslman and Helu [21] estimated the stress–strength reliability for the IWD under adaptive type II progressive hybrid censoring. Shawky and Khan [22] employed maximum likelihood estimation for a multi-component IWD stress–strength model, confirming its effectiveness via Monte Carlo simulations. Ren et al. [23] demonstrated that Bayesian estimation outperforms other methods for IWD under progressive type II censoring. However, no one has studied the statistical inference of the IWD under the JPC model. The research on this aspect is of great significance.

This study applies the JPC scheme to estimate two independent IWD samples in scenarios where no explanatory variables are available. Point and interval estimators are constructed using maximum likelihood estimation (MLE) and Bayesian methods. Asymptotic confidence intervals (ACIs) are derived from the observed information matrix, while Bootstrap-P (Boot-P) and Bootstrap-T (Boot-T) methods yield bootstrap confidence intervals (CIs). Gamma priors are assumed for both shape and scale parameters, with Bayes estimates computed via the Metropolis–Hastings (M-H) algorithm under squared error (SE) and linear exponential (LINEX) loss functions. Monte Carlo simulations and a real-data analysis are conducted to assess the performance of these estimators.

The structure of the paper is as follows. Section 2 derives the maximum likelihood estimators for the IWD parameters. Section 3 discusses approximate confidence intervals based on these estimators, while Section 4 focuses on bootstrap-based confidence intervals. The Bayesian analysis is presented in Section 5, followed by the simulation results in Section 6. Section 7 applies the proposed methods to real datasets and Section 8 concludes the paper.

2. The Joint Progressive Type II Censor Scheme and Maximum Likelihood Estimation

2.1. Model Description

We begin by introducing the IWD, which is frequently employed to model lifetime data. The cumulative distribution function (CDF) of the IWD is given by

$$F\left(x\right)=e^{-\beta x^{-\alpha }},x>0,\alpha ,\beta >0.$$

Figure 1 illustrates this CDF.

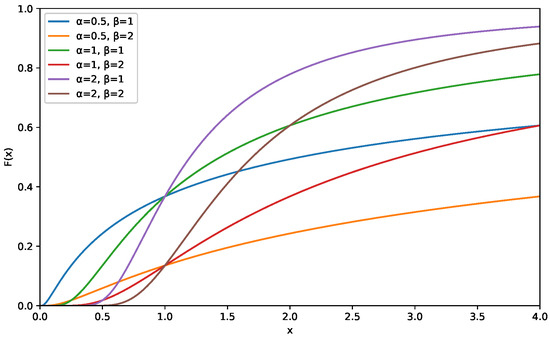
Figure 1. CDF of the inverse Weibull distribution.

The associated probability density function (PDF) is

$$f\left(x\right)=\alpha \beta x^{-(\alpha +1)}{e}^{-\beta x^{-\alpha }},$$

as shown in Figure 2, and it can be observed that the IWD exhibits a right-skewed, unimodal PDF with a heavy right tail, making it suitable for modeling extreme events and late-life failures.

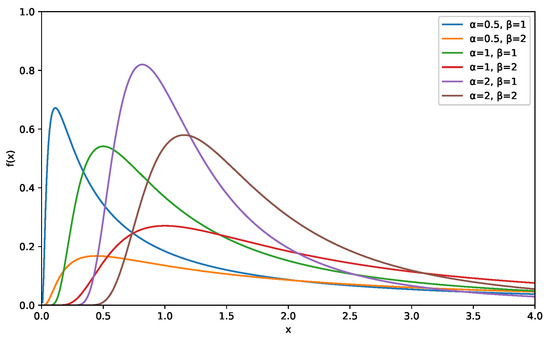
Figure 2. PDF of the inverse Weibull distribution.

This paper focuses on inference of the two-sample IWD under the JPC model. Following the idea of [24], for product A, let $X_1,X_2,\dots ,X_m$ denote the lifetimes of m units. These are assumed to be independent and identically distributed (i.i.d.) according to the IWD with a shape parameter ${\alpha }_1$ and scale parameter $\beta$. Similarly, for product B, let $Y_1,Y_2,\dots ,Y_n$ be the lifetimes of n units, which are also i.i.d. following the IWD with a shape parameter ${\alpha }_2$ and the same scale parameter $\beta$.

Let $K=m+n$ be the total sample size, with ${\lambda }_1\le \dots \le {\lambda }_K$ representing the order statistics of the random variables $\{X_1,X_2,\dots ,X_m;Y_1,Y_2,\dots ,Y_n\}$. In the JPC method, after the first failure, $R_1$ units are randomly removed from the remaining $K-1$ units. This procedure continues at the second failure, where $R_2$ units are randomly withdrawn from the remaining $K-R_1-2$ surviving units, and so forth. The process continues until exactly r failures have been observed, at which point all remaining units are withdrawn. This termination criterion aligns with the definition of type II censoring. At the r-th failure, all remaining units are withdrawn, with the number of withdrawn units given by $R_r=K-r-{\sum }_{i=1}^{r-1}{R}_i$. The scheme is denoted by $R=(R_1,R_2,\dots ,R_r)$, where r is the predetermined number of observed failures.

Let $R_i=s_i+t_i$ for $i=1,\dots ,r$, where $s_i$ and $t_i$ denote the number of units withdrawn at the i-th failure for the X and Y samples, respectively. Both $s_i$ and $t_i$ are random variables with unknown values. The observed data consist of $(H,\mathrm{\Lambda },S)$, where $H=(h_1,h_2,\dots ,h_r)$ indicates the source of failure, with $h_i=1$ if ${\lambda }_i$ corresponds to an X failure and $h_i=0$ if it corresponds to a Y failure. The vector $\mathrm{\Lambda }=({\lambda }_1,{\lambda }_2,\dots ,{\lambda }_r)$ contains the failure times, and $S=(s_1,s_2,\dots ,s_r)$ represents the number of units withdrawn from the X sample at each failure time. A concise overview of this type II censoring method is provided in Figure 3.

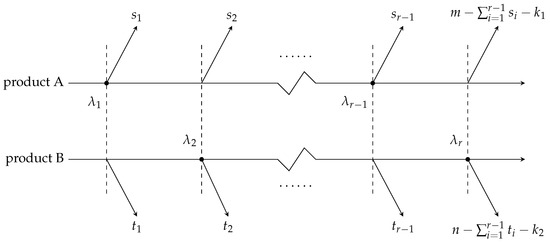
Figure 3. JPC scheme.

2.2. Maximum Likelihood Estimation

The likelihood function can be expressed based on the joint progressive censoring scheme as follows:

$$L({\alpha }_1,{\alpha }_2,\beta |H,\mathrm{\Lambda },S)=C\prod _{i=1}^r{\left[f\left({\lambda }_i\right)\right]}^{h_i}{\left[g\left({\lambda }_i\right)\right]}^{1-h_i}{\left[\overline{F}\left({\lambda }_i\right)\right]}^{s_i}{\left[\overline{G}\left({\lambda }_i\right)\right]}^{t_i}.$$

where $\overline{F}=1-F$, $\overline{G}=1-G$, ${\sum }_{i=1}^r{s}_i=m-m_r$, ${\sum }_{i=1}^r{t}_i=n-n_r$ and $C=D_1{D}_2$ with

$$D_1=\prod _{j=1}^r\left\{\left(m-\sum _{i=1}^{j-1}{h}_i-\sum _{i=1}^{j-1}{s}_i\right)h_i+\left(n-\sum _{i=1}^{j-1}\left(1-h_i\right)-\sum _{i=1}^{j-1}\left(R_i-s_i\right)\right)\left(1-h_i\right)\right\},$$

$$D_2=\prod _{j=1}^r\left\{{\displaystyle \frac{\left(\begin{array}{c}m-{\sum }_{i=1}^{j-1}{h}_i-{\sum }_{i=1}^{j-1}{s}_i\\ s_j\end{array}\right)\left(\begin{array}{c}n-{\sum }_{i=1}^{j-1}\left(1-h_i\right)-{\sum }_{i=1}^{j-1}\left(R_i-s_i\right)\\ t_j\end{array}\right)}{\left(\begin{array}{c}m+n-j-{\sum }_{i=1}^{j-1}{R}_i\\ R_j\end{array}\right)}}\right\}.$$

Therefore, the likelihood function becomes

$$\begin{array}{cc}\hfill L\left({\alpha }_1,{\alpha }_2,\beta |H,\mathrm{\Lambda },S\right)& =C\prod _{i=1}^r{\alpha }_1^{h_i}{\alpha }_2^{1-h_i}\beta {\lambda }_i^{-\left({\alpha }_1+1\right)h_i}{\lambda }_i^{-\left({\alpha }_2+1\right)\left(1-h_i\right)}\hfill \\ \hfill & \times {\left(e^{-\beta {\lambda }_i^{-{\alpha }_1}}\right)}^{h_i}{\left(e^{-\beta {\lambda }_i^{-{\alpha }_2}}\right)}^{1-h_i}{\left(1-e^{-\beta {\lambda }_i^{-{\alpha }_1}}\right)}^{s_i}{\left(1-e^{-\beta {\lambda }_i^{-{\alpha }_2}}\right)}^{t_i}\hfill \end{array}$$

(1)

By taking the logarithm of both sides of Function (1), we obtain the following log-likelihood function:

$$\begin{array}{cc}\hfill lnL& =lnC+m_{r}ln{\alpha }_1+n_{r}ln{\alpha }_2+rln\beta -\sum _{i=1}^r\left({\alpha }_1+1\right)h_{i}ln{\lambda }_i-\sum _{i=1}^r\left({\alpha }_2+1\right)\left(1-h_i\right)ln{\lambda }_i\hfill \\ \hfill & -\sum _{i=1}^r{h}_i\beta {\lambda }_1^{-{\alpha }_1}-\sum _{i=1}^r\left(1-h_i\right)\beta {\lambda }_i^{-{\alpha }_2}+\sum _{i=1}^r{s}_{i}ln\left(1-e^{-\beta {\lambda }_i^{-{\alpha }_1}}\right)+\sum _{i=1}^r{t}_{i}ln\left(1-e^{-\beta {\lambda }_i^{-{\alpha }_2}}\right)\hfill \end{array}$$

(2)

To obtain the MLEs of ${\alpha }_1,{\alpha }_2,\beta$, we take the first derivative of the log-likelihood Function (2) with respect to each parameter as follows:

$${\displaystyle \frac{\partial lnL}{\partial {\alpha }_1}}={\displaystyle \frac{m_r}{{\alpha }_1}}-\sum _{i-1}^r{h}_{i}ln{\lambda }_i+\sum _{i-1}^r{h}_i\beta {\lambda }_i^{-{\alpha }_1}ln{\lambda }_i-\sum _{i=1}^r{\displaystyle \frac{s_i\beta {\lambda }_i^{-{\alpha }_1}{e}^{-\beta {\lambda }_i^{-{\alpha }_1}}ln{\lambda }_i}{1-e^{-\beta {\lambda }_i^{-{\alpha }_1}}}}=0,$$

(3)

$${\displaystyle \frac{\partial lnL}{\partial {\alpha }_2}}={\displaystyle \frac{n_r}{{\alpha }_2}}-\sum _{i-1}^r\left(1-h_i\right)ln{\lambda }_i+\sum _{i-1}^r{h}_i\beta {\lambda }_i^{-{\alpha }_2}ln{\lambda }_i-\sum _{i=1}^r{\displaystyle \frac{t_i\beta {\lambda }_i^{-{\alpha }_2}{e}^{-\beta {\lambda }_i^{-{\alpha }_2}}ln{\lambda }_i}{1-e^{-\beta {\lambda }_i^{-{\alpha }_2}}}}=0,$$

(4)

$${\displaystyle \frac{\partial lnL}{\partial \beta }}={\displaystyle \frac{r}{\beta }}-\sum _{i-1}^r{h}_i{\lambda }_i^{-{\alpha }_1}-\sum _{i-1}^r\left(1-h_i\right){\lambda }_i^{-{\alpha }_2}+\sum _{i=1}^r{\displaystyle \frac{s_i{\lambda }_i^{-{\alpha }_1}{e}^{-\beta {\lambda }_i^{-{\alpha }_1}}}{1-e^{-\beta {\lambda }_i^{-{\alpha }_1}}}}+\sum _{i=1}^r{\displaystyle \frac{t_i{\lambda }_i^{-{\alpha }_2}{e}^{-\beta {\lambda }_i^{-{\alpha }_2}}}{1-e^{-\beta {\lambda }_i^{-{\alpha }_2}}}}=0.$$

(5)

Remark 1.

MLEs are computed only for cases where $0<m_r<r$ as this ensures that the likelihood function contains useful information for parameter estimation.

Obtaining analytical solutions for these equations is challenging, which makes closed-form expressions for the parameters difficult to derive. Hence, parameter values are typically estimated using numerical techniques like the Newton–Raphson iteration.

3. Approximate Confidence Interval

Proposition 1.

The asymptotic normality of the MLEs allows us to compute the approximate $100(1-\eta )\%$ ACIs for ${\alpha }_1,{\alpha }_2,\beta$ as follows:

$$\left({\widehat{\alpha }}_1-Z_{\eta /2}\sqrt{var\left({\widehat{\alpha }}_1\right)},{\widehat{\alpha }}_1+Z_{\eta /2}\sqrt{var\left({\widehat{\alpha }}_1\right)}\right),$$

$$\left({\widehat{\alpha }}_2-Z_{\eta /2}\sqrt{var\left({\widehat{\alpha }}_2\right)},{\widehat{\alpha }}_2+Z_{\eta /2}\sqrt{var\left({\widehat{\alpha }}_2\right)}\right),$$

$$\left(\widehat{\beta }-Z_{\eta /2}\sqrt{var\left(\widehat{\beta }\right)},\widehat{\beta }+Z_{\eta /2}\sqrt{var\left(\widehat{\beta }\right)}\right),$$

Here, $Z_{\eta /2}$ is the percentile of the standard normal distribution corresponding to a right-tail probability of $\eta /2$.

Proof. 

The asymptotic distribution of the MLE is utilized to derive confidence intervals for the unknown parameters ${\alpha }_1$, ${\alpha }_2$, and $\beta$. The second partial derivatives of the log-likelihood Function (2) are expressed as follows:

$${\displaystyle \frac{{\partial }^{2}lnL}{\partial {\alpha }_1^2}}=-{\displaystyle \frac{m_r}{{\alpha }_1^2}}-\sum _{i=1}^r{h}_i\beta {\lambda }_i^{-{\alpha }_1}{\left(ln{\lambda }_i\right)}^2-\sum _{i=1}^r{\displaystyle \frac{s_i{\left(\beta {\lambda }_i^{-{\alpha }_1}ln{\lambda }_i\right)}^2{e}^{-\beta {\lambda }_i^{-{\alpha }_1}}}{{\left(1-e^{-\beta {\lambda }_i^{-{\alpha }_1}}\right)}^2}},$$

(6)

$${\displaystyle \frac{{\partial }^{2}lnL}{\partial {\alpha }_2^2}}=-{\displaystyle \frac{n_r}{{\alpha }_2^2}}-\sum _{i=1}^r\left(1-h_i\right)\beta {\lambda }_i^{-{\alpha }_2}{\left(ln{\lambda }_i\right)}^2-\sum _{i=1}^r{\displaystyle \frac{t_i{\left(\beta {\lambda }_i^{-{\alpha }_2}ln{\lambda }_i\right)}^2{e}^{-\beta {\lambda }_i^{-{\alpha }_2}}}{{\left(1-e^{-\beta {\lambda }_i^{-{\alpha }_2}}\right)}^2}},$$

(7)

$${\displaystyle \frac{{\partial }^{2}lnL}{\partial {\beta }^2}}=-{\displaystyle \frac{r}{{\beta }^2}}-\sum _{i=1}^r{\displaystyle \frac{s_i{\lambda }_i^{-2{\alpha }_1}{e}^{-\beta {\lambda }_i^{-{\alpha }_1}}}{{\left(1-e^{-\beta {\lambda }_i^{-{\alpha }_1}}\right)}^2}}-\sum _{i=1}^r{\displaystyle \frac{t_i{\lambda }_i^{-2{\alpha }_2}{e}^{-\beta {\lambda }_i^{-{\alpha }_2}}}{{\left(1-e^{-\beta {\lambda }_i^{-{\alpha }_2}}\right)}^2}},$$

(8)

$${\displaystyle \frac{{\partial }^{2}lnL}{\partial {\alpha }_1\partial \beta }}=\sum _{i=1}^r{h}_i{\lambda }_i^{-{\alpha }_1}ln{\lambda }_i+\sum _{i=1}^r{s}_I{\lambda }_i^{-{\alpha }_1}{e}^{-\beta {\lambda }_i^{-{\alpha }_1}}ln{\lambda }_i\left(-{\displaystyle \frac{1}{1-e^{-\beta {\lambda }_i^{-{\alpha }_1}}}}+{\displaystyle \frac{\beta {\lambda }_i^{-{\alpha }_1}}{{\left(1-e^{-\beta {\lambda }_i^{-{\alpha }_1}}\right)}^2}}\right),$$

(9)

$${\displaystyle \frac{{\partial }^{2}lnL}{\partial {\alpha }_2\partial \beta }}=\sum _{i=1}^r\left(1-h_i\right){\lambda }_i^{-{\alpha }_2}ln{\lambda }_i+\sum _{i=1}^r{t}_i{\lambda }_i^{-{\alpha }_2}{e}^{-\beta {\lambda }_i^{-{\alpha }_2}}ln{\lambda }_i\left(-{\displaystyle \frac{1}{1-e^{-\beta {\lambda }_i^{-{\alpha }_2}}}}+{\displaystyle \frac{\beta {\lambda }_i^{-{\alpha }_2}}{{\left(1-e^{-\beta {\lambda }_i^{-{\alpha }_2}}\right)}^2}}\right),$$

(10)

$${\displaystyle \frac{{\partial }^{2}lnL}{\partial {\alpha }_1\partial {\alpha }_2}}={\displaystyle \frac{{\partial }^{2}lnL}{\partial {\alpha }_2\partial {\alpha }_1}}=0.$$

(11)

Taking the expectation of the negative second derivatives from Equations (6)–(11), the Fisher information matrix (FIM) is defined as $I_{ij}=-E\left(\begin{array}{c}{\displaystyle \frac{{\partial }^{2}L}{\partial {\delta }_i\partial {\delta }_j}}\end{array}\right)$, where $i,j=1,2,3$ and $({\delta }_1,{\delta }_2,{\delta }_3)=({\alpha }_1,{\alpha }_2,\beta )$. The observed information matrix is computed by replacing the expected value, such as $E\left({\displaystyle \frac{{\partial }^{2}L}{\partial {\alpha }^2}}\right)$, with ${\displaystyle \frac{{\partial }^{2}L}{\partial {\alpha }^2}}{|}_{\alpha =\widehat{\alpha }}$. Therefore, the observed Fisher information is given by the following:

$$I\left({\widehat{\alpha }}_1,{\widehat{\alpha }}_2,\widehat{\beta }\right)=-{\left(\begin{array}{ccc}{\displaystyle \frac{{\partial }^{2}L}{\partial {\alpha }_1^2}}& {\displaystyle \frac{{\partial }^{2}L}{\partial {\alpha }_1\partial {\alpha }_2}}& {\displaystyle \frac{{\partial }^{2}L}{\partial {\alpha }_1\partial \beta }}\\ {\displaystyle \frac{{\partial }^{2}L}{\partial {\alpha }_2\partial {\alpha }_1}}& {\displaystyle \frac{{\partial }^{2}L}{\partial {\alpha }_2^2}}& {\displaystyle \frac{{\partial }^{2}L}{\partial {\alpha }_2\partial \beta }}\\ {\displaystyle \frac{{\partial }^{2}L}{\partial \beta \partial {\alpha }_1}}& {\displaystyle \frac{{\partial }^{2}L}{\partial \beta \partial {\alpha }_2}}& {\displaystyle \frac{{\partial }^{2}L}{\partial {\beta }^2}}\end{array}\right)}_{{\alpha }_1={\widehat{\alpha }}_1,{\alpha }_2={\widehat{\alpha }}_2,\beta =\widehat{\beta }}.$$

The covariance matrix $Cov({\widehat{\alpha }}_1,{\widehat{\alpha }}_2,\widehat{\beta })$ can be calculated by inverting the FIM. Therefore, the asymptotic variance–covariance matrix for the MLEs is obtained by inverting the observed Fisher information, as shown below:

$$Cov\left({\widehat{\alpha }}_1,{\widehat{\alpha }}_2,\widehat{\beta }\right)=I^{-1}\left({\widehat{\alpha }}_1,{\widehat{\alpha }}_2,\widehat{\beta }\right)=\left(\begin{array}{ccc}var\left({\widehat{\alpha }}_1\right)& cov\left({\widehat{\alpha }}_1,{\widehat{\alpha }}_2\right)& cov\left({\widehat{\alpha }}_1,\widehat{\beta }\right)\\ cov\left({\widehat{\alpha }}_2,{\widehat{\alpha }}_1\right)& var\left({\widehat{\alpha }}_2\right)& cov\left({\widehat{\alpha }}_2,\widehat{\beta }\right)\\ cov\left(\widehat{\beta },{\widehat{\alpha }}_1\right)& cov\left(\widehat{\beta },{\widehat{\alpha }}_2\right)& var\left(\widehat{\beta }\right)\end{array}\right).$$

(12)

   □

4. Bootstrap Confidence Intervals

Bootstrap confidence intervals are an effective technique for measuring uncertainty in statistical analysis, especially when the underlying data distribution is complex or unknown. This method works by repeatedly resampling the observed data with replacements to create several “bootstrap samples”. Each of these samples generates a new estimate of the parameter of interest. By studying the spread and distribution of these estimates, bootstrap confidence intervals provide a range that likely contains the true value of the parameter. One of the key strengths of the bootstrap method is its flexibility, as it does not rely on assumptions about the specific form of the data distribution. This makes it particularly useful in real-world applications, where data may not follow standard parametric distributions.

We present bootstrap methods [25,26], which are particularly effective for small sample sizes. The steps outlined in Algorithms 1 and 2 are used to construct the Boot-P and Boot-T CI $100(1-\eta )\%$ for ${\alpha }_1,{\alpha }_2$, and $\beta$.

Algorithm 1 Generation process of Boot-P CIs

1: Based on the original sample $\mathrm{\Lambda }=({\lambda }_1,{\lambda }_2,\dots ,{\lambda }_n)$, and compute the MLEs of the parameters ${\alpha }_1,{\alpha }_2,\beta$ from Equations (3)–(5). 2: Utilizing the estimated values ${\widehat{\alpha }}_1,{\widehat{\alpha }}_2,\widehat{\beta }$ to generate a bootstrap JPC sample denoted as ${\mathrm{\Lambda }}^{*}$ by resampling from the original data, applying the estimated parameters to create new bootstrap samples. 3: Calculate the bootstrap estimation of ${\alpha }_1,{\alpha }_2$ and $\beta$ based on the bootstrap sample, named as ${\widehat{\alpha }}_1^{*},{\widehat{\alpha }}_2^{*},{\widehat{\beta }}^{*}$. 4: Repeat steps 2 and 3 for N iterations to obtain ${\widehat{\alpha }}_{j1}^{*},{\widehat{\alpha }}_{j2}^{*},\dots ,{\widehat{\alpha }}_{j{N}_{noot}}$ and ${\widehat{\beta }}_1^{*},{\widehat{\beta }}_2^{*},\dots ,{\widehat{\beta }}_{N_{noot}}$, $j=1,2$. 5: Sort ${\widehat{\alpha }}_{ji}^{*}$$(i=1,2,\dots ,N)$ and ${\widehat{\beta }}_i^{*}$$(i=1,2,\dots ,N)$ in ascending order as ${\widehat{\alpha }}_{\left(j1\right)}^{*},{\widehat{\alpha }}_{\left(j2\right)}^{*},\dots ,{\widehat{\alpha }}_{\left(jN\right)}$ and ${\widehat{\beta }}_{\left(1\right)}^{*},{\widehat{\beta }}_{\left(2\right)}^{*},\dots ,{\widehat{\beta }}_{\left(N\right)}$, where $j=1,2$. 6: The approximate Boot-P $100(1-\eta )\%$ CI of ${\alpha }_1$, ${\alpha }_2$ and $\beta$ are presented by $$\left({\widehat{\alpha }}_{\left(j\left[N(\eta /2)\right]\right)}^{*},{\widehat{\alpha }}_{\left(j\left[N(1-\eta /2)\right]\right)}^{*}\right),j=1,2,$$ $$\left({\widehat{\beta }}_{\left[N(\eta /2)\right]}^{*},{\widehat{\beta }}_{\left[N(1-\eta /2)\right]}^{*}\right).$$ The symbol [] represents the floor function, which rounds down to the largest integer less than or equal to the given value.

Algorithm 2 Generation process of Boot-T CIs

1: Using the same steps (1) to (3) as in the same steps Boot-P. 2: Compute the Boot-T statistics $T_{{\widehat{\alpha }}_1^{*}}$, $T_{{\widehat{\alpha }}_2^{*}}$ and $T_{{\widehat{\beta }}^{*}}$ follows: $$T_{{\widehat{\alpha }}_j^{*}}={\displaystyle \frac{({\widehat{\alpha }}_j^{*}-{\widehat{\alpha }}_j)}{\sqrt{\mathrm{var}\left({\widehat{\alpha }}_j^{*}\right)}}},T_{{\widehat{\beta }}^{*}}={\displaystyle \frac{({\widehat{\beta }}^{*}-\widehat{\beta })}{\sqrt{\mathrm{var}\left({\widehat{\beta }}^{*}\right)}}},j=1,2,$$ where $Cov({\widehat{\alpha }}_1^{*},{\widehat{\alpha }}_2^{*},{\widehat{\beta }}^{*})$ is given by Function (Section 3). 3: Repeat steps 2 and 3 for N iterations to obtain $T_{{\widehat{\alpha }}_{j1}^{*}},T_{{\widehat{\alpha }}_{j2}^{*}},\dots ,T_{{\widehat{\alpha }}_{jN}^{*}}$, $T_{{\widehat{\beta }}_1^{*}},T_{{\widehat{\beta }}_2^{*}}$, …, $T_{{\widehat{\beta }}_N^{*}}$, and $j=1,2$. 4: Sort $T_{{\widehat{\alpha }}_{ji}^{*}}$, $(i=1,2,\dots ,N)$ in ascending order as $T_{{\widehat{\alpha }}_{\left(j1\right)}^{*}},T_{{\widehat{\alpha }}_{\left(j2\right)}^{*}}$, …, $T_{{\widehat{\alpha }}_{\left(jN\right)}^{*}}$, $T_{{\widehat{\beta }}_{\left(1\right)}^{*}}$, $T_{{\widehat{\beta }}_{\left(2\right)}^{*}}$, …, $T_{{\widehat{\beta }}_{\left(N\right)}^{*}}$, where $j=1,2$. 5: The approximate Boot-t $100(1-\eta )\%$ CI for ${\alpha }_1,{\alpha }_2$ and $\beta$ are given by $$\left({\widehat{\alpha }}_j+T_{{\widehat{\alpha }}_{j\left[N\right(\eta /2\left)\right]}^{*}},{\widehat{\alpha }}_j+T_{{\widehat{\alpha }}_{j\left[N\right(1-\eta /2\left)\right]}^{*}}\right),j=1,2,$$ $$\left(\widehat{\beta }+T_{{\widehat{\beta }}_{\left[N\right(\eta /2\left)\right]}^{*}},\widehat{\beta }+T_{{\widehat{\beta }}_{\left[N\right(1-\eta /2\left)\right]}^{*}}\right).$$ The symbol [] represents the floor function, which rounds down to the largest integer less than or equal to the given value.

5. Bayesian Inference

5.1. Prior and Posterior Distribution

We assume that the parameters ${\alpha }_1$, ${\alpha }_2$, and $\beta$ of the IWD follow independent gamma priors with hyperparameters $a_1,b_1$; $a_2,b_2$, and $a_3,b_3$, respectively. Therefore, their joint prior distribution is expressed as

$$\pi \left({\alpha }_1,{\alpha }_2,\beta \right)\propto {\alpha }_1^{a_1-1}{e}^{-b_1{\alpha }_1}{\alpha }_2^{a_2-1}{e}^{-b_2{\alpha }_2}{\beta }^{a_3-1}{e}^{-b_3\beta }.$$

The joint posterior distribution can be formulated as

$$\pi ({\alpha }_1,{\alpha }_2,\beta \mid H,\mathrm{\Lambda },S)={\displaystyle \frac{\pi ({\alpha }_1,{\alpha }_2,\beta )L({\alpha }_1,{\alpha }_2,\beta \mid H,\mathrm{\Lambda },S)}{{\int }_0^{\infty }{\int }_0^{\infty }{\int }_0^{\infty }\pi ({\alpha }_1,{\alpha }_2,\beta )L({\alpha }_1,{\alpha }_2,\beta \mid H,\mathrm{\Lambda },S)d{\alpha }_{1}d{\alpha }_{2}d\beta }},$$

where $L({\alpha }_1,{\alpha }_2,\beta \mid H,\mathrm{\Lambda },S)$ represents the likelihood function, $H=(h_1,h_2,\dots ,h_r)$ indicates the source of failure, with $h_i=1$ if ${\lambda }_i$ corresponds to an X failure and $h_i=0$ if it corresponds to a Y failure. The vector $\mathrm{\Lambda }=({\lambda }_1,{\lambda }_2,\dots ,{\lambda }_r)$ contains the failure times, and $S=(s_1,s_2,\dots ,s_r)$ represents the number of units withdrawn from the X sample at each failure time.

Moreover, using the joint prior distribution and the likelihood function (1), the joint posterior distribution is given by

$$\begin{array}{cc}\hfill \pi \left({\alpha }_1,{\alpha }_2,\beta |H,\mathrm{\Lambda },S\right)\propto & {\alpha }_1^{m_r+a_1-1}{\alpha }_2^{n_r+a_2-1}{\beta }^{r+a_3-1}exp\{-{\alpha }_1\sum _{i=1}^r{h}_{i}ln{\lambda }_i-b_1{\alpha }_1\hfill \\ \hfill & -{\alpha }_2\sum _{i=1}^r\left(1-h_i\right)ln{\lambda }_i-b_2{\alpha }_2-\beta \sum _{i=1}^r{h}_i{\lambda }_i^{-{\alpha }_1}-\beta \sum _{i=1}^r\left(1-h_i\right){\lambda }_i^{-{\alpha }_2}\hfill \\ \hfill & -b_3\beta +\sum _{i=1}^r{s}_{i}ln\left(1-e^{-\beta {\lambda }_i^{-{\alpha }_1}}\right)+\sum _{i=1}^r{t}_{i}ln\left(1-e^{-\beta {\lambda }_i^{-{\alpha }_2}}\right)\}.\hfill \end{array}$$

(13)

5.2. Loss Functions

In this subsection, we emphasize the significance of selecting appropriate loss functions for parameter estimation within Bayesian inference. Specifically, we consider two types of loss functions: the SE loss function and the asymmetric LINEX loss function.

The SE loss function is represented by

$${\xi }_{SE}\left(\mathrm{\Delta }\right)\propto {\mathrm{\Delta }}^2={[u\left(\mathrm{\Phi }\right)-\widehat{u}\left(\mathrm{\Phi }\right)]}^2.$$

In this equation, $\mathrm{\Delta }=\widehat{u}\left(\mathrm{\Phi }\right)-u\left(\mathrm{\Phi }\right)$, $u\left(\mathrm{\Phi }\right)$ is any function of $\mathrm{\Phi }=({\alpha }_1,{\alpha }_2,\beta )$, and $\widehat{u}\left(\mathrm{\Phi }\right)$ represents the SE estimate of $u\left(\mathrm{\Phi }\right)$. Let $\widehat{u}{\left(\mathrm{\Phi }\right)}_{SE}$ denote the Bayesian estimate of $u\left(\mathrm{\Phi }\right)$ under the SE function, which is given by

$$\widehat{u}{\left(\mathrm{\Phi }\right)}_{SE}=E[u\left(\mathrm{\Phi }\right)\mid H,\mathrm{\Lambda },S]={\int }_0^{\infty }{\int }_0^{\infty }{\int }_0^{\infty }u\left(\mathrm{\Phi }\right)\pi (\mathrm{\Phi }\mid H,\mathrm{\Lambda },S)d{\alpha }_{1}d{\alpha }_{2}d\beta .$$

The SE loss function is widely used in the literature and is one of the most common loss functions. It is symmetric, treating overestimation and underestimation of parameters equally. However, in life-testing situations, one type of estimation error may have more severe consequences. To address this, we use the LINEX loss function, defined as follows:

$${\xi }_{\mathrm{LINEX}}\left(\mathrm{\Delta }\right)\propto e^{a\mathrm{\Delta }}-a\mathrm{\Delta }-1,a\ne 0.$$

Here, $\mathrm{\Delta }$ is as previously defined, and $\widehat{u}\left(\mathrm{\Phi }\right)$ represents the LINEX estimate of $u\left(\mathrm{\Phi }\right)$.

The shape parameter a controls the direction and degree of asymmetry in the loss function. When $a>0$, overestimation is penalized more heavily than underestimation, whereas the reverse is true when $a<0$. For values of a near zero, the LINEX loss function becomes similar to the SE loss function. When $a=1$, the function is highly asymmetric, with overestimation costing more than underestimation. If $a<0$, the loss increases almost exponentially for $\mathrm{\Delta }=\widehat{u}\left(\mathrm{\Phi }\right)-u\left(\mathrm{\Phi }\right)<0$ and decreases nearly linearly for $\mathrm{\Delta }=\widehat{u}\left(\mathrm{\Phi }\right)-u\left(\mathrm{\Phi }\right)>0$.

The Bayes estimate $\widehat{u}{\left(\mathrm{\Phi }\right)}_{LINEX}$ is obtained to be

$$\begin{array}{cc}\hfill \widehat{u}{\left(\mathrm{\Phi }\right)}_{LINEX}& =-{\displaystyle \frac{1}{a}}ln\left[E\left(e^{-a\widehat{u}\left(\mathrm{\Phi }\right)}\mid H,\mathrm{\Lambda },S\right)\right]\hfill \\ \hfill & =-{\displaystyle \frac{1}{a}}ln\left({\int }_0^{\infty }{\int }_0^{\infty }{\int }_0^{\infty }{e}^{-a\widehat{u}\left(\mathrm{\Phi }\right)}\pi ({\alpha }_1,{\alpha }_2,\beta \mid H,\mathrm{\Lambda },S)d{\alpha }_{1}d{\alpha }_{2}d\beta \right).\hfill \end{array}$$

We found that analytical solutions are not feasible for this problem. To address this, the Metropolis–Hastings algorithm is used to approximate explicit formulas for $\widehat{u}{\left(\mathrm{\Phi }\right)}_{SE}$ and $\widehat{u}{\left(\mathrm{\Phi }\right)}_{LINEX}$, as well as to construct the associated confidence intervals.

5.3. Metropolis–Hastings Algorithm

Proposition 2.

The Bayes estimates based on the SE loss function are as follows:

$${\widehat{\alpha }}_{1SE}={\displaystyle \frac{1}{N-N_0}}\sum _{i=N_0+1}^N{\alpha }_1^{\left(i\right)},$$

$${\widehat{\alpha }}_{2SE}={\displaystyle \frac{1}{N-N_0}}\sum _{i=N_0+1}^N{\alpha }_2^{\left(i\right)},$$

$${\widehat{\beta }}_{SE}={\displaystyle \frac{1}{N-N_0}}\sum _{i=N_0+1}^N{\beta }^{\left(i\right)}.$$

and the Bayes estimates based on the LINEX loss function are

$${\widehat{\alpha }}_{1LINEX}=-{\displaystyle \frac{1}{a}}ln\left[{\displaystyle \frac{1}{N-N_0}}\sum _{i=N_0+1}^N{e}^{-a{\alpha }_1^{\left(i\right)}}\right],$$

$${\widehat{\alpha }}_{2LINEX}=-{\displaystyle \frac{1}{a}}ln\left[{\displaystyle \frac{1}{N-N_0}}\sum _{i=N_0+1}^N{e}^{-a{\alpha }_2^{\left(i\right)}}\right],$$

$${\widehat{\beta }}_{LINEX}=-{\displaystyle \frac{1}{a}}ln\left[{\displaystyle \frac{1}{N-N_0}}\sum _{i=N_0+1}^N{e}^{-a{\beta }^{\left(i\right)}}\right].$$

where N denotes the total MCMC sample size and $N_0$ is the number of burn-in iterative values.

Proof. 

From Function (13), the conditional posterior density function of ${\alpha }_1,{\alpha }_2,\beta$ can be obtained as the following proportionality:

$$\begin{array}{cc}\hfill {\pi }_1^{*}\left({\alpha }_1|H,\mathrm{\Lambda },S\right)\propto & {\alpha }_1^{m_r+a_1-1}exp\{-{\alpha }_1\sum _{i=1}^r{h}_{i}ln{\lambda }_i\hfill \\ \hfill -& b_1{\alpha }_1-\beta \sum _{i=1}^r{h}_i{\lambda }_i^{-{\alpha }_1}+\sum _{i=1}^r{s}_{i}ln\left(1-e^{-\beta {\lambda }_i^{-{\alpha }_1}}\right)\},\hfill \end{array}$$

(14)

$$\begin{array}{cc}\hfill {\pi }_2^{*}\left({\alpha }_2|H,\mathrm{\Lambda },S\right)\propto & {\alpha }_2^{n_r+a_2-1}exp\{-{\alpha }_2\sum _{i=1}^r\left(1-h_i\right)ln{\lambda }_i\hfill \\ & -b_2{\alpha }_2-\beta \sum _{i=1}^r\left(1-h_i\right){\lambda }_i^{-{\alpha }_2}+\sum _{i=1}^r{t}_{i}ln\left(1-e^{-\beta {\lambda }_i^{-{\alpha }_2}}\right)\},\hfill \end{array}$$

(15)

$$\begin{array}{cc}\hfill {\pi }_3^{*}\left(\beta |H,\mathrm{\Lambda },S\right)\propto & {\beta }^{r+c+1}exp\{-\beta \sum _{i=1}^r{h}_i{\lambda }_i^{-{\alpha }_1}-\beta \sum _{i=1}^r\left(1-h_i\right){\lambda }_i^{-{\alpha }_2}-d\beta \hfill \\ \hfill & +\sum _{i=1}^r{s}_{i}ln\left(1-e^{-\beta {\lambda }_i^{-{\alpha }_1}}\right)+\sum _{i=1}^r{t}_{i}ln\left(1-e^{-\beta {\lambda }_i^{-{\alpha }_2}}\right)\}.\hfill \end{array}$$

(16)

It is crucial to highlight that the conditional posterior distributions for ${\alpha }_1$, ${\alpha }_2$, and $\beta$, as given in Functions (14)–(16), do not reduce to any familiar standard forms. This complexity makes direct sampling using conventional methods rather challenging. However, these distributions appear to resemble the normal distribution.

The proposed distribution of $\pi \left({\alpha }_1,{\alpha }_2,\beta |H,\mathrm{\Lambda },S\right)$ is assumed to be multivariate normal, and the MCMC sample is generated using the Metropolis–Hastings method outlined in Algorithm 3.    □

Sort ${\alpha }_{ji},{\beta }_i$ in ascending order to obtain $\{{\alpha }_{\left(j1\right)},{\alpha }_{\left(j2\right)},\dots ,{\alpha }_{\left(j(N-N_0)\right)}\}$. With that, the $100(1-\eta )\%$ credible interval of the unknown parameter is constructed as

$$({\alpha }_{j\left[(N-N_0)(\eta /2)\right]},{\alpha }_{j\left[(N-N_0)(1-\eta /2)\right]})\mathrm{and}({\beta }_{\left[(N-N_0)(\eta /2)\right]},{\beta }_{\left[(N-N_0)(1-\eta /2)\right]}),j=1,2$$

The shortest one of all the possible intervals with the length $\left[(N-N_0)(1-\eta )\right]$ is the highest posterior density credible interval.

Algorithm 3 Generating samples following the posterior distribution.

1: Choose initial values of $({\alpha }_1,{\alpha }_2,\beta )$ as $({\alpha }_1^{\left(0\right)},{\alpha }_2^{\left(0\right)},{\beta }^{\left(0\right)})$. 2: Generate $({\alpha }_1^{\prime },{\alpha }_2^{\prime },{\beta }^{\prime })$ by using the proposal normal distribution $N({\alpha }_1^{(i-1)},{\sigma }_1^2)$, $N({\alpha }_2^{(i-1)},{\sigma }_2^2)$ and $N({\beta }^{(i-1)},{\sigma }_3^2)$. Here, ${\sigma }_1^2$, ${\sigma }_2^2$, and ${\sigma }_3^2$ represent the variance of the MLEs of ${\alpha }_1$, ${\alpha }_2$, and $\beta$, respectively, which are obtained from the diagonal elements of the inverse Fisher information matrix. 3: Calculate $$P_1^{*}={\displaystyle \frac{\pi ({\alpha }_1^{\prime }\mid \beta ,H,\mathrm{\Lambda },S)}{\pi ({\alpha }_1^{(i-1)}\mid \beta ,H,\mathrm{\Lambda },S)}},$$ $$P_2^{*}={\displaystyle \frac{\pi ({\alpha }_2^{\prime }\mid \beta ,H,\mathrm{\Lambda },S)}{\pi ({\alpha }_2^{(i-1)}\mid \beta ,H,\mathrm{\Lambda },S)}},$$ and $$P_3^{*}={\displaystyle \frac{\pi ({\beta }^{\prime }\mid {\alpha }_1,{\alpha }_2,H,\mathrm{\Lambda },S)}{\pi ({\beta }^{(i-1)}\mid {\alpha }_1,{\alpha }_2,H,\mathrm{\Lambda },S)}}.$$ 4: Compute the acceptance probability $P_1=min\{1,P_1^{*}\}$, $P_2=min\{1,P_2^{*}\}$, and $P_3=min\{1,P_3^{*}\}$. 5: Generate samples $u_1$, $u_2$, and $u_3$ from the uniform distribution $U(0,1)$. If $u_1\le P_1$, accept ${\alpha }_1^{\left(i\right)}={\alpha }_1^{\prime }$; otherwise, set ${\alpha }_1^{\left(i\right)}={\alpha }_1^{(i-1)}$. The same applies to ${\alpha }_2^{\left(i\right)}$ and ${\beta }^{\left(i\right)}$ with $u_2$ and $u_3$. 6: Repeat Steps 2–5 for N iterations to obtain enough samples.

6. Simulation Study

In this section, we assess the performance of the methods by simulating parameter estimates across different JPC schemes. The simulation follows a structured approach, including data generation, parameter estimation, and result evaluation. We reference the approach outlined in [27].

First, we drew samples from two populations, namely, population A and population B, which follow the distributions $IW({\alpha }_1,\beta )$ and $IW({\alpha }_2,\beta )$, respectively. The true values of the parameters are set as ${\alpha }_1=1.5,{\alpha }_2=2$, and $\beta =1$. For the sample sizes $(m,n)$, we select the combinations $(20,20)$, $(20,30)$, $(30,30)$, $(30,40)$, and $(40,50)$, while the numbers of failures r are chosen as 20, 30, 40, 50, and 60. The procedure for generating JPC data is described in Algorithm 4.

Algorithm 4 The algorithm to generate samples under the JPC scheme.

1: Generate m samples for population A from $IW({\alpha }_1,\beta )$ and n samples for population B from $IW({\alpha }_2,\beta )$. Combine these samples and sort them in ascending order. 2: At the i-th failure, the smallest value of the joint samples is noted as ${\lambda }_i$. Then, it is determined whether this unit belongs to population A. If so, $h_i$ is set to 1; otherwise, it is set to 0. 3: Given that $R_i$ is predetermined, randomly assign values to $s_i$ and $t_i$ under the condition $s_i+t_i=R_i$. Then, $s_i$ units are randomly selected from population A and $t_i$ units from population B, respectively. 4: Store the data as $({\lambda }_i,h_i,s_i,t_i)$ and reconstruct the joint samples using the remaining information. 5: Repeat Steps 2–4 until the k-th failure occurs. There are $k_1={\sum }_{i=1}^k{h}_i$ failures from population A and $k_2=k-k_1$ from population B. At this point, withdraw all remaining units. Then, $s_k=m-{\sum }_{i=1}^{k-1}{s}_i-k_1$ and $t_k=n-{\sum }_{i=1}^{k-1}{t}_i-k_2$ are recorded.

Once the censored data are obtained, the MLEs of ${\alpha }_1,{\alpha }_2$, and $\beta$ are calculated using Function (1); then, we present the mean MSEs of the MLEs. The bootstrap method is used to compute the ACI for the parameters. The experiment was carried out using R, with the code written in RStudio version 2024.12.0+467. The RStudio environment was run on Windows 10 (64-bit), and the experimental computer was equipped with AMD Ryzen 7 5800H with Radeon Graphics and the NVIDIA GeForce GTX 1650 graphics card.

Here, $R=(0_{\left(19\right)},20)$ means $R_1=R_2=\dots =R_{19}=0,R_{20}=10$. For interval estimates, we construct $95\%$ ACIs, Boot-T CIs, and Boot-P CIs. Then, based on 1000 repetitions, we calculate the average lengths (ALs) and coverage probabilities (CPs) of these intervals. Table 1 and Table 2 demonstrate that the average estimates (AMLEs) of ${\alpha }_1$ and ${\alpha }_2$ exhibit bias for small sample sizes $m+n$. As the sample size increases, the estimates progressively converge to the true values. Table 3 indicates that the MSEs of $\widehat{\beta }$ are generally smaller than those of ${\widehat{\alpha }}_1$ and ${\widehat{\alpha }}_2$ in most cases. The ALs of the approximate confidence intervals are similar to those of the two bootstrap confidence intervals. Since the confidence probability of the bootstrap intervals consistently reaches 100%, the results are not included in the table.

Table 1. AMLEs, MSEs, ACIs, Boot-T CIs, and Boot-P CIs of ${\alpha }_1$.

$(\mathit{m},\mathit{n})$	r	$({\mathit{R}}_1,\dots ,{\mathit{R}}_{\mathit{r}})$	AMLE (MSE)	ACI		Boot-T AL	Boot-P AL
				AL	CP
(20, 20)	20	($0_{\left(19\right)}$, 20)	1.7027 (0.2309)	1.8360	89.5%	1.6794	1.7570
		($0_{\left(18\right)}$, 5, 15)	1.6513 (0.2244)	1.9249	91.3%	1.7832	1.8529
	30	($0_{\left(29\right)}$, 10)	1.5925 (0.1195)	1.3507	91.5%	1.2941	1.2804
		($0_{\left(28\right)}$, 8, 2)	1.6006 (0.1229)	1.3543	91.0%	1.2795	1.2911
(20, 30)	30	($0_{\left(29\right)}$, 20)	1.6548 (0.1670)	1.5465	88.7%	1.4923	1.5469
		($0_{\left(28\right)}$, 15, 5)	1.6215 (0.1108)	1.5157	89.6%	1.4284	1.4801
	40	($0_{\left(39\right)}$, 10)	1.6134 (0.1226)	1.3501	90.0%	1.2320	1.3142
		($0_{\left(38\right)}$, 5, 5)	1.4942 (0.0833)	1.1618	95.1%	1.0834	1.0957
(30, 30)	30	($0_{\left(29\right)}$, 30)	1.6257 (0.1253)	1.3572	91.5%	1.3277	1.3003
		($0_{\left(28\right)}$, 20, 10)	1.6046 (0.1264)	1.3640	91.7%	1.2984	1.3362
	40	($0_{\left(39\right)}$, 20)	1.5939 (0.0875)	1.1235	90.9%	1.0475	1.0692
		($0_{\left(38\right)}$, 20, 0)	1.6226 (0.0906)	1.1407	89.2%	1.1087	1.1204
(30, 40)	40	($0_{\left(39\right)}$, 30)	1.5855 (0.1014)	1.2148	91.0%	1.1601	1.2213
		($0_{\left(38\right)}$, 29, 1)	1.6173 (0.1118)	1.2625	89.3%	0.8930	1.1819
	50	($0_{\left(49\right)}$, 20)	1.5765 (0.0799)	1.0914	92.2%	1.0603	1.0860
		($0_{\left(48\right)}$, 15, 5)	1.5528 (0.0687)	1.0263	91.6%	0.9160	1.0000
(40, 50)	50	($0_{\left(49\right)}$, 40)	1.5595 (0.0754)	1.0515	92.6%	0.9260	1.0616
		($0_{\left(48\right)}$, 35, 5)	1.5817 (0.0728)	1.0436	92.7%	0.9270	1.0140
	60	($0_{\left(59\right)}$, 30)	1.5739 (0.0574)	0.9250	92.6%	0.9260	0.8984
		($0_{\left(58\right)}$, 25, 5)	1.5406 (0.0560)	0.9298	92.6%	0.9210	0.9249

Table 2. AMLEs, MSEs, ACIs, Boot-T CIs, and Boot-P CIs of ${\alpha }_2$.

$(\mathit{m},\mathit{n})$	r	$({\mathit{R}}_1,\dots ,{\mathit{R}}_{\mathit{r}})$	AMLE (MSE)	ACI		Boot-T AL	Boot-P AL
				AL	CP
(20, 20)	20	($0_{\left(19\right)}$, 20)	2.2568 (0.4263)	2.5265	89.1%	2.3058	2.3371
		($0_{\left(18\right)}$, 5, 15)	2.4729 (0.6462)	2.7021	84.6%	2.5468	2.5304
	30	($0_{\left(29\right)}$, 10)	2.1285 (0.1726)	1.6131	92.2%	1.5926	1.5996
		($0_{\left(28\right)}$, 2, 8)	2.2105 (0.2826)	1.9205	88.0%	1.8180	1.7945
(20, 30)	30	($0_{\left(29\right)}$, 20)	2.1136 (0.1569)	1.4982	90.2%	1.4357	1.4124
		($0_{\left(18\right)}$, 15, 5)	2.2705 (0.2505)	1.7822	87.9%	1.7199	1.6676
	40	($0_{\left(39\right)}$, 10)	2.1024 (0.1122)	1.2843	92.0%	1.2783	1.2660
		($0_{\left(38\right)}$, 5, 5)	2.2802 (0.2066)	1.4900	85.5%	1.4619	1.4794
(30, 30)	30	($0_{\left(29\right)}$, 30)	2.1330 (0.2243)	1.7878	90.3%	1.7324	1.7611
		($0_{\left(28\right)}$, 20, 10)	2.2581 (0.2875)	1.9045	87.5%	1.7720	1.7790
	30	($0_{\left(39\right)}$, 20)	2.1206 (0.1340)	1.4057	91.8%	1.3682	1.3687
		($0_{\left(28\right)}$, 20, 0)	2.1560 (0.1590)	1.4870	90.1%	1.4397	1.4210
(30, 40)	40	($0_{\left(39\right)}$, 30)	2.0866 (0.1098)	1.2793	91.6%	1.2428	1.2512
		($0_{\left(38\right)}$, 29, 1)	2.1423 (0.1422)	1.3821	89.9%	0.8990	1.3511
	50	($0_{\left(49\right)}$, 20)	2.0665 (0.0871)	1.1578	93.1%	1.1595	1.1305
		($0_{\left(48\right)}$, 15, 5)	2.15499 (0.1136)	1.2051	89.2%	0.8920	1.0000
(40, 50)	50	($0_{\left(49\right)}$, 40)	2.0872 (0.0907)	1.1492	91.0%	0.9200	1.1308
		($0_{\left(48\right)}$, 35, 5)	2.1518 (0.1080)	1.1880	89.4%	0.8940	1.1418
	60	($0_{\left(59\right)}$, 30)	2.0577 (0.0775)	1.0732	92.4%	0.9240	1.0263
		($0_{\left(58\right)}$, 25, 5)	2.1192 (0.0891)	1.1012	91.7%	0.9170	1.0738

Table 3. AMLEs, MSEs, ACIs, Boot-T CIs, and Boot-P CIs of $\beta$.

$(\mathit{m},\mathit{n})$	r	$({\mathit{R}}_1,\dots ,{\mathit{R}}_{\mathit{r}})$	AMLE (MSE)	ACI		Boot-T AL	Boot-P AL
				AL	CP
(20, 20)	20	($0_{\left(19\right)}$, 20)	1.0003 (0.0405)	0.8130	94.9%	0.8097	0.7918
		($0_{\left(18\right)}$, 5, 15)	0.9954 (0.0285)	0.6739	94.8%	0.6571	0.6537
	30	($0_{\left(29\right)}$, 10)	1.0326 (0.0343)	0.7336	93.0%	0.9300	0.7270
		($0_{\left(28\right)}$, 8, 2)	1.0057 (0.0320)	0.7173	93.9%	0.6808	0.6771
(20, 30)	30	($0_{\left(29\right)}$, 20)	1.0055 (0.0286)	0.6764	94.2%	0.6700	0.6645
		($0_{\left(28\right)}$, 15, 5)	0.9954 (0.0285)	0.6739	94.8%	0.6571	0.6537
	40	($0_{\left(39\right)}$, 10)	1.0079 (0.0258)	0.6397	94.2%	0.6302	0.6323
		($0_{\left(38\right)}$, 5, 5)	0.9949 (0.0257)	0.6405	94.7%	0.9470	0.6159
(30, 30)	30	($0_{\left(29\right)}$, 30)	0.9927 (0.0255)	0.6369	95.8%	0.6194	0.6155
		($0_{\left(28\right)}$, 20, 10)	0.9822 (0.0260)	0.6411	96.1%	0.6403	0.6233
	40	($0_{\left(39\right)}$, 20)	1.0116 (0.0220)	0.5902	95.0%	0.5793	0.5667
		($0_{\left(38\right)}$, 20, 0)	0.9980 (0.0245)	0.6248	95.2%	0.9520	0.5974
(30, 40)	40	($0_{\left(39\right)}$, 30)	0.9964 (0.0191)	0.5479	94.3%	0.9430	0.5538
		($0_{\left(38\right)}$, 29, 1)	0.9920 (0.0194)	0.5499	95.9%	0.9590	0.5399
	50	($0_{\left(49\right)}$, 20)	1.0113 (0.0179)	0.5275	93.5%	0.9350	0.5115
		($0_{\left(48\right)}$, 15, 5)	1.0038 (0.0187)	0.5436	94.8%	0.9480	0.5438
(40, 50)	50	($0_{\left(49\right)}$, 40)	1.0088 (0.0158)	0.4966	94.7%	0.9470	0.5138
		($0_{\left(48\right)}$, 35, 5)	0.9917 (0.0156)	0.4948	95.4%	0.9540	0.4892
	60	($0_{\left(59\right)}$, 30)	1.0033 (0.0137)	0.4624	94.9%	0.9490	0.4751
		($0_{\left(58\right)}$, 25, 5)	1.0028 (0.0139)	0.4661	94.8%	0.9510	0.4648

Under the Bayesian framework, we compute both the parameter estimates and their corresponding MSEs using the SE and LINEX loss functions, employing either gamma informative priors (IPs) or non-informative priors (NIPs).

To compare the performance of these Bayesian estimates, the hyperparameters for the IPs are set as $(a_1,a_2,b_1,b_2,c,d)=(15,10,10.5,5,10,10)$. We select these hyperparameters to ensure that the prior expectations of the two populations align closely with the true values. And for NIPs, we assign $a_1=a_2=b_1=b_2=c=d={10}^{-5}$.

Table 4 and Table 5 present the average Bayesian estimates (ABEs), MSEs, and ALs of the 95% credible intervals for ${\alpha }_1$ under both IPs and NIPs. The corresponding results for ${\alpha }_2$ and $\beta$ are provided in Appendix A, in Table A1, Table A2, Table A3 and Table A4. In particular, the MSEs for ${\widehat{\alpha }}_1$ remain consistently the lowest among the unknown parameters. Moreover, the Bayesian estimates under IPs tend to slightly underestimate the parameters, while those under NIP tend to slightly overestimate them. For the LINEX loss function with $a=-2$, the credible intervals have the shortest average lengths. Additionally, the ALs of the confidence intervals are quite similar across all three loss functions. Furthermore, under both IPs and NIPs, the CPs for ${\alpha }_1$ are consistently close to the nominal level of 95%, indicating reliable interval estimation for this parameter. However, the CPs for ${\alpha }_2$ and $\beta$ remain around 80%, suggesting that the current approach may not fully capture the uncertainty associated with this parameter. Future research is anticipated to explore appropriate methodologies to enhance the CPs, ensuring more robust and reliable interval estimation.

Table 4. Bayesian estimations of parameter ${\alpha }_1$ supposing informative priors $(a_1,a_2,b_1,b_2,c,d)=(15,10,10.5,5,10,10)$.

$(\mathit{m},\mathit{n})$	r	$({\mathit{R}}_1,\dots ,{\mathit{R}}_{\mathit{r}})$	SE		LINEX (a = −2)		LINEX (a = 2)
			ABE (MSE)	AL (CP)	ABE (MSE)	AL (CP)	ABE (MSE)	AL (CP)
(20, 20)	20	($0_{\left(19\right)}$, 20)	1.5540	1.0856	1.4627	1.0122	1.4212	1.0443
			(0.2319)	(98.0%)	(0.1806)	(100.0%)	(0.2106)	(100.0%)
		($0_{\left(18\right)}$, 5, 15)	1.4282	1.0479	1.4477	1.0722	1.4686	1.0198
			(0.1956)	(100.0%)	(0.2308)	(100.0%)	(0.1920)	(100.0%)
	30	($0_{\left(29\right)}$, 10)	1.4721	1.0263	1.4489	0.9893	1.5236	1.0107
			(0.1914)	(100.0%)	(0.1853)	(95.9%)	(0.1835)	(100.0%)
		($0_{\left(29\right)}$, 8, 2)	1.4773	0.9943	1.4517	1.0549	1.4624	1.0138
			(0.1852)	(100.0%)	(0.2119)	(100.0%)	(0.1923)	(97.96%)
(20, 30)	30	($0_{\left(29\right)}$, 20)	1.4851	0.9736	1.4665	0.9690	1.4283	0.9938
			(0.1693)	(100.0%)	(0.1710)	(97.96%)	(0.1840)	(100.0%)
		($0_{\left(28\right)}$, 15, 5)	1.4734	1.0072	1.4091	0.9971	1.4508	0.9837
			(0.1755)	(100.0%)	(0.1994)	(100.0%)	(0.1726)	(100.0%)
	40	($0_{\left(39\right)}$, 10)	1.5437	0.9858	1.5155	1.0384	1.4327	1.0452
			(0.1704)	(100.0%)	(0.2019)	(100.0%)	(0.2023)	(100.0%)
		($0_{\left(38\right)}$, 5, 5)	1.4175	1.04799	1.4096	0.9987	1.4462	1.0027
			(0.1946)	(100.0%)	(0.1742)	(100.0%)	(0.1820)	(100.0%)
(30, 30)	30	($0_{\left(29\right)}$, 30)	1.4717	0.9640	1.4930	0.9761	1.4912	0.9608
			(0.1699)	(97.96%)	(0.1731)	(97.96%)	(0.1736)	(97.96%)
		($0_{\left(28\right)}$, 20, 10)	1.5002	0.9997	1.5325	1.0172	1.4544	1.0484
			(0.1766)	(100.0%)	(0.1886)	(100.0%)	(0.2044)	(100.0%)
	40	($0_{\left(39\right)}$, 20)	1.4782	0.9419	1.4653	1.0049	1.4987	1.0303
			(0.1609)	(98.0%)	(0.1841)	(98.0%)	(0.1935)	(100.0%)
		($0_{\left(38\right)}$, 20, 0)	1.4769	1.0073	1.4924	1.0412	1.5021	1.0273
			(0.1797)	(100.0%)	(0.2009)	(100.0%)	(0.1902)	(100.0%)
(30, 40)	40	($0_{\left(39\right)}$, 30)	1.487	1.039	1.452	0.942	1.496	1.019
			(0.1902)	(100.0%)	(0.1586)	(98.0%)	(0.1857)	(100.0%)
		($0_{\left(39\right)}$, 29, 1)	1.4913	0.9877	1.4369	1.0116	1.5307	1.0151
			(0.1748)	(100.0%)	(0.1784)	(100.0%)	(0.1825)	(100.0%)
	50	($0_{\left(49\right)}$, 20)	1.4993	0.9816	1.4748	1.0207	1.4509	1.0532
			(0.1740)	(100.0%)	(0.1860)	(100.0%)	(0.2010)	(100.0%)
		($0_{\left(48\right)}$, 15, 5)	1.4526	1.0467	1.4565	1.0428	1.4391	1.0215
			(0.1966)	(100.0%)	(0.1974)	(100.0%)	(0.1903)	(100.0%)
(40, 50)	50	($0_{\left(49\right)}$, 40)	1.4862	1.0449	1.4922	1.0040	1.5055	1.0486
			(0.1940)	(100.0%)	(0.1771)	(100.0%)	(0.2009)	(100.0%)
		($0_{\left(48\right)}$, 35, 5)	1.5231	1.0125	1.4924	0.9742	1.4771	1.0412
			(0.1779)	(100.0%)	(0.1720)	(100.0%)	(0.1994)	(100.0%)
	60	($0_{\left(59\right)}$, 30)	1.4926	1.0105	1.4820	0.9905	1.4994	1.0187
			(0.1826)	(100.0%)	(0.1685)	(100.0%)	(0.1794)	(100.0%)
		($0_{\left(58\right)}$, 25, 5)	1.4740	1.0425	1.5041	1.0200	1.4719	1.0245
			(0.1929)	(100.0%)	(0.1828)	(100.0%)	(0.1831)	(100.0%)

Table 5. Bayesian estimations of parameter ${\alpha }_1$ supposing non-informative priors $a_1=a_2=b_1=b_2=c=d={10}^{-5}$.

$(\mathit{m},\mathit{n})$	r	$({\mathit{R}}_1,\dots ,{\mathit{R}}_{\mathit{r}})$	SE		LINEX (a = −2)		LINEX (a = 2)
			ABE (MSE)	AL (CP)	ABE (MSE)	AL (CP)	ABE (MSE)	AL (CP)
(20, 20)	20	($0_{\left(19\right)}$, 20)	1.5415	0.9974	1.5202	1.1238	1.5560	1.0223
			(0.1891)	(98.0%)	(0.2478)	(100.0%)	(0.2064)	(95.9%)
		($0_{\left(18\right)}$, 5, 15)	1.3973	1.1096	1.4134	1.0052	1.4864	1.1652
			(0.2565)	(100.0%)	(0.1947)	(95.9%)	(0.2797)	(100.0%)
	30	($0_{\left(29\right)}$, 10)	1.5459	1.0182	1.5821	1.0241	1.5657	1.0313
			(0.2048)	(98.0%)	(0.1954)	(100.0%)	(0.1936)	(100.0%)
		($0_{\left(29\right)}$, 8, 2)	1.5342	1.0839	1.4975	1.0356	1.5406	1.0968
			(0.2248)	(98.0%)	(0.1963)	(98.0%)	(0.2452)	(100.0%)
(20, 30)	30	($0_{\left(29\right)}$, 20)	1.5068	1.0485	1.4969	0.9977	1.5988	1.0299
			(0.2120)	(100.0%)	(0.1945)	(98.0%)	(0.1946)	(100.0%)
		($0_{\left(28\right)}$, 15, 5)	1.5275	1.1028	1.4590	1.0865	1.5836	1.0912
			(0.2460)	(100.0%)	(0.2205)	(100.0%)	(0.2500)	(98.0%)
	40	($0_{\left(39\right)}$, 10)	1.5544	1.0465	1.5168	1.0104	1.4995	1.0326
			(0.1981)	(100.0%)	(0.1808)	(100.0%)	(0.1987)	(98.0%)
		($0_{\left(28\right)}$, 5, 5)	1.4592	0.9943	1.4368	1.0164	1.4163	1.1130
			(0.1860)	(98.0%)	(0.1974)	(98.0%)	(0.2435)	(100.0%)
(30, 30)	30	($0_{\left(29\right)}$, 30)	1.5452	1.0391	1.5198	1.0611	1.6159	0.9741
			(0.2185)	(98.0%)	(0.2299)	(95.9%)	(0.1652)	(100.0%)
		($0_{\left(28\right)}$, 20, 10)	1.5250	1.0462	1.4700	1.0006	1.4882	1.0511
			(0.2010)	(100.0%)	(0.1809)	(100.0%)	(0.2093)	(100.0%)
	40	($0_{\left(39\right)}$, 20)	1.5112	1.0565	1.4932	1.0288	1.4970	1.0090
			(0.2065)	(100.0%)	(0.2073)	(98.0%)	(0.1920)	(95.9%)
		($0_{\left(38\right)}$, 20, 0)	1.5510	1.0584	1.5105	1.0100	1.5340	1.0369
			(0.2045)	(100.0%)	(0.1877)	(100.0%)	(0.2034)	(100.0%)
(30, 40)	40	($0_{\left(39\right)}$, 30)	1.6226	1.0623	1.4931	1.0384	1.5335	1.0430
			(0.2186)	(98.0%)	(0.1990)	(100.0%)	(0.1993)	(100.0%)
		($0_{\left(39\right)}$, 29, 1)	1.5016	0.9801	1.4981	1.0258	1.5474	1.0125
			(0.1733)	(100.0%)	(0.1882)	(100.0%)	(0.1988)	(98.0%)
	50	($0_{\left(49\right)}$, 20)	1.5536	1.0146	1.4953	0.9792	1.5270	1.0628
			(0.1907)	(100.0%)	(0.1738)	(100.0%)	(0.2026)	(100.0%)
		($0_{\left(48\right)}$, 15, 5)	1.5256	1.0128	1.4978	0.9998	1.4926	1.0616
			(0.1907)	(98.0%)	(0.1738)	(98.0%)	(0.2008)	(100.0%)
(40, 50)	50	($0_{\left(49\right)}$, 40)	1.4773	0.9553	1.5163	0.9957	1.4868	1.0291
			(0.1596)	(100.0%)	(0.1797)	(100.0%)	(0.1919)	(100.0%)
		($0_{\left(48\right)}$, 35, 5)	1.5283	1.0298	1.5067	1.0215	1.5188	1.0704
			(0.1918)	(100.0%)	(0.1924)	(100.0%)	(0.2128)	(100.0%)
	60	($0_{\left(59\right)}$, 30)	1.5016	0.9801	1.4780	1.0114	1.4594	0.9964
			(0.1678)	(100.0%)	(0.1822)	(100.0%)	(0.1738)	(100.0%)
		($0_{\left(58\right)}$, 25, 5)	1.4615	1.0400	1.5245	1.0407	1.5225	0.9925
			(0.1914)	(100.0%)	(0.1957)	(100.0%)	(0.1707)	(100.0%)

Histograms, cumulative mean plots, and estimation plots of the parameters produced by the MCMC method under gamma IPs and NIPs are shown in Figure 4, Figure 5, Figure 6, Figure 7, Figure 8 and Figure 9 (taking $(m,n)=(40,50)$, $R=(0_{\left(49\right)},40$) as an example). These plots demonstrate good convergence behavior, as evidenced by the stable cumulative means and well-mixed histograms.

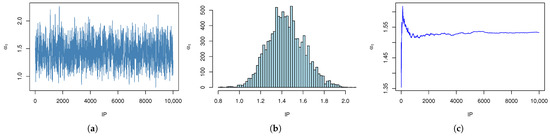
Figure 4. Simulation of ${\alpha }_1$ with IP.(a) The trace plot of MCMC samples of ${\alpha }_1$ with IPs. (b) Histogram of ${\alpha }_1$ with IPs. (c) Cumulative mean plots of ${\alpha }_1$ with IPs.

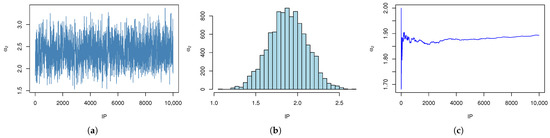
Figure 5. Simulation of ${\alpha }_2$ with IPs. (a) The trace plot of MCMC samples of ${\alpha }_2$ with IPs. (b) Histogram of ${\alpha }_2$ with IPs. (c) Cumulative mean plots of ${\alpha }_2$ with IPs.

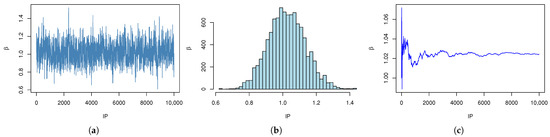
Figure 6. Simulation of $\beta$ with IPs. (a) The trace plot of MCMC samples of $\beta$ with IPs. (b) Histogram of $\beta$ with IPs. (c) Cumulative mean plots of $\beta$ with IPs.

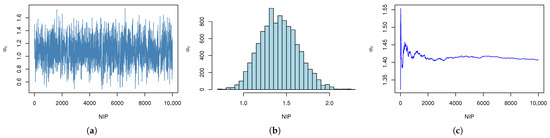
Figure 7. Simulation of ${\alpha }_1$ with NIPs. (a) The trace plot of MCMC samples of ${\alpha }_1$ with NIPs. (b) Histogram of ${\alpha }_1$ with NIPs. (c) Cumulative mean plots of ${\alpha }_1$ with NIPs.

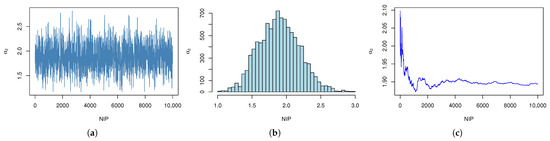
Figure 8. Simulation of ${\alpha }_2$ with NIPs. (a) The trace plot of MCMC samples of ${\alpha }_2$ with NIPs. (b) Histogram of ${\alpha }_2$ with NIPs. (c) Cumulative mean plots of ${\alpha }_2$ with NIPs.

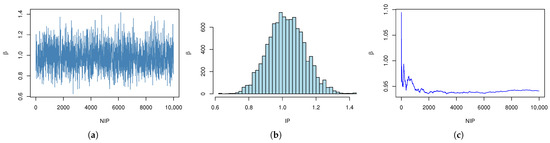
Figure 9. Simulation of $\beta$ with NIPs. (a) The trace plot of MCMC samples of $\beta$ with NIPs. (b) Histogram of $\beta$ with NIPs. (c) Cumulative mean plots of $\beta$ with NIPs.

7. Real-Data Analysis

7.1. Example 1

The following section presents an analysis of real data obtained from Balakrishnan et al. [28], which documents the breakdown time of electrical current under varying voltage levels. A detailed statistical examination of these data was later conducted by Ding and Gui [29]. For clearer demonstration, this study focuses on breakdown times recorded at voltage levels of 32 kV and 34 kV. The corresponding data are summarized in Table 6 for reference.

Table 6. Breakdown times at voltages of 32 and 34 kV.

Datasets	Breakdown Times
Breakdown at 32 kV	0.27	0.40	0.69	0.79	2.75
	3.91	9.88	13.95	15.93	27.80
	53.24	82.85	89.29	100.60	215.10
Breakdown at 34 kV	0.19	0.78	0.96	1.31	2.78
	3.16	4.15	4.67	4.85	6.50
	7.35	8.01	8.27	12.06	31.75
	32.53	33.91	36.71	72.89

The goodness of fit of the samples to the IWD is assessed using the Kolmogorov–Smirnov (K-S) test. For the first sample, the test yields a p-value of 0.2391, while the second sample produces a p-value of 0.5941. The test results are visually illustrated in Figure 10.

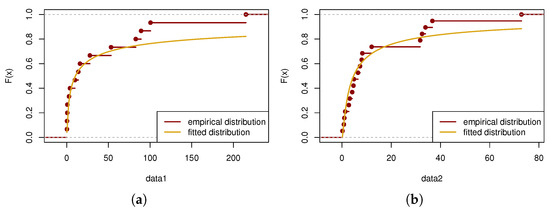
Figure 10. Fitness between the fitted distribution and the empirical distribution for example 1. (a) Fitness of dataset 1. (b) Fitness of dataset 2.

Using the datasets above, we generated the JPC sample based on the censoring scheme. Suppose that the first sample has a size of $m=15$ and $n=19$ for the second sample. By implementing JPC, where $K=m+n$ represents the total sample size, and setting $r=10,19$, with $R=(0_{\left(8\right)},12,12)$,$(0_{\left(17\right)},14,1)$, and $(0_{\left(17\right)},10,5)$, we proceed with the analysis.

The estimation results under different censoring schemes are presented in Table A5. The MLEs, MSEs, and AL for ${\alpha }_1$, ${\alpha }_2$, and $\beta$ demonstrate variations across the censoring schemes, with noticeable differences in the estimated values and corresponding MSEs. In particular, the estimates of ${\alpha }_1$ and ${\alpha }_2$ show sensitivity to the censoring structure, while $\beta$ remains relatively stable.

Table A6 and Table A7 in Appendix A further examine the influence of prior settings on parameter estimation, comparing the IP and NIP approaches. The hyperparameters for IPs are chosen based on the MLE results, ensuring that the prior mean approximates the MLE estimates. Table A6 presents the results under IPs with $a_1=4,b_1=10.5,a_2=10$, $b_2=20,c=18$, and $d=10$. In contrast, Table A7 in Appendix A reports the results using NIPs with $a_1=b_1=a_2=b_2=c=d={10}^{-5}$.

7.2. Example 2

The two datasets, each consisting of 30 observations $(m=n=30)$, pertain to the breaking strength of jute fiber glass laminate (JFGL) with diameters of 10 mm and 20 mm. The measurements are given in units of fiber strength (MPa). These data are from [30], and are presented in Table 7.

Table 7. Breaking strength of JFGL with 10 mm and 20 mm.

Datasets	Fiber Strength
10 mm	43.93	50.16	101.15	108.94	123.06	141.38
	151.48	163.40	177.25	183.16	212.13	257.44
	262.90	291.27	303.90	323.83	353.24	376.42
	383.43	422.11	506.60	530.55	590.48	637.66
	671.49	693.73	700.74	704.66	727.23	778.17
20 mm	36.75	45.58	48.01	71.46	83.55	99.72
	113.85	116.99	119.86	145.96	166.49	187.13
	187.85	200.16	244.53	284.64	350.70	375.81
	419.02	456.60	547.44	578.62	581.60	585.57
	594.29	662.66	688.16	707.36	756.70	765.14

A rescaling factor of 1000 is applied to the data to prevent the estimates from becoming excessively large or small. The K-S test is also employed to evaluate the fit of the samples to the IWD. The resulting p-values are 0.6781 for the first sample and 0.8081 for the second. A visual representation of the test outcomes is provided in Figure 11.

Figure 11. Fitness between the fitted distribution and the empirical distribution for example 2. (a) Fitness of dataset 1. (b) Fitness of dataset 2.

Based on the datasets described above, JPC samples are constructed under a specified censoring scheme. The analysis is conducted using different censoring settings: setting $r=30,40$ with $(0_{\left(28\right)},15,15)$, $R=(0_{\left(38\right)},15,5)$, and $R=(0_{\left(38\right)},10,10)$.

Table A8 displays the parameter estimates obtained under various censoring schemes. To assess the impact of prior selection, Appendix A includes Table A9 and Table A10, which present results from the IP and NIP settings. Specifically, Table A9 uses $a_1=10,b_1=10.5$, $a_2=9,b_2=20,c=2$, and $d=10$. In comparison, Table A10 in Appendix A reports the results using NIPs with $a_1=b_1=a_2=b_2=c=d={10}^{-5}$.

8. Conclusions

This paper investigates statistical inference for two inverse Weibull distributions under a joint progressive type II censoring scheme, assuming a common shape parameter with differing scale parameters. The Newton–Raphson method is used to derive maximum likelihood estimates, and asymptotic confidence intervals are constructed. Additionally, bootstrap techniques are applied to improve interval estimation. The foundation of our Bayesian analysis is the use of independent priors for the model parameters. We employ the MCMC algorithm to obtain Bayesian estimates under the squared error and LINEX loss functions, along with corresponding credible intervals. Through these procedures, we conduct simulations under various joint censoring schemes. Finally, we apply the proposed method to real datasets to demonstrate its practical implementation.

In this study, the populations are assumed to follow an inverse Weibull distribution with a common shape parameter. However, in practical applications, the shape parameters may vary across populations, highlighting the need for further investigation. Additionally, alternative approaches, such as the Jackknife method, could be explored by future researchers to further evaluate estimation performance and variability. Future research will also examine statistical inference methods for multiple populations, considering both identical and distinct lifetime distributions.