A Path-Planning Method Recommended for Multi-UAV Police Patrols Based on the Wolf Pack Optimization Algorithm Using CDRS and DRSS

Abstract

Multi-UAV path planning for police patrols plays an important role in public security work, and while many path-planning algorithms have been applied in this area, all of them possess various degrees of shortcomings. To further improve the accuracy and efficiency of multi-UAV path planning for police patrols, this paper proposes a multi-UAV police patrol path-planning method based on an improved wolf pack optimization algorithm using the strategies of Composite Directional Raid and Dynamic Random Search (PMU-3PM-IWPA). Firstly, a multi-UAV police patrol path-planning model was constructed to reflect the planning problem for multi-UAV police patrol paths (PMU-3PM). Moreover, to enhance the performance of the existing wolf pack optimization algorithm, this paper proposes an improved wolf pack optimization algorithm (for short CDR-DRS-WPOA), including the Composite-Directional Raid Strategy (CDRS), aimed at enhancing global exploration capability, as well as the Dynamic Random Search Strategy (DRSS), with a view to speeding up the convergence for simple problems and heightening the optimization accuracy for difficult problems. Finally, the improved wolf pack optimization algorithm was adopted to solve the issue of multi-UAV path planning for police patrols, and numerical experiments were carried out on 20 public classical datasets as well as PMU-3PM compared with GA, PSO, WDX-WPOA, and DAF-BRS-CWOA. The results indicate that CDR-DRS-WPOA took 20~80% less time and possessed more optimization accuracy, and that PMU-3PM-IWPA based on CDR-DRS-WPOA offers excellent performance.

1. Introduction

With the rapid development of unmanned aerial vehicle (for short, UAV) technology and the demand for police patrols for social security, police UAV patrols are widely used in the daily patrol work of public security. Drones are increasingly being used in policing in many countries, as they can help police detect hazards and respond to emergencies in a timely manner and at a low cost [1]. Furthermore, efficient and well-organized drone patrols can save time and police resources and maximize the chances of apprehending criminals [2]. However, how to rationally deploy drones is an important issue today, and drones need to be combined with advanced navigation algorithms and artificial intelligence technology to meet the challenges of operating in complex environments [3].

Many scholars have reflected on the development of police drone patrol policing modes and the optimization of drone patrol routes. In terms of drone policing patrols, Wang et al., proposed a multi-UAV patrol response strategy based on target clustering and combinatorial genetic algorithms based on crime prediction results [4]; Yang et al., studied a patrol solution based on air-ground cooperation between multiple UAVs and police vehicles [5]; Wang et al., used the area coverage traversal algorithm of multiple unmanned ships to study a large-scale maritime patrol task in which multiple unmanned ships cooperate to perform area coverage tasks [6]; Liu et al., proposed a whale algorithm based on chaos theory to plan the patrol tasks of multiple UAVs to solve the border patrol tasks in complex environments [7]; and Andrey V. Savkin et al., designed a model predictive control-based multi-UAV path-planning algorithm [8]. In terms of UAV path optimization, Xiao et al., proposed an enhanced dynamic group-based collaborative optimization to solve UAV path planning [9]; Bai et al., developed a new algorithm for UAV flight path planning based on improved A∗ and dynamic window algorithms [10]; Yu et al., developed a hybrid algorithm based on gray wolf optimizer and differential evolution for UAV path planning [11]; Zhu et al., proposed UCAV path planning for avoiding obstacles using cooperative co-evolution spider monkey optimization [12]; and Wang et al., proposed a Modified Mayfly Algorithm for UAV path planning [13].

In the past few years, the wolf pack optimization algorithm has attracted extensive attention from researchers due to its good global convergence and computational robustness in solving multi-modal complex functions [14]. For instance, Duan et al., developed a target allocation method based on the wolf behavior mechanism [15], which solves the problem of collaborative target allocation among UAV groups; Lai et al., proposed a discrete wolf pack optimization algorithm aimed at the no-wait flow shop scheduling problem [16]; and Wang et al., proposed ship automation collision avoidance tactics based on the quantum-behaved wolf pack optimization algorithm [17]. At the same time, many scholars have improved the performance of the wolf pack optimization algorithm by improving some of its shortcomings. Sun et al., proposed a new wolf intelligent optimization algorithm, which have a faster convergence speed and higher robustness [18]; Zhao et al., proposed an improved wolf pack optimization algorithm that provides scout wolves variable scouting directions and scouting step length that can be adjusted dynamically based on the Fibonacci Sequence to increase the global search capability [19]; and in paper [20], the researchers proposed a chaotic disturbance wolf pack optimization algorithm for solving ultrahigh-dimensional complex functions.

Therefore, the effective use of the wolf pack optimization algorithm prompts us to use an improved wolf pack optimization algorithm to solve the problem of police multi-UAV security patrol path optimization. This paper therefore proposes an improved wolf pack optimization algorithm (CDR-DRS-WPOA) and a discrete algorithm (PMU-3PM-IWPA) based on CDR-DRS-WPOA to optimize the police multi-UAV security patrol path. Moreover, this paper considers various factors, such as energy consumption, to construct a practical model (PMU-3PM). In addition, this paper demonstrates the advantages of this model through a series of comparative experiments with other existing algorithms, including the testing of 20 classical functions and the PMU-3PM model.

2. Related Works

2.1. Principle of WDX-WPOA

Many creatures in nature with limited individual abilities have shown amazing abilities through individual cooperation. Scientists have designed many swarm intelligence optimization algorithms by simulating the behavioral characteristics of these biological groups, and have optimized complex functions by mimicking simple rules and interactions between biological individuals; the wolf pack algorithm is a typical representative of this. The wolf pack optimization algorithm (WPOA) was first proposed by Yang et al. [21], and abstracts the five intelligent lines of Initialization, Migration, Summon-Raid, Siege, and Regeneration. The WDX-WPOA was proposed in 2018 by Wang et al., in [22], and is an efficient variant of the wolf pack optimization algorithm in the optimization field aimed at solving application problems efficiently. Its key steps are as follows.

Initialization: initialize the necessary parameters and assign the wolf pack to the solution space or definition domain of a function. Assuming that the number of wolves is N and the dimension of the solution space is D, then the position of wolf i is shown in Equation (1).

$$\left\{\begin{array}{c}{x}_i=\left(x_{i1},x_{i2},x_{i3},\dots \dots x_{iD}\right), \left(i=1, 2, \dots , N; d=1, 2, \dots , D\right)\\ x_{id-new}={rang}_{min}+rand\left(1\right)\ast \left({rang}_{max}-{rang}_{min}\right),\left(i=1, 2, \dots , N;d=1, 2, \dots , D\right)\end{array}\right.$$

(1)

where, rand (1) is variables randomly distributed in the interval [0, 1], and rang_max and rang_min are the upper and lower bounds of the solution space, respectively.

Migration: wolves roam in search of prey; for the current wolf, an adaptive mesh with D dimension is generated to reflect the local neighborhood space of the current position, (2 ∗ k + 1)^D points are generated according to Equation (2), and the optimal wolf is found to replace the current wolf.

$$\left\{\begin{array}{c}step\_a=\left[1-{\left(\frac{t-1}{T}\right)}^2\right]\ast step\_a_0, \left(i=1, 2, \dots , N; d=1, 2, \dots , D\right)\\ x_{id-new}=x_{id}+step\_c\ast k,\left(i=1, 2, \dots , N; d=1, 2, \dots , D,k=-K,-K+1\dots \dots K\right)\\ x_{i-new}=\left(x_{i1-new},x_{i2-new},x_{i3-new},\dots \dots x_{iD-new}\right), \left(i=1, 2, \dots , N; d=1, 2, \dots , D\right)\end{array}\right.$$

(2)

where, step_a₀ is the initial value of migration step size; t is the number of the current iteration; T is the maximum number of the current iteration; and K means the number of points taken in the same direction of each dimension.

Summon-Raid: once the wolf receives the summoning signal, it will move towards the lead wolf during the raid according to Equation (3), and at the same time look for prey. If the new location is a better fit than the current location, the current location is changed to the new position according to Equation (3).

$$\left\{\begin{array}{c}{x}_{id-opposition}=2\ast bestwolf-x_{id} ,\left(i=1, 2, \dots , N; d=1, 2, \dots , D\right)\\ x_{imid\_d}=\frac{\left(x_{id+bestwolf}\right)}{2}, \left(i=1, 2, \dots , N; d=1, 2, \dots , D\right)\\ x_i=(bestfitness\left[x_{i\_1},x_{i\_2},\dots \dots ,x_{i\_(D-1)},x_{i\_D}\right],\left[x_{i\_1},x_{i\_2},\dots \dots x_{i\_(d-1)},x_{imid\_D}\right],\dots \dots ,\\ \left[x_{i\_1},x_{imid\_2},\dots \dots ,x_{imid\_(D-1)},x_{imid\_D}\right],\left[x_{i\_1},x_{imid\_2},\dots \dots ,x_{imid\_(D-1)},x_{imid\_D}\right],\\ x_{id-opposition)}, \left(i=1,2, \dots ,N; d=1,2, \dots ,D; i\le num/2\right)\\ x_{id\_new}=\mathrm{bestwolf}+rand\left(1\right)\ast step\_b,\left(i=1, 2, \dots , N; d=1, 2, \dots , D;i>\frac{\mathrm{n}\mathrm{u}\mathrm{m}}{2}\right)\end{array}\right.$$

(3)

where, x_id is the coordinate of the wolf i; bestwolf means the coordinate of the best wolf at dimension d; x_{imid_d} means the position of the middle point between the wolf i and the best wolf; bestfitness means the best fitness of all points, with this line of formula representing the best fitness of x_i and x_{imid_d} after permutation; x_{id_opposition}; num means the number of the wolf population; and step_b means the raid step length.

Siege: All the wolves are ambushed around the lead wolf (the lead wolf position is considered the prey position). A D-dimensional mesh is generated to reflect the local neighborhood space of the current location according to Equation (4), and the optimal wolf is searched to replace the current wolf.

$$\left\{\begin{array}{c}step\_c_0=step\_c_{min}\ast \left(x_{d-max}-x_{d-min}\right)\ast \exp \left[\frac{t\ast \mathit{ln}\left(step\_c_{max}-step\_c_{min}\right)}{T}\right]\\ step\_c=\left[1-{\left(\frac{t-1}{T}\right)}^2\right]\ast rand\left(1\right)\ast step\_c_0\\ x_{id-new}=x_{id}+step\_c\ast k,\left(i=1, 2, \dots , N; d=1, 2, \dots , D,k=-K,-K+1\dots \dots K\right)\\ x_{i-new}=\left(x_{i1-new},x_{i2-new},x_{i3-new},\dots \dots x_{iD-new}\right), \left(i=1, 2, \dots , N; d=1, 2, \dots , D\right)\end{array}\right.$$

(4)

where, step_c_min means the minimum value of the siege step size; step_c_max means the maximum value of the siege step size; x_d−max means the maximum value of the wolves in d dimension; x_d−min means the minimum value of the wolves in d dimension; t means the current number of iterations; T is the maximum number of iterations; and K means the number of points taken in the same direction of each dimension.

Regeneration: according to the principle of food distribution based on the survival of the fittest, the strong will be prioritized for more food while the weak will starve to death and be eliminated, so the stronger wolves can continue to survive and the population has a better ability to adapt. According to the principle of survival of the fittest, wolves with less adaptability are eliminated according to Equation (5), and the same number of wolves are regenerated according to Equation (1).

$$x_{i\_worst}=worstfitness\left(x_1,x_2,x_3,\dots \dots x_1\right), \left(i=1, 2, \dots , N\right)$$

(5)

where, worstfitness means the five coordinate points with the worst fitness.

Finally, the overall algorithm will follow the above steps to cycle and determine whether the exit condition is reached, and when the stop condition is reached, the algorithm will exit and output the optimal value.

2.2. Datasets

In order to verify the excellent performance of the new proposed CDR-DRS-WPOA in solving the optimization problem, the functions with unique characteristics, such as measured functions, including multi-modal, highly complex, and multi-peak function as shown in Table 1, are selected as test datasets. The choice of 20 public datasets is solid, as it provides a broad basis for bench marking the algorithm. All test functions will go through 50 consecutive tests to obtain data, and calculate the optimal value, worst value, average value, standard deviation, number of iterations, average run time, and other indicators of 50 consecutive tests to fully reflect the performance of each algorithm.

Table 1. Datasets for performance validation.

Order	Function	Expression	Dimension	Range	Optimum
1	Ackley	$\mathrm{F}1=-20\mathit{exp}\left(-0.2\sqrt{\frac{1}{2}{\displaystyle \sum _{i=1}^2}{x}_i^2}\right)--\exp (\frac{1}{2}{\sum }_{i=1}^2\cos (2\pi x_i))+20+\exp (1)$	2	[−32.768, 32.768]	Min f = 0
2	Three-Hump-Camel	$\mathrm{F}2=2x_1^2-1.05x_1^4+\frac{x_1^6}{6}+x_1{x}_2+x_2^2$	2	[−5, 5]	Min f = 0
3	Drop-Wave	$F3=-\frac{1+\cos \left(12\sqrt{x_1^2+x_2^2}\right)}{0.5(x_1^2+x_2^2)+2}$	2	[−5.12, 5.12]	Min f = −1
4	Leon	$\mathrm{F}5=100{\left(x_2-x_1^3\right)}^2+{\left(x_2-1\right)}^2$	2	[−10, 10]	Min f = 0
5	Griewank	$\mathrm{F}7={\displaystyle \sum _{i=1}^2}\frac{x_i^2}{4000}-{\displaystyle \prod _{i=1}^2}cos\left(\frac{x_i}{\sqrt{i}}\right)+1$	2	[−600, 600]	Min f = 0
6	Levy	$F6={\sin }^2 (\pi w_1)+{\displaystyle \sum _{i=1}^{2-1}}{\left(w_i-1\right)}^2\left[1+10{\sin }^2\left(\pi w_i+1\right)\right]+{\left(w_2-1\right)}^2\left[1+{\sin }^2|\left(2\pi w_2\right)\right],\mathrm{where}{w}_i=1+\frac{x_i-1}{4},\mathrm{for}\mathrm{all}i=1,2$	2	[−10, 10]	Min f = 0
7	Levy13	$F11={\sin }^2\left(3\pi x_1\right)+{\left(x_1-1\right)}^2\left[1+{\sin }^2\left(3\pi x_2\right)\right]+{\left(x_2-1\right)}^2\left[1+{\sin }^2\left(2\pi x_2\right)\right]$	2	[−10, 10]	Min f = 0
8	Rastrigin	$\mathrm{F}12=10d+{\displaystyle \sum _{i=1}^2}\left[x_i^2-10cos\left(2\pi x_i\right)\right]$	2	[−5.12, 5.12]	Min f = 0
9	Schaffer2	$F9=0.5+\frac{{\mathrm{s}\mathrm{i}\mathrm{n}}^2(x_1^2-x_2^2)-0.5}{{\left[1+0.001(x_1^2+x_2^2)\right]}^2}$	2	[−100, 100]	Min f = 0
10	Bohachevsky1	$\mathrm{F}10=x_1^2+2x_2^2-{0.3}^{\ast }\cos \left(3\pi x_1\right)-{0.4}^{\ast }\cos \left(4\pi x_2\right)+0.7$	2	[−100, 100]	Min f = 0
11	Trecanni	$\mathrm{F}11=x_1^4+4x_1^3+4x_1^2+x_2^2$	2	[−5, 5]	Min f = 0
12	Rotated-Hyper-Ellipsoid	$\mathrm{F}12={\displaystyle \sum _{i=1}^2}{\displaystyle \sum _{j=1}^i}{x}_j^2$	2	[−65.536, 65.536]	Min f = 0
13	Sum-Squares	$\mathrm{F}13={\displaystyle \sum _{i=1}^2}i{x}_i^2$	2	[−10, 10]	Min f = 0
14	Trid	$\mathrm{F}14={\displaystyle \sum _{i=1}^2}{\left(x_i-1\right)}^2-{\displaystyle \sum _{i=2}^2}{x}_i{x}_{i-1}$	2	[−4, 4]	Min f = 2
15	Beale	$\mathrm{F}15={\left(1.5-x_1+x_1{x}_2\right)}^2+{\left(2.25-x_1+x_1{x}_2^2\right)}^2+{\left(2.625-x_1+x_1{x}_2^3\right)}^2$	2	[−4.5, 4.5]	Min f = 0
16	Matyas	$\mathrm{F}16=0.26\left(x_2^1+x_2^3\right)-0.48x_1{x}_2$	2	[−10, 10]	Min f = 0
17	Zakharov	$\mathrm{F}17={\displaystyle \sum _{i=1}^2}{x}_i^2+{\left({\displaystyle \sum _{i=1}^2}0.5i{x}_i\right)}^2+{\left({\displaystyle \sum _{i=1}^2}0.5i{x}_i\right)}^4$	2	[−5, 10]	Min f = 0
18	Easom	$\mathrm{F}18=-\cos {\left(\mathrm{x}1\right)}^{\ast }\cos {\left(\mathrm{x}2\right)}^{\ast }\exp \left[-{\left(\mathrm{x}1-\mathsf{\pi }\right)}^2-{\left(\mathrm{x}2-\mathsf{\pi }\right)}^2\right]$	2	[−100, 100]	Min f = −1
19	Eggcrate	$\mathrm{F}19={\mathrm{x}}_1^2+{\mathrm{x}}_2^2+{25}^{\ast }\left({\sin }^2 {\mathrm{x}}_1+{\sin }^2 {\mathrm{x}}_1\right)$	2	[−10, 10]	Min f = 0
20	Bohachevsky3	$\mathrm{F}20=x_1^2+2x_2^2-0.3\cos (3\pi x_1+4\pi x_2)+0.3$	2	[−100, 100]	Min f = 0

2.3. Police Multi-UAV Patrol Model Construction (PMU-3PM)

Police unmanned aerial vehicles have become an important means to improve the efficiency of police patrols of public security organs, with the wide application of unmanned aerial vehicles. Moreover, police drone patrols are an important measure for public security aircraft to maintain social stability and ensure the safety of people’s lives and property. According to the requirements of police patrols, public security organs need to patrol key areas and facilities, such as government seats, stations, commercial venues, schools, and so on. Assuming that the police drone departs from the police station and returns there after completing the patrol of each point, the patrol task is completed with the shortest total flight distance for multiple drones and the least number of drones according to the spatial distribution of key patrol places and areas within the jurisdiction of the police station and the time requirements for patrolling each area.

Suppose there are L locations that need to be patrolled in the jurisdiction of a police station and the endurance of a certain type of UAV is D kilometers, then the distance from the i-th patrol point to the j-th one is d_ij and the distance from the i-th patrol point to the police station is d_0i. Moreover, if R represents the flight path of the k-th drone, then the element r_ki in the path represents the i-th passing point of the k-th drone. It should be noted that the starting and ending points of the path are both police stations, the police station is r_k0, and n_k is the number of points passing through the kth drone (excluding the starting point and end point). Furthermore, there are no obstacles during the flight and there is no need to adjust the flight altitude up and down when the UAV always flies high enough, so the Euclidean distance is used to calculate the distance between two points, as shown in Equation (6). Therefore, if the shortest range is taken as the objective function, the following UAV patrol path optimization model can be established.

$$\mathrm{sign}\left(n_k\right)=\left\{\begin{array}{cc}1,& n_k\ge 1\\ 0,& \mathrm{others}\end{array}\right.$$

(6)

As in Equation (6), the equation indicates that when the patrol points of the k-th UAV are greater than or equal to 1, the UAV participates in the patrol and takes sign(n_k) = 1; when the patrol points of the k-th UAV are less than 1, the UAV does not participate in the patrol and takes sign(n_k) = 0.

$$\left\{\begin{array}{c}{\displaystyle \sum _{i=1}^{n_k}}\left[d_{r_{k(i-1)}{r}_{ki}}+d_{r_{k{n}_k}{r}_{k0}}\mathrm{sign}\left(n_k\right)\right]\le D\\ 0\le n_k\le L\\ {\displaystyle \sum _{k=1}^K} n_k=L\\ R_k=\left\{r_{ki}|r_{ki}\in \{1,2,\cdots ,L\},i=1,2,\cdots ,n_k\right\}\\ R_{k_1}\cap R_{k_2}=\varnothing ,k_1\ne k_2\end{array}\right.$$

(7)

Equation (7) above concerns the constraints. The first equation indicates that the flight distance of each drone does not exceed its maximum flight distance; the second equation indicates that the number of patrol points passed by each drone does not exceed the total number of patrol points; the third equation means that each patrol point needs to be patrolled but only needs to be patrolled once; the fourth equation indicates the patrol points contained in each patrol path; and the last equation indicates that there is no intersection between any two patrol paths, which means that only one drone needs to patrol each patrol point. Based on the above constraints, the following fitness function is constructed.

$$\left\{\begin{array}{c}{d}_{ij}=\sqrt{{\left(x_i-x_j\right)}^2+{\left(y_i-y_j\right)}^2}\\ minZ={\sum }_{k=1}^K \left\{{\sum }_{i=1}^{n_k}[d_{r_{k(i-1)}{r}_{ki}}+d_{r_{k{n}_k}{r}_{k0}}\mathrm{sign}(n_k)]\right\}\end{array}\right.$$

(8)

As in Equation (8), this accounts for a small proportion of the total flight distance because the police drone flies at a low altitude and the amplitude of the up-and-down flight is small but higher than the average building. Therefore, this paper ignores the up-and-down flight distance and flight obstacles to calculate the distance between two patrol points using the Euclidean distance in the two-dimensional plane. As a result, the objective function is constructed as shown in the third formula of Equation (8).

Police drones patrol a wide variety of routes with varying numbers and path lengths. As shown in Figure 1a, multiple UAVs are used to patrol key areas in an area and there is a police station, as shown by the red triangle. Moreover, unplanned patrol routes can be lengthy and require a large number of UAVs, as shown in Figure 1b. It is necessary to reasonably plan the patrol path to make the patrol path as short as possible while ensuring that it completely covers the key areas, so that the number of UAVs required is also lower, as shown in Figure 1c.

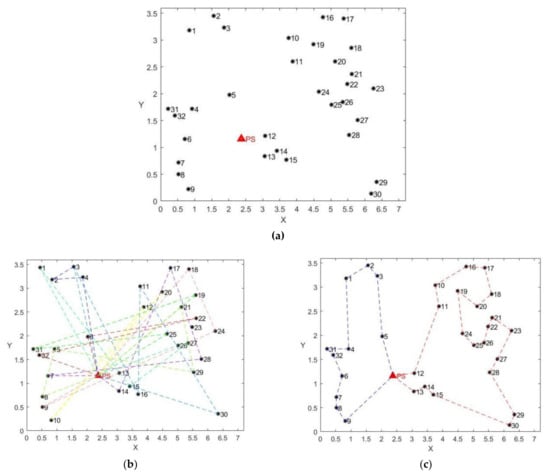
Figure 1. (a) Patrol Locations; (b) Randomly Arranged Security Patrol Path Planning; (c) Optimized Security Patrol Path Planning.

This paper takes a public case of a police station patrol location in a city in southern China, as shown in Figure 1a; there are 32 key areas to patrol and a police station, and a certain type of UAV is employed, with a maximum flight distance of no more than 18 km. Moreover, it is important to use as few drones as possible and to fly as far as possible to patrol the patrol point in the map and fly back to the police station. It is clear that the above description is a discrete problem, which is different from the dataset in Section 2.2. In order to solve this problem, this paper proposes a discrete algorithm according to the WPOA idea to solve the discrete problem.

3. Improvement and Design of the New Proposed Method

3.1. Composite-Directional Raid Strategy (CDRS)

In WDX-WPOA, half of the wolves will find the symmetrical coordinates of the current wolf with respect to the best wolf according to Equation (9). Then, the midpoint between the current wolf, the symmetrical wolf, and the best wolf will be found and arranged according to the dimensions. However, symmetrical coordinates can exceed boundary constraints. If a dimension of a symmetry coordinate exceeds the constraint boundary, the dimension value takes the value of the boundary. Half of the wolves will search for the above points, as shown in Figure 2a,b. Furthermore, the other half of the pack is airdropped directly around the current best wolf, as shown in Figure 2a,b. Moreover, DAF-BRS-CWOA [23] introduces the Balanced Raid Strategy and dynamic factor on the basis of WDX-WPOA; the number of wolves searched will decrease with the number of iterations and the number of wolves that are airdropped will increase. Moreover, searching wolves also search for the midpoint between the current wolf and the points where the current wolf is in the opposite position relative to the best wolf, as well as the points where the midpoint and the current point are arranged and combined according to the spatial dimension, as shown in Figure 2c,d.

$$wolf\_opposite=2\ast bestwolf-pop (i, :)$$

(9)

where, wolf_opposite means the opposite location of the current wolf while bestwolf means the current best wolf and pop (i, :) means the current wolf.

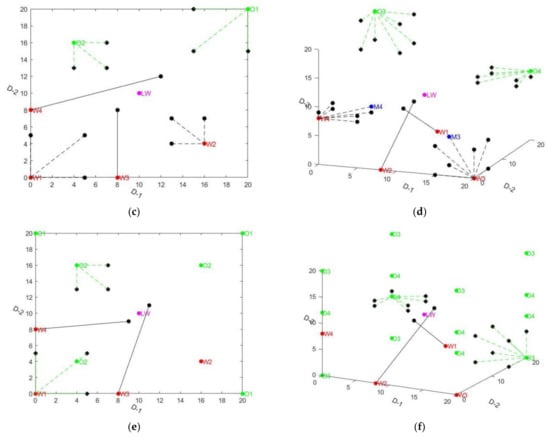
Figure 2. (a,b) the original raiding strategy in WDX-WPOA; (c,d) the old raiding strategy in DAF-BRS-CWOA; (e,f) the new adaptive raiding strategy in new algorithm (CDR-DRS-WPOA).

Additionally, this paper proposes a new optimal raid strategy based on the summon-raid strategy for DAF-BRS-CWOA, which not only checks the reverse position of the current wolf, but also arranges and combines the coordinates of the current wolf and the coordinates of the wolf in the opposite position, according to the dimensions, to make up the points in all directions. After that, the point with the best fitness among these points is identified, and then the midpoint between this and the best wolf coordinates is searched for, as well as the points where the midpoint and this point are arranged and combined according to the spatial dimensions of the search, as shown in Equation (10). The other part of the airdrop wolves still follows the summon-raid strategy for DAF-BRS-CWOA. This increases the probability of finding the global optimal solution and optimizes the computational resumption, as shown in Figure 2e,f.

$$\left\{\begin{array}{c}raid\_wolf\_ft=FitnessFunctionthe (raid\_wolf)\\ \left[raid\_\mathrm{bestwolf}\_\mathrm{ft},raid\_\mathrm{bestwolf}\_\mathrm{no}\right]=min(raid\_wolf\_ft)\\ res=original\_Summon\_Raid\_Mesh(raid\_wolf(raid\_\mathrm{bestwolf}\_no,:),bestwolf)\\ \left[summon\_\mathrm{bestwolf}\_\mathrm{ft},summon\_\mathrm{bestwolf}\_\mathrm{no}\right]=\min \left(\mathrm{Fitness}\mathrm{Function}\right(\mathrm{res}\left)\right)\\ tem\_bestwolf=\mathrm{res}\left(\mathrm{tem}\_\mathrm{bestwolf}\_\mathrm{no},:\right)\end{array}\right.$$

(10)

where, raid_wolf_ft means the fitness regarding raid_wolf; FitnessFunction is a fitness function; raid_wolf is the point where the pack needs to search; raid_bestwolf_ft means the best one in raid_wolf_ft and raid_bestwolf_no is the serial number of raid_bestwolf_ft in raid_wolf_ft; res represents the locations between raid_bestwolf and bestwolf according to the Summon-Raid rules while original_Summon_Raid_Mesh_Process is a function that returns some related locations determined by Summon-Raid rules in DAF-BRS-CWOA; summon_best_ft means the fitness regarding FitnessFunction(res); summon_bestwolf_no is the serial number of the best one in FitnessFunction(res); and tem_bestwolf is the best one corresponding to summon_best_ft in res.

3.2. Dynamic Random Search Strategy (DRSS)

According to the principle of WDX-WPOA and DAF-BRS-CWOA, during the migration or siege of the wolf pack, the position of the current wolf is the center, and at the same time, a uniformly distributed search is carried out in the num direction, assuming that the dimension of the solution space is D, and the total number of wolves is fixed at (2 ∗ num + 1)^D, as shown in Figure 3a,b. In the real world, however, a pack with a smaller number of wolves will be able to catch simple prey and more wolves will be summoned to besiege difficult prey. The wolves will summon more wolves to assist as the difficulty of migration or siege increases within a certain range. Abstracted into the model, the number of iterations is an important indicator of the difficulty of prey catching; simple fitness functions usually require fewer iterations to find the optimal value, while more complex fitness functions usually require more iterations to find the optimal value. According to this idea, this paper proposes a dynamic search strategy based on a specific threshold, in which the wolf population only searches along the diagonal of the search space in the first 10 iterations (then the total number of wolves is only D * num-D + 1), and more wolves are added to perform a randomly distributed search after more than 10 iterations and the number of wolves will reach (2 ∗ num + 1)^D in the end. The number of iterations does not exceed 10, as shown in Figure 3c,d, and the rest is shown in Figure 3e,f.

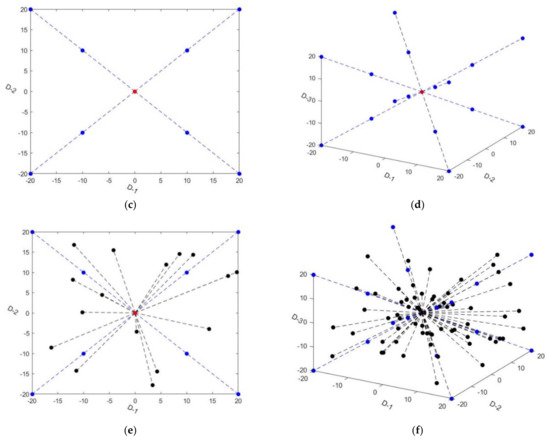
Figure 3. (a,b): about WDX-WPOA; (c,d) iterations do not exceed 10 in new algorithm (CDR-DRS-WPOA); (e,f) iterations exceed 10 in new algorithm (CDR-DRS-WPOA).

In summary, when the number of iterations exceeds 10, the number of wolves will increase with the number of iterations. The number of wolves randomly distributed after more than 10 iterations is shown in Equation (11). When the iterations reach 11, there will suddenly be a lot of wolves summoned to raid to help capture prey. However, the number of wolves increased each time was relatively stable in subsequent iterations. This idea can promote the algorithm to quickly iterate to solve simple problems in the early iteration process, and add search points in subsequent iterations to improve the global and computational accuracy to solve complex problems.

$$Increase\_number=\left\{\begin{array}{c}0,\left(t<10\right)\\ floor\left(\frac{2\left(\mathrm{t}-10\right)}{3\left(\mathrm{T}-10\right)}+\frac{1}{3}\right)\times {\left(2\ast K\right)}^D,\left(t\ge 10\right)\end{array}\right.$$

(11)

where, t means the number of current iterations; T means the number of the maximum iteration; floor means a function that returns the calculated result rounded down to ensure that wolf_number is an integer; K means the maximum number of wolves in a directional dimension; and D means the dimension of the solution space.

Simple test functions tend to require fewer iterations to find the optimal value, while complex test functions require more iterations. Therefore, this new search method will reduce a large number of search points for simple test functions to save a lot of calculations, and for complex test functions, a large number of wolves will be added in the middle and late stages to enhance the optimization effect. As a result, this search method not only reduces the optimization time of simple test functions, but also improves the calculation accuracy of complex functions.

3.3. Steps of Algorithms

On the basis of the strategy of dynamically increasing the number of wolves within a specific threshold in the process of migration and siege as well as of compound directional raid in the process of raid, the CWOA is improved and the CDR-DRS-WPOA algorithm is proposed.

All the steps are consistent with DAF-BRS-CWOA, with the exception of the use of PMU-3PM-IWPA during migration and siege and the use of composite directional raid strategies during raids, as detailed in Section 3.1 and Section 3.2. The steps of CDR-DRS-WPOA and how to implement the CDR-DRS-WPOA are shown in Figure 4. The overall algorithm will follow the above steps to determine whether the exit condition is met, and when the exit condition is met, the algorithm will exit. At the end of the loop, the wolf with the best fitness will be the global optimal value that the algorithm is committed to finding.

Figure 4. Flowchart for CDR-DRS-WPOA.

At the same time, this paper proposes a discrete algorithm (PMU-3PM-IWPA) to deal with multi-UAV path planning for police patrol problems based on CDR-DRS-WPOA, as shown in Figure 5.

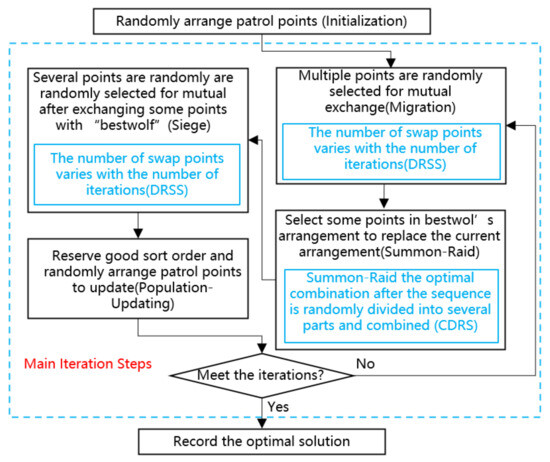
Figure 5. Flowchart for PMU-3PM-IWPA.

4. Experiments and Analysis

4.1. Experimental Environment & Comparative Algorithms

All the numerical experiments were conducted on a computer equipped with Windows 11 Home 22H2 operating system, Intel(R) Core (TM) i7-12700H processor (CA, American), 16 G memory, and the integrated development environment was MATLAB-2023b. To verify the optimization ability of CDR-DRS-WPOA, the genetic algorithm (GA), particle swarm optimization (PSO), and WDX-WPOA are adopted as comparative experiments, and 21 test functions, including PMU-3PM, were used as testing datasets.

A special toolbox in Matlab2023b was utilized for the GA experiment and a “PSOt” toolbox from Matlab2023b was used for the PSO experiment. The experiment concerning WDX-WPOA was carried out according to the process set out in reference [22] while the experiment relating to DAF-BRS-CWOA was conducted based on the process set out in reference [23]. CDR-DRS-WPOA was implemented based on the steps and approach set out in Section 3. Table 2 displays the configurations of the preceding algorithms, and each of the above algorithms was independently executed 50 times on 21 test datasets, including PMU-3PM, to verify the excellent performance of the new algorithm.

Table 2. Arithmetic Configuration.

Order	Algorithm Name	Configuration
1	GA	The crossover probability is 0.8, the mutation probability is 0.01, the max iteration T = 600, population size N = 50.
2	PSO	Inertia weight is 0.5, the cognitive coefficient is 1.5, the social coefficient is 1.5, the max iteration T = 600, population size N = 50.
3	WDX-WPOA	Initial value of search step size step_a0 = 1.5; the initial max value of sicge step size step_cmax = 1 × 106 and the minimum value of siege step size step_cmin = 1 × 10−40; the maximum iteration time T = 600; the wolf population N = 50.
4	DAF-BRS-CWOA	Initial value of search step size step_a0 = 1.5; the initial max value of sicge step size step_cmax = 1 × 106 and the minimum value of siege step size step_cmin = 1 × 10−40; the maximum iteration time T = 600; the wolf population N = 50.
5	CDR-DRS-WPOA	Initial value of search step size step_a0 = 1.5; the initial max value of siege step size step_cmax = 1 × 106 and the minimum value of siege step size step_cmin = 1 × 10−40; the maximum iteration time T = 600; the wolf population N = 50.

4.2. Test Function Results and Analysis

Firstly, the new proposed algorithm CDR-DRS-WPOA was conducted independently 50 times with four other algorithms on 20 test functions and the average value was taken, as shown in Table 3. Seen from the perspective of the optimal value and calculation accuracy, CDR-DRS-WPOA can find the theoretical optimal value of all test functions, as can DAF-BRS-CWOA and WDX-WPOA, but other methods cannot fully do so. Moreover, in terms of the worst and average values, CDR-DRS-WPOA performed best among the 5 algorithms (PSO, GA, WDX-WPOA, DAF-BRS-CWOA, and CDR-DRS-WPOA), and its worst and average values reached the theoretical optimal values while other algorithms did not have this ability. As a result, CDR-DRS-WPOA has better optimization accuracy.

Table 3. Raw data of experiments.

Function	Algorithm	Optimal Value	Worst Value	Average Value	Standard Deviation	Average Iteration	Average Time Spent
1. Ackley min f = 0	GA	7.92 × 10−6	1.28 × 10−4	5.17 × 10−5	6.95 × 10−10	600	0.23365
	PSO	1.71 × 10−5	5.72 × 10−4	1.14 × 10−4	6.89 × 10−9	600	0.046053
	WDX-WPOA	0	0	0	0	25.48	0.031144
	DAF-BRS-CWOA	0	0	0	0	22.12	0.028735
	CDR-DRS-WPOA	0	0	0	0	16.42	0.019348
2. Three-Hump-Camel min f = 0	GA	2.04 × 10−14	0.29864	0.035837	9.70 × 10−2	600	0.15705
	PSO	1.60 × 10−206	0.29864	0.011946	5.85 × 10−2	600	0.081915
	WDX-WPOA	0	0	0	0	24.32	0.063319
	DAF-BRS-CWOA	0	0	0	0	21.1	0.058633
	CDR-DRS-WPOA	0	0	0	0	16.44	0.027872
3. Drop-Wave min f = −1	GA	−0.99992	−0.78573	−0.93986	0.04808	600	0.034075
	PSO	−1	−0.93625	−0.98512	0.026965	218.6333	0.020236
	WDX-WPOA	−1	−1	−1	0	15.16	0.014995
	DAF-BRS-CWOA	−1	−1	−1	0	13.14	0.013978
	CDR-DRS-WPOA	−1	−1	−1	0	7.52	0.0075679
4. Leon min f = 0	GA	2.18 × 10−2	8.7913	2.1025	2.7501	600	0.024246
	PSO	0	1.26 × 10−19	4.20 × 10−21	2.26 × 10−20	595.3	0.10341
	WDX-WPOA	0	0	0	0	28.54	0.046596
	DAF-BRS-CWOA	0	0	0	0	24.12	0.044818
	CDR-DRS-WPOA	0	0	0	0	20.58	0.02608
5. Griewank min f = 0	GA	0.004788	0.31789	0.075813	0.063402	600	0.013661
	PSO	0	0.019719	0.0026303	0.0045421	339.3	0.0085504
	WDX-WPOA	0	0	0	0	16.8	0.018748
	DAF-BRS-CWOA	0	0	0	0	13.64	0.016633
	CDR-DRS-WPOA	0	0	0	0	8.36	0.0090338
6. Levy min f = 0	GA	0.00024335	1.1263	0.12324	0.21281	600	0.038618
	PSO	1.50 × 10−32	1.50 × 10−32	1.50 × 10−32	1.09 × 10−47	600	0.039204
	WDX-WPOA	0	8.59 × 10−8	1.72 × 10−9	1.20 × 10−8	551.54	0.67339
	DAF-BRS-CWOA	0	0.71613	0.024478	0.11739	509.82	0.61078
	CDR-DRS-WPOA	0	5.02 × 10−9	1.16 × 10−10	7.09 × 10−10	91.16	0.12264
7. Levy13 min f = 0	GA	0.011247	2.2797	0.22303	0.76184	600	0.01238
	PSO	0.00010961	−0.97283	−0.97283	3.33 × 10−16	600	0.012789
	WDX-WPOA	0	0	0	0	25.14	0.032147
	DAF-BRS-CWOA	0	0	0	0	21.66	0.02904
	CDR-DRS-WPOA	0	0	0	0	15.98	0.01774
8. Rastrigin min f = 0	GA	0.013678	6.3489	2.2711	1.7587	600	0.0119
	PSO	0	0.99496	0.066331	0.24819	110.4333	0.0023772
	WDX-WPOA	0	0	0	0	12.58	0.013655
	DAF-BRS-CWOA	0	0	0	0	10.74	0.012917
	CDR-DRS-WPOA	0	0	0	0	7.4	0.0077144
9. Schaffer2 min f = 0	GA	1.03 × 10−6	0.042464	0.010477	0.0093243	600	0.01321
	PSO	0	0	0	0	66.9667	0.012164
	WDX-WPOA	0	0	0	0	11.32	0.01139
	DAF-BRS-CWOA	0	0	0	0	9.78	0.010517
	CDR-DRS-WPOA	0	0	0	0	6.42	0.0061977
10. Bohachevsky3 min f = 0	GA	0.011268	0.91934	0.48134	0.25563	600	0.011984
	PSO	0	0	0	0	78.1667	0.015723
	WDX-WPOA	0	0	0	0	14.34	0.014551
	DAF-BRS-CWOA	0	0	0	0	11.94	0.013178
	CDR-DRS-WPOA	0	0	0	0	10.32	0.0099612
11. Trecanni min f = 0	GA	7.43 × 10−7	0.0038742	0.00037922	7.20 × 10−4	600	0.027606
	PSO	2.34 × 10−168	3.55 × 10−15	1.42 × 10−15	1.74 × 10−15	600	0.107907
	WDX-WPOA	0	0	0	0	24.48	0.062238
	DAF-BRS-CWOA	0	0	0	0	20.96	0.056577
	CDR-DRS-WPOA	0	0	0	0	16	0.026963
12. Rotated-Hyper-Ellipsoid min f = 0	GA	0.00039244	0.12985	0.034819	0.03493	600	0.012687
	PSO	1.96 × 10−134	1.02 × 10−129	8.56 × 10−131	2.28 × 10−130	600	0.013828
	WDX-WPOA	0	0	0	0	26.04	0.02325
	DAF-BRS-CWOA	0	0	0	0	22.66	0.021667
	CDR-DRS-WPOA	0	0	0	0	17.22	0.015096
13. Sum-Squares min f = 0	GA	2.42 × 10−6	0.0025094	0.00051005	0.00048937	600	0.012084
	PSO	5.91 × 10−137	2.18 × 10−132	3.76 × 10−133	5.82 × 10−133	600	0.013233
	WDX-WPOA	0	0	0	0	24.4	0.021132
	DAF-BRS-CWOA	0	0	0	0	20.98	0.021415
	CDR-DRS-WPOA	0	0	0	0	16.16	0.014255
14. Trid min f = −2	GA	−0.037736	−1.9991	−1.8925	0.11219	600	0.01241
	PSO	−2	−2	−2	0	523	0.014356
	WDX-WPOA	−2	−2	−2	0	10.92	0.010908
	DAF-BRS-CWOA	−2	−2	−2	0	9.22	0.0094853
	CDR-DRS-WPOA	−2	−2	−2	0	6.52	0.0065244
15. Beale min f = 0	GA	1.62 × 10−5	0.068489	0.021623	0.019766	600	0.022946
	PSO	0	0.76207	0.050805	0.19009	190.4333	0.030796
	WDX-WPOA	0	0	0	0	23.86	0.041922
	DAF-BRS-CWOA	0	0	0	0	20.12	0.037743
	CDR-DRS-WPOA	0	0	0	0	20.08	0.02635
16. Matyas min f = 0	GA	9.11 × 10−6	0.042161	0.010059	0.010711	600	0.01241
	PSO	1.76 × 10−120	2.71 × 10−116	2.87 × 10−117	5.48 × 10−117	600	0.013081
	WDX-WPOA	0	0	0	0	24.42	0.022231
	DAF-BRS-CWOA	0	0	0	0	20.72	0.020007
	CDR-DRS-WPOA	0	0	0	0	16.16	0.014232
17. Zakharov min f = 0	GA	2.32 × 10−6	0.0016735	0.00069625	0.00057972	600	0.015955
	PSO	3.10 × 10−137	7.27 × 10−131	3.57 × 10−132	1.30 × 10−131	600	0.016975
	WDX-WPOA	0	0	0	0	24.6	0.046247
	DAF-BRS-CWOA	0	0	0	0	21.26	0.040252
	CDR-DRS-WPOA	0	0	0	0	16.02	0.02342
18. Easom min f = −1	GA	−1	0	−0.75001	0.18749	72.91	0.084762
	PSO	−1	−6.30 × 10−61	−0.90001	0.089988	593.02	0.033852
	WDX-WPOA	−1	−1	−1	0	13.62	0.014799
	DAF-BRS-CWOA	−1	−1	−1	0	11.88	0.013726
	CDR-DRS-WPOA	−1	−1	−1	0	7.98	0.0080525
19. Eggcrate min f = 0	GA	1.13 × 10−11	3.20 × 10−8	4.13 × 10−9	4.66 × 10−17	600	0.085997
	PSO	6.23 × 10−24	1.42 × 10−8	1.42 × 10−10	1.99 × 10−18	597.56	0.030566
	WDX-WPOA	0	0	0	0	24.78	0.023696
	DAF-BRS-CWOA	0	0	0	0	21.68	0.021977
	CDR-DRS-WPOA	0	0	0	0	16.28	0.015303
20. Bohachevsky1 min f = 0	GA	0.0053751	2.2884	0.57643	0.42923	600	0.022766
	PSO	0	0	0	0	86.92	0.014321
	WDX-WPOA	0	0	0	0	14.38	0.016296
	DAF-BRS-CWOA	0	0	0	0	12.28	0.014996
	CDR-DRS-WPOA	0	0	0	0	8.6	0.0089217

Moreover, the standard deviation of the new algorithm in all test functions except function 6 “Levy” is zero. Nevertheless, in function 6 “Levy”, CDR-DRS-WPOA outperforms other algorithms in terms of Worst Value, Standard Deviation, and Runtime. Therefore, CDR-DRS-WPOA has good stability overall.

Furthermore, in terms of the average number of iterations, CDR-DRS-WPOA is the smallest of all test functions. Although there is almost no improvement in the number of iterations of DAF-BRS-CWOA in function 15, “Beale”, it is about the same as DAF-BRS-CWOA but has a shorter run time. This is made possible by the Composite-Directional Raid Strategy proposed in this paper. In general, CDR-DRS-WPOA has a better advantage in terms of iterations.

Finally, as shown in Table 3 in relation to average times, the average time spent on functions 6 “Levy”, 7 “Levy13”, 12 “Rotated-Hyper-Ellipsoid”, 13 “Sum-Squares”, 15 “Beale”, 16 “Matyas”, and 17 “Zakharov” CDR-DRS-WPOA was slightly longer for GA and PAO. However, the performance and accuracy of finding the optimal value are better than GA or PSO. Among the other test functions, CDR-DRS-WPOA requires the shortest time among the five algorithms, and has the best performance and accuracy in finding the optimal value. As shown in Table 4, CDR-DRS-WPOA is an improvement over DAF-BRS-CWOA and WDX-WPOA in all tested functions. Therefore, CDR-DRS-WPOA has a good convergence speed while also offering good computational accuracy.

Table 4. Time-Spent Comparison between DAF-BRS-CWOA, WDX-WPOA, and CDR-DRS-WPOA. (The Improvement Rate is CDR-DRS-WPOA compared to DAF-BRS-CWOA).

	Algorithm	WDX-WPOA	DAF-BRS-CWOA	CDR-DRS-WPOA	Improvement Rate
Function
F1: Ackley		0.031144	0.028735	0.019348	32.67%
F2: Three-Hump-Camel		0.063319	0.058633	0.027872	52.46%
F3: Drop-Wave		0.014995	0.013978	0.0075679	45.86%
F4: Leon		0.046596	0.044818	0.02608	41.81%
F5: Griewank		0.018748	0.016633	0.0090338	45.69%
F6: Levy		0.67339	0.61078	0.12264	79.92%
F7: Levy13		0.032147	0.02904	0.01774	38.91%
F8: Rastrigin		0.013655	0.012917	0.0077144	40.28%
F9: Schaffer2		0.01139	0.010517	0.0061977	41.07%
F10: Bohachevsky1		0.014551	0.013178	0.0099612	24.41%
F11: Trecanni		0.062238	0.056577	0.026963	52.34%
F12: Rotated-Hyper-Ellipsoid		0.02325	0.021667	0.015096	30.33%
F13: Sum-Squares		0.021132	0.021415	0.014255	33.43%
F14: Trid		0.010908	0.0094853	0.0065244	31.22%
F15: Beale		0.041922	0.037743	0.02635	30.19%
F16: Matyas		0.022231	0.020007	0.014232	28.86%
F17: Zakharov		0.046247	0.040252	0.02342	41.82%
F18: Easom		0.014799	0.013726	0.0080525	41.33%
F19: Eggcrate		0.023696	0.021977	0.015303	30.37%
F20: Bohachevsky3		0.016296	0.014996	0.0089217	40.51%

On the premise of maintaining accuracy and absolute global optimization capabilities, it can be seen from Table 4 and Figure 6 that CDR-DRS-WPOA takes less time and offers at least a 20% improvement for all test functions. Of these, only 2 test functions had the smallest improvement, between 20 and 30%, and they concentrated between 30 and 50% for most of the improvements. It is worth mentioning that the improvement rate of function 2 “Three-Hump-Camel”, function 6 “Levy”, and function 11 “Trecanni” is more than 50%, which means that the runtime of CDR-DRS-WPOA compared to DAF-BRS-CWOA has been reduced by more than half while maintaining absolute global optimization capabilities. In particular, the improvement rate of function 6 “Levy” is nearly 80%, and seen from the Optimal Value Worst Value, Average Value, and Standard Deviation in Table 3, CDR-DRS-WPOA has better indicators. This means that CDR-DRS-WPOA not only has higher global and computational accuracy, but also offers a much shorter time spent.

Figure 6. Histograms of improvement rate for time spent by comparing CDR-DRS-WPOA and DAF-BRS-CWOA on all 20 test functions in this paper. (Table 4 lists the functions corresponding to sequence numbers).

In a word, CDR-DRS-WPOA has the advantages of good optimization accuracy, stronger globality, less time spent, and fast convergence speed.

4.3. Test Results and Analysis of PMU-3PM

All the algorithms were conducted independently 50 times on PMU-3PM and the related raw data are shown in Table 5; Accordingly, it can be seen that PMU-3PM-IWPA has the best performance in terms of Optimal Value, Worst Value, and Average Value compared to PMU-3PM-GA, PMU-3PM-PSO, PMU-3PM-WDX-WPOA, and PMU-3PM-DAF-BRS-CWOA. Moreover, in terms of Standard Deviation, PMU-3PM-IWPA has a slightly higher value than WDX-WPOA and DAF-BRS-CWOA, but better than GA and PSO. As a whole, therefore, PMU-3PM-IWPA offers better stability and the best optimization accuracy.

Table 5. Raw Data for PMU-3PM.

Algorithm	Optimal Value	Worst Value	Average Value	Standard Deviation	Average Time
PMU-3PM-GA	47.031	77.8299	64.2782	6.4325	0.14386
PMU-3PM-PSO	34.909	53.9059	45.7949	4.1645	0.69808
PMU-3PM-WDX-WPOA	27.955	45.3993	32.9021	3.6069	11.2806
PMU-3PM-DAF-BRS-CWOA	27.242	44.722	34.6783	3.3169	10.4916
PMU-3PM-IWPA	25.082	42.0629	31.196	3.8514	8.8258

From the perspective of time spent, the WPOA family algorithm took much longer than GA and PSO to solve PMU-3PM, but what is exciting is that the WPOA family algorithm offers better performance in terms of optimization accuracy than GA and PSO, as shown in Table 5 and Figure 7. It is well-known that every coin has two different sides to it and a flaw cannot overshadow the brilliance of jade. Furthermore, it is a consolation that PMU-3PM-IWPA spent less time than PMU-3PM-WDX-WPOA and PMU-3PM-DAF-BRS-CWOA. In relation to optimization performance, as shown in Table 5 and Figure 7, PMU-3PM-IWPA is about 15.9% better than PMU-3PM-DAF-BRS-CWOA in terms of time spent, while ensuring better optimization accuracy. Therefore, it can be concluded that PMU-3PM-IWPA offers better performance in relation to time spent.

Figure 7. Time-spent comparison for solving PMU-3PM.

In short, PMU-3PM-IWPA has better stability, the best optimization accuracy, better performance in terms of time spent, and a faster convergence speed.

5. Conclusions

Multi-UAV path planning for police patrols plays an important role in public security work, and while many path-planning algorithms have been applied in this area, all of them possess various degrees of shortcomings. To further improve the accuracy and efficiency of multi-UAV path planning for police patrols, this paper proposed PMU-3PM-IWPA. Firstly, PMU-3PM was constructed to reflect the planning problem for multi-UAV police patrol paths. Moreover, to enhance the performance of current existing wolf pack optimization algorithms, this paper proposed an improved wolf pack optimization algorithm named CDR-DRS-WPOA, including CDRS, aimed at enhancing the global exploration capability, as well as DRSS, with a view to speeding up the convergence for simple problems and heighten the optimize accuracy for difficult problems. Finally, CDR-DRS-WPOA was adopted to solve PMU-3PM, and numerical experiments were carried out on 20 public classical datasets, as well as PMU-3PM compared with GA, PSO, WDX-WPOA, and DAF-BRS-CWOA. The results indicate that CDR-DRS-WPOA spent 20~80% less time and possessed greater optimization accuracy, and that PMU-3PM-IWPA based on CDR-DRS-WPOA offers excellent performance.

Unfortunately, nothing is perfect, and CDR-DRS-WPOA also has its own respective shortcomings, such as in terms of time spent. Although CDR-DRS-WPOA offered better optimization performance in solving PMU-3PM, it spent more time than GA and PSO, as shown in Table 5. To summarize the reasons, GA and PSO are suitable for fast and rough optimization calculations while CDR-DRS-WPOA is more suitable for optimization calculations with higher accuracy and requirements. Similarly, the stability of CDR-DRS-WPOA is slightly reduced compared to DAF-BRS-CWOA as a result of the fact that the distribution of wolves in the Dynamic Search Strategy based on a specific threshold is random, as shown in Table 5. However, none of this detracts from the fact that CDR-DRS-WPOA is an excellent algorithm.

In future work, we will continue to improve the new proposed algorithm by reducing its time spent and enhancing its stability with a view to ensuring superior performance.