Abstract
Marcolli, Chomsky, and Berwick described the minimalist program, proposed by Chomsky in generative linguistics, as an algebra of binary trees in an analogy of quantum physics on Feynman diagrams. In this paper, we proposed another model of the minimalist program based on simplicial Hodge theory by taking the relevant brain neural network into account. We focused on a long directed pathway connecting distant areas in the brain, and took the (abstract) simplex spanning the locations on the terminal area, which the signals going through the pathway can reach. The identity of each signal is represented by the symmetry of the corresponding face, consisting of locations receiving the signal simultaneously. Then, we showed that this model fits the minimalist program. Further, we calculated the spectrum and eigenspaces of the Hodge Laplacian in important cases and found their surprising rationality. According to this rationality, we could draw pictures of syntactic relations based only on the calculation without using linguistic knowledge. In addition, though word order depends on what language is used, and thus has nothing to do with the minimalist program, planar word arrangements are still possible and within the scope of our model.
1. Introduction
Human language has an instinctive aspect, in addition to intellectual and sociocultural aspects. Chomsky’s minimalist program [1,2] focused on the instinctive aspect. For the program to be fully successful, there must be an innate mechanism in our brain to perform Merge, which is supposed to be the minimal linguistic operation. Marcolli, Chomsky himself, and Berwick fixed the official mathematical model of the minimalist program ([3,4,5], and a forthcoming book from MIT Press). They described Merges as abstract rooted binary trees and investigated them in a way analogous to the study of Feynman diagrams in quantum physics. In this paper, we provide another mathematical model by taking the possible shape or topology of the related brain neural network into account.
Regarding networks in general, Eckermann’s simplicial Hodge theory [6] is the essence of various spectral graph theories (see [7]), and our model is also based on this. There are many relevant works (for example, Ref. [8], which further developed the theory itself, and Ref. [9], which applied it to the analysis of loops in neural circuits); however, few—possibly none—focused on cases with a small number of vertices like our present study. In this regard, it certainly appears that we are oversimplifying a faculty of the human brain. Thus, it is necessary to explain here why we study particularly small models.
We do not consider any network in a single area in the brain. Instead, we focus on instinctive activities involving interactions of distant brain areas via narrow pathways, such as human language (see [10] for a highlighted picture of such pathways), and consider primarily one-way transmission from an area to a set of a small number of distinct locations in another area, with only a certain amount of feedback, for simple operations like Merge to work. Since the pathway is narrow, the number of such locations is expected to be quite small. We notice that each edge or face does not represent a local communication, but rather a subset consisting of locations which information can equally reach.
We calculate the spectrum and eigenspaces of the Hodge Laplacian for low-dimensional cases, and observe that they are surprisingly all rational in the fundamental cases of the minimalist program. In particular, the rationality of the -dimensional data makes it possible to illustrate the gradient parts in the Helmholtz decomposition. Stacking the illustrations according to the height of their eigenvalues, we can restore the diagrams of syntactic relations without using any linguistic knowledge. The advantage of our model is in explaining the human language (and possibly other instinctive activities of animals, like birds singing, homing, etc.). We also point out that the remaining rotational parts of the decomposition relate to -dimensional data, and since there is a transverse -dimensional plane of the narrow pathway, some information about the planar arrangement of words should also be available. This contrasts with the fact that the linear word ordering is irrelevant in the core of the minimalist program, as it varies across languages.
2. The Model
2.1. Merges in the Brain
This is a model of the human brain dealing with a long tubular part which is small in volume. We suppose that there are distinct locations in a language area which are connected to a dictionary area by neural pathways in the tube. Let S denote the set of the locations. The pathways can spread into branches so that a single signal is transmitted to multiple locations. This defines a map f: or an oriented assembly consisting of perceptrons, each of which takes a value of . Now, for two signals x and y with and , we expect another signal z, with being the union to be generated. We use the term Merge if this expectation is met. More precisely, Merge requires that feedback from A and B triggers a signal in the dictionary area, which will be sent back to U, and furthermore, the signal is somehow specific to the situation of U, including A and B. This may be a linguistic situation that should be represented not simply as the union but rather as the doubleton in a set theory. To fully explain this, a precise mathematical argument is needed. In the model explained below, we regard A and B as weighted simplices contained in the simplex spanned by S, and consider Merge as adding weight 1 to each face with a positive dimension in the topological join , in response to a signal amplification between the pathways leading there. We also notice that S is not merely a set but also a planar arrangement presenting the relative positions on the transverse section of the pathways at the language terminal.
2.2. The Simplicial Hodge Theory
A non-empty subset of a finite set is called a face. If it consists of elements, we call it a k-face or a k-dimensional face. Let denote the family of all faces of S. A non-empty subfamily is called a simplicial complex if any non-empty subset of any face of C belongs to C. A member of C is called a face of C. In particular, a 0-face and a 1-face of C are, respectively, called a vertex and an edge. If a simplicial complex C contains a m-face , which coincides with the union of the family C, the complex C is called the m-simplex spanned by . Then, we have .
Example 1.
A solid tetrahedron, which is a -dimensional manifold homoemorphic to the ball is a geometric realization of the -simplex consisting of vertices, edges, triangular -faces, and tetrahedral -face, which have been named by their vertices since Ancient Greece. On the other hand, a hollow octahedron, which is a -dimensional manifold homeomorphic to the sphere, is not a simplex but a simplicial complex consisting of vertices, 12 edges, and -faces. The vertices span a -simplex, which is realized in the -dimensional space so that the units on the axes and the origin are the vertices. The hollow octahedron is also realized there. For the disjoint union of a solid tetrahedron and a hollow octahedron, we can add a -cell bridging them to obtain a connected simplicial complex which is not a manifold. Here and hereafter, the connectivity of a complex is that of its realization.
We suppose that a simplicial complex C is equipped with a non-negative integer weight . Then, the pair is called a weighted simplicial complex. The subset is the support of the weight. We also define the superlevel set for each . We have and . Note that w is positive if .
Example 2.
An abstract (i.e., non-planar) rooted full binary tree with leaf set S defines a positive weight of the n-simplex as follows. The root corresponds to putting the initial weight 1 all over . Then, the first branch separates S into two non-empty subsets and . We add 1 to the weight on the two simplices and . This process is repeated in each branch except after reaching a -simplex consisting of a leaf. Finally, we obtain the weight w corresponding to the tree. Its support is the whole of as well as that of the initial weight ().
Let (resp. ) denote the -vector space with a basis consisting of the k-faces of C (resp. ). We present a k-face as with an increasing function . The combinatorial number system provides the rank
of , which takes all integers from 0 to for the possibilities. Let (= for precision) denote the k-face with rank r. We present as
and obtain by putting certain factors equal to 0. Let (resp. ) be the dual space of (resp. ). Explicitly, we define linear functions by (Kronecker’s delta), and put
Using the presentation (), we put
for . We define the boundary operator (= by
and the coboundary operator (= by (). We restrict them to C and its dual space, respectively. In the case where the weight is positive, we can define the inner product by
We regard as a linear isomorphism , and define the weighed boundary operator by . Then, the Hodge theory is
Theorem 1
([6,7]). The two operators and each have the multiset of non-negative real eigenvalues, their images meet only at the origin, and the intersection of their kernels is the cohomology group of the realization of C. Furthermore, the multiset of the positive eigenvalues of coincides with that of .
3. Results
3.1. Definition of Merge
We give the precise definition of Merge.
Definition 1.
Each step of the following construction of a sequence of weighted simplices is called Merge. In the initial state, we suppose that the weight is equal to (m is a fixed positive integer) on the vertices of the n-simplex () and to 0 on the other faces. This implies that is fragmented into -simplices. Then, in each step, we choose either (i) or (ii) below. We can finish the sequence when holds.
- (i)
- External Merge: We choose two different connected components C and D of , and add 1 to the weight on , except at the vertices, to obtain a weight of . Here, ⊔ denotes the union of mutually disjointed sets.
- (ii)
- Internal Merge (of level-c): We choose a connected component C of and a connected component P of for some integer c with , under the condition that for all . We take the copy of P with the weight except at the vertices, and put . On the original part , we put except at the vertices. At the vertices of P and , we put (). Then, we add 1 to the weight on , except at the vertices, to obtain a new weight of (see Figure 1).
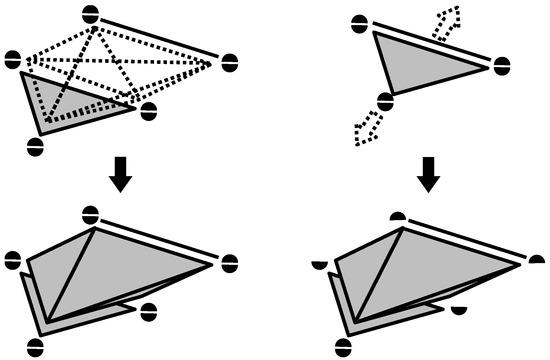 Figure 1. An External Merge (left) and Internal Merge (right). Here, 1, 2, and 4-simplices are depicted. The number of parallel faces presents the weight at single faces of dimension . Each half dot .
Figure 1. An External Merge (left) and Internal Merge (right). Here, 1, 2, and 4-simplices are depicted. The number of parallel faces presents the weight at single faces of dimension . Each half dot .
There is also the following weak version of Merge, including cases that do not occur. In this paper, we use the term Virtual Merge to distinguish it from the above Merge.
Definition 2.
Virtual Merge uses only the following (I) instead of the above, (i) and (ii):
- (I)
- Let C and D be connected components of . We take a connected component P (resp. Q) of a superlevel set of some level of the restriction (resp. ), so that holds for all (resp. ). If (resp. ), then we take the copy of P (resp. of Q) with weight (resp. ); change the weight of P (resp. Q) into (resp. ); and exceptionally set the weight of the vertices of and P (resp. and Q) to all m. Otherwise, we just put (resp. ). We put and extend as elsewhere on . Here, we choose C, D, P, Q so that . Then, we add 1 to on , except at the vertices, to obtain a new weight .
Both of the definitions imply the following regularity result.
Lemma 1.
Suppose that is obtained by a sequence of Merge or a sequence of Virtual Merge. Let be the modification of to take value at all of the vertices. Then, the superlevel set is a disjointed union of simplices or empty for .
Proof.
It is easy to inductively show that each connected component of the superlevel set is a simplex if we totally use the modified weight instead of in each definition. The cases in the actual construction are rather limited, hence the lemma. □
Virtual Merge is indeed a generalization of Merge.
Theorem 2.
Adding the following choices, (iii) to (v), to the definition of Merge, we obtain the definition of Virtual Merge.
- (iii)
- Sideward Merge of the first kind: We choose two different connected components C and D of . Then, we choose a connected component P (resp. Q) of the superlevel set of the restriction (resp. ) of some level so that the weight on the vertices is equal to . Here, we suppose that and . We take the copies and of P and Q, respectively, and define the weight on for , similarly to the case of Internal Merge. Then, we add 1 to on , except at the vertices, to obtain a new weight of .
- (iv)
- Sideward Merge of the second kind: We choose two different connected components C and D of . Then, we choose a connected component P of the superlevel set of the restriction of some level so that the weight on the vertices are equal to . Here, we suppose that . We take the copies of P and define the weight on for , similarly to the case of Internal Merge. Then, we add 1 to on , except at the vertices, to obtain a new weight of .
- (v)
- Sideward Merge of the third kind: We choose a connected component C of . Then, we choose a connected component P (resp. Q) of the superlevel set of the restriction of some level so that the weight on the vertices are equal to . Here, we suppose that . We take the copies and of P and Q, respectively, and define the weight on for , similarly to the case of Internal Merge. Then, we add 1 to on , except at the vertices, to obtain a new weight of .
Proof.
If and (), then (I) is equivalent to (i). If (or ), then (I) is equivalent to (i). If (or ), then (I) is equivalent to (iv). If and , then (I) is equivalent to (iii) (resp. (v)), provided that (resp ). □
According to this classification, Internal Merge and External Merge are special.
Theorem 3.
Among classes (i) to (v), only classes (i) and (ii) satisfy the following monotonicity condition in any case.
- Monotonicity: Take any sequence of so that is either or its copy. Let denote the dimension of the connected component of containing . We require the non-decreasing monotonicity for any choice of the sequence.
Proof.
It is clear that (i) and (ii) satisfy the monotonicity. It is also clear that (v) violates the monotonicity, except in non-essential cases where . In the remaining cases, (iii) and (iv) violate the monotonicity if . □
Theorem 4.
Adding the following maximality condition to the definition of Virtual Merge, we obtain the definition of Merge.
- Maximality: The identification of copies induces a partial order of from the partial order of with respect to the inclusion. We require that X is maximal on , and Y is maximal on , i.e., maximal except for X.
Proof.
The maximality condition implies (Internal Merge), (External Merge), (Internal Merge), or (External Merge). □
Remark 1.
Adding the mononicity condition to the definition of Virtual Merge does not imply the definition of Merge.
An Internal Merge is, linguistically, a Merge between the whole and a part of a phrase in a sentence. It clearly appears in such a sentence as “I know what you mean” (={I,{know, {what(copy), {you, {mean, what(original)}}}}}) (see Section 4 for the problem on the level of Internal Merge which forbids this naive understanding). On the other hand, in the case where Merges are performed only between mutually disjointed simplices, i.e., only External Merges are permitted, the final result of the Merges differs from the weight described in Example 2 only at the vertices, for example, as follows:
Example 3.
Consider the binary tree . We order the faces of the simplex spanned by as
Put the initial values of the weight at the faces. Then,
This differs only at the -faces from the binary tree weight of Example 2 calculated as
3.2. Calculations
Let be the identity of order k and ; the column with k entries equals 1. The coboundary operators () are the matrices
The weight corresponds to a diagonal matrix of order , which is assumed to be positive here. The weighted boundary operators are
The Laplacians and appear in the process of the calculation of the square of the Dirac operator
The total Laplacian is block diagonal because of the exactness of the (co)chain complex.
3.2.1. -Simplex: Merge Between -Simplices
A Merge between and yields the weight w of the -simplex:
satisfying , and presented by the dual metric
Then, the Dirac operator and the Laplace operators are
The eigenforms are
3.2.2. The Basic -Simplex: Merge Between - and -Simplices
A Merge between the result of Section 3.2.1 and yields the weight of the -simplex
presented by
Then, the Dirac operator and the Laplace operators are
The eigenforms are
Recall that the Hodge decomposition is a generalization of the Helmholtz decomposition of a -dimensional vector field into the rotation-free part coming from a scalar potential and the divergence-free part coming from a vector potential. In the above calculation on a simplicial Hodge decomposition, is -orthogonally decomposed as the direct sum of
To describe the scalar potential as an weight of vertices, we use the following parametrization:
In practice, the parameters a and b would be manipulated within the language area in the brain that contains the locations represented by the vertices. Further, the parameters would represent the direction of certain syntactic relations, namely the sign of a (resp. b), indicating which of - and (resp. and ) dominates. The fact that the eigenvalue is smaller than would mean that the dominance presented by a is coarser (i.e., longer in wavelength and carrying lesser energy) than that presented by b (see Figure 2).
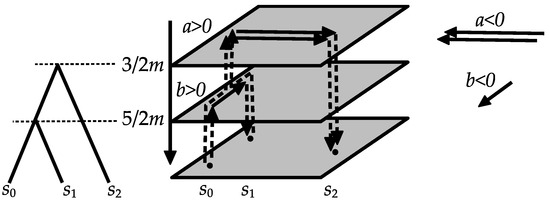
Figure 2.
Syntactic relations arising from the eigenvalues–eigenforms of the basic 2-simplex.
3.2.3. Level- Internal Merge of -Simplex
A merge between the result of Section 3.2.1 and the copy of the connected component of yields a weight on the -simplex presented by
Then, the Dirac operator and the Laplace operators are
The eigenforms are
The parametrization of the scalar potential is
Here, the sign of a (resp. b) indicates which of and (resp. and ) dominates. Since the eigenvalue is smaller than , we have the relations in Figure 3.
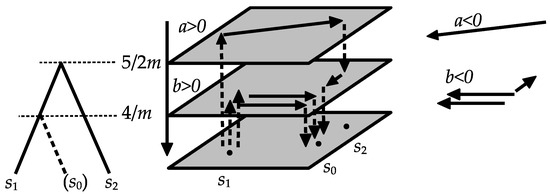
Figure 3.
Syntactic relations of the level-2 Internal Merge of 1-simplex.
3.2.4. Level- Internal Merge of the Basic -Simplex: The First Case
A Merge between the result of Section 3.2.2 and the copy of the component of yields the weight of the -simplex:
presented by with diagonal blocks , , , and . Then, the main operators are
Let denote the eigenspace of corresponding to the positive eigenvalue of . Then, we have and
The parametrization of the scalar potential is
We have the relations in Figure 4.
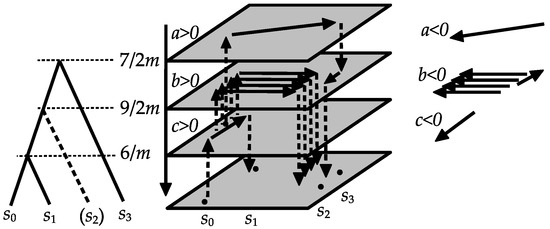
Figure 4.
Syntactic relations of the level-2 Internal Merge of 2-simplex: the first case.
3.2.5. Level- Internal Merge of the Basic -Simplex: The Second Case
A Merge between the result of Section 3.2.2 and the copy of the component of yields the -simplex with , , , , and . We have
Then, the eigenspaces are
The parametrization of the scalar potential is
We have the relations in Figure 5.
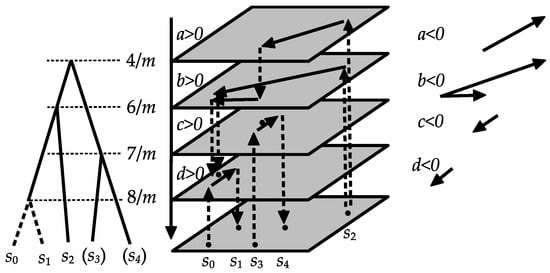
Figure 5.
Syntactic relations of the level-2 Internal Merge of 2-simplex (2).
3.2.6. Level- Internal Merge of the Basic -Simplex
In the case where , a Merge between the result of Section 3.2.2 and the copy of the connected component of yields the weight of the -simplex presented by , , , and . We have , ,
Then, we encounter the following irrationality, where is the positive spectrum.
4. Conclusions and Discussion
4.1. Conclusions
The materialistic approach in this paper complements the abstract algebraic results of the official model, and is not in conflict with them. We look at the signal pathways in the brain instead of the symbolic relations, since symbols must be in the brain. We proposed a model of a signal pathway and applied it to the minimalist program. Then, we obtained External and Internal Merges from the same operation under the monotonicity condition in Theorem 3 or the maximality conditions in Theorem 4. Although it is possible that both of the conditions follow from the economic constraint in the official theoretical model, we are more interested in how to construct (artificially, if possible) a system in each pathway. For this purpose, the maximality seems more realistic than the monotonicity, since real signals should have a tendency to leak out. Then, we calculated the Laplacian spectrum, especially for low-dimensional cases, since we considered only narrow pathways in the brain. Then, we found surprising spectrum rationality in such cases. According to the rationality, we illustrated the gradient parts of -dimensional data to restore the syntactic relations without using any linguistic knowledge.
4.2. Discussion of Internal Merge
The irrationality appearing in the calculation of Section 3.2.6 suggests that the Internal Merge of level would be forbidden (and we can avoid it just by setting in our model). Note that a high-level Internal Merge is necessary to understand phrases such as “know what you mean (what)” simply as the word connections (i.e., , , , ). However, if we perform the Internal Merge of Section 3.2.3 so that becomes the label of the Merged item , and, further, if we can rearrange the construction so that the labelled item becomes an elementary item carrying that label, it is possible to obtain the above phrase so that the label is the object of knowing. Namely, putting , and , we obtain the labelling , and replace the basic premise of the mapping f with and start over. Note that if we avoid Internal Merges of level in this way, any Internal Merge can be represented by doubletons as (labelled by A) or (labelled by B). Thus, the above irrationality may have something to do with the less obvious reason why linguists use doubletons.
4.3. Discussion of Word Arrangement
We considered a general phenomenon that is likely to occur at the terminal of a bundle of signal pathways that run through a narrow tubular part in the brain. Thus, considering the cross-section of the bundle at the terminal, we can see that the signal receivers make an arrangement of points on the oriented -dimensional plane. On the other hand, we parametrized the scalar potential of an element of by the variables a, b, etc., on specific lines in ; using them, we formally controlled the direction of each relation depicted in Figure 2, Figure 3, Figure 4 and Figure 5. Similarly, we can also parametrize the vector potential by lines in and use them to control the rotation direction of the corresponding eigenforms. What differs from the case of scalar potential is how to use the sign of the parameters. Since each -face carries the canonical sign induced by the orientation of the plane (see Figure 6), we can, in principle, obtain information about the planar arrangement from the change in the actual state corresponding to the change in the sign of each parameter. The minimalist program does not concern word order since it depends on specific language. However, planar word arrangement is now within its scope. The parameters probably depend on the operation of other systems. Although we only modeled one of the signal pathways, their interaction should be investigated in the future.
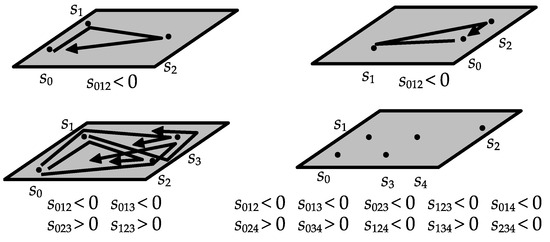
Figure 6.
The orientation of 2-faces determined by the planar arrangement of each case.
Funding
This research received no external funding.
Data Availability Statement
This is a theoretical research that does not use external data.
Acknowledgments
The comments of the referees helped to make this paper meaningful. The authors would like to thank the reviewers and the editorial staff for this opportunity.
Conflicts of Interest
The author declares no conflicts of interest.
References
- Chomsky, N. Some Puzzling Foundational Issues. Catalan J. Linguist. Spec. Issue 2019, 2019, 263–285. [Google Scholar] [CrossRef]
- Chomsky, N. The UCLA Lectures. 2019. Available online: https://ling.auf.net/lingbuzz/005485 (accessed on 1 November 2023).
- Marcolli, M.; Chomsky, N.; Berwick, R. Mathematical Structure of Syntactic Merge. arXiv 2023, arXiv:2305.18278. [Google Scholar]
- Marcolli, M.; Berwick, R.; Chomsky, N. Old and New Minimalism: A Hopf algebra comparison. arXiv 2023, arXiv:2306.10270. [Google Scholar]
- Marcolli, M.; Berwick, R.; Chomsky, N. Syntax-semantics interface: An algebraic model. arXiv 2023, arXiv:2311.06189. [Google Scholar]
- Eckmann, B. Harmonische Funktionen und Randwertaufgaben in einem Komplex. Comment. Math. Helv. 1944, 17, 240–255. [Google Scholar] [CrossRef]
- Horak, D.; Jost, J. Spectra of combinatorial Laplace operators on simplicial complexes. Adv. Math. 2013, 244, 303–336. [Google Scholar] [CrossRef]
- Anand, D.; Chung, M.K. Hodge Laplacian of Brain Networks. IEEE Trans. Med. Imaging 2023, 42, 1563–1573. [Google Scholar] [CrossRef]
- Grbić, J.; Wu, J.; Xia, K.; Wei, G.W. Aspects of topological approaches for data science. Found. Data Sci. 2022, 4, 165–216. [Google Scholar] [CrossRef]
- Tremblay, P.; Dick, A. Broca and Wernicke are dead, or moving past the classic model of language neurobiology. Brain Lang. 2016, 162, 60–71. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).