Abstract
A unified geometric framework for the full Lorentz group is introduced, based on a bounded angle parametrization of spacetime transformations within a hyper-spherical geometry. By mapping the unbounded hyperbolic angle to a bounded angle using the Gudermannian function, hyperbolic, causal, and Euclidean three-spheres are brought together into a single structure: hyper-spacetime. This structure unifies the Euclidean and Minkowski domains, incorporates discrete symmetries in a continuous way, and removes discontinuities at the lightlike boundary. Each three-sphere carries a natural spinor set, encoding symmetry, and acting as eigen-spinors of corresponding observables. These reproduce the Dirac spectrum while confining singular behavior to a scalar factor. The bounded angle parametrization therefore provides a continuous, closed representation of the full Lorentz group and a transparent geometric basis for spacetime symmetry.
1. Introduction
The Lorentz group [1,2,3,4,5,6] underlies the symmetries of spacetime and forms the mathematical backbone of both classical and quantum relativistic physics. In its standard formulation, spatial rotations are described by compact angles on the circle, while boosts are parameterized by the unbounded rapidity . Although effective, this conventional parametrization exhibits several structural limitations:
- Rapidity diverges at the lightlike boundary ;
- Discrete transformations remain algebraically disconnected from continuous Lorentz transformations;
- Euclidean and Minkowski spacetime structures are treated as fundamentally separate, linked only by analytic continuation or Wick rotation;
- Spinor solutions of the Dirac equation are usually derived analytically, rather than emerging directly from geometric structure.
- These issues motivate the need for a compact, continuous, and geometrically transparent representation of Lorentz symmetry, one that unifies continuous and discrete transformations while clarifying the relationship between Euclidean and Minkowski domains.
1.1. Motivation
The divergence of rapidity at the lightlike limit is not merely a coordinate inconvenience: it obscures geometric relations between boosts and rotations, interrupts continuity at , and masks the structural similarity between hyperbolic and circular symmetries. Moreover, discrete spacetime reflections remain isolated algebraic operations in the conventional Lorentz group, preventing smooth interpolation between parity P, time reversal T, and the identity component I. A compact parametrization that connects these sectors continuously would offer a coherent geometric understanding of the full Lorentz group.
At the same time, many modern formalisms, from path integrals to Euclidean field theory and particle classification, rely on controlled transitions between Minkowski and Euclidean metrics [7]. Standard Wick rotation introduces imaginary time as a technical device, but its geometric meaning remains conceptually opaque [8,9,10]. A structural framework that embeds both domains within a single real geometry would provide a transparent foundation for analytic continuation and symmetry-based reasoning.
These motivations converge in the search for a unified geometric representation capable of handling boosts, rotations, discrete symmetries, and Euclidean/Minkowski duality in a single continuous mathematical object.
1.2. Research Gap and Objectives
Despite extensive research on Lorentz geometry [11], no previous framework provides the following:
- A bounded and continuous parametrization covering the full Lorentz group.
- A real geometric structure unifying Euclidean and Minkowski domains.
- Spinor sets that simultaneously encode symmetry, discrete operations, and Dirac eigen-spinors.
- A compact angular coordinate that regularizes the lightlike boundary.
This paper aims to fill these gaps through the following objectives:
- Unify circular and hyperbolic symmetry via the bounded angle .
- Construct a triplet of three-spheres forming hyper-spacetime.
- Develop spinor sets that derive Dirac eigen-spinors geometrically.
- Provide a continuous representation of the full Lorentz group, including discrete reflections.
- Bridge Euclidean and Minkowski metrics through a natural geometric duality.
1.3. Central Idea: A Bounded Angular Parametrization
The key innovation of this work is the introduction of a bounded angular variable , obtained through the Gudermannian mapping [12,13,14] (Appendix B). This mapping transforms the unbounded rapidity parameter into a bounded angular domain, effectively compactifying the boost parameter space. In doing so, it closes the hyperbola into a hyperbolic one-sphere and provides a continuous, finite coordinate for Lorentz boosts [15,16]. Replacing rapidity with the bounded angle β produces several important consequences:
- The lightlike boundary becomes a regular point of the domain.
- Divergences in boosts are isolated in a scalar density, while spinors remain finite.
- Both branches of the hyperbola are traversed continuously.
- Temporal orientation changes correspond to smooth shifts in , turning a discrete transformation into a continuous operation.
This compactification unifies hyperbolic and circular symmetries, creating a single angular structure that links rotations, boosts and reflections across the full Lorentz group.
1.4. Hyper-Spacetime: A Unified Three-Sphere Geometry
Building on the bounded parametrization, this work introduces hyper-spacetime, a unified geometric structure constructed from a triplet of three-spheres: :
- is a hyperbolic unit sphere representing normalized momentum.
- is a causal sphere encoding spacetime intervals.
- is a Euclidean sphere preserving the same temporal and spatial orientation.
All three share a common temporal axis and a reciprocal temporal bivector plane, establishing a correspondence between spatial vectors in the Minkowski domain and temporal bivectors in the Euclidean domain, and vice versa. This duality creates a continuous geometric bridge linking the Minkowski and Euclidean representations.
1.5. Spinors, Observables, and the Dirac Spectrum
Within this unified geometry, spinor sets and arise directly from variations in the hyper-spherical coordinates . These spinor sets act simultaneously as:
- Symmetry generators preserving the three-spheres;
- Eigen-spinors of geometric observables ;
- Continuous representatives of the discrete operations ;
- A geometric reconstruction of the four Dirac plane-wave solutions.
Crucially, the Dirac spectrum emerges without solving a differential equation: it arises geometrically from the structure of hyper-spacetime, demonstrating that relativistic spinors are intrinsic to the unified geometry.
1.6. Novelty and Contribution
- The resulting framework provides the following:
- A closed, continuous, and bounded representation of the full Lorentz group ;
- A unified spinor structure generating the Dirac spectrum directly;
- Continuity across discrete symmetries and the lightlike boundary;
- A new geometric interpretation of Wick rotation;
- A compactified Lorentz parameter suitable for quantization and field-theoretic formulations;
- A pedagogically transparent geometric picture of spacetime symmetry.
The remainder of this work develops this structure rigorously, derives the related spinors and observables, and discusses both physical implications and potential applications.
1.7. Layout of the Paper
The core of the paper (Section 2, Section 3, Section 4, Section 5 and Section 6) develops the geometric framework. Section 2 and Section 3 present the bounded angular parametrization of Lorentz boosts that unifies circular and hyperbolic symmetry and applies naturally to special relativity, yielding harmonic relativistic proportionality factors [17,18]. Section 4 extends to four dimensions, a triplet of three-spheres is introduced that defines hyper-spacetime and shows how the full Lorentz group, with both continuous and discrete symmetries, emerges within its hyper-spherical coordinates. In Section 5 and Section 6, spinor sets are then constructed and analyzed as eigen-spinors of geometric observables, reproducing the Dirac spectrum while confining singularities to scalar factors. The final part of the paper (Section 7 and Section 8) turns to interpretation and outlook, discussing the physical implications of hyper-spacetime, and concludes with a summary of its unifying features.
1.8. Mathematical Formalism
The mathematical formalism throughout is based on the geometric algebra (GA) of spacetime (STA), as developed by Hestenes [19,20] (Appendix A). Its foundations trace back to Grassmann [21] and Clifford [22], whose work established a unified algebra of vectors, bivectors, and higher-grade multivectors. In this algebra, Lorentz transformations are expressed naturally through rotors, which generalize rotations and boosts in a coordinate-free manner [23,24,25,26,27]. In STA [19], a spacetime inertial frame is represented by four orthogonal basis vectors which satisfy the real Clifford-algebra [7,28] relation equivalent to the algebra of the Dirac gamma matrices [4]. This framework provides the natural setting for the bounded parametrization, the three-sphere geometry, and the spinor sets constructed later in the paper.
2. Hyperbolic Rotation
Lorentz boosts are conventionally expressed as hyperbolic rotations, parameterized by the unbounded angle (rapidity) (Figure 1a).
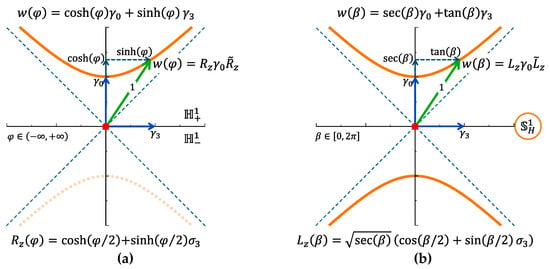
Figure 1.
Comparison of hyperbolic rotation. (a) In the unbounded parametrization, the rotor covers only one branch , with a discontinuity at lightlike boundaries. (b) Using the bounded angle , the rotor spans the full symmetry . The Gudermannian mapping ensures smooth continuity through infinity, closing the hyperbola into a one-sphere .
- A boost along the -axis (-axis) is generated by the hyperbolic rotor :
To cover the full hyperbolic symmetry in a single parameter domain, the unbounded angle is related to the bounded angle by using the Gudermannian function (Appendix B) [12,13]. Substituting this function into yields the rotor :
The scalar factor ensures normalization, while acts as a temporal spinor (Appendix C). Applying rotor to generates the boosted spacetime vector :
where the full hyperbolic symmetry is covered continuously (Figure 1b).
In summary, the bounded angle parametrization provides several advantages. It removes singularities by isolating them in the scalar density factor , while the associated spinor remains regular. At , the mapping passes smoothly through infinity, ensuring continuity across the lightlike boundary where crossing corresponds to a time reversal. The two disconnected hyperbolic branches and are thereby closed into a single hyperbolic one-sphere (Figure 1b). In this way, hyperbolic symmetry is unified within a single angular cycle.
3. Harmonic Relativistic Proportionality Factors
In special relativity, the relative speed is conventionally mapped to the unbounded angle (rapidity). Using instead the bounded angle introduced in Section 2, this mapping provides a harmonic set of relativistic proportionality factors:
These factors form a bridge between circular and hyperbolic symmetry:
Consequently, the bounded angle mapping unifies circular with hyperbolic symmetry (Figure 1b). A complete cycle on one-sphere corresponds one-to-one with a complete cycle on hyperbolic one-sphere . This includes a smooth passage through infinity at the lightlike boundaries .
To incorporate all the symmetries of the full Lorentz group , the framework must extend from the two-dimensional (2D) relation to a four-dimensional (4D) relation that unifies the Euclidean domain with the Minkowski domain .
4. One Unified Geometry Bridging and
The generalization from two to four dimensions is realized by the introduction of a triplet of three-spheres embedded in a Euclidean and a Minkowski domain (Appendix A). Accordingly, three distinct but related three-spheres are defined as follows:
Here,
Each of these three-spheres is preserved by a specific spinor structure (as defined in Section 4.1), which ensures that the geometry remains invariant under both Lorentzian and Euclidean transformations. In this way, every three-sphere is not only defined by its metric but also carries a natural spinor representation that encodes its symmetry.
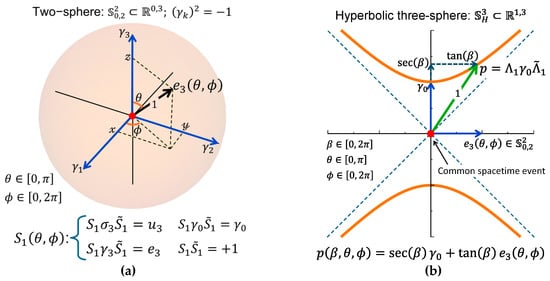
Figure 2.
(a) The spatial two-sphere , spanned by vectors , is preserved by the spatial spinor . (b) The hyperbolic three-sphere , spanned by vectors , is preserved by the spacetime rotor . The spatial vectors are all orthogonal to the temporal axis .
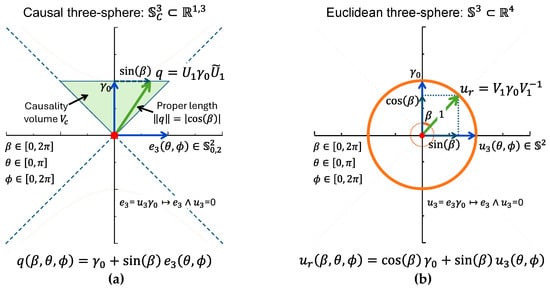
Figure 3.
(a) The causal three-sphere , spanned by vectors , is preserved by the spacetime spinor . (b) The Euclidean three-sphere , spanned by vectors , is preserved by the Euclidean spinor . In this structure, each of the aligned vectors and is orthogonal to the temporal axis in its respective domain, thereby fixing a reciprocal temporal bivector plane.
All three-spheres share the following: a common temporal axis , a common origin (spacetime event), and a reciprocal temporal bivector plane. They differ in their metric and spatial subspaces and (Equation (7)), which define two complementary two-spheres:
Both two-spheres are preserved by spatial spinor (Figure 2a):
Applying spinor to and generates the spatial unit vectors and :
They are orthogonal to , aligned , and define spatial direction. Moreover, they span a reciprocal temporal bivector plane , which is a cornerstone of the unified geometry. The Minkowski vector acts as a temporal bivector in the Euclidean domain, while the Euclidean vector act as a temporal bivector in the Minkowski domain. This geometrical duality specifies spatial direction while simultaneously encoding for temporal orientation in the opposite domain. Their associated dual spatial bivector planes belongs to the common three-dimensional even subalgebra (Appendix A), ensuring domain-independence of spatial orientation.
4.1. Definition of the Spinors , Rotor , and Vectors
The two spinors , and associated rotor , form a spinor structure that preserves the triplet of three-spheres (Figure 2 and Figure 3). Thus, every three-sphere carries a natural spinor representation that encodes its symmetry. The Euclidean spinor (preserving ) and spacetime spinor (preserving and ) are defined as
Here acts as a spatial spinor (Equation (9)), and act as temporal spinors (Appendix C), and the scalar factor ensures the unitarity of rotor , the normalized form of . Applying the spinors and yields the vectors spanning the three-spheres:
Here, is a hyperbolic unit vector, is a causal vector with variable norm, and is a Euclidean unit vector. The causal three-sphere covers the spacetime region bounded by the light cone of a past event (Figure 3a). Each causal vector is future pointing and its norm represents proper length, vanishing at the lightlike boundaries. In this way, integrates a natural form of causality in the triplet of three-spheres.
4.2. Geometric Duality
A central feature of hyper-spacetime is the geometric duality between the Minkowski and Euclidean domains, expressed directly through the spacetime spinor and the Euclidean spinor (Equation (11)). This duality is governed by the temporal spinors and , which are defined by the temporal bivectors
This relation shows that the temporal bivector acts as the spatial basis vector , while the temporal bivector acts as the spatial basis vector . With this structure in place, the only difference between and is the domain to which the temporal bivector resides. Their spatial component (Equations (9) and (11)) is identical in both cases, since the spatial bivectors belong to the shared three-dimensional even subalgebra common to both metrics (Appendix A).
This establishes the geometric duality transparently: a vector (spatial direction) in one domain corresponds to a bivector (orientation) in the other. The combined spinors and , therefore, encode the same orientation data, expressed within two different metric signatures. Each spinor preserves its associated three-spheres: preserves and , while preserves . Consequently, the same angular coordinates generate parallel spinor structures in both domains. This illustrates how the unified hyper-spacetime geometry emerges from the vector ↔ bivector duality linking the Euclidean and Minkowski representations.
In summary, the three-spheres (Equation (7)) exhibit the following features:
- A common temporal axis with a shared origin (spacetime event).
- Unit vectors and that encode spatial direction and temporal orientation through the reciprocal relation , expressing a geometric duality between domains.
- Domain-independent spatial bivector planes , common to both domains.
A complete cycle on the Euclidean three-sphere corresponds one-to-one with a complete cycle on hyperbolic three-sphere , thereby unifying and . The apparent boundary at infinity () is absorbed smoothly, making the entire structure closed and traversable. The unified geometry constructed from the triplet of three-spheres is referred to as hyper-spacetime :
Its coordinates are given by the hyper-spherical set , where the spatial angles encode direction, and the temporal angle encodes relative speed (Equation (5)). Hence, the familiar relativistic parameters of direction and speed are reformulated as angular variables in a closed domain, and continuity at the lightlike boundaries.
5. Full Lorentz Group
The full Lorentz group [29,30,31] contains the symmetries of spacetime that preserve the Minkowski metric. It includes the following: (1) continuous transformations as boosts and spatial rotations, and (2) spacetime event reflections : identity (I), parity (P), time-reversal (T), and spacetime-reversal (PT). Thus, the full Lorentz group is defined as
where is the proper orthochronous Lorentz subgroup connected to identity.
In the conventional formalism, boosts in are parameterized by the unbounded angle , leading to singularities at the lightlike boundaries. Moreover, the discrete reflections remain disconnected from identity. The standard way to extend the full Lorentz group is through its double cover , as it includes both proper and improper transformations [31]. However, even within , the discrete transformations remain disconnected from identity, leaving a gap between reflections and continuous transformations. This gap is closed by hyper-spacetime, in which continuous and discrete symmetries arise naturally within a unified geometry.
5.1. A Unified Geometry
In the hyper-spherical coordinates of hyper-spacetime (defined in Section 4), the spacetime event reflections manifest naturally as smooth angular transformations:
These transformations correspond to changes in temporal orientation ( sign changes or shifts in ) and spatial orientation ( shifts in ). Crucially, all four reflections are smoothly connected to identity, eliminating discontinuities.
5.2. Spinor Representations
The spinor structure of hyper-spacetime provides explicit representations of the transformations. Starting from the spacetime spinor , variations in the hyper-spherical coordinates generate the full set of spacetime spinors , where each of the spinors represents one of the transformations:
With . Similarly, changes in generate the full set of Euclidean spinors :
With . Note the algebraic closure: each of the spinors and can be a basis to generate the full set of transformations. The spatial spinors in and are generated from spatial spinor (Figure 2a) via a parity transformation:
This orthonormal set corresponds to the spatial Pauli spinors [32].
Each set and forms an orthonormal basis within its respective metric, and the discrete transformations remain continuously connected to the identity. The components of both sets are identical, differing only in their temporal bivector plane: in the Minkowski domain versus in the Euclidean domain.
5.3. Example: Continuous Time-Reversal in Hyper-Spacetime
The importance of representing the full Lorentz group becomes evident when considering time-reversal . In the conventional formulation, is an isolated discrete reflection that cannot be reached continuously from the identity transformation. In hyper-spacetime, however, time-reversal corresponds to a smooth angular shift in the bounded parameter :
As varies continuously, a boost can pass smoothly through the lightlike boundary and change temporal orientation without algebraic discontinuity. The boosted vector
thus evolves continuously into its time-reversed counterpart. This example illustrates why the full Lorentz group , —including the discrete reflections , , and —must be treated on equal geometric footing. These symmetries are essential in relativistic physics (e.g., CPT invariance [31,33,34]), and incorporating them continuously removes the traditional separation between boosts, rotations, and reflections. Hyper-spacetime provides this unified representation within a single angular domain.
- In summary, hyper-spacetime provides:
- A smooth, closed, continuous angular domain for the full Lorentz group .
- Discrete reflections , continuously connected to identity.
- Spinor sets forming orthonormal bases in their respective metrics, unifying the Euclidean domain with the Minkowski domain .
- A closed realization of the double cover through the spinor sets .
- Isolation of infinities at the lightlike boundaries into the scalar density factor (Equation (11)), while the spinors themselves remain regular.
This prepares the ground for Section 6, where the eigen-spinor and eigenvalue structure of physical observables in hyper-spacetime is developed.
6. Eigen-Spinors and Eigenvalues in the Geometry of Hyper-Spacetime
Analogous to how the observables of lie on the surface of one-sphere , the observables of hyper-spacetime reside on the surfaces of the three-spheres , each preserved by the spinor sets . These spinor sets act not only as symmetry generators, but also as eigen-spinors of the corresponding observables (Equation (12)). This follows directly from the geometric algebra eigen-spinor eigenvalue relation (Appendix D):
Here, is an observable, is a basis vector (reference observable, e.g., ), are the eigen-spinors of , and the corresponding eigenvalues. In hyper-spacetime, however, the spinor sets are generated geometrically by variations in the hyper-spherical coordinates (Equation (15)), rather than being obtained by solving an eigen-spinor eigenvalue equation explicitly (Appendix D).
6.1. Spatial Eigen-Spinors
The spatial spinor set (Equation (18)), generated from a parity transformation, act as eigen-spinors of the spatial unit vectors (Figure 2a) and (Equation (10)). They satisfy the GA eigen-spinor eigenvalue relations (Appendix D):
So, and are observables with eigen-spinors and eigenvalues . Physically, these correspond to spin-up or spin-down measurements along the spatial directions of and .
6.2. Spacetime Eigen-Spinors
The spacetime spinor set (Equation (16)) and Euclidean spinor set (Equation (17)) act as eigen-spinors of the hyper-spacetime observables (Equation (12)):
Here, the eigenvalues encodes two constant spin states combined with positive/negative temporal orientation in and , while the eigenvalues encodes two variable spin states combined with positive/negative temporal orientation in . Unlike , the values of depend on relative speed via angle (Equation (5)). Hence, a spin state in vanishes at the lightlike boundaries .
6.3. Null Spinors
At the lightlike boundaries (), the spacetime spinors reduce to null spinors:
These spinors have zero intensity but preserve direction, lying on the light cone of and . For the Euclidean spinors , the corresponding boundary form is
Thus, the Euclidean spinors keep their unit intensity, while the intensities of spacetime spinors become zero. Each spinor set pass smoothly through the lightlike boundary.
6.4. Correspondence with the Dirac Equation
The eigen-spinors (Equation (21)) and eigenvalues of the observable reproduce those of the Dirac equation [23] (two spin states combined with positive/negative temporal orientation, i.e., matter/antimatter) (Appendix E). This agreement is remarkable because in hyper-spacetime these eigen-spinors are generated geometrically (Equation (16)), rather than being obtained by solving an eigen-spinor eigenvalue equation (Appendix D). This establishes a direct geometric origin for the Dirac spectrum, demonstrating that the fundamental structure of spacetime eigen-spinors emerges naturally within the hyper-spacetime framework.
In summary, the eigen-spinor structure of hyper-spacetime reproduces the Dirac spectrum, isolates singularities into a scalar density, and reveals null spinors as natural lightlike states.
7. Discussion
The hyper-spacetime framework developed in this paper provides a compact, continuous, and geometrically transparent representation of Lorentz symmetry. By replacing the unbounded rapidity with the bounded angular coordinate , the structure of Lorentz boosts is reformulated in a closed domain in which both branches of the hyperbola, as well as the lightlike boundary, appear as regular geometric features. This compact parametrization enables boosts, rotations, and reflections to be expressed within a unified angular system, thereby revealing structural parallels between hyperbolic and circular symmetries that are hidden in the conventional rapidity formalism.
A central outcome is the introduction of a triplet of three-spheres (Figure 2 and Figure 3)
which encode hyperbolic, causal, and Euclidean structure within a shared geometric framework. The three-spheres possess a common temporal axis and a reciprocal temporal bivector plane, providing a continuous geometric bridge between Minkowski and Euclidean domains (Equation (10)). This real-domain duality constitutes an alternative to analytic continuation and offers a natural geometric basis for Wick-type transformations [8,9], in which transitions between signatures correspond to smooth variations in the bounded angle .
The unified geometry also clarifies the status of discrete symmetries. In the conventional Lorentz group, appear as isolated, algebraically imposed reflections. Here, they arise instead as continuous angular operations within the compact domain of hyper-spherical coordinates : shifts of and encode changes in temporal or spatial orientation. This continuity removes the algebraic disconnection between discrete and continuous transformations and provides a closed and unified representation of the full Lorentz group .
Spinor structure plays a central role in this unification. By treating spinors as geometric entities generated directly from variations in the hyper-spherical coordinates (Equation (15)), the spinor sets and (Equations (16) and (17)) act both as symmetry generators and as eigen-spinors of geometric observables . Remarkably, their eigenvalue structure reproduces the Dirac spectrum: two spin states combined with positive and negative temporal orientation, with null spinors emerging naturally at the lightlike boundary. In this formulation, Dirac spinors arise not from solving the Dirac differential equation but from the intrinsic geometry of hyper-spacetime.
A brief physical example illustrates this geometry in practice: the hyperbolic three-sphere parametrizes normalized relativistic momentum in bounded form, while the causal sphere simultaneously parametrizes normalized spacetime intervals (Appendix E). Their geometric product yields relativistic action, and the compact angular domain provides a clean representation of lightlike limits, where the action reduces to a null-spinor configuration. This highlights how the framework can be used to reformulate standard relativistic quantities in a bounded, continuous setting.
Finally, to place the work in its broader context [35,36], conventional treatments of Lorentz symmetry [37] are typically based on Lie-algebraic parametrizations [38], rapidity methods, or complex-analytic Wick rotations [8,10]. More recent studies examine compactifications or alternative parametrizations, but these typically apply only to restricted subgroups (e.g., ) or require analytic continuation to imaginary time [39,40,41]. In contrast, hyper-spacetime combines compactification, spinor unification, and Euclidean–Minkowski duality within a single four-dimensional real geometric construction.
8. Conclusions
This paper introduces a unified geometric framework—hyper-spacetime—that provides a bounded, continuous representation of the full Lorentz group. By replacing rapidity with a bounded angular parameter , the framework unifies circular and hyperbolic symmetry, eliminates divergences at the lightlike boundary, and reveals a continuous pathway through both branches of the Lorentz boost hyperbola. This compact domain enables discrete symmetries to be expressed as smooth angular transformations, providing a closed geometric picture of .
The construction of a triplet of three-spheres forms the core of hyper-spacetime. These spheres share a temporal axis and a reciprocal temporal bivector plane, establishing a real geometric duality between Minkowski and Euclidean representations. This duality offers a natural geometric interpretation of Wick rotation and clarifies how Euclidean and Lorentzian structures can be embedded within a single continuous geometry.
The associated spinor sets and (Equations (16) and (17)) reproduce the eigen-spinor structure of the Dirac equation, including null spinors at the lightlike boundary. In this sense, hyper-spacetime provides a geometric origin for Dirac spinors, where eigen-spinor behavior emerges directly from the geometry rather than from analytic solutions of a differential equation. Singularities are isolated in scalar density factors, allowing the spinors themselves to remain regular throughout the full angular domain.
Overall, the hyper-spacetime framework yields a closed and unified representation of Lorentz geometry, clarifies the role of discrete symmetries, and provides a continuous real-domain connection between Euclidean and Minkowski structures. Beyond its conceptual clarity, the framework suggests potential applications to geometric quantization, path-integral formulations, and the study of null-spinor behavior at the lightlike boundary. Future work may explore these directions, as well as the possibility of embedding interactions or gauge structures within the same compact geometric setting.
Funding
This research received no external funding.
Data Availability Statement
The original contributions presented in this article are included in the article. Further inquiries can be directed to the author.
Conflicts of Interest
The author declares no conflict of interest.
Appendix A. Spacetime Algebra

Table A1.
Spacetime algebra bridging and .
Table A1.
Spacetime algebra bridging and .
| # | Spacetime Algebra [19,23,42,43] | Description | ||
|---|---|---|---|---|
| 1 | Metric diagonal for Metric diagonal for | The four orthogonal basis vectors and span the same four-dimensional (4D) spacetime axes . The common temporal basis vector squares to plus one (+1). The spatial basis vectors square to minus one (−1). The spatial basis vectors square to plus one (+1). | ||
| 2 | The basis vectors satisfy the algebra of the Dirac gamma matrices, while the spatial basis vectors satisfy the algebra of three-dimensional space. | |||
| 3 | Grade (#) | Spacetime | Spacetime | The algebra of four-dimensional (4D) spacetime, unifying the Minkowski domain with the Euclidean domain , is a graded linear space with dimension . Multi-vectors are “geometric numbers” being scalars , vectors , bivectors , trivectors , and pseudoscalars . Both domains, and , share the following: scalar 1, temporal basis vector , three spatial bivectors , four trivectors , and pseudoscalar . The spatial basis vectors correspond to temporal bivectors in the Euclidean domain, while the spatial basis vectors correspond to temporal bivectors in the Minkowski domain. This geometric duality (spatial vector temporal bivector) unifies the two domains at the level of temporal bivector planes. |
| (1) | 1 | |||
| (4) (3) | ||||
| (3) (4) (1) | ||||
| 4 | Pseudoscalar in the Minkowski domain . Pseudoscalar in 3D space of the Euclidean domain . These pseudoscalars are equal. | |||
| 5 | The form of a general spacetime multi-vector . Revision operator—on top of a multi-vector is an invariant type of conjugation. | |||
| 6 | The even subalgebra (see item 7 in this table). The even subalgebra is closed under a geometric product (GP). The GP of gives a scalar plus a pseudoscalar . | |||
| 7 | Grade (#) | 3D even subalgebra | The three orthogonal basis vectors span the spatial axes of 3D space. Together with scalar , the spatial bivectors , and the pseudoscalar , they provide an eight-dimensional common 3D even subalgebra . The spatial basis vectors , orthogonal to the temporal basis vector , correspond to the temporal bivectors in the Minkowski domain. Both domains and , therefore, share the three spatial bivectors , ensuring domain-independence of spatial orientation. | |
| (1) | 1 | |||
| (6) | ||||
| (1) | ||||
Appendix B. Gudermannian Function
The Gudermannian* function [12,13] relates circular and hyperbolic functions without introducing complex arguments. In its primary form, it connects the unbounded hyperbolic angle to the bounded angle , through the following identity:
Within this interval, the associated identities
map the positive branch of the Lorentz-boost hyperbola
onto the trigonometric form
which preserves the Minkowski norm .
Periodic Extension and Coverage of Both Hyperbolic Branches
The primary Gudermannian mapping covers only the region where , corresponding to the positive branch of the Lorentz-boost hyperbola. However, a complete representation of Lorentz boosts must include the negative branch , where the hyperbolic functions reverse sign. This extension is achieved by exploiting the trigonometric periodicity.
which, when inserted into the Gudermannian relations,
produce precisely the negative hyperbolic functions
Therefore, shifting by maps the trigonometric functions onto the complementary branch of the hyperbola. Thus, combining the principal interval with the shifted interval yields a continuous coverage of both branches of the Lorentz hyperbola within the full periodic domain (Figure A1).
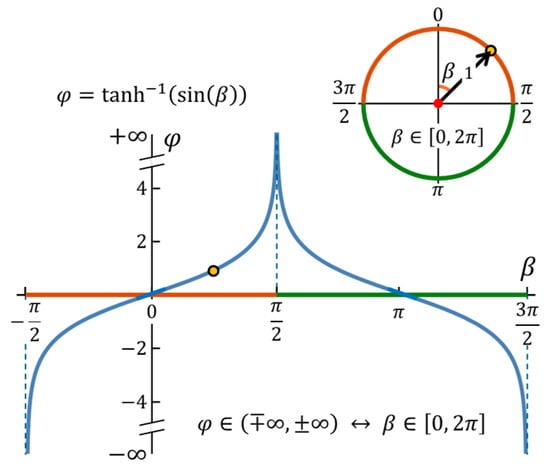
Figure A1.
The Gudermannian function provides a smooth mapping between the unbounded angle and the bounded angle .
This periodic extension is what closes the two disconnected hyperbolic branches and into the hyperbolic one-sphere , ensuring that boosts pass smoothly through the lightlike boundary () and that the complete Lorentz-boost structure is represented within a single bounded angular parameter.
- * Christoph Gudermann (25 March 1798–25 September 1852) introduced this function and the concept of uniform convergence. See Wikipedia.
Appendix C. Spinors and Rotors
In geometrical algebra (GA) the rotation of a multivector by a rotor is performed by a double-sided geometric product (GP):
This is a powerful generalization of rotation, as it applies in any dimension and to any multivector. A rotor can be written as a scalar density times a spinor :
Here, the unitarity of the rotor determines the scalar density . In general, for a spinor to define a proper rotor, its intensity must be a scalar:
Any nonzero additional grade contribution to the intensity would prevent normalization with a scalar density (Equation (A9)).
A spinor is characterized by its bivector, i.e., the plane of rotation. In hyper-spacetime, the Minkowski domain and the Euclidean domain share the three spatial bivectors (Appendix A). Hence, a general spatial spinor is as follows:
The three temporal bivectors in the Minkowski domain are . Hence, a general Minkowski temporal spinor is as follows:
The three temporal bivectors in the Euclidean domain are . Hence, a general Euclidean temporal spinor is
Both the spatial and the two temporal spinors are pure spinors, since their intensities reduce to scalar values.
The pure spinors (Equations (16) and (17)) preserving hyper-spacetime and acting as eigen-spinors, are geometrically generated from the spinors and (Equation (11)). Both are composed of a spatial spinor (Equation (9)) and the temporal spinors and :
The associated proper rotor , the normalized form of , is
The rotor associated with spinor is equal to , since its intensity satisfies . The same holds for the spatial spinor , which also has unit intensity.
The temporal spinors and (Equation (A14)), characterized by the temporal bivectors and , reveal the dual role of these temporal bivector planes across hyper-spacetime . In this dual relation, the temporal bivectors of the Euclidean domain appear as the spatial basis vectors of the Minkowski domain, while the temporal bivectors of the Minkowski domain play the same role in the Euclidean domain. This geometric duality unifies the two domains at the level of their temporal bivector planes. Moreover, the two domains share the three spatial bivectors (Equation (A11)), which belong to a common three-dimensional even subalgebra, ensuring that the spatial spinors remain domain independent.
Appendix D. Eigen-Spinors and Eigenvalues
The hyper-spacetime spinor sets (Equations (16) and (17)), which preserve the three-spheres , act also as eigen-spinors of the corresponding observables . Their connection is described by the geometric algebra eigen-spinor eigenvalue relation:
Here, is observable, is a basis vector (reference observable, e.g., ), is the eigen-spinor set of , and are the eigenvalues of . However, in hyper-spacetime, these spinor sets are geometrically generated (Equations (16) and (17)), rather than being obtained by solving an eigen-spinor eigenvalue equation.
To calculate eigen-spinors and eigenvalues in practice, one uses the linear algebra (LA) eigen-spinor eigenvalue equation:
where is the matrix representation of the observable, the column vector representation of the eigen-spinors, and the eigenvalues. A one-to-one conversion between GA and LA is obtained via the standard matrix representations of the basis vectors:
Using these, the observables become 4 by 4 matrices:
where is the 2 by 2 spatial spin observable matrix associated with the spatial unit vectors and (Equation (10)):
Solving the LA eigen-spinor eigenvalue Equation (A17) for gives the spatial eigen-spinors with eigenvalues :
Here, the set is the orthonormal spatial Pauli spinors [32]. Similarly, solving Equation (A17) for the observables yields the column vector eigen-spinor sets:
with eigenvalues and .
In summary, the eigen-spinors and obtained by solving the LA eigen-spinor eigenvalue equation are equal to the geometrically generated (Equation (15)) spacetime spinor sets (Equations (16) and (17)).
Appendix E. Dirac Equation
This appendix provides the explicit correspondence between (1) the spacetime spinors obtained as solutions of the Dirac equation and (2) the geometrically generated spacetime spinors (Equation (16)).
The observables , as elements of the three-spheres , are normalized vectors and can directly be linked to relativistic dynamics. The hyperbolic three-sphere vector corresponds to normalized momentum:
While the causal three-sphere vector corresponds to normalized distance:
The geometric product of and yields relativistic action [44,45]:
Treating action as a phase , a free particle plane-wave state [23] is defined as
where is the normalized action, and is a constant spacetime spinor. This plane-wave state is a solution of the Dirac equation in geometric algebra [23]:
which is equivalent to the linear algebra (LA) form [4]:
Substitution of the plane wave state in Equation (A27) shows that spinor satisfies the GA eigen-spinor eigenvalue relation:
Multiplying from the right with gives
Hence, a plane wave state (Equation (A26)) is a solution of the Dirac equation.
Finally, variations in the hyper-spherical coordinates of , encoded by the spacetime event reflections (Equation (15)), generate the four Dirac plane-wave solutions:
The orientation of action depends on the temporal angle , such that matter and antimatter solutions follow naturally from the spacetime event reflections . Each of these plane-waves is a valid solution of the Dirac equation, demonstrating the remarkable correspondence between the Dirac equation and the spacetime event reflections .
In addition to the four fermionic Dirac plane-wave solutions , these solutions also yield a lightlike boundary solution at :
This corresponds to a photon-like state with vanishing mass term. At the lightlike boundary, the fermionic plane-wave solutions reduce to null spinors with zero intensity while retaining directionality. Thus, the hyper-spacetime framework produces both fermionic (massive) and photonic (massless) solutions as limiting cases of a unified spinor structure.
Clifford-Algebra Structure and Lorentz-Invariant Spinors
The spacetime spinors (Equation (16)) naturally belong to the even subalgebra of the real Clifford-algebra generated by
which is isomorphic to , the double cover of the Lorentz group . Since Lorentz transformations are generated by bivectors in and implemented by rotors , the spinors (Equation (16)) are automatically Lorentz-covariant: their spatial part rotates within the shared spatial bivector plane (Appendix A), while the temporal part rotates in the Minkowski temporal plane . The geometric eigenvalue relation
is the Clifford-algebra analog of the Dirac equation’s operator form
Thus, the four spinors generated geometrically by variations in the hyper-spherical coordinates reproduce the four standard Dirac plane-wave spinors (two spin states, each with positive or negative temporal orientation). In this sense, the Dirac spectrum is not imposed but emerges directly from the hyper-spacetime geometry.
References
- Vaughan-Hankinson, B. 1 The Lorentz Group. 2019. Available online: https://researchers.ms.unimelb.edu.au/~nganter@unimelb/UndergraduateSeminar/lorentz.pdf (accessed on 11 October 2025).
- Gray, J. Henri Poincaré. In Henri Poincaré; Princeton University Press: Princeton, NJ, USA, 2012. [Google Scholar]
- Schwichtenberg, J. Physics from Symmetry; Springer: Berlin/Heidelberg, Germany, 2018. [Google Scholar]
- Thomson, M. Modern Particle Physics; Cambridge University Press: Cambridge, UK, 2013. [Google Scholar]
- Bonolis, L. From the rise of the group concept to the stormy onset of group theory in the new quantum mechanics: A saga of the invariant characterization of physical objects, events and theories. La Riv. Del Nuovo C. 2004, 27, 1–110. [Google Scholar]
- Cao, T.Y. Conceptual Development of 20th Century Field Theories; Cambridge University Press: Cambridge, UK, 2019. [Google Scholar]
- Roelfs, M.; Eelbode, D. Lepton Triptych I: Geometric Foundations of Electroweak Symmetry in the Real Clifford Algebra . arXiv 2025, arXiv:2510.13834. [Google Scholar]
- Kontsevich, M.; Segal, G. Wick Rotation and the Positivity of Energy in Quantum Field Theory. Q. J. Math. 2021, 72, 673–699. [Google Scholar] [CrossRef]
- Feynman, R.P.; Hibbs, A.R.; Styer, D.F. Quantum Mechanics and Path Integrals; Courier Corporation: North Chelmsford, MA, USA, 2010. [Google Scholar]
- Singh, R.; Kothawala, D. Geometric aspects of covariant Wick rotation. arXiv 2020, arXiv:2010.01822. [Google Scholar]
- Merz, T. Geometric Interpretation of the Minkowski Metric. 2024; preprints. [Google Scholar]
- Gambini, A.; Nicoletti, G.; Ritelli, D. A Structural Approach to Gudermannian Functions. Results Math. 2024, 79, 10. [Google Scholar] [CrossRef]
- Gudermann, C. Theorie der Modular-Functionen und der Modular-Integrale. J. Für Die Reine Und Angew. Math. (Crelles J.) 1838, 1838, 1–54. [Google Scholar]
- Kim, S.; Lawson, J. Unit balls, Lorentz boosts, and hyperbolic geometry. Results Math. 2013, 63, 1225–1242. [Google Scholar] [CrossRef]
- Long, G.; Lin, C.-Y. Geometric parametrization of SO (D + 1) phase space of all dimensional loop quantum gravity. Phys. Rev. D 2021, 103, 086016. [Google Scholar] [CrossRef]
- Coddens, G. A Lorentz Boost as a Product of Two Space-Time Reflections and Some Additional Results About Clifford Algebra. 2022. Available online: https://hal.science/hal-03864603v1/file/Lorentz-from-reflections-3.pdf (accessed on 21 November 2022).
- Brands, P.J. Hyperbolic Rotation with Euclidean Angle Illuminates Spacetime Spinors. J. Math. Tech. Comput. Math. 2023, 2, 456–478. [Google Scholar]
- Eckstein, D. Epstein Explains Einstein; Epubli GmbH: Berlin, Germany, 2013. [Google Scholar]
- Hestenes, D. Space-Time Algebra; Springer: Berlin/Heidelberg, Germany, 2015. [Google Scholar]
- Hestenes, D. Spacetime physics with geometric algebra. Am. J. Phys. 2003, 71, 691–714. [Google Scholar] [CrossRef]
- Grassmann, H. A New Branch of Mathematics: The “Ausdehnungslehre” of 1844 and Other Works; Open Court: Singapore, 1995. [Google Scholar]
- Chisholm, M. Such Silver Currents: The Story of William and Lucy Clifford, 1845–1929; The Lutterworth Press: Cambridge, UK, 2021; pp. 1–100. [Google Scholar]
- Doran, C.; Lasenby, A.; Lasenby, J. Geometric Algebra for Physicists; Cambridge University Press: Cambridge, UK, 2003. [Google Scholar]
- Dressel, J.; Bliokh, K.Y.; Nori, F. Spacetime algebra as a powerful tool for electromagnetism. Phys. Rep. 2015, 589, 1–71. [Google Scholar] [CrossRef]
- Hestenes, D. Vectors, spinors, and complex numbers in classical and quantum physics. Am. J. Phys. 1971, 39, 1013–1027. [Google Scholar] [CrossRef]
- Stubhaug, A. The Mathematician Sophus Lie: It was the Audacity of My Thinking; Springer: Berlin/Heidelberg, Germany, 2002. [Google Scholar]
- Hall, B.C.; Hall, B.C. Lie Groups, Lie Algebras, and Representations; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Roelfs, M.; De Keninck, S. Graded symmetry groups: Plane and simple. Adv. Appl. Clifford Algebras 2023, 33, 30. [Google Scholar] [CrossRef]
- McRae, C. A Convenient Representation Theory of Lorentzian Pseudo-Tensors. arXiv 2025, arXiv:2501.05400. [Google Scholar]
- Gerber, P.R.; Design, G.M. On Representations of the Lorentz Group. J. Adv. Math. Comput. Sci. 2023, 38, 76–82. [Google Scholar] [CrossRef]
- Berg, M.; DeWitt-Morette, C.; Gwo, S.; Kramer, E. The pin groups in physics: C, P and T. Rev. Math. Phys. 2001, 13, 953–1034. [Google Scholar] [CrossRef]
- Steane, A.M. An introduction to spinors. arXiv 2013, arXiv:1312.3824. [Google Scholar]
- Bediaga, I.; Frederico, T.; Lourenço, O. CP violation and CPT invariance in B ± decays with final state interactions. Phys. Rev. D 2014, 89, 094013. [Google Scholar] [CrossRef]
- Greenberg, O.W. CPT violation implies violation of Lorentz invariance. Phys. Rev. Lett. 2002, 89, 231602. [Google Scholar] [CrossRef] [PubMed]
- Shin, D.-C.; Hayward, T.M.; Fife, D.; Menon, R.; Sudhir, V. Active laser cooling of a centimeter-scale torsional oscillator. Optica 2025, 12, 473–478. [Google Scholar] [CrossRef]
- Tirole, R.; Vezzoli, S.; Galiffi, E.; Robertson, I.; Maurice, D.; Tilmann, B.; Maier, S.A.; Pendry, J.B.; Sapienza, R. Double-slit time diffraction at optical frequencies. Nat. Phys. 2023, 19, 999–1002. [Google Scholar] [CrossRef]
- Visser, M. Lorentz symmetry breaking as a quantum field theory regulator. Phys. Rev. D—Part. Fields Gravit. Cosmol. 2009, 80, 025011. [Google Scholar] [CrossRef]
- Ragone, M.; Bakalov, B.N.; Sauvage, F.; Kemper, A.F.; Marrero, C.O.; Larocca, M.; Cerezo, M. A Lie algebraic theory of barren plateaus for deep parameterized quantum circuits. Nat. Commun. 2024, 15, 7172. [Google Scholar] [CrossRef] [PubMed]
- Danciger, J.; Guéritaud, F.; Kassel, F. Geometry and topology of complete Lorentz spacetimes of constant curvature. Ann. Sci. De L Ecole Norm. Super. 2016, 49, 1–56. [Google Scholar] [CrossRef]
- Duboeuf, B. Kaluza-Klein Compactification, Exceptional Geometry and Holography. Ph.D. Dissertation, Ecole Normale Supérieure de Lyon-Ens Lyon, Lyon, France, 2024. [Google Scholar]
- Zenginoğlu, A. Hyperbolic times in Minkowski space. Am. J. Phys. 2024, 92, 965–974. [Google Scholar] [CrossRef]
- De Sabbata, V.; Datta, B.K. Geometric Algebra and Applications to Physics; CRC Press: Boca Raton, FL, USA, 2006. [Google Scholar]
- Lasenby, A.N. Geometric algebra as a unifying language for physics and engineering and its use in the study of gravity. Adv. Appl. Clifford Algebras 2017, 27, 733–759. [Google Scholar] [CrossRef]
- Goldstein, H. Classical Mechanics; Addison-Wesley Series in Physics: Boston, MA, USA, 1980. [Google Scholar]
- Friedman, Y. A unifying physically meaningful relativistic action. Sci. Rep. 2022, 12, 10843. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).