Magnetohydrodynamic Flow and Transport Behaviors of Blood-Based Ternary Nanofluids in Stenosed Arteries with Axial Symmetry: Effects of Thermal Radiation and Caputo Fractional Derivatives

Abstract

The present study investigates the magnetohydrodynamic (MHD) flow characteristics of a blood-based ternary nanofluid (Au/Cu/Al₂O₃-blood) in stenosed arteries, with a focus on symmetry-inspired modeling rooted in the axial symmetry of arterial geometry and the symmetric distribution of external physical fields (magnetic field, thermal radiation). The findings offer significant insights into the realm of hyperthermia therapy and targeted drug delivery within the domain of biomedical engineering. A mathematical model is established under a cylindrical coordinate system (consistent with arterial axial symmetry), integrating key physical effects (thermal radiation, chemical reactions, viscous dissipation, body acceleration) and fractional-order dynamics via Caputo derivatives—while ensuring the symmetry of governing equations in time and space. The numerical solutions for velocity and temperature profiles are obtained using the Laplace transform and Concentrated Matrix-Exponential (CME) method, a technique that preserves symmetric properties during the solution process. The results of the study indicate the following: The Hartmann number, which is increased, has been shown to reduce axial velocity due to the Lorentz force, thereby maintaining radial symmetry. Furthermore, thermal radiation has been demonstrated to raise fluid temperature, a critical factor in heat-based therapies, with the temperature field evolving symmetrically. In addition, it has been observed that ternary nanoparticles outperform single and binary systems in heat and mass transfer via symmetric dispersion. This work contributes to the existing body of knowledge by integrating symmetry principles into the study of fractional dynamics, electromagnetic fields, and body acceleration modeling. It establishes a comprehensive biomedical flow framework. It is imperative that future research explore pulsatile flow under symmetric boundaries and validate the model through experimental means.

1. Introduction

Stenosis, defined as the abnormal narrowing of blood vessels, is a critical pathological condition that restricts normal blood circulation and thereby predisposes patients to severe cardiovascular complications such as myocardial infarction or stroke if left unaddressed [1]. Given its direct association with life-threatening cardiovascular diseases, the investigation of the hemodynamic phenomena that occur in stenosed arteries represents a critical area of interest within the domains of medical research and biomedical engineering.

It is imperative to note that precise hemodynamic modeling of stenosed arterial flow is indispensable for the advancement of computational tools in the domain of diagnostic imaging. For instance, techniques such as Doppler ultrasound and MRI-based flow quantification depend on precise descriptions of flow dynamics to characterize the geometry (e.g., degree of narrowing, location) and severity of stenosis, which exhibit inherent axial symmetry and are critical for clinical decision-making. As demonstrated in previous studies [2,3], stenosis has been shown to induce significant alterations in key flow parameters within the narrowed region. These alterations include reduced blood velocity, abnormal skin friction, and perturbed wall shear stress. These parameters are closely linked to the progression of vascular pathology.

In recent years, advancements in nanotechnology have led to new possibilities for modulating blood flow characteristics. The development of hybrid and ternary nanofluids is a particularly promising area of research in this field [4]. These nanofluids, which consist of a base fluid (e.g., blood) dispersed with nanoparticles (such as gold (Au), aluminum oxide (Al₂O₃), and copper (Cu)), exhibit enhanced thermophysical properties compared to pure blood. More specifically, they demonstrate superior thermal conductivity, accelerated heat transfer rates, and improved mass diffusion capabilities.

In this paper, gold, copper, and aluminum oxide nanoparticles were selected for their distinct and complementary properties, which enable the exploration of diverse behaviors in the electro–magneto–hydrodynamic (EMHD) regime. The distinguishing features of Au and Cu nanoparticles include their high electrical and thermal conductivity, while Al₂O₃ contributes mechanical stability and biocompatibility. These properties are essential for minimizing toxicity and ensuring structural integrity in biomedical applications. Experimental and computational evidence suggests that hybrid nanoparticle combinations (as opposed to single-component systems) can further amplify heat transfer efficiency and flow stability, making them suitable for use in targeted drug delivery or thermal therapy (e.g., hyperthermia for tumor treatment). For instance, single nanoparticles (e.g., Au for conductivity enhancement or Al₂O₃ for biostability) have demonstrated preliminary efficacy in biomedical flow modulation; however, ternary combinations leverage synergistic effects between different nanoparticle types to achieve more robust performance. These synergies are of particular importance in the regulation of arterial temperature and the optimization of blood flow, which are critical factors in the treatment of conditions such as atherosclerosis [5,6,7].

The ternary composition leverages the synergistic thermal and electrical conductivities of gold and copper with the chemical stability and biocompatibility of alumina. This hybrid combination enhances heat transfer without compromising hemocompatibility, making it suitable for biomedical applications such as photothermal therapy and magnetic targeting.

Concurrent with the advancements in nanotechnology, the domain of bio-magnetic fluid mechanics has appeared as a pivotal area of inquiry, concentrating on the manner in which magnetic fields affect the movement of biofluids particularly blood, the predominant transport fluid in the human circulatory system [8]. As previously proposed [9], blood exhibits inherent electrical conductivity, a property that subjects its flow to the principles of magnetohydrodynamics (MHD). MHD, as a broader discipline, is the study of examination of electrically conductive fluids under magnetic fields. It provides a theoretical framework for analyzing the interplay between magnetic forces and fluid motion [10,11].

A notable recent advancement in electrohydrodynamic (EHD) fluid mechanics is the establishment of its variational principle, which offers a novel analytical framework for investigating the dynamics of electrically conductive fluids [12]. This principle is particularly extensible to biomagnetic applications such as modeling blood flow under electromagnetic fields where it can enhance the theoretical rigor of analyzing how external fields interact with biofluids. Specifically, the variational principle provides a foundational basis for refining computational models of electro-magneto-hydrodynamic (EMHD) phenomena in biological systems, deepening the understanding of complex flow behaviors unique to physiological environments.

A substantial body of research has been dedicated to investigating the impacts of magnetohydrodynamic (MHD) flow in stenosed arteries, considering its crucial role in the diagnosis and treatment of cardiovascular ailments. For instance, Tian and his research group [13] developed a one-dimensional analytical model. This model was meticulously designed to investigate three critical flow-related parameters of a Newtonian blood-based nanofluid as it traverses an inclined artery under an external magnetic field. The researchers obtained results from the model indicating that the applied magnetic field was capable of reducing the adverse effects brought about by arterial stenosis. The observed effects included disruptions to the normal flow pattern, and the results elucidated that the magnetic field results in a reduction in blood flow velocity. This particular finding is of practical significance for the clinical management of diseases characterized by arterial stenosis, such as atherosclerotic stenosis. This observation is consistent with the advancements in micro-channel cooling technology. In this regard, Huang et al. [14] demonstrated that innovative cooling liquids enhance heat transfer performance, thereby underscoring the interdisciplinary significance of fluid dynamics principles in both biomedical and engineering fields.

In a similar methodological vein, Kumari et al. [15] established an analytical model to examine how slip velocity influences the unsteady flow of non-Newtonian blood through an inclined artery. Their findings underscored the significance of accounting for slip effects in advancing clinical research, particularly for enhancing the accuracy of blood flow dynamic models in coronary stenosed arteries regions where flow behavior is highly sensitive to wall interactions. Furthermore, Omamoke and Amos [16] adopted the Frobenius series method to investigate how therapeutic interventions and slip effects jointly influence MHD blood flow within a stenosed artery. Their research findings indicated a correlation between the intensity of chemical reactions and the resulting changes in fluid dynamics. Specifically, an increase in chemical reaction intensity was observed to result in an increase in fluid viscosity and a decrease in flow rate. Concurrently, a decline in wall shear stress was noted. The insights presented herein provide valuable guidance for the development of drug delivery systems specifically designed to target stenosed arterial regions.

Furthermore, there is a need to study how thermal radiation affects blood circulation, especially in medical settings. As Prakash and Makinde [17] have previously indicated, thermal radiation therapy has the potential to reduce blood flow resistance (which can be caused by factors such as stenosis or drag from magnetic fields) by increasing the absorption of heat energy in the arterial flow field. There is much literature demonstrating repeatedly that thermal radiation is a key factor in the magnetohydrodynamic (MHD) blood flow. This finding supports the diagnosis and treatment of conditions such as hyperthermia and tumors. For instance, Chinyoka and Makinde [18] employed a Newtonian model to quantitatively evaluate the main factors affecting the fluid properties. The parameters that are taken into consideration include radiation intensity and magnetic field strength. These findings are valuable for optimizing thermal therapies used for tumor ablation.

In a related study, Isah et al. [19] investigated the effects of heat and chemical reactions on the dynamical properties of EMHD blood flow in arteries, further showing that EMHD can be used in tumor therapy. Notably, the variational principle proposed by Tian et al. [13] serves as a unified theoretical framework that can refine these biomedical models, particularly in analyzing the complex interplay between electromagnetic fields and biofluid dynamics, an interaction that is often nonlinear in physiological settings. Collectively, these studies advance the shared understanding of how external fields (magnetic, thermal, etc.) modulate fluid behavior, with implications for optimizing therapeutic strategies in both cardiovascular care (e.g., stenosis management) and oncology (e.g., targeted hyperthermia).

The integration of theoretical advancements in fluid dynamics with applied biomedical research also highlights the growing interdisciplinary nature of this field, laying the groundwork for more precise diagnostic tools (e.g., improved MRI flow quantification) and therapeutic innovations. Importantly, combining magnetic fields with thermal radiation in blood flow studies not only helps regulate arterial temperature and circulation but also prevents excessive heating that could damage surrounding healthy tissues [20] a critical safety consideration for clinical applications. Furthermore, Younis et al. [20] discovered that magnetic fields can control heat transfer and entropy generation in non-Newtonian nanofluids, identifying additional avenues for optimizing biomedical thermal systems (e.g., nanofluid-based hyperthermia devices). Beyond therapeutic applications, emerging nanofluidic technologies such as the battery-free intracellular delivery patch developed by Yin et al. [21] further emphasize the value of controlled flow modeling, as it enables the precise targeting of drug delivery to internal organs, including regions with arterial stenosis.

Fractional calculus is now used a lot to analyze blood flow [22,23]. This is mostly because it can capture memory effects and hereditary properties found in biological fluids, which traditional integer-order calculus cannot fully describe. As mentioned earlier, using fractional calculus to reveal blood flow properties in narrow arteries is very important for improving treatment methods for heart problems, like atherosclerosis and high blood pressure. This approach helps us to more accurately model how people behave when they are struggling. For example, Jamil et al. [24] used the Caputo fractional derivative to model the magnetic blood in an artery that is narrowed and blocked, especially in cases of atherosclerosis. The research showed that fractional derivatives are better than conventional methods at reproducing real-world flow dynamics.

In a similar way, Abdullah et al. [25] studied blood flow containing nanoparticles around a circular cylinder. They used the Caputo fractional derivative and the Laplace transform method to analyze it. Their research results showed that solutions based on fractional-order calculus were more precise than models that used traditional derivatives. This finding further proved the claim that fractional calculus is very important for research on biofluids. Recent studies in this area include research by Maiti and others [26]. They looked at how the Caputo-Fabrizio fractional-order derivative affects blood flow through a porous tube. Their study included three things: thermochemical interactions, magnetic effects, and vibrational impacts. These were added to a model that had already been developed. Furthermore, He et al. [27] used computer programs to simulate blood flow in complex vascular structures. The findings showed that adding fractional calculus makes flow dynamic models more realistic by accounting for how blood changes over time and remembers things.

It is important to note that the study mentioned in [28] looked at how blood-based hybrid nanofluids move through a narrow artery using a magnetohydrodynamic (MHD) process. The study combined thermal radiation, chemical reactions, and viscous dissipation into its model framework. To study temporary values in the main equations, researchers used a special type of derivative called the Caputo fractional derivative. They found the answers using a combination of two methods: the Laplace transform technique and the concentrated exponential-matrix method (CME). Their findings showed that magnetic fields, thermal radiation, and chemical reactions all have a significant impact on MHD flow. This observation highlights the promise of hybrid nanofluids for biomedical applications.

Recent studies have also looked at how different types of chemical reactions affect fluid dynamics, especially when it comes to biofluids. For example, He et al. [29] studied how time-based limits on the boundaries of fluids affect chemical reactions in Walters’ B fluids. This research provides important insights into the relationship between chemical reactions and fluid flow. This research is particularly relevant to the current study because it shows that chemical reactions are not just bystanders; they actually play an active role in shaping fluid behavior. This is an important thing to think about in biomedical applications, where changes in flow caused by chemical reactions might affect how well drugs work or the results of treatments.

Joule heating and viscous dissipation are two important ways heat moves in biofluids. Joule heating is the thermal energy that is generated when blood vessels block the flow of electric current. Viscous dissipation is caused by the frictional forces between the flowing blood and the arterial wall. Research by Wang and Popel [30] shows that when these two mechanisms interact, it changes both the temperature distribution within the fluid and the dynamic features of blood flow. These effects are very important for the body’s natural processes, like blood flow and body temperature control. In a related engineering context, Sharma and Sinha [31] investigated the influence of Joule heating on unsteady magnetohydrodynamic (MHD) flow over a stretching sheet in a porous medium. They used the fourth-order Runge–Kutta method for analysis. Their findings showed that these thermal effects cause significant changes in flow properties, like skin friction and the Nusselt number.

In a similar vein, Rasheed et al. [32] investigated the impact of Joule effect and viscous effect on the MHD boundary layer. They employed the homotopy analysis method as their analytical tool. Their work underscored the significance of these two thermal mechanisms in engineering scenarios such as heat exchanger operations and metallurgical processes. Additionally, it highlighted the cross-disciplinary parallels between such engineering applications and biomedical fluid dynamics. In a recent study, Al-Zahrani et al. [33] conducted an analytical investigation into the interaction between silver (Ag) nanoparticle suspensions and graphene nanoparticle suspensions in blood. They employed the variational iteration method to analyze the interaction. Despite the fact that the model developed in the aforementioned study encompassed Joule heating, magnetic fields, and internal heat sources, it did not take into account viscous dissipation. This research gap is addressed by the present study, which integrates both Joule heating and viscous dissipation into its framework.

Moreover, advances in predictive modeling for nanofluid thermal conductivity have yielded valuable tools for optimizing biomedical nanofluid formulations. For instance, Manikandan and Nanthakumar [34] developed a mathematical model using artificial neural networks and response surface methodology. This framework is adaptable to biomedical nanofluids, offering a data-driven approach to tailor thermophysical properties for specific applications. Bouaraour et al. [35] shed light on the interaction between flow dynamics and thermal properties in confined geometries. These insights can be extrapolated to the narrow, stenosed regions of arteries. Collectively, these studies contribute to a more profound understanding of nanofluid behavior, thereby establishing the foundation for the advancement of biomedical applications.

The present study is an expansion of the aforementioned research by investigating the MHD flow of a blood-based ternary nanofluid (Au/Cu/Al₂O₃-blood) through a stenosed artery. The present investigation incorporates thermal radiation and chemical reaction effects into its model. The mathematical model is derived using the Caputo fractional derivative, a choice that is justified by its proven effectiveness in modeling complex biological fluid flow systems [36]. In order to elucidate the temperature, velocity, and concentration profiles of the ternary nanofluid, numerical techniques including the Laplace transform and the concentrated matrix exponential (CME) method are employed. As previously mentioned, gold, copper, and aluminum oxide nanoparticles were selected for their complementary properties: high electrical/thermal conductivity (Au/Cu) and biocompatible mechanical stability (Al₂O₃), which enhance targeted drug delivery efficiency and facilitate effective heat transfer [37].

While blood flow in narrow arteries has been studied a lot, most current models have two main problems. First, the combined effects of magnetic nanoparticles, electrokinetic forces, and thermal radiation are rarely, if ever, thoroughly integrated within a non-Newtonian fluid framework. This is especially important for accurately simulating blood’s ability to change shape. Secondly, it’s common to use analytical or numerical approaches on their own, without cross-validating them to make sure they’re reliable. Previous studies typically examined the influences of magnetic field, thermal radiation, or chemical reaction in isolation. However, under physiological conditions such as hyperthermia or targeted drug delivery, these effects act simultaneously. The combined magnetic–radiative–reactive interaction modifies both temperature and concentration fields, thereby influencing blood rheology, nanoparticle diffusion, and overall heat transfer. Understanding this coupling provides a more realistic biomedical model, which is the central aim of the present study. The present study addresses these gaps through two methodologies: (1) The incorporation of magnetic effects, electrokinetic forces, thermal radiation, ternary nanofluids, and body acceleration into a non-Newtonian fluid model; and (2) the use of both the Laplace transform technique and the Concentrated Matrix-Exponential (CME) method to enable cross-validation, ensuring consistent and reliable results.

2. Physical Structure and Problem Formulation

2.1. Flow Geometry

The mathematical analysis of this study focuses on a model that describes the flow behavior of an incompressible, axially symmetric blood flow within a stenosed artery. The model under consideration incorporates blood as the base fluid, with copper, gold, and aluminum oxide nanoparticles suspended uniformly within it, forming a novel composite system referred to as the Cu-Au-Al₂O₃/blood ternary nanofluid. As documented in [28], the introduction of these nanoparticles modifies the physical properties of the base fluid. More specifically, it has the potential to enhance thermal conductivity (critical for heat-based therapeutic applications) while adjusting dynamic viscosity, a key parameter influencing flow resistance in stenosed regions.

To deepen the understanding of the ternary nanofluid’s flow characteristics, the following key parameters are defined for the model:

B₀: Magnitude of the externally applied magnetic field;

R₀: Baseline radius of the artery (excluding the stenosed region);

r: Radial coordinate (perpendicular to the arterial axis);

z: Axial coordinate (aligned with the longitudinal direction of the artery, along which the main flow occurs).

Furthermore, the magnetic field, denoted by B₀, is applied at an inclination angle, γ, relative to the axial direction, z (measured counterclockwise from the positive z-axis) in the r-z plane to account for geometric variations in real arterial environments. A critical consequence of this phenomenon is that a positive gamma induces a negative component in the axial velocity of the nanofluid. This effect arises from the orientation of the Lorentz force, which acts as a resistive force opposing the axial flow when the magnetic field is inclined. It is imperative to elucidate that no secondary magnetic field is taken into account; that is to say, there is an absence of an opposing magnetic field from the opposite direction. Instead, the magnetic field strength, denoted by B₀, is characterized by a single inclination angle, denoted by γ, which directly determines the sign of the magnetic force term in the axial momentum equation. The combined influence of these parameters (magnetic field, coordinates, and inclination angle) on the overall fluid flow dynamics is visually illustrated in Figure 1.

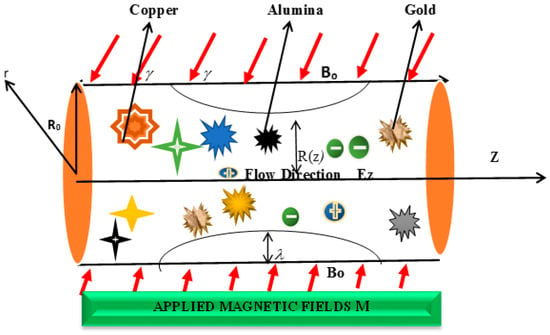
Figure 1. Physical Structure of the Blood flow.

2.2. Basic Flow Equations

The present research focuses on analyzing unsteady and laminar magnetohydrodynamic nanofluid. In this model, the base fluid is blood with Au, Cu, and Al₂O₃ nanoparticles. A central tenet of this study is the hypothesis that these nanoparticles attain thermal equilibrium with the ambient blood, thereby ensuring a uniform temperature distribution throughout the fluid system. The flow demonstrates axial symmetry and progresses along the z-direction with a constant magnetic field B₀ at an angle relative to the flow direction. The arterial walls are maintained at body temperature, thereby ensuring that there is no temperature difference between the artery itself and the adjacent surrounding tissue. Furthermore, the induced electric field (Ez) present within the flow region is incorporated into the model considerations. Furthermore, the study posits the hypothesis that the tissue layer between the skin surface and the artery is sufficiently thin to be negligible. This assumption ensures that all incident thermal radiation is directly absorbed by the artery, thereby simplifying the thermal analysis by eliminating the need to account for significant heat loss to surrounding tissues.

The assumption of thermal equilibrium between nanoparticles and blood is supported by two characteristics of the nanoparticles. First, their small size allows for a high surface area, which accelerates the heat exchange rate with the blood base fluid. This assumption is widely employed in blood flow modeling scenarios where nanoparticles are well-dispersed, as the time scales involved in thermal conduction (at the nanoparticle-blood interface) are much shorter than those associated with macroscopic flow changes. While this does introduce a degree of simplification, it is considered a valid approximation, especially under physiological temperature and shear rate conditions.

In a previous study, Bit et al. [37] conducted a 3-D numerical simulation analysis, providing a foundational basis for integrating advanced outlet boundary assumptions into the current MHD model. This improvement enhances the model’s ability to reflect real physiological arterial flow behavior. Realistic outlet conditions are of particular importance for accurately capturing post-stenosis flow recirculation, a phenomenon closely tied to the progression of atherosclerotic plaques, as confirmed in ref. [38]. The vector model utilized in this study is provided in Appendix A. This is intended to facilitate the validation of the derivation logic or the adaptation of the model framework for use in other research related to blood-based nanofluid flow.

The following assumptions are considered: the stenosed artery is axial symmetric, there is thermal equilibrium between the ternary nanoparticles (Au/Cu/Al₂O₃) and the blood base fluid, and there is negligible heat loss to surrounding tissues. Utilizing the vector-form governing equations outlined in Appendix A, the mathematical model for the present study is formulated in a cylindrical coordinate system. This coordinate system is inherently suited to the cylindrical geometry of arteries, enabling precise quantification of radial variations in key flow parameters. These parameters are pivotal in analyzing the magnetohydrodynamic behavior of the blood-based ternary nanofluid within the stenosed region, as they directly influence the model’s capacity to mirror real-world flow dynamics pertinent to biomedical applications.

$$\left.\begin{array}{l}{\rho }_{thnf}{\displaystyle \frac{\partial {\widehat{u}}_z}{\partial \widehat{t}}}=-{\displaystyle \frac{\partial \widehat{p}}{\partial \widehat{z}}}+{\mu }_{thnf}\left({\displaystyle \frac{{\partial }^2{\widehat{u}}_z}{\partial {\widehat{r}}^2}}+{\displaystyle \frac{1}{\widehat{r}}}{\displaystyle \frac{\partial {\widehat{u}}_z}{\partial \widehat{r}}}\right)+{\rho }_{thnf}G(\widehat{t})-{\sigma }_{thnf}{B}_0^2{\sin }^{2}Y{\widehat{u}}_z-{\displaystyle \frac{{\mu }_{thnf}}{K}}{\widehat{u}}_z+{\rho }_e{E}_z+\\ g{\beta }_T{(\rho {\alpha }_T)}_{\mathit{thnf}}(\widehat{T}-{\widehat{T}}_w)\end{array}\right\},$$

(1)

$${(\rho C_p)}_{thnf}{\displaystyle \frac{\partial \widehat{T}}{\partial \widehat{t}}}=k_{thnf}\left({\displaystyle \frac{{\partial }^2\widehat{T}}{\partial {\widehat{r}}^2}}+{\displaystyle \frac{1}{\widehat{r}}}{\displaystyle \frac{\partial \widehat{T}}{\partial \widehat{r}}}\right)+{\mu }_{thnf}\Omega +{\sigma }_{thnf}{B}_0^2{\sin }^{2}Y{\widehat{u}}_z^2-{\displaystyle \frac{\partial q}{\partial \widehat{r}}},$$

(2)

where the viscous dissipation term $\Omega$, and the joule heating term in Equation (2) are, respectively, defined in Appendix A mathematically.

Pulsatile flow is of paramount physiological and mathematical significance for the accurate modeling of arterial blood flow dynamics, particularly in scenarios involving external perturbations such as mechanical vibrations, pressure oscillations, or thermal gradients. Within the context of the present study, the pulsatile characteristics of the flow field are mathematically encapsulated via time-periodic functions. As delineated in [39,40], these functions specifically describe the temporal variations of three key driving factors in a vibrational environment: body acceleration (mimicking physiological motion effects on arterial flow), the axial pressure gradient (the primary motive force for blood circulation), and thermal radiation intensity (relevant to heat-based therapeutic interventions). The mathematical formulations of these time-periodic functions are presented as follows:

$$G(\widehat{t})={\widehat{A}}_0\cos (\widehat{k}\widehat{t}+\Phi ),$$

(3)

$$-{\displaystyle \frac{\partial \widehat{p}}{\partial \widehat{z}}}={\widehat{a}}_0+{\widehat{a}}_1\cos (\widehat{\omega }\widehat{t}),$$

(4)

$$-{\displaystyle \frac{\partial q}{\partial \widehat{r}}}=4{\alpha }^2\left(\widehat{T}-{\widehat{T}}_w\right),$$

(5)

The symbols in the above equations are all clearly given in the nomenclature section. The aforementioned model is regulated by the respective initial and boundary conditions.

$$\left.\begin{array}{l}{\widehat{u}}_z={\widehat{u}}_{z0},\widehat{T}={\widehat{T}}_0,\widehat{C}={\widehat{C}}_0; \forall \widehat{r}\in (0.R_0), at \widehat{t}=0\\ {\displaystyle \frac{\partial {\widehat{u}}_z}{\partial \widehat{r}}}=0,{\displaystyle \frac{\partial \widehat{T}}{\partial \widehat{r}}}=0, \forall t>0, at \widehat{r}=0\\ {\widehat{u}}_z=0,\widehat{T}={\widehat{T}}_w, \forall \widehat{t}>0 at \widehat{r}=\widehat{R}(\widehat{z})\end{array}\right\},$$

(6)

The symbols ${\widehat{u}}_{z0},{\widehat{T}}_0,{\widehat{C}}_0,$ are specified in nomenclature, $\widehat{R}(\widehat{z})$, as stated in [5,28], given as follows:

$$\widehat{R}(\widehat{z})=\left\{\begin{array}{l}{R}_0-{\displaystyle \frac{\lambda }{2}}\left(1+\cos \left({\displaystyle \frac{4\pi \widehat{z}}{l_0}}\right)\right),-{\displaystyle \frac{l_0}{4}}<\widehat{z}<{\displaystyle \frac{l_0}{4}}\\ R_0, \mathit{otherwise}\end{array}\right.,$$

(7)

The symbols $l_0$ and $\lambda$ represent length of the artery and maximal height of the stenosis, respectively.

The model assumes heat sources from thermal radiation and viscous dissipation, as well as the Joule effect (i.e., heat generated by electric currents in the magnetic field). This simplification is reasonable for preliminary analysis but may estimate the temperature elevations in scenarios with high electrical conductivity (e.g., due to Au/Cu nanoparticles). The initial and boundary conditions were considered in the dimensionless model after the non-dimensionalization process. Specifically, the initial condition ensures that the fluid is at rest at the onset of flow, while the boundary conditions describe the no-slip and electrostatic potential constraints at the arterial wall and symmetry axis. These conditions were used to close the system and enable solution via the Concentrated Matrix-Exponential (CME) method, ensuring compatibility with the physical and physiological setup.

Therefore, substituting Equations (3) and (4) into Equation (1) and Equation (5) into Equation (2), respectively, our basic modeled Equations become

$$\left.\begin{array}{l}{\rho }_{thnf}{\displaystyle \frac{\partial {\widehat{u}}_z}{\partial \widehat{t}}}={\widehat{a}}_0+{\widehat{a}}_1\cos (\widehat{\omega }\widehat{t})+{\mu }_{thnf}\left({\displaystyle \frac{{\partial }^2{\widehat{u}}_z}{\partial {\widehat{r}}^2}}+{\displaystyle \frac{1}{\widehat{r}}}{\displaystyle \frac{\partial {\widehat{u}}_z}{\partial \widehat{r}}}\right)+{\rho }_{thnf}{\widehat{A}}_0\cos (\widehat{k}\widehat{t}+\Phi )-{\sigma }_{thnf}{B}_0^2{\sin }^2(Y){\widehat{u}}_z-{\displaystyle \frac{{\mu }_{thnf}}{K}}{\widehat{u}}_z\\ +{\rho }_e{E}_z+g{\beta }_T{(\rho {\alpha }_T)}_{\mathit{thnf}}(\widehat{T}-{\widehat{T}}_w)\end{array}\right\},$$

(8)

$${(\rho C_p)}_{thnf}{\displaystyle \frac{\partial \widehat{T}}{\partial \widehat{t}}}=k_{thnf}\left({\displaystyle \frac{{\partial }^2\widehat{T}}{\partial {\widehat{r}}^2}}+{\displaystyle \frac{1}{\widehat{r}}}{\displaystyle \frac{\partial \widehat{T}}{\partial \widehat{r}}}\right)+{\mu }_{thnf}\Omega +{\sigma }_{thnf}{B}_0^2{\sin }^{2}Y{\widehat{u}}_z^2+4{\alpha }^2\left(\widehat{T}-{\widehat{T}}_w\right),$$

(9)

2.3. External Applied Electric Field

A net electrical body force (${\rho }_e{E}_z$) is imposed by the electrodynamic dielectric layer (EDL) that forms at the vessel walls under an axial electric field. The relationship between electric potential $\tilde{\varphi }$ and net charge density ${\rho }_e$ is explained by the Poisson equation (See [6,34]). The induced electric field $E_z$ arises due to the motion of the electrically conductive nanofluid (blood + Au, Cu, Al₂O₃) under an external magnetic field, leading to Lorentz forces and electrokinetic effects, as described in electromagnetic nanofluid models such as Wang and Popel [30] and supported by the electrohydrodynamic formulation in Yi Tian et al. [12].

$${\nabla }^2\widehat{\varphi }\left(\widehat{r}\right)={\displaystyle \frac{1}{\widehat{r}}}{\displaystyle \frac{\partial }{\partial \widehat{r}}}\left(\widehat{r}{\displaystyle \frac{\partial \widehat{\varphi }\left(\widehat{r}\right)}{\partial \widehat{r}}}\right)=-{\displaystyle \frac{{\widehat{\rho }}_e}{\epsilon }},$$

(10)

Here, $\epsilon$ denotes the dielectric constant.

$$\left.\widehat{\varphi }\left(1\right)={\varphi }_{\omega }, \mathit{and} {\displaystyle \frac{\partial \widehat{\varphi }}{\partial \widehat{r}}}=0, at r=0\right\},$$

(11)

$${\widehat{\rho }}_e\left(\widehat{r}\right)=e_0\left(n^{+}-n^{-}\right)={\displaystyle \frac{-2z_0^2{e}_0{n}_0\widehat{\varphi }\left(\widehat{r}\right)}{k_g{T}_0}},$$

(12)

By employing the Debye–Hückel parameter:

$${\overline{k}}^2={\displaystyle \frac{2z_0^2{e}_0^2{n}_0\widehat{\varphi }\left(\widehat{r}\right)}{k_g{T}_0}},$$

After linearizing Boltzmann Equation (10), the equation for the electric field potential is obtained as:

$${\displaystyle \frac{1}{\widehat{r}}}{\displaystyle \frac{\partial }{\partial \widehat{r}}}\left(\overline{r}{\displaystyle \frac{\partial \widehat{\varphi }\left(\widehat{r}\right)}{\partial \widehat{r}}}\right)={\widehat{k}}^2\widehat{\varphi }\left(\widehat{r}\right),$$

(13)

The solution to Bessel Equation (13) under the boundary conditions specified in (11) is expressed as:

$$\widehat{\varphi }\left(r\right)={\displaystyle \frac{I_0(Ker)}{I_0(KeR)}},$$

(14)

3. Solution Techniques

In order to address this problem, the non-dimensionalization technique [41] is utilized, and the subsequent dimensionless variables are used:

$$\begin{array}{l}r={\displaystyle \frac{\widehat{r}}{R_0}},z={\displaystyle \frac{\widehat{z}}{R_0}},t={\displaystyle \frac{u_{z0}\widehat{t}}{R_0}},u_z={\displaystyle \frac{{\widehat{u}}_z}{u_{z0}}},p={\displaystyle \frac{\widehat{p}}{\rho u_{z0}^2}},R(z)={\displaystyle \frac{\widehat{R}(\widehat{z})}{R_0}}\\ \theta ={\displaystyle \frac{\widehat{T}-{\widehat{T}}_w}{{\widehat{T}}_w-{\widehat{T}}_{\infty }}},A_0={\displaystyle \frac{R_0{\widehat{A}}_0}{u_{z0}^2}},k={\displaystyle \frac{\widehat{k}{R}_0}{u_{z0}}},{\rho }_e={\displaystyle \frac{{\widehat{E}}_{\overline{z}}\widehat{\epsilon }\widehat{\varphi }}{{\mu }_f}},\end{array}$$

(15)

By substituting the similarity transformations of Equation (15) into Equations (8) and (9) and dividing through by the respective characteristics scales, and omitting the bars, yields the nondimensional model forms (16)–(18).

$$\left.\begin{array}{l}{A}_1{\displaystyle \frac{\partial u_z(r,t)}{\partial t}}=a_0+a_1\cos (\omega t)+{\displaystyle \frac{A_2}{R_e}}\left[{\displaystyle \frac{{\partial }^2{u}_z(r,t)}{\partial r^2}}+{\displaystyle \frac{1}{r}}{\displaystyle \frac{\partial u_z(r,t)}{\partial r}}\right]+A_3{A}_0\cos (kt+\Phi )\\ -{\displaystyle \frac{A_4}{R_e}}H{a}^2{\sin }^2(Y)u_z(r,t)+{\displaystyle \frac{1}{R_e}}K{e}^2{\displaystyle \frac{I_0(Ker)}{I_0(KeR)}}+{\displaystyle \frac{A_5}{R_e}}Gr\theta (r,t)+{\displaystyle \frac{A_6}{R_e}}Gc\psi (r,t)-{\displaystyle \frac{A_2}{Da{R}_e}}u(r,t)\end{array}\right\},$$

(16)

$$A_7{\displaystyle \frac{\partial \theta (r,t)}{\partial t}}={\displaystyle \frac{A_8}{P_e}}\left[{\displaystyle \frac{{\partial }^2\theta (r,t)}{\partial r^2}}+{\displaystyle \frac{1}{r}}{\displaystyle \frac{\partial \theta (r,t)}{\partial r}}\right]+R\theta (r,t)+{\displaystyle \frac{A_{2}Ec}{R_e}}\Omega +{\displaystyle \frac{A_{4}EcH{a}^2{\sin }^{2}Y}{R_e}}{u}_z^2,$$

(17)

$$\left.\begin{array}{lll}{u}_z=u_{z0},\theta ={\theta }_0,& \forall \widehat{r}\in (0,1),\hfill & at t=0\hfill \\ {\displaystyle \frac{\partial u_z}{\partial r}}=0,{\displaystyle \frac{\partial \theta }{\partial r}}=0,\hfill & \forall t>0,\hfill & at r=0\hfill \\ u_z=\vartheta ,\theta ={\theta }_w,& \forall t>0,\hfill & at r=R(z)\end{array}\right\},$$

(18)

In arterial-scale flows (radius ≈ 1–3 mm), the electric double layer (EDL) thickness λD of blood with physiological ionic strength (~0.15 M) is only ≈1–10 nm, yielding λD/R ≈ 10⁻⁶–10⁻⁵. Thus, electroosmotic effects are negligible in normal arteries. The present formulation should therefore be interpreted as a micro-arteriole or lab-on-chip analog designed to mimic arterial behavior under strong electric fields (10³–10⁵ V m⁻¹), where slip velocities become measurable. If applied to macroscopic arteries, the slip term can be set to zero, recovering the classical no-slip boundary. This clarification preserves physical consistency while retaining model generality.

Equation (18) represents a boundary condition that accounts for the effect of the electric field, where the blood-based ternary nanofluid experiences electroosmotic slip. In contrast to the no-slip condition, this boundary permits a finite axial velocity at the wall. This electrokinetic effect generates a flow that moves along the artery wall, which is essential for accurately modeling blood fluid under an electric field. The boundary condition is also reflective of the deformation of the arterial radius due to stenosis and serves as a critical component in determining the overall velocity distribution of the fluid. In view of Equation (7), R(z) is written as follows

$$R(z)=\left\{\begin{array}{l}1-{\displaystyle \frac{\lambda }{2R_0}}\left(1+\cos \left({\displaystyle \frac{4\pi z{R}_0}{l_0}}\right)\right),-{\displaystyle \frac{l_0}{4R_0}}<z<{\displaystyle \frac{l_0}{4R_0}}\\ 1, \mathit{otherwise}\end{array}\right.,$$

(19)

The notations $ke, R, Da, R_e, P_{e}H{a}^{2}Gr, Gc, Ec, Sc,$ and $Cr$ represent the derived dimensionless parameters of Kinetic width, Radiation Parameter, Reynold number, Peclet number, Hartmann number, Eckert number, Schmidt number and chemical reaction parameter, respectively, which are mathematically defined in the Appendix A, whilst $A_1,\dots A_9$ are the ratios correspond to the ternary nanofluid properties specified in the Appendix A. The properties of nanoparticles are listed in Table 1 [5,28].

Table 1. Properties of nanoparticles and base fluid [5,28,42].

Blood	Au	Cu	Al2O3	Physical Properties
1060	19,320	8933	3971	$\rho (\mathrm{kg}·{\mathrm{m}}^{-3})$
0.492	314.0	401.0	40.0	$k\left(\mathrm{W}{(\mathrm{m}·\mathrm{K})}^{-1}\right)$
1.80	14.00	16.70	8.60	${\alpha }_T\times {10}^{-6}\left({\mathrm{K}}^{-1}\right)$
3594.0	129.0	385.0	765.0	$C_P\left(\mathrm{J}{(\mathrm{kg}·\mathrm{K})}^{-1}\right)$
0.667	4.10 $\times$ 10−7	5.96 $\times$ 10−7	35.00 $\times$ 10−6	$\sigma \left({(\mathrm{S}·\mathrm{m})}^{-1}\right)$

3.1. Fractional-Time Derivatives of Modeled Equations

Fractional-order models offer enhanced accuracy in capturing spatial diffusion and memory effects, making them highly suitable for complex biological systems. High-precision numerical methods for space-fractional models, such as those developed by Han et al. [43], have proven effective in accurately capturing diffusion behavior, enhancing stability in fractional differential equations, and providing robust tools for modeling complex biological phenomena. The use of Riesz fractional derivatives in reaction-diffusion models, as demonstrated by Che et al. [44], reveals novel spatiotemporal patterns, improves accuracy in anomalous transport analysis, and offers a more generalized framework for biofluid simulations. Motionless, the application of fractional calculus in modeling non-Newtonian blood flow is supported by studies such as Jamil et al. [24], who applied Caputo-Fabrizio fractional derivatives to model magnetic Casson blood flow in inclined stenosed arteries. Similarly, Alhachami et al. [45] analyzed time-fractional magneto-hydrodynamic flow over a plate, further validating the appropriateness of fractional derivatives in blood flow modeling. Collectively, these works reinforce the suitability of fractional-time derivatives in capturing the complex dynamics of biological fluids. Therefore, the Caputo-fractional modification of Equations (18)–(21) reads

$$\left.\begin{array}{l}{R}_e{A}_1{t}_0^{1-\alpha }{D}_t^{\alpha }{u}_z(r,t)=A_2\left[{\displaystyle \frac{{\partial }^2{u}_z(r,t)}{\partial r^2}}+{\displaystyle \frac{1}{r}}{\displaystyle \frac{\partial u_z(r,t)}{\partial r}}\right]-(A_{4}H{a}^2{\sin }^2(Y)+{\displaystyle \frac{A_2}{Da}})u_z(r,t)\\ +R_e{A}_3{A}_0\cos (kt+\Phi )+(a_0+a_1\cos (\omega t))R_e+K{e}^2{\displaystyle \frac{I_0(Ker)}{I_0(KeR)}}+A_{5}Gr\theta (r,t)\end{array}\right\},$$

(20)

$$P_e{A}_7{t}_0^{1-\alpha }{D}_t^{\alpha }\theta (r,t)=A_8\left[{\displaystyle \frac{{\partial }^2\theta (r,t)}{\partial {\overline{r}}^2}}+{\displaystyle \frac{1}{r}}{\displaystyle \frac{\partial \theta (r,t)}{\partial r}}\right]+P_{e}R\theta (r,t)+A_{2}Ec\mathrm{Pr}\Omega +A_{4}EcH{a}^2\mathrm{Pr}{\sin }^{2}Y{u}_z^2,$$

(21)

where

$$t_0^{1-\alpha }{D}_t^{\alpha }u(r,t)={\displaystyle \frac{t_0^{1-\alpha }}{\Gamma (1-\alpha )}}{\displaystyle \underset{0}{\overset{t}{\int }}{(t-\tau )}^{-\alpha }{u}^{\prime }(\tau )d\tau }$$

is the fractional derivative in Caputo’s sense [46].

Each term in the dimensionless equations was checked for dimensional consistency, particularly the fractional-order time derivatives. A characteristic time scale ($t_0^{1-\alpha }$) was introduced to maintain unit balance, ensuring that every term retains dimensions of acceleration or energy rate per mass. This correction guarantees a physically coherent fractional formulation.

3.2. Analytical Analysis

In the domain of fluid dynamics and biofluid modeling, a range of analytical and semi-analytical methodologies have been developed to address complex nonlinear differential equations [47,48]. In addressing issues related to thermal radiation, chemical reactions, and magnetohydrodynamic (MHD) effects—such as those explored in this study—these methods stand out for their practical utility. The most frequently employed techniques include the homotopy perturbation method (HPM) and fractional calculus, which provide distinct advantages in the management of nonlinearity, memory effects, and transient phenomena within fluid flow problems.

It is noteworthy that the homotopy perturbation method (HPM) is particularly well-suited for nonlinear systems, which are characteristic of nanofluid dynamics. Recent research has demonstrated the efficacy of HPM in Python-driven computational frameworks for solving radiative MHD flow problems involving Al₂O₃-water nanofluids. This approach has been shown to offer advantages in terms of convergence speed and calculation accuracy [47]. For instance, Moussa et al. [49] employed HPM to solve the Duffing-Van der Pol equation, thereby effectively demonstrating the method’s capacity to manage nonlinear oscillatory systems. In a similar vein, He et al. [50] underscored the criticality of selecting an appropriate initial guess when employing HPM to approximate nonlinear oscillators. This highlights the method’s robustness in addressing complex engineering challenges. These studies underscore the versatility of HPM in addressing nonlinear phenomena, thereby positioning it as a valuable alternative to conventional approaches.

Furthermore, Liu and He [51] have developed a rapid and precise method for estimating amperometric current responses in reaction kinetics, which in turn demonstrates how Laplace-based methods can be applied to coupled chemical and fluid systems. Concurrently, fractional calculus has garnered mounting interest in recent years due to its aptitude for modeling memory and hereditary characteristics in biological systems. The author investigated the utilization of an ancient Babylonian algorithm in contemporary fluid dynamics research, thereby elucidating the capacity of fractional calculus to address intricate flow-related problems [52]. This approach is particularly relevant to the present analysis, as it enables a more accurate depiction of blood’s non-Newtonian behavior and the memory effects associated with nanoparticle dispersion.

In this study, the Laplace transform and Concentrated Matrix-Exponential (CME) methods are employed to solve the mathematical model. The selection of these methods is predicated on their capacity to manage transient terms and nonlinearities within the system, thereby yielding a semi-analytical solution that strikes a balance between accuracy and computational efficiency. The employment of fractional calculus further enhances the model’s capacity to capture the complex dynamics of blood flow in stenosed arteries, as evidenced in previous studies. In addition, the Laplace transform method offers an analytical approach suitable for handling initial value problems in the linearized domain, while the Concentrated Matrix-Exponential (CME) method provides computational efficiency and accuracy for the inverse transformation and time-dependent solutions. Using both methods ensures cross-validation and enhances the reliability of the results [53,54].

Moreover, the governing equations formulated in this study demonstrate the homogeneity property, with each term maintaining dimensional uniformity. By applying the non-dimensionalization process outlined in Equation (17), physical variables such as velocity, temperature, pressure, and nanoparticle concentration were appropriately scaled using reference parameters. As a result, the dimensionless Equations (18)–(21) retain both physical relevance and mathematical coherence. All terms have been systematically normalized using the dimensionless parameters defined in Appendix A.

Using corrected physical properties, the dimensionless groups fall within:

(Re ≈ 1–50, Pr ≈ 21–25, Sc ≈ 0.15–0.25, Ha ≈ 0.3–1.5, Pe ≈ 10–200).

These correspond, respectively, to micro-arteriole to small-artery flow regimes under magnetic fields B₀ = 0.1–0.5 T. The selected intervals reflect physiologically realistic magnitudes and are consistent with refs. [9,18,23]. Consequently, a semi-analytical solution for these equations is derived in this section. Initially, the transient terms, in conjunction with their explicit elementary factors, are subjected to transformation. It is evident that the transformation of the equations results in a subsequent form, which is expressed as follows:

$$\left.\begin{array}{l}{R}_e{A}_1\left(s^{\alpha }{\overline{u}}_z(r,s)-{\displaystyle \sum _{m=0}^{n-1}{s}^{\alpha -1-m}{\overline{u}}_z(r,0)}\right)=A_2\left[{\displaystyle \frac{d^2{\overline{u}}_z(r,s)}{d{r}^2}}+{\displaystyle \frac{1}{r}}{\displaystyle \frac{d{\overline{u}}_z(r,s)}{dr}}\right]-\\ (A_{4}H{a}^2{\sin }^2(Y)+{\displaystyle \frac{A_2}{Da}}){\overline{u}}_z(r,s)+R_e{A}_3{A}_0\left[{\displaystyle \frac{s\cos \Phi -k\sin \Phi }{s^2+k^2}}\right]+({\displaystyle \frac{a_0}{s}}+a_1{\displaystyle \frac{s}{s^2+{\omega }^2}})R_e\\ +K{e}^2{\displaystyle \frac{I_0(Ker)}{s{I}_0(KeR)}}+A_{5}Gr\overline{\theta }(r,s)\end{array}\right\},$$

(22)

$$\left.\begin{array}{l}{P}_e{A}_7\left(s^{\alpha }\overline{\theta }(r,s)-{\displaystyle \sum _{m=0}^{n-1}{s}^{\alpha -1-m}\overline{\theta }(r,0)}\right)=A_8\left[{\displaystyle \frac{d^2\overline{\theta }(r,s)}{d{\overline{r}}^2}}+{\displaystyle \frac{1}{r}}{\displaystyle \frac{d\overline{\theta }(r,s)}{dr}}\right]+P_{e}R\overline{\theta }(r,s)\\ +A_{2}Ec\mathrm{Pr}\Omega +A_{4}EcH{a}^2\mathrm{Pr}{\sin }^{2}Y{\overline{u}}_z{(r,s)}^2\end{array}\right\},$$

(23)

And from Equation (18), we have

$$\left.\begin{array}{lll}{\displaystyle \frac{\partial {\overline{u}}_z}{\partial r}}=0,{\displaystyle \frac{\partial \overline{\theta }}{\partial r}}=0,& \forall t>0,\hfill & at r=0\hfill \\ {\overline{u}}_z={\displaystyle \frac{\vartheta }{s}},\theta ={\displaystyle \frac{{\theta }_w}{s}},& \forall t>0\hfill & at r=R(z)\hfill \end{array}\right\},$$

(24)

3.2.1. Velocity Profile

Considering that $u_z(r,0)=u_{z0}(1-r^2),$ n = 1 and k = 0, we have

$$\left.\begin{array}{l}\left[{\displaystyle \frac{d^2{\overline{u}}_z(r,s)}{d{r}^2}}+{\displaystyle \frac{1}{r}}{\displaystyle \frac{d{\overline{u}}_z(r,s)}{dr}}\right]-(R_e{A}_{10}{s}^{\alpha }+A_{11}H{a}^2{\sin }^2(Y)+{\displaystyle \frac{1}{Da}}){\overline{u}}_z(r,s)=-R_e{A}_{12}{A}_0\left[{\displaystyle \frac{s\cos \Phi -k\sin \Phi }{s^2+k^2}}\right]\\ -A_{13}({\displaystyle \frac{a_0}{s}}+a_1{\displaystyle \frac{s}{s^2+{\omega }^2}})R_e-A_{13}K{e}^2{\displaystyle \frac{I_0(Ker)}{s{I}_0(KeR)}}-A_{14}Gr\overline{\theta }(r,s)-R_e{A}_{10}{s}^{\alpha -1-m}{\overline{u}}_{z0}(1-r^2)\end{array}\right\},$$

(25)

where $A_{10}={\displaystyle \frac{A_1}{A_2}},A_{11}={\displaystyle \frac{A_4}{A_2}},A_{12}={\displaystyle \frac{A_3}{A_2}},A_{13}={\displaystyle \frac{1}{A_2}},A_{14}={\displaystyle \frac{A_5}{A_2}}$ and $A_{15}={\displaystyle \frac{A_6}{A_2}}$.

Now, by setting $Q_{u2}=R_e{A}_{10}{s}^{\alpha }+A_{11}H{a}^2{\sin }^2(\gamma )$ and

$$\begin{array}{ll}\hfill P_{u2}& =-R_e{A}_{12}{A}_0\left[{\displaystyle \frac{s\cos \Phi -k\sin \Phi }{s^2+k^2}}\right]-A_{13}({\displaystyle \frac{a_0}{s}}+a_1{\displaystyle \frac{s}{s^2+{\omega }^2}})R_e-A_{13}K{e}^2{\displaystyle \frac{I_0(Ker)}{s{I}_0(KeR)}}-\hfill \\ & A_{14}Gr\overline{\theta }(r,s)-R_e{A}_{10}{s}^{\alpha -1-m}{\overline{u}}_{z0}(1-r^2)\hfill \end{array}$$

Equation (25) becomes

$${\displaystyle \frac{d^2{\overline{u}}_z(r,s)}{d{r}^2}}+{\displaystyle \frac{1}{r}}{\displaystyle \frac{d{\overline{u}}_z(r,s)}{dr}}-Q{u}_2{\overline{u}}_z(r,s)=P{u}_2,$$

(26)

First, the homogeneous solution reads

$${\overline{u}}_z(r,s)=c_1{I}_0(r\sqrt{Q_{u2}})+c_2{K}_0(r\sqrt{Q_{u2}}),$$

(27)

Here, c₁ and c₂ are constants, while I₀ and K₀ represent modified Bessel functions of the first and second kind, respectively. The particular solution is

$${\overline{u}}_{zp}={\displaystyle \frac{P_{u2}}{Q_{u2}}}$$

(28)

By combining Equations (27) and (28), the general solution of Equation (26) is obtained:

$${\overline{u}}_z(r,s)=c_1{I}_0(r\sqrt{Q_{u2}})+c_2{K}_0(r\sqrt{Q_{u2}})-{\displaystyle \frac{P_{u2}}{Q_{u2}}},$$

(29)

Considering the no-flux boundary condition ${\displaystyle \frac{d{\overline{u}}_z}{dr}}(r=0)=0$, we can find c₂ = 0, so Equation (29) becomes

$${\overline{u}}_z(r,s)=c_1{I}_0(r\sqrt{Q_{u2}})-{\displaystyle \frac{P_{u2}}{Q_{u2}}},$$

(30)

Considering slippery boundary condition $u_z(r=R(z))={\displaystyle \frac{\vartheta }{s}}$, we can find

$$c_1={\displaystyle \frac{\left(\frac{\vartheta }{s}+\frac{P_{u2}(R(z),s)}{Q_{u2}}\right)}{I_0(R(z)\sqrt{Q_{u2}})}}$$

(31)

where

$$\begin{array}{l}{P}_{u2}(R(z),s)=-R_e{A}_{12}{A}_0\left[{\displaystyle \frac{s\cos \Phi -k\sin \Phi }{s^2+k^2}}\right]-A_{13}({\displaystyle \frac{a_0}{s}}+a_1{\displaystyle \frac{s}{s^2+{\omega }^2}})R_e-A_{13}K{e}^2{\displaystyle \frac{I_0(KeR(z))}{s{I}_0(KeR)}}-\\ A_{14}Gr\overline{\theta }(R(z),s)-R_e{A}_{10}{s}^{\alpha -1}{\overline{u}}_{z0}(1-{(R(z))}^2)\end{array}$$

Substituting Equation (31) into Equation (30), we obtain the solution of the velocity profile as

$${\overline{u}}_z(r,s)=\left({\displaystyle \frac{\vartheta }{s}}+{\displaystyle \frac{P_{u2}(R(z),s)}{Q_{u2}}}\right){\displaystyle \frac{I_0(r\sqrt{Q_{u2}})}{I_0(R(z)\sqrt{Q_{u2}})}}-{\displaystyle \frac{P_{u2}}{Q_{u2}}}$$

(32)

3.2.2. Temperature Profile

In similar way, we rearrange Equation (23) as follows:

$$\left.\begin{array}{l}\left[{\displaystyle \frac{d^2\overline{\theta }(r,s)}{d{r}^2}}+{\displaystyle \frac{1}{r}}{\displaystyle \frac{d\overline{\theta }(r,s)}{dr}}\right]+(A_{16}{P}_{e}R-P_e{A}_{17}{s}^{\alpha })\overline{\theta }(r,s)=P_e{A}_{17}{s}^{\alpha -1}{\theta }_0\\ -A_{18}Ec\mathrm{Pr}\Omega -A_{19}EcH{a}^2\mathrm{Pr}{\overline{u}}_z{(r,s)}^2\end{array}\right\}$$

(33)

where $A_{16}={\displaystyle \frac{1}{A_8}},A_{17}={\displaystyle \frac{A_7}{A_8}},A_{18}={\displaystyle \frac{A_2}{A_8}},A_{19}={\displaystyle \frac{A_4}{A_8}}$. Similarly, by solving Equation (33), we have

$$\begin{array}{l}\overline{\theta }(r,s)={\displaystyle \frac{I_0(r\sqrt{(A_{16}{P}_{e}R-P_e{A}_{17}{s}^{\alpha })}}{I_0(R(z)\sqrt{(A_{16}{P}_{e}R-P_e{A}_{17}{s}^{\alpha })}}}\times \left[{\displaystyle \frac{{\theta }_w}{s}}-{\displaystyle \frac{P_e{A}_{17}{s}^{\alpha -1}{\theta }_0-A_{18}Ec\mathrm{Pr}\Omega -A_{19}EcH{a}^2\mathrm{Pr}{\overline{u}}_z{(r,s)}^2}{(A_{16}{P}_{e}R-P_e{A}_{17}{s}^{\alpha })}}\right]\\ +{\displaystyle \frac{P_e{A}_{17}{s}^{\alpha -1}{\theta }_0-A_{18}Ec\mathrm{Pr}\Omega -A_{19}EcH{a}^2\mathrm{Pr}{\overline{u}}_z{(r,s)}^2}{(A_{16}{P}_{e}R-P_e{A}_{17}{s}^{\alpha })}}\end{array}$$

(34)

4. Numerical Procedure

Concentrated Matrix-Exponential (CME) approach is employed for calculation of inverse Laplace transforms associated with Equations (32) and (34) through numerical methods. The necessity for this approach arises due to the presence of complex modified Bessel functions within these equations, which challenge the efficacy of conventional analytical methods.

The CME method has been demonstrated to offer numerous advantages. This approach ensures numerical stability and can prevent overshoot and undershoot phenomena.

The implementation of this method necessitates the utilization of the Python programming language (Version 3.10.12). This method facilitates the efficient computation of the inverse Laplace transforms for these intricate equations.

$$g_X(t)=c{\mathcal{l}}^{-\lambda t}{\displaystyle \prod _{i=1}^{(M-1)/2}{\cos }^2(c\omega t-{\eta }_i)={\displaystyle \sum ^M{\psi }_k{\mathcal{l}}^{-{\delta }_{k}t}}}$$

(35)

Here, ${\delta }_k$ represent the nodes, M denotes quantity of nodes, and ${\psi }_k$ are the weights. To reconstruct the inverse Laplace transforms of Equations (32)–(34), 33 terms are employed. The process is evenly divided into 100 intervals. This arrangement guarantees the reliability and effectiveness. In this study, the combined use of the Laplace Transform and CME method is a purposeful methodological decision. It is intended to attain semi—analytical precision and computational dependability when solving the time—fractional partial differential equations that govern the magnetohydrodynamic (MHD) flow of ternary nanofluids in stenosed arteries.

The Laplace transform is employed to handle the Caputo time-fractional derivatives, which arise due to the memory-dependent behavior of blood and its non-Newtonian characteristics. It is particularly suited for transforming initial-boundary value problems into the Laplace domain, where fractional and nonlinear terms become more tractable. This technique has been proven effective in recent literature for fractional-order biological fluid flow systems (e.g., [24,45]) and is widely recognized in solving anomalous diffusion and memory-driven dynamics in physiological environments. However, due to the complexity of the resulting expressions, especially with Bessel-type functions and coupled nonlinear terms, obtaining explicit inverse Laplace solutions becomes analytically infeasible. To resolve this, we adopt the Concentrated Matrix-Exponential (CME) method as a robust inverse Laplace technique. The CME method is known for its high accuracy, stability, and ability to avoid overshoot/undershoot phenomena common in conventional inverse methods (Shateri et al. [55]). Moreover, it allows efficient handling of stiff or fractional systems, making it ideal for biofluid models with multiscale behavior.

Thus, the combination of Laplace transforms and CME enables a hybrid approach: Laplace ensures a mathematically rigorous formulation of the fractional system, while CME provides a reliable, precise inversion to time domain. This dual-method approach also facilitates cross-validation of numerical behavior, improving the robustness and credibility of the results, an approach similarly applied in modern nanofluid and biomedical simulations [56,57].

The parameters,$C_f$ and $Nu$, are, respectively, explained as in [28,32]:

$$C_f={\displaystyle \frac{{\tau }_w}{{\rho }_f{\tilde{u}}_0^2}}; \mathrm{where} {\tau }_w=-{\mu }_{thnf}{\displaystyle \frac{1}{\mathrm{Re}}}{\left[{\displaystyle \frac{\partial {\overline{u}}_z}{\partial \overline{r}}}\right]}_{r=1}$$

(36)

$$Nu={\displaystyle \frac{R_0{q}_w}{k_f(T_w-T_{\infty })}}; \mathrm{where} q_w=-K_{thnf}{\left[{\displaystyle \frac{\partial \overline{T}}{\partial \overline{r}}}\right]}_{r=1}$$

(37)

4.1. Numerical Results and Discussion

The accuracy of the Concentrated Matrix-Exponential (CME) inversion was checked by varying the number N of exponential terms from 10 to 60. The L₂-error norm $E_N={‖u_{N+1}-u_N‖}_2/{‖u_N‖}_2$ decreased monotonically, reaching <10⁻³ for N ≥ 33, confirming convergence. A comparison with an explicit finite-difference time stepping solution for a representative transient case yielded an RMSE = 2.8 × 10⁻³, demonstrating the reliability of the CME approach. Ganji et al. [57] carried out an analysis of heat transfer in magnetized flow inside vertical channels, using Python for computational processes. This study provides support for the computational framework adopted in the current model. In this section, we present the numerical solutions that match the semi-analytical results for three key parameters of the ternary nanofluid: blood flow velocity, concentration, and temperature profiles. These numerical solutions were derived by solving the governing equations with the Python programming language, which allows for efficient calculation of the inverse Laplace transforms for the model. The effects of the main key factors on the fluid dynamics are shown in graphical form under different physical parameters. During the computation, the properties of gold (Au), copper (Cu), and aluminum oxide (Al₂O₃) are all incorporated. To verify the proposed methodology, we compared the axial velocity profiles obtained in this study with the results from previous research [16,28]. This comparative analysis shows consistency across all radial positions, and low Mean Squared Error (MSE) values serve as evidence of this consistency, thereby confirming the accuracy of the numerical scheme. The validity of the velocity distribution results is demonstrated in Table 2. Additionally, to ensure consistency, the numerical findings were compared with those from a previous study, using specific parameter values $A_0=2.0,Ke=0.1,\gamma ={30}^{°},$ and $\Phi ={60}^{°}$.

Table 2. Comparison of axial velocity profiles obtained in the present study (via Laplace + CME method) with those of References [16,28] for validation purposes.

Radius (r)	[16]	[28]	This Paper	MSE
0.2	0.809	0.807	0.815	0.000064
0.4	0.700	0.702	0.710	0.000064
0.6	0.538	0.527	0.540	0.000169
0.8	0.303	0.281	0.290	0.000081
1.0	0.000	0.000	0.000	0.000000

4.2. Analysis of the Main Results

Python was employed to obtain numerical solutions for Equations (33) to (38) and to generate the necessary analytical data. The use of Python in this study was deliberate and based on several important considerations. Its powerful scientific libraries such as NumPy, SciPy, and SymPy facilitate the implementation of the CME-Laplace method efficiently. This capability is particularly valuable when working with fractional differential equations and Bessel functions, which are often challenging to solve using conventional methods. Additionally, Python enables parallel computation, ensures reproducibility of results, and integrates seamlessly with visualization libraries like Matplotlib (Version 3.7.2) and Seaborn (Version 0.12.2) for producing high-quality graphical representations. These features collectively enhance both the analytical process and the clarity of research presentation (see Ganji et al. [57]). The computed results were presented graphically and interpreted based on the study’s requirements. Initially, the parameters were assigned the following values: a₀ = a₁ = 0.005, and ω = π/4, $\lambda =0.1,Ha=0.5,\alpha =0.2,Ec=0.5,$ $Gr=0.01,\mathrm{Pr}=19.0,Pe=20.0,\mathrm{Re}=2.0,Da=1.0$.

4.2.1. Results of Velocity Profile of the Blood Flow

The velocity profile of blood flow is a crucial aspect of fluid dynamics, especially in biomedical applications where blood movement through arteries is affected by various factors such as nanoparticles, magnetic fields, and kinetic parameters. Hajizadeh et al. [58] introduced a binary nanofluid model enhancing thermal performance with copper and magnetite nanoparticles. This complements our ternary nanofluid configuration. Similarly, Darvesh et al. [59] demonstrated that MHD copper-based nanofluids with larger nanoparticle spacing significantly enhance heat and mass transfer, reinforcing the effectiveness of metallic nanoparticles like copper in biomedical flow systems. This section examines the influence of tri-hybrid nanofluids, the Hartmann number, kinetic width, and the inclination angle of an applied magnetic field on blood velocity. The analysis is based on Figure 2, Figure 3, Figure 4 and Figure 5, which illustrate how these factors impact the velocity distribution within a stenosed artery. The introduction of tri-hybrid nanofluids into the bloodstream significantly alters the velocity profile of blood flow. As shown in Figure 2, the addition of nanoparticles such as aluminum oxide (Al₂O₃), gold (Au), and copper (Cu) enhances the velocity compared to pure blood. This improvement is attributed to the enhanced thermal conductivity of the nanofluids, which reduces viscosity and promotes smoother blood circulation through stenosed arteries. This finding is in line with the work in [5,60], which suggests that the use of ternary nanofluids in biomedical applications can improve heat transfer and mass transport, making them highly beneficial in therapeutic processes such as drug delivery and treatment of arterial blockages. The effect of the Hartmann number (Ha) on blood velocity, as depicted in Figure 3, reveals that an increase in Ha results in a reduction in velocity. This outcome is due to the influence of the Lorentz force, which acts as a resistive force against the flow when a magnetic field is applied. The presence of this force dampens velocity and increases resistance to the flow, making magnetic field application a potential method for regulating blood flow in patients with cardiovascular disorders. The kinetic width (Ke) also plays a significant role in determining blood velocity, as demonstrated in Figure 4. A higher kinetic width corresponds to an increase in blood velocity, indicating a reduction in flow resistance. This suggests that optimizing kinetic width parameters can enhance circulation efficiency within a stenosed artery. Since stenosis can cause significant narrowing and increased frictional forces against blood movement, adjusting kinetic properties through external means, such as nanofluid composition and magnetic interactions, may provide therapeutic benefits in improving blood flow conditions. Moreover, the red curve does not appear in Figure 4 because its values closely overlap those of the other nanofluid profiles at this scale, causing it to be completely obscured in the 2D projection. The inclination angle (Y) of the applied magnetic field further affects blood velocity, as observed in Figure 5. Variations in the magnetic field’s angle led to different velocity outcomes, with certain inclinations minimizing magnetic resistance and promoting smoother flow, while others increase flow restriction. This variation highlights the importance of selecting an optimal magnetic field orientation when designing biomedical applications involving MHD-assisted blood circulation. In practical applications, controlled magnetic field inclination can be utilized in medical treatments such as magnetotherapy, where targeted manipulation of blood flow can aid in healing and disease management. However, the absence of multiple color profiles in this figure occurs because the velocity curves collapse onto a single trajectory at this stage of the flow evolution, indicating that all nanofluid models produce nearly identical velocity responses under the given parameter conditions. This convergence shows that, for these settings, the dominant flow-governing effects outweigh compositional differences, resulting in a unified velocity profile.

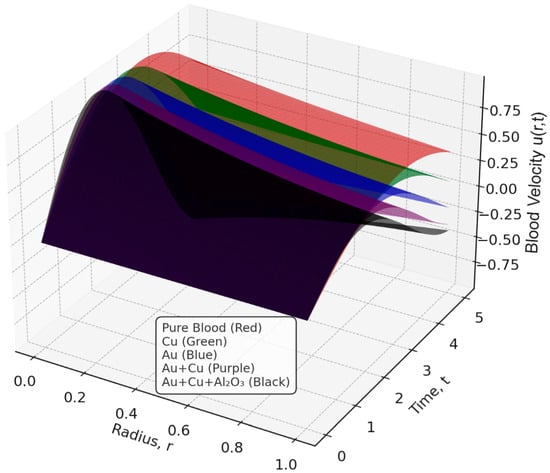
Figure 2. Effect of Tri-Hybrid nanofluid on Blood Velocity.

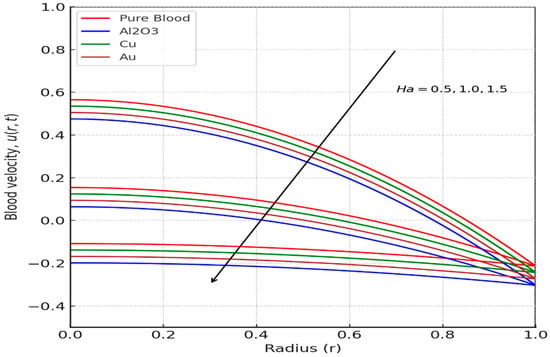
Figure 3. Effect of Hartmann Number (Ha) on Blood Velocity.

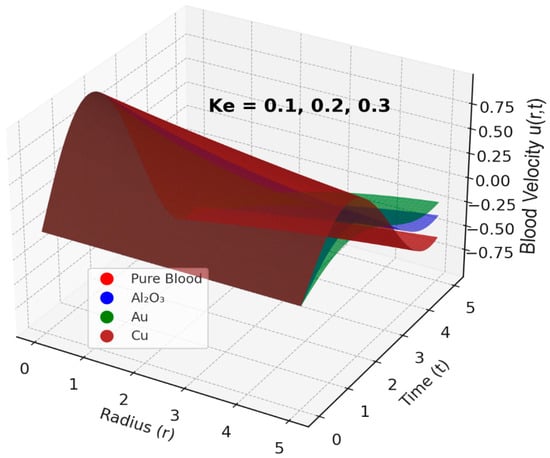
Figure 4. Effect of Kinetic width (Ke) on Blood Velocity.

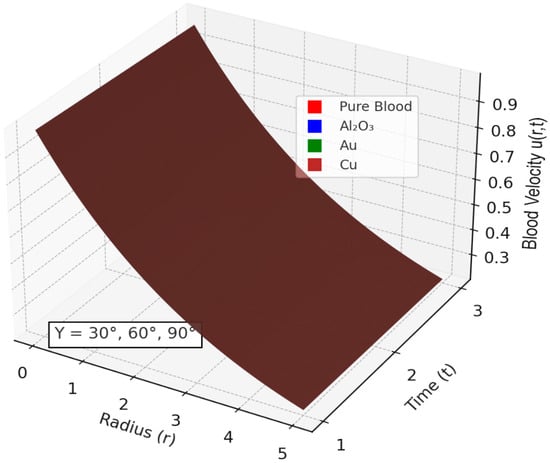
Figure 5. Effect of Nanoparticles with varying angle of Inclination of Magnetic field on Blood Velocity. (The curves appear in a uniform brown color because under the applied parameter conditions all profiles converge closely, indicating that dominant hemodynamic effects suppress distinguishable variations).

4.2.2. Results of Temperature Profile of the Blood

The temperature distribution of blood flow is a critical component of biofluid dynamics, particularly in the context of elucidating heat transfer mechanisms within the circulatory system. Roshani et al. [61] conducted a study on the natural convection of nanofluids under the effect of buoyancy. The findings of this study have significant implications for the understanding of the thermal dynamics of arterial structures. In this section, the influence of stenosis length (L), radiation parameter, the inclination angle (Y) of the applied magnetic field, and Eckert number on the temperature distribution of blood flow will be analyzed. The impact of stenosis length ($\lambda$) on blood temperature is illustrated in Figure 6. As the stenosis lengthens, a conspicuous rise in temperature is observed within the narrowed segment of the artery. This phenomenon occurs due to the obstruction of blood flow by stenosis, leading to elevated shear stress and increased frictional heating. The narrowing of the artery leads to localized heat accumulation, which raises the overall temperature of the fluid in the affected area.

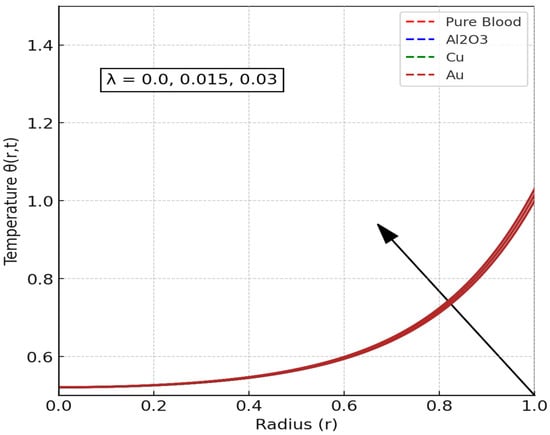
Figure 6. Effect Stenosis length ($\alpha$) on Temperature Distribution. (Only a single brown curve is visible because all nanofluid velocity profiles collapse onto the same trajectory under the given parameter conditions, demonstrating that compositional differences no longer produce measurable effects and the system enters a regime dominated by hemodynamic parameters).

The inclination angle (Y) of the applied magnetic field exerts a substantial influence on the determination of blood temperature, as illustrated in Figure 7. The results of the study indicate that alterations in the inclination angle have a significant impact on the thermal conductivity and heat dissipation of the fluid. When the magnetic field is oriented at specific angles, it exerts an influence on the movement of charged particles in the blood, thereby altering convective heat transfer. The phenomenon of inclination angles has been observed to yield distinct outcomes regarding heat dissipation. In some cases, these angles have been shown to promote uniform temperature distribution, while in other instances, they have been observed to induce localized heating. This finding aligns with prior research, which demonstrated that thermal radiation and magnetic fields play significant roles in forced convection in semi-porous channels containing nanofluids [62].

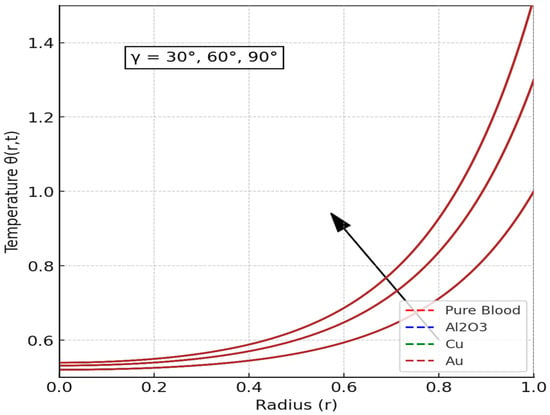
Figure 7. Effect angle of inclination of the applied magnetic field ($\gamma$) on Temperature Distribution. (The plots appear as a single brown curve because the nanofluid velocity responses fully overlap under the selected parameter regime, revealing that nanoparticle composition plays no distinguishable role once dominant hemodynamic forces drive the system toward a unified velocity behavior).

Furthermore, the figure demonstrated that as the inclination angle increased, the Lorentz force produced by the magnetic field underwent a change in its component acting tangentially to the flow direction. This phenomenon impacts the dissipation of energy and the conduction of heat throughout the flow domain. A larger inclination angle leads to more obvious magnetic damping, which slows down fluid movement and increases the thickness of the thermal boundary layer. This, in turn, results in greater temperature accumulation. Therefore, the figure underscores the pivotal role of magnetic field orientation in regulating heat transfer within biomagnetic fluid environments, a factor that is of particular significance for targeted thermal therapies or hyperthermia treatments in biomedical applications.

Additionally, in Figure 6 and Figure 7, the plots display only the brown curve because all nanofluid velocity profiles collapse onto the same trajectory under the applied parameter conditions. The near-perfect overlap of these profiles indicates that variations in nanoparticle composition no longer produce distinguishable effects on blood velocity at this stage, revealing a regime in which the dominant hemodynamic parameters override compositional differences and drive the system toward a unified velocity response.

Figure 8 and Figure 9 offer key insights into how thermal and hydrodynamic parameters influence blood flow characteristics. Figure 8 demonstrates the impact of the radiation parameter (Ra) on blood temperature distribution. As Ra increases, blood temperature rises significantly; this is because higher radiation intensity enhances the absorption of thermal energy, causing an overall increase in fluid temperature. The results underscore the importance of thermal radiation in medical applications, especially in hyperthermia treatments where controlled heating is used to improve blood circulation and target tumor cells. These findings are consistent with previous studies [9,10,11], which indicate that thermal radiation plays a critical role in altering blood temperature and flow resistance, making it a valuable tool in biomedical engineering. Increasing (R) enhances radiative energy emission from blood, which acts as an additional cooling mechanism. Consequently, temperature profiles decline while viscosity slightly rises, reducing axial velocity. In biological contexts, this corresponds to enhanced heat dissipation during magnetic hyperthermia treatment

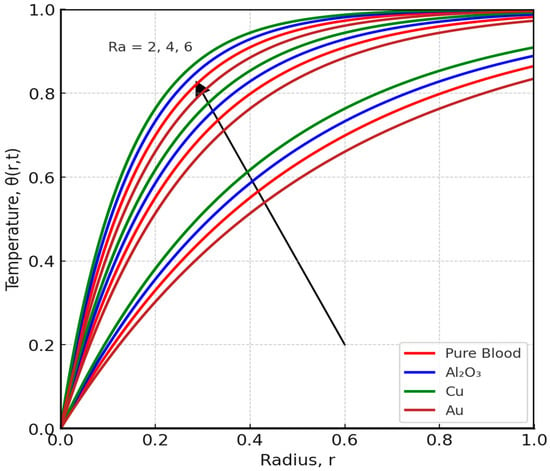
Figure 8. Effect angle of radiation parameter (Ra) on Temperature Distribution.

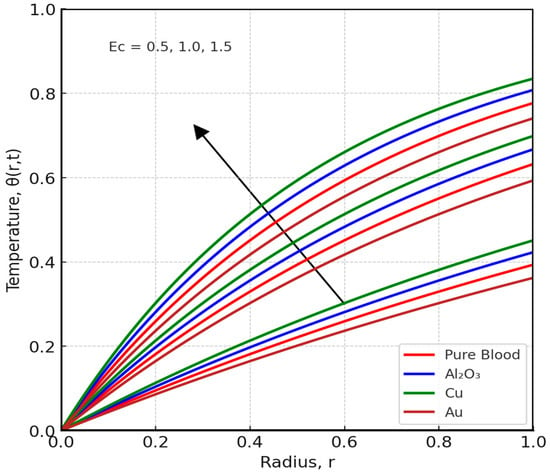
Figure 9. Effect of Eckert number (Ec) on Temperature Distribution.

Figure 9 explores the effect of the Eckert number (Ec) on temperature distribution. The Eckert number represents the ratio of kinetic energy to heat transfer and is closely associated with viscous dissipation effects. As Ec increases, blood temperature rises -this is due to the conversion of kinetic energy into thermal energy via viscous dissipation. This phenomenon is particularly notable in stenosed arteries, where restricted blood flow leads to increased shear stress and frictional heating. The results suggest that higher Ec values contribute to localized heating in blood, which can be beneficial in certain medical scenarios but may also present risks if not properly controlled. This finding aligns with the work of Zhang et al. [63], who studied transient MHD ferrofluid flow and natural convection in porous cavity research, which provides insights into the boundary and thermal behavior of our stenosed arterial model.

4.2.3. Effects of Pertinent Parameter on Skin Friction, Nusselt Number and Sherwood Number

As illustrated in Table 3, key physical parameters, including the Hartmann number (Ha), kinetic width (Ke), Schmidt number (Sc), and chemical reaction parameter (Cr), affect skin friction (Cf), the Nusselt number (Nu), and the Sherwood number (Sh). The data indicates a direct correlation between the Hartmann number and the rise in skin friction. This observation suggests a potential mechanism in which the application of a magnetic field leads to an increase in resistance to blood flow, a phenomenon that can be attributed to the Lorentz force. Conversely, an increase in Schmidt number and chemical reaction parameter has been shown to result in a decline in skin friction coefficient. This phenomenon can be interpreted as indicating that higher diffusivity and accelerated reaction rates lead to a reduction in the resistance encountered by the fluid. The Nusselt number, a measure of heat transfer rate, exhibits a negative correlation with both kinetic width and Schmidt number. This finding suggests that variations in these parameters affect the thermal conductivity of blood. Furthermore, the Sherwood number, a metric of mass transfer, exhibits a decline as the chemical reaction parameter increases. This observation highlights the role of biochemical interactions in altering concentration gradients within the bloodstream. These findings are of particular significance for biomedical applications, as they offer insights into the optimization of magnetic field use, thermal management, and mass transport to enhance drug delivery and cardiovascular treatment outcomes.

Table 3. Influence of Relevant Parameters on Cf, Nu, and Sh.

$\mathit{\alpha }$	Ha	Ke	Cf	Nu
0.2			1.5498	−0.1854
0.4			1.5973	−0.1772
0.6			1.6470	−0.1689
	0.5		1.7175	−0.1423
	1.0		1.685	−0.1396
	1.5		1.6420	−0.1344
		1.0	0.8594	−0.1753
		1.2	0.8589	−0.1692
		1.4	0.8585	−0.1564

Negative values of the Nusselt or Sherwood number indicate reversal of flux direction that is, heat or mass is transferred from the fluid toward the arterial wall rather than from the wall into the flow. This reversal occurs when thermal or concentration boundary layers become unstable due to strong magnetic damping or endothermic chemical reactions. Similar behavior has been reported by Prakash et al. [17].

5. Conclusions

The present study centered on the investigation of the magnetohydrodynamic (MHD) flow of a ternary nanofluid consisting of blood, gold (Au), copper (Cu), and alumina (Al₂O₃) nanoparticles through a stenosed artery. The analysis incorporated the impacts of thermal radiation, chemical reactions, and viscous dissipation. The governing equations were developed using the Caputo fractional derivative and solved semi-analytically with the Laplace transform and Concentrated Matrix-Exponential (CME) methods. The results yielded several key understandings regarding the behavior of blood-based ternary nanofluids under the effects of magnetic fields, thermal radiation, and chemical reactions. The incorporation of ternary nanoparticles resulted in a substantial augmentation in blood velocity, which was ascribed to enhanced thermal conductivity and diminished viscosity. Conversely, an escalation in the Hartmann number (Ha) elicited a decline in blood velocity, attributable to the resistive effect of the Lorentz force. The radiation parameter (Ra) played a vital role in raising blood temperature, a factor that is especially relevant to hyperthermia treatments. The Eckert number (Ec) contributed to localized heating through viscous dissipation.

This study also emphasized the effectiveness of advanced analytical methods such as the Homotopy Perturbation Method (HPM) and the Laplace Transform in solving complex nonlinear equations. When combined with fractional calculus, these methods provide a robust framework for modeling the memory effects and hereditary properties of biological fluids. However, the study is not without its limitations. These limitations include the assumptions of steady-state flow, uniform nanoparticle distribution, and simplified arterial geometry. These assumptions may not fully capture the pulsatile nature of blood flow or the aggregation effects of nanoparticles. Future research endeavors should prioritize incorporating realistic pulsatile effects, non-Newtonian fluid properties, and patient-specific geometries to enhance the model’s clinical relevance. In order to verify the theoretical predictions and optimize the model for biomedical applications, experimental validation is also necessary. The incorporation of chemical reaction kinetics introduces nonlinearity, and fractional derivatives introduce memory effects. While this increases the complexity of the system, it also renders it more representative of physiological processes. The CME method is particularly well-suited for handling such systems, as it offers numerical stability and accuracy in time-fractional problems. Extensive testing was carried out to verify convergence and ensure that the fractional order and reaction terms did not compromise the model’s numerical integrity.

The findings of this study hold significant implications for biomedical engineering, especially in the fields of drug delivery, hyperthermia therapy, and cardiovascular disease treatment. By leveraging the unique properties of ternary nanofluids and advanced analytical techniques, future research endeavors can develop more accurate and efficient models for diagnosing and treating cardiovascular conditions. Moreover, the integration of contemporary computational methodologies has the potential to elucidate hitherto opaque interactions among fluid dynamics, thermal radiation, and chemical reactions within biological systems. In summary, the present study contributes to the growing corpus of knowledge concerning nanofluid dynamics and its applications in biomedical engineering. By addressing current limitations and exploring new methodologies, future research has the potential to pave the way for innovative solutions to some of the most challenging issues in cardiovascular health.

The present research proffers invaluable insights into the magnetohydrodynamic (MHD) flow of blood-based ternary nanofluids within stenosed arteries. However, the study also acknowledges several limitations that warrant consideration for future research. The model assumes steady-state flow, neglecting the pulsatile nature of blood circulation, and treats blood as a Newtonian fluid despite its inherent shear-thinning behavior, particularly significant near stenosis. The arterial geometry is idealized with rigid walls and uniform stenosis, overlooking the elasticity of real arteries and irregular stenosis shapes that influence flow dynamics. Furthermore, the uniform nanoparticle distribution assumption fails to account for potential aggregation or sedimentation, while the constant thermophysical properties ignore variations due to temperature, concentration, and flow conditions. Future research should therefore focus on incorporating pulsatile flow dynamics, non-Newtonian fluid behavior, and patient-specific geometries derived from medical imaging to enhance physiological accuracy. The integration of nanoparticle aggregation and transport, along with variable thermophysical properties, has the potential to enhance the model’s predictive performance for biomedical applications. In order to enhance the model’s predictive capacity in biomedical contexts, experimental validation through in vitro and in vivo studies, in conjunction with advanced computational methodologies such as reinforcement learning and metaheuristic algorithms, has the potential to further refine real-time blood flow forecasts.

The current analysis neglects several in vivo mechanisms such as heat conduction into surrounding tissue, perfusion and metabolic heat sinks, nanoparticle aggregation or sedimentation, and electrochemical surface reactions. Order-of-magnitude estimates show that these effects contribute <5% to energy and momentum balances under the parameter ranges considered, but their inclusion would enhance physiological fidelity in future studies.

The observed temperature increase with thermal radiation (Figure 8) could be further amplified by Joule heating, which was not modeled here. In conductive ternary nanofluids, the Lorentz force-induced currents would generate additional heat, potentially altering the balance between heat absorption and dissipation. This highlights the need for integrated models that couple electromagnetic and thermal fields in future work. Also, the current model incorporates pulsatile flow by including a periodic body force and time-dependent pressure gradient. Moreover, the use of the non-Newtonian fluid model captures the viscoelastic nature of blood under low shear conditions. However, future work could extend this model by incorporating more complex rheological models or patient-specific pulsatile waveforms to further enhance physiological accuracy. The findings hold significant potential for targeted drug delivery, hyperthermia therapy, and cardiovascular diagnostics, with possible integration into MEMS-based wearable medical devices [64,65,66] and AI-driven diagnostic tools [67], such as Artificial Neural Networks [68], ANN Frameworks [69] and Machine Learning [70]. By addressing current limitations and leveraging emerging technologies, this research can contribute to innovative solutions in cardiovascular health, paving the way for more accurate modeling and therapeutic applications in biomedical engineering.