Generalized Padovan Numbers

Abstract

In this paper, we study a generalization of Padovan numbers. We define a generating function and matrix generators for the generalized Padovan sequence. Moreover, using graph methods and a special family of generalized Padovan sequences, we derive a multinomial formula for generalized Padovan numbers. We also prove some identities that generalize known formulae for the classical Padovan numbers.

1. Introduction

The Fibonacci sequence $\left\{F_n\right\}$, given by the formula $F_n=F_{n-1}+F_{n-2}$ for $n\ge 2$ with initial conditions $F_0=F_1=1$, is one of the most celebrated sequences defined recursively. Its terms, known as Fibonacci numbers, occur in nature, art, architecture, and many branches of modern science. The ratio of consecutive Fibonacci numbers tends to the golden number $\varphi ={\displaystyle \frac{1+\sqrt{5}}{2}}\approx 1.618$, which is sometimes considered the source of all beauty, harmony, and symmetry in the world. In the shadow of the Fibonacci sequence lies the Padovan sequence, a relatively young sequence exhibiting similarly surprising and interesting properties to its golden cousin.

The Padovan sequence $\left\{Pv\right(n\left)\right\}$, named after the contemporary architect Richard Padovan, is defined by the third-order linear recurrence relation

$$Pv\left(n\right)=Pv(n-2)+Pv(n-3),\mathrm{for}n\ge 3\mathrm{and}Pv\left(0\right)=Pv\left(1\right)=Pv\left(2\right)=1.$$

(1)

Formula (1) generates the sequence 1, 1, 1, 2, 2, 3, 4, 5, 7, 9, 14, 16, …whose terms are called Padovan numbers, and the ratio of consecutive Padovan numbers tends to a constant $p\approx 1.3247$, known as the plastic number. The plastic number was discovered in 1924 by a French student of architecture, G. Cordonnier, and independently in 1928 by a Dutch architect, D. H. van der Laan, as an analog of the golden number in three-dimensional space. In 1994 R. Padovan, in his essay devoted to van der Laan and his architectonic ideas (see [1]), presented the virtues of the plastic number as a design tool that constraints the growth rate of the recursion (1) and its applications, not only in architecture but also in other fields. Many similarities between the Fibonacci and the Padovan sequences were discussed by I. Steward in [2], while B.M.M. Weger in [3] pointed out some crucial differences between them. Some properties and identities for the classical Padovan numbers were described in [4,5,6]; for others we refer readers to The Online Encyclopedia of Integer Sequences A000931 [7]. Modern applications of the Padovan sequence include graph theory [8,9], computer science [10], and cryptography [11].

Analogously to the Fibonacci sequence, the Padovan sequence has been generalized in various directions. Some of these generalizations arise from combinatorial interpretations. In [12] a generalization of the Padovan sequence was introduced as a consequence of counting special subsets of the set of n integers, while in [13] the Padovan sequence was generalized via tiling and in [14] via decompositions of a number n. A natural way to generalize the recursion (1) is to replace the sum of two terms used to obtain Padovan numbers with a sum involving a larger number of terms. V. Iliopoulos in [15] investigated the recurrence relation of the form $Pv\left(n\right)=Pv(n-2)+Pv(n-3)+\dots Pv(n-k)$ for $k\ge 3$ and $n\ge k$, with initial conditions $Pv\left(0\right)=Pv\left(1\right)=\dots =Pv(k-1)=1$. The same recursion, but with different initial conditions, was considered by J. J. Bravo and J. L. Herrera in [16]. The main focus of the authors in [15,16] was the characteristic polynomial associated with the generalized Padovan sequence and the roots of that polynomial, and interesting results were obtained by combining combinatorics with analytic methods. In this paper, we propose a generalization of Padovan numbers based on a similar idea, but we combine combinatorial properties with matrix theory and graph theory.

Let $k\ge 2$ be an integer. We define generalized Padovan numbers $Pv(k,n)$ by the following recurrence relation:

$$Pv(k,n)=Pv(k,n-k)+\cdots +Pv(k,n-(2k-1\left)\right),\mathrm{for}n\ge 2k-1$$

(2)

with initial conditions $Pv(k,n)=\left\{\begin{array}{c}Pv(k,0)=1,\hfill \\ Pv(k,1)=\dots =Pv(k,k-1)=0,\hfill \\ Pv(k,k)=\dots =Pv(k,2k-2)=1.\hfill \end{array}\right.$

In Table 1 we present $Pv(k,n)$ numbers for some fixed n and k.

Table 1. Generalized Padovan numbers $Pv(k,n)$.

n	0	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17
$Pv(2,n)$	1	0	1	1	1	2	2	3	4	5	7	9	12	16	21	28	37	49
$Pv(3,n)$	1	0	0	1	1	1	1	2	3	3	4	6	8	10	13	18	24	31
$Pv(4,n)$	1	0	0	0	1	1	1	1	1	2	3	4	4	5	7	10	13	16
$Pv(5,n)$	1	0	0	0	0	1	1	1	1	1	1	2	3	4	5	5	6	8
$Pv(6,n)$	1	0	0	0	0	0	1	1	1	1	1	1	1	2	3	4	5	6
$Pv(7,n)$	1	0	0	0	0	0	0	1	1	1	1	1	1	1	1	2	3	4
$Pv(8,n)$	1	0	0	0	0	0	0	0	1	1	1	1	1	1	1	1	1	2

We can observe that for $k=2$ we get the shifted Padovan sequence, i.e., $Pv(2,n)=Pv(n-2)$. For $k=3$ we obtain the sequence denoted in [7] by A017818, connected with a combinatorial model of a settlement along a coastline known as the Riviera model.

Numbers $Pv(k,n)$ can be extended for negative integers. If $k\ge 2$ is an integer and

$$Pv(k,n)=\left\{\begin{array}{c}1 \mathrm{if} n=0,k,k+1,\dots ,2k-2,\hfill \\ 0 \mathrm{if} n=1,2,\dots ,k-1,\hfill \end{array}\right.$$

then

$$Pv(k,-n)=Pv(k,-n+(2k-1\left)\right)-\cdots -Pv(k,-n+1),\mathrm{for}n>0.$$

(3)

In Table 2 we present $Pv(k,n)$ numbers for some negative n.

Table 2. Generalized Padovan numbers $Pv(k,-n)$.

n	−15	−14	−13	−12	−11	−10	−9	−8	−7	−6	−5	−4	−3	−2	−1	0
$Pv(2,n)$	0	−3	4	−3	1	1	−2	2	−1	0	1	−1	1	0	0	1
$Pv(3,n)$	2	−3	2	0	−1	1	−1	1	0	−1	1	0	0	0	0	1
$Pv(4,n)$	−1	1	0	−1	1	0	0	−1	1	0	0	0	0	0	0	1
$Pv(5,n)$	−1	1	0	0	0	−1	1	0	0	0	0	0	0	0	0	1
$Pv(6,n)$	0	0	0	−1	1	0	0	0	0	0	0	0	0	0	0	1
$Pv(7,n)$	0	−1	1	0	0	0	0	0	0	0	0	0	0	0	0	1
$Pv(8,n)$	1	0	0	0	0	0	0	0	0	0	0	0	0	0	0	1

In this paper, we establish several properties of the generalized Padovan sequence defined by the recursion (2). We define its matrix generators as a product of a generalized Q-matrix and a symmetric matrix of initial conditions. We also show how digraphs can be used to obtain direct formulae for generalized Padovan numbers.

2. Generating Function and Some Identities

A linear recurrence equation with constant coefficients is typically used in conjunction with a generating function, which is an elegant tool for studying it and establishing a connection between number sequences and algebraic expressions.

For the sequence $\left\{Pv\right(k,n\left)\right\}$ the generating function can be determined using the definition of a generating function and the generalized Padovan recurrence relation.

Theorem 1. 

If $n\ge 0$, $k\ge 2$ are integers, then the generating function of $\left\{Pv\right(k,n\left)\right\}$ has the following form:

$$f\left(x\right)={\displaystyle \frac{-1}{x^{2k-1}+\cdots +x^k-1}}.$$

Proof. 

Let $f\left(x\right)={\displaystyle \sum _{n=0}^{\infty }}Pv(k,n)x^n$. Using the recurrence relation (2), we get

$$f\left(x\right)=Pv(k,0)+\sum _{n=1}^{k-1}Pv(k,n)x^n+\sum _{n=k}^{2k-2}Pv(k,n)x^n+\sum _{n=2k-1}^{\infty }Pv(k,n)x^n$$

$$=1+\sum _{n=k}^{2k-2}{x}^n+\sum _{n=2k-1}^{\infty }[Pv(k,n-k)+\dots +Pv(k,n-(2k-1))]x^n$$

$$=1+\sum _{n=k}^{2k-2}{x}^n+\sum _{n=2k-1}^{\infty }Pv(k,n-k)x^n+\dots +\sum _{n=2k-1}^{\infty }Pv(k,n-(2k-1))x^n$$

$$=1+\sum _{n=k}^{2k-2}{x}^n+\sum _{n=k-1}^{\infty }Pv(k,n)x^{n+k}+\dots +\sum _{n=0}^{\infty }Pv(k,n)x^{n+2k-1}$$

$$=1+\sum _{n=k}^{2k-2}{x}^n+x^k\sum _{n=k-1}^{\infty }Pv(k,n)x^n+\dots +x^{2k-1}\sum _{n=0}^{\infty }Pv(k,n)x^n$$

$$=1+\sum _{n=k}^{2k-2}{x}^n+x^k\left(\sum _{n=0}^{\infty }Pv(k,n)x^n-1\right)+\dots +x^{2k-1}\sum _{n=0}^{\infty }Pv(k,n)x^n$$

$$=1+x^k\sum _{n=0}^{\infty }Pv(k,n)x^n+\dots +x^{2k-1}\sum _{n=0}^{\infty }Pv(k,n)x^n.$$

Thus,

$$f\left(x\right)-x^{k}f\left(x\right)-\cdots -x^{2k-1}f\left(x\right)=1,$$

and hence

$$f\left(x\right)={\displaystyle \frac{-1}{x^{2k-1}+\cdots +x^k-1}},$$

which completes the proof. □

Some identities related to the generalized Padovan sequence are shown below.

Theorem 2. 

For integers $n\ge 2k$ and $k\ge 2$,

$$Pv(k,n)-Pv(k,n-1)=Pv(k,n-k)-Pv(k,n-2k).$$

Proof. 

Let $n\ge 2k$, $k\ge 2$. Using the definition of the generalized Padovan sequence, we have

$$\begin{array}{cc}\hfill Pv(k,n)& =Pv(k,n-k)+Pv(k,n-k-1)+\cdots +Pv(k,n-(2k-1\left)\right)\hfill \\ \hfill & =Pv(k,n-2k)+Pv(k,n-2k-1)+\cdots +Pv(k,n-(3k-1\left)\right)\hfill \\ \hfill & +Pv(k,n-k-1)+\cdots +Pv(k,n-(2k-1\left)\right)\hfill \\ \hfill & =Pv(k,n-1)+Pv(k,n-2k-1)+\cdots +Pv(k,n-(3k-1\left)\right)\hfill \\ \hfill & +Pv(k,n-2k)-Pv(k,n-2k)\hfill \\ \hfill & =Pv(k,n-1)+Pv(k,n-k)-Pv(k,n-2k).\hfill \end{array}$$

Thus, the proof is complete. □

Theorem 3. 

If $n\ge 0$, $k\ge 2$ are integers, then

$$\sum _{i=0}^{n}Pv(k,i)={\displaystyle \frac{1}{k-1}}\left(Pv(n+3k-1)-\sum _{j=1}^{k-2}(k-1-j)Pv(k,n+j)-1\right).$$

Proof. 

(By induction on n). If $n=0$, then the theorem immediately follows, because by the recursion (2) we have

$$\sum _{i=0}^{n+1}Pv(k,i)={\displaystyle \frac{1}{k-1}}\left(Pv(n+3k-1)-\sum _{j=1}^{k-2}(k-1-j)Pv(k,n+j)-1\right)+Pv(k,n+1)=$$

$${\displaystyle \frac{1}{k-1}}\left(Pv(n+3k-1)-\sum _{j=1}^{k-2}(k-1-j)Pv(k,n+j)-1+(k-1)Pv(k,n+1)\right)$$

Since ${\displaystyle \sum _{j=1}^{k-2}}(k-1-j)Pv(k,n+j)=(k-2)Pv(k,n+1)+{\displaystyle \sum _{j=2}^{k-2}}(k-1-j)Pv(k,n+j)$, we get

$$\sum _{i=0}^{n+1}Pv(k,i)={\displaystyle \frac{1}{k-1}}\left(Pv(n+3k-1)+Pv(k,n+1)-\sum _{j=2}^{k-2}(k-1-j)Pv(k,n+j)-1\right)=$$

$${\displaystyle \frac{1}{k-1}}(Pv(n+2k-1)+Pv(k,n+2k-2)+\dots +Pv(k,n+k+1)+Pv(k,n+k)+$$

$$Pv(k,n+2k)-Pv(k,n+k)-\dots -Pv(k,n+2)-\sum _{j=2}^{k-2}(k-1-j)Pv(k,n+j)-1)=$$

$$={\displaystyle \frac{1}{k-1}}\left(Pv(k,n+3k)-\sum _{j=1}^{k-2}(k-1-j)Pv(k,n+1+j)-1\right),$$

which ends the proof. □

From the above theorem we obtain the following identities for special cases $k\in \{2,3,4,5\}$.

$$\sum _{i=0}^{n}Pv(2,i)=Pv(2,n+5)-1.$$

$$\sum _{i=0}^{n}Pv(3,i)={\displaystyle \frac{1}{2}}(Pv(3,n+8)-Pv(3,n+1)-1).$$

$$\sum _{i=0}^{n}Pv(4,i)={\displaystyle \frac{1}{3}}(Pv(4,n+11)-2Pv(4,n+1)-Pv(4,n+2)-1).$$

$$\sum _{i=0}^{n}Pv(5,i)={\displaystyle \frac{1}{4}}(Pv(5,n+14)-3Pv(5,n+1)-2Pv(5,n+2)-Pv(3,n+3)-1).$$

In particular, if $k=2$ then we obtain the well-known identity for Padovan numbers.

Proving analogously to Theorem 3, we can also obtain the following identity.

Theorem 4. 

Let $n\ge 0$, $k\ge 2$ be integers.

$$\sum _{i=0}^{n}Pv(k,i)={\displaystyle \frac{1}{k-1}}\left(Pv(k,n+2k+1)+\sum _{j=0}^{k-3}(k-2-j)Pv(k,n-j)-1\right).$$

If $k\in \{3,4,5\}$, then we obtain the identities of the form

$$\sum _{i=0}^{n}Pv(3,i)={\displaystyle \frac{1}{2}}(Pv(3,n+7)+Pv(3,n)-1),$$

$$\sum _{i=0}^{n}Pv(4,i)={\displaystyle \frac{1}{3}}(Pv(4,n+9)+2Pv(4,n)+Pv(4,n-1)-1),$$

$$\sum _{i=0}^{n}Pv(5,i)={\displaystyle \frac{1}{4}}(Pv(5,n+11)+3Pv(5,n)+2Pv(5,n-1)+Pv(5,n-2)-1).$$

3. Matrix Generators, Graph Interpretation, and Multinomial Formula

There is a long tradition of applying matrices, determinants, and permanents to study sequences of the Fibonacci type; see, for example, [17,18,19,20]. The concept of the Q-matrix as a matrix generator of the Fibonacci sequence was introduced by Ch. King in his master’s thesis, and since then the Q-matrix method has become an important tool in the analysis of Fibonacci properties; for historical details, see [21]. The Q-matrices for the classical Padovan sequence have also been examined in the literature; see, for instance, [6,22,23]. In this section, we define matrix generators for generalized Padovan sequences $\left\{Pv\right(k,n\left)\right\}$.

Based on the recursion (2), let us define a square matrix $Q_k={\left[q_{i,j}\right]}_{m\times m}$, where $k\ge 2$ and $m=2k-1$ as follows. For $i=1,2\dots ,m$, and $j=1$, an element $q_{i,j}$ of the matrix $Q_k$ is equal to the coefficient of $Pv(k,n)$ on the right-hand side of Equation (2). For $i=1,2\dots m$ and $2\le j\le m$, we put

$$q_{i,j}=\left\{\begin{array}{cc}1\hfill & if j=i+1,\hfill \\ 0\hfill & \mathrm{otherwise}.\hfill \end{array}\right.$$

For $k\ge 2$ the above definition gives matrices of the form

$Q_2=\left[\begin{array}{ccc}0& 1& 0\\ 1& 0& 1\\ 1& 0& 0\end{array}\right]$, $Q_3=\left[\begin{array}{ccccc}0& 1& 0& 0& 0\\ 0& 0& 1& 0& 0\\ 1& 0& 0& 1& 0\\ 1& 0& 0& 0& 1\\ 1& 0& 0& 0& 0\end{array}\right]$, $Q_4=\left[\begin{array}{ccccccc}0& 1& 0& 0& 0& 0& 0\\ 0& 0& 1& 0& 0& 0& 0\\ 0& 0& 0& 1& 0& 0& 0\\ 1& 0& 0& 0& 1& 0& 0\\ 1& 0& 0& 0& 0& 1& 0\\ 1& 0& 0& 0& 0& 0& 1\\ 1& 0& 0& 0& 0& 0& 0\end{array}\right]$,

$Q_5=\left[\begin{array}{ccccccccc}0& 1& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 1& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 1& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 1& 0& 0& 0& 0\\ 1& 0& 0& 0& 0& 1& 0& 0& 0\\ 1& 0& 0& 0& 0& 0& 1& 0& 0\\ 1& 0& 0& 0& 0& 0& 0& 1& 0\\ 1& 0& 0& 0& 0& 0& 0& 0& 1\\ 1& 0& 0& 0& 0& 0& 0& 0& 0\end{array}\right]$, $Q_k=\left[\begin{array}{ccccccc}0& 1& 0& 0& 0& \cdots & 0\\ ⋮& ⋮& \ddots & ⋮& ⋮& ⋮& ⋮\\ 0& 0& 0& 1& 0& \cdots & 0\\ 1& 0& 0& 0& 1& \cdots & 0\\ ⋮& ⋮& ⋮& ⋮& ⋮& \ddots & ⋮\\ 1& 0& 0& 0& 0& \cdots & 1\\ 1& 0& 0& 0& 0& \cdots & 0\end{array}\right]$.

Using a cofactor expansion across the last row of the matrix $Q_k$, we immediately obtain the following result.

Theorem 5. 

Let $k\ge 2$ be an integer. Then $det{Q}_k=1$.

For the classical Fibonacci sequence, as well as for the classical Padovan sequence, the powers of the Q-matrix generate the terms of the sequence directly. In the case of generalized Fibonacci-type sequences, to be able to generate the terms of such a sequence, we usually need an additional matrix called the matrix of initial conditions. For the sequence $\left\{Pv\right(k,n\left)\right\}$, we define a square matrix $P_k$ of size $2k-1$ as the matrix of initial conditions as follows.

$$P_k=\left[\begin{array}{ccccc}Pv(k,4k-4)& Pv(k,4k-5)\hfill & \cdots & Pv(k,2k-1)& Pv(k,2k-2)\\ Pv(k,4k-5)& Pv(k,4k-6)\hfill & \cdots & Pv(k,2k-1)& Pv(k,2k-3)\\ ⋮& ⋮\hfill & \ddots & ⋮& ⋮\\ Pv(k,2k-1)& Pv(k,2k-2)\hfill & \cdots & Pv(k,2)& Pv(k,1)\\ Pv(k,2k-2)& Pv(k,2k-3)\hfill & \cdots & Pv(k,1)& Pv(k,0)\end{array}\right].$$

For $k=2,3,4$ by the above definition we obtain the following symmetric matrices.

$P_2=\left[\begin{array}{ccc}1& 1& 1\\ 1& 1& 0\\ 1& 0& 1\end{array}\right]$, $P_3=\left[\begin{array}{ccccc}3& 2& 1& 1& 1\\ 2& 1& 1& 1& 1\\ 1& 1& 1& 1& 0\\ 1& 1& 1& 0& 0\\ 1& 1& 0& 0& 1\end{array}\right]$, $P_4=\left[\begin{array}{ccccccc}4& 4& 3& 2& 1& 1& 1\\ 4& 3& 2& 1& 1& 1& 1\\ 3& 2& 1& 1& 1& 1& 1\\ 2& 1& 1& 1& 1& 1& 0\\ 1& 1& 1& 1& 1& 0& 0\\ 1& 1& 1& 1& 0& 0& 0\\ 1& 1& 1& 0& 0& 0& 1\end{array}\right]$.

Theorem 6. 

Let $k\ge 2$, $n\ge 1$ be integers. Then

$$P_k{Q}_k^n=\left[\begin{array}{ccccc}Pv(k,n+4k-4)& Pv(k,n+4k-5)\hfill & \cdots & Pv(k,n+2k-1)& Pv(k,n+2k-2)\\ Pv(k,n+4k-5)& Pv(k,n+4k-6)\hfill & \cdots & Pv(k,n+2k-1)& Pv(k,n+2k-3)\\ ⋮& ⋮\hfill & \ddots & ⋮& ⋮\\ Pv(k,n+2k)& Pv(k,n+2k-1)\hfill & \cdots & Pv(k,n+2)& Pv(k,n+1)\\ Pv(k,n+2k-2)& Pv(k,n+2k-3)\hfill & \cdots & Pv(k,n+1)& Pv(k,n+0)\end{array}\right].$$

(4)

Proof. 

(By induction on n). If $n=1$, then by (2) and simple calculations the result immediately follows. Assume that the formula (4) holds for n; we will prove it for $n+1$. Since $P_k{Q}_k^{n+1}=\left(P_k{Q}_k^n\right)Q_k$, by our assumption and by the recurrence (2) we obtain $P_k{Q}_k^{n+1}=$

$$\left[\begin{array}{cccc}Pv(k,n+4k-4)& Pv(k,n+4k-5)\hfill & \cdots & Pv(k,n+2k-2)\\ Pv(k,n+4k-5)& Pv(k,n+4k-6)\hfill & \cdots & Pv(k,n+2k-3)\\ ⋮& ⋮\hfill & \ddots & ⋮\\ Pv(k,n+2k-1)& Pv(k,n+2k-1)\hfill & \cdots & Pv(k,n+1)\\ Pv(k,n+2k-2)& Pv(k,n+2k-2)\hfill & \cdots & Pv(k,n+0)\end{array}\right]\left[\begin{array}{ccccccc}0& 1& 0& 0& 0& \cdots & 0\\ ⋮& ⋮& \ddots & ⋮& ⋮& ⋮& ⋮\\ 0& 0& 0& 1& 0& \cdots & 0\\ 1& 0& 0& 0& 1& \cdots & 0\\ ⋮& ⋮& ⋮& ⋮& ⋮& \ddots & ⋮\\ 1& 0& 0& 0& 0& \cdots & 1\\ 1& 0& 0& 0& 0& \cdots & 0\end{array}\right].$$

By matrix multiplication and Equation (2), it follows that

$$P_k{Q}_k^{n+1}=\left[\begin{array}{ccccc}Pv(k,n+4k-3)& Pv(k,n+4k-4)\hfill & \cdots & Pv(k,n+2k)& Pv(k,n+2k-1)\\ Pv(k,n+4k-4)& Pv(k,n+4k-5)\hfill & \cdots & Pv(k,n+2k-1)& Pv(k,n+2k-2)\\ ⋮& ⋮\hfill & \ddots & ⋮& ⋮\\ Pv(k,n+2k)& Pv(k,n+2k-1)\hfill & \cdots & Pv(k,n+3)& Pv(k,n+2)\\ Pv(k,n+2k-1)& Pv(k,n+2k-2)\hfill & \cdots & Pv(k,n+2)& Pv(k,n+1)\end{array}\right],$$

which ends the proof. □

We use the matrix $Q_k$ to determine the explicit formula for $Pv(k,n)$. In [20] M. C. Er introduced a family of k sequences $\{\left\{g_n^i\right\},i\in \{1,\dots ,k\}\}$ of generalized Fibonacci numbers in the following way.

Let $k\ge 2$ and $c_1,\dots ,c_k$ be integers. Then for each $i\in \{1,\dots ,k\}$, a sequence $\left\{g_n^i\right\}$ consists of generalized Fibonacci numbers $g_n^i$ defined as

$$g_n^i=\sum _{j=1}^k{c}_j{g}_{n-j}^i\mathrm{for}n>0$$

(5)

with initial conditions $g_n^i=\left\{\begin{array}{cc}1\hfill & \mathrm{if}i=1-n,\hfill \\ 0\hfill & \mathrm{otherwise},\hfill \end{array}\right.$ for $1-k\le n\le 0$.

If $k=2$ and $c_1=c_2=1$, then $g_{n-1}^1=g_n^2=F_n$, where $F_n$ is nth Fibonacci number.

Based on an approach taken by D. Kalman [19], M. C. Er used a square matrix A of size k of the form

$$A=\left[\begin{array}{cccc}{c}_1& c_2& \dots & c_k\\ 1& 0& \dots & 0\\ ⋮& \ddots & \ddots & ⋮\\ 0& 0& 1& 0\end{array}\right]$$

and next showed that elements of sequences $\left\{g_n^i\right\}$ can be generated by $A^n$, namely

$$A^n=\left[\begin{array}{cccc}{g}_n^1\hfill & g_n^2\hfill & \cdots & g_n^k\hfill \\ g_{n-1}^1\hfill & g_{n-1}^2\hfill & \cdots & g_{n-1}^k\hfill \\ ⋮\hfill & ⋮\hfill & \ddots & ⋮\hfill \\ g_{n-k+1}^1\hfill & g_{n-k+1}^2\hfill & \cdots & g_{n-k+1}^k\hfill \end{array}\right].$$

(6)

In [8] a special case of generalized Fibonacci numbers related to elements of sequences $\left\{g_n^i\right\}$ was considered. For an integer $k\ge 2$ and non-negative integers $c_1,\dots ,c_k$ such that at least two of $c_j$ are positive, the following recursion was defined:

$$f_n=c_1{f}_1+\dots +c_k{f}_{n-k}\mathrm{for}n>0$$

(7)

with non-negative integers $f_{1-k},\dots ,f_{-1},f_0$ and $f_j>0$ for some $j\in \{1-k,\dots ,0\}$ as initial values.

Let us observe that for special values of $c_1$, $c_2$, $c_3$ and $f_j$, $j\in \{1-k,\dots ,0\}$, we obtain definitions of well-known sequences of the Fibonacci type.

In Table 3 we present the well-known recurrence relations, which follow from (7).

Table 3. Special cases of sequences $\left\{f_n\right\}$.

k	${\mathit{c}}_1$	${\mathit{c}}_2$	${\mathit{c}}_3$	${\mathit{f}}_{-2}$	${\mathit{f}}_{-1}$	${\mathit{f}}_0$	$\left\{{\mathit{f}}_{\mathit{n}}\right\}$ and Other Sequences	Name of the Sequence
2	1	1			0	1	$f_n=F_{n+1}$ for $n\ge -1$	$\left\{F_n\right\}$-Fibonacci seq.
2	1	1			2	1	$f_n=L_{n+1}$ for $n\ge -1$	$\left\{L_n\right\}$-Lucas seq.
2	2	1			0	1	$f_n=P_{n+1}$ for $n\ge -1$	$\left\{P_n\right\}$-Pell seq.
2	1	2			0	1	$f_n=J_{n+1}$ for $n\ge -1$	$\left\{J_n\right\}$-Jacobsthal seq.
3	1	1	1	0	0	1	$f_n=T_{n+2}$ for $n\ge -2$	$\left\{T_n\right\}$-Tribonacci seq.
3	0	1	1	1	1	1	$f_n=Pv(n+2)$ for $n\ge -2$	$\left\{Pv\right(n\left)\right\}$-Padovan seq.
3	0	1	1	3	0	2	$f_n=Pr(n+2)$ for $n\ge -2$	$\left\{Pr\right(n\left)\right\}$-Perrin seq.

In [8] the relation between numbers $f_n$ and elements of sequences $\left\{g_n^i\right\}$ was proved.

Theorem 7 

([8]). If $k\ge 2$ and $n\ge 1-k$ are integers, then $f_n={\displaystyle \sum _{i=1}^k}{f}_{1-i}{g}_n^i$.

Let us now consider a family ${\mathcal{F}}_k=\{\left\{Pv(k,n,i)\right\},i\in \{1,\dots ,2k-1\}\}$, $k\ge 2$ of sequences defined by the recurrence relation (2),

$$Pv(k,n,i)=Pv(k,n-k,i)+\cdots +Pv(k,n-(2k-1),i),\mathrm{for}n>2k-1$$

(8)

with initial conditions $Pv(k,n,i)=\left\{\begin{array}{c}1 \mathrm{if} n=i \mathrm{or} (n=0 \mathrm{and} i=k),\hfill \\ 0 \mathrm{otherwise},\hfill \end{array}\right.$ for $0\le n\le 2k-1$.

For clarity, if $k=3$, then $i\in \{1,2,3,4,5\}$, so the family ${\mathcal{F}}_3$ includes five sequences. From the recurrence (8) we obtain that ${\mathcal{F}}_3=\{\left\{Pv(3,n,1)\right\},\left\{Pv(3,n,2)\right\},\dots ,\left\{Pv(3,n,5)\right\}\}$.

Table 4 presents some initial words of sequences $\left\{Pv\right(3,n,i\left)\right\}$ for $i\in \{1,2,3,4,5\}$ and a few initial terms of the sequence $\left\{Pv\right(3,n\left)\right\}$.

Table 4. Sequences $\left\{Pv\right(3,n,i\left)\right\}$ for $i\in \{1,2,3,4,5\}$.

n	0	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16
$Pv(3,n,1)$	0	1	0	0	0	0	1	0	0	1	1	1	1	2	3	3	4
$Pv(3,n,2)$	0	0	1	0	0	0	1	1	0	1	2	2	2	3	5	6	7
$Pv(3,n,3)$	1	0	0	1	0	0	1	1	1	1	2	3	3	4	6	8	10
$Pv(3,n,4)$	0	0	0	0	1	0	0	1	1	1	1	2	3	3	4	6	8
$Pv(3,n,5)$	0	0	0	0	0	1	0	0	1	1	1	1	2	3	3	4	6
$Pv(3,n)$	1	0	0	1	1	1	1	2	3	3	4	6	8	10	13	18	24

We can observe that $Pv(3,n)=Pv(3,n+6,1)=Pv(3,n+i,i)$ for $i\in \{3,4,5\}$. Moreover, the sequence $\left\{Pv\right(3,n\left)\right\}$ is a sum of sequences $\left\{Pv\right(3,n,i\left)\right\}$ for indices $i\in \{3,4,5\}$. The same relations hold for the sequence $\left\{Pv\right(k,n\left)\right\}$ with an arbitrary $k\ge 2$ and corresponding sequences $\left\{Pv\right(k,n,i\left)\right\}$, where $i\in \{k,\dots ,2k-1\}$.

By definitions of numbers $Pv(k,n)$ and $Pv(n,k,i)$, the following immediately follows.

Theorem 8. 

If $k\ge 2$ and $n\ge 0$ are integers, then

(i) 

$Pv(k,n)=Pv(k,n+2k,1)$;

(ii) 

$Pv(k,n)=Pv(k,n+i,i)$ for $i\in \{k,\dots ,2k-1\}$.

We prove that $Pv(k,n)$ is a sum of elements of sequences $\left\{Pv\right(k,n,i\left)\right\}$ for $i\in \{k,\dots ,2k-1\}$.

Theorem 9. 

Let $k\ge 2$ and $n\ge 0$ be integers. Then

$$Pv(k,n)=\sum _{i=k}^{2k-1}Pv(k,n,i).$$

(9)

Proof. 

(By induction on n). If $0\le n<k$, then

$$\sum _{i=k}^{2k-1}Pv(k,n,i)=Pv(k,n,k)=Pv(k,n).$$

If $k\le n\le 2k-1$, then

$$\sum _{i=k}^{2k-1}Pv(k,n,i)=Pv(k,n,k)+Pv(k,n,k+1)+\cdots +Pv(k,n,2k-1)=Pv(k,n,n)=Pv(k,n).$$

Assume that $n\ge 0$ and ${\displaystyle Pv(k,n)=\sum _{i=k}^{2k-1}Pv(k,n,i).}$ We shall show that

$$\sum _{i=k}^{2k-1}Pv(k,n+1,i)=Pv(k,n+1).$$

$$\begin{array}{cc}\hfill \sum _{i=k}^{2k-1}Pv(k,n,i)& =Pv(k,n-k,k)+Pv(k,n-k-1,k)+\cdots +Pv(k,n-(2k-1),k)\hfill \\ \hfill & =Pv(k,n-k,k+1)+Pv(k,n-k-1,k+1)+\cdots +Pv(k,n-(2k-1),k+1)\hfill \\ \hfill & ⋮\hfill \\ \hfill & =Pv(k,n-k,2k-1)+Pv(k,n-k-1,2k-1)+\cdots +Pv(k,n-(2k-1),2k-1)\hfill \\ \hfill & =\sum _{i=k}^{2k-1}Pv(k,n-k,i)+\sum _{i=k}^{2k-1}Pv(k,n-k-1,i)+\cdots +\sum _{i=k}^{2k-1}Pv(k,n-(2k-1),i)\hfill \\ \hfill & =Pv(k,n-k+1)+Pv(k,n-k-1+1)+\cdots +Pv(k,n-(2k-1)+1)\hfill \\ \hfill & =Pv(k,n+1).\hfill \end{array}$$

So the proof is complete. □

Terms of sequences $\left\{Pv\right(k,n,i\left)\right\}$ for $i\in \{1,\dots ,k-1\}$ can be used to derive a multinomial formula for $Pv(k,n)$.

Let A be a square matrix of size $2k-1$ associated with recurrence (8) as follows:

$$A=\left[\begin{array}{ccccccc}0& \dots & 0& 1& \dots & 1& 1\\ 1& \dots & 0& 0& \dots & 0& 0\\ 0& \ddots & 0& 0& \dots & 0& 0\\ 0& \dots & 1& 0& \dots & 0& 0\\ 0& \dots & 0& 1& \dots & 0& 0\\ ⋮& ⋮& ⋮& ⋮& \ddots & ⋮& ⋮\\ 0& \dots & 0& 0& \dots & 1& 0\end{array}\right].$$

It can be easily verified that the nth power, $n\ge 1$, of the matrix A has the form

$$A^n=\left[\begin{array}{cccc}Pv(k,n+2k-1,2k-1)\hfill & \dots & Pv(k,n+2k-1,2)& Pv(k,n+2k-1,1)\\ Pv(k,n+2k-2,2k-1)\hfill & \dots & Pv(k,n+2k-2,2)& Pv(k,n+2k-2,1)\\ ⋮\hfill & \ddots & ⋮& ⋮\\ Pv(k,n+1,2k-1)\hfill & \dots & Pv(k,n+1,2)& Pv(k,n+1,1)\end{array}\right].$$

(10)

Note that $A={\left(Q_k\right)}^T$, and therefore

$$A^n={\left(Q_k^n\right)}^T.$$

(11)

The matrix $Q_k$ can be considered as the adjacency matrix of a special directed graph $D_k$ with the set of vertices $V\left(D_k\right)=\{v_1,\dots ,v_{2k-1}\}$. Moreover, there is an arc $v_i{v}_j\in E\left(D_k\right)$ if $q_{ij}=1$. The directed graph $D_k$ is presented in Figure 1.

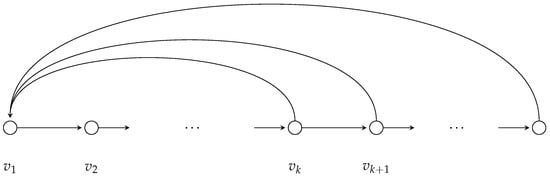
Figure 1. Digraph $D_k$.

From a well-known fact in graph theory, it follows that the entry $q_{ij}$ of the matrix $Q_k^n$ is equal to the number of all distinct paths of length n between the vertices $v_i$ and $v_j$. Therefore, by (8) and the equality (11), we obtain that $Pv(k,n,i)$ is the total number of distinct paths of length n from $v_i$ to $v_1$.

To give a multinomial formula for $Pv(k,n)$ numbers, it is sufficient to consider a single sequence from the family ${\mathcal{F}}_k$. Before obtaining such a formula, recall that if n is a non-negative integer, and $k_1,\dots ,k_m$ are integers satisfying $k_1+\dots +k_m=n$, then multinomial coefficients are defined as follows:

$$\left({\displaystyle \genfrac{}{}{0pt}{}{n}{k_1,\dots ,k_m}}\right)=\left\{\begin{array}{c}{\displaystyle \frac{n!}{k_1!\cdots k_m!}}\mathrm{if} \mathrm{each}{k}_i\ge 0,\hfill \\ 0\mathrm{otherwise}.\hfill \end{array}\right.$$

Theorem 10. 

If $k\ge 2$, $n\ge 1$, $1\le i\le 2k-1$ are integers, then

$$Pv(k,n+2k-1,2k-1)=\sum _{\begin{array}{c}{\alpha }_k,\dots ,{\alpha }_{2k-1}\\ k{\alpha }_k+\cdots +(2k-1){\alpha }_{2k-1}=n\end{array}}\left({\displaystyle \genfrac{}{}{0pt}{}{{\alpha }_k+\cdots +{\alpha }_{2k-1}}{{\alpha }_k,\dots ,{\alpha }_{2k-1}}}\right).$$

(12)

Proof. 

Let $D_k$ be a digraph shown in Figure 1. From the graph interpretation of the number $Pv(k,n,i)$, it follows that, in order to prove the multinomial Formula (12), we must count all paths of length n between vertices $v_1$ and $v_1$. Each such path consists of elementary cycles arranged in an arbitrary order. The cycles have the form $C_i=v_1-v_2-\cdots -v_i-v_1$ and have lengths i, $i\in \{k,\dots ,2k-1\}$. Suppose that the path contains the cycle $C_i$ exactly ${\alpha }_i$-times. Clearly, ${\alpha }_i\ge 0$, $i\in \{k,\dots ,2k-1\}$. Each such path then corresponds to an ordering, with repetitions allowed, of cycles from the set $\{C_k,...,C_{2k-1}\}$ in an arbitrary order. Then the length of this path is $k{\alpha }_k+\cdots +(2k-1){\alpha }_{2k-1}=n$. The cycle $C_i$, $k\le i\le 2k-1$, can be placed in the path in

$$\left({\displaystyle \genfrac{}{}{0pt}{}{{\alpha }_k+\cdots +{\alpha }_{2k-1}}{{\alpha }_i}}\right)$$

ways. Hence, there are

$$\left({\displaystyle \genfrac{}{}{0pt}{}{{\alpha }_k+\cdots +{\alpha }_{2k-1}}{{\alpha }_k}}\right)\left({\displaystyle \genfrac{}{}{0pt}{}{{\alpha }_{k+1}+\cdots +{\alpha }_{2k-1}}{{\alpha }_{k+1}}}\right)\cdots \left({\displaystyle \genfrac{}{}{0pt}{}{{\alpha }_{2k-1}}{{\alpha }_{2k-1}}}\right)=\left({\displaystyle \genfrac{}{}{0pt}{}{{\alpha }_k+\cdots +{\alpha }_{2k-1}}{{\alpha }_k,\dots ,{\alpha }_{2k-1}}}\right)$$

such paths in the digraph $D_k$. Summing over all collections ${\alpha }_k,\dots ,{\alpha }_{2k-1}$ satisfying the equation $k{\alpha }_k+\dots +(2k-1){\alpha }_{2k-1}=n$, we obtain the total number of such paths, which is equal to

$$\sum _{\begin{array}{c}{\alpha }_k,\dots ,{\alpha }_{2k-1}\\ k{\alpha }_k+\cdots +(2k-1){\alpha }_{2k-1}=n\end{array}}\left({\displaystyle \genfrac{}{}{0pt}{}{{\alpha }_k+\cdots +{\alpha }_{2k-1}}{{\alpha }_k,\dots ,{\alpha }_{2k-1}}}\right),$$

and this completes the proof. □

Based on Theorem 8 and using Equation (12), we immediately obtain a most convenient expression.

Corollary 1. 

For integers $k\ge 2$ and $n\ge 1$,

$$Pv(k,n)=\sum _{\begin{array}{c}{\alpha }_k,\dots ,{\alpha }_{2k-1}\\ k{\alpha }_k+\dots +(2k-1){\alpha }_{2k-1}=n\end{array}}\left({\displaystyle \genfrac{}{}{0pt}{}{{\alpha }_k+\dots +{\alpha }_{2k-1}}{{\alpha }_k,\dots ,{\alpha }_{2k-1}}}\right).$$

(13)

An equivalent form is

$$Pv(k,n)=\sum _{\begin{array}{c}{\alpha }_k,\dots ,{\alpha }_{2k-1}\\ k{\alpha }_k+\cdots +(2k-1){\alpha }_{2k-1}=n\end{array}}{\displaystyle \frac{({\alpha }_k+\cdots +{\alpha }_{2k-1})!}{{\alpha }_k!\cdots {\alpha }_{2k-1}!}}.$$

(14)

To illustrate Corollary 1, let us compute $Pv(3,15)$. Using (13), we obtain

$$Pv(3,15)=\sum _{\begin{array}{c}{\alpha }_3,{\alpha }_4,{\alpha }_5\\ 3{\alpha }_3+4{\alpha }_4+5{\alpha }_5=15\end{array}}\left({\displaystyle \genfrac{}{}{0pt}{}{{\alpha }_3+{\alpha }_4+{\alpha }_5}{{\alpha }_3,{\alpha }_4,{\alpha }_5}}\right).$$

The triples satisfying the equation $3{\alpha }_3+4{\alpha }_4+5{\alpha }_5=15$ are $(5,0,0),(2,1,1),(1,3,0),(0,0,3)$. Therefore,

$$Pv(3,15)=\left({\displaystyle \genfrac{}{}{0pt}{}{5+0+0}{5,0,0}}\right)+\left({\displaystyle \genfrac{}{}{0pt}{}{2+1+1}{2,1,1}}\right)\left({\displaystyle \genfrac{}{}{0pt}{}{1+3+0}{1,3,0}}\right)+\left({\displaystyle \genfrac{}{}{0pt}{}{0+0+3}{0,0,3}}\right)=1+12+4+1=18.$$

4. Conclusions

In this paper, we introduced generalized Padovan numbers and established several of their properties. Futhermore, we showed that the Q-matrix associated with the generalized Padovan recursion can be viewed not only as a matrix generator but also as the adjacency matrix of a particular digraph, yielding interesting results that arise from combining matrix theory, combinatorics, and graph theory. As a direction for further research, it would be worthwhile to consider the characteristic polynomial associated with the generalization of the Padovan sequence defined here, as well as the roots of the polynomial, following approaches similar to those in [15,16]. It also seems interesting to find a connection between generalized Padovan numbers and Pascal’s triangle and to extend the notion of generalized Padovan numbers to polynomials. Applications of matrix generators of Fibonacci-type sequences in coding theory, initiated by work of A.P. Stakhov [24] and subsequently developed by other authors, have opened a new area of investigations. We hope that the matrix generators we have defined in this paper for generalized Padovan numbers will likewise find applications in cryptography, where such matrices are used in encoding and decoding algorithms.