Regret Psychology-Driven Information Propagation and Behavioral Adoption in Complex Social Networks
Abstract
1. Introduction
2. Model Description
3. Theoretical Analysis
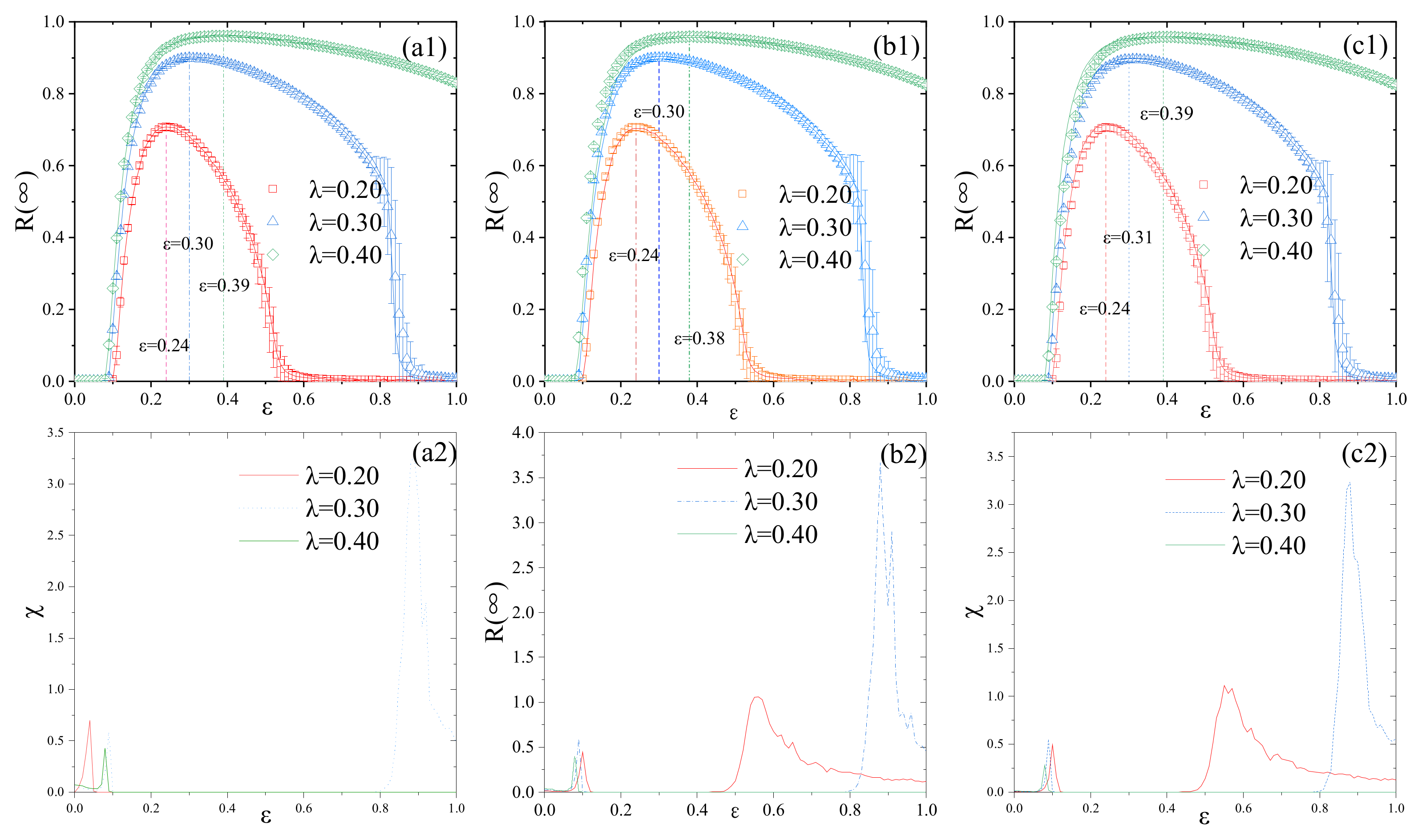
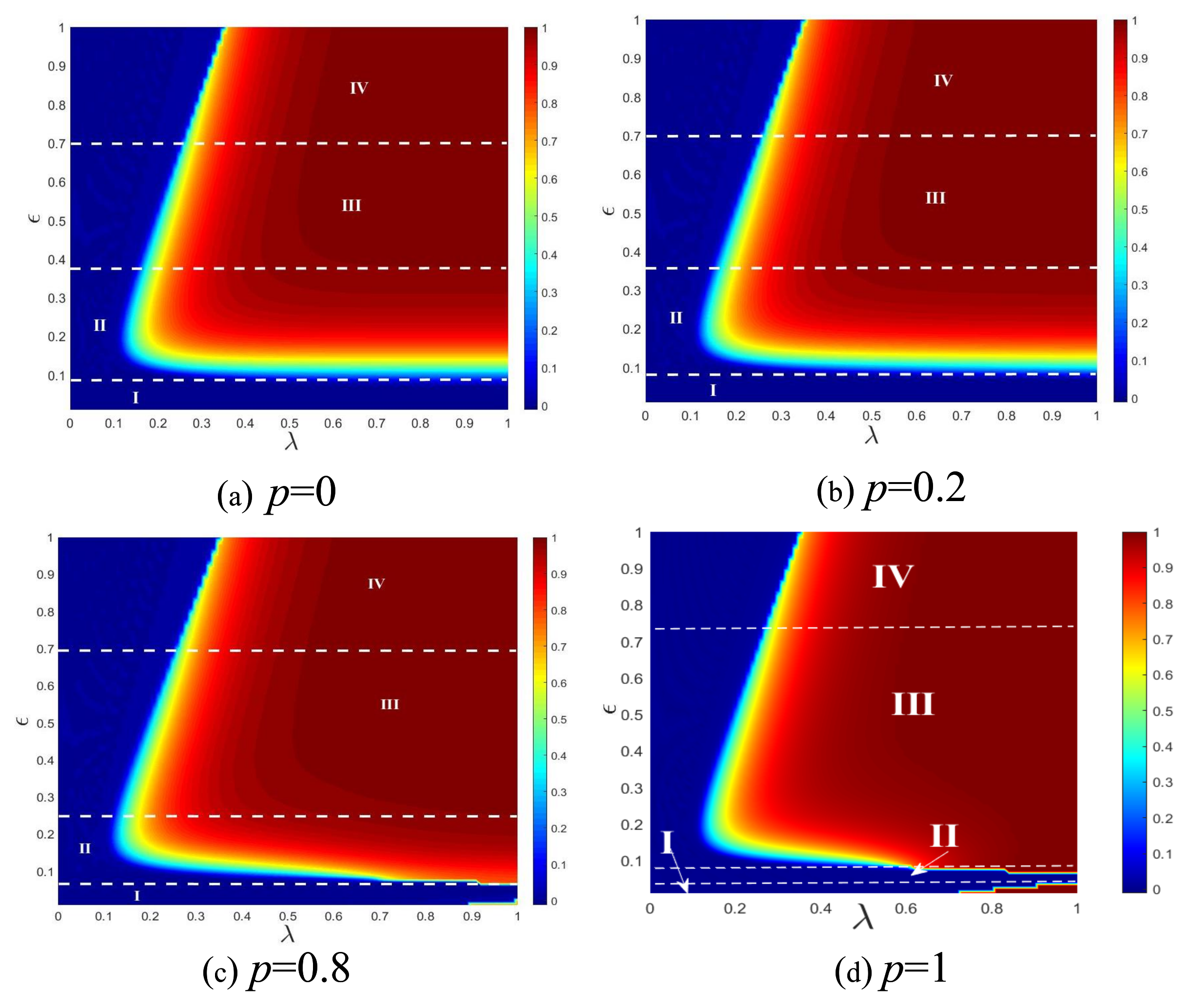
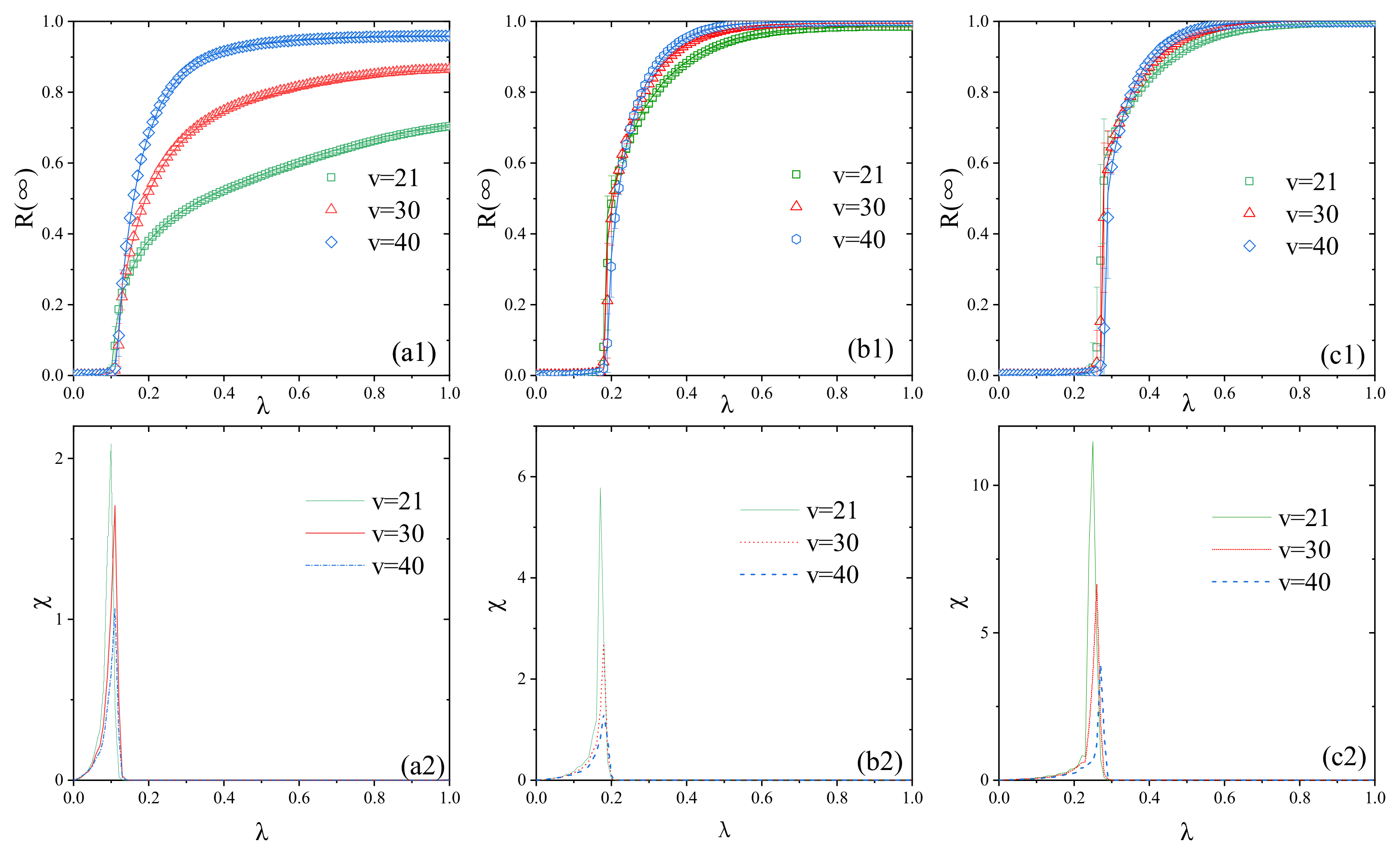
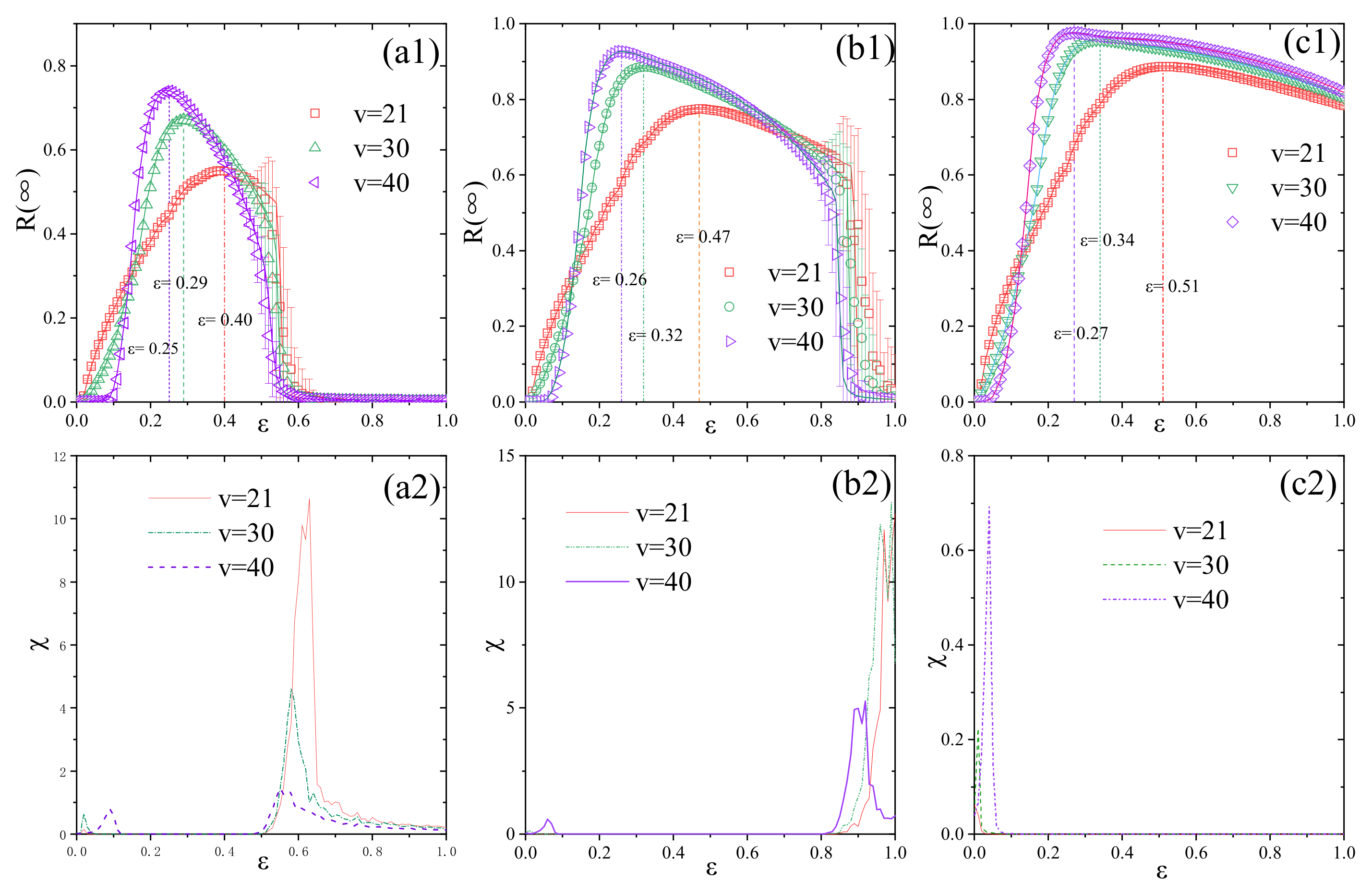
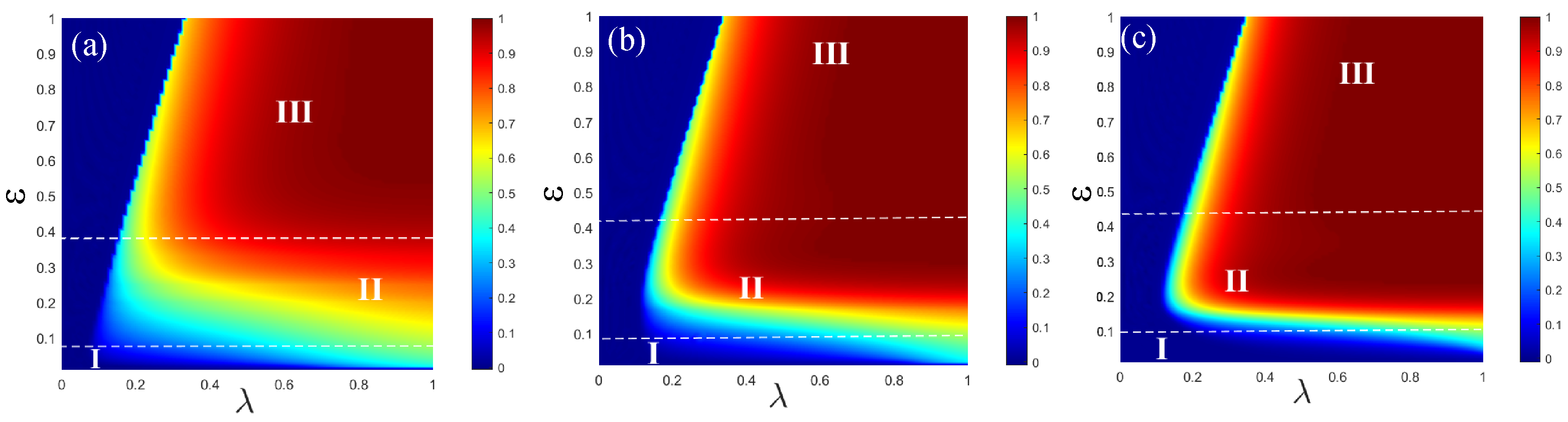
4. Results and Discussions
4.1. The Information Propagation on ER Social Network
4.2. The Information Propagation on SF Network
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Derivation Details of the Model
References
- Thapliyal, K.; Thapliyal, M.; Thapliyal, D. Social media and health communication: A review of advantages, challenges, and best practices. In Emerging Technologies for Health Literacy and Medical Practice; IGI Global Scientific Publishing: Hershey, PA, USA, 2024; pp. 364–384. [Google Scholar]
- Avalle, M.; Di Marco, N.; Etta, G.; Sangiorgio, E.; Alipour, S.; Bonetti, A.; Alvisi, L.; Scala, A.; Baronchelli, A.; Cinelli, M.; et al. Persistent interaction patterns across social media platforms and over time. Nature 2024, 628, 582–589. [Google Scholar] [CrossRef]
- Ishfaq, U.; Khan, H.U.; Shabbir, D. Exploring the role of sentiment analysis with network and temporal features for finding influential users in social media platforms. Soc. Netw. Anal. Min. 2024, 14, 241. [Google Scholar] [CrossRef]
- Ruggeri, K.; Vanderslott, S.; Yamada, Y.; Argyris, Y.A.; Većkalov, B.; Boggio, P.S.; Fallah, M.P.; Stock, F.; Hertwig, R. Behavioural interventions to reduce vaccine hesitancy driven by misinformation on social media. BMJ 2024, 384, e076542. [Google Scholar] [CrossRef] [PubMed]
- Shah, S.S.; Asghar, Z. Dynamics of social influence on consumption choices: A social network representation. Heliyon 2023, 9, e17146. [Google Scholar] [CrossRef] [PubMed]
- Souki, G.Q.; Oliveira, A.S.d.; Guerreiro, M.M.M.; Mendes, J.d.C.; Moura, L.R.C. Do memorable restaurant experiences affect eWOM? The moderating effect of consumers’ behavioural engagement on social networking sites. TQM J. 2023, 35, 2255–2281. [Google Scholar] [CrossRef]
- Du, K.; Fan, R. SHI1I2R competitive information spreading model in online and offline two-layer networks in emergencies. Expert Syst. Appl. 2024, 235, 121225. [Google Scholar] [CrossRef]
- Wu, J.; Wang, S.; Chiclana, F.; Herrera-Viedma, E. Two-fold personalized feedback mechanism for social network consensus by uninorm interval trust propagation. IEEE Trans. Cybern. 2021, 52, 11081–11092. [Google Scholar] [CrossRef]
- Saad, F.; Benzehoua, H.; Belafhal, A. Propagation behavior of a generalized Hermite cosh-Gaussian laser beam through marine environment. Opt. Quantum Electron. 2024, 56, 130. [Google Scholar] [CrossRef]
- Goodarzi, S.; Masini, A.; Aflaki, S.; Fahimnia, B. Right information at the right time: Reevaluating the attitude–behavior gap in environmental technology adoption. Int. J. Prod. Econ. 2021, 242, 108278. [Google Scholar] [CrossRef]
- Peng, H.; Peng, W.; Zhao, D.; Wang, W. Impact of the heterogeneity of adoption thresholds on behavior spreading in complex networks. Appl. Math. Comput. 2020, 386, 125504. [Google Scholar] [CrossRef]
- Wang, Z.; Rui, X.; Yuan, G.; Cui, J.; Hadzibeganovic, T. Endemic information-contagion outbreaks in complex networks with potential spreaders based recurrent-state transmission dynamics. Phys. A Stat. Mech. Its Appl. 2021, 573, 125907. [Google Scholar] [CrossRef]
- Hu, Y.; Pan, Q.; Hou, W.; He, M. Rumor spreading model with the different attitudes towards rumors. Phys. A Stat. Mech. Its Appl. 2018, 502, 331–344. [Google Scholar] [CrossRef]
- Wang, W.; Tang, M.; Zhang, H.F.; Lai, Y.C. Dynamics of social contagions with memory of nonredundant information. Phys. Rev. E 2015, 92, 012820. [Google Scholar] [CrossRef] [PubMed]
- Leng, H.; Zhao, Y.; Wang, D. Message passing approach for social contagions based on the trust probability with multiple influence factors. Phys. A Stat. Mech. Its Appl. 2022, 587, 126510. [Google Scholar] [CrossRef]
- Zhang, Y.X.; Zou, L. Research on information dissemination on social networks based on edge-based compartmental theory. Int. J. Mod. Phys. B 2021, 35, 2150249. [Google Scholar] [CrossRef]
- Han, L.; Lin, Z.; Tang, M.; Zhou, J.; Zou, Y.; Guan, S. Impact of contact preference on social contagions on complex networks. Phys. Rev. E 2020, 101, 042308. [Google Scholar] [CrossRef]
- Hosni, A.I.E.; Li, K.; Ahmad, S. Minimizing rumor influence in multiplex online social networks based on human individual and social behaviors. Inf. Sci. 2020, 512, 1458–1480. [Google Scholar] [CrossRef]
- Centola, D.; Eguíluz, V.M.; Macy, M.W. Cascade dynamics of complex propagation. Phys. A Stat. Mech. Its Appl. 2007, 374, 449–456. [Google Scholar] [CrossRef]
- Abella, D.; San Miguel, M.; Ramasco, J.J. Aging in binary-state models: The Threshold model for complex contagion. Phys. Rev. E 2023, 107, 024101. [Google Scholar] [CrossRef]
- Li, X.; Hsee, C.K. The psychology of marginal utility. J. Consum. Res. 2021, 48, 169–188. [Google Scholar] [CrossRef]
- Cui, Y.; Wei, R.; Tian, Y.; Tian, H.; Zhu, X. Information propagation influenced by individual fashion-passion trend on multi-layer weighted network. Chaos Solitons Fractals 2022, 160, 112200. [Google Scholar] [CrossRef]
- Tian, Y.; Tian, H.; Cui, Y.; Zhu, X.; Cui, Q. Influence of behavioral adoption preference based on heterogeneous population on multiple weighted networks. Appl. Math. Comput. 2023, 446, 127880. [Google Scholar] [CrossRef]
- Huo, L.; Pan, M.; Wei, Y. Impact of individual activity on behavior adoption in complex networks: A two-layer generalized SAR model analysis. Chaos Solitons Fractals 2024, 186, 115198. [Google Scholar] [CrossRef]
- Iacopini, I.; Petri, G.; Barrat, A.; Latora, V. Simplicial models of social contagion. Nat. Commun. 2019, 10, 2485. [Google Scholar] [CrossRef] [PubMed]
- Zhao, Y.; Li, C.; Shi, D.; Chen, G.; Li, X. Ranking cliques in higher-order complex networks. Chaos Interdiscip. J. Nonlinear Sci. 2023, 33, 073139. [Google Scholar] [CrossRef]
- Zhao, X.; Yu, H.; Li, S.; Liu, S.; Zhang, J.; Cao, X. Effects of memory on spreading processes in non-Markovian temporal networks based on simplicial complex. Phys. A Stat. Mech. Its Appl. 2022, 606, 128073. [Google Scholar] [CrossRef]
- Centola, D. The spread of behavior in an online social network experiment. Science 2010, 329, 1194–1197. [Google Scholar] [CrossRef]
- Zhu, X.; Wang, W.; Cai, S.; Stanley, H.E. Optimal imitation capacity and crossover phenomenon in the dynamics of social contagions. J. Stat. Mech. Theory Exp. 2018, 2018, 063405. [Google Scholar] [CrossRef]
- Tian, Y.; Tian, H.; Cui, Q.; Zhu, X. Phase transition phenomena in social propagation with dynamic fashion tendency and individual contact. Chaos Solitons Fractals 2024, 178, 114366. [Google Scholar] [CrossRef]
- Wang, W.; Li, W.; Lin, T.; Wu, T.; Pan, L.; Liu, Y. Generalized k-core percolation on higher-order dependent networks. Appl. Math. Comput. 2022, 420, 126793. [Google Scholar] [CrossRef]
- Kobayashi, T. Trend-driven information cascades on random networks. Phys. Rev. E 2015, 92, 062823. [Google Scholar] [CrossRef]
- Granovetter, M. Threshold models of collective behavior. Am. J. Sociol. 1978, 83, 1420–1443. [Google Scholar] [CrossRef]
- Karampourniotis, P.D.; Sreenivasan, S.; Szymanski, B.K.; Korniss, G. The impact of heterogeneous thresholds on social contagion with multiple initiators. PLoS ONE 2015, 10, e0143020. [Google Scholar] [CrossRef] [PubMed]
- Fink, C.; Schmidt, A.; Barash, V.; Kelly, J.; Cameron, C.; Macy, M. Investigating the observability of complex contagion in empirical social networks. In Proceedings of the International AAAI Conference on Web and Social Media, Cologne, Germany, 17–20 May 2016; Volume 10, pp. 121–130. [Google Scholar]
- Juul, J.S.; Porter, M.A. Synergistic effects in threshold models on networks. Chaos Interdiscip. J. Nonlinear Sci. 2018, 28, 013115. [Google Scholar] [CrossRef]
- Bellomo, N.; Burini, D.; Dosi, G.; Gibelli, L.; Knopoff, D.A.; Outada, N.; Terna, P.; Virgillito, M.E. What is life? A perspective of the mathematical kinetic theory of active particles. Math. Model. Methods Appl. Sci. 2021, 31, 1821–1866. [Google Scholar] [CrossRef]
- Bellomo, B.; Esfahanian, M.; Secchini, V.; Terna, P. What is life? Active particles tools towards behavioral dynamics in social-biology and economics. Phys. Life Rev. 2022, 43, 189–207. [Google Scholar] [CrossRef]
- Bellomo, N.; Gibelli, L.; Quaini, A.; Reali, A. Towards a mathematical theory of behavioral human crowds. Math. Model. Methods Appl. Sci. 2022, 32, 321–358. [Google Scholar] [CrossRef]
- Bellomo, N.; Liao, J.; Quaini, A.; Russo, L.; Siettos, C. Human behavioral crowds. Review, critical analysis, and research perspectives. Math. Model. Methods Appl. Sci. 2023, 33, 1611–1659. [Google Scholar] [CrossRef]
- Miller, J.C.; Slim, A.C.; Volz, E.M. Edge-based compartmental modelling for infectious disease spread. J. R. Soc. Interface 2012, 9, 890–906. [Google Scholar] [CrossRef]
- Karrer, B.; Newman, M.E.J.; Zdeborová, L. Percolation on Sparse Networks. Phys. Rev. Lett. 2014, 113, 208702. [Google Scholar] [CrossRef]
- Erdös, P.; Rényi, A. On the evolution of random graphs. Publ. Math. Inst. Hung. Acad. Sci 1960, 5, 17–60. [Google Scholar]
- Catanzaro, M.; Boguná, M.; Pastor-Satorras, R. Generation of uncorrelated random scale-free networks. Phys. Rev. E 2005, 71, 027103. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, N.; Cui, Y.; Tian, Y.; Hu, C.; Zhu, X.; Hu, S. Regret Psychology-Driven Information Propagation and Behavioral Adoption in Complex Social Networks. Symmetry 2025, 17, 2008. https://doi.org/10.3390/sym17112008
Li N, Cui Y, Tian Y, Hu C, Zhu X, Hu S. Regret Psychology-Driven Information Propagation and Behavioral Adoption in Complex Social Networks. Symmetry. 2025; 17(11):2008. https://doi.org/10.3390/sym17112008
Chicago/Turabian StyleLi, Nana, Yajuan Cui, Yang Tian, Chenxi Hu, Xuzhen Zhu, and Simin Hu. 2025. "Regret Psychology-Driven Information Propagation and Behavioral Adoption in Complex Social Networks" Symmetry 17, no. 11: 2008. https://doi.org/10.3390/sym17112008
APA StyleLi, N., Cui, Y., Tian, Y., Hu, C., Zhu, X., & Hu, S. (2025). Regret Psychology-Driven Information Propagation and Behavioral Adoption in Complex Social Networks. Symmetry, 17(11), 2008. https://doi.org/10.3390/sym17112008






