Residual-Based Improved Uncertain Maximum Likelihood Estimation for Uncertain Delay Differential Equations

Abstract

As a powerful tool for characterizing the time-evolution behavior of dynamic systems with delay characteristics, the parameter estimation problem for uncertain delay differential equations has always been a research hotspot in the field of uncertain statistics. In order to eliminate the impact of outliers on the relevant results during parameter estimation, this paper proposes the improved uncertain maximum likelihood estimation and the generalized improved uncertain maximum likelihood estimation for uncertain delay differential equations based on symmetric statistical invariants, named residuals. After that, a numerical algorithm is also designed to solve the numerical solutions of the corresponding estimators. Finally, two numerical examples and an empirical study on stock price modeling are provided to illustrate the effectiveness of the methods proposed in this paper.

1. Introduction

The early research on delay differential equations dates back to the 18th century, when mathematicians such as Euler and Bernoulli encountered the issue of time delays in the calculus of variations. After that, delay differential equations received widespread attention from scholars in the 20th century and were formally developed into a theoretical branch of differential equations. A key turning point was in the 1950s, when American mathematician Cooke [1] and Soviet mathematician Myshkis [2] laid the foundation regarding the current theory framework of delay differential equations, which encompasses the fundamental characteristics of their solutions, such as the existence and uniqueness of solutions, and stability theory. However, in practical situations, time-delay dynamic systems often operate in an indeterminate environment, and the deterministic models often fail. This further promotes the development of stochastic delay differential equations based on Itô integration proposed by Itô [3]. Up to now, stochastic delay differential equations have been widely applied in fields such as physiology, engineering control, and economics.

The mathematical foundation of stochastic delay differential equations is probability theory (established by Kolmogorov [4]) for characterizing random phenomena, in which the prerequisite for effectively modeling in practice is that the non-deterministic factors affecting the research object must satisfy the properties required by the operational laws of probability theory; namely, the frequency must be stable enough. However, this is often difficult to meet in practice, as the real world is constantly changing, and the non-deterministic factors affecting the research object are also constantly changing. In particular, when the research object is affected by sudden events such as stimulus policies, extreme weather, and public opinion news, its historical data becomes invalid, and the distribution function (sometimes also called the estimated frequency) generated based on historical data no longer closely approximates the future frequency. That is to say, the fluctuation characteristics of the studied system deviate from the steady state, and its frequency domain characteristics exhibit a persistent tendency of instability. Under these conditions, it will be difficult for the traditional stochastic delay differential equations established based on the probability theory framework to accurately describe the dynamic behavior of the system. The applicability and predictive performance of the original modeling methods will significantly decrease.

To verify the above phenomenon through actual data, many researchers have conducted empirical analyses based on actual observational data. Taking the field of social sciences as an example, Liu [5] introduced uncertain differential equations to construct a dynamic prediction model when analyzing the changing patterns of China’s population structure. Subsequently, Yang and Liu [6] further expanded the modeling tools to uncertain partial differential equations, systematically examining the frequency instability characteristics of the population system under the influence of random factors. These studies started from actual data and revealed the effectiveness and limitations of stochastic models in describing the frequency domain characteristics of complex social systems. In the field of data analysis for ride-hailing platforms, Liu et al. [7] through rigorous mathematical deduction discovered that when using a random renewal process to simulate passenger booking orders on ride-hailing platforms, a systematic paradox contrary to intuitive understanding would occur. This finding raises significant doubts about the validity of traditional traffic demand prediction models. At the same time, Gao et al. [8] made breakthrough progress in population dynamic modeling. They innovatively used uncertain differential equations to construct a model for the evolution of the student population scale in Chinese universities, and based on this model, they revealed that the fluctuations in the number of students in the education system still exhibit frequency instability. In the field of natural science research, several scholars have conducted systematic explorations of the fluctuation patterns of China’s grain production through various modeling methods. Ye and Kang [9] constructed an uncertain time series model, while Liu [10] employed a method of uncertain regression analysis to establish a prediction model for China’s grain production. Both studies were based on grain production data within a random framework and confirmed the frequency instability phenomenon exhibited by this system. At the same time, Chen [11] analyzed the per capita output data by constructing an uncertain autoregressive model and also verified this statistical characteristic that the frequency of corresponding economic indicators remains unstable under the influence of random environments. In the field of financial and economic research, Ye and Liu [12] employed an uncertain regression model to model China’s macroeconomic data. Their research results further revealed the widespread prevalence of frequency instability in the economic system. The above empirical studies indicate that frequency instability has become a common statistical feature in actual data across multiple fields. In the face of this widespread phenomenon, the academic community urgently needs to establish a mathematical theoretical framework based on a brand-new axiomatic system to provide more effective analytical tools and methodological support. Fortunately, uncertainty theory provides a rigorous mathematical framework for addressing the issue of possibility measurement in frequency instability phenomena, which is a brand-new axiomatic system founded by Liu [13] and perfected by Liu [14]. This theory can accurately depict the quantitative assessment of the likelihood of an event occurring under conditions of frequency instability. Based on this theory, Barbacioru [15] proposed uncertain delay differential equations, which further provide a powerful analytical tool for studying the evolution laws of time-delay dynamic systems in the environment of frequency instability. This method is particularly suitable for describing the complex system behaviors that are simultaneously influenced by the effects of time delay and frequency domain instability.

For the sake of addressing the research gap in the parameter estimation of uncertain delay differential equations regarding the handling of outliers and to enhance the robustness of the estimation results against outliers, this study innovatively incorporates the influence of outliers into the parameter estimation framework. By extending the improved uncertain maximum likelihood method to the symmetric statistical invariants (i.e., residuals) of uncertain delay differential equations, two new estimation methods are proposed: the improved uncertain maximum likelihood estimation based on residuals and the generalized improved uncertain maximum likelihood estimation. These contributions fill the gap in the field of parameter inference for uncertain delay differential equations regarding estimation methods that are resistant to outliers and enrich the theoretical system of uncertain statistical estimation. The specific innovative contributions of this paper are as follows:

•

The improved uncertainty maximum likelihood method is applied to the symmetric statistical invariants (residuals) of uncertain delay differential equations, thereby developing two innovative estimation methods: the improved uncertain maximum likelihood estimation and the generalized improved uncertain maximum likelihood estimation of uncertain delay differential equations. This pioneering integration not only addresses the vulnerability of existing estimation methods to outliers, but also extends the application scope of the improved uncertain maximum likelihood method to uncertain dynamic systems with delays.

•

A specialized numerical algorithm is designed to efficiently solve the proposed estimators using the observed data. This algorithm fully takes into account the delay characteristics of the uncertain dynamic system and the structural characteristics of the new estimation methods, ensuring a feasible and stable numerical solution, which lays a practical foundation for the application of the proposed method.

•

In order to verify the effectiveness and practical value of the proposed methods, two numerical examples with different delay conditions are constructed, and an empirical study on stock price modeling is also conducted using real financial data. These case studies comprehensively demonstrate the effectiveness of the proposed method in adapting to complex systems in the real world.

2. Methodological Approaches of Parameter Estimation for Uncertain Differential Equations

As a unique subclass within the broader category of uncertain differential equations, uncertain delay differential equations introduce specific delays into their dynamic structure. Therefore, the parameter estimation problem for systems with delays of this type fundamentally falls under a special case within the general framework of parameter estimation for uncertain differential equations. Therefore, this section will conduct a corresponding literature review on the parameter estimation problem for uncertain differential equations.

In the analysis and modeling of the evolution process of dynamic systems, when the environment in which the system is located has significant uncertainty, how to construct an effective mathematical model becomes a key issue. To address such problems, Liu [16] first proposed a theoretical framework of uncertain differential equations based on the Liu process as the source of uncertainty. This theory is based on the unique mathematical properties of the Liu process and can more accurately describe complex scenarios, such as inaccurate observation data, a limited sample size, or dynamic changes in the population distribution in the evolution laws of the system. Therefore, this theoretical tool has shown unique advantages in addressing the challenges of modeling uncertain systems and has gradually attracted widespread attention from the academic community. With the continuous exploration by numerous scholars in this field, the theoretical system of uncertain differential equations has been continuously improved, and the related research methods have become increasingly mature.

Currently, the core issue in the field of uncertain differential equations is focused on the parameter estimation problem, which serves as a crucial link connecting theoretical exploration and practical engineering applications. To address this challenge, Yao and Liu [17] pioneered the construction of statistical invariants following the difference scheme of uncertain differential equations and, based on this, proposed a moment estimation method based on the difference scheme. However, when there are many parameters to be estimated, the high-dimensional equation systems corresponding to the traditional moment estimation method are often difficult to solve, resulting in a computational bottleneck. To overcome this limitation, Liu [18] further proposed a generalized moment estimation method based on the difference scheme, achieving parameter estimation by minimizing the sum of the squared deviations between sample moments and population moments. Based on the theory of statistical invariant in difference schemes, Sheng et al. [19] drew on the idea of least squares and constructed the corresponding least squares estimation method. Subsequently, Liu and Liu [20] introduced the concept of maximum likelihood estimation and proposed the uncertain maximum likelihood estimation method. Moreover, Yang et al. [21], based on the $\alpha$ path theory of uncertain differential equations, established the minimum coverage estimation method. Xu and Dong [22], starting from the difference scheme and the least squares criterion, systematically studied the parameter estimation problem for general uncertain differential equations. Although the existing results are quite abundant, it should be pointed out that almost all of the above research methods are based on the theoretical framework of the difference scheme of uncertain differential equations. The approximate error of the difference scheme is closely related to the time step of the observed data and is strictly constrained by it. In practical application scenarios, due to objective factors such as the performance of observation equipment and policy regulations, it is often difficult to control the time step of the observed data within the ideal range, resulting in significant errors in the estimation methods based on the difference scheme in practical applications, and this limitation urgently needs to be overcome through subsequent research.

To overcome the limitations of the existing parameter estimation methods based on the difference scheme and to establish a more accurate correspondence between uncertain differential equations and observed data, Liu and Liu [23], based on the analytical solution of updated uncertain differential equations, constructed a new type of statistical invariant that follows a linear uncertainty distribution and clearly defined it as the residual term of the uncertain differential equation. On this basis, the two scholars further proposed the residual-based moment estimation method and its generalized form. Subsequently, Liu and Liu in the papers [24] and [25], respectively, introduced the improved maximum likelihood estimation idea and the least squares theory and systematically proposed the improved residual-based uncertain maximum likelihood estimation method and the residual-based least squares estimation method. Apart from the general form of uncertain differential equations, many scholars have also expanded their research perspectives to other types of equation systems. In the field of multi-factor uncertain differential equation research, Yao and Sheng [26] proposed a residual-based moment estimation method, Wu and Liu [27] deeply explored the residual-based least squares estimation theory, and Liu et al. [28] conducted a systematic study on the residual-based uncertain maximum likelihood estimation method. In the area of partial differential uncertain equations, Yang and Liu [6] and [29], respectively, proposed a residual-based moment estimation method and a least squares estimation method. Furthermore, the estimation of initial values for uncertain differential equations is also a highly regarded research direction. To effectively identify the initial state of the system from the observed data, Lio and Liu [30] proposed an initial value estimation method based on the $\alpha$ region. Subsequently, Lio and Liu [31] further explored the initial time estimation theory based on residuals, providing a new technical path for the development of this field.

As the literature review above demonstrates, residual-based parameter estimation methods have become a research hotspot in the current field of uncertain differential equations. As an important mathematical tool for studying time-delay dynamical systems, the parameter estimation problem for uncertain time-delay differential equations has attracted the attention of the academic community. Several scholars have already explored this issue, such as the moment estimation method proposed by Gao et al. [32], the least squares estimation method studied by Wei [33], and the maximum likelihood estimation method discussed by Xu [34]. However, it should be noted that all these existing methods are based on the difference scheme of uncertain delay differential equations, and the final estimated results obtained by them all have significant systematic errors that cannot be ignored. Currently, in the specific direction of parameter estimation for uncertain delay differential equations based on residuals, only one paper by Jin and Liu [35] has conducted a preliminary discussion on this. From the overall perspective of the research landscape, this field is still in a state of theoretical lack, the research system is not yet complete, and more scholars are still needed to conduct in-depth exploration. This research situation is precisely the core motivation and innovative entry point for the research work carried out in this paper.

3. The Method of Improved Uncertain Maximum Likelihood Estimation

The method of uncertain maximum likelihood estimation is one of the core methods for parameter estimation in the field of uncertain statistics, whose core idea is to infer the uncertainty distribution parameters that are most likely to generate a group of samples based on the observed samples by using the operational rules of uncertainty theory.

Specifically, assume that $\xi$ is an uncertain variable that follows the regular uncertainty distribution ${\Phi }_{\theta }$, where ${\Phi }_{\theta }$: $\mathbb{R}\to [0,1]$ serves as the population distribution function and $\theta$ is a vector of unknown parameters. Furthermore, assume that a set of independent observations $x_1,x_2,\cdots ,x_n$ (here n is the samples size) for the uncertain variable $\xi$ has been obtained. To estimate the unknown parameter vector $\theta$ based on these observations, Lio and Liu [36] proposed the uncertain likelihood function within the axiomatic system of uncertainty theory and deduced that the uncertain likelihood function for the unknown parameter vector $\theta$ corresponding to the population distribution ${\Phi }_{\theta }$ and the observed data $x_1,x_2,\cdots ,x_n$ is

$$L\left(\theta \right|x_1,x_2,\cdots ,x_n)=\underset{i=1}{\overset{n}{\bigwedge }}{\Phi }_{\theta }^{\prime }\left(x_i\right),$$

(1)

where

$${\Phi }_{\theta }^{\prime }\left(x\right)={\displaystyle \frac{\mathrm{d}{\Phi }_{\theta }\left(x\right)}{\mathrm{d}x}}$$

is the derived function of the population distribution function ${\Phi }_{\theta }$. Based on the above results, Lio and Liu [36] also suggested that the uncertain maximum likelihood estimation of the unknown parameter vector $\theta$ should be the optimal solution of the following optimization problem:

$$\underset{\theta }{max}L\left(\theta \right|x_1,x_2,\cdots ,x_n)=\underset{\theta }{max}\underset{i=1}{\overset{n}{\bigwedge }}{\Phi }_{\theta }^{\prime }\left(x_i\right).$$

Example 1. 

Let ξ be a linear uncertain variable with uncertainty distribution $L(a,b)$, and let $x_1,x_2,\cdots ,x_n$ be a set of observed data for the uncertain variable ξ. Then the uncertainty distribution function of ξ is

$${\Phi }_{a,b}\left(x\right)=\left\{\begin{array}{cc}{\displaystyle 0,}\hfill & ifx<a,\hfill \\ {\displaystyle \frac{x-a}{b-a},}\hfill & ifa\le x\le b,\hfill \\ {\displaystyle 1,}\hfill & ifx>b,\hfill \end{array}\right.$$

and the derived function of ${\Phi }_{a,b}\left(x\right)$ is

$${\Phi }_{a,b}^{\prime }\left(x\right)=\left\{\begin{array}{cc}{\displaystyle \frac{1}{b-a},}\hfill & ifa\le x\le b,\hfill \\ {\displaystyle 0,}\hfill & otherwise.\hfill \end{array}\right.$$

It follows from (1) that the uncertain likelihood function for the unknown parameters a and b corresponding to the population distribution ${\Phi }_{a,b}\left(x\right)$ and the observed data $x_1,x_2,\cdots ,x_n$ is

$$L(a,b|x_1,x_2,\cdots ,x_n)=\underset{i=1}{\overset{n}{\bigwedge }}{\displaystyle \frac{1}{b-a}}{\mathbb{I}}_{a\le x_i\le b}={\displaystyle \frac{1}{b-a}}{\mathbb{I}}_{a\le x_1,x_2,\cdots ,x_n\le b},$$

where

$${\mathbb{I}}_{x\in A}=\left\{\begin{array}{cc}{\displaystyle 1,}\hfill & ifx\in A,\hfill \\ {\displaystyle 0,}\hfill & otherwise,\hfill \end{array}\right.$$

is the indicator function. Thus the uncertain maximum likelihood estimations of a and b should solve the following optimization problem:

$$\underset{a,b}{max}L(a,b|x_1,x_2,\cdots ,x_n)=\underset{a,b}{max}{\displaystyle \frac{1}{b-a}}{\mathbb{I}}_{a\le x_1,x_2,\cdots ,x_n\le b}.$$

In order to ensure that the objective function

$${\displaystyle \frac{1}{b-a}}{\mathbb{I}}_{a\le x_1,x_2,\cdots ,x_n\le b}$$

of the above optimization problem can reach its maximum value, we must have

$$a\le x_i\le b,i=1,2,\cdots ,n.$$

That is, it should be met that

$$a\le \underset{i=1}{\overset{n}{\bigwedge }}{x}_i,\underset{i=1}{\overset{n}{\bigvee }}{x}_i\le b.$$

Based on the monotonicity of

$${\displaystyle \frac{1}{b-a}}{\mathbb{I}}_{a\le x_1,x_2,\cdots ,x_n\le b}$$

with respect to $b-a$, it is easy to conclude that the maximum value must be obtained when $b-a$ attains the minimum value. Thus the optimal solutions are

$$\left\{\begin{array}{cc}{\displaystyle \widehat{a}=\underset{i=1}{\overset{n}{\bigwedge }}{x}_i,}\hfill & \\ {\displaystyle \widehat{b}=\underset{i=1}{\overset{n}{\bigvee }}{x}_i,}\hfill \end{array}\right.$$

(2)

which are also the uncertain maximum likelihood estimations of a and b.

For the uncertain maximum likelihood estimations $\widehat{a}$ and $\widehat{b}$ determined in (2), the estimated linear uncertainty distribution is $L\left({\displaystyle \underset{i=1}{\overset{n}{\bigwedge }}{x}_i,\underset{i=1}{\overset{n}{\bigvee }}{x}_i}\right)$, which implies that there are at least two outliers in the observed data $x_1,x_2,\cdots ,x_n$ and is unreasonable in practice. In order solve this problem, Liu and Liu [24] proposed the improved uncertain maximum likelihood estimation and proved the the improved uncertain maximum likelihood estimations are

$$\left\{\begin{array}{cc}{\displaystyle \widehat{a}=\frac{2-\alpha }{2\left(1-\alpha \right)}{x}_{\widehat{i}}^{\prime }-\frac{\alpha }{2\left(1-\alpha \right)}{x}_{\widehat{i}+\widehat{k}-1}^{\prime }}\hfill & \\ {\displaystyle \widehat{b}=\frac{2-\alpha }{2\left(1-\alpha \right)}{x}_{\widehat{i}+\widehat{k}-1}^{\prime }-\frac{\alpha }{2\left(1-\alpha \right)}{x}_{\widehat{i}}^{\prime }}\hfill \end{array}\right.$$

(3)

in Example 1, where $\alpha$ is a given detection level with $0\le \alpha \le 0.1$, $\{x_1^{\prime },x_2^{\prime },\cdots ,x_n^{\prime }\}$ with $x_1^{\prime }\le x_2^{\prime }\le \cdots \le x_n^{\prime }$ is a rearrangement of $\{x_1,x_2,\cdots ,x_n\}$, $\widehat{k}=\lceil n(1-\alpha )\rceil$, and $\widehat{i}$ is the optimal solution of

$$\underset{1\le i\le n-\widehat{k}+1}{min}{x}_{i+\widehat{k}-1}^{\prime }-x_i^{\prime }.$$

4. Improved Uncertain Maximum Likelihood Estimation for Uncertain Delay Differential Equations

In this section, we consider the following uncertain delay differential equation:

$$\left\{\begin{array}{cc}\mathrm{d}{X}_t=f(t,X_t,X_{t-\tau }|\theta )\mathrm{d}t+g(t,X_t|\theta )\mathrm{d}{C}_t\hfill & \\ X_t=\varphi \left(t\right),t\in [-\tau ,0],\hfill \end{array}\right.$$

(4)

where the coefficients f and g satisfy the linear growth condition

$$\begin{array}{c}\hfill \left|f(t,x,y|\theta )\right|+\left|g(t,x|\theta )\right|\le L\left(1 + \left|x\right| + \left|y\right|\right)\end{array}$$

for any $t\ge 0$, $x,y\in \mathbb{R}$ and each $\theta$, and the Lipschitz condition

$$\begin{array}{c}\hfill |f(t,x_1,y_1|\theta )-f(t,x_2,y_2|\theta )| + |g(t,x_1|\theta )-g(t,x_2|\theta )| \le L\left(|x_1-x_2| + |y_1-y_2|\right)\end{array}$$

for any $t\ge 0$, $x_1,x_2,y_1,y_2\in \mathbb{R}$ and each $\theta$, where L is a constant, $\varphi \left(t\right)$ is a continuous and bounded function, $\tau$ is a positive real number representing the time delay, $C_t$ is a Liu process, and $\theta$ is a vector of unknown parameters. Furthermore, in order to ensure the solvability of the inverse uncertainty distribution of the solution of uncertain delay differential Equation (4), it is necessary to make the following assumptions:

(1) The coefficient $f(t,x,y|\theta )$ is a monotonically increasing function with respect to y for each $\theta$;

(2) Uncertain delay differential Equation (4) satisfies the regular condition for each $\theta$; that is,

$$g(t,X_t|\theta )>0,\forall t\ge 0$$

holds almost everywhere for each $\theta$.

Based on the above background and assumptions, we further assume that the solution $X_t$ of uncertain delay differential Equation (4) is observed at time points $t_1,t_2,\cdots ,t_n$, satisfying the sequential relationship of $t_1<t_2<\cdots <t_n$, and a set of observed data is obtained as

$$x_{t_1},x_{t_2},\cdots ,x_{t_n}.$$

(5)

By defining a number as

$$i^{*}=inf\left\{i|t_i-t_1-\tau \ge 0,i=1,2,\cdots ,n\right\},$$

(6)

and assuming that $i^{*}<n$, the subset $\{x_{t_{i^{*}+1}},\cdots ,x_{t_n}\}$ of the observed data (5) can be regarded as the observations obtained with the previous observed data before the current moment, used as the initial values. That is, for each index i with $i^{*}+1\le i\le n$, the observed data $x_{t_i}$ can be regarded as the observation of the solution of the following updated uncertain delay differential equation:

$$\left\{\begin{array}{cc}\mathrm{d}{X}_t=f(t,X_t,X_{t-\tau }|\theta )\mathrm{d}t+g(t,X_t|\theta )\mathrm{d}{C}_t\hfill & \\ X_{t_j}=x_{t_j},j=1,2,\cdots ,i-1\hfill \end{array}\right.$$

(7)

at time $t_i$. However, the solution of updated uncertain delay differential Equation (7) is not unique because its initial values do not satisfy the conditions of continuity and boundedness. In order to overcome this problem, Jin and Liu [35] performed linear interpolation on $x_{t_j},j=1,2,\cdots ,i-1$ to obtain the fitted boundary condition, which is

$${\widehat{\varphi }}_i\left(t\right)=\sum _{j=2}^{i-1}\left(x_{t_{j-1}}+{\displaystyle \frac{x_{t_j}-x_{t_{j-1}}}{t_j-t_{j-1}}}(t-t_{j-1})\right){\mathbf{I}}_{[t_{j-1},t_j]}\left(t\right).$$

(8)

Thus the observed data $x_{t_i}$ can also be regarded as the observation of the solution of the following updated uncertain delay differential equation:

$$\left\{\begin{array}{cc}\mathrm{d}{X}_t=f(t,X_t,X_{t-\tau }|\theta )\mathrm{d}t+g(t,X_t|\theta )\mathrm{d}{C}_t\hfill & \\ X_t={\widehat{\varphi }}_i\left(t\right),t\in [t_1,t_{i-1}]\hfill \end{array}\right.$$

(9)

at time $t_i$. By solving the above updated uncertain delay differential Equation (9) to obtain the solution $X_{t_i}$ and its uncertainty distribution ${\Phi }_{t_i}\left(x\right|\theta )$, Jin and Liu [35] also proved that

$${\epsilon }_i\left(\theta \right)={\Phi }_{t_i}\left(x_{t_i}\right|\theta )$$

(10)

is a sample of the linear uncertainty distribution $L(0,1)$ and is called the i-th residual of uncertain delay differential Equation (4) corresponding to observed data (5). Thus we can always obtain a set of residuals as

$${\epsilon }_{i^{*}+1}\left(\theta \right),{\epsilon }_{i^{*}+2}\left(\theta \right),\cdots ,{\epsilon }_n\left(\theta \right)$$

and always have

$${\epsilon }_{i^{*}+1}\left(\theta \right),{\epsilon }_{i^{*}+2}\left(\theta \right),\cdots ,{\epsilon }_n\left(\theta \right)\sim L(0,1).$$

(11)

Based on (11), the following theorem provides the improved uncertain maximum likelihood estimation $\widehat{\theta }$ of an unknown parameter vector in uncertain delay differential Equation (4).

Theorem 1. 

Consider the following uncertain delay differential equation:

$$\left\{\begin{array}{cc}\mathrm{d}{X}_t=f(t,X_t,X_{t-\tau }|\theta )\mathrm{d}t+g(t,X_t|\theta )\mathrm{d}{C}_t\hfill & \\ X_t=\varphi \left(t\right),t\in [-\tau ,0],\hfill \end{array}\right.$$

and let $x_{t_1},x_{t_2},\cdots ,x_{t_n}$ be a set of observed data of some uncertain process $X_t$ that follows the above uncertain delay differential equation. Let α ($0\le \alpha \le 0.1$) be a detection level; then the improved uncertain maximum likelihood estimation $\widehat{\theta }$ of the unknown parameter vector θ solves the following system of equations:

$$\left\{\begin{array}{cc}{\displaystyle {\epsilon }_{\widehat{i}\left(\theta \right)}^{\prime }\left(\theta \right)=\frac{\alpha }{2}}\hfill & \\ {\displaystyle 1-{\epsilon }_{\widehat{i}\left(\theta \right)+\widehat{k}-1}^{\prime }\left(\theta \right)=\frac{\alpha }{2},}\hfill \end{array}\right.$$

(12)

where $\widehat{i}\left(\theta \right)$ is the solution of the following minimization problem:

$$\underset{i^{*}+1\le i\le n-\widehat{k}+1}{min}{\epsilon }_{i+\widehat{k}-1}^{\prime }\left(\theta \right)-{\epsilon }_i^{\prime }\left(\theta \right)$$

${\epsilon }_i\left(\theta \right)$ is determined by (10) for $i=i^{*}+1,\cdots ,n$, $i^{*}$ is determined by (6),

$$\{{\epsilon }_{i^{*}+1}^{\prime }\left(\theta \right),\cdots ,{\epsilon }_n^{\prime }\left(\theta \right)\}$$

with

$${\epsilon }_{i^{*}+1}^{\prime }\left(\theta \right)\le \cdots \le {\epsilon }_n^{\prime }\left(\theta \right)$$

is a rearrangement of

$$\{{\epsilon }_{i^{*}+1}\left(\theta \right),\cdots ,{\epsilon }_n\left(\theta \right)\},$$

and $\widehat{k}=\lceil (n-i^{*})(1-\alpha )\rceil$.

Proof. 

Firstly, we regard the $n-i^{*}$ residual values ${\epsilon }_{i^{*}+1}\left(\theta \right),\cdots ,{\epsilon }_n\left(\theta \right)$ as a set of samples from the linear uncertain distribution $L(a,b)$, where a and b are the two unknown parameters to be estimated. Based on this set of residual samples, the improved uncertain maximum likelihood estimates of the parameters a and b can be further derived, and it follows from (3) that the improved uncertain maximum likelihood estimates of the parameters a and b are, respectively,

$$\left\{\begin{array}{cc}{\displaystyle \widehat{a}\left(\theta \right)=\frac{2-\alpha }{2\left(1-\alpha \right)}{\epsilon }_{\widehat{i}}^{\prime }\left(\theta \right)-\frac{\alpha }{2\left(1-\alpha \right)}{\epsilon }_{\widehat{i}+\widehat{k}-1}^{\prime }\left(\theta \right)}\hfill & \\ {\displaystyle \widehat{b}\left(\theta \right)=\frac{2-\alpha }{2\left(1-\alpha \right)}{\epsilon }_{\widehat{i}+\widehat{k}-1}^{\prime }\left(\theta \right)-\frac{\alpha }{2\left(1-\alpha \right)}{\epsilon }_{\widehat{i}}^{\prime }\left(\theta \right).}\hfill \end{array}\right.$$

Since ${\epsilon }_{i^{*}+1}\left(\theta \right),\cdots ,{\epsilon }_n\left(\theta \right)$ are actually $n-i^{*}$ samples of linear uncertain variable $L(0,1)$, we must ensure that

$$\left\{\begin{array}{cc}{\displaystyle \frac{2-\alpha }{2\left(1-\alpha \right)}{\epsilon }_{\widehat{i}\left(\theta \right)}^{\prime }\left(\theta \right)-\frac{\alpha }{2\left(1-\alpha \right)}{\epsilon }_{\widehat{i}\left(\theta \right)+\widehat{k}-1}^{\prime }\left(\theta \right)=0}\hfill & \\ {\displaystyle \frac{2-\alpha }{2\left(1-\alpha \right)}{\epsilon }_{\widehat{i}\left(\theta \right)+\widehat{k}-1}^{\prime }\left(\theta \right)-\frac{\alpha }{2\left(1-\alpha \right)}{\epsilon }_{\widehat{i}\left(\theta \right)}^{\prime }\left(\theta \right)=1,}\hfill \end{array}\right.$$

which can be rewritten as

$$\left\{\begin{array}{cc}{\displaystyle {\epsilon }_{\widehat{i}\left(\theta \right)}^{\prime }\left(\theta \right)=\frac{\alpha }{2}}\hfill & \\ {\displaystyle 1-{\epsilon }_{\widehat{i}\left(\theta \right)+\widehat{k}-1}^{\prime }\left(\theta \right)=\frac{\alpha }{2},}\hfill \end{array}\right.$$

and the theorem is proved immediately. □

Remark 1. 

Due to the nonlinear relationship between the residuals ${\epsilon }_{i^{*}+1}\left(\theta \right),\cdots ,{\epsilon }_n\left(\theta \right)$ of uncertain delay differential Equation (4) with parameters and the unknown parameter vector θ, the system of Equation (12) is sometimes difficult to solve or may have no solution at all. In such cases, we can obtain the generalized improved uncertain maximum likelihood estimation of the unknown parameter vector θ by solving the following optimization problem:

$$\begin{array}{c}\hfill \underset{\theta }{min}\left({\left({\epsilon }_{\widehat{i}\left(\theta \right)}^{\prime }\left(\theta \right)-{\displaystyle \frac{\alpha }{2}}\right)}^2+{\left({\epsilon }_{\widehat{i}\left(\theta \right)+\widehat{k}-1}^{\prime }\left(\theta \right)-1+{\displaystyle \frac{\alpha }{2}}\right)}^2\right).\end{array}$$

(13)

The purpose of the proposed improved uncertain maximum likelihood estimation and the generalized improved uncertain maximum likelihood estimation for uncertain delay differential equations is to eliminate the influence of outliers in the observed data on the parameter estimation results. Therefore, the identifiable conditions of the methods proposed in this paper mainly consist of two aspects: one is that it is an uncertain dynamic system with time delay and the other is that the observed data contain outliers (or it cannot be determined that the observed data do not contain outliers). Regarding the handling effect of outliers by the improved maximum likelihood estimation method used here, interested readers can refer to Liu and Qin [37] and Liu and Qin [38].

For the sake of obtaining the numerical solution of the generalized improved uncertain maximum likelihood estimation, we can design an effective numerical algorithm based on the important conclusion proved by Liu [39]. Specifically, this study, through rigorous theoretical derivation, confirms that the inverse uncertain distribution ${\Phi }_t^{-1}\left(\alpha |\theta \right)$ of the solution to the uncertain delay differential Equation (4) can actually be obtained by solving the following form of the system of ordinary differential equations:

$$\left\{\begin{array}{cc}\mathrm{d}{\Phi }_t^{-1}\left(\alpha |\theta \right)=f\left(t,{\Phi }_t^{-1}\left(\alpha |\theta \right),{\Phi }_{t-\tau }^{-1}\left(\alpha |\theta \right)|\theta \right)\mathrm{d}t+\left|g\left(t,{\Phi }_t^{-1}\left(\alpha |\theta \right)|\theta \right)\right|{\Psi }^{-1}\left(\alpha \right)\mathrm{d}t\hfill & \\ {\Phi }_t^{-1}\left(\alpha |\theta \right)=\varphi \left(t\right),t\in [-\tau ,0],\alpha \in (0,1),\hfill \end{array}\right.$$

where

$${\Psi }^{-1}\left(\alpha \right)={\displaystyle \frac{{\displaystyle \sqrt{3}ln\frac{\alpha }{1-\alpha }}}{\pi }},$$

which provides a crucial theoretical basis for constructing the numerical algorithm. Based on the above theoretical results, we are able to establish a numerical implementation approach for calculating the residuals of the uncertain delay differential Equation (4). At first, we can obtain the inverse uncertainty distribution of the solution of the uncertain delay differential Equation (4) by numerically solving the above family of ordinary differential equations. Based on this, the uncertainty distribution of the solution can also be derived, and then the corresponding residual sequence can also be obtained. Based on this calculation framework, we can construct the following numerical algorithm to solve the numerical solution of the generalized improved uncertain maximum likelihood estimation.

The numerical solutions obtained through Algorithm 1 mainly manifest in the Euler difference scheme used for calculating the $\alpha$ path of the uncertain delay differential equation. Essentially, the $\alpha$ path of the uncertain delay differential equation is the solution of a certain ordinary differential equation with a delay term. Therefore, the error analysis and convergence analysis of Algorithm 1 are actually related analyses of the numerical solutions of the Euler difference scheme for the ordinary differential equation with a delay term, which has already formed a mature theoretical foundation in the classical numerical solution method system of ordinary differential equations. Based on the existing achievements of classical numerical analysis theory, the global truncation error of this algorithm satisfies a linear relationship with the calculation step size h. Based on this characteristic, the global truncation error brought by the Euler difference scheme can be effectively controlled in two ways: one is to directly adjust the step size by reducing the step size to improve the accuracy of the numerical solution; the other is to replace the traditional explicit Euler scheme with a more accurate difference scheme (such as the implicit Euler difference scheme, Runge–Kutta difference scheme, etc.). From the perspective of numerical performance, the convergence speed of Algorithm 1 reaches first-order accuracy, and the computational complexity is $O(T/h)$, where T represents the time scale for discussion.

Algorithm 1. Numerical Solution of the Generalized Improved Uncertain Maximum Likelihood Estimation

Step 0: Input the coefficients $f(t,x,y|\theta )$ and $g(t,x|\theta )$, time delay $\tau$, the observed data $x_{t_1},x_{t_2},\cdots ,x_{t_n}$, and the detection level $\alpha$.

Step 1: Set a precision of $\delta =0.0001$ and a step size of $h=0.0001$.

Step 2: Determine the feasible region $\Theta$ of unknown parameter vector $\theta$.

Step 3: Compute $i^{*}$ by $$i^{*}=inf\left\{i|t_i-t_1-\tau \ge 0,i=1,2,\cdots ,n\right\},$$ and $\widehat{\varphi }\left(t\right)$ by $$\widehat{\varphi }\left(t\right)=\sum _{j=2}^{i^{*}-1}\left(x_{t_{j-1}}+{\displaystyle \frac{x_{t_j}-x_{t_{j-1}}}{t_j-t_{j-1}}}(t-t_{j-1})\right){\mathbf{I}}_{[t_{j-1},t_j]}\left(t\right).$$ Step 4: For each $\theta \in \Theta$, set $i=i^{*}+1$.

Step 5: Compute $\widehat{\varphi }\left(t\right)$ by $$\widehat{\varphi }\left(t\right)=\widehat{\varphi }\left(t\right)+\left(x_{t_{i-2}}+{\displaystyle \frac{x_{t_{i-1}}-x_{t_{i-2}}}{t_{i-1}-t_{i-2}}}(t-t_{i-2})\right){\mathbf{I}}_{[t_{i-2},t_{i-1}]}\left(t\right).$$ Step 6: Set $l=0$, $r=1$, and ${\Phi }_t^{-1}\left(\alpha \right)=\widehat{\varphi }\left(t\right)$ for $t\in [t_1,t_{i-1}]$.

Step 7: Set ${\displaystyle \alpha =(l+r)/2}$ and $j=1$.

Step 8: Compute ${\Phi }_{t_{i-1}+j\times h}^{-1}\left(\alpha \right)$ by $$\begin{array}{cc}\hfill {\Phi }_{t_{i-1}+j\times h}^{-1}\left(\alpha |\theta \right)=& {\Phi }_{t_{i-1}+(j-1)\times h}^{-1}\left(\alpha |\theta \right)\hfill \\ \hfill & +f\left(t_{i-1}+\left(j-1\right)\times h,{\Phi }_{t_{i-1}+(j-1)\times h}^{-1}\left(\alpha |\theta \right),{\Phi }_{t_{i-1}+(j-1)\times h-\tau }^{-1}\left(\alpha |\theta \right)\right)\times h\hfill \\ \hfill & +\left|g\left(t_{i-1}+\left(j-1\right)\times h,{\Phi }_{t_{i-1}+(j-1)\times h}^{-1}\left(\alpha |\theta \right)\right)\right|{\Psi }^{-1}\left(\alpha \right)\times h,\hfill \end{array}$$ and set $j=j+1$.

Step 9: If $j\le \lfloor \left(t_i-t_{i-1}\right)/h\rfloor$, then go to Step 8. Otherwise, set $${\Phi }_{t_i}^{-1}\left(\alpha |\theta \right)={\Phi }_{t_{i-1}+j\times h}^{-1}\left(\alpha |\theta \right),$$ and go to Step 10.

Step 10: If ${\Phi }_{t_i}^{-1}\left(\alpha |\theta \right)<x_{t_i}$, then set $l=\alpha$. Otherwise, set $r=\alpha$.

Step 11: If $|l-r|>\delta$, then go to Step 7. Otherwise, go to Step 12.

Step 12: Set ${\epsilon }_i\left(\theta \right)=(l+r)/2$ and $i=i+1$.

Step 13: If $i\le n$, then go to Step 5. Otherwise, go to Step 14.

Step 14: Compute the objective function $Obj\left(\theta \right)$ of optimization problem (13) by $$Obj\left(\theta \right)={\left({\epsilon }_{\widehat{i}\left(\theta \right)}^{\prime }\left(\theta \right)-{\displaystyle \frac{\alpha }{2}}\right)}^2+{\left({\epsilon }_{\widehat{i}\left(\theta \right)+\widehat{k}-1}^{\prime }\left(\theta \right)-1+{\displaystyle \frac{\alpha }{2}}\right)}^2.$$ Step 15: Find $\widehat{\theta }$ such that $Obj\left(\theta \right)$ reaches its minimum value.

Step 16: Output $\widehat{\theta }$.

5. Numerical Examples

This section will provide two numerical examples to illustrate the method of improved uncertain maximum likelihood estimation for uncertain delay differential equations proposed in this paper.

Example 2. 

Consider the following exponential uncertain delay differential equation:

$$\mathrm{d}{X}_t={\mu }_1{X}_t+{\mu }_2{X}_{t-0.5}\mathrm{d}t+\sigma X_t\mathrm{d}{C}_t,$$

where ${\mu }_1$, ${\mu }_2$, and σ are unknown parameters to be estimated. Suppose also that there are 58 sets of observed data $(t_i,x_{t_i})$, $i=1,2,\cdots ,58$ of some uncertain process $X_t$ following the above exponential uncertain delay differential equation, as shown in Table 1.

Table 1. The observed data in Example 2.

${\mathit{t}}_{\mathit{i}}$	${\mathit{x}}_{{\mathit{t}}_{\mathit{i}}}$	${\mathit{t}}_{\mathit{i}}$	${\mathit{x}}_{{\mathit{t}}_{\mathit{i}}}$	${\mathit{t}}_{\mathit{i}}$	${\mathit{x}}_{{\mathit{t}}_{\mathit{i}}}$	${\mathit{t}}_{\mathit{i}}$	${\mathit{x}}_{{\mathit{t}}_{\mathit{i}}}$	${\mathit{t}}_{\mathit{i}}$	${\mathit{x}}_{{\mathit{t}}_{\mathit{i}}}$
0.39	1.0753	1.96	1.2789	3.53	2.9297	5.30	3.3479	7.04	5.9531
0.40	1.0786	2.13	1.3917	3.80	3.0309	5.41	3.4352	7.11	5.8050
0.61	1.1957	2.29	1.4783	3.84	3.0928	5.67	3.8250	7.38	6.1024
0.75	1.2681	2.31	1.4790	4.02	2.8408	5.88	3.8724	7.66	5.7359
0.94	1.2730	2.61	1.7640	4.12	3.3646	6.07	4.1840	7.84	5.7022
1.17	1.2088	2.69	1.8952	4.34	3.3687	6.11	4.3055	7.95	5.8698
1.41	0.9581	2.78	2.0402	4.50	3.6403	6.14	4.3569	8.13	5.3700
1.42	0.9552	2.87	2.1233	4.57	3.6872	6.40	5.5972	8.33	6.0798
1.65	1.0128	2.88	2.1344	4.72	4.0331	6.52	5.4999	8.60	6.9791
1.82	1.1484	3.04	2.4759	4.98	3.3925	6.67	5.7115	8.62	6.9690
1.85	1.1551	3.12	2.5280	5.20	3.1581	6.81	5.7896
1.92	1.1965	3.24	2.5564	5.26	3.3766	6.96	6.2135

It follows from $\tau =0.5$ and the observation time data in Table 1 that

$$i^{*}=inf\left\{i|t_i-0.39-0.5\ge 0,i=1,2,\cdots ,58\right\}=5.$$

Then for each given parameter vector $({\mu }_1,{\mu }_2,\sigma )$, we can always calculate the 53 residuals

$${\epsilon }_6({\mu }_1,{\mu }_2,\sigma ),{\epsilon }_7({\mu }_1,{\mu }_2,\sigma ),\cdots ,{\epsilon }_{58}({\mu }_1,{\mu }_2,\sigma )$$

of the above exponential uncertain delay differential equation corresponding to observed data shown in Table 1 according to Algorithm 1. Taking the value of the detection level as $\alpha =0.05$, we can obtain

$$\widehat{k}=\lceil (58-5)\times (1-0.05)\rceil =51.$$

Then the system of Equation (12) becomes

$$\left\{\begin{array}{cc}{\displaystyle {\epsilon }_{\widehat{i}({\mu }_1,{\mu }_2,\sigma )}^{\prime }({\mu }_1,{\mu }_2,\sigma )=0.025}\hfill & \\ {\displaystyle {\epsilon }_{\widehat{i}({\mu }_1,{\mu }_2,\sigma )+50}^{\prime }({\mu }_1,{\mu }_2,\sigma )=0.975}\hfill & \\ \widehat{i}({\mu }_1,{\mu }_2,\sigma )=\underset{6\le i\le 8}{argmin}{\epsilon }_{i+50}^{\prime }({\mu }_1,{\mu }_2,\sigma )-{\epsilon }_i^{\prime }({\mu }_1,{\mu }_2,\sigma )\hfill \end{array}\right.$$

whose solutions are

$$\widehat{i}=8,{\widehat{\mu }}_1=0.3281,{\widehat{\mu }}_2=0.2817,\widehat{\sigma }=0.5539.$$

Thus the estimated exponential uncertain delay differential equation is also obtained as

$$\mathrm{d}{X}_t=0.3281X_t+0.2817X_{t-0.5}\mathrm{d}t+0.5539X_t\mathrm{d}{C}_t.$$

(14)

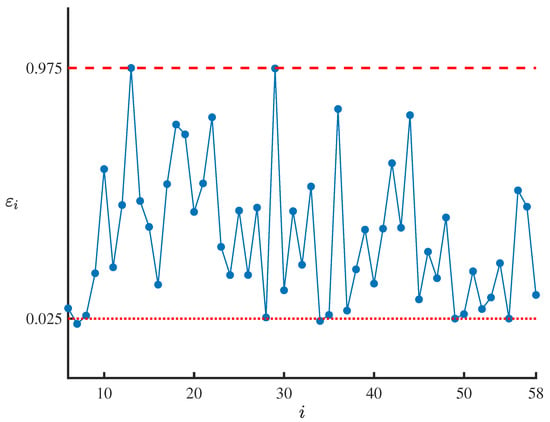
By substituting the obtained residual-based improved uncertain maximum likelihood estimations ${\widehat{\mu }}_1$, ${\widehat{\mu }}_2$, and $\widehat{\sigma }$ into ${\epsilon }_6({\mu }_1,{\mu }_2,\sigma ),{\epsilon }_7({\mu }_1,{\mu }_2,\sigma ),\cdots ,{\epsilon }_{58}({\mu }_1,{\mu }_2,\sigma )$, we can generate 53 residuals ${\epsilon }_6,{\epsilon }_7,\cdots ,{\epsilon }_{58}$, which are shown in Table 2 and Figure 1. In order to test whether the obtained residual-based improved uncertain maximum likelihood estimations ${\widehat{\mu }}_1$, ${\widehat{\mu }}_2$, and $\widehat{\sigma }$ are appropriate, we first take the significance level as $\beta =0.05$. Then it follows from $\beta \times 53=2.65$ and the work of Ye and Liu [40] that the test is

$$\begin{array}{cc}\hfill W=\left\{\right(z_6,z_7,\cdots ,& z_{58}):there are at least 3 of indexes i^{\prime }s with\hfill \\ \hfill & 6\le i\le 58 such that z_i<0.025 or z_i>0.975\}.\hfill \end{array}$$

As shown in Table 2 and Figure 1, it can be seen that only

$${\epsilon }_7,{\epsilon }_{34}\notin [0.025,0.975].$$

Thus we have

$$({\epsilon }_6,{\epsilon }_7,\cdots ,{\epsilon }_{58})\notin W,$$

and it can be concluded that the obtained residual-based improved uncertain maximum likelihood estimations ${\widehat{\mu }}_1$, ${\widehat{\mu }}_2$, and $\widehat{\sigma }$ pass the uncertain hypothesis testing. Therefore, the estimated exponential uncertain delay differential Equation (14) fits the observed data shown in Table 1 well immediately.

Table 2. Residual data in Example 2.

0.0641	0.0048	0.0364	0.1968	0.5917	0.2195	0.4554	0.9750	0.4708	0.3726
0.1536	0.5349	0.7606	0.7232	0.4294	0.5374	0.7882	0.2970	0.1899	0.4343
0.1903	0.4456	0.0293	0.9732	0.1323	0.4322	0.2289	0.5258	0.0161	0.0389
0.8194	0.0553	0.2116	0.3621	0.1577	0.3660	0.6141	0.3693	0.7962	0.0978
0.2786	0.1781	0.4084	0.0250	0.0420	0.2043	0.0611	0.1050	0.2352	0.0251
0.5111	0.4491	0.1147

Figure 1. Residual data in Example 2.

Example 3. 

Consider the following uncertain delay differential equation:

$$\mathrm{d}{X}_t=\left(\mu -c_{1}ln{X}_t+c_{2}ln{X}_{t-1}\right)\mathrm{d}t+\sigma X_t\mathrm{d}{C}_t,$$

where μ, $c_1$, $c_2$, and σ are unknown parameters to be estimated. Suppose also that there are 69 sets of observed data $(t_i,x_{t_i})$, $i=1,2,\cdots ,69$ of some uncertain process $X_t$ following the above uncertain delay differential equation, as shown in Table 3.

Table 3. The observed data in Example 3.

${\mathit{t}}_{\mathit{i}}$	${\mathit{x}}_{{\mathit{t}}_{\mathit{i}}}$	${\mathit{t}}_{\mathit{i}}$	${\mathit{x}}_{{\mathit{t}}_{\mathit{i}}}$	${\mathit{t}}_{\mathit{i}}$	${\mathit{x}}_{{\mathit{t}}_{\mathit{i}}}$	${\mathit{t}}_{\mathit{i}}$	${\mathit{x}}_{{\mathit{t}}_{\mathit{i}}}$	${\mathit{t}}_{\mathit{i}}$	${\mathit{x}}_{{\mathit{t}}_{\mathit{i}}}$
0.35	1.1228	3.47	4.2394	5.53	5.9583	7.18	9.2414	9.46	7.5970
0.65	1.6902	3.57	4.3555	5.59	6.1476	7.31	9.3566	9.51	7.9640
0.90	1.8032	3.63	4.1855	5.67	6.1292	7.47	9.6602	9.76	7.3664
1.14	1.8775	3.78	4.5185	5.90	7.2681	7.72	7.8613	9.97	7.5303
1.34	2.1452	3.79	4.5359	6.00	7.4196	7.91	8.1667	10.18	8.4612
1.50	2.1296	4.04	4.8896	6.18	7.2452	7.98	8.3266	10.45	8.7112
1.61	2.4161	4.12	4.8324	6.24	7.1790	8.25	8.6066	10.70	9.6548
1.86	3.0392	4.32	5.2653	6.27	7.3309	8.48	7.3404	10.86	9.1610
2.04	3.0914	4.56	5.8235	6.36	7.3136	8.65	7.5448	10.87	9.1909
2.27	3.1401	4.76	5.7942	6.43	7.1335	8.92	6.2069	10.89	9.3302
2.57	3.5871	4.96	4.8923	6.70	8.9087	9.03	6.6414	11.05	8.8089
2.81	3.9983	5.03	5.1181	6.98	9.5927	9.13	6.8174	11.33	8.8876
3.06	4.5919	5.17	5.4899	6.99	9.7083	9.32	7.3058	11.59	7.1555
3.21	4.7890	5.45	5.7691	7.17	9.1920	9.34	7.3509

It follows from $\tau =1$ and the observation time data in Table 3 that

$$i^{*}=inf\left\{i|t_i-0.35-1\ge 0,i=1,2,\cdots ,69\right\}=6.$$

Then for each given parameter vector $(\mu ,c_1,c_2,\sigma )$, we can always calculate the 63 residuals

$${\epsilon }_7(\mu ,c_1,c_2,\sigma ),{\epsilon }_8(\mu ,c_1,c_2,\sigma ),\cdots ,{\epsilon }_{69}(\mu ,c_1,c_2,\sigma )$$

of the above uncertain delay differential equation corresponding to observed data shown in Table 3 according to Algorithm 1. Taking the value of the detection level as $\alpha =0.05$, we can obtain

$$\widehat{k}=\lceil (69-6)\times (1-0.05)\rceil =60.$$

Then the system of Equation (12) becomes

$$\left\{\begin{array}{cc}{\displaystyle {\epsilon }_{\widehat{i}(\mu ,c_1,c_2,\sigma )}^{\prime }(\mu ,c_1,c_2,\sigma )=0.025}\hfill & \\ {\displaystyle {\epsilon }_{\widehat{i}(\mu ,c_1,c_2,\sigma )+59}^{\prime }(\mu ,c_1,c_2,\sigma )=0.975}\hfill & \\ \widehat{i}(\mu ,c_1,c_2,\sigma )=\underset{7\le i\le 10}{argmin}{\epsilon }_{i+59}^{\prime }(\mu ,c_1,c_2,\sigma )-{\epsilon }_i^{\prime }(\mu ,c_1,c_2,\sigma )\hfill \end{array}\right.$$

whose solutions are

$$\widehat{i}=9,\widehat{\mu }=0.7778,{\widehat{c}}_1=0.2704,{\widehat{c}}_2=0.1771,\widehat{\sigma }=0.4402.$$

Thus the estimated uncertain delay differential equation is also obtained as

$$\mathrm{d}{X}_t=\left(0.7778-0.2704ln{X}_t+0.1771ln{X}_{t-1}\right)\mathrm{d}t+0.4402X_t\mathrm{d}{C}_t.$$

(15)

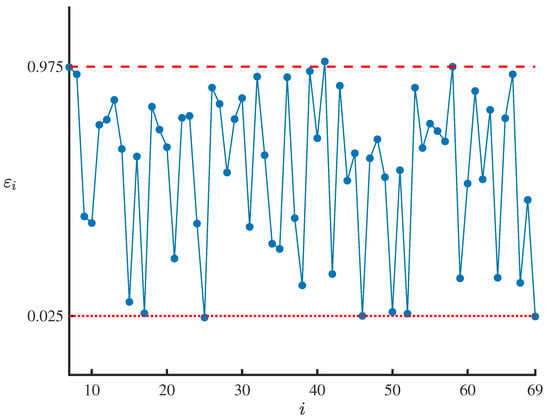
By substituting the obtained residual-based improved uncertain maximum likelihood estimations $\widehat{\mu }$, ${\widehat{c}}_1$, ${\widehat{c}}_2$, and $\widehat{\sigma }$ into ${\epsilon }_7(\mu ,c_1,c_2,\sigma ),{\epsilon }_8(\mu ,c_1,c_2,\sigma ),\cdots ,{\epsilon }_{69}(\mu ,c_1,c_2,\sigma )$, we can generate 63 residuals ${\epsilon }_7,{\epsilon }_8,\cdots ,{\epsilon }_{69}$, which are shown in Table 4 and Figure 2. In order to test whether the obtained residual-based improved uncertain maximum likelihood estimations $\widehat{\mu }$, ${\widehat{c}}_1$, ${\widehat{c}}_2$, and $\widehat{\sigma }$ are appropriate, we first take the significance level as $\beta =0.05$. Then it follows from $\beta \times 63=3.15$ and the work of Ye and Liu [40] that the test is

$$\begin{array}{cc}\hfill W=\left\{\right(z_7,z_8,\cdots ,& z_{69}):there are at least 4 of indexes i^{\prime }s with\hfill \\ \hfill & 7\le i\le 69 such that z_i<0.025 or z_i>0.975\}.\hfill \end{array}$$

As shown in Table 4 and Figure 2, it can be seen that only

$${\epsilon }_{25},{\epsilon }_{40},{\epsilon }_{69}\notin [0.025,0.975].$$

Thus we have

$$({\epsilon }_7,{\epsilon }_8,\cdots ,{\epsilon }_{69})\notin W,$$

and it can be concluded that the obtained residual-based improved uncertain maximum likelihood estimations $\widehat{\mu }$, ${\widehat{c}}_1$, ${\widehat{c}}_2$, and $\widehat{\sigma }$ pass the uncertain hypothesis testing. Therefore, the estimated uncertain delay differential Equation (15) fits the observed data shown in Table 3 well immediately.

Table 4. Residual data in Example 3.

0.9730	0.9460	0.4041	0.3790	0.7532	0.7728	0.8484	0.6614	0.0785	0.6327
0.0347	0.8224	0.7352	0.6682	0.2437	0.7800	0.7874	0.3771	0.0189	0.8951
0.8330	0.5714	0.7749	0.8551	0.3644	0.9371	0.6376	0.3000	0.2804	0.9349
0.3978	0.1414	0.9575	0.7021	0.9949	0.1845	0.9022	0.5406	0.6450	0.0250
0.6257	0.6983	0.5538	0.0403	0.5804	0.0333	0.8949	0.6652	0.7580	0.7295
0.6903	0.9750	0.1682	0.5295	0.8822	0.5457	0.8103	0.1704	0.7785	0.9459
0.1511	0.4672	0.0228

Figure 2. Residual data in Example 3.

6. Case Study: Modeling of Stock Prices

Stock prices are dynamically influenced by a variety of factors, including the macroeconomy, market sentiment, and historical trading data. Traditional uncertain differential equation modeling methods often assume that stock prices are influenced only by immediate factors, ignoring the delay effect; that is, past trading behaviors, policy changes, etc., will continue to affect the current price. In practice, there is a time delay phenomenon in stock price adjustments. For example, it takes time for the market to digest information after a company’s financial report is released, and technical indicators (such as moving averages) essentially reflect the lagging influence of historical data on current decisions. These time delays make it difficult for traditional uncertain differential equation models to accurately capture price fluctuations. Uncertain delay differential equations can quantify the persistent impact of historical information by introducing a delay term, adapting to the dynamic delay characteristics of stock prices. Therefore, their application to stock price modeling has important practical implications for improving price forecast accuracy, optimizing investment decisions, and managing risk and is a research hotspot in financial engineering.

6.1. Data Source

As a core provider of AI computing power, NVIDIA’s stock prices are driven by multiple lagging factors, the shipment of Blackwell chips, the value signal of the repurchase plan, export control, and quarterly financial reports, which form a dynamic game and exhibit certain cyclical characteristics. It is difficult for traditional uncertain differential equations to accurately characterize these lagged relationships and uncertainties. Therefore, we collected the closing price data of NVIDIA Corporation Common stock reported by Nasdaq from 2 January 2025 to 3 October 2025 (unit: US dollars) and organized it into weekly average data, as shown in Table 5.

Table 5. The weekly average closing price data of NVIDIA Corporation Common stock reported by Nasdaq from 2 January 2025 to 3 October 2025 (unit: US dollars).

138.6400	141.3975	134.5020	144.4350	123.1660	123.7320	134.3300	138.2925
126.6520	114.1220	113.7460	117.7420	115.3920	105.0120	105.3540	107.2225
103.1900	110.5560	115.6880	131.7000	133.1740	136.1575	140.4460	143.2780
144.5350	151.8300	156.9700	162.0280	170.3100	171.2860	176.6240	180.2300
181.8560	177.2040	179.5060	170.0200	174.2780	175.1660	178.9780	186.4360

6.2. Uncertain Stock Price Model

The 5-day moving average line is one of the most commonly used methods for analyzing the short-term trend of stock prices. Therefore, here we can assume that the time delay of NVIDIA Corporation Common stock price data is 5 trading days. On a weekly average time scale, we denote the time delay as $\tau =1$. Additionally, mean reversion is the most important property of stock prices. Thus we choose the following mean reversion uncertain delay differential equation:

$$\mathrm{d}{X}_t=\left(m-{\mu }_1{X}_t+{\mu }_2{X}_{t-1}\right)\mathrm{d}t+\sigma \mathrm{d}{C}_t,$$

to model the weekly average closing price data in Table 5, where m, ${\mu }_1$, ${\mu }_2$, and $\sigma$ are unknown parameters to be estimated.

Let $i=1,2,\cdots ,40$ denote the weeks from 2 January 2025 to 3 October 2025, and let

$$x_1,x_2,\cdots ,x_{40}$$

(16)

denote the weekly average closing price data in Table 5. It follows from $\tau =1$ and the observation time data $i=1,2,\cdots ,40$ that

$$i^{*}=inf\left\{i|t_i-1-1\ge 0,i=1,2,\cdots ,40\right\}=2.$$

Then for each given parameter vector $(m,{\mu }_1,{\mu }_2,\sigma )$, we can always calculate the 38 residuals

$${\epsilon }_3(m,{\mu }_1,{\mu }_2,\sigma ),{\epsilon }_3(m,{\mu }_1,{\mu }_2,\sigma ),\cdots ,{\epsilon }_{40}(m,{\mu }_1,{\mu }_2,\sigma )$$

of the above mean reversion uncertain delay differential equation corresponding to observed data (16) according to Algorithm 1. Taking the value of the detection level as $\alpha =0.05$, we can obtain

$$\widehat{k}=\lceil (40-2)\times (1-0.05)\rceil =37.$$

Then the system of Equation (12) becomes

$$\left\{\begin{array}{cc}{\displaystyle {\epsilon }_{\widehat{i}(m,{\mu }_1,{\mu }_2,\sigma )}^{\prime }(m,{\mu }_1,{\mu }_2,\sigma )=0.025}\hfill & \\ {\displaystyle {\epsilon }_{\widehat{i}(m,{\mu }_1,{\mu }_2,\sigma )+36}^{\prime }(m,{\mu }_1,{\mu }_2,\sigma )=0.975}\hfill & \\ \widehat{i}(m,{\mu }_1,{\mu }_2,\sigma )=\underset{3\le i\le 4}{argmin}{\epsilon }_{i+36}^{\prime }(m,{\mu }_1,{\mu }_2,\sigma )-{\epsilon }_i^{\prime }(m,{\mu }_1,{\mu }_2,\sigma )\hfill \end{array}\right.$$

whose solutions are

$$\widehat{i}=4,\widehat{m}=27.8944,{\widehat{\mu }}_1=0.2020,{\widehat{\mu }}_2=0.0011,\widehat{\sigma }=8.0679.$$

Thus the estimated uncertain stock price model is also obtained as

$$\mathrm{d}{X}_t=\left(27.8944-0.2020X_t+0.0011X_{t-1}\right)\mathrm{d}t+8.0679\mathrm{d}{C}_t.$$

(17)

6.3. Uncertain Hypothesis Testing

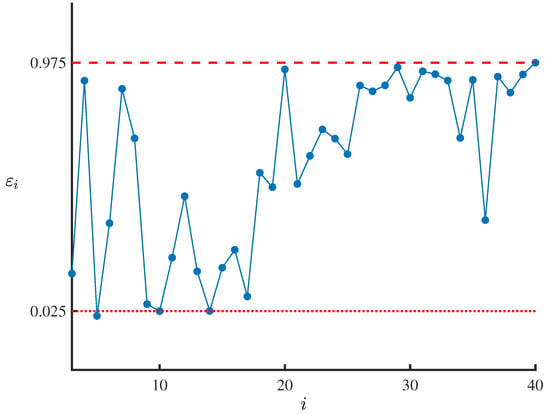
By substituting the obtained residual-based improved uncertain maximum likelihood estimations $\widehat{m}$, ${\widehat{\mu }}_1$, ${\widehat{\mu }}_2$, and $\widehat{\sigma }$ into ${\epsilon }_3(m,{\mu }_1,{\mu }_2,\sigma ),{\epsilon }_4(m,{\mu }_1,{\mu }_2,\sigma ),\cdots ,{\epsilon }_{40}(m,{\mu }_1,{\mu }_2,\sigma )$, we can generate 38 residuals ${\epsilon }_3,{\epsilon }_4,\cdots ,{\epsilon }_{40}$, which are shown in Table 6 and Figure 3. In order to test whether the obtained residual-based improved uncertain maximum likelihood estimations $\widehat{m}$, ${\widehat{\mu }}_1$, ${\widehat{\mu }}_2$, and $\widehat{\sigma }$ are appropriate, we first take the significance level as $\beta =0.05$. Then it follows from $\beta \times 38=1.9$ and the work of Ye and Liu [40] that the test is

$$\begin{array}{cc}\hfill W=\left\{\right(z_3,z_4,\cdots ,& z_{40}):there are at least 2 of indexes i^{\prime }s with\hfill \\ \hfill & 3\le i\le 40 such that z_i<0.025 or z_i>0.975\}.\hfill \end{array}$$

Table 6. Residual data of the estimated uncertain stock price model (17) corresponding to observed data (16).

0.1684	0.9062	0.0065	0.3610	0.8752	0.6857	0.0514	0.0250	0.2293	0.4645
0.1770	0.0257	0.1908	0.2593	0.0809	0.5541	0.4991	0.9493	0.5111	0.6187
0.7197	0.6846	0.6252	0.8877	0.8656	0.8884	0.9570	0.8407	0.9421	0.9309
0.9065	0.6872	0.9091	0.3730	0.9215	0.8606	0.9299	0.9750

Figure 3. Residual data of the estimated uncertain stock price model (17) corresponding to observed data (16).

As shown in Table 6 and Figure 3, it can be seen that only

$${\epsilon }_5\notin [0.025,0.975].$$

Thus we have

$$({\epsilon }_3,{\epsilon }_4,\cdots ,{\epsilon }_{40})\notin W,$$

and it can be concluded that the obtained residual-based improved uncertain maximum likelihood estimations $\widehat{m}$, ${\widehat{\mu }}_1$, ${\widehat{\mu }}_2$, and $\widehat{\sigma }$ pass the uncertain hypothesis testing. Therefore, the estimated uncertain stock price model (17) fits the observed data shown in Table 5 well immediately.

7. Conclusions

For the purpose of addressing the problem of the adverse impact of outliers on the estimation results in the parameter estimation of uncertain delay differential equations, which has long existed in uncertain dynamic delay systems, this paper innovatively proposed two new estimation methods by combining the improved uncertain maximum likelihood method with the symmetric statistical invariants (i.e., residuals) of uncertain delay differential equations. These methods uniquely incorporate the outlier-resistant mechanism into the uncertain statistical inference framework of uncertain dynamic delay systems, effectively reducing the adverse impact of abnormal observations on the estimation results, while adapting to the inherent delay characteristics of uncertain delay differential equations, thereby filling the gap in the research on parameter estimation of such systems. For the sake of facilitating the practical application of the proposed methods, this paper specially designed a numerical algorithm to solve the non-convex optimization problems corresponding to these estimators. This algorithm fully takes into account the structural complexity of the improved uncertain likelihood function and the delay effect of the uncertain delay differential equations, thereby ensuring the stable and efficient acquisition of numerical solutions from the observed data. To verify the effectiveness of the proposed methods, this paper also constructed two numerical examples and conducted an empirical study on stock price modeling using real financial market data.

In conclusion, this study has enriched the theoretical framework for parameter estimation of uncertain delay differential equations, provided a new technical path for robust parameter inference in complex uncertain dynamic systems, and offered practical methodological support in fields such as financial risk modeling, engineering system identification, and propagation dynamics analysis. Future research will focus on using numerical approximation techniques to explore the asymptotic statistical properties of the proposed estimators and extend the proposed framework to high-dimensional uncertain delay differential equations to address more complex practical problems.