A Chaos-Initiated and Adaptive Multi-Guide Control-Based Crayfish Optimization Algorithm for Image Analysis

Abstract

Image clustering analysis faces the curse of dimensionality, distance concentration, multimodal landscapes, and rapid diversity loss that challenge meta-heuristics. Meanwhile, the standard Crayfish Optimization Algorithm (COA) has shown notable potential but often suffers from poor convergence speed and premature convergence. To address these issues, this paper introduces a Chaos-initiated and Adaptive Multi-guide Control-based COA (CMCOA). First, a chaotic initialization strategy is employed by explicitly exploiting the reflection symmetry of logistic-map chaotic sequences together with opposition-based learning, which enhances population diversity and facilitates early exploration of promising regions. Second, a fitness-feedback adaptive parameter control mechanism, motivated by the general idea of the MIT rule, is integrated to dynamically balance exploration and exploitation, thereby accelerating convergence while mitigating premature stagnation. Furthermore, a multi-guide stage-switching strategy is designed to avoid being trapped in local optima by promoting adaptive transitions between exploration phases and exploitation phases. CMCOA is benchmarked against competing algorithms on ten challenging test functions drawn from CEC2017, CEC2019, CEC2020, and CEC2022 suites. We also conducted multispectral clustering, where class differences often lie in reflectance magnitude; we adopt Euclidean distance for its efficiency and suitability in capturing such variations. Compared with other algorithms, CMCOA shows faster convergence, higher accuracy, and improved robustness, revealing its broader potential for image analysis tasks.

1. Introduction

High-dimensional image analysis, especially in multispectral and hyperspectral clustering, faces unique challenges for meta-heuristic optimizers. The curse of dimensionality and distance concentration weaken similarity measures and obscure cluster boundaries, reducing the effectiveness of traditional distance metrics as dimensionality increases [1,2]. Additionally, the objective landscapes are highly non-convex and multi-modal, often resembling ridges, which can cause premature convergence in many population-based methods unless diversity is actively preserved [3,4,5]. Population diversity itself tends to diminish under leader-biased update rules, further increasing the risk of mode trapping; recent diversity-guided and multi-level learning strategies only partially address this problem [6]. Fixed or manually tuned schedules also find it difficult to balance exploration and exploitation across different stages, motivating the use of adaptive parameter control and stage-aware strategies in evolutionary computation [7,8]. Furthermore, unequal cluster sizes in real hyperspectral scenes are common and can lead to over-segmentation or collapsed clusters, prompting methods that combine subspace or graph modeling with imbalance-aware learning [9,10]. These interconnected challenges limit the effectiveness of mainstream optimizers when directly applied to high-dimensional image data. To counter these issues, this paper proposes a unified framework that improves initialization coverage, incorporates adaptive stage control, and includes anti-bias guidance to enhance robustness and clustering accuracy in imagery.

Among many meta-heuristic techniques, the Crayfish Optimization Algorithm (COA) [11] has gained attention for its simple design and biologically inspired phase structure, which—through summer-resort, competition, and foraging stages—provides a natural way to switch between exploration and exploitation. Empirically, COA achieves competitive results on various benchmarks and engineering problems, and its temperature-driven schedule offers an understandable method to adjust search behavior. However, these practical advantages do not guarantee consistent performance across all problem types: in high-dimensional or highly deceptive landscapes, the usual COA initialization and leader-biased updates can lead to inadequate search-space coverage and faster diversity loss, raising the chance of premature stagnation. These limitations highlight specific areas for improvement while keeping the useful phase structure that makes COA a good base for improvement.

In response to the limitations of the standard COA mentioned earlier, several researchers have proposed various improvements to enhance its performance. Shikoun et al. [12] introduced the Binary Crayfish Optimization Algorithm (BinCOA), which uses refracted opposition-based learning and crisscross strategies to improve the algorithm’s exploitation capability and convergence accuracy in feature selection tasks. To address performance decline and local stagnation observed in later iterations of COA, Jia et al. [13] proposed the Modified Crayfish Optimization Algorithm (MCOA), which includes an environmental renewal mechanism and a ghost-antagonism-based learning strategy. Their results show significant improvements in avoiding local optima, especially in constrained engineering design and feature selection scenarios. To further enhance the standard COA, Elhosseny et al. [14] introduced the Adaptive Dynamic COA with a Locally enhanced escape operator (AD-COA-L), which leverages the Bernoulli map for population initialization, an adaptive dynamic inertia weight, and a local escape operator to better balance exploration and exploitation and prevent premature convergence. Table 1 summarizes the mathematical mechanisms across COA variants.

Table 1. Comparative table summarizing mathematical mechanisms across COA variants.

Mechanism	CMCOA	AD-COA-L	BinCOA	MCOA
Initialization	Uses a chaotic system (Logistic Map).	Uses a Bernoulli map for initialization.	Uses refracted opposition-based learning to select a better starting point.	Standard random initialization.
Adaptation	Dynamically adjusts the key control parameter C based on the population’s fitness change, replacing $C_2$.	Introduces a dynamic inertia weight to balance exploration and exploitation.	A special mechanism for binary problems, converting continuous values to binary.	Guides the algorithm to seek a better “environment” based on a fitness-related “water quality” factor.
Update Rule	Guides the search using the average position of the elites and switches between exploration and exploitation.	Encourages information sharing and helps escape local optima via random movement.	A crossover mechanism that averages two random individuals’ positions to increase diversity.	A strategy to escape local optima by generating and evaluating an “opposite” solution.

Many studies collectively emphasize COA’s potential in solving feature selection and engineering optimization problems [15]. However, there is a growing demand for more efficient and robust optimization algorithms. Recent research has extended COA and its variants into the fields of image processing and recognition. Padmashree et al. [16] used COA to optimize similarity-navigated graph neural networks (SNGNNs) for brain tumor image analysis, resulting in significant improvements in diagnostic accuracy. Dinh [17] employed COA to control texture layer fusion in the Medical Image Fusion based on the Bilateral Texture Filter and Transfer Learning with the ResNet-101 network, addressing issues such as limited training data, inadequate feature representation, and contrast loss. Their approach enhanced the visual quality of fused medical images, highlighting the algorithm’s usefulness in critical clinical imaging tasks.

Among these techniques, chaotic systems have gained increasing attention as initialization methods due to their sensitivity to initial conditions and ergodic, pseudo-random dynamics, which increase dispersion in the initial population and therefore help to reduce the risk of premature convergence. Practically, chaotic initializers can be viewed in three classes: simple one-dimensional maps that provide low-cost, tunable diversification; higher-order and hyperchaotic generators that produce stronger mixing for rugged search landscapes; and fractional-order or hybrid schemes that introduce memory effects or combine chaotic sequences with Lévy/quantum operators to enhance exploration under constraints. Recent research has explored their integration into various applications: Lévy-augmented chaotic PSO has been shown to improve energy-efficient cluster routing in industrial WSNs [18], while a chaotic-quantum hybrid was employed successfully for berth-crane scheduling under tidal constraints [19]. In the image-security domain, fractional-order chaotic Hopfield networks and hybrid-domain chaotic encryption have been proposed for high-performance protection of medical and social images [20,21], and tailored quadratic polynomial hyperchaotic maps combined with pixel-fusion strategies have demonstrated superior randomness and efficiency in image encryption [22]. Together, these results both motivate and guide our choice of a chaotic initializer: match the map complexity to problem difficulty.

However, directly using chaotic sequences for population initialization in high-dimensional clustering is insufficient: distance concentration persists, and cluster balance is not guaranteed. To address this gap, the proposed CMCOA simultaneously acts on initialization, parameter adaptation, and guidance diversity. Initialization is reworked through logistic-map chaos coupled with opposition-based selection [23], which increases initial sample dispersion and convergence speed; the adaptive parameter control, inspired by the general concept of the MIT rule [24] and implemented here as a population-level, non-gradient fitness-feedback controller, replaces the fixed temperature schedule with a state-driven step-size controller that scales exploitation intensity according to relative improvement; finally, a multi-guide stage-switching mechanism distributes search pressure among several elites and employs a diversity threshold to trigger phase transitions, thereby avoiding single-leader dominance while permitting focused refinement when warranted. Each of these components targets one of the identified failure modes and is integrated so that early broad exploration is preserved while late exploitation is stabilized, yielding lower final objective values in image clustering benchmarks.

The effectiveness of CMCOA is demonstrated through benchmark functions and clustering experiments on multispectral image datasets. Empirical results show that the proposed algorithm delivers improvements in convergence speed, clustering precision, and intra-cluster balance. Notably, CMCOA is able to extract semantically meaningful structures from complex images, producing segmentation results that align well with human visual interpretation. These findings support CMCOA’s applicability to image analysis tasks and reinforce its value as a robust tool for advanced image analysis.

This paper’s contributions are summed up as follows:

• We present CMCOA, an improved optimization algorithm that integrates chaotic initialization and adaptive multi-guide control, showing consistent gains in exploration, convergence speed, and robustness on benchmarks and multispectral datasets.
• CMCOA combines logistic-map chaos with opposition-based learning to enhance initial diversity and accelerate early search, while an MIT-inspired adaptive mechanism adjusts parameters to maintain a balance between exploration and exploitation.
• A multi-guide stage-switching strategy enables flexible transitions across search phases, reducing leader bias and supporting more reliable solution quality.
• Applied to multispectral image clustering, CMCOA improves cluster balance and texture preservation, yielding meaningful segmentation with practical efficiency in high-dimensional tasks.

2. The Chaotic Initialization and Adaptive Multi-Guide Control-Based Crayfish Optimization Algorithm

2.1. Overview of the Original Crayfish Optimization Algorithm

The Crayfish Optimization Algorithm is a nature-inspired meta-heuristic that mimics the social and survival behaviors of crayfish. These behaviors mainly include summer avoidance, competition, and foraging, which are reflected as different search phases in the algorithm. Each crayfish in the algorithm represents a possible solution within the multi-dimensional search space, with its position being updated iteratively based on these behaviors. The algorithm goes through multiple iterations, aiming to reach an optimal solution by imitating the collective intelligence and adaptive strategies seen in crayfish populations.

2.1.1. Initialization

In the original COA, the initialization of individuals in the population is typically performed using a uniform random distribution. Each individual’s position vector is generated independently within the problem’s lower and upper bounds:

$$X_{i,j}={lb}_j+rand(1,d)\cdot ({ub}_j-{lb}_j)$$

(1)

where $X_{i,j}$ represents the position of the $i^{th}$ individual and $j^{th}$ dimension, $d$ is the problem dimension, and $rand\left(1,d\right)$ denotes a d-dimensional vector whose entries are generated uniformly at random from the interval [0, 1]. ${lb}_j$ and ${ub}_j$ denote the lower and upper bounds of the $j^{th}$ dimension search space, respectively. While effective for basic coverage, purely random initialization lacks structural diversity and may limit exploration from the outset.

2.1.2. Temperature Schedule

The behavior of crayfish is significantly influenced by variations in temperature, which in turn dictate the specific behavioral stages undertaken by the organisms. The definition of temperature can be expressed as Equation (2). When temperatures exceed 30 °C, crayfish are observed to seek cooler refuges, exhibiting a summer escape behavior. Conversely, under optimal temperature conditions, foraging activities are initiated. The quantity of food consumed by crayfish is directly impacted by ambient temperature. It has been established that the optimal foraging temperature range for crayfish lies between 15 °C and 30 °C, with peak intake observed around 25 °C. Consequently, the foraging intake of crayfish can be approximated by a normal distribution, reflecting its dependence on temperature fluctuations.

$$\mathit{temp}=20+15\times rand$$

(2)

$rand$ is generated uniformly at random from the interval [0, 1].

2.1.3. Summer Resort Stage

If temp > 30, each crayfish seeks a safe cave location. The “cave” position is defined as the midpoint between the global best and the individual’s local best:

$$X_{\mathit{shade}}={\displaystyle \frac{X_G+X_L}{2}}$$

(3)

The fitness of each agent is evaluated to determine the global best solution $X_G$ and each local best $X_L$. Subsequently, with a probability of 0.5, indicating the absence of competition, the crayfish directly relocates to the cave position. Otherwise, in the presence of competition for the same cave, it moves toward the cave by taking a fractional step in its direction:

$$X_{i,j}^{t+1}=X_{i,j}^t+C_2·rand·\left(X_{\mathit{shade}}-X_{i,j}^t\right)$$

(4)

$$C_2=2-t/T$$

(5)

where $C_2$ is the linearly decreasing coefficient, with total iterations $T$ and current iteration $t$. This update pulls the crayfish toward the cave, enhancing exploitation as they converge on high-quality regions.

2.1.4. Competition Stage

When temp > 30 and another crayfish is contesting the cave, modeled by the random coin flip, a competition update is used. A random competitor $X_z$ is chosen from the population, and the current agent moves toward it:

$$Z =\mathit{round}(\mathit{rand}·(N - 1\left)\right) + 1$$

(6)

$$X_{i,j}^{t+1}=X_{i,j}^t-X_{z,j}^t+X_{\mathrm{shade}}$$

(7)

This exchange encourages diversity by having agents interact and spread out, expanding the search.

2.1.5. Foraging Stage

If temp ≤ 30, the environment is suitable for feeding. All crayfish move toward the food at the current global best position $X_{\mathit{food}}=X_G$. Each crayfish computes a food-size measure $Q$:

$$Q=C_3\hspace{0.17em}·\mathit{rand}·{\displaystyle \frac{f_i}{f_{\mathit{food}}}}$$

(8)

where $f_i$ is the fitness of crayfish $i$, $f_{\mathit{food}}$ is the fitness at $X_{\mathit{food}}$, and $C_3=3$ is a constant “food factor”. This ratio measures how large or small the food is relative to the crayfish’s current solution. Two feeding behaviors ensue:

• Shredding (when $Q>{\displaystyle \frac{C_3+1}{2}}$): If the food is large relative to the agent’s state, the crayfish first “shreds” it. The global best position is scaled to simulate processing:

  $$X_{\mathit{food}}=\mathrm{e}\mathrm{x}\mathrm{p}(-{\displaystyle \frac{1}{Q}}){·X}_{\mathit{food}}$$

  (9)

  Then the crayfish advances toward the food with an alternating step:

  $$X_{i,j}^{t+1}=X_{i,j}^t+X_{\mathit{food}}·p·\left(\mathrm{c}\mathrm{o}\mathrm{s}\left(2\pi \mathit{rand}\right)-sin\left(2\pi \mathit{rand}\right)\right)$$

  (10)

  Here $p$ is the food intake proportion, determined by a Gaussian function of the temperature:

  $$p={\displaystyle \frac{C_1}{\sigma \sqrt{2\pi }}}·exp\left(-{\displaystyle \frac{{\left(\mathit{temp}-\mu \right)}^2}{2{\sigma }^2}}\right)$$

  (11)

  Among them, µ refers to the temperature most suitable for crayfish, σ and $C_1$ are used to control the intake of crayfish at different temperatures, where $C_1=0.2,$ $\mu ={25 }^{\circ }\mathrm{C}$ and $\sigma =3$ in the original COA formulation. The sine-cosine term is designed to emulate the alternating use of claws when manipulating larger food items, thereby enabling fine-grained local search behavior within the optimization process.
• Direct Feeding (when $Q\le {\displaystyle \frac{C_3+1}{2}}$): If the food is small enough, the crayfish moves directly toward it:

  $$X_{i,j}^{t+1}=\left(X_{i,j}^t-X_{\mathit{food}}\right)·p+p·\mathit{rand}·X_{i,j}^t$$

  (12)

  This accelerates convergence by exploiting the gradient toward the best solution. These stages are repeated until the iteration limit T is reached. Throughout, the algorithm updates global and local bests. In summary, COA embeds exploration and exploitation within a unified framework.

2.2. Improved Strategy Framework of CMCOA

To address the identified drawbacks of the standard COA, a novel enhanced version named CMCOA was developed. CMCOA integrates three specifically designed strategies to improve population diversity, balance exploration with exploitation, and enhance convergence robustness.

2.2.1. Chaotic Initialization Strategy

Instead of purely random initialization, CMCOA adopts a chaotic initialization strategy in which logistic mapping is utilized to construct the initial population. In this process, chaotic sequences are applied not primarily for their randomness but for their inherent symmetric properties within the unit interval [0, 1]. By coupling each candidate solution with its symmetric counterpart, the coverage of the search space is reinforced, and population diversity is preserved from the outset. The logistic formulation is then employed as a generator of such symmetric mappings, defined by:

$$x_{n+1}=L·x_n·\left(1-x_n\right)$$

(13)

With $L$ chosen as 4 and the chaotic value $x_n\in \left(0,1\right)$. For $L$ = 4, the Logistic map admits the invariant distribution:

$$\rho (x)={\displaystyle \frac{1}{\pi \sqrt{x\left(1-x\right)}}},x\in (0,1)$$

(14)

$$E\left[X\right]={\int }_0^1 x\rho \left(x\right)dx={\displaystyle \frac{1}{\pi }}{\int }_0^1 {\displaystyle \frac{x}{\sqrt{x\left(1-x\right)}}}dx$$

(15)

$$\mathrm{V}\mathrm{a}\mathrm{r}\left(X\right)=\mathrm{E}\left[X^2\right]-\mathrm{E}[X{]}^2$$

(16)

$$\lambda ={\int }_0^1 \mathrm{l}\mathrm{n}\left|f^{\prime }\left(x\right)\right|\rho (x)dx={\int }_0^1 \mathrm{l}\mathrm{n}\left|4(1-2x)\right|\rho (x)dx$$

(17)

This distribution yields mean E[X] = 0.5 and variance Var(X) = 1/8, which is larger than that of the uniform distribution (1/12), implying stronger boundary coverage and greater spread of samples. Its positive Lyapunov exponent λ = ln2 > 0 ensures chaotic sensitivity and ergodicity. This recurrence generates a pseudo-random sequence that is ergodic on [0, 1]. To initialize a solution, one takes a chaotic value $x_n$ and maps it into the search space for each dimension $j:$

$$X_{i,j}=l{b}_j+x_n\left(u{b}_j-l{b}_j\right),j=1,\dots ,dim$$

(18)

By applying initialization independently to each individual, a well-distributed and diverse initial population can be obtained. Compared with uniform random sampling, chaotic sequences provide more comprehensive coverage of the search space, as they traverse the domain in a deterministic yet non-repetitive manner. To further accelerate convergence, opposition-based learning has also been incorporated, whereby for each candidate solution $X$, an opposite solution $X^{\mathit{op}}$ is generated, and the superior of the two is retained.

$$X_j^{op}=l{b}_j+u{b}_j-X_j$$

(19)

The expected distance between $X$ and $X^{\mathit{op}}$ is 0.5 under uniform sampling and 2/π ≈ 0.6366 under the logistic invariant measure, both larger than the expected distance between two independent uniform samples (1/3). This operator yields antipodal pairs whose midpoint is the domain center. From a geometric standpoint, evaluating such antipodal pairs reduces directional bias introduced by single-point sampling and increases the effective angular coverage around potential optima. In stochastic terms, the expected pairwise distance under the logistic invariant measure exceeds that of uniform sampling, which empirically accelerates the early-stage basin discovery.

2.2.2. Adaptive Parameter Control Rule

In the original COA, the transition between different behavioral stages is mainly governed by a random temperature variable: temp. When temp > 30, the algorithm enters the summer resort or competition stage; otherwise, it performs foraging. While this mechanism introduces stochasticity, it lacks sensitivity to the actual optimization state, which may result in either premature convergence or excessive randomness.

To overcome this limitation, CMCOA replaces the random temperature-driven mechanism with a state-driven adaptive rule. Although the update mechanism used in this paper is not the same as the classical MIT rule in Model Reference Adaptive Control—which typically adjusts parameters through gradient-based adaptation with respect to a reference model—our design is inspired by its underlying idea of error-driven adjustment. Specifically, CMCOA adopts a fitness-feedback approach: the control parameter is updated according to the relative difference between the population mean fitness and the current best fitness, with projection onto a bounded interval to ensure stability. This mechanism is computationally efficient, model-free, and automatically balances exploration and exploitation during the search process.

Specifically, a control parameter $C$ is introduced to govern the step size, initially set as 2, replacing $C_2$ in Equation (4). Instead of being linearly decreasing, $C$ is dynamically adjusted according to the optimization progress. The updated law is given by:

$$e={\displaystyle \frac{F_{avg}\left(\mathrm{i}\right)-F_{avg}(\mathrm{i}-1)}{\mid F_{avg}(\mathrm{i}-1)\mid +{10}^{-8}}}$$

(20)

$$C=max(0.01,min(2,C+\eta \cdot e\left)\right)$$

(21)

$F_{avg}\left(\mathrm{i}\right)$ denotes the average fitness value of the $i^{th}$ generation population, $e$ measures the relative deviation between the population average and the best solution, $\eta$ is a learning rate controlling the update speed set as 0.03, and the projection operator max (0.01, min (2, ⋅)) ensures that $C$ always remains within the bounded interval [0.01, 2].

When the population quality is poor, $e$ < 0, which decreases $C$. This reduces the exploitation intensity and introduces exploratory behavior, thereby mitigating premature convergence. When the population tends to converge, $e$ > 0, leading to an increase in $C$. This encourages stronger exploitation by amplifying the attraction toward promising regions.

Furthermore, the projection operator guarantees boundedness, since by construction $C$∈ [0.01, 2] at every iteration. When the algorithm converges, we have $e$→0. Thus, the increments $\eta \cdot e$ vanish, and the update stabilizes at a fixed point within the bounded interval. Therefore, the adaptive update law ensures both stability and convergence under practical conditions.

2.2.3. Multi-Guide and Stage-Switching Update Mechanism

To further improve search robustness, CMCOA enhances the update mechanism by introducing multiple elite guides and a diversity-driven stage-switching rule, which operate in synergy with the adaptive parameter control.

• Multi-guide update

Instead of relying on a single global best, CMCOA aggregates several top-performing solutions. Let E $=\left\{X_{\left(1\right)},X_{\left(2\right)},\dots ,X_{\left(N_e\right)}\right\}$ denote the elite set of size $N_e=[0.2\cdot N]$, where $X_{\left(i\right)}$ is the $i^{th}$ best solution. The elite ratio was set to 20% as a balanced choice: smaller values reduce diversity, while larger value weakens selection pressure. Our preliminary tests indicated that performance is stable within 10–30%, with 20% giving slightly better results overall. This parameter is tunable and not a strict requirement of the algorithm. The guiding position $X_g$ is formed by a convex combination:

$$X_g=\alpha \cdot X_{food}+\beta \cdot {\displaystyle \frac{1}{N_e}}\cdot {\sum }_{i=1}^{N_e}{X}_{\left(i\right)}$$

(22)

$$\alpha ={\displaystyle \frac{1}{1+D_N\left(t\right)}},\beta ={\displaystyle \frac{D_N\left(t\right)}{1+D_N\left(t\right)}}$$

(23)

$$D_N\left(t\right)=\mathit{std}(f_1,\dots ,f_N)$$

(24)

where $X_{food}$ is the global best solution. $X_g$ will replace $X_{\mathit{shade}}$ in Equation (4). The weights $\alpha , \beta$ are adaptively chosen based on the population state. $D_N\left(t\right)$ stands for $t^{th}$ generation population fitness standard deviation. Thus, when diversity is high, $\beta$ increases, giving more emphasis to multiple elites; when diversity collapses, $\alpha$ dominates, and the algorithm relies on the global best. The adaptive weighting balances robustness and intensification: at high population diversity, the global best may be an outlier, so using the elite centroid gives a more robust search direction; at low diversity, the population has converged, and the global best is more reliable, so emphasizing it enhances exploitation. This is a heuristic design intended to improve practical robustness; a protocol for empirical comparison with alternative schemes is provided in the supplement.

Suppose all elite solutions $X_{\left(i\right)}$ lie in the feasible domain $\Omega \subseteq R^d$, which is convex. Then the convex combination $X_g$ also lies in $\Omega$. Hence, the multi-guide rule preserves feasibility. Moreover, by mixing different elite directions, the update direction variance is enlarged, thereby enhancing exploration before convergence.

By weighing multiple elite guides, the algorithm explores along different promising directions simultaneously, which can reduce over-convergence on a single leader and maintain diversity in exploitation.

• Stage-switching rule

Stage-switching means that CMCOA can alternate between different update formulas as the search progresses. Concretely, one can define two update functions $F_{\mathit{explore}}$, $F_{\mathit{exploit}}$ and a threshold:

$$t_s=0.05\cdot \mathrm{m}\mathrm{a}\mathrm{x}(\left|F_{avg}\left(\mathrm{t}\right)\right|, {10}^{-8})$$

(25)

$$X_{i,j}^{t+1}=\left\{\begin{array}{ll}{F}_{\mathit{explore}}\left(X_{i,j}^t\right),& D_N\left(t\right)>t_s,\\ F_{\mathit{exploit}}\left(X_{i,j}^t\right),& D_N\left(t\right)\le t_s\end{array}\right.$$

(26)

$$F_{\mathit{explore}}\left(X_{i,j}^t\right)=\left\{\begin{array}{ll}{X}_{i,j}^{t+1}=X_{i,j}^t-X_{z,j}^t+X_g,& \mathit{rand}>0.5,\\ X_{i,j}^{t+1}=X_{i,j}^t+C·\mathit{rand}·\left(X_g-X_{i,j}^t\right),& \mathit{rand}\le 0.5\end{array}\right.$$

(27)

$$F_{\mathit{exploit}}\left(X_{i,j}^t\right)=\left\{\begin{array}{ll}{X}_{i,j}^{t+1}=X_{i,j}^t+X_{\mathit{food}}·p·\left(\mathrm{c}\mathrm{o}\mathrm{s}\left(2\pi \mathit{rand}\right)-\mathrm{s}\mathrm{i}\mathrm{n}\left(2\pi \mathit{rand}\right)\right),& Q>{\displaystyle \frac{C_3+1}{2}},\\ X_{i,j}^{t+1}=\left(X_{i,j}^t-X_{\mathit{food}}\right)·p+p·\mathit{rand}·X_{i,j}^t& Q\le {\displaystyle \frac{C_3+1}{2}}\end{array}\right.$$

(28)

Specifically, the switching threshold is set as $t_s$, and the allowable fitness fluctuation equals 5% of the current mean fitness. The switching threshold is chosen as a small relative tolerance. Using normalized/relative thresholds to decide stage switches or convergence is common in population-based methods, and thresholds in practice typically lie on the order of 1–10% depending on problem scale. This practice aligns with previous work that uses population variance or normalized tolerances to guide search dynamics. Thus, $t_s$ can be interpreted as a practical relative rule that exhibits scale-insensitive behavior in practice, balancing the risk of premature switching against the need for timely exploitation.

When diversity is high, multiple elite guides promote global exploration; once diversity drops below the adaptive switching point $t_s$, the algorithm shifts to local exploitation led by the global best. This stage-switching mechanism works in tandem with the adaptive parameter control: the former selects the update mode, while the latter adjusts the step intensity via $C$. Together, they replace the fixed scheduling of the original COA with a responsive, state-driven balance between exploration and exploitation.

2.3. Complexity Analysis

The time complexity of CMCOA is related to the number of crayfish population size (N), the dimension of the problem (D), the number of iterations (T), and the cost of a single objective function evaluation (EC). Therefore, the time complexity of CMCOA can be expressed as follows:

$$\begin{gathered} O\left(\mathrm{CMCOA}\right)=O(\mathrm{parameter} \mathrm{initialization}) + O(\mathrm{population} \mathrm{initialization}) + \\ O(\mathrm{fitness} \mathrm{evaluation}) + O(\mathrm{population} \mathrm{update}) \end{gathered}$$

(29)

Specifically, parameter initialization requires only $O$(1), chaotic initialization of the population requires $O$(N × D), and the initial fitness evaluation of the population requires $O$(N × EC). During the iterative process, adaptive parameter control and diversity estimation introduce an additional $O$(N); the update of population positions requires $O$(T × N × D), and the fitness evaluation of candidate solutions requires $O$(T × N × EC). Therefore, the overall time complexity of CMCOA can be described as:

$$O\left(CMCOA\right)=O(1+N\times D+N\times EC+T\times N\times (EC+D\left)\right)$$

(30)

Since the number of iterations T is usually large, and fitness evaluations dominate the runtime of population-based metaheuristics practically, whereas the vector operations in position updates are of order $O$(D) and comparatively minor. The term T × N × (EC + D) dominates the complexity, Equation (30) can be simplified into:

$$O\left(CMCOA\right)\approx O(T\times N\times (EC+D\left)\right)$$

(31)

This demonstrates that the time complexity of CMCOA remains polynomial. Compared with the standard COA, the proposed CMCOA introduces chaotic initialization, adaptive parameter control, and stage-switching mechanisms, which slightly increase the computational overhead in constant terms. Nevertheless, the overall computational efficiency of CMCOA is maintained, and the algorithm can be regarded as an effective optimization method with acceptable computational complexity.

2.4. Pseudo Code and Flow Chart of CMCOA

The pseudo code of CMCOA is presented as Algorithm 1:

Algorithm 1: The CMCOA algorithm

1. Define iterations T, population size N, dimension dim, upper bound ub, and lower bound lb. 2. Initialize population using chaotic initialization by Equation (18). 3. Evaluate the fitness of all individuals. 4. t = 1; While t ≤ $T$ do 5. Compute average fitness, $F_{avg}\left(\mathrm{t}\right)$, and diversity measure $e$ by Equation (20). 6. Update control parameter $C$ by Equation (21). 7. Sort the population by fitness and select the top 20% as elite individuals E. 8. Compute the guiding position $X_g$ by Equation (22) and set the global best position as $X_{food}$. 9. Compute population diversity $D_N$ by Equation (24) and set dynamic threshold $t_s$ by Equation (25). 10. For i = 1: N 11. If $D$ > $t_s$ 12. If rand < 0.5 13. Update by summer resort stage: $X_{i,j}^{t+1}=X_{i,j}^t+C·rand·\left(X_g-X_{i,j}^t\right)$; 14. Else 15. For j = 1: dim 16. Conduct the competition stage by Equation (6) and update the new solution: 17. $X_{i,j}^{t+1}=X_{i,j}^t-X_{z,j}^t+X_g$ 18. End 19. End 20. Else 21. Compute the foraging intensity coefficient $Q$ 22. If Q$>{\displaystyle \frac{C_3+1}{2}}$ 23. Use the shredding strategy to update: $X_{i,j}^{t+1}=X_{i,j}^t+X_{\mathit{food}}·p·\left(\mathrm{c}\mathrm{o}\mathrm{s}\left(2\pi \mathit{rand}\right)-\mathrm{s}\mathrm{i}\mathrm{n}\left(2\pi \mathit{rand}\right)\right)$ 24. Else 25. Use the direct feeding strategy: $X_{i,j}^{t+1}=\left(X_{i,j}^t-X_{\mathit{food}}\right)·p+p·\mathit{rand}·X_{i,j}^t$ 26. End 27. End 28. End 29. Ensure the population $\overrightarrow{X}$ are within [lb, ub] 30. Update fitness values and global best fitness 31. $t+1$; $F_{avg}\left(t-1\right)=F_{avg}\left(t\right)$ 32. End

The flow chart of CMCOA is shown in Figure 1.

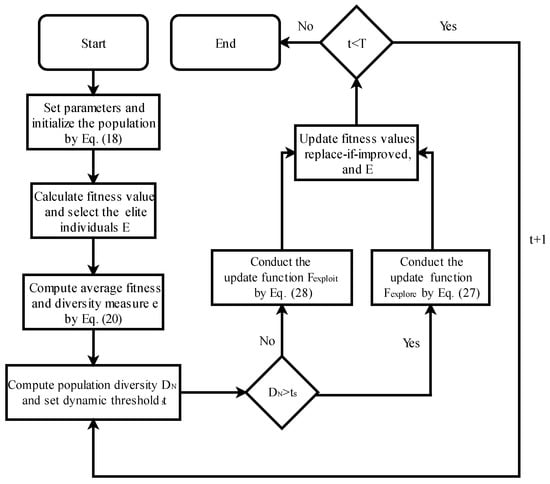
Figure 1. Flow chart of CMCOA.

2.5. Numeric Experiments

Numerical experiments were conducted to evaluate the performance of the proposed CMCOA against several other algorithms, including Differential Evolution (DE) [25], Hippopotamus Optimization (HO) [26], Whale Optimization Algorithm (WOA) [27], Ivy Algorithm (IVY) [28], the original COA [11], MCOA [13], and AD-COA-L [14]. These algorithms have attracted considerable attention in the field of meta-heuristic optimization and are recognized for their commendable optimization performance and representativeness. Compared with them, CMCOA demonstrates significant superiority. The parameter configurations for all algorithms are provided in Table 2.

Table 2. Parameter setting of each algorithm.

Algorithm	Parameter	Value
DE	F	0.8
	CR	0.9
HO	ϑ	1.5
WOA	a	Linear reduction 2 to 0
	r	[0, 1]
	l	[−1, 1]
IVY	β	[1, 1.5]
COA	$C_1$	0.2
	$C_3$	3
	µ	25
	σ	3
CMCOA	$L$	4
	$\eta$	0.03

The experimental setup utilized test functions from the IEEE Congress on Evolutionary Computation (CEC) competitions, specifically CEC2017 [29], CEC2019 [30], CEC2020 [31], and CEC2022 [32]. Ten representative test functions were selected, encompassing unimodal, hybrid, and composition types, as summarized in Table 3. We selected the CEC benchmark functions to comprehensively evaluate the algorithm’s performance. Unimodal functions assess convergence and precision in high-dimensional spaces, hybrid functions capture problems with multiple distinct features, and composition functions mimic multi-modal and non-separable complexities. This combination forms a widely accepted benchmark, providing a robust and realistic assessment of algorithm capability. Hybrid functions and composition functions are constructed from multiple basic functions, and M in the table denotes the number of basic functions. All algorithms were executed under identical conditions to ensure fair comparison. The population size was uniformly set to 30, a standard value in the meta-heuristic community that balances the need for sufficient population diversity to explore the search space and computational efficiency. Similarly, a maximum of 500 iterations was chosen as the termination criterion. This value provides adequate time for the algorithms to converge on most test functions while preventing unnecessarily long run times.

Table 3. Characteristics of 10 test functions.

	No.	Functions	Dimension	Search Range	Optimum
Unimodal Functions	1	Shifted and Rotated Bent Cigar Function	30	[−100, 100]	100
	2	Shifted and Rotated Sum of Different Power Functions	30	[−100, 100]	200
	3	Weierstrass Function	10	[−100, 100]	1
	4	Shifted and full Rotated Zakharov Function	20	[−100, 100]	300
Hybrid Functions	5	Hybrid Function 1 (M = 3)	30	[−100, 100]	1200
	6	Hybrid Function 2 (M = 4)	30	[−100, 100]	1400
	7	Hybrid Function 3 (M = 5)	20	[−100, 100]	2100
Composition Functions	8	Composition Function 1 (M = 5)	30	[−100, 100]	2600
	9	Composition Function 2 (M = 3)	30	[−100, 100]	3000
	10	Composition Function 3 (M = 4)	20	[−100, 100]	2400

2.5.1. Algorithm Performance Analysis on Test Functions

The performance of the algorithms is evaluated in two ways: Figure 2 displays the comparative convergence curves of the different algorithms across ten test functions, and Table 4 provides the statistical results, showing the mean and standard deviation, as well as the average total runtime in seconds for each algorithm on each function, obtained from 30 independent runs. A careful examination of these data underscores the superior performance of CMCOA across a wide range of test functions. On the unimodal F1, CMCOA’s mean and on F2 are substantially better than those of the baseline COA and other competitors, indicating a stronger and more reliable drive toward the global optimum. On more deceptive hybrid and composition landscapes, the advantage persists: CMCOA’s performance on the hybrid F5 and on composition F8 is significantly improved compared with COA, which suggests that the algorithm’s enhanced diversity maintenance and adaptive exploitation mechanisms more effectively cope with multi-modality and landscape heterogeneity.

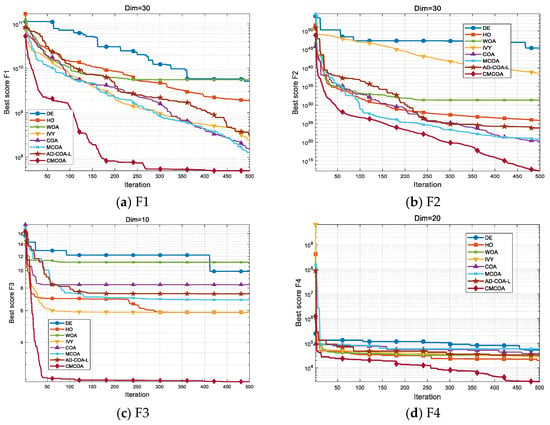
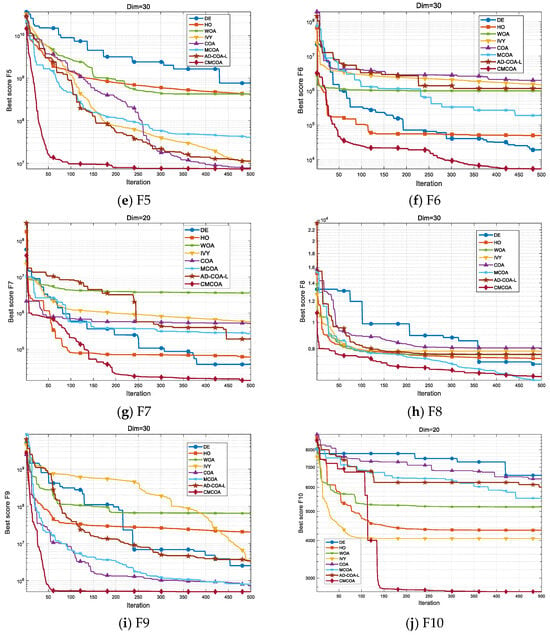
Figure 2. Comparison of convergence curves of the eight optimization algorithms on test functions.

Table 4. Detailed performance metrics of the eight optimization algorithms.

Function		DE [25]	HO [26]	WOA [27]	IVY [28]	COA [11]	MCOA [13]	AD-COA-L [14]	CMCOA
F1	$\mathrm{M}\mathrm{E}\mathrm{A}\mathrm{N}$	1.88 × 1010	2.72 × 108	2.32 × 109	6.3 × 107	1.09 × 108	9.56 × 107	1.70 × 108	1.30 × 108
	$\mathrm{S}\mathrm{T}\mathrm{D}$	5.58 × 109	2.69 × 108	9.68 × 108	1.50 × 108	1.54 × 108	3.08 × 1016	1.10 × 1016	1.73 × 107
	TIME	0.208	3.192	0.0913	0.589	0.123	0.120	0.187	0.0957
F2	$\mathrm{M}\mathrm{E}\mathrm{A}\mathrm{N}$	2.33 × 1046	1.55 × 1031	4.33 × 1039	4.39 × 1039	5.56 × 1024	2.72 × 1022	9.22 × 1023	7.38 × 1013
	$\mathrm{S}\mathrm{T}\mathrm{D}$	8.36 × 1046	6.35 × 1031	2.37 × 1040	2.20 × 1040	2.99 × 1025	9.79 × 1045	1.39 × 1049	3.13 × 1014
	TIME	0.239	3.103	0.0972	0.525	0.136	0.140	0.215	0.108
F3	$\mathrm{M}\mathrm{E}\mathrm{A}\mathrm{N}$	10.4946	6.264	8.7262	5.7342	9.9109	4.4447	5.3074	4.3841
	$\mathrm{S}\mathrm{T}\mathrm{D}$	0.70196	1.3226	1.9108	2.0109	0.9925	1.9738	2.0936	1.536
	TIME	1.639	4.681	0.779	1.223	1.292	1.308	2.077	1.236
F4	$\mathrm{M}\mathrm{E}\mathrm{A}\mathrm{N}$	154,587.69	17,565.24	26,152.7	36,470.94	41,746.72	40,935.48	26,690.80	4910.69
	$\mathrm{S}\mathrm{T}\mathrm{D}$	1364.85	5347.51	11,212.3	14,025.44	15,320.54	1.08 × 108	3.106 × 107	1923.38
	TIME	0.184	2.502	0.0694	0.527	0.0952	0.095	0.150	0.0758
F5	$\mathrm{M}\mathrm{E}\mathrm{A}\mathrm{N}$	2.59 × 109	1.09 × 108	2.01 × 108	3.23 × 106	8.08 × 106	9.24 × 106	8.36 × 106	1.7 × 106
	$\mathrm{S}\mathrm{T}\mathrm{D}$	8.64 × 108	9.46 × 107	1.39 × 108	2.46 × 106	8.21 × 106	2.76 × 1013	1.28 × 1014	1.7 × 106
	TIME	0.271	3.005	0.113	0.572	0.163	0.185	0.274	0.147
F6	$\mathrm{M}\mathrm{E}\mathrm{A}\mathrm{N}$	1.02 × 105	3.33 × 105	2.95 × 106	1.37 × 106	3.73 × 105	2.61 × 105	4.19 × 105	47,615.86
	$\mathrm{S}\mathrm{T}\mathrm{D}$	51,916.22	4.63 × 105	2.86 × 106	1.21 × 106	3.46 × 105	4.52 × 1010	1.81 × 1011	26,653.6
	TIME	0.313	3.016	0.136	0.608	0.198	0.201	0.325	0.141
F7	$\mathrm{M}\mathrm{E}\mathrm{A}\mathrm{N}$	2.24 × 105	51,662.08	1.22 × 106	7.99 × 105	2.19 × 105	2.21 × 105	5.11 × 105	1.08 × 105
	$\mathrm{S}\mathrm{T}\mathrm{D}$	1.11 × 105	34,314.9	1.21 × 106	8.26 × 105	2.80 × 105	3.85 × 105	8.63 × 105	81,411.68
	TIME	0.224	2.606	0.0902	0.541	0.122	0.135	0.206	0.0957
F8	$\mathrm{M}\mathrm{E}\mathrm{A}\mathrm{N}$	7476.37	7192.30	8559.44	5756.80	5994.25	5561.52	5948.29	5719.08
	$\mathrm{S}\mathrm{T}\mathrm{D}$	533.74	1361.35	675.96	1778.69	1348.80	1672.66	2732.49	182.09
	TIME	0.675	3.731	0.327	0.772	0.488	0.500	0.807	0.317
F9	$\mathrm{M}\mathrm{E}\mathrm{A}\mathrm{N}$	1.44 × 107	2.09 × 107	3.98 × 107	61,498.20	5.25 × 105	4.43 × 105	7.12 × 105	1.1 × 105
	$\mathrm{S}\mathrm{T}\mathrm{D}$	8.07 × 106	2.21 × 107	2.68 × 107	41,016.21	6.54 × 105	2.44 × 105	2.85 × 105	1.5 × 105
	TIME	1.242	4.521	0.611	1.095	1.007	1.046	1.635	0.715
F10	$\mathrm{M}\mathrm{E}\mathrm{A}\mathrm{N}$	6688.12	4028.24	4829.55	3774.09	4300.92	3585.02	2862.07	3369.18
	$\mathrm{S}\mathrm{T}\mathrm{D}$	1124.06	1088.57	1076.81	281,291.09	2258.22	1351.52	5908.71	945.03
	TIME	0.334	2.761	0.138	0.606	0.211	0.214	0.330	0.202

These numeric trends are supported by the convergence curves shown in Figure 2: CMCOA typically exhibits a steeper early decline followed by a smoother late-stage descent, which reflects two complementary effects of the proposed modifications. The chaotic initialization accelerates early discovery of promising basins, producing the rapid early decrease visible on most curves, while the MIT rule-inspired adaptive control, together with multi-guide stage-switching, stabilizes the later iterations and prevents premature stagnation, as evidenced by reduced variance across independent runs and by a tighter final spread in Table 3. Finally, the additional computational overhead introduced by these strategies is modest: average runtimes remain comparable to lightweight methods and are frequently in the sub-second or low-second range on the tested functions, indicating that improved search behavior has been achieved without prohibitive cost. This combination of faster initial exploration and controlled, diversity-aware exploitation explains why CMCOA achieves robust gains across unimodal, hybrid, and composition classes.

2.5.2. Analysis of Non-Parametric Statistical Significance Test of CMCOA

To further validate the statistical reliability of the observed performance differences, a Wilcoxon rank-sum test was carried out against all comparative algorithms. The p-values reported in Table 5 show that CMCOA achieves statistically significant improvements (p < 0.05) on the vast majority of benchmark functions, with many cases reaching p < 0.01. This confirms that the observed advantages are not due to random effects but stem from its enhanced search strategy. Only a few functions yield p > 0.05, where CMCOA remains competitive but not significantly better. Overall, the results provide strong statistical evidence that the proposed chaotic initialization, adaptive parameter control, and multi-guide stage-switching mechanisms substantially improve the reliability and superiority of CMCOA over other algorithms.

Table 5. Experimental results of the Wilcoxon rank-sum test on test functions.

Function	CMCOA vs. DE	CMCOA vs. HO	CMCOA vs. WOA	CMCOA vs. IVY	CMCOA vs. COA	CMCOA vs. MCOA	CMCOA vs. AD-COA-L
F1	1.73 × 10−6	1.73 × 10−6	1.73 × 10−6	4.28 × 10−6	1.73 × 10−6	0.845	0.198
F2	1.73 × 10−6	1.73 × 10−6	1.73 × 10−6	1.73 × 10−6	1.73 × 10−6	3.88 × 10−6	1.73 × 10−6
F3	1.73 × 10−6	0.000174	2.12 × 10−6	0.503	0.0936	0.0185	2.16 × 10−5
F4	1.73 × 10−6	1.73 × 10−6	1.73 × 10−6	1.73 × 10−6	1.73 × 10−6	1.73 × 10−6	1.73 × 10−6
F5	1.73 × 10−6	1.73 × 10−6	1.73 × 10−6	3.72 × 10−5	1.23 × 10−5	0.05709	0.00196
F6	1.92 × 10−6	1.92 × 10−6	1.73 × 10−6	1.73 × 10−6	1.92 × 10−6	5.75 × 10−6	1.23 × 10−5
F7	8.18 × 10−5	0.115	1.73 × 10−6	5.75 × 10−6	1.79 × 10−5	0.00773	3.88 × 10−6
F8	1.73 × 10−6	0.00499	1.92 × 10−6	0.318	0.845	0.0147	0.2802
F9	1.73 × 10−6	1.73 × 10−6	1.73 × 10−6	0.749	1.97 × 10−5	0.000331	0.00984
F10	0.00927	0.00499	0.428	0.000528	0.00159	0.781	0.141

2.5.3. Engineering Design Problems

To further demonstrate the general-purpose capability of CMCOA beyond benchmark functions, two widely used engineering design problems are investigated: the gear train design problem and the cantilever beam design problem. These problems are classical constrained optimization benchmarks that have been extensively employed to assess the effectiveness of metaheuristic algorithms in both discrete and continuous domains.

• Gear Train Design Problem

The gear train design problem aims to minimize the squared error between the actual gear ratio and the desired target ratio R = 1/6.931. The decision variables represent the number of teeth of four gears $X_1$, $X_2$, $X_3$, $X_4$ ($12\le X_i\le 60$), which must be positive integers. The objective function can be formulated as:

$$\mathrm{M}\mathrm{i}\mathrm{n}\mathrm{i}\mathrm{m}\mathrm{i}\mathrm{z}\mathrm{e} f(X)={\left({\displaystyle \frac{1}{6.931}}-{\displaystyle \frac{X_2{X}_3}{X_1{X}_4}}\right)}^2$$

(32)

• Cantilever Beam Design Problem

The cantilever beam design problem is a classical continuous constrained optimization benchmark. The objective is to minimize the material volume of a beam consisting of five segments, subject to stress and deflection constraints. The five design variables correspond to the cross-sectional dimensions of the beam $X_1$, $X_2$, $X_3$, $X_4$, $X_5$. The mathematical model can be formulated as:

$$\mathrm{M}\mathrm{i}\mathrm{n}\mathrm{i}\mathrm{m}\mathrm{i}\mathrm{z}\mathrm{e} f\left(X\right)=0.0624{\sum }_{i=1}^5 X_i$$

(33)

The problem is subject to a maximum stress/deflection constraint which must not exceed the allowable limit, represented by the value of 1 in the constraint function $g_1\left(X\right)\le 0$. The constraint formulation is:

$$g_1(X)={\displaystyle \frac{61}{X_1^3}}+{\displaystyle \frac{37}{X_2^3}}+{\displaystyle \frac{19}{X_3^3}}+{\displaystyle \frac{7}{X_4^3}}+{\displaystyle \frac{1}{X_5^3}}-1\le 0$$

(34)

• Experimental analysis

In addition to the baseline algorithms already considered, we further compare CMCOA with four recently proposed methods that have shown strong performance on engineering design benchmarks: Symmetric Projection Optimizer (SPO) [33], Genghis Khan Shark Optimizer (GKSO) [34], Surrogate Ensemble-Assisted Hyper-Heuristic Algorithm (SEA-HHA) [35], and Surrogate-assisted Hybrid Evolutionary Algorithm with Local Estimation of Distribution (SHEALED) [36]. These methods were included to provide a more comprehensive benchmark in both discrete and continuous engineering optimization problems.

For the discrete optimization problem of gear train design, as detailed in Table 6, CMCOA successfully identified the optimal integer solution, achieving a minimum objective function value. This outcome not only significantly outperforms all variants of COA and numerous mainstream metaheuristics but also perfectly matches the best-known results reported in the literature by state-of-the-art methods like SPO and GKSO. This superior performance indicates that CMCOA’s chaotic initialization strategy and multi-guide mechanism exhibit powerful exploration and precise convergence capabilities within the discrete search space, effectively overcoming the complexities introduced by integer variables. Furthermore, the convergence curves presented in Figure 3 confirm that CMCOA demonstrates a fast convergence rate, rapidly escaping local optima and approaching the global best solution.

Table 6. Optimal results of algorithms on the gear train design problem.

Algorithm	Optimal Objective Value	Optimal Variables
DE	2.3078 × 10−11	[51, 30, 13, 53]
HO	2.3576 × 10−9	[39, 12, 15, 32]
WOA	2.3078 × 10−11	[53, 15, 26, 51]
IVY	1.8274 × 10−8	[37, 12, 12, 27]
COA	2.3576 × 10−9	[48, 12, 15, 26]
MCOA	9.9399 × 10−11	[49, 31, 13, 57]
AD-COA-L	6.6021 × 10−10	[56, 23, 13, 37]
CMCOA	2.7009 × 10−12	[49, 16, 19, 43]
SPO [33]	2.7009 × 10−12	[43, 16, 19, 49]
GKSO [34]	2.7009 × 10−12	[49, 19, 16, 43]

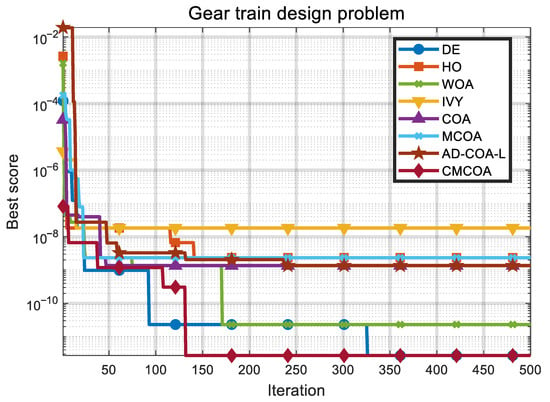
Figure 3. Convergence curves of CMCOA and competitor algorithms on the gear train design problem.

Turning to the continuous constrained optimization problem of Cantilever Beam Design, as shown in Table 7 and Figure 4. While this result is highly competitive with benchmark algorithms such as DE and HO, the critical advantage lies in CMCOA’s ability to achieve this minimal volume while strictly satisfying all constraint conditions. Notably, CMCOA’s performance also proved to be more consistent and effective compared to recent surrogate-assisted methods, which often struggle with solution consistency across multiple runs or sacrifice precision for accelerated convergence.

Table 7. Optimal results of algorithms on the cantilever beam design problem.

Algorithm	Optimal Objective Value	Optimal Variables
DE	1.3400	[6.0160, 5.3092, 4.4943, 3.5015, 2.1527]
HO	1.3400	[6.0288, 5.3229, 4.4922, 3.4981, 2.1322]
WOA	1.4092	[6.2557, 4.6792, 4.0823, 4.5797, 2.9872]
IVY	1.3402	[6.0974, 5.2295, 4.4873, 3.5063, 2.1578]
COA	1.3400	[5.9890, 5.3216, 4.4963, 3.5137, 2.1537]
MCOA	1.3400	[6.0098, 5.3300, 4.4990, 3.4804, 2.1551]
AD-COA-L	1.3401	[6.0183, 5.3328, 4.4474, 3.5215, 2.1555]
CMCOA	1.3400	[6.0329, 5.3202, 4.4808, 3.5072, 2.1332]
SEA-HHA [35]	1.4037	[5.3868, 5.4171, 5.1441, 3.3892, 3.1576]
SHEALED [36]	1.3540	[5.7524, 5.7174, 4.1701, 3.9365, 2.1216]

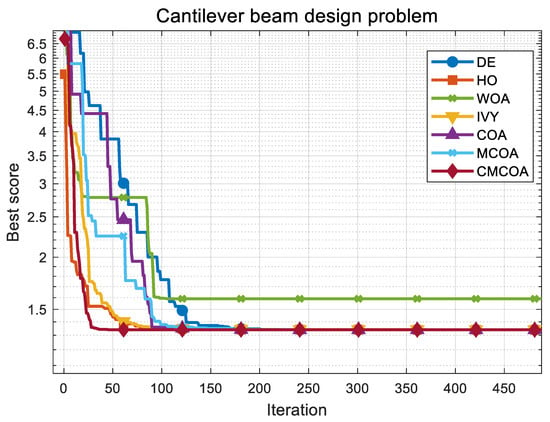
Figure 4. Convergence curves of CMCOA and competitor algorithms on the cantilever beam design problem.

In summary, the comprehensive assessment across both discrete and constrained continuous engineering design problems provides compelling evidence for the versatility, efficacy, and robustness of the CMCOA algorithm. By achieving competitive or superior results against both classic and state-of-the-art optimizers, the experiments validate that the proposed enhancements—chaotic initialization, adaptive parameter control, and multi-guide phase switching—serve as effective, general strategies for comprehensively boosting the optimization performance of the underlying algorithm.

3. Application and Evaluation of CMCOA for Image Analysis

3.1. Experimental Setup

To assess the clustering capability of the proposed CMCOA on realistic high-dimensional imagery, two test images were used. Test image 1, as shown in Figure 5, is a multispectral scene with pronounced local texture and color variation, while test image 2, as shown in Figure 6, is drawn from the UC Merced Land Use dataset [37] and consists of satellite aerial imagery captured at high spatial resolution. The two images induce different clustering challenges: the first emphasizes fine-grained intra-object variation, whereas the second presents large-scale land use patterns and more clearly separated spectral modes.

Figure 5. Test image 1 in the experiment.

Figure 6. Test image 2 in the experiment.

All optimizers were executed under identical control settings—population size 30, maximum iterations 500, search bounds [0, 255], and a fixed random seed to ensure reproducibility. The original three-dimensional image data were first transformed into a two-dimensional matrix, where each row represents a pixel’s feature vector across all bands. This transformation allowed the clustering task to be formulated as a numerical optimization problem, with the goal of locating a set of optimal cluster centers. A cost function $Fit$ was established to minimize the sum of Euclidean distances between each pixel and its nearest cluster center, thereby ensuring spectral compactness within clusters.

$$Fit={\sum }_{i=1}^I \stackrel{K}{\underset{k=1}{min}} |\left|x_i-c_k\right|{|}^2$$

(35)

where $x_i$ denotes the feature vector of the i-th pixel, and $c_k$ represents the k-th cluster center. $I$ and $K$ represent the total number of pixels and cluster centers, respectively. During the clustering experiments, each algorithm was executed independently to obtain a final set of cluster centers. We set the number of cluster centers to 6 in test image 1 and 8 in test image 2. Pixels were subsequently assigned to their respective nearest centers, and segmented images were reconstructed accordingly. The best fitness value at each iteration was recorded to generate convergence curves and analyze the algorithms’ optimization behavior over time.

To ensure experimental reproducibility and statistical reliability, we presented the final objective function value $Fit$, and an external validity metric—the mean silhouette coefficient (Silhouette)—in Table 8. We additionally added the most basic and widely used standard clustering algorithms in this field, K-Means [38], to fully demonstrate the practical value and effectiveness of the proposed optimization-based approach. The K-Means baseline was implemented with k-means++ initialization and 50 restarts to mitigate sensitivity to initial centroids; other meta-heuristic algorithms used the parameter settings reported in Table 2 and were run with the same random-seed strategy to ensure comparability. Silhouettes were computed in the original pixel multiband feature space using Euclidean distance. Pixel preprocessing was limited to standard normalization, and no additional dimensionality reduction or spatial priors were introduced so that the performance of the optimizers themselves in the spectral space could be assessed objectively.

Table 8. Comparison of quantitative metrics for different algorithms in image clustering.

Test Image 1	DE [25]	HO [26]	WOA [27]	IVY [28]	COA [11]	K-Means [38]	CMCOA
Fit Silhouette	458,837.75	541,011.41	508,927.69	438,185.77	437,017.73	445,498.86	424,886.16
	0.6021	0.6101	0.4040	0.5910	0.5990	0.6128	0.6432
Test Image 2	DE [25]	HO [26]	WOA [27]	IVY [28]	COA [11]	K-Means [38]	CMCOA
Fit Silhouette	958,164.06	1,490,353.64	1,349,062.02	1,026,513.97	1,232,848.03	780,546.27	746,342.75
	0.6423	0.5719	0.6219	0.4575	0.6348	0.6722	0.6623

3.2. Analysis of Experimental Results

Across both test images, the proposed CMCOA produced a consistently faster early decline in the objective value and a more restrained late-stage descent, a pattern that aligns with the intended effects of the chaotic initialization and adaptive control mechanisms. On test image 1, the final mean Fit obtained by CMCOA was 424,886.16, which improved upon the classical COA and the K-Means baseline. This reduction in the optimization objective was accompanied by a clear gain in external validity: CMCOA’s mean silhouette rose to 0.6432, exceeding the nearest competitor by a comfortable margin. The steep initial drop in the convergence curve is attributed to the chaotic, opposition-enhanced initialization that populated promising regions early, while the adaptive parameter control rule moderated step sizes as the population approached better basins, preventing premature stagnation and yielding a tighter final spread in successive runs.

Results on the UC Merced satellite image, test image 2, present a complementary picture. CMCOA attained the lowest Fit among all methods, indicating superior minimization of the spectral compactness objective in a higher-complexity setting. The silhouette score for CMCOA was marginally lower than the highest silhouette produced by K-Means. This divergence is informative: K-Means’ objective biases it toward spherical, well-separated clusters and therefore it can occasionally produce slightly higher silhouette figures when the underlying class geometry matches that bias; CMCOA, in contrast, optimizes the same Euclidean objective while maintaining richer intra-cluster texture and avoiding collapsed centroids, which explains the lower Fit but the very similar silhouette performance. Visual inspection of the segmentation confirms that CMCOA preserves subtle boundaries and intra-class heterogeneity that are desirable in remote-sensing interpretation, while still delivering compact spectral clusters. Clustering fitness convergence curves of seven optimization algorithms on images 1 and 2 are shown in Figure 7 and Figure 8.

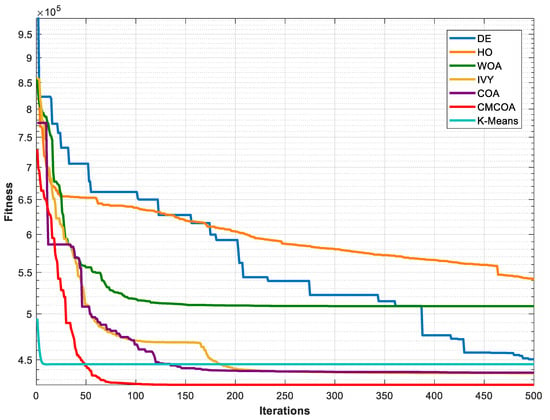
Figure 7. Clustering fitness convergence curves of seven optimization algorithms on image 1.

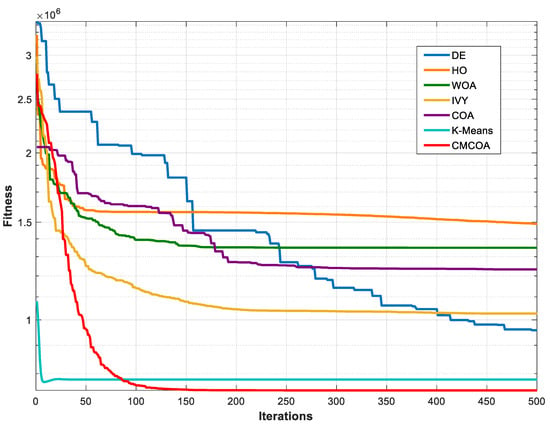
Figure 8. Clustering fitness convergence curves of seven optimization algorithms on image 2.

Figure 9 and Figure 10 present the clustering results produced by the seven algorithms on the test images.

Figure 9. Comparison of the visualized clustering results of the seven algorithms on image 1.

Figure 10. Comparison of the visualized clustering results of the seven algorithms on image 2.

Qualitative comparisons further emphasize the differences in segmentation performance. DE and HO could outline the general shape, but failed to capture internal details, leading to blurred boundaries and some background misclassification. WOA delivered improved contour detection and better separation, but lacked accuracy in capturing finer textures. IVY was less effective, with irregular segmentation and significant background misclassification. The original COA, serving as CMCOA’s baseline, showed better structural differentiation and cleaner backgrounds, confirming its suitability for these tasks.

In contrast, CMCOA achieved the most advanced segmentation, clearly distinguishing between petal regions and accurately preserving subtle structural and color variations, especially near the flower’s center. This level of detail retention and color consistency is particularly useful in digital printing workflows, where precise boundary detection, minimal color bleeding, and accurate tone reproduction are crucial for maintaining print quality and visual appeal. CMCOA’s strong performance in balancing cluster sizes further ensures even ink distribution, reducing the risk of over-saturation or under-printing in different image areas.

Overall, CMCOA generated segmentation results that closely matched human perception of semantic regions, effectively decomposing the image into distinct and meaningful components. This validates its potential in unsupervised image recognition. With stable convergence, accurate clustering, and strong visual interpretability, CMCOA proves to be a compelling approach for image analysis. In addition, it should be noted that ground truth segmentations for the experimental images are not available. As a result, standard image segmentation metrics could not be computed. This represents a limitation of the present study. Consequently, our evaluation relies on qualitative visual inspection and clustering-related indices. Future work will incorporate datasets with available ground truth masks to enable a more comprehensive and objective assessment.

4. Conclusions

This paper presented CMCOA, an improved framework for image clustering that integrates chaotic initialization, fitness-feedback adaptive parameter controller inspired by the MIT-rule, and a multi-guide stage-switching mechanism. These strategies were designed to strengthen global exploration, maintain a dynamic exploration-exploitation balance, and mitigate premature convergence. Experimental results on CEC benchmark functions and multispectral image datasets showed that CMCOA achieves notable gains in convergence speed, clustering accuracy, and intra-cluster compactness compared with several state-of-the-art meta-heuristics, while maintaining competitive computational efficiency.

Although the results are encouraging, some limitations remain. The adaptive parameter control is still designed empirically and may not be equally effective across all problem scales. While the multi-guide strategy reduces the risk of stagnation, convergence on problems with many local optima may still be challenging. More importantly, the current evaluation has been largely limited to clustering and multispectral imagery. The generalization of CMCOA to other image analysis tasks—such as segmentation, classification, or feature extraction—and its performance on different modalities, including medical, satellite, and natural images, remains to be systematically investigated.

Future work will focus on improving adaptability and extending applicability. Potential directions include refining adaptive parameter dynamics, incorporating parallel computing to reduce runtime, and combining CMCOA with deep learning or graph-based models for richer semantic representation. Furthermore, extending validation to diverse image domains and tasks will be essential for assessing robustness and transferability, paving the way for CMCOA to serve as a versatile tool in complex and dynamic optimization scenarios.