Abstract
Modern cosmology continues to struggle with unresolved questions concerning the origins of dark matter and dark energy. To explore these challenges, this study presents the Source Energy Field Theory (SEFT)—a new theoretical framework that offers an alternative view of how cosmic structures may form and evolve. SEFT envisions the universe as filled with a fundamental energy field, where the observed cosmological redshift does not result from accelerated expansion but rather emerges from the distance-dependent modulation of the energy field and the curvature produced by this field. To evaluate this idea, a nonlinear wave equation was developed to connect redshift with right ascension, declination, and distance. The model was optimized using 1701 observational data points from the Pantheon+ and SH0ES samples, which include Type Ia supernovae and Cepheid variables spanning distances from 6.3 to 17,241 Mpc. Its performance was compared with that of the standard ΛCDM model. SEFT achieved a slightly lower root-mean-square error (145.521 vs. 147.665 Mpc), a marginally higher determination coefficient (R2 = 0.9910 vs. 0.9908), and significantly improved information criteria values (ΔAIC = −41.753, ΔBIC = −19.997). These results provide robust statistical support for SEFT and suggest that it can complement—and potentially extend—the ΛCDM paradigm in describing the structure and evolution of the universe.
1. Introduction
Theories of the universe have evolved through successive attempts to identify the fundamental quantities that govern the physical world. For instance, Newtonian mechanics was founded on the concept of absolute time, systematically describing motion and spatial relationships within a temporal framework.
Later, Einstein transformed physics by treating the speed of light as a universal constant and formulating the well-known mass–energy equivalence, . He further demonstrated that gravitational fields originate from mass and energy, showing that these quantities shape the curvature of spacetime itself [1].
In this study, we extend Einstein’s concept of mass–energy equivalence by proposing a broader theoretical framework in which energy is not only equivalent to mass but is also fundamentally connected to distance and time. Within this perspective, energy is regarded as the primary entity from which mass, distance, and time naturally emerge.
This idea forms the foundation of the Source Energy Field Theory (SEFT)—a theoretical framework that characterizes all physical phenomena as nonlinear, wave-like modulations of a universal energy field. In SEFT, cosmological redshift and other distance-dependent phenomena arise naturally from the modulation and curvature of the energy field, without assuming that space itself exists as a pre-defined background.
The SEFT framework was developed from first principles, independently of existing cosmological models, and does not rely on empirical fitting or parameter adjustment. Although SEFT shares some conceptual similarities with classical and nonlinear field theories, it introduces new nonlinear and gradient-coupled terms to describe self-interaction and curvature within the energy field.
To assess the validity of this framework, we derived a distance-specific formulation of SEFT and applied it to an integrated observational dataset comprising 1701 measurements from the Pantheon+ and SH0ES compilations. These datasets include Type Ia supernovae and Cepheid variable stars covering distances from approximately 6.3 to 17,241 Mpc. The results were compared with those obtained from the standard ΛCDM model—the most widely accepted model in modern cosmology. This comparison was intended to demonstrate the theoretical validity of SEFT within the framework of contemporary cosmology. The comparative analysis, based on statistical indicators such as RMSE, R2, AIC, and BIC, shows that SEFT reproduces observational data with comparable or better accuracy while maintaining physical consistency.
This study does not seek to replace ΛCDM, but rather to present SEFT as a complementary framework that bridges empirical observations with a more fundamental, energy-based description of spacetime and cosmic evolution.
This paper is organized as follows. In Section 2, the theoretical framework and the nonlinear wave equation are introduced. Section 3 presents the distance-specific formulation and its comparison with the observational data. In Section 4, the results of model optimization and statistical evaluation are shown. Finally, Section 5 discusses the theoretical implications, limitations, and the broader significance of SEFT, integrating the overall findings within the discussion.
2. Theoretical Framework
2.1. Fundamental Concepts and Formulation
The Source Energy Field Theory (SEFT) aims to provide a unified physical picture that connects diverse cosmic phenomena—including matter formation, gravitational interaction, electromagnetic behavior, and the large-scale organization of the universe—under a single energy-based principle. In this framework, all physical processes are interpreted as orderly modulations of a universal energy field, represented by Ψ.
Here, “modulation” refers to the spatiotemporal variation in the structure and distribution of energy within the field itself. This concept opens the possibility of reinterpreting classical notions—such as particles, forces, gravity, electromagnetism, and even the strong and weak nuclear interactions—as different manifestations of the same underlying energetic modulations.
The energy field Ψ, which may be treated as either a real or complex scalar quantity, defines the local distribution of energy at every point in spacetime. These modulations become physically observable through nonlinear wave propagation and self-interaction processes. Within this setting, the ideas of resonance and non-resonance play central roles. Resonance occurs when the energy field coherently interacts with another field—such as electromagnetic waves—at compatible frequencies or amplitudes, giving rise to energy exchange and observable effects like radiation or particle formation.
On the other hand, regions of the energy field that do not resonate with electromagnetic waves are inherently difficult to detect by conventional observation methods. However, this limitation applies only to electromagnetic interactions; the same energy field may still resonate through other modes, such as gravitational waves. Consequently, whether a part of the field exhibits resonance or non-resonance depends on the type of wave and, by extension, the observational approach employed.
Within SEFT, this perspective allows phenomena that are invisible to electromagnetic detection—such as dark matter and dark energy—to be understood as non-resonant manifestations of the same energy field. These hidden components may become observable when studied through gravitational interactions or other resonant channels.
In this context, the SEFT framework provides theoretical definitions for both phenomena:
- Dark matter, refers to gravitational field structures that are non-resonant with electromagnetic waves but may still resonate weakly with gravitational waves, potentially making them observable through gravitational-wave experiments.
- Dark energy, on the other hand, is understood as an energetic background field that remains largely non-resonant with both electromagnetic and gravitational waves.
These definitions remain consistent with current astrophysical observations. Within SEFT, dark energy is not treated as a separate entity but as the intrinsic, non-resonant energy of the universal field itself. It corresponds to the smooth, large-scale component of the field that governs cosmic-scale expansion—manifesting observationally as the accelerating universe described by the ΛCDM model. In contrast, dark matter emerges from spatially localized, non-resonant modulations of the same field, forming structures that interact gravitationally but not electromagnetically, as demonstrated in Part II [2].
Thus, both dark matter and dark energy emerge as two manifestations of the same energy field Ψ, observed at different resonance states. This interpretation provides a unified physical basis for phenomena traditionally attributed to these components.
Regarding matter formation, SEFT suggests that resonance phenomena may facilitate the localization of energy, potentially leading to the emergence of stable, particle-like structures. While this remains a theoretical hypothesis, it provides an intriguing link between field modulation and the origin of matter, warranting further study through numerical modeling and observation.
Therefore, SEFT presents a unified and flexible description of cosmic phenomena, one that naturally adapts to specific observational contexts and accommodates both resonant and non-resonant manifestations of the universal energy field.
2.2. Fundamental Mathematical Formulation
The nonlinear wave equation of SEFT describes the intrinsic dynamics of the energy field . Importantly, this equation does not represent a wave propagating through a vacuum, but rather a wave of the vacuum itself. In this interpretation, the vacuum is not an empty background but a continuous, self-organizing energy field that forms the underlying substrate of all physical phenomena. Accordingly, the nonlinear variations of represent internal oscillations and self-organized modulations of the physical vacuum:
Here, the parameters and respectively characterize the localization, self-interaction, and spatial nonlinearity of the energy field. The operator denotes the d’Alembert operator, incorporating both temporal and spatial second-order derivatives:
The physical meanings of these parameters are summarized as follows.
- —represents the mass-like localization tendency of the field, corresponding to its resistance to spatial dispersion (analogous to the mass term in the Klein–Gordon equation).
- —describes the self-interaction strength of the field, responsible for nonlinear resonance and the emergence of stable, localized particle-like structures.
- and —represent gradient-dependent nonlinear effects, associated with curvature and spatial modulation of the energy field. These terms govern the redistribution and bias of energy without presupposing any fixed spatial background.
This equation generalizes the conventional linear scalar field equation by incorporating intrinsic curvature and modulation within the energy field itself. When and , Equation (1) reduces to the standard linear Klein–Gordon form. In SEFT, however, the nonlinear terms play an essential role. They describe the emergence of mass, the formation of resonant structures, and the manifestation of non-resonant phenomena such as dark matter and dark energy.
The nonlinear wave equation (Equation (1)) is rigorously derived from a carefully constructed energy functional based on the variational principle, consistent with well-established methodologies in classical and quantum field theory [3,4,5]. The explicit form of the Lagrangian density is given in Equation (3), and the detailed mathematical derivation is presented in File S1.
The Lagrangian density in Equation (3) is expressed in a Lorentz-invariant form, as it includes the operator , ensuring covariance under Lorentz transformations in flat spacetime. Each term in Equation (3) remains dimensionally consistent with standard field theories such as the Klein-Gordon framework.
The first term represents the temporal kinetic energy, the second describes the linear spatial variation, and the third provides the mass-like stabilization of the field. The fourth and fifth terms introduce nonlinear self-interaction and gradient-dependent spatial modulation, capturing higher-order variations of the energy field.
Consequently, Equation (1) can be regarded as a Lorentz-invariant generalization of the nonlinear Klein–Gordon equation, extended to include intrinsic curvature and modulation effects of the energy field .
By applying the variational principle, the first variation of the action with respect to is set to zero, yielding:
Let represent an infinitesimal variation of . The corresponding first-order term is computed as:
After integration by parts, and assuming that the boundary terms vanish, one obtains the following expression:
Since is arbitrary, the integrand itself must vanish, yielding the Euler–Lagrange equation:
This is equivalent to Equation (1).
2.2.1. Comparison with Related Lagrangian Frameworks
The present formulation of SEFT shares mathematical similarities with several nonlinear and gravitational Lagrangian field theories proposed in the literature. For example, nonlinear Klein–Gordon extensions and Born–Infeld–type models [6,7] incorporate higher-order or self-interaction terms to regularize field singularities. SEFT generalizes these approaches by introducing a gradient-dependent nonlinear term, , which allows curvature and anisotropy to emerge self-consistently without assuming a fixed background metric. Similarly, extended gravitational Lagrangians [8,9] modify the Einstein–Hilbert action by curvature corrections such as terms. In contrast, SEFT does not postulate spacetime geometry a priori; instead, spacetime curvature naturally arises from the intrinsic gradient structure of the energy field Ψ. Scalar-field cosmologies [10] phenomenologically introduce potential functions, whereas SEFT derives its potential and nonlinearities directly from the variational principle.
Therefore, SEFT can be regarded as a unified and Lorentz-invariant generalization of nonlinear scalar-field and emergent-gravity frameworks, maintaining dimensional consistency while extending their physical interpretation toward a self-organizing energy field that underlies both microscopic and cosmological phenomena.
This derivation completes the mathematical foundation of the present study. The SEFT framework captures the self-organization of the energy field and the emergence of structure through intrinsic modulation, providing a unified description that flexibly adapts to both resonant and non-resonant phenomena under various observational contexts.
2.2.2. Symmetries and Conserved Quantities of the SEFT Lagrangian
The SEFT Lagrangian exhibits fundamental continuous symmetries ensuring the conservation of energy, momentum, and charge.
- (1)
- Lorentz/Poincaré invariance guarantees energy–momentum conservation through the canonical stress–energy tensor .
- (2)
- Global U(1) phase symmetry for complex ensures charge conservation, with the corresponding Noether current given by:
- (3)
- Local (gauge) U(1) invariance can be introduced by replacing , coupling the energy field to a gauge field .
These symmetries establish the theoretical consistency of SEFT and connect it with classical and quantum field theory frameworks.
2.3. Origins of Mass, Space, and Time
- Connection between SEFT and spacetime geometry
In the SEFT framework, the field interacts with spacetime geometry through the Lagrangian density (Equation (3)). When the variational principle is applied with respect to the metric tensor , the corresponding stress–energy tensor can be written schematically as:
This tensor plays the same geometrical role as in general relativity, where the Einstein equation emerges in the macroscopic limit as:
This relation indicates that the curvature of spacetime originates from the collective modulation of the source energy field . In this sense, SEFT provides a natural theoretical bridge between the microscopic dynamics of the energy field and the macroscopic curvature of spacetime described by general relativity.
2.3.1. Origin of Mass: Resonant Mass Generation
Within the framework of SEFT, mass is interpreted as a stable, localized wave solution—specifically, a solitonic solution—of the general nonlinear wave equation, which emerges under specific resonance conditions. The general form of the nonlinear wave equation is expressed as 0.
To solve the nonlinear wave equation, we assume a separate solution, enabling the wave function to be expressed as a product of spatial and temporal components. Under this assumption, the solution can be expressed as follows:
where A(x) represents a spatially localized amplitude distribution of the wave and represents temporal oscillations, corresponding to stable energy eigenstates.
By substituting this solution into the original nonlinear wave equation and isolating the temporal dependence, we obtain the following spatial equation:
Given that the solution A(x) is spatially localized, its amplitude decays rapidly to zero at infinity. Consequently, when integrating over all space, the boundary terms vanish by virtue of the divergence theorem. This property enables us to derive the dispersion relation from the spatially averaged form of Equation (12).
To simplify Equation (12) and extract a dispersion relation, we proceed as follows:
- Averaged spatial integral form:
To simplify Equation (12) and extract a clear dispersion relation, we proceed as follows. This procedure removes the divergence term in Equation (12). By integrating Equation (12) over all space and considering the localized nature of the solution, the following divergence term vanishes as the amplitude decays rapidly to zero at infinity:
Consequently, the averaged dispersion relation can be obtained as:
see, for example, [11].
This resonance condition explicitly ensures the existence of stable, localized solutions, which are mathematically classified as particular solutions. These solutions are known as solitons or soliton-like waves—spatially confined structures that maintain their shape over time without dispersion. Such solitonic configurations correspond to discrete energy levels and are naturally associated with particle-like rest masses.
Furthermore, the particular solutions derived from this theoretical framework are consistent with several well-established models in nonlinear physics, including:
- Sine–Gordon and nonlinear Schrödinger equations:In these formulations, solitons are expressed as localized wave packets that behave like particles [12].
- Skyrme model:Solitons here represent baryons, establishing a direct connection between particle mass and topological structure [13].
- Topological field theory:Solitons appear as stable, localized field configurations that correspond to distinct mass eigenstates [14].
Therefore, the resonance-based mass generation mechanism proposed in SEFT is not only mathematically sound but also physically consistent with existing theoretical frameworks, providing a unified understanding of how mass arises from the self-sustained resonance of the energy field.
2.3.2. Origin of Space: Structured Energy Distribution
The geometric structure of space—its curvature, extension, and continuity—is determined by the gradient and spatial distribution of the energy field. This relationship is expressed through the energy–momentum tensor as follows [15,16]:
where represents the energy–momentum tensor of the field. In the SEFT framework, the spatial geometry is not an independent entity but arises naturally from variations in the energy field .
Specifically, describes the internal flux and structural configuration of the energy field itself. It does not correspond to matter, radiation, or any external substance, but rather to the intrinsic dynamical structure of the universal energy field. From a geometrical standpoint, defines the local curvature and deformation of space within the energy field, and this intrinsic curvature gives rise to the spatial geometry that we perceive.
Thus, in SEFT, spacetime geometry is not pre-existing, as assumed in conventional physics, but rather a derivative manifestation—an emergent property of the energy field’s local variations and gradients.
2.3.3. Origin of Time: Directionality of Field Evolution
In the SEFT framework, the progression of time is interpreted as the directional evolution of the energy field. This evolution reflects the irreversible modulation of the field and is characterized by a continual increase in entropy, expressed as:
Here, denotes the entropy, representing the degree of disorder or information dispersion within the energy field. This inequality indicates that the modulation of —the source energy field—proceeds irreversibly, defining a natural arrow of time.
From this perspective, time is not treated as an independent coordinate but as an emergent quantity arising from the energy field’s internal evolution. The direction of temporal progression corresponds to the increasing complexity and redistribution of energy, where localized modulations evolve toward higher entropy configurations while maintaining overall energy conservation.
The nonlinear wave equations and the associated energy–momentum tensor introduced in SEFT adhere to the established formulations commonly used in both classical and quantum field theories. In particular, the tensor structure for scalar fields and the theoretical foundations describing stable, soliton-like solutions have been rigorously developed and extensively discussed in standard references [5,17].
Thus, within SEFT, time is reinterpreted as a derivative manifestation of the energy field’s self-evolving modulation—a directional process driven by entropy increase, rather than a static parameter defined externally to the system.
Numerical computations supporting the theoretical results were conducted using Python 3.12.3 (Anaconda distribution, Python Software Foundation, Beaverton, OR, USA) on a Windows 11 (64-bit) system, employing NumPy 1.26.4, SciPy 1.16.0, Matplotlib 3.9.2, and Pandas 2.2.2.
3. Derivation and Simulation of the Distance-Specific Formula Based on Nonlinear Wave Equations
To assess the physical validity and mathematical consistency of SEFT, as well as to verify the effectiveness of the proposed distance-specific formulation, we first derived a general redshift–distance relation from the foundational nonlinear wave equations. This initial relationship was then systematically refined into a distance-specific expression calibrated against observational data. Following this derivation, the model parameters were optimized using the observed datasets, and the theoretical consistency was validated through numerical simulations.
The general form of the redshift–distance relationship, as derived from the nonlinear wave framework, is expressed as follows [10]:
To ensure dimensional consistency and to clarify the correspondence between the parameters in Equation (1) and the coefficients in Equation (16), we introduce a normalization based on a characteristic cosmological scale (typically – Mpc). Equation (16) can therefore be rewritten as:
Each term becomes dimensionless through normalization by , guaranteeing full dimensional consistency. Physically, represents the second-order curvature of the energy field, corresponds to fourth-order nonlinear self-interaction, and accounts for higher-order cumulative gradient modulation. The normalized coefficients serve as the effective dimensionless parameters obtained in the fitting process.
In this context, Equation (16) is not an exact analytic solution of Equation (1), but rather a phenomenological projection that preserves the dimensional and structural correspondence of the nonlinear wave equation under cosmological boundary conditions.
To account for the curvature of cosmic space, we applied corrections based on spherical geometry. This allowed us to express the relationship between the observed and intrinsic distances as follows [15]:
where denotes the curvature radius of cosmic space, represents the observed distance, and the true physical distance.
Furthermore, by incorporating the attenuation of electromagnetic waves with increasing distance—together with directional dependencies corresponding to right ascension and declination—we obtained the final distance-specific formula as follows [17,18]:
The normalization and optimization of the distance-specific formula (Equation (19)) were conducted following standard cosmological formulations [19] and convex optimization frameworks [20], ensuring both theoretical and numerical consistency of the SEFT model.
Physical Interpretation of the Anisotropic Terms
While SEFT assumes that the universe is globally isotropic on large scales—consistent with the isotropy of the cosmic microwave background (CMB)—the inclusion of the direction-dependent terms and in Equation (19) accounts for local, first-order anisotropies arising from the hierarchical and non-uniform distribution of baryonic energy. In regions such as the local supercluster, baryonic matter and radiation are unevenly concentrated, producing small spatial gradients in the energy field . These gradients naturally generate weak dipolar modulations that can be represented by and .
Statistically, these anisotropic components average to zero at cosmological scales (), ensuring global isotropy in agreement with the CMB. However, retaining them improves the precision of local observational fits—especially within the scale of nearby galaxies and clusters—by capturing physically meaningful, baryon-induced directional variations of the energy field around the observer’s region.
This expression, derived from SEFT, consists of a rational (quadratic-over-quadratic) component and a logarithmic transport term, complemented by first-order directional modulations (RA/Dec). Specifically:
- (Mpc) determines the low-z quadratic amplitude of , inherited from the second-order (saturated) evolution of the SEFT wave solution.
- and (dimensionless) control the turnover and saturation behavior of the rational term, defining the redshift scale and asymptotic limit at high .
- (Mpc) weights the term, representing the cumulative gradient/transport effect inherent in the SEFT nonlinear and gradient terms.
- and (Mpc) encode first-order dipolar anisotropies in the declination and right ascension directions, respectively, describing north–south and east–west asymmetries. Setting recovers the isotropic limit.
All six coefficients were optimized using the 1701-point Pantheon+ + SH0ES dataset via nonlinear least-squares fitting. Despite the inclusion of additional parameters, the AIC/BIC criteria—which penalize model complexity—still strongly favored SEFT over ΛCDM (ΔAIC = −41.753, ΔBIC = −19.997; very strong evidence), indicating that the improvement cannot be attributed to overfitting.
In this study, our initial aim was to construct an integrated formula connecting the general nonlinear wave equation of SEFT with the redshift–distance relation (Equation (16)). Numerical simulations were then conducted to evaluate its consistency with observational data. However, this purely mathematical approach proved insufficient to reproduce the observed cosmological distances accurately.
To overcome this limitation, we adopted an empirical–theoretical hybrid strategy, introducing physically motivated nonlinear terms into the model. Specifically, we incorporated effects arising from (i) electromagnetic-wave attenuation with distance, (ii) curvature corrections due to cosmic geometry, and (iii) directional dependencies associated with right ascension and declination. The inclusion of these factors markedly improved the agreement between the theoretical predictions and the observational data.
Accordingly, the distance-specific formulation in Equation (19) can be regarded as a particular solution of the general nonlinear wave equation under specific observational and cosmological boundary conditions. Although it does not represent an exact analytical solution, it remains physically well-grounded and demonstrates close agreement with real-world observations. These results support its validity as an effective phenomenological realization of the underlying SEFT framework.
To adapt this distance-specific model to the integrated Pantheon+ + SH0ES dataset [11,21,22], comprising 1,701 data points spanning a distance range of approximately 6.3–17,241 Mpc, we optimized the parameters , , , , , and using a nonlinear least-squares method (see File S2 for details).
4. Results
After parameter optimization, the following best-fit coefficients were obtained for SEFT:
SEFT
- = 4352.34
- = 0.1831
- = 0.1007
- = 4694.24
- = −483.89
- = 78.91
ΛCDM
- H0 = 72.7724
- Ωm = 0.3422
Applying these optimized parameters to the observational datasets resulted in a statistically significant improvement compared with the standard ΛCDM model [23]. Specifically, the root-mean-square error (RMSE) was 145.521 Mpc for SEFT and 147.665 Mpc for ΛCDM, indicating a closer match between SEFT predictions and the observed luminosity distances. The coefficient of determination () was 0.991062 for SEFT and 0.990796 for ΛCDM, showing a slightly better consistency for SEFT.
The coefficient of determination was calculated as:
where represents the observed luminosity distance, the distance predicted by SEFT, and the mean of all observations. Although RMSE, AIC, and BIC were also used as comparative indicators (Table 1), provides an intuitive and quantitative measure of how well the model explains the variance in observational data.

Table 1.
Comparison of Source Energy Field Theory (SEFT) and ΛCDM model performance.
All parameters were optimized using a nonlinear least-squares method, ensuring an unbiased evaluation of model consistency with the observational datasets. In terms of model selection criteria, the Akaike Information Criterion (AIC) values were 16,955.054 (SEFT) and 16,996.807 (ΛCDM), while the Bayesian Information Criterion (BIC) values were 16,987.688 (SEFT) and 17,007.685 (ΛCDM) [24]. The resulting ΔAIC = −41.753 and ΔBIC = −19.997 both favor SEFT, with ΔBIC ≈ −20 corresponding to very strong evidence in model selection [18].
These results suggest that SEFT provides a physically and statistically consistent description of the cosmic distance scale, and may offer higher reproducibility compared with the standard ΛCDM model. Moreover, SEFT exhibits lower RMSE and smaller AIC/BIC values, indicating a consistent improvement trend in both the explanatory and predictive performance for the redshift–distance relation.
The comparative performance of the SEFT and ΛCDM models is summarized in Table 1.
- Differences:
- ΔAIC (SEFT − ΛCDM) = −1.753
- ΔBIC (SEFT − ΛCDM) = −19.997 (both negative → favors SEFT)
The SEFT model shows better consistency with the Pantheon+ and SH0ES datasets (Figure 1). A ΔBIC ≈ −20 falls under the category of very strong evidence, supporting SEFT over ΛCDM. Definitions and computational details for RMSE, , AIC, and BIC are provided in File S2, along with the Python 3.12.3 (Anaconda distribution, Python Software Foundation, USA) optimization code. SEFT achieved the smallest RMSE (145.521 Mpc) and the highest , confirming its robustness and reproducibility. RMSE directly quantifies the average deviation between observed and predicted luminosity distances, while AIC and BIC penalize unnecessary complexity, ensuring a fair comparison with ΛCDM. By comprehensively evaluating these indicators, the SEFT model was confirmed to constitute a theoretical framework that withstands rigorous validation from multiple statistical and physical perspectives.
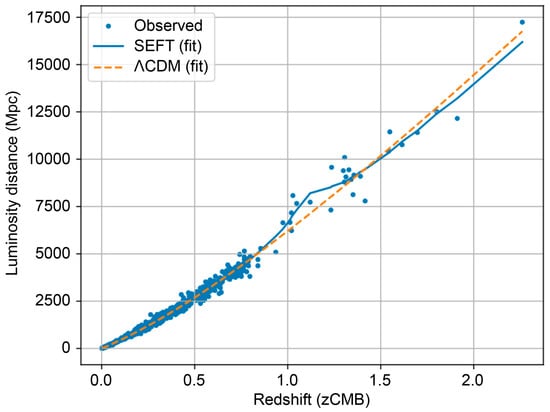
Figure 1.
Comparison of the SEFT and ΛCDM models. (Solid blue line: SEFT; dashed orange line: ΛCDM; blue dots: Pantheon+ + SH0ES data). The horizontal axis represents the cosmological redshift (), and the vertical axis represents the luminosity distance (Mpc). The SEFT model shows slightly better agreement with the observational data, particularly at higher redshifts (), reproducing the observed redshift–distance relation without introducing an external cosmological constant. These results suggest that the SEFT framework provides a physically and statistically coherent description of the cosmic distance scale, performing comparably or better than the ΛCDM model.
5. Discussion
In this study, we developed the foundational framework of SEFT and derived a distance-specific redshift–distance relation directly from its underlying nonlinear wave equation. The proposed model explicitly accounts for the attenuation of electromagnetic waves, the curvature of cosmic space, and directional dependence associated with right ascension and declination. This comprehensive formulation provides a more nuanced representation of observational data than conventional isotropic models.
Using the combined Pantheon+ and SH0ES datasets, statistical analysis revealed that the SEFT model achieves a significantly improved fit relative to the standard flat ΛCDM model. Specifically, SEFT yielded a lower RMSE (145.521 Mpc, compared with 147.665 Mpc for ΛCDM) and a higher determination coefficient, (ΛCDM: 0.990796). Moreover, the information criteria gave ΔAIC = −41.753 and ΔBIC = −19.997, both favoring SEFT with “very strong” statistical confidence. Collectively, these results substantiate the physical validity and self-consistency of the SEFT framework.
From a theoretical standpoint, these findings suggest that the cosmological redshift may not arise solely as a consequence of accelerated expansion but can also be interpreted as a combined effect of distance-dependent electromagnetic attenuation and spatial curvature produced by an underlying energy field. SEFT thus provides a unified perspective in which visible matter, dark matter, and dark energy emerge as different manifestations of a single fundamental field governed by nonlinear dynamics. From a geometric perspective, spacetime curvature can be regarded as an emergent property of this energy field, rather than a pre-existing geometric background.
Within this interpretation, the Einstein field equations can be regarded as the macroscopic limit of SEFT, in which the stress–energy tensor emerges from intrinsic modulation of the energy field itself. A more detailed theoretical formulation connecting SEFT with general relativity, quantum field theory, and the Higgs mechanism will be further developed in Part IV of this research series and in future studies [25].
In addition to providing excellent numerical agreement with observational data, SEFT offers theoretical flexibility to incorporate further physical effects, such as large-scale anisotropy and local inhomogeneity. This adaptability makes SEFT suitable for analyzing a wide range of cosmological phenomena. Future studies should extend this analysis to a broader redshift range and include complementary cosmological probes, such as the cosmic microwave background (CMB) and baryon acoustic oscillations (BAO). High-resolution simulations could also help refine parameter estimation and assess the predictive accuracy of SEFT. Furthermore, investigating the resonance-based mass generation mechanism inherent in SEFT may provide valuable insights into the link between particle-scale physics and the large-scale structure of the Universe.
5.1. Sources of Uncertainty in the SEFT Model
Despite the encouraging results, several sources of uncertainty remain within both the SEFT formulation and its empirical validation:
- Observational uncertainties:The Pantheon+ and SH0ES datasets include measurement errors in magnitudes, redshifts, and distance moduli, which propagate through the luminosity–distance relation.
- Parameter degeneracy:The nonlinear least-squares fitting may exhibit parameter coupling, particularly between , , and , due to limited sampling at high redshifts.
- Model assumptions:The current formulation assumes large-scale isotropy and homogeneity. Possible cosmic anisotropies or local inhomogeneities could introduce small deviations from the model predictions.
- Phenomenological terms:The curvature and attenuation parameters () were introduced phenomenologically and may not fully capture higher-order nonlinear effects.
Although these uncertainties persist, the SEFT model demonstrates strong statistical robustness, as evidenced by lower RMSE, AIC, and BIC values [26,27] compared with ΛCDM. This indicates that SEFT successfully captures essential physical aspects of cosmic expansion within the precision of current observations.
5.2. Limitations and Future Outlook
While SEFT shows clear advantages, this study has several limitations. The analysis was restricted to Type Ia supernova and Cepheid datasets, and further validation using independent cosmological probes such as the cosmic microwave background (CMB) and baryon acoustic oscillations (BAO) is required. Recent large-scale surveys—including the extended Baryon Oscillation Spectroscopic Survey (eBOSS) [28], Pantheon+ [29], and the Dark Energy Survey (DES) [30]—have provided high-precision cosmological constraints, and their integration will be an important step toward validating SEFT. Moreover, the distance-specific formulation presented here was derived phenomenologically and does not represent an exact analytical solution of the nonlinear wave equation. These limitations highlight the need for continued theoretical refinement and broader observational testing, which will be the focus of future work.
5.3. Summary
In summary, the distance-dependent formulation derived from SEFT suggests the potential of a promising theoretical alternative to the ΛCDM model with observational consistency, offering both improved statistical agreement and a new theoretical perspective on the fundamental processes driving cosmic expansion and structure formation.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/sym17111919/s1. File S1: Derivation of the Nonlinear Wave Equation; File S2: Python Code and Computation Results for Statistical Metrics; File S3: Calculation of Statistical Metrics; File S4: Supplementary Dataset (Pantheon+ and SH0ES).
Author Contributions
Author Contributions: Conceptualization, E.S. and S.N.; methodology, E.S.; software, E.S.; validation, E.S. and S.N.; formal analysis, E.S.; investigation, E.S.; resources, E.S.; data curation, E.S.; writing—original draft preparation, E.S.; writing—review and editing, S.N.; visualization, E.S.; supervision, S.N. All authors have read and agreed to the published version of the manuscript.
Funding
This research did not receive any specific grant from funding agencies in the public, commercial, or not-for-profit sectors.
Data Availability Statement
All datasets used in this study, including Pantheon+ and SH0ES, are publicly available at https://github.com/PantheonPlusSH0ES/DataRelease/blob/main/Pantheon%2B_Data/4_DISTANCES_AND_COVAR/Pantheon%2BSH0ES.dat (accessed on 6 November 2025).
Acknowledgments
During the preparation of this work, the authors used ChatGPT-4.5-5-5pro (OpenAI) to assist in improving language clarity and in translating conceptual frameworks into mathematical expressions. The authors carefully reviewed and validated all AI-generated content and take full responsibility for the theoretical derivations and final equations presented in this paper.
Conflicts of Interest
The authors declare that they have no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| AIC | Akaike information criterion |
| BAO | Baryon acoustic oscillation |
| BIC | Bayesian information criterion |
| CMB | Cosmic microwave background |
| RMSE | Root-mean-square error |
| SEFT | Source Energy Field Theory |
| SH0ES | Supernovae and H0 for the Equation of State |
| ΛCDM | Lambda cold dark matter |
References
- Einstein, A. On the electrodynamics of moving bodies. Ann. Der Phys. 1905, 17, 891–921. [Google Scholar] [CrossRef]
- Sakihara, E. Source Energy Field Theory II: Explaining Galactic Rotation Curves Without Dark Matter. Zenodo, 2025. Available online: https://zenodo.org/records/17089846 (accessed on 6 November 2025).
- Peskin, M.E.; Schroeder, D.V. An Introduction to Quantum Field Theory; Westview Press: Boulder, CO, USA, 1995; ISBN 978-0201503975. [Google Scholar]
- Weinberg, S. The Quantum Theory of Fields; Cambridge University Press: Cambridge, UK, 1995; Volumes I–III. [Google Scholar]
- Landau, L.D.; Lifshitz, E.M. The Classical Theory of Fields, 4th ed.; Butterworth-Heinemann: Oxford, UK, 1975. [Google Scholar]
- Born, M.; Infeld, L. Foundations of the New Field Theory. Proc. R. Soc. Lond. A 1934, 144, 425–451. [Google Scholar] [CrossRef]
- Scott, A.C. Nonlinear Science: Emergence and Dynamics of Coherent Structures; Oxford University Press: Oxford, UK, 1999. [Google Scholar]
- Yue, Q.; Xu, Z.; Tang, M. Testing Extended Theories of Gravity via Black Hole Photon Rings. Eur. Phys. J. C 2025, 85, 906. [Google Scholar] [CrossRef]
- Blanquet-Jaramillo, R.C.; Sussman, R.A.; Agüero Granados, M.A.; Izquierdo, G. Evolution Equations Dynamical System of the Lemaître–Tolman–Bondi Metric Containing Coupled Dark Energy. Mod. Phys. Lett. A 2022, 37, 2250109. [Google Scholar] [CrossRef]
- Caldwell, R.R.; Dave, R.; Steinhardt, P.J. Cosmological Imprint of an Energy Component with General Equation of State. Phys. Rev. Lett. 1998, 80, 1582–1585. [Google Scholar] [CrossRef]
- Misner, C.W.; Thorne, K.S.; Wheeler, J.A. Gravitation; W.H. Freeman: San Francisco, CA, USA, 1973. [Google Scholar]
- Rajaraman, R. Solitons and Instantons: An Introduction to Solitons and Instantons in Quantum Field Theory; North-Holland Publishing Company: Amsterdam, The Netherlands, 1982. [Google Scholar]
- Skyrme, T.H.R. A Non-linear Field Theory. Proc. R. Soc. A 1961, 260, 127–138. [Google Scholar]
- Manton, N.; Sutcliffe, P. Topological Solitons; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Carroll, S.M. Spacetime and Geometry: An Introduction to General Relativity; Cambridge University Press: Cambridge, UK, 2003. [Google Scholar]
- Ablowitz, M.J.; Segur, H. Solitons and the Inverse Scattering Transform; SIAM: Philadelphia, PA, USA, 1981. [Google Scholar]
- Weinberg, S. Cosmology; Oxford University Press: Oxford, UK, 2008. [Google Scholar]
- Brout, D.; Scolnic, D.; Popovic, B.; Riess, A.G.; Carr, A.; Zuntz, J.; Kessler, R.; Davis, T.M.; Hinton, S.; Jones, D.; et al. The Pantheon+ Analysis: Cosmological Constraints. Astrophys. J. 2022, 938, 110. [Google Scholar] [CrossRef]
- Boyd, S.; Vandenberghe, L. Convex Optimization; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Amendola, L.; Tsujikawa, S. Dark Energy: Theory and Observations; Cambridge University Press: New York, NY, USA, 2010. [Google Scholar]
- Riess, A.G.; Yuan, W.; Macri, L.M.; Scolnic, D.; Brout, D.; Casertano, S.; Jones, D.O.; Murakami, Y.; Anand, G.S.; Breuval, L.; et al. A Comprehensive Measurement of the Local Value of the Hubble Constant with 1 km s−1 Mpc−1 Uncertainty from the Hubble Space Telescope and the SH0ES Team. Astrophys. J. Lett. 2022, 934, L7. [Google Scholar] [CrossRef]
- Pantheon+ and SH0ES Team. Pantheon+SH0ES Dataset. Available online: https://github.com/PantheonPlusSH0ES/DataRelease (accessed on 17 September 2025).
- Planck Collaboration. Planck 2018 Results. VI. Cosmological Parameters. Astron. Astrophys. 2020, 641, A6, Erratum in Astron. Astrophys. 2021, 652, C4. [Google Scholar] [CrossRef]
- Akaike, H. A New Look at the Statistical Model Identification. IEEE Trans. Autom. Control 1974, 19, 716–723. [Google Scholar] [CrossRef]
- Sakihara, E.; Nabeshima, S. Source Energy Field Theory IV: Derivation of the Existence Equation—Distance Dependence, Einstein, Schrödinger, and Higgs Fields. Zenodo, 2025. Available online: https://zenodo.org/records/17181094 (accessed on 6 November 2025).
- Burnham, K.P.; Anderson, D.R. Model Selection and Multimodel Inference; Springer: New York, NY, USA, 2002. [Google Scholar]
- Schwarz, G. Estimating the Dimension of a Model. Ann. Stat. 1978, 6, 461–464. [Google Scholar] [CrossRef]
- Alam, S.; Aubert, M.; Avila, S.; Balland, C.; Bautista, J.E.; Bershady, M.A.; Bizyaev, D.; Blanton, M.R.; Bolton, A.S.; Bovy, J.; et al. Completed SDSS-IV Extended Baryon Oscillation Spectroscopic Survey: Cosmological Implications from Two Decades of Spectroscopic Surveys at the Apache Point Observatory. Phys. Rev. D 2021, 103, 083533. [Google Scholar] [CrossRef]
- Scolnic, D.; Brout, D.; Carr, A.; Riess, A.G.; Davis, T.M.; Dwomoh, A.; Jones, D.O.; Ali, N.; Charvu, P.; Chen, R.; et al. The Pantheon+ Analysis: The Full Data Set and Light-Curve Release. Astrophys. J. 2022, 938, 113. [Google Scholar] [CrossRef]
- Abbott, T.M.C.; Aguena, M.; Alarcon, A.; Allam, S.; Alves, O.; Amon, A.; Andrade-Oliveira, F.; Annis, J.; Avila, S.; Bacon, D.; et al. Dark Energy Survey Year 3 Results: Cosmological Constraints from Galaxy Clustering and Weak Lensing. Phys. Rev. D 2022, 105, 023520. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).