On Local Fractional Topological Indices and Entropies for Hyper-Chordal Ring Networks Using Local Fractional Metric Dimension

Abstract

An algebraic graph is defined in terms of graph theory as a graph with related algebraic structures or characteristics. If the vertex set of a graph $\mathcal{G}$ is a group, a ring, or a field, then $\mathcal{G}$ is called an algebraic structure graph. This work uses an algebraic structure graph based on the modular ring ${\mathbb{Z}}_n$, known as a hyper-chordal ring network. The lower and upper bounds of the local fractional metric dimension are computed for certain families of hyper-chordal ring networks. Utilizing the cardinalities of local fractional resolving sets, local fractional resolving (LFR)M-polynomials are computed for hyper-chordal ring networks. Further, new topological indices based on (LFR)M-polynomials are established for the proposed networks. The local fraction entropies are developed by modifying the first three kinds of Zagreb entropies, which are calculated for the chosen hyper-chordal ring networks. Furthermore, numerical and graphical comparisons are discussed to observe the order between newly computed topological indices.

1. Introduction

An algebraic graph theory and topological indices focus on graph research and its applications in physical science, information technology, and media platforms. A mutual return in graphical research and presentation links topological indices and algebraic graph theory. Topological indices have a specific set of mathematical computations generated from graph topology, algebraic graph theory, and graph features studied using mathematics tools and symbols, which may be used to analyze and identify them. A polynomial, matrix, numerical sequence, or numeric number representing the whole graph may be used to identify it.

The metric dimension has various applications in the field of cryptography and network theory. To find the family of networks that has a particular number of metric dimensions is a hard problem. Further, computing the local fractional metric dimension is an NP-hard problem. The applications of metric dimensions in fields such as network theory, graph theory, and optimization have been discussed in [1,2,3]. Initially, the concept of metric dimension in graph theory was given by Melter and Harary [4]. The resolving set was the minimum number of vertices which was uniquely determined by the distances from all other vertices described in [5]. The initial idea about fractional metric dimension (FMD) given by Arumugam and Mathew contributed to an enhanced comprehension of the FMD. They computed the FMD for complicated structures of lexicographic, classified, Cartesian, corona, and corona-comb networks. Concerning LMD, especially product operations, these networks have been studied in [6].

The FMD of improved Jahangir networks and conversion systems has been studied earliest in the research conducted by Wang and Feng [7,8] and Liu et al. [9]. When accomplishing the estimation, these methodologies were used when considering the landscapes of FMDs and other calculation measures in multiple network topologies. In their study, Aisyah planned the FMD limits in metal-organic graphs [10,11]. However, as Raza pointed out, the FMD can be known with other types of graphs belonging to other categories as well. They proposed to use the Local Fractional Metric Dimension (LFMD), which is a localized version of the metric dimension, in the corona product of systems. In the area of LFMD exploration, remarkable incursions have been achieved by Liu et al. [12]. Ali and Falcn, with other researchers, recently conducted a study on the LFMD of circular symmetric planar networks [13]. More related information can be found in [14]. A similar approach was used by Aisyah [11] as one of the innovators of using the LFMD to characterize the corona product of systems.

A molecular graph displays a molecule’s formation and relationships. The physical and chemical characteristics of molecules are determined by molecular graphs. Research on QSAR and QSPR relies on several applications, including digital screens [15,16]. Molecular graphs are characterized using several topological indices, including effective graph descriptors [17,18]. Various topological indices are used to describe molecular graphs, and several have been shown to interact with natural, chemical, or physical features of molecules [19,20,21,22,23,24,25,26]. Topological indices play a crucial role in understanding and predicting molecular activity and characteristics in diverse chemical and medical settings.

Mathematics is used to study chemical structures in mathematical chemistry. In mathematical chemistry, chemical graph theory models chemical processes mathematically using chemical diagrams. In principle, a molecular network is straightforward: a graph with many edges and no loops that represents atoms and their chemical bonding by their vertices and edges. In mathematics, atoms are graph vertices while chemical bonds are edges. A molecular graph shows a molecule’s formation and connections in a topological representation. Molecular graphs are analyzed using several topological indices, including degree, distance, and derived ones. Distance-based topological indices are important in chemical graph theory, especially chemistry. Each topological index provides unique statistics of molecular graphs and offers many representations for studying chemical compound properties [27,28]. Degree-based topological indices have been investigated extensively and shown to correlate with molecular compound characteristics. Those indexes are strongly linked. In a prior study [29], degree-based topological indices were the most often used variations. Numerical values relate molecular structures to physical properties, chemical compound reactions, and biological reactivities. Topological indices and mathematical values link molecular structure with physical properties, synthetic operations, and biological processes [30,31].

Some topological indices are difficult to calculate. To solve this problem, several academics have developed algebraic polynomials to effectively calculate topological indices. These polynomials are intended to differentiate, integrate, or both, at a point to provide the correct topological index. These algebraic polynomials may considerably minimize the processing effort needed to construct topological indices. The generating function M-polynomial gives the number of graph walks of varying lengths. It helps research molecular graphs and other complicated network topologies. An NM-polynomial is a modified M-polynomial that accounts for non-adjacent vertices in a graph [32,33]. Shannon introduced the entropy theory in 1948 in his landmark paper [34]. While entropies use a probability distribution, they only measure information certainty. Entropy, initially presented in thermodynamics, is now used in information theory, computer theory, physics, and chemistry. Entropy is used to evaluate steam engines and optical fiber data transport capacity. Entropy is usually connected with information theory, but it may also be used to investigate networks, composite systems, graph patterns, and algebraic construction. A broad study of entropy’s applications in algebraic structures and other domains. The degree of each atom is crucial, leading to basic analysis in graph and network theory, revealing constants for scientific studies [35,36,37,38,39,40]. Several researchers have used graph entropy estimates to analyze biological and chemical networks sequentially [41,42,43]. Das and colleagues investigated topological indices and entropies in their study. Graphs based on algebraic structures such as group and number theory are crucial in this study [44,45,46,47,48].

Finding the local fractional metric dimension of a graph, especially an algebraic structure graph, is not an easy task. The upper bound of the local fractional metric dimension is important because in various cases where we cannot compute the exact values of the local fractional metric dimension in the cases, upper bounds give the information that we cannot use objects above the upper bounds. If we cannot have an upper bound for a certain structure, then it is difficult to use the minimum number of objects to cover the whole network uniquely. In this paper, we consider hyper-chordal ring networks, which are based on algebraic structure modular groups. Using a local fractional metric resolving the mapping of cardinalities, we establish a novel local resolving M polynomial and then define some new topological indices based on that polynomial. Further, some new entropies that are based on local fraction metric dimensions are established.

The rest of the article is arranged as follows: In Section 2, the hyper-chordal ring networks and their upper bounds for LFMD are established. In Section 3, local fractional topological indices are computed by using LFRM polynomials. The local fractional entropies are developed for the proposed hyper-chordal ring networks in Section 4. In Section 5, concluding remarks about the proposed work are given.

2. Hyper-Chordal Ring Networks and Their Upper Bounds for LFMD

In this section, hyper-chordal networks and lower- and upper-bound sequences are computed for the local fractional metric dimension.

Definition 1.

Let $V\left(\mathcal{G}\right)={\mathbb{Z}}_n$ be the vertex set of the graph $\mathcal{G}$ and $S=\{s_1,s_2,\cdots ,s_k\}$ be the set of parameters which is the subset of ${\mathbb{Z}}_n$. The hyper-chordal network is denoted by ${\mathbb{CRZ}}_n\left(S\right)$, and their edge set is defined as

$$E\left({\mathbb{CRZ}}_n\left(S\right)\right)=\{i\equiv s_t+j\left(\mathit{mod}n\right)\}\cup \{i\equiv j-s_t\left(\mathit{mod}n\right)\}$$

where $s_t\in S$ and $i,j\in {\mathbb{Z}}_n.$

Some hyper-chordal networks are given in Figure 1.

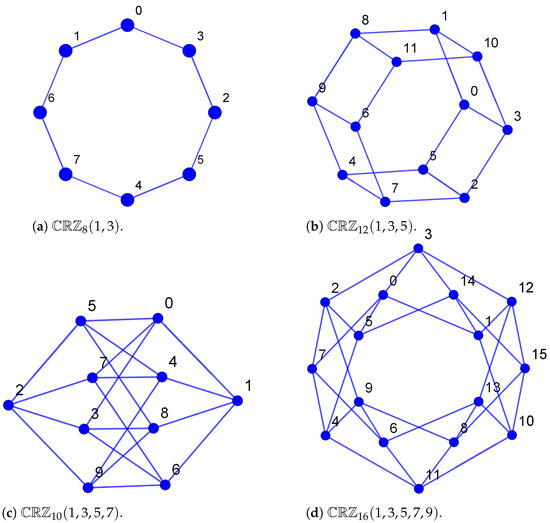
Figure 1. Four hyper-chordal networks with different parameters.

The mapping r from the set of vertex to the closed interval $[0,1]$ is known as a resolving mapping [49] if

$$\sum _{\nu \in \mathcal{R}\{\mu ,\omega \}}r\left(\nu \right)\ge 1,\mu ,\omega \in V.$$

The FMD of a graph $\mathcal{G}$ is

$$F_d\left(\mathcal{G}\right):=min\left\{\sum _{\mu \in V}r\left(\mu \right):r \mathrm{is} \mathrm{the} \mathrm{resolving} \mathrm{mapping} \mathrm{on} V\left(\mathcal{G}\right)\right\}.$$

The LFMD of a graph $\mathcal{G}$ is defined as;

$${\mathcal{L}}_{fmd}\left(\mathcal{G}\right):=min\left\{\sum _{\mu \in V}r\left(\mu \right):r \mathrm{is} \mathrm{the} \mathrm{resolving} \mathrm{mapping} \mathrm{on} V\left(\mathcal{G}\right)\right\}.$$

Further, $\mathfrak{l}\left(\mathcal{G}\right)=min\{\left|\mathcal{R}\left\{\mu ,\omega \right\}\right|:\mu \omega \in E\}$. Lemma 1 and Theorem 1 are very useful in this manuscript.

Lemma 1

([11,50]). Let $\mathcal{G}$ be a finite graph whose order is greater than two; then, we have

$${\displaystyle \frac{O\left(\mathcal{G}\right)}{O\left(\mathcal{G}\right)-{\mathrm{L}}_d\left(\mathcal{G}\right)+1}}\le {\mathrm{L}}_{fd}\left(\mathcal{G}\right)\le {\displaystyle \frac{O\left(\mathcal{G}\right)}{\mathfrak{l}\left(\mathcal{G}\right)}}$$

(1)

where

$$\mathfrak{l}\left(\mathcal{G}\right)=min\{\left|\mathcal{R}\left\{\mu ,\omega \right\}\right|:\mu \omega \in E\}.$$

Theorem 1.

Let $\mathcal{G}$ be a simple graph; then, we have ${\displaystyle \frac{O\left(\mathcal{G}\right)}{\gamma \left(\mathcal{G}\right)}}\le {\mathrm{L}}_f\left(\mathcal{G}\right).$ Where $\gamma \left(\mathcal{G}\right)=max\{\left|\mathcal{R}\left\{a\right\}\right|:a\in E\},2\le \gamma \left(\mathcal{G}\right)\le O\left(\mathcal{G}\right)$ [51].

Theorem 2.

Let ${\mathbb{CRZ}}_{2⋎+1}(1,3,5)$ be a chordal ring network; the lower and upper limits of the local fractional metric dimension are

$$1\le {\mathcal{L}}_{fmd}\left({\mathbb{CRZ}}_{2⋎+1}(1,3,5)\right)\le {\displaystyle \frac{2⋎+1}{2⋎-1}}.$$

Proof. 

Let ${\mathbb{CRZ}}_{2⋎+1}(1,3,5)$ be a chordal ring network; there are three cases of sequences for resolving sets for adjacent vertices. The numerical computing of these cases is given in Table 1, Table 2 and Table 3 respectively.

Case (a):

When $⋎\equiv 1\left(\mathrm{mod}4\right)$:

Table 1. The LFRMs and their cardinalities when $⋎\equiv 1\left(\mathrm{mod}4\right)$.

${⋋}_1$	${⋋}_2$	${{\mathcal{R}}^{\prime }}_{\mathit{l}}^{\mathit{f}}\{{⋋}_1,{⋋}_2\}$	$|{\mathcal{R}}_{\mathit{l}}^{\mathit{f}}\{{⋋}_1,{⋋}_2\}|$
0	1	$\left\{⋎-3,⋎-1\right\}$	$2⋎-1$
0	3	$\left\{⋎-1,⋎+2\right\}$	$2⋎-1$
0	5	$\left\{⋎+2,⋎+4\right\}$	$2⋎-1$
0	$2⋎-4$	$\left\{⋎-3,⋎-1\right\}$	$2⋎-1$
0	$2⋎-2$	$\left\{⋎-1,⋎+2\right\}$	$2⋎-1$
2	$2⋎-2$	$\left\{⋎-1,⋎+1\right\}$	$2⋎-1$
0	$2⋎$	$\left\{⋎+2,⋎+4\right\}$	$2⋎-1$
2	$2⋎$	$\left\{⋎+1,⋎+4\right\}$	$2⋎-1$
4	$2⋎$	$\left\{⋎+1,⋎+3\right\}$	$2⋎-1$
Otherwise	Otherwise	∅	$2⋎+1$

Table 1. The LFRMs and their cardinalities when $⋎\equiv 1\left(\mathrm{mod}4\right)$.

${⋋}_1$	${⋋}_2$	${{\mathcal{R}}^{\prime }}_{\mathit{l}}^{\mathit{f}}\{{⋋}_1,{⋋}_2\}$	$|{\mathcal{R}}_{\mathit{l}}^{\mathit{f}}\{{⋋}_1,{⋋}_2\}|$
0	1	$\left\{⋎-3,⋎-1\right\}$	$2⋎-1$
0	3	$\left\{⋎-1,⋎+2\right\}$	$2⋎-1$
0	5	$\left\{⋎+2,⋎+4\right\}$	$2⋎-1$
0	$2⋎-4$	$\left\{⋎-3,⋎-1\right\}$	$2⋎-1$
0	$2⋎-2$	$\left\{⋎-1,⋎+2\right\}$	$2⋎-1$
2	$2⋎-2$	$\left\{⋎-1,⋎+1\right\}$	$2⋎-1$
0	$2⋎$	$\left\{⋎+2,⋎+4\right\}$	$2⋎-1$
2	$2⋎$	$\left\{⋎+1,⋎+4\right\}$	$2⋎-1$
4	$2⋎$	$\left\{⋎+1,⋎+3\right\}$	$2⋎-1$
Otherwise	Otherwise	∅	$2⋎+1$

Case (b):

When $⋎\equiv 3\left(\mathrm{mod}4\right)$:

Table 2. The LFRMs and their cardinalities when $⋎\equiv 2\left(\mathrm{mod}4\right)$.

${⋋}_1$	${⋋}_2$	${{\mathcal{R}}^{\prime }}_{\mathit{l}}^{\mathit{f}}\{{⋋}_1,{⋋}_2\}$	$|{\mathcal{R}}_{\mathit{l}}^{\mathit{f}}\{{⋋}_1,{⋋}_2\}|$
0	1	$\left\{⋎,⋎+2\right\}$	$2⋎-1$
0	3	$\left\{⋎-1,⋎+2\right\}$	$2⋎-1$
0	5	$\left\{⋎-1,⋎+1\right\}$	$2⋎-1$
0	$2⋎-4$	$\left\{⋎,⋎+1\right\}$	$2⋎-1$
0	$2⋎-2$	$\left\{⋎-1,⋎+2\right\}$	$2⋎-1$
2	$2⋎-2$	$\left\{⋎+2,⋎+4\right\}$	$2⋎-1$
0	$2⋎$	$\left\{⋎-1,⋎+1\right\}$	$2⋎-1$
2	$2⋎$	$\left\{⋎+1,⋎+4\right\}$	$2⋎-1$
4	$2⋎$	$\left\{⋎+4,⋎+6\right\}$	$2⋎-1$
Otherwise	Otherwise	∅	$2⋎+1$

Table 2. The LFRMs and their cardinalities when $⋎\equiv 2\left(\mathrm{mod}4\right)$.

${⋋}_1$	${⋋}_2$	${{\mathcal{R}}^{\prime }}_{\mathit{l}}^{\mathit{f}}\{{⋋}_1,{⋋}_2\}$	$|{\mathcal{R}}_{\mathit{l}}^{\mathit{f}}\{{⋋}_1,{⋋}_2\}|$
0	1	$\left\{⋎,⋎+2\right\}$	$2⋎-1$
0	3	$\left\{⋎-1,⋎+2\right\}$	$2⋎-1$
0	5	$\left\{⋎-1,⋎+1\right\}$	$2⋎-1$
0	$2⋎-4$	$\left\{⋎,⋎+1\right\}$	$2⋎-1$
0	$2⋎-2$	$\left\{⋎-1,⋎+2\right\}$	$2⋎-1$
2	$2⋎-2$	$\left\{⋎+2,⋎+4\right\}$	$2⋎-1$
0	$2⋎$	$\left\{⋎-1,⋎+1\right\}$	$2⋎-1$
2	$2⋎$	$\left\{⋎+1,⋎+4\right\}$	$2⋎-1$
4	$2⋎$	$\left\{⋎+4,⋎+6\right\}$	$2⋎-1$
Otherwise	Otherwise	∅	$2⋎+1$

Case (c):

When $⋎\equiv 0,2\left(\mathrm{mod}4\right)$:

Table 3. The LFRMs and their cardinalities when $⋎\equiv 3\left(\mathrm{mod}4\right)$.

${⋋}_1$	${⋋}_2$	${{\mathcal{R}}^{\prime }}_{\mathit{l}}^{\mathit{f}}\{{⋋}_1,{⋋}_2\}$	$|{\mathcal{R}}_{\mathit{l}}^{\mathit{f}}\{{⋋}_1,{⋋}_2\}|$
0	1	$\left\{⋎-2,⋎+1\right\}$	$2⋎-1$
0	5	$\left\{⋎,⋎+3\right\}$	$2⋎-1$
0	$2⋎-4$	$\left\{⋎-2,⋎+1\right\}$	$2⋎-1$
2	$2⋎-2$	$\left\{⋎,⋎+3\right\}$	$2⋎-1$
0	$2⋎$	$\left\{⋎,⋎+3\right\}$	$2⋎-1$
4	$2⋎$	$\left\{⋎+2,⋎+5\right\}$	$2⋎-1$
Otherwise	Otherwise	∅	$2⋎+1$

Table 3. The LFRMs and their cardinalities when $⋎\equiv 3\left(\mathrm{mod}4\right)$.

${⋋}_1$	${⋋}_2$	${{\mathcal{R}}^{\prime }}_{\mathit{l}}^{\mathit{f}}\{{⋋}_1,{⋋}_2\}$	$|{\mathcal{R}}_{\mathit{l}}^{\mathit{f}}\{{⋋}_1,{⋋}_2\}|$
0	1	$\left\{⋎-2,⋎+1\right\}$	$2⋎-1$
0	5	$\left\{⋎,⋎+3\right\}$	$2⋎-1$
0	$2⋎-4$	$\left\{⋎-2,⋎+1\right\}$	$2⋎-1$
2	$2⋎-2$	$\left\{⋎,⋎+3\right\}$	$2⋎-1$
0	$2⋎$	$\left\{⋎,⋎+3\right\}$	$2⋎-1$
4	$2⋎$	$\left\{⋎+2,⋎+5\right\}$	$2⋎-1$
Otherwise	Otherwise	∅	$2⋎+1$

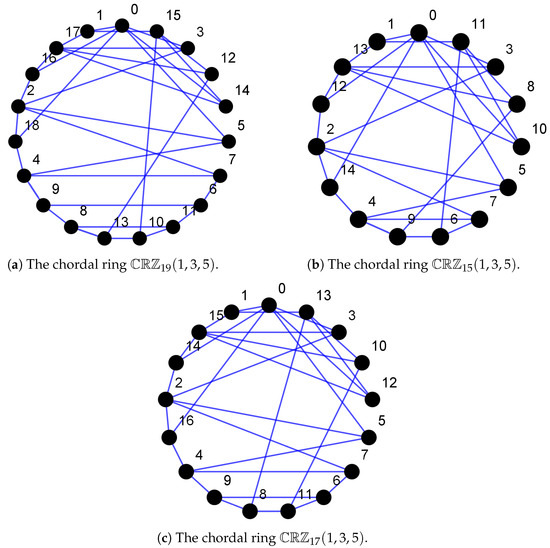
To better understand the proof of Theorem 2, the following networks and their LFRMs are given. Three hyper-chordal networks with parameters $(1,3,5)$ for $⋎=19,15,17$ are shown in Figure 2.

Figure 2. Three hyper-chordal networks with parameters $(1,3,5)$ for $⋎=19,15,17$.

For case (a), $⋎\equiv 1\left(\mathrm{mod}3\right)$, the chordal network ${\mathbb{CRZ}}_{19}(1,3,5)$ is shown in Figure 2a. The local fractional resolving sets for chordal ring ${\mathbb{CRZ}}_{19}(1,3,5)$ are calculated as follows:

$$\begin{array}{cccccc}\hfill & {{\mathcal{R}}^{\prime }}_l^f\{1,0\}=\{6,8\},\hfill & \hfill & {{\mathcal{R}}^{\prime }}_l^f\{3,0\}=\{8,11\},\hfill & \hfill & {{\mathcal{R}}^{\prime }}_l^f\{5,0\}=\{11,13\},\hfill \\ \hfill & {{\mathcal{R}}^{\prime }}_l^f\{14,0\}=\{6,8\},\hfill & \hfill & {{\mathcal{R}}^{\prime }}_l^f\{16,0\}=\{8,11\},\hfill & \hfill & {{\mathcal{R}}^{\prime }}_l^f\{16,2\}=\{8,10\},\hfill \\ \hfill & {{\mathcal{R}}^{\prime }}_l^f\{18,0\}=\{11,13\},\hfill & \hfill & {{\mathcal{R}}^{\prime }}_l^f\{18,2\}=\{10,13\},\hfill & \hfill & {{\mathcal{R}}^{\prime }}_l^f\{18,4\}=\{10,12\}.\hfill \end{array}$$

${{\mathcal{R}}^{\prime }}_l^f=\varnothing$ for all other edges. Since $|{\mathcal{R}}_l^f\{{⋋}_1,{⋋}_2\}|=V\left({\mathbb{CRZ}}_{19}(1,3,5)\right)\setminus {{\mathcal{R}}^{\prime }}_l^f\{{⋋}_1,{⋋}_2\}$, the minimum and maximum cardinalities are 17 and 19, respectively. Thus, by using Lemma 1 and Theorem 1, we have

$$1\le {\mathcal{L}}_{fmd}\left({\mathbb{CRZ}}_{19}(1,3,5)\right)\le {\displaystyle \frac{19}{17}}.$$

For case (b), $⋎\equiv 0\left(\mathrm{mod}3\right)$, the chordal network ${\mathbb{CRZ}}_{15}(1,3,5)$ is shown in Figure 2b. The local fractional resolving sets for chordal ring ${\mathbb{CRZ}}_{15}(1,3,5)$ are calculated as follows:

$$\begin{array}{cccccc}\hfill & {{\mathcal{R}}^{\prime }}_l^f\{1,0\}=\{7,9\},\hfill & \hfill & {{\mathcal{R}}^{\prime }}_l^f\{3,0\}=\{6,9\},\hfill & \hfill & {{\mathcal{R}}^{\prime }}_l^f\{5,0\}=\{6,8\},\hfill \\ \hfill & {{\mathcal{R}}^{\prime }}_l^f\{10,0\}=\{7,9\},\hfill & \hfill & {{\mathcal{R}}^{\prime }}_l^f\{12,0\}=\{6,9\},\hfill & \hfill & {{\mathcal{R}}^{\prime }}_l^f\{14,0\}=\{6,8\},\hfill \\ \hfill & {{\mathcal{R}}^{\prime }}_l^f\{12,2\}=\{6,11\},\hfill & \hfill & {{\mathcal{R}}^{\prime }}_l^f\{14,2\}=\{8,11\},\hfill & \hfill & {{\mathcal{R}}^{\prime }}_l^f\{14,4\}=\{11,13\}.\hfill \end{array}$$

${{\mathcal{R}}^{\prime }}_l^f=\varnothing$ for all other edges. Since $|{\mathcal{R}}_l^f\{{⋋}_1,{⋋}_2\}|=V\left({\mathbb{CRZ}}_{15}(1,3,5)\right)\setminus {{\mathcal{R}}^{\prime }}_l^f\{{⋋}_1,{⋋}_2\}$, the minimum and maximum cardinalities are 17 and 19, respectively. Thus, by using Lemma 1 and Theorem 1, we have

$$1\le {\mathcal{L}}_{fmd}\left({\mathbb{CRZ}}_{15}(1,3,5)\right)\le {\displaystyle \frac{19}{17}}.$$

For case (c), $⋎\equiv 2\left(\mathrm{mod}3\right)$, the chordal network ${\mathbb{CRZ}}_{17}(1,3,5)$ is shown in Figure 2c. The local fractional resolving sets for chordal ring ${\mathbb{CRZ}}_{17}(1,3,5)$ are calculated as follows:

$$\begin{array}{cccccc}\hfill & {{\mathcal{R}}^{\prime }}_l^f\{1,0\}=\{6,9\},\hfill & \hfill & {{\mathcal{R}}^{\prime }}_l^f\{5,0\}=\{8,11\},\hfill & \hfill & {{\mathcal{R}}^{\prime }}_l^f\{12,0\}=\{6,9\},\hfill \\ \hfill & {{\mathcal{R}}^{\prime }}_l^f\{14,2\}=\{8,11\},\hfill & \hfill & {{\mathcal{R}}^{\prime }}_l^f\{16,0\}=\{8,11\},\hfill & \hfill & {{\mathcal{R}}^{\prime }}_l^f\{16,4\}=\{10,13\},\hfill \end{array}$$

${{\mathcal{R}}^{\prime }}_l^f=\varnothing$ for all other edges. Since $|{\mathcal{R}}_l^f\{{⋋}_1,{⋋}_2\}|=V\left({\mathbb{CRZ}}_{17}(1,3,5)\right)\setminus {{\mathcal{R}}^{\prime }}_l^f\{{⋋}_1,{⋋}_2\}$, the minimum and maximum cardinalities are 17 and 19, respectively. Thus, by using Lemma 1 and Theorem 1, we have

$$1\le {\mathcal{L}}_{fmd}\left({\mathbb{CRZ}}_{17}(1,3,5)\right)\le {\displaystyle \frac{19}{17}}.$$

□

Theorem 3.

Let ${\mathbb{CRZ}}_{⋎}(1,3,5,7)$ be a chordal ring network; the lower and upper bounds of the local fractional metric dimension are

$$1\le {\mathcal{L}}_{fmd}\left({\mathbb{CRZ}}_{⋎}(1,3,5,7)\right)\le {\displaystyle \frac{⋎}{⋎-3}},$$

where ⋎ is an odd number but $3\nmid ⋎$

Proof. 

Let ${\mathbb{CRZ}}_{⋎}(1,3,5,7)$ be a chordal ring network; there are two cases of sequences for resolving sets for adjacent vertices. The numerical computing of these cases is given in Table 4 and Table 5 respectively.

Case (a):

When $⋎\equiv 1\left(\mathrm{mod}4\right)$:

Table 4. The LFRMs and their cardinalities when $⋎\equiv 1\left(\mathrm{mod}4\right)$.

${⋋}_1$	${⋋}_2$	${{\mathcal{R}}^{\prime }}_{\mathit{l}}^{\mathit{f}}\{{⋋}_1,{⋋}_2\}$	$|{\mathcal{R}}_{\mathit{l}}^{\mathit{f}}\{{⋋}_1,{⋋}_2\}|$
0	1	$\left\{{\displaystyle \frac{⋎-9}{2}},{\displaystyle \frac{⋎-5}{2}},{\displaystyle \frac{⋎+1}{2}}\right\}$	$⋎-3$
0	3	$\left\{{\displaystyle \frac{⋎-5}{2}}\right\}$	$⋎-1$
0	5	$\left\{{\displaystyle \frac{⋎+5}{2}}\right\}$	$⋎-1$
0	7	$\left\{{\displaystyle \frac{⋎-1}{2}},{\displaystyle \frac{⋎+5}{2}},{\displaystyle \frac{⋎+9}{2}}\right\}$	$⋎-3$
0	$⋎-7$	$\left\{{\displaystyle \frac{⋎-9}{2}},{\displaystyle \frac{⋎-5}{2}},{\displaystyle \frac{⋎+1}{2}}\right\}$	$⋎-3$
0	$⋎-5$	$\left\{{\displaystyle \frac{⋎-5}{2}}\right\}$	$⋎-1$
2	$⋎-5$	$\left\{{\displaystyle \frac{⋎-5}{2}},{\displaystyle \frac{⋎-1}{2}},{\displaystyle \frac{⋎+5}{2}}\right\}$	$⋎-3$
0	$⋎-3$	$\left\{{\displaystyle \frac{⋎+5}{2}}\right\}$	$⋎-1$
2	$⋎-3$	$\left\{{\displaystyle \frac{⋎-1}{2}}\right\}$	$⋎-1$
4	$⋎-3$	$\left\{{\displaystyle \frac{⋎-1}{2}},{\displaystyle \frac{⋎+3}{2}},{\displaystyle \frac{⋎+9}{2}}\right\}$	$⋎-3$
0	$⋎-1$	$\left\{{\displaystyle \frac{⋎-1}{2}},{\displaystyle \frac{⋎+5}{2}},{\displaystyle \frac{⋎+9}{2}}\right\}$	$⋎-3$
2	$⋎-1$	$\left\{{\displaystyle \frac{⋎+9}{2}}\right\}$	$⋎-1$
4	$⋎-1$	$\left\{{\displaystyle \frac{⋎+3}{2}}\right\}$	$⋎-1$
6	$⋎-1$	$\left\{{\displaystyle \frac{⋎+3}{2}},{\displaystyle \frac{⋎+7}{2}},{\displaystyle \frac{⋎+13}{2}}\right\}$	$⋎-3$
Otherwise	Otherwise	∅	⋎

Table 4. The LFRMs and their cardinalities when $⋎\equiv 1\left(\mathrm{mod}4\right)$.

${⋋}_1$	${⋋}_2$	${{\mathcal{R}}^{\prime }}_{\mathit{l}}^{\mathit{f}}\{{⋋}_1,{⋋}_2\}$	$|{\mathcal{R}}_{\mathit{l}}^{\mathit{f}}\{{⋋}_1,{⋋}_2\}|$
0	1	$\left\{{\displaystyle \frac{⋎-9}{2}},{\displaystyle \frac{⋎-5}{2}},{\displaystyle \frac{⋎+1}{2}}\right\}$	$⋎-3$
0	3	$\left\{{\displaystyle \frac{⋎-5}{2}}\right\}$	$⋎-1$
0	5	$\left\{{\displaystyle \frac{⋎+5}{2}}\right\}$	$⋎-1$
0	7	$\left\{{\displaystyle \frac{⋎-1}{2}},{\displaystyle \frac{⋎+5}{2}},{\displaystyle \frac{⋎+9}{2}}\right\}$	$⋎-3$
0	$⋎-7$	$\left\{{\displaystyle \frac{⋎-9}{2}},{\displaystyle \frac{⋎-5}{2}},{\displaystyle \frac{⋎+1}{2}}\right\}$	$⋎-3$
0	$⋎-5$	$\left\{{\displaystyle \frac{⋎-5}{2}}\right\}$	$⋎-1$
2	$⋎-5$	$\left\{{\displaystyle \frac{⋎-5}{2}},{\displaystyle \frac{⋎-1}{2}},{\displaystyle \frac{⋎+5}{2}}\right\}$	$⋎-3$
0	$⋎-3$	$\left\{{\displaystyle \frac{⋎+5}{2}}\right\}$	$⋎-1$
2	$⋎-3$	$\left\{{\displaystyle \frac{⋎-1}{2}}\right\}$	$⋎-1$
4	$⋎-3$	$\left\{{\displaystyle \frac{⋎-1}{2}},{\displaystyle \frac{⋎+3}{2}},{\displaystyle \frac{⋎+9}{2}}\right\}$	$⋎-3$
0	$⋎-1$	$\left\{{\displaystyle \frac{⋎-1}{2}},{\displaystyle \frac{⋎+5}{2}},{\displaystyle \frac{⋎+9}{2}}\right\}$	$⋎-3$
2	$⋎-1$	$\left\{{\displaystyle \frac{⋎+9}{2}}\right\}$	$⋎-1$
4	$⋎-1$	$\left\{{\displaystyle \frac{⋎+3}{2}}\right\}$	$⋎-1$
6	$⋎-1$	$\left\{{\displaystyle \frac{⋎+3}{2}},{\displaystyle \frac{⋎+7}{2}},{\displaystyle \frac{⋎+13}{2}}\right\}$	$⋎-3$
Otherwise	Otherwise	∅	⋎

Case (b):

When $⋎\equiv 3\left(\mathrm{mod}4\right)$, then

Table 5. The LFRMs and their cardinalities when $⋎\equiv 3\left(\mathrm{mod}4\right)$.

${⋋}_1$	${⋋}_2$	${{\mathcal{R}}^{\prime }}_{\mathit{l}}^{\mathit{f}}\{{⋋}_1,{⋋}_2\}$	$|{\mathcal{R}}_{\mathit{l}}^{\mathit{f}}\{{⋋}_1,{⋋}_2\}|$
0	1	$\left\{{\displaystyle \frac{⋎-7}{2}},{\displaystyle \frac{⋎-1}{2}},{\displaystyle \frac{⋎+3}{2}}\right\}$	$⋎-3$
0	3	$\left\{{\displaystyle \frac{⋎+3}{2}}\right\}$	$⋎-1$
0	5	$\left\{{\displaystyle \frac{⋎-3}{2}}\right\}$	$⋎-1$
0	7	$\left\{{\displaystyle \frac{⋎-3}{2}},{\displaystyle \frac{⋎+1}{2}},{\displaystyle \frac{⋎+7}{2}}\right\}$	$⋎-3$
0	$⋎-7$	$\left\{{\displaystyle \frac{⋎-7}{2}},{\displaystyle \frac{⋎-1}{2}},{\displaystyle \frac{⋎+3}{2}}\right\}$	$⋎-3$
0	$⋎-5$	$\left\{{\displaystyle \frac{⋎+3}{2}}\right\}$	$⋎-1$
2	$⋎-5$	$\left\{{\displaystyle \frac{⋎-3}{2}},{\displaystyle \frac{⋎+3}{2}},{\displaystyle \frac{⋎+7}{2}}\right\}$	$⋎-3$
0	$⋎-3$	$\left\{{\displaystyle \frac{⋎-3}{2}}\right\}$	$⋎-1$
2	$⋎-3$	$\left\{{\displaystyle \frac{⋎+7}{2}}\right\}$	$⋎-1$
4	$⋎-3$	$\left\{{\displaystyle \frac{⋎+1}{2}},{\displaystyle \frac{⋎+7}{2}},{\displaystyle \frac{⋎+11}{2}}\right\}$	$⋎-3$
0	$⋎-1$	$\left\{{\displaystyle \frac{⋎-3}{2}},{\displaystyle \frac{⋎+1}{2}},{\displaystyle \frac{⋎+7}{2}}\right\}$	$⋎-3$
2	$⋎-1$	$\left\{{\displaystyle \frac{⋎+1}{2}}\right\}$	$⋎-1$
4	$⋎-1$	$\left\{{\displaystyle \frac{⋎+11}{2}}\right\}$	$⋎-1$
6	$⋎-1$	$\left\{{\displaystyle \frac{⋎+5}{2}},{\displaystyle \frac{⋎+11}{2}},{\displaystyle \frac{⋎+15}{2}}\right\}$	$⋎-3$
Otherwise	Otherwise	∅	⋎

Table 5. The LFRMs and their cardinalities when $⋎\equiv 3\left(\mathrm{mod}4\right)$.

${⋋}_1$	${⋋}_2$	${{\mathcal{R}}^{\prime }}_{\mathit{l}}^{\mathit{f}}\{{⋋}_1,{⋋}_2\}$	$|{\mathcal{R}}_{\mathit{l}}^{\mathit{f}}\{{⋋}_1,{⋋}_2\}|$
0	1	$\left\{{\displaystyle \frac{⋎-7}{2}},{\displaystyle \frac{⋎-1}{2}},{\displaystyle \frac{⋎+3}{2}}\right\}$	$⋎-3$
0	3	$\left\{{\displaystyle \frac{⋎+3}{2}}\right\}$	$⋎-1$
0	5	$\left\{{\displaystyle \frac{⋎-3}{2}}\right\}$	$⋎-1$
0	7	$\left\{{\displaystyle \frac{⋎-3}{2}},{\displaystyle \frac{⋎+1}{2}},{\displaystyle \frac{⋎+7}{2}}\right\}$	$⋎-3$
0	$⋎-7$	$\left\{{\displaystyle \frac{⋎-7}{2}},{\displaystyle \frac{⋎-1}{2}},{\displaystyle \frac{⋎+3}{2}}\right\}$	$⋎-3$
0	$⋎-5$	$\left\{{\displaystyle \frac{⋎+3}{2}}\right\}$	$⋎-1$
2	$⋎-5$	$\left\{{\displaystyle \frac{⋎-3}{2}},{\displaystyle \frac{⋎+3}{2}},{\displaystyle \frac{⋎+7}{2}}\right\}$	$⋎-3$
0	$⋎-3$	$\left\{{\displaystyle \frac{⋎-3}{2}}\right\}$	$⋎-1$
2	$⋎-3$	$\left\{{\displaystyle \frac{⋎+7}{2}}\right\}$	$⋎-1$
4	$⋎-3$	$\left\{{\displaystyle \frac{⋎+1}{2}},{\displaystyle \frac{⋎+7}{2}},{\displaystyle \frac{⋎+11}{2}}\right\}$	$⋎-3$
0	$⋎-1$	$\left\{{\displaystyle \frac{⋎-3}{2}},{\displaystyle \frac{⋎+1}{2}},{\displaystyle \frac{⋎+7}{2}}\right\}$	$⋎-3$
2	$⋎-1$	$\left\{{\displaystyle \frac{⋎+1}{2}}\right\}$	$⋎-1$
4	$⋎-1$	$\left\{{\displaystyle \frac{⋎+11}{2}}\right\}$	$⋎-1$
6	$⋎-1$	$\left\{{\displaystyle \frac{⋎+5}{2}},{\displaystyle \frac{⋎+11}{2}},{\displaystyle \frac{⋎+15}{2}}\right\}$	$⋎-3$
Otherwise	Otherwise	∅	⋎

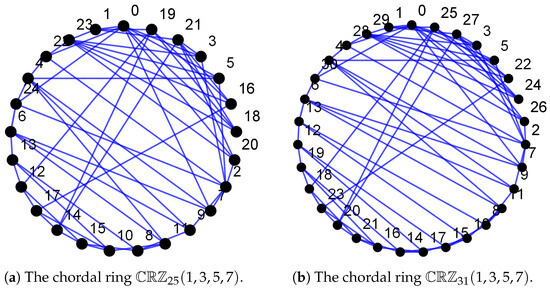
To better understand the proof of Theorem 3, the following networks and their LFRMs are given. Two hyper-chordal networks with parameters $(1,3,5,7)$ for $⋎=25,31$ are shown in Figure 3.

Figure 3. Two hyper-chordal networks with parameters $(1,3,5,7)$ for $⋎=25,31$.

For case (a), $⋎\equiv 0\left(\mathrm{mod}3\right)$, the chordal network ${\mathbb{CRZ}}_{25}(1,3,5,7)$ is shown in Figure 3a. The local fractional resolving sets for chordal ring ${\mathbb{CRZ}}_{25}(1,3,5,7)$ are calculated as follows:

$$\begin{array}{cccccc}\hfill & {{\mathcal{R}}^{\prime }}_l^f\{1,0\}=\{8,10,13\},\hfill & \hfill & {{\mathcal{R}}^{\prime }}_l^f\{3,0\}=\left\{10\right\},\hfill & \hfill & {{\mathcal{R}}^{\prime }}_l^f\{5,0\}=\left\{15\right\},\hfill \\ \hfill & {{\mathcal{R}}^{\prime }}_l^f\{7,0\}=\{12,15,17\},\hfill & \hfill & {{\mathcal{R}}^{\prime }}_l^f\{18,0\}=\{8,10,13\},\hfill & \hfill & {{\mathcal{R}}^{\prime }}_l^f\{20,0\}=\left\{10\right\},\hfill \\ \hfill & {{\mathcal{R}}^{\prime }}_l^f\{20,2\}=\{10,12,15\},\hfill & \hfill & {{\mathcal{R}}^{\prime }}_l^f\{22,0\}=\left\{15\right\},\hfill & \hfill & {{\mathcal{R}}^{\prime }}_l^f\{22,2\}=\left\{12\right\},\hfill \\ \hfill & {{\mathcal{R}}^{\prime }}_l^f\{22,4\}=\{12,14,17\},\hfill & \hfill & {{\mathcal{R}}^{\prime }}_l^f\{24,0\}=\{12,15,17\},\hfill & \hfill & {{\mathcal{R}}^{\prime }}_l^f\{24,2\}=\left\{17\right\},\hfill \\ \hfill & {{\mathcal{R}}^{\prime }}_l^f\{24,4\}=\left\{14\right\},\hfill & \hfill & {{\mathcal{R}}^{\prime }}_l^f\{24,6\}=\{14,16,19\}.\hfill \end{array}$$

${{\mathcal{R}}^{\prime }}_l^f=\varnothing$ for all other edges. Since $|{\mathcal{R}}_l^f\{{⋋}_1,{⋋}_2\}|=V\left({\mathbb{CRZ}}_{25}(1,3,5,7)\right)\setminus {{\mathcal{R}}^{\prime }}_l^f\{{⋋}_1,{⋋}_2\}$, the minimum and maximum cardinalities are 22 and 25, respectively. Thus, by using Lemma 1 and Theorem 1, we have

$$1\le {\mathcal{L}}_{fmd}\left({\mathbb{CRZ}}_{25}(1,3,5,7)\right)\le {\displaystyle \frac{25}{22}}.$$

For case (b), $⋎\equiv 3\left(\mathrm{mod}4\right)$, the chordal network ${\mathbb{CRZ}}_{31}(1,3,5,7)$ is shown in Figure 3b. The local fractional resolving sets for chordal ring ${\mathbb{CRZ}}_{31}(1,3,5,7)$ are calculated as follows:

$$\begin{array}{cccccc}\hfill & {{\mathcal{R}}^{\prime }}_l^f\{1,0\}=\{12,15,17\},\hfill & \hfill & {{\mathcal{R}}^{\prime }}_l^f\{3,0\}=\left\{17\right\},\hfill & \hfill & {{\mathcal{R}}^{\prime }}_l^f\{5,0\}=\left\{14\right\},\hfill \\ \hfill & {{\mathcal{R}}^{\prime }}_l^f\{7,0\}=\{14,16,19\},\hfill & \hfill & {{\mathcal{R}}^{\prime }}_l^f\{24,0\}=\{12,15,17\},\hfill & \hfill & {{\mathcal{R}}^{\prime }}_l^f\{26,0\}=\left\{17\right\},\hfill \\ \hfill & {{\mathcal{R}}^{\prime }}_l^f\{26,2\}=\{14,17,19\},\hfill & \hfill & {{\mathcal{R}}^{\prime }}_l^f\{28,0\}=\left\{14\right\},\hfill & \hfill & {{\mathcal{R}}^{\prime }}_l^f\{28,2\}=\left\{19\right\},\hfill \\ \hfill & {{\mathcal{R}}^{\prime }}_l^f\{28,4\}=\{16,19,21\},\hfill & \hfill & {{\mathcal{R}}^{\prime }}_l^f\{30,0\}=\{14,16,19\},\hfill & \hfill & {{\mathcal{R}}^{\prime }}_l^f\{30,2\}=\left\{16\right\},\hfill \\ \hfill & {{\mathcal{R}}^{\prime }}_l^f\{30,4\}=\left\{21\right\},\hfill & \hfill & {{\mathcal{R}}^{\prime }}_l^f\{30,6\}=\{18,21,23\}.\hfill \end{array}$$

${{\mathcal{R}}^{\prime }}_l^f=\varnothing$ for all other edges. Since $|{\mathcal{R}}_l^f\{{⋋}_1,{⋋}_2\}|=V\left({\mathbb{CRZ}}_{31}(1,3,5,7)\right)\setminus {{\mathcal{R}}^{\prime }}_l^f\{{⋋}_1,{⋋}_2\}$, the minimum and maximum cardinalities are 28, and 31, respectively. Thus, by using Lemma 1 and Theorem 1, we have

$$1\le {\mathcal{L}}_{fmd}\left({\mathbb{CRZ}}_{31}(1,3,5,7)\right)\le {\displaystyle \frac{28}{31}}.$$

□

Theorem 4.

Let ${\mathbb{CRZ}}_{⋎}(1,3,5,7)$ be a chordal ring network; the lower and upper bounds of local fractional metric dimension are

$$1\le {\mathcal{L}}_{fmd}\left({\mathbb{CRZ}}_{⋎}(1,3,5,7)\right)\le {\displaystyle \frac{⋎}{⋎-3}},$$

where ⋎ is an odd number and divisible by 3.

Proof. 

Let ${\mathbb{CRZ}}_{⋎}(1,3,5,7)$ be a chordal ring network; there are two cases of sequences for resolving sets for adjacent vertices. The numerical computing of these cases is given in Table 6 and Table 7 respectively.

Case (a):

When $⋎\equiv 3\left(\mathrm{mod}4\right)$:

Table 6. The LFRMs and their cardinalities when $⋎\equiv 1\left(\mathrm{mod}4\right)$.

${⋋}_1$	${⋋}_2$	${{\mathcal{R}}^{\prime }}_{\mathit{l}}^{\mathit{f}}\{{⋋}_1,{⋋}_2\}$	$|{\mathcal{R}}_{\mathit{l}}^{\mathit{f}}\{{⋋}_1,{⋋}_2\}|$
0	1	$\left\{{\displaystyle \frac{⋎-11}{2}},{\displaystyle \frac{⋎-7}{2}},{\displaystyle \frac{⋎-3}{2}}\right\}$	$⋎-3$
0	3	$\left\{{\displaystyle \frac{⋎-7}{2}},{\displaystyle \frac{⋎-3}{2}},{\displaystyle \frac{⋎+3}{2}}\right\}$	$⋎-3$
0	5	$\left\{{\displaystyle \frac{⋎-3}{2}},{\displaystyle \frac{⋎+3}{2}},{\displaystyle \frac{⋎+7}{2}}\right\}$	$⋎-3$
0	7	$\left\{{\displaystyle \frac{⋎+3}{2}},{\displaystyle \frac{⋎+7}{2}},{\displaystyle \frac{⋎+11}{2}}\right\}$	$⋎-3$
0	$⋎-7$	$\left\{{\displaystyle \frac{⋎-11}{2}},{\displaystyle \frac{⋎-7}{2}},{\displaystyle \frac{⋎-3}{2}}\right\}$	$⋎-3$
0	$⋎-5$	$\left\{{\displaystyle \frac{⋎-7}{2}},{\displaystyle \frac{⋎-3}{2}},{\displaystyle \frac{⋎+3}{2}}\right\}$	$⋎-3$
2	$⋎-5$	$\left\{{\displaystyle \frac{⋎-7}{2}},{\displaystyle \frac{⋎-3}{2}},{\displaystyle \frac{⋎+1}{2}}\right\}$	$⋎-3$
0	$⋎-3$	$\left\{{\displaystyle \frac{⋎-3}{2}},{\displaystyle \frac{⋎+3}{2}},{\displaystyle \frac{⋎+7}{2}}\right\}$	$⋎-3$
2	$⋎-3$	$\left\{{\displaystyle \frac{⋎-3}{2}},{\displaystyle \frac{⋎+1}{2}},{\displaystyle \frac{⋎+7}{2}}\right\}$	$⋎-3$
4	$⋎-3$	$\left\{{\displaystyle \frac{⋎-3}{2}},{\displaystyle \frac{⋎+1}{2}},{\displaystyle \frac{⋎+5}{2}}\right\}$	$⋎-3$
0	$⋎-1$	$\left\{{\displaystyle \frac{⋎+3}{2}},{\displaystyle \frac{⋎+7}{2}},{\displaystyle \frac{⋎+11}{2}}\right\}$	$⋎-3$
2	$⋎-1$	$\left\{{\displaystyle \frac{⋎+1}{2}},{\displaystyle \frac{⋎+7}{2}},{\displaystyle \frac{⋎+11}{2}}\right\}$	$⋎-3$
4	$⋎-1$	$\left\{{\displaystyle \frac{⋎+1}{2}},{\displaystyle \frac{⋎+5}{2}},{\displaystyle \frac{⋎+11}{2}}\right\}$	$⋎-3$
6	$⋎-1$	$\left\{{\displaystyle \frac{⋎+1}{2}},{\displaystyle \frac{⋎+5}{2}},{\displaystyle \frac{⋎+9}{2}}\right\}$	$⋎-3$
Otherwise	Otherwise	∅	⋎

Table 6. The LFRMs and their cardinalities when $⋎\equiv 1\left(\mathrm{mod}4\right)$.

${⋋}_1$	${⋋}_2$	${{\mathcal{R}}^{\prime }}_{\mathit{l}}^{\mathit{f}}\{{⋋}_1,{⋋}_2\}$	$|{\mathcal{R}}_{\mathit{l}}^{\mathit{f}}\{{⋋}_1,{⋋}_2\}|$
0	1	$\left\{{\displaystyle \frac{⋎-11}{2}},{\displaystyle \frac{⋎-7}{2}},{\displaystyle \frac{⋎-3}{2}}\right\}$	$⋎-3$
0	3	$\left\{{\displaystyle \frac{⋎-7}{2}},{\displaystyle \frac{⋎-3}{2}},{\displaystyle \frac{⋎+3}{2}}\right\}$	$⋎-3$
0	5	$\left\{{\displaystyle \frac{⋎-3}{2}},{\displaystyle \frac{⋎+3}{2}},{\displaystyle \frac{⋎+7}{2}}\right\}$	$⋎-3$
0	7	$\left\{{\displaystyle \frac{⋎+3}{2}},{\displaystyle \frac{⋎+7}{2}},{\displaystyle \frac{⋎+11}{2}}\right\}$	$⋎-3$
0	$⋎-7$	$\left\{{\displaystyle \frac{⋎-11}{2}},{\displaystyle \frac{⋎-7}{2}},{\displaystyle \frac{⋎-3}{2}}\right\}$	$⋎-3$
0	$⋎-5$	$\left\{{\displaystyle \frac{⋎-7}{2}},{\displaystyle \frac{⋎-3}{2}},{\displaystyle \frac{⋎+3}{2}}\right\}$	$⋎-3$
2	$⋎-5$	$\left\{{\displaystyle \frac{⋎-7}{2}},{\displaystyle \frac{⋎-3}{2}},{\displaystyle \frac{⋎+1}{2}}\right\}$	$⋎-3$
0	$⋎-3$	$\left\{{\displaystyle \frac{⋎-3}{2}},{\displaystyle \frac{⋎+3}{2}},{\displaystyle \frac{⋎+7}{2}}\right\}$	$⋎-3$
2	$⋎-3$	$\left\{{\displaystyle \frac{⋎-3}{2}},{\displaystyle \frac{⋎+1}{2}},{\displaystyle \frac{⋎+7}{2}}\right\}$	$⋎-3$
4	$⋎-3$	$\left\{{\displaystyle \frac{⋎-3}{2}},{\displaystyle \frac{⋎+1}{2}},{\displaystyle \frac{⋎+5}{2}}\right\}$	$⋎-3$
0	$⋎-1$	$\left\{{\displaystyle \frac{⋎+3}{2}},{\displaystyle \frac{⋎+7}{2}},{\displaystyle \frac{⋎+11}{2}}\right\}$	$⋎-3$
2	$⋎-1$	$\left\{{\displaystyle \frac{⋎+1}{2}},{\displaystyle \frac{⋎+7}{2}},{\displaystyle \frac{⋎+11}{2}}\right\}$	$⋎-3$
4	$⋎-1$	$\left\{{\displaystyle \frac{⋎+1}{2}},{\displaystyle \frac{⋎+5}{2}},{\displaystyle \frac{⋎+11}{2}}\right\}$	$⋎-3$
6	$⋎-1$	$\left\{{\displaystyle \frac{⋎+1}{2}},{\displaystyle \frac{⋎+5}{2}},{\displaystyle \frac{⋎+9}{2}}\right\}$	$⋎-3$
Otherwise	Otherwise	∅	⋎

Case (b):

When $⋎\equiv 1\left(\mathrm{mod}4\right)$:

Table 7. The LFRMs and their cardinalities when $⋎\equiv 1\left(\mathrm{mod}4\right)$.

${⋋}_1$	${⋋}_2$	${{\mathcal{R}}^{\prime }}_{\mathit{l}}^{\mathit{f}}\{{⋋}_1,{⋋}_2\}$	$|{\mathcal{R}}_{\mathit{l}}^{\mathit{f}}\{{⋋}_1,{⋋}_2\}|$
0	1	$\left\{{\displaystyle \frac{⋎-3}{2}},{\displaystyle \frac{⋎+1}{2}},{\displaystyle \frac{⋎+5}{2}}\right\}$	$⋎-3$
0	3	$\left\{{\displaystyle \frac{⋎-5}{2}},{\displaystyle \frac{⋎+1}{2}},{\displaystyle \frac{⋎+5}{2}}\right\}$	$⋎-3$
0	5	$\left\{{\displaystyle \frac{⋎-5}{2}},{\displaystyle \frac{⋎-1}{2}},{\displaystyle \frac{⋎+5}{2}}\right\}$	$⋎-3$
0	7	$\left\{{\displaystyle \frac{⋎-5}{2}},{\displaystyle \frac{⋎-1}{2}},{\displaystyle \frac{⋎+3}{2}}\right\}$	$⋎-3$
0	$⋎-7$	$\left\{{\displaystyle \frac{⋎-3}{2}},{\displaystyle \frac{⋎+1}{2}},{\displaystyle \frac{⋎-5}{2}}\right\}$	$⋎-3$
0	$⋎-5$	$\left\{{\displaystyle \frac{⋎-5}{2}},{\displaystyle \frac{⋎+1}{2}},{\displaystyle \frac{⋎+5}{2}}\right\}$	$⋎-3$
2	$⋎-5$	$\left\{{\displaystyle \frac{⋎+1}{2}},{\displaystyle \frac{⋎+5}{2}},{\displaystyle \frac{⋎+9}{2}}\right\}$	$⋎-3$
0	$⋎-3$	$\left\{{\displaystyle \frac{⋎-5}{2}},{\displaystyle \frac{⋎-1}{2}},{\displaystyle \frac{⋎+5}{2}}\right\}$	$⋎-3$
2	$⋎-3$	$\left\{{\displaystyle \frac{⋎-1}{2}},{\displaystyle \frac{⋎+5}{2}},{\displaystyle \frac{⋎+9}{2}}\right\}$	$⋎-3$
4	$⋎-3$	$\left\{{\displaystyle \frac{⋎+5}{2}},{\displaystyle \frac{⋎+9}{2}},{\displaystyle \frac{⋎+13}{2}}\right\}$	$⋎-3$
0	$⋎-1$	$\left\{{\displaystyle \frac{⋎-5}{2}},{\displaystyle \frac{⋎-1}{2}},{\displaystyle \frac{⋎+3}{2}}\right\}$	$⋎-3$
2	$⋎-1$	$\left\{{\displaystyle \frac{⋎-1}{2}},{\displaystyle \frac{⋎+3}{2}},{\displaystyle \frac{⋎+9}{2}}\right\}$	$⋎-3$
4	$⋎-1$	$\left\{{\displaystyle \frac{⋎+3}{2}},{\displaystyle \frac{⋎+9}{2}},{\displaystyle \frac{⋎+13}{2}}\right\}$	$⋎-3$
6	$⋎-1$	$\left\{{\displaystyle \frac{⋎+9}{2}},{\displaystyle \frac{⋎+13}{2}},{\displaystyle \frac{⋎+17}{2}}\right\}$	$⋎-3$
Otherwise	Otherwise	∅	⋎

Table 7. The LFRMs and their cardinalities when $⋎\equiv 1\left(\mathrm{mod}4\right)$.

${⋋}_1$	${⋋}_2$	${{\mathcal{R}}^{\prime }}_{\mathit{l}}^{\mathit{f}}\{{⋋}_1,{⋋}_2\}$	$|{\mathcal{R}}_{\mathit{l}}^{\mathit{f}}\{{⋋}_1,{⋋}_2\}|$
0	1	$\left\{{\displaystyle \frac{⋎-3}{2}},{\displaystyle \frac{⋎+1}{2}},{\displaystyle \frac{⋎+5}{2}}\right\}$	$⋎-3$
0	3	$\left\{{\displaystyle \frac{⋎-5}{2}},{\displaystyle \frac{⋎+1}{2}},{\displaystyle \frac{⋎+5}{2}}\right\}$	$⋎-3$
0	5	$\left\{{\displaystyle \frac{⋎-5}{2}},{\displaystyle \frac{⋎-1}{2}},{\displaystyle \frac{⋎+5}{2}}\right\}$	$⋎-3$
0	7	$\left\{{\displaystyle \frac{⋎-5}{2}},{\displaystyle \frac{⋎-1}{2}},{\displaystyle \frac{⋎+3}{2}}\right\}$	$⋎-3$
0	$⋎-7$	$\left\{{\displaystyle \frac{⋎-3}{2}},{\displaystyle \frac{⋎+1}{2}},{\displaystyle \frac{⋎-5}{2}}\right\}$	$⋎-3$
0	$⋎-5$	$\left\{{\displaystyle \frac{⋎-5}{2}},{\displaystyle \frac{⋎+1}{2}},{\displaystyle \frac{⋎+5}{2}}\right\}$	$⋎-3$
2	$⋎-5$	$\left\{{\displaystyle \frac{⋎+1}{2}},{\displaystyle \frac{⋎+5}{2}},{\displaystyle \frac{⋎+9}{2}}\right\}$	$⋎-3$
0	$⋎-3$	$\left\{{\displaystyle \frac{⋎-5}{2}},{\displaystyle \frac{⋎-1}{2}},{\displaystyle \frac{⋎+5}{2}}\right\}$	$⋎-3$
2	$⋎-3$	$\left\{{\displaystyle \frac{⋎-1}{2}},{\displaystyle \frac{⋎+5}{2}},{\displaystyle \frac{⋎+9}{2}}\right\}$	$⋎-3$
4	$⋎-3$	$\left\{{\displaystyle \frac{⋎+5}{2}},{\displaystyle \frac{⋎+9}{2}},{\displaystyle \frac{⋎+13}{2}}\right\}$	$⋎-3$
0	$⋎-1$	$\left\{{\displaystyle \frac{⋎-5}{2}},{\displaystyle \frac{⋎-1}{2}},{\displaystyle \frac{⋎+3}{2}}\right\}$	$⋎-3$
2	$⋎-1$	$\left\{{\displaystyle \frac{⋎-1}{2}},{\displaystyle \frac{⋎+3}{2}},{\displaystyle \frac{⋎+9}{2}}\right\}$	$⋎-3$
4	$⋎-1$	$\left\{{\displaystyle \frac{⋎+3}{2}},{\displaystyle \frac{⋎+9}{2}},{\displaystyle \frac{⋎+13}{2}}\right\}$	$⋎-3$
6	$⋎-1$	$\left\{{\displaystyle \frac{⋎+9}{2}},{\displaystyle \frac{⋎+13}{2}},{\displaystyle \frac{⋎+17}{2}}\right\}$	$⋎-3$
Otherwise	Otherwise	∅	⋎

To better understand the proof of Theorem 4, the following networks and their LFRMs are given. Two hyper-chordal networks with parameters $(1,3,5,7)$ for $⋎=27,21$ are shown in Figure 4.

Figure 4. Two hyper-chordal networks with parameters $(1,3,5,7)$ for $⋎=27,21$.

For case (a), $⋎\equiv 3\left(\mathrm{mod}4\right)$, the chordal network ${\mathbb{CRZ}}_{27}(1,3,5,7)$ is shown in Figure 4a. The local fractional resolving sets for chordal ring ${\mathbb{CRZ}}_{27}(1,3,5,7)$ are calculated as follows:

$$\begin{array}{cccccc}\hfill & {{\mathcal{R}}^{\prime }}_l^f\{1,0\}=\{8,10,12\},\hfill & \hfill & {{\mathcal{R}}^{\prime }}_l^{f}f\{3,0\}=\{10,12,15\},\hfill & \hfill & {{\mathcal{R}}^{\prime }}_l^{f}f\{5,0\}=\{12,15,17\},\hfill \\ \hfill & {{\mathcal{R}}^{\prime }}_l^f\{7,0\}=\{15,17,19\},\hfill & \hfill & {{\mathcal{R}}^{\prime }}_l^f\{20,0\}=\{8,10,12\},\hfill & \hfill & {{\mathcal{R}}^{\prime }}_l^f\{22,0\}=\{10,12,15\},\hfill \\ \hfill & {{\mathcal{R}}^{\prime }}_l^f\{22,2\}=\{10,12,14\},\hfill & \hfill & {{\mathcal{R}}^{\prime }}_l^f\{24,0\}=\{12,15,17\},\hfill & \hfill & {{\mathcal{R}}^{\prime }}_l^f\{24,2\}=\{12,14,17\},\hfill \\ \hfill & {{\mathcal{R}}^{\prime }}_l^f\{24,4\}=\{12,14,16\},\hfill & \hfill & {{\mathcal{R}}^{\prime }}_l^f\{26,0\}=\{15,17,19\},\hfill & \hfill & {{\mathcal{R}}^{\prime }}_l^f\{26,2\}=\{14,17,19\},\hfill \\ \hfill & {{\mathcal{R}}^{\prime }}_l^f\{26,4\}=\{14,16,19\},\hfill & \hfill & {{\mathcal{R}}^{\prime }}_l^f\{26,6\}=\{14,16,18\}.\hfill \end{array}$$

${{\mathcal{R}}^{\prime }}_l^f=\varnothing$ for all other edges. Since $|{\mathcal{R}}_l^f\{{⋋}_1,{⋋}_2\}|=V\left({\mathbb{CRZ}}_{27}(1,3,5,7)\right)\setminus {{\mathcal{R}}^{\prime }}_l^f\{{⋋}_1,{⋋}_2\}$, the minimum and maximum cardinalities are 24 and 27, respectively. Thus, by using Lemma 1 and Theorem 1, we have

$$1\le {\mathcal{L}}_{fmd}\left({\mathbb{CRZ}}_{27}(1,3,5,7)\right)\le {\displaystyle \frac{27}{24}}.$$

For case (b), $⋎\equiv 1\left(\mathrm{mod}4\right)$, the chordal network ${\mathbb{CRZ}}_{21}(1,3,5,7)$ is shown in Figure 4b. The local fractional resolving sets for chordal ring ${\mathbb{CRZ}}_{21}(1,3,5,7)$ are calculated as follows:

$$\begin{array}{cccccc}\hfill & {{\mathcal{R}}^{\prime }}_l^f\{1,0\}=\{9,11,13\},\hfill & \hfill & {{\mathcal{R}}^{\prime }}_l^f\{3,0\}=\{8,11,13\},\hfill & \hfill & {{\mathcal{R}}^{\prime }}_l^f\{5,0\}=\{8,10,13\},\hfill \\ \hfill & {{\mathcal{R}}^{\prime }}_l^f\{7,0\}=\{8,10,12\},\hfill & \hfill & {{\mathcal{R}}^{\prime }}_l^f\{14,0\}=\{9,11,13\},\hfill & \hfill & {{\mathcal{R}}^{\prime }}_l^f\{16,0\}=\{8,11,13\},\hfill \\ \hfill & {{\mathcal{R}}^{\prime }}_l^f\{16,2\}=\{11,13,15\},\hfill & \hfill & {{\mathcal{R}}^{\prime }}_l^f\{18,0\}=\{8,10,13\},\hfill & \hfill & {{\mathcal{R}}^{\prime }}_l^f\{18,2\}=\{10,13,15\},\hfill \\ \hfill & {{\mathcal{R}}^{\prime }}_l^f\{18,4\}=\{13,15,17\},\hfill & \hfill & {{\mathcal{R}}^{\prime }}_l^f\{20,0\}=\{8,10,12\},\hfill & \hfill & {{\mathcal{R}}^{\prime }}_l^f\{20,2\}=\{10,12,15\},\hfill \\ \hfill & {{\mathcal{R}}^{\prime }}_l^f\{20,4\}=\{12,15,17\},\hfill & \hfill & {{\mathcal{R}}^{\prime }}_l^f\{20,6\}=\{15,17,19\}.\hfill \end{array}$$

${{\mathcal{R}}^{\prime }}_l^f=\varnothing$ for all other edges. Since $|{\mathcal{R}}_l^f\{{⋋}_1,{⋋}_2\}|=V\left({\mathbb{CRZ}}_{21}(1,3,5,7)\right)\setminus {{\mathcal{R}}^{\prime }}_l^f\{{⋋}_1,{⋋}_2\}$, the minimum and maximum cardinalities are 19 and 21, respectively. Thus, by using Lemma 1 and Theorem 1, we have

$$1\le {\mathcal{L}}_{fmd}\left({\mathbb{CRZ}}_{21}(1,3,5,7)\right)\le {\displaystyle \frac{21}{19}}.$$

□

3. Local Fractional Resolving M-Polynomials and Topological Indices

In this section, we define new local fractional resolving M-polynomials and then some new topological indices that are based on local fractional resolving set cardinalities. These M-polynomials are defined as follows:

$${\mathcal{M}}_l^{fr}(\mathcal{G},u,v)=\sum _{i\in \left|\mathcal{R}\right(E\left(\mathcal{G}\right)\left)\right|}{\alpha }_i{u}^i{v}^i,$$

where ${\alpha }_i$ is the cardinality mapping on $\left|\mathcal{R}\right(E\left(\mathcal{G}\right)\left)\right|$. The relationship between the LFR-M polynomial and certain topological indices is given by

$$\begin{array}{ccc}\hfill {\mathcal{M}}_1^{LFR}\left(\mathcal{G}\right)& =& ({\mathcal{D}}_u+{\mathcal{D}}_v){|}_{u=v=1}\hfill \\ \hfill {\mathcal{M}}_2^{LFR}\left(\mathcal{G}\right)& =& \left({\mathcal{D}}_u{\mathcal{D}}_v\right){|}_{u=v=1}\hfill \\ \hfill {}^m\mathcal{M}_2^{\mathit{LFR}}\left(\mathcal{G}\right)& =& \left({\delta }_u{\delta }_v\right){|}_{u=v=1}\hfill \\ \hfill SS{D}_3^{LFR}\left(\mathcal{G}\right)& =& {\mathcal{D}}_u{\mathcal{D}}_v\left({\mathcal{D}}_u+{\mathcal{D}}_v\right){|}_{u=v=1}\hfill \\ \hfill SS{D}_5^{LFR}\left(\mathcal{G}\right)& =& {\mathcal{D}}_u{\delta }_v+{\delta }_u{\mathcal{D}}_v{|}_{u=v=1}\hfill \\ \hfill F^{LFR}\left(\mathcal{G}\right)& =& \left({\mathcal{D}}_u^2+{\mathcal{D}}_v^2\right){|}_{u=v=1}\hfill \end{array}$$

where ${\mathcal{D}}_u={\displaystyle \frac{\partial f(u,v)}{\partial u}}u,{\mathcal{D}}_v={\displaystyle \frac{\partial f(u,v)}{\partial v}}v,{\delta }_v={\int }_0^v{\displaystyle \frac{f(u,t)}{t}}\mathrm{d}t,{\delta }_u={\int }_0^u{\displaystyle \frac{f(t,v)}{t}}\mathrm{d}t$.

Lemma 2.

Let ${\mathbb{CRZ}}_{⋎}(1,3,5,7)$ be a chordal ring network; the local fractional resolving M-polynomial is

$${\mathcal{M}}_l^{fr}({\mathbb{CRZ}}_{⋎}(1,3,5,7);u,v)=u^{⋎-3}{v}^{⋎-3}\left(2(⋎-3)u^3{v}^3+7u^2{v}^2+7\right).$$

where ⋎ is an odd number but $3\nmid ⋎$.

Proof. 

Let ${\mathbb{CRZ}}_{⋎}(1,3,5,7)$ be a chordal ring network; the edge partition mapping concerning the cardinalities of local resolving sets are computed in Table 4 and Table 5.

$$\begin{array}{c}\hfill r_i=\left\{\begin{array}{c}\begin{array}{cc}7,\hfill & \mathrm{if}i=⋎-3,\hfill \\ 7,\hfill & \mathrm{if}i=⋎-1,\hfill \\ 2⋎-6,\hfill & \mathrm{if}i=⋎.\hfill \end{array}\hfill \end{array}\right.\end{array}$$

(2)

By using relation (2), we have

$$\begin{array}{ccc}\hfill {\mathcal{M}}_l^{fr}({\mathbb{CRZ}}_{⋎}(1,3,5,7);u,v)& =& \sum _{i\in \left|\mathcal{R}\right(E\left({\mathbb{CRZ}}_{⋎}(1,3,5,7)\right)\left)\right|}{r}_i{u}^i{v}^i\hfill \\ & =& 7u^{⋎-3}{v}^{⋎-3}+7u^{⋎-3}{v}^{⋎-3}+(2⋎-6)u^{⋎}{v}^{⋎}\hfill \\ & =& u^{⋎-3}{v}^{⋎-3}\left(2(⋎-3)u^3{v}^3+7u^2{v}^2+7\right).\hfill \end{array}$$

□

Theorem 5.

Let ${\mathbb{CRZ}}_{⋎}(1,3,5,7)$ be a chordal ring network; the topological indices are

$$\begin{array}{ccc}\hfill {\mathcal{M}}_1^{LFR}\left({\mathbb{CRZ}}_{⋎}(1,3,5,7)\right)& =& 4{⋎}^2+16⋎-56\hfill \\ \hfill {\mathcal{M}}_2^{LFR}\left({\mathbb{CRZ}}_{⋎}(1,3,5,7)\right)& =& 2{⋎}^3+8{⋎}^2-56⋎+70\hfill \\ \hfill {}^m\mathcal{M}_2^{\mathit{LFR}}\left({\mathbb{CRZ}}_{⋎}(1,3,5,7)\right)& =& -{\displaystyle \frac{6}{{⋎}^2}}+{\displaystyle \frac{7}{{(⋎-1)}^2}}+{\displaystyle \frac{2}{⋎}}+{\displaystyle \frac{7}{{(⋎-3)}^2}}\hfill \end{array}$$

$$\begin{array}{ccc}\hfill SS{D}_3^{LFR}\left({\mathbb{CRZ}}_{⋎}(1,3,5,7)\right)& =& 4{⋎}^4+16{⋎}^3-168{⋎}^2+420⋎-392\hfill \\ \hfill SS{D}_5^{LFR}\left({\mathbb{CRZ}}_{⋎}(1,3,5,7)\right)& =& -{\displaystyle \frac{7⋎}{1-⋎}}-{\displaystyle \frac{7⋎}{{(1-⋎)}^2}}+{\displaystyle \frac{7⋎}{⋎-3}}+4⋎+{\displaystyle \frac{7}{{(1-⋎)}^2}}-{\displaystyle \frac{21}{⋎-3}}+2\hfill \\ \hfill F^{LFR}\left({\mathbb{CRZ}}_{⋎}(1,3,5,7)\right)& =& 4{⋎}^3+16{⋎}^2-112⋎+140\hfill \end{array}$$

Proof. 

Let ${\mathbb{CRZ}}_{⋎}(1,3,5,7)$ be a chordal ring network, the local fractional resolving M-polynomial is

$$\begin{array}{ccc}\hfill f(u,v)& =& {\mathcal{M}}_l^{fr}({\mathbb{CRZ}}_{⋎}(1,3,5,7);u,v)=u^{⋎-3}{v}^{⋎-3}\left(2(⋎-3)u^3{v}^3+7u^2{v}^2+7\right).\hfill \end{array}$$

(3)

where ⋎ is an odd number but $3\nmid ⋎$. Taking the partial derivative concerning u and v of Equation (3), we have

$$\begin{array}{ccc}& & {\mathcal{D}}_u={\displaystyle \frac{\partial f(u,v)}{\partial u}}u,{\mathcal{D}}_v={\displaystyle \frac{\partial f(u,v)}{\partial v}}v\hfill \\ & & {\mathcal{D}}_u={\mathcal{D}}_v=2{⋎}^2{u}^{⋎}{v}^{⋎}+7⋎u^{⋎-3}{v}^{⋎-3}-21u^{⋎-3}{v}^{⋎-3}+7⋎u^{⋎-1}{v}^{⋎-1}\hfill \\ & -& 7u^{⋎-1}{v}^{⋎-1}-6⋎u^{⋎}{v}^{⋎}\hfill \end{array}$$

$$\begin{array}{ccc}\hfill {\mathcal{M}}_1^{LFR}\left({\mathbb{CRZ}}_{⋎}(1,3,5,7)\right)& =& ({\mathcal{D}}_u+{\mathcal{D}}_v){|}_{u=v=1}\hfill \\ & =& 4{⋎}^2{u}^{⋎}{v}^{⋎}+14⋎u^{⋎-3}{v}^{⋎-3}-42u^{⋎-3}{v}^{⋎-3}+14⋎u^{⋎-1}{v}^{⋎-1}\hfill \\ & -& 14u^{⋎-1}{v}^{⋎-1}-12⋎u^{⋎}{v}^{⋎}{|}_{u=v=1}\hfill \\ & =& 4{⋎}^2+16⋎-56.\hfill \end{array}$$

$$\begin{array}{ccc}\hfill {\mathcal{D}}_u{\mathcal{D}}_v& =& u{\displaystyle \frac{\partial f(u,v)}{\partial u}}\left({\mathcal{D}}_v\right)\hfill \\ & =& 2{⋎}^3{u}^{⋎}{v}^{⋎}+7{⋎}^2{u}^{⋎-3}{v}^{⋎-3}+7{⋎}^2{u}^{⋎-1}{v}^{⋎-1}-6{⋎}^2{u}^{⋎}{v}^{⋎}-42⋎u^{⋎-3}{v}^{⋎-3}\hfill \\ & +& 63u^{⋎-3}{v}^{⋎-3}-14⋎u^{⋎-1}{v}^{⋎-1}+7u^{⋎-1}{v}^{⋎-1}\hfill \end{array}$$

$$\begin{array}{ccc}\hfill {\mathcal{M}}_2^{LFR}\left({\mathbb{CRZ}}_{⋎}(1,3,5,7)\right)& =& \left({\mathcal{D}}_u{\mathcal{D}}_v\right){|}_{u=v=1}\hfill \\ & =& 2{⋎}^3{u}^{⋎}{v}^{⋎}+7{⋎}^2{u}^{⋎-3}{v}^{⋎-3}+7{⋎}^2{u}^{⋎-1}{v}^{⋎-1}-6{⋎}^2{u}^{⋎}{v}^{⋎}\hfill \\ & +& 63u^{⋎-3}{v}^{⋎-3}-14⋎u^{⋎-1}{v}^{⋎-1}+7u^{⋎-1}{v}^{⋎-1}\hfill \\ & -& 42⋎u^{⋎-3}{v}^{⋎-3}{|}_{u=v=1}\hfill \\ & =& 2{⋎}^3+8{⋎}^2-56⋎+70.\hfill \end{array}$$

$$\begin{array}{ccc}\hfill {\delta }_v& =& {\int }_0^v{\displaystyle \frac{f(u,t)}{t}}\mathrm{d}t=u^{⋎}{v}^{⋎}\left({\displaystyle \frac{7}{(⋎-3)u^3{v}^3}}-{\displaystyle \frac{7}{uv-⋎uv}}-{\displaystyle \frac{6}{⋎}}+2\right)\hfill \\ \hfill {\delta }_u{\delta }_v& =& {\int }_0^u{\displaystyle \frac{{\delta }_v}{t}}\mathrm{d}t=v^{⋎}\left(u^{⋎}\left(-{\displaystyle \frac{6}{{⋎}^2}}+{\displaystyle \frac{7}{{(⋎-3)}^2{u}^3{v}^3}}+{\displaystyle \frac{2}{⋎}}\right)+{\displaystyle \frac{7u^{⋎-1}}{{(⋎-1)}^{2}v}}\right)\hfill \end{array}$$

$$\begin{array}{ccc}\hfill {}^m\mathcal{M}_2^{\mathit{LFR}}\left({\mathbb{CRZ}}_{⋎}(1,3,5,7)\right)& =& {\delta }_u{\delta }_v{\left)\right|}_{u=v=1}\hfill \\ & =& v^{⋎}\left(u^{⋎}\left(-{\displaystyle \frac{6}{{⋎}^2}}+{\displaystyle \frac{7}{{(⋎-3)}^2{u}^3{v}^3}}+{\displaystyle \frac{2}{⋎}}\right)+{\displaystyle \frac{7u^{⋎-1}}{{(⋎-1)}^{2}v}}\right){|}_{u=v=1}\hfill \\ & =& -{\displaystyle \frac{6}{{⋎}^2}}+{\displaystyle \frac{7}{{(⋎-1)}^2}}+{\displaystyle \frac{2}{⋎}}+{\displaystyle \frac{7}{{(⋎-3)}^2}}.\hfill \end{array}$$

$$\begin{array}{ccc}\hfill {\mathcal{D}}_v\left({\mathcal{D}}_u+{\mathcal{D}}_v\right)& =& 4{⋎}^3{u}^{⋎}{v}^{⋎}+14{⋎}^2{u}^{⋎-3}{v}^{⋎-3}+14{⋎}^2{u}^{⋎-1}{v}^{⋎-1}-12{⋎}^2{u}^{⋎}{v}^{⋎}\hfill \\ & -& 84⋎u^{⋎-3}{v}^{⋎-3}+126u^{⋎-3}{v}^{⋎-3}-28⋎u^{⋎-1}{v}^{⋎-1}+14u^{⋎-1}{v}^{⋎-1}\hfill \\ \hfill {\mathcal{D}}_u{\mathcal{D}}_v\left({\mathcal{D}}_u+{\mathcal{D}}_v\right)& =& 4{⋎}^4{u}^{⋎}{v}^{⋎}+14{⋎}^3{u}^{⋎-3}{v}^{⋎-3}+14{⋎}^3{u}^{⋎-1}{v}^{⋎-1}-12{⋎}^3{u}^{⋎}{v}^{⋎}\hfill \\ & -& 126{⋎}^2{u}^{⋎-3}{v}^{⋎-3}-42{⋎}^2{u}^{⋎-1}{v}^{⋎-1}+378⋎u^{⋎-3}{v}^{⋎-3}-378u^{⋎-3}{v}^{⋎-3}\hfill \\ & +& 42⋎u^{⋎-1}{v}^{⋎-1}-14u^{⋎-1}{v}^{⋎-1}.\hfill \end{array}$$

$$\begin{array}{lll}\hfill SS{D}_3^{LFR}\left({\mathbb{CRZ}}_{⋎}(1,3,5,7)\right)& =& {\mathcal{D}}_u{\mathcal{D}}_v\left({\mathcal{D}}_u+{\mathcal{D}}_v\right){|}_{u=v=1}\hfill \\ & =& 4{⋎}^4{u}^{⋎}{v}^{⋎}+14{⋎}^3{u}^{⋎-3}{v}^{⋎-3}+14{⋎}^3{u}^{⋎-1}{v}^{⋎-1}-12{⋎}^3{u}^{⋎}{v}^{⋎}\hfill \\ & -& 126{⋎}^2{u}^{⋎-3}{v}^{⋎-3}-42{⋎}^2{u}^{⋎-1}{v}^{⋎-1}+378⋎u^{⋎-3}{v}^{⋎-3}\hfill \\ & -& 378u^{⋎-3}{v}^{⋎-3}\hfill \\ & +& 42⋎u^{⋎-1}{v}^{⋎-1}-14u^{⋎-1}{v}^{⋎-1}{|}_{u=v=1}\hfill \\ & =& 4{⋎}^4+16{⋎}^3-168{⋎}^2+420⋎-392\hfill \\ \hfill {\mathcal{D}}_u{\delta }_v& =& u{\displaystyle \frac{\partial }{\partial u}}\left({\delta }_v\right)\hfill \\ & =& {\displaystyle \frac{7⋎u^{⋎-3}{v}^{⋎-3}}{⋎-3}}-{\displaystyle \frac{21u^{⋎-3}{v}^{⋎-3}}{⋎-3}}-{\displaystyle \frac{7⋎u^{⋎+1}{v}^{⋎+1}}{{(uv-⋎uv)}^2}}\hfill \\ & & \begin{array}{lll}& +& {\displaystyle \frac{7u^{⋎+1}{v}^{⋎+1}}{{(uv-⋎uv)}^2}}+2⋎u^{⋎}{v}^{⋎}\hfill \\ & -& 6u^{⋎}{v}^{⋎}-{\displaystyle \frac{7⋎u^{⋎}{v}^{⋎}}{uv-⋎uv}}\hfill \\ \hfill {\delta }_u{\mathcal{D}}_v& =& 7u^{⋎-3}{v}^{⋎-3}+7u^{⋎-1}{v}^{⋎-1}+2⋎u^{⋎}{v}^{⋎}-6u^{⋎}{v}^{⋎}\hfill \end{array}\end{array}$$

By adding ${\mathcal{D}}_u{\delta }_v$ and ${\delta }_u{\mathcal{D}}_v$, we have

$$\begin{array}{ccc}\hfill {\mathcal{D}}_u{\delta }_v+{\delta }_u{\mathcal{D}}_v& =& {\displaystyle \frac{7⋎u^{⋎-3}{v}^{⋎-3}}{⋎-3}}+7u^{⋎-3}{v}^{⋎-3}-{\displaystyle \frac{21u^{⋎-3}{v}^{⋎-3}}{⋎-3}}+7u^{⋎-1}{v}^{⋎-1}\hfill \\ & -& {\displaystyle \frac{7⋎u^{⋎+1}{v}^{⋎+1}}{{(uv-⋎uv)}^2}}+{\displaystyle \frac{7u^{⋎+1}{v}^{⋎+1}}{{(uv-⋎uv)}^2}}+4⋎u^{⋎}{v}^{⋎}-12u^{⋎}{v}^{⋎}-{\displaystyle \frac{7⋎u^{⋎}{v}^{⋎}}{uv-⋎uv}}\hfill \end{array}$$

$$\begin{array}{ccc}\hfill SS{D}_5^{LFR}\left({\mathbb{CRZ}}_{⋎}(1,3,5,7)\right)& =& {\mathcal{D}}_u{\delta }_v+{\delta }_u{\mathcal{D}}_v{|}_{u=v=1}\hfill \\ & =& {\displaystyle \frac{7⋎u^{⋎-3}{v}^{⋎-3}}{⋎-3}}+7u^{⋎-3}{v}^{⋎-3}-{\displaystyle \frac{21u^{⋎-3}{v}^{⋎-3}}{⋎-3}}+7u^{⋎-1}{v}^{⋎-1}\hfill \\ & -& {\displaystyle \frac{7⋎u^{⋎+1}{v}^{⋎+1}}{{(uv-⋎uv)}^2}}+{\displaystyle \frac{7u^{⋎+1}{v}^{⋎+1}}{{(uv-⋎uv)}^2}}+4⋎u^{⋎}{v}^{⋎}-12u^{⋎}{v}^{⋎}\hfill \\ & -& {\displaystyle \frac{7⋎u^{⋎}{v}^{⋎}}{uv-⋎uv}}{|}_{u=v=1}\hfill \\ & =& -{\displaystyle \frac{7⋎}{1-⋎}}-{\displaystyle \frac{7⋎}{{(1-⋎)}^2}}+{\displaystyle \frac{7⋎}{⋎-3}}+4⋎+{\displaystyle \frac{7}{{(1-⋎)}^2}}-{\displaystyle \frac{21}{⋎-3}}+2.\hfill \end{array}$$

$$\begin{array}{lll}{F}^{LFR}\left({\mathbb{CRZ}}_{⋎}(1,3,5,7)\right)\hfill & =& \left({\mathcal{D}}_u^2+{\mathcal{D}}_v^2\right){|}_{u=v=1}\hfill \\ & =& 4{⋎}^3{u}^{⋎}{v}^{⋎}+14{⋎}^2{u}^{⋎-3}{v}^{⋎-3}+14{⋎}^2{u}^{⋎-1}{v}^{⋎-1}-12{⋎}^2{u}^{⋎}{v}^{⋎}\hfill \\ & -& 84⋎u^{⋎-3}{v}^{⋎-3}+126u^{⋎-3}{v}^{⋎-3}-28⋎u^{⋎-1}{v}^{⋎-1}\hfill \\ & & \begin{array}{ccc}& +& 14u^{⋎-1}{v}^{⋎-1}{|}_{u=v=1}\hfill \\ & =& 4{⋎}^3+16{⋎}^2-112⋎+140.\hfill \end{array}\end{array}$$

□

The graphical comparison of Table 8 in Figure 5.

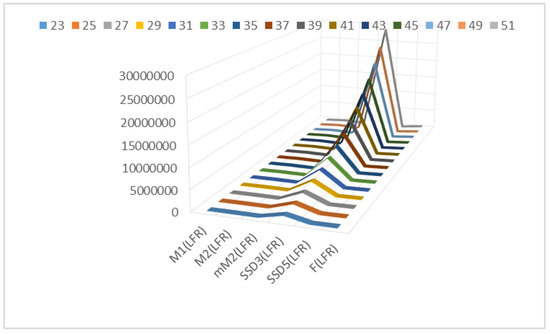
Figure 5. The graphical comparison of Table 8.

Table 8. Numerical comparison between topological indices.

⋎	${\mathcal{M}}_1^{\mathit{LFR}}$	${\mathcal{M}}_2^{\mathit{LFR}}$	${}^{\mathit{m}}\mathcal{M}_2^{\mathit{LFR}}$	${\mathit{SSD}}_3^{\mathit{LFR}}$	${\mathit{SSD}}_5^{\mathit{LFR}}$	${\mathit{F}}^{\mathit{LFR}}$
23	2428	27,348	0.107577	1,234,432	108	54,696
25	2844	34,920	0.0970156	1,717,608	116	69,840
27	3292	43,756	0.0883514	2,329,168	124	87,512
29	3772	53,952	0.0811148	3,089,848	132	107,904
31	4284	65,604	0.074979	4,021,920	140	131,208
33	4828	78,808	0.0697101	5,149,192	148	157,616
35	5404	93,660	0.0651362	6,497,008	156	187,320
37	6012	110,256	0.0611279	8,092,248	164	220,512
39	6652	128,692	0.0575862	9,963,328	172	257,384
41	7324	149,064	0.0544338	12,140,200	180	298,128
43	8028	171,468	0.0516099	14,654,352	188	342,936
45	8764	196,000	0.0490654	17,538,808	196	392,000
47	9532	222,756	0.0467609	20,828,128	204	445,512
49	10,332	251,832	0.0446637	24,558,408	212	503,664
51	11,164	283,324	0.0427471	28,767,280	220	566,648

Table 8. Numerical comparison between topological indices.

⋎	${\mathcal{M}}_1^{\mathit{LFR}}$	${\mathcal{M}}_2^{\mathit{LFR}}$	${}^{\mathit{m}}\mathcal{M}_2^{\mathit{LFR}}$	${\mathit{SSD}}_3^{\mathit{LFR}}$	${\mathit{SSD}}_5^{\mathit{LFR}}$	${\mathit{F}}^{\mathit{LFR}}$
23	2428	27,348	0.107577	1,234,432	108	54,696
25	2844	34,920	0.0970156	1,717,608	116	69,840
27	3292	43,756	0.0883514	2,329,168	124	87,512
29	3772	53,952	0.0811148	3,089,848	132	107,904
31	4284	65,604	0.074979	4,021,920	140	131,208
33	4828	78,808	0.0697101	5,149,192	148	157,616
35	5404	93,660	0.0651362	6,497,008	156	187,320
37	6012	110,256	0.0611279	8,092,248	164	220,512
39	6652	128,692	0.0575862	9,963,328	172	257,384
41	7324	149,064	0.0544338	12,140,200	180	298,128
43	8028	171,468	0.0516099	14,654,352	188	342,936
45	8764	196,000	0.0490654	17,538,808	196	392,000
47	9532	222,756	0.0467609	20,828,128	204	445,512
49	10,332	251,832	0.0446637	24,558,408	212	503,664
51	11,164	283,324	0.0427471	28,767,280	220	566,648

Lemma 3.

Let ${\mathbb{CRZ}}_{2⋎+1}(1,3,5)$ be a chordal ring network; the local fractional resolving M-polynomial is

$${\mathcal{M}}_l^{fr}({\mathbb{CRZ}}_{2⋎+1}(1,3,5);u,v)=u^{2⋎-1}{v}^{2⋎-1}\left(3(⋎-1)u^2{v}^2+9\right).$$

Theorem 6.

Let ${\mathbb{CRZ}}_{2⋎+1}(1,3,5)$ be a chordal ring network; the topological indices are

$$\begin{array}{ccc}\hfill {\mathcal{M}}_1^{LFR}\left({\mathbb{CRZ}}_{2⋎+1}(1,3,5)\right)& =& 12{⋎}^2+30⋎-24\hfill \\ \hfill {\mathcal{M}}_2^{LFR}\left({\mathbb{CRZ}}_{2⋎+1}(1,3,5)\right)& =& 12{⋎}^3+36{⋎}^2-45⋎+6\hfill \\ \hfill {}^m\mathcal{M}_2^{\mathit{LFR}}\left({\mathbb{CRZ}}_{2⋎+1}(1,3,5)\right)& =& 3\left({\displaystyle \frac{⋎-1}{{(2⋎+1)}^2}}+{\displaystyle \frac{3}{{(1-2⋎)}^2}}\right)\hfill \\ \hfill SS{D}_3^{LFR}\left({\mathbb{CRZ}}_{2⋎+1}(1,3,5)\right)& =& 48{⋎}^4+168{⋎}^3-252{⋎}^2+78⋎+12\hfill \\ \hfill SS{D}_5^{LFR}\left({\mathbb{CRZ}}_{2⋎+1}(1,3,5)\right)& =& {\displaystyle \frac{24{⋎}^2}{4{⋎}^2-1}}-{\displaystyle \frac{3⋎}{4{⋎}^2-1}}-{\displaystyle \frac{6}{4{⋎}^2-1}}+{\displaystyle \frac{12{⋎}^3}{4{⋎}^2-1}}+3⋎+6\hfill \\ \hfill F^{LFR}\left({\mathbb{CRZ}}_{2⋎+1}(1,3,5)\right)& =& 24{⋎}^3+72{⋎}^2-90⋎+12\hfill \end{array}$$

The graphical comparison of Table 9 in Figure 6.

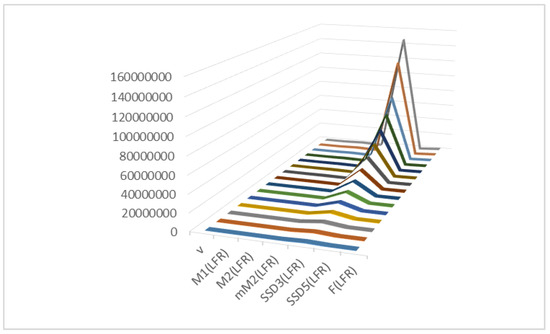
Figure 6. The graphical comparison of Table 9.

Table 9. Numerical comparison between topological indices.

⋎	${\mathcal{M}}_1^{\mathit{LFR}}$	${\mathcal{M}}_2^{\mathit{LFR}}$	${}^{\mathit{m}}\mathcal{M}_2^{\mathit{LFR}}$	${\mathit{SSD}}_3^{\mathit{LFR}}$	${\mathit{SSD}}_5^{\mathit{LFR}}$	${\mathit{F}}^{\mathit{LFR}}$
11	1758	19,839	0.0771189	896,754	78	39,678
13	2394	31,869	0.0637827	1,698,462	90	63,738
15	3126	47,931	0.054406	2,941,482	102	95,862
17	3954	68,601	0.0474481	4,762,902	114	137,202
19	4878	94,455	0.0420771	7,318,242	126	188,910
21	5898	126,069	0.0378039	10,781,454	138	252,138
23	7014	164,019	0.0343222	15,344,922	150	328,038
25	8226	208,881	0.0314301	21,219,462	162	417,762
27	9534	261,231	0.0289891	28,634,322	174	522,462
29	10,938	321,645	0.0269011	37,837,182	186	643,290
31	12,438	390,699	0.0250944	49,094,154	198	781,398
33	14,034	468,969	0.0235158	62,689,782	210	937,938
35	15,726	557,031	0.0221244	78,927,042	222	1,114,062
39	19,398	764,835	0.0197843	120,630,522	246	1,529,670
41	21,378	885,729	0.0187908	146,794,854	258	1,771,458

Table 9. Numerical comparison between topological indices.

⋎	${\mathcal{M}}_1^{\mathit{LFR}}$	${\mathcal{M}}_2^{\mathit{LFR}}$	${}^{\mathit{m}}\mathcal{M}_2^{\mathit{LFR}}$	${\mathit{SSD}}_3^{\mathit{LFR}}$	${\mathit{SSD}}_5^{\mathit{LFR}}$	${\mathit{F}}^{\mathit{LFR}}$
11	1758	19,839	0.0771189	896,754	78	39,678
13	2394	31,869	0.0637827	1,698,462	90	63,738
15	3126	47,931	0.054406	2,941,482	102	95,862
17	3954	68,601	0.0474481	4,762,902	114	137,202
19	4878	94,455	0.0420771	7,318,242	126	188,910
21	5898	126,069	0.0378039	10,781,454	138	252,138
23	7014	164,019	0.0343222	15,344,922	150	328,038
25	8226	208,881	0.0314301	21,219,462	162	417,762
27	9534	261,231	0.0289891	28,634,322	174	522,462
29	10,938	321,645	0.0269011	37,837,182	186	643,290
31	12,438	390,699	0.0250944	49,094,154	198	781,398
33	14,034	468,969	0.0235158	62,689,782	210	937,938
35	15,726	557,031	0.0221244	78,927,042	222	1,114,062
39	19,398	764,835	0.0197843	120,630,522	246	1,529,670
41	21,378	885,729	0.0187908	146,794,854	258	1,771,458

Lemma 4.

Let ${\mathbb{CRZ}}_{⋎}(1,3,5,7)$ be a chordal ring network; the local fractional resolving M-polynomial is

$${\mathcal{M}}_l^{fr}({\mathbb{CRZ}}_{⋎}(1,3,5,7);u,v)=2u^{⋎-3}{v}^{⋎-3}\left((⋎-3)u^3{v}^3+7\right),$$

where ⋎ is a multiple of 3.

Theorem 7.

Let ${\mathbb{CRZ}}_{⋎}(1,3,5,7)$ be a chordal ring network; the topological indices are

$$\begin{array}{ccc}\hfill {\mathcal{M}}_1^{LFR}\left({\mathbb{CRZ}}_{⋎}(1,3,5,7)\right)& =& 4{⋎}^2+16⋎-84\hfill \\ \hfill {\mathcal{M}}_2^{LFR}\left({\mathbb{CRZ}}_{⋎}(1,3,5,7)\right)& =& 2{⋎}^3+8{⋎}^2-84⋎+126\hfill \\ \hfill {}^m\mathcal{M}_2^{\mathit{LFR}}\left({\mathbb{CRZ}}_{⋎}(1,3,5,7)\right)& =& 2\left(-{\displaystyle \frac{3}{{⋎}^2}}+{\displaystyle \frac{1}{⋎}}+{\displaystyle \frac{7}{{(⋎-3)}^2}}\right)\hfill \\ \hfill SS{D}_3^{LFR}\left({\mathbb{CRZ}}_{⋎}(1,3,5,7)\right)& =& 4{⋎}^4+16{⋎}^3-252{⋎}^2+756⋎-756\hfill \\ \hfill SS{D}_5^{LFR}\left({\mathbb{CRZ}}_{⋎}(1,3,5,7)\right)& =& {\displaystyle \frac{14⋎}{⋎-3}}+4⋎-{\displaystyle \frac{42}{⋎-3}}+2\hfill \\ \hfill F^{LFR}\left({\mathbb{CRZ}}_{⋎}(1,3,5,7)\right)& =& 4{⋎}^3+16{⋎}^2-168⋎+252\hfill \end{array}$$

The graphical comparison of Table 10 in Figure 7.

Figure 7. The graphical comparison of Table 10.

Table 10. Numerical comparison between topological indices.

⋎	${\mathcal{M}}_1^{\mathit{LFR}}$	${\mathcal{M}}_2^{\mathit{LFR}}$	${}^{\mathit{m}}\mathcal{M}_2^{\mathit{LFR}}$	${\mathit{SSD}}_3^{\mathit{LFR}}$	${\mathit{SSD}}_5^{\mathit{LFR}}$	${\mathit{F}}^{\mathit{LFR}}$
23	2400	26,760	0.110614	1,197,360	108	53,520
25	2816	34,276	0.0993256	1,673,144	116	68,552
27	3264	43,056	0.0901492	2,276,640	124	86,112
29	3744	53,196	0.0825412	3,028,584	132	106,392
31	4256	64,792	0.0761298	3,951,248	140	129,584
33	4800	77,940	0.070652	5,068,440	148	155,880
35	5376	92,736	0.0659168	6,405,504	156	185,472
37	5984	109,276	0.061782	7,989,320	164	218,552
39	6624	127,656	0.0581397	9,848,304	172	255,312
41	7296	147,972	0.0549065	12,012,408	180	295,944
43	8000	170,320	0.0520166	14,513,120	188	340,640
45	8736	194,796	0.049418	17,383,464	196	389,592
47	9504	221,496	0.0470684	20,658,000	204	442,992
49	10,304	250,516	0.0449336	24,372,824	212	501,032
51	11,136	281,952	0.0429853	28,565,568	220	563,904

Table 10. Numerical comparison between topological indices.

⋎	${\mathcal{M}}_1^{\mathit{LFR}}$	${\mathcal{M}}_2^{\mathit{LFR}}$	${}^{\mathit{m}}\mathcal{M}_2^{\mathit{LFR}}$	${\mathit{SSD}}_3^{\mathit{LFR}}$	${\mathit{SSD}}_5^{\mathit{LFR}}$	${\mathit{F}}^{\mathit{LFR}}$
23	2400	26,760	0.110614	1,197,360	108	53,520
25	2816	34,276	0.0993256	1,673,144	116	68,552
27	3264	43,056	0.0901492	2,276,640	124	86,112
29	3744	53,196	0.0825412	3,028,584	132	106,392
31	4256	64,792	0.0761298	3,951,248	140	129,584
33	4800	77,940	0.070652	5,068,440	148	155,880
35	5376	92,736	0.0659168	6,405,504	156	185,472
37	5984	109,276	0.061782	7,989,320	164	218,552
39	6624	127,656	0.0581397	9,848,304	172	255,312
41	7296	147,972	0.0549065	12,012,408	180	295,944
43	8000	170,320	0.0520166	14,513,120	188	340,640
45	8736	194,796	0.049418	17,383,464	196	389,592
47	9504	221,496	0.0470684	20,658,000	204	442,992
49	10,304	250,516	0.0449336	24,372,824	212	501,032
51	11,136	281,952	0.0429853	28,565,568	220	563,904

4. Local Fractional Entropies for Hyper-Chordal Networks

The historical background of entropies was first introduced by a German physicist named Rudolf Clausius in the mid-19th century within the branch of thermodynamics, delivered as a measuring instrument of disorder or randomness within a system. Entropies show what quantity of energy is not accessible to producing work. The more disorganized a structure is and the higher the entropies, the less is the amount of energy of a structure accessible for work. In the branch of chemistry, entropy is connected to the distribution of matter and energy in a system. Entropy is used in biological systems, statistical interpretation, information theory, and thermodynamic perspective. Some newly defined local fractional entropies are

$$\begin{array}{ccc}\hfill LFRZ{G}_1\left(\mathcal{G}\right)& =& \sum _{e_i\in E}{\displaystyle \frac{2r_{e_i}}{r_{e_i}^2}}\hfill \end{array}$$

(4)

$$\begin{array}{ccc}\hfill LFRZ{G}_2\left(\mathcal{G}\right)& =& \sum _{e_i\in E}{\displaystyle \frac{r_{e_i}^2}{2r_{e_i}}}\hfill \end{array}$$

(5)

$$\begin{array}{ccc}\hfill LFRZ{G}_3\left(\mathcal{G}\right)& =& \sum _{e_i\in E}\left(r_{e_i}^2\right)\left(2r_{e_i}\right)\hfill \end{array}$$

(6)

$$\begin{array}{ccc}\hfill EN{T}_{LFRZ{G}_1}\left(\mathcal{G}\right)& =& log\left(LFRZ{G}_1\left(\mathcal{G}\right)\right)-{\displaystyle \frac{1}{LFRZ{G}_1\left(\mathcal{G}\right)}}log\{\prod _{x_i{y}_j\epsilon E\left(G\right)}{\left[{\displaystyle \frac{2r_{e_i}}{r_{e_i}^2}}\right]}^{{\displaystyle \frac{2r_{e_i}}{r_{e_i}^2}}}\}\hfill \end{array}$$

(7)

$$\begin{array}{ccc}\hfill EN{T}_{LFRZ{G}_2}\left(\mathcal{G}\right)& =& log\left(LFRZ{G}_2\left(\mathcal{G}\right)\right)-{\displaystyle \frac{1}{LFRZ{G}_2\left(\mathcal{G}\right)}}log\{\prod _{x_i{y}_j\in E\left(G\right)}{\left[{\displaystyle \frac{r_{e_i}^2}{2r_{e_i}}}\right]}^{{\displaystyle \frac{r_{e_i}^2}{2r_{e_i}}}}\}\hfill \\ \hfill EN{T}_{LFRZ{G}_3}\left(\mathcal{G}\right)& =& log\left(LFRZ{G}_3\left(\mathcal{G}\right)\right)\hfill \end{array}$$

(8)

$$\begin{array}{ccc}& -& {\displaystyle \frac{1}{LFRZ{G}_3\left(\mathcal{G}\right)}}log\{\prod _{x_i{y}_j\in E\left(G\right)}{\left[\left(r_{e_i}^2\right)\left(2r_{e_i}\right)\right]}^{\left(r_{e_i}^2\right)\left(2r_{e_i}\right)}\}\hfill \end{array}$$

(9)

For more detail, see the Appendix A.

Lemma 5.

Let ${\mathbb{CRZ}}_{⋎}(1,3,5,7)$ be a chordal ring network; then,

$$\begin{array}{ccc}\hfill LFRZ{G}_1\left({\mathbb{CRZ}}_{⋎}(1,3,5,7)\right)& =& {\displaystyle \frac{14⋎}{{(⋎-3)}^2}}+{\displaystyle \frac{14⋎}{{(⋎-1)}^2}}-{\displaystyle \frac{42}{{(⋎-3)}^2}}-{\displaystyle \frac{14}{{(⋎-1)}^2}}-{\displaystyle \frac{12}{⋎}}+4\hfill \end{array}$$

$$\begin{array}{ccc}\hfill LFRZ{G}_2\left({\mathbb{CRZ}}_{⋎}(1,3,5,7)\right)& =& {\displaystyle \frac{7{⋎}^2}{2⋎-6}}+{\displaystyle \frac{7{⋎}^2}{2⋎-2}}+{⋎}^2-{\displaystyle \frac{42⋎}{2⋎-6}}-{\displaystyle \frac{14⋎}{2⋎-2}}-3⋎\hfill \\ & +& {\displaystyle \frac{63}{2⋎-6}}+{\displaystyle \frac{7}{2⋎-2}}\hfill \\ \hfill LFRZ{G}_3\left({\mathbb{CRZ}}_{⋎}(1,3,5,7)\right)& =& 4{⋎}^4+16{⋎}^3-168{⋎}^2+420⋎-392\hfill \end{array}$$

Proof. 

Let ${\mathbb{CRZ}}_{⋎}(1,3,5,7)$ be a chordal ring network; the edge partition mapping concerning the cardinalities of local resolving sets computed in Table 4 and Table 5 is given in relation (2). By using relation (2), we have

$$\begin{array}{ccc}\hfill LFRZ{G}_1\left({\mathbb{CRZ}}_{⋎}(1,3,5,7)\right)& =& \sum _{e_i\in E}{\displaystyle \frac{2r_{e_i}}{r_{e_i}^2}}\hfill \end{array}$$

$$\begin{array}{ccc}& =& {\displaystyle \frac{7(2⋎-6)}{{(⋎-3)}^2}}+{\displaystyle \frac{2(2⋎-6)}{⋎}}+{\displaystyle \frac{7(2⋎-2)}{{(⋎-1)}^2}}\hfill \\ & =& {\displaystyle \frac{14⋎}{{(⋎-3)}^2}}+{\displaystyle \frac{14⋎}{{(⋎-1)}^2}}-{\displaystyle \frac{42}{{(⋎-3)}^2}}-{\displaystyle \frac{14}{{(⋎-1)}^2}}-{\displaystyle \frac{12}{⋎}}+4.\hfill \end{array}$$

$$\begin{array}{ccc}\hfill LFRZ{G}_2\left({\mathbb{CRZ}}_{⋎}(1,3,5,7)\right)& =& \sum _{e_i\in E}{\displaystyle \frac{r_{e_i}^2}{2r_{e_i}}}\hfill \\ & =& {\displaystyle \frac{7{(⋎-3)}^2}{2⋎-6}}+{\displaystyle \frac{1}{2}}⋎(2⋎-6)+{\displaystyle \frac{7{(⋎-1)}^2}{2⋎-2}}\hfill \\ & =& {\displaystyle \frac{7{⋎}^2}{2⋎-6}}+{\displaystyle \frac{7{⋎}^2}{2⋎-2}}+{⋎}^2-{\displaystyle \frac{42⋎}{2⋎-6}}-{\displaystyle \frac{14⋎}{2⋎-2}}-3⋎+{\displaystyle \frac{63}{2⋎-6}}\hfill \\ & +& {\displaystyle \frac{7}{2⋎-2}}.\hfill \end{array}$$

$$\begin{array}{ccc}\hfill LFRZ{G}_3\left({\mathbb{CRZ}}_{⋎}(1,3,5,7)\right)& =& \sum _{e_i\in E}\left(r_{e_i}^2\right)\left(2r_{e_i}\right)\hfill \\ & =& 2(2⋎-6){⋎}^3+7{(⋎-3)}^2(2⋎-6)+7{(⋎-1)}^2(2⋎-2)\hfill \\ & =& 4{⋎}^4+16{⋎}^3-168{⋎}^2+420⋎-392.\hfill \end{array}$$

□

Theorem 8.

Let ${\mathbb{CRZ}}_{⋎}(1,3,5,7)$ be a chordal ring network; then,

$$\begin{array}{ccc}\hfill EN{T}_{LFRZ{G}_1}\left({\mathbb{CRZ}}_{⋎}(1,3,5,7)\right)& =& log\left({\displaystyle \frac{{⋎}^3+⋎-9}{⋎\left({⋎}^2-4⋎+3\right)}}\right)-{\displaystyle \frac{1}{4\left({⋎}^3+⋎-9\right)}}(⋎-3)(⋎-1)\hfill \\ & & \times ⋎log\left({\displaystyle \frac{2^{\frac{28(⋎-2)}{{⋎}^2-4⋎+3}-\frac{12}{⋎}+8}{7}^{\frac{28(⋎-2)}{{⋎}^2-4⋎+3}}{\left(2-\frac{6}{⋎}\right)}^{-12/⋎}{\left(\frac{1}{⋎-3}\right)}^{\frac{14}{⋎-3}-4}{\left(\frac{1}{⋎-1}\right)}^{\frac{14}{⋎-1}}}{{⋎}^4}}\right)+log\left(4\right)\hfill \end{array}$$

$$\begin{array}{ccc}\hfill EN{T}_{LFRZ{G}_2}\left({\mathbb{CRZ}}_{⋎}(1,3,5,7)\right)& =& log\left({⋎}^2+4⋎-14\right)\hfill \\ & -& {\displaystyle \frac{log\left({\left(\frac{7}{2}\right)}^{7(⋎-2)}{(⋎-3)}^{\frac{7(⋎-3)}{2}}{(⋎-1)}^{\frac{7(⋎-1)}{2}}{((⋎-3)⋎)}^{(⋎-3)⋎}\right)}{{⋎}^2+4⋎-14}}\hfill \end{array}$$

$$\begin{array}{ccc}\hfill EN{T}_{LFRZ{G}_3}\left({\mathbb{CRZ}}_{⋎}(1,3,5,7)\right)& =& log\left(4{⋎}^4+16{⋎}^3-168{⋎}^2+420⋎-392\right)\hfill \\ & -& {\displaystyle \frac{1}{4{⋎}^4+16{⋎}^3-168{⋎}^2+420⋎-392}}\hfill \\ & & \times log\left(2^{2{⋎}^3(2⋎-6)}{7}^{7(2⋎-6){(⋎-3)}^2+7{(⋎-1)}^2(2⋎-2)}\right.\hfill \\ & & \times {\left({(⋎-3)}^2(2⋎-6)\right)}^{7{(⋎-3)}^2(2⋎-6)}\hfill \\ & & \left.\times {\left({⋎}^3(2⋎-6)\right)}^{2{⋎}^3(2⋎-6)}{\left({(⋎-1)}^2(2⋎-2)\right)}^{7{(⋎-1)}^2(2⋎-2)}\right)\hfill \end{array}$$

5. Conclusions

It is difficult to determine the local fractional metric dimension of a graph, particularly one with an algebraic structure. The local fractional metric dimension’s upper bound is crucial because in several situations when we are unable to determine the precise values of the local fractional metric dimension, upper bounds indicate that we are not permitted to employ objects larger than the upper bounds. It is challenging to employ the smallest number of objects to cover the whole network uniquely if we are unable to establish an upper bound for a certain structure. In this work, the hyper-chordal network was studied, and then the lower and upper bounds of the local fractional metric dimension were computed. These bounds were

•

$$1\le {\mathcal{L}}_{fmd}\left({\mathbb{CRZ}}_{2⋎+1}(1,3,5)\right)\le {\displaystyle \frac{2⋎+1}{2⋎-1}}$$

•

$$1\le {\mathcal{L}}_{fmd}\left({\mathbb{CRZ}}_{⋎}(1,3,5,7)\right)\le {\displaystyle \frac{⋎}{⋎-3}}.$$

Further, we defined a new LFR-M-polynomial based on the cardinalities of LFR sets. Using LFR-M-polynomial, various new topological indices were computed. The local fraction entropies were developed by modifying the first three kinds of Zagreb entropies; then, those were calculated for chosen hyper-chordal ring networks. Furthermore, numerical and graphical comparisons were given to observe the order between newly computed topological indices. The order between computed topological indices were

$${}^m\mathcal{M}_2^{\mathit{LFR}}<SS{D}_5^{LFR}{\mathcal{M}}_1^{LFR}<{\mathcal{M}}_2^{LFR}<F^{LFR}<SS{D}_3^{LFR}.$$

For future work, the lower and upper bound for the general hyper-chordal ring ${\mathbb{CRZ}}_{⋎}(r_1,r_2,\cdots ,r_k))$ is still an open problem.