Some Identities on (p,q)-Analog of the Generalized Hyperharmonic Polynomials of Order ν

Abstract

In this paper, $\left(p,q\right)$-analogues of the generalized harmonic polynomials and the generalized hyperharmonic polynomials of order $\nu$ are defined. We found new sums of these numbers by using combinatorial operations. We also obtained the generating function and used it to reproduce new equations. The applications of matrices are made in the end.

1. Introduction

Recently, many researchers have studied the applications of q-numbers and ($p,q$)-numbers. q-calculus has an important place in mathematics, and it is inclusive of many different study areas. First discovered by Euler [1], the q-calculus is exceedingly substantial in number theory, combinatorics and other branches of mathematics [2,3]. There has been considerable additions and improvements in q-calculus, which provide an insight to its complexity and usage in the past years. Mathematicians continue to study this topic, discover new methods and try to find relations with other branches of mathematics. So, the research of q-calculus is still an operative study that has many contributers who explores its mysteries and connections in modern mathematical study. The researchers from quantum mechanics, physics and mathematics have investigated the applying theory extensively. In particular, mathematicians from combinatorics, number theory and special functions have recently studied this topic [4,5,6]. There are also various studies in the literature on matrix analysis [7,8,9].

The ($p,q$)-analogue is a powerful generalization tool in mathematics that arises by extending classical structures with two parameters (p and q). This generalization makes structures such as q-series, special functions and differential equations more flexible, making important contributions to both theoretical and applied mathematics. Since 1991, a large number of mathematicians and physicists have extensively researched and developed the theory of ($p,q$) calculus as well as the introduction of ($p,q$) numbers. In particular, in quantum mechanics and quantum algebra, ($p,q$)-analogs generalize quantum groups and oscillators, allowing the symmetry and behavior of quantum systems to be studied in a broader framework. It also opens up new relations and generalized counting functions in combinatorics and number theory, which can be used in areas such as coding theory and cryptography. In coding theory, generalized counting functions play a critical role in structuring codes and developing efficient algorithms. In cryptography, these functions are an important tool for determining the size of key spaces used in encryption algorithms and for designing complex cryptographic structures. There are specific functions that are important for solving the different kinds of problems in physics and engineering. The (p, q)-analog enables us to generalize these functions that lead to more sophisticated tools to form physical facts. These tools are mathematical methods such as generalized special functions, orthogonal polynomials and differential equations developed with ($p,q$)-analogs. These tools enable the more precise modeling of complex dynamics, such as signal processing and control systems in engineering and physics. In short, ($p,q$)-analogs extend the limits of classical mathematical tools, enabling more in-depth analysis and solutions in many fields. ($p,q$)-analogs enable us to obtain generalized forms in modeling dynamic systems in engineering and physics that have special tools as differential and difference equations. By combining two parameters, these analogs can be used to model more complicated systems compared to their classical matches.

Let $p,q$ be real numbers with $0<q<p\le 1.$ The $\left(p,q\right)$ -analog of a non-negative integer ℓ is defined by

$${\left[\ell \right]}_{p,q}:={\displaystyle \frac{p^{\ell }-q^{\ell }}{p-q}}.$$

The definition of symmetry property allows us to write

$${\left[\ell \right]}_{p,q}={\left[\ell \right]}_{q,p}.$$

For $p=1,$ ${\left[\ell \right]}_{1,q}={\left[\ell \right]}_q$ and ${lim}_{q\to 1}{\left[\ell \right]}_q=\ell .$

The well-known binomial identities, which are widely used and widely applied in mathematics, also have ($p,q$)-analogues, which under certain conditions appear as a generalized form of the classical binomial identities.

Let $\ell ,\mathbb{k}$ be integers. The $\left(p,q\right)$-Gaussian binomial coefficient is defined by

$${\left[{\displaystyle \genfrac{}{}{0pt}{}{\ell }{\mathbb{k}}}\right]}_{p,q}=\left\{\begin{array}{cc}{\displaystyle \frac{{\left[\ell \right]}_{p,q}!}{{\left[\mathbb{k}\right]}_{p,q}!{\left[\ell -\mathbb{k}\right]}_{p,q}!}}& \mathrm{if}0\le \mathbb{k}\le \ell ,\\ 0& \mathrm{otherwise},\end{array}\right.$$

where ${\left[\ell \right]}_{p,q}!={\left[1\right]}_{p,q}{\left[2\right]}_{p,q}\dots {\left[\ell \right]}_{p,q}$ [5]. If we take $p=1,$ it is clear that the first equation simplifies to the triangular recurrence relation of the q-binomial coefficient, as previously shown.

The $\left(p,q\right)$-analogues of the binomial identities are expressed as follows:

$${\left[{\displaystyle \genfrac{}{}{0pt}{}{\ell +1}{\mathbb{k}}}\right]}_{p,q}=q^{\mathbb{k}}{\left[{\displaystyle \genfrac{}{}{0pt}{}{\ell }{\mathbb{k}}}\right]}_{p,q}+p^{\ell -\mathbb{k}+1}{\left[{\displaystyle \genfrac{}{}{0pt}{}{\ell }{\mathbb{k}-1}}\right]}_{p,q},$$

$${\left[{\displaystyle \genfrac{}{}{0pt}{}{\ell +1}{\mathbb{k}}}\right]}_{p,q}=p^{\mathbb{k}}{\left[{\displaystyle \genfrac{}{}{0pt}{}{\ell }{\mathbb{k}}}\right]}_{p,q}+q^{\ell -\mathbb{k}+1}{\left[{\displaystyle \genfrac{}{}{0pt}{}{\ell }{\mathbb{k}-1}}\right]}_{p,q},$$

$$\sum _{\mathbb{k}}{p}^{\left(\mathbb{k}-\ell \right)\left(\mathbb{k}-\nu \right)}{q}^{\mathbb{k}\left(\mathbb{k}-\nu +w\right)}{\left[{\displaystyle \genfrac{}{}{0pt}{}{w}{\nu -\mathbb{k}}}\right]}_{p,q}{\left[{\displaystyle \genfrac{}{}{0pt}{}{\ell }{\mathbb{k}}}\right]}_{p,q}={\left[{\displaystyle \genfrac{}{}{0pt}{}{\ell +w}{\nu }}\right]}_{p,q},$$

(1)

$$\sum _{\mathbb{k}=0}^{\nu -1}{p}^{\mathbb{k}}{q}^{\mathbb{k}\left(w-\ell \right)}{\left[{\displaystyle \genfrac{}{}{0pt}{}{\ell +\mathbb{k}-w-1}{\mathbb{k}}}\right]}_{p,q}=q^{\left(\nu -1\right)\left(w-\ell \right)}{\left[{\displaystyle \genfrac{}{}{0pt}{}{\ell +\nu -w-1}{\nu -1}}\right]}_{p,q},$$

(2)

and

$$\sum _{\mathbb{k}=a}^{\ell -b}{p}^{\left(\ell -b-\mathbb{k}\right)\left(a+1\right)}{q}^{\left(\mathbb{k}-a\right)\left(b+1\right)}{\left[{\displaystyle \genfrac{}{}{0pt}{}{\mathbb{k}}{a}}\right]}_{p,q}{\left[{\displaystyle \genfrac{}{}{0pt}{}{\ell -\mathbb{k}}{b}}\right]}_{p,q}={\left[{\displaystyle \genfrac{}{}{0pt}{}{\ell +1}{a+b+1}}\right]}_{p,q}.$$

(3)

In [10,11], two types of the $\left(p,q\right)$-exponential functions are presented as below

$$\sum _{\ell =0}^{\infty }{p}^{\left({\displaystyle \genfrac{}{}{0pt}{}{\ell }{2}}\right)}{\displaystyle \frac{t^{\ell }}{{\left[\ell \right]}_{p,q}!}}=e_{p,q}\left(t\right),$$

and

$$\sum _{\ell =0}^{\infty }{q}^{\left({\displaystyle \genfrac{}{}{0pt}{}{\ell }{2}}\right)}{\displaystyle \frac{t^{\ell }}{{\left[\ell \right]}_{p,q}!}}=E_{p,q}\left(t\right).$$

The $\left(p,q\right)$-version of the polylogarithm function, denoted as $L{i}_{\mu ,p,q}$, is recognized as

$$L{i}_{\mu ,p,q}\left(t\right)=\sum _{\ell =0}^{\infty }{\displaystyle \frac{t^{\ell }}{{\left[\ell \right]}_{p,q}^{\mu }}}\left(\mu \in \mathbb{Z}\right).$$

(4)

The $\left(p,q\right)$-Pochhammer symbol is given by

$${\left(t;p,q\right)}_0=1\mathrm{and}{\left(t;p,q\right)}_{\ell }=\prod _{\widehat{\mathsf{ı}}=0}^{\ell -1}\left(1-t{p}^{\widehat{\mathsf{ı}}}{q}^{-\widehat{\mathsf{ı}}}\right).$$

It is clear that

$${\left(t;p,q\right)}_{\ell }=\sum _{\widehat{\mathsf{ı}}=0}^{\ell }{\left(-1\right)}^{\widehat{\mathsf{ı}}}{q}^{\left({\displaystyle \genfrac{}{}{0pt}{}{\widehat{\mathsf{ı}}+1}{2}}\right)-\ell \widehat{\mathsf{ı}}}{p}^{\left({\displaystyle \genfrac{}{}{0pt}{}{\widehat{\mathsf{ı}}}{2}}\right)}{\left[{\displaystyle \genfrac{}{}{0pt}{}{\ell }{\widehat{\mathsf{ı}}}}\right]}_{p,q}{t}^{\widehat{\mathsf{ı}}},$$

(5)

and

$${\displaystyle \frac{1}{{\left(t;p,q\right)}_{\ell }}}=\sum _{\widehat{\mathsf{ı}}=0}^{\ell }{q}^{-\widehat{\mathsf{ı}}\left(\ell -1\right)}{\left[{\displaystyle \genfrac{}{}{0pt}{}{\ell +\widehat{\mathsf{ı}}-1}{\widehat{\mathsf{ı}}}}\right]}_{p,q}{t}^{\widehat{\mathsf{ı}}}.$$

(6)

In [6], the authors described $\left(q,\upsilon ,w\right)-$ Stirling numbers. Naturally, the generalized series of $\left(p,q\right)$-Stirling numbers of the second kind can be defined as follows

$$\sum _{\ell =\widehat{\mathsf{ı}}}^{\infty }{S}_{p,q,\upsilon ,w}\left(\ell +\upsilon +w,\widehat{\mathsf{ı}}+\upsilon +w\right){\displaystyle \frac{t^{\ell }}{{\left[\ell \right]}_{p,q}!}}={\displaystyle \frac{{\left(e_{p,q}\left(t\right)-1\right)}^{\widehat{\mathsf{ı}}}}{{\left[\widehat{\mathsf{ı}}\right]}_{p,q}!}}{e}_{p,q}\left(\upsilon t\right)E_{p,q}\left(wt\right).$$

By taking $\upsilon =w=0,$ the generating function can be obtained as below

$${\displaystyle \frac{{\left(e_{p,q}\left(t\right)-1\right)}^{\widehat{\mathsf{ı}}}}{{\left[\widehat{\mathsf{ı}}\right]}_{p,q}!}}=\sum _{\ell =\widehat{\mathsf{ı}}}^{\infty }{S}_{p,q}\left(\ell ,\widehat{\mathsf{ı}}\right){\displaystyle \frac{t^{\ell }}{{\left[\ell \right]}_{p,q}!}}.$$

(7)

The fully modified $\left(p,q\right)$ poly-Bernoulli polynomials ${\tilde{B}}_{\ell ,p,q}^{\left(\mu \right)}\left(y\right)$ of the first type and $\left(p,q\right)$-Bernoulli polynomials of order m $B_{\ell ,p,q}^{\left(m\right)}\left(y\right)$ are defined by, respectively,

$$\sum _{\ell =0}^{\infty }{\tilde{B}}_{\ell ,p,q}^{\left(\mu \right)}\left(y\right){\displaystyle \frac{t^{\ell }}{\ell !}}={\displaystyle \frac{L{i}_{\mu ,p,q}\left(1-e_{p,q}\left(-t\right)\right)}{e_{p,q}\left(t\right)-1}}{e}_{p,q}\left(yt\right)$$

(8)

and

$$\sum _{\ell =0}^{\infty }{B}_{\ell ,p,q}^{\left(m\right)}\left(y\right){\displaystyle \frac{t^{\ell }}{\ell !}}={\left({\displaystyle \frac{t}{e_{p,q}\left(t\right)-1}}\right)}^m{e}_{p,q}\left(yt\right),$$

(9)

where $m\in {\mathbb{Z}}^{+},$$\mu \in \mathbb{Z}$ [4]. For $m=1,$$B_{\ell ,p,q}^{\left(1\right)}\left(y\right)=B_{\ell ,p,q}\left(y\right).$

The fully modified $\left(p,q\right)$-poly-tangent polynomials ${\tilde{T}}_{\ell ,p,q}^{\left(\mu \right)}\left(y\right)$ of the first type and $\left(p,q\right)$-tangent polynomials $T_{\ell ,p,q}\left(y\right)$ of the first type are identified by, respectively,

$$\sum _{\ell =0}^{\infty }{\tilde{T}}_{\ell ,p,q}^{\left(\mu \right)}\left(y\right){\displaystyle \frac{t^{\ell }}{\ell !}}={\displaystyle \frac{{\left[2\right]}_{p,q}L{i}_{\mu ,p,q}\left(1-e_{p,q}\left(-t\right)\right)}{t\left(e_{p,q}\left(2t\right)+1\right)}}{e}_{p,q}\left(yt\right),$$

(10)

and

$$\sum _{\ell =0}^{\infty }{T}_{\ell ,p,q}\left(y\right){\displaystyle \frac{t^{\ell }}{{\left[\ell \right]}_{p,q}!}}={\displaystyle \frac{{\left[2\right]}_{p,q}}{e_{p,q}\left(2t\right)+1}}{e}_{p,q}\left(yt\right),$$

(11)

where $\mu \in \mathbb{Z}$ [4].

The definition of harmonic numbers is

$$H_0=0,H_{\ell }=\sum _{\widehat{\mathsf{ı}}=1}^{\ell }{\displaystyle \frac{1}{\widehat{\mathsf{ı}}}}\mathrm{for}\ell =1,2,...,$$

and their generating function is

$${\displaystyle \frac{-ln\left(1-t\right)}{1-t}}=\sum _{\ell =0}^{\infty }{H}_{\ell }{t}^{\ell }.$$

Harmonic numbers have been investigated in various areas of number theory and combinatorial problems. There are some generalized versions of $H_{\ell }$ harmonic numbers. In this context, an extension known as hyperharmonic numbers has been introduced [12,13,14,15,16,17,18,19,20,21,22]. Recently, q-analogs of these numbers have been studied.

Hyperharmonic numbers generalize harmonic numbers by introducing a parameter $\nu$, where $\nu$ is a positive integer. The hyperharmonic number, denoted $H_{\ell }^{\nu },$ is recursively defined as follows:

$$H_{\ell }^{\nu }=\sum _{\widehat{\mathsf{ı}}=1}^{\ell }{H}_{\widehat{\mathsf{ı}}}^{\nu -1}.$$

In this recursive formula, each hyperharmonic number of order $\nu$ is built from the sums of the hyperharmonic numbers of order $\nu -1$. This leads to a layered structure of summation, which gives the hyperharmonic numbers their generalized form.

Hyperharmonic numbers represent a natural and elegant generalization of harmonic numbers with applications spanning across number theory, combinatorics, analysis, and even physics. Their recursive definition and closed-form expression allow them to be used in a variety of mathematical problems, particularly those involving sums, series, and recursive structures. By providing a deeper understanding of harmonic-type sums, hyperharmonic numbers serve as a valuable tool in both theoretical and applied mathematics.

2. A $\left(\mathit{p},\mathit{q}\right)$-Analog of the Generalized Hyperharmonic Polynomials

In this section, firstly, we will begin by presenting the definitions of $\left(p,q\right)$-analogues of the generalized harmonic polynomials of order $\mu$, $H_{\ell ,\mu }\left(p,q,x\right)$ and the generalized hyperharmonic polynomials of order $\nu ,$ $H_{\ell ,\mu }^{\nu }\left(p,q,x\right)$. We found new sums of these polynomials by using combinatorial operations. We also obtained the generating function and used it to reproduce new equations. The applications of matrices are made in the end.

Definition 1. 

For $\ell ,\mu \ge 1,$ we have

$$H_{0,\mu }\left(p,q,x\right)=0\mathit{and}{H}_{\ell ,\mu }\left(p,q,x\right)=\sum _{\widehat{\mathsf{ı}}=1}^{\ell }{\displaystyle \frac{x^{\widehat{\mathsf{ı}}}}{{\left[\widehat{\mathsf{ı}}\right]}_{p,q}^{\mu }}}.$$

Definition 2. 

For $\mu \ge 1,$ we have

$$\underset{\ell ,\mu }{\overset{\nu }{H}}\left(p,q,x\right)=\left\{\begin{array}{cc}{\displaystyle \sum _{\overline{\mathsf{ı}}=1}^{\ell }}{q}^{\overline{\mathsf{ı}}}{p}^{\left(\ell -\overline{\mathsf{ı}}\right)\left(\nu -1\right)}{H}_{\overline{\mathsf{ı}},\mu }^{\nu -1}\left(p,q,x\right),& if\ell ,\nu \ge 1,\\ {\displaystyle \frac{q^{-\ell }{x}^{\ell }}{{\left[\ell \right]}_{p,q}^{\mu }}},& if\nu =0,\\ 0,& if\nu <0or\ell \le 0.\end{array}\right.$$

(12)

It is clear that for $\ell ,\nu ,\mu ⩾1,$

$$H_{\ell ,\mu }^{\nu }\left(p,q,x\right)=q^{\ell }{H}_{\ell ,\mu }^{\nu -1}\left(p,q,x\right)+p^{\nu -1}{H}_{\ell -1,\mu }^{\nu }\left(p,q,x\right).$$

(13)

Lemma 1. 

For $\ell ,\nu \ge 1,$ we have

$$\sum _{\widehat{\mathsf{ı}}=1}^{\nu }{q}^{\ell \left(\nu -\widehat{\mathsf{ı}}\right)}{p}^{\widehat{\mathsf{ı}}-1}{H}_{\ell -1,\mu }^{\widehat{\mathsf{ı}}}\left(p,q,x\right)=H_{\ell ,\mu }^{\nu }\left(p,q,x\right)-q^{\ell \left(\nu -1\right)}{\displaystyle \frac{x^{\ell }}{{\left[\ell \right]}_{p,q}^{\mu }}}.$$

Proof. 

Double induction must be used on ℓ and $\nu$ in order to prove this sum. It is clear from Definition 2 when $\ell =\nu =1$. Let us assume that the proposition holds for $\ell \ge 1$. For $\ell +1,$ using induction assumption and Definition 2, we have

$$\begin{array}{ccc}& & H_{\ell ,\mu }\left(p,q,x\right)+{\displaystyle \frac{x^{\ell +1}}{{\left[\ell +1\right]}_{p,q}^{\mu }}}\hfill \\ & =& H_{\ell -1,\mu }\left(p,q,x\right)+{\displaystyle \frac{x^{\ell }}{{\left[\ell \right]}_{p,q}^{\mu }}}+{\displaystyle \frac{x^{\ell +1}}{{\left[\ell +1\right]}_{p,q}^{\mu }}}\hfill \\ & =& \cdots \hfill \\ & =& H_{0,\mu }\left(p,q,x\right)+{\displaystyle \frac{x^1}{{\left[1\right]}_{p,q}^{\mu }}}+\cdots +{\displaystyle \frac{x^{\ell }}{{\left[\ell \right]}_{p,q}^{\mu }}}+{\displaystyle \frac{x^{\ell +1}}{{\left[\ell +1\right]}_{p,q}^{\mu }}}\hfill \\ & =& \sum _{\widehat{\mathsf{ı}}=1}^{\ell +1}{\displaystyle \frac{x^{\widehat{\mathsf{ı}}}}{{\left[\widehat{\mathsf{ı}}\right]}_{p,q}^{\mu }}}=H_{\ell +1,\mu }\left(p,q,x\right).\hfill \end{array}$$

Finally, let us suppose that $\nu \ge 1,$ and let us assume that the proposition is true for $\nu -1.$ In that for all $\ell \ge 1,$

$$\sum _{\widehat{\mathsf{ı}}=1}^{\nu -1}{q}^{\ell \left(\nu -\widehat{\mathsf{ı}}-1\right)}{p}^{\widehat{\mathsf{ı}}-1}{H}_{\ell -1,\mu }^{\widehat{\mathsf{ı}}}\left(p,q,x\right)=H_{\ell ,\mu }^{\nu -1}\left(p,q,x\right)-q^{\ell \left(\nu -2\right)}{\displaystyle \frac{x^{\ell }}{{\left[\ell \right]}_{p,q}^{\mu }}}.$$

We want to prove that the claim holds for $\nu .$ Using the induction assumption and (13), we can write the following expression.

$$\begin{array}{ccc}& & \sum _{\widehat{\mathsf{ı}}=1}^{\nu }{q}^{\ell \left(\nu -\widehat{\mathsf{ı}}\right)}{p}^{\widehat{\mathsf{ı}}-1}{H}_{\ell -1,\mu }^{\widehat{\mathsf{ı}}}\left(p,q,x\right)\hfill \\ & =& p^{\nu -1}{H}_{\ell -1,\mu }^{\nu }\left(p,q,x\right)+q^{\ell }\sum _{\widehat{\mathsf{ı}}=1}^{\nu -1}{q}^{\ell \left(\nu -\widehat{\mathsf{ı}}-1\right)}{p}^{\widehat{\mathsf{ı}}-1}{H}_{\ell -1,\mu }^{\widehat{\mathsf{ı}}}\left(p,q,x\right)\hfill \\ & =& p^{\nu -1}{H}_{\ell -1,\mu }^{\nu }\left(p,q,x\right)+q^{\ell }\left(H_{\ell ,\mu }^{\nu -1}\left(p,q,x\right)-q^{\ell \left(\nu -2\right)}{\displaystyle \frac{x^{\ell }}{{\left[\ell \right]}_{p,q}^{\mu }}}\right)\hfill \\ & =& H_{\ell ,\mu }^{\nu }\left(p,q,x\right)-q^{\ell \left(\nu -1\right)}{\displaystyle \frac{x^{\ell }}{{\left[\ell \right]}_{p,q}^{\mu }}}.\hfill \end{array}$$

Based on principle of double induction, we show that for all values of $\ell \ge 1$ and $\nu \ge 1,$ the result we want to obtain is true. In this case, the proof is complete since the necessary conditions are satisfied. □

Theorem 1. 

For every ordered pair $\left(x,\nu \right)\in {\mathbb{R}}^{+}\times {\mathbb{Z}}^{+},$ then

$$H_{\ell ,\mu }^{\nu }\left(p,q,x\right)=\sum _{\widehat{\mathsf{ı}}=1}^{\ell }{\left[{\displaystyle \genfrac{}{}{0pt}{}{\ell +\nu -\widehat{\mathsf{ı}}-1}{\nu -1}}\right]}_{p,q}{\displaystyle \frac{q^{\left(\nu -1\right)\widehat{\mathsf{ı}}}}{{\left[\widehat{\mathsf{ı}}\right]}_{p,q}^{\mu }}}{x}^{\widehat{\mathsf{ı}}}.$$

(14)

Proof. 

(Principle of Double Induction on ℓ and $\nu$). For $\ell =\nu =1$ and $\ell =1$, $\nu >1,$ Definition 2, it is clear. Let us assume that the proposition holds for $\ell -1$. Thus, we show that the claim holds also for ℓ. By the induction assumption, Lemma 1 and (2), we have

$$\begin{array}{ccc}& & H_{\ell ,\mu }^{\nu }\left(p,q,x\right)\hfill \\ & =& q^{\ell \left(\nu -1\right)}{\displaystyle \frac{x^{\ell }}{{\left[\ell \right]}_{p,q}^{\mu }}}+\sum _{\widehat{j}=1}^{\nu }{q}^{\ell \left(\nu -\widehat{j}\right)}{p}^{\widehat{j}-1}{H}_{\ell -1,\mu }^{\widehat{j}}\left(p,q,x\right)\hfill \\ & =& q^{\ell \left(\nu -1\right)}{\displaystyle \frac{x^{\ell }}{{\left[\ell \right]}_{p,q}^{\mu }}}+\sum _{\widehat{j}=1}^{\nu }{q}^{\ell \left(\nu -\widehat{j}\right)}{p}^{\widehat{j}-1}\sum _{\widehat{\mathsf{ı}}=1}^{\ell -1}{\left[{\displaystyle \genfrac{}{}{0pt}{}{\ell +\widehat{j}-\widehat{\mathsf{ı}}-2}{\widehat{j}-1}}\right]}_{p,q}{\displaystyle \frac{q^{\left(\widehat{j}-1\right)\widehat{\mathsf{ı}}}}{{\left[\widehat{\mathsf{ı}}\right]}_{p,q}^{\mu }}}{x}^{\widehat{\mathsf{ı}}}\hfill \\ & =& q^{\ell \left(\nu -1\right)}{\displaystyle \frac{x^{\ell }}{{\left[\ell \right]}_{p,q}^{\mu }}}+\sum _{\widehat{\mathsf{ı}}=1}^{\ell -1}{\displaystyle \frac{q^{\ell \nu -\ell }}{{\left[\widehat{\mathsf{ı}}\right]}_{p,q}^{\mu }}}{x}^{\widehat{\mathsf{ı}}}\sum _{\widehat{j}=0}^{\nu -1}{p}^{\widehat{j}}{q}^{\widehat{j}\left(\widehat{\mathsf{ı}}-\ell \right)}{\left[{\displaystyle \genfrac{}{}{0pt}{}{\ell +\widehat{j}-\widehat{\mathsf{ı}}-1}{\widehat{j}}}\right]}_{p,q}\hfill \\ & =& q^{\ell \left(\nu -1\right)}{\displaystyle \frac{x^{\ell }}{{\left[\ell \right]}_{p,q}^{\mu }}}+\sum _{\widehat{\mathsf{ı}}=1}^{\ell -1}{\left[{\displaystyle \genfrac{}{}{0pt}{}{\ell +\nu -\widehat{\mathsf{ı}}-1}{\nu -1}}\right]}_{p,q}{\displaystyle \frac{q^{\left(\nu -1\right)\widehat{\mathsf{ı}}}}{{\left[\widehat{\mathsf{ı}}\right]}_{p,q}^{\mu }}}{x}^{\widehat{\mathsf{ı}}}\hfill \\ & =& \sum _{\widehat{\mathsf{ı}}=1}^{\ell }{\left[{\displaystyle \genfrac{}{}{0pt}{}{\ell +\nu -\widehat{\mathsf{ı}}-1}{\nu -1}}\right]}_{p,q}{\displaystyle \frac{q^{\left(\nu -1\right)\widehat{\mathsf{ı}}}}{{\left[\widehat{\mathsf{ı}}\right]}_{p,q}^{\mu }}}{x}^{\widehat{\mathsf{ı}}}.\hfill \end{array}$$

At the end of these steps, thanks to the operations performed and the assumptions used, the desired equality is proved to be valid, and we have reached the result we were looking for. □

Some basic elementary operations will be used to obtain the following theorem:

Theorem 2. 

For $0<w<\nu <\ell ,$ we have

$$\sum _{\widehat{\mathsf{ı}}=1}^w{p}^{\left(\widehat{\mathsf{ı}}-w\right)\left(\widehat{\mathsf{ı}}-\nu +1\right)}{q}^{\widehat{\mathsf{ı}}(\ell -w+\widehat{\mathsf{ı}})}{\left[{\displaystyle \genfrac{}{}{0pt}{}{w}{\widehat{\mathsf{ı}}}}\right]}_{p,q}{H}_{\ell -w+\widehat{\mathsf{ı}},\mu }^{\nu -\widehat{\mathsf{ı}}}(p,q,x)=H_{\ell ,\mu }^{\nu }(p,q,x)-p^{w\left(\nu -1\right)}{H}_{\ell -w,\mu }^{\nu }(p,q,x).$$

Proof. 

By (14), we have

$$\begin{array}{ccc}& & \sum _{\widehat{\mathsf{ı}}=1}^w{p}^{\left(\widehat{\mathsf{ı}}-w\right)\left(\widehat{\mathsf{ı}}-\nu +1\right)}{q}^{\widehat{\mathsf{ı}}(\ell -w+\widehat{\mathsf{ı}})}{\left[{\displaystyle \genfrac{}{}{0pt}{}{w}{\widehat{\mathsf{ı}}}}\right]}_{p,q}{H}_{\ell -w+\widehat{\mathsf{ı}},\mu }^{\nu -\widehat{\mathsf{ı}}}(p,q,x)\hfill \\ & =& \sum _{\widehat{\mathsf{ı}}=1}^w{p}^{\left(\widehat{\mathsf{ı}}-w\right)\left(\widehat{\mathsf{ı}}-\nu +1\right)}{q}^{\widehat{\mathsf{ı}}(\ell -w+\widehat{\mathsf{ı}})}{\left[{\displaystyle \genfrac{}{}{0pt}{}{w}{\widehat{\mathsf{ı}}}}\right]}_{p,q}\sum _{\widehat{j}=1}^{\ell -w+\widehat{\mathsf{ı}}}{\left[{\displaystyle \genfrac{}{}{0pt}{}{\ell +\nu -w-\widehat{j}-1}{\nu -\widehat{\mathsf{ı}}-1}}\right]}_{p,q}{\displaystyle \frac{q^{(\nu -\widehat{\mathsf{ı}}-1)\widehat{j}}}{{\left[\widehat{j}\right]}_{p,q}^{\mu }}}{x}^{\widehat{j}}\hfill \\ & =& \sum _{\widehat{j}=1}^{\ell -w}{\displaystyle \frac{q^{(\nu -1)\widehat{j}}}{{\left[\widehat{j}\right]}_{p,q}^{\mu }}}{x}^{\widehat{j}}\sum _{\widehat{\mathsf{ı}}=1}^w{p}^{\left(\widehat{\mathsf{ı}}-w\right)\left(\widehat{\mathsf{ı}}-\nu +1\right)}{q}^{\widehat{\mathsf{ı}}(\ell -w+\widehat{\mathsf{ı}}-\widehat{j})}{\left[{\displaystyle \genfrac{}{}{0pt}{}{w}{\widehat{\mathsf{ı}}}}\right]}_{p,q}{\left[{\displaystyle \genfrac{}{}{0pt}{}{\ell +\nu -w-\widehat{j}-1}{\nu -\widehat{\mathsf{ı}}-1}}\right]}_{p,q}\hfill \\ & & +\sum _{\widehat{\mathsf{ı}}=1}^w{p}^{\left(\widehat{\mathsf{ı}}-w\right)\left(\widehat{\mathsf{ı}}-\nu +1\right)}{q}^{\widehat{\mathsf{ı}}(\ell -w+\widehat{\mathsf{ı}})}{\left[{\displaystyle \genfrac{}{}{0pt}{}{w}{\widehat{\mathsf{ı}}}}\right]}_{p,q}\sum _{\widehat{j}=1}^{\widehat{\mathsf{ı}}}{\left[{\displaystyle \genfrac{}{}{0pt}{}{\nu -\widehat{j}-1}{\nu -\widehat{\mathsf{ı}}-1}}\right]}_{p,q}{\displaystyle \frac{q^{(\nu -\widehat{\mathsf{ı}}-1)\left(\widehat{j}+\ell -w\right)}}{{\left[\widehat{j}+\ell -w\right]}_{p,q}^{\mu }}}{x}^{\widehat{j}+\ell -w}\hfill \\ & =& \sum _{\widehat{j}=1}^{\ell -w}{\displaystyle \frac{q^{(\nu -1)\widehat{j}}}{{\left[\widehat{j}\right]}_{p,q}^{\mu }}}{x}^{\widehat{j}}\sum _{\widehat{\mathsf{ı}}=1}^w{p}^{\left(\widehat{\mathsf{ı}}-w\right)\left(\widehat{\mathsf{ı}}-\nu +1\right)}{q}^{\widehat{\mathsf{ı}}(\ell -w+\widehat{\mathsf{ı}}-\widehat{j})}{\left[{\displaystyle \genfrac{}{}{0pt}{}{w}{\widehat{\mathsf{ı}}}}\right]}_{p,q}{\left[{\displaystyle \genfrac{}{}{0pt}{}{\ell -w+\nu -\widehat{j}-1}{\nu -\widehat{\mathsf{ı}}-1}}\right]}_{p,q}\hfill \\ & & +\sum _{\widehat{j}=\ell -w+1}^{\ell }{\displaystyle \frac{q^{(\nu -1)\widehat{j}}}{{\left[\widehat{j}\right]}_{p,q}^{\mu }}}{x}^{\widehat{j}}\sum _{\widehat{\mathsf{ı}}=\widehat{j}-\ell +w}^w{p}^{\left(\widehat{\mathsf{ı}}-w\right)\left(\widehat{\mathsf{ı}}-\nu +1\right)}{q}^{\widehat{\mathsf{ı}}(\widehat{\mathsf{ı}}-\widehat{j}+\ell -w)}{\left[{\displaystyle \genfrac{}{}{0pt}{}{w}{\widehat{\mathsf{ı}}}}\right]}_{p,q}{\left[{\displaystyle \genfrac{}{}{0pt}{}{\ell +\nu -\widehat{j}-w-1}{\nu -\widehat{\mathsf{ı}}-1}}\right]}_{p,q}\hfill \\ & =& \sum _{\widehat{j}=1}^{\ell -w}{\displaystyle \frac{q^{(\nu -1)\widehat{j}}}{{\left[\widehat{j}\right]}_{p,q}^{\mu }}}{x}^{\widehat{j}}\sum _{\widehat{\mathsf{ı}}=1}^w{p}^{\left(\widehat{\mathsf{ı}}-w\right)\left(\widehat{\mathsf{ı}}-\nu +1\right)}{q}^{\widehat{\mathsf{ı}}(\ell -w+\widehat{\mathsf{ı}}-\widehat{j})}{\left[{\displaystyle \genfrac{}{}{0pt}{}{w}{\widehat{\mathsf{ı}}}}\right]}_{p,q}{\left[{\displaystyle \genfrac{}{}{0pt}{}{\ell -w+\nu -\widehat{j}-1}{\nu -\widehat{\mathsf{ı}}-1}}\right]}_{p,q}\hfill \\ & & +\sum _{\widehat{j}=\ell -w+1}^{\ell }{\displaystyle \frac{q^{(\nu -1)\widehat{j}}}{{\left[\widehat{j}\right]}_{p,q}^{\mu }}}{x}^{\widehat{j}}\sum _{\widehat{\mathsf{ı}}=0}^{\ell -\widehat{j}}{p}^{\left(\widehat{\mathsf{ı}}-\ell +\widehat{j}\right)\left(\widehat{\mathsf{ı}}-\ell +w+\widehat{j}-\nu +1\right)}{q}^{\widehat{\mathsf{ı}}\left(\widehat{\mathsf{ı}}-\ell +w+\widehat{j}\right)}\hfill \\ & & \times {\left[{\displaystyle \genfrac{}{}{0pt}{}{w}{\widehat{\mathsf{ı}}-\ell +w+\widehat{j}}}\right]}_{p,q}{\left[{\displaystyle \genfrac{}{}{0pt}{}{\ell +\nu -\widehat{j}-w-1}{\widehat{\mathsf{ı}}}}\right]}_{p,q}\hfill \\ & =& \sum _{\widehat{j}=1}^{\ell -w}{\displaystyle \frac{q^{(\nu -1)\widehat{j}}}{{\left[\widehat{j}\right]}_{p,q}^{\mu }}}{x}^{\widehat{j}}\sum _{\widehat{\mathsf{ı}}=0}^w{p}^{\left(\widehat{\mathsf{ı}}-w\right)\left(\widehat{\mathsf{ı}}-\nu +1\right)}{q}^{\widehat{\mathsf{ı}}(\ell -w+\widehat{\mathsf{ı}}-\widehat{j})}{\left[{\displaystyle \genfrac{}{}{0pt}{}{w}{\widehat{\mathsf{ı}}}}\right]}_{p,q}{\left[{\displaystyle \genfrac{}{}{0pt}{}{\ell -w+\nu -\widehat{j}-1}{\nu -\widehat{\mathsf{ı}}-1}}\right]}_{p,q}\hfill \\ & & -p^{w\left(\nu -1\right)}\sum _{\widehat{j}=1}^{\ell -w}{\displaystyle \frac{q^{(\nu -1)\widehat{j}}}{{\left[\widehat{j}\right]}_{p,q}^{\mu }}}{x}^{\widehat{j}}{\left[{\displaystyle \genfrac{}{}{0pt}{}{\ell -w+\nu -\widehat{j}-1}{\nu -1}}\right]}_{p,q}\hfill \\ & & +\sum _{\widehat{j}=\ell -w+1}^{\ell }{\displaystyle \frac{q^{(\nu -1)\widehat{j}}}{{\left[\widehat{j}\right]}_{p,q}^{\mu }}}{x}^{\widehat{j}}\sum _{\widehat{\mathsf{ı}}=0}^{\ell -\widehat{j}}{p}^{\left(\widehat{\mathsf{ı}}-\ell +\widehat{j}\right)\left(\widehat{\mathsf{ı}}-\ell +w+\widehat{j}-\nu +1\right)}{q}^{\widehat{\mathsf{ı}}\left(\widehat{\mathsf{ı}}-\ell +w+\widehat{j}\right)}\hfill \\ & & \times {\left[{\displaystyle \genfrac{}{}{0pt}{}{w}{\widehat{\mathsf{ı}}-\ell +w+\widehat{j}}}\right]}_{p,q}{\left[{\displaystyle \genfrac{}{}{0pt}{}{\ell +\nu -\widehat{j}-w-1}{\widehat{\mathsf{ı}}}}\right]}_{p,q}.\hfill \end{array}$$

From (1), we write

$$\begin{array}{ccc}& & \sum _{\widehat{\mathsf{ı}}=1}^w{q}^{\widehat{\mathsf{ı}}(\ell -w+\widehat{\mathsf{ı}})}{p}^{\left(\widehat{\mathsf{ı}}-w\right)\left(\widehat{\mathsf{ı}}-\nu +1\right)}{\left[{\displaystyle \genfrac{}{}{0pt}{}{w}{\widehat{\mathsf{ı}}}}\right]}_{p,q}{H}_{\ell -w+\widehat{\mathsf{ı}},\mu }^{\nu -\widehat{\mathsf{ı}}}(p,q,x)\hfill \\ & =& \sum _{\widehat{j}=1}^{\ell -w}{\left[{\displaystyle \genfrac{}{}{0pt}{}{\ell +\nu -\widehat{j}-1}{\nu -1}}\right]}_{p,q}{\displaystyle \frac{q^{(\nu -1)\widehat{j}}}{{\left[\widehat{j}\right]}_{p,q}^{\mu }}}{x}^{\widehat{j}}-p^{w\left(\nu -1\right)}\sum _{\widehat{j}=1}^{\ell -w}{\left[{\displaystyle \genfrac{}{}{0pt}{}{\ell +\nu -w-\widehat{j}-1}{\nu -1}}\right]}_{p,q}{\displaystyle \frac{q^{(\nu -1)\widehat{j}}}{{\left[\widehat{j}\right]}_{p,q}^{\mu }}}{x}^{\widehat{j}}\hfill \\ & & +\sum _{\widehat{j}=\ell -w+1}^{\ell }{\left[{\displaystyle \genfrac{}{}{0pt}{}{\ell +\nu -\widehat{j}-1}{\nu -1}}\right]}_{p,q}{\displaystyle \frac{q^{(\nu -1)\widehat{j}}}{{\left[\widehat{j}\right]}_{p,q}^{\mu }}}{x}^{\widehat{j}}\hfill \\ & =& \sum _{\widehat{j}=1}^{\ell }{\left[{\displaystyle \genfrac{}{}{0pt}{}{\ell +\nu -\widehat{j}-1}{\nu -1}}\right]}_{p,q}{\displaystyle \frac{q^{(\nu -1)\widehat{j}}}{{\left[\widehat{j}\right]}_{p,q}^{\mu }}}{x}^{\widehat{j}}-p^{w\left(\nu -1\right)}\sum _{\widehat{j}=1}^{\ell -w}{\displaystyle \frac{q^{(\nu -1)\widehat{j}}}{{\left[\widehat{j}\right]}_{p,q}^{\mu }}}{x}^{\widehat{j}}{\left[{\displaystyle \genfrac{}{}{0pt}{}{\ell +\nu -w-\widehat{j}-1}{\nu -1}}\right]}_{p,q}\hfill \\ & =& H_{\ell ,\mu }^{\nu }(p,q,x)-p^{w\left(\nu -1\right)}{H}_{\ell -w,\mu }^{\nu }(p,q,x).\hfill \end{array}$$

With this, we have concluded all necessary steps and verified each part, thereby completing the proof. □

Lemma 2. 

For $\ell ,\mu \ge 1,$ we have

$$\sum _{\ell =1}^{\infty }{H}_{\ell ,\mu }\left(p,q,x\right)t^{\ell }={\displaystyle \frac{1}{1-t}}L{i}_{\mu ,p,q}\left(xt\right).$$

Proof. 

By Definition 1 and (4), observe that

$$\begin{array}{ccc}\hfill \sum _{\ell =1}^{\infty }{H}_{\ell ,\mu }\left(p,q,x\right)t^{\ell }& =& \sum _{\ell =1}^{\infty }\sum _{\widehat{\mathsf{ı}}=1}^{\ell }{\displaystyle \frac{x^{\widehat{\mathsf{ı}}}}{{\left[\widehat{\mathsf{ı}}\right]}_{p,q}^{\mu }}}{t}^{\ell }=\sum _{\widehat{\mathsf{ı}}=1}^{\infty }{\displaystyle \frac{x^{\widehat{\mathsf{ı}}}}{{\left[\widehat{\mathsf{ı}}\right]}_{p,q}^{\mu }}}\sum _{\ell =\widehat{\mathsf{ı}}}^{\infty }{t}^{\ell }\hfill \\ & =& \sum _{\widehat{\mathsf{ı}}=1}^{\infty }{\displaystyle \frac{x^{\widehat{\mathsf{ı}}}}{{\left[\widehat{\mathsf{ı}}\right]}_{p,q}^{\mu }}}\left(\sum _{\ell =0}^{\infty }{t}^{\ell }-\sum _{\ell =0}^{\widehat{\mathsf{ı}}-1}{t}^{\ell }\right)\hfill \\ & =& {\displaystyle \frac{1}{1-t}}\sum _{\widehat{\mathsf{ı}}=1}^{\infty }{\displaystyle \frac{x^{\widehat{\mathsf{ı}}}}{{\left[\widehat{\mathsf{ı}}\right]}_{p,q}^{\mu }}}{t}^{\widehat{\mathsf{ı}}}={\displaystyle \frac{1}{1-t}}L{i}_{\mu ,p,q}\left(xt\right).\hfill \end{array}$$

□

Theorem 3. 

For $\ell ,\mu ,\nu \ge 1,$ we have

$$\sum _{\ell =1}^{\infty }{q}^{-\ell \left(\nu -1\right)}{H}_{\ell ,\mu }^{\nu }\left(p,q,x\right)t^{\ell }={\displaystyle \frac{1}{{\left(t;p,q\right)}_{\nu }}}L{i}_{\mu ,p,q}\left(xt\right).$$

(15)

Proof. 

From (4), (6) and (14), we have

$$\begin{array}{ccc}\hfill {\displaystyle \frac{1}{{\left(t;p,q\right)}_{\nu }}}L{i}_{\mu ,p,q}\left(xt\right)& =& \sum _{\ell =0}^{\infty }{q}^{-\ell \left(\nu -1\right)}{\left[{\displaystyle \genfrac{}{}{0pt}{}{\nu +\ell -1}{\ell }}\right]}_{p,q}{t}^{\ell }\sum _{\ell =1}^{\infty }{\displaystyle \frac{x^{\ell }}{{\left[\ell \right]}_{p,q}^{\mu }}}{t}^{\ell }\hfill \\ & =& \sum _{\ell =1}^{\infty }\sum _{\widehat{\mathsf{ı}}=1}^{\ell }{q}^{\left(\widehat{\mathsf{ı}}-\ell \right)\left(\nu -1\right)}{\left[{\displaystyle \genfrac{}{}{0pt}{}{\ell +\nu -\widehat{\mathsf{ı}}-1}{\nu -1}}\right]}_{p,q}{\displaystyle \frac{x^{\widehat{\mathsf{ı}}}}{{\left[\widehat{\mathsf{ı}}\right]}_{p,q}^{\mu }}}{t}^{\ell }\hfill \\ & =& \sum _{\ell =1}^{\infty }{q}^{-\ell \left(\nu -1\right)}{H}_{\ell ,\mu }^{\nu }\left(p,q,x\right)t^{\ell }.\hfill \end{array}$$

□

The new equations will be given by the help of the generating function that obtained Theorem 3.

Theorem 4. 

For $\ell ,\mu ,\nu \ge 1,$ we have

$${\displaystyle \frac{x^{\ell }}{{\left[\ell \right]}_{p,q}^{\mu }}}=q^{-\ell \left(\nu -1\right)}\sum _{\widehat{\mathsf{ı}}=1}^{\ell }{\left(-1\right)}^{\ell -\widehat{\mathsf{ı}}}{p}^{\left({\displaystyle \genfrac{}{}{0pt}{}{\ell -\widehat{\mathsf{ı}}}{2}}\right)}{q}^{\left({\displaystyle \genfrac{}{}{0pt}{}{\ell -\widehat{\mathsf{ı}}}{2}}\right)}{\left[{\displaystyle \genfrac{}{}{0pt}{}{\nu }{\ell -\widehat{\mathsf{ı}}}}\right]}_{p,q}{H}_{\widehat{\mathsf{ı}},\mu }^{\nu }\left(p,q,x\right),$$

(16)

and

$$\begin{array}{ccc}\hfill {\displaystyle \frac{x^{\ell }}{{\left[\ell \right]}_{p,q}^{\mu }}}& =& q^{-\ell \left(\nu +w-1\right)}\sum _{\widehat{\mathsf{ı}}=1}^{\ell }\sum _{\hat{j}=1}^{\hat{\mathsf{ı}}}{\left(-1\right)}^{\ell -\widehat{\mathsf{ı}}}{p}^{\left({\displaystyle \genfrac{}{}{0pt}{}{\ell -\widehat{\mathsf{ı}}}{2}}\right)+\nu \left(\widehat{\mathsf{ı}}-\widehat{j}\right)}{q}^{\left({\displaystyle \genfrac{}{}{0pt}{}{\ell -\widehat{\mathsf{ı}}}{2}}\right)+\widehat{j}w}{\left[{\displaystyle \genfrac{}{}{0pt}{}{\nu +w}{\ell -\widehat{\mathsf{ı}}}}\right]}_{p,q}\hfill \\ & & \times {\left[{\displaystyle \genfrac{}{}{0pt}{}{w+\widehat{\mathsf{ı}}-\widehat{j}-1}{w-1}}\right]}_{p,q}{H}_{\widehat{j},\mu }^{\nu }\left(p,q,x\right).\hfill \end{array}$$

(17)

Proof. 

We will give proof of (17). By (4) and (15), we have

$$\sum _{\ell =1}^{\infty }{\displaystyle \frac{x^{\ell }}{{\left[\ell \right]}_{p,q}^{\mu }}}{t}^{\ell }=L{i}_{\mu ,p,q}\left(xt\right)={\left(t;p,q\right)}_{\nu }\sum _{\ell =1}^{\infty }{q}^{-\ell \left(\nu -1\right)}{H}_{\ell ,\mu }^{\nu }\left(p,q,x\right)t^{\ell }.$$

With the help of the (5) and (6), we can rewrite

$$\begin{array}{ccc}& & \sum _{\ell =1}^{\infty }{\displaystyle \frac{x^{\ell }}{{\left[\ell \right]}_{p,q}^{\mu }}}{t}^{\ell }\hfill \\ & =& L{i}_{\mu ,p,q}\left(xt\right)={\left(t;p,q\right)}_{\nu }\sum _{\ell =1}^{\infty }{q}^{-\ell \left(\nu -1\right)}{H}_{\ell ,\mu }^{\nu }\left(p,q,x\right)t^{\ell }\hfill \\ & =& {\left(t;p,q\right)}_{\nu +w}{\displaystyle \frac{1}{{\left(t{p}^{\nu }{q}^{-\nu };p,q\right)}_w}}\sum _{\ell =1}^{\infty }{q}^{-\ell \left(\nu -1\right)}{H}_{\ell ,\mu }^{\nu }\left(p,q,x\right)t^{\ell }\hfill \\ & =& \sum _{\widehat{\mathsf{ı}}=0}^{\nu +w}{\left(-1\right)}^{\widehat{\mathsf{ı}}}{p}^{\left({\displaystyle \genfrac{}{}{0pt}{}{\widehat{\mathsf{ı}}}{2}}\right)}{q}^{\left({\displaystyle \genfrac{}{}{0pt}{}{\widehat{\mathsf{ı}}+1}{2}}\right)-\widehat{\mathsf{ı}}\left(\nu +w\right)}{\left[{\displaystyle \genfrac{}{}{0pt}{}{\nu +w}{\widehat{\mathsf{ı}}}}\right]}_{p,q}{t}^{\widehat{\mathsf{ı}}}\hfill \\ & & \times \sum _{\widehat{\mathsf{ı}}=0}^w{p}^{\nu \widehat{\mathsf{ı}}}{q}^{-\widehat{\mathsf{ı}}\left(\nu +w-1\right)}{\left[{\displaystyle \genfrac{}{}{0pt}{}{w+\widehat{\mathsf{ı}}-1}{\widehat{\mathsf{ı}}}}\right]}_{p,q}{t}^{\widehat{\mathsf{ı}}}\sum _{\widehat{\mathsf{ı}}=1}^{\infty }{q}^{-\widehat{\mathsf{ı}}\left(\nu -1\right)}{H}_{\widehat{\mathsf{ı}},\mu }^{\nu }\left(p,q,x\right)t^{\widehat{\mathsf{ı}}}\hfill \\ & =& \sum _{\widehat{\mathsf{ı}}=0}^{\infty }{\left(-1\right)}^{\widehat{\mathsf{ı}}}{p}^{\left({\displaystyle \genfrac{}{}{0pt}{}{\widehat{\mathsf{ı}}}{2}}\right)}{q}^{\left({\displaystyle \genfrac{}{}{0pt}{}{\widehat{\mathsf{ı}}+1}{2}}\right)-\widehat{\mathsf{ı}}\left(\nu +w\right)}{\left[{\displaystyle \genfrac{}{}{0pt}{}{\nu +w}{\widehat{\mathsf{ı}}}}\right]}_{p,q}{t}^{\widehat{\mathsf{ı}}}\hfill \\ & & \times \sum _{\ell =1}^{\infty }\sum _{\widehat{\mathsf{ı}}=1}^{\ell }{p}^{\nu \left(\ell -\widehat{\mathsf{ı}}\right)}{q}^{-\ell \left(\nu +w-1\right)+\widehat{\mathsf{ı}}w}{\left[{\displaystyle \genfrac{}{}{0pt}{}{w+\ell -\widehat{\mathsf{ı}}-1}{w-1}}\right]}_{p,q}{H}_{\widehat{\mathsf{ı}},\mu }^{\nu }\left(p,q,x\right)t^{\ell }\hfill \\ & =& \sum _{\ell =0}^{\infty }\sum _{\widehat{\mathsf{ı}}=1}^{\ell }\sum _{\widehat{j}=1}^{\widehat{\mathsf{ı}}}{\left(-1\right)}^{\ell -\widehat{\mathsf{ı}}}{p}^{\left({\displaystyle \genfrac{}{}{0pt}{}{\ell -\widehat{\mathsf{ı}}}{2}}\right)+\nu \left(\widehat{\mathsf{ı}}-\widehat{j}\right)}{q}^{\left({\displaystyle \genfrac{}{}{0pt}{}{\ell -\widehat{\mathsf{ı}}}{2}}\right)-\ell \left(\nu +w-1\right)+\widehat{j}w}{\left[{\displaystyle \genfrac{}{}{0pt}{}{\nu +w}{\ell -\widehat{\mathsf{ı}}}}\right]}_{p,q}\hfill \\ & & \times {\left[{\displaystyle \genfrac{}{}{0pt}{}{w+\widehat{\mathsf{ı}}-\widehat{j}-1}{w-1}}\right]}_{p,q}{H}_{\widehat{j},\mu }^{\nu }\left(p,q,x\right)t^{\ell }.\hfill \end{array}$$

To prove (16), the methods that we practiced for the proof of (17) can be used. □

Theorem 5. 

For $\ell ,\mu ,\nu \ge 1,$ we have

$$\begin{array}{ccc}& & H_{\ell ,\mu }^w\left(p,q,x\right)\hfill \\ & =& \sum _{\widehat{\mathsf{ı}}=1}^{\ell }\sum _{\widehat{j}=1}^{\widehat{\mathsf{ı}}}{\left(-1\right)}^{\widehat{\mathsf{ı}}-\widehat{j}}{p}^{\left({\displaystyle \genfrac{}{}{0pt}{}{\widehat{\mathsf{ı}}-\widehat{j}}{2}}\right)}{q}^{\left({\displaystyle \genfrac{}{}{0pt}{}{\widehat{\mathsf{ı}}-\widehat{j}}{2}}\right)-\widehat{\mathsf{ı}}\left(\nu -w\right)}{\left[{\displaystyle \genfrac{}{}{0pt}{}{\nu }{\widehat{\mathsf{ı}}-\widehat{j}}}\right]}_{p,q}{\left[{\displaystyle \genfrac{}{}{0pt}{}{\ell +w-\widehat{\mathsf{ı}}-1}{w-1}}\right]}_{p,q}{H}_{\widehat{j},\mu }^{\nu }(p,q,x),\hfill \end{array}$$

and

$$\begin{array}{ccc}\hfill H_{\ell ,\mu }^a\left(p,q,x\right)& =& \sum _{\widehat{\mathsf{ı}}=1}^{\ell }\sum _{\widehat{j}=1}^{\widehat{\mathsf{ı}}}\sum _{\mathbb{k}=1}^{\widehat{j}}{\left(-1\right)}^{\widehat{\mathsf{ı}}-\widehat{j}}{p}^{\left({\displaystyle \genfrac{}{}{0pt}{}{\widehat{\mathsf{ı}}-\widehat{j}}{2}}\right)+\nu \left(\widehat{j}-\mathbb{k}\right)}{q}^{\left({\displaystyle \genfrac{}{}{0pt}{}{\widehat{\mathsf{ı}}-\widehat{j}}{2}}\right)+\mathbb{k}w-\widehat{\mathsf{ı}}\left(\nu +w-a\right)}{\left[{\displaystyle \genfrac{}{}{0pt}{}{\nu +w}{\widehat{\mathsf{ı}}-\widehat{j}}}\right]}_{p,q}\hfill \\ & & \times {\left[{\displaystyle \genfrac{}{}{0pt}{}{w+\widehat{j}-\mathbb{k}-1}{w-1}}\right]}_{p,q}{\left[{\displaystyle \genfrac{}{}{0pt}{}{a+\ell -\widehat{\mathsf{ı}}-1}{a-1}}\right]}_{p,q}{H}_{\mathbb{k},\mu }^{\nu }(p,q,x).\hfill \end{array}$$

Proof. 

From (6) and (16), we obtain

$$\begin{array}{ccc}& & \sum _{\ell =1}^{\infty }{q}^{-\ell \left(w-1\right)}{H}_{\ell ,\mu }^w\left(p,q,x\right)t^{\ell }\hfill \\ & =& {\displaystyle \frac{1}{{\left(t;p,q\right)}_w}}L{i}_{\mu ,p,q}\left(xt\right)\hfill \\ & =& \sum _{\widehat{j}=0}^w{q}^{-\widehat{j}\left(w-1\right)}{\left[{\displaystyle \genfrac{}{}{0pt}{}{w+\widehat{j}-1}{\widehat{j}}}\right]}_{p,q}{t}^{\widehat{j}}\hfill \\ & & \times \sum _{\ell =1}^{\infty }\sum _{\widehat{j}=1}^{\ell }{\left(-1\right)}^{\ell -\widehat{j}}{p}^{\left({\displaystyle \genfrac{}{}{0pt}{}{\ell -\widehat{j}}{2}}\right)}{q}^{\left({\displaystyle \genfrac{}{}{0pt}{}{\ell -\widehat{j}}{2}}\right)-\ell \left(\nu -1\right)}{\left[{\displaystyle \genfrac{}{}{0pt}{}{\nu }{\ell -\widehat{j}}}\right]}_{p,q}{H}_{\widehat{j},\mu }^{\nu }\left(p,q,x\right)t^{\ell }\hfill \\ & =& \sum _{\ell =1}^{\infty }\sum _{\widehat{\mathsf{ı}}=1}^{\ell }\sum _{\widehat{j}=1}^{\widehat{\mathsf{ı}}}{\left(-1\right)}^{\widehat{\mathsf{ı}}-\widehat{j}}{p}^{\left({\displaystyle \genfrac{}{}{0pt}{}{\widehat{\mathsf{ı}}-\widehat{j}}{2}}\right)}{q}^{\left({\displaystyle \genfrac{}{}{0pt}{}{\widehat{\mathsf{ı}}-\widehat{j}}{2}}\right)-\widehat{\mathsf{ı}}\left(\nu -w\right)-\ell \left(w-1\right)}{\left[{\displaystyle \genfrac{}{}{0pt}{}{\nu }{\widehat{\mathsf{ı}}-\widehat{j}}}\right]}_{p,q}\hfill \\ & & \times {\left[{\displaystyle \genfrac{}{}{0pt}{}{\ell +w-\widehat{\mathsf{ı}}-1}{w-1}}\right]}_{p,q}{H}_{\widehat{j},\mu }^{\nu }\left(p,q,x\right)t^{\ell }.\hfill \end{array}$$

From the coefficients on the each sides of the equation, the proof is complete. Similarly, the other equality can be obtained. □

Theorem 6. 

For $\ell ,\mu ,\nu \ge 1,$ we have

$$\begin{array}{ccc}\hfill {\tilde{B}}_{\ell ,p,q}^{\left(\mu \right)}\left(y\right)& =& \sum _{\mathbb{k}=0}^{\ell }\sum _{\widehat{j}=1}^{\mathbb{k}+1}\sum _{\widehat{\mathsf{ı}}=1}^{\widehat{j}}{\left(-1\right)}^{\widehat{\mathsf{ı}}+\mathbb{k}+1}{x}^{-\widehat{j}}{p}^{\left({\displaystyle \genfrac{}{}{0pt}{}{\widehat{j}-\widehat{\mathsf{ı}}}{2}}\right)}{q}^{\left({\displaystyle \genfrac{}{}{0pt}{}{\widehat{j}-\widehat{\mathsf{ı}}}{2}}\right)-\widehat{j}\left(\nu -1\right)}\mathbb{k}!{\displaystyle \frac{{\left[\widehat{j}\right]}_{p,q}!}{{\left[\mathbb{k}+1\right]}_{p,q}!}}\left({\displaystyle \genfrac{}{}{0pt}{}{\ell }{\mathbb{k}}}\right)\hfill \\ & & \times {\left[{\displaystyle \genfrac{}{}{0pt}{}{\nu }{\widehat{j}-\widehat{\mathsf{ı}}}}\right]}_{p,q}{H}_{\widehat{\mathsf{ı}},\mu }^{\nu }(p,q,x)S_{p,q}\left(\mathbb{k}+1,\widehat{j}\right)B_{\ell -\mathbb{k},p,q}\left(y\right),\hfill \end{array}$$

and

$$\begin{array}{ccc}& & {\tilde{B}}_{\ell ,p,q}^{\left(\mu \right)}\left(y\right)\hfill \\ & =& \sum _{\xi =0}^{\ell }\sum _{\mathbb{k}=1}^{\xi +1}\sum _{\widehat{j}=1}^{\mathbb{k}}\sum _{\widehat{\mathsf{ı}}=1}^{\widehat{j}}{\left(-1\right)}^{\xi +\widehat{j}+1}{x}^{-\mathbb{k}}{p}^{\left({\displaystyle \genfrac{}{}{0pt}{}{\mathbb{k}-\widehat{j}}{2}}\right)+\nu \left(\widehat{j}-\widehat{\mathsf{ı}}\right)}{q}^{\left({\displaystyle \genfrac{}{}{0pt}{}{\mathbb{k}-\widehat{j}}{2}}\right)+\widehat{\mathsf{ı}}w-\mathbb{k}\left(\nu +w-1\right)}\xi !{\displaystyle \frac{{\left[\mathbb{k}\right]}_{p,q}!}{{\left[\xi +1\right]}_{p,q}!}}\left({\displaystyle \genfrac{}{}{0pt}{}{\ell }{\xi }}\right)\hfill \\ & & \times {\left[{\displaystyle \genfrac{}{}{0pt}{}{\nu +w}{\mathbb{k}-\widehat{j}}}\right]}_{p,q}{\left[{\displaystyle \genfrac{}{}{0pt}{}{w+\widehat{j}-\widehat{\mathsf{ı}}-1}{w-1}}\right]}_{p,q}{H}_{\widehat{\mathsf{ı}},\mu }^{\nu }(p,q,x)S_{p,q}\left(\xi +1,\mathbb{k}\right)B_{\ell -\xi ,p,q}\left(y\right).\hfill \end{array}$$

Proof. 

By (16), we have

$$L{i}_{\mu ,p,q}\left(xt\right)=\sum _{\ell =1}^{\infty }\sum _{\widehat{\mathsf{ı}}=1}^{\ell }{\left(-1\right)}^{\ell -\widehat{\mathsf{ı}}}{p}^{\left({\displaystyle \genfrac{}{}{0pt}{}{\ell -\widehat{\mathsf{ı}}}{2}}\right)}{q}^{\left({\displaystyle \genfrac{}{}{0pt}{}{\ell -\widehat{\mathsf{ı}}}{2}}\right)-\ell \left(\nu -1\right)}{\left[{\displaystyle \genfrac{}{}{0pt}{}{\nu }{\ell -\widehat{\mathsf{ı}}}}\right]}_{p,q}{H}_{\widehat{\mathsf{ı}},\mu }^{\nu }\left(p,q,x\right)t^{\ell },$$

and here if we take ${\displaystyle \frac{1-e_{p,q}\left(-t\right)}{x}}$ instead of $t,$ and also by (7), we obtain

$$\begin{array}{ccc}& & L{i}_{\mu ,p,q}\left(1-e_{p,q}\left(-t\right)\right)\hfill \\ & =& \sum _{\widehat{j}=1}^{\infty }\sum _{\widehat{\mathsf{ı}}=1}^{\widehat{j}}{\left(-1\right)}^{\widehat{\mathsf{ı}}}{x}^{-\widehat{j}}{p}^{\left({\displaystyle \genfrac{}{}{0pt}{}{\widehat{j}-\widehat{\mathsf{ı}}}{2}}\right)}{q}^{\left({\displaystyle \genfrac{}{}{0pt}{}{\widehat{j}-\widehat{\mathsf{ı}}}{2}}\right)-\widehat{j}\left(\nu -1\right)}{\left[\widehat{j}\right]}_{p,q}!{\left[{\displaystyle \genfrac{}{}{0pt}{}{\nu }{\widehat{j}-\widehat{\mathsf{ı}}}}\right]}_{p,q}\hfill \\ & & \times H_{\widehat{\mathsf{ı}},\mu }^{\nu }\left(p,q,x\right){\displaystyle \frac{{\left(e_{p,q}\left(-t\right)-1\right)}^{\widehat{j}}}{{\left[\widehat{j}\right]}_{p,q}!}}\hfill \\ & =& \sum _{\widehat{j}=1}^{\infty }\sum _{\widehat{\mathsf{ı}}=1}^{\widehat{j}}{\left(-1\right)}^{\widehat{\mathsf{ı}}}{x}^{-\widehat{j}}{p}^{\left({\displaystyle \genfrac{}{}{0pt}{}{\widehat{j}-\widehat{\mathsf{ı}}}{2}}\right)}{q}^{\left({\displaystyle \genfrac{}{}{0pt}{}{\widehat{j}-\widehat{\mathsf{ı}}}{2}}\right)-\widehat{j}\left(\nu -1\right)}{\left[\widehat{j}\right]}_{p,q}!{\left[{\displaystyle \genfrac{}{}{0pt}{}{\nu }{\widehat{j}-\widehat{\mathsf{ı}}}}\right]}_{p,q}\hfill \\ & & \times H_{\widehat{\mathsf{ı}},\mu }^{\nu }\left(p,q,x\right)\sum _{\ell =\widehat{j}}^{\infty }{\left(-1\right)}^{\ell }{S}_{p,q}\left(\ell ,\widehat{j}\right){\displaystyle \frac{t^{\ell }}{{\left[\ell \right]}_{p,q}!}}\hfill \\ & =& t\sum _{\ell =0}^{\infty }\sum _{\widehat{j}=1}^{\ell +1}\sum _{\widehat{\mathsf{ı}}=1}^{\widehat{j}}{\left(-1\right)}^{\ell +\widehat{\mathsf{ı}}+1}{x}^{-\widehat{j}}{p}^{\left({\displaystyle \genfrac{}{}{0pt}{}{\widehat{j}-\widehat{\mathsf{ı}}}{2}}\right)}{q}^{\left({\displaystyle \genfrac{}{}{0pt}{}{\widehat{j}-\widehat{\mathsf{ı}}}{2}}\right)-\widehat{j}\left(\nu -1\right)}{\displaystyle \frac{{\left[\widehat{j}\right]}_{p,q}!}{{\left[\ell +1\right]}_{p,q}!}}\hfill \\ & & \times {\left[{\displaystyle \genfrac{}{}{0pt}{}{\nu }{\widehat{j}-\widehat{\mathsf{ı}}}}\right]}_{p,q}{H}_{\widehat{\mathsf{ı}},\mu }^{\nu }\left(p,q,x\right)S_{p,q}\left(n+1,\widehat{j}\right)t^{\ell }.\hfill \end{array}$$

(18)

From (8), (9) and (18), we can write

$$\begin{array}{ccc}& & \sum _{\ell =0}^{\infty }{\tilde{B}}_{\ell ,p,q}^{\left(\mu \right)}\left(y\right){\displaystyle \frac{t^{\ell }}{\ell !}}\hfill \\ & =& {\displaystyle \frac{L{i}_{\mu ,p,q}\left(1-e_{p,q}\left(-t\right)\right)}{e_{p,q}\left(t\right)-1}}{e}_{p,q}\left(yt\right)\hfill \\ & =& \sum _{\ell =0}^{\infty }{B}_{\ell ,p,q}\left(y\right){\displaystyle \frac{t^{\ell }}{\ell !}}\sum _{\ell =0}^{\infty }\sum _{\widehat{j}=1}^{\ell +1}\sum _{\widehat{\mathsf{ı}}=1}^{\widehat{j}}{\left(-1\right)}^{\ell +\widehat{\mathsf{ı}}+1}{x}^{-\widehat{j}}{p}^{\left({\displaystyle \genfrac{}{}{0pt}{}{\widehat{j}-\widehat{\mathsf{ı}}}{2}}\right)}{q}^{\left({\displaystyle \genfrac{}{}{0pt}{}{\widehat{j}-\widehat{\mathsf{ı}}}{2}}\right)-\widehat{j}\left(\nu -1\right)}\hfill \\ & & \times {\displaystyle \frac{{\left[\widehat{j}\right]}_{p,q}!}{{\left[\ell +1\right]}_{p,q}!}}{\left[{\displaystyle \genfrac{}{}{0pt}{}{\nu }{\widehat{j}-\widehat{\mathsf{ı}}}}\right]}_{p,q}{H}_{\widehat{\mathsf{ı}},\mu }^{\nu }\left(p,q,x\right)S_{p,q}\left(\ell +1,\widehat{j}\right)t^{\ell }\hfill \\ & =& \sum _{\ell =0}^{\infty }\sum _{\mathbb{k}=0}^{\ell }\sum _{\widehat{j}=1}^{\mathbb{k}+1}\sum _{\widehat{\mathsf{ı}}=1}^{\widehat{j}}{\left(-1\right)}^{\mathbb{k}+\widehat{\mathsf{ı}}+1}{x}^{-\widehat{j}}{p}^{\left({\displaystyle \genfrac{}{}{0pt}{}{\widehat{j}-\widehat{\mathsf{ı}}}{2}}\right)}{q}^{\left({\displaystyle \genfrac{}{}{0pt}{}{\widehat{j}-\widehat{\mathsf{ı}}}{2}}\right)-\widehat{j}\left(\nu -1\right)}{\displaystyle \frac{{\left[\widehat{j}\right]}_{p,q}!}{{\left[\mathbb{k}+1\right]}_{p,q}!}}\hfill \\ & & \times {\left[{\displaystyle \genfrac{}{}{0pt}{}{\nu }{\widehat{j}-\widehat{\mathsf{ı}}}}\right]}_{p,q}{H}_{\widehat{\mathsf{ı}},\mu }^{\nu }\left(p,q,x\right)S_{p,q}\left(\mathbb{k}+1,\widehat{j}\right)B_{\ell -\mathbb{k},p,q}\left(y\right){\displaystyle \frac{t^{\ell }}{\left(\ell -\mathbb{k}\right)!}}.\hfill \end{array}$$

In this way, by carefully comparing the coefficients on both sides of the equation, we can derive the first equality as a direct result. Following a similar approach and applying the same reasoning, the second equality is also obtained in a straightforward manner. □

Theorem 7. 

For $\ell ,\mu ,\nu \ge 1,$ we have

$$\begin{array}{ccc}& & {\displaystyle \frac{{\left[\ell +1\right]}_{p,q}!}{\ell !}}{\tilde{T}}_{\ell ,p,q}^{\left(\mu \right)}\left(y\right)\hfill \\ & =& \sum _{\mathbb{k}=0}^{\ell }\sum _{\widehat{j}=1}^{\mathbb{k}+1}\sum _{\widehat{\mathsf{ı}}=1}^{\widehat{j}}{\left(-1\right)}^{\widehat{\mathsf{ı}}+\mathbb{k}+1}{x}^{-\widehat{j}}{p}^{\left({\displaystyle \genfrac{}{}{0pt}{}{\widehat{j}-\widehat{\mathsf{ı}}}{2}}\right)}{q}^{\left({\displaystyle \genfrac{}{}{0pt}{}{\widehat{j}-\widehat{\mathsf{ı}}}{2}}\right)-\widehat{j}\left(\nu -1\right)}{\left[\widehat{j}\right]}_{p,q}!{\left[{\displaystyle \genfrac{}{}{0pt}{}{\ell +1}{\mathbb{k}+1}}\right]}_{p,q}\hfill \\ & & \times {\left[{\displaystyle \genfrac{}{}{0pt}{}{\nu }{\widehat{j}-\widehat{\mathsf{ı}}}}\right]}_{p,q}{H}_{\widehat{\mathsf{ı}},\mu }^{\nu }(p,q,x)S_{p,q}\left(\mathbb{k}+1,\widehat{j}\right)T_{\ell -\mathbb{k},p,q}\left(y\right),\hfill \end{array}$$

and

$$\begin{array}{ccc}& & {\displaystyle \frac{{\left[\ell +1\right]}_{p,q}!}{\ell !}}{\tilde{T}}_{\ell ,p,q}^{\left(\mu \right)}\left(y\right)\hfill \\ & =& \sum _{\xi =0}^{\ell }\sum _{\mathbb{k}=1}^{\xi +1}\sum _{\widehat{j}=1}^{\mathbb{k}}\sum _{\widehat{\mathsf{ı}}=1}^{\widehat{j}}{\left(-1\right)}^{\xi +\widehat{j}+1}{x}^{-\mathbb{k}}{p}^{\left({\displaystyle \genfrac{}{}{0pt}{}{\mathbb{k}-\widehat{j}}{2}}\right)+\nu \left(\widehat{j}-\widehat{\mathsf{ı}}\right)}{q}^{\left({\displaystyle \genfrac{}{}{0pt}{}{\mathbb{k}-\widehat{j}}{2}}\right)+\widehat{\mathsf{ı}}w-\mathbb{k}\left(\nu +w-1\right)}{\left[\mathbb{k}\right]}_{p,q}!{\left[{\displaystyle \genfrac{}{}{0pt}{}{\ell +1}{\xi +1}}\right]}_{p,q}\hfill \\ & & \times {\left[{\displaystyle \genfrac{}{}{0pt}{}{\nu +w}{\mathbb{k}-\widehat{j}}}\right]}_{p,q}{\left[{\displaystyle \genfrac{}{}{0pt}{}{w+\widehat{j}-\widehat{\mathsf{ı}}-1}{w-1}}\right]}_{p,q}{H}_{\widehat{\mathsf{ı}},\mu }^{\nu }(p,q,x)S_{p,q}\left(\xi +1,\mathbb{k}\right)T_{\ell -\xi ,p,q}\left(y\right).\hfill \end{array}$$

Proof. 

Using (8), (9), the proof of Theorem 7 follows a similar approach to the proof of Theorem 6. Similar mathematical techniques and methods were used in both theorems, which suggests that the same methodological framework was applied to show the truth of Theorem 7. □

Now, the matrices of order $n,$ which are $n\times n$ matrices $A_n=\left[a_{\widehat{\mathsf{ı}},\widehat{j}}\right]$ and $C_n=\left[c_{\widehat{\mathsf{ı}},\widehat{j}}\right]$ such that $a_{\widehat{\mathsf{ı}},\widehat{j}}=H_{\widehat{\mathsf{ı}},\mu }^{\nu }(p,q,\widehat{j})$ and $c_{\widehat{\mathsf{ı}},\widehat{j}}=H_{\widehat{\mathsf{ı}},\mu }^w(p,q,\widehat{j})$, are defined. In this case, as a next step, we can state the following theorem:

Theorem 8. 

For any positive integer $n,$ we have

$$A_n=F_n{C}_n,$$

(19)

where the $n\times n$ matrix $F_n=\left[f_{\widehat{\mathsf{ı}},\widehat{j}}\right]$ with

$$f_{\widehat{\mathsf{ı}},\widehat{j}}=\left\{\begin{array}{cc}{p}^{w\left(\widehat{\mathsf{ı}}-\widehat{j}\right)}{q}^{\widehat{j}(\nu -w)}{\left[{\displaystyle \genfrac{}{}{0pt}{}{\widehat{\mathsf{ı}}-\widehat{j}+\nu -w-1}{\widehat{\mathsf{ı}}-\widehat{j}}}\right]}_{p,q}& if\widehat{\mathsf{ı}}\ge \widehat{j},\\ 0& \mathit{otherwise},\end{array}\right.$$

where $0\le w\le \nu -1.$

Proof. 

It is clearly $a_{1,1}=q^{\nu -1}=H_{1,\mu }^{\nu }(p,q,1)$ for $\widehat{\mathsf{ı}}=1,\widehat{j}=1.$ For $\widehat{\mathsf{ı}}=1,$$\widehat{j}>1,$ we write

$$\begin{array}{ccc}& & \sum _{\mathbb{k}=1}^n{f}_{1,\mathbb{k}}{c}_{\mathbb{k},\widehat{j}}\hfill \\ & =& \sum _{\mathbb{k}=1}^n{q}^{\mathbb{k}(\nu -w)}{p}^{w\left(1-\mathbb{k}\right)}{\left[{\displaystyle \genfrac{}{}{0pt}{}{\nu -w-\mathbb{k}}{1-\mathbb{k}}}\right]}_{p,q}{H}_{\mathbb{k},\mu }^w(p,q,\widehat{j})\hfill \\ & =& q^{\nu -w}{H}_{1,\mu }^w(p,q,\widehat{j})=q^{\nu -w}{\displaystyle \frac{q^{w-1}}{{\left[1\right]}_{p,q}^{\mu }}}\widehat{j}=H_{1,\mu }^{\nu }(p,q,\widehat{j})=a_{1,\widehat{j}}.\hfill \end{array}$$

For $\widehat{\mathsf{ı}}>1$ and $\widehat{j}\ge 1,$ we obtain

$$\begin{array}{ccc}& & \sum _{\mathbb{k}=1}^n{f}_{\widehat{\mathsf{ı}},\mathbb{k}}{c}_{\mathbb{k},\widehat{j}}\hfill \\ & =& \sum _{\mathbb{k}=1}^n{q}^{\mathbb{k}(\nu -w)}{p}^{w\left(\widehat{\mathsf{ı}}-\mathbb{k}\right)}{\left[{\displaystyle \genfrac{}{}{0pt}{}{\widehat{\mathsf{ı}}+\nu -w-\mathbb{k}-1}{\widehat{\mathsf{ı}}-\mathbb{k}}}\right]}_{p,q}{H}_{\mathbb{k},\mu }^w(p,q,\widehat{j})\hfill \\ & =& \sum _{\mathbb{k}=1}^{\widehat{\mathsf{ı}}}{q}^{\mathbb{k}(\nu -w)}{p}^{w\left(\widehat{\mathsf{ı}}-\mathbb{k}\right)}{\left[{\displaystyle \genfrac{}{}{0pt}{}{\widehat{\mathsf{ı}}+\nu -w-\mathbb{k}-1}{\widehat{\mathsf{ı}}-\mathbb{k}}}\right]}_{p,q}\sum _{l=1}^{\mathbb{k}}{\left[{\displaystyle \genfrac{}{}{0pt}{}{\mathbb{k}+w-l-1}{w-1}}\right]}_{p,q}{\displaystyle \frac{q^{\left(w-1\right)l}}{{\left[l\right]}_{p,q}^{\mu }}}{\widehat{j}}^l\hfill \\ & =& \sum _{l=1}^{\widehat{\mathsf{ı}}}{\displaystyle \frac{q^{\left(\nu -1\right)l}}{{\left[l\right]}_{p,q}^{\mu }}}{\widehat{j}}^l\sum _{\mathbb{k}=l}^{\widehat{\mathsf{ı}}}{q}^{(\mathbb{k}-l)(\nu -w)}{p}^{w\left(\widehat{\mathsf{ı}}-\mathbb{k}\right)}{\left[{\displaystyle \genfrac{}{}{0pt}{}{\widehat{\mathsf{ı}}+\nu -w-\mathbb{k}-1}{\widehat{\mathsf{ı}}-\mathbb{k}}}\right]}_{p,q}{\left[{\displaystyle \genfrac{}{}{0pt}{}{\mathbb{k}+w-l-1}{w-1}}\right]}_{p,q}\hfill \\ & =& \sum _{l=1}^{\widehat{\mathsf{ı}}}{\displaystyle \frac{q^{\left(\nu -1\right)l}}{{\left[l\right]}_{p,q}^{\mu }}}{\widehat{j}}^l\sum _{\mathbb{k}=w-1}^{\widehat{\mathsf{ı}}-l+w-1}{q}^{(\mathbb{k}-w+1)(\nu -w)}{p}^{w\left(\widehat{\mathsf{ı}}+w-\mathbb{k}-l-1\right)}{\left[{\displaystyle \genfrac{}{}{0pt}{}{\mathbb{k}}{w-1}}\right]}_{p,q}{\left[{\displaystyle \genfrac{}{}{0pt}{}{\widehat{\mathsf{ı}}+\nu -l-\mathbb{k}-2}{\nu -w-1}}\right]}_{p,q}\hfill \\ & =& a_{\widehat{\mathsf{ı}},\widehat{j}}.\hfill \end{array}$$

Taking $w-1=a,$$\widehat{\mathsf{ı}}-l-2+\nu =\ell$ and $\nu -w-1=b$ in (3), we obtain

$$\sum _{l=1}^{\widehat{\mathsf{ı}}}{\left[{\displaystyle \genfrac{}{}{0pt}{}{\widehat{\mathsf{ı}}+\nu -l-1}{\nu -1}}\right]}_{p,q}{\displaystyle \frac{q^{\left(\nu -1\right)l}}{{\left[l\right]}_{p,q}^{\mu }}}{\widehat{j}}^l=H_{\widehat{\mathsf{ı}},\mu }^{\nu }(p,q,\widehat{j})=a_{\widehat{\mathsf{ı}},\widehat{j}},$$

as claimed. □

For example, for $n=w=2,p={\displaystyle \frac{1}{2}},q={\displaystyle \frac{1}{3}},\mu =\nu =4,$ we write

$$\begin{array}{c}\hfill A_2=\left[\begin{array}{cc}{\displaystyle \frac{1}{27}}& {\displaystyle \frac{2}{27}}\\ & \\ {\displaystyle \frac{50993}{3645000}}& {\displaystyle \frac{61361}{1822500}}\end{array}\right]=\left[\begin{array}{cc}{\displaystyle \frac{1}{9}}& 0\\ & \\ {\displaystyle \frac{5}{216}}& {\displaystyle \frac{1}{81}}\end{array}\right]\left[\begin{array}{cc}{\displaystyle \frac{1}{3}}& {\displaystyle \frac{2}{3}}\\ & \\ {\displaystyle \frac{5717}{11250}}& {\displaystyle \frac{8309}{5625}}\end{array}\right]=F_2{C}_2.\end{array}$$

We can form the next identity as a result of Theorem 8.

Corollary 1. 

For $0<\ell$ and $x\in {\mathbb{R}}^{+},$ then

$$H_{\ell ,\mu }^{\nu }\left(p,q,x\right)=\sum _{\widehat{\mathsf{ı}}=1}^{\ell }{q}^{\widehat{\mathsf{ı}}(\nu -w)}{p}^{w\left(\ell -\widehat{\mathsf{ı}}\right)}{\left[{\displaystyle \genfrac{}{}{0pt}{}{\ell +\nu -w-\widehat{\mathsf{ı}}-1}{\ell -\widehat{\mathsf{ı}}}}\right]}_{p,q}{H}_{\widehat{\mathsf{ı}},\mu }^w(p,q,x),$$

(20)

where $0\le w\le \nu -1.$

Proof. 

Equating $\left(\ell ,x\right)$-entries of (19) gives the claimed result. □

3. Graphical Behavior of $H_{\ell ,\mu }^{\nu }\left(p,q,x\right)$

In this section, the numerical behavior of $H_{\ell ,\mu }^{\nu }\left(p,q,x\right)$ has been analyzed using Mathematica 11.2. Specifically, the independent parameter p is examined within the range $0<p<1$ for fixed values of $\ell =3,\mu =7,\nu =2,$ and $x=2$, while keeping q constant for each case. The resulting polynomial behavior of $H_{3,7}^2\left(p,q,2\right)$ is illustrated in Figure 1. When visualizing q values of $0.69,0.7,0.71,0.72,0.73$, and $0.74$, it is observed that the polynomial exhibits a higher magnitude for smaller p values $(p\to 0)$ and decreases rapidly as p approaches 1.

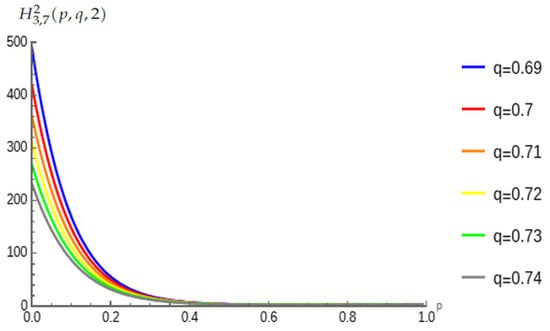
Figure 1. $H_{3,7}^2\left(p,q,2\right)$ values for some fixed q.

4. Conclusions

In conclusion, we define $\left(p,q\right)$-analogues of the generalized harmonic polynomials of order $\mu$, $H_{\ell ,\mu }\left(p,q,x\right)$ and the generalized hyperharmonic polynomials of order $\nu ,$ $H_{\ell ,\mu }^{\nu }\left(p,q,x\right)$. As an application, this paper has provided important insights in the field of applications of ($p,q$)-generalized hyperharmonic polynomials of order $\nu$. New equations involving Stirling numbers, Bernoulli polynomials, and target polynomials have been obtained. The proof methods and results developed in this research paper are expected to make significant contributions to the solution of problems in combinatorics, algebra and other mathematical disciplines in future research. In the study, new sums of certain numbers and polynomials are obtained using combinatorial operations, and the properties of these numbers and polynomials are analyzed in detail. In addition, generating functions are obtained and new and more complex equations are constructed by means of these functions, thus gaining a more comprehensive understanding of the deep mathematical structures of the related number sequences. Finally, a new equation is given using matrix multiplication. It is foreseen that these methods will have a wide range of applications in advanced mathematics studies and many applications. In addition to the contributions presented in this study, future research could explore several promising directions. One potential avenue is the extension of ($p,q$)-analogues to other families of polynomials and special functions, such as Hermite, Laguerre, and Chebyshev polynomials, which are widely used in mathematical physics and engineering. Additionally, the exploration of ($p,q$)-analogues in higher dimensions or in the context of multi-parameter generalizations could open new perspectives in both theoretical and applied mathematics. Another intriguing area is the development of numerical algorithms to compute ($p,q$)-generalized functions and polynomials efficiently. Such algorithms could facilitate their application in areas like numerical analysis, optimization, and machine learning. Furthermore, the connection between ($p,q$)-analogues and quantum mechanics, particularly in modeling quantum systems with deformed symmetries, remains an exciting domain that warrants deeper investigation. Overall, these future directions underscore the versatility and depth of ($p,q$)-analogues, promising a wide range of contributions across disciplines.