Intuitionistic Fuzzy Sequential Three-Way Decision Model in Incomplete Information Systems

Abstract

As an effective method for uncertain knowledge discovery and decision-making, the three-way decisions model has attracted extensive attention from scholars. However, in practice, the existing sequential three-way decision model often faces challenges due to factors such as missing data and unbalanced attribute granularity. To address these issues, we propose an intuitionistic fuzzy sequential three-way decision (IFSTWD) model, which introduces several significant contributions: (1) New intuitionistic fuzzy similarity relations. By integrating possibility theory, our model defines similarity and dissimilarity in incomplete information systems, establishing new intuitionistic fuzzy similarity relations and their cut relations. (2) Granulation method innovation. We propose a density neighborhood-based granulation method to partition decision attributes and introduce a novel criterion for evaluating attribute importance. (3) Enhanced decision process. By incorporating sequential three-way decision theory and developing a multi-level granularity structure, our model replaces the traditional equivalent relation in the decision-theoretic rough sets model, thus advancing the model’s applicability and effectiveness. The practical utility of our model is demonstrated through an example analysis of “Chinese + vocational skills” talent competency and validated through simulation experiments on the UCI dataset, showing superior performance compared to existing methods.

1. Introduction

In many real-world applications, decision-making is complicated by incomplete or uncertain information, making it difficult to achieve accurate outcomes using traditional methods. Conventional two-way decision models, which rely on binary classifications, often struggle to balance risk and uncertainty, leading to incorrect decisions in the presence of ambiguous data. To address these challenges, Yao [1] proposed the three-way decision model based on decision-theoretic rough sets [2], which introduces a third decision option to handle uncertainty more effectively. Unlike traditional two-way decisions, the three-way decisions model divides the domain into three mutually exclusive regions: the positive region (POS), the negative region (NEG), and the boundary region (BND). This approach mitigates the risk associated with making direct decisions when information is insufficient. To further handle objects in the boundary region, Yao [3] introduced the sequential three-way decisions model, which constructs a multi-granularity space using a sequence of attribute sets. During the sequential decision-making process, the boundary region is gradually reduced until a definitive decision is reached.

In recent years, the study of sequential three-way decisions models has attracted significant attention from scholars [4,5], particularly in the context of managing uncertainty in decision-making environments. Notably, Cui et al. [6] proposed a malware detection model integrating sequential three-way decisions with convolutional neural networks, while Qian et al. [7] developed a hierarchical multi-attribute decision-making method. On the other hand, intuitionistic fuzzy set (IFS) theory [8] is an extension of fuzzy set theory proposed by Atanassov, which enhances decision-making by accounting for degrees of uncertainty in incomplete information systems. Integrating IFS with three-way decision models [9,10,11], as explored in works such as Liu et al. [12] and Tiwari et al. [13], offers improved approaches to handling uncertainty and attribute importance. Additionally, new approaches leveraging fuzzy and intuitionistic fuzzy sets have emerged, as exemplified by Gohain et al. [14], who explored fuzzy similarity measures for decision-making. To make scientific decisions with incomplete information systems [15], it is necessary to reasonably handle the missing data, typically through three methods: imputation [16], deletion [17], and model extension [18]. In practice, the first two methods inevitably disrupt the original information in the data, potentially leading to inaccurate classification results. Therefore, scholars prefer the model extension method, which generalizes equivalence relations to similarity or tolerance relations. Wei et al. [19] constructed a logistic regression classifier and Wang et al. [20] proposed a three-way decision method based on regret theory in fuzzy incomplete information systems. In summary, the expansion or optimization of similarity relations effectively promotes the deep integration of incomplete information systems with intuitionistic fuzzy set theory.

In reality, data often come with incompleteness and fuzziness, and decision classification problems are influenced by multi-level granularity information, which may prevent optimal decision-making. Although recent studies have considered the impact of data missingness and multi-granularity fuzzy information on three-way decisions models, challenges remain in handling complex multi-granularity fuzzy information. Inspired by these ideas, this paper proposes a granulation method based on density neighborhoods in incomplete information systems, combining similarity and dissimilarity to divide the decision attribute set. Specifically, it primarily uses a multi-level structure to analyze incomplete information systems progressively, incorporating the effects of secondary condition attribute information into the constructed intuitionistic fuzzy similarity relations. Therefore, constructing a new attribute importance evaluation criterion and integrating the nuanced depiction of uncertain information by intuitionistic fuzzy similarity relations into the sequential decision-making process of three-way decisions can enhance the comprehensive expression of uncertain information in complex environments. This study makes the following contributions:

(1) We propose a novel granulation method based on density neighborhoods for handling incomplete information systems;

(2) We introduce a new attribute importance evaluation criterion that enhances decision-making accuracy in fuzzy environments;

(3) We develop an intuitionistic fuzzy sequential three-way decision model to manage multi-granular information more effectively, improving the comprehensiveness of uncertain information expression.

The remaining parts of this study are structured as follows. In Section 2, some basic knowledge is reviewed. Section 3 introduces a new attribute importance evaluation criterion based on attribute dependency and decision cost. Section 4 utilizes intuitionistic fuzzy similarity relations and cutoff relations to obtain similar classes, constructing the IFSTWD model based on incomplete information systems and providing the partitioning rules for each level. In Section 5, the proposed method is elaborated through a concrete example and compared with several methods on UCI data sets, and, finally, summarizes this article.

2. Preliminaries

2.1. Intuitionistic Fuzzy Set

Definition 1

[21]. Let $U$ be a finite domain. An intuitionistic fuzzy set on $U$ is defined as $S=\{\left.<x,{\mu }_S(x),{\nu }_S(x)>\right|x\in U\}$, where ${\mu }_S(x):U\to [0,1]$ represents the membership degree of $S$, and ${\nu }_S(x):U\to [0,1]$ represents the non-membership degree of $S$. $\forall x\in U$, $0\le {\mu }_S(x)+{\nu }_S(x)\le 1$ holds. The hesitation degree of $S$ is ${\pi }_S(x)=1-{\mu }_S(x)-{\nu }_S(x)$, where ${\pi }_S(x)\in [0,1]$.

For convenience, $({\mu }_S,{\nu }_S)$ is used when the membership and non-membership functions of $<x,{\mu }_S(x),{\nu }_S(x)>$ are real numbers, and $({\mu }_S,{\nu }_S)$ is called an intuitionistic fuzzy number.

Definition 2

[21]. Let $S$ and $T$ be intuitionistic fuzzy sets on the domain $U$. The operations of $S$ and $T$ are defined as follows:

(1)	$S\cup T=\{\left.<x,{\mu }_S(x)\vee {\mu }_T(x),{\nu }_S(x)\wedge {\nu }_T(x)>\right|\forall x\in U\}$;
(2)	$S\cap T=\{\left.<x,{\mu }_S(x)\wedge {\mu }_T(x),{\nu }_S(x)\vee {\nu }_T(x)>\right|\forall x\in U\}$;
(3)	$S\subseteq T=\{\left.<x,{\mu }_S(x)\le {\mu }_T(x),{\nu }_S(x)\ge {\nu }_T(x)>\right|\forall x\in U\}$;
(4)	$S=T=\{\left.<x,{\mu }_S(x)={\mu }_T(x),{\nu }_S(x)={\nu }_T(x)>\right|\forall x\in U\}$;
(5)	$S^C=\{\left.<x,\nu (x),\mu (x)>\right|x\in R\}$.

Definition 3

[22]. Let $sim(S,T)$ denote the similarity degree between intuitionistic fuzzy sets $S$ and $T$. The similarity degree satisfies the following properties:

(1)	$0\le sim(S,T)\le 1$;
(2)	$sim(S,T)=1\iff S=T$;
(3)	$sim(S,T)=sim(T,S)$;
(4)	If $S\subseteq T\subseteq W$, then $sim(S,W)\le min(sim(S,T),sim(T,W))$.

Definition 4

[21]. Let the quadruple $IIS=(U,AT,V,f)$ represents an intuitionistic fuzzy information system, where $U$ is a finite non-empty universe, $AT$ is a finite non-empty set of attributes, $V$ is the range of attribute values, $V=\{\left.<x,{\mu }_a(x),{\nu }_a(x)>\right|\forall x\in U,0\le {\mu }_a(x)+{\nu }_a(x)\le 1,{\mu }_a(x)\in [0,1],{\nu }_a(x)\in [0,1]\}$, $V_a$ is the set of membership and non-membership values for attribute $a$ $(V_a\subseteq V)$, and $f:U\times AT\to V$ is an information function, where $\forall a\in AT, x\in U, f(x,a)\in V_a$.

Definition 5

[14]. Let $U_1$ and $U_2$ be finite non-empty domain. The intuitionistic fuzzy binary relation $I$ between $U_1$ and $U_2$ is defined as:

$$I(x,y)=\{\left.{\mu }_I(x,y),v_I(x,y)\right|x\in U_1,y\in U_2\}$$

(1)

where ${\mu }_I:U_1\times U_2\to [0,1]$ and $v_I:U_1\times U_2\to [0,1]$, satisfying $0\le {\mu }_I(x,y)+v_I(x,y)\le 1$. $IFR(U_1\times U_2)$ denotes all the intuitionistic fuzzy binary relations on $U_1\times U_2$.

Definition 6

[23]. For $\forall x,y,z\in U$, $R_1\in IFR(U\times U)$, $R_1$ is called a similarity relation, and it has the following properties:

(1)

Reflexivity: $\mu (x,x)=(1,0)$, $\nu (x,x)=(0,1)$;

(2)

Symmetry: $R_1(x,y)=R_1(y,x)$, where ${\mu }_{R1}(x,y)={\mu }_{R1}(y,x)$, ${\nu }_{R1}(x,y)={\nu }_{R1}(y,x)$;

(3)

Transitivity: If $x\subseteq y\subseteq z$, then $R_1(x,z)\subseteq R_1(x,y)$, $R_1(x,z)\subseteq R_1(y,z)$.

2.2. Rough Set

Definition 7

[24]. Let $IIS=(U,AT,V,f)$ be an intuitionistic fuzzy information system, where $R$ denotes an equivalence relation on $U$. For $\forall X\subseteq U$, the lower and upper approximation sets of $X$ with respect to the equivalence relation $R$ can be described as follows:

$$\underset{¯}{R}(X)=\{x\in U\left|{\left[x\right]}_R\subseteq X\right.\};$$

(2)

$$\overline{R}(X)=\{x\in U\left|{\left[x\right]}_R\cap X\ne \varnothing \right.\}$$

(3)

Theorem 1

[24]. The properties related to the rough set are as follows:

(1)

$\underset{¯}{R}(X)\subseteq X\subseteq \overline{R}(X)$;

(2)

$\underset{¯}{R}(\varnothing )=\overline{R}(\varnothing )=\varnothing$, $\underset{¯}{R}(U)=\overline{R}(U)=U$;

(3)

If $X\subseteq Y$, then $\overline{R}(X)\subseteq \overline{R}(Y)$, $\underset{¯}{R}(X)\subseteq \underset{¯}{R}(Y)$;

(4)

$\overline{R}(X\cup Y)\supseteq \overline{R}(X)\cup \overline{R}(Y)$, $\overline{R}(X\cap Y)\subseteq \overline{R}(X)\cap \overline{R}(Y)$;

(5)

$\underset{¯}{R}(X\cup Y)\supseteq \underset{¯}{R}(X)\cup \underset{¯}{R}(Y)$, $\underset{¯}{R}(X\cap Y)\subseteq \underset{¯}{R}(X)\cap \underset{¯}{R}(Y)$;

(6)

$\overline{R}(X^C)={(\overline{R}(X))}^C$, $\underset{¯}{R}(X^C)={(\underset{¯}{R}(X))}^C$.

Here, $X$ and $Y$ are subsets of $U$, and $X^C$ is the complement of $X$.

2.3. Classic Three-Way Decisions Model

Definition 8

[2,25]. Let $U$ be a finite domain, $R$ an equivalence relation on $U$, and its equivalence class partition be $U/R=\{\left.{[x]}_R\right|x\in U\}$, where ${[x]}_R$ is the equivalence class of $x$. Given the threshold values $\overline{\alpha }$, $\overline{\beta }$, and $0\le \overline{\beta }<\overline{\alpha }\le 1$, the positive, boundary, and negative regions are defined as follows:

$$POS(X)=\{\left.x\in U\right|P(\left.X\right|{[x]}_R)\ge \overline{\alpha }\};$$

$$BND(X)=\{\left.x\in U\right|\overline{\beta }<P(\left.X\right|{[x]}_R)<\overline{\alpha }\};$$

$$NEG(X)=\{\left.x\in U\right|P(\left.X\right|{[x]}_R)\le \overline{\beta }\}$$

where $POS(X)$ represents the set of objects that accept the decision, $NEG(X)$ represents the set of objects that reject the decision, and $BND(X)$ represents the set of objects that delay the decision. Based on the Bayesian decision process, Yao proposes a three-way decision model. Suppose the state set is $\Omega =\{X,X^C\}$, where $X$ and $X^C$ represent belonging and not belonging, respectively, and the action set is ${\rm K}=\{a_P,a_B,a_N\}$, where $a_P, a_B$, and $a_N$ represent $x\in NEG(X)$. Suppose that ${\lambda }_{PP}$, ${\lambda }_{BP}$, and ${\lambda }_{NP}$ represent the loss functions of selected actions $a_P, a_B$, and $a_N$ when $x\in X$. Similarly, suppose that ${\lambda }_{PN}$, ${\lambda }_{BN}$, and ${\lambda }_{NN}$ represent the loss functions for choosing three actions when $x\in X^C$. The corresponding loss functions for different actions are shown in Table 1.

Table 1. Loss functions corresponding to different actions.

	X	XC
$a_P$	${\lambda }_{PP}$	${\lambda }_{PN}$
$a_B$	${\lambda }_{BP}$	${\lambda }_{BN}$
$a_N$	${\lambda }_{NP}$	${\lambda }_{NN}$

Expected loss calculation:

$$R(\left.a_P\right|{[x]}_R)={\lambda }_{PP}P(\left.X\right|{[x]}_R)+{\lambda }_{PN}P(\left.X^C\right|{[x]}_R);$$

(4)

$$R(\left.a_B\right|{[x]}_R)={\lambda }_{BP}P(\left.X\right|{[x]}_R)+{\lambda }_{BN}P(\left.X^C\right|{[x]}_R);$$

(5)

$$R(\left.a_N\right|{[x]}_R)={\lambda }_{NP}P(\left.X\right|{[x]}_R)+{\lambda }_{NN}P(\left.X^C\right|{[x]}_R)$$

(6)

According to the Bayesian decision process, the minimum risk rule is as follows:

Acceptance rule (P1): $R(\left.a_P\right|{[x]}_R)\le R(\left.a_B\right|{[x]}_R)\wedge R(\left.a_P\right|{[x]}_R)\le R(\left.a_N\right|{[x]}_R)$, $x\in POS(X)$;

Deferment rule (B1): $R(\left.a_B\right|{[x]}_R)\le R(\left.a_P\right|{[x]}_R)\wedge R(\left.a_B\right|{[x]}_R)\le R(\left.a_N\right|{[x]}_R)$, $x\in BND(X)$;

Rejection rule (N1): $R(\left.a_N\right|{[x]}_R)\le R(\left.a_P\right|{[x]}_R)\wedge R(\left.a_N\right|{[x]}_R)\le R(\left.a_B\right|{[x]}_R)$, $x\in NEG(X)$.

The corresponding decision rules are as follows:

(P2) If $P(\left.X\right|{[x]}_R)\ge \overline{\alpha }$, then $x\in POS(X)$;

(B2) If $\overline{\beta }<P(\left.X\right|{[x]}_R)<\overline{\alpha }$, then $x\in BND(X)$;

(N2) If $P(\left.X\right|{[x]}_R)\le \overline{\beta }$, then $x\in NEG(X)$.

Here,

$$\overline{\alpha }={\displaystyle \frac{{\lambda }_{PN}-{\lambda }_{BN}}{({\lambda }_{PN}-{\lambda }_{BN})+({\lambda }_{BP}-{\lambda }_{PP})}},$$

$$\overline{\beta }={\displaystyle \frac{{\lambda }_{BN}-{\lambda }_{NN}}{({\lambda }_{BN}-{\lambda }_{NN})+({\lambda }_{NP}-{\lambda }_{BP})}}$$

2.4. Sequential Three-Way Decisions Model

Definition 9

[26,27]. Let $LS=(U,AT=C\cup D,V,f)$ represent an intuitionistic fuzzy decision information system where $U$ is a finite domain, $AT$ is a non-empty finite set of attributes, $V$ is the range of attribute values, and $f:U\times AT\to V$ is an information mapping function. $C=\{a_1,a_2,a_3\dots a_n\}$ represents the set of condition attributes and $D$ represents the set of decision attributes. Suppose $C_0=\left\{a_1\right\}$, $C_1=\{a_1,a_2\}$, $C_n=\{a_1,a_2,\dots ,a_n\}$ is a sequence of nested attribute sets that satisfy $C_0\subset C_1\subset \dots \subset C_n\dots \subseteq C$. The multi-level granularity structure based on the condition attribute set is denoted as $GI$, and the $i$-th$(i=1,2,\dots ,n)$ level granularity structure is denoted as $G{I}_i$, then the sequential three-way decision is expressed as follows:

$$GI=\{G{I}_1,G{I}_2,\dots ,G{I}_n\};$$

(7)

$$G{I}_i=(U_i,A{T}_i=C_i\cup D_i,V_i,f_i)$$

(8)

where $C_i$ represents the subset of condition attributes in the $i$-th level granularity structure, $U_i$ represents the domain of discourse of the $i$-th level granularity structure, $A{T}_i$ is the union of $C_i$ and the decision attribute subset $D_i$, $V_i$ is the attribute value range of the $i$-th level granularity structure, and $f_i$ is the information mapping function of the $i$-th level granularity structure.

Definition 10

[26,27]. Let $LS=(U,AT=C\cup D,V,f)$ and let a nested attribute set sequence satisfy $C_0\subset C_1\subset \dots \subset C_n\dots \subseteq C$, where $C$ is the set of condition attributes and $C_i(i=1,2,3\dots )$ is a subset of condition attributes. Let ${\pi }_D=\{D_1,D_2,\dots ,D_m\}$ be the set of decision classes and let $D_i^j(j=1,2,\dots ,m)$ be a subset of decision classes under the multi-level granularity structure $G{I}_i$. The positive, boundary, and negative regions of the $D_i^j$ with respect to the threshold pair $({\overline{\alpha }}_i,{\overline{\beta }}_i)(0\le {\overline{\beta }}_i<{\overline{\alpha }}_i\le 1)$ are defined follows:

$$\begin{array}{l}POS(D_i^j)=\{\left.x\in U_i\right|P(\left.D_i^j\right|{[x]}_{C_i})\ge {\overline{\alpha }}_i\};\\ BND(D_i^j)=\{\left.x\in U_i\right|{\overline{\beta }}_i<P(\left.D_i^j\right|{[x]}_{C_i})<{\overline{\alpha }}_i\};\\ NEG(D_i^j)=\{\left.x\in U_i\right|P(\left.D_i^j\right|{[x]}_{C_i})\le {\overline{\beta }}_i\}.\end{array}$$

2.5. Possibility Theory

Definition 11

[28]. Let $Nec$ and $Plt$ represent the necessity measure and possibility measure, respectively, and $U$ is a non-empty finite domain. For $\forall S\in U$, $Nec$ and $Plt$ satisfy:

(1)

$Nec(S)=1-Plt(S^C)$, and $S^C$ is the complement of $S$;

(2)

$Plt({\cup }_i{S}_i)=Su{p}_i(Plt(S_i))(i=1,2\dots )$, $Nec({\cap }_i{S}_i)=in{f}_i(Nec(S_i))(i=1,2\dots )$;

(3)

$0\le Nec(S)\le 1,0\le Plt(S)\le 1$;

(4)

$Plt(S)\ge Nec(S)$.

3. Intuitionistic Fuzzy Similarity Relations under Incomplete Information Systems

This section mainly puts forward the intuitionistic fuzzy similarity degree and dissimilarity degree based on possibility theory under an incomplete information system, proves their related properties, and constructs the corresponding intuitionistic fuzzy similarity relation.

3.1. Intuitionistic Fuzzy Similarity Relation Based on Possibility Theory

Definition 12.

For $\forall x\in U$, the necessity measure of element $x$ in $S$ is defined as:

$$Ne{c}_S(x)=inf{\mu }_S(x)$$

(9)

Definition 13.

For $\forall x\in U$, the possibility measure of element $x$ in $S$ is defined as:

$$Pl{t}_S(x)=sup(1-{\nu }_S(x))$$

(10)

Theorem 2.

Let $Nec$ and $Plt$ respectively denote the necessity measure and the possibility measure. $U$ is a finite domain, and $\forall x,y\in U$, $S$ and $T$ are intuitionistic fuzzy subsets on $U$. If $S\subseteq T$, then $Ne{c}_S(x)\le Ne{s}_T(x)$ and $Pl{t}_S(x)\le Pl{t}_T(x)$.

Proof .

Since $S\subseteq T$, it follows that ${\mu }_S(x)\le {\mu }_T(x)$ and ${\nu }_S(x)\ge {\nu }_T(x)$. Therefore, $inf{\mu }_S(x)\le inf{\mu }_T(x)$ and $sup(1-{\nu }_S(x))\le sup(1-{\nu }_T(x))$, thus $Ne{c}_S(x)\le Ne{c}_T(x)$ and $Pl{t}_S(x)\le Pl{t}_T(x)$. □

Definition 14.

Let $LS=(U,AT=C\cup D,V,f)$, $\forall x,y\in U$, $S=\{\left.f(x,a)\right|a\in AT\}$, and $T=\{\left.f(y,a)\right|a\in AT\}$ represent the intuitionistic fuzzy set of $x$ and $y$ under the conditional attribute set $AT$. $f(x,a)$ and $f(y,a)$ represent the values of $x$ and $y$ under attribute $a$. The intuitionistic fuzzy similarity degree $S{I}_a(x,y)$ and dissimilarity degree $D{I}_a(x,y)$ between $x$ and $y$ with respect to the attribute set $AT$ are defined as:

$$S{I}_a(x,y)=\left\{\begin{array}{ll}1,& f(x,a)=f(y,a)\\ min\left\{1-|Pl{t}_S(a)-Pl{t}_T(a)|,1-|Ne{c}_S(a)-Ne{c}_T(a)|\right\},& f(x,a)\ne f(y,a)\end{array}\right.$$

(11)

$$D{I}_a(x,y)=\left\{\begin{array}{ll}0,& f(x,a)=f(y,a)\\ max\left\{|Pl{t}_S(a)-Pl{t}_T(a)|, |Ne{c}_S(a)-Ne{c}_T(a)|\right\}, & f(x,a)\ne f(y,a)\end{array}\right.$$

(12)

Proof .

By Definition 11, $S{I}_a(x,y)$ satisfies properties 1–3 of Definition 3.

If $S\subseteq T\subseteq W$, according to Definition 11 and Theorem 2, it follows that:

$$\begin{array}{l}Pl{t}_S(a)\le Pl{t}_T(a)\le Pl{t}_W(a), \\ Ne{c}_S(a)\le Ne{s}_T(a)\le Ne{s}_W(a),\\ max\left\{\left|Pl{t}_S(a)-Pl{t}_T(a)\right|,\left|Ne{c}_S(a)-Ne{c}_T(a)\right|\right\}\le max\left\{\left|Pl{t}_S(a)-Pl{t}_W(a)\right|,\left|Ne{c}_S(a)-Ne{c}_W(a)\right|\right\},\\ max\left\{\left|Pl{t}_T(a)-Pl{t}_W(a)\right|,\left|Ne{c}_T(a)-Ne{c}_W(a)\right|\right\}\le max\left\{\left|Pl{t}_S(a)-Pl{t}_W(a)\right|,\left|Ne{c}_S(a)-Ne{c}_W(a)\right|\right\}.\end{array}$$

Thus, $D{I}_a(x,z)\ge max\{D{I}_a(x,y),D{I}_a(y,z)\}$ and $S{I}_a(x,z)$$\le min\{S{I}_a(x,y),S{I}_a(y,z)\}$. □

Theorem 3.

Let $IIS=(U,AT,V,f)$, $\forall x,y\in U$, $\forall a\in AT$, $S{I}_a(x,y)$, and $D{I}_a(x,y)$ represent the similarity degree and dissimilarity degree of $x$ and $y$ with respect to $a$, and where $S{R}_a(x,y)=(S{I}_a(x,y),D{I}_a(x,y))$ is the intuitionistic fuzzy similarity.

Proof .

(1) If $\forall x\in U$, $S{I}_a(x,x)=1$, and $D{I}_a(x,x)=0$, then $x=y$.

(2) If $\forall x,y\in U$ and $S{R}_a(x,y)=(S{I}_a(x,y),D{I}_a(x,y))$, then $S{I}_a(x,y)=S{I}_a(y,x)$, $D{I}_a(x,y)=D{I}_a(y,x)$, and $S{R}_a(x,y)=S{R}_a(y,x)$.

(3) $0\le S{I}_a(x,y)\le 1$ and $0\le D{I}_a(x,y)\le 1$ if $x=y$, and $S{I}_a(x,y)+D{I}_a(x,y)=1+0=1$. If $x\ne y$, then we have

$$S{I}_a(x,y)+D{I}_a(x,y)=max\left\{\left|Pl{t}_S(a)-Pl{t}_T(a)\right|,\left|Ne{c}_S(a)-Ne{c}_T(a)\right|\right\}+min\left\{1-\left|Pl{t}_S(a)-Pl{t}_T(a)\right|\right.,$$

$$\left.1-\left|Ne{c}_S(a)-Ne{c}_T(a)\right|\right\}=max\left\{\left|Pl{t}_S(a)-Pl{t}_T(a)\right|,\left|Ne{c}_S(a)-Ne{c}_T(a)\right|\right\}+1-max\left\{\left|Pl{t}_S(a)-Pl{t}_T(a)\right|,\right.$$

$$\left.\left|Ne{c}_S(a)-Ne{c}_T(a)\right|\right\}\le 1.$$

(4) $S{I}_a(x,z)\le S{I}_a(x,y)$, $S{I}_a(x,z)\le S{I}_a(y,z)$, $D{I}_a(x,z)\ge D{I}_a(x,y)$, and $D{I}_a(x,z)\ge D{I}_a(x,y)$ can be known from $\forall x,y,z\in U$, $x\subseteq y\subseteq z$, and $S{I}_a(x,z)\le min\left\{S{I}_a(x,y),S{I}_a(y,z)\right\}$, so $S{R}_a(x,z)\subseteq S{R}_a(x,y)$ and $S{R}_a(x,z)\subseteq S{R}_a(y,z)$. □

In summary, $S{R}_a(x,y)=(S{I}_a(x,y),D{I}_a(x,y))$ is the intuitionistic fuzzy similarity relation between $x$ and $y$ with respect to attribute $a$.

3.2. Intuitionistic Fuzzy Similarity Relations under Incomplete Information Systems

Definition 15.

Let $ILS=(U,AT=C\cup D,V,*,f)$ be an intuitionistic fuzzy incomplete decision information system as shown in Table 2, where the domain of discourse $U=\{x_1,x_2,\dots ,x_n\}$ and $x,y,z\in U$. The attribute set $AT$ contains the condition attribute set $C=\{a_1,a_2,a_3\dots a_n\}$ and the decision attribute $D$, $V$ is the range of attribute values, * is the missing data, and $f:U\times AT\to \{V,*\}$ is the information mapping function.

Table 2. ILS example (* is the missing data).

	a1	a2	a3	D
$x_1$	(0.2, 0.7)	(0.6, 0.3)	(0.4, 0.5)	(0.2, 0.7)
$x_2$	(0.6, *)	(0.8, 0.1)	(*, 0.4)	(0.7, 0.3)
$x_3$	(0.2, 0.7)	(*, * )	(0.6, 0.3)	(0.2, 0.7)
$x_4$	(0.5, 0.4)	(*, 0.4)	(0.7, 0.2)	(0.5, 0.0)

(1) If $f(x,a)=({\mu }_a(x),{\nu }_a(x))$ and $f(y,a)=({\mu }_a(y),{\nu }_a(y))$, then $S{I}_a(x,y)$ and $D{I}_a(x,y)$ are as follows:

$$S{I}_a(x,y)=\left\{\begin{array}{ll}1,& f(x,a)=f(y,a)\\ min\left\{1-|Pl{t}_x(a)-Pl{t}_y(a)|,1-|Ne{c}_x(a)-Ne{c}_y(a)|\right\},& f(x,a)\ne f(y,a)\end{array}\right.$$

$$D{I}_a(x,y)=\left\{\begin{array}{ll}0,& f(x,a)=f(y,a)\\ max\left\{|Pl{t}_x(a)-Pl{t}_y(a)|, |Ne{c}_x(a)-Ne{c}_y(a)|\right\},& f(x,a)\ne f(y,a)\end{array}\right.$$

(2) If $f(x,a)=({\mu }_a(x),*)$, $f(y,a)=({\mu }_a(y),*)$, then $S{I}_a(x,y)$ and $D{I}_a(x,y)$ are as follows:

$$S{I}_a(x,y)=\left\{\begin{array}{ll}1,& f(x,a)=f(y,a)\\ min\left\{1-max(1-{\nu }_{x_i}(a)),1-|Ne{c}_x(a)-Ne{c}_y(a)|\right\},& f(x,a)\ne f(y,a)\end{array}\right.$$

(13)

$$D{I}_a(x,y)=\left\{\begin{array}{ll}0,& f(x,a)=f(y,a)\\ max\left\{max(1-{\nu }_{x_i}(a)), |Ne{c}_x(a)-Ne{c}_y(a)|\right\},& f(x,a)\ne f(y,a)\end{array}\right.$$

(14)

where $x_i\in U$.

Proof .

(a) For $\forall x,y\in U$, $S{I}_a(x,y)=min\{min({\nu }_{x_i}(a)),1-\left|Ne{c}_x(a)-Ne{c}_y(a)\right|\}$ and $S{I}_a(y,x)=min\{min$$({\nu }_{x_i}(a)),1-\left|Ne{c}_y(a)-Ne{c}_x(a)\right|\}$. So $S{I}_a(x,y)=S{I}_a(y,x)$;

Similarly, $D{I}_a(x,y)=D{I}_a(y,x)$. For $\forall x\in U$, if $S{I}_a(x,x)=1$ and $D{I}_a(x,x)=0$, then $x=y$.

(b) For $\forall x,y\in U$, $S{D}_a(x,y)=(S{I}_a(x,y),D{I}_a(x,y))$, with $S{I}_a(x,y)=S{I}_a(y,x)$, $D{I}_a(x,y)=D{I}_a(y,x)$, and $S{R}_a(x,y)=S{R}_a(y,x)$;

(c) By $0\le {\nu }_{S_i}(a)\le 1$ and $0\le \left|Ne{c}_x(a)-Ne{c}_y(a)\right|\le 1$, $0\le S{I}_a(x,y)\le 1$ and $0\le D{I}_a(x,y)\le 1$;

If $x=y$, then $S{I}_a(x,y)+D{I}_a(x,y)=1+0=1$;

If $x\ne y$, then $S{I}_a(x,y)+D{I}_a(x,y)=min\left\{1-max\right.(1-{\nu }_{x_i}(a)),$$\left.1-\left|Ne{c}_x(a)-Ne{c}_y(a)\right|\right\}+$$max\left\{max(1-{\nu }_{x_i}(a)),\left|Ne{c}_x(a)-Ne{c}_y(a)\right|\right\}=1-max\left\{max(1-{\nu }_{x_i}(a)),\left|Ne{c}_x(a)-Ne{c}_y(a)\right|\right\}+$$max\left\{max(1-{\nu }_{S_i}(a)),\left|Ne{c}_x(a)-Ne{c}_y(a)\right|\right\}\le 1$;

(d) For $x\subseteq y\subseteq z$ and $S{I}_a(x,z)\le min\{S{I}_a(x,y),S{I}_a(y,z)\}$, $S{I}_a(x,z)\le S{I}_a(y,z)$, $S{I}_a(x,z)\le S{I}_a(x,y)$, $D{I}_a(x,z)\ge D{I}_a(x,y)$, and $D{I}_a(x,z)\ge D{I}_a(y,z)$. Thus, $S{R}_a(x,z)\subseteq S{R}_a(x,y)$ and $S{R}_a(x,z)\subseteq S{R}_a(y,z)$.

In summary, $S{R}_a(x,y)=(S{I}_a(x,y),D{I}_a(x,y))$ is the intuitionistic fuzzy similarity relation between $x$ and $y$ with respect to attribute $a$.

(3) If $f(x,a)=({\mu }_a(x),*)$ and $f(y,a)=({\mu }_a(y),{\nu }_a(y))$, then $S{I}_a(x,y)$ and $D{I}_a(x,y)$ are $S{I}_a(x,y)=0$ and $D{I}_a(x,y)=1$;

(4) If $f(x,a)=(*,{\nu }_a(x))$ and $f(y,a)=({\mu }_a(y),{\nu }_a(y))$, then $S{I}_a(x,y)$ and $D{I}_a(x,y)$ are $S{I}_a(x,y)=0$ and $D{I}_a(x,y)=1$;

(5) If $f(x,a)=(*,{\nu }_a(x))$ and $f(y,a)=(*,{\nu }_a(y))$, then $S{I}_a(x,y)$ and $D{I}_a(x,y)$ are as follows:

$$S{I}_a(x,y)=\left\{\begin{array}{ll}1,& {\nu }_a(x)={\nu }_a(y)\\ min\left\{1-|Pl{t}_x(a)-Pl{t}_y(a)|, 1-min({\mu }_{x_i}(a))\right\},& {\nu }_a(x)\ne {\nu }_a(y)\end{array}\right.$$

(15)

$$D{I}_a(x,y)=\left\{\begin{array}{ll}1,& {\nu }_a(x)={\nu }_a(y)\\ max\left\{|Pl{t}_x(a)-Pl{t}_y(a)|,min({\mu }_{x_i}(a))\right\},& {\nu }_a(x)\ne {\nu }_a(y)\end{array}\right.$$

(16)

Similarly, $S{R}_a(x,y)=(S{I}_a(x,y),D{I}_a(x,y))$ is the intuitionistic fuzzy similarity relation between $x$ and $y$ with $a$;

(6) If $f(x,a)=(*,*)$ and $f(y,a)=({\mu }_a(y),{\nu }_a(y))$, then $S{I}_a(x,y)=0$ and $D{I}_a(x,y)=1$;

(7) If $f(x,a)=(*,{\nu }_a(x))$ and $f(y,a)=({\mu }_a(y),*)$, then $S{I}_a(x,y)=0$ and $D{I}_a(x,y)=1$;

(8) If $f(x,a)=(*,{\nu }_a(x))$ and $f(y,a)=(*,*)$, then $S{I}_a(x,y)=0$ and $D{I}_a(x,y)=1$;

(9) If $f(x,a)=({\mu }_a(x),*)$ and $f(y,a)=(*,*)$, then $S{I}_a(x,y)=0$ and $D{I}_a(x,y)=1$;

(10) If $f(x,a)=(*,*)$ and $f(y,a)=(*,*)$, then $S{I}_a(x,y)=1$ and $D{I}_a(x,y)=0$. □

4. Sequential Three-Way Decisions Based on Intuitionistic Fuzzy Similarity Relations under ILS

In this section, a decision partition method based on density neighborhood is proposed, and a new attribute importance evaluation criterion is given according to attribute dependency and decision cost, and the IFSTWD model is constructed by combining the sequential thought. The corresponding framework is shown in Figure 1.

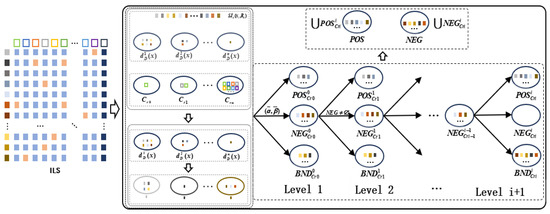
Figure 1. Overall framework of IFSTWD.

4.1. IFSTWD Model Construction

Definition 16.

Let $ILS=(U,AT=C\cup D,V,*,f)$, $N_D\left(x\right)$ represent the similarity degree of intuitionistic fuzzy decisions, where $x\in U$. The similarity degree between object $x_i$ and $R_D$ with respect to the $D$ is $S{I}_D(x_i,R_D)$, where $R_D=(max({\mu }_D(x_i)),min({\nu }_D(x_i))$. Sort the objects from small to large according to their similarity degree, and the sorting result can be obtained as follows:

$$N_D(x)=\{x_{r1},x_{r2},x_{r3}\dots x_{rn}\}$$

(17)

where $x_{r1}$ and $x_{rn}$ are the objects with minimum and maximum similarity degrees, and $\{x_{r1},x_{r2},x_{r3}\dots x_{rn}\}=U$.

Definition 17.

Let $ILS=(U,AT=C\cup D,V,*,f)$. $d_D(x)$ represents the density neighborhood of the object on decision attribute $D$, calculated as:

$$d_D(x)=\{x_{r1},x_{r2},x_{r3}\dots x_{rn}|△(x_{rk},x_{rk+1})<k△avg\}$$

(18)

where $△avg={\displaystyle \frac{max(S{I}_D(x_i,R_D))-min(S{I}_D(x_i,R_D))}{n-1}}$, $△(x_{rk},x_{rk+1})=D{I}_D(x_{rk},x_{rk+1})$, and $k$ is the given value.

Definition 18.

Let $ILS=(U,AT=C\cup D,V,*,f)$. The decision partition of domain $U$ based on density neighborhood is as follows:

$$U/d_D(x)=\{d_D^1(x),d_D^2(x),\dots d_D^n(x)\}$$

(19)

The consistent relation [29] induced by the conditional attribute $C$ is as follows:

$$T_C=\{\left.(x,y)\in U\times U\right|\forall a\in C,f(x,a)=f(x,a)\vee f(y,a)=*\vee f(y,a)=*\}$$

The consistent relation $T_C$ relates the missing values and the clear values equally, which satisfies the reflexivity and symmetry but has no transitivity, and mainly describes the element similarity of incomplete information systems.

The lower and upper approximations of $d_D(x)$ are as follows:

$$\begin{array}{l}\underset{¯}{FD}(d_D(x))=\{\left.x\in U\right|{[x]}_C\subseteq d_D(x)\},\\ \overline{FD}(d_D(x))=\{\left.x\in U\right|{[x]}_C\cap d_D(x)\ne \varnothing \}.\end{array}$$

where ${[x]}_C=\left\{\left.y\in U\right|x{T}_{C}y\right\}(x\in U)$. Based on the above definition, the positive, boundary, and negative regions relative to $U/d_D(x)$ are defined as follows:

$$\begin{array}{l}PO{S}_C(d_D(x))=\underset{¯}{FD}(d_D(x))=\{\left.x\in U\right|{[x]}_C\subseteq d_D(x)\};\\ BN{D}_C(d_D(x))=\overline{FD}(d_D(x))-\underset{¯}{FD}(d_D(x))=\{\left.x\in U\right|{[x]}_C\cap d_D(x)\ne \varnothing \wedge \neg ({[x]}_C\subseteq d_D(x))\};\\ NE{G}_C(d_D(x))=U-\overline{FD}(d_D(x))=\left\{\left.x\in U\right|{[x]}_C\cap d_D(x)=\varnothing \right\}.\end{array}$$

Definition 19.

Let $ILS=(U,AT=C\cup D,V,*,f)$. $d_D(x)$ represents the density neighborhood of the object in $D$. The dependency of attribute $a_i\in C$ is defined as:

$${\phi }_{a_i}(d_D(x))={\displaystyle \frac{\left|PO{S}_C(d_D(x))\right|}{\left|U\right|}}$$

(20)

Definition 20.

Let $ILS=(U,AT=C\cup D,V,*,f)$, $A\subseteq C$, and $SR$ be the intuitionistic fuzzy similarity relation and the domain $U=\{x_1,x_2,\dots ,x_n\}$, then the intuitionistic fuzzy granularity structure on the domain $U$ is as follows:

$$K(S{R}_A)=\{F_{S{R}_A}(x_1),F_{S{R}_A}(x_2),\dots F_{S{R}_A}(x_n)\}$$

(21)

where $F_{S{R}_A}(x_i)={\displaystyle \frac{S{R}_A(x_i,x_1)}{x_1}}+{\displaystyle \frac{S{R}_A(x_i,x_2)}{x_2}}+\dots {\displaystyle \frac{S{R}_A(x_i,x_n)}{x_n}},1\le i\le n$.

Definition 21.

Let $ILS=(U,AT=C\cup D,V,*,f)$, $A\subseteq C$, and the intuitionistic fuzzy granularity structure derived from the intuitionistic fuzzy similarity relation $S{R}_A$ is $K(S{R}_A)=\{F_{S{R}_A}(x_1),F_{S{R}_A}(x_2),\dots ,F_{S{R}_A}(x_n)\}$, then the intuitionistic fuzzy information entropy $H\left(A\right)$ is as follows:

$$H(A)=-{\displaystyle \frac{1}{\left|U\right|}}{\displaystyle \sum _{i=1}^{\left|U\right|}\log \frac{\left|F_{S{R}_A}(x_i)\right|}{\left|U\right|}}$$

(22)

Definition 22.

Let $ILS=(U,AT=C\cup D,V,*,f)$, $A\subseteq C$, and the intuitionistic fuzzy granularity structure derived from the intuitionistic fuzzy similarity relation $S{R}_A$ is $K(S{R}_A)=\{F_{S{R}_A}(x_1),F_{S{R}_A}(x_2),\dots ,F_{S{R}_A}(x_n)\}$, and the decisions derived from the equivalence relation are divided into $U/D=\{{[x]}_D:x\in U\}$. Then the intuitionistic fuzzy conditional entropy of $A$ relative to $D$ is as follows: 

$$H(D\left|A\right.)=-{\displaystyle \frac{1}{\left|U\right|}}{\displaystyle \sum _{i=1}^{\left|U\right|}\left|F_{S{R}_A}(x_i)\cap {[x_i]}_D\right|\log \frac{\left|F_{S{R}_A}(x_i)\cap {[x_i]}_D\right|}{\left|U\right|}}$$

(23)

Definition 23.

Let $ILS=(U,AT=C\cup D,V,*,f)$. The attribute testing cost loss is $TC:C\to {ℝ}^{+}\cup \left\{0\right\}$, where ${ℝ}^{+}$ is the set of positive real numbers.

Definition 24

[30]. Let $ILS=(U,AT=C\cup D,V,*,f)$, $C_i\in C(i=1,2,3\dots ,n)$, and ${\pi }_D=\{D_1,D_2,\dots ,D_m\}$ is the decision class set. Assuming the test costs for each attribute are independent, the test cost for the condition attribute is given by:

$$T{C}_{a_i}=k\cdot H(D,a_i)=k\cdot (H(D)-H(D\left|a_i\right.))$$

(24)

Definition 25.

Let $ILS=(U,AT=C\cup D,V,*,f)$. $U/d_D(x)$ represents the fuzzy decision set, $\forall d_D^j(x)\in U/d_D(x)$, and $\forall a_i\in C$, ${\phi }_{a_i}(d_D^j(x))$ is the dependence of attribute $a_i$ on the decision subset, then the importance of attribute $a_i$ is as follows:

$$SIG(a_i,C,D,TC)={\phi }_C(d_D^j(x))-{\phi }_{C-\left\{a_i\right\}}(d_D^j(x))-T{C}_{a_i}$$

(25)

Definition 26.

Let $GI=\left\{G{I}_1,G{I}_2,\dots ,G{I}_n\right\}$ be an n-level granular structure, where $G{I}_i=(U_i,A{T}_i=C_i\cup D_i,V_i,f_i)$. For $\forall x,y\in U$, give the threshold pair of level $i$ $\left({\lambda }_{i1},{\lambda }_{i2}\right)$, where $\forall {\lambda }_{i1},{\lambda }_{i2}\in [0,1]$ and $0\le {\lambda }_{i1}+{\lambda }_{i2}\le 1$. $S{R}_{C_{ri}}(x,y)$ is the $i$-th level intuitionistic fuzzy similarity relation on $U_i$, and $S{R}_{C_{ri}}\subseteq \dots \subseteq S{R}_{C_{r2}}\subseteq S{R}_{C_{r1}}$, then the $\left({\lambda }_{i1},{\lambda }_{i2}\right)$-cut set $S{R}_{C_{ri}}^{\left({\lambda }_{i1},{\lambda }_{i2}\right)}$ under intuitionistic fuzzy similarity relation $S{R}_{C_{ri}}$ is defined as follows:

$$S{R}_{C_{ri}}^{\left({\lambda }_{i1},{\lambda }_{i2}\right)}=\{\left.(x,y)=U_i\times U_i\right|{\displaystyle \sum _{a\in AT}\frac{S{I}_{a_i}(x,y)}{n}}\ge {\lambda }_{i1},{\displaystyle \sum _{a\in AT}\frac{D{I}_{a_i}(x,y)}{n}}\le {\lambda }_{i2}\}$$

(26)

The similar class of $x$ under $\left({\lambda }_{i1},{\lambda }_{i2}\right)$-cut sets is follows:

$${[x]}_{S{R}_{C_{ri}}^{\left({\lambda }_{i1},{\lambda }_{i2}\right)}}=\{\left.y\in U\right|(x,y)\in S{R}_{C_{ri}}^{\left({\lambda }_{i1},{\lambda }_{i2}\right)}\}$$

(27)

The $\left({\lambda }_{i1},{\lambda }_{i2}\right)$-cut sets $S{R}_{C_{ri}}^{\left({\lambda }_{i1},{\lambda }_{i2}\right)}$ under the intuitionistic fuzzy similarity relation $S{R}_{C_{ri}}$ has $S{R}_{C_{ri}}^{\left({\lambda }_{i1},{\lambda }_{i2}\right)}\subseteq \dots \subseteq S{R}_{C_{r1}}^{\left({\lambda }_{i1},{\lambda }_{i2}\right)}$ at the $i$-th level on $U_i$.

Definition 27.

Let $ILS=(U,AT=C\cup D,V,*,f)$, the attributes of high importance are added in turn to form the attribute subset $C_{rn}(n=0,1,2,\dots ,n\dots ,k)$, and $C_{r0}\subset C_{r1}\subset \dots \subset C_{rn}\dots \subseteq C$. The sequential three-way decisions model is outlined as follows:

$$g(C_{rn})=(U_n,A{T}_n=C_n\cup D_n,V_n,*,f_n,TC), g(C)=(g(C_{r0}),g(C_{r1})\dots g(C_{rk})).$$

where, $g(C_{r0})$ is the fuzzy decision information table on the first level which is independent of the test cost. If the fuzzy decision is divided into $d_D^j(x)\in d_D(x)$ and the threshold pair is $({\overline{\alpha }}_i,{\overline{\beta }}_i)$, for $\forall x_i\in U$, the sequential three-way model with more than $n$ levels is expressed as follows:

$$\begin{array}{l}PO{S}_{C_{rn}}(d_D^j(x))=\{x\in BN{D}_{n+1}|P(d_D^j(x)|{[x]}_{C_{rn}})\ge {\overline{\alpha }}_i\};\\ BN{D}_{C_{rn}}(d_D^j(x))=\{x\in BN{D}_{n+1}|{\overline{\beta }}_i<P(d_D^j(x)|{[x]}_{C_{rn}})<{\overline{\alpha }}_i\};\\ NE{G}_{C_{rn}}(d_D^j(x))=\{x\in BN{D}_{n+1}|P(d_D^j(x)|{[x]}_{C_{rn}})\le {\overline{\beta }}_i\}.\end{array}$$

Assuming that the threshold pairs $({\overline{\alpha }}_i,{\overline{\beta }}_i)$ have the same value at all levels, $P(d_D^j(x)|{[x]}_{C_{rn}})={\displaystyle \frac{\left|d_D^j(x)\cap {[x]}_{C_{rn}}\right|}{\left|{[x]}_{C_{rn}}\right|}}$, ${[x]}_{C_{rn}}={\left[x\right]}_{SR({\lambda }_1,{\lambda }_2)}=\{y\in \left.U\right|(x,y)\in S{R}_{({\lambda }_1,{\lambda }_2)}\}$, the three regions actually obtained are as follows:

$PO{S}_{C_{rn}}^n={\displaystyle \underset{i=0}{\overset{n}{\cup }}PO{S}_{C_{rn}}(d_D^j(x))};BN{D}_{C_{rn}}^n=BN{D}_{C_{rn}}(d_D^j(x));NE{G}_{C_{rn}}^n={\displaystyle \underset{i=0}{\overset{n}{\cup }}NE{G}_{C_{rn}}(d_D^j(x))}.$

At the n + 1 level, it should be noted that the three-way decision is transformed into a two-way decision using a specified threshold $\gamma$, which yields the following two regions:

$$\begin{array}{l}PO{S}_{C_{rn}}(d_D^j(x))=\{x\in BN{D}_{n-1}|P(d_D^j(x)|{[x]}_{C_n})\ge \overline{\gamma }\};\\ NE{G}_{Cn}(d_D^j(x))=\{x\in BN{D}_{n-1}|P(d_D^j(x)|{[x]}_{C_{rn}}<\overline{\gamma }\}.\end{array}$$

According to the decision rule, the decision process consists of two states of belonging and not belonging, $(X_i, X_i^C)$, and three actions, $(a_{P_i}, a_{B_i}, a_{N_i})$, of accepting the decision, delaying the decision, and rejecting the decision. Assuming that the losses associated with various decision actions across different states are expressed as intuitionistic fuzzy values, Table 3 presents the risk losses for the three decision actions at the i−th level.

Table 3. Intuitionistic fuzzy risk loss matrix.

	Xi	XiC
$a_{P_i}$	${\lambda }_{PP}^i=(\mu ({\lambda }_{PP}^i),v({\lambda }_{PP}^i))$	${\lambda }_{PN}^i=(\mu ({\lambda }_{PN}^i),v({\lambda }_{PN}^i))$
$a_{B_i}$	${\lambda }_{BP}^i=(\mu ({\lambda }_{BP}^i),v({\lambda }_{BP}^i))$	${\lambda }_{BN}^i=(\mu ({\lambda }_{BN}^i),v({\lambda }_{BN}^i))$
$a_{N_i}$	${\lambda }_{NP}^i=(\mu ({\lambda }_{NP}^i),v({\lambda }_{NP}^i))$	${\lambda }_{NN}^i=(\mu ({\lambda }_{NN}^i),v({\lambda }_{NN}^i))$

Reasonable case of intuitionistic fuzzy risk loss function:

$\mu ({\lambda }_{PP}^i)<\mu ({\lambda }_{BP}^i)<\mu ({\lambda }_{NP}^i)$, $\nu ({\lambda }_{NP}^i)<\nu ({\lambda }_{BP}^i)<\nu ({\lambda }_{PP}^i)$,

$\mu ({\lambda }_{NN}^i)<\mu ({\lambda }_{BN}^i)<\mu ({\lambda }_{PN}^i)$, $\nu ({\lambda }_{PN}^i)<\nu ({\lambda }_{BN}^i)<\nu ({\lambda }_{NN}^i)$.

Then the following decision rules can be obtained:

(P1) If $P(d_D^i(x)|{[x]}_{C_{rn}})\ge {\overline{\alpha }}_i$ and $P(d_D^i(x)|{[x]}_{C_{rn}})\ge {\overline{\gamma }}_i$, then $x\in POS(X)$;

(N1) If $P(d_D^i(x)|{[x]}_{C_{rn}})\le {\overline{\beta }}_i$ and $P(d_D^i(x)|{[x]}_{C_{rn}})\le {\overline{\gamma }}_i$, then $x\in NEG(X)$;

(B1) If $P(d_D^i(x)|{[x]}_{C_{rn}})\le {\overline{\alpha }}_i$ and $P(d_D^i(x)|{[x]}_{C_{rn}})\ge {\overline{\beta }}_i$, then $x\in BND(X)$.

Thus,

(P1) If $P(d_D^i(x)|{[x]}_{C_{rn}})\ge max\{{\overline{\alpha }}_i,{\overline{\beta }}_i,{\overline{\gamma }}_i\}$, then $x\in POS(X)$;

(N1) If $P(d_D^i(x)|{[x]}_{C_{rn}})\le min\{{\overline{\alpha }}_i,{\overline{\beta }}_i,{\overline{\gamma }}_i\}$, then $x\in NEG(X)$;

(B1) If $x\in U-POS(X)-NEG(X)$, then $x\in BND(X)$.

Here,

$${\overline{\alpha }}_i={\displaystyle \frac{\mu ({\lambda }_{PN}^i)-\mu ({\lambda }_{BN}^i)+v({\lambda }_{BN}^i)-v({\lambda }_{PN}^i)}{\mu ({\lambda }_{PN}^i)-\mu ({\lambda }_{BN}^i)+\mu ({\lambda }_{BP}^i)-\mu ({\lambda }_{PP}^i)+\nu ({\lambda }_{BN}^i)-\nu ({\lambda }_{PN}^i)+\nu ({\lambda }_{PP}^i)-\nu ({\lambda }_{BP}^i)}},$$

(28)

$${\overline{\beta }}_i={\displaystyle \frac{\mu ({\lambda }_{BN}^i)-\mu ({\lambda }_{NN}^i)+v({\lambda }_{NN}^i)-v({\lambda }_{BN}^i)}{\mu ({\lambda }_{BN}^i)-\mu ({\lambda }_{NN}^i)+\mu ({\lambda }_{NP}^i)-\mu ({\lambda }_{BP}^i)+\nu ({\lambda }_{NN}^i)-\nu ({\lambda }_{BN}^i)+\nu ({\lambda }_{BP}^i)-\nu ({\lambda }_{NP}^i)}},$$

(29)

$${\overline{\gamma }}_i={\displaystyle \frac{\mu ({\lambda }_{PN}^i)-\mu ({\lambda }_{NN}^i)+v({\lambda }_{NN}^i)-v({\lambda }_{PN}^i)}{\mu ({\lambda }_{PN}^i)-\mu ({\lambda }_{NN}^i)+\mu ({\lambda }_{NP}^i)-\mu ({\lambda }_{PP}^i)+\nu ({\lambda }_{NN}^i)-\nu ({\lambda }_{PN}^i)+\nu ({\lambda }_{PP}^i)-\nu ({\lambda }_{NP}^i)}}.$$

(30)

4.2. Key Steps and Algorithms

According to the similarity relation in incomplete information systems and the decision rules of sequential three-way decisions, the key steps and algorithms of the IFSTWD model in the incomplete information system are given as:

Step 1 Calculate the attribute similarity degree on the decision attribute $D$;

Step 2 Based on density neighborhood, obtain the partition of fuzzy decision $d_D(x)$;

Step 3 Calculate attribute importance;

Step 4 Sort the attributes and construct a nested sequence of attribute subsets;

Step 5 Calculate $\overline{\alpha }$, $\overline{\beta }$, $\overline{\gamma }$;

Step 6 Calculate the similarity relation of the object in attribute subset, and the similarity and the dissimilarity matrix;

Step 7 Add attributes step by step according to step 4, construct multi-level granular structure, and divide the objects under this attribute into $POS$, $NEG$, and $BND$.

The corresponding pseudocode is shown in Algorithm 1.

Based on Algorithm 1, the time complexity of $H(D|C)$ is $O(n^2)$, and the time complexity of $T{C}_{a_j}$ is $O(n)$. Consequently, the overall time complexity of the attribute importance $SIG(a_i,C,D,TC)$ is $O(n^2)+O(n)$, and $U/d_D(x)$ has a time complexity of $O(n^3)$. Similarly, the time complexity for constructing the nested sequence of subsets is $O(nm)$. Then, by continually refining the granularity of sequential three-way decisions and dividing all elements in the $n$ levels into three disjoint regions, the time complexity is $O({\displaystyle {\sum }_{n=0}^{m}n\cdot \left|U_n\right|}\left|C_{rn}\right|)$, which is $O(n^{2}m)$. Therefore, Algorithm 1 has a time complexity of $O(n^3)+O(n^{2}m)+2O(n^2)+2O(n)$, corresponding to $O(n^3)$.

Algorithm 1. IFSTWD algorithm in an incomplete information system

Input: $ILS=(U,AT,V,*,f)$, ${\lambda }_1$, ${\lambda }_2$. Output: $POS(X), BND(X), NEG(X)$. 1. for each $a_i\in C$ do 2. Calculate information entropy $H(D|C)$ and $H(D)$, decision cost loss $TC$ and attribute importance $SIG(a_i,C,D,TC)$. 3. Calculate fuzzy decision partitioning $U/d_D(x)$. 4. Construct a nested sequence of attribute subsets: $C_{r0}\subset C_{r1}\subset \dots \subset C_{rn}\dots \subseteq C$. 5. Input ${\lambda }_{PP},{\lambda }_{BP},{\lambda }_{NP},{\lambda }_{PN},{\lambda }_{BN},{\lambda }_{NN}$. and calculate $\overline{\alpha },\overline{\beta },\overline{\gamma }$. 6. The similarity relation $SR(x_m,x_n)$ of objects in attribute subset $C_{rn}$ about attribute $a_i$ and $\mathit{S}{\mathit{I}}_{C_{r0}}(x_m,x_n)$ and $\mathit{D}{\mathit{I}}_{C_{r0}}(x_m,x_n)$ are calculated. 7. while $U_n\ne \varnothing$ and $0\le n\le m(m=\left|C\right|)$. 8. for each $x\in U_n$ do 9.  compute the similarity relation $SR(x_m,x_n)$ of objects in attribute subset $C_{rn}$ with respect to attribute $a_i$. 10. if $P(d_D^j(x)|{[x]}_{C_{rn}})\ge max(\overline{\alpha },\overline{\beta },\overline{\gamma })$, then $x_i\in POS(X)$, $PO{S}_{C_{rn}}^n(d_D^j(x))=PO{S}_{C_{rn}}^n(d_D^j(x))\cup {\left[x\right]}_{C_{rn}}$. 11. if $P(d_D^j(x)|{[x]}_{C_{rn}})\le min(\overline{\alpha },\overline{\beta },\overline{\gamma })$, then $x_i\in NEG(X)$, $NE{G}_{C_{rn}}^n(d_D^j(x))=NE{G}_{C_{rn}}^n(d_D^j(x))\cup {\left[x\right]}_{C_{rn}}$. 12. else $x_i\in BND(X)$, $BN{D}_{C_{rn}}^n(d_D^j(x))=U_n-PO{S}_{C_{rn}}^n(d_D^j(x))-NE{G}_{C_{rn}}^n(d_D^j(x))$, $U_n=BN{D}_{C_{rn}}^n(d_D^j(x)).$ 13. if n = m do 14.   for each ${\left[x\right]}_C\in U_n$ do 15.    if $P(d_D^j(x)|{[x]}_{C_C})\ge \overline{\gamma }$, then $x_i\in POS(X)$, $POS=POS\cup {\left[x\right]}_{C_c}$. 16.    if $P(d_D^j(x)|{[x]}_{C_{rn}})<\overline{\gamma }$, then $x_i\in NEG(X)$, $NEG=NEG\cup {\left[x\right]}_{C_c}$. 17. $POS=POS\cup PO{S}_{C_{rn}}^n(d_D^j(x))$. 18. $NEG=NEG\cup NE{G}_{C_{rn}}^n(d_D^j(x))$. 19. $BND=BN{D}_{C_{rn}}^n(d_D^j(x))$. 20. Return $POS$, $NEG$ and $BND$.

5. Examples and Experimental Comparative Analysis

In this section, the decision-making process of the proposed model is demonstrated through an example analysis. Furthermore, experiments are performed using six UCI datasets to verify the model’s effectiveness by comparing it with several other methods.

5.1. The Example Analysis

Recently, global interest in learning Chinese has been further stimulated by the release of products such as the game “Black Myth: Wukong.” As of the end of 2023, Chinese language education has been established in over 180 countries and regions. In the context of digital transformation, the integration of “Chinese + vocational skills” offers a promising avenue for international learners to boost their language proficiency and professional skills. Consequently, methods for assessing these competencies have also gained significant attention. An overseas company needs to recruit a number of employees who understand both auto repair and Chinese, based on China’s vocational Chinese proficiency level standards and national vocational skill standards,. Next, 10 overseas students are evaluated for talent competency, that is $U=\{x_1,x_2,x_3,x_4,x_5,x_6,x_7,x_8,x_9,x_{10}\}$. Experts selected three main criteria: Chinese language ability, professional quality, and cross-cultural communication ability, that is, the standard set is $AT=\{a_1,a_2,a_3,D\}$, where $D$ is the decision-making attribute. For a risk that is acceptable, set h = 0.5. Next, comprehensively consider the risk of employment and select relatively better personnel. Table 4 shows the data for 10 participants, with missing data due to objective or subjective reasons denoted by “*”, and each evaluation value is an intuitive ambiguity number, including membership and non-membership.

Table 4. Comprehensive ability information table of candidates.

	a1	a2	a3	D
$x_1$	(0.2, 0.7)	(0.6, 0.4)	(0.8, 0.1)	(0.2, 0.7)
$x_2$	(0.6, *)	(0.2, 0.7)	(*, 0.5)	(0.7, 0.3)
$x_3$	(0.2, 0.7)	(*, *)	(0.8, 0.1)	(0.2, 0.7)
$x_4$	(0.5, 0.4)	(0.3, 0.6)	(0.6, 0.4)	(0.5, 0.0)
$x_5$	(0.4, 0.6)	(0.8, 0.1)	(0.5, 0.3)	(0.2, 0.6)
$x_6$	(0.4, 0.0)	(*, 0.5)	(0.3, 0.7)	(0.5, 0.0)
$x_7$	(0.3, 0.3)	(0.7, 0.1)	(0.7, 0.3)	(0.3, 0.6)
$x_8$	(0.0, 0.7)	(0.7, 0.2)	(0.0, 1.0)	(0.3, 0.7)
$x_9$	(0.1, 0.7)	(*, 0.7)	(0.0, 0.4)	(0.1, 0.7)
$x_{10}$	(*, 0.0)	(0.6, 0.1)	(0.2, 0.8)	(0.8, 0.1)

Step 1 Calculate the similarity degree. $S{I}_d(x_i,R_d)$: $R_d=(max({\mu }_d(x_i)), min({\nu }_d(x_i))=(0.8,0.0)$,

$$S{I}_d(x_1,R_d)=0.3, S{I}_d(x_2,R_d)=0.7, S{I}_d(x_3,R_d)=0.3, S{I}_d(x_4,R_d)=0.7, S{I}_d(x_5,R_d)=0.4,$$

 

$$S{I}_d(x_6,R_d)=0.7, S{I}_d(x_7,R_d)=0.4, S{I}_d(x_9,R_d)=0.3, S{I}_d(x_8,R_d)=0.3, S{I}_d(x_{10},R_d)=0.9.$$

Step 2 Sort the objects according to the similarity degree of the decision values from smallest to largest: $N_D(x)=\{x_1,x_3,x_8,x_9,x_5,x_7,x_2,x_4,x_6,x_{10}\}$. According to Definition 17, the average distance can be obtained as follows: $△avg=(0.9-0.3)/9=0.067$.

The distance between two adjacent objects can be obtained at the same time as follows: $△(x_{rk},x_{rk+1})=(0,0.1,0.1,0.1,0.1,0.4,0.3,0,0.3)$.

Assuming the density parameter $k=2$, $△(x_7,x_2)=0.4>k△avg=0.134$, $x_7$ to start changing to $x_2$, then it can be divided into two equivalence classes $d_D^1=\{x_1,x_3,x_8,x_9,x_5,x_7\}$ and $d_D^2=\{x_2,x_4,x_6,x_{10}\}$. The decision attribute can be divided into:

$$U/d_D(x)=\left\{\right\{x_1,x_3,x_8,x_9,x_5,x_7\},\{x_2,x_4,x_6,x_{10}\left\}\right\}=\left\{\right\{x_1,x_3,x_5,x_7,x_8,x_9\},\{x_2,x_4,x_6,x_{10}\left\}\right\}.$$

Step 3 Calculate attribute importance. According to Definition 18, the lower approximation on the condition attribute $C$ is $\underset{¯}{FD}(d_D(x))=\{x_1,x_2,x_3,x_4,x_5,x_6,x_7,x_8,x_9,x_{10}\}$, $PO{S}_C(d_D(x))=\underset{¯}{FD}(d_D(x))=\{x_1,x_2,x_3,x_4,x_5,x_6,x_7,$$x_8,x_9,x_{10}\}$. According to Definition 19, the dependency of the conditional attribute $C$ is ${\phi }_C(d_D(x))=1$. Similarly, the attribute dependence of attribute $a_i$ can be obtained as ${\phi }_{a_1}(d_D(x))=0.8$, ${\phi }_{a_2}(d_D(x))=0.7$, and ${\phi }_{a_3}(d_D(x))=0.9$. $\overline{\alpha }=0.65$, $\overline{\beta }=0.33$, and $\overline{\gamma }=0.52$ are calculated from Table 5 and Formulas (28)–(30). Further, the conditional entropy of decision set $D$ is obtained as follows: $H(D)=0.978$, $H(D\left|a_1\right.)=0.968$, $H(D\left|a_2\right.)=0.909$, and $H(D\left|a_3\right.)=0.959$.

Table 5. Intuitive fuzzy loss cost matrix.

	X	XC
$a_P$	(0.1, 0.9)	(0.9, 0.1)
$a_B$	(0.3, 0.5)	(0.3, 0.6)
$a_N$	(0.8, 0.2)	(0.1, 0.8)

The testing cost is set to k = 1 and the importance of $T{C}_{a_1}=0.01$, $T{C}_{a_2}=0.069$, and $T{C}_{a_3}=0.019$, and the importance of the attribute is as follows:

$$\begin{array}{l}SIG(a_1,C,D,TC)={\phi }_C(d_D^j(x))-{\phi }_{C-\left\{a_1\right\}}(d_D^j(x))-T{C}_{a_1}=0.79,\\ SIG(a_2,C,D,TC)={\phi }_C(d_D^j(x))-{\phi }_{C-\left\{a_2\right\}}(d_D^j(x))-T{C}_{a_2}=0.631,\\ SIG(a_3,C,D,TC)={\phi }_C(d_D^j(x))-{\phi }_{C-\left\{a_3\right\}}(d_D^j(x))-T{C}_{a_3}=0.881\end{array}$$

.

According to Definition 27, a granular structure based on attribute importance is constructed to obtain a three-level granularity structure, and the attribute set of each level is: $C_{r0}=\left\{a_3\right\}$, $C_{r1}=\left\{a_3,a_1\right\}$, $C_{r2}=\left\{a_3,a_1,a_2\right\}$.

Step 4 Similar class partition. Level 1: the partition of the domain $U$ with respect to the decision attribute set $D$ is as follows:

$$U/d_D^0(x)=\left\{\right\{x_1,x_3,x_5,x_7,x_8,x_9\},\{x_2,x_4,x_6,x_{10}\left\}\right\}$$

.

Then, we have $S{R}_{C_{r0}}(x_m,x_n)=({\displaystyle \frac{1}{n}}{\displaystyle \sum _{a_3\in AT}S{I}_{a_3}(x_m,x_n)},{\displaystyle \frac{1}{n}}{\displaystyle \sum _{a_3\in AT}D{I}_{a3}(x_m,x_n)})$, and the similarity matrix and dissimilarity matrix are as follows:

$\mathit{S}{\mathit{I}}_{C_{r0}}(x_m,x_n)={({\displaystyle \frac{1}{n}}{\displaystyle \sum _{a_3\in AT}S{I}_{a_3}(x_m,x_n)})}_{m\times n}$, $\mathit{D}{\mathit{I}}_{C_{r0}}(x_m,x_n)={({\displaystyle \frac{1}{n}}{\displaystyle \sum _{a_3\in AT}D{I}_{a3}(x_m,x_n)})}_{m\times n}$.

The similarity matrix $\mathit{S}{\mathit{I}}_{C_{r0}}(x_m,x_n)$ and the dissimilarity matrix $\mathit{D}{\mathit{I}}_{C_{r0}}(x_m,x_n)$$(m=(1,2\dots 10),n=(1,2\dots 10))$ are as follows:

$$\begin{array}{l}\mathit{S}{\mathit{I}}_{C_{r0}}(x_m,x_n)=({\displaystyle \frac{1}{n}}{\displaystyle \sum _{a_1\in AT}S{I}_{a_3}(x_m,x_n)}{)}_{m\times n}=\left[\begin{array}{llllllllll}1.0\hfill & 0.0\hfill & 1.0\hfill & 0.7\hfill & 0.7\hfill & 0.4\hfill & 0.4\hfill & 0.1\hfill & 0.2\hfill & 0.3\hfill \\ 0.0\hfill & 1.0\hfill & 0.0\hfill & 0.0\hfill & 0.0\hfill & 0.0\hfill & 0.0\hfill & 0.0\hfill & 0.0\hfill & 0.0\hfill \\ 1.0\hfill & 0.0\hfill & 1.0\hfill & 0.7\hfill & 0.7\hfill & 0.4\hfill & 0.4\hfill & 0.1\hfill & 0.2\hfill & 0.3\hfill \\ 0.7\hfill & 0.0\hfill & 0.7\hfill & 1.0\hfill & 0.9\hfill & 0.7\hfill & 0.7\hfill & 0.4\hfill & 0.4\hfill & 0.6\hfill \\ 0.7\hfill & 0.0\hfill & 0.7\hfill & 0.9\hfill & 1.0\hfill & 0.6\hfill & 0.6\hfill & 0.3\hfill & 0.5\hfill & 0.5\hfill \\ 0.4\hfill & 0.0\hfill & 0.4\hfill & 0.7\hfill & 0.6\hfill & 1.0\hfill & 1.0\hfill & 0.7\hfill & 0.7\hfill & 0.9\hfill \\ 0.4\hfill & 0.0\hfill & 0.4\hfill & 0.7\hfill & 0.6\hfill & 1.0\hfill & 1.0\hfill & 0.7\hfill & 0.7\hfill & 0.9\hfill \\ 0.1\hfill & 0.0\hfill & 0.1\hfill & 0.4\hfill & 0.3\hfill & 0.7\hfill & 0.7\hfill & 1.0\hfill & 0.4\hfill & 0.8\hfill \\ 0.2\hfill & 0.0\hfill & 0.2\hfill & 0.4\hfill & 0.5\hfill & 0.7\hfill & 0.7\hfill & 0.4\hfill & 1.0\hfill & 0.6\hfill \\ 0.3\hfill & 0.0\hfill & 0.3\hfill & 0.6\hfill & 0.5\hfill & 0.9\hfill & 0.9\hfill & 0.8\hfill & 0.6\hfill & 1.0\hfill \end{array}\right],\\ \mathit{D}{\mathit{I}}_{C_{r0}}(x_m,x_n)=({\displaystyle \frac{1}{n}}{\displaystyle \sum _{a_1\in AT}D{I}_{a3}(x_m,x_n){)}_{m\times n}}=\left[\begin{array}{llllllllll}0.0\hfill & 1.0\hfill & 0.0\hfill & 0.3\hfill & 0.3\hfill & 0.6\hfill & 0.6\hfill & 0.9\hfill & 0.8\hfill & 0.7\hfill \\ 1.0\hfill & 0.0\hfill & 1.0\hfill & 1.0\hfill & 1.0\hfill & 1.0\hfill & 1.0\hfill & 1.0\hfill & 1.0\hfill & 1.0\hfill \\ 0.0\hfill & 1.0\hfill & 0.0\hfill & 0.3\hfill & 0.3\hfill & 0.6\hfill & 0.6\hfill & 0.9\hfill & 0.8\hfill & 0.7\hfill \\ 0.3\hfill & 1.0\hfill & 0.3\hfill & 0.0\hfill & 0.1\hfill & 0.3\hfill & 0.3\hfill & 0.6\hfill & 0.6\hfill & 0.4\hfill \\ 0.3\hfill & 1.0\hfill & 0.3\hfill & 0.1\hfill & 0.0\hfill & 0.4\hfill & 0.4\hfill & 0.7\hfill & 0.5\hfill & 0.5\hfill \\ 0.6\hfill & 1.0\hfill & 0.6\hfill & 0.3\hfill & 0.4\hfill & 0.0\hfill & 0.0\hfill & 0.3\hfill & 0.3\hfill & 0.1\hfill \\ 0.6\hfill & 1.0\hfill & 0.6\hfill & 0.3\hfill & 0.4\hfill & 0.0\hfill & 0.0\hfill & 0.3\hfill & 0.3\hfill & 0.1\hfill \\ 0.9\hfill & 1.0\hfill & 0.9\hfill & 0.6\hfill & 0.7\hfill & 0.3\hfill & 0.3\hfill & 0.0\hfill & 0.6\hfill & 0.2\hfill \\ 0.8\hfill & 1.0\hfill & 0.8\hfill & 0.6\hfill & 0.5\hfill & 0.3\hfill & 0.3\hfill & 0.6\hfill & 0.0\hfill & 0.4\hfill \\ 0.7\hfill & 1.0\hfill & 0.7\hfill & 0.4\hfill & 0.5\hfill & 0.1\hfill & 0.1\hfill & 0.2\hfill & 0.4\hfill & 0.0\hfill \end{array}\right].\end{array}$$

The values of ${\lambda }_1$ and ${\lambda }_2$ are 0.6 and 0.4, respectively, then similar classes of each object are as follows:

$$\begin{array}{l}{[x_1]}_{S{R}_{C_{r0}}({\lambda }_{01},{\lambda }_{02})}=\{x_1,x_3,x_4,x_5\}, {[x_2]}_{S{R}_{C_{r0}}({\lambda }_{01},{\lambda }_{02})}=\{x_2\}, {[x_3]}_{S{R}_{C_{r0}}({\lambda }_{01},{\lambda }_{02})}=\{x_1,x_3,x_4,x_5\}, \\ {[x_4]}_{S{R}_{C_{r0}}({\lambda }_{01},{\lambda }_{02})}=\{x_1,x_3,x_4,x_5,x_6,x_7\}, {[x_5]}_{S{R}_{C_{r0}}({\lambda }_{01},{\lambda }_{02})}=\{x_1,x_3,x_4,x_5\}, \\ {[x_6]}_{S{R}_{C_{r0}}({\lambda }_{01},{\lambda }_{02})}=\{x_4,x_6,x_7,x_8,x_9,x_{10}\}, {[x_7]}_{S{R}_{C_{r0}}({\lambda }_{01},{\lambda }_{02})}=\{x_4,x_6,x_7,x_8,x_9,x_{10}\}, \\ {[x_8]}_{S{R}_{C_{r0}}({\lambda }_{01},{\lambda }_{02})}=\{x_6,x_7,x_8,x_{10}\}, {[x_9]}_{S{R}_{C_{r0}}({\lambda }_{01},{\lambda }_{02})}=\{x_6,x_7,x_9\}, {[x_{10}]}_{S{R}_{C_{r0}}({\lambda }_{01},{\lambda }_{02})}=\{x_6,x_7,x_8,x_{10}\}.\end{array}$$

For each object $x_i\in U$, the corresponding conditional probability is determined as follows:

$P(d_D^0(x)|{[x_1]}_{C_{r0}})=0.75$, $P(d_D^0(x)|{[x_2]}_{C_{r0}})=0$, $P(d_D^0(x)|{[x_3]}_{C_{r0}})=0.75$, $P(d_D^0(x)|{[x_4]}_{C_{r0}})=0.67$, $P(d_D^0(x)|{[x_5]}_{C_{r0}})=0.75$, $P(d_D^0(x)|{[x_6]}_{C_{r0}})=0.5$, $P(d_D^0(x)|{[x_7]}_{C_{r0}})=0.5$, $P(d_D^0(x)|{[x_8]}_{C_{r0}})=0.5$, $P(d_D^0(x)|{[x_9]}_{C_{r0}})=0.67$, $P(d_D^0(x)|{[x_{10}]}_{C_{r0}})=0.5$.

The decision threshold pair $(\overline{\alpha },\overline{\beta })$ is $(0.65,0.33)$, $P(d_D^0(x)|{[x_1]}_{C_{r0}})>0.65$, then $x_1\in PO{S}_{C_{r0}}$. Similarly, $PO{S}_{C_{r0}}=\{x_1,x_3,x_4,x_5,x_9\}$, $NE{G}_{C_{r0}}=\{x_2\}$, and $BN{D}_{C_{r0}}=\{x_6,x_7,x_8,x_{10}\}$. The granularity partition of the first level can be obtained as follows:

$$\begin{array}{l}PO{S}_{C_{r0}}^0={\displaystyle \underset{i=0}{\overset{0}{\cup }}PO{S}_{C_{ri}}}=\{x_1,x_3,x_4,x_5,x_9\};\\ NE{G}_{C_{r0}}^0={\displaystyle \underset{i=0}{\overset{0}{\cup }}NE{G}_{C_{ri}}}=\{x_2\};\\ BN{D}_{C_{r0}}^0={\displaystyle \underset{i=0}{\overset{0}{\cup }}BN{D}_{C_{ri}}}=\{x_6,x_7,x_8,x_{10}\}.\end{array}$$

Under the second set of attributes $C_{r1}$, only the objects in $BN{D}_{C{r}_0}^0$ need to be decided, and $BN{D}_{C{r}_0}^0$ is divided into ${\displaystyle \frac{U}{d_D^1(x)}}=\{\{x_7,x_8\},\{x_6,x_{10}\}\}$ relative to the decision attribute $D$.

Similar classes of objects can be found:

$$\begin{array}{l}{[x_6]}_{S{R}_{C_{r1}}({\lambda }_{11},{\lambda }_{12})}=\{x_6,x_7,x_8\}, {[x_7]}_{S{R}_{C_{r1}}({\lambda }_{11},{\lambda }_{12})}=\{x_6,x_7,x_8\}, \\ {[x_8]}_{S{R}_{C_{r1}}({\lambda }_{11},{\lambda }_{12})}=\{x_6,x_7,x_8\}, {[x_{10}]}_{S{R}_{C_{r1}}({\lambda }_{11},{\lambda }_{12})}=\{x_{10}\}.\end{array}$$

Determine the conditional probability for the object within set $BN{D}_{C{r}_0}^0$:

$P(d_D^1(x)|{[x_6]}_{C_{r1}}^1)=0.67$, $P(d_D^1(x)|{[x_7]}_{C_{r1}}^1)=0.67$,

$P(d_D^1(x)|{[x_8]}_{C_{r1}}^1)=0.67$, $P(d_D^1(x)|{[x_{10}]}_{C_{r1}}^1)=0$.

The decision for the object in $BN{D}_{C{r}_0}^0$ at the second level of granularity is $PO{S}_{C_{r1}}=\{x_6,x_7,x_8\}$, $NE{G}_{C_{r1}}=\{x_{10}\}$, and $BN{D}_{C_{r1}}=\varnothing$.

Calculate the three areas of the second level:

$$\begin{array}{l}PO{S}_{C_{r1}}^1={\displaystyle \underset{i=0}{\overset{1}{\cup }}PO{S}_{C_{ri}}}=\{x_1,x_3,x_4,x_5,x_6,x_7,x_8,x_9\};\\ NE{G}_{C_{r1}}^1={\displaystyle \underset{i=0}{\overset{1}{\cup }}NE{G}_{C_{ri}}}=\{x_2,x_{10}\};\\ BN{D}_{C_{r1}}^1={\displaystyle \underset{i=0}{\overset{1}{\cup }}BN{D}_{C_{ri}}}=\varnothing .\end{array}$$

Under the third level of attribute set $C_{r2}$, only the objects in $BN{D}_{Cr1}^1$ need to be decided, and since $BN{D}_{C_{r1}}^1=\varnothing$, the objects in $BN{D}_{C{r}_1}^1$ are divided in the second level. In summary, the three decisions in $U$ are divided into:

$$\begin{array}{l}POS(X)=\{x_1,x_3,x_4,x_5,x_6,x_7,x_8,x_9\};\\ BND(X)=\varnothing ;\\ NEG(X)=\{x_2,x_{10}\}.\end{array}$$

Ultimately, the candidate objects in the $POS$ domain are optional. In practice, attribute importance also has an impact on the results, and attributes with high attribute importance are generally preferred for decision classification, so as to reduce the cost. In the above example, the detection steps are sorted according to the importance of the attributes to improve the testing efficiency. Otherwise, there may be some unnecessary testing steps that increase the cost of testing; for example, if the candidate only understands cross-cultural communication and does not understand relevant skills and Chinese. Furthermore, the scale of $BND$ shows a monotonically decreasing trend, while the scale of $POS$ (or $NEG$) exhibits a monotonically increasing trend. This can be primarily attributed to the fact that certain properties may become reducible. As granularity becomes more refined, the number of objects in $POS$ (or $NEG$) grows steadily, leading to a corresponding reduction in the number of objects in $BND$. In this paper, the decision of incomplete information is made through the similarity relationship, which reduces the data loss of the original fuzzy decision information system and improves the classification accuracy. When the sequential three-way decision is used to divide the objects, only the similarity relationship between the objects needs to be calculated under the attributes, and the similarity relationship of all attributes between the objects is not calculated, so as to improve the decision-making efficiency and reduce the calculation time.

5.2. Experimental Comparison and Analysis

The experimental data are from the UCI dataset (http://archive.ics.uci.edu/, accessed on 1 June 2023), and the specific description is shown in Table 6.

Table 6. Description of experimental data set.

Data Set	Missing Value	Number of Objects	Number of Attribute
Boot	Yes	500	19
Fish	Yes	908	7
Craft	No	3395	20
Aquatic	Yes	546	9
Servo	Yes	167	4
Productivity	Yes	1197	15

All experiments were performed on a platform with a Windows 10 operating system, Intel (R) Core (TM) i5-6500 CPU@3.2 GHz and 8 GB memory, and on the development platform of Python 3.6. The fuzzy decisions of the six selected datasets were normalized, and the values were adjusted to [0, 1]. In addition, to verify the effectiveness and feasibility, the IFSTWD is compared with three other different particle size partition models. Meanwhile, the performance is evaluated by CCA [31] and ECR [32]. Accordingly, the two measures are calculated as follows:

$$CCA={\displaystyle \frac{{\displaystyle \sum _{j=1}^m\left|POS(D_i)\cap D_i\right|/\left|POS(D_i)\right|}}{m}},$$

(31)

$$ECR={\displaystyle \frac{{\displaystyle \sum _{j=1}^m\left[\frac{\left|POS(D_i)\cap \neg D_i\right|+\left|NEG(D_i)\cap D_i\right|}{\left|POS(D_i)\right|+\left|NEG(D_i)\right|}\right]}}{m}}.$$

(32)

where $D_i$ and $\neg D_i$ respectively represent the set of objects in decision classes $D_i$ and $\neg D_i$, $POS(D_i)$, and $NEG(D_i)$ respectively represent the set of objects belonging to positive and negative fields in $D_i$.

Firstly, the influence of granularity parameters on the model is analyzed. In order to reflect the ability of fuzzy decision-making to deal with incomplete information systems, the IFSTWD model proposed in this paper is compared with the three granularity partition models of CSTWD [33], DSTWD [34], and TSTWD [35]. Among them, CSTWD is a classical sequential three-way decision model, and DSTWD and TSTWD are sequential three-way decision models based on dependency and tolerance relations, respectively. To ensure experimental fairness, we assume that the threshold remains constant across all particle size levels. In incomplete information systems, the label’s granularity parameter is closely tied to the classification performance of the proposed sequential three-way decision. To further demonstrate the impact of the particle size parameter $t$ on grading performance, $t$ is set to 10 with a step size of 1. The variation curves of particle size parameter $t$ under different methods are illustrated in Figure 2 and Figure 3.

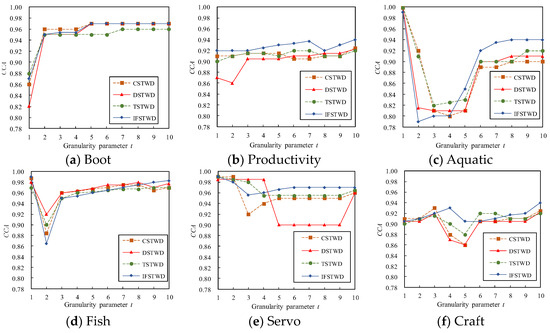
Figure 2. CCA results of different methods.

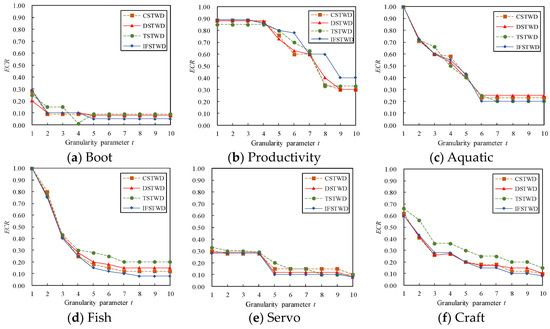
Figure 3. ECR results of different methods.

From Figure 2, the trends of TSTWD and CSTWD exhibit similar behavior when $t\in [1,3]$. However, when $t\ge 3$, the CCA curves of IFSTWD on the Boot and Productivity datasets show slower changes compared to the other datasets. At $t\ge 4$, the CCA of IFSTWD is significantly higher than the other three methods. Finally, when $t=10$, all four methods reach a steady state on the Boot, Aquatic, and Fish datasets. On the Servo dataset, all three methods reach a steady state, except for DSTWD. Similarly, Figure 3 illustrates that the ECR curves for different methods decrease as $t$ increases. When $t$ approaches 10, the ECR curves for the other five datasets gradually converge, with the exception of the Productivity dataset. In addition, the ECR curves of Boot and Servo decline relatively slowly. When $t\in [1,4]$, the ECR curves of IFSTWD and DSTWD are similar to those of Productivity, Fish, Servo, and Craft. However, at $t>6$, the ECR curves of Boot, Aquatic, and Servo tend to be similar under four different particle size partitioning methods. When $t>5$, the ECR curves of IFSTWD are the lowest in Boot, Aquatic, Fish, Serv and Craft, and the ECR curves of the other four datasets are significantly lower than those of the other three methods, except for the Aquatic dataset. On the Aquatic dataset, the ECR curves of IFSTWD and TSTWD are the lowest. In summary, the CCA curves of the four methods on the six datasets gradually increase with the increase of t, while the ECR curves are the opposite. The performance of the proposed IFSTWD model surpasses the other three methods, as demonstrated by the CCA curve, which shows a steady improvement as the particle size parameter $t$ increases.

6. Conclusions

In this paper, we introduced intuitionistic fuzzy similarity relations and their cut relations to construct similarity classes, replacing equivalence relations in incomplete information systems. Recognizing that the granularity structure in sequential three-way decisions is influenced by the attribute connection order, we proposed a new attribute importance evaluation criterion that combines attribute correlation with decision cost. Attributes with higher importance are then selected to construct the next level of granular structure. To optimize the granularity of information, we also proposed a density neighborhood-based granulation method, which captures implicit connections between different objects, and discussed the construction of the IFSTWD model based on intuitionistic fuzzy similarity relations.

For future research, several potential directions can be considered. First, as this study focuses on relatively simple data types, future work could explore extending the proposed model to mixed information systems that involve multiple data types such as categorical, and interval data [36]. This would enhance the model’s ability to handle more complex and heterogeneous environments. Second, while this paper predefines the thresholds for dividing equivalence classes at each level, future studies could investigate dynamic threshold adjustment mechanisms. These mechanisms could be based on real-time changes in the boundary regions or other data characteristics, potentially using adaptive algorithms or machine learning methods to optimize threshold determination. Third, future research could further examine the impact of varying levels of granularity on decision accuracy and computational efficiency. Understanding the trade-offs between finer and coarser granularity could provide deeper insights into optimizing decision outcomes in complex environments [37]. Additionally, extending the proposed model to handle temporal or dynamic data would be a valuable direction for future studies. This would allow the model to be applied in real-time decision-making scenarios, where information evolves over time, such as monitoring systems or predictive analytics. Lastly, while the theoretical model presented in this paper offers significant insights, future work could focus on its practical application in real-world domains such as medical diagnosis [38], financial forecasting, and industrial decision-making [39]. Evaluating the model’s robustness and performance in practical settings would not only validate its utility but also suggest further refinements.