Existence and Uniqueness of Solution Represented as Fractional Power Series for the Fractional Advection–Dispersion Equation

Abstract

The fractional advection–dispersion equation is used in groundwater hydrology for modeling the movements of contaminants/solute particles along with flowing groundwater at the seepage velocity in porous media. This model is used for the prediction of the transport of nonreactive dissolved contaminants in groundwater. This paper establishes the existence and the uniqueness of solutions represented as fractional bi-variate power series of some initial-value problems and boundary-value problems for the fractional advection–dispersion equation. Moreover, a method to approximate the solutions using fractional polynomials in two variables and to evaluate the errors in a suitable rectangle is designed. Illustrative examples showing the applicability of the theoretical results are presented.

1. Introduction

Advection–dispersion is the transport process of groundwater contaminants. The movement of contaminants along with flowing groundwater at the seepage velocity in porous media is called advection, and the process caused by velocity variations in the porous media defines the dispersion. The advection–dispersion equation (ADE) for solute transport is derived from the law of conservation of mass (see [1,2]).

A space–time fractional advection–dispersion equation (FADE) is a generalization of the classical ADE in which the integer-order derivatives are replaced with fractional derivatives. The time-fractional advection–dispersion equation describes particles’ motion with memory in time [3].

Generally, fractional differential equations are a very useful instrument for modeling many phenomena in various fields of science and engineering (see, for example, [4,5,6,7,8]). Applications of fractional calculus require fractional derivatives of different kinds, leading to generalizations or modifications of some classical fractional derivatives (see [9] for some generalizations of the Riemann–Liouville derivative, [10] for an illustrative application of the Caputo–Fabrizio derivative, or [11] for an innovative approach rooted in the fusion of conformable and Caputo fractional calculus).

In our work, we use the Caputo fractional derivative, which is the most common type of fractional derivative used for the advection–dispersion equation (see, for instance, [12,13,14] or [15], where the two-dimensional fractional advection–dispersion equation is studied). However, there are also studies employing other fractional derivative operators, such as: the Riesz derivative [16,17,18], Atagana–Baleanu derivative [19], or Hilfer derivative, which generalizes both the Caputo and Riemann–Liouville operators [2]. We also mention some papers that use the Caputo fractional derivative for the time variable and another type of fractional derivative for the space variable (Riemann–Liouville in [20,21] or Riesz–Feller in [22,23]).

A number of methods that are used to approximate solutions of ordinary differential equations (ODEs) or partial differential equations (PDEs) have been extended to fractional ordinary differential equations (FODEs) and fractional partial differential equations (FPDEs). Particularly, for the fractional advection–dispersion equation, the following methods have been employed: Laplace, Mellin, and Fourier transforms ([23,24,25,26,27]), Adomian’s decomposition method and variational iteration method ([12,13]), analytic algorithms based on a homotopy analysis method or optimal homotopy asymptotic method ([28,29]), or the representation of solutions by means of particular series ([20]).

The power series method is a well-known tool to approximate the solutions of ordinary differential equations or partial differential equations. One of the main advantages of the method is that the accuracy of the approximate solution can be evaluated directly by replacing it in the equation and in the initial or boundary conditions. Thus, whenever there exists a solution that is represented as a power series, this method of approximation is highly recommended.

The method has been extended to fractional power series, where it has been employed to approximate solutions of fractional ordinary (as well as partially) differential equations (see, for instance, [30,31,32,33]). However, there are only a few theoretical results regarding the existence and the uniqueness of solutions for FODEs or FPDEs subjected to initial or boundary conditions.

Motivated by this lack of theoretical results, in this paper, we analyze some initial-value and boundary-value problems for the fractional space–time advection–dispersion equation with Caputo fractional derivatives and establish sufficient conditions for the existence and the uniqueness of the solution represented as fractional power series. The method can be also applied for other fractional derivatives or for other fractional differential equations.

The outline of this paper is as follows. In Section 2, we present some basic results regarding fractional derivatives and fractional power series. Theorem 1 states the fundamental properties of the $\alpha$-fractional power series. Section 3 presents the main results of the paper. As a basic subject, we consider three problems associated with the one-dimensional fractional advection–dispersion equation. Theorems 2 and 3 study two Cauchy problems and show that they have solutions represented as two-dimensional fractional power series—solutions that are uniquely determined by the initial conditions. Theorem 4 establishes conditions for the existence of the solution for a boundary-value problem. Section 4 contains the proofs of the theorems stated in Section 3 and, in addition, some comments and remarks regarding the solutions of the problems. We show, for instance, that all the hypotheses of Theorem 2 are necessary to obtain the result (see Remark 1). The proofs of the theorems outline the method to approximate the solution and also to obtain an estimation of the error in a suitable region. Section 5 deals with two illustrative examples, and the steps for error estimation are also described (see Example 1). The conclusions of our work are summarized in the last section of the paper.

2. Preliminaries

We present in this section some basic definitions and results regarding the Caputo fractional derivatives and the fractional power series (see [4,5,6,7,8]).

Definition 1 

([4]). Let I be a real interval, $I=(x_0,a]$, and μ be a real number. A function $f:I\to \mathbb{R}$ is said to be of class $C_{\mu ,x_0+}\left(I\right)$ if there exists $p>\mu$ such that $f\left(x\right)={(x-x_0)}^{p}g\left(x\right)$ for all $x\in I$, where $g:[x_0,a]\to \mathbb{R}$ is a continuous function. The function f is said to be of class $C_{\mu ,x_0+}^{\left(n\right)}\left(I\right)$, $n\in \mathbb{N}$, if there exists $f^{\left(n\right)}\left(x\right)$ for every $x\in I$ and $f^{\left(n\right)}\in C_{\mu ,x_0+}\left(I\right)$.

If $\alpha >0$ and $m=\lceil \alpha \rceil$, where $⌈x⌉=min\left\{z\in \mathbb{Z}:z\ge x\right\}$ denotes the ceiling function, the (left-sided) Caputo fractional derivative of order $\alpha$ of a function f is defined as follows.

Definition 2 

([4]). Let $I=(x_0,a]$ be a real interval, $\alpha >0$, $m=\lceil \alpha \rceil$, and let $f:I\to \mathbb{R}$ be a function of class $C_{-1,x_0+}^{\left(m\right)}\left(I\right)$. The left-sided Caputo fractional derivative of order α of f is defined as

$$\left(D_{x_0+}^{\alpha }f\right)\left(x\right)=\left\{\begin{array}{cc}{\displaystyle \frac{1}{\Gamma (m-\alpha )}}\underset{x_0}{\overset{x}{\int }}{\displaystyle \frac{f^{\left(m\right)}\left(t\right)dt}{{(x-t)}^{\alpha -m+1}}},& \mathrm{if}\alpha \notin \mathbb{N}\\ f^{\left(\alpha \right)}\left(x\right),& \mathrm{if}\alpha \in \mathbb{N}\end{array}\right.$$

We denote by

$$\left({\widehat{D}}_{x_0+}^{n\alpha }f\right)\left(x\right):=\underset{n-times}{\underbrace{(D_{x_0+}^{\alpha }{D}_{x_0+}^{\alpha }\dots D_{x_0+}^{\alpha }}}f)\left(x\right)$$

the sequential Caputo fractional derivative of order n. Let ${\widehat{C}}_{x_0+}^n\left(I\right)$ be the set of all the functions having sequential left-sided Caputo fractional derivatives of order k, and ${\widehat{D}}_{x_0+}^{k\alpha }f$ is continuous on $\overline{I}$ for every $k\le n$.

We remark that, in general, ${\widehat{D}}_{x_0+}^{n\alpha }f\ne D_{x_0+}^{n\alpha }f$: for instance, if $f\left(x\right)=\sqrt{x}$ and $\alpha ={\displaystyle \frac{1}{2}}$, then $\left({\widehat{D}}_{0+}^{2\alpha }f\right)\left(x\right)=D_{0+}^{{\displaystyle \frac{1}{2}}}\left(D_{0+}^{{\displaystyle \frac{1}{2}}}\sqrt{x}\right)=D_{0+}^{{\displaystyle \frac{1}{2}}}(\sqrt{\pi }/2)=0$, while $\left(D_{0+}^{2\alpha }f\right)\left(x\right)=D_{0+}^1\sqrt{x}={\left(\sqrt{x}\right)}^{\prime }={\displaystyle \frac{1}{2\sqrt{x}}}$.

By Definition 2, it follows that

$$D_{x_0+}^{\alpha }{(x-x_0)}^{i\alpha }=\left\{\begin{array}{cc}{\displaystyle \frac{\Gamma (i\alpha +1)}{\Gamma \left(\right(i-1)\alpha +1)}}{(x-x_0)}^{(i-1)\alpha },& \mathrm{if}i\ge 1\\ 0,& \mathrm{if}i=0.\end{array}\right.$$

(1)

Obviously, for a function of two variables $u(x,y)$, the Caputo fractional partial derivatives ${\displaystyle \frac{{\partial }_{x_0+}^{\alpha }u}{\partial x^{\alpha }}}$, ${\displaystyle \frac{{\partial }_{y_0+}^{\beta }u}{\partial y^{\beta }}}$ can be defined in a similar way.

A series of the form

$$\sum _{i=0}^{+\infty }{a}_i{(x-x_0)}^{i\alpha },x\ge x_0,$$

(2)

where the coefficients $a_i$ are real numbers, $\alpha >0$, and $x,x_0\in \mathbb{R}$, is said to be an α-fractional power series about $x_0$.

By using a substitution, fractional power series can be transformed into ordinary power series, so the basic results known for classical power series can be also proved for the fractional case. Thus, the following theorem establishes the basic properties of $\alpha$-fractional power series.

Theorem 1 

([30,32]). Let (2) be an α-fractional power series, with $\alpha \in (0,1)$ and $R={\displaystyle \frac{1}{\underset{i\to \infty }{lim\; sup}\sqrt[i]{|a_i|}}}$. Then $r=\left\{\begin{array}{c}{R}^{{\displaystyle \frac{1}{\alpha }}},\mathrm{if}R<+\infty \\ +\infty ,\mathrm{if}R=+\infty ,\end{array}\right.$ is called the radius of convergence of the series (2). If $r>0$, then:

(i) For all $b\in (0,r)$, the series (2) converges absolutely and uniformly on $\left[x_0,x_0+b\right]$, and there exists a positive integer $i\left(b\right)$ such that

$$|a_i|\le b^{-i\alpha },\mathrm{for}\mathrm{all}i\ge i\left(b\right).$$

If $f:[x_0,x_0+r)\to \mathbb{R}$ is the sum of the α-fractional power series (2), then f is a continuous function.

(ii) There exists the Caputo fractional derivative $\left(D_{x_0+}^{\alpha }f\right):(x_0,x_0+r)\to \mathbb{R}$. Moreover, the series of the Caputo fractional derivatives

$$\sum _{i=0}{a}_i{D}_{x_0+}^{\alpha }\left({(x-x_0)}^{i\alpha }\right)=\sum _{i=1}^{\infty }{a}_i{\displaystyle \frac{\Gamma (i\alpha +1)}{\Gamma \left((i-1)\alpha +1\right)}}{(x-x_0)}^{(i-1)\alpha },$$

(3)

converges absolutely and uniformly on $\left[x_0,x_0+b\right]$ for any $b\in (0,r)$, and $\left(D_{x_0+}^{\alpha }f\right)\left(x\right)$ is the sum of the series (3) for all $x\in \left(x_0,x_0+r\right)$.

We notice that a series of results from classical calculus do not hold in a similar form in the case of fractional calculus. For example, one can define in the fractional case an analytic function as in classical calculus.

Definition 3 

([34]). Let I be an open interval and $\alpha \in (0,1]$. A real function f defined on I is called α-fractional analytic on I if for every $x_0\in I$, there exists $\epsilon >0$ such that $J_{x_0,\epsilon }=[x_0,x_0+\epsilon )\subset I$ and f can be represented as an α-fractional power series (2) about $x_0$ on $J_{x_0,\epsilon }$.

It is known (see, for instance, [35]) in classical calculus that the sum of a power series is an analytic function. In the fractional case, the sum of an $\alpha$-fractional power series is an $\alpha$-analytic function if and only if $\alpha ={\displaystyle \frac{1}{n}}$, where n is a positive integer (see [34]).

Finally, since we need to express a function of two variables as a bi-variate fractional power series, we discuss in the following some particular features of this kind of series. First of all, we introduce the following relation of order on ${\mathbb{N}}^2$.

Let $\mathbf{i}=(i_1,i_2)$ be an element from ${\mathbb{N}}^2$. We denote by $\left|\mathbf{i}\right|=i_1+i_2$, and we order the elements of ${\mathbb{N}}^2$ such that for $\mathbf{i}\ne {\mathbf{i}}^{\prime }$, $\mathbf{i}=\left(i_1,i_2\right)$ and ${\mathbf{i}}^{\prime }=\left(i_1^{\prime },i_2^{\prime }\right)$, we have

$$\begin{array}{cc}\hfill \mathbf{i}\prec {\mathbf{i}}^{\prime }& \mathrm{if}\left|\mathbf{i}\right|<\left|{\mathbf{i}}^{\prime }\right|\hfill \\ & \mathrm{or}\left|\mathbf{i}\right|=\left|{\mathbf{i}}^{\prime }\right|\mathrm{and}{i}_2<i_2^{\prime }.\hfill \end{array}$$

(4)

A series of the form

$$\begin{array}{c}\sum _{\mathbf{i}⪰\mathbf{0}}{c}_{(i_1,i_2)}{\left(x_1-x_1^{\left(0\right)}\right)}^{i_1{\alpha }_1}{\left(x_2-x_2^{\left(0\right)}\right)}^{i_2{\alpha }_2}=c_{(0,0)}+c_{(1,0)}{\left(x_1-x_1^{\left(0\right)}\right)}^{{\alpha }_1}\hfill \\ \hfill +c_{(0,1)}{\left(x_2-x_2^{\left(0\right)}\right)}^{{\alpha }_2}+c_{(2,0)}{\left(x_1-x_1^{\left(0\right)}\right)}^{2{\alpha }_1}+c_{(1,1)}{\left(x_1-x_1^{\left(0\right)}\right)}^{{\alpha }_1}{\left(x_2-x_2^{\left(0\right)}\right)}^{{\alpha }_2}+\dots ,\end{array}$$

(5)

where $c_{(i_1,i_2)}\in \mathbb{R}$, $\mathit{\alpha }:=({\alpha }_1,{\alpha }_2)\succ \mathbf{0}$, and the terms are ordered by (4), is called an $\mathit{\alpha }$-fractional power series in two variables about ${\mathbf{x}}^{\left(0\right)}=(x_1^{\left(0\right)},x_2^{\left(0\right)})$.

For any $\alpha >0$, an $\alpha$-fractional power series is also an ${\alpha }^{\prime }$-fractional power series (where ${\alpha }^{\prime }={\displaystyle \frac{\alpha }{\lceil \alpha \rceil }}\in (0,1]$), so we can consider ${\alpha }_1,{\alpha }_2\in (0,1].$

Consider ${\mathbf{x}}^{\left(0\right)},{\mathbf{x}}^{\left(1\right)}\in {\mathbb{R}}^2$ such that $x_i^{\left(0\right)}<x_i^{\left(1\right)}$ for $i=1,2$. Denote by $[{\mathbf{x}}^{\left(0\right)},{\mathbf{x}}^{\left(1\right)}]:=\{\mathbf{x}\in {\mathbb{R}}^2:x_i^{\left(0\right)}\le x_i\le x_i^{\left(1\right)},i=1,2\}$ the rectangle defined by ${\mathbf{x}}^{\left(0\right)},{\mathbf{x}}^{\left(1\right)}$. If the series (5) converges on $[{\mathbf{x}}^{\left(0\right)},{\mathbf{x}}^{\left(1\right)}]$, then we say that its sum $u=u(x_1,x_2)$ is representable as a fractional power series about ${\mathbf{x}}^{\left(0\right)}$ on the rectangle defined by ${\mathbf{x}}^{\left(0\right)},{\mathbf{x}}^{\left(1\right)}$.

3. Main Results

We study two initial-value problems (Problems 1 and 2) and a boundary-value problem (Problem 3) for the fractional advection–dispersion equation, focusing on the existence and the uniqueness of the solutions representable as fractional power series.

Consider the one-dimensional fractional space–time advection–dispersion equation of the form (see, for example, [13])

$${\displaystyle \frac{{\partial }_{0+}^{\beta }c}{\partial t^{\beta }}}=-\nu {\displaystyle \frac{{\partial }_{0+}^{\alpha }c}{\partial x^{\alpha }}}+\kappa {\displaystyle \frac{{\widehat{\partial }}_{0+}^{2\alpha }c}{\partial x^{2\alpha }}},x>0,t>0,$$

(6)

where $c=c(x,t)$ is the solute concentration, x is the spatial variable, t is the time, $\nu$ and $\kappa$ are positive constants representing the average fluid velocity and the dispersion coefficient, respectively, and $\alpha ,\beta \in (0,1]$ are parameters describing the order of Caputo fractional derivatives with respect to x and t, respectively.

If $\alpha =\beta =1$, then Equation (6) becomes the classical advection–dispersion equation. The boundary conditions (and/or the initial conditions) are crucial for the existence and the uniqueness of the solution. Thus, as shown in [36], the classical advection–dispersion equation with the boundary conditions ${\displaystyle \frac{\partial c}{\partial x}}(0,t)={\displaystyle \frac{\nu }{\kappa }}c(0,t)$ and ${\displaystyle \frac{\partial c}{\partial x}}(L,t)=0$ (where L is a fixed positive number) has an infinite number of solutions.

3.1. Problem 1

Consider the one-dimensional fractional advection–dispersion Equation (6) subjected to the initial conditions

$$c(0,t)=f_1\left(t\right),$$

(7)

$${\displaystyle \frac{{\partial }_{0+}^{\alpha }c}{\partial x^{\alpha }}}(0,t)=f_2\left(t\right),$$

(8)

where $f_j\left(t\right)={\displaystyle \sum _{i=0}^{\infty }}{a}_i^{\left(j\right)}{t}^{i\beta }$, $j=1,2$, are represented as a $\beta$-fractional power series about 0 on an interval $[0,A_j]$, with $A_j$ being positive constants. For simplicity, without loss of generality, we can consider $A_1=A_2=A$.

Theorem 2 

(Existence and uniqueness of the solution of the Cauchy problem (6)–(8)). If $\beta \le 2\alpha$, then there exist a rectangle $\mathcal{R}=[\mathbf{0},\mathbf{y}]$ and a unique function $c=c(x,t)$ that is representable as an $(\alpha ,\beta )$-fractional power series about $\mathbf{0}$ on $\mathcal{R}$ and is a solution of Equation (6) that also satisfies conditions (7) and (8).

3.2. Problem 2

Consider now the one-dimensional fractional advection–dispersion Equation (6) subjected to the initial condition

$$c(x,0)=f_3\left(x\right),$$

(9)

where $f_3\left(x\right)={\displaystyle \sum _{i=0}^{\infty }}{a}_i^{\left(3\right)}{x}^{i\alpha }$ is represented as an $\alpha$-fractional power series about 0 on an interval $[0,A]$, with A being a positive constant.

Theorem 3 

(Existence and uniqueness of the solution the Cauchy problem (6) and (9)). If $2\alpha \le \beta$, then there exist a rectangle $\mathcal{R}=[\mathbf{0},\mathbf{y}]$ and a unique function $c=c(x,t)$ that is representable as an $(\alpha ,\beta )$-fractional power series about $\mathbf{0}$ on $\mathcal{R}$ and is a solution of Equation (6) that also satisfies condition (9).

3.3. Problem 3

Theorem 4. 

Consider the problem defined by (6)–(8) and (9). Suppose that $2\alpha =\beta$ and the functions $f_j$, $j=1,2,3$, are representable as α-fractional power series about 0 on $[0,A]$. Then there exist a rectangle $\mathcal{R}=[\mathbf{0},\mathbf{y}]$ and a unique function $c=c(x,t)$ that is representable as an $(\alpha ,\alpha )$-fractional power series about $\mathbf{0}$ on $\mathcal{R}$ and is a solution of Equation (6) that also satisfies conditions (7)–(9) if and only if $a_0^{\left(3\right)}=a_0^{\left(1\right)}$ and $a_1^{\left(3\right)}={\displaystyle \frac{a_0^{\left(2\right)}}{\Gamma (\alpha +1)}}$ and every $a_i^{\left(3\right)}$ can be written as a linear combination of the coefficients of $f_1$ and $f_2$ in the following form:

$$\begin{array}{c}{a}_i^{\left(3\right)}={\displaystyle \frac{1}{\Gamma (i\alpha +1){\kappa }^{i-1}}}\left(\sum _{j=0}^{⌊{\displaystyle \frac{i-2}{2}}⌋}\left({\displaystyle \genfrac{}{}{0pt}{}{i-2-j}{j}}\right){\kappa }^j{\nu }^{i-2-2j}\Gamma ((j+1)\beta +1)a_{j+1}^{\left(1\right)}\right.\hfill \\ \hfill \left.+\sum _{j=0}^{⌊{\displaystyle \frac{i-1}{2}}⌋}\left({\displaystyle \genfrac{}{}{0pt}{}{i-1-j}{j}}\right){\kappa }^j{\nu }^{i-1-2j}\Gamma (j\beta +1)a_j^{\left(2\right)}\right).\end{array}$$

(10)

4. Proofs of the Main Results and Comments

In this section, we present the proofs of Theorems 2–4 together with some comments and remarks regarding each problem and its (unique) solution represented as a fractional power series.

4.1. Problem 1

Proof of Theorem 2. 

We prove that problem (6)–(8) has a solution $c(x,t)$ that is representable as an $(\alpha ,\beta )$-fractional power series of the form

$$c(x,t)=\sum _{\mathbf{i}⪰\mathbf{0}}{c}_{(i_1,i_2)}{x}^{i_1\alpha }{t}^{i_2\beta }.$$

(11)

By using (6)–(8), we compute the coefficients $c_{(i_1,i_2)}$ such that the series (11) converges absolutely and uniformly in a suitable rectangle $\mathcal{R}=[\mathbf{0},\mathbf{y}]$. Thus, by Theorem 1, it follows that

$${\displaystyle \frac{{\partial }_{0+}^{\beta }c}{\partial t^{\beta }}}=\sum _{\mathbf{i}⪰\mathbf{0}}{c}_{(i_1,i_2+1)}{\displaystyle \frac{\Gamma ((i_2+1)\beta +1)}{\Gamma (i_2\beta +1)}}{x}^{i_1\alpha }{t}^{i_2\beta },$$

(12)

$${\displaystyle \frac{{\partial }_{0+}^{\alpha }c}{\partial x^{\alpha }}}=\sum _{\mathbf{i}⪰\mathbf{0}}{c}_{(i_1+1,i_2)}{\displaystyle \frac{\Gamma ((i_1+1)\alpha +1)}{\Gamma (i_1\alpha +1)}}{x}^{i_1\alpha }{t}^{i_2\beta }$$

(13)

and

$${\displaystyle \frac{{\widehat{\partial }}_{0+}^{2\alpha }c}{\partial x^{2\alpha }}}=\sum _{\mathbf{i}⪰\mathbf{0}}{c}_{(i_1+2,i_2)}{\displaystyle \frac{\Gamma ((i_1+2)\alpha +1)}{\Gamma (i_1\alpha +1)}}{x}^{i_1\alpha }{t}^{i_2\beta }.$$

(14)

By the initial conditions, we have

$$c_{(0,i_2)}=a_{i_2}^{\left(1\right)},c_{(1,i_2)}={\displaystyle \frac{a_{i_2}^{\left(2\right)}}{\Gamma (\alpha +1)}}.$$

(15)

Then, by (6) and (12)–(14), it follows that for every $i_1,i_2\ge 0$,

$$c_{(i_1+2,i_2)}={\displaystyle \frac{\nu }{\kappa }}·{\displaystyle \frac{\Gamma ((i_1+1)\alpha +1)}{\Gamma ((i_1+2)\alpha +1)}}{c}_{(i_1+1,i_2)}+{\displaystyle \frac{1}{\kappa }}·{\displaystyle \frac{\Gamma (i_1\alpha +1)}{\Gamma ((i_1+2)\alpha +1)}}·{\displaystyle \frac{\Gamma ((i_2+1)\beta +1)}{\Gamma (i_2\beta +1)}}{c}_{(i_1,i_2+1)}.$$

(16)

By (15) and (16), we have

$$c_{(2,i_2)}={\displaystyle \frac{\nu }{\kappa }}·{\displaystyle \frac{\Gamma (\alpha +1)}{\Gamma (2\alpha +1)}}{c}_{(1,i_2)}+{\displaystyle \frac{1}{\kappa }}·{\displaystyle \frac{\Gamma \left(1\right)}{\Gamma (2\alpha +1)}}·{\displaystyle \frac{\Gamma ((i_2+1)\beta +1)}{\Gamma (i_2\beta +1)}}{c}_{(0,i_2+1)}$$

$$={\displaystyle \frac{1}{\Gamma (2\alpha +1)}}\left({\displaystyle \frac{\nu a_{i_2}^{\left(2\right)}}{\kappa }}+{\displaystyle \frac{\Gamma ((i_2+1)\beta +1)a_{i_2+1}^{\left(1\right)}}{\kappa \Gamma (i_2\beta +1)}}\right),$$

$$c_{(3,i_2)}={\displaystyle \frac{\nu }{\kappa }}·{\displaystyle \frac{\Gamma (2\alpha +1)}{\Gamma (3\alpha +1)}}{c}_{(2,i_2)}+{\displaystyle \frac{1}{\kappa }}·{\displaystyle \frac{\Gamma (\alpha +1)}{\Gamma (3\alpha +1)}}·{\displaystyle \frac{\Gamma ((i_2+1)\beta +1)}{\Gamma (i_2\beta +1)}}{c}_{(1,i_2+1)}$$

$$={\displaystyle \frac{1}{\Gamma (3\alpha +1)}}\left({\displaystyle \frac{{\nu }^2{a}_{i_2}^{\left(2\right)}}{{\kappa }^2}}+{\displaystyle \frac{\nu \Gamma ((i_2+1)\beta +1)a_{i_2+1}^{\left(1\right)}}{{\kappa }^2\Gamma (i_2\beta +1)}}+{\displaystyle \frac{\Gamma ((i_2+1)\beta +1)a_{i_2+1}^{\left(2\right)}}{\kappa \Gamma (i_2\beta +1)}}\right),\dots .$$

Since the series ${\displaystyle \sum _{i=0}^{\infty }}{a}_i^{\left(j\right)}{t}^{i\beta }$, $j=1,2$, converges on $[0,A]$, there exists a positive constant C such that, for every $i=0,1,\dots$ and $j=1,2$,

$$|a_i^{\left(j\right)}|\le {\displaystyle \frac{C}{A^{i\beta }}}.$$

Hence, $|c_{(0,i_2)}|\le {\displaystyle \frac{C}{A^{i_2\beta }}}$, $|c_{(1,i_2)}|\le {\displaystyle \frac{C}{\Gamma (\alpha +1)A^{i_2\beta }}}$, $|c_{(2,i_2)}|\le {\displaystyle \frac{C}{\Gamma (2\alpha +1)A^{i_2\beta }}}\left({\displaystyle \frac{\nu }{\kappa }}+{\displaystyle \frac{\Gamma ((i_2+1)\beta +1)}{\kappa \Gamma (i_2\beta +1)A^{\beta }}}\right)$, $|c_{(3,i_2)}|\le {\displaystyle \frac{C}{\Gamma (3\alpha +1)A^{i_2\beta }}}\left({\displaystyle \frac{{\nu }^2}{{\kappa }^2}}+({\displaystyle \frac{\nu }{{\kappa }^2}}+{\displaystyle \frac{1}{\kappa }}){\displaystyle \frac{\Gamma ((i_2+1)\beta +1)}{\kappa \Gamma (i_2\beta +1)A^{\beta }}}\right)$ and so on.

Now, we prove that there exists a positive constant B such that, for every $i_1,i_2\ge 0$,

$$|c_{(i_1,i_2)}|\le {\displaystyle \frac{C{B}^{(i_1+i_2)\beta }}{{\kappa }^{i_1}{A}^{(i_2+\lfloor \frac{i_1}{2}\rfloor )\beta }}}·{\displaystyle \frac{\Gamma ((i_2+\lfloor \frac{i_1}{2}\rfloor )\beta +1)}{\Gamma (i_2\beta +1)\Gamma (i_1\alpha +1)}},$$

(17)

where $⌊x⌋=max\left\{z\in \mathbb{Z}:z\le x\right\}$ denotes the floor function.

The function $\Gamma \left(x\right)$ has a minimum value on $(0,\infty )$ at $x_{min}\approx 1.4616$ and it is strictly decreasing on $(0,x_{min}]$ and strictly increasing on $[x_{min},+\infty )$. We denote

$$\gamma ={\displaystyle \frac{1}{min\Gamma \left(x\right)}}={\displaystyle \frac{1}{\Gamma \left(x_{min}\right)}}\approx 1.129173.$$

(18)

We can see that for any $1<x<y$, the following inequality holds:

$$\Gamma \left(x\right)\le \gamma \Gamma \left(y\right).$$

(19)

We choose B such that

$$B^{\beta }\ge max\{1,A^{\beta },\gamma \nu max\{A^{\beta },1\}+\kappa \},$$

(20)

and we prove inequality (17) by induction on $i_1$.

If $i_1=0$, for every $i_2$, (17) becomes $|c_{(0,i_2)}|\le {\displaystyle \frac{C{B}^{i_2\beta }}{A^{i_2\beta }}}$. Since $|c_{(0,i_2)}|\le {\displaystyle \frac{C}{A^{i_2\beta }}}$, by (20), it follows that (17) is true for $i_1=0$ and for every $i_2$.

Similarly, if $i_1=1$, for every $i_2$, (17) becomes $|c_{(1,i_2)}|\le {\displaystyle \frac{C{B}^{(i_2+1)\beta }}{\kappa A^{i_2\beta }\Gamma (\alpha +1)}}$. Since $|c_{(1,i_2)}|\le {\displaystyle \frac{C}{\Gamma (\alpha +1)A^{i_2\beta }}}$, it follows that (17) is also true for $i_1=1$ and for every $i_2$.

We assume that the inequality (17) is true for every $i_1\le m+1$ and every $i_2\ge 0$. Then, by (16), (19), (20) and by the induction hypothesis, we have

$$|c_{(m+2,i_2)}|\le {\displaystyle \frac{\nu \Gamma \left(\right(m+1)\alpha +1)}{\kappa \Gamma \left(\right(m+2)\alpha +1)}}|c_{(m+1,i_2)}|+{\displaystyle \frac{\Gamma (m\alpha +1)}{\kappa \Gamma \left(\right(m+2)\alpha +1)}}·{\displaystyle \frac{\Gamma ((i_2+1)\beta +1)}{\Gamma (i_2\beta +1)}}|c_{(m,i_2+1)}|$$

$$\le {\displaystyle \frac{\nu }{\kappa }}·{\displaystyle \frac{\Gamma \left(\right(m+1)\alpha +1)}{\Gamma \left(\right(m+2)\alpha +1)}}·{\displaystyle \frac{C{B}^{(m+1+i_2)\beta }}{{\kappa }^{m+1}{A}^{(i_2+\lfloor \frac{m+1}{2}\rfloor )\beta }}}·{\displaystyle \frac{\Gamma ((i_2+\lfloor \frac{m+1}{2}\rfloor )\beta +1)}{\Gamma (i_2\beta +1)\Gamma ((m+1)\alpha +1)}}$$

$$+{\displaystyle \frac{1}{\kappa }}·{\displaystyle \frac{\Gamma (m\alpha +1)}{\Gamma \left(\right(m+2)\alpha +1)}}·{\displaystyle \frac{\Gamma ((i_2+1)\beta +1)}{\Gamma (i_2\beta +1)}}{\displaystyle \frac{C{B}^{(m+i_2+1)\beta }}{{\kappa }^m{A}^{(i_2+1+\lfloor \frac{m}{2}\rfloor )\beta }}}·{\displaystyle \frac{\Gamma ((i_2+1+\lfloor \frac{m}{2}\rfloor )\beta +1)}{\Gamma ((i_2+1)\beta +1)\Gamma (m\alpha +1)}}$$

$$={\displaystyle \frac{C{B}^{(m+1+i_2)\beta }\left(\nu A^{(\lfloor \frac{m+2}{2}\rfloor -\lfloor \frac{m+1}{2}\rfloor )\beta }\Gamma ((i_2+\lfloor \frac{m+1}{2}\rfloor )\beta +1)+\kappa \Gamma ((i_2+1+\lfloor \frac{m}{2}\rfloor )\beta +1)\right)}{{\kappa }^{m+2}{A}^{(i_2+\lfloor \frac{m+2}{2}\rfloor )\beta }\Gamma (i_2\beta +1)\Gamma ((m+2)\alpha +1)}}$$

$$\le {\displaystyle \frac{C{B}^{(m+1+i_2)\beta }\Gamma ((i_2+\lfloor \frac{m+2}{2}\rfloor )\beta +1)\left(\gamma \nu A^{(\lfloor \frac{m+2}{2}\rfloor -\lfloor \frac{m+1}{2}\rfloor )\beta }+\kappa \right)}{{\kappa }^{m+2}{A}^{(i_2+\lfloor \frac{m+2}{2}\rfloor )\beta }\Gamma (i_2\beta +1)\Gamma ((m+2)\alpha +1)}}$$

$$\le {\displaystyle \frac{C{B}^{(m+1+i_2)\beta }\Gamma ((i_2+\lfloor \frac{m+2}{2}\rfloor )\beta +1)\left(\gamma \nu max\{A^{\beta },1\}+\kappa \right)}{{\kappa }^{m+2}{A}^{(i_2+\lfloor \frac{m+2}{2}\rfloor )\beta }\Gamma (i_2\beta +1)\Gamma ((m+2)\alpha +1)}}$$

$$\le {\displaystyle \frac{C{B}^{(m+2+i_2)\beta }\Gamma ((i_2+\lfloor \frac{m+2}{2}\rfloor )\beta +1)}{{\kappa }^{m+2}{A}^{(i_2+\lfloor \frac{m+2}{2}\rfloor )\beta }\Gamma (i_2\beta +1)\Gamma ((m+2)\alpha +1)}}.$$

Hence, the inequality (17) holds for every $i_1,i_2\ge 0$.

Since $\beta \le 2\alpha$, we obtain using (19) that $\Gamma ((i_2+\lfloor {\displaystyle \frac{i_1}{2}}\rfloor )\beta +1)\le \gamma \Gamma ((i_2\beta +i_1\alpha +1)$. Moreover, because $B\ge 1$, ${\displaystyle \frac{B}{A}}\ge 1$, $\left({\displaystyle \genfrac{}{}{0pt}{}{n}{k}}\right)\le 2^{n-1}$, and $\gamma <2$, by (17), we have:

$$|c_{(i_1,i_2)}|\le {\displaystyle \frac{\gamma C{B}^{(i_1+i_2)\beta }}{{\kappa }^{i_1}{A}^{(i_2+\lfloor \frac{i_1}{2}\rfloor )\beta }}}·{\displaystyle \frac{\Gamma (i_2\beta +i_1\alpha +1)}{\Gamma (i_2\beta +1)\Gamma (i_1\alpha +1)}}\le {\displaystyle \frac{\gamma C{B}^{(i_1+i_2)\beta }}{{\kappa }^{i_1}{A}^{(i_2+\lfloor \frac{i_1}{2}\rfloor )\beta }}}·{\displaystyle \frac{\Gamma (i_2+i_1+1)}{\Gamma (i_2+1)\Gamma (i_1+1)}}$$

$$\le {\displaystyle \frac{C{2}^{i_1+i_2}{B}^{(i_1+i_2)\beta }}{{\kappa }^{i_1}{A}^{(i_2+\lfloor \frac{i_1}{2}\rfloor )\beta }}}\le {\displaystyle \frac{C{2}^{i_1+i_2}{B}^{(i_1-\lfloor \frac{i_1}{2}\rfloor )\beta }}{{\kappa }^{i_1}}}·{\left({\displaystyle \frac{B}{A}}\right)}^{i_2\beta }{\left({\displaystyle \frac{B}{A}}\right)}^{\lfloor {\displaystyle \frac{i_1}{2}}\rfloor \beta }$$

$$\le {\displaystyle \frac{C{2}^{i_1+i_2}{B}^{(i_1+1)\alpha }}{{\kappa }^{i_1}}}·{\left({\displaystyle \frac{B}{A}}\right)}^{i_2\beta }{\left({\displaystyle \frac{B}{A}}\right)}^{i_1\alpha }=C{B}^{\alpha }{\left({\displaystyle \frac{B^2{2}^{\frac{1}{\alpha }}}{A{\kappa }^{\frac{1}{\alpha }}}}\right)}^{i_1\alpha }{\left({\displaystyle \frac{B{2}^{\frac{1}{\beta }}}{A}}\right)}^{i_2\beta }.$$

We denote $M_1={\displaystyle \frac{B^2{2}^{\frac{1}{\alpha }}}{A{\kappa }^{\frac{1}{\alpha }}}}$ and $M_2={\displaystyle \frac{B{2}^{\frac{1}{\beta }}}{A}}$. Hence, by choosing $y_1<{\displaystyle \frac{1}{M_1}}$ and $y_2<{\displaystyle \frac{1}{M_2}}$, it follows that the series (11) converges absolutely and uniformly on $\mathcal{R}=[\mathbf{0},\mathbf{y}]$.

Thus, we proved that function (11) with the coefficients $c_{i_1,i_2}$ defined by Equations (15) and (16) is a solution of the Cauchy problem (6)–(8). Moreover, we have shown that a fractional power series of the form (11) that satisfies the fractional differential equation (6) and the initial conditions (7) and (8) has the coefficients $c_{i_1,i_2}$ that are uniquely determined by Equations (15) and (16), and so the theorem is proved. □

Remark 1. 

The condition $\beta \le 2\alpha$ cannot be removed from the hypotheses of Theorem 2. To give a counterexample, we consider $\beta =1$ and $\alpha \in (0,1/2).$ Under the previous notations, we choose $a_i^{\left(1\right)}=a_i^{\left(2\right)}=1$ for all i, $\nu =\kappa =1$, and $A={\displaystyle \frac{1}{2}}.$ Then, for all $i_2$, we have $c_{(0,i_2)}=1$ and $c_{(1,i_2)}={\displaystyle \frac{1}{\Gamma (\alpha +1)}}$.

To prove the statement, we assume by contradiction that the theorem holds in this case. Then, by (16), it follows that all $c_{(i_1,i_2)}$ are positive real numbers, and we have:

$$c_{(2,i_2)}={\displaystyle \frac{\Gamma (\alpha +1)}{\Gamma (2\alpha +1)}}{c}_{(1,i_2)}+{\displaystyle \frac{\Gamma \left(1\right)}{\Gamma (2\alpha +1)}}(i_2+1)c_{(0,i_2+1)}={\displaystyle \frac{i_2+2}{\Gamma (2\alpha +1)}}>{\displaystyle \frac{i_2}{\Gamma (2\alpha +1)}},$$

$$c_{(3,i_2)}={\displaystyle \frac{\Gamma (2\alpha +1)}{\Gamma (3\alpha +1)}}{c}_{(2,i_2)}+{\displaystyle \frac{\Gamma (\alpha +1)}{\Gamma (3\alpha +1)}}(i_2+1)c_{(1,i_2+1)}>{\displaystyle \frac{1}{\Gamma (3\alpha +1)}}(i_2+i_2+1)>{\displaystyle \frac{i_2}{\Gamma (3\alpha +1)}},$$

$$c_{(4,i_2)}={\displaystyle \frac{\Gamma (3\alpha +1)}{\Gamma (4\alpha +1)}}{c}_{(3,i_2)}+{\displaystyle \frac{\Gamma (2\alpha +1)}{\Gamma (4\alpha +1)}}(i_2+1)c_{(2,i_2+1)}>{\displaystyle \frac{i_2+{(i_2+1)}^2}{\Gamma (4\alpha +1)}}>{\displaystyle \frac{i_2^2}{\Gamma (4\alpha +1)}},\dots .$$

Thus, by recurrence, we have

$$c_{(i_1,i_2)}>{\displaystyle \frac{i_2^{⌊\frac{i_1}{2}⌋}}{\Gamma (i_1\alpha +1)}},\mathrm{for}\mathrm{all}{i}_1,i_2\ge 0.$$

(21)

Since for every positive real number x,

$$\Gamma (x+1)<\sqrt{2\pi }{x}^{x+1/2}{e}^{-x+{\displaystyle \frac{1}{12x}}},$$

taking $i_1=i_2=i$ in (21), we obtain:

$$c_{(i,i)}>{\displaystyle \frac{i^{\frac{i-1}{2}}}{\sqrt{2\pi }{\left(i\alpha \right)}^{i\alpha +1/2}{e}^{-i\alpha +\frac{1}{12i\alpha }}}}>u_i:={\displaystyle \frac{i^{i(\frac{1}{2}-\alpha )-1}}{\sqrt{2\pi e\alpha }}}{\left({\displaystyle \frac{e}{\alpha }}\right)}^{i\alpha },\mathit{for}\mathit{all}i>{\displaystyle \frac{1}{6\alpha }}.$$

(22)

Since

$$u_i^{{\displaystyle \frac{1}{i}}}={\displaystyle \frac{i^{\frac{1}{2}-\alpha -\frac{1}{i}}}{{\left(2\pi e\alpha \right)}^{\frac{1}{2i}}}}{\left({\displaystyle \frac{e}{\alpha }}\right)}^{\alpha },$$

it follows that

$$\underset{i\to +\infty }{lim}{u}_i^{{\displaystyle \frac{1}{i}}}=+\infty .$$

Hence, for every positive real number y, the sequence ${\left\{u_i{y}^i\right\}}_{i\ge 0}$ is unbounded. Thus, by (22), it follows that the series (11) diverges on any rectangle $\mathcal{R}=[\mathbf{0},\mathbf{y}]$, so the conclusion of Theorem 2 does not hold in this case.

Remark 2. 

The coefficients $c_{(i_1,i_2)}$ of the fractional power series $c(x,t)$ that satisfies Equation (6) and the initial conditions (7)–(8) can be expressed using the coefficients $a_i^{\left(1\right)}$ and $a_i^{\left(2\right)}$ of the functions $f_1\left(x\right)$ and $f_2\left(x\right)$. Thus, it can be proved by mathematical induction on $i_1$ that for every $i_1\ge 2$ and $i_2\ge 0$, we have:

$$c_{(i_1,i_2)}={\displaystyle \frac{1}{{\kappa }^{i_1-1}\Gamma (i_1\alpha +1)\Gamma (i_2\beta +1)}}\left(P^{\left(1\right)}(i_1,i_2)+P^{\left(2\right)}(i_1,i_2)\right),$$

(23)

where

$$\begin{array}{cc}\hfill P^{\left(1\right)}(i_1,i_2)& =\sum _{j=0}^{⌊{\displaystyle \frac{i_1-2}{2}}⌋}F(i_1-2,j){\kappa }^j{\nu }^{i_1-2-2j}\Gamma ((j+i_2+1)\beta +1)a_{j+i_2+1}^{\left(1\right)},i_1\ge 2\hfill \end{array}$$

(24)

$$\begin{array}{cc}\hfill P^{\left(2\right)}(i_1,i_2)& =\sum _{j=0}^{⌊{\displaystyle \frac{i_1-1}{2}}⌋}F(i_1-1,j){\kappa }^j{\nu }^{i_1-1-2j}\Gamma ((j+i_2)\beta +1)a_{j+i_2}^{\left(2\right)},i_1\ge 1,\hfill \end{array}$$

(25)

and $F(n,j)=\left({\displaystyle \genfrac{}{}{0pt}{}{n-j}{j}}\right)$ for all $n\ge 0$, and $0\le j\le ⌊{\displaystyle \frac{n}{2}}⌋$ are the coefficients of the Fibonacci polynomials (sequence A011973 in the On-line Encyclopedia of Integer Sequences [37]).

Taking $P^{\left(1\right)}(1,i_2)=0$ for every $i_2\ge 0$, relation (23) can be easily verified for $i_1=1,2$. We suppose it is true for any $i_1\le m+1$ and $i_2\ge 0$. Then, from the recurrence relation (16) and the induction hypothesis, we can write:

$$c_{(m+2,i_2)}={\displaystyle \frac{\nu P^{\left(1\right)}(m+1,i_2)+\nu P^{\left(2\right)}(m+1,i_2)+\kappa P^{\left(1\right)}(m,i_2+1)+\kappa P^{\left(2\right)}(m,i_2+1)}{{\kappa }^{m+1}\Gamma ((m+2)\alpha +1)\Gamma (i_2\beta +1)}}.$$

From the relations (24) and (25), it follows that

$$\nu P^{\left(i\right)}(i_1+1,i_2)+\kappa P^{\left(i\right)}(i_1,i_2+1)=P^{\left(i\right)}(i_1+2,i_2)$$

for $i=1,2$, so we have

$$c_{(m+2,i_2)}={\displaystyle \frac{1}{{\kappa }^{m+1}\Gamma ((m+2)\alpha +1)\Gamma (i_2\beta +1)}}\left(P^{\left(1\right)}(m+2,i_2)+P^{\left(2\right)}(m+2,i_2)\right),$$

and the relation (23) holds for any $i_1\ge 2$ and $i_2\ge 0$.

4.2. Problem 2

Proof of Theorem 3. 

As in the proof of Theorem 2, we show that the problem (6), (9) has a solution $c(x,t)$ that is representable as an $(\alpha ,\beta )$-fractional power series of the form (11). By using (6) and (9), we find the coefficients $c_{(i_1,i_2)}$ such that the series (11) converges absolutely and uniformly in a suitable rectangle $\mathcal{R}=[\mathbf{0},\mathbf{y}]$.

Thus, by the initial condition (9), we have

$$c_{(i_1,0)}=a_{i_1}^{\left(3\right)}.$$

(26)

Then, by (6) and (12)–(14), it follows that (16) can be written in the form

$$c_{(i_1,i_2+1)}={\displaystyle \frac{\Gamma (i_2\beta +1)}{\Gamma ((i_2+1)\beta +1)}}\left(-{\displaystyle \frac{\nu \Gamma ((i_1+1)\alpha +1)}{\Gamma (i_1\alpha +1)}}{c}_{(i_1+1,i_2)}+{\displaystyle \frac{\kappa \Gamma ((i_1+2)\alpha +1)}{\Gamma (i_1\alpha +1)}}{c}_{(i_1+2,i_2)}\right).$$

(27)

By (26) and (27), we have

$$c_{(i_1,1)}={\displaystyle \frac{\Gamma \left(1\right)}{\Gamma (\beta +1)}}\left(-{\displaystyle \frac{\nu \Gamma ((i_1+1)\alpha +1)}{\Gamma (i_1\alpha +1)}}{c}_{(i_1+1,0)}+{\displaystyle \frac{\kappa \Gamma ((i_1+2)\alpha +1)}{\Gamma (i_1\alpha +1)}}{c}_{(i_1+2,0)}\right)$$

$$={\displaystyle \frac{1}{\Gamma (\beta +1)}}\left(-{\displaystyle \frac{\nu \Gamma ((i_1+1)\alpha +1)}{\Gamma (i_1\alpha +1)}}{a}_{i_1+1}^{\left(3\right)}+{\displaystyle \frac{\kappa \Gamma ((i_1+2)\alpha +1)}{\Gamma (i_1\alpha +1)}}{a}_{i_1+2}^{\left(3\right)}\right),$$

$$c_{(i_1,2)}={\displaystyle \frac{\Gamma (\beta +1)}{\Gamma (2\beta +1)}}\left(-\nu {\displaystyle \frac{\Gamma ((i_1+1)\alpha +1)}{\Gamma (i_1\alpha +1)}}{c}_{(i_1+1,1)}+\kappa {\displaystyle \frac{\Gamma ((i_1+2)\alpha +1)}{\Gamma (i_1\alpha +1)}}{c}_{(i_1+2,1)}\right).$$

$$={\displaystyle \frac{1}{\Gamma (2\beta +1)}}\left({\displaystyle \frac{{\nu }^2\Gamma ((i_1+2)\alpha +1)}{\Gamma (i_1\alpha +1)}}{a}_{i_1+2}^{\left(3\right)}-{\displaystyle \frac{2\nu \kappa \Gamma ((i_1+3)\alpha +1)}{\Gamma (i_1\alpha +1)}}{a}_{i_1+3}^{\left(3\right)}\right.$$

$$\left.+{\displaystyle \frac{{\kappa }^2\Gamma ((i_1+4)\alpha +1)}{\Gamma (i_1\alpha +1)}}{a}_{i_1+4}^{\left(3\right)}\right),$$

$$c_{(i_1,3)}={\displaystyle \frac{\Gamma (2\beta +1)}{\Gamma (3\beta +1)}}\left(-\nu {\displaystyle \frac{\Gamma ((i_1+1)\alpha +1)}{\Gamma (i_1\alpha +1)}}{c}_{(i_1+1,2)}+\kappa {\displaystyle \frac{\Gamma ((i_1+2)\alpha +1)}{\Gamma (i_1\alpha +1)}}{c}_{(i_1+2,2)}\right).$$

$$={\displaystyle \frac{1}{\Gamma (3\beta +1)}}\left(-{\displaystyle \frac{{\nu }^3\Gamma ((i_1+3)\alpha +1)}{\Gamma (i_1\alpha +1)}}{a}_{i_1+3}^{\left(3\right)}+{\displaystyle \frac{3{\nu }^2\kappa \Gamma ((i_1+4)\alpha +1)}{\Gamma (i_1\alpha +1)}}{a}_{i_1+4}^{\left(3\right)}\right.$$

$$\left.-{\displaystyle \frac{3\nu {\kappa }^2\Gamma ((i_1+5)\alpha +1)}{\Gamma (i_1\alpha +1)}}{a}_{i_1+5}^{\left(3\right)}+{\displaystyle \frac{{\kappa }^3\Gamma ((i_1+6)\alpha +1)}{\Gamma (i_1\alpha +1)}}{a}_{i_1+6}^{\left(3\right)}\right),\dots .$$

Since the series ${\displaystyle \sum _{i=0}^{\infty }}{a}_i^{\left(3\right)}{x}^{i\alpha }$ converges on $[0,A]$, there exists a positive constant C such that for every i,

$$|a_i^{\left(3\right)}|\le {\displaystyle \frac{C}{A^{i\alpha }}}.$$

(28)

Hence,

$$\begin{array}{cc}\hfill |c_{(i_1,0)}|& \le \frac{C}{A^{i_1\alpha }},\hfill \\ \hfill |c_{(i_1,1)}|& \le \frac{C}{\Gamma (\beta +1)A^{(i_1+1)\alpha }}\left(\frac{\nu \Gamma ((i_1+1)\alpha +1)}{\Gamma (i_1\alpha +1)}+\frac{\kappa \Gamma ((i_1+2)\alpha +1)}{\Gamma (i_1\alpha +1)A^{\alpha }}\right),\hfill \\ \hfill |c_{(i_1,2)}|& \le \frac{C}{\Gamma (2\beta +1)A^{(i_1+2)\alpha }}\left(\frac{{\nu }^2\Gamma ((i_1+2)\alpha +1)}{\Gamma (i_1\alpha +1)}+\frac{2\nu \kappa \Gamma ((i_1+3)\alpha +1)}{\Gamma (i_1\alpha +1)A^{\alpha }}+\frac{{\kappa }^2\Gamma ((i_1+4)\alpha +1)}{\Gamma (i_1\alpha +1)A^{2\alpha }}\right),\hfill \\ \hfill |c_{(i_1,3)}|& \le \frac{C}{\Gamma (3\beta +1)A^{(i_1+3)\alpha }}\left(\frac{{\nu }^3\Gamma ((i_1+3)\alpha +1)}{\Gamma (i_1\alpha +1)}+\frac{3{\nu }^2\kappa \Gamma ((i_1+4)\alpha +1)}{\Gamma (i_1\alpha +1)A^{\alpha }}+\frac{3\nu {\kappa }^2\Gamma ((i_1+5)\alpha +1)}{\Gamma (i_1\alpha +1)A^{2\alpha }}+\frac{{\kappa }^3\Gamma ((i_1+6)\alpha +1)}{\Gamma (i_1\alpha +1)A^{3\alpha }}\right),\hfill \end{array}$$

and so on.

Now, we prove that there exists a positive constant B such that for every $i_1,i_2\ge 0$,

$$|c_{(i_1,i_2)}|\le {\displaystyle \frac{C{B}^{i_2\alpha }}{\Gamma (i_2\beta +1)A^{(i_1+i_2)\alpha }}}·{\displaystyle \frac{\Gamma ((i_1+2i_2)\alpha +1)}{\Gamma (i_1\alpha +1)}}.$$

(29)

We choose the constant B such that

$$B^{\alpha }=max\left\{A^{\alpha },\gamma \nu +{\displaystyle \frac{\kappa }{A^{\alpha }}}\right\},$$

(30)

where $\gamma$ is defined by (18), and we prove the inequality (29) by induction on $i_2$.

If $i_2=0$, then (29) becomes $|c_{(i_1,0)}|\le {\displaystyle \frac{C}{A^{i_1\alpha }}}$, which is true for every $i_1$.

Similarly, if $i_2=1$, then (29) becomes $|c_{(i_1,1)}|\le {\displaystyle \frac{C{B}^{\alpha }}{\Gamma (\beta +1)A^{(i_1+1)\alpha }}}·{\displaystyle \frac{\Gamma ((i_1+2)\alpha +1)}{\Gamma (i_1\alpha +1)}}.$ Since $|c_{(i_1,1)}|\le {\displaystyle \frac{C}{\Gamma (\beta +1)A^{(i_1+1)\alpha }}}\left({\displaystyle \frac{\nu \Gamma ((i_1+1)\alpha +1)}{\Gamma (i_1\alpha +1)}}+{\displaystyle \frac{\kappa \Gamma ((i_1+2)\alpha +1)}{\Gamma (i_1\alpha +1)A^{\alpha }}}\right)\le {\displaystyle \frac{C(\gamma \nu +\frac{\kappa }{A^{\alpha }})}{\Gamma (\beta +1)A^{(i_1+1)\alpha }}}·{\displaystyle \frac{\Gamma ((i_1+2)\alpha +1)}{\Gamma (i_1\alpha +1)}}$ it follows that (29) is true also for $i_2=1$ and for every $i_1$.

We assume that the inequality (29) holds for every $i_2\le m+1$ and every $i_1$. Then, by (27), (30) and by the induction hypothesis, we have:

$$|c_{(i_1,m+2)}|\le {\displaystyle \frac{\Gamma \left(\right(m+1)\beta +1)}{\Gamma \left(\right(m+2)\beta +1)}}\left({\displaystyle \frac{\nu \Gamma ((i_1+1)\alpha +1)}{\Gamma (i_1\alpha +1)}}|c_{(i_1+1,m+1)}|+{\displaystyle \frac{\kappa \Gamma ((i_1+2)\alpha +1)}{\Gamma (i_1\alpha +1)}}·|c_{(i_1+2,m+1)}|\right)$$

$$\le {\displaystyle \frac{\Gamma \left(\right(m+1)\beta +1)}{\Gamma \left(\right(m+2)\beta +1)}}\left({\displaystyle \frac{\nu \Gamma ((i_1+1)\alpha +1)}{\Gamma (i_1\alpha +1)}}·{\displaystyle \frac{C{B}^{(m+1)\alpha }}{\Gamma ((m+1)\beta +1)A^{(i_1+m+2)\alpha }}}·{\displaystyle \frac{\Gamma ((i_1+1+2(m+1))\alpha +1)}{\Gamma ((i_1+1)\alpha +1)}}\right.$$

$$+\left.{\displaystyle \frac{\kappa \Gamma ((i_1+2)\alpha +1)}{\Gamma (i_1\alpha +1)}}·{\displaystyle \frac{C{B}^{(m+1)\alpha }}{\Gamma ((m+1)\beta +1)A^{(i_1+m+3)\alpha }}}·{\displaystyle \frac{\Gamma ((i_1+2+2(m+1))\alpha +1)}{\Gamma ((i_1+2)\alpha +1)}}\right)$$

$$={\displaystyle \frac{C{B}^{(m+1)\alpha }}{\Gamma ((m+2)\beta +1)A^{(i_1+m+2)\alpha }}}\left({\displaystyle \frac{\nu \Gamma ((i_1+2m+3)\alpha +1)}{\Gamma (i_1\alpha +1)}}+{\displaystyle \frac{\kappa \Gamma ((i_1+2m+4)\alpha +1)}{\Gamma (i_1\alpha +1)A^{\alpha }}}\right)$$

$$\le {\displaystyle \frac{C{B}^{(m+1)\alpha }\Gamma ((i_1+2m+4)\alpha +1)}{\Gamma ((m+2)\beta +1)A^{(i_1+m+2)\alpha }\Gamma (i_1\alpha +1)}}\left(\gamma \nu +{\displaystyle \frac{\kappa }{A^{\alpha }}}\right)$$

$$\le {\displaystyle \frac{C{B}^{(m+2)\alpha }\Gamma ((i_1+2m+4)\alpha +1)}{\Gamma ((m+2)\beta +1)A^{(i_1+m+2)\alpha }\Gamma (i_1\alpha +1)}}.$$

Hence, the inequality (29) holds for every $i_1,i_2\ge 0$.

Since $\alpha \le \beta /2$, it follows that $\Gamma ((i_1+2i_2)\alpha +1)\le \gamma \Gamma ((i_1\alpha +i_2\beta +1)$. Then, by (29), we have

$$\begin{array}{cc}\hfill |c_{(i_1,i_2)}|& \le {\displaystyle \frac{C{B}^{i_2\alpha }\gamma }{\Gamma (i_2\beta +1)A^{(i_1+i_2)\alpha }}}·{\displaystyle \frac{\Gamma (i_1\alpha +i_2\beta +1)}{\Gamma (i_1\alpha +1)}}\hfill \\ \hfill & \le {\displaystyle \frac{C{2}^{i_1+i_2}{B}^{i_2\alpha }}{A^{(i_1+i_2)\alpha }}}\le C{2}^{i_1+i_2}{\left({\displaystyle \frac{1}{A}}\right)}^{i_1\alpha }{\left(\sqrt{{\displaystyle \frac{B}{A}}}\right)}^{i_2\beta }.\hfill \end{array}$$

By choosing $y_1<2^{-{\displaystyle \frac{1}{\alpha }}}A$ and $y_2<2^{-{\displaystyle \frac{1}{\beta }}}\sqrt{{\displaystyle \frac{A}{B}}}$, it follows that the series (11) converges absolutely and uniformly on $\mathcal{R}=[\mathbf{0},\mathbf{y}]$, which implies the theorem. □

Remark 3. 

The coefficients $c_{(i_1,i_2)}$ of the fractional power series $c(x,t)$ that satisfies Equation (6) can be expressed explicitly using the coefficients $a_i^{\left(3\right)}$ of the function $f_3\left(x\right)$ from the initial condition (9). Thus, it can be easily proved by mathematical induction on $i_2=0,1,\dots$ that

$$c_{(i_1,i_2)}={\displaystyle \frac{1}{\Gamma (i_1\alpha +1)\Gamma (i_2\beta +1)}}\sum _{j=0}^{i_2}{(-1)}^{i_2-j}\left({\displaystyle \genfrac{}{}{0pt}{}{i_2}{j}}\right){\kappa }^j{\nu }^{i_2-j}\Gamma ((i_1+i_2+j)\alpha +1)a_{i_1+i_2+j}^{\left(3\right)}.$$

(31)

4.3. Problem 3

This last problem has boundary conditions defined on the two bounds ($x=0$ and $t=0$) of the space–time domain.

Proof of Theorem 4. 

By Theorem 2, the problem (6)–(8) has a solution

$$c(x,t)=\sum _{\mathbf{i}⪰\mathbf{0}}{c}_{(i_1,i_2)}{x}^{i_1\alpha }{t}^{2i_2\alpha },$$

where $c_{(i_1,i_2)}$ are uniquely determined by (15) and (16). By (28), we have for every $i_1$,

$$c_{(i_1,0)}=a_{i_1}^{\left(3\right)}.$$

Then, by (15), we have $a_0^{\left(3\right)}=a_0^{\left(1\right)}$ and $a_1^{\left(3\right)}={\displaystyle \frac{a_0^{\left(2\right)}}{\Gamma (\alpha +1)}}$.

The general expression (10) follows from Remark 2 by taking $i_2=0$ and $i_1=i$ in (23)–(25). □

Remark 4. 

Notice that if Problem 1 is also studied on the left side of the straight line $x=0$ (a symmetric problem), then it is useful to replace the fractional power series (5) with the fractional power moduli series of the form

$$\sum _{(i_1,i_2)⪰(0,0)}{c}_{(i_1,i_2)}{|x|}^{i_1\alpha }{t}^{i_2\beta }$$

and left-sided Caputo fractional derivatives with two-sided Caputo fractional derivatives (see [34]).

5. Numerical Illustration and Discussion of Results

In this section, we illustrate the method from Section 3 by two numerical examples. We remark that similar initial-value problems have been studied, for instance, in [12,13,28,29]. What is significant in our work is that the matter of the existence and uniqueness of the solution is addressed, and at the same time, the accuracy of the approximation is discussed.

We use in the initial conditions the Mittag–Leffler function with one parameter.

Definition 4 

([38]). The function $E_{\alpha }\left(z\right)$ defined by the series (that is convergent for any $z\in \mathbb{C}$)

$$E_{\alpha }\left(z\right)=\sum _{k=0}^{\infty }{\displaystyle \frac{z^k}{\Gamma (k\alpha +1)}}$$

(32)

is called the Mittag–Leffler function with parameter α.

As can easily be seen, $D_{0+}^{\alpha }\left(E_{\alpha }\left(z^{\alpha }\right)\right)=E_{\alpha }\left(z^{\alpha }\right)$, so the function ${\mathrm{Exp}}_{\alpha }\left(z\right)=E_{\alpha }\left(z^{\alpha }\right)$ is also known as the $\alpha$-fractional exponential function (see [39]).

Example 1. 

Consider the one-dimensional advection–dispersion equation

$${\displaystyle \frac{{\partial }_{0+}^{\beta }c}{\partial t^{\beta }}}=-\nu {\displaystyle \frac{{\partial }_{0+}^{\alpha }c}{\partial x^{\alpha }}}+\kappa {\displaystyle \frac{{\widehat{\partial }}_{0+}^{2·\alpha }c}{\partial x^{2·\alpha }}},x\in (0,0.2],t\in (0,2]$$

(33)

and the initial conditions

$$c(0,t)=E_{\beta }(-t^{\beta })=\sum _{j=0}^{+\infty }{\displaystyle \frac{{(-1)}^j{t}^{j\beta }}{\Gamma (j\beta +1)}},$$

(34)

$${\displaystyle \frac{{\partial }_{0+}^{\alpha }c}{\partial x^{\alpha }}}(0,t)=-0.01t^{\beta }.$$

(35)

Suppose that $\nu =0.1$ and $\kappa =0.2$.

By Theorem 2, if $\beta \le 2\alpha$, the problem (33)–(35) has a solution that can be uniquely determined. We approximate the exact solution of the problem by the following partial sum of the series (11):

$$S_{(n_1,n_2)}(x,t)=\sum _{\left(0.0\right)⪯(i_1,i_2)⪯(n_1,n_2)}{c}_{(i_1,i_2)}{x}^{i_1\alpha }{t}^{i_2\beta }.$$

The coefficients $c_{(0,i_2)}$ and $c_{(1,i_2)}$ are obtained from the initial conditions (34) and (35):

$$c_{(0,i_2)}={\displaystyle \frac{{(-1)}^{i_2}}{\Gamma (i_2\beta +1)}},i_2\ge 0,$$

$$c_{(1,1)}=-{\displaystyle \frac{0.01}{\Gamma (\beta +1)}},\mathrm{and}{c}_{(1,i_2)}=0,\mathit{for}\mathit{all}{i}_2\ne 1.$$

For $i_1\ge 2$, the coefficients $c_{(i_1,i_2)}$ are computed by the recurrence relation (16).

We take $n_1=0$, $n_2=20$ and approximate $c(x,t)$ by the partial sum $S_{(0,20)}(x,t)$.

We discuss three cases relative to the values of the parameters $\alpha ,\beta \in (0,1]$:

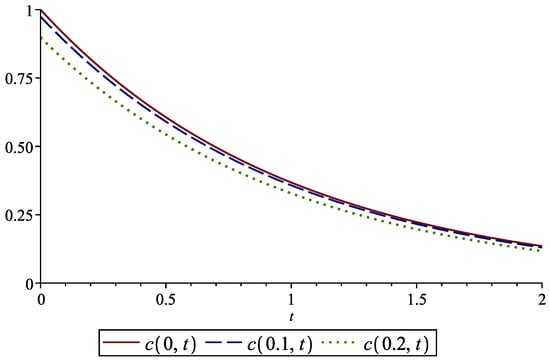
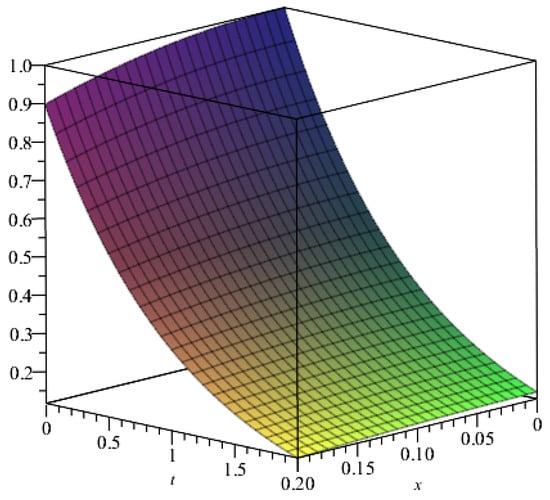
Case I: $\alpha =1$, $\beta =1$. In this case, Equation (33) is the classical advection–dispersion equation.

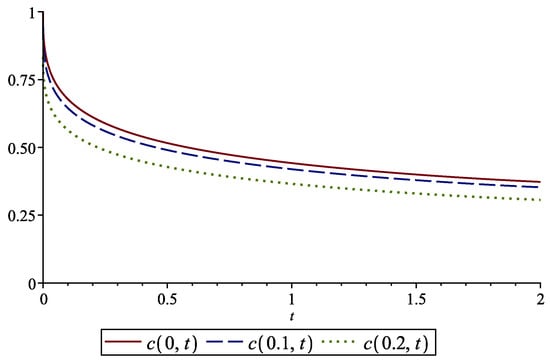
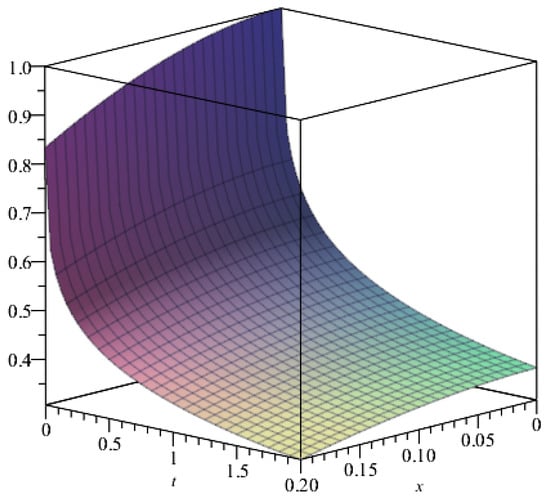
Figure 1 shows the variation of the concentration in time at the points $x=0$, $x=0.1$, and $x=0.2$. A spatial representation of the approximate solution $c(x,t)\approx S_{(0,20)}(x,t)$ is given in Figure 2. Table 1 contains the numerical values of the approximate solution.

Figure 1. Concentration varying in time at $x=0$, $x=0.1$, and $x=0.2$ for Example 1 with $\alpha =1$, $\beta =1$.

Figure 2. Representation of the approximate solution $c(x,t)$ from Example 1 with $\alpha =1$, $\beta =1$.

Table 1. The values of the approximate solution $c(x,t)$ from Example 1 with $\alpha =1$, $\beta =1$.

t	$\mathit{c}(0,\mathit{t})$	$\mathit{c}(0.1,\mathit{t})$	$\mathit{c}(0.2,\mathit{t})$
0.0	1.000000	0.974676	0.898236
0.5	0.606531	0.590655	0.543728
1.0	0.367880	0.357531	0.328297
1.5	0.223131	0.215936	0.197213
2.0	0.135339	0.129854	0.117299

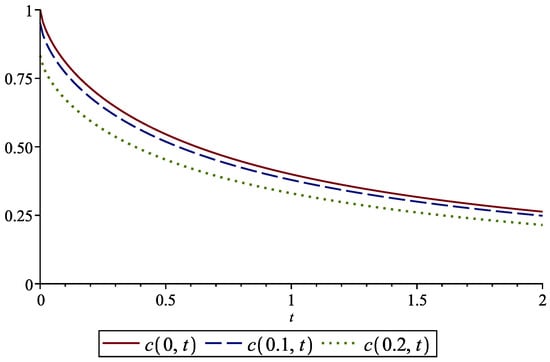
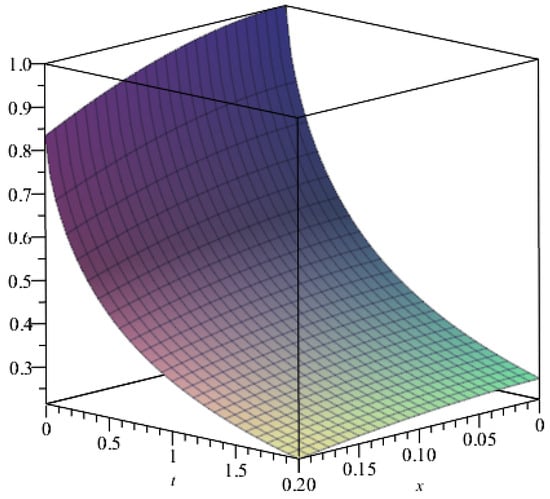
Case II: $\alpha =0.9$, $\beta =0.7$.

Figure 3 shows the variation of the concentration in time at the points $x=0$, $x=0.1$, and $x=0.2$. A spatial representation of the approximate solution $c(x,t)\approx S_{(0,20)}(x,t)$ is given in Figure 4.

Figure 3. Concentration varying in time at $x=0$, $x=0.1$, and $x=0.2$ for Example 1 with $\alpha =0.9$, $\beta =0.7$.

Figure 4. Representation of the approximate solution $c(x,t)$ for Example 1 with $\alpha =0.9$, $\beta =0.7$.

Case III: $\alpha =0.9$, $\beta =0.4$.

Figure 5 shows the variation of the concentration in time at the points $x=0$, $x=0.1$, and $x=0.2$. A spatial representation of the approximate solution $c(x,t)\approx S_{(0,20)}(x,t)$ is given in Figure 6.

Figure 5. Concentration varying in time at $x=0$, $x=0.1$, and $x=0.2$ for Example 1 with $\alpha =0.9$, $\beta =0.4$.

Figure 6. Representation of the approximate solution $c(x,t)$ for Example 1 with $\alpha =0.9$, $\beta =0.4$.

Table 2 shows a comparison between the numerical values of the approximate solution $c(x,t)$ when $\alpha =0.9$ is fixed and the order β of the fractional derivative with respect to time has two different values: $\beta =0.7$ (Case II) and $\beta =0.4$ (Case III). It can be noticed that the concentration at a fixed point x decreases with time.

Table 2. The values of the approximate solution $c(x,t)$ for Example 1 with $\alpha =0.9$ and $\beta =0.7$, $\beta =0.4$, respectively.

t	$\mathit{c}(0,\mathit{t})$		$\mathit{c}(0.1,\mathit{t})$		$\mathit{c}(0.2,\mathit{t})$
	$\mathit{\beta }=\mathbf{0.7}$	$\mathit{\beta }=\mathbf{0.4}$	$\mathit{\beta }=\mathbf{0.7}$	$\mathit{\beta }=\mathbf{0.4}$	$\mathit{\beta }=\mathbf{0.7}$	$\mathit{\beta }=\mathbf{0.4}$
0.0	1.000000	1.000000	0.951972	0.951973	0.833140	0.833143
0.5	0.545825	0.515872	0.518764	0.490055	0.453071	0.427742
1.0	0.399613	0.442070	0.379045	0.419471	0.330220	0.365608
1.5	0.316917	0.399915	0.299869	0.379073	0.260458	0.329949
2.0	0.263189	0.372733	0.248331	0.352823	0.214920	0.306396

Finally, we remark that the method presented in the proof of Theorem 2 provides an estimation of the error in a suitable rectangle $\mathcal{R}=[\mathbf{0},\mathbf{y}]$.

Consider, for instance, the case $\alpha =0.9$, $\beta =0.7$. As noticed above, the coefficients $c_{(i_1,i_2)}$ are obtained from the initial conditions for $i_2=0,1$ and by using the recurrence relation (16) for $i_2\ge 2$. Thus, we obtain: $c_{(0,0)}=1$, $c_{(1,0)}=0$, $c_{(0,1)}\approx -1.10055$, $c_{(2,0)}\approx -2.98242$, $c_{(1,1)}\approx -0.0104$, $c_{(0,2)}\approx 0.80504$, $c_{(3,0)}\approx -0.61032$, $c_{(2,1)}\approx 3.27931$, $c_{(1,2)}=0$, $c_{(0,3)}\approx -0.45504$, and so on.

By using the notations from the proof of Theorem 2, since the series associated with the functions $f_1\left(t\right)$ and $f_2\left(t\right)$ converge for every t, we may choose, for example, $A=1$. Since, for $y>0$, ${\displaystyle \frac{1}{\Gamma (\beta y+1)}}<1.2$, we can take $C=1.2$ and $B=1$, and so we find $M_1\approx 12.915496$, $M_2\approx 2.691800$, ${\displaystyle \frac{1}{M_1}}\approx 0.077426$, and ${\displaystyle \frac{1}{M_2}}\approx 0.371498$. Thus, we may choose, for instance, $y_1=0.07$ and $y_2=0.37$, and consider $(x,t)\in \mathcal{R}=[\mathbf{0},\mathbf{y}]$. To estimate the error of the approximation, we evaluate the remainder $R_{(0,20)}(x,t)=c(x,t)-S_{(0,20)}(x,t)$ for $(x,t)$ in a suitable rectangle ${\mathcal{R}}^{\left(1\right)}=[\mathbf{0},{\mathbf{y}}^{\left(1\right)}]\subset \mathcal{R}=[\mathbf{0},\mathbf{y}]$. Since

$$R_{(0,20)}(x,t)=\sum _{j=21}^{+\infty }\sum _{i=0}^j{c}_{(j-i,i)}{x}^{(j-i)\alpha }{t}^{i\beta },$$

it follows that for any $(x,t)\in \mathcal{R}$, we have:

$$|R_{(0,20)}(x,t)|\le \sum _{j=21}^{+\infty }\sum _{i=0}^j|c_{(j-i,i)}|x^{(j-i)\alpha }{t}^{i\beta }\le C{B}^{\alpha }\sum _{j=21}^{+\infty }\sum _{i=0}^j{\left(M_{1}x\right)}^{(j-i)\alpha }{\left(M_{2}t\right)}^{i\beta }.$$

We take ${\rho }_1=0.6<{\left(M_1{y}_1\right)}^{\alpha }\approx 0.913246$ and ${\rho }_2=0.6<{\left(M_2{y}_2\right)}^{\beta }\approx 0.997174$ and consider $y_1^{\left(1\right)}={\displaystyle \frac{{\rho }_1^{1/\alpha }}{M_1}}\approx 0.043892$ and $y_2^{\left(1\right)}={\displaystyle \frac{{\rho }_2^{1/\beta }}{M_2}}\approx 0.179073$. Hence, for any $(x,t)\in {\mathcal{R}}^{\left(1\right)}$, we have

$$|R_{(0,20)}(x,t)|\le C{B}^{\alpha }\sum _{j=21}^{+\infty }\sum _{i=0}^j{\rho }_1^{j-i}{\rho }_2^i=C{B}^{\alpha }\sum _{j=21}^{+\infty }(j+1){\rho }_1^j=C{B}^{\alpha }{\displaystyle \frac{22{\rho }_1^{21}-21{\rho }_1^{22}}{{(1-{\rho }_1)}^2}}\le 0.00155.$$

Example 2. 

Consider the one-dimensional advection–dispersion equation

$${\displaystyle \frac{\partial c}{\partial t}}=-\nu {\displaystyle \frac{{\partial }_{0+}^{0.4}c}{\partial x^{0.4}}}+\kappa {\displaystyle \frac{{\widehat{\partial }}_{0+}^{2·0.4}c}{\partial x^{2·0.4}}},x\in (0,1],t\in (0,1]$$

(36)

and the initial condition

$$c(x,0)=E_{0.4}(-x^{0.4})=\sum _{j=0}^{\infty }{\displaystyle \frac{{(-1)}^j{x}^{0.4j}}{\Gamma (0.4j+1)}},$$

(37)

where $\nu =0.1$ and $\kappa =0.2$.

By Theorem 3, since $\alpha =0.4$ and $\beta =1>2\alpha$, we know that the problem (36), (37) has a unique solution of the form (11), where the coefficients $c_{(i_1,i_2)}$ are given by the formula (31). Since in our case, $a_j^{\left(3\right)}={\displaystyle \frac{{(-1)}^j}{\Gamma (\alpha j+1)}}$ for every $j\ge 0$, we obtain that

$$c_{(i_1,i_2)}={\displaystyle \frac{1}{\Gamma (i_1\alpha +1)\Gamma (i_2\beta +1)}}\sum _{j=0}^{i_2}{(-1)}^{i_2-j}\left({\displaystyle \genfrac{}{}{0pt}{}{i_2}{j}}\right){\kappa }^j{\nu }^{i_2-j}{(-1)}^{i_1+i_2+j}={\displaystyle \frac{{(-1)}^{i_1}{(\kappa +\nu )}^{i_2}}{\Gamma (i_1\alpha +1)\Gamma (i_2\beta +1)}},$$

for all $i_1,i_2\ge 0$. Hence,

$$c(x,t)=\sum _{(i_1,i_2)⪰\mathbf{0}}{\displaystyle \frac{{(-1)}^{i_1}}{\Gamma (i_1\alpha +1)}}·{\displaystyle \frac{{(\kappa +\nu )}^{i_2}}{\Gamma (i_2\beta +1)}}·x^{i_1\alpha }{t}^{i_2\beta }.$$

(38)

Since we know that the double series (38) is absolutely convergent, it follows that the order of summation does not matter, so we have (using $\beta =1$):

$$c(x,t)=\sum _{i_1\ge 0}\left({\displaystyle \frac{{(-x^{\alpha })}^{i_1}}{\Gamma (i_1\alpha +1)}}\sum _{i_2\ge 0}{\displaystyle \frac{{(\kappa +\nu )}^{i_2}{t}^{i_2}}{i_2!}}\right)=e^{t(\kappa +\nu )}\sum _{i_1\ge 0}{\displaystyle \frac{{(-x^{\alpha })}^{i_1}}{\Gamma (i_1\alpha +1)}}.$$

Hence, the exact solution of the problem is

$$c(x,t)=e^{t(\kappa +\nu )}{E}_{\alpha }(-x^{\alpha })=e^{0.3t}{E}_{0.4}(-x^{0.4}).$$

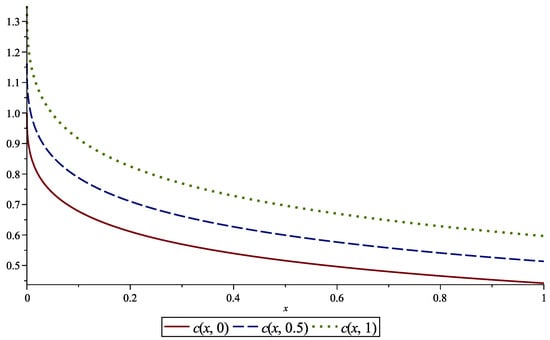
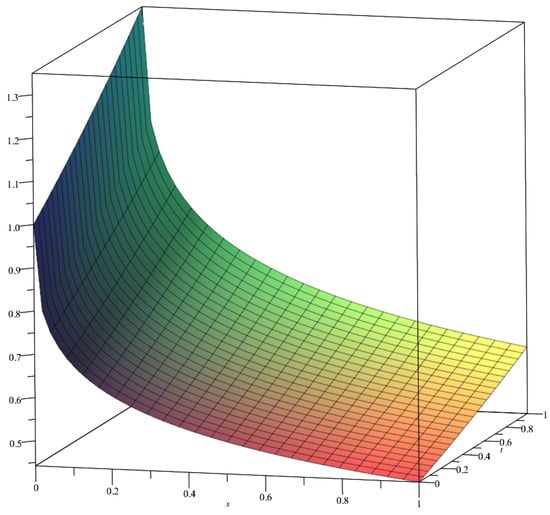
In Figure 7 the variation of the concentration for $x\in [0,1]$ is represented at times $t=0$, $t=0.5$, and $t=1$. A spatial representation of the solution $c(x,t)$ is given in Figure 8.

Figure 7. Concentration variation at $t=0$, $t=0.5$, and $t=1$ for Example 2.

Figure 8. Representation of the solution $c(x,t)$ for Example 2.

6. Conclusions

In this paper, we have demonstrated three theorems on the existence and the uniqueness of solutions represented as fractional power series for initial-value and boundary-value problems associated with the one-dimensional fractional advection–dispersion equation. Our research extends the well-known power series method to the domain of fractional calculus. The proofs of the theorems not only present the details of the methodology of approximating the solutions but also introduce a systematic method to estimate the associated error, providing a powerful and rigorous tool for researchers in the field.

Beyond the framework of the fractional advection–dispersion equation, the main results of our work can be extended to a broader range of initial-value and boundary-value problems that model various physical phenomena. Thus, in a forthcoming paper, we intend to highlight similar results for other complex problems associated with fractional partial differential equations. Moreover, our future research will also investigate different fractional derivatives, as we believe that the fractional power series method is strong enough to be applied in most contexts encountered by scientist dealing with fractional PDEs.

In summary, our research is not only a contribution to the theoretical background of fractional calculus but also an exploration of new insights and strategies for approaching complex systems governed by fractional differential equations.