On Some Formulas for Single and Double Integral Transforms Related to the Group SO(2, 2)

Abstract

We present a novel proof, using group theory, for a Meijer transform formula. This proof reveals the formula as a specific case of a broader generalized result. The generalization is achieved through a linear operator that intertwines two representations of the connected component of the identity of the group $\mathrm{SO}(2,2)$. Using this same approach, we derive a formula for the sum of three double integral transforms, where the kernels are represented by Bessel functions. It is particularly noteworthy that the group $\mathrm{SO}(2,2)$ is connected to symmetry in several significant ways, especially in mathematical physics and geometry.

1. Introduction

One approach to studying special functions in mathematical physics involves using integral transforms. For instance, the commonly utilized Euler gamma function, $\mathsf{\Gamma }\left(x\right):=\underset{0}{\overset{\infty }{\int }}{e}^{-t}{t}^{x-1}\mathrm{d}t$ $(\Re (x)>0)$ (see, for example, [1], Entries 8.31–8.33), can be interpreted as the value of the Laplace transform $L_{s}f\left(t\right)=\underset{0}{\overset{+\infty }{\int }}f\left(t\right){\mathrm{e}}^{-st}\mathrm{d}t$ for $s=1$ and elementary functions $f\left(t\right)=t^{x-1}$. The generalized hypergeometric function, ${}_{p}F_q$$(p,q\in {\mathbb{Z}}_{⩾0})$, is defined by (see [2], p. 73; see, also, [3]):

$$\begin{gathered} {}_{p}F_q\left[\begin{array}{c}{\alpha }_1,\dots ,{\alpha }_p;\\ {\beta }_1,\dots ,{\beta }_q;\end{array}z\right]=\sum _{n=0}^{\infty }{\displaystyle \frac{{\left({\alpha }_1\right)}_n\cdots {\left({\alpha }_p\right)}_n}{{\left({\beta }_1\right)}_n\cdots {\left({\beta }_q\right)}_n}}{\displaystyle \frac{z^n}{n!}} \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em} ={}_{p}F_q({\alpha }_1,\dots ,{\alpha }_p;{\beta }_1,\dots ,{\beta }_q;z), \end{gathered}$$

where ${\left(\lambda \right)}_{\nu }$ denotes the Pochhammer symbol or the shifted factorial, which is defined (for $\lambda ,\nu \in \mathbb{C}$) in terms of the gamma function $\mathsf{\Gamma }$ by the following:

$${\left(\lambda \right)}_{\nu }:={\displaystyle \frac{\mathsf{\Gamma }(\lambda +\nu )}{\mathsf{\Gamma }\left(\lambda \right)}}=\left\{\begin{array}{l}1(\nu =0;\lambda \in \mathbb{C}\setminus \{0\left\}\right)\\ \lambda (\lambda +1)\cdots (\lambda +n-1)\hspace{1em}(\nu =n\in \mathbb{N};\lambda \in \mathbb{C}),\end{array}\right.$$

It is understood conventionally that ${\left(0\right)}_0:=1$. The generalized hypergeometric function ${}_{p}F_q$ plays a crucial role in the class of special functions in mathematical physics. Here and throughout, $\mathbb{N}$, $\mathbb{Z}$, $\mathbb{R}$, and $\mathbb{C}$ represent the sets of positive integers, integers, real numbers, and complex numbers, respectively. Also, let ${\mathbb{Z}}_{⩾0}:=\mathbb{N}\cup \left\{0\right\}$. This function can be seen as an extension of the elementary function $e^x$, which is represented by ${}_{0}F_0\left(x\right)$ through the composition of Laplace transforms and their inverses. Integral transforms emerge in the context of infinite-dimensional representation spaces of Lie groups, particularly when composing transformations of bases, decomposing matrix elements of a representation into those of the same representation in a different basis, and similar processes. Through group-theoretic constructions, not only do well-known integral transformations emerge, but also new ones, including those involving multiple integrals. Multiple integral transforms are primarily discussed in works focused on solving partial differential equations [4,5,6,7].

Shilin and Choi [8] explored the quasi-regular representation of the group SO(2, 2), applying it to specific diagonal and cell-diagonal matrices. Through this approach, they derived elegant double integral representations for various special functions. Notably, they provided double integral formulas for the products $W_{\nu ,\mu }(z+w)W_{\nu ,\kappa }(z-w)$ of two Whittaker functions of the second kind. In [9], they obtained explicit formulas involving Bessel functions, which describe the kernels of integral operators of the $\mathrm{SO}(2,2)$ representation in a space of functions defined in a $2\times 4$-matrix cone.

In this work, we will explore the group-theoretic aspect of double integral transformations for the first time; specifically, the connection between the group $\mathrm{SO}(2,2)$ and double integral transformations whose kernels are Bessel functions of order $\nu$ and argument z, the first and second kind, denoted, respectively, by the following:

$$J_{\nu }\left(z\right):={\displaystyle \frac{z^{\nu }}{2^{\nu }}}\sum _{k=0}^{\infty }{\displaystyle \frac{{(-1)}^k{z}^{2k}}{2^{2k}k!\mathsf{\Gamma }(\nu +k+1)}}\left(\right|argz|<\pi ,\nu \in \mathbb{C})$$

(see, for example, [1], Entries 8.4–8.5; see, also, [10], Section 3.1) and

$$Y_{\nu }\left(z\right):={\displaystyle \frac{1}{sin\nu \pi }}\left[cos\nu \pi J_{\nu }\left(z\right)-J_{-\nu }\left(z\right)\right]\left(\right|argz|<\pi ,\nu \in \mathbb{C}\setminus \mathbb{Z}),$$

which are also called Neumann functions (see, for instance, [1], Entry 8.403; see, also, [10], p. 64, Equation (1)), as well as the Macdonald function (more commonly known as the modified Bessel function of the second kind), $K_{\nu }\left(z\right)$ (see, for instance, [10], p. 78; see, also, [11], pp. 373–374). The function $K_{\nu }\left(z\right)$ is defined by the following (see, for instance, [1], pp. 900–901):

$$K_{\nu }\left(z\right)=\left\{\begin{array}{cc}{\displaystyle \frac{\pi \mathbf{i}}{2}}{e}^{\frac{\pi }{2}\nu \mathbf{i}}{H}_{\nu }^{\left(1\right)}\left(z{e}^{\frac{\pi \mathbf{i}}{2}}\right)\hfill & \left(-\pi <argz⩽{\displaystyle \frac{\pi }{2}}\right),\hfill \\ {\displaystyle \frac{-\pi \mathbf{i}}{2}}{e}^{\frac{-\pi }{2}\nu \mathbf{i}}{H}_{-\nu }^{\left(2\right)}\left(z{e}^{-\frac{\pi \mathbf{i}}{2}}\right)\hfill & \left(-{\displaystyle \frac{\pi }{2}}<argz⩽\pi \right).\hfill \end{array}\right.$$

Here, $H_{\nu }^{\left(1\right)}\left(z\right)$ and $H_{\nu }^{\left(2\right)}\left(z\right)$ are Bessel functions of the third kind (also called Hankel’s functions), defined by the following:

$$H_{\nu }^{\left(1\right)}\left(z\right)=J_{\nu }\left(z\right)+\mathbf{i}{Y}_{\nu }\left(z\right)$$

and

$$H_{\nu }^{\left(2\right)}\left(z\right)=J_{\nu }\left(z\right)-\mathbf{i}{Y}_{\nu }\left(z\right).$$

Here and throughout, $\mathbf{i}=\sqrt{-1}$. The double integral transform with the Macdonald function as the kernel (Meijer transform) was previously studied in [12]. Additionally, we will provide a new (group-theoretic) proof of a well-known formula for the ordinary Meijer transform and a generalization of this formula where the Macdonald function is replaced by the Whittaker function of the second kind, $W_{\mu ,\nu }\left(z\right)$ (see, for example, [1], Entries 9.22–9.23; see, also, [11], Chapter XVI). One of various integral representations of the function $W_{\mu ,\nu }\left(z\right)$ is recalled (see, for example, [1], Entry 9.222-1):

$$\begin{gathered} W_{\mu ,\nu }\left(z\right)={\displaystyle \frac{z^{\nu +\frac{1}{2}}{e}^{-z/2}}{\mathsf{\Gamma }(\nu -\mu +\frac{1}{2})}}\underset{0}{\overset{\infty }{\int }}{e}^{-zt}{t}^{\nu -\mu -\frac{1}{2}}{(1+t)}^{\nu -\mu -\frac{1}{2}}\mathrm{d}t \\ \left(\Re (\nu -\mu )>-\frac{1}{2},|argz|<\frac{\pi }{2}\right). \end{gathered}$$

To derive all the formulas, we will use a linear operator that intertwines two representations of the group $G\subset \mathrm{SO}(2,2)$ (refer to the sentence between Equations (1) and (2)).

2. The Group G and Some of Its Subgroups

Let us represent each matrix g belonging to the following group (see [13]):

$$\mathrm{SO}(2,2)=\{g\in \mathrm{GL}(4,\mathbb{R})\mid g\mathrm{diag}(1,1,-1,-1)g^T=\mathrm{diag}(1,1,-1,-1)\},$$

in the following form:

$$g=\left(\begin{array}{cc}A& B\\ C& D\end{array}\right),$$

(1)

where A is a matrix of size $2\times 2$. Considering $\mathrm{SO}(2,2)$ as a topological group, we obtain the connected component G of the identity matrix, which is a subgroup defined by the condition that the determinants of the submatrices A and D are both greater than zero (see [14]):

$$detA>0,detD>0.$$

(2)

Clearly, the cone $\mathcal{X}=\{x\mid x_1^2+x_2^2-x_3^2-x_4^2=0\}$ and hyperboloids ${\mathcal{Y}}_r=\{y\mid y_1^2+y_2^2-y_3^2-y_4^2=r,r\ne 0\}$ are invariant under the action of the group G.

To construct a tangent (at the point $\mathrm{id}$) space of the group G, we utilize six one-parameter subgroups. Two of these subgroups involve rotations $h_{1,2}\left(\phi \right)$ and $h_{3,4}\left(\phi \right)$, rotating through an angle $\phi$ in the planes $\mathrm{O}{x}_1{x}_2$ and $\mathrm{O}{x}_3{x}_4$, respectively. The remaining four subgroups consist of hyperbolic rotations $h_{i,j}\left(\varphi \right)$ in the planes $\mathrm{O}{x}_i{x}_j$, where $i⩽2<j⩽4$. The corresponding tangent vectors satisfy the following commutation relations:

$$\begin{array}{lll}[e_{1,2},e_{3,4}]=0,& [e_{1,2},e_{1,3}]=e_{2,3},& [e_{1,2},e_{1,4}]=e_{2,4},\\ [e_{1,2},e_{2,3}]=-e_{1,3},& [e_{1,2},e_{2,4}]=-e_{1,4},& [e_{3,4},e_{1,3}]=e_{1,4},\\ [e_{3,4},e_{1,4}]=-e_{1,3},& [e_{3,4},e_{2,3}]=e_{2,4},& [e_{3,4},e_{2,4}]=-e_{2,3},\\ [e_{1,3},e_{1,4}]=-e_{3,4},& [e_{1,3},e_{2,3}]=-e_{1,2},& [e_{1,3},e_{2,4}]=0,\\ [e_{1,4},e_{2,3}]=0,& [e_{1,4},e_{2,4}]=-e_{1,2},& [e_{2,3},e_{2,4}]=-e_{3,4}.\end{array}$$

(3)

These vectors form the basis E of the tangent space.

The linear space ${\mathfrak{g}}_0=\mathrm{Span}(e_{1,2},e_{3,4})$ forms a subalgebra within the tangent algebra $\mathfrak{g}$ generated by vectors in E. We require the subgroup $H_1$, which is the exponential image of ${\mathfrak{g}}_0$. Given that the real rank of G is 2 [15], any maximal commutative subalgebra in $\mathfrak{g}$ can be generated by two linearly independent vectors $v_1$ and $v_2$ not in ${\mathfrak{g}}_0$. Choosing $v_1=e_{1,3}$ and $v_2=e_{2,4}$, we find the eigenvalues of the adjoint operators $\mathrm{ad}{e}_{1,3}$ and $\mathrm{ad}{e}_{2,4}$ to be 0, 1, and $-1$.

The subspace in $\mathfrak{g}$, consisting of the zero vector and the eigenvectors corresponding to the eigenvalue 1, forms a maximal nilpotent subalgebra generated by the vectors $e_{1,2}-e_{1,4}$ and $e_{2,3}-e_{3,4}$. We need the subgroup $H_2$, which is the exponential image of this nilpotent subalgebra. Another choice of $v_1$ and $v_2$ results in a subgroup isomorphic to $H_2$.

The subgroup $H_1$ consists of matrices $h_1({\phi }_1,{\phi }_2)=\mathrm{diag}(A_1,A_2)$, where

$$A_i=\left(\begin{array}{cc}\hfill cos{\phi }_i& \hfill -sin{\phi }_i\\ \hfill sin{\phi }_i& \hfill cos{\phi }_i\end{array}\right),$$

and $H_2$ consists of matrices $h_2=h^{\left(1\right)}{h}^{\left(2\right)}$, where

$$\begin{array}{c}{h}^{\left(1\right)}\left(\phi \right)=exp\left({\phi }_1(e_{1,2}-e_{1,4})\right)={\displaystyle \frac{1}{2}}\left(\begin{array}{cccc}2& -2\phi & 0& -2\phi \\ 2\phi & 2-{\phi }^2& 0& -{\phi }^2\\ 0& 0& 2& 0\\ -2\phi & {\phi }^2& 0& 2+{\phi }^2\end{array}\right),\\ h^{\left(2\right)}\left(\phi \right)=exp\left(\phi (e_{2,3}-e_{3,4})\right)={\displaystyle \frac{1}{2}}\left(\begin{array}{cccc}2& 0& 0& 0\\ 0& 2+{\phi }^2& 2\phi & {\phi }^2\\ 0& 2\phi & 2& 2\phi \\ 0& -{\phi }^2& -2\phi & 2-{\phi }^2\end{array}\right).\end{array}$$

It is evident that $H_1$ and $H_2$ act transitively on the subsets ${\gamma }_1:x_1^2+x_2^2=1$ and ${\gamma }_2:x_2+x_4=1$ within the cone $\mathcal{X}$.

Lemma 1.

The group G acts transitively on the punctured cone ${\mathcal{X}}^{\circ }:=\mathcal{X}\setminus \left\{(0,0,0,0)\right\}$.

Proof. 

For any point $x=(rcos\alpha ,rsin\alpha ,rcos\beta ,rsin\beta )\in {\mathcal{X}}^{\circ }$, where $r>0$, we can express it as:

$$g_{1,2}\left(\alpha \right)g_{3,4}\left({\displaystyle \frac{3\pi }{2}}-\beta \right)g_{1,4}(lnr)(1,0,0,1)=x.$$

Since the matrix

$$g=g_{1,2}\left(\alpha \right)g_{3,4}\left({\displaystyle \frac{3\pi }{2}}-\beta \right)g_{1,4}(lnr)=\left(\begin{array}{cc}A& B\\ C& D\end{array}\right),$$

where $detA=detD={\displaystyle \frac{r^2+1}{2r}}>0$ (by (2)), we conclude $g\in G$. Therefore, for any $\tilde{x}\in {\mathcal{X}}^{\circ }$, there exists a transformation $\tilde{g}\in G$ such that $\tilde{g}(1,0,0,1)=\tilde{x}$. Consequently, $\tilde{g}{g}^{-1}x=\tilde{x}$ and $\tilde{g}{g}^{-1}\in G$. □

3. Some Linear Spaces and Their Bases

Fix $\sigma \in \mathbb{C}$. A function f is called $\sigma$-homogeneous if $f\left(\lambda x\right)={\left|\lambda \right|}^{\sigma }f\left(x\right)$. We denote by $L_1$ the linear space of $\sigma$-homogeneous, infinitely differentiable functions on ${\mathcal{X}}^{\circ }$. Similarly, we denote by $L_2$ the space of $\sigma$-homogeneous functions on ${\mathcal{Y}}_1$ that belong to the kernel of the operator ${\Delta }_{2,2}={\displaystyle \frac{{\partial }^2}{\partial y_1^2}}+{\displaystyle \frac{{\partial }^2}{\partial y_2^2}}-{\displaystyle \frac{{\partial }^2}{\partial y_3^2}}-{\displaystyle \frac{{\partial }^2}{\partial y_4^2}}$. For any $g\in G$, we consider the linear operators $T_i\left(g\right):L_i\to L_i$ defined by the formula $f\left(x\right)\mapsto f\left(gx\right)$. If $f\left(gx\right)$ is the zero function, then for any x, at the point $g^{-1}x$, we have $f\left(g{g}^{-1}x\right)=f\left(x\right)=0$. Therefore, $T_i\left(g\right)$ are non-degenerate operators. For any $g,\tilde{g}\in G_0$, we have $T_i\left(g\right)T_i\left(\tilde{g}\right)f\left(x\right)=T_i\left(g\tilde{g}\right)f\left(x\right)$; thus, $T_i\left(g\right)$ is a representation of the group G in $L_i$.

Consider the infinitesimal operators ${\mathfrak{d}}_{ij}=\mathbf{i}\underset{t\to 0}{lim}{\displaystyle \frac{T\left(exp\left(t{e}_{ij}\right)\right)f\left(x\right)-f\left(x\right)}{t}}$, which correspond to vectors from E. In spherical coordinates $x_1=cos\alpha$, $x_2=sin\alpha$, $x_3=cos\beta$, $x_4=sin\beta$, where $\alpha ,\beta \in [-\pi ,\pi ]$, on ${\gamma }_1$, we have ${\mathfrak{d}}_{1,2}=-\mathbf{i}{\displaystyle \frac{\partial }{\partial \alpha }}$ and ${\mathfrak{d}}_{3,4}=-\mathbf{i}{\displaystyle \frac{\partial }{\partial \beta }}$. In view of relations (3), we have

$$[{\mathfrak{d}}_{1,2}{\mathfrak{d}}_{3,4},{\mathfrak{d}}_{1,2}]={\mathfrak{d}}_{1,2}{\mathfrak{d}}_{3,4}{\mathfrak{d}}_{1,2}-{\mathfrak{d}}_{1,2}^2{\mathfrak{d}}_{3,4}={\mathfrak{d}}_{1,2}[{\mathfrak{d}}_{3,4},{\mathfrak{d}}_{1,2}]=0$$

and $[{\mathfrak{d}}_{1,2}{\mathfrak{d}}_{3,4},{\mathfrak{d}}_{3,4}]=0$. This implies that ${\mathfrak{d}}_{1,2}$ and ${\mathfrak{d}}_{3,4}{\mathfrak{d}}_{1,2}$ are Casimir operators corresponding to the reduction $G\supset H_1\supset H_{1,2}$, where the subgroup $H_{1,2}$ consists of rotations $h_{1,2}$. By separating the variables in the restriction of their joint eigenfunction to ${\gamma }_1$, we find that this restriction coincides with ${\mathrm{e}}^{\mathbf{i}(n\alpha +m\beta )}$, where $n,m\in \mathbb{Z}$. These restrictions form a basis of the space of restrictions of functions from $L_1$ to ${\gamma }_1$. For any $x\in {\mathcal{X}}^{\circ }$, we have $x_1^2+x_2^2\ne 0$. Therefore, for any $f\in L_1$, we obtain the following:

$$f\left(x\right)={(x_1^2+x_2^2)}^{\sigma /2}{f}_{\downarrow ,{\gamma }_1}\left({\displaystyle \frac{x_1}{\sqrt{x_1^2+x_2^2}}},{\displaystyle \frac{x_2}{\sqrt{x_1^2+x_2^2}}},{\displaystyle \frac{x_3}{\sqrt{x_1^2+x_2^2}}},{\displaystyle \frac{x_4}{\sqrt{x_1^2+x_2^2}}}\right),$$

where $f_{\downarrow ,{\gamma }_1}$ is the restriction of f to ${\gamma }_1$. This implies that the following extensions:

$$\begin{array}{cc}\hfill f_{(n,m)}^{\left(1\right)}& ={(x_1^2+x_2^2)}^{\sigma /2}{\mathrm{e}}^{\mathbf{i}(n\alpha +m\beta )}\hfill \\ & ={(x_1^2+x_2^2)}^{\sigma /2}{(cos\alpha +\mathbf{i}sin\alpha )}^n{(cos\beta +\mathbf{i}sin\beta )}^n\hfill \\ & ={(x_1^2+x_2^2)}^{\sigma /2}{\left({\displaystyle \frac{x_1}{\sqrt{x_1^2+x_2^2}}}+{\displaystyle \frac{\mathbf{i}{x}_2}{\sqrt{x_1^2+x_2^2}}}\right)}^n{\left({\displaystyle \frac{x_3}{\sqrt{x_1^2+x_2^2}}}+{\displaystyle \frac{\mathbf{i}{x}_4}{\sqrt{x_1^2+x_2^2}}}\right)}^m\hfill \\ & ={(x_1^2+x_2^2)}^{(\sigma -n-m)/2}{(x_1+\mathbf{i}{x}_2)}^n{(x_3+\mathbf{i}{x}_4)}^m,\hfill \end{array}$$

of joint eigenfunctions form the basis $B_1$ in $L_1$.

Let us introduce the orispherical coordinates on ${\gamma }_2$: $x_1=\alpha$, $x_2={\displaystyle \frac{1-{\alpha }^2+{\beta }^2}{2}}$, $x_3=\beta$, $x_4={\displaystyle \frac{1+{\alpha }^2-{\beta }^2}{2}}$, where $\alpha ,\beta \in \mathbb{R}$.

Note that the principle of constructing a horospherical coordinate system (in which the Laplace operator admits separation of variables) is described in detail in ref. [16], subsection 10.5.3.

At these coordinates, we have ${\mathfrak{d}}_{1,2}-{\mathfrak{d}}_{1,4}=\mathbf{i}{\displaystyle \frac{\partial }{\partial \alpha }}$ and ${\mathfrak{d}}_{2,3}-{\mathfrak{d}}_{3,4}=-\mathbf{i}{\displaystyle \frac{\partial }{\partial \beta }}$. Referring to (3), we obtain the following:

$$\begin{array}{l}[({\mathfrak{d}}_{1,2}-{\mathfrak{d}}_{1,4})({\mathfrak{d}}_{2,3}-{\mathfrak{d}}_{3,4}),{\mathfrak{d}}_{1,2}-{\mathfrak{d}}_{1,4}]\\ =({\mathfrak{d}}_{1,2}-{\mathfrak{d}}_{1,4})({\mathfrak{d}}_{2,3}-{\mathfrak{d}}_{3,4})({\mathfrak{d}}_{1,2}-{\mathfrak{d}}_{1,4})-{({\mathfrak{d}}_{1,2}-{\mathfrak{d}}_{1,4})}^2({\mathfrak{d}}_{2,3}-{\mathfrak{d}}_{3,4})\\ =({\mathfrak{d}}_{1,2}-{\mathfrak{d}}_{1,4})[{\mathfrak{d}}_{2,3}-{\mathfrak{d}}_{3,4},{\mathfrak{d}}_{1,2}-{\mathfrak{d}}_{1,4}]\\ =[{\mathfrak{d}}_{2,3},{\mathfrak{d}}_{1,2}]-[{\mathfrak{d}}_{2,3},{\mathfrak{d}}_{1,4}]-[{\mathfrak{d}}_{3,4},{\mathfrak{d}}_{1,2}]+[{\mathfrak{d}}_{3,4},{\mathfrak{d}}_{1,4}]\\ ={\mathfrak{d}}_{1,3}+0+0-{\mathfrak{d}}_{1,3}=0\end{array}$$

and $[({\mathfrak{d}}_{1,2}-{\mathfrak{d}}_{1,4})({\mathfrak{d}}_{2,3}-{\mathfrak{d}}_{3,4}),{\mathfrak{d}}_{2,3}-{\mathfrak{d}}_{3,4}]=0$. Thus, ${\mathfrak{d}}_{2,3}-{\mathfrak{d}}_{3,4}$ and $({\mathfrak{d}}_{1,2}-{\mathfrak{d}}_{1,4})({\mathfrak{d}}_{2,3}-{\mathfrak{d}}_{3,4})$ are Casimir operators corresponding to the reduction $G\supset H_2\supset H^{\left(2\right)}$, where $H^{\left(2\right)}$ denotes the subgroup consisting of matrices $h^{\left(2\right)}$.

Let f be their joint eigenfunction defined on ${\gamma }_2$. Representing this function as $f=\mathrm{A}\left(\alpha \right)\mathrm{B}\left(\beta \right)$, we obtain $f={\mathrm{e}}^{\mathbf{i}(\lambda \alpha +\mu \beta )}$, where $\lambda ,\mu \in \mathbb{R}$. For any $x\in {\mathcal{X}}^{\circ }$ such that $x_2+x_4\ne 0$, we have

$$f\left(x\right)=|x_2+x_4{|}^{\sigma }{f}_{\downarrow ,{\gamma }_2}\left({\displaystyle \frac{x_1}{x_2+x_4}},{\displaystyle \frac{x_2}{x_2+x_4}},{\displaystyle \frac{x_3}{x_2+x_4}},{\displaystyle \frac{x_4}{x_2+x_4}}\right),$$

where $f_{\downarrow ,{\gamma }_2}$ is the restriction of f to ${\gamma }_2$. Thus, the extensions

$$f_{(\lambda ,\mu )}^{\left(2\right)}=|x_2+x_4{|}^{\sigma }{\mathrm{e}}^{\mathbf{i}(\lambda \alpha +\mu \beta )}={|x_2+x_4|}^{\sigma }exp{\displaystyle \frac{\mathbf{i}(\lambda x_1+\mu x_3)}{x_2+x_4}}$$

form the basis $B_2$ in $L_1$. By analogy, we obtain the basis $B_3$ consisting of functions

$$f_{(\lambda ,\mu )}^{\left(3\right)}=|x_2+x_3{|}^{\sigma }{\mathrm{e}}^{\mathbf{i}(\lambda \alpha +\mu \beta )}={|x_2+x_3|}^{\sigma }exp{\displaystyle \frac{\mathbf{i}(\lambda x_1+\mu x_4)}{x_2+x_3}},$$

where $\lambda ,\mu \in \mathbb{R}$. Further, we will need the subset ${\gamma }_3:x_2+x_3=1$ of the punctured cone ${\mathcal{X}}^{\circ }$, which is a homogeneous space of the subgroup $H_3$ of G consisting of matrices

$$h_3({\phi }_1,{\phi }_2)={\displaystyle \frac{1}{2}}\left(\begin{array}{cccc}2& -2{\phi }_1& -2{\phi }_1& 0\\ 2{\phi }_1& 2+{\phi }_2^2-{\phi }_1^2& {\phi }_2^2-{\phi }_1^2& 2{\phi }_2\\ -2{\phi }_1& {\phi }_1^2-{\phi }_2^2& 2+{\phi }_1^2-{\phi }_2^2& -2{\phi }_2\\ 0& 2{\phi }_2& 2{\phi }_2& 2\end{array}\right).$$

In orispherical coordinates $x_1=\alpha$, $x_2={\displaystyle \frac{1-{\alpha }^2+{\beta }^2}{2}}$, $x_2={\displaystyle \frac{1+{\alpha }^2-{\beta }^2}{2}}$, $x_4=\beta$, where $\alpha ,\beta \in \mathbb{R}$, on ${\gamma }_3$, the restriction of the $f_{(\lambda ,\mu )}^{\left(3\right)}$ to ${\gamma }_3:x_2+x_3=1$ coincides with ${\mathrm{e}}^{\mathbf{i}(\lambda \alpha +\mu \beta )}$.

4. The Intertwining Operator Q

Let us assume that the linear space $L_1^{*}$ differs from $L_1$ by replacing $\sigma$ with $-\sigma -2$. For each function $f\in L_1$ and basis $B_i$, we denote their analogues in $L_1^{*}$ by $f^{*}$ and $B_i^{*}$, respectively. We define the bilinear functionals ${\mathsf{F}}_i:L_1\times L_1^{*}⟶\mathbb{C}$ by the formula $(f,f^{*})⟼\underset{{\gamma }_i}{\int }f\left(x\right)f^{*}\left(x\right)\mathrm{d}x$, where $\mathrm{d}x$ denotes the $H_i$-invariant measure on ${\gamma }_i$. Clearly, $\mathrm{d}x=\mathrm{d}\alpha \mathrm{d}\beta$ for any i.

The following lemma states that the bilinear functionals ${\mathsf{F}}_i$ (for $i=1,2,3$) are identical.

Lemma 2.

${\mathsf{F}}_1={\mathsf{F}}_2={\mathsf{F}}_3$.

Proof. 

For the orispherical coordinates on ${\gamma }_2$, we define $\omega ={\displaystyle \frac{1}{2}}\sqrt{4{\alpha }^2+{(1-{\alpha }^2+{\beta }^2)}^2}$. Supposing $\omega =0$, we obtain $1+{\beta }^2=0$; therefore, $\omega \ne 0$. Given this, we can express ${\mathsf{F}}_2(f,f^{*})$ as follows:

$$\begin{gathered} {\mathsf{F}}_2(f,f^{*})=\underset{{\mathbb{R}}^2}{\int \int }{\omega }^{-2}f\left({\displaystyle \frac{\alpha }{\omega }},{\displaystyle \frac{1-{\alpha }^2+{\beta }^2}{2\omega }},{\displaystyle \frac{\beta }{\omega }},{\displaystyle \frac{1+{\alpha }^2-{\beta }^2}{2\omega }}\right) \\ \times f^{*}\left({\displaystyle \frac{\alpha }{\omega }},{\displaystyle \frac{1-{\alpha }^2+{\beta }^2}{2\omega }},{\displaystyle \frac{\beta }{\omega }},{\displaystyle \frac{1+{\alpha }^2-{\beta }^2}{2\omega }}\right)\mathrm{d}\beta \mathrm{d}\beta . \end{gathered}$$

Introducing new variables $\widehat{\alpha }$ and $\widehat{\beta }$ such that $cos\widehat{\alpha }={\displaystyle \frac{\alpha }{\omega }}$ and $cos\widehat{\beta }={\displaystyle \frac{\beta }{\omega }}$, we note that ${\displaystyle \frac{\partial (\widehat{\alpha },\widehat{\beta })}{\partial (\alpha ,\beta )}}={\omega }^{-2}$. This implies a bijective mapping between the integration domain ${\mathbb{R}}^2$ and ${[-\pi ,\pi ]}^2$. Therefore, we can conclude that ${\mathsf{F}}_2(f,f^{*})={\mathsf{F}}_1(f,f^{*})$.

The equality ${\mathsf{F}}_3(f,f^{*})={\mathsf{F}}_1(f,f^{*})$ can be proven in the same way. □

Let $F\left({\mathcal{Y}}_1\right)$ be the set of functions defined on ${\mathcal{Y}}_1$. Given a fixed $y\in {\mathcal{Y}}_1$, we define the mapping $Q:L_1^{*}⟶F\left({\mathcal{Y}}_1\right)$ by $Q{f}^{*}={\mathsf{F}}_i\left(q{(x,y)}^{\sigma },f^{*}\right)$, where $q(x,y)=|x_1{y}_1+x_2{y}_2-x_3{y}_3-x_4{y}_4|$.

The following lemma asserts that the space $L_2$ contains $Q{L}_1$.

Lemma 3.

$Q{L}_1\subset L_2$.

Proof. 

It is evident that $Q{f}^{*}$ represents a $\sigma$-homogeneous function. Additionally, ${\Delta }_{2,2}Q{f}^{*}\left(y\right)$ can be simplified as follows:

$$\begin{array}{cc}\hfill {\Delta }_{2,2}Q{f}^{*}\left(y\right)& =\underset{{\gamma }_i}{\int }{\Delta }_{2,2}{\left[q(x,y)\right]}^{\sigma }{f}^{*}\left(x\right)\mathrm{d}x\hfill \\ & =({\sigma }^2-\sigma ){\displaystyle \sum _{k=1}^4}{(-1)}^{1{\delta }_{1,k}}\underset{{\gamma }_i}{\int }{x}_k^2{\left[q(x,y)\right]}^{\sigma -2}{f}^{*}\left(x\right)\mathrm{d}x\hfill \\ & =({\sigma }^2-\sigma )\underset{{\gamma }_i}{\int }(x_1^2+x_2^2-x_3^2-x_4^2){\left[q(x,y)\right]}^{\sigma -2}{f}^{*}\left(x\right)\mathrm{d}x=0,\hfill \end{array}$$

since $x\in {\mathcal{X}}^{\circ }$. □

In applications of representation theory to the physics of the atomic nucleus, the concept of equivalence of representations, as well as the weaker concept of intertwining representations, play a crucial role. Let us demonstrate that Q functions as an intertwining operator for the representations $T_1^{*}$ and $T_2$ (see [17], Chapter 2).

Lemma 4.

For every $g\in G$, $Q{T}_1^{*}\left(g\right)=T_2\left(g\right)Q$.

Proof. 

It is straightforward to determine that the stabilizer S of the point $y=(1,0,0,0)\in {\mathcal{Y}}_1$ is isomorphic to the connected component $SO{(1,2)}_0$ of the identity in the group $SO(1,2)$. Using Lemma 1 from [18] and the definitions of the current paper, for any $g_0\in S$, we can write $g_0=g_0({\phi }_1,{\phi }_2,{\phi }_3)=h_{3,4}\left({\phi }_3\right)h_{2,3}\left({\phi }_2\right)h_{3,4}\left({\phi }_1\right)$. Since ${\mathcal{Y}}_1=G/S$, by considering an arbitrary point of ${\mathcal{Y}}_1$, we find that a generating element $g_1$ of the coset $g_{1}S$ can be represented as $g_1=h_{1,2}\left({\phi }_6\right)h_{3,4}\left({\phi }_5\right)h_{1,3}\left({\phi }_4\right)$. Using the obtained expressions for $g_0$ and $g_1$ and Lemma 2, for any $g\in G$ and any i, we derive ${\mathsf{F}}_i(T_1\left(g\right)\left(f\right),f^{*})={\mathsf{F}}_i(f,T_1^{*}\left(g^{-1}\right)\left(f^{*}\right))$. Then,

$$\begin{array}{cc}\hfill Q\left(T_1^{*}\left(g\right)f^{*}\right)\left(y\right)& ={\mathsf{F}}_i\left(T_1\left(g^{-1}\right){\left[q(x,y)\right]}^{\sigma },T_1^{*}\left(g^{-1}\right)T_1^{*}\left(g\right)f^{*}\right)\hfill \\ & ={\mathsf{F}}_i\left(T_1\left(g^{-1}\right){\left[q(x,y)\right]}^{\sigma },f^{*}\right).\hfill \end{array}$$

(4)

On the other hand, considering $T_2\left(g\right)\left(Q{f}^{*}\right)\left(y\right)$, we have

$$\begin{array}{cc}\hfill T_2\left(g\right)\left(Q{f}^{*}\right)\left(y\right)& =T_2\left(g\right)\underset{{\gamma }_i}{\int }{\left[q(x,y)\right]}^{\sigma }{f}^{*}\left(x\right)\mathrm{d}x\hfill \\ & =\underset{{\gamma }_i}{\int }{T}_2\left(g\right){\left[q(x,y)\right]}^{\sigma }{f}^{*}\left(x\right)\mathrm{d}x\hfill \\ & ={\mathsf{F}}_i\left(T_2\left(g\right){\left[q(x,y)\right]}^{\sigma },f^{*}\right).\hfill \end{array}$$

(5)

Since for an arbitrary $g=\left(g_{ij}\right)\in G$ from (1), we have

$$g^{-1}=\left(\begin{array}{cc}\hfill A& \hfill -B\\ \hfill -C& \hfill D\end{array}\right),$$

therefore,

$$\begin{array}{l}{T}_1\left(g^{-1}\right){\left[q(x,y)\right]}^{\sigma }=M\\ \equiv [(g_{11}{x}_1+g_{21}{x}_2-g_{31}{x}_3-g_{41}{x}_4)y_1\\ +(g_{12}{x}_1+g_{22}{x}_2-g_{32}{x}_3-g_{42}{x}_4)y_2\\ -(-g_{13}{x}_1-g_{23}{x}_2+g_{33}{x}_3+g_{43}{x}_4)y_3\\ -(-g_{14}{x}_1-g_{24}{x}_2+g_{34}{x}_3)y_3+g_{44}{x}_4)y_4{]}^{\sigma }.\end{array}$$

(6)

Since $T_2\left(g\right){\left[q(x,y)\right]}^{\sigma }=M$, from (4) to (6), we derive

$$Q\left(T_1^{*}\left(g\right)f^{*}\right)\left(y\right)=T_2\left(g\right)\left(Q{f}^{*}\right)\left(y\right).$$

□

Lemma 4 can be used to derive integral relations between special functions. By understanding the connection between two functions in $L_1\ast$, one can deduce the corresponding relation between their Q-images in $L_2$. Below, we will apply this to the simplest case, where $g=\mathrm{id}$.

5. A New Derivation for a Formula of the Meijer Transform: A Generalization of This Formula

Theorem 1.

Let $\Re \left(\sigma \right)>-1$. For odd n values, $Q{f}_{(n,0)}^{\left(1\right)\ast }\left(y\right)=0$. For even n values,

$$Q{f}_{(n,0)}^{\left(1\right)\ast }\left(y\right)={\displaystyle \frac{{(-1)}^n{\pi }^{3/2}\left|n\right|!\mathsf{\Gamma }\left(\frac{\sigma +\left|n\right|+1}{2}\right)}{2^{\left|n\right|-2}\mathsf{\Gamma }\left(\frac{\sigma +\left|n\right|}{2}+1\right)}}{C}_{\left|n\right|}^{\left(\right(1+\sigma -\left|n\right|)/2)}\left(1\right),$$

where $C_n^{\nu }\left(x\right)$$(n\in {\mathbb{Z}}_{⩾0})$ are Gegenbauer polynomials, which are essentially equivalent to ultraspherical polynomials, defined by the generating relation:

$${(1-2xt+t^2)}^{-x}=\sum _{n=0}^{\infty }{C}_n^{\nu }\left(x\right)t^n(\nu ,x\in \mathbb{C})$$

(see, for instance, [2], Chapter 17; see, also, [3], Entry 7.3.1.203). One of the numerous properties and identities for these polynomials is recalled (see [2], pp. 277, 279):

$$\begin{array}{cc}\hfill C_n^{\nu }\left(x\right)& ={\displaystyle \sum _{k=0}^{[n/2]}}{\displaystyle \frac{{(-1)}^k{\left(\nu \right)}_{n-k}{\left(2x\right)}^{n-2k}}{k!(n-2k)!}}\hfill \\ & ={\displaystyle \frac{{\left(2\nu \right)}_n}{n!}}{}_{2}F_1\left[\begin{array}{c}\hfill -n,2\nu +n;\\ \hfill \nu +\frac{1}{2};\end{array}{\displaystyle \frac{1-x}{2}}\right].\hfill \end{array}$$

Here and throughout, $\left[\nu \right]$ represents the integer part of a real number ν.

Proof. 

Indeed,

$$\begin{array}{cc}\hfill Q{f}_{(n,m)}^{\left(1\right)\ast }\left(y\right)& ={\mathsf{F}}_1\left(|x_1{y}^1+x_2{y}_2-x_3{y}_3-x_4{y}_4{|}^{\sigma },f_{(n,m)}^{\left(1\right)\ast }\right)\hfill \\ & =\underset{-\pi }{\overset{\pi }{\int }}{|cos\alpha |}^{\sigma }{\mathrm{e}}^{\mathbf{i}n\alpha }\mathrm{d}\alpha \underset{-\pi }{\overset{\pi }{\int }}{\mathrm{e}}^{\mathbf{i}m\beta }\mathrm{d}\beta .\hfill \end{array}$$

Using formulae [19], Entry 2.1.2.76

$$\underset{0}{\overset{\pi }{\int }}f(sinx,cosx)\mathrm{d}x=\underset{0}{\overset{\pi /2}{\int }}\left[f(sinx,cosx)+f(sinx,-cosx)\right]\mathrm{d}x$$

and [19], Appl. I.1.1

$$cos\left(\right|n\left|\alpha \right)=\sum _{k=0}^{[n/2]}{(-1)}^k\left({\displaystyle \genfrac{}{}{0pt}{}{n}{2k}}\right){cos}^{n-2k}\alpha {sin}^{2k}\alpha ,$$

we have

$$\begin{array}{cc}\hfill Q{f}_{(n,0)}^{\left(1\right)\ast }\left(y\right)& =4\pi \underset{0}{\overset{\pi }{\int }}{|cos\alpha |}^{\sigma }cos\left(\right|n\left|\alpha \right)\mathrm{d}\alpha \hfill \\ & =\left\{\begin{array}{cc}8\pi \underset{0}{\overset{\pi /2}{\int }}{|cos\alpha |}^{\sigma }cos\left(\right|n\left|\alpha \right)\mathrm{d}\alpha \hfill & \mathrm{for}\mathrm{even}n,\hfill \\ 0\hfill & \mathrm{for}\mathrm{odd}n.\hfill \end{array}\right..\hfill \end{array}$$

Referring to [19], 2.5.12.26, we obtain

$$\begin{array}{cc}\hfill Q{f}_{(n,0)}^{\left(1\right)\ast }\left(y\right)& =8\pi {\displaystyle \sum _{k=0}^{\left[\right|n|/2]}}{(-1)}^k\left({\displaystyle \genfrac{}{}{0pt}{}{\left|n\right|}{2k}}\right)\underset{0}{\overset{\pi /2}{\int }}{cos}^{\sigma +\left|n\right|-2k}\alpha {sin}^{2k}\alpha \mathrm{d}\alpha \hfill \\ & =4\pi {\displaystyle \sum _{k=0}^{\left[\right|n|/2]}}{(-1)}^k\left({\displaystyle \genfrac{}{}{0pt}{}{\left|n\right|}{2k}}\right)\mathrm{B}\left({\displaystyle \frac{\sigma +\left|n\right|+1}{2}}-k,k+{\displaystyle \frac{1}{2}}\right),\hfill \end{array}$$

where $\mathrm{B}(\alpha ,\beta )$ is the classical Beta function, defined by

$$\mathrm{B}(\alpha ,\beta )=\left\{\begin{array}{l}{\int }_0^1{t}^{\alpha -1}{(1-t)}^{\beta -1}\mathrm{d}t(\Re \left(\alpha \right)>0,\Re \left(\beta \right)>0)\\ {\displaystyle \frac{\mathsf{\Gamma }\left(\alpha \right)\mathsf{\Gamma }\left(\beta \right)}{\mathsf{\Gamma }(\alpha +\beta )}}\left(\alpha ,\beta \in \mathbb{C}\setminus {\mathbb{Z}}_{⩽0}\right).\end{array}\right.$$

(7)

(see, for example, [20], p. 8, Equation (43)). Since

$$\begin{array}{c}\mathsf{\Gamma }(2k+1)=2^{2k}k!{(1/2)}_k,\\ \mathsf{\Gamma }\left(k+{\displaystyle \frac{1}{2}}\right)=\left\{\begin{array}{cc}\sqrt{\pi }\hfill & \mathrm{for}k=0,\hfill \\ 2^{-k}\sqrt{\pi }(2k-1)!!\hfill & \mathrm{for}k>0,\hfill \end{array}\right.\\ \mathsf{\Gamma }(1+|n|-2k)={\displaystyle \frac{2^{-2k}\left|n\right|!}{{\left(-\frac{\left|n\right|}{2}\right)}_k{\left(\frac{1-\left|n\right|}{2}\right)}_k}},\\ \mathsf{\Gamma }\left({\displaystyle \frac{\sigma +\left|n\right|+1}{2}}-k\right)={\displaystyle \frac{{(-1)}^k\mathsf{\Gamma }\left(\frac{\sigma +\left|n\right|+1}{2}\right)}{{\left(\frac{1-\sigma -\left|n\right|}{2}\right)}_k}},\end{array}$$

we obtain

$$\begin{array}{cc}\hfill Q{f}_{(n,0)}^{\left(1\right)\ast }\left(y\right)& ={\displaystyle \frac{4{\pi }^{3/2}\mathsf{\Gamma }\left(\frac{\sigma +\left|n\right|+1}{2}\right)}{\mathsf{\Gamma }\left(\frac{\sigma +\left|n\right|}{2}+1\right)}}{\displaystyle \sum _{k=0}^{\left[\right|n|/2]}}{\displaystyle \frac{{\left(-\frac{\left|n\right|}{2}\right)}_k{\left(\frac{1-\left|n\right|}{2}\right)}_k}{k!{\left(\frac{1-\left|n\right|-\sigma }{2}\right)}_k}}\hfill \\ & ={\displaystyle \frac{4{\pi }^{3/2}\mathsf{\Gamma }\left(\frac{\sigma +\left|n\right|+1}{2}\right)}{\mathsf{\Gamma }\left(\frac{\sigma +\left|n\right|}{2}+1\right)}}{}_{2}F_1\left(-{\displaystyle \frac{\left|n\right|}{2}},{\displaystyle \frac{1-\left|n\right|}{2}};{\displaystyle \frac{1-\left|n\right|-\sigma }{2}};1\right).\hfill \end{array}$$

Here, $(2n+1)!!:=1·3\cdots (2n+1)$$(n\in {\mathbb{Z}}_{⩾0})$; $\left(2n\right)!!:=2·4\cdots \left(2n\right)$$(n\in \mathbb{N})$; $0!!:=1$; and $(-1)!!:=1.$ Using the Gegenbauer polynomial (see, for instance, [3], Entry 7.3.1.203), we complete the proof. □

Let us demonstrate that at point $\widehat{y}=(1,0,0,0)$, the Q-image of the function belonging to the basis $B_2^{*}$ is a generalized function.

Theorem 2.

For $-1<\Re \left(\sigma \right)<0$,

$$Q{f}_{(\lambda ,\mu )}^{\left(2\right)\ast }\left(\widehat{y}\right)=-4\pi {\left|\lambda \right|}^{-\sigma -1}sin{\displaystyle \frac{\sigma \pi }{2}}\mathsf{\Gamma }(\sigma +1)\delta \left(\mu \right),$$

where δ is the Dirac delta function.

Proof. 

We have

$$Q{f}_{(\lambda ,\mu )}^{\left(2\right)\ast }={\mathsf{F}}_2\left(|x_1{y}^1+x_2{y}_2-x_3{y}_3-x_4{y}_4{|}^{\sigma },f_{(\lambda ,\mu )}^{\left(2\right)\ast }\right)=2\underset{0}{\overset{+\infty }{\int }}{\alpha }^{\sigma }cos\left|\lambda \right|\alpha \mathrm{d}\alpha \underset{-\infty }{\overset{+\infty }{\int }}{\mathrm{e}}^{\mathbf{i}\mu \beta }\mathrm{d}\beta .$$

Using the known formula ([19], Entry 2.5.3.10) for the Fourier cosine transform and the integral representation of the delta function, we complete the proof. □

Remark 1.

In 1926, Dirac introduced the delta function, denoted as $\delta \left(x\right)$, characterized by the following properties:

$$\delta \left(x\right)=0(x\ne 0)\mathrm{and}\underset{-\infty }{\overset{\infty }{\int }}\delta \left(x\right)\mathrm{d}\mathrm{x}=1.$$

The Dirac delta function, $\delta \left(x\right)$ is defined such that for any well-behaved function $f\left(x\right)$, the integral

$$\underset{-\infty }{\overset{\infty }{\int }}\delta \left(x\right)f\left(x\right)\mathrm{d}\mathrm{x}=\mathrm{f}\left(0\right).$$

Notably, there is no conventional function that directly corresponds to the delta function. For a detailed exploration of the various properties and applications of the Dirac delta function, one can refer to the source cited on pages 27–35 and 80–81 in [21].

Theorem 3.

Let $n\equiv 0(mod2)$ and $-1<\Re \left(\sigma \right)<0$. Then,

$$\begin{gathered} \underset{0}{\overset{+\infty }{\int }}{\lambda }^{-1}\left[{\displaystyle \frac{W_{n/2,(\sigma +1)/2}^2\left(\lambda \right)}{{\mathsf{\Gamma }}^2\left(\frac{\sigma +n}{2}+1\right)}}+{\displaystyle \frac{W_{-n/2,(\sigma +1)/2}^2\left(\lambda \right)}{{\mathsf{\Gamma }}^2\left(\frac{\sigma -n}{2}+1\right)}}\right]\mathrm{d}\lambda \\ ={\displaystyle \frac{{(-1)}^{n+1}{2}^{\sigma -\left|n\right|}\sqrt{\pi }\left|n\right|!\mathsf{\Gamma }\left(\frac{\sigma +\left|n\right|+1}{2}\right)}{sin\frac{\sigma \pi }{2}\mathsf{\Gamma }(\sigma +1)\mathsf{\Gamma }\left(\frac{\sigma +\left|n\right|}{2}+1\right)}}{C}_{\left|n\right|}^{\left(\right(1+\sigma -\left|n\right|)/2)}\left(1\right), \end{gathered}$$

where $W_{n/2,(\sigma +1)/2}$ is the Whittaker function of the second kind (see, for example, [11], Chapter XVI).

Proof. 

Let us consider the integral operator

$$f_{(n,m)}^{\left(1\right)\ast }=\underset{{\mathbb{R}}^2}{\int \int }k(n,m,\lambda ,\mu )f_{(\lambda ,\mu )}^{\left(2\right)\ast }\mathrm{d}\lambda \mathrm{d}\mu .$$

(8)

Since

$$\begin{array}{cc}\hfill {\mathsf{F}}_2(f_{(\tilde{\lambda },\tilde{\mu })}^{\left(2\right)},f_{(n,m)}^{\left(1\right)\ast })& =\underset{{\mathbb{R}}^2}{\int \int }k(n,m,\lambda ,\mu ){\mathsf{F}}_2(f_{(\tilde{\lambda },\tilde{\mu })}^{\left(2\right)},f_{(\lambda ,\mu )}^{\left(2\right)\ast })\mathrm{d}\lambda \mathrm{d}\mu \hfill \\ & =4{\pi }^2\underset{{\mathbb{R}}^2}{\int \int }k(n,m,\lambda ,\mu )\delta (\lambda +\tilde{\lambda })\delta (\mu +\tilde{\mu })\mathrm{d}\lambda \mathrm{d}\mu ,\hfill \end{array}$$

where $\delta$ is the Dirac delta function, we have

$$\begin{array}{l}k(n,m,\lambda ,\mu )={\left(4{\pi }^2\right)}^{-1}{\mathsf{F}}_2(f_{(-\lambda ,-\mu )}^{\left(2\right)},f_{(n,m)}^{\left(1\right)\ast })\\ ={\displaystyle \frac{2^{\sigma }}{{\pi }^2}}\underset{-\infty }{\overset{+\infty }{\int }}{\mathrm{e}}^{-\mathbf{i}\lambda \alpha }\mathrm{d}\alpha \underset{-\infty }{\overset{+\infty }{\int }}{\mathrm{e}}^{-\mathbf{i}\mu \beta }{(1+{\alpha }^4+{\beta }^4+2{\alpha }^2+2{\beta }^2-2{\alpha }^2{\beta }^2)}^{(\sigma -n-m)/2}\\ \times {(1-{\alpha }^2+{\beta }^2+2\mathbf{i}\alpha )}^n{(1+{\alpha }^2-{\beta }^2+2\mathbf{i}\beta )}^m\mathrm{d}\beta \\ ={\displaystyle \frac{2^{\sigma -1}}{{\pi }^2}}{\displaystyle \prod _{k=0}^1}\underset{-\infty }{\overset{+\infty }{\int }}{\mathrm{e}}^{-\mathbf{i}(\lambda +{(-1)}^k\mu )t/2}{(1+\mathbf{i}t)}^{(\sigma +n+{(-1)}^{k}m)/2}{(1-\mathbf{i}t)}^{(\sigma -n+{(-1)}^{k+1}m)/2}\mathrm{d}t.\end{array}$$

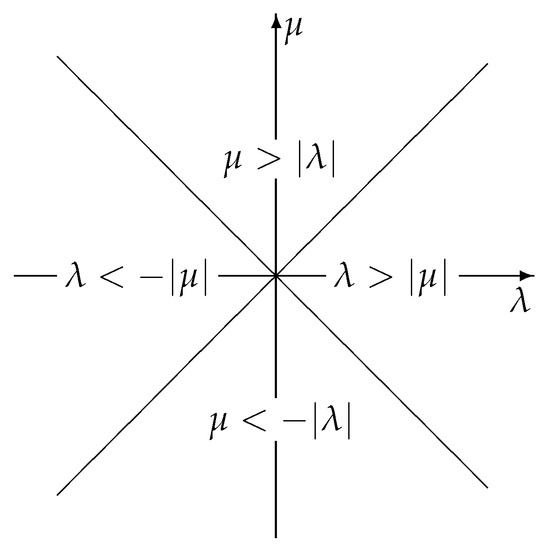
Let us divide the plane $O\lambda \mu$ into the following five equivalence classes: $\lambda >\left|\mu \right|$, $\mu >\left|\lambda \right|$, $\lambda <-\left|\mu \right|$, $\mu <-\left|\lambda \right|$, and $\left|\lambda \right|=\left|\mu \right|$ (Figure 1).

Figure 1. Equivalence classes in the $(\lambda ,\mu )$ plane.

According to formula [1], Entry 3.384.9, we obtain the following for the different classes:

For the class $\lambda >\left|\mu \right|$,

$$k(n,m,\lambda ,\mu )={\displaystyle \frac{2^{-\sigma -2}{({\lambda }^2-{\mu }^2)}^{-\sigma /2-1}}{\mathsf{\Gamma }\left(\frac{\sigma +n+m}{2}+1\right)\mathsf{\Gamma }\left(\frac{\sigma +n-m}{2}+1\right)}}{W}_{{\displaystyle \frac{n+m}{2}},{\displaystyle \frac{\sigma +1}{2}}}(\lambda +\mu )W_{{\displaystyle \frac{n-m}{2}},{\displaystyle \frac{\sigma +1}{2}}}(\lambda -\mu );$$

(9)

For the class $\mu >\left|\lambda \right|$,

$$k(n,m,\lambda ,\mu )=-{\displaystyle \frac{2^{-\sigma -2}{({\mu }^2-{\lambda }^2)}^{-\sigma /2-1}}{\mathsf{\Gamma }\left(\frac{\sigma +n+m}{2}+1\right)\mathsf{\Gamma }\left(\frac{\sigma +m-n}{2}+1\right)}}{W}_{{\displaystyle \frac{m+n}{2}},{\displaystyle \frac{\sigma +1}{2}}}(\mu +\lambda )W_{{\displaystyle \frac{m-n}{2}},{\displaystyle \frac{\sigma +1}{2}}}(\mu -\lambda );$$

For the class $\lambda <-\left|\mu \right|$,

$$k(n,m,\lambda ,\mu )={\displaystyle \frac{2^{-\sigma -2}{({\mu }^2-{\lambda }^2)}^{-\sigma /2-1}}{\mathsf{\Gamma }\left(\frac{\sigma +m-n}{2}+1\right)\mathsf{\Gamma }\left(\frac{\sigma -n-m}{2}+1\right)}}{W}_{{\displaystyle \frac{m-n}{2}},{\displaystyle \frac{\sigma +1}{2}}}(\mu -\lambda )W_{-{\displaystyle \frac{m+n}{2}},{\displaystyle \frac{\sigma +1}{2}}}(-\mu -\lambda );$$

(10)

For the class $\mu <-\left|\lambda \right|$,

$$k(n,m,\lambda ,\mu )=-{\displaystyle \frac{2^{-\sigma -2}{({\lambda }^2-{\mu }^2)}^{-\sigma /2-1}}{\mathsf{\Gamma }\left(\frac{\sigma +n-m}{2}+1\right)\mathsf{\Gamma }\left(\frac{\sigma -n-m}{2}+1\right)}}{W}_{{\displaystyle \frac{n-m}{2}},{\displaystyle \frac{\sigma +1}{2}}}(\lambda -\mu )W_{-{\displaystyle \frac{m+n}{2}},{\displaystyle \frac{\sigma +1}{2}}}(-\mu -\lambda ).$$

From (8) and Theorem 2, we have the following:

$$\begin{array}{cc}\hfill Q{f}_{(n,0)}^{\left(1\right)\ast }\left(\widehat{y}\right)& =\underset{{\mathbb{R}}^2}{\int \int }k(n,0,\lambda ,\mu )Q{f}_{(\lambda ,\mu )}^{\left(2\right)\ast }\left(\widehat{y}\right)\mathrm{d}\lambda \mathrm{d}\mu \hfill \\ & =-4\pi sin\left({\displaystyle \frac{\sigma \pi }{2}}\right)\mathsf{\Gamma }(\sigma +1)\underset{-\infty }{\overset{+\infty }{\int }}{\left|\lambda \right|}^{-\sigma -1}k(n,0,\lambda ,0)\mathrm{d}\lambda .\hfill \end{array}$$

In view of Formulas (9) and (10), we obtain the following:

$$\begin{array}{l}-4\pi sin\left({\displaystyle \frac{\sigma \pi }{2}}\right)\mathsf{\Gamma }(\sigma +1)[{\mathsf{\Gamma }}^{-2}\left({\displaystyle \frac{\sigma +n}{2}}+1\right)\underset{0}{\overset{+\infty }{\int }}{\lambda }^{-1}{W}_{n/2,(\sigma +1)/2}^2\left(\lambda \right)\mathrm{d}\lambda \\ +{\mathsf{\Gamma }}^{-2}\left({\displaystyle \frac{\sigma -n}{2}}+1\right)\underset{-\infty }{\overset{0}{\int }}{(-\lambda )}^{-1}{W}_{-n/2,(\sigma +1)/2}^2(-\lambda )\mathrm{d}\lambda ]=Q{f}_{(n,0)}^{\left(1\right)\ast }\left(\widehat{y}\right).\end{array}$$

Using Theorem 1, we complete the proof. □

Remark 2.

Letting $n=0$ in Theorem 3 and using the known formula $W_{0,\nu }\left(z\right)$ = $\sqrt{z/\pi }{K}_{\nu }(z/2)$, where $K_{\nu }$ is the Macdonald function, we obtain the following identity:

$$\underset{0}{\overset{+\infty }{\int }}{\left[K_{{\displaystyle \frac{\sigma +1}{2}}}\left(t\right)\right]}^2\mathrm{d}t=-{\displaystyle \frac{2^{\sigma -2}{\pi }^{3/2}\mathsf{\Gamma }\left(\frac{\sigma +1}{2}\right)\mathsf{\Gamma }\left(\frac{\sigma }{2}+1\right)}{sin\frac{\sigma \pi }{2}\mathsf{\Gamma }(\sigma +1)}}.$$

(11)

This formula coincides with the particular case

$$\underset{0}{\overset{+\infty }{\int }}{\left[K_{{\displaystyle \frac{\sigma +1}{2}}}\left(t\right)\right]}^2\mathrm{d}t=2^{-2}\pi \mathsf{\Gamma }(-\sigma /2)\mathsf{\Gamma }(1+\sigma /2)$$

(12)

of the known formula [22], Entry 2.16.33.2, since

$$\begin{array}{c}\mathsf{\Gamma }(\sigma +1)=2^{\sigma }{\pi }^{-1/2}\mathsf{\Gamma }\left({\displaystyle \frac{\sigma +1}{2}}\right)\mathsf{\Gamma }\left({\displaystyle \frac{\sigma }{2}}+1\right),\\ \mathsf{\Gamma }(-\sigma /2)\mathsf{\Gamma }(1+\sigma /2)=-{\displaystyle \frac{\pi }{sin\frac{\sigma \pi }{2}}}\end{array}$$

and, therefore,

$$\begin{array}{c}{\displaystyle \frac{2^{\sigma -2}{\pi }^{3/2}\mathsf{\Gamma }\left(\frac{\sigma +1}{2}\right)\mathsf{\Gamma }\left(\frac{\sigma }{2}+1\right)}{sin\frac{\sigma \pi }{2}\mathsf{\Gamma }(\sigma +1)}}={\displaystyle \frac{{\pi }^2}{4sin\frac{\sigma \pi }{2}}},\\ 2^{-2}\pi \mathsf{\Gamma }(-\sigma /2)\mathsf{\Gamma }(1+\sigma /2)=-{\displaystyle \frac{{\pi }^2}{4sin\frac{\sigma \pi }{2}}}.\end{array}$$

This means that Theorem 3 is a generalization of Formula (11) (and (12)) for the Meijer integral transform.

6. A Sum of Double Integral Transforms Whose Kernels Are Bessel Functions

In this section, we assume $\tilde{y}=(0,1,0,0)$.

Theorem 4.

Let $-1<\Re \left(\sigma \right)<0$. For $\left|\mu \right|<\left|\lambda \right|$,

$$\begin{array}{cc}\hfill Q{f}_{(\lambda ,\mu )}^{\left(2\right)\ast }\left(\tilde{y}\right)=& -4\pi {({\lambda }^2-{\mu }^2)}^{-\sigma /2-1/2}sin{\displaystyle \frac{\sigma \pi }{2}}\mathsf{\Gamma }(\sigma +1)\hfill \\ & \times \left[sin{\displaystyle \frac{\sigma \pi }{2}}{Y}_{-\sigma -1}\left(\sqrt{{\lambda }^2-{\mu }^2}\right)+cos{\displaystyle \frac{\sigma \pi }{2}}{J}_{-\sigma -1}\left(\sqrt{{\lambda }^2-{\mu }^2}\right)\right].\hfill \end{array}$$

For $\left|\lambda \right|<\left|\mu \right|$,

$$Q{f}_{(\lambda ,\mu )}^{\left(2\right)\ast }\left(\tilde{y}\right)=8{sin}^2{\displaystyle \frac{\sigma \pi }{2}}{({\mu }^2-{\lambda }^2)}^{-\sigma /2-1/2}\mathsf{\Gamma }(\sigma +1)K_{-\sigma -1}\left(\sqrt{{\mu }^2-{\lambda }^2}\right).$$

Proof. 

Indeed,

$$\begin{array}{cc}\hfill Q{f}_{(\lambda ,\mu )}^{\left(2\right)\ast }\left(\tilde{y}\right)& ={\mathsf{F}}_2\left(\right|x_1{\tilde{y}}_1+x_2{\tilde{y}}_2-x_3{\tilde{y}}_3-x_4{\tilde{y}}_4{|}^{\sigma },f_{(\lambda ,\mu )}^{\left(2\right)\ast })\hfill \\ & =2^{1-\sigma }\underset{-\infty }{\overset{+\infty }{\int }}{\mathrm{e}}^{\mathbf{i}\mu \beta }\mathrm{d}\beta \underset{0}{\overset{+\infty }{\int }}|1+{\beta }^2-{\alpha }^2{|}^{\sigma }cos\left(\right|\lambda \left|\alpha \right)\mathrm{d}\alpha .\hfill \end{array}$$

According to formulae [19], Entry 2.5.6.1–2,

$$\begin{array}{c}\underset{0}{\overset{\sqrt{1+{\beta }^2}}{\int }}{(1+{\beta }^2-{\alpha }^2)}^{\sigma }cos\left(\right|\lambda \left|\alpha \right)\mathrm{d}\alpha =w{J}_{\sigma +1/2}(\left|\lambda \right|\sqrt{1+{\beta }^2}),\\ \underset{\sqrt{1+{\beta }^2}}{\overset{+\infty }{\int }}{({\alpha }^2-{\beta }^2-1)}^{\sigma }cos\left(\right|\lambda \left|\alpha \right)\mathrm{d}\alpha =-w{Y}_{-\sigma -1/2}(\left|\lambda \right|\sqrt{1+{\beta }^2}),\end{array}$$

where

$$w=2^{\sigma -1/2}\sqrt{\pi }{\left(\sqrt{1+{\beta }^2}\right)}^{\sigma +1/2}{\left|\lambda \right|}^{-\sigma -1/2}\mathsf{\Gamma }(\sigma +1).$$

Therefore,

$$\begin{array}{cc}\hfill Q{f}_{(\lambda ,\mu )}^{\left(2\right)\ast }\left(\tilde{y}\right)=& \sqrt{8\pi }\mathsf{\Gamma }(\sigma +1){\left|\lambda \right|}^{-\sigma -1/2}\hfill \\ & \times \underset{1}{\overset{+\infty }{\int }}{\displaystyle \frac{t^{\sigma +3/2}}{\sqrt{t^2-1}}}cos\left(\left|\mu \right|\sqrt{t^2-1}\right)\left(J_{\sigma +1/2}\left(\right|\lambda \left|t\right)-Y_{-\sigma -1/2}\left(\right|\lambda \left|t\right)\right)\mathrm{d}t.\hfill \end{array}$$

According to formulae [22], 2.12.22.7 and [22], 2.13.8.14, we have the following, respectively:

$$\begin{array}{l}\underset{1}{\overset{+\infty }{\int }}{\displaystyle \frac{t^{\sigma +3/2}}{\sqrt{t^2-1}}}cos\left(\left|\mu \right|\sqrt{t^2-1}\right)J_{-\sigma -1/2}\left(\right|\lambda \left|t\right)\mathrm{d}t\\ =\left\{\begin{array}{cc}v{J}_{-\sigma -1}\left(\sqrt{{\lambda }^2-{\mu }^2}\right)\hfill & \mathrm{for}\left|\mu \right|<\left|\lambda \right|,\hfill \\ 0\hfill & \mathrm{for}\left|\lambda \right|<\left|\mu \right|\hfill \end{array}\right.\end{array}$$

and

$$\begin{array}{l}\underset{1}{\overset{+\infty }{\int }}{\displaystyle \frac{t^{\sigma +3/2}}{\sqrt{t^2-1}}}cos\left(\left|\mu \right|\sqrt{t^2-1}\right)Y_{-\sigma -1/2}\left(\right|\lambda \left|t\right)\mathrm{d}t\\ =\left\{\begin{array}{cc}v{Y}_{-\sigma -1}\left(\sqrt{{\lambda }^2-{\mu }^2}\right)\hfill & \mathrm{for}\left|\mu \right|<\left|\lambda \right|,\hfill \\ -{\displaystyle \frac{2v}{\pi }}{K}_{-\sigma -1}\left(\sqrt{{\mu }^2-{\lambda }^2}\right)\hfill & \mathrm{for}\left|\lambda \right|<\left|\mu \right|,\hfill \end{array}\right.\end{array}$$

where

$$v=\sqrt{2^{-1}\pi }{\left|\lambda \right|}^{\sigma +1/2}{|{\lambda }^2-{\mu }^2|}^{-\sigma /2-1/2}.$$

Taking the identity ([23], 7.4.26a)

$$J_{-\nu }\left(z\right)=J_{\nu }\left(z\right)cos\left(\nu \pi \right)-Y_{\nu }\left(z\right)sin\left(\nu \pi \right),$$

we obtain

$$\begin{array}{cc}\hfill Q{f}_{(\lambda ,\mu )}^{\left(2\right)\ast }\left(\tilde{y}\right)=& 2\pi {({\lambda }^2-{\mu }^2)}^{-\sigma /2-1/2}\mathsf{\Gamma }(\sigma +1)\hfill \\ & \times \left[\left(cos\left(\sigma \pi \right)-1\right)Y_{-\sigma -1}\left(\sqrt{{\lambda }^2-{\mu }^2}\right)-sin\left(\sigma \pi \right)J_{-\sigma -1}\left(\sqrt{{\lambda }^2-{\mu }^2}\right)\right]\hfill \end{array}$$

for the case $\left|\mu \right|<\left|\lambda \right|$, and

$$Q{f}_{(\lambda ,\mu )}^{\left(2\right)\ast }\left(\tilde{y}\right)=4\left(1-cos\left(\sigma \pi \right)\right){({\mu }^2-{\lambda }^2)}^{-\sigma /2-1/2}\mathsf{\Gamma }(\sigma +1)K_{-\sigma -1}\left(\sqrt{{\lambda }^2-{\mu }^2}\right)$$

for the case $\left|\lambda \right|<\left|\mu \right|$. □

Theorem 5.

For $-1<\Re \left(\sigma \right)<-{\displaystyle \frac{1}{2}}$,

$$Q{f}_{(0,0)}^{\left(3\right)\ast }\left(\tilde{y}\right)=2^{-\sigma }\mathrm{B}\left(-\sigma -1,{\displaystyle \frac{1}{2}}\right)\left[\mathrm{B}\left(\sigma +1,{\displaystyle \frac{1}{2}}\right)+\mathrm{B}\left(\sigma +1,-\sigma -{\displaystyle \frac{1}{2}}\right)\right].$$

Proof. 

Indeed, according to [19], Entry 2.2.3.1 and [19], Entry 2.2.3.4,

$$\begin{array}{cc}\hfill Q{f}_{(0,0)}^{\left(3\right)\ast }\left(\tilde{y}\right)& ={\mathsf{F}}_3\left(\right|x_1{\tilde{y}}_1+x_2{\tilde{y}}_2-x_3{\tilde{y}}_3-x_4{\tilde{y}}_4{|}^{\sigma },f_{(0,0)}^{\left(3\right)\ast })\hfill \\ & =2^{1-\sigma }\underset{-\infty }{\overset{+\infty }{\int }}\mathrm{d}\beta \left[\underset{0}{\overset{\sqrt{1+{\beta }^2}}{\int }}{(1+{\beta }^2-{\alpha }^2)}^{\sigma }\mathrm{d}\alpha +\underset{\sqrt{1+{\beta }^2}}{\overset{+\infty }{\int }}{({\alpha }^2-{\beta }^2-1)}^{\sigma }\mathrm{d}\alpha \right]\hfill \\ & =2^{1-\sigma }\left[\mathrm{B}\left(\sigma +1,{\displaystyle \frac{1}{2}}\right)+\mathrm{B}\left(\sigma +1,-\sigma -{\displaystyle \frac{1}{2}}\right)\right]\underset{0}{\overset{+\infty }{\int }}{(1+{\beta }^2)}^{\sigma +1/2}\mathrm{d}\sigma .\hfill \end{array}$$

This integral can be evaluated using formula ([19], Entry 2.2.3.5). □

Theorem 6.

For $-1<\Re \left(\sigma \right)<-{\displaystyle \frac{1}{2}}$,

$$\begin{array}{l}2sin{\displaystyle \frac{\sigma \pi }{2}}\underset{\left|\lambda \right|<\left|\mu \right|}{\int \int }{({\mu }^2-{\lambda }^2)}^{(\sigma +1)/2}{\mathrm{e}}^{\mathbf{i}\mu }{K}_{-\sigma -1}\left(\sqrt{{\mu }^2-{\lambda }^2}\right)\mathrm{d}\lambda \mathrm{d}\mu \\ -\pi \underset{\left|\mu \right|<\left|\lambda \right|}{\int \int }{({\lambda }^2-{\mu }^2)}^{(\sigma +1)/2}{\mathrm{e}}^{\mathbf{i}\mu }[cos{\displaystyle \frac{\sigma \pi }{2}}{J}_{-\sigma -1}\left(\sqrt{{\lambda }^2-{\mu }^2}\right)\\ +sin{\displaystyle \frac{\sigma \pi }{2}}{Y}_{-\sigma -1}\left(\sqrt{{\lambda }^2-{\mu }^2}\right)]\mathrm{d}\lambda \mathrm{d}\mu \\ =\pi sin{\displaystyle \frac{\sigma \pi }{2}}{\left[\mathsf{\Gamma }(-\sigma -1)\right]}^{-1}.\end{array}$$

(13)

Proof. 

Considering the linear operator

$$f_{(0,0)}^{\left(3\right)\ast }=\underset{{\mathbb{R}}^2}{\int \int }l(\lambda ,\mu )f_{\lambda ,\mu }^{\left(2\right)\ast }\mathrm{d}\lambda \mathrm{d}\mu ,$$

(14)

we obtain the following:

$$\begin{array}{cc}\hfill l(\lambda ,\mu )& ={\left(2\pi \right)}^{-2}{\mathsf{F}}_2(f_{-(\lambda ,\mu )}^{\left(2\right)},f_{(0,0)}^{\left(3\right)\ast })\hfill \\ & =2^{\sigma }{\pi }^{-2}\underset{{\mathbb{R}}^2}{\int \int }|{(1+\beta )}^2-{\alpha }^2{|}^{-\sigma -2}{\mathrm{e}}^{-\mathbf{i}(\lambda \alpha +\mu \beta )}\mathrm{d}\alpha \mathrm{d}\beta \hfill \\ & =2^{\sigma +1}{\pi }^{-2}{\mathrm{e}}^{\mathbf{i}\mu }\underset{-\infty }{\overset{+\infty }{\int }}{\mathrm{e}}^{-\mathbf{i}\mu u}\mathrm{d}u\underset{0}{\overset{+\infty }{\int }}|u^2-{\alpha }^2{|}^{-\sigma -2}cos\left(\right|\lambda \left|\alpha \right)\mathrm{d}\alpha .\hfill \end{array}$$

According to formulae ([19], Entry 2.5.6.1–2),

$$\begin{array}{c}\underset{0}{\overset{\left|u\right|}{\int }}{(u^2-{\alpha }^2)}^{-\sigma -2}cos\left(\right|\lambda \left|\alpha \right)\mathrm{d}\alpha =c{J}_{-\sigma -3/2}\left(\right|u\lambda \left|\right),\\ \underset{\left|u\right|}{\overset{+\infty }{\int }}{({\alpha }^2-u^2)}^{-\sigma -2}cos\left(\right|\lambda \left|\alpha \right)\mathrm{d}\alpha =-c{Y}_{\sigma +3/2}\left(\right|u\lambda \left|\right),\end{array}$$

where

$$c=2^{-(\sigma +5)/2}\sqrt{\pi }{\left|\lambda \right|}^{\sigma +3/2}{\left|u\right|}^{-\sigma -3/2}\mathsf{\Gamma }(-\sigma -1),$$

we find

$$\begin{array}{cc}\hfill l(\lambda ,\mu )=\hfill & {\displaystyle \frac{{\left|\lambda \right|}^{\sigma +3/2}{\mathrm{e}}^{\mathbf{i}\mu }\mathsf{\Gamma }(-\sigma -1)}{\sqrt{2{\pi }^3}}}\hfill \\ & \times \underset{0}{\overset{+\infty }{\int }}{u}^{-\sigma -3/2}cos\left(\right|\mu \left|u\right)\left(J_{-\sigma -3/2}\left(\right|\lambda \left|u\right)-Y_{\sigma +3/2}\left(\right|\lambda \left|u\right)\right)\mathrm{d}u.\hfill \end{array}$$

According to formulae [22], Entry 2.12.15.5–6 and [22], Entry 2.13.8.2, respectively, we have the following:

$$\begin{array}{l}\underset{0}{\overset{+\infty }{\int }}{u}^{-\sigma -3/2}cos\left(\right|\mu \left|u\right)J_{-\sigma -3/2}\left(\right|\lambda \left|u\right)\mathrm{d}u\\ =\left\{\begin{array}{cc}d{({\lambda }^2-{\mu }^2)}^{\sigma +1}\hfill & \mathrm{for}\left|\mu \right|<\left|\lambda \right|,\hfill \\ -dcos\pi \sigma {({\mu }^2-{\lambda }^2)}^{\sigma +1}\hfill & \mathrm{for}\left|\lambda \right|<\left|\mu \right|,\hfill \end{array}\right.\end{array}$$

and

$$\begin{array}{l}\underset{0}{\overset{+\infty }{\int }}{u}^{-\sigma -3/2}cos\left(\right|\mu \left|u\right)Y_{\sigma +3/2}\left(\right|\lambda \left|u\right)\mathrm{d}u\\ =\left\{\begin{array}{cc}dcos\pi \sigma {({\lambda }^2-{\mu }^2)}^{\sigma +1}\hfill & \mathrm{for}\left|\mu \right|<\left|\lambda \right|,\hfill \\ -d{({\mu }^2-{\lambda }^2)}^{\sigma +1}\hfill & \mathrm{for}\left|\lambda \right|<\left|\mu \right|,\hfill \end{array}\right.\end{array}$$

where

$$d={\left(2\right|\lambda \left|\right)}^{-\sigma -3/2}{\pi }^{-1/2}\mathsf{\Gamma }(-\sigma -1).$$

Thus,

$$l(\lambda ,\mu )=2^{-\sigma -1}{\pi }^{-2}{|{\mu }^2-{\lambda }^2|}^{\sigma +1}{\mathrm{e}}^{\mathbf{i}\mu }{sin}^2{\displaystyle \frac{\pi \sigma }{2}}{\mathsf{\Gamma }}^2(-\sigma -1).$$

Using the identity (14) and Theorems 4 and 5, we complete the proof. □

7. Concluding Remarks

We presented a novel proof using group theory for a Meijer transform formula. This proof unveils the formula as a special case of a broader, generalized result. The generalization is achieved through a linear operator that connects two representations of the connected component of the identity of the group $\mathrm{SO}(2,2)$. Using this innovative approach, we derived a formula for the sum of three double integral transforms, with kernels represented by Bessel functions.

We can interpret (13) as a formula representing the sum of three double integral transforms: Meijer–Clifford, Hankel–Clifford, and Neumann–Clifford [24,25,26,27]. By introducing new variables in the left side, this formula achieves a more symmetric form, resulting in a combination of Meijer, Hankel, and Neumann integral transforms [28]. For instance, by letting $s=\sqrt{\mu +\lambda }$ and $t=\sqrt{\mu -\lambda }$, we have the following:

$$\begin{array}{l}\underset{\mu >\left|\lambda \right|}{\int \int }{({\lambda }^2-{\mu }^2)}^{(\sigma +1)/2}{\mathrm{e}}^{\mathbf{i}\mu }{K}_{-\sigma -1}\left(\sqrt{{\mu }^2-{\lambda }^2}\right)\mathrm{d}\lambda \mathrm{d}\mu \\ =2\underset{s,t>0}{\int \int }{\left(st\right)}^{\sigma +2}{\mathrm{e}}^{\mathbf{i}(s^2+t^2)/2}{K}_{\sigma +1}\left(st\right)\mathrm{d}s\mathrm{d}t.\end{array}$$

Reference [29] established connections among various well-known functions, including exponential, trigonometric, hyperbolic, and Bessel functions, by expressing them as generalized Meijer G-functions and solving an integral involving modified Bessel functions. Reference [30] extended various fractional Laplace transform results to matrix-valued functions, using them to derive valuable theorems on piecewise continuous functions with conformable exponential order and the conditions for obtaining the fractional Laplace transform of matrix-valued functions. Reference [31] introduced a novel cryptosystem called Deoxyribose Nucleic Acid (DNA) secret writing, which utilizes the Laplace transform of the Mittag–Leffler function.