Riemannian SVRG Using Barzilai–Borwein Method as Second-Order Approximation for Federated Learning
Abstract
1. Introduction
1.1. Related Work
1.2. Our Contributions
- We propose the Barzilai–Borwein approximation as second-order information to control the variance with lower computational cost (RFedSVRG-2BB). In addition, we incorporate the Barzilai–Borwein step size for RFedSVRG-2BB and lead the RFedSVRG-2BBS.
- We present the convergence results and the corresponding convergence rate of the proposed methods for the strongly geodesically convex objective function and non-convex objective function, respectively.
- We conduct numerical experiments for the proposed methods on solving the PCA, kPCA and PSD Karcher mean problems in some datasets. The numerical results show that our methods are better than RFedSVRG and other algorithms.
2. Preliminaries on Riemannian Optimization
3. RFedSVRG with Barzilai–Borwein Approximation as Second-Order Information
3.1. The RFedSVRG Method
- Uniformly sample clients to obtain the set , and the clients receive and from the server;
- The clients in take the local updatesto obtain , where is the constant step size specified by users, and ;
- The central sever aggregates the updated points from the clients to obtain by tangent space mean
- Property 1: unbiased estimate of B and , that is,
- Property 2: approximation of B and such that
3.2. Barzilai–Borwein Method
3.3. RFedSVRG with Barzilai–Borwein Method as Second-Order Information (RFedSVRG-2BB)
3.4. RFedSVRG-2BB with Barzilai–Borwein Step Size (RFedSVRG-2BBS)
| Algorithm 1: Framework of RFedSVRG-2BB |
 |
4. Convergence Analysis
5. Numerical Experiments
5.1. Experiments on Synthetic Data
- (a)
- (b)
- the communication exceeds the specified number of rounds.
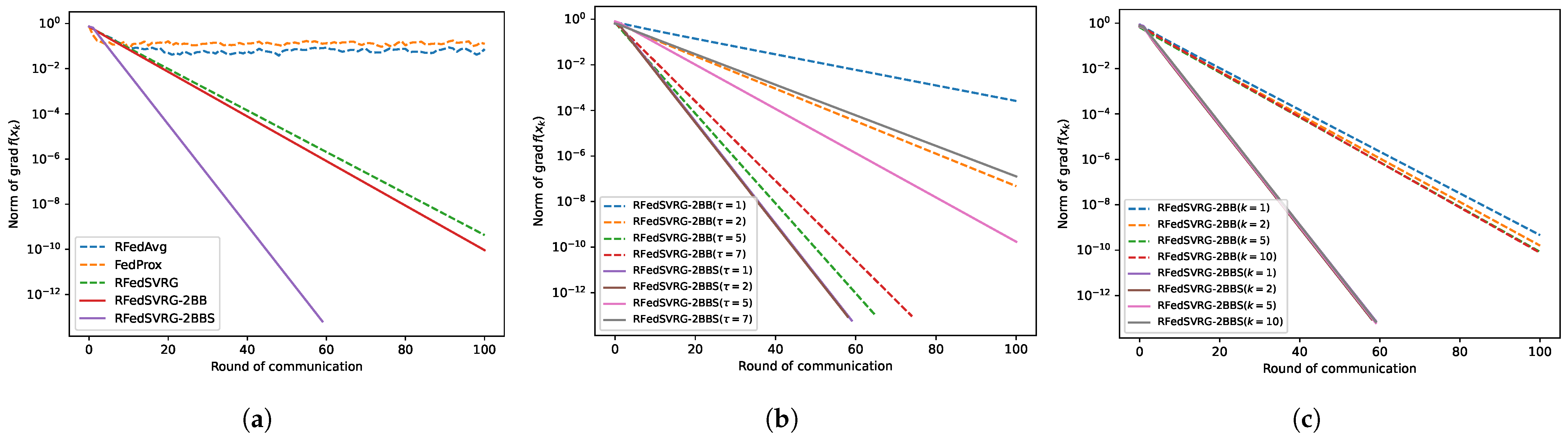
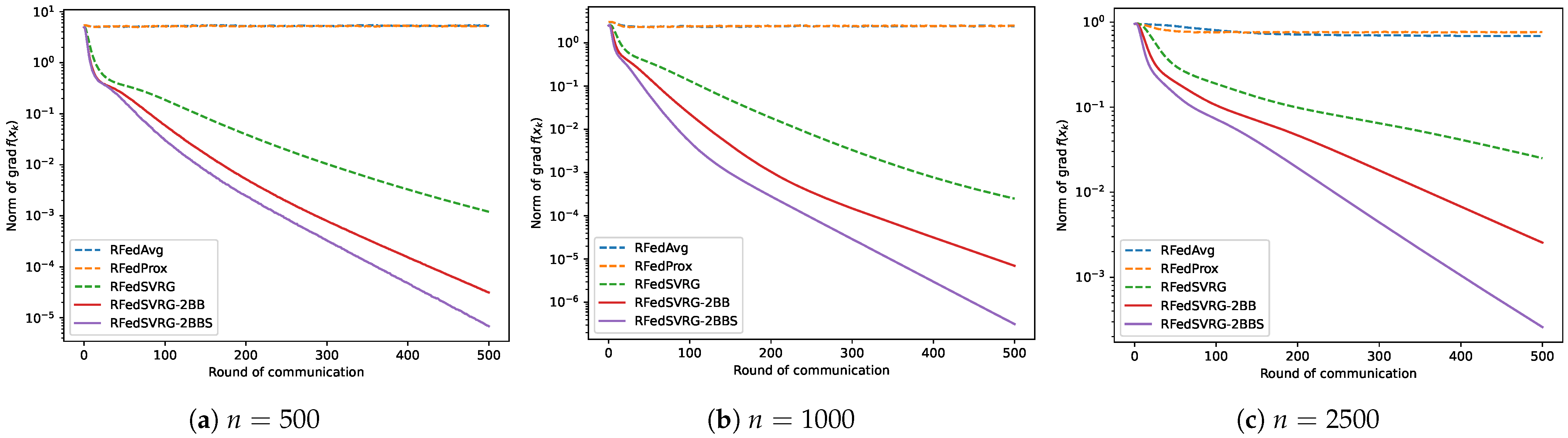
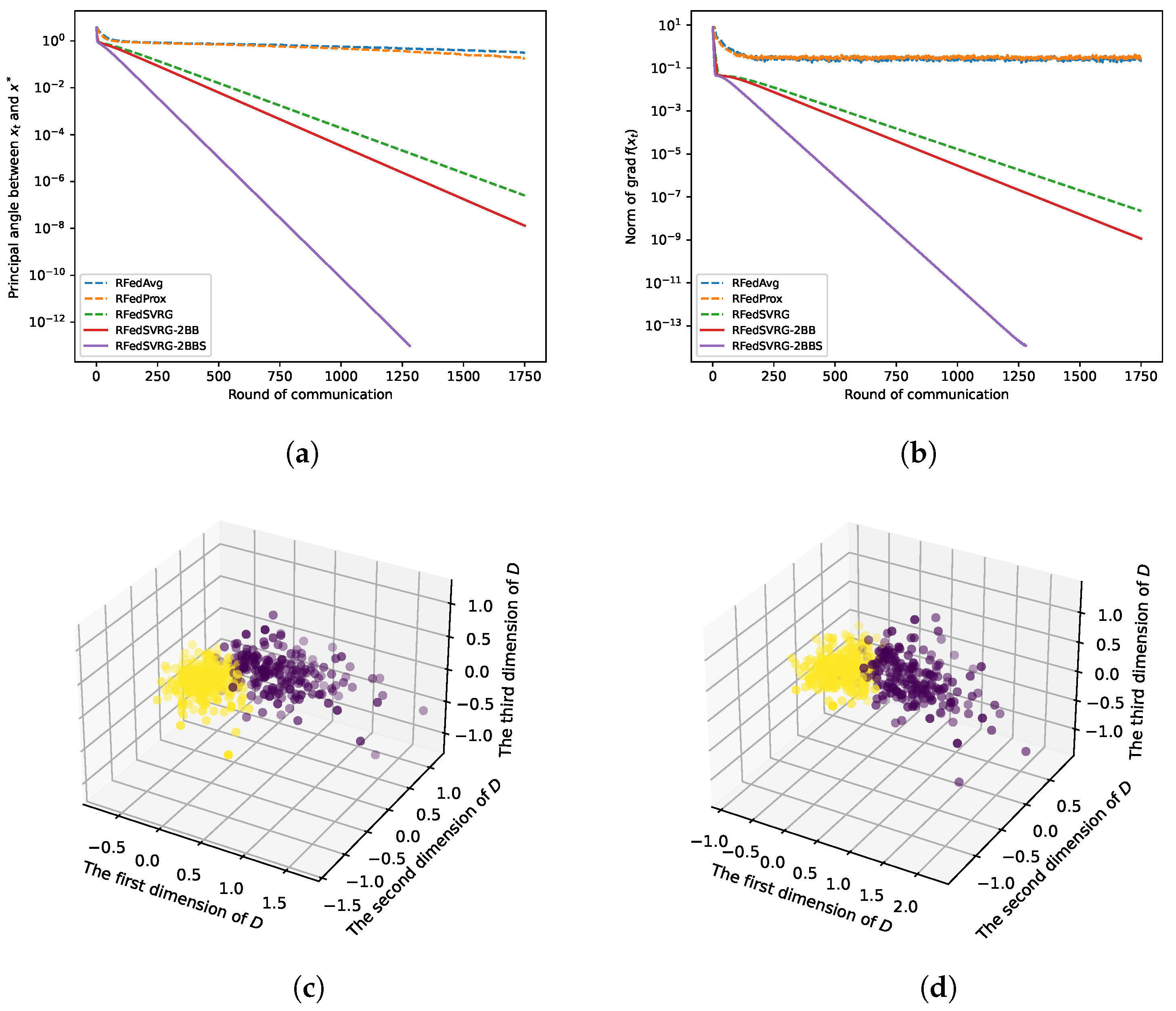
5.1.1. Experiments on PSD Karcher Mean
5.1.2. Experiments on PCA
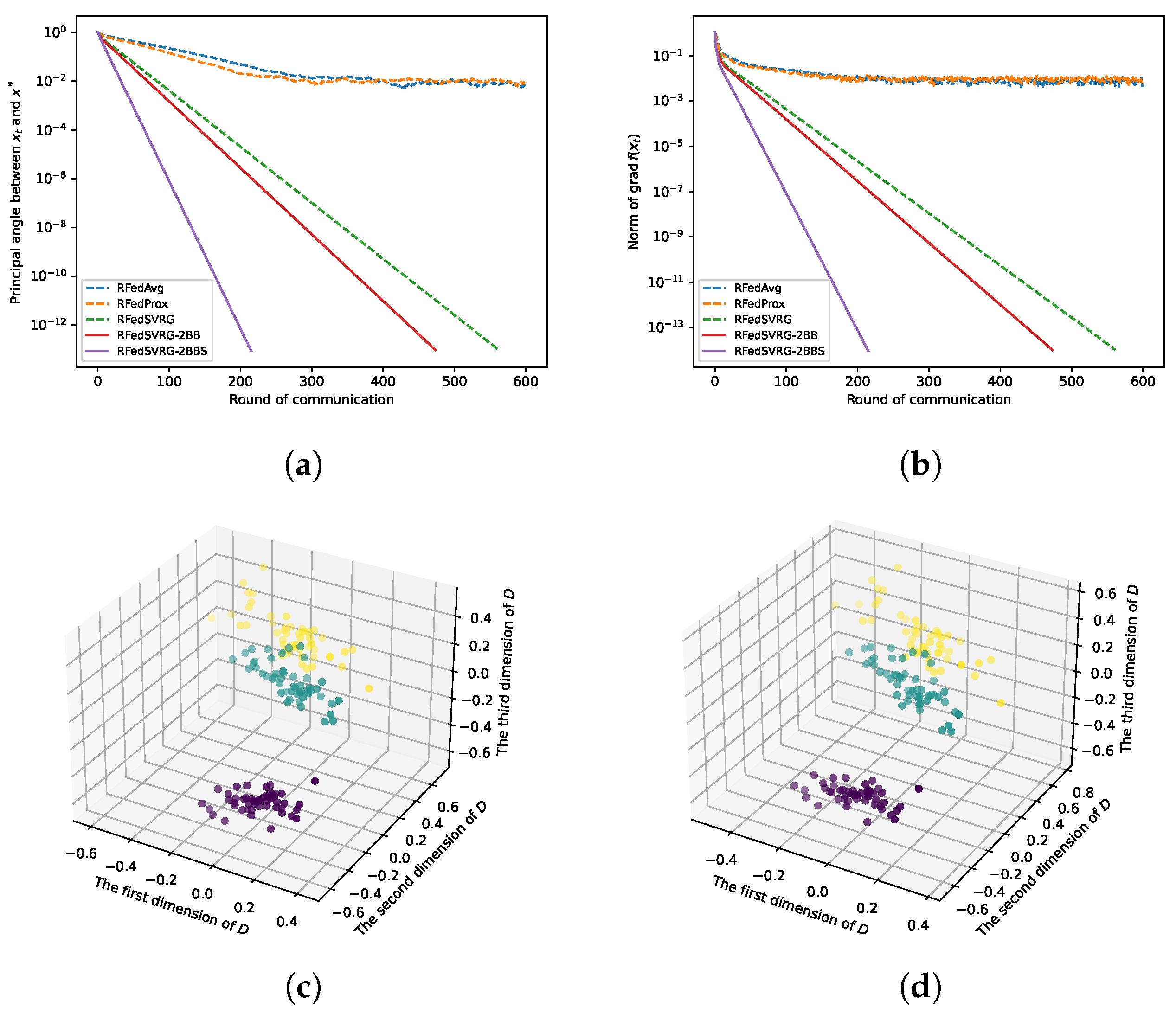
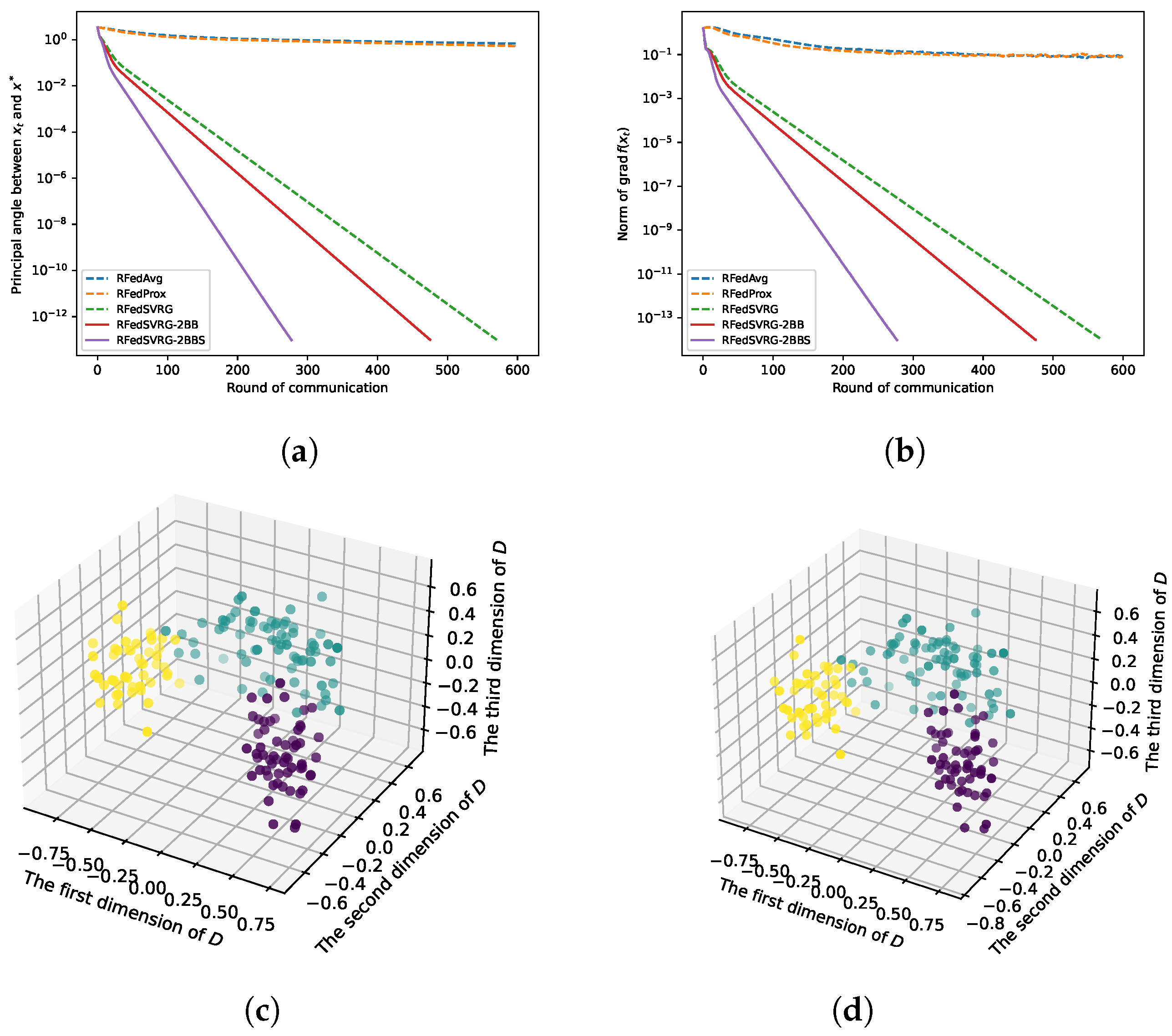
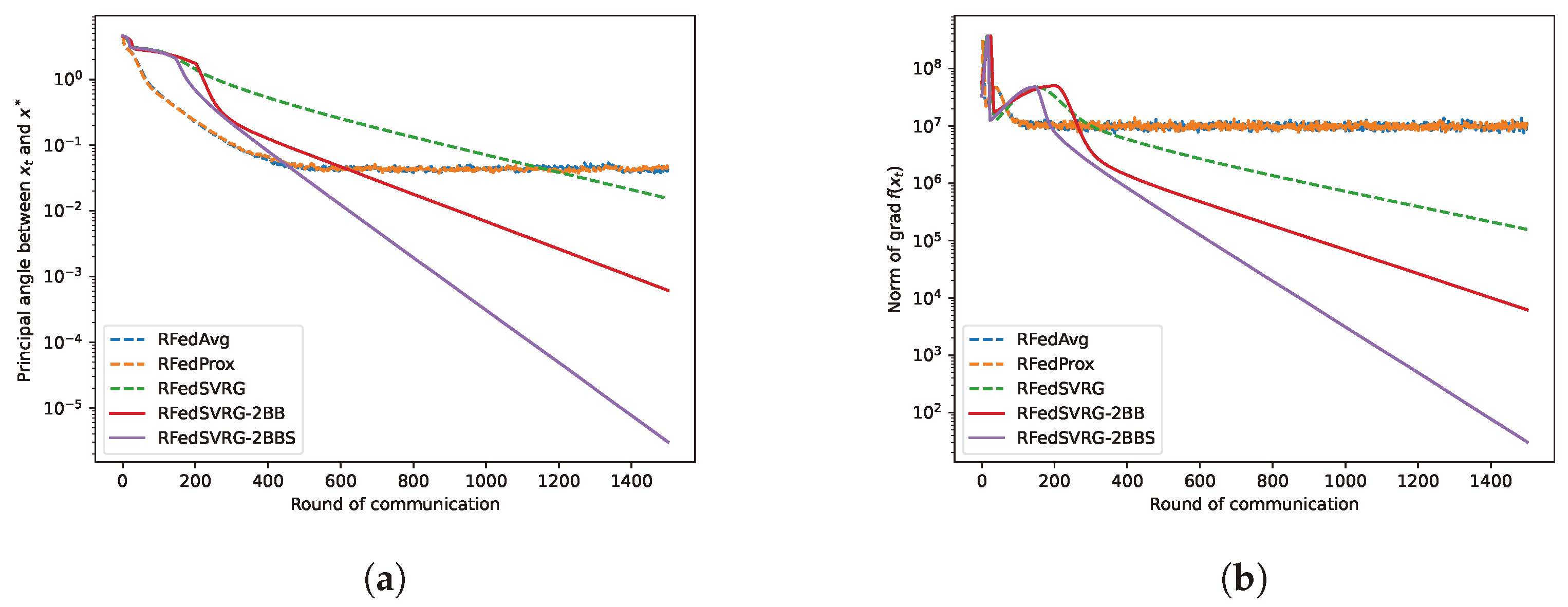
5.2. Experiments on Real Data
- and the principal angle between and is less than ;
- the communication exceeds the specified number of rounds.
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- McMahan, B.; Moore, E.; Ramage, D.; Hampson, S.; Arcas, B.A.y. Communication-Efficient Learning of Deep Networks from Decentralized Data. In Proceedings of the 20th International Conference on Artificial Intelligence and Statistics, Fort Lauderdale, FL, USA, 20–22 April 2017; PMLR: New York, NY, USA, 2017; Volume 54, pp. 1273–1282. [Google Scholar]
- Konecný, J.; McMahan, H.; Ramage, D.; Richtárik, P. Federated Optimization: Distributed Machine Learning for On-Device Intelligence. arXiv 2016, arXiv:1610.02527. [Google Scholar]
- Li, J.; Ma, S. Federated Learning on Riemannian Manifolds. Appl. Set-Valued Anal. Optim. 2023, 5, 213–232. [Google Scholar]
- Zhang, H.; Sra, S. First-order Methods for Geodesically Convex Optimization. In Proceedings of the 29th Annual Conference on Learning Theory, New York, New York, USA, 23–26 June 2016; PMLR: New York, NY, USA, 2016; Volume 49, pp. 1617–1638. [Google Scholar]
- Härdle, W.; Simar, L. Applied Multivariate Statistical Analysis; Springer: Cham, Switzerland, 2019. [Google Scholar]
- Cheung, Y.; Lou, J.; Yu, F. Vertical Federated Principal Component Analysis on Feature-Wise Distributed Data. In Web Information Systems Engineering, Proceedings of the 22nd International Conference on Web Information Systems Engineering, WISE 2021, Melbourne, VIC, Australia, 26–29 October 2021; WISE: Cham, Switzerland, 2021; pp. 173–188. [Google Scholar]
- Boumal, N.; Absil, P.A. Low-rank matrix completion via preconditioned optimization on the Grassmann manifold. Linear Algebra Its Appl. 2015, 475, 200–239. [Google Scholar] [CrossRef]
- Pennec, X.; Fillard, P.; Ayache, N. A Riemannian Framework for Tensor Computing. Int. J. Comput. Vis. 2005, 66, 41–66. [Google Scholar] [CrossRef]
- Fletcher, P.; Joshi, S. Riemannian geometry for the statistical analysis of diffusion tensor data. Signal Process. 2007, 87, 250–262. [Google Scholar] [CrossRef]
- Rentmeesters, Q.; Absil, P. Algorithm comparison for Karcher mean computation of rotation matrices and diffusion tensors. In Proceedings of the 19th European Signal Processing Conference, Barcelona, Spain, 29 August–2 September 2011; pp. 2229–2233. [Google Scholar]
- Cowi, S.; Yang, G. Averaging anisotropic elastic constant data. J. Elast. 1997, 46, 151–180. [Google Scholar]
- Massart, E.; Chevallier, S. Inductive Means and Sequences Applied to Online Classification of EEG. In Geometric Science of Information, Proceedings of the Third International Conference, GSI 2017, Paris, France, 7–9 November 2017; Springer International Publishing: Berlin/Heidelberg, Germany, 2017; pp. 763–770. [Google Scholar]
- Magai, G. Deep Neural Networks Architectures from the Perspective of Manifold Learning. In Proceedings of the 2023 IEEE 6th International Conference on Pattern Recognition and Artificial Intelligence (PRAI), Haikou, China, 18–20 August 2023; pp. 1021–1031. [Google Scholar]
- Yerxa, T.; Kuang, Y.; Simoncelli, E.; Chung, S. Learning Efficient Coding of Natural Images with Maximum Manifold Capacity Representations. In Proceedings of the Advances in Neural Information Processing Systems; Oh, A., Naumann, T., Globerson, A., Saenko, K., Hardt, M., Levine, S., Eds.; Curran Associates, Inc.: New Orleans, LA, USA, 2023; Volume 36, pp. 24103–24128. [Google Scholar]
- Chen, S.; Ma, S.; Man-Cho So, A.; Zhang, T. Proximal Gradient Method for Nonsmooth Optimization over the Stiefel Manifold. SIAM J. Optim. 2020, 30, 210–239. [Google Scholar] [CrossRef]
- Boumal, N. An Introduction to Optimization on Smooth Manifolds; Cambridge University Press: Cambridge, UK, 2022. [Google Scholar]
- Zhang, H.; Reddi, S.; Sra, S. Riemannian svrg: Fast stochastic optimization on riemannian manifolds. Adv. Neural Inf. Process. Syst. 2016, 29, 4599–4607. [Google Scholar]
- Li, T.; Sahu, A.K.; Zaheer, M.; Sanjabi, M.; Talwalkar, A.; Smith, V. Federated Optimization in Heterogeneous Networks. Proc. Mach. Learn. Syst. 2020, 2, 429–450. [Google Scholar]
- Pathak, R.; Wainwright, M. FedSplit: An algorithmic framework for fast federated optimization. Adv. Neural Inf. Process. Syst. 2020, 33, 7057–7066. [Google Scholar]
- Wang, J.; Liu, Q.; Liang, H.; Joshi, G.; Poor, H.V. Tackling the objective inconsistency problem in heterogeneous federated optimization. In Proceedings of the 34th International Conference on Neural Information Processing Systems, NIPS ’20, Vancouver, BC, Canada, 6–12 December 2020; Curran Associates, Inc.: Red Hook, NY, USA, 2020. [Google Scholar]
- Mitra, A.; Jaafar, R.; Pappas, G.; Hassani, H. Linear Convergence in Federated Learning: Tackling Client Heterogeneity and Sparse Gradients. Adv. Neural Inf. Process. Syst. 2021, 34, 14606–14619. [Google Scholar]
- Karimireddy, S.P.; Kale, S.; Mohri, M.; Reddi, S.J.; Stich, S.U.; Suresh, A.T. SCAFFOLD: Stochastic controlled averaging for federated learning. In Proceedings of the 37th International Conference on Machine Learning, ICML’20, Virtual Event, 13–18 July 2020. [Google Scholar]
- Yuan, H.; Zaheer, M.; Reddi, S. Federated Composite Optimization. In Proceedings of the Machine Learning Research, 38th International Conference on Machine Learning, 18–24 July 2021; Meila, M., Zhang, T., Eds.; PMLR: New York, NY, USA, 2021; Volume 139, pp. 12253–12266. [Google Scholar]
- Bao, Y.; Crawshaw, M.; Luo, S.; Liu, M. Fast Composite Optimization and Statistical Recovery in Federated Learning. In Proceedings of the Machine Learning Research, 39th International Conference on Machine Learning, Baltimore, MD, USA, 17–23 July 2022; Chaudhuri, K., Jegelka, S., Song, L., Szepesvari, C., Niu, G., Sabato, S., Eds.; PMLR: New York, NY, USA, 2022; Volume 162, pp. 1508–1536. [Google Scholar]
- Tran Dinh, Q.; Pham, N.H.; Phan, D.; Nguyen, L. FedDR–Randomized Douglas-Rachford Splitting Algorithms for Nonconvex Federated Composite Optimization. Neural Inf. Process. Syst. 2021, 34, 30326–30338. [Google Scholar]
- Zhang, J.; Hu, J.; Johansson, M. Composite Federated Learning with Heterogeneous Data. In Proceedings of the ICASSP 2024—2024 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Seoul, Republic of Korea, 14–19 April 2023; pp. 8946–8950. [Google Scholar]
- Zhang, J.; Hu, J.; So, A.M.; Johansson, M. Nonconvex Federated Learning on Compact Smooth Submanifolds With Heterogeneous Data. arXiv 2024, arXiv:2406.08465. [Google Scholar] [CrossRef]
- Charles, Z.; Konečný, J. Convergence and Accuracy Trade-Offs in Federated Learning and Meta-Learning. In Proceedings of the 24th International Conference on Artificial Intelligence and Statistics, Virtual, 13–15 April 2021; Banerjee, A., Fukumizu, K., Eds.; PMLR: New York, NY, USA, 2021; Volume 130, pp. 2575–2583. [Google Scholar]
- Johnson, R.; Zhang, T. Accelerating stochastic gradient descent using predictive variance reduction. In Proceedings of the 26th International Conference on Neural Information Processing Systems, NIPS’13, Lake Tahoe, NV, USA, 5–10 December 2013; Curran Associates Inc.: Red Hook, NY, USA, 2013; Volume 1, pp. 315–323. [Google Scholar]
- Huang, Z.; Huang, W.; Jawanpuria, P.; Mishra, B. Federated Learning on Riemannian Manifolds with Differential Privacy. arXiv 2024, arXiv:2404.10029. [Google Scholar]
- Nguyen, T.A.; Le, L.T.; Nguyen, T.D.; Bao, W.; Seneviratne, S.; Hong, C.S.; Tran, N.H. Federated PCA on Grassmann Manifold for IoT Anomaly Detection. IEEE/ACM Trans. Netw. 2024, 1–16. [Google Scholar] [CrossRef]
- Gower, R.; Le Roux, N.; Bach, F. Tracking the gradients using the Hessian: A new look at variance reducing stochastic methods. In Proceedings of the Machine Learning Research, Twenty-First International Conference on Artificial Intelligence and Statistics, Playa Blanca, Lanzarote, Spain, 9–11 April 2018; Storkey, A., Perez-Cruz, F., Eds.; PMLR: New York, NY, USA, 2018; Volume 84, pp. 707–715. [Google Scholar]
- Tankaria, H.; Yamashita, N. A stochastic variance reduced gradient using Barzilai-Borwein techniques as second order information. J. Ind. Manag. Optim. 2024, 20, 525–547. [Google Scholar] [CrossRef]
- Roux, R.; Schmidt, M.; Bach, F. A Stochastic Gradient Method with an Exponential Convergence Rate for Finite Training Sets. In Proceedings of the 25th International Conference on Neural Information Processing Systems, NIPS’12, Lake Tahoe, NV, USA, 3–6 December 2012; Curran Associates Inc.: Red Hook, NY, USA, 2012; Volume 2, pp. 2663–2671. [Google Scholar]
- Tan, C.; Ma, S.; Dai, Y.; Qian, Y. Barzilai-Borwein step size for stochastic gradient descent. In Proceedings of the 30th International Conference on Neural Information Processing Systems, NIPS’16, Barcelona, Spain, 5–10 December 2016; Curran Associates Inc.: Red Hook, NY, USA, 2016; pp. 685–693. [Google Scholar]
- Barzilai, J.; Borwein, J. Two-Point Step Size Gradient Methods. IMA J. Numer. Anal. 1988, 8, 141–148. [Google Scholar] [CrossRef]
- Francisco, J.; Bazán, F. Nonmonotone algorithm for minimization on closed sets with applications to minimization on Stiefel manifolds. J. Comput. Appl. Math. 2012, 236, 2717–2727. [Google Scholar] [CrossRef]
- Jiang, B.; Dai, Y. A framework of constraint preserving update schemes for optimization on Stiefel manifold. Math. Program. 2013, 153, 535–575. [Google Scholar] [CrossRef]
- Wen, Z.; Yin, W. A feasible method for optimization with orthogonality constraints. Math. Program. 2013, 142, 397–434. [Google Scholar] [CrossRef]
- Iannazzo, B.; Porcelli, M. The Riemannian Barzilai–Borwein method with nonmonotone line search and the matrix geometric mean computation. IMA J. Numer. Anal. 2017, 38, 495–517. [Google Scholar] [CrossRef]
- Absil, P.; Mahony, R.; Sepulchre, R. Optimization Algorithms on Matrix Manifolds; Princeton University Press: Princeton, NJ, USA, 2007. [Google Scholar]
- Lee, J.M. Introduction to Riemannian Manifolds, 2nd ed.; Springer International Publishing: Cham, Switzerland, 2018; pp. 225–262. [Google Scholar]
- Petersen, P. Riemannian Geometry; Springer: Berlin/Heidelberg, Germany, 2006; Volume 171. [Google Scholar]
- Tu, L. An Introduction to Manifolds; Springer: New York, NY, USA, 2011. [Google Scholar]
- Nocedal, J.; Wright, S. Numerical Optimization; Springer: New York, NY, USA, 1999. [Google Scholar]
- Townsend, J.; Koep, N.; Weichwald, S. Pymanopt: A Python Toolbox for Optimization on Manifolds using Automatic Differentiation. J. Mach. Learn. Res. 2016, 17, 4755–4759. [Google Scholar]
- Absil, P.; Malick, J. Projection-like Retractions on Matrix Manifolds. SIAM J. Optim. 2012, 22, 135–158. [Google Scholar] [CrossRef]
- Kaneko, T.; Fiori, S.; Tanaka, T. Empirical Arithmetic Averaging Over the Compact Stiefel Manifold. IEEE Trans. Signal Process 2013, 61, 883–894. [Google Scholar] [CrossRef]
- Zhu, P.; Knyazev, A. Angles between subspaces and their tangents. J. Numer. Math. 2013, 21, 325–340. [Google Scholar] [CrossRef]
- Forina, M.; Leardi, R.; Armanino, C.; Lanteri, S. PARVUS: An Extendable Package of Programs for Data Exploration. J. Chemom. 1990, 4, 191–193. [Google Scholar]
- Street, W.N.; Wolberg, W.H.; Mangasarian, O.L. Nuclear feature extraction for breast tumor diagnosis. In Proceedings of the Biomedical Image Processing and Biomedical Visualization, San Jose, CA, USA, 1–4 February 1993; Acharya, R.S., Goldgof, D.B., Eds.; International Society for Optics and Photonics, SPIE: Bellingham, WA, USA, 1993; Volume 1905, pp. 861–870. [Google Scholar]
- Lecun, Y.; Bottou, L.; Bengio, Y.; Haffner, P. Gradient-based learning applied to document recognition. Proc. IEEE 1998, 86, 2278–2324. [Google Scholar] [CrossRef]
| Properties of f | Algorithm | Convergence Rate | Parameter Source and Conditions |
|---|---|---|---|
| L-smooth and -strongly g-convex | RFedSVRG-2BB | Theorem 1 | |
| L-smooth and -strongly g-convex | RFedSVRG-2BBS | Theorem 2 | |
| L-smooth and h-gradient dominated | RFedSVRG-2BB | Theorem 5 | |
| L-smooth and h-gradient dominated | RFedSVRG-2BBS | Theorem 6 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xiao, H.; Yan, T.; Wang, K. Riemannian SVRG Using Barzilai–Borwein Method as Second-Order Approximation for Federated Learning. Symmetry 2024, 16, 1101. https://doi.org/10.3390/sym16091101
Xiao H, Yan T, Wang K. Riemannian SVRG Using Barzilai–Borwein Method as Second-Order Approximation for Federated Learning. Symmetry. 2024; 16(9):1101. https://doi.org/10.3390/sym16091101
Chicago/Turabian StyleXiao, He, Tao Yan, and Kai Wang. 2024. "Riemannian SVRG Using Barzilai–Borwein Method as Second-Order Approximation for Federated Learning" Symmetry 16, no. 9: 1101. https://doi.org/10.3390/sym16091101
APA StyleXiao, H., Yan, T., & Wang, K. (2024). Riemannian SVRG Using Barzilai–Borwein Method as Second-Order Approximation for Federated Learning. Symmetry, 16(9), 1101. https://doi.org/10.3390/sym16091101




