An Integrated Bayesian Best–Worst Method and Consensus-Based Intuitionistic Fuzzy Evaluation Based on Distance from Average Solution Approach for Evaluating Alternative Aircraft Models from a Sustainability Perspective

Abstract

Sustainability in transportation is vital for lessening environmental effects and ensuring the long-term viability of the transportation industry. The aviation sector, a significant player in sustainable transport, has encountered obstacles in reducing its ecological footprint, especially in aircraft design and operation. Symmetry and asymmetry exist widely in the aviation sector, as in other industrial applications. Multicriteria decision making (MCDM) is an important research topic that is widely applied to practical decision-making problems and is considered a complex tool with which to balance the symmetry between goals and conflicting criteria. This research assesses different airplane models in order to pinpoint the most environmentally friendly options using the Bayesian best–worst (BWM) method for evaluating criteria and the consensus-based intuitionistic fuzzy evaluation based on distance from average solution (IF EDAS) method for assessing alternatives. The Bayesian BWM approach facilitates group decision making on criteria evaluation and systematically evaluates factors like fuel efficiency, emissions, and noise levels, offering a holistic view of each airplane model’s sustainability performance. Conversely, consensus-based IF EDAS allows for the ranking of alternatives based on their distance to the average solution for a sustainable airplane model while concurrently considering multiple criteria, guiding decisionmakers to a consensus and eliminating the asymmetry between opinions before the final decision. This study reveals that technical features are the critical criteria for airplanes and significantly influence alternative rankings. The findings indicate that the chosen decision criteria greatly impact the selection of the most sustainable airplane model as part of a sustainable transportation system, potentially altering ranking orders.

1. Introduction

Sustainable transportation is an aspect of modern urban planning and global environmental initiatives. It considers and evaluates all fields of transportation—infrastructure, vehicles and operations—in such a way that the primary sustainable development factors are satisfied. Sustainable transportation represents a change in how societies think about planning and implementing transportation systems. The main goal of transportation is to find a balance between the need for mobility, economic growth, and environmental protection. When designing and developing transportation systems, sustainable transportation takes into account factors such as energy efficiency, reduced emissions, fair accessibility, and social inclusivity.

The United Nations (UN) Department of Economic and Social Affairs recognizes transportation as being aligned with the broader global agenda outlined in the Sustainable Development Goals (SDGs). These SDGs are composed of 17 interconnected goals adopted by UN member nations in order to tackle global challenges by 2030. Sustainable transportation plays a role in achieving several of these goals by supporting economic prosperity, promoting social equality, and reducing environmental impact [1].

The interdependent relationship between transportation and the aviation sector is crucial in the broader conversation about taking care of our environment and embracing technological progress. While aviation has long been praised for connecting people and driving economic growth, we must urgently reconsider its ecological impact due to traditional aircraft operations. Given the changing landscape that requires a shift away from carbon-intensive practices, sustainable transportation has become key to aligning aviation with a low carbon future.

Sustainable transportation within the aviation industry involves commitments such as reducing greenhouse gas emissions (GHGs), improving fuel efficiency, and lessening the environmental consequences of air travel [2]. Recognizing its contribution to global emissions, the aviation industry has increasingly become a focal point for transformative initiatives that aim to merge technological advancements with environmental responsibility. As air travel demand continues to rise it is not a strategic objective but an ethical imperative to identify, assess, and implement sustainable alternatives to conventional aircraft models.

As the global aviation industry grapples with the challenge of reconciling its growth with the need for environmental sustainability, it faces a crucial moment where innovation and responsibility intersect [3]. Traditionally associated with speed, connectivity, and economic vitality, the aviation sector now finds itself navigating a set of challenges dominated by the demand for eco-friendly and energy-efficient solutions. In this era of heightened awareness and climate consciousness, there is an increasing focus on sustainable transportation. As a result, the evaluation of airplane models has become a key focal point for driving transformative change.

Multiple-criteria decision-making (MCDM) techniques, which balance the symmetry between goals and conflicting criteria involved in a decision problem, find application in the field of sustainable transportation research, helping to address the intricate decision-making process involved in planning, implementing, and evaluating transportation systems [4]. Sustainable transportation encompasses aspects such as economic feasibility, social fairness, and environmental impact. Due to its multiobjective nature, it presents a complex challenge. MCDM methods provide an approach for analyzing and prioritizing alternatives based on multiple criteria. This aids decision makers (DMs) in identifying sustainable and efficient solutions.

This study embarks on an exploration into sustainable aviation by employing the following MCDM methodologies: the Bayesian best–worst method (Bayesian BWM) [5], consensus model [6], and the intuitionistic fuzzy evaluation based on distance from the average solution (IF EDAS) [7].

With the aviation industry at a crossroads, facing mounting concerns and stricter regulatory measures, assessment and adoption of sustainable airplane models have become not only strategically important but also morally imperative.

The Bayesian BWM and the consensus-based IF EDAS were chosen as the pillars of our proposed novel solution framework. The best–worst method, introduced by Rezaei [5], has proven its effectiveness in unraveling complex decision-making processes. This approach helps identify the strengths and weaknesses of options, giving insight into the relative importance of each criterion. This relative importance approach allows for the elimination of unnecessary pairwise comparison so as to determine the weight of the determined criteria. The reason that Bayesian BWM is preferred over the original BWM is because it can ensure that evaluations of each decision maker are considered without losing the effect of individual views. Bayesian BWM is regarded as the group decision-making version of the original BWM. On the other hand, for evaluations on the alternatives, it is important to incorporate a consensus model before integrating the rating of the decisionmakers in the selection model [8]. Several studies in the literature propose different consensus models for MCDM problems with or without fuzzy set extensions [9,10]. As the intuitionistic fuzzy set is used in this study, the model proposed by Zhang et al. [6] is adopted. IF EDAS, proven by Kahraman et al. [7] as an extension of the EDAS technique, incorporates intuitionistic fuzzy set theory to handle uncertainties for the evaluation of complex systems [11,12]. In this study, a consensus-based IF EDAS method is proposed to ensure evaluation distance of the decisionmakers for each alternative. The EDAS method has also proven its efficacy and robustness with plentiful applications in the sustainable transportation literature, which we also discuss in Section 2.

In the case study, this novel framework is applied to evaluate various airplane models in the aviation industry. The aviation sector presents a challenge when it comes to sustainability. We need to balance the symmetry between fuel efficiency, reduced carbon emissions, economic viability, and technological feasibility due to technological advancements. By combining Bayesian BWM and a consensus-based IF EDAS we can overcome the complexities and uncertainties involved in this decision-making procedure.

The goal of this research is to address the pressing need for a comprehensive approach to evaluating alternative airplane models in the aviation industry from a sustainability perspective. Through Bayesian BWM and consensus-based IF EDAS, our goal is to provide a novel technique for a nuanced understanding of how criteria such as cost of ownership, technical features, operational characteristics, reliability, maintenance, and safety features, sustainability features, and end-of-life vehicle characteristics interact with each other by considering their trade-offs and synergies in terms of the alternatives.

Combining Bayesian BWM and consensus-based IF EDAS for evaluating aircraft models effectively improves sustainability assessment for the precision in the sustainability criterion, robust handling of uncertainty, and dynamic adaptability. To ensure the precision in sustainability criterion, Bayesian BWM is utilized to obtain accurate weighting of this criterion among other critical criteria during the decision-making process of the multiple experts for the ideal aircraft model. Unlike the original BWM, Bayesian BWM provides a way to integrate the judgments of multiple experts with a probabilistic approach, which avoids losing the impact of singular opinions of the DMs [13]. Consensus-based IF EDAS considers the internal uncertainty and subjectivity in the assessment of the sustainability features criterion as well as in the assessment of other criteria. Consensus-based IF EDAS enables DMs to address their choices through different levels of confidence and hesitation, which is important for evaluating such complex criteria as sustainability features. While the IF logic provides a framework for the DMs for the ambiguity that is faced during the decision-making process, especially for sustainability, the method, which is integrated into the process to obtain a consensus, overcomes the subjectivity within DMs; thus, the final decision can be considered valid and acceptable by all.

The combination of Bayesian BWM and consensus-based IF EDAS introduces an innovative combination of probabilistic and intuitionistic fuzzy logic methods in decision making. This approach advances the current literature by presenting a novel approach that improves the accuracy and robustness of MCDM. By pitching the restrictions of conventional MCDM techniques, particularly subjectivity and uncertainty, the proposed decision-making framework contributes to the literature with a more advanced and reliable approach. The proposed framework presents a robust approach for aviation industry stakeholders to have well-defined and structured procedures for the evaluation of aircraft models. By assessing sustainability as a criterion among other critical criteria, companies in the industry can have a prioritization on selecting airplanes that support their long-term environmental and financial objectives. Airline companies and manufacturers can utilize this framework to improve their competitiveness, which will help them to prove a commitment to sustainability, which becomes more crucial to customers, governments, and investors day by day. The proposed framework contributes to certain Sustainable Development Goals (SDGs) by decreasing the aviation industry’s reliance on fossil fuels by considering energy-efficient aircraft models (to Goal 7, Affordable and Clean Energy); by fostering sustainable aircraft models, thus encouraging investment in new technologies (to Goal 9, Industry, Innovation, and Infrastructure); by helping the stakeholders to have a decision framework, which is in favor of sustainable production and responsible resource use (to Goal 12, Responsible Consumption and Production); by prioritizing the aircraft models with low carbon emissions (to Goal 13, Climate Action); and. Finally. by minimizing the GHG emissions and other pollutants with sustainable aircraft to protect the terrestrial habitat.

The benefits of the proposed integrated approach can be summarized as follows:

• Utilizing Bayesian BWM decreases the number of pairwise comparisons between criteria set with the use of relative importance assessment of reference comparisons based on determined best and worst criteria.
• Including Bayesian BWM also enables the incorporation of opinions of multiple decisionmakers without the loss of any DMs’ effect on the decision process.
• Intuitionistic fuzzy (IF) extension of the EDAS method considers the hesitancy levels of DMs.
• IF extension of EDAS successfully captures dual decision-making through membership and non-membership levels, which provides a more detailed and precise presentation of real-life decision preferences.
• Consensus model for group decision making in the IF environment gives a systematic structure that evaluates multiple criteria; the model’s goal is to construct harmonious intersecting opinions and navigate the decision group to a consensus that reveals the expertise of the group.
• The consensus model also strengthens the legitimacy and acceptance of the final decision reached by the group since the consensus is obtained considering each DM’s opinion with revisions, which handles asymmetry between individuals’ views.

The organization of this study is as follows: Section 2 gives related work on sustainable transportation, Section 3 provides detailed information about the methodologies that are used for the proposed framework, Section 4 focuses on a case study for an airline company, Section 5 supplies a comparative analysis with the proposed methodology and the alternative ones, and, finally, Section 6 completes the study with conclusions.

2. Related Works

2.1. Literature on Sustainable Transportation

In the recent past, a significant number of studies have been conducted on the topic of sustainable transportation. An important number of these studies have focused on the difficulties posed by multicriteria decision-making approaches, while others have explored alternative methods to tackle the challenges in this research area. Figure 1 shows keyword co-occurrence analysis for the relationship of the terms for different concepts and sustainable transportation in the literature. This investigation clarifies the relationships between sustainable transportation and related concepts in the literature. The aim is to reveal the thematic structure of sustainable transportation by uncovering the connections and clusters of related topics. The figure shows that MCDM techniques have a high-level connection with sustainable transportation, which led us to conduct a comprehensive literature survey about MCDM in this research area. During this study, we reviewed sixty articles for studies with MCDM techniques on sustainable transportation as a research area. The most related and recent articles from the last six years of the sustainable transportation literature are selected and presented with MCDM classification in this section.

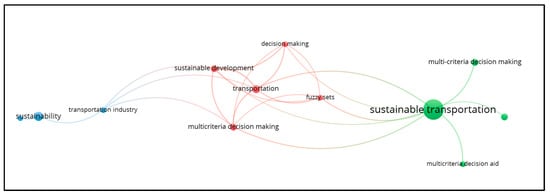
Figure 1. Connections of terms with sustainable transportation in the literature.

2.1.1. Hierarchical Methods

In MCDM, hierarchical approaches are employed to organize complex decision scenarios, facilitating the analysis and comparison of diverse options. By breaking down the decision process into a structured hierarchy of criteria and subcriteria, these methods simplify the process of assessing and ranking various alternatives. This includes methodologies such as the analytic hierarchy process (AHP) and the analytic network process (ANP). The reviewed articles, which utilize hierarchical methods, are explained briefly in this section.

Liang et al. [14] conducted a linear goal programming priority-oriented fuzzy AHP method to decide the weights of the assessment factor for the sustainability evaluation of alternative fuel vehicles (AFVs). They also used fuzzy group multi-attribute decision analysis (MADA) to propose a fuzzy group decision support system for prioritizing the sustainability of AFVs. They verified the outcomes by fuzzy technique for order of preference by similarity to ideal solution (TOPSIS) technique, and to evaluate the impacts of the evaluation criteria weights, a sensitivity analysis was applied.

Semanjski et al. [15] utilized the AHP to combine route sustainability into the procedure for city logistics routing. Firstly, they used a traffic sign database to derive sustainability substance. Secondly, this sustainability substance was incorporated into the cost computations of the routes using the MCDM method. With the help of the Dijkstra technique, they assessed the proposed method on a real-world problem and proved its applicability and effectiveness.

Gulcimen et al. [16] proposed a methodology to evaluate urban sustainable transportation alternatives in urban planning. Their methodology consisted of hesitant fuzzy AHP (HF-AHP) and a multiple attribute utility model (MAUT). In their results, they emphasized that the “number of fatalities or injuries” is the most important factor in the selection process. Low-motorized vehicles (low-MVs) turned out to be the best among the sustainable urban transportation alternatives according to their utility score.

Hierarchical methods are powerful when it is important to use a well-structured and intuitive approach for decision making. The methods also make consistency checks possible. However, subjective evaluations are one of the main limitations of these methods. Additionally, pairwise comparisons for the evaluations create a vast amount, resulting in a complex and time-inefficient process for decision making. Our proposed method is agile enough to eliminate those limitations. By utilizing Bayesian BWM, there is no need for pairwise comparisons through leveraging primary and secondary comparisons. Additionally, our proposed framework is strong enough to overcome subjectivity using a consensus-based IF EDAS approach to evaluate the alternatives.

2.1.2. Literature on Compromise Methods

The methods of compromise involve an interactive approach to multiple-criteria decision making (MCDM) that involves aggregating features that contribute to the optimal solution and serve as a basis for discussions on decision making, taking into account factors such as TOPSIS, Vise Kriterijumska Optimizacija I Kompromisno Resenje (VIKOR), complex proportional assessment (COPRAS), EDAS, weighted aggregated sum product assessment (WASPAS), and simple additive weighting (SAW). The reviewed articles, which use various compromise techniques, are explained briefly in this section.

Ecer [17] focused their study on the performance evaluation of the battery electric buses. Eleven criteria were utilized to evaluate ten different battery electric vehicle (BEV) models. The researchers conducted the simultaneous evaluation of criteria and alternatives (SECA) method to determine the criteria weights. Afterward, the researchers undertook SECA, measurement of alternatives and ranking according to compromise solution (MARCOS), multiattributive ideal-real comparative analysis (MAIRCA), combined compromise solution (CoCoSo), additive ratio assessment (ARAS), and COPRAS techniques for the ranking of the alternative BEV models. The results showed that the most important factors in deciding between different BEV models are price, permitted load, and energy consumption. Tesla Model S was the ideal alternative. They validated the results with several other MCDM approaches.

Sadrani et al. [18] studied the electrical battery charging strategy. They established economic, environmental, social, operational, and quality-of-service as a criteria set. These criteria were given weights using the fuzzy BWM. The alternative strategies were evaluated using the fuzzy ranking of alternatives through functional mapping of criterion subintervals into a single interval (FRAFSI) approach. Their case study was centered on the EBs of Munich City, Germany. As a result, they found the most important criterion: the economic one. The evaluation of alternatives showed that overnight charging is the best strategy. The robustness of the results was assessed using a comparative analysis with fuzzy TOPSIS and fuzzy EDAS methods.

Even though the EDAS method is among the compromise methods, it still has certain advantages over the other compromise techniques. The EDAS technique provides better distinction between alternatives by examining average distances and ensures sensitivity to negative criteria and equitable assessment for both positive and negative distances. The EDAS uses a less complex parameter determination method than VIKOR. Moreover, it is more robust in dealing with extreme values than COPRAS. Compared to the SAW method, the main benefit of using the EDAS is reducing score inflation, which is a common issue with other MCDM techniques. WASPAS integrates two distinct techniques: the weighted sum model (WSM) and the weighted product model (WPM). While BWM and IF EDAS utilize more detailed and reliable paths suitable for complex problems, WASPAS includes additive and multiplicative operations, which are more straightforward compared to them. Each compromise method has its advantages and disadvantages on a selection between them and these should be assessed carefully regarding those attributes. For the proposed framework, the comparative analysis of the results is undertaken in Section 5 through these methods, which are within the same MCDM classification.

2.1.3. Literature on Multiobjective Decision-Making Methods

The methods for making decisions with multiple objectives, such as best–worst method (BWM), data envelopment analysis (DEA), and goal programming (GP), are often referred to as continuous methods or mathematical programming methods. These approaches handle multiple goals at once without a distinct focus on what pertains to performance and what relates to issues. They use a mathematical optimization solver to aim for the simultaneous optimization of more than one objective function. The reviewed articles that use multiobjective decision-making methods are explained briefly in this section.

Mahmoudi et al. [19] proposed assessment factors for the evaluation of the sustainability of urban transportation network (UTN). They also utilized the BWM to assess and prioritize sustainability aspects and assessment factors.

Gupta et al. [20] conducted a broad approach, which formulates a combined multiobjective optimization model for an extended capacitated sustainable transportation problem in a coal mining industry using AHP and DEA methods. (1) The AHP method was utilized to determine the weights of various alternative vehicles listed as one of the alternatives for transport. (2) The DEA method was utilized to compute the efficiency rates of vehicles on several routes through inputs and outputs determined as important, especially for the mining sector. Moreover, they decreased dependency on carbon-oriented vehicles for transport that reduce GHG emissions. (3) A fuzzy interactive optimization framework was proposed to obtain compromise transportation solutions, which include the optimal number of vehicles selected for sustainable transport. (4) The case study focused on the mining sector in India. They explored whether they could apply the proposed optimization framework and solution procedure. Furthermore, several comparisons were made with current transportation models to establish the advantages of their model.

A multiobjective robust possibilistic programming approach (RPP^∗) was presented by utilizing the reciprocal fuzzy programming technique because of the lack of information on the exact value of various traveler discomfort degrees and vagueness in demand by Günay et al. [21]. Other than other robust possibilistic methods, RPP* optimized the average of the objective function and chance limitation contraventions, and the risk score was obtained by vague metrics by taking into account the absolute deviation of the objective function.

Fathi et al. [22] proposed a novel network data envelopment analysis (NDEA) model to handle the bidirectional connections, considering the bounded connectivity to assess sustainable supply chains.

Hmamed et al. [23] focused their study on waste transportation. The proposed framework included two methodologies, namely, AHP and DEA. With AHP, they first identified the evaluation criteria for route selection of waste transportation companies. The efficiencies of the routes were computed through the DEA method using the inputs and outputs of a system.

The decision for a selection within BWM, DEA, and GP techniques as MCDM tools is dependent on the requirements of those techniques. BWM provides a consistency check and is beneficial to use with fewer pairwise comparisons based on structure that include primary and secondary comparisons obtained by the determining the most and the least important criteria, which gives clear insight into the weighting process. The DEA method is strong enough to provide an objective and efficient evaluation structure. However, it requires highly detailed data. GP provides an important flexibility when dealing with multiple goals. On the other hand, the method’s one crucial limitation is subjective weighting between these multiple and generally contradicting goals.

2.1.4. Literature on Outranking Methods

The outranking techniques, referred to as partially compensatory or preference aggregation methods, assess a series of preferences to establish if one choice is as good as another, such as PROMETHEE and ELECTRE. The reviewed articles that use outranking methods are explained briefly in this section.

Ziemba [24] introduced a novel hybrid methodology for the evaluation of alternative electric cars in Poland. Their methodology was based on the integration of a new easy approach to fuzzy PROMETHEE (NEAT F-PROMETHEE), Monte Carlo method, and stochastic multicriteria acceptability analysis (SMAA). During the decision-making process, while the NEAT F-PROMETHEE method considered the score of a single decisionmaker, stochastic methods made it possible for them to simulate the opinion of the Polish community.

Turoń [25] presented a method to describe the best alternative car models for car sharing as a sustainable transportation mode. The study used ELECTRE III as a multiple-criteria decision-making tool to report the solution. The case study of the proposed approach was conducted in Poland and showed that the best alternative vehicles are the large and well-equipped ones with electric drive, classified as D in European standards.

The outranking methods, such as PROMETHEE and ELECTRE, enable a selection where comparing alternatives is not directly possible. The PROMETHEE approach is powerful in resolving highly conflicting criteria, and ELECTRE methods can rank and sort the alternatives. However, the application of PROMETHEE depends on adequate preference function, which can result in subjectivity, and for ELECTRE, a similar subjectivity problem might occur while determining the thresholds. The proposed method is more efficient regarding the computational complexity of weight calculations. It provides balanced evaluations between alternatives, resulting in a reduction in bias compared to these outranking methods.

2.1.5. Literature on Other MCDM Methods

The final group, referred to as other MCDM methods, includes distinct techniques that do not fall neatly into the hierarchical, compromise, multiobjective, or outranking categories because of their intricate nature. Examples of such methods include the DEMATEL, LBWA, MA, MAV, SMART, and UTAUT techniques. The reviewed articles that use these decision-making methods are explained briefly in this section.

Dwivedi et al. [26] described and formulated the readjustment metrics of sustainable freight transport (SFT) after the COVID-19 pandemic. In their work, 13 crucial readjustment metrics were decided with the help of the professional team. A combined grey decision-making trial and evaluation laboratory (DEMATEL) was utilized to prioritize and introduce the causal nexus among the described crucial readjustment metrics. They explored sensitivity analysis to evaluate the validity of the presented model.

Karuppiah et al. [27] utilized the Pareto diagram method. The research established 20 enablers through the list of 25 enablers for location decisions and assessed the enablers for sustainable transport. The ultimate enablers were placed first, and their dependencies were unfolded utilizing the grey DEMATEL technique. They used sensitivity analysis to decide the impact of professionals’ weight on the outcomes of the study.

Rajak et al. [28] explored the burdens of achieving the sustainable transportation goal in India. Their proposed methodology consisted of two well-known techniques. The first one was the grey-theory-based method, and this method handles the ambiguity of data obtained by the decisionmakers. The second one was DEMATEL, in which they undertook this method to design the cause and effect relationship between 22 determined burdens.

Trivedi et al. [29] focused on the burdens of applying inland waterway transports in India by introducing and assessing the complicated relationship between them. DEMATEL and interpretive structural modeling (ISM) methods were conducted to assess the cause–effect relationship among the burdens, and they further described the fundamental impactful burdens from a determined set of criteria.

Alternative fuel vehicles (AFVs) are generally considered among the sustainable transportation alternatives. In this area, Raj et al. [30] proposed a combined DEMATEL and TOPSIS approach to evaluate the feasibility of the EVs. Fourteen factors, such as economic sustainability and end-of-life options, were considered during the decision-making process. Those factors’ weights were calculated using the DEMATEL method, and the alternatives were ranked through the TOPSIS method. The case study in India showed that electric vehicles (EVs) are accepted as the most preferred among AFV alternatives to take the place of gasoline vehicles.

LBWA is used to simplify the weight calculations, and MA gives an interactive framework for the decision-making process. MAV and SMART provide well-structured assessments, and UTAUT is utilized specifically for the technology adoption problems. DEMATEL is specifically beneficial in comprehending interdependencies within criteria. Additionally, DEMATEL supports prioritizing criteria according to their influence within the network. This method can resolve conflicts between criteria in complex problems. However, this method is complex to implement and can take a lot of time to obtain a solution for large-scale problems. On the other hand, our proposed approach requires less computational complexity and provides balanced and objective results in evaluating alternatives compared to DEMATEL. Nevertheless, it lacks interdependency analysis and does not offer a way to resolve the conflict as DEMATEL does.

2.2. Literature on Fuzzy Extensions of MCDM Approaches

Fuzzy set theory, which was pioneered by Zadeh [31], was applied by Bellman and Zadeh [32] to a decision-making environment to handle uncertainty, and posed the first example of it. Ever since, many researchers have proposed extensions to MCDM techniques with various fuzzy sets. This section presents selected articles that demonstrate the integration of the two approaches.

Turskis et al. [33] proposed a hybrid method with WASPAS and AHP with a case study on the construction site selection area for a shopping mall in Vilnius. Their approach included qualitative as well as quantitative criteria, which required the use of fuzzy logic. While the fuzzy AHP method is utilized to assign weight to the criteria, the fuzzy WASPAS method is also undertaken to decide the ideal alternative among a certain set of locations.

Yanmaz et al. [34] introduced a novel method to the car selection problem. The proposed framework consisted of the EDAS method with interval-valued Pythagorean fuzzy extension to offer a larger domain to experts. It was described that the new extension does not force experts to give a membership score in relatively narrow areas, and the main advantage of EDAS to overcome the uncertainty of data is further improved with this fuzzy set. The results were compared with interval-valued fuzzy extension of the same method and concluded the same outcome.

Fermatean fuzzy sets (FFSs) were first presented by Senapati and Yager [35,36] with their basic operations. FFSs provide an enhanced model for dealing with uncertainty and improved decision support with hesitation inclusion and three-dimensional structure. In their work [36], a novel method was proposed, which introduces the Fermatean fuzzy extension of the WPM method.

Rouyendegh et al. [37] proposed the intuitionistic fuzzy TOPSIS method with a case study in a green supplier selection problem area in Ankara city of Turkey. Their study was the first to embark on the IF extension of the TOPSIS methodology. In the case study, four supplier alternatives were evaluated under ten criteria with the aid of three decisionmakers.

Sun et al. [38] presented a study on multigranulation rough set theory and the three-way decision principle in group decision making. They placed the combination of multigranulation rough set method with three-way decision-making in the center of their research. In a similar perspective, Ma et al. [39] brought decision-theoretic rough set (DTRS) with hesitant fuzzy data for multiple-criteria group decision-making problems. Jiubing et al. [40] proposed a method for weight-updating to obtain a consensus in the group decision-making process with linguistic intuitionistic fuzzy evaluations. Loss functions are important for three-way decision making since they try to minimize the loss by selecting the best option during the process.

The literature review showed us that one of the efficient methods regarding the evaluation process of the selected criteria is BWM due to the relative importance concept. The BWM eliminates the unnecessary number of pairwise comparisons within criteria. The novel version of the method, namely, Bayesian BWM, also makes it possible to merge the opinions of multiple decisionmakers successfully utilizing a probabilistic view.

These studies inferred that the IF extension of the EDAS method is one of the outstanding methods for handling vague data. Kahraman et al. [7] proved its effectiveness with a case study in solid waste disposal site selection, illustrating how the technique deals with uncertain data in the evaluation procedure. Mahmood et al. [41] validated its ability by implementing it in factor analysis in the robotic industry, emphasizing its benefit with intuitionistic fuzzy rough Yager operators. Chen [42] considered a circular intuitionistic fuzzy assessment approach, underlining how the EDAS technique reinforces intelligent decision making incorporating uncertainty. Das and Chakraborty [43] implemented the EDAS technique to optimize hybrid machining procedures in an intuitionistic fuzzy setting, illustrating its practical implementation in dealing with uncertain data. These studies collectively highlight the IF EDAS method’s capability to effectively process vague and uncertain data across various application domains.

The combination of Bayesian BWM and IF EDAS is chosen over any other potential pairings such as the integration of AHP and TOPSIS methods or the integration of ANP and TOPSIS methods. Bayesian BWM presents a robust approach for determining criteria weights with high consistency and resilience. In contrast with conventional techniques such as AHP or ANP, which are frequently integrated with TOPSIS, Bayesian BWM includes the decisionmaker’s uncertainty via probabilistic modeling. It ensures more reliable weight estimation [5]. Compared to AHP or ANP, BWM drastically decreases the cognitive load on experts by evaluating fewer pairwise comparisons [44]. Thus, it provides relatively more efficacy and fewer tendencies for inconsistency.

The IF EDAS is specifically efficient in dealing with uncertainty and imprecision observed in real-life decision-making instances. The technique takes advantage of intuitionistic fuzzy sets through the presence of both membership and non-membership degrees, assuring a more detailed evaluation of alternatives [7]. The IF EDAS improves the discrimination functionality between alternatives by taking into account the positive and negative distances from the average solution, which conveys more accurate rankings for the alternatives [45].

The synergetic effect of the Bayesian BWM and IF EDAS combination benefits the essentials of both techniques. Bayesian BWM’s robust weight estimation completes IF EDAS’s ability to deal with uncertainty, constructing a complete and flexible decision-making approach. This combination overcomes the limitations of utilizing TOPSIS, for example, its deterministic essence and capacitated ability to deal with uncertainty in both criteria weights and alternative evaluations [46].

When we compare our proposed method with ANP + TOPSIS, ANP presents dependencies within criteria, which appears to be a strength over the proposed approach. Nevertheless, the complexity of the computation and the large number of pairwise comparisons in ANP are burdensome. On the contrary, Bayesian BWM facilitates a procedure with fewer comparisons while still ensuring a robust weight determination for criteria [44]. On the other hand, for alternative evaluation, TOPSIS considers the relative closeness of alternatives to the ideal solution. EDAS handles the assessment by the distances to average solution. The EDAS method enhances the distinction within alternatives through positive and negative distances from the average solution, and this distinction derives more accurate and reliable results compared to TOPSIS [45].

When we compare our proposed method with AHP + TOPSIS, AHP introduces a basic hierarchical formation within criteria, which is straightforward to understand and implement. However, as in ANP, AHP needs a larger number of pairwise comparisons, which may result in an exhaustive procedure and lead to inconsistency [47]. Bayesian BWM decreases this load through fewer comparisons with the concept of primary and secondary relations described in criteria and including decision-maker uncertainty [44]. While TOPSIS does not include uncertainty, EDAS seizes the imprecision in the assessment procedure by analyzing both positive and negative distances [45].

Compared to AHP + TOPSIS or ANP + TOPSIS, our proposed approach presents a more intricate framework to handle decisionmakers’ uncertainty and evaluation of the alternatives. Despite being efficient, TOPSIS lacks the consideration of uncertainty while determining criteria weights or alternative rankings as completely as IF EDAS does [46,47].

Integrating Bayesian BWM and EDAS methods with IF extension ensures a robust approach for MCDM by combining rigorous weight computation with advanced yet practical evaluation of alternatives. The Bayesian BWM is robust for weight calculation in group decision making. However, this method is required to be combined with one of the other methods for alternative evaluations. IF EDAS is an enhanced method that seeks balanced decisions with consideration of the distances to positive and negative distances to the average solution, which is more detailed compared to the classical TOPSIS method, yet is practical and contributes to the robustness of Bayesian BWM. The consensus technique integrated into the proposed framework improves the reduction in bias in the decision-making process. This integration also ensures a result that will be considered valid and acceptable by all parties of the decision process. Together, they provide a comprehensive and complete framework that improves the effectiveness of the decision-making process.

This study introduces a novel method that brings the Bayesian BWM with the consensus-based IF EDAS together to thoroughly evaluate different alternatives with their selection criteria. In the case study application of the proposed method, firstly, for the problem of selecting airplane models, six criteria are determined and evaluated by using Bayesian BWM, which is a multiple-criteria group decision-making tool, which also offers an ability to handle uncertainty effectively among members of the decision-making group and reduce biases in the decision-making process. Secondly, the alternatives are ranked utilizing the consensus-based IF EDAS method, which is a valuable tool for decisionmakers facing complex and uncertain decision environments that search for a consensus to eliminate asymmetry between opinions. This proposed combined approach is presented to fill in the gap in the literature to identify the most desirable alternative using an integrated approach between Bayesian BWM and consensus-based IF EDAS in Section 3 and Section 4; a case study on selection of airplane models proves its efficacy and robustness.

3. Methodologies

3.1. Bayesian Best–Worst Method

In this study, a relatively novel methodology called Bayesian BWM, which is proved by Rezai [5], is used to evaluate the weight of the criteria to leverage its strength to assess the individual opinions of the group decision-making process.

The Bayesian BWM approach involves the following steps to determine the weights of the criteria:

Step 1. Define the set of criteria $\{c_1,c_2,\dots ,c_n\}$ that are relevant to the decision-making process and need to be prioritized by the literature and DMs’ opinions.

Step 2. Identify the best (e.g., most desirable, most important) and worst (e.g., least desirable, least important) criteria for each DM. The best and the worst criteria for DM k are denoted by $C_B^k$ and $C_W^k$, respectively.

Step 3. Compare the best criterion with other criteria using a scale between 1 and 9, and best-to-others vectors ($A_B^k$) are constructed for each expert.

$$\begin{array}{cc}{A}_B^k=(A_{B1}^k,A_{B2}^k,A_{B3}^k,\dots ,A_{Bm}^k),& k=1,2,\dots ,K\end{array}$$

(1)

In this formula, K represents the number of DMs, while $A_{Bi}^k$ is the pairwise comparison between the best and other criteria $c_i$ by DM k.

Step 4. Compare the worst criterion with the remaining criteria utilizing a scale between 1 and 9, and others-to-worst vectors ($A_W^k$) are constructed for each expert.

$$\begin{array}{cc}{A}_W^k=(A_{1W}^k,A_{2W}^k,A_{3W}^k,\dots ,A_{mW}^k),& k=1,2,\dots ,K\end{array}$$

(2)

In this formula, K represents the number of DMs, and $A_{jW}^k$ is the pairwise comparison between the worst and other criteria $c_j$ by DM k.

The structure of Bayesian BWM is in line with the original BWM. However, criterion weights of multiple DMs are aggregated by Bayesian BWM utilizing a probabilistic approach.

During the construction of the Bayesian BWM process, the dependencies between variables are crucial and are shown in Figure 2. As a convention, dependent variables are shown with circular nodes, and independent variables are depicted with rectangular nodes. In the Bayesian deduction, the Dirichlet distribution is utilized as the prior to the multinomial distribution. It can be undertaken as a weight set due to the properties of non-negativity and sum-to-one.

$$\begin{array}{cc}(w^k)\sim Multinominal\left({\displaystyle \frac{1}{w}}\right),& k=1,2,\dots ,K\end{array}$$

(3)

$$\begin{array}{cc}\left(w^k\right)\sim Multinominal\left(w^k\right),& k=1,2,\dots ,K\end{array}$$

(4)

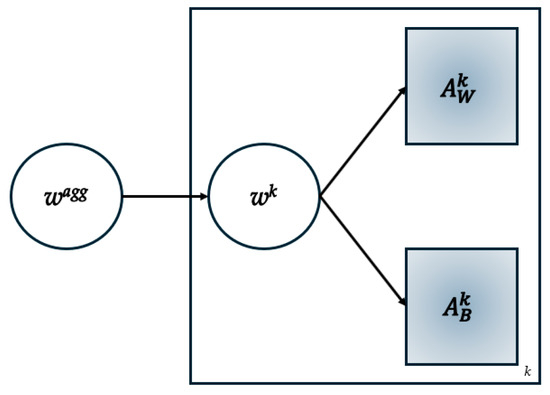
Figure 2. The dependencies of the probabilistic model of the Bayesian BWM. Adapted with permission from Ref. [5]. 2024 Elsevier.

Here, Multinomial represents the multinomial distribution.

$$\begin{array}{cc}\left(w^{*}\right)\sim Dir\left(\gamma x{w}^{*}\right),& k=1,2,\dots ,K\end{array}$$

(5)

$$\gamma \sim Gamma\left(\mathrm{0.1,0.1}\right)$$

(6)

A gamma value of 0.1 often presents an adequate degree of uncertainty and fuzziness in the experts’ opinions and it also reflects a conservative estimation as a hyperparameter that one assumes a certain variability while avoiding an overestimation. When Dirichlet is utilized as the prior and multinomial as the likelihood, the posterior distribution becomes Dirichlet as well, with the posterior parameter ${\alpha }_{post}=\alpha +A_W$.

Then, the prior distribution for aggregated weights, denoted by w^agg, is established by employing an uninformative Dirichlet distribution with the parameter α = 1, represented as follows:

$$w^{agg}\sim Dir\left(1\right)$$

(7)

The aggregated weight matrix is $w^{agg}=(w_1^{*},w_2^{*},w_3^{*},\dots ,w_n^{*})$. Dir(1) and Gamma(0.1, 0.1) represent the Dirichlet and Gamma distributions, respectively. The proposed model does not offer a solution in closed form. Consequently, Markov-chain Monte Carlo (MCMC) methods are required to calculate the posterior distribution. Specifically, the “just another Gibbs sampler” (JAGS) is used for MCMC sampling purposes in the solution procedure of the case study. The valuable result of the model is the posterior distribution of weights for each decisionmaker and the aggregated weights, w^agg.

3.2. Intuitionistic Fuzzy Sets

Fuzzy set theory, pioneered by Zadeh [30] to address scenarios where uncertainty is present, has been applied to integrate imprecise information into decision-making processes. A fuzzy set $\stackrel{\sim }{A}$ can be mathematically characterized by a membership function ${\mu }_{\stackrel{\sim }{A}}\left(x\right)$, which assigns a real number within the range of [0, 1] to each element x belonging to the universe of discourse X [48]. Because of the hesitation levels of the elements, non-membership degree is not always equal to 1. For this purpose, Atanassov [48] presented an intuitionistic fuzzy set (IFS) that incorporates this hesitancy level.

Here are some basic concepts about IFS [49]:

If X is not equal to the empty set, then

$$\tilde{A}=\{<x,{\mu }_{\tilde{A}}\left(x\right),{\nu }_{\tilde{A}}\left(x\right)>;x\in X\},$$

(8)

${\mu }_{\tilde{A}}:X\to [0,1]$ and also $v_{\tilde{A}}:X\to \left[0,1\right]$ are in line with the following condition:

$$0\le {\mu }_{\tilde{A}}\left(x\right)+v_{\tilde{A}}\left(x\right)\le 1,$$

(9)

The above interval is valid for every x ∈ X. Then hesitancy equals to $1-({\mu }_{\tilde{A}}\left(x\right)+v_{\tilde{A}}\left(x\right))$.

Intuitionistic fuzzy numbers (IFNs) are shown as $\tilde{A}$ and $\tilde{B}$ has the following properties:

$$\tilde{A}=\left\{<x_l,{\mu }_{\tilde{A}}\left(x_l\right),{\nu }_{\tilde{A}}\left(x_l\right)>|x_l\in X\right\}$$

(10)

$$\tilde{B}=\left\{<x_l,{\mu }_{\tilde{B}}\left(x_l\right),{\nu }_{\tilde{B}}\left(x_l\right)>|x_l\in X\right\}$$

(11)

$${\pi }_{\tilde{A}}\left(x_l\right)=1-{\mu }_{\tilde{A}}\left(x_l\right)-{\nu }_{\tilde{A}}\left(x_l\right){\pi }_{\tilde{B}}\left(x_l\right)=1-{\mu }_{\tilde{B}}\left(x_l\right)-{\nu }_{\tilde{B}}\left(x_l\right).$$

(12)

Then, we can compute the Euclidean distance between these two numbers as follows:

$$d(\tilde{A},\tilde{B})=\sqrt{{\displaystyle \frac{1}{2}}{\sum }_{l=1}^n[{({\mu }_{\tilde{A}}\left(x_l\right)-{\mu }_{\tilde{B}}\left(x_l\right))}^2+{({\nu }_{\tilde{A}}\left(x_l\right)-{\nu }_{\tilde{B}}\left(x_l\right))}^2+{({\pi }_{\tilde{A}}\left(x_l\right)-{\pi }_{\tilde{B}}\left(x_l\right))}^2]}.$$

(13)

3.3. Proposed Consensus-Based Intuitionistic Fuzzy EDAS Methodology

This research presents a novel technique that combines the Bayesian BWM with consensus-based IF EDAS. This method aids in group decision making by effectively managing uncertainty, promoting consensus among decisionmakers, and minimizing biases in decision making.

In the first step of this proposed framework, the weights of criteria are computed utilizing Bayesian BWM. Afterwards, the consensus-based IF EDAS method is applied to rank the alternatives. IF EDAS was first established by Kahraman et al. [7]. Before directly integrating the gathered evaluations of the DMs, the integration of the consensus model under the intuitionistic fuzzy environment’s procedure, which was presented by Zhang et al. [6], is proposed as an initial phase of the IF EDAS method.

The proposed methodology that is depicted with a flow diagram in Figure 3 aims to fill the gap in the decision-making literature. There is no prior study that reveals the effective collaboration of Bayesian BWM and consensus-based IF EDAS methodologies to prove the harmony for handling group decision-making processes for criteria evaluation, resolving the uncertainty, ensuring consensus, and, thus, eliminating asymmetry between experts’ evaluations on alternatives, respectively.

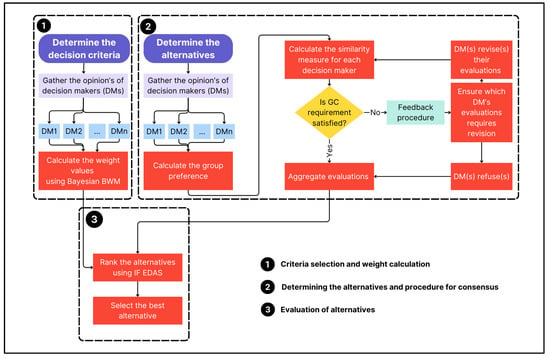
Figure 3. The flowchart of the proposed methodology.

The steps of the proposed “Integrated Bayesian BWM with Consensus-Based IF EDAS framework” are as follows:

Step 1. Define the alternatives and criteria for assessment.

Step 2. The preference data on criteria are gathered from the DMs.

Step 3. Employ the Bayesian BWM in Section 3.1 to compute the criteria weights.

Step 4. Collect the linguistic ratings of alternatives concerning criteria from the DMs.

Step 5. Convert the linguistic ratings into IFNs.

Step 6. Apply the consensus model utilizing Equation (14), and obtain the group preference vector ($A_i^G(i=1,2,\dots ,m)$),

$$A_i^G=\left\{\begin{array}{c}<C_1,\left({\displaystyle \frac{1}{p}}\sum _{k=1}^p{\mu }_{C_1}^k,{\displaystyle \frac{1}{p}}\sum _{k=1}^p{\nu }_{C_1}^k\right)>,\\ <C_2,\left({\displaystyle \frac{1}{p}}\sum _{k=1}^p{\mu }_{C_2}^k,{\displaystyle \frac{1}{p}}\sum _{k=1}^p{\nu }_{C_2}^k\right)>,\dots ,<C_n,\left({\displaystyle \frac{1}{p}}\sum _{k=1}^p{\mu }_{C_n}^k,{\displaystyle \frac{1}{p}}\sum _{k=1}^p{\nu }_{C_n}^k\right)>\end{array}\right\},$$

(14)

where $A_i(i=1,2,...,m)$ for each alternative.

Step 7. Compute the similarity measures $S_i^k$ between $A_i^k(k=1,2,\dots ,p)$ and $A_i^G$ for each alternative, using Equation (15):

$$S(A,B)={\displaystyle \frac{1}{2}}\left[{\displaystyle \frac{1}{n}}{\sum }_{i=1}^n{\displaystyle \frac{2\left({\mu }_A\right(x_i\left){\mu }_B\right(x_i)+{\nu }_A(x_i\left){\nu }_B\right(x_i\left)\right)}{\left({\mu }_A^2\left(x_i\right)+{\nu }_A^2\left(x_i\right)\right)+\left({\mu }_B^2\left(x_i\right)+{\nu }_B^2\left(x_i\right)\right)}}+{\displaystyle \frac{1}{n}}{\sum }_{i=1}^n{\displaystyle \frac{{\mu }_A\left(x_i\right){\mu }_B\left(x_i\right)+{\nu }_A\left(x_i\right){\nu }_B\left(x_i\right)}{\sqrt{{\mu }_A^2\left(x_i\right)+{\nu }_A^2\left(x_i\right)}\sqrt{{\mu }_B^2\left(x_i\right)+{\nu }_B^2\left(x_i\right)}}}\right].$$

(15)

where A and B are two IFNs and S(A,B) represents the similarity measure between A and B.

Step 8. Calculate the deviations on the decisions of DMs, denoted as $D_i=(D_i^1,D_i^2,\dots ,D_i^p)$, for each alternative, utilizing Equation (16).

$$D_i^k=|S_i^k-S_i|,$$

(16)

where $S_i={\displaystyle \frac{1}{p}}{\sum }_{k=1}^p{S}_i^k,{ S}_i$ is defined as the group similarity measure for the alternative $A_i$.

Step 9. Determine a threshold value δ and compare it with each $D_i^k$ and follow the procedure until each $D_i^k<\delta ,i=(1,2,\dots ,m)$.

The DM determines the threshold value $\delta$. If $D_i^k⩾\delta ,i=(1,2,\dots ,m)$, the DM is requested to revise the preference information about $A_i$, and after obtaining revised preference information, go to Step 3, until $D_i^k<\delta ,i=(1,2,\dots ,m)$. If the DM who is asked to revise on his/her judgment, declines to adjust his/her judgment, aggregate his/her opinion to the remaining part of the group.

Step 10. Build the aggregated intuitionistic fuzzy decision matrix (IFDM) with the ratings of DMs.

Assume that ${\left(r_{ij}^{\left(k\right)}\right)}_{m\times n}$is IFDM for every decisionmaker and λ = {λ₁, λ₂, λ₃, …, λ_l} is set the of DM weights. Therefore, one can easily define that ${\sum }_{k=1}^l{\lambda }_k=1,{\lambda }_k\in [0,1]$. Each decisionmaker’s evaluation is required to be added to group evaluation to build aggregated IFDM. To achieve that, Xu [50] presented the intuitionistic fuzzy weighted averaging (IFWA) technique.

$$\begin{gathered} r_{ij}={IFWA}_{\lambda }(r_{ij}^{\left(1\right)},r_{ij}^{\left(2\right)},\dots ,r_{ij}^{\left(l\right)})={\lambda }_1{r}_{ij}^{\left(1\right)}\oplus {\lambda }_2{r}_{ij}^{\left(2\right)}\oplus {\lambda }_3{r}_{ij}^{\left(3\right)}\oplus \cdots \oplus {\lambda }_l{r}_{ij}^{\left(l\right)} \\ =\left[1-\stackrel{l}{\prod _{k=1}}{\left(1-{\mu }_{ij}^{\left(k\right)}\right)}^{{\lambda }_k},\stackrel{l}{\prod _{k=1}}{\left({\nu }_{ij}^{\left(k\right)}\right)}^{{\lambda }_k},\stackrel{l}{\prod _{k=1}}{\left(1-{\mu }_{ij}^{\left(k\right)}\right)}^{{\lambda }_k}-\stackrel{l}{\prod _{k=1}}{\left({\nu }_{ij}^{\left(k\right)}\right)}^{{\lambda }_k}\right] \end{gathered}$$

(17)

$$r_{ij}=\left({\mu }_{A_i}\right(x_j),{\nu }_{A_i}(x_j),{\pi }_{A_i}(x_j\left)\right)(i=1,2\dots ,m;j=1,2,\dots ,n)$$

(18)

Aggregated IFDM is defined as follows:

$$R=\left[\begin{array}{cccc}\left({\mu }_{A_1}\left(x_1\right),{\nu }_{A_1}\left(x_1\right),{\pi }_{A_1}\left(x_1\right)\right)& \left({\mu }_{A_1}\left(x_2\right),{\nu }_{A_1}\left(x_2\right),{\pi }_{A_1}\left(x_2\right)\right)& \cdots & \left({\mu }_{A_1}\left(x_n\right),{\nu }_{A_1}\left(x_n\right),{\pi }_{A_1}\left(x_n\right)\right)\\ \left({\mu }_{A_2}\left(x_1\right),{\nu }_{A_2}\left(x_1\right),{\pi }_{A_2}\left(x_1\right)\right)& \left({\mu }_{A_2}\left(x_2\right),{\nu }_{A_2}\left(x_2\right),{\pi }_{A_2}\left(x_2\right)\right)& \cdots & \left({\mu }_{A_2}\left(x_n\right),{\nu }_{A_2}\left(x_n\right),{\pi }_{A_2}\left(x_n\right)\right)\\ ⋮& ⋮& \ddots & ⋮\\ \left({\mu }_{A_m}\left(x_1\right),{\nu }_{A_m}\left(x_1\right),{\pi }_{A_m}\left(x_1\right)\right)& \left({\mu }_{A_m}\left(x_2\right),{\nu }_{A_m}\left(x_2\right),{\pi }_{A_m}\left(x_2\right)\right)& \cdots & \left({\mu }_{A_m}\left(x_n\right),{\nu }_{A_m}\left(x_n\right),{\pi }_{A_m}\left(x_n\right)\right)\end{array}\right]$$

(19)

$$R=\left[\begin{array}{ccccc}{r}_{11}& r_{12}& r_{13}& \dots & r_{1m}\\ r_{21}& r_{22}& r_{23}& \dots & r_{2m}\\ r_{31}& r_{32}& r_{33}& \dots & r_{3m}\\ ⋮& ⋮& ⋮& \ddots & ⋮\\ r_{n1}& r_{n2}& r_{n3}& \dots & r_{nm}\end{array}\right]$$

(20)

Step 11. Create the aggregated weighted IFDM.

Once the weights are calculated and aggregated IFDM is obtained, the aggregated weighted IFDM is built utilizing the definition below by [51]:

$$R\otimes W=\left\{<x,{\mu }_{A_i}\left(x\right)·{\mu }_W\left(x\right),{\nu }_{A_i}\left(x\right)+{\nu }_W\left(x\right)-{\nu }_{A_i}\left(x\right)·{\nu }_W\left(x\right)>|x\in X\right\}$$

(21)

Also,

$${\pi }_{A_i·W}\left(x\right)=1-{\nu }_{A_i}\left(x\right)-{\nu }_W\left(x\right)-{\mu }_{A_i}\left(x\right)·{\mu }_W\left(x\right)+{\nu }_{A_i}\left(x\right)·{\nu }_W\left(x\right)$$

(22)

Afterwards, the aggregated weighted IFDM is constructed as follows:

$$R^{\prime }=\left[\begin{array}{cccc}\left({\mu }_{A_{1}W}\left(x_1\right),{\nu }_{A_{1}W}\left(x_1\right),{\pi }_{A_{1}W}\left(x_1\right)\right)& \left({\mu }_{A_{1}W}\left(x_2\right),{\nu }_{A_{1}W}\left(x_2\right),{\pi }_{A_{1}W}\left(x_2\right)\right)& \cdots & \left({\mu }_{A_{1}W}\left(x_n\right),{\nu }_{A_{1}W}\left(x_n\right),{\pi }_{A_{1}W}\left(x_n\right)\right)\\ \left({\mu }_{A_{2}W}\left(x_1\right),{\nu }_{A_{2}W}\left(x_1\right),{\pi }_{A_{2}W}\left(x_1\right)\right)& \left({\mu }_{A_{2}W}\left(x_2\right),{\nu }_{A_{2}W}\left(x_2\right),{\pi }_{A_{2}W}\left(x_2\right)\right)& \cdots & \left({\mu }_{A_{2}W}\left(x_n\right),{\nu }_{A_{2}W}\left(x_n\right),{\pi }_{A_{2}W}\left(x_n\right)\right)\\ ⋮& ⋮& \ddots & ⋮\\ \left({\mu }_{A_{m}W}\right(x_1),{\nu }_{A_{m}W}(x_1),{\pi }_{A_{m}W}(x_1\left)\right)& \left({\mu }_{A_{m}W}\left(x_2\right),{\nu }_{A_{m}W}\left(x_2\right),{\pi }_{A_{m}W}\left(x_2\right)\right)& \cdots & \left({\mu }_{A_{m}W}\left(x_n\right),{\nu }_{A_{m}W}\left(x_n\right),{\pi }_{A_{m}W}\left(x_n\right)\right)\end{array}\right]$$

(23)

$$R^{\prime }=\left[\begin{array}{ccccc}{r}_{11}^{\prime }& r_{12}^{\prime }& r_{13}^{\prime }& \dots & r_{1j}^{\prime }\\ r_{21}^{\prime }& r_{22}^{\prime }& r_{23}^{\prime }& \dots & r_{2j}^{\prime }\\ r_{31}^{\prime }& r_{32}^{\prime }& r_{33}^{\prime }& \dots & r_{3j}^{\prime }\\ ⋮& ⋮& ⋮& \ddots & ⋮\\ r_{i1}^{\prime }& r_{i2}^{\prime }& r_{i3}^{\prime }& \dots & r_{ij}^{\prime }\end{array}\right]$$

$r_{ij}^{\prime }=({\mu }_{ij}^{\prime },{\nu }_{ij}^{\prime },{\pi }_{ij}^{\prime })=\left({\mu }_{A_{i}W}\right(x_j),{\nu }_{A_{i}W}(x_j),{\pi }_{A_{i}W}(x_j\left)\right)$ is an element of the aggregated weighted IFDM.

Step 12. Compute the average solution values (AVs).

The average solution values are determined using the IF-weighted arithmetic mean IWAM operator, as described in [52]. The average solution value is derived through the calculations outlined in Equation (24).

$${\mathrm{AV}}_J=\mathrm{IWAM}(x_{ij})=[1-{\prod }_{k=1}^l{(1-{\mu }_{ij})}^{1/l},{\prod }_{k=1}^l{\left({\nu }_{ij}\right)}^{1/l}]$$

(24)

Step 13. Determine the positive distance from the average solution (PDA) and the negative distance from the average solution (NDA), which involves applying the formula provided below.

$${\mathrm{PDA}}_{\dot{\mathrm{I}}J}={\left[{\mathrm{PDA}}_{\dot{\mathrm{I}}J}\right]}_{mxn}{\displaystyle \frac{\max (0,(S\left(x_{ij}\right)-S\left({AV}_j\right)\left)\right)}{S{(AV}_j)}}$$

(25)

$${\mathrm{NDA}}_{\dot{\mathrm{I}}J}={\left[{\mathrm{NDA}}_{\dot{\mathrm{I}}J}\right]}_{mxn}={\displaystyle \frac{\max (0,(S\left({AV}_j\right)-S\left(x_{ij}\right)\left)\right)}{S{(AV}_j)}}$$

(26)

Step 14. The total positive distance from the average solution and the negative distance from the average solution ${(SP}_i,{SN}_i)$ for each alternative are calculated using Equations (27) and (28), respectively.

$${SP}_{\mathrm{i}}={\sum }_{j=1}^m{w}_j{PDA}_{ij}$$

(27)

$${SN}_i={\sum }_{j=1}^m{w}_j{NDA}_{ij}$$

(28)

Step 15. Normalize the weighted sum values of the alternatives (${NSP}_i,{NSN}_i)$ using Equations (29) and (30), as outlined.

$${NSP}_i={\displaystyle \frac{{SP}_i}{{\mathrm{Max}}_i\left({SP}_i\right)}}$$

(29)

$${NSN}_i=1-{\displaystyle \frac{{SN}_i}{{\mathrm{Max}}_i\left({SN}_i\right)}}$$

(30)

Step 16. Determine the ranking involves calculating the assessment score (AS) for each option. To finalize this process, all alternative assessment scores are computed using Equation (31). The options are then arranged based on their AS values, with the highest value indicating the best alternative.

$${AS}_i={\displaystyle \frac{1}{2}}\left({\mathrm{NSP}}_i+{\mathrm{NSN}}_i\right) \mathrm{w}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{e} 0\le {AS}_i\le 1.$$

(31)

Thus, the proposed approach is terminated by selecting the highest valued ${AS}_i$ as the best alternative. For overviewing the proposed approach, the Algorithm 1 is provided below with the main algorithm stages.

Algorithm 1 Pseudocode for the proposed approach

Stage 1: Input Define criteria, alternatives, and decisionmakers

1. Criteria = [C1, C2, …, Cn]

2. Alternatives = [A1, A2, …, Am]

3. DecisionMakers = [DM1, DM2, …, DMo]

Stage 2: Bayesian BWM to determine criteria weights

1. Function Bayesian_BWM(Criteria):

2.       PairwiseComparisons = CollectPairwiseComparisons(Criteria)

3.       Return CalculatePosteriorWeights(PairwiseComparisons)

Stage 3: Technique to consensus among decision-makers

1. Function EnsureConsensus(Evaluations):

2.       While not IsConsensusAchieved(Evaluations):

3.          For each DM in DecisionMakers:

4.             If not IsScoreWithinThreshold(Evaluations[DM]):

5.                If DM refuses to reevaluate:

6.                   Continue # Use current scores

7.                Else:

8.                   Update Evaluations[DM]

9.       Return Evaluations

Stage 4: Consensus-Based IF EDAS for evaluating alternatives

1. Function Intuitionistic_Fuzzy_EDAS(Criteria, Alternatives, Weights, Evaluations):

2.       Evaluations = EnsureConsensus(Evaluations)

3.       Scores = CalculateEDAS(Criteria, Alternatives, Weights, Evaluations)

4.       Return Rank(Scores)

Stage 5: Main Function to Integrate The Prior Stages

1. Function Main():

2.       Weights = Bayesian_BWM(Criteria)

3.       Evaluations = CollectEvaluations(Criteria, Alternatives, DecisionMakers)

4.       Rankings = Intuitionistic_Fuzzy_EDAS(Criteria, Alternatives, Weights, Evaluations)

The time complexity analysis of the algorithms is often crucial for the application purposes. The time complexity of the proposed approach might be examined in the algorithmic stages of the given pseudocode. For Stage 2, the selection of the best and the worst criteria requires O(n) to iterate over all criteria. To handle the pairwise comparisons, O(n) amount of time is needed, and to calculate the posterior weights, another O(n) is required, resulting in O(n) time complexity for Bayesian BWM overall. For Stage 3, with o amount of decisionmakers, each giving scores for m alternatives on n criteria, it produces O(o × m × n). If we assume k as the number of opinion-gathering processes until a consensus is reached, then the time complexity is O(k × o × m × n). Since k is a small valued constant, the overall complexity results in O(o × m × n). For Stage 4, the calculation of the average solution, positive and negative distances, normalization of the distances, and aggregation of the computed scores take O(m × n) for each of those steps, and the overall time complexity returns O(m × n). Finally, for Stage 5, since the time complexities for Bayesian BWM, consensus technique, and IF EDAS are O(n), O(o × m × n), and O(m × n), respectively, the dominant term is O(o × m × n), which leads us to the overall time complexity of the proposed approach.

4. Case Study

The case study focuses on the sustainable decision-making process of the airplanes of one of the largest companies in the airline industry. For airline industries, since the economic, environmental, and social factors of sustainability are all crucial, it is important to make a reliable decision in terms of all three aspects. A literature review study was undertaken to meet all three elements from the company’s perspective.

A broad literature review was conducted to identify the possible criteria. Then, the criteria were reviewed with the three experts from the company. The formation of the expert team was decided under two conditions. The first condition to be in the expert team is to have experience in the aviation sector of at least 5 years. The second condition is to be a graduate of an engineering faculty of a reputable university. Eight candidates were selected to be part of the team. Then, five of them were eliminated because they were not able to satisfy the experience year condition, so only three remained in the team. All three decisionmakers have a bachelor’s degree in aircraft engineering. Two of them also hold master’s degrees: one of them is in project management and the other one is in business administration. These experts are from the managerial board of the aircraft systems department in the respective company.

First, the criteria were listed from the related literature on sustainable transportation. Then, all the listed criteria were evaluated by expert decisionmakers in the aviation industry, who are described above. Thus, the criteria set that was utilized in the case study was determined with the help of the broad literature review and the expert DMs combined.

The first criterion was determined to be the cost of ownership, which includes purchase, registration, insurance, fuel/km, preventive maintenance, and spare parts costs. The second criterion was the technical features, and this criterion evaluates engine capacity and power, travel length, maximum speed, full tank capacity, overall length and width, ergonomics of controls, and seat and auxiliary features. The third criterion was decided to be the operational characteristics, and this criterion considers features such as fuel efficiency, payload capacity, driving comfort, and NVH (noise, vibration, and harshness) characteristics. The reliability, maintenance, and safety features criterion was the fourth criterion, and this criterion takes into account properties like warranty period, maintainability, service period, service network, and inbuilt safety devices. The fifth criterion of the sustainability features was decided to evaluate important sustainability factors such as CO₂ and GHG emissions, other air pollutants, use of green technology, and energy-efficient systems. The sixth and final criterion was selected as the end-of-life vehicle characteristics to convey the important end-of-life features such as resale value and manufacturability, reusability, and recyclability of systems.

After the determination of the criteria, the problem was defined as follows:

The airline company needs to prioritize airplanes. Following an initial assessment, eight options, labeled as $A_1, A_2$,$A_3$, $A_4$, $A_5$, $A_6$, $A_7$, and $A_8$, were left for further examination. A committee consisting of three decisionmakers, referred to as DM₁, DM₂, and DM₃, was assembled to conduct interviews and determine the best choice. Six criteria were considered for this selection process, and are given in Table 1.

Table 1. The list of the criteria.

Index of Criterion	Criterion Name	Criterion Notation	Related Literature
1	Cost of ownership	C1	Khisty and Lall [53], Zhao and Melaina [54], Bodziony et al. [55], Bai et al. [56]
2	Technical features	C2	Baykasoğlu et al. [57], Bodziony et al. [55], Bai et al. [56], Jesus et al. [58]
3	Operational characteristics	C3	Litman and Burwell [59], Litman [60], Jesus et al. [58]
4	Reliability, maintenance, and safety features	C4	Byrne and Polonsky [61], Abkowitz [62], Baykasoğlu et al. [57], Bai et al. [56], Jesus et al. [58]
5	Sustainability features	C5	Zhao and Melaina [54], Gehin et al. [63], Awasthi et al. [64]
6	End-of-life vehicle characteristics	C6	Gehin et al. [63], Amelia et al. [65], Vermeulen et al. [66], Jesus et al. [58], James et al. [67]

All criteria are considered as the performance rating in the evaluation scale. Thus, high scores represent a better performance, and low scores represent a worse performance for each criterion.

The technical features criterion (C₂) was selected as the best criterion and sustainability features criterion (C₅) was selected as the worst criterion by the decisionmakers (DMs) for the initiation of the Bayesian BWM. The DMs then used a scale of 1 to 9 to undertake primary comparisons of the criteria; this is explained in detail in Section 3. The primary comparisons are given in Table 2 and Table 3 using the best criterion and the worst criterion, respectively.

Table 2. The reference comparisons to the best criterion.

	C1	C2	C3	C4	C5	C6
DM1	1	1	2	3	5	4
DM2	1	1	3	4	5	4
DM3	2	1	3	2	5	4

Table 3. The reference comparisons to the worst criterion.

	C1	C2	C3	C4	C5	C6
DM1	5	5	4	3	1	2
DM2	6	5	5	2	1	2
DM3	5	5	4	3	1	2

The Bayesian BWM explained in Section 3 was conducted, and the optimal criteria weights were computed, as in Table 4.

Table 4. The aggregated weights that are obtained from Bayesian BWM.

	C1	C2	C3	C4	C5	C6
wagg	0.2578	0.2675	0.1819	0.1269	0.0703	0.0956

After applying Bayesian BWM, it was proven that the most important criterion is “technical features”, with 0.2675 of weight value. The criterion “cost of ownership” followed it, with 0.2578 of weight value. Then “operational characteristics”, “reliability, maintenance, and safety features”, “end-of-life vehicle characteristics”, and “sustainability features” criteria were ranked as third, fourth, fifth, and sixth regarding their weight values of 0.1819, 0.1269, 0.0956, and 0.0703, respectively. Even though the sustainability features criterion affected the results less than the remaining criteria, it still has essential importance during the evaluation process.

To evaluate the alternatives, the decisionmakers used the linguistic term set in Table 5.

Table 5. The linguistic evaluations scale and corresponding abbreviations and IFNs.

Linguistic Terms	Abbreviations	IFN
Extremely Poor	EP	(0.05, 0.95, 0.00)
Very Poor	VP	(0.15, 0.80, 0.05)
Poor	P	(0.25, 0.65, 0.10)
Slightly Poor	SP	(0.35, 0.55, 0.10)
Fair	F	(0.50, 0.40, 0.10)
Slightly Good	SG	(0.65, 0.25, 0.10)
Good	G	(0.75, 0.15, 0.10)
Very Good	VG	(0.85, 0.10, 0.05)
Extremely Good	EG	(0.95, 0.05, 0.00)

The evaluations of the decisionmakers on the alternatives with respect to the decision criteria are provided in Table 6.

Table 6. The alternative ranking of decisionmakers with respect to the defined criteria.

		C1	C2	C3	C4	C5	C6
DM1
	A1	P	SP	SP	SG	F	VG
	A2	G	VG	VG	SG	EG	SG
	A3	G	VG	VG	G	G	SG
	A4	VG	G	VG	EG	G	G
	A5	VP	SP	SP	SG	F	VG
	A6	EG	G	EG	VG	G	F
	A7	VG	VG	EG	EG	VG	SG
	A8	SG	EG	SG	G	EG	G
DM2
	A1	VP	SP	SP	G	F	EG
	A2	G	SG	VG	G	VG	F
	A3	VG	VG	VG	SG	G	SG
	A4	G	G	VG	EG	SG	G
	A5	EP	F	SP	G	F	VG
	A6	VG	SG	EG	VG	SG	F
	A7	VG	G	EG	EG	VG	G
	A8	G	EG	F	G	EG	SG
DM3
	A1	P	SP	F	SP	F	EG
	A2	G	G	VG	SG	VG	SG
	A3	G	EG	VG	G	SG	SG
	A4	VG	VG	VG	VG	SG	G
	A5	VP	F	SP	SG	SP	VG
	A6	VG	G	VG	G	SG	F
	A7	VG	G	EG	VG	VG	F
	A8	SG	VG	F	G	EG	G

After the evaluations were obtained, a consensus model for MCGDM was conducted to evaluate the scores of individual DMs’ preferences for consensus. Using Equation (18), the $A_i^G$ vector was calculated, and the results are given in Table 7.

Table 7. Group preference vector ($A_i^G$).

	C1	C2	C3	C4	C5	C6
A1	(0.217, 0.700)	(0.350, 0.550)	(0.400, 0.500)	(0.583, 0.317)	(0.500, 0.400)	(0.917, 0.067)
A2	(0.750, 0.150)	(0.750, 0.167)	(0.850, 0.100)	(0.683, 0.217)	(0.883, 0.083)	(0.600, 0.300)
A3	(0.783, 0.133)	(0.883, 0.083)	(0.850, 0.100)	(0.717, 0.183)	(0.717, 0.183)	(0.650, 0.250)
A4	(0.817, 0.117)	(0.783, 0.133)	(0.850, 0.100)	(0.917, 0.067)	(0.683, 0.217)	(0.750, 0.150)
A5	(0.117, 0.850)	(0.450, 0.450)	(0.350, 0.550)	(0.683, 0.217)	(0.450, 0.450)	(0.850, 0.100)
A6	(0.883, 0.083)	(0.717, 0.183)	(0.917, 0.067)	(0.817, 0.117)	(0.683, 0.217)	(0.500, 0.400)
A7	(0.850, 0.100)	(0.783, 0.133)	(0.950, 0.050)	(0.917, 0.067)	(0.850, 0.100)	(0.633, 0.267)
A8	(0.683, 0.217)	(0.917, 0.067)	(0.550, 0.350)	(0.750, 0.150)	(0.950, 0.050)	(0.717, 0.183)

After obtaining $A_i^G$, similarity measures $S_i^k$ were computed with Equation (14) and are given in Table 8.

Table 8. Similarity measures ($S_i^k$).

${\mathit{S}}_{\mathit{i}}^{\mathit{k}}$	Value	${\mathit{S}}_{\mathit{i}}^{\mathit{k}}$	Value	${\mathit{S}}_{\mathit{i}}^{\mathit{k}}$	Value
$S_1^1$	0.974	$S_3^3$	0.998	$S_6^2$	0.998
$S_1^2$	0.997	$S_4^1$	0.999	$S_6^3$	0.998
$S_1^3$	0.989	$S_4^2$	0.999	$S_7^1$	0.993
$S_2^1$	0.999	$S_4^3$	0.999	$S_7^2$	0.999
$S_2^2$	0.997	$S_5^1$	0.994	$S_7^3$	0.996
$S_2^3$	0.993	$S_5^2$	0.994	$S_8^1$	0.998
$S_3^1$	0.998	$S_5^3$	0.996	$S_8^2$	0.996
$S_3^2$	0.999	$S_6^1$	0.998	$S_8^3$	0.996

After the computation of $S_i^k$, the group similarity measures ($S_i$) were calculated using Equation (15) and can be found in Table 9.

Table 9. Group similarity measures ($S_i$).

${\mathit{S}}_{\mathit{i}}$	Value
$S_1$	0.9857
$S_2$	0.9962
$S_3$	0.9984
$S_4$	0.9987
$S_5$	0.9948
$S_6$	0.9982
$S_7$	0.9961
$S_8$	0.9968

Then, using$S_i$, decision deviations of DMs ($D_i^k$) were obtained utilizing Equation (16), and are shown in Table 10.

Table 10. Decision deviations of DMs ($D_i^k$).

${\mathit{D}}_{\mathit{i}}^{\mathit{k}}$	Value	${\mathit{D}}_{\mathbf{i}}^{\mathbf{k}}$	Value	${\mathit{D}}_{\mathbf{i}}^{\mathbf{k}}$	Value
$D_1^1$	0.0012	$D_3^3$	0.0005	$D_6^2$	0.0002
$D_1^2$	0.0099	$D_4^1$	0.0000	$D_6^3$	0.0001
$D_1^3$	0.0024	$D_4^2$	0.0002	$D_7^1$	0.0031
$D_2^1$	0.0025	$D_4^3$	0.0002	$D_7^2$	0.0033
$D_2^2$	0.0010	$D_5^1$	0.0005	$D_7^3$	0.0001
$D_2^3$	0.0035	$D_5^2$	0.0005	$D_8^1$	0.0013
$D_3^1$	0.0004	$D_5^3$	0.0009	$D_8^2$	0.0010
$D_3^2$	0.0009	$D_6^1$	0.0002	$D_8^3$	0.0003

Since none of the decision deviations of DMs are greater than the determined threshold value of 0.05, the consensus was ensured so the evaluations of DMs could be utilized in the alternatives’ ranking method, IF EDAS.

The aggregated fuzzy decision matrix was obtained, and it is presented in Table 11.

Table 11. Aggregate intuitionistic fuzzy decision matrix $({\mu }_{A_i}\left(x_j\right),{\nu }_{A_i}\left(x_j\right))$.

	C1	C2	C3	C4	C5	C6
A1	(0.218, 0.697)	(0.350, 0.550)	(0.404, 0.495)	(0.615, 0.274)	(0.500, 0.400)	(0.928, 0.063)
A2	(0.750, 0.262)	(0.764, 0.202)	(0.850, 0.177)	(0.687, 0.211)	(0.896, 0.126)	(0.606, 0.146)
A3	(0.789, 0.131)	(0.896, 0.079)	(0.850, 0.100)	(0.720, 0.178)	(0.720, 0.178)	(0.650, 0.250)
A4	(0.822, 0.114)	(0.789, 0.131)	(0.850, 0.100)	(0.928, 0.063)	(0.687, 0.211)	(0.750, 0.150)
A5	(0.118, 0.847)	(0.454, 0.445)	(0.350, 0.550)	(0.687, 0.211)	(0.454, 0.445)	(0.850, 0.100)
A6	(0.896, 0.079)	(0.720, 0.178)	(0.928, 0.063)	(0.822, 0.114)	(0.687, 0.211)	(0.500, 0.400)
A7	(0.850, 0.100)	(0.789, 0.131)	(0.950, 0.050)	(0.928, 0.063)	(0.850, 0.100)	(0.648, 0.247)
A8	(0.687, 0.211)	(0.928, 0.063)	(0.556, 0.342)	(0.750, 0.150)	(0.950, 0.050)	(0.720, 0.178)

For the ranking of the alternative airplane models, the IF EDAS methodology was applied. The final rankings of alternatives are shown in Table 12.

Table 12. The rankings that were obtained from IF EDAS.

Alternative No.	Rank Values	Rank Order
A1	0.083	7
A2	0.484	6
A3	0.854	3
A4	0.875	2
A5	0.049	8
A6	0.839	4
A7	0.988	1
A8	0.698	5

According to the final rankings obtained by the IF EDAS technique, the best alternative is “Alternative 7”, with the ranking value of 0.988. Alternative 7, which has top weight values among all criteria, has good scores in terms of cost of ownership and technical features criteria as well, of 0.2578 and 0.2675, respectively.

Although Alternative 4, which appeared as the second-best alternative as a result, has equilibrium with Alternative 7 on the cost of ownership and the technical features criteria, which are the most important ones, Alternative 7 has dominant scores in terms of C₃, which is operational characteristics.

On the other hand, Alternative 5 has good scores by means of the end-of-life vehicle characteristics. Nevertheless, the criterion weight is small, and it is ranked in the eighth position.

Even though Alternative 7 has high scores across all criteria compared to the other alternatives, it has relatively low scores in sustainability features. This depicts an important gap as an improvement area.

Alternatives 2 and 8 achieved the best scores for sustainability features among alternatives, which led them to the mid position in the overall ranking, 6th and 5th positions, respectively, because of their relatively low scores in the remaining factors. It should be noted that those alternatives have strong strategies for the reduction in environmental effects, usage of innovative and sustainable technologies, and usage of energy-efficient systems.

Sustainable development in the aviation sector requires a comprehensive and balanced strategy. The alternatives that received good scores in terms of sustainability can take further steps towards Sustainable Development Goals, and alternatives that had a balanced performance regarding sustainability can take important steps for investments in areas such as energy-efficient systems and use of green technology to reduce their carbon footprint.

The proposed method aimed to bridge the existing gap by selecting the most eco-friendly aircraft and leveraging the benefits of Bayesian BWM as a group decision-making tool to determine weights and rank the alternatives with the consensus-based IF EDAS method as a novel group decision-making method in the case study. The case study shows that the proposed approach is robust at computing the criteria weights, evaluating and ranking the alternatives, and detecting improvement areas to achieve those goals for a sustainable future.

5. Comparative Analysis

The proposed method was compared against other well-known MCDM techniques, namely, the intuitionistic fuzzy technique for order preference by similarity to ideal solution (IF TOPSIS) [68], the intuitionistic fuzzy weighted product method (IF WPM) [69], and the intuitionistic fuzzy weighted aggregated sum product assessment (IF WASPAS) [70]. As described in Section 2, these techniques were chosen for the comparative analysis because they are all compromise methods, since the proposed methodology utilizes EDAS, which also falls under this MCDM category. The comparison between these methods produced robust and significant results since these approaches for the alternatives’ selection process seek proximity regarding dealing with the ambiguity of the data given by the DMs. The comparative analysis revealed insights into their performance in selecting alternatives. Table 13 provides an overview of the results of the described methodologies.

Table 13. The comparison of the proposed method’s results with other IF techniques.

	IF EDAS		IF TOPSIS		IF WPM		IF WASPAS
Alternative No.	Rank Values	Rank Order	Rank Values	Rank Order	Rank Values	Rank Order	Rank Values	Rank Order
A1	0.083	7	0.307	7	0.384	7	0.488	7
A2	0.484	6	0.730	4	0.757	5	0.782	6
A3	0.854	3	0.764	3	0.798	3	0.840	3
A4	0.875	2	0.811	2	0.813	2	0.851	2
A5	0.049	8	0.261	8	0.342	8	0.452	8
A6	0.839	4	0.681	6	0.781	4	0.833	4
A7	0.988	1	0.820	1	0.838	1	0.874	1
A8	0.698	5	0.726	5	0.744	6	0.808	5

The comparison indicates that the ranking orders of the alternatives have symmetry and are similar across different methodologies, highlighting the robustness of the proposed selection procedure.

Alternative 7 is favored as the best one among all the rankings, with IF EDAS giving it a top rank value of 0.988. IF TOPSIS, IF WPM, and IF WASPAS techniques also place Alternative 7 at the top position, assigning the rank values of 0.820, 0.838, and 0.874, respectively.

When we compare our proposed IF EDAS approach with IF TOPSIS, we observe that the resulting rank orders of both techniques are close to each other, taking only two alternatives (4 and 6) in the swapped positioning in the ranking. The rank value ranges differ significantly since IF TOPSIS ranges within [0.261, 0.820] and IF EDAS within [0.049, 0.988], making the range values of IF EDAS method more spread out.

Regarding occurrence numbers, more differences are observed between IF TOPSIS and IF WPM for the middle-ranked alternatives. While IF TOPSIS places Alternative 2 in the fourth ranking, IF WPM places Alternative 6 in that place, similar cases also apply to the fifth and the sixth rankings, too. However, for the remaining positions, the methods produce the same results. IF WPM rank values range within [0.342, 0.838], which makes it closer to the IF TOPSIS results than IF EDAS.

The results, which are from the IF WASPAS method, are the same as IF EDAS in terms of rankings. Moreover, the rank values of IF WASPAS results are within [0.452, 0.874], which is closer to IF TOPSIS than IF EDAS in terms of value proximity.

Since these rankings were obtained with slight changes from different methods, we utilized the Spearman correlation analysis [71]. However, the calculated pairwise correlation coefficients between methods also proved the strong relationship and symmetry between the results calculated from methods, as shown in Figure 4. In Figure 4, white circles represent the plots for rankings from different methods, whereas red lines represent the overall tendencies. The “*” signs right next to the correlation coefficient values represent the correlation significance. An increase in the number of “*” signs depicts a stronger relationship.

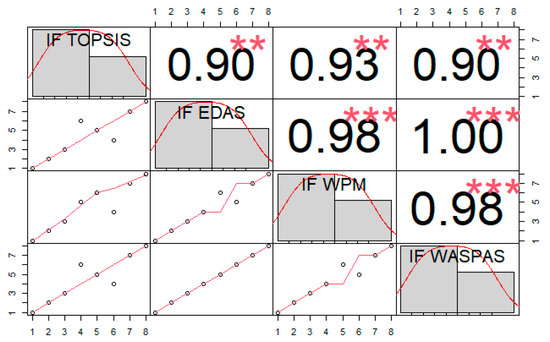
Figure 4. Plots and correlation coefficients between rankings using Spearman method.

As a result, despite methodological differences, the results show a significant level of alignment among the approaches used. This result indicates that the proposed method is robust enough to generate reliable rankings even when compared with established MCDM techniques.

6. Conclusions

Sustainable transportation plays a role in promoting responsibility and reducing our impact on the environment. It helps combat climate change, improve air quality, and preserve resources. Prioritizing transportation solutions can lead to the creation of vibrant cities, lower carbon emissions, and enhance the overall wellbeing of both current and future generations. As the aviation industry is one of the key agents of burdens against sustainable transportation, the focus of this study was to determine a selection framework of airplane models. In conclusion, utilizing Bayesian BWM and IF EDAS for evaluating airplane models provides a decision-making framework within the aviation industry. These approaches take into account the uncertainties and complexities in assessing airplanes, offering a reliable evaluation process. The proposed novel framework leverages Bayesian BWM’s ability to incorporate viewpoints of multiple decisionmakers and eliminate unnecessary numbers of pairwise comparisons with the creation of relative importance vectors between them. The framework also utilizes IF EDAS’s capacity to handle imprecise data using the membership function, which leverages symmetry so that it can effectively rank airplane models based on sustainability standards. This integrated approach contributes to promoting sustainability in the aviation industry by encouraging the adoption of environmentally friendly fuel for airplane models. The consensus model integration to IF EDAS fosters the DMs to reach a consensus before directly aggregating the ratings of the DM in the decision process through IF EDAS. The consensus model also enhances the acceptance of the final decision since it incorporates the DMs’ opinions after consensus based on each alternative.

After determining the criteria weights using Bayesian BWM, it appeared that the most significant criterion for the evaluation of the airplane models was technical features. The criterion of sustainability features, which enhances the company’s decision to better incorporate the sustainability goals of the company, has limited effect as the weight. However, it still gains a significant appearance during the decision-making process. In the evaluations of the alternatives using IF EDAS, it was observed that when the alternative airplane models gather similar scores from the experts regarding other decision factors, sustainability features become a decisive factor for the selection. As a final decision, an airplane model that is named Alternative 7 was selected as the best among alternatives.

The results also show us that there is an important trade-off between the cost of ownership criterion and the sustainability criterion. Since sustainability can be assured through investments in innovative technologies and energy-efficient systems, the cost of ownership for those airplane models might seem undesirable for short-term decisions. However, for the aviation industry, the decision for aircraft selection is long-term and strategic. Thus, sustainability factors become crucial in achieving the Sustainable Development Goals of the companies and being in line with governmental regulations that become stricter each year. The proposed approach provides a complete tool for this important trade-off.

While the proposed solution framework poses various benefits and valuable outcomes, it has also limitations encountered during the implementation of the model. First, the experiences and background of the decisionmakers are important crucial factors. Thus, the formation of experts affects the reliability and accuracy of the outcomes. Therefore, effectively managing this process is necessary to solve the decision-making problem accurately. Second, the difficulty in collecting unbiased data is another limitation of this study. Since the collected data in decision-making problems should reflect the decisionmakers’ subjective evaluation without any manipulation, preventing bias in group decision-making approaches is an important property. A consensus model in group decision-making problems is adopted in the proposed model to overcome this problem. Third, the data of the case study were obtained from three experts. The increase in the number of experts may change the obtained results and those experts must thoroughly understand the existing problem and give correct opinions accordingly. During the data collection phase of this study, decisionmakers sometimes experienced hesitation regarding linguistic variables. Therefore, this phase took a long time. This limitation is addressed by employing intuitionistic fuzzy sets. Moreover, the original BWM assesses the consistency of the criteria evaluations, and Bayesian BWM lacks this property. The final limitations of the study can be listed as a lack of risk assessment and refined consensus procedure.

In future studies, applications should integrate various methods similar to this study in the aviation industry. The proposed approach does not consider the interrelationships between criteria, which may impact the results. A new MCDM method might be developed to consider interrelationships among criteria to resolve this issue. In addition, since all three decisionmakers had similar backgrounds, the weights were assumed to be equal in the study. Future studies might focus on giving different weights to the decisionmakers. Furthermore, to handle linguistic term sets, the analysis can incorporate some flexible and valuable approaches, such as the two-tuple linguistic modeling, the ordinal linguistic approach, and the unbalanced linguistic approach. Ensuring the connection of these linguistic models to BWM is an intriguing and potential area for further research. Moreover, increasing the number of decisionmakers in the data collection phase and employing a large-scale group decision-making consensus model might be the subject of future research. Additionally, a consistency evaluation method might be presented for criteria weights. Finally, as a future work, the three-way group decision-making method can be utilized to refine the consensus-building procedure and to enhance the risk assessment by evaluating the likelihood of multiple scenarios, resulting in an improved and transparent risk-averse decision-making perspective.