The Pedal Curves Generated by Alternative Frame Vectors and Their Smarandache Curves

Abstract

In this paper, pedal-like curves are defined resulting from the orthogonal projection of a fixed point on the alternative frame vectors of a given regular curve. For each pedal curve, the Frenet vectors, the curvature and the torsion functions are found to provide the common relations among the main curve and its pedal curves. Then, Smarandache curves are defined by using the alternative frame vectors of each pedal curve as position vectors. The relations of the Frenet apparatus are also established for the pedal curves and their corresponding Smarandache curves. Finally, the expressions of the alternative frame apparatus of each Smarandache curves are given in terms of the alternative frame elements of the pedal curves. Thus, a set of new symmetric curves are introduced that contribute to the vast curve family.

1. Introduction

Curves are natural figures that always exist in nature. Scientists have formulated these figures, examined their characteristics and obtained some theories. Curve theory has been one of the fields of study that best represents differential geometry and makes it most interesting. More information and theory can be obtained when an orthonormal system is established on a curve. Following such an orthonormal system, the curvatures which are the invariants of a curve can be established. Thus, one can characterize a given curve by these invariants. For example, if the second curvature (torsion) of a curve is zero, then the curve is a planar curve; if the torsion is different from zero, then the curve is a space curve. If the harmonic curvature, which is the ratio of the torsion to curvature, is constant, then the curve is a general helix. If the curvature is a constant and the torsion is a function, the curve is a Salkowski curve [1,2].

Another useful aspect of curve theory is to associate some curves to each other. Any two curves can be related to one another by some specific and symmetrical methods. Such methods of symmetry are based on translations, scaling, rotations and reflections. For example, a Bertrand pair has common principal normal vectors, that is to say, the principal normal vector of a Bertrand curve is translated and its mate curve accepts this translated principal normal vector. As a consequence, the resulting Bertrand pair has the relation of scale symmetry (see Figure 1). Similarly, a Mannheim curve pair possesses such translational symmetry between the principal normal and binormal vectors, whereas a successor curve has the translational symmetry between the tangent vector and principal normal vector. However, the involute–evolute curves have a 90-degree rotary symmetry relation between their tangent vectors [3]. There are many studies on these curves; see [4] and the references therein.

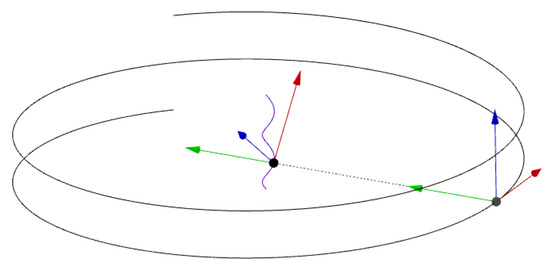
Figure 1. A helix curve (purple) and its Bertrand mate (black). The principal normal vectors (green) have a translational symmetry, whereas the resulting pair of curves have a scale symmetry relation between them. To see the animated version of this figure, please visit https://www.geogebra.org/m/ndjktahz, accessed on 9 July 2024.

Further, generating new curves is an important matter for the theory of curves. Smarandache geometry is one way of creating new curves [5,6,7]. In addition, a pedal curve is another type of curve which is derived by a given specific curve and a fixed point. That is, a pedal (resp., contrapedal) curve is defined as the geometric location of the projection points on the tangent (resp., normal vector) of a curve from a point that is not on the curve. This way of deriving new curves is also considered as a symmetric procedure; see [3]. Many studies exist on these curves such as [8,9,10] and the references therein. Further, research on such curves has been carried out using different frames in many spaces, and similar works continue today [11,12,13,14,15,16].

In this study, pedal curves belonging to the alternative frame vectors of a space curve are defined, and their Frenet apparatus is calculated. Next, Smarandache curves are defined by taking alternative frame elements of each pedal curve as the position vectors. Finally, the corresponding alternative frame apparatus are obtained and expressed in terms of the main curve. In the following lines, we recall the basic concepts that we use throughout the paper. For a given differentiable curve $\alpha \left(t\right):I\subset R\to R^3$, the formulae of Frenet vector fields and curvature functions are defined as follows:

$$\begin{array}{cc}\hfill T& ={\displaystyle \frac{{\alpha }^{\prime }}{∥{\alpha }^{\prime }∥}},N=B\wedge T={\displaystyle \frac{\left({\alpha }^{\prime }\wedge {\alpha }^{″}\right)\wedge {\alpha }^{\prime }}{∥{\alpha }^{\prime }\wedge {\alpha }^{″}∥∥{\alpha }^{\prime }∥}},B={\displaystyle \frac{{\alpha }^{\prime }\wedge {\alpha }^{″}}{∥{\alpha }^{\prime }\wedge {\alpha }^{″}∥}},\hfill \end{array}$$

(1)

$$\begin{array}{cc}\hfill \kappa & ={\displaystyle \frac{∥{\alpha }^{\prime }\wedge {\alpha }^{″}∥}{{∥{\alpha }^{\prime }∥}^3}},\tau ={\displaystyle \frac{det\left({\alpha }^{\prime },{\alpha }^{″},{\alpha }^{‴}\right)}{{∥{\alpha }^{\prime }\wedge {\alpha }^{″}∥}^2}},\hfill \end{array}$$

(2)

$$\begin{array}{cc}\hfill T^{\prime }& =v\kappa N,N^{\prime }=v\left(-\kappa T+\tau B\right),B^{\prime }=-v\tau N,\hfill \end{array}$$

(3)

where $∥ ∥$ is the norm, “∧” is the vector product operator, and $v=∥{\alpha }^{\prime }∥$ [10,17]. Frenet vectors make a rotational motion along the curve around an axis. This axis is called the Darboux rotational axis, and it is defined by the relation $W_0=\tau T+\kappa B$. If the unit Darboux vector is denoted by W, then, for $\varphi =\measuredangle (B,W_0)$, we have the following equation.

$$W=\sin \varphi T+\cos \varphi B,$$

(4)

where ${\displaystyle \cos \varphi =\frac{\kappa }{\sqrt{{\kappa }^2+{\tau }^2}}}$ and ${\displaystyle \sin \varphi =\frac{\tau }{\sqrt{{\kappa }^2+{\tau }^2}}.}$ Since W is a vector lying in the rectifying plane, it is clear that $N\perp W.$ Thus, a new orthonormal system on a curve can be established with the set of vectors $\{N,C=N\wedge W,W\}.$ The new moving frame is called the alternative frame for the curve. We have the following relations among Frenet and alternative frame vectors.

$$N=N,C=-cos\varphi T+sin\varphi B,W=sin\varphi T+cos\varphi B.$$

(5)

Further, similar to the Frenet formulae given in (3), we have the alternative formulae as follows:

$$N^{\prime }=v\beta C,C^{\prime }=v\left(-\beta N+{\varphi }^{\prime }W\right),W^{\prime }=-v{\varphi }^{\prime }C,$$

(6)

where ${\displaystyle {\varphi }^{\prime }={\left(\frac{\tau }{\kappa }\right)}^{\prime }\left(\frac{{\kappa }^2+{\tau }^2}{{\kappa }^2}\right)}$, and $\beta =\kappa \sqrt{{\kappa }^2+{\tau }^2}.$

2. The Alternative $\mathbf{N}$-Pedal Curve and Its Smarandache Curves

In this section of the study, we first define the alternative N-pedal curve considering the principal normal vector of a given curve as an element of the alternative frame. Second, we find the Frenet apparatus of the alternative N-pedal curve and establish the relationship among the alternative frame vectors of both the main curve and its corresponding alternative N-pedal curve. Then, we examine four possible Smarandache curves of the alternative N-pedal curve whose position vectors are the linear combinations of the alternative frame elements. We also support the results by giving an example and the graphs of the curves.

Definition 1. 

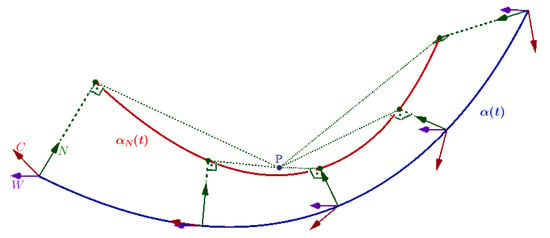
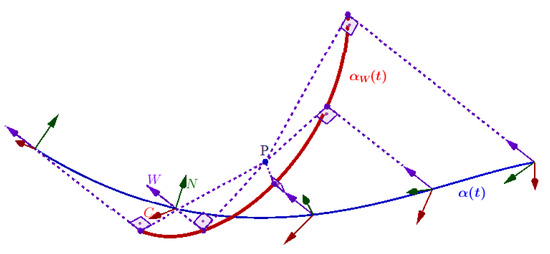
Let $\alpha :I\subset R\to R^3$ be a regular curve in $E^3$, and $\{N,C,W\}$ denote the set of its alternative frame vectors. Then, the locus of the perpendicular projection points of a fixed point P that is not on α onto the alternative frame vector N is called the alternative N-pedal curve for α according to P (see Figure 2).

Figure 2. The alternative N-pedal curve (red) of the curve $\alpha \left(t\right)$ (blue) according to a fixed point P.

Theorem 1. 

The equation of the alternative N-pedal curve of the curve α is given as follows:

$${\alpha }_N\left(t\right)=\alpha \left(t\right)+⟨P-\alpha \left(t\right),N\left(t\right)⟩N\left(t\right).$$

(7)

Proof. 

Let $P^{\prime }$ be the perpendicular projection point onto the normal vector $\overrightarrow{N}$ from the fixed point P that is not on the curve $\alpha$. By using the definition of vector projections, we compute the perpendicular projection vector denoted by $\overrightarrow{\alpha P^{\prime }}$ as follows:

$$\overrightarrow{\alpha P^{\prime }}={\displaystyle \frac{⟨\overrightarrow{\alpha P},\overrightarrow{N}⟩}{⟨\overrightarrow{N},\overrightarrow{N}⟩}}\overrightarrow{N}.$$

Thus, with the motion of the frame vectors along the curve, the geometric location of the point $P^{\prime }$ constructs a new curve that is called the alternative N-pedal curve and denoted by ${\alpha }_N\left(t\right)$. Accordingly, we have the following equations:

$$\begin{array}{cc}\hfill \overrightarrow{\alpha P}=\overrightarrow{\alpha P^{\prime }}+\overrightarrow{P^{\prime }P}& \Rightarrow \overrightarrow{\alpha P}={\displaystyle \frac{⟨\overrightarrow{\alpha P},\overrightarrow{N}⟩}{{∥\overrightarrow{N}∥}^2}}\overrightarrow{N}+\overrightarrow{P^{\prime }P}\hfill \\ & \Rightarrow P^{\prime }=\alpha \left(t\right)+⟨\overrightarrow{\alpha P},\overrightarrow{N}⟩\overrightarrow{N}\hfill \\ & \Rightarrow {\alpha }_N\left(t\right)=\alpha \left(t\right)+⟨P-\alpha \left(t\right),N\left(t\right)⟩N\left(t\right),\hfill \end{array}$$

by which the proof is completed. □

If specifically $⟨P-\alpha \left(t\right),N\left(t\right)⟩=u\left(t\right)$, then Relation (7) can clearly be simplified as follows:

$${\alpha }_N\left(t\right)=\alpha \left(t\right)+u\left(t\right)N\left(t\right).$$

(8)

Theorem 2. 

Let ${\alpha }_N$ be the alternative N-pedal curve of a unit speed curve α, and $\{T_1,N_1,B_1\}$ denote the Frenet vectors of the alternative N-pedal curve. Then, we have the following relations:

$$\begin{array}{cc}\hfill T_1=& {\omega }_1{u}^{\prime }N+{\omega }_1\left(uv\beta -cos\phi \right)C+{\omega }_{1}sin\phi W,\hfill \\ \hfill N_1=& B_1\wedge T_1,\hfill \\ \hfill B_1=& {\eta }_1\left(x_{3}uv\beta -x_{3}cos\phi -x_{2}sin\phi \right)N+{\eta }_1\left(x_{1}sin\phi -u^{\prime }{x}_3\right)C\hfill \\ & +{\eta }_1\left(u^{\prime }{x}_2-x_{1}uv\beta +x_{1}cos\phi \right)W,\hfill \end{array}$$

where

$$\begin{array}{cc}\hfill x_1=& u^{″}-v^2\beta \left(u\beta -cos\phi \right),\hfill \\ \hfill x_2=& v\left(u^{\prime }\beta -v{\phi }^{\prime }sin\phi \right)+{\left(uv\beta -vcos\phi \right)}^{\prime },\hfill \\ \hfill x_3=& v^2{\phi }^{\prime }\left(u\beta -cos\phi \right)+{\left(vsin\phi \right)}^{\prime },\hfill \\ \hfill {\omega }_1=& {\displaystyle \frac{1}{\sqrt{{\left(u^{\prime }\right)}^2+{\left(uv\beta -vcos\phi \right)}^2+{\left(vsin\phi \right)}^2}}},\hfill \\ \hfill {\eta }_1=& {\displaystyle \frac{1}{\sqrt{{\left(x_{3}uv\beta -x_{3}vcos\phi -x_{2}vsin\phi \right)}^2+{\left(x_{1}vsin\phi -u^{\prime }{x}_3\right)}^2+{\left(u^{\prime }{x}_2-x_{1}uv\beta +x_{1}vcos\phi \right)}^2}}}.\hfill \end{array}$$

Proof. 

By considering the relations in (5), we have the derivatives up to the third degree for Relation (8) as follows:

$$\begin{array}{cc}\hfill {\alpha }_N^{\prime }=& u^{\prime }N+v\left(u\beta -cos\phi \right)C+vsin\phi W,\hfill \\ \hfill {\alpha }_N^{″}=& x_{1}N+x_{2}C+x_{3}W,\hfill \\ \hfill {\alpha }_N^{‴}=& \left(x_1^{\prime }-x_{2}v\beta \right)N+\left(x_2^{\prime }+x_{1}v\beta -x_{3}v{\phi }^{\prime }\right)C+\left(x_{2}v{\phi }^{\prime }+x_3^{\prime }\right)W.\hfill \end{array}$$

(9)

Further, if we perform the required vector product operations and take the norms, the following relations are obtained:

$$\begin{array}{cc}\hfill {\alpha }_N^{\prime }\wedge {\alpha }_N^{″}=& \left(u{x}_{3}v\beta -x_{2}vsin\phi -x_{3}vcos\phi \right)N+\left(x_{1}vsin\phi -x_3{u}^{\prime }\right)C\hfill \\ \hfill & +\left(x_2{u}^{\prime }-u{x}_{1}v\beta +x_{1}vcos\phi \right)W,\hfill \\ \hfill \\ \hfill det\left({\alpha }_N^{\prime },{\alpha }_N^{″},{\alpha }_N^{‴}\right)=& \left(-x_{2}vsin\phi +u{x}_{3}v\beta -x_{3}vcos\phi \right)\left(x_1^{\prime }-x_{2}v\beta \right)\hfill \\ \hfill & +\left(x_{1}sin\phi -u^{\prime }{x}_3\right)\left(x_{1}v\beta +x_2^{\prime }-x_{3}v{\phi }^{\prime }\right)\hfill \\ \hfill & +\left(x_2{u}^{\prime }-u{x}_{1}v\beta +x_{1}vcos\phi \right)\left(x_{2}v{\phi }^{\prime }+x_3^{\prime }\right),\hfill \end{array}$$

(10)

$$\begin{array}{cc}\hfill ∥{\alpha }_N^{\prime }∥=& \sqrt{{u^{\prime }}^2+v^2+v^{2}u\beta \left(u\beta -cos\phi \right)},\hfill \\ \hfill ∥{\alpha }_N^{\prime }\wedge {\alpha }_N^{″}∥=& \sqrt{\begin{array}{c}{\left(u{x}_{3}v\beta -x_{2}vsin\phi -x_{3}vcos\phi \right)}^2+{\left(x_{1}vsin\phi -x_3{u}^{\prime }\right)}^2\hfill \\ +{\left(u^{\prime }{x}_2-x_{1}uv\beta +x_{1}vcos\phi \right)}^2\hfill \end{array}}·\hfill \end{array}$$

(11)

If Equations (9)–(11) are substituted in (1), the proof is completed. □

Theorem 3. 

Let ${\alpha }_N$ be the alternative N-pedal curve of the unit speed curve α, and ${\kappa }_1$ and ${\tau }_1$ denote its curvature and torsion functions, respectively. Then, we have the following relations among the curvatures:

$$\begin{array}{cc}\hfill {\kappa }_1=& {\displaystyle \frac{\sqrt{{\left(x_{3}uv\beta -x_{3}cos\phi -x_{2}sin\phi \right)}^2+{\left(x_{1}sin\phi -u^{\prime }{x}_3\right)}^2+{\left(u^{\prime }{x}_2-x_{1}uv\beta +x_{1}cos\phi \right)}^2}}{\left({u^{\prime }}^2+v^2+v^{2}u\beta \left(u\beta -cos\phi \right)\right)\sqrt{{u^{\prime }}^2+v^2+v^{2}u\beta \left(u\beta -cos\phi \right)}}},\hfill \\ \hfill {\tau }_1=& {\displaystyle \frac{\begin{array}{c}\left(-x_{2}vsin\phi +u{x}_{3}v\beta -x_{3}vcos\phi \right)\left(x_1^{\prime }-x_{2}v\beta \right)+\left(x_{1}sin\phi -u^{\prime }{x}_3\right)\left(x_{1}v\beta +x_2^{\prime }-x_{3}v{\phi }^{\prime }\right)\hfill \\ +\left(x_2{u}^{\prime }-u{x}_{1}v\beta +x_{1}vcos\phi \right)\left(x_{2}v{\phi }^{\prime }+x_3^{\prime }\right)\hfill \end{array}}{{\left(u{x}_{3}v\beta -x_{2}vsin\phi -x_{3}vcos\phi \right)}^2+{\left(x_{1}vsin\phi -x_3{u}^{\prime }\right)}^2+{\left(u^{\prime }{x}_2-x_{1}uv\beta +x_{1}vcos\phi \right)}^2}}.\hfill \end{array}$$

Proof. 

We substitute the relations given in (10) and (11) in (2) and complete the proof. □

Remark 1. 

The alternative frame for the alternative N-pedal curve ${\alpha }_N$ is established by the following equations:

$$N_1=N_1,C_1=-cos\partial T_1+sin\partial B_1,W_1=sin\partial T_1+cos\partial B_1,$$

(12)

where ${\displaystyle \partial =\measuredangle \left(B_1,W_1\right),}$${\displaystyle cos\partial =\frac{{\kappa }_1}{\sqrt{{\kappa }_1^2+{\tau }_1^2}},}$ and ${\displaystyle sin\partial =\frac{{\tau }_1}{\sqrt{{\kappa }_1^2+{\tau }_1^2}}.}$

Corollary 1. 

The alternative frame formulae for the alternative N-pedal curve is given as follows:

$$N_1^{\prime }={\mu }_1{\beta }_1{C}_1,{C^{\prime }}_1=-{\mu }_1{\beta }_1{N}_1+{\mu }_1{\partial }^{\prime }{W}_1,{W_1}^{\prime }=-{\mu }_1{\partial }^{\prime }{C}_1,$$

(13)

where ${\displaystyle {\mu }_1=∥{\alpha }_N^{\prime }∥,{\partial }^{\prime }={\left(\frac{{\tau }_1}{{\kappa }_1}\right)}^{\prime }\left(\frac{{\kappa }_1^2+{\tau }_1^2}{{\kappa }_1^2}\right),{\beta }_1={\mu }_1\sqrt{{\kappa }_1^2+{\tau }_1^2}.}$

Definition 2. 

The $N_1{C}_1$ Smarandache curve of the alternative N-pedal curve whose position vector is the linear combination of the two vectors $N_1$ and $C_1$ is defined by the following parametrization:

$${\alpha }_1={\displaystyle \frac{N_1+C_1}{\sqrt{2}}}.$$

(14)

Theorem 4. 

Let $\{N_{{\alpha }_1},C_{{\alpha }_1},W_{{\alpha }_1}\}$ denote the alternative frame for the $N_1{C}_1$ Smarandache curve. Then, we have the following relations among the Frenet vectors:

$$\begin{array}{cc}\hfill T_{{\alpha }_1}=& {\displaystyle \frac{\sqrt{2}\left(-{\beta }_1{N}_1+{\beta }_1{C}_1+{\partial }^{\prime }{W}_1\right)}{\sqrt{2{\beta }_1^2+{{\partial }^{\prime }}^2}}},\hfill \\ \hfill N_{{\alpha }_1}=& B_{{\alpha }_1}\wedge T_{{\alpha }_1},\hfill \\ \hfill B_{{\alpha }_1}=& {\displaystyle \frac{\left(x_6{\beta }_1-x_5{\partial }^{\prime }\right)N_1+\left(x_6{\beta }_1+x_4{\partial }^{\prime }\right)C_1-\left({\beta }_1{x}_4+{\beta }_1{x}_5\right)W_1}{\sqrt{{\left(x_6{\beta }_1-x_5{\partial }^{\prime }\right)}^2+{\left(x_6{\beta }_1+x_4{\partial }^{\prime }\right)}^2+{\left({\beta }_1{x}_4+{\beta }_1{x}_5\right)}^2}}},\hfill \end{array}$$

where ${\displaystyle x_4=-\frac{{\left({\mu }_1{\beta }_1\right)}^{\prime }+{\mu }_1^2{\beta }_1^2}{\sqrt{2}},x_5=\frac{{\left({\mu }_1{\beta }_1\right)}^{\prime }-{\mu }_1^2\left({\beta }_1^2+{{\partial }^{\prime }}^2\right)}{\sqrt{2}},x_6=\frac{{\left({\mu }_1{\partial }^{\prime }\right)}^{\prime }+{\mu }_1^2{\beta }_1{\partial }^{\prime }}{\sqrt{2}}.}$

Proof. 

If Relation (13) is taken into account, and the required derivatives for the $N_1{C}_1$ curve given in (14) are taken, we have

$$\begin{array}{cc}\hfill {\alpha }_1^{\prime }=& {\displaystyle \frac{-{\mu }_1{\beta }_1{N}_1+{\mu }_1{\beta }_1{C}_1+{\mu }_1{\partial }^{\prime }{W}_1}{\sqrt{2}}},\hfill \\ \hfill {\alpha }_1^{″}=& x_4{N}_1+x_5{C}_1+x_6{W}_1,\hfill \\ \hfill {\alpha }_1^{‴}=& \left(x_4^{\prime }-x_5{\mu }_1{\beta }_1\right)N_1+\left(x_5^{\prime }+x_4{\mu }_1{\beta }_1-x_6{\mu }_1{\partial }^{\prime }\right)C_1+\left(x_6^{\prime }+x_5{\mu }_1{\partial }^{\prime }\right)W_1.\hfill \end{array}$$

(15)

Moreover, if the vector products, determinants and norms are taken, we obtain:

$$\begin{array}{cc}\hfill {\alpha }_1^{\prime }\wedge {\alpha }_1^{″}=& {\displaystyle \frac{{\mu }_1}{\sqrt{2}}}\left(\left(x_6{\beta }_1-x_5{\partial }^{\prime }\right)N_1+\left(x_6{\beta }_1+x_4{\partial }^{\prime }\right)C_1-{\beta }_1\left(x_4+x_5\right)W_1\right),\hfill \\ \hfill det\left({\alpha }_1^{\prime },{\alpha }_1^{″},{\alpha }_1^{‴}\right)=& {\displaystyle \frac{{\mu }_1}{\sqrt{2}}}\left(\begin{array}{c}\left(x_4^{\prime }-x_5{\mu }_1{\beta }_1\right)\left(x_6{\beta }_1-x_5{\partial }^{\prime }\right)\hfill \\ +\left(x_5^{\prime }+x_4{\mu }_1{\beta }_1-x_6{\mu }_1{\partial }^{\prime }\right)\left(x_6{\beta }_1+x_4{\partial }^{\prime }\right)\hfill \\ -{\beta }_1\left(x_4+x_5\right)\left(x_6^{\prime }+x_5{\mu }_1{\partial }^{\prime }\right)\hfill \end{array}\right),\hfill \end{array}$$

(16)

and

$$\begin{array}{cc}\hfill ∥{\alpha }_1^{\prime }∥=& {\displaystyle \frac{{\mu }_1}{\sqrt{2}}}\sqrt{2{\beta }_1^2+{{\partial }^{\prime }}^2},\hfill \\ \hfill ∥{\alpha }_1^{\prime }\wedge {\alpha }_1^{″}∥=& {\displaystyle \frac{{\mu }_1}{\sqrt{2}}}\sqrt{{\left(x_6{\beta }_1-x_5{\partial }^{\prime }\right)}^2+{\left(x_6{\beta }_1+x_4{\partial }^{\prime }\right)}^2+{\left(x_4{\beta }_1+x_5{\beta }_1\right)}^2}·\hfill \end{array}$$

(17)

Finally, by substituting Relations (15)–(17) into (1), we complete the proof. □

Theorem 5. 

Let ${\kappa }_{{\alpha }_1}$ and ${\tau }_{{\alpha }_1}$ be the curvature and the torsion functions for the $N_1{C}_1$ Smarandache curve, respectively. Then, we have the following relations among the curvatures:

$$\begin{array}{cc}\hfill {\kappa }_{{\alpha }_1}=& {\displaystyle \frac{2\sqrt{{\left(x_6{\beta }_1-x_5{\partial }^{\prime }\right)}^2+{\left(x_6{\beta }_1+x_4{\partial }^{\prime }\right)}^2+{\left({\beta }_1{x}_4+{\beta }_1{x}_5\right)}^2}}{{\mu }_1^2\left(2{\beta }_1^2+{{\partial }^{\prime }}^2\right)\sqrt{2{\beta }_1^2+{{\partial }^{\prime }}^2}}},\hfill \\ \hfill {\tau }_{{\alpha }_1}=& {\displaystyle \frac{\sqrt{2}\left(\begin{array}{c}\left(x_4^{\prime }-x_5{\mu }_1{\beta }_1\right)\left(x_6{\beta }_1-x_5{\partial }^{\prime }\right)+\left(x_5^{\prime }+x_4{\mu }_1{\beta }_1-x_6{\mu }_1{\partial }^{\prime }\right)\left(x_6{\beta }_1+x_4{\partial }^{\prime }\right)\hfill \\ -{\beta }_1\left(x_4+x_5\right)\left(x_6^{\prime }+x_5{\mu }_1{\partial }^{\prime }\right)\hfill \end{array}\right)}{{\mu }_1\left({\left(x_6{\beta }_1-x_5{\partial }^{\prime }\right)}^2+{\left(x_6{\beta }_1+x_4{\partial }^{\prime }\right)}^2+{\left({\beta }_1{x}_4+{\beta }_1{x}_5\right)}^2\right)}}.\hfill \end{array}$$

Proof. 

By using (16) and (17) and substituting them into (2), we complete the proof. □

Remark 2. 

The alternative frame for the $N_1{C}_1$ Smarandache curve ${\alpha }_1$ is established by the following equations:

$$N_{{\alpha }_1}=N_{{\alpha }_1},C_{{\alpha }_1}=-cos{\partial }_1{T}_{{\alpha }_1}+sin{\partial }_1{B}_{{\alpha }_1},W_{{\alpha }_1}=sin{\partial }_1{T}_{{\alpha }_1}+cos{\partial }_1{B}_{{\alpha }_1},$$

where ${\displaystyle {\partial }_1=\measuredangle \left(B_{{\alpha }_1},W_{{\alpha }_1}\right),}$${\displaystyle cos{\partial }_1=\frac{{\kappa }_{{\alpha }_1}}{\sqrt{{\kappa }_{{\alpha }_1}^2+{\tau }_{{\alpha }_1}^2}},}$ and ${\displaystyle sin{\partial }_1=\frac{{\tau }_{{\alpha }_1}}{\sqrt{{\kappa }_{{\alpha }_1}^2+{\tau }_{{\alpha }_1}^2}}.}$

Definition 3. 

The $N_1{W}_1$ Smarandache curve of the alternative N-pedal curve whose position vector is the linear combination of the two vectors $N_1$ and $W_1$ is defined by the following parametrization:

$${\alpha }_2={\displaystyle \frac{N_1+W_1}{\sqrt{2}}}.$$

(18)

Theorem 6. 

Let $\{N_{{\alpha }_2},C_{{\alpha }_2},W_{{\alpha }_2}\}$ denote the alternative frame for the $N_1{W}_1$ Smarandache curve. Then, we have the following relations among the Frenet vectors:

$$T_{{\alpha }_2}=C_1,N_{{\alpha }_2}={\displaystyle \frac{-{\beta }_1{N}_1+{\partial }^{\prime }{W}_1}{\sqrt{{{\partial }^{\prime }}^2+{\beta }_1^2}}},B_{{\alpha }_2}={\displaystyle \frac{{\partial }^{\prime }{N}_1+{\beta }_1{W}_1}{\sqrt{{{\partial }^{\prime }}^2+{\beta }_1^2}}},$$

where ${\partial }^{\prime }$ and ${\beta }_1$ are as given in Corollary 1.

Proof. 

If Relation (13) is taken into account, and the required derivatives for the $N_1{W}_1$ curve given in (18) are taken, we have

$$\begin{array}{cc}\hfill {\alpha }_2^{\prime }=& {\displaystyle \frac{{\mu }_1\left({\beta }_1-{\partial }^{\prime }\right)C_1}{\sqrt{2}}},\hfill \\ \hfill {\alpha }_2^{″}=& {\displaystyle \frac{-{\mu }_1^2{\beta }_1\left(\beta -{\partial }^{\prime }\right)N_1+{\left({\mu }_1{\beta }_1-{\mu }_1{\partial }^{\prime }\right)}^{\prime }{C}_1+{\mu }_1^2{\partial }^{\prime }\left({\beta }_1-{\partial }^{\prime }\right)W_1}{\sqrt{2}}},\hfill \\ \hfill {\alpha }_2^{‴}=& {\displaystyle \frac{\begin{array}{c}-\left({\left({\mu }_1^2{\beta }_1\left({\beta }_1-{\partial }^{\prime }\right)\right)}^{\prime }+{\mu }_1{\beta }_1{\left({\mu }_1{\beta }_1-{\mu }_1{\partial }^{\prime }\right)}^{\prime }\right)N_1\hfill \\ +\left({\left({\mu }_1{\beta }_1-{\mu }_1{\partial }^{\prime }\right)}^{″}-{\mu }_1^3\left({\beta }_1-{\partial }^{\prime }\right)\left({\beta }_1^2+{\left({{\partial }_1}^{\prime }\right)}^2\right)\right)C_1\hfill \\ +\left({\left({\mu }_1^2{\partial }^{\prime }\left({\beta }_1-{\partial }^{\prime }\right)\right)}^{\prime }+{\mu }_1{\partial }^{\prime }{\left({\mu }_1{\beta }_1-{\mu }_1{\partial }^{\prime }\right)}^{\prime }\right)W_1\hfill \end{array}}{\sqrt{2}}}.\hfill \end{array}$$

(19)

In addition, if the vector products, determinants and norms are taken, we obtain:

$$\begin{array}{cc}\hfill {\alpha }_2^{\prime }\wedge {\alpha }_2^{″}=& {\displaystyle \frac{{\mu }_1^3{\partial }^{\prime }{\left({\beta }_1-{\partial }^{\prime }\right)}^2{N}_1+{\mu }_1^3{\beta }_1{\left({\beta }_1-{\partial }^{\prime }\right)}^2{W}_1}{2}},\hfill \\ \hfill det\left({\alpha }_2^{\prime },{\alpha }_2^{″},{\alpha }_2^{‴}\right)=& {\displaystyle \frac{{\mu }_1^5{\left({\beta }_1-{\partial }^{\prime }\right)}^3\left({\beta }_1{\partial }^{″}-{\partial }^{\prime }{\beta }_1^{\prime }\right)}{2\sqrt{2}}},\hfill \end{array}$$

(20)

and

$$\begin{array}{cc}\hfill ∥{\alpha }_2^{\prime }∥=& {\displaystyle \frac{{\mu }_1\left({\beta }_1-{\partial }^{\prime }\right)}{\sqrt{2}}},\hfill \\ \hfill ∥{\alpha }_2^{\prime }\wedge {\alpha }_2^{″}∥=& {\displaystyle \frac{{\left({\beta }_1-{\partial }^{\prime }\right)}^2{\mu }_1^3\sqrt{{{\partial }^{\prime }}^2+{\beta }_1^2}}{2}}.\hfill \end{array}$$

(21)

Finally, by substituting Relations (19)–(21) into (1), we complete the proof. □

Theorem 7. 

Let ${\kappa }_{{\alpha }_2}$ and ${\tau }_{{\alpha }_2}$ be the curvature and the torsion functions for the $N_1{W}_1$ Smarandache curve, respectively. Then, we have the following relations among the curvatures:

$${\kappa }_{{\alpha }_2}={\displaystyle \frac{\sqrt{2}\sqrt{{{\partial }^{\prime }}^2+{\beta }_1^2}}{{\beta }_1-{\partial }^{\prime }}},{\tau }_{{\alpha }_2}={\displaystyle \frac{\sqrt{2}\left({\beta }_1{\partial }^{″}-{\partial }^{\prime }{\beta }_1^{\prime }\right)}{{\mu }_1\left({\beta }_1-{\partial }^{\prime }\right)\left({{\partial }^{\prime }}^2+{\beta }_1^2\right)}}$$

Proof. 

By using (20) and (21) and substituting them into (2), we complete the proof. □

Remark 3. 

The alternative frame for the $N_1{W}_1$ Smarandache curve ${\alpha }_2$ is established by the following equations:

$$N_{{\alpha }_2}=N_{{\alpha }_2},C_{{\alpha }_2}=-cos{\partial }_2{T}_{{\alpha }_2}+sin{\partial }_2{B}_{{\alpha }_2},W_{{\alpha }_2}=sin{\partial }_2{T}_{{\alpha }_2}+cos{\partial }_2{B}_{{\alpha }_2}$$

where ${\displaystyle {\partial }_2=\measuredangle \left(B_{{\alpha }_2},W_{{\alpha }_2}\right),}$${\displaystyle cos{\partial }_2=\frac{{\kappa }_{{\alpha }_2}}{\sqrt{{\kappa }_{{\alpha }_2}^2+{\tau }_{{\alpha }_2}^2}},}$ and ${\displaystyle sin{\partial }_2=\frac{{\tau }_{{\alpha }_2}}{\sqrt{{\kappa }_{{\alpha }_2}^2+{\tau }_{{\alpha }_2}^2}}.}$

Definition 4. 

The $C_1{W}_1$ Smarandache curve of the alternative N-pedal curve whose position vector is the linear combination of the two vectors $C_1$ and $W_1$ is defined by the following parametrization:

$${\alpha }_3={\displaystyle \frac{C_1+W_1}{\sqrt{2}}}.$$

(22)

Theorem 8. 

Let $\{N_{{\alpha }_3},C_{{\alpha }_3},W_{{\alpha }_3}\}$ denote the alternative frame for the $C_1{W}_1$ Smarandache curve. Then, we have the following relations among the Frenet vectors:

$$\begin{array}{cc}\hfill T_{{\alpha }_3}=& {\displaystyle \frac{-{\beta }_1{N}_1-{\partial }^{\prime }{C}_1+{\partial }^{\prime }{W}_1}{\sqrt{{\beta }_1^2+2{{\partial }^{\prime }}^2}}},\hfill \\ \hfill N_{{\alpha }_3}=& B_{{\alpha }_3}\wedge T_{{\alpha }_3},\hfill \\ \hfill B_{{\alpha }_3}=& {\displaystyle \frac{-\left({\partial }^{\prime }{x}_9+{\partial }^{\prime }{x}_8\right)N_1+\left({\beta }_1{x}_9+{\partial }^{\prime }{x}_7\right)C_1+\left({\partial }^{\prime }{x}_7-{\beta }_1{x}_8\right)W_1}{\sqrt{{\left({\partial }^{\prime }{x}_9+{\partial }^{\prime }{x}_8\right)}^2+{\left({\beta }_1{x}_9+{\partial }^{\prime }{x}_7\right)}^2+{\left({\partial }^{\prime }{x}_7-{\beta }_1{x}_8\right)}^2}}},\hfill \end{array}$$

where ${\displaystyle x_7=\frac{{\mu }_1^2{\partial }^{\prime }{\beta }_1-{\left({\mu }_1{\beta }_1\right)}^{\prime }}{\sqrt{2}},x_8=-\frac{{\left({\mu }_1{\partial }^{\prime }\right)}^{\prime }+{\mu }_1^2\left({\beta }_1^2+{{\partial }^{\prime }}^2\right)}{\sqrt{2}},x_9=\frac{{\left({\mu }_1{\partial }^{\prime }\right)}^{\prime }-{\mu }_1^2{{\partial }^{\prime }}^2}{\sqrt{2}}.}$

Proof. 

If Relation (13) is taken into account, and the required derivatives for the $C_1{W}_1$ curve given in (22) are taken, we have

$$\begin{array}{cc}\hfill {\alpha }_3^{\prime }=& {\displaystyle \frac{-{\mu }_1{\beta }_1{N}_1-{\mu }_1{\partial }^{\prime }{C}_1+{\mu }_1{\partial }^{\prime }{W}_1}{\sqrt{2}}},\hfill \\ \hfill {\alpha }_3^{″}=& x_7{N}_1+x_8{C}_1+x_9{W}_1,\hfill \\ \hfill {\alpha }_3^{‴}=& \left(x_7^{\prime }-x_8{\mu }_1{\beta }_1\right)N_1+\left(x_8^{\prime }+x_7{\mu }_1{\beta }_1-x_9{\mu }_1{\partial }^{\prime }\right)C_1+\left(x_9^{\prime }+x_8{\mu }_1{\partial }^{\prime }\right)W_1.\hfill \end{array}$$

(23)

In addition, if the vector products, determinants and norms are taken, we obtain:

$$\begin{array}{cc}\hfill {\alpha }_3^{\prime }\wedge {\alpha }_3^{″}=& {\displaystyle \frac{{\mu }_1\left(-\left({\partial }^{\prime }{x}_9+{\partial }^{\prime }{x}_8\right)N_1+\left({\beta }_1{x}_9+{\partial }^{\prime }{x}_7\right)C_1+\left({\partial }^{\prime }{x}_7-{\beta }_1{x}_8\right)W_1\right)}{\sqrt{2}}},\hfill \\ \hfill det\left({\alpha }_3^{\prime },{\alpha }_3^{″},{\alpha }_3^{‴}\right)=& {\displaystyle \frac{{\mu }_1}{\sqrt{2}}}\left(\begin{array}{c}\left({\partial }^{\prime }{x}_7-{\beta }_1{x}_8\right)\left(x_9^{\prime }+x_8{\mu }_1{\partial }^{\prime }\right)-\left({\partial }^{\prime }{x}_9+{\partial }^{\prime }{x}_8\right)\left(x_7^{\prime }-x_8{\mu }_1{\beta }_1\right)\hfill \\ +\left({\beta }_1{x}_9+{\partial }^{\prime }{x}_7\right)\left(x_8^{\prime }+x_7{\mu }_1{\beta }_1-x_9{\mu }_1{\partial }^{\prime }\right)\hfill \end{array}\right),\hfill \end{array}$$

(24)

and

$$\begin{array}{cc}\hfill ∥{\alpha }_3^{\prime }∥=& {\displaystyle \frac{{\mu }_1}{\sqrt{2}}}\sqrt{{\beta }_1^2+2{{\partial }^{\prime }}^2},\hfill \\ \hfill ∥{\alpha }_3^{\prime }\wedge {\alpha }_3^{″}∥=& {\displaystyle \frac{{\mu }_1}{\sqrt{2}}}\sqrt{{\left({\partial }^{\prime }{x}_9+{\partial }^{\prime }{x}_8\right)}^2+{\left({\beta }_1{x}_9+{\partial }^{\prime }{x}_7\right)}^2+{\left({\partial }^{\prime }{x}_7-{\beta }_1{x}_8\right)}^2}·\hfill \end{array}$$

(25)

Finally, by substituting Relations (23)–(25) into (1), we complete the proof. □

Theorem 9. 

Let ${\kappa }_{{\alpha }_3}$ and ${\tau }_{{\alpha }_3}$ be the curvature and the torsion functions for the $C_1{W}_1$ Smarandache curve, respectively. Then, we have the following relations among the curvatures:

$$\begin{array}{cc}\hfill {\kappa }_{{\alpha }_3}=& {\displaystyle \frac{2\sqrt{{\left({\partial }^{\prime }{x}_9+{\partial }^{\prime }{x}_8\right)}^2+{\left({\beta }_1{x}_9+{\partial }^{\prime }{x}_7\right)}^2+{\left({\partial }^{\prime }{x}_7-{\beta }_1{x}_8\right)}^2}}{{\mu }_1^2\left({\beta }_1^2+2{{\partial }^{\prime }}^2\right)\sqrt{{\beta }_1^2+2{{\partial }^{\prime }}^2}}},\hfill \\ \hfill {\tau }_{{\alpha }_3}=& {\displaystyle \frac{\sqrt{2}\left(\begin{array}{c}\left({\partial }^{\prime }{x}_7-{\beta }_1{x}_8\right)\left(x_9^{\prime }+x_8{\mu }_1{\partial }^{\prime }\right)-\left({\partial }^{\prime }{x}_9+{\partial }^{\prime }{x}_8\right)\left(x_7^{\prime }-x_8{\mu }_1{\beta }_1\right)\hfill \\ +\left({\beta }_1{x}_9+{\partial }^{\prime }{x}_7\right)\left(x_8^{\prime }+x_7{\mu }_1{\beta }_1-x_9{\mu }_1{\partial }^{\prime }\right)\hfill \end{array}\right)}{{\mu }_1\left({\left({\partial }^{\prime }{x}_9+{\partial }^{\prime }{x}_8\right)}^2+{\left({\beta }_1{x}_9+{\partial }^{\prime }{x}_7\right)}^2+{\left({\partial }^{\prime }{x}_7-{\beta }_1{x}_8\right)}^2\right)}}·\hfill \end{array}$$

Proof. 

By using (24) and (25) and substituting them into (2), we complete the proof. □

Remark 4. 

The alternative frame for the $C_1{W}_1$ Smarandache curve ${\alpha }_3$ is established by the following equations:

$$N_{{\alpha }_3}=N_{{\alpha }_3},C_{{\alpha }_3}=-cos{\partial }_3{T}_{{\alpha }_3}+sin{\partial }_3{B}_{{\alpha }_3},W_{{\alpha }_3}=sin{\partial }_3{T}_{{\alpha }_3}+cos{\partial }_3{B}_{{\alpha }_3}$$

where ${\displaystyle {\partial }_3=\measuredangle \left(B_{{\alpha }_3},W_{{\alpha }_3}\right),}$${\displaystyle cos{\partial }_3=\frac{{\kappa }_{{\alpha }_3}}{\sqrt{{\kappa }_{{\alpha }_3}^2+{\tau }_{{\alpha }_3}^2}},}$ and ${\displaystyle sin{\partial }_3=\frac{{\tau }_{{\alpha }_3}}{\sqrt{{\kappa }_{{\alpha }_3}^2+{\tau }_{{\alpha }_3}^2}}.}$

Definition 5. 

The $N_1{C}_1{W}_1$ Smarandache curve of the alternative N-pedal curve whose position vector is the linear combination of the vectors $N_1$, $C_1$ and $W_1$ is defined by the following parametrization:

$${\alpha }_4={\displaystyle \frac{N_1+C_1+W_1}{\sqrt{3}}}.$$

(26)

Theorem 10. 

Let $\{N_{{\alpha }_4},C_{{\alpha }_4},W_{{\alpha }_4}\}$ denote the alternative frame for the $N_1{C}_1{W}_1$ Smarandache curve. Then, we have the following relations among the Frenet vectors:

$$\begin{array}{cc}\hfill T_{{\alpha }_4}=& {\displaystyle \frac{-{\beta }_1{N}_1+\left({\beta }_1-{\partial }^{\prime }\right)C_1+{\partial }^{\prime }{W}_1}{\sqrt{2}\sqrt{{\beta }_1^2-{\beta }_1{\partial }^{\prime }+{{\partial }^{\prime }}^2}}},\hfill \\ \hfill N_{{\alpha }_4}=& B_{{\alpha }_4}\wedge T_{{\alpha }_4},\hfill \\ \hfill B_{{\alpha }_4}=& {\displaystyle \frac{-\left(x_{11}{\partial }^{\prime }-x_{12}\left({\beta }_1-{\partial }^{\prime }\right)\right)N_1+\left(x_{10}{\partial }^{\prime }+x_{12}{\beta }_1\right)C_1-\left(x_{11}{\beta }_1+x_{10}\left({\beta }_1-{\partial }^{\prime }\right)\right)W_1}{\sqrt{{\left(x_{11}{\partial }^{\prime }-x_{12}\left({\beta }_1-{\partial }^{\prime }\right)\right)}^2+{\left(x_{10}{\partial }^{\prime }+x_{12}{\beta }_1\right)}^2+{\left(x_{11}{\beta }_1+x_{10}\left({\beta }_1-{\partial }^{\prime }\right)\right)}^2}}},\hfill \end{array}$$

where ${\displaystyle x_{10}=\frac{{\left({\mu }_1{\beta }_1\right)}^{\prime }+{\mu }_1^2{\beta }_1\left({\beta }_1-{\partial }^{\prime }\right)}{\sqrt{3}},x_{11}=\frac{{\left({\mu }_1\left({\beta }_1-{\partial }^{\prime }\right)\right)}^{\prime }-{\mu }_1^2\left({\beta }_1^2+{\left({{\partial }_1}^{\prime }\right)}^2\right)}{\sqrt{3}},}$${\displaystyle x_{12}=\frac{{\left({\mu }_1{\partial }^{\prime }\right)}^{\prime }+{\mu }_1^2{\partial }^{\prime }\left({\beta }_1-{\partial }^{\prime }\right)}{\sqrt{3}}.}$

Proof. 

If Relation (13) is taken into account, and the required derivatives for the $N_1{C}_1{W}_1$ curve given in (22) are taken, we have

$$\begin{array}{cc}\hfill {\alpha }_4^{\prime }=& {\displaystyle \frac{{\mu }_1\left(-{\beta }_1{N}_1+\left({\beta }_1-{\partial }^{\prime }\right)C_1+{\partial }^{\prime }{W}_1\right)}{\sqrt{3}}},\hfill \\ \hfill {\alpha }_4^{″}=& x_{10}{N}_1+x_{11}{C}_1+x_{12}{W}_1,\hfill \\ \hfill {\alpha }_4^{‴}=& \left(x_{10}-x_{11}{\mu }_1{\beta }_1\right)N_1+\left(x_{11}+x_{10}{\mu }_1{\beta }_1-x_{12}{\mu }_1{\partial }^{\prime }\right)C_1+\left(x_{12}+x_{11}{\mu }_1{\partial }^{\prime }\right)W_1.\hfill \end{array}$$

(27)

In addition, if the vector products, determinants and norms are taken, we obtain:

$$\begin{array}{cc}\hfill {\alpha }_4^{\prime }\wedge {\alpha }_4^{″}=& {\displaystyle \frac{{\mu }_1\left(\begin{array}{c}-\left(x_{11}{\partial }^{\prime }-x_{12}\left({\beta }_1-{\partial }^{\prime }\right)\right)N_1+\left(x_{10}{\partial }^{\prime }+x_{12}{\beta }_1\right)C_1\hfill \\ -\left(x_{11}{\beta }_1+x_{10}\left({\beta }_1-{\partial }^{\prime }\right)\right)W_1\hfill \end{array}\right)}{\sqrt{3}}},\hfill \\ \hfill det\left({\alpha }_4^{\prime },{\alpha }_4^{″},{\alpha }_4^{‴}\right)=& {\displaystyle \frac{{\mu }_1}{\sqrt{3}}}\left(\begin{array}{c}-\left(x_{11}{\partial }^{\prime }-x_{12}\left({\beta }_1-{\partial }^{\prime }\right)\right)\left(x_{10}-x_{11}{\mu }_1{\beta }_1\right)\hfill \\ +\left(x_{10}{\partial }^{\prime }+x_{12}{\beta }_1\right)\left(x_{11}+x_{10}{\mu }_1{\beta }_1-x_{12}{\mu }_1{\partial }^{\prime }\right)\hfill \\ -\left(x_{11}{\beta }_1+x_{10}\left({\beta }_1-{\partial }^{\prime }\right)\right)\left(x_{12}+x_{11}{\mu }_1{\partial }^{\prime }\right)\hfill \end{array}\right),\hfill \end{array}$$

(28)

and

$$\begin{array}{cc}\hfill ∥{\alpha }_4^{\prime }∥=& {\displaystyle \frac{\sqrt{6}{\mu }_1}{3}}\sqrt{{\beta }_1^2-{\beta }_1{\partial }^{\prime }+{{\partial }^{\prime }}^2},\hfill \\ \hfill ∥{\alpha }_4^{\prime }\wedge {\alpha }_4^{″}∥=& {\displaystyle \frac{{\mu }_1}{\sqrt{3}}}\sqrt{\begin{array}{c}{\left(x_{11}{\partial }^{\prime }-x_{12}\left({\beta }_1-{\partial }^{\prime }\right)\right)}^2+{\left(x_{10}{\partial }^{\prime }+x_{12}{\beta }_1\right)}^2\hfill \\ +{\left(x_{11}{\beta }_1+x_{10}\left({\beta }_1-{\partial }^{\prime }\right)\right)}^2\hfill \end{array}}·\hfill \end{array}$$

(29)

Finally, by substituting Relations (27)–(29) into (1), we complete the proof. □

Theorem 11. 

Let ${\kappa }_{{\alpha }_4}$ and ${\tau }_{{\alpha }_4}$ be the curvature and the torsion functions for the $N_1{C}_1{W}_1$ Smarandache curve, respectively. Then, we have the following relations among the curvatures:

$${\kappa }_{{\alpha }_4}={\displaystyle \frac{3\sqrt{2}}{4}}{\displaystyle \frac{\sqrt{\begin{array}{c}{\left(x_{11}{\partial }^{\prime }-x_{12}\left({\beta }_1-{\partial }^{\prime }\right)\right)}^2+{\left(x_{10}{\partial }^{\prime }+x_{12}{\beta }_1\right)}^2+{\left(x_{11}{\beta }_1+x_{10}\left({\beta }_1-{\partial }^{\prime }\right)\right)}^2\hfill \end{array}}}{{\mu }_1^2\left({\beta }_1^2-{\beta }_1{\partial }^{\prime }+{{\partial }^{\prime }}^2\right)\sqrt{{\beta }_1^2-{\beta }_1{\partial }^{\prime }+{{\partial }^{\prime }}^2}}},$$

$${\tau }_{{\alpha }_4}={\displaystyle \frac{\sqrt{3}\left(\begin{array}{c}-\left(x_{11}{\partial }^{\prime }-x_{12}\left({\beta }_1-{\partial }^{\prime }\right)\right)\left(x_{10}-x_{11}{\mu }_1{\beta }_1\right)\hfill \\ +\left(x_{10}{\partial }^{\prime }+x_{12}{\beta }_1\right)\left(x_{11}+x_{10}{\mu }_1{\beta }_1-x_{12}{\mu }_1{\partial }^{\prime }\right)\hfill \\ -\left(x_{11}{\beta }_1+x_{10}\left({\beta }_1-{\partial }^{\prime }\right)\right)\left(x_{12}+x_{11}{\mu }_1{\partial }^{\prime }\right)\hfill \end{array}\right)}{{\mu }_1\left({\left(x_{11}{\partial }^{\prime }-x_{12}\left({\beta }_1-{\partial }^{\prime }\right)\right)}^2+{\left(x_{10}{\partial }^{\prime }+x_{12}{\beta }_1\right)}^2+{\left(x_{11}{\beta }_1+x_{10}\left({\beta }_1-{\partial }^{\prime }\right)\right)}^2\right)}}.$$

Proof. 

By using (28) and (29) and substituting them into (2), we complete the proof. □

Remark 5. 

The alternative frame for the $N_1{C}_1{W}_1$ Smarandache curve ${\alpha }_4$ is established by the following equations:

$$N_{{\alpha }_4}=N_{{\alpha }_4},C_{{\alpha }_4}=-cos{\partial }_4{T}_{{\alpha }_4}+sin{\partial }_4{B}_{{\alpha }_4},W_{{\alpha }_4}=sin{\partial }_4{T}_{{\alpha }_4}+cos{\partial }_4{B}_{{\alpha }_4}$$

where ${\displaystyle {\partial }_4=\measuredangle \left(B_{{\alpha }_4},W_{{\alpha }_4}\right),}$${\displaystyle cos{\partial }_4=\frac{{\kappa }_{{\alpha }_4}}{\sqrt{{\kappa }_{{\alpha }_4}^2+{\tau }_{{\alpha }_4}^2}},}$ and ${\displaystyle sin{\partial }_4=\frac{{\tau }_{{\alpha }_4}}{\sqrt{{\kappa }_{{\alpha }_4}^2+{\tau }_{{\alpha }_4}^2}}.}$

Example 1. 

Let us consider the polynomial general helix curve parameterized as $\zeta \left(t\right)=(6s,3s^2,s^3)$. The alternative frame vectors and their corresponding pedal curves according to the point $P=(1,1,1)$ are given as follows:

$$\begin{array}{cc}\hfill N=& {\displaystyle \frac{\left(-2s,-s^2+2,2s\right)}{\sqrt{s^2+2}}},C={\displaystyle \frac{\left(s^2-2,-4s,-s^2+2\right)}{\sqrt{2}(s^2+2)}},W={\displaystyle \frac{\left(1,0,1\right)}{\sqrt{2}}},\hfill \end{array}$$

$$\begin{array}{cc}\hfill N-Pedal\Rightarrow {\alpha }_N=& {\displaystyle \frac{\left(s^4+3s^2+6,2s^2\left(s^4+4s^2+12\right),s^3\left(s^4+6s^2+16\right)\right)}{{\left(s^2+2\right)}^2}},\hfill \\ \hfill C-Pedal\Rightarrow {\alpha }_C=& {\displaystyle \frac{\left(s\left(s^6+14s^4+52s^2+24\right),2s^2\left(s^4+4s^2-12\right),s\left(s^6+6s^4+4s^2+24\right)\right)}{2{\left(s^2+2\right)}^2}},\hfill \\ \hfill W-Pedal\Rightarrow {\alpha }_W=& {\displaystyle \frac{\left(4s\left(s^4+6s^2+6\right),s^2\left(3s^4+16s^2+12\right),s^5\left(s^2+4\right)\right)}{{\left(s^2+2\right)}^2}}.\hfill \end{array}$$

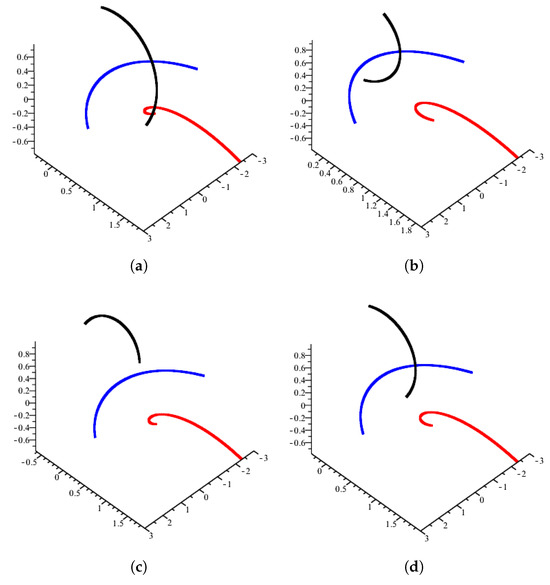
In Figure 3, the four of the Smarandache curves of the alternative N-pedal curve according to the point $P(1,1,1)$ are illustrated.

Figure 3. Smarandache curves (black) of the alternative N-pedal curve (red) of the curve $\zeta \left(t\right)$ (blue) according to the fixed point $P(1,1,1)$ where $t\in [-0.5,0.5]$. (a) $N_1{C}_1$ Smarandache curve; (b) $N_1{W}_1$-Smarandache curve; (c) $C_1{W}_1$ Smarandache curve; (d) $N_1{C}_1{W}_1$ Smarandache curve.

3. The Alternative $\mathbf{C}$-Pedal Curve and Its Smarandache Curves

Similar to the previous section, first, the alternative C-pedal curve resulting from the orthogonal projections of the alternative frame vector C of a given curve according to a fixed point P is defined. Second, we provide the Frenet apparatus of the alternative C-pedal curve and identify the relations among the alternative frame vectors of both the main curve and its corresponding alternative C-pedal curve. Then, we examine four new possible Smarandache curves of the alternative C-pedal curve where the position vectors are taken as the linear combinations of the alternative frame elements. We provide Example 1 and the graphs of these curves.

Definition 6. 

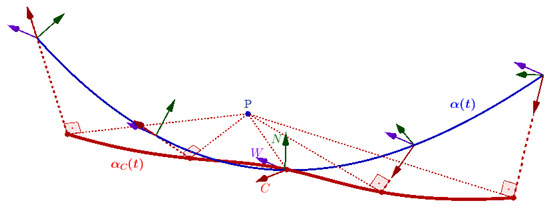
Let $\alpha :I\subset R\to R^3$ be a regular curve in $E^3$ and $\{N,C,W\}$ denote the set of its alternative frame vectors. Then, the locus of the perpendicular projection points of a fixed point P that is not on α onto the alternative frame vector C is called the alternative C-pedal curve for α according to P (Figure 4).

Figure 4. The alternative C-pedal curve (red) of the curve $\alpha \left(t\right)$ (blue) according to a fixed point P.

Theorem 12. 

The equation of the alternative C-pedal curve of the curve α is given as follows:

$${\alpha }_C\left(t\right)=\alpha \left(t\right)+⟨P-\alpha \left(t\right),C\left(t\right)⟩C\left(t\right).$$

(30)

Proof. 

Let $P^{\prime }$ be the perpendicular projection point onto the vector $\overrightarrow{C}$ from the fixed point P that is not on the curve $\alpha$. By using the definition of vector projections, we compute the perpendicular projection vector denoted by $\overrightarrow{\alpha P^{\prime }}$ as follows:

$$\overrightarrow{\alpha P^{\prime }}={\displaystyle \frac{⟨\overrightarrow{\alpha P},\overrightarrow{C}⟩}{⟨\overrightarrow{C},\overrightarrow{C}⟩}}\overrightarrow{C}.$$

Thus, with the motion of the frame vectors along the curve, the geometric location of point $P^{\prime }$ constructs a new curve that is called the alternative C-pedal curve and denoted by ${\alpha }_C\left(t\right)$. Accordingly, we have the following equations.

$$\begin{array}{cc}\hfill \overrightarrow{\alpha P}=\overrightarrow{\alpha P^{\prime }}+\overrightarrow{P^{\prime }P}& \Rightarrow \overrightarrow{\alpha P}={\displaystyle \frac{⟨\overrightarrow{\alpha P},\overrightarrow{C}⟩}{{∥\overrightarrow{C}∥}^2}}\overrightarrow{C}+\overrightarrow{P^{\prime }P}\hfill \\ & \Rightarrow P^{\prime }=\alpha \left(t\right)+⟨\overrightarrow{\alpha P},\overrightarrow{C}⟩\overrightarrow{C}\hfill \\ & \Rightarrow {\alpha }_C\left(t\right)=\alpha \left(t\right)+⟨P-\alpha \left(t\right),C\left(t\right)⟩C\left(t\right),\hfill \end{array}$$

by which the proof is completed. □

If $⟨P-\alpha \left(t\right),C\left(t\right)⟩=\chi \left(t\right)$, then Relation (30) can be expressed as follows:

$${\alpha }_C\left(t\right)=\alpha \left(t\right)+\chi \left(t\right)C\left(t\right).$$

(31)

Theorem 13. 

Let ${\alpha }_C$ be the alternative C-pedal curve of a unit speed curve α, and $\{T_2,N_2,B_2\}$ denote the Frenet vectors of the alternative C-pedal curve. Then, we have the following relations:

$$\begin{array}{cc}\hfill T_2=& -{\omega }_2\chi \beta N+{\omega }_2\left({\chi }^{\prime }-vcos\phi \right)C+{\omega }_2\left(v\chi {\phi }^{\prime }+vsin\phi \right)W\hfill \\ \hfill N_2=& B_2\wedge T_2\hfill \\ \hfill B_2=& {\eta }_2\left(y_3\left({\chi }^{\prime }-vcos\phi \right)-y_2\left(v\chi {\phi }^{\prime }+vsin\phi \right)\right)N+{\eta }_2\left(y_3\chi \beta +y_1\left(v\chi {\phi }^{\prime }+vsin\phi \right)\right)C\hfill \\ & -{\eta }_2\left(y_2\chi \beta +y_1\left({\chi }^{\prime }-vcos\phi \right)\right)W\hfill \end{array}$$

where

$$\begin{array}{cc}\hfill y_1=& -\beta \left(\chi +v{\chi }^{\prime }-v^{2}cos\phi \right),y_2={\chi }^{\prime }-vcos\phi -\chi v{\beta }^2-v^2{\phi }^{\prime }\left(\chi {\phi }^{\prime }+sin\phi \right),\hfill \\ \hfill y_3=& v{\phi }^{\prime }\left({\chi }^{\prime }-vcos\phi \right)+v\left(\chi {\phi }^{\prime }+sin\phi \right),\hfill \\ \hfill {\omega }_2=& {\displaystyle \frac{1}{\sqrt{{\left(\chi \beta \right)}^2+{\left({\chi }^{\prime }-vcos\phi \right)}^2+{\left(v\chi {\phi }^{\prime }+vsin\phi \right)}^2}}},\hfill \\ \hfill {\eta }_2=& {\displaystyle \frac{1}{\sqrt{\begin{array}{c}{\left(y_3\left({\chi }^{\prime }-vcos\phi \right)-y_2\left(v\chi {\phi }^{\prime }+vsin\phi \right)\right)}^2+{\left(y_3\chi \beta +y_1\left(v\chi {\phi }^{\prime }+vsin\phi \right)\right)}^2\hfill \\ +{\left(y_2\chi \beta +y_1\left({\chi }^{\prime }-vcos\phi \right)\right)}^2\hfill \end{array}}}}·\hfill \end{array}$$

Proof. 

By considering the relations in (5), we have the derivatives up to the third degree for Relation (31) as follows:

$$\begin{array}{cc}\hfill {\alpha }_C^{\prime }=& -\chi \beta N+\left({\chi }^{\prime }-vcos\phi \right)C+\left(v\chi {\phi }^{\prime }+vsin\phi \right)W,\hfill \\ \hfill {\alpha }_C^{″}=& y_{1}N+y_{2}C+y_{3}W,\hfill \\ \hfill {\alpha }_C^{‴}=& \left(y_1^{\prime }-v{y}_2\beta \right)N+\left(y_2^{\prime }+y_{1}v\beta -y_{3}v{\phi }^{\prime }\right)C+\left(y_3^{\prime }+y_{2}v{\phi }^{\prime }\right)W.\hfill \end{array}$$

(32)

Further, if we perform the required vector product operations and take the norms, the following relations are obtained:

$$\begin{array}{cc}\hfill {\alpha }_C^{\prime }\wedge {\alpha }_C^{″}=& \left(y_3\left({\chi }^{\prime }-vcos\phi \right)-y_2\left(v\chi {\phi }^{\prime }+vsin\phi \right)\right)N+\left(y_3\chi \beta +y_1\left(v\chi {\phi }^{\prime }+vsin\phi \right)\right)C\hfill \\ \hfill & -\left(y_2\chi \beta +y_1\left({\chi }^{\prime }-vcos\phi \right)\right)W,\hfill \\ \hfill det\left({\alpha }_C^{\prime },{\alpha }_C^{″},{\alpha }_C^{‴}\right)=& \left(y_3\left({\chi }^{\prime }-vcos\phi \right)-y_2\left(v\chi {\phi }^{\prime }+vsin\phi \right)\right)\left(y_1^{\prime }-v{y}_2\beta \right)\hfill \\ \hfill & +\left(y_3\chi \beta +y_1\left(v\chi {\phi }^{\prime }+vsin\phi \right)\right)\left(y_2^{\prime }+y_{1}v\beta -y_{3}v{\phi }^{\prime }\right)\hfill \\ \hfill & -\left(y_2\chi \beta +y_1\left({\chi }^{\prime }-vcos\phi \right)\right)\left(y_3^{\prime }+y_{2}v{\phi }^{\prime }\right)\hfill \end{array}$$

(33)

$$\begin{array}{cc}\hfill ∥{\alpha }_C^{\prime }∥=& \sqrt{{\left(\chi \beta \right)}^2+{\left({\chi }^{\prime }-vcos\phi \right)}^2+{\left(v\chi {\phi }^{\prime }+vsin\phi \right)}^2},\hfill \\ \hfill ∥{\alpha }_C^{\prime }\wedge {\alpha }_C^{″}∥=& \sqrt{\begin{array}{c}{\left(y_3\left({\chi }^{\prime }-vcos\phi \right)-y_2\left(v\chi {\phi }^{\prime }+vsin\phi \right)\right)}^2+{\left(y_3\chi \beta +y_1\left(v\chi {\phi }^{\prime }+vsin\phi \right)\right)}^2\hfill \\ +{\left(y_2\chi \beta +y_1\left({\chi }^{\prime }-vcos\phi \right)\right)}^2\hfill \end{array}}·\hfill \end{array}$$

(34)

If Equations (32)–(34) are substituted in (1), the proof is completed. □

Theorem 14. 

Let ${\alpha }_C$ be the alternative C-pedal curve of the unit speed curve α, and ${\kappa }_2$ and ${\tau }_2$ denote its curvature and torsion functions, respectively. Then, we have the following relations among the curvatures:

$$\begin{array}{cc}\hfill {\kappa }_2=& {\displaystyle \frac{\sqrt{\begin{array}{c}{\left(y_3\left({\chi }^{\prime }-vcos\phi \right)-y_2\left(v\chi {\phi }^{\prime }+vsin\phi \right)\right)}^2+{\left(y_3\chi \beta +y_1\left(v\chi {\phi }^{\prime }+vsin\phi \right)\right)}^2\hfill \\ +{\left(y_2\chi \beta +y_1\left({\chi }^{\prime }-vcos\phi \right)\right)}^2\hfill \end{array}}}{{\left({\left(\chi \beta \right)}^2+{\left({\chi }^{\prime }-vcos\phi \right)}^2+{\left(v\chi {\phi }^{\prime }+vsin\phi \right)}^2\right)}^{\frac{3}{2}}}},\hfill \\ \hfill {\tau }_2=& {\displaystyle \frac{\begin{array}{c}\left(y_3\left({\chi }^{\prime }-vcos\phi \right)-y_2\left(v\chi {\phi }^{\prime }+vsin\phi \right)\right)\left(y_1^{\prime }-v{y}_2\beta \right)\hfill \\ +\left(y_3\chi \beta +y_1\left(v\chi {\phi }^{\prime }+vsin\phi \right)\right)\left(y_2^{\prime }+y_{1}v\beta -y_{3}v{\phi }^{\prime }\right)\hfill \\ -\left(y_2\chi \beta +y_1\left({\chi }^{\prime }-vcos\phi \right)\right)\left(y_3^{\prime }+y_{2}v{\phi }^{\prime }\right)\hfill \end{array}}{\begin{array}{c}{\left(y_3\left({\chi }^{\prime }-vcos\phi \right)-y_2\left(v\chi {\phi }^{\prime }+vsin\phi \right)\right)}^2+{\left(y_3\chi \beta +y_1\left(v\chi {\phi }^{\prime }+vsin\phi \right)\right)}^2\hfill \\ +{\left(y_2\chi \beta +y_1\left({\chi }^{\prime }-vcos\phi \right)\right)}^2\hfill \end{array}}}·\hfill \end{array}$$

Proof. 

We substitute the relations given in (33) and (34) in (2) and complete the proof. □

Remark 6. 

The alternative frame for the alternative C-pedal curve ${\alpha }_C$ is established by the following equations:

$$N_2=N_2,C_2=-cos\Delta T_2+sin\Delta B_2,W_2=sin\Delta T_2+cos\Delta B_2,$$

(35)

where ${\displaystyle \Delta =\measuredangle \left(B_2,W_2\right),}$${\displaystyle cos\Delta =\frac{{\kappa }_2}{\sqrt{{\kappa }_2^2+{\tau }_2^2}},}$ and ${\displaystyle sin\Delta =\frac{{\tau }_2}{\sqrt{{\kappa }_2^2+{\tau }_2^2}}.}$

Corollary 2. 

The alternative frame formulae for the alternative C-pedal curve is given as follows:

$$N_2^{\prime }={\mu }_2{\beta }_2{C}_2,{C^{\prime }}_2=-{\mu }_2{\beta }_2{N}_2+{\mu }_2{\Delta }^{\prime }{W}_2,{W_2}^{\prime }=-{\mu }_2{\Delta }^{\prime }{C}_2,$$

(36)

where ${\displaystyle {\mu }_2=∥{\alpha }_C^{\prime }∥,{\Delta }^{\prime }={\left(\frac{{\tau }_2}{{\kappa }_2}\right)}^{\prime }\left(\frac{{\kappa }_2^2+{\tau }_2^2}{{\kappa }_2^2}\right),{\beta }_2={\mu }_2\sqrt{{\kappa }_2^2+{\tau }_2^2}.}$

Definition 7. 

The $N_2{C}_2$ Smarandache curve of the alternative C-pedal curve whose position vector is the linear combination of the two vectors $N_2$ and $C_2$ is defined by the following parametrization:

$${\delta }_1={\displaystyle \frac{N_2+C_2}{\sqrt{2}}}.$$

(37)

Theorem 15. 

Let $\{N_{{\delta }_1},C_{{\delta }_1},W_{{\delta }_1}\}$ denote the alternative frame for the $N_2{C}_2$ Smarandache curve. Then, we have the following relations among the Frenet vectors:

$$\begin{array}{cc}\hfill T_{{\delta }_1}=& {\displaystyle \frac{\sqrt{2}\left(-{\beta }_2{N}_2+{\beta }_2{C}_2+{\Delta }^{\prime }{W}_2\right)}{\sqrt{2{\beta }_2^2+{{\Delta }^{\prime }}^2}}},\hfill \\ \hfill N_{{\delta }_1}=& B_{{\delta }_1}\wedge T_{{\delta }_1},\hfill \\ \hfill B_{{\delta }_1}=& {\displaystyle \frac{\left(y_6{\beta }_1-y_5{\Delta }^{\prime }\right)N_2+\left(y_6{\beta }_2+y_4{\Delta }^{\prime }\right)C_2-\left({\beta }_2{y}_4+{\beta }_2{y}_5\right)W_2}{\sqrt{{\left(y_6{\beta }_1-y_5{\Delta }^{\prime }\right)}^2+{\left(y_6{\beta }_2+y_4{\Delta }^{\prime }\right)}^2+{\left({\beta }_2{y}_4+{\beta }_2{y}_5\right)}^2}}},\hfill \end{array}$$

where ${\displaystyle y_4=-\frac{{\left({\mu }_2{\beta }_2\right)}^{\prime }+{\mu }_2^2{\beta }_2^2}{\sqrt{2}},y_5=\frac{{\left({\mu }_2{\beta }_2\right)}^{\prime }-{\mu }_2^2\left({\beta }_2^2+{{\Delta }^{\prime }}^2\right)}{\sqrt{2}},y_6=\frac{{\left({\mu }_2{\Delta }^{\prime }\right)}^{\prime }+{\mu }_2^2{\beta }_2{\Delta }^{\prime }}{\sqrt{2}}.}$

Proof. 

If Relation (36) is taken into account, and the required derivatives for the $N_2{C}_2$ curve given in (37) are taken, we have

$$\begin{array}{cc}\hfill {\delta }_1^{\prime }=& {\displaystyle \frac{-{\mu }_2{\beta }_2{N}_2+{\mu }_2{\beta }_2{C}_2+{\mu }_2{\Delta }^{\prime }{W}_2}{\sqrt{2}}},\hfill \\ \hfill {\delta }_1^{″}=& y_4{N}_2+y_5{C}_2+y_6{W}_2,\hfill \\ \hfill {\delta }_1^{‴}=& \left(y_4^{\prime }-y_5{\mu }_2{\beta }_2\right)N_2+\left(y_5^{\prime }+y_4{\mu }_2{\beta }_2-y_6{\mu }_2{\Delta }^{\prime }\right)C_2+\left(y_6^{\prime }+y_5{\mu }_2{\Delta }^{\prime }\right)W_2,\hfill \end{array}$$

(38)

Moreover, if the vector products, determinants and norms are taken, we obtain:

$$\begin{array}{cc}\hfill {\delta }_1^{\prime }\wedge {\delta }_1^{″}=& {\displaystyle \frac{{\mu }_2}{\sqrt{2}}}\left(\left(y_6{\beta }_2-y_5{\Delta }^{\prime }\right)N_2+\left(y_6{\beta }_2+y_4{\Delta }^{\prime }\right)C_2-{\beta }_2\left(y_4+y_5\right)W_2\right),\hfill \\ \hfill det\left({\delta }_1^{\prime },{\delta }_1^{″},{{\delta }^{‴}}_1\right)=& {\displaystyle \frac{{\mu }_2}{\sqrt{2}}}\left(\begin{array}{c}\left(y_4^{\prime }-y_5{\mu }_2{\beta }_2\right)\left(y_6{\beta }_2-y_5{\Delta }^{\prime }\right)\hfill \\ +\left(y_5^{\prime }+y_4{\mu }_2{\beta }_2-y_6{\mu }_2{\Delta }^{\prime }\right)\left(y_6{\beta }_2+y_4{\Delta }^{\prime }\right)\hfill \\ -{\beta }_2\left(y_4+y_5\right)\left(y_6^{\prime }+y_5{\mu }_2{\Delta }^{\prime }\right)\hfill \end{array}\right),\hfill \end{array}$$

(39)

and

$$\begin{array}{cc}\hfill ∥{\delta }_1^{\prime }∥=& {\displaystyle \frac{{\mu }_2}{\sqrt{2}}}\sqrt{2{\beta }_2^2+{{\Delta }^{\prime }}^2},\hfill \\ \hfill ∥{\delta }_1^{\prime }\wedge {\delta }_1^{″}∥=& {\displaystyle \frac{{\mu }_2}{\sqrt{2}}}\sqrt{{\left(y_6{\beta }_2-y_5{\Delta }^{\prime }\right)}^2+{\left(y_6{\beta }_1+y_4{\Delta }^{\prime }\right)}^2+{\left({\beta }_2{y}_4+{\beta }_2{y}_5\right)}^2}·\hfill \end{array}$$

(40)

Finally, by substituting Relations (38)–(40) into (1), we complete the proof. □

Theorem 16. 

Let ${\kappa }_{{\delta }_1}$ and ${\tau }_{{\delta }_1}$ be the curvature and the torsion functions for the $N_2{C}_2$ Smarandache curve, respectively. Then, we have the following relations among the curvatures:

$$\begin{array}{cc}\hfill {\kappa }_{{\delta }_1}=& {\displaystyle \frac{2\sqrt{{\left(y_6{\beta }_2-y_5{\Delta }^{\prime }\right)}^2+{\left(y_6{\beta }_1+y_4{\Delta }^{\prime }\right)}^2+{\left({\beta }_2{y}_4+{\beta }_2{y}_5\right)}^2}}{{\mu }_2^2\left(2{\beta }_2^2+{{\Delta }^{\prime }}^2\right)\sqrt{2{\beta }_2^2+{{\Delta }^{\prime }}^2}}},\hfill \\ \hfill {\tau }_{{\delta }_1}=& {\displaystyle \frac{\sqrt{2}\left(\begin{array}{c}\left(y_4^{\prime }-y_5{\mu }_2{\beta }_2\right)\left(y_6{\beta }_2-y_5{\Delta }^{\prime }\right)+\left(y_5^{\prime }+y_4{\mu }_2{\beta }_2-y_6{\mu }_2{\Delta }^{\prime }\right)\left(y_6{\beta }_2+y_4{\Delta }^{\prime }\right)\hfill \\ -{\beta }_2\left(y_4+y_5\right)\left(y_6^{\prime }+y_5{\mu }_2{\Delta }^{\prime }\right)\hfill \end{array}\right)}{{\mu }_2\left({\left(y_6{\beta }_2-y_5{\Delta }^{\prime }\right)}^2+{\left(y_6{\beta }_1+y_4{\Delta }^{\prime }\right)}^2+{\left({\beta }_2{y}_4+{\beta }_2{y}_5\right)}^2\right)}}.\hfill \end{array}$$

Proof. 

By using (39) and (40) and substituting them into (2), we complete the proof. □

Remark 7. 

The alternative frame for the $N_2{C}_2$ Smarandache curve ${\delta }_1$ is established by the following equations:

$$N_{{\delta }_1}=N_{{\delta }_1},C_{{\delta }_1}=-cos{\Delta }_1{T}_{{\delta }_1}+sin{\Delta }_1{B}_{{\delta }_1},W_{{\delta }_1}=sin{\Delta }_1{T}_{{\delta }_1}+cos{\Delta }_1{B}_{{\delta }_1},$$

where ${\displaystyle {\Delta }_1=\measuredangle \left(B_{{\delta }_1},W_{{\delta }_1}\right),}$${\displaystyle cos{\Delta }_1=\frac{{\kappa }_{{\delta }_1}}{\sqrt{{\kappa }_{{\delta }_1}^2+{\tau }_{{\delta }_1}^2}},}$ and ${\displaystyle sin{\Delta }_1=\frac{{\tau }_{{\delta }_1}}{\sqrt{{\kappa }_{{\delta }_1}^2+{\tau }_{{\delta }_1}^2}}.}$

Definition 8. 

The $N_2{W}_2$ Smarandache curve of the alternative C-pedal curve whose position vector is the linear combination of the two vectors $N_2$ and $W_2$ is defined by the following parametrization:

$${\delta }_2={\displaystyle \frac{N_2+W_2}{\sqrt{2}}}.$$

(41)

Theorem 17. 

Let $\{N_{{\delta }_2},C_{{\delta }_2},W_{{\delta }_2}\}$ denote the alternative frame for the $N_2{W}_2$ Smarandache curve. Then, we have the following relations among the Frenet vectors:

$$T_{{\delta }_2}=C_2,N_{{\delta }_2}={\displaystyle \frac{-{\beta }_2{N}_2+{\Delta }^{\prime }{W}_2}{\sqrt{{{\Delta }^{\prime }}^2+{\beta }_2^2}}},B_{{\delta }_2}={\displaystyle \frac{{\Delta }^{\prime }{N}_2+{\beta }_2{W}_2}{\sqrt{{{\Delta }^{\prime }}^2+{\beta }_2^2}}}.$$

Proof. 

If Relation (36) is taken into account, and the required derivatives for the $N_2{W}_2$ curve given in (41) are taken, we have

$$\begin{array}{cc}\hfill {\delta }_2^{\prime }=& {\displaystyle \frac{{\mu }_2\left({\beta }_2-{\Delta }^{\prime }\right)C_2}{\sqrt{2}}},\hfill \\ \hfill {\delta }_2^{″}=& {\displaystyle \frac{-{\mu }_2^2{\beta }_2\left({\beta }_2-{\Delta }^{\prime }\right)N_2+{\left({\mu }_2\left({\beta }_2-{\Delta }^{\prime }\right)\right)}^{\prime }{C}_2+{\mu }_2^2{\Delta }^{\prime }\left({\beta }_2-{\Delta }^{\prime }\right)W_2}{\sqrt{2}}},\hfill \\ \hfill {{\delta }^{‴}}_2=& {\displaystyle \frac{\begin{array}{c}-\left({\left({\mu }_2^2{\beta }_2\left({\beta }_2-{\Delta }^{\prime }\right)\right)}^{\prime }+{\mu }_2{\beta }_2{\left(\left({\mu }_2{\beta }_2-{\mu }_2{\Delta }^{\prime }\right)\right)}^{\prime }\right)N_2\hfill \\ +\left({\left(\left({\mu }_2{\beta }_2-{\mu }_2{\Delta }^{\prime }\right)\right)}^{″}-{\mu }_2^3\left({\beta }_2^2+{{\Delta }^{\prime }}^2\right)\left({\beta }_2-{\Delta }^{\prime }\right)\right)C_2\hfill \\ +\left({\mu }_2{\Delta }^{\prime }{\left({\mu }_2\left({\beta }_2-{\Delta }^{\prime }\right)\right)}^{\prime }+{\left({\mu }_2^2{\Delta }^{\prime }\left({\beta }_2-{\Delta }^{\prime }\right)\right)}^{\prime }\right)W_2\hfill \end{array}}{\sqrt{2}}}.\hfill \end{array}$$

(42)

Moreover, if the vector products, determinants and norms are taken, we obtain:

$$\begin{array}{cc}\hfill {\delta }_2^{\prime }\wedge {\delta }_2^{″}=& {\displaystyle \frac{{\mu }_2^3{\Delta }^{\prime }{\left({\beta }_2-{\Delta }^{\prime }\right)}^2{N}_2+{\mu }_2^3{\beta }_2{\left({\beta }_2-{\Delta }^{\prime }\right)}^2{W}_2}{2}},\hfill \\ \hfill det\left({\delta }_2^{\prime },{\delta }_2^{″},{\delta }_2^{‴}\right)=& {\displaystyle \frac{{\mu }_2^5{\left({\beta }_2-{\Delta }^{\prime }\right)}^3\left({\beta }_2{\Delta }^{″}-{\Delta }^{\prime }{\beta }_2^{\prime }\right)}{2\sqrt{2}}},\hfill \end{array}$$

(43)

and

$$\begin{array}{cc}\hfill ∥{\delta }_2^{\prime }∥=& {\displaystyle \frac{{\mu }_2\left({\beta }_2-{\Delta }^{\prime }\right)}{\sqrt{2}}},\hfill \\ \hfill ∥{\delta }_2^{\prime }\wedge {\delta }_2^{″}∥=& {\displaystyle \frac{{\left({\beta }_2-{\Delta }^{\prime }\right)}^2{\mu }_2^3\sqrt{{{\Delta }^{\prime }}^2+{\beta }_2^2}}{2}}.\hfill \end{array}$$

(44)

Finally, by substituting Relations (42)–(44) into (1), we complete the proof. □

Theorem 18. 

Let ${\kappa }_{{\delta }_2}$ and ${\tau }_{{\delta }_2}$ be the curvature and the torsion functions for the $N_2{W}_2$ Smarandache curve, respectively. Then, we have the following relations among the curvatures:

$${\kappa }_{{\delta }_2}={\displaystyle \frac{\sqrt{2}\sqrt{{{\Delta }^{\prime }}^2+{\beta }_2^2}}{{\beta }_2-{\Delta }^{\prime }}},{\tau }_{{\delta }_2}={\displaystyle \frac{\sqrt{2}\left({\beta }_2{\Delta }^{″}-{\Delta }^{\prime }{\beta }_2^{\prime }\right)}{{\mu }_2\left({\beta }_2-{\Delta }^{\prime }\right)\left({{\Delta }^{\prime }}^2+{\beta }_2^2\right)}}.$$

Proof. 

By using (43) and (44) and substituting them into (2), we complete the proof. □

Remark 8. 

The alternative frame for the $N_2{W}_2$ Smarandache curve ${\delta }_2$ is established by the following equations:

$$N_{{\delta }_2}=N_{{\delta }_2},C_{{\delta }_2}=-cos{\Delta }_2{T}_{{\delta }_2}+sin{\Delta }_2{B}_{{\delta }_2},W_{{\delta }_2}=sin{\Delta }_2{T}_{{\delta }_2}+cos{\Delta }_2{B}_{{\delta }_2},$$

where ${\displaystyle {\Delta }_2=\measuredangle \left(B_{{\delta }_2},W_{{\delta }_2}\right),}$${\displaystyle cos{\Delta }_2=\frac{{\kappa }_{{\delta }_2}}{\sqrt{{\kappa }_{{\delta }_2}^2+{\tau }_{{\delta }_2}^2}},}$ and ${\displaystyle sin{\Delta }_2=\frac{{\tau }_{{\delta }_2}}{\sqrt{{\kappa }_{{\delta }_2}^2+{\tau }_{{\delta }_2}^2}}.}$

Definition 9. 

The $C_2{W}_2$ Smarandache curve of the alternative C-pedal curve whose position vector is the linear combination of the two vectors $C_2$ and $W_2$ is defined by the following parametrization:

$${\delta }_3={\displaystyle \frac{C_2+W_2}{\sqrt{2}}}.$$

(45)

Theorem 19. 

Let $\{N_{{\delta }_3},C_{{\delta }_3},W_{{\delta }_3}\}$ denote the alternative frame for the $C_2{W}_2$ Smarandache curve. Then, we have the following relations among the Frenet vectors:

$$\begin{array}{cc}\hfill T_{{\delta }_3}=& {\displaystyle \frac{-{\beta }_2{N}_2-{\Delta }^{\prime }{C}_2+{\Delta }^{\prime }{W}_2}{\sqrt{{\beta }_2^2+2{{\Delta }^{\prime }}^2}}},\hfill \\ \hfill N_{{\delta }_3}=& B_{{\delta }_3}\wedge T_{{\delta }_3},\hfill \\ \hfill B_{{\delta }_3}=& {\displaystyle \frac{-\left({\Delta }^{\prime }{y}_9+{\Delta }^{\prime }{y}_8\right)N_2+\left({\beta }_2{y}_9+{\Delta }^{\prime }{y}_7\right)C_2+\left({\Delta }^{\prime }{y}_7-{\beta }_2{y}_8\right)W_2}{\sqrt{{\left({\Delta }^{\prime }{y}_9+{\Delta }^{\prime }{y}_8\right)}^2+{\left({\beta }_2{y}_9+{\Delta }^{\prime }{y}_7\right)}^2+{\left({\Delta }^{\prime }{y}_7-{\beta }_2{y}_8\right)}^2}}},\hfill \end{array}$$

where ${\displaystyle y_7=\frac{{\mu }_2^2{\Delta }^{\prime }{\beta }_2-{\left({\mu }_2{\beta }_2\right)}^{\prime }}{\sqrt{2}},y_8=-\frac{{\left({\mu }_2{\Delta }^{\prime }\right)}^{\prime }+{\mu }_2^2\left({\beta }_2^2+{{\Delta }^{\prime }}^2\right)}{\sqrt{2}},y_9=\frac{{\left({\mu }_2{\Delta }^{\prime }\right)}^{\prime }-{\mu }_2^2{{\Delta }^{\prime }}^2}{\sqrt{2}}.}$

Proof. 

If Relation (36) is taken into account, and the required derivatives for the $C_2{W}_2$ curve given in (45) are taken, we have

$$\begin{array}{cc}\hfill {\delta }_3^{\prime }=& {\displaystyle \frac{-{\mu }_2{\beta }_2{N}_2-{\mu }_2{\Delta }^{\prime }{C}_2+{\mu }_2{\Delta }^{\prime }{W}_2}{\sqrt{2}}},\hfill \\ \hfill {\delta }_3^{″}=& y_7{N}_2+y_8{C}_2+y_9{W}_2,\hfill \\ \hfill {\delta }_3^{‴}=& \left(y_7^{\prime }-y_8{\mu }_2{\beta }_2\right)N_2+\left(y_8^{\prime }+y_7{\mu }_2{\beta }_2-y_9{\mu }_2{\Delta }^{\prime }\right)C_2+\left(y_9^{\prime }+y_8{\mu }_2{\Delta }^{\prime }\right)W_2.\hfill \end{array}$$

(46)

Moreover, if the vector products, determinants and norms are taken, we obtain:

$$\begin{array}{cc}\hfill {\delta }_3^{\prime }\wedge {\delta }_3^{″}=& {\displaystyle \frac{{\mu }_2\left(-{\Delta }^{\prime }\left(y_9+y_8\right)N_2+\left({\beta }_2{y}_9+{\Delta }^{\prime }{y}_7\right)C_2+\left({\Delta }^{\prime }{y}_7-{\beta }_2{y}_8\right)W_2\right)}{\sqrt{2}}},\hfill \\ \hfill det\left({\delta }_3^{\prime },{\delta }_3^{″},{\delta }_3^{‴}\right)=& {\displaystyle \frac{{\mu }_2}{\sqrt{2}}}\left(\begin{array}{c}\left({\Delta }^{\prime }{y}_7-{\beta }_2{y}_8\right)\left(y_9^{\prime }+y_8{\mu }_2{\Delta }^{\prime }\right)-{\Delta }^{\prime }\left(y_9+y_8\right)\left(y_7^{\prime }-y_8{\mu }_2{\beta }_2\right)\hfill \\ +\left({\beta }_2{y}_9+{\Delta }^{\prime }{y}_7\right)\left(y_8^{\prime }+y_7{\mu }_2{\beta }_2-y_9{\mu }_2{\Delta }^{\prime }\right)\hfill \end{array}\right),\hfill \end{array}$$

(47)

and

$$\begin{array}{cc}\hfill ∥{\delta }_3^{\prime }∥=& {\displaystyle \frac{{\mu }_2}{\sqrt{2}}}\sqrt{{\beta }_2^2+2{{\Delta }^{\prime }}^2},\hfill \\ \hfill ∥{\delta }_3^{\prime }\wedge {\delta }_3^{″}∥=& {\displaystyle \frac{{\mu }_2}{\sqrt{2}}}\sqrt{{\left({\Delta }^{\prime }{y}_9+{\Delta }^{\prime }{y}_8\right)}^2+{\left({\beta }_2{y}_9+{\Delta }^{\prime }{y}_7\right)}^2+{\left({\Delta }^{\prime }{y}_7-{\beta }_2{y}_8\right)}^2}·\hfill \end{array}$$

(48)

Finally, by substituting Relations (46)–(48) into (1), we complete the proof. □

Theorem 20. 

Let ${\kappa }_{{\delta }_3}$ and ${\tau }_{{\delta }_3}$ be the curvature and the torsion functions for the $C_2{W}_2$ Smarandache curve, respectively. Then, we have the following relations among the curvatures:

$$\begin{array}{cc}\hfill {\kappa }_{{\delta }_3}=& {\displaystyle \frac{2\sqrt{{\left({\Delta }^{\prime }{y}_9+{\Delta }^{\prime }{y}_8\right)}^2+{\left({\beta }_2{y}_9+{\Delta }^{\prime }{y}_7\right)}^2+{\left({\Delta }^{\prime }{y}_7-{\beta }_2{y}_8\right)}^2}}{{\mu }_2^2\left({\beta }_2^2+2{{\Delta }^{\prime }}^2\right)\sqrt{{\beta }_2^2+2{{\Delta }^{\prime }}^2}}},\hfill \\ \hfill {\tau }_{{\delta }_3}=& {\displaystyle \frac{\sqrt{2}\left(\begin{array}{c}\left({\Delta }^{\prime }{y}_7-{\beta }_2{y}_8\right)\left(y_9^{\prime }+y_8{\mu }_2{\Delta }^{\prime }\right)-{\Delta }^{\prime }\left(y_9+y_8\right)\left(y_7^{\prime }-y_8{\mu }_2{\beta }_2\right)\hfill \\ +\left({\beta }_2{y}_9+{\Delta }^{\prime }{y}_7\right)\left(y_8^{\prime }+y_7{\mu }_2{\beta }_2-y_9{\mu }_2{\Delta }^{\prime }\right)\hfill \end{array}\right)}{{\mu }_2\left({\left({\Delta }^{\prime }{y}_9+{\Delta }^{\prime }{y}_8\right)}^2+{\left({\beta }_2{y}_9+{\Delta }^{\prime }{y}_7\right)}^2+{\left({\Delta }^{\prime }{y}_7-{\beta }_2{y}_8\right)}^2\right)}}.\hfill \end{array}$$

Proof. 

By using (47) and (48) and substituting them into (2), we complete the proof. □

Remark 9. 

The alternative frame for the $C_2{W}_2$ Smarandache curve ${\delta }_3$ is established by the following equations:

$$N_{{\delta }_3}=N_{{\delta }_3},C_{{\delta }_3}=-cos{\Delta }_3{T}_{{\delta }_3}+sin{\Delta }_3{B}_{{\delta }_3},W_{{\delta }_3}=sin{\Delta }_3{T}_{{\delta }_3}+cos{\Delta }_3{B}_{{\delta }_3},$$

where ${\displaystyle {\Delta }_3=\measuredangle \left(B_{{\delta }_3},W_{{\delta }_3}\right),}$${\displaystyle cos{\Delta }_3=\frac{{\kappa }_{{\delta }_3}}{\sqrt{{\kappa }_{{\delta }_3}^2+{\tau }_{{\delta }_3}^2}},}$ and ${\displaystyle sin{\Delta }_3=\frac{{\tau }_{{\delta }_3}}{\sqrt{{\kappa }_{{\delta }_3}^2+{\tau }_{{\delta }_3}^2}}.}$

Definition 10. 

The $N_2{C}_2{W}_2$ Smarandache curve of the alternative C-pedal curve whose position vector is the linear combination of the vectors $N_2$, $C_2$ and $W_2$ is defined by the following parametrization:

$${\delta }_4={\displaystyle \frac{N_2+C_2+W_2}{\sqrt{3}}}.$$

(49)

Theorem 21. 

Let $\{N_{{\delta }_4},C_{{\delta }_4},W_{{\delta }_4}\}$ denote the alternative frame for the $N_2{C}_2{W}_2$ Smarandache curve. Then, we have the following relations among the Frenet vectors:

$$\begin{array}{c}{T}_{{\delta }_4}={\displaystyle \frac{-{\beta }_2{N}_2+\left({\beta }_2-{\Delta }^{\prime }\right)C_2+{\Delta }^{\prime }{W}_2}{\sqrt{2}\sqrt{{\beta }_2^2-{\beta }_2{\Delta }^{\prime }+{{\Delta }^{\prime }}^2}}},\hfill \\ N_{{\delta }_4}=B_{{\alpha }_4}\wedge T_{{\delta }_4},\hfill \\ B_{{\delta }_4}={\displaystyle \frac{-\left(y_{11}{\Delta }^{\prime }-y_{12}\left({\beta }_2-{\Delta }^{\prime }\right)\right)N_2+\left(y_{10}{\Delta }^{\prime }+y_{12}{\beta }_2\right)C_2-\left(y_{11}{\beta }_2+y_{10}\left({\beta }_2-{\Delta }^{\prime }\right)\right)W_2}{\sqrt{{\left(y_{11}{\Delta }^{\prime }-y_{12}\left({\beta }_2-{\Delta }^{\prime }\right)\right)}^2+{\left(y_{10}{\Delta }^{\prime }+y_{12}{\beta }_2\right)}^2+{\left(y_{11}{\beta }_2+y_{10}\left({\beta }_2-{\Delta }^{\prime }\right)\right)}^2}}}\hfill \end{array}$$

where ${\displaystyle y_{10}=\frac{{\left({\mu }_1{\beta }_1\right)}^{\prime }+{\mu }_1^2{\beta }_1\left({\beta }_1-{\partial }^{\prime }\right)}{\sqrt{3}},y_{11}=\frac{{\left({\mu }_1\left({\beta }_1-{\partial }^{\prime }\right)\right)}^{\prime }-{\mu }_1^2\left({\beta }_1^2+{\left({{\partial }_1}^{\prime }\right)}^2\right)}{\sqrt{3}},}$${\displaystyle y_{12}=\frac{{\left({\mu }_1{\partial }^{\prime }\right)}^{\prime }+{\mu }_1^2{\partial }^{\prime }\left({\beta }_1-{\partial }^{\prime }\right)}{\sqrt{3}}.}$

Proof. 

If Relation (36) is taken into account, and the required derivatives for the $N_2{C}_2{W}_2$ curve given in (49) are taken, we have

$$\begin{array}{cc}\hfill {\delta }_4^{\prime }=& {\displaystyle \frac{{\mu }_2\left(-{\beta }_2{N}_2+\left({\beta }_2-{\Delta }^{\prime }\right)C_2+{\Delta }^{\prime }{W}_2\right)}{\sqrt{3}}},\hfill \\ \hfill {\delta }_4^{″}=& y_{10}{N}_2+y_{11}{C}_2+y_{12}{W}_2,\hfill \\ \hfill {\delta }_4^{‴}=& \left(y_{10}-y_{11}{\mu }_2{\beta }_2\right)N_2+\left(y_{11}+y_{10}{\mu }_2{\beta }_2-y_{12}{\mu }_2{\Delta }^{\prime }\right)C_2+\left(y_{12}+y_{11}{\mu }_2{\Delta }^{\prime }\right)W_2.\hfill \end{array}$$

(50)

Moreover, if the vector products, determinants and norms are taken, we obtain:

$$\begin{array}{cc}\hfill {\delta }_4^{\prime }\wedge {\delta }_4^{″}=& {\displaystyle \frac{{\mu }_2\left(\begin{array}{c}-\left(y_{11}{\Delta }^{\prime }-y_{12}\left({\beta }_2-{\Delta }^{\prime }\right)\right)N_2+\left(y_{10}{\Delta }^{\prime }+y_{12}{\beta }_2\right)C_2\hfill \\ -\left(y_{11}{\beta }_2+y_{10}\left({\beta }_2-{\Delta }^{\prime }\right)\right)W_2\hfill \end{array}\right)}{\sqrt{3}}},\hfill \\ \hfill det\left({\delta }_4^{\prime },{\delta }_4^{″},{\delta }_4^{‴}\right)=& {\displaystyle \frac{{\mu }_2}{\sqrt{3}}}\left(\begin{array}{c}-\left(y_{11}{\Delta }^{\prime }-y_{12}\left({\beta }_2-{\Delta }^{\prime }\right)\right)\left(y_{10}-y_{11}{\mu }_2{\beta }_2\right)\hfill \\ +\left(y_{10}{\Delta }^{\prime }+y_{12}{\beta }_2\right)\left(y_{11}+y_{10}{\mu }_2{\beta }_2-y_{12}{\mu }_2{\Delta }^{\prime }\right)\hfill \\ -\left(y_{11}{\beta }_2+y_{10}\left({\beta }_2-{\Delta }^{\prime }\right)\right)\left(y_{12}+y_{11}{\mu }_2{\Delta }^{\prime }\right)\hfill \end{array}\right),\hfill \end{array}$$

(51)

and

$$\begin{array}{cc}\hfill ∥{\delta }_4^{\prime }∥=& {\displaystyle \frac{\sqrt{6}{\mu }_2}{3}}\sqrt{{\beta }_2^2-{\beta }_2{\Delta }^{\prime }+{{\Delta }^{\prime }}^2},\hfill \\ \hfill ∥{\delta }_4^{\prime }\wedge {\delta }_4^{″}∥=& {\displaystyle \frac{{\mu }_2}{\sqrt{3}}}\sqrt{{\left(y_{11}{\Delta }^{\prime }-y_{12}\left({\beta }_2-{\Delta }^{\prime }\right)\right)}^2+{\left(y_{10}{\Delta }^{\prime }+y_{12}{\beta }_2\right)}^2+{\left(y_{11}{\beta }_2+y_{10}\left({\beta }_2-{\Delta }^{\prime }\right)\right)}^2}.\hfill \end{array}$$

(52)

Finally, by substituting Relations (50)–(52) into (1), we complete the proof. □

Theorem 22. 

Let ${\kappa }_{{\delta }_4}$ and ${\tau }_{{\delta }_4}$ be the curvature and the torsion functions for the $N_2{C}_2{W}_2$ Smarandache curve, respectively. Then, we have the following relations among the curvatures:

$$\begin{array}{cc}\hfill {\kappa }_{{\delta }_4}=& {\displaystyle \frac{3\sqrt{2}}{4}}{\displaystyle \frac{\sqrt{{\left(y_{11}{\Delta }^{\prime }-y_{12}\left({\beta }_2-{\Delta }^{\prime }\right)\right)}^2+{\left(y_{10}{\Delta }^{\prime }+y_{12}{\beta }_2\right)}^2+{\left(y_{11}{\beta }_2+y_{10}\left({\beta }_2-{\Delta }^{\prime }\right)\right)}^2}}{{\mu }_2^2\left({\beta }_2^2-{\beta }_2{\Delta }^{\prime }+{{\Delta }^{\prime }}^2\right)\sqrt{{\beta }_2^2-{\beta }_2{\Delta }^{\prime }+{{\Delta }^{\prime }}^2}}},\hfill \\ \hfill {\tau }_{{\delta }_4}=& {\displaystyle \frac{\sqrt{3}\left(\begin{array}{c}-\left(y_{11}{\Delta }^{\prime }-y_{12}\left({\beta }_2-{\Delta }^{\prime }\right)\right)\left(y_{10}-y_{11}{\mu }_2{\beta }_2\right)\hfill \\ +\left(y_{10}{\Delta }^{\prime }+y_{12}{\beta }_2\right)\left(y_{11}+y_{10}{\mu }_2{\beta }_2-y_{12}{\mu }_2{\Delta }^{\prime }\right)\hfill \\ -\left(y_{11}{\beta }_2+y_{10}\left({\beta }_2-{\Delta }^{\prime }\right)\right)\left(y_{12}+y_{11}{\mu }_2{\Delta }^{\prime }\right)\hfill \end{array}\right)}{{\mu }_2\left({\left(y_{11}{\Delta }^{\prime }-y_{12}\left({\beta }_2-{\Delta }^{\prime }\right)\right)}^2+{\left(y_{10}{\Delta }^{\prime }+y_{12}{\beta }_2\right)}^2+{\left(y_{11}{\beta }_2+y_{10}\left({\beta }_2-{\Delta }^{\prime }\right)\right)}^2\right)}}·\hfill \end{array}$$

Proof. 

By using (51) and (52) and substituting them into (2), we complete the proof. □

Remark 10. 

The alternative frame for the $N_2{C}_2{W}_2$ Smarandache curve ${\delta }_4$ is established by the following equations:

$$N_{{\delta }_4}=N_{{\delta }_4},C_{{\delta }_4}=-cos{\Delta }_4{T}_{{\delta }_4}+sin{\Delta }_4{B}_{{\delta }_4},W_{{\delta }_4}=sin{\Delta }_4{T}_{{\delta }_4}+cos{\Delta }_4{B}_{{\delta }_4},$$

where ${\Delta }_4=\measuredangle \left(B_{{\delta }_4},W_{{\delta }_4}\right),$$cos{\Delta }_4={\displaystyle \frac{{\kappa }_{{\delta }_4}}{\sqrt{{\kappa }_{{\delta }_4}^2+{\tau }_{{\delta }_4}^2}}},$ and $sin{\Delta }_4={\displaystyle \frac{{\tau }_{{\delta }_4}}{\sqrt{{\kappa }_{{\delta }_4}^2+{\tau }_{{\delta }_4}^2}}}.$

By using Example 1, Smarandache curves of the alternative C-pedal curve according to the point $P(1,1,1)$ are illustrated in Figure 5.

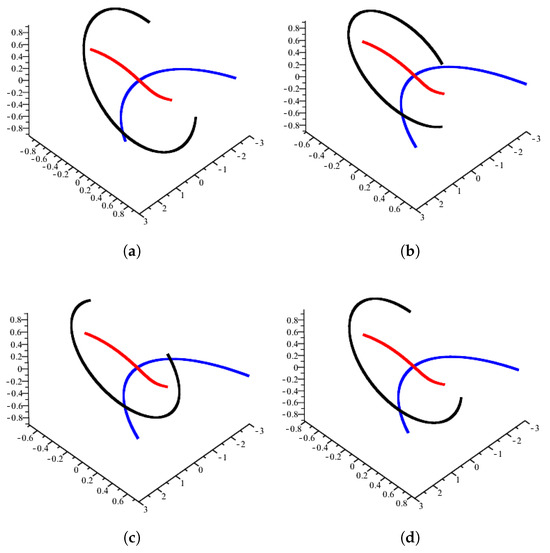
Figure 5. Smarandache curves (black) of the alternative C-pedal curve (red) of the curve $\zeta \left(t\right)$ (blue) according to the fixed point $P(1,1,1)$ where $t\in [-0.5,0.5]$. (a) $N_2{C}_2$ Smarandache curve; (b) $N_2{W}_2$ Smarandache curve; (c) $C_2{W}_2$ Smarandache curve; (d) $N_2{C}_2{W}_2$ Smarandache curve.

4. The Alternative $\mathbf{W}$-Pedal Curve and Its Smarandache Curves

We deal with the last vector W of alternative frame to define the alternative W-pedal curve in this section and determine the Frenet apparatus of this curve. Similarly, the relations among the alternative frame vectors of both the main curve and the alternative W-pedal curve are computed, and the Smarandache curves of the alternative W-pedal curve are defined. The invariants of each Smarandache curve are expressed by the invariants of the alternative W-pedal curve. Example 1 is applied to the alternative W-pedal curve and each curve is illustrated.

Definition 11. 

Let $\alpha :I\subset R\to R^3$ be a regular curve in $E^3$ and $\{N,C,W\}$ denote the set of its alternative frame vectors. Then, the locus of the perpendicular projection points of a fixed point P that is not on α onto the alternative frame vector W is called the alternative W-pedal curve for α according to P (Figure 6).

Figure 6. The alternative W-pedal curve (red) of the curve $\alpha \left(t\right)$ (blue) according to a fixed point P.

Theorem 23. 

The equation of the alternative W-pedal curve of the curve α is given as follows:

$${\alpha }_W\left(t\right)=\alpha \left(t\right)+⟨P-\alpha \left(t\right),W\left(t\right)⟩W\left(t\right).$$

(53)

Proof. 

Let $P^{\prime }$ be the perpendicular projection point onto the vector $\overrightarrow{W}$ from the fixed point P that is not on the curve $\alpha$. By using the definition of vector projections, we compute the perpendicular projection vector denoted by $\overrightarrow{\alpha P^{\prime }}$ as follows:

$$\overrightarrow{\alpha P^{\prime }}={\displaystyle \frac{⟨\overrightarrow{\alpha P},\overrightarrow{W}⟩}{⟨\overrightarrow{W},\overrightarrow{W}⟩}}\overrightarrow{W}.$$

Thus, with the motion of the frame vectors along the curve, the geometric location of point $P^{\prime }$ constructs a new curve that is called the alternative W-pedal curve and denoted by ${\alpha }_W\left(t\right)$. Accordingly, we have the following equations:

$$\begin{array}{cc}\hfill \overrightarrow{\alpha P}=\overrightarrow{\alpha P^{\prime }}+\overrightarrow{P^{\prime }P}& \Rightarrow \overrightarrow{\alpha P}={\displaystyle \frac{⟨\overrightarrow{\alpha P},\overrightarrow{W}⟩}{{∥\overrightarrow{W}∥}^2}}\overrightarrow{W}+\overrightarrow{P^{\prime }P}\hfill \\ & \Rightarrow P^{\prime }=\alpha \left(t\right)+⟨\overrightarrow{\alpha P},\overrightarrow{W}⟩\overrightarrow{W}\hfill \\ & \Rightarrow {\alpha }_W\left(t\right)=\alpha \left(t\right)+⟨P-\alpha \left(t\right),W\left(t\right)⟩W\left(t\right),\hfill \end{array}$$

by which the proof is completed. □

If $⟨P-\alpha \left(t\right),W\left(t\right)⟩=\varsigma \left(t\right)$, then Relation (53) can be expressed as follows:

$${\alpha }_W\left(t\right)=\alpha \left(t\right)+\varsigma \left(t\right)W\left(t\right).$$

(54)

Theorem 24. 

Let ${\alpha }_W$ be the alternative W-pedal curve of a unit speed curve α, and $\{T_3,N_3,B_3\}$ denote the Frenet vectors of the alternative W-pedal curve. Then, we have the following relations:

$$\begin{array}{cc}\hfill T_3=& -{\omega }_3\varsigma \beta N+{\omega }_3\left({\varsigma }^{\prime }-vcos\phi \right)C+{\omega }_3\left(v\varsigma {\phi }^{\prime }+vsin\phi \right)W,\hfill \\ \hfill N_3=& B_3\wedge T_3,\hfill \\ \hfill B_3=& {\eta }_3\left(z_3\left({\varsigma }^{\prime }-vcos\phi \right)-z_2\left(v\varsigma {\phi }^{\prime }+vsin\phi \right)\right)N+{\eta }_2\left(z_3\varsigma \beta +z_1\left(v\varsigma {\phi }^{\prime }+vsin\phi \right)\right)C\hfill \\ & -{\eta }_3\left(z_2\varsigma \beta +z_1\left({\varsigma }^{\prime }-vcos\phi \right)\right)W,\hfill \end{array}$$

where

$$\begin{array}{cc}\hfill z_1=& -\beta \left(\varsigma +v{\varsigma }^{\prime }-v^{2}cos\phi \right),z_2={\varsigma }^{\prime }-vcos\phi -\varsigma v{\beta }^2-v^2{\phi }^{\prime }\left(\varsigma {\phi }^{\prime }+sin\phi \right),\hfill \\ \hfill z_3=& v{\phi }^{\prime }\left({\varsigma }^{\prime }-vcos\phi \right)+v\left(\varsigma {\phi }^{\prime }+sin\phi \right),\hfill \\ \hfill {\omega }_3=& {\displaystyle \frac{1}{\sqrt{{\left(\varsigma \beta \right)}^2+{\left({\varsigma }^{\prime }-vcos\phi \right)}^2+{\left(v\varsigma {\phi }^{\prime }+vsin\phi \right)}^2}}},\hfill \\ \hfill {\eta }_3=& {\displaystyle \frac{1}{\sqrt{\begin{array}{c}{\left(z_3\left({\varsigma }^{\prime }-vcos\phi \right)-z_2\left(v\varsigma {\phi }^{\prime }+vsin\phi \right)\right)}^2+{\left(z_3\varsigma \beta +z_1\left(v\varsigma {\phi }^{\prime }+vsin\phi \right)\right)}^2\hfill \\ +{\left(z_2\varsigma \beta +z_1\left({\varsigma }^{\prime }-vcos\phi \right)\right)}^2\hfill \end{array}}}}.\hfill \end{array}$$

Proof. 

By considering the relations in (5), we have the derivatives up to the third degree for Relation (54) as follows:

$$\begin{array}{cc}\hfill {\alpha }_W^{\prime }=& -\varsigma \beta N+\left({\varsigma }^{\prime }-vcos\phi \right)C+\left(v\varsigma {\phi }^{\prime }+vsin\phi \right)W,\hfill \\ \hfill {\alpha }_W^{″}=& z_{1}N+z_{2}C+z_{3}W,\hfill \\ \hfill {\alpha }_W^{‴}=& \left(z_1^{\prime }-v{z}_2\beta \right)N+\left(z_2^{\prime }+z_{1}v\beta -z_{3}v{\phi }^{\prime }\right)C+\left(z_3^{\prime }+z_{2}v{\phi }^{\prime }\right)W,\hfill \end{array}$$

(55)

Further, if we perform the required vector product operations and take the norms, the following relations are obtained.

$$\begin{array}{cc}\hfill {\alpha }_W^{\prime }\wedge {\alpha }_W^{″}=& \left(z_3\left({\varsigma }^{\prime }-vcos\phi \right)-z_2\left(v\varsigma {\phi }^{\prime }+vsin\phi \right)\right)N\hfill \\ \hfill & +\left(z_3\varsigma \beta +z_1\left(v\varsigma {\phi }^{\prime }+vsin\phi \right)\right)C\hfill \\ \hfill & -\left(z_2\varsigma \beta +z_1\left({\varsigma }^{\prime }-vcos\phi \right)\right)W,\hfill \\ \hfill det\left({\alpha }_W^{\prime },{\alpha }_W^{″},{\alpha }_W^{‴}\right)=& \left(z_3\left({\varsigma }^{\prime }-vcos\phi \right)-z_2\left(v\varsigma {\phi }^{\prime }+vsin\phi \right)\right)\left(z_1^{\prime }-v{z}_2\beta \right)\hfill \\ \hfill & +\left(z_3\varsigma \beta +z_1\left(v\varsigma {\phi }^{\prime }+vsin\phi \right)\right)\left(z_2^{\prime }+z_{1}v\beta -z_{3}v{\phi }^{\prime }\right)\hfill \\ \hfill & -\left(z_2\varsigma \beta +z_1\left({\varsigma }^{\prime }-vcos\phi \right)\right)\left(z_3^{\prime }+z_{2}v{\phi }^{\prime }\right),\hfill \end{array}$$

(56)

$$\begin{array}{cc}\hfill ∥{\alpha }_W^{\prime }∥=& \sqrt{{\left(\varsigma \beta \right)}^2+{\left({\varsigma }^{\prime }-vcos\phi \right)}^2+{\left(v\varsigma {\phi }^{\prime }+vsin\phi \right)}^2},\hfill \\ \hfill ∥{\alpha }_W^{\prime }\wedge {\alpha }_W^{″}∥=& \sqrt{\begin{array}{c}{\left(z_3\left({\varsigma }^{\prime }-vcos\phi \right)-z_2\left(v\varsigma {\phi }^{\prime }+vsin\phi \right)\right)}^2+{\left(z_3\varsigma \beta +z_1\left(v\varsigma {\phi }^{\prime }+vsin\phi \right)\right)}^2\hfill \\ +{\left(z_2\varsigma \beta +z_1\left({\varsigma }^{\prime }-vcos\phi \right)\right)}^2\hfill \end{array}}.\hfill \end{array}$$

(57)

If Equations (55)–(57) are substituted in (1), the proof is completed. □

Theorem 25. 

Let ${\alpha }_W$ be the alternative W-pedal curve of the unit speed curve α, and ${\kappa }_3$ and ${\tau }_3$ denote its curvature and torsion functions, respectively. Then, we have the following relations among the curvatures.

$$\begin{array}{cc}\hfill {\kappa }_3=& {\displaystyle \frac{\sqrt{\begin{array}{c}{\left(z_3\left({\varsigma }^{\prime }-vcos\phi \right)-z_2\left(v\varsigma {\phi }^{\prime }+vsin\phi \right)\right)}^2+{\left(z_3\varsigma \beta +z_1\left(v\varsigma {\phi }^{\prime }+vsin\phi \right)\right)}^2\hfill \\ +{\left(z_2\varsigma \beta +z_1\left({\varsigma }^{\prime }-vcos\phi \right)\right)}^2\hfill \end{array}}}{{\left({\left(\varsigma \beta \right)}^2+{\left({\varsigma }^{\prime }-vcos\phi \right)}^2+{\left(v\varsigma {\phi }^{\prime }+vsin\phi \right)}^2\right)}^{\frac{3}{2}}}},\hfill \\ \hfill {\tau }_3=& {\displaystyle \frac{\begin{array}{c}\left(z_3\left({\varsigma }^{\prime }-vcos\phi \right)-z_2\left(v\varsigma {\phi }^{\prime }+vsin\phi \right)\right)\left(z_1^{\prime }-v{z}_2\beta \right)\hfill \\ +\left(z_3\varsigma \beta +z_1\left(v\varsigma {\phi }^{\prime }+vsin\phi \right)\right)\left(z_2^{\prime }+z_{1}v\beta -z_{3}v{\phi }^{\prime }\right)\hfill \\ -\left(z_2\varsigma \beta +z_1\left({\varsigma }^{\prime }-vcos\phi \right)\right)\left(z_3^{\prime }+z_{2}v{\phi }^{\prime }\right)\left(y_3^{\prime }+y_{2}v{\phi }^{\prime }\right)\hfill \end{array}}{\begin{array}{c}{\left(z_3\left({\varsigma }^{\prime }-vcos\phi \right)-z_2\left(v\varsigma {\phi }^{\prime }+vsin\phi \right)\right)}^2+{\left(z_3\varsigma \beta +z_1\left(v\varsigma {\phi }^{\prime }+vsin\phi \right)\right)}^2\hfill \\ +{\left(z_2\varsigma \beta +z_1\left({\varsigma }^{\prime }-vcos\phi \right)\right)}^2\hfill \end{array}}}·\hfill \end{array}$$

Proof. 

We substitute the relations given in (56) and (57) in (2) and complete the proof. □

Remark 11. 

The alternative frame for the alternative W-pedal curve ${\alpha }_W$ is established by the following equations:

$$N_3=N_3,C_3=-cos\psi T_3+sin\psi B_3,W_2=sin\psi T_3+cos\psi B_3,$$

(58)

where ${\displaystyle \psi =\measuredangle \left(B_3,W_3\right),}$${\displaystyle cos\psi =\frac{{\kappa }_3}{\sqrt{{\kappa }_3^2+{\tau }_3^2}},}$ and ${\displaystyle sin\psi =\frac{{\tau }_3}{\sqrt{{\kappa }_3^2+{\tau }_3^2}}.}$

Corollary 3. 

The alternative frame formulae for the alternative W-pedal curve is given as follows:

$$N_3^{\prime }={\mu }_3{\beta }_3{C}_3,C_3^{\prime }=-{\mu }_3{\beta }_3{N}_3+{\mu }_3{\psi }^{\prime }{W}_3,{W_3}^{\prime }=-{\mu }_3{\psi }^{\prime }{C}_3,$$

(59)

where ${\displaystyle {\mu }_3=∥{\alpha }_W^{\prime }∥,{\psi }^{\prime }={\left(\frac{{\tau }_3}{{\kappa }_3}\right)}^{\prime }\left(\frac{{\kappa }_3^2+{\tau }_3^2}{{\kappa }_3^2}\right),{\beta }_3={\mu }_3\sqrt{{\kappa }_3^2+{\tau }_3^2}.}$

Definition 12. 

The $N_3{C}_3$ Smarandache curve of the alternative W-pedal curve whose position vector is the linear combination of the two vectors $N_3$ and $C_3$ is defined by the following parametrization:

$${\xi }_1={\displaystyle \frac{N_3+C_3}{\sqrt{2}}}.$$

(60)

Theorem 26. 

Let $\{N_{{\xi }_1},C_{{\xi }_1},W_{{\xi }_1}\}$ denote the alternative frame for the $N_3{C}_3$ Smarandache curve. Then, we have the following relations among the Frenet vectors:

$$\begin{array}{cc}\hfill T_{{\xi }_1}=& {\displaystyle \frac{\sqrt{2}\left(-{\beta }_3{N}_3+{\beta }_3{C}_3+{\psi }^{\prime }{W}_3\right)}{\sqrt{2{\beta }_3^2+{{\psi }^{\prime }}^2}}},\hfill \\ \hfill N_{{\xi }_1}=& B_{{\xi }_1}\wedge T_{{\xi }_1},\hfill \\ \hfill B_{{\xi }_1}=& {\displaystyle \frac{\left(z_6{\beta }_3-z_5{\psi }^{\prime }\right)N_3+\left(z_6{\beta }_3+z_4{\psi }^{\prime }\right)C_3-\left(z_4{\beta }_3+z_5{\beta }_3\right)W_3}{\sqrt{{\left(z_6{\beta }_3-z_5{\psi }^{\prime }\right)}^2+{\left(z_6{\beta }_3+z_4{\psi }^{\prime }\right)}^2+{\left(z_4{\beta }_3+z_5{\beta }_3\right)}^2}}},\hfill \end{array}$$

where ${\displaystyle z_4=-\frac{{\left({\mu }_3{\beta }_3\right)}^{\prime }+{\mu }_3^2{\beta }_3^2}{\sqrt{2}},z_5=\frac{{\left({\mu }_3{\beta }_3\right)}^{\prime }-{\mu }_3^2\left({\beta }_3^2+{{\psi }^{\prime }}^2\right)}{\sqrt{2}},z_6=\frac{{\left({\mu }_3{\psi }^{\prime }\right)}^{\prime }+{\mu }_3^2{\beta }_3{\psi }^{\prime }}{\sqrt{2}}.}$

Proof. 

If Relation (59) is taken into account, and the required derivatives for the $N_3{C}_3$ curve given in (60) are taken, we have

$$\begin{array}{cc}\hfill {\xi }_1^{\prime }=& {\displaystyle \frac{-{\mu }_3{\beta }_3{N}_2+{\mu }_3{\beta }_3{C}_2+{\mu }_3{\Delta }^{\prime }{W}_2}{\sqrt{2}}},\hfill \\ \hfill {\xi }_1^{″}=& z_4{N}_3+z_5{C}_3+z_6{W}_3,\hfill \\ \hfill {\xi }_1^{‴}=& \left(z_4^{\prime }-z_5{\mu }_3{\beta }_3\right)N_3+\left(z_5^{\prime }+z_4{\mu }_3{\beta }_3-z_6{\mu }_3{\psi }^{\prime }\right)C_3+\left(z_6^{\prime }+z_5{\mu }_3{\psi }^{\prime }\right)W_3.\hfill \end{array}$$

(61)

Moreover, if the vector products, determinants and norms are taken, we obtain:

$$\begin{array}{c}{\xi }_1^{\prime }\wedge {\xi }_1^{″}={\displaystyle \frac{{\mu }_3}{\sqrt{2}}}\left(\left(z_6{\beta }_3-z_5{\psi }^{\prime }\right)N_3+\left(z_6{\beta }_3+z_4{\psi }^{\prime }\right)C_3-{\beta }_3\left(z_4+z_5\right)W_3\right),\hfill \\ det\left({\xi }_1^{\prime },{\xi }_1^{″},{\xi }_1^{‴}\right)={\displaystyle \frac{{\mu }_3}{\sqrt{2}}}\left(\begin{array}{c}\left(z_4^{\prime }-z_5{\mu }_3{\beta }_3\right)\left(z_6{\beta }_3-z_5{\psi }^{\prime }\right)\hfill \\ +\left(z_5^{\prime }+z_4{\mu }_3{\beta }_3-z_6{\mu }_3{\psi }^{\prime }\right)\left(z_6{\beta }_3+z_4{\psi }^{\prime }\right)\hfill \\ -{\beta }_3\left(z_4+z_5\right)\left(z_6^{\prime }+z_5{\mu }_3{\psi }^{\prime }\right)\hfill \end{array}\right),\hfill \end{array}$$

(62)

and

$$\begin{array}{c}∥{\xi }_1^{\prime }∥={\displaystyle \frac{{\mu }_3}{\sqrt{2}}}\sqrt{2{\beta }_3^2+{{\psi }^{\prime }}^2},\hfill \\ ∥{\xi }_1^{\prime }\wedge {\xi }_1^{″}∥={\displaystyle \frac{{\mu }_3}{\sqrt{2}}}\sqrt{{\left(z_6{\beta }_3-z_5{\psi }^{\prime }\right)}^2+{\left(z_6{\beta }_3+z_4{\psi }^{\prime }\right)}^2+{\left(z_4{\beta }_3+z_5{\beta }_3\right)}^2}.\hfill \end{array}$$

(63)

Finally, by substituting Relations (61)–(63) into (1), we complete the proof. □

Theorem 27. 

Let ${\kappa }_{{\xi }_1}$ and ${\tau }_{{\xi }_1}$ be the curvature and the torsion functions for the $N_3{C}_3$ Smarandache curve, respectively. Then, we have the following relations among the curvatures:

$$\begin{array}{cc}\hfill {\kappa }_{{\xi }_1}=& {\displaystyle \frac{2\sqrt{{\left(z_6{\beta }_3-z_5{\psi }^{\prime }\right)}^2+{\left(z_6{\beta }_3+z_4{\psi }^{\prime }\right)}^2+{\left(z_4{\beta }_3+z_5{\beta }_3\right)}^2}}{{\mu }_3^2\left(2{\beta }_3^2+{{\psi }^{\prime }}^2\right)\sqrt{2{\beta }_3^2+{{\psi }^{\prime }}^2}}},\hfill \\ \hfill {\tau }_{{\xi }_1}=& {\displaystyle \frac{\sqrt{2}\left(\begin{array}{c}\left(z_4^{\prime }-z_5{\mu }_3{\beta }_3\right)\left(z_6{\beta }_3-z_5{\psi }^{\prime }\right)+\left(z_5^{\prime }+z_4{\mu }_3{\beta }_3-z_6{\mu }_3{\psi }^{\prime }\right)\left(z_6{\beta }_3+z_4{\psi }^{\prime }\right)\hfill \\ -{\beta }_3\left(z_4+z_5\right)\left(z_6^{\prime }+z_5{\mu }_3{\psi }^{\prime }\right)\hfill \end{array}\right)}{{\mu }_3\left({\left(z_6{\beta }_3-z_5{\psi }^{\prime }\right)}^2+{\left(z_6{\beta }_3+z_4{\psi }^{\prime }\right)}^2+{\left(z_4{\beta }_3+z_5{\beta }_3\right)}^2\right)}}.\hfill \end{array}$$

Proof. 

By using (62) and (63) and substituting them into (2), we complete the proof. □

Remark 12. 

The alternative frame for the $N_3{C}_3$ Smarandache curve ${\xi }_1$ is established by the following equations:

$$N_{{\xi }_1}=N_{{\xi }_1},C_{{\xi }_1}=-cos{\Delta }_1{T}_{{\xi }_1}+sin{\Delta }_1{B}_{{\xi }_1},W_{{\xi }_1}=sin{\Delta }_1{T}_{{\xi }_1}+cos{\Delta }_1{B}_{{\xi }_1},$$

where ${\displaystyle {\Delta }_1=\measuredangle \left(B_{{\xi }_1},W_{{\xi }_1}\right),}$${\displaystyle cos{\Delta }_1=\frac{{\kappa }_{{\xi }_1}}{\sqrt{{\kappa }_{{\xi }_1}^2+{\tau }_{{\xi }_1}^2}},}$ and ${\displaystyle sin{\Delta }_1=\frac{{\tau }_{{\xi }_1}}{\sqrt{{\kappa }_{{\xi }_1}^2+{\tau }_{{\xi }_1}^2}}.}$

Definition 13. 

The $N_3{W}_3$ Smarandache curve of the alternative W-pedal curve whose position vector is the linear combination of the two vectors $N_3$ and $W_3$ is defined by the following parametrization:

$${\xi }_2={\displaystyle \frac{N_3+W_3}{\sqrt{2}}}.$$

(64)

Theorem 28. 

Let $\{N_{{\xi }_2},C_{{\xi }_2},W_{{\xi }_2}\}$ denote the alternative frame for the $N_3{W}_3$ Smarandache curve. Then, we have the following relations among the Frenet vectors:

$$T_{{\xi }_2}=C_2,N_{{\xi }_2}={\displaystyle \frac{-{\beta }_3{N}_3+{\psi }^{\prime }{W}_3}{\sqrt{{{\psi }^{\prime }}^2+{\beta }_3^2}}},B_{{\xi }_2}={\displaystyle \frac{{\psi }^{\prime }{N}_3+{\beta }_3{W}_3}{\sqrt{{{\psi }^{\prime }}^2+{\beta }_3^2}}}.$$

Proof. 

If Relation (59) is taken into account, and the required derivatives for the $N_3{W}_3$ curve given in (64) are taken, we have

$$\begin{array}{cc}\hfill {\xi }_2^{\prime }=& {\displaystyle \frac{{\mu }_3\left({\beta }_3-{\psi }^{\prime }\right)C_3}{\sqrt{2}}},\hfill \\ \hfill {\xi }_2^{″}=& {\displaystyle \frac{-{\mu }_3^2{\beta }_3\left({\beta }_3-{\psi }^{\prime }\right)N_3+{\left({\mu }_3\left({\beta }_3-{\psi }^{\prime }\right)\right)}^{\prime }{C}_3+{\mu }_3^2{\psi }^{\prime }\left({\beta }_3-{\psi }^{\prime }\right)W_3}{\sqrt{2}}},\hfill \\ \hfill {\xi }_2^{‴}=& {\displaystyle \frac{\begin{array}{c}-\left({\left({\mu }_3^2{\beta }_3\left({\beta }_3-{\psi }^{\prime }\right)\right)}^{\prime }+{\mu }_3{\beta }_3{\left(\left({\mu }_3{\beta }_3-{\mu }_3{\psi }^{\prime }\right)\right)}^{\prime }\right)N_3\hfill \\ +\left({\left(\left({\mu }_3{\beta }_3-{\mu }_3{\psi }^{\prime }\right)\right)}^{″}-{\mu }_3^3\left({\beta }_3^2+{{\psi }^{\prime }}^2\right)\left({\beta }_3-{\psi }^{\prime }\right)\right)C_3\hfill \\ +\left({\mu }_3{\psi }^{\prime }{\left({\mu }_3\left({\beta }_3-{\psi }^{\prime }\right)\right)}^{\prime }+{\left({\mu }_3^2{\psi }^{\prime }\left({\beta }_3-{\psi }^{\prime }\right)\right)}^{\prime }\right)W_3\hfill \end{array}}{\sqrt{2}}}.\hfill \end{array}$$

(65)

Moreover, if the vector products, determinants and norms are taken, we obtain:

$$\begin{array}{cc}\hfill {\xi }_2^{\prime }\wedge {\xi }_2^{″}=& {\displaystyle \frac{{\mu }_3^3{\psi }^{\prime }{\left({\beta }_3-{\psi }^{\prime }\right)}^2{N}_3+{\mu }_3^3{\beta }_3{\left({\beta }_3-{\psi }^{\prime }\right)}^2{W}_3}{2}},\hfill \\ \hfill det\left({\xi }_2^{\prime },{\xi }_2^{″},{\xi }_2^{‴}\right)=& {\displaystyle \frac{{\mu }_3^5{\left({\beta }_3-{\psi }^{\prime }\right)}^3\left({\beta }_3{\psi }^{″}-{\psi }^{\prime }{\beta }_3^{\prime }\right)}{2\sqrt{2}}},\hfill \end{array}$$

(66)

and

$$\begin{array}{cc}\hfill ∥{\xi }_2^{\prime }∥=& {\displaystyle \frac{{\mu }_3\left({\beta }_3-{\psi }^{\prime }\right)}{\sqrt{2}}},\hfill \\ \hfill ∥{\xi }_2^{\prime }\wedge {\xi }_2^{″}∥=& {\displaystyle \frac{{\left({\beta }_3-{\psi }^{\prime }\right)}^2{\mu }_3^3\sqrt{{{\psi }^{\prime }}^2+{\beta }_3^2}}{2}}.\hfill \end{array}$$

(67)

Finally, by substituting Relations (65)–(67) into (1), we complete the proof. □

Theorem 29. 

Let ${\kappa }_{{\xi }_2}$ and ${\tau }_{{\xi }_2}$ be the curvature and the torsion functions for the $N_3{W}_3$ Smarandache curve, respectively. Then, we have the following relations among the curvatures:

$${\kappa }_{{\xi }_2}={\displaystyle \frac{\sqrt{2}\sqrt{{{\Delta }^{\prime }}^2+{\beta }_2^2}}{{\beta }_2-{\Delta }^{\prime }}},{\tau }_{{\xi }_2}={\displaystyle \frac{\sqrt{2}\left({\beta }_3{\psi }^{″}-{\psi }^{\prime }{\beta }_3^{\prime }\right)}{{\mu }_3\left({\beta }_3-{\psi }^{\prime }\right)\left({{\psi }^{\prime }}^2+{\beta }_3^2\right)}}.$$

Proof. 

By using (66) and (67) and substituting them into (2), we complete the proof. □

Remark 13. 

The alternative frame for the $N_3{W}_3$ Smarandache curve ${\xi }_2$ is established by the following equations:

$$N_{{\xi }_2}=N_{{\xi }_2},C_{{\xi }_2}=-cos{\Delta }_2{T}_{{\xi }_2}+sin{\Delta }_2{B}_{{\xi }_2},W_{{\xi }_2}=sin{\Delta }_2{T}_{{\xi }_2}+cos{\Delta }_2{B}_{{\xi }_2},$$

where ${\displaystyle {\Delta }_2=\measuredangle \left(B_{{\xi }_2},W_{{\xi }_2}\right),}$${\displaystyle cos{\Delta }_2=\frac{{\kappa }_{{\xi }_2}}{\sqrt{{\kappa }_{{\xi }_2}^2+{\tau }_{{\xi }_2}^2}},}$ and ${\displaystyle sin{\Delta }_2=\frac{{\tau }_{{\xi }_2}}{\sqrt{{\kappa }_{{\xi }_2}^2+{\tau }_{{\xi }_2}^2}}.}$

Definition 14. 

The $C_3{W}_3$ Smarandache curve of the alternative W-pedal curve whose position vector is the linear combination of the two vectors $C_3$ and $W_3$ is defined by the following parametrization:

$${\xi }_3={\displaystyle \frac{C_3+W_3}{\sqrt{2}}}.$$

(68)

Theorem 30. 

Let $\{N_{{\xi }_3},C_{{\xi }_3},W_{{\xi }_3}\}$ denote the alternative frame for the $C_3{W}_3$ Smarandache curve. Then, we have the following relations among the Frenet vectors:

$$\begin{array}{cc}\hfill T_{{\xi }_3}=& {\displaystyle \frac{-{\beta }_3{N}_3-{\psi }^{\prime }{C}_3+{\psi }^{\prime }{W}_3}{\sqrt{{\beta }_3^2+2{{\psi }^{\prime }}^2}}},\hfill \\ \hfill N_{{\xi }_3}=& B_{{\xi }_3}\wedge T_{{\xi }_3},\hfill \\ \hfill B_{{\xi }_3}=& {\displaystyle \frac{-\left({\psi }^{\prime }{z}_9+{\psi }^{\prime }{z}_8\right)N_3+\left({\beta }_3{z}_9+{\psi }^{\prime }{z}_7\right)C_3+\left({\psi }^{\prime }{z}_7-{\beta }_3{z}_8\right)W_3}{\sqrt{{\left({\psi }^{\prime }{z}_9+{\psi }^{\prime }{z}_8\right)}^2+{\left({\beta }_3{z}_9+{\psi }^{\prime }{z}_7\right)}^2+{\left({\psi }^{\prime }{z}_7-{\beta }_3{z}_8\right)}^2}}},\hfill \end{array}$$

where ${\displaystyle z_7=\frac{{\mu }_3^2{\psi }^{\prime }{\beta }_3-{\left({\mu }_3{\beta }_3\right)}^{\prime }}{\sqrt{2}},z_8=-\frac{{\left({\mu }_3{\psi }^{\prime }\right)}^{\prime }+{\mu }_3^2\left({\beta }_3^2+{{\psi }^{\prime }}^2\right)}{\sqrt{2}},z_9=\frac{{\left({\mu }_3{\psi }^{\prime }\right)}^{\prime }-{\mu }_3^2{{\psi }^{\prime }}^2}{\sqrt{2}}.}$

Proof. 

If Relation (59) is taken into account, and the required derivatives for the $C_3{W}_3$ curve given in (68) are taken, we have

$$\begin{array}{cc}\hfill {\xi }_3^{\prime }=& {\displaystyle \frac{-{\mu }_3{\beta }_3{N}_3-{\mu }_3{\psi }^{\prime }{C}_3+{\mu }_3{\psi }^{\prime }{W}_3}{\sqrt{2}}},\hfill \\ \hfill {\xi }_3^{″}=& z_7{N}_3+z_8{C}_3+z_9{W}_3,\hfill \\ \hfill {\xi }_3^{‴}=& \left(z_7^{\prime }-z_8{\mu }_3{\beta }_3\right)N_3+\left(z_8^{\prime }+z_7{\mu }_3{\beta }_3-z_9{\mu }_3{\psi }^{\prime }\right)C_3+\left(z_9^{\prime }+z_8{\mu }_3{\psi }^{\prime }\right)W_3.\hfill \end{array}$$

(69)

Moreover, if the vector products, determinants and norms are taken, we obtain:

$$\begin{array}{cc}\hfill {\xi }_3^{\prime }\wedge {\xi }_3^{″}=& {\displaystyle \frac{{\mu }_3\left(-{\psi }^{\prime }\left(z_9+z_8\right)N_3+\left({\beta }_3{z}_9+{\psi }^{\prime }{z}_7\right)C_3+\left({\psi }^{\prime }{z}_7-{\beta }_3{z}_8\right)W_3\right)}{\sqrt{2}}},\hfill \\ \hfill det\left({\xi }_3^{\prime },{\xi }_3^{″},{\xi }_3^{‴}\right)=& {\displaystyle \frac{{\mu }_3}{\sqrt{2}}}\left(\begin{array}{c}\left({\psi }^{\prime }{z}_7-{\beta }_3{z}_8\right)\left(z_9^{\prime }+z_8{\mu }_3{\Delta }^{\prime }\right)-{\psi }^{\prime }\left(z_9+z_8\right)\left(z_7^{\prime }-z_8{\mu }_3{\beta }_3\right)\hfill \\ +\left({\beta }_3{z}_9+{\psi }^{\prime }{z}_7\right)\left(z_8^{\prime }+z_7{\mu }_3{\beta }_3-z_9{\mu }_3{\psi }^{\prime }\right)\hfill \end{array}\right),\hfill \end{array}$$

(70)

and

$$\begin{array}{cc}\hfill ∥{\xi }_3^{\prime }∥=& {\displaystyle \frac{{\mu }_3}{\sqrt{2}}}\sqrt{{\beta }_3^2+2{{\psi }^{\prime }}^2},\hfill \\ \hfill ∥{\xi }_3^{\prime }\wedge {\xi }_3^{″}∥=& {\displaystyle \frac{{\mu }_3}{\sqrt{2}}}\sqrt{{\left({\psi }^{\prime }{x}_9+{\psi }^{\prime }{x}_8\right)}^2+{\left({\beta }_3{z}_9+{\psi }^{\prime }{z}_7\right)}^2+{\left({\psi }^{\prime }{z}_7-{\beta }_3{z}_8\right)}^2}.\hfill \end{array}$$

(71)

Finally, by substituting Relations (69)–(71) into (1), we complete the proof. □

Theorem 31. 

Let ${\kappa }_{{\xi }_3}$ and ${\tau }_{{\xi }_3}$ be the curvature and the torsion functions for the $C_3{W}_3$ Smarandache curve, respectively. Then, we have the following relations among the curvatures:

$$\begin{array}{cc}\hfill {\kappa }_{{\xi }_3}=& {\displaystyle \frac{2\sqrt{{\left({\psi }^{\prime }{z}_9+{\psi }^{\prime }{z}_8\right)}^2+{\left({\beta }_3{z}_9+{\psi }^{\prime }{z}_7\right)}^2+{\left({\psi }^{\prime }{z}_7-{\beta }_3{z}_8\right)}^2}}{{\mu }_3^2\left({\beta }_3^2+2{{\psi }^{\prime }}^2\right)\sqrt{{\beta }_3^2+2{{\psi }^{\prime }}^2}}},\hfill \\ \hfill {\tau }_{{\xi }_3}=& {\displaystyle \frac{\sqrt{2}\left(\begin{array}{c}\left({\psi }^{\prime }{z}_7-{\beta }_3{z}_8\right)\left(z_9^{\prime }+z_8{\mu }_3{\Delta }^{\prime }\right)-{\psi }^{\prime }\left(z_9+z_8\right)\left(z_7^{\prime }-z_8{\mu }_3{\beta }_3\right)\hfill \\ +\left({\beta }_3{z}_9+{\psi }^{\prime }{z}_7\right)\left(z_8^{\prime }+z_7{\mu }_3{\beta }_3-z_9{\mu }_3{\psi }^{\prime }\right)\hfill \end{array}\right)}{{\mu }_3\left({\left({\psi }^{\prime }{z}_9+{\psi }^{\prime }{z}_8\right)}^2+{\left({\beta }_3{z}_9+{\psi }^{\prime }{z}_7\right)}^2+{\left({\psi }^{\prime }{z}_7-{\beta }_3{z}_8\right)}^2\right)}}.\hfill \end{array}$$

Proof. 

By using (70) and (71) and substituting them into (2), we complete the proof. □

Remark 14. 

The alternative frame for the $C_3{W}_3$ Smarandache curve ${\xi }_3$ is established by the following equations:

$$N_{{\xi }_3}=N_{{\xi }_3},C_{{\xi }_3}=-cos{\Delta }_3{T}_{{\xi }_3}+sin{\Delta }_3{B}_{{\xi }_3},W_{{\xi }_3}=sin{\Delta }_3{T}_{{\xi }_3}+cos{\Delta }_3{B}_{{\xi }_3},$$

where ${\displaystyle {\Delta }_3=\measuredangle \left(B_{{\xi }_3},W_{{\xi }_3}\right),}$${\displaystyle cos{\Delta }_3=\frac{{\kappa }_{{\xi }_3}}{\sqrt{{\kappa }_{{\xi }_3}^2+{\tau }_{{\xi }_3}^2}},}$ and ${\displaystyle sin{\Delta }_3=\frac{{\tau }_{{\xi }_3}}{\sqrt{{\kappa }_{{\xi }_3}^2+{\tau }_{{\xi }_3}^2}}.}$

Definition 15. 

The $N_3{C}_3{W}_3$ Smarandache curve of the alternative W-pedal curve whose position vector is the linear combination of the vectors $N_3$, $C_3$ and $W_3$ is defined by the following parametrization:

$${\xi }_4={\displaystyle \frac{N_3+C_3+W_3}{\sqrt{2}}}.$$

(72)

Theorem 32. 

Let $\{N_{{\xi }_4},C_{{\xi }_4},W_{{\xi }_4}\}$ denote the alternative frame for the $N_3{C}_3{W}_3$ Smarandache curve. Then, we have the following relations among the Frenet vectors:

$$\begin{array}{cc}\hfill T_{{\xi }_4}=& {\displaystyle \frac{-{\beta }_3{N}_3+\left({\beta }_3-{\psi }^{\prime }\right)C_3+{\psi }^{\prime }{W}_3}{\sqrt{2}\sqrt{{\beta }_3^2-{\beta }_3{\psi }^{\prime }+{{\psi }^{\prime }}^2}}},\hfill \\ \hfill N_{{\xi }_4}=& B_{{\xi }_4}\wedge T_{{\xi }_4},\hfill \\ \hfill B_{{\xi }_4}=& {\displaystyle \frac{-\left(z_{11}{\psi }^{\prime }-z_{12}\left({\beta }_3-{\psi }^{\prime }\right)\right)N_3+\left(z_{10}{\psi }^{\prime }+z_{12}{\beta }_3\right)C_3-\left(z_{11}{\beta }_3+z_{10}\left({\beta }_3-{\psi }^{\prime }\right)\right)W_2}{\sqrt{{\left(z_{11}{\psi }^{\prime }-z_{12}\left({\beta }_3-{\psi }^{\prime }\right)\right)}^2+{\left(z_{10}{\psi }^{\prime }+z_{12}{\beta }_3\right)}^2+{\left(z_{11}{\beta }_3+z_{10}\left({\beta }_3-{\psi }^{\prime }\right)\right)}^2}}},\hfill \end{array}$$

where ${\displaystyle z_{10}=\frac{{\left({\mu }_3{\beta }_3\right)}^{\prime }+{\mu }_3^2{\beta }_3\left({\beta }_3-{\psi }^{\prime }\right)}{\sqrt{3}},z_{11}=\frac{{\left({\mu }_3\left({\beta }_3-{\psi }^{\prime }\right)\right)}^{\prime }-{\mu }_3^2\left({\beta }_3^2+{{\psi }^{\prime }}^2\right)}{\sqrt{3}},}$ ${\displaystyle z_{12}=\frac{{\left({\mu }_3{\psi }^{\prime }\right)}^{\prime }+{\mu }_3^2{\psi }^{\prime }\left({\beta }_3-{\psi }^{\prime }\right)}{\sqrt{3}}.}$

Proof. 

If Relation (59) is taken into account, and the required derivatives for the $N_3{C}_3{W}_3$ curve given in (72) are taken, we have

$$\begin{array}{cc}\hfill {\xi }_4^{\prime }=& {\displaystyle \frac{{\mu }_3\left(-{\beta }_3{N}_3+\left({\beta }_3-{\psi }^{\prime }\right)C_3+{\psi }^{\prime }{W}_3\right)}{\sqrt{3}}},\hfill \\ \hfill {\xi }_4^{″}=& z_{10}{N}_3+z_{11}{C}_3+z_{12}{W}_3,\hfill \\ \hfill {\xi }_4^{‴}=& \left(z_{10}-z_{11}{\mu }_3{\beta }_3\right)N_3+\left(z_{11}+z_{10}{\mu }_3{\beta }_3-z_{12}{\mu }_3{\psi }^{\prime }\right)C_3+\left(z_{12}+z_{11}{\mu }_3{\psi }^{\prime }\right)W_3.\hfill \end{array}$$

(73)

Moreover, if the vector products, determinants and norms are taken, we obtain:

$$\begin{array}{cc}\hfill {\xi }_4^{\prime }\wedge {\xi }_4^{″}=& {\displaystyle \frac{{\mu }_3\left(\begin{array}{c}-\left(z_{11}{\psi }^{\prime }-z_{12}\left({\beta }_2-{\psi }^{\prime }\right)\right)N_3+\left(z_{10}{\psi }^{\prime }+z_{12}{\beta }_3\right)C_3\hfill \\ -\left(z_{11}{\beta }_3+z_{10}\left({\beta }_3-{\psi }^{\prime }\right)\right)W_3\hfill \end{array}\right)}{\sqrt{3}}},\hfill \\ \hfill det\left({\xi }_4^{\prime },{\xi }_4^{″},{\xi }_4^{‴}\right)=& {\displaystyle \frac{{\mu }_3}{\sqrt{3}}}\left(\begin{array}{c}-\left(z_{11}{\psi }^{\prime }-z_{12}\left({\beta }_3-{\psi }^{\prime }\right)\right)\left(z_{10}-z_{11}{\mu }_3{\beta }_3\right)\hfill \\ +\left(z_{10}{\psi }^{\prime }+z_{12}{\beta }_3\right)\left(z_{11}+z_{10}{\mu }_3{\beta }_3-z_{12}{\mu }_3{\psi }^{\prime }\right)\hfill \\ -\left(z_{11}{\beta }_3+z_{10}\left({\beta }_3-{\psi }^{\prime }\right)\right)\left(z_{12}+z_{11}{\mu }_3{\psi }^{\prime }\right)\hfill \end{array}\right),\hfill \end{array}$$

(74)

and

$$\begin{array}{cc}\hfill ∥{\xi }_4^{\prime }∥=& {\displaystyle \frac{\sqrt{6}{\mu }_3}{3}}\sqrt{{\beta }_3^2-{\beta }_3{\psi }^{\prime }+{{\psi }^{\prime }}^2},\hfill \\ \hfill ∥{\xi }_4^{\prime }\wedge {\xi }_4^{″}∥=& {\displaystyle \frac{{\mu }_3}{\sqrt{3}}}\sqrt{{\left(z_{11}{\psi }^{\prime }-z_{12}\left({\beta }_2-{\psi }^{\prime }\right)\right)}^2+{\left(z_{10}{\psi }^{\prime }+z_{12}{\beta }_3\right)}^2+{\left(z_{11}{\beta }_3+z_{10}\left({\beta }_3-{\psi }^{\prime }\right)\right)}^2}.\hfill \end{array}$$

(75)

Finally, by substituting Relations (73)–(75) into (1), we complete the proof. □

Theorem 33. 

Let ${\kappa }_{{\xi }_4}$ and ${\tau }_{{\xi }_4}$ be the curvature and the torsion functions for the $N_3{C}_3{W}_3$ Smarandache curve, respectively. Then, we have the following relations among the curvatures:

$$\begin{array}{cc}\hfill {\kappa }_{{\xi }_4}=& {\displaystyle \frac{3\sqrt{2}}{4}}·{\displaystyle \frac{\sqrt{{\left(z_{11}{\psi }^{\prime }-z_{12}\left({\beta }_2-{\psi }^{\prime }\right)\right)}^2+{\left(z_{10}{\psi }^{\prime }+z_{12}{\beta }_3\right)}^2+{\left(z_{11}{\beta }_3+z_{10}\left({\beta }_3-{\psi }^{\prime }\right)\right)}^2}}{{\mu }_3^2\left({\beta }_3^2-{\beta }_3{\psi }^{\prime }+{{\psi }^{\prime }}^2\right)\sqrt{{\beta }_3^2-{\beta }_3{\psi }^{\prime }+{{\psi }^{\prime }}^2}}},\hfill \\ \hfill {\tau }_{{\xi }_4}=& {\displaystyle \frac{\sqrt{3}\left(\begin{array}{c}-\left(z_{11}{\psi }^{\prime }-z_{12}\left({\beta }_3-{\psi }^{\prime }\right)\right)\left(z_{10}-z_{11}{\mu }_3{\beta }_3\right)+\left(z_{10}{\psi }^{\prime }+z_{12}{\beta }_3\right)\left(z_{11}+z_{10}{\mu }_3{\beta }_3-z_{12}{\mu }_3{\psi }^{\prime }\right)\hfill \\ -\left(z_{11}{\beta }_3+z_{10}\left({\beta }_3-{\psi }^{\prime }\right)\right)\left(z_{12}+z_{11}{\mu }_3{\psi }^{\prime }\right)\hfill \end{array}\right)}{{\mu }_3\left({\left(z_{11}{\psi }^{\prime }-z_{12}\left({\beta }_2-{\psi }^{\prime }\right)\right)}^2+{\left(z_{10}{\psi }^{\prime }+z_{12}{\beta }_3\right)}^2+{\left(z_{11}{\beta }_3+z_{10}\left({\beta }_3-{\psi }^{\prime }\right)\right)}^2\right)}}·\hfill \end{array}$$

Proof. 

By using (74) and (75) and substituting them into (2), we complete the proof. □

Remark 15. 

The alternative frame for the $N_3{C}_3{W}_3$ Smarandache curve ${\xi }_4$ is established by the following equations:

$$N_{{\xi }_4}=N_{{\xi }_4},C_{{\xi }_4}=-cos{\Delta }_4{T}_{{\xi }_4}+sin{\Delta }_4{B}_{{\xi }_4},W_{{\xi }_4}=sin{\Delta }_4{T}_{{\xi }_4}+cos{\Delta }_4{B}_{{\xi }_4},$$

where ${\displaystyle {\Delta }_4=\measuredangle \left(B_{{\xi }_4},W_{{\xi }_4}\right),}$${\displaystyle cos{\Delta }_4=\frac{{\kappa }_{{\xi }_4}}{\sqrt{{\kappa }_{{\xi }_4}^2+{\tau }_{{\xi }_4}^2}},}$ and ${\displaystyle sin{\Delta }_4=\frac{{\tau }_{{\xi }_4}}{\sqrt{{\kappa }_{{\xi }_4}^2+{\tau }_{{\xi }_4}^2}}.}$

By using Example 1, Smarandache curves of the alternative W-pedal curve according to the point $P(1,1,1)$ are illustrated in Figure 7.

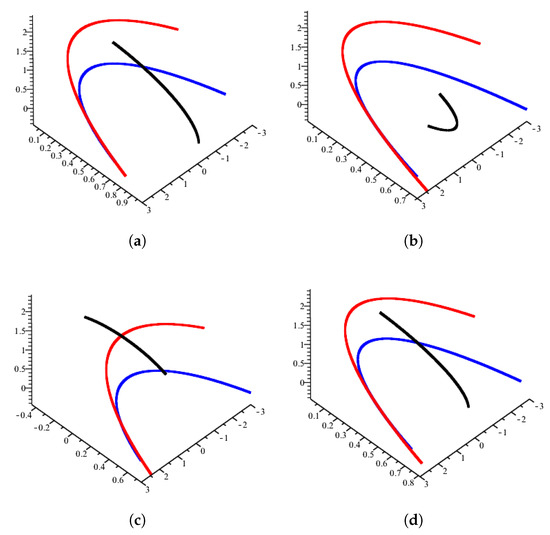
Figure 7. Smarandache curves (black) of the alternative W-pedal curve (red) of the curve $\zeta \left(t\right)$ (blue) according to the fixed point $P(1,1,1)$ where $t\in [-0.5,0.5]$. (a) $N_3{C}_3$ Smarandache curve; (b) $N_3{W}_3$ Smarandache curve; (c) $C_3{W}_3$ Smarandache curve; (d) $N_3{C}_3{W}_3$ Smarandache curve.

5. Conclusions

The theory of curves is the most fundamental concept in differential geometry. Therefore, generating new curves is important as well as providing their characteristics mostly by moving frames along the curve and by its invariant curvatures. Pedal curves and Smarandache curves are two ways of defining new curves. In this study, we defined pedal-type curves by using the moving alternative frame vectors along the curve. Second, we established the relations among the alternative frame apparatus for the main curve and its pedal curve. Next, we introduced the Smarandache curves of the new pedal curves. Thus, we examined twelve new curves for one fixed point. A set of new curves could be investigated to expand the literature on the theory of curves by having different points and more curves added to the field. Finally, since symmetry as a concept is more relevant for real-world applications, with this paper, it is believed that the obtained formulas and definitions for the new curves can be useful for some design and modeling purposes. We also encourage researchers to examine possible pedal-like surfaces from this study.