A Conjecture for the Clique Number of Graphs Associated with Symmetric Numerical Semigroups of Arbitrary Multiplicity and Embedding Dimension

Abstract

A subset $\mathcal{S}$ of non-negative integers ${\mathbb{N}}_o$ is called a numerical semigroup if it is a submonoid of ${\mathbb{N}}_o$ and has a finite complement in ${\mathbb{N}}_o$. An undirected graph $G\left(\mathcal{S}\right)$ associated with $\mathcal{S}$ is a graph having $V\left(G\left(\mathcal{S}\right)\right)=\{v_i:i\in {\mathbb{N}}_o\setminus \mathcal{S}\}$ and $E\left(G\left(\mathcal{S}\right)\right)=\{v_i{v}_j\iff i+j\in \mathcal{S}\}$. In this article, we propose a conjecture for the clique number of graphs associated with a symmetric family of numerical semigroups of arbitrary multiplicity and embedding dimension. Furthermore, we prove this conjecture for the case of arbitrary multiplicity and embedding dimension 7.

1. Introduction and Preliminaries

An important field of mathematics called graph theory uses graph representations to study the interactions between pairs of objects. Recent developments in mathematics led to new studies into the relationship between algebraic objects and graphs. In the past, scholars have developed links between graphs and other algebraic structures, enhancing mathematical analysis [1,2,3]. The Cayley graph, zero divisor graph, and nilpotent graphs are important ideas in this field [4,5,6]. Numerous features of a graph related to numerical semigroups and their ideals were studied by Binyamin et al. [7,8].

A graph H is said to be an induced subgraph of G if $V\left(H\right)\subseteq V\left(G\right)$ and $E\left(H\right)\subseteq E\left(G\right)$. A graph is said to be complete if each pair of distinct vertices is connected by an edge. A clique $cl\left(G\right)$ in a graph G is a complete subgraph, and the largest possible clique in G is referred to as the maximal clique. The size of the maximal clique in G is termed the clique number, denoted by $\omega \left(G\right)$.

The most significant clique problem involves determining the largest clique or maximum complete subgraph. Numerous disciplines, including electrical engineering, chemistry, biology, medicine, image processing, and network analysis, have used this problem in the past. For instance, Ref. [9] proposed a bottom-up clustering technique based on incrementally collapsing small cliques within a system for VLSI architecture. Szabó [10] reformulated the graph coloring problem as a k-clique problem and also introduced symmetry-breaking techniques. In [11], Seda proposed modifications in integer models that improve time complexity for solving the maximum clique problem by using GAMS. In [12], the relevance to the gas sector is discussed, while [13] proposed a clique-based strategy for recognizing protein clusters (see Figure 1), Ref. [14] offers a method using graph theory for finding cliques for the comparative modeling of protein structures.

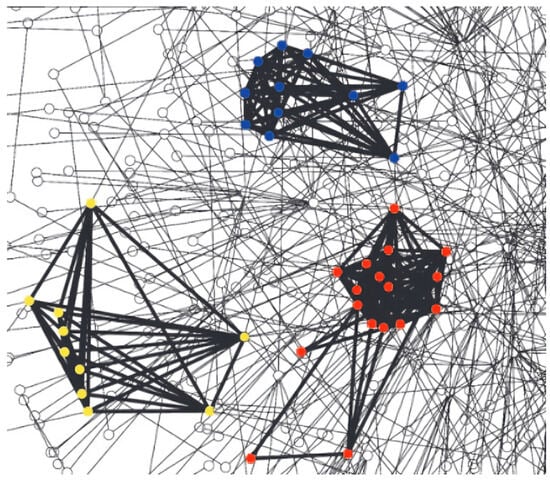
Figure 1. Fragment of the protein network, nodes, and interactions in discovered clusters are shown in bold. Nodes are colored by functional categories in MIPS $\left(20\right)$; red, transcription regulation; blue, cell cycle/cell fate control; green, RNA processing; and yellow, protein transport [13]. Reprinted with permission from Ref. [13], Copyright 2003 Victor Spirin and Leonid A. Mirny.

Cliques inside an image are used in [15] to compute clique potentials with the objective of segmenting the entire image. A brain tumor picture receives treatment as a graph segment in [16], which uses a clique-based strategy to perform multi-modal segmentation of brain tumors. Additionally, Ref. [17] analyzes the brain’s synaptic networks and finds a large number of neuron cliques within gaps that facilitate correlated activity (see Figure 2).

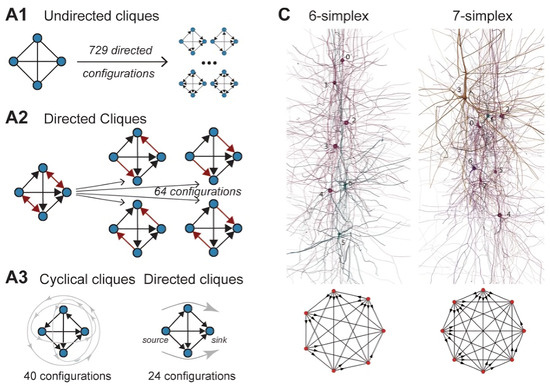
Figure 2. Examples of neurons forming high-dimensional simplices in the reconstruction and their representation as directed graphs [17].

Cliques are another way that social networks identify groups of people who are acquainted with each other. Group members (or cliques) may have asymmetric relationships with anyone outside the group, while symmetric ties with one another belong to all by members. This is due to the fact that some individuals outside the clique are not connected at all, while others may be connected by an edge, implying exclusive relationships. The maximum clique constrained to visibility graphs of a simple polygon, computed using dynamic programming, is described in [18] (see Figure 3).

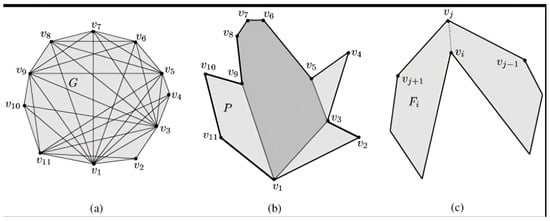
Figure 3. The maximum clique in G and vertices of the largest convex polygon in P consist of vertices $v_1,v_3,v_5,v_6,v_7,v_8,v_9$, which are shown in (a) and (b), respectively. (c) No vertex of $V_{ij}$ can see any vertex of $V_{ji}$ in the fan $F_i$.

In [19], it is restricted to one-planar graphs, in [20] to dense graphs, and in [21] to graphs without long cycles. To generate different partitions on graphs, Tomescu et al. [22] employed counting, sequence, and layer matrices, along with proposed modifications and extensions. These partitions were then used to produce visual representations of the graphs.

A numerical semigroup $\mathcal{S}$ is a cofinite subset of non-negative integers ${\mathbb{N}}_o$ having additive binary operation and identity element. If $X\subseteq {\mathbb{N}}_0$, we can view the submonoid of $({\mathbb{N}}_0,+)$, generated by X as

$$⟨X⟩=\{x_1{c}_1+\cdots +x_n{c}_n:x_i\ge 0\},$$

where $X=\{c_1,\dots ,c_n\}$. If $\mathcal{S}=⟨X⟩$ is a numerical semigroup, then gcd$(c_1,\dots ,c_n)=1$. If no proper subset of X generates the numerical semigroup $\mathcal{S}$, then X is called the minimal set of generators and its cardinality is called embedding dimension e. The multiplicity m is the smallest non-zero element that belongs to the $\mathcal{S}$ and the largest integer $y\notin \mathcal{S}$ is called the Frobenius number $\mathcal{F}$. Rosales and Branco introduced that a numerical semigroup $\mathcal{S}$ is irreducible if it is not expressible as the intersection of two numerical semigroups properly containing $\mathcal{S}$. Additionally, if a numerical semigroup has an odd Frobenius number and is irreducible, then it is symmetric. The main objective of this article is to propose a conjecture for the clique number of graphs associated with symmetric numerical semigroups of arbitrary multiplicity and embedding dimension and prove it for the case of $m=2q+7.$

2. Clique Number of Graphs Associated with Symmetric Numerical Semigroups

In this section, we compute the clique number of $G\left(\mathcal{S}\right)$, where $\mathcal{S}$ is a symmetric numerical semigroup of arbitrary multiplicity and embedding dimension discussed in [23]. Let $\mathcal{L}\subseteq \mathcal{S}$, then a graph associated with $\mathcal{L}$ is said to be an induced subgraph of $\mathcal{S}$, represented by $G_{\mathcal{L}}.$

Lemma 1

([24]). Let $\mathcal{S}=⟨m,m+1,\dots ,m+u⟩$ be a numerical semigroup with $1\le u<m.$ Then $n\in \mathcal{S}$ if and only if $n=qm+i$ with $q\in \mathbb{N}$ and $i\in \{0,\dots ,qu\}.$

Let $\mathcal{S}=⟨m,m+1,qm+2q+2,\dots ,qm+(m-1)⟩$, where $m\ge 2q+7$ and $e=m-2q$. We define the following sets as:

$${\mathcal{C}}_1=\{\mathcal{F}-pm:p\in \{0,\dots ,q\}\},$$

$${\mathcal{C}}_2=\{\mathcal{F}-t:t\in \{qm+2q+2,\dots ,qm+m+q-\lfloor \frac{m}{2}\rfloor \}\},$$

$${\mathcal{C}}_3=\{\mathcal{F}-(am+(a+b)):a\in \{1,\dots ,\lfloor \frac{q}{2}\rfloor \},b\in \{qm+2q+2,\dots ,qm+q+m-\lceil \frac{m}{2}\rceil -a\}\}.$$

If $q\ge 3$ is an odd integer, then we consider

$${\mathcal{C}}_4=\{\mathcal{F}-((a+b)m+b)):a\in \{0,\dots ,\frac{q-1}{2}\},b\in \{1,\dots ,q\}ora=q,b\in \{1,\dots ,\frac{q+1}{2}\}$$

or

$$a=\frac{q-1}{2}+l,b\in \{1,\dots ,q-l\},l=1,\dots \frac{q-1}{2}\}$$

and if $q=1$ or $q\ge 2$ is an even integer, then

$${\mathcal{C}}_4=\{\mathcal{F}-((a+b)m+b)):a\in \{0,\dots ,\lfloor \frac{q}{2}\rfloor \},b\in \{1,\dots ,q\}ora=\lfloor \frac{q}{2}\rfloor +l,b\in \{1,\dots ,q-l\},l=1,\dots ,\lfloor \frac{q}{2}\rfloor \}.$$

Proposition 1.

Let $G\left(\mathcal{S}\right)$ be a graph associated with numerical semigroup $\mathcal{S}$. Then ${\mathcal{C}}_k\subseteq V\left(G\left(\mathcal{S}\right)\right)$, for every $k\in \{1,\dots ,4\}$.

Proof. 

Since $m\ge 2q+7$, therefore $m+q-\lfloor \frac{m}{2}\rfloor <m-1$. Furthermore, for $i\in \{1,\dots ,\frac{q}{2}-1\}$, we have $m+q-\lfloor \frac{m}{2}\rfloor -i<m-1$. Note that for every $a\ge 0$ and $b\in \{qm+2q+2,\dots ,qm+m-1\}$,

$$am+(a+b)=a(m+1)+b\in \mathcal{S}$$

and for every $a,b\ge 0$

$$(a+b)m+b=am+b(m+1)\in \mathcal{S}.$$

Above discussion implies $pm,t,am+(a+b),(a+b)m+b\in \mathcal{S}$ for given conditions. Since $\mathcal{S}$ is symmetric and $\mathcal{F}=2qm+2q+1$ is the Frobenius number of $\mathcal{S}$, therefore $\mathcal{F}-pm,\mathcal{F}-t,\mathcal{F}-(am+(a+b\left)\right),\mathcal{F}-\left(\right(a+b)m+b)\notin \mathcal{S}$.

Now, we need to show that $\mathcal{F}-pm,\mathcal{F}-t,\mathcal{F}-(am+(a+b\left)\right),\mathcal{F}-\left(\right(a+b)m+b)$, are positive integers for given conditions. To show this, we consider the following cases:

(1)

For ${\mathcal{C}}_1$:

Since the maximum value of p is q, then

$$\mathcal{F}-qm=qm+2q+1>0.$$

This implies $F-pm>0$, for $p\in \{0,\dots ,q\}$.

(2)

For ${\mathcal{C}}_2$:

As the maximum value of t is $qm+m+q-\lfloor \frac{m}{2}\rfloor$, therefore

$$\mathcal{F}-(qm+m+q-\lfloor \frac{m}{2}\rfloor )=(q-1)m+q+1+\lfloor \frac{m}{2}\rfloor >0.$$

This gives $\mathcal{F}-t>0$, for $t\in \{qm+2q+2,\dots ,qm+m+q-\lfloor \frac{m}{2}\rfloor \}$.

(3)

For ${\mathcal{C}}_3$:

Note that for each a, the maximum of b is $qm+q+m-\lceil \frac{m}{2}\rceil -a$. Then,

$$\mathcal{F}-(am+(a+qm+q+m-\lceil \frac{m}{2}\rceil -a))=(q-(a+1))m+q+1+\lceil \frac{m}{2}\rceil >0,$$

since $q\ge \frac{q}{2}$, therefore $q\ge a+1$. This implies $\mathcal{F}-(am+(a+b\left)\right)>0$ for $a\in \{1,\dots ,\lfloor \frac{q}{2}\rfloor \}$ and $b\in \{qm+2q+2,\dots ,qm+q+m-\lceil \frac{m}{2}\rceil -a\}$.

(4)

For ${\mathcal{C}}_4$:

If $a\in \{0,\dots ,\lfloor \frac{q}{2}\rfloor \}$ and $b\in \{1,\dots ,q\}$, then

$$\mathcal{F}-((\lfloor \frac{q}{2}\rfloor +q)m+q)=(q-\lfloor \frac{q}{2}\rfloor )m+q+1>0.$$

Now, if $a=\lfloor \frac{q}{2}\rfloor +l$ and $b\in \{1,\dots ,q-l\}$, where $l=1,\dots ,\lfloor \frac{q}{2}\rfloor$, then

$$\mathcal{F}-((\lfloor \frac{q}{2}\rfloor +q)m+q-l)=(q-\lfloor \frac{q}{2}\rfloor )m+q+l+1>0.$$

If q is odd, $a=q$ and $b\in \{1,\dots ,\frac{q+1}{2}\}$, then

$$\mathcal{F}-((q+\left(\frac{q+1}{2}\right))m+\frac{q+1}{2})=\left(\frac{q-1}{2}\right)m+\frac{3q+1}{2}+1>0.$$

These imply that $\mathcal{F}-\left(\right(a+b)m+b))$ is a positive integer for all possibilities of a and b. Consequently, we obtain ${\mathcal{C}}_k\subseteq V\left(G\left(\mathcal{S}\right)\right)$ for every $k\in \{1,\dots ,4\}$. □

Proposition 2.

Let $G_i$ be an induced subgraph of $G\left(\mathcal{S}\right)$ such that $V\left(G_i\right)={\mathcal{C}}_i,$ where $i\in \{1,\dots 4\}$. Then, $G_i\cong K_{|{\mathcal{C}}_i|}$.

Proof. 

To prove ${\mathcal{C}}_i$ to be a complete graph, we have to show that $r_1+r_2\in \mathcal{S}forall{r}_1,r_2\in {\mathcal{C}}_i$

Case 1: 

If $r_1=\mathcal{F}-p_{1}m,$ and $r_2=\mathcal{F}-p_{2}m,$ then

$$r_1+r_2=2\mathcal{F}-(p_1+p_2)m=\mathcal{F}+m(2q-(p_1+p_2))+2q+1$$

Since $p_1,p_2\le q$ and $p_1\ne p_2$, therefore $p_1+p_2<2q.$ This implies $r_1+r_2\in \mathcal{S}.$

Case 2: 

If $r_1=\mathcal{F}-t_1,$ and $r_2=\mathcal{F}-t_2,$ then

$$r_1+r_2=2\mathcal{F}-(t_1+t_2).$$

We can write

$$t_1+t_2=2q(m+1)+(x_1+x_2),q+2\le x_1\ne x_2\le m-\lfloor \frac{m}{2}\rfloor .$$

This gives

$$2\mathcal{F}-(t_1+t_2)=\mathcal{F}+1-(x_1+x_2).$$

Consider $\mathcal{F}-(\mathcal{F}+1-(x_1+x_2))=(x_1+x_2)-1.$ Since $2q+5\le x_1+x_2\le m-1,$ therefore $(x_1+x_2)-1\in g\left(\mathcal{S}\right)$. This implies $\mathcal{F}+1-(x_1+x_2)\in \mathcal{S}.$ Hence, $r_1+r_2\in \mathcal{S}.$

Case 3: 

Let $r_1=\mathcal{F}-(a_{1}m+(a_1+b_1))$ and $r_2=\mathcal{F}-(a_{2}m+(a_2+b_2)).$ Let $b_i=qm+q+m-\lceil \frac{m}{2}\rceil -a_i-x_i,$ where $i\in \{1,2\}$ and $0\le x_i\le m-\lceil \frac{m}{2}\rceil -q-2.$ Consider

$$r_1+r_2=2F-(a_1+a_2)m-(a_1+a_2+b_1+b_2)$$

$$=2qm+2q+2-2m+(x_1+x_2)-(a_1+a_2)m+2\left(\lceil \frac{m}{2}\rceil \right).$$

If m is even, then

$$r_1+r_2=qm+2q+2+(x_1+x_2)+(q-(1+a_1+a_2))m.$$

Since $1\le (x_1+x_2)\le m-2q-3$ and $a_1+a_2\le q-2,$ therefore $r_1+r_2\in \mathcal{S},$ and if m is odd, then

$$r_1+r_2=qm+2q+3+(x_1+x_2)+(q-(1+a_1+a_2))m.$$

Since $1\le (x_1+x_2)\le m-2q-4$ and $a_1+a_2\le q-2,$ therefore $r_1+r_2\in \mathcal{S}.$

Case 4: 

Assume that $r_1=\mathcal{F}-((a_1+b_1)m+b_1)$, $r_2=\mathcal{F}-((a_2+b_2)m+b_2)$, then

$$r_1+r_2=2\mathcal{F}-(a_1+a_2+b_1+b_2)m-(b_1+b_2),$$

$$=(3q-(a_1+a_2+b_1+b_2))m+2q-(b_1+b_2)+(qm+2q+2).$$

(1)

$a_1\ne a_2\in \{0,\dots ,\lfloor \frac{q}{2}\rfloor \}$ and $b_1\ne b_2\in \{1,\dots ,q\}$:

We can write

$$3q-(a_1+a_2+b_1+b_2)=(2q-(b_1+b_2))+(q-(a_1+a_2)).$$

If q is even, then $a_1+a_2\in \{1,\dots ,q-1\}$, and if q is odd, then $a_1+a_2\in \{1,\dots ,q-2\}$ and also, $b_1+b_2\in \{3,\dots ,2q-1\}$. This implies $q-(a_1+a_2)\ge 0$ and $2q-(b_1+b_2)>0$ and therefore

$$3q-(a_1+a_2+b_1+b_2)>2q-(b_1+b_2).$$

By Lemma 1, $(3q-(a_1+a_2+b_1+b_2))m+2q-(b_1+b_2)\in \mathcal{S}.$ This gives

$$r_1+r_2=(3q-(a_1+a_2+b_1+b_2))m+2q-(b_1+b_2)+(qm+2q+2)\in \mathcal{S}.$$

(2)

$a_1=a_2=\lfloor \frac{q}{2}\rfloor +l$ and $b_1\ne b_2\in \{1,\dots ,q-l\},l=1,\dots ,\lfloor \frac{q}{2}\rfloor$:

It is easy to see that for every q and for each l, $a_1+a_2+b_1+b_2\le 3q$. This implies

$$3q-(a_1+a_2+b_1+b_2)\ge 0.$$

If $2q-(b_1+b_2)\le m-q-1$, then consider

$$2q-(b_1+b_2)=m-q-1-x,$$

where $0\le x\le q+1.$ This implies

$$2q-(b_1+b_2)+(qm+2q+2)=(q+1)m+(q+1-x).$$

By Lemma 1, $r_1+r_2\in \mathcal{S}.$

Now, if $2q-(b_1+b_2)>m-q-1$, then consider

$$2q-(b_1+b_2)-(m-q-1)=3q+1-m-(b_1+b_2).$$

We can write

$$r_1+r_2=[(3q-(a_1+a_2+b_1+b_2))m+(3q+1-m-(b_1+b_2))]+[(qm+2q+2)+(m-q-1)].$$

Note that

$$3q-(a_1+a_2+b_1+b_2)-(3q+1-m-(b_1+b_2))=m-(a_1+a_2+1)>0,$$

as $a_1+a_2\le 2q.$ By Lemma 1, $(3q-(a_1+a_2+b_1+b_2))m+(3q+1-m-(b_1+b_2))\in \mathcal{S}$. Furthermore, $(qm+2q+2)+(m-q-1)\in \mathcal{S}$, from the above case. Consequently, we obtain $r_1+r_2\in \mathcal{S}$.

(3)

q is odd, $a_1=a_2=q$ and $b_1\ne b_2\in \{1,\dots ,\frac{q+1}{2}\}$:

Since $a_1+a_2=2q$ and $b_1+b_2\le q$, therefore

$$3q-(a_1+a_2+b_1+b_2)\ge 0.$$

If $2q-(b_1+b_2)\le m-q-1$, then consider

$$2q-(b_1+b_2)=m-q-1-x,where0\le x\le q+1.$$

This implies

$$(qm+2q+2)+(2q-(b_1+b_2))=(q+1)m+(q+1-x)\in \mathcal{S}.$$

By using Lemma 1, we obtain $r_1+r_2\in \mathcal{S}.$

Now, if $2q-(b_1+b_2)>m-q-1$, then consider

$$2q-(b_1+b_2)-(m-q-1)=3q+1-m-(b_1+b_2).$$

We can write

$$r_1+r_2=[(3q-(a_1+a_2+b_1+b_2))m+(3q+1-m-(b_1+b_2))]+[(qm+2q+2)+(m-q-1)].$$

Note that

$$3q-(a_1+a_2+b_1+b_2)-(3q+1-m-(b_1+b_2))=m-(2q+1)>0.$$

By using Lemma 1, $(3q-(a_1+a_2+b_1+b_2))m+(3q+1-m-(b_1+b_2))\in \mathcal{S}$. Furthermore, $(qm+2q+2)+(m-q-1)\in \mathcal{S}$, from the above case. Consequently, we obtain $r_1+r_2\in \mathcal{S}$. □

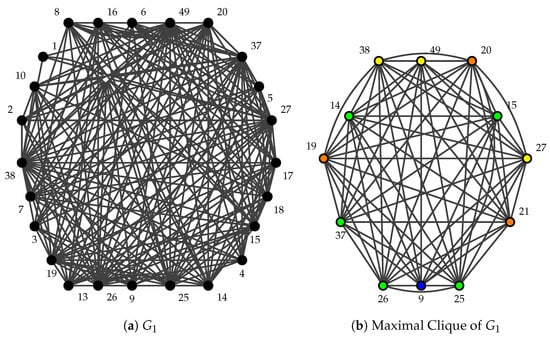
Example 1.

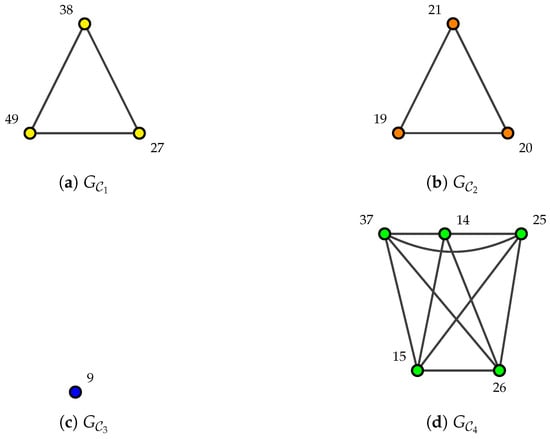
Let $G\left(\mathcal{S}\right)$ be a graph associated with $\mathcal{S}=⟨11,12,28,29,30,31,32⟩$ then $V\left(G\right(\mathcal{S}\left)\right)=\{1,2,3,5,6,7,8,9,10,13,14,15,16,17,18,19,20,21,25,26,27,37,38,49\}.$ By Proposition 2, ${\mathcal{C}}_1=\{49,38,27\}$, ${\mathcal{C}}_2=\{21,20,19\}$, ${\mathcal{C}}_3=\left\{9\right\},$ and ${\mathcal{C}}_4=\{37,26,25,15,14\}.$ The corresponding graphs $G_{{\mathcal{C}}_1},G_{{\mathcal{C}}_2},G_{{\mathcal{C}}_3},G_{{\mathcal{C}}_4}$ are shown in Figure 4.

Figure 4. The graphs associated with vertex partitions $C_i$ of numerical semigroup $\mathcal{S}=⟨11,12,28,29,30,31,32⟩$.

Proposition 3.

Let $G_{ij}$ be an induced subgraph of $G\left(\mathcal{S}\right)$ such that $V\left(G_{ij}\right)={\mathcal{C}}_i\cup {\mathcal{C}}_j$, where $i\ne j$. Then

$$G_{ij}\cong K_{|{\mathcal{C}}_i|}+K_{|{\mathcal{C}}_j|}\cong K_{|{\mathcal{C}}_i|+|{\mathcal{C}}_j|}.$$

Proof. 

To prove ${\mathcal{C}}_i\cup {\mathcal{C}}_j$ is a complete graph where $i\ne j$, we have to show that $c_i+c_j\in \mathcal{S}$ for $c_i\in {\mathcal{C}}_i$ and $c_j\in {\mathcal{C}}_j.$

Case 1: 

If $c_i=\mathcal{F}-pm$ and $c_j=\mathcal{F}-t$, where $p\in \{0,\dots ,q\},$ and $t=qm+q+x$, where $x\in \{q+2,\dots ,m-\lfloor \frac{m}{2}\rfloor \},$ then

$$c_i+c_j=2\mathcal{F}-(pm+t)=(q-p)m+qm+2q+2+qm+q-x.$$

If $qm+q-x\le m-q-1$, then consider

$$qm+q-x=m-q-1-s,where0\le s\le q+1.$$

This implies

$$(qm+2q+2)+(qm+q-x)=(q+1)m+(q+1-s)\in \mathcal{S}.$$

Now, if $qm+q-x>m-q-1$, then consider

$$qm+q-x-(m-q-1)=2q+1+(q-1)m-x.$$

We can write

$$c_i+c_j=[(q-p+q-1)m+(2q+1-x)]+[(qm+2q+2)+(m-q-1)].$$

Note that

$$(q-p+q-1)-(2q+1-x)=x-(p+2)\ge 0.$$

By Lemma 1, $(q-p+q-1)m+(2q+1-x)\in \mathcal{S}$. Furthermore, $(qm+2q+2)+(m-q-1)\in \mathcal{S}$. Consequently, we obtain $c_i+c_j\in \mathcal{S}$.

Case 2: 

If $c_i=\mathcal{F}-pm$ and $c_j=\mathcal{F}-(am+(a+b))$, where $p\in \{0,\dots ,q\},$ and $a\in \{1,\dots ,\lceil \frac{q}{2}\rceil -1\},b\in \{qm+2q+2,\dots ,qm+q+m-\lceil \frac{m}{2}\rceil -a\}$ then

$$c_i+c_j=2\mathcal{F}-((p+a)m+(a+b))=(2q-(p+a))m+qm+2q+2+qm+2q-(a+b).$$

Since $a+b=qm+q+m-\lceil \frac{m}{2}\rceil -x,$ where $0\le x\le m-\lceil \frac{m}{2}\rceil -q-2,$ then $qm+2q-(a+b)=q+x+\lceil \frac{m}{2}\rceil -m.$ If $q+x+\lceil \frac{m}{2}\rceil -m\le m-q-1,$ then consider

$$q+x+\lceil \frac{m}{2}\rceil -m=m-q-1-s,where0\le s\le q+1.$$

This implies

$$(qm+2q+2)+(q+x+\lceil \frac{m}{2}\rceil -m)=(q+1)m+(q+1-s)\in \mathcal{S}.$$

So, we obtain $c_i+c_j\in \mathcal{S}.$

Now, if $q+x+\lceil \frac{m}{2}\rceil -m>m-q-1$, then consider

$$q+x+\lceil \frac{m}{2}\rceil -m-(m-q-1)=2q+1-2m+\lceil \frac{m}{2}\rceil +x.$$

We can write

$$c_i+c_j=[(2q-(p+a))m+(2q+1+x+\lceil \frac{m}{2}\rceil -2m)]+[(qm+2q+2)+(m-q-1)].$$

Note that

$$(2q-(p+a))-(2q+1+x+\lceil \frac{m}{2}\rceil -2m)=2m-(p+a+1+x+\lceil \frac{m}{2}\rceil )\ge 0,$$

because $p+a+1+x+\lceil \frac{m}{2}\rceil -2m)\le m+\lceil \frac{q}{2}\rceil -2.$ This implies $(2q-(p+a))m+(2q+1+x+\lceil \frac{m}{2}\rceil -2m)\in \mathcal{S}$. Furthermore, $(qm+2q+2)+(m-q-1)\in \mathcal{S}$. Consequently, we obtain $c_i+c_j\in \mathcal{S}$.

Case 3: 

If $c_i=\mathcal{F}-pm$ and $c_j=\mathcal{F}-((a+b)m+b)$, where $p\in \{0,\dots ,q\},$ and $a\in \{0,\dots ,\lfloor \frac{q}{2}\rfloor \},b\in \{1,\dots ,q\}ora=q,b\in \{1,\dots ,\frac{q+1}{2}\}ora=\lfloor \frac{q}{2}\rfloor +l,b\in \{1,\dots ,q-l\},l=1,\dots ,\lfloor \frac{q}{2}\rfloor$ then

$$c_i+c_j=2\mathcal{F}-((p+a+b)m+b)=(3q-(p+a+b))m+qm+2q+2+2q-b.$$

(1)

$a\in \{0,\dots ,\lfloor \frac{q}{2}\rfloor \}$ and $b\in \{1,\dots ,q\}$:

We can see that $2q-b<m-q-1,$ therefore $qm+2q+2+(2q-b)\in \{qm+2q+2,\dots ,qm+m-1\}.$ Hence $c_i+c_j\in \mathcal{S}.$

(2)

$a=\lfloor \frac{q}{2}\rfloor +l$, $b\in \{1,\dots ,q-l\}$ and $l=1,\dots ,\lfloor \frac{q}{2}\rfloor$ or $a=q,b\in \{1,\dots ,\frac{q+1}{2}\}$:

If $2q-b\le m-q-1,$ then $qm+2q+2+(2q-b)\in \{qm+2q+2,\dots ,qm+m-1\}.$ If $2q-b>m-q-1,$ then consider $2q-b-(m-q-1)=3q-m-b+1.$ We can write

$$c_i+c_j=[(3q-(p+a+b))m+(3q+1-b-m)]+[(qm+2q+2)+(m-q-1)].$$

Note that

$$(3q-(p+a+b\left)\right)-(3q+1-b-m)=m-(p+a+1)\ge 0.$$

By Lemma 1, $(2q-(p+a))m+(2q+1+x+\lceil \frac{m}{2}\rceil -2m)\in \mathcal{S}$. Furthermore, $(qm+2q+2)+(m-q-1)\in \mathcal{S}$. Consequently, we obtain $c_i+c_j\in \mathcal{S}$.

Case 4: 

If $c_i=\mathcal{F}-t$ and $c_j=\mathcal{F}-(am+(a+b))$, where $t=qm+q+x\&x\in \{q+2,\dots ,m-\lfloor \frac{m}{2}\rfloor \}$ and $a\in \{1,\dots ,\lceil \frac{q}{2}\rceil -1\},b\in \{qm+2q+2,\dots ,qm+q+m-\lceil \frac{m}{2}\rceil -a\}$, then

$$c_i+c_j=2\mathcal{F}-t-((am+(a+b))=(q-a-1)m+qm+2q+2+2qm+2q+m-(a+b+t).$$

If $2qm+2q+m-(a+b+t)\le m-q-1,$ then consider

$$2qm+2q+m-(a+b+t)=m-q-1-s,where0\le s\le q+1.$$

This implies

$$(qm+2q+2)+(2qm+2q+m-(a+b+t\left)\right)=(q+1)m+(q+1-s)\in \mathcal{S}.$$

So, we obtain $c_i+c_j\in \mathcal{S}.$

Now, if $2qm+2q+m-(a+b+t)>m-q-1$, then consider

$$2qm+2q+m-(a+b+t)-(m-q-1)=2qm+3q+1-(t+a+b).$$

We can write

$$c_i+c_j=[(q-(a+1))m+(2qm+3q+1-(t+a+b))]+[(qm+2q+2)+(m-q-1)].$$

Note that

$$(q-(a+1\left)\right)-(2qm+3q+1-(t+a+b\left)\right)=q+t+b-(2qm+3q+2)\ge 0,$$

as $t+b\ge 2qm+4q+4.$ This implies $(q-(a+1\left)\right)m+(2qm+3q+1-(t+a+b\left)\right)\in \mathcal{S}$. Furthermore, $(qm+2q+2)+(m-q-1)\in \mathcal{S}$. Consequently, we obtain $c_i+c_j\in \mathcal{S}$.

Case 5: 

If $c_i=\mathcal{F}-t$ and $c_j=\mathcal{F}-((a+b)m+b)$, where $t=qm+q+m-\lfloor \frac{m}{2}\rfloor -x\&x\in \{0,\dots ,m-\lfloor \frac{m}{2}\rfloor -q-2\}$ and $a\in \{0,\dots ,\lfloor \frac{q}{2}\rfloor \},b\in \{1,\dots ,q\}ora=q,b\in \{1,\dots ,\frac{q+1}{2}\}ora=\lfloor \frac{q}{2}\rfloor +l,b\in \{1,\dots ,q-l\},l=1,\dots ,\lfloor \frac{q}{2}\rfloor$ then

$$c_i+c_j=2\mathcal{F}-t-((a+b)m+b)=(2q-(a+b+1))m+qm+2q+2+q+x-b+\lfloor \frac{m}{2}\rfloor .$$

If $\lfloor \frac{m}{2}\rfloor +q+x-b\le m-q-1$, then consider

$$\lfloor \frac{m-1}{2}\rfloor +q+x-b=m-q-1-s,where0\le s\le q+1.$$

This implies

$$(qm+2q+2)+(\lfloor \frac{m}{2}\rfloor +q+x-b)=(q+1)m+(q+1-s)\in \mathcal{S}.$$

Now, if $\lfloor \frac{m}{2}\rfloor +q+x-b>m-q-1$, then consider

$$\lfloor \frac{m}{2}\rfloor +q+x-b-(m-q-1)=2q+x-b+1-\lceil \frac{m}{2}\rceil .$$

We can write

$$c_i+c_j=[(2q-(a+b+1))m+(2q+x-b+1-\lceil \frac{m}{2}\rceil )]+[(qm+2q+2)+(m-q-1)].$$

Note that

$$(2q-(a+b+1)-(2q+x-b+1-\lceil \frac{m}{2}\rceil )=\lceil \frac{m}{2}\rceil -(a+x+2)\ge 0.$$

By Lemma 1, $(2q-(a+b+1))m+(x-b-1-\lceil \frac{m}{2}\rceil )\in \mathcal{S}$. Furthermore, $(qm+2q+2)+(m-q-1)\in \mathcal{S}$. Consequently, we obtain $c_i+c_j\in \mathcal{S}$.

Case 6: 

If $c_i=\mathcal{F}-(rm+(r+j))$ and $c_j=\mathcal{F}-((a+b)m+b)$, where $r\in \{1,\dots ,\lceil \frac{q}{2}\rceil -1\},j\in \{qm+2q+2,\dots ,qm+q+m-\lceil \frac{m}{2}\rceil -r\}$ and $a\in \{0,\dots ,\lfloor \frac{q}{2}\rfloor \},b\in \{1,\dots ,q\}ora=\lfloor \frac{q}{2}\rfloor +l,b\in \{1,\dots ,q-l\},l=1,\dots ,\lfloor \frac{q}{2}\rfloor$ then

$$c_i+c_j=2\mathcal{F}-((r+a+b)m+(r+j+b))=(2q(r+a+b)+1)m+qm+2q+2+qm+2q+m$$

$$-(b+r+j).$$

If $qm+2q+m-(b+r+j)\le m-q-1,$ then consider

$$qm+2q+m-(b+r+j)=m-q-1-s,where0\le s\le q+1.$$

This implies

$$(qm+2q+2)+(qm+2q+m-(b+r+j\left)\right)=(q+1)m+(q+1-s)\in \mathcal{S}.$$

So, we obtain $c_i+c_j\in \mathcal{S}.$

Now, if $qm+2q+m-(b+r+j)>m-q-1$, then consider

$$qm+2q+m-(b+r+j)-(m-q-1)=qm+3q+1-(b+r+j).$$

We can write

$$c_i+c_j=[(q-(a+1))m+(qm+3q+1-(b+r+j))]+[(qm+2q+2)+(m-q-1)].$$

Note that

$$(2q-(a+b+r+1\left)\right)-(qm+3q+1-(b+r+j\left)\right)=j-(qm+q+a+2)\ge 0.$$

This implies $(2q-(a+b+r+1\left)\right)m+(qm+3q+1-(b+r+j\left)\right)\in \mathcal{S}$. Furthermore, $(qm+2q+2)+(m-q-1)\in \mathcal{S}$. Consequently, we obtain $c_i+c_j\in \mathcal{S}$.

□

Example 2.

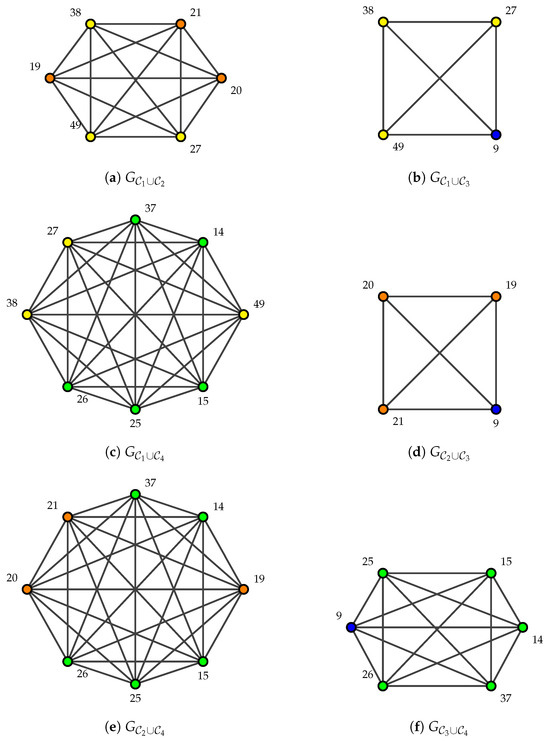
Let $G\left(\mathcal{S}\right)$ be a graph associated with $\mathcal{S}=⟨11,12,28,29,30,31,32⟩$, then

$$V\left(G\right(\mathcal{S}\left)\right)=\{1,2,3,5,6,7,8,9,10,13,14,15,16,17,18,19,20,21,25,26,27,37,38,49\}.$$

By Proposition 3, ${\mathcal{C}}_1\cup {\mathcal{C}}_2=\{49,38,27,21,20,19\}$, ${\mathcal{C}}_1\cup {\mathcal{C}}_3=\{49,38,27,9\}$, ${\mathcal{C}}_1\cup {\mathcal{C}}_4=\{49,38,37,27,26,25,15,14\},$${\mathcal{C}}_2\cup {\mathcal{C}}_3=\{21,20,19,9\},$${\mathcal{C}}_2\cup {\mathcal{C}}_4=\{37,26,25,21,20,19,15,14\},$ and ${\mathcal{C}}_3\cup {\mathcal{C}}_4=\{37,26,25,15,14,9\}.$ The corresponding graphs $G_{{\mathcal{C}}_1\cup {\mathcal{C}}_2},$$G_{{\mathcal{C}}_1\cup {\mathcal{C}}_3},$$G_{{\mathcal{C}}_1\cup {\mathcal{C}}_4},$$G_{{\mathcal{C}}_2\cup {\mathcal{C}}_3},$$G_{{\mathcal{C}}_2\cup {\mathcal{C}}_4},$$G_{{\mathcal{C}}_3\cup {\mathcal{C}}_4}$ are shown in Figure 5, respectively.

Figure 5. The complete graphs associated with $C_i\cup C_j$ for $i\ne j$.

Theorem 1.

Let $G_{\Sigma }$ be an induced subgraph of $G\left(\mathcal{S}\right)$ such that $V\left(G_{\Sigma }\right)={\cup }_{i=1}^4{\mathcal{C}}_i$. Then, $G_{\Sigma }\cong {\oplus }_{i=1}^4{K}_{|{\mathcal{C}}_i|}.$ Moreover,

1. 

$|G_{\Sigma }|=m-\lfloor \frac{m}{2}\rfloor -1+\frac{{(q+1)}^2}{2}+{\sum }_{a=1}^{\frac{q-1}{2}}(m-\lceil \frac{m}{2}\rceil -q-1-a)+{\sum }_{l=1}^{\frac{q-1}{2}}(q-l)$, if $q\ge 3$ is odd.

2. 

$|G_{\Sigma }|=m-\lfloor \frac{m}{2}\rfloor -1+q(\lfloor \frac{q}{2}\rfloor +1)+{\sum }_{a=1}^{\lfloor \frac{q}{2}\rfloor }(m-\lceil \frac{m}{2}\rceil -q-1-a)+{\sum }_{l=1}^{\lfloor \frac{q}{2}\rfloor }(q-l),$ if $q=1$ or $q\ge 2$ is even.

Proof. 

This follows from Proposition 3 that $G_{\Sigma }\cong {\sum }_{i=1}^4{K}_{|{\mathcal{C}}_i|},$ so we need to show ${\mathcal{C}}_i\cap {\mathcal{C}}_j=\varnothing$ for $i\ne j$. For this, we have to discuss the following cases:

Case 1: 

If $pm=t$, then t is not a minimal generator, which is a contradiction. Therefore ${\mathcal{C}}_1$ and ${\mathcal{C}}_2$ must be disjoint sets. Similar reasons imply ${\mathcal{C}}_2\cap {\mathcal{C}}_3=\varnothing$ and ${\mathcal{C}}_2\cap {\mathcal{C}}_4=\varnothing .$

Case 2: 

If $x\in {\mathcal{C}}_1\cap {\mathcal{C}}_3$, then $pm-b=a(m+1)$. Since $qm<b\le qm+2q+2,$ therefore $pm-b<0$. As we know that $a\ge 1$ and $m+1>0$, therefore ${\mathcal{C}}_1$ and ${\mathcal{C}}_3$ are disjoint.

Case 3: 

If $x\in {\mathcal{C}}_1\cap {\mathcal{C}}_4$, then $pm=am+b(m+1)$ and therefore $(p-a)m=b(m+1)$. If $p-a<0,$ then $b(m+1)+(a-p)m=0,$ this gives $a-p=0$ and $b=0$, which is a contradiction. If $p-a>0,$ then $(p-a)m=b(m+1)$, and gcd$(m,m+1)=1$, therefore $m+1|p-a.$ This gives $m+1<p-a$, which is a contradiction as $0\le (p-a)\le q<m+1$. This implies ${\mathcal{C}}_1$ and ${\mathcal{C}}_4$ are disjoint.

Case 4: 

If $x\in {\mathcal{C}}_3\cap {\mathcal{C}}_4$, then $j=(am+(b-r\left)\right(m+1\left)\right)$. If $b-r\ge 0$, then $j\in ⟨m,m+1⟩$, which is a contradiction, as j is a generator. If $b-r<0,$ then $am-j=(r-b)(m+1)$. Since $qm<j\le qm+2q+2,$ therefore $am-j<0,$ and we also know that $(r-b)(m+1)>0$. Therefore, ${\mathcal{C}}_3\cap {\mathcal{C}}_4=\varnothing .$

This implies $G_{\Sigma }\cong {\oplus }_{i=1}^4{K}_{|{\mathcal{C}}_i|}$, and therefore

$$|G_{\Sigma }|=|{\mathcal{C}}_1|+|{\mathcal{C}}_2|+|{\mathcal{C}}_3|+|{\mathcal{C}}_4|.$$

It is easy to see that if $q\ge 3$ is odd then

$$|G_{\Sigma }|=m-\lfloor \frac{m}{2}\rfloor -1+\frac{{(q+1)}^2}{2}+\sum _{a=1}^{\frac{q-1}{2}}(m-\lceil \frac{m}{2}\rceil -q-1-a)+\sum _{l=1}^{\frac{q-1}{2}}(q-l)$$

if $q=1$ or $q\ge 2$ is even then

$$|G_{\Sigma }|=m-\lfloor \frac{m}{2}\rfloor -1+q(\lfloor \frac{q}{2}\rfloor +1)+\sum _{a=1}^{\lfloor \frac{q}{2}\rfloor }(m-\lceil \frac{m}{2}\rceil -q-1-a)+\sum _{l=1}^{\lfloor \frac{q}{2}\rfloor }(q-l).$$

□

Conjucture: Let $G\left(\mathcal{S}\right)$ be a graph associated with numerical semigroup $\mathcal{S}$. If $q\ge 3$ is odd then

$$\omega \left(G\left(\mathcal{S}\right)\right)=m-\lfloor \frac{m}{2}\rfloor -1+\frac{{(q+1)}^2}{2}+\sum _{a=1}^{\frac{q-1}{2}}(m-\lceil \frac{m}{2}\rceil -q-1-a)+\sum _{l=1}^{\frac{q-1}{2}}(q-l),$$

and if $q=1$ or $q\ge 2$ is even then

$$\omega \left(G\left(\mathcal{S}\right)\right)=m-\lfloor \frac{m}{2}\rfloor -1+\frac{q(q+2)}{2}+\sum _{a=1}^{\frac{q-2}{2}}(m-\lceil \frac{m}{2}\rceil -q-1-a)+\sum _{l=1}^{\frac{q}{2}}(q-l).$$

We prove this conjucture for the case, when $m=2q+7$. For this, we only need to show that $G_{\Sigma }$ is a maximal clique of $G\left(\mathcal{S}\right)$.

Theorem 2.

Let $m=2q+7$, then $G_{\Sigma }$ is a maximal clique of $G\left(\mathcal{S}\right)$.

Proof. 

Let $\mathcal{F}-(xm+y(m+1)+c{t}_j)\in g\left(\mathcal{S}\right)\setminus {\cup }_{i=1}^4{C}_i$, where $x,y,c\ge 0.$

Case-1: 

If $x=q+z,z\in \{1,\dots ,q\},y=0,c=0,$ then for $\mathcal{F}-(qm+2q+2)\in {\cup }_{i=1}^4{C}_i$

$$\mathcal{F}-(mq+mz)+\mathcal{F}-(qm+2q+2)=2qm+2q-mz.$$

Since $\mathcal{F}-(2qm+2q-mz)=mz+1\in \mathcal{S}$ (by Lemma 1), therefore $2qm+2q-mz\notin \mathcal{S}.$

Case-2: 

If $x=q+z,z\in \{1,\dots ,q-1\},y=q-s,s\in \{0,\dots ,q-1\},c=0,$ then

$$\mathcal{F}-(mq+mz+mq-ms+q-s)+\mathcal{F}-(qm+2q+2)=(q+s)(m+1)-mz.$$

Since $\mathcal{F}-\left(\right(q+s\left)\right(m+1)-mz)=(q+z-s)m+(q+1-s)\in \mathcal{S},$ therefore $(q+s)(m+1)-mz\notin \mathcal{S}.$

Case-3: 

If $x=q-z,z\in \{0,\dots ,q\},y=q+s,s\in \{1,\dots ,q\},c=0,$ then for $\mathcal{F}-q(m+1)\in {\cup }_{i=1}^4{C}_i$

$$\mathcal{F}-(qm-mz+qm+ms+q+s)+\mathcal{F}-(qm+q)=(q+z)m-s(m+1)+2q+2.$$

Since $\mathcal{F}-(q+z)m-s(m+1)+2q+2=(q+s-z)m+(s-1)\in \mathcal{S}$ (by Lemma 1), therefore $(q+z)m-s(m+1)+2q+2\notin \mathcal{S}.$

Case-4: 

If $x=0,y=0,c=1$ and $t_j=qm+2q+5+u,$$u\in \{0,1\}$, then

$$\mathcal{F}-(qm+2q+5+u)+\mathcal{F}-(qm+2q+3)=2qm-6-u.$$

Since $\mathcal{F}-(2qm-6-u)=2q+7+u=m+u\in S$, therefore $2qm-6-u\notin \mathcal{S}.$

Case-5: 

If $x=0,$ $y=q-s,s\in \{1,\dots ,q-1\}$, $c=1$, and $t_i=2q^2+9q+5+u,u\in \{0,1\}$, then

$$\mathcal{F}-(qm+q-ms-s+2q^2+9q+5+u)+\mathcal{F}-(qm+2q+3)=qm+ms+s-q-6-u.$$

Since $\mathcal{F}-(qm+ms+s-q-6-u)=m(q+1-s)+(q+u-s)\in \mathcal{S}$ (by Lemma 1), therefore $qm+ms+s-q-6-u\notin \mathcal{S}.$

Case-6: 

If $x=q-z,z\in \{1,\dots ,q\},y=0,c=1$, and $t_i=2q^2+9q+5+u,u\in \{0,1\}$, then

$$\mathcal{F}-(qm-mz+2q^2+9q+5+u)+\mathcal{F}-(qm+2q+3)=qm+mz-6-u.$$

Since $\mathcal{F}-(qm+mz-6-u)=m(q+1-z)+u\in \mathcal{S}$ (by Lemma 1), therefore $qm+mz-6-u\notin \mathcal{S}.$ □

Example 3.

Let $G\left(\mathcal{S}\right)$ be a graph associated with $\mathcal{S}=⟨11,12,28,29,30,31,32⟩$, then

$$V\left(G\right(\mathcal{S}\left)\right)=\{1,2,3,5,6,7,8,9,10,13,14,15,16,17,18,19,20,21,25,26,27,37,38,49\}.$$

Proposition 1 and Theorem 1 imply

$$cl\left(G\right(\mathcal{S}\left)\right)=\{9,14,15,19,20,21,25,26,27,37,38,49\}$$

and so,

$$\omega \left(G\right(\mathcal{S}\left)\right)=12.$$

The graph $G\left(\mathcal{S}\right)$ and a maximal clique of $G\left(\mathcal{S}\right)$ are given in Figure 6a and Figure 6b, respectively.

Figure 6. The graph $G_1$ associated with numerical semigroup $\mathcal{S}=⟨11,12,28,29,30,31,32⟩$ and its maximal clique.

3. Discussion

In this work, we proposed a conjecture for the clique number of graphs associated with symmetric numerical semigroups of arbitrary multiplicity and embedding dimension. We elaborate this conjecture to relate back to the existing results characterizing the structural and algebraic properties of numerical semigroups dictated by their ass-commutation, which would further clarify some of these deeply involved connections with graph theory. We give evidence of this claim by studying a large number of examples of symmetric numerical semigroups with arbitrary multiplicities and embedding dimensions. The conjecture is supported extremely well by empirical data, and the proposed function turns out to be a very good predictor of the clique number in these cases. We have also verified the conjecture with computational techniques for a wider range of numerical semigroups giving our points another layer of evidence in favor of this hypothesis. The main focus for future research is to mathematically prove our conjecture. This will involve thoroughly studying the structure of symmetric numerical semigroups and their graphs, as well as developing new theoretical approaches and methods, and while our conjecture mainly applies to symmetric numerical semigroups, it would also be valuable to explore if similar outcomes can be obtained for non-symmetric numerical semigroups. Examining this wider category might uncover more connections and characteristics, thus enhancing the theory as a whole.

4. Conclusions

In this article, we compute the maximal clique of graphs associated with symmetric numerical semigroup of arbitrary multiplicity and embedding dimension 7. Moreover, we give a conjecture on the clique number of $G\left(\mathcal{S}\right),$ where $\mathcal{S}$ is a symmetric numerical semigroup of arbitrary multiplicity and embedding dimension. In the future, we will compute the clique number of other classes of numerical semigroups and on this basis we will discuss the several invariants of $G\left(\mathcal{S}\right)$.