Numerical Approach Based on the Haar Wavelet Collocation Method for Solving a Coupled System with the Caputo–Fabrizio Fractional Derivative

Abstract

In the present paper, we consider an effective computational method to analyze a coupled dynamical system with Caputo–Fabrizio fractional derivative. The method is based on expanding the approximate solution into a symmetry Haar wavelet basis. The Haar wavelet coefficients are obtained by using the collocation points to solve an algebraic system of equations in mathematical physics. The error analysis of this method is characterized by a good convergence rate. Finally, some numerical examples are presented to prove the accuracy and effectiveness of this method.

1. Introduction

Recently, various problems in the applied mathematics, physical, biological, and engineering sciences are modeled using fractional calculus. Due to its property of memory effect, this concept has received a great response in the applied sciences. In this regard, many definitions have been given for both the integral and the fractional derivatives, such as the Riemann–Liouville [1], Caputo [2] and Caputo–Fabrizio fractional integrals and derivatives [1,2,3,4,5]. However, the concepts of Riemann–Liouville and Caputo were used to model the phenomena first, which have singularity in their kernels. For this reason, many new definitions of integrals and fractional derivatives have been introduced in the literature. For instance, the Caputo–Fabrizio fractional integral and derivative [1] avoid the singularity problem; this property makes it popular in the scientific community. The main problem facing researchers in solving Caputo–Fabrizio fractional differential equations and systems [6] is the difficulty in finding an analytical solution, which leads them to use numerical methods. In fact, it is known that in many numerical methods, the solutions contain discontinuities at some points, which negatively affects the accuracy and convergence rate. Currently, the Haar wavelet method [7] is a common strategy that aims to improve the convergence rate according to exponential decay. Confirming this, we find that it has been applied to solve many problems, such as ODEs [8] and time-PDEs [9,10], differential equations [11,12,13,14], and fractional differential equations (FDEs) [15,16,17,18,19,20,21]. Indeed, the Haar wavelet has the advantages of simplicity, orthogonality, and compact support. As a support for the Haar wavelet method, in the present paper, we apply and investigate it to solve the following system [6] for $0\le t\le 1$:

$$\left\{\begin{array}{c}{}^{CF}D^{\left(\nu \right)}u\left(t\right)=c_{1}u\left(t\right)+c_{2}v\left(t\right)+f\left(t\right),\hfill \\ {}^{CF}D^{\left(\nu \right)}v\left(t\right)=c_{3}u\left(t\right)+c_{4}v\left(t\right)+h\left(t\right),\hfill \\ \multicolumn{1}{c}{u(t=0)=v(t=0)=0,}\end{array}\right.$$

(1)

where $0<\nu <1$, f and h are two continuous functions, whereas the operator ${}^{CF}D^{\left(\nu \right)}$ is the Caputo–Fabrizio derivative of order $\nu$, and $c_i$ $\left(i=1,\dots ,4\right)$ are real constants.

In fact, Ikram Mansouri et al. [6] considered the questions of the existence of a unique solution for this system, where the Adomian Decomposition Method (ADM) is applied to provide an approximate solution to it. However, the Adomian Decomposition Method has a polynomial decay of the convergence rate, and it is expensive to compute its terms and requires a large number of terms to obtain the exact solution. To overcome these defects, the Haar wavelet collocation method is suitable in terms of computation costs and convergence rates. As far as we know, the Haar wavelet approximation method has not been applied to a coupled system with the Caputo–Fabrizio fractional derivative before.

This paper is structured as follows: In the second Section 2, we remember the definition of the Caputo–Fabrizio fractional derivative and the associated fractional integral. In Section 3, we introduce the Haar wavelet family that is associated with our proposed numerical method of the solution. In Section 4, we give illustrative examples to prove the accuracy and effectiveness of our proposed method. Finally, we finish this paper with a concluding section.

2. Basic Knowledge

2.1. Caputo–Fabrizio Fractional Integral and Derivative

We state and recall some definitions and the main properties related to the Caputo–Fabrizio fractional integral and derivative.

Definition 1 

([6]). Assume that the function $f\in H^1(a,b)$ and a constant $\nu \in (0,1)$; then, the Caputo–Fabrizio fractional derivative is defined by

$${}^{CF}D_a^{\left(\nu \right)}f\left(x\right)=\frac{M\left(\nu \right)}{1-\nu }\underset{a}{\overset{x}{\int }}{f}^{\prime }\left(\tau \right)exp\left(-\nu {\displaystyle \frac{t-\tau }{1-\nu }}\right)d\tau ,$$

(2)

and the associated fractional integral is defined as

$${}^{CF}I_a^{\nu }f\left(x\right)=\frac{1}{M\left(\nu \right)}\left[\left(1-\nu \right)\left(f\left(x\right)-f\left(a\right)\right)+\nu \underset{a}{\overset{x}{\int }}f\left(\tau \right)d\tau \right],$$

(3)

where M is a normalization function such as

$$M(\nu =0)=M(\nu =1)=1.$$

Lemma 1 

([6]). Assume that

$$\nu \in \left(n,n+1\right),n=\left[\nu \right]\ge 0.$$

Let $f\in C^n\left(\left[a,b\right]\right)$; then,

1. If $f\left(a\right)=0,$ then

$${}^{CF}D_a^{\left(\nu \right)}\left({}^{CF}I_a^{\nu }f\left(x\right)\right)=f\left(x\right).$$

2. We have

$${}^{CF}I_a^{\nu }\left({}^{CF}D_a^{\left(\nu \right)}f\left(x\right)\right)=f\left(x\right)+\sum _{i=0}^n{a}_i{x}^i,a_i\in \mathbb{R},i=0,\dots ,n.$$

3. If $\nu \in \left(0,1\right),$ then

$${}^{CF}I_a^{\nu }\left({}^{CF}D_a^{\left(\nu \right)}f\left(x\right)\right)=f\left(x\right)-f\left(a\right).$$

In the following theorem and in our study, it is assumed that $M=1.$

Theorem 1 

([6]). Let us define $L_1\left(t,u,v\right)=c_{1}u+c_{2}v,$ $L_2\left(t,u,v\right)=c_{3}u+c_{4}v.$ Suppose that $L_1$ and $L_2$ are continuous functions; then, the system (1) has a unique solution such that

$$\mu ={\mu }_1+{\mu }_2<1,$$

(4)

where ${\mu }_1=max\left(\left|c_1\right|,\left|c_2\right|\right),$ ${\mu }_2=max\left(\left|c_3\right|,\left|c_4\right|\right).$

2.2. Haar Wavelet Basis

As in [1,7], the Haar wavelets basis on $\left[0,1\right)$ consists of the following functions:

The scaling function on $\left[0,1\right)$ is $g_1\left(t\right)=1$ for $0\le t<1$ and also the wavelets functions

$$g_i\left(t\right)=\left\{\begin{array}{c}1,ift\in \left[{\varrho }_1,{\varrho }_2\right),\hfill \\ \multicolumn{1}{c}{-1,ift\in \left[{\varrho }_2,{\varrho }_3\right),}\\ \multicolumn{1}{c}{0,otherwise,}\end{array}\right.$$

(5)

where ${\varrho }_1=\frac{\kappa }{m},$ ${\varrho }_2=\frac{\kappa +0.5}{m}$, and ${\varrho }_3=\frac{\kappa +1}{m},$ $m=2^j,$ $j=0, 1, \dots , J$, and J is considered as resolution level for wavelet approximation and $\kappa =0, \dots , m-1$ is a translation parameter where $i=m+\kappa +1.$ The value i can take $i=2M,$ $M=2^J$ as a maximum value.

Any function $f\in L^2\left(\left[0,1\right)\right)$ can be expanded as

$$f\left(t\right)=\sum _{i=1}^{+\infty }{a}_i{g}_i\left(t\right),$$

(6)

where

$$a_i=\underset{0}{\overset{1}{\int }}f\left(t\right)g_i\left(t\right)dt.$$

In reality, note that the first $2M$ terms of (6) can be considered, where M is a power of 2 $\left(M=2^J\right).$ That is,

$$f\left(t\right)\equiv f_{2M}\left(t\right)=\sum _{i=1}^{2M}{a}_i{g}_i\left(t\right).$$

(7)

The integration $\beta$ times of $g_1\left(t\right)$ together with (5) is as follows:

$$F_{i,\beta }\left(t\right)=\underset{0}{\overset{t}{\int }}\underset{0}{\overset{t}{\int }}\dots \underset{0}{\overset{t}{\int }}{g}_i\left(t\right)d{t}^{\beta },$$

(8)

and we obtain the following formula [1]: $F_{1,\beta }\left(t\right)=\frac{t^{\beta }}{\beta !}$ and $\forall i\ge 2,$

$$F_{i,\beta }\left(t\right)=\frac{1}{\beta !}\left\{\begin{array}{ccc}0,\hfill & if& t\in \left[0,{\varrho }_1\right),\\ {\left(t-{\varrho }_1\right)}^{\beta },\hfill & if& t\in \left[{\varrho }_1,{\varrho }_2\right),\\ {\left(t-{\varrho }_1\right)}^{\beta }-2{\left(t-{\varrho }_2\right)}^{\beta },\hfill & if& t\in \left[{\varrho }_2,{\varrho }_3\right),\\ {\left(t-{\varrho }_1\right)}^{\beta }-2{\left(t-{\varrho }_2\right)}^{\beta }+{\left(t-{\varrho }_3\right)}^{\beta },\hfill & if& t\in \left[{\varrho }_3,1\right).\end{array}\right.$$

(9)

3. Haar Wavelet Approximation Method

Here, we propose our new numerical method.

3.1. Method of Solution

Consider the system (1) for $0\le t\le 1$:

$$\left\{\begin{array}{c}{}^{CF}D^{\left(\nu \right)}u\left(t\right)=c_{1}u\left(t\right)+c_{2}v\left(t\right)+f\left(t\right),\\ {}^{CF}D^{\left(\nu \right)}v\left(t\right)=c_{3}u\left(t\right)+c_{4}v\left(t\right)+h\left(t\right),\\ \multicolumn{1}{c}{u(t=0)=v(t=0)=0.}\end{array}\right.$$

(10)

Suppose that

$$\left\{\begin{array}{c}{}^{CF}D^{\left(\nu \right)}u\left(t\right)\equiv \widetilde{{}^{CF}D^{\left(\nu \right)}}u\left(t\right)={\displaystyle \sum _{i=1}^{2M}}{a}_i{g}_i\left(t\right),\hfill \\ {}^{CF}D^{\left(\nu \right)}v\left(t\right)\equiv \widetilde{{}^{CF}D^{\left(\nu \right)}}v\left(t\right)={\displaystyle \sum _{i=1}^{2M}}{b}_i{g}_i\left(t\right),\hfill \end{array}\right.$$

(11)

where $a_i, b_i,$ $i=1, \dots , 2M$ are the Haar wavelet coefficients to be determined.

By integrating (11) in the Caputo–Fabrizio sense and taking into account that $u(t=0)=v(t=0)=0$, we obtain

$$\left\{\begin{array}{c}u\left(t\right)\equiv u_{2M}\left(t\right)={\displaystyle \sum _{i=1}^{2M}}{a}_i{I}^{\nu }{g}_i\left(t\right),\hfill \\ v\left(t\right)\equiv v_{2M}\left(t\right)={\displaystyle \sum _{i=1}^{2M}}{b}_i{I}^{\nu }{g}_i\left(t\right).\hfill \end{array}\right.$$

(12)

Using (3), we have

$$I^{\left(\nu \right)}{g}_i\left(t\right)=\left(1-\nu \right)(g_i\left(t\right)-g_i\left(0\right))+\nu F_{i,1}\left(t\right),\forall i=1,\dots ,2M.$$

(13)

Substituting (13) in (12), we find

$$\left\{\begin{array}{c}u\left(t\right)\equiv u_{2M}\left(t\right)={\displaystyle \sum _{i=1}^{2M}}{a}_i\left[\left(1-\nu \right)(g_i\left(t\right)-g_i\left(0\right))+\nu F_{i,1}\left(t\right)\right],\hfill \\ v\left(t\right)\equiv v_{2M}\left(t\right)={\displaystyle \sum _{i=1}^{2M}}{b}_i\left[\left(1-\nu \right)(g_i\left(t\right)-g_i\left(0\right))+\nu F_{i,1}\left(t\right)\right].\hfill \end{array}\right.$$

(14)

Using (11) and (14) and (10), we obtain the next system of equations:

$$\left\{\begin{array}{c}{\displaystyle \sum _{i=1}^{2M}}{a}_{i}L(i,t)+{\displaystyle \sum _{i=1}^{2M}}{b}_{i}G(i,t)=-f\left(t\right),\hfill \\ {\displaystyle \sum _{i=1}^{2M}}{a}_i\tilde{L}(i,t)+{\displaystyle \sum _{i=1}^{2M}}{b}_i\tilde{G}(i,t)=-h\left(t\right),\hfill \end{array}\right.$$

(15)

where

$$\left\{\begin{array}{c}L(i,t)=(c_1\left(1-\nu \right)-1)g_i\left(t\right)+\nu c_1{F}_{i,1}\left(t\right)-c_1\left(1-\nu \right)g_i\left(0\right),\hfill \\ G(i,t)=c_2\left(1-\nu \right)g_i\left(t\right)+\nu c_2{F}_{i,1}\left(t\right)-c_2\left(1-\nu \right)g_i\left(0\right),\hfill \\ \tilde{L}(i,t)=c_3\left(1-\nu \right)g_i\left(t\right)+\nu c_3{F}_{i,1}\left(t\right)-c_3\left(1-\nu \right)g_i\left(0\right),\hfill \\ \multicolumn{1}{c}{\tilde{G}(i,t)=(c_4\left(1-\nu \right)-1)g_i\left(t\right)+\nu c_4{F}_{i,1}\left(t\right)-c_4\left(1-\nu \right)g_i\left(0\right).}\end{array}\right.$$

(16)

Define the collocation points $t_{\ell }=\frac{\ell -0.5}{2M},$ $\ell =1, \dots , 2M,$ and replace them in the system (15); we have the following $4M\times 4M$ linear system of equations:

$$\left\{\begin{array}{c}{\displaystyle \sum _{i=1}^{2M}}{a}_{i}L(i,t_{\ell })+{\displaystyle \sum _{i=1}^{2M}}{b}_{i}G(i,t_{\ell })=-f\left(t_{\ell }\right),\ell =1,\dots ,2M,\hfill \\ {\displaystyle \sum _{i=1}^{2M}}{a}_i\tilde{L}(i,t_{\ell })+{\displaystyle \sum _{i=1}^{2M}}{b}_i\tilde{G}(i,t_{\ell })=-h\left(t_{\ell }\right),\ell =1,\dots ,2M.\hfill \end{array}\right.$$

(17)

By solving this system, we obtain the unknown coefficients $a_i, b_i,$ $i=1, \dots , 2M,$ and by substituting them into (14), we obtain the numerical solution of the system (1).

3.2. Analysis of Error Estimations

The error of approximation using our proposed method of the solution is studied here.

Lemma 2 

([12]). Let $f\in L^2\left([0,1)\right)$ be a differentiable function; then, $f^{\prime }$ is bounded on $\left(0,1\right)$ and $\tilde{f}$ is its Haar wavelet approximation, defined by (7); then,

$${∥f-\tilde{f}∥}_{L^2\left([0,1)\right)}\le C{2}^{-J},$$

(18)

where C is a constant.

The Haar wavelet coefficients that are given in (11) can be estimated as follows:

$$a_i=\mathcal{O}\left(\frac{1}{2^{j+1}}\right),i=2^j+\kappa +1.$$

(19)

Proof. 

We have, first,

$$\begin{array}{ccc}\hfill a_i& =& \underset{0}{\overset{1}{\int }}{}^{CF}D^{\left(\nu \right)}u\left(t\right)g_i\left(t\right)dt\hfill \\ & =& \underset{{\varrho }_1}{\overset{{\varrho }_2}{\int }}{}^{CF}D^{\left(\nu \right)}u\left(t\right)dt-\underset{{\varrho }_2}{\overset{{\varrho }_3}{\int }}{}^{CF}D^{\left(\nu \right)}u\left(t\right)dt\hfill \\ & =& \left({\varrho }_2-{\varrho }_1\right){}^{CF}D^{\left(\nu \right)}u\left({\eta }_1\right)-\left({\varrho }_3-{\varrho }_2\right){}^{CF}D^{\left(\nu \right)}u\left({\eta }_2\right),\hfill \end{array}$$

where ${\eta }_1\in \left[{\varrho }_1,{\varrho }_2\right]$ and ${\eta }_2\in \left[{\varrho }_2,{\varrho }_3\right].$

Since ${\varrho }_2-{\varrho }_1={\varrho }_3-{\varrho }_2=\frac{1}{2m}=\frac{1}{2^{j+1}},$

$$a_i=\frac{\left({\eta }_1-{\eta }_2\right)}{2^{j+1}}\frac{d{}^{CF}D^{\left(\nu \right)}u}{dt}\left(\vartheta \right),\vartheta \in \left[{\eta }_1,{\eta }_2\right],$$

which implies that

$$\left|a_i\right|\le \frac{1}{2^{j+1}}{∥\frac{d{}^{CF}D^{\left(\nu \right)}u}{dt}∥}_{\infty }.$$

(20)

On the other hand,

$$\begin{array}{ccc}\hfill \frac{d{}^{CF}D^{\left(\nu \right)}u}{dt}\left(t\right)& =& \frac{1}{1-\nu }\left[u^{\prime }\left(t\right)+\underset{0}{\overset{t}{\int }}{u}^{\prime }\left(\tau \right)\left(\frac{-\nu }{1-\nu }\right)exp(-\nu \frac{t-\tau }{1-\nu })d\tau \right]\hfill \\ & =& \frac{1}{1-\nu }\left[u^{\prime }\left(t\right)-\nu {}^{CF}D^{\left(\nu \right)}u\left(t\right)\right].\hfill \end{array}$$

This expression leads to

$${∥\frac{d{}^{CF}D^{\left(\nu \right)}u}{dt}∥}_{\infty }\le \frac{1}{1-\nu }{∥u^{\prime }∥}_{\infty }+\frac{\nu }{1-\nu }{∥{}^{CF}D^{\left(\nu \right)}u∥}_{\infty }.$$

(21)

Now, for ${∥{}^{CF}D^{\left(\nu \right)}u∥}_{\infty }$, we have

$$\begin{array}{ccc}\hfill \left|{}^{CF}D^{\left(\nu \right)}u\left(t\right)\right|& \le & \frac{1}{1-\nu }{∥u^{\prime }∥}_{\infty }\underset{0}{\overset{t}{\int }}exp(-\nu \frac{t-\tau }{1-\nu })d\tau \hfill \\ & \le & \frac{{∥u^{\prime }∥}_{\infty }}{\nu }\left[1-exp(-\nu \frac{t}{1-\nu })\right]\hfill \\ & \le & \frac{{∥u^{\prime }∥}_{\infty }}{\nu }\left[1-exp\left(\frac{-\nu }{1-\nu }\right)\right],\hfill \end{array}$$

and thus,

$${∥{}^{CF}D^{\left(\nu \right)}u\left(t\right)∥}_{\infty }\le \frac{{∥u^{\prime }∥}_{\infty }}{\nu }\left[1-exp\left(\frac{-\nu }{1-\nu }\right)\right],$$

(22)

and inserting (22) into (21) yields

$${∥\frac{d{}^{CF}D^{\left(\nu \right)}u}{dt}∥}_{\infty }\le \frac{2-exp\left(\frac{-\nu }{1-\nu }\right)}{1-\nu }{∥u^{\prime }∥}_{\infty }.$$

Therefore,

$$\left|a_i\right|\le \left(\frac{2-exp\left(\frac{-\nu }{1-\nu }\right)}{1-\nu }{∥u^{\prime }∥}_{\infty }\right)\frac{1}{2^{j+1}}.$$

□

Lemma 3. 

The function $F_{i,1}$ for $i\ge 2$ verifies the following inequality:

$${∥F_{i,1}∥}_{\infty }\le \frac{1}{2^{j+1}},i=2^j+\kappa +1.$$

(23)

Proof. 

From (9), we have, $i\ge 2$

$$F_{i,1}\left(t\right)=\left\{\begin{array}{ccc}0,\hfill & if& t\in \left[0,{\varrho }_1\right),\\ t-{\varrho }_1,\hfill & if& t\in \left[{\varrho }_1,{\varrho }_2\right),\\ -t+2{\varrho }_2-{\varrho }_1,\hfill & if& t\in \left[{\varrho }_2,{\varrho }_3\right),\\ 2{\varrho }_2-{\varrho }_3-{\varrho }_1,\hfill & if& t\in \left[{\varrho }_3,1\right).\end{array}\right.$$

Note that in the interval $\left[{\varrho }_1,{\varrho }_2\right),$ the function $F_{i,1}$ is positive and increasing; then, $\left|F_{i,1}\right|\le {\varrho }_2-{\varrho }_1=\frac{1}{2^{j+1}}.$

In the interval $\left[{\varrho }_2,{\varrho }_3\right),$ the function $F_{i,1}$ is positive and decreasing; then, $\left|F_{i,1}\right|\le {\varrho }_2-{\varrho }_1=\frac{1}{2^{j+1}}.$

Otherwise, the function $F_{i,1}$ is null.

Thus, ${∥F_{i,1}∥}_{\infty }\le \frac{1}{2^{j+1}}.$ □

Lemma 4. 

For $i\ge 2$, we define the function $q_i$ as

$$q_i\left(t\right)=(1-\nu )\left(g_i\left(t\right)-g_i\left(0\right)\right)+\nu F_{i,1}\left(t\right),i=2^j+\kappa +1,0\le t<1.$$

(24)

Then, we have

1. $\forall i\ge 2,$ $\left|q_i\left(t\right)\right|\le 2-\nu .$

2. If $\kappa \ne 0,$ then $\underset{0}{\overset{1}{\int }}\left|q_i\left(t\right)\right|dt\le \left(1-\frac{\nu }{2}\right)\frac{1}{2^j}.$

Proof. 

1. $\forall i\ge 2$; we have

$$\begin{array}{ccc}\hfill \left|q_i\left(t\right)\right|& \le & (1-\nu )\left|g_i\left(t\right)-g_i\left(0\right)\right|+\nu {∥F_{i,1}\left(t\right)∥}_{\infty }\hfill \\ & \le & 2(1-\nu )+\nu \frac{1}{2^{j+1}}\hfill \\ & \le & 2(1-\nu )+\nu =2-\nu .\hfill \end{array}$$

2. If $\kappa \ne 0,$ then $g_i\left(0\right)=0$, and we have

$$\underset{0}{\overset{1}{\int }}\left|q_i\left(t\right)\right|dt\le (1-\nu )\underset{0}{\overset{1}{\int }}\left|g_i\left(t\right)\right|dt+\nu \underset{0}{\overset{1}{\int }}{∥F_{i,1}\left(t\right)∥}_{\infty }dt.$$

Note that

$$\underset{0}{\overset{1}{\int }}\left|g_i\left(t\right)\right|dt=\underset{{\varrho }_1}{\overset{{\varrho }_2}{\int }}dt+\underset{{\varrho }_2}{\overset{{\varrho }_3}{\int }}dt=\frac{1}{2^j}.$$

Hence,

$$\begin{array}{ccc}\hfill \underset{0}{\overset{1}{\int }}\left|q_i\left(t\right)\right|dt& \le & (1-\nu )\frac{1}{2^j}+\nu \frac{1}{2^{j+1}}\hfill \\ & \le & (1-\frac{\nu }{2})\frac{1}{2^j}.\hfill \end{array}$$

□

Theorem 2. 

Let $\left(u,v\right)$ be the exact solution of (1), and let $\left(u_{2M},v_{2M}\right)$ be its approximation formula, which is expressed in (14), so the convergence rate is estimated by

$${∥u-u_{2M}∥}_{L^2\left(\left[0,1\right)\right)}=\mathcal{O}\left(\frac{1}{\sqrt{M}}\right),$$

(25)

and

$${∥v-v_{2M}∥}_{L^2\left(\left[0,1\right)\right)}=\mathcal{O}\left(\frac{1}{\sqrt{M}}\right).$$

(26)

Proof. 

From (14), the error square at the $Jth$-level resolution for the function u can be written as

$$\begin{array}{ccc}\hfill E_M^2\left(u\right)& =& {∥u-u_{2M}∥}_{L^2\left(\left[0,1\right)\right)}^2={∥\sum _{i=2M+1}^{+\infty }{a}_i\left[\left(1-\nu \right)(g_i\left(t\right)-g_i\left(0\right))+\nu F_{i,1}\left(t\right)\right]∥}_{L^2\left(\left[0,1\right)\right)}^2\hfill \\ & =& \sum _{\ell =2M+1}^{+\infty }\sum _{i=2M+1}^{+\infty }{a}_i{a}_{\ell }\underset{0}{\overset{1}{\int }}{q}_i\left(t\right)q_{\ell }\left(t\right)dt.\hfill \end{array}$$

By putting $i=2^j+\kappa +1$ and $\ell =2^r+s+1,$ we obtain

$$\begin{array}{ccc}\hfill E_M^2\left(u\right)& =& \sum _{r=J+1}^{+\infty }\sum _{s=0}^{2^r-1}\sum _{j=J+1}^{+\infty }\sum _{\kappa =0}^{2^j-1}{a}_{2^j+\kappa +1}{a}_{2^r+s+1}\underset{0}{\overset{1}{\int }}{q}_{2^j+\kappa +1}\left(t\right)q_{2^r+s+1}\left(t\right)dt\hfill \\ & =& \sum _{r=J+1}^{+\infty }\sum _{j=J+1}^{+\infty }{a}_{2^j+1}{a}_{2^r+1}\underset{0}{\overset{1}{\int }}{q}_{2^j+1}\left(t\right)q_{2^r+1}\left(t\right)dt\hfill \\ & & +\sum _{r=J+1}^{+\infty }\sum _{s=1}^{2^r-1}\sum _{j=J+1}^{+\infty }{a}_{2^j+1}{a}_{2^r+s+1}\underset{0}{\overset{1}{\int }}{q}_{2^j+1}\left(t\right)q_{2^r+s+1}\left(t\right)dt\hfill \\ & & +\sum _{r=J+1}^{+\infty }\sum _{j=J+1}^{+\infty }\sum _{\kappa =1}^{2^j-1}{a}_{2^j+\kappa +1}{a}_{2^r+1}\underset{0}{\overset{1}{\int }}{q}_{2^j+\kappa +1}\left(t\right)q_{2^r+1}\left(t\right)dt\hfill \\ & & +\sum _{r=J+1}^{+\infty }\sum _{s=1}^{2^r-1}\sum _{j=J+1}^{+\infty }\sum _{\kappa =1}^{2^j-1}{a}_{2^j+\kappa +1}{a}_{2^r+s+1}\underset{0}{\overset{1}{\int }}{q}_{2^j+\kappa +1}\left(t\right)q_{2^r+s+1}\left(t\right)dt.\hfill \end{array}$$

This implies that

$$\begin{array}{ccc}\hfill E_M^2& \le & \sum _{r=J+1}^{+\infty }\sum _{j=J+1}^{+\infty }\left|a_{2^j+1}\right|\left|a_{2^r+1}\right|\underset{0}{\overset{1}{\int }}\left|q_{2^j+1}\left(t\right)\right|\left|q_{2^r+1}\left(t\right)\right|dt\hfill \\ & & +\sum _{r=J+1}^{+\infty }\sum _{s=1}^{2^r-1}\sum _{j=J+1}^{+\infty }\left|a_{2^j+1}\right|\left|a_{2^r+s+1}\right|\underset{0}{\overset{1}{\int }}\left|q_{2^j+1}\left(t\right)\right|\left|q_{2^r+s+1}\left(t\right)\right|dt\hfill \\ & & +\sum _{r=J+1}^{+\infty }\sum _{j=J+1}^{+\infty }\sum _{\kappa =1}^{2^j-1}\left|a_{2^j+\kappa +1}\right|\left|a_{2^r+1}\right|\underset{0}{\overset{1}{\int }}\left|q_{2^j+\kappa +1}\left(t\right)\right|\left|q_{2^r+1}\left(t\right)\right|dt\hfill \\ & & +\sum _{r=J+1}^{+\infty }\sum _{s=1}^{2^r-1}\sum _{j=J+1}^{+\infty }\sum _{\kappa =1}^{2^j-1}\left|a_{2^j+\kappa +1}\right|\left|a_{2^r+s+1}\right|\underset{0}{\overset{1}{\int }}\left|q_{2^j+\kappa +1}\left(t\right)\right|\left|q_{2^r+s+1}\left(t\right)\right|dt.\hfill \end{array}$$

By using Lemma (2), Lemma (3), and Lemma (4), we obtain

$$\begin{array}{ccc}\hfill E_M^2\left(u\right)& \le & \sum _{r=J+1}^{+\infty }\sum _{j=J+1}^{+\infty }C\frac{1}{2^{j+1}}\frac{1}{2^{r+1}}\underset{0}{\overset{1}{\int }}{(2-\nu )}^{2}dt\hfill \\ & & +\sum _{r=J+1}^{+\infty }\sum _{s=1}^{2^r-1}\sum _{j=J+1}^{+\infty }C\frac{1}{2^{j+1}}\frac{1}{2^{r+1}}\underset{0}{\overset{1}{\int }}\left(2-\nu \right)\left|q_{2^r+s+1}\left(t\right)\right|dt\hfill \\ & & +\sum _{r=J+1}^{+\infty }\sum _{j=J+1}^{+\infty }\sum _{\kappa =1}^{2^j-1}C\frac{1}{2^{j+1}}\frac{1}{2^{r+1}}\underset{0}{\overset{1}{\int }}\left(2-\nu \right)\left|q_{2^j+\kappa +1}\left(t\right)\right|dt\hfill \\ & & +\sum _{r=J+1}^{+\infty }\sum _{s=1}^{2^r-1}\sum _{j=J+1}^{+\infty }\sum _{\kappa =1}^{2^j-1}C\frac{1}{2^{j+1}}\frac{1}{2^{r+1}}\sqrt{\underset{0}{\overset{1}{\int }}{\left|q_{2^j+\kappa +1}\left(t\right)\right|}^{2}dt\underset{0}{\overset{1}{\int }}{\left|q_{2^r+s+1}\left(t\right)\right|}^{2}dt}.\hfill \end{array}$$

Note that

$$\sqrt{\underset{0}{\overset{1}{\int }}{\left|q_{2^j+\kappa +1}\left(t\right)\right|}^{2}dt\underset{0}{\overset{1}{\int }}{\left|q_{2^r+s+1}\left(t\right)\right|}^{2}dt}=$$

$$\begin{array}{cc}\hfill & \sqrt{\underset{0}{\overset{1}{\int }}\left|q_{2^j+\kappa +1}\left(t\right)\right|\left|q_{2^j+\kappa +1}\left(t\right)\right|dt\underset{0}{\overset{1}{\int }}\left|q_{2^r+s+1}\left(t\right)\right|\left|q_{2^r+s+1}\left(t\right)\right|dt}\hfill \\ \hfill & \le \left(2-\nu \right)\sqrt{\underset{0}{\overset{1}{\int }}\left|q_{2^j+\kappa +1}\left(t\right)\right|dt\underset{0}{\overset{1}{\int }}\left|q_{2^r+s+1}\left(t\right)\right|dt}\hfill \\ \hfill & \le \left(2-\nu \right)\left(1-\frac{\nu }{2}\right)\frac{1}{2^{\frac{j}{2}}}\frac{1}{2^{\frac{r}{2}}}.\hfill \end{array}$$

Then,

$$\begin{array}{ccc}\hfill E_M^2\left(u\right)& \le & \sum _{r=J+1}^{+\infty }\sum _{j=J+1}^{+\infty }C\frac{1}{2^{j+1}}\frac{1}{2^{r+1}}{(2-\nu )}^2\hfill \\ & & +\sum _{r=J+1}^{+\infty }\sum _{s=1}^{2^r-1}\sum _{j=J+1}^{+\infty }C\frac{1}{2^{j+1}}\frac{1}{2^{r+1}}\left(2-\nu \right)\left(1-\frac{\nu }{2}\right)\frac{1}{2^r}\hfill \\ & & +\sum _{r=J+1}^{+\infty }\sum _{j=J+1}^{+\infty }\sum _{\kappa =1}^{2^j-1}C\frac{1}{2^{j+1}}\frac{1}{2^{r+1}}\left(2-\nu \right)\left(1-\frac{\nu }{2}\right)\frac{1}{2^j}\hfill \\ & & +\sum _{r=J+1}^{+\infty }\sum _{j=J+1}^{+\infty }C\frac{1}{2^{\frac{j}{2}+1}}\frac{1}{2^{\frac{r}{2}+1}}\left(2-\nu \right)\left(1-\frac{\nu }{2}\right)\hfill \\ & \le & \frac{C{(2-\nu )}^2}{4}{\left(\frac{1}{2^J}\right)}^2+\frac{C\left(2-\nu \right)\left(1-\frac{\nu }{2}\right)}{4}{\left(\frac{1}{2^J}\right)}^2\hfill \\ & & +\frac{C\left(2-\nu \right)\left(1-\frac{\nu }{2}\right)}{4}{\left(\frac{1}{2^J}\right)}^2+\frac{C\left(2-\nu \right)\left(1-\frac{\nu }{2}\right)}{4{\left(\sqrt{2}-1\right)}^2}{\left(\frac{1}{2^{\frac{J}{2}}}\right)}^2\hfill \\ & \le & \left[\frac{C{(2-\nu )}^2}{4}+\frac{C\left(2-\nu \right)\left(1-\frac{\nu }{2}\right)}{2}+\frac{C\left(2-\nu \right)\left(1-\frac{\nu }{2}\right)}{4{\left(\sqrt{2}-1\right)}^2}\right]{\left(\frac{1}{2^{\frac{J}{2}}}\right)}^2.\hfill \end{array}$$

Therefore,

$$E_M\left(u\right)=\mathcal{O}\left(\frac{1}{\sqrt{M}}\right).$$

In a similar way, we prove that $E_M\left(v\right)=\mathcal{O}\left(\frac{1}{\sqrt{M}}\right).$

Now, to verify the convergence analysis, we must prove that the following system converges to the system (1):

$$\left\{\begin{array}{c}\widetilde{{}^{CF}D^{\left(\nu \right)}}u\left(t\right)=c_1{u}_{2M}\left(t\right)+c_2{v}_{2M}\left(t\right)+f\left(t\right)+R_M^1\left(t\right),0\le t\le 1,\\ \widetilde{{}^{CF}D^{\left(\nu \right)}}v\left(t\right)=c_3{u}_{2M}\left(t\right)+c_4{v}_{2M}\left(t\right)+h\left(t\right)+R_M^2\left(t\right),0\le t\le 1,\end{array}\right.$$

(27)

where $R_M^1$ and $R_M^2$ represent the remainders.

By subtracting (27) from (1), we obtain

$$\left\{\begin{array}{c}{R}_M^1\left(t\right)=c_1(u\left(t\right)-u_{2M}\left(t\right))+c_2(v\left(t\right)-v_{2M}\left(t\right))-\left({}^{CF}D^{\left(\nu \right)}u\left(t\right)-\widetilde{{}^{CF}D^{\left(\nu \right)}}u\left(t\right)\right),0\le t\le 1,\\ R_M^2\left(t\right)=c_3(u\left(t\right)-u_{2M}\left(t\right))+c_4(v\left(t\right)-v_{2M}\left(t\right))-\left({}^{CF}D^{\left(\nu \right)}v\left(t\right)-\widetilde{{}^{CF}D^{\left(\nu \right)}}v\left(t\right)\right),0\le t\le 1.\end{array}\right.$$

(28)

Then,

$$\left\{\begin{array}{c}{∥R_M^1∥}_{L^2\left(\left[0,1\right]\right)}\le c_1{∥u-u_{2M}∥}_{L^2\left(\left[0,1\right]\right)}+c_2{∥v-v_{2M}∥}_{L^2\left(\left[0,1\right]\right)}+{∥{}^{CF}D^{\left(\nu \right)}u-\widetilde{{}^{CF}D^{\left(\nu \right)}}u∥}_{L^2\left(\left[0,1\right]\right)},\\ {∥R_M^2∥}_{L^2\left(\left[0,1\right]\right)}\le c_3{∥u-u_{2M}∥}_{L^2\left(\left[0,1\right]\right)}+c_4{∥v-v_{2M}∥}_{L^2\left(\left[0,1\right]\right)}+{∥{}^{CF}D^{\left(\nu \right)}v-\widetilde{{}^{CF}D^{\left(\nu \right)}}v∥}_{L^2\left(\left[0,1\right]\right)},\end{array}\right.$$

when $M\to +\infty ,$ we obtain ${∥u-u_{2M}∥}_{L^2\left(\left[0,1\right]\right)}\to 0,$ ${∥v-v_{2M}∥}_{L^2\left(\left[0,1\right]\right)}\to 0,$

${∥{}^{CF}D^{\left(\nu \right)}u-\widetilde{{}^{CF}D^{\left(\nu \right)}}u∥}_{L^2\left(\left[0,1\right]\right)}\to 0$ and ${∥{}^{CF}D^{\left(\nu \right)}v-\widetilde{{}^{CF}D^{\left(\nu \right)}}v∥}_{L^2\left(\left[0,1\right]\right)}\to 0.$

Therefore, ${∥R_M^1∥}_{L^2\left(\left[0,1\right]\right)}\to 0$ and ${∥R_M^2∥}_{L^2\left(\left[0,1\right]\right)}\to 0.$ □

4. Numerical Examples

Here, we examine examples of the problem (1) to show the efficiency of our proposed method. All computations are performed using Matlab, and the numerical results are represented in Figure 1, Figure 2, Figure 3 and Figure 4.

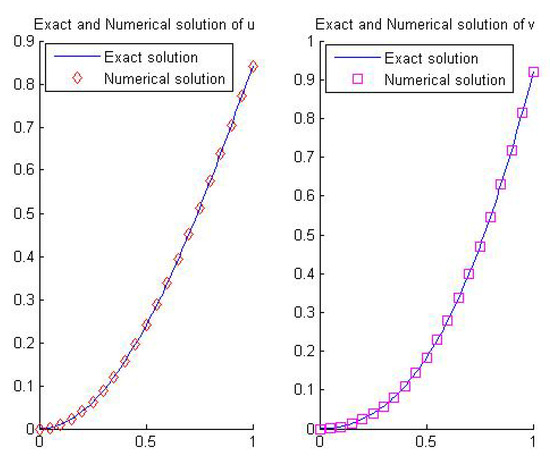
Figure 1. Numerical solution of Example 1 at level J = 3.

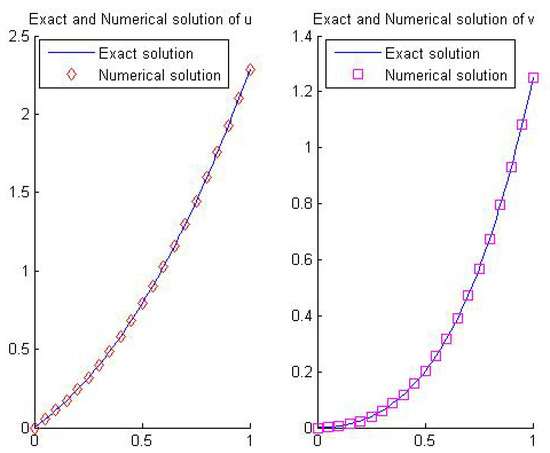
Figure 2. Numerical solution to Example 2 at level J = 3.

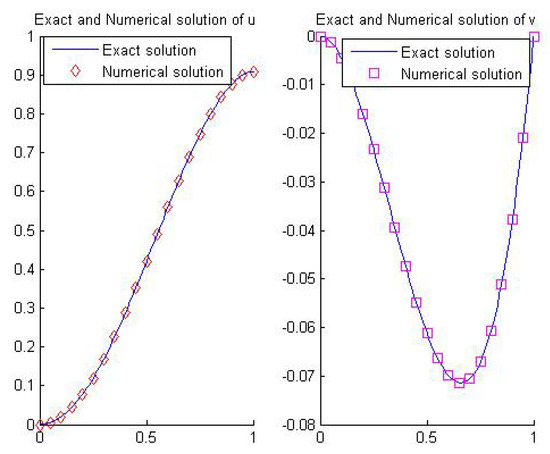
Figure 3. Numerical solution of Example 3 at level J = 3.

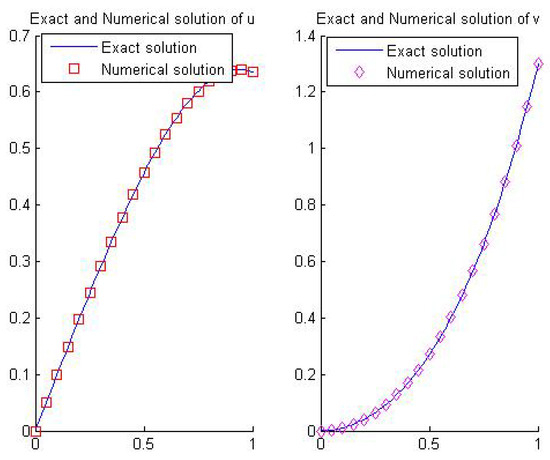
Figure 4. Numerical solution to Example 4 at the level J = 3.

Example 1. 

The next coupled system is considered for $0\le t\le 1$:

$$\left\{\begin{array}{c}{}^{CF}D^{\left(\mathrm{0.25}\right)}u\left(t\right)=-\frac{1}{2}u\left(t\right)+\frac{1}{2}v\left(t\right)+f\left(t\right),\hfill \\ \multicolumn{1}{c}{{}^{CF}D^{\left(\mathrm{0.25}\right)}v\left(t\right)=-\frac{1}{4}u\left(t\right)+\frac{1}{4}v\left(t\right)+h\left(t\right),}\\ u(t=0)=v(t=0)=0,\hfill \end{array}\right.$$

where

$$f\left(t\right)=\left(\frac{17}{10}t-\frac{8}{25}\right)sin\left(t\right)+\left(\frac{13}{50}+\frac{9}{10}t\right)cos\left(t\right)+\frac{6}{25}{e}^{-\frac{t}{3}}-\frac{1}{2}\left(1+t\right),$$

and

$$h\left(t\right)=\left(\frac{4}{25}+\frac{13}{20}t\right)sin\left(t\right)+\left(\frac{-63}{100}-\frac{19}{20}t\right)cos\left(t\right)-\frac{78}{25}{e}^{-\frac{t}{3}}-\frac{t}{4}+\frac{15}{4}.$$

The exact solution is given by

$$u\left(t\right)=tsin\left(t\right),$$

and

$$v\left(t\right)=(1+t)(1-cos(t\left)\right).$$

Example 2. 

Let us consider the problem for $0\le t\le 1$:

$$\left\{\begin{array}{c}{}^{CF}D^{\left(\mathrm{0.5}\right)}u\left(t\right)=\frac{1}{3}u\left(t\right)-\frac{1}{2}v\left(t\right)+f\left(t\right),\hfill \\ {}^{CF}D^{\left(\mathrm{0.5}\right)}v\left(t\right)=\frac{1}{8}u\left(t\right)+\frac{1}{6}v\left(t\right)+h\left(t\right),\hfill \\ u(t=0)=v(t=0)=0,\hfill \end{array}\right.$$

where

$$f\left(t\right)=\left(-\frac{1}{10}cos\left(t\right)+\frac{13}{15}sin\left(t\right)+\frac{1}{2}\right)e^t-\frac{2}{5}{e}^{-t},$$

and

$$h\left(t\right)=\left(-\frac{31}{30}cos\left(t\right)+\frac{11}{40}sin\left(t\right)+\frac{5}{6}\right)e^t+\frac{1}{5}{e}^{-t}.$$

The exact solution is defined as

$$u\left(t\right)=sin\left(t\right)e^t,$$

and

$$v\left(t\right)=(1-cos\left(t\right))e^t.$$

Example 3. 

Let the next problem for $0\le t\le 1$ be

$$\left\{\begin{array}{c}{}^{CF}D^{\left(\mathrm{0.75}\right)}u\left(t\right)=-\frac{1}{5}u\left(t\right)+\frac{2}{3}v\left(t\right)+f\left(t\right),\hfill \\ {}^{CF}D^{\left(\mathrm{0.75}\right)}v\left(t\right)=\frac{1}{6}u\left(t\right)+\frac{1}{12}v\left(t\right)+h\left(t\right),\hfill \\ u(t=0)=v(t=0)=0,\hfill \end{array}\right.$$

where

$$\begin{array}{ccc}\hfill f\left(t\right)& =& \left(\frac{60}{169}+\frac{93}{65}t\right)sin\left(2t\right)+\left(\frac{48}{13}t-\frac{288}{169}\right){cos}^2\left(t\right)\hfill \\ & +& \frac{144}{169}{e}^{-3t}-\frac{24}{13}t+\frac{144}{169}-\frac{2}{3}(t-1)(1-cos\left(t\right)),\hfill \end{array}$$

and

$$\begin{array}{ccc}\hfill h\left(t\right)& =& \left(-\frac{48}{25}+\frac{6}{5}t\right)sin\left(t\right)+\left(-\frac{14}{25}-\frac{2}{5}t\right)cos\left(t\right)-\frac{1}{6}tsin\left(2t\right)-\frac{58}{75}{e}^{-3t}\hfill \\ & -& \frac{1}{12}\left(t-1\right)\left(1-cos\left(t\right)\right)+\frac{4}{3}.\hfill \end{array}$$

The exact solution is given by

$$u\left(t\right)=tsin\left(2t\right),$$

and

$$v\left(t\right)=\left(t-1\right)(1-cos\left(t\right)).$$

Example 4. 

We consider the following problem:

$$\left\{\begin{array}{c}{}^{CF}D^{\mathrm{0.9}}u\left(t\right)=-\frac{1}{3}u\left(t\right)+\frac{2}{7}\nu \left(t\right)+f\left(t\right),\\ {}^{CF}D^{\mathrm{0.9}}\nu \left(t\right)=\frac{1}{11}u\left(t\right)+\frac{5}{13}\nu \left(t\right)+h\left(t\right),\\ u(t=0)=\nu (t=0)=0,\end{array}\right.$$

where

$$\begin{array}{ccc}\hfill f\left(t\right)& =& \frac{1}{1313}\left[\frac{715e^{2t}cos\left(t\right)-585e^{2t}sin\left(t\right)+707cos\left(t\right)+909sin\left(t\right)}{e^t}\right]\hfill \\ & & -\frac{1422}{1313}{e}^{-9t}+\frac{1}{3}cos\left(t\right)sinh\left(t\right)-\frac{2}{7}tsin\left(t\right)cosh\left(t\right),\hfill \\ \hfill h\left(t\right)& =& \frac{1}{8619845e^t}[-4641455tsin\left(t\right)+5783967sin\left(t\right)\hfill \\ & & +4693975e^{2t}tsin\left(t\right)+5967585tcos\left(t\right)]\hfill \\ & & -\frac{1}{8619845e^t}[1468944cos\left(t\right)+3764475e^{2t}sin\left(t\right)\hfill \\ & & -760500e^{2t}cos\left(t\right)+3840525t{e}^{2t}cos\left(t\right)Big]\hfill \\ & & +\frac{2229444}{8619845}{e}^{-9t}-\frac{1}{11}cos\left(t\right)sinh\left(t\right)-\frac{5}{13}tsin\left(t\right)cosh\left(t\right).\hfill \end{array}$$

The exact solution is given by

$$u\left(t\right)=cos\left(t\right)sinh\left(t\right)$$

and

$$\nu \left(t\right)=tsin\left(t\right)cosh\left(t\right)$$

We have computed the maximum absolute errors $L_{\infty }$ and the rate of convergence $R_M$, which is defined by

$$R_M=\frac{log(E_{\infty }\left(M/2\right)/E_{\infty }\left(M\right))}{log2},$$

of our proposed method; then, we have obtained the above results, which are presented in Table 1, Table 2, Table 3 and Table 4.

Table 1. Comparison of the $L_{\infty }$ norm with the proposed and ADM methods for Example 1.

J	M	$2\mathit{M}$	${\mathit{L}}_{\mathit{\infty }}\left(\mathit{M}\right)=max\left|{\mathit{u}}_{\mathit{i}}-{\tilde{\mathit{u}}}_{\mathit{i}}\right|$	${\mathit{R}}_{\mathit{M}}$ of Proposed Method	${\mathit{L}}_{\mathit{\infty }}$ of ADM
0	1	2	$3.14\times {10}^{-2}$		$3.02\times {10}^{-1}$
1	2	4	$1.06\times {10}^{-2}$	$1.5656$	$1.32\times {10}^{-1}$
2	4	8	$3.15\times {10}^{-3}$	$1.7485$	$4.28\times {10}^{-2}$
3	8	16	$8.02\times {10}^{-4}$	$1.9709$	$1.52\times {10}^{-2}$
4	16	32	$2.01\times {10}^{-4}$	$1.9964$	$4.19\times {10}^{-3}$

Table 2. Comparison of the $L_{\infty }$ norm with the proposed and ADM methods for Example 2.

J	M	$2\mathit{M}$	${\mathit{L}}_{\mathit{\infty }}\left(\mathit{M}\right)=max\left|{\mathit{\nu }}_{\mathit{i}}-{\tilde{\mathit{\nu }}}_{\mathit{i}}\right|$	${\mathit{R}}_{\mathit{M}}$ of Proposed Method	${\mathit{L}}_{\mathit{\infty }}$ of ADM
0	1	2	$4.01\times {10}^{-2}$		$2.50\times {10}^{-1}$
1	2	4	$1.25\times {10}^{-2}$	$1.6781$	$1.15\times {10}^{-1}$
2	4	8	$3.8\times {10}^{-3}$	$1.7137$	$3.92\times {10}^{-2}$
3	8	16	$9.8\times {10}^{-4}$	$1.9523$	$1.27\times {10}^{-2}$
4	16	32	$2.50\times {10}^{-4}$	$1.9709$	$3.50\times {10}^{-3}$

Table 3. Comparison of the $L_{\infty }$ norm with the proposed and ADM methods for Example 3.

J	M	$2\mathit{M}$	${\mathit{L}}_{\mathit{\infty }}\left(\mathit{M}\right)=max\left|{\mathit{\nu }}_{\mathit{i}}-{\tilde{\mathit{\nu }}}_{\mathit{i}}\right|$	${\mathit{R}}_{\mathit{M}}$ of Proposed Method	${\mathit{L}}_{\mathit{\infty }}$ of ADM
0	1	2	$3.23\times {10}^{-2}$		$4.11\times {10}^{-1}$
1	2	4	$1.15\times {10}^{-2}$	$1.4854$	$1.75\times {10}^{-1}$
2	4	8	$3.55\times {10}^{-3}$	$1.6915$	$4.90\times {10}^{-2}$
3	8	16	$9.0\times {10}^{-4}$	$1.9781$	$1.65\times {10}^{-2}$
4	16	32	$2.4\times {10}^{-4}$	$1.9069$	$4.8\times {10}^{-3}$

Table 4. Comparison of the $L_{\infty }$ norm with the proposed and ADM methods for Example 4.

J	M	$2\mathit{M}$	${\mathit{L}}_{\mathit{\infty }}\left(\mathit{M}\right)=max\left|{\mathit{\nu }}_{\mathit{i}}-{\tilde{\mathit{\nu }}}_{\mathit{i}}\right|$	${\mathit{R}}_{\mathit{M}}$ of Proposed Method	${\mathit{L}}_{\mathit{\infty }}$ of ADM
0	1	2	$3.80\times {10}^{-2}$		$3.41\times {10}^{-1}$
1	2	4	$1.16\times {10}^{-2}$	$1.7093$	$1.12\times {10}^{-1}$
2	4	8	$3.35\times {10}^{-3}$	$1.7908$	$3.20\times {10}^{-2}$
3	8	16	$9.01\times {10}^{-4}$	$1.8914$	$1.02\times {10}^{-2}$
4	16	32	$2.30\times {10}^{-4}$	$1.9672$	$3.11\times {10}^{-3}$

5. Conclusions

In this work, the Haar wavelet collocation method has been used to solve coupled dynamical systems with the Caputo–Fabrizio fractional derivative. Error analysis shows that our proposed method has an exponential convergence rate. Furthermore, for four examples, the numerical solutions agree very well with the exact solutions. In addition, this method is effective and recommended. As our next work, we will apply the symmetry Haar wavelet collocation method to solve different types of the Caputo–Fabrizio implicit fractional differential equations and coupled systems; see [22,23]. The Haar wavelet collocation method is preferred to investigate the discussed problem. The advantages of this method compared to the conventional collocation method (see [24,25,26]), like, for example, shooting methods, are as follows:

• It can decrease computational efforts and is suitable in terms of computation costs and the convergence rate.
• It is suitable for the analysis of the dynamical system with fractional derivatives.
• The convergence properties of this class of methods are very helpful.
• The error analysis of this method is characterized by a good convergence rate.
• Unlike the collocation method, other methods have several limitations in their applications to unlimited classes of singular problems.